Characterizing model errors in chemical transport modeling of methane: using GOSAT XCH₄ data with weak-constraint four-dimensional variational data assimilation

We examined biases in the global GEOS-Chem chemical transport model for the period of February–May 2010 using weak-constraint (WC) four-dimensional variational (4D-Var) data assimilation and dry-air mole fractions of CH₄ (XCH₄) from the Greenhouse gases Observing SATellite (GOSAT). The ability of the observations and the WC 4D-Var method to mitigate model errors in CH₄ concentrations was first investigated in a set of observing system simulation experiments (OSSEs). We then assimilated the GOSAT XCH₄ retrievals and found that they were capable of providing information on the vertical structure of model errors and of removing a significant portion of biases in the modeled CH₄ state. In the WC 4D-Var assimilation, corrections were added to the modeled CH₄ state at each model time step to account for model errors and improve the model fit to the assimilated observations. Compared to the conventional strong-constraint (SC) 4D-Var assimilation, the WC method was able to significantly improve the model fit to independent observations. Examination of the WC state corrections suggested that a significant source of model errors was associated with discrepancies in the model CH₄ in the stratosphere. The WC state corrections also suggested that the model vertical transport in the troposphere at middle and high latitudes is too weak. The problem was traced back to biases in the uplift of CH₄ over the source regions in eastern China and North America. In the tropics, the WC assimilation pointed to the possibility of biased CH₄ outflow from the African continent to the Atlantic in the mid-troposphere. The WC assimilation in this region would greatly benefit from glint observations over the ocean to provide additional constraints on the vertical structure of the model errors in the tropics. We also compared the WC assimilation at 4^∘ × 5^∘ and 2^∘ × 2.5^∘ horizontal resolutions and found that the WC corrections to mitigate the model errors were significantly larger at 4^∘ × 5^∘ than at 2^∘ × 2.5^∘ resolution, indicating the presence of resolution-dependent model errors. Our results illustrate the potential utility of the WC 4D-Var approach for characterizing model errors. However, a major limitation of this approach is the need to better characterize the specified model error covariance in the assimilation scheme.

1 Introduction

Atmospheric concentrations of methane (CH₄), the second most important anthropogenic greenhouse gas, have been rapidly raising since 1850 (Etheridge et al., 1992). However, atmospheric measurements in recent decades show that the rate of CH₄ increase in the atmosphere has varied, and its behavior is not well understood (Dlugokencky et al., 2009). Significant effort has been put into characterizing surface emissions of CH₄ in order to attribute its recent trends. In this context, a number of satellites have been launched to measure atmospheric CH₄ in order to constrain its sources. These include Envisat carrying the Scanning Imaging Absorption Spectrometer for Atmospheric Cartography (SCIAMACHY; Schneising et al., 2011), the Greenhouse Gases Observing Satellite (GOSAT) carrying the Thermal And Near-infrared Sensor for carbon Observation Fourier Transport Spectrometer (TANSO-FTS; Kuze et al., 2009), Sentinel-5p with the Tropospheric Monitoring Instrument (TROPOMI) on board (Veefkind et al., 2012), and the Greenhouse Gases Satellite (GHGSat). Proposed missions include the Methane Remote Sensing Lidar Mission (MERLIN; Kiemle et al., 2014), GOSAT-2 (Nakajima et al., 2017), the Geostationary Carbon Cycle Observatory (GeoCARB; Polonsky et al., 2014), and the recently announced MethaneSat. However, current regional CH₄ emissions remain largely uncertain (e.g., Saunois et al., 2016). One of the biggest challenges for reducing uncertainty in emission estimates is the relatively weak signal of emissions in the atmospheric column of CH₄, which puts tight requirements on the accuracy of satellite measurements. However, while future satellite instruments and improved spectroscopy are expected to provide better CH₄ measurements, errors in the atmospheric models used to simulate CH₄ remain poorly characterized. While random model errors can be accounted for in flux inversion analyses, the impact of biases in chemistry and transport are often neglected or accounted for using various ad hoc approaches. In the case of CH₄, which is a relatively long-lived gas with an atmospheric lifetime of about 9 years (Prather et al., 2012), chemistry plays a critical role in long-term trends (McNorton et al., 2016), whereas transport, alone or coupled with chemistry, defines how total surface emissions are distributed on a regional scale. Therefore, transport errors, such as those produced by numerical advection schemes, biases and uncertainties of meteorological fields, and parametrization of sub-grid-scale processes, may significantly undermine our ability to use models to relate emissions to atmospheric observations and thus our ability to improve CH₄ emission estimates (Prather et al., 2008; Locatelli et al., 2015; Patra et al., 2011).

One potential solution is to apply a bias correction to the model in the context of the inversion analysis. Simple bias correction schemes with uniform or latitudinally dependent bias estimates have been attempted before (Bergamaschi et al., 2009; Fraser et al., 2013; Monteil et al., 2013; Alexe et al., 2015; Locatelli et al., 2015), mostly to correct poor descriptions of the modeled stratosphere. Here we explore the utility of a “weak-constraint” (WC) four-dimensional variational (4D-Var) data assimilation method to characterize forward model errors. In contrast to the traditional “strong-constraint” (SC) 4D-Var method, the WC scheme does not assume that the model evolution is perfect. The WC 4D-Var method was introduced by Sasaki (1970) and used in numerical weather prediction (NWP) models by Derber (1989), Zupanski (1997), and Trémolet (2006, 2007). It was first applied by Keller (2014) in the GEOS-Chem simulation of atmospheric carbon monoxide (CO) to characterize model bias. One of the first attempts to apply bias correction in chemical data assimilation was done in the framework of the suboptimal Kalman filter by Lamarque et al. (2004), who used the bias estimation approach of Dee and Da Silva (1998) to constrain the CO state using measurements from the Measurement of Pollution in the Troposphere (MOPITT) instrument. The study pointed to the possibility of errors in the model vertical transport; however, most of the estimated biases were attributed to poor a priori estimates of CO surface emissions in the model. The major challenge for this type of analysis for CH₄ is the limited information available about the global vertical distribution of CH₄ in the atmosphere. There are satellite observations that contain information about the CH₄ distribution in the middle and upper troposphere, such as the thermal infrared CH₄ retrievals from the Tropospheric Emission Spectrometer (TES) on board the NASA Aura satellite (Worden et al., 2012), and in the stratosphere, such as the solar occultation measurements from the Atmospheric Chemistry Experiment Fourier Transform Spectrometer (ACE-FTS; Bernath et al., 2005) on board SCISAT. However, the accuracy of these measurements, based on validation studies (for example, De Mazière et al., 2008; Wecht et al., 2012), may not be sufficient to detect model errors. The most accurate satellite measurements are those of the total dry-air mole fraction of CH₄ in the total atmospheric column (XCH₄) obtained by TANSO-FTS on board GOSAT. However, these measurements provide less vertical information on CH₄ than those from TES and ACE-FTS, although the latter are less sensitive to surface emissions. Highly accurate aircraft or AirCore CH₄ profile measurements would be an ideal source of information, but they are limited in space and time. We explore the information content of GOSAT CH₄ observations and show that despite being designed to constrain surface emissions, they contain sufficient information to help characterize possible model errors. We assimilate the GOSAT observations using the WC 4D-Var data assimilation approach to estimate biases in GEOS-Chem. This approach is shown to provide a valuable tool for diagnosing and determining the origin of model errors.

This paper is organized as follows. Section 2 gives an overview of the forward model, the observations, and the WC 4D-Var method. It also contains a description of the various sensitivity studies conducted through a series of observing system simulation experiments (OSSEs). In Sect. 3, we present the results of the sensitivity experiments and the results of the assimilation of real GOSAT observations. Section 4 provides an interpretation of the pattern of model biases estimated from the GOSAT assimilation. Finally, conclusions are given in Sect. 5.

2 Data and methods

2.1 The GEOS-Chem model

For all assimilation experiments we use version v35 of the GEOS-Chem adjoint, which is based on version v8-02-01 of the forward model, with updates up to v9-02 (Henze et al., 2007). The GEOS-Chem chemical transport model (CTM) (http://www.geos-chem.org, last access: 21 May 2021) is driven by archived meteorological fields from the Goddard Earth Observing System (GEOS-5.2.0) produced by the NASA Global Modeling and Assimilation Office (GMAO). The meteorological fields are regridded from their native resolution of 0.5^∘ × 0.67^∘ with 72 vertical levels to 4^∘ × 5^∘ and 2^∘ × 2.5^∘ with 47 vertical levels. The vertical grid spacing in the troposphere varies from about 150 m in the lower part to about 1 km in the upper part. CH₄ is advected using the multidimensional flux-form semi-Lagrangian (FFSL) scheme by Lin and Rood (1996). Convection is implemented based on the relaxed Arakawa–Schubert scheme (Moorthi and Suarez, 1992). The model uses a simple treatment of turbulent mixing in the boundary layer by instantaneously mixing species from the surface to the top of the planetary boundary layer (PBL). The GEOS-Chem CH₄ sources and sinks used here are described in detail in Wecht et al. (2014). Anthropogenic CH₄ sources include emissions from natural gas and oil extraction, coal mining, livestock, landfills, wastewater treatment, rice cultivation, biofuel burning, and other minor sources based on the 2004 anthropogenic inventory from the Emission Database for Global Atmospheric Research (EDGAR) v4.2 (European Commission Joint Research Centre/Netherlands Environmental Assessment Agency, 2009). Natural CH₄ sources include wetland emissions after Kaplan (2002) and Pickett-Heaps et al. (2011), termite emissions (Fung et al., 1991), and open fire emissions from the daily Global Fire Emissions Database version 3 (GFED3) (van der Werf et al., 2010; Mu et al., 2011). The CH₄ emissions at 4^∘ × 5^∘ and 2^∘ × 2.5^∘ resolutions are slightly different due to the dependence of wetland emissions on the meteorological fields. Therefore, for consistency of the analysis of model errors, the emissions were regridded from the coarser to the finer resolution. The main loss of CH₄ (about 90 % of the total loss) in the atmosphere is due to oxidation by OH, with the remaining 10 % sink mainly due to soil absorption and oxidation in the stratosphere. CH₄ chemistry is performed in offline mode in which changes in CH₄ concentrations do not feed back on other species. Tropospheric OH fields in the model are prescribed as a three-dimensional monthly mean climatology from a tropospheric chemistry simulation in GEOS-Chem v5-03 (Park et al., 2004). Stratospheric CH₄ loss frequencies are from archived climatology of the NASA Global Modeling Initiative (GMI) (Murray et al., 2012).

The adjoint model is described by Henze et al. (2007) and has been used for assimilation of CH₄ observations by Wecht et al. (2012, 2014), Turner et al. (2015), Bousserez et al. (2016), and Tan et al. (2016). For the analysis presented here, we focus on the period of 1 February to 31 May 2010. The CH₄ fields were spun up at a resolution of 4^∘ × 5^∘ and 2^∘ × 2.5^∘ for about 5.5 years until July 2009. From July 2009 to January 2010 we assimilated the GOSAT proxy XCH₄ retrievals (Parker et al., 2015) to obtain monthly mean emission estimates at 4^∘ × 5^∘ resolution. The optimized emissions were then regridded and used to perform forward model simulations at 2^∘ × 2.5^∘ resolution for the same period from July 2009 to January 2010. The updated model fields on 1 February 2010 at both model resolutions were taken as initial condition for the analysis period. As a result, the initial conditions at both resolutions contain similar amounts of CH₄ in the atmosphere. However, CH₄ is distributed differently, reflecting the balance between emissions and transport at each model resolution.

2.2 Measurements

2.2.1 GOSAT

We obtain information about the CH₄ distribution in the atmosphere from XCH₄ retrievals from the TANSO-FTS on board GOSAT, which has a 3 d repeat orbit period. The instrument has a surface footprint of 10.5 km in diameter and records spectra at about 13:00 local time. We use version 5.2 of the University of Leicester (UoL) GOSAT proxy XCH₄ data product. The retrieval algorithm is explained in detail in Parker et al. (2011, 2015). In this algorithm, simplified spectral retrievals of XCO₂ and XCH₄ are obtained in spectral bands centered at 1.65 and 1.61 µm, respectively. The final total column-averaged dry-air mole fraction of CH₄ is obtained by multiplying the retrieved XCH₄ $/$ XCO₂ ratio by modeled XCO₂ fields. This is useful for canceling out common spectral features caused by light path modifications due to thin clouds, aerosol scattering, and instrumental artifacts in close spectral bands. However, reliable knowledge of the XCO₂ data is required. The proxy method provides significantly greater observational coverage, especially in tropical areas, compared to “full-physics” retrievals. The weakness of the approach is in the fact that the modeled CO₂ fields may still contain biases that are not accounted for in the final XCH₄ product. Version 5.2 of the XCH₄ data does not include retrievals from spectra recorded over oceans (glint observations). This is in contrast to the later versions 6 and 7, which use the same algorithm for XCH₄ retrievals over land. Furthermore, in our analysis we exclude all retrievals over Greenland and poleward of 75^∘ (including retrievals over snow).

The original XCH₄ retrievals utilized XCO₂ fields based on the median of three models: GEOS-Chem (from the University of Edinburgh), LMDZ/MACC-II, and CarbonTracker (National Oceanic and Atmospheric Administration, NOAA) smoothed with GOSAT CO₂ averaging kernels (Parker and the GHG-CCI group, 2016). CO₂ fields in all three models were produced by assimilating in situ surface CO₂ observations. In this work, we replaced the original modeled CO₂ fields with optimized CO₂ fields from a GEOS-Chem CO₂ surface flux assimilation analysis that used GOSAT XCO₂ retrievals over land (Deng et al., 2014). For the period of interest (February–May 2010), the XCH₄ retrievals using both proxy CO₂ fields are unbiased against each other with a scatter of 3 ppb and a correlation of R=0.99. Sensitivity tests that were conducted showed that a posteriori inversion results using the new CO₂ fields and the original fields generally produced comparable fits to independent CH₄ measurements from the Total Carbon Column Observing Network (TCCON; Wunch et al., 2011) and from the NOAA Earth System Research Laboratory (ESRL) global cooperative air sampling network (Dlugokencky et al., 2016). The use of the alternative CO₂ fields did not change any of the findings about model errors in our study.

GOSAT CH₄ retrievals contain about 1 degree of freedom for signal (DOFS) and have relatively flat averaging kernels in the troposphere that slowly decrease in the stratosphere (Yoshida et al., 2011). Therefore, they contain little vertical information about the atmosphere at the time of measurement. We use these averaging kernels to smooth the GEOS-Chem CH₄ fields and map them into the measurement space of the GOSAT retrievals using the expression

$$\begin{array}{}\text{(1)}& {\mathrm{XCH}}_{\mathrm{4}}={\mathrm{XCH}}_{\mathrm{4}}^{\mathrm{a}}+{\mathit{a}}^T\left({\mathit{z}}_{\mathrm{mod}}-{\mathit{z}}_{\mathrm{a}}\right),\end{array}$$

where z_mod is the GEOS-Chem CH₄ profile, z_a is the GOSAT a priori profile, a^T is the GOSAT column averaging kernel, and XCH${}_{\mathrm{4}}^{\mathrm{a}}$ is the a priori XCH₄ based on z_a. The absence of vertical information in the measurements is a challenge for constraining the 3D structure of model errors, but we expect vertical structure to emerge from atmospheric transport patterns.

Errors in GOSAT proxy XCH₄ retrievals with the original XCO₂ data were assessed against co-located TCCON ground-based measurements by Hewson et al. (2015). That validation study found that GOSAT retrievals contain random errors of 12.55 ppb and systematic errors of 4.8 ppb (although per-site biases ranged from −2.15 ppb in Wollongong to 13.44 ppb in Garmisch). However, errors away from TCCON sites could be larger. Overall, GOSAT and TCCON were highly correlated, with a correlation coefficient of 0.86. Buchwitz et al. (2017) obtained similar results with random errors of 11.9 ppb and systematic errors of 5.7 ppb for GOSAT proxy XCH₄ retrievals against co-located TCCON retrievals. Such precision, combined with spatial and temporal aggregation of the data, could be enough to improve knowledge about CH₄ a priori surface emissions in regions such as North America, where the XCH₄ enhancements above the background are about 10 ppb (Sheng et al., 2018). However, the presence of potential model errors significantly undermines this assumption. Therefore, here we explore the potential utility of the weak-constraint 4D-Var scheme to discern model biases using the XCH₄ data.

2.2.2 Validation data

The a priori and constrained model CH₄ fields are validated against in situ NOAA-ESRL CH₄ measurements (Dlugokencky et al., 2016) as well as measurements from the third HIAPER Pole-to-Pole Observations (HIPPO-3) aircraft campaign (Wofsy et al., 2011), TCCON ground-based XCH₄ retrievals (Wunch et al., 2011), and ACE-FTS space-based CH₄ retrievals (Boone et al., 2005).

The NOAA network operates by collecting air flask samples, which are later analyzed by gas chromatography with flame ionization detection. At stationary sites, samples are collected once per week. Shipborne samples from sites in the Pacific Ocean and the South China Sea are collected once every 3 weeks and weekly, respectively, per latitude band. Measurements are reported relative to the NOAA X2004A CH₄ scale. The absolute uncertainty of the scale is 0.2 % (about 3 ppb), and measurements are reproducible to within 1–3 ppb.

Airborne data are provided by the HIPPO-3 aircraft campaign, which took place between 20 March and 20 April 2010. The campaign sampled the atmospheric curtain from the North Pole to the coast of Antarctica through the central Pacific Ocean and from the surface to 14 km of altitude. We used CH₄ measurements performed by a quantum cascade laser spectrometer (QCLS) at 1 Hz frequency. QCLS measurements have a precision of 0.5 ppb and accuracy of 1 ppb, while the mean bias relative to simultaneous flask-based measurements is 0.44 ppb (Santoni et al., 2014). We exploited the merged 10 s meteorology, atmospheric chemistry, and aerosol data product (Wofsy et al., 2012), which was derived from 1 s measurements, by applying a median filter.

TCCON is a global network of ground-based high-resolution Fourier transform infrared (FTIR) spectrometers retrieving XCH₄ from solar absorption spectra in the near-infrared band. We used the GGG2014 version of TCCON XCH₄ data from multiple stations around the globe (Kivi and Heikkinen, 2016; Kivi et al., 2017; Blumenstock et al., 2017; Griffith et al., 2017; Hase et al., 2017; Notholt et al., 2017; Sherlock et al., 2017; Sussmann and Rettinger., 2017; Warneke et al., 2017; Wennberg et al., 2017b, a). The estimated accuracy and precision of XCH₄ retrievals are less than 0.5 % and 0.3 %, respectively (Wunch et al., 2015). Retrievals are bias-corrected based on comparisons with calibrated aircraft and AirCore profiles.

ACE-FTS on board SCISAT performs solar occultation measurements over a range of tangent heights. The satellite makes 15 occultations for both sunrise and sunset per day separated by about 24^∘ in longitude. Measurements cover an altitude range from the cloud tops in the upper troposphere up to 150 km. Spectra are recorded continuously during 2 s scans, which implies that the altitude and tangent point change slightly during the scan. As a result, the instrument has a low horizontal resolution of about 300 km in the limb direction. The vertical resolution determined by the instrument field of view is about 3 km at a tangent point 3000 km away from the satellite. However, vertical sampling ranges from 2 to 6 km depending on viewing geometry. In this study, we use the most recent v3.6 CH₄ retrievals with geolocation information (Boone et al., 2013; Waymark et al., 2013). Version 3.6 only differs from version 3.5 in that a local computer was used to process v3.5, while a shared supercomputing system was used for v3.6. Olsen et al. (2017) compared ACE-FTS v3.5 and MIPAS CH₄ vertical profiles coincident with TANSO-FTS measurements and found small differences above the tropopause except in the tropics. The mean differences were larger than 20 % below about 450 hPa, within 5 % between 450 and 40 hPa, and larger than 5 % above 40 hPa.

2.3 The weak-constraint 4D-Var approach

The estimation of surface emissions of CH₄ using the strong-constraint 4D-Var scheme is achieved by minimizing the strong-constraint cost function:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}J\left(\mathit{p}\right)& =\sum _{i=\mathrm{0}}^N{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\mathit{y}}_i-{\mathbf{H}}_i{\mathit{x}}_i\right)}^T{\mathbf{R}}_i^{-\mathrm{1}}\left({\mathit{y}}_i-{\mathbf{H}}_i{\mathit{x}}_i\right)\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(\mathit{p}-{\mathit{p}}_{\mathrm{a}}\right)}^T{\mathbf{B}}^{-\mathrm{1}}\left(\mathit{p}-{\mathit{p}}_{\mathrm{a}}\right),\end{array}\end{array}$$

where N is the number of 1-hourly time steps, y_i is the vector of XCH₄ observations during the time step i, x_i∈ℝⁿ is the model state at time step i that is represented by a 3D field of CH₄ concentrations, p∈ℝ^p is the vector of surface emissions of CH₄, and p_a∈ℝ^p is the a priori estimate of the CH₄ emissions. Here, H is the observation operator that maps the modeled CH₄ state into the measurement space at the location of the GOSAT XCH₄ observations, R_i represents the observation error covariance matrix, and B is the a priori error covariance matrix. In minimizing J, we solve for monthly mean emission estimates over the specified assimilation period. The evolution of the model state in Eq. (2) is performed by the GEOS-Chem model, which can be represented by an operator M that acts on the model state x_i and emissions p at time step i to produce a new model state x_i+1 at the next time step as follows:

$$\begin{array}{}\text{(3)}& {\mathit{x}}_{i+\mathrm{1}}=M\left({\mathit{x}}_i,\mathit{p}\right).\end{array}$$

In Eq. (3), it is assumed that there are no errors in propagating the state forward in time. This is the assumption that is implicit in Eq. (2), and thus the optimization is referred to as strong-constraint 4D-Var; the model trajectory is used as a strong constraint in the optimization.

As described by Trémolet (2006), Eq. (3) can be modified to account for model errors by adding corrections u_i+1 to the CH₄ state at time step i+1 so that the model forecast becomes

$$\begin{array}{}\text{(4)}& {\mathit{x}}_{i+\mathrm{1}}=M\left({\mathit{x}}_i,\mathit{p}\right)+\mathbf{G}{\mathit{u}}_{i+\mathrm{1}},\end{array}$$

where G is an operator that maps corrections u∈ℝ^m into the model state. Here, the corrections u are referred to as forcing terms, which is distinct from the adjoint forcing commonly used in 4D-Var. The operator G can also be understood as a mask that defines the spatial regions in the 3D model state in which corrections need to be applied. Hence, the second term in Eq. (4) represents additional sources and sinks of CH₄ in the region of the atmosphere defined by G. In the case in which G represents the whole atmosphere, m=n and u will have the same dimension as x. The sources and sinks could arise from errors in the model transport or chemistry. In minimizing Eq. (2) we solve only for the surface emissions. However, because of Eq. (4) we have the means of solving for the surface emissions as well as the 3D distribution of sources and sinks. In this case, the 4D-Var cost function, which is minimized with respect to both surface emissions (p) and state corrections (u), is expressed as

$$\begin{array}{}\text{(5)}& \begin{array}{rl}J(\mathit{p},{\mathit{u}}_i)& =\sum _{i=\mathrm{0}}^N{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\mathit{y}}_i-{\mathbf{H}}_i{\mathit{x}}_i\right)}^T{\mathbf{R}}_i^{-\mathrm{1}}\left({\mathit{y}}_i-{\mathbf{H}}_i{\mathbf{x}}_i\right)+\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(\mathit{p}-{\mathit{p}}_{\mathrm{a}}\right)}^T{\mathbf{B}}^{-\mathrm{1}}\left(\mathit{p}-{\mathit{p}}_{\mathrm{a}}\right)\\ & +\sum _{i=\mathrm{1}}^N{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{u}}_i^T{\mathbf{Q}}_i^{-\mathrm{1}}{\mathit{u}}_i,\end{array}\end{array}$$

where Q_i defines the a priori model error covariance matrix. This is the weak-constraint 4D-Var cost function, which is similar to Eq. 2, except for the addition of the third term that accounts for the errors in the evolution of the model state. This approach provides a means of capturing the model errors in the context of the 4D-Var formalism, whereas other approaches may try to account for these errors by including u in p. As described by Trémolet (2006), u_i can be considered to represent model errors on timescales as short as each model time step or as long as the full assimilation period, and it is assumed to be constant over the appropriate interval. In the case in which the forcing is estimated over the full assimilation window, the optimized forcing will represent a constant model bias over the whole model trajectory. For the results presented here, u_i changes in time, but we assume that Q is constant.

The WC 4D-Var approach was implemented into the GEOS-Chem model by Keller (2014), and here we describe that approach. The cost function (Eq. 5) is minimized subject to the equality constraints in Eq. (4) by adding the model constraints to the cost function to create the following Lagrangian function:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\mathcal{L}(\mathit{p},{\mathit{x}}_i,{\mathit{\lambda }}_i,{\mathit{u}}_i)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(\mathit{p}-{\mathit{p}}_{\mathrm{a}}\right)}^T{\mathbf{B}}^{-\mathrm{1}}\left(\mathit{p}-{\mathit{p}}_{\mathrm{a}}\right)\\ & +\sum _{i=\mathrm{0}}^N{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\mathit{y}}_i-{\mathbf{H}}_i{\mathit{x}}_i\right)}^T{\mathbf{R}}_i^{-\mathrm{1}}\left({\mathit{y}}_i-{\mathbf{H}}_i{\mathit{x}}_i\right)\\ & +\sum _{i=\mathrm{1}}^N{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{u}}_i^T{\mathbf{Q}}_i^{-\mathrm{1}}{\mathit{u}}_i\\ & -\sum _{i=\mathrm{1}}^N{\mathit{\lambda }}_i^T\left[{\mathit{x}}_i-M\left({\mathit{x}}_{i-\mathrm{1}},\mathit{p}\right)-\mathbf{G}{\mathit{u}}_i\right],\end{array}\end{array}$$

where λ_i represents the Lagrange multipliers. We define gradients of the Lagrangian ℒ with respect to x_i, p, and u_i by the following system of equations:

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\partial \mathcal{L}}{\partial {\mathit{x}}_i}}=-{\mathbf{H}}_i^T{\mathbf{R}}_i^{-\mathrm{1}}\left[{\mathit{y}}_i-{\mathbf{H}}_i{\mathit{x}}_i\right]-{\mathit{\lambda }}_i+{\left({\displaystyle \frac{\partial M}{\partial {\mathit{x}}_i}}\right)}^T{\mathit{\lambda }}_{i+\mathrm{1}},\text{(8)}& {\displaystyle \frac{\partial \mathcal{L}}{\partial {\mathit{x}}_N}}=-{\mathbf{H}}_i^T{\mathbf{R}}_i^{-\mathrm{1}}\left[{\mathit{y}}_N-{\mathbf{H}}_i{\mathit{x}}_N\right]-{\mathit{\lambda }}_N,\text{(9)}& {\displaystyle \frac{\partial \mathcal{L}}{\partial \mathit{p}}}={\mathbf{B}}^{-\mathrm{1}}\left(\mathit{p}-{\mathit{p}}_{\mathrm{a}}\right)+\sum _{i=\mathrm{1}}^N{\left({\displaystyle \frac{\partial M}{\partial \mathit{p}}}\left({\mathit{x}}_{i-\mathrm{1}},\mathit{p}\right)\right)}^T{\mathit{\lambda }}_i,\text{(10)}& {\displaystyle \frac{\partial \mathcal{L}}{\partial {\mathit{u}}_i}}={\mathbf{Q}}_i^{-\mathrm{1}}{\mathit{u}}_i+{\mathbf{G}}^T{\mathit{\lambda }}_i,\end{array}$$

where ${\mathbf{M}}^T={\left(\frac{\partial M}{\partial {\mathit{x}}_i}\right)}^T$ is the adjoint of the tangent linear model M. At the minimum, the ℒ gradients are equal to zero. In this case, Eqs. (7)–(8) give the adjoint model equations:

$$\begin{array}{}\text{(11)}& \begin{array}{rl}& {\mathit{\lambda }}_N=-{\mathbf{H}}_i^T{\mathbf{R}}_i^{-\mathrm{1}}\left[{\mathit{y}}_N-{\mathbf{H}}_i{\mathit{x}}_N\right],\\ & {\mathit{\lambda }}_i={\left({\displaystyle \frac{\partial M}{\partial {\mathbf{x}}_i}}\right)}^T{\mathit{\lambda }}_{i+\mathrm{1}}-{\mathbf{H}}_i^T{\mathbf{R}}_i^{-\mathrm{1}}\left[{\mathit{y}}_i-{\mathbf{H}}_i{\mathbf{x}}_i\right].\end{array}\end{array}$$

Values of λ_i are derived from the forward and adjoint model integrations and are substituted into Eqs. (9)–(10). In general, $\frac{\partial \mathcal{L}}{\partial {\mathit{u}}_i}$ and $\frac{\partial \mathcal{L}}{\partial \mathit{p}}$ do not equal zero as the minimum has yet to be reached by iteratively minimizing the Lagrangian function ℒ. In GEOS-Chem this is done using the L-BFGS-B algorithm (Byrd et al., 1995). Finally, the entire optimization algorithm consists of the following steps.

1. Run the forward model (Eq. 4) from time t₁ to t_N using the current estimates of p and u_i.

2. Run the adjoint model and simultaneously accumulate the estimate of λ_i based on Eq. (11).

3. Calculate the gradients of ℒ with respect to p and u_i using Eqs. (9)–(10) and estimates of λ_i.

4. Update the estimates of p and u_i using the L-BFGS-B optimization algorithm based on the descent direction defined by $\frac{\partial \mathcal{L}}{\partial {\mathit{u}}_i}$ and $\frac{\partial \mathcal{L}}{\partial \mathit{p}}$.

5. Repeat steps 1–4 until convergence is reached.

For the assimilation configurations employed here, it took about 20 iterations for the SC scheme to converge and 30–35 iterations to obtain convergence with the WC scheme. Generally, at some point during the convergence process the inversion will start fitting the noise in GOSAT observations. This can be prevented by stopping the iterative algorithm when the reduced chi-squared value for the fitted model approximately equals unity. In practice, the real uncertainty in GOSAT XCH₄ retrievals is unknown due to errors in the CO₂ fields that are unaccounted for, for example, so we used a different approach. For each WC inversion that was performed, we monitored the evolution of the optimized model fields and compared them to independent observations (from TCCON, the NOAA in situ network, and the HIPPO-3 aircraft campaign). The iterative process was terminated when the fit to independent observations did not improve any further or started to get worse based on the assumption that after this threshold the optimization began to fit noise in GOSAT observations. On average, the level of noise was estimated to correspond to GOSAT XCH₄ uncertainty of about 10 ppb, which produced a reduced χ²≈1 for the model fit to the GOSAT observations.

We assumed that the observation errors are uncorrelated so that R was assumed to be diagonal. In constructing R, we utilized the reported uncertainty in the GOSAT XCH₄ retrievals (with the median value of approximately 10 ppb) and inflated it to match the GOSAT scatter against TCCON observations (approximately 13 ppb). The a priori error covariance matrix B was also assumed to be diagonal, with 50 % uncertainty in CH₄ emissions in each surface grid box. Emissions were not split into separate categories but optimized as monthly totals in each surface grid box. GOSAT provides global coverage with a period of 3 d. Therefore, we did not attempt to characterize the global pattern of model errors on shorter timescales and explored keeping the forcing terms constant over a time interval that varied from a minimum of 3 d up to 1 month. Little is known about the a priori structure of the model errors, so in the design of the cost function, a priori estimates of model errors were set to zero (u=0 at the beginning of the assimilation).

The WC algorithm optimizes scaling factors (SFs) for both the forcing terms and the model parameters (surface emissions). Emission SFs are ratios of optimized emissions to a priori emissions, while forcing SFs are the ratios of optimized forcing terms to a constant scaling parameter $\stackrel{\mathrm{̃}}{u}$. The WC inverse method becomes sensitive to the choice of the scaling parameter when working with multidimensional problems. This choice does not affect the Lagrangian ℒ (Eq. 6); however, it does change the relative magnitude of ℒ gradients with respect to forcing terms $\frac{\partial \mathcal{L}}{\partial {\mathit{u}}_i}$ (Eq. 10) and to surface emissions $\frac{\partial \mathcal{L}}{\partial \mathit{p}}$ (Eq. 9). The state vector of the WC inversion is largely dominated by the number of forcing SFs as opposed to the emission SFs (with a ratio of up to 500 : 1). Due to the high dimensionality of the problem, the L-BFGS-B optimization algorithm can search only a fraction of parameter space in the direction of the largest gradient descent. Therefore, it becomes sensitive to the relative magnitude of the forcing gradients $\frac{\partial \mathcal{L}}{\partial {\mathit{u}}_i}$ versus the emission gradients $\frac{\partial \mathcal{L}}{\partial \mathit{p}}$. For large values of $\stackrel{\mathrm{̃}}{u}$ (for example, $\stackrel{\mathrm{̃}}{u}>\mathrm{50}$ ppb), the algorithm descends in the direction of the forcing gradient and the WC inversion is transformed into the so-called “full state assimilation”. Meanwhile, small values of $\stackrel{\mathrm{̃}}{u}$ (for example, $\stackrel{\mathrm{̃}}{u}<\mathrm{0.05}$ ppb) force the algorithm to minimize the cost function in the direction of emission gradients (“flux assimilation”). The value of $\stackrel{\mathrm{̃}}{u}=\mathrm{1.0}$ ppb was empirically chosen to perform simultaneous optimization of the emissions and forcing terms (“flux+state assimilation”).

Application of the WC 4D-Var method is sensitive to the specification of the covariance matrix Q, which is difficult to characterize (Trémolet, 2007). We adopted a diagonal structure of matrix Q as our standard option. This implies that there was no explicit temporal or spatial correlation assumed between model errors. However, some correlation is implicitly present in the model and emerges from both atmospheric transport patterns and the definition of the constant forcing time window. Still, assigning adequate model error uncertainty is one of the major challenges for using the WC method. Generally, there is no single recipe for that, as model errors come from a variety of sources with different characteristics and, moreover, vary on daily to seasonal timescales. Additionally, in practice, there is usually no way to properly validate whether the inversion correctly attributed biases in CH₄ fields as being caused by surface emissions, model errors, or observational biases. This latter statement is related to the fact that surface emissions, observational bias, and some model errors may leave similar signatures in the CH₄ fields that would not be easy to distinguish even with perfect observational coverage. The situation may even be worse for CH₄ biases if incorrect emissions and model errors mask each other and do not show up in the model comparison with the GOSAT data.

Given these issues, our focus here is not on estimating surface emissions of CH₄. Instead, we use the WC 4D-Var method to optimally constrain the 3D corrections to the CH₄ state and explore the structure of the errors in the model. We performed two types of inversions: full state assimilation, in which we estimate only the 3D corrections (u) to the model state, and flux+state assimilation, in which we estimate the surface emissions (p) and the 3D corrections. Given that little is known about the distribution of model errors in CH₄ in the troposphere, in both cases we chose a uniform spatial and temporal structure of model error uncertainty q so that the model error covariance is defined as Q=q²I.

We conducted a series of parameter tuning experiments in which the WC 4D-Var analysis was performed using values of q ranging from 0.05 ppb to about 2000 ppb, and optimized CH₄ fields were validated against independent observations. The experiments showed that for larger values of q above 50 ppb, the fit of optimized CH₄ fields to independent observations did not change noticeably. However, for values of q below 50 ppb, the fit deteriorated as q became smaller. Therefore, q was set to 50 ppb. It is important to note that the magnitude of estimated forcing terms changes with changing q, but the general pattern of positive and negative corrections was not significantly affected by the choice of q. As shown in the experiments described in Sect. 2.4, the WC method was able to improve the model and capture the bias in the CH₄ state with q set to 50 ppb. Therefore, we considered a uniform structure for Q to be a satisfactory assumption for this initial assessment of model errors in the context of the WC 4D-Var analysis.

2.4 Configuration of the OSSEs

We conducted three OSSEs in order to evaluate the performance of the WC 4D-Var method in regards to mitigating artificially introduced model errors for February–May 2010. In particular, we investigated model biases due to vertical transport, chemical loss, and initial conditions. The “true” model state was defined as optimized CH₄ global fields obtained from an inversion analysis to constrain estimates of monthly CH₄ fluxes using GOSAT XCH₄ proxy retrievals during the same time period. We also refer to these constrained fluxes as true CH₄ surface emissions. The CH₄ initial conditions are described in Sect. 2.1. This true model state was used to produce pseudo-GOSAT XCH₄ measurements by sampling at the corresponding times and locations of the real GOSAT measurements and then convolving them with GOSAT averaging kernels. No noise was added to pseudo-observations. The perturbed model was defined by introducing bias in the true model from one of the three specified sources of model bias. Then the pseudo-observations were used to constrain and mitigate biases in the perturbed model CH₄ state. It should be noted that these are “perfect model” experiments since we are using GEOS-Chem to simulate the pseudo-data as well as for the inversions. The performance of the pseudo-inversion was evaluated by comparing the recovered CH₄ fields to the true ones. The analyses were conducted for the standard period of 4 months (February–May 2010), but most of the results are presented for the second month of the assimilation period, March 2010. This gives the model errors time to accumulate during February and provides 2 months of pseudo-data, for April and May, to constrain the CH₄ state in March. Given that and the fact that, usually, the state is most optimally constrained in the middle of the assimilation period, we believe that the OSSEs should reveal the best performance of the WC method.

In the first and second OSSEs, the bias in vertical transport and chemistry was introduced by turning off convection and chemistry, respectively, in the model for the duration of the assimilation period. In the third OSSE, a bias in initial conditions was introduced by replacing the true initial conditions with the ones obtained by running the forward model without convection and with 70 % of the a priori emissions from 1 July 2009 to 1 February 2010, the beginning of the assimilation period. The applied biases for these three OSSEs were intentionally designed to be extreme; for real-world applications, we expect less extreme model errors.

We configured the WC method to carry out a full state assimilation (as described in Sect. 2.3) to enable the optimization to independently determine the location and magnitude of the bias in the modeled state. The constant forcing time window was set to 3 d and the forcing terms were optimized throughout the entire atmosphere (the mask G equals unity everywhere). This particular configuration may not be optimal to mitigate a specific type of bias in a real assimilation with limited observational coverage. Here, we intend to investigate the performance of the measurements and the assimilation method when no information is given about the sources and magnitude of model errors.

2.5 Configuration of the assimilation with real GOSAT data

For the assimilation of the real GOSAT CH₄ data, the model error corrections to the CH₄ state were constrained during the standard 4-month period of February–May 2010. The CH₄ initial conditions are as described in Sect. 2.1. We conducted four sets of experiments, which are described below, to assess the sensitivity of the results to the WC 4D-Var configuration. Additionally, we compared results of the WC inversions with results of the SC surface flux assimilation.

The a priori model validation presented in Sect. 3.2.2, as well as the results of Saad et al. (2016), pointed to the fact that the stratosphere in GEOS-Chem at the 4^∘ × 5^∘ resolution, particularly at high latitudes, may be positively biased. The OSSE results also suggested that the WC assimilation may benefit from additional constraints on stratospheric forcing terms. Therefore, for the assimilation of the real GOSAT data we imposed a negativity bound in the L-BFGS-B algorithm for the optimization of the forcing terms in the extratropical stratosphere (above about 210 hPa and poleward of 44^∘) to remove the known bias at 4^∘ × 5^∘ resolution. No bound was imposed on forcing terms in the 2^∘ × 2.5^∘ resolution assimilation.

In the first set of experiments, we performed a full state assimilation and changed the length of the time window over which the forcing terms are held constant in the assimilation. In these experiments, the forcing mask G comprised the entire atmosphere, and biases in the CH₄ state potentially induced by incorrect surface emissions were treated as just another source of model errors included in forcing terms. The length for the forcing window was varied from 3 to 30 d. Short time windows (less than 2 d, for example) would be more appropriate if the model were affected by temporally changing biases such as those related to transient mesoscale eddies. However, the observations may not be able to constrain the short timescales. Also, for short temporal correlation length scales, there is a higher risk that the inversion will fit noise or possible biases in observations. In contrast, the use of long time windows introduces additional temporal correlations between forcing terms that may be suitable only for mitigation of stationary systematic biases in the model, such as those related to surface emissions, chemistry, or stationary transport errors.

In the second set of experiments, we carried out a WC 4D-Var source+state assimilation and explored the sensitivity of the results to the vertical extent of the forcing mask G. Here, the forcing window was set to 3 d. The algorithm was configured to optimize the 3D forcing terms on model levels (1) above the surface (the whole atmosphere), (2) above 750 hPa, (3) above 500 hPa, and (4) above 200 hPa. Then in the third set of experiments, the horizontal extent of G was modified. Forcing terms were applied (1) globally throughout the stratosphere and (2) in the troposphere only over the following four regions: the three regions defined by the boundaries of the GEOS-Chem nested model domains (North America – NA, Europe – EU, and China with Southeast Asia – CH) and over equatorial Africa (EQAf). In these experiments we also attempted to identify the origin of the biases affecting the model at the location of the TCCON and NOAA measurement sites.

All the above experiments were conducted at the 4^∘ × 5^∘ model resolution. In the fourth experiment, we applied the WC 4D-Var full state assimilation to constrain errors in GEOS-Chem at 2^∘ × 2.5^∘ resolution. We used the standard configuration with a forcing time window of 3 d. The only difference between the 4^∘ × 5^∘ and 2^∘ × 2.5^∘ assimilation was in the initial conditions, which are described in Sect. 2.1.

3 Results

3.1 OSSEs

In the first OSSE, we investigated the ability of the WC 4D-Var method to mitigate errors in vertical transport by turning off convection in the model. The spatial patterns of the estimated model corrections are shown in Fig. 1. As can be seen, the assimilation resulted in enhanced CH₄ concentrations in the lower troposphere and reduced CH₄ in the upper troposphere over the main source regions. Furthermore, the positive CH₄ anomalies in the lower troposphere were partly advected downstream. For example, over equatorial Africa and South America, instead of being convectively lifted over the continent, CH₄ emissions were transported westward in the lower and middle troposphere (see Fig. 1, first column, third row). As shown in the figure, the state corrections capture the general structure of the a priori bias, which consists of excessive CH₄ in the lower troposphere and a deficit in the upper troposphere. The largest corrections are co-located with the regions of deep convection. Positive corrections are found in the upper troposphere and negative corrections in the lower. Still, this was not sufficient to fully mitigate the extreme bias associated with turning off convection, but the results show that GOSAT retrievals contain information to enable us to capture vertical transport bias even when the sources and magnitude of model errors are unknown.

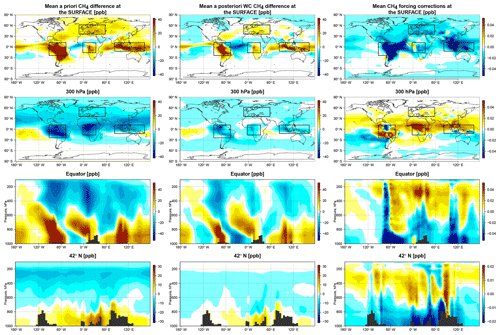
Figure 1 Mean differences in the CH₄ distribution in March 2010 in the OSSE with biased convection. Left column: mean differences between the a priori CH₄ state and the true CH₄ state. Middle column: mean differences between the WC optimized CH₄ state and the true CH₄ state. Right column: the mean WC state corrections (the forcing terms) in parts per billion (ppb). Shown are the latitude–longitude differences at (top row) the surface and (second row) at 300 hPa, as well as the altitude–longitude differences (third row) along the Equator and (bottom row) along 42^∘ N. The black boxes indicate the four domains considered for the regional analysis discussed in the text and shown in Fig. 2.

Figure 2 shows the mean vertical distribution of the a priori and a posteriori residual biases in the CH₄ state over equatorial South America, equatorial Africa, equatorial Southeast Asia, and Europe. In midlatitudes over Europe, the convection bias was much weaker than over the tropics and reached just about 16 ppb near the surface. At altitudes above 600 hPa the WC 4D-Var method was able to strongly mitigate this bias, and below 800 hPa it reduced the bias by more than a factor of 2. The worst results in terms of the fractional reduction of the bias were achieved over equatorial Southeast Asia, most likely due to fewer GOSAT retrievals over this region and limited constraints on the CH₄ distribution in the outflow region over the ocean. The assimilation also removed a large fraction of the bias in the CH₄ fields over equatorial Africa and South America, particularly in the middle and upper troposphere over Africa and in the lower troposphere over South America.

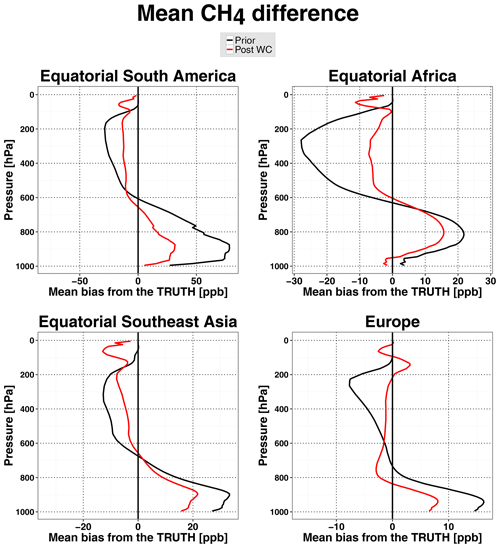
Figure 2 Mean vertical profiles of the CH₄ differences in March 2010 in the OSSE with biased convection for the four regions depicted in Fig. 1. The differences are between (black lines) the a priori and the true CH₄ state and between (red lines) the WC optimized state and the true CH₄ state.

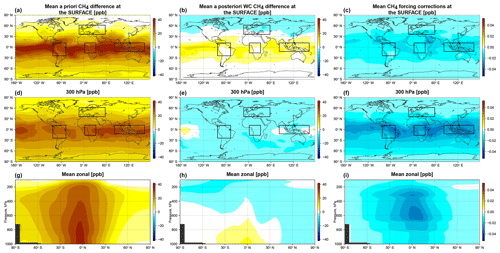
Figure 3 Mean differences in the CH₄ distribution in March 2010 in the OSSE with biased chemistry. (a, d, g) Mean differences between the a priori CH₄ state and the true CH₄ state. (b, e, h) Mean differences between the WC optimized CH₄ state and the true CH₄ state. (c, f, i) The mean WC state corrections (the forcing terms) in parts per billion (ppb). Shown are the latitude–longitude differences at (a–c) the surface and (d–f) at 300 hPa, as well as the altitude–longitude differences (g–i) along the Equator. The black boxes indicate the four domains considered for the regional analysis discussed in the text and shown in Fig.  4.

The second OSSE, in which a chemistry bias was created by turning off the reaction of CH₄ with OH, was the least challenging bias for the WC 4D-Var scheme to mitigate. This bias was rather smooth in the troposphere and did not contain small-scale features. Although the actual chemistry bias in the model may have a more complex vertical structure, we do not expect chemical biases to be as strongly localized as the biases associated with emissions and vertical transport. The a priori and a posteriori residual biases, as well as WC forcing terms, are shown in Fig. 3. The WC state optimization performed best over land where the a priori biases were almost completely removed. The optimization was least successful over the oceans in the lower troposphere. This situation is consistent with the fact that the assimilation of GOSAT data has lower sensitivity to variations in CH₄ in the lower troposphere compared to the upper troposphere, due in part to the absence of GOSAT observations over oceans in our analysis as well as to different transport patterns and stronger winds in the upper troposphere. Shown in Fig. 4 are the mean vertical profiles of the prior and posterior bias over the same four regions considered in Fig. 2. The model does indeed successfully mitigate the bias. Over the convection regions in the tropics, there are some compensatory corrections in the lower troposphere and in the upper troposphere and lower stratosphere (UTLS), which is probably due to the fast vertical transport in these regions and the limited vertical information in the GOSAT retrievals.

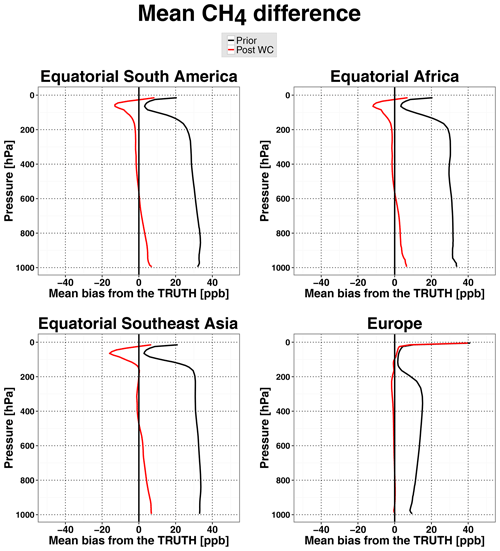
Figure 4 Mean vertical profiles of the CH₄ differences in March 2010 in the OSSE with biased chemistry for the four regions depicted in Fig. 3. The differences are between (black lines) the a priori and the true CH₄ state and between (red lines) the WC optimized state and the true CH₄ state.

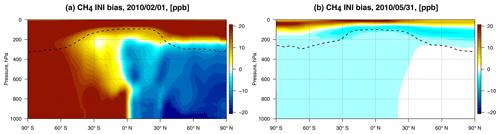
Figure 5 Results of the OSSE with biased initial conditions. (a) A priori bias in initial conditions. (b) A posteriori bias at the end of the assimilation window. The dashed line represents the mean tropopause height on 31 May 2010 taken from GEOS-5 meteorological fields.

In the third OSSE, with biased initial conditions, the initial condition bias is shown in the left panel in Fig. 5. The stratosphere and southern troposphere were positively biased, whereas the northern troposphere was negatively biased. The right panel shows the structure of the a posteriori bias after the WC assimilation on the last day of the assimilation window, 31 May. It shows that the CH₄ state converged to the true concentrations everywhere except in the upper stratosphere; the positive upper-stratospheric bias was compensated for in the column by a small negative CH₄ bias in the troposphere and the lower stratosphere. Examination of the evolution of the initial condition bias (not shown) indicates that different regions of the atmosphere converged to the true CH₄ mass at different rates, with levels above 200 hPa converging the slowest, such that by the third month the CH₄ mass had not fully recovered at these levels.

3.2 Assimilation of real GOSAT retrievals

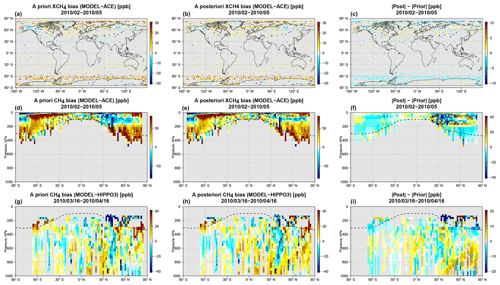
The bias between the GOSAT data and the 4^∘ × 5^∘ a priori and a posteriori model is shown in Fig. 6. Here we will refer to the a posteriori results as the WC_4x5 assimilation, which is our standard WC 4D-Var assimilation at 4^∘ × 5^∘ resolution with a 3 d forcing time window and a forcing mask G comprising the entire vertical extent of the atmosphere. As can be seen, there are large positive a priori biases at high latitudes in the Northern Hemisphere and in some low-latitude regions, such as equatorial Africa and eastern China. The WC_4x5 assimilation successfully reduces the a priori bias. There is some residual high-latitude bias, which resembles noise or bias in the GOSAT observations. In a companion analysis (Stanevich et al., 2020) in which we examine the impact of model resolution on the modeled CH₄ distribution, we showed that the large positive a priori CH₄ bias over China may partly be explained by weakening of the vertical transport in the model due to the coarse 4^∘ × 5^∘ resolution. In Stanevich et al. (2020), we also showed that a significant fraction of the high-latitude bias comes from the stratosphere and is a consequence of running the model at 4^∘ × 5^∘ resolution. As a result, here we repeated the GOSAT WC assimilation at the higher resolution of 2^∘ × 2.5^∘. The results, which are shown in Fig. 7, reveal that the high-latitude a priori bias is indeed smaller in the 2^∘ × 2.5^∘ model. At the higher resolution, the WC assimilation also successfully reduces the model bias. For comparison, we repeated the assimilation at 4^∘ × 5^∘ but optimized the emissions instead of the CH₄ state. The results for this experiment, referred to as SC_4x5, are shown in Fig. 8. As can be seen, the SC assimilation leaves significantly larger residual biases. The pattern of the residual bias indicates that there were other biases that the assimilation could not fit at the expense of the emissions. We will investigate possible sources for these biases in the sections below.

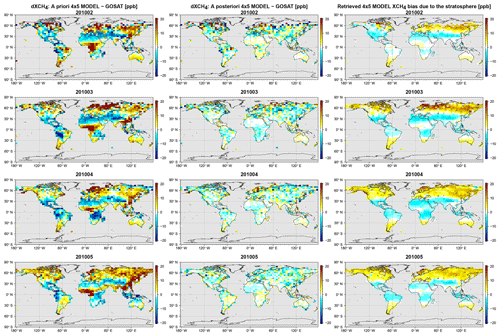
Figure 6 Monthly mean fields from the 4^∘ × 5^∘ resolution model for February–May 2010. First column: differences between the GEOS-Chem a priori XCH₄ state and the GOSAT data. Middle column: differences between the a posteriori WC_4x5 XCH₄ state and the GOSAT data. Right column: the optimized stratospheric XCH₄ bias correction calculated as the difference between the model simulation with optimized forcing corrections everywhere and the model simulation with the forcing corrections estimated only in the troposphere. The rows represent results for (top row) February, (second row) March, (third row) April, and (bottom row) May 2010. All model simulations were sampled at the locations and times of the GOSAT observations and smoothed with the GOSAT averaging kernels.

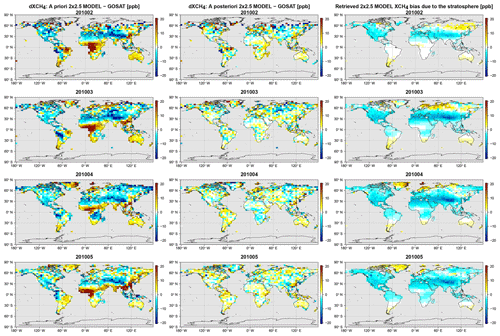
Figure 7 Same as Fig. 6 but for the 2^∘ × 2.5^∘ resolution model.

Figure 8 Monthly mean differences between the GEOS-Chem a posteriori XCH₄ state and GOSAT. Left column: differences between the a posteriori state from the SC flux assimilation at 4^∘ × 5^∘ (SC_4x5) and GOSAT. Right column: differences between the a posteriori state from the SC flux assimilation at 2^∘ × 2.5^∘ (SC_2x25) and GOSAT. The rows represent results for (top row) February, (second row) March, (third row) April, and (bottom row) May 2010.

The signal of surface emissions is mixed with possible model errors in the troposphere, such as those related to vertical transport. Biases in the CH₄ fields caused by incorrect surface emissions will in some cases have an identical structure as those caused by biased vertical transport, which may complicate the interpretation of WC 4D-Var state corrections in the troposphere. On the other hand, it takes much longer for the surface emission signal to mix into the stratosphere. We therefore assumed that, on the short (4-month) timescale of the simulation, optimized forcing corrections u_i in the stratosphere can be considered independent from the influence of surface emissions. The third column in Figs. 6 and 7 shows the actual mean monthly bias in the a priori CH₄ fields that was corrected by the stratospheric forcing terms. The bias corrections in the 2^∘ × 2.5^∘ CH₄ simulation are smaller than for the 4^∘ × 5^∘ simulation, which is consistent with Stanevich et al. (2020), who suggested that part of the stratospheric bias at 4^∘ × 5^∘ resolution is due to the model resolution itself. The WC inversion results suggest that the 4^∘ × 5^∘ model is positively biased in the stratosphere at high latitudes and weakly negatively biased in the tropics. In contrast, the 2^∘ × 2.5^∘ model is mainly negatively biased in the stratosphere, particularly around 30–40^∘ N, except for a few high-latitude regions, possibly related to the polar vortex.

3.2.1 Evaluation with TCCON and NOAA data

Table 1 presents the results of the evaluation of the SC_4x5 and WC_4x5 assimilation with the in situ and TCCON data, whereas Table 2 gives the comparison results at individual TCCON sites. Based on the OSSE results in Sect. 3.1 and provided that the only model bias is due to incorrect surface emissions, we would anticipate the WC assimilation to produce generally worse fits to the surface measurements than the SC assimilation. The comparisons show that both approaches produced similar improvements in the fit to the NOAA in situ observations, with slightly better performance from the WC method. The WC assimilation had a significant impact on the overall fit to the TCCON XCH₄ retrievals, whereas the SC assimilation had a much more limited impact. Table 2 shows the benefits of using the WC method at the individual TCCON sites. With the exception of Park Falls and Lamont, the WC assimilation significantly improved the correlation and reduced the bias between the model and the TCCON observations. The results suggest that the GEOS-Chem a priori CH₄ simulation suffered from biases that were not only related to incorrect surface emissions.

Table 1 Evaluation of a priori, SC_4x5, and WC_4x5 optimized CH₄ fields using TCCON XCH₄ from the stations listed in Table 2 and NOAA surface in situ observation (mean statistics for the period of February–May 2010). The first, second, and third columns represent the mean difference, standard deviation, and correlation between the model and measurements, respectively. The fourth column represents the slope of the regression line, with modeled data on the y axis and measurements on the x axis.

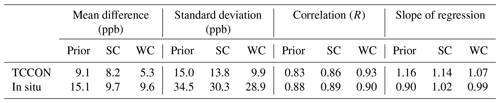
Table 2 Evaluation of a priori, SC_4x5, and WC_4x5 optimized CH₄ fields using TCCON XCH₄ (mean station-wise statistics for the period of February–May 2010). The first, second, and third columns represent the mean difference, standard deviation, and correlation between the model and measurements, respectively.

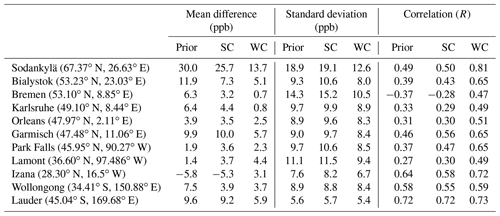
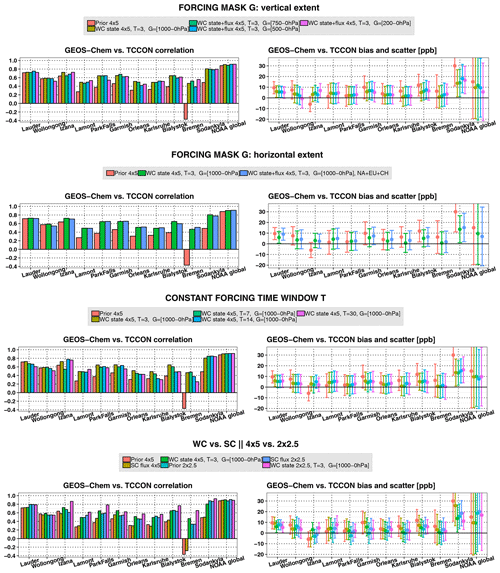
Figure 9 Evaluation of the mean (February–May 2010) a priori and optimized CH₄ fields using TCCON XCH₄ and NOAA surface in situ observations. Results are shown for the four experiments described in Sect. 2.5. For each set of experiments (each row), the left column shows the correlation with respect to the TCCON and NOAA data, whereas the right column shows the mean bias and scatter. Top row: comparison of (red) the a priori fields, (light green) the standard WC assimilation, and the WC assimilation with the forcing terms estimated at altitudes above (dark green) 750 hPa, (blue) 500 hPa, and (purple) 200 hPa. Second row: comparison of (red) the a priori fields, (dark green) the standard WC assimilation, and (blue) the WC assimilation with joint estimation of the state and surface emissions with forcing terms estimated only over North America, Europe, and Asia. Third row: comparison of (red) the a priori fields, (light green) the standard WC assimilation, and the WC assimilation with a constant forcing window of (dark green) 7 d, (blue) 14 d, and (purple) 30 d. Bottom row: comparison of the a priori fields at (red) 4^∘ × 5^∘ and (light blue) 2^∘ × 2.5^∘, the SC assimilation at (light green) 4^∘ × 5^∘ and (dark blue) 2^∘ × 2.5^∘, and the WC assimilation at (dark green) 4^∘ × 5^∘ and (purple) 2^∘ × 2.5^∘.

The evaluation of the WC sensitivity experiments is summarized in Fig. 9. The series of WC experiments described in Sect. 2.5 were organized into four groups. The most sensitive indicator of the quality of the model–observation fit is the correlation. The scatter was close to the level of the GOSAT measurement noise and did not change much among the different assimilation experiments. In the set of experiments (first panel in Fig. 9) in which we changed the vertical extent of the forcing mask G, we found that restricting the optimized forcing to the stratosphere (altitudes above 200 hPa) resulted in correlation statistics that were only slightly worse than when we optimized the forcing throughout the whole atmosphere. This suggests that a significant part of model errors above all TCCON stations may be related to the representation of the stratosphere in the model. In addition, the bias and scatter plots show that optimization of forcing terms above 200 hPa produced the best fit to NOAA surface observations. In the experiments (second panel in Fig. 9) in which we modified the horizontal extent of the forcing mask G, we found that optimization of the forcing throughout the stratosphere and only over North America, Europe, China, and equatorial Africa in the troposphere, as described in Sect. 2.5, produced almost identical fits to the case of the full state assimilation. These four regions are major sources of CH₄, and our results suggest that at the TCCON sites the model was likely affected by errors in emissions and the transport of the emission signal over these regions. Henceforth, we refer to these assimilation results as WC_4REG_4x5. In the experiments (see the third panel in Fig. 9) in which we varied the length of the forcing window from 3 to 7, 14, and 30 d, we found that the agreement at some of the stations, such as Lamont, Park Falls, and Sodankylä, was generally insensitive to increasing the length of the forcing window, which could suggest that the model above these stations was affected by slowly varying biases. The model fit at other stations, particularly Bialystok, Bremen, and Karlsruhe, degraded when the window length was increased. The latter three stations are located close to each other and are probably affected by similar model errors on synoptic timescales of about 1 week.

In the last group of experiments (see the fourth panel in Fig. 9), we compared the performance of the two 4D-Var assimilation modeling approaches (WC full state assimilation and SC flux assimilation) at the two model resolutions (4^∘ × 5^∘ and 2^∘ × 2.5^∘). The comparison suggested that, in the absence of a priori bias correction, the SC method brings limited improvements to the a prior CH₄ fields at both resolutions. Indeed, we conclude that the SC assimilation at the 4^∘ × 5^∘ resolution is futile as the a priori model at 2^∘ × 2.5^∘ resolution produces a better fit to the TCCON observations than the SC 4^∘ × 5^∘ assimilation. The performance of the SC assimilation at the 2^∘ × 2.5^∘ resolution was similar to but was surpassed by the “best-fit” WC state assimilation at the 4^∘ × 5^∘ resolution in term of its fit to TCCON and NOAA in situ measurements. Overall, the WC state assimilation at 2^∘ × 2.5^∘ resolution generated the best model fit to TCCON observations. However, in all 2^∘ × 2.5^∘ resolution experiments the model bias against NOAA surface measurements was larger compared to the 4^∘ × 5^∘ experiments. For example, the smallest WC a posteriori bias at 4^∘ × 5^∘ was about 10 ppb, whereas at 2^∘ × 2.5^∘ it was about 17 ppb.

Another important conclusion can be drawn from the fact that the WC assimilation at both model resolutions significantly improved the model fit to Izana measurements (see the fourth panel in Fig. 9). The Izana station is located at an altitude of 2370 m above sea level on a small island near the coast of Africa that has no local CH₄ emission sources. The model at 2^∘ × 2.5^∘ and 4^∘ × 5^∘ resolutions is not able to resolve the topography of the island. Therefore, the model transport in the vicinity of this high-altitude station, particularly in the lower troposphere, may be subject to similar errors at both the 2^∘ × 2.5^∘ and 4^∘ × 5^∘ resolutions. Hence, the improvement in the assimilated CH₄ fields may be related to the corrected model errors in the upper troposphere and the stratosphere rather than in the lower troposphere where topography-related errors would be dominant.

The WC full state assimilation at 4^∘ × 5^∘ leaves weak positive biases in the GEOS-Chem fields against the TCCON observations (excluding Sodankylä) in most of the experiments. Mean a posteriori inter-station bias at 4^∘ × 5^∘ (2^∘ × 2.5^∘) resolution is 3.4 ppb (4.0 ppb) (excluding Sodankylä), while the scatter is 8.6 ppb (7.3 ppb) (excluding Sodankylä). It is not clear if the GOSAT data are positively biased or if this could be caused by differences between the GOSAT and TCCON averaging kernels in the stratosphere and the fact that, for example, the stratospheric model bias was not fully recovered by the assimilation, particularly during the first couple of months of the assimilation period. The results also do not indicate the presence of a latitudinal bias between TCCON and GEOS-Chem and hence between TCCON and GOSAT.

There is a larger positive XCH₄ bias between the model and Sodankylä measurements of 12.6 and 11.2 ppb for the WC assimilation at 4^∘ × 5^∘ and 2^∘ × 2.5^∘ resolution, respectively; however, the correlation is also high at 0.81 and 0.93, respectively. Tukiainen et al. (2016) and Ostler et al. (2014) pointed to the fact that polar vortex conditions at high-latitude stations may induce biases in TCCON XCH₄ retrievals. It has been claimed that a priori profiles in the retrievals do not account for and are not adjusted to these dynamic conditions; hence, they significantly deviate from the real CH₄ profiles. When there is not enough information in the spectra to correct for such discrepancies, the XCH₄ retrievals can be systematically biased. It is possible that both GOSAT and TCCON could have been affected by the polar vortex conditions during some days in February–April 2010 so that the biases in co-located retrievals are partially canceled. It should also be noted that the negative a priori correlation between the model and Bialystok XCH₄ measurements is partly caused by the limited number (84) of measurements during the 4-month assimilation time window.

3.2.2 Evaluation with ACE-FTS and HIPPO-3 data

Figures  and 10 show the results of the GEOS-Chem comparison with the ACE-FTS and HIPPO-3 data. Model versus ACE-FTS data are shown only in the stratosphere in order to exclude potentially biased data due to interference with clouds in the upper troposphere. The mean XCH₄ difference between GEOS-Chem and ACE-FTS that is shown was obtained by artificially extending the ACE-FTS CH₄ profiles down into the troposphere using the GEOS-Chem fields and then applying the GOSAT column averaging kernels. Consistent with Saad et al. (2016), the CH₄ differences reveal that the a priori 4^∘ × 5^∘ model has a positive stratospheric bias that can be as large as 250 ppb averaged zonally (see Fig. ). The HIPPO-3 comparison also showed that the 4^∘ × 5^∘ model is positively biased in the stratosphere and slightly negative in the troposphere. Wang et al. (2017) showed that similar positive CH₄ biases at middle and high latitudes exist in TM3, TM5, and Laboratoire de Météorologie Dynamique (LMDz) CTMs. The 4^∘ × 5^∘ WC assimilation reduced the positive stratospheric bias with respect to both HIPPO-3 and ACE-FTS, but it did not remove it completely. For example, the maximum model minus ACE-FTS XCH₄ bias due to the stratosphere was reduced from about 40 to 30 ppb. The average negative tropospheric CH₄ bias relative to HIPPO-3 was reduced. It is possible that the WC method was not able to properly localize the stratospheric bias. However, the validation analysis may also reflect the influence of the slow recovery of the stratospheric CH₄ fields from the bias in the initial conditions. Therefore, discrepancies in the stratospheric CH₄ field from the initial conditions in the first 2 months of the WC assimilation could be contributing to the observed HIPPO-3 and ACE-FTS bias. Unfortunately, the measurements are either too sparse or limited in space and time to verify this assumption.

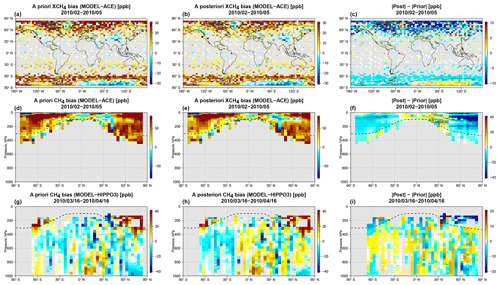
Figure 10 Evaluation of the mean (February–May 2010) a priori and WC_4x5 optimized CH₄ fields using ACE-FTS and HIPPO-3 CH₄ measurements. Shown are (a, d, g) the a priori bias, (b, e, h) the a posteriori bias, and (c, f, i) the reduction in absolute bias. (a–c) XCH₄ bias between GEOS-Chem and ACE-FTS. (d–f) Zonally averaged CH₄ bias between GEOS-Chem and ACE-FTS. (g–i) CH₄ bias between GEOS-Chem and HIPPO-3. We used ACE-FTS retrievals only in the stratosphere. The XCH₄ bias between GEOS-Chem and ACE-FTS was obtained by augmenting the ACE-FTS profile in the stratosphere with the GEOS-Chem profile in the troposphere and smoothing the vertical CH₄ profile with mean meridional GOSAT averaging kernels. The dashed line represents the mean tropopause height.

Figure 11 Same as Fig.  but for the 2^∘ × 2.5^∘ resolution model.

The positive a priori stratospheric bias relative to ACE-FTS and HIPPO-3 was significantly smaller at 2^∘ × 2.5^∘ than at the 4^∘ × 5^∘ resolution (see Fig. 10); however, it was not completely removed. Stratospheric CH₄ fields in the Northern Hemisphere (NH) above 200 hPa even became negatively biased at 2^∘ × 2.5^∘, particularly around 30–40^∘ N, where the absolute bias became larger than at 4^∘ × 5^∘. The WC assimilation at 2^∘ × 2.5^∘ further corrected the positive biases and significantly reduced the negative bias around 30–40^∘ N. As can be inferred from Fig. 7, the latter covered the entire latitudinal band but was particularly pronounced over the Himalayas. Despite the reduction of the stratospheric bias, the 2^∘ × 2.5^∘ WC assimilation introduces a positive CH₄ bias relative to HIPPO-3 in the NH lower troposphere.

4 Discussion of model biases

4.1 Stratospheric bias

The sensitivity experiments carried out in Sect. 2.4 suggest that a stratospheric bias introduced in the system through the initial conditions has the slowest correction rate. However, by the start of the last month of the assimilation, May 2010, the bias is either removed or does not change much with time. Therefore, we focus the discussion here on the stratosphere in the month of May 2010, with the assumption that the model is free of the influence of the initial conditions. Figure 11 compares the a priori CH₄ fields to the optimized fields from the WC_4x5 and SC_4x5 assimilations. The top panel shows that corrections in the stratospheric CH₄ abundance are the most pronounced feature of the WC optimized CH₄ fields and that changes are smaller in the zonal mean tropospheric fields. The bottom panel is presented to contrast the behavior of the two 4D-Var approaches. It shows that the SC assimilation attempts to correct the positive high-latitude stratospheric CH₄ bias at the expense of surface emissions. This results in a negative CH₄ bias in the lower troposphere, while the surface signal hardly impacts the stratosphere. In the WC assimilation, stratospheric CH₄ was significantly reduced at high latitudes and increased in the tropics relative to the a priori, which is consistent with the correction of the biases shown in Figs.  and 10. The changes are more substantial in the Northern Hemisphere due to the asymmetrically larger number of GOSAT measurements in the Northern Hemisphere since we are assimilating data only over land.

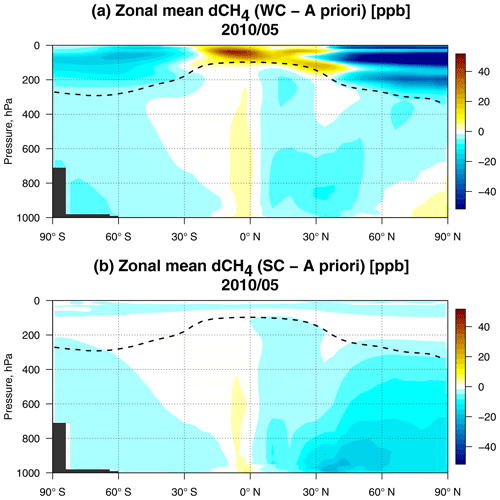
Figure 12 Zonal mean CH₄ differences (in ppb) in May 2010 between (a) the WC_4x5 optimized state and the a priori fields and (b) between the SC_4x5 optimized state and the a priori fields. The dashed line represents the mean monthly tropopause height.

Large biases in the stratosphere were previously identified in GEOS-Chem (Saad et al., 2016) and in other chemistry transport models (Strahan and Polansky, 2006; Patra et al., 2011; Ostler et al., 2016). The problem was mainly linked to biases in the meridional Brewer–Dobson circulation in the stratosphere and in the rate of troposphere–stratosphere exchange. However, neither mechanism was analyzed in detail. Indeed, the observed changes in Fig. 11 may partly reflect discrepancies in the Brewer–Dobson circulation projected from the initial conditions. In particular, meridional overturning that is too rapid in the months prior to the assimilation would have transported excess CH₄ from the tropics and to the high latitudes. In the companion study, Stanevich et al. (2020) show that the stratospheric bias in GEOS-Chem can also be due to increased numerical diffusion at the coarse horizontal model resolution. This leads to additional unphysical horizontal mixing between the troposphere and the stratosphere and between the high latitudes and the tropics in the stratosphere.

4.2 Tropospheric bias

4.2.1 Pattern of forcing terms

The forcing terms are corrections applied to the CH₄ fields at each model time step. This time step is 30 and 15 min for the 4^∘ × 5^∘ and 2^∘ × 2.5^∘ simulations, respectively. In order to compare the forcing terms in the two simulations, we added together the state corrections at two successive 2^∘ × 2.5^∘ time steps. Therefore, all forcing terms discussed in this section are presented for 30 min time intervals. The first column in Fig. 12 presents forcing terms in the troposphere optimized by the WC_4x5 assimilation. The observed structure of the forcing terms simultaneously mitigated model errors from multiple sources. In this section, we attempt to give the most likely explanation for the retrieved pattern of the state correction and identify sources of regional biases.

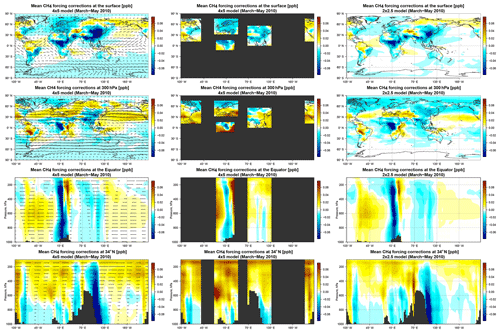
Figure 13 Mean optimized forcing terms (in ppb) for March–May 2010. Left column: WC_4x5 assimilation at 4^∘ × 5^∘. Middle column: WC_4REG_4x5 assimilation at 4^∘ × 5^∘. Right column: WC_2x25 inversion at 2^∘ × 2.5^∘. Top row: forcing terms at the surface. Second row: forcing terms at 300 hPa. Third row: altitude–longitude distribution of the forcing terms along the Equator. Bottom row: altitude–longitude distribution of the forcing terms along 34^∘ N. In the plots in the left column, arrows represent the direction and relative magnitude of horizontal winds.

In general, the original a priori CH₄ fields can be affected by model errors that either occurred during the assimilation period or were projected onto the assimilation window from the initial conditions. Here, we investigate the former case. Given the results of the OSSE with biased initial conditions in Sect. 3.1, we focus in Fig. 12 on the mean forcing terms in the last 3 months of the assimilation (March–May 2010) as they are much more likely to be related to recent model errors than to biases in the initial conditions. The temporally averaged structure also gives insight into systematic model errors and is easier to interpret. Figure 12 (first column) shows that negative forcing terms dominate near the surface and in the lower troposphere, particularly over Europe, equatorial Africa, and East Asia. The CH₄ reduction at the surface is consistent with NOAA observations. Positive state corrections are more frequently found in the upper troposphere, mainly at midlatitudes over the Pacific and Atlantic oceans as well as over Europe and a significant part of Russia. There are also several regions, such as eastern China and equatorial Africa, where the forcing terms are negative throughout the entire tropospheric column. Vertical slices over midlatitudes (bottom right panel) show that strong negative corrections over the east coast of Asia and North America are accompanied by positive corrections in the upper troposphere downwind of the continents. Forcing terms are generally weaker in the lower troposphere over the oceans where we lack GOSAT observations.

Generally, corrections of one sign with monotonically decaying magnitude from the surface to the upper troposphere could be associated with biases in the surface emissions, while the dipole structures with corrections of the opposite sign in the upper and lower troposphere could be related to errors in vertical transport. However, it is not feasible to uniquely identify the origin of model errors from the pattern of forcing terms because model errors from separate sources are mixed in the atmosphere and the estimation of the forcing terms is an under-constrained inverse problem.

Still, we may try to identify possible sources of model errors. For example, initial assessment of the state corrections pointed to potential issues in vertical transport. Indeed, the dipole structure of the forcing terms could indicate that upward transport of CH₄ at midlatitudes may be insufficient, particularly over regions with strong vertical CH₄ gradients that are present over large sources of CH₄. At NH midlatitudes the major CH₄ source regions are China, the US, and Europe. Moreover, the eastern parts of China and North America are located in regions of significant extratropical cyclone activity (Stohl, 2001; Shaw et al., 2016), where CH₄ emitted from the surface is being lifted into the free troposphere in warm conveyor belts associated with these cyclones (Kowol-Santen et al., 2001; Li et al., 2005; Sinclair et al., 2008; Lin et al., 2010). Moist convection over land could also contribute to the total transport bias; however, convective transport is not strong over these midlatitude regions during the months of February–May.

A similar vertical structure in the forcing terms was identified above and downwind of eastern North America and China (see the first column, fourth row of Fig. 12). The WC method applied negative corrections over land from the surface to the upper troposphere, large positive corrections in the upper troposphere, and weakly negative corrections in the lower troposphere over the oceans downwind of the continents. The WC method may suggest that vertical transport over eastern parts of the continents has to be stronger. In such a case, more CH₄ emitted from local sources reaches the middle to upper troposphere and is transported away from the continents by strong westerly winds. Meanwhile, CH₄ concentrations in the entire atmospheric column over land and in the lower troposphere over the adjacent oceans are reduced. Therefore, the large positive a priori bias between the model and GOSAT over China shown in Fig. 6 (first column) may be partly attributed to weak local uplift of CH₄.

Another region of interest, as suggested by the WC assimilation (Fig. 12, first column, third row), is equatorial Africa. Similar to China, a large positive a priori model XCH₄ bias was found here. However, due to the observational coverage, there are limited direct constraints on the CH₄ outflow from equatorial Africa except for sparse GOSAT observations over South America. While the African XCH₄ bias could be related to positively biased local a priori surface emissions, the WC assimilation also suggested another transport-related explanation. The WC assimilation applied negative CH₄ forcing terms over central Africa and positive forcing terms downwind in the middle troposphere (between 400 and 800 hPa) over the Atlantic Ocean. Such a pattern of state correction could point to potential errors in CH₄ outflow from the African continent. Southern Africa is characterized by a persistent high-pressure system that drives easterly outflow from southern tropical Africa to the Atlantic in the lower to middle troposphere (Garstang et al., 1996). In their analysis of the sources of moisture in the Congo Basin, Dyer et al. (2017) showed that there is a strong export of moisture from southern tropical Africa to the Atlantic between 800 and 500 hPa. Furthermore, Arellano et al. (2006) found, in their inversion analysis of carbon monoxide (CO) data from the MOPITT instrument, a discrepancy between their a posteriori CO and observations at Ascension Island, which they speculated could be due to errors in the altitude dependence of the outflow from Africa in the GEOS-Chem model. It is possible that too much CH₄ is being convectively lifted to the upper troposphere over central Africa and not enough is exported out over the Atlantic in the lower troposphere. Figure 1 (first column) displays the bias in CH₄ fields when convection was turned off in the model. This caused CH₄ emitted over Africa to take a different transport pathway. Instead of being lifted up over the continent, more CH₄ was transported out to the Atlantic in the lower to middle troposphere between 500 and 900 hPa. Under such conditions, CH₄ is simultaneously depleted over the continent and increased over the Atlantic, which is similar to what the WC forcing terms suggest. We cannot determine the exact origin of the XCH₄ bias over Africa, but the forcing terms do suggest the presence of a transport bias.

The estimation of the forcing terms is an under-constrained inverse problem. Consequently, here we evaluate the impact of reducing the dimensionality of the inverse problem by limiting the region of the atmosphere where the forcing terms should be applied. This was done in the WC_4REG_4x5 assimilation, in which we restricted the forcing optimization to the stratosphere and only over the main CH₄ anthropogenic emission regions in the troposphere. The results presented in Sect. 3.2.1 suggest that the WC_4x5 and WC_4REG_4x5 assimilations produced similar fits to the independent observations. Therefore, errors affecting the model, at least at the location of the validation stations, could emerge from the NA, CH, EU, EQAf, or STRAT regions. The second column in Fig. 12 presents the structure of optimized forcing terms from the WC_4REG_4x5 assimilation in which the number of optimized variables was reduced using the forcing mask G. Over China and North America, the forcing terms acquired a better-defined dipole structure with a positive correction in the upper troposphere and a negative correction in the lower troposphere. Over equatorial Africa, the region of positive corrections in the mid-troposphere moved closer to the continent.

4.2.2 Dependence of the forcing terms on model resolution

Coarsening the model resolution from 2^∘ × 2.5^∘ to 4^∘ × 5^∘ can be considered equivalent to introducing errors in the finer-resolution model. Yu et al. (2018) and Stanevich et al. (2020) showed that at coarse resolution vertical transport in GEOS-Chem is weakened due to loss of eddy mass flux and air mass flux in the regridding of the meteorological fields. Stanevich et al. (2020) also showed that the efficiency of transport barriers is reduced due to increased numerical diffusion, which causes unphysical mixing between the interior and the exterior of the polar vortex, mixing of CH₄ between the tropical and extratropical branch of the Brewer–Dobson circulation that is too rapid, and increased troposphere–stratosphere exchange. Thus, in Fig. 12 we compare the forcing terms from the 4^∘ × 5^∘ assimilation (WC_4x5) with those from the 2^∘ × 2.5^∘ WC assimilation (WC_2x25). Differences between the 2^∘ × 2.5^∘ and 4^∘ × 5^∘ forcing represent the response of the WC method to the resolution-induced transport errors. We found that the magnitude of the negative forcing term was reduced in the lower troposphere, particularly over China. Similarly, the magnitude of positive forcing terms was reduced in the upper troposphere. The pattern of forcing terms on the vertical slice at midlatitudes became significantly weaker. Comparison of Figs. 6 and 7 also suggests smaller stratospheric corrections at the 2^∘ × 2.5^∘ resolution. At the same time, the structure and magnitude of forcing terms at the Equator (particularly over equatorial Africa) were not significantly affected by the increase in resolution.

Several conclusions follow from Fig. 12. First, the results suggest that a large fraction of model errors at 4^∘ × 5^∘ resolution, particularly in the stratosphere and over midlatitudes in the troposphere, are resolution-induced. Second, although the magnitude of the forcing terms at the 2^∘ × 2.5^∘ resolution is smaller, the pattern remains similar, which implies that the 2^∘ × 2.5^∘ resolution model may still be affected by the same type of transport errors. Third, the assumptions made about sources of model errors in the tropics, particularly over equatorial Africa, still apply to the 2^∘ × 2.5^∘ simulation as the structure and magnitude of forcing terms remained unresponsive to the model resolution. It is possible that these regions are dominated by discrepancies in moist convective transport that are large at 2^∘ × 2.5^∘ and 4^∘ × 5^∘.

5 Conclusions

In this study, we assessed errors in the global GEOS-Chem chemistry transport model during the 4-month period of February–May 2010 using the weak-constraint 4D-Var data assimilation method at model resolutions of 4^∘ × 5^∘ and 2^∘ × 2.5^∘. This was done by constraining simulated CH₄ fields with GOSAT XCH₄ retrievals. This represents the first application of the WC 4D-Var scheme for assimilation of GOSAT XCH₄ retrievals to characterize model errors in a CTM.

An analysis of the sensitivity of the GOSAT measurements to the atmospheric CH₄ state found that the XCH₄ retrievals are most sensitive to CH₄ mass changes in the stratosphere and in the upper troposphere in the Northern Hemisphere, which was explained by the GOSAT observational coverage and stronger horizontal winds in the UTLS, allowing the CH₄ perturbations to be observed by a larger number of measurements. Sensitivity at the Equator was about half that at northern midlatitudes. In a series of OSSEs, the observations and the WC method were tested to determine the ability of the system to recover “unknown” errors in CH₄ fields associated with artificially introduced biases in convection, chemistry, and initial conditions. We found that when not supplied with any information about the errors, the WC method was able to significantly mitigate biases in the CH₄ fields with slowly changing spatial structures, but it was not able to correct strongly localized biases, particularly those in the boundary layer. Despite having almost flat averaging kernels in the troposphere, our analysis showed that the GOSAT XCH₄ retrievals could help constrain the vertical distribution of model errors when convection was turned off in the model. The WC method needed about a month to recover the bias introduced in the initial condition in the troposphere and about 2 months to do so in the stratosphere. Generally, the method was successful in mitigating model errors of unknown origin and magnitude. However, more optimal performance could be achieved by supplying the method with additional information about model errors, such as their temporal and spatial correlation, using the model error covariance matrix Q. However, characterizing these correlations will be challenging.

The WC method was tuned in a set of experiments to diagnose real model errors in the GEOS-Chem CTM at the 4^∘ × 5^∘ resolution. The a posteriori model fit to independent observations, such as ACE-FTS, HIPPO-3, TCCON, and NOAA surface measurements, was used to evaluate the assimilation. Initial comparisons suggested that GEOS-Chem was affected by biases not solely related to discrepancies in surface emissions. Results suggested that the modeled CH₄ fields at the location of most NH TCCON stations were affected by slowly varying biases. However, a few stations, such as Bialystok, Bremen, and Karlsruhe, were more likely influenced by errors varying on timescales of 1 week. The evaluations pointed to a large positive bias in the stratosphere relative to ACE-FTS and HIPPO-3 measurements and a weakly negative bias in the middle to upper troposphere relative to HIPPO-3 data. The WC assimilation was able to mitigate the negative tropospheric bias and partly removed the stratosphere bias. We found that the SC 4D-Var assimilation that optimized the surface emissions had only a limited impact on the model fits. Furthermore, the WC assimilation at 4^∘ × 5^∘ resolution performed better than the SC assimilation at 2^∘ × 2.5^∘ resolution. Meanwhile, the results showed that running the a priori model at 2^∘ × 2.5^∘ resolution produced better agreement with TCCON observations than the a posteriori fields from the SC 4D-Var surface emission optimization at 4^∘ × 5^∘.

State corrections at the 4^∘ × 5^∘ resolution also explicitly pointed to issues with vertical transport, suggesting that vertical transport of CH₄ at midlatitudes over the large CH₄ source regions of eastern China and North America is too weak. In the tropics, the WC inversion corrected for large positive XCH₄ biases over equatorial Africa. From the pattern of forcing terms, it remained unclear whether the bias over Africa was related to surface emissions. However, the WC method suggested the possibility of biased CH₄ outflow from the African continent to the Atlantic Ocean in the mid-troposphere, which could be related to a discrepancy in the partitioning between deep convection transport to the upper troposphere and shallow outflow to the Atlantic Ocean.

In a companion analysis, Stanevich et al. (2020) examined the impact of model resolution on CH₄ simulation and found larger model biases at 4^∘ × 5^∘ compared to 2^∘ × 2.5^∘. We found that assimilating the GOSAT data at the higher resolution of 2^∘ × 2.5^∘ produced state corrections that were similar to those obtained at 4^∘ × 5^∘. However, the magnitude of these corrections in the stratosphere and in the midlatitude troposphere was significantly reduced at the higher resolution. This suggests that the model at both resolutions was affected by transport errors of similar origin, although less so at the 2^∘ × 2.5^∘ resolution. The WC assimilation also corrected for the negative CH₄ bias relative the ACE-FTS and HIPPO in the northern midlatitude stratosphere, which was found only at the 2^∘ × 2.5^∘ resolution, and located this bias particularly over the Himalayas. However, the origin of this bias remained unclear.

In our analysis, we used only GOSAT CH₄ data over land. However, XCH₄ glint measurements over oceans could help better constrain the vertical structure of the model errors. The WC 4D-Var assimilation of shorter-lived species, such as CO, could also help better diagnose model errors, especially when transport and emission errors mask each other in CH₄ fields, although shorter-lived species may also be more strongly affected by errors in chemistry. The advantage of CH₄ is its longer memory of model transport; however, shorter-lived gases are more strongly affected by, and hence may be more sensitive to, the same model errors. Clearly, the detected transport error at the 4^∘ × 5^∘ resolution would have a considerable impact on inferred emissions if the evolution of the model state were assumed to be perfect, as is the case in SC 4D-Var. Instead of reducing the positive high-latitude bias in the stratosphere, the 4^∘ × 5^∘ SC 4D-Var surface flux assimilation negatively biased the lower troposphere. The SC inversion also significantly reduced Chinese CH₄ emissions by incorrectly attributing model errors in vertical transport to emissions. Some of the detected transport errors were significantly smaller at the 2^∘ × 2.5^∘ resolution, while others remained resolution-independent. The effect of these remaining errors at the 2^∘ × 2.5^∘ resolution has to be further investigated.

In the context of optimizing fluxes, potentially any CTM may be improved if the signal from the surface emissions can be separated from other model errors. This would be a rather challenging task for GOSAT XCH₄ measurements. Further analysis is needed on this problem, particularly on the design of the model error covariance matrix Q. For example, Trémolet (2007) proposed a design based on statistics of model tendencies. The Q matrix had a rather primitive structure in our analysis, although it is sufficient for the objectives of this work. Based on our initial assessment of model errors, the structure of Q can be further improved. In the meantime, the WC 4D-Var method has a number of immediately useful applications. In general, it is a valuable instrument for diagnosing model errors. It can also be used as a tool to produce a better estimate of the CH₄ state in a model in order to provide boundary and initial conditions for forecasting purposes or regional-scale analysis at higher spatial resolution.