Comment on “Climate consequences of hydrogen emissions” by Ocko and Hamburg (2022)

In this commentary, we provide additional context for Ocko and Hamburg (2022) related to the climate consequences of replacing fossil fuels with clean hydrogen alternatives. We first provide a tutorial for the derivations of underlying differential equations that describe the radiative forcing of hydrogen emissions, which differ slightly from equations relied on by previous studies. Ocko and Hamburg (2022) defined a metric based on time-integrated radiative forcing from continuous emissions. To complement their analysis, we further present results for temperature and radiative forcing over the next centuries for unit pulse and continuous emissions scenarios. Our results are qualitatively consistent with previous studies, including Ocko and Hamburg (2022). Our results clearly show that for the same quantity of emissions, hydrogen shows a consistently smaller climate impact than methane. As with other short-lived species, the radiative forcing from a continuous emission of hydrogen is proportional to emission rates, whereas the radiative forcing from a continuous emission of carbon dioxide is closely related to cumulative emissions. After a cessation of hydrogen emissions, the Earth cools rapidly, whereas after a cessation of carbon dioxide emissions, the Earth continues to warm somewhat and remains warm for many centuries. Regardless, our results support the conclusion of Ocko and Hamburg (2022) that, if methane were a feedstock for hydrogen production, any possible near-term consequences will depend primarily on methane leakage and secondarily on hydrogen leakage.

1 Introduction

In a recent paper, Ocko and Hamburg (2022) examined the climate consequences of replacing fossil fuel technologies with clean hydrogen alternatives. The paper accounted for a range of hydrogen and methane emission rates for two types of clean hydrogen production pathways, i.e., green hydrogen produced via renewables and water, and blue hydrogen produced via steam methane reforming with carbon capture, usage, and storage (CCUS). They calculated the time-integrated radiative forcing using equations derived recently for hydrogen based on chemistry–climate modeling experiments (Warwick et al., 2022). Ocko and Hamburg (2022) found that high emission rates of hydrogen could diminish net climate benefits of clean hydrogen technologies, and high emission rates of methane might lead to net climate disbenefits for blue hydrogen in the near term (e.g., 20-year timescale).

Here, we provide context for understanding the results of Ocko and Hamburg (2022) in three different ways: (1) we present equations underlying the time evolution of hydrogen and its radiative and thermal consequences and solve them analytically for unit pulse and continuous hydrogen emissions scenarios; (2) we present global mean temperature and radiative forcing in the time domain covering 500 years; and (3) we examine three scenarios, including a unit pulse, a limited duration (square wave), and a continuous emissions framework. Our aim here is to complement Ocko and Hamburg (2022), which emphasizes the near term, with an analysis that places greater emphasis on long-term outcomes using newly developed equations.

2 Methods and equations

We derive and apply equations underlying the estimate of radiative forcing from hydrogen (H₂) emissions as presented by Warwick et al. (2022), relying heavily on parameter values from Ocko and Hamburg (2022) (Table S1 in the Supplement). Equations describing the radiative forcing of carbon dioxide (CO₂) and methane (CH₄) are based on Myhre et al. (2013). We estimate the global mean temperature change from emissions of CO₂, CH₄, or H₂ using a linearized Green's function approach and apply these equations to simple idealized cases. The calculation of the global mean temperature response is based on Gasser et al. (2017).

2.1 Indirect forcing from hydrogen

The system that describes the radiative forcing from H₂ emissions modeled by Warwick et al. (2022) and later used in Ocko and Hamburg (2022) is a representation of the following differential equations.

The change of H₂ molar mass relative to an unperturbed background condition, as a function of the time horizon t in units of year, is represented by a source function $f_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)$ and a decay term $\frac{m_{{\mathrm{H}}_{\mathrm{2}}}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}$, where $m_{{\mathrm{H}}_{\mathrm{2}}}$ is the molar mass of H₂ and ${\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}$ is the perturbation lifetime of H₂:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}{m}_{{\mathrm{H}}_{\mathrm{2}}}}{\mathrm{d}t}}=f_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)-{\displaystyle \frac{m_{{\mathrm{H}}_{\mathrm{2}}}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}.\end{array}$$

The presence of additional H₂ in the atmosphere changes the decay of atmospheric CH₄ and also results in the production of ozone (O₃) and stratospheric water vapor (H₂O). Underlying equations for perturbations to atmospheric molar masses of CH₄, O₃, and stratospheric H₂O induced from additional atmospheric H₂ (denoted by superscripts) are

$$\begin{array}{}\text{(2a)}& {\displaystyle \frac{\mathrm{d}{m}_{{\mathrm{CH}}_{\mathrm{4}}}^{{\mathrm{H}}_{\mathrm{2}}}}{\mathrm{d}t}}=a_{{\mathrm{CH}}_{\mathrm{4}}}{m}_{{\mathrm{H}}_{\mathrm{2}}}-{\displaystyle \frac{m_{{\mathrm{CH}}_{\mathrm{4}}}^{{\mathrm{H}}_{\mathrm{2}}}}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}},\text{(2b)}& {\displaystyle \frac{\mathrm{d}{m}_{{\mathrm{O}}_{\mathrm{3}}}^{{\mathrm{H}}_{\mathrm{2}}}}{\mathrm{d}t}}=a_{{\mathrm{O}}_{\mathrm{3}}}{m}_{{\mathrm{H}}_{\mathrm{2}}}-{\displaystyle \frac{m_{{\mathrm{O}}_{\mathrm{3}}}^{{\mathrm{H}}_{\mathrm{2}}}}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}}},\text{(2c)}& {\displaystyle \frac{\mathrm{d}{m}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{{\mathrm{H}}_{\mathrm{2}}}}{\mathrm{d}t}}=a_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{m}_{{\mathrm{H}}_{\mathrm{2}}}-{\displaystyle \frac{m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{{\mathrm{H}}_{\mathrm{2}}}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}.\end{array}$$

Here, $m_{{\mathrm{CH}}_{\mathrm{4}}}^{{\mathrm{H}}_{\mathrm{2}}}$, $m_{{\mathrm{O}}_{\mathrm{3}}}^{{\mathrm{H}}_{\mathrm{2}}}$, and $m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{{\mathrm{H}}_{\mathrm{2}}}$ are the respective molar masses of CH₄, O₃, and H₂O resulting from additional atmospheric H₂; $a_{{\mathrm{CH}}_{\mathrm{4}}}$, $a_{{\mathrm{O}}_{\mathrm{3}}}$, and $a_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ are factors representing the impact of remaining H₂ in the atmosphere on the atmospheric molar mass of these respective species; and ${\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}$, ${\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}$, and ${\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ are perturbation lifetimes of these respective species.

For the special case of a unit pulse perturbation of H₂ into an unperturbed background condition at time zero, these equations can be solved analytically. The respective solutions to Eqs. (1) and (2) under conditions $m_{{\mathrm{H}}_{\mathrm{2}}}\left(\mathrm{0}\right)=\mathrm{1}$, $f_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)=\mathrm{0}$, $m_{{\mathrm{CH}}_{\mathrm{4}}}^{{\mathrm{H}}_{\mathrm{2}}}\left(\mathrm{0}\right)=\mathrm{0}$, $m_{{\mathrm{O}}_{\mathrm{3}}}^{{\mathrm{H}}_{\mathrm{2}}}\left(\mathrm{0}\right)=\mathrm{0}$, and $m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{{\mathrm{H}}_{\mathrm{2}}}\left(\mathrm{0}\right)=\mathrm{0}$ are

$$\begin{array}{}\text{(3)}& m_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)=e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}},\end{array}$$

and

$$\begin{array}{}\text{(4a)}& {\displaystyle }{m}_{{\mathrm{CH}}_{\mathrm{4}}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)={\displaystyle \frac{a_{{\mathrm{CH}}_{\mathrm{4}}}}{\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}\right)-\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}\right)}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}-e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right),\text{(4b)}& {\displaystyle }{m}_{{\mathrm{O}}_{\mathrm{3}}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)={\displaystyle \frac{a_{{\mathrm{O}}_{\mathrm{3}}}}{\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}\right)-\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}}\right)}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}}}-e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right),\text{(4c)}& {\displaystyle }{m}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)={\displaystyle \frac{a_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}\right)-\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}\right)}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}-e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right).\end{array}$$

The corresponding radiative forcing is the product of the resulted molar mass and scaling factors $A_{{\mathrm{CH}}_{\mathrm{4}}}$, $A_{{\mathrm{O}}_{\mathrm{3}}}$, and $A_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ that convert molar mass to watts per meter squared (W m⁻²). The chemically adjusted radiative forcing, $A_{{\mathrm{CH}}_{\mathrm{4}}}^{\ast }$, for CH₄ uses factors f₁ and f₂ (Myhre et al., 2013) to represent the effect on O₃ and stratospheric H₂O:

$$\begin{array}{}\text{(5)}& A_{{\mathrm{CH}}_{\mathrm{4}}}^{\ast }=(\mathrm{1}+f_{\mathrm{1}}+f_{\mathrm{2}})A_{{\mathrm{CH}}_{\mathrm{4}}}.\end{array}$$

The indirect radiative forcing from a unit pulse emission of H₂, $R_{{\mathrm{H}}_{\mathrm{2}}}$, is thus the sum of radiative forcing from all three radiatively active perturbations:

6a$$\begin{array}{}\text{(6a)}& {\displaystyle }{R}_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)=A_{{\mathrm{CH}}_{\mathrm{4}}}^{\ast }{m}_{{\mathrm{CH}}_{\mathrm{4}}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)+A_{{\mathrm{O}}_{\mathrm{3}}}{m}_{{\mathrm{O}}_{\mathrm{3}}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)+A_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{m}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{{\mathrm{H}}_{\mathrm{2}}}\left(t\right).\end{array}$$

Inserting Eq. (4), we have

$$\begin{array}{}\text{(6b)}& \begin{array}{rl}{R}_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)& ={\displaystyle \frac{A_{{\mathrm{CH}}_{\mathrm{4}}}^{\ast }{a}_{{\mathrm{CH}}_{\mathrm{4}}}}{\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}\right)-\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}\right)}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}-e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right)\\ & +{\displaystyle \frac{A_{{\mathrm{O}}_{\mathrm{3}}}{a}_{{\mathrm{O}}_{\mathrm{3}}}}{\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}\right)-\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}}\right)}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}}}-e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right)\\ & +{\displaystyle \frac{A_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{a}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}\right)-\left(\frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}\right)}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}-e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right).\end{array}\end{array}$$

For a 1 kg unit pulse emission case, the time-integrated radiative forcing to a specified time horizon, H, is defined to be the absolute global warming potential (AGWP) (Myhre et al., 2013). Thus, AGWP can be represented as

$$\begin{array}{}\text{(7a)}& {\mathrm{AGWP}}_{{\mathrm{H}}_{\mathrm{2}}}\left(H\right)=\underset{\mathrm{0}}{\overset{H}{\int }}{R}_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)\mathrm{d}t,\end{array}$$

which can be rewritten as

7b$$\begin{array}{}\text{(7b)}& {\displaystyle }\begin{array}{rl}& {\mathrm{AGWP}}_{{\mathrm{H}}_{\mathrm{2}}}\left(H\right)=\\ & {\displaystyle \frac{A_{{\mathrm{CH}}_{\mathrm{4}}}^{\ast }{a}_{{\mathrm{CH}}_{\mathrm{4}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}\left({\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}\right)-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right)\right)}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\\ & +{\displaystyle \frac{A_{{\mathrm{O}}_{\mathrm{3}}}{a}_{{\mathrm{O}}_{\mathrm{3}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}\left({\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}}}\right)-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right)\right)}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\\ & +{\displaystyle \frac{A_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{a}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left({\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}\right)-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right)\right)}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}.\end{array}\end{array}$$

Equation (7) is the response to a unit pulse emission of H₂ taking into consideration radiative forcing adjustments to CH₄ as in Ocko and Hamburg (2022). Because we are considering a linear system, we can use this impulse response function to derive the radiative forcing from an arbitrary H₂ emission function $f_{{\mathrm{H}}_{\mathrm{2}}}$:

$$\begin{array}{}\text{(8)}& \widehat{R_{{\mathrm{H}}_{\mathrm{2}}}}\left(t\right)=\underset{\mathrm{0}}{\overset{t}{\int }}{f}_{{\mathrm{H}}_{\mathrm{2}}}\left(\mathit{\tau }\right)R_{{\mathrm{H}}_{\mathrm{2}}}(t-\mathit{\tau })\mathrm{d}\mathit{\tau }.\end{array}$$

Considering a continuous unit emission scenario where

$$\begin{array}{}\text{(9)}& f_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)=\mathrm{1},\end{array}$$

this leads to radiative forcing under a continuous emission scenario:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}& R_{{\mathrm{H}}_{\mathrm{2}},\text{cont}}\left(t\right)=\\ & {\displaystyle \frac{A_{{\mathrm{CH}}_{\mathrm{4}}}^{\ast }{a}_{{\mathrm{CH}}_{\mathrm{4}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}\left({\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}-\mathrm{1}\right)-{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}-\mathrm{1}\right)\right)}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\\ & +{\displaystyle \frac{A_{{\mathrm{O}}_{\mathrm{3}}}{a}_{{\mathrm{O}}_{\mathrm{3}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}\left({\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}-\mathrm{1}\right)-{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}}}-\mathrm{1}\right)\right)}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\\ & +{\displaystyle \frac{A_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{a}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left({\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}-\mathrm{1}\right)-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left(e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}-\mathrm{1}\right)\right)}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}.\end{array}\end{array}$$

In a linear system, the time-integrated radiative forcing from a unit pulse emission to some time horizon t₀ is mathematically equivalent to the radiative forcing at time t₀ from continuous unit emissions:

$$\begin{array}{}\text{(11)}& {\mathrm{AGWP}}_{{\mathrm{H}}_{\mathrm{2}}}\left(t_{\mathrm{0}}\right)=R_{{\mathrm{H}}_{\mathrm{2}},\text{cont}}\left(t_{\mathrm{0}}\right).\end{array}$$

Ocko and Hamburg (2022) used a metric that is equal to the time-integrated radiative forcing of continuous emissions to time horizon H. Since the AGWP has been defined as the time-integrated radiative forcing from the instantaneous release of 1 kg of a trace substance (Myhre et al., 2013), here we define the time-integrated radiative forcing under a continuous emission scenario as continuous absolute global warming potential (CAGWP):

$$\begin{array}{}\text{(12a)}& {\displaystyle }{\mathrm{CAGWP}}_{{\mathrm{H}}_{\mathrm{2}}}\left(H\right)& {\displaystyle }=\underset{\mathrm{0}}{\overset{H}{\int }}{R}_{{\mathrm{H}}_{\mathrm{2}},\text{cont}}\left(t\right)\mathrm{d}t,\text{(12b)}& {\displaystyle }& {\displaystyle }=\underset{\mathrm{0}}{\overset{H}{\int }}\underset{\mathrm{0}}{\overset{t}{\int }}{R}_{{\mathrm{H}}_{\mathrm{2}}}\left(\mathit{\tau }\right)\mathrm{d}\mathit{\tau }\mathrm{d}t,\text{(12c)}& {\displaystyle }& {\displaystyle }=\underset{\mathrm{0}}{\overset{H}{\int }}\underset{t}{\overset{H}{\int }}{R}_{{\mathrm{H}}_{\mathrm{2}}}\left(\mathit{\tau }\right)\mathrm{d}t\mathrm{d}\mathit{\tau },\text{(12d)}& {\displaystyle }& {\displaystyle }=\underset{\mathrm{0}}{\overset{H}{\int }}\left(\underset{t}{\overset{H}{\int }}\mathrm{d}t\right)R_{{\mathrm{H}}_{\mathrm{2}}}\left(\mathit{\tau }\right)\mathrm{d}\mathit{\tau },\text{(12e)}& {\displaystyle }& {\displaystyle }=\underset{\mathrm{0}}{\overset{H}{\int }}(H-t)R_{{\mathrm{H}}_{\mathrm{2}}}\left(t\right)\mathrm{d}t.\end{array}$$

Comparing Eq. (12) with Eq. (7a), we can see that the CAGWP metric is equivalent to the AGWP metric, except that the radiative forcing at time 0 is weighted by H, and the radiative forcing at time H is weighted at 0, with a linear ramping of weights in between by the number of years to the end of the time horizon. Equation (12) illustrates that time-integrated metrics under continuous emissions put heavy weights on the short-term effect.

Expanding Eq. (12), we have

$$\begin{array}{}\text{(13)}& \begin{array}{rl}& {\mathrm{CAGWP}}_{{\mathrm{H}}_{\mathrm{2}}}\left(H\right)=\\ & {\displaystyle \frac{\begin{array}{l}{A}_{{\mathrm{CH}}_{\mathrm{4}}}^{\ast }{a}_{{\mathrm{CH}}_{\mathrm{4}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}\left({\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}^{\mathrm{2}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right)\right.\\ \left.-{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}^{\mathrm{2}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}\right)+H\left({\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\right)\right)\end{array}}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\\ & +{\displaystyle \frac{\begin{array}{l}{A}_{{\mathrm{O}}_{\mathrm{3}}}{a}_{{\mathrm{O}}_{\mathrm{3}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}\left({\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}^{\mathrm{2}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right)\right.\\ \left.-{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}^{\mathrm{2}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}}}\right)+H\left({\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\right)\right)\end{array}}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{3}}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\\ & +{\displaystyle \frac{\begin{array}{l}{A}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{a}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left({\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}^{\mathrm{2}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}\right)\right.\\ \left.-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{2}}\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}\right)+H\left({\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}\right)\right)\end{array}}{{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}-{\mathit{\tau }}_{{\mathrm{H}}_{\mathrm{2}}}}}.\end{array}\end{array}$$

Equations (10) and (13) consider continuous emissions through the whole period. Equations considering a continuous emission to time tp are shown in Sect. S1 in the Supplement. Reproductions of the three components in Warwick et al. (2022) and Ocko and Hamburg (2022) are shown in Sect. S2. When used to estimate radiative forcing for identical cases, numerical differences between our equations and equations presented by Warwick et al. (2022) are small and are unlikely to make a material difference.

2.2 Forcing from CO₂ and CH₄

Here, we show radiative forcing and time-integrated radiative forcing functions for CO₂ and CH₄. Parameters are defined and values are given in Table S1. Radiative forcing for a unit pulse emission of CO₂ and CH₄ is represented as (Myhre et al., 2013)

$$\begin{array}{}\text{(14)}& {\displaystyle }{R}_{{\mathrm{CO}}_{\mathrm{2}}}\left(t\right)=A_{{\mathrm{CO}}_{\mathrm{2}}}\left(a_{\mathrm{0}}+\sum _{i=\mathrm{1}}^{\mathrm{3}}{a}_i{e}^{-\frac{t}{{\mathit{\tau }}_i}}\right),\text{(15)}& {\displaystyle }{R}_{{\mathrm{CH}}_{\mathrm{4}}}\left(t\right)=(\mathrm{1}+f_{\mathrm{1}}+f_{\mathrm{2}})A_{{\mathrm{CH}}_{\mathrm{4}}}{e}^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}.\end{array}$$

The AGWP for a unit pulse emission is

$$\begin{array}{}\text{(16)}& {\displaystyle }{\mathrm{AGWP}}_{{\mathrm{CO}}_{\mathrm{2}}}\left(H\right)=A_{{\mathrm{CO}}_{\mathrm{2}}}\left(a_{\mathrm{0}}H+\sum _{i=\mathrm{1}}^{\mathrm{3}}{a}_i{\mathit{\tau }}_i\left(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_i}}\right)\right),\text{(17)}& {\displaystyle }{\mathrm{AGWP}}_{{\mathrm{CH}}_{\mathrm{4}}}\left(H\right)=(\mathrm{1}+f_{\mathrm{1}}+f_{\mathrm{2}})A_{{\mathrm{CH}}_{\mathrm{4}}}{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}(\mathrm{1}-e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}).\end{array}$$

Radiative forcing for continuous emissions of CO₂ and CH₄ can be represented as

$$\begin{array}{}\text{(18)}& {\displaystyle }{R}_{{\mathrm{CO}}_{\mathrm{2}},\text{cont}}\left(t\right)=A_{{\mathrm{CO}}_{\mathrm{2}}}\left(a_{\mathrm{0}}t+\sum _{i=\mathrm{1}}^{\mathrm{3}}{a}_i{\mathit{\tau }}_i\left(\mathrm{1}-e^{-\frac{t}{{\mathit{\tau }}_i}}\right)\right),\text{(19)}& {\displaystyle }{R}_{{\mathrm{CH}}_{\mathrm{4}},\text{cont}}\left(t\right)=(\mathrm{1}+f_{\mathrm{1}}+f_{\mathrm{2}})A_{{\mathrm{CH}}_{\mathrm{4}}}{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}(\mathrm{1}-e^{-\frac{t}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}).\end{array}$$

And the corresponding CAGWP is

$$\begin{array}{}\text{(20)}& {\displaystyle }\begin{array}{rl}{\mathrm{CAGWP}}_{{\mathrm{CO}}_{\mathrm{2}}}\left(H\right)& =A_{{\mathrm{CO}}_{\mathrm{2}}}({\displaystyle \frac{a_{\mathrm{0}}{H}^{\mathrm{2}}}{\mathrm{2}}}\\ & +\sum _{i=\mathrm{1}}^{\mathrm{3}}{a}_i{\mathit{\tau }}_i\left(H+{\mathit{\tau }}_i\left(e^{-\frac{H}{{\mathit{\tau }}_i}}-\mathrm{1}\right)\right))\end{array},\text{(21)}& {\displaystyle }\begin{array}{rl}{\mathrm{CAGWP}}_{{\mathrm{CH}}_{\mathrm{4}}}\left(H\right)& =(\mathrm{1}+f_{\mathrm{1}}+f_{\mathrm{2}})A_{{\mathrm{CH}}_{\mathrm{4}}}{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}\\ & \times \left(H+{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}\left(e^{-\frac{H}{{\mathit{\tau }}_{{\mathrm{CH}}_{\mathrm{4}}}}}-\mathrm{1}\right)\right).\end{array}\end{array}$$

2.3 The global mean temperature response

For a linear system, the absolute global temperature change potential (AGTP), defined as the change of global mean surface temperature realized at a given time horizon from a pulse or continuous emissions of any gas i, can be represented as a convolution function (Myhre et al., 2013; Gasser et al., 2017):

$$\begin{array}{}\text{(22)}& {\mathrm{AGTP}}_i\left(H\right)=\underset{\mathrm{0}}{\overset{H}{\int }}{R}_i\left(t\right)T(H-t)\mathrm{d}t.\end{array}$$

In Eq. (22), R_i(t) is the radiative forcing for unit pulse or continuous emissions of gas i and T(t) indicates the temperature response to a unit forcing that can be represented as a sum of exponentials:

$$\begin{array}{}\text{(23)}& T\left(t\right)=\mathit{\lambda }\sum _{j=\mathrm{1}}^M{\displaystyle \frac{c_j}{d_j}}{e}^{-\frac{t}{d_j}},\end{array}$$

where λ is a constant that corresponds to the equilibrium climate sensitivity, $\sum _{j=\mathrm{1}}^M{c}_j=\mathrm{1}$, and d_j is the response time. Two exponential terms (M=2) are normally used in previous studies, with the first term associated with the response of the ocean mixed layer and the higher order associated with the response of the deep ocean (Gasser et al., 2017). In our central cases, we focus on using the equation from Geoffroy et al. (2013):

$$\begin{array}{}\text{(24)}& T\left(t\right)=\mathrm{0.885}\left({\displaystyle \frac{\mathrm{0.587}}{\mathrm{4.1}}}{e}^{-\frac{t}{\mathrm{4.1}}}+{\displaystyle \frac{\mathrm{0.413}}{\mathrm{249}}}{e}^{-\frac{t}{\mathrm{249}}}\right).\end{array}$$

Uncertainty in the temperature response function is shown in Sect. S3.

2.4 Simulations and assumptions

As in Ocko and Hamburg (2022), we focus on comparing the climate impact of replacing fossil fuel technologies with clean hydrogen alternatives. Climate impacts from hydrogen or fossil fuels are the summation of climate impacts of one or more components in a linear system (Sect. S4).

In this commentary, we analyze the climate impact per 1 kg consumption of green and blue H₂ and corresponding impacts from the avoided CO₂ emissions. We consider consistent assumptions as in Ocko and Hamburg (2022). For example, the kilogram amount of CH₄ required to produce blue H₂ is 3 times the kilogram amount of H₂ used, 1 kg consumption of H₂ would avoid 11 kg of CO₂ emissions (additional cases, i.e., 5 or 15 kg of avoided CO₂ emissions, are examined as well), and burning 1 kg of CH₄ would emit 2.75 kg of CO₂. Also, we take the same consistent leakage rate assumptions for CH₄ and H₂ to generate two central cases: a low-leakage case with 1 % H₂ and 1 % CH₄ leakage rates, and a high-leakage case with 10 % H₂ and 3 % CH₄ leakage rates (see detailed discussion underlying these assumptions in their paper).

We focus our discussions on three H₂ consumption scenarios: a 1 kg pulse consumption, 0.01 kg yr⁻¹ continuous consumption lasting for 100 years, and 0.01 kg yr⁻¹ continuous consumption lasting for 500 years. Results for 20-, 100-, and 500-year horizons are summarized in Tables S2 to S5.

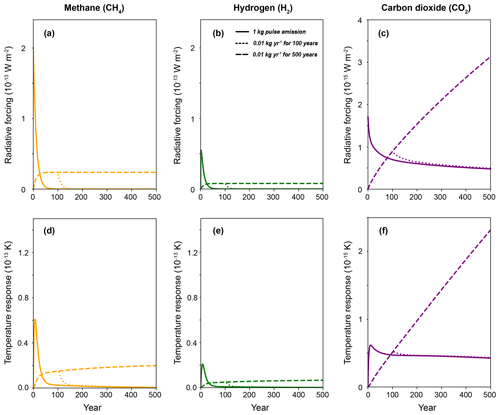
Figure 1 Climate impact from emissions of respective species. Radiative forcing (a–c) and global mean temperature response (d–f) caused by emissions of methane (CH₄), hydrogen (H₂), and carbon dioxide (CO₂). Three emission scenarios are considered: a 1 kg pulse emission, 0.01 kg yr⁻¹ continuous emissions lasting for 100 years, and 0.01 kg yr⁻¹ continuous emissions lasting for 500 years. CH₄ and H₂ share the same y axis, the maximum value of which is 60 times relative to that of CO₂. Radiative forcing from continuous emissions of H₂ and CH₄ is proportional to the emission rate and decays rapidly once ceased, whereas radiative forcing from CO₂ is closely related to the cumulative amount and will last for longer timescales. Figures showing only 100-year results are plotted in Fig. S12.

3 Results

3.1 Climate impact of individual gas

We first examine the time-evolving climate impact from emissions of carbon dioxide (CO₂), methane (CH₄), and hydrogen (H₂), respectively. Similarly, we consider three emission scenarios: a 1 kg pulse emission, 0.01 kg yr⁻¹ continuous emissions lasting for 100 years, and 0.01 kg yr⁻¹ continuous emissions lasting for 500 years.

Figure 1 shows the climate impact of individual species under various emission scenarios. Results showing ratios of CH₄ and H₂ to CO₂ are plotted in Fig. S1 in the Supplement. For the 1 kg pulse emission scenario, all species produce the largest climate impacts within the first few years and decay over time. Soon after emission, per kilogram emitted, CH₄ and H₂ show much larger impacts compared to CO₂. The global warming potential is typically defined for a 1 kg pulse emission of gas (Myhre et al., 2013), which will lead to different immediate changes in their atmospheric concentration when viewed on a molar basis. Figure S2 shows that when considering a 1 ppb increase of these gases, CH₄ still generates a much larger warming potential, whereas H₂ and CO₂ show the same order of magnitude impacts on radiative forcing and temperature in the first decade.

The climate impact of CH₄ and H₂ decays substantially faster than CO₂ along with their concentrations (perturbation lifetime used is 11.8 years for CH₄ and 1.9 years for H₂). For example, the radiative forcing of CH₄ and H₂ for the 1 kg pulse emission scenario is smaller than that of CO₂ after ∼ 65 and 50 years and approaches zero after 100 years. We do not consider conversions of the decayed CH₄ to CO₂, which will add more long-term impacts for CH₄ emissions (Forster et al., 2021) as shown in Fig. S3. This conversion should not be considered in the case of CH₄ perturbations brought about by H₂ emissions, because there is no net addition of carbon to the atmosphere in this case. In contrast, the radiative forcing of CO₂ is still 28 % of its maximum value at the 500-year time horizon. Temperature response behaves similarly to radiative forcing but at a slower rate due to the inertia of the climate system. Impacts of considering different H₂ perturbation lifetimes (i.e., 1.4 and 2.5 years) are shown in Fig. S4.

For 0.01 kg yr⁻¹ continuous emission cases, there is an accumulation of CO₂ concentration in the atmosphere, leading to monotonic increases in radiative forcing and temperature. If emissions stop abruptly after 100 years, the climate impacts of CO₂ slowly converge with those under the 1 kg emission case and stay roughly stable, because the effects of atmospheric concentration decrease are approximately offset by the effects of ocean warming. Due to the shorter perturbation lifetime of CH₄ and H₂, their atmospheric concentrations reach equilibrium under continuous emission scenarios with magnitudes depending on the emission rates, and radiative forcing reaches a stable level after a few decades. Global mean temperature continues to increase slowly due to the thermal inertia of the climate system. If emissions stop abruptly after 100 years, their concentrations would decrease rapidly and reach zero within decades. The longer perturbation lifetime of CO₂ results in more prominent longer-term climate impacts under both pulse and continuous emission scenarios.

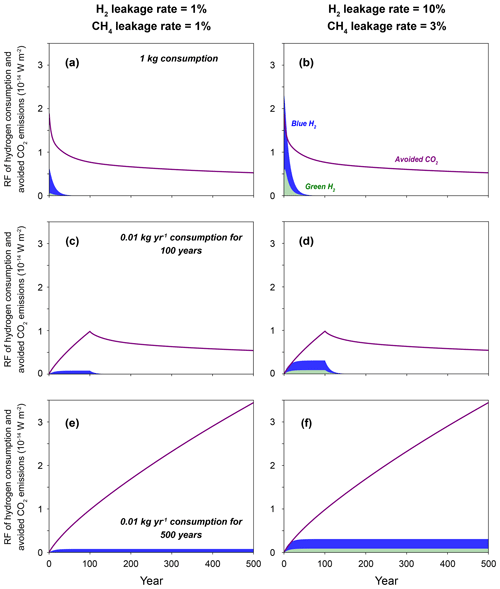
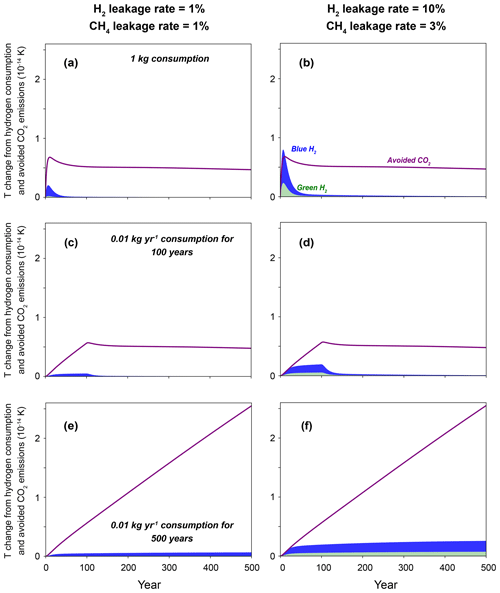
Figure 2 Radiative forcing from consumption of green hydrogen (H₂), blue H₂, and avoided CO₂ emissions. Three cases are considered: (a, b) a 1 kg consumption of H₂, (c, d) 0.01 kg yr⁻¹ continuous consumption of H₂ lasting for 100 years, and (e, f) 0.01 kg yr⁻¹ continuous consumption of H₂ lasting for 500 years. Panels (a), (c), and (e) show cases with 1 % H₂ and 1 % CH₄ leakage rates, and panels (b), (d), and (f) show cases with 10 % H₂ and 3 % CH₄ leakage rates. CH₄ leakage contributes primarily to the warming potential of blue H₂ consumption, while H₂ leakage plays a secondary role. For the longer term, radiative forcing from carbon dioxide is substantially larger than that from clean H₂ alternatives. Figures showing only 100-year results are plotted in Fig. S13.

Figure 3 Same as Fig. 2 but for the global mean temperature response. Figures showing only 100-year results are plotted in Fig. S14.

3.2 Climate impact of hydrogen and fossil fuels

Under the low-leakage scenario (i.e., 1 % H₂ and 1 % CH₄ leakage rate), both green and blue H₂ produce smaller radiative forcing and global mean temperature increases compared to the avoided CO₂ emissions (Figs. 2 and 3), indicating net climate benefits of replacing fossil fuels with clean hydrogen alternatives. Compared to green H₂, leakages of CH₄ from blue H₂ add substantial additional warming within the first few decades. For the 1 kg pulse consumption scenario, the climate impact of green and blue H₂ decays rapidly to zero within the first few decades (conversion of decayed CH₄ to CO₂ not included), whereas the climate impact of avoided CO₂ emissions becomes roughly stable with time. Continuous consumption of H₂ would lead to stable radiative forcing and temperature change at longer timescales with magnitudes depending on consumption levels, and such impacts will adjust quickly if future leakage rates change. Meanwhile, continuous consumption of fossil fuels leads to accumulation of CO₂ concentration and increasing climate responses. Even if CO₂ consumption is ceased, its impacts would last for hundreds of years.

Under the high-leakage scenario, the additional leakage of H₂ (i.e., 10 % vs. 1 % H₂ leakage rate) reduces the short-term climate benefits of green H₂, and the additional leakage of CH₄ (i.e., 3 % vs. 1 % CH₄ leakage rate) further leads to net disbenefits for blue H₂ in the first few years, when compared to avoided CO₂ emissions (Figs. 2 and 3). In both the low- and high-leakage cases, CH₄ adds more warming than H₂ does (Fig. S5). Because of the shorter lifetimes of H₂ and CH₄, net climate benefits for blue H₂ are observed after ∼ 12 and 20 years under different emission scenarios for the high-leakage case. The climate impacts of H₂ become orders of magnitude smaller than that of CO₂ emissions as time evolves.

In our central cases, we do not include CH₄ leakages when calculating climate impacts for the avoided CO₂ emissions, which are included for blue H₂. Under all emission scenarios, using the same CH₄ leakage rates for CH₄ combustion and H₂ production (Figs. S6 and S7) substantially increases the warming potentials from the avoided CO₂ emissions, especially for the short-term results, leading to net climate benefits for both clean hydrogen alternatives. Consideration of conversion of the decayed CH₄ to CO₂ further increases the long-term climate impacts for both blue H₂ and the avoided CO₂ emission cases that contain CH₄ leakage (Figs. S6 and S7). As in Ocko and Hamburg (2022), considering that different amounts of avoided CO₂ emission for per kilogram of H₂ consumption (e.g., 5 or 15 kg CO₂ avoided per kilogram of H₂ consumption) can affect both short-term and long-term climate impacts (Fig. S8). In contrast, considering different H₂ perturbation lifetimes or climate response functions has minor effects (Figs. S6, S7, and S9). Here, we do not cover all uncertainties but give some first-level impressions of how different parameters can affect results presented in this analysis.

Finally, Ocko and Hamburg (2022) quantified the net climate benefits of consuming H₂ compared to the avoided CO₂ emissions by comparing the time-integrated radiative forcing from continuous emissions of both gases. This metric overpredicts the amount of warming that would be produced by CH₄ and H₂ leakage relative to the warming that would have been caused by the avoided CO₂ emissions over time (Fig. S10). This result is similar to that of Allen et al. (2016) showing that, for pulse emissions and any time horizon longer than a decade, the global mean relative temperature response metric (i.e., GTP) would be lower than values of the time-integrated relative radiative forcing (i.e., GWP).

4 Discussion

The radiative forcing calculation presented here is a linear approximation, with radiative forcing increasing linearly with concentration, when in fact absorption bands become increasingly saturated at higher concentrations, and this results in less sensitivity at higher concentrations. The radiative forcing calculation assumes an unchanging background atmospheric composition, whereas it is likely that the climate impact of an emission will depend on the background climate state (Duan et al., 2019; Robrecht et al., 2019). For instance, the indirect radiative forcing of hydrogen (H₂) through its effect on the lifetime of methane (CH₄) might depend on the background CH₄ concentration. The effectiveness of radiative forcing at affecting temperature can vary substantially from gas to gas (Hansen et al., 1997; Modak et al., 2018). In addition, the framework used here only compares H₂ with the avoided carbon dioxide (CO₂) emissions, while fossil fuel adoptions are associated with emissions of other radiatively active species and air pollutants (IPCC, 2018).

Many important uncertainties persist. For example, we considered the chemical adjustment to radiative forcing for CH₄ due to effects on ozone (O₃) and stratospheric water vapor (H₂O), as considered by Ocko and Hamburg (2022). There are other effects that have been included in previous works, which would affect the warming impact of CH₄ emissions (Boucher et al., 2009; Shindell et al., 2009). There are uncertainties related to cloud radiative effects from thermodynamic adjustments and aerosol–cloud interactions (O'Connor et al., 2022). There are additional uncertainties related to the fast physical radiative forcing adjustments to dioxide, O₃, and other radiatively active gases (Smith et al., 2018). Co-emissions from fossil fuel combustions (e.g., aerosol precursors) can also affect climate and public health (Lelieveld et al., 2019). Unlike long-lived CO₂, the climate impact of short-lived forcers might depend on locations of emissions (Persad and Caldeira, 2018; Burney et al., 2022). While their radiative forcing might diminish quickly after emission ceasing, indirect impacts from these short-lived forcers (e.g., by affecting carbon sinks and atmospheric CO₂ levels) could last longer, introducing additional uncertainties (Fu et al., 2020). None of these considerations are expected to be of sufficient magnitudes to qualitatively alter key conclusions presented here.

Ocko and Hamburg (2022) propose a metric, which we call CAGWP, that involves the integral of radiative forcing for continuous emissions, which differs from the standard GWP metric based on a unit emission of 1 kg of gas. While the GWP metric has been widely used to compare the climate impact of different greenhouse gases, it may not be the best predictor of climate impacts. For example, Allen et al. (2016) have argued that the GWP metric overemphasizes the long-term climate effect of short-lived gases such as CH₄. The CAGWP metric proposed by Ocko and Hamburg (2022) emphasizes short-lived gases to an even greater extent than the customary GWP metric. We have shown that the CAGWP metric is equivalent to a front-loaded weighted integral of a pulse emission. The 100-year CAGWP metric weights the 1st year after an emission 99 times, whereas it weights the 99th year after an emission only once.

There are different motivations for reducing warming at various timescales. One motivation is to avoid near-term climate damage that might come, for example, from increasing storm or drought intensity. Another motivation is to avoid long-term climate damage that might come, for example, from the melting of the large ice sheets (Pattyn et al., 2018) or from making parts of the tropics effectively uninhabitable (Dunne et al., 2013; Sun et al., 2019). Decision-making can balance near-term and long-term risks and identify opportunities to address both kinds of risk simultaneously.

Different climate forcing agents differ in their degrees of reversibility. To a close approximation, on the timescale of decades or more, temperature change from CH₄ or H₂ emissions are proportional to rates of emission, whereas temperature change from CO₂ is proportional to cumulative emission (Jones et al., 2006; Allen et al., 2009). This important distinction is not captured by the CAGWP metric proposed by Ocko and Hamburg (2022).

Considering how different market sizes would affect the overall impact of H₂ is beyond the scope of this analysis. Blue H₂, despite its larger climate impacts, is currently the dominant way of producing H₂. Meanwhile, the additional climate benefits from green H₂ have been recognized that will likely play a greater role in some regions (EUR-Lex, 2022) in the future. It is clear that electrolytic H₂ made with carbon-emission-free electricity would produce less climate change than H₂ made using CH₄ as a feedstock; people use steam–methane reforming to produce H₂ typically because it costs less than electrolysis.

5 Conclusions

Our analysis confirms the results of Ocko and Hamburg (2022) under consistent assumptions but complements their presentation with additional uncertainty analysis and a longer-term perspective. While we confirm the results presented in Ocko and Hamburg (2022), it is clear that over longer time horizons (e.g., 100 years), substituting blue or green hydrogen (H₂) for fossil fuels will result in much less climate change.

We have developed a tutorial for the derivations of underlying differential equations that describe the radiative forcing of H₂ emissions, which differ slightly from equations relied on by previous studies. In line with previous studies (Fuglestvedt et al., 2010; Allen et al., 2016; Balcombe et al., 2018), both the radiative forcing and global mean temperature response from H₂ and methane (CH₄) are proportional to the underlying emission rates, whereas climate impacts from carbon dioxide (CO₂) are closely related to cumulative emissions. For the same quantity of emissions, H₂ shows consistently smaller climate impact than CH₄. High leakage rates of CH₄ contribute primarily to the high warming potential of methane-derived H₂ production, with high H₂ leakage rates playing a secondary role. As shown by Ocko and Hamburg (2022), blue H₂ with a CH₄ leakage rate of 3 % and a H₂ leakage rate of 10 % could produce more warming in the first 20 years after the release. However, even with these high-leakage rates, warming from blue H₂ 100 years later would be only a small portion of the warming from the fossil fuels it replaced. In contrast to the climate impact of CO₂ emissions, which persist for many millennia (Archer, 2005; Solomon et al., 2009), climate impacts decay on the timescale of decades after a cessation of CH₄ or H₂ emissions.

Consideration of CH₄ leakage associated with burning natural gas can have a substantial effect on results. Including the CH₄ leakage associated with fossil fuel combustion would increase its short-term impact and might lead to net short-term climate benefit for blue H₂ under greater leakage rates. Other factors, including the H₂ lifetime and different climate response functions, are relatively less important.

Ocko and Hamburg (2022) propose that the climate impact of blue and green H₂ be evaluated with the use of a metric that strongly weights near-term radiative forcing relative to long-term radiative forcing from individual pulse emissions.

We emphasize that to attain near-term climate benefits from “blue” H₂ that dominates current markets depends critically on achieving low CH₄ leakage rates. “Green” H₂ produced by electrolysis using carbon-emission-free electricity has a small climate impact relative to the impact of the fossil fuels that H₂ would replace, while very high H₂ leakage rates could pose some climate concern and undercut accomplishing net zero emission goals. Safety and cost considerations may motivate the reduction of hydrogen leakage (Nugroho et al., 2022). In all cases considered, relative to fossil fuel combustion and associated emissions, both blue and green H₂ show large long-term climate benefits even with high-leakage rates.