Large-eddy-simulation study on turbulent particle deposition and its dependence on atmospheric-boundary-layer stability

It is increasingly recognized that atmospheric-boundary-layer stability (ABLS) plays an important role in eolian processes. While the effects of ABLS on particle emission have attracted much attention and been investigated in several studies, those on particle deposition have so far been less well studied. By means of large-eddy simulation, we investigate how ABLS influences the probability distribution of surface shear stress and hence particle deposition. Statistical analysis of the model results reveals that the shear stress can be well approximated using a Weibull distribution, and the ABLS influences on particle deposition can be estimated by considering the shear stress fluctuations. The model-simulated particle depositions are compared with the predictions of a particle-deposition scheme and measurements, and the findings are then used to improve the particle-deposition scheme. This research represents a further step towards developing deposition schemes that account for the stochastic nature of particle processes.

1 Introduction

Dry deposition is the removal of particulates and gases at the air–surface interface by turbulent transfer and gravitational settling (Sehmel, 1980; Droppo, 2006; Hicks et al., 2016). Because it is the only process for the removal of particles from the atmosphere in the absence of precipitation, developing reliable methods for estimating dry deposition of particles has attracted much interest since the early 1940s (Gregory, 1945; Chamberlain, 1953; Slinn and Slinn, 1980; Slinn, 1982; Walcek et al., 1986; Zhang et al., 2001; Petroff and Zhang, 2010; Zhang and Shao, 2014; Seinfeld et al., 2016). Several particle-deposition schemes have been proposed (Slinn, 1982; Walcek et al., 1986; Zhang and Shao, 2014; Zhang et al., 2001) for regional and global models, which are driven using several environmental parameters, including the Reynolds surface shear stress (typically averaged over 15–30 min). However, field observations indicate that the use of Reynolds stress as the only wind-related parameter in such schemes may not be sufficient to achieve accurate estimates of particle deposition because of the nonlinear relationship between deposition velocity and wind shear. Observations using the eddy correlation method show that particle-deposition velocity has strong spatiotemporal variations associated with the fluctuations of wind speed (Connan et al., 2018; Damay et al., 2009; Lamaud et al., 1994; Wesely et al., 1983, 1985). It is also observed that when the background wind speeds are similar, dry deposition velocities under convective conditions are larger than under neutral and stable conditions (Fowler et al., 2009). Pellerin et al. (2017) suggested that cospectral similarities exist between heat and particle-deposition fluxes and that atmospheric turbulence plays a role in particle deposition. It is therefore necessary to find a link between instantaneous wind and particle deposition and to correctly represent this link in particle-deposition schemes, i.e., to introduce and account for the effect of turbulence on particle deposition.

Some eolian processes, e.g., turbulent particle emission (Klose and Shao, 2012, 2013) and intermittent saltation (Li et al., 2020; Liu et al., 2018; Rana et al., 2020), have been under development. To the best of our knowledge, although turbulent particle deposition is now perceived to be important, a scheme is yet to be constructed for its quantitative estimate.

The turbulent wind flow in a particle-deposition scheme is reflected in the turbulent shear stress (or vertical momentum flux) (Fowler et al., 2009; Zhang and Shao, 2014). It is well known that apart from gravitational settling, particle deposition is driven by turbulent diffusion, which is intimately related to the vertical momentum transfer in the atmospheric boundary layer (ABL) (Wyngaard, 2010). Based on the Prandtl mixing-length theory, the shear stress can be parameterized in neutral conditions. However, it is known that for a given mean wind speed (at a reference height) in the ABL, both the mean value and the perturbations of shear stress depend on the atmospheric-boundary-layer stability (ABLS); for instance, shear stress shows generally larger fluctuations in convective ABLS. Klose and Shao (2013) pointed out the following:

In a convective atmospheric boundary layer, large eddies have coherent structures of dimensions comparable to boundary-layer depth, which are efficient entities in generating localized momentum fluxes to the surface. Although the eddies only occupy fractions of time and space, the momentum fluxes to these fractions can be many times the average. (p. 49)

Hicks et al. (2016) mentioned that ABLS is of immediate concern in the micrometeorological community because of its influences on the intermittency, gustiness and diurnal cycle of particle deposition. Similar to turbulent dust emission and intermittent sand saltation, intermittent particle deposition also occurs as a result of fluctuating surface shear stress. The current particle-deposition schemes only consider the mean behavior of wind (Slinn, 1982; Zhang and Shao, 2014; Zhang et al., 2001) and how this mean behavior varies with ABLS via the Monin–Obukhov similarity theory (Monin et al., 2007; Monin and Obukhov, 1954) but not the fluctuations of the associated shear stress and how they vary with ABLS.

We argue that focusing only on the effects of ABLS on mean wind is insufficient to accurately model particle deposition. In this study, we explore the influences of ABLS on the turbulent behavior of particle deposition and attempt to improve an existing particle-deposition scheme. A large-eddy-simulation (LES) model is used here to simulate turbulence and particle deposition under various ABLS conditions, and parts of the study design follow Klose and Shao (2013). The particle depositions simulated using the LES model and predicted using the particle-deposition scheme of Zhang and Shao (2014, ZS14 hereafter) are compared with each other and with measurements. Specifically, we address the following three issues: (1) how ABLS affects the probability distribution of surface shear stress, (2) how ABLS impacts particle deposition and (3) how the ZS14 scheme can be improved to account for the ABLS effect. On this basis, an improvement to the ZS14 scheme (also applicable to other schemes) is proposed. The remaining part of the paper is organized as follows: Sect. 2 gives a brief description of the Weather Research and Forecasting – Large-Eddy-Simulation Model with Dust module (WRF-LES/D), the ZS14 scheme and the design of the numerical experiments. Section 3 discusses the findings of the numerical simulations and the improvement to the ZS14 scheme. The concluding remarks are given in Sect. 4.

2 Model/method

2.1 WRF-LES/D

The WRF-LES/D used here is initially developed by Shao et al. (2013) and Klose and Shao (2013) by coupling the WRF-LES (Moeng et al., 2007; Skamarock et al., 2008) with a land-surface module and dust module. As demonstrated in the earlier studies, WRF-LES/D is a well-established system for applications of simulating turbulence, turbulent particle emission and transport for various ABLS conditions. WRF-LES is a three-dimensional and non-hydrostatic model for fully compressible flow. The model separates the turbulent flow into a grid-resolved component and a subgrid component. The k−l subgrid closure (Deardorff, 1980) together with the turbulent kinetic energy (TKE) equation (Skamarock et al., 2008) is used here. The governing equations in WRF-LES/D include the equations of motion, continuity equation, enthalpy equation, equation of state and the particle conservation equation, as shown below:

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial u_i}{\partial t}}& +{\displaystyle \frac{\partial u_i{u}_j}{\partial x_j}}=-{\mathit{\delta }}_{i\mathrm{3}}g+{\mathit{\epsilon }}_{ij\mathrm{3}}f{u}_j-{\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{a}}}}{\displaystyle \frac{\partial p}{\partial x_i}}+\mathit{\nu }{\displaystyle \frac{{\partial }^{\mathrm{2}}{u}_i}{\partial x_j{x}_j}}\\ & -{\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{a}}}}{\displaystyle \frac{\partial {\mathit{\tau }}_{ij}}{\partial x_j}}\end{array}\text{(2)}& {\displaystyle \frac{\partial {\mathit{\rho }}_{\mathrm{a}}}{\partial t}}+{\displaystyle \frac{\partial \left({\mathit{\rho }}_{\mathrm{a}}{u}_j\right)}{\partial x_j}}=\mathrm{0}\text{(3)}& {\displaystyle \frac{\partial c_{\mathrm{p}}T}{\partial t}}+{\displaystyle \frac{\partial \left(c_{\mathrm{p}}{u}_{j}T\right)}{\partial x_j}}={\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{a}}}}{\displaystyle \frac{\partial H_j}{\partial x_j}}+s_T\text{(4)}& {\displaystyle }p={\mathit{\rho }}_{\mathrm{a}}{R}_{\mathrm{a}}T\text{(5)}& {\displaystyle \frac{\partial c}{\partial t}}+u_j{\displaystyle \frac{\partial c}{\partial x_j}}-w_{\mathrm{t}}{\displaystyle \frac{\partial c}{\partial z}}=-{\displaystyle \frac{\partial F_j}{\partial x_j}}+s_r,\end{array}$$

where $u_i(u,v,w)$ is the grid-resolved flow velocity along x_i (x, y, z), referring to the streamwise, spanwise and vertical directions, respectively; g is the acceleration due to gravity; ρ_a is the air density; f is the Coriolis parameter; p is the air pressure; τ_ij is the subgrid stress tensor modeled using an eddy viscosity approach, where the eddy viscosity is represented as the product of a length scale and a velocity scale characterizing the subgrid-scale (SGS) turbulent eddies (Dupont et al., 2013), with the velocity scale being derived from the SGS TKE and the length scale from the grid spacing (Skamarock et al., 2008); ν is the kinematic viscosity; δ_i3 is the Kronecker operator; ε_i3 is the alternating operator; c_p is the specific heat of air at constant pressure; T is air temperature; H_j is the jth component of subgrid heat flux; R_a is the specific gas constant of air; c is particle concentration; w_t is the particle terminal velocity; F_j is the jth component of subgrid particle flux; and s_T and s_r are the source or sink terms for heat and particles, respectively. The subgrid eddy diffusivity is set to subgrid eddy viscosity divided by the Prandtl number. For the surface layer, an important parameterization to solve the governing equations for high-Reynolds-number turbulence is embedded in the surface boundary condition, which computes the instantaneous local surface shear stress using the bulk-transfer method (Kalitzin et al., 2008; Kawai and Larsson, 2012; Piomelli et al., 2002; Zheng et al., 2020) as follows:

$$\begin{array}{}\text{(6)}& \mathit{\tau }={\mathit{\rho }}_{\mathrm{a}}{K}_m{\displaystyle \frac{\partial V}{\partial z}},\end{array}$$

with

$$\begin{array}{}\text{(7)}& K_m={\displaystyle \frac{\mathit{\kappa }{u}_{\ast }z}{{\mathit{\phi }}_{\mathrm{m}}}},\end{array}$$

where K_m is the eddy viscosity, φ_m is the Monin–Obukhov similarity theory (MOST) stability function, $V=\sqrt{u^{\mathrm{2}}+v^{\mathrm{2}}}$, and κ is the von Karman constant. Even though Shao et al. (2013) questioned the application of the MOST in LES, it is still used here, as our emphasis is on the variance of shear stress in the simulation domain. Several land-surface models (LSMs) can be selected (e.g., Chen and Dudhia, 2000; Pleim and Xiu, 2003) in WRF-LES/D, and the 5-layer thermal diffusion (Dudhia, 1996) is used in this study. Furthermore, the surface heat flux, denoted H₀, is specified. The dry deposition flux to the ground for each grid, denoted F_d, is obtained by multiplying the deposition velocity V_d and particle concentration c in the lowest layer, and V_d is estimated using the ZS14 deposition scheme.

2.2 Particle-deposition scheme of ZS14

The particle deposition on the surface is more complicated than the momentum flux as the change of particle concentration close to the surface is unclear. To solve the particle conservation equation (Eq. 5), the emission and deposition fluxes at the surface need to be specified. The problem of particle emission has been dealt with elsewhere (e.g., Shao, 2004, focuses on the particle emission without turbulence effects; Klose et al., 2014, and Klose and Shao, 2012, emphasize the turbulent particle emission) and is not considered here. For our purpose, particle emission is assumed to be zero. This section gives the parameterization scheme proposed by ZS14. The details of the scheme are described in ZS14; only the main results are given here for completeness. In general, we can express the particle-deposition flux F_d as

$$\begin{array}{}\text{(8)}& F_{\mathrm{d}}=-\left(K_{\mathrm{p}}+k_{\mathrm{p}}\right){\displaystyle \frac{\partial c}{\partial z}}-w_{\mathrm{t}}\cdot c,\end{array}$$

where K_p and k_p are the eddy diffusivity and the molecular diffusivity, respectively. By analogy with the bulk-transfer formulation of scalar fluxes in ABL, F_d can be parameterized as

$$\begin{array}{}\text{(9)}& F_{\mathrm{d}}=-V_{\mathrm{d}}\left(z\right)\cdot c\left(z\right),\end{array}$$

where c(z) is the particle concentration at height z (the center height of the lowest model level in this study), and V_d(z) is the corresponding dry deposition velocity.

The surface layer is divided into an inertial layer and a roughness layer. Integrating Eq. (8) into the inertial layer and substituting Eq. (9) into it, V_d(z) is obtained as follows:

$$\begin{array}{}\text{(10)}& V_{\mathrm{d}}\left(z\right)={\left(r_{\mathrm{g}}+{\displaystyle \frac{r_s-r_{\mathrm{g}}}{\exp \left(r_{\mathrm{a}}/r_{\mathrm{g}}\right)}}\right)}^{-\mathrm{1}},\end{array}$$

with r_g being the gravitational resistance, r_s being the collection resistance, and r_a being the aerodynamic resistance for the inertial layer.

The gravitational resistance r_g is defined as the reciprocal of the gravitational settling velocity w_t and depends mainly on particle size and density. A free-falling particle is subject to gravitational and aerodynamic drag forces. When these forces are in equilibrium, the gravitational settling velocity of the particle smaller than 20 µm can be reasonably accurately calculated according to the Stokes formula (Malcolm and Raupach, 1991; Seinfeld and Pandis, 2006):

$$\begin{array}{}\text{(11)}& w_{\mathrm{t}}={\displaystyle \frac{C_u{\mathit{\rho }}_{\mathrm{p}}{D}_{\mathrm{p}}^{\mathrm{2}}g}{\mathrm{18}{\mathit{\mu }}_{\mathrm{a}}}}=r_{\mathrm{g}}^{-\mathrm{1}},\end{array}$$

where D_p is the particle diameter, ρ_p is the particle density, μ_a is the air dynamic viscosity, and C_u is the Cunningham correction factor that accounts for the slipping effect affecting the fine particles.

Using the MOST, the aerodynamic resistance is calculated as

$$\begin{array}{}\text{(12)}& r_{\mathrm{a}}={\displaystyle \frac{S{c}_T}{\mathit{\kappa }{u}_{\ast }}}\left[\ln \left({\displaystyle \frac{z-z_{\mathrm{d}}}{h-z_{\mathrm{d}}}}\right)-{\mathit{\psi }}_m\right],\end{array}$$

where z_d is the displacement height, h is the height of roughness element, ψ_m is the integral of stability function in the inertial layer, and $S{c}_T=K_m/K_p$ (Csanady, 1963).

In the roughness layer, the collection process is reflected in collection resistance, defined by $r_s=-\frac{c\left(h\right)}{F_{\mathrm{d}}}$, with an assumption that particle concentration is zero on roughness elements or the ground. In addition to the meteorological factors and land-use category, Zhang and Shao (2014) established a relationship between aerodynamic and surface collection processes using an analogy between the drag partition and deposition flux partition, which can describe surface heterogeneity.

$$\begin{array}{}\text{(13)}& r_s={\left[R\cdot {\displaystyle \frac{\mathit{\tau }}{{\mathit{\rho }}_{\mathrm{a}}{u}_h}}\left({\displaystyle \frac{E}{C_{\mathrm{d}}}}{\displaystyle \frac{{\mathit{\tau }}_c}{\mathit{\tau }}}+\left(\mathrm{1}+{\displaystyle \frac{{\mathit{\tau }}_c}{\mathit{\tau }}}\right)S{c}^{-\mathrm{1}}+{\mathrm{10}}^{\frac{-\mathrm{3}}{\widehat{T}}}\right)+w_{\mathrm{t}}\right]}^{-\mathrm{1}},\end{array}$$

where R is the reduction in collection caused by particle rebound; u_h is the wind speed at the top of roughness layer; E is the collection coefficient of roughness elements, and it includes the collection efficiency from Brownian motion (E_B), impaction (E_im), and interception (E_in); C_d is the drag coefficient for isolated roughness element; ${\mathit{\tau }}_c/\mathit{\tau }$ describes the drag partition, with τ_c being the pressure drag (the force exerted on roughness elements); Sc is the Schmidt number, which is the ratio of air viscosity to molecular diffusion; and ${\mathrm{10}}^{-\mathrm{3}/\widehat{T}}{T}_{\mathrm{p},\mathit{\delta }}^{+}$ represents the turbulent impaction efficiency, with $\widehat{T}$ being the dimensionless particle relaxation time. E_B, E_im, E_in, and R are expressed as

$$\begin{array}{}\text{(14)}& {\displaystyle }{E}_{\mathrm{B}}=C_{B}S{c}^{-\mathrm{2}/\mathrm{3}}R{e}^{n_B-\mathrm{1}}\text{(15)}& {\displaystyle }{E}_{\mathrm{im}}={\left({\displaystyle \frac{St}{\mathrm{0.6}+St}}\right)}^{\mathrm{2}}\text{(16)}& {\displaystyle }{E}_{\mathrm{in}}=u_{\ast }{\mathrm{10}}^{-St}{\displaystyle \frac{\mathrm{2}{D}_{\mathrm{p}}}{d_c}}\text{(17)}& {\displaystyle }R=\exp (-\sqrt{St}),\end{array}$$

where Re is the roughness element Reynolds number, C_B and n_B are parameters depending on Re, d_c is the diameter of the roughness element, and St is the Stokes number.

The ratio ${\mathit{\tau }}_c/\mathit{\tau }$ can be calculated according to Yang and Shao (2006), as follows:

$$\begin{array}{}\text{(18)}& {\displaystyle \frac{{\mathit{\tau }}_c}{\mathit{\tau }}}={\displaystyle \frac{{\mathit{\beta }}_{\mathrm{1}}{\mathit{\lambda }}_e}{\mathrm{1}+{\mathit{\beta }}_{\mathrm{1}}{\mathit{\lambda }}_e}}\end{array}$$

and

$$\begin{array}{}\text{(19)}& {\mathit{\lambda }}_e={\displaystyle \frac{\mathit{\lambda }}{{\left(\mathrm{1}-\mathit{\eta }\right)}^{\mathrm{6}}}}\cdot \exp \left(-{\displaystyle \frac{\mathit{\lambda }}{\mathrm{10}\cdot {\left(\mathrm{1}-\mathit{\eta }\right)}^{\mathrm{6}}}}\right),\end{array}$$

with β₁(= 200) being the ratio of the drag coefficient for isolated roughness element to that for bare surface, λ being the frontal area index of the roughness elements, and η being the basal area index or the fraction of cover.

From Eqs. (10) to (19), it can be seen that V_d and τ are nonlinearly related. For example, for particles with a diameter of 1 µm, analysis shows that V_d is dominated by w_t when τ is small. As τ increases, w_t and τ are both important to V_d. With τ increasing further, the effect of τ becomes much greater than gravitational settling; thus the V_d is mainly determined by τ.

2.3 Simulation setup

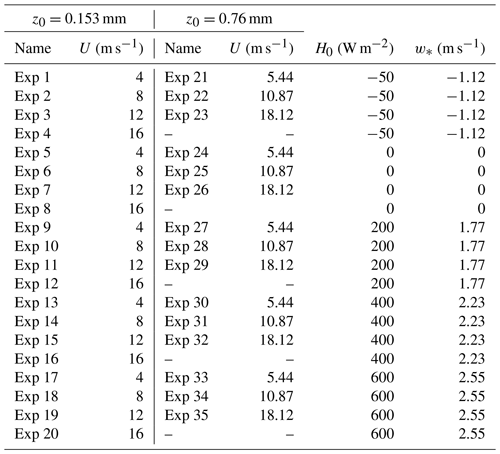
Numerical experiments are carried out with WRF-LES/D for various atmospheric stability and background wind conditions for two different roughness lengths (Table 1). Similar to Klose and Shao (2013), the domain of the simulation is $\mathrm{2000}\times \mathrm{2000}\times \mathrm{1500}$ m³, and the number of grid points is $\mathrm{200}\times \mathrm{200}\times \mathrm{90}$, corresponding to a horizontal resolution $\mathrm{\Delta }x=\mathrm{\Delta }y=\mathrm{10}$ m. The Arakawa-C staggered grid is used. The depth of the lowest model layer is 1 m, and the grid above is stretched following a logarithmic function of z. The simulation time is 90 min, with a time step of 0.05 s, and the output interval is 10 s. The first 30 min of the simulation is the model spin-up time, and the data of the remaining 60 min are used for the analysis.

For model initialization, the wind and particle (ρ_p=2650 kg m⁻³) concentration (Chamberlain, 1967; Monin, 1970; Kind, 1992) are assumed to be logarithmic in the vertical and uniform in the horizontal direction. For each experiment, a constant surface heat flux is specified. A 300 m deep Rayleigh damping layer is used at the upper boundary with a damping coefficient of 0.01. The wind speed at the top boundary, U, is given in Table 1. The surface heat flux, H₀, increases from −50 to 600 W m⁻², and for each surface heat flux, the top wind speed increases from 4 to 16 m s⁻¹ in Exp (1–20) and from 5.44 to 18.12 m s⁻¹ in Exp (21–35). The roughness length z₀ for sand surface used in Exp (1–20) is 0.153 mm following wind tunnel experiments (Zhang and Shao, 2014) but 0.76 mm in Exp (21–35) according to field observations (Bergametti et al., 2018). The lateral boundary conditions are periodic, which allows for the simulation of a well-developed boundary layer. The vertical scaling velocity is estimated using the heat flux, $w_{\ast }={\left(\frac{g}{\stackrel{\mathrm{‾}}{\mathit{\theta }}}\frac{H_{\mathrm{0}}}{{\mathit{\rho }}_{\mathrm{a}}{c}_{\mathrm{p}}}{z}_l\right)}^{\frac{\mathrm{1}}{\mathrm{3}}}$, with $\stackrel{\mathrm{‾}}{\mathit{\theta }}$ being the mean potential temperature and z_l=1000 m the boundary-layer inversion height. Usually, w_∗ is not used for stable ABLS, but it is used here as an indicator for the suppression of turbulence by negative buoyancy.

Table 1 List of numerical experiments with z₀=0.153 mm for Exp (1–20) in wind tunnel experiments (Zhang and Shao, 2014) and z₀=0.76 mm for Exp (21–35) in field observations (Bergametti et al., 2018) for the sand surface.

3 Results

3.1 Turbulent shear stress

In the first set of analyses, we examine the impact of atmospheric stability on shear stress fluctuations. Early particle-deposition studies considered only the time average of surface shear stress, τ_r, with the assumption that shear stress is horizontally homogeneous. In WRF-LES/D, the corresponding mean resultant shear stress τ_r can be obtained as

$$\begin{array}{}\text{(20)}& {\mathit{\tau }}_{\mathrm{r}}=\sqrt{{\stackrel{\mathrm{‾}}{\mathit{\tau }}}_{xz}^{\mathrm{2}}+{\stackrel{\mathrm{‾}}{\mathit{\tau }}}_{yz}^{\mathrm{2}}}.\end{array}$$

The shorthand notation $\stackrel{\mathrm{‾}}{f}=\frac{\mathrm{1}}{N_x{N}_y{N}_t}\sum _{n_x{n}_y{n}_t}f(n_x,n_y,n_t)$ is introduced to represent the space and time average over the simulation domain and time period (hereafter ensemble mean) with N_x (i.e., 200) and N_y (i.e., 200) being the numbers of grid points in the x and y direction, respectively, and N_t (i.e., 360) the time steps of model output.

Figure 1a–c show the instantaneous shear stress, τ, of a sample grid (n_x=198, n_y=41) over a 1 h period for the runs with z₀=0.153 mm, U=4 m s⁻¹ and various ABL stabilities (H₀=0, 200, 600 W m⁻²). Figure 1d–f are the same as Fig. 1a–c but for U=16 m s⁻¹. The panel shows that τ is not a constant, and the mean resultant shear stress, as well as the shear stress fluctuations, increases with increasing atmospheric instability. In addition, the inset plots in Fig. 1 show that the autocorrelation function (ACF) oscillates during the decrease. The oscillation periodicity is longer under weak wind conditions (Fig. 1a–c) than strong wind (Fig. 1d–f). The ACF in neutral conditions decreases more rapidly than in convective conditions. Recall the definition of coherent motion given by Robinson (1991) – the correlation of variables over a range of long time larger than the smallest scales of flow is evidence of coherent oscillating motion. Thus, the regular oscillation and a long-time correlation of τ are closely related to the evolvement of the coherent structure. This indicates that in a convective ABL, stronger large-scale coherent structures exist, even under weak wind conditions.

To gain insight into the behavior of the unsteady shear stress field, we introduce the turbulence intensity of surface shear stress (TI-S), defined as the ratio of the standard deviation of fluctuating surface shear stress, σ_τ, to the mean resultant stress τ_r, i.e., ${\mathit{\sigma }}_{\mathit{\tau }}/{\mathit{\tau }}_{\mathrm{r}}$. Analysis shows that ${\mathit{\sigma }}_{\mathit{\tau }}/{\mathit{\tau }}_{\mathrm{r}}$ increases as atmospheric conditions become more unstable and decreases with increasing wind speed (e.g., Fig. 1). High wind speeds tend to force the ratio to be more similar to that in neutral ABLS, as the mean-wind-induced shear stress becomes dominant over the large-eddy-induced shear stress fluctuations. For a weak TI-S, τ is dominated by τ_r, and the stress fluctuations are small compared to τ_r. As TI-S increases, the contribution of momentum transport by large eddies becomes significant because in unstable ABLS, buoyancy-generated large eddies penetrate to high levels and intermittently enhance the momentum transfer to the surface.

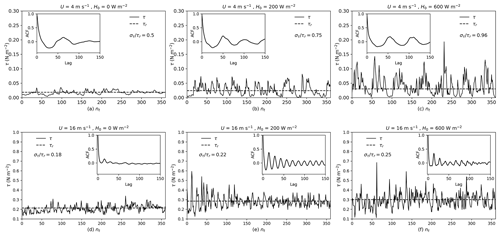
Figure 1 Time evolution of surface shear stress τ with different H₀ values and z₀=0.153 mm at the grid point n_x=198 and n_y=41 (a–c) for U=4 m s⁻¹ and (d–f) for U=16 m s⁻¹; the inset plots are the autocorrelation functions of τ.

The intermittent surface shear stress can directly cause localized particle deposition. Therefore, particle deposition is also intermittent in space and time. However, to the best of our knowledge, in existing particle-deposition schemes (e.g., ZS14 used here), the particle-deposition velocity is calculated using only the mean resultant shear stress τ_r instead of the instantaneous shear stress. We denote this deposition velocity as $V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}$. The mean deposition velocity simulated by WRF-LES/D, denoted as V_d,LES, is estimated via the ratio of the ensemble mean of particle-deposition flux and the ensemble mean of particle concentration:

$$\begin{array}{}\text{(21)}& V_{\mathrm{d},\mathrm{LES}}=-{\displaystyle \frac{{\stackrel{\mathrm{‾}}{F}}_d}{\stackrel{\mathrm{‾}}{c}}},\end{array}$$

which is consistent with the methods commonly used in field observations and wind tunnel experiments.

Figure 2a and b, with the same wind conditions and surface heat fluxes as in Fig. 1c and f, show the time evolution of the instantaneous deposition velocity V_d for particles with a diameter of 1.46 µm. This size is chosen because it is the most sensitive to turbulent diffusion compared to the other four sizes (2.8, 4.8, 9, 16 µm) used in Exp (1–20). As shown, the fluctuating behavior of V_d is consistent with that of τ. Moreover, Fig. 2a shows a substantial difference between V_d,LES and $V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}$, while Fig. 2b shows $V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}$ is similar with V_d,LES. This suggests that the ZS14 scheme can more accurately estimate the deposition velocity for weak TI-S but underestimates the deposition velocity for strong TI-S. The reason for this is that in the case of strong TI-S, particle deposition caused by the gusty wind plays an important role as V_d and τ are nonlinearly related, which is not reflected in $V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}$. Since τ fluctuates and sometimes strongly, a bias always exists in conventional particle-deposition schemes, and the magnitude of the bias depends on turbulence intensity. Therefore, in order to estimate particle deposition accurately, we need to first describe and parameterize the shear stress.

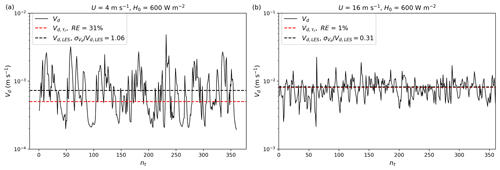
Figure 2 Time evolution of deposition velocity V_d at grid point n_x=198, n_y=41 when H₀=600 W m⁻², z₀=0.153 mm and (a) U=4 m s⁻¹ and (b) U=16 m s⁻¹. RE $=\left|\frac{V_{\mathrm{d},\mathrm{LES}}-V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}}{V_{\mathrm{d},\mathrm{LES}}}\right|\times \mathrm{100}\mathit{\%}$ is the relative error between $V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}$ and V_d,LES, and ${\mathit{\sigma }}_{V_{\mathrm{d}}}/V_{\mathrm{d},\mathrm{LES}}$ is the ratio of the standard deviation of simulated instantaneous deposition velocity V_d and mean deposition velocity, V_d,LES.

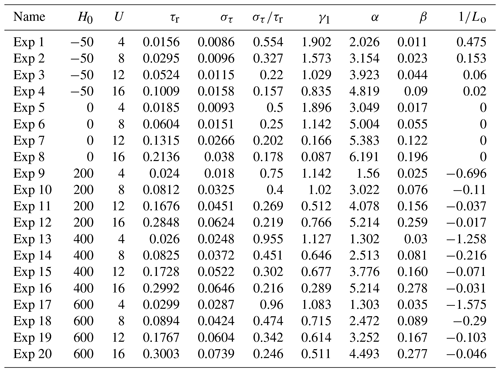
As a main predisposing factor for eolian processes, turbulent shear stress has attracted increasing attention in recent years (e.g., Klose et al., 2014; Li et al., 2020; Liu et al., 2018; Rana et al., 2020; Zheng et al., 2020). Similar to previous studies, we use the probability density function (pdf) p(τ) to characterize the stochastic variable τ. Figure 3 shows that the variability of τ increases as atmospheric instability increases in different wind conditions. The statistic moments of τ, including its mean resultant value τ_r, standard deviation σ_τ, and skewness γ₁ of Exp (1–20) are listed in Table 2. σ_τ and τ_r increase with increased instability, and the distribution is positively skewed. Positive skewness is characterized by the distribution having a longer positive tail as compared with the negative tail, and the distribution appears as a left-leaning (i.e., tends toward low values) curve. This indicates that large negative fluctuations are not as frequent as large positive fluctuations. The data also show that γ₁ generally shows a downward trend as TI-S decreases, which is consistent with Monahan (2006); i.e., as TI-S decreases, p(τ) becomes increasingly Gaussian.

Table 2 Statistics of shear stress for numerical experiments Exp (1–20).

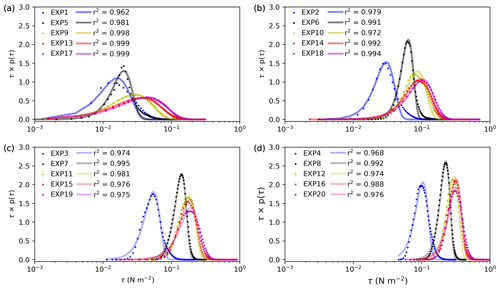
Figure 3 Probability density functions derived from WRF-LES/D simulated surface shear stress τ (dots) and the corresponding fitted Weibull density functions (solid lines, r² is the coefficients of determination) for different surface heat fluxes and different wind speeds: (a) U=4 m s⁻¹, (b) U=8 m s⁻¹, (c) U=12 m s⁻¹, and (d) U=16 m s⁻¹ with z₀=0.153 mm.

The parameterization of surface shear stress has attracted intense interest; for example, Klose et al. (2014) reported that τ in unstable conditions is Weibull-distributed based on large-eddy simulations. Shao et al. (2020) found that p(τ) is skewed to small τ values (i.e., positively skewed) based on field observations. Li et al. (2020) suggested that τ in neutral conditions is Gauss-distributed based on a wind tunnel experiment. Colella and Keith (2003) explained that in turbulent shear flows, the nonlinear interaction between the eddies gives rise to a departure from Gaussian behavior. Our results show that the Gaussian approximation is inadequate in representing the skewed p(τ), especially for the conditions of strong turbulence intensity (e.g., unstable cases in Fig. 3a). Therefore, p(τ) here is approximated using a Weibull distribution, i.e.,

$$\begin{array}{}\text{(22)}& p\left(\mathit{\tau }\right)={\displaystyle \frac{\mathit{\alpha }}{\mathit{\beta }}}{\left({\displaystyle \frac{\mathit{\tau }}{\mathit{\beta }}}\right)}^{\mathit{\alpha }-\mathrm{1}}\exp \left(-{\left(\mathit{\tau }/\mathit{\beta }\right)}^{\mathit{\alpha }}\right),\end{array}$$

where α and β are the shape and scale parameters, respectively. The values of α and β for the numerical experiments Exp (1–20) are listed in Table 2. It can be seen that both α and β depend on wind speed and atmospheric stability. However, β is mainly determined by wind conditions when the wind is strong, while it is affected by ABL stability when the wind is weak. The behavior of α and β is shown in Fig. 4. $\left|\mathrm{1}/L_{\mathrm{o}}\right|$ is the absolute value of the reciprocal of the Obukhov length L_o, which can be calculated using

$$\begin{array}{}\text{(23)}& L_{\mathrm{o}}=-{\displaystyle \frac{\stackrel{\mathrm{‾}}{\mathit{\theta }}{u}_{\ast }^{\mathrm{3}}}{\mathit{\kappa }g\frac{H_{\mathrm{0}}}{{\mathit{\rho }}_{\mathrm{a}}{c}_{\mathrm{p}}}}}.\end{array}$$

In both stable and unstable atmospheric conditions, analysis shows that the scale parameter α is related to ABL stability as the power of $\left|\mathrm{1}/L_{\mathrm{o}}\right|$. Figure 4a shows that α decreases with the $\left|\mathrm{1}/L_{\mathrm{o}}\right|$, satisfying Eq. (24) approximately. For neutral conditions, L_o goes to infinity, and Eq. (24) no longer applies. Therefore, the shape parameter obtained by the fitting was directly used for pdf reproduction for the neutral cases instead of the approximated α used for stable and unstable conditions. As Fig. 4b shows, the β parameter increases almost linearly with $u_{\ast r}^{\mathrm{2}}+\mathrm{0.001}\cdot w_{\ast }^{\mathrm{2}}$ but can be best approximated using Eq. (25), with $u_{\ast r}=\sqrt{{\mathit{\tau }}_{\mathrm{r}}/{\mathit{\rho }}_{\mathrm{a}}}$.

$$\begin{array}{}\text{(24)}& {\displaystyle }\mathit{\alpha }=\mathrm{5.39}\cdot \exp \left(-\mathrm{5.43}{\left({\displaystyle \frac{\mathrm{1}}{L_{\mathrm{o}}}}\right)}^{\mathrm{2}/\mathrm{3}}\right)+\mathrm{1.42}\text{(25)}& {\displaystyle }\mathit{\beta }=\mathrm{1.058}\cdot (u_{\ast r}^{\mathrm{2}}+\mathrm{0.001}{w}_{\ast }^{\mathrm{2}})\end{array}$$

Using Eqs. (22)–(25), we can approximately describe the turbulent surface shear stress in non-neutral cases.

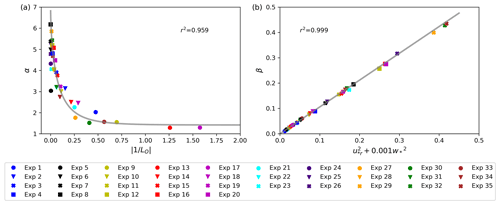
Figure 4 (a) Dependency of the shape parameter α on $L_{\mathrm{o}}^{-\mathrm{1}}$ for all numerical experiments Exp (1–35). (b) Dependency of scaling parameter β on $\left(u_{\ast r}^{\mathrm{2}}+\mathrm{0.001}{w}_{\ast }^{\mathrm{2}}\right)$ for Exp (1–35).

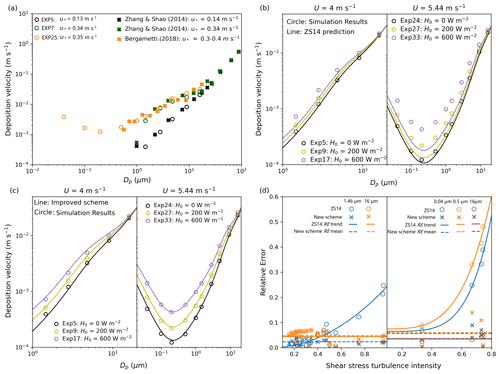
Figure 5 (a) Validation of the simulated deposition velocity from WRF-LES/D (circles) by comparing with the observation data (crosses). (b) The comparison of the predicted result by ZS14 scheme (lines) with the simulated value (circles) of Exp (5, 9, 17) (left) and Exp (24, 27, 33) (right). (c) The comparison of the predicted result by the improved scheme (lines) with the simulated value (circles) of Exp (5, 9, 17) (left) and Exp (24, 27, 33) (right). (d) Comparison of relative error as a function of shear stress turbulence intensity (TI-S), estimated by ZS14 scheme (circles) and the improved scheme (crosses) for Exp (1–20) (left) and Exp (24, 27, 30, 33) (right).

3.2 Improvement to particle-deposition scheme

Figure 5a shows the performance of WRF-LES/D by comparing the simulated deposition velocity, V_d,LES, with wind tunnel experiments (Zhang and Shao, 2014) and field observation (Bergametti et al., 2018). The observed data are measured under neutral conditions and similar wind flow. As shown, the simulation results agree well with the observed data. On this basis, by further evaluating the performance of the ZS14 scheme, we found that the accuracy of the ZS14 scheme decreases with increasing instability. For example, Fig. 5b compares the deposition velocities of Exp (5, 9, 17) and Exp (24, 27, 33), V_d,LES, with those calculated by the ZS14 scheme using τ_r from the corresponding experiments, $V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}$. It shows that under weak wind conditions, $V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}$ predicts the deposition well under neutral conditions and underestimates the deposition under convective conditions, especially for particles that are not dominated by molecular diffusion and gravity, and the underestimation increases with the atmospheric instability. To predict the deposition velocity more accurately for convective conditions, we need to account for the effect of shear stress fluctuations, i.e., the instantaneous shear stress distribution. Thus, the dry deposition scheme can be improved as

$$\begin{array}{}\text{(26)}& V_{\mathrm{d},\mathit{\tau }}=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{V}_{\mathrm{d}}\left(\mathit{\tau }\right)p\left(\mathit{\tau }\right)\mathrm{d}\mathit{\tau },\end{array}$$

with p(τ) as given by Eqs. (22)–(25). As Fig. 5c shows, the improved scheme results V_d,τ and the simulation value V_d,LES show a remarkable congruence.

To make the comparison more clear, the relative errors (REs) of the predicted deposition velocity by the ZS14 scheme and improved scheme are compared with the WRF-LES/D simulation value and are calculated as below:

$$\begin{array}{}\text{(27)}& \mathrm{RE}=\left|{\displaystyle \frac{V_{\mathrm{d},\mathrm{LES}}-V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}\left(\mathrm{or}{V}_{\mathrm{d},\mathit{\tau }}\right)}{V_{\mathrm{d},\mathrm{LES}}}}\right|\times \mathrm{100}\mathit{\%}.\end{array}$$

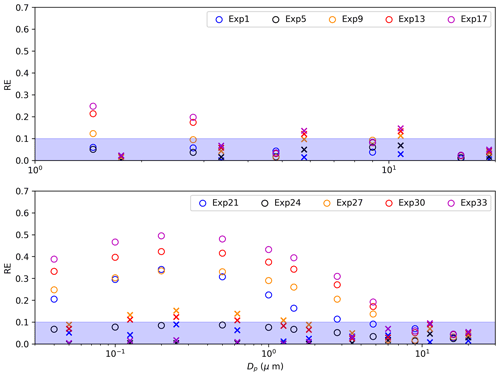
Analysis shows that the value of relative error (RE) depends on surface conditions, wind conditions, atmospheric stabilities, and particle sizes. It increases obviously with increased atmospheric instability under weak wind conditions, while it becomes less sensitive to stability when the wind is strong. Through the analysis, we find that the RE of the ZS14 scheme generally increases with the shear stress turbulence intensity, TI-S, and the value depends on particle size, as shown in Fig. 5d (left). Thus, we compared the RE of some different sized particles to investigate the particle in which size range is strongly affected (Fig. A2). The result shows that the RE first increases and then decreases with increasing particle size, and the particles with size normally in the range of 0.01 to 5 µm are strongly affected by turbulent shear stress, and p(τ) needs to be considered. After modification, the errors are limited to less than 10 % or approximately 10 %. For example, the relative error of Exp (17; i.e., U =4 m s⁻¹ and H₀=600 W m⁻²) for particles of 1.46 µm is reduced from ∼25 % to ∼3 %. The relative error of Exp (33; i.e., U =5.44 m s⁻¹ and H₀=600 W m⁻²) for particles of 0.5 µm is reduced from ∼50 % to ∼12 %.

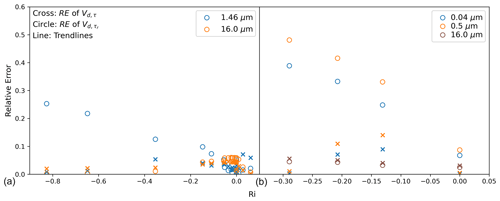
To further analyze if the RE of ZS14 in unstable conditions is dominated by kinetic instability or dynamic instability, the Richardson number is calculated. Analysis shows that TI-S is positively correlated to gradient Richardson number Ri (Eq. A1). Under unstable conditions associated with strong vertical motion and weak winds, the RE of ZS14 increases with the increasing magnitude of Richardson number Ri (Fig. A3). The relationship between Ri and TI-S needs further study. Consequently, the results illustrate that the modified scheme V_d,τ tends to be more accurate than the unmodified scheme $V_{\mathrm{d},{\mathit{\tau }}_{\mathrm{r}}}$.

4 Conclusions

The present study was designed to determine the effect of ABL stability on particle deposition. For this purpose, the WRF-LES/D was used to model atmospheric-boundary-layer turbulence under the presence of atmospheric stability effects to recover statistics of shear stress variability. We then presented an improved particle-deposition scheme with the consideration of turbulent shear stress. While ABLS can broadly represent levels of atmospheric turbulence, its effect on particle deposition is wind-speed-dependent. Through a series of numerical experiments, we have shown the turbulent characteristics of particle-deposition velocity caused by the turbulent wind flow and pointed out the shortcomings of the ZS14 scheme in representing particle deposition under convective conditions. The relative error (RE) increases as the ABL instability increases for low wind conditions; i.e., the RE increases with shear stress turbulence intensity, especially for a certain size range of particles.

Since the dependency of particle deposition on micrometeorology is embedded in the application of the surface shear stress, we believe that the dependency of particle deposition on ABL stability is ultimately attributed to the statistical behavior of shear stress τ. Therefore, in this study, a model including the effects of surface shear fluctuations is proposed and validated by numerical experiments. Additionally, the fluctuations of surface shear caused by turbulence can be approximated with a Weibull distribution. The shape parameter decreases exponentially with the reciprocal of Monin–Obukhov length, and the scale parameter increases linearly with $u_{\ast r}^{\mathrm{2}}+\mathrm{0.001}{w}_{\ast }^{\mathrm{2}}$. After statistically revising the original scheme, an improved model is obtained. Using the modified model, the deposition velocity tends towards numerical experimental results.

The project is the first comprehensive investigation of the turbulent characteristics of particle deposition, and the findings will be of interest to improve the accuracy of particle-deposition predictions on regional or global scales. One source of weakness in this study is that the variation of τ may be changed by surface roughness and needs further study, as the roughness length does not fully reflect the effect of the surface topography on the turbulence structure. In spite of this limitation, the study adds to our understanding of the influence caused by ABLS on particle deposition.

Appendix A

Figure A1 shows the probability density distribution of surface shear stress for experiments (21–35); Fig. A2 shows the changing of relative error with particle size; Fig. A3 shows the variation of relative error (RE) of the ZS14 scheme (Eq. 10) and improved scheme (Eq. 26) with gradient Richardson number Ri.

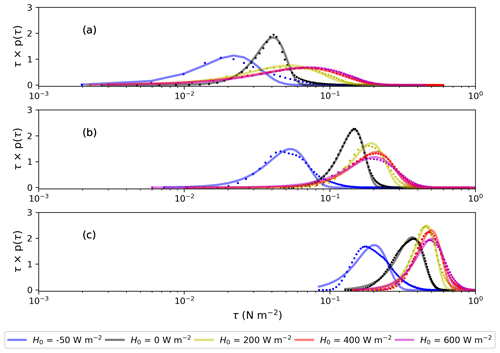
Figure A1 Probability distributions of simulated surface shear stress τ (dots) and the corresponding fitted Weibull density distribution (solid lines) with different surface heat flux for different wind conditions: (a) U=5.44 m s⁻¹, (b) U=10.87 m s⁻¹, and (c) U=18.12 m s⁻¹.

Figure A2 RE changes with particle size under weak wind conditions.

$$\begin{array}{}\text{(A1)}& R_i=-{\displaystyle \frac{g}{\stackrel{\mathrm{‾}}{\mathit{\theta }}}}\mathit{\kappa }z{\displaystyle \frac{{\mathit{\phi }}_h}{{\mathit{\phi }}_{\mathrm{m}}^{\mathrm{2}}}}{\displaystyle \frac{H_{\mathrm{0}}}{{\mathit{\rho }}_{\mathrm{a}}{c}_{\mathrm{p}}{u}_{\ast }^{\mathrm{3}}}},\end{array}$$

where z is the center height of the lowest layer, and $\stackrel{\mathrm{‾}}{\mathit{\theta }}$ is the potential temperature of the lowest layer.

Figure A3 Comparison of relative error as a function of Ri, estimated by ZS14 scheme (circles) and the improved scheme (crosses) for Exp (1–20) (a) and Exp (24, 27, 30, 33) (b).