Equilibrium climate sensitivity increases with aerosol concentration due to changes in precipitation efficiency

How Earth's climate reacts to anthropogenic forcing is one of the most burning questions faced by today's scientific community. A leading source of uncertainty in estimating this sensitivity is related to the response of clouds. Under the canonical climate-change perspective of forcings and feedbacks, the effect of anthropogenic aerosols on clouds is categorized under the forcing component, while the modifications of the radiative properties of clouds due to climate change are considered in the feedback component. Each of these components contributes the largest portion of uncertainty to its relevant category and is largely studied separately from the other. In this paper, using idealized cloud-resolving radiative–convective-equilibrium simulations, with a slab ocean model, we show that aerosol–cloud interactions could affect cloud feedback. Specifically, we show that equilibrium climate sensitivity increases under high aerosol concentration due to an increase in the short-wave cloud feedback. The short-wave cloud feedback is enhanced under high-aerosol conditions due to a stronger increase in the precipitation efficiency with warming, which can be explained by higher sensitivity of the droplet size and the cloud water content to the CO₂ concentration rise. These results indicate a possible connection between cloud feedback and aerosol–cloud interactions.

1 Introduction

Estimating Earth's equilibrium climate sensitivity (ECS), defined as the steady-state global-mean temperature increase for a doubling of CO₂, is considered to be a first-order, fundamental milestone on the way to understanding and predicting anthropogenically driven climate change (Sherwood et al., 2020). Decades of research have tried to accurately quantify ECS, with only limited success. The most probable current ECS estimates are in the range of 2.3–4.5 K (Sherwood et al., 2020). The largest source of uncertainty in estimating ECS is related to the response of clouds to the externally forced warming and the feedback of these changes on the climate system (Sherwood et al., 2020; Ceppi et al., 2017; Schneider et al., 2017). Clouds strongly modulate Earth's radiation budget by reflecting the incoming short-wave radiation from the sun and by absorbing and re-emitting the terrestrial long-wave radiation (Loeb et al., 2018). Thus, changes in the cloud macro-physical properties (such as coverage and vertical extent) and micro-physical properties (such as liquid/ice partition and hydrometeors size) due to anthropogenically driven climate change could significantly alter the climate system's response (Gettelman and Sherwood, 2016; Nuijens and Siebesma, 2019; Schneider et al., 2017).

An important factor in determining cloud feedback magnitude is the sensitivity of the precipitation efficiency (ϵ) (Lutsko and Cronin, 2018; Lutsko et al., 2021; Li et al., 2022). ϵ quantifies the fraction of condensed water in a cloud to reach the surface as precipitation. Using idealized cloud-resolving simulations, it was shown that ϵ is expected to increase with temperature (Lutsko and Cronin, 2018). The increase in ϵ with warming was shown to be mostly driven by an increase in the efficiency with which cloud condensate is converted into precipitation, while changes in the evaporation of falling precipitation were shown to play a smaller role (Lutsko and Cronin, 2018).

An increase in ϵ with warming represents more efficient depletion of the water from the clouds, thus affecting the radiation budget. On the one hand, increase in ϵ with warming was suggested to reduce the anvil cloud coverage and hence increase the outgoing long-wave radiation (Lindzen et al., 2001; Mauritsen and Stevens, 2015), thus producing negative feedback. On the other hand, however, it was recently shown that the long-wave effect of an ϵ increase is over-compensated for by changes in the short-wave flux (Li et al., 2019); i.e. a large reduction in the cloud optical depth, driving a reduction in the short-wave cooling effect of clouds, dominates the response.

The efficiency with which cloud condensate is converted into precipitation is closely linked to the micro-physical properties of the clouds. The autoconversion of cloud droplets into rain becomes significant when liquid water amount and/or droplet radii reach a critical threshold (Freud and Rosenfeld, 2012). An important factor influencing the droplet radii (and also the liquid water amount, to some degree) is the amount of available cloud condensation nuclei (CCN). Generally, an increase in aerosol concentration drives an increase in CCN concentration, which results in more numerous and smaller droplets in the cloud (Twomey, 1974; Warner and Twomey, 1967). The smaller droplets require longer time (or equivalently larger vertical distance) in the clouds to grow by diffusion to the critical size enabling precipitation, thus delaying the initial warm-rain formation (Rosenfeld, 2000; Dagan et al., 2015b). In addition, aerosols were suggested to enhance the vertical velocities and the cloud top heights of deep convective clouds (due to the so-called invigoration mechanism; Abbott and Cronin, 2021; Koren et al., 2005; Rosenfeld et al., 2008), which in turn can result in precipitation enhancement (Koren et al., 2012). Therefore, aerosols could affect ϵ (Khain, 2009).

In addition to the effect on rain, aerosols could modify the radiative properties of clouds by modifying the droplet concentration and size distribution (Twomey, 1974) and by affecting the clouds' macro-physical properties (Albrecht, 1989; Bellouin et al., 2019). These changes to the radiative properties of clouds result in radiative forcing that could affect the sea surface temperature (SST; Bellouin et al., 2019). Using cloud-resolving radiative–convective-equilibrium simulations with interactive SST, Khairoutdinov and Yang (2013) showed that the surface temperature decreases by 1.5 K with each 10-fold increase in aerosol concentration, an effect quite comparable to a 2.1–2.3 K SST warming obtained in a simulation with given (low-)aerosol conditions but doubled CO₂ concentration.

It has been suggested that cloud feedback and aerosol forcing are not independent of each other (Mülmenstädt and Feingold, 2018; Igel and van den Heever, 2021). In addition, the strong links between ϵ and cloud feedback and between ϵ and aerosol concentration merit a dedicated study on the potential mutual CO₂ and aerosol effect on clouds and thus also on ECS, which is the aim of the current study.

2 Methods

2.1 Model description and experimental design

The model used herein is the System of Atmospheric Modeling (SAM; Khairoutdinov and Randall, 2003) version 6.11.7. Subgrid-scale fluxes are parameterized using Smagorinsky's eddy diffusivity model, and gravity waves are damped at the top of the domain. The microphysics scheme used is the two-moment bulk microphysics of Morrison et al. (2005). The cloud droplet number concentration (CDNC) source assumes that the number of activated CCN depends on the super-saturation (S – which is estimated diagnostically in the model as the model assumes saturation adjustment) according to a power law: CDNC = N_aS^k, where N_a is the prescribed concentration of CCN active at 1 % super-saturation, and k is a constant (set in this study to 0.4 – a typical value for maritime conditions). Changes in N_a serve as a proxy for the change in aerosol concentration. Three levels of N_a are considered here, covering an extreme range of conditions – 20, 200 and 2000 cm⁻³. While this wide range of conditions is unlikely to exist at any given geographical location, they are used here in order to cover the range of possible conditions at different locations and to maximize the effect for establishing better physical understanding. The activation of CCN at the cloud base is parameterized following Twomey (1959), using the vertical velocity and CCN spectrum parameters. The model is configured to pass cloud water and ice-crystal effective radii from the microphysics scheme to the radiation scheme; thus, the Twomey effect (Twomey, 1977) of both liquid and ice is considered. Direct interactions between aerosols and radiation are not considered here.

The simulations are conducted in a radiative–convective-equilibrium (RCE) mode and generally follow the RCEMIP (RCE Model Intercomparison Project; Wing et al., 2018) small-domain instructions (but with interactive SST and changes in the CO₂ and aerosol concentration). The simulations were performed on a square, doubly periodic domain. In this case, we want to avoid the effect of convective self-aggregation on ϵ; thus, the domain size is set to 96×96 km², which was shown to be small enough to prevent convective self-aggregation (Muller and Held, 2012; Lutsko and Cronin, 2018; Yanase et al., 2020). The horizontal grid spacing is set to 1 km, and 68 vertical levels are used, between 25 m and 31 km, with vertical grid spacing increasing from 50 m near the surface to roughly 1 km at the domain top. We note that while shallow clouds are present in the simulations, the grid spacing used here is too coarse for a full representation of these clouds. A time step of 10 s is used, and radiative fluxes are calculated every 5 min using the CAM radiation scheme (Collins et al., 2006). The output resolution for all fields is 1 h (3-D fields are saved as snapshots, while domain statistics are saved as hourly averages). The incoming solar radiation is fixed at 551.58 W m⁻², with a zenith angle of 42.05^∘ (Wing et al., 2018), producing a net insolation close to the tropical-mean value. Convection is initialized with a small thermal noise added near the surface at the beginning of the simulation. The initial conditions for the simulations are as in Wing et al. (2018).

Greenhouse gases are varied for three different levels: pre-industrial level (280 ppm; 1× CO₂), 2 times the pre-industrial level (2× CO₂) and 4 times the pre-industrial level (4× CO₂). As in the case of the aerosol concentrations, the large range of CO₂ conditions covered here are used to examine the clouds' sensitivity to greenhouse gas concentrations under a wide range of conditions. Nine different simulations, with all possible combinations of N_a and CO₂ concentrations, were conducted. The O₃ vertical profile is similar to Wing et al. (2018) and represents a typical tropical atmosphere. The effect of other trace gases (such as CH₄ and N₂O) is neglected for simplicity.

In all simulations, the SST is interactive and predicted by a slab ocean model (SOM). The SOM's mixed layer depth is set to 5 m, which represented a compromise between a relatively deep layer (≥ 10 m), which reduces SST noise (Khairoutdinov and Yang, 2013), and a relatively shallow layer (≪ 1 m), which requires a shorter computation time for equilibrium (Romps, 2020). As in Romps (2020), the SOM is cooled at a rate of 112 W m⁻² in order to ensure that the simulations with 1× CO₂ are kept at around the initial SST of 300 K (Fig. 1). Each simulation was run for 1800 d, which is sufficient for reaching close to equilibrium (the surface energy imbalance is ≤ 0.1 W m⁻² in all simulations during the last 150 d). The last 150 d of each run is used for statistical sampling (grey shading in Fig. 1).

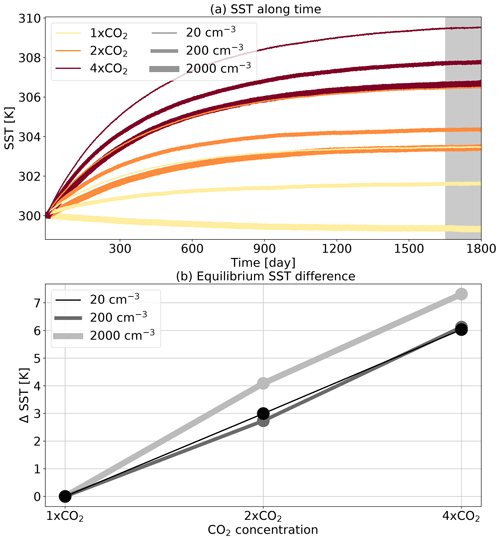
Figure 1 (a) The sea surface temperature (SST) along time for the different simulations conducted under different aerosol and CO₂ concentrations. The shaded grey area is referred to as equilibrium conditions. (b) Change in equilibrium SST due to a change in CO₂ concentration (compared to the 1× CO₂ case of each aerosol concentration), for the different aerosol concentrations (the different curves).

3 Results

Figure 1 presents the SST of the different simulations along time (panel a) and the change in the equilibrium SST with the CO₂ concentration for the different N_a cases (panel b). As expected, the equilibrium SST (grey shading in Fig. 1a) increases with the CO₂ concentration and decreases with N_a concentration. However, the rate of increase in equilibrium SST with CO₂ concentration increases under extremely high N_a concentrations (2000 cm⁻³), compared with the low and medium N_a concentrations (20 and 200 cm⁻³, respectively; Fig. 1b). Calculating the average ECS based on the three combinations available for each N_a condition (2× CO₂ − 1× CO₂, 4× CO₂ − 2× CO₂ and (4× CO₂ − 1× CO${}_{\mathrm{2}})/\mathrm{2}$) demonstrates that it increases with N_a from 3.0 K at the lowest N_a to 3.7 K at the highest N_a (i.e. a 23 % increase; Table 1).

Table 1 Average equilibrium climate sensitivity (ECS), cloud feedback parameter (λ_cloud), hydrological sensitivity (η) and change in precipitation efficiency (Δϵ) of the three combinations available for each N_a condition (2× CO₂ − 1× CO₂, 4× CO₂ − 2× CO₂ and 4× CO₂ − 1× CO₂). For the calculation of the average ECS, the difference between 4× CO₂ and 1× CO₂ is divided by 2. The rest of the quantities are normalized by the SST change between the relevant simulations. Please refer to the text for the definitions of these quantities.

Figure 2 presents the time- and domain-mean vertical profiles of temperature and water vapour mixing ratio (q_v) in the different simulations (panels a and b) and their difference from the simulation with the lowest N_a and CO₂ concentrations (panels c and d). It demonstrates, as expected, that the vertical profile of air temperature is set by the surface temperature (increases with CO₂ concentrations and decreases with N_a) with an amplification of the change at the upper troposphere, as the profiles follow the moist adiabatic lapse rate. It also shows that q_v increases with the temperature, as expected (Held and Soden, 2006).

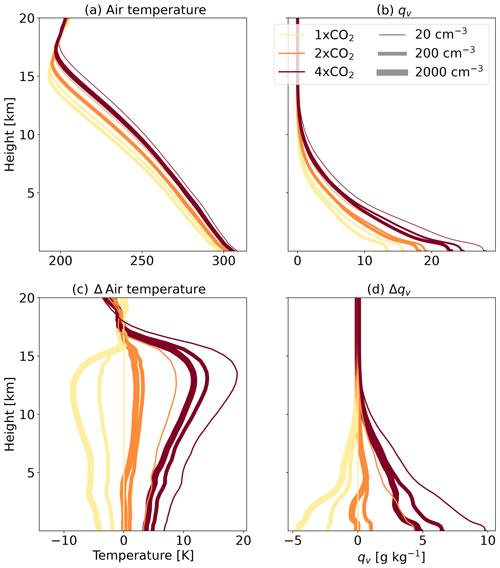
Figure 2 Time- and domain-mean vertical profiles of air temperature and water vapour mixing ratio (q_v) in the different simulations (a, b) and how they differ from the simulation with the lowest N_a and CO₂ concentrations (c, d).

In order to understand the increase in ECS with N_a, we next examine the top-of-atmosphere (TOA) energy budget. Figure 3 presents the change in the net short-wave and long-wave TOA energy gain (R^SW and R^LW, respectively) with the CO₂ concentration for the different N_a conditions. In addition, Fig. 3 presents the change in the cloud radiative effect (CRE) with increasing the CO₂ concentration, where CRE is computed by subtracting the clear-sky from the all-sky TOA radiative fluxes (R−R_clear-sky), again for the short wave and long wave separately (CRE^SW and CRE^LW, respectively). Figure 3a and b demonstrate that under equilibrium conditions R^SW increases, while R^LW decreases with the CO₂ concentration. However, the rate of change in both R^SW and R^LW is much faster under the high-N_a conditions than under the low- and medium-N_a conditions. The trend in CRE^SW under the different N_a conditions (Fig. 3c) resembles the trend in R^SW, suggesting that the clouds' response dominates the changes in the TOA short-wave fluxes. CRE^LW, on the other hand, decreases at a similar rate with CO₂ concentration for the different N_a conditions (Fig. 3d). Thus, the different decrease rates in R^LW with CO₂ concentration for the different N_a conditions (Fig. 3b) must be driven by clear-sky changes (specifically, the plank, the lapse rate and the water vapour feedbacks; see Fig. 2 above).

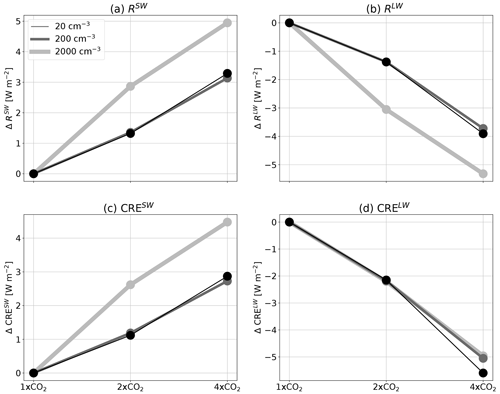
Figure 3 The change in the net top-of-atmosphere energy gain (R) in the short wave (a) and in the long wave (b) and the change in the cloud radiative effect (CRE) in the short wave (c) and in the long wave (d), due to a change in the CO₂ concentration (compared to the 1× CO₂ case of each aerosol concentration), for the different aerosol concentrations (the different curves).

In Table 1 above, we estimate the average cloud radiative feedback (λ_cloud) as the change in CRE with increasing surface temperature, i.e. λ_cloud= dCRE $/$ dT, for the different N_a conditions. The table shows that λ_cloud becomes less negative with the increase in N_a, leading to higher climate sensitivity. The differences in the values of λ_cloud between the different N_a conditions are mostly derived from the short-wave part of the spectrum (Fig. 3).

Thus far, we have seen that the ECS increases with N_a (Fig. 1 and Table 1) and that this increase can be explained by changes in λ_cloud (Table 1) and specifically in CRE^SW (Fig. 3). To understand the changes in the cloud properties driving the changes in λ_cloud, and hence also in ECS, under the different N_a conditions, in Fig. 4 we present the change in cloud liquid water path (CWP), ice water path (IWP), rainwater path (RWP) and cloud fraction (CF) with increasing CO₂ concentrations for the different N_a conditions. The figure shows that the CWP decreases with the CO₂ concentrations at a much faster rate (about 3 times faster) under the highest-N_a conditions compared to the low- and medium-N_a conditions (Fig. 4a). The changes in the IWP, on the other hand, are about an order of magnitude smaller than the changes in CWP and are not consistent in sign for the different N_a conditions (Fig. 4b). The RWP increases with the CO₂ concentrations at a slightly faster rate (about 20 % faster) under the highest-N_a conditions compared to the low- and medium-N_a conditions (however the response is non-monotonic with N_a; Fig. 4c). The CF decreases with the CO₂ concentrations at a similar rate for the different N_a conditions (about 1.5 % decrease in CF for each doubling of the CO₂ concentrations; Fig. 4d).

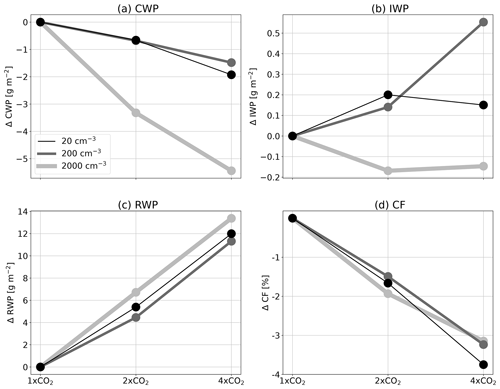
Figure 4 The change in (a) cloud liquid water path (CWP), (b) ice water path (IWP), (c) rainwater path (RWP) and (d) cloud fraction (CF) due to a change in the CO₂ concentration (compared to the 1× CO₂ case of each aerosol concentration), for the different aerosol concentrations (the different curves).

The faster decrease in CWP with CO₂ concentrations under high-N_a conditions drives the faster increase in CRE^SW as the clouds become less opaque in the short wave. We note that the difference in CRE^SW trend under different N_a conditions could not be explained by the minor differences in the CF trends. In addition, the small differences in the IWP between the different N_a conditions are consistent with the small differences in the CRE^LW seen above. The general increase in RWP with CO₂ concentrations is consistent with an increase in precipitation efficiency with warming (Lutsko and Cronin, 2018), as elaborated below.

Figure 4 suggests that the largest difference in the cloud response to CO₂ under different N_a conditions is due to changes in CWP. The higher sensitivity of CWP to CO₂ concentration under higher-N_a conditions can explain the higher λ_cloud and thus also the larger ECS. Hence, the question arises: what causes the faster reduction in CWP with CO₂ concentration under high-N_a conditions? A major sink for CWP is via precipitation. Hence, in Fig. 5 we present the change in the mean surface precipitation rate, the hydrological sensitivity (η – the rate of change in the surface precipitation per 1 K increase in surface temperature) and the precipitation efficiency (ϵ – calculated following Li et al., 2022, as the ratio of surface precipitation to condensed water path, i.e. CWP + IWP + RWP). Please note that the precipitation efficiency definition used here, following Li et al. (2022), is slightly different from the definition used in Lutsko and Cronin (2018). However, the two different definitions were shown to be tightly correlated (Li et al., 2022); thus, the exact definition used is not expected to change the main conclusions. In addition, the use of this definition will enable easier comparison with observations and global climate models in the future.

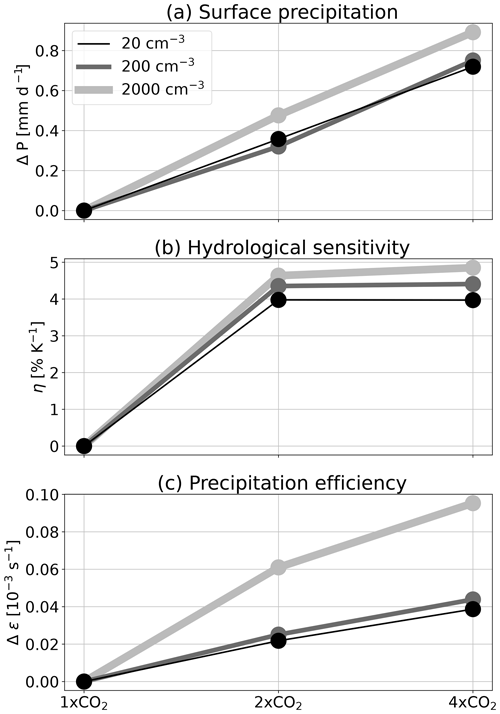
Figure 5 The change in (a) surface precipitation, (b) hydrological sensitivity (η) and (c) precipitation efficiency (ϵ) due to a change in the CO₂ concentration (compared to the 1× CO₂ case of each aerosol concentration), for the different aerosol concentrations (the different curves).

As expected, Fig. 5 demonstrates that the surface precipitation increases with CO₂ (i.e. η is positive), and so does ϵ (Lutsko and Cronin, 2018). This is true for all N_a conditions. However, the rates of increase in surface precipitation and ϵ with CO₂ concentration are higher under the highest-N_a conditions (see also Table 1). We note that the larger rate of increase in surface precipitation under the highest-N_a conditions is not solely due to the higher surface temperature increase, as η also increases with N_a.

The much larger (more than double; Table 1) rate of increase in ϵ with the CO₂ concentration under the highest-N_a conditions represents more efficient depletion of the cloud water from the atmosphere, leading to a faster reduction in CWP with CO₂ concentration (Fig. 4), which in turn leads to higher λ_cloud and ECS. The faster increase in RWP with CO₂ concentration under the highest-N_a conditions presented in Fig. 4c is consistent with this explanation.

The last open question is why ϵ increases faster with CO₂ concentration under the highest-N_a conditions. The increase in ϵ with warming was shown to be mostly driven by an increase in the efficiency with which cloud condensate is converted into precipitation (Lutsko and Cronin, 2018). As mentioned in the introduction, the conversion of cloud condensate into precipitation (or autoconversion of cloud droplets) becomes significant only when liquid water amount and/or droplet radii reach a critical threshold (Freud and Rosenfeld, 2012). To understand the faster ϵ increases with CO₂ concentration under the highest-N_a conditions, we present the histograms over the domain and time (during the last 150 d of the simulations based on 3-D output in 1 h resolution) of liquid cloud droplet mixing ratio (q_c; Fig. 6) and mean cloud droplet radii ($\stackrel{\mathrm{‾}}{r_{\mathrm{c}}}$; Fig. 7) around the height of the maximum in cloud droplet effective radii (1950 m) and its mean sensitivity to doubling of CO₂ concentration for each N_a condition.

Figure 6 demonstrates that the cut-off of the q_c distribution (the mixing ratio for which the probability density function starts to decrease sharply) increases with the CO₂ concentration and decreases with the aerosol concentration. However, the sensitivity of the relatively large q_c to CO₂ concentration is significantly larger under high aerosol concentrations compared to the lower aerosol concentrations (Fig. 6b). The larger relative increase in high q_c promotes the autoconversion process and hence enhances ϵ, more so under high aerosol concentrations than under low aerosol concentrations.

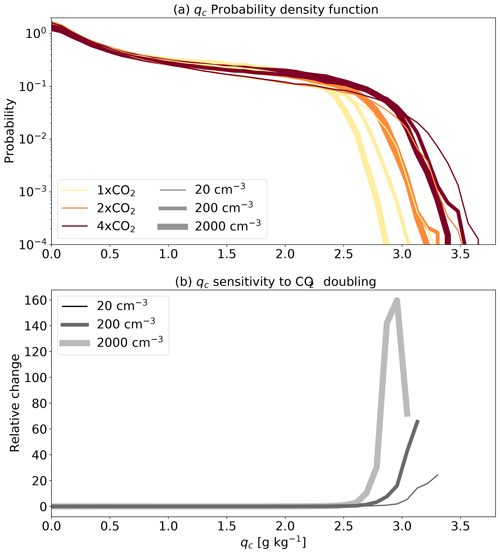
Figure 6 Probability density functions (PDFs) of the cloud droplet mixing ratio (q_c) for the different simulations (a) and the mean sensitivity of the q_c PDF to a doubling of the CO₂ concentration based on the three combinations available for each N_a condition (2× CO₂ − 1× CO₂, 4× CO₂ − 2× CO₂ and (4× CO₂ − 1× CO₂) $/\mathrm{2}$) (b), calculated for the heights around which the cloud droplet effective radii reach a maximum (1950 m) and using 3-D files output every hour of the last 150 d of the simulations. Note the logarithmic scales for the y axes of (a).

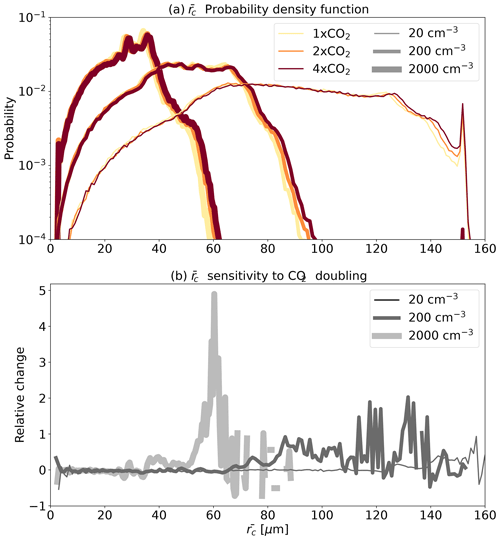
Figure 7 Probability density functions (PDFs) of cloud droplet mean radii ($\stackrel{\mathrm{‾}}{r_{\mathrm{c}}}$) for the different simulations (a) and the mean sensitivity of the $\stackrel{\mathrm{‾}}{r_{\mathrm{c}}}$ PDF to a doubling of the CO₂ concentration based on the three combinations available for each N_a condition (2× CO₂ − 1× CO₂, 4× CO₂ − 2× CO₂ and (4× CO₂ − 1× CO₂) $/\mathrm{2}$) (b), calculated for the heights around which the cloud droplet effective radii reach a maximum (1950 m) and using 3-D files output every hour of the last 150 d of the simulations. Note the logarithmic scales for the y axes of (a).

Figure 7 demonstrates, in line with expectations, that N_a has a strong effect on $\stackrel{\mathrm{‾}}{r_{\mathrm{c}}}$. In addition, it shows that under all N_a conditions, $\stackrel{\mathrm{‾}}{r_{\mathrm{c}}}$ increases with the CO₂ concentration. This could be explained by the increase in the availability of water vapour (Fig. 2), which, for given N_a conditions, enables larger diffusional growth of the droplets. This trend could also be understood from the increase in q_c with warming (Fig. 6; Lutsko and Cronin, 2018), which under given N_a conditions implies larger $\stackrel{\mathrm{‾}}{r_{\mathrm{c}}}$. Here again, the highest-N_a conditions demonstrate the largest sensitivity of $\stackrel{\mathrm{‾}}{r_{\mathrm{c}}}$ to CO₂ concentration, especially on the right-hand side of the distribution (Fig. 7b). This could be explained by the fact that under these high-N_a conditions, the cloud droplet growth is primarily limited by the availability of water vapour, as a large number of droplets compete for the available water vapour (Koren et al., 2014; Dagan et al., 2015a; Reutter et al., 2009). Thus, an increase in the availability of water vapour with CO₂ concentration (Fig. 2) under polluted conditions results in a larger increase in $\stackrel{\mathrm{‾}}{r_{\mathrm{c}}}$ compared with clean conditions. However, the reasons behind this trend, as well as behind the larger increase in q_c in high-N_a simulations, deserve further exploration in the future. Similarly to the q_c case, the larger relative increase in the relatively large droplets promotes the autoconversion process and hence enhances ϵ, more so under high aerosol concentrations than under lower aerosol concentrations.

4 Summary and conclusions

The role of clouds in climate change is manifested by two pathways: (1) effects of anthropogenic aerosol on clouds and (2) feedback that clouds exert on the changing climate. These two pathways are usually studied separately, and even by different scientific communities. In this paper, we demonstrate that the two pathways are closely linked to each other and should be examined concurrently.

Using long, idealized RCE simulations over a small domain with a slab ocean model, we demonstrate that the ECS, i.e. the increase in surface temperature under equilibrium conditions due to doubling of the CO₂ concentration, increases with the aerosol concentration. The ECS increase is explained by a faster increase in precipitation efficiency with warming under high aerosol concentrations, which represents a more efficient depletion of the water from the cloud and thus is manifested as an increase in the cloud feedback parameter. The precipitation efficiency increases faster under high aerosol concentration due to a higher sensitivity of the relatively high liquid water mixing ratios and the relatively large mean droplet sizes to a CO₂ concentration increase. We note that the increase in the total (short wave plus long wave) cloud feedback parameter with the increase in precipitation efficiency is a result of a stronger short-wave effect (Li et al., 2019) than a long-wave effect (Lindzen et al., 2001) in the simulations presented here. Future work should examine the robustness of this trend in different models and with different microphysical and radiative schemes. Moreover, the response of precipitation to changes in aerosol concentration might be microphysical-representation-dependent (White et al., 2017) and hence should be examined in the future under different microphysical schemes (conceivably in a multi-model intercomparison project focusing on aerosol effect on RCE simulations).

The results presented here are based on idealized simulations over a small domain. Under more realistic conditions, other processes, not included here, that could affect the precipitation efficiency and hence the general trend will be introduced. In particular, convective self-aggregation could be of interest as, while it is inhibited in the small domain used here, it was shown to affect precipitation efficiency (Lutsko et al., 2021) and to be affected by aerosols (Nishant et al., 2019). Other processes that should be accounted for in future research include the presence of large-scale circulation and direct aerosol radiative effects (Dagan et al., 2019; Dingley et al., 2021). In addition, the results presented here suggest that the sensitivity of ECS to aerosol loading might not be linear (Table 1). Hence, the dynamical aerosol range present at different geographical locations would affect the total ECS trend.

The results presented here suggest a possible connection between cloud feedback and aerosol–cloud interactions. The regulation of aerosol emissions is known to be more effective than the effort to reduce greenhouse gas emissions. This, together with the short lifetime of aerosols in the atmosphere, has resulted in a reduction in the value of the global-mean aerosol effective radiative forcing in recent years (Quaas et al., 2022). If the conclusions of this paper hold under higher levels of complexity (e.g. large-scale circulation, convective self-aggregation, etc.) this might mean that the reduction in global aerosol emissions could lead to a reduction in ECS, which could compensate, at least partially, for the reduction in the negative forcing induced by aerosols (Quaas et al., 2022; Bellouin et al., 2019), thus providing yet additional motivation for reducing aerosol emissions globally.