An updated microphysical model for particle activation in contrails: the role of volatile plume particles

Global simulations suggest the mean annual contrail cirrus net radiative forcing is comparable to that of aviation's accumulated CO₂ emissions. Currently, these simulations assume non-volatile particulate matter (nvPM) and ambient particles are the only source of condensation nuclei, omitting activation of volatile particulate matter (vPM) formed in the nascent plume. Here, we extend a microphysical model to include vPM and benchmark this against a more advanced parcel model (pyrcel) modified to treat contrail formation. We explore how the apparent emission index (EI) of contrail ice crystals (AEI_ice) scales with EI_nvPM, vPM properties, ambient temperature, and aircraft/fuel characteristics. We find model agreement within 10 %–30 % in the previously defined “soot-poor” regime. However, discrepancies increase non-linearly (up to 60 %) in the “soot-rich” regime, due to differing treatment of droplet growth. Both models predict that, in the “soot-poor” regime, AEI_ice approaches 10¹⁶ kg⁻¹ for low ambient temperatures (< 210 K) and sulfur-rich vPM, which is comparable to estimates in the “soot-rich” regime. Moreover, our sensitivity analyses suggest that the point of transition between the “soot-poor” and “soot-rich” regimes is a dynamic threshold that ranges from 10¹³–10¹⁶ kg⁻¹ and depends sensitively on ambient temperature and vPM properties, underlining the need for vPM emission characterisation measurements. We suggest that existing contrail simulations omitting vPM activation may underestimate AEI_ice, especially for flights powered by lean-burn engines. Furthermore, our results imply that, under these conditions, AEI_ice might be reduced by (i) reducing fuel sulfur content, (ii) minimising organic emissions, and/or (iii) avoiding cooler regions of the atmosphere.

1 Introduction

The aviation industry contributes approximately 3.5 % towards global anthropogenic effective radiative forcing (ERF) (Lee et al., 2021). This share is projected to increase, as the sector is comparatively challenging to decarbonise (Grewe et al., 2021), notwithstanding anticipated compound annual growth in global passenger traffic of 3.6 % from 2027–2043 (Airbus, 2024). Estimates for 2018 indicate that the largest contribution towards net aviation ERF (+100.9 m Wm⁻²) is from contrail cirrus (+57.4 m Wm⁻²), with remaining contributions from accumulated CO₂ emissions (+34.3 m Wm⁻²), followed by NO_x (+17.5 m Wm⁻²) (Lee et al., 2021). The sign and magnitude of the contrail cirrus ERF depend inter alia on optical thickness and spatiotemporal coverage (Kärcher, 2018; Schumann et al., 2012), which are determined by ice crystal microphysics and hence the contrail formation pathway.

Provided the aircraft exhaust plume satisfies the Schmidt–Appleman Criterion (SAC), linear contrail formation occurs within 1 s behind the engine exit plane (Schumann, 1996). In the nascent plume, exhaust gases mix with cooler ambient air, resulting in a locally water-supersaturated environment. Under these conditions, particles in the plume can activate to form water droplets, which later nucleate ice homogeneously to form contrail ice crystals. Hence, this pathway is regulated by the number concentration of particles able to activate, which is controlled by their particle size distribution characteristics and chemical composition (Petters and Kreidenweis, 2007). If fewer particles are able to activate, the resulting ice crystals will be larger and less numerous (Teoh et al., 2022), which may decrease both the optical thickness and the spatiotemporal coverage of the cloud. Therefore, contrail cirrus ERF is inherently sensitive to the characteristics of particles in the mixing plume.

Particles within an exhaust plume are either released by the engine (aircraft mode) or entrained during atmospheric mixing (ambient mode). Aircraft mode particles that evaporate (above) below 350 °C (623 K) (Saffaripour et al., 2020) are defined as (non-)volatile particulate matter, (n)vPM. The largest vPM particles are formed from chemi-ions, which are generated during the combustion process (Yu and Turco, 1997). These chemi-ions scavenge sulfuric acid–water clusters and/or condensable particulate organic matter (POM) in the cooling plume to generate liquid aerosol particles with a number emission index EI_vPM ∼ 10¹⁷ kg⁻¹ (Yu et al., 1998). A smaller, more numerous population of vPM is generated from binary homogeneous nucleation of sulfuric acid and water (Kärcher and Fahey, 1997). However, these particles are efficiently scavenged by the larger particles, enhancing their growth depending on available sulfuric acid and/or POM (Kärcher et al., 2000). They are therefore unlikely to compete with the larger population for plume supersaturations, so we consider the larger population to be plume vPM within this work. The geometric mean diameter (d_g) and hygroscopicity of plume vPM depend on the nature and availability of condensable gases in the aircraft exhaust (Kärcher et al., 2000); d_g,vPM is typically < 5 nm (Schumann et al., 2002) prior to contrail formation. Depending on the engine architecture, (semi-)vPM lubrication oil may also be released as larger droplets or gaseous emissions, with the latter capable of either nucleating new particles or contributing towards the condensable organic fraction (Decker et al., 2024; Ungeheuer et al., 2022). By contrast, EI_nvPM and d_g,nvPM do not change in young exhaust plumes, besides a minor increase to d_g,nvPM by accretion of condensable material. Under cruise thrust settings, $d_{\mathrm{g},\mathrm{nvPM}}\sim \mathrm{35}$ nm (Durdina et al., 2024) and exhibits dependence on fuel and combustor type (Moore et al., 2017; Voigt et al., 2021).

EI_nvPM varies by several orders of magnitude depending on the fuel and engine type (EASA, 2025), with most engines operating in the “soot-rich” regime, where the majority of contrail ice crystals form via nvPM particles (Kärcher and Yu, 2009). Larger nvPM particles (d_g,nvPM > d_g,vPM) activate preferentially in the plume and can suppress water uptake on plume vPM particles, defining “soot-rich” baseline conditions of approximately EI_nvPM>10¹⁵ kg⁻¹ (Kärcher, 2018). Upon reducing EI_nvPM, size differences no longer compensate for differences in relative abundance, and concentrations of activated nvPM and plume vPM become comparable, characterising the “transition regime” (Kärcher and Yu, 2009). Here, baseline conditions depend sensitively on the characteristics of all particle species. Recent developments in lean-burn technology have been shown to further reduce EI_nvPM into the “soot-poor” regime, where activated number concentrations become independent of EI_nvPM as EI_nvPM decreases. “Soot-poor” baseline conditions have been shown to depend on the relative concentration of ambient particles and the characteristics of plume vPM, including EI_vPM and d_g,vPM (Yu et al., 2024). Nevertheless, while the role of vPM has been evidenced in model simulations of individual contrails, these effects have not yet been incorporated into global mean contrail cirrus ERF estimates (Bier and Burkhardt, 2022; Teoh et al., 2024).

Generally, two complementary classes of models are used to describe contrail formation (Bier et al., 2022): those that focus on jet dynamics and those that focus on plume microphysics. The former include 3D large eddy simulations (LESs), which provide insight into the spatial heterogeneity within contrail mixing plumes (Lewellen et al., 2014). Inevitably, the high spatial resolution achieved in these simulations is achieved at the expense of detailed microphysical descriptions (Ferreira et al., 2024). To that end, several LES models prescribe water saturation as the critical condition for contrail ice formation (Paoli et al., 2013; Picot et al., 2015) or heterogeneous ice nucleation as the primary formation pathway (Khou et al., 2017, 2015), both of which have been rejected by in situ observations (Kärcher et al., 2015). More representative microphysical treatment can be achieved using 0D box- and parcel model simulations (Bier et al., 2022; Rojo et al., 2015; Yu et al., 2024). Here, the dilution of a parcel of exhaust air is simulated, and microphysical phase transitions, such as particle activation and homogeneous ice nucleation, are tracked. While these models are unable to incorporate feedback between different plume parcels, which may otherwise lead to a diversity of particle history (Lewellen, 2020), they are configured for sophisticated treatment of complex ice microphysics, which is critical for describing contrail properties (Yu et al., 2024).

Here, we undertake a literature review of the microphysical pathway to contrail formation, to better understand the role of plume vPM in contrail formation. We then extend two parcel models using detailed microphysics to account for the activation of plume vPM. In both models, we prescribe plume vPM properties at the time of droplet formation and ice nucleation (0.1–1 s after emission) rather than explicitly modelling their formation. The two models include (i) a minimal microphysical framework developed by Kärcher et al. (2015), henceforth referred to using the shorthand K15, and (ii) a more complex numerical parcel model (pyrcel) developed by Rothenberg and Wang (Rothenberg and Wang, 2016). The extended K15 model is designed for future integration into global contrail simulations, while the modified pyrcel model serves as a benchmark to highlight model discrepancies. After examining these discrepancies, we use the modified pyrcel model to perform a suite of sensitivity analyses, studying the influence of the prescribed vPM size distribution characteristics and hygroscopicity, ambient temperature, and aircraft/fuel properties.

In Sect. 2, we provide an overview of elementary contrail thermodynamics (Sect. 2.1), a description of particle activation in contrail mixing plumes (Sect. 2.2), and implications for the SAC (Sect. 2.3). Next, we provide an overview of the underlying model framework (Sect. 3.1) and extensions (Sect. 3.2 and 3.3) and of the assumed particle characteristics used in this work (Sect. 3.4). We then evaluate the two models in Sect. 4.1 and 4.2, justifying the use of the modified pyrcel model for several sensitivity analyses (Sect. 4.3–4.6). Finally, we comment on several implications for future modelling studies and wider impacts (Sect. 5).

2 Background

Here, we review the thermodynamic pathway to contrail formation and define the SAC framework (Sect. 2.1). We describe several fundamental principles of particle activation (Sect. 2.2) and use these to justify an extension to the original SAC framework (Sect. 2.3). Finally, we provide a theoretical framework for the parcel models used within this work (Sect. 2.4).

2.1 Thermodynamics of contrail formation

A cruising aircraft releases combustion emissions at a typical engine exhaust temperature T_E∼600 K, which depends on the engine architecture and bypass ratio (Cumpsty, 2003). The emissions are dispersed into the turbulent jet plume of the aircraft and are rapidly diluted by upper-tropospheric air, cooling to the ambient temperature (T_A) within 1 s. We can use the partial pressure of water in the mixing plume (p_v,M) to navigate the transition between exhaust and ambient conditions. For isobaric conditions, this property scales linearly between exhaust and ambient conditions (Rogers and Yau, 1996):

$$\begin{array}{}\text{(1)}& G={\displaystyle \frac{\mathrm{d}{p}_{\mathrm{v},\mathrm{M}}}{\mathrm{d}T}}={\displaystyle \frac{p_{\mathrm{v},\mathrm{E}}-p_{\mathrm{v},\mathrm{A}}}{T_{\mathrm{E}}-T_{\mathrm{A}}}},\end{array}$$

where p_v,E and p_v,A represent the partial pressure of water in the exhaust and ambient air, respectively, and G is the gradient of the mixing line. Provided we know the ambient conditions (p_v,A, T_A) and T_E, to fully constrain Eq. (1), we must also define either p_v,E or G. Conveniently, the latter has been shown to depend on the aircraft and fuel properties (Schumann, 1996):

$$\begin{array}{}\text{(2)}& G={\displaystyle \frac{c_p{\mathrm{EI}}_{\mathrm{w}}{P}_{\mathrm{T}}}{\mathit{\epsilon }Q(\mathrm{1}-\mathit{\eta })}},\end{array}$$

where P_T is the ambient air pressure, c_p is the isobaric specific heat of air (1004 J kg⁻¹), EI_w is the mass emission index of water vapour, ε is the ratio of gas constants for water vapour and dry air (0.622), and η is the overall efficiency such that (1–η) represents the fraction of the total heat released per mass of fuel burned (Q) that is transferred to the exhaust gas. We can describe p_v,M by re-arranging Eq. (1):

$$\begin{array}{}\text{(3)}& p_{\mathrm{v},\mathrm{M}}=p_{\mathrm{v},\mathrm{A}}+G\left(T-T_{\mathrm{A}}\right).\end{array}$$

Often, it is useful to describe how the water or ice saturation ratio of the plume (S_v,M and S_i,M, respectively) evolves during the mixing process (Fig. 1). Here, we define S_v,M and S_i,M within the mixing plume as follows:

$$\begin{array}{}\text{(4)}& {\displaystyle }{S}_{\mathrm{v},\mathrm{M}}={\displaystyle \frac{p_{\mathrm{v},\mathrm{M}}}{p_{\mathrm{liq}}\left(T\right)}},\text{(5)}& {\displaystyle }{S}_{\mathrm{i},\mathrm{M}}={\displaystyle \frac{p_{\mathrm{v},\mathrm{M}}}{p_{\mathrm{ice}}\left(T\right)}}.\end{array}$$

p_liq(T) and p_ice(T) represent the saturation vapour pressure above a plane surface of supercooled liquid water or ice, respectively (Murphy and Koop, 2005). In turn, we use Eq. (4) to define the liquid water supersaturation within the contrail mixing plume as s_v,M = S_v,M − 1.

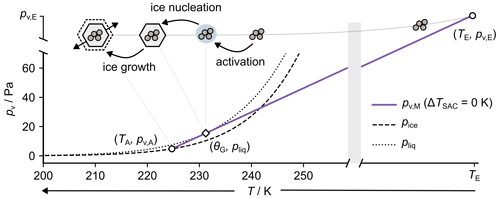
Figure 1 Partial pressure of water vapour (p_v) and temperature of the plume (T) during contrail mixing (purple line) under threshold conditions (T_A=T_SAC). Saturation vapour pressures above ice (p_ice) and water (p_liq) are also shown. Finally, a schematic representation of particle emission, activation, and ice nucleation is shown. The latter two occur simultaneously within the original SAC framework. Here, we assume typical aircraft and fuel properties of P_T, EI_w, Q, and η of 25 kPa, 1.23 kg kg⁻¹, 43.2 MJ, and 0.3 for temperatures T_A and T_E of ∼224 and 600 K, respectively.

To illustrate several features associated with contrail formation, we have shown an example of mixing behaviour for typical aircraft and fuel properties; see Fig. 1. The first feature is the crux of the SAC: contrail formation can only occur if S_v,M > 1 (s_v,M > 0). However, this represents only an approximate requirement for the activation of particles into liquid droplets, which we will discuss further in Sect. 2.2 and 2.3. Nevertheless, as originally defined, the SAC may be interpreted quantitatively as

$$\begin{array}{}\text{(6)}& {\left.{\displaystyle \frac{\mathrm{d}{p}_{\mathrm{liq}}\left(T\right)}{\mathrm{d}T}}\right|}_{{\mathit{\theta }}_G}=G,\end{array}$$

where θ_G is the temperature at which the contrail mixing line tangentially intersects p_liq. Under this definition, θ_G represents the highest temperature at which contrail formation can occur in a water-saturated plume. For ambient relative humidities below water saturation $(p_{\mathrm{v},\mathrm{A}}<p_{\mathrm{liq}})$, this corresponds to a projected ambient temperature known as the Schmidt–Appleman threshold temperature (T_SAC) (Schumann et al., 1996). Accordingly, T_SAC represents the highest ambient temperature at which contrail formation can occur. The mixing behaviour presented in Fig. 1 is consistent with this threshold condition. Notably, for lower T_A and fixed p_v,A, the mixing line would be translated towards cooler T by an amount ΔT_SAC, and the plume would become supersaturated during mixing. Hence, the parameter ΔT_SAC provides a useful indicator for the degree of supersaturation experienced by a contrail mixing plume. Importantly, the SAC implies that the activation of particles into liquid droplets occurs before ice nucleation takes place.

This water saturation constraint is consistent with observations of young contrails (Kärcher et al., 2015) and implies a formation pathway of condensation followed by homogeneous ice nucleation (Murray et al., 2012). As such, we omit heterogeneous ice nucleation in our analysis, which would otherwise contradict this mechanism. The water saturation constraint is also motivated by particle properties because (a) aircraft-emitted nvPM particles have previously been shown as inactive heterogeneous ice nuclei (Testa et al., 2024); (b) only a small subset of ambient tropospheric aerosol particles (mineral dust, ammonium sulfate, and amorphous organic) are efficient heterogeneous ice nuclei (Kärcher et al., 2023), and these have low number concentrations at cruise altitudes (relative to lean-burn EI_nvPM); and (c) plume vPM is likely to be at least partly soluble and therefore inactive as heterogeneous ice nuclei. Therefore, in the context of nvPM, the water saturation constraint implies that particles first activate to form water droplets, after which they act as passive inclusions, with rates of homogeneous ice nucleation controlled by the ambient temperature and volume of adsorbed water. In the context of plume vPM and ambient particles, we extend this analysis and demonstrate that the process of ice formation is again strictly sequential, with particle activation occurring before homogeneous ice nucleation; see Sect. S1 in the Supplement. For this reason, contrail formation is dictated by the conditions under which particle activation takes place, which are addressed in Sect. 2.2.

2.2 Aerosol particle activation and the κ–Köhler framework

The equilibrium saturation ratio over a particle may be described as a balance of two interactions (Seinfeld and Pandis, 2016). The first of these is the Kelvin (also commonly referred to as the “surface curvature”) effect. Consider the situation whereby a particle with a (dry-particle) diameter d_d is activated to form a pure liquid droplet with a (wet-particle) diameter of d_w. Due to surface tension at the water–air interface, a decrease in the droplet diameter leads to an increase in the partial pressure of water vapour at the droplet surface and hence to an increase in the water saturation ratio (S_v). This effect is parameterised as

$$\begin{array}{}\text{(7)}& S_{\mathrm{v}}=a_{\mathrm{w}}{e}^{\left(\frac{\mathrm{4}{\mathit{\sigma }}_{\mathrm{s}}{M}_{\mathrm{w}}}{\mathrm{RT}{\mathit{\rho }}_{\mathrm{w}}{d}_{\mathrm{w}}}\right)},\end{array}$$

where σ_s is the surface tension of the liquid–air interface, M_w is the molar mass of water, ρ_w is the density of the liquid, R is the global gas constant, T is the temperature, and a_w is the activity of water in solution (Petters and Kreidenweis, 2007). For particles that are entirely insoluble, the liquid surrounding the particle will be pure water, and we can approximate a_w=1, reducing Eq. (7) to the Kelvin equation (Pruppacher and Klett, 2010). This simplified treatment of insoluble particle activation has been revisited by several studies that consider multilayer adsorption mechanisms (Kumar et al., 2009; Sorjamaa and Laaksonen, 2007), although the application of these approaches is limited by the availability of experimental data. In contrast, if the particle is not entirely insoluble (for example, the insoluble core may contain a soluble coating), the value of a_w (and S_v) is reduced, thus defining the second, solute effect. In this case, the activity of water in solution may be treated using the parameterisation proposed by Petters and Kreidenweis (2007). Here, the particle is described using a hygroscopicity parameter (κ), which is related to the bulk material solubility (Sullivan et al., 2009), and a_w is given by

$$\begin{array}{}\text{(8)}& a_{\mathrm{w}}={\displaystyle \frac{d_{\mathrm{w}}^{\mathrm{3}}-d_{\mathrm{d}}^{\mathrm{3}}}{d_{\mathrm{w}}^{\mathrm{3}}-d_{\mathrm{d}}^{\mathrm{3}}\left(\mathrm{1}-\mathit{\kappa }\right)}},\end{array}$$

where, for an internally mixed particle, κ is given as a volume-weighted sum over the individual components. Note that Eq. (7) collapses to a_w=1 if κ=0, which is the approximate limit for a non-hygroscopic (insoluble) particle. Above this limit, κ is typically represented on a logarithmic scale, with slightly hygroscopic materials (κ<0.01) less capable of water uptake than very hygroscopic materials (κ>0.5) (Petters and Kreidenweis, 2007). Combining Eqs. (7) and (8), we recover the final form of κ-Köhler theory,

$$\begin{array}{}\text{(9)}& S_{\mathrm{v}}={\displaystyle \frac{d_{\mathrm{w}}^{\mathrm{3}}-d_{\mathrm{d}}^{\mathrm{3}}}{d_{\mathrm{w}}^{\mathrm{3}}-d_{\mathrm{d}}^{\mathrm{3}}\left(\mathrm{1}-\mathit{\kappa }\right)}}{e}^{\left(\frac{\mathrm{4}{\mathit{\sigma }}_{\mathrm{s}}{M}_{\mathrm{w}}}{\mathrm{RT}{\mathit{\rho }}_{\mathrm{w}}{d}_{\mathrm{w}}}\right)}.\end{array}$$

According to Eq. (9), S_v increases with d_w up to a maximum at (d_w,c, S_v,c), beyond which it declines; see Fig. 2a. These critical parameters may be estimated for a given particle type and at a given T by setting the derivative of Eq. (9) equal to zero and solving numerically. In the context of particle activation, it is more instructive to explore how d_w depends on the ambient saturation ratio, remaining mindful that the inverse function d_w=d_w(S_v) is multivalued. To that end, as the ambient S_v is increased over a particle, growth is initially regulated by the solute effect, and the particle diameter increases by slow, hygroscopic growth. Upon further increasing S_v, the relative magnitudes of the Kelvin and solute effects balance at the critical point $(S_{\mathrm{v},\mathrm{c}},d_{\mathrm{w},\mathrm{c}})$ (Seinfeld and Pandis, 2016). Here, the particle is said to have been activated, and subsequent growth is regulated by kinetic droplet growth outlined in Sect. S2. In summary, a particle is considered activated to form a water droplet once the ambient S_v exceeds S_v,c.

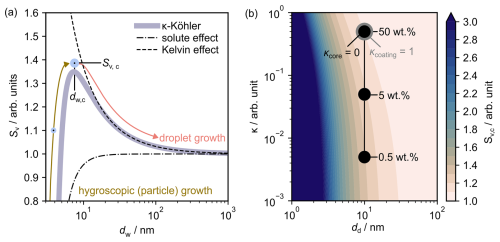
Figure 2 (a) Water saturation ratio (S_v) with increasing wet-particle diameter (d_w) as the combination of the solute and Kelvin effects. The critical diameter (d_w,c) and the associated critical saturation ratio (S_v,c) mark the point at which a particle is considered activated. (b) S_v,c is shown as a function of the dry-particle diameter (d_d) and particle hygroscopicity. Values for insoluble (κ=0) particles with variable highly soluble (κ=1) coatings have been shown for reference.

Figure 2b shows that S_v,c exhibits three key trends: (i) it increases with both d_d and κ; (ii) it is more sensitive to changes in d_d than κ (i.e. $\frac{\mathrm{d}{S}_{\mathrm{v},\mathrm{c}}}{\mathrm{d}{d}_{\mathrm{d}}}\gg \frac{\mathrm{d}{S}_{\mathrm{v},\mathrm{c}}}{\mathrm{d}\mathit{\kappa }}$); and (iii) it approaches 1 in the limit $(\mathit{\kappa },d_{\mathrm{p}})\to (\mathrm{1},\mathrm{\infty }$), $S_{\mathrm{v},\mathrm{c}}\to \mathrm{1}$, for which additional justification is provided in Sect. S3. In Fig. 2b, we also show how S_v,c varies for a series of mixed particles with insoluble (κ=0) cores and variable coatings of hygroscopic (κ=1) material (0.5 wt %–50 wt %) with similar total dry-particle diameters d_d=10 nm. These highlight the importance of soluble coatings when considering plume particle activation, which is a feature we return to in Sect. 4.5.

2.3 Extended Schmidt–Appleman framework

As discussed in Sect. 2.1, the SAC assumes that contrails are formed if the mixing line becomes (super)saturated with respect to water during plume evolution (S_v≥1). However, as outlined in Sect. S3, this criterion cannot be reconciled with the minimum requirement for (even hygroscopic) particle activation.

Instead, suppose that a contrail mixing contains a single particle mode with properties (d_d, κ). Now, the criterion for contrail formation is that the contrail mixing line must contact p_liq ⋅ S_v,c $\left(T,d_{\mathrm{d}},\mathit{\kappa }\right)$ at least once during the mixing process. Figure 3a shows that, when these particle properties are included, the threshold requirement for activation (previously water-saturated conditions, dotted black line) is elevated (grey/green dotted line). Using Eq. (9), the particle dependence of ΔT_SAC=ΔT_SAC $\left(T,d_{\mathrm{d}},\mathit{\kappa }\right)$ can be determined and is shown in Fig. 3b. Alternatively, we can reframe the parameter ΔT_SAC $\left(T,d_{\mathrm{d}},\mathit{\kappa }\right)$ presented in Fig. 3b to be an effective Schmidt–Appleman temperature, T_SAC (d_d,κ), the ambient temperature below which contrail formation takes place when the plume contains particles with properties d_d and κ. Figure 3b also enables us to estimate for which particle types the SAC framework (as outlined in Sect. 2.1) remains applicable, under a specified temperature uncertainty.

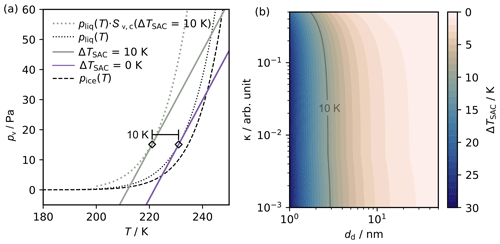
Figure 3 (a) Saturation vapour pressure above water (p_liq) (purple, dotted) and a contrail mixing line (purple, solid) for threshold conditions, ΔT_SAC=0 K. Particle properties (d_d, κ) have been chosen so that the modified saturation vapour pressure above water p_liq ⋅ S_v,c (d_d, κ) (grey/green, dotted) translates threshold conditions by 10 K, so ΔT_SAC=10 K (grey/green, solid). (b) Extension of panel (a) to show dependence of ΔT_SAC on d_d and κ. Combinations of particle properties resulting in ΔT_SAC=10 K are shown (grey/green, solid). In all cases, S_v,c is estimated conservatively using T=220 K.

For particles with κ>0.6 and/or d_d>20 nm, ΔT_SAC $\left(T,d_{\mathrm{d}},\mathit{\kappa }\right)<\mathrm{2}$ K, which is close to the typical uncertainty associated with low-altitude temperature measurements during in situ campaigns, $\mathrm{\Delta }T=\pm \mathrm{1.9}$ K (Bräuer et al., 2021). Therefore, for “soot-rich” emissions, where the typical nvPM particles have d_d>20 nm, the condition for applying the original SAC is valid within measurement uncertainty. This explains the success of this approach over the past decades and across various measurement campaigns (Schumann et al., 2017). However, with reduced soot emissions, exhaust material will be enriched with smaller plume vPM particles. Under these circumstances, the SAC is less effective at predicting the temperature at which most particles activate; see Fig. 3b.

3 Model

Here, we outline the fundamental relations used to describe a parcel model for contrail formation (Sect. 3.1), including a basic overview of the original K15 model. Next, we outline several extensions made to the K15 model so that it can be applied to treat plume vPM activation (Sect. 3.2). Then, we outline modifications made to a pre-existing cloud parcel model, pyrcel (Rothenberg and Wang, 2016), to simulate the early stages of contrail formation (Sect. 3.3). Finally, we describe the parameter space used in our model simulations (Sect. 3.4).

3.1 Contrail parcel model

As discussed in Sect. 2.2, the critical parameter governing the uptake of water onto particles is the water saturation ratio, S_v. The water saturation ratio within a parcel of air can be described as

$$\begin{array}{}\text{(10)}& S_{\mathrm{v}}={\displaystyle \frac{P_T}{p_{\mathrm{liq}}(\mathit{\epsilon }+w_{\mathrm{v}})}}{w}_{\mathrm{v}},\end{array}$$

where ε (=0.622) is the ratio of the molar mass of water (18.02 g mol⁻¹) to the molar mass of dry air (28.97 g mol⁻¹) and w_v is the water vapour mixing ratio, the mass of water vapour per unit mass of dry air contained within the parcel. We can simplify Eq. (10) further using several features of contrail mixing. Within a contrail, the maximum partial pressure of water vapour in the plume is given by the maximum of S_v⋅p_liq. This is bounded by $S_{\mathrm{v},\mathrm{M}}\cdot p_{\mathrm{liq}}$, since isobaric mixing is the only process that acts to increase the parcel saturation ratio. Assuming that the ambient environment is ice-saturated, we also know that p_v,M is bounded by (p_v,M)_max = $p_{\mathrm{ice}}\left(T_{\mathrm{A}}\right)+G\cdot (T_{\mathrm{E}}-T_{\mathrm{A}}$), provided we prescribe an anomalously-low T_A of 200 K. Rearranging Eq. (10), we can therefore bound w_v as

$$\begin{array}{}\text{(11)}& w_{\mathrm{v}}<{\displaystyle \frac{\mathit{\epsilon }{\left(p_{\mathrm{v},\mathrm{M}}\right)}_{\max }}{P_{\mathrm{T}}-{\left(p_{\mathrm{v},\mathrm{M}}\right)}_{\max }}}.\end{array}$$

Using T_E=600 K, T_SAC=224 K, G=1.64 PaK⁻¹, and P_T=23 000 Pa, we have w_v<0.02. Therefore, the inequality w_v≪ε is satisfied for all conditions, which enables us to simplify Eq. (10) as

$$\begin{array}{}\text{(12)}& S_{\mathrm{v}}={\displaystyle \frac{P_T}{p_{\mathrm{liq}}\mathit{\epsilon }}}{w}_{\mathrm{v}}.\end{array}$$

Next, we assume that contrail mixing occurs at constant atmospheric pressure so that, upon differentiating Eq. (12) with respect to time and collecting like terms, we have

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}}={\displaystyle \frac{P_{\mathrm{d}}T}{p_{\mathrm{liq}}\mathit{\epsilon }}}{\displaystyle \frac{\mathrm{d}{w}_{\mathrm{v}}}{\mathrm{d}t}}-S_{\mathrm{v}}{\displaystyle \frac{\mathrm{1}}{p_{\mathrm{liq}}}}{\displaystyle \frac{\mathrm{d}{p}_{\mathrm{liq}}}{\mathrm{d}t}},\end{array}$$

$$\begin{array}{}\text{(14)}& {\displaystyle \frac{\mathrm{d}{w}_{\mathrm{v}}}{\mathrm{d}t}}=-{\left({\displaystyle \frac{\mathrm{d}{w}_{\mathrm{c}}}{\mathrm{d}t}}\right)}_{\mathrm{microphysical}}+{\left({\displaystyle \frac{\mathrm{d}{w}_{\mathrm{v},\mathrm{M}}}{\mathrm{d}t}}\right)}_{\mathrm{mixing}}.\end{array}$$

Equation (14) is a statement of mass conservation: any change in the water vapour content of the parcel must result either from particle microphysical processes (i.e. particle activation and droplet/ice crystal growth) or from plume mixing vapour. Using Eq. (10), we can express the mixing term as

$$\begin{array}{}\text{(15)}& {\left({\displaystyle \frac{\mathrm{d}{w}_{\mathrm{v},\mathrm{M}}}{\mathrm{d}t}}\right)}_{\mathrm{mixing}}=\dot{T}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}T}}\left({\displaystyle \frac{\mathit{\epsilon }{p}_{\mathrm{v},\mathrm{M}}}{P_T}}\right)={\displaystyle \frac{\mathit{\epsilon }}{P_T}}G\dot{T},\end{array}$$

where $\dot{T}$ is the cooling rate in the plume. Then, combining Eqs. (12)–(15), we arrive at the governing equation

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{1}}{p_{\mathrm{liq}}}}G\dot{T}-S_{\mathrm{v}}{\displaystyle \frac{\mathrm{1}}{p_{\mathrm{liq}}}}{\displaystyle \frac{\mathrm{d}{p}_{\mathrm{liq}}}{\mathrm{d}t}}-{\displaystyle \frac{P_T}{p_{\mathrm{liq}}\mathit{\epsilon }}}{\displaystyle \frac{\mathrm{d}{w}_{\mathrm{c}}}{\mathrm{d}t}}.\end{array}$$

This is almost identical to the result given by Kärcher et al. (2015). However, we find that, on the right-hand side of Eq. (16), the actual plume saturation ratio (S_v) is present rather than the saturation ratio assumed from mixing alone (S_v,M). This equation can be solved numerically, for example, by using a numerical parcel model. However, the equation cannot be solved analytically. Under these circumstances, a solution may be derived by firstly approximating $S_{\mathrm{v}}\sim S_{\mathrm{v},\mathrm{M}}$ on the right-hand side of Eq. (16) as in the original K15 model, which effectively decouples the equation. In this purely analytical case, we can generalise Eq. (16) in the form

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}}=P_{\mathrm{w}}-L_{\mathrm{w}},\end{array}$$

where P_w represents the rate of change of the water saturation ratio without particles in the plume and L_w represents the rate of change of the water saturation ratio resulting from (a) particle activation to form water droplets and (b) the growth of droplets and/or ice crystals. The description for P_w follows from the description of contrail mixing outlined in Sect. 2.1 and is given by Kärcher et al. (2015):

$$\begin{array}{}\text{(18)}& P_{\mathrm{w}}={\displaystyle \frac{\mathrm{1}}{p_{\mathrm{liq}}}}G\dot{T}-S_{\mathrm{v},\mathrm{M}}{\displaystyle \frac{\mathrm{1}}{p_{\mathrm{liq}}}}{\displaystyle \frac{\mathrm{d}{p}_{\mathrm{liq}}}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{d}{S}_{\mathrm{v},\mathrm{M}}}{\mathrm{d}t}}.\end{array}$$

Using the description of mixing provided by Kärcher et al. (2015), next we will outline the equations necessary to estimate the cooling rate. For a full description of the parameters and underlying approximations, the reader is directed to the original text and references therein. The contrail mixing plume cools as it is diluted with ambient air according to the dilution factor

$$\begin{array}{}\text{(19)}& D\left(T\right)={\displaystyle \frac{T-T_{\mathrm{A}}}{T_{\mathrm{E}}-T_{\mathrm{A}}}},\end{array}$$

which describes how the cross-sectional area of the plume decreases with decreasing ambient temperature. The temporal evolution of the plume is then described by

$$\begin{array}{}\text{(20)}& {\displaystyle \frac{\mathrm{d}T}{\mathrm{d}t}}=-\mathit{\beta }{\displaystyle \frac{T_{\mathrm{E}}-T_{\mathrm{A}}}{{\mathit{\tau }}_{\mathrm{m}}}}{D}^{\mathrm{1}+\mathrm{1}/\mathit{\beta }},\text{(21)}& {\displaystyle }t={\mathit{\tau }}_{\mathrm{m}}{D}^{-\mathrm{1}/\mathit{\beta }},\end{array}$$

where τ_m is the timescale over which the contrail mixing parcel is unaffected by entrainment and β is a constant dilution parameter. Note that we choose to omit effects associated with latent heat within our simulations, which we found to have a negligible impact on projected ice crystal number concentrations. Therefore, if we have knowledge of the aircraft and ambient conditions, using Eqs. (19)–(21), we are now able to describe P_w within the contrail mixing parcel at a given temperature. These relations also govern particle dilution within the cooling contrail mixing parcel. To that end, the total particle number concentration of aircraft (n_T) and ambient (n_a,T) particle modes are, respectively,

$$\begin{array}{}\text{(22)}& {\displaystyle }{n}_{\mathrm{T}}={\displaystyle \frac{D\left(T\right){\mathit{\rho }}_{\mathrm{a}}\left(T\right)}{N_{\mathrm{0}}}}\mathrm{EI},\text{(23)}& {\displaystyle }{n}_{\mathrm{a},T}={\displaystyle \frac{T_{\mathrm{A}}}{T}}\left[\mathrm{1}-D\left(T\right)\right]n_{\mathrm{a},\mathrm{0}},\end{array}$$

where ρ_a is the mass density of ambient air, EI represents the emission index of the aircraft mode, n_a,0 represents the ambient number concentration far from the plume, and N₀ is the mass-based mixing ratio according to the K15 model. Particle types are assumed to conform to lognormal particle size distributions and described using a fixed (total) hygroscopicity parameter, κ. For this reason, only a fraction of the total particles within a given mode will be able to activate under a given set of ambient conditions. The activated number concentration can be estimated by integrating over the particle size distribution using Eq. (9), using a methodology outlined in Sect. S4. The second term in Eq. (17), L_w, may be expressed as in Korolev and Mazin (2003):

$$\begin{array}{}\text{(24)}& L_{\mathrm{w}}={\displaystyle \frac{P_{\mathrm{T}}}{p_{\mathrm{liq}}\mathit{\epsilon }}}{\displaystyle \frac{\mathrm{d}{w}_{\mathrm{c}}}{\mathrm{d}t}};{\displaystyle \frac{\mathrm{d}{w}_{\mathrm{c}}}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{a}}}}\sum _{i=\mathrm{1}}^n{n}_{\mathrm{w},\mathrm{i}}{r}_{\mathrm{w},\mathrm{i}}^{\mathrm{2}}{\dot{r}}_{\mathrm{w},\mathrm{i}},\end{array}$$

where n_w,i is the number concentration of droplets, r_w,i is the droplet radius, and ${\dot{r}}_{\mathrm{w},\mathrm{i}}$ is the droplet growth rate of these droplets; see Sect. S2. In Eq. (24), we summed contributions from each of the droplets at a given time t. Another useful formulation of Eq. (24) is

$$\begin{array}{}\text{(25)}& \begin{array}{rl}{L}_{\mathrm{w}}& ={\displaystyle \frac{P_{\mathrm{T}}}{p_{\mathrm{liq}}\mathit{\epsilon }}}{\displaystyle \frac{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{a}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathrm{d}{r}_{\mathrm{0}}{\displaystyle \frac{\mathrm{d}{n}_{\mathrm{w}}}{\mathrm{d}{r}_{\mathrm{0}}}}\underset{-\mathrm{\infty }}{\overset{t}{\int }}{\dot{n}}_{\mathrm{w}}\left(t_{\mathrm{0}}\right)r_{\mathrm{w}}^{\mathrm{2}}\left(t,t_{\mathrm{0}}\right)\\ & {\dot{r}}_{\mathrm{w}}(t,t_{\mathrm{0}})\mathrm{d}{t}_{\mathrm{0}},\end{array}\end{array}$$

where ${\dot{n}}_{\mathrm{w}}\left(t_{\mathrm{0}}\right)\mathrm{d}{t}_{\mathrm{0}}$ is the number density of aerosol particles that activate between times t₀ and t + dt₀, $\mathrm{4}\mathit{\pi }{r}_{\mathrm{w}}^{\mathrm{2}}\left(t,t_{\mathrm{0}}\right)$ is related to the volumetric flux of water towards water droplets at time t that first formed at time t₀<t, and ${\dot{r}}_{\mathrm{w}}\left(t,t_{\mathrm{0}}\right)$ is the growth rate of these droplets at time t (Kärcher and Lohmann, 2002a). We also integrated over the size distribution of activated particles, $\frac{\mathrm{d}{n}_{\mathrm{w}}}{\mathrm{d}{r}_{\mathrm{0}}}$. In Eq. (25), rather than summing over contributions from each droplet at a given time t, we have instead integrated over each time t₀<t and estimated the projected contribution towards the final time t. Equations (24) and (25) are therefore equivalent representations that are suited to different applications.

Finally, the contrail mixing behaviour can be described using P_w in combination with either expression for L_w. The formulation in Eq. (24) is used in traditional cloud parcel models using discretised particle and droplet size distributions, which enables Eq. (17) to be solved iteratively as a function of time. This forms the basis for the pyrcel model, which is described in more detail in Sect. 3.3. On the other hand, in the K15 model, the formulation in Eq. (25) is solved analytically at each time step, assuming that particle activation and droplet growth at time t<t₀ do not affect S_v at time t₀. At each time t, we estimate the critical droplet number concentration required to prevent any further change in the plume saturation ratio $\left(\frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}=\mathrm{0}\right)$. Using Eq. (25), we can define the mean supersaturation loss rate per droplet as R_w = $L_{\mathrm{w}}/n_{\mathrm{w}}\left(t\right)$ and reformulate this critical droplet number concentration as $n_{\mathrm{w}}^{\left(\mathrm{2}\right)}\left(t\right)=\frac{P_{\mathrm{w}}}{R_{\mathrm{w}}}$. As time evolves and S_v increases, so too will the number concentration of droplets, $n_{\mathrm{w}}^{\left(\mathrm{1}\right)}\left(t\right)$. At some threshold time, the number concentration of droplets will be equal to the critical droplet number concentration; i.e. $n_{\mathrm{w}}^{\left(\mathrm{1}\right)}\left(t\right)=n_{\mathrm{w}}^{\left(\mathrm{2}\right)}\left(t\right)$. Assuming the plume saturation ratio has equilibrated, no further activation can take place after this time (Twomey, 1959). Hence, this condition defines a lower bound for the maximum number of water droplets that can form during the mixing process, providing an estimate for the contrail ice crystal number concentration. This process forms the basis of the K15 model approach, for which several extensions are described in Sect. 3.3.

3.2 Model extensions for K15

The original K15 model only considers aircraft-emitted nvPM and ambient particles, both of which contain a single particle type and are described using assumed lognormal particle size distribution characteristics and κ. This approach is applicable to nvPM particles because their size distribution characteristics do not change significantly over time and because κ is dominated by the insoluble nvPM fraction. This approach is also applicable to ambient solution droplets because, once entrained into the plume, these droplets are readily activated due to the high (S_v≫1) plume supersaturations. Therefore, small changes in their size distribution characteristics that are not captured by the K15 model are relatively insignificant. Considering this, our first extension to the K15 model is to introduce plume vPM (Yu et al., 1998) as an additional particle type. We define plume vPM to consist of condensable gaseous material, including (but not limited to) sulfuric acid, organic material, and engine lubrication oil. Simulations show that the size distribution characteristics of plume vPM evolve over time due to condensational growth and coagulation (Kärcher et al., 2000). However, here we are concerned with the contrail formation phase 0.1–1 s into plume dilution, so we prescribe plume vPM properties expected at these timescales. As such, our model cannot be used to predict the properties of plume vPM. Instead, we prescribe plume vPM using a fixed emission index, κ, and particle size distribution characteristics, and we evaluate the model sensitivity to these variables under typical ranges. In Sect. S5, we also investigate the use of a more complex ambient particle description comprising seven independent particle types. The particle size distribution characteristics and hygroscopicity of these particle types are estimated using outputs from the global aerosol–climate model ECHAM-HAM (Zhang et al., 2012). Overall, we suggest that incorporating these additional ambient particle types could enhance AEI_ice by 1 order of magnitude when most ice crystals form via ambient particles. Next, there are several microphysical processes within the K15 model which are described using analytical approximations. Our extensions focus on either improving the accuracy of these approximations or removing them altogether in favour of numerical solutions. Firstly, the analytical approximation used to estimate the activated number concentrations for a given particle type can lead to overpredictions for $S_{\mathrm{v}}<S_{\mathrm{v},\mathrm{c}}$ (d_g, κ, T) (Sect. S6). To address this, we updated the methodology to estimate activated particle number concentrations using an exact analytical solution.

Secondly, the K15 model estimates $S_{\mathrm{v},\mathrm{c}}\left(T,d_{\mathrm{d}},\mathit{\kappa }\right)$ using an approximate analytical solution derived from Eq. (9). We compared this with the full numerical solution and show that the K15 approximation systematically underpredicts critical supersaturations for κ (<0.2), with larger discrepancies upon reducing d_g (Sect. S7). Hence, we solve Eq. (9) numerically when identifying critical supersaturations, in line with Bier and Burkhardt (2022).

The aforementioned approximations each indirectly relate to the P_w term; however, the final approximation relates to the L_w term. The methodology for estimating contrail ice crystal number concentrations outlined in K15 relies on analytical solutions for both P_w and L_w. In Sect. S8, we provide an overview of the relevant equations used to estimate L_w and give an account of the various approximations used in its derivation. After considering these, we suggest the following modification. The solution to L_w provided in K15 is valid only for when particle activation occurs more quickly than droplet growth, i.e. the “slow-growth” regime (Kärcher and Lohmann, 2002b). After incorporating a plume vPM particle mode, this condition is not necessarily satisfied, so we use a regime-independent analytical solution (Kärcher et al., 2006).

There are two outstanding limitations in the extended K15 model that cannot be resolved. Firstly, we found no means of introducing the Kelvin correction into the solution for L_w (via the droplet growth equation). Omitting the Kelvin effect in the droplet growth equation acts to increase the radial growth rate (Sect. S2). Hence, the ability for droplets to deplete the plume supersaturation is increased, so a lower droplet number concentration is required to quench the ambient supersaturation. This effect is relevant for smaller particles such as plume vPM, where the magnitude of the Kelvin correction is increased. Secondly, an analytical solution for the inner integral of Eq. (25) requires that L_w is independent of the plume supersaturation so that droplet formation at time t₀<t does not deplete the plume supersaturation at time t. However, as defined in Eq. (25), L_w is coupled to the plume supersaturation via the droplet growth equation. We anticipate this may be problematic when two or more particle types with comparable number concentrations but different S_v,c coexist. Here, one particle type will preferentially activate and grow, subsequently depleting the supersaturation available for the second particle type and thereby inhibiting its activation and growth. For this reason, the extended K15 does not account for the temporal depletion of supersaturation or competition between particle types.

3.3 Model modifications for pyrcel

pyrcel is a 0D cloud parcel model used to simulate the evolution of a parcel of air as it ascends adiabatically at a constant updraft speed (Rothenberg and Wang, 2016). The model is initialised by defining the aerosol population using lognormal particle size distributions, which are discretised into bins. These particle properties are used in combination with the initial ambient conditions to establish an equilibrium wet-particle size distribution. Next, the conservation relations Eqs. (11), (13), and (21) are iterated forward in time, and the wet-particle radii within each bin are tracked using a Lagrangian grid. For a fuller description of the underlying model mechanics, the reader is directed to the original paper and references therein (Rothenberg and Wang, 2016). In contrast to the K15 model, pyrcel explicitly considers the feedback of water vapour between different droplet populations and P_w. However, pyrcel was originally written to describe the formation of warm-phase clouds; therefore, several modifications were made for application to contrail formation.

Firstly, we replace the original P_w term (deriving from parcel updraft) with the definition in Eq. (18). Secondly, we remove the time dependence of altitude and pressure, under the assumption of an adiabatic expansion at constant atmospheric pressure as described in Sect. 3.1. Finally, we derive initial particle number concentrations for the aircraft modes from the associated emission indices using Eqs. (18) and (19). After these changes, the modified pyrcel model and extended K15 models provide an identical description of P_w. However, the coupling of P_w to L_w is fully represented only within the modified pyrcel model.

Additionally, we also extended pyrcel to include homogeneous ice nucleation within growing water droplets. For a complete description of the relations used to arrive at an estimate for the homogeneous ice nucleation temperature, the reader is directed to Sect. S1. In brief, we estimate the rate of homogeneous ice nucleation within a droplet using its water activity (Koop et al., 2000), identified using Eq. (8) as in Lewellen (2020). The probability for ice nucleation within the droplet is then determined by assuming a pulse-like freezing process according to the methodology employed in K15. If the probability equals unity, we assume that the supercooled droplet freezes. The growth of ice crystals by deposition of (ice) supersaturated water vapour is then described using equations analogous to those in Sect. S2, where water saturation in the numerator is replaced with ice saturation, which represents the driving force for vapour deposition. For additional information on the exact form of these expressions, the reader is directed towards Pruppacher and Klett (2010). As outlined above, our implementation is sufficiently flexible to capture homogeneous ice nucleation events within droplets that may not (yet) be considered activated ($d_{\mathrm{w}}<d_{\mathrm{w},\mathrm{c}}$).

3.4 Assumed particle properties

We use a conservative parameter space for the properties of each particle mode; see Table 1. We note that both EI_nvPM and the particle size distribution characteristics can change with the use of sustainable aviation fuel (SAF) (Märkl et al., 2024; Schripp et al., 2022); however, these fall within larger uncertainties in our simulations. Recently, contrail parcel model simulations have been performed assuming a smaller d_g,nvPM, consistent with the primary particle diameter rather than the aggregate particle diameter (Yu et al., 2024). While the ice-nucleating ability of larger soot particles has been shown to depend on particle morphology (Marcolli et al., 2021), there is a paucity of data available for activation and ice nucleation on surrogate aircraft nvPM. Therefore, here we choose to identify d_g,nvPM as the aggregate particle diameter in line with other studies (Kärcher et al., 2015). Nevertheless, we evaluate the model sensitivity to the choice of nvPM primary particle or aggregate diameter in detail (see Sect. S10) and find that (i) AEI_ice predictions agree within 40 % and that (ii) the functional behaviour is similar. Finally, we assume that the nvPM mode contains a 1 wt % coating of soluble material as observed for ground-based emissions testing at moderate fuel sulfur content (FSC) (Gysel et al., 2003) and is therefore characterised by κ = 0.005 in accordance with the original K15.

The properties of the ambient mode are taken directly from the original K15 model inputs. We argue that these properties are sufficient to investigate the competition between the three modes under most conditions; however, a more sophisticated description would be required to examine sensitivity if most ice crystals formed via ambient particles (Bier et al., 2024); see Sect. S5.

For the plume vPM mode, we identify a provisional size range of 1 < d_g,vPM $/$ nm < 4 and a σ_g,vPM of 1.3 (Kärcher et al., 2000; Yu et al., 1998). Similarly, we assume a fixed emission index EI_vPM=10¹⁷ kg⁻¹ in line with modelling and observational evidence (Arnold et al., 2000; Haverkamp et al., 2004; Schumann et al., 2002; Sorokin and Mirabel, 2001). This is also supported by newer observational evidence (Voigt et al., 2025) that the total particle emission index (particle sizes > 5 nm) is on the order 10¹⁵ kg⁻¹, which is consistent with EI_vPM=10¹⁷ kg⁻¹ if $d_{\mathrm{g},\mathrm{vPM}}=\mathrm{2.7}$ nm and $d_{\mathrm{g},\mathrm{vPM}}=\mathrm{1.3}$. Concerning particle hygroscopicity, we assume a mixed plume vPM mode comprising sulfuric acid (κ=0.5) and condensable POM, for which we use a conservative lower bound of κ=0 in line with measurements of non-hygroscopic lubrication oil droplets (Ponsonby et al., 2024). However, we acknowledge that the value of κ for condensable POM is likely to vary with changes in fuel and/or engine architecture. To that end, we evaluate our sensitivity analyses in the extreme cases of both sulfur-rich plume vPM (volume mixing ratio of 95:5 sulfuric acid : condensable POM; 0.05⋅κ_POM + $\mathrm{0.95}\cdot {\mathit{\kappa }}_{\mathrm{H}\mathrm{2}\mathrm{SO}\mathrm{4}}\sim \mathrm{0.5}$) and organic-rich plume vPM (volume mixing ratio of 5:95 for sulfuric acid : condensable POM; 0.95⋅κ_POM + $\mathrm{0.05}\cdot {\mathit{\kappa }}_{\mathrm{H}\mathrm{2}\mathrm{SO}\mathrm{4}}\sim \mathrm{0.01}$). In Sect. S9, we investigate the impact of assuming all plume vPM particles have the same chemical composition (κ). To achieve this, we divide the plume vPM mode into two distinct plume vPM modes, prescribing these with identical physical characteristics but dissimilar κ. We find that the results of the two-mode system are similar to those of the single-mode system, with a modified value of κ. Therefore, we argue that our range of κ is sufficient to capture a degree of variation in chemical composition between vPM particles.

In the above, we have described vPM characteristics at the timescale of particle activation and droplet growth in the nascent contrail mixing plume (∼ 1 s). Separately, we can also estimate the (maximum) equilibrium plume vPM diameters (d_eq,vPM) that would be reached at t≫1 s using a mass balance. Among other factors, the characteristics of the plume vPM particle size distribution are constrained by the quantity of available sulfuric acid and POM. The former contribution is produced by oxidation of FSC,

$$\begin{array}{}\text{(26)}& {\mathrm{EI}}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}={\displaystyle \frac{\mathrm{98}}{\mathrm{32}}}{\mathit{\epsilon }}_s\mathrm{FSC},\end{array}$$

where ε_s is the conversion efficiency of sulfur to sulfuric acid, which is typically on the order of 3 % (Yu et al., 2024). The latter contribution represents the sum of condensable gaseous emissions, which has previously been estimated in the range 1–40 mg kg⁻¹ for relevant, combustion-related organics (Yu et al., 1999) in addition to potential non-combustion lubrication oil emissions of 110 mg kg⁻¹ (Decker et al., 2024). As outlined in Sect. 1, we can assume that the plume vPM mode can be treated as monomodal, as the smaller mode (i) requires a higher critical supersaturation for activation and (ii) is effectively scavenged by the larger mode. Conservation of mass enables us to estimate d_eq,vPM for the plume vPM mode (Kärcher et al., 2000):

$$\begin{array}{}\text{(27)}& {\displaystyle \frac{\mathit{\pi }}{\mathrm{6}}}{d}_{\mathrm{eq},\mathrm{vPM}}^{\mathrm{3}}{\mathit{\rho }}_{\mathrm{vPM}}{\mathrm{EI}}_{\mathrm{vPM}}={\displaystyle \frac{\mathrm{98}}{\mathrm{32}}}{\mathit{\epsilon }}_{\mathrm{s}}\mathrm{FSC}+{\mathrm{EI}}_{\mathrm{POM}},\end{array}$$

where ρ_vPM is the density of the volatile mode. Using Eq. (27), we can therefore estimate d_eq,vPM for given EI_POM and FSC, which is explored in Sect. 4.5.

Table 1 Assumed characteristics and associated ranges for each particle type used within our parcel model simulations. List of references in the table: [1] Arnold et al. (2000); [2] Haverkamp et al. (2004); [3] Schumann et al. (2002); [4] Sorokin and Mirabel (2001); [5] Kärcher et al. (2000); [6] Yu et al. (1998); [7] Ponsonby et al. (2024); [8] EASA (2025); [9] Durdina et al. (2024); [10] Petzold et al. (2005); [11] Kärcher et al. (2015).

4 Results

Here, we present the results of both the extended K15 model and the modified pyrcel models. Based on these results, we then use the modified pyrcel models to run a set of sensitivity analyses and explore how the apparent emission index of ice crystals (AEI_ice) within a contrail depends upon particle properties (Sect. 4.3 and 4.5), T_A (Sect. 4.4), and aircraft parameters (Sect. 4.6).

4.1 Contrail mixing behaviour

Figure 4 shows the typical mixing behaviour as predicted by extended K15 and modified pyrcel models. These are compared to profiles in the absence of any particle intervention (SAC-type mixing behaviour), which is encapsulated by P_w. In both the extended K15 model and the modified pyrcel model, the partial pressure of water within the plume follows a similar trend. When the conditions in the plume are subsaturated (i.e. S_v<1), both models align with SAC-type mixing behaviour, since very few particles can activate. Hence, L_w∼0, and the mixing is dominated by P_w. However, once the plume becomes supersaturated, a proportion of the particles activate to form aqueous solution/water droplets. Here, L_w gradually increases to a maximum, before equilibrating with P_w at water-saturated conditions.

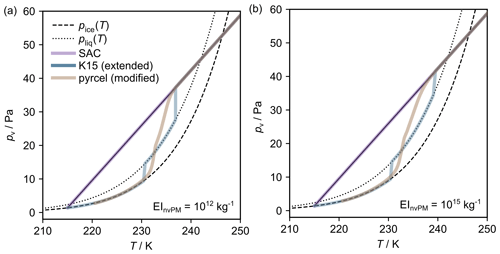
Figure 4 Contrail mixing lines simulated with assumed EI_nvPM of (a) 10¹² kg⁻¹ and (b) 10¹⁵ kg⁻¹. For both scenarios, the mixing lines are simulated using the original SAC framework (purple lines), the extended K15 model (blue lines), and the modified pyrcel model (brown lines). Each of the simulations has been set to terminate at ice-saturated conditions. These model predictions have been made with plume vPM (EI_vPM=10¹⁷ kg⁻¹).

This process of “activation–relaxation” (see warmer-temperature vertical regions of the blue lines in Fig. 4) is approximated within the extended K15 model by estimating the supersaturation at which this takes place and an associated timescale; see Sect. S8. Note that, because particles require supersaturated conditions to activate ($S_{\mathrm{v},\mathrm{c}}>\mathrm{1}$), the onset temperature for “activation–relaxation” within the extended K15 model occurs after the point of intersection between the contrail mixing line and p_liq. These findings are in qualitative agreement with the modified pyrcel outputs, although they cannot be directly compared. Moreover, the temperature difference is more pronounced for lower EI_nvPM (∼2, 5 K for EI_nvPM=10¹⁵ kg⁻¹, 10¹² kg⁻¹), as the number-weighted particle diameter is smaller, which increases S_v,c. This again highlights the importance of considering particle properties when determining the point at which most particles activate (see Sect. 2.3).

4.2 Peak plume supersaturation

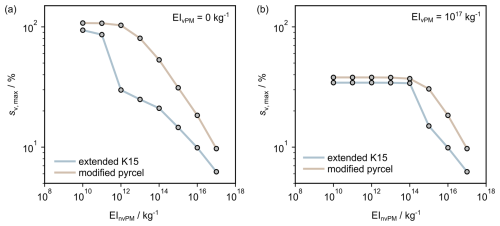
On average across EI_nvPM, the maximum plume supersaturations predicted by the extended K15 model are ∼10 %–70 % lower than those predicted by the modified pyrcel model; see Fig. 5. Without plume vPM, the largest discrepancies occur when competition between nvPM and ambient particles is largest (at EI_nvPM∼10¹² kg⁻¹; see Fig. 5a). However, when vPM is included, model discrepancies are largest when most contrail ice crystals form via nvPM; see Fig. 5b. Given that both pyrcel and the extended K15 model employ an identical treatment of P_w (Eq. 18), these model discrepancies must arise from the treatment of L_w. It follows that underestimating the supersaturation at which activation relaxation takes place implies the extended K15 likely overestimates the ability for water droplets to deplete the plume supersaturation. In the final part of Sect. 3.2, we comment on a fundamental limitation of the extended (and original) K15 model that could lead to this discrepancy, which centres around the treatment of L_w. In brief, preparing an analytical solution to Eq. (25) demands that (a) the plume supersaturation is unaffected by particle activation and subsequent droplet growth between adjacent time steps and that (b) the Kelvin effect is discarded from the droplet growth equations. A combination of these effects accounts for the observed behaviour shown in Fig. 5, which underlines the principal limitations of the extended K15 model.

Figure 5 The maximum plume supersaturation (s_v,max) across a range of EI_nvPM as predicted by the modified pyrcel (brown lines) and extended K15 (blue lines) models. These model predictions have been made (a) without and (b) with the presence of plume vPM (EI_vPM=10¹⁷ kg⁻¹).

4.3 Sensitivity to EI_nvPM

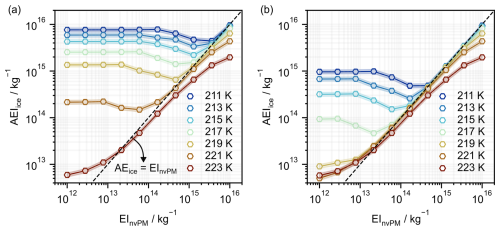
In Fig. 6, we show how the ice crystal number concentration scales with EI_nvPM in both the extended K15 and modified pyrcel models. This is presented in terms of AEI_ice, using Eq. (22), so that the results can be more readily compared to other model predictions. Without plume vPM, we find the model agreement for AEI_ice is within 35 % when EI_nvPM<10¹⁶ kg⁻¹; see Fig. 6a. When plume vPM is included, we find that, under this range of EI_nvPM, differences in model predictions for AEI_ice and s_v,max exhibit similar trends; see Fig. 5b. Note that AEI_ice predictions made using the modified pyrcel model were found to have a maximum uncertainty of ±10 %; see Sect. S11. These derive principally from discretising the vPM mode, which necessarily approximates the analytic particle size distribution; see Sect. S4. These errors are shown in Fig. 6 and in future analysis, where appropriate.

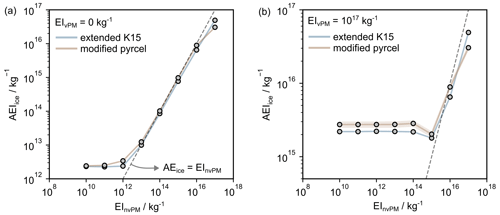
Figure 6 The dependence of contrail AEI_ice on EI_nvPM as predicted by the modified pyrcel and extended K15 models. Model predictions have been made without (a) and with (b) the inclusion of plume vPM.

For EI_nvPM≥10¹⁶ kg⁻¹, the extended K15 predicts higher AEI_ice than the modified pyrcel model because the extended K15 model does not consider feedback of water vapour between water droplets and ice crystals. To illustrate this effect, suppose we identify a temperature that is warm enough to avoid homogeneous ice nucleation but nonetheless cool enough to promote substantial particle activation, we find that the characteristics of the activated nvPM particles are different in the limit of small and large EI_nvPM. Note that these limiting values depend on particle size distribution characteristics and properties specified for the contrail mixing line; however, in the case of Fig. 6b, they are separated at EI_nvPM∼10¹⁶ kg⁻¹. To that end, for EI_nvPM≥10¹⁶ kg⁻¹, the available water vapour in the plume is distributed among many particles, and activated nvPM particles typically have values $d_{\mathrm{w}}-d_{\mathrm{d}}<\mathrm{200}$ nm. Comparatively, for EI_nvPM<10¹⁶ kg⁻¹, the nvPM wet-particle diameters are distributed quasi-normally and have values $d_{\mathrm{w}}-d_{\mathrm{d}}>\mathrm{200}$ nm. For this reason, the condition for homogeneous ice nucleation is satisfied for each activated nvPM particle for EI_nvPM<10¹⁶ kg⁻¹, since this is sensitive to the relative difference between wet- and dry-particle diameters, d_w−d_d. Hence, we find that the AEI_ice is always at least as large as the apparent emission index of activated particles. By comparison, for EI_nvPM≥10¹⁶ kg⁻¹, given that the smaller activated nvPM particles have comparatively low d_w−d_d, their size is more sensitive to changes in local supersaturation. Therefore, when the largest activated nvPM particles begin to nucleate ice, this can result in smaller activated nvPM particles evaporating at their expense. In general terms, this is referred to as the Wegener–Bergeron–Findeisen (WBF) process (Korolev, 2007) and provides a rationale for the opposite trend observed in Figs. 6 and 5 for EI_nvPM≥10¹⁶ kg⁻¹.

We have previously discussed the importance of vapour feedback between growing droplets and the evolving contrail mixing plume as a source of model agreement, highlighting the coupled nature of growing droplets. These effects are exacerbated by the WBF process, which implies that coupled feedback of water vapour occurring between ice crystals and growing droplets can also contribute to model disagreement. Only the modified pyrcel model is able to describe the kinetic treatment of vapour feedback between hydrometeors and the contrail mixing plume. For this reason, we can place more confidence in model predictions made by the modified pyrcel model than the extended K15 model. Additionally, inclusion of the Kelvin effect in the radial growth equation is only represented in the modified pyrcel model, which is critical for describing water uptake on plume vPM. Hence, we choose to use the modified pyrcel model for the following sensitivity studies.

4.4 Sensitivity to ambient temperature

An evaluation of the modified pyrcel model sensitivity across a range of T_A and EI_nvPM revealed several key findings (Fig. 7). Firstly, AEI_ice follows a quasi-linear relationship with EI_nvPM only when EI_nvPM exceeds a temperature-dependent threshold that ranges between 10¹³ and 10¹⁶ kg⁻¹. In this quasi-linear region, most ice crystals form via nvPM particles, which defines the “soot-rich” regime. Increasing T_A decreases the peak plume supersaturation so that a reduced proportion of the nvPM particles can activate (Bräuer et al., 2021), which has a similar effect to decreasing d_g,nvPM (see Sect. S10). The threshold EI_nvPM marks the point at which an equal number of contrail ice crystals are formed via nvPM particles and other particles in the plume. Therefore, below this threshold, EI_nvPM, the majority of ice crystals do not form via nvPM particles, which defines the “soot-poor” regime. Owing to the results in Fig. 7, “soot-poor” conditions always satisfy the baseline condition EI_nvPM≤10¹² kg⁻¹. Here, for warmer T_A (∼T_SAC), most contrail ice crystals form via ambient particles, and AEI_ice approaches an asymptotic limit governed by the assumed ambient particle number concentration. Recall that most ambient particles assumed in our simulations (see Table 1) are able to activate at ΔT_SAC<1 K (see Fig. 3). As T_A is reduced further (<T_SAC), the increased peak plume supersaturation enables a greater proportion of plume vPM particles to activate (in addition to the ambient particles), and the limiting value of AEI_ice increases. Generally, the position of the threshold EI_nvPM increases with decreasing T_A as a larger proportion of vPM particles can activate and therefore compete with nvPM particles for the plume supersaturation (Yu et al., 2024). These findings suggest that the EI_nvPM threshold separating the “soot-rich” and “soot-poor” regime should not be treated as a fixed value but rather as a dynamic threshold that varies with T_A.

Figure 7 The dependence of contrail AEI_ice on T_A (211–223 K, corresponding to ΔT_SAC of 2–13 K) and EI_nvPM for (a) sulfur-rich and (b) organic-rich plume vPM.

4.5 Sensitivity to plume vPM properties

Before continuing with our analysis, we emphasise that d_eq,vPM calculated using Eq. (27) provide us with an upper bound on the diameter of the volatile mode prior to maximum plume supersaturation; due to the kinetics of particle growth, this diameter is likely reached only after a timescale of minutes to hours (Kärcher et al., 2000). Furthermore, it is possible that some volatile material may condense on nvPM (if present), which would further reduce d_eq,vPM. Therefore, the equilibrium plume vPM diameters quoted in Fig. 8a should only be interpreted as upper bounds.

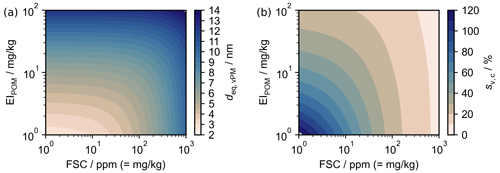
Figure 8 (a) Equilibrium volatile particle modal diameter as a function of fuel sulfur content and the emission index of organic particulate matter, assuming a monomodal distribution and omitting the condensation of plume vPM on nvPM. (b) Peak plume supersaturation required to activate volatile particles described in panel (a). We have approximated ${\mathrm{EI}}_{\mathrm{vPM}}=\mathrm{1}\times {\mathrm{10}}^{\mathrm{17}}$, ε=3 %, and ρ_vPM as a mass-weighted sum of the densities of sulfuric acid and POM (1800 and 1000 kg m⁻³, respectively), assuming ideal mixing.

Figure 8a shows that d_vPM increases with EI_POM and FSC. For high FSC values (∼1000 ppm), d_eq,vPM can reach values upwards of 10 nm. By contrast, for low FSC, the size becomes limited by POM, without which d_eq,vPM reaches 2–3 nm at most. In Fig. 8b, we use the hygroscopicity parameter for sulfuric acid and POM (assuming κ_POM=0) to show how the critical saturation ratio depends on both FSC and POM. For low FSC and EI_POM, critical supersaturations exceeding 100 % are required for particle activation. However, the presence of nvPM typically precludes such high supersaturations (see Fig. 5); therefore, given that $d_{\mathrm{g},\mathrm{vPM}}\le d_{\mathrm{eq},\mathrm{vPM}}$, volatile contributions to AEI_ice are likely low in the “soot-rich” regime. On the other hand, with increasing FSC, plume vPM activation becomes increasingly likely, as there are fewer nvPM particles available to quench the plume supersaturation.

As discussed, the results presented above are valid only for providing insight into the approximate equilibrium behaviour of plume vPM formation. Within a real contrail mixing plume, the time available for volatile particle growth by accretion of POM and/or sulfuric acid is reduced, and kinetics become important. To that end, the dependence of volatile mode characteristics on POM (including lubrication oil) and FSC has previously been investigated in simulations performed at cruise (Cantin et al., 2025; Rojo et al., 2015) and ground level (Jones and Miake-Lye, 2024; Wong et al., 2014, 2015). Next, we investigate the dependence of contrail AEI_ice on prescribed vPM properties in the modified pyrcel model

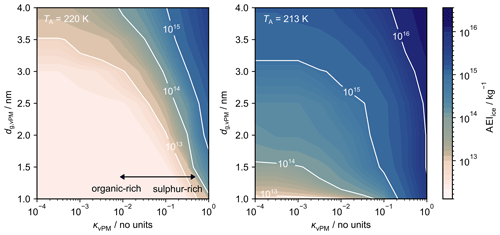
Figure 9 The dependence of contrail AEI_ice on the plume vPM properties (d_g,vPM and κ_vPM) at ambient temperatures of (a) 220 K and (b) 213 K. For both scenarios, the assumed particle properties are outlined in Table 1; EI_vPM and EI_nvPM are assumed to be 10¹⁷ and 10¹² kg⁻¹, respectively (in line with the “soot-poor” baseline conditions described in Sect. 4.4); and the contrail AEI_ice is simulated using the modified pyrcel model with model time steps of 0.1 ms and a maximum duration of 0.5 s.

Figure 9 demonstrates the sensitivity of the modified pyrcel model to the properties of the plume vPM mode in the “soot-poor” regime, subject to our assumptions on the hygroscopicity of the condensable POM. Our results suggest that a sulfur-rich plume vPM mode can lead to AEI_ice>10¹⁵ kg⁻¹, even when $d_{\mathrm{g},\mathrm{vPM}}<\mathrm{2}$ nm. Conversely, when the plume vPM mode is organic-rich, the AEI_ice only rises above 10¹⁵ kg⁻¹ under extremal conditions (i.e. low T_A and high d_g,vPM). For most other cases, AEI_ice≪10¹⁵ kg⁻¹, and the organic-rich plume vPM mode competes with ambient particles for plume supersaturation. Therefore, if soot particle emissions could be reduced in the vicinity of 10¹² kg⁻¹, provided the volatile particle mode is largely composed of sulfuric acid, we anticipate only a small reduction in AEI_ice values relative to “soot-rich” exhausts. On the other hand, if the volatile particle mode is largely composed of organic material, we find that AEI_ice values could be reduced by a factor of up to 100, with benefits ultimately constrained by the size of the plume vPM particles and the properties of entrained ambient particles.

4.6 Sensitivity to aircraft parameters

The final sensitivity analysis will focus on the gradient of the SAC contrail mixing line (Kärcher et al., 2015), which contains important information about aircraft and fuel properties; see Sect. 2.1. Simultaneously, we will explore the sensitivity to ambient temperature so that the resulting output, AEI_ice (G,T_A), provides a useful reference for estimating AEI_ice for various combinations of aircraft properties and ambient conditions under “soot-poor” conditions, as defined in Sect. 4.4. For both these scenarios, a sulfur-rich volatile mode was prescribed, as in Sect. 3.4.

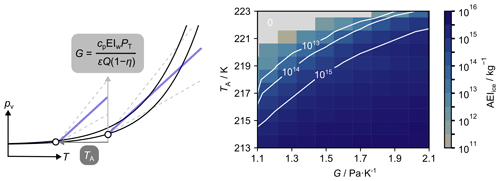
Figure 10 The dependence of contrail AEI_ice on T_A and the gradient of the contrail mixing line, as defined in Eq. (1). The simulation was performed for sulfur-rich plume vPM and EI_nvPM of 10¹² kg⁻¹, in line with the “soot-poor” baseline conditions described in Sect. 4.4. The region shaded in grey corresponds to AEI_ice = 0. Physically, this represents mixing lines that do not intersect the water saturation line.

Figure 10 shows how the AEI_ice varies as a function of G and T_A for “soot-poor” baseline conditions as described in Sect. 4.4 and sulfur-rich plume vPM. For a fixed ambient temperature, increasing G leads to an increased peak plume supersaturation and hence an increase in AEI_ice. For ambient temperatures with ΔT_SAC>10 K (here, T_A>215 K), enhancements of up to 3 orders of magnitude are observed within the prospective range of G values for kerosene-based fuel (1.1–2.2). This aligns with results from the original SAC framework, namely that parameters such as overall efficiency (Schumann, 2000), cruise altitude (Gryspeerdt et al., 2024), and water vapour emissions are critical for estimating the resulting contrail ice crystal properties and hence the radiative impact of contrail cirrus.

5 Implications

Here, we contextualise several of the key findings from Sect. 4 for global contrail simulations (Sect. 5.1), contrail mitigation (Sect. 5.2), and engine and fuel technologies (Sect. 5.3).

5.1 Global contrail simulations

Several contrail simulations rely on nvPM (and ambient particle) properties to parameterise AEI_ice in young contrails (Bier and Burkhardt, 2022; Teoh et al., 2024). In the “soot-poor” regime, we find that including the activation of plume vPM might enhance AEI_ice by up to 3 orders of magnitude. Increased AEI_ice is correlated with contrail RF (Burkhardt et al., 2018), implying that these current global contrail simulations may underestimate global contrail forcing. Importantly, as the AEI_ice predictions are sensitive to the assumed properties of plume vPM and as these are highly uncertain at present, a global contrail simulation relying on the extended K15 model would serve only as a sensitivity study.

5.2 Contrail mitigation

Operational contrail mitigation has hitherto focused on circumventing regions where s_i>0 in order to mitigate contrail persistence. Our simulations imply that, under “soot-poor” conditions and for flights within 5 K of T_SAC, increasing the ambient temperature by 2 K may reduce AEI_ice by up to a factor of 10 (see Fig. 9). If this behaviour could be experimentally validated, an analogous strategy might be possible by circumventing cooler regions of the upper troposphere, to mitigate contrail formation under “soot-poor” conditions. Moreover, maximum predictive biases between the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 atmospheric reanalysis model and In-service Aircraft for A Global Observing System (IAGOS) observations of T_A and s_i are −0.2 % and −5.5 %, respectively (Wolf et al., 2025), which implies that atmospheric requirements for contrail formation can be predicted more accurately than for contrail persistence. Assuming an upper-tropospheric lapse rate of −6.5 K km⁻¹ per the ICAO standard atmosphere (ICAO, 1993), a 2 K temperature difference corresponds to approximately 10 flight levels (1000 ft or 305 m). This is equivalent to the reduced vertical separation minima between aircraft in the FL 290–FL 410 flight band (ICAO, 2012), which implies that it might be possible to adjust T_A by making relatively small changes in elevation. Using T_A data from ECMWF, we explore this further in Sect. S12. Nevertheless, avoidance of local cold spots would likely involve reducing aircraft cruise altitudes, which may increase (a) the likelihood for aircraft emissions to perturb clouds in the mixed-phase regime, (b) the number of turbulence events (Dehghan et al., 2014), and (c) direct emissions of CO₂. Therefore, we reiterate that this approach is subject to both inherent model uncertainties and the aforementioned concerns (a)–(c), which need to be resolved before this is explored further.

5.3 Engine and fuel technologies

Aircraft powered by lean-burn combustors have EI_nvPM that range between 10¹⁰ and 10¹² kg⁻¹ (EASA, 2025), which coincides with our definition for the “soot-poor” regime given in Sect. 4.4. Under these conditions, AEI_ice is controlled by the properties of plume vPM emissions and T_A (see Fig. 9). Therefore, AEI_ice can be reduced practically by (a) avoiding cooler ambient temperatures (see Sect. 5.1) and (b) reducing the mass of condensable volatile material. To that end, we suggest the removal of lubrication oil emissions and diminution of FSC. In Sect. 4.4, we demonstrate that FSC scales with the mass of condensable sulfuric acid. Therefore, for fixed EI_vPM, increasing FSC may produce plume vPM particles with higher d_g,vPM and higher κ_vPM. This intuition agrees with results collated across various flight campaigns, showing that EI_vPM for particles larger than 5 nm increases with increasing FSC (Schumann et al., 2002). In the “soot-poor” regime, AEI_ice and hence the potential contrail climate impact increase with d_g,vPM and κ_vPM. Therefore, we would advise that FSC is reduced as low as practicably possible, as FSC levels of several ppm (assuming EI_POM=0 kg⁻¹) are sufficient to produce plume vPM particles with d_eq,vPM on the order of several nm (see Sect. 4.5). We note that comparable FSC reductions have been successfully demonstrated in other sectors (IMO, 2022) and that the largest benefits would be achieved if low-FSC fuels were used in lean-burn engines, where AEI_ice values are most sensitive to the properties of plume vPM emissions.

Finally, measurements show that SAF can reduce both EI_nvPM and d_g,nvPM relative to conventional fuel (Moore et al., 2017; Voigt et al., 2021). Under conditions where most contrail ice crystals form via nvPM particles, both changes would reduce AEI_ice, as fewer particles are able to activate at a given supersaturation. These effects have previously been reported using contrail parcel model simulations to compare with ECLIF (Emission and CLimate Impact of alternative Fuels) measurements (Yu et al., 2024). Additionally, for variable EI_nvPM and fixed plume vPM properties, decreasing d_g,nvPM would increase the position of the minimum in Fig. 9 (see Sect. S10).

6 Conclusions

Here, we extended two parcel models to describe particle microphysics during the early stages (t < 1 s) of contrail plume evolution. Firstly, the minimal framework originally developed by Kärcher et al. (2015) was extended to account for plume vPM by incorporating an additional particle mode. We replaced several analytical approximations with numerical solutions and increased the accuracy of others so that the model could be more applicable for describing the activation of plume vPM. Secondly, using similar parameterisations for the mixing process but a higher-fidelity description of L_w, a cloud parcel model (pyrcel) (Rothenberg and Wang, 2016) was modified to treat contrail formation and used as a benchmark for model comparison.

We found the extended K15 model systematically underpredicted the peak plume supersaturations when compared to the modified pyrcel model. This is likely because it does not incorporate the Kelvin effect and therefore overpredicts droplet growth rates. Generally, the estimated AEI_ice from both models are within 35 % for EI_nvPM≤10¹⁶ kg⁻¹, when activation of plume vPM is excluded. However, when plume vPM activation is included, the modified pyrcel model predicts higher ice crystal number concentrations by 10 %–30 % for EI_nvPM≤10¹³ kg⁻¹. Discrepancies are more pronounced for EI_nvPM>10¹³ kg⁻¹ due to differing treatment of kinetics and water vapour competition between hydrometeors between models.

Using the modified pyrcel model, we performed several sensitivity studies and found that, across EI_nvPM, the AEI_ice decreases with decreasing peak plume supersaturations as predicted by the original SAC mixing line. This is controlled by the ambient relative humidity, T_A, and the gradient of the mixing line. Therefore, decreasing the overall efficiency and water vapour emissions results in fewer contrail ice crystals being produced. Also, we find that the threshold between “soot-rich” and “soot-poor” conditions (as defined in Sect. 4.4) is sensitive to the properties of plume vPM (EI_vPM, d_g,vPM, κ_vPM) and T_A and should therefore be treated as a dynamic threshold. Notably, we find that the threshold EI_nvPM increases with decreasing T_A as an increasing proportion of vPM particles are able to compete with nvPM particles for the plume supersaturation. In the “soot-poor” regime, including plume vPM activation leads to AEI_ice enhancements by up to 3 orders of magnitude; these are maximised if the material is highly hygroscopic (e.g. sulfur-rich).

As the aviation industry reduces EI_nvPM and therefore approaches the “soot-poor” regime, we find that existing contrail cirrus models that do not extend to include plume vPM activation will underestimate AEI_ice and therefore global climate forcing. Future research should be directed towards (i) ground-based and in situ measurements focusing on the “soot-poor” regime and its transition towards the “soot-rich” regime, with near-field characterisation of both nvPM and plume vPM properties; (ii) laboratory measurements of the activation properties and/or ice-nucleating ability of particles representative of plume vPM present in nascent contrail exhausts; and (iii) validation of plume aerosol and contrail formation models (parcel model/LES simulations) using in situ observations.

Appendix A: Notation

SAC	Schmidt–Appleman Criterion
nvPM	Non-volatile particulate matter
vPM	Volatile particulate matter
EIvPM, EInvPM	Number emission index of vPM, nvPM
SAF	Sustainable aviation fuel
dg	Geometric mean diameter
σg	Geometric standard deviation
K15	Microphysical model developed by Kärcher et al. (2015)
TE	Gas temperature at the engine exit plane
TA	Ambient temperature
T	Plume temperature
G	Gradient of average contrail mixing line
pv,M	Partial pressure of water vapour in the contrail mixing plume
pv,E	Partial pressure of water vapour at the engine exit plane
pv,A	Partial pressure of water vapour in the ambient environment
cp	Isobaric specific heat capacity of air
EIw	Mass emission index of water vapour
PT	Total air pressure
ε	Ratio of gas constants for water vapour and dry air
Q	Total heat released per mass of fuel burned
η	Overall aircraft efficiency
pliq, pice	Saturation vapour pressure above a plane surface of supercooled water, ice
Sv,M, Si,M	Water, ice saturation ratio in a contrail mixing plume
sv,M	Water supersaturation in a contrail mixing plume
TSAC	SAC temperature
ΔTSAC	Difference between the ambient and SAC temperatures (TSAC–TA)
Sv	Water saturation ratio above a liquid droplet
aw	Water activity
σs	Surface tension at the droplet–air interface
Mw	Molar mass of water
ρw	Density of water
R	Global gas constant
dw	Wet-particle diameter
dd	Dry-particle diameter
κ	Hygroscopicity parameter
dw,c, rw,c	Critical wet-particle diameter, radius
Sv,c	Critical water saturation ratio
wv	Water vapour mixing ratio
wc	Mixing ratio of condensed water vapour
Pw	Water (super)saturation production rate in the absence of particles
Lw	Water (super)saturation depletion rate due to particle activation and droplet growth
β	Plume dilution parameter
D	Plume dilution factor
τm	Timescale over which contrail mixing is unaffected by entrainment
N0	Mass-based mixing factor

nT	Total number concentration of aircraft-mode particles
na,T	Total number concentration of ambient-mode particles
na,0	Ambient particle number concentration
ρa	Mass density of ambient air
${\dot{r}}_{\mathrm{w}}$	Radial droplet growth rate
nw	Droplet number concentration
${\dot{n}}_{\mathrm{w}}$	Rate of change of droplet number concentration
FSC	Fuel sulfur content
POM	Particulate organic matter
${\mathrm{EI}}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$	Mass emission index of sulfuric acid
EIPOM	Mass emission index of POM
εs	Conversion efficiency of sulfur to sulfuric acid
deq,vPM	vPM equilibrium diameter
ρvPM	Density of condensed vPM
θG	threshold contrail formation temperature at pliq