the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A thermodynamic framework for bulk–surface partitioning in finite-volume mixed organic–inorganic aerosol particles and cloud droplets
Ryan Schmedding
Atmospheric aerosol particles and their interactions with clouds are among the largest sources of uncertainty in global climate modeling. Aerosol particles in the ultrafine size range with diameters less than 100 nm have very high surface-area-to-volume ratios, with a substantial fraction of molecules occupying the air–droplet interface. The partitioning of surface-active species between the interior bulk of a droplet and the interface with the surrounding air plays a large role in the physicochemical properties of a particle and in the activation of ultrafine particles, especially those of less than 50 nm diameter, into cloud droplets. In this work, a novel and thermodynamically rigorous treatment of bulk–surface equilibrium partitioning is developed through the use of a framework based on the Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients (AIOMFAC) model in combination with a finite-depth Guggenheim interface region on spherical, finite-volume droplets. We outline our numerical implementation of the resulting modified Butler equation, including accounting for challenging extreme cases when certain compounds have very limited solubility in either the surface or the bulk phase. This model, which uses a single, physically constrained interface thickness parameter, is capable of predicting the size-dependent surface tension of complex multicomponent solutions containing organic and inorganic species. We explore the impacts of coupled surface tension changes and changes in bulk–surface partitioning coefficients for aerosol particles ranging in diameters from several micrometers to as small as 10 nm and across atmospherically relevant relative humidity ranges. The treatment of bulk–surface equilibrium leads to deviations from classical cloud droplet activation behavior as modeled by simplified treatments of the Köhler equation that do not account for bulk–surface partitioning. The treatments for bulk–surface partitioning laid out in this work, when applied to the Köhler equation, are in agreement with measured critical supersaturations of a range of different systems. However, we also find that challenges remain in accurately modeling the growth behavior of certain systems containing small dicarboxylic acids, especially in a predictive manner. Furthermore, it was determined that the thickness of the interfacial phase is a sensitive parameter in this treatment; however, constraining it to a meaningful range allows for predictive modeling of aerosol particle activation into cloud droplets, including cases with consideration of co-condensation of semivolatile organics.
- Article
(3668 KB) - Full-text XML
-
Supplement
(1583 KB) - BibTeX
- EndNote
Atmospheric aerosols are suspensions of condensed particles and the gas which surrounds them. They can be a major contributor to poor indoor and outdoor air quality. Exposure to poor air quality is the leading environmental risk factor for premature mortality globally (Cohen et al., 2017; Burnett et al., 2018). Beyond their public health effects, the role of atmospheric aerosols and aerosol–cloud interactions in the global climate system remains one of the least understood processes in climate models (Boucher et al., 2013). Some light-absorbing aerosols exhibit a positive direct radiative forcing, while others mostly scatter solar radiation and exhibit negative direct radiative forcing. The magnitude and sign of the local or regional direct radiative forcing depend on numerous factors, including an aerosol's composition, size distribution, geographic location, season, and altitude in the atmosphere (Bellouin et al., 2020). Furthermore, atmospheric aerosols interact with clouds and precipitation, thereby contributing to important indirect effects on Earth's climate that are poorly constrained (Seinfeld et al., 2016). Therefore, it is of the utmost importance to understand the physicochemical properties and microphysical processes of aerosol particles, including aerosol–cloud–radiation interactions, as these drive their impacts on the climate system.
Aerosol particles exist over a broad range of sizes. Differently sized particles frequently originate from distinct sources or form through unique processes. Particles in the nucleation mode are primarily formed via the spontaneous condensation of gaseous compounds to create or extend a tiny condensed phase. Similarly, Aitken mode particles may form by the continued growth of nucleation mode particles through condensation of gaseous species or coagulation of condensed particles. Particles in the nucleation mode or Aitken mode are collectively referred to as ultrafine particles. Accumulation mode particles form through coagulation and agglomeration of smaller Aitken mode particles in the air. The largest aerosols, such as mineral dust and sea spray particles, are primarily composed of inorganic compounds and typically form via mechanical processes.
As aerosol particles decrease in size, they are more likely to originate from and grow through complex multiphase chemical reactions. Many fine and ultrafine aerosol particles are composed of organic compounds that form via oxidation reactions of volatile organic compounds (VOCs) or intermediate-volatility organic compounds (IVOCs) in the gas phase. Many of the products of these reactions are lower in volatility and partition into condensed particles. Semivolatile and low-volatility organic compounds (SVOCs and LVOCs) may also be emitted and partition into particles with minimal processing in the gas phase. Organic aerosol particles, or components thereof, formed through gas-phase or multiphase chemistry are known as secondary organic aerosols (SOAs) (Jimenez et al., 2009; Hallquist et al., 2009); for a complete list of abbreviations and symbols, please refer to Tables S1 and S2 of the Supplement. Within a condensed phase additional chemical reactions may proceed. This is particularly notable in low-viscosity aqueous aerosol particles and cloud droplets; those droplets provide aqueous media wherein numerous laboratory and field observations have observed the formation or transformation of SOAs through chemical processing (e.g., Ervens et al., 2011). For certain species these reactions can further reduce their volatility, effectively “trapping” said species in the particle phase. For example, isoprene epoxydiols (IEPOXs) are known to undergo acid-catalyzed reactions in aqueous -containing particle phases (Surratt et al., 2010). The IVOCs and VOCs which lead to the formation of SOAs can be biogenic (e.g., isoprene or monoterpenes) or anthropogenic (e.g., toluene, xylene, naphthalene) (Ng et al., 2007; Chan et al., 2009). Observational studies have concluded that the majority of SOA material is derived from biogenic precursors (Zhang et al., 2007).
The internal mixing state and geometries of aerosol particles are varied. Aerosol particles that are emitted by primary emission from biomass burning often take the shape of long agglomerations of individual spherical particles (Pokhrel et al., 2021), while aqueous inorganic-rich particles and soluble SOAs are thought to be approximately spherical. The frequent presence of liquid–liquid-phase separation (LLPS) can complicate the shape aspect. LLPS particles may form radially symmetric structures with an organic-rich “shell” (phase β) covering an inorganic-rich “core” (phase α) or other geometrically more complex structures, such as a partially engulfed morphology, wherein the particle is no longer radially symmetric nor perfectly spherical. In a partially engulfed particle, phase β does not spread completely over phase α and leaves a portion of phase α exposed (Song et al., 2013, 2012; Ciobanu et al., 2009; Shiraiwa et al., 2013). These particles are also called “Russian dolls” or “janus particles” and interact with radiation differently than their core–shell counterparts (Lang-Yona et al., 2010). Furthermore, should phase β of core–shell-phase-separated particles become a highly viscous liquid or even glassy, it can limit the reactive uptake of different species (Schmedding et al., 2020, 2019; Zhou et al., 2019; Kuwata and Martin, 2012).
Since the surface-area-to-volume ratio of a sphere scales with the inverse of its radius, said ratio becomes of great importance for ultrafine particles. If the assumption is made that the surface of a particle is represented by a monolayer of molecules in contact with the gas phase, an assumption further explored in this study, then spherical particles with a diameter less than 100 nm will have a non-negligible quantity of molecules present at their surface. For example, in a pure water droplet with a diameter of 50 nm, ∼4 % of the water molecules will be present in the surface monolayer, while more than half of the water molecules in a pure droplet with a diameter of 3 nm will be present in the surface monolayer.
Many ultrafine aerosol particles are complex multicomponent systems and contain numerous surfactant and tensoionic species in differing concentrations. These species modify the surface tension of a particle (Sorjamaa et al., 2004; Nozière et al., 2014; Gérard et al., 2016; Petters and Petters, 2016; Ruehl et al., 2016; Ovadnevaite et al., 2017; Kroflič et al., 2018; Malila and Prisle, 2018; Gérard et al., 2019). In finite-volume systems, surfactants may become depleted out of the particle interior; likewise tensoionic species may become increasingly concentrated in the particle interior. This may influence the equilibrium morphology of an aerosol particle for a given size. Even in macroscopic systems, it is possible for LLPS particles to adopt non-spherical partially engulfed morphologies based on their surface properties (Binyaminov et al., 2021). The surface enrichment and depletion of species may affect the conditions under which an aerosol particle will activate and quickly grow into a cloud droplet.
The impact of surface tension modification by surfactants on cloud droplet activation has been known and studied for decades (Facchini et al., 1999, 2000; Topping et al., 2007; Ovadnevaite et al., 2017). The conditions under which a hygroscopically growing aerosol particle will activate into a cloud droplet were first stated by Köhler (1936), recognizing the importance of the global maximum of a particle's equilibrium saturation ratio, Scrit, as expressed by the following equation:
Here, σ denotes the effective surface tension of the particle at the air–liquid interface. Mw and ρw are the molar mass and density of water, respectively. R is the gas constant, T is the temperature, and Dp is the diameter of the particle. The so-called solute or Raoult effect is captured by the water activity, aw, whereas the exponential factor captures the Kelvin effect. These two effects are often considered to be in competition with one another, since the Raoult effect decreases the supersaturation necessary for an aerosol (or cloud condensation nucleus, CCN) to reach activation into a cloud droplet, while the Kelvin effect increases the critical supersaturation. Note that values of S are often reported as percentages, in which case the value of Eq. (1) is multiplied by 100 %. A common reason for considering this a competition is the following: as surface-active species are depleted from a droplet's interior “bulk” to populate the surface during hygroscopic droplet growth, their lowered concentration in the bulk will typically raise the value of aw while simultaneously decreasing the value of σ by lowering the effective surface tension. However, we note that there is not necessarily a competition. In particular, in multicomponent organic–inorganic particles with substantial nonideal mixing, such as in cases with LLPS, the bulk–surface partitioning of low-polarity surfactants can lead to a relative lowering of both surface tension and aw (e.g., Ovadnevaite et al., 2017).
In an effort to simplify calculations of aerosol water uptake and CCN activation, Petters and Kreidenweis (2007) developed a single-parameter model of hygroscopic growth, commonly known as κ-Köhler theory, wherein aw can be related to the current volume of water in the particle Vw and the starting dry particle (solute) volume, Vdry, through the following equation:
The value of κ for a multicomponent solution can be found from a volume-fraction-based linear weighting of the κ values of individual components. The combination of Eqs. (1) and (2), along with an assumption about σ, allows for the calculation of critical supersaturations of aerosol particles given only their composition and dry sizes (Petters and Kreidenweis, 2007); however, the utility of κ-Köhler theory is thought to be more limited for ultrafine particles (Topping et al., 2016).
While κ-Köhler theory may provide reasonable predictions for many systems, including particles in the accumulation mode or of even larger sizes that are composed of highly soluble components, its neglect of bulk–surface partitioning treatments in combination with the high surface-area-to-volume ratios of ultrafine particles is worth exploring in greater detail. There are numerous methods for determining the surface composition at a gas–liquid interface, all of which rely on various assumptions, such as the location and dimensionality of said interface and the inclusion of various system-dependent fit parameters. One of the classical methods is the Gibbs 2-dimensional (2D) dividing surface (or plane) approach, which relates the change in surface tension of a solution (dσ) to the surface excess concentration (Γi) and change in chemical potential dμi of component i in the bulk solution via (Gibbs, 1874)
The term surface excess concentration may be misleading in this case, since it is defined as the difference between the concentration of i on the Gibbs dividing plane and that in the interior volume of a bulk phase adjacent to the plane. Thus negative values of Γi are possible if i partitions preferentially into the bulk of a solution and consequently has a lower concentration at the surface. The definition of the location of the Gibbs surface is of the utmost importance when utilizing this approach. Its location is typically selected such that the surface excess concentration of the first species (usually the main solvent, e.g., water) is precisely 0, thus making that 2D plane location a system-specific as well as composition- and size-dependent parameter. Determining the location of the Gibbs dividing plane presents additional challenges, since the location of the surface is defined to be located within the interfacial region between two phases but may not necessarily be found at the same radial position as that of the “outside” edge of the monolayer of molecules found at the boundary of a phase.
From the theoretical framework laid out by Gibbs, the semi-empirical Szyszkowski–Langmuir isotherm for bulk–surface partitioning was developed (Szyszkowski, 1908):
Here, σw is the surface tension of pure water at the temperature of interest, ASL and BSL are system-dependent fit parameters, and is the concentration of solute i in the bulk liquid of the system. While simpler as an approach and adequate in many system-specific cases (such as the interpretation of laboratory studies), the predictive power of this equation is limited due to the inclusion of two fit parameters for each chemical system.
A third treatment for modeling bulk–surface partitioning of different species was introduced by Jura and Harkins (1946). It combined semi-empirical fitted models, relating surface concentrations to surface tension as follows:
This equation describes an insoluble compressed film (CF) at the interface between a liquid and a gas with a 2D equation of state for bulk–surface partitioning. is the maximum surface adsorption possible, is the current surface adsorption of i, and mσ is a term relating the change in surface tension to the change in surface concentration. This equation, when coupled with an isotherm relating bulk and surface concentrations, is capable of describing the surface tension as aerosol particles grow hygroscopically when exposed to increasing relative humidity (RH) (Ruehl et al., 2016). In macroscopic systems, the approaches of Szyszkowski (1908) and Jura and Harkins (1946) assume that the enrichment or depletion of species at the particle surface has a negligible effect on the bulk particle composition; however, in ultrafine particles, depletion of surface-active species from the bulk phase may become important. This bulk depletion effect has recently come under scrutiny (Prisle et al., 2010; Bzdek et al., 2020; Lin et al., 2020) and has already been considered previously by Sorjamaa et al. (2004), who considered binary systems of water and the surfactant sodium dodecyl sulfate (SDS). They noted that Köhler curve calculations should include the effect of bulk depletion, since neglecting this effect led to unrealistically low critical supersaturation conditions. These results were supported by laboratory measurements of ternary water–SDS–sodium-chloride systems taken by Prisle et al. (2008).
While many organic species present in the atmosphere are expected to be strongly surface active, there are others classified as weak surfactants, including organosulfates (Hansen et al., 2015), certain components in mixtures of marine SOA and POA (Ovadnevaite et al., 2017), and aliphatic dicarboxylic acids (Ruehl et al., 2016). The surface enrichment of these compounds is difficult to predict, currently inaccessible experimentally (for airborne particles), and potentially showing complex interactions with particle size (Sorjamaa et al., 2004; Sorjamaa and Laaksonen, 2007; Davies et al., 2019; Ovadnevaite et al., 2017).
Prior treatments of bulk–surface partitioning in aerosol systems
There have been numerous methods developed for predicting the bulk–surface partitioning of aerosol chemical species; the following is a summary of recent works. Briefly, Sorjamaa et al. (2004) used an approach based on the 2D Gibbs dividing surface theory and found that the depletion of water-soluble surfactants may have a substantial impact on Köhler curves through both surface tension depression and modification of the Raoult effect as surfactants are depleted from the bulk. They report that failing to account for both surface and bulk effects in growing aerosol particles may lead to under-predictions of the critical supersaturation, particularly at higher organic mass fractions. Prisle et al. (2008) used the semi-empirical Szyszkowski equation (Szyszkowski, 1908) to model the bulk–surface partitioning of various fatty acids with increasing carbon chain length. Importantly, they noted that using the surface tension of pure water while accounting for changes to the Raoult effect from bulk–surface partitioning led to good agreement with experimental data and less costly calculations; however, the use of accurate values of aw that accounted for bulk–surface partitioning was critical. These assumptions were more thoroughly explored by Prisle et al. (2010), wherein they found that particles with at least 50 % of their mass composed of surfactant species required more accurate treatments of surface tension depression than considering σ to be the same as that of pure water. In systems with lower concentrations of surfactants it was noted that the surface tension may be similar to that of pure water at the point of CCN activation. Despite this, an evolving surface tension depression in growing aerosol particles that have not yet activated may play a role in their growth and activation behavior (Ovadnevaite et al., 2017; Davies et al., 2019). Further complicating the issue is a lack of measurements of surface tension on sub-500 nm diameter particles.
Romakkaniemi et al. (2011) included a Szyszkowski–Langmuir treatment of bulk–surface partitioning to droplets containing methylglyoxal, a semivolatile species and moderate surfactant. They found that treating the surface as a hypothetical 2D plane that mixes ideally led to an over 1 order of magnitude increase in the total particle-phase concentration of methylglyoxal, further confirming the importance of bulk–surface exchange treatments. Beyond Szyszkowski–Langmuir isotherm-based treatments of bulk–surface partitioning, other equations of state have been employed, including 2D Van der Waals models, compressed film models, and LLPS-based models of bulk–surface partitioning (Ruehl and Wilson, 2014; Ruehl et al., 2016; Ovadnevaite et al., 2017). The compressed film model of Jura and Harkins (1946) (Ruehl et al., 2016) was also utilized by Forestieri et al. (2018) to examine long-chain fatty acid coatings on sodium chloride particles to mimic sea spray aerosols. It was found that different surfactant species may have large effects on CCN activation through both their impacts on σ and the effective hygroscopic growth parameter κ under high-RH conditions. They note that compounds traditionally thought of as highly surface active, like the fatty acids in their study, may not have as large of an impact on CCN activation as others (Forestieri et al., 2018).
The treatment of bulk–surface partitioning was also studied using an AIOMFAC-based coupled liquid–liquid equilibrium and gas–particle partitioning calculation (Ovadnevaite et al., 2017; Davies et al., 2019). The effective surface tension was estimated based on the predicted LLPS phase compositions and the surface coverage by an organic-rich shell phase, constrained to be of a defined minimum thickness δβ,min. This approach found that LLPS aerosols can be strongly affected by surface tension reductions, yet weakly by changes to the Raoult effect following bulk–surface partitioning (Ovadnevaite et al., 2017; Davies et al., 2019). The treatment of bulk–surface partitioning in the LLPS-based approach was primarily due to bulk equilibrium LLPS, organic surface coverage, and gas–particle partitioning, which directly account for substantial nonideal mixing. However, other more detailed effects, such as a size-dependent feedback from bulk–surface partitioning on LLPS phase compositions as well as liquid–liquid–interfacial-phase partitioning and energy effects were not accounted for. Furthermore, this approach did not depend on any assumptions about the maximum thickness of the interfacial region, only a prescribed minimum thickness (Ovadnevaite et al., 2017). Likewise, a subsequent study by Davies et al. (2019) compared a compressed film model and three versions of AIOMFAC-based bulk–surface partitioning models. The first AIOMFAC-based approach involved using a full (unconstrained) liquid–liquid equilibrium calculation. This methodology assumed that the organic-rich phase β would form a spherical shell around phase α if there was sufficient material; otherwise phase β formed a partial spherical shell of thickness δβ,min over phase α. An area-weighted mean of pure-component surface tensions based on the areas of each phase exposed to the gas phase was used to determine the effective droplet surface tension. The second approach involved assuming a complete phase separation among organics and aqueous inorganic electrolytes, with only water allowed to partition between both phases and the assumption that the organic species formed a film, i.e., a partial monolayer or up to multiple molecular layers at the droplet surface. In the case of insufficient organic material for forming a complete monolayer over the droplet, the effective surface tension of the droplet is computed as the surface coverage area-weighted average of the pure organic species surface tension and the surface tension of water. These two treatments of surface tension provided a good and predictive estimate of the upper and lower bounds of the measured critical supersaturation of a CCN, given the initial dry composition of the particle.
Malila and Prisle (2018) developed a semi-empirical monolayer-based bulk–surface partitioning model based on an extension of an earlier method developed by Laaksonen and Kulmala (1991) wherein the surface tension of a droplet was related to a surface-composition-weighted average of pure-component surface tensions (σi∘):
Here, 𝒱i and are the molar volumes and surface mole fractions of i, respectively. Coupled with mass conservation, this equation must be solved iteratively from a given droplet size and overall composition. It is important to note that pseudo-binary approximations must be made for Eq. (6) for systems with three or more components and that the iterative solution must be optimized for each system tested, which somewhat limits the utility of this approach as a predictive tool.
Vepsäläinen et al. (2022) conducted a comparative study examining the differences between the 2D Gibbs adsorption model of Prisle et al. (2011), the simplified complete partitioning model of Prisle et al. (2011), the compressed film model of Ruehl et al. (2016), a partial monolayer model based on Ovadnevaite et al. (2017), the monolayer model of Malila and Prisle (2018), and a simple bulk-composition-based model that did not allow for bulk–surface partitioning. In their study, the hygroscopic growth of 50 nm particles of different moderately surface-active dicarboxylic acid species was modeled. It was noted that the more complex models for bulk–surface partitioning, those which allowed for the partial partitioning of species between the bulk and surface, had the best agreement with measured critical supersaturations. Despite the agreement between the more complex models with measured critical supersaturations as a function of dry particle size, they predicted varying degrees of bulk–surface partitioning for different species and, thus, different equilibrium compositions for the bulk and surface of the droplet. A related model comparison by Vepsäläinen et al. (2023) was also extended to systems including stronger surfactant species, such as myristic acid. In that recent work, it was also noted that the various bulk–surface partitioning treatments from Vepsäläinen et al. (2022) were in agreement at low surfactant mass fractions; however, there was disagreement at higher surfactant mass fractions.
Other recent work with thermodynamics-based models has attempted to predict the degree to which surfactants may cover an aerosol particle (surface) at equilibrium, with many surfactant species expected to have a surface coverage on the order of 60 %–85 %, while some surfactant remains dissolved in the particle bulk, for compositions both below and above the critical micelle concentration (McGraw and Wang, 2021).
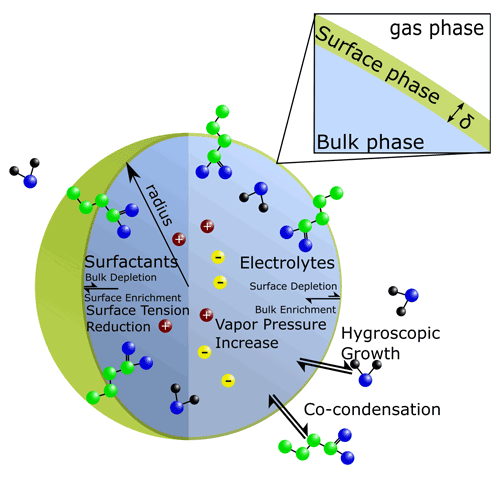
While simplifying assumptions about bulk–surface partitioning are reasonable for macroscopic systems, in the case of ultrafine particles, the competing effects of interior bulk-phase depletion and surface accumulation are complex and must be considered. Recent experimental findings have highlighted that even for larger droplets on the order of several micrometers, which contain non-ionic surfactant species similar to those found in atmospheric aerosols, varying surface tensions may be exhibited across particle sizes (Bzdek et al., 2020). Thus, a rigorous framework for determining the equilibrium bulk–surface partitioning of a droplet is necessary to better understand the size dependency of bulk–surface partitioning and related surface tension impacts in aerosol systems. Ideally, such a framework is predictive in design; i.e., it does not need to be fine-tuned or fitted specifically for every system or size range of interest. In the following, we introduce and evaluate such a framework by extending the AIOMFAC-based gas–particle partitioning calculations to include a distinct surface phase present between aerosol particles and the surrounding gas phase; see Fig. 1.
In his seminal works, Gibbs (1874) defined the following equation capable of expressing the so-called “free” energy of a thermodynamic system (G) with negligible energetic contributions from surfaces and interfaces as
Here, U is the internal energy of the system, T is temperature, S is entropy, P is pressure, and V is the volume of the system. Taking the derivative of Eq. (7) and then integrating with respect to the number of moles of i in the system (ni) at constant T and P gives the following equation for a system with k components:
Using the information given in Eq. (8), the equilibrium composition of a closed multiphase system can be found when its energy is at its global minimum. However, in order to accurately predict the chemical potential of each component in a system, physicochemical mixing models must be employed to account for non-ideal mixing effects on the chemical potential of i in a liquid-state bulk phase b as given by
where is the standard chemical potential, R is the gas constant, and is the (chemical) activity of i. The activity of a species is a unitless value which represents the “effective concentration” of component i on a chosen composition scale (e.g., mole fraction or molality) as determined by non-ideal mixing in a given phase of a system. Under equilibrium conditions, the chemical potentials of a component must be equivalent across all phases (e.g., Zuend et al., 2010). A useful choice, often employed when calculating μi for multiple phases of a system, is that μi∘ is defined to be identical for all phases. With that definition, the activities of a species must also be equal in all coexisting phases for a system at equilibrium. In order to accurately predict the various values over a wide range of solution compositions, complex mixing models, such as the AIOMFAC model, must be employed to account for molecular interactions and shape and size differences.
The AIOMFAC model is a state-of-the-art thermodynamic mixing model capable of accurately predicting the chemical activity of species in atmospheric aerosol systems in a thermodynamically rigorous and consistent manner. AIOMFAC can be considered to be a major extension of the UNIversal quasichemical Functional Group Activity Coefficients (UNIFAC) model by Fredenslund et al. (1975), since AIOMFAC includes the treatment of aqueous electrolytes and interactions between ions and organic molecules. UNIFAC itself is a group-contribution model derived from the UNIversal QUAsi-Chemical (UNIQUAC) theory of liquid mixtures developed by Abrams and Prausnitz (1975). The UNIQUAC theory and model represent a local composition model for mixtures of non-electrolyte components that generalizes the original quasi-chemical theory of Guggenheim (1952) to mixtures consisting of molecules of various shapes and sizes (while Guggenheim's quasi-chemical lattice model was restricted to spherical molecules of approximately equal sizes). The UNIQUAC model, the UNIFAC group-contribution version, and subsequently extended variants like AIOMFAC are therefore all deeply rooted in an advanced statistical mechanics treatment of mixing and interactions among different molecules in solution based on the local composition principle and are more rigorous than Guggenheim's two-component lattice gas model. AIOMFAC has been updated numerous times to include many atmospherically relevant inorganic cations, anions, and organic functional groups so that this model can represent a large number of mixed organic–inorganic aerosol systems, including systems with tens to thousands of components (Zuend et al., 2008, 2011; Yin et al., 2022).
If two or more distinct phases (phases are here indexed by superscript ϕ) are present in a system at constant temperature and pressure, Eq. (8) may need to be expanded to account for the energy associated with the boundaries between the phases. This can be achieved via the addition of a term accounting for the interfacial energy per unit area (σ) scaled by the area of the interface (A) (e.g., Aston and Herrington, 1991):
The interfacial Gibbs energy contribution can be important for microscopic systems, in which the contribution gains in magnitude relative to the collective energy content of the bulk volume of the phases. This interfacial Gibbs energy is therefore of interest in the context of small aerosol particles and cloud droplets. In the case of macroscopic systems, the interfacial energy term can usually be neglected due to its comparably tiny contribution.
Gibbs defined interfacial energy (or tension) as the excess energy attributed to the 2D boundary present between two phases. However, the choice to describe the boundary between two phases as a 2D surface and deciding its exact location presented several problems because real systems may exhibit concentration gradients near an interface. To account for this, Guggenheim introduced the concept of a 3-dimensional (3D) interfacial phase, which includes the boundary between two distinct phases and the concentration gradients of species therein (Guggenheim, 1940). While often on the order of a molecular monolayer or bilayer in depth, such an interfacial compartment can be treated as a distinct phase and must abide by the thermodynamic equilibrium conditions. Given the abovementioned challenges when using Gibbs' 2D surface treatment and in order to more easily connect geometrically confined interfacial and bulk phases in a mass-conserving finite-volume system, the approach of Guggenheim's 3D interface is adopted in our framework. Thus, for application to fine and ultrafine particles, we introduce an interface with a small but finite thickness (δ). We will focus in the following derivations on particles of spherical shape (droplets).
Following the approach of Cai and Griffin (2005), species adsorbed onto or absorbed into the surface of an aerosol particle contribute to the total volume of the particle. Thus, the interface only extends from the limit of the particle's radius inward, and the total number of condensed-phase molecules of i () is defined as the sum of the number of molecules of i in the bulk () and in the surface ():
If the surface of an aerosol is chemically distinct from the underlying bulk phase, then a particle with one condensed (here liquid) bulk phase, a distinct surface phase, and the surrounding gas phase will satisfy the criterion of equivalency of chemical potentials at equilibrium, as mentioned previously. As described by Aston and Herrington (1991), the chemical potential of a surface can be defined by differentiating Eq. (10) for a surface phase with respect to the molar amount of component i in the surface :
This leads to the following expression for the chemical potential of a surface phase:
where is the surface energy per unit surface area of the solution (i.e., the interfacial energy per unit area of the gas–liquid interface), and is the partial molar area of i. 𝒜i can be found for a finite-depth Guggenheim surface phase of a spherical particle as follows:
Here, the change in surface area of a sphere with respect to its radius is
and the volume of the finite-depth surface phase on a spherical droplet is
Differentiating Eq. (16) with respect to the particle radius assuming a constant surface depth leads to
Equation (17) can be converted into an expression for with the inclusion of the molar volume of i in the surface (). This value is assumed to be the same as the bulk molar volume of pure i, which can be calculated by dividing the molar mass (Mi) by the liquid-state density (ρi). This yields
Combining Eqs. (15) and (18) along with the assumption that the molar volumes are additive in order to determine leads to Eq. (19) for the partial molar area 𝒜i:
In the extreme case of the depth of the interface approaching the value of a droplet's radius, of Eq. (19) reduces to . In the opposite limiting case of a macroscopic system, in which δ≪r and δ2≈0, the of Eq. (19) is . Integrating partial molar areas by Euler's theorem leads to
for a multicomponent system with different species present. Note that for cases in which the surface phase extends beyond monolayer thickness, Eq. (20) indicates that the 𝒜i values will not necessarily correspond to the area per molecule located directly at the 2D gas–liquid surface.
Returning to Eq. (13), the intrinsic chemical potential, , of components in the surface phase can be formulated analogously to that of a liquid phase (Aston and Herrington, 1991):
Here, is the intrinsic standard chemical potential, and is the activity of i in the surface phase. In the case of pure component i, Eq. (13) yields
where σi∘ is the surface energy per unit area of pure component i. For a more general multicomponent surface phase, Eq. (13) becomes
Assuming that under all conditions, defining , and further requiring that at equilibrium the chemical potentials of species across phases are equal, the effective surface tension of a multicomponent solution can be isolated to form the following equation:
At equilibrium all σi values must be equivalent to a common value, the effective solution surface tension (σ) . In this case, Eq. (24) can be recognized as the Butler equation (Butler and Kendall, 1932; Sprow and Prausnitz, 1966). Employing Eq. (24) for each component in a system, along with Eq. (11), leads to a system of equations for the equilibrium composition of a 3D Guggenheim interface. These equations can be solved iteratively in a nested manner in combination with the AIOMFAC-based gas–particle partitioning and liquid–liquid-phase-separation algorithms laid out in Zuend et al. (2010) and Zuend and Seinfeld (2013).
2.1 Calculation of surface composition
In order to determine the composition of the surface phase in practice, a system of equations which allows maximum freedom of variable ranges, yet simultaneously satisfies the volume balance constraints of the 3D interface, is required. Furthermore those equations must not modify variables that should be held constant during the calculation of partial derivatives. For this purpose, we have developed a conforming implementation within the extended AIOMFAC equilibrium model. We begin by introducing a term representing the fractional amount of component i relative to the total amount of i in the particle phase:
where denotes the molar amount in the surface phase, and is the total molar amount of i available for partitioning (a constant during partitioning calculations). From the values of rp and δ, the total volume of the surface phase is calculated according to Eq. (16). Likewise , ρi, and Mi can be used to determine the volume of i in the surface phase. The fraction of the total surface volume occupied by i is given by
We now define a new variable, ζi, expressing the fraction of i in the surface relative to its assigned volume range such that
where , and and are the respective maximum and minimum possible surface volume contributions. is the unnormalized surface volume contribution of i. The values of ζi can vary in the range from 0.0 to 1.0; however, there can be non-zero values for some components (e.g., for water at very high RH) in order to achieve volume closure between the targeted geometric surface shell volume and the (unnormalized) volume as calculated by summing up the surface quantities such that and . For a given particle composition, rp, and δ, both and are species-specific constants. As such, can be determined depending on whether all other components j≠i can occupy all of the surface volume if they are at their maximum abundance in the surface. If this is the case, then . Otherwise, . This leads to
Here, is the maximum possible volume in the surface phase, less than or equal to vs, such that
Returning to ζi, Eq. (27) can be rearranged as
For a given value of ζi, can be computed and then normalized to find fi via
and a value for can be determined via
We note that such calculated fi and values may violate the condition that . This issue is remedied by introducing the relative deviation of actual to targeted surface-phase volume, an additional equation (constraint) to be solved alongside the equations describing the partitioning of k−1 components. From , variables and εi can be computed via and then applied in Eq. (25) to obtain εi.
2.2 Initial guess generation
An initial guess for the surface composition of a given particle can be derived from a first calculation for a non-partitioning (superscript “np”) case. In this trivial case, the relative compositions of the surface and bulk phases are set to be identical such that and . From this case, an estimation of can be computed given that
and
to yield
Given the definition that ai=xiγi for neutral components (and for electrolytes), Eq. (24) can be rearranged to the following form:
As long as the same nonideal mixing model is used for bulk and surface activity coefficients (in this case, AIOMFAC), the activity coefficient ratio on the right-hand side of Eq. (36) is equal to 1 (only in this non-partitioning case). For a spherical particle of known surface volume vs as well as and 𝒱i values, the non-partitioning assumption enables the calculation of the molar-phase amounts and the surface-to-bulk-molar ratios, . Using a composition-weighted mean of the pure-component surface tensions for σ allows for the evaluation of Eq. (36), which yields . For neutral components (mole fraction scale), the obtained mole fraction ratios can then be converted into a (new) guess for the set of εi values as follows:
For electrolyte components with activities defined on molality scale, the corresponding bulk–surface partitioning guess is generated via scaling by the surface-to-bulk-phase mass ratio,
where the summation index l covers non-electrolyte components (i.e., solvents) only. Using the determined set of values, Eq. (24) can be evaluated to obtain updated activity coefficient ratios, , as well as an updated weighted mean estimate of the surface tension, which can then once more be evaluated with Eq. (36) and processed to obtain an updated εguess vector. If desired, one can expand on this approach by using the determined activity coefficient ratios (in this case kept fixed) together with a set of distinct guesses for potential equilibrium σ values in Eq. (36), yielding a set of initial guesses for the εi values. Systematically generating more than one initial guess is useful when the subsequent numerical solution of the system of nonlinear equations, given by Eqs. (24) or (40), is unsuccessful in the case of the first initial guess evaluated – or to further explore whether more than one solution may exist. In our modern Fortran implementation, the system of equations is solved by a modified, bound-constrained version of Powell's hybrid method (Moré et al., 1980, 1984). Our extensive numerical testing suggests that this approach results in a fast and robust method for finding the equilibrium bulk–surface partitioning state for a given overall particle composition, radius, and interfacial thickness.
2.3 Model assumptions
A key piece of information that is necessary to solve Eq. (24) is the liquid-state pure-component surface tension, σi∘, at given temperature. In this work, σi∘ values of organic components were taken from published data (Hyvärinen et al., 2006; Riipinen et al., 2007; Booth et al., 2009) or, in the case of glutaric acid, extrapolated from high-concentration data of binary aqueous solutions (Booth et al., 2009). For inorganic electrolyte components, σi∘ was calculated using the approach for estimating pure molten salt surface tensions as described in Dutcher et al. (2010). Organic compounds with poorly constrained σi∘ values were assumed to have values of 35 mJ m−2. In addition, there are physical constraints applied to the surface-phase thickness δ in this study. The lower limit of δ was selected to be 0.15 nm or the approximate length of a single alkane C−C bond. The upper bound for δ was selected to be 1.0 nm for all systems tested, which is the approximate length of three water molecule diameters. An alternative assumption was also tested: a treatment where δ is a function of particle- or surface-phase composition; however, there is limited information on how exactly δ should change as a function of composition. Therefore, in this test case it was assumed that a simple weighted average of molecular lengths based on the surface mole fraction in the particle phase could be used. These molecular lengths were computed based on 𝒱i for each species and the assumption that the molecular length scale can be approximated by the side length of a volume-equivalent cube. Following the calculation of the surface composition, δ was updated, and the surface composition was recalculated. This process was repeated iteratively until convergence (within a set tolerance) to a stable δ value. It is also important to note that Eqs. (24) and (40) cannot be solved directly for a species which is completely insoluble in either the surface or the bulk phase. As such, the relative surface tension deviations, to be solved for from these equations, are scaled by a smooth (∼ rectangular step) weighting factor expressed by the following function:
Here, ϵ is the floating point machine precision employed, the weighted mean surface tension, and τσ a tolerance value, typically set to 0.1 J m−2. The weighting factor (expression after ×) on the right-hand side of Eq. (39) is evaluated to be near 1.0 in most cases and smoothly transitions to substantially smaller values only as i becomes very close to insoluble in either the surface phase or the bulk phase, in which case εi approaches either 1 or 0. Therefore, in cases of extremely limited solubility of i in the surface or bulk, the contribution of i to the system of equations used to solve for bulk–surface equilibrium is diminished (a desired property, since the numerical uncertainty grows near the limits of solubility, and numerical precision limitations become substantial). We note that the weighting factor is computed prior to (but not during) numerically solving the system of equations and is only updated if deemed necessary afterwards, such as when the solver was unsuccessful for set numerical tolerances and the equation solving needed to be repeated. Furthermore, a closely related weighting factor, which is normalized by the sum of weightings such that the resulting fractional weights sum to 1.0, is used in the calculation of the weighted mean value during the process of iteratively solving the system of equations (i.e., simultaneously solving Eq. 39 via Eq. 24 for all components).
An additional assumption made in this study concerns the computation of activity coefficients. It is assumed that there are no modifications to the calculation (by AIOMFAC) of activity coefficients in the surface phase compared to the bulk phase. Lane (1983) introduced a common exponential correction factor, t, which is applied to the calculated activity coefficients of a surface phase such that . The introduction of such an exponent is motivated by the idea that activity coefficients in a surface, affected by some limitations in the molecular packing options, may deviate slightly from those calculated for a bulk phase of identical composition and temperature. However, estimated values of t are system-dependent, yet often close to unity (Lane, 1983). Because the inclusion of additional semi-empirical terms limits the flexibility of the targeted predictive capability of the model developed in this work, it is assumed that t=1 for all systems.
Returning to Eq. (24), if an alternate assumption is made about the partial molar areas, specifically that , then the expressions previously leading to Eq. (24) result in
and 𝒜i∘ can be found for a pure droplet of i analogous to Eq. (19), with the only modification being that the interfacial thickness used is that of the pure component, i.e., set . If it is assumed that only a monolayer of molecules forms the surface of a pure-component droplet, then δi∘ can be estimated based on the molecular size of i. With this information, Eq. (40) can be employed with Eqs. (11) and (39) in the same manner as Eq. (24) to form a system of equations for numerically solving the equilibrium bulk–surface partitioning problem.
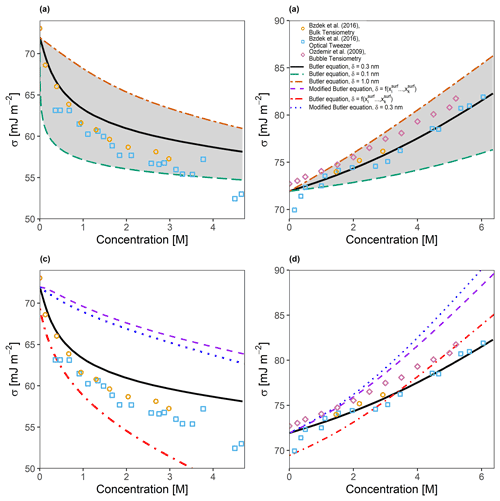
Figure 2Predicted and measured surface tensions for (a) a binary water–glutaric acid system and (b) a binary water–sodium-chloride system as a function of solute concentration in water at 298 K. The area shaded in grey represents the predicted surface tension bounded by the proposed limits for δ of 0.1 and 1.0 nm. The solid black line is the predicted surface tension for δ=0.3 nm. Also shown in (c) and (d) are the same systems as (a) and (b), respectively, but with the assumption that , leading to a modified form of the Butler equation (Eq. 40) and the testing of the surface-composition-based approach for determining δ.
3.1 Comparison of measured and predicted surface tension
In order to determine the validity of the described predictive model, comparisons were made to measurements for a selection of atmospherically relevant binary systems. Figure 2a shows the predicted surface tension (utilizing AIOMFAC with Eq. 24) as a function of the total particle-phase concentration of glutaric acid in a binary water–glutaric acid droplet that was allowed to grow hygroscopically from a starting dry diameter of 5 µm to the point of cloud droplet activation, corresponding to a diameter of approximately 10 µm. This scenario allowed us to compare predicted surface tensions to the bulk tensiometry and optical tweezer measurements taken by Bzdek et al. (2016). The three curves shown in Fig. 2a correspond to three different values of δ: 0.1 nm, which is the approximate length of a single carbon–carbon bond; 0.3 nm, which is the approximate length scale of a single water molecule (the same value was also used as a minimum thickness in models by Davies et al., 2019 and Ovadnevaite et al., 2017); and 1.0 nm, which corresponds to the approximate size of a single glutaric acid molecule along its longest axis. It is shown that assuming a thinner interfacial thickness value leads to a surface tension curve which is highly sensitive to the overall concentration of glutaric acid in the droplet. Analogously, an interfacial thickness that is larger will require greater changes in the total particle-phase concentration of an organic species in order to observe a similar decrease in surface tension. In addition to the binary water–glutaric acid system, Bzdek et al. (2016) also analyzed a binary water–sodium-chloride system of the same size using the bulk tensiometry and optical tweezer approaches. Shown along with these data in Fig. 2b are bulk measurements by Ozdemir et al. (2009). While the surface tension increases with salt concentration in this case, a similar behavior can be seen in the surface tension vs. concentration curves for the inorganic electrolyte system, wherein the curve is sensitive to the selection of δ. However, for the system shown in Fig. 2b, the sensitivity of the modeled surface tension to the value of δ is opposite of that for surface-active organic species. This is likely due to the fact that electrolytes preferentially partition into the bulk phase; therefore, a thinner interface will contain a higher mole fraction of water (at a specific wet diameter) and requires greater concentrations of electrolytes to increase a droplet's surface tension. Additional sensitivity comparisons were performed to determine the effect of modifying σi∘ by ±10 %. It was found that glutaric acid was more sensitive to modifications in the value of σglutaric∘ than NaCl, which was very weakly sensitive to increases in σNaCl∘ and somewhat sensitive to reductions in σNaCl∘. Overall, using δ=0.3 nm leads to surface tension predictions in better agreement with the measurements shown for large droplets or macroscopic solutions. This suggests that a molecular monolayer assumption for representing the surface phase is a relatively good model, at least for the systems shown in Fig. 2a and b.
Figure 2c and d show the effects of exploring different assumptions of Eq. (24) along with the same measurements from Fig. 2a and b. The modified Butler equation, which assumes that (Eq. 40 in this work), consistently overestimates the surface tension of the water–glutaric-acid system and only agrees with the water–NaCl system at very low concentrations. Assuming that δ is surface composition-dependent also leads to poor agreement with experimental data at high concentrations for the water–glutaric-acid system and better agreement at low concentrations. For the water–NaCl system, it can be seen that the opposite is true; the composition-dependent δ leads to good agreement at higher concentrations than at lower concentrations. The combination of Eq. (40) and a surface-composition-dependent δ leads to poor agreement across all concentrations shown for the water–glutaric-acid system and only gives good agreement for the water–NaCl system at low concentrations.
It is important to note that the sizes of the droplets analyzed in Bzdek et al. (2016) are large relative to the more numerous but substantially smaller atmospheric aerosol particles of importance in cloud formation. However, there is a paucity of surface tension data available for droplets in the sub-500 nm size range, since it is extremely difficult to measure the surface tension of atmospherically relevant aerosol particles that are freely suspended while at sizes near or below the wavelengths of visible light. Recent developments in atomic force microscopy have allowed surface tension measurements of sub-500 nm particles to be taken (Lee et al., 2017) directly and are indeed promising as a source of measurement data at that size scale. In the present study, such measurements were not analyzed because placing the droplet on a glass substrate introduces a second interface, the substrate–droplet interface, which may modify the partitioning behavior of different species as well as affect the geometry of the droplet from spherical to approximately semi-spherical. At the moment, the framework laid out in this work is only capable of handling spherical geometries with a single gas–droplet surface; the inclusion of interfaces between two condensed phases and the treatment of non-spherical geometries are the subject of future work.
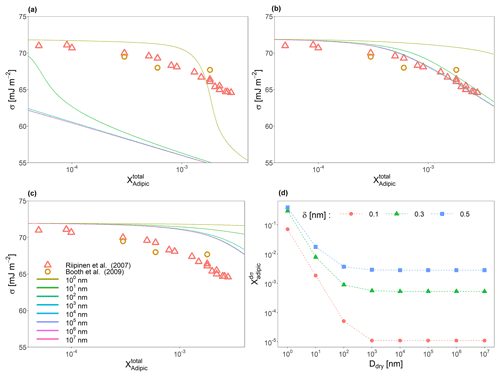
Figure 3Predicted surface tensions of a binary water–adipic acid system across 8 orders of magnitude in dry particle diameter (see legend in panel c) for interfacial thickness values of (a) 0.1 nm, (b) 0.3 nm, and (c) 0.5 nm. (d) The specific concentrations of adipic acid for which the surface tension is the most sensitive to change in the overall mole fraction of adipic acid as a function of dry diameter and δ. Also shown in (a), (b), and (c) are measurements taken by Riipinen et al. (2007) and Booth et al. (2009).
3.2 Bulk-phase depletion
While the measured particles associated with the data from Fig. 2 are large, the effects of bulk-phase depletion cannot be neglected entirely. Figure 3a, b, and c show surface tension as a function of particle size and δ for binary water–adipic acid systems of particles with dry diameters of 1.0 nm, 10 nm, 100 nm, 1 µm, 10 µm, 100 µm, 1 mm, and 1 cm (ranging over 8 orders of magnitude). It is shown that even highly diluted particles with dry diameters below 100 µm have different surface tensions at the same total mole fraction of adipic acid in the condensed phase. If the value of δ decreases, the surface tension curves for larger dry diameters converge, and bulk-phase depletion is only noticeable for the smallest particles. If δ is increased to be more similar to the molecular length scale of the solute species (∼0.45 nm), there is better agreement between modeled and measured surface tension values in the larger-sized droplets. Increases in δ also increase the minimum concentration of solute necessary to decrease the surface tension from that of pure water for all particle sizes; however, smaller particle sizes are more responsive to this change than larger ones. A method for determining this dependence is by taking the concentration of solute () at which the change in surface tension with each additional molecule of solute added is the greatest, in other words, the global extrema (minimum for surfactant species and maximum for tensoionic species) of . Figure 3d shows how varies as a function of size for the binary water–adipic acid system. Droplets with initial dry diameters on the order of 1 µm may still experience mild bulk depletion effects depending on the selection of the interfacial thickness value, with larger δ values leading to more pronounced bulk-phase depletion effects at larger sizes. Moreover, we note that the value of is strongly dependent on δ at larger sizes compared to smaller ones, with a doubling of the interfacial thickness from 0.15 to 0.3 nm leading to approximately 3 orders of magnitude increase in the value of for particles with dry diameters larger than 1 µm. This same change in δ for particles with dry sizes below 100 nm leads to differences of about 2 orders of magnitude or less. Thus, we demonstrate that bulk-phase depletion may modify surface tension as a function of particle composition on particles up to the micrometer size scale.
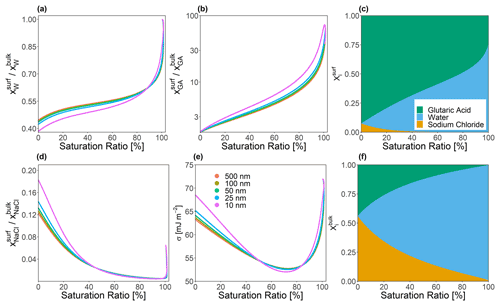
Figure 4Predicted bulk–surface partitioning coefficient () of (a) water, (b) glutaric acid, and (d) sodium chloride present in a forced single-bulk-phase particle at T=298 K. A molar dry solute ratio of 1:1 was used in all cases. (d) Predicted effective surface tension for several particle dry diameters as indicated by color. Right column (composition bar graphs): shown are the mole fractions of each species in the surface and the bulk phase (α) for a particle of 25 nm dry diameter.
The bulk–surface concentration ratio is independent of the volume ratio and represents the physicochemical partitioning coefficient. Figure 4 shows these mole fraction ratios for each species in a ternary water–glutaric-acid–sodium-chloride system as a function of equilibrium saturation ratio (S). Monodisperse particles consisting of a 1:1 molar ratio of glutaric acid to sodium chloride, with dry diameter values ranging from 10 to 500 nm, were allowed to grow hygroscopically until the point of cloud droplet activation (while maintaining the same solute masses, i.e., no gas–particle partitioning of glutaric acid considered). In this test, a forced one-phase calculation was performed (only allowing a single bulk liquid phase to exist), which prevented the particles from undergoing LLPS at compositions where that would be favorable. The value of δ was held constant at 0.3 nm, and Eq. (24) was employed. It can be seen that glutaric acid, while only a weakly surface-active compound compared to lower-polarity organics, is nevertheless strongly enriched in the surface of the particle across all particle sizes, especially at higher values of S. The predicted surface tension for each particle is also shown. The difference in σ of particles is the largest at both very low and very high values of S, with all of the σ values being the most similar for saturation ratios between 0.675 and 0.725. However, particles with diameters below 25 nm exhibit greater deviations from the behavior of their larger counterparts. These smallest particles achieve both a slightly lower minimum surface tension and a slightly higher surface tension value under low-aw conditions. This may be driven by the fact that under these conditions, more tensoionic species must be present in the surface due to limited amounts of both water and organic species. However, this effect is still quite weak even at such small particle sizes.
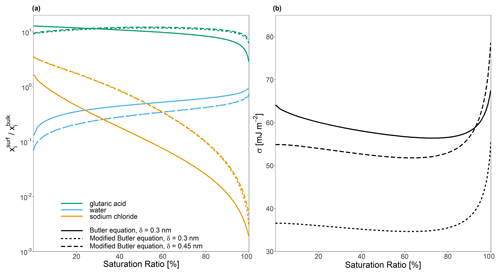
Figure 5The effect of implementing a modified form of the Butler equation (Eq. 40) with the assumption that for a water–glutaric-acid–sodium-chloride system with a 1:1 water-free molar ratio of glutaric acid to sodium chloride on (a) the bulk–surface partitioning coefficient, , and (b) predicted surface tension, σ. All calculations were performed at a temperature of 298 K.
If Eq. (40) is employed for bulk–surface equilibrium predictions, the δi∘ values for water, glutaric acid, and sodium chloride are calculated based on their molecular sizes. This leads to modified bulk–surface partitioning behavior as shown in Fig. 5a and b. The assumption that effectively modifies the value of σi∘ by multiplying it by the ratio . In the macroscopic case, where r≫δ, then , again showing an important effect of the calculated or assumed value of δ. In the case of species for which , a stronger affinity for the surface results, while for , it is expected that species i would have a weaker affinity for the surface phase. Notably, the feedbacks on the partitioning behavior of one species can still modify the bulk–surface partitioning of other species, since modifications to the composition of the surface phase will modify the activity coefficients for all species in the phase. As such, in Fig. 5, it can be seen that the assumption that leads to decreased partitioning of water, as both glutaric acid and sodium chloride show an increased affinity for the surface phase. This also modifies the effective solution surface tension. In the case where , σ is consistently lower than the values predicted by Eq. (24). In the case where δ lies between all of the values of δi∘, σ predicted by Eq. (40) is lower than the value predicted by Eq. (24) when the solution is highly concentrated in both organic and inorganic solutes (low aw) and higher than Eq. (24) in more dilute cases (high aw). These findings suggest that it is best to assume that for most systems.
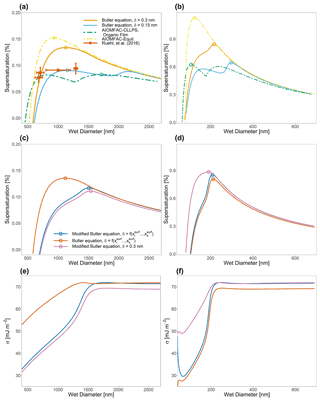
Figure 6Köhler curves for ternary water–suberic-acid–ammonium-sulfate particles at 298 K at an organic volume fraction of 0.88 and with a water-free diameter of (a) 150 nm and (b) 40 nm. Also shown in (a) are the measured SScrit and the critical wet diameter measured by Ruehl et al. (2016). Panels (c) and (d) show the calculated Köhler curves if the assumption is made that , leading to the modified Butler equation (Eq. 40), as well as the effect of modifying δ as a function of overall particle composition. Panels (e) and (f) show the calculated σ values for the systems shown in (c) and (d). A complete list of SScrit and Dcrit values for this system and the system shown in Fig. 7 can be found in Table 2.
3.3 Köhler curves
Numerous different test systems have been used in laboratory experiments and modeling studies to better understand the role of bulk–surface partitioning in the behavior of CCN both before and after activation. One such system that will now be considered has been studied in experiments and theory by Ruehl et al. (2016). They generated 150 nm (dry diameter) mixed suberic-acid–ammonium-sulfate particles corresponding to a spherical 50 nm diameter ammonium sulfate core coated with a 50 nm layer of suberic acid. Figure 6a shows the Köhler curve calculated via Eq. (1) with the assumption that aw in that equation is determined from the bulk-phase composition of the particle. Figure 6b also shows a particle with the same organic volume fraction as Fig. 6a but of a water-free diameter of 40 nm instead of 150 nm. Different interfacial thicknesses (δ) are shown, including the values determined by the compressed film model used in Ruehl et al. (2016). The resulting behavior of the Köhler curve is highly sensitive to the value of δ, particularly as δ approaches the lower limit of physically realistic values. The shapes of these Köhler curves are determined by the point at which the surface tension of the particle becomes similar to that of pure suberic acid relative to a given saturation ratio. In systems with δ values that are smaller, the surface remains are enriched in suberic acid at higher S values than in systems with larger δ values. This lowered surface tension at high S values may lead to modifications of the shape of the Köhler curve, including the branch at sizes greater than the critical wet diameter for CCN activation. Such behavior can be seen in the blue curve of Fig. 6a. Also shown in panels (a) and (b) of Fig. 6 are AIOMFAC-based predictive treatments of bulk–surface partitioning and CCN activation for such systems, as discussed in prior work (Ovadnevaite et al., 2017; Davies et al., 2019). These prior treatments both assume a surface with adjustable depth; consideration of LLPS; and, in the presence or absence of bulk LLPS at higher aw values, the calculation of an effective surface tension using a volume-fraction-weighted mixing rule of the pure-component surface tension values based on the bulk-liquid-phase compositions (and area fractions in the case of LLPS) in contact with the droplet surface. In this case, both simulations used δ=0.3 nm and the same pure-component surface tension values as used in the more detailed approach developed in this work. Briefly, these are two thermodynamic model variants for the computation of droplet surface tension as a function of composition, size, and temperature, introduced by Ovadnevaite et al. (2017) (see their supplementary information) and also discussed and applied by Davies et al. (2019). AIOMFAC-Equil is a full bulk equilibrium model, including gas–particle partitioning and liquid–liquid-phase separation (LLPS), but without consideration of bulk–surface partitioning. In the context of surface tension predictions, a procedure for the post-processing of model outputs has been introduced by Ovadnevaite et al. (2017), which assumes a core–shell droplet morphology in the case of LLPS. The AIOMFAC-Equil model treats the droplet surface tension as the surface-area-fraction-weighted average of the surface tensions of the present liquid phases (when no complete shell is formed by an organic-rich phase). The initial surface tensions of those phases are computed based on a volume-fraction-weighted mean of the pure-component surface tensions. The AIOMFAC-CLLPS with organic film model variant assumes complete LLPS among organics and inorganics (except for water) at all RH levels. It further assumes that all organic species in the droplet are present in a water-free layer at the surface of the droplet, while all electrolytes are present in an (aqueous) core phase of the droplet. The surface tension of the droplet in this model is equal to the surface tension of the organic film (phase), assuming complete coverage by the organic phase, or the surface-area-fraction-weighted average of the organic phase and the electrolyte-rich aqueous phase, should there be insufficient organic material to completely cover the droplet (Davies et al., 2019). The AIOMFAC-Equil prediction leads to substantially higher critical supersaturations than observed because this model variant ignores bulk–surface partitioning in the case of a single bulk phase present at higher RH, as in the system of Fig. 6. In contrast, the AIOMFAC-CLLPS variant with an imposed organic film assumption agrees reasonably well with the measured critical supersaturations. Indeed, if δ is assumed to be 0.3 nm for both prior AIOMFAC-based treatments (in those cases setting the minimum thickness of the surface phase), then the calculation by the AIOMFAC-CLLPS variant with an organic film represents the measured data better than the approach laid out in this work. However, if the δ value is lowered, then the bulk–surface equilibrium approach from this study shows excellent agreement with the measured peak supersaturation and, importantly, does not rely on the same simplifying assumptions as the organic-film-based calculation. Figure 6b demonstrates the effect of particle size (dry diameter of 40 nm) and bulk–surface partitioning on CCN activation, since the deviations from classical Köhler curve behavior (using a fixed surface tension, that of pure water) are more pronounced in both the δ=0.3 nm and δ=0.15 nm cases. In the example of Fig. 6, the AIOMFAC-Equil prediction is representative of a classical Köhler curve, since that model does not predict LLPS in the high-aw range close to the CCN activation point for this system. Clearly, in the case of ultrafine particles, a more detailed treatment of bulk–surface partitioning and associated surface tension evolution leads to notable deviations from classical behavior. Indeed a more detailed and thermodynamically rigorous treatment of bulk–surface partitioning leads to better agreement of the activation conditions in comparison to laboratory studies of water–suberic-acid–ammonium-sulfate particles than previous AIOMFAC-based treatments.
To further demonstrate the predictive power of the model developed in this work, an isoprene SOA system was considered as well. This system consists of water and 21 semivolatile isoprene photo-oxidation products, as proposed for a simplified isoprene-derived SOA representation in previous modeling work (Rastak et al., 2017; Gervasi et al., 2020). Because of the higher volatility of some of the isoprene SOA species, the effects of organic co-condensation (or more generally gas–particle partitioning) during hygroscopic growth should also be analyzed to better understand atmospheric implications of such aerosol systems. Concentrations simulated by the Master Chemical Mechanism (Jenkin et al., 2015, 1997, 2012) were used as inputs for the “co-condensation-enabled” case (Rastak et al., 2017) (see Table S3 in the Supplement). A distinct case, in which the organic composition of the particle was fixed, termed the “co-condensation-disabled” case, was also used for comparison. In that case, the equilibrium composition of the particle was taken from a bulk equilibrium gas–particle partitioning calculation at 0.1 % RH and then fixed for the organics (essentially rendering them nonvolatile) such that only water could partition between the gas and particle phases in subsequent computations. We note that for this isoprene SOA system, the values of the various σi∘ values have not been measured. We therefore assumed that for all species, which is in line with the assumptions made in Davies et al. (2019) and Ovadnevaite et al. (2017) (see Fig. S7 in the Supplement for an analysis of the framework sensitivity to σi∘ values). Based on experiments and AIOMFAC LLPS equilibrium computations for bulk solutions, this system is not expected to undergo LLPS at any RH (Rastak et al., 2017).
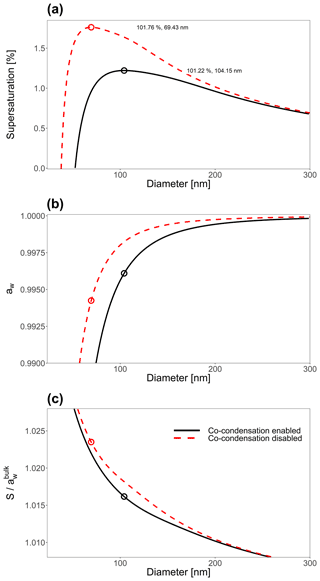
Figure 7(a) The effect of including co-condensation of SVOC species for an aqueous 21-component system of isoprene-derived SOA (Rastak et al., 2017; Gervasi et al., 2020) with Ddry=23 nm. (b) The bulk-phase water activity, corresponding to the contribution of the Raoult effect to the Köhler curves shown in (a). Panel (c) shows the Kelvin effect term's contribution to the curves in (a). For the co-condensation-disabled case, the particle's water-free composition was taken at RH=0.1 %, and then only water was allowed to partition to and from particles with this dry composition. For a detailed description of the system components, see Table S1.
Figure 7a shows the Köhler curve for a particle of 25 nm in dry diameter with co-condensation enabled and disabled. Figure 7b shows the contribution of the Raoult effect for both systems shown in Fig. 7a. Likewise Fig. 7c shows the contribution of the Kelvin effect for the same system. The inclusion of co-condensation of organic species leads to substantial reductions in Scrit for this system through modifications to both the Raoult effect and the Kelvin effect.
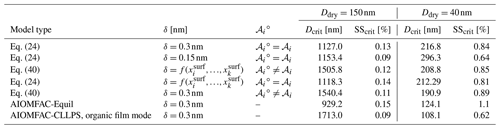
Goldsack and White (1983)Table 1Partial molar areas (m2 mol−1) of different organic species calculated using a simplified geometric approach based on the values given in Topping et al. (2007) and the model developed by Goldsack and White (1983), as well as by Eq. (19) of this study for particle diameters of 5, 50, and 5000 nm and two distinct δ values (0.15 or 1.0 nm).
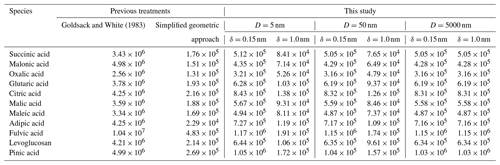
Table 2Critical wet diameter and supersaturations for the Köhler curves shown in Fig. 6.
4.1 Theoretical implications
One source of uncertainty in the approaches to bulk–surface partitioning described in Sect. 1 is determining the effective partial molar area of a given species, 𝒜i, in a mixed-surface phase and how that value may differ from the molar area of pure i, 𝒜i∘. A common assumption is that the apparent molar area can be calculated from the molar volume (𝒱i) of a species as and that the molar area of a species in solution is the same as its pure-component value . Table 1 lists the partial molar areas of numerous organic species calculated using Eq. (19) for particles of three distinct diameters and δ=0.15 nm or δ=1.0 nm. Those diameter choices serve to demonstrate a size dependence in this parameter when calculated via Eq. (19). Also shown are the size-independent partial molar areas when computed under the assumption or with the empirical approach developed by Goldsack and White (1983):
where 𝒱c,i and 𝒱b,i are the critical and bulk molar volumes. It should be noted that the scaling factor in Eq. (41) requires that the values of 𝒱c,i and 𝒱b,i are input in units of cm3 mol−1; the equation then returns 𝒜i in units of cm2 mol−1. In the mathematically sound framework developed in this work, the values of 𝒜i are weak functions of particle radius rp; however, they are stronger functions of the value of δ, with smaller δ values leading to smaller 𝒜i values.
Another important assumption made regarding the treatment of 𝒜i is the assumption that the density of i in the surface phase () is equivalent to that of the pure-component value of a (bulk) liquid state. Currently, all AIOMFAC-based bulk solution calculations make the assumption that the 𝒱i and related ρi of a species do not change as a function of solution composition and that the total volume of a phase is a linearly additive function of the individual component molar volumes times their molar abundance. Other studies have noted that may differ from and that lower values of may lead to better agreement between surface tension models and experimental data (Defay et al., 1966).
It should also be noted that deviations in activity coefficients are possible when comparing surface versus bulk phases of the same molar composition. As mentioned in Sect. 2.3, the introduction of a single exponential scaling factor (t) for all component activity coefficients in the surface phase has been used in the past as a fit parameter in order for binary solution surface tension curves to better match experimental data without violating the Gibbs–Duhem relation. This t value may be thought of as treating the surface-phase nonideality as taking place at a different temperature than that of the bulk phase, since . Therefore, one may argue that the value of t should be constrained such that the temperature change remains physically realistic. Thus, a value of t=25 is physically unrealistic for a system at 298 K which shows substantial nonideal mixing, since it would mean that the surface-phase nonideality would be behaving as if it were at 7450 K. The inclusion of t also introduces an additional fit parameter that is likely unique for each system, thus limiting the predictive power of the model introduced in this work. Use of exponent t in combination with an unconstrained fit leads to better agreement with points below cloud droplet activation for some of the Köhler curves presented in Ruehl et al. (2016), such as ternary water–succinic-acid–ammonium-sulfate, water–pimelic-acid–ammonium-sulfate, and water–glutaric-acid–ammonium-sulfate particles. However, those fitted t values must be combined with rather extreme values of δ and σorg for good agreement with the experimental data both at the CCN activation point and at points below activation (see Figs. S4–S6 for examples). In addition, the framework laid out in this work is incapable of simultaneously matching the growth data points and critical supersaturation point reported by Ruehl et al. (2016) for water–malonic-acid–ammonium-sulfate particles (see Fig. S3). Further explorations of variations in the activity coefficients of species in the surface phase are warranted to better understand how these activity coefficients may differ in value from those of a bulk solution with the same molar composition. Likewise, the explicit treatment of the dissociation of organic acids under dilute aqueous conditions is not considered in regard to its role in bulk–surface partitioning in this study. Under highly diluted conditions, such as those found in activating CCN, many dicarboxylic acids may partially or fully dissociate. It is possible that consideration of such acid dissociation may lead to modifications of both the surface enrichment and the bulk depletion of different species as well as to enhancements of the solute effect via an increase in dissolved ionic species. Explicit treatments of organic acid dissociation and resulting interactions among various additional ions in an AIOMFAC-based model framework are thus a direction to be explored in future work.
An alternative approach to using the framework laid out in this work is to use other statistical mechanics models to predict the surface tension as a function of bulk solution composition. A simplified statistical-mechanics-based approach for surface tension predictions was developed by Wexler and Dutcher (2013), which relies on a single physically constrained fitted parameter, r, which represents the average number of water molecules displaced by a solute molecule at the surface. As shown in Fig. S6, this model had a root mean square error of 2.90 mJ m−2 in comparison to measurements of surface tension for a (macroscopic) binary water–ethanol system (Ernst et al., 1935). In comparison, the model developed in this work has a root mean square error of 2.930 mJ m−2, when using our default assumption that the thickness of the interface is δ=0.3 nm. The fitted value of r as reported by Wexler and Dutcher (2013) is 3.00. If the number of water molecules displaced by an ethanol molecule at the surface of a droplet is assumed to be determined based on the respective values of 𝒜water and 𝒜ethanol, then the number of water molecules displaced by an ethanol molecule in the surface phase is 3.02. Despite both models being in good agreement in the macroscopic case, it is important to note that their statistical mechanical model does not directly account for bulk-phase depletion in volume-constrained systems. For a comparison of various other frameworks for estimating the surface tension of liquid solutions and/or atmospheric aerosol particles, we refer the reader to the recent work by Kleinheins et al. (2023) and Vepsäläinen et al. (2022, 2023).
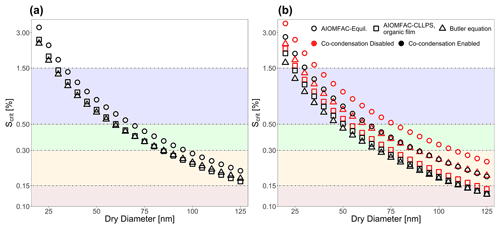
Figure 8Critical supersaturations vs. dry diameter as predicted by the AIOMFAC-Equil model, the AIOMFAC-CLLPS with organic film model, and a model from this work (Eq. 24) for (a) water–suberic-acid–ammonium-sulfate particles and (b) water–isoprene SOA particles. The horizontal shaded bands represent distinct regimes of maximum supersaturations encountered by aerosols in either marine (blue), clean continental (green), background (orange-yellow), or urban polluted (brown) conditions at cloud base conditions, as reported by Pinsky et al. (2014).
4.2 Atmospheric implications
The effect of bulk–surface partitioning on Köhler curve shapes is evident for submicron-sized aerosol particles. Even the use of relatively “thick”, yet reasonable, δ values (>0.5 nm) still exhibits substantial suppression of the critical supersaturation and modifications to the shape of the Köhler curve for the particle size range prior to reaching the CCN activation point under growth conditions. The inclusion of the thermodynamic treatment of equilibrium bulk–surface partitioning outlined in this study leads to simulated droplets that will grow to larger diameters at lower relative humidities than classical Köhler theory would otherwise suggest. If the value of δ is lowered, Köhler curves may exhibit a second local maximum as the CCN surface tension approaches that of pure water after the point of droplet activation. This behavior suggests that particles with very thin surface phases are more likely to activate into cloud droplets (for a given dry diameter). Clouds which form from rising air parcels populated by surfactant-containing particles may exhibit substantially higher cloud droplet number concentrations than those forming from air parcels of comparable particle size distributions but lacking aerosol particles of lowered (yet evolving) surface tensions. Figure 8a shows the critical supersaturation for CCN activation of particles with the same condensed-phase composition as those of Fig. 6, with Ddry values ranging from 25 to 130 nm. Similarly, Fig. 8b shows particles that grow under the same input parameters as used for Fig. 7, with dry sizes from 25 to 130 nm. The colored horizontal bands shown in Fig. 8 correspond to the typical supersaturation values experienced by aerosol particles in marine (blue), clean continental (green), background (orange), and urban polluted (brown) cloud base conditions, according to the classification by Pinsky et al. (2014). If the AIOMFAC-Equil model is used to determine the CCN activation conditions, particles with Ddry between approximately 60 and 75 nm would not be predicted to activate in continental clouds for both systems shown. For the isoprene-derived SOA system, in particular, the inclusion of both equilibrium co-condensation of SVOCs and bulk–surface partitioning leads to larger modifications in predicted Scrit, especially for Ddry>50 nm. This can have important implications for both the radiative forcing effects of resulting clouds and for the precipitation formation microphysics in these clouds, since lowering the critical dry diameter for typical peak supersaturation experienced at cloud base conditions may lead to substantially increased cloud droplet number concentrations (depending on the present aerosol number–size distribution) (Ovadnevaite et al., 2017). It is also important to note that the new framework introduced in this study to date has only considered impacts of organic components on CCN activation, yet does not consider the role that bulk–surface partitioning may play (if any) in ice-nucleating particles in cirrus clouds or mixed-phase clouds. Likewise, the interplay of bulk–surface partitioning and co-condensation with liquid–liquid equilibria is not yet considered in a fully coupled manner. For example, in the case of phase separation, such interactions may influence particle morphology and the RH range within which LLPS occurs. Consequently, coupled size and LLPS effects may also change the interactions between aerosol particles and light.
The surface-area-to-volume ratio of atmospheric aerosol particles increases substantially as particle diameter decreases in the fine and ultrafine size ranges. Any unique properties of the exterior surface of an aerosol particle must be accounted for in order to accurately model the behavior of the smallest (sub-100 nm sized) particles. This study builds on the finite-depth Guggenheim surface-phase treatment in combination with variants of the Butler equation and AIOMFAC-based vapor–liquid equilibrium computations to create a thermodynamically rigorous treatment of bulk–surface partitioning in spherical aerosol particles with diameters as low as 10 nm. This model relies on one adjustable, loosely constrained parameter, the surface-phase thickness δ, and applies it consistently to any number of species in multicomponent organic–inorganic aerosol systems. The approach is capable of representing experimentally measured surface tension data for atmospherically relevant systems across a range of relative humidities. The inclusion of a thermodynamically sound treatment of interfacial regions leads to modified Köhler curve predictions that are in agreement with measured data, including for cases for which simpler approaches with fixed surface tension fail. For particles with diameters larger than ∼ 100 nm, the simpler AIOMFAC-CLLPS model variant with an organic film assumption agrees reasonably well with the more thermodynamically sound model in terms of predicted SScrit values and may serve as a good approximation when computational efficiency is a key concern. For smaller particles, where bulk-phase depletion may play a larger role, larger disagreement arises between the AIOMFAC-CLLPS model with organic film and the approaches laid out in this work.
While measurements of physicochemical properties of particles, such as surface tension and chemical composition, in the size range below 1 µm and especially below 100 nm are rare or nonexistent, there have been numerous measurements made on larger particles. Models trained on data from bulk measurements and large microscopic droplets have been used to study sub-100 nm particles. Frequently, those measurements were done on droplets exhibiting a single liquid (bulk) phase and spherical shape when freely suspended, but phase separation and associated phase boundaries can affect the particle shape. Indeed, many systems have been modeled or observed to adopt more complex, non-spherical morphologies, in some cases involving multiple liquid phases (Huang et al., 2021; Kwamena et al., 2010; Reid et al., 2011). The basic thermodynamic theory introduced in Sect. 2 is generally applicable; however, we show that when applied to finite-volume droplets, geometric considerations introduce shape- and mass-balance constraints which impact the bulk–surface partitioning, particularly in submicron-sized particles. In this study, we have outlined the detailed expressions for spherical single-bulk-phase particles, which were implemented in our AIOMFAC-based bulk–surface partitioning model. To date, this model has not accounted for non-spherical shape or feedback effects from energy stored in liquid–liquid interfaces. However, our model provides a basis for future extensions to account for size-dependent feedback between droplet size, liquid–liquid interfaces, non-sphericity, and size effects on LLPS onset. Furthermore, the use of Eq. (24) or (40) for gas–liquid interfaces requires accurate measurements or predictions of a reference state value of σ, usually pure-component surface tension, for many atmospherically relevant species. These data do not exist or, in the case of inorganic electrolytes, are disputed as to what the correct value should be. This may limit the systems for which our approach can be used – or requires assumptions to be made. Therefore, this study highlights the need for, and benefit of, reliable data for pure-component surface tension. A key goal for applications of thermodynamic multiphase aerosol models in atmospheric chemistry is achieving predictive capability, unrestricted by system- and size-dependent fit parameters. The model introduced here marks a major step toward this goal. It enables us to better quantify the role of interfacial properties in environmental systems on the nanometer and micrometer size scales. Models like those introduced in this study can serve as a bridge between the measurable particle size range and the presently experimentally inaccessible ultrafine size range of interest for cloud formation.
The experimental data and model outputs underlying all figures shown are provided in the Supplement. The bulk–surface partitioning code is available upon request from the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-23-7741-2023-supplement.
RS performed model development and simulations, visualized model outputs, and wrote the paper. AZ conceived the project, assisted with model development, co-wrote the paper, was responsible for supervision, and secured funding for the work.
The contact author has declared that neither of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We would like to acknowledge Judith Kleinheins, Nadia Shardt, Claudia Marcolli, and Thomas Peter for their helpful feedback and discussions in the preparation of this manuscript.
This project was undertaken with financial support from the government of Canada through the federal Department of Environment and Climate Change (grant no. GCXE20S049) and the Natural Sciences and Engineering Research Council of Canada (NSERC grant no. RGPIN-2021-02688). Ryan Schmedding was also supported by a doctoral scholarship from the Fonds de recherche du Québec – Nature et technologies (FRQNT; scholarship no. 314186) and a Mitacs Globalink research award (IT27170).
This paper was edited by Markus Ammann and reviewed by two anonymous referees.
Abrams, D. S. and Prausnitz, J. M.: Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems, AIChE Journal, 21, 116–128, https://doi.org/10.1002/aic.690210115, 1975. a
Aston, M. S. and Herrington, T. M.: The effect of added electrolyte on surface pressure/area per molecule isotherms, J. Colloid Interf. Sci., 141, 50–59, 1991. a, b, c
Bellouin, N., Quaas, J., Gryspeerdt, E., Kinne, S., Stier, P., Watson-Parris, D., Boucher, O., Carslaw, K. S., Christensen, M., Daniau, A.-L., Dufresne, J.-L., Feingold, G., Fiedler, S., Forster, P., Gettelman, A., Haywood, J. M., Lohmann, U., Malavelle, F., Mauritsen, T., McCoy, D. T., Myhre, G., Mülmenstädt, J., Neubauer, D., Possner, A., Rugenstein, M., Sato, Y., Schulz, M., Schwartz, S. E., Sourdeval, O., Storelvmo, T., Toll, V., Winker, D., and Stevens, B.: Bounding Global Aerosol Radiative Forcing of Climate Change, Rev. Geophys., 58, e2019RG000660, https://doi.org/10.1029/2019RG000660, 2020. a
Binyaminov, H., Abdullah, F., Zargarzadeh, L., and Elliott, J. A. W.: Thermodynamic Investigation of Droplet–Droplet and Bubble–Droplet Equilibrium in an Immiscible Medium, J. Phys. Chem. B, 125, 8636–8651, https://doi.org/10.1021/acs.jpcb.1c02877, 2021. a
Booth, A. M., Topping, D. O., McFiggans, G., and Percival, C. J.: Surface tension of mixed inorganic and dicarboxylic acid aqueous solutions at 298.15 K and their importance for cloud activation predictions, Phys. Chem. Chem. Phys., 11, 8021–8028, https://doi.org/10.1039/B906849J, 2009. a, b, c
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V. M., Kondo, Y., Liao, H., Lohmann, U., Rasch, P., Satheesh, S. K., Sherwood, S., Stevens, B., and Zhang, X. Y.: Clouds and aerosols, Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 571–657, https://doi.org/10.1017/CBO9781107415324.016, 2013. a
Burnett, R., Chen, H., Szyszkowicz, M., Fann, N., Hubbell, B., Pope, C. A., Apte, J. S., Brauer, M., Cohen, A., Weichenthal, S., Coggins, J., Di, Q., Brunekreef, B., Frostad, J., Lim, S. S., Kan, H., Walker, K. D., Thurston, G. D., Hayes, R. B., Lim, C. C., Turner, M. C., Jerrett, M., Krewski, D., Gapstur, S. M., Diver, W. R., Ostro, B., Goldberg, D., Crouse, D. L., Martin, R. V., Peters, P., Pinault, L., Tjepkema, M., van Donkelaar, A., Villeneuve, P. J., Miller, A. B., Yin, P., Zhou, M., Wang, L., Janssen, N. A. H., Marra, M., Atkinson, R. W., Tsang, H., Quoc Thach, T., Cannon, J. B., Allen, R. T., Hart, J. E., Laden, F., Cesaroni, G., Forastiere, F., Weinmayr, G., Jaensch, A., Nagel, G., Concin, H., and Spadaro, J. V.: Global estimates of mortality associated with long-term exposure to outdoor fine particulate matter, P. Natl. Acad. Sci. USA, 115, 9592–9597, https://doi.org/10.1073/pnas.1803222115, 2018. a
Butler, J. A. V. and Kendall, J. P.: The thermodynamics of the surfaces of solutions, P. Roy. Soc. Lond. A, 135, 348–375, https://doi.org/10.1098/rspa.1932.0040, 1932. a
Bzdek, B. R., Power, R. M., Simpson, S. H., Reid, J. P., and Royall, C. P.: Precise, contactless measurements of the surface tension of picolitre aerosol droplets, Chem. Sci., 7, 274–285, https://doi.org/10.1039/C5SC03184B, 2016. a, b, c
Bzdek, B. R., Reid, J. P., Malila, J., and Prisle, N. L.: The surface tension of surfactant-containing, finite volume droplets, P. Natl. Acad. Sci. USA, 117, 8335–8343, https://doi.org/10.1073/pnas.1915660117, 2020. a, b
Cai, X. and Griffin, R. J.: Theoretical Modeling of the Size-Dependent Influence of Surface Tension on the Absorptive Partitioning of Semi-Volatile Organic Compounds, J. Atmos. Chem., 50, 139–158, https://doi.org/10.1007/s10874-005-2364-2, 2005. a
Chan, A. W. H., Kautzman, K. E., Chhabra, P. S., Surratt, J. D., Chan, M. N., Crounse, J. D., Kürten, A., Wennberg, P. O., Flagan, R. C., and Seinfeld, J. H.: Secondary organic aerosol formation from photooxidation of naphthalene and alkylnaphthalenes: implications for oxidation of intermediate volatility organic compounds (IVOCs), Atmos. Chem. Phys., 9, 3049–3060, https://doi.org/10.5194/acp-9-3049-2009, 2009. a
Ciobanu, V. G., Marcolli, C., Krieger, U. K., Weers, U., and Peter, T.: Liquid–Liquid Phase Separation in Mixed Organic/Inorganic Aerosol Particles, J. Phys. Chem. A, 113, 10966–10978, https://doi.org/10.1021/jp905054d, 2009. a
Cohen, A. J., Brauer, M., Burnett, R., Anderson, H. R., Frostad, J., Estep, K., Balakrishnan, K., Brunekreef, B., Dandona, L., Dandona, R., Feigin, V., Freedman, G., Hubbell, B., Jobling, A., Kan, H., Knibbs, L., Liu, Y., Martin, R., Morawska, L., Pope, C. A., Shin, H., Straif, K., Shaddick, G., Thomas, M., van Dingenen, R., van Donkelaar, A., Vos, T., Murray, C. J. L., and Forouzanfar, M. H.: Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: an analysis of data from the Global Burden of Diseases Study 2015, The Lancet, 389, 1907–1918, https://doi.org/10.1016/S0140-6736(17)30505-6, 2017. a
Davies, J. F., Zuend, A., and Wilson, K. R.: Technical note: The role of evolving surface tension in the formation of cloud droplets, Atmos. Chem. Phys., 19, 2933–2946, https://doi.org/10.5194/acp-19-2933-2019, 2019. a, b, c, d, e, f, g, h, i, j
Defay, R., Prigogine, I., and Bellemans, A.: Surface tension and adsorption, Longmans, London, ark:/13960/s2ffcbbxv31, 1966. a
Dutcher, C. S., Wexler, A. S., and Clegg, S. L.: Surface Tensions of Inorganic Multicomponent Aqueous Electrolyte Solutions and Melts, J. Phys. Chem. A, 114, 12216–12230, https://doi.org/10.1021/jp105191z, 2010. a
Ernst, R. C., Watkins, C. H., and Ruwe, H.: The Physical Properties of the Ternary System Ethyl Alcohol–Glycerin–Water, J. Phys. Chem., 40, 627–635, 1935. a
Ervens, B., Turpin, B. J., and Weber, R. J.: Secondary organic aerosol formation in cloud droplets and aqueous particles (aqSOA): a review of laboratory, field and model studies, Atmos. Chem. Phys., 11, 11069–11102, https://doi.org/10.5194/acp-11-11069-2011, 2011. a
Facchini, M. C., Mircea, M., Fuzzi, S., and Charlson, R. J.: Cloud albedo enhancement by surface-active organic solutes in growing droplets, Nature, 401, 257–259, https://doi.org/10.1038/45758, 1999. a
Facchini, M. C., Decesari, S., Mircea, M., Fuzzi, S., and Loglio, G.: Surface tension of atmospheric wet aerosol and cloud/fog droplets in relation to their organic carbon content and chemical composition, Atmos. Environ., 34, 4853–4857, https://doi.org/10.1016/S1352-2310(00)00237-5, 2000. a
Forestieri, S. D., Staudt, S. M., Kuborn, T. M., Faber, K., Ruehl, C. R., Bertram, T. H., and Cappa, C. D.: Establishing the impact of model surfactants on cloud condensation nuclei activity of sea spray aerosol mimics, Atmos. Chem. Phys., 18, 10985–11005, https://doi.org/10.5194/acp-18-10985-2018, 2018. a, b
Fredenslund, A., Jones, R. L., and Prausnitz, J. M.: Group-contribution estimation of activity coefficients in nonideal liquid mixtures, AIChE Journal, 21, 1086–1099, https://doi.org/10.1002/aic.690210607, 1975. a
Gérard, V., Nozière, B., Baduel, C., Fine, L., Frossard, A. A., and Cohen, R. C.: Anionic, Cationic, and Nonionic Surfactants in Atmospheric Aerosols from the Baltic Coast at Askö, Sweden: Implications for Cloud Droplet Activation, Environ. Sci. Technol., 50, 2974–2982, https://doi.org/10.1021/acs.est.5b05809, 2016. a
Gérard, V., Noziere, B., Fine, L., Ferronato, C., Singh, D. K., Frossard, A. A., Cohen, R. C., Asmi, E., Lihavainen, H., Kivekäs, N., Aurela, M., Brus, D., Frka, S., and Cvitešić Kušan, A.: Concentrations and Adsorption Isotherms for Amphiphilic Surfactants in PM1 Aerosols from Different Regions of Europe, Environ. Sci. Technol., 53, 12379–12388, https://doi.org/10.1021/acs.est.9b03386, 2019. a
Gervasi, N. R., Topping, D. O., and Zuend, A.: A predictive group-contribution model for the viscosity of aqueous organic aerosol, Atmos. Chem. Phys., 20, 2987–3008, https://doi.org/10.5194/acp-20-2987-2020, 2020. a, b
Gibbs, J. W.: On the Equilibrium of Heterogeneous Substances, Am. J. Sci., s3-16, 441–458, https://doi.org/10.2475/ajs.s3-16.96.441, 1874. a, b
Goldsack, D. E. and White, B. R.: An iterative technique for calculating surface tensions of -on-electrolyte solutions, Can. J. Chem., 61, 1725–1729, https://doi.org/10.1139/v83-295, 1983. a, b, c
Guggenheim, E. A.: The thermodynamics of interfaces in systems of several components, T. Faraday Soc., 35, 397–412, https://doi.org/10.1039/TF9403500397, 1940. a
Guggenheim, E. A.: Mixtures; the theory of the equilibrium properties of some simple classes of mixtures, solutions and alloys, The International series of monographs on physics, Clarendon Press, Oxford, ark:/13960/s20q1n7jcr8, 1952. a
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009. a
Hansen, A. M. K., Hong, J., Raatikainen, T., Kristensen, K., Ylisirniö, A., Virtanen, A., Petäjä, T., Glasius, M., and Prisle, N. L.: Hygroscopic properties and cloud condensation nuclei activation of limonene-derived organosulfates and their mixtures with ammonium sulfate, Atmos. Chem. Phys., 15, 14071–14089, https://doi.org/10.5194/acp-15-14071-2015, 2015. a
Hyvärinen, A.-P., Lihavainen, H., Gaman, A., Vairila, L., Ojala, H., Kulmala, M., and Viisanen, Y.: Surface Tensions and Densities of Oxalic, Malonic, Succinic, Maleic, Malic, and cis-Pinonic Acids, J. Chem. Eng. Data, 51, 255–260, https://doi.org/10.1021/je050366x, 2006. a
Huang, Y., Mahrt, F., Xu, S., Shiraiwa, M., Zuend, A., and Bertram, A. K.: Coexistence of three liquid phases in individual atmospheric aerosol particles, P. Natl. Acad. Sci. USA, 118, e2102512118, https://doi.org/10.1073/pnas.2102512118, 2021. a
Jenkin, M. E., Saunders, S. M., and Pilling, M. J.: The tropospheric degradation of volatile organic compounds: a protocol for mechanism development, Atmos. Environ., 31, 81–104, https://doi.org/10.1016/S1352-2310(96)00105-7, 1997. a
Jenkin, M. E., Wyche, K. P., Evans, C. J., Carr, T., Monks, P. S., Alfarra, M. R., Barley, M. H., McFiggans, G. B., Young, J. C., and Rickard, A. R.: Development and chamber evaluation of the MCM v3.2 degradation scheme for β-caryophyllene, Atmos. Chem. Phys., 12, 5275–5308, https://doi.org/10.5194/acp-12-5275-2012, 2012. a
Jenkin, M. E., Young, J. C., and Rickard, A. R.: The MCM v3.3.1 degradation scheme for isoprene, Atmos. Chem. Phys., 15, 11433–11459, https://doi.org/10.5194/acp-15-11433-2015, 2015. a
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., null null, Dunlea, J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of Organic Aerosols in the Atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009. a
Jura, G. and Harkins, W. D.: Surfaces of Solids. XIV. A Unitary Thermodynamic Theory of the Adsorption of Vapors on Solids and of Insoluble Films on Liquid Subphases, J. Am. Chem. Soc., 68, 1941–1952, https://doi.org/10.1021/ja01214a022, 1946. a, b, c
Kleinheins, J., Shardt, N., El Haber, M., Ferronato, C., Nozière, B., Peter, T., and Marcolli, C.: Surface tension models for binary aqueous solutions: a review and intercomparison, Phys. Chem. Chem. Phys., 25, 11055–11074, https://doi.org/10.1039/D3CP00322A, 2023. a
Köhler, H.: The nucleus in and the growth of hygroscopic droplets, T. Faraday Soc., 32, 1152–1161, https://doi.org/10.1039/TF9363201152, 1936. a
Kroflič, A., Frka, S., Simmel, M., Wex, H., and Grgić, I.: Size-Resolved Surface-Active Substances of Atmospheric Aerosol: Reconsideration of the Impact on Cloud Droplet Formation, Environ. Sci. Technol., 52, 9179–9187, https://doi.org/10.1021/acs.est.8b02381, 2018. a
Kuwata, M. and Martin, S. T.: Phase of atmospheric secondary organic material affects its reactivity, P. Natl. Acad. Sci. USA, 109, 17354–17359, https://doi.org/10.1073/pnas.1209071109, 2012. a
Kwamena, N. O. A., Buajarern, J., and Reid, J. P.: Equilibrium Morphology of Mixed Organic/Inorganic/Aqueous Aerosol Droplets: Investigating the Effect of Relative Humidity and Surfactants, J. Phys. Chem. A, 114, 5787–5795, https://doi.org/10.1021/jp1003648, 2010. a
Laaksonen, A. and Kulmala, M.: An explicit cluster model for binary nuclei in water–alcohol systems, J. Chem. Phys., 95, 6745–6748, https://doi.org/10.1063/1.461513, 1991. a
Lane, J.: Surface Activity Coefficients, Adsorption from Solution, Academic Press, London, 115, 51–64, https://doi.org/10.1016/B978-0-12-530980-6.50008-5, 1983. a, b
Lang-Yona, N., Abo-Riziq, A., Erlick, C., Segre, E., Trainic, M., and Rudich, Y.: Interaction of internally mixed aerosols with light, Phys. Chem. Chem. Phys., 12, 21–31, https://doi.org/10.1039/B913176K, 2010. a
Lee, H. D., Estillore, A. D., Morris, H. S., Ray, K. K., Alejandro, A., Grassian, V. H., and Tivanski, A. V.: Direct Surface Tension Measurements of Individual Sub-Micrometer Particles Using Atomic Force Microscopy, J. Phys. Chem. A, 121, 8296–8305, https://doi.org/10.1021/acs.jpca.7b04041, 2017. a
Lin, J. J., Kristensen, T. B., Calderón, S. M., Malila, J., and Prisle, N. L.: Effects of surface tension time-evolution for CCN activation of a complex organic surfactant, Environ. Sci.-Processes and Impacts, 22, 271–284, https://doi.org/10.1039/C9EM00426B, 2020. a
Malila, J. and Prisle, N. L.: A Monolayer Partitioning Scheme for Droplets of Surfactant Solutions, J. Adv. Model. Earth Sy., 10, 3233–3251, https://doi.org/10.1029/2018MS001456, 2018. a, b, c
McGraw, R. and Wang, J.: Surfactants and cloud droplet activation: A systematic extension of Köhler theory based on analysis of droplet stability, J. Chem. Phys., 154, 024707, https://doi.org/10.1063/5.0031436, 2021. a
Moré, J. J., Garbow, B. S., and Hillstrom, K. E.: User Guide for MINPACK-1, Argonne National Laboratory Report ANL-80-74, http://www.netlib.org/minpack/ (last access: 16 May 2028), 1980. a
Moré, J. J., Sorensen, D. C., Hillstrom, K. E., and Garbow, B. S.: The MINPACK Project, in: Sources and Development of Mathematical Software, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, United States, ark:/13960/t07x3kd4r, 1984. a
Ng, N. L., Kroll, J. H., Chan, A. W. H., Chhabra, P. S., Flagan, R. C., and Seinfeld, J. H.: Secondary organic aerosol formation from m-xylene, toluene, and benzene, Atmos. Chem. Phys., 7, 3909–3922, https://doi.org/10.5194/acp-7-3909-2007, 2007. a
Nozière, B., Baduel, C., and Jaffrezo, J.-L.: The dynamic surface tension of atmospheric aerosol surfactants reveals new aspects of cloud activation, Nat. Commun., 5, 3335, https://doi.org/10.1038/ncomms4335, 2014. a
Ovadnevaite, J., Zuend, A., Laaksonen, A., Sanchez, K. J., Roberts, G., Ceburnis, D., Decesari, S., Rinaldi, M., Hodas, N., Facchini, M. C., Seinfeld, J. H., and O’ Dowd, C.: Surface tension prevails over solute effect in organic-influenced cloud droplet activation, Nature, 546, 637–641, https://doi.org/10.1038/nature22806, 2017. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q
Ozdemir, O., Karakashev, S. I., Nguyen, A. V., and Miller, J. D.: Adsorption and surface tension analysis of concentrated alkali halide brine solutions, Miner. Eng., 22, 263–271, https://doi.org/10.1016/j.mineng.2008.08.001, 2009. a
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. a, b
Petters, S. S. and Petters, M. D.: Surfactant effect on cloud condensation nuclei for two-component internally mixed aerosols, J. Geophys. Res.-Atmos., 121, 1878–1895, https://doi.org/10.1002/2015JD024090, 2016. a
Pinsky, M., Mazin, I. P., Korolev, A., and Khain, A.: Supersaturation and diffusional droplet growth in liquid clouds: Polydisperse spectra, J. Geophys. Res.-Atmos., 119, 12872–12887, https://doi.org/10.1002/2014JD021885, 2014. a, b
Pokhrel, R. P., Gordon, J., Fiddler, M. N., and Bililign, S.: Impact of combustion conditions on physical and morphological properties of biomass burning aerosol, Aerosol Sci. Technol., 55, 80–91, https://doi.org/10.1080/02786826.2020.1822512, 2021. a
Prisle, N. L., Raatikainen, T., Sorjamaa, R., Svenningsson, B., Laaksonen, A., and Bilde, M.: Surfactant partitioning in cloud droplet activation: a study of C8, C10, C12 and C14 normal fatty acid sodium salts, Tellus B, 60, 416–431, https://doi.org/10.1111/j.1600-0889.2008.00352.x, 2008. a, b
Prisle, N. L., Raatikainen, T., Laaksonen, A., and Bilde, M.: Surfactants in cloud droplet activation: mixed organic-inorganic particles, Atmos. Chem. Phys., 10, 5663–5683, https://doi.org/10.5194/acp-10-5663-2010, 2010. a, b
Prisle, N. L., Dal Maso, M., and Kokkola, H.: A simple representation of surface active organic aerosol in cloud droplet formation, Atmos. Chem. Phys., 11, 4073–4083, https://doi.org/10.5194/acp-11-4073-2011, 2011. a, b
Rastak, N., Pajunoja, A., Acosta Navarro, J. C., Ma, J., Song, M., Partridge, D. G., Kirkevåg, A., Leong, Y., Hu, W. W., Taylor, N. F., Lambe, A., Cerully, K., Bougiatioti, A., Liu, P., Krejci, R., Petäjä, T., Percival, C., Davidovits, P., Worsnop, D. R., Ekman, A. M. L., Nenes, A., Martin, S., Jimenez, J. L., Collins, D. R., Topping, D., Bertram, A. K., Zuend, A., Virtanen, A., and Riipinen, I.: Microphysical explanation of the RH-dependent water affinity of biogenic organic aerosol and its importance for climate, Geophys. Res. Lett., 44, 5167–5177, https://doi.org/10.1002/2017GL073056, 2017. a, b, c, d
Reid, J. P., Dennis-Smither, B. J., Kwamena, N.-O. A., Miles, R. E. H., Hanford, K. L., and Homer, C. J.: The morphology of aerosol particles consisting of hydrophobic and hydrophilic phases: hydrocarbons, alcohols and fatty acids as the hydrophobic component, Phys. Chem. Chem. Phys., 13, 15559–15572, https://doi.org/10.1039/C1CP21510H, 2011. a
Riipinen, I., Koponen, I. K., Frank, G. P., Hyvärinen, A.-P., Vanhanen, J., Lihavainen, H., Lehtinen, K. E. J., Bilde, M., and Kulmala, M.: Adipic and Malonic Acid Aqueous Solutions: Surface Tensions and Saturation Vapor Pressures, J. Phys. Chem. A, 111, 12995–13002, https://doi.org/10.1021/jp073731v, 2007. a, b
Romakkaniemi, S., Kokkola, H., Smith, J. N., Prisle, N. L., Schwier, A. N., McNeill, V. F., and Laaksonen, A.: Partitioning of semivolatile surface-active compounds between bulk, surface and gas phase, Geophys. Res. Lett., 38, L03807, https://doi.org/10.1029/2010GL046147, 2011. a
Ruehl, C. R. and Wilson, K. R.: Surface Organic Monolayers Control the Hygroscopic Growth of Submicrometer Particles at High Relative Humidity, J. Phys. Chem. A, 118, 3952–3966, https://doi.org/10.1021/jp502844g, 2014. a
Ruehl, C. R., Davies, J. F., and Wilson, K. R.: An interfacial mechanism for cloud droplet formation on organic aerosols, Science, 351, 1447–1450, https://doi.org/10.1126/science.aad4889, 2016. a, b, c, d, e, f, g, h, i, j, k
Schmedding, R., Ma, M., Zhang, Y., Farrell, S., Pye, H. O. T., Chen, Y., Wang, C.-t., Rasool, Q. Z., Budisulistiorini, S. H., Ault, A. P., Surratt, J. D., and Vizuete, W.: alpha-Pinene-Derived organic coatings on acidic sulfate aerosol impacts secondary organic aerosol formation from isoprene in a box model, Atmos. Environ., 213, 456–462, https://doi.org/10.1016/j.atmosenv.2019.06.005, 2019. a
Schmedding, R., Rasool, Q. Z., Zhang, Y., Pye, H. O. T., Zhang, H., Chen, Y., Surratt, J. D., Lopez-Hilfiker, F. D., Thornton, J. A., Goldstein, A. H., and Vizuete, W.: Predicting secondary organic aerosol phase state and viscosity and its effect on multiphase chemistry in a regional-scale air quality model, Atmos. Chem. Phys., 20, 8201–8225, https://doi.org/10.5194/acp-20-8201-2020, 2020. a
Seinfeld, J. H., Bretherton, C., Carslaw, K. S., Coe, H., DeMott, P. J., Dunlea, E. J., Feingold, G., Ghan, S., Guenther, A. B., Kahn, R., Kraucunas, I., Kreidenweis, S. M., Molina, M. J., Nenes, A., Penner, J. E., Prather, K. A., Ramanathan, V., Ramaswamy, V., Rasch, P. J., Ravishankara, A. R., Rosenfeld, D., Stephens, G., and Wood, R.: Improving our fundamental understanding of the role of aerosol−cloud interactions in the climate system, P. Natl. Acad. Sci. USA, 113, 5781–5790, https://doi.org/10.1073/pnas.1514043113, 2016. a
Shiraiwa, M., Zuend, A., Bertram, A. K., and Seinfeld, J. H.: Gas-particle particle partitioning of atmospheric aerosols: interplay of physical state, non-ideal mixing and morphology, Phys. Chem. Chem. Phys., 15, 11441–11453, https://doi.org/10.1039/C3CP51595H, 2013. a
Song, M., Marcolli, C., Krieger, U. K., Zuend, A., and Peter, T.: Liquid-liquid phase separation and morphology of internally mixed dicarboxylic acids/ammonium sulfate/water particles, Atmos. Chem. Phys., 12, 2691–2712, https://doi.org/10.5194/acp-12-2691-2012, 2012. a
Song, M., Marcolli, C., Krieger, U. K., Lienhard, D. M., and Peter, T.: Morphologies of mixed organic/inorganic/aqueous aerosol droplets, Faraday Discuss., 165, 289–316, https://doi.org/10.1039/C3FD00049D, 2013. a
Sorjamaa, R. and Laaksonen, A.: The effect of H2O adsorption on cloud drop activation of insoluble particles: a theoretical framework, Atmos. Chem. Phys., 7, 6175–6180, https://doi.org/10.5194/acp-7-6175-2007, 2007. a
Sorjamaa, R., Svenningsson, B., Raatikainen, T., Henning, S., Bilde, M., and Laaksonen, A.: The role of surfactants in Köhler theory reconsidered, Atmos. Chem. Phys., 4, 2107–2117, https://doi.org/10.5194/acp-4-2107-2004, 2004. a, b, c, d
Sprow, F. B. and Prausnitz, J. M.: Surface tensions of simple liquid mixtures, T. Faraday Soc., 62, 1105–1111, https://doi.org/10.1039/TF9666201105, 1966. a
Surratt, J. D., Chan, A. W. H., Eddingsaas, N. C., Chan, M., Loza, C. L., Kwan, A. J., Hersey, S. P., Flagan, R. C., Wennberg, P. O., and Seinfeld, J. H.: Reactive intermediates revealed in secondary organic aerosol formation from isoprene, P. Natl. Acad. Sci. USA, 107, 6640–6645, https://doi.org/10.1073/pnas.0911114107, 2010. a
Szyszkowski, B. V.: Experimentelle Studien über kapillare Eigenschaften der wässerigen Lösungen von Fettsäuren, Zeitschrift für Physikalische Chemie 385–414, https://doi.org/10.1515/zpch-1908-6425, 1908. a, b, c
Topping, D., Barley, M., Bane, M. K., Higham, N., Aumont, B., Dingle, N., and McFiggans, G.: UManSysProp v1.0: an online and open-source facility for molecular property prediction and atmospheric aerosol calculations, Geosci. Model Dev., 9, 899–914, https://doi.org/10.5194/gmd-9-899-2016, 2016. a
Topping, D. O., McFiggans, G. B., Kiss, G., Varga, Z., Facchini, M. C., Decesari, S., and Mircea, M.: Surface tensions of multi-component mixed inorganic/organic aqueous systems of atmospheric significance: measurements, model predictions and importance for cloud activation predictions, Atmos. Chem. Phys., 7, 2371–2398, https://doi.org/10.5194/acp-7-2371-2007, 2007. a, b
Vepsäläinen, S., Calderón, S. M., Malila, J., and Prisle, N. L.: Comparison of six approaches to predicting droplet activation of surface active aerosol – Part 1: moderately surface active organics, Atmos. Chem. Phys., 22, 2669–2687, https://doi.org/10.5194/acp-22-2669-2022, 2022. a, b, c
Vepsäläinen, S., Calderón, S. M., and Prisle, N. L.: Comparison of six approaches to predicting droplet activation of surface active aerosol – Part 2: strong surfactants, EGUsphere [preprint], https://doi.org/10.5194/egusphere-2022-1188, 2023. a, b
Wexler, A. S. and Dutcher, C. S.: Statistical Mechanics of Multilayer Sorption: Surface Tension, J. Phys. Chem. Lett., 4, 1723–1726, https://doi.org/10.1021/jz400725p, 2013. a, b
Yin, H., Dou, J., Klein, L., Krieger, U. K., Bain, A., Wallace, B. J., Preston, T. C., and Zuend, A.: Extension of the AIOMFAC model by iodine and carbonate species: applications for aerosol acidity and cloud droplet activation, Atmos. Chem. Phys., 22, 973–1013, https://doi.org/10.5194/acp-22-973-2022, 2022. a
Zhang, Q., Jimenez, J. L., Canagaratna, M. R., Allan, J. D., Coe, H., Ulbrich, I., Alfarra, M. R., Takami, A., Middlebrook, A. M., Sun, Y. L., Dzepina, K., Dunlea, E., Docherty, K., DeCarlo, P. F., Salcedo, D., Onasch, T., Jayne, J. T., Miyoshi, T., Shimono, A., Hatakeyama, S., Takegawa, N., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Williams, P., Bower, K., Bahreini, R., Cottrell, L., Griffin, R. J., Rautiainen, J., Sun, J. Y., Zhang, Y. M., and Worsnop, D. R.: Ubiquity and dominance of oxygenated species in organic aerosols in anthropogenically-influenced Northern Hemisphere midlatitudes, Geophys. Res. Lett., 34, 13, https://doi.org/10.1029/2007GL029979, 2007. a
Zhou, S., Hwang, B. C. H., Lakey, P. S. J., Zuend, A., Abbatt, J. P. D., and Shiraiwa, M.: Multiphase reactivity of polycyclic aromatic hydrocarbons is driven by phase separation and diffusion limitations, P. Natl. Acad. Sci. USA, 116, 11658–11663, https://doi.org/10.1073/pnas.1902517116, 2019. a
Zuend, A. and Seinfeld, J. H.: A practical method for the calculation of liquid–liquid equilibria in multicomponent organic–water–electrolyte systems using physicochemical constraints, Fluid Phase Equilibr., 337, 201–213, https://doi.org/10.1016/j.fluid.2012.09.034, 2013. a
Zuend, A., Marcolli, C., Luo, B. P., and Peter, T.: A thermodynamic model of mixed organic-inorganic aerosols to predict activity coefficients, Atmos. Chem. Phys., 8, 4559–4593, https://doi.org/10.5194/acp-8-4559-2008, 2008. a
Zuend, A., Marcolli, C., Peter, T., and Seinfeld, J. H.: Computation of liquid-liquid equilibria and phase stabilities: implications for RH-dependent gas/particle partitioning of organic-inorganic aerosols, Atmos. Chem. Phys., 10, 7795–7820, https://doi.org/10.5194/acp-10-7795-2010, 2010. a, b
Zuend, A., Marcolli, C., Booth, A. M., Lienhard, D. M., Soonsin, V., Krieger, U. K., Topping, D. O., McFiggans, G., Peter, T., and Seinfeld, J. H.: New and extended parameterization of the thermodynamic model AIOMFAC: calculation of activity coefficients for organic-inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups, Atmos. Chem. Phys., 11, 9155–9206, https://doi.org/10.5194/acp-11-9155-2011, 2011. a