the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Molecular-level nucleation mechanism of iodic acid and methanesulfonic acid
Lin Ji
Both iodic acid (HIO3, IA) and methanesulfonic acid (CH3S(O)2OH, MSA) have been identified by field studies as important precursors of new particle formation (NPF) in marine areas. However, the mechanism of NPF in which IA and MSA are jointly involved is still unclear. Hence, we investigated the IA-MSA nucleation system under different atmospheric conditions and uncovered the corresponding nucleating mechanism at the molecular level for the first time, using a quantum chemical approach and Atmospheric Cluster Dynamics Code (ACDC). The findings show that the pure-IA nucleation rate was much lower than the results of CLOUD (Cosmics Leaving Outdoor Droplets) experiments. MSA can promote IA cluster formation through stabilizing IA via both hydrogen and halogen bonds, especially under conditions with lower temperatures, sparse IA, and rich MSA. However, the nucleation rate of the IA-MSA mechanism is much lower than that of field observations, indicating that the effect of additional nucleation precursors needs to be considered (e.g., H2SO4, HIO2, NH3, and amines). The IA-MSA nucleation mechanism revealed in this study may help to gain insight into the joint effect of marine sulfur- and iodine-containing components on marine NPF.
- Article
(3534 KB) - Full-text XML
-
Supplement
(1798 KB) - BibTeX
- EndNote
Marine aerosols, being the primary natural aerosol system (O'Dowd and De Leeuw, 2007), significantly affect global radiation balance and climate by regulating cloud properties as cloud condensation nuclei (CCN) (Takegawa et al., 2020; IPCC, 2013). Nearly half of the CCN originate from new particle formation (NPF) via the gas-to-particle conversion (Merikanto et al., 2009; Yu and Luo, 2009). As a major source of CCN globally, NPF mainly consists of the nucleation of gaseous molecules and the subsequent growth of the formed clusters (Kulmala et al., 2013; Kulmala, 2003; Zhang, 2010). Although extensive studies have provided observational evidence of NPF events in the coastal zone, open ocean, and even ice-covered polar regions (Zheng et al., 2021; Sipilä et al., 2016; Yu et al., 2019; Baccarini et al., 2020), the corresponding NPF mechanisms at the molecular level remain poorly understood, stemming from the lack of chemical speciation in the initial nucleating steps.
Marine NPF, particularly in remote marine areas, is more affected by biological emissions compared to inland ones with anthropogenic influence (Kerminen et al., 2018). Historically, sulfur-containing species originating from ocean-emitted dimethyl sulfide (DMS) have long been identified as significant components of marine aerosols (Charlson et al., 1987; Shaw, 1983; Bates et al., 1992). Methanesulfonic acid (CH3S(O)2OH, MSA), as a well-known oxidation product of DMS (Chen et al., 2018; Hatakeyama et al., 1982), is widely dispersed throughout the world's oceans and has considerable atmospheric concentrations (Chen et al., 2018), comparable to or higher than sulfuric acid (SA), i.e., [MSA] [SA] = 10 %–250 % (Berresheim et al., 2002; Davis et al., 1998; Eisele and Tanner, 1993). Moreover, MSA has been experimentally demonstrated to be a significant nucleating precursor in coastal and remote oceans (Dawson et al., 2012; Hodshire et al., 2019; Karl et al., 2007). Along with stricter global controls on anthropogenic SO2 emissions, the impact of MSA on NPF will become increasingly significant in the future (Perraud et al., 2015), particularly in marine areas.
In addition to the above sulfur precursors, recent experimental and theoretical studies (He et al., 2021; Martín et al., 2020; Xia et al., 2020; Rong et al., 2020) have also recognized the critical role of iodine compounds in marine NPF processes. According to the field studies (O'Dowd et al., 2002; Sipilä et al., 2016), the observed intense NPF events occur during low tide and are accompanied by a significant increase in iodic acid (HIO3, IA) concentration in the coastal Mace Head, Ireland, indicating that the coastal NPF is primarily driven by subsequential addition of IA and involves the participation of I2O5. More recently, He et al. (2021) demonstrated experimentally that, in addition to IA and I2O5, iodous acid (HIO2) and I2O4 are also involved in the cluster formation process, with HIO2 playing a key role in the stabilization of neutral IA clusters. Also, recent evidence suggests that the NPF events in the sea-ice-covered Arctic region are also mainly driven by IA (Baccarini et al., 2020). Notably, in addition to IA, significant concentrations of MSA were observed during marine NPF events (Beck et al., 2021). Although MSA and IA were detected in the smallest clusters (Beck et al., 2021), it is still unknown whether they could be simultaneously involved in the early nucleation process. If so, their joint nucleation mechanism and the corresponding regions affected by that mechanism need to be further elucidated.
Herein, the high-level quantum chemical calculations combined with Atmospheric Cluster Dynamics Code (ACDC) (McGrath et al., 2012) were employed to simulate the nucleating process of the (IA)x ⋅ (MSA)y system (where , , ). Under different atmospheric conditions (temperature and precursor concentration), a series of ACDC simulations were carried out to explore (i) the binding nature of IA and MSA, (ii) the joint effects of IA and MSA on the nucleation, and (iii) which conditions are more affected by the IA-MSA mechanism. The current work may contribute to developing a more comprehensive marine NPF mechanism and explaining some missing sources of particles in marine environments.
2.1 Quantum chemistry calculation
All structure optimizations with tight convergence criteria and frequency calculations with density functional theory (DFT) were carried out by the Gaussian 09 package (Frisch et al., 2009). Considering the variety of possible isomers of multimolecular clusters, a systematic multistep conformation search was employed here to locate the lowest-energy cluster structures. The structures of the pure-IA clusters employed in this study refer to those in the study by Rong et al. (2020). A new (IA)6 cluster with lower energy was found here. For each studied IA-MSA cluster, the artificial bee algorithm combining the UFF force field (Rappé et al., 1992) was adopted to yield 1000 initial configurations from 5000 generations by ABCluster software (Zhang and Dolg, 2015). After pre-optimization by the PM7 semiempirical method (Stewart, 2013) with MOPAC2016 (Stewart, 2016), the 100 structures with lower energies were left for further optimization at the ωB97X-D/6-31 + G* + Lanl2DZ (for iodine) level of theory due to the best performance of the ωB97X-D functional in studying atmospheric clusters (Elm and Kristensen, 2017; Schmitz and Elm, 2020). The final global minima were reoptimized by ωB97X-D functional with the 6-311 G(3df,3pd) (Francl et al., 1982) basis set for H, C, O, and S atoms and aug-cc-pVTZ-PP with ECP28MDF for I atom (Peterson et al., 2003), and they were identified with the lowest Gibbs formation free energy (ΔG). It is noteworthy that the larger aug-cc-pVTZ-PP basis set (for iodine) was employed in the present study compared to the aug-cc-pVDZ-PP basis set (for iodine) in our previous work (Rong et al., 2020), because higher level of theory usually implies a better calculation accuracy.
The single-point correction was further performed by the RI-CC2 method (Hattig and Weigend, 2000) with aug-cc-pVTZ (for H, C, O) + aug-cc-pV(T+d)Z (for S) + aug-cc-pVTZ-PP with ECP28MDF (for I) basis set using the TURBOMOLE program (Dunning et al., 2001; Ahlrichs et al., 1989), since the ACDC simulations based on RI-CC2 values are in good agreement with the experimental results (Lu et al., 2020; Kürten et al., 2018; Li et al., 2020; Almeida et al., 2013). Herein, the Gibbs formation free energies (ΔG, kcal mol−1) of the studied clusters were calculated as Eq. (1):
where ΔERI-CC2 is the electronic contribution and is the thermal contribution to Gibbs free energy. For subsequent clustering kinetic simulations at different temperatures, the ΔG values of clusters ranging from 218 to 298 K were calculated by Shermo 2.0 (Lu and Chen, 2021) and collected in Table S3.
2.2 Wave function analysis
To better understand the interactions between IA and MSA, the bonding nature was investigated through wave function analysis using Multiwfn 3.7 (Lu and Chen, 2012). Specifically, the molecular electrostatic potential (ESP) was calculated for IA and MSA, which facilitates understanding their potential interaction sites. Moreover, natural bond orbital (NBO) analysis (Reed et al., 1988) was carried out to give a detailed insight into intermolecular interactions. Based on the final identified stable clusters, the NBO information calculated by Gaussian 09 is resolved by Multiwfn, and the key interactive orbitals are visualized by VMD 1.9.3 (Humphrey et al., 1996). To further quantify the binding strength, electron density ρ(r), Laplacian electron density ∇2ρ(r), energy density H(r) at corresponding bond critical points (BCPs) based on atoms in molecules (AIM) theory (Becke, 2007; Lane et al., 2013) were also calculated in this work (Table S1 in the Supplement).
2.3 Atmospheric cluster dynamic simulations
Simulation of the nucleation process of the IA-MSA system is achieved by the Atmospheric Clusters Dynamic Code (ACDC) (McGrath et al., 2012). Specifically, the ACDC derives the steady-state concentration and cluster formation rates by solving the birth–death equations (Eq. 2).
where Ci refers to the cluster i concentration, βi,j is the collision rate coefficient between clusters i and j, γi→j is the evaporation rate coefficient of smaller cluster j from the parent cluster i, and Qi and Si are the outside source and loss term of cluster i, respectively. βi,j is calculated based on the kinetic gas theory, which is given as
where Vi and mi are the volume and mass of cluster i, respectively. kB is the Boltzmann constant, and T is the temperature. Equation (3) is derived from the hard-sphere collision theory where . The diameter Di of cluster i is calculated by Multiwfn (Lu and Chen, 2012). Evaporation rate coefficients, , are derived from ΔG of clusters and the corresponding collision rate coefficients based on the detailed balance assumption (McGrath et al., 2012):
where Pref is the reference pressure (1 atm) at which the Gibbs free energies were determined, and ΔGi is the Gibbs formation free energy of the formation of cluster i from the corresponding monomers.
In the present study, the ACDC simulations only modeled the neutral cluster formation process and did not consider the charge nor the effect of water. Since IA is weakly bound to water, it is less inclined to exist as hydration of IA in tropospheric conditions (Khanniche et al., 2016). Meanwhile, the nucleation efficiency of MSA and water is low (Arquero et al., 2017). Thus, the effect of water on the conclusion in this study is limited. The settings of the boundary conditions of the ACDC simulations are discussed in Sect. S1 (Supplement) and summarized in Table S5.
3.1 Cluster conformational analysis
The obtained most stable structures of (IA)x ⋅ (MSA)y (, , ) clusters are presented in Fig. S1 in the Supplement, and the corresponding Cartesian coordinates are collected in Table S7 in the Supplement. To investigate the intermolecular bonding potential of IA and MSA, the electrostatic potential (ESP) was calculated to analyze their potential interaction sites.
As shown in Fig. 1a, IA has positive ESPs (red region) surrounding its −OH group, with a maximum value of +59.04 kcal mol−1, making the −OH group an effective hydrogen bond (HB) donor. And IA's two terminal oxygens with negative ESPs (−29.09 and −29.47 kcal mol−1) can serve as HB acceptors. Similarly, the −OH group of MSA has the strongest electrophilicity (ESP value of +63.86 kcal mol−1) as the HB donor, while its terminal O atom has strong nucleophilicity as the HB acceptor, due to its lone pair of electrons. In this case, IA and MSA can directly bind with each other via HBs. Moreover, IA possesses positive charge localization (the so-called δ hole) with a maximal ESP value of +51.87 kcal mol−1 at the end of the iodine atom along the O–I direction. This electron-deficient region tends to attract the electron-rich oxygen atom of the MSA to form the halogen bonds (XBs) O–I…O (green band line in Fig. 1a). From the skeletal formula presented in Fig. 1a, we can know that a formed (IA)1 ⋅ (MSA)1 cluster is stabilized by both HBs and XBs. A similar situation has also been found in the larger IA-MSA clusters in Fig. S1.
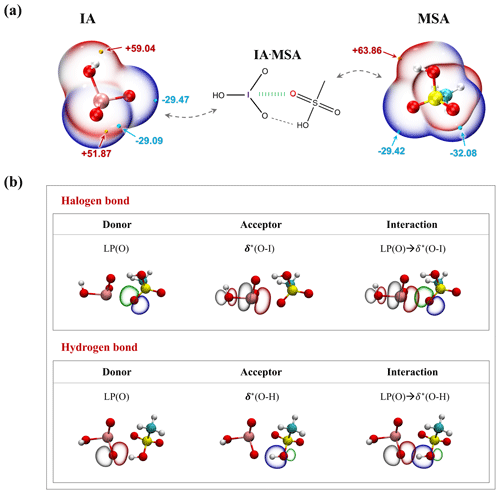
Figure 1(a) The ESP-mapped molecular vdW (van der Waals) surfaces of iodic acid (IA) and methanesulfonic acid (MSA). The pink, red, yellow, cyan, and white spheres represent I, O, S, C, and H atoms, respectively. The yellow and cyan dots indicate the positions of maximums and minimums of ESP (in kcal mol−1), respectively. (b) The donor–acceptor NBOs involved in the (IA)1 ⋅ (MSA)1 cluster. LP indicates the lone-pair orbitals, and δ∗ indicates the antibonding orbitals.
Additionally, as illustrated in Fig. 1b, natural bond orbital (NBO) analysis was performed to reveal the bonding nature of IA and MSA. For the formed O–I…O halogen bond, the lone-pair orbital LP(O) in the terminal oxygen atom of MSA acts as an electron donor, while the antibonding orbital δ∗(O–I) in IA is the electron acceptor. Essentially, halogen bonding originates from the interactions between LP(O) and δ∗(O–I) orbitals, accompanied by intermolecular charge transferring from LP(O) to δ∗(O–I). In the case of the O–H…O hydrogen bond, the LP(O) of IA serves as the donor orbital, and δ∗(O–H) of MSA is the acceptor orbital; the charge shifts from LP(O) to δ∗(O–H). The ESP and NBO results indicate that IA and MSA are capable of forming both HBs and XBs and have the potential to form stable clusters.
To quantify the bonding strength of HBs or XBs within the studied IA-MSA clusters (Fig. S1), the bonding properties, including electron density ρ(r), Laplacian electron density ∇2ρ(r), and energy density H(r) at the bond critical points (BCPs), are calculated based on the AIM methodology (Becke, 2007; Lane et al., 2013) and collected in Table S1. For O–I…O XBs, the ρ(r), ∇2ρ(r), and H(r) values at the BCPs are in the ranges of 0.0143 to 0.0849, 0.0409 to 0.1589, and −0.0265 to 0.0019 a.u., respectively. As for O–H…O HBs, the ρ(r), ∇2ρ(r), and H(r) values at the BCPs are in the ranges of 0.0178 to 0.0796, 0.0615 to 0.1141, and −0.0032 to −0.0332 a.u., respectively. The electron density ρ(r) is generally positively correlated with the bond strength, and the ρ(r) values (Table S1) are well within the specified ρ(r) range of HBs (0.002 to 0.040 a.u.) (Grabowski, 2004; Koch and Popelier, 1995), indicating that all the O–H…O non-covalent interactions are indeed HBs. Moreover, according to the classification of HBs (Rozas et al., 2000), all the HBs formed within IA-MSA clusters are medium HBs (12.0<E (interaction energy) <24.0 kcal mol−1) with ∇2ρ(r)>0 and H(r)<0. Overall, the conformational analysis suggests that MSA can stabilize IA clusters by forming relatively strong non-covalent interactions such as HBs and XBs and thus has the potential to form relatively stable clusters with IA.
3.2 Cluster stability analysis
To evaluate the thermodynamic stability of formed IA-MSA clusters, the Gibbs formation free energy (ΔG, kcal mol−1) of each studied (IA)x ⋅ (MSA)y (, , ) cluster at T = 218–298 K ranging from boundary layer to free troposphere (Williamson et al., 2019) and p=1 atm was calculated by Eq. (1) and shown in Table S3. In the present study, the analysis and discussion of the simulation results are mainly at T=278 K.
As shown in Fig. 2a, the ΔG values of IA-MSA clusters at 278 K decrease with increasing cluster size, indicating that the cluster growth process is energetically favorable. And the same trend is also observed at 298 K (Fig. S2) and 258 K (Fig. S3). The ΔG of the (IA)x ⋅ (MSA)1 (x = 1–5) clusters, are 7.71–15.67 kcal mol−1 lower than those of the corresponding (IA)x clusters, indicating that pure-IA clusters could potentially grow by binding with MSA. Moreover, the corresponding total evaporation rate coefficients (∑γ, s−1) of clusters were calculated at 278 K by Eq. (4) and presented in Fig. 2b and Table S4. In general, a lower ∑γ value indicates greater cluster stability. As shown in Fig. 2b, the ∑γ values of larger clusters, (IA)4–6 and (IA)3–4 ⋅ (MSA)2, are significantly lower than those of the corresponding initial, small-sized clusters, indicating that the stability increases during the cluster growth. Considering the competition between collision and evaporation during the clustering process, the ratio of collision frequencies versus total evaporation rate coefficients () was calculated to access the probability of cluster growth. If , further growth of cluster by colliding IA or MSA molecules can be assumed to dominate over cluster evaporation (details in the Sect. S1 of the Supplement). Figure 2c presents the minimum values of for the studied clusters at lowest CIA (106 molec. cm−3), where βIA is the rate coefficient of cluster collision with IA monomer, and CIA is the concentration of IA monomer. Figure 2d presents the results of the collision with MSA (). Similarly, the minimum values of at 298 and 258 K are presented in Figs. S2 and S3, respectively. Among these clusters, the largest (IA)4 ⋅ (MSA)2 and (IA)6 clusters () incline to collide with IA monomer (or MSA monomer) to grow out of the simulated system. As a result, the fluxes for clusters with larger size than (IA)4 ⋅ (MSA)2 and (IA)6 are counted in the cluster formation rate J.
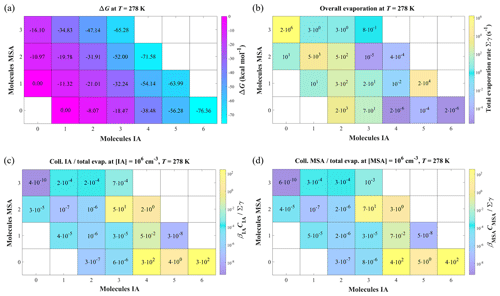
Figure 2(a) Gibbs formation free energy (ΔG, kcal mol−1) of the (IA)x ⋅ (MSA)y (, , ) clusters calculated at the RI-CC2/aug-cc-pV(T+d)Z(-PP)//ωB97X-D/6-311 G(3df,3pd) + aug-cc-pVTZ-PP level of theory; T=278 K, and p=1 atm. (b) The total evaporation rate coefficients (∑γ, s−1) and the ratios of collision frequencies with (c) IA monomer or (d) MSA monomer versus total evaporation rate coefficients ( or ) of the corresponding clusters. β is the rate coefficient of cluster collision with monomer, and C is the monomer concentration.
3.3 Cluster formation rates
To comprehensively explore the effect of MSA on IA cluster formation kinetically, the IA-MSA cluster formation rate J (cm−3 s−1) was simulated under different atmospheric conditions using ACDC. Herein, we first explored the changes of J after the intervention of different concentrations of MSA ([MSA]), using the pure-IA system as a reference. Based on the field measurement, [IA] in the ACDC simulation is set to be in the range of 106–108 molec. cm−3 (Sipilä et al., 2016); [MSA] = 106, 107, and 108 molec. cm−3 (Chen et al., 2018; Berresheim et al., 2002; Davis et al., 1998). As for the setting of condensation sink coefficient (CS), the different CS values (–2.6 × 10−3 s−1) have an impact on the simulated J, especially in the case of low J (Fig. S4), but less on presenting the promotion of MSA on IA cluster formation and the main conclusions of this study. Hence, the CS is chosen as a typical coastal value ( s−1) (Dal Maso et al., 2002), which is uniform for all clusters.
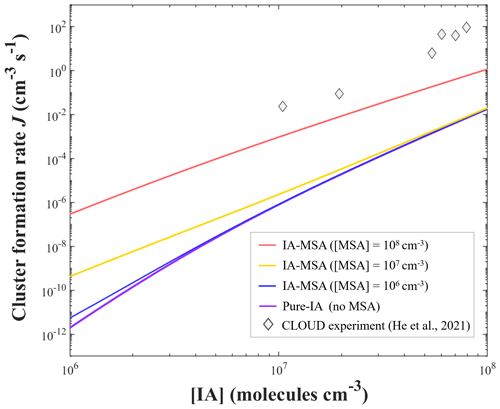
Figure 3Simulated cluster formation rates J (cm−3 s−1) as a function of iodic acid concentration [IA], with different concentrations of methanesulfonic acid [MSA] of 106 (blue), 107 (yellow), 108 (red), and 0 molec. cm−3 (purple, “pure-IA”), at T = 278 K, and CS = s−1. The gray diamonds are the measured rate data from the CLOUD experiment at T=283 K (He et al., 2021).
As shown in Fig. 3, the simulated J of pure-IA nucleation (purple line) is much lower than the rate obtained from the CLOUD experiment (He et al., 2021). The J values of the IA-MSA system with varying [MSA] (red, yellow, and blue lines) are all higher than those of the pure-IA system (purple line). Particularly, at a lower [IA] of 106 molec. cm−3, the involvement of MSA results in a greater boost in J. Briefly, MSA can promote J of IA clusters to a higher level, which is a reflection of the stabilizing effect of MSA on IA clusters. However, the J of IA-MSA nucleation was still much less than the experimental results (He et al., 2021), even at a high [MSA] (108 molec. cm−3). The large rate difference suggests that MSA stabilizes IA less efficiently than the potential iodine-containing components.
To quantify such enhancement of MSA on J, here we defined an enhancement strength R as the following Eq. (5):
where JIA-MSA and Jpure-IA indicate the J of IA-MSA and pure-IA nucleating systems, respectively. x and y are the atmospheric concentrations of IA and MSA, respectively.
During nucleating processes, variations in ambient conditions (precursor concentration and temperature) can affect JIA-MSA and Jpure-IA as well as the R of MSA. Herein, the simulations were performed in a wide range of atmospheric temperatures (T = 218 to 298 K) and concentrations of IA (106–108 molec. cm−3) and MSA (106 to 108 molec. cm−3).
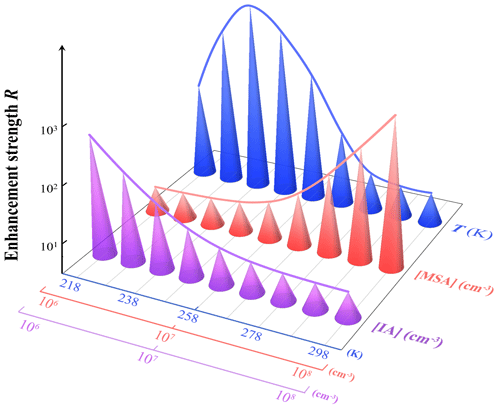
Figure 4Enhancement strength R of MSA on cluster formation rates under different atmospheric conditions: T = 218 to 298 K (blue cones, [IA] = 107 and [MSA] = 107 molec. cm−3), [MSA] = 106 to 108 molec. cm−3 (red cones, T = 278 K and [IA] = 107 molec. cm−3), [IA] = 106 to 108 molec. cm−3 (purple cones, T = 278 K and [MSA] = 107 molec. cm−3), and CS = 2.0 × 10−3 s−1.
As shown in Fig. 4, the enhancement strength, R, of MSA decreases with increasing [IA] (106 → 108 molec. cm−3), under the condition of T = 278 K and [MSA] = 107 molec. cm−3 (purple line). The specific R values are summarized in Table S6. This is because the contribution of pure-IA clusters to nucleation becomes higher with increasing [IA], thereby diminishing that of IA-MSA clusters (smaller R). Conversely at lower [IA] (106 molec. cm−3), the effect of R of MSA on J could reach 211-fold, even when [MSA] is only at a median value (107 molec. cm−3). The R increases with increasing [MSA] (106 → 108 molec. cm−3) (orange line) due to more IA-MSA clusters formed. Interestingly, as the temperature decreases from 298 to 218 K (blue line), R first increases (298 → 238 K) and then decreases (238 → 218 K). During the temperature range from 298 to 238 K, the decrease in temperature diminishes cluster evaporation (Eq. 4), which in turn promotes IA-MSA cluster formation and leads to an increase in R. When the temperature is very low, between 218 and 238 K, the effect of cluster evaporation is almost negligible, and the nucleation process is primarily limited by collisions between clusters or molecules, namely, the kinetic limit process. In this case, the lower T reduces the collision rate and thus results in a decrease in R. The numerator, JIA-MSA, in Eq. (5) is affected by the formation of both pure-IA clusters and IA-MSA clusters, while the denominator, Jpure-IA, is only affected by the formation of pure-IA clusters. When the overall intermolecular collision rate between IA and IA, as well as IA and MSA, is reduced due to the decrease in temperature, the numerator would be affected more than the denominator in Eq. (5), which in turn leads to a reduced R. As a result of the above analysis, the effect of the IA-MSA system on the nucleation process varies with the [IA], [MSA], and T, and this is particularly important in regions with lower T, sparse IA, and rich MSA.
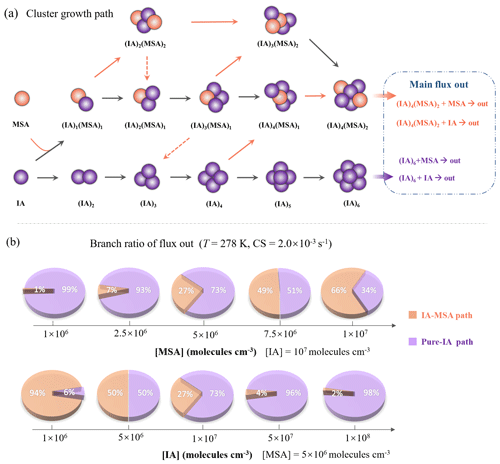
Figure 5(a) Main cluster growth pathway of the IA-MSA nucleating system at T=278 K, CS = s−1, [IA] = 107, and [MSA] = 5×106 molec. cm−3. The black and orange arrows refer to the pathways of colliding with IA and MSA, respectively, where the dashed arrows indicate the evaporation of MSA. (b) Branch ratio of IA-MSA (orange pieces) and pure-IA (purple pieces) growth pathway under varying [MSA] (106–107 molec. cm−3) and [IA] (106–108 molec. cm−3).
3.4 Cluster growth pathways
According to the analysis above, MSA can stabilize IA clusters, thereby enhancing cluster formation rate. However, the mechanism of how MSA and IA jointly contribute to cluster formation is still unclear. Thus, the detailed cluster growth pathways were tracked by ACDC and shown in Fig. 5a.
The main clustering pathways can be divided into two types: (i) IA self-nucleation and (ii) IA-MSA cluster formation. The studied clusters that did not appear in the cluster growth pathway are mainly due to their low stability. For the IA self-nucleation pathway, cluster growth proceeds mainly via the collisional binding of IA monomers ((IA)), which is consistent with the reported pure-IA nucleation mechanism (Rong et al., 2020). For the IA-MSA pathway, it starts from the heterodimer (IA)1 ⋅ (MSA)1 and then grows primarily through IA addition, resulting in the (IA)4 ⋅ (MSA)2 clusters with sufficient stability to grow out of the simulated system (Fig. 2c). The results suggest that MSA can directly participate in the IA-involved nucleation by forming relatively stable IA-MSA clusters.
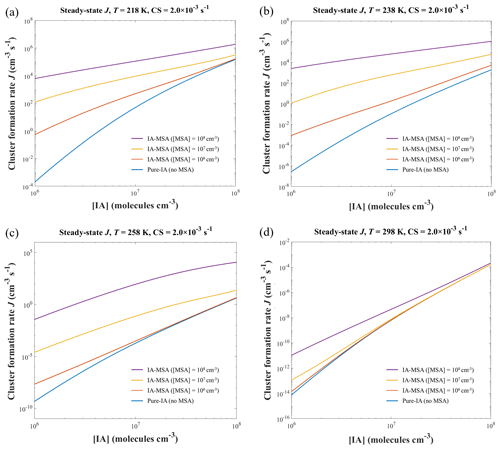
Figure 6The simulated cluster formation rate J (cm−3 s−1) of the IA-MSA system at different temperatures (a) 218, (b) 238, (c) 258, and (d) 298 K; [IA] = 106–108 molec. cm−3; [MSA] = 0, 106, 107, and 108 molec. cm−3; and CS = s−1.
In the atmosphere, the distribution of IA and MSA varies by region, affecting the contribution of IA-MSA clustering pathways accordingly. Hence, the branch ratios of flux out through the IA-MSA path (orange pieces) and pure-IA path (purple pieces) at varying [MSA] (106–107 molec. cm−3) and [IA] (106–108 molec. cm−3) are presented in Fig. 5b to access the impact of the IA-MSA mechanism. As shown in Fig. 5b, the branch ratio of IA-MSA and pure-IA path is highly dependent on [MSA] and [IA]. At the conditions of T = 278 K, CS = s−1, and [IA] = 107 molec. cm−3, the contribution of the IA-MSA path increases from 1 % to 66 % with increasing [MSA]. Additionally, given the uneven distribution of IA, the analysis was further carried out within the atmospherically relevant range of [IA] (106–108 molec. cm−3). The results show that the contribution of the IA-MSA path decreases from 94 % to 2 % with increasing [IA] (106–108 molec. cm−3). These findings indicate that the IA-MSA mechanism contributes more in regions with higher [MSA] and lower [IA]. Furthermore, the branch ratio was calculated based on field conditions (temperatures and [IA]) reported by He et al. (2021) and presented in Fig. S5. The results indicate that the IA-MSA mechanism does have stronger effects in polar regions than in mid-latitude coastal regions due to lower temperatures, which is also consistent with the above findings.
Most of the analysis above was performed at 278 K. To further probe the impact of temperature on J systematically, Fig. 6 presents the simulated J at additional temperatures (218, 238, 258 and 298 K), [IA] = 106–108 molec. cm−3, [MSA] = 106 (red line), 107 (yellow line), and 108 molec. cm−3 (purple line). At a relatively high T=298 K (Fig. 6d), the improvement on J by the addition of MSA was not significant compared to the pure-IA system, except at higher [MSA] = 108 molec. cm−3 and relatively lower [IA]. At lower T=258 K (Fig. 6c), the enhancement in J by MSA is stronger in all cases except at lowest [MSA] = 106 molec. cm−3. Moreover, such a boost in J was further enhanced at 238 K (Fig. 6b). Lower concentrations of MSA (106 molec. cm−3) also significantly promote the formation of IA clusters, mainly because the low temperature weakens the cluster evaporation.
Interestingly, the comparison of the simulations at 218 K (Fig. 6a) and 238 K (Fig. 6b) shows that the decrease in temperature does not further improve J to a higher level. Instead, there is a decrease of the enhancement of MSA at higher [IA] = 107–108 molec. cm−3. The reason for this phenomenon, which was also discussed in Sect. 3.3, is that at such low temperatures cluster growth is more dependent on collisions and less on evaporation. And the low temperature reduces the rate of collision between clusters or molecules.
Compared to the field observations at Mace Head (Sipilä et al., 2016) and Arctic sites (Beck et al., 2021), the rate of the IA-MSA mechanism is also significantly lower. This indicates that the contribution of MSA to IA particle formation under atmospheric conditions is relatively limited, and a more efficient stabilizer for IA should be involved in the nucleating process, such as other iodine-containing components such as HIO2 or iodine oxides (I2O4 and I2O5). Moreover, considering the complexity of the marine atmosphere, other non-iodine nucleation precursors, such as SA, NH3, amines, etc., may also affect the nucleation process. This is particularly true with SA, because MSA and SA coexist in the air and both are formed during the oxidation of DMS in the marine atmosphere. Therefore, in future studies, the influence of the above factors on the nucleation mechanism of marine aerosols will also be considered.
The present work systematically investigates the joint nucleation mechanisms of two critical marine nucleation precursors, i.e., methanesulfonic acid (MSA) and iodic acid (IA), using the quantum chemical approach and Atmospheric Cluster Dynamics Code (ACDC). The results suggest that the self-nucleation rate of IA is much lower than that of the CLOUD experiment, indicating the importance of stabilizers for IA in the nucleation process. We find that MSA can stabilize IA cluster via both hydrogen and halogen bonds and thus promote IA cluster formation rate, especially in low-temperature environments with sparse IA and rich MSA. The corresponding IA-MSA nucleating mechanism can be described by two distinct pathways: (i) pure-IA cluster formation and (ii) IA-MSA cluster formation, indicating that IA and MSA can jointly nucleate. The IA-MSA nucleation is highly dependent on the distribution of MSA and IA in the marine atmosphere. However, IA-MSA nucleation rates are far from sufficient to explain the field observations, indicating that additional essential precursors need to be considered (e.g., H2SO4, HIO2, NH3, and amines). Nucleation among these components is likely to be synergistic, with only varying magnitudes of contribution. For example, both SA and MSA originate from the oxidation of DMS, so their coexistence in the atmosphere may synergistically promote the formation of IA clusters, which is worthy of future studies.
The current study provides molecular-level evidence that IA and MSA can jointly nucleate, and the IA-MSA joint nucleation is more efficient than the IA self-nucleation. More broadly, this finding helps to construct a more comprehensive marine multicomponent nucleation model.
The data in this article are available from the corresponding author upon request (zhangxiuhui@bit.edu.cn).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-22-6103-2022-supplement.
XZ designed the research. AN performed the quantum chemistry calculations and the ACDC simulations. AN, LL, and LJ analyzed data. AN and XZ wrote the paper with contributions from all of the other co-authors.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We acknowledge the National Supercomputing Center in Shenzhen for providing the computational resources and the TURBOMOLE program.
This work was supported by the National Natural Science Foundation of China (grant no. 21976015). Ling Liu was supported by the China Postdoctoral Science Foundation (grant no. 2020M680013) and the National Natural Science Foundation of China (grant no. 4210050126).
This paper was edited by Markku Kulmala and reviewed by three anonymous referees.
Ahlrichs, R., Bär, M., Häser, M., Horn, H., and Kölmel, C.: Electronic-Structure Calculations on Workstation Computers: The program system turbomole, Chem. Phys. Lett., 162, 165–169, https://doi.org/10.1016/0009-2614(89)85118-8, 1989.
Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurtén, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppä, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petäjä, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamäki, H., and Kirkby, J.: Molecular understanding of sulphuric acid–amine particle nucleation in the atmosphere, Nature, 502, 359–363, https://doi.org/10.1038/nature12663, 2013.
Arquero, K. D., Xu, J., Gerber, R. B., and Finlayson-Pitts, B. J.: Particle formation and growth from oxalic acid, methanesulfonic acid, trimethylamine and water: a combined experimental and theoretical study, Phys. Chem. Chem. Phys., 19, 28286–28301, https://doi.org/10.1039/C7CP04468B, 2017.
Baccarini, A., Karlsson, L., Dommen, J., Duplessis, P., Vüllers, J., Brooks, I. M., Saiz-Lopez, A., Salter, M., Tjernström, M., Baltensperger, U., Zieger, P., and Schmale, J.: Frequent new particle formation over the high Arctic pack ice by enhanced iodine emissions, Nat. Commun., 11, 4924, https://doi.org/10.1038/s41467-020-18551-0, 2020.
Bates, T. S., Lamb, B. K., Guenther, A., Dignon, J., and Stoiber, R. E.: Sulfur emissions to the atmosphere from natural sourees, J. Atmos. Chem., 14, 315–337, https://doi.org/10.1007/BF00115242,1992.
Beck, L. J., Sarnela, N., Junninen, H., Hoppe, C. J. M., Garmash, O., Bianchi, F., Riva, M., Rose, C., Peräkylä, O., Wimmer, D., Kausiala, O., Jokinen, T., Ahonen, L., Mikkilä, J., Hakala, J., He, X., Kontkanen, J., Wolf, K. K. E., Cappelletti, D., Mazzola, M., Traversi, R., Petroselli, C., Viola, A. P., Vitale, V., Lange, R., Massling, A., Nøjgaard, J. K., Krejci, R., Karlsson, L., Zieger, P., Jang, S., Lee, K., Vakkari, V., Lampilahti, J., Thakur, R. C., Leino, K., Kangasluoma, J., Duplissy, E., Siivola, E., Marbouti, M., Tham, Y. J., Saiz-Lopez, A., Petäjä, T., Ehn, M., Worsnop, D. R., Skov, H., Kulmala, M., Kerminen, V., and Sipilä, M.: Differing Mechanisms of New Particle Formation at Two Arctic Sites, Geophys. Res. Lett., 48, e2020GL091334, https://doi.org/10.1029/2020GL091334, 2021.
Becke, A.: The quantum theory of atoms in molecules: from solid state to DNA and drug design, John Wiley & Sons, https://doi.org/10.1002/9783527610709, 2007.
Berresheim, H., Elste, T., Tremmel, H. G., Allen, A. G., Hansson, H. C., Rosman, K., Dal Maso, M., Makela, J. M., Kulmala, M., and O'Dowd, C. D.: Gas-aerosol relationships of H2SO4, MSA, and OH: Observations in the coastal marine boundary layer at Mace Head, Ireland, J. Geophys. Res.-Atmos., 107, PAR 5-1–PAR 5-12 https://doi.org/10.1029/2000jd000229, 2002.
Charlson, R. J., Lovelock, J. E., Andreae, M. O., and Warren, S. G.: Oceanic Phytoplankton, Atmospheric Sulfur, Cloud Albedo and Climate, Nature, 326, 655–661, https://doi.org/10.1038/326655a0, 1987.
Chen, Q., Sherwen, T., Evans, M., and Alexander, B.: DMS oxidation and sulfur aerosol formation in the marine troposphere: a focus on reactive halogen and multiphase chemistry, Atmos. Chem. Phys., 18, 13617–13637, https://doi.org/10.5194/acp-18-13617-2018, 2018.
Dal Maso, M., Kulmala, M., Lehtinen, K. E. J., Makela, J. M., Aalto, P., and O'Dowd, C. D.: Condensation and coagulation sinks and formation of nucleation mode particles in coastal and boreal forest boundary layers, J. Geophys. Res.-Atmos., 107, PAR 2-1–PAR 2-10, https://doi.org/10.1029/2001jd001053, 2002.
Davis, D., Chen, G., Kasibhatla, P., Jefferson, A., Tanner, D., Eisele, F., Lenschow, D., Neff, W., and Berresheim, H.: DMS oxidation in the Antarctic marine boundary layer: Comparison of model simulations and field observations of DMS, DMSO, DMSO2, H2SO4(g), MSA(g), and MSA(p), J. Geophys. Res.-Atmos., 103, 1657–1678, https://doi.org/10.1029/97jd03452, 1998.
Dawson, M. L., Varner, M. E., Perraud, V., Ezell, M. J., Gerber, R. B., and Finlayson-Pitts, B. J.: Simplified mechanism for new particle formation from methanesulfonic acid, amines, and water via experiments and ab initio calculations, P. Natl. Acad. Sci. USA, 109, 18719–18724, https://doi.org/10.1073/pnas.1211878109, 2012.
Dunning, T. H., Peterson, K. A., and Wilson, A. K.: Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited, J. Chem. Phys., 114, 9244–9253, https://doi.org/10.1063/1.1367373, 2001.
Eisele, F. L. and Tanner, D. J.: Measurement of the gas phase concentration of H2SO4 and methane sulfonic acid and estimates of H2SO4 production and loss in the atmosphere, J. Geophys. Res.-Atmos., 98, 9001–9010, https://doi.org/10.1029/93JD00031, 1993.
Elm, J. and Kristensen, K.: Basis set convergence of the binding energies of strongly hydrogen-bonded atmospheric clusters, Phys. Chem. Chem. Phys., 19, 1122–1133, https://doi.org/10.1039/C6CP06851K, 2017.
Francl, M. M., Pietro, W. J., Hehre, W. J., Binkley, J. S., Gordon, M. S., DeFrees, D. J., and Pople, J. A.: Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements, J. Chem. Phys., 77, 3654–3665, https://doi.org/10.1063/1.444267, 1982.
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Men nucci, B., Petersson, G. A., Nakatsuji, H., Caricato, M., Li, X.,Hratchian, H. P., Izmaylov, A. F., Bloino, J., Zheng, G., Son nenberg, J. L., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J.,Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Montgomery, J. A. Jr., Peralta, J. E., Ogliaro, F., Bearpark, M.,Heyd, J. J., Brothers, E., Kudin, K. N., Staroverov, V. N., Kobayashi,R., Normand, J., Raghavachari, K., Rendell, A., Burant, J. C., Iyengar, S. S., Tomasi, J., Cossi, M., Rega, N., Millam, J. M., Klene, M., Knox, J. E., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochter ski, J. W., Martin, R. L., Morokuma, K., Zakrzewski, V. G., Voth, G. A., Salvador, P., Dannenberg, J. J., Dapprich, S., Daniels, A. D., Farkas, O., Foresman, J. B., Ortiz, J. V., Cioslowski, J., and Fox, D. J.: Gaussian 09, Revision A.02, Gaussian Inc., Wallingford, CT, https://gaussian.com/g09citation/ (last access: 7 May 2022), 2009.
Grabowski, S. J.: Hydrogen bonding strength – measures based on geometric and topological parameters, J. Phys. Org. Chem., 17, 18–31, https://doi.org/10.1002/poc.685, 2004.
Hatakeyama, S., Okuda, M., and Akimoto, H.: Formation of sulfur dioxide and methanesulfonic acid in the photooxidation of dimethyl sulfide in the air, Geophys. Res. Lett., 9, 583–586, https://doi.org/10.1029/GL009i005p00583, 1982.
Hattig, C. and Weigend, F.: CC2 excitation energy calculations on large molecules using the resolution of the identity approximation, J. Chem. Phys., 113, 5154–5161, https://doi.org/10.1063/1.1290013, 2000.
He, X.-C., Tham, Y. J., Dada, L., Wang, M., Finkenzeller, H., Stolzenburg, D., Iyer, S., Simon, M., Kürten, A., Shen, J., Rörup, B., Rissanen, M., Schobesberger, S., Baalbaki, R., Wang, D. S., Koenig, T. K., Jokinen, T., Sarnela, N., Beck, L. J., Almeida, J., Amanatidis, S., Amorim, A., Ataei, F., Baccarini, A., Bertozzi, B., Bianchi, F., Brilke, S., Caudillo, L., Chen, D., Chiu, R., Chu, B., Dias, A., Ding, A., Dommen, J., Duplissy, J., El Haddad, I., Gonzalez Carracedo, L., Granzin, M., Hansel, A., Heinritzi, M., Hofbauer, V., Junninen, H., Kangasluoma, J., Kemppainen, D., Kim, C., Kong, W., Krechmer, J. E., Kvashin, A., Laitinen, T., Lamkaddam, H., Lee, C. P., Lehtipalo, K., Leiminger, M., Li, Z., Makhmutov, V., Manninen, H. E., Marie, G., Marten, R., Mathot, S., Mauldin, R. L., Mentler, B., Möhler, O., Müller, T., Nie, W., Onnela, A., Petäjä, T., Pfeifer, J., Philippov, M., Ranjithkumar, A., Saiz-Lopez, A., Salma, I., Scholz, W., Schuchmann, S., Schulze, B., Steiner, G., Stozhkov, Y., Tauber, C., Tomé, A., Thakur, R. C., Väisänen, O., Vazquez-Pufleau, M., Wagner, A. C., Wang, Y., Weber, S. K., Winkler, P. M., Wu, Y., Xiao, M., Yan, C., Ye, Q., Ylisirniö, A., Zauner-Wieczorek, M., Zha, Q., Zhou, P., Flagan, R. C., Curtius, J., Baltensperger, U., Kulmala, M., Kerminen, V.-M., Kurtén, T., Donahue, N. M., Volkamer, R., Kirkby, J., Worsnop, D. R., and Sipilä, M.: Role of iodine oxoacids in atmospheric aerosol nucleation, Science, 371, 589–595, https://doi.org/10.1126/science.abe0298, 2021.
Hodshire, A. L., Campuzano-Jost, P., Kodros, J. K., Croft, B., Nault, B. A., Schroder, J. C., Jimenez, J. L., and Pierce, J. R.: The potential role of methanesulfonic acid (MSA) in aerosol formation and growth and the associated radiative forcings, Atmos. Chem. Phys., 19, 3137–3160, https://doi.org/10.5194/acp-19-3137-2019, 2019.
Humphrey, W., Dalke, A., and Schulten, K.: VMD: Visual molecular dynamics, J. Mol. Graphics, 14, 33–38, https://doi.org/10.1016/0263-7855(96)00018-5, 1996.
IPCC: Long-term climate change: projections, commitments and irreversibility, in: Climate Change 2013 – The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, 1029–1136, 2013.
Karl, M., Gross, A., Leck, C., and Pirjola, L.: Intercomparison of dimethylsulfide oxidation mechanisms for the marine boundary layer: Gaseous and particulate sulfur constituents, J. Geophys. Res.-Atmos., 112, D15304, https://doi.org/10.1029/2006jd007914, 2007.
Kerminen, V.-M., Chen, X., Vakkari, V., Petäjä, T., Kulmala, M., and Bianchi, F.: Atmospheric new particle formation and growth: review of field observations, Environ. Res. Lett., 13, 103003, https://doi.org/10.1088/1748-9326/aadf3c, 2018.
Khanniche, S., Louis, F., Cantrel, L., and Černušák, I.: A theoretical study of the microhydration of iodic acid (HOIO2), Comput. Theor. Chem., 1094, 98–107, https://doi.org/10.1016/j.comptc.2016.09.010, 2016.
Koch, U. and Popelier, P. L. A.: Characterization of CHO hydrogen bonds on the basis of the charge density, J. Phys. Chem., 99, 9747–9754, https://doi.org/10.1021/j100024a016, 1995.
Kulmala, M.: How particles nucleate and grow, Science, 302, 1000–1001, https://doi.org/10.1126/science.1090848, 2003.
Kulmala, M., Kontkanen, J., Junninen, H., Lehtipalo, K., Manninen, H. E., Nieminen, T., Petäjä, T., Sipilä, M., Schobesberger, S., Rantala, P., Franchin, A., Jokinen, T., Järvinen, E., Äijälä, M., Kangasluoma, J., Hakala, J., Aalto, P. P., Paasonen, P., Mikkilä, J., Vanhanen, J., Aalto, J., Hakola, H., Makkonen, U., Ruuskanen, T., Mauldin, R. L., III, Duplissy, J., Vehkamäki, H., Bäck, J., Kortelainen, A., Riipinen, I., Kurtén, T., Johnston, M. V., Smith, J. N., Ehn, M., Mentel, T. F., Lehtinen, K. E. J., Laaksonen, A., Kerminen, V.-M., and Worsnop, D. R.: Direct Observations of Atmospheric Aerosol Nucleation, Science, 339, 943–946, https://doi.org/10.1126/science.1227385, 2013.
Kürten, A., Li, C., Bianchi, F., Curtius, J., Dias, A., Donahue, N. M., Duplissy, J., Flagan, R. C., Hakala, J., Jokinen, T., Kirkby, J., Kulmala, M., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Onnela, A., Rissanen, M. P., Simon, M., Sipilä, M., Stozhkov, Y., Tröstl, J., Ye, P., and McMurry, P. H.: New particle formation in the sulfuric acid–dimethylamine–water system: reevaluation of CLOUD chamber measurements and comparison to an aerosol nucleation and growth model, Atmos. Chem. Phys., 18, 845–863, https://doi.org/10.5194/acp-18-845-2018, 2018.
Lane, J. R., Contreras-García, J., Piquemal, J.-P., Miller, B. J., and Kjaergaard, H. G.: Are bond critical points really critical for hydrogen bonding?, J. Chem. Theory Comput., 9, 3263–3266, https://doi.org/10.1021/ct400420r, 2013.
Li, H., Ning, A., Zhong, J., Zhang, H., Liu, L., Zhang, Y., Zhang, X., Zeng, X. C., and He, H.: Influence of atmospheric conditions on sulfuric acid-dimethylamine-ammonia-based new particle formation, Chemosphere, 245, 125554, https://doi.org/10.1016/j.chemosphere.2019.125554, 2020.
Lu, T. and Chen, F. W.: Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 33, 580–592, https://doi.org/10.1002/jcc.22885, 2012.
Lu, T. and Chen, Q.: Shermo: A general code for calculating molecular thermochemistry properties, Comput. Theor. Chem., 1200, 113249, https://doi.org/10.1016/j.comptc.2021.113249, 2021.
Lu, Y., Liu, L., Ning, A., Yang, G., Liu, Y., Kurtén, T., Vehkamäki, H., Zhang, X., and Wang, L.: Atmospheric sulfuric acid-dimethylamine nucleation enhanced by trifluoroacetic acid, Geophys. Res. Lett., 47, e2019GL085627, https://doi.org/10.1029/2019GL085627, 2020.
Martín, J. C. G., Lewis, T. R., Blitz, M. A., Plane, J. M., Kumar, M., Francisco, J. S., and Saiz-Lopez, A.: A gas-to-particle conversion mechanism helps to explain atmospheric particle formation through clustering of iodine oxides, Nat. Commun., 11, 4521, https://doi.org/10.1038/s41467-020-18252-8, 2020.
McGrath, M. J., Olenius, T., Ortega, I. K., Loukonen, V., Paasonen, P., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 12, 2345–2355, https://doi.org/10.5194/acp-12-2345-2012, 2012.
Merikanto, J., Spracklen, D. V., Mann, G. W., Pickering, S. J., and Carslaw, K. S.: Impact of nucleation on global CCN, Atmos. Chem. Phys., 9, 8601–8616, https://doi.org/10.5194/acp-9-8601-2009, 2009.
O'Dowd, C. D. and de Leeuw, G.: Marine aerosol production: a review of the current knowledge, Philos. T. R. Soc. A, 365, 1753–1774, https://doi.org/10.1098/rsta.2007.2043, 2007.
O'Dowd, C. D., Jimenez, J. L., Bahreini, R., Flagan, R. C., Seinfeld, J. H., Hämeri, K., Pirjola, L., Kulmala, M., Jennings, S. G., and Hoffmann, T.: Marine aerosol formation from biogenic iodine emissions, Nature, 417, 632–636, https://doi.org/10.1038/nature00775, 2002.
Perraud, V., Horne, J. R., Martinez, A. S., Kalinowski, J., Meinardi, S., Dawson, M. L., Wingen, L. M., Dabdub, D., Blake, D. R., Gerber, R. B., and Finlayson-Pitts, B. J.: The future of airborne sulfur-containing particles in the absence of fossil fuel sulfur dioxide emissions, P. Natl. Acad. Sci. USA, 112, 13514–13519, https://doi.org/10.1073/pnas.1510743112, 2015.
Peterson, K. A., Figgen, D., Goll, E., Stoll, H., and Dolg, M.: Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements, J. Chem. Phys., 119, 11113–11123, https://doi.org/10.1063/1.1622924, 2003.
Reed, A. E., Curtiss, L. A., and Weinhold, F.: Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 88, 899–926, https://doi.org/10.1021/cr00088a005, 1988.
Rong, H., Liu, J., Zhang, Y., Du, L., Zhang, X., and Li, Z.: Nucleation mechanisms of iodic acid in clean and polluted coastal regions, Chemosphere, 253, 126743, https://doi.org/10.1016/j.chemosphere.2020.126743, 2020.
Rozas, I., Alkorta, I., and Elguero, J.: Behavior of ylides containing N, O, and C atoms as hydrogen bond acceptors, J. Am. Chem. Soc., 122, 11154–11161, https://doi.org/10.1021/ja0017864, 2000.
Rappé, A. K., Casewit, C. J., Colwell, K. S., Goddard III, W. A., and Skiff, W. M.: UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 114, 10024–10035, https://doi.org/10.1021/ja00051a040, 1992.
Schmitz, G. and Elm, J.: Assessment of the DLPNO Binding Energies of Strongly Noncovalent Bonded Atmospheric Molecular Clusters, ACS omega, 5, 7601–7612, https://doi.org/10.1021/acsomega.0c00436, 2020.
Shaw, G. E.: Bio-Controlled Thermostasis Involving the Sulfur Cycle, Climatic Change, 5, 297–303, https://doi.org/10.1007/Bf02423524, 1983.
Sipilä, M., Sarnela, N., Jokinen, T., Henschel, H., Junninen, H., Kontkanen, J., Richters, S., Kangasluoma, J., Franchin, A., Peräkylä, O., Rissanen, M. P., Ehn, M., Vehkamäki, H., Kurten, T., Berndt, T., Petäjä, T., Worsnop, D., Ceburnis, D., Kerminen, V.-M., Kulmala, M., and O'Dowd, C.: Molecular-scale evidence of aerosol particle formation via sequential addition of HIO3, Nature, 537, 532–534, https://doi.org/10.1038/nature19314, 2016.
Stewart, J. J. P.: Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters, J. Mol. Model., 19, 1–32, https://doi.org/10.1007/s00894-012-1667-x, 2013.
Stewart, J. J. P.: MOPAC2016, Colorado Springs, CO (USA), http://openmopac.net/MOPAC2016.html (last access: 7 May 2022), 2016.
Takegawa, N., Seto, T., Moteki, N., Koike, M., Oshima, N., Adachi, K., Kita, K., Takami, A., and Kondo, Y.: Enhanced new particle formation above the marine boundary layer over the Yellow Sea: Potential impacts on cloud condensation nuclei, J. Geophys. Res.-Atmos., 125, e2019JD031448, https://doi.org/10.1029/2019JD031448, 2020.
Williamson, C. J., Kupc, A., Axisa, D., Bilsback, K. R., Bui, T., Campuzano-Jost, P., Dollner, M., Froyd, K. D., Hodshire, A. L., Jimenez, J. L., Kodros, J. K., Luo, G., Murphy, D. M., Nault, B. A., Ray, E. A., Weinzierl, B., Wilson, J. C., Yu, F., Yu, P., Pierce, J. R., and Brock, C. A.: A large source of cloud condensation nuclei from new particle formation in the tropics, Nature, 574, 399–403, https://doi.org/10.1038/s41586-019-1638-9, 2019.
Xia, D., Chen, J., Yu, H., Xie, H., Wang, Y., Wang, Z., Xu, T., and Allen, D. T.: Formation Mechanisms of Iodine–Ammonia Clusters in Polluted Coastal Areas Unveiled by Thermodynamics and Kinetic Simulations, Environ. Sci. Technol., 54, 9235–9242, https://doi.org/10.1021/acs.est.9b07476, 2020.
Yu, F. and Luo, G.: Simulation of particle size distribution with a global aerosol model: contribution of nucleation to aerosol and CCN number concentrations, Atmos. Chem. Phys., 9, 7691–7710, https://doi.org/10.5194/acp-9-7691-2009, 2009.
Yu, H., Ren, L., Huang, X., Xie, M., He, J., and Xiao, H.: Iodine speciation and size distribution in ambient aerosols at a coastal new particle formation hotspot in China, Atmos. Chem. Phys., 19, 4025–4039, https://doi.org/10.5194/acp-19-4025-2019, 2019.
Zhang, J. and Dolg, M.: ABCluster: the artificial bee colony algorithm for cluster global optimization, Phys. Chem. Chem. Phys., 17, 24173–24181, https://doi.org/10.1039/c5cp04060d, 2015.
Zhang, R.: Atmospheric science. Getting to the critical nucleus of aerosol formation, Science, 328, 1366–1367, https://doi.org/10.1126/science.1189732, 2010.
Zheng, G., Wang, Y., Wood, R., Jensen, M. P., Kuang, C., McCoy, I. L., Matthews, A., Mei, F., Tomlinson, J. M., Shilling, J. E., Zawadowicz, M. A., Crosbie, E., Moore, R., Ziemba, L., Andreae, M. O., and Wang, J.: New particle formation in the remote marine boundary layer, Nat. Commun., 12, 1–10, https://doi.org/10.1038/s41467-020-20773-1, 2021.





