An interactive stratospheric aerosol model intercomparison of solar geoengineering by stratospheric injection of SO₂ or accumulation-mode sulfuric acid aerosols

Studies of stratospheric solar geoengineering have tended to focus on modification of the sulfuric acid aerosol layer, and almost all climate model experiments that mechanistically increase the sulfuric acid aerosol burden assume injection of SO₂. A key finding from these model studies is that the radiative forcing would increase sublinearly with increasing SO₂ injection because most of the added sulfur increases the mass of existing particles, resulting in shorter aerosol residence times and aerosols that are above the optimal size for scattering. Injection of SO₃ or H₂SO₄ from an aircraft in stratospheric flight is expected to produce particles predominantly in the accumulation-mode size range following microphysical processing within an expanding plume, and such injection may result in a smaller average stratospheric particle size, allowing a given injection of sulfur to produce more radiative forcing. We report the first multi-model intercomparison to evaluate this approach, which we label AM-H₂SO₄ injection. A coordinated multi-model experiment designed to represent this SO₃- or H₂SO₄-driven geoengineering scenario was carried out with three interactive stratospheric aerosol microphysics models: the National Center for Atmospheric Research (NCAR) Community Earth System Model (CESM2) with the Whole Atmosphere Community Climate Model (WACCM) atmospheric configuration, the Max-Planck Institute's middle atmosphere version of ECHAM5 with the HAM microphysical module (MAECHAM5-HAM) and ETH's SOlar Climate Ozone Links with AER microphysics (SOCOL-AER) coordinated as a test-bed experiment within the Geoengineering Model Intercomparison Project (GeoMIP). The intercomparison explores how the injection of new accumulation-mode particles changes the large-scale particle size distribution and thus the overall radiative and dynamical response to stratospheric sulfur injection. Each model used the same injection scenarios testing AM-H₂SO₄ and SO₂ injections at 5 and 25 Tg(S) yr⁻¹ to test linearity and climate response sensitivity. All three models find that AM-H₂SO₄ injection increases the radiative efficacy, defined as the radiative forcing per unit of sulfur injected, relative to SO₂ injection. Increased radiative efficacy means that when compared to the use of SO₂ to produce the same radiative forcing, AM-H₂SO₄ emissions would reduce side effects of sulfuric acid aerosol geoengineering that are proportional to mass burden. The model studies were carried out with two different idealized geographical distributions of injection mass representing deployment scenarios with different objectives, one designed to force mainly the midlatitudes by injecting into two grid points at 30^∘ N and 30^∘ S, and the other designed to maximize aerosol residence time by injecting uniformly in the region between 30^∘ S and 30^∘ N. Analysis of aerosol size distributions in the perturbed stratosphere of the models shows that particle sizes evolve differently in response to concentrated versus dispersed injections depending on the form of the injected sulfur (SO₂ gas or AM-H₂SO₄ particulate) and suggests that prior model results for concentrated injection of SO₂ may be strongly dependent on model resolution. Differences among models arise from differences in aerosol formulation and differences in model dynamics, factors whose interplay cannot be easily untangled by this intercomparison.

1 Introduction

Deliberate modification of Earth's albedo has been proposed to counteract some of the longwave radiative forcing from increased concentrations of CO₂ and other greenhouse gases (GHGs) caused by human emissions (Budyko, 1974; Crutzen, 2006). In light of the complexity of the climate system and the inherent risks of climate manipulation, the effects of hypothesized solar radiation modification (SRM) are being studied with Earth system models to examine the potential benefits and possible adverse effects (e.g. Aquila et al., 2014; Richter et al., 2017; Tilmes et al., 2017), while simultaneously improving our knowledge of climate interactions and feedback processes. The most studied SRM proposals involve a deliberate enhancement of the Earth's stratospheric sulfuric acid aerosol layer by injection of sulfur-bearing gases or sulfuric acid aerosol into the stratosphere. Potential SRM scenarios could help to mitigate climate change risks by slowing the rate of change of climate over decades to a century, allowing time for emission mitigation, adaptation or GHG removal.

Many SRM model experiments have used alteration of the solar constant as a simple proxy for exploring the climate response to a geoengineering-enhanced stratospheric aerosol layer (Kravitz et al., 2015; Kalidindi et al., 2015). Of the global climate model (GCM) studies that have explicitly simulated alteration of stratospheric aerosols, almost all have either injected SO₂ or directly prescribed an increase in the sulfuric acid aerosol burden (IPCC, 2001). Simulations of SO₂ injection are motivated, in part, from an analogy to volcanoes, which are found to cool the surface climate and warm the stratosphere as a result of the increase in stratosphere aerosol loading (Robock, 2000). Volcanic injections and their effects on climate have been a major motivation for the inclusion of stratospheric sulfuric acid aerosols in global climate models. Yet, stratospheric solar geoengineering scenarios differ from volcanic aerosol injections because emissions will be continuous in time, producing different microphysical behaviour (Heckendorn et al., 2009; Niemeier and Timmreck, 2015).

It is well established (e.g. Pinto et al., 1989) that greater emission of SO₂ leads to larger sulfuric acid aerosol particles with shorter residence times in the stratosphere. Studies of SRM by injection of gas-phase SO₂ have found limitations including (1) reduced radiative efficacy at higher loading due to larger particles (less efficient shortwave scattering) and shortened aerosol residence time with possible limitations on achievable radiative forcing (Niemeier and Timmreck, 2015; Kleinschmitt et al., 2018), (2) depletion of stratospheric ozone (Tilmes et al., 2009; Pitari et al., 2014), (3) stratospheric heating which also perturbs stratospheric circulation and water vapour (Ferraro et al., 2011; Aquila et al., 2014; Richter et al., 2017; Niemeier and Schmidt, 2017; Franke et al., 2021), (4) enhanced diffuse light at the Earth's surface (Kravitz et al., 2012) and (5) impacts on upper tropospheric ice clouds (Kuebbeler et al., 2012; Visioni et al., 2018a). Limitations (3) and (4) might be addressed through use of various solid aerosol particles for SRM (e.g. Pope et al., 2012; Weisenstein et al., 2015); alternatively, limitation (1) may be addressed with geoengineering strategies designed to achieve a sulfuric acid aerosol layer with a size distribution that optimizes shortwave scattering.

Aerosol particle residence time is decreased with increased SO₂ injection because most of the added sulfur increases the mass of existing particles rather than forming new accumulation-mode particles. Pierce et al. (2010) proposed that addition of accumulation-mode particles could be used to steer the overall large-scale aerosol size distribution towards the size range that produces the most radiative forcing per unit mass of injected sulfur (termed radiative efficacy). New particles would be formed when H₂SO₄ or SO₃ vapour is released into an aircraft wake; coagulation within the confined plume would result in a distribution of sulfuric acid particles in the accumulation size range (0.05–0.2 µm radius). Injecting SO₃ or H₂SO₄ vapour into the stratosphere presents technical challenges not encountered in the release of SO₂ gas (Smith et al., 2018; Janssens et al., 2020) and would require engineering studies as well as atmospheric modelling. The global impact of this proposed methodology was tested in a global three-dimensional model of aerosol microphysics by English et al. (2012), who found larger stratospheric aerosol burdens with injection of accumulation-mode particles rather than equivalent emissions of SO₂ or gas-phase H₂SO₄. Later, Vattioni et al. (2019) used a three-dimensional interactive chemistry–climate–aerosol model and found improved radiative efficacy of SRM by accumulation-mode sulfuric acid aerosol injection over that of SO₂ injection.

The Geoengineering Model Intercomparison Project (GeoMIP) was formed in 2011 to coordinate a common set of experiments for the purpose of assessing climate model responses and sensitivities to solar radiation management (Kravitz et al., 2011, 2015). GeoMIP scenarios have included uniform reductions in solar radiation as well as specified injections of SO₂ into the tropical stratosphere or globally specified aerosol distributions (Tilmes et al., 2015). This study represents a GeoMIP test-bed experiment in which three of the participating GeoMIP models ran identical scenarios exploring the impacts of controlled accumulation-mode sulfuric acid aerosol injection, which we refer to as AM-H₂SO₄ injection, into GCMs.

The evolution of aerosol particles after injection of H₂SO₄ into the stratosphere would include the initial formation of nucleation-mode particles by homogeneous nucleation of H₂SO₄ gas and the subsequent formation of accumulation-mode particles by coagulation of the nucleation mode. Our study does not address these plume-scale microphysical processes. We simply specify a size distribution of H₂SO₄ aerosol that is delivered at the scale of each model's numerical grid. The constant size distribution used by the models in the coordinated modelling simulations is consistent with Pierce et al. (2010) and Benduhn et al. (2016), who modelled plume microphysics and found that sulfuric acid aerosol size distributions in the 0.1–0.15 µm radius size range could potentially be produced. Detailed modelling of potential plume-scale evolution under a full range of stratospheric physical, chemical and microphysical conditions awaits further studies. For the temporal and spatial scale beyond plume models, global GCMs such as those participating in the Interactive Stratospheric Aerosol Model Intercomparison Project (ISA-MIP; Timmreck et al., 2018) have the functionality to explore how the stratospheric aerosol layer responds with global dispersion of the geoengineering injections. Those models with microphysical aerosol schemes can also address the key issue of how the particle size distribution evolves, this being a key determinant of subsequent global aerosol burden and radiative forcing. As input, the global models would take a mass flux of particles with the size distributions generated by aircraft plume model studies, or any hypothetical source of particles at a specified rate. The input size distribution is simplified here by using a lognormal distribution with a constant mode radius and mode width for all injection grid points and times.

Three GCMs with interactive aerosol microphysics participated in this experiment: the National Center for Atmospheric Research (NCAR) Community Earth System Model (CESM2) with the Whole Atmosphere Community Climate Model (WACCM) atmospheric configuration, the Max-Planck Institute's middle atmosphere version of ECHAM5 with the HAM microphysical module (MAECHAM5-HAM) and the SOlar Climate Ozone Links model with AER microphysics (SOCOL-AER) version 2 model developed at ETH Zurich and Physikalisch-Meteorologisches Observatorium Davos (PMOD). These three models are participants in both the GeoMIP and ISA-MIP model intercomparisons. The CESM2 and MAECHAM5-HAM models employ a modal scheme to prescribe the aerosol size distributions, while the SOCOL-AER model uses a size-resolving sectional scheme. The CESM2 and SOCOL-AER models interactively couple the aerosol and ozone through photochemistry and heterogeneous reactions, whereas the MAECHAM5-HAM model uses prescribed and precalculated ozone and OH concentrations when calculating sulfur chemistry to predict aerosol. The MAECHAM5-HAM and CESM2 models internally generate a quasi-biennial oscillation (QBO), while the SOCOL-AER model uses nudging to simulate QBOs. As this study focuses on stratospheric responses to the sulfur injections, all were run with specified sea surface temperatures, simplifying the interpretation of inter-model differences. Section 2 includes a description of these models and of the scenario calculations, while Sect. 3 presents results and Sect. 4 a summary and discussion.

2 Description of models and emission scenarios

All three models in this intercomparison are three-dimensional dynamic general circulation models. All include sulfur chemistry and interactive microphysics for prognostically calculating the size distribution of stratospheric aerosol. All models allow radiative heating from aerosols to alter dynamics and thus the transport of aerosols and trace gases. Table 1 summarizes the most relevant aspects of the models. The CESM2 (Donabasoglu et al., 2016) and MAECHAM5-HAM (Stier et al., 2005) models employ a modal representation of the aerosol size distributions, utilizing three (for CESM2) or four (for MAECHAM5-HAM) lognormal modes to describe the size range of sulfuric acid aerosols from nanometre to micrometre scale. CESM2 includes four modes total but only three modes represent sulfuric acid aerosol (Liu et al., 2016), omitting the nucleation mode included in MAECHAM5-HAM. CESM2 generates new particles according to nucleation rates from Sihto et al. (2006), which are adjusted according to a parameterization from Kerminen and Kumala (2002) and added to the Aitken mode. The two modal schemes also differ in the size ranges and assumed lognormal widths, σ, of the modes, with the CESM2 model utilizing a coarse mode with radius greater than 0.5 µm, whereas the MAECHAM5-HAM model considers the coarse mode with radius greater than 0.2 µm. The CESM2 modal scheme used here, unlike previous versions of the same scheme, allows for growth of sulfuric acid aerosols also in the coarse mode for a more proper representation of stratospheric processes (Mills et al., 2016). The SOCOL-AER version 2 model (Feinberg et al., 2019; Sheng et al., 2015) employs a sectional aerosol scheme that calculates size distributions in 40 bins for sulfuric acid aerosols representing dry radii from 0.39 nm to 3.2 µm with no a priori assumptions on the distribution shape. Both schemes have been shown to be capable of prognostically generating realistic aerosol distributions (Weisenstein et al., 2007; Kokkola et al., 2009), though modal schemes require a priori assumptions on the width of the lognormal modes which may differ for background and perturbed conditions. Sectional schemes generate numerical diffusion in size space (Wu and Biswas, 1998), though this numerical diffusion has been significantly reduced in SOCOL-AERv2 relative to SOCOL-AERv1 (Feinberg et al., 2019).

Table 1 Models used in this study, their horizontal resolution, number of levels and model top height, aerosol formulation, dynamical core, chemical interactivity and QBO interactivity.

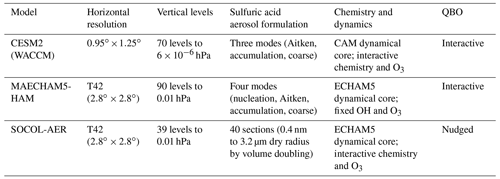
The MAECHAM5-HAM (Niemeier et al., 2020; Niemeier and Timmreck, 2015; Stier et al., 2005) and SOCOL-AER models (Feinberg et al., 2019; Stenke et al., 2013) share the same dynamical core from MAECHAM5 (Roeckner et al., 2003, 2006) and used the same horizontal resolution (T42 or $\mathrm{2.8}{}^{\circ }\times \mathrm{2.8}{}^{\circ }$ in longitudes and latitudes) and model top (0.01 hPa or approximately 80 km). However, the MAECHAM5-HAM model uses 90 vertical levels and internally generates a quasi-biennial oscillation (QBO), which has been found in several studies to modify the effects of geoengineering injections (Aquila et al., 2014; Richter et al., 2017; Niemeier et al., 2020, Franke et al., 2021). The SOCOL-AER model uses 39 vertical levels and employs nudging to reproduce a QBO that does not vary with geoengineering scenario. The CESM2 model (Donabasoglu et al., 2016) in the WACCM6 configuration (Gettelman et al., 2019) uses a finer horizontal resolution ($\mathrm{0.95}{}^{\circ }\times \mathrm{1.25}{}^{\circ }$ in longitude and latitude) than the other models and has a higher model top ($\mathrm{6}\times {\mathrm{10}}^{-\mathrm{6}}$ hPa or approximately 130 km) with 70 vertical levels. The vertical resolution of CESM2 allows for an internally generated QBO.

SOCOL-AER employs fully interactive chemistry from MEZON (Stenke et al., 2013), while the MAECHAM5-HAM model includes SO₂ oxidation chemistry only with OH, NO₂ and O₃ concentrations prescribed and invariant between the baseline and geoengineering scenarios, thus missing potential chemical–dynamical feedbacks due to geoengineering injections. The version of CESM2 used here has a reduced set of tropospheric reactions but full interactive chemistry in the stratosphere, mesosphere and lower thermosphere (known as the middle atmosphere version) with 98 chemical species simulated and with prognostic stratospheric aerosols. The SOCOL-AER model simulates 90 chemical species.

Boundary conditions for GHGs and ozone-depleting substances (ODSs) use the 2040 projection values from the SSP5-8.5 scenario (O'Neill et al., 2016). All the models used a configuration with annually repeating monthly mean climatological sea surface temperatures (SSTs) and sea ice boundary conditions derived from an average of the years 1988–2007 of the CMIP5 PCMDI-AMIP-1.1.0 SST/Sea Ice dataset (Taylor et al., 2000). We used prescribed SSTs because not all models used in this intercomparison can utilize a coupled ocean and because prescribing SSTs allows shorter integration times to achieve a given signal-to-noise ratio. This also simplifies interpretation of changes in radiative forcing and stratospheric temperature, since it removes differences due to the model's climate sensitivity. The combination of SSTs averaged from 1988 to 2007 and GHGs from 2040 was selected so that, with radiative forcing from increased GHG roughly cancelled by the sulfuric acid aerosol burden of a 5 Tg(S) yr⁻¹ injection, the overall model disequilibrium between atmosphere and sea surface was minimal.

Models were run for 10 years (13 years for SOCOL-AER) for each scenario, with the first 2 years (5 years for SOCOL-AER) considered spin-up and the final 8 years averaged and used in our analysis. The 2-year spin-up was found to be adequate for all scenarios presented here except for the 25 Tg yr⁻¹ injection scenarios using AM-H₂SO₄ for which a 4- to 5-year spin-up would have been more appropriate. However, the difference in averaged quantities (comparing averaging the final 5 or 6 years versus averaging the final 8 years of the 10-year simulations) is only 2 %–3 % and does not affect our analysis or conclusions. Our choice of 8-year averages was a balance between the need to remove interannual variability (i.e. QBO) and to provide adequate statistics while avoiding the spin-up period.

The calculations performed for this intercomparison include a baseline or reference scenario with 2040 GHGs and SSTs as described above but without geoengineering and 8–12 perturbation scenarios including stratospheric sulfur injection. The perturbation scenario parameters chosen are shown in Table 2. Sulfur was injected in one of two forms, either as SO₂ gas or as accumulation-mode H₂SO₄ (AM-H₂SO₄) aerosol particles of specified size. The sectional model SOCOL-AER assumed a lognormal distribution for the injected AM-H₂SO₄ with dry mode radius of 0.1 µm, wet mode radius 0.12 µm and mode width σ of 1.5. The modal models (CESM2 and MAECHAM5-HAM) input the AM-H₂SO₄ particles into their accumulation-mode: for the CESM2 model, the input size distribution has a dry mode radius of 0.1 µm and wet mode radius of 0.12 µm with σ=1.5, while MAECHAM5-HAM has an input dry mode radius of 0.075 µm and wet mode radius of 0.1 µm with σ=1.59.

Table 2 Each model ran a total of 8 (or 12) geoengineering scenarios, plus a reference scenario with no geoengineering. The geoengineering scenarios included two injection forms (SO₂ gas or AM-H₂SO₄ particulate) and two geographical distributions of injection mass for each of two or three injection rates.

Two different geographical distributions of injection mass were chosen: either uniformly distributed in a broad tropical region between 30^∘ S and 30^∘ N, with a 2 km thickness centred around 20 km, and across all longitudes (hereinafter called regional injections), or narrowly injected at two model grid points located at 30^∘ S and 30^∘ N, at 20 km (CESM2 and SOCOL-AER) or 18–20 km (MAECHAM5-HAM) and at 180^∘ E longitude (hereinafter called 2point injections) outside the tropics. The regional injections are designed to utilize the Brewer–Dobson circulation to distribute emissions globally and maximize their residence time, as has been observed for volcanic aerosol clouds (Dyer and Hicks, 1968; Grant et al., 1996). The 2point injections occur outside the tropical stratospheric reservoir (Grant et al., 1996; Tilmes et al., 2017) and are meant to concentrate geoengineering impacts at higher latitudes and to explore microphysical differences when injections are more concentrated spatially. All models simulated injections of 5 and 25 Tg(S) yr⁻¹, and the MAECHAM5-HAM and SOCOL-AER models also simulated a 10 Tg(S) yr⁻¹ injection. The combination of two injection forms, two geographical distributions of injection mass and two (or three) injection rates yielded 8 (or 12) perturbation scenarios. The same set of model calculations (excluding SOCOL-AER due to lack of an internally generated QBO) has been analysed for changes in the QBO by Franke et al. (2021).

3 Results

We analyse changes in global aerosol properties and radiative forcing to determine whether the use of AM-H₂SO₄ can increase (compared to SO₂) the radiative efficacy per unit of material injected across a range of models. If so, can this be attributed to increased stratospheric lifetime of the aerosols, improved scattering efficacy or some other factor? What contributes to inter-model differences, and what can these differences tell us about uncertainty in the response to the aerosol injections? Finally, we examine some of the side effects of increasing stratospheric aerosol and explore how they differ with AM-H₂SO₄ versus SO₂ injection and with geographical distribution of injection mass.

3.1 Changes in global aerosol properties

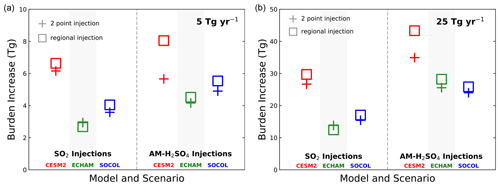
Figure 1 Global sulfuric acid aerosol burden increase (90^∘ S–90^∘ N; stratosphere and troposphere) in Tg of sulfur due to geoengineering injection of (a) 5 Tg(S) yr⁻¹ and (b) 25 Tg(S) yr⁻¹. Panels (a) and (b) show the three models, CESM2 in red, MAECHAM5-HAM (labelled ECHAM) in green and SOCOL-AER in blue, with the left side of each panel representing injection as SO₂ and the right side of each panel representing injection as accumulation-mode H₂SO₄. Square symbols represent injection into a region around the Equator from 30^∘ S to 30^∘ N, 19–21 km and all longitudes. Plus symbols represent injection into two model grid points at 30^∘ S and 30^∘ N, 20 km and 180^∘ E longitude.

We start by examining the aerosol burden using the global (troposphere and stratosphere) rather than stratospheric burden to reduce uncertainties that would arise from inconsistent diagnoses of tropopause height and because the troposphere represents less than 10 % of the total burden increase in our scenarios. Injections of 5 Tg(S) yr⁻¹ in the form of SO₂ yield increases in the global aerosol burden of 2.7 to 6.6 Tg of sulfur while injections of 5 Tg(S) yr⁻¹ as AM-H₂SO₄ yield increases in aerosol burden of 4.2 to 8.1 Tg of sulfur (Fig. 1). Accumulation-mode particle injection produces a larger burden increase than SO₂ injection in all cases except for the CESM2 model using 2point injections of 5 Tg(S) yr⁻¹. Inter-model differences are roughly a factor of 2 larger than difference between SO₂ and AM-H₂SO₄. Differences arise in part from dynamics including the QBO which may influence microphysics by changing tropical confinement (Visioni et al., 2018b). The CESM2 model in all cases shows the highest burden increases and the MAECHAM5-HAM model the lowest in most cases. The SOCOL-AER model, with the same dynamical core as the MAECHAM5-HAM model, produces burden increases closer to that model than to CESM2. For 25 Tg(S) yr⁻¹ injections, most results scale proportionately, though in this case the MAECHAM5-HAM model produces a larger burden than SOCOL-AER with AM-H₂SO₄ injections. A previous intercomparison of geoengineering results between the MAECHAM5-HAM and CESM2 models (Niemeier et al., 2020) found significantly larger aerosol burden increases for equatorial injection of SO₂ with CESM2 than with MAECHAM5-HAM and attributed the greater CESM2 burden to greater vertical advection in the CESM2 model. Differences in global aerosol burden due to the chosen geographical distribution (2point or region) are modest except with the CESM2 model injecting AM-H₂SO₄. In most cases, regional injections produce slightly greater global burdens.

Figure 2 shows the zonal mean of vertically integrated aerosol mass increase (troposphere and stratosphere) as a function of latitude relative to the reference scenario for each model. Significant increases in aerosol column burden are seen at all latitudes for all scenarios; however, the latitudinal pattern is different for regional and 2point injections. Regional injections which evenly spread the injection mass in a region centred around the Equator between 30^∘ S and 30^∘ N result in aerosol column burden peaks over the Equator and at 45^∘ N and 45^∘ S, and minima at 30^∘ S and 30^∘ N at the subtropical barrier zone (see, e.g. Strahan and Douglas, 2004). The 2point injections at 30^∘ S and 30^∘ N show minimal increases in aerosol column burden at the Equator and maximum aerosol column increases at about 45–50^∘ S and 45–50^∘ N. The hemispheres differ due to the stronger polar vortex in the Southern Hemisphere that inhibits mixing of midlatitude and polar air resulting in a strong contrast between the two regions in this hemisphere. Of these two geographical distributions of injection mass, the regional injections (30^∘ S–30^∘ N) yield more uniform global distributions of aerosol, whereas the 2point injections at 30^∘ S and 30^∘ N concentrate more aerosol at midlatitudes and high latitudes which could concentrate geoengineering effects toward the high latitudes which are warming fastest. Figure 2 explains the significant differences in total burden between the 2point and regional injections of AM-H₂SO₄ seen in the CESM2 model in Fig. 1 as a strong subtropical barrier minimizing the impact of extratropical injections on the tropics and tropical upwelling enhancing the impact of tropical injections in the same region. Because SO₂ injections yield larger particle sizes, the tropical upwelling has less impact on the aerosol burden in that case. The MAECHAM5-HAM and SOCOL-AER models, which share the same dynamical core, have weaker subtropical barriers.

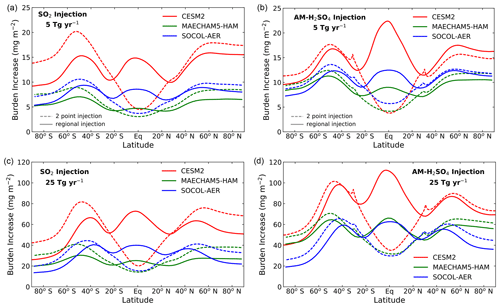
Figure 2 Zonal mean aerosol column burden increase above background (mg m⁻²) with 5 Tg(S) yr⁻¹ injections (a, b) and 25 Tg(S) yr⁻¹ injections (c, d) as a function of latitude for SO₂ injections (a, c) and AM-H₂SO₄ injections (b, d). Regional injections are shown with solid lines and 2point injections with dashed lines.

The global aerosol burdens normalized by the injection rate are shown in Fig. 3 as a function of injection rate. The normalized burden has units of time and can be considered the residence time of injected sulfur, which varies from 0.5 to 1.3 years for SO₂ injections and from 0.8 to 1.7 years for AM-H₂SO₄ injections. Regional injections have longer residence time than 2point injections in most cases. The CESM2 model shows longer residence times than the other models, consistent with its greater burdens. The SO₂ injections (Fig. 3, left panel) all show decreasing residence time with increasing injection rate. This is consistent with other studies (Niemeier and Timmreck, 2015; Heckendorn et al., 2009) showing decreasing injection efficiency with increasing injection amount, which has been found to result from substantial increases in mean particle size and thus sedimentation rates. However, injections of AM-H₂SO₄ (Fig. 3, right panel) show increasing residence time with increasing injection for the CESM2 and MAECHAM5-HAM models. The AM-H₂SO₄ scenarios were designed to minimize the growth in average particle size as a function of injection rate, since sulfur is added to each grid box as particles of approximately 0.1 µm radius which grow mainly by coagulation. In addition, aerosol heating in the tropical lower stratosphere increases the strength of the Brewer–Dobson circulation, resulting in greater lofting in the tropical stratosphere. For accumulation mode and smaller particles, (Niemeier et al., 2020), lofting can prolong the residence time for 25 Tg(S) yr⁻¹ injections relative to 5 Tg(S) yr⁻¹ injections, though the details of this process are model dependent and include changes in the QBO for the CESM2 and MAECHAM5-HAM models (Franke et al., 2021). The SOCOL-AER model, which uses a sectional aerosol scheme, may transfer aerosol mass into larger particle sizes more efficiently than the two modal models and thus yield more sedimentation at higher loadings.

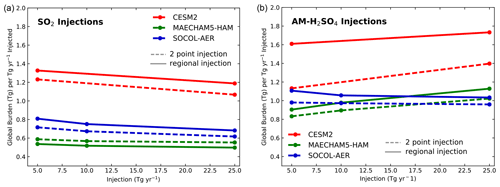
Figure 3 Increase in global sulfuric acid aerosol burden normalized by geoengineering injection rate in units of Tg(S) per (Tg(S) yr⁻¹) as a function of injection rate. The y axis also represents the residence time in years of injected sulfur as aerosol. SO₂ injections (a) show decreasing residence time with increasing injection rate, whereas AM-H₂SO₄ injections (b) show increasing residence time with increasing injection rate for the CESM2 and MAECHAM5-HAM models. Regional injections (solid lines) show longer residence times than 2point injections (dashed lines) in most cases.

Globally averaged effective wet radius (R_eff) at 60 hPa near the injection region and where these values maximize is shown in Fig. 4 (left panel) for background conditions and for injections of 5 and 25 Tg(S) yr⁻¹ of SO₂ or AM-H₂SO₄. The effective radius at 60 hPa after continuous injection of AM-H₂SO₄ results in R_eff from 0.27 to 0.39 µm with 5 Tg(S) yr⁻¹ injections, whereas SO₂ injections yield R_eff of 0.40 to 0.52 µm for the same annual sulfur injection. The SO₂ injections consistently yield larger average particles than the AM-H₂SO₄ injections. As has been seen in other studies (English et al., 2012; Vattioni et al., 2019), injection of SO₂ results in substantial particle size growth since most of the injected sulfur condenses onto the larger existing particles or nucleates and preferentially coagulates onto the larger background particles. The assumed lognormal size of the input AM-H₂SO₄ particles in our scenarios is equivalent to a wet R_eff of 0.18 µm (0.16 for MAECHAM5-HAM) and the additional particle growth is due to coagulation with both background and other injected particles. For 5 Tg(S) yr⁻¹ injections of AM-H₂SO₄ particles, the resulting global averaged R_eff at 60 hPa is within or smaller than the optimal R_eff for scattering (blue band in the figure), whereas the R_eff resulting from SO₂ injections is larger than optimal for scattering, particularly for regional injections. Increasing the injection rate from 5 to 25 Tg(S) yr⁻¹ results in larger mean particles in all cases, with the SO₂ injection scenarios responding more strongly than the AM-H₂SO₄ scenarios. The MAECHAM5-HAM model shows only small increases in R_eff for the AM-H₂SO₄ scenarios as a function of injection rate. The SO₂ injection scenarios all produce larger R_eff with regional injections, while the AM-H₂SO₄ injection scenarios produce larger R_eff with 2point injections. Based on injection location and aerosol lifetime alone, we would expect the regional injections into the tropical stratospheric reservoir to produce larger particles in all cases.

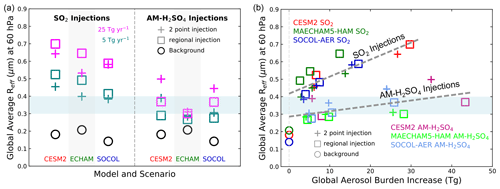
Figure 4 Global average effective radius (µm) at 60 hPa (a) for the three models with SO₂ injections of 5 and 25 Tg(S) yr⁻¹ (left side) and with AM-H₂SO₄ injections of 5 and 25 Tg(S) yr⁻¹ (right side). Scatter plot of global average effective radius (µm) at 60 hPa plotted against the global increase in aerosol burden in Tg(S) (b). Regression lines are shown for both SO₂ (R²=0.74) and AM-H₂SO₄ (R²=0.34) injections. Injections into regions are shown by open squares, while injections at two points are shown with plus symbols and for background conditions with open circles. The light blue shaded region represents the optimal effective radius for scattering of solar radiation assuming a lognormal distribution and σ between 1.1 and 1.8 (John Dykema, personal communication, 2019).

Figure 4 (right panel) shows the same R_eff parameter at 60 hPa plotted against the increase in global aerosol burden for each case, including the 5, 10 and 25 Tg(S) yr⁻¹ scenarios. Linear regression lines are plotted for SO₂ injections and AM-H₂SO₄ injections (equal weighting of plotted points for all models), showing that the relationship between burden and R_eff is close to linear though more steeply sloped for SO₂ injections. R² values are 0.74 for SO₂ injection and 0.34 for the AM-H₂SO₄ injections. SO₂ injection cases all lie above the AM-H₂SO₄ injection cases, with the latter yielding smaller R_eff and larger burden for the same annual injection amount and even greater burdens with similar R_eff values. The MAECHAM5-HAM model exhibits a somewhat flatter regression slope than the other models with AM-H₂SO₄ injections (smaller sensitivity of R_eff to burden) and an upward offset on the regression line with SO₂ for regional injections.

Particle size distributions for the 30^∘ S–30^∘ N region at 60 hPa are shown in Fig. 5 for SO₂ injections (left panels) and AM-H₂SO₄ injections (right panels) of 5 Tg(S) yr⁻¹. Note that the CESM2 model includes only three sulfuric acid aerosol modes, omitting the nucleation mode and transferring the mass of freshly nucleated particles into the Aitken mode. The SO₂ injection scenarios result in an increase in nucleation-mode particles relative to background levels (dotted lines in Fig. 5) in the MAECHAM5-HAM model, particularly with regional injections in the tropics and a decrease in the nucleation mode in the SOCOL-AER model. In these scenarios, the SOCOL-AER model results reflect a predominance of condensation, while the MAECHAM5-HAM results reflect a larger role for nucleation. An analysis with the SOCOL-AER model revealed that concentrations of nucleation-mode particles are sensitive to the order of calculation of nucleation and condensation, the time-splitting scheme and the time step, though this does not affect conclusions concerning the overall differences between SO₂ and AM-H₂SO₄ injections.

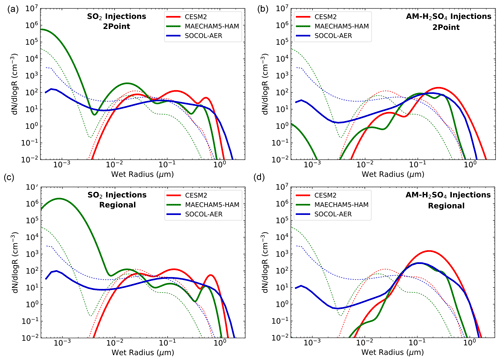
Figure 5 Size distributions (d$N/$d₁₀log R, particles cm⁻³ µm⁻¹) averaged between 30^∘ S and 30^∘ N at 60 hPa for the three models with SO₂ (a, c) and AM-H₂SO₄ (b, d) injections of 5 Tg(S) yr⁻¹ and with 2point injections (a, b) and regional injections (c, d). Background size distributions are shown as dotted lines.

Large increases in the accumulation mode and coarse mode are seen for all models with SO₂ injection. The coarse modes have mode radii values (R_g) of 0.4 to 0.7 µm, with MAECHAM5-HAM having the smallest coarse mode R_g but also the smaller background distribution in the coarse mode. AM-H₂SO₄ injections decrease the nucleation-mode and Aitken-mode particles as many of these particles are scavenged by the injected accumulation-mode particles. Coagulation with background particles and with other injected particles moves the accumulation-mode particle size distribution from an R_g of 0.1–0.12 µm upon injection to 0.2–0.3 µm for the CESM2 and SOCOL-AER models with 2point injections, while the MAECHAM5-HAM model retains a mode at 0.1 µm and also grows the coarse mode at 0.3 µm. The size distributions with regional injections of AM-H₂SO₄ tend to maintain a mode close to the accumulation-mode injection size.

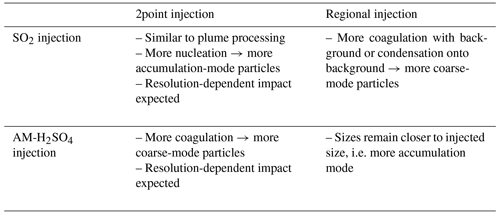
The size distributions respond differently to 2point rather than regional injections depending on whether SO₂ gas or AM-H₂SO₄ particulate is injected. These results suggest the way aerosol microphysics drives differences between AM-H₂SO₄ and SO₂ injection scenarios (see Table 3). For AM-H₂SO₄, 2point injections produce larger R_eff (Fig. 4) and smaller global burdens (Fig. 1) than regional injections. The regional AM-H₂SO₄ injection cases have size distributions (see Fig. 4) which remain closer to their injected size distributions. We expect that injection of AM-H₂SO₄ into points increases the coalescence rate, driving the radius up and the lifetime down due to sedimentation of large particles. In contrast, SO₂ regional injections yield larger coarse-mode particle sizes than the 2point injections, resulting in a larger R_eff. The 30 d conversion time from SO₂ to H₂SO₄ leads to H₂SO₄ condensation onto existing background particles that favours coarse-mode growth, particularly with dispersed regional injections. Small freshly nucleated particles in this scenario preferentially coagulate with the larger background particles, also favouring coarse-mode growth. Point injections of SO₂ are more likely to create locally high densities of nucleation-mode particles that would coagulate among themselves, thus lowering the average size relative to regional injections. This effect is somewhat akin to injections into an aircraft plume but on a very different scale. We expected this effect will be strongly dependent on model resolution which may partly explain the model discrepancies. Given our chosen scenarios, some of the differences between regional and 2point injections are likely due to the interaction of dynamics with injection location – injections outside the tropics will less efficiently be transported in the upward branch of the Brewer–Dobson circulation, which could lead to faster stratospheric removal and lower global burdens for 2point injections.

Table 3 Matrix explaining 2point vs. regional injection effects.

3.2 Changes in radiative forcing and stratospheric temperature

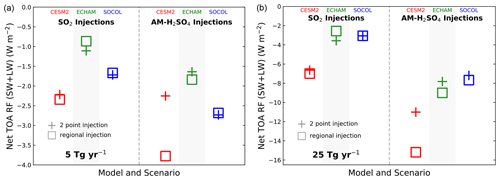
Figure 6 Globally averaged change in net top-of-atmosphere shortwave and longwave radiative forcing (W m⁻²) due to geoengineering injection of (a) 5 Tg(S) yr⁻¹ and (b) 25 Tg(S) yr⁻¹. Colours and symbols are as in Fig. 1.

Changes in the top-of-atmosphere (TOA) radiative forcing (RF) of shortwave (SW, solar) and longwave (LW, thermal) bands combined are shown in Fig. 6 for our simulations with 5 and 25 Tg(S) yr⁻¹ injections under all-sky conditions. RF changes range from −0.9 to −2.5 W m⁻² with SO₂ injections of 5 Tg(S) yr⁻¹ and from −1.6 to −3.8 W m⁻² with AM-H₂SO₄ injections of 5 Tg(S) yr⁻¹. For comparison, approximately −4 W m⁻² forcing would be needed to offset a doubling of CO₂ (Etminan et al., 2016). Inter-model differences encompass a factor of 3 and are larger than differences due to injection form (AM-H₂SO₄ vs. SO₂) and geographical distribution of injection mass (2point vs. regional) in the 5 Tg(S) yr⁻¹ case (left panel), but differences due to injection form are of a similar magnitude as inter-model differences with 25 Tg(S) yr⁻¹ (right panel). The efficacy (RF reduction per Tg of sulfur injected annually) is shown in Fig. 7 as a function of injection rate. The efficacy is reduced with increasing injection rate for SO₂ injection scenarios, a consequence of the larger particles generated at high injection rates that both increase sedimentation and decreases the shortwave scattering efficiency, which is consistent with previous studies (Heckendorn et al., 2009; Kleinschmitt et al., 2018). Efficacy is also reduced with increasing injection rate for AM-H₂SO₄ injections with the SOCOL-AER model but stays roughly constant with injection rate in the CESM2 (2point injection only) and MAECHAM5-HAM models. Even though the normalized aerosol burden increases with increasing AM-H₂SO₄ injection rate for these models (Fig. 2), the RF efficacy is insensitive to injection rate, possibly due to the offsetting effects of aerosol heating on circulation and stratospheric water vapour and more modest changes in particle size.

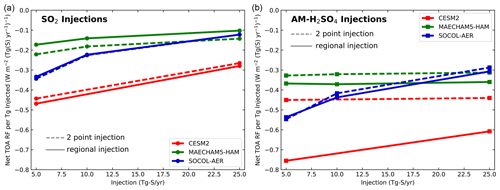
Figure 7 Globally averaged change in net top-of-atmosphere shortwave and longwave radiative forcing (W m⁻²) per unit annual injection (Tg(S) yr⁻¹) due to geoengineering injection as a function of injection rate for (a) SO₂ injections and (b) AM-H₂SO₄ injections.

Figure 8 shows a scatter plot of the change in SW and LW TOA RF plotted against the increase in global aerosol burden. The upper left panel of Fig. 8 expands the region from 0 to 18 Tg(S) burden increase. Linear regression lines for the SO₂ injections and AM-H₂SO₄ injections are shown, with R² values greater than 0.9 in both cases, indicating that global burden is a good predictor of change in TOA RF. For the same burden increase, the AM-H₂SO₄ injection scenarios show somewhat greater RF changes than the SO₂ injection scenarios, which we can attribute to a more optimal size distribution after AM-H₂SO₄ injections. Model differences in RF are, for the most part, contained in the differences in calculated burdens, with differences in size distributions yielding different linear fits for SO₂ vs. particulate injection, consistent with results for R_eff.

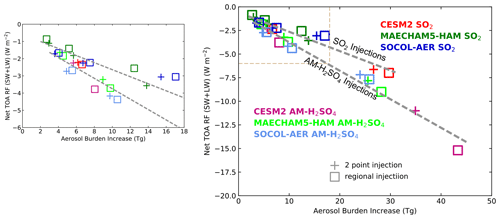
Figure 8 Scatter plot of globally averaged net top-of-atmosphere shortwave and longwave radiative forcing (W m⁻²) due to geoengineering injection relative to the corresponding increase in global aerosol burden (Tg(S)). The smaller left panel is a finer scale for the upper left corner of the main plot. Regression lines are shown for SO₂ injections (R²=0.93) and for AM-H₂SO₄ injections (R²=0.98).

Figure 9 shows the latitudinal variation in net TOA SW and LW radiative forcing for both 5 and 25 Tg(S) yr⁻¹ injections. The MAECHAM5-HAM model shows less variability of RF with latitude than the other models, while the CESM2 model shows much more variability. The SOCOL-AER model shows near-zero RF change, and sometimes positive RF change, in the high latitudes. The 2point injections in most cases produce greater RF change at midlatitudes and high latitudes as expected, while the regional injections produce a much greater impact on RF in the tropics. Compared to latitudinal changes in aerosol burden (Fig. 3), changes in RF exhibit more small-scale variability, a result of the high variability in tropospheric cloudiness.

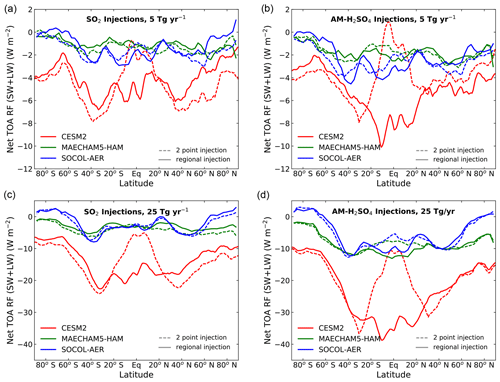
Figure 9 Zonal mean net top-of-atmosphere shortwave and longwave radiative forcing (W m⁻²) with 5 Tg(S) yr⁻¹ injections (a, b) and 25 Tg(S) yr⁻¹ injections (c, d) as a function of latitude for SO₂ injections (a, c) and AM-H₂SO₄ injections (b, d).

Next, we look at the vertical profiles of changes in tropical temperature (30^∘ S–30^∘ N) in Fig. 10. Sulfuric acid aerosols absorb in the longwave and lead to atmospheric heating, which would lead to an enhancement in the Brewer–Dobson circulation and to increased transport of H₂O into the stratosphere. Increased stratospheric water vapour could lead to ozone losses via an enhanced HO_x cycle in the upper stratosphere (Tilmes et al., 2018). Thus, aerosol heating in the tropical lower stratosphere is considered a serious risk of geoengineering. Previous studies indicate that such stratospheric changes could impact tropospheric climate (Simpson et al., 2019; Jiang et al., 2019), though we do not explore that here. Maximum model-calculated temperature changes in this region range from 1.7 K for the MAECHAM5-HAM model to 5.3 K for the CESM2 model with SO₂ injections of 5 Tg(S) yr⁻¹. With AM-H₂SO₄ injections of the same magnitude, model-calculated tropical temperature changes range from 2.1 to 6.4 K for the same two models. The SOCOL-AER model results are similar to the CESM2 model results with SO₂ injections of the same magnitude and geographic distribution (2point vs. region), though this similarity does not extend to AM-H₂SO₄ injections. The larger temperature changes with AM-H₂SO₄ likely reflect the greater stratospheric burden for the same sulfur injection amount, a result seen in all three models (Fig. 1).

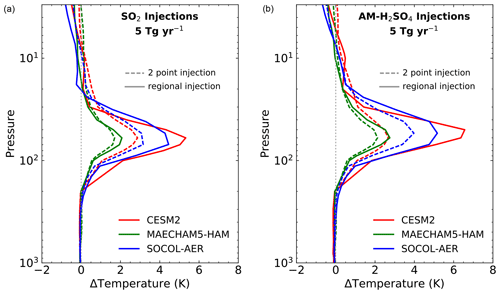
Figure 10 Change in atmospheric temperature (K) averaged between 30^∘ S and 30^∘ N due to 5 Tg(S) yr⁻¹ of geoengineering injection as a function on height for (a) injections of SO₂ and (b) injections of AM-H₂SO₄.

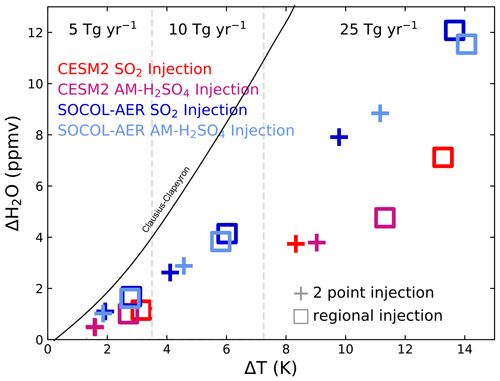
In Fig. 11, we look at the changes in H₂O and changes in temperature at 90 hPa in the tropics, shown as a scatter plot including injections of 5, 10 and 25 Tg(S) yr⁻¹. A value of 90 hPa is close to the cold-point temperature which determines H₂O concentration entering the stratosphere, though the actual cold point could vary from model to model and from low to high injection rates. MAECHAM5-HAM results are not shown as H₂O was not calculated diagnostically in this model. Plotting H₂O against temperature shows that 90 hPa tropical water vapour mixing ratio is determined by 90 hPa tropical temperature, though with different relationships for the SOCOL-AER and CESM2 models. Since we plot these quantities averaged over time and spatial volumes, they do not follow the Clausius–Clapeyron equation but fall below it. Compared to control runs with H₂O values of about 4 ppmv in the tropics at this altitude, injections of 25 Tg(S) yr⁻¹ of SO₂ or AM-H₂SO₄ yield H₂O increases of 3.7 to 12 ppmv, which represents increases of factors of 2–4. The SOCOL-AER model has larger increases in 90 hPa water vapour per degree of heating than the CESM2 model. As the H₂O vapour crossing the 90 hPa surface in the tropics largely determines H₂O concentrations throughout the stratosphere, this would be expected to significantly perturb stratospheric chemistry and ozone.

Figure 11 Scatter plot of water vapour change (ppmv) relative to change in temperature (K) at 90 hPa and averaged between 30^∘ S and 30^∘ N for injections of 5, 10 and 25 Tg(S) yr⁻¹ of SO₂ or AM-H₂SO₄. Results from CESM2 and SOCOL-AER only are shown, as the MAECHAM5-HAM model used fixed H₂O.

3.3 Chemical changes

Increases in stratospheric water vapour concentration are expected to modify OH concentration in the stratosphere as well. However, OH chemistry is complex and HO_x cycles interconnect with those of NO_x, ClO_x and BrO_x. The CESM2 and SOCOL-AER models show significant increases in tropical OH concentration above 50 hPa, up to a 15 % increase for SOCOL-AER and a 10 % increase for CESM2 with 5 Tg(S) yr⁻¹ injection. These relative increases in OH are consistent with relative increases in H₂O at 90 hPa. Analysis of our SO₂ injection scenarios shows that 7 %–10 % of the additional global sulfur (SO₂ + H₂SO₄) burden remains as SO₂ in the SOCOL-AER model, 5 %–8 % in the CESM2 model and 20 %–22 % for MAECHAM5-HAM. Derived residence times of the excess SO₂ burden (burden/SO₂ injection rate) are 18–28 d for SOCOL-AER, 25–37 d for CESM2 and 50–60 d for MAECHAM5-HAM. The long residence time for the MAECHAM5-HAM model results from the prescribed OH field employed in these calculations. SO₂ residence times in all models change very little with injection rate from 5 to 25 Tg(S) yr⁻¹, indicating that OH is not depleted by these large continuous injections of SO₂, as this effect is counterbalanced by increases in stratospheric H₂O due to heating of the tropical tropopause region.

Next, we evaluate the impacts on ozone, which are shown as zonal mean total ozone column (TOC) changes as a function of latitude in Fig. 12 for the 5 Tg(S) yr⁻¹ case for the two models which include HO_x chemistry (SOCOL-AER and CESM2). In agreement with previous studies (Pitari et al., 2014; see their Fig. 14c), we find that SO₂ injections lead to a TOC decrease, which maximizes in midlatitudes and high latitudes. However, we find larger polar losses in the Southern Hemisphere (20–30 DU) because of the larger sulfur injections in our study (5 vs. 2.5 Tg(S) yr⁻¹ in their study). Most of the column depletion occurs because of changes in the lower stratosphere, where the primary mechanism is N₂O₅ hydrolysis and consequent formation of nitric acid (HNO₃), thus decreasing ozone loss due to NO_x cycles and increasing it due to ClO_x and HO_x cycles. In addition, chlorine is activated via heterogeneous reaction of ClONO₂ and H₂O on stratospheric aerosols, contributing to most of the ozone depletion in polar latitudes. Both chemical pathways are enhanced via enhanced aerosol burden and consequently greater surface area density (SAD). The impact of chlorine on ozone is a function of the simulation year (2040) and future projection chosen, with our 2040 simulations containing 2.4 ppbv of total chlorine. Changes in dynamics, such as increased tropical upwelling (and consequent tropical lower stratospheric ozone decreases), modified stratosphere–troposphere exchange and chemical changes such as OH increases (and consequent enhancement of HO_x depletion cycles), also contribute to ozone changes.

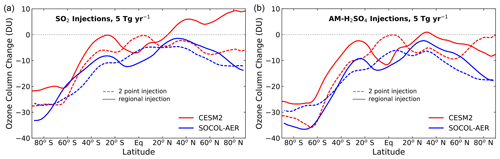
Figure 12 Change in zonal average column ozone (Dobson units) due to geoengineering injection as a function of latitude for (a) 5 Tg(S) yr⁻¹ of SO₂ injection and (b) 5 Tg(S) yr⁻¹ of AM-H₂SO₄ injection.

Ozone decreases in the lower stratosphere are partly offset by ozone increases in the middle stratosphere (10–50 hPa), due to weakened NO_x depletion cycles, in agreement with other studies (Heckendorn et al., 2009). As atmospheric chlorine concentrations decrease into the future and N₂O emissions continue, NO_x-mediated depletion will become dominant (Ravishankara et al., 2009) and the impact of increasing sulfuric acid aerosol on ozone is expected to become predominantly positive. The CESM2 model, in fact, shows increases in total ozone poleward of 30^∘ N with regional injections of SO₂ in 2040. AM-H₂SO₄ injections lead to a very similar TOC pattern as SO₂ injections in both models, although depletions are slightly larger (by 10 %–20 %) with AM-H₂SO₄ due to larger sulfuric acid aerosol burdens (Fig. 1) with smaller mean particle size and consequently larger SAD throughout the stratosphere. Hence, more surface area is available for heterogeneous reactions, leading to larger ozone depletion in the case of AM-H₂SO₄ rather than SO₂ injections, consistent with previous findings (Vattioni et al., 2019). Note that while the CESM2 model has larger increases in aerosol burden than the SOCOL-AER model, it nevertheless shows smaller changes in total ozone.

Geoengineering by stratospheric sulfur injection can have a strong impact on Arctic and Antarctic ozone depletion (Tilmes et al., 2009). However, this effect is generally less severe in the Arctic and is strongly modulated by interannual variations in the polar vortex strength. Both models produce Antarctic ozone depletion of 20–35 DU, while the Arctic shows smaller depletion (up to 18 DU) for SOCOL-AER. The CESM2 model shows minimal Arctic ozone depletion (up to 8 DU) for most cases but an increase in Arctic column ozone with SO₂ regional injections where positive changes in the middle stratosphere dominate negative changes in the lower stratosphere. Longer simulations than those considered here (8 years) would be needed to robustly detect dynamical and chemical effects on the Arctic stratosphere.

Figure 13 shows the correlation between global ozone change and global aerosol burden (left panel) or net TOA RF (right panel). Changes in total ozone column are a mix of both positive and negative local changes, and the global average includes large depletions in the Antarctic and small-to-moderate depletions elsewhere. The correlations with burden and net TOA RF are fairly compact for the SOCOL-AER model (R²=0.95 for burden, 0.90 for RF) but less so for the CESM2 model (R²=0.58 for burden, 0.72 for RF) which is much more sensitive to injection form and location. Regression lines for the SOCOL-AER model are much steeper than those for the CESM2 model, indicating different ozone sensitivities in the two models. A −4 W m⁻² change in net TOA RF corresponds to global ozone changes of from −1.5 % to −5 % among our two models and four injection scenarios, indicating large model uncertainties in ozone response to SRM.

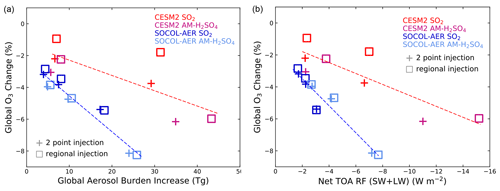
Figure 13 Global average change in column ozone (%) due to geoengineering injection plotted against (a) the global average aerosol burden increase (Tg(S)) and (b) the global average change in SW and LW radiative forcing (W m⁻²). Regression lines are shown for each model with R² values of 0.95 and 0.90 for SOCOL-AER (burden and RF, respectively) and 0.58 and 0.72 for CESM2.

4 Summary and discussion

Most obviously, the fact that all three models show that use of AM-H₂SO₄ particles can aid in controlling the large-scale particle size distribution strengthens the case that this method might be useful for sulfuric acid aerosol SRM. Improved control of particle size can, in turn, allow use of less sulfur to achieve the same radiative forcing, or it could allow higher levels of radiative forcing with less nonlinear saturation. Our three-model intercomparison increases the confidence in this general result while simultaneously demonstrating the significant uncertainty that arises from differences in model dynamics and model treatment of aerosol microphysics and chemistry. We note first there are large inter-model differences in both absolute quantities such as aerosol burden and radiative forcing and in derivative quantities such as aerosol lifetime and the change in radiative forcing with injection rate. Nevertheless, the intra-model differences in the impact of SO₂ vs. AM-H₂SO₄ show systematic agreement among the models. The inter-model differences in radiative forcing and R_eff are consistent with the inter-model differences in aerosol burden as diagnosed by the compact relationships among these quantities. And the significant difference in correlation slopes between SO₂ and AM-H₂SO₄ injection scenarios indicates that the different size distributions resulting from the different injection forms also play a significant role in determining the radiative forcing and radiative forcing per unit of injected mass flux, i.e. RF efficacy.

Perhaps the most interesting result is the systematic differences in radiative efficacy achieved over the 2×2 matrix of cases formed by the choice of SO₂ vs. AM-H₂SO₄ and regional vs. 2point injections, which are summarized in Table 3. These results hint at the limitations that come from the unresolved spatial scales between the injection plume and the model grid boxes, limitations that are common to these three models along with all other global models that have been used for studying SRM. For AM-H₂SO₄, 2point injections produce larger particles and lower radiative efficacies than regional injections. This is consistent with the expectation that point injections will drive up coagulation rates producing larger particles.

Results are less consistent for SO₂. All models find that 2point injections decrease particle size relative to regional injections, but the models do not agree on the sign of the difference in radiative efficacy between 2point and regional injections. The decrease in particle size may be due to point injections in the GCMs providing the same physical mechanism that is simulated in plume models in which new accumulation-mode particles are created by high densities of SO₂ and subsequently H₂SO₄ gas and locally high densities of nucleation-mode particles. But while the physical mechanism is similar, the length scales and timescales differ by many orders of magnitude from the plume scale (timescale of minutes and horizontal length scale of tens of metres). If SO₂ were actually injected from aircraft, it would form high aspect ratio plumes that observations suggest remain coherent for timescales of at least a week, and these plumes might have chemical and microphysical dynamics that are quite different from those simulated on the scale of a typical model grid box. This illustrates the limits of uniformly gridded Eulerian models in simulating the range of scales from injection plume to global circulation.

The most surprising and puzzling result is the increase in aerosol burden per unit AM-H₂SO₄ injected with increasing injection rate for two of the models (CESM2 and MAECHAM5-HAM). This may reflect the balance between increased tropical upwelling due to aerosol heating and increased sedimentation as a function of particle size and may be influenced by interactive changes in the QBO. This result, however, may depend on the initial size distribution of the AM-H₂SO₄ input to the GCMs as well as details of the model's resolution and transport processes and their interaction with aerosol microphysics. The SOCOL-AER model, which employs a sectional aerosol scheme, may remove the largest particles by sedimentation more efficiently than the modal schemes employed in the other models, thus leading to a decrease in aerosol burden per unit AM-H₂SO₄ injected with increasing injection rate in this model.

We have examined two side effects of geoengineering in this study: changes in lower stratospheric tropical temperature and changes in ozone. The use of AM-H₂SO₄ injections rather than SO₂ injections does not ameliorate these side effects when comparing equal injection amounts by sulfur weight. Yet we do find that the total aerosol mass burden needed to achieve a given RF is reduced by ∼35 % with AM-H₂SO₄ rather than SO₂ (Fig. 8). This may mean that, for the same RF, AM-H₂SO₄ injections would produce less stratospheric heating than SO₂ injections. For ozone the inter-model differences are larger than any systematic difference between AM-H₂SO₄ and SO₂ injection (Fig. 13).

This study is a step towards systematic study of the effectiveness and limitations of using AM-H₂SO₄ to influence the particle size distribution during a hypothetical deployment of SRM. Yet it is only one small step, and our results are subject to significant limitations including the following:

• The treatment of aerosol microphysics is inconsistent in that two of the models used a modal scheme (CESM2 and MAECHAM5-HAM) and one of them used a sectional scheme (SOCOL-AER). And the size boundary between accumulation mode and coarse mode differs between the two modal models. We find these model differences to be especially problematic in the large size tail of the size distribution that most influences the overall sedimentation rate.

• Results undoubtedly depend on resolution, and resolution varied significantly across models used here (see Table 2). CESM2 has a much finer horizontal resolution than the other two models, and the SOCOL-AER model was noticeably coarser in vertical resolution. The coarse vertical resolution of SOCOL-AER precluded interactive QBOs that are known to influence SRM simulation results (Niemeier and Schmidt, 2017; Franke et al., 2021).

• Our results on AM-H₂SO₄ aerosols depend on the aerosol size distribution we provided as input to the models. This distribution is intended to represent the distribution that would arise following processing within an aircraft plume and dispersal of that plume into a well-mixed grid box. But that process is not resolved in these models and is deeply uncertain. We do not know how that distribution would depend on the specifics of injection including location, local temperature and turbulence, injection rate and aircraft characteristics and the aerosol size distribution in the background air. Finally, this distribution implicitly assumes that the AM-H₂SO₄ is introduced by an aircraft plume.

• Observations (Murphy et al., 1998) suggest that the actual composition of lower stratospheric aqueous aerosols is not purely sulfuric acid but may contain a significant amount of secondary organics and minor amounts of meteoritic and other materials. The presence of secondary organic aerosols may be expected to change both chemical and optical properties of sulfuric acid aerosols. These processes are not accounted for in any of our models and are likely to vary spatially and seasonally.

• All these models may suffer from limitations in stratospheric dynamics and mixing (Linz et al., 2017; Niemeier et al., 2020; Dietmüller et al., 2018). For example, we expect substantial differences between mixing dynamical processes in the relatively low-vertical-resolution SOCOL-AER and the high-resolution CESM2.

Improved understanding of the effectiveness of stratospheric sulfur injection and the role of plume-scale formation of accumulation-mode particles may require use of modelling methods such as plume-in-grid or adaptive mesh to better capture the multi-scale problem from injection plume to the global circulation. Such methods may allow future interactive stratospheric aerosol model experiments to link directly with plume-scale model experiments and seek to realistically represent potential alternative deployment scenarios. Nonlinear interactions between aerosols and chemical species need to be explored across spatial scales. Small-scale field studies of aerosol dispersion and growth in the stratosphere under various conditions could reduce uncertainty. However, uncertainties will remain in predicting the performance and impact of any solar geoengineering technology.