the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Four-dimensional variational assimilation for SO2 emission and its application around the COVID-19 lockdown in the spring 2020 over China
Yiwen Hu
Zengliang Zang
Yi Li
Yanfei Liang
Wei You
Xiaobin Pan
Zhijin Li
Emission inventories are essential for modelling studies and pollution control, but traditional emission inventories are usually updated after a few years based on the statistics of “bottom-up” approach from the energy consumption in provinces, cities, and counties. The latest emission inventories of multi-resolution emission inventory in China (MEIC) was compiled from the statistics for the year 2016 (MEIC_2016). However, the real emissions have varied yearly, due to national pollution control policies and accidental special events, such as the coronavirus disease (COVID-19) pandemic. In this study, a four-dimensional variational assimilation (4DVAR) system based on the “top-down” approach was developed to optimise sulfur dioxide (SO2) emissions by assimilating the data of SO2 concentrations from surface observational stations. The 4DVAR system was then applied to obtain the SO2 emissions during the early period of COVID-19 pandemic (from 17 January to 7 February 2020), and the same period in 2019 over China. The results showed that the average MEIC_2016, 2019, and 2020 emissions were 42.2×106, 40.1×106, and 36.4×106 kg d−1. The emissions in 2020 decreased by 9.2 % in relation to the COVID-19 lockdown compared with those in 2019. For central China, where the lockdown measures were quite strict, the mean 2020 emission decreased by 21.0 % compared with 2019 emissions. Three forecast experiments were conducted using the emissions of MEIC_2016, 2019, and 2020 to demonstrate the effects of optimised emissions. The root mean square error (RMSE) in the experiments using 2019 and 2020 emissions decreased by 28.1 % and 50.7 %, and the correlation coefficient increased by 89.5 % and 205.9 % compared with the experiment using MEIC_2016. For central China, the average RMSE in the experiments with 2019 and 2020 emissions decreased by 48.8 % and 77.0 %, and the average correlation coefficient increased by 44.3 % and 238.7 %, compared with the experiment using MEIC_2016 emissions. The results demonstrated that the 4DVAR system effectively optimised emissions to describe the actual changes in SO2 emissions related to the COVID lockdown, and it can thus be used to improve the accuracy of forecasts.
- Article
(6620 KB) - Full-text XML
- BibTeX
- EndNote
Sulfur dioxide (SO2) causes acid rain through the formation of sulfuric acid, which destroys infrastructure and harms aquatic and terrestrial ecosystems (Saikawa et al., 2017; Zheng et al., 2018). SO2 is also a precursor of sulfate aerosols, which directly affect the radiation budget and indirectly modulate clouds and precipitation, and also cause haze pollution (Qin et al., 2022). Thus, SO2 emission impacts the ecological environment. SO2 pathway in the atmosphere is generally investigated using chemistry transport models (CTMs) to estimate the three-dimensional changes of SO2 concentrations. Thus, accurately estimating SO2 emissions is important for understanding spatiotemporal distribution of SO2 concentrations in CTMs (Zeng and Wu, 2021).
SO2 emissions are generally estimated using the “bottom-up” approach, which requires direct observations of the activities and emissions factors from all possible sources (Zhao et al., 2020). However, the estimates are subject to substantial uncertainties because of limited available observations, with the differences among existing inventories as high as 42 % (Granier et al., 2011). Saikawa et al. (2017) compared five types of emission inventories and found a significant difference in SO2 emissions from the power sector due to the difference in the assumed installation period of flue gas desulfurisation in coal-fired power plants. Moreover, most “bottom-up” emissions are recorded annually or monthly amounts, which need to be spatiotemporally allocated into the hourly gridded emissions for use in regional air quality models, and thus can cause uncertainties (Peng et al., 2017, 2018; Zeng and Wu, 2018). China has implemented several control strategies, such as strengthening emission standards, phasing out obsolete industrial capacity, and establishing small but high-emitting factories (Zheng et al., 2018), all of these have markedly reduced the emissions. However, these policies have been applied to varying extents in different regions, so that emission changes vary spatiotemporally (Chen et al., 2019; Dai et al., 2021). Such complex changes in SO2 emission were not reflected in the “bottom-up” estimates. Differences in the spatiotemporal control also caused additional uncertainties in gridded hourly emissions reducing their accuracy (Zeng et al., 2020).
In contrast to the “bottom-up” approach, data assimilation (DA) provides a “top-down” approach, where the ensemble Kalman filter (EnKF) and four-dimensional variational DA (4DVAR) are two of the most explored algorithms to optimise emissions (Cohen and Wang, 2014; Wang et al., 2022). The EnKF method uses flow-dependent covariance generated by an ensemble of model outputs to convert observational information into emissions (Tang et al., 2013; Ma et al., 2019), and has been used to estimate regional and global aerosols and gas-phase emissions, such as SO2, NOx, CO, and particulate matter. (Huneeus et al., 2012, 2013; Miyazaki et al., 2012, 2014; Tang et al., 2013, 2016; Chu et al., 2018). For example, Dai et al. (2021) developed a four-dimensional regional ensemble transform Kalman filter and showed that SO2 emissions over China in November 2016 decreased by 49.4 % in comparison to the 2010 background emission due to the implementation of emission control policies (Zheng et al., 2018). Peng et al. (2017, 2018) developed an EnKF system to include more spatiotemporal emission characteristics over China using hourly surface observations as constraints, and the forecasting results with optimised emissions are more accurate than those with the background emissions. The SO2 forecasts with the optimised emissions were improved for the forecast out to 72 h, and the root mean square errors (RMSEs) decreased by 30 % in comparison to the forecasts with the background emission. Feng et al. (2020) quantitatively optimised the gridded CO emissions in China using hourly surface CO measurements and EnKF algorithm with the weather research and forecasting (WRF)/Community Multiscale Air Quality (CMAQ) model, and found the optimised CO emissions in December 2017 17 % lower than those in December 2013.
A 4DVAR method has been used to estimate emissions based on the adjoint model of a CTM and is known as an inverse process (Bao et al., 2019; Yumimoto and Uno, 2006, 2007; Wang et al., 2022). Several studies have shown that 4DVAR is a promising approach to derive the emission rates (Dubovik et al., 2008; Hakami et al., 2005; Müller and Stavrakou, 2005; Elbern et al., 2007; Yumimoto et al., 2007, 2008). Stavrakou and Müller (2006) estimated CO and NOx emissions with a 4DVAR system using satellite data as a constraint, and showed that the optimised CO emission was 2900 Tg yr−1, which was about 5 % higher than the background emission. Henze et al. (2007) developed an adjoint model based on the GEOS-Chem model, and used it to optimise the SOx, NOx, and NH3 emissions. The model was also used to investigate the sensitivity of modelled aerosol concentrations to their precursor emissions, suggesting that their relationship strongly depended on thermodynamic competition. Qu et al. (2019) estimated SO2 emissions by assimilating Ozone Monitoring Instrument (OMI) observations using the GEOS-Chem model and its adjoint model, and found that the SO2 emissions decreased by 48 % over China from 2008 to 2016. The emissions based on a “top-down” approach can reduce the uncertainty of “bottom-up” emissions and provide a more accurate emission related to a special event than traditional emissions.
Emergence of the coronavirus disease (COVID-19) pandemic during the period from the end of 2019 through the beginning of 2020 (Wang et al., 2020) impacted more than 200 countries. To slow and stop the rapid spread of the virus, Wuhan was the first city to implement a lockdown on 23 January 2020, followed by the entire Hubei province 1 d later (Wuhan is capital of the Hubei province). Subsequently, all provinces in China successively implemented a national emergency to respond to major public health emergencies. The pollutant emissions decreased because human activities reduced during the lockdown (Filonchyk et al., 2020; Forster et al., 2020; Ghahremanloo et al., 2021; Keller et al., 2021; Li et al., 2020, 2021; Miyazaki et al., 2020; Huang et al., 2021a; Zhan and Xie, 2022; Zhang et al., 2020). For example, Huang et al. (2021b) estimated NOx emissions over China during this period, and found a decreased trend owing to human activity reduction.
In this study, we developed a 4DVAR system to estimate SO2 emissions, using the WRF model coupled with chemistry (WRF–Chem; Grell et al., 2005). Some physical and chemical processes, including transport, dry/wet deposition, emission, vertical mixing, and SO2 chemicals, were implemented to describe the pathway of SO2 in WRF–Chem. The 4DVAR system was applied to investigate the changes in SO2 emissions over China during the COVID-19 lockdown. Hourly surface SO2 observations were assimilated.
This paper is organised as follows. Section 2 describes the methodology, including the WRF–Chem and 4DVAR system configurations and their adjoint model, as well as observational data. In Sect. 3, the spatiotemporal changes in SO2 emission during the COVID-19 lockdown are estimated. SO2 simulations using optimised emissions are also verified against observations to show the improvements in emission data. Finally, a discussion and conclusions are presented in Sect. 4.
2.1 WRF–Chem model
WRF–Chem is an online coupled air quality model (Grell et al., 2005), which includes sophisticated and comprehensive physical and chemical processes such as transport, turbulence, emission, chemical transformation, photolysis, radiation, and more. The WRF–Chem version 3.9.1 was used in this study. The WRF–Chem domain (Fig. 1a) is centred at 101.5∘ E, 37.5∘ N, and covers all of China with 27 km horizontal resolution. There are totally 169×211 grid points. In the vertical, 40 vertical layers extend from the surface to 50 hPa, with high resolution near the surface. Meteorological initial and boundary conditions were derived from the National Centers for Environmental Prediction Global Final Analysis data at a 6 h frequency. Most of the WRF–Chem settings follow Hu et al. (2022; Table 1). Those settings include the WRF Lin microphysics scheme (Lin et al., 1983), rapid radiative transfer model longwave (Mlawer et al., 1997), Goddard shortwave radiation schemes (Chou, 1994), Yonsei University (YSU) boundary layer scheme (Hong et al., 2006), Noah land surface model (Chen et al., 2010), and Grell-3D cumulus parameterisation (Grell, 1993; Grell and Dévényi, 2002). Aerosol and gas-phase chemistry schemes are the aerosol interactions and chemistry (MOSAIC-4 bin) and carbon bond mechanism-Z (CBMZ; Zaveri and Peters, 1999; Zaveri et al., 2008). The heterogeneous SO2 reaction is also added to the WRF–Chem (Sha et al., 2019). The anthropogenic emissions from the multi-resolution emission inventory for China (MEIC) in 2016 are used as the background emission input.
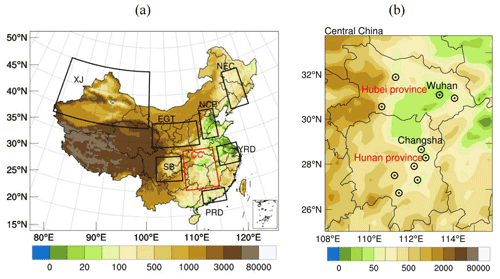
Figure 1(a) Maps of the WRF modelling domain and (b) central China. The colour bars represent the terrain altitude. The black rectangles in (a) are North China Plain (NCP), northeastern China (NEC), Energy Golden Triangle (EGT), Xinjiang (XJ), Sichuan Basin (SB), Yangtze River Delta (YRD), and Pearl River Delta (PRD). The red rectangle in (a) represents central China (CC). (b) The details of CC. Black circle with dots in (b) represent the locations of large cities. The red characters in (b) are the name of provinces, and the black characters are the name of capital cities. Wuhan and Changsha are the capitals of Hubei and Hunan provinces. Inset in (a): South China Sea. Units: m.
2.2 4DVAR system
4DVAR is a continuous data assimilation method to simultaneously assimilate a time series of observations over a time window. It produces an analysis that fit a set of observations taken over the time window. The time evolution of the concerning quantities is governed using a deterministic model as a strong constraint. The cost function of 4DVAR can be written as follows:
where c0 and ei are the control variables to denote the initial concentration vector and the emission to estimate. is the background concentration at zero time, and is the background emission. The subscripts of the variables represent time levels, and n is the time window. The first term in Eq. (1) is the background term due to the initial concentration field, and the second term is the background term for emissions in the time window. Bc and are the background error covariances (BECs) for the initial concentrations and background emissions. The third term is the observation term, where is the observation vector at time i. Hi is the observation operator mapping the control variables to the observations, and Ri is the observation error covariance matrix. The concentration ci is governed by a model.
where represents the model time integration for one time step from time i−1 to i. The increment field of the initial SO2 concentration can be written as , and the increment field of SO2 emission as . The innovation vector is denoted as , which is the difference between the observations and the model equivalent state. Thus, the cost function Eq. (1) can be written in an incremental form as follows:
Using a linearisation approximation, Eq. (2) becomes
where and Γi−1 are Jacobians of with respect to δci−1 and δei−1, and . Thus, with a time integration, Eq. (4) can be presented as
where Li,0 denotes the tangent linear model operator of the CTM acting on δc0, and the subscript is the time step from i to the initial time. Li,lΓl ( is the operator acting on δel, and Γl is an operator that converts emissions to concentrations.
There are several numerical algorithms available to minimise the cost function in Eq. (3) (Courtier et al., 1994; Li and Navon, 2001). For the algorithms to minimise Eq. (3) with large dimensions, the gradient of the cost function is required. The gradient with respect to δc0 and δei ( can be written as
Here, for i=0, where I is an identity matrix. A time window of 6 h is typically used in operational synoptic-scale numerical weather predictions. Since a SO2 lifetime in a model grid is usually less than 6 h (Fioletov et al., 2015), we still use a window of 6 h (n=6) in the experiments presented in the following sections.
Equations (6) and (7) include three types of adjoint operators, that is, ΓTLT and HT, which are derived from the tangent linear model operator ΓL, and observation operator H, respectively. The tangent linear operators Γ and L from WRF–Chem are very complex and computationally demanding, we simplify the CTM to focus on SO2.
WRF–Chem is an online coupled air quality model with sophisticated and comprehensive physical and chemical processes. Focusing on SO2, the governing equation for the concentration can be written as
where c is the gas/aerosol concentration, and u, v, and w denote the wind in x, y, and z directions, respectively. Thus, the is a transport term. Kx, Ky, and Kz are turbulent exchange coefficients in x, y, and z directions, respectively, based on K theory of turbulence, and is the turbulent term. In the study, the horizontal grid spacing is 27 km, thus the can be neglected. But the vertical turbulence term should be retained since the vertical grid spacing is generally less 200 m in the lower and middle layers. denotes the wet deposition term, where Λ is the loss rate (Grell and Dévényi, 2002) and e is the base of natural logarithms (=0.272), is the chemical term, where r is the chemical reaction rate of the species, and is the emission term, where e denotes the emission source of the species. m3 mol−1 is the molar gas volume, ρ is the air density of the actual atmosphere (kg m−3), ρair is the standard air density indicating the molar volume, and ΔS is the grid area.
From the simplified Eq. (8), the model operators of Γ and L can be written as
Using tangent linear coding techniques, we could derive the code for the discretised tangent linear operators L and Γ (Eqs. 9–10) from the source code built in WRF–Chem. Once the source code is available for the tangent linear operators, we use the adjoint coding technique to derive the adjoint operator. The adjoint coding technique are detailed in Hoffman et al. (1992).
2.3 Observational and background error covariances
Ri in Eq. (1) is the observational error covariance for a set of observations (yi), where Bc and are the BECs for the concentrations and emissions, respectively. In a DA system, Ri and BEC play important roles in successful assimilation. The observational errors include the measurement error (observed value error) and representative error (error of observation operator H). The observation error is defined as below:
where εo is the measurement error, and εr is the representative error. The measurement error εo is the systematic error generated during monitoring by the instrument at each environmental monitoring station. Therefore, the measurement error εo of SO2 observation in this study is 1.0 µg m−3, similar to that reported by Chen et al. (2019).
The representative error εr is caused by converting the model variable to the observation variable (Schwartz et al., 2012) and can be expressed as
where γ is an adjustable parameter scaling εo. γ=0.5 was used in accordance with that used in Dai et al. (2021). Furthermore, dx is the grid spacing (27 km in this study) and L is the radius of influence of an observation, which was taken as 2 km according to that reported by Chen et al. (2019). Then, εr=1.8 µg m−3 is calculated from Eq. (12).
BECs (Bc and in Eq. 1) are the error covariance matrices of SO2 concentrations and emissions. Practically, the BEC is overly large for handling numerically. Thus, we followed the method used by Li et al. (2013) and Zang et al. (2016) to simplify B:
where D is the RMSE matrix and C is the correlation matrix.
C can be simplified by the Cholesky factorisation and Kronecker product method (Li et al., 2013) as
For , the standard deviation is diagonal with a 200 % error (Wang et al., 2012) and is a block diagonal matrix, with the main diagonal blocks being the correlation matrices of SO2 emission. The main diagonal blocks of is 1.0 because the emission in each grid point is independent of that in other grids.
The National Meteorological Center method (Parrish and Derber, 1992) was used to estimate the BEC of SO2 concentrations. The differences between 48 and 24 h forecasts were generated from 17 January to 18 February 2020. The first initial chemical field at 00:00 UTC on 17 January 2020 was obtained from a 10 d forecast in consideration of spin-up. The subsequent initial chemical fields were derived from the former forecast 1 d prior. The horizontal length scale was used to determine the magnitude of SO2 variance in the horizontal direction. This scale can be estimated by the curve of the horizontal correlation with distances, and the horizontal correlation is approximately expressed by a Gaussian function (e is the base of natural logarithms equal to 0.272). Here, x1 and x are two points, and Ls is the horizontal length scale. According to Zang et al. (2016), when the intersection of the decline curve reaches , the distance can be approximated as the horizontal length scale in Fig. 2a. The horizontal length scale was 81 km in this study. The vertical variance of SO2 concentrations was considered by the vertical correlations in the BEC. A strong relationship was observed in the boundary layer (approximately below the 20th model layer) in the vertical direction (Fig. 2b). The standard deviation demonstrates the reliability of the forecasting model, and the standard deviation for the vertical distribution of SO2 concentrations decreased with increasing height in the Bc (Fig. 2c).
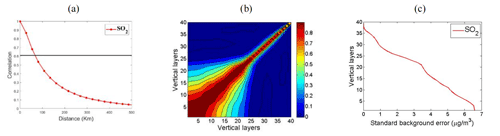
Figure 2Background error covariation of SO2 concentrations. (a) Vertical distribution of the horizontal correlation; the horizontal thin black line is the reference line () used to determine the horizontal correlation scales. (b) Vertical correlations. (c) Vertical distribution of the standard deviation.
2.4 Observation and emission data
Hourly SO2 data obtained from the website of the China National Environmental Monitoring Center (http://www.cnemc.cn/en/, last access: 28 September 2022) were used for assimilation and evaluation. There were 1933 stations in China in January 2020. Most observational stations were located in central and eastern China, whereas the stations in the west were relatively sparse. The sites were gridded into the model grid (27×27 km2). If more than two stations were in the same grid, one station was randomly selected to verify the improvements relating to using optimised emissions, and the remaining sites were used for assimilation. In this study, 508 sites were selected for verification, and the remaining 1425 stations were used for assimilation. A strict criterion was used to remove SO2 observations with values exceeding 650 µg m−3 to ensure data quality (Chen et al., 2019).
The background anthropogenic emissions data were obtained from the MEIC (http://www.meicmodel.org/, last access: 28 September 2022) developed by Tsinghua University, with a resolution and 2016 as the base year. The MEIC is a “bottom-up” emission inventory that covers 31 provinces on the Chinese mainland, and includes eight major chemical species (Zhang et al., 2009), and counts anthropogenic emissions from sources in five sectors (power, industry, residential, transportation, and agriculture). Details of the technology-based approach and source classifications have been reported by Zhang et al. (2009). The actual emission inventory () was pre-processed to match the model grid spacing (27 km).
2.5 Experimental design
Figure 4 shows a flowchart of the procedure used to optimise SO2 emissions in a single time step of i. First, a forecast was performed using the WRF–Chem model and background emissions to generate the meteorological and chemical fields, which were recorded every 10 min and then used in the 4DVAR system. Then, the 4DVAR system performed every 6 h to obtain SO2-optimised emissions and initial concentrations by assimilating the hourly SO2 observations. For example, the observations during 00:00–06:00 UTC were assimilated using Eq. (1). The assimilated SO2 concentration initial field (00:00 UTC) and the optimised SO2 emissions during 00:00–05:00 UTC were obtained.
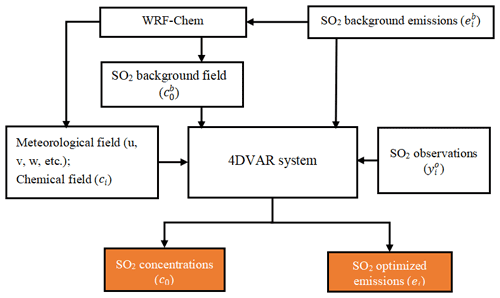
Figure 4Flow chart of the SO2 emissions optimisation procedure in a single time step of i. The orange boxes represent the SO2-optimised emissions and SO2 concentrations of output. The , c0, , ei, and are the mathematical symbols from Eq. (1).
The SO2 emissions during the COVID-19 lockdown over China were optimised to evaluate the performance of the 4DVAR system, and to analyse the reduction of SO2 emissions related to the COVID-19 lockdown. The national lockdown was imposed in Wuhan and surrounding cities of Hubei provinces on 23 and 24 January 2020, respectively. Then, the Chinese mainland implemented the national lockdown policies on 26 January 2020. We selected the study period from 17 January to 6 February 2020, which covered the time before and during lockdown. The latest available MEIC emission inventory is based on the statistics of 2016. However, the changes of emissions between 2020 and 2016 are both related to the emissions reduction policies and COVID-19 lockdown. The difference between 2019 and 2020 emissions during the same period reflected the influence of COVID-19 lockdown on SO2 emissions. Thus, the SO2 emissions during the study period in 2019 was also optimised.
Table 2 summarises the details of DA emissions experiments. For the set of Emi_2019 experiments, the first DA process started on 17 January 2019, and the observations during 00:00–06:00 UTC of 17 January 2019 were assimilated by the 4DVAR system. Then, the optimised initial SO2 concentration field (00:00 UTC) and SO2 emissions during 00:00–05:00 UTC were obtained. Before conducting Emi_2019 experiment, 24 h forecasts were performed by WRF–Chem with MEIC_2016 emissions every 00:00 UTC from 17 January to 7 February 2019 to provide the physical and chemical parameters. The daily chemical initial conditions were obtained from the 24 h forecast of the previous day. For the 24 h forecast, the meteorological initial and boundary conditions were provided by the National Centers for Environmental Prediction (NCEP) global final analysis data at a 6 h frequency. The chemical boundary fields were not considered because the domain used in this study was wider than that in China. For the Emi_2019 experiment, the emissions of 2019 were optimised by the 4DVAR system every 6 h with the background emissions of MEIC_2016. The physical and chemical parameters used in this DA process were obtained from the WRF–Chem forecast. For the Emi_2020 experiment, the DA process settings were similar to those of the Emi_2019 experiment. The optimised emissions for 2020 were obtained with the emission 2019 as background emission.
To estimate the improvement of SO2 forecasts using optimised emissions, three sets of forecast experiments were performed using the MEIC_2016 emissions and the optimised emissions for 2019 and 2020, respectively, labelled Ctr_2016, DA_2019, and DA_2020, respectively (see Table 3). The three experiments were run daily with 24 h forecasts from 17 January to 7 February 2020 using the same WRF–Chem domain settings and physiochemical parameters. The SO2 initial condition (IC) at 00:00 UTC on 17 January was based on the spin-up forecasts initialised at 00:00 UTC on 7 January 2020 for all three forecast experiments. The SO2 ICs were later obtained from the 24 h forecast of the previous day for the three experiments, respectively. For example, the SO2 IC of the experiment beginning at 00:00 UTC on 18 January was taken from the 24 h forecast result of the experiment beginning at 00:00 UTC of 17 January, and so on. Meteorological initial and boundary conditions were provided by the NCEP global final analysis data at a 6 h frequency. The chemical boundary fields were not considered.
3.1 Results of 4DVAR emission experiments
3.1.1 4DVAR test case
The first day (17 January 2019) was used as a test case to determine the effectiveness of using 4DVAR. The experiment employed MEIC_2016 as the background emissions and assimilated the hourly surface SO2 observations during 00:00–06:00 UTC of 17 January 2019. The observed SO2 concentrations in Fig. 5a indicated the heavy polluted areas with SO2 concentrations exceeding 80 µg m−3 were mostly located in the North China Plain and northeast China. The areas lightly polluted with SO2 concentrations below 40 µg m−3 were mostly located in southern China. Compared with the observed concentrations, the background concentrations (Fig. 5b) were underestimated in North China Plain and northeast China but overestimated in central China and the Sichuan Basin. Figure 5c shows the increment field of SO2 concentrations (analysed field minus background field). Positive values in most of northern China and negative in central China and the Sichuan Basin were observed, suggesting that the optimised IC is more consistent with the observed SO2 concentrations than the background concentrations. The evaluations of the optimised IC and background concentrations are shown in Fig. 5d. Compared with the background field, the mean bias in analysis field improved from −2.76 to 1.79 µg m−3 and RMSE decreased from 23.12 to 11.81 µg m−3, and the correlation coefficient (CORR) of analysis field increased from 0.19 to 0.84. The result indicates that the accuracy of the ICs of SO2 concentrations were improved after using the 4DVAR method. The forecast accuracy can be improved using optimised ICs (Peng et al., 2017, 2018), but the emission is the most important factor influencing the forecast accuracy. The emissions and IC concentrations were simultaneously optimised in the EMI_2019 experiment using our 4DVAR system.
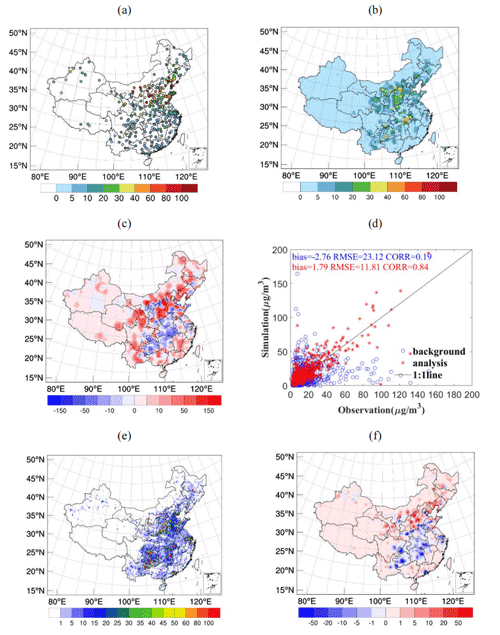
Figure 5Simulated and observed SO2 concentrations at 00:00 UTC, 17 January 2019. (a) Observations, (b) background concentrations, (c) SO2 concentrations increment, (d) scatter plots, (e) background emissions, and (f) SO2 emissions increment. Units: µg m−3 for (a)–(d), and mol km−2 h−1 for (e) and (f). Insets: South China Sea.
Figure 5e presents the background emission of MEIC_2016 at 00:00 UTC. According to Fig. 5a and b, MEIC_2016 emissions underestimated in most of northern China and overestimated in central China and Sichuan Basin. Figure 5f shows the increment of SO2 emissions at 00:00 UTC 17 January 2019 by using the 4DVAR system. There were positive increment in North China Plain and northeast China, and negative increment in central China and Sichuan Basin. The distribution of the incremental SO2 emissions was consistent with that of the incremental SO2 concentration (Fig. 5c). There is a reasonable relationship between the two increments since the underestimated/overestimated emission may result in underestimated/overestimated simulation of concentration.
3.1.2 Spatial distribution of emissions
Compared with MEIC_2016 (Fig. 6a), the emissions for 2019 and 2020 (Fig. 6b and c) from the 4DVAR experiments of Emi_2019 and Emi_2020 decreased in the area with heavy emissions, particularly in North China Plain and central China. The reduction in emissions between 2019 and MEIC_2016 may primarily result from the national pollution control policy. However, the reduction of emissions between 2020 and 2019 may primarily result from the COVID 2019 lockdown, including school and workplace closures, event and public gathering cancellation, and restrictions on public transport.
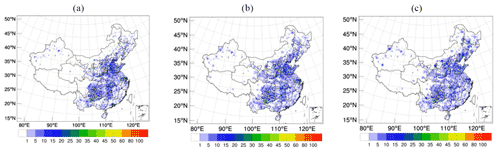
Figure 6Emissions in China for (a) MEIC_2016, (b) 2019, and (c) 2020. Units: mol km−2 h−1. Insets: South China Sea.
Figure 7a shows the difference in emissions between 2020 and 2019. The negative values were seen in most of the areas with strict lockdown, such as North China Plain, central China, Yangtze River Delta, and Pearl River Delta. It indicates that the 2020 emission substantially decrease, compared with the 2019 emission due to the COVID-19 lockdown. The reducing ratio of emission was averaged in China as 9.2 % (Fig. 7b), but over 40.0 % in most areas of north China and central China. Zheng et al. (2021) have found that SO2 emissions in China decreased by 12.0 % in January and February 2020 compared to values in 2019. Fan et al. (2020) have also reported the SO2 concentration decreased by 20.0 %–50.0 % over China during the COVID-19 lockdown period in the spring of 2020 based on TROPOMI satellite data. Our results are similar to those of previous studies. In addition, SO2 emissions increased in some areas of northeast China, Tibetan Plateau, Yunnan province, and the southeast coastal areas, where the epidemic was weaker than that in other areas (Kraemer et al., 2020; Tian et al., 2020). Most of the increase in SO2 was <10 mol km−2 h−1, but the positive ratios were >100.0 %, suggesting that new emission sources were generated. It is suggested that these newly generated emissions were probably due to relocating power plants and factories from cities to the surrounding villages (Chen et al., 2019).
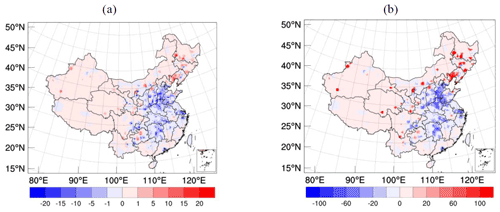
Figure 7(a) Difference between 2020 and 2019 emissions, and (b) ratios of (2020–2019) emissions in China. Units are mol km−2 h−1 for (a) and percent (%) for (b). Insets: South China Sea.
Figure 8 shows the similar analyses as in Fig. 6, but for central China. Wuhan first implemented the first-level response to COVID-19 with strict lockdown policies on 23 January 2020, and the entire Hubei province implemented lockdown on 24 January 2020. The heavy emissions exceeding 20.0 mol km−2 h−1 were most located around large cities from the emissions of 2019 and 2020 (Fig. 8b and c). Figure 9a shows the difference between 2020 and 2019 emissions in central China. The average emission value in Wuhan was 43.0 mol km−2 h−1 in 2019 and 34.0 mol km−2 h−1 in 2020, showing a reduction of 21.0 % compared with the emissions for 2019. Al-qaness et al. (2021) have also found approximately 15 % decrease in SO2 concentrations with 15 % around Wuhan. Furthermore, almost all emissions around the large cities decreased by 5–10 mol km−2 h−1 (Fig. 9a), and the negative ratios were >20.0 % (Fig. 9b). The large reduction in SO2 emissions were related to the decrease in industrial and domestic coal combustion and power plants during the COVID-19 lockdown (Zheng et al., 2018, 2021; Bian et al., 2019; van der A et al., 2017).
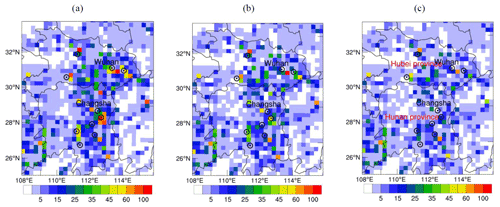
Figure 8Emissions in central China for (a) MEIC_2016, (b) 2019, and (c) 2020. Black circles with dots are the locations of large cities. The red characters in (c) are the name of provinces, and the black characters are the name of cities. Wuhan and Changsha are the capitals of Hubei and Hunan provinces, respectively. Unit: mol km−2 h−1.
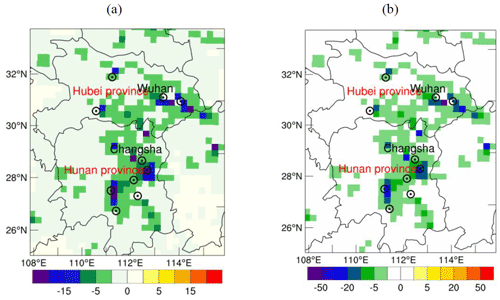
Figure 9(a) Difference between 2020 and 2019 emissions, and (b) ratios of (2020–2019) emissions in central China. Black circles with dots are the location of large cities. The red characters are the name of provinces, and the black characters are the name of cities. Wuhan and Changsha are the capitals of Hubei and Hunan provinces, respectively. Units: mol km−2 h−1 for (a) and percent (%) for (b).
3.1.3 Temporal evolution of emissions
Figure 10 shows the daily SO2 emissions for MEIC_2016, Emi_2019, and Emi_2020 over all grid points. The average emissions in the Chinese mainland (Fig. 10a) from MEIC_2016, Emi_2019, and Emi_2020 were 42.2×106, 40.1×106, and 36.4×106 kg d−1 during the same period from 17 January to 7 February. The emissions for 2020 decreased by 9.2 % compared with those for 2019, indicating a decrease between 2020 and 2019 due to the COVID-19-related lockdown. In Emi_2019 emissions, the lowest emissions occurred on 1 February 2019, but increased during 4–6 February 2019, mainly attributed to the traditional firework displays during Spring Festival (Wang et al., 2007; Zhang et al., 2020; Huang et al., 2021a). Complex changes in SO2 emission trends were observed in 2020 in relation to reduced human activity. For example, a peak of 40.1×106 kg d−1 occurred on 24 January 2020, in relation to firework displays (Fig. 10a), after which the SO2 emissions decreased because of the COVID-19 lockdown. For central China, the average SO2 emissions were 5.7×106, 4.2×106 and 3.1×106 kg d−1 during the same period from 17 January to 7 February (Fig. 10b). The SO2 emissions peaked at 3.5×106 kg d−1 on 24 January 2020 due to firework displays, and a reduction began from 26 January 2020 because of the national lockdown.
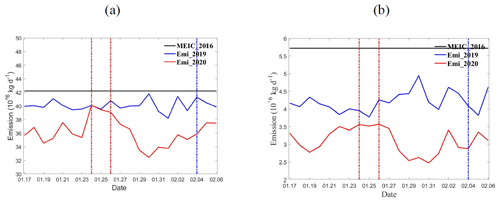
Figure 10Time series of daily SO2 emissions in (a) China and (b) central China. The red dotted lines represent the dates of the start of national lockdown and the Chinese Spring Festival in 2020. The blue dotted line represents the Chinese Spring Festival in 2019. Units: 106 kg d−1.
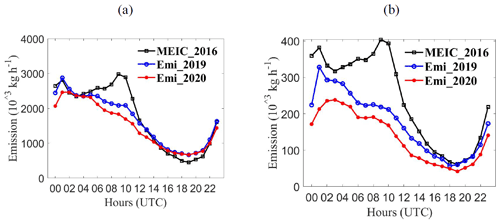
Figure 11 shows the average hourly emissions for MEIC_2016, Emi_2019, and Emi_2020 emissions from 17 January to 7 February over all grid points. The hourly factors for MEIC_2016 were obtained from power plant report, with two peaks during the day at 01:00 UTC (09:00 BJ time – Beijing time) and 09:00 UTC (17:00 BJ time) to reflect the emissions at rush hours (Chen et al., 2019; Hu et al., 2022). In the Chinese mainland (Fig. 11a), the emissions of 2019 and 2020 were lower than those of MEIC_2016 during 06:00–12:00 UTC. This is primarily due to the recent implementation of China's emission reduction policies and the COVID-19 lockdown. Previous studies have shown that the second peak (09:00 UTC) of SO2 emissions had weakened (Chen et al., 2019), which was also reflected in our hourly emission analysis. The emissions for Emi_2019 and Emi_2020 were higher than those of MEIC_2016 during 16:00–20:00 UTC, but remain almost unchanged between Emi_2019 and Emi_2020 emissions. During this time period, most factories were closed and human activities were reduced. The SO2 emissions are primarily emitted from power plants, and the changes in emissions are small between different years (Zheng et al., 2018, 2021; Hu et al., 2022). Thus, the increase in Emi_2019 and Emi_2020 emissions during 16:00–20:00 UTC are mainly due to the uncertainties of MEIC_2016 (Chen et al., 2019). Compared with the average emissions for Emi_2019, those for Emi_2020 emissions decreased by 18.0 %, reflecting the reduction due to the COVID-19 lockdown. The emissions in 2019 and 2020 in central China were lower than those in MEIC_2016 for 24 h period, with a maximum reduction at 09:00 UTC (Fig. 9b). Compared with the emissions in 2019, the emissions in 2020 appreciably decreased by 22.3 %–42.1 %. The first peak of the emissions in 2020 was delayed and occurred at 02:00 UTC because of the national lockdown policies. The most substantial reduction between 2019 and 2020 emissions was kg h−1 at 01:00 UTC, reflecting the change in human activities at the first peak. Additionally, although there was only a moderate decrease in SO2 emissions ( kg h−1) at 13:00 UTC, the reduction ratio (−54.5 %) was the largest during 24 h.
3.2 Results of forecast experiments
Using the emissions of MEIC_2016, Emi_2019, and Emi_2020, three forecast experiments (Ctrl_2016, DA_2019, and DA_2020 in Table 3) were implemented to further demonstrate the effect of optimised emissions. Figure 12 shows the average 24 h forecast of SO2 concentrations of the three forecast experiments over all stations in China during the study period from 17 January to 7 February 2020. The DA_2020 experiment with the 2020 emissions performed much better than the Ctrl_2016 and DA_2019 experiments, indicating that the emission is one of the most important factors for 24 h forecasts. The SO2 concentrations in Ctrl_2016 and DA_2019 were overestimated, particularly during 08:00–18:00 UTC (Fig. 12a), while the SO2 concentrations in DA_2020 are similar to the observed concentrations. The result showed the 4DVAR system effectively optimises emissions and improves the accuracy of forecasts. The average RMSEs of the three experiments were 21.7, 15.6, and 10.7 µg m−3, respectively. Compared to the average RMSE of Ctrl_2016 experiment, the RMSEs of the DA_2019 and DA_2020 decreased by 28.1 % and 50.7 %. The average CORRs for the Ctrl_2016, DA_2019, and DA_2020 experiments were 0.20, 0.38, and 0.61, respectively. Thus, the average CORRs for DA_2019 and DA_2020 experiments increased by 89.5 % and 205.9 % from the CORR for Ctrl_2016 experiment. The average bias of Ctrl_2016, DA_ 2019, and DA_2020 experiments were 5.9, 4.9, and −0.1 µg m−3, respectively. It is suggested that the optimised emissions could substantially improve forecast accuracy, and the 4DVAR approach is effective to optimise daily and hourly emissions during an accidental special event.
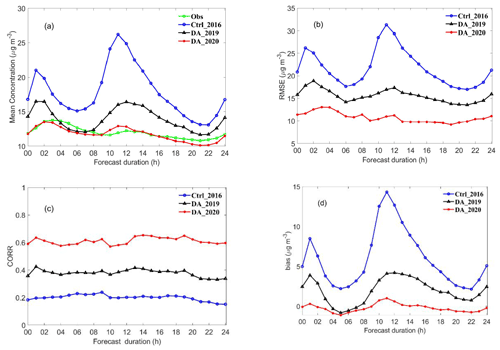
Figure 12Forecast accuracy of SO2 concentrations in China for the Ctrl_2016, DA_2019, and DA_2020 experiments during the study period in 2020: (a) mean concentration, (b) RMSE, (c) CORR, and (d) bias. Unit: µg m−3 for (a), (b), and (d). Obs: observation.
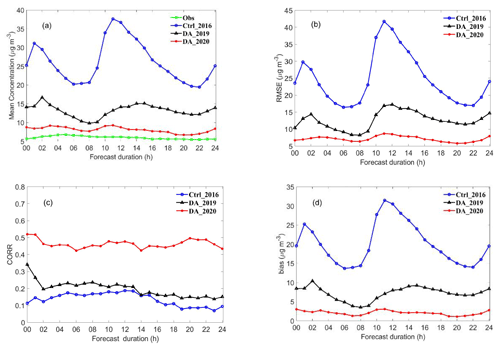
Figure 13Forecast accuracy of SO2 concentrations in central China using the Ctrl_2016, DA_2019, and DA_2020 experiments during the study period in 2020. (a) Mean concentration, (b) root mean square error (RMSE), (c) correlation coefficient (CORR), and (d) bias. Unit: µg m−3 for (a), (b), and (d). Obs: observation.
Figure 13 shows the same analyses as those presented in Fig. 12, but for central China. It also showed that the forecast accuracies of the DA_2019 and DA_2020 experiments were higher than those of Ctrl_2016. The average observation concentration was <10 µg m−3, which is substantially lower than that for Chinese mainland (Fig. 12a). The mean concentration of DA_2020 was close to the observed concentration in central China. The above results suggest that although the 2020 optimised emissions were generally consistent with the real emissions, they were slightly higher than the real emissions. In the 4DVAR optimisation process, each grid will be influenced by surrounding grids because of the advection and vertical mixing. The theory of 4DVAR method is to take a balance between the observations and background field, and to obtain the optimised field. Therefore, when the observations are lower and the background fields are higher, the value of the optimised field will be higher than the observation. Compared to that of Ctrl_2016, the average bias of the DA_2019 and DA_2020 experiments decreased from 20.1 to 12.6 and 3.5 µg m−3. The average RMSE decreased by 48.8 % and 77.0 %, and the average CORR increased by 44.3 % and 238.7 %. This indicates that the forecast accuracy substantially improved after using optimised emissions.
In this study, we developed a 4DVAR system based on the WRF–Chem model to estimate SO2 emissions, where the initial SO2 concentration and emissions were set as the state variables to estimate SO2 emissions. An adjoint operator was derived from the WRF–Chem model, focusing on the processes of transport, dry/wet deposition, vertical turbulence, and SO2 chemical reactions. Hourly SO2 concentration observations were assimilated to optimise SO2 emissions, which were used to improve the SO2 forecasting accuracy.
The 4DVAR system was applied to investigate SO2 emission changes during the COVID-19 lockdown in China, particularly focusing on central China. The MEIC_2016 emissions were set as the background values. The average emissions of MEIC_2016, 2019, and 2020 were 42.2×106, 40.1×106, and 36.4×106 kg d−1, namely 2020 emissions decreased by 9.2 % compared with those in 2019, indicating a substantial decrease between 2019 and 2020 due to the COVID-19 related lockdown. The average 2020 emissions in central China dropped by 21.0 % compared to the 2019 emissions, owing to the strict lockdown policy during COVID-19. The largest decrease in emissions occurred in Wuhan (decline of 57.0 %), which COVID-19 had heavily affected by this time. Hourly average emissions were analysed to estimate the changes between 2019 and 2020. Compared with 2019 emissions, the average 2020 emissions decreased by 18.0 %, reflecting lockdown-associated reduction in SO2 emissions. The 2020 emissions in central China decreased by 22.3 %–42.1 % compared with the 2019 emissions.
Three sets of forecast experiments for 2020, using MEIC_2016, Emi_2019, and Emi_2020 emissions, were conducted to illustrate the effects of the optimised emissions. The experiment with MEIC_2016 emissions overestimated the SO2 concentration forecast, whereas the experiment with 2019 optimised emissions decreased the concentrations but still overestimated the values. The forecast accuracy of the experiment with the 2020 emissions was the closest to the observation. The RMSE of the experiments with the emissions in 2019 and 2020 decreased from 21.7 to 15.6, and 10.7 µg m−3, respectively, and the correlation coefficient increased from 0.20 to 0.38 and 0.61, respectively, compared with those of the experiment with MEIC_2016 emissions. For central China, the average RMSE and correlation coefficient of the experiment with MEIC_2016 were 24.6 µg m−3 and 0.1. Compared with the average RMSE of the experiment with MEIC_2016, those of the experiments with 2019 and 2020 emissions decreased by 48.8 % and 77.0 %, and the average correlation coefficient increased by 44.3 % and 238.7 %.
Though our 4DVAR system could effectively optimise real time emission as a “top-down” approach, some limitations still remain. Only hourly surface SO2 observations were used to constrain the emission sources. The spatial distribution of surface observation sites was uneven with fewer sites in the northwest and southwest regions, resulting in limited adjustments to emission sources in these regions. In future, satellite data will be used to adjust the emission source to address the lack of surface observation data. Furthermore, the simultaneous optimisation of SO2 concentrations and emissions will be implemented in a 4DVAR system, and multi-source observation data will be used to improve its performance.
NCEP FNL reanalysis data were downloaded from https://rda.ucar.edu/datasets/ds083.2/ (National Centers for Environmental Prediction/National Weather Service/NOAA/US Department of Commerce, 2022). The MEIC 2016 emission sources can be found at http://meicmodel.org/?page_id=541&lang=en (Tsinghua University, 2022). The hourly SO2 observations were downloaded from http://www.cnemc.cn/en/ (China National Environmental Monitoring Centre, 2022).
ZZ designed the overall research; YH performed experiments; YaL, WY, ZiL and XP contributed to the development of the DA system; ZZ and XM provided funds; YH, ZZ, and XM wrote the paper with contributions from all co-authors; and XM, ZZ, and ZL developed the mathematical formulation and reviewed the paper. All authors have read and agreed to the published version of the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research has been supported by the National Natural Science Foundation of China (grant nos. 41975167, 41775123, 41975002, and 42061134009) and the National Key Scientific and Technological Infrastructure project “Earth System Science Numerical Simulator Facility” (EarthLab).
This paper was edited by Matthias Tesche and reviewed by three anonymous referees.
Al-qaness, M. A. A., Fan, H., Ewees, A. A., Yousri, D., and Abd Elaziz, M.: Improved ANFIS model for forecasting Wuhan City Air Quality and analysis COVID-19 lockdown impacts on air quality, Environ. Res., 194, 110607, https://doi.org/10.1016/j.envres.2020.110607, 2021.
Bao, Y., Zhu, L., Guan, Q., Guan, Y., Lu, Q., Petropoulos, G. P., Che, H., Ali, G., Dong, Y., Tang, Z., Gu, Y., Tang, W., and Hou, Y.: Assessing the impact of Chinese FY-3/MERSI AOD data assimilation on air quality forecasts: Sand dust events in northeast China, Atmos. Environ., 205, 78–89, https://doi.org/10.1016/j.atmosenv.2019.02.026, 2019.
Bian, Y., Huang, Z., Ou, J., Zhong, Z., Xu, Y., Zhang, Z., Xiao, X., Ye, X., Wu, Y., Yin, X., Li, C., Chen, L., Shao, M., and Zheng, J.: Evolution of anthropogenic air pollutant emissions in Guangdong Province, China, from 2006 to 2015, Atmos. Chem. Phys., 19, 11701–11719, https://doi.org/10.5194/acp-19-11701-2019, 2019.
Chen, D., Liu, Z., Ban, J., and Chen, M.: The 2015 and 2016 wintertime air pollution in China: SO2 emission changes derived from a WRF-Chem/EnKF coupled data assimilation system , Atmos. Chem. Phys., 19, 8619–8650, https://doi.org/10.5194/acp-19-8619-2019, 2019.
Chen, Y., Yang, K., Zhou, D., Qin, J., and Guo, X.: Improving the Noah Land Surface Model in Arid Regions with an Appropriate Parameterization of the Thermal Roughness Length, J. Hydrometeorol., 11, 995–1006, https://doi.org/10.1175/2010JHM1185.1, 2010.
China National Environmental Monitoring Centre: Real-time national air quality, CNEMC [data set], http://www.cnemc.cn/en/, last access: 28 September 2022.
Chou, M. and Suarez, M.: An efficient thermal infrared radiation parameterization for use in general circulation models, http://purl.fdlp.gov/GPO/gpo60401 (last access: 28 September 2022), 1994.
Chu, K., Peng, Z., Liu, Z., Lei, L., Kou, X., Zhang, Y., Bo, X., and Tian, J.: Evaluating the Impact of Emissions Regulations on the Emissions Reduction During the 2015 China Victory Day Parade With an Ensemble Square Root Filter, J. Geophys. Res.-Atmos., 123, 4122–4134, https://doi.org/10.1002/2017JD027631, 2018.
Cohen, J. B. and Wang, C.: Estimating global black carbon emissions using a top-down Kalman Filter approach, J. Geophys. Res.-Atmos., 119, 307–323, https://doi.org/10.1002/2013JD019912, 2014.
Courtier, P., Thépaut, J. N., and Hollingsworth, A.: A strategy for operational implementation of 4D-Var, using an incremental approach, Q. J. Roy. Meteor. Soc., 120, 1367–1387, https://doi.org/10.1002/qj.49712051912, 1994.
Dai, T., Cheng, Y., Goto, D., Li, Y., Tang, X., Shi, G., and Nakajima, T.: Revealing the sulfur dioxide emission reductions in China by assimilating surface observations in WRF-Chem, Atmos. Chem. Phys., 21, 4357–4379, https://doi.org/10.5194/acp-21-4357-2021, 2021.
Dubovik, O., Lapyonok, T., Kaufman, Y. J., Chin, M., Ginoux, P., Kahn, R. A., and Sinyuk, A.: Retrieving global aerosol sources from satellites using inverse modeling, Atmos. Chem. Phys., 8, 209–250, https://doi.org/10.5194/acp-8-209-2008, 2008.
Elbern, H., Strunk, A., Schmidt, H., and Talagrand, O.: Emission rate and chemical state estimation by 4-dimensional variational inversion, Atmos. Chem. Phys., 7, 3749–3769, https://doi.org/10.5194/acp-7-3749-2007, 2007.
Fan, C., Li, Y., Guang, J., Li, Z., Elnashar, A., Allam, M., and de Leeuw, G.: The Impact of the Control Measures during the COVID-19 Outbreak on Air Pollution in China, Remote Sens., 12, 1613, https://doi.org/10.3390/rs12101613, 2020.
Feng, S., Jiang, F., Wu, Z., Wang, H., Ju, W., and Wang, H.: CO Emissions Inferred From Surface CO Observations Over China in December 2013 and 2017, J. Geophys. Res.-Atmos., 125, e2019JD031808, https://doi.org/10.1029/2019JD031808, 2020.
Filonchyk, M., Hurynovich, V., Yan, H., Gusev, A., and Shpilevskaya, N.: Impact Assessment of COVID-19 on Variations of SO2, NO2, CO and AOD over East China, Aerosoll Air. Qual. Res., 20, 1530–1540, https://doi.org/10.4209/aaqr.2020.05.0226, 2020.
Fioletov, V. E., McLinden, C. A., Krotkov, N., and Li, C.: Lifetimes and emissions of SO2 from point sources estimated from OMI, Geophys. Res. Lett., 42, 1969–1976, https://doi.org/10.1002/2015GL063148, 2015.
Forster, P. M., Forster, H. I., Evans, M. J., Gidden, M. J., Jones, C. D., Keller, C. A., Lamboll, R. D., Quéré, C. L., Rogelj, J., Rosen, D., Schleussner, C.-F., Richardson, T. B., Smith, C. J., and Turnock, S. T.: Current and future global climate impacts resulting from COVID-19, Nat. Clim. Change, 10, 913–919, https://doi.org/10.1038/s41558-020-0883-0, 2020.
Ghahremanloo, M., Lops, Y., Choi, Y., and Mousavinezhad, S.: Impact of the COVID-19 outbreak on air pollution levels in East Asia, Sci. Total Environ., 754, 142226, https://doi.org/10.1016/j.scitotenv.2020.142226, 2021.
Granier, C., Bessagnet, B., Bond, T., D'Angiola, A., Denier van der Gon, H., Frost, G. J., Heil, A., Kaiser, J. W., Kinne, S., Klimont, Z., Kloster, S., Lamarque, J.-F., Liousse, C., Masui, T., Meleux, F., Mieville, A., Ohara, T., Raut, J.-C., Riahi, K., Schultz, M. G., Smith, S. J., Thompson, A., van Aardenne, J., van der Werf, G. R., and van Vuuren, D. P.: Evolution of anthropogenic and biomass burning emissions of air pollutants at global and regional scales during the 1980–2010 period, Clim. Change, 109, 163, https://doi.org/10.1007/s10584-011-0154-1, 2011.
Grell, G. A.: Prognostic Evaluation of Assumptions Used by Cumulus Parameterizations, Mon. Weather Rev., 121, 764–787, https://doi.org/10.1175/1520-0493(1993)121<0764:PEOAUB>2.0.CO;2, 1993.
Grell, G. A. and Dévényi, D.: A generalized approach to parameterizing convection combining ensemble and data assimilation techniques, Geophys. Res. Lett., 29, 3831–3834, https://doi.org/10.1029/2002GL015311, 2002.
Grell, G. A., Peckham, S. E., Schmitz, R., McKeen, S. A., Frost, G., Skamarock, W. C., and Eder, B.: Fully coupled “online” chemistry within the WRF model, Atmos. Environ., 39, 6957–6975, https://doi.org/10.1016/j.atmosenv.2005.04.027, 2005.
Hakami, A., Henze, D. K., Seinfeld, J. H., Chai, T., Tang, Y., Carmichael, G. R., and Sandu, A.: Adjoint inverse modeling of black carbon during the Asian Pacific Regional Aerosol Characterization Experiment, J. Geophys. Res.-Atmos., 110, D14301, https://doi.org/10.1029/2004jd005671, 2005.
Henze, D. K., Hakami, A., and Seinfeld, J. H.: Development of the adjoint of GEOS-Chem, Atmos. Chem. Phys., 7, 2413–2433, https://doi.org/10.5194/acp-7-2413-2007, 2007.
Hoffman, R., Louis, J. F., and Nehrkorn, T.: A method for implementing adjoint calculations in the discrete case, Technical memorandum, ECMWF, Shinfield Park, Reading, https://www.ecmwf.int/node/9906 (last access: 28 September 2022), 1992.
Hong, S.-Y., Noh, Y., and Dudhia, J.: A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes, Mon. Weather Rev., 134, 2318–2341, https://doi.org/10.1175/mwr3199.1, 2006.
Hu, Y., Zang, Z., Chen, D., Ma, X., Liang, Y., You, W., Pan, X., Wang, L., Wang, D., and Zhang, Z.: Optimization and Evaluation of SO2 Emissions Based on WRF-Chem and 3DVAR Data Assimilation, Remote Sens., 14, 220, https://doi.org/10.3390/rs14010220, 2022.
Huang, C., Wang, T., Niu, T., Li, M., Liu, H., and Ma, C.: Study on the variation of air pollutant concentration and its formation mechanism during the COVID-19 period in Wuhan, Atmos. Environ., 251, 118276, https://doi.org/10.1016/j.atmosenv.2021.118276, 2021a.
Huang, X., Ding, A., Gao, J., Zheng, B., Zhou, D., Qi, X., Tang, R., Wang, J., Ren, C., Nie, W., Chi, X., Xu, Z., Chen, L., Li, Y., Che, F., Pang, N., Wang, H., Tong, D., Qin, W., Cheng, W., Liu, W., Fu, Q., Liu, B., Chai, F., Davis, S. J., Zhang, Q., and He, K.: Enhanced secondary pollution offset reduction of primary emissions during COVID-19 lockdown in China, Nat. Sci. Rev., 8, nwaa137, https://doi.org/10.1093/nsr/nwaa137, 2021b.
Huneeus, N., Chevallier, F., and Boucher, O.: Estimating aerosol emissions by assimilating observed aerosol optical depth in a global aerosol model, Atmos. Chem. Phys., 12, 4585–4606, https://doi.org/10.5194/acp-12-4585-2012, 2012.
Huneeus, N., Boucher, O., and Chevallier, F.: Atmospheric inversion of SO2 and primary aerosol emissions for the year 2010, Atmos. Chem. Phys., 13, 6555–6573, https://doi.org/10.5194/acp-13-6555-2013, 2013.
Keller, C. A., Evans, M. J., Knowland, K. E., Hasenkopf, C. A., Modekurty, S., Lucchesi, R. A., Oda, T., Franca, B. B., Mandarino, F. C., Díaz Suárez, M. V., Ryan, R. G., Fakes, L. H., and Pawson, S.: Global impact of COVID-19 restrictions on the surface concentrations of nitrogen dioxide and ozone, Atmos. Chem. Phys., 21, 3555–3592, https://doi.org/10.5194/acp-21-3555-2021, 2021.
Kraemer, M. U. G., Yang, C.-H., Gutierrez, B., Wu, C.-H., Klein, B., Pigott David, M., null, n., du Plessis, L., Faria Nuno, R., Li, R., Hanage William, P., Brownstein John, S., Layan, M., Vespignani, A., Tian, H., Dye, C., Pybus Oliver, G., and Scarpino Samuel, V.: The effect of human mobility and control measures on the COVID-19 epidemic in China, Science, 368, 493–497, https://doi.org/10.1126/science.abb4218, 2020.
Li, L., Li, Q., Huang, L., Wang, Q., Zhu, A., Xu, J., Liu, Z., Li, H., Shi, L., Li, R., Azari, M., Wang, Y., Zhang, X., Liu, Z., Zhu, Y., Zhang, K., Xue, S., Ooi, M. C. G., Zhang, D., and Chan, A.: Air quality changes during the COVID-19 lockdown over the Yangtze River Delta Region: An insight into the impact of human activity pattern changes on air pollution variation, Sci. Total Environ., 732, 139282, https://doi.org/10.1016/j.scitotenv.2020.139282, 2020.
Li, M., Wang, T., Xie, M., Li, S., Zhuang, B., Fu, Q., Zhao, M., Wu, H., Liu, J., Saikawa, E., and Liao, K.: Drivers for the poor air quality conditions in North China Plain during the COVID-19 outbreak, Atmos. Environ., 246, 118103, https://doi.org/10.1016/j.atmosenv.2020.118103, 2021.
Li, Z. and Navon, I. M.: Optimality of variational data assimilation and its relationship with the Kalman filter and smoother, Q. J. Roy. Meteor. Soc., 127, 661–683, https://doi.org/10.1002/qj.49712757220, 2001.
Li, Z., Zang, Z., Li, Q. B., Chao, Y., Chen, D., Ye, Z., Liu, Y., and Liou, K. N.: A three-dimensional variational data assimilation system for multiple aerosol species with WRF/Chem and an application to PM2.5 prediction, Atmos. Chem. Phys., 13, 4265–4278, https://doi.org/10.5194/acp-13-4265-2013, 2013.
Lin, Y., Farley, R., and Orville, H.: Bulk Parameterization of the Snow Field in a Cloud Model, J. Clim. Appl. Meteorol., 22, 1065–1092, https://doi.org/10.1175/1520-0450(1983)022<1065:BPOTSF>2.0.CO;2, 1983.
Ma, C., Wang, T., Mizzi, A. P., Anderson, J. L., Zhuang, B., Xie, M., and Wu, R.: Multiconstituent Data Assimilation With WRF-Chem/DART: Potential for Adjusting Anthropogenic Emissions and Improving Air Quality Forecasts Over Eastern China, J. Geophys. Res.-Atmos., 124, 7393–7412, https://doi.org/10.1029/2019jd030421, 2019.
Miyazaki, K., Eskes, H. J., and Sudo, K.: Global NOx emission estimates derived from an assimilation of OMI tropospheric NO2 columns, Atmos. Chem. Phys., 12, 2263–2288, https://doi.org/10.5194/acp-12-2263-2012, 2012.
Miyazaki, K., Eskes, H. J., Sudo, K., and Zhang, C.: Global lightning NOx production estimated by an assimilation of multiple satellite data sets, Atmos. Chem. Phys., 14, 3277–3305, https://doi.org/10.5194/acp-14-3277-2014, 2014.
Miyazaki, K., Bowman, K., Sekiya, T., Jiang, Z., Chen, X., Eskes, H., Ru, M., Zhang, Y., and Shindell, D.: Air Quality Response in China Linked to the 2019 Novel Coronavirus (COVID-19) Lockdown, Geophys. Res. Lett., 47, e2020GL089252, https://doi.org/10.1029/2020GL089252, 2020.
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res.-Atmos., 102, 16663–16682, https://doi.org/10.1029/97JD00237, 1997.
Müller, J.-F. and Stavrakou, T.: Inversion of CO and NOx emissions using the adjoint of the IMAGES model, Atmos. Chem. Phys., 5, 1157–1186, https://doi.org/10.5194/acp-5-1157-2005, 2005.
National Centers for Environmental Prediction/National Weather Service/NOAA/US Department of Commerce: NCEP FNL Operational Model Global Tropospheric Analyses, NCAR [data set], https://rda.ucar.edu/datasets/ds083.2/, last access: 28 September 2022.
Parrish, D. F. and Derber, J. C.: The National Meteorological Center's Spectral Statistical-Interpolation Analysis System, Mon. Weather Rev., 120, 1747–1763, https://doi.org/10.1175/1520-0493(1992)120<1747:TNMCSS>2.0.CO;2, 1992.
Peng, Z., Liu, Z., Chen, D., and Ban, J.: Improving PM2.5 forecast over China by the joint adjustment of initial conditions and source emissions with an ensemble Kalman filter, Atmos. Chem. Phys., 17, 4837–4855, https://doi.org/10.5194/acp-17-4837-2017, 2017.
Peng, Z., Lei, L., Liu, Z., Sun, J., Ding, A., Ban, J., Chen, D., Kou, X., and Chu, K.: The impact of multi-species surface chemical observation assimilation on air quality forecasts in China, Atmos. Chem. Phys., 18, 17387–17404, https://doi.org/10.5194/acp-18-17387-2018, 2018.
Qin, K., He, Q., Zhang, Y., Cohen, J. B., Tiwari, P., and Lolli, S.: Aloft Transport of Haze Aerosols to Xuzhou, Eastern China: Optical Properties, Sources, Type, and Components, Remote Sens., 14, 1589, https://doi.org/10.3390/rs14071589, 2022.
Qu, Z., Henze, D. K., Theys, N., Wang, J., and Wang, W.: Hybrid Mass Balance/4D-Var Joint Inversion of NOx and SO2 Emissions in East Asia, J. Geophys. Res.-Atmos., 124, 8203–8224, https://doi.org/10.1029/2018JD030240, 2019.
Saikawa, E., Kim, H., Zhong, M., Avramov, A., Zhao, Y., Janssens-Maenhout, G., Kurokawa, J.-I., Klimont, Z., Wagner, F., Naik, V., Horowitz, L. W., and Zhang, Q.: Comparison of emissions inventories of anthropogenic air pollutants and greenhouse gases in China, Atmos. Chem. Phys., 17, 6393–6421, https://doi.org/10.5194/acp-17-6393-2017, 2017.
Schwartz, C. S., Liu, Z., Lin, H.-C., and McKeen, S. A.: Simultaneous three-dimensional variational assimilation of surface fine particulate matter and MODIS aerosol optical depth, J. Geophys. Res.-Atmos., 117, D13202, https://doi.org/10.1029/2011JD017383, 2012.
Sha, T., Ma, X., Jia, H., Tian, R., Chang, Y., Cao, F., and Zhang, Y.: Aerosol chemical component: Simulations with WRF-Chem and comparison with observations in Nanjing, Atmos. Environ., 218, 116982, https://doi.org/10.1016/j.atmosenv.2019.116982, 2019.
Stavrakou, T. and Müller, J.-F.: Grid-based versus big region approach for inverting CO emissions using Measurement of Pollution in the Troposphere (MOPITT) data, J. Geophys. Res.-Atmos., 111, D15304, https://doi.org/10.1029/2005JD006896, 2006.
Tang, X., Zhu, J., Wang, Z. F., Wang, M., Gbaguidi, A., Li, J., Shao, M., Tang, G. Q., and Ji, D. S.: Inversion of CO emissions over Beijing and its surrounding areas with ensemble Kalman filter, Atmos. Environ., 81, 676–686, https://doi.org/10.1016/j.atmosenv.2013.08.051, 2013.
Tang, X., Zhu, J., Wang, Z., Gbaguidi, A., Lin, C., Xin, J., Song, T., and Hu, B.: Limitations of ozone data assimilation with adjustment of NOx emissions: mixed effects on NO2 forecasts over Beijing and surrounding areas, Atmos. Chem. Phys., 16, 6395–6405, https://doi.org/10.5194/acp-16-6395-2016, 2016.
Tian, H., Liu, Y., Li, Y., Wu, C. H., Chen, B., Kraemer, M. U. G., Li, B., Cai, J., Xu, B., Yang, Q., Wang, B., Yang, P., Cui, Y., Song, Y., Zheng, P., Wang, Q., Bjornstad, O. N., Yang, R., Grenfell, B. T., Pybus, O. G., and Dye, C.: An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China, Science, 368, 638–642, https://doi.org/10.1126/science.abb6105, 2020.
Tsinghua University: MEICv1.0-v1.3, Tsinghua University [data set], http://meicmodel.org/?page_id=541&lang=en, last access: 28 September 2022.
van der A, R. J., Mijling, B., Ding, J., Koukouli, M. E., Liu, F., Li, Q., Mao, H., and Theys, N.: Cleaning up the air: effectiveness of air quality policy for SO2 and NOx emissions in China, Atmos. Chem. Phys., 17, 1775–1789, https://doi.org/10.5194/acp-17-1775-2017, 2017.
Wang, D., You, W., Zang, Z., Pan, X., Hu, Y., and Liang, Y.: A three-dimensional variational data assimilation system for aerosol optical properties based on WRF-Chem v4.0: design, development, and application of assimilating Himawari-8 aerosol observations, Geosci. Model Dev., 15, 1821–1840, https://doi.org/10.5194/gmd-15-1821-2022, 2022.
Wang, J., Xu, X., Henze, D. K., Zeng, J., Ji, Q., Tsay, S.-C., and Huang, J.: Top-down estimate of dust emissions through integration of MODIS and MISR aerosol retrievals with the GEOS-Chem adjoint model, Geophys. Res. Lett., 39, L08802, https://doi.org/10.1029/2012gl051136, 2012.
Wang, P., Chen, K., Zhu, S., Wang, P., and Zhang, H.: Severe air pollution events not avoided by reduced anthropogenic activities during COVID-19 outbreak, Resour. Conserv. Recycl., 158, 104814, https://doi.org/10.1016/j.resconrec.2020.104814, 2020.
Wang, S., Cohen, J. B., Deng, W., Qin, K., and Guo, J.: Using a New Top-Down Constrained Emissions Inventory to Attribute the Previously Unknown Source of Extreme Aerosol Loadings Observed Annually in the Monsoon Asia Free Troposphere, Earth's Future, 9, e2021EF002167, https://doi.org/10.1029/2021EF002167, 2021.
Wang, Y., Zhuang, G., Xu, C., and An, Z. J. A. E.: The air pollution caused by the burning of fireworks during the lantern festival in Beijing, Atmos. Environ., 41, 417–431, https://doi.org/10.1016/j.atmosenv.2006.07.043, 2007.
Yumimoto, K. and Uno, I.: Adjoint inverse modeling of CO emissions over Eastern Asia using four-dimensional variational data assimilation, Atmos. Environ., 40, 6836–6845, https://doi.org/10.1016/j.atmosenv.2006.05.042, 2006.
Yumimoto, K., Uno, I., Sugimoto, N., Shimizu, A., and Satake, S.: Adjoint inverse modeling of dust emission and transport over East Asia, Geophys. Res. Lett., 34, L08806, https://doi.org/10.1029/2006gl028551, 2007.
Yumimoto, K., Uno, I., Sugimoto, N., Shimizu, A., Liu, Z., and Winker, D. M.: Adjoint inversion modeling of Asian dust emission using lidar observations, Atmos. Chem. Phys., 8, 2869–2884, https://doi.org/10.5194/acp-8-2869-2008, 2008.
Zang, Z., Li, Z., Pan, X., Hao, Z., and You, W.: Aerosol data assimilation and forecasting experiments using aircraft and surface observations during CalNex, Tellus B, 68, 29812, https://doi.org/10.3402/tellusb.v68.29812, 2016.
Zaveri, R. A. and Peters, L. K.: A new lumped structure photochemical mechanism for large-scale applications, J. Geophys. Res.-Atmos., 104, 30387–30415, https://doi.org/10.1029/1999jd900876, 1999.
Zaveri, R. A., Easter, R. C., Fast, J. D., and Peters, L. K.: Model for Simulating Aerosol Interactions and Chemistry (MOSAIC), J. Geophys. Res., 113, D13204, https://doi.org/10.1029/2007jd008782, 2008.
Zhan, C. and Xie, M.: Land use and anthropogenic heat modulate ozone by meteorology: a perspective from the Yangtze River Delta region, Atmos. Chem. Phys., 22, 1351–1371, https://doi.org/10.5194/acp-22-1351-2022, 2022.
Zhao, J., Cohen, J. B., Chen, Y., Cui, W., Cao, Q., Yang, T., and Li, G.: High-resolution spatiotemporal patterns of China’s FFCO2 emissions under the impact of LUCC from 2000 to 2015, Environ. Res. Lett., 15, 044007, https://doi.org/10.1088/1748-9326/ab6edc, 2020.
Zeng, Q. and Wu, L.: Optimal reduction of anthropogenic emissions for air pollution control and the retrieval of emission source from observed pollutants ?. Application of incomplete adjoint operator, Sci. China Earth Sci., 61, 951–956, https://doi.org/10.1007/s11430-017-9199-2, 2018.
Zeng, Q., Wu, L., and Fei, K.: Optimal reduction of anthropogenic emissions for air pollution control and the retrieval of emission source from observed pollutants II: Iterative optimization using a positive-negative discriminant, Sci. China Earth Sci., 63, 726–730, https://doi.org/10.1007/s11430-018-9568-5, 2020.
Zeng, Q. and Wu, L.: Optimal reduction of anthropogenic emissions for air pollution control and the retrieval of emission source from observed pollutants III: Emission source inversion using a double correction iterative method, Sci. China Earth Sci., 45, 553–555, https://doi.org/10.1007/s11430-020-9860-7, 2021.
Zhang, Q., Streets, D. G., Carmichael, G. R., He, K. B., Huo, H., Kannari, A., Klimont, Z., Park, I. S., Reddy, S., Fu, J. S., Chen, D., Duan, L., Lei, Y., Wang, L. T., and Yao, Z. L.: Asian emissions in 2006 for the NASA INTEX-B mission, Atmos. Chem. Phys., 9, 5131–5153, https://doi.org/10.5194/acp-9-5131-2009, 2009.
Zhang, R., Zhang, Y., Lin, H., Feng, X., Fu, T.-M., and Wang, Y.: NOx Emission Reduction and Recovery during COVID-19 in East China, Atmosphere, 11, 433, https://doi.org/10.3390/atmos11040433, 2020.
Zheng, B., Tong, D., Li, M., Liu, F., Hong, C., Geng, G., Li, H., Li, X., Peng, L., Qi, J., Yan, L., Zhang, Y., Zhao, H., Zheng, Y., He, K., and Zhang, Q.: Trends in China's anthropogenic emissions since 2010 as the consequence of clean air actions, Atmos. Chem. Phys., 18, 14095–14111, https://doi.org/10.5194/acp-18-14095-2018, 2018.
Zheng, B., Zhang, Q., Geng, G., Chen, C., Shi, Q., Cui, M., Lei, Y., and He, K.: Changes in China's anthropogenic emissions and air quality during the COVID-19 pandemic in 2020, Earth Syst. Sci. Data, 13, 2895–2907, https://doi.org/10.5194/essd-13-2895-2021, 2021.