Vertical dependence of horizontal variation of cloud microphysics: observations from the ACE-ENA field campaign and implications for warm-rain simulation in climate models

In the current global climate models (GCMs), the nonlinearity effect of subgrid cloud variations on the parameterization of warm-rain process, e.g., the autoconversion rate, is often treated by multiplying the resolved-scale warm-rain process rates by a so-called enhancement factor (EF). In this study, we investigate the subgrid-scale horizontal variations and covariation of cloud water content (q_c) and cloud droplet number concentration (N_c) in marine boundary layer (MBL) clouds based on the in situ measurements from a recent field campaign and study the implications for the autoconversion rate EF in GCMs. Based on a few carefully selected cases from the field campaign, we found that in contrast to the enhancing effect of q_c and N_c variations that tends to make EF > 1, the strong positive correlation between q_c and N_c results in a suppressing effect that tends to make EF < 1. This effect is especially strong at cloud top, where the q_c and N_c correlation can be as high as 0.95. We also found that the physically complete EF that accounts for the covariation of q_c and N_c is significantly smaller than its counterpart that accounts only for the subgrid variation of q_c, especially at cloud top. Although this study is based on limited cases, it suggests that the subgrid variations of N_c and its correlation with q_c both need to be considered for an accurate simulation of the autoconversion process in GCMs.

1 Introduction

Marine boundary layer (MBL) clouds cover about one-fifth of Earth's surface and play an important role in the climate system (Wood, 2012). A faithful simulation of MBL clouds in the global climate model (GCM) is critical for the projection of future climate (Bony and Dufresne, 2005; Bony et al., 2015; Boucher et al., 2013) and understanding of aerosol–cloud interactions (Carslaw et al., 2013; Lohmann and Feichter, 2005). Unfortunately, this turns out to be an extremely challenging task. Among others, an important reason is that many physical processes in MBL clouds occur on spatial scales that are much smaller than the typical resolution of GCMs.

Of particular interest in this study is the warm-rain processes that play an important role in regulating the lifetime, water budget, and therefore integrated radiative effects of MBL clouds. In the bulk cloud microphysics schemes that are widely used in GCMs (Morrison and Gettelman, 2008), continuous cloud particle spectrum is often divided into two modes. Droplets smaller than the separation size r^∗ are classified into the cloud mode, which is described by two moments of droplet size distribution (DSD), the droplet number concentration N_c (0th moment of DSD), and droplet liquid water content q_c (proportional to the third moment). Droplets larger than r^∗ are classified into a precipitation mode (drizzle or rain), with properties denoted by drop concentration and water content (N_r and q_r). In a bulk microphysics scheme, the transfer of mass from the cloud to rain modes as a result of the collision–coalescence process is separated into two terms, autoconversion and accretion:${\left(\frac{\partial q_{\mathrm{r}}}{\partial t}\right)}_{\mathrm{coal}}={\left(\frac{\partial q_{\mathrm{r}}}{\partial t}\right)}_{\mathrm{auto}}+{\left(\frac{\partial q_{\mathrm{r}}}{\partial t}\right)}_{\mathrm{acc}}$. Autoconversion is defined as the rate of mass transfer from the cloud to rain mode due to the coalescence of two cloud droplets with $r<r^{\ast }$. Accretion is defined as the rate of mass transfer due to the coalescence of a rain drop with $r>r^{\ast }$ with a cloud droplet. A number of autoconversion and accretion parameterizations have been developed, formulated either through numerical fitting of droplet spectra obtained from bin microphysics LES or parcel model (Khairoutdinov and Kogan, 2000), or through an analytical simplification of the collection kernel to arrive at expressions that link autoconversion and accretion with the bulk microphysical variables (Liu and Daum, 2004). For example, a widely used scheme developed by Khairoutdinov and Kogan (2000) (“KK scheme” hereafter) relates the autoconversion with N_c and q_c as follows:

$$\begin{array}{}\text{(1)}& {\left({\displaystyle \frac{\partial q_{\mathrm{r}}}{\partial t}}\right)}_{\mathrm{auto}}=f_{\mathrm{auto}}\left(q_{\mathrm{c}},N_{\mathrm{c}}\right)=C{q}_{\mathrm{c}}^{{\mathit{\beta }}_q}{N}_{\mathrm{c}}^{{\mathit{\beta }}_N},\end{array}$$

where q_c and N_c have units of kg kg⁻¹ and cm⁻³, respectively; the parameter C=1350 and the two exponents β_q=2.47 and ${\mathit{\beta }}_N=-\mathrm{1.79}$ are obtained through a nonlinear regression between the variables q_c and N_c and the autoconversion rate derived from large-eddy simulation (LES) with bin-microphysics spectra.

Having a highly accurate microphysical parameterization – specifically, highly accurate local microphysical process rates – is not sufficient for an accurate simulation of warm-rain processes in GCMs. Clouds can have significant structures and variations at the spatial scale much smaller than the typical grid size of GCMs (10–100 km) (Barker et al., 1996; e.g., Cahalan and Joseph, 1989; Lebsock et al., 2013; Wood and Hartmann, 2006; Zhang et al., 2019). Therefore, GCMs need to account for these subgrid-scale variations in order to correctly calculate grid-mean autoconversion and accretion rates. Pincus and Klein (2000) nicely illustrate this dilemma. Given subgrid-scale variability represented as a distribution P(x) of some variable x, for example the q_c in Eq. (1), a grid-mean process rate is calculated as $\langle f\left(x\right)\rangle =\int f\left(x\right)P\left(x\right)\mathrm{d}x$ , where f(x) is the formula for the local process rate. For nonlinear process rates such as autoconversion and accretion, the grid-mean process rates calculated from the subgrid-scale variability do not equal the process rate calculated from the grid-mean value of x, i.e., 〈f(x)〉≠f(〈x〉). Therefore, calculating autoconversion and accretion from grid-mean quantities introduces biases arising from subgrid-scale variability. To take this effect into account, a parameter E is often introduced as part of the parameterization such that $\langle f\left(x\right)\rangle =E\cdot f(\langle x\rangle )$. Following the convention of previous studies, E is referred to as the enhancement factor (EF) here. Given the autoconversion parameterization scheme, the magnitude of EF is primarily determined by cloud horizontal variability within a GCM grid. Unfortunately, because most GCMs do not resolve subgrid cloud variation, the value of EF is often simply assumed to be a constant for the lack of better options. In the previous generation of GCMs, the EF for the KK autoconversion scheme due to subgrid q_c variation is often simply assumed to be a constant. For example, in the widely used Community Atmosphere Model (CAM) version 5 (CAM5) the EF for autoconversion is assumed to be 3.2 (Morrison and Gettelman, 2008).

A number of studies have been carried out to better understand the horizontal variations of cloud microphysics in MBL cloud and the implications for warm-rain simulations in GCMs. Most of these studies have been focused on the subgrid variation of q_c. Morrison and Gettelman (2008) and several later studies (Boutle et al., 2014; Hill et al., 2015; Lebsock et al., 2013; Zhang et al., 2019) showed that the subgrid variability q_c and thereby the EF are dependent on cloud regime and cloud fraction (f_c). They are generally smaller over the closed-cell stratocumulus regime with higher f_c and larger over the open-cell cumulus regime that often has a relatively small f_c. The subgrid variance of q_c is also dependent on the horizontal scale (L) of a GCM grid. Based on the combination of in situ and satellite observations, Boutle et al. (2014) found that the subgrid q_c variance first increases quickly with L when L is below about 20 km, then increases slowly and seems to approach to an asymptotic value for larger L. Similar spatial dependence is also reported in Huang et al. (2014), Huang and Liu (2014), Xie and Zhang (2015), and Wu et al. (2018), which are based on the ground radar retrievals from the Department of Energy (DOE) Atmospheric Radiation Measurement (ARM) sites. The cloud-regime and horizontal-scale dependences have inspired a few studies to parameterize the subgrid q_c variance as a function of either f_c or L or a combination of the two (e.g., Ahlgrimm and Forbes, 2016; Boutle et al., 2014; Hill et al., 2015; Xie and Zhang, 2015; Zhang et al., 2019). Inspired by these studies, several latest-generation GCMs have adopted the cloud-regime-dependent and scale-aware parameterization schemes to account for the subgrid variability of q_c and thereby the EF (Walters et al., 2019).

However, the aforementioned studies have an important limitation. They consider only the impacts of subgrid q_c variations on the EF but ignore the impacts of subgrid variation of N_c and its covariation with q_c. Based on cloud fields from large-eddy simulation, Larson and Griffin (2013) and later Kogan and Mechem (2014, 2016) elucidated that it is important to consider the covariation of q_c and N_c to derive a physically complete and accurate EF for the autoconversion parameterization. Lately, on the basis of MBL cloud observations from the Moderate Resolution Imaging Spectroradiometer (MODIS), Zhang et al. (2019) (hereafter referred to as Z19) have elucidated that the subgrid variation of N_c tends to further increase the EF for the autoconversion process in addition to the EF due to q_c variation. The effect of q_c–N_c covariation on the other hand depends on the sign of the q_c–N_c correlation. A positive q_c–N_c correlation would lead to an EF < 1 that partly offsets the effects of q_c and N_c variations. Although Z19 shed important new light on the EF problem for the warm-rain process, their study also suffers from limitations due to the use of satellite remote sensing data. First, as a passive remote sensing technique, the MODIS cloud product can only retrieve the column-integrated cloud optical thickness and the cloud droplet effective radius at cloud top, from which the column-integrated cloud liquid water path (LWP) is estimated. As a result of using LWP, instead vertically resolved observations the vertical dependence of the q_c and N_c horizontal variabilities are ignored in Z19. Second, the N_c retrieval from MODIS is based on several important assumptions, which can lead to large uncertainties (see review by Grosvenor et al., 2018). Furthermore, the MODIS cloud retrieval product is known to suffer from several inherent uncertainties, such as the three-dimensional radiative effects(e.g., Zhang and Platnick, 2011; Zhang et al., 2012, 2016), which in turn can lead to large uncertainties in the estimated EF.

This study is a follow-up of Z19. To overcome the limitations of satellite observations, we use the in situ measurements of MBL cloud from a recent DOE field campaign, the Aerosol and Cloud Experiments in the Eastern North Atlantic (ACE-ENA), to investigate the subgrid variations of q_c and N_c, as well as their covariation, and the implications for the simulation of autoconversion simulation in GCMs. A main focus of this investigation is to understand the vertical dependence of the q_c and N_c horizontal variations within the MBL clouds. This aspect has been neglected in Z19 as well as most previous studies (Boutle et al., 2014; Lebsock et al., 2013; Xie and Zhang, 2015). A variety of microphysical processes, such as adiabatic growth, collision–coalescence, and entrainment mixing, can influence the vertical structure of MBL clouds. At the same time, these processes also vary horizontally at the subgrid scale of GCMs. As a result, the horizontal variations of q_c and N_c, as well as their covariation, and therefore the EFs may depend on the vertical location inside the MBL clouds. It is important to understand this dependence for several reasons. First, the warm-rain process is usually initialized at cloud top where the autoconversion process of the cloud droplets gives birth to embryo drizzle drops. The accretion process is, on the other hand, more important in the lower part of the cloud (Wood, 2005b). Thus, a better understanding of the vertical dependence of horizontal variations of q_c and N_c inside MBL clouds could help us understand how the EF should be modeled in the GCMs for both autoconversion and accretion. Second, a good understanding of the vertical dependence of q_c and N_c variation inside MBL clouds will also help us understand the limitations in the previous studies, such as Z19, that use the column-integrated products for the study of EF. Finally, this investigation may also be useful for modeling other processes, such as aerosol–cloud interactions, in the GCMs.

Therefore, our main objectives in this study are to (1) better understand the horizontal variations of q_c and N_c, their covariation, and the dependence on vertical height in MBL clouds; and (2) elucidate the implications for the EF of the autoconversion parameterization in GCMs. The rest of the paper is organized as follows: we will describe the data and observations used in this study in Sect. 2 and explain how we select the cases from the ACE-ENA campaign for our study in Sect. 3. We will present case studies in Sects. 4 and 5. Finally, the results and findings from this study will be summarized and discussed in Sect. 6.

2 Data and observations

The data and observations used for this study are from two main sources: the in situ measurements from the ACE-ENA campaign and the ground-based observations from the ARM ENA site. The ENA region is characterized by persistent subtropical MBL clouds that are influenced by different seasonal meteorological conditions and a variety of aerosol sources (Wood et al., 2015). A modeling study by Carslaw et al. (2013) found the ENA to be one of the regions over the globe with the largest uncertainty of aerosol indirect effect. As such, the ENA region attracted substantial attention over the past few decades for aerosol–cloud interaction studies. From April 2009 to December 2010 the DOE ARM program deployed its ARM Mobile Facility (AMF) to Graciosa Island (39.09^∘ N, 28.03^∘ W) for a measurement field campaign targeting the properties of cloud, aerosol, and precipitation in the MBL (CAP-MBL) in the Azores region of ENA (Wood et al., 2015). The measurements from the CAP-MBL campaign have proved highly useful for a variety of purposes, from understanding the seasonal variability of clouds and aerosols in the MBL of the ENA region (Dong et al., 2014; Rémillard et al., 2012) to improving cloud parameterizations in the GCMs (Zheng et al., 2016) to validating the spaceborne remote sensing products of MBL clouds (Zhang et al., 2017). The success of the CAP-MBL revealed that the ENA has an ideal mix of conditions to study the interactions of aerosols and MBL clouds. In 2013 a permanent measurement site was established by the ARM program on Graciosa Island and is typically referred to as the ENA site (Voyles and Mather, 2013).

2.1 In situ measurements from the ACE-ENA campaign

The Aerosol and Cloud Experiments in ENA (ACE-ENA) project was “motivated by the need for comprehensive in situ characterizations of boundary-layer structure and associated vertical distributions and horizontal variabilities of low clouds and aerosol over the Azores” (Wang et al., 2016). The ARM Aerial Facility (AAF) Gulfstream-1 (G-1) aircraft was deployed during two intensive observation periods (IOPs), the summer 2017 IOP from 21 June to 20 July 2017 and the winter 2018 IOP from 15 January to 18 February 2018. Over 30 research flights (RFs) were carried out during the two IOPs around the ARM ENA site on Graciosa Island that sampled a large variety of cloud and aerosol properties along with the meteorological conditions.

Table 1 summarizes the in situ measurements from the ACE-ENA campaign used in this study. The location and velocity of G-1 aircraft and the environmental and meteorological conditions during the flight (temperature, humidity, and wind velocity) are taken from Aircraft-Integrated Meteorological Measurement System 20 Hz (AIMMS-20) dataset (Beswick et al., 2008). The size distribution of cloud droplets and the corresponding q_c and N_c are obtained from the fast cloud droplet probe (FCDP) measurement. The FCDP measures the concentration and size of cloud droplets in the diameter size range from 1.5 to 50 µm in 20 size bins with an overall uncertainty of size around 3 µm (Lance et al., 2010; SPEC, 2019). Following previous studies (Wood, 2005a), we adopt $r^{\ast }=\mathrm{20}$ µm as the threshold to separate cloud droplets from drizzle drops; i.e., drops with $r<r^{\ast }$ are considered cloud droplets. After the separation, the q_c and N_c are derived from the FCDP droplet size distribution measurements. As an evaluation, we compared our FCDP-derived q_c results with the direct measurements of q_c from the multi-element water content system (WCM-2000; Matthews and Mei, 2017) also flown during the ACE-ENA and found a reasonable agreement (e.g., biases within 20 %). We also performed a few sensitivity tests in which we perturbed the value of r^∗ from 15 up to 50 µm. The perturbation shows little impact on the results shown in Sects. 4 and 5. The cloud droplet spectrum from the FCDP is available at a frequency of 10 Hz, which is used in this study. We have also done a sensitivity study, in which we averaged the FCDP data to 1 Hz and got almost identical results. Since the typical horizontal speed of the G-1 aircraft during the in-cloud leg is about 100 m s⁻¹, the spatial sampling rate these instruments is on the order of 10 m for the FCDP at 10 Hz.

Table 1 In situ cloud instruments from ACE-ENA campaign used in this study.

2.2 Ground observations from the ARM ENA site

In addition to the in situ measurements, ground measurements from the ARM ENA site are also used to provide ancillary data for our studies. In particular, we will use the Active Remote Sensing of Cloud Layers product (ARSCL; Clothiaux et al., 2000; Kollias et al., 2005) which blends radar observations from the Ka-band ARM zenith cloud radar (KAZR), the micropulse lidar (MPL), and the ceilometer to provide information on cloud boundaries and the mesoscale structure of cloud and precipitation. The ARSCL product is used to specify the vertical location of the G-1 aircraft and thereby the in situ measurements with respect to the cloud boundaries, i.e., cloud base and top (see example in Fig. 1). In addition, the radar reflectivity observations from KAZR, alone with in situ measurements, are used to select the precipitating cases for our study. Note that the ARSCL product is from the vertically pointing instruments, which sometimes are not collocated with the in situ measurements from G-1 aircraft. As explained later in the next section, only those cases with a reasonable collocation are selected for our study.

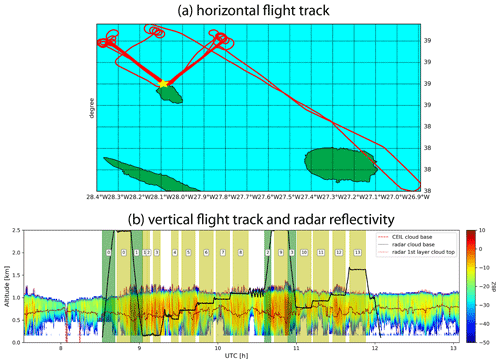
Figure 1 (a) Horizontal flight track of the G-1 aircraft (red) during the 18 July 2017 RF around the DOE ENA site (yellow star) on Graciosa Island. (b) The vertical flight track of G-1 (thick black line) overlaid on the radar reflectivity contour by the ground-based KZAR. The dotted lines in the figure indicate the cloud base and top retrievals from ground-based radar and CEIL instruments. The yellow-shaded regions are the “hlegs” and green-shaded regions are the “vlegs”. See text for their definitions.

3 Case selections

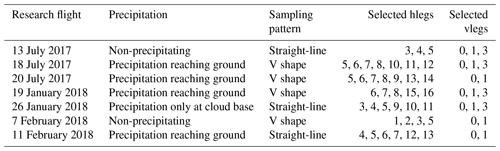
3.1 ACE-ENA flight pattern

The section provides a brief overview of the G-1 aircraft flight patterns during the ACE-ENA and explains the method for case selections for our study using the 18 July 2017 RF as an example. As shown in Table 2, a variety of MBL conditions were sampled during the two IOPs of the ACE-ENA campaign, from mostly clear sky to thin stratus and drizzling stratocumulus. The basic flight patterns of G-1 aircraft in the ACE-ENA included spirals to obtain vertical profiles of aerosol and clouds, as well as legs at multiple altitudes, including below cloud, inside cloud, at the cloud top, and in the free troposphere. As an example, Fig. 1a shows the horizontal location of the G-1 aircraft during the 18 July 2017 RF, which is the “golden case” for our study as explained in the next section. The corresponding vertical track of the aircraft is shown in Fig. 1b overlaid on the reflectivity curtain of the ground-based KAZR. In this RF, the G-1 aircraft repeated the horizontal level runs multiple times in a V shape at different vertical levels inside, above, and below the MBL (see Fig. 1b). The lower tip of the V shape is located at the ENA site on Graciosa Island. The average wind in the upper MBL (i.e., 900 mbar) is approximately Northwest. So, the west side of the V-shape horizontal level runs is along the wind and the east side across the wind. Note that the horizontal velocity of the G-1 aircraft is approximately 100 m s⁻¹. Since the duration of these selected V-shaped hlegs is between 580 and 700 s, their total horizontal length is roughly 60 km, with each side of the V shape ∼ 30 km. These V-shape horizontal level runs, with one side along and the other across the wind, are a common sampling strategy used in the ACE-ENA to observe the properties of aerosol and cloud at different vertical levels of the MBL. In our study we use the vertical location of the G-1 aircraft from the AIMMS to identify continuous horizontal flight tracks which are referred to as the “hlegs”. For the 18 July 2017 case, a total of 13 hlegs are identified as shown in Fig. 1b. Among them, hlegs 5, 6, 7, 8, 10, 11, and 12 are the seven V-shape horizontal level runs inside the MBL cloud. Together they provide an excellent set of samples of the MBL cloud properties at different vertical levels of a virtual GCM grid box of about 30 km. As previously mentioned, Boutle et al. (2014) found that the horizontal variance of q_c increases with the horizontal scale L slowly when L is larger than about 20 km. Therefore, although the horizontal sampling of the selected hlegs is only about 30 km, the lessons learned here could yield useful insights for larger GCM grid sizes. In addition to the hlegs, we also identified the vertical penetration legs in each flight, referred to as the “vlegs”, from which we will obtain the vertical structure of the MBL, along with the properties of cloud and aerosol.

Table 2 Conditions of MBL sampled during the two IOPs of the ACE-ENA campaign. Dates are given in month and day (m/dd) format.

3.2 Case selection

As illustrated in Fig. 1a and b for the 18 July 2017 RF, the criteria we used to select the RF cases and the hlegs within the RF can be summarized as follows:

• The RF samples multiple continuous in-cloud hlegs at different vertical levels with the horizontal length of at least 10 km and cloud fraction larger than 10 % (i.e., the fraction of an hleg with q_c > 0.01 g m⁻³must exceed 10 % of the total length of that hleg). It is important to note here that, unless otherwise specified, all the analyses of q_c and N_c are based on in-cloud observations (i.e., in the regions with q_c > 0.01 g m⁻³).

• Moreover, the selected hlegs must sample the same region (i.e., the same virtual GCM grid box) repeatedly in terms of horizontal track but different vertical levels in terms of vertical track. Take the 18 July 2017 case as an example. The hlegs 5, 6, 7, and 8 follow the same V-shaped horizontal track (see Fig. 1a) but sample different vertical levels of the MBL clouds (see Fig. 1b). Such hlegs provide us the horizontal sampling needed to study the subgrid horizontal variations of the cloud properties and, at the same time, the chance to study the vertical dependence of the horizontal cloud variations.

• Finally, the RF needs to have at least one vleg, and the cloud boundary derived from the vleg is largely consistent with that derived from the ground-based measurements. This requirement is to ensure that the vertical locations of the selected hlegs with respect to cloud boundaries can be specified. For example, as shown in Fig. 1b according to the ground-based observations, hlegs 5 and 10 of the 18 July 2017 case are close to cloud base, while hlegs 8 and 12 are close to cloud top (see also Fig. 4).

The above requirements together pose a strong constraint on the observation. Fortunately, thanks to the careful planning of the RF, which had already taken studies like ours into consideration, we are able to select a total of seven RF cases as summarized in Table 3. The plots of the flight tracks and ground-based radar observations for the six other RF cases are provided in the Supplement (Figs. S1–S6). We will first focus on the golden case – 18 July 2017 RF – and then investigate if the lessons learned from the 18 July 2017 RF also apply to the other three cases.

Table 3 A summary of selected RFs and the selected hlegs and vlegs within each RF.

4 A study of the 18 July 2017 case

4.1 Horizontal and vertical variations of cloud microphysics

On 18 July 2017, the North Atlantic is controlled by the Icelandic low to the north and the Azores high to the south (see Fig. 2b), which is a common pattern of large-scale circulation during the summer season in this region (Wood et al., 2015). The Azores is at the southern tip of the cold air sector of a frontal system where the fair-weather low-level stratocumulus clouds are dominant (see satellite image in Fig. 2a). The RF on this day started around 08:30 UTC and ended around 12:00 UTC. As explained in the previous section, we selected seven hlegs from this RF that horizontally sampled the same region repeatedly in a similar V-shaped track but vertically at different levels. The radar reflectivity observation from the ground-based KAZR during the same period peaks around 10 dBZ, indicating the presence of significant drizzle inside the MBL clouds.

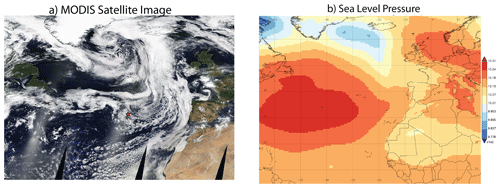
Figure 2 (a) The real color satellite image of the ENA region on 18 July 2017 from MODIS. The small red star marks the location of the ARM ENA site on Graciosa Island. (b) The averaged sea level pressure (SLP) of the ENA region on 18 July 2017 from the MERRA-2 reanalysis.

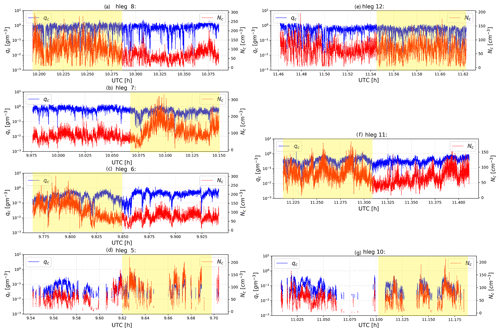
Figure 3 The horizontal variations of q_c (red) and N_c (blue) for each selected hleg derived from the in situ FCDP instrument. The yellow-shaded time period in each plot corresponds to the cross-wind side of the V-shaped flight track, and the unshaded part corresponds to the along-wind part. Note that plots are ordered such that (a) hleg 8 and (e) hleg 12 are close to cloud top; (b) hleg 6, (c) hleg 7, and (f) hleg 11 are sampled in the middle of clouds; and (d) hleg 5 and (g) hleg 10 are close to cloud base.

Among the seven selected hlegs, hlegs 5, 6, 7, and 8 constitute one set of four consecutive V-shaped tracks, with hlegs 5 close to cloud base and hleg 8 close to cloud top. The hlegs 10, 11, and 12 are another set of consecutive V-shaped tracks with hlegs 10 and 12 close to cloud base and top, respectively (see Fig. 1). Using q_c>0.01 g m⁻³ as a threshold for cloud, the cloud fraction (f_c) of all these hlegs is close to unity (i.e., overcast), except for the two hlegs close to cloud base (f_c= 46 % for hleg 5 and f_c= 51 % for hleg 10). The q_c and N_c derived from the in situ FCDP measurements for these selected hlegs are plotted in Fig. 3 as a function of UTC time. It is evident from Fig. 3 that both q_c and N_c have significant horizontal variations. At cloud base (see Fig. 3d for hleg 5 and Fig. 3g for hleg 10) the q_c varies from 0.01 g m⁻³ (i.e., the lower threshold) up to about 0.4 g m⁻³ and the N_c from 25 up to 150 cm⁻³, with the mean in-cloud values around 0.08 g m⁻³ and 65 cm⁻³, respectively. Such strong variations of cloud microphysics could be contributed by a number of factors. One can see from the ground radar and lidar observations in Fig. 1b that the height of cloud base varies significantly. As a result, the horizonal legs may not really sample the cloud base. In addition, the variability in updraft at cloud base could lead to the variability in the activation and growth of cloud condensation nuclei (CCN). In the middle of the MBL cloud, i.e., hleg 6 (Fig. 3c), 7 (Fig. 3b) and 11 (Fig. 3f), the mean value of q_c is significantly larger than that of cloud base hlegs while the variability is reduced. The mean value of q_c keeps increasing toward cloud top to ∼ 0.73 g m⁻³ in hleg 8 (Fig. 3a) and to ∼ 0.53 g m⁻³ in hleg 12 (Fig. 3e), respectively. In contrast, the horizontal variability of q_c seems to increase in comparison to those observed in mid-level hlegs.

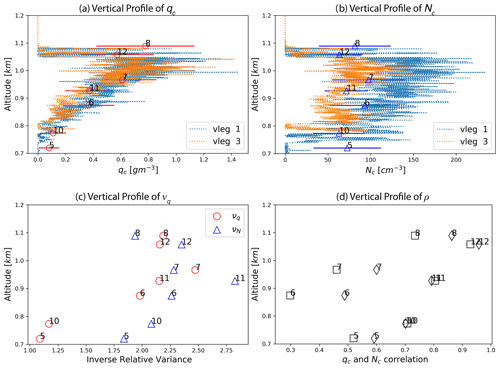
Figure 4 (a) The vertical profiles of q_c derived from the vlegs (dotted lines) of the 18 July 2017 case. The overplotted red error bars indicate the mean values and standard deviations of the q_c derived from the selected hlegs at different vertical levels. (b) Same as panel (a) except for N_c. (c) The vertical profile of the inverse relative variances (i.e., mean divided by standard deviation) of N_c (red circle) and N_c (blue triangle) derived from the hleg; (d) the vertical profile of the linear correlation coefficient between ln (q_c) and ln (N_c), i.e., ρ_L (square), and the linear correlation coefficient between q_c and N_c, i.e., ρ (diamond).

To obtain a further understanding of the vertical variations of cloud microphysics, we analyzed the cloud microphysics observations from the two green-shaded vlegs 1 and 3 in Fig. 1b. The vertical profiles of the mean q_c and N_c from these two vlegs are shown in Fig. 4a and b, respectively, with the mean and standard deviation of the q_c and N_c derived from the seven selected hlegs overplotted. Overall, the vertical profiles of the q_c and N_c are qualitatively aligned with the classic adiabatic MBL cloud structure (Brenguier et al., 2000; Martin et al., 1994). That is, the N_c remains relatively constant (see Fig. 4b), while the q_c increases approximately linearly with height from cloud base upward as a result of condensation growth (see Fig. 4a,), except for the very top of the cloud, i.e., the entrainment zone where the dry air entrained from above mixes with the humid cloudy air in the MBL. In previous studies, a so-called inverse relative variance, ν, is often used to quantify the subgrid variations of cloud microphysics. It is defined as follows:

$$\begin{array}{}\text{(2)}& {\mathit{\nu }}_X={\displaystyle \frac{\langle x{\rangle }^{\mathrm{2}}}{{\mathit{\sigma }}_X^{\mathrm{2}}}},\end{array}$$

where X is either q_c (i.e., ${\mathit{\nu }}_X={\mathit{\nu }}_{q_{\mathrm{c}}}$) or N_c (i.e., ${\mathit{\nu }}_X={\mathit{\nu }}_{N_{\mathrm{c}}}$) (Barker et al., 1996; Lebsock et al., 2013; Zhang et al., 2019). 〈x〉 and σ_X are the mean value and standard deviation of X, respectively. As such, the smaller the ν value, the larger the horizontal variation of X in comparison to the mean value. As shown in Fig. 4c, the ${\mathit{\nu }}_{q_{\mathrm{c}}}$ and ${\mathit{\nu }}_{N_{\mathrm{c}}}$ derived from the selected hlegs follow a similar vertical pattern: they both increase first from cloud base upward and then decrease in the entrainment zone, with the turning point somewhere around 1 km (i.e., around hleg 7 and 11). It indicates that both q_c and N_c have significant horizontal variabilities at cloud base which may be a combined result of horizontal fluctuations of dynamics (e.g., updraft) and thermodynamics (e.g., temperature and dynamics), as well as horizontal variations of aerosols. The horizontal variabilities of both q_c and N_c both decrease upward toward cloud top until the entrainment zone where both variabilities increase again.

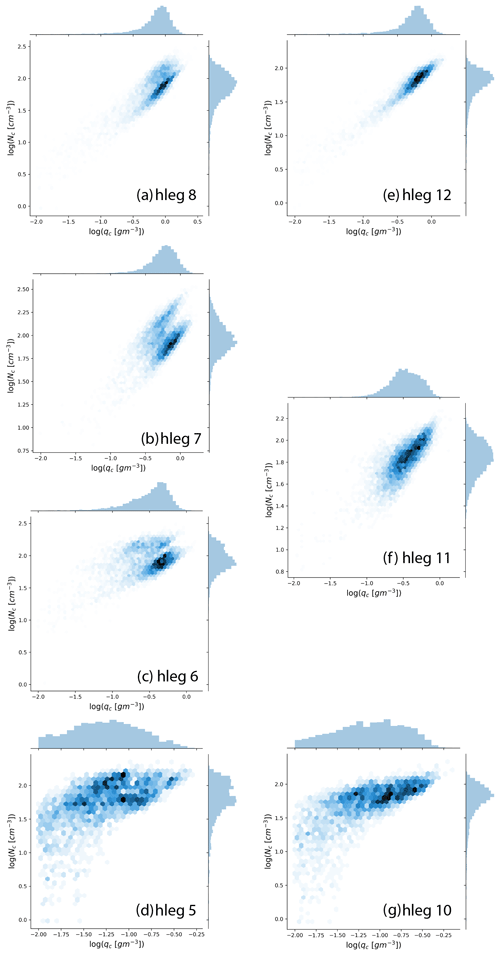
Figure 5 The joint distributions of q_c and N_c, along with the marginal histograms, for the seven selected hlegs from the 18 July 2017 RF. As in Fig. 3, the plots are ordered such that (a) hleg 8 and (e) hleg 12 are close to cloud top; (b) hleg 6, (c) hleg 7, and (f) hleg 11 are sampled in the middle of clouds; and (d) hleg 5 and (g) hleg 10 are close to cloud base.

So far, in all the analyses above, the variations of q_c and N_c have been considered separately and independently. As pointed out in several previous studies, the covariation of q_c and N_c could have an important impact on the EF for the autoconversion process in GCMs (Kogan and Mechem, 2016; Larson and Griffin, 2013; Zhang et al., 2019). This point will be further elucidated in detail in the next section. Figure 5 shows the joint distributions of q_c and N_c for the seven selected hlegs, and the corresponding linear correlation coefficients as a function of height are shown in Fig. 4d. For the sake of reference, the linear correlation coefficient between ln (q_c) and ln (N_c) , i.e., the ρ_L that will be introduced later in Eq. (4), is also plotted in Fig. 4d. Looking first at hlegs 10, 11, and 12, i.e., the second group of consecutive V-shaped legs, there is a clear increasing trend of the correlation between q_c and N_c from cloud bottom (ρ=0.75 for hleg 10) to cloud top (ρ=0.95 for hleg 12). The picture based on hlegs 5, 6, 7, and 8 is more complex. As shown in Fig. 5, the joint distributions of q_c and N_c of hleg 6 (Fig. 5b), hleg 7 (Fig. 5c), and, to a less extent, hleg 8 (Fig. 5d) all exhibit a clear bimodality. Further analysis reveals that each of the two modes in these bimodal distributions approximately corresponds to one side of the V-shaped track. To illustrate this, the east side (i.e., across wind) of the hleg is shaded in yellow in Fig. 3. It is intriguing to note that the N_c values from the east side of the hleg are systematically larger than those from the west side, while their q_c values are largely similar. It is unlikely that the bimodality is caused by the along-wind and across-wind difference between the two sides of the V-shaped track. It is most likely just a coincidence. On the other hand, the bimodal joint distribution between q_c and N_c is real, which could be a result of subgrid variations of updraft, precipitation, and/or aerosols.

As a result of the bimodality of N_c, the correlation coefficients between q_c and N_c is significantly smaller for hlegs 6 (ρ=0.22) and 7 (ρ=0.31) in comparison to other hlegs. However, if the two sides of the V-shaped tracks are considered separately, then q_c and N_c become more correlated, except for the east side of hleg 6, which still exhibits to some degree a bimodal joint distribution of q_c and N_c. In spite of the bimodality, there is evidently a general increasing trend of the correlation between q_c and N_c from cloud base toward cloud top. At the cloud top, the q_c and N_c correlation coefficient can be as high as ρ=0.95 for hleg 12 (see Fig. 5e). As explained in the next section, this close correlation between q_c and N_c has important implications for the simulation of the autoconversion enhancement factor.

As a summary, the above phenomenological analysis of the 18 July 2017 RF reveals the following features of the horizontal and vertical variations of cloud microphysics. Vertically, the mean values of q_c and N_c qualitatively follow the adiabatic structure of MBL cloud; i.e., q_c increases linearly with height and N_c remains largely invariant above cloud base. Even though the joint distribution of q_c and N_c exhibits a bimodality in several hlegs, their correlation generally increases with height and can be as high as ρ=0.95 at cloud top. Horizontally, both q_c and N_c have a significant variability at cloud base, which tends to first decrease upward and then increase in the uppermost part of cloud close to the entrainment zone. Finally, we have to point out a couple of important caveats in the above analysis. First, as seen from Fig. 1 the selected hlegs are sampled at different vertical locations and also at different times. For example, hleg 5 at cloud base is more than 1 h apart from hleg 8 at cloud top (Fig. 1a). As a result, the temporal evolution of clouds is a confounding factor and might be misinterpreted as vertical variations of clouds. On the other hand, as shown below, we also observed similar vertical structure of q_c and N_c in other cases. It seems highly unlikely that the temporal evaluations of the clouds in all selected cases conspire to confound our results in the same way. Based on this consideration, we assume that the temporal evolution of clouds is an uncertainty that could lead to random errors but does not impact the overall vertical trend. The second caveat is that due to the very limited vertical sampling rate of hlegs (i.e., only 3–4 samples), we cannot possibly resolve the detailed vertical variation of ν_q, ν_N, and ρ. Although we have used the word “trend” in the above analysis, it should be noted that the vertical profile of these parameters may, but more likely may not, be linear. So, the word “trend” here indicates only the large pattern that can be resolved by the hlegs. Obviously these two caveats also apply to the analysis below the EF, which is also derived from the hlegs.

4.2 Implications for the EF for the autoconversion rate parameterization

As explained in the introduction, in GCMs the autoconversion process is usually parameterized as a highly nonlinear function of q_c and N_c, e.g., the KK scheme in Eq. (1). In such a parameterization, an EF is needed to account for the bias caused by the nonlinearity effect. A variety of methods have been proposed and used in the previous studies to estimate the EF (Larson and Griffin, 2013; Lebsock et al., 2013; Pincus and Klein, 2000; Zhang et al., 2019). The methods used in this study are based on Z19. Only the most relevant aspects are recapped here. Readers are referred to Z19 for detail.

If the subgrid variations of q_c and N_c, as well as their covariation, are known, then the EF can be estimated based on its definition as follows:

$$\begin{array}{}\text{(3)}& E={\displaystyle \frac{{\int }_{N_{\mathrm{c},\min }}^{\mathrm{\infty }}{\int }_{q_{\mathrm{c},\min }}^{\mathrm{\infty }}{q}_{\mathrm{c}}^{{\mathit{\beta }}_q}{N}_{\mathrm{c}}^{{\mathit{\beta }}_N}P\left(q_{\mathrm{c}},N_{\mathrm{c}}\right)\mathrm{d}{q}_{\mathrm{c}}\mathrm{d}{N}_{\mathrm{c}}}{\langle q_{\mathrm{c}}{\rangle }^{{\mathit{\beta }}_q}\langle N_{\mathrm{c}}{\rangle }^{{\mathit{\beta }}_N}}},\end{array}$$

where 〈q_c〉 and 〈N_c〉 are the grid-mean value, P(q_c,N_c) is the joint probability density function (PDF) of q_c and N_c. q_c,min and N_c,min are the lower limits of the in-cloud value (e.g., $q_{\mathrm{c},\min }=\mathrm{0.01}$ g m⁻³). Some previous studies approximate the P(q_c,N_c) as a bivariate lognormal distribution as follows:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& P\left(q_{\mathrm{c}},N_{\mathrm{c}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }{q}_{\mathrm{c}}{N}_{\mathrm{c}}{\mathit{\sigma }}_{q_{\mathrm{c}}}{\mathit{\sigma }}_{N_{\mathrm{c}}}\sqrt{\mathrm{1}-{\mathit{\rho }}_{\mathrm{L}}^{\mathrm{2}}}}}\exp \left(-{\displaystyle \frac{\mathit{\zeta }}{\mathrm{2}}}\right)\\ & \mathit{\zeta }={\displaystyle \frac{\mathrm{1}}{\mathrm{1}-{\mathit{\rho }}_{\mathrm{L}}^{\mathrm{2}}}}\left[{\left({\displaystyle \frac{\ln q_{\mathrm{c}}-{\mathit{\mu }}_{q_{\mathrm{c}}}}{{\mathit{\sigma }}_{q_{\mathrm{c}}}}}\right)}^{\mathrm{2}}\right.\\ & -\mathrm{2}\mathit{\rho }\left({\displaystyle \frac{\ln q_{\mathrm{c}}-{\mathit{\mu }}_{q_{\mathrm{c}}}}{{\mathit{\sigma }}_{q_{\mathrm{c}}}}}\right)\left({\displaystyle \frac{\ln N_{\mathrm{c}}-{\mathit{\mu }}_{N_{\mathrm{c}}}}{{\mathit{\sigma }}_{N_{\mathrm{c}}}}}\right)\\ & \left.+{\left({\displaystyle \frac{\ln N_{\mathrm{c}}-{\mathit{\mu }}_{N_{\mathrm{c}}}}{{\mathit{\sigma }}_{N_{\mathrm{c}}}}}\right)}^{\mathrm{2}}\right],\end{array}\end{array}$$

where μ_X and σ_X are, respectively, the mean and standard deviation of ln (X), where X is either q_c or N_c. ρ_L is the linear correlation coefficient between ln (q_c) and ln (N_c) (Larson and Griffin, 2013; Lebsock et al., 2013; Zhang et al., 2019). It should be noted here that ρ_L is fundamentally different from ρ (i.e., the linear correlation coefficient between q_c and N_c). On the other hand, we found that for all the selected hlegs, ρ and ρ_L are in an excellent agreement (see Fig. 4d). In fact, ρ and ρ_L can be used interchangeably in the context of this study without any impact on the conclusions. Nevertheless, interested readers may find more detailed discussion of the relationship between ρ and ρ_L in Larson and Griffin (2013).

Substituting P(q_c,N_c) in Eq. (4) into Eq. (3) yields a formula for EF that consists of the following three terms:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}E& =E_q\left({\mathit{\nu }}_{q_{\mathrm{c}}},{\mathit{\beta }}_q\right)\cdot E_N\left({\mathit{\nu }}_{N_{\mathrm{c}}},{\mathit{\beta }}_N\right)\\ & \cdot E_{\mathrm{COV}}\left({\mathit{\rho }}_{\mathrm{L}},{\mathit{\beta }}_q,{\mathit{\beta }}_N{\mathit{\nu }}_{q_{\mathrm{c}}},{\mathit{\nu }}_{N_{\mathrm{c}}}\right),\end{array}\end{array}$$

where $E_q\left({\mathit{\nu }}_{q_{\mathrm{c}}},{\mathit{\beta }}_q\right)$ corresponds to the enhancing effect of the subgrid variation of q_c, if q_c follows a marginal lognormal distribution, i.e., $P\left(x\right)=\frac{\mathrm{1}}{\sqrt{\mathrm{2}\mathit{\pi }}x\mathit{\sigma }}\exp \left(-\frac{{\left(\ln x-\mathit{\mu }\right)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}\right)$. It is a function of the inverse relative variance ν_q in Eq. (2) as follows:

$$\begin{array}{}\text{(6)}& E_q\left({\mathit{\nu }}_{q_{\mathrm{c}}},{\mathit{\beta }}_q\right)={\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{{\mathit{\nu }}_{q_{\mathrm{c}}}}}\right)}^{\frac{{\mathit{\beta }}_q^{\mathrm{2}}-{\mathit{\beta }}_q}{\mathrm{2}}}.\end{array}$$

Similarly, the $E_N\left({\mathit{\nu }}_{N_{\mathrm{c}}},{\mathit{\beta }}_N\right)$ below corresponds to the enhancing effect of the subgrid variation of N_c, if N_c follows a marginal lognormal distribution:

$$\begin{array}{}\text{(7)}& E_N\left(v_{N_{\mathrm{c}}},{\mathit{\beta }}_N\right)={\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{{\mathit{\nu }}_{N_{\mathrm{c}}}}}\right)}^{\frac{{\mathit{\beta }}_N^{\mathrm{2}}-{\mathit{\beta }}_N}{\mathrm{2}}}.\end{array}$$

The third term $E_{\mathrm{COV}}\left({\mathit{\rho }}_{\mathrm{L}},{\mathit{\beta }}_q,{\mathit{\beta }}_N{\mathit{\nu }}_{q_{\mathrm{c}}},{\mathit{\nu }}_{N_{\mathrm{c}}}\right)$ in Eq. (5),

$$\begin{array}{}\text{(8)}& E_{\mathrm{COV}}\left({\mathit{\rho }}_{\mathrm{L}},{\mathit{\beta }}_q,{\mathit{\beta }}_N,v_{q_{\mathrm{c}}},v_{N_{\mathrm{c}}}\right)=\exp \left({\mathit{\rho }}_{\mathrm{L}}{\mathit{\beta }}_q{\mathit{\beta }}_N{\mathit{\sigma }}_{q_{\mathrm{c}}}{\mathit{\sigma }}_{N_{\mathrm{c}}}\right),\end{array}$$

corresponds to the impact of the covariation of q_c and N_c on the EF. Because β_q>0 and β_N<0, if q_c and N_c are negatively correlated (i.e., ρ_L<0), then the E_COV>1 and acts as an enhancing effect on the autoconversion rate computation. In contrast, if q_c and N_c are positively correlated (i.e., ρ_L>0), then the E_COV<1, which becomes a suppressing effect on the autoconversion rate computation.

As previously mentioned, most previous studies of the EF consider only the impact of subgrid q_c variation (i.e., only the E_q term). The impacts of subgrid N_c variation as well as its covariation with q_c have been largely overlooked in observational studies, in which the E_q is often derived from the observed subgrid variation of q_c based on the definition of EF, i.e.,

$$\begin{array}{}\text{(9)}& E_q={\displaystyle \frac{{\int }_{q_{\mathrm{c},\min }}^{\mathrm{\infty }}{q}_{\mathrm{c}}^{{\mathit{\beta }}_q}P\left(q_{\mathrm{c}}\right)\mathrm{d}{q}_{\mathrm{c}}}{\langle q_{\mathrm{c}}{\rangle }^{{\mathit{\beta }}_q}}},\end{array}$$

where P(q_c) is the observed subgrid PDF of q_c. Alternatively, E_q has also been estimated from the inverse relative variance ν_q by assuming the subgrid variation of q_c follows the lognormal distribution, in which case E_q is given in Eq. (6).

Similar to E_N, if only the effect of subgrid N_c is considered, the corresponding E_N can be derived from the following two ways: one from the observed subgrid PDF P(N_c) based on the definition of EF, i.e.,

$$\begin{array}{}\text{(10)}& E_N={\displaystyle \frac{{\int }_{N_{\mathrm{c},\min }}^{\mathrm{\infty }}{N}_{\mathrm{c}}^{{\mathit{\beta }}_N}P\left(N_{\mathrm{c}}\right)\mathrm{d}{N}_{\mathrm{c}}}{\langle N_{\mathrm{c}}{\rangle }^{{\mathit{\beta }}_N}}},\end{array}$$

and the other based on Eq. (7) from the relative variance ${\mathit{\nu }}_{N_{\mathrm{c}}}$ by assuming the subgrid N_c variation follows the lognormal distribution.

Now, we put the in situ q_c and N_c observations from the selected hlegs in the theoretical framework of EF described above and investigate the following questions:

1. What is the (observation-based) EF derived based on Eq. (3) from the observed joint PDF P(q_c,N_c)?

2. How well does the (bi-logarithmic) EF derived based on Eq. (5) by assuming that the covariation of q_c and N_c follows a bivariate lognormal agree with the observation-based EF?

3. What is the relative importance of the E_q, E_N, and E_COV terms in Eq. (5) in determining the value of EF?

4. What is the error of considering only E_q and omitting the E_N and E_COV terms?

5. How do the observation-based EFs from Eq. (3) and the E_q, E_N, and E_COV terms vary with vertical height in cloud?

These questions are addressed in the rest of this section. Focusing first on the E_q in Fig. 6a, the E_q derived from observation based on Eq. (9) (solid circle) shows a clear decreasing trend with height between cloud base at around 700 m to about 1 km, with a value reduced from about 3 to about 1.2. Then, the value of E_q increases slightly in the cloud top hlegs 8 and 12. The E_q derived based on Eq. (6) by assuming lognormal distribution (open circle) has a very similar vertical pattern, although the value is slightly overestimated on average by 0.07 in comparison to the observation-based result. The vertical pattern of E_q can be readily explained by the subgrid variation of q_c in Fig. 4c. The E_N derived from observation (solid triangle) in Fig. 6b shows a similar vertical pattern as E_q, i.e., first decreasing with height from cloud base to about 1.2 km and then increasing with height in the uppermost part of cloud. The E_N derived based on Eq. (7) by assuming a lognormal distribution (open triangle) significantly underestimates the observation-based values (mean bias of −4.3), especially at cloud base (i.e., hleg 5 and 10) and cloud top (i.e., hleg 8 and 12).

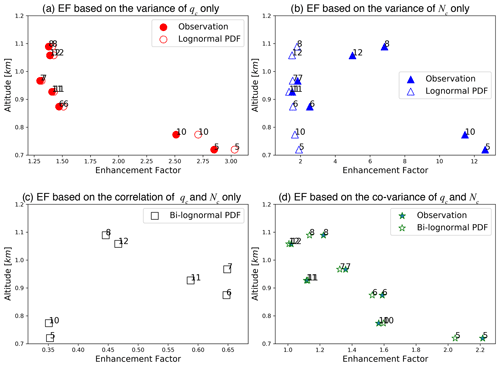
Figure 6 (a) E_q as a function of height derived from observation based on Eq. (9) (solid circle) and from the inverse relative variance ν_q assuming lognormal distribution based on Eq. (6) (open circle). (b) E_N as a function of height derived from observation based on Eq. (10) (solid triangle) and from the inverse relative variance ν_N assuming lognormal distribution based on Eq. (7) (open triangle). (c) E_COV derived based on Eq. (8) as a function of height. (d) E as a function of height derived from observation based on Eq. (3) (solid star) and based on Eq. (5) assuming a bi-lognormal distribution (open star). The numbers beside the symbols in the figure correspond to the numbers of the seven selected hlegs.

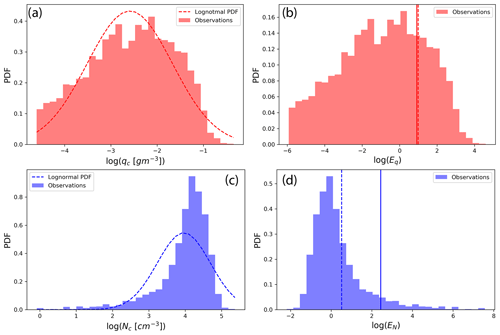
Figure 7 (a) Histogram of ln (q_c) based on observations from hleg 10 (bars) and the lognormal PDF (dashed line) based on the ${\mathit{\mu }}_{q_{\mathrm{c}}}$ and ${\mathit{\sigma }}_{q_{\mathrm{c}}}$ of hleg 10. (b) The histogram of ln (E_q) diagnosed from the observed q_c based on Eq. (9). The two vertical lines correspond to the leg-averaged ln (E_q) derived based on the observed q_c (solid) and the lognormal PDF (dashed line), respectively. (c) Histogram of ln (N_c) based on observations from hleg 10 (bars) and the lognormal PDF (dashed line) based on the ${\mathit{\mu }}_{N_{\mathrm{c}}}$ and ${\mathit{\sigma }}_{N_{\mathrm{c}}}$ of hleg 10. (d) The histogram of ln (E_N) diagnosed from the observed q_c based on Eq. (10). The two vertical lines correspond to the leg-averaged ln (E_N) derived based on the observed N_c (solid) and the lognormal PDF (dashed line), respectively.

Using hleg 10 as an example, we further investigated the cause for the error in lognormal-based EFs in comparison to those diagnosed from the observation. As shown in Fig. 7a the observed q_c is slightly negatively skewed in logarithmic space by the small values. Because the autoconversion rate is proportional to $q_{\mathrm{c}}^{\mathrm{2.47}}$, the negatively skewed q_c also leads to a negatively skewed E_q in Fig. 7b. As a result, the leg-averaged E_q diagnosed from the observation is slightly smaller than that derived based on Eq. (6) by assuming a lognormal distribution. The negative skewness also explains the large error in E_N for hleg 10 seen on Fig. 6b. As shown in Fig. 7c the observed N_c is also negatively skewed to a much larger extent in comparison to q_c. Because the autoconversion rate is proportional to $N_{\mathrm{c}}^{-\mathrm{1.79}}$, the highly negatively skewed N_c results in a highly positively skewed E_N in Fig. 7d. As a result, the E_N diagnosed from the observation is much larger than that derived based on Eq. (7) by assuming a lognormal distribution.

The E_q and E_N reflect only the individual contributions of subgrid q_c and N_c variations to the EF. The effect of the covariation of q_c and N_c, i.e., the E_COV, is shown in Fig. 6c. Interestingly, the value of E_COV is smaller than unity for all the selected hlegs. As explained in Eq. (8), E_COV<1 is a result of a positive correlation between q_c and N_c, as seen in Fig. 4d. Therefore, in these hlegs the covariation of the q_c and N_c has a suppressing effect on the EF, in contrast to the enhancing effect of E_q and E_N. This result is qualitatively consistent with Z19, who found that the vertically integrated liquid water path (LWP) of MBL clouds is in general positively correlated with the N_c estimated from the MODIS cloud retrieval product and, as a result, E_COV<1 over most of the tropical oceans. Because of the relationship in Eq. (8), the value E_COV is evidently negatively proportional to the correlation coefficient ρ_L in Fig. 4d. The largest value is seen in hleg 6 and 7, in which the bimodal joint distribution of q_c and N_c results in a small ρ_L. A rather small value of E_COV∼0.45 is seen for cloud top hleg 8 and 12, as result of a strong correlation between q_c and N_c (ρ_L>0.9) and moderate σ_q and σ_N.

Finally, the EF that accounts for all factors, including the individual variations of q_c and N_c, as well as their covariation, is shown in Fig. 6d. Focusing first on the observation-based results (solid star), i.e., E in Eq. (3), evidently there is a decreasing trend from cloud base (e.g., E=2.2 for hleg 5 and E=1.59 for hleg 10) to cloud top (e.g., E=1.20 for hleg 8 and E=1.02 for hleg 12). The E values derived based on Eq. (5) by assuming the bivariate lognormal distribution between q_c and N_c (i.e., open star in Fig. 6d) are in reasonable agreement with the observation-based results, with a mean bias of −0.09. It is intriguing to note that the value of $E=E_q\cdot E_N\cdot E_{\mathrm{COV}}$ in Fig. 6d is comparable to E_q in Fig. 6a, which indicates that the enhancing effect of E_N>1 in Fig. 6b is partially canceled by the suppressing effect of E_COV<1 in Fig. 6c. As previously mentioned, many previous studies of the EF consider only the effect of E_q but overlook the effect of E_N and E_COV. The error in the studies would be quite large if it were not for a fortunate error cancellation.

5 Other selected cases

In addition to the 18 July 2017 RF, we also found another six RFs that meet our criteria as described in Sect. 3 for case selection, from non-precipitating (e.g., 13 July 2017 case in Fig. S1) to weakly (e.g., 26 January 2018 case in Fig. S4) and heavily precipitating cloud (11 February 2018 case in Fig. S6). Due to limited space, we cannot present the detailed case studies of these RFs. Instead, we view them collectively and investigate whether the lessons learned from the 18 July 2017 RF, especially those about the EF in Sect. 4.2, also apply to the other cases.

In order to compare the hlegs from different RFs, we first normalize the altitude of each hleg with respect to the minimum and maximum values of all selected hlegs in each RF as follows:

$$\begin{array}{}\text{(11)}& z_{\mathrm{hleg}}^{\ast }={\displaystyle \frac{z_{\mathrm{hleg}}-z_{min}}{z_{max}-z_{min}}},\end{array}$$

where $z_{\mathrm{hleg}}^{\ast }$ is the normalized altitude for each hleg in a RF, and z_min and z_max are the altitude of the lowest and highest hleg in the corresponding RF. Defined this way, $z_{\mathrm{hleg}}^{\ast }$ is bounded between 0 and 1. Alternatively, $z_{\mathrm{hleg}}^{\ast }$ could also be defined with respect to the averaged cloud top (z_top) and base (z_base) as inferred from the KAZR or vlegs. However, because of the variation of cloud top and cloud base heights, as well as the collocation error, the $z_{\mathrm{hleg}}^{\ast }$ would often become significantly larger than 1 or smaller than 0, if $z_{\mathrm{hleg}}^{\ast }$ were defined with respect to z_top and z_base, making results confusing and difficult to interpret.

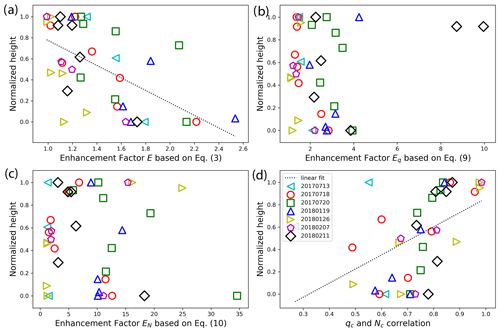
Figure 8 (a) The observation-based E derived from Eq. (3) that accounts for the covariation of q_c and N_c. (b) The observation-based E_q derived from Eq. (9) that accounts for only the subgrid variation of q_c. (c) The observation-based E_N derived from Eq. (10) that accounts for only the subgrid variation of N_c. (d) The correlation coefficient between q_c and N_c. All quantities are plotted as a function of the normalized height $z_{\mathrm{hleg}}^{\ast }$ in Eq. (11). The dashed lines correspond to a linear fit of the data when the fitting is statistically significant (i.e., P value < 0.05).

Figure 8 shows the observation-based EFs for all the selected hlegs from the seven selected RFs as a function of the $z_{\mathrm{hleg}}^{\ast }$. As shown in Fig. 8a, the E derived based on Eq. (3) that accounts for the covariation of q_c and N_c has a decreasing trend from cloud base to cloud top. This is consistent with the result from the 18 July 2017 case in Fig. 6d. However, neither the E_q in Fig. 8b nor the E_N in Fig. 8c shows a clear dependence on $z_{\mathrm{hleg}}^{\ast }$ in comparison to the results of the 18 July 2017 case in Fig. 6a and b. Note that the E_q and E_N are influenced by a number of factors, such as horizontal distance and cloud fraction, in addition to vertical height. It is possible that the differences in other factors outweigh the vertical dependence here. Interestingly, the linear correlation coefficient ρ between q_c and N_c in Fig. 8d shows an increasing trend with $z_{\mathrm{hleg}}^{\ast }$ that is statistically significant (R value =0.50 and P value = 0.02), despite a few outliers. This is consistent with what we found in the 18 July 2017 case (see Fig. 4d). As evident from Eq. (8), an increase in ρ_L would lead to a decrease in E_COV. Since neither E_q nor E_N shows a clear dependence on $z_{\mathrm{hleg}}^{\ast }$, the decrease in E_COV with $z_{\mathrm{hleg}}^{\ast }$ seems to play an important role in the determining the value of E. Another line of evidence supporting this role is the fact that both E_q and E_N are quite large for the cloud top hlegs, while in contrast the values of the corresponding E that accounts for the covariation of q_c and N_c are much smaller. For example, the E_q for two hlegs from the 11 February 2018 RF exceeds 8, but the corresponding E values are smaller than 1.2, which is evidently a result of large ρ_L and thereby small E_COV.

As previously mentioned, many previous studies of the EF for the autoconversion rate parameterization consider only the effect of subgrid q_c variation but ignore the effects of subgrid N_c variation and its covariation with q_c. To understand the potential error, we compared the E_q and E both derived based on observations in Fig. 9. Apparently, E_q is significantly larger than E for most of the selected hlegs, which implies that considering only subgrid q_c variation would likely lead to an overestimation of EF. This is an interesting result. Note that E_N≥1 by definition and therefore E_q>E is possible only when the covariation of q_c and N_c has a suppressing effect, instead of enhancing. Once again, this result demonstrates the importance of understanding the covariation of q_c and N_c for understanding the EF for autoconversion rate parameterization.

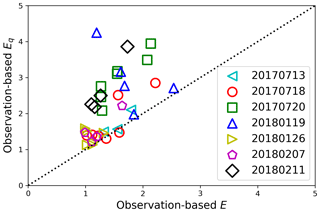
Figure 9 A comparison of observation-based E and observation-based E_q for all the selected hlegs from all four selected RFs.

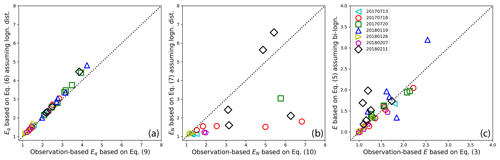
Figure 10 (a) A comparison of observation-based E_q derived based on Eq. (9) and E_q derived based on Eq. (6) assuming lognormal distribution for subgrid q_c observations for all the selected hlegs. (b) A comparison of observation-based E_N derived based on Eq. (10) and E_N derived based on Eq. (7) assuming lognormal distribution or all the selected hlegs. (c) A comparison of observation-based E derived based on Eq. (3) and E derived based on Eq. (5) assuming bivariate lognormal distribution for the subgrid joint distribution of q_c and N_c.

Having looked at the observation-based EFs, we now check if the EFs derived based on assumed PDFs (e.g., lognormal or bivariate lognormal distributions) agree with the observation-based results. As shown in Fig. 10a, the E_q based on Eq. (6) that assumes a lognormal distribution for the subgrid variation of q_c is in an excellent agreement with the observation-based results. In contrast, the comparison is much worse for the E_N in Fig. 10b, which is not surprising given the results from the 18 July 2017 case in Fig. 6b. As one can see from Fig. 5, the marginal PDF of N_c is often broad and sometimes even bimodal. The deviation of the observed N_c PDF from the lognormal distribution is probably the reason for the large difference of E_N in Fig. 10b. As shown in Fig. 10c, the E values derived based on Eq. (5) by assuming a bivariate lognormal function for the joint distribution of q_c and N_c are in good agreement with observation-based values, which is consistent with the results from the 18 July 2017 case in Fig. 6.

6 Summary and discussion

In this study we derived the horizontal variations of q_c and N_c, as well as their covariations in MBL clouds based on the in situ measurements from the recent ACE-ENA campaign, and investigated the implications of subgrid variability as it relates to the enhancement of autoconversion rates. The main findings can be summarized as follows:

• In the 18 July 2017 case, the vertical variation of the mean values of q_c and N_c roughly follows the adiabatic structure. The horizontal variances of q_c and N_c first decrease from cloud base upward toward the middle of the cloud and then increase near cloud top. The correlation between of q_c and N_c generally increases from cloud base to cloud top.

• In other selected cases, the horizontal variances of q_c and N_c show no statistically significant dependence on the vertical height in cloud. However, the increasing trend of the correlation between q_c and N_c from cloud base to cloud top remains robust.

• In a few selected V-shaped hlegs, the q_c and N_c follow a bimodal joint distribution which leads to a weak linear correlation between them.

• The observation-based physically complete E that accounts for the covariation of q_c and N_c has a robust decreasing trend from cloud base to cloud top, which can be explained by the increasing trend of the q_c and N_c correlation from cloud base to cloud top.

• The E estimated by assuming a monomodal bivariate lognormal joint distribution between q_c and N_c agrees well with the observation-based results.

These results provide the following two new understandings of the EF for the autoconversion parameterization that have potentially important implications for GCM. First, our study indicates that the physically complete E has a robust decreasing trend from cloud base to cloud top. Because the autoconversion process is most important at the cloud top, this vertical dependence of EF should be taken into consideration in the GCM parametrization scheme. Second, our study indicates that effect of the q_c and N_c correlation plays a critical role in determining the EF. Lately a few novel modeling techniques have been developed to provide the coarse-resolution GCM information of subgrid cloud variation, such as the PDF-based higher-order turbulence closure method – Cloud Layer Unified By Binormals (CLUBB; Golaz et al., 2002; Guo et al., 2015; Larson et al., 2002). These models are able to provide the parameterized subgrid variance of q_c, which can be used in turn to estimate E_q. However, as shown in our study the E_q tends to overestimate the EF.

Our study has a few important limitations. First of all, our results are based on a handful cases from a single field campaign. The lessons learned here need to be further examined based on more data or tested in modeling studies. Second, as pointed out in Sect. 4.1, due to the inherent sampling limitation of airborne measurements, the temporal evolution of clouds is an important uncertainty and a confounding factor in this study, which needs to be quantified in future studies. Third, our study provides only a phenomenological analysis of the horizontal variations of cloud microphysics in the MBL clouds and the implications for the EF. Ongoing modeling research based on a comprehensive LES model is being conducted to identify and elucidate the process-level physical mechanisms behind our observational results. Finally, this study is focused on the KK parameterization in estimating the enhancement factors resulting from subgrid variability of q_c, N_c, and q_c–N_c covariance. The specific values are expected to differ when applied to other autoconversion parameterizations with different power-law exponents.