the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Supercooled liquid water and secondary ice production in Kelvin–Helmholtz instability as revealed by radar Doppler spectra observations
Alexei Korolev
Dmitri Moisseev
Mixed-phase clouds are globally omnipresent and play a major role in the Earth's radiation budget and precipitation formation. The existence of liquid droplets in the presence of ice particles is microphysically unstable and depends on a delicate balance of several competing processes. Understanding mechanisms that govern ice initiation and moisture supply are important to understand the life cycle of such clouds. This study presents observations that reveal the onset of drizzle inside a ∼ 600 m deep mixed-phase layer embedded in a stratiform precipitation system. Using Doppler spectral analysis, we show how large supercooled liquid droplets are generated in Kelvin–Helmholtz (K–H) instability despite ice particles falling from upper cloud layers. The spectral width of the supercooled liquid water mode in the radar Doppler spectrum is used to identify a region of increased turbulence. The observations show that large liquid droplets, characterized by reflectivity values larger than −20 dBZ, are generated in this region. In addition to cloud droplets, Doppler spectral analysis reveals the production of columnar ice crystals in the K–H billows. The modeling study estimates that the concentration of these ice crystals is 3–8 L−1, which is at least 1 order of magnitude higher than that of primary ice-nucleating particles. Given the detail of the observations, we show that multiple populations of secondary ice particles are generated in regions where larger cloud droplets are produced and not at some constant level within the cloud. It is, therefore, hypothesized that K–H instability provides conditions favorable for enhanced droplet growth and formation of secondary ice particles.
- Article
(7727 KB) - Full-text XML
- BibTeX
- EndNote
Clouds strongly influence the Earth's radiation budget (Baker, 1997; Baker and Peter, 2008; Morrison et al., 2012; Tan et al., 2016) and hydrological cycle (Mülmenstädt et al., 2015). A large fraction of clouds are mixed phase (Hogan et al., 2004), i.e., contain both liquid water droplets and ice particles. Such clouds exist in an unstable equilibrium. Liquid water droplets can rapidly convert into ice particles via the Wegener–Bergeron–Findeisen process or riming (Korolev et al., 2017). This transition significantly changes the radiative and microphysical properties of these clouds (Sun and Shine, 1994; Lamb and Verlinde, 2011). Climate and numerical weather prediction models, however, struggle to accurately represent mixed-phase clouds (Klein et al., 2009; McCoy et al., 2016; Barrett et al., 2017). They tend to underestimate cloud liquid water content (Klein et al., 2009; Barrett et al., 2017), which seems to be linked to the modeled ice production (Klein et al., 2009; Barrett et al., 2017). The number of ice crystals is typically controlled by ice-nucleating particles (INPs) (DeMott et al., 2010; Kanji et al., 2017). However, in some cases, the observed ice crystal number concentration largely exceeds the concentration of INPs (Mossop, 1985; Field et al., 2017). There are several secondary ice production (SIP) mechanisms that explain the production of additional ice particles (e.g., Hallett and Mossop, 1974; Lauber et al., 2018; Field et al., 2017). Their importance and occurrence, however, is still a topic of current scientific interest (Field et al., 2017; Korolev et al., 2020; Morrison et al., 2020; Shaw et al., 2020; Luke et al., 2021).
The existence of supercooled liquid water in mixed-phase clouds necessitates the sufficient supply of water vapor to replenish its depletion due to ice particles. For single-layered mixed-phase clouds, the water vapor supply may benefit from a number of processes (Morrison et al., 2012) such as the adiabatic cooling of air parcels due to turbulence (Korolev and Field, 2008) and cloud-scale updrafts (Shupe et al., 2008b), radiative cooling of the liquid cloud layer (Pinto, 1998), entrainment of upper moist air (Solomon et al., 2011), and feedbacks with the surface (Morrison and Pinto, 2006). While multilayered clouds, where a supercooled liquid water layer is embedded in an ice-precipitating cloud, occur frequently (Shupe et al., 2006; Intrieri et al., 2002) and may produce drizzle-sized drops (Majewski and French, 2020) as well as secondary ice particles (Hallett and Mossop, 1974; Lauber et al., 2018; Luke et al., 2021), they are much less studied owing to the complexity of the microphysical processes that are taking place.
Past studies have highlighted the importance of upward air motions, such as shear-induced turbulence (Hill et al., 2014), orographic forcing (Lohmann et al., 2016) and periodic supersaturation variations (Korolev, 1995; Majewski and French, 2020), for the growth of liquid droplets in multilayered mixed-phase clouds. In addition to these mechanisms, isobaric mixing (Korolev and Isaac, 2000) and inhomogeneous mixing (Pobanz et al., 1994), which usually take place in dynamically unstable regions such as Kelvin–Helmholtz (K–H) clouds, seem to also favor the formation of large supercooled droplets. However, there seems to be a lack of observations with a detailed depiction of vertical air motions, which are critical for analyzing the driver of the mixing process (Majewski and French, 2020). Aircraft measurements have been widely utilized for analyzing the growth of liquid drops in mixed-phase clouds (e.g., Korolev and Isaac, 2000; Hogan et al., 2002; Majewski and French, 2020); however, they are only available along the aircraft tracks and cannot resolve the vertical profiles of different hydrometeors. To provide a larger-scale view of the clouds, radar observations are often used (e.g., Petre and Verlinde, 2004; Barnes et al., 2018; Luce et al., 2012; Geerts and Miao, 2010; Houser and Bluestein, 2011; Medina and Houze Jr, 2016; Conrick et al., 2018; Grasmick and Geerts, 2020; Gehring et al., 2020). Because radar observations are more sensitive to larger hydrometeors, it is often impossible to separate echoes from ice particles and water droplets at the same time.
For vertically pointing radars, the recorded Doppler spectra split radar returns over a range of sampled Doppler velocities (Kollias et al., 2011) and can be used to separate echoes from different hydrometeor types in a radar sampling volume Shupe et al. (e.g., 2004); Luke and Kollias (e.g., 2013). The utilization of the polarimetric spectral analysis technique (Spek et al., 2008; Moisseev et al., 2015; Luke et al., 2010; Oue et al., 2015; Kalesse et al., 2016; Li and Moisseev, 2020; Luke et al., 2021; Li et al., 2021) allows for the identification of supercooled liquid water, which is indicative of vertical air motions, and ice columns, thereby facilitating the analysis of different hydrometeor populations and vertical air motions simultaneously. In this study, this data analysis method is used to uncover the K–H billows of supercooled liquid water and ice columns embedded in a stratiform precipitation event.
The paper is organized as follows: Sect. 2 introduces the data used in this study; an overview of a stratiform precipitation event is shown in Sect. 3; Sect. 4 demonstrates the methods used to analyze this event; the dynamics and microphysics of embedded K–H billows are shown in Sect. 5; and discussions and conclusions are given in Sects. 6 and 7, respectively.
In this study, measurements from several radars supplemented by radiosonde observations are used to study microphysical and dynamical properties of a stratiform precipitation event that took place on 18 April 2018. The vertically pointing C- and W-band radars (HYDRA-C and -W) deployed at the University of Helsinki's Hyytiälä station (61.845∘ N, 24.287∘ E) (Hari and Kulmala, 2005; Petäjä et al., 2016) are aided by a scanning weather radar. This radar setup provides various observing views over Hyytiälä, facilitating the synthetic analysis of clouds and precipitation (Li et al., 2020; Sinclair et al., 2016). The closest sounding station to the Hyytiälä station is located at Jokioinen, which is around 123 km to the southwest of Hyytiälä. The sounding is launched twice a day at around 00:00 and 12:00 UTC. The radiosonde observations at 23:30 UTC (the 00:00 UTC sounding) were used in our analysis
Both vertically pointing radars, HYDRA-C and -W, operate in the linear depolarization ratio (LDR) mode. HYDRA-C is a container-based weather radar that was transported to Hyytiälä in the summer of 2016. Prior to its deployment at the Hyytiälä station, HYDRA-C was operating in Järvenpää (Moisseev et al., 2015). HYDRA-W is a frequency-modulated continuous-wave radar (Küchler et al., 2017) and has been deployed at the Hyytiälä station since November 2017.
The Doppler radar moments (e.g., reflectivity, LDR, Doppler velocity and spectral width) were recorded by both radars. The pulse length of HYDRA-C is 0.5 µs, resulting in a range resolution of 75 m, which was oversampled to 50 m. HYDRA-W employs dynamic range resolutions of 25.5 and 34 m for range gates lower and higher than 3577 m, respectively. The Doppler spectra of HYDRA-W were calculated by applying a fast Fourier transform with 1024 points (Vmax, W=10.24 m s−1) below and 512 points (Vmax, W=5.12 m s−1) above 996 m. The spectral compression mode was used for HYDRA-W and the background noise was removed by applying a noise filter factor that is characterized by the standard deviation of the Doppler spectrum. The archived W-band polarimetric spectra data enable the analysis of spectral LDR. The time resolutions of HYDRA-C and -W are 1.37 and 3.35 s, respectively. All observations were binned into the time resolution of HYDRA-C and the range resolution of HYDRA-W. The beam widths of HYDRA-C and -W are 0.48 and 1∘, respectively.
Most of the presented analysis is based on HYDRA-W observations. The C/W dual-wavelength observations at the cloud top were used to compute the path-integrated attenuation (Li and Moisseev, 2019; Tridon et al., 2020). This attenuation was then used to estimate the supercooled liquid water path (SLWP) (Hogan et al., 2005).
The scanning C-band dual-polarization weather radar is located in Ikaalinen (IKA), 64 km west of Hyytiälä station, and is operated by the Finnish Meteorological Institute (FMI). The Ikaalinen C-band radar performs range–height indicator (RHI) scans over Hyytiälä every 15 min. As part of the data analysis, the Ikaalinen radar raw data were processed using the Python ARM Radar Toolkit (Helmus and Collis, 2016). In this study, the Doppler velocity observations of Ikaalinen radar were employed to identify the radial wind shear over the Hyytiälä station.
As the Ikaalinen radar is routinely calibrated, its reflectivity measurements were also used to calibrate HYDRA-C. The calibration of HYDRA-W was then cross-checked by matching HYDRA-C and HYDRA-W reflectivity values at cloud tops where the Rayleigh approximation applies at both bands (Hogan et al., 2005; Kneifel et al., 2015; Falconi et al., 2018; Li and Moisseev, 2019; Tridon et al., 2020).
A stratiform precipitation system passed over Hyytiälä between 17:00 UTC on 18 April and 04:00 UTC on 19 April 2018. The time–height evolution of this stratiform precipitation captured by HYytiälä Doppler RAdar-W (HYDRA-W; Li and Moisseev, 2020) between 20:00 and 22:30 UTC on 18 April 2018 is presented in Fig. 1a, b and c. As shown in Fig. 1a, the precipitation intensifies after 21:45 UTC. C-band radar reflectivity at 400 m (not shown) increased from ∼ 5 to ∼ 20 dBZ with the rain rate increasing from 0.1 to 0.7 mm h−1. During the presented time period, the cloud top stays at ∼ 4 km, where the air temperature is around −15 ∘C. The snow-generating cells at the cloud top can be identified by the positive Doppler velocities (Fig. 1c). About 1 km below the radar-detected cloud top, the fall streaks visible in the reflectivity observations change their direction, indicating the presence of a wind shear layer. It is noteworthy that below the wind shear layer, a region of enhanced spectral width, as can be seen in Fig. 1b, is present between 21:00 and 21:50 UTC. From 20:20 through 21:20 UTC, the HYDRA-W-measured mean Doppler velocity exhibits visible oscillations between 2.3 and 3.2 km (Fig. 1c), implying the presence of an embedded convection.
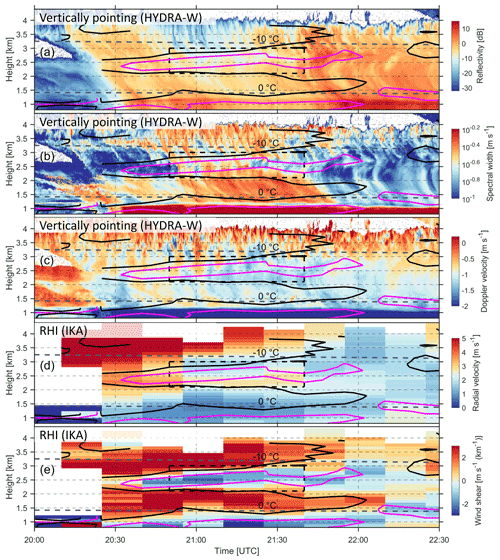
Figure 1Radar observations collected on 18 April 2018 between 20:00 and 22:30 UTC showing vertically pointing HYDRA-W reflectivity (a), spectral width (b) and mean Doppler velocity (c). Panels (d) and (e) present vertical profiles of radial Doppler velocity and vertical wind shear derived from the range–height indicator (RHI) scans of Ikaalinen radar (IKA), respectively. Purple and black contours depict the wind shear of −1 and 1 m s−1 (km−1), respectively. The 0 and −10 ∘C isotherms are marked by gray dashed lines. The black dashed box shows the region where the spectral analysis has identified the presence of supercooled liquid, as shown in Fig. 4.
To verify if the environmental conditions were favorable for the formation of the K–H instability, the radio sounding data were used. Observations from the radiosonde launched at 23:30 UTC on 18 April 2018 are shown in Fig. 2. The Richardson number (Ri) was computed in both dry and moist conditions following the method used by Hogan et al. (2002). The air between 0.3 and 3.1 km was almost saturated, and the moist Ri from 1.7 to 3.5 km was mostly below 0.25, indicating that the necessary conditions for the development of the K–H instability were met.
Because the radio sounding station is not very close to Hyytiälä, the Doppler velocity observations from Ikaalinen radar were used as additional auxiliary information to support the hypothesis of the formation of the K–H instability. From the RHI measurements, vertical profiles of the Doppler velocity observations above the station were extracted. The time series of these profiles is shown in Fig. 1d and e. One can observe that IKA radial velocity observations detect a wind shear of 1–2 m s−1 (km−1) in the region where the vertical velocity oscillations occur. This wind shear is strongest between 20:40 and 21:40 UTC. It more or less disappears after that. The observed duration of the wind shear is an important observation that potentially explains the evolution of the K–H billows, as will be discussed below. We should also point out that the snow-generating cells, clearly visible in Fig. 1a, may affect stability of the layer where we believe the oscillations have formed. This, in turn, may affect the properties of the K–H instability, and it may not have a “classic” appearance. However, the correlation between the K–H instability and wind shear indicates that shear may play a dominant role in formation of the K–H wave.
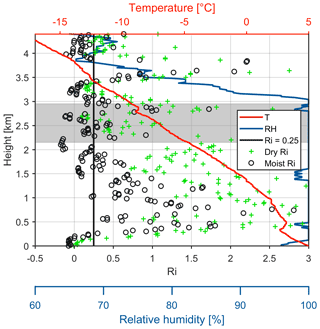
Figure 2Radiosonde observations at 23:30 UTC on 18 April 2018 from the Jokioinen station. This figure shows the air temperature (T, red line), relative humidity (RH, blue line), and dry (green cross) and moist (black circle) Ri numbers derived from the radiosonde data. The vertical black line indicates the critical Richardson number Ri = 0.25. The gray shaded area in this figure corresponds to the heights as marked by the black dashed box in Fig. 1.
4.1 HYDRA-W Doppler spectra analysis
In a radar volume, hydrometeors with different fall velocities are typically present. Multilayered mixed-phase clouds are a good example of conditions where hydrometeors with diverse fall velocities are present in a radar volume (Rambukkange et al., 2011; Verlinde et al., 2013; Kalesse et al., 2016). In such cases, the analysis of Doppler radar spectra measured by a vertically pointing radar can be used to separate radar echoes of these particles. The sizes of typical supercooled liquid droplets range from 5 to 20 µm (Shupe et al., 2008b). The terminal velocities are in the order of 0.03 and 0.07 m s−1 for 10 and 50 µm liquid droplets, respectively (Kollias et al., 2001). Given their negligible fall velocities, these cloud droplets can be used as tracers for air motions. In Doppler radar spectra, the radar returns from liquid cloud droplets can be identified as a narrow peak around 0 m s−1. The mean velocity of this peak can be used to derive vertical air motion (Shupe et al., 2004).
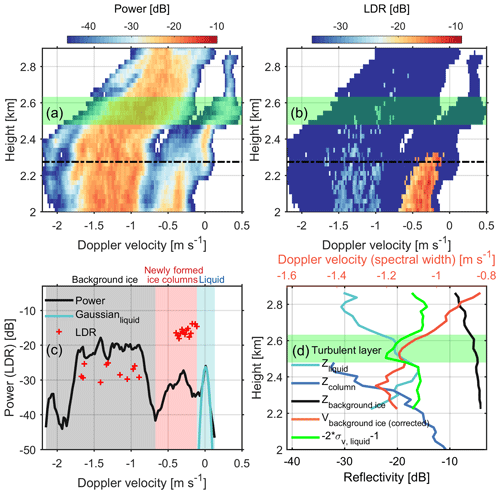
Figure 3Vertical Doppler spectra profiles at 21:08:43 UTC for (a) power and (b) LDR. Panel (c) presents a zoomed-in view of the spectral power and LDR as marked by the dot-dash lines in panels (a) and (b). Panel (d) presents vertical profiles of the scaled spectral width of the supercooled liquid water mode (green line) in the Doppler spectra (σv, liquid), the Doppler velocity of background ice (Vbackground ice) after correcting air motions retrieved from liquid water, and radar reflectivity of supercooled liquid water (Zliquid), columnar ice (Zcolumn) and background ice (Zbackground ice). The gray, red and blue shaded areas in panel (c) indicate background ice from above, newly formed ice columns and supercooled liquid, respectively. The green shaded areas in panels (a), (b) and (d) indicate the turbulent layer as characterized by the increased σv, liquid. Negative velocity indicates downward.
In multilayered mixed-phase clouds, more than one population of ice may exist (Zawadzki et al., 2001; Verlinde et al., 2013; Spek et al., 2008). In some cases, the presence of new ice particles is indicative of SIP (Zawadzki et al., 2001). At vertical incidence, LDR can be used to discriminate between columns and other types of ice (Matrosov, 1991; Matrosov et al., 1996; Oue et al., 2015; Li et al., 2021). The columnar crystals will produce LDR values as large as −16 to −13 dB. Figures 3a and b present vertical profiles of W-band radar Doppler spectral power and LDR, respectively. The supercooled liquid water, with relatively weak and narrow spectral mode (Shupe et al., 2004, 2008b; Luke et al., 2010), exists between 2.2 and 2.85 km. Ice crystals with a spectral LDR around −15 dB and Doppler velocity lower than 0.8 m s−1 are attributed to the columnar ice (Oue et al., 2015). The spectral power of the background ice falling from upper clouds is much larger than that of liquid water droplets and ice columns. A close-up of the measurements at a height of 2.28 km is shown in Fig. 3c. The background ice, newly generated ice columns and supercooled liquid in the Doppler spectrum are shown using gray, yellow and blue shading, respectively. As can be seen, the spectral LDR of ice columns is much higher than background ice, whereas the LDR signals for supercooled liquid water are below the noise level.
The Doppler spectra components of different hydrometeor types, present during this event, can be identified using Doppler velocity and spectral LDR, as discussed above. Despite the straightforward identification of different ice particle types in the Doppler spectrum, deriving their spectral moments, like reflectivity, Doppler velocity and spectral width, is complicated because of the overlap of the spectral modes. This overlap is enhanced if there is significant spectral broadening due to the horizontal and vertical wind shears, and turbulence. As the size distribution of liquid droplets is relatively narrow, their spectrum can be closely approximated by a Gaussian model (Luke and Kollias, 2013). If individual Doppler spectra of different particles can be modeled using Gaussian shapes, their spectral moments can be estimated using Gaussian mixture models (Nguyen et al., 2008). However, the Doppler spectra of ice particles do not necessarily follow this functional form. Nevertheless, the Gaussian model is a good approximation for the Doppler spectrum of liquid cloud droplets (Luke and Kollias, 2013). As the right slope of the liquid cloud droplet mode in the Doppler spectrum is less affected by the ice mode, the Gaussian model can still be fitted to the right part of the cloud droplet spectrum (Luke and Kollias, 2013). As shown in Fig. 3c, the Gaussian model fits the spectral peak of supercooled liquid water well. Using such a Gaussian fit, the reflectivity, spectral width and Doppler velocity of supercooled liquid water were derived. The reflectivity of the columnar ice mode in the Doppler spectrum was calculated directly from the spectrum, as we expect that the impact of the liquid mode on the reflectivity of columnar ice is not significant enough to affect our study of the evolution of ice columns (Oue et al., 2015; Kalesse et al., 2016).
4.2 Estimation of the supercooled liquid water path
The retrieval of the SLWP was mainly based on the differential attenuation between C- and W-band radar reflectivity (Hogan et al., 2005).This event was observed by two radars, namely W-band cloud and C-band precipitation radars. While the attenuation due to rain, the melting layer, ice particles and supercooled liquid water is negligible for the C-band radar signal, it may have a strong impact on W-band radar observations (Hogan et al., 2005; Li and Moisseev, 2019). The differential attenuation between C- and W-band radar observations caused by supercooled liquid water is proportional to the liquid water content (Hogan et al., 2005). Therefore, if the attenuation due to other attenuation sources can be mitigated, the differential attenuation measurements can be used to estimate the SLWP.
For HYDRA-W, the observed reflectivity is affected by the attenuation from the atmosphere and the wet radome. Using the reflectivity observations from HYDRA-C, the atmospheric attenuation due to rain and the melting layer at the W-band was removed by applying reflectivity–attenuation relations (Li and Moisseev, 2019). It was found that the attenuation due to rain and the melting layer is relatively small, less than 1 dB, and the uncertainties in attenuation estimation were, in the order of 0.5 dB (Li and Moisseev, 2019). Given the weak rain intensity, the attenuation due to ice particles is negligible (Leinonen et al., 2011). The gaseous attenuation can be calculated from the Millimeter-wave Propagation Model (Liebe, 1985). The wet radome attenuation should be minimized, as the antenna of HYDRA-W is protected by a hydrophobic cover and the blower further reduces radome wetting. After the attenuation due to rain and the melting layer was removed from W-band reflectivity, the differential attenuation was derived by matching C- and W-band reflectivities at the cloud top, where ice particles are expected to be small enough to satisfy the Rayleigh approximation in both radar bands. The SLWP was then converted from the differential attenuation which is mainly caused by the liquid attenuation at W-band (Hogan et al., 2005).
The following discussion is focused on the analysis of dynamics and microphysical properties of the cloud region inside the black rectangle in Fig. 1a, b and c (20:50–21:40 UTC). This period will be analyzed with the help of specifically derived radar reflectivity (Zliquid), spectral width (σv, liquid) and Doppler velocity of the supercooled liquid water (Vliquid); reflectivity of ice columns (Zcolumn); and the SLWP. It should be noted that the rectangle in the abovementioned figure panels depicts the region where the supercooled liquid water was detected. The Doppler analysis was also performed on the regions outside of the rectangle, but no supercooled water or columnar ice production was detected there.
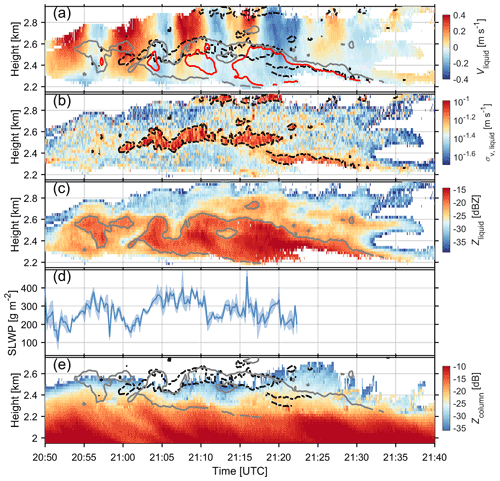
Figure 4The (a) Doppler velocity, (b) spectral width and (c) reflectivity of supercooled liquid cloud droplets, (d) the SLWP above the melting layer estimated from the differential attenuation between C- and W-bands, and (e) the reflectivity of ice columns are shown. The blank regions in panels (a), (b), (c) and (e) are where no significant supercooled liquid mode (a, b, c) or columnar ice mode (e) can be identified in the radar Doppler spectrum. Red and gray isolines indicate the reflectivity of −18 and −21 dBZ for supercooled liquid water, respectively. Black dashed isolines indicate the spectral width of 0.06 m s−1 for supercooled liquid water. The shaded areas in panel (d) indicate the standard deviation of the SLWP in 13.7 s. After 21:23 UTC, no SLWP retrieval was made. This was caused by the rapid changes in the observed C-band reflectivity at cloud top, which hindered the identification of Rayleigh scattering regions.
5.1 Doppler velocity and the spectral width of supercooled liquid water
A layer of supercooled liquid water persisted during the entire period (Fig. 4). As the cloud droplet fall velocity does not usually exceed a few centimeters per second (∼ 0.03 m s−1 for the diameter of 10 µm), Vliquid is used for the assessment of the vertical velocity of air motion (Shupe et al., 2004). Figure 4a reveals periodic air circulations with the amplitude of approximately 0.4 m s−1. It should be noted that the K–H instability may not be the only factor modulating air motions, since the wind shear layer is so close to the cloud top. However, we argue that the oscillation of air motions at around 2.8 km is mainly caused by the K–H instability. Firstly, the wind shear layer, which is inductive to vertical air motions, at 2.8 km was clearly present from 20:50 to 21:40 UTC (Fig. 1e). Secondly, after 22:00 UTC, when the wind shear layer has almost disappeared, there are no identifiable signatures of air oscillations at 2.8 km (Fig. 1c).
A wave train of enhanced σv, liquid at around 2.5 km is colocated with vertical air perturbations (Fig. 4b). Specifically, the upward branches of the waves coincide with updrafts, and the crests of waves are close to the transitional regions of upward and downward velocities. Such colocation of K–H billows and vertical air motions bears a good resemblance to previous vertically pointing radar records of K–H clouds (Petre and Verlinde, 2004; Geerts and Miao, 2010; Luce et al., 2012). Despite the lower amplitude of the vertical velocities in the present observations, both temporal (∼ 5 min) and spatial (∼ 300 m) scales of each wave are very similar to those K–H billows observed in the convective outflow anvil (Petre and Verlinde, 2004). In addition, σv, liquid is enhanced along the central axis (Barnes et al., 2018) rather than only around the crests of K–H waves (Houser and Bluestein, 2011).
The enhanced σv, liquid can be caused by the broadening of the drop size distribution as well as the enhanced turbulence within the radar volume. If it was attributed to the former, the increase in σv, liquid would not be only 100 to 200 m in depth and would not vanish just below 2.4 km. Therefore, we conclude that the sharp increase in σv, liquid was mainly caused by the velocity fluctuations and that mixing was taking place between 2.4 and 2.6 km.
5.2 Reflectivity of supercooled liquid water
The regions of enhanced Zliquid manifest themselves as well-defined K–H billows (see the gray solid isolines in Fig. 4c), especially between 21:00 and 21:13 UTC. The crests of the K–H billows are around the transitional regions of upward and downward velocities and protrude to downdrafts. Just below the turbulent layer, as characterized by the increased σv, liquid, there is a region of enhanced Zliquid which is as high as −16 dBZ, indicating the onset of drizzle in this region (Frisch et al., 1995).
Interestingly, the K–H billows of Zliquid (gray solid isolines) are colocated with the enhanced σv, liquid (black dashed isolines), as shown in Fig. 4a. This colocation resembles what has been observed in rain where the perturbation from the K–H instability is expected to facilitate the coalescence of raindrops and leads to increased radar reflectivity (Barnes et al., 2018).
Previous observational studies have shown that K–H billows embedded in precipitation can be characterized by the fluctuations in radar reflectivity and spectral width colocating with Doppler velocities (Petre and Verlinde, 2004; Geerts and Miao, 2010; Barnes et al., 2018). In this event, such signatures are hardly identifiable in conventional radar reflectivity and spectral width observations (Fig. 1a, b), despite the evidence of air circulations as indicated by mean Doppler velocities (Fig. 1c). This difference may be explained by much weaker vertical air motions and the potential impact of snow-generating cells at the cloud top in this study.
5.3 Supercooled liquid water path
As shown in Fig. 4d, the SLWP presents a wave-like pattern as well. The estimated SLWP ranges from 150 to 400 g m−2 between 21:00 and 21:15 UTC. In general, the SLWP is larger in downdrafts than in updrafts, somewhat resembling aircraft observations presented by Majewski and French (2020). The oscillations in the SLWP and observed supercooled liquid droplet velocities do not fully coincide. This discrepancy can be attributed to presence of supercooled liquid at the other altitudes, i.e., at around 1.5 km (not shown) and potentially at the top of the snow-generating cells.
5.4 Generation of ice columns
Zcolumn was derived from the columnar ice mode in radar Doppler spectrum observations. As shown in Fig. 4e, the detected ice columns initiate at about 2.5 km, coinciding with the enhanced σv, liquid. Once generated, these ice particles grow rapidly from about −30 to −15 dBZ within ∼ 0.3 km. Interestingly, several fall streaks of ice columns present below the K–H billows, and each of them (around 21:04, 21:10 and 21:22 UTC, respectively) corresponds to a crest in the K–H billows as indicated by the enhanced Zliquid and σv, liquid.
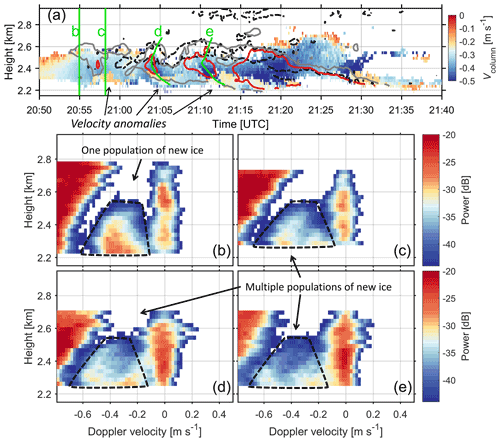
Figure 5(a) The Doppler velocity of ice columns after the air motion correction. For the green lines labeled (b), (c), (d) and (e), the corresponding Doppler spectral power observations after the air motion correction are shown in panels (b), (c), (d) and (e), respectively. Red and gray isolines in panel (a) indicate the reflectivity of −18 and −21 dBZ for supercooled liquid water, respectively. Black dashed isolines in panel (a) indicate the spectral width of 0.06 m s−1 for supercooled liquid water. Black arrows point to the regions of velocity anomalies in panel (a). Populations of new ice in panels (b), (c), (d) and (e) are marked by black dashed curves.
5.5 Multiple populations of ice columns
Based on the air motions estimated from the Vliquid, we have been able to estimate the terminal Doppler velocity of ice columns (Vcolumn), as shown in Fig. 5a. Before 20:56 UTC, Vcolumn increases as ice columns fall toward the ground. This is expected, as the mass of ice columns increases during riming (if they are not too small) and depositional growth, leading to increased terminal velocity (Lamb and Verlinde, 2011). After 20:56 UTC, an intermittent slowdown of Vcolumn at around 2.3 km occurred (black arrows). This anomalous decrease in Vcolumn is surprising, given the fact that the air motion has already been corrected. In addition, the velocity anomalies are well colocated with the areas of high Zliquid (above −18 dBZ, red isolines).
Further inspection of the radar Doppler spectra observations was carried out. Figure 5b, c, d and e show the observed Doppler spectral power of the green lines labeled b, c, d and e in Fig. 5a, respectively. The green lines labeled d and e were identified by tracing the peaks of Zliquid. It is anticipated that the green lines are representative of the quasi-Lagrangian trajectories of ice columns. As expected, there seems to be one population of ice columns in Fig. 5b that corresponds to the period with no velocity anomaly. In contrast, multiple populations of ice columns can be identified in Fig. 5c, d and e. At a height of 2.3 km, the velocity of faster falling columnar ice is 0.5–0.6 m s−1, whereas the velocity of slower falling columnar ice is 0.2–0.3 m s−1. Figure 5d and e suggest that the generation of the faster falling ice columns coincides with the turbulent layer at around 2.55 km, whereas the slower ones were formed at around 2.4 km, which corresponds to the region of enhanced Zliquid.
6.1 Generation of large droplets
As shown in Fig. 4c, the reflectivity of supercooled liquid water can be as high as −18 to −15 dBZ, which exceeds (or is close to) the expected reflectivity of drizzle, e.g., −20 dBZ (Kato et al., 2001), −17 dBZ (Kogan et al., 2005) and −15 dBZ (Chin et al., 2000). Generally, the reflectivity of liquid clouds seldom exceeds −18 dBZ (Frisch et al., 1995). Thus, this indicates the onset of drizzle that is taking place in the K–H billows.
One of the striking observations is that the level where velocity oscillations are most intensive is obviously higher than the regions of enhanced reflectivity of supercooled liquid water. This suggests that droplet growth at quasi-steady supersaturation formed in adiabatically ascending cloud is not the only mechanism responsible for drizzle formation (Houze Jr and Medina, 2005; Shupe et al., 2008b; Houser and Bluestein, 2011; Morrison et al., 2012). Given the apparent presence of enhanced turbulence (Fig. 4b), we speculate that drizzle formation could be associated with isobaric mixing. The supersaturation caused by isobaric mixing of saturated air parcels with different temperatures can facilitate the generation of drizzle (Korolev and Isaac, 2000). Figure 2 shows the presence of the inversion around 1.5 ∘C embedded in the liquid layer at ∼ 2.75 km. Vertical transport of cloud parcels forced by the wind shear to the levels below and above the inversion will result in temperature fluctuations in a saturated environment required for the generation of cloud volumes with high supersaturation formed due to isobaric mixing. The mixing process is supported by the enhanced spectral width (Fig. 4b) which is indicative of strong sub-radar-volume velocity fluctuations. The colocation of the enhanced spectral width and reflectivity further indicates the strong link between the mixing and large-drop formation. The relatively high SLWP values during downdrafts seem to further corroborate this hypothesis. The temperature fluctuation of 2.5 ∘C can lead to a supersaturation of 0.5 % (Korolev and Isaac, 2000) which is favorable for the generation and growth of supercooled liquid droplets. Although the observed inversion over the radiosonde station is relatively weak and the temperature difference between the air masses below and above the inversion is around 1.5 ∘C, we speculate that the actual inversion over the Hyytiälä station might be stronger.
The inhomogeneous mixing in the K–H instability can also contribute to the generation of large supercooled droplets (Pobanz et al., 1994). As soon as the liquid droplets meet with dry air, they evaporate until saturation is reached or until liquid water is depleted. This mixing process facilitates the formation of large droplets due to the depletion of small liquid droplets; hence, more excess water vapor is available to grow large cloud droplets (Lamb and Verlinde, 2011). The circulation of this process allows for the continuous growth of liquid droplets (Korolev, 1995), as supported by recent aircraft observations (Majewski and French, 2020). After overcoming the mechanistic gap around the diameter of 40 µm (Lamb and Verlinde, 2011), these liquid drops grow more efficiently during the collision–coalescence process (Korolev and Isaac, 2000).
6.2 Secondary ice production
As follows from Fig. 4, the first radar echo of ice columns was detected at approximately 2.5–2.6 km. As ice crystals must grow for some time in order to become detectable by the radar, the actual level of the columns’ origin is most likely located at the top of the mixed-phase layer at 2.65 km. The temperature at this altitude was around −8 ∘C, which is expected for the columnar growth. During their fall through the mixed-phase layer, the columns grew and the average fall velocity reached approximately 0.35 m s−1, as derived from the Doppler spectrum at 2.2 km. To assess the back trajectory of ice crystals, a simulation of free-falling growing ice columns was performed (see the Appendix). In this simulation, the cloud environment was considered to be saturated over liquid water.
Figure 6 shows the modeled changes in mass, maximum length (Lmax) and Vcolumn between 2.2 and 2.7 km for columnar crystals with aspect ratios of 2, 4 and 8. The radar observed Vcolumn between 21:08:20 and 21:08:50 UTC during which one population of ice columns presented was used for the assessment (black curve in Fig. 6c). In order for the simulated Vcolumn to be consistent with radar measurements, the aspect ratio (AR) of ice columns formed at 2.6–2.7 km should be 4–8, which implies that the mass of these columns (m) was 2– g at around 2.2 km. At this level, Zcolumn (Fig. 3d) is −15 to −18 dB. Hence, the ice water content of ice columns (IWC) was 0.009–0.014 g m−3 based on the parameterization IWC = 0.167Z0.712, derived using aircraft observations within the temperature range of −12 to −3 ∘C (Korolev et al., 2020). Therefore, the number concentration of ice columns () is in the range of 3–8 L−1. Interestingly, the N estimated from the temperature-dependent IWC-Z parameterization (Hogan et al., 2006) is within the same magnitude (4.7 ± 3.7 L−1 for Zcolumn of −10 dB at 2 km, −5 ∘C). The estimated primary INPs based on the parameterization of DeMott et al. (2010) is about 0.3 L−1 at −8 ∘C. The INP parameterization from Schneider et al. (2021) derived from measurements obtained at the Hyytiälä station yields the primary INP concentration of L−1 at −8 ∘C. These values are about 1–5 orders of magnitude lower than the estimated ice number concentration. Therefore, the estimated concentration of columns cannot be explained by primary nucleation. In addition, their origin in the mixed-phase layer cannot be explained by the seeding ice from above, as the columnar shape is not consistent with the environmental conditions in the cloud above. As a result, SIP is the most likely explanation for the observed columnar ice. Considering that smaller ice columns contribute less to the radar reflectivity, the actual concentration of columns is expected to be even higher than the estimation. This provides additional support for ice initiation via SIP.
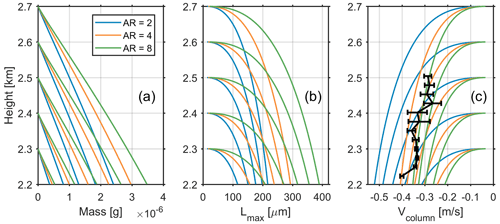
Figure 6Simulated (a) mass, (b) maximum length (Lmax) and (c) fall velocity (Vcolumn) of ice columns with aspect ratios (AR) of 2, 4 and 8. Vcolumn was calculated based on the Kajikawa (1976) parameterization. Ice particles were considered to grow at saturation over liquid water. Observations from the radiosonde launched at 23:30 UTC were used as inputs. The radar-observed Vcolumn (black) from 21:08:20 to 21:08:50 UTC is shown in panel (c), and the error bars indicate the standard deviation of Vcolumn during this period.
There are two potential mechanisms to explain SIP in our observations: the Hallett–Mossop (H–M) process (Hallett and Mossop, 1974; Mossop and Hallett, 1974) and droplet breakup during freezing (Field et al., 2017; Lauber et al., 2018, 2021; Keinert et al., 2020). Activation of the H–M process requires a set of necessary conditions: (a) the presence of droplets larger than 24 µm, (b) an environmental temperature of −8 to −3 ∘C and (c) the presence of rimed snow flakes. As follows from the discussion above, conditions (a) and (b) are satisfied in the mixed-phase layer. The presence of graupel and heavily rimed ice is supported by the observed Doppler velocity (around 2 m s−1 after compensating for air motions; Fig. 3a). Therefore, the environmental conditions required for the initiation of the H–M process were satisfied in the mixed-phase layer. The presence of drizzle-sized drops and background ice is also favorable for SIP via droplet breakup during freezing (Lauber et al., 2018; Keinert et al., 2020). This is very possible given that Luke et al. (2021) recently proposed that droplet breakup is more efficient than the H–M process in natural clouds. The background ice particles in this case can play the role of INPs. Hence, it is concluded that both mechanisms may be responsible for the observed SIP.
For the first time, multiple populations of newly generated ice particles have been identified in K–H billows. The spectral analysis method presented in study shows the potential of remote sensing techniques for studying the evolution of a SIP event. In particular, although the spatially separated SIP cloud regions can be identified from the “needle-like” aircraft penetrations (e.g., Hogan et al., 2002; Korolev et al., 2020), our understanding of their distribution is rather limited (Field et al., 2017). Summarizing the obtained observations, it could be stated that K–H instability embedded in a relatively deep mixed-phase layer may create conditions favorable for enhanced growth of large droplets, which facilitate the initiation of SIP. Several past observations suggest that, in many cases, SIP was spatially associated with dynamically active cloud regions (Korolev et al., 2020; Lasher-Trapp et al., 2016; Rauber et al., 2019). The present study supports this previously attained finding. As a result, we advocate that more efforts should be devoted to addressing the microphysical impact of SIP, as currently poorly parameterized in models (Morrison et al., 2020), associated with the K–H instability.
On 18 April 2014 between 20:50 and 21:40 UTC, a K–H cloud embedded in stratiform precipitation was observed over the University of Helsinki measurement site in Hyytiälä, Finland. The observations were collected using three radars, two vertically pointing C- and W-band radars located at the site and a scanning weather radar operated by FMI. The FMI radar is located 64 km west of the site and performed RHI scans every 15 min over Hyytiälä. Although oscillations of mean vertical Doppler velocity are visible in the data, no obvious signatures of K–H waves were identified from radar reflectivity and spectral width observations.
To unmask the cloud, radar Doppler spectra analysis was performed on the W-band radar observations. The analysis showed the presence of supercooled cloud embedded in the precipitation. The mean Doppler velocities of the cloud droplets, which can be used as tracers of air motion, exhibited a well-defined oscillation with a magnitude of 0.4 m s−1. The FMI weather radar observations detected the presence of a vertical shear layer coinciding with the supercooled liquid cloud layer. Given that the lifetime of the cloud coincides with the lifetime of the shear, we speculate that this cloud is mainly formed due to the K–H instability. It should be noted, however, that other processes could also contribute to the formation of the atmospheric wave, i.e., air motion associated with the snow-generating cells that are present about 0.5 km above the studied layer.
The presented observations and analysis show that K–H clouds are capable of producing large liquid droplets, despite the competition for moisture with ice particles falling from above. In some regions, the observed K–H cloud reflectivity values exceeded −20 dBZ, which is typically associated with the onset of drizzle. Furthermore, spectral linear depolarization ratio observations identified the presence of ice columns. These columns appeared to form in the supercooled liquid cloud regions. In the pockets where larger cloud droplets were formed, multiple populations of columnar ice particles were observed. The estimated number concentration of ice columns is at least 1 order of magnitude higher than the expected concentration of primary ice-nucleating particles. This implies that the secondary ice production is the most likely source of the observed columnar ice.
Overall, the presented observations and analysis indicate that even not very strong wind shears may result in the formation of K–H instability, which could lead to the formation of conditions favorable for the onset of supercooled drizzle and SIP.
The diffusional growth of columnar ice particles was simulated with the help of an electrostatic approximation of the ice crystal shapes by capacitance. The mass growth rate was described as (e.g., Pruppacher and Klett, 1997)
Here, Si is the supersaturation over ice, A1 and A2 are the coefficients dependent on temperature T and pressure P (e.g., Pruppacher and Klett, 1997), C is the capacitance equivalent to the particle shape, and fv is the ventilation factor. The columnar shapes of ice particles were approximated by prolate spheroids with an aspect ratio of AR = , where ra and rb are major and minor axes of the prolate spheroid, respectively (ra>rb). The aspect ratio of the particle remained constant during simulation. The capacitance of the prolate spheroid was calculated as
The ventilation factor was calculated as (Wang and Ji, 1992)
where . Here, Sc is the Schmidt number, and Re is the Reynolds number in which U is the particle fall velocity and v is the kinematic viscosity. is the effective aerodynamic particle size, where s is the surface area of the prolate spheroid and p is the perimeter of the maximum projection of the spheroid. Following the observational study by Kajikawa (1976), the terminal fall velocity of columnar ice crystals was parameterized as
where P0=880 mbar and a and b are dependent on the AR of columns. Thus, for the calculations, it was assumed that b=0.271, a=2.53 for AR = 2, a=1.87 for AR = 4, and a=1.55 for AR = 8. In Eq. (A4), the particle mass m is in milligrams (mg) and the fall velocity U is in meters per second (m s−1). The altitude of falling particles was integrated from the equation dz=Udt. The temperature profile T as a function of height z employed in the simulation was adapted from the observations, as in Fig. 2. As the cloud environment in the modeling domain (2.2–2.7 km) was in a mixed-phase state, the water vapor pressure E in this altitude range can be considered, with high accuracy, to be saturated with respect to water Esw (Korolev and Mazin, 2003). Therefore, at each time step, the supersaturation over ice in Eq. (A1) was calculated as , where Esi is the saturation water vapor pressure of ice at T.
Radiosonde observations can be accessed at http://weather.uwyo.edu/upperair/sounding.html (last access: 5 July 2020). The radar data used in this study are available at https://doi.org/10.5281/zenodo.4019602 (Haoran, 2020).
HL and DM conceptualized the study and wrote the paper. HL performed the majority of the data analysis. All the authors took part in the interpretation of the results. AK performed the ice particle growth modeling and reviewed and edited the paper.
The authors declare that they have no conflict of interest.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Ice nucleation in the boreal atmosphere”. It is not associated with a conference.
We thank Matti Leskinen for his excellent work on the instrument maintenance. Jussi Tiira is acknowledged for his help in processing radar data.
This research has been supported by the Horizon 2020 project (grant nos. ERA-PLANET – The European network for observing our changing planet (689443); ACTRIS-2 – Aerosols, Clouds, and Trace gases Research InfraStructure (654109); ACTRIS PPP – ACTRIS PPP – Aerosols, Clouds and Trace gases Preparatory Phase Project (739530); and ACTRIS IMP – Aerosol, Clouds and Trace Gases Research Infrastructure Implementation Project (871115)), the Academy of Finland (grant nos. 328616, 329274, 307331 and 337549).
Open-access funding was provided by the Helsinki University Library.
This paper was edited by Paul Zieger and reviewed by two anonymous referees.
Baker, M.: Cloud microphysics and climate, Science, 276, 1072–1078, 1997. a
Baker, M. B. and Peter, T.: Small-scale cloud processes and climate, Nature, 451, 299–300, 2008. a
Barnes, H. C., Zagrodnik, J. P., McMurdie, L. A., Rowe, A. K., and Houze Jr, R. A.: Kelvin–Helmholtz Waves in Precipitating Midlatitude Cyclones, J. Atmos. Sci., 75, 2763–2785, 2018. a, b, c, d
Barrett, A. I., Hogan, R. J., and Forbes, R. M.: Why are mixed-phase altocumulus clouds poorly predicted by large-scale models?, Part 1. Physical processes, J. Geophys. Res.-Atmos., 122, 9903–9926, 2017. a, b, c
Chin, H.-N. S., Rodriguez, D. J., Cederwall, R. T., Chuang, C. C., Grossman, A. S., Yio, J. J., Fu, Q., and Miller, M. A.: A microphysical retrieval scheme for continental low-level stratiform clouds: Impacts of the subadiabatic character on microphysical properties and radiation budgets, Mon. Weather Rev., 128, 2511–2527, 2000. a
Conrick, R., Mass, C. F., and Zhong, Q.: Simulated Kelvin–Helmholtz waves over terrain and their microphysical implications, J. Atmos. Sci., 75, 2787–2800, 2018. a
DeMott, P. J., Prenni, A. J., Liu, X., Kreidenweis, S. M., Petters, M. D., Twohy, C. H., Richardson, M., Eidhammer, T., and Rogers, D.: Predicting global atmospheric ice nuclei distributions and their impacts on climate, P. Natl. Acad. Sci. USA, 107, 11217–11222, 2010. a, b
Falconi, M. T., von Lerber, A., Ori, D., Marzano, F. S., and Moisseev, D.: Snowfall retrieval at X, Ka and W bands: consistency of backscattering and microphysical properties using BAECC ground-based measurements, Atmos. Meas. Tech., 11, 3059–3079, https://doi.org/10.5194/amt-11-3059-2018, 2018. a
Field, P., Lawson, R. P., Brown, P. R. A., Lloyd, G., Westbrook, C.,Moisseev, D., Miltenberger, A., Nenes, A., Blyth, A., Choularton, T., Connolly, P., Buehl, J., Crosier, J., Cui, Z., Dearden, C.,DeMott, P., Flossmann, A., Heymsfield, A., Huang, Y., Kalesse,H., Kanji, Z. A., Korolev, A., Kirchgaessner, A., Lasher-Trapp, S., Leisner, T., McFarquhar, G., Phillips, V., Stith, J., and Sullivan, S.: Secondary ice production: Current state of the science and recommendations for the future, Meteorol. Monogr., 58, 7–1, 2017. a, b, c, d, e
Frisch, A., Fairall, C., and Snider, J.: Measurement of stratus cloud and drizzle parameters in ASTEX with a Kα-band Doppler radar and a microwave radiometer, J. Atmos. Sci., 52, 2788–2799, 1995. a, b
Geerts, B. and Miao, Q.: Vertically pointing airborne Doppler radar observations of Kelvin–Helmholtz billows, Mon. Weather Rev., 138, 982–986, 2010. a, b, c
Gehring, J., Oertel, A., Vignon, É., Jullien, N., Besic, N., and Berne, A.: Microphysics and dynamics of snowfall associated with a warm conveyor belt over Korea, Atmos. Chem. Phys., 20, 7373–7392, https://doi.org/10.5194/acp-20-7373-2020, 2020. a
Grasmick, C. and Geerts, B.: Detailed dual-Doppler structure of Kelvin-Helmholtz waves from an airborne profiling radar over complex terrain. Part I: Dynamic structure, J. Atmos. Sci., 77, 1761–1782, https://doi.org/10.1175/JAS-D-19-0108.1, 2020. a
Hallett, J. and Mossop, S.: Production of secondary ice particles during the riming process, Nature, 249, 26–28, 1974. a, b, c
Haoran, L.: Supercooled liquid water and secondary ice production in Kelvin–Helmholtz instability, ZENODO [data set], https://doi.org/10.5281/zenodo.4019602, 2020. a
Hari, P. and Kulmala, M.: Station for Measuring Ecosystem-Atmosphere Relations (SMEAR II), Bor. Environ. Res., 10, 315–322, 2005. a
Helmus, J. J. and Collis, S. M.: The Python ARM Radar Toolkit (Py-ART), a library for working with weather radar data in the Python programming language, Journal of Open Research Software, 4, 2016. a
Hill, A., Field, P., Furtado, K., Korolev, A., and Shipway, B.: Mixed-phase clouds in a turbulent environment. Part 1: Large-eddy simulation experiments, Q. J. Roy. Meteor. Soc., 140, 855–869, 2014. a
Hogan, R. J., Field, P., Illingworth, A., Cotton, R., and Choularton, T.: Properties of embedded convection in warm-frontal mixed-phase cloud from aircraft and polarimetric radar, Q. J. Roy. Meteor. Soc., 128, 451–476, 2002. a, b, c
Hogan, R. J., Behera, M. D., O'Connor, E. J., and Illingworth, A. J.: Estimate of the global distribution of stratiform supercooled liquid water clouds using the LITE lidar, Geophys. Res. Lett., 31, https://doi.org/10.1029/2003GL018977, 2004. a
Hogan, R. J., Gaussiat, N., and Illingworth, A. J.: Stratocumulus liquid water content from dual-wavelength radar, J. Atmos. Ocean. Tech., 22, 1207–1218, 2005. a, b, c, d, e, f
Hogan, R. J., Mittermaier, M. P., and Illingworth, A. J.: The retrieval of ice water content from radar reflectivity factor and temperature and its use in evaluating a mesoscale model, J. Appl. Meteorol. Clim., 45, 301–317, 2006. a
Houser, J. L. and Bluestein, H. B.: Polarimetric Doppler radar observations of Kelvin–Helmholtz waves in a winter storm, J. Atmos. Sci., 68, 1676–1702, 2011. a, b, c
Houze Jr, R. A. and Medina, S.: Turbulence as a mechanism for orographic precipitation enhancement, J. Atmos. Sci., 62, 3599–3623, 2005. a
Intrieri, J., Shupe, M., Uttal, T., and McCarty, B.: An annual cycle of Arctic cloud characteristics observed by radar and lidar at SHEBA, J. Geophys. Res.-Oceans, 107, C108030, https://doi.org/10.1029/2000JC000423, 2002. a
Kajikawa, M.: Observation of falling motion of columnar snow crystals, J. Meteorol. Soc. Jpn., 54, 276–284, 1976. a, b
Kalesse, H., Szyrmer, W., Kneifel, S., Kollias, P., and Luke, E.: Fingerprints of a riming event on cloud radar Doppler spectra: observations and modeling, Atmos. Chem. Phys., 16, 2997–3012, https://doi.org/10.5194/acp-16-2997-2016, 2016. a, b, c
Kanji, Z. A., Ladino, L. A., Wex, H., Boose, Y., Burkert-Kohn, M., Cziczo, D. J., and Krämer, M.: Overview of ice nucleating particles, Meteorol. Monogr., 58, https://doi.org/10.1175/AMSMONOGRAPHS-D-16-0006.1, 2017. a
Kato, S., Mace, G. G., Clothiaux, E. E., Liljegren, J. C., and Austin, R. T.: Doppler cloud radar derived drop size distributions in liquid water stratus clouds, J. Atmos. Sci., 58, 2895–2911, 2001. a
Keinert, A., Spannagel, D., Leisner, T., and Kiselev, A.: Secondary ice production upon freezing of freely falling drizzle droplets, J. Atmos. Sci., 77, 2959–2967, 2020. a, b
Klein, S. A., McCoy, R., Morrison, H., Ackerman, A., Avramov,A., de Boer, G., Chen, M., Cole, J., DelGenio, A. D., Falk, M.,Foster, M., Fridlind, A., Golaz, J.-C., Hashino, T., Harrington,J., Hoose, C., Khairoutdinov, M., Larson, V., Liu, X., Luo, Y.,McFarquhar, G., Menon, S., Neggers, R., Park, S., von Salzen,K., Schmidt, J. M., Sednev, I., Shipway, B., Shupe, M., Spangenberg, D., Sud, Y., Turner, D., Veron, D., Walker, G., Wang,Z., Wolf, A., Xie, S., Xu, K.-M., Yang, G., and Zhang, G.: Intercomparison of model simulations of mixed-phase clouds observed during the ARM Mixed-Phase Arctic Cloud Experiment, I: Single-layer cloud, Q. J. Roy. Meteor. Soc., 135, 979–1002, 2009. a, b, c
Kneifel, S., von Lerber, A., Tiira, J., Moisseev, D., Kollias, P., and Leinonen, J.: Observed relations between snowfall microphysics and triple-frequency radar measurements, J. Geophys. Res.-Atmos., 120, 6034–6055, 2015. a
Kogan, Z. N., Mechem, D. B., and Kogan, Y. L.: Assessment of variability in continental low stratiform clouds based on observations of radar reflectivity, J. Geophys. Res.-Atmos., 110, https://doi.org/10.1029/2005JD006158, 2005. a
Kollias, P., Albrecht, B. A., Lhermitte, R., and Savtchenko, A.: Radar observations of updrafts, downdrafts, and turbulence in fair-weather cumuli, J. Atmos. Sci., 58, 1750–1766, 2001. a
Kollias, P., Rémillard, J., Luke, E., and Szyrmer, W.: Cloud radar Doppler spectra in drizzling stratiform clouds: 1. Forward modeling and remote sensing applications, J. Geophys. Res.-Atmos., 116, https://doi.org/10.1029/2010JD015237, 2011. a
Korolev, A. and Field, P. R.: The effect of dynamics on mixed-phase clouds: Theoretical considerations, J. Atmos. Sci., 65, 66–86, 2008. a
Korolev, A., McFarquhar, G., Field, P. R., Franklin, C., Lawson,P., Wang, Z., Williams, E., Abel, S. J., Axisa, D., Borrmann,S., Crosier, J., Fugal, J., Krämer, M., Lohmann, U., Schlenczek,O., Schnaiter, M., and Wendisch, M.: Mixed-Phase Clouds: Progress and Challenges, Meteorol. Monogr., 58, 1–50, https://doi.org/10.1175/amsmonographs-d-17-0001.1, 2017. a
Korolev, A., Heckman, I., Wolde, M., Ackerman, A. S., Fridlind, A. M., Ladino, L. A., Lawson, R. P., Milbrandt, J., and Williams, E.: A new look at the environmental conditions favorable to secondary ice production, Atmos. Chem. Phys., 20, 1391–1429, https://doi.org/10.5194/acp-20-1391-2020, 2020. a, b, c, d
Korolev, A. V.: The influence of supersaturation fluctuations on droplet size spectra formation, J. Atmos. Sci., 52, 3620–3634, 1995. a, b
Korolev, A. V. and Isaac, G. A.: Drop growth due to high supersaturation caused by isobaric mixing, J. Atmos. Sci., 57, 1675–1685, 2000. a, b, c, d, e
Korolev, A. V. and Mazin, I. P.: Supersaturation of water vapor in clouds, J. Atmos. Sci., 60, 2957–2974, 2003. a
Küchler, N., Kneifel, S., Löhnert, U., Kollias, P., Czekala, H., and Rose, T.: A W-Band radar–radiometer system for accurate and continuous monitoring of clouds and precipitation, J. Atmos. Ocean. Tech., 34, 2375–2392, 2017. a
Lamb, D. and Verlinde, J.: Physics and chemistry of clouds, Cambridge University Press, https://doi.org/10.1017/CBO9780511976377, 2011. a, b, c, d
Lasher-Trapp, S., Leon, D. C., DeMott, P. J., Villanueva-Birriel, C. M., Johnson, A. V., Moser, D. H., Tully, C. S., and Wu, W.: A multisensor investigation of rime splintering in tropical maritime cumuli, J. Atmos. Sci., 73, 2547–2564, 2016. a
Lauber, A., Kiselev, A., Pander, T., Handmann, P., and Leisner, T.: Secondary ice formation during freezing of levitated droplets, J. Atmos. Sci., 75, 2815–2826, 2018. a, b, c, d
Lauber, A., Henneberger, J., Mignani, C., Ramelli, F., Pasquier, J. T., Wieder, J., Hervo, M., and Lohmann, U.: Continuous secondary-ice production initiated by updrafts through the melting layer in mountainous regions, Atmos. Chem. Phys., 21, 3855–3870, https://doi.org/10.5194/acp-21-3855-2021, 2021. a
Leinonen, J., Moisseev, D., Chandrasekar, V., and Koskinen, J.: Mapping radar reflectivity values of snowfall between frequency bands, IEEE T. Geosci. Remote, 49, 3047–3058, 2011. a
Li, H. and Moisseev, D.: Melting Layer Attenuation at Ka-and W-Bands as Derived From Multifrequency Radar Doppler Spectra Observations, J. Geophys. Res.-Atmos., 124, 9520–9533, 2019. a, b, c, d, e
Li, H. and Moisseev, D.: Two layers of melting ice particles within a single radar bright band: Interpretation and implications, Geophys. Res. Lett., 47, e2020GL087499, https://doi.org/10.1029/2020GL087499, 2020. a, b
Li, H., Tiira, J., von Lerber, A., and Moisseev, D.: Towards the connection between snow microphysics and melting layer: insights from multifrequency and dual-polarization radar observations during BAECC, Atmos. Chem. Phys., 20, 9547–9562, https://doi.org/10.5194/acp-20-9547-2020, 2020. a
Li, H., Möhler, O., Petäjä, T., and Moisseev, D.: Multiyear statistics of columnar ice production in stratiform clouds over Hyytiälä, Finland, Atmos. Chem. Phys. Discuss. [preprint], https://doi.org/10.5194/acp-2021-332, in review, 2021. a, b
Liebe, H. J.: An updated model for millimeter wave propagation in moist air, Radio Science, 20, 1069–1089, 1985. a
Lohmann, U., Henneberger, J., Henneberg, O., Fugal, J., Bühl, J., and Kanji, Z. A.: Persistence of orographic mixed-phase clouds, Geophys. Res. Lett., 43, 10–512, 2016. a
Luce, H., Nishi, N., Caccia, J.-L., Fukao, S., Yamamoto, M. K., Mega, T., Hashiguchi, H., Tajiri, T., and Nakazato, M.: Kelvin-Helmholtz billows generated at a cirrus cloud base within a tropopause fold/upper-level frontal system, Geophys. Res. Lett., 39, https://doi.org/10.1029/2011GL050120, 2012. a, b
Luke, E. P. and Kollias, P.: Separating cloud and drizzle radar moments during precipitation onset using Doppler spectra, J. Atmos. Ocean. Tech., 30, 1656–1671, 2013. a, b, c, d
Luke, E. P., Kollias, P., and Shupe, M. D.: Detection of supercooled liquid in mixed-phase clouds using radar Doppler spectra, J. Geophys. Res.-Atmos., 115, https://doi.org/10.1029/2009JD012884, 2010. a, b
Luke, E. P., Yang, F., Kollias, P., Vogelmann, A. M., and Maahn, M.: New insights into ice multiplication using remote-sensing observations of slightly supercooled mixed-phase clouds in the Arctic, P. Natl. Acad. Sci. USA, 118, https://doi.org/10.1073/pnas.2021387118, 2021. a, b, c, d
Majewski, A. and French, J. R.: Supercooled drizzle development in response to semi-coherent vertical velocity fluctuations within an orographic-layer cloud, Atmos. Chem. Phys., 20, 5035–5054, https://doi.org/10.5194/acp-20-5035-2020, 2020. a, b, c, d, e, f
Matrosov, S. Y.: Theoretical study of radar polarization parameters obtained from cirrus clouds, J. Atmos. Sci., 48, 1062–1070, 1991. a
Matrosov, S. Y., Reinking, R. F., Kropfli, R. A., and Bartram, B. W.: Estimation of ice hydrometeor types and shapes from radar polarization measurements, J. Atmos. Ocean. Tech., 13, 85–96, 1996. a
McCoy, D. T., Tan, I., Hartmann, D. L., Zelinka, M. D., and Storelvmo, T.: On the relationships among cloud cover, mixed-phase partitioning, and planetary albedo in GCMs, J. Adv. Model. Earth Sy., 8, 650–668, 2016. a
Medina, S. and Houze Jr, R. A.: Kelvin–Helmholtz waves in extratropical cyclones passing over mountain ranges, Q. J. Roy. Meteor. Soc., 142, 1311–1319, 2016. a
Moisseev, D. N., Lautaportti, S., Tyynela, J., and Lim, S.: Dual-polarization radar signatures in snowstorms: Role of snowflake aggregation, J. Geophys. Res.-Atmos., 120, 12644–12655, 2015. a, b
Morrison, H. and Pinto, J.: Intercomparison of bulk cloud microphysics schemes in mesoscale simulations of springtime Arctic mixed-phase stratiform clouds, Mon. Weather Rev., 134, 1880–1900, 2006. a
Morrison, H., De Boer, G., Feingold, G., Harrington, J., Shupe, M. D., and Sulia, K.: Resilience of persistent Arctic mixed-phase clouds, Nat. Geosci., 5, 11, https://doi.org/10.1038/NGEO1332, 2012. a, b, c
Morrison, H., van Lier-Walqui, M., Fridlind, A. M., Grabowski, W. W., Harrington, J. Y., Hoose, C., Korolev, A., Kumjian, M. R., Milbrandt, J. A., Pawlowska, H., et al.: Confronting the challenge of modeling cloud and precipitation microphysics, J. Adv. Model. Earth Sys., 12, e2019MS001689, https://doi.org/10.1029/2019MS001689, 2020. a, b
Mossop, S.: Secondary ice particle production during rime growth: The effect of drop size distribution and rimer velocity, Q. J. Roy. Meteor. Soc., 111, 1113–1124, 1985. a
Mossop, S. and Hallett, J.: Ice crystal concentration in cumulus clouds: Influence of the drop spectrum, Science, 186, 632–634, 1974. a
Mülmenstädt, J., Sourdeval, O., Delanoë, J., and Quaas, J.: Frequency of occurrence of rain from liquid-, mixed-, and ice-phase clouds derived from A-Train satellite retrievals, Geophys. Res. Lett., 42, 6502–6509, 2015. a
Nguyen, C. M., Moisseev, D. N., and Chandrasekar, V.: A parametric time domain method for spectral moment estimation and clutter mitigation for weather radars, J. Atmos. Ocean. Tech., 25, 83–92, 2008. a
Oue, M., Kumjian, M. R., Lu, Y., Verlinde, J., Aydin, K., and Clothiaux, E. E.: Linear depolarization ratios of columnar ice crystals in a deep precipitating system over the Arctic observed by zenith-pointing Ka-band Doppler radar, J. Appl. Meteorol. Clim., 54, 1060–1068, 2015. a, b, c, d
Petäjä, T., O’Connor, E. J., Moisseev, D., Sinclair, V. A., Manninen, A. J., Väänänen, R., von Lerber, A., Thornton, J. A., Nicoll, K., Petersen, W., Chandrasekar, V., Smith, J. N., Winkler, P. M., Krüger, O., Hakola, H., Timonen, H., Brus, D., Laurila, T., Asmi, E., Riekkola, M.-L., Mona, L., Massoli, P., Engelmann, R., Komppula, M., Wang, J., Kuang, C., Bäck, J., Virtanen, A., Levula, J., Ritsche, M., and Hickmon, N.: BAECC: A field campaign to elucidate the impact of biogenic aerosols on clouds and climate, B. Am. Meteorol. Soc., 97, 1909–1928, 2016. a
Petre, J. M. and Verlinde, J.: Cloud radar observations of Kelvin–Helmholtz instability in a Florida anvil, Mon. Weather Rev., 132, 2520–2523, 2004. a, b, c, d
Pinto, J. O.: Autumnal mixed-phase cloudy boundary layers in the Arctic, J. Atmos. Sci., 55, 2016–2038, 1998. a
Pobanz, B. M., Marwitz, J. D., and Politovich, M. K.: Conditions associated with large-drop regions, J. Appl. Meteorol., 33, 1366–1372, 1994. a, b
Pruppacher, H. and Klett, J.: Microphysics of clouds and precipitation, Kluwer Acad, Kluwer Academic Publishers, Dordrecht, 954 pp., 1997. a, b
Rambukkange, M. P., Verlinde, J., Eloranta, E. W., Flynn, C. J., and Clothiaux, E. E.: Using Doppler Spectra to Separate Hydrometeor Populations and Analyze Ice Precipitation in Multilayered Mixed-Phase Clouds, IEEE T. Geosci. Remote, 8, 108–112, https://doi.org/10.1109/LGRS.2010.2052781, 2011. a
Rauber, R. M., Geerts, B., Xue, L., French, J., Friedrich, K., Rasmussen, R. M., Tessendorf, S. A., Blestrud, D. R., Kunkel, M. L., and Parkinson, S.: Wintertime Orographic Cloud Seeding – A Review, J. Appl. Meteorol. Clim., 58, 2117–2140, 2019. a
Schneider, J., Höhler, K., Heikkilä, P., Keskinen, J., Bertozzi, B., Bogert, P., Schorr, T., Umo, N. S., Vogel, F., Brasseur, Z., Wu, Y., Hakala, S., Duplissy, J., Moisseev, D., Kulmala, M., Adams, M. P., Murray, B. J., Korhonen, K., Hao, L., Thomson, E. S., Castarède, D., Leisner, T., Petäjä, T., and Möhler, O.: The seasonal cycle of ice-nucleating particles linked to the abundance of biogenic aerosol in boreal forests, Atmos. Chem. Phys., 21, 3899–3918, https://doi.org/10.5194/acp-21-3899-2021, 2021. a
Shaw, R. A., Cantrell, W., Chen, S., Chuang, P., Donahue, N., Feingold, G., Kollias, P., Korolev, A., Kreidenweis, S., Krueger, S., et al.: Cloud–Aerosol–Turbulence Interactions: Science Priorities and Concepts for a Large-Scale Laboratory Facility, B. Am. Meteorol. Soc., 101, 1026–1035, 2020. a
Shupe, M. D., Kollias, P., Matrosov, S. Y., and Schneider, T. L.: Deriving mixed-phase cloud properties from Doppler radar spectra, J. Atmos. Ocean. Tech., 21, 660–670, 2004. a, b, c, d
Shupe, M. D., Matrosov, S. Y., and Uttal, T.: Arctic mixed-phase cloud properties derived from surface-based sensors at SHEBA, J. Atmos. Sci., 63, 697–711, 2006. a
Shupe, M. D., Kollias, P., Persson, P. O. G., and McFarquhar, G. M.: Vertical motions in Arctic mixed-phase stratiform clouds, J. Atmos. Sci., 65, 1304–1322, 2008b. a, b, c, d
Sinclair, V. A., Moisseev, D., and von Lerber, A.: How dual-polarization radar observations can be used to verify model representation of secondary ice, J. Geophys. Res.-Atmos., 121, 10–954, 2016. a
Solomon, A., Shupe, M. D., Persson, P. O. G., and Morrison, H.: Moisture and dynamical interactions maintaining decoupled Arctic mixed-phase stratocumulus in the presence of a humidity inversion, Atmos. Chem. Phys., 11, 10127–10148, https://doi.org/10.5194/acp-11-10127-2011, 2011. a
Spek, A., Unal, C., Moisseev, D., Russchenberg, H., Chandrasekar, V., and Dufournet, Y.: A new technique to categorize and retrieve the microphysical properties of ice particles above the melting layer using radar dual-polarization spectral analysis, J. Atmos. Ocean. Tech., 25, 482–497, 2008. a, b
Sun, Z. and Shine, K. P.: Studies of the radiative properties of ice and mixed-phase clouds, Q. J. Roy. Meteor. Soc., 120, 111–137, 1994. a
Tan, I., Storelvmo, T., and Zelinka, M. D.: Observational constraints on mixed-phase clouds imply higher climate sensitivity, Science, 352, 224–227, 2016. a
Tridon, F., Battaglia, A., and Kneifel, S.: Estimating total attenuation using Rayleigh targets at cloud top: applications in multilayer and mixed-phase clouds observed by ground-based multifrequency radars, Atmos. Meas. Tech., 13, 5065–5085, https://doi.org/10.5194/amt-13-5065-2020, 2020. a, b
Verlinde, J., Rambukkange, M. P., Clothiaux, E. E., McFarquhar, G. M., and Eloranta, E. W.: Arctic multilayered, mixed-phase cloud processes revealed in millimeter-wave cloud radar Doppler spectra, J. Geophys. Res.-Atmos., 118, 13–199, 2013. a, b
Zawadzki, I., Fabry, F., and Szyrmer, W.: Observations of supercooled water and secondary ice generation by a vertically pointing X-band Doppler radar, Atmos. Res., 59, 343–359, 2001. a, b





