The response of stratospheric water vapor to climate change driven by different forcing agents

We investigate the response of stratospheric water vapor (SWV) to different forcing agents within the Precipitation Driver and Response Model Intercomparison Project (PDRMIP) framework. For each model and forcing agent, we break down the SWV response into a slow response, which is coupled to surface temperature changes, and a fast response, which is the response to external forcing but before the sea surface temperatures have responded. Our results show that, for most climate perturbations, the slow SWV response dominates the fast response. The slow SWV response exhibits a similar sensitivity to surface temperature across all climate perturbations. Specifically, the sensitivity is 0.35 ppmv K⁻¹ in the tropical lower stratosphere (TLS), 2.1 ppmv K⁻¹ in the northern hemispheric lowermost stratosphere (LMS), and 0.97 ppmv K⁻¹ in the southern hemispheric LMS. In the TLS, the fast SWV response only dominates the slow SWV response when the forcing agent radiatively heats the cold-point region – for example, black carbon, which directly heats the atmosphere by absorbing solar radiation. The fast SWV response in the TLS is primarily controlled by the fast adjustment of cold-point temperature across all climate perturbations. This control becomes weaker at higher altitudes in the tropics and altitudes below 150 hPa in the LMS.

1 Introduction

Stratospheric water vapor (SWV) plays an important role in global climate change. It is an important greenhouse gas (GHG), which affects the Earth's radiative budget (Forster and Shine, 2002; Solomon et al., 2010), and it also plays an important role in stratospheric ozone chemistry (Solomon et al., 1986; Dvortsov and Solomon, 2001).

SWV in the overworld (above the 380 K isentropic surface) (e.g., Hoskins, 1991) and SWV in the extratropical lowermost stratosphere (LMS, between the extratropical tropopause and the 380 K isentropic surface) (e.g., Holton et al., 1995) are distinguished according to different mechanisms that control them. Overworld SWV is primarily controlled by the temperatures in the tropical tropopause layer (TTL) as air is transported through it (e.g., Mote et al., 1996; Fueglistaler et al., 2009) and by production from oxidation of methane (e.g., Brasseur and Solomon, 2005). The LMS SWV is controlled by three major sources, including the transport of overworld air by the downward branch of the Brewer–Dobson circulation, adiabatic quasi-horizontal transport from the tropical upper troposphere, and diabatic cross-tropopause transport due to deep convection (Dessler et al., 1995; Holton et al., 1995; Plumb, 2002; Gettelman et al., 2011).

The response of SWV to climate change can be partitioned into two components: the fast response and slow response. The addition of a radiatively active constituent to the atmosphere can influence the atmosphere even before the surface temperature changes, leading to changes in SWV. This is often referred to as an “adjustment” to the forcing and is generally considered part of the external forcing (e.g., Sherwood et al., 2015). We will refer to this as the “fast response” of SWV to the forcing. The slow response is the component in the SWV change that is coupled to changes in the surface temperature, which occur on longer timescales. This slow response means that SWV could be an important positive feedback to global warming (Forster and Shine, 2002; Dessler et al., 2013; Huang et al., 2016; Banerjee et al., 2019). Banerjee et al. (2019) have shown that, when CO₂ is abruptly quadrupled, the change in SWV mainly consists of the slow response and that the fast response is less important.

Previous studies have shown that climate models, which are able to accurately reproduce observed interannual variations in SWV (Dessler et al., 2013; Smalley et al., 2017), robustly project a positive long-term trend in overworld SWV at entry level with a warming climate due to increasing GHGs (Gettelman et al., 2010; Dessler et al., 2013; Smalley et al., 2017). This is mainly due to a warmer tropopause (Thuburn and Craig, 2002; Gettelman et al., 2010; Lin et al., 2017; Smalley et al., 2017; Xia et al., 2019), which is controlled, to some extent at least, by the warming surface (Gettelman et al., 2010; Shu et al., 2011; Dessler et al., 2013; Huang et al., 2016; Revell et al., 2016; Lin et al., 2017; Smalley et al., 2017; Banerjee et al., 2019). Dessler et al. (2016) suggested that increases in convective injection into the stratosphere due to a warming climate may also be contributing to the trend in entry SWV. In the LMS, climate models show larger increases in SWV (Dessler et al., 2013; Huang et al., 2016; Banerjee et al., 2019). It is not known how SWV responds to different forcing agents. Hodnebrog et al. (2019) investigated the response of global integrated water vapor to different forcing agents but focused on the troposphere.

The goal of this study is to investigate the response of both overworld and LMS SWV to forcing agents with different physical properties. We will explicitly investigate the fast and slow responses in SWV and compare them. We will also investigate how SWV responds to surface temperature change when the climate is forced by different forcing agents.

2 Method

2.1 The PDRMIP setup

In this paper, we analyze nine models from the Precipitation Driver and Response Model Intercomparison Project (PDRMIP) (Samset et al., 2016; Myhre et al., 2017; Tang et al., 2018, 2019). These are Coupled Model Intercomparison Project phase 5 (CMIP5) era models (Table 1), and each performed a baseline and multiple climate perturbation experiments (Table 1). This subset of the CMIP5 ensemble has a multi-model mean equilibrium climate system (ECS) of 3.6 K, close to the ensemble average ECS of the entire CMIP5 ensemble (3.3 K) (Zelinka et al. 2020).

Table 1 Columns 1–6: description of PDRMIP models (Myhre et al., 2017). © American Meteorological Society. Used with permission. Column 7: list of perturbation experiments used in this study.

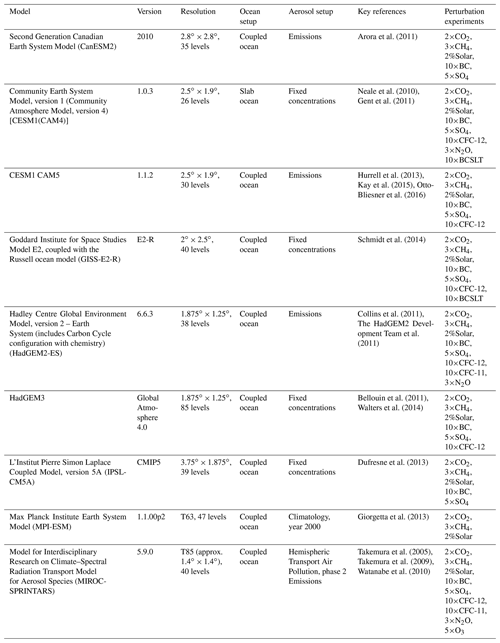
In the perturbation experiments, perturbations on a global scale are applied abruptly at the beginning of the model simulation. The five core experiments include a doubling of CO₂ concentration (2×CO₂), a tripling of CH₄ concentration (3×CH₄), a 2 % increase in solar irradiance (2%Solar), an increase in present-day black carbon concentration or emission by a factor of 10 (10×BC), and an increase in present-day SO₄ concentration or emission by a factor of 5 (5×SO₄). In addition to the five core experiments, a subset of models also performed additional perturbation experiments: an increase in CFC-11 concentration from 535 ppt to 5 ppb (hereafter, 10×CFC-11), an increase in CFC-12 concentration from 653.45 ppt to 5 ppb (hereafter, 10×CFC-12), an increase in N₂O concentration from 316 ppb to 1 ppm (hereafter, 3×N₂O), an increase in tropospheric O₃ concentration used in MacIntosh et al. (2016) by a factor of 5 (5×O₃), and an increase in present-day black carbon with a shorter lifetime by a factor of 10 (10×BCSLT). We note that indirect chemical effects are not included in the 3×CH₄ experiment. Table 1 provides details about the models and the perturbations each one simulated.

The perturbations in GHGs and solar irradiance are relative to the models' baseline simulations, in which the concentrations of GHGs and solar irradiance are either at present-day levels or preindustrial levels. The perturbations in the aerosols depend on whether it is possible to prescribe aerosol concentrations in the models. For models that are able to prescribe aerosol concentrations, the aerosol perturbations are based on a multi-model mean baseline aerosol concentration in 2000 obtained from the AeroCom Phase II initiative (Myhre et al., 2013a). For those that are only able to produce aerosols through emissions, the perturbation is applied by increasing the emissions by the factors listed above. The 10×BCSLT experiment is performed only by models that are able to prescribe aerosol concentrations.

Each perturbation experiment is performed in two configurations: a fixed sea surface temperatures simulation (“fixed SST”) and a fully coupled (slab ocean for CAM4 only) simulation. The fixed SST simulations use the SST climatology at either the present-day or preindustrial level. The fixed SST simulations are at least 15 years, and the coupled simulations are at least 100 years.

2.2 Fast response and slow response

When available, the SWV mixing ratio is obtained directly from the specific humidity output by each model simulation. For the models that do not output specific humidity (CAM5, GISS-E2-R, and MIROC-SPRINTARS), we calculate specific humidity by multiplying the models' relative humidity by the saturation mixing ratio with respect to ice calculated using model temperature and pressure. Responses of specific humidity and relative humidity in the PDRMIP have been investigated by Hodnebrog et al. (2019), but they focused on water vapor in the troposphere.

We define ΔSWV, the change in the SWV mixing ratio in response to a particular perturbation, to be the difference between SWV in the perturbed coupled run and that in the baseline coupled run. As discussed above, the ΔSWV can then be broken down into the two components: the fast response (ΔSWV_fast) and slow response (ΔSWV_slow). We compute results in the tropical lower stratosphere (70 hPa, 30^∘ N–30^∘ S, hereafter, TLS), in the northern hemispheric (NH) lowermost stratosphere (50–90^∘ N at 200 hPa, hereafter, NH LMS), and in the southern hemispheric (SH) lowermost stratosphere (50–90^∘ S at 200 hPa, hereafter, SH LMS). Most previous studies have focused on the response of water vapor in the TLS (e.g., Gettelman et al., 2010; Shu et al., 2011; Smalley et al., 2017). But recent studies report that the climate is most sensitive to changes in water vapor in the LMS (Solomon et al., 2010; Dessler et al., 2013; Banerjee et al., 2019), so we also investigate that region.

We use the fixed SST simulations to get ΔSWV_fast, the rapid adjustment in SWV before sea surface temperature changes. ΔSWV_fast is the difference between the SWV mixing ratio averaged over the last 10 years in the fixed SST run with the forcing perturbation and the SWV mixing ratio averaged over the last 10 years in the fixed SST baseline simulation. The fixed SST runs have some warming of the land surface, meaning that our fast response includes a contribution from a warming land surface. We expect this will have a small impact on our results, but it remains one of the uncertainties in our analysis.

We calculate ΔSWV_slow as ΔSWV minus ΔSWV_fast. To estimate the time series of ΔSWV_slow, we use annual mean ΔSWV time series over the entire coupled run period (at least 100 years) minus the 10-year average ΔSWV_fast. To estimate equilibrium ΔSWV_slow, we use a regression method similar to the methodology introduced by Gregory et al. (2004). The basic concept is that we regress the annual mean global average net downward radiative flux (R) at the top of the atmosphere (TOA) against the annual mean ΔSWV averaged at TLS, NH LMS, or SH LMS. The equilibrium ΔSWV is where the linear fit intercepts at R=0. Then we simply subtract ΔSWV_fast from the equilibrium ΔSWV to estimate equilibrium ΔSWV_slow.

These regressions can be very noisy and yield highly uncertain parameters, particularly for perturbations with relatively small amounts of radiative forcing and warming. To account for this, we first fit the R and ΔSWV time series using an exponential function ($y\left(t\right)=b+a\mathrm{1}\cdot e^{-t/\mathit{\tau }\mathrm{1}}+a\mathrm{2}\cdot e^{-t/\mathit{\tau }\mathrm{2}}$) and then do the regression using the fitted time series. For fully coupled models, we constrain τ1 to be within the range of 4±2 years and τ2 to be within the range of 250±70 years; for CAM4, in which the atmosphere is coupled to a slab ocean, we constrain τ1 to be within the range of 4±2 years. We then compute the best fit of all parameters. The ranges for the time constants are based on previous estimations of climate system timescales (Geoffroy et al., 2013). We estimate the ΔSWV intercept at R=0 by regressing the fitted R and ΔSWV data over the last 30 years, since the relation between R and ΔSWV is not necessarily linear over the entire 100-year period. The slow and fast responses of other variables, such as global average surface temperatures and cold-point temperatures, are computed using the same method.

We tested this method in a climate model that nearly reaches the equilibrium climate state. We analyzed runs of the fully coupled Max Planck Institute Earth System Model version 1.1 (MPI-ESM1.1) (Maher et al., 2019), which has a transient climate response and an effective climate sensitivity near the middle of the CMIP5 ensemble range (Adams and Dessler, 2019; Dessler, 2020). It includes a 2000-year preindustrial control run and a 2614-year abruptly quadrupled CO₂ run. The values of ΔSWV averaged over the last 30 years of the 4×CO₂ run relative to the control run are 4.60 ppmv in the TLS, 22.40 ppmv in the NH LMS, and 9.69 ppmv in the SH LMS. We expect this to be close to equilibrium ΔSWV because the trend in global average surface temperature over the last 500 years of the 4×CO₂ run is 0.02 K per century. We use the regression method to estimate the equilibrium ΔSWV using MPI-ESM1.1 water vapor mixing ratio time series over the first 100 years and obtain estimates of 4.38 ppmv in the TLS, 20.01 ppmv in the NH LMS, and 9.07 ppmv in the SH LMS; these yield differences of 0.22 ppmv in the TLS, 2.39 ppmv in the NH LMS, and 0.62 ppmv in the SH LMS. Thus, our method underestimates the true equilibrium value by 5 % in the TLS, 11 % in the NH LMS, and 6 % in the SH LMS.

Uncertainty for slow and fast responses of different quantities shown in this paper is obtained from Monte Carlo samples as follows: for each perturbation, we randomly sample with replacement 100 000 times for each model that performed that perturbation and from these samples compute the 2.5–97.5 percentiles.

3 Results

3.1 The slow stratospheric water vapor response

We show equilibrium ΔSWV_slow and its percentage contribution to the total equilibrium ΔSWV in Fig. 1. We show results in the TLS (Fig. 1a and d), in the NH LMS (Fig. 1b and e), and the SH LMS (Fig. 1c and f). In evaluating the absolute magnitude of ΔSWV_slow in the first column of Fig. 1, we normalize the equilibrium ΔSWV_slow using effective radiative forcing (ERF) so that differences in the magnitude of the forcing do not confound our results.

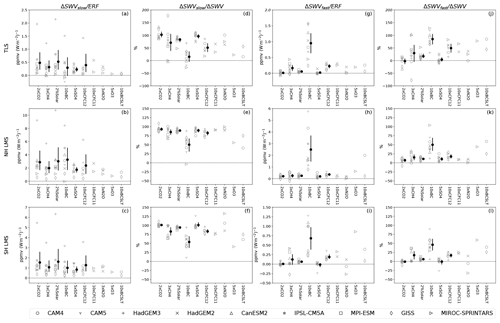
Figure 1 (a–c) Equilibrium ΔSWV_slow normalized by ERF (ppmv (W m⁻²)⁻¹) in TLS (70 hPa, 30^∘ N–30^∘ S), NH LMS (200 hPa, 50–90^∘ N), and SH LMS (200 hPa, 50–90^∘ S). (d–f) Contribution (%) of equilibrium ΔSWV_slow to total equilibrium ΔSWV. (g–i) ΔSWV_fast normalized by ERF (ppmv (W m⁻²)⁻¹). (j–l) Contribution (%) of ΔSWV_fast to total equilibrium ΔSWV. The marker shapes indicate results from different models. For perturbations that are performed by more than three models, the solid circles and error bars for each perturbation plotted in solid black are the multi-model mean and 2.5–97.5 percentiles of the model samples. Note that in the second and fourth columns, we took out models with extremely small ΔSWV magnitudes that yield extremely large ΔSWV_slow ∕ ΔSWV and ΔSWV_fast ∕ ΔSWV ratios.

ERF values used in the construction of Fig. 1 are plotted in Fig. 2a; they are calculated as the difference in net radiation at the top of the atmosphere (TOA) averaged over the last 10 years between the fixed SST perturbed and baseline simulation. Previous studies have computed the ERF in the PDRMIP using various methods (Richardson et al., 2019; Tang et al., 2019). The ERF calculation in our paper uses the same method as the ERF_sst in Richardson et al. (2019). We directly compared our ERF with the ERF_sst listed in Richardson et al. (2019), which shows good agreement and can be found in the Supplement (Table S3). The equilibrium global averaged surface temperature changes (ΔT_s), estimated using the regression method described in Sect. 2.2 and normalized by ERF, are plotted in Fig. 2b. The multi-model mean ΔT_s ∕ ERF shows general agreement across different perturbations. This quantity is the inverse of the feedback parameter λ (e.g., Dessler and Zelinka, 2015), so Fig. 2b implies that the climate sensitivity to these different perturbations is similar, which also agrees with Richardson et al. (2019). We list the ERF and ΔT_s quantities for each model and perturbation in Table S1.

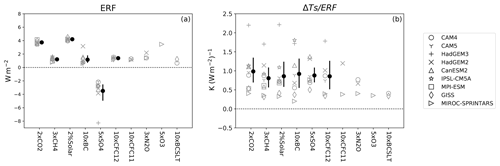
Figure 2 (a) Global average ERF (W m⁻²) at the top of the atmosphere. (b) Global averaged surface temperature change per unit ERF (K (W m⁻²)⁻¹). The marker shapes indicate results from different models. For perturbations that are performed by more than three models, the solid circles and error bars for each perturbation plotted in solid black are the multi-model mean and 2.5–97.5 percentiles of the model samples.

In each region, the magnitude of multi-model mean ΔSWV_slow ∕ ERF shows general agreement for different perturbations. The magnitudes of ΔSWV_slow ∕ ERF in the LMS are larger than those in the TLS (Fig. 1b–c). This is consistent with previous studies, which showed that the long-term trend in SWV over the century in climate models is largest near the LMS tropopause (Dessler et al., 2013; Huang et al., 2016; Banerjee et al., 2019). This reflects different transport pathways into the LMS, including downward transport by the Brewer–Dobson circulation, quasi-horizontal isentropic mixing from the tropical troposphere, and convective influence (Dessler et al., 1995; Holton et al., 1995; Plumb, 2002; Gettelman et al., 2011).

In the LMS, the multi-model mean ΔSWV_slow ∕ ΔSWV ratio is close to 100 % for many perturbations (Fig. 1e–f). The latitude band (50–90^∘) we choose is somewhat arbitrary, so in the Supplement (Fig. S1), we also show ΔSWV_slow ∕ ERF and ΔSWV_slow ∕ ΔSWV ratios for water vapor averaged at 200 hPa between 30^∘ and 50^∘ latitudes in the Northern Hemisphere and Southern Hemisphere, respectively, which also show that the ΔSWV_slow plays a dominant role and contributes to close to 100 % of the total ΔSWV for most perturbations. In the TLS, the multi-model mean ΔSWV_slow ∕ ΔSWV ratio is generally above 50 %, with a few exceptions. We will discuss this in detail in Sect. 3.3.

We note that inter-model variability in ΔSWV_slow ∕ ERF and ΔSWV_slow is generally consistent for different perturbations. For example, HadGEM3 produces larger responses than the rest of the models for most perturbations (Fig. 1a–c, Table S1). GISS-E2-R and MIROC-SPRINTARS have ΔSWV_slow ∕ ERF and ΔSWV_slow values generally below the rest of the models (Fig. 1a–c, Table S1). We have not further investigated the causes of these differences among models; this clearly warrants further investigation.

We also note that CAM5, CanESM2, and MIROC-SPRINTARS produce negative TLS ΔSWV_slow ∕ ERF for 10×BC. These negative values are partly contributed by artifacts of the method we use to estimate equilibrium ΔSWV_slow, which is the residual of the total equilibrium ΔSWV minus ΔSWV_fast. When differencing two numbers with similar magnitudes, the residual may be quite uncertain. So, the negative values here do not necessarily mean that a BC-induced surface warming results in a negative SWV slow response. The direct regression between ΔSWV_slow and surface temperature change described in the next section more accurately describes the relationship for these cases.

3.2 The slow stratospheric water vapor response and the surface temperature change

Our results show that, in most climate perturbations analyzed in this study, the equilibrium response of water vapor in both the TLS and the LMS is dominated by ΔSWV_slow, which is the component mediated by sea surface temperature change. To directly quantify how SWV responds to surface temperature across a range of different climate change mechanisms, we linearly regress the time series of annual mean ΔSWV_slow over the entire period of the coupled simulations (at least 100 years) against the time series of annual mean global averaged surface temperature change (ΔT_s). We do this regression for each model and perturbation separately. This is similar to the analysis of Banerjee et al. (2019), who did this for quadrupled CO₂ perturbation, but we do this for multiple perturbations.

The scatter plot for each perturbation and model is shown in the Supplement (Figs. S3–S5). For most perturbations and models, the ΔSWV_slow time series in both the TLS and the LMS is positively correlated with the ΔT_s time series, supporting the hypothesis that the surface temperature change contributes to the long-term trend in SWV for most cases.

Figure 3 shows the slopes of the regression for all perturbations and models. The corresponding slope values are listed in Table S4. We also list slopes in the unit of percent per Kelvin (% K⁻¹) in Table S5. The uncertainty of the slopes is obtained from Monte Carlo samples: for each model and perturbation, we first randomly sample the slope 100 000 times, assuming a Gaussian distribution. Then, for each perturbation, we sample from the slope distributions with replacement 100 000 times for each model that performed that perturbation and from these samples compute the 2.5–97.5 percentiles.

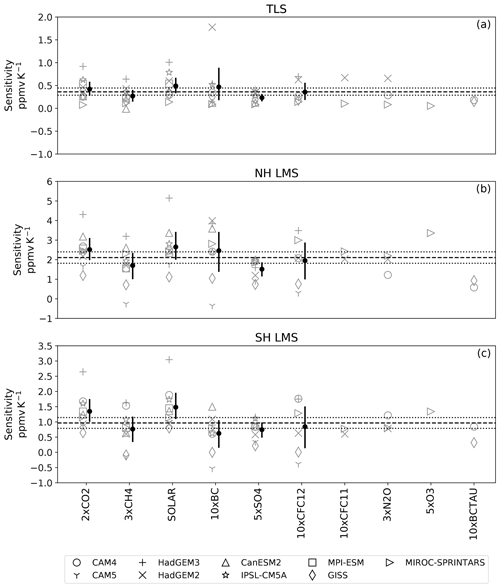
Figure 3 Slopes (ppmv K⁻¹) from the linear regression between annual mean ΔSWV_slow time series and annual mean ΔT_s time series. The marker shapes indicate results from different models. For perturbations that are performed by more than three models, the solid circles and error bars for each perturbation plotted in solid black are the multi-model mean and 2.5–97.5 percentiles of the model samples. The horizontal dashed line is the multi-model mean of all slopes, and the horizontal dotted lines are 2.5–97.5 percentiles of the model samples.

In both the TLS and LMS, the slopes from different perturbations show general agreement (Fig. 3); this is also true for water vapor averaged at 200 hPa between 30^∘ and 50^∘ latitudes in the Northern Hemisphere and Southern Hemisphere (Fig. S2). In the TLS, the multi-model and multi-perturbation average slope is 0.35 ppmv K⁻¹, with a 95 % confidence interval of 0.28–0.44 ppmv K⁻¹ (Fig. 3a). The LMS ΔSWV_slow time series has stronger correlations with the ΔT_s time series (Figs. S3–S5) and produces larger sensitivities (Fig. 3b–c). Specifically, the multi-model and multi-perturbation mean slope is 2.1 ppmv K⁻¹ in the Northern Hemisphere and 0.97 ppmv K⁻¹ in the Southern Hemisphere, with 95 % confidence intervals of 1.82–2.39 ppmv K⁻¹ and 0.79–1.15 ppmv K⁻¹, respectively. Our results are similar to those of Dessler et al. (2013) and Smalley et al. (2017) despite the fact that they used 500 hPa temperature as their regressor.

We show that the relation between ΔSWV_slow and ΔT_s time series can be extended to the entire stratosphere (Fig. 4a). We regridded the zonal mean ΔSWV_slow from all models and perturbations onto the same pressure–latitude grid (10 hPa above 100 hPa and 50 hPa below 100 hPa, 4^∘ latitude) and regressed the ΔSWV_slow time series at each grid point against global average ΔT_s time series. The multi-model and multi-perturbation average slope of the linear fit at each grid point is shown in Fig. 4a (figures for each individual perturbation are shown in Fig. S6). Since the vertical gradient of water vapor is large, we plot the percentage change in the mixing ratio per Kelvin relative to the baseline. Lapse rate tropopause, the lowest level where the lapse rate decreases to 2 K km⁻¹, also plotted, is obtained using the atmospheric temperatures from the baseline coupled run and multi-model mean.

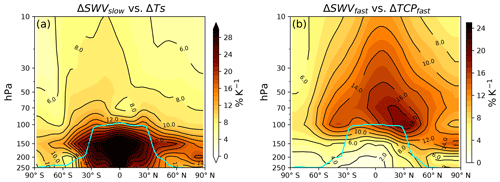
Figure 4 (a) Multi-model and multi-perturbation mean slope (% K⁻¹) from the regression between annual mean time series of ΔSWV_slow (at each latitude grid point and pressure level) and annual mean time series of global average ΔT_s. (b) Slope (% K⁻¹) from the regression between ΔSWV_fast (ppmv) (at each latitude grid point and pressure level) and ΔTCP_fast (K). The solid cyan line is the multi-model mean lapse rate tropopause derived from the baseline simulations.

We clearly see the larger sensitivity of ΔSWV_slow to ΔT_s in the LMS than in the overworld. In the LMS, the slope has a hemispheric asymmetry, with larger values in the Northern Hemisphere. This is consistent with previous studies, which showed that isentropic transport brings more tropospheric water vapor to the NH than the SH (Pan et al., 1997, 2000; Dethof et al., 1999, 2000; Ploeger et al., 2013). In addition, convective moistening may be more important to the NH due to more land in the Northern Hemisphere and, consequently, more convection (Dessler and Sherwood, 2004; Smith et al., 2017; Ueyama et al., 2018; Wang et al., 2019). We also see large responses in the tropical upper troposphere, which is the main part of the tropospheric water vapor feedback. The sensitivity declines as one ascends through the TTL. Once above the TTL, the sensitivity in the overworld is relatively uniform with altitude.

3.3 The fast stratospheric water vapor response

Figure 1 also shows the ΔSWV_fast normalized by the ERF (Fig. 1g–i) and its contribution to total equilibrium ΔSWV (Fig. 1j–l). As discussed previously, ΔSWV_fast is the rapid adjustment in SWV before the sea surface temperatures respond. For most perturbations, especially in the LMS, ΔSWV_fast ∕ ERF is smaller than ΔSWV_slow ∕ ERF, with a magnitude of a few tenths of a part per million by volume per watt per square meter (ppmv (W m⁻²)⁻¹).

For 2×CO₂, the near-zero TLS ΔSWV_fast ∕ ERF is the result of cancellation between cooling by a strengthening Brewer–Dobson circulation and increased local radiative heating (Lin et al., 2017). Some other GHG forcing agents, however, produce larger TLS ΔSWV_fast ∕ ERF and contributions in the TLS. For both 10×CFC-12 and 10×CFC-11 the multi-model mean ΔSWV_fast contributes about half of the total ΔSWV (Fig. 1j). This is a consequence of halocarbons producing more TTL warming per watt per square meter (W m⁻²) by efficiently absorbing upwelling longwave radiation from the troposphere in the atmospheric window (Forster et al., 1997; Jain et al., 2000; Forster and Joshi, 2005). Figure 5 shows the fast temperature response per unit ERF due to different perturbations, and it shows heating in the TTL for both 10×CFC-12 and 10×CFC-11.

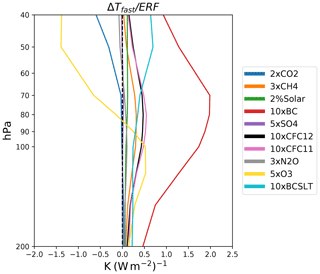
Figure 5 Profiles of fast temperature response normalized by ERF (K (W m⁻²)⁻¹) between 200 and 40 hPa, averaged over 30^∘ N–30^∘ S. The color coding indicates results from different perturbations. Each profile is the multi-model mean.

The 3×CH₄ also includes some models that produce large TLS ΔSWV_fast ∕ ERF magnitudes. This is likely due to TTL heating (Fig. 5) by CH₄ shortwave absorption, which is explicitly treated in some models, including CAM5, CanESM2, MPI-ESM, and MIROC-SPRINTARS (Smith et al., 2018). These models are also the ones that produce the largest TLS ΔSWV_fast contributions (Fig. 1g and j).

Increases in tropospheric O₃ (in the 5×O₃ experiment) reduce the upwelling longwave radiation, which cools the stratosphere (Ramaswamy and Bowen, 1994; Berntsen et al., 1997; Forster et al., 1997). The longwave radiation absorbed heats the TTL region (Fig. 5), resulting in larger TLS ΔSWV_fast ∕ ERF magnitude than ΔSWV_slow ∕ ERF and larger contributions to total equilibrium ΔSWV (77 %) (Fig. 1g and j). There is also heating in the LMS, resulting in larger LMS ΔSWV_fast ∕ ERF magnitude than ΔSWV_slow ∕ ERF (Fig. 1h–i and k–l). We note that our conclusion on 5×O₃ is based on only one model, MIROC-SPRINTARS.

ΔSWV_fast from 10×BC dominates total equilibrium ΔSWV in the TLS, with a multi-model mean contribution of 84 %. The magnitude of the multi-model mean ΔSWV_fast ∕ ERF from 10×BC is also larger than any other perturbations in each region. This occurs because the 10×BC strongly absorbs shortwave radiation, causing large heating of the tropopause region in both the tropics and extratropics. Figure 5 shows that the 10×BC gives by far the most warming per unit ERF, which is consistent with the vertical profile of fast temperature response shown in Stjern et al. (2017).

The 10×BC ΔSWV_fast ∕ ERF in the NH and SH LMS contributes about 50 % of the total equilibrium ΔSWV, with smaller magnitudes in the Southern Hemisphere (Fig. 1h–i and k–l). This is because the total amount of black carbon is smaller in the Southern Hemisphere (Myhre et al., 2017), since black carbon is a combustion product and is predominantly emitted over the NH continents (Ramanathan and Carmichael, 2008). The 10×BCSLT ΔSWV_fast also contributes about 50 % of the total 10×BCSLT ΔSWV. The 10×BCSLT does not produce as strong a ΔSWV_fast ∕ ERF as 10×BC, since the reduction in BC lifetime leads to less BC in the TTL and therefore less heating per unit ERF.

We quantify control of TLS ΔSWV_fast by the fast TTL temperature adjustments across a range of different climate perturbations by regressing the TLS ΔSWV_fast against the fast response of the cold-point temperature (ΔTCP_fast). To estimate ΔTCP_fast in the models, we first find the minimum temperature in the profile at each grid point in the fixed SST runs (no interpolation is done; we simply find the minimum temperature on the output model levels). These minimum temperatures are then averaged between 30^∘ N and 30^∘ S to yield TCP_fast in each run. ΔTCP_fast is the difference between TCP_fast in the perturbed model run and that in the baseline runs.

We find that TLS ΔSWV_fast is strongly correlated with ΔTCP_fast across all perturbations and models (Fig. 6a), with a slope of 0.52 ppmv K⁻¹ and a 95 % confidence interval of 0.43 to 0.61 ppmv K⁻¹. Randel and Park (2019) pointed out that the slope from the Clausius–Clapeyron relationship evaluated near the tropical tropopause is close to this value, about 0.5 ppmv K⁻¹. We also tested the relationship between TLS ΔSWV_slow and the slow response of the cold-point temperature (ΔTCP_slow) across all perturbations and models, yielding a slope of 0.72 ppmv K⁻¹. However, for the slow response, correlation does not necessarily prove causality, since Dessler et al. (2016) showed that, in two climate models at least, a significant fraction of the long-term trend was due to increases in convective moistening, which bypasses the TTL cool trap. Therefore, this relationship for the slow response could arise from either TCP control, a process that correlates with it, such as deep convective injection of ice, or some combination.

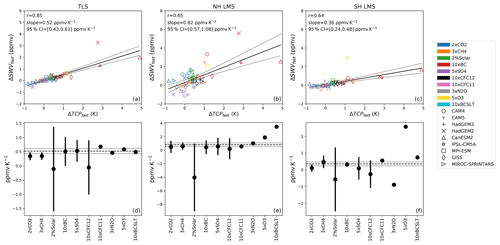
Figure 6 (a–c) Linear regression between ΔSWV_fast (ppmv) and ΔTCP_fast (K) from all models and perturbations. The color coding indicates different perturbations, while the marker shapes indicate results from different models. The black solid line is the linear fit of the regression. The black dotted lines indicate the linear fits within the 95 % confidence interval, estimated using a t test. (d–f) Slopes and their 95 % confidence intervals (for perturbations that are performed by more than three models) obtained from linear regression between ΔSWV_fast (ppmv) and ΔTCP_fast (K) for each individual perturbation. The black dashed lines and dotted lines are the slopes and their 95 % confidence intervals of the regressions in (a)–(c).

We also separately plot the slopes between ΔSWV_fast and ΔTCP_fast for each perturbation (Fig. 6d–f). For the perturbations that have more than five participating models, including 2×CO₂, 3×CH₄, 2%Solar, 10×BC, 5×SO₄, and 10×CFC-12, we calculate the linear regression between ΔSWV_fast and ΔTCP_fast from the models and show the slopes and 95 % confidence intervals. For the perturbations that have fewer participating models, including 10×CFC11, 3×N₂O, 5×O₃, and 10×BCSLT, we plot the ratio ΔSWV_fast ∕ ΔTCP_fast and show only the multi-model mean. The slopes produced by different perturbations show general agreement (Fig. 6d). The larger uncertainty in the slopes produced by 2%Solar and 10×CFC-12 occurs because both the ΔTCP_fast and ΔSWV_fast produced by different models are similar, and therefore the slope of the linear regression is uncertain. Overall, we find that the fast response of TTL temperature is a good predictor for the TLS ΔSWV_fast across a range of different climate mechanisms and across multiple models.

For the LMS ΔSWV_fast, the ΔTCP_fast does not show a control as strong as that in the TLS (Fig. 6b–c) due to the fact that TTL temperatures are only one factor that influences the LMS. In addition, the regression between ΔSWV_fast and ΔTCP_fast across all perturbations at each grid point in the pressure–latitude domain shows that the slope (% K⁻¹) follows the transport pattern of the Brewer–Dobson circulation (BDC) (Fig. 4b). The slope is large in the tropical overworld stratosphere and becomes weaker as one moves poleward and downward in the extratropics below 150 hPa. The value is lower in the LMS, again consistent with the fact that water vapor in the LMS is controlled by several processes, not just TTL cold-point temperature. Clearly, more work on this is warranted.

4 Historical changes in SWV

Given the importance of SWV change, we now ask whether our results can help us understand historical variations in TLS ΔSWV over 1980–2010 (Fig. 7). To do this, we estimate historical values of ΔSWV_slow and ΔSWV_fast based on the PDRMIP results, historical surface temperature change, and historical radiative forcing. For the slow component (blue in Fig. 7a), we multiply 0.35 ppmv K⁻¹, the multi-model multi-perturbation mean sensitivity of the PDRMIP TLS ΔSWV_slow to ΔT_s, by the historical surface temperature change over 1980–2010. For the fast component (orange in Fig. 7a), we multiply the multi-model mean PDRMIP TLS ΔSWV_fast ∕ ERF value for each perturbation by the corresponding historical radiative forcing and then sum it up. We also show the fast component of the historical ΔSWV contributed by each historical forcing agent in Fig. 7b. This is similar to the analysis done by Hodnebrog et al. (2019) in their Fig. 6, where they used this method to estimate the historical water vapor lifetime change based on the PDRMIP results.

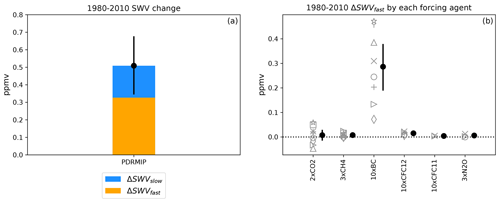
Figure 7 (a) TLS (30^∘ S–30^∘ N, 70 hPa) SWV change over 1980–2010 estimated using PDRMIP results. Blue indicates the component contributed by the slow response, while orange indicates the component contributed by the fast response. (b) The fast component of the PDRMIP-estimated 1980–2010 SWV change contributed by each historical forcing agent. The solid circles are the multi-model mean. The error bars are 2.5–97.5 percentiles of the model samples; in (b) they are shown for perturbations that are performed by more than three models.

The historical surface temperature change and radiative forcing data used in this analysis are listed in Table 2. The historical radiative forcing we use here is defined as the change in net downward radiative flux at the tropopause after adjustments in the stratospheric temperatures, while the surface and troposphere are held unperturbed (Myhre et al., 2013b). This is different from the ERF we use in the PDRMIP calculations, which introduces uncertainties in the fast component of the historical ΔSWV we estimate based on PDRMIP.

Table 2 Historical global average surface temperature change and radiative forcing (RF) by greenhouse gases (GHGs) and halocarbons over 1980–2010. The SWV change over 1980–2010 estimated using PDRMIP results is also listed, including the total SWV change, the slow component, and the fast component. For the fast component of SWV change contributed by each forcing agent, multi-model mean results are listed. The uncertainties are 2.5–97.5 percentiles of the model samples.

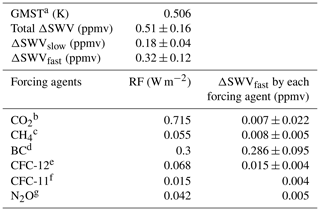
^a We used NOAA Merged Land Ocean Global Surface Temperature Analysis V5 (Zhang et al., 2020) to compute the global surface temperature change. We use values averaged over 2005–2015 minus those averaged over 1975–1985. ${}^{\mathrm{b},\mathrm{c},\mathrm{e},\mathrm{f},\mathrm{g}}$ We compute the RFs using the formulae listed in Table 3 of Myhre et al. (1998). These formulae were also used to compute RFs of CO₂, CH₄, and N₂O in IPCC reports (Myhre et al., 2013b). ${}^{\mathrm{b},\mathrm{c},\mathrm{g}}$ Concentrations of GHGs were used to compute RFs. CO₂ and CH₄ are samples collected in glass flasks at Cold Bay, Alaska, United States (CBA), from the ERSL GML website (Dlugokencky et al., 2020a, b). N₂O is from the combined nitrous oxide data from the NOAA/ESRL Global Monitoring Division. For CO₂, concentrations averaged over 2005–2015 and averaged over 1978–1985 are used. For CH₄, concentrations averaged over 2005–2015 and averaged over 1983–1985 are used. For N₂O, concentrations averaged over 2005–2015 and averaged over 1977–1985 are used. ^e–f Concentrations of CFC-12 and CFC-11 were used to compute RFs. We use CFC-12 and CFC-11 data from combined stations from the NOAA/ESRL Global Monitoring Division. Concentrations averaged over 2005–2015 and averaged over 1977–1985 are used. ^d We use 0.4 W m⁻², the BC RF between 1750 and 2011 reported in IPCC AR5, minus 0.1 W m⁻², the BC RF between 1750 and 1993 reported in the 1995 IPCC report (see Table 8.4 of Myhre et al., 2013b).

Figure 7a shows our estimate that climate change over 1980–2010 has increased TLS SWV by 0.51±0.16 ppmv (Fig. 7a); 36 % is due to the slow component, although this is probably an overestimate because our sensitivity value estimated using the PDRMIP results is for the long term. We find that the rest of the ΔSWV, 64 %, is due to the fast component, mainly from black carbon. We have also calculated the SWV sensitivity and SWV fast response over 35–45^∘ N between 100 and 80 hPa to estimate the historical 1980–2010 ΔSWV using the same method, which is 0.65±0.20 ppmv. This value shows reasonable agreement with the SWV increase measured by Hurst et al. (2011) of 0.71±0.26 ppmv over Boulder between 16 and 18 km over 1980–2010.

Dessler et al. (2014) and Hegglin et al. (2014) argue that there is not a detectible trend over this period. Such a conclusion is not inconsistent with ours because any actual trend estimate has to contend with short-term interannual variability (i.e., like that from the quasi-biennial oscillation and Brewer–Dobson circulation variability), which can mask a small trend. Our estimate of the trend is based on sensitivity estimated from 100-year run, and therefore short-term interannual variability has a small impact. Given a continuous, reliable, long-term SWV observation record in the future, one will be able to better test the model-predicted values.

For the fast component of the estimated historical ΔSWV, radiative forcing by BC plays the dominant role (Fig. 7b). Uncertainties exist in the historical BC radiative forcing we use in this analysis, which is shown in the IPCC AR5 (Myhre et al., 2013b). In addition, Allen et al. (2019) pointed out that the radiative effect by BC in the PDRMIP is different from that shown in models using observationally constrained aerosol forcing, which may overestimate the heating in the upper troposphere–lower stratosphere region. However, Allen et al. (2019) also noted that uncertainties exist in their observationally constrained aerosol forcing. The uncertainties in the impact of BC forcing on SWV clearly merit more analysis in the future.

5 Conclusions

It is of great interest for the climate community to understand how SWV changes when the climate changes since SWV plays an important role in the Earth's radiative budget and stratospheric ozone chemistry (Solomon et al., 1986, 2010; Dvortsov and Solomon, 2001; Forster and Shine, 2002). In this study, we investigate the response of stratospheric water vapor (SWV) to a range of different climate forcing mechanisms using a multi-model and multiple-forcing-agent framework. We use output from nine CMIP5 models participating in the PDRMIP. Each model performs a baseline and up to 10 climate perturbation experiments, including 2×CO₂, 3×CH₄, 2%Solar, 10×BC, 5×SO₄, 10×CFC-11, 10×CFC-12, 3×N₂O, 5×O₃, and 10×BCSLT (Table 1). Each perturbation is performed in two configurations, including fixed SST simulations (at least 15 years) and fully coupled simulations (at least 100 years).

To better understand the SWV response (ΔSWV), we partition it into two parts: the slow response (ΔSWV_slow) and the fast response (ΔSWV_fast). The ΔSWV_fast is the change in response to a perturbation on short timescales before the surface temperature has responded. ΔSWV_slow occurs on longer timescales and is coupled to the surface temperature change. Our results show that, for most perturbations, ΔSWV in the tropical lower stratosphere (TLS) and in the lowermost stratosphere (LMS) (200 hPa, 50–90^∘ N and 50–90^∘ S) is dominated by ΔSWV_slow (Fig. 1).

Analysis of ΔSWV_slow shows that a warming surface increases SWV (Figs. S3–S5). Furthermore, the response of SWV to the surface temperature change has a similar sensitivity across different climate perturbations in both the overworld stratosphere and the lowermost stratosphere (Figs. 3 and 4a). Specifically, the multi-model and multi-perturbation mean slope is 0.35 ppmv K⁻¹ in the TLS, 2.1 ppmv K⁻¹ in the northern hemispheric (NH) LMS, and 0.97 ppmv K⁻¹ in the southern hemispheric (SH) LMS (Fig. 3).

ΔSWV_slow in the LMS is more sensitive to ΔT_s than the tropical overworld, reflecting different transport pathways into the LMS compared to the overworld (Dessler et al., 1995; Holton et al., 1995; Plumb, 2002; Gettelman et al., 2011). The ΔSWV_slow in the NH LMS is more sensitive than the SH LMS, consistent with hemispheric asymmetries in the isentropic transport and convective moistening reported by previous studies (Pan et al., 1997, 2000; Dethof et al., 1999, 2000; Dessler and Sherwood, 2004; Ploeger et al., 2013; Smith et al., 2017; Ueyama et al., 2018; Wang et al., 2019).

The fast response of SWV from most perturbations is weak compared to the slow response and therefore plays a smaller role in ΔSWV (Fig. 1). In the TLS, for forcing agents that directly heat tropopause levels (Fig. 5), ΔSWV_fast makes a larger contribution to ΔSWV. In particular, when the climate is perturbed by 10×BC, the ΔSWV_fast dominates the ΔSWV_slow and has a larger magnitude than any other perturbed simulations. This occurs because black carbon absorbs shortwave radiation in the atmosphere and directly heats the temperatures at tropopause levels. Other forcing agents also heat the tropopause levels and increase ΔSWV_fast through absorption of shortwave radiation or longwave radiation at the atmospheric window range (3×CH₄, 5×O₃, 10×BCSLT, 10×CFC-12, 10×CFC-11), but these are not as strong as 10×BC.

The TLS ΔSWV_fast is controlled by the fast response of the cold-point temperature across different climate change mechanisms (Fig. 6), with a slope of 0.52 ppmv K⁻¹, which is consistent with the Clausius–Clapeyron relationship evaluated near the tropical tropopause (Randel and Park, 2019). Control of the cold-point temperature fast response over ΔSWV_fast is stronger in the tropical overworld and becomes weaker at higher latitudes and altitudes below 150 hPa in the LMS (Fig. 4b).