Dependence between the photochemical age of light aromatic hydrocarbons and the carbon isotope ratios of atmospheric nitrophenols

Concepts were developed to establish relationships between the stable carbon isotope ratios of nitrophenols in the atmosphere and the photochemical processing of their precursors, light aromatic volatile organic compounds. These concepts were based on the assumption that nitrophenols are formed dominantly from the photo-oxidation of aromatic volatile organic compounds (VOCs). A mass balance model as well as various scenarios based on the proposed mechanism of nitrophenol formation were formulated and applied to derive the time-integrated exposure of the precursors to processing by OH radicals (∫[OH]dt) from ambient observations made between 2009 and 2012 in Toronto, Canada. The mechanistic model included the possibility of isotopic fractionation during intermediate steps, rather than only during the initial reaction step. This model takes kinetic isotope effects for the reaction of the precursor VOC with the hydroxyl radical and their respective rate constants into account, as well as carbon isotope ratio source signatures. While many of these values are known, there are some, such as the kinetic isotope effects of reactions of first- and second-generation products, which are unknown. These values were predicted in this study based on basic principles and published laboratory measurements of kinetic carbon isotope effects and were applied to the mechanistic model. Due to the uncertainty of the estimates based on general principles, three scenarios were used with different values for isotope effects that were not known from laboratory studies. Comparison of the dependence between nitrophenol carbon isotope ratios and ∫[OH]dt with published results of laboratory studies and ambient observations was used to narrow the range of plausible scenarios for the mechanistic model. The results also suggests that mass-balance-based models do not adequately describe the dependence between nitrophenol carbon isotope ratios and ∫[OH]dt.

1 Introduction

Secondary organic aerosols (SOA) in the atmosphere formed from the photo-oxidation of both anthropogenic and biogenic volatile organic compounds (VOCs) are poorly understood. Products formed from these reactions are only partly known, and apart from the composition of SOA little is known about its atmospheric processing. It has been proposed that the use of concentration measurements in conjunction with stable carbon isotope ratio measurements can be used to gain insight into this topic (Goldstein and Shaw, 2003; Rudolph, 2007; Gensch et al., 2014). The compounds of interest in this study are nitrophenols, which have been proposed to be formed specifically from the gas-phase photo-oxidation of aromatic VOCs (Forstner et al., 1997; Atkinson, 2000; Jang and Kamens, 2001; Hamilton et al., 2005; Sato et al., 2007). Once toluene, for example, is emitted from its anthropogenic sources, it is expected to react according to the proposed reaction mechanism (Forstner et al., 1997) to produce methylnitrophenols (Fig. 1). As it is formed specifically from identified reactions, the stable carbon isotope ratio of the product can be linked back to the precursor and its source. Based on laboratory observations (Irei et al., 2011), methylnitrophenols were found to have an average isotope ratio that is close to the isotope ratio of the sum of all products calculated from the mass balance. The aqueous phase production of nitrophenols, specifically 4-nitrophenol, has also been proposed to occur via a reaction pathway involving the NO₃ radical (Herrmann et al., 1995; Harrison et al., 2005). This pathway is thought to be quite a significant source of 4-nitrophenol in the presence of clouds with a high liquid water content but has been modelled to contribute less than 2 % when the liquid water content is low (Harrison et al., 2005). Ambient measurements in the Toronto area (Saccon et al., 2015) indicate that nitrophenols are second-generation products due to their depletion in ¹³C relative to the carbon isotope ratio of the precursor.

Figure 1 Proposed formation mechanism of 2-methyl-4-nitrophenol from toluene oxidation (adapted from Forstner et al., 1997).

The carbon isotope ratio of a species, which will be referred to as the delta value (δ¹³C), is defined using Eq. (1), where (¹³C∕¹²C)_VPDB is the internationally accepted Vienna Peedee Belemnite (VPDB) value of 0.0112372. As differences in isotope ratios between species are small, delta values are expressed in per mille notation. Limited studies using the carbon isotope ratio of atmospheric trace components, including several aromatic VOCs and nitrophenols, have been applied to differentiate between sources and to trace components back to their precursors, respectively (Moukhtar et al., 2011; Kornilova et al., 2013; Saccon et al., 2013). The concept of deriving information on photochemical processing of trace constituents from isotope ratios is based on the kinetic isotopic effect (KIE), which describes the dependence of the rate constant of a reaction on the atomic mass of isotopologues. In this work, the KIE will be referred to as ε (Eq. 2), where k₁₂ and k₁₃ are the rate constants for ¹²C only and for one ¹³C containing isotopologues, respectively. Normal KIE, which occurs when ε is positive, is exhibited when a compound reacts in the atmosphere and the remaining compound is enriched in heavier isotopes, for example ¹³C. Like delta values, ε is also expressed in per mille notation.

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}={\displaystyle \frac{({}^{\mathrm{13}}\mathrm{C}/{}^{\mathrm{12}}\mathrm{C}{)}_{\text{sample}}-({}^{\mathrm{13}}\mathrm{C}/{}^{\mathrm{12}}\mathrm{C}{)}_{\mathrm{VPDB}}}{({}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}\mathrm{C}{)}_{\mathrm{VPDB}}}}\times \mathrm{1000}\mathrm{‰}\text{(2)}& {\displaystyle }& {\displaystyle }\mathit{\epsilon }={\displaystyle \frac{k_{\mathrm{12}}-k_{\mathrm{13}}}{k_{\mathrm{13}}}}\times \mathrm{1000}\mathrm{‰}\end{array}$$

Among other factors, the concentration of a species in the atmosphere depends on its reactivity and the time over which it is exposed to reactants. For many VOCs and semi-volatile organic compounds (SVOCs) the most important reactant is the OH radical, and the time-integrated OH-radical concentration is often referred to as the photochemical age (PCA). The combination of laboratory experiments and ambient measurements can allow for the determination of the PCA of a specific component in SOA. The PCA for an air mass has previously been used to quantify the extent of the processing of a precursor using the hydrocarbon clock and the mixing ratios of VOCs (Parrish et al., 1992, 2007; Jobson et al., 1998, 1999; Kleinman et al., 2003). A more recently developed method uses the carbon isotope ratio of an atmospheric VOC with emissions as the only relevant source; the KIE and the isotope ratio source signature are utilized to determine the PCA of this VOC. This approach is often referred to as the isotope hydrocarbon clock (Rudolph and Czuba, 2000; Rudolph et al., 2003; Thompson, 2003; Stein and Rudolph, 2007; Kornilova, 2012; Kornilova et al., 2016). The PCA of a species can be calculated using Eq. (3), where δ¹³C_pre is the carbon isotope ratio of the measured ambient precursor, δ¹³C₀ is the carbon isotope ratio of the emissions, and ∫[OH]dt is the time-integrated OH concentration (PCA). It has been shown that the concept of ascribing a PCA to an air mass (Parrish et al., 1992) is only meaningful if all VOC emissions that contribute to the observed VOC mixing ratios have been subject to an identical extent of processing. In cases where air masses mix that contain VOC emissions which have been subject to a different extent of processing, the concept of a PCA for an air mass has to be replaced by the concept of a PCA for an individual VOC (Kornilova et al., 2016). Rudolph and Czuba (2000) showed that VOC carbon isotope ratio measurements can be used to determine the concentration weighted average of the photochemical age of individual VOCs provided that the variability of the carbon isotope ratio of the emissions is small compared to the change in the carbon isotope ratio resulting from atmospheric removal reactions.

The carbon isotope ratios of the emissions of many important anthropogenic VOC precursors have previously been measured, and their uncertainty is typically below 1 ‰ (Czapiewski et al., 2002; Rudolph et al., 2002; Rudolph, 2007; Gensch et al., 2014). The change in the VOC mixing ratios due to reaction with OH radicals can be described by Eq. (4), where χ_amb and χ₀ are the mixing ratios of the ambient precursor and the mixing ratio that would be observed in the absence of reaction with OH radicals, respectively. Consequently, a combination of carbon isotope ratio measurements and concentration measurements allows for separation between the impact of atmospheric reactions and changes in source strength or atmospheric mixing and dilution.

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{pre}}={{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{0}}+k_{\mathrm{12}}\mathit{\epsilon }\int \left[\mathrm{OH}\right]\mathrm{d}t\text{(4)}& {\displaystyle }& {\displaystyle }{\mathit{\chi }}_{\mathrm{amb}}={\mathit{\chi }}_{\mathrm{0}}\exp (-k_{\mathrm{12}}\int \left[\mathrm{OH}\right]\mathrm{d}t)\end{array}$$

Comparison of the difference between χ₀ and χ_amb with the ambient concentrations of the products of the photochemical reactions of VOCs will provide insight into the yield of the secondary pollutants from the reactions. In the case of mixing air masses containing VOCs with different PCAs, Eq. (3) is still a very good approximation for the concentration weighted average ∫[OH]dt of the precursor VOC (Rudolph and Czuba, 2000). However, Eq. (4) is only a valid approximation if the variability in the PCAs is small compared to the average PCA. Otherwise Eq. (4) will underestimate the average of χ₀ (Rudolph and Czuba, 2000). Consequently, yield estimates derived from combining results derived from Eqs. (3) and (4) with measured ambient concentrations of reaction products will be an upper limit. In principle this limitation can be avoided by using the carbon isotope ratio of the reaction product to derive ∫[OH]dt, as the average of ∫[OH]dt derived from the carbon isotope ratios of the reaction products will be weighted according to the concentration of the products, which will accumulate as a result of the photochemical reaction of the precursor. However, due to the simultaneous formation and removal of the reaction products, the relation between the carbon isotope ratio of the reaction product and the extent of photochemical processing is more complex than the simple relation between the carbon isotope ratio of the precursor and ∫[OH]dt as described by Eq. (3). The reported carbon isotope ratio measurements of nitrophenols in the solid and the gas phases from Saccon et al. (2015) showed that, although the average isotope ratios are consistent with laboratory studies, a significant number of delta values are between 2 ‰ and 3 ‰ lower than predicted from mass balance. This difference cannot be explained by the uncertainty of the carbon isotope ratios of precursor emission or measurement errors. However, a simple mass balance only considers the KIE for the first step of the reaction mechanism (shown in Fig. 1). It must be accepted that further fractionation can occur in reaction steps following the initial reaction of the aromatic VOC with the OH radical. In this work, we will present calculations using a mechanism based on the formation and removal of nitrophenols from the atmosphere that describe the dependence between the photochemical processing of light aromatic hydrocarbons and the carbon isotope ratio of nitrophenols, which are products of atmospheric reactions of light aromatic hydrocarbons. Different scenarios using a range of isotope fractionation effects for a simple mechanistic model will be discussed using the carbon isotope ratios of nitrophenols published by Saccon et al. (2015) and the laboratory studies published by Irei et al. (2015). From this comparison, the magnitude of isotope fractionation effects following the initial reaction of light aromatic VOCs with OH radicals can be constrained. PCAs derived from nitrophenol carbon isotope ratios will be compared with PCAs derived from carbon isotope ratios of the precursors (Kornilova et al., 2016).

2 Materials and method

The experimental method used in this work is described in detail by Saccon et al. (2013), which is based on methods developed by Moukhtar et al. (2011) and Irei et al. (2013). The results of the carbon isotope ratio measurements have been presented by Saccon et al. (2015); therefore, we will only briefly describe the experimental procedure. Sample collection was carried out at York University in Toronto, Canada, using 20.32 cm × 25.4 cm quartz-fiber filters (Pallflex^® Tissuquartz^™ filters – 2500 QAT – Pall Gelman Sciences) on high-volume air samplers (TE-6001 from Tisch Environmental Inc.) equipped with PM_2.5 heads. Uncoated quartz filters were used to collect particulate matter (PM) alone, with an average sampling time of 1–3 days, and filters coated with XAD-4^™ resin were used for the collection of both the gas phase and PM, with an average sampling time of 1 day. Filter samples were collected between March 2009 and August 2012. The analysis of the filters included extraction in acetonitrile, and HPLC separation and solid-phase extraction were used as sample clean-up steps. Concentration measurements were undertaken using a HP 5890 GC equipped with a HP 5972 mass spectrometer; carbon isotope ratio measurements were carried out using an Micromass IsoPrime isotope ratio mass spectrometer (Isomass Scientific, Inc.). Method performance characteristics are given in Saccon et al. (2013, 2015).

3 Determination of PCA

Laboratory experiments studying the carbon isotope ratios of secondary particulate organic matter (POM) formed by the gas-phase oxidation of toluene showed that the δ¹³C value of total secondary POM can be approximated by mass balance (Irei et al., 2006, 2011). However, compound-specific measurements also indicate that in some cases detailed mechanistic considerations are required to explain the observed δ¹³C values of secondary phenols that are lower than expected from mass balance alone (Irei et al., 2015).

3.1 PCA from mass balance

Mass balance calculations allow a straightforward determination of the dependence between the δ¹³C of the total of secondary POM and the PCA. This requires the assumption that the carbon isotope ratio of the gas-phase reaction products in the atmosphere is identical to the carbon isotope ratio of secondary POM observed in laboratory studies (Irei et al., 2006, 2011). Furthermore, for compound-specific carbon isotope ratio measurements it also has to be assumed that the carbon isotope ratio of the individual products is representative of the carbon isotope ratio of all secondary POM. In this case the dependence between the PCA of the precursors and the product isotope ratio (Eq. 5) can be derived from Eqs. (3) and (4). Here, k_OH is the averaged rate constant of all isotopomers of the precursor reacting with OH and, for practical purposes, is equal to k₁₂.

$$\begin{array}{ll}{\displaystyle }{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\text{prod}}=& {\displaystyle \frac{{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{o}}-\exp (-k_{\mathrm{OH}}\int \left[\mathrm{OH}\right]\mathrm{d}t)}{\mathrm{1}-\exp }}\\ \text{(5)}& {\displaystyle }& {\displaystyle \frac{({{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{o}}+k_{\mathrm{12}\mathrm{OH}}\mathit{\epsilon }\int \left[\mathrm{OH}\right]\mathrm{d}t)}{(-k_{\mathrm{OH}}\int \left[\mathrm{OH}\right]\mathrm{d}t)}}\end{array}$$

It should be noted that, similar to the conventional hydrocarbon clock, in the case of mixing of air masses with different PCAs, the PCA from Eq. (5) is a combination of the PCAs of the individual air masses, which is not always easy to interpret. Equation (5) also neglects possible isotope fractionation resulting from the loss of secondary POM. The values for rate constants, the carbon isotope ratio of precursor VOC emissions, and the kinetic isotope effects used are listed in Table 1.

Table 1 Parameters, including the rate constant of the precursor with the OH radical (k_OH), the KIE, and the carbon isotope ratio of emissions (δ¹³C₀) used for the determination of the PCA by Eq. (5). The uncertainty of the parameter is given in parentheses.

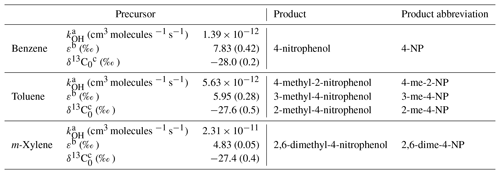
^a Calvert et al. (2002), uncertainty not included as the uncertainty resulting from the error in the rate constants is small compared with uncertainties derived from the error in the carbon isotope ratio and KIE. ^b Anderson et al. (2004). ^c Rudolph et al. (2002); for m-xylene the value reported for p+m-xylene is given.

3.2 PCA from detailed mechanistic concepts

The reaction sequence resulting in the formation of nitrophenols from the oxidation of toluene proposed by Forstner et al. (1997) is shown in Fig. 1. It does not include the details of the various branching reactions and alternate pathways resulting in other products or isotope fractionation due to loss reactions of secondary POM. While in many cases branching ratios are known, there is little direct knowledge on isotope fractionation resulting from branching reactions. Nevertheless, isotope effects for specific pathways can be estimated from the type of reaction and known principles of isotope fractionation. For example, after the formation of the cresol first-generation product (Fig. 1), the probability that an OH radical is added to the ring is 92 % (Atkinson et al., 1980), whereas reaction at the phenolic OH group, which is expected to result in formation of nitrophenols, occurs in 8 % of all reactions. The reaction of the phenolic OH group is expected to result in negligible carbon isotope fraction as it is a secondary isotope effect, whereas the OH-radical addition will have a carbon isotope effect similar to that of other OH addition reactions to aromatic rings. Similarly, the main gas-phase loss process of nitrophenols is expected to be via reaction with the OH radical, which occurs through an OH addition to the ring more than 80 % of the time (Bejan et al., 2007). As an OH radical is added to the ring, fractionation typical for reaction at the six carbon atoms of an aromatic ring is expected to occur for 80 % of the loss reactions. Reaction at the alkyl group or the phenolic OH results in a much lower KIE than for addition to the aromatic ring and therefore their contribution to the KIE is negligible.

Another complication is the distribution of nitrophenols between the gas phase and PM. It is assumed that there are no chemical losses when nitrophenols partition into PM, and that there is equilibrium between the gas and particle phases. As phase distribution processes typically have very small isotope effects, partitioning between the gas phase and PM is expected to have only a marginal impact on the carbon isotope ratio. This is consistent with the findings of Saccon et al. (2015). However, partitioning will influence the loss rate for SVOCs, as it is assumed that there is little to no chemical loss in the PM phase. It has been reported that phenols can be oxidized in aqueous solutions under conditions somewhat similar to atmospheric conditions in fog or cloud water (Yu et al., 2016). However, these reactions are very slow compared to the reaction of nitrophenols with OH radicals in the gas phase (for details see Sect. S1 of the Supplement). Uncertainty in phase partitioning will only result in minor uncertainties of the photochemical nitrophenol loss rate, as it has been reported that only approximately 20 % of the nitrophenols partition into the particle phase (Saccon et al., 2013, 2015). There is no information available that would allow for the estimation of the rate of exchange of nitrophenols between the gas phase and PM. It is assumed that phase partitioning is fast compared to gas-phase reactions. There are indications that in some cases exchange between the gas phase and PM is slower than the formation or loss reactions of SVOCs in the gas phase (Saccon et al., 2015), but the reported average of the difference in carbon isotope ratios between the gas phase and PM is negligible (0.3±0.5 ‰).

Reaction rate constants for which no laboratory measurements are available are estimated on the following principles. The rate constant for 3-methyl-4-nitrophenol is estimated based on the position of its substituents on the aromatic ring relative to other isomers that have known rate constants, such as 3-methyl-2-nitrophenol and 4-methyl-2-nitrophenol. For 2,6-dimethyl-4-nitrophenol it is assumed that loss reactions due to the addition of the OH radical to the aromatic ring are negligible as the nitro and hydroxyl substituents both direct reactions to positions that are already occupied by other substituents; furthermore, reactions at positions three or five are unlikely to occur. It should be noted that reaction at the phenolic OH group of 2,6-dimethyl-4-nitrophenol will not directly impact the carbon isotope ratio as this secondary carbon isotope effect will be negligible, independent of the rate of this reaction.

Using these assumptions, a set of differential equations is derived that describe the change in the concentration of the isotopologues of the precursor, the first-generation product (phenols), and the second-generation product (nitrophenols) (Eqs. 6 to 8). Here, ¹²C_prod/int/pre and ¹³C_prod/int/pre are the concentrations of each of the ¹²C and ¹³C isotopologues of the second-generation nitrophenol, first-generation phenolic compound, and aromatic precursor, respectively. ${}_{\text{int}}^{\mathrm{12}}Y$ and ${}_{\text{int}}^{\mathrm{13}}Y$ are the yields of the first-generation product from reaction of the precursor, and ${}_{\text{prod}}^{\mathrm{12}}Y$ and ${}_{\text{prod}}^{\mathrm{13}}Y\mathrm{are}\mathrm{the}\mathrm{yields}\mathrm{of}$ nitrophenols from the reaction of the phenol. The rate constants k¹² and k¹³ for different isotopologues are calculated from constants and the KIE.

$$\begin{array}{}\text{(6a)}& {\displaystyle }{{\mathrm{d}}^{\mathrm{12}}\mathrm{C}}_{\text{prod}}=-{{}^{\mathrm{12}}\mathrm{C}}_{\text{prod}}{k}_{\text{prod}}^{\mathrm{12}}\left[\mathrm{OH}\right]\mathrm{d}t+{}_{\text{prod}}^{\mathrm{12}}{Y}^{\mathrm{12}}{C}_{\text{int}}{k}_{\text{int}}^{\mathrm{12}}\left[\mathrm{OH}\right]\mathrm{d}t\text{(6b)}& {\displaystyle }{{\mathrm{d}}^{\mathrm{13}}\mathrm{C}}_{\text{prod}}=-{{}^{\mathrm{13}}\mathrm{C}}_{\text{prod}}{k}_{\text{prod}}^{\mathrm{13}}\left[\mathrm{OH}\right]\mathrm{d}t+{}_{\text{prod}}^{\mathrm{13}}{Y}^{\mathrm{13}}{C}_{\text{int}}{k}_{\text{int}}^{\mathrm{13}}\left[\mathrm{OH}\right]\mathrm{d}t\end{array}$$

$$\begin{array}{}\text{(7a)}& {\displaystyle }{{\mathrm{d}}^{\mathrm{12}}\mathrm{C}}_{\text{int}}={{-}^{\mathrm{12}}\mathrm{C}}_{\text{int}}{k}_{\text{int}}^{\mathrm{12}}\left[\mathrm{OH}\right]\mathrm{d}t+{}_{\text{int}}^{\mathrm{12}}{Y}^{\mathrm{12}}{C}_{\text{pre}}{k}_{\text{pre}}^{\mathrm{12}}\left[\mathrm{OH}\right]\mathrm{d}t\text{(7b)}& {\displaystyle }{{\mathrm{d}}^{\mathrm{13}}\mathrm{C}}_{\text{int}}={{-}^{\mathrm{13}}\mathrm{C}}_{\text{int}}{k}_{\text{int}}^{\mathrm{13}}\left[\mathrm{OH}\right]\mathrm{d}t+{}_{\text{int}}^{\mathrm{13}}{Y}^{\mathrm{13}}{C}_{\text{pre}}{k}_{\text{pre}}^{\mathrm{13}}\left[\mathrm{OH}\right]\mathrm{d}t\end{array}$$

$$\begin{array}{}\text{(8a)}& {\displaystyle }{{\mathrm{d}}^{\mathrm{12}}\mathrm{C}}_{\text{pre}}={{-}^{\mathrm{12}}\mathrm{C}}_{\text{pre}}{k}_{\text{pre}}^{\mathrm{12}}\left[\mathrm{OH}\right]\mathrm{d}t\text{(8b)}& {\displaystyle }{{\mathrm{d}}^{\mathrm{13}}\mathrm{C}}_{\text{pre}}={{-}^{\mathrm{13}}\mathrm{C}}_{\text{pre}}{k}_{\text{pre}}^{\mathrm{13}}\left[\mathrm{OH}\right]\mathrm{d}t\end{array}$$

Details regarding the numerical integration of these coupled differential equations are described in Sect. S2. The largest uncertainty arises from the possible isotope dependence of the yields in Eqs. (6) and (7), but uncertainty in the kinetic isotope effects will also contribute to uncertainty in the calculated carbon isotope ratio. Equations (6)–(8) only describe the fractionation relative to the carbon isotope ratio of the precursor emissions. In order to determine carbon isotope ratios that can be compared with observations we use the carbon isotope ratios for emissions reported by Rudolph et al. (2002). To obtain insight into the possible impact of uncertainties in model parameters we utilize different scenarios.

As the yields of nitrophenols from the reaction of light aromatic VOCs are small, the feedback of the differences in yields for isotopologues of the product on the carbon isotope ratio of the first-generation product is very small. It cannot be distinguished if the isotope fractionation occurs during the formation of the first- or the second-generation product. The consequence is that at low PCA values the reaction channel specific isotope fractionation for the formation of nitrophenols is determined by the following equation:

$$\begin{array}{}\text{(9)}& {\displaystyle }{\mathrm{KIE}}_{\text{For}}={\displaystyle \frac{{}_{\text{prod}}^{\mathrm{13}}Y{k}_{\text{int}}^{\mathrm{13}}{}_{\text{int}}^{\mathrm{13}}Y{k}_{\text{pre}}^{\mathrm{13}}}{{}_{\text{prod}}^{\mathrm{12}}Y{k}_{\text{int}}^{\mathrm{12}}{}_{\text{int}}^{\mathrm{12}}Y{k}_{\text{pre}}^{\mathrm{12}}}},\end{array}$$

where KIE_For represents the total isotope fractionation during the formation of nitrophenols following the initial reaction of the precursor with the OH radical (for details see Sect. S3). This greatly reduces the number of scenarios that need to be considered.

The basic parameters used for solving these differential equations are listed in Table 2. The rate constants are for 298 K for consistency with data available for comparison from published literature. Rate constants for this temperature were used in the determination of the PCA from carbon isotope ratios of light aromatic VOCs (Kornilova et al., 2016). The laboratory studies of the formation of methylnitrophenols (Irei et al., 2015) from toluene were conducted at room temperature. To understand uncertainties arising from the assumptions made to estimate the KIEs, which were not determined experimentally, different scenarios are used. In the first scenario (Scenario 1) it is assumed that formation of nitrophenols occurs entirely via the abstraction of a hydrogen atom from the phenolic OH group and that, as it is a secondary KIE, there is no isotope fractionation from this reaction step. It is also assumed that there is no reaction channel specific isotope fractionation for the formation of the phenolic intermediate from the precursor. This is equivalent to the assumption that ${}_{\text{int}}^{\mathrm{12}}Y={}_{\text{int}}^{\mathrm{13}}Y{}_{\text{prod}}^{\mathrm{12}}Y{k}_{\text{int}}^{\mathrm{12}}={}_{\text{prod}}^{\mathrm{13}}Y{k}_{\text{int}}^{\mathrm{13}}$ and ${}_{\text{int}}^{\mathrm{12}}Y={}_{\text{int}}^{\mathrm{13}}Y$.

Table 2 Parameters used to determine the PCA for individual products. Units of k (rate constant) are in cm³ molecules⁻¹ s⁻¹. As 80 % of the phenols are in the gas phase (Saccon et al., 2013), the rate constant for the product loss was adjusted to 80 % of the gas-phase rate constant. If available, the uncertainty of the parameter is given in parentheses.

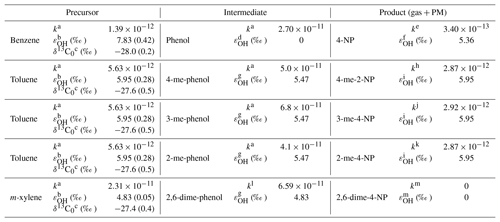
^a Reaction rate constant taken from Calvert et al. (2002). ^b Kinetic isotope effects taken from Anderson et al. (2004). ^c Carbon isotope ratio of emissions taken from Rudolph et al. (2002) and Kornilova et al. (2016); for m-xylene the value reported for p+m-xylene is given. ^d Reaction occurs via OH abstraction (Atkinson et al., 1992) and the secondary carbon isotope effect is assumed to be negligible. ^e Rate constant from Grosjean (1991). ^f Estimated based on the loss reaction proceeding mostly by addition to the aromatic ring (Grosjean, 1991) and the carbon kinetic isotope effects reported by Anderson et al. (2004). ^g Estimated on the assumption that reaction proceeds primarily through an addition pathway (Atkinson et al., 1980). The kinetic isotope effect for the addition of OH radicals to an aromatic ring are based on the kinetic isotope effects reported by Anderson et al. (2004). ^h Rate constant from Bejan et al. (2007). ⁱ Estimate based on the carbon kinetic isotope effects for reactions of aromatic VOCs reported by Anderson et al. (2004). ^j Rate constant assumed to be the average of the rate constants for 3-me-2-NP ($\mathrm{3.69}\times {\mathrm{10}}^{-\mathrm{12}}$ cm³ molecules⁻¹ s⁻¹) and 4-me-2-NP reported by Bejan et al. (2007). ^k Rate constant estimated to be identical to the rate constant reported for 4-me-2-NP by Bejan et al. (2007). ^l Reaction rate constant from Atkinson and Aschmann (1990). ^m Assumed to have no loss reaction that results in carbon isotope fractionation (see text).

Another scenario (Scenario 2) is based on the assumptions that the isotope fractionation for the formation of nitrophenols from the intermediate is identical to the fractionation for all reactions of the intermediate and that there is no reaction channel specific isotope fractionation. It should be noted that for the formation of nitrophenol from the reaction of benzene, the two scenarios will be identical as the reaction of phenol with the OH radical occurs predominantly via abstraction from the OH group (Atkinson et al., 1992); it is also assumed that this secondary carbon isotope effect is negligible ($k_{\text{int}}^{\mathrm{12}}=k_{\text{int}}^{\mathrm{13}}$). For the reactions of toluene and xylene, these two scenarios represent an estimate for the upper and lower limit of carbon isotope fractionation resulting from reactions of the first-generation product.

The third scenario (Scenario 3) is based on laboratory studies of the formation of nitrophenols from gas-phase reactions of toluene in the presence of NO₂ (Irei et al., 2011, 2015) and the lower end of atmospheric observations of nitrophenol carbon isotope ratios reported by Saccon et al. (2015). Details of how these observations can be used to constrain the isotope fractionation during the formation of nitrophenols from aromatic VOCs and the uncertainties of these constraints are given in Sect. S4. Scenario 3 uses an overall isotope fractionation that is 3 ‰ greater than in Scenario 1. It should also be noted that this does not necessarily imply a specific process for the formation of nitrophenols from phenols.

The results of the numerical integration are plotted in Fig. 2 for 2,6-dimethyl-4-nitrophenol, 4-nitrophenol, and 2-methyl-4-nitrophenol in addition to predictions from mass balance. For comparison, the median, the 10th and the 90th percentiles, and the lowest and highest carbon isotope ratios reported by Saccon at al. (2015) are also shown. For 2-methyl-4-nitrophenol the results of laboratory studies reported by Irei et al. (2015) are included.

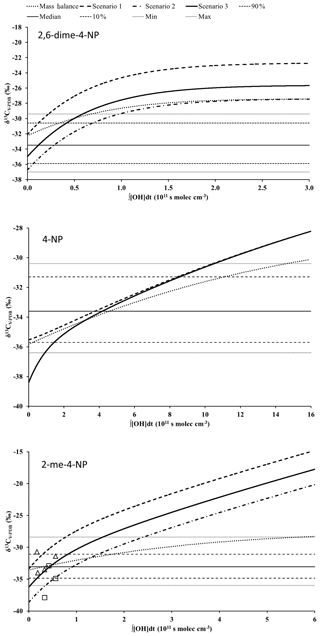
Figure 2 Dependence between the carbon isotope ratio and the PCA (∫[OH]dt) for several nitrophenols calculated for different scenarios using a mechanistic model and mass balance. Also shown are the median, the 10th and 90th percentiles, and the lowest and highest carbon isotope ratios measured by Saccon at al. (2015) in an urban area. The triangles and squares represent the carbon isotope ratios of 3-methyl-4-nitrophenol and 2-methyl-4-nitrophenol, respectively, reported by Irei et al. (2015) for laboratory studies.

The predictions from the mechanistic model are very similar for the methylnitrophenol isomers (see the example in Fig. S1), and for a wide range of PCAs the difference in predicted carbon isotope ratios between the isomers is less than the estimated accuracy of 0.5 ‰ for carbon isotope ratio measurements of methylnitrophenols (Saccon et al., 2013).

For methylnitrophenols and 2,6-dimethyl-4-nitrophenol in all three scenarios the shape of the functions describing the dependence between the carbon isotope ratio and ∫[OH]dt is very similar; the difference in the intercept with the y axis is determined by the isotope fractionation specific for the reaction channel resulting in the formation of nitrophenols and the kinetic isotope effect for the reaction of the precursor as well as the carbon isotope ratio of precursor emissions.

The steep increase in δ¹³C at low values of ∫[OH]dt is the result of the high reactivity of the phenolic first-generation product and the resulting rapid increase in its carbon isotope ratio (Fig. 3). The exception is Scenario 1 for nitrophenol which assumes that the kinetic isotope effect for the reaction of phenol with the OH radical is negligible.

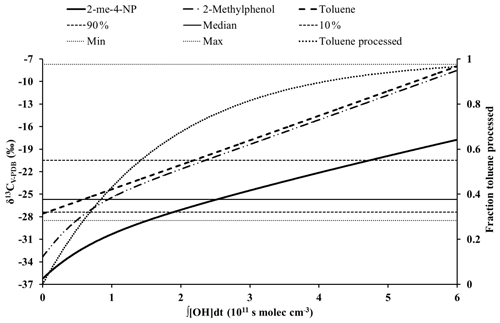
Figure 3 Dependence between the carbon isotope ratio and the PCA (∫[OH]dt) for 2-methyl-4-nitrophenol, its precursor (toluene), and the phenolic intermediate calculated for Scenario 3. Also shown are the median, the 10th and 90th percentiles, and the lowest and highest carbon isotope ratios for toluene reported by Kornilova et al. (2016) for an urban area in Toronto, Canada.

At high PCAs the dependence between the carbon isotope ratio and the PCA is nearly linear, representing conditions where the first-generation phenol is in quasi-steady state between formation from the precursor and loss reactions (Fig. 3). The PCA (∫[OH]dt) for the transition between the initial steep increase and the nearly linear range depends primarily on the reaction rate constants of the phenolic intermediates. At high values of ∫[OH]dt the slope of the dependence between δ¹³C and ∫[OH]dt is mainly determined by the rate constant and the kinetic isotope effect for the reaction of nitrophenol with the OH radical as most of the aromatic precursor has been consumed (Fig. 3). Nevertheless, due to the continuing formation of nitrophenols from the precursor and the increase in δ¹³C of the precursor this slope is slightly steeper than predicted by the rate constant and the kinetic isotope effect for the reaction of the nitrophenol alone. It should be noted that the carbon isotope ratios of the precursor predicted by our mechanistic model are fully consistent with the range of carbon isotope ratios of aromatic VOCs in the atmosphere reported by Kornilova et al. (2016) (Fig. 3).

3.3 Comparison of predicted carbon isotope ratios with laboratory and ambient measurements

For 2,6-dimethyl-4-nitrophenol and methylnitrophenols, the lower end of the mass balance predictions is substantially heavier than the lower end of ambient observations; however, for methylnitrophenols mass balance predicts carbon isotope ratios well within the range of the laboratory results reported by Irei et al. (2015). The lower end of carbon isotope ratios predicted by Scenario 1 for 2,6-dimethyl-4-nitrophenol and methylnitrophenols is 3 ‰ to 4 ‰ heavier than the lower end of ambient observations reported by Saccon et al. (2015). Furthermore, six out of the seven carbon isotope ratios of methylnitrophenols observed in laboratory studies by Irei et al. (2015) are more than 2 ‰ lighter than predictions based on Scenario 1.

For 4-nitrophenol at small values of the precursor's PCA (∫[OH]dt≤10¹¹ s molecules cm⁻³), Scenario 3 predicts that the carbon isotope ratios are lower than the lower limit of ambient observations in an urban area of Toronto (Saccon et al., 2015). Similarly, the methylnitrophenol carbon isotope ratios predicted by Scenario 2 for a ∫[OH]dt of less than 3×10¹⁰ s molecules cm⁻³ are lighter than the lowest ambient observations (Saccon et al., 2015). Kornilova et al. (2016) report that 25 % of PCAs derived from carbon isotope ratio measurements of benzene and toluene are below 1.1×10¹¹ and 1.6×10¹⁰ s molecules cm⁻³, respectively. However, it has to be taken into account that the PCA derived from carbon isotope ratios of the precursor and the reaction product-based PCA are not necessarily identical for mixing air masses with different PCAs (see Sect. 3.5).

For high PCAs mass balance predicts a substantially lower slope for the dependence between the PCA and carbon isotope ratios than all three scenarios based on a mechanistic model. This is due to the conceptual limitation of the mass balance, which does not include the change in the carbon isotope ratio resulting from the atmospheric reaction of nitrophenols; consequently, it cannot be expected that a mass balance can correctly predict carbon isotope ratios at high PCAs.

Most of the observed nitrophenol carbon isotope ratios correspond to PCAs at the lower end of the PCAs predicted by Scenario 3 (Fig. 2). For this range a linear approximation can be used (Sect. S5). The estimated accuracy of the nitrophenol carbon isotope ratio measurements published by Saccon et al. (2015) is ±0.5 ‰. This corresponds to uncertainty in ∫[OH]dt in the range from 6×10⁹ to 9×10⁹ s molecules cm⁻³. This is similar to the sensitivity of ∫[OH]dt derived from the measurement of carbon isotope ratios of toluene (Kornilova et al., 2016). However, for PCAs derived from nitrophenol carbon isotope ratios, the uncertainty of model predictions will also contribute to the overall uncertainty. The overall uncertainty can be described as an uncertainty independent of the PCA and a contribution proportional to the PCA. Detailed estimates of uncertainty are given in Sect. S6.

3.4 PCA determined from carbon isotope ratios of nitrophenols

Based on the dependence between the PCA and the carbon isotope ratio of VOC reaction products (Fig. 3), ∫[OH]dt can be determined from measured carbon isotope ratios of ambient nitrophenols under the assumption of a uniform PCA for the observed nitrophenols. In Table 3, the average PCA determined from product carbon isotope ratios is compared with ∫[OH]dt values calculated directly from precursor isotope ratios, which were published by Kornilova (2012) and Kornilova et al. (2016). The nitrophenol-derived PCA is based on Scenario 3. It should be noted that, although collected at locations only 3 km apart, precursor and product samples were not collected simultaneously in most cases, and in some cases they were even collected in different years. Nevertheless, the substantial number of samples in most of the data sets and the low uncertainty of the mean PCA justify a comparison of averages and the distribution of precursor-derived PCA with ∫[OH]dt values calculated from second-generation product carbon isotope ratios.

Table 3 Averages and uncertainty of the mean PCA for nitrophenols in both PM and the gas phase in addition to PM calculated for Scenario 3. Also shown are the average carbon isotope ratios. The number of data points used is shown in parentheses. For comparison, the PCA calculated from the carbon isotope ratios of the precursor VOCs reported by Kornilova et al. (2016) for Toronto are included.

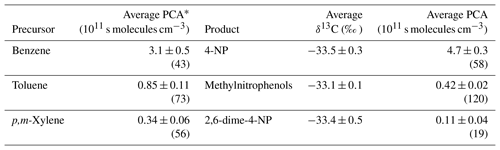
^∗ The average carbon isotope ratio and PCA determined by Kornilova (2012) and Kornilova et al. (2016).

Similar to the precursor carbon isotope ratio-based PCAs the product isotope ratio-derived PCAs increase substantially with decreasing precursor reactivity. This was explained by Kornilova et al. (2016) in terms of the mixing of air masses with different PCAs, which results in a lower weight for VOCs with high reactivity in aged air due to the faster photochemical removal. However, the weighting of contributions from different air masses differs between precursor isotope ratio-derived PCAs and product isotope ratio-derived PCAs. Details will be discussed in Sect. 3.5.

All precursor carbon isotope ratio-derived PCAs differ significantly from the PCAs determined from nitrophenol carbon isotope ratios. Toluene and xylene precursor-derived PCAs are lower than second-generation product-derived PCAs by approximately 4×10¹⁰ and 3×10¹⁰ s molecules cm⁻³, respectively. The average PCA derived from 4-nitrophenol carbon isotope ratios is approximately 50 % higher than the average PCA calculated from benzene carbon isotope ratios.

The uncertainty in the calculated average PCA can result from uncertainty in the parameters used to calculate PCAs from carbon isotope ratios. The 10th and 90th percentiles of the second-generation product carbon isotope ratios range from approximately −36 ‰ to −31 ‰. For this range, errors in the rate constants and the kinetic isotope effects for reactions of the precursors or the second-generation product only have a small impact on the dependence between the PCA and carbon isotope ratio (Figs. S2 and S3); therefore, these factors cannot explain the difference in average PCA. However, uncertainties in the carbon isotope ratios of VOC emissions as well as the isotope fractionation for reactions or branching of the intermediates in the reaction sequence resulting in nitrophenol formation can have a significant impact on PCAs calculated from nitrophenol carbon isotope ratios (Tables S5, S6).

However, PCAs derived from precursor's carbon isotope ratio measurements also strongly depend on the carbon isotope ratios of the emissions (Kornilova et al., 2016). For a 1 ‰ decrease in the emission isotope ratios, the PCAs derived from the carbon isotope ratios of benzene, toluene, and m-xylene increase by 0.9×10¹¹, 0.3×10¹¹, and 0.09×10¹¹ s molecules cm⁻³, respectively. Consequently, a 1 ‰ decrease in the carbon isotope ratio of emissions would reduce the difference between the precursor- and product-derived PCAs for benzene, toluene, and m-xylene by approximately 0.7×10¹¹, 0.15×10¹¹ s molecules cm⁻³, and less than 0.01×10¹¹ s molecules cm⁻³, respectively. A decrease of approximately 3 ‰ in the carbon isotope ratio of toluene emissions would be able to explain the difference in PCAs derived from toluene carbon isotope ratios and methylnitrophenol carbon isotope ratios. Similarly, a 2.5 ‰ increase in the carbon isotope ratio of benzene emissions would eliminate the difference between benzene and 4-nitrophenol-derived PCAs. However, a 2–3 ‰ error in the carbon isotope ratio of emissions is substantially larger than the uncertainty derived from VOC emission studies (Rudolph et al., 2002; Rudolph, 2007; Kornilova et al., 2016). Moreover, a carbon isotope ratio of benzene emissions that is 2.5 ‰ heavier than the value used in our calculations (Table 2) would not be compatible with the lower end of ambient benzene carbon isotope ratios reported by Kornilova et al. (2016). The discrepancies between the m,p-xylene and 2,6-dimethyl-4-nitrophenol-derived PCA cannot be explained by the uncertainty of the carbon isotope ratios of xylene emissions. However, it should be noted that the precursor-based PCA is derived from ambient observations of the combined isotope ratios of p-xylene and m-xylene, whereas only m-xylene is a precursor of 2,6-dimethyl-4-nitrophenol.

An increase in the carbon isotope fractionation specific for the formation of nitrophenols from the intermediate phenol of approximately 3 ‰ would result in very good agreement between precursor and second-generation product-derived PCA for toluene and xylene. However, for the conditions of the laboratory studies reported by Irei et al. (2015), a model with an additional isotope fractionation for the formation of nitrophenols from reaction of the intermediate such as this would predict carbon isotope ratios that were 2.5 ‰ lighter on average than the measured values. Based on the reported average experimental uncertainty of less than 1 ‰ this difference is significant at a confidence level higher than 99.9 %.

For the formation of 2,6-dimethyl-4-nitrophenol from m-xylene, no laboratory results are available that would allow for the constraint of the carbon isotope fractionation for reactions of the intermediate phenol. However, it is unlikely that carbon isotope fractionation for reactions of the intermediate dimethyl phenol are substantially larger than for the cresol intermediates.

The formation of 4-nitrophenol from the atmospheric oxidation of benzene proceeds via phenol, which reacts with OH radicals, in contrast to methyl substituted phenols, which primarily form by H-abstraction from the phenol group. Consequently, a reaction channel specific carbon isotope fractionation substantially different from that for reactions of methyl-substituted phenols cannot be ruled out. However, a model scenario that would result in good agreement between precursor and second-generation product-derived average PCAs for benzene also predicts that the lowest carbon isotope ratio for 4-nitrophenol exceeds approximately 30 % of the measured ambient carbon isotope ratios reported by Saccon et al. (2015) by more than the measurement uncertainty.

In addition to the formation of nitrophenols via OH-radical initiated oxidation, the reaction of the intermediate cresol with NO₃ also has to be considered as a possible reaction pathway for the formation of the methylnitrophenols (Carter et al., 1981). Here, it was proposed that at NO_x levels greater than 20 ppb and O₃ levels much larger than NO levels, the reaction with NO₃ would dominate over the proposed reaction with OH radicals. However, as [OH] and [NO₃] each exhibit very pronounced diurnal cycles, with [OH] peaking during the day and [NO₃] peaking at night (due to its fast photolysis during daytime), reactions with NO₃ during the day can be ignored. The proposed reaction pathway of the cresol + NO₃ reaction is via an addition reaction, which results in a similar estimated KIE to the addition of the OH group. Consequently, the carbon isotope ratio of nitrophenols formed via this reaction pathway will not depend significantly on the formation pathway. However, due to the possible nighttime processing of the phenolic intermediate in the presence of NO₃ this may create a difference between the true value for ∫[OH]dt and the PCA derived from the carbon isotope ratio of the nitrophenol. To determine this possible bias Scenario 3 was modified. At a value for ∫[OH]dt corresponding to the average carbon isotope ratios reported by Saccon et al. (2015), the OH-radical concentration was set to zero and replaced by a mechanism representing the reaction of the intermediate at 1 pmol mol⁻¹ of NO₃ until the phenolic intermediate was nearly completely depleted. The resulting average bias in ∫[OH]dt corresponds to less than 0.2 ‰ in the carbon isotope ratio for all of the methylnitrophenol isomers when compared with the unmodified Scenario 3.

The reactions of cresols with OH radicals are substantially faster than the formation of cresols from the reaction of toluene with OH radicals. This does not allow for the build-up of high concentrations of cresols during the day, and limits the possible role of the NO₃ reaction pathway. For the same reason it is unlikely that the NO₃ reaction pathway plays a substantial role in the formation of 4-nitrophenol or 2,6-dimethyl-4-nitrophenol.

Figure 4 shows the frequency distributions for PCAs determined from the carbon isotope ratios of 4-nitrophenol (Fig. 4a) and methylnitrophenols (Fig. 4b) using Scenario 3. For comparison, percentiles for PCAs derived from carbon isotope ratios of benzene (Fig. 4a) and toluene (Fig. 4b) reported by Kornilova et al. (2016) are also shown. Consistent with the difference in the average PCA (Table 3), PCAs derived from 4-nitrophenol carbon isotope ratios are shifted approximately 2×10¹¹ s molecules cm⁻³ towards higher values than PCAs derived from benzene carbon isotope ratios, but the width of the two PCA distributions are very similar (Fig. 4a). The PCA-independent uncertainty for the 4-nitrophenol carbon isotope ratio-derived PCA is only 7×10¹¹ s molecules cm⁻³ (Table S5), which cannot explain the difference in the average PCA. The PCA-dependent relative uncertainty is 32 % (Table S5). Combined with the PCA-independent uncertainty this could explain the difference in the average PCA. However, such a scenario also predicts a more than 30 % narrower distribution for 4-nitrophenol-derived PCAs than the best estimate. A distribution such as this would be substantially narrower than the distribution of PCAs derived from benzene carbon isotope ratios.

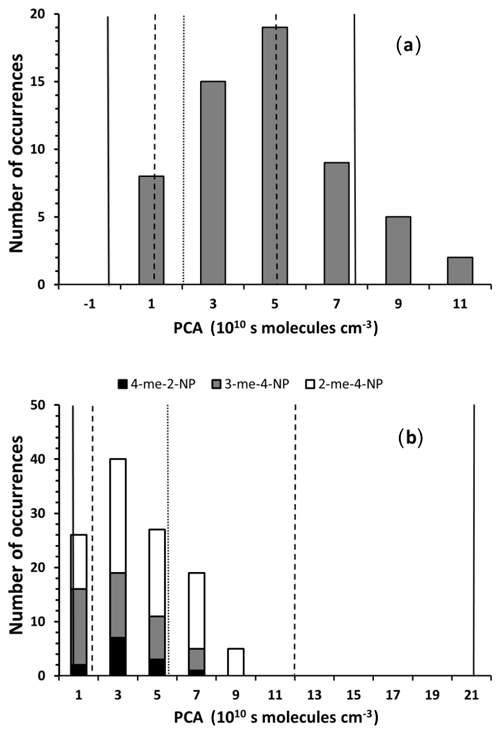
Figure 4 Frequency distribution of PCAs determined from the carbon isotope ratios of 4-nitrophenol (a) and methylnitrophenols (b) using Scenario 3. For comparison the median (dotted line), the 75th and 25th percentiles (dashed line), and the 10th and 90th percentiles (solid line) determined by Kornilova et al. (2016) from carbon isotope ratios of benzene (a) and toluene (b) are included.

The PCA distribution derived for methylnitrophenols is, compared to the toluene-derived distribution, not only shifted to lower values, but also much narrower (Fig. 4b). This discrepancy cannot be explained by the uncertainty of PCAs derived from methylnitrophenol carbon isotope ratios.

3.5 Average PCA and mixing of air masses

Based on the measurement of carbon isotope ratios of several aromatic VOCs, Kornilova et al. (2016) concluded that the mixing ratios and average PCAs of aromatic VOCs in Toronto are typically determined by the mixing of air masses with VOCs of different origin and different PCAs. While ∫[OH]dt values determined from the carbon isotope ratios of aromatic VOCs represent, for all practical purposes, the correct concentration weighted average PCA for the VOC studied (Rudolph and Czuba, 2000; Kornilova et al., 2016), the situation is different for PCAs derived from carbon isotope ratios of VOC reaction products such as nitrophenols. In the case of atmospheric mixing of VOCs and VOC reaction products the PCAs derived from product carbon isotope ratios can differ from the ∫[OH]dt calculated for VOC isotope ratios for several reasons.

For nitrophenols with different PCAs the decrease in the sensitivity of the PCA–carbon isotope ratio dependence outside of the linear range will reduce the apparent PCA derived from nitrophenols compared to the VOC-derived PCA. Conversely, with increasing PCA the VOC precursor concentrations will not only decrease due to atmospheric dilution but also due to chemical reactions, which reduce their weight for the average PCA. In contrast, nitrophenols are formed as a result of precursor reactions, which will counteract the effect of atmospheric dilution. However, in opposition to light aromatic hydrocarbons the polar nitrophenols are water-soluble and are found in both the particle and gas phase (Saccon et al., 2013). Consequently, they will be removed not only by chemical reactions, but also by wet and dry deposition. Carbon isotope fractionation resulting from physical removal processes is much smaller than isotope fractionation during chemical reactions and therefore will have little direct impact on the carbon isotope ratio of nitrophenols. However, physical removal processes will reduce the contribution of aged air masses to nitrophenol concentrations and therefore reduce the weight of aged air in samples representing air masses with different PCAs. Combined, these effects have the potential to create a complex situation with substantial differences in PCAs derived from precursor carbon isotope ratios compared with nitrophenol-derived PCAs.

Consequently, the mixing of aged air with fresh emissions of light aromatic VOCs can result in discrepancies between precursor carbon isotope ratio-derived PCAs and benzene carbon isotope ratio-derived PCAs. Lower values for precursor-derived PCAs can be expected if fresh emissions are mixed with aged air masses under conditions which allow for the accumulation of reaction products (Fig. S7a). The accumulation of polar low-volatility reaction products is not only limited by gas-phase reactions, but also by deposition (an example of the principle of the impact of deposition on PCAs is given in Sect. S7 in the Supplement).

While conceptually, mixing of two air masses with different PCAs explains the difference in the frequency of observations of between precursor- and product-derived PCAs, it can be expected that a range of PCAs will be a more realistic situation for urban sites. For the average precursor-derived PCA the distribution for individual PCA observations is known (Kornilova et al., 2016). We use these distributions to calculate the PCA distribution for 4-nitrophenol and understand the source of differences in the average PCA.

Figure 5 shows the resulting PCA distributions calculated for different depositional loss rates of 4-nitrophenol. With increasing loss by deposition, the centres of the distributions shift towards lower PCAs and become narrower, which is the consequence of decreasing contributions of air masses with high PCAs. The centre of the distribution resulting from a depositional loss rate five times faster than loss due to reaction with the OH radical has its maximum at a value for [OH]dt of approximately 5×10¹¹ s molecules cm⁻³, which is close to the average of PCAs derived from observed 4-nitrophenol carbon isotope ratios (Table 3).

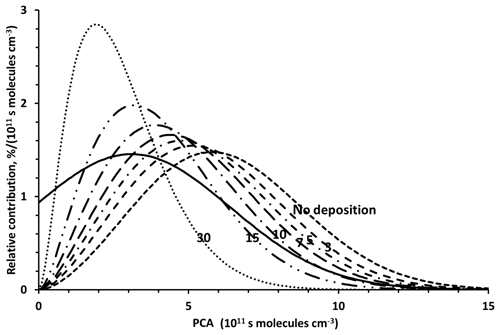
Figure 5 PCA distributions calculated for different depositional loss rates of 4-nitrophenol. The depositional loss rates are given as multiples of the chemical loss rate of 4-nitrophenol due to reaction with OH radicals. For comparison, the PCA distribution determined from the precursor carbon isotope ratio distribution (Kornilova et al., 2016) is also shown (solid line). The numbers on the graph indicate the OH-loss rates (similar to Fig. 6).

A comparison of the calculated distributions with the carbon isotope ratio-derived PCA distributions shows that not only the averages but also the widths of the distributions agree for depositional loss rates of 4-nitrophenol between three and seven times faster than reaction with the OH radical (Fig. 6) within the statistical errors of the observations. Based on an average OH-radical concentration of 10⁶ radicals cm⁻³ the 4-nitrophenol loss by deposition corresponds to a lifetime in the range of 6 days to 2 weeks. This is at the lower end of the atmospheric residence time of PM. However, only a small fraction of atmospheric 4-nitrophenol is found in the particle phase (Saccon et al., 2013), which explains the fact that the atmospheric residence time of 4-nitrophenol exceeds the average residence time of PM in the lower troposphere. Isotopic evidence does not allow for differentiation between different processes unless the isotope fractionation resulting from these processes differs. There are, consequently, no or very small isotope fractionation effects. To our knowledge there are no published values for wet or dry deposition rates of 4-nitrophenol. Consequently, we cannot identify the contribution of specific types of physical deposition processes. Based on current knowledge, chemical reactions in the condensed phase are too slow to contribute to the atmospheric loss of 4-nitrophenol (see the detailed estimate in Sect. S1 in the Supplement).

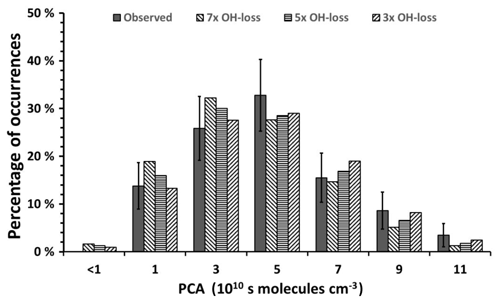
Figure 6 Comparison of the PCA distributions calculated for different depositional loss rates of 4-nitrophenol. The depositional loss rates are given as multiples of the chemical loss rate of 4-nitrophenol due to reaction with OH radicals. For comparison, the PCA distributions determined from the 4-nitrophenol carbon isotope ratios reported by Saccon et al. (2015) are also shown. The error bars represent the statistical uncertainty resulting from the limited number of observations.

The contribution of an air mass with a given PCA derived from 4-nitrophenol carbon isotope ratios depends on the deposition rate relative to the rate of the reaction of 4-nitrophenol and the benzene precursor with the OH radical (Sect. S7). However, there is no direct connection between deposition rates and the reaction rate with OH radicals; therefore, the ratio of the depositional loss rate over the impact of OH-radical chemistry can vary substantially for individual observations. For example, during rain events it is expected that deposition will be faster than average, whereas removal as well as formation of 4-nitrophenol due to reaction with OH radicals will be slower.

Indeed, rain has a substantial impact on the atmospheric concentrations of nitrophenols in the particle phase as well as in the gas phase. Substantial precipitation during sampling or on the day before sampling, reduces the nitrophenol concentrations by a factor of between 3 and 6 (Fig. 7a). In contrast, precipitation has no significant impact on the PCA (Fig. 7b). Changes in the PCA are within the uncertainty of the averages for different precipitation conditions and, except for 4-methyl-2-nitrophenol, are below 25 %. Precipitation during or immediately before sampling reduces contributions from air masses with different PCAs independent of the PCAs of the air masses. This reduces the atmospheric concentrations, but does not significantly impact the average PCA.

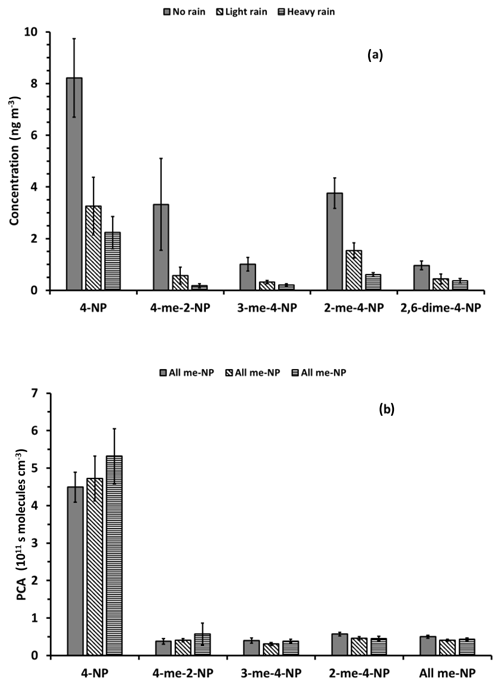
Figure 7 Average nitrophenol concentrations (a) and PCA (b) determined from carbon isotope ratios reported by Saccon et al. (2015) using Scenario 3 for different precipitation conditions during and before sampling. No rain refers to a total precipitation of less than 1 mm on the day of sampling and the day before; light rain refers to between 1 and 10 mm precipitation on the day of sampling or a total of >4 mm on the day of sampling and the day before; and heavy rain refers to >20 mm precipitation on the day of sampling or >10 mm on the day of sampling and >20 mm on the day before. Historical meteorological data were acquired from Environment Canada, Toronto North York site (http://climate.weather.gc.ca/historical_data/search_historic_data_e.html, last access: 23 April 2019).

For the precursor of methylnitrophenols, toluene, the PCA distribution is very different from the distribution observed for benzene, the precursor of 4-nitrophenol (Kornilova et al., 2016). The average PCA for toluene is only approximately one third of the benzene PCA, and the distribution peaks at a PCA close to zero, indicating a strong influence from very recent toluene emissions. The different behaviour of benzene and toluene is explained by the difference in reactivity and the different geographical distribution of emission sources (Kornilova et al., 2016). There are substantial sources of toluene within the Toronto metropolitan area, whereas most major sources of benzene are located in the surrounding regions.

The low average PCA derived from methylnitrophenol carbon isotope ratios is consistent with a dominant role of local emissions of toluene and demonstrates that air masses containing methylnitrophenols with high PCAs are of limited importance in determining the methylnitrophenol-derived PCAs. This is supported by the dependence of methylnitrophenol concentrations, carbon isotope ratios, and PCAs on wind speed shown in Figs. 8 and 9.

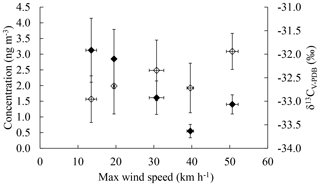
Figure 8 Plot of concentrations (black diamonds, left axis) and carbon isotope ratios (open diamonds, right axis) of 2-methyl-4-nitrophenol as a function of the maximum wind speed during sampling (Environment Canada, Historical Weather Data, Toronto North York site). Points were sorted in order of increasing wind speed, and each point is an average of 10 filter samples; the samples collected while there was precipitation were excluded. Error bars are the errors of the mean.

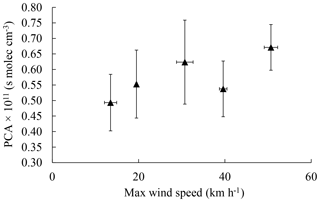
Figure 9 The PCA of 2-methyl-4-nitrophenol as a function of the maximum wind speed during sampling (Environment Canada, Historical Data, Toronto North York site). Points were sorted in order of increasing wind speed and each point is an average of 10 filter samples; the samples collected while there was precipitation were excluded. Error bars are the errors of the mean.

Figure 8 indicates that when the maximum wind speed over the sampling period is lowest, concentrations for 2-methyl-4-nitrophenol are highest and the corresponding carbon isotope ratios are lowest, indicating that methylnitrophenols may be dominantly produced from local emissions with limited mixing. This is consistent with the observed PCA (Fig. 9), which is lowest when the wind speed is lowest and increases with increasing wind speed. This can be explained by a decrease in the impact of local emissions resulting in a larger relative contribution of aged 2-methyl-4-nitrophenol originating from further away. A similar trend is observed for 3-methyl-4-nitrophenol, whereas 4-methyl-2-nitrophenol and 2,6-dimethyl-4-nitrophenol were not considered due to the small number of samples. 4-nitrophenol did not show any systematic trend. This is consistent with the lower reactivity of benzene compared to toluene, the 4-nitrophenol precursor, and the lower local emission rates for benzene (Kornilova et al., 2016). Both factors will greatly diminish the role of local emission and local photochemistry on the average PCA derived from 4-nitrophenol carbon isotope ratios.

4 Summary and conclusions

Similar to primary emissions of VOCs for secondary pollutants PCAs derived from carbon isotope ratios decrease with increasing reactivity of the precursor. However, for the nitrophenols studied here the reactivity of the secondary pollutant is highly correlated with the reactivity of the primary pollutant. Consequently, the available experimental evidence does not allow for a distinction between the impacts of the reactivity of primary or secondary pollutants. However, this evidence does allow for probing of the atmospheric processing of pollutants at different timescales and, consequently, differentiation between impacts from local emissions and long-range transport. In principle carbon isotope ratios of secondary organic pollutants provide better insight into the formation of secondary products than carbon isotope ratios of precursors. However, the use of carbon isotope ratios of secondary organic pollutants is currently limited by uncertainties and gaps in the understanding of formation mechanism and carbon isotope fractionation during the reaction sequence.

Available ambient observations of the carbon isotope ratios of precursor and second-generation products provide constraints for the parameters and their uncertainty in a mechanistic model, describing the dependence between the carbon isotope ratio and the PCA of second-generation products formed by the photo-oxidation of light aromatic VOCs. Predictions by this mechanistic model are consistent with the results of laboratory experiments studying the formation of methylnitrophenols from the photo-oxidation of toluene.

Mixing of air masses with nitrophenols that have different ∫[OH]dt values plays an important role in determining their carbon isotope ratios and needs to be considered in the interpretation of carbon isotope ratios of secondary organic pollutants and in the relation between concentrations and carbon isotope ratios. Loss processes such as physical processes based on diffusion, solubility, or chemical reactions, such as secondary isotope effects that cause only very small isotope fractionation, can still have a strong indirect impact on the carbon isotope ratio of nitrophenols if they play a major role in determining their atmospheric residence time. Consequently, the dependence between the atmospheric residence time and the carbon isotope ratios of nitrophenols results in a strong dependence between the average nitrophenol PCA and the deposition rate. The dependence of the deposition rate on factors only weakly related to the photochemical reactivity of the atmosphere can explain the absence of a significant dependence between the concentration of nitrophenols and their carbon isotope ratios. Similarly, dispersion in the atmosphere has an indirect but visible impact not only on the concentration of nitrophenols but also on their carbon isotope ratios. These results are based on observations in a major urban area with substantial local and regional nitrophenol precursor emissions. Due to the increasing uncertainty of the predictions of the mechanistic model with increasing PCAs and the non-linearity of the dependence between nitrophenol carbon isotope ratios and PCAs any extrapolation of these results to regions without substantial emission sources for the light aromatic compounds may be highly uncertain.