the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Assessing uncertainties of a geophysical approach to estimate surface fine particulate matter distributions from satellite-observed aerosol optical depth
Arlene M. Fiore
Gabriele Curci
Alexei Lyapustin
Kevin Civerolo
Michael Ku
Aaron van Donkelaar
Randall V. Martin
Health impact analyses are increasingly tapping the broad spatial coverage of satellite aerosol optical depth (AOD) products to estimate human exposure to fine particulate matter (PM2.5). We use a forward geophysical approach to derive ground-level PM2.5 distributions from satellite AOD at 1 km2 resolution for 2011 over the northeastern US by applying relationships between surface PM2.5 and column AOD (calculated offline from speciated mass distributions) from a regional air quality model (CMAQ; 12×12 km2 horizontal resolution). Seasonal average satellite-derived PM2.5 reveals more spatial detail and best captures observed surface PM2.5 levels during summer. At the daily scale, however, satellite-derived PM2.5 is not only subject to measurement uncertainties from satellite instruments, but more importantly to uncertainties in the relationship between surface PM2.5 and column AOD. Using 11 ground-based AOD measurements within 10 km of surface PM2.5 monitors, we show that uncertainties in modeled PM2.5∕AOD can explain more than 70 % of the spatial and temporal variance in the total uncertainty in daily satellite-derived PM2.5 evaluated at PM2.5 monitors. This finding implies that a successful geophysical approach to deriving daily PM2.5 from satellite AOD requires model skill at capturing day-to-day variations in PM2.5∕AOD relationships. Overall, we estimate that uncertainties in the modeled PM2.5∕AOD lead to an error of 11 µg m−3 in daily satellite-derived PM2.5, and uncertainties in satellite AOD lead to an error of 8 µg m−3. Using multi-platform ground, airborne, and radiosonde measurements, we show that uncertainties of modeled PM2.5∕AOD are mainly driven by model uncertainties in aerosol column mass and speciation, while model representation of relative humidity and aerosol vertical profile shape contributes some systematic biases. The parameterization of aerosol optical properties, which determines the mass extinction efficiency, also contributes to random uncertainty, with the size distribution being the largest source of uncertainty and hygroscopicity of inorganic salt the second largest. Future efforts to reduce uncertainty in geophysical approaches to derive surface PM2.5 from satellite AOD would thus benefit from improving model representation of aerosol vertical distribution and aerosol optical properties, to narrow uncertainty in satellite-derived PM2.5.
- Article
(4035 KB) - Full-text XML
-
Supplement
(1316 KB) - BibTeX
- EndNote
Exposure to ambient fine particulate matter (PM2.5) is estimated to cause more than 8 million attributable deaths worldwide in 2015 (Burnett et al., 2018) and is associated with an increase in the risk of cardiovascular and respiratory disease (Dominici et al., 2006; Peng et al., 2009). Evidence is emerging that exposure to PM2.5 has adverse health effects even at low concentrations (Crouse et al., 2012; Shi et al., 2015). Early studies relied on the nearest ground-based monitors to estimate PM2.5 exposure (e.g., Dockery et al., 1993; Laden et al., 2006), but lack of resolution of spatial and temporal gradients in population exposure may lead to substantial errors in health impact analyses.
Satellite remote sensing, which fills a spatial gap in ground-based networks, is playing an increasingly important role in PM2.5 exposure assessment (Cohen et al., 2017; Jerrett et al., 2017). Aerosol optical depth (AOD), a measure of the sum of light extinction by aerosols within the atmospheric column, is retrieved from a number of satellite instruments. The Moderate Resolution Imaging Spectroradiometer (MODIS) on board Terra and Aqua has provided twice-daily global AOD data for nearly 2 decades, and the Multi-Angle Implementation of Atmospheric Correction (MAIAC) product has refined the spatial resolution retrieved from MODIS to 1 km (Lyapustin et al., 2011, 2012; Lyapustin and Wang, 2018), offering the potential to reveal aerosol spatial variability within urban cores (Hu et al., 2014). A big challenge to inferring near-surface PM2.5 from column AOD retrieved from satellite instruments is to accurately describe the nonlinear and spatiotemporally varying relationship between PM2.5 and AOD, which depends on aerosol chemical composition, vertical profiles, aerosol optical properties, and the ambient environment (Griffin et al., 2012). Approaches to link satellite AOD with PM2.5 exposures are often classified into two categories: statistical (e.g., Di et al., 2016; Hu et al., 2014; Kloog et al., 2014) and geophysical (e.g., van Donkelaar et al., 2010, 2006). A two-stage process is also used with a geophysical approach followed by a statistical approach (e.g., van Donkelaar et al., 2015; de Hoogh et al., 2016; Shaddick et al., 2017).
Statistical approaches fit an optimized relationship between ground-based PM2.5 and satellite AOD along with other predictors (e.g., land use, meteorology, traffic density) using methods such as multiple linear regression (e.g., Gupta and Christopher, 2009; Lee et al., 2016), geographic regression (Hu et al., 2014), generalized additive models (e.g., Kloog et al., 2014), or machine learning (Di et al., 2016). In regions with high monitor density, the statistical methods generally agree better with ground-based observations than PM2.5 derived with a geophysical approach, but statistical methods rely on the availability of ground-based monitors to train the statistical model and are thus limited to regions with dense monitoring networks.
The geophysical approach that has been applied to AOD is a process-based forward approach that uses chemical transport models to explicitly simulate the spatially and temporally varying relationship between column AOD and PM2.5 (van Donkelaar et al., 2006). The satellite-derived PM2.5 is calculated by taking the product of satellite AOD with the modeled ratio of PM2.5 to AOD (van Donkelaar et al., 2006):
This geophysical approach has the advantage of broad spatial coverage that is not limited by the availability of in situ measurements (van Donkelaar et al., 2006) and thus has been integral for studying the global burden of disease attributable to ambient air pollution (Cohen et al., 2017). Van Donkelaar et al. (2010) estimate global annual average PM2.5 using AOD observed from both MODIS and MISR (Multi-angle Imaging SpectroRadiometer) by PM2.5–AOD relationships from a global chemical transport model (GEOS-Chem). They estimate an overall uncertainty of around 25 % for annual average satellite-derived PM2.5, but the uncertainty of the geophysical approach on short timescales is expected to be larger (van Donkelaar et al., 2012).
The overall uncertainty in deriving surface PM2.5 with the geophysical approach consists of uncertainty in the satellite AOD as well as the modeled PM2.5∕AOD. First, satellite observations of AOD are subject to uncertainties due to the viewing geometry, the presence of clouds and snow, and choices involved in modeling optical aerosol and surface properties (Superczynski et al., 2017; Toth et al., 2014). Second, since the relationship between PM2.5 and AOD is nonlinear and multivariate, modeled PM2.5∕AOD is subject to model uncertainties in aerosol vertical distributions, aerosol speciation, and the ambient environment. Third, even if a model accurately simulates the aerosol mass distribution, calculating AOD in models generally requires assumptions regarding the aerosol size distribution, aerosol species density, refractive index, and hygroscopic growth factors, all of which are sources of uncertainties (Curci et al., 2015). The ability of a particle to scatter and absorb light largely depends on its size, which varies significantly in nature (Stanier et al., 2004). As resolving the size distribution is computationally expensive (Adams, 2002), aerosols are typically assumed to follow a certain distribution (e.g., lognormal), which can introduce error. Moreover, aerosol water uptake (hygroscopicity) affects the aerosol size and optical properties, but the representation of hygroscopic factors in models varies considerably (Chin et al., 2002; Curci et al., 2015; Drury et al., 2010). The hygroscopic growth factor for organic carbon (OC) is especially uncertain, varying by organic species, and is poorly represented in models (Ming et al., 2005; Jimenez et al., 2009; Latimer and Martin, 2018). The impacts of these uncertainties on aerosol radiative forcing have been studied extensively, but their impacts on deriving surface PM2.5 from satellite-based column AOD have not yet been quantified.
Here, we estimate PM2.5 distributions over the northeastern US for 2011 using a geophysical approach that combines MAIAC AOD data with modeled PM2.5∕AOD relationships simulated with a regional air quality model, the Community Multiscale Air Quality (CMAQ) Modeling System. Compared to the global GEOS-Chem model used by van Donkelaar et al. (2016), CMAQ has finer spatial resolution (12×12 km2) and a locally refined emission inventory (see Sect. 2.2). We use an ensemble of surface, aircraft, and radiosonde measurements to evaluate different sources of uncertainties in satellite-derived PM2.5, especially at the daily scale. To evaluate the sensitivities of satellite-derived PM2.5 to the parameterization of aerosol optical properties, we conduct a series of sensitivity tests in an offline AOD calculation package (FlexAOD). The overarching goal of the comprehensive uncertainty analysis is to assess the relative importance of each uncertain factor, thereby advancing the process-level understanding of the relationship between satellite AOD and surface PM2.5 air quality.
2.1 Satellite AOD products
We use the high-resolution (1 km) daily AOD products retrieved from the MODIS instruments on board the Terra and Aqua satellites with the MAIAC algorithm, which applies time series analysis and image processing techniques (Lyapustin et al., 2011, 2018; Lyapustin and Wang, 2018). The spatial resolution of MAIAC (1 km) is finer than the conventional MODIS Dark Target and Deep Blue AOD products (10 km). The MAIAC algorithm improved upon the earlier Dark Target retrieval algorithm (MOD04) by explicitly including bidirectional reflectance (rather than the parameterized Dark Target approach), which improves accuracy over brighter surfaces, with similar accuracy over dark and vegetated surfaces (Lyapustin et al., 2011).
Using the quality flags provided, we filtered out pixels with or adjacent to cloud, snow, or ice. We follow the approach of Hu et al. (2014) to combine daily MAIAC AOD from Terra (overpasses around 10:30 local time) and Aqua (overpasses around 13:30 local time). For the pixels for which both Terra and Aqua have valid data, we take the average to reflect the mean daytime AOD. For pixels for which only one instrument has valid data, AOD may be biased accordingly towards morning or afternoon conditions. We find, on average, Terra MAIAC AOD is higher than Aqua MAIAC AOD by 0.005 (about 5 % of the annual average AOD) over the northeastern US in 2011, reflecting diurnal variations in AOD (Green et al., 2012) and potential calibration differences (Levy et al., 2018). To account for these differences, we fit two linear equations (R=0.87) between Terra MAIAC (AODT) and Aqua MAIAC AOD (AODA):
We use Eqs. (2) and (3) to predict the AOD from the other instrument when one of them is missing and then take the average. We find little seasonal variation in the linear relationship.
2.2 CMAQ model
The CMAQ is a regional multipollutant air quality model developed and maintained by the U.S. Environmental Protection Agency (EPA). We use the CMAQ (v5.0.2) model simulations for 2011 conducted at the New York State Department of Environmental Conservation (NYSDEC) for air quality planning purposes. The simulations are conducted for the eastern US with 12 km horizontal resolution and 35 vertical layers extending up to 50 hPa. The meteorological fields to drive CMAQ are provided by annual Weather Research and Forecasting (WRF) v3.4 model simulations over the continental US. Chemical boundary conditions are from the GEOS-Chem () global chemical transport model (Bey et al., 2001, version 8) generated by the EPA. The emission inventory is based on the 2011 National Emissions Inventory (NEI) and processed through the Sparse Matrix Operator Kernel Emissions (SMOKE; Houyoux et al., 2000). Biogenic emissions are generated with the Biogenic Emission Inventory System (BEIS) v3.61 (Pierce et al., 2002). Prescribed burning and wildfire emissions are computed using the SmartFire 2 (Raffuse et al., 2009). Mobile emissions are produced from the EPA's MOtor Vehicle Emission Simulator (MOVES) 2014a (US EPA, MOVES2014a). The gas-phase chemical mechanism is CB05, and the aerosol module is AERO6. Appel et al. (2013, 2017) provide details on the calculation of total PM2.5 mass and speciated aerosol mass, as well as model evaluation.
2.3 Offline AOD calculation
We calculate hourly AOD from the CMAQ model (AODCMAQ) offline from the archived hourly three-dimensional, speciated aerosol (i.e., sulfate, nitrate, ammonium, black carbon (BC), OC, sea salt, soil dust) distribution and meteorological fields (i.e., relative humidity, hereafter RH) using the Flexible Aerosol Optical Depth (FlexAOD) post-processing tool. FlexAOD was originally developed to calculate aerosol optical properties for the GEOS-Chem model. It is based on the NASA Codes for Computation of Bidirectional Reflectance of Flat Particulate Layers and Rough Surfaces (Mishchenko et al., 1999). We adapt FlexAOD to CMAQ by matching the aerosol speciation with GEOS-Chem based on Appel et al. (2013). Under the assumption of spherical particles, aerosol optical properties are calculated based on Mie theory. Given size distributions for each aerosol species, aerosol light extinction (EXTl) at a given model layer is calculated as follows (Curci, 2015):
where i refers to the species, N is the number of aerosol species (N=5: sulfate–nitrate–ammonium (SNA), OC, BC, dust, sea salt), is the Mie extinction efficiency of species i averaged over the dry size distribution, is the hygroscopic growth factor of species i at given RHl, ρi is aerosol density of species i, Mi,l is the aerosol mass of species i at layer l, and is the dry effective radius. AODCMAQ is then calculated as the vertical integral of EXTl across all model layers:
We use the recommended values of Drury et al. (2010) for aerosol density. The refractive index (m) in the default run is adapted from the Optical Properties of Aerosols and Clouds (OPAC) database (Hess et al., 1998). As CMAQ does not explicitly simulate the size distribution of aerosols, we assume lognormal distributions for all species except for dust (assumed to be a gamma distribution). The effective radius (re), or the area-weighted mean radius of lognormal size distribution can be derived as
where r0 is the specific modal radius, and σg is the geometric standard deviation. For the aerosol size distribution and density, we follow the recommended values of Drury et al. (2010) in the default run. We apply the single parameter κ to represent the hygroscopic growth of SNA and OC, as developed by Petters and Kreidenweis (2007) based on the κ-Kohler theory, which is the most commonly used function in the literature (Brock et al., 2016; Snider et al., 2016). The hygroscopic growth factor can be simplified as a function of parameter κ and RH (Snider et al., 2016):
Koehler et al. (2006) suggest κ for SNA (κSNA) ranges from 0.33 to 0.72, with a mean of 0.53. The hygroscopic growth factor of OC (κOC) varies with species and is correlated with the age of organics (Duplissy et al., 2011). Duplissy et al. (2011) and Jimenez et al. (2009) suggest κ for OC typically ranges from 0 to 0.2. We apply κSNA=0.53, and κOC=0.1. For BC and sea salt, we apply the hygroscopic growth factors reported in Chin et al. (2002). In addition to the default values, we test the sensitivities of the derived PM2.5 to uncertainties in aerosol optical property parameterization by varying each parameter across a range of values reported in the literature, as specified in Table 1.
Table 1Optical properties used to calculate AODCMAQ in FlexAOD. Values in square brackets represent the range of uncertainties for each parameter, which we used in FlexAOD sensitivity tests to quantify their impacts on the satellite-derived PM2.5.
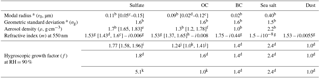
a Assuming lognormal distributions for all aerosol species except for dust. The effective radius is calculated as . b Drury et al. (2010). c Highwood et al. (2009). d Chin et al. (2002). e Sarangi et al. (2016). f Park et al. (2006). g OPAC (Hess et al., 1998). h Moise et al. (2015). i κ parameter (Petters and Kreidenweis, 2007). The hygroscopic factor (f) is calculated as f(RH) following Snider et al. (2016), where κ=0.53 in the default run, κ=0.33 for the low end, and κ=0.72 for the high end. j Calculated from the κ parameter equation, where κ=0.1 in the default run, and κ=0.2 for the high end (Jimenez et al., 2009; Duplissy et al., 2011). k Empirical hygroscopic growth factors used by the revised IMPROVE algorithm (Hand and Malm, 2006) to calculate light extinction (http://vista.cira.colostate.edu/Improve/the-improve-algorithm/, last access: 9 January 2019). The revised IMPROVE algorithm assumes no hygroscopic growth for OC.
2.4 Ground-based observations
The AErosol RObotic NETwork (AERONET) is a federated instrument network that provides ground-based information about aerosols including AOD, derived from sun photometer measurements of direct solar radiation (Holben et al., 1998). We use Level-2 (cloud screened and quality assured) daily average data from 13 sites over the northeastern US. We also include observed AOD from the Distributed Regional Aerosol Gridded Observation Networks (DRAGON)-USA 2011 field campaign, co-located with the DISCOVER-AQ aircraft campaign. The DRAGON campaign provides extensive sun photometer measurements of AOD at 38 sites along the flight path of DISCOVER-AQ from 1 July to 15 August 2011, which were incorporated into the AERONET database. To allow direct comparison with AODMAIAC and AODCMAQ, AERONET AOD measurements at 0.44 and 0.675 µm were interpolated to 0.55 µm using the Ångström exponent (the first derivative of AOD with wavelength, on a logarithmic scale) provided.
We use ground-based measurements of daily 24 h average PM2.5 from 152 EPA Air Quality System (AQS) sites over the northeastern US. Of the 152 sites, 13 sites have AERONET sites within 10 km of them (about the resolution of CMAQ). We consider these 13 sites to be “co-located” and use them to evaluate uncertainties in modeled PM2.5∕AOD relationships. We also use AQS aerosol speciation data at 54 sites, which include the Chemical Speciation Network (CSN) and the Interagency Monitoring of Protected Visual Environments (IMPROVE) visibility monitoring network.
To evaluate the modeled vertical profile of ambient RH, we use ground-based soundings from six radiosonde sites over the northeastern US. Aggregated daily data at 00:00 and 12:00 UTC are acquired from the NOAA Integrated Global Radiosonde Archive (IGRA), and modeled vertical profiles are sampled concurrently with radiosonde observations. We use the RH data calculated from vapor pressure, saturation vapor pressure, and ambient air pressure (Durre and Yin, 2008).
2.5 NASA DISCOVER-AQ 2011 field campaign
The NASA DISCOVER-AQ (Deriving Information on Surface conditions from Column and Vertically Resolved Observations Relevant for Air Quality) aircraft campaign over Baltimore–Washington, D.C. in July 2011 provides extensive, systematic, concurrent measurements of aerosol chemical, optical, and microphysical properties. The NASA P-3B aircraft performed 14 flights, which include 247 profiles (typically extending from 0.4 to 3.2 km above the surface) over six DRAGON sites (Crumeyrolle et al., 2014). We use the simultaneous measurements of aerosol composition (SNA, OC, BC), scattering, absorption, and extinction coefficients in dry (RH < 40 %), ambient, and wet (RH > 80 %) environments. To reduce the random uncertainties of individual observations and to allow direct comparison with CMAQ and ground-based observations, we aggregate the daily aircraft profiles horizontally to six locations corresponding to the six sites, and vertically to CMAQ model layers, and then we sample CMAQ modeled values consistently with observations.
3.1 Deriving surface PM2.5 from satellite observations
We derive satellite-based PM2.5 (hereafter PM2.5_MAIAC) over the northeastern US for 2011 by taking the product of daily average CMAQ modeled PM2.5∕AOD relationships (PM2.5_CMAQ∕AODCMAQ) with MAIAC AOD (AODMAIAC, Eq. 1). These unconstrained PM2.5 estimates (Fig. 1) are independent of surface observations. As PM2.5_MAIAC is determined as the product of observed AODMAIAC and modeled PM2.5_CMAQ∕AODCMAQ, the spatial patterns of PM2.5_MAIAC will be affected by the spatial variations in both AODMAIAC and PM2.5_CMAQ∕AODCMAQ. Figure 1a shows the summertime average (June, July, and August, JJA) AODMAIAC at 1 km resolution overlaid with AERONET observed AOD. While we find high AOD over some populated urban areas such as New York City (NYC), high AODMAIAC is also found over central New York State (NYS), away from major anthropogenic sources. In CMAQ, PM2.5 (PM2.5_CMAQ) occurs over regions with major anthropogenic sources such as NYC. AODCMAQ also shows a latitudinal dependence, with higher AOD at lower latitudes, which reflects (1) relatively high emissions of aerosol and its precursors from anthropogenic and biogenic sources over Maryland, Pennsylvania, and NYC and (2) latitudinal variations in RH that affect aerosol hygroscopic growth. The modeled PM2.5_CMAQ∕AODCMAQ varies spatially (1 standard deviation (SD) is 45 µg m−3 per unit of AOD), mainly driven by the spatial variations in PM2.5_CMAQ (R=0.86). We find the overall spatial pattern of satellite-derived PM2.5 correlates more strongly with modeled PM2.5_CMAQ∕AODCMAQ (R=0.97) than observed AODMAIAC (R=0.8), suggesting that the large-scale spatial variability reflects modeled rather than satellite-based distributions, at least under our framework for the northeastern US in summer. The temporal variability in PM2.5_MAIAC is also mainly driven by variability in PM2.5_CMAQ∕AODCMAQ (R=0.61), with little temporal correlation between regional average AODMAIAC and PM2.5_MAIAC (R=0.05, Fig. 2). At short timescales, the daily variability in regional average PM2.5_MAIAC shows stronger correlation with PM2.5_CMAQ∕AODCMAQ in all seasons except for JJA, when PM2.5_MAIAC values are driven by variability in both AODMAIAC (R=0.5) and PM2.5_CMAQ∕AODCMAQ (R=0.4, Fig. 2). Summertime AODMAIAC is higher than wintertime AOD by 50 %, while summertime PM2.5_MAIAC is lower than in winter by 46 %. Previous studies also found inconsistent seasonal cycles in AOD and PM2.5 (Ford et al., 2013; Kim et al., 2015). We attribute the opposite seasonal cycle in PM2.5_MAIAC and AODMAIAC to three factors: (1) weak boundary layer ventilation in winter that leads to sharp vertical gradients of aerosol distribution (Kim et al., 2015), (2) higher RH in summer that leads to larger hygroscopic growth, and (3) model overestimates of PM2.5 (especially OC) in wintertime and underestimates of PM2.5 in summertime, leading to an overestimate of the winter-to-summer decrease in PM2.5_CMAQ∕AODCMAQ (see Sect. 3.3).
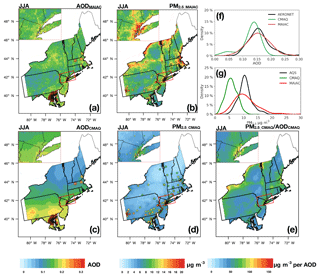
Figure 1Summertime (JJA) average (a) MAIAC AOD (AODMAIAC), (b) satellite-derived PM2.5 (PM2.5_MAIAC), (c) CMAQ model AOD (AODCMAQ), (d) CMAQ model PM2.5 (PM2.5_CMAQ), and (e) CMAQ modeled PM2.5∕AOD (PM2.5_CMAQ∕AODCMAQ) ratio overlaid with ground-based observations (AERONET, AQS, co-located AERONET and AQS sites) over the northeastern US with zoom-in maps over the New York City region in the upper left corner. (f) Density plot of AOD showing the distribution of MAIAC, CMAQ, and AERONET observed AOD sampled at AERONET sites. (g) Density plot of PM2.5 showing the distribution of satellite-derived, CMAQ, and AQS observed PM2.5 sampled at AQS sites.
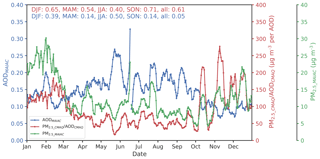
Figure 2Regional 10-day running average of (a) MAIAC AOD (AODMAIAC, blue), (b) CMAQ modeled PM2.5∕AOD relationship (PM2.5_CMAQ∕AODCMAQ, red), and (c) satellite-derived PM2.5 (PM2.5_MAIAC, green). The numbers on the upper left corner show the Pearson correlation coefficients (R) of PM2.5_MAIAC with PM2.5_CMAQ∕AODCMAQ (red) and AODMAIAC (blue).
While at larger spatial scales PM2.5_CMAQ∕AODCMAQ contributes more to the spatial and temporal variability in PM2.5_MAIAC than AODMAIAC, at smaller scales, over which we assume the spatial variability in PM2.5∕AOD is homogenous, incorporating fine-resolution satellite data reveals stronger spatial gradients (e.g., enhancements along industrial corridors) than PM2.5_CMAQ (Fig. 1b). In addition to refining spatial resolution, satellite-derived PM2.5 can correct model summertime biases in PM2.5. Observed AOD from AERONET and PM2.5 from AQS indicate an overall underestimate in both AODCMAQ (Fig. 1c; normalized mean bias (NMB) = −44 %) and PM2.5_CMAQ (Fig. 1d; NMB = −17 %) in summer. We find PM2.5_CMAQ∕AODCMAQ is overall consistent with the observed PM2.5∕AOD sampled at co-located AQS–AERONET sites (NMB = 0.9 %) as the ratio largely cancels out the model underestimates in both PM2.5 and AOD. AOD distributions retrieved from MODIS (AODMAIAC) agree better with AERONET AOD than AODCMAQ (NMB = 5 %, Fig. 1f), though we find small low biases at two sites in NYC and at most DRAGON sites over Maryland. Our derived distribution of PM2.5_MAIAC is thus closer to PM2.5 observed at AQS sites than PM2.5_CMAQ (NMB = 4.7 % vs. 44 % for PM2.5_CMAQ, Fig. 1g). However, the PM2.5_MAIAC distribution is wider than observed at AQS: the lowest 5 % is 5 vs. 7 µg m−3 for PM2.5_MAIAC vs. AQS PM2.5, and the highest 5 % is 16 vs. 13 µg m−3. We find that PM2.5_MAIAC is biased high over NYC, coastal regions of Massachusetts, the borders of upstate New York, and northern Vermont. Evaluation of PM2.5_MAIAC in other seasons shows larger biases and uncertainties (Fig. S1 in the Supplement). In the following sections, we examine sources of uncertainties and biases in satellite-derived PM2.5. We quantify the uncertainties in terms of bias (systematic) and random uncertainty. The bias uncertainty is linked to the overall accuracy, while the random uncertainty reflects random fluctuations in the measurements or the imprecision of the model resulting from imperfect modeling assumptions and simplifications.
3.2 Evaluation of satellite-observed AOD products
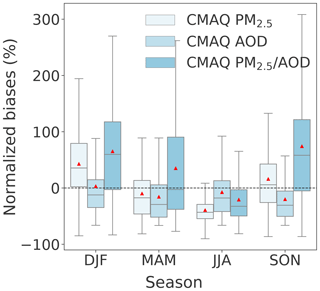
AODMAIAC in general agrees well with AERONET observations (spatial R=0.83, temporal R=0.85, MB = −0.01, and RMSE = 0.07). The performance of AODMAIAC evaluated at northeastern US AERONET sites is consistent with the evaluation of Superczynski et al. (2017) over North America (R=0.82, MB = −0.008). We find, however, that AODMAIAC in winter (December, January, and February, DJF) is biased high by 49 % () on average. The wintertime overestimate is likely due to residual snow contamination, which is below the detection limit, even though we applied a stringent data quality filter to remove pixels flagged as snow. We find the wintertime overestimate is most evident over northern latitudes (e.g., AERONET sites in Massachusetts; NMB ranges from 80 % to 180 %), where snow occurs more often. The NMBs of AODMAIAC are 15 % in March, April, and May (MAM), −5 % in JJA, and 17 % in September, October, and November (SON), though the quantile range of the error is large, suggesting that single observations have large random uncertainties (Fig. 3). Taking the 1σ standard deviation of the normalized biases as a metric of random uncertainty, we estimate the uncertainties of daily satellite observations to be around 80 % in DJF, 60 % in MAM and SON, and 50 % in JJA. Spatial and/or temporal averaging can reduce these random errors of satellite observations, which is evidenced as the smaller spread of errors than for monthly averages at the same spatial resolution, or daily data at coarser (10 km) resolution, but it does not reduce the overall MB between AODMAIAC and AODAERONET (Fig. 3). We find that spatially averaging AODMAIAC to 10 km leads to an overall increase in AODMAIAC. Temporal averaging, however, leads to an overall decrease in AODMAIAC except for DJF, leading to a smaller positive MB in SON (7 %) and MAM (7 %), but larger negative MB in JJA (−8 %) and positive MB (67 %) in DJF.
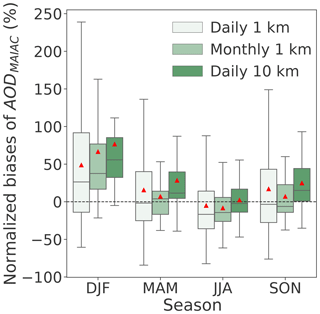
Figure 3Distribution of normalized biases of AODMAIAC evaluated at 52 AERONET (including DRAGON, only available for JJA) sites in four seasons of 2011 over the northeastern US using daily MAIAC AOD at 1 km resolution and 10 km resolution and monthly average MAIAC AOD composite (only including days when both satellite and AERONET measurements are available) at 1 km resolution. The box shows the interquartile range (IQR) while the whiskers extend to show the rest of the distribution with outliers (points that are either 1.5× IQR or more above the third quantile or below the first quantile) removed. The red triangles show the seasonal mean normalized biases. Note that the normalized bias is an asymmetric metric, for which model overestimates are unbounded, whereas model underestimates are bounded by −100 %; therefore the mean of normalized biases is typically higher than the median of the normalized biases.
3.3 Evaluation of modeled PM2.5∕AOD relationships
Three factors contribute to the overall uncertainty in the modeled PM2.5∕AOD relationship: (1) PM2.5_CMAQ, (2) AODCMAQ, and (3) the relation between (1) and (2). We evaluate uncertainties of the three factors at 13 paired AQS–AERONET sites (within 10 km of each other; about the resolution of CMAQ). Figure 4 shows the distribution of the biases of modeled daily PM2.5_CMAQ, AODCMAQ, and PM2.5_CMAQ∕AODCMAQ compared with observations. Generally, PM2.5_CMAQ biases vary seasonally: from +42 % in DJF to −39 % in JJA on average. In contrast, AODCMAQ biases show weaker seasonality. The NMBs of AODCMAQ are 3 % in DJF, −16 % in MAM, −7 % in JJA, and −20 % in SON. On the daily scale, biases of AODCMAQ are weakly correlated with the biases of PM2.5_CMAQ (R=0.14), suggesting model biases in AOD do not necessarily reflect biases in modeled PM2.5. This is in contrast with prior analysis of annual means for which emission biases drive similar biases in AOD and PM2.5 (van Donkelaar et al., 2013). The better accuracy of emissions in the northeastern US than elsewhere in the world allows processes other than emissions to be more important for the northeastern US. We find the seasonal biases in modeled PM2.5 are retained in the PM2.5_CMAQ∕AODCMAQ ratio, which exceeds the biases of PM2.5_CMAQ in DJF, MAM, and SON. As both PM2.5_CMAQ and AODCMAQ are biased low in JJA, the modeled PM2.5∕AOD bias (−20 %) is smaller than that of PM2.5_CMAQ (−39 %). Biases in PM2.5_CMAQ and AODCMAQ are oppositely signed in fall, leading to the largest mean biases of modeled PM2.5∕AOD (+74 %). The spread of the biases of PM2.5_CMAQ∕AODCMAQ is larger than that of PM2.5_CMAQ and AODCMAQ, with the standard deviation ranging from 50 % in JJA to 100 % in SON.
3.4 Relative importance of satellite AOD versus modeled PM2.5∕AOD to uncertainties in satellite-derived PM2.5
We have shown that both satellite AOD and modeled PM2.5∕AOD are subject to large uncertainties at the daily timescale. To directly compare the relative importance of the biases of satellite AOD vs. model PM2.5∕AOD for the satellite-derived PM2.5, we scale the biases of modeled PM2.5∕AOD with daily AODMAIAC, so that the biases are expressed in units of PM2.5 (µg m−3):
We then scale the biases of AODMAIAC with the daily modeled PM2.5∕AOD relationship:
We can also interpret ΔPM2.5_AOD and ΔPM2.5_Rel as the changes in derived PM2.5 if we use “true” observed AOD or PM2.5∕AOD instead of AODMAIAC or modeled PM2.5∕AOD. As shown in Fig. 5a, mean biases caused by modeled PM2.5∕AOD are +9.2 µg m−3 in DJF, +2.8 µg m−3 in MAM, −3.3 µg m−3 in JJA, and +7.7 µg m−3 in SON, which introduces larger biases to the derived PM2.5 than the MAIAC satellite product in all seasons (7.6 µg m−3 in DJF, +1.3 µg m−3 in MAM, −0.7 µg m−3 in JJA, and 0.9 µg m−3 in SON). Using the root-mean-squared ΔPM2.5_AOD to quantify the random uncertainty, satellite AOD contributes an overall random error of 8.3 µg m−3 to daily satellite PM2.5_MAIAC with the smallest error in JJA (5.1 µg m−3) and largest error in DJF (13.2 µg m−3), while modeled PM2.5∕AOD contributes an error of 10.8 µg m−3 (root-mean-squared ΔPM2.5_Rel), with the smallest error in JJA (6.5 µg m−3) and largest error in SON (15.2 µg m−3). The spread of the biases is larger for modeled PM2.5∕AOD than that for MAIAC AOD except for DJF. Our findings are consistent with Ford and Heald (2016), who use a higher-resolution (nested) version of the GEOS-Chem model and MODIS Dark Target AOD (Collection 6) to estimate 2 times larger uncertainties in surface PM2.5 resulting from modeled PM2.5∕AOD relationships than in satellite AOD.
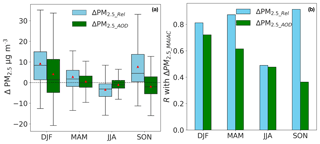
Figure 5(a) Box plots comparing the distribution of biases in daily PM2.5_MAIAC due to observational uncertainties in AODMAIAC (green, ΔPM2.5_AOD) versus model uncertainties in PM2.5_CMAQ∕AODCMAQ (blue, ΔPM2.5_Rel), evaluated consistently at 11 co-located AQS–AERONET sites over the northeastern US. (b) Pearson correlation coefficient between the biases in daily satellite-derived PM2.5 (ΔPM2.5_MAIAC, evaluated with AQS observations) and the biases in PM2.5_AOD attributed to observational uncertainties in AODMAIAC (ΔPM2.5_AOD) versus model uncertainties in PM2.5_CMAQ∕AODCMAQ (ΔPM2.5_Rel). ΔPM2.5_AOD is calculated by multiplying the biases of AODMAIAC with daily modeled PM2.5∕AOD relationships (Eq. 8). ΔPM2.5_Rel is calculated by multiplying the modeled PM2.5∕AOD biases with daily AODMAIAC (Eq. 9). The red triangles show the seasonal mean biases.
At the daily timescale, both ΔPM2.5_AOD and ΔPM2.5_Rel show large day-to-day variability: the 1σ standard deviation is 10.5 µg m−3 for daily ΔPM2.5_AOD and 8.3 µg m−3 for daily ΔPM2.5_Rel. Next, we evaluate the dependence of the biases of satellite-derived PM2.5 (denoted as ΔPM2.5_MAIAC; evaluated with AQS observed PM2.5) on ΔPM2.5_Rel versus ΔPM2.5_AOD by evaluating the Pearson correlation coefficients (R). Overall, ΔPM2.5_MAIAC is more strongly correlated with ΔPM2.5_Rel (R=0.85) than with ΔPM2.5_AOD (R=0.53), indicating the uncertainties of modeled PM2.5∕AOD are a more important driving factor to the uncertainties of daily satellite-derived PM2.5, which could explain 72 % variance (R2) in ΔPM2.5_MAIAC. In JJA, however, ΔPM2.5_MAIAC is moderately correlated with both ΔPM2.5_AOD (R=0.48) and ΔPM2.5_Rel (R=0.49), suggesting uncertainties of modeled PM2.5∕AOD and satellite AOD contribute equally to the uncertainties of satellite-derived PM2.5. We note that there is no statistically significant correlation between ΔPM2.5_Rel and ΔPM2.5_AOD, with R ranging from −0.4 in SON to 0.23 in JJA, which suggests that the errors caused by modeled PM2.5∕AOD and by satellite AOD are independent of each other.
3.5 Factors leading to uncertainties in modeled PM2.5∕AOD relationship
Uncertainties in the modeled PM2.5∕AOD relationship mainly reflect uncertain aerosol speciation, aerosol vertical profiles, ambient RH, and parameterizations for aerosol optical properties including aerosol density, size distribution, refractive index, and hygroscopic growth. Here we quantify the uncertainties from each factor and evaluate their impacts on the derived PM2.5.
3.5.1 Aerosol speciation
Aerosol optical properties vary with chemical composition. Model biases in the aerosol composition also affect the overall representation of particle hygroscopicity. For the same PM2.5 abundance, variations in the aerosol composition may alter the particle optical properties, especially hygroscopicity, and consequently the PM2.5∕AOD relationship. Figure 6a compares the modeled aerosol composition with ground-based observations averaged for each season. High biases in PM2.5_CMAQ in winter are largely due to model overestimates of OC by a factor of 3, and low biases in summer are due to a combination of underestimated SNA and OC. As a result, CMAQ overestimates the fraction of OC by about 20 % in DJF, 15 % in MAM, and less than 10 % in other seasons, while it underestimates the fraction of SNA by 5 % to 20 % in all seasons.
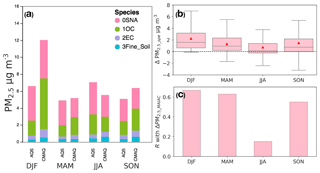
Figure 6(a) Seasonal average PM2.5 speciation from CMAQ vs. AQS observations in 2011 evaluated at 54 CSN and IMPROVE sites. (b) Box plots showing the distribution of estimated biases of daily satellite-derived PM2.5 due to model biases in PM2.5 speciation (ΔPM2.5_spe) by season for 2011. Red triangles show the seasonal mean biases. (c) Pearson correlation coefficient between the biases in PM2.5_MAIAC (ΔPM2.5_MAIAC) and ΔPM2.5_spe.
To estimate the impacts of model biases in aerosol speciation on AODCMAQ and PM2.5_MAIAC, we keep the total aerosol mass the same and redistribute AOD (AODCMAQ_ir) of each species i based on the observed fraction of each species (i.e., SNA, OC, elemental carbon (EC), soil dust; sea salt was excluded due to the limited ground-based measurements and its negligible contribution):
where PMTOT_obs and PMTOT_CMAQ are the total aerosol mass from observations and CMAQ, respectively, which are reconstructed by summing up SNA, OC, EC, and soil dust. Next, we estimate the uncertainty due to speciation as the differences in derived PM2.5_MAIAC (ΔPM2.5_spe) using the redistributed AODCMAQ_ir instead of the original AODCMAQ, shown in Fig. 6b. As SNA generally has the largest mass extinction efficiency (MEE), a low bias in SNA leads to an overall underestimate of AODCMAQ and therefore an overestimate of PM2.5_MAIAC, which is largest in winter (MB = 2.2 µg m−3, SD = 2.6 µg m−3) and smallest in summer (MB = 0.7 µg m−3, SD = 3.0 µg m−3). The estimated biases due to speciation show seasonal cycles similar to those of the modeled PM2.5∕AOD biases (Fig. 4), suggesting that aerosol speciation errors contribute to the seasonality in modeled PM2.5∕AOD biases. Overall, model–observation discrepancy in speciation causes an error (root-mean-squared ΔPM2.5_spe) of 4.0 µg m−3. On a daily basis, the correlation (R) between ΔPM2.5_spe and ΔPM2.5_MAIAC is over 0.5 for all seasons except JJA, which means model biases in speciation alone can explain more than 25 % variance (R2) in ΔPM2.5_MAIAC. Biases in speciation in JJA have relatively smaller impacts on the derived PM2.5, which contribute less than 1 µg m−3 MB and show weak correlation with ΔPM2.5_MAIAC (R=0.15).
3.5.2 Aerosol vertical profile
A caveat on the results in the Sect. 3.5.1 is that we assume the model errors in speciation are constant across all vertical layers, as AQS sites only provide observations near the surface. The DISCOVER-AQ aircraft campaign measured vertical variations in aerosol composition, although spatial and temporal coverage is limited. Figure 7a compares the modeled and observed vertical distributions of SNA, OC, and BC averaged over the DISCOVER-AQ campaign. We do not discuss sea salt and dust here since they contribute a negligible portion of the total aerosol mass in this region. Both the model and observations show SNA contributes more than half of the total aerosol across all vertical layers (Fig. 7). Aircraft observations show SNA decreases gradually with altitude with a nearly constant vertical gradient, while SNACMAQ is well mixed below 1.5 km and starts to decline at the same rate as SNAaircraft above 1.5 km (Fig. 7). CMAQ underestimates SNA below 1.5 km but overestimates SNA at higher altitudes. The positive model bias of SNA at higher altitudes may be due to excessive vertical transport or overestimation of RH (Sect. 3.4.3) and consequently overestimation of SO2 oxidation rate and aerosol water uptake. OC, however, is biased low at all altitudes, which is likely due to inaccurate treatment of the production of secondary organic aerosol (SOA) (Zhang et al., 2009). The newer version of CMAQv5.1 shows higher SOA concentration in summer with the introduction of new SOA species (Appel et al., 2017). BC is generally low during the campaign (typically lower than 0.3 µg m−3). BCCMAQ generally agrees well with BCaircraft, though BCCMAQ tends to overestimate BC between 1 and 3 km. Figure 7b compares CMAQ modeled and observed total aerosol mass (SNA + OC + BC) averaged during the campaign. CMAQ modeled aerosol mass is on average biased low below 2 km and biased high at higher altitudes (Fig. 7b).
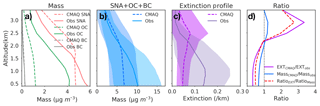
Figure 7Campaign-mean vertical profiles of (a) aerosol composition, (b) total mass (SNA + OC + BC), and (c) extinction from CMAQ vs. observations from the DISCOVER-AQ 2011 Baltimore–Washington, D.C. campaign. (d) Campaign-mean vertical profile of the model-to-observation ratio of extinction (RatioEXT), total aerosol mass (RatioMass), and RatioEXT∕RatioMass. Aircraft observations are first aggregated to match model layers, and corresponding model values are sampled concurrently with the time of observations. CMAQ modeled extinction is estimated with FlexAOD using the default parameters in Table 1. The shading in (b) and (c) shows the standard deviation of the day-to-day variability.
Next, we evaluate how the vertical distribution of aerosols relates to extinction. Figure 7c compares the modeled and observed average vertical extinction profiles. We find, consistent with the biases in mass, a low bias in the modeled extinction profile below 2 km and a high bias above (Fig. 7c). The biases in extinction and the biases in mass have the same signs for more than 80 % of data pairs and are strongly correlated (R=0.85). This suggests that the aerosol vertical profile of extinction is mainly indicative of mass distribution. However, column AOD measures the vertical integral of light extinction by aerosols, which means the modeled AOD biases would be proportional to modeled surface PM2.5 biases only if the biases in extinction are constant across all vertical layers. Since the biases of extinction change sign at higher altitude, the AOD biases reflect the competing effects of negative biases near the surface and positive biases at high altitudes, which lead to an overall negative bias of the PM2.5∕AOD relationship, consistent with the negative NMB of PM2.5∕AOD in July shown in Fig. 4.
To explore the causes of the model–observation discrepancy in extinction and the resulting impacts on the satellite-derived surface PM2.5, we calculate the vertical extinction profile in CMAQ by replacing the modeled aerosol mass distribution (SNA, OC, BC), total MEE (ratio of total mass to extinction), or RH with those of the aircraft observations, as shown in Fig. 8a. Replacing the modeled aerosol mass with observations, we find a decrease in extinction at high altitudes (above 2.5 km) and increase at low altitudes (below 2.5 km), but replacing the aerosol mass alone does not explain all of the model–observation differences. At high altitudes, only replacing the modeled total MEE without changing the mass captures the observed extinction. We attribute the model overestimate of extinction to model overestimation of extinction efficiency at high altitudes. A major contributor to the model overestimate of total MEE is its excessive RH at high altitudes, which leads to an overestimate of the hygroscopic growth. Replacing RH with observations largely corrects the high biases aloft but does not correct the low biases below 2 km (Fig. 8a). At lower altitudes, the model low biases are due to model underestimates of both aerosol mass and total MEE. Model underestimates of MEE are likely due to (1) uncertain optical properties, (2) other aerosols or gases (e.g., NO2, O3), or liquid clouds that can scatter or absorb light.
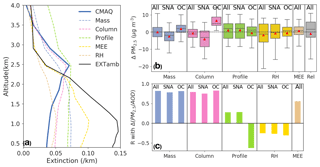
Figure 8(a) Campaign-mean vertical profiles of extinction calculated from CMAQ speciated aerosol fields using FlexAOD and those calculated by replacing modeled speciated aerosol mass (Mass), total column mass (Column), vertical profile shape (Profile), total mass extinction efficiency (MEE), and relative humidity (RH) with those observed during the DISCOVER-AQ 2011 Baltimore–Washington, D.C. campaign. EXTamb is the aircraft observed vertical extinction profile. (b) Box plots of the distribution of biases of PM2.5_MAIAC attributed to each factor shown in (a), and the biases of PM2.5_MAIAC attributed to modeled PM2.5∕AOD (Rel). Red triangles show the mean biases. (c) Pearson correlation coefficient between the biases in modeled PM2.5∕AOD relationships and the biases in modeled PM2.5∕AOD attributed to individual factors shown in (b).
Figure 8b shows the biases of PM2.5_MAIAC due to model uncertainties in vertical profiles of aerosol mass or MEE or RH, estimated by calculating the changes in PM2.5 when we replace the model vertical profiles with observations. Since the aircraft altitude ranges from 0.3 to 3.4 km, we use modeled values for the layers below 0.3 and above 3.4 km while attempting to minimize the discontinuity at both boundaries through vertical interpolation. As SNA and OC contribute most to extinction, we also evaluate the biases of vertical profiles of SNA and OC separately. We find that replacing modeled aerosol mass with observed mass leads to small positive biases in PM2.5_MAIAC (MB = 0.05 µg m−3, SD = 4.3 µg m−3), due to the combined effects of negative biases from SNA (MB = −2.5 µg m−3, SD = 4.7 µg m−3) and positive biases from OC (MB = +1.9 µg m−3, SD = 4.3 µg m−3).
We further separate the model–observation discrepancy in the vertical profiles as differences in total column mass versus in vertical profile shape by (1) keeping the modeled vertical distribution but adjusting the mass of each species uniformly so that the total column mass is equal to observation and (2) keeping the total column mass the same as in the model but redistributing the aerosol based on the observed vertical profiles. We find that redistributing the aerosol vertical profile leads to a positive mean bias in PM2.5_MAIAC (MB = 1.1 µg m−3, SD = 4.9 µg m−3), while the model–observation discrepancy in column mass leads to a negative mean bias (MB = −0.6 µg m−3, SD = 3.6 µg m−3) (Fig. 8b). The positive biases in the profile shape are mainly attributed to model biases of the vertical profile of SNA (MB = 1.2 µg m−3, SD = 5.0 µg m−3), which shows a larger fraction of SNA at higher altitude where aerosol is less effective at scattering light due to lower RH. The negative MB of column mass reflects a combination of negative biases of SNA (MB = −4.1 µg m−3, SD = 5.6 µg m−3) due to model overestimates of SNA column mass and positive bias of OC (MB = 6.7 µg m−3, SD = 4.4 µg m−3) due to model underestimates of column mass of OC. Model biases in MEE lead to a small positive MB of 0.6 µg m−3.
Using the observed PM2.5∕AOD acquired from paired AQS–AERONET sites, we estimate that model biases in modeled PM2.5∕AOD lead to a negative MB of −0.9 µg m−3 with large day-to-day variability (SD = 9.8 µg m−3) during the DISCOVER-AQ campaign, reflecting the model biases from different sources as discussed above. Next, we evaluate which factor drives the daily variability in the modeled PM2.5∕AOD biases the most by evaluating the R value between the estimated biases in modeled PM2.5∕AOD versus that attributed to individual factors. We find model bias in aerosol mass is the most deterministic factor for the biases in modeled PM2.5∕AOD (R=0.82, Fig. 8c). Model biases in aerosol mass can be due to either biases in column mass or vertical profile shape. We find model biases in modeled PM2.5∕AOD are more dependent on the biases in aerosol column mass (R=0.79), instead of vertical profile shape. Model biases in MEE show moderate correlation with model biases of PM2.5∕AOD (R=0.56). While model uncertainties in RH lead to an overall negative bias (MB = −1.7 µg m−3, SD = 7.4 µg m−3) to PM2.5_MAIAC, they are negatively correlated with model biases of PM2.5∕AOD ().
3.5.3 RH
Figure 8 suggests model biases in RH contribute a negative bias to the derived PM2.5_MAIAC during the DISCOVER-AQ aircraft campaign. Here we evaluate the impacts of modeled RH (RHCMAQ) biases on derived PM2.5 throughout the year using six atmospheric soundings over the northeastern US. We only assess the impacts of RH on the optical properties (i.e., hygroscopic growth) of aerosols. Comparing RHCMAQ with observed RH (RHobs), RHCMAQ is overall biased high with the largest biases in winter. To evaluate the resulting impacts on AODCMAQ, we recalculate the extinction using observed ambient RH from the soundings instead of RHCMAQ in Eq. (4). Replacing RHCMAQ with RHobs decreases extinction by ∼50 % on average from the surface to 5 km in both JJA and DJF (black lines in Fig. 9a and b). As AOD is the vertical integral of extinction, the total area between EXTsonde and EXTCMAQ (gray shading in Fig. 9a and b) indicates the differences in AOD due to differences in RH. The differences in RH below 3 km in DJF, MAM, and SON contribute more than 80 % to the total differences in AOD. In JJA, the contribution from higher versus lower altitudes is similar, despite small model RH biases below 2 km.
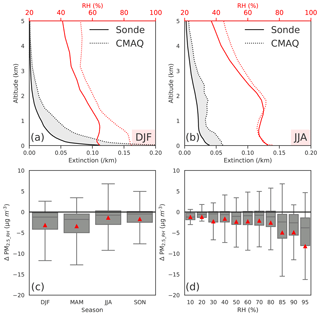
Figure 9(a) DJF and (b) JJA average vertical profiles of the CMAQ modeled versus observed RH at six atmospheric soundings over the northeastern US, and the modeled extinction versus that calculated by replacing modeled RH with observed values. The gray area shows the difference in the two extinction profiles, with the total area being the difference in AOD. (c) Box plots showing the impacts of model bias of RH on the derived PM2.5_MAIAC (ΔPM2.5_RH) in four seasons of 2011, which are calculated by comparing the PM2.5_MAIAC minus the one calculated using observed RH. (d) Box plots show the influence of model RH biases on the derived PM2.5_MAIAC (ΔPM2.5_RH) as a function of observed near-surface RH.
We evaluate how the model–observation discrepancy in RH affects the derived PM2.5 by calculating the changes in PM2.5_MAIAC (ΔPM2.5_RH) if EXTsonde is used instead of EXTCMAQ. As expected, model errors in RH lead to a negative bias in derived PM2.5_MAIAC of 3 µg m−3 on average (Fig. 9c). The negative biases in PM2.5_MAIAC due to RH are largest in spring (−3.5 µg m−3) and smallest in summer (−1.6 µg m−3). The hygroscopic growth factor is nonlinearly correlated with RH, which increases more rapidly at high RH (> 80 %) than at low to median RH (< 80 %, Fig. S2). Compared with median RH conditions, model RH errors lead to more than double ΔPM2.5_RH (−6.4 µg m−3 vs. 3 µg m−3) when observed near-surface RH > 80 % (Fig. 9d). At RH > 95 %, we find that the ΔPM2.5_RH can be as large as −20 µg m−3 (Fig. 9d). Despite the large impacts of model errors of RH at humid conditions, there is no significant correlation between ΔPM2.5_RH and ΔPM2.5_MAIAC (R=0.18, evaluated at nearby sites within 10 km), suggesting that uncertainty in RH is not a main contributor to the random uncertainties in satellite-derived PM2.5.
3.5.4 Uncertainties in the parameterization of aerosol optical properties
In previous sections, we demonstrated that the satellite-derived PM2.5 depends on the accuracy of the model simulation. Even with a perfect simulation, satellite-derived PM2.5 will be sensitive to the parameterization of aerosol optical properties, which would affect the MEE. We evaluate the uncertainties associated with the parameterization of aerosol optical properties by varying each parameter (Table 1), and we calculate the corresponding changes in the derived PM2.5_MAIAC. Figure 10 shows the range of uncertainty in annual average PM2.5_MAIAC due to uncertain aerosol size distributions, hygroscopicity, refractive index, and aerosol species density.
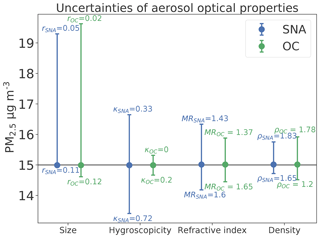
Figure 10Uncertainties in annual average satellite-derived PM2.5_MAIAC due to uncertainties of size distribution, hygroscopicity, refractive index, and aerosol species density of sulfate–nitrate–ammonium (SNA; blue) and organic carbon (OC; green) sampled over AQS sites. The circle shows the annual average satellite-derived PM2.5_MAIAC using the default parameters to calculate AODCMAQ in FlexAOD (Table 1). The error bars represent the range of PM2.5_MAIAC using different values for each parameter. The labels indicate the corresponding minimum or maximum parameter values that produce the range shown in PM2.5_MAIAC. The horizontal line at 15 µg m−3 indicates the annual average PM2.5_MAIAC calculated using default values for each aerosol optical property in the base FlexAOD.
The size of a particle is a defining characteristic of aerosol light extinction (Mishchenko et al., 1999). To evaluate model sensitivities to the uncertainties in size distribution, we vary the r0 of SNA from 0.05 to 0.15 with a 0.02 increase each time to cover the range of values reported in the literature. For OC, we calculate AODCMAQ with r0=0.02, 0.06, 0.09, and 0.12 µm, all values used in previous studies (Hess et al., 1998; Chin et al., 2002; Highwood, 2009; Drury et al., 2010). Annual average PM2.5_MAIAC could vary by up to 5 µg m−3 (32 %) with the choice of a modal radius of either rSNA or rOC, which is the largest source of uncertainty among the four parameters (Fig. 10). We find that AODCMAQ reaches a maximum with rSNA=0.07 µm (reff=0.12 µm) and minimum with rSNA=0.05 (reff=0.15 µm), while PM2.5_MAIAC reaches a maximum with rSNA=0.05 (reff=0.09 µm) and minimum with rSNA=0.11 (reff=0.19 µm), suggesting the impacts of size distribution are nonlinear and nonuniform (Fig. S3). Mie scattering of a particle tends to be most effective when the particle's diameter is near the wavelength of interest (0.55 µm). As hygroscopic particle growth also affects the size distribution, depending on ambient RH and the hygroscopic growth factor, reducing (or increasing) the dry effective radius could move the bulk aerosol size either closer to or further from 0.55 µm and thus either increase or decrease the extinction. For OC, as the effective radius and the hygroscopic growth factor are smaller than for SNA, increasing the modal radius leads to more effective scattering, and thus larger AODCMAQ and smaller PM2.5_MAIAC. Relative to the default rOC=0.09 µm assumed by Drury et al. (2010), using the rOC (0.02 µm) recommended by Chin et al. (2002a) increases PM2.5_MAIAC by 5 µg m−3 (32 %) on average, worsening the positive biases of PM2.5_MAIAC. Increasing rOC to 0.12 µm as recommended by Highwood et al. (2009) has little effect, decreasing PM2.5_MAIAC by 2 % on average.
The uncertainty of hygroscopicity lies in two aspects: (1) the function shape and (2) the parameters. Figure S2 compares the κ function shape with the hygroscopic growth factors used by the IMPROVE network (Hand and Malm, 2006), the default algorithm used to calculate AOD online in CMAQ, with that proposed by Chin et al. (2002) (Table 1). Using the DISCOVER-AQ aircraft data to evaluate the parameterization of hygroscopic growth, we find that the κ parameter best characterizes the observed hygroscopic growth factor (Fig. S2c). Latimer and Martin (2018) similarly found that implementing a κ formulation instead of hygroscopic growth based on OPAC improved the GEOS-Chem representation of mass scattering efficiency. Thus, we choose the κ parameter to represent the hygroscopic growth factor, and the uncertainty estimate here only reflects uncertainties in the κ parameter. In practice, changes in aerosol composition could have even larger effects on hygroscopicity than uncertainties in κ as discussed in Sect. 3.5.1.
To test the sensitivity of satellite-derived PM2.5 to uncertainties in the κ parameter, we compute AODCMAQ using the low (0.33) and high end of κ (0.72) for SNA as suggested by Koehler et al. (2006). As the hygroscopic properties of inorganic salts are relatively well known, the range of uncertainty for f(RH) of SNA is 30 % at most (Fig. S2b). OC, however, is composed of thousands of species with distinct hygroscopicities. Assuming κOC ranges from 0 (non-hygroscopic) to 0.2 (Jimenez et al., 2009; Duplissy et al., 2011), the range of f(RH) of OC can be as large as a factor of 2 at high RH > 96 % (Fig. S2a). Despite the larger uncertainty of κOC, we find the overall impacts of the uncertainties of κOC on the derived PM2.5 (0.3 µg m−3, 2 % of annual average PM2.5_MAIAC) are smaller than those of κSNA (1.6 µg m−3, 11 % of annual average PM2.5_MAIAC). The small impacts of κOC reflect the relatively small portion and the less hygroscopic nature of OC. For single observations, varying κSNA leads to a maximum increase in PM2.5_MAIAC by 20 % and a maximum decrease by 28 %. Varying κOC increases PM2.5_MAIAC by 10 % or decreases PM2.5_MAIAC by 18 % at most. The overall impact of the uncertainties of κSNA ranks second among the four parameters for SNA, while κOC has the smallest impacts on the derived PM2.5 (Fig. 10).
The refractive index (m) determines the Mie extinction efficiency, which is subject to uncertainties mostly due to the lack of measurements (Kanakidou et al., 2005). mSNA in OPAC (default value) is slightly different from that recommended in Chin et al. (2002) and Highwood (2009). Moise et al. (2015) suggest mOC varies by species, with its real part ranging from 1.37 to 1.65. We calculated another version of AODCMAQ by varying the real part of mSNA and mOC using the lowest and highest values reported in the literature. We find the annual average PM2.5_MAIAC decreased by 0.8 µg m−3 (6 %) using the high end of mR_SNA, while it increased by 1.3 µg m−3 (9 %) on average using the low end. Though mR_OC has a wider range of uncertainty, its impacts on PM2.5_MAIAC (−4 % to +6 %) are smaller than that of mR_SNA. While the overall impacts on PM2.5_MAIAC due to uncertainties of mR_SNA are generally within 10 % for single observations, PM2.5_MAIAC can change by more than 20 % under SNA-dominated and high-RH environments. The overall uncertainty due to mR_OC is generally within 5 % for single observations, with a few cases (< 10 % of the total data) in which the relative change in PM2.5_MAIAC can exceed 10 %.
As aerosol density (ρ) is assumed to be constant for each species, varying ρ has the same effect on the extinction of given species. We vary the aerosol density of SNA from 1.65 to 1.83 g cm−3 based on the uncertainty estimate from a laboratory study of Sarangi et al. (2016), which translates to an uncertainty of −3 % to 7 % for AODSNA, and the aerosol density of OC from 1.2 to 1.78 g cm−3 following Park et al. (2006), which translates to an uncertainty in AODOC ranging from −8 % to 37 %. We find aerosol species density, in general, contributes least to the overall uncertainty in satellite-derived PM2.5. Varying ρOC across the range in Table 1 increases annual average PM2.5_MAIAC by 0.9 µg m−3 (6 %) or decreases it by 0.6 µg m−3 (3 %) at most. As the aerosol density of inorganic salt is less uncertain, varying ρsulf leads to negligible changes in annual average PM2.5_MAIAC at both the high (0.7 µg m−3, 5 %) and low (−0.5 µg m−3, −2 %) ends.
We derive surface PM2.5 distributions from satellite observations of AOD (MAIAC products) at 1 km resolution for 2011 over the northeastern US using a geophysical approach that simulates the relationship between surface PM2.5 and AOD with a regional air quality model (CMAQ) and offline AOD calculation package (FlexAOD). We find that the fine spatial resolution of MAIAC AOD reveals more spatial detail (“hot spots”), including over populated urban areas or along major roadways. While the geophysical approach has shown promise for mapping the PM2.5 exposure at seasonal to annual scales (van Donkelaar et al., 2010, 2016), we show that estimating PM2.5 from satellite AOD at the daily scale is not only subject to large measurement uncertainty in satellite AOD products, but more importantly, to uncertainty in daily variations in the relationship between surface PM2.5 and column AOD. We take advantage of multi-platform in situ observations available over the northeastern US to quantify different sources of uncertainties in the satellite-derived PM2.5, with a particular focus on the daily scale. We use observed AOD from AERONET sun photometers to quantify uncertainties in satellite and modeled AOD; co-located AQS PM2.5 and AERONET sites to evaluate modeled PM2.5∕AOD relationships; IMPROVE and CSN aerosol speciation data to evaluate model uncertainties of aerosol composition; and atmospheric soundings to evaluate modeled RH, as well as their impacts on PM2.5 derivation. To assess the uncertainties associated with aerosol vertical profiles, we use the extensive concurrent measurements of extinction and aerosol composition available from the NASA DISCOVER-AQ 2011 campaign over Baltimore–Washington, D.C. Finally, we estimate intrinsic uncertainties associated with the model parameterization of optical properties by testing sensitivities of satellite-derived PM2.5 to variations in each individual parameter across ranges reported in the literature using FlexAOD.
As the relationship between surface PM2.5 and column AOD is nonlinear and spatiotemporally heterogeneous, satellite AOD alone is unable to fully resolve the spatial and temporal variability in ground-level PM2.5. We find that large-scale spatial and temporal variability in satellite-derived PM2.5 correlates more strongly with the variability in modeled PM2.5∕AOD than with satellite-derived AOD. At the daily scale over the northeastern US, modeled PM2.5∕AOD introduces larger mean biases to satellite-derived PM2.5 than the satellite retrievals. Uncertainties in modeled PM2.5∕AOD explain more than 70 % variance in the uncertainties of satellite-derived PM2.5, suggesting that the precision of daily satellite-derived PM2.5 depends on the capability of models to simulate the day-to-day variability in the relationship between PM2.5 and AOD.
Uncertainties in modeled PM2.5∕AOD relationships can be attributed to several factors, including uncertain model aerosol speciation, vertical profiles, RH, and the parameterization of aerosol optical properties. We find that seasonally varying biases in modeled PM2.5∕AOD reflect biases in aerosol speciation, particularly OC, which is overestimated in the cold season and underestimated by CMAQ in the warm season. Biases in aerosol composition in turn affect aerosol hygroscopicity. The CMAQ model generally overestimates RH, especially above 2 km, contributing to an overall negative bias to satellite-derived PM2.5, particularly for more humid conditions. Using concurrent measurements of vertical profiles of aerosol extinction and composition available from the DISCOVER-AQ 2011 aircraft campaign, we show that the aerosol extinction is indicative of mass distributions. Biases in modeled extinction, however, vary with altitude, such that model biases in vertically integrated column AOD do not necessarily reflect model biases in surface PM2.5. We find that model uncertainties in column mass and in the MEE drive the variability in overall uncertainty in modeled PM2.5∕AOD, while RH and aerosol vertical profile shape contribute some systematic bias.
Even with a model that perfectly simulates the distribution of aerosols, calculating AOD is subject to additional uncertainties in aerosol size distributions, hygroscopic growth factor refractive indices, and aerosol density. Our uncertainty analysis involving a series of sensitivity tests in FlexAOD indicates that for SNA, the uncertainties in size distributions contribute most to uncertainty in the derived PM2.5 (32 %), followed by the hygroscopicity parameter κ (11 %), refractive index (9 %), and aerosol density (5 %). For OC, size distribution is also the largest source of uncertainty in the derived PM2.5 (32 %). Despite the large uncertainty of the hygroscopicity of OC, its impact on the satellite-derived PM2.5 is negligible (2 %), even smaller than uncertainties associated with the refractive index and aerosol density (6 % each).
Based on this uncertainty analysis, we identify opportunities and directions to develop the applications of satellite-derived PM2.5 using the geophysical approach, especially at finer spatial and temporal scales. Van Donkelaar et al. (2016) found that calibration with ground-based PM2.5 measurements improves the performance of satellite-based PM2.5 at the annual scale, although such calibration is more challenging at short timescales (van Donkelaar et al., 2012). As the uncertainties in satellite-derived PM2.5 reflect multiple factors, calibration targeting specific sources of uncertainty would help further refine the geophysical approach. Additional collocated measurements of both PM2.5 and AOD would be valuable to further evaluate the relationship between surface PM2.5 and satellite AOD (Snider et al., 2015). Routine measurements of aerosol vertical profiles would aid uncertainty attribution and likely lead to improved models and thereby reduce the overall uncertainty in satellite-derived PM2.5. Quantifying source-specific uncertainties would not only facilitate future model improvement but more importantly benefit applications of the satellite-derived PM2.5 products to health studies.
Data and code behind the figures are provided in the Columbia University Academic Commons (Jin, 2018). The CMAQ model output can be obtained by contacting Xiaomeng Jin (xjin@ldeo.columbia.edu). The FlexAOD code is available upon request by contacting Gabriele Curci (gabriele.curci@aquila.infn.it).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-295-2019-supplement.
XJ, AMF, AvD, and RVM designed the experiments. GC developed the FlexAOD code for CMAQ. AL provided MAIAC AOD data. KC and MK conducted the CMAQ simulation. XJ carried out the data analysis and prepared the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
Although this paper was reviewed internally, it does not necessarily reflect the views or policies of the New York State Department of Environmental Conservation.
Support for this study was provided by the New York State Energy Research and
Development Authority (grant number 91268) and NASA Health and Air Quality
Applied Sciences Team (HAQAST, grant NNX16AQ20G). This is Lamont-Doherty
Earth Observatory contribution 8279. The authors thank Melanie Follette-Cook
of NASA GSFC and Morgan State University for her help in obtaining the
DISCOVER-AQ aircraft data. The authors thank Gus Correa for his help in
obtaining, processing, and archiving CMAQ data. We acknowledge useful
discussions with Yang Liu from Emory University and Dan Westervelt from
Lamont-Doherty Earth Observatory of Columbia University.
Edited by: Robert Harley
Reviewed by: two anonymous referees
Adams, P. J.: Predicting global aerosol size distributions in general circulation models, J. Geophys. Res., 107, 4370, https://doi.org/10.1029/2001JD001010, 2002.
Appel, K. W., Pouliot, G. A., Simon, H., Sarwar, G., Pye, H. O. T., Napelenok, S. L., Akhtar, F., and Roselle, S. J.: Evaluation of dust and trace metal estimates from the Community Multiscale Air Quality (CMAQ) model version 5.0, Geosci. Model Dev., 6, 883–899, https://doi.org/10.5194/gmd-6-883-2013, 2013.
Appel, K. W., Napelenok, S. L., Foley, K. M., Pye, H. O. T., Hogrefe, C., Luecken, D. J., Bash, J. O., Roselle, S. J., Pleim, J. E., Foroutan, H., Hutzell, W. T., Pouliot, G. A., Sarwar, G., Fahey, K. M., Gantt, B., Gilliam, R. C., Heath, N. K., Kang, D., Mathur, R., Schwede, D. B., Spero, T. L., Wong, D. C., and Young, J. O.: Description and evaluation of the Community Multiscale Air Quality (CMAQ) modeling system version 5.1, Geosci. Model Dev., 10, 1703–1732, https://doi.org/10.5194/gmd-10-1703-2017, 2017.
Bey, I., Jacob, D. J., Yantosca, R. M., Logan, J. A., Field, B. D., Fiore, A. M., Li, Q. B., Liu, H., Mickley, L. J., and Schultz, M. G.: Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation, J. Geophys. Res.-Atmos., 106, 23073–23095, https://doi.org/10.1029/2001JD000807, 2001.
Brock, C. A., Wagner, N. L., Anderson, B. E., Attwood, A. R., Beyersdorf, A., Campuzano-Jost, P., Carlton, A. G., Day, D. A., Diskin, G. S., Gordon, T. D., Jimenez, J. L., Lack, D. A., Liao, J., Markovic, M. Z., Middlebrook, A. M., Ng, N. L., Perring, A. E., Richardson, M. S., Schwarz, J. P., Washenfelder, R. A., Welti, A., Xu, L., Ziemba, L. D., and Murphy, D. M.: Aerosol optical properties in the southeastern United States in summer – Part 1: Hygroscopic growth, Atmos. Chem. Phys., 16, 4987–5007, https://doi.org/10.5194/acp-16-4987-2016, 2016.
Burnett, R., Chen, H., Szyszkowicz, M., Fann, N., Hubbell, B., Pope, C. A., Apte, J. S., Brauer, M., Cohen, A., Weichenthal, S., Coggins, J., Di, Q., Brunekreef, B., Frostad, J., Lim, S. S., Kan, H., Walker, K. D., Thurston, G. D., Hayes, R. B., Lim, C. C., Turner, M. C., Jerrett, M., Krewski, D., Gapstur, S. M., Diver, W. R., Ostro, B., Goldberg, D., Crouse, D. L., Martin, R. V., Peters, P., Pinault, L., Tjepkema, M., van Donkelaar, A., Villeneuve, P. J., Miller, A. B., Yin, P., Zhou, M., Wang, L., Janssen, N. A. H., Marra, M., Atkinson, R. W., Tsang, H., Quoc Thach, T., Cannon, J. B., Allen, R. T., Hart, J. E., Laden, F., Cesaroni, G., Forastiere, F., Weinmayr, G., Jaensch, A., Nagel, G., Concin, H., and Spadaro, J. V.: Global estimates of mortality associated with long-term exposure to outdoor fine particulate matter, P. Natl. Acad. Sci. USA, 115, 9592–9597, https://doi.org/10.1073/pnas.1803222115, 2018.
Chin, M., Ginoux, P., Kinne, S., Torres, O., Holben, B. N., Duncan, B. N., Martin, R. V., Logan, J. A., Higurashi, A., and Nakajima, T.: Tropospheric aerosol optical thickness from the GOCART model and comparisons with satellite and Sun photometer measurements, J. Atmos. Sci., 59, 461–483, https://doi.org/10.1175/1520-0469(2002)059<0461:TAOTFT>2.0.CO;2, 2002.
Cohen, A. J., Brauer, M., Burnett, R., Anderson, H. R., Frostad, J., Estep, K., Balakrishnan, K., Brunekreef, B., Dandona, L., Dandona, R., Feigin, V., Freedman, G., Hubbell, B., Jobling, A., Kan, H., Knibbs, L., Liu, Y., Martin, R., Morawska, L., Pope III, C. A., Shin, H., Straif, K., Shaddick, G., Thomas, M., van Dingenen, R., van Donkelaar, A., Vos, T., Murray, C. J. L., and Forouzanfar, M. H.: Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: an analysis of data from the Global Burden of Diseases Study 2015, The Lancet, 389, 1907–1918, https://doi.org/10.1016/S0140-6736(17)30505-6, 2017.
Crouse, D. L., Peters, P. A., van Donkelaar, A., Goldberg, M. S., Villeneuve, P. J., Brion, O., Khan, S., Atari, D. O., Jerrett, M., Pope, C. A., Brauer, M., Brook, J. R., Martin, R. V., Stieb, D., and Burnett, R. T.: Risk of Nonaccidental and Cardiovascular Mortality in Relation to Long-term Exposure to Low Concentrations of Fine Particulate Matter: A Canadian National-Level Cohort Study, Environ. Health Perspect., 120, 708–714, https://doi.org/10.1289/ehp.1104049, 2012.
Crumeyrolle, S., Chen, G., Ziemba, L., Beyersdorf, A., Thornhill, L., Winstead, E., Moore, R. H., Shook, M. A., Hudgins, C., and Anderson, B. E.: Factors that influence surface PM2.5 values inferred from satellite observations: perspective gained for the US Baltimore–Washington metropolitan area during DISCOVER-AQ, Atmos. Chem. Phys., 14, 2139–2153, https://doi.org/10.5194/acp-14-2139-2014, 2014.
Curci, G., Hogrefe, C., Bianconi, R., Im, U., Balzarini, A., Baró, R., Brunner, D., Forkel, R., Giordano, L., Hirtl, M., Honzak, L., Jiménez-Guerrero, P., Knote, C., Langer, M., Makar, P. A., Pirovano, G., Pérez, J. L., José, R. S., Syrakov, D., Tuccella, P., Werhahn, J., Wolke, R., Žabkar, R., Zhang, J., and Galmarini, S.: Uncertainties of simulated aerosol optical properties induced by assumptions on aerosol physical and chemical properties: An AQMEII-2 perspective, Atmos. Environ., 115, 541–552, https://doi.org/10.1016/j.atmosenv.2014.09.009, 2015.
de Hoogh, K., Gulliver, J., Donkelaar, A. V., Martin, R. V., Marshall, J. D., Bechle, M. J., Cesaroni, G., Pradas, M. C., Dedele, A., Eeftens, M., Forsberg, B., Galassi, C., Heinrich, J., Hoffmann, B., Jacquemin, B., Katsouyanni, K., Korek, M., Künzli, N., Lindley, S. J., Lepeule, J., Meleux, F., de Nazelle, A., Nieuwenhuijsen, M., Nystad, W., Raaschou-Nielsen, O., Peters, A., Peuch, V.-H., Rouil, L., Udvardy, O., Slama, R., Stempfelet, M., Stephanou, E. G., Tsai, M. Y., Yli-Tuomi, T., Weinmayr, G., Brunekreef, B., Vienneau, D., and Hoek, G.: Development of West-European PM2.5 and NO2 land use regression models incorporating satellite-derived and chemical transport modelling data, Environ. Res., 151, 1–10, https://doi.org/10.1016/j.envres.2016.07.005, 2016.
Di, Q., Kloog, I., Koutrakis, P., Lyapustin, A., Wang, Y., and Schwartz, J.: Assessing PM2.5 Exposures with High Spatiotemporal Resolution across the Continental United States, Environ. Sci. Technol., 50, 4712–4721, https://doi.org/10.1021/acs.est.5b06121, 2016.
Dockery, D. W., Pope, C. A., Xu, X., Spengler, J. D., Ware, J. H., Fay, M. E., Ferris Jr., B. G., and Speizer, F. E.: An Association between Air Pollution and Mortality in Six U.S. Cities, N. Engl. J. Med., 329, 1753–1759, https://doi.org/10.1056/NEJM199312093292401, 1993.
Dominici, F., Peng, R. D., Bell, M. L., Pham, L., McDermott, A., Zeger, S. L., and Samet, J. M.: Fine Particulate Air Pollution and Hospital Admission for Cardiovascular and Respiratory Diseases, JAMA, 295, 1127–1134, https://doi.org/10.1001/jama.295.10.1127, 2006.
Drury, E., Jacob, D. J., Spurr, R. J. D., Wang, J., Shinozuka, Y., Anderson, B. E., Clarke, A. D., Dibb, J., McNaughton, C., and Weber, R.: Synthesis of satellite (MODIS), aircraft (ICARTT), and surface (IMPROVE, EPA-AQS, AERONET) aerosol observations over eastern North America to improve MODIS aerosol retrievals and constrain surface aerosol concentrations and sources, J. Geophys. Res.-Atmos. (1984–2012), 115, D14204, https://doi.org/10.1029/2009JD012629, 2010.
Duplissy, J., DeCarlo, P. F., Dommen, J., Alfarra, M. R., Metzger, A., Barmpadimos, I., Prevot, A. S. H., Weingartner, E., Tritscher, T., Gysel, M., Aiken, A. C., Jimenez, J. L., Canagaratna, M. R., Worsnop, D. R., Collins, D. R., Tomlinson, J., and Baltensperger, U.: Relating hygroscopicity and composition of organic aerosol particulate matter, Atmos. Chem. Phys., 11, 1155–1165, https://doi.org/10.5194/acp-11-1155-2011, 2011.
Durre, I. and Yin, X.: Enhanced Radiosonde Data for Studies of Vertical Structure, B. Am. Meteorol. Soc., 89, 1257–1262, 2008.
Ford, B. and Heald, C. L.: Aerosol loading in the Southeastern United States: reconciling surface and satellite observations, Atmos. Chem. Phys., 13, 9269–9283, https://doi.org/10.5194/acp-13-9269-2013, 2013.
Ford, B. and Heald, C. L.: Exploring the uncertainty associated with satellite-based estimates of premature mortality due to exposure to fine particulate matter, Atmos. Chem. Phys., 16, 3499–3523, https://doi.org/10.5194/acp-16-3499-2016, 2016.
Green, M., Kondragunta, S., Ciren, P., and Xu, C.: Comparison of GOES and MODIS Aerosol Optical Depth (AOD) to Aerosol Robotic Network (AERONET) AOD and IMPROVE PM2.5 Mass at Bondville, Illinois, J. Air Waste Manage. Assoc., 59, 1082–1091, https://doi.org/10.3155/1047-3289.59.9.1082, 2012.
Griffin, D., Naumova, E., McEntee, J., Castronovo, D., Durant, J., Lyles, M., Faruque, F., and Lary, D.: Air quality and human health, in: Environmental Tracking for Public Health Surveillance, 129–185, CRC Press, Leiden, the Netherlands, 2012.
Gupta, P. and Christopher, S. A.: Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: Multiple regression approach, J. Geophys. Res., 114, D14205, https://doi.org/10.1029/2008JD011496, 2009.
Hand, J. and Malm, W. C.: Review of the IMPROVE equation for estimating ambient light extinction coefficients, Colorado State University, Fort Colins, 2006.
Hess, M., Koepke, P., and Schult, I.: Optical Properties of Aerosols and Clouds: The Software Package OPAC, B. Am. Meteorol. Soc., 79, 831–844, https://doi.org/10.1175/1520-0477(1998)079<0831:OPOAAC>2.0.CO;2, 1998.
Highwood, E. J.: Suggested Refractive Indices and Aerosol Size Parameters for Use in Radiative Effect Calculations and Satellite Retrievals, ADIENT/APPRAISE CP2 Technical Report, DRAFT V2, available at: http://www.met.rdg.ac.uk/~adient/refractiveindices.html (last access: 8 December 2018), 2009.
Holben, B. N., Eck, T. F., Slutsker, I., Tanre, D., Buis, J. P., Setzer, A., Vermote, E., Reagan, J. A., Kaufman, Y. J., Nakajima, T., Lavenu, F., Jankowiak, I., and Smirnov, A.: AERONET – A federated instrument network and data archive for aerosol characterization, Remote Sens. Environ., 66, 1–16, https://doi.org/10.1016/S0034-4257(98)00031-5, 1998.
Houyoux, M. R., Vukovich, J. M., Coats Jr., C. J., Wheeler, N. J. M., and Kasibhatla, P. S.: Emission inventory development and processing for the Seasonal Model for Regional Air Quality (SMRAQ) project, J. Geophys. Res., 105, 9079–9090, https://doi.org/10.1029/1999JD900975, 2000.
Hu, X., Waller, L. A., Lyapustin, A., Wang, Y., and Liu, Y.: 10-year spatial and temporal trends of PM2.5 concentrations in the southeastern US estimated using high-resolution satellite data, Atmos. Chem. Phys., 14, 6301–6314, https://doi.org/10.5194/acp-14-6301-2014, 2014.
Jerrett, M., Turner, M. C., Beckerman, B. S., Pope, C. A., van Donkelaar, A., Martin, R. V., Serre, M., Crouse, D., Gapstur, S. M., Krewski, D., Diver, W. R., Coogan, P. F., Thurston, G. D., and Burnett, R. T.: Comparing the Health Effects of Ambient Particulate Matter Estimated Using Ground-Based versus Remote Sensing Exposure Estimates, Environ. Health. Perspect., 125, 1–8, https://doi.org/10.1289/EHP575, 2017.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., E., Dunlea, J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of Organic Aerosols in the Atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Jin, X.: Assessing uncertainties of a geophysical approach to estimate surface fine particulate matter distributions from satellite observed aerosol optical depth: Data and code, https://doi.org/10.7916/d8-x9h1-cg54, 2018.
Kanakidou, M., Seinfeld, J. H., Pandis, S. N., Barnes, I., Dentener, F. J., Facchini, M. C., van Dingenen, R., Ervens, B., Nenes, A., Nielsen, C. J., Swietlicki, E., Putaud, J. P., Balkanski, Y., Fuzzi, S., Horth, J., Moortgat, G. K., Winterhalter, R., Myhre, C. E. L., Tsigaridis, K., Vignati, E., Stephanou, E. G., and Wilson, J.: Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 5, 1053–1123, https://doi.org/10.5194/acp-5-1053-2005, 2005.
Kim, P. S., Jacob, D. J., Fisher, J. A., Travis, K., Yu, K., Zhu, L., Yantosca, R. M., Sulprizio, M. P., Jimenez, J. L., Campuzano-Jost, P., Froyd, K. D., Liao, J., Hair, J. W., Fenn, M. A., Butler, C. F., Wagner, N. L., Gordon, T. D., Welti, A., Wennberg, P. O., Crounse, J. D., St. Clair, J. M., Teng, A. P., Millet, D. B., Schwarz, J. P., Markovic, M. Z., and Perring, A. E.: Sources, seasonality, and trends of southeast US aerosol: an integrated analysis of surface, aircraft, and satellite observations with the GEOS-Chem chemical transport model, Atmos. Chem. Phys., 15, 10411–10433, https://doi.org/10.5194/acp-15-10411-2015, 2015.
Kloog, I., Chudnovsky, A. A., Just, A. C., Nordio, F., Koutrakis, P., Coull, B. A., Lyapustin, A., Wang, Y., and Schwartz, J.: A new hybrid spatio-temporal model for estimating daily multi-year PM2.5 concentrations across northeastern USA using high resolution aerosol optical depth data, Atmos. Environ., 95, 581–590, https://doi.org/10.1016/j.atmosenv.2014.07.014, 2014.
Koehler, K. A., Kreidenweis, S. M., DeMott, P. J., Prenni, A. J., Carrico, C. M., Ervens, B., and Feingold, G.: Water activity and activation diameters from hygroscopicity data – Part II: Application to organic species, Atmos. Chem. Phys., 6, 795–809, https://doi.org/10.5194/acp-6-795-2006, 2006.
Laden, F., Schwartz, J., Speizer, F. E., and Dockery, D. W.: Reduction in Fine Particulate Air Pollution and Mortality, Am J Respir Crit Care Med, 173, 667–672, https://doi.org/10.1164/rccm.200503-443OC, 2006.
Latimer, R. N. C. and Martin, R. V.: Interpretation of Measured Aerosol Mass Scattering Efficiency Over North America Using a Chemical Transport Model, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2018-459, in review, 2018.
Lee, H. J., Chatfield, R. B., and Strawa, A. W.: Enhancing the Applicability of Satellite Remote Sensing for PM2.5 Estimation Using MODIS Deep Blue AOD and Land Use Regression in California, United States, Environ. Sci. Technol., 50, 6546–6555, https://doi.org/10.1021/acs.est.6b01438, 2016.
Levy, R. C., Mattoo, S., Sawyer, V., Shi, Y., Colarco, P. R., Lyapustin, A. I., Wang, Y., and Remer, L. A.: Exploring systematic offsets between aerosol products from the two MODIS sensors, Atmos. Meas. Tech., 11, 4073–4092, https://doi.org/10.5194/amt-11-4073-2018, 2018.
Lyapustin, A. and Wang, Y.: MCD19A2 MODIS/Terra+Aqua Land Aerosol Optical Depth Daily L2G Global 1 km SIN Grid V006 [Data set], NASA EOSDIS Land Processes DAAC, https://doi.org/10.5067/MODIS/MCD19A2.006, 2018.
Lyapustin, A., Martonchik, J., Wang, Y., Laszlo, I., and Korkin, S.: Multiangle implementation of atmospheric correction (MAIAC): 1. Radiative transfer basis and look-up tables, J. Geophys. Res.-Atmos., 116, D03210, https://doi.org/10.1029/2010JD014985, 2011.
Lyapustin, A. I., Wang, Y., Laszlo, I., Hilker, T., G Hall, F., Sellers, P. J., Tucker, C. J., and Korkin, S. V.: Multi-angle implementation of atmospheric correction for MODIS (MAIAC): 3. Atmospheric correction, Remote Sens. Environ., 127, 385–393, 2012.
Lyapustin, A., Wang, Y., Korkin, S., and Huang, D.: MODIS Collection 6 MAIAC algorithm, Atmos. Meas. Tech., 11, 5741–5765, https://doi.org/10.5194/amt-11-5741-2018, 2018.
Ming, Y., Ramaswamy, V., Ginoux, P. A., and Horowitz, L. H.: Direct radiative forcing of anthropogenic organic aerosol, J. Geophys. Res., 110, 1097–1112, https://doi.org/10.1029/2004JD005573, 2005.
Mishchenko, M. I., Dlugach, J. M., Yanovitskij, E. G., and Zakharova, N. T.: Bidirectional reflectance of flat, optically thick particulate layers: an efficient radiative transfer solution and applications to snow and soil surfaces, J. Quant. Spectrosc. Ra., 63, 409–432, https://doi.org/10.1016/S0022-4073(99)00028-X, 1999.
Moise, T., Flores, J. M., and Rudich, Y.: Optical Properties of Secondary Organic Aerosols and Their Changes by Chemical Processes, Chem. Rev., 115, 4400–4439, https://doi.org/10.1021/cr5005259, 2015.
Park, S.-K., Marmur, A., Kim, S. B., Tian, D., Hu, Y., McMurry, P. H., and Russell, A. G.: Evaluation of Fine Particle Number Concentrations in CMAQ, Aerosol Sci. Technol., 40, 985–996, https://doi.org/10.1080/02786820600907353, 2006.
Peng, R. D., Bell, M. L., Geyh, A. S., McDermott, A., Zeger, S. L., Samet, J. M., and Dominici, F.: Emergency Admissions for Cardiovascular and Respiratory Diseases and the Chemical Composition of Fine Particle Air Pollution, Environ. Health Perspect., 117, 957–963, 2009.
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007.
Pierce, T., Geron, C., Pouliot, G., Kinnee, E., and Vukovich, J.: Integration of the Biogenic Emissions Inventory System (BEIS3) into the Community Multiscale Air Quality (CMAQ) Modeling System, Proceedings of the AMS 4th Urban Environment Symposium, 20–23 May, Norfolk, Virginia, 2002.
Raffuse, S. M., Pryden, D. A., Sullivan, D. C., Larkin, N. K., Strand, T., and Solomon, R.: SMARTFIRE algorithm description, Paper prepared for the U.S. Environmental Protection Agency, Research Triangle Park, NC, by Sonoma Technology, Inc., Petaluma, CA, and the U.S. Forest Service, AirFire Team, Pacific Northwest Research Laboratory, Seattle, WA STI-905517-3719, October, 2009.
Sarangi, B., Aggarwal, S. G., Sinha, D., and Gupta, P. K.: Aerosol effective density measurement using scanning mobility particle sizer and quartz crystal microbalance with the estimation of involved uncertainty, Atmos. Meas. Tech., 9, 859–875, https://doi.org/10.5194/amt-9-859-2016, 2016.
Shaddick, G., Thomas, M. L., Green, A., Brauer, M., van Donkelaar, A., Burnett, R., Chang, H. H., Cohen, A., Dingenen, R. V., Dora, C., Gumy, S., Liu, Y., Martin, R., Waller, L. A., West, J., Zidek, J. V., and Prüss-Ustün, A.: Data integration model for air quality: a hierarchical approach to the global estimation of exposures to ambient air pollution, J. R. Stat. Soc. C, 67, 231–253, https://doi.org/10.1111/rssc.12227, 2017.
Shi, L., Zanobetti, A., Kloog, I., Coull, B. A., Koutrakis, P., Melly, S. J., and Schwartz, J. D.: Low-Concentration PM2.5 and Mortality: Estimating Acute and Chronic Effects in a Population-Based Study, Environ. Health Perspect., 124, 1–30, https://doi.org/10.1289/ehp.1409111, 2015.
Snider, G., Weagle, C. L., Martin, R. V., van Donkelaar, A., Conrad, K., Cunningham, D., Gordon, C., Zwicker, M., Akoshile, C., Artaxo, P., Anh, N. X., Brook, J., Dong, J., Garland, R. M., Greenwald, R., Griffith, D., He, K., Holben, B. N., Kahn, R., Koren, I., Lagrosas, N., Lestari, P., Ma, Z., Vanderlei Martins, J., Quel, E. J., Rudich, Y., Salam, A., Tripathi, S. N., Yu, C., Zhang, Q., Zhang, Y., Brauer, M., Cohen, A., Gibson, M. D., and Liu, Y.: SPARTAN: a global network to evaluate and enhance satellite-based estimates of ground-level particulate matter for global health applications, Atmos. Meas. Tech., 8, 505–521, https://doi.org/10.5194/amt-8-505-2015, 2015.
Snider, G., Weagle, C. L., Murdymootoo, K. K., Ring, A., Ritchie, Y., Stone, E., Walsh, A., Akoshile, C., Anh, N. X., Balasubramanian, R., Brook, J., Qonitan, F. D., Dong, J., Griffith, D., He, K., Holben, B. N., Kahn, R., Lagrosas, N., Lestari, P., Ma, Z., Misra, A., Norford, L. K., Quel, E. J., Salam, A., Schichtel, B., Segev, L., Tripathi, S., Wang, C., Yu, C., Zhang, Q., Zhang, Y., Brauer, M., Cohen, A., Gibson, M. D., Liu, Y., Martins, J. V., Rudich, Y., and Martin, R. V.: Variation in global chemical composition of PM2.5: emerging results from SPARTAN, Atmos. Chem. Phys., 16, 9629–9653, https://doi.org/10.5194/acp-16-9629-2016, 2016.
Stanier, C. O., Khlystov, A. Y., and Pandis, S. N.: Ambient aerosol size distributions and number concentrations measured during the Pittsburgh Air Quality Study (PAQS), Atmos. Environ., 38, 3275–3284, https://doi.org/10.1016/j.atmosenv.2004.03.020, 2004.
Superczynski, S. D., Kondragunta, S., and Lyapustin, A. I.: Evaluation of the multi-angle implementation of atmospheric correction (MAIAC) aerosol algorithm through intercomparison with VIIRS aerosol products and AERONET, J. Geophys. Res.-Atmos., 122, 3005–3022, https://doi.org/10.1002/2016JD025720, 2017.
Toth, T. D., Zhang, J., Campbell, J. R., Hyer, E. J., Reid, J. S., Shi, Y., and Westphal, D. L.: Impact of data quality and surface-to-column representativeness on the PM2.5/satellite AOD relationship for the contiguous United States, Atmos. Chem. Phys., 14, 6049–6062, https://doi.org/10.5194/acp-14-6049-2014, 2014.
US EPA, MOVES2014a: Latest version of MOtor Vehicle Emission Simulator (MOVES): https://www.epa.gov/moves/moves2014a-latest-version-motor-vehicle-emission-simulator-moves, last access: April 2018.
van Donkelaar, A., Martin, R. V., and Park, R. J.: Estimating ground-level PM2.5 using aerosol optical depth determined from satellite remote sensing, J. Geophys. Res., 111, D21201, https://doi.org/10.1029/2005JD006996, 2006.
van Donkelaar, A., Martin, R. V., Brauer, M., Kahn, R., Levy, R., Verduzco, C., and Villeneuve, P. J.: Global Estimates of Ambient Fine Particulate Matter Concentrations from Satellite-Based Aerosol Optical Depth: Development and Application, Environ. Health Perspect., 118, 847–855, https://doi.org/10.1289/ehp.0901623, 2010.
van Donkelaar, A., Martin, R. V., Pasch, A. N., Szykman, J. J., Zhang, L., Wang, Y. X., and Chen, D.: Improving the Accuracy of Daily Satellite-Derived Ground-Level Fine Aerosol Concentration Estimates for North America, Environ. Sci. Technol., 46, 11971–11978, https://doi.org/10.1021/es3025319, 2012.
van Donkelaar, A., Martin, R. V., Spurr, R. J. D., Drury, E., Remer, L. A., Levy, R. C., and Wang, J.: Optimal estimation for global ground-level fine particulate matter concentrations, J. Geophys. Res.-Atmos., 118, 5621–5636, https://doi.org/10.1002/jgrd.50479, 2013.
van Donkelaar, A., Martin, R. V., Spurr, R. J. D., and Burnett, R. T.: High-Resolution Satellite-Derived PM2.5 from Optimal Estimation and Geographically Weighted Regression over North America, Environ. Sci. Technol., 49, 10482–10491, https://doi.org/10.1021/acs.est.5b02076, 2015.
van Donkelaar, A., Martin, R. V., Brauer, M., Hsu, N. C., Kahn, R. A., Levy, R. C., Lyapustin, A., Sayer, A. M., and Winker, D. M.: Global Estimates of Fine Particulate Matter using a Combined Geophysical-Statistical Method with Information from Satellites, Models, and Monitors, Environ. Sci. Technol., 50, 3762–3772, https://doi.org/10.1021/acs.est.5b05833, 2016.
Zhang, Y., Vijayaraghavan, K., Wen, X.-Y., Snell, H. E., and Jacobson, M. Z.: Probing into regional ozone and particulate matter pollution in the United States: 1, A 1 year CMAQ simulation and evaluation using surface and satellite data, J. Geophys. Res., 114, D22304, https://doi.org/10.1029/2009JD011898, 2009.