the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantifying uncertainty from aerosol and atmospheric parameters and their impact on climate sensitivity
Christopher G. Fletcher
Ben Kravitz
Bakr Badawy
Climate sensitivity in Earth system models (ESMs) is an emergent property that is affected by structural (missing or inaccurate model physics) and parametric (variations in model parameters) uncertainty. This work provides the first quantitative assessment of the role of compensation between uncertainties in aerosol forcing and atmospheric parameters, and their impact on the climate sensitivity of the Community Atmosphere Model, Version 4 (CAM4). Running the model with prescribed ocean and ice conditions, we perturb four parameters related to sulfate and black carbon aerosol radiative forcing and distribution, as well as five atmospheric parameters related to clouds, convection, and radiative flux. In this experimental setup where aerosols do not affect the properties of clouds, the atmospheric parameters explain the majority of variance in climate sensitivity, with two parameters being the most important: one controlling low cloud amount, and one controlling the timescale for deep convection. Although the aerosol parameters strongly affect aerosol optical depth, their impacts on climate sensitivity are substantially weaker than the impacts of the atmospheric parameters, but this result may depend on whether aerosol–cloud interactions are simulated. Based on comparisons to inter-model spread of other ESMs, we conclude that structural uncertainties in this configuration of CAM4 likely contribute 3 times more to uncertainty in climate sensitivity than parametric uncertainties. We provide several parameter sets that could provide plausible (measured by a skill score) configurations of CAM4, but with different sulfate aerosol radiative forcing, black carbon radiative forcing, and climate sensitivity.
- Article
(4490 KB) - Full-text XML
- BibTeX
- EndNote
Climate models are exceptional tools for understanding contributions of different forcing agents to climate change. When forced with observed climate forcings (e.g., greenhouse gases and aerosols), they are skillful at reproducing past climate change (Flato et al., 2013). Their ability to do so builds confidence that climate models can provide plausible projections of future climate change under various assumptions about ranges of changes in forcing agents (i.e., emissions scenarios).
At the core of these projections is the climate sensitivity (CS) of the model, which is an emergent property of a model that describes how much global warming will be simulated by the model for a prescribed change in the carbon dioxide (CO2) concentration. Variations in CS arise due to structural uncertainty (how models represent the underlying physics of the climate system) and parametric uncertainty (how the simulation varies with model parameters, typically those associated with subgrid-scale parameterizations). Each parameter in a model parameterization has an associated uncertainty due to deficiencies in representing model physics with these parameterizations, or a lack of available observational data to constrain the physics. A third source of uncertainty comes from the emissions of climate forcings – particularly anthropogenic and natural aerosols – which are also uncertain to some degree, and have plausible ranges (Ban-Weiss et al., 2011; Bond et al., 2013; Samset and Myhre, 2015).
Reducing the uncertainty in CS is a key focus of climate science research. Fortunately, there are tools available to provide constraints on the estimates. Kiehl (2007), and more recently Forster et al. (2013), observed that there is a statistical relationship among climate models (the “Kiehl curve”), where models that are the most sensitive to CO2 also tend to show largest historical radiative forcing by aerosols. As such, by exploring uncertainties in key model parameters and/or aerosol emissions rates, we expect to be able to alter a model's climate sensitivity, effectively moving the model along the Kiehl curve. With a sufficiently large number of such parameter sets, we can identify which versions of the model (i.e., sets of parameters or emissions rates) produce plausible climates. We hypothesize that, through this procedure, it may be possible to create multiple versions of a single climate model that plausibly reproduce observations but have discernibly different climate sensitivities.
The idea of obtaining multiple plausible versions of a model with different climate sensitivities was also explored by Mauritsen et al. (2012) for the Max Planck Institute for Meteorology's climate model. These authors found that the CS was not as sensitive to parameters as expected; however, they did not attempt to explore uncertainty in the forcing. Similarly, Golaz et al. (2013) altered the settings of a cloud detrainment parameter in the deep convection scheme, and produced three versions of the GFDL CM3 model with very different climate sensitivities, but again did not vary the forcing, and so two of the candidate versions were not able to reproduce the transient evolution of historical global mean surface air temperature. A recent, and highly relevant, contribution is that of Regayre et al. (2018), who show that uncertainties in historical aerosol radiative forcing, and top-of-atmosphere shortwave radiative flux, in a comprehensive chemistry-climate model are controlled by a combination of aerosol parameters and emissions, as well as uncertain atmospheric parameters. Their results show that, particularly in recent decades, constraining aerosol and atmospheric parameters allows regional climate impacts of aerosols to be more faithfully reproduced.
This area of research is closely related to uncertainty quantification (UQ), and to the more applied topic of model tuning (see also: Gent et al., 2011; Hourdin et al., 2013, 2016; Watanabe et al., 2010; Zhao M. et al., 2018). Modern climate and Earth system models (ESMs) are so complex, and with so many tunable parameters, that running comprehensive calibration schemes with the full dynamical model is impractical. The typical approach is to conduct one-at-a-time (OAT) tests, where a single uncertain parameter is varied while holding all other parameters at their default value (Covey et al., 2013). While a lot can be learned about a model in OAT mode, this approach neglects potentially important parameter interactions, which can only be studied in vastly more expensive all-at-a-time (AAT) sampling designs. A very useful approach, therefore, is to construct a statistical emulator trained on output from the dynamical model, which is used to predict unsampled outputs from the dynamical model. Many recent studies have used Gaussian process (GP) emulators to sample an almost infinitely large number of parameter combinations in climate and atmospheric models (Carslaw et al., 2013; Lee et al., 2011; McNeall et al., 2016; Regayre et al., 2018). The GP emulator is a Bayesian statistical technique that fits a smooth nonlinear function to a set of training data based on some prior information and assumptions, and provides an estimate of its own posterior uncertainty for each prediction (Lee et al., 2011).
The main goal of this paper is to quantify how much variation in climate sensitivity within a single climate model (CAM4, the atmospheric component of CCSM4/CESM-CAM4; see Sect. 2.1 below) is a function of uncertainties in aerosol forcing and atmospheric parameters. We will use statistical emulation to test 105 combinations of parameters and forcing, to identify those combinations that yield plausible climates, but with different climate sensitivities. In other words, we seek to quantify the degree of equifinality in CAM4's climate sensitivity. This work differs in focus from the recent study of Regayre et al. (2018), because here we explicitly assess the combined impact of parametric uncertainty and forcing uncertainty on climate sensitivity. While the conceptual idea of the Kiehl curve has existed for more than a decade, this work is, to our knowledge, the first explicit attempt to move a single climate model to different parts of the curve, and to quantify the impact on climate sensitivity. We stress that this contribution does not tackle the problem of calibration to observations: all simulations are conducted as perturbations to preindustrial (pre-1850) conditions, and are compared to the default version of CAM4 as a reference. The idea from this proof-of-concept study is to configure a series of candidate models with high and low CS, which could then be run with interactive ocean components, to produce transient RCP-type simulations (historical and future scenarios) beginning in the preindustrial era.
2.1 CAM4 model and atmospheric parameters
We use the National Center for Atmospheric Research (NCAR) Community Atmosphere Model Version 4 (CAM4), the atmospheric component of the Community Climate System Model Version 4 (CCSM4) and the Community Earth System Model Version 1.0.4 (CESM1), fully documented by Gent et al. (2011) and Collins et al. (2006). Hereafter, we refer to this model simply as “CAM4”. In this proof-of-concept study, CAM4 is run at coarse horizontal resolution (3.75∘ longitude × 3.75∘ latitude) with 26 vertical layers extending from the surface to 3 hPa (∼40 km). The coarse horizontal resolution is selected to increase computational efficiency and is appropriate to represent the broad-scale features of the climate response described in this study (Shields et al., 2012). In addition, we note that this model configuration includes a crude representation of the stratosphere (only four layers are located above 100 hPa); however, since our primary focus is on radiation, and not circulation, we consider this resolution to be sufficient for the purpose of separating the radiative effects of aerosols in the troposphere and stratosphere. This is also the same vertical resolution that was employed in a similar manner by Ban-Weiss et al. (2011). All simulations are performed in preindustrial (pre-1850) mode: the CO2 concentration is fixed at 284 ppmv, while other atmospheric constituents are prescribed from a monthly varying climatology. For natural and anthropogenic aerosols the climatology is taken from a simulation using interactive (i.e., prognostic) chemistry (Lamarque et al., 2010), and the output is taken as the mean of all realizations. The uncertainty due to atmospheric and oceanic initial conditions is estimated using the standard deviation of the realizations.
We assess CS in CAM4 using the method proposed by Cess et al. (1989), where a uniform 2 K warming is applied to global sea surface temperatures (SSTs). The Cess CS is then , where ΔTs is the change in global annual mean near-surface air temperature (K), and ΔF is the change in global annual mean top-of-atmosphere net radiative flux (ΔF, W m−2). The changes are evaluated as the difference between the simulation with warmed SSTs and the simulation with preindustrial SSTs. The λ diagnostic is useful for model calibration and tuning because it can be run with atmospheric general circulation models using prescribed SSTs (Golaz et al., 2013; Zhao M. et al., 2018), and it is highly correlated with the transient climate response and the equilibrium climate sensitivity of the same models run with coupled interactive ocean (Medeiros et al., 2014).
2.2 Perturbations to aerosol forcing and atmospheric parameters
We focus on two aerosol species, sulfate and black carbon (BC), and we perturb the radiative forcing from both species simultaneously. Current best estimates of aerosol radiative forcing (ARF) are −1.9 to 0.1 W m−2 with medium confidence (Boucher et al., 2013), with by far the dominant source of uncertainty arising from interactions with clouds (Regayre et al., 2018; Stevens, 2015). Sulfate exerts a well-known and strong negative radiative forcing on climate due to direct scattering of solar radiation, and through interactions with cloud properties (Boucher et al., 2013). By contrast, BC is an absorbing aerosol that generally exerts a positive ARF, although the sign depends on whether the BC layers are above (negative) or below (positive) cloud layers (Ban-Weiss et al., 2011; Kim et al., 2015; Regayre et al., 2018). The largest uncertainties in BC ARF are due to an incomplete inventory of emissions, as well as poor understanding of aging and scavenging rates, vertical and horizontal transport, and deposition (Bond et al., 2013).
Table 1List of parameters that are perturbed in this study, including for each parameter a description, the range of perturbed values, and the default value in CAM4 (where applicable).
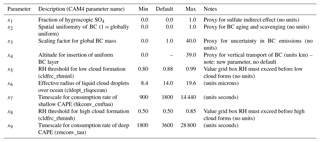
To examine uncertainty due to sulfate and BC forcing in CAM4, we introduced four new parameters to the model (x1–x4; see Table 1), with x1 controlling sulfate and x2–x4 controlling BC. CAM4 does not include aerosol–cloud interactions, yet sulfate aerosols are known to be effective cloud condensation nuclei. As a proxy, parameter x1 attempts to mimic these interactions by specifying the fraction of the sulfate mass that uses optical properties for sulfate in “hygroscopic mode”, i.e., a pure SO4 molecule grown hygroscopically (following Köhler theory) corresponding to a relative humidity of 99 %. The optical properties for the resulting sulfate aerosol (single scattering albedo, asymmetry parameter, and extinction coefficient) are given by , where kdefault indicates the default sulfate aerosol parameters in CAM4, and khygro indicates the parameters corresponding to this hygroscopic aerosol. This procedure ensures that the total mass of sulfate, and its geographic location, are the same in all cases, and the only perturbation is the fraction of sulfate that is water-coated (regardless of the atmospheric humidity profile in the vicinity of the sulfate molecules).
To perturb BC forcing we assume that the optical properties are known, but that the total mass and horizontal and vertical distributions are uncertain, broadly consistent with the conclusions of Bond et al. (2013). We define three parameters x2 (horizontal distribution), x3 (mass scaling) and x4 (vertical distribution) that control the distribution and amount of BC mass in the model. More specifically, x2 describes linear interpolation between the default horizontal distribution for BC mass (x2=0) and BC being uniformly distributed throughout the globe (x2=1). This parameter addresses the uncertainty associated with BC aging and transport: the longer that BC particles are able to survive in the atmosphere without being scavenged, the further the distribution should spread into pristine marine and polar environments. x3 takes values between 0 and 40 and simply serves as a multiplier on the BC distribution, indicating uncertainties in total emissions and hence total mass loading. x4 corresponds to an altitude (0–40 km), indicating where a “layer” of BC (with mass equal to the total default mass) is added to the model, and then the total mass is rescaled to be the appropriate value per parameter x3. This parameter addresses uncertainties associated with large-scale transport of BC by the atmospheric circulation, which is known to be poorly simulated, especially when model spatial resolution is low (Lamarque et al., 2010).
We also investigate the sensitivity to five uncertain atmospheric parameters in CAM4 that are related to clouds and convection. The parameters (denoted x5–x9) were identified as highly important in a previous one-at-a-time sensitivity analysis (Covey et al., 2013), and are described in Table 1. Two parameters, x5 and x8, control the threshold of atmospheric relative humidity that must be achieved before low and high clouds form, respectively; increasing either of these parameters will reduce the amount of low, or high, cloud in the model. Parameter x6 changes the radius of liquid cloud droplets over the ocean, with smaller radii associated with brighter marine clouds, which are known to be highly important for climate sensitivity (Sherwood et al., 2014; Stevens, 2015). Parameters x7 and x9 are the timescales for shallow and deep convection, respectively; increasing either parameter will result in longer-duration convective precipitation. These parameters exert a large control on the mean climate in CAM4, but they are also expected to influence the climate sensitivity (Bony et al., 2015; Gent et al., 2011; Sherwood et al., 2014). We therefore vary these five atmospheric parameters in tandem with changes to the aerosol forcing to identify plausible climates with different climate sensitivities.
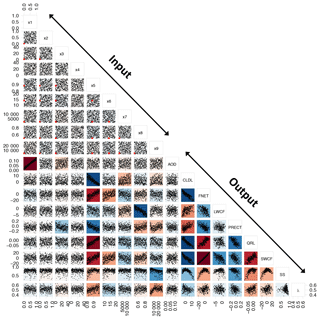
Figure 1Scatter plot matrix showing the relationship between all input parameters (x1–x9) and all output variables (names defined in the text) in the n=350 training cases run with CAM4. Red points show the default values for all input parameters except x4, which has no default. The background shading of each panel indicates the strength and sign of the correlation between a particular pair of variables, with reds indicating positive and blues indicating negative correlations, and stronger correlations indicated by darker shading. For example, there is a strong positive correlation between x5 and FNET, and a weak negative correlation between x9 and FNET.
2.3 Emulation
For the nine parameters described in Sect. 2.2, we would need to perform at least 105 simulations with CAM4 to adequately sample the parameter space in a typical all-at-a-time mode. Even running CAM4 at relatively low resolution, this would be impractical. The solution is to train an efficient statistical emulator of the dynamical model, which can be used to predict the climate output for any combination of parameter values, provided that the parameters lie within the range over which the emulator has been trained.
Following Lee et al. (2012) and McNeall et al. (2016), we construct a GP emulator of CAM4 using the R package diceKriging (Roustant et al., 2012), which fits an N-dimensional nonlinear regression model to predict an output y based on a series of k predictors (input parameters x1–x9). Alternative methods of emulation have been used for climate modeling applications, including generalized linear models (Yang et al., 2017) and artificial neural networks (Sanderson et al., 2008). However, the GP model has two attractive properties that make it highly applicable to this type of problem: it can capture nonlinear interactions between the output and multiple inputs, and it provides an estimate of its posterior uncertainty.
We begin by defining n=350 combinations of parameter values (x1–x9) for the training points in the nine-parameter space, using a Latin hypercube design that ensures good distribution of cases, even in the corners of the hypercube (McKay et al., 1979). For each training point, we produce three 1-year realizations of CAM4, each using different atmospheric and oceanic initial conditions drawn from a 500-year control integration of the coupled ocean–atmosphere version of CAM4 at the same resolution (see Sect. 2.1). The mean of the resulting outputs from the three realizations is used to train the emulator, which reduces the noise arising from internal climate variability. To quantify the impact of the parameters on climate sensitivity, the training process must be repeated twice: once using prescribed preindustrial SSTs, and then again using warmed SSTs (see Sect. 2.1). For each training point, the necessary simulations take approximately 6 h on a single eight-core node of a high-performance computing cluster, giving a total computing time of core hours. Applying the emulator to predict an output variable at 105 or 106 uniformly sampled points in parameter space takes less than 30 s on a single core of a modern desktop computer. This is many orders of magnitude faster than it would take to run a set of 105 or 106 simulations with the dynamical model.
The output from the training simulations are used to construct the emulator. We make standard assumptions to configure the GP model, using a linear prior and the default Matérn covariance function (Lee et al., 2011; Roustant et al., 2012), although we have verified that our conclusions are insensitive to these choices. Before the emulator can be used for prediction, its performance is validated using leave-one-out cross-validation (LOOCV): each case from the n=350 training set is left out in turn, and the emulator is rebuilt using the remaining n=349 cases. The resulting model is then used to predict the output for the case that was left out, and so on until each case has been predicted. The performance metric used here is the correlation coefficient between the n=350 outputs simulated by CAM4 and the n=350 predictions from the emulator run in LOOCV mode. The validation results are presented in Sect. 4.1.
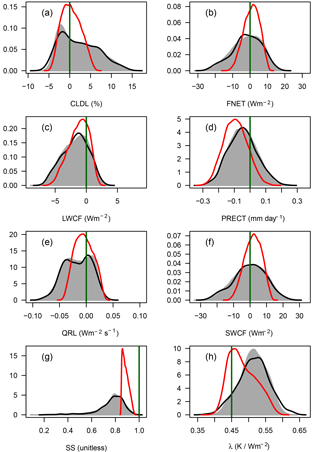
Figure 2The black line shows the density distribution of simulated values from CAM4 for (a) CLDL, (b) FNET, (c) LWCF, (d) PRECT, (e) QRL, (f) SWCF, (g) multivariate skill score (SS), and (h) Cess climate sensitivity (λ), from the n=350 training cases (variable names are defined in the text). The gray shaded region shows the density distribution from 100 000 emulated samples of each variable, and the red line shows the density distribution for the subset of emulated samples that is most plausible (see Sect. 4.3). Note the different x axis scales in each panel. The dark green vertical line in each panel indicates the location of CAM4 with its default parameter settings.
2.4 Quantifying the plausibility of candidate models
The plausibility of the climate produced by a particular combination of input parameters is assessed using a multivariate skill score (SS), based on Pierce et al. (2009):
where for a spatial grid of particular output variable X (e.g., precipitation, low cloud amount), p denotes a perturbed model, and d denotes the default (reference) model, rp,d is the anomaly (pattern) correlation between X in p and d, σ is the spatial standard deviation of X, and overlines denote the spatial mean of X.
The SS quantifies the mean bias, spatial correlation, and spatial variance of six key simulated variables for each perturbed model relative to the default version of CAM4. The variables included in SS are low cloud fraction (CLDL), total precipitation (PRECT), net top-of-the-atmosphere (TOA) radiative flux (FNET), shortwave cloud forcing (SWCF), longwave cloud forcing (LWCF), and global vertically integrated longwave heating rate (QRL). We calculate SS for each variable separately, and then average the SS values to obtain the final SS for each perturbed model. To obtain a high value of SS (SS ∼ 1), a parameter combination must produce a simulated climate that is simultaneously close to that of the default model in all of these fields. We apply a stringent threshold of SS > 0.85 to determine whether a particular perturbed model is plausible, which equates to approximately the 85th percentile of the SS distribution. We compute SS for the n=350 training cases, and then use the emulator to predict SS for all possible parameter combinations (see Sect. 4.1).
3.1 Relationship between inputs and outputs
Figure 1 presents the relationships between all inputs (perturbed parameters x1–x9) and all outputs, for the n=350 training simulations run with CAM4. The Latin hypercube sampling of input parameters (Sect. 2.3) ensures an even sampling of values across each input parameter's full range (see Table 1). Correlations between parameter values are very weak, which provides confidence that each training case is an independent event drawn from the parameter population. The default values in CAM4 of parameters x5 and x6 are located within the center of their distributions, while the values for aerosol parameters x1–x3 and atmospheric parameters x7–x9 are at the lower end. For the sensitivity parameter for high clouds (x8), the default is also the minimum value (0.5); however, we note that the default value varies considerably with horizontal resolution, and at the 2∘ resolution used, for example, by Covey et al. (2013), its value is 0.80. No default exists in CAM4 for the new BC altitude parameter x4.
The marginal relationships between inputs and outputs can provide an indication of which parameters may be important for emulating the outputs. Intuitively, the aerosol optical depth output (AOD) is a strong function of the sulfate hygroscopic fraction (x1), and a weaker function of BC mass scaling (x3), but it shows no obvious relationships with the other aerosol-related parameters (x2 or x4), and most other atmospheric outputs are not strongly correlated with any of the aerosol parameters. One exception is total precipitation, which appears to decrease as a function of BC mass scaling (x3), presumably because of a reduction in precipitating clouds induced by so-called semi-direct effects (Bond et al., 2013). For the atmospheric parameters, there are clear relationships between inputs and the output variable(s) directly related to the parameter being perturbed. For example, there is a strong negative relationship between low cloud amount (CLDL) and the sensitivity parameter for low clouds (x5), and longwave cloud forcing (LWCF) is negatively correlated with the sensitivity parameter for high clouds (x8). Most apparent from Fig. 1 is the interconnectedness of the outputs; for example, low cloud, net radiation and shortwave cloud forcing are highly correlated. Parameter x5 strongly affects CLDL, and this produces knock-on effects to all other outputs: positive correlations with FNET, QRL and SWCF, and negative correlations with LWCF and PRECT.
The multivariate skill score (see Sect. 2.4) shows no obvious relationships with any aerosol parameters, nor with the majority of the atmospheric parameters. Exceptions are the nonlinear relationship with x5 (higher values of x5 are inconsistent with low SS), and the deep convective timescale (x9), which is negatively correlated with, and sets an upper bound on, SS. This suggests that it is not feasible to achieve a climate that is consistent with the default model when the timescale for deep convection is longer than 3–4 h (the default value of x9 in CAM4 is 1 h). Similar results are seen for the Cess climate sensitivity (λ), which shows no relationship to the aerosol parameters or atmospheric parameters x6–x8. A positive correlation is found between λ and x5: higher x5 produces less low cloud, and high-x5 cases are, on average, slightly more sensitive to warming, which is consistent with expectations based on comprehensive ESMs (Siler et al., 2018). Lastly, we note an interesting nonlinear impact of x9 on λ, where λ increases linearly with x9 up to about a 4 h timescale, then becomes much more variable and begins to decrease again.
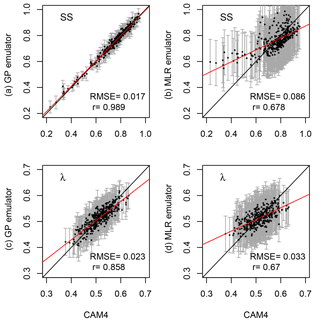
Figure 3Points show predictions from the emulator (y axis) against CAM4 simulated values (x axis) for SS (a) and λ (b) for each case in the n=350 training set, using the statistical emulator in LOOCV mode (see Sect. 4.1). Panels (a) and (c) show predictions made using the GP emulator, and the panels (b) and (d) show predictions made using the MLR emulator. Gray error bars show the 95 % prediction interval for each case. The red line is a least-squares linear fit of the predicted against simulated values, and the black solid line shows the 1:1 line.
3.2 Probability distribution of output variables
The black lines in Fig. 2 show the distribution of global mean outputs based on the n=350 training cases from CAM4, for the six variables that comprise the SS, and λ. The six variables are expressed as biases relative to the default model, so that a value of zero represents a case that perfectly reproduces the default model's global mean for that variable. Their distributions are unimodal and straddle zero, indicating that the majority of cases produce climates reasonably close to the default CAM4. However, for most variables the tails of the distribution are much longer than a Gaussian distribution, indicating a large number of climates that are far from the default model. Indeed, the full range of climates produced in this ensemble is dramatic: the spread in TOA net radiative flux (FNET) is between −30 and +20 W m−2, which is an order of magnitude larger than the FNET response expected due to a doubling of the atmospheric CO2 concentration (Andrews et al., 2012). The distributions of CLDL and FNET are also shifted toward positive and negative values, respectively, indicating a tendency for the perturbations to increase low cloud in the model, increasing shortwave flux to space. Fig. 1 shows that this effect is controlled almost entirely by parameter x5, the sensitivity parameter for low clouds, which has previously been identified as very important in CAM4 (Covey et al., 2013). The impact of x5 may also be asymmetric: reducing x5 by 0.01 from its default value of 0.88 is likely to have a greater impact on cloudiness than increasing x5 by the same amount, because x5 is a relative humidity (RH) threshold, and the distribution of RH is heavily skewed toward lower values.
The distribution of SS is bounded by 0 and 1, by construction, with a single peak at around 0.8, a maximum SS of 0.953, and a long left tail. The peak in the distribution of SS at 0.8, and the fact that max(SS)<1.0, implies that all the cases within our ensemble are – to a greater or lesser extent – imperfect representations of the default model. This is mostly explained by the parameter x4 (the altitude of injection of a uniform layer of BC): no perturbed case can produce a climate exactly like the default model, because the default model does not include x4, and the experimental design specifies that a BC layer is always injected somewhere between 0 and 40 km. We reiterate that the emphasis here is on identifying plausible candidate models with altered aerosol and atmospheric parameters, not on tuning or calibration to make the default model more realistic (relative to observations). The distribution of λ shows a range between 0.35 and 0.65 K W−1 m2, meaning that around 90 % of all candidate models produce a higher climate sensitivity than the default value of 0.45 K W−1 m2. The input parameters driving these changes are explored in Sect. 5.
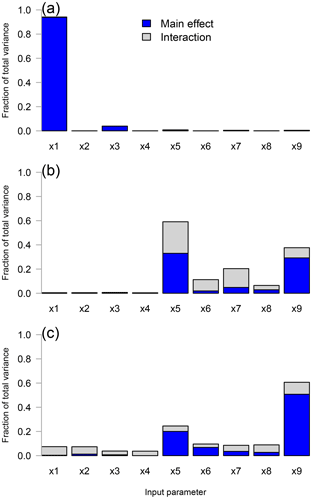
Figure 4Fraction of total variance explained by each input parameter, for (a) AOD, (b) SS, and (c) λ. The light gray portion of each bar represents the contribution of interaction terms, while the blue portion represents the main effect. The full height of each bar represents the total variance explained by each input parameter, with more influential parameters explaining a higher fraction of variance.
4.1 Validating the emulator
Relative to modern ensembles with comprehensive ESMs (Kay et al., 2014), our sample of n=350 training cases provides a large ensemble of cases with which to study the effects on CS from aerosol forcing and atmospheric parameters (Figs. 1–2). However, the nine parameters x1–x9 map onto a vast parameter space that is computationally impractical to sample adequately using CAM4 itself. A more practical way to explore the response space (i.e., to fill in the unsampled regions for the output variables in Fig. 1) is by using a statistical emulator.
Using the emulator of CAM4 described in Sect. 2.3, we make predictions for each output variable shown in Fig. 2 using fine-resolution uniform sampling over the full range of each parameter x1–x9. The emulated results are shown as the gray shaded regions in Fig. 2, and it is immediately apparent that the emulator does a very good job at reproducing the simulated distribution for each variable. The close agreement in all cases indicates that the uncertainty in the emulator is small, which provides confidence that the emulator is a useful tool to explore the parameter space of CAM4. However, we first conduct a more quantitative validation of the emulator, by performing LOOCV to sequentially leave out, and then predict, each individual case from the n=350 training sample. The results of this LOOCV procedure are shown in Fig. 3 and reveal that the emulator is, in general, highly successful at predicting model outputs for unseen parameter combinations.
Taking into account emulator uncertainty (shown by the 95 % confidence interval on each prediction), the agreement between the emulated and simulated values of the multivariate SS is close to perfect (r>0.98). For the Cess climate sensitivity (λ), while there is greater uncertainty on each prediction (margin of error ∼0.05 K W−1 m2), and the emulated values show a general tendency to be slightly underpredicted, root-mean-square error (RMSE) is very low (0.023 K W−1 m2) and the correlation skill is high (r=0.86). A final demonstration of the value of using the Gaussian Process emulator is shown by repeating the emulation using a multiple least-squares linear regression (MLR) model. Figure 3b and d show that the MLR emulator performs substantially worse than the GP emulator in terms of both RMSE and correlation skill.
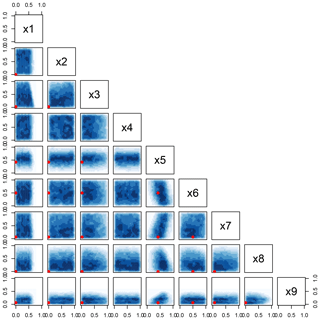
Figure 5The blue shading in each panel indicates the density of plausible cases for each pair of input parameters (x1–x9), displayed in standardized units. Plausible cases are defined as the subset of n=100 000 emulated samples with SS > 0.85, and dAOD < 0.08. Darker shading indicates higher density, and white areas indicate very low density. The default values for each parameter in CAM4 are indicated by red dots in each panel (except for x4, which has no default).
4.2 Parameter sensitivity and importance
Parameter sensitivity is quantified following Carslaw et al. (2013) and McNeall et al. (2016) using the so-called FAST methodology (Saltelli et al., 1999), in the R package sensitivity (Pujol et al., 2017). This method separates the contribution to the total response from “main effects”, that are directly attributable to variations in each (normalized) parameter, and interactions between parameters, which are calculated as the residual: interaction = total − main effect.
Figure 4 reveals that atmospheric parameters x5 and x9 are the most influential for the outputs SS and λ, explaining a combined total of ∼75 % of the total variance in each output. The variation in output AOD is explained almost entirely by x1 (sulfate hygroscopic fraction), with a small residual contribution by x3 (BC mass scaling). No other aerosol parameters are influential for any of the output variables shown, and there are small (<10 %) contributions from atmospheric parameters x6–x8 for SS and λ. In general, the main effects are dominant; however, non-negligible parameter interactions are found for SS, where they make up almost half of the total variance explained by x5. While difficult to directly interpret, we hypothesize that this emphasis on the interaction terms is due to the interrelated nature of the parameters x5–x9, all of which influence clouds, precipitation, and radiative flux (i.e., all of the variables assessed in computing SS) in some form. These results agree closely with previous work examining the sensitivity to atmospheric parameters in CAM4. For example, Covey et al. (2013) show that x5 and x9 are highly influential parameters for top-of-atmosphere radiative flux, although their one-at-a-time methodology did not permit an examination of parameter interactions.
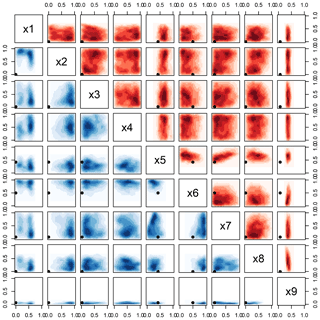
Figure 6As Fig. 5, except that panels with blue shading (lower triangle) are for the subset of cases with low values of Cess climate sensitivity (λ<0.418 K W−1 m2), and panels with red shading (upper triangle) are for the subset of cases with high values of λ (λ>0.538 K W−1 m2). The default values for each parameter in CAM4 are indicated by black dots in each panel (except for x4, which has no default).
4.3 Identifying a plausible set of input parameters
In this section, we use the statistical emulator to identify regions of the nine-dimensional parameter space that produce plausible climates, which are defined as those similar to the climate of the default CAM4. We begin by using the emulator to construct a set of n=100 000 cases for output variables SS, AOD and λ, based on a uniform sample of the distributions of each parameter (x1–x9). Applying first the threshold SS > 0.85 eliminates ∼85 % of cases, and adding a second constraint (AOD < 0.08) eliminates a further 6 % of cases whose AOD is too far from that of default CAM4. The threshold for AOD represents a trade-off between finding a sufficiently large sample of cases, and their fidelity to the default model. Since present-day AOD in default CAM4 tends to be biased low (satellite observations from MODIS and MISR for the present day show AOD ∼ 0.16, compared to 0.11 for CAM4; Remer et al., 2008), and the aerosol perturbations x1–x4 tend to increase AOD, the threshold ensures that plausible cases maintain a global mean AOD that is within 50 % uncertainty of the default CAM4. After applying both thresholds, only ∼9 % of the original parameter space remains plausible, and the density distributions of parameters for this remaining space are shown in Fig. 5.
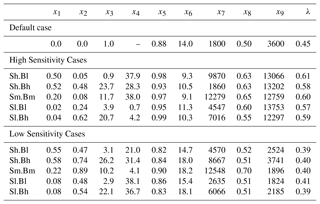
Table 2Each row shows the input parameter values (columns 2–10), and the Cess climate sensitivity (λ, units K Wm−2; column 11) predicted by the emulator for that combination of parameters. The first column denotes the strength of aerosol radiative forcing (ARF) in a case from sulfate (S) and Black Carbon (B): h = high, m = medium and l = low (defined in the text). For reference, the default parameter values in CAM4, and the associated λ, are shown toward the top.
Next we attempt to constrain the parameter ranges by examining the regions of parameter space in Fig. 5 that produce higher or lower densities of plausible outputs. The only aerosol parameter that can be constrained is x1, where all values above 0.6 are implausible. The BC mass scaling parameter x3 shows a slightly reduced density of plausible cases for very high BC mass; however, even very high BC mass cannot be ruled out completely, because 15 % of cases remain plausible with x3>32. For the atmospheric parameters (x5–x9), the range of x5 is compressed toward a central value that is slightly higher than the default value in CAM4 (denoted by the red points in Fig. 5). For x8 (high cloud sensitivity) there is a tendency for most plausible cases to have higher parameter values than default, but very high values are ruled out. The parameter x9 (deep CAPE timescale) is dramatically constrained from its original range: all values above ∼4 h are ruled out, and the default value is located well within the plausible range. Parameters x6 (liquid drop radius over ocean) and x7 (shallow CAPE timescale) do not show any obvious reduction in their plausible ranges.
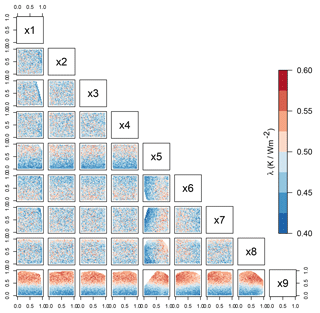
Figure 7Color shading shows Cess climate sensitivity (λ, units K Wm−2) for plausible cases as a function of each pair of input parameters (x1–x9). White areas indicate regions of parameter space where there are no plausible cases.
Finally, we examine the emulated outputs associated with the subset of plausible cases. The red line in each panel of Fig. 2 shows the distribution of output values only for the plausible cases, which provides an estimate of how much our candidate model versions differ from the default CAM4. For all variables the spread for the plausible subset is often considerably smaller than the spread for all cases, and tends to be shifted toward a mean of zero (a perfect representation of the global mean from the default model). This indicates that our threshold-based approach to plausibility is working as desired: the outputs from the plausible models should be closer to the default model, by construction. Interestingly, high values of λ become much less likely after imposing the thresholds. It could be argued that λ is directly influenced by the variables in the SS, and so it is not independent of our thresholding approach; however, we consider λ to be an emergent property of the model and, therefore, this result could not have been predicted a priori.
Running the CAM4 model with its default (unperturbed) settings for parameters x5–x9, and without perturbations to the additional aerosol parameters x1–x4, we find λ=0.45 K W−1 m2. The median value of λ for all n=100 000 emulated cases is 0.51 K W−1 m2, which implies that the net effect of the perturbations to the aerosol parameters (x1–x4) is to increase λ. The 95 % interval of λ for the 9 % of emulated cases that are plausible is 0.418 K W−1 m2 (7 % lower than default) to 0.538 K W−1 m2 (20 % higher than default). This shows that, to some extent, λ is a tunable quantity; however, this range is only about 25 % of the range in λ across an ensemble of CMIP5 models by Medeiros et al. (2014), and only about 16 % of the range found for a much earlier set of models in a slightly different experimental configuration (Cess et al., 1989). This suggests that structural uncertainty (not sampled here) is probably more important than parametric uncertainty in explaining the intermodel spread of λ.
We next examine the distribution of aerosol and atmospheric parameters that are associated with high (λ>0.538 K W−1 m2) and low (λ<0.418 K W−1 m2) sensitivity cases, i.e., plausible cases with λ in the upper and lower 2.5 % of all plausible cases. Figure 6 shows little difference in the distribution of the aerosol parameters (x1–x4) for high or low sensitivity, suggesting that neither the hygroscopicity of sulfate, nor the mass and spatial distribution of BC, are important for determining λ in this model. Much larger differences between the high and low sensitivity cases are found for the atmospheric parameters. As suggested from Fig. 1, high sensitivity is associated with higher values of x5 (less low cloud), x8 (less high cloud) and x9 (longer deep convection), and lower values of x6 (smaller liquid cloud droplets). The parameter x7 (shallow CAPE timescale) appears to have little influence on λ. The situation for low sensitivity is broadly the inverse, and the narrow ranges for some parameters (e.g., x5 and x9) provide clear constraints on radiative–convective processes that control climate sensitivity in this model. The speckled blue–yellow–red nature of the panels for x1–x4 in Fig. 7 shows that the spread of λ is very similar for all values of the aerosol parameters. This suggests that, in tandem with the right combination of atmospheric parameters, any value of λ within the model's range can be achieved for any strength of aerosol forcing. Figure 7 also reveals multiple effects of x9 on λ: the main effect (cf. Fig. 4) is a strong linear gradient in λ from low to high parameter values, in addition to clear nonlinear interactions with parameters x6 and x8.
Collectively, these results suggest that our overall objective of configuring different, but equally plausible, versions of CAM4 with varying strengths of aerosol forcing and climate sensitivity (λ) is eminently achievable. To this end, we conclude this section by presenting examples in Table 2 of parameters with very different aerosol forcings selected from the emulated cases, which produce λ values across the full range for this model. To extract these cases we apply joint thresholds to parameters x1 (sulfate hygroscopicity) and x3 (BC mass scaling) to identify combinations with high (“h”) and low (“l”) sulfate (“S”) and BC (“B”) forcing; for example, Sh.Bl denotes cases with high sulfate, and low BC, forcing. After extracting a distribution of cases for each combination of sulfate and BC forcing, we record the parameters that produce the minimum (low sensitivity), and maximum (high sensitivity), value of λ.
As expected from Fig. 7 and the discussion above, we are able to identify both high and low sensitivity cases for all combinations of aerosol forcing. Comparing pairs of rows for the same aerosol forcing at high and low sensitivity reveals that, by construction, they tend to have similar aerosol parameters. However, clear differences emerge in the atmospheric parameters: the high sensitivity cases tend to have higher x5, x8 and x9, and lower x6. Only x7 appears unrelated to λ, perhaps due to its influence on shallow cumulus clouds, which are more likely to be overlain by higher clouds and, therefore, have limited influence on the top-of-atmosphere energy budget. This table provides a prototype for a future study to test a suite of cases in CAM4 with a fully interactive ocean, to determine the relationship between ARF, λ and the transient climate response (Golaz et al., 2013; Zhao M. et al., 2018).
We employ a statistical emulation procedure to sample the parameter–response space of the atmospheric general circulation model NCAR CESM-CAM4. The influence of four aerosol parameters controlling the aerosol radiative forcing (ARF) from sulfate and black carbon, and five atmospheric parameters controlling clouds and convection, are assessed in combination across their full range of uncertainty. A multivariate skill score is used to determine the plausibility of each combination of parameters, and thus to constrain plausible parameter ranges, and the spread of an important emergent property of the model: its climate sensitivity (λ). We find that atmospheric parameters explain more than 85 % of the variance in λ, and two parameters are most important: x5 controls the amount of low cloud in the model, and x9 controls the timescale for deep convection. The aerosol parameters have little impact on λ in our model configuration, making it equally possible to identify cases with high or low ARF that have high, or low, λ (Table 2).
However, while we attempt to quantify the impact of aerosol–cloud interactions (ACIs) through the hygroscopicity parameter for sulfate aerosols x1, the CAM4 model does not include direct simulation of ACI, which would be expected to substantially increase the importance of the aerosol parameters (Regayre et al., 2018). Future work should quantify the importance of uncertainties in parameters related to subgrid-scale activation of cloud droplets by aerosols in newer versions of the CESM-CAM models that include these processes, and quantify their impacts on ACI and λ (Golaz et al., 2013). In addition, our study focuses entirely on sulfate and black carbon aerosols, but important contributions to aerosol radiative forcing could be expected from uncertainties in the distribution of organic, sea salt, dust and nitrate aerosol, and the representation of their aging properties, as well as activation of cloud droplets (Chen and Penner, 2005). Therefore, while we expect the overall importance of parameters x5 and x9 to be robust, we recommend caution in interpreting the precise numerical details of these results (for example, the 85 % variance explained by atmospheric parameters), since these figures could be highly sensitive to the details of the model configuration.
Our results indicate that the climate sensitivity of CAM4 can be modified, and possibly constrained, through adjustments to select uncertain atmospheric parameters, primarily x5 and x9. These results can be compared with previous studies that examined the impact of tuning parameters on climate sensitivity (λ) in ESMs. We find a plausible spread of λ between 0.418 K W−1 m2 and 0.538 K W−1 m2, which spans approximately 25 % of the range derived from a suite of CMIP5 models that performed a similar experiment (Medeiros et al., 2014). This is in good agreement with previous studies that found that the spread in λ for a single ESM (with either interactive or prescribed ocean components) due to uncertain tuning parameters related to clouds and convection was smaller than the spread among the ensemble of CMIP models (Golaz et al., 2013; Mauritsen et al., 2012). This body of work, therefore, suggests that structural deficiencies in the configuration of ESMs contribute more to the uncertainty in λ than parametric uncertainty. Of the ∼25 % of the spread in λ due to parametric uncertainty, our study indicates that atmospheric parameters explain the vast majority, with only a minor role for aerosol parameters. The major new finding from this work is that a given model's position on the Kiehl curve can be varied through compensating adjustments to atmospheric parameters and radiative forcing, although perhaps only by a relatively modest amount compared to structural uncertainty.
This study explores only the question of whether plausible alternative versions of CAM4 can be configured (through uncertain aerosol and atmospheric parameters) to have different climate sensitivities, relative to CAM4 at the same horizontal resolution with its default parameter settings. Using the default model to determine plausibility explicitly avoids the question of plausibility relative to observations, or finding parameter combinations to “improve” CAM4. That would be an exercise in model tuning or calibration, which is beyond the scope of this study. However, our opinion is that the range of plausible solutions that have been revealed through the emulation procedure makes it highly likely that parameter combinations exist within the sampled parameter–response space that provide better matches to the observed climate than the default settings. This hypothesis will be examined in a future study.
All data and scripts will be made available through the lead author's GitHub repository at https://doi.org/10.5281/zenodo.1400612 (Fletcher, 2018).
CF conceived of the study, completed the simulations and wrote the manuscript. BK helped to design the simulations, ran the Mie code, and contributed to the manuscript. BB helped to run the simulations.
The authors declare that they have no conflict of interest.
This article is part of the special issue “NETCARE (Network on Aerosols and Climate: Addressing Key Uncertainties in Remote Canadian Environments) (ACP/AMT/BG inter-journal SI)”. It is not associated with a conference.
Christopher G. Fletcher and Bakr Badawy were supported by the Network on Climate and Aerosols: Addressing
Key Uncertainties in Remote Canadian Environments. The authors are grateful
for valuable discussions with Jason Blackstock (UCL), and data processing and
analysis performed by graduate student Alex Vukandinovic at the University of
Waterloo. We thank Doug McNeall (UKMO) for making his R code publicly
available at https://github.com/dougmcneall/famous-git (last access: 4 October 2018). The Pacific
Northwest National Laboratory is operated for the US Department of Energy by
Battelle Memorial Institute under contract DE-AC05-76RL01830. We thank the referees for their insightful comments.
Edited by: Farahnaz Khosrawi
Reviewed by: three anonymous referees
Andrews, T., Gregory, J. M., Webb, M. J., and Taylor, K. E.: Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere-cean climate models, Geophys. Res. Lett., 39, L09712, https://doi.org/10.1029/2012GL051607, 2012. a
Ban-Weiss, G. A., Cao, L., Bala, G., and Caldeira, K.: Dependence of climate forcing and response on the altitude of black carbon aerosols, Clim. Dynam., 38, 897–911, https://doi.org/10.1007/s00382-011-1052-y, 2011. a, b, c
Bond, T. C., Doherty, S. J., Fahey, D. W., Forster, P. M., Berntsen, T., DeAngelo, B. J., Flanner, M. G., Ghan, S., Kärcher, B., Koch, D., Kinne, S., Kondo, Y., Quinn, P. K., Sarofim, M. C., Schultz, M. G., Schulz, M., Venkataraman, C., Zhang, H., Zhang, S., Bellouin, N., Guttikunda, S. K., Hopke, P. K., Jacobson, M. Z., Kaiser, J. W., Klimont, Z., Lohmann, U., Schwarz, J. P., Shindell, D., Storelvmo, T., Warren, S. G., and Zender, C. S.: Bounding the role of black carbon in the climate system: A scientific assessment, J. Geophys. Res.-Atmos., 118, 5380–5552, https://doi.org/10.1002/jgrd.50171, 2013. a, b, c, d
Bony, S., Stevens, B., Frierson, D. M. W., Jakob, C., Kageyama, M., Pincus, R., Shepherd, T. G., Sherwood, S. C., Siebesma, A. P., Sobel, A. H., Watanabe, M., and Webb, M. J.: Clouds, circulation and climate sensitivity, Nat. Geosci., 8, 261–268, https://doi.org/10.1038/ngeo2398, 2015. a
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V.-M., Kondo, Y., Liao, H., Lohmann, U., Rasch, P., Satheesh, S., Sherwood, S., Stevens, B., and Zhang, X.: Clouds and Aerosols, book section 7, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 571–658, https://doi.org/10.1017/CBO9781107415324.016, 2013. a, b
Carslaw, K. S., Lee, L. A., Reddington, C. L., Pringle, K. J., Rap, A., Forster, P. M., Mann, G. W., Spracklen, D. V., Woodhouse, M. T., Regayre, L. A., and Pierce, J. R.: Large contribution of natural aerosols to uncertainty in indirect forcing, Nature, 503, 67–71, https://doi.org/10.1038/nature12674, 2013. a, b
Cess, R. D., Potter, G. L., Blanchet, J. P., Boer, G. J., Ghan, S. J., Kiehl, J. T., Treut, H. L., Li, Z.-X., Liang, X.-Z., Mitchell, J. F. B., Morcrette, J.-J., Randall, D. A., Riches, M. R., Roeckner, E., Schlese, U., Slingo, A., Taylor, K. E., Washington, W. M., Wetherald, R. T., and Yagai, I.: Interpretation of cloud-climate feedback as produced by 14 atmospheric general circulation models, Science, 245, 513–516, https://doi.org/10.1126/science.245.4917.513, 1989. a, b
Chen, Y. and Penner, J. E.: Uncertainty analysis for estimates of the first indirect aerosol effect, Atmos. Chem. Phys., 5, 2935–2948, https://doi.org/10.5194/acp-5-2935-2005, 2005. a
Collins, W. D., Rasch, P. J., Boville, B. A., Hack, J. J., McCaa, J. R., Williamson, D. L., Briegleb, B. P., Bitz, C. M., Lin, S.-J., and Zhang, M.: The Formulation and Atmospheric Simulation of the Community Atmosphere Model Version 3 (CAM3), J. Clim., 19, 2144–2161, https://doi.org/10.1175/JCLI3760.1, 2006. a
Covey, C., Lucas, D. D., Tannahill, J., Garaizar, X., and Klein, R.: Efficient screening of climate model sensitivity to a large number of perturbed input parameters, J. Adv. Model. Earth Syst., 5, 598–610, 2013. a, b, c, d, e
Flato, G., Marotzke, J., Abiodun, B., Braconnot, P., Chou, S., Collins, W., Cox, P., Driouech, F., Emori, S., Eyring, V., Forest, C., Gleckler, P., Guilyardi, E., Jakob, C., Kattsov, V., Reason, C., and Rummukainen, M.: Evaluation of climate models, Cambridge University Press, 741–882, 2013. a
Fletcher, C. G.: FKB2018, https://doi.org/10.5281/zenodo.1400612date, last access: 8 December 2018.
Forster, P. M., Andrews, T., Good, P., Gregory, J. M., Jackson, L. S., and Zelinka, M.: Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models, J. Geophys. Res.-Atmos., 118, 1139–1150, https://doi.org/10.1002/jgrd.50174, 2013. a
Gent, P. R., Danabasoglu, G., Donner, L. J., Holland, M. M., Hunke, E. C., Jayne, S. R., Lawrence, D. M., Neale, R. B., Rasch, P. J., Vertenstein, M., Worley, P. H., Yang, Z.-L., and Zhang, M.: The Community Climate System Model Version 4, J. Clim., 24, 4973–4991, https://doi.org/10.1175/2011JCLI4083.1, 2011. a, b, c
Golaz, J.-C., Golaz, J.-C., and Levy, H.: Cloud tuning in a coupled climate model: Impact on 20th century warming, Geophys. Res. Lett., 40, 2246–2251, https://doi.org/10.1002/grl.50232, 2013. a, b, c, d, e
Hourdin, F., Foujols, M.-A., Codron, F., Guemas, V., Dufresne, J.-L., Bony, S., Denvil, S., Guez, L., Lott, F., Ghattas, J., Braconnot, P., Marti, O., Meurdesoif, Y., and Bopp, L.: Impact of the LMDZ atmospheric grid configuration on the climate and sensitivity of the IPSL-CM5A coupled model, Clim. Dynam., 40, 2167–2192, https://doi.org/10.1007/s00382-012-1411-3, 2013. a
Hourdin, F., Mauritsen, T., Gettelman, A., Golaz, J.-C., Balaji, V., Duan, Q., Folini, D., Ji, D., Klocke, D., Qian, Y., Rauser, F., Rio, C., Tomassini, L., Watanabe, M., and Williamson, D.: The art and science of climate model tuning, Bull. Am. Meteor. Soc., March 2017, 589–602, https://doi.org/10.1175/BAMS-D-15-00135.1, 2016. a
Kay, J. E., Deser, C., Phillips, A., Mai, A., Hannay, C., Strand, G., Arblaster, J. M., Bates, S. C., Danabasoglu, G., Edwards, J., Holland, M., Kushner, P., Lamarque, J.-F., Lawrence, D., Lindsay, K., Middleton, A., Munoz, E., Neale, R., Oleson, K., Polvani, L., and Vertenstein, M.: The community earth system model (cesm) large ensemble project: a community resource for studying climate change in the presence of internal climate variability, Bull. Am. Meteor. Soc., 96, 1333–1349, https://doi.org/10.1175/BAMS-D-13-00255.1, 2014. a
Kiehl, J. T.: Twentieth century climate model response and climate sensitivity, Geophys. Res. Lett., 34, L22710, https://doi.org/10.1029/2007GL031383, 2007. a
Kim, H., Kang, S. M., Hwang, Y.-T., and Yang, Y.-M.: Sensitivity of the Climate Response to the Altitude of Black Carbon in the Northern Subtropics in an Aquaplanet GCM, J. Clim., 28, 6351–6359, https://doi.org/10.1175/JCLI-D-15-0037.1, 2015. a
Lamarque, J.-F., Bond, T. C., Eyring, V., Granier, C., Heil, A., Klimont, Z., Lee, D., Liousse, C., Mieville, A., Owen, B., Schultz, M. G., Shindell, D., Smith, S. J., Stehfest, E., Van Aardenne, J., Cooper, O. R., Kainuma, M., Mahowald, N., McConnell, J. R., Naik, V., Riahi, K., and van Vuuren, D. P.: Historical (1850–2000) gridded anthropogenic and biomass burning emissions of reactive gases and aerosols: methodology and application, Atmos. Chem. Phys., 10, 7017–7039, https://doi.org/10.5194/acp-10-7017-2010, 2010. a, b
Lee, L. A., Carslaw, K. S., Pringle, K. J., Mann, G. W., and Spracklen, D. V.: Emulation of a complex global aerosol model to quantify sensitivity to uncertain parameters, Atmos. Chem. Phys., 11, 12253–12273, https://doi.org/10.5194/acp-11-12253-2011, 2011. a, b, c
Lee, L. A., Carslaw, K. S., Pringle, K. J., and Mann, G. W.: Mapping the uncertainty in global CCN using emulation, Atmos. Chem. Phys., 12, 9739–9751, https://doi.org/10.5194/acp-12-9739-2012, 2012. a
Mauritsen, T., Stevens, B., Roeckner, E., Crueger, T., Esch, M., Giorgetta, M., Haak, H., Jungclaus, J., Klocke, D., Matei, D., Mikolajewicz, U., Notz, D., Pincus, R., Schmidt, H., and Tomassini, L.: Tuning the climate of a global model, J. Adv. Model. Earth Syst., 4, M00A01, https://doi.org/10.1029/2012MS000154, 2012. a, b
McKay, M. D., Beckman, R. J., and Conover, W. J.: A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code, Technometrics, 21, 239–245, https://doi.org/10.2307/1268522, 1979. a
McNeall, D., Williams, J., Booth, B., Betts, R., Challenor, P., Wiltshire, A., and Sexton, D.: The impact of structural error on parameter constraint in a climate model, Earth Syst. Dynam., 7, 917–935, https://doi.org/10.5194/esd-7-917-2016, 2016. a, b, c
Medeiros, B., Stevens, B., and Bony, S.: Using aquaplanets to understand the robust responses of comprehensive climate models to forcing, Clim. Dynam., 44, 1957–1977, https://doi.org/10.1007/s00382-014-2138-0, 2014. a, b, c
Pierce, D. W., Barnett, T. P., Santer, B. D., and Gleckler, P. J.: Selecting global climate models for regional climate change studies, P. Natl. Acad. Sci. USA, 106, 8441–8446, https://doi.org/10.1073/pnas.0900094106, 2009. a
Pujol, G., Iooss, B., Boumhaout, A. J. w. c. f. K., Veiga, S. D., Delage, T., Fruth, J., Gilquin, L., Guillaume, J., Gratiet, L. L., Lemaitre, P., Nelson, B. L., Monari, F., Oomen, R., Ramos, B., Roustant, O., Song, E., Staum, J., Touati, T., and Weber, F.: sensitivity: Global Sensitivity Analysis of Model Outputs, available at: https://CRAN.R-project.org/package=sensitivity (last access: 8 December 2018), 2017. a
Regayre, L. A., Johnson, J. S., Yoshioka, M., Pringle, K. J., Sexton, D. M. H., Booth, B. B. B., Lee, L. A., Bellouin, N., and Carslaw, K. S.: Aerosol and physical atmosphere model parameters are both important sources of uncertainty in aerosol ERF, Atmos. Chem. Phys., 18, 9975–10006, https://doi.org/10.5194/acp-18-9975-2018, 2018. a, b, c, d, e, f
Remer, L. A., Kleidman, R. G., Levy, R. C., Kaufman, Y. J., Tanré, D., Mattoo, S., Martins, J. V., Ichoku, C., Koren, I., Yu, H., and Holben, B. N.: Global aerosol climatology from the MODIS satellite sensors, J. Geophys. Res., 113, D14S07, https://doi.org/10.1029/2007JD009661, 2008. a
Roustant, O., Ginsbourger, D., and Deville, Y.: DiceKriging , DiceOptim: Two R Packages for the Analysis of Computer Experiments by Kriging-Based Metamodeling and Optimization, J. Stat. Softw., 51, 1–55, https://doi.org/10.18637/jss.v051.i01, 2012. a, b
Saltelli, A., Tarantola, S., and Chan, K. P.-S.: A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output, Technometrics, 41, 39–56, https://doi.org/10.1080/00401706.1999.10485594, 1999. a
Samset, B. H. and Myhre, G.: Climate response to externally mixed black carbon as a function of altitude: BC climate response vs altitude, J. Geophys. Res.-Atmos., 120, 2913–2927, https://doi.org/10.1002/2014JD022849, 2015. a
Sanderson, B. M., Knutti, R., Aina, T., Christensen, C., Faull, N., Frame, D. J., Ingram, W. J., Piani, C., Stainforth, D. A., Stone, D. A., and Allen, M. R.: Constraints on Model Response to Greenhouse Gas Forcing and the Role of Subgrid-Scale Processes, J. Clim., 21, 2384–2400, https://doi.org/10.1175/2008JCLI1869.1, 2008. a
Sherwood, S. C., Bony, S., and Dufresne, J.-L.: Spread in model climate sensitivity traced to atmospheric convective mixing, Nature, 505, 37–42, https://doi.org/10.1038/nature12829, 2014. a, b
Shields, C. A., Bailey, D. A., Danabasoglu, G., Jochum, M., Kiehl, J. T., Levis, S., and Park, S.: The Low-Resolution CCSM4, J. Clim., 25, 3993–4014, https://doi.org/10.1175/JCLI-D-11-00260.1, 2012. a
Siler, N., Po-Chedley, S., and Bretherton, C. S.: Variability in modeled cloud feedback tied to differences in the climatological spatial pattern of clouds, Clim. Dynam., 50, 1209–1220, https://doi.org/10.1007/s00382-017-3673-2, 2018. a
Stevens, B.: Rethinking the Lower Bound on Aerosol Radiative Forcing, J. Clim., 28, 4794–4819, https://doi.org/10.1175/JCLI-D-14-00656.1, 2015. a, b
Watanabe, M., Suzuki, T., O'ishi, R., Komuro, Y., Watanabe, S., Emori, S., Takemura, T., Chikira, M., Ogura, T., Sekiguchi, M., Takata, K., Yamazaki, D., Yokohata, T., Nozawa, T., Hasumi, H., Tatebe, H., and Kimoto, M.: Improved climate simulation by miroc5: mean states, variability, and climate sensitivity, J. Clim., 23, 6312–6335, https://doi.org/10.1175/2010JCLI3679.1, 2010. a
Yang, B., Qian, Y., Berg, L. K., Ma, P.-L., Wharton, S., Bulaevskaya, V., Yan, H., Hou, Z., and Shaw, W. J.: Sensitivity of turbine-height wind speeds to parameters in planetary boundary-layer and surface-layer schemes in the weather research and forecasting model, Bound.-Lay. Meteorol., 162, 117–142, https://doi.org/10.1007/s10546-016-0185-2, 2017. a
Zhao, M., Golaz, J.-C., Held, I. M., Guo, H., Balaji, V., Benson, R., Chen, J.-H., Chen, X., Donner, L. J., Dunne, J. P., Dunne, K., Durachta, J., Fan, S.-M., Freidenreich, S. M., Garner, S. T., Ginoux, P., Harris, L. M., Horowitz, L. W., Krasting, J. P., Langenhorst, A. R., Liang, Z., Lin, P., Lin, S.-J., Malyshev, S. L., Mason, E., Milly, P. C. D., Ming, Y., Naik, V., Paulot, F., Paynter, D., Phillipps, P., Radhakrishnan, A., Ramaswamy, V., Robinson, T., Schwarzkopf, D., Seman, C. J., Shevliakova, E., Shen, Z., Shin, H., Silvers, L. G., Wilson, J. R., Winton, M., Wittenberg, A. T., Wyman, B., and Xiang, B.: The GFDL global atmosphere and land model AM4.0/LM4.0: 2. model description, sensitivity studies, and tuning strategies, J. Adv. Model. Earth Syst., 10, 735–769, https://doi.org/10.1002/2017MS001209, 2018. a, b, c
- Abstract
- Introduction
- Data, models and methods
- Controls on climate sensitivity in the CAM4 training simulations
- Exploring the parameter space through emulation
- Impact on climate sensitivity
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- References
- Abstract
- Introduction
- Data, models and methods
- Controls on climate sensitivity in the CAM4 training simulations
- Exploring the parameter space through emulation
- Impact on climate sensitivity
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- References





