Molecular dynamics simulation of the surface tension of aqueous sodium chloride: from dilute to highly supersaturated solutions and molten salt

Sodium chloride (NaCl) is one of the key components of atmospheric aerosols. The surface tension of aqueous NaCl solution (σ_NaCl,sol) and its concentration dependence are essential to determine the equilibrium water vapor pressure of aqueous NaCl droplets. Supersaturated NaCl solution droplets are observed in laboratory experiments and under atmospheric conditions, but the experimental data for σ_NaCl,sol are mostly limited up to subsaturated solutions. In this study, the surface tension of aqueous NaCl is investigated by molecular dynamics (MD) simulations and the pressure tensor method from dilute to highly supersaturated solutions. We show that the linear approximation of concentration dependence of σ_NaCl,sol at molality scale can be extended to the supersaturated NaCl solution until a molality of ∼10.7 mol kg⁻¹ (i.e., solute mass fraction (x_NaCl) of ∼0.39). Energetic analyses show that this monotonic increase in surface tension is driven by the increase in excess surface enthalpy (ΔH) as the solution becomes concentrated. After that, the simulated σ_NaCl,sol remains almost unchanged until x_NaCl of ∼0.47 (near the concentration upon efflorescence). The existence of the “inflection point” at x_NaCl of ∼0.39 and the stable surface tension of x_NaCl between ∼0.39 and ∼0.47 can be attributed to the nearly unchanged excess surface entropy term (T⋅ΔS) and the excess surface enthalpy term (ΔH). After a “second inflection point” at x_NaCl of ∼0.47, the simulated σ_NaCl,sol gradually regains the growing momentum with a tendency to approach the surface tension of molten NaCl (∼175.58 mN m⁻¹ at 298.15 K, MD simulation-based extrapolation). This fast increase in σ_NaCl,sol at x_NaCl>0.47 is a process driven by excess surface enthalpy and excess surface entropy. Our results reveal different regimes of concentration dependence of the surface tension of aqueous NaCl at 298.15 K: a water-dominated regime (x_NaCl from 0 to ∼0.39), a transition regime (x_NaCl from ∼0.39 to ∼0.47) and a molten NaCl-dominated regime (x_NaCl from ∼0.47 to 1).

1 Introduction

Sodium chloride (NaCl) is one of the most important components of atmospheric aerosol particles (Finlayson-Pitts, 2003; Lewis and Schwartz, 2004). The aqueous NaCl solution droplet could participate in many atmospheric processes, such as phase transition, cloud activation, ice crystallization, long-range transport and chemical aging (Martin, 2000; Finlayson-Pitts, 2003; Ghorai et al., 2014; Wagner et al., 2015; Chen et al., 2016). To better understand these processes, the concentration-dependent surface tension of aqueous NaCl solution (σ_NaCl,sol) is essential to determine the equilibrium between NaCl solution droplet and water vapor (Jarvis and Scheiman, 1968; Dutcher et al., 2010).

Below the saturation point (∼6.15 mol kg⁻¹), σ_NaCl,sol shows a near-linear dependence on molality (Jarvis and Scheiman, 1968; Johansson and Eriksson, 1974; Aveyard and Saleem, 1976; Weissenborn and Pugh, 1995; Matubayasi et al., 2001) with a slope of 1.73±0.17 (Pegram and Record, 2006, 2007). Because of the energy barrier of crystallization during dehydration and size effects at the nanoscale (Martin, 2000; Biskos et al., 2006; Cheng et al., 2015), supersaturated aqueous NaCl solution droplets can exist under atmospheric conditions. However, direct measurements of surface tension of supersaturated droplets are challenging due to technical difficulties (Harkins and Brown, 1919; Vargaftik et al., 1983; Richardson and Snyder, 1994; Kumar, 2001). Only recently, Bzdek et al. (2016) overcame these limitations with an optical tweezer method and extended the concentration range to ∼8 mol kg⁻¹, where the near-linear relationship still holds (Bzdek et al., 2016).

It is a matter of debate to what extent the approximation of a near-linear dependence of surface tension on molality can still be used for NaCl droplets. Cheng et al. (2015) used the differential Köhler analyses (DKA) method to retrieve the surface tension of NaCl aqueous droplets, and revealed a large deviation from the near-linear increase at a molality of ∼10 mol kg⁻¹. In literature, such a deviation in concentrated solution has also been found for other compounds, such as HNO₃ (Weissenborn and Pugh, 1996), and it is believed to be typically true for most highly soluble electrolytes (Dutcher et al., 2010). The reason for such deviation remains unclear.

Several models about surface tension have been developed for highly concentrated solutions, e.g., Li and Lu (2001), Li et al. (1999) and Levin and Flores-Mena (2001). Li and Lu (2001) developed a model based on the Gibbs dividing surface concept, where the adsorption and desorption rate constants, saturated surface excess, stoichiometric coefficient of ions and mean ionic activity coefficient are needed. For NaCl aqueous solutions, this model is suitable for solutions with concentrations up to ∼5.5 mol kg⁻¹. Li et al. (1999) uses a Debye–Hückel parameter, osmotic coefficient and a proportionality constant from the fitting of measured values to calculate the surface tension, which covers the concentration until the saturation point of bulk NaCl aqueous solutions. The remaining models are mostly only suitable for the dilute electrolyte solutions, such as the one proposed by Levin and Flores-Mena (2001). In their valid concentration range, these surface tension models produce linear or near-linear concentration dependence of σ_NaCl,sol that agrees well with currently available observations.

One surface tension model that is able to predict σ_NaCl,sol in the whole concentration range from infinitely dilute (x_NaCl=0) to highly supersaturated solution to molten salts (x_NaCl=1) was proposed by Dutcher et al. (2010), which has been adopted into the widely used Extended Aerosol Inorganics Model (E-AIM; Wexler and Clegg, 2002). This model is based on the following concept: ions are solvated by the water at low salt concentrations, which means that water molecules form hydration shells around the ions; while at very high salt concentration the water is considered as “solute” that is solvated by the ions, which means that ions form shells around the water molecules (Dutcher et al., 2010). Accordingly, for a diluted solution, the surface tension of water dominates and the surface tension of the solution equals the surface tension of water adjusted by a term that is proportional to the solute concentration. For a highly supersaturated solution, a similar relationship can be applied with the surface tension of molten salt as governing element. Legitimately, the model is then constrained by the surface tensions of water and molten salt. The parameterization of this model is obtained by fitting the data of subsaturated solutions. When the aqueous NaCl solution gets concentrated, this model shows a nonlinear monotonically increasing trend of σ_NaCl,sol generally in good agreement with observations, but no inflection point was introduced. It should be noted that the surface tension as a function of mole fraction of NaCl according to the Dutcher et al. (2010) model is essentially a linear interpolation between the surface tensions of water and molten NaCl.

In this study, we applied molecular dynamics (MD) simulations and the pressure tensor method to calculate the concentration dependence of σ_NaCl,sol from infinitely dilute (x_NaCl=0) to highly supersaturated solution to molten salt (x_NaCl=1). The concentration dependence of σ_NaCl,sol is divided into 3 regimes: a water-dominated regime, a transition regime and a molten NaCl-dominated regime. We compare our results with the Dutcher et al. (2010) model, and present the principal underlying physical chemistry (driving forces) behind the change of surface tension along concentration changes.

Table 1 Concentrations of solution studied in our simulation and the calculated values of surface tension.

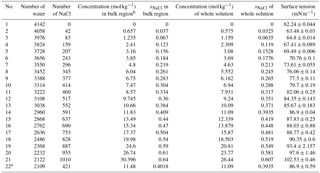
^a The solution slab in this system is $\mathrm{3}\mathrm{nm}\times \mathrm{3}\mathrm{nm}\times \mathrm{10}\mathrm{nm}$ and the simulation box is $\mathrm{3}\mathrm{nm}\times \mathrm{3}\mathrm{nm}\times \mathrm{30}\mathrm{nm}$.
^b There is a little difference between the concentration in the bulk region and the one of the whole system due to surface effects. The values used in the main text are the ones in the bulk region.

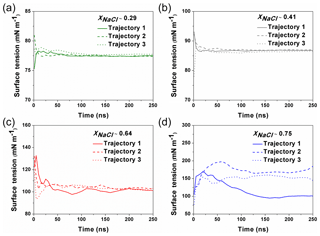
Figure 1 The calculated surface tension at different simulation time from different trajectories. For the solution with x_NaCl≤0.64 (a–c), the surface tension become steadily stabilized after ∼100–150 ns, and different individual simulation runs converge to a similar result. When x_NaCl>0.64 (d; here x_NaCl=0.75), the surface tension keeps fluctuating and the final values from different individual simulations cannot be converged even after 250 ns.

2 Methods

2.1 MD simulation

MD simulations were carried out with the GROMACS 5.1 package (Abraham et al., 2015). The Na⁺ ions, Cl⁻ ions and water molecules were added into a cubic box (L=5 nm) to imitate the NaCl solution. The concentrations of simulated solutions are summarized in Table 1. To simulate the surface tension of supersaturated NaCl aqueous solution, we make use of the time window in the MD simulations before the crystallization starts in the system. The highest x_NaCl we can reach is ∼0.64 (the corresponding concentration is ∼30.39 mol kg⁻¹), below which the simulated surface tensions in three independent runs stably converge after 50 to 100 ns (Fig. 1). For more concentrated solutions, stable convergence cannot be reached, e.g., large fluctuations are shown in Fig. 1d at x_NaCl of 0.75.

According to Dutcher et al. (2010), surface tension of liquid or molten NaCl at 298.15 K (corresponding x_NaCl is 1, infinite concentrated solution) can be regarded as the upper boundary of σ_NaCl,sol. However, a direct simulation of surface tension of molten NaCl at 298.15 K would not be possible, due to excessively large relaxation times of this system at this temperature. It has been found that surface tensions of a very wide range of molten salts can be well described by linear functions of temperature (Sada et al., 1984; Horvath, 1985; Janz, 1988; Dutcher et al., 2010). We thus follow the approach of Dutcher et al. (2010) assuming a linear relationship between surface tension of molten NaCl and temperature. With this approach, we retrieve the surface tension of molten NaCl at 298.15 K by extrapolating the simulated surface tension of molten NaCl in the temperature range of 1000 to 1700 K. Note that, in principle, non-linearity could still be possible at very high degrees of supercooling (e.g., close to or at room temperature) for the molten salts, which may introduce uncertainties to the offset obtained by the extrapolation.

Figure 2 Schematic diagram of the different steps performed in the MD simulation.

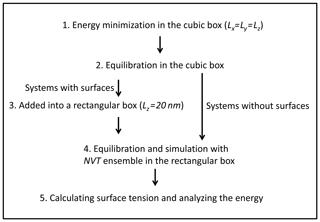
The simulation procedure we followed is the following (Fig. 2): (1) systems were firstly energetically minimized by the steepest descent method (Stillinger and Weber, 1985). (2) Solutions were equilibrated in the NVT ensemble (constant-temperature, constant-volume) and NPT ensemble (constant-temperature, constant-pressure) (pressure=1 bar) with periodic boundary conditions in three directions. The temperature was controlled by using the Nosé–Hoover thermostat (Nosé, 1984; Hoover, 1985). The box volume change due to the variation in density at different temperatures, and in our case the length of the cubic box varied from 4.9 to 5.1 nm. (3) The box was elongated along the z direction with L_z=20 nm to create two interfacial regions. (4) The solution was equilibrated and simulated with the NVT ensemble in the rectangular parallelepiped box at the corresponding temperature. (5) Systems without surfaces were also simulated for further energy analysis, and the trajectories obtained from step 2 were simulated with NPT ensemble. (6) All simulations were carried out for at least 200 ns, which is much longer than that in previous studies (a few nanoseconds; Jungwirth and Tobias, 2000; Neyt et al., 2013), because the system that we were dealing with is much more concentrated. A 1 fs time step was adopted and conformations for analysis were saved every 2 ps. Both electrostatic interactions and van der Waals interactions were calculated using the particle mesh Ewald (PME) algorithm, which has been proven to be a good choice for accurate calculation of long-range interactions (Essmann et al., 1995; Fischer et al., 2015). To test the reproducibility, all the systems were simulated 3 times, and the respective statistical error bars were provided.

In our simulation, the Joung–Cheatham (JC) force field for NaCl (Joung and Cheatham III, 2009) with SPC/E water model (Berendsen et al., 1987) was applied to simulate the NaCl solution and molten NaCl. The solubility at 298.15 K based on the JC force field with SPC/E model has been determined as 3.7±0.2 mol kg⁻¹ (Moučka et al., 2013; Mester and Panagiotopoulos, 2015; Espinosa et al., 2016), which to the best of our knowledge is the value closest to the experimental value of solubility (∼6.15 mol kg⁻¹). Therefore, this force field is appropriate to use to study the concentration dependence of properties. More details about the history of the attempts to correctly calculate the quantity by molecular simulation can be found in the review by Nezbeda et al. (2016).

2.2 Calculation of surface tension

Based on results from MD simulations, the surface tension was calculated by using the mechanical definition of the atomic pressure (Alejandre et al., 1995):

$$\begin{array}{}\text{(1)}& {\mathit{\sigma }}_{\mathrm{MD}}=\mathrm{0.5}{L}_z\left[\langle P_{zz}\rangle -\mathrm{0.5}\left(\langle P_{xx}\rangle +\langle P_{yy}\rangle \right)\right],\end{array}$$

where σ_MD can represent the surface tension of molten NaCl (σ_NaCl), NaCl solution (σ_NaCl,sol) or pure water (σ_water); L_z is the length of the simulation cell in the longest direction (along z axis) and P_aa (a=x, y, z) denotes the diagonal component of the pressure tensor. The 〈…〉 refers to the time average. The factor 0.5 outside the squared brackets takes into account the two interfaces in the system. Only the stable values were taken as our calculated surface tension.

2.3 Energy analysis

The excess surface enthalpy denotes the additional enthalpy in the system due to the creation of surfaces. It can be calculated as the difference of enthalpy between solutions with and without surfaces (Bahadur et al., 2007),

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }H=H_{b\mathit{\_}s}-H_b,\end{array}$$

where H_{b_s} is the total enthalpy of simulated systems with surfaces and H_b is the total enthalpy of simulated systems without surfaces. As the kinetic energy is the same for systems with or without surfaces and the difference of pV can be ignored, ΔH can be presented as

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }H=E_{b\mathit{\_}s}-E_b,\end{array}$$

where E_{b_s} and E_b are the potential energy of the system with and without surfaces.

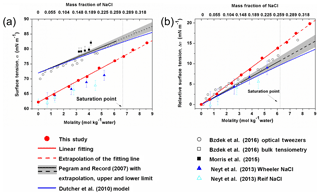
Figure 3 Surface tension (a) and relative surface tension (b) defined as $\mathrm{\Delta }\mathit{\sigma }={\mathit{\sigma }}_{\mathrm{solution}}-{\mathit{\sigma }}_{\mathrm{water}}$ as a function of the concentration of NaCl. The σ_water in the Morris et al. (2015) study was not determined, thus the corresponding Δσ is not shown in (b).

Then the surface tension can be determined by the excess surface free energy per unit area as in Eq. (4) (Davidchack and Laird, 2003):

$$\begin{array}{}\text{(4)}& \mathit{\sigma }={\displaystyle \frac{\mathrm{\Delta }G}{A}}={\displaystyle \frac{\mathrm{\Delta }H-T\cdot \mathrm{\Delta }S}{A}},\end{array}$$

where ΔG is the increased part of free energy due to the creation of surfaces, A is the total area of the surface we created, so $A=\mathrm{2}\times a$ and a is the area of each created surface. ΔS is the excess surface entropy. We then can retrieve ΔS by using the data of enthalpy and surface tension:

$$\begin{array}{}\text{(5)}& \mathrm{\Delta }S={\displaystyle \frac{\mathrm{\Delta }H-\mathit{\sigma }\cdot A}{T}},\end{array}$$

where ΔH and T⋅ΔS per unit area ($\frac{\mathrm{\Delta }H}{A}$ and $\frac{T\cdot \mathrm{\Delta }S}{A}$) are obtained as the enthalpic and entropic part of the contributions to the net surface tension, which will be used to explain the change of surface tension along with the mass fraction of NaCl (x_NaCl).

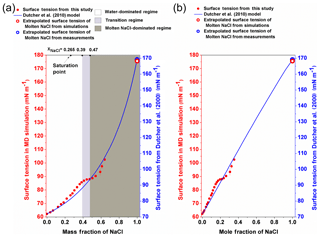
Figure 4 The surface tension of different-concentration NaCl solution. (a) The surface tension of NaCl solution against the mass fraction of NaCl. The left red y axis is for the data from MD simulation (red circle), and the right blue y axis is for the Dutcher et al. (2010) model (blue solid line). The white, light grey and dark grey areas shade the water-dominated, transition and molten NaCl-dominated regimes, respectively. (b) The surface tension of NaCl solution is plotted against the mole fraction of NaCl.

3 Results and discussion

3.1 Water-dominated regime ($x_{\mathrm{NaCl}}<\sim \mathrm{0.39}$)

In Fig. 3a, the calculated surface tension of NaCl aqueous solution (σ_NaCl,sol) is compared with experimentally determined values (Jarvis and Scheiman, 1968; Johansson and Eriksson, 1974; Aveyard and Saleem, 1976; Weissenborn and Pugh, 1995; Matubayasi et al., 2001; Pegram and Record, 2006, 2007; Morris et al., 2015; Bzdek et al., 2016) in the subsaturated concentration range (molality of NaCl solution from 0 to 6.15 mol kg⁻¹ and x_NaCl from 0 to ∼0.265). At 298.15 K, both model simulation (red solid points and fit line in Fig. 3a) and experimental observation (black line in Fig. 3a) reveal a linear dependence of surface tension on solution concentration at molality scale, with a very similar slope (2.1 versus 1.73±0.17, respectively). Systematic underestimation, however, exists in the simulated σ_NaCl,sol. The previous MD simulations by Neyt et al. (2013) have also reported a similar result for the solution whose concentration ranges from 0 to 5.2 mol kg⁻¹ by using the same water model (SPC/E) but two different NaCl force fields, i.e., Wheeler NaCl (solid dark-blue triangle in Fig. 3a) and Relf NaCl (open light-blue triangle in Fig. 3a). Bhatt et al. (2004) also used the Wheeler NaCl model and SPC/E water model revealing a linear dependence and underestimation. We also subtracted the experimentally determined and the MD-simulated surface tension of pure water (σ_water) from the observed and modeled σ_NaCl,sol, respectively. The relative increase in surface tension ($\mathrm{\Delta }\mathit{\sigma }={\mathit{\sigma }}_{\mathrm{NaCl},\mathrm{sol}}-{\mathit{\sigma }}_{\mathrm{water}}$) from models and experiments converge nicely (Fig. 3b), and the former is only a little higher than the latter. The MD simulation is able to reproduce the increment in the growth of surface tension from pure water due to the addition of solute NaCl, although the predicted absolute value of σ_NaCl,sol is systematically underestimated, which may mainly be attributed to the discrepancy between observed σ_water and the modeled ones from the SPC/E water model.

By performing MD simulations in the supersaturated concentration range, we found that this linear relationship still holds beyond the saturation point until x_NaCl of ∼0.39 (Fig. 4). As mentioned above, the laboratory experiments with elevated NaCl aqueous droplet and the optical tweezer method show that the linear relationship between σ_NaCl,sol and NaCl concentration (molality scale) can be extended to ∼8 mol kg⁻¹ (Fig. 3; Bzdek et al., 2016), corresponding to x_NaCl of ∼0.33 (Fig. 4), which is consistent with our simulations.

3.2 Transition regime (x_NaCl from ∼0.39 to ∼0.47)

It was often found that surface tensions of single inorganic electrolyte aqueous solutions were linear functions of concentration (at the molality scale) over the moderate concentration range (Horvath, 1985; Dutcher et al., 2010). However, these simple relationships may not hold when the solutions become more concentrated. As shown in Fig. 4, starting from x_NaCl∼0.39, the simulated σ_NaCl,sol remains almost unchanged until x_NaCl of ∼0.47 (concentration upon efflorescence). This inflection point of σ_NaCl,sol at x_NaCl of ∼0.39 is supported by those determined by the DKA approach (Cheng et al., 2015), where there is a large deviation of surface tension from the monotonic linear increase. Note that beyond x_NaCl of ∼0.47, the simulated surface tension increases again (Fig. 4). This second inflection point, right at the concentration upon efflorescence, may imply a potential correlation with crystallization processes.

3.3 Molten NaCl-dominated regime ($x_{\mathrm{NaCl}}>\sim \mathrm{0.47}$)

Beyond the second inflection point (x_NaCl>0.47), the simulated σ_NaCl,sol gradually increases more and more strongly (Fig. 4). Unfortunately, due to the large fluctuation in the surface tension simulation (Fig. 1), we are not able to extend our surface tension calculation in this way beyond x_NaCl of ∼0.64. However, according to Dutcher et al. (2010), it is expected that the surface tension of the solution would ultimately approach the surface tension of the hypothetical molten solute (i.e., x_NaCl=1) at the same temperature. This hypothesis has been found to be consistent with the DKA retrieval for a highly concentrated ammonium sulfate aqueous solution with molality of ∼380 mol kg⁻¹ (Cheng et al., 2015). We thus also try to constrain the growth of σ_NaCl,sol by MD-simulated surface tension of molten NaCl (σ_NaCl) at 298.15 K.

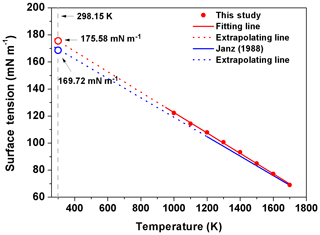
Figure 5 The surface tension of molten NaCl at different temperatures. The equation in Janz's study (1988) is ${\mathit{\sigma }}_{\mathrm{NaCl}}=-\mathrm{0.07188}\cdot T+\mathrm{191}$ (blue solid line). The fitting line based on our data is ${\mathit{\sigma }}_{\mathrm{NaCl}}=-\mathrm{0.0755}\cdot T+\mathrm{198.09}$ (red solid line). The red and blue open circles represent the extrapolated value of surface tension in simulation and reality, respectively.

Similar to the experimental results of Janz (1988), the simulated σ_NaCl is also linearly correlated with temperature from 1000 K (the simulated melting point of NaCl) to 1700 K, as shown in Fig. 5. Following Dutcher et al. (2010), a surface tension of ∼175.58 mN m⁻¹ is obtained for the hypothetical molten NaCl at 298.15 K by linear extrapolation of the MD simulated σ_NaCl at higher temperature, which is very close to the ∼169.7 mN m⁻¹ extrapolated from the experimental results (Dutcher et al., 2010). Combined with ${\mathit{\sigma }}_{\mathrm{NaCl}}={\mathit{\sigma }}_{\mathrm{NaCl},\mathrm{sol}}(x_{\mathrm{NaCl}}=\mathrm{1})=\sim \mathrm{175.58}$ mN m⁻¹, the simulated σ_NaCl,sol in the concentration range of x_NaCl>0.47 shows the tendency to ultimately approach the surface tension of melting NaCl at 298.15 K, similar to the blue curve in Fig. 4 from the Dutcher et al. (2000) study.

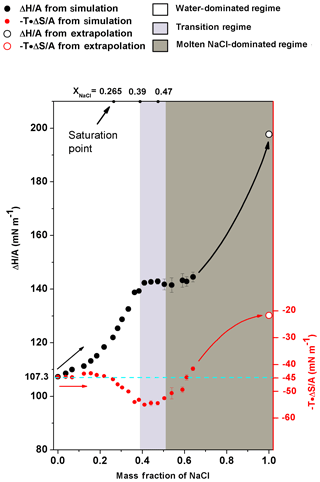
Figure 6 The excess surface enthalpy and entropy per unit area ($\frac{\mathrm{\Delta }H}{A}$ and $\frac{T\cdot \mathrm{\Delta }S}{A}$) of different NaCl solution concentrations. $\frac{\mathrm{\Delta }H}{A}$ (black circles) and $-\frac{T\cdot \mathrm{\Delta }S}{A}$ (red circles) are shown as a function of mass fraction of NaCl. The solid circles are obtained from simulation directly, and the open circles are obtained from the extrapolation of corresponding properties of molten NaCl. The cyan dashed line is only an auxiliary line for clearer view. Shaded areas are the same as in Fig. 4.

3.4 Physical chemistry behind the regimes

In energetic analyses, surface tension was decomposed into excess surface enthalpy ($\frac{\mathrm{\Delta }H}{A})$ and excess surface entropy ($\frac{T\cdot \mathrm{\Delta }S}{A}$). Note that the increase in excess surface entropy ($\frac{T\cdot \mathrm{\Delta }S}{A}$) or decrease in $-\frac{T\cdot \mathrm{\Delta }S}{A}$ will negatively contribute to the growth of σ_NaCl,sol. The analyses show that the monotonic increase in surface tension in water-dominated concentration ranges (x_NaCl from 0 to ∼0.39) is driven by the increase in $\frac{\mathrm{\Delta }H}{A}$ when the solution becomes concentrated (Fig. 6). When the solution gets concentrated, $\frac{\mathrm{\Delta }H}{A}$ first increases slightly with enhanced increasing rate at $x_{\mathrm{NaCl}}>\sim \mathrm{0.2}$ and in the supersaturated regime up to x_NaCl of ∼0.39. $-\frac{T\cdot \mathrm{\Delta }S}{A}$ behaves differently, it remains almost constant at about −45 mN m⁻¹ first and only starts to decrease at x_NaCl∼0.2. This way, in this concentration range (x_NaCl from 0 to ∼0.39), the increase in excess surface enthalpy outnumbers the increase in excess surface entropy and thus this physicochemical regime can be understood as an excess surface enthalpy-driving process.

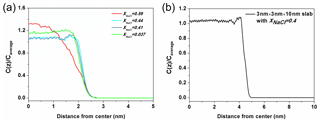
Figure 7 The ratio of Na⁺ concentration at different positions (C_z) to the average concentration of the whole system (C_average). (a) The solution with x_NaCl=0.59 (red line) is on behalf of the solution in the molten NaCl-dominated regime (red line), the solution x_NaCl=0.44 and 0.41 (blue lines) represent the solution in transition regime and the solution x_NaCl=0.037 (green line) represents the solution in the water-dominated regime. (b) The density profile obtained from a $\mathrm{3}\mathrm{nm}\times \mathrm{3}\mathrm{nm}\times \mathrm{10}\mathrm{nm}$ solution slab in which NaCl mass fraction is about 0.4.

The stable surface tension in the transition-regime concentration range (x_NaCl from ∼0.39 to ∼0.47) is attributed to the fact that $-\frac{T\cdot \mathrm{\Delta }S}{A}$ and $\frac{\mathrm{\Delta }H}{A}$ are both almost unchanged. Figure 6 shows that in the concentration above x_NaCl of ∼0.39, the increase in $\frac{\mathrm{\Delta }H}{A}$ significantly slows down and stabilizes at ∼145 mN m⁻¹ when the mass fraction approaches the efflorescence point. During this period, $-\frac{T\cdot \mathrm{\Delta }S}{A}$ keeps nearly unchanged, which results in a corresponding σ_NaCl,sol almost independent of the solution concentration change.

Here, we present a potential explanation for the stability of surface tension in this region from the structural analysis. The ratio of Na⁺ concentration at different positions to the average concentration of the whole system (C_z∕C_average) in different solutions is shown in Fig. 7a. The three blue-toned lines represent the ratio of solution in the transition regime with x_NaCl from ∼0.39 to ∼0.47. All of them have apophyses (significant rise) near the surface and these apophyses almost overlap with each other. This phenomenon suggests that the solute in these solutions enriches close to the surface and the degree of enrichment is almost the same for the different-concentration solution. Here, we denote the significant difference of the solute concentration in bulk region and on surface as a type of liquid–liquid partitioning. To check if this partitioning is dependent on the size of the solution slab, we calculate the corresponding value of a $\mathrm{3}\mathrm{nm}\times \mathrm{3}\mathrm{nm}\times \mathrm{10}\mathrm{nm}$ solution slab with x_NaCl of 0.4 (Fig. 7b). There is still an apophysis near the surface, thus we can claim that the partitioning is independent of the size of the solution slab in the simulation. Note that this surface enrichment of NaCl does not mean that NaCl is enriched right on top of the solution surface. Actually the density profile of water extends about 0.2 nm beyond that of NaCl towards the vapor region. By contrast, the solution with x_NaCl>0.47 or <0.39 do not have this type of partitioning as shown by the red and green lines. This comparison implies that the stability of surface tension of solution with x_NaCl from ∼0.39 to ∼0.47 is related to the “bulk-surface” partitioning. This interpretation is only a conjecture, and more studies are needed to further examine this phenomenon and interpretation. The shallow minimum in the density profile for x_NaCl between 0.39 and 0.47 to the left of the maximum is somewhat unexpected, and one might expect equilibration problems. However, we have checked that this structural feature develops already during the first 10 ns of the MD simulation, and does not change at all during the residual 200 ns. Surface enrichment of NaCl can be expected, however, when the solubility limit of the water-rich solution in the bulk is reached. Very roughly, such phenomena are analogous to interfacial wetting phenomena such as surface melting of crystals (Frenken and Van der Veen, 1985), which is sometimes observed when the temperature is raised towards the triple point. In our case, the enrichment zone of NaCl (which is about 0.4 nm thick in Fig. 7) would be a precursor effect to the (metastable) NaCl-rich bulk solution. Tentatively, one may correlate the formation of the enrichment zone with the stability of the surface entropy in this region via the entropy of mixing. At the same time, the surface enhancement of ions may be related to the phenomenon of efflorescence.

As shown in Fig. 6, when a solution gets more concentrated from x_NaCl of ∼0.47 to ∼0.64, the $\frac{\mathrm{\Delta }H}{A}$ slightly increases from the plateau of ∼145 mN m⁻¹ but the change is only ∼5 mN m⁻¹. The $-\frac{T\cdot \mathrm{\Delta }S}{A}$ keeps increasing. So during this period, both the surface excess enthalpy and entropy terms contribute to the growth of σ_NaCl,sol. To constrain the energetic analyses, the $\frac{T\cdot \mathrm{\Delta }S}{A}$ and $\frac{\mathrm{\Delta }H}{A}$ were also calculated for the molten NaCl at 298.15 K. According to Fig. 5, we have ${\mathit{\sigma }}_{\mathrm{NaCl}}=-\mathrm{0.0755}\cdot T+\mathrm{198.09}$; then we can get $\frac{\mathrm{\Delta }{S}_{\mathrm{NaCl}}}{A}=\mathrm{0.0755}$ $\mathrm{mN}{\mathrm{m}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$ because of $\frac{\mathrm{\Delta }S\left(T\right)}{A}=\frac{-\mathrm{d}\mathit{\sigma }\left(T\right)}{\mathrm{d}T}$ (Landau and Lifshitz, 1969). Therefore, for molten NaCl (x_NaCl=1.0), $\frac{T\cdot \mathrm{\Delta }{S}_{\mathrm{NaCl}}}{A}$ at 298.16 K is 22.15 mN m⁻¹, and $\frac{\mathrm{\Delta }{H}_{\mathrm{NaCl}}}{A}$ at 298.15 K is 198.09 mN m⁻¹ (Fig. 6). Here, we used the derivative of the temperature–surface tension relation to calculate the excess surface entropy, and more discussions about the comparison of these methods can be found in the Supplement (Fig. S1). As can be seen in Fig. 6, it is expected that the excess surface enthalpy term will still have a large amount (about more than 50 mN m⁻¹) to grow until approaching $\frac{\mathrm{\Delta }H}{A}$ of molten NaCl at 298.15 K. It is similar for the surface excess entropy term while the increment is smaller. Thus, the fast increase in σ_NaCl,sol in the concentration of x_NaCl from ∼0.47 to 1 can be assumed to be a process driven by excess surface enthalpy and excess surface entropy.

4 Conclusion

The analysis based on the calculated surface tension confirms the basic concept of the Dutcher et al. (2010) semiempirical model, while unfolding a more detailed global landscape of concentration dependence of surface tension of aqueous NaCl solution and its driving forces: (1) a water-dominated regime (x_NaCl from 0 to ∼0.39; at low concentrations ions are solvated by the water molecules, which means that water-structures/hydration shells are formed around ions); (2) a transition regime (x_NaCl from ∼0.39 to ∼0.47); and (3) a molten NaCl-dominated regime (x_NaCl from ∼0.47 to 1, at very high salt concentration water molecules are solvated by the ions, which means that a salt-structure is formed around the water molecules). Note that our result may not exactly reflect the real mode of surface tension of NaCl solution along the concentration, but it does imply the concept of a non-monotonic change of surface tension. One must be aware that for nucleation processes in the atmosphere other chemical compounds also matter, and will require future study. Also, mixed salt solutions would be very interesting, and can in principle be studied with similar simulation methods as applied here; however, this task must be left to future work.