Initiation of secondary ice production in clouds

Disparities between the measured concentrations of ice-nucleating particles (INPs) and in-cloud ice crystal number concentrations (ICNCs) have led to the hypothesis that mechanisms other than primary nucleation form ice in the atmosphere. Here, we model three of these secondary production mechanisms – rime splintering, frozen droplet shattering, and ice–ice collisional breakup – with a six-hydrometeor-class parcel model. We perform three sets of simulations to understand temporal evolution of ice hydrometeor number (N_ice), thermodynamic limitations, and the impact of parametric uncertainty when secondary production is active. Output is assessed in terms of the number of primarily nucleated ice crystals that must exist before secondary production initiates ($N_{\text{INP}}^{\left(\text{lim}\right)}$) as well as the ICNC enhancement from secondary production and the timing of a 100-fold enhancement. N_ice evolution can be understood in terms of collision-based nonlinearity and the “phasedness” of the process, i.e., whether it involves ice hydrometeors, liquid ones, or both. Ice–ice collisional breakup is the only process for which a meaningful $N_{\text{INP}}^{\left(\text{lim}\right)}$ exists (0.002 up to 0.15 L⁻¹). For droplet shattering and rime splintering, a warm enough cloud base temperature and modest updraft are the more important criteria for initiation. The low values of $N_{\text{INP}}^{\left(\text{lim}\right)}$ here suggest that, under appropriate thermodynamic conditions for secondary ice production, perturbations in cloud concentration nuclei concentrations are more influential in mixed-phase partitioning than those in INP concentrations.

1 Background

Number concentrations of ice-nucleating particles (INPs, N_INP) in the atmosphere span orders of magnitude from a few per cubic meter up to hundreds per liter DeMott et al. (e.g.,  2010). At temperatures greater than about −15 ^∘C, these concentrations remain low: only one particle in every 10³ or 10⁴ will nucleate an ice crystal (Rogers et al., 1998; Chubb et al., 2013; DeMott et al., 2015). However, even when INP concentrations are low at warm subzero temperatures, in-cloud ice crystal number concentrations (ICNCs) can be orders of magnitude higher Hallett and Mossop (e.g.,  1974); Heymsfield and Willis (e.g.,  2014); Lasher-Trapp et al. (e.g.,  2016); Taylor et al. (e.g.,  2016); Ladino et al. (e.g.,  2017), particularly in tropical maritime clouds (Koenig, 1963, 1965; Hobbs and Rangno, 1990).

This discrepancy may be explained in some cases by shattering upon cloud probe tips (Field et al., 2003; Heymsfield, 2007; McFarquhar et al., 2007), but even as instrumentation and algorithms have been developed to minimize these artifacts (Korolev et al., 2013; Korolev and Field, 2015), the disparity has remained, supporting several hypothesized secondary ice production processes. Hallett and Mossop (1974) proposed rime splintering in which ice hydrometeors collide with and freeze supercooled droplets to form rime, which then splinters off as the hydrometeor continues to fall. Droplets in cases of rime splintering tend to be both less than 13 µm and greater than 25 µm in diameter, and temperatures fall between −3 and −8 ^∘C (Mossop, 1978, 1985; Heymsfield and Mossop, 1984); however, ICNC enhancement, i.e., an increase in ICNC beyond that generated by primary nucleation, exists even outside of these conditions.

Another hypothesized mechanism is the shattering of droplets with a diameter of 50 to 100 µm upon freezing (Mason and Maybank, 1960; Cannon et al., 1974; Korolev et al., 2004; Fridlind et al., 2007; Rangno, 2008; Leisner et al., 2014; Lawson et al., 2015; Wildeman et al., 2017). At sufficiently cold temperatures, latent heat release leads to the formation of a liquid core–ice shell structure that eventually shatters upon internal pressure buildup. A third mechanism, independent of the liquid phase, is breakup upon mechanical collision of ice hydrometeors. Vardiman (1978) calculated the fragment number generated during ice–ice collisional breakup from a change in momentum, and Takahashi et al. (1995) later conducted experiments with a rotating ice sphere in a cloud chamber to estimate the number of ice crystals ejected vs. temperature. Yano and Phillips (2011), and more recently Yano et al. (2015), have identified “explosive regimes” defined by nondimensional parameters, where ice–ice collisional breakup may enhance ICNC by as much as 10⁴.

Laboratory and in situ data of these processes are difficult to obtain, and their fragment generation functions and temperature dependence remain uncertain (Field et al., 2017). Given these uncertainties, implementation of secondary ice production parameterizations in large-scale models is still premature. Instead, small-scale, more controllable modeling provides a good tool to estimate variability in secondarily produced ICNC with these parameters, as well as the minimum number of INPs needed to initiate secondary production. We call this latter variable $N_{\text{INP}}^{\left(\text{lim}\right)}$ hereafter.

Some previous studies have estimated $N_{\text{INP}}^{\left(\text{lim}\right)}$ on the basis of in situ data. For example, in a study of ice initiation in cumulus, Beard (1992) found that a nucleated ICNC of 0.001 L⁻¹ could trigger raindrop freezing around −5 ^∘C. More recently, Crawford et al. (2012), with Aerosol Properties, PRocesses And Influences (APPRAISE) campaign data, and Huang et al. (2017), with ICE and Precipitation Initiation in Cumulus (ICEPIC) campaign data, identified a primarily nucleated ICNC of 0.01 L⁻¹ as sufficient to initiate rime splintering. Connolly et al. (2006) found that the rime splintering tendency increased with increasing primarily nucleated ICNC, but this result was based upon adjusting the primary nucleation rate rather than the absolute N_INP. Clark et al. (2005) also adjusted the primary nucleation rate relative to the rime splintering one but gave no approximate $N_{\text{INP}}^{\left(\text{lim}\right)}$ values or thermodynamic constraints. These studies have also considered only rime splintering, despite evidence that multiple processes occur simultaneously (Rangno and Hobbs, 2001). We provide more comprehensive estimates of $N_{\text{INP}}^{\left(\text{lim}\right)}$ here for three secondary production processes over a range of thermodynamic conditions and fragment numbers.

2 Parcel model

To estimate ICNC enhancement and $N_{\text{INP}}^{\left(\text{lim}\right)}$, we run a parcel model with six hydrometeor classes for small ice crystals and droplets, small and large graupel, and medium and large droplets (Sullivan et al., 2017). The number in these classes is denoted N_i, N_d, N_g, N_G, N_r, and N_R, respectively. The hydrometeors in each class are assumed to be monodisperse, but their sizes are tracked over time as a function of temperature and supersaturation. N_ice is used to denote the summation of the number in the three ice hydrometeor classes. The bin microphysics consists of primary nucleation and secondary production by ice–ice collisional breakup, rime splintering, and frozen droplet shattering. These processes are included in an ice generation function with units of ${\mathrm{m}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$:

$$\begin{array}{ll}\text{(1)}& {\displaystyle }& {\displaystyle }{G}_{\text{ice}}={\displaystyle \frac{\mathrm{d}{N}_{\mathrm{i}}}{\mathrm{d}t}}{|}_{\text{NUC}}+{\displaystyle \frac{\mathrm{d}{N}_{\mathrm{i}}}{\mathrm{d}t}}{|}_{\text{BR}}+{\displaystyle \frac{\mathrm{d}{N}_{\mathrm{i}}}{\mathrm{d}t}}{|}_{\text{RS}}+{\displaystyle \frac{\mathrm{d}{N}_{\mathrm{i}}}{\mathrm{d}t}}{|}_{\text{DS}}{\displaystyle }& {\displaystyle }=c_{\mathrm{0}}{f}_{\text{imm}}+{\mathit{\eta }}_{\text{BR}}{K}_{\text{BR}}{\mathrm{\aleph }}_{\text{BR}}{N}_{\mathrm{g}}{N}_{\mathrm{G}}\\ \text{(2)}& {\displaystyle }& {\displaystyle }+{\mathit{\eta }}_{\text{RS}}{\mathrm{\aleph }}_{\text{RS}}[K_{\text{RS,g}}{N}_{\mathrm{g}}+K_{\text{RS,G}}{N}_{\mathrm{G}}]N_R+{\mathit{\eta }}_{\text{DS}}{\mathrm{\aleph }}_{\text{DS}}{N}_R.\end{array}$$

NUC stands for nucleation, BR for ice–ice collisional breakup, RS for rime splintering, and DS for droplet shattering. c₀ is the primary nucleation rate derived from the temperature dependence of the immersion INP concentration given in DeMott et al. (2010); η_X is the weighting for process X, either 100 % when the process is active or 0 % when it is inactive; K_X is a gravitational collection kernel for process X; and ℵ_X is the fragment number generated by process X. More specifically, the nucleation rate is calculated as the product of updraft velocity, an assumed lapse rate of 6 K km⁻¹, and the temperature derivative of the INP concentration: $u_z\mathrm{\Gamma }\mathrm{d}/\mathrm{d}T\left[a_{\mathrm{1}}\text{exp}\right(a_{\mathrm{2}}(T-a_{\mathrm{3}})\left)\right]$. The factor f_imm indicates the fraction of these INPs that nucleate immediately in cloud droplets. This formulation requires no explicit treatment of aerosol.

Hallett and Mossop (1974)Takahashi et al. (1995)Paukert et al. (2017)Lawson et al. (2015)Mossop (1978, 1985)Zhang et al. (2014)Reinking (1975)(Hegg et al., 1992)(Korolev and Field, 2007)

Table 1 Default parameter values from simulations and their sources. 𝒩(μ,σ) indicates a normal distribution with mean µ and SD σ.

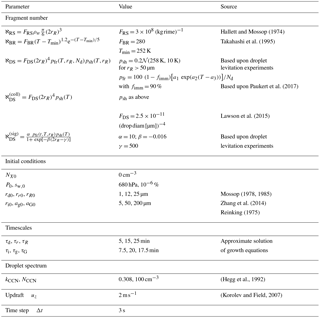
Expressions for ℵ_X are given in Table 1: ℵ_RS is taken from the laboratory experiments of Hallett and Mossop (1974), and ℵ_BR is based upon those of Takahashi et al. (1995). η_RS is set to 1 % outside an optimal temperature zone of −3 to −8 ^∘C to allow for cases in which local temperature gradients may still permit rime splintering at the hydrometeor surface. ℵ_DS contains a product of droplet freezing and shattering probabilities, p_fr and p_sh, and either polynomial (as in Lawson et al., 2015) or sigmoidal dependence on large droplet size. p_fr synthesizes the INP concentration from DeMott et al. (2010) with the particle accumulation simulations of Paukert et al. (2017). The remaining INPs that do not nucleate immediately as given by f_imm are found in cloud droplets that undergo about 100 collisions before they form a “shatter-able” drop. p_sh is nonzero for drops of radii greater than 50 µm and has Gaussian temperature dependence centered at 258 K on the basis of droplet levitation experiments. The droplet shattering tendency is later modified to represent a collisional process with a product of large droplet and ice crystal numbers and then denoted DScoll.

For the liquid phase, a droplet generation function consists simply of droplet activation, calculated from a Twomey power-law formulation. This formulation is supersaturation-dependent and, again, requires no explicit aerosol. The number balance in each class is then the generation function at the current time as a source and the generation function at a time delay as the sink, along with aggregation and coalescence losses. For example, the number in the ice crystal class is given by

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle \frac{\mathrm{d}{N}_{\mathrm{i}}}{\mathrm{d}t}}=G_{\text{ice}}\left(t\right)-G_{\text{ice}}(t-{\mathit{\tau }}_{\mathrm{i}})-{\mathit{\eta }}_{\text{agg}}{K}_{\text{agg}}{N}_{\mathrm{i}}{N}_{\mathrm{g}}.\end{array}$$

The time delays, τ_X, quantify how long depositional, riming, or condensational growth to the next hydrometeor class will take and are approximately solved for from growth equations. Newly produced ice crystals are assumed to be spherical with bulk ice density, while graupel is assumed to be spheroidal with a deposition density and non-unit capacitance as in Chen and Lamb (1994). The coalescence efficiency is assumed to be unity between small and medium droplets (Klett and Davis, 1973). A basic representation of large droplet coalescence is employed at temperatures above 273 K, given the importance of droplet size distribution broadening to droplet shattering (Lawson et al., 2017): N_d is reduced by 5 % every minute due to coalescence, and the mass is redistributed among the remaining large droplets.

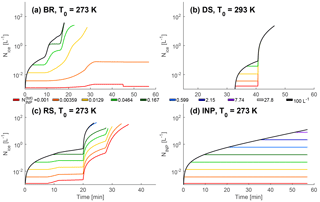
Figure 1 Evolution of the total ice hydrometeor (summation of ice crystal and small and large graupel numbers) number for default simulations with a range of $N_{\text{INP}}^{\left(\text{tot}\right)}$ from 0.001 up to 100 L⁻¹: (a) ice–ice collisional breakup only, (b) droplet shattering only, (c) rime splintering only, and (d) a control run when only primary nucleation is active. These default simulations are run for u_z of 2 m s⁻¹ and T₀ values given in each panel.

The six hydrometeor number tendencies are solved with an explicit Runge–Kutta (2,3) pair for delay differential equations (Bogacki and Shampine, 1989) and coupled to moist thermodynamic equations for pressure, temperature, supersaturation, mixing ratios, and hydrometeor sizes. This second set of equations is solved with a Rosenbrock formula of order 2 (Rosenbrock, 1963). The model microphysics is shown schematically in Fig. S1 in the Supplement, and parameter values and sources are given in Table 1. Model assumptions, thermodynamic tendencies and correlations, and collection kernels are more thoroughly described in Sullivan et al. (2017) and their effects more thoroughly discussed below in Sect. 4.

3 Simulations

The three rows of Table 2 show three sets of simulations with the parcel model. First we investigate the evolution of the total ice hydrometeor number, N_ice, i.e., the summation of N_i, N_g, and N_G, in default simulations with fixed fragment numbers and thermodynamic conditions. Simulation acronyms include BR for ice–ice collisional breakup, DS for droplet shattering, or RS for rime splintering. These runs address how the value of $N_{\text{INP}}^{\left(\text{lim}\right)}$ and enhancement magnitude or timing vary when different processes are active. We quantify enhancement from secondary production as the ratio of the total ICNC to the number generated by primary nucleation when the simulation ends, i.e., when the parcel becomes water subsaturated or reaches a temperature of 237 K above which no homogeneous nucleation occurs: N_ice(t_end)∕N_INP(t_end). An enhancement of 10 can be understood as at least a 10-fold increase in ICNC due to secondary production, as an aggregation sink is also active in the simulations. In the absence of secondary production, ICNC enhancement does not exceed one.

Table 2 All simulations with parameters adjusted from the default values in Table 1. A control run with no secondary production, i.e., ${\mathit{\eta }}_{\text{DS}}={\mathit{\eta }}_{\text{BR}}={\mathit{\eta }}_{\text{RS}}$ = 0 %, is denoted INP in Fig. 1. Simulations run with combinations (BRDS, BRRS, and DSRS) or all (ALL and ALLth) of the processes are shown in the Supplement and detailed in Table S1.

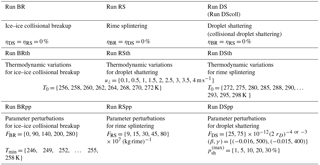
The second set of simulations considers the effect of updraft velocity and initial temperature in the parcel; this set is denoted “th” for thermodynamics. The updraft is varied from 0.1 up to 5 m s⁻¹ to simulate both stratiform and convective conditions, while the initial parcel temperature is adjusted from a quite warm cloud base temperature of 295 K down to the temperature at the droplet shattering probability peak of 256 K. Then parameter perturbations are performed in a final set, denoted “pp”. In particular, we vary the leading coefficient of the fragment number generated per collision and per kilogram of rime, F_BR and F_RS, respectively; the minimum temperature for which ice–ice collisional breakup occurs, T_min; the functional form of the fragment number generated per shattering droplet, F_DS(β,γ); and the maximum of the temperature-dependent droplet shattering probability distribution, $p_{\text{sh}}^{\left(\text{max}\right)}$. The effect of these parameters on the generated fragment numbers is shown in Fig. S2, and the alternate sigmoid functions for ℵ_DS are shown in Fig. S3.

Figure 2 Evolution of N_ice at different cloud base temperatures, 290 K in (a) and 288 K in (b), and a collisional formulation with (c) 10 fragments generated $\left({\mathrm{\aleph }}_{\text{DS}}^{\left(\text{coll}\right)}=\mathrm{10}\right)$ and (d) 2 fragments generated per collision $\left({\mathrm{\aleph }}_{\text{DS}}^{\left(\text{coll}\right)}=\mathrm{2}\right)$. Otherwise, $p_{\text{sh},max}$ = 20 %, u_z = 2 m s⁻¹ as in Fig. 1. Coloring indicates the $N_{\text{INP}}^{\left(\text{tot}\right)}$ value as in Fig. 1.

3.1 Hydrometeor number evolution

The temporal evolution of N_ice in the default simulations is shown in Fig. 1. Each simulation is carried out for a range of total INP numbers within the parcel, $N_{\text{INP}}^{\left(\text{tot}\right)}$. A base run with only nucleation shows the $N_{\text{INP}}^{\left(\text{tot}\right)}$ thresholds in panel Fig. 1d. The structure in the number evolution can be understood by considering whether the process is collisional and its “phasedness”, i.e., whether it involves hydrometeors in the liquid or ice phase or both. The ice mass mixing ratio and ice crystal radius evolution are also shown in Figs. S5 and S6, but analysis focuses on N_ice below.

When the process involves a product of hydrometeor numbers, as for breakup and rime splintering, the N_ice evolution is nonlinear. Independent of $N_{\text{INP}}^{\left(\text{tot}\right)}$, N_ice grows steadily throughout the simulation for these collisional secondary production processes. Even as graupel or large droplets are consumed, those hydrometeors still in the parcel continue to grow by deposition or condensation, respectively. This ongoing hydrometeor growth increases the secondary production tendencies via their collection kernels, and this link itself is nonlinear because both hydrometeor terminal velocity and collisional cross section increase with growth. This idea is shown qualitatively in the red and blue traces of Fig. 8a.

When the process involves a single hydrometeor number, as for droplet shattering here, the N_ice evolution is almost linear and increases suddenly. This threshold behavior occurs when the temperature becomes cold enough for non-negligible shattering and freezing probabilities. Although these factors control the initiation, the fragment and large droplet numbers, ℵ_DS and N_R, control the enhancement magnitude from the droplet shattering. As a result, the traces in Fig. 1b do not exhibit direct dependence on $N_{\text{INP}}^{\left(\text{tot}\right)}$: all DS simulations reach an $N_{\text{ice}}^{\left(\text{max}\right)}$ of 29 L⁻¹ in about 46 min. But the implicit dependence on a nonzero $N_{\text{INP}}^{\left(\text{tot}\right)}$ should be pointed out: in the absence of INPs, p_fr is always zero and no droplet shattering occurs. As soon as p_fr becomes nonzero, the other terms in the droplet shattering tendency are large enough to produce an ICNC enhancement. Below in Sect. 3.1.1, we discuss cloud base temperature dependence and a collisional mechanism (DScoll). The DS and DScoll trends are also shown qualitatively in the green traces of Fig. 8a.

Because breakup and rime splintering involve the ice phase, increasing $N_{\text{INP}}^{\left(\text{tot}\right)}$ boosts their rates of generation and yields large enhancement sooner. For ice–ice collisional breakup, a parcel with 0.0129 L⁻¹ INP reaches 10 L⁻¹ N_ice in 23 min, while that with 0.167 L⁻¹ INP reaches the same value in 17 min. For rime splintering, the same increase in INPs shifts the time to reach 10 L⁻¹N_ice from 30 min back to 25. While these differences in enhancement timing sound small, they can help infer which secondary production processes are active from in situ N_INP and ICNC data. For example, ICNC on the order of hundreds per liter can form within 10 to 15 min (Hobbs and Rangno, 1990; Rangno and Hobbs, 1991, 1994). This timing is too rapid to be explained by rime splintering alone (Mason, 1996), in agreement with our rime splintering simulation. Simulations with ice–ice collisional breakup and rime splintering in combination, however, are sufficiently rapid (Fig. S4b).

Higher $N_{\text{INP}}^{\left(\text{tot}\right)}$ only increases the ice generation rates from ice–ice collisional breakup and rime splintering up to a certain point, however. Beyond an $N_{\text{INP}}^{\left(\text{tot}\right)}$ of about 0.599 L⁻¹, additional INPs do not increase $N_{\text{ice}}^{\left(\text{max}\right)}$. The parcel is in a supersaturation-limited regime, for which it becomes subsaturated before the effect of additional primary nucleation can be felt by secondary production.

Finally, nonlinearity and hydrometeor phases involved determine enhancement magnitude. The ice–ice collisional breakup tendency is proportional to the product of two ice hydrometeor numbers, N_g and N_G, so the impact of varying $N_{\text{INP}}^{\left(\text{tot}\right)}$ is most pronounced for the ice–ice collisional breakup simulations. Increasing $N_{\text{INP}}^{\left(\text{tot}\right)}$ by 2 orders of magnitude (0.001 to 0.167 L⁻¹) increases $N_{\text{ice}}^{\left(\text{max}\right)}$ by 4 orders of magnitude (0.0023 to 37.6 L⁻¹). The rime splintering and droplet shattering tendencies are proportional to N_R, which is around 10⁶ times as large as N_g or N_G. Thus, the impact of $N_{\text{INP}}^{\left(\text{tot}\right)}$ for these processes is diluted. For the purely liquid-phase droplet shattering, the increase in $N_{\text{INP}}^{\left(\text{tot}\right)}$ of 2 orders of magnitude has no significant impact on $N_{\text{ice}}^{\left(\text{max}\right)}$. For rime splintering, it actually translates to a 2-fold decrease in $N_{\text{ice}}^{\left(\text{max}\right)}$ (30.58 to 16.67 L⁻¹). This decrease is the result of an increasing denominator in the $N_{\text{ice}}^{\left(\text{max}\right)}/N_{\text{INP}}\left(t_{\text{end}}\right)$ expression (see also the rime splintering panels of Figs. 3 and 4). The rime splintering tendency is strong enough that it always generates additional ice crystals, so that increasing $N_{\text{INP}}^{\left(\text{tot}\right)}$ actually decreases enhancement. The total INP number does, however, affect which rimers contribute to enhancement: when $N_{\text{INP}}^{\left(\text{tot}\right)}$ exceeds 0.167 L⁻¹, only rime splintering of small graupel can occur before subsaturation of the parcel.

3.1.1 Droplet shattering formulation

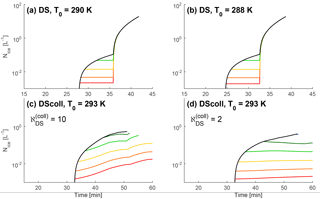
For droplet shattering, we additionally investigate the impact of T₀ and the underlying physical mechanism. First, recent experimental evidence indicates the importance of warm cloud base temperature and the warm rain process to any subsequent droplet shattering (Lawson et al., 2015; Taylor et al., 2016; Lawson et al., 2017). Although the model with its six monodisperse hydrometeor classes cannot fully represent droplet size distribution broadening, we implement simplified large droplet coalescence whereby the large droplet number is reduced by 5 % every minute above the freezing level. Liquid mass is conserved by redistribution among the remaining drops. Without this process, the condensational growth from a diameter of 50 µm up to about 100 µm is very slow, and an appropriate dependence on T₀ is not reproduced.

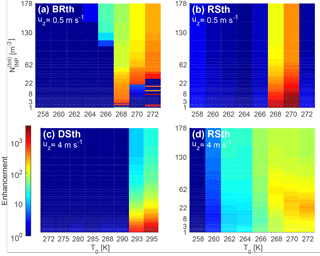
Figure 3 ICNC enhancement, i.e., N_ice(t_end)∕N_INP(t_end), for the thermodynamics simulations with fixed updraft u_z at various values of the total INP number in the parcel $N_{\text{INP}}^{\left(\text{tot}\right)}$ and initial temperature T₀. Red indicates a larger enhancement per INP. Panels (a, b) show the enhancement for ice–ice collisional breakup and rime splintering at a low, stratiform-like updraft of 0.5 m s⁻¹. The lowest updraft of 0.1 m s⁻¹ is not shown because only very small enhancements occur. Panels (c, d) show the enhancement for droplet shattering and rime splintering at a higher, convective-like updraft of 4 m s⁻¹. No meaningful enhancements are generated by ice–ice collisional breakup at the larger updraft or by droplet shattering at the lower one. Note the different temperature scale for the DSth simulation.

Figure 2a and b show the impact of lowering T₀ to 290 or 288 K from the 293 K level shown in Fig. 1. The colder this cloud base temperature becomes, the sooner the temperature threshold for non-negligible p_fr and p_sh is reached. But as T₀ drops, the resultant $N_{\text{ice}}^{\left(\text{max}\right)}$ also drops. At 293 K, N_ice of 29.2 L⁻¹ is produced in 46.3 min; at 290 K, 19.4 L⁻¹ in 41.8 min; and at 288 K, 15.1 L⁻¹ in 38.7 min. Once T₀ drops to 285 K or below at this updraft, droplet shattering is no longer effective because the large droplets do not have sufficient time to grow, either by coalescence or condensation, to a size at which they can shatter. There is also an upper bound to warmer T₀. At 298 K, $N_{\text{ice}}^{\left(\text{max}\right)}$ increases to 86.1 L⁻¹ after 53 min, but beyond that, the droplets begin to sediment before the parcel reaches sufficiently cold temperatures for their shattering. These u_z−T₀ dependencies are shown qualitatively in Figs. 8b and 9 and described in greater detail in Sect. 3.2.

Then, the exact mechanism underlying this droplet shattering remains uncertain, and it has been hypothesized that it initiates via collision between a large droplet and a small ice crystal. In this case, the droplet shattering tendency is proportional to both N_R and N_i, rather than just N_R, in the final term of Eq. (2):

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle \frac{\mathrm{d}{N}_{\mathrm{i}}}{\mathrm{d}t}}{|}_{\text{DS}}={\mathit{\eta }}_{\text{DS}}{\mathrm{\aleph }}_{\text{DS}}^{\left(\text{coll}\right)}{K}_{\text{DS}}{N}_R{N}_{\mathrm{i}}.\end{array}$$

The fragment numbers from Lawson et al. (2015) ($F_{\text{DS}}{D}_R^{\mathrm{4}}$) or from a sigmoidal function, along with p_sh, are retained as in the droplet shattering simulation, but p_fr is removed with the understanding that collision with the ice surface initiates freezing.

In Fig. 2c and d, the threshold behavior of the enhancement in the droplet shattering simulation is replaced by a steady increase similar to that from the rime splintering or ice–ice collisional breakup simulation in Fig. 1. This formulation yields a smaller $N_{\text{ice}}^{\left(\text{max}\right)}$ than droplet shattering, up to 0.39 L⁻¹ when ${\mathrm{\aleph }}_{\text{DS}}^{\left(\text{coll}\right)}$ = 2 or 0.53 L⁻¹ when ${\mathrm{\aleph }}_{\text{DS}}^{\left(\text{coll}\right)}$ = 10. Enhancement timing is also slowed, with $N_{\text{ice}}^{\left(\text{max}\right)}$ reached after 54 min for ${\mathrm{\aleph }}_{\text{DS}}^{\left(\text{coll}\right)}$ = 2 and 51 min for ${\mathrm{\aleph }}_{\text{DS}}^{\left(\text{coll}\right)}$ = 10. The simultaneous consumption and generation of crystals during collisions now means that $\mathrm{d}{N}_{\mathrm{i}}/\mathrm{d}t\propto N_{\mathrm{i}}$, and the process will never generate the super-exponential increases as from ice–ice collisional breakup in Fig. 1a. The dual source–sink of N_i also means that $N_{\text{INP}}^{\left(\text{tot}\right)}$ has a large effect on enhancement magnitude. From an $N_{\text{INP}}^{\left(\text{tot}\right)}$ of 0.001 L⁻¹ up to 0.6 L⁻¹, there is a difference of 2 orders of magnitude in the ultimate N_ice. However, given the slower N_ice generation rate of this collisional process, initiation of non-collisional droplet shattering by immersed INPs is likely to be the more influential process.

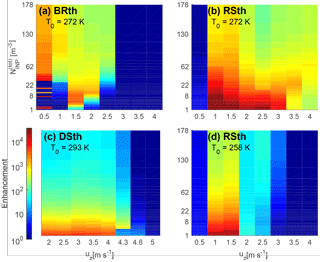
Figure 4 ICNC enhancement, i.e., N_ice(t_end)∕N_INP(t_end), for the thermodynamics simulations with fixed initial temperature T₀ at various values of the total INP number in the parcel $N_{\text{INP}}^{\left(\text{tot}\right)}$ and updraft velocity u_z. Red indicates a larger enhancement per INP. Panels (a, b) show the enhancement for ice–ice collisional breakup and rime splintering at a cloud base temperature of 272 K. Panels (c, d) show the enhancement for droplet shattering and rime splintering at colder and warmer cloud base temperatures of 293 and 258 K, respectively. No meaningful enhancement is generated by ice–ice collisional breakup at the warmer T₀ or by droplet shattering at the colder ones.

3.2 Varying thermodynamics

Secondary enhancement from the simulations with varying thermodynamics are shown in Figs. 3 and 4. Runs are performed for a range of updraft velocities and initial temperatures given in Table 2, but we focus on the extremes.

Figure 3a, b show enhancement for stratiform conditions, i.e., u_z of 0.5 m s⁻¹, and a range of cloud base temperatures T₀. Clear $N_{\text{INP}}^{\left(\text{lim}\right)}$ values for ice–ice collisional breakup can be seen in Fig. 3a. As T₀ decreases from 272 to 270 to 268 K, $N_{\text{INP}}^{\left(\text{lim}\right)}$ drops from 32.8 to 21.5 to 2.1 m⁻³. At 266 K, $N_{\text{INP}}^{\left(\text{lim}\right)}$ increases again, reaching an 𝒪(10²) enhancement only for an INP concentration of 0.143 L⁻¹. Larger ICNCs occur only at these warmer T₀ values because the parcel remains in the mixed-phase temperature range long enough that large graupel can form by riming (see also Fig. 8b). For rime splintering, there is no $N_{\text{INP}}^{\left(\text{lim}\right)}$ value greater than 1 m⁻³: the enhancement is largest at the lowest value of $N_{\text{INP}}^{\left(\text{tot}\right)}$ in Fig. 3 and decreases with higher values of $N_{\text{INP}}^{\left(\text{tot}\right)}$.

Then when u_z is increased to 4 m s⁻¹ in Fig. 3c and d, rime splintering occurs over an expanded range of T₀ but with a reduced enhancement magnitude. As the parcel moves faster, it is more likely to pass through the optimal rime splintering temperature zone of 267 to 269 K or obtain higher p_sh or p_fr, but it also spends less time in these optimal zones. This idea is also true for the DSth runs shown in Fig. 3c: a faster-moving parcel must initiate at a warmer temperature for sufficiently large droplets to form before the freezing level. No enhancement occurs from ice–ice collisional breakup at these faster updrafts because there is always insufficient time for graupel to form. The general favorability of modest updrafts is shown in Fig. 8b.

If instead we fix T₀ and look at a range of u_z values as in Fig. 4, ice–ice collisional breakup remains the only process with a defined $N_{\text{INP}}^{\left(\text{lim}\right)}$. This threshold value decreases from 32.8 m⁻³ at 0.5 m s⁻¹ down to 1.52 m⁻³ at 1.5 m s⁻¹. At 2.5 m s⁻¹, it increases back up to 50 m⁻³, and at the fastest updraft velocities, no enhancement from ice–ice collisional breakup occurs again because graupel does not form. In this case, not only is the parcel too short-lived for graupel formation, diffusional growth is also slowed significantly at such low temperatures.

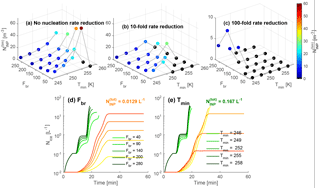
Figure 5 Results from the parameter perturbation simulations with ice–ice collisional breakup. The top panels show $N_{\text{INP}}^{\left(\text{lim}\right)}$ to obtain a 100-fold ICNC enhancement for various values of F_BR and T_min within the ice–ice collisional breakup parameterization. Dots are also colored by $N_{\text{INP}}^{\left(\text{lim}\right)}$, where black indicates no 100-fold enhancement ever occurring. From (a–c), the nucleation rate decreases by 2 orders of magnitude; note that the y axis in (c) has a smaller range than the others. Panels (d, e) show the temporal evolution of N_ice for the various values of F_BR and T_min with a $N_{\text{INP}}^{\left(\text{tot}\right)}$ of 0.167 L⁻¹ (green traces) and 0.012 L⁻¹ (yellow traces). The light-to-dark gradient in green and yellow corresponds to the same parameter values. These parameter perturbations are run for u_z of 2 m s⁻¹ and T₀ of 272 K.

Although there is no meaningful $N_{\text{INP}}^{\left(\text{lim}\right)}$ for droplet shattering or rime splintering, N_INP still affects enhancement from these processes. In fact, increasing $N_{\text{INP}}^{\left(\text{tot}\right)}$ generally decreases enhancement for all u_z−T₀ conditions. This can be understood in terms of a sort of INP efficiency: the highest ICNC per INP is produced when $N_{\text{INP}}^{\left(\text{tot}\right)}$ is lowest. Mathematically, increasing $N_{\text{INP}}^{\left(\text{tot}\right)}$ increases the denominator of the enhancement ratio without a corresponding increase in the numerator. Physically, a higher $N_{\text{INP}}^{\left(\text{tot}\right)}$ depletes supersaturation more rapidly, as many small ice crystals grow by deposition, or it may keep the parcel warmer with latent heating. Fragment numbers, ℵ_DS and ℵ_RS, also depend on the large droplet radius or rimed mass, which are reduced at lower supersaturation. Previous work corroborates this understanding: Connolly et al. (2006) found that increasing primary nucleation led to a decrease in the freezing of rain in cloud-resolving simulations. Other studies have also emphasized the importance of liquid hydrometeor formation, rather than primary nucleation, to ice generation from rime splintering (Mossop, 1978, 1985; Hobbs and Rangno, 1985; Heymsfield and Willis, 2014).

Figure 4c and d show enhancement from droplet shattering at a warmer T₀ and from rime splintering at a colder T₀, respectively. The idea of a “sweet spot” in u_z reappears: the updraft must be strong enough that large droplets form by coalescence or condensation but modest enough that these droplets remain in an appropriate temperature range to rime or shatter. These trends are summarized in the first panel of Fig. 9 and, for rime splintering, agree generally with Mossop (1985) in which enhancement was possible down to 0.55 m s⁻¹ but highest around 1.8 to 2 m s⁻¹. Mossop used a shell-fracture hypothesis to explain this optimum: too high a velocity and the riming drop spreads across the ice surface rather than forming a fragile protuberance, and too small a velocity and an incomplete ice shell may form around the riming drop. Although not a validation of this hypothesis, the simplified model is, interestingly, able to reproduce this u_z behavior without such detailed rime physics.

3.3 Parameter perturbations

Lastly we use the insight about N_ice evolution and approximate enhancement from the simulations above to investigate the impact of adjustable parameters. In particular, we look at the effect of generated fragment numbers and temperature dependencies on $N_{\text{INP}}^{\left(\text{lim}\right)}$ and enhancement magnitude or timing.

First the effect of nucleation rate is investigated on the $N_{\text{INP}}^{\left(\text{lim}\right)}$ value for breakup, as illustrated in Fig. 5a, b, c. Runs are performed with a default nucleation rate and ones reduced by factors of 10 and 100, and the conditions for which no enhancement occurs are shown in black. The number of these points increases dramatically as the nucleation rate decreases from left to right (8 to 32 to 84 %). Then as T_min increases, the temperature range over which ice–ice collisional breakup occurs shrinks, and $N_{\text{INP}}^{\left(\text{lim}\right)}$ increases: more ice crystals are needed initially to ultimately reach a 100-fold enhancement. As F_BR increases, more fragments are formed per collision, and $N_{\text{INP}}^{\left(\text{lim}\right)}$ decreases. This second effect of F_BR is the larger of the two. These $N_{\text{INP}}^{\left(\text{lim}\right)}$ trends for ice–ice collisional breakup occur until a sufficiently low F_BR or sufficiently high T_min is reached, beyond which enhancement does not occur for any value of $N_{\text{INP}}^{\left(\text{tot}\right)}$ (up to 300 L⁻¹).

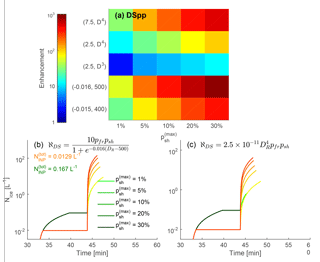
Figure 6 Results from the parameter perturbation simulations with droplet shattering. Panel (a) shows how the enhancement magnitude shifts with $p_{\text{sh}}^{\left(\text{max}\right)}$ and the various fragmentation functions, both polynomial and sigmoidal. Panels (b, c) show the temporal evolution of N_ice for the various values of $p_{\text{sh}}^{\left(\text{max}\right)}$ with a $N_{\text{INP}}^{\left(\text{tot}\right)}$ of 0.167 L⁻¹ (green traces) and 0.012 L⁻¹ (yellow traces) and for a sigmoidal and polynomial fragmentation function, respectively. These parameter perturbations are run for u_z of 2 m s⁻¹ and T₀ of 293 K.

Figure 5d and e show N_ice evolution for various values of F_BR and T_min and for $N_{\text{INP}}^{\left(\text{tot}\right)}$ of 0.0129 L⁻¹ (in yellow) and 0.167 L⁻¹ (in green). The effect of both parameters is much larger when $N_{\text{INP}}^{\left(\text{tot}\right)}$ is small. Increasing F_BR from 40 to 280 increases N_ice by a factor of 200 when $N_{\text{INP}}^{\left(\text{tot}\right)}$ is 0.0129 L⁻¹ and by only a factor of 3 when $N_{\text{INP}}^{\left(\text{tot}\right)}$ is 0.167 L⁻¹. Similarly, decreasing T_min from 258 to 246 K increases N_ice by a factor of 230 when $N_{\text{INP}}^{\left(\text{tot}\right)}$ is 0.0129 L⁻¹ and by only a factor of 1.5 when $N_{\text{INP}}^{\left(\text{tot}\right)}$ is 0.167 L⁻¹. The parameters primarily affect the enhancement magnitude not its timing.

Then the effect of shattering probability and generated fragment number are investigated for droplet shattering. We triple the leading coefficient F_DS and alter the diameter dependence from quartic to cubic within the Lawson et al. (2015) formulation. We also use two sigmoids shown in Fig. S3, which generate higher ℵ_DS at small D_R and lower ℵ_DS at large D_R relative to Lawson et al. (2015), based upon the results of droplet levitation experiments. As above, there is no meaningful $N_{\text{INP}}^{\left(\text{lim}\right)}$ here, so we focus on the maximum enhancement from these various cases, shown in Fig. 6.

In Fig. 6a, by far the smallest enhancement occurs for a $D_R^{\mathrm{3}}$ dependence in ℵ_DS. Independent of $p_{\text{sh}}^{\left(\text{max}\right)}$ these simulations never produce an ICNC enhancement greater than about 50. The largest enhancement comes from sigmoidal dependence on D_R as this yields higher fragment numbers than the polynomial dependence for droplets of less than about 350 µm diameter, which dominate in our simulation. The situation would be reversed for very large droplets with millimeter diameters: the polynomial function of D_R would predict higher fragment numbers than the sigmoidal one. In all cases, increasing $p_{\text{sh}}^{\left(\text{max}\right)}$ increases enhancement with a similar, linear effect throughout its range as expected: a 2-fold increase in $p_{\text{sh}}^{\left(\text{max}\right)}$ from 5 to 10 % has the same quantitative impact as a 2-fold increase from 10 to 20 %.

Figure 6b and c show N_ice evolution for various values of $p_{\text{sh}}^{\left(\text{max}\right)}$ and the sigmoidal and default $D_R^{\mathrm{4}}$ and ℵ_DS forms, respectively. The yellow traces show this evolution for $N_{\text{INP}}^{\left(\text{tot}\right)}$ of 0.0129 L⁻¹ and the green for 0.167 L⁻¹, but these INP concentrations do not make a significant difference. This evolution confirms that the sigmoidal ℵ_DS calculates more fragments than the polynomial one: $N_{\text{ice}}^{\left(\text{max}\right)}$ is 143.2 L⁻¹ in Fig. 6b and 42.1 L⁻¹ in Fig. 6c. And increasing $p_{\text{sh}}^{\left(\text{max}\right)}$ by a factor of 10 from 1 to 10 % translates linearly to a factor 10 increase in $N_{\text{ice}}^{\left(\text{max}\right)}$.

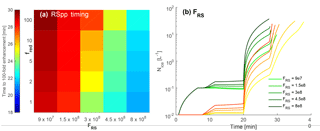
Figure 7 Results from the parameter perturbation simulations with rime splintering. Panel (a) shows how time of a 100-fold enhancement shifts with the fragment number per kilogram rime F_RS and the nucleation reduction rate f_red. Panel (b) shows the temporal evolution of N_ice for various values of F_RS with $N_{\text{INP}}^{\left(\text{tot}\right)}$ values of 0.167 L⁻¹ (green traces) and 0.012 L⁻¹ (yellow traces). The light-to-dark gradient in green and yellow corresponds to the same parameter values. These parameter perturbations are run for u_z of 2 m s⁻¹ and T₀ of 272 K.

Finally, we investigate the impact of the fragment number from rime splintering, F_RS. Here we consider enhancement timing because the thermodynamic simulations show that there is no meaningful $N_{\text{INP}}^{\left(\text{lim}\right)}$ and the default ones show that the enhancement magnitude stays more or less constant. Figure 7a shows how the enhancement timing varies with the nucleation rate and fragment number F_RS. Slower nucleation rates are quantified by a reduction factor f_red on the y axis. Along with lower F_RS, slower nucleation yields longer enhancement times, by about 8 min relative to the highest nucleation rate and F_RS. F_RS is the more influential factor in timing. Its impact on N_ice evolution is shown in Fig. 7b, where a given enhancement is obtained over a shorter period for a higher F_RS. As for ice–ice collisional breakup, the effect of the parameter is much larger when $N_{\text{INP}}^{\left(\text{tot}\right)}$ is smaller in the yellow traces.

4 Observational comparison and discussion

In the first set of simulations, we investigated N_ice temporal evolution. For breakup and rime splintering at the higher values of $N_{\text{INP}}^{\left(\text{lim}\right)}$, 100-fold enhancement is formed within 15 to 25 min. These values are in agreement with the timescales measured during the COnvective Precipitation Experiment: no single process was definitely active, but drizzle drops formed in 20 min and glaciation occurred in 12 to 15 min after first ice nucleation (Taylor et al., 2016). In observations of maritime cumuliform clouds, Hobbs and Rangno (1990) measured 100-fold increases in N_ice over 9 min. These clouds had tops no colder than −8 ^∘C, so rime splintering was the active process, and a similar ice formation rate can be seen in Fig. 1c between about 20 and 30 min.

These rates are somewhat faster than those measured during the Ice in Clouds Experiment-Tropical campaign in which ice crystal concentrations of about 10 L⁻¹ were formed over half an hour (Heymsfield and Willis, 2014). The model also predicts somewhat faster rates than those in some laboratory studies. For example, Vardiman (1978) measured a 10-fold increase in ice crystal number over 20 min with $N_{\text{INP}}^{\left(\text{lim}\right)}$ of 3 L⁻¹. The breakup simulation with $N_{\text{INP}}^{\left(\text{lim}\right)}$ of 2.15 L⁻¹ (Fig. 1a) shows must faster evolution. Whereas Hallett and Mossop (1974) measured a linear increase between 10 and 20 min, Fig. 1c shows exponential increase. These larger rates are due, in part, to the Lagrangian nature of the simulations. By following a single parcel of air, we track colder and colder temperatures and ice accumulation, which both lead to more efficient ice generation.

We have also considered the impact of varying thermodynamics, particularly cloud base temperature and updraft, and INP concentrations. In situ measurements of breakup are hard to definitively obtain, but our simulations confirm the strong modulation of ultimate N_ice by the initial crystal concentration, reported in the laboratory experiments of Vardiman (1978) (his Fig. 1). Rangno and Hobbs (2001) also saw about 47 % fragmented ice in their measurements of supercooled Arctic clouds, whose cloud base temperatures were around 1  ^∘C and top temperatures were around −15 to −18 ^∘C. These conditions were appropriate for breakup and associated with a pristine columnar ice concentration of 0.1 to 3 L⁻¹. These values fall in the range of $N_{\text{INP}}^{\left(\text{tot}\right)}$ for which we predict active breakup in Fig. 1b.

Then for processes involving the liquid phase, observations indicate low values of $N_{\text{INP}}^{\left(\text{lim}\right)}$. For example, Crawford et al. (2012) note a $N_{\text{INP}}^{\left(\text{lim}\right)}$ of 0.01 L⁻¹ for rime splintering, while Lawson et al. (2015) report INP concentrations of 10⁻⁴ to 0.01 L⁻¹ prior to secondary enhancement. Beard (1992) notes a $N_{\text{INP}}^{\left(\text{lim}\right)}$ of 1 m⁻³ in his measurements of warm-base convective clouds. The essentially negligible values of $N_{\text{INP}}^{\left(\text{lim}\right)}$ from our simulations reflect these measurements qualitatively. Quantitatively, the simulated estimates may be lower because the model does not represent continuous sedimentation or advection of existing ice outside the parcel.

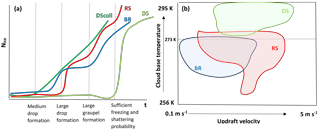
Figure 8 Qualitative summary of the findings from the default and varying thermodynamic simulations in Sect. 3.1 and 3.2. Panel (a) summarizes N_ice evolution for the different processes, particularly the instances of influential hydrometeor formation and whether the process exhibits gradual or threshold increases. Panel (b) shows which processes are possible for conditions in the T₀-u_z space.

For rime splintering, both our simulations and observations show the favorability of modest u_z for rime splintering (Heymsfield and Willis, 2014). Moderate updrafts hold the hydrometeors in the appropriate temperature zone for a longer period of time. Conversely, for droplet shattering, increasing u_z accelerates droplet growth by condensation or coalescence and enhancement, at least up to a certain point, in our simulations. Lawson et al. (2015) also observed the highest N_ice enhancement in high-updraft convective cores during ICE-T. In updating model formulations, we have also found that a representation of droplet size distribution broadening is a crucial factor to reproduce behavior from recent observational studies Taylor et al. (e.g., 2016); Lawson et al. (e.g., 2017). Without a basic implementation of the warm rain process, our model does not give realistic dependence of N_ice on T₀. Unrealistic coalescence rates in a monodisperse-class hydrometeor scheme should lead to underestimations of secondary ice production since the largest-diameter droplets are omitted. This reflects an important limitation of the model in its assumption of monodispersity. Large droplets shatter more effectively, and large graupel will have a larger sweep-out kernel for ice–ice collisional breakup. As more observational constraints become available, secondary production processes should be implemented into more complete microphysics schemes to quantify the importance of hydrometeor size distribution tails to their tendencies.

Other more advanced features of a real-world parcel, like ventilation effects, spatial phase separation, and continuous sedimentation, could also alter the simulation results (Sullivan et al., 2017). For example, droplet or ice hydrometeor growth will be enhanced by the stronger vapor density gradient generated by their in-cloud motion. Omitting additional hydrometeor growth should again underestimate secondary production. If “pockets” of ice phase exist within mixed-phase cloud, then the values of $N_{\text{INP}}^{\left(\text{lim}\right)}$ will be more influential as the ice–ice collisional breakup contribution will increase relative to rime splintering or droplet shattering. If a continuous formulation of sedimentation were substituted for the threshold one used here, the largest enhancement in Figs. 3 and 4 should shift to higher updrafts. Large hydrometeors would be held aloft by these higher updrafts and their numbers would feed into the secondary production tendencies.

5 Summary and outlook

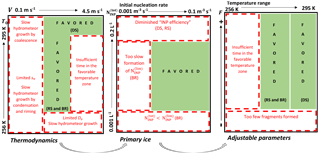
Figure 9 Summary of thermodynamic, primary ice, and adjustable parameter trends affecting ICNC enhancement from secondary production. F denotes the leading coefficient of a fragment number function for process X, ℵ_X. Regions in red indicate that secondary production may be limited, and those in green indicate that conditions are favorable. If the limitation is applicable only to one process, this is indicated in parentheses. The INP efficiency mentioned in the primary ice panel refers to the idea that lower secondary enhancement per INP is produced as the INP concentration increases.

We have performed three sets of simulations with a parcel model with six hydrometeor classes, considering the effect of thermodynamics and parameter perturbations on $N_{\text{INP}}^{\left(\text{lim}\right)}$, as well as ICNC enhancement and timing. Our findings can be summarized in three points:

1. The evolution of N_ice from secondary production is determined by collision-based nonlinearity and single- vs. two-phasedness.

   N_ice increases gradually for the collision-based processes of breakup and rime splintering, whereas for non-collisional droplet shattering, N_ice increases abruptly, when p_fr and p_sh become large enough at cold enough temperatures. $N_{\text{INP}}^{\left(\text{tot}\right)}$ affects both the enhancement magnitude and timing for ice–ice collisional breakup. For rime splintering, $N_{\text{INP}}^{\left(\text{tot}\right)}$ affects timing to obtain a given N_ice(t_end), while for droplet shattering, it has almost no impact on either magnitude or timing. These trends are summarized qualitatively in Fig. 8a.

2. $N_{\text{INP}}^{\left(\text{lim}\right)}$ can be as large as 0.15 L⁻¹ for ice–ice collisional breakup. Rime splintering or droplet shattering enhancement is determined by a thermodynamic sweet spot rather than by $N_{\text{INP}}^{\left(\text{lim}\right)}$.

   $N_{\text{INP}}^{\left(\text{lim}\right)}$ increases for ice–ice collisional breakup as the fragment number decreases or the temperature range shrinks, particularly for $N_{\text{INP}}^{\left(\text{tot}\right)}$ values of 0.01 L⁻¹ or less. At faster nucleation rates, the fragment number and temperature range are also more influential: enhancement occurs for 90 % of the parameter space at a default nucleation rate and just 10 % of the space at a rate 100 times slower. These trends are visualized in the “primary ice” panel of the summary schematic (Fig. 9).

   For rime splintering or droplet shattering, ICNC enhancement of 10² or 10³ is possible even for slow nucleation rates and $N_{\text{INP}}^{\left(\text{tot}\right)}$ values as low as 1 m⁻³. For these processes involving the liquid phase, an intermediate updraft for which hydrometeors grow fast enough but also spend long enough in the appropriate temperature zone is more important. For droplet shattering, a representation of the warm rain process and a warm enough initial temperature are also crucial to reproduce observations. These trends are summarized visually in Fig. 8b.

3. No single secondary ice production process dominates ICNC enhancement.

   At higher nucleation rates, low u_z, and warm T₀, the contribution from ice–ice collisional breakup is large. If INPs are limited, u_z is somewhat higher, and T₀ is above the freezing level, droplet shattering is most important. And if temperature falls around the optimal zone of 268 to 270 K with an intermediate u_z, the rime splintering contribution will be large. These “thermodynamic spaces” where one process dominates are visualized in Fig. 8b.

More generally, the role of INPs in secondary production reflects how changing aerosol emissions will affect cloud phase partitioning. The low or nonexistent values of $N_{\text{INP}}^{\left(\text{lim}\right)}$ calculated in this study indicate that perturbations in cloud condensation nuclei concentrations are more influential on mixed-phase partitioning than those in INP concentrations, with the caveat that thermodynamic conditions are appropriate for secondary production. If the mixed-phase cloud is polluted by more cloud condensation nuclei, the higher droplet number will mean that fewer droplets reach a sufficient size to shatter or rime efficiently (This last factor has been called the riming indirect effect (Borys et al., 2003; Lance et al., 2011; Lohmann, 2017)). And in these cases, the supercooled liquid fraction remains higher, and the cloud reflects more shortwave radiation. More pollution by cloud condensation nuclei could also yield a thermodynamic indirect effect in which latent heat is released at high altitudes and strengthens the upward movement of the cloud; Koren et al. (2005) have called this cloud invigoration. Our simulations have shown that beyond a certain updraft, secondary production is no longer favored. In this way, the liquid portion of a mixed-phase cloud could also remain higher.

The impact of INP concentrations could be larger for deep convective clouds in which anvil spreading is caused by generation of many small crystals at cloud top (Fan et al., 2013). If the cloud is polluted by more INPs, more vigorous secondary production by ice–ice collisional breakup may occur under conditions of fast enough nucleation rate but modest enough updraft and warmer subzero cloud base temperatures. These conditions can be found in deep convective clouds, for example at the edges of rising turrets or tops of eroding ones (Beard, 1992). In contrast to the riming or thermodynamic indirect effects mentioned above, an ICNC increase at the deep convective cloud top, a kind of “anvil enhancement effect”, would radiatively warm the surface.

A systematic quantification of $N_{\text{INP}}^{\left(\text{lim}\right)}$ is also relevant for the growing field of bioaerosol. Primary biological aerosol particles (PBAPs) exist in the atmosphere at much lower number concentrations than dust or black carbon. But they also nucleate at warmer subzero temperatures (Hoose and Möhler, 2012; Fröhlich-Nowoisky et al., 2016), and small biological residues can intermix with dust particles to boost ice nucleation activity (Conen et al., 2011; O'Sullivan et al., 2015; Steinke et al., 2016). Even when their contribution to primarily nucleated ICNC is small, they may remain influential via initiation of secondary ice production. For example, the ice active fraction of 10⁻⁴ for Pseudomonas syringae measured by Möhler et al. (2008) around −8 ^∘C could provide the 0.01 L⁻¹ seed concentration from Crawford et al. (2012) for concentrations of 10⁵ m⁻³, although this is an upper bound for bioaerosol number. From our calculations, it could also provide the $N_{\text{INP}}^{\left(\text{lim}\right)}$ necessary for ice–ice collisional breakup to occur. Bioaerosol could also be sufficient to initiate rime splintering, given that this process occurs even for N_INP below 1 m⁻³ in our simulations. A climatically important linkage has also been hypothesized between PBAPs, in-cloud ICNC, and cold-phase-initiated rain and is often termed the “bioprecipitation feedback” (Huffman et al., 2013; Morris et al., 2014). The possibility of secondary production with a low $N_{\text{INP}}^{\left(\text{lim}\right)}$ means that even a few bioaerosols could trigger generation of many small ice hydrometeors from larger droplets or graupel and suppress precipitation.

As a summary of our findings, we present an organizational framework for future studies of secondary production in Fig. 9. Favorable conditions for large ICNC enhancement are shown in green, e.g., intermediate updraft in the thermodynamic panel or higher nucleation rate for ice–ice collisional breakup in the primary ice panel. This classification, along with the T₀−u_z space in Fig. 8b, can be used to determine where signatures of secondary production are likely to be found in in situ or remote sensing data. And as more experimental studies to quantify the fragment number and temperature dependencies of these processes are performed, more quantitative bounds can be established in the final adjustable parameter panel.

Appendix A

Notation
aX	Spheroidal axis of hydrometeor of type X
β	Adjustable parameter in the sigmoidal function for the fragment number generated from shattering
c0	Primary ice nucleation rate based upon DeMott et al. (2010)
𝒟v	Diffusion coefficient of water vapor
FBR	Leading coefficient of the fragment number generated per collision based upon data from Takahashi et al. (1995)
FDS	Leading coefficient of the fragment number generated per shattering droplet as in Lawson et al. (2015)
fimm	Fraction of INPs that immediately immerse nucleate droplets, rather than later after coalescence
fred	Factor for nucleation rate reduction
FRS	Leading coefficient of the fragment number per kilogram of rime as in Hallett and Mossop (1974)
γ	Adjustable parameter in the sigmoidal function for the fragment number generated from shattering
Γ	Atmospheric lapse rate
ICNC	In-cloud ice crystal number concentration
INP	Ice-nucleating particle
KX	Gravitational collection kernel for process X
ℵBR	Fragment number from ice–ice collisional breakup per large and small graupel number
Nd	Small droplet number concentration in the parcel
ℵDS	Fragment number from droplet shattering per large droplet number
${\mathrm{\aleph }}_{\text{DS}}^{\left(\text{coll}\right)}$	Fragment number from collisional droplet shattering per large droplet and small ice crystal number
Ni	Ice crystal number concentration in the parcel
Nice	Total ice hydrometeor number within the parcel, i.e., the summation of ice crystal and small and large graupel numbers
$N_{\text{ice}}^{\left(\text{max}\right)}$	Maximum Nice formed within the parcel during a given simulation
$N_{\text{INP}}^{\left(\text{lim}\right)}$	Limiting ice-nucleating particle number concentration to initiate secondary production
$N_{\text{INP}}^{\left(\text{tot}\right)}$	Total number of ice-nucleating particles within the parcel available for primary nucleation. This value is fixed by the
	user beforehand.
Ng	Small graupel number concentration in the parcel
NG	Large graupel number concentration in the parcel
Nr	Medium droplet number concentration in the parcel
NR	Large droplet number concentration in the parcel
ℵRS	Fragment number from rime splintering per large droplet and large or small graupel number
ρw	Density of liquid water
$p_{\text{fr}}(t,T,r)$	Temperature- and INP-dependent probability that a large droplet freezes based upon Paukert et al. (2017)
psh(T)	Temperature-dependent probability that a frozen large droplet shatters, with $p_{\text{sh}}^{\left(\text{max}\right)}$ being the maximum of this distribution
rX	Radius of hydrometeor of type X
sw	Supersaturation with respect to liquid water in the parcel
τX	Time delay for a hydrometeor in class X to grow by deposition, riming, or condensation to the next class
T0	Cloud base temperature or the initial temperature of the parcel
tend	Time when the simulation is terminated, either because the parcel has become water subsaturated or the temperature
	has reached 237 K where homogeneous nucleation can occur
Tmin	Minimum temperature for ice–ice collisional breakup to occur
uz	Updraft velocity of the parcel