Representation of solar tides in the stratosphere and lower mesosphere in state-of-the-art reanalyses and in satellite observations

Atmospheric solar tides in the stratosphere and the lower mesosphere are investigated using temperature data from five state-of-the-art reanalysis data sets (MERRA-2, MERRA, JRA-55, ERA-Interim, and CFSR) as well as TIMED SABER and Aura MLS satellite measurements. The main focus is on the period 2006–2012 during which the satellite observations are available for direct comparison with the reanalyses. Diurnal migrating tides, semidiurnal migrating tides, and nonmigrating tides are diagnosed. Overall the reanalyses agree reasonably well with each other and with the satellite observations for both migrating and nonmigrating components, including their vertical structure and the seasonality. However, the agreement among reanalyses is more pronounced in the lower stratosphere and relatively weaker in the upper stratosphere and mesosphere. A systematic difference between SABER and the reanalyses is found for diurnal migrating tides in the upper stratosphere and the lower mesosphere; specifically, the amplitude of trapped modes in reanalyses is significantly smaller than that in SABER, although such difference is less clear between MLS and the reanalyses. The interannual variability and the possibility of long-term changes in migrating tides are also examined using the reanalyses during 1980–2012. All the reanalyses agree in exhibiting a clear quasi-biennial oscillation (QBO) in the tides, but the most significant indications of long-term changes in the tides represented in the reanalyses are most plausibly explained by the evolution of the satellite observing systems during this period. The tides are also compared in the full reanalyses produced by the Japan Meteorological Agency (i.e., JRA-55) and in two parallel data sets from this agency: one (JRA-55C) that repeats the reanalysis procedure but without any satellite data assimilated and one (JRA-55AMIP) that is a free-running integration of the model constrained only by observed sea surface temperatures. Many aspects of the tides are closer in JRA-55C and JRA-55AMIP than these are to the full reanalysis JRA-55, demonstrating the importance of the assimilation of satellite data in representing the diurnal variability of the middle atmosphere. In contrast to the assimilated data sets, the free-running model has no QBO in equatorial stratospheric mean circulation and our results show that it displays no quasi-biennial variability in the tides.

1 Introduction

Atmospheric solar tides are global-scale inertia-gravity waves with periods that are integer fractions of a solar day (Chapman and Lindzen, 1970). They are primarily driven by diurnally varying diabatic heating, such as the absorption of solar radiation by tropospheric water and stratospheric ozone, and the latent heat release associated with tropical convection. The diurnal (S₁) and semidiurnal (S₂) variations around the globe can be decomposed into zonal harmonics with the “migrating” (Sun-synchronous) components for the S₁ and S₂ tides represented by westward-propagating wavenumber one and two, respectively. The remainder of the tidal zonal harmonics are “nonmigrating components” and are excited mainly by zonally asymmetric variations in (local time) heat sources or topography. Tides propagate vertically with amplitudes typically reaching a maximum in the mesosphere and lower thermosphere (MLT) region. There have been many studies of the tides in MLT as seen in ground-based measurements, satellite measurements, and numerical simulations (e.g., Lieberman, 1991; Hagan et al., 1995; Forbes and Wu, 2006; Zhang et al., 2006; Ward et al., 2010).

The amplitudes of tidal variations in the region from the troposphere to the lower mesosphere are generally smaller than in the MLT and so fewer studies have investigated the tides in this lower altitude region. Nevertheless, tidal variations in the lower atmosphere are worth investigating not only because they provide a “lower boundary condition” for tides in upper air but also because the tide and the resultant diurnal cycle in stratospheric ozone (Sakazaki et al., 2013a) need to be considered when constructing a homogenized data set of temperature and ozone from different satellites with different measurement local times (e.g., Zou et al., 2014; WMO, 2014; Nash and Saunders, 2015; Sakazaki et al., 2015c). Also it is now established that tides excited in the stratosphere can play a significant role in tropospheric meteorology, particularly in the diurnal cycle of tropical rainfall (Woolnough et al., 2004; Sakazaki et al., 2017).

The global pattern of stratospheric tides was investigated based on temperature data from ground-based (radiosondes, lidars) and satellite measurements (e.g., Wallace and Hartranft, 1969; Keckhut et al., 1996; Leblanc et al., 1999; Xu et al., 2009; Mukharov et al., 2009; Huang et al., 2010; see also Sakazaki et al., 2012 and references therein). However, the available direct measurements have important limitations in temporal and spatial coverage. For example, SABER, which is so far the most commonly used data set for tidal studies, has difficulty detecting tides in regions poleward of ∼50^∘. Meteorological reanalyses that provide temporally and spatially homogeneous data over the globe could be a useful data set for a tidal study. Using a fixed assimilation–forecast model system, the reanalyses provide best estimates of past atmospheric states in many dynamical variables. Currently available reanalyses from major centers provide estimates of atmospheric variables from the surface to the upper stratosphere or the lower mesosphere with time resolutions of 3 or 6 h.

Reanalyses for relatively high-frequency features such as the tide are particularly challenging in the region above the usual ∼10 hPa upper boundary of conventional balloon soundings. Above the middle stratosphere the reanalyses must rely on direct observations only from satellites (e.g., Fujiwara et al., 2017), which have limited local time and space coverage, so the reanalysis representation of tides in this region may be particularly dependent on the tidal simulation in the forecast models employed.

Previous studies evaluating the representation of solar tides in the stratosphere and the lower mesosphere in reanalyses have mainly considered only S₁ (24 h) tides. An early study by Swinbank et al. (1999) investigated the S₁ migrating tide in the stratosphere as represented in the Goddard Earth Observing System (GEOS) version 2 analysis data (one of the predecessors of MERRA and MERRA-2 reanalyses). They found that the GEOS-2 tidal amplitude in the free-running model is reduced by assimilating satellite data, particularly data from the stratospheric sounding unit (SSU). Sakazaki et al. (2012, hereafter referred to as S12) compared S₁ migrating tides in the stratosphere by using data from TIMED SABER and six types of reanalysis data: MERRA, ERA-Interim, CFSR, JRA-25–JCDAS, NCEP1, and NCEP2. They found that the overall latitude–altitude structure and its seasonality was reproduced qualitatively by the newer three reanalyses (MERRA, ERA-Interim, and CFSR), but the amplitude in the reanalyses was 30–50 % underestimated in the upper stratosphere and lower mesosphere.

Only a few studies have examined S₂ tides in reanalyses (although the solar S₂ surface pressure oscillation has been more extensively studied; e.g., Ray and Ponte, 2003; Saha et al., 2010; Díaz-Argandoña et al., 2016; Hamilton and Sakazaki, 2017). Hsu and Hoskins (1989) and Kohyama and Wallace (2014) derived S₂ migrating tides in the stratosphere by using the ECMWF operational analysis and the ERA-Interim, respectively. Li et al. (2015) used CFSR reanalysis to examine the seasonality of S₂ migrating tides. Kopp et al. (2015) compared the S₂ tides derived from lidar measurements over Kühlungsborn (54^∘ N, 12^∘ E) with those from MERRA reanalysis. Note that no intercomparison of the S₂ tides as represented in different reanalyses has so far been performed. Note also that nonmigrating tides have not been examined with reanalysis data as far as the authors are aware.

Since the study of S12, several new reanalysis data sets have been released including MERRA-2 and JRA-55. The present study is a follow-up to S12 including these new reanalyses and extending the analysis to the S₂ migrating tides and to nonmigrating tides. The Japan Meteorological Agency has produced a unique resource in which the full state-of-the-art JRA-55 reanalysis is supplemented with two additional global data sets (collectively called the JRA-55 family): JRA-55C, which assimilates only conventional surface and balloon sounding observations, and JRA-55AMIP, which employs a free-running version of the forecast model. The comparison of JRA-55 family members enables us to investigate the effects of data assimilation on the representation of tides in the global data sets. In addition to SABER data, data from Aura MLS (only assimilated in MERRA-2) will be also analyzed as a measure of S₁ migrating tides.

The remainder of the paper is organized as follows. Section 2 describes the reanalysis and observational data sets employed, while Sect. 3 describes our method to extract tidal components. Section 4 shows the results for S₁ migrating tides, S₂ migrating tides, and nonmigrating tides (mainly for S₁). Section 5 examines the long-term changes in migrating tides as represented in the reanalyses over the last 3 decades, while major findings are summarized in Sect. 6. The work described in the present paper contributes to the SPARC Reanalysis Intercomparison Project (S-RIP), chap. 11: “Upper stratosphere and lower mesosphere” (see Fujiwara et al., 2017, for details about S-RIP).

2 Data sets

We analyze and compare data from global reanalyses and two satellite observational data sets: SABER (not assimilated in any reanalyses) and Aura MLS (only assimilated in MERRA-2). In Sect. 5 below we intercompare several reanalyses over a long period (1980–2012) that includes most of the modern era in which satellite radiances have been assimilated. However, our detailed evaluation will focus on the 7-year period 2006–2012 during which it seems that the satellite data sources used in the global assimilations were fairly stable (e.g., Kawatani et al., 2016; Fujiwara, 2017) and during which we have two other satellite data sets (SABER and Aura MLS) not included in most of the assimilations and thus providing independent estimates of the diurnal variability of temperature in the stratosphere and mesosphere. Note that all the reanalysis data sets employed extended over the full 1980–2012 period with the exception of CFSR, whose integration with the original CDAS-T382 system ends in December 2010 (see Fujiwara et al., 2017).

2.1 Reanalyses

We compare results in satellite data sets with those from seven different global gridded data sets produced at major meteorological centers. Five of these are standard state-of-the-art global atmospheric reanalyses: (1) MERRA-2 (Gelaro et al., 2017), (2) MERRA (Rienecker et al., 2011), (3) JRA-55 (Kobayashi et al., 2015), (4) ERA-Interim (Dee et al., 2011), and (5) CFSR (Saha et al., 2010). We will not consider the JRA-25, ERA-40, and NCEP1/2 reanalyses, which are the predecessors of JRA-55, ERA-Interim, and CFSR, respectively. S12 showed that the global structure and seasonality of the S₁ migrating tide represented in JRA-25 and NCEP1/2 were less consistent with available observations than the newer reanalyses data sets.

In addition to the five full reanalyses we also analyze the tides in two other gridded products produced by the Japan Meteorological Agency that are parallel to their full JRA-55 reanalysis. One (JRA-55C) repeats the reanalysis procedure but assimilating surface and upper-air conventional data but not satellite data, and the other (JRA-55AMIP) is a free-running integration of the forecast model constrained only by observed sea surface temperatures (Kobayashi et al., 2014). Here we refer to the three JMA data sets (JRA-55, JRA-55C, and JRA-55AMIP) as the JRA-55 family. The comparison of these family members will help us examine the effects of data assimilation on the representation of the solar tides.

Each reanalysis system is comprehensively described by Fujiwara et al. (2017) and thus only key aspects are summarized here (see also Table 1). Data are available on a 3-hourly basis at 00:00, 03:00, 06:00, 09:00, 12:00, 15:00, 18:00, and 21:00 UTC for MERRA and MERRA-2 and on a 6-hourly basis at 00:00, 06:00, 12:00, and 18:00 UTC for the remaining data sets. Data provided on the output pressure levels are used for MERRA and MERRA-2, CFSR, and JRA-55AMIP, with the number of levels being 42 (up to 0.1 hPa), 37 (up to 1 hPa), and 37 (up to 1 hPa), respectively. For JRA-55, JRA-55C, and ERA-Interim, we interpolated data provided on model levels onto the 42 MERRA and MERRA-2 pressure levels up to 0.1 hPa.

Table 1 List of reanalyses used in this study. Also included is the JRA-55AMIP data set, which represents the results of a free-running version of the forecast model used to produce the JRA-55 and JRA-55C reanalyses.

2.2 Satellite measurements

2.2.1 SABER

The SABER instrument is onboard the TIMED satellite, which was launched on 7 December 2001 (Russell et al., 1999). It measures CO₂ infrared limb radiance to retrieve the kinematic temperature profiles between 20 and 120 km (Remsberg et al., 2008). Data are continuously obtained between 53^∘ S and 53^∘ N. The TIMED satellite is not in a Sun-synchronous orbit, and the local time of SABER measurements changes by about 12 min per day, meaning that a full diurnal cycle (24 h in local time) is covered over a period of 60 days using ascending and descending nodes. Note that data are not acquired by SABER near local noon. The vertical resolution of the measurements is ∼2 km.

In our study, version 2.0 temperature data on pressure levels are analyzed for January 2006 through December 2012 (S12 analyzed version 1.07 data). As described by Sakazaki et al. (2015b), before further analysis, data were averaged in bins of 15^∘ longitude, 5^∘ latitude, and 2 km in log-pressure vertical coordinates for each day and for each ascending and descending node. We emphasize that SABER data were not assimilated into any of the reanalyses used in this study.

2.2.2 Aura MLS

The MLS instrument is onboard the Aura satellite, which was launched in July 2004. It uses the microwave limb sounding technique to observe atmospheric dynamical parameters and chemical constituents (Waters et al., 2006). The Aura orbit is Sun synchronous at 705 km of altitude with 98^∘ of inclination, and the Equator-crossing local time is 13:45 for the ascending nodes. The MLS fields of view look in the forward direction (an almost north–south direction) and vertically scan the limb of the atmosphere. In the tropics (10^∘ S–10^∘ N), the actual measurement local times were 13:45 and 01:45 on average for the ascending and descending nodes, respectively.

MLS temperature is retrieved from bands near O₂ spectral lines for the region between 261 and 0.001 hPa pressure levels with a vertical resolution of 3–6 km. In this study, version 4.2 and 3.3 data are utilized after a data screening performed based on the criteria shown by Livesey et al. (2017) and Livesey et al. (2011), respectively. The MLS measurements were assimilated into the MERRA-2 data set at pressure levels less than 5 hPa (after 2004; McCarty et al., 2016, their Table 1; Gelaro et al., 2017), but not into any of the other reanalyses that we employed.

3 Analysis methods

3.1 Migrating and nonmigrating tides

In this study, the (1) diurnal (S₁) migrating tide, (2) semidiurnal (S₂) migrating tide, and (3) nonmigrating tides are extracted and diagnosed individually. The analysis procedure to extract these three components basically follows the method proposed by Sakazaki et al. (2015b) as briefly explained below.

First, all diurnal variations, which includes both migrating and nonmigrating components, are calculated based on universal time (UT) as follows. For SABER data, since 24 local times are covered by 60-day measurements by ascending and descending nodes, a time series of the 60-day running mean that can be regarded as the daily mean is calculated for each latitude–longitude bin; this is then subtracted from the original temperatures for each day, for each bin, and for each descending and ascending node to produce the anomaly from the daily mean. These anomaly temperatures are binned and averaged into hourly UT time bins to obtain 1-hourly diurnal variations. For reanalyses, 3- or 6-hourly diurnal variations in UT are extracted at each grid point through composite analysis based on UT after the subtraction of the daily mean; in fact, we downloaded and analyzed the diurnal monthly mean (monthly mean for each UTC snapshot) data provided by each reanalysis center (e.g., for JRA-55, diurnal monthly mean data are the monthly averages for 00:00, 06:00, 12:00, and 18:00 UTC). Clearly the 6-hourly data (ERA-Interim, JRA-55, and CFSR) cannot resolve S₂ at each grid point, but the “migrating component” of S₂ can be extracted by using data at grid points on the same latitude belt, as explained in the following (Ray and Ponte, 2003; Díaz-Argandoña et al., 2016; Hamilton and Sakazaki, 2017).

Next, by averaging data at the same local time (LT) for each latitude band, migrating tides that are a function of LT are calculated; for example, for 6-hourly reanalyses, data at 00:00 LT are the average of data points at 00:00 UT (0^∘ E), 06:00 UT (90^∘ E), 12:00 UT (180^∘ E), and 18:00 UT (270^∘ E). Then, the harmonic fitting is performed for the diurnal variations in LT to extract the migrating S₁ and S₂ components. Finally, nonmigrating tides are calculated by subtracting migrating tides (for reanalyses, the S₁ plus S₂ migrating tides are used for actual calculation) from the total tidal variations.

For nonmigrating tides, the zonal wavenumber decomposition is also applied for the S₁ component, following the method proposed by Dai and Wang (1999). Before the analysis, the tidal component (X) at any longitude (λ), latitude (θ), and vertical pressure level (z) was decomposed into the symmetric (X_S) and antisymmetric (X_A) components with respect to the Equator as

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }X(\mathit{\lambda },\mathit{\theta },z)=X_S(\mathit{\lambda },\mathit{\theta },z)+X_A(\mathit{\lambda },\mathit{\theta },z),\end{array}$$

where

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }{X}_S(\mathit{\lambda },\mathit{\theta },z)\equiv {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left\{X(\mathit{\lambda },\mathit{\theta },z)+X(\mathit{\lambda },-\mathit{\theta },z)\right\},\text{(3)}& {\displaystyle }& {\displaystyle }{X}_A(\mathit{\lambda },\mathit{\theta },z)\equiv {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left\{X(\mathit{\lambda },\mathit{\theta },z)-X(\mathit{\lambda },-\mathit{\theta },z)\right\}.\end{array}$$

Figure 1 Latitude–altitude distribution of amplitude for annual mean diurnal (S₁) migrating tide in temperature, as derived from (a) SABER, (b) JRA-55, (c) JRA-55C, (d) JRA-55AMIP, (e) MERRA-2, (f) MERRA, (g) ERA-Interim, and (h) CFSR.

3.2 Difference between ascending minus descending nodes for MLS (A–D difference)

The difference between the ascending (A) and descending (D) nodes of MLS temperature measurements is calculated in the tropics (10^∘ S–10^∘ N) as a measure of tidal amplitude (hereafter referred to as the A–D difference). Since the measurement times are fixed and are 12 h apart in local time (i.e., ∼ 01:45 and 13:45), the zonal mean A–D difference can be caused by odd harmonics of the migrating tides (24 h, 8 h components, etc.). In addition, because the S₁ component is predominant over the higher-order harmonics (e.g., the ratio of 8 h to 24 h components in SABER data was <30 % for most parts in the tropical stratosphere and in the lower mesosphere), the A–D difference can be mostly attributed to the S₁ migrating tide. The same quantity is calculated for the other data sets as well (i.e., SABER and reanalyses) by using the migrating tides (i.e., diurnal variations in LT) in each data set (for reanalyses, migrating tides reconstructed from S₁, S₂ and terdiurnal harmonic components are considered).

Figure 2 As for Fig. 1 but for phase (LT at which the S₁ temperature variation is maximum).

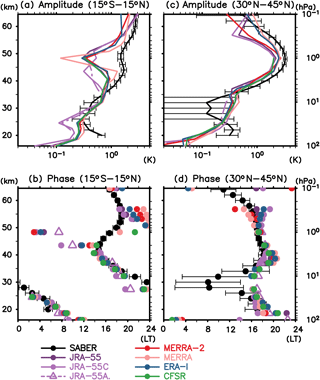
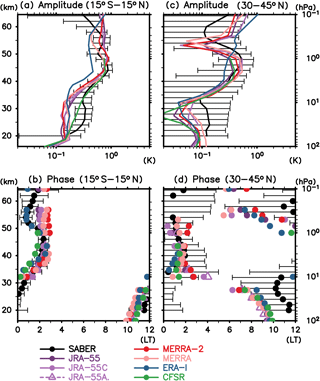
Figure 3 Vertical profile of the (a, c) amplitude and (b, d) phase of the annual mean diurnal (S₁) migrating tide averaged for (a, b) 15^∘ S–15^∘ N and (c, d) 30–45^∘ N, derived from different data sets. Horizontal bars show 95 % confidential levels in a t test for SABER results. For the statistical test, the error is defined as the 95 % confidential level for the daily anomaly (composite value) at each hourly universal time; this quantity has been propagated to the error of amplitude and phase for diurnal migrating tides following the error propagation theory.

4 Results

4.1 Diurnal (S₁) migrating tide

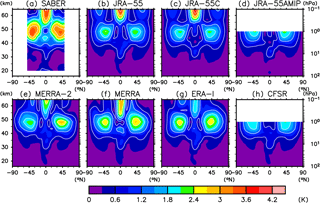
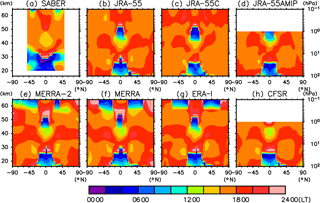
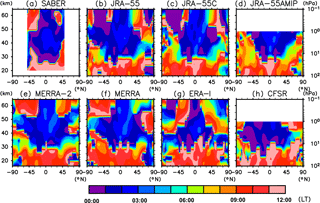
Figures 1 and 2 show the latitude–altitude distribution of amplitude and phase, respectively, for annual mean S₁ migrating temperature tides computed from SABER data and from the various reanalyses during 2006–2012. Figure 3 compares the vertical profile of amplitude and phase averaged over 15^∘ S–15^∘ N (tropics) and 30–45^∘ N (midlatitudes). All data sets show that the tidal amplitude increases with altitude in the tropics (up to ∼4 K in the lower mesosphere in the SABER data, somewhat less in the various reanalyses). The amplitude has maxima in the upper stratosphere (45–50 km or 1 hPa) at ∼3.5 K for SABER (again somewhat less in the reanalyses) in the extratropics of both hemispheres. Over the tropics, the phase shows a downward progression (except for SABER at 40–55 km; see below for further discussion). At extratropical latitudes, on the other hand, the phase is almost constant around 18:00 LT except for the region above ∼55 km (0.3 hPa).

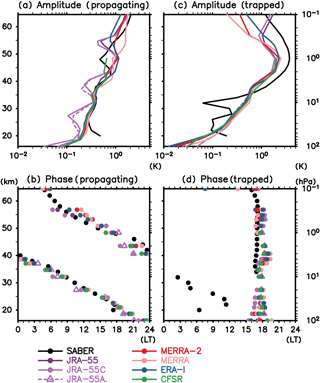
Figure 4 Vertical profile of the (a, c) amplitude and (b, d) phase of (a, b) the first propagating Hough mode and (c, d) the first trapped Hough mode for the annual mean diurnal (S₁) migrating tide.

There is quite a good agreement among the full reanalysis data sets below ∼45 km, while the spread among the reanalysis results becomes larger above the upper stratosphere. It is inferred that the reanalyses may be well constrained by satellite measurements up to the upper stratosphere while being somewhat more model dependent in the lower mesosphere.

Apart from the difference among different reanalyses, we see a systematic difference between SABER and all the reanalyses both for amplitude and phase above 40 km. Notably, (1) the amplitude in SABER is ∼1 K larger than that in the reanalyses (see, e.g., the extratropical maximum at ∼45 km in Fig. 3c) and (2) the phase is locally constant (or shows an upward progression) in the tropics for SABER at 40–55 km, while it shows a continuous downward progression for most reanalyses. The present SABER results, including the extratropical maxima at 45–50 km and the phase stagnation at 40–50 km, are quantitatively consistent with previous studies using SABER, even though earlier investigators used a different procedure to extract tides (Mukhtarov et al., 2009; Xu et al., 2009; Huang et al., 2010).

In Fig. 3 it is apparent that the JRA-55C and JRA-55AMIP results for the S₁ migrating tide stand out from those obtained with the full reanalyses. Notably, the JRA-55C and JRA-55AMIP results are close together and differ substantially from the JRA-55 results. The amplitude in JRA-55C and JRA-55AMIP is no larger than that in JRA-55 for the entire stratosphere and is substantially smaller in some regions. This suggests that, contrary to the finding by Swinbank et al. (1999), the assimilation of satellite measurements does not act to damp the tidal amplitude in JRA-55, at least for the recent period (Swinbank et al. analyzed data in the early 1990s).

We analyzed these results further with some guidance from the expectations of so-called classical tidal theory, which solves for the linear response of the global atmosphere to monochromatic heating ignoring mean winds and horizontal temperature gradients in the mean state. The classical tidal theory equations are separable in the zonal, vertical, and meridional directions and conventionally the solutions are written as the product of zonal harmonics and meridional modes known as Hough functions (e.g., Chapman and Lindzen, 1970). As shown by Sakazaki et al. (2013b), the S₁ migrating tide in the stratosphere can be reasonably well represented by a superposition of only a few (∼4) Hough modes each of which has its own vertical propagation characteristics. For the annual mean tidal temperatures, which are almost symmetric about the Equator (Fig. 1), even the two symmetric Hough modes (the (1, 1) mode and (1, −1) mode shown in Fig. A1a) are enough to represent the overall structures. That is, the S₁ migrating tidal temperatures ($T_{S_{\mathrm{1}}\text{-mig}}$) determined from SABER and each of the reanalyses are approximated as

$$\begin{array}{ll}\text{(4)}& {\displaystyle }& {\displaystyle }{T}_{S_{\mathrm{1}}\text{-mig}}(\mathit{\theta },z,t)=\stackrel{\mathrm{‾}}{T}(\mathit{\theta },z)\cos \left(\mathit{\omega }\right(t-\stackrel{\mathrm{‾}}{\mathit{\alpha }}(\mathit{\theta },z)\left)\right){\displaystyle }& {\displaystyle }\cong \sum _{n=\mathrm{1}}^{\mathrm{2}}{\stackrel{\mathrm{̃}}{T}}_n^{\mathrm{1}}\left(z\right){\mathrm{\Theta }}_n^{\mathrm{1}}\left(\mathit{\theta }\right)\cos \left(\mathit{\omega }\right(t-{\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_n^{\mathrm{1}}\left(z\right)\left)\right),\end{array}$$

where t is local time (hr); $\stackrel{\mathrm{‾}}{T}$ and $\stackrel{\mathrm{‾}}{\mathit{\alpha }}$ are amplitude (K) and phase (LT), respectively, at each latitude and pressure level; $\mathit{\omega }=\mathrm{2}\mathit{\pi }/\mathrm{24}$ (hr⁻¹); and ${\stackrel{\mathrm{̃}}{T}}_n^{\mathrm{1}}$ and ${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_n^{\mathrm{1}}$ are the amplitude (K) and phase (LT) of the nth Hough mode (${\mathrm{\Theta }}_n^{\mathrm{1}}$; in this case, n=1 is the (1, 1) mode and n=2 is the (1, −1) mode). Note that the equatorially trapped (1, 1) mode is associated with vertical phase propagation, while the (1, −1) mode represents disturbances we expect to be vertically trapped.

Figure 4 shows the vertical profile of amplitude and phase of the two modes (i.e., ${\stackrel{\mathrm{̃}}{T}}_n^{\mathrm{1}}\left(z\right)$ and ${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_n^{\mathrm{1}}\left(z\right)$ of Eq. (4), respectively). For the propagating (1, 1) mode, the amplitude grows exponentially with increasing altitude and the phase shows a downward progression. The vertical wavelength is ∼25 km, which is quite consistent with the prediction by classical tidal theory (∼28 km; Chapman and Lindzen, 1970). For the trapped (1, −1) mode, the amplitude is localized around the peak ozone heating region (∼50 km) and the phase is almost constant with altitude at around 18:00 LT. Notably, the systematic difference between SABER and the reanalyses seen in Fig. 3 is projected mostly onto the amplitude of the trapped mode (Fig. 4c); the amplitude of the trapped mode in the reanalyses is 1.5–2.5 K, which is significantly smaller than that in SABER (3–4 K). For the propagating mode, by contrast, there is no clear systematic difference between SABER and the reanalyses (Fig. 4a and b). Because the magnitude of the trapped mode is smaller in reanalyses compared to SABER, the amplitude is small at all latitudes and the phase can propagate vertically in the tropics (i.e., in SABER, the phase is almost constant at 40–55 km as affected by the strong trapped mode; Fig. 3). The magnitude of the trapped mode in SABER is consistent with the analysis by Mukhtarov (2009; ∼4 K peak both in March and July). These findings imply two possible reasons for the SABER–reanalyses difference: (1) (if SABER is “true”) the ozone heating, which is largely responsible for the trapped mode in the upper stratosphere, may be underestimated in the reanalyses, or (2) (if reanalyses are “true”) SABER might have a bias that is dependent on local time and has a similar latitudinal structure similar to the trapped mode (i.e., almost constant with latitude).

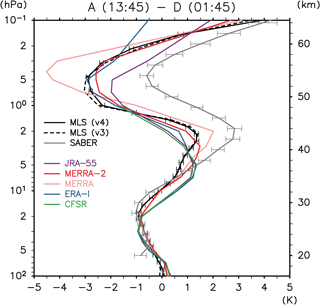
Figure 5 Vertical profile of the difference between ascending and descending profiles of temperature in MLS measurements compared to the 13:45 minus 01:45 LT temperature difference sampled from the SABER data and various reanalysis data sets (average between 10^∘ S and 10^∘ N). For MLS, solid and dashed curves show the results from v4.2 and v3.3, respectively. Horizontal bars show 95 % confidential levels with t test (only for MLS (v4.2) and SABER). Results are annual means for the 7-year period 2006–2012.

To supplement the above discussion concerning the S₁ migrating tide, we examined the A–D difference (i.e., 13:45 LT minus 01:45 LT) in MLS temperature measurements. As mentioned in Sect. 2, the zonal mean A–D difference is expected to result from S₁ migrating tides (if there is no “instrumental” bias between A and D profiles). The vertical profile of the 13:45 LT minus 01:45 LT difference averaged over 10^∘ S–10^∘ N is shown in Fig. 5 for the MLS determinations (both for versions 4.2 and 3.3) and for the SABER data and each of the reanalyses. The A–D difference in MLS and all the reanalyses, but not SABER, basically changes its sign vertically, with its absolute value increasing with altitude. This feature means that the amplitude increases with altitude and the phase shows a vertical progression. The profile by SABER, by contrast, is mostly positive over the entire upper stratospheric region; this corresponds to the fact that the phase from SABER shows little vertical progression at 40–55 km (Fig. 3b).

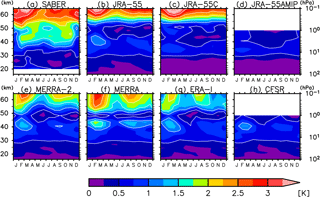
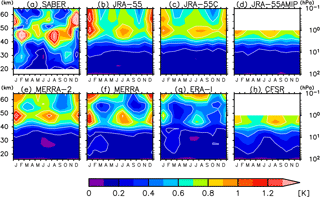
Figure 6 Month–altitude distribution of the amplitude of diurnal (S₁) migrating tides averaged between 15^∘ S and 15^∘ N from (a) SABER, (b) JRA-55, (c) JRA-55C, (d) JRA-55AMIP, (e) MERRA-2, (f) MERRA, (g) ERA-Interim, and (h) CFSR.

It may be worth comparing the present results with previous findings, especially for the upper stratosphere and the lower mesosphere. Wu et al. (1998) analyzed temperature measurements from the MLS onboard the UARS. In the tropics (15^∘ S–15^∘ N), they showed that the amplitude of S₁ migrating tides is ∼1 K at 1 hPa (see their Fig. 2); this is between our SABER (∼1.5 K) and reanalyses (∼0.3 K) results (Fig. 3a). Swinbank et al. (1999) also analyzed MLS measurements (in 1992 only) and showed that the extratropical maxima in the upper stratosphere is 3–3.5 K in January; our analysis showed that it is >4 K for SABER and ∼3 K in the reanalyses in January (for 2006–2012 mean; not shown). Keckhut et al. (1996) reported that UARS MLS results are quite consistent with lidar measurements over a station in southern France (at 44^∘ N). This latitude is close to the location of the amplitude maxima in the extratropical upper stratosphere that we find for the S₁ migrating tide (Fig. 1). Huang et al. (2010) pointed out that the local upward phase progression between 35 and 60 km in SABER (Fig. 3b) is not observed in the measurements from the CRISTA during 5–11 November 1994 (Oberheide et al., 2000); the CRISTA results look similar to the present tidal determinations in the various reanalysis data sets. To summarize, it seems that there is enough uncertainty concerning the S₁ migrating tide represented in the SABER data that further investigation may be needed before attributing the systematic differences we found between SABER and the reanalyses considered here.

The seasonal variation in the amplitude of S₁ migrating tides averaged in the tropics (15^∘ S–15^∘ N) is shown in Fig. 6. Monthly tides during 2006–2012 are calculated both for SABER and the reanalyses, but for SABER, the results of each month are derived from 60-day data (e.g., the results in January are from 15 December through 15 February). All data sets show that the amplitude maximizes in February–March and again in July–August–September in the stratosphere and the lower mesosphere; this semiannual variation is consistent with previous studies (e.g., Mukhtarov et al., 2009; Huang et al., 2010; SA12). Such seasonality has been attributed to the antisymmetric Hough-mode strengthening due to the meridional gradient of the zonal-mean zonal wind in the tropics (McLandress, 2002; Sakazaki et al., 2013b). In the extratropics, on the other hand, all data sets show that the amplitude maximizes in local summer in the stratosphere (not shown), presumably due to the enhanced ozone heating in the summer hemisphere.

Figure 7 As for Fig. 1 but for semidiurnal (S₂) migrating tide.

Figure 8 As for Fig. 2 but for the semidiurnal (S₂) migrating tide.

Figure 9 As for Fig. 3 but for the semidiurnal (S₂) migrating tide.

4.2 Semidiurnal (S₂) migrating tide

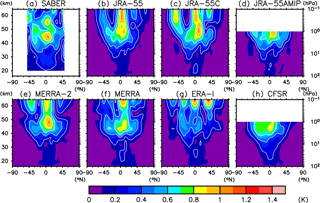
Figures 7 and 8 show the latitude–altitude distribution of amplitude and phase, respectively, for annual mean S₂ migrating tides in temperature. Figure 9 compares the vertical profiles of S₂ amplitude and phase averaged over 15^∘ S–15^∘ N and 30–45^∘ N. The amplitude is largest in the tropics, showing a local maximum at around 45 km (up to ∼1.2 K), i.e., close to the location of ozone heating maximum. In the tropics, the phase shows a slight upward progression below ∼40 km (Fig. 9b), indicating that the energy propagates downward from the ozone heating layer. Above ∼40 km, the phase is almost constant, at least in the tropics. The long vertical wavelength and the significant downward energy propagation from the stratosphere are consistent with classical tidal theory for S₂ migrating tides (Chapman and Lindzen, 1970).

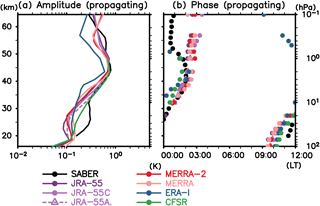
Figure 10 As for Fig. 4 but for the gravest symmetric Hough mode (2, 2) of the semidiurnal (S₂) migrating tide.

The vertical profiles of amplitude and phase are in good agreement among the data sets, particularly below ∼45 km, except that the ERA-Interim shows a smaller amplitude in the tropics (Fig. 9a). Above ∼45 km, the phase diverges among the data sets (Fig. 9b and d). In contrast to the S₁ migrating tide, there is no systematic difference between SABER and the reanalyses in the upper stratosphere and the lower stratosphere, but the amplitude in the reanalyses is systematically smaller than that in SABER between 20 and 30 km of altitude (Fig. 9a). Note that the S₂ tides in the stratosphere have not been examined in detail except for some ground-based lidar measurements (e.g., Keckhut et al., 1996; Leblanc et al., 1999; Kopp et al., 2015); our study demonstrated its meridional-vertical structure for the first time.

Figure 10 shows the vertical profiles of amplitude and phase for the temperature projected onto the (2, 2) mode (${\mathrm{\Theta }}_{\mathrm{2}}^{\mathrm{2}}$), i.e., the gravest symmetric S₂ Hough mode (see Fig. A1b for the structure of this mode). That is, the S₂ migrating tide is approximated by ${\stackrel{\mathrm{̃}}{T}}_{\mathrm{2}}^{\mathrm{2}}\left(z\right){\mathrm{\Theta }}_{\mathrm{2}}^{\mathrm{2}}\left(\mathit{\theta }\right)\cos \left(\mathrm{2}\mathit{\omega }\right(t-{\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{2}}^{\mathrm{2}}\left(z\right)\left)\right)$ and the vertical profiles of ${\stackrel{\mathrm{̃}}{T}}_{\mathrm{2}}^{\mathrm{2}}\left(z\right)$ and ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{2}}^{\mathrm{2}}\left(z\right)$ are shown. Note that classical tidal theory predicts that the S₂ tidal response should consist of only modes with vertical propagation in contrast to S₁. The profiles of this mode are similar to the observed profiles over the tropics (Fig. 9a and b), meaning that this mode dominates the S₂ migrating tide over the tropics. All data sets show that the amplitude maximizes in the upper stratosphere, although the amplitude in ERA-Interim is again smaller than the other data sets. The phase is in good agreement among the data sets below 45 km, but it shows a difference above 45 km. As for S₁ migrating tides, the variance among reanalyses becomes large in the upper stratosphere and the lower mesosphere even for such a large-scale structure.

Figure 11 As for Fig. 6 but for the semidiurnal (S₂) migrating tide.

Figure 11 shows the month–altitude distribution of amplitude for S₂ migrating tides. Although the SABER results are noisy, all data sets basically show that the amplitude maximizes twice in December–January–February and in June–July–August in the upper stratosphere and the lower mesosphere. In the lower and middle stratosphere, by contrast, the amplitude minimizes during June–July–August; notably, this is similar to the seasonality of surface pressure tides (e.g., Díaz-Argandoña et al., 2016; Hamilton and Sakazaki, 2017). Such seasonality in the stratosphere was reported earlier by Li et al. (2015) using the CFSR reanalysis.

Figure 12 Longitude–altitude distribution of annual mean nonmigrating temperature tides at 00:00 UTC averaged between 10^∘ S and 10^∘ N, as derived from (a) SABER, (b) JRA-55, (c) JRA-55C, (d) JRA-55AMIP, (e) MERRA-2, (f) MERRA, (g) ERA-Interim, and (h) CFSR.

4.3 Nonmigrating tides

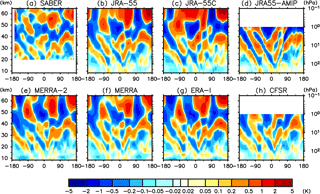
Figure 12 shows the longitude–altitude distribution of annual mean nonmigrating temperature tides at 00:00 UTC averaged between 10^∘ S and 10^∘ N. It is clear that through the upper troposphere to the lower stratosphere, the wave signals are the strongest around the South America (80–40^∘ W) and Africa (10–40^∘ E) and are the second largest around the Maritime continent (90–150^∘ E); both westward- and eastward-tilting waves emanate from these locations. This horizontal pattern indicates that nonmigrating tides are interpreted as the superposition of gravity waves from these geographically localized sources, which is consistent with the findings by Sakazaki et al. (2015b, their Sect. 4), who analyzed data from a high-resolution GCM as well as SABER and COSMIC GPS radio occultation measurements. We also see that westward-tilting (eastward-tilting) waves correspond to the westward-propagating (eastward-propagating) waves that are clear in the western (eastern) hemisphere below ∼40 km. Such asymmetry may be explained by two factors. First, the major excitation regions are confined around −60 to +20^∘ E (see also Sakazaki et al., 2015b); because waves are subject to dissipation during the horizontal propagation, westward waves are likely dominant to the west of −60^∘ E and eastward waves are dominant to the east of 20^∘ E. Secondly, westward signals are clearer between −60 and +20^∘ E, even though in this region both westward waves (from Africa) and eastward waves (from South America) might be equally important. This asymmetry is likely because westward waves (mainly wavenumber 5) are more efficiently excited by tropospheric heating than eastward waves (mainly wavenumber 3; see also Fig. 15) due to the difference in their typical vertical wavelengths (e.g., Williams and Avery, 1996).

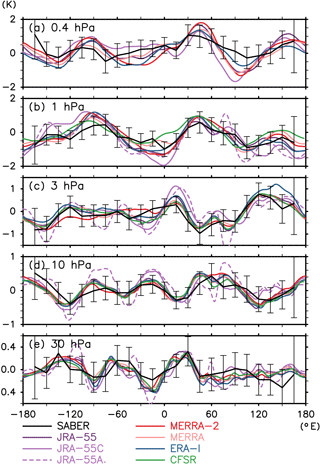
Figure 13 Longitudinal variation of annual mean nonmigrating tides at 00:00 UTC averaged between 10^∘ S and 10^∘ N at (a) 0.4 hPa, (b) 1 hPa, (c) 3 hPa, (d) 10 hPa, and (e) 30 hPa. Vertical bars show the 95 % confidence level estimated by a t test.

Figure 13 compares in detail the longitudinal variations of nonmigrating tides at several pressure levels. We see that the longitudinal variations agree well among the data sets. There is no systematic difference between SABER and the reanalyses. The biggest outliers are JRA-55C and JRA-55AMIP, which seem to display somewhat larger amplitudes than the full reanalyses. It may be worth mentioning that Sakazaki et al. (2015b) also noted that the amplitude in their model (a free-running model) was significantly larger than that for SABER and COSMIC.

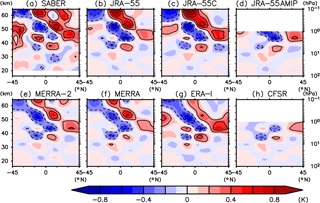
Figure 14 Latitude–altitude distribution of annual mean zonally uniform nonmigrating tides (zonal wavenumber 0 component) at 00:00 UTC, as derived from (a) SABER, (b) JRA-55, (c) JRA-55C, (d) JRA-55AMIP, (e) MERRA-2, (f) MERRA, (g) ERA-Interim, and (h) CFSR. Contour interval is 0.2 K.

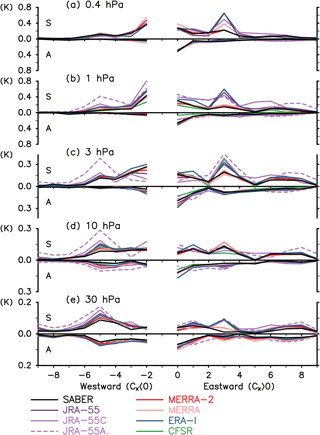
Figure 15 Amplitudes for each zonal wavenumber component of annual mean diurnal (S₁) nonmigrating tides for the region between 10^∘ S and 10^∘ N, at (a) 0.4 hPa, (b) 1 hPa, (c) 3 hPa, (d) 10 hPa, and (e) 30 hPa. The top and bottom half of each panel show the results of symmetric and antisymmetric components, respectively. Positive and negative wavenumbers are for the eastward- and westward-traveling waves, respectively. The S₁ migrating tide (westward wavenumber 1) is not shown.

We note that averaging data between 10^∘ S and 10^∘ N as was done in Figs. 12 and 13 only extracts the symmetric components with respect to the Equator. Sakazaki et al. (2015a) showed that antisymmetric components near the Equator (i.e., as revealed by taking the difference between the 10^∘ S–0^∘ average and the 0–10^∘ N average) have a clear zonally uniform component (zonal wavenumber 0) as do the gravity wave patterns emanating from the continents (Sakazaki et al., 2015a). Figure 14 shows our present results for the latitude–altitude structure of the annual mean, zonal wavenumber 0 component (zonal mean temperature anomaly from the daily mean) at 00:00 UTC. As found by Kuroda and Chiba (1995) and Sakazaki et al. (2015a), the antisymmetric structure with respect to the Equator is dominant, with a vertical wavelength of ∼15 km and confined mainly to within about 15^∘ of the Equator.

Figure 15 shows the zonal wavenumber dependence for the annual mean S₁ (24 h) harmonic of nonmigrating tides for each symmetric and antisymmetric component (see Sect. 3.1). All data sets show that zonal wavenumber 0 (so-called D0; particularly for antisymmetric components as seen in Fig. 14), westward zonal wavenumbers 5 and 2 (DW5 and DW2), and eastward zonal wavenumber 3 (DE3) are dominant, which is consistent with previous studies (Forbes and Wu., 2006; Zhang et al., 2006; Sakazaki et al., 2015b). Particularly, DW5 in the stratosphere corresponds to the clear westward-tilting waves in Fig. 12 (Sakazaki et al., 2015b). Although the dominant wavenumbers agree among the data sets, their magnitudes display some differences. A marked difference is seen for DE3; the MERRA and MERRA-2 results are close to the SABER but the other reanalyses have larger amplitudes than SABER above the middle stratosphere (pressures less than 3 hPa).

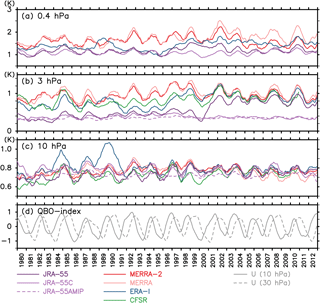
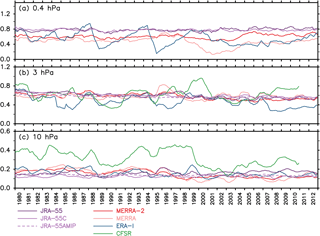
Figure 16 (a–c) Long-term changes in the amplitude of the diurnal (S₁) migrating tide averaged between 10^∘ S and 10^∘ N after applying a 12-month moving average at (a) 0.4 hPa, (b) 3 hPa, and (c) 10 hPa, as derived from reanalyses. (d) Two QBO indices defined as the deseasonalized (12-month moving average), normalized zonal wind over Singapore at (solid gray curve) 10 hPa and (dashed gray curve) 30 hPa.

Figure 17 As for Fig. 16a–c but for the semidiurnal (S₂) migrating tide.

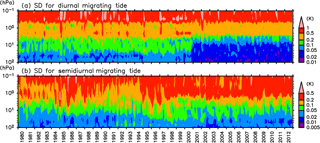
Figure 18 Time–altitude distributions of SD among the four reanalyses (MERRA, MERRA-2, ERA-Interim, and JRA-55) for the (a) amplitude of the diurnal (S₁) migrating tide and (b) the amplitude of the semidiurnal (S₂) migrating tide averaged over 10^∘ S–10^∘ N.

Sakazaki et al. (2015b) in their study of nonmigrating tides found that the westward-propagating waves from the continents penetrate deeply into the mesosphere during equinox but they are dissipated near the stratopause around the solstice season, likely due to filtering by the zonal wind associated with the stratospheric semiannual oscillation (SAO). In the present project we confirmed that such features are discernable in all reanalysis data sets (not shown). For the zonally uniform pattern discussed above (i.e., D0 tide), Sakazaki et al. (2015a) showed that it is most clear in June–July–August; this was also confirmed in all data sets in the present study (not shown).

5 Interannual variations and long-term trends in reanalysis representation of tides

This section examines the interannual variations and long-term changes in S₁ and S₂ migrating tides as represented in the various reanalyses over the extended 1980–2012 period. Figure 16a–c show the monthly amplitude of S₁ migrating tide averaged over 10^∘ S–10^∘ N at selected pressure levels in the stratosphere and the lower mesosphere (0.4, 3, and 10 hPa). The seasonal variations have been removed by applying a 12-month running mean. First, all reanalyses show similar interannual variations with a peak-to-peak difference of up to 0.5 K. The time series of two quasi-biennial oscillation (QBO) indices, the zonal wind at 10 and 30 hPa over Singapore after the deseasonalization (12-month running mean) and normalization, are shown in Fig. 16d. It is clear that the main interannual variations in tides are synchronized with the QBO cycle in stratospheric zonal wind. The modulation of S₁ tides by tropical stratospheric QBO in mean winds has been reported in satellite measurements from the stratosphere through the MLT (e.g., Burrage et al., 1995; Mukhtarov et al., 2009). The QBO in zonal wind itself is represented quite well in the reanalyses considered here (including JRA-55C; Konayashi et al., 2014; Kawatani et al., 2016). Note that the free-running JRA-55AMIP model does not generate a QBO in the tropical stratospheric mean circulation (Kobayashi et al., 2014), and correspondingly there is no QBO apparent in the S₁ tidal amplitudes (Fig. 16b and c).

The difference in tidal amplitudes among the reanalyses depends on vertical level, and it changes through the full period. In the lower mesosphere at 0.4 hPa (Fig. 16a), the amplitudes for MERRA and MERRA-2 are larger than that for ERA-Interim and JRA-55. This pattern continues for the 3 decades except that the MERRA-2 amplitude became smaller after ∼2004, likely corresponding to the assimilation of MLS temperature starting in 2004. Since no other measurements are assimilated in the lower mesosphere, the reanalyses in this altitude region are presumably strongly dependent on the tides simulated in the forecast model used to produce each reanalysis. Figure 18a shows the variance in the amplitude of S₁ migrating tides averaged over 10^∘ S–10^∘ N among the four reanalyses, MERRA-2, MERRA, JRA-55, and ERA-Interim (CFSR is not included because its CDAS-T382 integration ended in December 2010), plotted as a function of altitude and time. In the lower mesosphere the variance among the reanalysis data sets is large (∼1 K) and fairly steady throughout the entire record

In the upper stratosphere at 3 hPa, it is clear that the variance among the reanalyses was much larger before 2000 than after 2000 (Figs. 16b and 18a). Notably, the amplitude in JRA-55 increases abruptly in ∼2000 to approach the results of other reanalyses, while the JRA-55C does not show any systematic changes even after $\sim \mathrm{2000}.$ This clearly indicates that the satellite observations, which are assimilated for JRA-55 but not for JRA-55C, are responsible for the drastic improvement around 2000. Actually, the years around 2000 correspond to the timing of the TOVS-to-ATOVS transition. ATOVS has the AMSU-A/B, which has more channels in the upper stratosphere with narrower weighting functions compared to the SSU on TOVS, so that the representation of the stratospheric dynamical fields significantly improved at this time (see Fujiwara et al., 2017, their Sect. 5.2 for more details). For JRA-55, SSU was assimilated until ∼2000, while AMSU started to be assimilated in ∼1999 (both SSU and AMSU were assimilated during 1999–2000; see Fig. 8 of Fujiwara et al., 2017). Artificial jumps around 2000 have been reported for other features of the circulation in the reanalysis data sets, such as climatological temperature (Long et al., 2017) and the zonal wind in the tropical stratosphere (Kawatani et al., 2016).

Finally, in the middle to lower stratosphere at 10 hPa, the variance is relatively small for the entire period compared to that at higher vertical levels. As at the 3 hPa level, an abrupt decrease in variance is observed after ∼2000 (Figs. 16c and 18a). In the 1990s, quite large amplitudes are sometimes observed in ERA-Interim.

Figure 17 shows the monthly amplitude of the S₂ migrating tide averaged over 10^∘ S–10^∘ N, while the variance in this quantity among the four reanalyses is shown in Fig. 18b. The QBO-related variation observed for S₁ migrating tides (Fig. 16) is not clear for the S₂ tide. An abrupt change due to the TOVS-to-ATOVS transition around 2000 does not seem clear for the S₂ tidal amplitudes, expect possibly for the CFSR data set, which is a strong outlier at 10 hPa before ∼1999 and somewhat more consistent with the other reanalyses after ∼1999 (Fig. 17c; for CFSR, SSU was assimilated until ∼1998; see Fig. 8 of Fujiwara et al., 2017). However, other strange interannual variations are observed, particularly before 2000. Notably, the ERA-Interim shows a “saw-tooth” pattern of changes at 0.4 and 3 hPa until $\sim \mathrm{2000}.$ This is likely caused by the orbital drift of TOVS and the transition between different NOAA satellites carrying the TOVS (e.g., Zou et al., 2014). For example, TOVS was onboard NOAA-9 between 1985 and 1988 and was onboard NOAA-11 between 1988 and 1994; the orbital drift of NOAA-9 (NOAA-11) likely corresponds to the gradual increase in S₂ amplitude over 1985–1988 (1988–1994), and the transition between the two satellites likely corresponds to the abrupt reduction seen in the ERA-Interim representation of S₂ amplitude in 1988 at the 0.4 hPa level (Fig. 17a).

6 Summary and discussion

This study investigated the solar tides seen in the temperature in the stratosphere and the lower mesosphere using state-of-the-art reanalysis data sets included in the S-RIP intercomparison project and compared with independent SABER measurements during 2006–2012. Diurnal (S₁) migrating tides, semidiurnal (S₂) migrating tides, and nonmigrating tides are extracted and discussed individually. Overall, the reanalysis results are found to be quite consistent with those from SABER in a qualitative way, such as the three-dimensional structure, dominant wavenumbers (for nonmigrating tides), and their seasonality. The spread among the reanalyses increases with altitude and is fairly large in the lower mesosphere where few actual observations are assimilated, leaving the reanalysis fields dependent on the tides simulated in the forecast model used in each reanalysis procedure.

A marked systematic difference between SABER and the reanalyses is seen for the amplitude and phase profiles for S₁ migrating tides above 40 km. S12 noticed this issue using MERRA, ERA-Interim, CFSR, and JRA-25, but this study confirmed such a difference for the more recent reanalyses (MERRA-2 and JRA-55) as well. Swinbank et al. (1999) found that the assimilation of SSU measurements damps the representation of the tidal amplitude in a reanalysis in the upper stratosphere. The comparison of JRA-55 family data sets in our study, however, suggests that the assimilation does not degrade tides, at least in the present day (i.e., 2006–2012 period) and in the JRA-55 system. A Hough-mode decomposition further showed that such SABER reanalyses differences can be attributed primarily to the amplitude of the trapped (1, −1) mode response in the stratosphere. This could be explained if either the stratospheric ozone heating is underestimated in the forecast models used to produce the reanalyses or SABER temperatures have some systematic local time biases. We also compared the vertical profile of ascending–descending temperature differences from Aura MLS measurements, which is a good indicator of the magnitude of S₁ migrating tides, to reanalysis temperatures sampled at the same local times. Our results suggest that the S₁ tides in the reanalyses are closer to those derived from Aura MLS than SABER observations. An intercomparison with available ground-based measurements may be helpful to resolve this issue.

The evolution of tidal amplitudes derived from the reanalyses over the extended 1980–2012 period shows a clear QBO signal except for JRA-55AMIP data, which have no QBO in equatorial stratospheric mean circulation. On the other hand, it is suggested that any long-term changes are primarily artificial and are driven by several changes in the input data employed. The largest impact is caused by the TOVS-to-ATOVS transition and the changes in NOAA satellites carrying TOVS. The tides as represented in MERRA-2 reanalyses are also affected by the incorporation of MLS data starting in 2004. How much influence these changes have on tides depend on each reanalysis system and also on the tidal frequency (i.e., S₁ or S₂). This finding indicates that the intercomparison results depend on the analysis period and artificial discontinuities in the data stream that were assimilated make it quite difficult to detect natural long-term trends of the tides in the middle atmosphere.

Some current global atmospheric models cover the region from the surface up to the MLT (often referred to as “whole-atmosphere models”). Such models are sometimes integrated with several dynamical variables nudged toward reanalysis data in order to reproduce the realistic day-to-day variations in the upper atmosphere that are often connected to tidal variations (e.g., Jin et al., 2012; Pedatella et al., 2014). In this respect, tides in reanalysis data provide an important “lower boundary condition” for simulations of upper-air dynamics. Tides in reanalyses are also used for correcting the diurnal anomaly or drift seen in Sun-synchronous satellite measurements. Zou et al. (2014) corrected the local time drift in SSU temperature measurements by using temperature tides in MERRA. The present evaluation of stratospheric tides should thus be helpful for estimating the uncertainty associated with using reanalyses for such applications.

Appendix A: Major abbreviations and terms

AMSU: Advanced Microwave Sounding Unit

Aura: a satellite in the EOS A-Train satellite constellation

ATOVS: Advanced TIROS Operational Vertical Sounder

CFSR: Climate Forecast System Reanalysis of NCEP

COSMIC: Constellation Observing System for Meteorology, Ionosphere, and Climate

CRISTA: CRyogenic Infrared Spectrometers and Telescopes for the Atmosphere

ECMWF: European Centre for Medium-Range Weather Forecasts

ERA-Interim: ECMWF interim reanalysis

JCDAS: JMA Climate Data Assimilation System

JRA-25: Japanese 25-year Reanalysis

JRA-55: Japanese 55-year Reanalysis

JRA-55AMIP: Japanese 55-year Reanalysis based on AMIP-type simulations

JRA-55C: Japanese 55-year Reanalysis assimilating Conventional observations only

MERRA: Modern Era Retrospective Analysis for Research

MLS: Microwave Limb Sounder

NCAR: National Center for Atmospheric Research

NCEP: National Centers for Environmental Prediction of NOAA

NOAA: National Oceanic and Atmospheric Administration

SABER: Sounding of the Atmosphere using Broadband Emission Radiometry

SPARC: Stratosphere–troposphere Processes And their Role in Climate

SSU: Stratospheric Sounding Unit

TIMED: Thermosphere–Ionosphere–Mesosphere Energetics and Dynamics

UARS: Upper Atmosphere Research Satellite

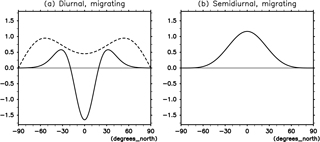
Figure A1 Meridional structure of Hough modes for (a) diurnal (S₁) migrating temperature tides (westward-propagating, zonal wavenumber 1, diurnal component) and (b) semidiurnal (S₂) migrating temperature tides (westward-propagating, zonal wavenumber 2, semidiurnal component). (a) The leading gravest (solid) and trapped (dashed) modes and (b) the gravest symmetric mode.