Influencing factors of the gas–particle distribution of oxygenated organic molecules in the urban atmosphere and deviation from equilibrium partitioning: a random forest model study

Gas–particle partitioning governs the fate of oxygenated organic molecules (OOMs) and the formation of organic aerosols. We employed a Chemical Ionization Mass Spectrometer equipped with a Filter Inlet for Gases and AEROsol (FIGAERO-CIMS) to measure the gas–particle distribution of OOMs in a winter campaign in the urban atmosphere. The observed gas–particle ($\mathrm{G}/\mathrm{P}$) ratios show a narrower range than the equilibrium $\mathrm{G}/\mathrm{P}$ ratios predicted from saturation mass concentration C^* and organic aerosol content. The difference between observed and equilibrium $\mathrm{G}/\mathrm{P}$ ratios could be up to 10 orders of magnitude, depending on the C^* parameterization selection. Our random forest models identified relative humidity (RH), aerosol liquid water content (LWC), temperature, and ozone as four influential factors driving the deviations of partitioning from the equilibrium state. Random forest models with satisfactory performance were developed to predict the observed $\mathrm{G}/\mathrm{P}$ ratios. Intrinsic molecule features far outweigh meteorological and chemical composition features in the model's predictions. For a given OOM species, particle chemical composition features, including pH, RH, LWC, organic carbon, potassium, and sulfate, dominate over meteorological and gaseous chemical composition features in predicting the $\mathrm{G}/\mathrm{P}$ ratios. We identified the positive or negative effects as well as the sensitive ranges of these influential features using SHapley Additive exPlanations (SHAP) analysis and curve fitting with a generalized additive model (GAM). Our models found that temperature does not emerge as a significant factor influencing the observed $\mathrm{G}/\mathrm{P}$ ratios, suggesting that other factors, most likely associated with particle composition, inhibit the gas–particle partitioning of OOMs in response to temperature change.

1 Introduction

Oxygenated organic molecules (OOMs) are ubiquitous in the atmosphere. They are key constituents of organic aerosols (OA) and play a critical role in particle formation and growth (Yuan et al., 2024). The distribution of an OOM between the gas and particle phases not only reflects its volatility or water solubility but also governs its formation pathways, atmospheric transport, and deposition. Therefore, understanding the phase distribution of OOMs is essential for gaining insights into their volatility, transformation processes, and environmental impacts in the atmosphere.

Gas–particle ($\mathrm{G}/\mathrm{P}$) ratios of OOMs measured by laboratory (e.g., ozonolysis products from Δ³-carene, Li et al., 2024a) or field studies (e.g., in the Hyytiälä forest, Finland, Lutz et al., 2019) were sometimes used to derive saturation mass concentrations (C^*) or partitioning coefficients (K_i), assuming that the observed $\mathrm{G}/\mathrm{P}$ ratios represent an equilibrium partitioning state (Priestley et al., 2024; Li et al., 2024a; Lutz et al., 2019; Stark et al., 2017). However, the $\mathrm{G}/\mathrm{P}$ ratio of an OOM under atmospheric conditions is influenced by not only intrinsic OOM physicochemical properties but also external factors such as meteorological shifts (Hildebrandt et al., 2009), precursor oxidation (Pankow, 1994; Seinfeld and Pankow, 2003), particle chemical composition, morphology, and particle-phase reactions (Jang et al., 2002; George et al., 2007). As a result, OOMs rarely achieve equilibrium partitioning between the gas and particle phases (Roldin et al., 2014; Li et al., 2024b).

Gas–particle partitioning kinetics have been incorporated into many atmospheric aerosol models, such as aerosol dynamics models (Liu et al., 2019; Zaveri et al., 2014) and kinetic multilayer models (Fowler et al., 2018; Roldin et al., 2014), which accounted for molecular transfer rates, interphase interactions, and environmental variability (Shiraiwa and Pöschl, 2021) in the gas–particle transfer process. The development of these models has advanced our understanding of the distribution and transport of organic compounds. However, existing theories and models often rely on parameter simplifications or assumptions, and there is a lack of systematic studies examining the factors influencing the phase distribution of OOMs under real atmospheric conditions. In recent years, machine learning methods have been applied successfully for a variety of purposes, including compound identification (Franklin et al., 2022; Boiko et al., 2022), aerosol classification (Christopoulos et al., 2018; Bland et al., 2022), precursor apportionment (Pande et al., 2022; Wang et al., 2021), and property prediction (Gong et al., 2022; Ruiz-Jimenez et al., 2021). Machine learning has proven to be a powerful, data-driven approach capable of uncovering complex and nonlinear relationships between variables (Lin et al., 2022; Zhu et al., 2019). Unlike physical or chemical models, machine learning does not rely on predefined assumptions or simplifications, which enables it to unveil previously unrecognized interactions.

In this work, we employed a Chemical Ionization Mass Spectrometer equipped with a Filter Inlet for Gases and AEROsol (FIGAERO-CIMS) in an urban location to measure the concentrations of OOMs in both the gas and particle phases. By building data-driven machine learning models with the $\mathrm{G}/\mathrm{P}$ ratio as the target variable, we explored the influencing factors of the gas–particle distribution of OOMs and examined the factors that contribute to the deviations from equilibrium gas–particle partitioning. This study offered new insights and provided the foundation for future studies on the atmospheric behavior of OOMs.

2 Methodology

2.1 OOM measurement

Hourly measurements of OOMs in both the gas and particle phases were conducted during a winter campaign from 5 December 2022 to 8 January 2023, using an iodide-based FIGAERO-CIMS (Aerodyne Research Inc., USA) at a suburban site in Wuhan, a megacity in central China (30.4577° N, 114.6157° E). The site is located on the campus of China University of Geosciences, which is surrounded by a residential and agricultural mixed area. The nearest urban center and industrial area are about 25 km west of the measurement site. The nearest highways and major roads lie about 2 km north and south of the site. The site is the only provincial supersite operated by a local environmental authority to monitor air quality in Wuhan and can thus be regarded as a receptor site influenced by wide ranges of emission sources from neighboring regions. We obtained valid data of 594 h, during which meteorological parameters (e.g., relative humidity RH and temperature T), particulate chemical components (e.g., organic carbon OC and sulfate ions SO${}_{\mathrm{4}}^{\mathrm{2}-}$), and gaseous components (e.g., sulfur dioxide SO₂ and ozone O₃) were routinely monitored. Detailed information about these routine measurements is shown in the Supplement (Text S1).

The design of FIGAERO-CIMS for hourly OOM measurement has been described by previous studies (Zhao et al., 2024; Lopez-Hilfiker et al., 2014; Lee et al., 2014). Briefly, FIGAERO operated in a measurement cycle of 1 h, alternating between gas-phase and particle-phase modes. In the gas-phase mode, ambient air was drawn at a flow rate of 2 L min⁻¹ directly into the ion–molecule reactor (IMR), where gaseous molecules were ionized and subsequently detected as adduct ions with the reagent ion I⁻. Simultaneously, another flow of ambient air was pulled through a PM_2.5 cyclone (URG-2000-30EN, URG Corp.) and then a PTFE filter (2 µm Zefluor, 25 mm, Pall Corp.), where particles smaller than 2.5 µm were collected. During the subsequent particle-phase mode, the molecules on the PTFE filter underwent thermal desorption in a heated ultrahigh-purity (UHP) nitrogen flow, which was kept at room temperature for 2 min, heated to 200° for 15 min, kept at 200° for an additional 15 min to ensure the desorption of the majority of OOMs (Lopez-Hilfiker et al., 2014), and then cooled to room temperature within 4 min. The desorbed molecules were directed into a turbulent-flow IMR. A field blank sample was collected every 24 h. According to our earlier investigation (Wang et al., 2024), the OOM measured with FIGAERO-CIMS stands for only those polar and moderate-volatility organic species being desorbed below 200 °C and accounted for only 26 ± 8 % of the total OA (OC × 1.4) measured with the thermal–optical method using the IMPROVE protocol.

2.2 OOM identification and selection

OOMs were identified using a non-target strategy. Mass calibration was performed using ions such as NO${}_{\mathrm{3}}^{-}$, C₂F₃O${}_{\mathrm{2}}^{-}$, IC₂H₂O${}_{\mathrm{2}}^{-}$, IC₂F₃HO${}_{\mathrm{2}}^{-}$, IC₃F₅HO${}_{\mathrm{2}}^{-}$, and I${}_{\mathrm{3}}^{-}$, covering a mass range from 62 to 381 $m/z$. The spectra peaks were iteratively fitted with multiple peaks using a custom peak shape until the residual was reduced to less than 5 % (Lee et al., 2014; Stark et al., 2015). Subsequently, the exact masses of these multiple peaks were matched with the most probable elemental formulas within the ranges of C₁₋₃₀H₁₋₆₀O₀₋₂₀N₀₋₂S₀₋₂X₀₋₂I${}_{\mathrm{0}-\mathrm{1}}^{-}$, where “X” stands for halogen atoms, with mass errors smaller than 10 ppm (mass resolution of ∼ 6000). Isotope distribution was inspected to match the theoretical isotope pattern. The elemental ratio and double-bond-equivalent (DBE) limits of the formulas were 0.3 ≤ $\mathrm{H}/\mathrm{C}$ ≤ 3, $\mathrm{N}/\mathrm{C}$ ≤ 0.5, $\mathrm{O}/\mathrm{C}$ ≤ 3, $\mathrm{S}/\mathrm{C}$ ≤ 1, and 0 ≤ DBE ≤ 20 (Kind and Fiehn, 2007; Lee et al., 2018; Kind and Fiehn, 2006).

In order to obtain reliable concentrations and thus $\mathrm{G}/\mathrm{P}$ ratios, only those OOMs with a unit mass peak area ratio of > 20 % and a sample-to-blank ratio of > 2 were included for further analysis. This filtered out the OOMs with low concentrations in the atmosphere as well as those extremely high- or low-volatility OOMs that are predominantly in only one phase. Thermal desorption may cause OOM decomposition in the particle phase. According to our earlier study on the same dataset using a K-means clustering method (Wang et al., 2024), on average, 25.1 % of the particle-bound OOM species number and 26.8 % of the OOM mass detected by FIGAERO-CIMS could be attributed to thermal decomposition fragments (Text S2). These fragments were excluded from the gas–particle partitioning analysis. The overlap of non-fragment particle-bound OOM species with those gas-phase OOM species resulted in 123 species, which were chosen as the target species for subsequent partitioning analysis. Based on our previous work (Fig. S1) (Wang et al., 2024), these 123 OOM species were classified as 41 aromatic species (33.7 %), 35 monoterpene-derived species (28.3 %), 14 isoprene-derived species (11.4 %), 11 aliphatic species (8.7 %), 10 biomass burning tracers (8.1 %), 3 sulfur-containing species (2.4 %), and 9 other unknown species (7.3 %). Notably, we cannot rule out the possibility that some of these 123 OOMs underwent partial thermal decomposition in the particle phase to an unknown extent. This could lead to an underestimation of their particle-phase concentrations and, in turn, bias the results towards higher $\mathrm{G}/\mathrm{P}$ ratios.

2.3 Observed $\mathrm{G}/\mathrm{P}$ ratios of OOMs

The concentrations of an OOM species in the gas phase and particle phase are calculated as

$$\begin{array}{}\text{(1)}& {\displaystyle }{C}_{\mathrm{g}}={\displaystyle \frac{{\mathrm{signal}}_{\mathrm{g}}}{S\times t_{\mathrm{g}}\times Q_{\mathrm{g}}}}\times \mathrm{1000},\text{(2)}& {\displaystyle }{C}_{\mathrm{p}}={\displaystyle \frac{{\mathrm{signal}}_{\mathrm{p}}}{S\times t_{\mathrm{p}}\times Q_{\mathrm{p}}}}\times \mathrm{1000},\end{array}$$

where C_g (ng m⁻³) and C_p (ng m⁻³) are the average concentrations of a species in the gas phase and particle phase, respectively, in a measurement interval (e.g., 1 h in our campaign). signal_g is the integrated signal (unit: counts) of this species during the 21 min gas-phase measurement time (t_g) in a measurement interval. t_p is the particle sampling time (24 min) in a measurement interval. signal_p is the integrated signal of the particle-phase species during the thermal desorption (30 min) period. Q_g and Q_p are the sampling flow rates for the gas phase and particle phase, respectively (L min⁻¹). S is the sensitivity of the species (counts per nanogram). The observed $\mathrm{G}/\mathrm{P}$ ratio ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ can be calculated as

$$\begin{array}{}\text{(3)}& {\left({\displaystyle \frac{\mathrm{G}}{\mathrm{P}}}\right)}_{\mathrm{obs}}={\displaystyle \frac{C_{\mathrm{g}}}{C_{\mathrm{p}}}}={\displaystyle \frac{{\mathrm{signal}}_{\mathrm{g}}\times t_{\mathrm{p}}\times Q_{\mathrm{p}}}{{\mathrm{signal}}_{\mathrm{p}}\times t_{\mathrm{g}}\times Q_{\mathrm{g}}}}.\end{array}$$

2.4 Comparison with the equilibrium $\mathrm{G}/\mathrm{P}$ ratios

According to the modified Raoult law, the saturation ratio of an organic species in the gas phase (i.e., $\frac{C_{\mathrm{g}}}{C^{*}}$) equals the mass fraction of the species in organic aerosol with mass concentration $C_{\mathrm{OA}}(\mathrm{ie}\frac{C_{\mathrm{p}}}{C_{\mathrm{OA}}}$), under the assumptions of equilibrium absorptive partitioning of the species over an ideal organic solution and that the species has a molecular weight similar to that of the organic solution (Donahue et al., 2009; Epstein et al., 2010). The equilibrium $\mathrm{G}/\mathrm{P}$ ratio ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ can thus be estimated from the saturated mass concentration C^* and the mass concentration of organic aerosol C_OA(C_OA=C_OC × 1.4) using Eq. (4):

$$\begin{array}{}\text{(4)}& {\left({\displaystyle \frac{\mathrm{G}}{\mathrm{P}}}\right)}_{\mathrm{eq}}={\displaystyle \frac{C^{*}\left(T\right)}{C_{\mathrm{OA}}}}.\end{array}$$

C^* at 300 K of OOMs was calculated using four different parameterizations reported by Mohr et al. (2019), Peräkylä et al. (2020), Ren et al. (2022), and Priestley et al. (2024). Based on the saturation concentrations of highly oxygenated molecules (HOMs) modeled by Tröstl et al. (2016), Mohr et al. (2019) applied an updated version of the SIMPOL-type parameterization described by Donahue et al. (2011) to estimate C^* from the numbers of carbon, oxygen, and nitrogen atoms of an organic species (n_C, n_O, and n_N) but emphasizing the increased importance of OOH groups. This parameterization likely produces C^* of pure compounds without considering the effect of the particle matrix. Ren et al. (2022) obtained the C^* of OOMs via calibrated C^*–T_max (the thermal desorption temperature at which the maximum signal intensity occurs) correlations in the thermal desorption process. A similar parameterization formula between C^* and n_C, n_O, and n_N was then derived using multivariate regression. Peräkylä et al. (2020) parameterized the dependence of C^* on n_C, n_O, n_N, and the number of hydrogen atoms (n_H) by comparing steady-state gas-phase concentrations of α-pinene ozonolysis products with and without seed addition in a chamber. This parameterization predicts much lower sensitivities of HOM volatility to oxygen-containing functional groups than SIMPOL. The parameterization of Priestley et al. (2024) was based on measured gas- and particle-phase concentrations, at an assumed equilibrium state, in residential wood burning emissions. The C^* values of the products were obtained via Eq. (4), and a parameterization was obtained between C^* and n_C, n_O, n_N, and n_H. The four C^* parameterizations are listed in Text S3. A temperature correction was made based on Eqs. (5) and (6) to convert C^*(300 K) into C^*(T) at observed temperatures (Epstein et al., 2010; Li et al., 2024a):

$$\begin{array}{}\text{(5)}& {\displaystyle }{C}^{*}\left(T\right)=C^{*}\left(\mathrm{300}\mathrm{K}\right)\times \exp \left({\displaystyle \frac{\mathrm{\Delta }{H}_{\mathrm{vap}}}{R}}\left({\displaystyle \frac{\mathrm{1}}{\mathrm{300}\mathrm{K}}}-{\displaystyle \frac{\mathrm{1}}{T}}\right)\right),\text{(6)}& {\displaystyle }\mathrm{\Delta }{H}_{\mathrm{vap}}=-\mathrm{11}\times {\log }_{\mathrm{10}}{C}^{*}\left(\mathrm{300}\mathrm{K}\right)+\mathrm{129},\end{array}$$

where ΔH_vap is the enthalpy of vaporization. R is the gas constant. T is the observed temperature for every hour. C^*(T) was then used in Eq. (4) to estimate the equilibrium $\mathrm{G}/\mathrm{P}$ ratios.

2.5 Random forest models

2.5.1 Build random forest models

Complex interactions and potential nonlinear dependencies exist among OOM gas–particle partitioning, atmospheric chemistry, and environmental variables. We employed random forest models to investigate the influencing factors of gas–particle partitioning.

Our selection of influencing factors (i.e., features) is based on a comprehensive literature review. We categorized 30 features into four groups: (1) 9 molecular features of the OOMs – n_C, n_O, n_N, n_H, molecular weight (Mw), DBE, hydrogen-to-carbon atom ratios ($\mathrm{H}/\mathrm{C}$), oxygen-to-carbon atom ratios ($\mathrm{O}/\mathrm{C}$), and the oxidation state of carbon (OSc); (2) seven meteorological features – RH, T, wind speed (WS), wind direction (represented by sine and cosine functions to preserve the periodicity, denoted as WD_sin and WD_cos), ultraviolet A (UV-A), ultraviolet B (UV-B), and J_HONO; (3) 4 gaseous composition features – SO₂ concentration, O₃ concentration, nitrogen dioxide (NO₂) concentration, and ammonia (NH₃) concentration; and (4) 10 particle composition features – OC concentration, elemental carbon (EC) concentration, SO${}_{\mathrm{4}}^{\mathrm{2}-}$ concentration, nitrate ion (NO₃) concentration, chloride ion (Cl) concentration, ammonium ion (NH${}_{\mathrm{4}}^{+}$) concentration, PM_2.5 concentration, potassium ion (K⁺) concentration, and aerosol-phase pH and liquid water content (LWC). Calculation details of pH and LWC using the ISORROPIA-II model (Fountoukis and Nenes, 2007) are provided in Text S4. This feature selection scheme guarantees a balanced representation of pertinent factors while preserving the simplicity and predictive efficacy of the models. Unlike neural networks and other machine learning algorithms, the random forest model used in this study is an ensemble model made up of multiple decision trees. During training, each tree splits using a randomly chosen subset of features. Because each tree uses different feature subsets, this randomness in feature selection reduces the model's reliance on any single feature, making it less likely to be severely impacted by multicollinearity. To further ensure model stability, we also conducted a 5-fold cross-validation to confirm the robustness of the model.

First, we developed a multispecies model involving 123 OOM species to predict the ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ of OOMs from molecule features, meteorological features, and gas and particle composition features. A total of 73 062 ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ values for 123 species with hourly resolution were collected in the winter campaign. Outliers can indeed exacerbate modeling errors and potentially affect the model's outcomes. Therefore, they should be removed (Leong et al., 2020). Outlier removal is described in Text S5. The data used for modeling were randomly divided into training data (85 % of the total) for model training and test data (15 % of the total) to evaluate the model generalization.

Second, we selected six typical OOMs, including more volatile (C₅H₈O₄, C₆H₁₀O₄, C₆H₅NO₃, and C₇H₇NO₃; C^* range: 10^3.90–10^6.53 µg m⁻³) and less volatile (C₁₀H₁₆O₄ and C₁₂H₂₁NO₉; C^* range: 10^−4.73–10^1.18 µg m⁻³) species according to the C^* parameterization of Mohr et al. (2019). C₅H₈O₄ (glutaric acid, Lee et al., 2014; Reyes-Villegas et al., 2018) and C₆H₁₀O₄ (adipic acid, Ye et al., 2021; Lee et al., 2014) are small dicarboxylic acids (C ≤ 6) typically formed through photochemical degradation of reactions of alkenes, aldehydes, longer-chain acids (Kawamura and Sakaguchi, 1999), or other low-oxygen organic compounds (Grosjean and Friedlander, 1980) in the urban atmosphere (Kawamura and Ikushima, 1993). C₆H₅NO₃ (Huang et al., 2019; Cai et al., 2022) and C₇H₇NO₃ (Huang et al., 2019; Cai et al., 2022) are nitrophenols directly emitted either from vehicle exhaust (Tremp et al., 1993), coal and wood combustion (Huang et al., 2019), or industrial processes (Harrison et al., 2005) or formed through the nitration of phenol in the gas or liquid phase (Lüttke and Levsen, 1997). C₁₀H₁₆O₄ is primarily derived from the oxidation of monoterpenes (Ye et al., 2019; Barreira et al., 2021). C₁₂H₂₁NO₉ is an organic nitrate from long-chain alkane oxidation under high-NO_x conditions (Wang and Ruiz, 2018).

Third, single-species models were tailored to predict the gas–particle partitioning behaviors of these six individual OOMs under varying meteorological and gas–particle composition conditions. We also built random forest models to investigate how the ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ values of the six OOMs deviate from ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ under varying meteorological conditions and gas–particle compositions. In this study, we did not build a random forest model to predict absolute gas- or particle-phase concentrations of OOMs, due to their strong dependencies on diverse emission sources from neighboring regions. We lack reliable features for quantifying the variable strengths of unknown sources and atmospheric aging processes during transport, which are key factors influencing the OOM concentrations.

2.5.2 Model optimization, evaluation, and feature importance analysis

To optimize and evaluate the model's performance, we applied a combination of grid search and cross-validation methods. First, we employed a grid search to tune the hyperparameters of the random forest model. The search space included the following hyperparameters: n_estimators (the number of decision trees), max_depth (the maximum depth of each tree), max_features (the number of features considered for splitting at each node), and min_samples_split (the minimum number of samples required to split an internal node). For each combination of hyperparameters, we used 5-fold cross-validation in the training set with a coefficient of determination (R²) as the primary metric to assess model performance and identify the best configuration. The specific hyperparameter settings used in the grid search are provided in the Supplement in Table S1.

After selecting the optimal hyperparameters, we further evaluated the final model using 5-fold cross-validation to assess the model's generalization ability and ensure that it was not overfitted. In this evaluation, both R² and the root mean square error (RMSE) were used as metrics: R² indicates the proportion of variance in the $\mathrm{G}/\mathrm{P}$ ratio explained by the model. The RMSE, on the other hand, quantifies the average prediction error and is calculated as the square root of the average squared differences between the predicted and actual values. The final model performance was determined by averaging the R² and RMSE values across the five validation sets. All model tunings and evaluations were conducted using Python (v.3.8).

To quantify the influence of each feature on the $\mathrm{G}/\mathrm{P}$ ratio, we computed a SHAP (SHapley Additive exPlanations) value for each feature and sample (i.e., at each hour) using the SHAP package (v.0.40.0) in Python (v.3.8). A positive SHAP value indicates that the feature contributes positively to the $\mathrm{G}/\mathrm{P}$ ratio, while a negative SHAP value means that it makes a negative contribution. The SHAP values versus feature values were then fitted with a generalized additive model (GAM) using the pygam package (v.0.8.0) to further identify the sensitivity ranges where the changes in feature values significantly affect the SHAP values. For more details, please refer to Text S6. We utilized two-way partial dependence plots (PDPs) (Chen et al., 2024a; Shi et al., 2023; Zhang et al., 2022) to analyze the joint effects of T and RH on the predicted $\mathrm{G}/\mathrm{P}$ ratio. This analysis yielded a comprehensive understanding of how simultaneous changes in T and RH affect the observed $\mathrm{G}/\mathrm{P}$ ratio, thereby unveiling the complex dynamics among these variables. For more details, please refer to Text S7.

3 Results and discussion

Despite the overall improvement in air quality in recent years, PM_2.5 episodes still occur frequently in December and January in most Chinese cities, contributing to the majority of the PM_2.5 exceedance days of a year. During the winter observation period of this study, PM_2.5 concentrations ranged from 20 to 150 µg m⁻³, spanning both clean and severe pollution conditions. Organic aerosol (C_OA= C_OC × 1.4) comprised 10 %–76 % of PM_2.5, emerging as a critical bottleneck when eliminating PM_2.5 episodes. Time series of the other criterion pollutants and key meteorological parameters are presented in Fig. S2. The data collected during the observation period herein are considered representative of winter PM_2.5 pollution characteristics in Wuhan.

3.1 Observed $\mathrm{G}/\mathrm{P}$ ratios of OOMs and comparison with equilibrium partitioning

As shown in Fig. 1a, although $\mathrm{G}/\mathrm{P}$ ratios generally decrease with increasing molecular weight, the observed $\mathrm{G}/\mathrm{P}$ ratios ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ show a narrower range (10⁻¹–10^1.5) than the equilibrium $\mathrm{G}/\mathrm{P}$ ratios ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ predicted from Eq. (4). The differences could be up to 10 orders of magnitude, depending on the C^* parameterization. Of all the methods, Mohr et al. (2019) predicted the steepest dependence of ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ on Mw. Their ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ values are higher than ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ for the OOMs with n_C= 2–5 and lower than ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ for the OOMs with n_C > 8 (Fig. 1b). It has been recognized by Kurtén et al. (2016) and subsequent publications that SIMPOL-derived parameterizations predict an overly steep dependence of C^* on Mw and oxygen content. Moreover, the parameterization of Mohr et al. (2019) likely produces C^* of pure compounds. Without considering the effect of the particle matrix, it may be unrealistic to predict $\mathrm{G}/\mathrm{P}$ ratios using their C^* parameterization. On the basis of the thermal desorption temperature, Ren et al. (2022) predicted lower equilibrium $\mathrm{G}/\mathrm{P}$ ratios than all other parameterizations and our observation. The weakness of Ren et al. (2022) is that thermal desorption may result in the formation of decomposed fragments, which could be misidentified as OOM species. As a result, the T_max of OOM formulas tends to be overestimated and the C^* tends to be underestimated in their parameterization. Although Peräkylä et al. (2020) also predicted lower $\mathrm{G}/\mathrm{P}$ ratios, their ratios are much closer to our observation than Ren et al. (2022). Of all the predictions, the one by Priestley et al. (2024) is closest to our observation. This is because their C^* parameterization is based on the measured gas- and particle-phase concentrations of OOMs in fresh or aged residential wood burning emissions. Their predicted $\mathrm{G}/\mathrm{P}$ ratio is thus inherently consistent with the observed $\mathrm{G}/\mathrm{P}$ ratios in our study. This also highlights the risks of estimating volatility (C^*) using the partitioning method, which is based on measuring equilibrium gas- and particle-phase concentrations of OOMs. Two key issues arise: (1) OOMs may not achieve the assumed equilibrium state under real atmospheric or chamber conditions, introducing substantial uncertainty into calculations of ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$; and (2) the method fails for compounds with extremely high or low volatility, as their gas- or particle-phase concentrations often fall below the detection limits of mass spectrometers. These limitations explain why the partitioning method typically reports a narrow volatility range (Voliotis et al., 2021; Chen et al., 2024b).

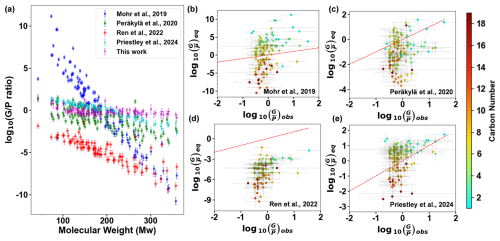
Figure 1 Comparison of the ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ of 123 OOMs with the corresponding ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ predicted by Eq. (4). C^* was estimated from the parameterizations of Mohr et al. (2019), Peräkylä et al. (2020), Ren et al. (2022), and Priestley et al. (2024), respectively. The error bars of ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ denote the range of $\mathrm{G}/\mathrm{P}$ ratios observed under varying conditions for 594 samples (i.e., 594 h). The error bars of ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ denote the variations with temperature and C_OA. The color scales in panels (b)–(e) denote the carbon numbers of the OOM species. The dashed red lines in panels (b)–(e) denote a 1:1 correspondence.

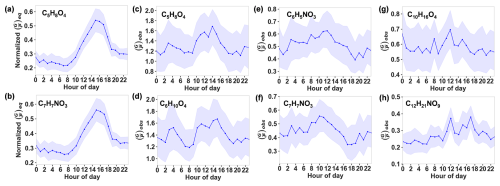
In theory, no matter which C^* parameterization is used in Eq. (4), the temporal variation of ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ for an OOM species depends solely on C_OA and temperature. Therefore, we are able to obtain a normalized ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$, which is independent of C^* parameterization, by dividing the ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ of an OOM by its maximum value. Diurnal variations of the normalized ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ of C₅H₈O₄ and C₇H₇NO₃ are shown in Fig. 2a, b, and those of the other four selected OOMs are shown in Fig. S3. We found similar diurnal variations for all six OOMs: a peak $\mathrm{G}/\mathrm{P}$ ratio appeared in the afternoon, which is attributed to a higher temperature. In contrast, we observed different patterns of ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ diurnal variations for the six OOM species during the campaign, as shown in Fig. 2c–h. This indicates that the extent of the deviation of actual gas–particle partitioning from the equilibrium state fluctuates randomly over time, driven by other unknown factors. In this study, we will first examine the influencing factors of the gas–particle distribution of OOMs in the urban atmosphere during the winter campaign (Sect. 3.2), followed by an investigation into the factors contributing to the discrepancies between the observed and equilibrium $\mathrm{G}/\mathrm{P}$ ratios (Sect. 3.3).

Figure 2 Diurnal variations of (a–b) the normalized equilibrium $\mathrm{G}/\mathrm{P}$ ratios for the selected species (C₅H₈O₄ and C₇H₇NO₃) and (c–h) the observed $\mathrm{G}/\mathrm{P}$ ratios during the campaign. The solid line denotes the average value, and the filled area denotes the 95 % confidence intervals of the mean.

3.2 Influencing factors of the observed $\mathrm{G}/\mathrm{P}$ ratios of OOMs

3.2.1 Multispecies model performance and key features

The 5-fold cross-validation demonstrates that a predictive multispecies model with a satisfactory generalization performance was developed, achieving R²=0.88 ± 0.02 and RMSE = 1.76 ± 0.13 in the test set (Fig. S4). Mean absolute SHAP values indicate the average importance of each feature in predicting the observed $\mathrm{G}/\mathrm{P}$ ratios (Fig. 3a). The model highlights that intrinsic molecule features, such as n_C, Mw, n_H, and DBE, far outweigh meteorological and chemical composition features in the model's predictions. Of the nine molecular features, eight are ranked as highly important, with n_N being comparatively less influential.

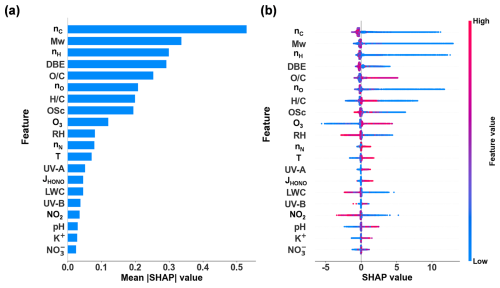
Figure 3 Multispecies model: (a) feature importance based on the mean of the absolute SHAP values calculated for 594 samples (i.e., 594 h) for predicting the $\mathrm{G}/\mathrm{P}$ ratio. (b) Distribution of SHAP values in 594 samples for the top 20 features.

Figure 3b shows the SHAP value distribution for each feature. For molecular features, such as n_C, Mw,n_H, and n_O, high feature values are associated with negative SHAP values, while low feature values are associated with positive SHAP values. This suggests that large molecules with high n_C, Mw, n_H, and n_O and consequently lower volatility are more likely to partition into the particle phase, thereby reducing the $\mathrm{G}/\mathrm{P}$ ratio.

However, the molecular features related to oxidation state and unsaturation degree did not show consistent effects on the observed $\mathrm{G}/\mathrm{P}$ ratios. For example, OSc has a negative effect on the $\mathrm{G}/\mathrm{P}$ ratios, whereas $\mathrm{O}/\mathrm{C}$ has a positive effect. DBE has a negative effect on the $\mathrm{G}/\mathrm{P}$ ratios, whereas $\mathrm{H}/\mathrm{C}$ shows a mixed positive and negative effect. This is due to the fact that these features are dependent variables as a function of n_C, n_H, n_N, and n_O. To isolate the effects of oxidation- and unsaturation-related features, we utilized the trained random forest model to predict $\mathrm{G}/\mathrm{P}$ ratios of modified C₁₀ monocarboxylic acid with varying numbers of the hydroxyl group and DBE (Fig. 4b and c). Other features in the model were fixed at average daytime or nighttime values observed during the campaign (see Tables S2 and S3). For comparison, the isolated effect of the carbon atom number is also plotted (Fig. 4a).

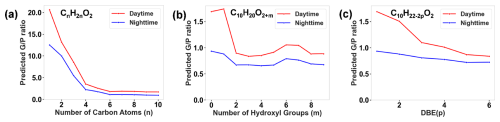
Figure 4 Predicted $\mathrm{G}/\mathrm{P}$ ratios using the developed multispecies model for (a) monocarboxylic acids as a function of the number of carbon atoms, (b) modified 10-carbon monocarboxylic acids as a function of the number of additional hydroxyl groups, and (c) modified 10-carbon monocarboxylic acids as a function of DBE values, under average daytime and nighttime environmental and gas–particle composition conditions.

Figure 4 demonstrates that the number of carbon atoms exerts the most significant influence on the predicted $\mathrm{G}/\mathrm{P}$ ratio, which decreases sharply as the carbon atom number increases from 1 to 4. Beyond this point, the ratio levels off. For modified 10-carbon monocarboxylic acids, $\mathrm{G}/\mathrm{P}$ ratios are high when there is one or no hydroxyl group (Fig. 4b). The $\mathrm{G}/\mathrm{P}$ ratio levels off when the number of hydroxyl groups exceeds two. The $\mathrm{G}/\mathrm{P}$ ratio decreases with an increasing DBE value (Fig. 4c). When the DBE value exceeds five, the $\mathrm{G}/\mathrm{P}$ ratio change becomes minimal. In all of the subplots, the $\mathrm{G}/\mathrm{P}$ ratio during nighttime is consistently lower than that during daytime, which could be attributed to enhanced partitioning from gases to particles at a lower nighttime temperature.

3.2.2 Identification of the key features and sensitivity analyses in single-species models

By excluding molecule features, single-species models focus on the prediction of observed gas–particle partitioning behaviors of individual OOMs from meteorological and gas–particle composition features. The evaluation results and optimal parameters of the six single-species models in the test set are presented in Table S4. All of the models show an acceptable generalization ability (R²= 0.51–0.88). For all six OOMs, particle composition features dominate over meteorological and gaseous composition features in predicting the $\mathrm{G}/\mathrm{P}$ ratios (Fig. 5). Particle composition features LWC, OC, K⁺, SO${}_{\mathrm{4}}^{\mathrm{2}-}$, and pH as well as RH consistently play important roles in influencing the $\mathrm{G}/\mathrm{P}$ ratios of these species. This is roughly in line with the correlation analysis between the features and the observed $\mathrm{G}/\mathrm{P}$ ratios of the six selected OOMs (Fig. S5), which show that pH, RH, LWC, and SO${}_{\mathrm{4}}^{\mathrm{2}-}$ exhibited strong positive or negative correlations with the $\mathrm{G}/\mathrm{P}$ ratios. Below, we (1) examined the positive or negative effects of these features one by one (Fig. 6a) and (2) identified the sensitive ranges of these features by fitting SHAP values against feature values using a GAM (Fig. 7).

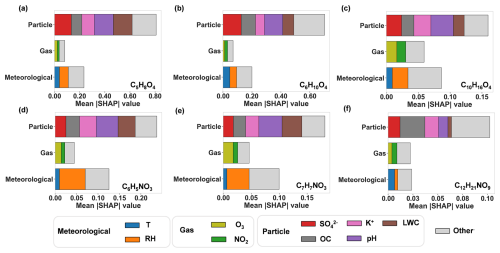
Figure 5 SHAP value analysis of three categories of features. The mean |SHAP| denotes the mean absolute SHAP values calculated for 594 samples (i.e., 594 h): (a) glutaric acid (C₅H₈O₄), (b) adipic acid (C₆H₁₀O₄), (c) monoterpene oxidation products (C₁₀H₁₆O₄), (d, e) nitrophenol (C₆H₅NO₃ and C₇H₇NO₃), and (f) nitrated aliphatic acid (C₁₂H₂₁NO₉).

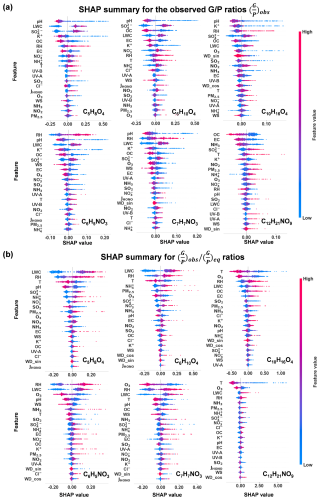
Figure 6 SHAP summary plots for feature importance based on the random forest model for glutaric acid (C₅H₈O₄), adipic acid (C₆H₁₀O₄), the monoterpene oxidation product (C₁₀H₁₆O₄), nitrophenol (C₆H₅NO₃ and C₇H₇NO₃), and nitrated aliphatic acid (C₁₂H₂₁NO₉). Features are prioritized in descending order based on their importance. (a) SHAP summary for the observed $\mathrm{G}/\mathrm{P}$ ratios ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$. (b) SHAP summary for the ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}/(\frac{\mathrm{G}}{\mathrm{P}}{)}_{\mathrm{eq}}$ ratios.

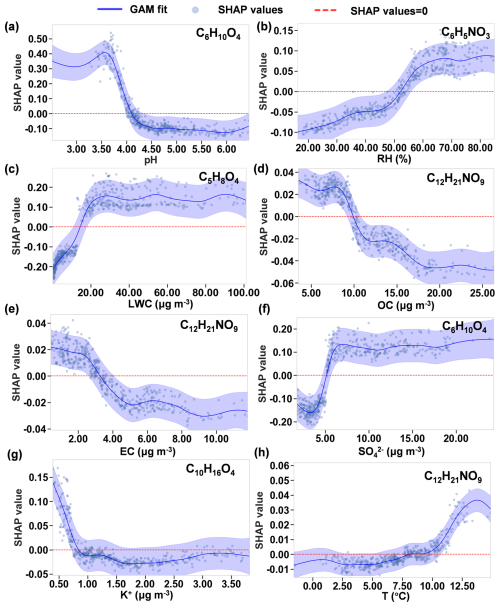
Figure 7 Curve fitting of SHAP values versus features using a GAM, illustrating the sensitivity ranges where the changes in feature values significantly affect the SHAP values. Only those OOM species most affected by the eight features are shown. (a) pH for C₆H₁₀O₄. (b) RH for C₆H₅NO₃. (c) LWC for C₅H₈O₄. (d) OC for C₁₂H₂₁NO₉. (e) EC for C₁₂H₂₁NO₉. (f) SO${}_{\mathrm{4}}^{\mathrm{2}-}$ for C₆H₁₀O₄. (g) K⁺ for C₁₀H₁₆O₄. (h) Temperature for C₁₂H₂₁NO₉. The blue line denotes the GAM fit. The shaded area indicates the 95 % confidence interval. The dots are the SHAP values for 594 samples (i.e., 594 h). The red dashed line denotes a SHAP value of 0.

pH is one of the two most influential factors in the gas–particle partitioning of five species (C₅H₈O₄, C₆H₁₀O₄, C₆H₅NO₃, C₇H₇NO₃, and C₁₀H₁₆O₄), with a sensitivity range of 3.5–4.5 (as illustrated for C₆H₁₀O₄ in Fig. 7a). Within this range, the contribution to the $\mathrm{G}/\mathrm{P}$ ratio decreases by 0.5 from pH 3.5 to 4.5. Beyond pH 4.5, the $\mathrm{G}/\mathrm{P}$ ratio stabilizes at −0.1. An increase in pH results in a pronounced decrease in the $\mathrm{G}/\mathrm{P}$ ratio. This phenomenon can be attributed to the enhanced partitioning of OOMs with acidic functional groups from gases to particles with elevated pH (Su et al., 2020).

RH has a positive effect, ranking among the top five significant features, on the $\mathrm{G}/\mathrm{P}$ ratios of the three OOMs C₆H₅NO₃, C₇H₇NO₃, and C₁₀H₁₆O₄ (Fig. 6a). The SHAP value is sensitive to RH across the full RH range (20 %–80 %, illustrated by the example C₆H₅NO₃ in Fig. 7b). LWC also has a significant positive effect for C₅H₈O₄, C₆H₁₀O₄, C₆H₅NO₃, and C₇H₇NO₃. For example, in the case of C₅H₈O₄, a sharp increase of 0.35 in the $\mathrm{G}/\mathrm{P}$ ratio is observed within the LWC range below 20 µg m⁻³. Above 20 µg m⁻³, the contribution to the $\mathrm{G}/\mathrm{P}$ ratio stabilizes at 0.15 (Fig. 7c). The underlying mechanism of this behavior is unclear. One explanation is that the low RH and LWC in particles may facilitate the reversible formation of oligomers (Shen et al., 2018) and suppress their hydrolysis (Liu et al., 2012), thereby increasing the concentration of these OOMs in the particle phase. It is also possible that the thermal desorption and subsequent detection of particle-bound OOMs were inhibited in aerosol particles with more moisture.

OC has a significant negative impact (i.e., ranking among the top five) on the $\mathrm{G}/\mathrm{P}$ ratios of all six species, consistent with Eq. (4), where the equilibrium $\mathrm{G}/\mathrm{P}$ ratios are inversely proportional to C_OA. Taking C₁₂H₂₁NO₉ as an example (Fig. 7d), the SHAP values decrease monotonically with C_OA by 0.08 in the entire C_OA range (5–25 µg m⁻³). For this compound, EC ranks as the second-most influential factor, exerting a notable negative impact below 4 µg m⁻³. A significant $\mathrm{G}/\mathrm{P}$ decrease of 0.05 was observed in this range (Fig. 7e).

SO${}_{\mathrm{4}}^{\mathrm{2}-}$ has a positive effect (i.e., ranking among the top five) on the $\mathrm{G}/\mathrm{P}$ ratios of C₅H₈O₄, C₆H₁₀O₄, C₁₀H₁₆O₄, and C₁₂H₂₁NO₉. For example, in the case of C₆H₁₀O₄, the $\mathrm{G}/\mathrm{P}$ ratio rises rapidly by 0.30, with increasing SO${}_{\mathrm{4}}^{\mathrm{2}-}$ concentrations below 6 µg m⁻³ (Fig. 7f). Above 6 µg m⁻³, the contribution to the $\mathrm{G}/\mathrm{P}$ ratio stabilizes at 0.1. This may partly be related to the fact that SO${}_{\mathrm{4}}^{\mathrm{2}-}$ is a highly hydrophilic component (Thaunay et al., 2015), which makes its effect similar to that of LWC. In addition, an increase in sulfate in aerosols is often associated with enhanced acidity and a decrease in pH (Zhang et al., 2007), which drives OOM from the particle to gas phases, as we have explained above.

K⁺ has a negative effect on the $\mathrm{G}/\mathrm{P}$ ratios of C₅H₈O₄, C₁₀H₁₆O₄, C₆H₅NO₃, and C₇H₇NO₃. Taking C₁₀H₁₆O₄ as an example, the $\mathrm{G}/\mathrm{P}$ ratio decreases rapidly by 0.15, with K⁺ in the concentration range below 1 µg m⁻³. Above 1 µg m⁻³, its contribution to the $\mathrm{G}/\mathrm{P}$ ratio stabilizes at −0.03 (Fig. 7g). K⁺ is considered a tracer of biomass burning. The increase in K⁺ is generally associated with higher pollution levels and higher OC concentrations in the study region (Zhao et al., 2024). The effect of K⁺ on the $\mathrm{G}/\mathrm{P}$ ratio is thus similar to that of OC.

In general, temperature is supposed to be an important influential factor in the $\mathrm{G}/\mathrm{P}$ ratio, because the saturation vapor pressure of OOMs increases with temperature. Temperature ranged from −1.6 to 14.9 °C during the winter campaign. Although temperature increase tends to elevate the $\mathrm{G}/\mathrm{P}$ ratios, as expected (Fig. 6a), the models show that temperature did not rank as an important feature for five of the six OOM species. We evaluated the effect of temperature on $\mathrm{G}/\mathrm{P}$ ratios using two-way partial dependence plots (Fig. S6). The $\mathrm{G}/\mathrm{P}$ ratio is sensitive to temperature change only for two dicarboxylic acids (C₅H₈O₄ and C₆H₁₀O₄, Fig. S6a–b) and for C₁₂H₂₁NO₉ in a narrow temperature range of 10–13 °C (Figs. S6f and 7h). The $\mathrm{G}/\mathrm{P}$ ratios of C₆H₅NO₃, C₇H₇NO₃, and C₁₀H₁₆O₄ are not sensitive to temperature across most of the RH range. This behavior may be attributed to the aerosol coating of inorganic salts and other aerosol components that hinder the rapid equilibrium partitioning of OOMs when temperature changes. In addition, the influence of temperature may be obscured due to the dominant effect of particle composition features (e.g., LWC, pH, OC, SO${}_{\mathrm{4}}^{\mathrm{2}-}$, and K⁺), as discussed above.

As shown in Fig. 6a, wind speed and direction rank relatively low in terms of feature importance for the six OOMs. This suggests that, while wind direction and speed might influence the source areas of OOMs, they have a minimal impact on the $\mathrm{G}/\mathrm{P}$ ratios of OOMs.

3.3 Identifying key factors driving the deviations of gas–particle partitioning from the equilibrium state

To investigate the deviations of the observed gas–particle partitioning from the equilibrium state, we first calculate the ratios of ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ to the normalized ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ for every hour for the six selected OOM species. The normalized ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ was used here in order to offset the effect of the C^* parameterization selection. We then developed new random forest models to investigate the effects of meteorological and gas–particle composition features on the ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}/{\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ ratios. All of the models show an acceptable generalization performance (R²= 0.52–0.83) (Table S5) in the test set.

Figure 6b presents the SHAP analysis results for the ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}/(\frac{\mathrm{G}}{\mathrm{P}}{)}_{\mathrm{eq}}$ ratios of the six OOMs. The models identify RH, LWC, O₃, and temperature as four influential factors driving the deviations from equilibrium partitioning. Positive correlations are observed between the SHAP values of ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}/(\frac{\mathrm{G}}{\mathrm{P}}{)}_{\mathrm{eq}}$ and the RH and LWC for all six compounds. This indicates that RH and LWC have a stronger positive effect on ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ than their effect on ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$, which should be negligible according to Eq. (4). Temperature is shown to be a negative factor driving the deviation from equilibrium partitioning, suggesting that temperature has a stronger influence on ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$ than ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$. This is consistent with our earlier result that ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$ is not sensitive to temperature. Surprisingly, O₃ is identified as an important influential factor with a negative effect, particularly for the three nitrophenols and the monoterpene oxidation product C₁₀H₁₆O₄. Since O₃ is not expected to change ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{eq}}$, the negative impact of O₃ on the ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}/(\frac{\mathrm{G}}{\mathrm{P}}{)}_{\mathrm{eq}}$ ratio could be explained by the speculation (Kaur Kohli et al., 2023) that high O₃ concentrations are likely to deplete gas-phase OOMs at a faster rate than particle-phase OOMs, thereby reducing ${\left(\frac{\mathrm{G}}{\mathrm{P}}\right)}_{\mathrm{obs}}$.

4 Conclusions

We measured the $\mathrm{G}/\mathrm{P}$ ratios of OOM species using FIGAERO-CIMS in the urban atmosphere during a winter campaign. The observed $\mathrm{G}/\mathrm{P}$ ratios show a narrower range than the equilibrium $\mathrm{G}/\mathrm{P}$ ratios predicted from C^* and C_OA. The difference between the observed and equilibrium $\mathrm{G}/\mathrm{P}$ ratios could be up to 10 orders of magnitude, depending on the C^* parameterization. Our observed $\mathrm{G}/\mathrm{P}$ ratio is inherently closer to the equilibrium $\mathrm{G}/\mathrm{P}$ ratios predicted from the C^* parameterization by Priestley et al. (2024), which was derived from measured $\mathrm{G}/\mathrm{P}$ ratios in wood burning emissions. Our random forest models identified RH, LWC, O₃, and temperature as four influential factors driving the deviations of gas–particle partitioning from the equilibrium state.

Random forest models with satisfactory performance were developed to predict observed $\mathrm{G}/\mathrm{P}$ ratios. Intrinsic molecule features, such as n_C, Mw, n_H, and DBE, far outweigh meteorological and chemical composition features in the model's predictions. Large molecules with high n_C, Mw, n_H, n_O, and consequently lower volatility are more likely to partition into the particle phase, thereby reducing the $\mathrm{G}/\mathrm{P}$ ratio. As dependent variables, oxidation state and unsaturation do not show consistently positive or negative effects on the observed $\mathrm{G}/\mathrm{P}$ ratios. If other variables are fixed, the model predicts that $\mathrm{G}/\mathrm{P}$ ratios generally decrease with the addition of oxygen atoms and the DBE.

Particle composition features dominate over meteorological and gaseous composition features in predicting the $\mathrm{G}/\mathrm{P}$ ratio of a given OOM species. Among these particle features, pH, RH, LWC, OC, K⁺, and SO${}_{\mathrm{4}}^{\mathrm{2}-}$ consistently play important roles in influencing the $\mathrm{G}/\mathrm{P}$ ratios of the six selected OOM species, showing either positive or negative effects. We also identified the sensitivity ranges where the changes in these features significantly affect the SHAP values and provided valuable insights for future research in atmospheric chemistry. It is surprising that temperature does not emerge as an important factor influencing the $\mathrm{G}/\mathrm{P}$ ratios for five of the six selected OOM species. Our model suggests that other factors, most likely associated with the particle composition, inhibit the gas–particle partitioning of OOMs in response to temperature change.

Finally, the random forest models developed in this study have certain limitations. (1) Aerosol particle coating may serve as an inhibitory factor in gas–particle partitioning. However, the mixing state and morphology of aerosol particles were not considered in the model due to the challenges in quantifying these features with high resolution. (2) The OOMs with extremely high or low volatility might be underrepresented in this study, because their gas- or particle-phase concentrations often fall below the limit of quantification of FIGAERO-CIMS. (3) Isomers were not differentiated in the measurement of FIGAERO-CIMS in this study. The observed $\mathrm{G}/\mathrm{P}$ ratio was contributed by isomers sharing the same chemical formula. The machine learning model built in this study did not account for the effect of isomerization on the gas–particle distribution of OOMs. (4) The model was based solely on the data collected during the winter season and for specific groups of OOM species present in the urban atmosphere. To enhance the robustness of the gas–particle partitioning model, future data collection under a broader range of atmospheric conditions is recommended.