the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Measurement report: Influence of particle density on secondary ice production by graupel and frozen drop collisions
Sudha Yadav
Lilly Metten
Pierre Grzegorczyk
Alexander Theis
Subir K. Mitra
Collision-induced fragmentation of atmospheric ice particles is a crucially important but understudied secondary ice production mechanism in clouds. We present a laboratory study dedicated to fragmentation due to graupel–graupel and frozen drop–frozen drop collisions and the role of these collisions in augmenting the ice particle concentration in clouds. For this, graupel particles of different sizes and densities were created utilizing dry growth conditions in a cold chamber at −7 and −15 °C using a setup that simulates the natural rotation and tumbling motion of freely falling graupel. Ice spheres, as proxies for frozen drops and ice pellets, were generated by freezing purified water in 3D-printed spherical molds. We conducted collision experiments inside the cold chamber utilizing a fall tube that ensures the central and repeatable collision of ice particles at different collision kinetic energies. The number of fragments generated in the collisions was analyzed, following a theoretical framework, as a function of the collision kinetic energy. The detection limit of our experiments was 30 µm; thus, fragments with sizes lower than 30 µm could not be detected. The observed number of fragments varied between 1 and 20 and was, thus, comparable to or higher than the number of fragments resulting from drop freezing experiments. Our results revealed a strong dependency of the fragment number on the density of the colliding ice particles, which can be attributed to the particles' structure. The sizes of the fragments that we detected were in the submillimeter range for graupel and up to 3 mm for ice spheres. Another set of experiments, focusing on the multiple collision of graupel revealed that the number of fragments generated decreases significantly and approaches zero when a particle undergoes more than three collisions in a row.
- Article
(1612 KB) - Full-text XML
- BibTeX
- EndNote
Ice particles are formed in the atmosphere via either primary processes, like homogeneous freezing or heterogeneous ice nucleation from the liquid or vapor phase, or secondary ice production (SIP), which refers to the generation of ice crystals during processes that involve preexisting ice particles. There is a general consensus that SIP (also known as ice multiplication) is responsible for the observed discrepancy between the number of detected ice crystals and ice-nucleating particles (INPs) in the atmosphere at temperatures between −5 and −15 °C (Field et al., 2017; Ladino et al., 2017; Sullivan et al., 2017; Korolev et al., 2022). In a recent study, Korolev et al. (2022) provided in situ evidence of SIP occurring at −27 °C aloft. During an ice pellet storm, Lachapelle and Thériault (2022) attributed the observed discrepancy between INP and ice crystal number concentrations to SIP. Despite their crucial importance, a basic understanding of SIP is still lacking due to the scarcity of systematic laboratory studies (Korolev and Leisner, 2020). Currently, seven different mechanisms are distinguished as possible SIP processes. For decades, the most prominent has been rime splintering (also known as the Hallett–Mossop process, hereinafter abbreviated as the H–M process), in which ice splinters are produced upon accretion of D<13 µm and D>24 µm (where D denotes diameter) droplets by ice particles at between −3 and −8 °C (e.g., Hallett and Mossop, 1974; Mossop, 1976, 1985; Choularton et al., 1978, 1980; Heymsfield and Mossop, 1984). However, the relevance of this process in the atmosphere has recently become a topic of debate. Seidel et al. (2024) conducted rime-splintering experiments under H–M conditions and detected no ice crystal formation. The second promising SIP process is fragmentation during freezing (Lauber et al., 2018; Keinert et al., 2020). Lauber et al. (2018) distinguished between ice particle ejection and splitting during drop freezing. Although the number of the generated secondary ice particles is strongly dependent on the drop size, it can exceed unity (∼2.4), especially bubble bursting might be very productive. Further SIP processes, like ice fragmentation due to sublimation (Oraltay and Hallett, 1989), due to the activation of INPs in transient supersaturation (Prabhakaran et al., 2020), due to thermal shock (Dye and Hobbs, 1968), and during the breakup of freezing droplets on impact with ice particles (James et al., 2021), have been supported experimentally but currently remained uncharacterized.
In a recent study (Grzegorczyk et al., 2023), we investigated another prominent SIP: fragmentation due to the collision of ice particles. That study was, in some sense, a follow-up experiment to the earlier investigations of Takahashi et al. (1995) and Vardiman (1978). Motivated by the analysis of the dendritic growth zone using the long-term radar observations of von Terzi et al. (2022), the collision of snowflake proxies was studied. For that, we used (1) graupel particles with dendritic crystals grown on their surface and (2) natural-like snowflakes produced from dendritic crystals grown in an aquarium setup. Our prior study (Grzegorczyk et al., 2023) revealed that hundreds of ice fragments can be generated when particles with dendritic crystal structures break apart upon collision. The fragment numbers were characterized in terms of the collision kinetic energy (CKE), which is defined as
where m1 and m2 are the masses of the colliding particles and Δv is their fall velocity difference.
Phillips et al. (2017) introduced a full physical formulation of the mechanical breakup of ice particles due to collision, which is based on an energy conservation principle. In this theoretical framework, the number of fragments N generated by collision is calculated as
where α is the surface area of the smaller colliding particle; A is the number of breakable asperities per unit area; and C is the asperity-fragility coefficient, which is an inverse measure of the average work to break each branch or other asperity. Both A and C are dependent on the morphology of the more fragile particle in the collision and, thus, on temperature, maximum dimension, rime fraction, and particle type (i.e., graupel, snow, or hail). In Grzegorczyk et al. (2023) and in its corrigendum, we provided the parameters A, C, and γ for graupel particles with dendrites on their surface, bare-graupel particles, and snowflakes. In that study, we presented indications of a dependency of the fragmentation on the particle structure, i.e., if the graupel particle had dendritic crystals on their surface or not.
Grzegorczyk et al. (2023) also revealed that bare-graupel particles, i.e., those that were produced by riming only, are able to produce fragments when they collide. In their experimental study, Griggs and Choularton (1986) pointed out that the fragility of rime increases as the temperature is lowered. Moreover, they suggested that, in a subsaturated environment, sublimation would further weaken the structure, making the rimed graupel more fragile. Similarly, the morphology of ice particles, in terms of their rime fraction, was suggested to affect the number of fragments produced during collision in a recent study by Gautam et al. (2024).
In the present paper, we aim to systematically investigate the effect of the bare-ice-particle structure on the fragmentation during collision using low- and moderate-density graupel as well as frozen drops (representative of ice pellets). This study extends our earlier investigation (Grzegorczyk et al., 2023) of graupel particles with dendritic crystals grown on their surface. Furthermore, we investigate the effect of multiple collisions of graupel particles on the ice multiplication mechanism.
The experimental studies were performed inside the walk-in chamber of the Mainz Vertical Wind Tunnel laboratory. Graupel and ice sphere generation and collisions were carried out at −5, −7, and −15 °C. These temperatures correspond to regions where rimed particles are observed in mixed-phase clouds (Waitz et al., 2022). Furthermore riming can also occur at even lower temperatures (e.g., down to −20 °C; see in Tridon et al., 2022). The graupel particles generated at −7 and −15 °C (as in Grzegorczyk et al., 2023) possess different morphological structures and, therefore, different densities. This is because supercooled droplets freeze faster at lower temperatures than at higher temperatures, leading to more air inclusion into the graupel structure and making its density lower (Enzmann et al., 2011).
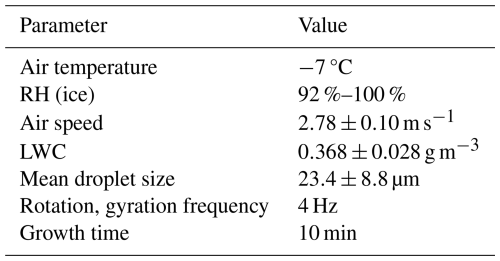
2.1 Graupel generation
Rimed lump graupel particles were generated using the GEORG (GEnerator instrument Of Rimed Graupel) graupel generator, which was described in detail in Grzegorczyk et al. (2023) and originally introduced in Theis et al. (2022). Graupel generation is performed inside a 2 m high flow tube with a 17 cm × 17 cm cross-sectional area. The parameters used for generating the graupel particles in the present study are summarized in Table 1. A small epoxy sphere acts as an ice embryo; this embryo is exposed to a supercooled droplet stream, and graupel then grows by riming. Droplets with diameters of 23.4 ± 8.8 µm are produced by an ultrasonic atomizer (US 2/58 Hz, Lechler GmbH, Germany) using a 30 L min−1 nitrogen flux, and they are injected to form a central droplet stream inside the flow tube. A blower is mounted at the top of the equipment and ensures a flow speed of 2.78 ± 0.10 m s−1 to simulate graupel free fall. The liquid water content (LWC) was 0.368 ± 0.028 g m−3; this LWC establishes dry growth conditions and represents typical conditions in mixed-phase clouds. To minimize the effect of turbulence inside GEORG, which was very likely responsible for a relatively large scatter in graupel size and density during the preparation phase of our experiments, a honeycomb structure was placed at the bottom of GEORG, from where the air is sucked in. The setup can simulate the falling and tumbling motion of graupel in natural clouds by a double-gyration motor apparatus to which the graupel is attached. This apparatus consists of one motor rotating around the vertical axis at 4 Hz and a second one fixed at 45° angle with respect to the first one and rotating at the same rotational speed.

Figure 1Microscope images of graupel particles with (a) a diameter of 2.23 mm and a density of 0.334 g cm−3, grown at −15 °C and 0.723 g m−3 LWC for 10 min in Grzegorczyk et al. (2023); (b) a diameter of 2.4 mm and a density of 0.558 g cm−3, grown at −7 °C and 0.368 g m−3 LWC for 5 min in the present study; and (c) an ice sphere of 5 mm diameter and a density of 0.89 g cm−3, generated at −15 °C. The red scale bar indicates 1 mm.
For the present experiments, we generated graupel particles at −7 °C that had an average diameter of 2.45 ± 0.28 mm and a density of 0.558 ± 0.02 g cm−3. In the experiments of Grzegorczyk et al. (2023), graupel particles were 2.48 ± 0.17, 2.12 ± 0.1, and 4.0 ± 0.2 mm in diameter with densities of 0.21 ± 0.05, 0.334 ±0.062, and 0.51 ± 0.07 g cm−3. The low density of 0.21 g cm−3 was achieved by growing dendritic crystals on the surface of the graupel particle (see Grzegorczyk et al., 2023, for details). Furthermore, the Grzegorczyk et al. (2023) experiments were conducted at −15 °C. Images of graupel particles generated for the current measurements and those generated in Grzegorczyk et al. (2023) are depicted in Fig. 1b and a, respectively.
2.2 Generation of frozen drops
Ice spheres, as proxies for frozen drops, were generated by freezing Milli-Q water in a 3D-printed spherical mold inside a deep freezer at −70 °C. Before the collision experiments, the mold was kept at the cold-room temperature of either −5 or −15 °C for several minutes and then briefly held and warmed in both palms to facilitate its easy removal. The ice spheres used in the collision experiments were 5 mm (shown in Fig. 1c) and 7 mm in diameter, and they had densities of 0.89 ± 0.02 g cm−3, i.e., corresponding to atmospheric small-hail densities (Lachapelle and Thériault, 2022). The different experimental temperatures enabled a systematic study of the effect of temperature and structural variations in ice on fragmentation.
The collision experiments were carried out using the same setup as in Grzegorczyk et al. (2023) (see their Fig. 6), which consists of a “collision tube” and a “fall tube”. In the measurements, one particle is falling, while the other is kept stationary in the collision tube using a thin plastic wire fitted into a cannula. The wire is flexible and possesses a small aerodynamic resistance; therefore, the particle can freely move after collision. Hence, the collision energy is not consumed by the mounting and fed only into the kinetic energies of the colliding particles and into fragmentation, which we could prove using high-speed video recordings. The 8 mm thin fall tube guides the falling particle to the impact point and ensures a central collision between the two particles.
Table 2Main characteristics of the collision experiments. The collision types are denoted as follows: GG – graupel–graupel collisions; II – ice sphere–ice sphere collisions; GI – graupel–ice sphere collisions; MC – multiple collisions. (Note that ice spheres were used as proxies for frozen drops in the atmosphere.)
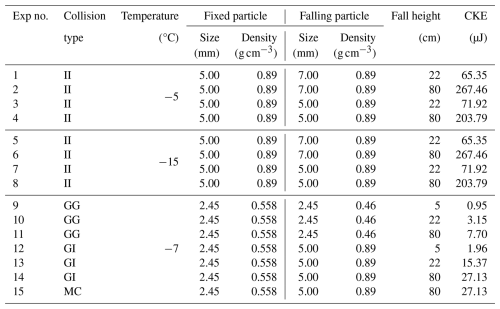
One aim of the present study was to derive a relationship between CKE and the number of fragments generated. Therefore, collisions with different CKEs but the same particle types and masses were carried out. For that, the falling particle was released from different heights of 5, 22, and 80 cm. For each particle type and size and for each fall height, the particles' velocities were determined from high-speed (2000-frame-per-second) images recorded in a characterization set of measurements. The masses and sizes of the graupel particles were also measured during the characterization measurements after producing several particles in GEORG under predefined conditions of −7 °C temperature, 0.368 g cm−3 LWC, and 10 min growth time. In the case of ice spheres, masses of 5 and 7 mm diameter particles were measured and averaged. Densities were calculated from the particle mass and size. During the test experiments, we observed that the epoxy inside a falling graupel modified the center of mass of the particle. This resulted in a fall orientation in which the unrimed epoxy hit the fixed graupel. In order to avoid this unnatural collision mode, we removed the epoxy from the falling graupel particle before the collision experiments. Therefore, the density of the falling graupel was 0.46 g cm−3, i.e., less than that of the fixed one (see Table 2).
To investigate the effect of a graupel particle experiencing multiple collisions with other ice particles in the cloud, we conducted experiments in which a 2.45 mm graupel particle and a 5 mm ice particle collided up to six times. The multiple-collision experiments were performed between graupel particles and ice spheres at the highest CKE, i.e., at a fall height of 80 cm, in order to account for the maximum possible number of fragments that produced. The number of collision repetitions was determined based on the observation that no new fragments were observed (considering the detection limit of approx. 25 µm) after a certain number of collisions, regardless of further collisions. For each subsequent collision, a new frozen drop was used as the falling particle. The fall tube ensured that the falling particles hit the fixed one at approximately the same position.
In total, we conducted 15 series of experiments (as listed in Table 2). Each series of experiments consisted of at least three individual collisions. The colliding particles were either ice spheres and ice spheres (II), graupel and graupel (GG), or graupel and ice spheres (GI). Particle sizes, densities, and the corresponding CKEs for each experimental series can be taken from Table 2. Uncertainties associated with these quantities were 2.5 % for the size and 4 % for the density and for CKE. CKEs for graupel particles and spheres match the atmospheric values of these sizes when calculating the fall velocities using, e.g., the parameterization in Heymsfield et al. (2020), although they represent the highest end of the possible natural collision kinetic energies.
The ice fragments generated by collision were collected into a Petri dish that was filled with food grade mineral oil (density equal to 0.78 g cm−3 at room temperature) and placed at the bottom of the collision tube. The ice fragments were then analyzed under a microscope. In the case of multiple collisions, the Petri dish was immediately removed after the collection of fragments during each collision, and the images were analyzed at the end of the experiment. For all collisions, the total number of fragments and the fragment sizes were determined following the procedure described in Grzegorczyk et al. (2023). We note here that the number of fragments with detectable sizes was low for all collision types; therefore, it was not possible to provide any fragment size distribution information from this study. Instead, we will provide the minimum and maximum fragment sizes detected for each collisions. The size resolution of the applied optical setup was 3.8 µm per pixel. Nevertheless, we could not prevent the oil bath from being contaminated by dust particles (see Fig. 8b in Grzegorczyk et al., 2023). This results in a detection limit for our analysis of 25 to 30 µm. Ice fragments larger than this size could be identified as ice particles with high reliability.
4.1 Number of fragments after collision
Figure 2 shows the variation in the average number of fragments generated during the collisions as a function of the CKE. The ice sphere–ice sphere collisions are presented in blue in Fig. 2a, whereas graupel–graupel and graupel–ice sphere collisions are shown in green in Fig. 2b. The average number of fragments released in each series of experiments is also provided in Table 3 along with the associated maximum and minimum values.
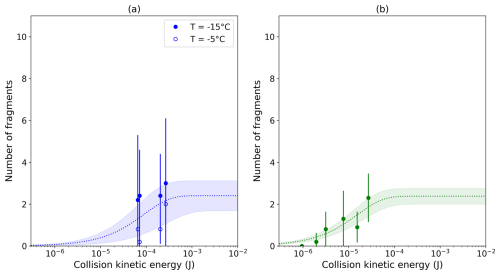
Figure 2Number of fragments generated as a function of CKE during (a) ice sphere–ice sphere collisions at −5 and −15 °C (Exp nos. 1–8) and (b) during graupel–graupel and graupel–ice sphere collisions at −7 °C (Exp nos. 9–14). The dashed lines represent fits to data using Eq. (2), while the shaded areas are the 1σ standard deviation intervals of the fits. (Note that ice spheres were used as proxies for frozen drops in the atmosphere.)
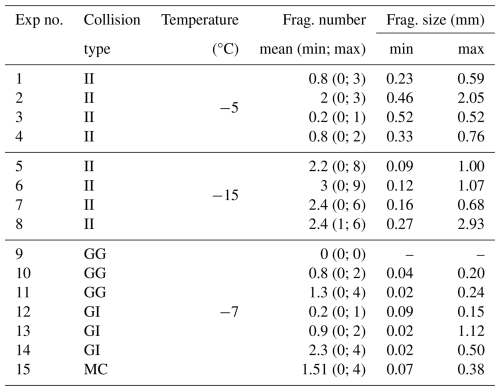
Table 3Average, minimum, and maximum number of fragments and the minimum and maximum fragment sizes produced in each series of experiments. Collision type and temperature are also indicated.
As expected, in both series of collisions, the average number of fragments was observed to increase with increasing CKE. The data were fitted with the parameterization given in Eq. (2) and are represented by blue and green dashed lines in Fig. 2. The shaded areas in the two plots represent a 1σ standard deviation interval of the best-fit curves. For fitting, the shape parameter γ was held constant at 0.78, which was also derived in Grzegorczyk et al. (2023) for graupel–graupel with dendrites and graupel–snowflake collisions. Fitting the other parameters provided values of A = 30 610 m−2 and C = 26 534.5 J−1 for ice sphere–ice sphere collisions and values of A = 126 168 m−2 and C = 150 597 J−1 for graupel–graupel collisions.
Ice sphere–ice sphere collisions were conducted at two different temperatures, namely, at −15 °C (shown using filled symbols in Fig. 1a) and at −5 °C (shown using open symbols in Fig. 1a). There seems to be a temperature dependency of the number of fragments, and this dependency shows a trend toward a higher number of fragments at lower temperatures in the investigated temperature range (see also Table 3). This temperature dependency is similar to that found by Takahashi et al. (1995). Nevertheless, the difference between the number of fragments at these two temperatures is within the error of the experiments. Therefore, we combined the two dataset for further discussion.
The minimum and maximum sizes of fragments produced are also listed in Table 3. Fragments during graupel–graupel collisions have a minimum size of 0.02 mm and a maximum size of 0.24 mm, whereas graupel–ice sphere collisions produced fragments with 0.02 mm minimum and 1.12 mm maximum sizes. In the case of collisions between ice spheres, there were no more than three fragments on an average (see Table 3), with fragments having a maximum average size of 1.2 mm and a minimum average size of 0.27 mm. For these ice sphere–ice sphere collisions, there seems to be a slight dependence of particle size on CKE. The minimum sizes are comparable to the ice crystal maximum dimensions in Grzegorczyk et al. (2023), but there are very large fragments within the maximum observed sizes for these collisions. This can most probably be attributed to high CKEs.
4.2 Compilation of the current results with Grzegorczyk et al. (2023)
Figure 3 depicts a composite plot of the results obtained in this work and the bare-graupel–bare-graupel collision results obtained in Grzegorczyk et al. (2023). For the Grzegorczyk et al. (2023) plot, all collisions are taken into account, whereas for the current results, average values over the collisions for each CKE are shown. The dashed lines represent the best fits using Eq. (2). For the sake of consistency, we employed the same shape parameter γ=0.78 for the Grzegorczyk et al. (2023) bare-graupel data points as used for the current graupel–graupel and ice sphere–ice sphere data. Grzegorczyk et al. (2023) found the best fit to the data if the shape parameter was 0.78 for graupel–snowflake and graupel–graupel with dendrites collisions, while a value of γ=0.55 was revealed as the best fit for bare-graupel–bare-graupel collisions. Nevertheless, when we set γ to 0.78, it modified the curve somewhat, but this change was insignificant and well within the measurement error. From Fig. 3, it is obvious that the average fragment number as a function of CKE is dependent on the particle density. The fragment number tends to decrease as the particle density increases. This can be attributed to the fact that the particle's structural integrity and surface properties change with the temperature at which they were generated. The higher-density graupel particles generated at −7 °C are structurally more integrated (see Fig. 1b) than those produced at −15°C (Fig. 1a), thereby reducing the chance of breaking and generating less fragments during collision. Certainly, ice spheres produce the lowest number of fragments due to their more compact structure.
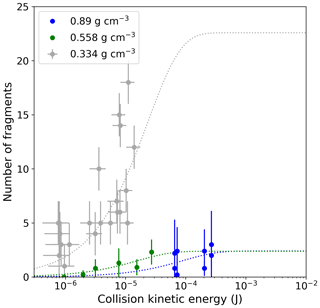
Figure 3Number of fragments generated in bare-graupel–bare-graupel collisions. Data are color-coded as follows: blue – current study, ice sphere–ice sphere collisions (−5 and −15 °C); green – current study, graupel–graupel collisions (−7 °C); gray – Grzegorczyk et al. (2023), bare-graupel–bare-graupel collisions (−15 °C). Dashed lines represent the best fits using Eq. (2).
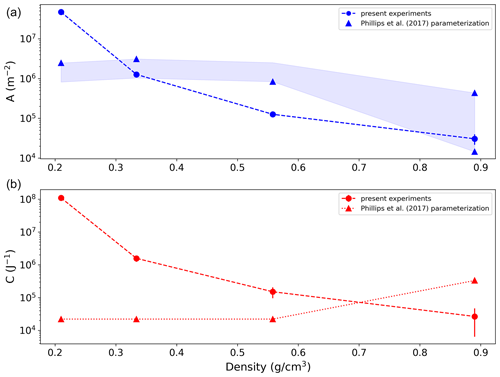
Figure 4Experimentally determined surface density of breakable asperities A (a, blue dots) and the asperity-fragility coefficient C (b, red dots) as a function of particle density. Blue and red triangles depict A and C, respectively, using the Phillips et al. (2017) parameterization. The shaded area corresponds to a temperature variation from −5 to −15 °C using the Phillips et al. (2017) parameterization.
The change in particle morphology can also be expressed in terms of the surface density (A) and fragility (C) of breakable asperities on the particle's surface (see Eq. 2). The surface property of the particles mainly determines the available number of breakable asperities on the surface. If graupel has a lower density, i.e., more air bubble inclusions are formed when the particle is generated (Enzmann et al., 2011), it has more asperities than a higher-density one. This is also obvious from Fig. 1: graupel generated at −15 °C has a rougher surface (e.g., crevices) and, hence, a greater number of breakable asperities than the relatively smooth graupel generated at −7 °C. As the structure of a low-density particle is more loose and fluffy, those asperities are also more fragile, i.e., require less energy to break them off. Consequently, both parameters, A and C, should increase with decreasing graupel density. This is reflected in Fig. 4 which shows the variation in A and C as a function of density calculated from the fit curves in Fig. 3. The lowest-density particle in Fig. 4 is the graupel with dendrites in Grzegorczyk et al. (2023), whereas the one with the highest density is the ice sphere. The parameters A and C, together with their errors, are given in Table 4.
Table 4Number density of breakable asperities, A, and the asperity-fragility coefficient, C, together with their errors from fits to our experimental data in Fig. 3 and Grzegorczyk et al. (2023) for different particle densities.

In their theoretical framework, Phillips et al. (2017) proposed the parameters A and C fitted to the experimental data of Takahashi et al. (1995). Following Table 1 of Phillips et al. (2017) for Type I collisions, one can calculate to 18.6×106 m−2, depending on the graupel size and temperature, and C = 22 050 J−1 and C = 331 000 J−1 for graupel–graupel and ice sphere–ice sphere collisions, respectively. In the Phillips et al. (2017) parameterization, both A and C are independent of the particle density. In contrast to these findings, we could demonstrate that A and C are dependent on the density of the colliding particles, thereby refining and improving upon the previous parameterization. This finding is in accordance with the study of Gautam et al. (2024), who presented an improved parameter set for graupel–snowflake collisions.
One has to note here that we did not carry out any systematic investigation of the temperature dependency of the fragment numbers. The experiments of Takahashi et al. (1995) indicated a strong variation with temperature, which was also taken into account in the parameterization of Phillips et al. (2017). In agreement with Takahashi et al. (1995) and Phillips et al. (2017), in our opinion, this temperature dependency can be attributed to the temperature dependency of the crystal habit, crystal surface density, and crystal size of crystals grown on the graupel's surface. For bare graupel and ice spheres, such a strong temperature dependency is not expected, but some structural or morphological change is very likely.
The sizes of the graupel particles corresponding to the three lowest densities investigated in our study were approximately the same. Thus, the largest variation in the generated number of fragments or in the parameters A and C stems from the temperature variation. In the Phillips et al. (2017) parameterization, C is invariant with respect to the temperature. Values of A were calculated for the particle sizes and temperature range of our experiments and are indicated by the shaded area in Fig. 4. As this variation is far less than the observed change in A over the different particle types, one can indeed attribute the systematic decrease in A to the density of the particles.
In Fig. 4, A for ice spheres shows the lowest value both in our experiments and in the Phillips et al. (2017) parameterization, having very good agreement at −5 °C. Nevertheless, the predicted temperature dependency of Phillips et al. (2017) could not be proven in our measurements. As can be seen in Fig. 2a, any potential temperature dependency is within the range of our experimental error. As mentioned above, the temperature dependency in the Phillips et al. (2017) parameterization might be attributed to the temperature dependency of the crystal growth on the ice sphere's surface. As solely the internal structure of the ice spheres can vary due to any temperature change in our experiments, the resulting temperature dependency becomes minor.
The fragility coefficient C shows similar dependency on the particle density to A in our experiments, but it behaves very differently to that of Phillips et al. (2017) when employing their Type I parameterization corresponding to graupel–graupel or hail–hail collisions. Nevertheless, the Phillips et al. (2017) parameterization was based on a very limited dataset available at that time, thereby preventing the resolution of the full dependencies of C on the temperature, size, and rimed fraction. Our experimental data shed light on the dependency of C at least on particle structure (i.e., rimed fraction) and probably temperature.
4.3 Multiple collisions
In the multiple-collision experiments, 2.45 mm diameter graupel particles were repeatedly hit by 5 mm diameter ice spheres until no more fragments were generated on subsequent collisions. In these experiments, it took two to four collisions to cease generating any additional fragments. An average of 1.5 fragments and a maximum of 4 fragments were released during these series of multiple collisions, which match the fragment numbers of single collisions (see Table 3). The number of released fragments was the highest for the very first collision in each set of measurements. The subsequent collisions did not show any clear tendency toward a decreasing or increasing number of fragments. Thus, the majority of the breakable asperities apparently broke at the very first collision, and none of them remained after the fourth collision. The maximum fragment dimension was 0.384 mm, whereas the minimum fragment dimension was 0.072 mm; these values also match the results for single collisions (Table 3). Hence, if a graupel particle undergoes multiple collisions, it behaves in the same way as a particle involved in a single-collision event, but it stops generating additional fragments after a few collisions. Nevertheless, if the graupel particle is in the mixed-phase zone of a cloud, i.e., it can continuously grow by riming, its structure is retained in the sense that breakable asperities are continuously produced. Considering the relatively long time between two collisions when compared to the growth rate by riming, the single collision of graupel particles can be taken into account when considering secondary ice production.
The main goal of the experiments was to gather more measurement data to improve the understanding and characterization of secondary ice production after the collision of ice particles. The focus was on the effect of the morphological structure of the colliding particles on the number of fragments generated, by exploring the most compact structures of spherical graupel and frozen droplets (ice spheres). We intended to simulate atmospheric ice particles in terms of size, morphology, fragility, and collision kinetic energy. Certainly, this experimental study also has some constraints and limitations. They can be considered in modeling studies and in future laboratory experiments. These limitations are as follows:
-
The graupel particles were generated using epoxy spheres as embryos. In the vicinity of the site where the embryo was connected to the double-gyration apparatus, no riming occurred. Therefore, the center of mass of the particle was offset from its geometric center. Due to this eccentricity, the particle was falling with the embryo facing down, and this would have affected the number of fragments generated during collision. Therefore, the embryos were removed from the falling graupel particles. After removing the embryo, a hollow space remained inside the graupel that modified its density (from 0.558 to 0.46 g cm−3). As the collision occurred at the rimed side of the fixed graupel, such a removal of the embryo from that graupel was not necessary.
-
The ice spheres were produced by freezing water at very low temperatures, i.e., at −70 °C, and then equilibrated at the experimental temperature. This method was used in order to get a rather homogeneous ice structure with a bulk ice density of 0.91 g cm−3. Hence, the internal ice structure (e.g., appearance, concentration, and distribution of air bubbles inside the particle) might be different compared to spheres frozen directly at −5 or −15 °C.
-
We examined central collisions between the particles, but we cannot rule out any oblique collisions. In Grzegorczyk et al. (2023), we found that oblique collisions between graupel and snowflakes result in significantly less fragments than central collisions (around a 50 % decrease), because some amount of energy was fed into the rotation of the snowflake and not into fragmentation. For graupel and ice sphere collisions, we do not expect such large differences in fragment numbers, as the torque is less than for snowflakes in this case and, consequently, less energy would be fed into the rotation of the particle. Furthermore, the total number of fragments observed is also of an order of magnitudes less than in the case of the more fragile snowflakes.
-
In the present experiments, CKEs represent the highest end of the natural CKE values, and the high particle densities reflect the most compact ice structures. This limits the direct applicability of our results in model simulations. Nevertheless, the main objective of the study was to reveal a relationship of the number of fragments generated due to collision with the CKE and the particle density (structure). In the experiments, we could capture the lower CKE limits for producing fragments (e.g., close to 10−6 J for 0.558 g cm−3 density graupel particles). Similarly, we identified the upper CKE limits above which no extra fragments were generated. Hence, we could cover the CKE range in which fragmentation due to collisions of the investigated particles in the atmosphere could occur. The same holds for particle densities, which represent a wide range of atmospheric ice particle structures, and allows the derivation of a dependency of the number of fragments on this feature.
-
The detection limit of our measurements was approximately 25 to 30 µm. Hence, it is possible that some small ice fragments remained undetected. However, the previous measurement of Grzegorczyk et al. (2023) showed that the fragment size distribution peaks at 75 and 400 µm, i.e., well above the detection limit. Certainly, whether small ice particles (less then 20 µm) survive in the atmosphere depends strongly on the humidity of the environment. In general, most experimental studies suffer from the relatively poor spatial resolution of the applied optical detection (Lauber et al., 2018; Keinert et al., 2020) and the challenge of distinguishing small ice fragments from dust particles (Grzegorczyk et al., 2023). Therefore, any comparison of the fragment number derived in the current study with earlier freezing fragmentation (Lauber et al., 2018; Keinert et al., 2020) or with collision-induced fragmentation measurements (Takahashi, 1993; Vardiman, 1978) should be interpreted with caution.
Building upon the collision studies by Grzegorczyk et al. (2023), we investigated the collision between graupel particles of different densities, specifically in the absence of fragile ice crystal growth on their surfaces. Collisions involving (1) graupel particles, grown at different temperatures by riming under dry growth conditions, and (2) ice spheres, as proxies frozen drops generated as frozen water, were investigated. Combining the dataset of the present study with data from Grzegorczyk et al. (2023), in which the graupel particles had densities of between approximately 0.2 and 0.34 g cm−3, revealed a direct dependency of the number of fragments generated by collision on the particle's density. This effect can be attributed to the morphological structure of the particles, which ultimately determines both their fragility and their density. Phillips et al. (2017) noted that the number of fragments generated increases with the degree of rime on graupel particles. This increase is explicable in terms of the number density of breakable branches, A, as our study also suggests. Our findings contradict the experimental study of Griggs and Choularton (1986), who suggested that fragmentation of rime is very unlikely to occur in natural clouds due to the high energy required to break the structure. Nevertheless, they pointed out that the evaporation of rime in an unsaturated (with respect to ice) environment of the cloud would weaken the structure making the rimed graupel more fragile.
Phillips et al. (2017) provided a temperature-dependent parameterization of the number of fragments produced after collision. We did not observed as much temperature dependency as Phillips et al. (2017); however, the graupel particles' structure is determined by the temperature at which the growth occurs. Hence, from this point of view, one can argue that our results also revealed an indirect temperature dependency. This suggests that the internal structural integrity of the particle varies with temperature, thereby altering its susceptibility to fracture. Nevertheless, the temperature dependency in Phillips et al. (2017) might also be attributed to the temperature dependency of the crystal growth on the ice particle surface in the experiment of Takahashi et al. (1995).
The observed number of fragments produced by graupel–graupel collisions is within the range of or higher than those observed in other secondary ice processes during drop freezing (Lauber et al., 2018; Keinert et al., 2020), at least for the sizes detectable by the applied optical imaging techniques. However, as shown in Grzegorczyk et al. (2023) for graupel–snowflake and graupel–graupel with dendrites collisions, when ice particles possess vapor-grown fragile ice structures, the number of ice fragments can rise up to hundreds for one collision. The typical cloud regime range for the collision-induced fragmentation of frozen drops might coincide with that for the fragmentation of drops during freezing (Lachapelle and Thériault, 2022), whereas the fragmentation of graupel particles would occur at lower cloud regimes and at temperatures of between −5 and −20 °C. This regime coincides with the typical H–M range of −3 to −8 °C (Hallett and Mossop, 1974); however, the observed number of fragments is far lower than those suggested from H–M processes. Therefore, we suggest sensitivity studies using cloud models to explore the role of the collision-induced fragmentation of graupel particles in the H–M regime in ice multiplication and cloud and precipitation development. Although numerous studies have highlighted the important role of the collision-induced fragmentation of ice particles in convective (Waman et al., 2022; Han et al., 2024; Grzegorczyk et al., 2024), Arctic (Sotiropoulou et al., 2020, 2021; Karalis et al., 2022), and orographic mixed-phase clouds (Dedekind et al., 2021; Georgakaki et al., 2022), further laboratory investigations are needed to quantify this process under varying atmospheric conditions that influence particle properties.
The data used to generate the figures are provided in the tables of this paper or in Grzegorczyk et al. (2023) or Yadav et al. (2024).
The paper was written by MS and SY, with support and assistance from all co-authors. PG made significant contributions to the data evaluation and provided comments on the results, discussion, and conclusion. SY performed graupel growth and collision experiments and evaluated the data. LM performed ice sphere collision experiments and analyzed the data. AT constructed the graupel generator and designed the graupel growth experiments. SKM and SY designed the graupel growth and collision experiments and characterized the setups. MS designed the experiments and analyzed the data.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We gratefully acknowledge help from Christoph Sievert (German Weather Service), who aided us with the calculation of the collision kinetic energy of atmospheric graupel and ice particles. Pierre Grzegorczyk is now funded by the French National Research Agency (ANR; ACME ANR-21-CE01-0003 project contract).
This research has been supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation; project no. 492234709). We also gratefully acknowledge funding from the DFG within the framework of the Priority Program “Polarimetric Radar Observations meet Atmospheric Modelling (PROM) – Fusion of Radar Polarimetry and Numerical Atmospheric Modelling Towards an Improved Understanding of Cloud and Precipitation Processes” (SPP 2115).
This open-access publication was funded by Johannes Gutenberg University Mainz.
This paper was edited by Luis A. Ladino and reviewed by four anonymous referees.
Choularton, T., Latham, J., and Mason, B. J.: A possible mechanism of ice splinter production during riming, Nature, 274, 791–792, 1978. a
Choularton, T. W., Griggs, D. J., Humood, B. Y., and Latham, J.: Laboratory studies of riming, and its relation to ice splinter production, Q. J. Roy. Meteor. Soc., 106, 367–374, https://doi.org/10.1002/qj.49710644809, 1980. a
Dedekind, Z., Lauber, A., Ferrachat, S., and Lohmann, U.: Sensitivity of precipitation formation to secondary ice production in winter orographic mixed-phase clouds, Atmos. Chem. Phys., 21, 15115–15134, https://doi.org/10.5194/acp-21-15115-2021, 2021. a
Dye, J. E. and Hobbs, P. V.: The influence of environmental parameters on the freezing and fragmentation of suspended water drops, J. Atmos. Sci., 25, 82–96, 1968. a
Enzmann, F., Miedaner, M. M., Kersten, M., von Blohn, N., Diehl, K., Borrmann, S., Stampanoni, M., Ammann, M., and Huthwelker, T.: 3-D imaging and quantification of graupel porosity by synchrotron-based micro-tomography, Atmos. Meas. Tech., 4, 2225–2234, https://doi.org/10.5194/amt-4-2225-2011, 2011. a, b
Field, P. R., Lawson, R. P., Brown, P. R. A., Lloyd, G., Westbrook, C., Moisseev, D., Miltenberger, A., Nenes, A., Blyth, A., Choularton, T., Connolly, P., Buehl, J., Crosier, J., Cui, Z., Dearden, C., DeMott, P., Flossmann, A., Heymsfield, A., Huang, Y., Kalesse, H., Kanji, Z. A., Korolev, A., Kirchgaessner, A., Lasher-Trapp, S., Leisner, T., McFarquhar, G., Phillips, V., Stith, J., and Sullivan, S.: Chapter 7. Secondary Ice Production – current state of the science and recommendations for the future, Meteor. Mon., 58, 7.1–7.20, https://doi.org/10.1175/amsmonographs-d-16-0014.1, 2017. a
Gautam, M., Waman, D., Patade, S., Deshmukh, A., Phillips, V., Jackowicz-Korczynski, M., Paul, F. P., Smith, P., and Bansemer, A.: Fragmentation in Collisions of Snow with Graupel/Hail: New Formulation from Field Observations, J. Atmos. Sci., 81, 2149–2164, https://doi.org/10.1175/JAS-D-23-0122.1, 2024. a, b
Georgakaki, P., Sotiropoulou, G., Vignon, É., Billault-Roux, A.-C., Berne, A., and Nenes, A.: Secondary ice production processes in wintertime alpine mixed-phase clouds, Atmos. Chem. Phys., 22, 1965–1988, https://doi.org/10.5194/acp-22-1965-2022, 2022. a
Griggs, D. J. and Choularton, T. W.: A laboratory study of secondary ice particle production by the fragmentation of rime and vapour-grown ice crystals, Q. J. Roy. Meteor. Soc., 112, 149–163, https://doi.org/10.1002/qj.49711247109, 1986. a, b
Grzegorczyk, P., Yadav, S., Zanger, F., Theis, A., Mitra, S. K., Borrmann, S., and Szakáll, M.: Fragmentation of ice particles: laboratory experiments on graupel–graupel and graupel–snowflake collisions, Atmos. Chem. Phys., 23, 13505–13521, https://doi.org/10.5194/acp-23-13505-2023, 2023. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac, ad, ae
Grzegorczyk, P., Wobrock, W., Canzi, A., Niquet, L., Tridon, F., and Planche, C.: Investigating secondary ice production in a deep convective cloud with a 3D bin microphysics model: Part I – Sensitivity study of microphysical processes representations, Atmos. Res., 313, 107774, https://doi.org/10.1016/j.atmosres.2024.107774, 2024. a
Hallett, J. and Mossop, S. C.: Production of secondary ice particles during the riming process, Nature, 249, 26–28, https://doi.org/10.1038/249026a0, 1974. a, b
Han, C., Hoose, C., and Dürlich, V.: Secondary Ice Production in Simulated Deep Convective Clouds: A Sensitivity Study, J. Atmos. Sci., 81, 903–921, https://doi.org/10.1175/jas-d-23-0156.1, 2024. a
Heymsfield, A., Szakáll, M., Jost, A., Giammanco, I., Wright, R., and Brimelow, J.: CORRIGENDUM, J. Atmos. Sci., 77, 405–412, https://doi.org/10.1175/JAS-D-19-0185.1, 2020. a
Heymsfield, A. J. and Mossop, S. C.: Temperature dependence of secondary ice crystal production during soft hail growth by riming, Q. J. Roy. Meteor. Soc., 110, 765–770, https://doi.org/10.1002/qj.49711046512, 1984. a
James, R. L., Phillips, V. T. J., and Connolly, P. J.: Secondary ice production during the break-up of freezing water drops on impact with ice particles, Atmos. Chem. Phys., 21, 18519–18530, https://doi.org/10.5194/acp-21-18519-2021, 2021. a
Karalis, M., Sotiropoulou, G., Abel, S. J., Bossioli, E., Georgakaki, P., Methymaki, G., Nenes, A., and Tombrou, M.: Effects of secondary ice processes on a stratocumulus to cumulus transition during a cold-air outbreak, Atmos. Res., 277, 106302, https://doi.org/10.1016/j.atmosres.2022.106302, 2022. a
Keinert, A., Spannagel, D., Leisner, T., and Kiselev, A.: Secondary Ice Production upon Freezing of Freely Falling Drizzle Droplets, J. Atmos. Sci., 77, 2959–2967, https://doi.org/10.1175/JAS-D-20-0081.1, 2020. a, b, c, d
Korolev, A. and Leisner, T.: Review of experimental studies of secondary ice production, Atmos. Chem. Phys., 20, 11767–11797, https://doi.org/10.5194/acp-20-11767-2020, 2020. a
Korolev, A., DeMott, P. J., Heckman, I., Wolde, M., Williams, E., Smalley, D. J., and Donovan, M. F.: Observation of secondary ice production in clouds at low temperatures, Atmos. Chem. Phys., 22, 13103–13113, https://doi.org/10.5194/acp-22-13103-2022, 2022. a, b
Lachapelle, M. and Thériault, J. M.: Characteristics of Precipitation Particles and Microphysical Processes during the 11–12 January 2020 Ice Pellet Storm in the Montréal Area, Québec, Canada, Mon. Weather Rev., 150, 1043–1059, https://doi.org/10.1175/MWR-D-21-0185.1, 2022. a, b, c
Ladino, L. A., Korolev, A., Heckman, I., Wolde, M., Fridlind, A. M., and Ackerman, A. S.: On the role of ice-nucleating aerosol in the formation of ice particles in tropical mesoscale convective systems, Geophys. Res. Lett., 44, 1574–1582, https://doi.org/10.1002/2016GL072455, 2017. a
Lauber, A., Kiselev, A., Pander, T., Handmann, P., and Leisner, T.: Secondary Ice Formation during Freezing of Levitated Droplets, J. Atmos. Sci., 75, 2815–2826, https://doi.org/10.1175/JAS-D-18-0052.1, 2018. a, b, c, d, e
Mossop, S. C.: Production of secondary ice particles during the growth of graupel by riming, Q. J. Roy. Meteor. Soc., 102, 45–57, https://doi.org/10.1002/qj.49710243104, 1976. a
Mossop, S. C.: The Origin and Concentration of Ice Crystals in Clouds, B. Am. Meteorol. Soc., 66, 264–273, https://doi.org/10.1175/1520-0477(1985)066<0264:TOACOI>2.0.CO;2, 1985. a
Oraltay, R. G. and Hallett, J.: Evaporation and melting of ice crystals: A laboratory study, Atmos. Res., 24, 169–189, 1989. a
Phillips, V. T. J., Yano, J.-I., and Khain, A.: Ice Multiplication by Breakup in Ice–Ice Collisions. Part I: Theoretical Formulation, J. Atmos. Sci., 74, 1705–1719, https://doi.org/10.1175/JAS-D-16-0224.1, 2017. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r
Prabhakaran, P., Kinney, G., Cantrell, W., Shaw, R. A., and Bodenschatz, E. High supersaturation in the wake of falling hydrometeors: Implications for cloud invigoration and ice nucleation, Geophys. Res. Lett., 47, e2020GL088055, https://doi.org/10.1029/2020GL088055, 2020. a
Seidel, J. S., Kiselev, A. A., Keinert, A., Stratmann, F., Leisner, T., and Hartmann, S.: Secondary ice production – no evidence of efficient rime-splintering mechanism, Atmos. Chem. Phys., 24, 5247–5263, https://doi.org/10.5194/acp-24-5247-2024, 2024. a
Sotiropoulou, G., Sullivan, S., Savre, J., Lloyd, G., Lachlan-Cope, T., Ekman, A. M. L., and Nenes, A.: The impact of secondary ice production on Arctic stratocumulus, Atmos. Chem. Phys., 20, 1301–1316, https://doi.org/10.5194/acp-20-1301-2020, 2020. a
Sotiropoulou, G., Ickes, L., Nenes, A., and Ekman, A. M. L.: Ice multiplication from ice–ice collisions in the high Arctic: sensitivity to ice habit, rimed fraction, ice type and uncertainties in the numerical description of the process, Atmos. Chem. Phys., 21, 9741–9760, https://doi.org/10.5194/acp-21-9741-2021, 2021. a
Sullivan, S. C., Hoose, C., and Nenes, A.: Investigating the contribution of secondary ice production to in-cloud ice crystal numbers, J. Geophys. Res.-Atmos., 122, 9391–9412, https://doi.org/10.1002/2017JD026546, 2017. a
Takahashi, T.: High ice crystal production in winter cumuli over the Japan Sea, Geophys. Res. Lett., 20, 451–454, https://doi.org/10.1029/93GL00613, 1993. a
Takahashi, T., Nagao, Y., and Kushiyama, Y.: Possible High Ice Particle Production during Graupel–Graupel Collisions, J. Atmos. Sci., 52, 4523–4527, https://doi.org/10.1175/1520-0469(1995)052<4523:phippd>2.0.co;2, 1995. a, b, c, d, e, f
Theis, A., Szakáll, M., Diehl, K., Mitra, S. K., Zanger, F., Heymsfield, A., and Borrmann, S.: Vertical Wind Tunnel Experiments and a Theoretical Study on the Microphysics of Melting Low-Density Graupel, J. Atmos. Sci., 79, 1069–1087, https://doi.org/10.1175/jas-d-21-0162.1, 2022. a
Tridon, F., Silber, I., Battaglia, A., Kneifel, S., Fridlind, A., Kalogeras, P., and Dhillon, R.: Highly supercooled riming and unusual triple-frequency radar signatures over McMurdo Station, Antarctica, Atmos. Chem. Phys., 22, 12467–12491, https://doi.org/10.5194/acp-22-12467-2022, 2022. a
Vardiman, L.: The Generation of Secondary Ice Particles in Clouds by Crystal–Crystal Collision, J. Atmos. Sci., 35, 2168–2180, https://doi.org/10.1175/1520-0469(1978)035<2168:tgosip>2.0.co;2, 1978. a, b
von Terzi, L., Dias Neto, J., Ori, D., Myagkov, A., and Kneifel, S.: Ice microphysical processes in the dendritic growth layer: a statistical analysis combining multi-frequency and polarimetric Doppler cloud radar observations, Atmos. Chem. Phys., 22, 11795–11821, https://doi.org/10.5194/acp-22-11795-2022, 2022. a
Waitz, F., Schnaiter, M., Leisner, T., and Järvinen, E.: In situ observation of riming in mixed-phase clouds using the PHIPS probe, Atmos. Chem. Phys., 22, 7087–7103, https://doi.org/10.5194/acp-22-7087-2022, 2022. a
Waman, D., Patade, S., Jadav, A., Deshmukh, A., Gupta, A. K., Phillips, V. T. J., Bansemer, A., and DeMott, P. J.: Dependencies of Four Mechanisms of Secondary Ice Production on Cloud-Top Temperature in a Continental Convective Storm, J. Atmos. Sci., 79, 3375–3404, https://doi.org/10.1175/jas-d-21-0278.1, 2022. a
Yadav, S., Metten, L., Grzegorczyk, P., Theis, A., Mitra, S. K., and Szakáll, M.: Experimental data for “Measurement Report: Influence of particle density on secondary ice production by graupel and ice pellet collisions”, Zenodo [data set], https://doi.org/10.5281/zenodo.14140846, 2024. a