Partitioning of ionic surfactants in aerosol droplets containing glutaric acid, sodium chloride, or sea salts

Sea spray is the largest contributor to atmospheric aerosol by mass and contains mixtures of inorganic salts and organics. The chemically complex organic fraction can contain soluble, highly surface-active organics, and field studies commonly identify ionic surfactants in aerosol samples. In macroscopic solutions, divalent cations present in sea spray can alter the partitioning of ionic surfactants. Furthermore, the high surface area-to-volume (SA $/$ V) ratio of aerosol droplets may lead to depletion of surfactant from the bulk, requiring more surfactant, relative to its volume, to lower the surface tension of a droplet compared to a macroscopic solution. Here, we investigate the partitioning of model ionic surfactants (sodium dodecyl sulfate, an anionic surfactant, and cetrimonium bromide, a cationic surfactant) in 6–10 µm radius droplets containing glutaric acid, NaCl, or sea spray mimic cosolutes. Surface tension measurements are compared to two independent partitioning models accounting for the SA $/$ V ratio of the droplets. Salting out of the ionic surfactants leads to strong bulk depletion in 6–10 µm radius droplets, with no observable difference in droplet surface tension between NaCl and sea spray mimic cosolutes. The total ionic surfactant concentration required to reach the minimum surface tension for these droplets was 2.0 ± 0.5 mM, consistent with previous observations in droplets containing strong surfactants. Modeling results suggest that surfactant concentrations on the order of tens to hundreds of millimolar are required to significantly reduce surface tension in 100 nm droplets. These results have implications for cloud droplet activation and chemistry occurring at the interface of sea spray aerosol.

1 Introduction

Aerosol in the atmosphere can scatter and absorb radiation, directly affecting climate, as well as altering cloud microphysics by serving as cloud condensation nuclei (CCN), indirectly impacting climate. Sea spray is a major source of surfactants in atmospheric aerosol (De Leeuw et al., 2011). Ambient aqueous aerosol contains a complex mixture of organic and inorganic species. For example, the sea surface microlayer contains salts as well as a high concentration of organic molecules. Bubble bursting and jet drop aerosol generation pathways have been shown to produce droplets enriched in surfactant compared to the sea surface microlayer (Bertram et al., 2018; Burdette et al., 2022; Cochran et al., 2016; Frossard et al., 2019; Wang et al., 2017). Surfactants are known to reduce surface tension at macroscopic aqueous interfaces and may also lower the surface tension of microscopic droplets if present in sufficiently high quantities (Bain et al., 2023b; Bzdek et al., 2020; Jacobs et al., 2024). Field studies often find ionic surfactants make up more than half of the total surfactant fraction (Gérard et al., 2016, 2019). Seawater is also a source of divalent ions like calcium, magnesium, and sulfate. Bridging interactions (i.e., the tethering of organics to divalent cations) between Ca²⁺ and anionic surfactants leads to co-adsorption at interfaces and can result in an excess of both Ca²⁺ and surface-active material at interfaces (Carter-Fenk et al., 2021; Hasenecz et al., 2019; Jayarathne et al., 2016).

For an aerosol droplet to become activated into a cloud droplet, it must grow to a critical size, which requires critical supersaturation in atmospheric relative humidity. The Köhler equation is commonly used in atmospheric science to predict this activation barrier for droplets of a known size and composition. The Köhler equation consists of two terms: the Raoult term, which accounts for the solute effect, and the Kelvin term, which accounts for the surface curvature (Seinfeld et al., 2016). The Kelvin term includes the surface tension of the droplet, which is often assumed to be equal to the value for pure water during activation (Tao et al., 2012). This assumption is historically considered reasonable because, near the point of cloud droplet activation, the droplet becomes very dilute (Sorjamaa et al., 2004), but it is at odds with field measurements that find highly surface-active material can lower the surface tension of macroscopic solutions with millimolar range concentrations in collected aerosol samples (Burdette and Frossard, 2021; Gérard et al., 2016, 2019). Furthermore, a growing number of field studies comparing the number of predicted CCN using the Köhler equation to the number of measured CCN have found that lowering the surface tension to 40–60 mN m⁻¹ (thereby lowering the barrier to cloud droplet formation) results in better agreement between predictions and measurements (Fan et al., 2024; Good et al., 2010; Irwin et al., 2010; Ovadnevaite et al., 2017). Accurate representations of aerosol surface tension during hygroscopic growth are necessary as shortwave cloud radiative forcing predictions are sensitive to descriptions of aerosol surface tension (Prisle et al., 2012).

Salts greatly affect the surface partitioning of ionic surfactants in macroscopic solutions. For example, the partitioning kinetics of ionic surfactants sodium dodecyl sulfate (SDS) and cetrimonium bromide (CTAB) are impacted by the concentration of NaCl in solution (Nozière et al., 2014; Qazi et al., 2020; Rohde and Sackmann, 1979; Weinheimer et al., 1980). Moreover, the addition of NaCl to SDS or CTAB solutions also greatly impacts the critical micelle concentration (CMC) and enhances the equilibrium surface concentration, commonly referred to as salting out (Prosser and Franses, 2001; Qazi et al., 2020). Additionally, divalent cations such as Ca²⁺ are known to alter the surface properties of anionic surfactants in solution (Cross and Jayson, 1994; Penfold and Thomas, 2022).

Predicting the surface tension of macroscopic aqueous mixtures of organics and inorganics is non-trivial and cannot be accomplished with simple mass or volume fraction mixing rules (Boyer et al., 2017; Kleinheins et al., 2024; May et al., 2018; Tuckermann, 2007; Wu et al., 2019). Compared to macroscopic solutions, predicting the surface tension of aerosol becomes even more challenging. The surface-active nature of organic molecules, in addition to the small size, and therefore large surface area-to-volume (SA $/$ V) ratio, of aerosol droplets means that surfactants can become depleted in the droplet bulk (Bain et al., 2023b; Bzdek et al., 2020; Jacobs et al., 2024; Prisle, 2021). This depletion has been experimentally observed for droplets in air containing nonionic surfactants spanning a wide range of chemical structures and surfactant properties. Models predicting surfactant partitioning in droplets have also been tested against droplet measurements for these nonionic surfactants (Bain et al., 2023b, 2024a; Bzdek et al., 2020). However, both nonionic and ionic surfactants have been characterized and quantified in ambient aerosol samples (Frossard et al., 2019; Gérard et al., 2016, 2019).

In this work, we investigate the surface tension of aqueous aerosol droplets containing atmospheric proxy anionic or cationic surfactants mixed with glutaric acid, NaCl, or a sea spray mimic. We measure the surface tensions of picoliter-volume droplets suspended in air as well as of macroscopic solutions, systematically altering the surfactant composition, and compare these results to predictions from two independent partitioning models. This systematic, bottom-up approach provides a framework to understand the partitioning of ionic surfactants in realistic aerosol droplets, which contain complex mixtures of surfactants and cosolutes.

2 Methods

2.1 Sample preparation

Solutions containing cosolutes and one surfactant were prepared for macroscopic and droplet surface tension measurements. NaCl (Sigma-Aldrich BioXtra, > 99.5 %) and glutaric acid (Sigma-Aldrich, 99 %) cosolutes were used without further purification. Sea spray mimic (herein referred to as sea spray) was made up from NaCl (Sigma-Aldrich BioXtra, > 99.5 %), MgCl₂ (MgCl₂ ⋅ 6H₂O, G-Biosciences), CaCl₂ (CaCl₂ ⋅ 2H₂O, Acros Organics, 99+ % ACS reagent), Na₂SO₄ (Fisher Scientific), and MgSO₄ (Fisher Scientific). Sea spray was made to match the inorganic ion ratios using the five most abundant ions of the fine-fraction sea spray aerosol as reported in the literature (Jayarathne et al., 2016) (ion mole fractions of 0.493 Cl⁻, 0.410 Na⁺, 0.057 Mg²⁺, 0.012 Ca²⁺, and 0.028 SO${}_{\mathrm{4}}^{\mathrm{2}-}$). The cationic surfactant CTAB (Sigma-Aldrich BioXtra, > 99 %) was used without further purification, but the anionic surfactant SDS (ultra-pure, MP Biomedicals, LLC) was purified by three consecutive recrystallization steps before use. After recrystallization, surface tension measurements of SDS no longer showed a dip in surface tension around the CMC, indicating the surface-active impurity had been removed. Solutions for macroscopic and droplet measurements contained one surfactant (SDS or CTAB) at a range of concentrations and one cosolute (0.9 M glutaric acid, 0.5 M NaCl, or 0.48 M sea spray). The sea spray concentration was chosen to be 0.48 M total salt so that the molar quantities of anions and cations would be equal to the amount of 0.5 M NaCl. These concentrations were chosen to represent water activity near saturation (a_w=0.99 for each cosolute), providing information about the surface tension of aerosol droplets near the point of cloud droplet activation. All solutions were prepared with deionized water.

2.2 Droplet surface tension measurements

The surface tension of single droplets was determined by the coalescence method using holographic optical tweezers, which has been previously described (Bain et al., 2023a, b; Bzdek et al., 2016, 2020). Aerosol was generated using a mesh grid medical nebulizer (MicroAIR, Omron). The surface tension of the droplet (σ, Eq. 1) is related to the oscillation frequency (ω_l) of the surface mode order l, which is excited upon droplet coalescence, as well as the droplet's radius (r) and density (ρ). The radius and refractive index are determined by fitting the cavity-enhanced Raman spectrum of the composite droplet (Preston and Reid, 2013, 2015). The droplet's density and viscosity were then determined using parameterizations.

$$\begin{array}{}\text{(1)}& \mathit{\sigma }={\displaystyle \frac{r^{\mathrm{3}}\mathit{\rho }{\mathit{\omega }}_l^{\mathrm{2}}}{l\left(l-\mathrm{1}\right)\left(l+\mathrm{2}\right)}}\end{array}$$

The observed oscillation frequency (${\mathit{\omega }}_l^{\ast }$) is corrected for viscous damping (η), assuming the viscosity of the surfactant-containing droplet is equal to that of a droplet with the same concentration of primary solute (NaCl, glutaric acid, or sea spray).

$$\begin{array}{}\text{(2)}& {\displaystyle }{\mathit{\omega }}_l^{\ast }=\sqrt{{\mathit{\omega }}_l^{\mathrm{2}}-{\mathit{\tau }}_l^{-\mathrm{2}}}\text{(3)}& {\displaystyle }{\mathit{\tau }}_l={\displaystyle \frac{r^{\mathrm{2}}\mathit{\rho }}{(l-\mathrm{1})(\mathrm{2}l+\mathrm{1})\mathit{\eta }}}\end{array}$$

Parameterizations for the density, viscosity, and composition of glutaric acid and NaCl droplets were taken from the literature (Bzdek et al., 2016; Rumble, 2021; Song et al., 2016). Parameterizations for sea spray (Table S1 and Fig. S1) were determined by fitting density (density meter, Densito, METTLER TOLEDO) and refractive index (n(589 nm), Palm Abbe digital refractometer (PA201, MISCO)) measurements of the sea spray mimic. The viscosity of sea spray is assumed to be equal to the viscosity of NaCl for the same total molar concentration. This assumption is reasonable because the solute is dilute (a_w=0.99) in all droplets. The concentration of surfactant in the droplet was then determined using the molar ratio of surfactant to cosolute in the nebulized solution (Bain et al., 2023b; Bzdek et al., 2020).

2.3 Macroscopic surface tension measurements

The equilibrium surface tension of macroscopic solutions containing surfactant and cosolute was measured with the Wilhelmy plate method (Krüss, K100) at 25 ± 1 °C. Reported surface tensions are an average of three repeat measurements. The macroscopic data were fit in the region of decreasing surface tension with increasing surfactant concentration to the Langmuir isotherm and equation of state (Eq. 4).

$$\begin{array}{}\text{(4)}& \begin{array}{rl}\mathit{\sigma }& ={\mathit{\sigma }}_{\mathrm{0}}+nRT{\mathrm{\Gamma }}_{\max }\ln \left(\mathrm{1}-{\displaystyle \frac{\mathrm{\Gamma }}{{\mathrm{\Gamma }}_{\max }}}\right)\\ & ={\mathit{\sigma }}_{\mathrm{0}}+nRT{\mathrm{\Gamma }}_{\max }\ln \left(\mathrm{1}-{\displaystyle \frac{K_{\mathrm{eq}}c}{\mathrm{1}+K_{\mathrm{eq}}c}}\right)\end{array}\end{array}$$

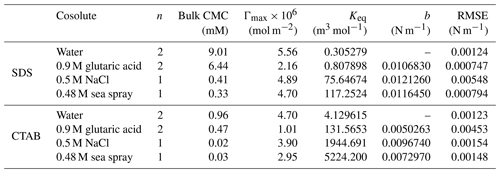
In the Langmuir isotherm, Γ is the equilibrium surface excess at a specific surfactant concentration, Γ_max is the maximum surface excess, K_eq is the equilibrium partitioning constant, c is the surfactant concentration, σ₀ is the surface tension without surfactant present, R is the gas constant, T is the temperature, and n is the van't Hoff factor for the surfactant at the surface. n is typically set to 2 for ionic surfactants in water but 1 in the presence of excess electrolyte. Here, n=1 for surfactant mixtures with NaCl or sea spray and n=2 for surfactant mixtures with glutaric acid. Glutaric acid is a weak diprotic acid with pK_a1=4.35 at room temperature. For a formal concentration of 0.9 M, we expect only about 7 % of the acid to be dissociated. The surface tension without surfactant present is set to 63.0 mN m⁻¹ for ternary mixtures with 0.9 M glutaric acid and to 72.0 mN m⁻¹ for ternary mixtures with 0.5 M NaCl or sea spray. The partitioning models are not sensitive to small differences in the choice of σ₀. Macroscopic measurements in the region of the surface tension plateau (concentration > CMC) were fit with a straight line. The CMC is then taken as the intersection of this straight line with the Langmuir isotherm, and the surface tension at surfactant concentrations greater than the CMC where the minimum surface tension has been reached (σ^min) is taken to be the average of all the surface tensions in this region.

2.4 Droplet bulk depletion

2.4.1 Simple kinetic partitioning framework

The bulk surfactant concentration in picoliter-volume and smaller-volume droplets can become depleted due to the high SA $/$ V ratio. The simple kinetic model, first developed by Alvarez et al. (2012), uses a mass balance for surfactant partitioned to the interface and dissolved in the bulk in combination with an isotherm model to express the depleted bulk concentration at equilibrium (Eq. 5) (Alvarez et al., 2012; Bain et al., 2024a).

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{C_{\mathrm{eff}}}{C_i}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\mathrm{1}-\mathit{\zeta }-{\displaystyle \frac{\mathit{\zeta }}{f}}\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sqrt{{\left(\mathrm{1}-\mathit{\zeta }-{\displaystyle \frac{\mathit{\zeta }}{f}}\right)}^{\mathrm{2}}+\mathrm{4}{\displaystyle \frac{\mathit{\zeta }}{f}}}\end{array}$$

The depleted bulk concentration, or effective concentration (C_eff), is normalized by the initial bulk concentration (C_i, i.e., total surfactant concentration) and is written as a function of two dimensionless parameters, f and ζ. ζ is a dimensionless parameter that represents the maximum fractional potential mass lost to the interface, and f is the ratio of the minimum bulk concentration needed to populate the interface at maximum packing. For the case of a spherical droplet with surfactant dissolved in the interior (Alvarez et al., 2012),

$$\begin{array}{}\text{(6)}& {\displaystyle }f={\displaystyle \frac{\mathrm{3}{K}_{\mathrm{eq}}{\mathrm{\Gamma }}_{\max }}{r}},\text{(7)}& {\displaystyle }\mathit{\zeta }={\displaystyle \frac{\mathrm{3}{\mathrm{\Gamma }}_{\max }}{C_{i}r}},\end{array}$$

where r is the radius of the droplet. The parameters Γ_max and K_eq can be found by fitting macroscopic surface tension measurements to the Langmuir isotherm (Eq. 4) (Eastoe and Dalton, 2000).

To predict the surface tension in a droplet with depleted surfactant concentration due to bulk-to-surface partitioning, c in Eq. (4) is replaced with C_eff. Note, as the droplet radius increases and C_eff approaches C_i, the predicted surface tension approaches the macroscopic surface tension from the Langmuir isotherm fit. When the predicted surface tension becomes equal to the average surface tension measured for macroscopic solutions at concentrations greater than the CMC, the surface tension is set equal to this average value for all larger surfactant concentrations, since the droplet size is not expected to alter the surface tension after the droplet bulk CMC is reached for the picoliter-volume droplets studied here.

2.4.2 Monolayer partitioning framework

The monolayer model developed by Malila and Prisle (2018) calculates the surface tension of aqueous droplets based on the composition of the bulk phase, which is determined from the total droplet composition by accounting for size-dependent bulk-to-surface partitioning (Malila and Prisle, 2018). In the monolayer model, a finite-sized spherical droplet with radius r is comprised of a surface monolayer with thickness δ and an interior (bulk) of radius r−δ. The surface is described as a separate liquid phase with a composition distinct from that of the bulk.

The compositions of the droplet bulk (superscript “b”) ${\mathit{\chi }}^{\mathrm{b}}=({\mathit{\chi }}_{\mathrm{1}}^{\mathrm{b}},{\mathit{\chi }}_{\mathrm{2}}^{\mathrm{b}}$, etc.) and surface (superscript “s”) ${\mathit{\chi }}^{\mathrm{s}}=({\mathit{\chi }}_{\mathrm{1}}^{\mathrm{s}},{\mathit{\chi }}_{\mathrm{2}}^{\mathrm{s}}$, etc.) are calculated iteratively using the semi-empirical relation

$$\begin{array}{}\text{(8)}& \mathit{\sigma }\left({\mathit{\chi }}^{\mathrm{b}}\right)={\displaystyle \frac{\sum _i{\mathit{\chi }}_i^{\mathrm{s}}{v}_i{\mathit{\sigma }}_i}{{\sum }_i{\mathit{\chi }}_i^{\mathrm{s}}{v}_i}}\end{array}$$

between the droplet surface tension parameterized in terms of the composition of the bulk (left side Eq. 8) and pure component surface tensions weighted by the volumes of individual components in the surface (right side Eq. 8). Here, ${\mathit{\chi }}_i^{\mathrm{b}}$ and ${\mathit{\chi }}_i^{\mathrm{s}}$ are the bulk and surface mole fractions, corresponding to molar amounts $n_i^{\mathrm{b}}$ and $n_i^{\mathrm{s}}$, respectively; v_i denotes the molecular volumes; and σ_i denotes the pure-compound surface tensions of each droplet component i. Details of model assumptions and boundary conditions have been described previously (Bain et al., 2023b; Bzdek et al., 2020; Malila and Prisle, 2018).

Here, Eq. (4) was used to parameterize surface tension for the left-hand side of Eq. (8). We simplify Eq. 4 by setting b=nRTΓ_max. Surface tensions when the surfactant concentration is zero (σ₀) were again set to 63.0 mN m⁻¹ for ternary mixtures with glutaric acid and 72.0 mN m⁻¹ for ternary mixtures with NaCl and sea spray mimic. Pure-component physical parameters required for all components of the droplet are provided in Table S2. In the case of sea spray, the E-AIM (Dutcher et al., 2010; E-AIM online model, 2023) predictions of the surface tension using the ion mole ratios and the measured densities are extrapolated to the pure component. We treat sea spray as a single cosolute, using its mole-averaged molecular mass. The surface tensions of pure, non-aqueous surfactants are not known and are approximated by the surface tensions at the CMC of the surfactant in a binary aqueous solution, σ_CMC. This assumption corresponds to assuming that a pure monolayer with ${\mathit{\chi }}_{\mathrm{surfactant}}^{\mathrm{s}}=\mathrm{1}$ has formed at the CMC and may therefore in some cases lead to discontinuous changes in droplet surface tension σ and ${\mathit{\chi }}_i^{\mathrm{s}}$ when ${\mathit{\chi }}_{\mathrm{surfactant}}^{\mathrm{b}}$ reaches the CMC.

Figure S2 shows the macroscopic experimental datasets fit with the Langmuir isotherm. Monolayer model predictions for large-radius droplets (100 µm and 100 cm) are also overlaid to show that as the droplet radius is increased, the monolayer model predictions tend towards the original parameterization.

2.5 Droplet bulk depletion

The agreement between the experimentally determined surface tensions and model predictions are quantified with the mean absolute error (MAE), defined as

$$\begin{array}{}\text{(9)}& \mathrm{MAE}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^n\left|M_i-E_i\right|,\end{array}$$

where M_i and E_i are the model prediction and experimental surface tension, respectively, for data point i and N is the total number of data points. If $M_i^{\mathrm{10}}<E_i<M_i^{\mathrm{6}}$ (where $M_i^{\mathrm{6}}$ and $M_i^{\mathrm{10}}$ are the model predictions for 6 and 10 µm radii, respectively), the residual is set to zero. If $E_i>M_i^{\mathrm{6}}$, the residual is $M_i^{\mathrm{6}}-E_i$; if $E_i<M_i^{\mathrm{10}}$, the residual is $M_i^{\mathrm{10}}-E_i$. The MAEs are calculated after removing data points where the concentration is greater than the average of the effective droplet CMCs (i.e., the concentration where the surface tension plateaus). When the concentration is greater than the effective droplet CMC, nonequilibrium surface concentrations impact the measured surface tension (Bain et al., 2023b).

The MAE ratio is used to compare the models' abilities to predict the experimental data against one another:

$$\begin{array}{}\text{(10)}& {\mathrm{MAE}}_{\mathrm{ratio}}={\displaystyle \frac{{\mathrm{MAE}}_{\mathrm{monolayer}}}{{\mathrm{MAE}}_{\mathrm{simple}\mathrm{kinetic}}}}.\end{array}$$

3 Results and discussion

In this work, CTAB and SDS were chosen as commercially available cationic and anionic representatives of atmospheric surfactants. SDS is particularly environmentally relevant due to its widespread use in soaps and cleaning agents and later release during water treatment (Cochran et al., 2016; Radke, 2005). To date, cationic surfactants found in aerosol and sea surface microlayer samples during field campaigns have been quantified, but their chemical structures have not yet been identified (Burdette et al., 2022; Burdette and Frossard, 2021; Gérard et al., 2016, 2019). Generally, oxygen-to-carbon (O : C) and hydrogen-to-carbon (H : C) ratios measured with mass spectrometry show the presence of aliphatic surfactants as well as lignin-like and carboxyl-rich alicyclic molecules (Burdette et al., 2022). The O : C and H : C ratios of SDS and CTAB are in the range of surface-active organics collected in field measurements (Burdette and Frossard, 2021), and their CMCs are within the range of CMCs reported for PM₁ aerosol collected in Lyon, France (Gérard et al., 2019). Glutaric acid and NaCl were chosen as cosolutes. Glutaric acid represents a soluble organic molecule that is often used in laboratory experiments as a proxy for oxidized organic material, and it has also been identified in ambient aerosol (Bondy et al., 2018; Wu et al., 2019). NaCl is the most abundant salt in seawater and therefore sea spray aerosol (Gong et al., 2002; Jayarathne et al., 2016). Since sea spray contains a mixture of ions, including Ca²⁺ and Mg²⁺, a sea spray mimic was used as an additional cosolute to determine if the concentrations of divalent ions in sea spray aerosol near the point of cloud droplet activation would alter the partitioning of surfactants in droplets. Sea spray was made up to have the inorganic ion composition of fine-mode sea spray droplets, which have the greatest enhancement of divalent cation concentration relative to seawater (Jayarathne et al., 2016).

Figure S3 shows macroscopic surface tension data for SDS and CTAB, each with the three studied cosolutes. Macroscopic measurements of aqueous SDS and CTAB without a cosolute agree well with literature results (Zdziennicka et al., 2012). The NaCl and sea spray mimic cosolutes clearly influence partitioning of SDS and CTAB, resulting in CMCs and Langmuir isotherm parameters (Table 1) that differ by orders of magnitude from the parameters associated with the respective binary aqueous solution, as well as with glutaric acid cosolute solutions. The properties of ionic surfactants can be substantially altered by salts (Eastoe et al., 2000; El Haber et al., 2024; Iyota and Krastev, 2009; Kumar et al., 2012; Prosser and Franses, 2001; Qazi et al., 2020). Solutions containing the counter ion of the ionic surfactant reduce the surfactant's solubility, lowering the CMC. Anionic surfactant properties are also affected by divalent cations (Eastoe et al., 2000; Eastoe and Dalton, 2000; Penfold and Thomas, 2022). The effect of cosolute on the surfactant parameters is larger here for ionic surfactants than previously observed with nonionic surfactants. For nonionic surfactants, glutaric acid increased the CMC in macroscopic solutions (generally within a factor of 4), while NaCl slightly reduced it (within a factor of 2.5) (Bain et al., 2023b). In contrast, for the ionic surfactants SDS and CTAB, the addition of 0.9 M glutaric acid reduces the CMC (by approximately 30 % for SDS and 50 % for CTAB), whereas in solutions containing 0.5 M NaCl or 0.5 M cations/anions, the macroscopic CMC is reduced by more than an order of magnitude compared to the binary aqueous surfactant case.

Table 1 Langmuir isotherm parameters, calculated CMCs, and fitting parameters for the monolayer model.

Experimentally determined surface tensions for 6–10 µm radius droplets containing either SDS or CTAB and one of three cosolutes are shown in Fig. 1 along with droplet surface tension predictions from the simple kinetic model (Alvarez et al., 2012) and the monolayer model (Malila and Prisle, 2018). The predicted surface tensions shown in Fig. 1 are for droplets at 6 µm (solid) and 10 µm (dashed) radius, with the shaded region between these two predictions encompassing the experimental droplet measurement range. Vertical lines indicate the CMC determined from macroscopic measurements. The uncertainty in the droplet surface tension measurements, propagated from the uncertainty in the droplet radius and oscillation frequency, is less than 0.5 mN m⁻¹.

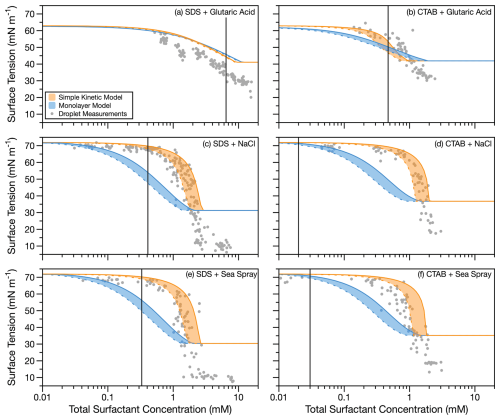
Figure 1 Comparing simple kinetic and monolayer partitioning models to experimentally measured surface tension for droplets of 6–10 µm radius. Shaded areas are predictions for droplets in this size range, with boundaries of 6 µm (solid lines) and 10 µm (dashed lines) radius. Vertical lines indicate the CMC determined from macroscopic measurements. Uncertainties in droplet surface tension measurements are smaller than the data markers.

When bulk surfactant depletion occurs, more surfactant is required to reach the CMC in the droplet bulk because a substantial fraction of molecules is removed from the bulk to populate the interface. Here we use the term “effective CMC” to describe the total surfactant concentration required to reach a plateau in droplet surface tension measurements. For SDS with glutaric acid cosolute (Fig. 1a), the macroscopic CMC and effective CMC are in close agreement (note the log scale is required to show the total surfactant concentration range for all systems, but this compresses the plateau region in panel a). This agreement indicates that there is little bulk depletion of SDS in these droplets, consistent with previous observations for surfactants with CMCs above about 5 mM (Bain et al., 2023b). In Fig. 1b–f, larger differences between the macroscopic CMCs and the effective CMC are observed, with the droplet measurements for these systems exhibiting a mean effective CMC of 2.0 ± 0.5 mM (Table 2). These effective CMCs are consistent with previous measurements for effective CMC in 6–9 µm radius droplets containing strong nonionic surfactants (effective CMC = 2.0 ± 0.3 mM when macroscopic CMC < 5 mM) (Bain et al., 2023b, 2024a). Figure S4 shows the predicted magnitude of depletion for the ionic surfactant–cosolute systems over the experimental radii and total surfactant concentrations investigated for each surfactant system. Only the SDS–glutaric acid system shows minimal depletion over the investigated radius and concentration range.

Table 2 Droplet-phase surfactant parameters. Calculated differences between droplet and macroscopic surface tension plateaus (Δσ^min) for mixtures with SDS and CTAB. Effective droplet CMC is determined from the intersection of the 6 µm radius droplet bulk depletion prediction and the macroscopic surface tension plateau region curves. Experimental effective droplet CMCs estimated from droplet measurements as the point where the surface tension reaches its minimum value. The effective CMC is also predicted for 6 µm radius droplets following the methodology from Jacobs et al. (2024).

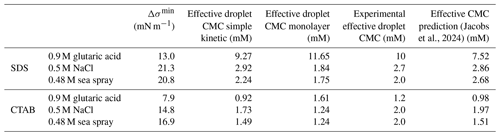
Model predictions for 6–10 µm radius droplets from both the monolayer model and the simple kinetic model in Fig. 1 reach the minimum surface tension at approximately the same total surfactant concentration as the estimated apparent CMC from the experimental droplet data (Table 2). Figure 2 compares the effective droplet CMCs predicted by the two models to those observed in the droplet measurements. The effective CMC predicted by the simple kinetic model is generally closer to the experimentally determined effective CMC, but both models agree with the experimental data within a factor of 2. Additionally, we predict the apparent CMCs for 6 µm radius droplets following the approach outlined by Jacobs et al. (2024). In their work, Jacobs et al. (2024) also use a kinetic approach based on the Langmuir isotherm. These predictions are generally in close agreement with the apparent CMCs determined from the simple kinetic model (Table 2).

Figure 2 Comparison of the apparent CMC predictions for 6 µm radius droplets from the simple kinetic and monolayer models to the experimentally determined apparent CMCs. The black 1:1 line indicates where model predictions and experimental observations are identical. Error bars have been omitted for clarity, but uncertainty in the CMC is generally within 10 %.

Although both models predict bulk depletion and similar total surfactant concentrations to reach the minimum surface tension for each surfactant system in Fig. 1, the surfactant-concentration-dependent trends in surface tension for each model are different. Generally, at low surfactant concentrations, before the effective CMC, the monolayer model predicts the reduction in surface tension with increased concentration to begin at lower concentrations and occur more gradually than the droplet measurements and the simple kinetic model predictions. For SDS and glutaric acid (Fig. 1a), the monolayer model slightly overpredicts the measured surface tension (by about 5 mN m⁻¹). For this one mixture, the droplet data appear to be biased low as the droplet measurements are also slightly lower than the macroscopic measurements. The simple kinetic model also slightly overpredicts the surface tension in the SDS and glutaric acid mixtures, but in panels (b)–(f), the simple kinetic model is in good agreement with the experimental data below the effective CMC. The mean absolute errors (MAEs) for the simple kinetic model (Table 3) are within 3.5 mN m⁻¹. Interestingly, if the macroscopic surface tension minimum limit is not imposed, the surface tension prediction from the simple kinetic model continues to capture the trend in the experimental data (Fig. S5). The general agreement between the measured surface tensions of micrometer-sized droplets and the simple kinetic model at surfactant concentrations below the effective CMC observed here is further validated by the recent work from Jacobs et al. (2024), who measured the surface tensions of SDS- and CTAB-containing droplets in an electrodynamic balance without the need for a coalescence step.

Table 3 Mean absolute error (MAE, mN m⁻¹) for model–measurement agreement and MAE ratios. Droplet datasets were cut at the effective droplet CMC before calculating MAE.

Surface tension measurements in 6–10 µm radius droplets, as well as monolayer and simple kinetic model predictions, show little difference when NaCl cosolute is replaced with sea spray (Fig. 1). Trends in experimentally determined surface tensions and model predictions are similar for NaCl and sea spray cosolutes for each surfactant. For SDS, the monolayer and simple kinetic models predict differences in effective CMCs between NaCl and sea spray cosolutes of 0.09 and 0.68 mM, respectively. For CTAB, the monolayer model and experimental data agree exactly for the effective CMC, and the difference in effective CMC is 0.24 mM for the simple kinetic model and experimental data. The effective CMCs determined experimentally for NaCl and sea spray cosolutes are separated by 0.7 mM for surfactant SDS and are identical for CTAB. The low divalent ion concentration in the sea spray droplets at a_w=0.99 does not significantly impact the surfactant partitioning in these droplets, indicating that NaCl cosolute can be used to approximate the salt component of sea spray aerosol to understand the partitioning of surfactants in aerosol containing ionic surfactants near the point of cloud droplet activation.

When the total surfactant concentration is sufficient to lower the droplet surface tension to the minimum value, large discrepancies are observed between the models (which are limited by the minimum surface tension of the macroscopic solutions) and the experimental measurements. Under high surface concentrations, droplet coalescence is expected to form a compressed film at the droplet surface (Bain et al., 2023b; Bzdek et al., 2020). Figure 3 shows the difference in minimum surface tension ($\mathrm{\Delta }{\mathit{\sigma }}^{\min }={\mathit{\sigma }}_{\mathrm{bulk}}^{\min }-{\mathit{\sigma }}_{\mathrm{droplet}}^{\min }$) as a function of macroscopic CMC. For nonionic surfactants, a clear trend in Δσ^min with CMC was previously observed (Bain et al., 2023b). The CTAB systems investigated here follow this trend closely. SDS systems also show a trend in increased Δσ^min with decreasing CMC. However, the absolute values are offset higher compared to the rest of the surfactants. The affinity for the surface appears to play a role in the divergence observed in the minimum surface tension in droplets using the droplet coalescence method. However, further investigation is required to understand the offset for droplets containing SDS.

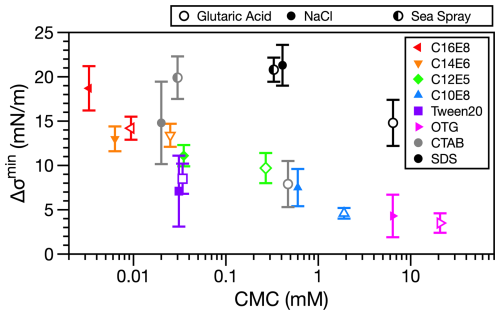
Figure 3 Difference between minimum surface tension in macroscopic measurements and droplet measurements as a function of the critical micelle concentration for each solution. Ionic surfactant systems investigated in this work are overlaid with the nonionic surfactant data from Bain et al. (2023b) and Bzdek and Bain (2023). (CmEn surfactants are linear poly(oxyethylene) alkyl ethers, Tween20 is a commercial surfactant also known as polyoxyethylene (20) sorbitan monolaurate, and OTG is octyl-β-d-thioglucopyranoside.)

MAEs for the agreements of the models with the experimentally measured droplet surface tensions and MAE ratio were calculated to compare the two models' abilities to predict the experimental data. MAEs and the MAE ratio are shown in Table 3. Generally, the simple kinetic model has lower MAEs than the monolayer model, resulting in MAE ratios between 1.33 and 6.50. SDS with glutaric acid as well as CTAB with glutaric acid and sea spray had MAE ratios > 2, indicating that the models agree or disagree with the experimental data about as equally well as one another. The remaining systems have MAE ratios > 2 indicating that the simple kinetic model agrees with the experimental data more than twice as well as the monolayer model. The underprediction of surface tension for micrometer-sized droplets containing ionic surfactants and salt cosolutes is likely due to an incomplete description of salting out. The monolayer model assumes that both the ionic surfactant and its counter ion partition to the interface together, which may not be the case under high-ionic-strength conditions. The monolayer model also uses a spherical approximation to determine the volume of the surfactant monomers, which may overestimate the amount of space each monomer occupies at the interface, resulting in an overestimate of surface coverage and thus an underprediction of surface tension. Additionally, the monolayer model uses the subcooled density of pure surfactants as an input parameter, which may not describe the density of the surfactants at the droplet interface well. Although the Langmuir isotherm does not include an interaction parameter to describe the salting out of surfactants by ionic solutes, here, the fitting parameters are found from data of the same total composition as the aerosol droplets, which accounts for any salting out. Further development of the monolayer model will seek to better describe the salting out of ionic surfactants.

Figure 4 compares the surface tension and fractional surface coverage for SDS with 0.5 M NaCl cosolute in a macroscopic solution and in a 10, 1.0, and 0.1 µm radius droplet using the simple kinetic model, which agrees well with experimental measurements. The macroscopic solution surface tension and fractional surface coverage are calculated from the Langmuir isotherm (Eq. 4) using the parameters in Table 1. Fractional surface coverage is defined as $\mathrm{\Theta }=\frac{K_{\mathrm{eq}}c}{\mathrm{1}+K_{\mathrm{eq}}c}$. In Fig. 4a, depletion of surfactant in the droplet bulk is observed as a shift to the higher total surfactant concentrations required to decrease the surface tension as the droplet radius is decreased. In this example, the difference in surface tension between a macroscopic solution and even the 10 µm radius droplet can be as high as 40 mN m⁻¹. Figure 4b shows the fractional surface coverage as a function of total surfactant concentration for the macroscopic solution and droplet. As expected from the observed difference in surface tension at total concentrations < 2 mM, more total surfactant is required to cover the same fraction of the surface in a 10 µm radius droplet than in a macroscopic solution. The total concentration required to reach a full surface coverage increases to greater than 10 and 100 mM for a 1 and 0.1 µm wet radius, respectively.

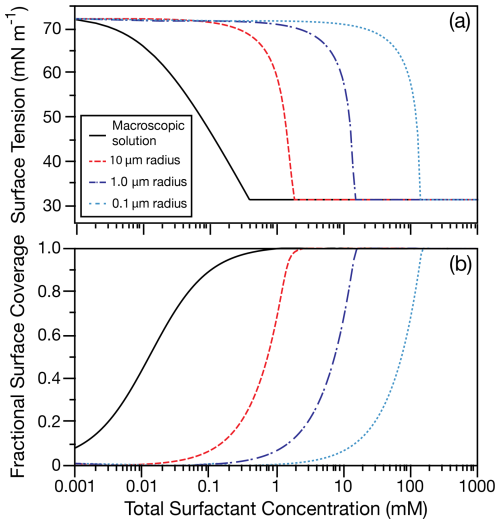
Figure 4 (a) Surface tension and (b) fractional surface coverage as a function of the total surfactant concentration for SDS with 0.5 M NaCl cosolute in a macroscopic solution from the Langmuir isotherm (black lines) and for a 10, 1.0, and 0.1 µm wet-radius droplet. Size-dependent surfactant partitioning is calculated using the simple kinetic model. At the CMC, the fractional surface coverage is 0.9998.

It is crucial to our understanding of many aerosol processes that, at equilibrium, the number of surface sites occupied in aerosol droplets is not equal to that of a macroscopic solution. Previous work has shown that the surfactant partitioning dynamics can reduce the surfactant concentration at the droplet surface (Bain et al., 2024b), but bulk depletion can also reduce the equilibrium surface concentration (Malila and Prisle, 2018). Even at a total concentration equivalent to the macroscopic CMC, a microscopic droplet containing a strong surfactant is unlikely to have all surface sites occupied. In Fig. 4b, for SDS in 0.5 M NaCl, at a total concentration equivalent to the macroscopic CMC, a 10 µm radius droplet is predicted to have a fractional surface coverage of only 0.16. Assuming the fraction of sites occupied by surface-active molecules at a 10 µm radius droplet interface is approximated by the fraction of occupied sites at the interface of a macroscopic solution would greatly overestimate the number of occupied surface sites. As the droplet radius decreases further (and SA $/$ V increases), these differences in surface tension and surface coverage widen. Such inaccuracies in surface concentration will affect predictions of reaction rates for chemical reactions at the droplet interface in addition to affecting predictions of droplet surface tension.

The results presented in this work have focused on droplets in the micrometer size range, but ambient aerosol particles that act as CCN are typically orders of magnitude smaller. Figure 5 shows predictions of the total surfactant concentration required to reach the minimum surface tension (i.e., the plateau surface tensions in Table S2) in 0.1 and 1.0 µm wet-radius droplets. Data presented here for SDS and CTAB with glutaric acid, NaCl, and sea spray cosolutes are included, in addition to the 12 nonionic surfactant systems presented by Bain et al. (2023b). These surfactants have a wide range of surface activities, with macroscopic CMCs between 1 µM and 10 mM. The box plot shows that total surfactant concentrations in the range of tens to the low hundreds of millimolar are required for accumulation-mode aerosol droplets to reach their minimum surface tension, regardless of surfactant strength. These concentrations are in line with previously reported surfactant concentrations from field studies (Gérard et al., 2016, 2019), suggesting that the surface tension of ambient aerosol could be lowered by the presence of surfactants during hygroscopic growth. However, in order to determine the impact on cloud droplet activation, we must also consider the impact of this bulk-to-surface partitioning on the droplet's water activity, which is beyond the scope of this work.

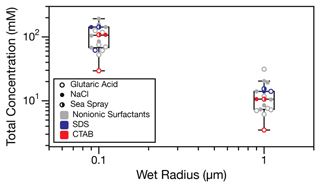
Figure 5 Box plot showing the total surfactant concentration required to reach the minimum surface tension in droplets with wet radii of 0.1 and 1 µm, using the simple kinetic partitioning model. A total of 18 surfactant systems are included, 12 nonionic ones (Bain et al., 2023b) and the 6 ionic ones from this work. Overlaid total surfactant concentration data points for each system are offset to improve clarity.

4 Conclusions

We experimentally measured the surface tensions of 6–10 µm radius aerosol droplets containing ionic surfactants and cosolutes and compared the results to two independent partitioning models. The macroscopic CMCs of ionic surfactants are greatly reduced in the presence of salts, which enhances the surface activity of the surfactants. In sea spray aerosol, which includes both salts and ionic surfactants, interactions between salts and surfactants result in more bulk depletion than for a droplet of the same size and surfactant concentration but containing an organic cosolute. Bulk surfactant depletion was observed for all systems except for glutaric acid–SDS in this droplet size range. The total ionic surfactant concentrations required to reach the minimum surface tension agree with previous observations and predictions for nonionic surfactants, providing additional evidence that as the SA $/$ V ratio increases, the size of the surfactant molecules at the interface plays a larger role than the surface affinity of the surfactant in determining surface coverage. This phenomenon is due to bulk surfactant depletion and further highlights that macroscopic measurements are insufficient to predict the equilibrium surface coverage and surface tension of picoliter-volume and smaller-volume droplets containing strong ionic surfactants and salts without applying partitioning models that account for the SA $/$ V ratio of the droplet.

For aerosol droplets containing ionic surfactants and cosolutes, the simple kinetic model better described the changing surface tension with total surfactant concentration in the experimental data than the monolayer model, likely due to an incomplete description of salting out in the monolayer model or overestimation of the volume taken up by the surfactant at the interface. However both models predicted similar total surfactant concentrations to reach the effective droplet CMC. Although Ca²⁺ ions have been shown to affect the partitioning of ionic surfactants in macroscopic solution, at the low concentrations in aerosol droplets containing the ratio of ions expected from sea spray under high-relative-humidity conditions (water activity = 0.99), no difference was observed in the partitioning of SDS or CTAB between NaCl-containing and sea-spray-mimic-containing droplets. These observations suggest that, at least near the point of cloud droplet activation, the impact of divalent ions on the surface tension and surface coverage of ionic-surfactant-containing droplets is likely small, and NaCl is an acceptable surrogate for sea spray in laboratory studies of surface tension. Surface concentrations of sea spray containing strong, ionic surfactants in dilute droplets can be determined using a partitioning model based on mixtures of NaCl and surfactants rather than sea spray mimic, potentially simplifying required laboratory experiments and modeling efforts aiming to understand surface chemistry at the interfaces of sea spray aerosol. Regardless of cosolute or surfactant identity, the simple kinetic model predicts that surfactant concentrations in the range of tens to the low hundreds of millimolar are required to reduce accumulation-mode aerosol surface tension to its minimum value. These concentrations are in line with surfactant concentrations found in aerosol samples collected during field studies, suggesting that there is sufficient surfactant in some ambient aerosol to reduce its surface tension during hygroscopic growth.