the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Desorption lifetimes and activation energies influencing gas–surface interactions and multiphase chemical kinetics
Daniel A. Knopf
Markus Ammann
Thomas Berkemeier
Ulrich Pöschl
Adsorption and desorption of gases on liquid or solid substrates are involved in multiphase processes and heterogeneous chemical reactions. The desorption energy (), which depends on the intermolecular forces between adsorbate and substrate, determines the residence time of chemical species at interfaces. We show how and temperature influence the net uptake or release of gas species, the rates of surface–bulk exchange and surface or bulk reactions, and the equilibration timescales of gas–particle partitioning. Using literature data, we derive a parameterization to estimate for a wide range of chemical species based on the molecular mass, polarizability, and oxygen-to-carbon ratio of the desorbing species independent of substrate-specific properties, which is possible because of the dominant role of the desorbing species' properties. Correlations between and the enthalpies of vaporization and solvation are rooted in molecular interactions. The relation between and desorption kinetics reflects the key role of interfacial exchange in multiphase processes. For small molecules and semi-volatile organics (VOC, IVOC, SVOC), values around 10–100 kJ mol−1 correspond to desorption lifetimes around nanoseconds to days at room temperature. Even higher values up to years are obtained at low temperatures and for low volatile organic compounds (LVOC, ELVOC/ULVOC) relevant for secondary organic aerosols (SOA). Implications are discussed for SOA formation, gas–particle partitioning, organic phase changes, and indoor surface chemistry. We expect these insights to advance the mechanistic and kinetic understanding of multiphase processes in atmospheric and environmental physical chemistry, aerosol science, materials science, and chemical engineering.
- Article
(10129 KB) - Full-text XML
-
Supplement
(1447 KB) - BibTeX
- EndNote
The interaction of gases with condensed phase matter via heterogeneous or multiphase reactions is of importance for a variety of disciplines such as chemical engineering, catalysis, materials science, and environmental and atmospheric chemistry (Cussler, 2009; Chorkendorff and Niemantsverdriet, 2007; Finlayson-Pitts and Pitts, 2000; Ravishankara, 1997; Solomon, 1999; Hoffmann et al., 1995; Beller et al., 2012; Hanefeld and Lefferts, 2018). In the atmosphere, gas–particle interactions and multiphase chemical processes involve gaseous and condensed-phase species manifesting in condensation, gas–particle partitioning, and alteration in the physicochemical properties of aerosol particles and cloud droplets (Pöschl et al., 2007; Kolb et al., 2010; Rudich et al., 2007; George and Abbatt, 2010; Pöschl and Shiraiwa, 2015; Moise et al., 2015; Ammann et al., 2013; Crowley et al., 2013; Kroll et al., 2011; Donahue et al., 2011; Jimenez et al., 2009; Abbatt and Ravishankara, 2023; Ravishankara, 1997; Penkett et al., 1979; Hoffmann and Edwards, 1975; Davidovits et al., 2006). The dramatic effects of multiphase reactions in the atmosphere are most impressively demonstrated by the large-scale stratospheric ozone depletion (ozone hole) over the South Pole during Antarctic winter and spring, where inactive gaseous chlorine species are converted to active gas species on cloud particles (Solomon, 1999; Rowland, 1991; Peter, 1997; Koop et al., 1997; Müller et al., 1997; Carslaw et al., 1997).
Atmospheric aerosol particles and environmental interfaces are often chemically complex systems comprising multiple components in multiple phases. The large compositional variety of airborne particulate matter and gas species including reactive radicals, oxidants, and volatile inorganic and volatile organic compounds (VOCs), in addition to the wide temperature and humidity range present in the atmosphere, poses challenges to resolve multiphase chemical kinetics on a molecular level. The underlying molecular processes are important for the scientific understanding and reliable description of gas uptake and chemical transformation of aerosols (Shiraiwa et al., 2011a; Berkemeier et al., 2013; Zhou et al., 2013; Abbatt et al., 2012; Kolb et al., 2010; Schwartz, 1986; Hanson and Lovejoy, 1995; Hanson et al., 1996; Shen et al., 2022; Willis and Wilson, 2022), the chemical evolution of secondary organic aerosol (SOA) including the partitioning of semivolatile species (Shiraiwa and Seinfeld, 2012; Shiraiwa et al., 2013b; Perraud et al., 2012; Donahue et al., 2011; Ingram et al., 2021), and the impact of multiphase reactions on the particles' activation as cloud condensation nuclei (CCN) or ice-nucleating particles (INPs) (Slade et al., 2015, 2017; Petters et al., 2006; Wang et al., 2012; Wang and Knopf, 2011; Knopf et al., 2018; Knopf and Alpert, 2023).
Atmospheric multiphase reactions usually involve an adsorbed state of gas species at the surface of a liquid or solid material (Langmuir, 1915, 1916, 1918; IUPAC, 1997), which can be regarded as physisorption or chemisorption depending on the nature and intensity of the surface interaction. Physisorption is caused by weak intermolecular interactions (van der Waals, hydrogen bond, ionic and hydrophobic interactions, Table 1) with energies up to ∼50 kJ mol−1, whereas chemisorption involves changes of chemical bonds with higher interaction energies (Desjonqueres and Spanjaard, 1996; Masel, 1996; Pöschl et al., 2007). The phenomenon of reversible adsorption is easiest to depict on solid surfaces but applies also to liquid surfaces, where it is coupled to the exchange with the bulk liquid (Langmuir, 1915, 1916, 1918; Nathanson, 2004; Ringeisen et al., 2002a, b; Behr et al., 2001; Morris et al., 2000; Masel, 1996; Nathanson et al., 1996; Rettner et al., 1996; Donaldson and Anderson, 1999; Donaldson et al., 1995; Donaldson, 1999; Pöschl et al., 2007).
According to the Frenkel equation, the desorption lifetime (τdes) of a surface-adsorbed chemical species (adsorbate) follows an Arrhenius-type behavior (Arrhenius, 1889a, b; Laidler, 1949; Frenkel, 1924; Laidler et al., 1940):
where kdes is a first-order desorption rate coefficient, Ades is a pre-exponential factor, in more detail discussed below, R is the gas constant, and T is the temperature. is the desorption energy with the energy reference of the gas molecule at rest at T=0 K. is referred to as the activation energy of desorption. In terms of the theory of the kinetics of desorption, desorption is always considered an activated process, independent of whether corresponds to just the energy difference between gas and adsorbed state or also include an energy barrier on top of that (Knopf and Ammann, 2021). In case of physisorption, is equal to the negative value of the enthalpy of adsorption with a correction for the change in degree of freedom between gas and adsorbed phase (see below and Knopf and Ammann, 2021; Kolasinski, 2012). In turn, in the other direction, for the kinetics of the process from the gas phase to the adsorbed state, the adsorption rate normalized to the gas kinetic collision rate is often expressed as the surface accommodation coefficient as discussed below.
Atmospheric trace gases and water vapor adopt reversibly adsorbed states on aerosol, cloud, and ground surfaces over a wide range of temperatures from below 200 to above 300 K. The rate of interfacial processes, which may involve reversible, reactive, and catalytic steps, generally depends on the concentration of surface-adsorbed reactants and hence on τdes. Especially at low temperatures, high values of τdes can (over)compensate for the low rates of thermally activated chemical reactions and diffusion and thereby enhance the overall gas uptake (Ammann et al., 2013; Crowley et al., 2013; Kolb et al., 2010; Pöschl et al., 2007).
Factors influencing gas uptake are competitive co-adsorption of other species (Pöschl et al., 2001, 2007; Slade and Knopf, 2014; Kaiser et al., 2011; Springmann et al., 2009; Shiraiwa et al., 2009), solvent dynamics and polarization effects (Ringeisen et al., 2002b; Morris et al., 2000; Klassen et al., 1997; Nathanson et al., 1996; Jungwirth et al., 2006), thermodynamics and kinetics of surface–bulk exchange and bulk diffusivity in viscous liquids (Lakey et al., 2016; Berkemeier et al., 2016; Steimer et al., 2015; Shiraiwa et al., 2013a, 2014; Houle et al., 2018; Wiegel et al., 2017; Davies and Wilson, 2015; Marshall et al., 2016, 2018), and phase separations or heterogeneous structures in the condensed phase (You and Bertram, 2015; You et al., 2012, 2014; Bertram et al., 2011; Huang et al., 2021).
Apart from adsorption and desorption, further processes influencing gas–particle interactions and multiphase chemical kinetics include mass transport to the condensed phase by gas-phase diffusion and accommodation at the interface; chemical reactions at the surface following Langmuir–Hinshelwood or Eley–Rideal type mechanisms; and dissolution, diffusion, and chemical reactions in the bulk. Together with desorption, these processes may proceed sequentially or in parallel for multiple chemical species, which can be described by appropriate differential equations and numerical models (Shiraiwa et al., 2009, 2010, 2012; Ammann and Pöschl, 2007; Pöschl et al., 2007; Wilson et al., 2022).
Traditionally, the uptake of trace gases by solid and liquid particles or substrates has often been analyzed by the so-called resistor model, treating each of the above processes in analogy to parallel or serial resistors in an electrical circuit (Schwartz, 1986; Worsnop et al., 2002; Hanson and Lovejoy, 1995; Hanson et al., 1994; Ammann et al., 2013; Crowley et al., 2010). Despite constraints and limitations such as the required approximations regarding steady state and mixing, and a limited capability to describe multicomponent systems, the resistor model has proven to be useful for the investigation and characterization of various processes and substrates, including mineral dust, ice, sulfuric acid, and organic and inorganic particles (Pöschl et al., 2007; Hanson, 1997; Davidovits et al., 2006; Crowley et al., 2010; Kolb et al., 2010; Hanson et al., 1994; Ammann et al., 2003, 2013; Knopf et al., 2005; Li and Knopf, 2021; Schwartz, 1986). In the resistor model approach, the uptake of a gas species with reaction at the surface and in the bulk is described by the following or equivalent equations (Pöschl et al., 2007):
Here, γ is the uptake coefficient, defined as the overall loss rate from the gas phase normalized to the gas kinetic collision rate, and αs is the surface accommodation coefficient, which represents the probability for a gas molecule colliding with the surface to be accommodated at the surface for period longer than the duration of an elastic scattering process (Pöschl et al., 2007). This parameter thus represents the adsorption rate normalized to the gas kinetic collision rate. The term Γs represents the normalized loss rate due to surface reaction, Γsb is the normalized rate of surface to bulk transfer, and Γb is the normalized loss rate in the bulk phase induced by solubility, diffusion, and reaction (Hanson et al., 1994; Ammann et al., 2013; Crowley et al., 2013; Kolb et al., 2010; Ammann and Pöschl, 2007; Pöschl et al., 2007; Wilson et al., 2022; Shiraiwa and Pöschl, 2021). By virtue of the coupled nature of the involved elementary processes, the desorption rate coefficient can influence the rates of all other surface and bulk processes involving this species; i.e., kdes can influence Γs, Γsb, and Γb (Pöschl et al., 2007). For example, the terms Γs, Γsb, and Γb governed by the competition between desorption and surface reaction, between desorption and surface to bulk transfer, or between desorption and surface to bulk transfer coupled to reaction and diffusion, respectively, are inversely proportional to kdes and can be expressed as follows:
Here, ks is a first-order rate coefficient of chemical reaction at the surface; ksb is a first-order rate coefficient for the transfer of molecules from the surface into the bulk (solvation); kb is a first-order rate coefficient of chemical reaction in the bulk; Db is the diffusion coefficient of the trace gas in the bulk; kbs is a first-order rate coefficient for the transfer of molecules from the bulk to the surface. Even though the rate coefficients for these elementary processes is independent of kdes, the overall normalized rates of Γs, Γsb, and Γb are. Similarly, the overall rate of transfer of a gas molecule into the bulk of a liquid or (semi)solid particle (independent of whether diffusion and reaction therein contributes to loss) also depends on kdes and can be expressed by the bulk accommodation coefficient, αb (Pöschl et al., 2007; Edwards et al., 2022):
Hence, the desorption rate coefficient is a critical parameter influencing the overall rates involved in the uptake of a gas species by condensed matter (Li and Knopf, 2021).
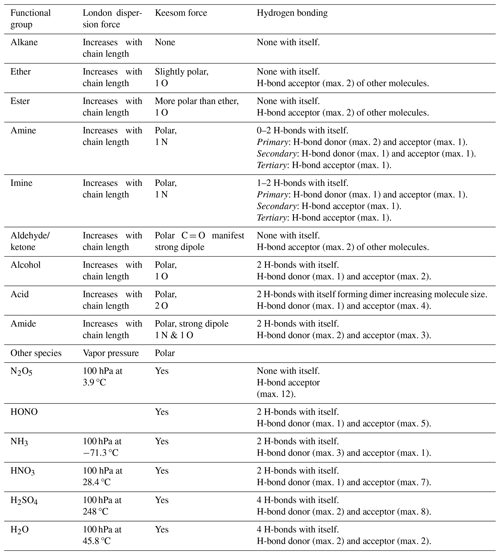
Table 1Intermolecular forces for selected functional groups and gases (Jeffrey, 1997; Jeffrey and Saenger, 1991; Vinogradov and Linnell, 1971; IUPAC, 1997).
The role of reversible adsorption and desorption has been addressed in many studies of gas uptake and heterogeneous chemistry in particular for the decoupling of mass transport and chemical reaction (Kolb et al., 1995; Hanson and Ravishankara, 1991; Kolb et al., 2010; Ammann et al., 2013; Crowley et al., 2013; Pöschl and Shiraiwa, 2015; Tabazadeh et al., 1994; Peter, 1997; Carslaw et al., 1997; Hanson et al., 1994; Hanson and Lovejoy, 1995). More recently, kinetic multilayer model analyses of measured uptake coefficients for OH radicals on levoglucosan substrates (Arangio et al., 2015) and the heterogeneous reaction of ozone with shikimic acid (Berkemeier et al., 2016; Steimer et al., 2015) and oleic acid aerosol (Berkemeier et al., 2021) demonstrated the complex dependency of the reactive uptake coefficient on the elementary steps, such as surface accommodation, desorption, surface reaction, and bulk diffusion by virtue of Eqs. (3)–(5). The range of experimental conditions was not sufficient to constrain the associated coefficients unambiguously. To determine a best estimate for the surface reaction rate coefficient, it was thus necessary to assume a realistic value for αs and τdes derived from molecular dynamics simulations (Vieceli et al., 2005; von Domaros et al., 2020). Li and Knopf (2021) made use of the temperature-dependent measurement of OH uptake to decouple τdes from surface reactivity. The intimate coupling of adsorption and desorption with other multiphase processes has also been discussed in the context of many other reaction systems. Ground-breaking work driving much of the developments of the kinetic concepts introduced above was directed at halogen activation on stratospheric aerosol and polar stratospheric clouds (Tabazadeh et al., 1994; Peter, 1997; Carslaw et al., 1997; Hanson et al., 1994; Hanson and Lovejoy, 1995). Others include the uptake of SO2 into sulfuric acid (Jayne et al., 1990; Ammann and Pöschl, 2007), adsorption of acetone on ice and HNO3 on mineral dust (Bartels-Rausch et al., 2005; Vlasenko et al., 2009; Cwiertny et al., 2008; Usher et al., 2003), ozonolysis in liquid, viscous, and solid particles (Knopf et al., 2005; Berkemeier et al., 2016; Steimer et al., 2015; Shiraiwa et al., 2011a; Hearn and Smith, 2007; Pöschl et al., 2001; Shiraiwa et al., 2009; Zhou et al., 2013; Kahan et al., 2006; Kwamena et al., 2004; Mu et al., 2018; Knopf et al., 2011; Willis and Wilson, 2022), and gas–particle partitioning of SOA (Shiraiwa et al., 2013a; Ingram et al., 2021; Schervish and Shiraiwa, 2023). Accordingly, the design and interpretation of heterogeneous and multiphase reaction rate measurements should include a careful assessment of whether reversible adsorption is an important or even rate-limiting step, whereby the applicable kinetic regime may vary with reaction time and conditions (Berkemeier et al., 2013, 2016; Shiraiwa et al., 2014; Ingram et al., 2021; Willis and Wilson, 2022). Hence, desorption lifetimes and related activation energies are important for describing the interaction of gas phase and condensed phase species.
To address and elucidate these issues, the remainder of this article is structured as follows: in Sect. 2, we discuss the molecular interactions underlying adsorption and desorption, and we outline the relevant thermodynamic and kinetic equations and parameters. In Sect. 3, we compile and present a comprehensive set of desorption energies and thermodynamic parameters for environmentally and atmospherically relevant gas species and substrates. In Sect. 4, we evaluate the role of the desorption energy in reactive and non-reactive gas uptake by solid and liquid substrates considering characteristic tropospheric temperatures by exploratory kinetic flux model simulations. In Sect. 5, we develop and present a simplified parameterization for estimating based on the gas species' polarizability and oxygen-to-carbon (O : C) ratio. Section 6 outlines the role of in selected atmospheric implications including the formation and properties of viscous secondary organic aerosol (SOA). We conclude the document with a summary and open questions.
A detailed discussion of the microscopic and thermodynamic treatments of adsorption and desorption and implications for uncertainties in is given in Knopf and Ammann (2021). Here we provide the key relationships and concepts needed to follow our assumptions when applying literature-obtained values for derivation of a parameterization.
Typically, the adsorption rate is a measure of the number of gas molecules that adsorb on the surface as a consequence of gas kinetic collisions. As mentioned above, in the atmospheric sciences this is often expressed with the surface accommodation coefficient αs (Kolb et al., 2010), operationally defined as the probability that a gas kinetic collision leads to adsorption. The adsorbed molecules may be considered an ideal 2D gas, meaning that the molecules have equilibrated with the surface in terms of the degrees of freedom perpendicular to the surface but may still retain some kinetic energy parallel to the surface. Alternatively, the adsorbed molecules may be considered an ideal 2D lattice gas, where the degrees of freedom in the horizontal plane are restricted to vibrations. Also, other models describing intermediate situations have been suggested (Savara et al., 2009; Campbell et al., 2016; Kisliuk, 1957). Here, we use αs to describe the rate of adsorption into either adsorbed state. The term thermal accommodation coefficient, αt, is commonly used for the case where the adsorbed molecule is fully thermally equilibrated with the substrate, thus close to the case of the ideal 2D lattice gas. Adsorption can be considered a non-activated process, though in the presence of an energy barrier, adsorption has to be treated as an activated process (Knopf and Ammann, 2021). The corresponding energy barrier directly impacts αs (Knopf and Ammann, 2021). In contrast, desorption is always treated as an activated process, even in the absence of an energy barrier. The explicit treatment of an additional energy barrier when deriving adsorption and desorption rates is given in Knopf and Ammann (2021). Here we solely consider as reported in the literature, independent of whether an additional activation barrier was included in the analysis. As discussed below, the choice of adsorbate model and standard state will impact the value and uncertainties in (Knopf and Ammann, 2021; Savara, 2013; Campbell et al., 2016).
Adsorption proceeds spontaneously and this implies an exergonic process with the thermodynamic condition (Bolis, 2013):
where represents the standard Gibbs free energy change of adsorption, is the standard enthalpy change of adsorption (in this case negatively defined), is the standard entropy change of adsorption, and T is temperature. Adsorption of a gas on a substrate results in an increase of order, thus, . This is because the degrees of freedom of the adsorbed molecules are more constrained than in the gas phase. Often, the adsorbed molecule may be considered a 2D ideal gas, a 2D ideal lattice gas, or an ideal hindered translator on the surface, with the motion perpendicular to the surface strongly constrained but with varying freedom parallel to the surface (Hill, 1986; Campbell et al., 2016; Savara et al., 2009; Sprowl et al., 2016). Since , the change in enthalpy has to be negative. The adsorption enthalpy is determined by the binding energy of a gas on the surface, thus on the molecular interactions between gas species and substrates, including hydrogen bonds and van der Waals forces (Poe et al., 1988; Valsaraj and Thibodeaux, 1988; Valsaraj, 1988a, b; Nguyen et al., 2005; Goss, 1993, 1994b; Valsaraj, 1994; Valsaraj et al., 1993). The van der Waals forces comprise London dispersion forces between instantaneously induced dipoles, Debye forces between permanent and induced dipoles, and Keesom forces between permanent dipoles (IUPAC, 1997). For organic molecules, the strength of both van der Waals and hydrogen bonds depends on the polarity of functional groups and commonly follows the order (Jeffrey, 1997; Jeffrey and Saenger, 1991; Vinogradov and Linnell, 1971)
Table 1 gives an overview of intermolecular forces active among functional groups present in typical gas- and condensed-phase atmospheric species. While all molecules exhibit van der Waals forces, their thermodynamic properties are largely determined by the number and type of hydrogen bonds they can form. The presence of charged groups, e.g., due to a dipole moment, can significantly increase binding energy. The hydrogen bond strength in liquid water is around 10–19 kJ mol−1 (Hakem et al., 2007), and with a few exceptions, usually involving fluorine, the energies associated with hydrogen bonding are typically less than 20–25 kJ mol−1 per hydrogen bond (Steiner, 2002; Jeffrey, 1997; Jeffrey and Saenger, 1991; Brini et al., 2017; IUPAC, 1997).
The complexity of the interaction between adsorbate and substrate can go beyond the 2D ideal gas, 2D ideal lattice gas, and hindered translator model depending on how physisorption and chemisorption are considered. For example, the Kisliuk precursor mechanism allows for more complex configurations of the adsorbate that could include adsorbate–adsorbate interactions (Kisliuk, 1957, 1958; Tully, 1994; Campbell et al., 2016). Hence, the overall adsorbate–substrate binding energy may involve contributions from adsorbate–surface as well as adsorbate–adsorbate interactions (see, e.g., Meyer et al., 2001). Moreover, the binding energy may vary between different types of adsorption sites co-existing on real surfaces, depending on the morphology and chemical heterogeneities of the substrate (Kolasinski, 2012). In view of the complex mixture of substances present in the atmosphere, such effects and variations are not explicitly resolved in this study. Instead, we assume that the energetics of reversible adsorption on atmospheric surfaces can be approximated by effective average values characterizing the binding energy to the substrate. The assumption of reversible adsorption has been crucial in studies of gas uptake and heterogeneous or multiphase chemical reactions when decoupling mass transport and chemical reaction (Kolb et al., 2010; Hanson and Ravishankara, 1991; Ammann et al., 2013; Crowley et al., 2013; Pöschl and Shiraiwa, 2015; Li and Knopf, 2021). The assumption of reversible adsorption directly leads to and , where and represent the changes in the desorption enthalpy and entropy, respectively.
The free energy change is the driving force for desorption from the thermodynamic point of view. The Frenkel equation, given by Eq. (1), is usually applied to describe the kinetics of desorption. By itself it does not differentiate between physisorption and chemisorption. For the description and understanding of atmospheric heterogeneous and multiphase kinetics, it is useful to treat chemisorption as a chemical reaction following physisorption (Pöschl et al., 2007; Hanson et al., 1994; George and Abbatt, 2010), as expressed in Eqs. (2) to (5). We note that the energy range of 50 kJ mol−1 mentioned above to distinguish between physisorption and chemisorption is not necessarily appropriate, if chemisorption is reflecting the fact that chemical bonds are formed or disrupted. Large molecules may undergo a multitude of van der Waals and hydrogen bonds adding up to large interaction energies, which would still be considered physisorption. As outlined above, for these cases we regard the adsorption process to be reversible.
Knopf and Ammann (2021) have provided the thermodynamic and microscopic equations, the latter based on conventional transition state (TS) theory, that are implicitly included in the Frenkel equation, while accounting for the choice of standard states. For example, for the case of a 2D ideal gas as adsorbate model, the desorption rate expressed in thermodynamic quantities is
where κ is a transmission coefficient giving the probability with which an activated complex proceeds to desorption (Kolasinski, 2012), kB is the Boltzmann constant, and h is the Planck constant. Furthermore, we assume the standard concentration of molecules in the TS, , is equal to the standard concentration of adsorbed molecules, , i.e., .
In microscopic quantities, kdes is derived as
where and are the standard partition functions for the TS and adsorbate, respectively, evaluated using standard molar volume and area. Equations (8) and (9) clearly demonstrate the importance of the choice of standard state when comparing measured kdes and evaluated .
Looking at the equations for kdes allows one to derive the pre-exponential factor of the Frenkel equation as (Knopf and Ammann, 2021)
where and qads,2D are the partition functions for the TS and adsorbate, respectively. The microscopic interpretation of Ades shows that Ades depends on temperature and the choice of adsorbate model, expressed as partition functions. The thermodynamic interpretation of Ades demonstrates its dependency on standard concentrations and the change in entropy when desorbing from the substrate surface into the activated TS.
We can now interpret Ades for the case of a 2D ideal gas adsorbate model. If we assume κ≈1, and adsorbate and TS are 2D ideal gases with similar degrees of freedom (neglecting vibrations), i.e., , then we obtain s−1 at room temperature (298 K). This is the commonly applied value for the pre-exponential factor. In this case, Eq. (10) demonstrates that the change in must be negligible. However, significant deviations from this benchmark factor can occur. For example, if going from the adsorbate state to the activated TS coincides with , and thus , implying more degrees of freedom in the TS, then Ades>1013 s−1. In contrast, if the TS is more constrained, e.g., only a limited number of molecular orientations are allowed, then . This yields , and as a consequence Ades<1013 s−1. A similar analysis has been provided for the 2D ideal lattice gas adsorbate model (Knopf and Ammann, 2021). Ades varies between 180 and 300 K for a 2D ideal gas and 2D ideal lattice gas adsorbate model by about a factor of 2 and 3, respectively, indicating minor temperature effects (Knopf and Ammann, 2021). However, Ades can differ by about 3 orders of magnitude between the 2D ideal gas and 2D ideal lattice gas adsorbate models.
Experimental studies usually yield pre-exponential factors in the range between 1×1011 and 1×1012 s−1 for smaller molecules such as methane and 1×1013 s−1 for larger alkanes (Fichthorn and Miron, 2002). For large adsorbates, Ades can be several orders of magnitude larger (Fichthorn and Miron, 2002). For example, adsorption of benzene and toluene by graphite surfaces exhibit Ades of about 1015 and 1019 s−1, respectively (Ulbricht et al., 2006). In general, the larger the adsorbate molecule, the larger the Ades (Ulbricht et al., 2006).
Nevertheless, for this study and the compilation of literature data of , we have assumed a constant pre-exponential factor s−1, being aware of the underlying assumptions discussed above. We justify this approach by noting that our aim is to derive estimates for complex substrate systems, including multicomponent and multiphase aerosol particles, which will impose additional uncertainties in . Due to the involvement of entropic contributions to the pre-exponential factor, experimentally derived Ades values often contain not well-documented implicit standard-state assumptions (related to experimental surface-to-volume ratios) (Donaldson et al., 2012a; Campbell et al., 2016; Savara, 2013) and thus carry more uncertainty than the obtained from the slope of temperature-dependent data.
Figure 1 displays the dependency of τdes on and temperature using Eq. (1). As illustrated in Fig. 1a, the temperature dependency of τdes increases with increasing . Calculations have been performed with Ades= 1013 s−1, while the shading represents the application of Ades being 1 order of magnitude greater or smaller, thereby covering the typical temperature dependency of Ades. Clearly, temperature can significantly increase the residence time of a molecule on the substrate surface, by several orders of magnitude, thereby, potentially, allowing different reaction pathways. It is also evident that uncertainties in Ades directly translate into corresponding uncertainties in τdes. Hence, assuming Ades=1013 s−1 in the analysis of literature data will yield uncertainties in values. For example, 1 order of magnitude uncertainty in Ades changes by ∼ 4–6 kJ mol−1 over a temperature range of 210 to 300 K. Conversely, an uncertainty of by 5 kJ mol−1 imposes an uncertainty in τdes of about a factor of ∼ 7–17 for a similar temperature range. These interdependencies are further outlined in Fig. 1b showing typical τdes for given temperatures and , again derived assuming Ades=1013 s−1. This discussion implies an uncertainty in our values of about ±5 kJ mol−1. However, as outlined in detail in Knopf and Ammann (2021), additional uncertainties in can arise when the appropriate adsorbate model is not known and if the surface coverage of the adsorbate is uncertain. For example, for a given τdes, can differ by 10–15 kJ mol−1 when assuming either a 2D ideal gas or 2D ideal lattice gas adsorbate model. If a surface is assumed to be pristine but actual coverage is about 20 %, may be uncertain by 10–20 kJ mol−1. In summary, literature values applied in this analysis, assuming a conservative estimate, may be uncertain by up to ∼ ±15 kJ mol−1.
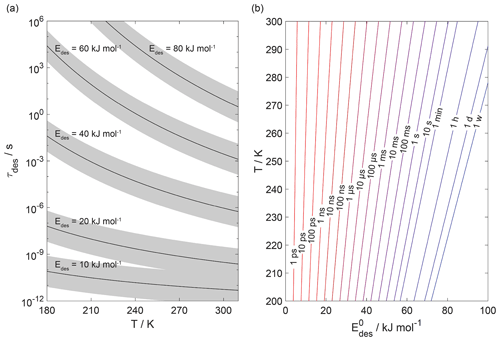
Figure 1The dependence of the desorption lifetime (τdes) on temperature (T) and desorption energy (). (a) τdes as a function of T for various values. The shaded area covers the range of the pre-exponential factor (Ades) varied by ±1 order of magnitude. (b) Iso-τdes lines for various combination of T and . All presented data calculated applying Eq. (1) and using s−1.
In the formulation of the kinetic and thermodynamic concepts and expressions, we have not made an explicit assumption about the physical state of the condensed phase – solid, liquid, crystalline, or amorphous. Lattice gas statistics can be applied generally in different dimensions and has been used for liquids, sorption of ions to proteins, or polymer wires (Hill, 1986). In spite of the simplifying assumptions, we use the equations summarized above and derived in more detail in Knopf and Ammann (2021) for all substrates, including liquids. This is straightforward for poorly soluble gases. For soluble gases, however, the full thermochemical cycle also involves the dissolved state (Donaldson, 1999). We also note that the system free energy change upon adsorption of a gas on a liquid manifests in a surface tension change, with the Gibbs adsorption isotherm relating the surface tension change to surface excess (Kolasinski, 2012; Donaldson, 1999). The manifestation of the change in surface tension convolutes the complex response of structure and dynamics at a liquid interface to an adsorbing molecule (Brini et al., 2017). Depending on the polarity of the adsorbate, the structural features of the interface may then also deviate significantly from that of an adsorbate on a solid surface, as exemplified in recent theory work by Cruzeiro et al. (2022) and Galib and Limmer (2021) for the interaction of N2O5 with water.
To derive a parameterization of applicable to typical gas–aerosol particle systems, literature values of reflecting typical atmospheric constituents or serving as aerosol surrogates have been compiled. If available, reflects values derived from lowest surface coverage, preferentially below one monolayer. Tables A1–A7, A8, and A9–A15 provide thermodynamic and physicochemical literature values for gas-to-solid, gas-to-ice, and gas-to-liquid substrate interactions, respectively. For derivation of and τdes values, we use Eq. (1) and assume Ades=1013 s−1, if not otherwise noted. We assume the temperature effect on Ades (proportional to T, see Eq. 10) and changes in the desorption entropy to be negligible compared to the Arrhenius factor (Eq. 9). The tables include the parameters , τdes, and for the gas species the molar mass (M), enthalpy of vaporization (ΔHvap), polarizability (α), dipole moment (μ), O : C, and enthalpy of solvation (ΔHsol). Lastly, the dielectric constant or relative permittivity of the substrate (εr) is given. values are obtained from different experimental techniques and theoretical studies described briefly below.
3.1 Experimental and theoretical techniques yielding desorption energies
Temperature programmed desorption (TPD), sometimes also termed thermal desorption spectroscopy (TDS), is an experimental technique where the flux of desorbing molecules is observed as the surface temperature is increased. TDS can yield coverages, activation energies, and pre-exponential factors for desorption (Ulbricht et al., 2006). Thermal gravimetry with differential scanning calorimetry (TG-DSC) determines the amount and rate (velocity) of change in the mass of a sample as a function of temperature or time in a controlled atmosphere in addition to thermophysical and thermoplastic properties derived by DSC (Giraudet et al., 2006). In general, if heats of adsorption are measured experimentally by, e.g., calorimetric methods, the accurate thermodynamic definitions have to be applied since heat is not a state function (Bolis, 2013). In Knudsen cells and diffusion tubes coupled to mass spectrometric detection (KN), the rate of molecules desorbing from a substrate can be selectively measured (Caloz et al., 1997; Koch and Rossi, 1998b; Tolbert et al., 1987; Alcala-Jornod et al., 2000). Scattering experiments of molecular beams (MBs) are applied to directly measure desorption from and adsorption of gas species to solid or liquid substrates (Thomson et al., 2011; Morris et al., 2000; Nathanson et al., 1996). While straightforward in use and interpretation for solid surfaces in high vacuum, the development around using MB techniques for atmospherically relevant volatile liquids is experimentally challenging, and also data interpretation with respect to desorption is less straightforward (Nathanson, 2004; Ringeisen et al., 2002b; Morris et al., 2000; Klassen et al., 1997; Nathanson et al., 1996; Gao and Nathanson, 2022), as discussed below. Inverse gas chromatography (IGC) applies the solid of interest as the chromatographic sorbent (stationary phase) and yields sorption coefficients of gas species (Mader et al., 1997). Vacuum microbalance (VM) determines the change in weight due to adsorbed gases (Rouquerol and Davy, 1978; Thomas and Williams, 1965). The desorption rate can be determined by measuring the time evolution of the adsorbed phase by using diffuse reflectance infrared Fourier transform spectroscopy (DRIFT), while the gas phase is monitored by selected-ion flow-tube mass spectrometry (SIFT−MS) and long-path transmission Fourier transform infrared spectroscopy (FTIR) (Romanias et al., 2016). Since measurement of the desorption rate requires pressures in the molecular flow regime, this is only straightforward for low vapor pressure materials, such as mineral dust or dry salts. For high vapor pressure materials (aqueous or organic liquids and ice) or materials featuring complex microstructure (mineral dust, soot), complications arise from the convolutions of pore space (Woodill et al., 2013; Keyser et al., 1991), bulk liquid diffusion (Koop et al., 2011; Pöschl et al., 2007), gas-phase diffusion (Knopf et al., 2015; Fuchs and Sutugin, 1971; Fuchs, 1964; Seinfeld and Pandis, 1998; Pöschl et al., 2007), and other coupled processes, making the determination of desorption lifetime an indirect and often difficult task. Kinetic uptake (KU) experiments operated in the molecular flow regime can yield estimates of species' surface residence times (Alcala-Jornod et al., 2000; Koch and Rossi, 1998a; Koch et al., 1997). KU experiments using laminar flow tube reactors can also yield estimates of the residence time of adsorbed species via determination of the Langmuir equilibrium constant (Pöschl et al., 2001; von Hessberg et al., 2008; Slade and Knopf, 2013). Vibrational spectroscopy (VS) is used to study the interaction of molecules with, e.g., ice surfaces, by examining the shifted dangling hydrogen bond of ice in presence of an adsorbed molecule (Silva and Devlin, 1994). Surface tension (ST) measurements of adsorbing gases on liquid substrates can yield directly the thermodynamic parameters describing adsorption (Hauxwell and Ottewill, 1968; Donaldson, 1999), and the molecular level relationship between surface excess and surface coverage can be assessed by direct spectroscopy (Lee et al., 2016).
IGC derives sorption coefficients which can yield estimates of via the van 't Hoff equation (Goss and Eisenreich, 1996). For experimental TPD and TDS desorption data analysis usually the Redhead equation (Redhead, 1962) is applied that considers the heating rate and gas species surface coverage. kdes derived from DRIFT studies yields τdes, which allows derivation of according to Eq. (1), with similar constraints with respect to effusion times from packed powder samples (Woodill et al., 2013; Keyser et al., 1991). MB methods allow one to uniquely differentiate thermal desorption of molecules from those undergoing elastic or inelastic scattering, or from those undergoing exchange with the bulk and/or reaction. For solid surfaces the interpretation is straightforward, and corresponding desorption lifetimes can directly be observed. For liquid surfaces, this is less straightforward, since the trajectory of a desorbing molecule may involve diffusion into and out of the near-surface bulk layers (Faust et al., 2013), so that the “surface residence time” is not strictly a true desorption lifetime. Equilibrium measurements of surface tension as a function of partial pressure of the trace gas allow one to determine and , if the latter is assumed to be independent of temperature (Donaldson, 1999).
The choice of standard states can impact data interpretation. Standard free energies of formation are typically referenced to 1 bar or 1 mol L−1 (at 298 K) (Donaldson et al., 2012a). Commonly, it can be assumed that standard enthalpy values are not strongly dependent on the choice of standard state, because the dependence of enthalpy on pressure is weak (Donaldson et al., 2012a). However, the standard entropies of phase transfer will depend on the choice of the standard state (Donaldson et al., 2012a; Knopf and Ammann, 2021; Campbell et al., 2016; Savara, 2013). Further complications arise when choosing standard states for different adsorbate–surface interactions (Campbell et al., 2016). This can impact standard-state surface concentrations, equilibrium constants, and rate constants and renders the adsorbate chemical potential dependent on surface coverage (Campbell et al., 2016; Savara, 2013).
Molecular dynamics (MD) simulations can provide estimates of the residence time of gas species at a surface or interface (Vieceli et al., 2005; von Domaros et al., 2020). MD simulations can yield residence times at the interface or substrate surface and as such an estimate of τdes. Then, for given Ades and temperature, can be estimated using Eq. (1). Monte Carlo (MC) methods based on computational algorithms rely on repeated random sampling to obtain numerical results (Remorov and Bardwell, 2005). Grand canonical Monte Carlo (GCMC) simulations account for density fluctuations at fixed volume and temperature and represent the preferred choice for the investigation of interfacial phenomena (Croteau et al., 2009; Collignon et al., 2005). Density functional theory (DFT) and coupled cluster (CC) theory are computational quantum mechanical modeling methods to compute the electronic structure of matter (Meng et al., 2004; Zhang and Grüneis, 2019). Coupled cluster singles and doubles theory including perturbative triples (CCSD(T)) is a commonly used level of theory and has been applied to describe adsorption processes (Voloshina et al., 2011). Embedded cluster theory (ECT) can be used for the description of the electronic structure of molecules adsorbed on solid surfaces and surface reactions (Whitten, 1993), allowing ab initio calculations of molecular properties of the lattice–absorbate system. The dipped adcluster model (DAM) is applied to study chemisorption and surface reactions in which an adcluster (admolecule + cluster) is dipped onto the electron bath of a solid metal (Nakatsuji, 1987). This treatment allows one to derive adsorption energies (Hu and Nakatsuji, 1999).
3.2 Atmospherically relevant gas–substrate systems
3.2.1 Gas adsorption by solid substrates
Gas adsorption and desorption is important when describing the reactivity between trace gases and solid interfaces in terms of removal rates and gas–particle partitioning (Kolb et al., 2010; Pöschl et al., 2007). It also constitutes a significant removal process of gaseous organic compounds by partitioning between gas and solid phases (Goss and Eisenreich, 1996; Goss, 1993). Mineral dust particles are the most abundant aerosol particles globally by mass, providing ample solid surface area for adsorption of gaseous species (Usher et al., 2003; Tang et al., 2016). Atmospheric soot particles also represent a solid surface, which allows for multiphase chemistry involving adsorption and reaction of atmospheric oxidants (Pöschl et al., 2001; Shiraiwa et al., 2009; Kaiser et al., 2011; Springmann et al., 2009), though soot can be complex consisting of solid graphite structures coated by organic carbon, the latter being amorphous or soft in nature (Bond et al., 2013; China et al., 2013; Cappa et al., 2012). Also, amorphous solid organic particles (Virtanen et al., 2010; Koop et al., 2011; Shiraiwa et al., 2017a) provide solid substrates that serve as adsorption and reactive sites for trace gas species (Knopf et al., 2018; Slade et al., 2017; Slade and Knopf, 2014, 2013; Houle et al., 2018; Hearn and Smith, 2007; Lakey et al., 2016; Berkemeier et al., 2016; Steimer et al., 2015; Shiraiwa et al., 2011a; Li and Knopf, 2021; Li et al., 2020).
In the atmosphere, adsorbing trace gases including oxidants, radicals, and VOCs compete with adsorbing water for substrate surface sites. A mineral dust surface is usually hydroxylated and covered by a monolayer of water at about 20 %–30 % relative humidity (Usher et al., 2003; Tang et al., 2016; Goss, 1994a). Adsorption of water by mineral dust is also crucial for our understanding of the ability of dust particles to serve as CCN (Tang et al., 2016) and INPs (Kanji et al., 2017; Knopf et al., 2018; Knopf and Koop, 2006; Hoose and Möhler, 2012; Knopf and Alpert, 2023). Since water vapor is abundant in our environment, adsorption of a reactive or non-reactive gas species will likely always proceed in competition with co-adsorbing water molecules (Kaiser et al., 2011; Springmann et al., 2009). Reactive uptake of O3 and OH radicals by insoluble organic aerosol surfaces has been shown to decrease as humidity increases, following a Langmuir–Hinshelwood mechanism, where water vapor co-adsorbs and competes for surface sites (Pöschl et al., 2001; Slade and Knopf, 2014). Condensation of water may lead to dissolution of soluble gas species and coating material on top of solid substrates, e.g., present as an aqueous organic coating on soot (Charnawskas et al., 2017). Those cases should then be considered as a solid substrate covered by a liquid layer, and adsorption or uptake processes should be treated as proceeding on a liquid substrate. Tables A1–A7 present a compilation of and other molecular parameters for a selection of atmospherically relevant reactive and non-reactive trace gases interacting with various solid substrates serving as surrogates of aerosol particles.
3.2.2 Gas adsorption by ice
Ice is among the most abundant solid materials on Earth's surface. Roughly 50 % of the northern hemispheric landmass is covered by ice and snow in winter (Bartels-Rausch, 2013). Adsorption and desorption of trace gases on ice impact gas-phase chemistry in the stratosphere and upper troposphere (Solomon, 1999; Borrmann et al., 1996; Voigt et al., 2006; Huthwelker et al., 2006), snow chemistry and boundary-layer gas-phase chemistry over perennial and permanent snowpacks, and gas-phase chemistry above sea ice (Bartels-Rausch et al., 2014; Artiglia et al., 2017; Raso et al., 2017; George et al., 2015; McNeill et al., 2012; Abbatt et al., 2012; Jeong et al., 2022; McNamara et al., 2021). Partitioning of gases to ice in polar and high-alpine snow also results in signals in ice cores used to reconstruct past climates and environmental conditions (Vega et al., 2015). In comparison to other solid materials, ice is a high-temperature material existing in the environment at temperatures relatively close to its melting point. As in other molecular solids this leads to surface premelting and thus a disordered interface, also referred to as quasi-liquid layer, the properties of which are a matter of ongoing debate (Bartels-Rausch et al., 2014; Asakawa et al., 2016; Cho et al., 2002; Slater and Michaelides, 2019). Since this layer is the interface with which adsorbing gases interact, the mutual interplay between the properties of the disordered interface and the nature of the interaction of gases have spurred speculations about whether it should be treated as a thin aqueous solution layer or a purely solid surface. Recent spectroscopic evidence indicates that soluble gases form solvation shells similar as in liquid water without, however, modifying the remaining ice structure significantly (Bartels-Rausch et al., 2017). Thus under typical atmospherically relevant conditions with low coverages of volatile gases, the surface remains dominated by the properties of ice. A template for this may be the case of HCl adsorption on ice (Huthwelker et al., 2006), for which singly hydrogen-bonded HCl is adsorbed at the outermost surface (Kong et al., 2017), while upon hydration and dissociation, chloride enters deeper into the interface (Zimmermann et al., 2016; McNeill et al., 2006, 2007). This is in accord with a low desorption energy and thus low coverage with molecular HCl (Table A8). This behavior can mask the weak temperature dependence of the total coverage by HCl (molecular and dissociated). Similar conclusions come from MB experiments, e.g., with NOy compounds, where the desorption kinetics are characterized directly (Lejonthun et al., 2014). An exception may be the case of H2O itself, where the MB experiments may not have been able to resolve singly hydrogen-bonded H2O desorbing, but only completely hydrated ones desorbing more slowly (Kong et al., 2014a, b). Therefore, adsorption on ice may well be considered as adsorption within the simplified scheme adopted in this work even for very soluble and more straightforwardly for less soluble molecules. Table A8 summarizes the thermodynamic literature data on gas species adsorption by ice substrates applied in this study.
3.2.3 Gas adsorption by water and aqueous solutions
Liquid water and aqueous solutions are a dominant form of condensed matter in the environment including aerosol particles, clouds, or ocean surfaces. In aerosol particles, aqueous solutions may range from dilute solutions at very high humidity and at or close to the point of activation into a cloud droplet to very concentrated supersaturated solutions at low relative humidity. High solute strength solutions may yield highly viscous, semi-solid, and glassy particle phase states occurring throughout the atmosphere (Shiraiwa et al., 2017a; Koop et al., 2011; Mikhailov et al., 2009; Zobrist et al., 2008; Klassen et al., 1998). Decreasing bulk diffusivity in these viscous phases increases the relative importance of the desorption lifetime as exchange with the bulk is retarded (Behr et al., 2009; Knox and Phillips, 1998; Li and Knopf, 2021) (see Eq. 4).
The notion that adsorbed molecules on liquid surfaces represent a distinct feature comes from both spectroscopic and kinetic evidence. MB experiments of HCl on deuterated sulfuric acid clearly identified collision, adsorption, and desorption trajectories (Behr et al., 2001; Morris et al., 2000; Gao and Nathanson, 2022), as a direct and unique manifestation of Langmuir's view of adsorption (Langmuir, 1918). The time the HCl molecule spends on the surface is directly related to and Ades. In other cases studied by the MB technique, the picosecond scale hydrogen bond exchange dynamics and fast diffusion (nanoseconds–microseconds for diffusion into and out of depths of several nanometers) prevented unambiguous separation of pure desorption from trajectories including entry into the liquid (Ringeisen et al., 2002a, b; Brastad et al., 2009; Faust and Nathanson, 2016; Faust et al., 2016; Faust et al., 2013). A comparable situation as for HCl has been documented through the MB technique for N2O5 (Shaloski et al., 2017). Later high-level theory work established the interaction of this important trace gas with the hydrogen bonding network of water that then subsequently controls hydrolysis (Cruzeiro et al., 2022; Galib and Limmer, 2021). Similar conclusions about adsorption–desorption trajectories in the case of H2O(g) on liquid water may be drawn from different isotope exchange kinetics for HDO with H2O and HO with H2O that require different degrees of hydration on the water surface (Davidovits et al., 2006, 2011). The suggestion that a distinct population of H2O molecules exists that is singly hydrogen bonded at the liquid water surface comes from detailed interpretation of IR spectra in line with theory (Devlin et al., 2000). The high vapor pressure of environmentally relevant liquids and other difficulties (including those related to fast exchange with the bulk liquid) prevent direct determination of desorption kinetics for many relevant trace gas–substrate pairs. In spite of this situation, we suggest to apply the same concept of converting desorption energies (derived from partitioning or chromatographic methods) into desorption lifetimes as for solid surfaces.
The fact that molecules at the aqueous solution or liquid water–air interface experience a different environment than in the bulk liquid is straightforward. The density drops over molecular length scales, and the hydrogen bond dynamics and orientation in water and aqueous solutions on average lead to a strongly asymmetric environment at the interface (Brini et al., 2017; Ahmed et al., 2021; Hao et al., 2022). The extension of the interface depends on the type of solutes and adsorbates present, as molecules with larger hydrophobic moieties or when charges are present at the adsorbate interacting with solute ions, which may establish a larger interfacial thickness (Brini et al., 2017; Zhao et al., 2020). The asymmetric environment at the interface leads to specific molecular interaction options (as described above) and in turn to specific binding energies as a result of these. Changes to the equilibrium surface tension of aqueous solutions in response to adsorption of gases are the consequence of the changes in the surface free energy. Its temperature dependence is reflecting the energy gain as a result of the sum of these interactions. Tables A9 to A15 are a compilation of for a range of inorganic and organic trace gases on pure water or on aqueous solutions. The simplest case, H2O(g) on H2O(l), exhibits a single hydrogen bond and a corresponding low value. Among the given families of species, interaction energies scale with molar mass or the degree of substitution with functional groups that alter the number of weak or strong molecular interactions. The degree of substitution may be represented by the dipole moment (μ) and O : C for organic molecules as outlined in the discussion of parameterized . The presence of hydrophilic functional groups with strong hydrogen bonding interaction options leads to correspondingly larger . Since these groups also interact with the hydrogen bonding network of water, these interactions are sensitive to the presence of other solutes or, especially, ions (Demou and Donaldson, 2002; Lee et al., 2019; Ohrwall et al., 2015; Ekholm et al., 2018).
To assess the impact of τdes on multiphase chemical kinetics, the kinetic multilayer models of aerosol surface and bulk chemistry (K2-SURF, KM-SUB) are applied (Shiraiwa et al., 2009, 2010). These models are based on the Pöschl–Rudich–Ammann (PRA) framework (Ammann and Pöschl, 2007; Pöschl et al., 2007) and describe the gas–particle interface by implementation of several model compartments and molecular layers in which species can undergo mass transport and chemical reactions. Here, the compartments included are gas phase, near-surface gas phase, sorption layer, quasi-static surface layer, and a number of bulk layers.
Gas-phase diffusion of a species X from the gas phase to the near-surface gas-phase surrounding the particle is treated by the net flux of gas-phase diffusion:
where dp is the particle diameter, λ is the mean free path, Dg is the gas diffusivity, and [X]g and [X]gs are concentrations of X in the gas and near-surface gas phases, respectively (Pöschl et al., 2007; Knopf et al., 2015; Li et al., 2018). The mass balance and rate equation for X in the near-surface gas phase can be described as
where As is the particle surface area and Vgs is the volume of the near-surface gas phase. Jdes,X is the desorption flux defined as . Jads,X is the adsorption flux defined as , where αs,X represents the surface accommodation coefficient, and the collision flux is defined as with ωX being the mean thermal velocity of X.
The surface-layer reaction (SLR), involving only the adsorbed species, X(s), or components of the quasi-static layer, Y(ss), such as X(s) + Y(ss) → products, is described by the second-order rate coefficient kSLR. The surface reaction rate is described as Ls=kSLR[X]s[Y]ss. The mass balance and rate equations for X in the near-surface gas phase and at the surface can be described as below:
where and are the fluxes from the surface to the near-surface bulk and from the near-surface bulk to the surface of X, respectively ( in the absence of bulk diffusion), and treated as a function of the bulk diffusion coefficient. The reactive uptake coefficient, γ, is usually the experimentally accessible parameter and the one used in atmospheric modeling studies. γ of a gas species X is defined as
4.1 Simulation of reactive gas uptake by solid substrates
We apply the kinetic double-layer model of aerosol surface chemistry (K2-SURF; Shiraiwa et al., 2009) to investigate the sensitivity of γ to the desorption lifetime for a solid substrate. The surface reaction of an adsorbed species X with condensed species Y is considered, while surface–bulk exchange and bulk diffusion and reaction are not considered for simplicity. The αs on an adsorbate-free substrate is assumed to be 1 for all simulations. Figure 2 shows the dependence of γ on τdes and kSLR at constant temperature. γ values represent steady-state values. Higher kSLR leads to higher γ at fixed τdes due to faster surface reaction rates. At fixed kSLR, longer τdes leads to higher surface concentrations of X and consequently to higher surface reaction rates and γ. In turn, with sufficiently long residence times of the adsorbed gas species, low kSLR can still lead to high values of γ. It is evident that different pairs of τdes and kSLR can yield the same γ value. Furthermore, when kSLR is known, uncertainties in τdes can result in large differences in γ. This exercise demonstrates that experimentally derived γ values do not sufficiently constrain the heterogeneous reaction process to yield unambiguous τdes and kSLR values, unless a significant parameter space is covered by the experiment to constrain them individually. For instance, at large enough gas-phase partial pressure the surface gets saturated (fully covered by the adsorbate), which leads to decoupling of τdes and kSLR (Knopf et al., 2011; Artiglia et al., 2017; Berkemeier et al., 2016; Steimer et al., 2015). However, this is often not possible due to technical constraints. Therefore, constraining τdes by application of , or best estimates of , can significantly improve our molecular understanding of the underlying processes in multiphase chemical kinetics and support the development of parameterizations for modeling purposes.
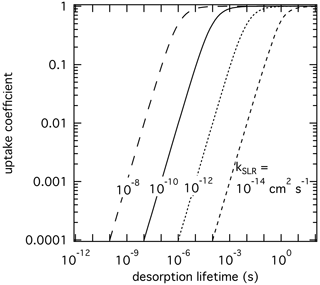
Figure 2The response in reactive uptake coefficient of a reactive gas species X with a condensed-phase species Y when varying the desorption lifetime and second-order rate coefficients derived by the numerical diffusion model K2-SURF. The gas-phase concentration of X and the surface concentration of Y remained fixed during the calculations. The surface accommodation coefficient is assumed to be equal to 1.
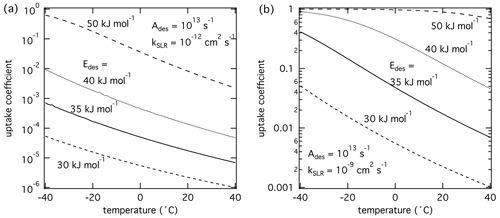
Figure 3The response of the reactive uptake coefficient as temperature and adsorption energy are varied for two different second-order rate coefficients derived by K2-SURF. The gas-phase concentration of X remained fixed during the calculations. The pre-exponential factor Ades is fixed for both cases. The surface accommodation coefficient is assumed to be 1.
Figure 3 displays the temperature dependence of γ with of 30–50 kJ mol−1. The pre-exponential frequency factor Ades was set to 1013 s−1, and kSLR was set to (a) 10−12 and (b) 10−9 cm2 s−1. Temperature dependence of kSLR was not considered in these simulations to evaluate only the effects of temperature-dependent τdes on γ. The modeling results suggest that γ depends strongly on temperature, where lower temperatures yield higher γ values. This is because lower temperatures lead to longer τdes and hence higher surface concentrations of X and reaction rates. Generally, γ is more temperature-dependent at higher values of . However, if is close to values typical for chemisorption (∼ 50 kJ mol−1), γ is close to 1 in this calculation. Further away from this special case and natural cap of γ=1, γ increases by about 2 orders of magnitude over a temperature range of 80 K. These modeling results indicate that extrapolating multiphase chemical kinetics acquired at room temperature to lower temperatures can result in significantly different reactive uptake coefficients. Clearly, a detailed understanding of the molecular processes is necessary when applying multiphase reaction kinetics to environmental and atmospheric conditions.
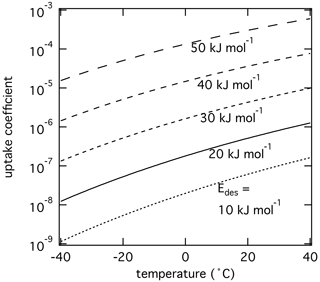
Figure 4The response of the reactive uptake coefficient of O3 by PAH coated on soot including formation of reactive oxygen intermediates (ROIs) following Shiraiwa et al. (2011b) as temperature and adsorption energy are varied using the numerical diffusion model K2-SURF. ROI formation and oxidation reaction rates are adjusted using an Arrhenius-based temperature scaling. The pre-exponential factor Ades is fixed at 1013 s−1.
Even though the above simulations clearly suggest potentially large effects of the temperature dependence of τdes on γ, surface reaction rate coefficients are also temperature dependent, which in turn affect γ as well (Li and Knopf, 2021; Li et al., 2020). To further investigate the role of temperature on heterogeneous reaction kinetics, we apply the K2-SURF model to heterogeneous reactions between O3 and polycyclic aromatic hydrocarbons (PAHs) adsorbed on soot. This reaction proceeds with a multi-step Langmuir–Hinshelwood mechanism that includes (R1) O3 physisorption, (R2) decomposition of O3 into long-lived reactive oxygen intermediates (ROIs, O atoms), and (R3) reactions of O atoms with PAHs (Shiraiwa et al., 2011b):
The activation energy for physisorbed O3 to dissociate into chemisorbed O (Ea,pc) is ∼40 kJ mol−1, and the activation energy for O reacting to oxidation products (Eox) is ∼80 kJ mol−1 (Berkemeier et al., 2016; Shiraiwa et al., 2011b). Temperature dependence of the reaction rate coefficients of Reactions (R2) and (R3) is considered using an Arrhenius equation. We examine the response of this reaction system to changes in initial of O3 (Reaction R1) and temperature.
Figure 4 shows the results of such simulations. Higher yields higher surface concentrations of physisorbed O3, and hence higher concentrations of O and reaction rates, yielding higher γ values. γ decreases as temperature decreases, which is in contrast to above sensitivity studies shown in Fig. 3. This is because the overall temperature dependency of the gas uptake is mostly determined by the temperature dependency of the rate-limiting Reaction (R3) and also influenced by thermally activated chemical Reaction (R2). Although physisorbed O3 molecules can reside significantly longer on the PAH surface at lower temperatures, the decrease in the formation rate of ROIs and subsequent oxidation reaction rate govern γ, suggesting lower γ values at lower temperatures.
Clearly, and activation energies for chemical reactions are crucial parameters to predict multiphase chemical kinetic processes under tropospheric conditions. Conducting temperature-dependent reactive uptake experiments of known reaction systems can be used to determine coupled desorption lifetimes and reaction rates (e.g., Kerbrat et al., 2010; Li and Knopf, 2021). For example, Li and Knopf (2021) measured the reactive uptake of OH radicals by triacontane for temperatures between 213 and 293 K. By having a temperature-dependent multiphase kinetics data set, and kSLR could be decoupled and individually assessed.
4.2 Non-reactive gas uptake into liquids
To demonstrate the effect of τdes on the equilibration timescale of non-reactive gas uptake by a liquid substrate, the kinetic multilayer model for aerosol surface and bulk chemistry (KM-SUB) (Shiraiwa et al., 2010) was applied (Fig. 5). We simulate non-reactive uptake of species X with a constant gas-phase concentration of 1 ppb into a particle with 100 nm diameter that initially contains no amount of X. Henry's law constant of X was set to be mol cm−3 atm−1 at 298 K, and its temperature dependence was considered using the van 't Hoff equation with a solvation enthalpy of 20 kJ mol−1; these values are chosen to be comparable with ozone solvation into water (Sander, 2015, 2023). The temperature dependence of Henry's law constant is shown in Fig. S1. The particle is assumed to be liquid with a temperature-dependent bulk diffusion coefficient following the parameterization of Zobrist et al. (2011) for pure water, which varies from – cm2 s−1 in this temperature range. values in the range of 10–80 kJ mol−1 were used, and the temperature dependence of τdes was considered using the Frenkel equation (see Eq. (1) and Fig. 1). Here, X can be regarded as a small molecule with moderate water solubility such as ozone for the simulations at low or a carboxylic acid with similar water solubility (e.g., nonanoic acid) for the simulations at high . The equilibration time is defined as the time after which the surface and particle bulk concentrations deviate by less than a factor of from their equilibrium or steady-state value.
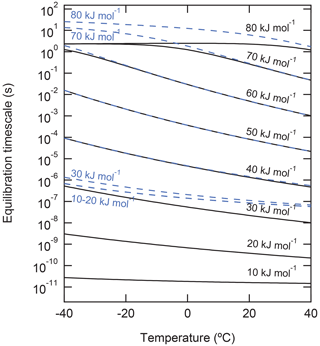
Figure 5Equilibration timescale of non-reactive uptake of gas molecules onto the surface (solid black lines) and into the particle phase (dashed blue lines) of liquid particles with a diameter of 100 nm for different desorption energies. Gas-phase mixing ratio is fixed to be 1 ppb.
The simulations show that equilibration times can vary over many orders of magnitude in the investigated range of (Fig. 5). For < 30 kJ mol−1, the timescales of surface equilibration (black solid lines) are shorter than the timescale of bulk equilibration (blue dashed lines). The convergence of the blue lines at low (< 30 kJ mol−1) reflects the kinetic limitation of gas–particle equilibration by diffusion inside the particle bulk ( s−1; Shiraiwa et al., 2011a). At higher , the increase of desorption lifetime leads to the increase of the equilibration times, as a larger amount of X is needed to saturate the surface; in fact, at kJ mol−1, the majority of molecules reside on the surface and the partitioning is governed by the surface processes in this simulation.
In the range of around 40 to 60 kJ mol−1, surface and bulk equilibration times coincide, as the simulated 100 nm particles are well-mixed and non-reactive uptake is limited by interfacial transport from the gas phase. The flattening and convergence of the black lines at > 60 kJ mol−1 reflects the kinetic limitation of gas–particle equilibration by interfacial transport (surface adsorption and surface–bulk exchange) if the surface gets fully covered by the adsorbate. The bulk equilibration (blue lines) and thus also the overall gas–particle equilibration time still increase for > 60 kJ mol−1 with decreasing temperature, because interfacial transport is slowed by the high surface propensity of X and its full surface coverage. Note that the slowing of bulk equilibration time as a consequence of sorption layer coverage is a direct consequence of using a Langmuir adsorption model. In case of multilayer adsorption and bulk condensation, especially at high , results may differ, which will be explored in follow-up studies (see also Sect. “Gas-particle partitioning of secondary organic aerosol”). Also note that the increased surface propensity of X with increasing is not a general rule but a consequence of the fixed Henry's law solubility coefficient in this sensitivity study.
The calculations for Fig. 5 represent an open system in which the gas-phase concentration of X is held constant. Wilson et al. (2021) investigated equilibration timescales for gas uptake of PAHs on soot surfaces in the closed system, i.e., where a fixed amount of X is distributed between the gas and particulate phases. In that study, equilibration timescales were either controlled by the adsorption or by the desorption process, depending on whether the particle surface was under- or oversaturated with X at the start of the model simulations, respectively. Temperature strongly influenced equilibration timescales in the desorption-controlled regime, whereas particle number concentrations influenced adsorption-controlled systems. Note that in the presence of chemical reactions in the gas phase or on the surface, the partitioning equilibrium can be perturbed and adopt a quasi-stationary state that differs from thermodynamic equilibrium.
For reactions occurring in liquids, the same features apply as for the case of surface reactions on solids; i.e., the temperature dependence of an activated reaction may counteract the temperature dependencies of desorption and solubility, e.g., for the reactions on sulfuric acid aerosol of HCl with HONO (Longfellow et al., 1998; Ammann et al., 2013) or with ClONO2 (Shi et al., 2001). These cold and viscous sulfuric acid aerosols, as well as viscous aqueous organic aerosols, are also at the same time high solute strength systems. The situation then is very complex since viscosity is modulated by temperature and humidity, thereby impacting diffusion and salting out effects, and thus, ultimately, solubility and kinetics (Edebeli et al., 2019; Li and Knopf, 2021; Li and Shiraiwa, 2019).
Thermodynamic and chemical parameters given in Tables A1–A15 provide the basis to derive estimates for application in multiphase chemical kinetics involving atmospheric gas species and aerosol particles. This analysis includes over 500 gas species-substrate systems. As discussed above, we note the underlying caveats in this analysis. The pre-exponential factor is set to 1013 s−1. The dependence of on absorbate model and surface coverage is neglected. Thus, a highly accurate prediction of is not possible. However, the goal here is to provide a best estimate of in agreement with this training data set (Tables A1–A15) to enable improved analyses of environmental multiphase chemical kinetics under the wide range of thermodynamic conditions encountered in Earth's environment. Furthermore, it would be desirable to predict from commonly measured and accessible parameters, e.g., derived by mass spectroscopy, such as molar mass, molecular structure, and oxidation state.
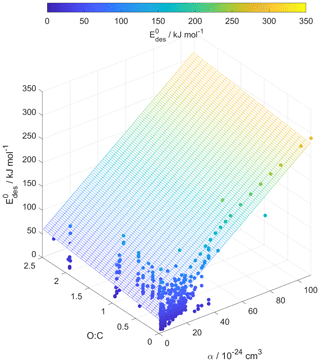
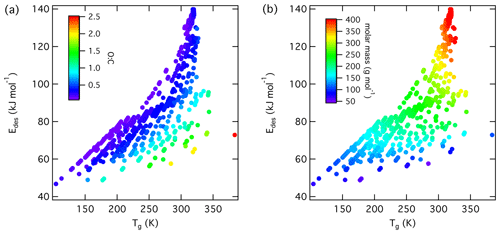
Figure 6Multilinear regression analysis of , oxygen-to-carbon ratio of gas species expressed as O : C, and gas species polarizability (α) using data from Tables A1–A15. Gridded surface shows regression model, and color shading indicates changes in .
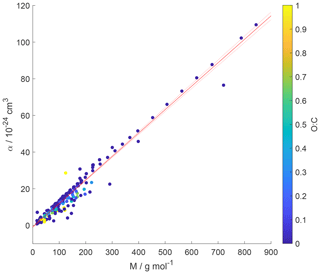
Figure 7Gas species polarizability (α) as a function of molar mass (M) and its dependence on oxygen-to-carbon ratio expressed as O : C. O : C given as color shading. Red solid and dotted lines represent a linear fit to the data and its 95 % prediction bands, respectively. Note that three gas species with O : C > 1 (CO2, formic acid, and peroxyacetyl nitrate) are included in this plot as having O : C =1 to allow for better visualization of entire data set.
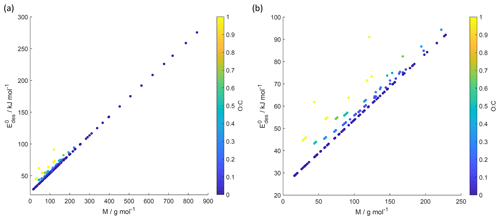
Figure 8 values derived from the new parameterization (Eq. 16) applying the training data set of gas species with molar mass (M) and O : C, the latter coded as symbol color described by the color bar. Panel (b) is an enlarged view of (a). Note that three gas species with O : C >1 (CO2, formic acid, and peroxyacetyl nitrate) are included in these plots as having to allow for better visualization of entire data set.
Following our previous discussion on the intermolecular bonding between adsorbate and substrate, gas species polarizability, α, should serve as a predictor of . Larger α should, in general, coincide with an increase in . The oxidation state of an organic gas species, represented in a simplified way by the ratio O : C, reflects the number of oxygenated functional groups, typically monitored by mass spectrometry (Isaacman-VanWertz et al., 2018). An increase in the gas species' oxidation state should also yield an increase in . Figure 6 displays a multilinear regression analysis using all available data including solid, ice, and liquid substrates (Tables A1–A15) to derive a relationship between , α, and O : C. Figure S2 depicts the same data in more detail as two separate plots. Figure 6 indicates that increases with increasing α and O : C, as one would expect from considerations of intermolecular bonding discussed above. This is also corroborated by a principal component analysis given in Fig. S3, showing significant correlation between and α. The regression analysis yields the following model (with an R2=0.559 and a root mean square error (RMSE) = 25.4):
where is in units kJ mol−1 and α is in units 10−24 cm3.
Figure 7 shows α as a function of molar mass and . Note that the few data for the three gas species with , namely CO2 (Table A3), formic acid (Table A7), and peroxyacetyl nitrate, PAN (Table A8), are colored as for better visibility of the overall training set. Figure 6 shows the few data points for . The data show a strong linear correlation between α and M, where O : C appears to play a less significant role. This can be understood by realizing that a carbon atom in a molecule contributes 3 times more to α than an oxygen atom (Bosque and Sales, 2002), discussed in more detail below. Hence, the number of methylene groups can dominate α for larger molecules. Thus, the polarizability can be described, applying regression analysis, as a linear function of molar mass (R2=0.952 and RMSE = 2.765):
where M is in units g mol−1. The linear regression is shown as a red line in Fig. 7.
We can now combine Eqs. (15) and (16) to obtain a parameterization to calculate from knowledge of the gas species' molar mass and O : C:
Figure 8 shows values derived from Eq. (17) using M and O : C values given by the training data sets as input. Similarly to Fig. 7, we have color-coded O : C for values up to 1 for better data visibility. Figure S4 shows values derived from the training data set separated by different substrate types, corroborating the correlation displayed in Fig. 8. Figure S5 shows values derived from Eq. (17) using arbitrary M and O : C values. For application of inorganic gas species with C=0, O : C should be set to zero. shows a linear relationship with M where deviation from linearity is only found at M < 250 g mol−1. Figure 8b demonstrates that gas species with larger O : C show larger . To understand this trend in the data, we have to address the role of the gas species' dipole moment and substrate in the derivation of the values. Equation (17) provides estimates of without specifically addressing substrate properties. As discussed, its dependency solely on M and O : C is advantageous for application to complex gas species–particle composition data. Considering the underlying uncertainties due to unknown applied standard states, absorbate model, and assumed pre-factor, this parameterization is accurate within those limits. However, one would expect that gas species' μ and the substrate's εr impact .
We recommend application of this parameterization (Eq. 17) for gas species with . Due to the few data points at , could be significantly under- or overestimated in this range. For example, for CO2 (Table A3), tabulated kJ mol−1, while the parameterization yields 61.8 kJ mol−1. In the case of formic acid (Table A7), the tabulated kJ mol−1, while the parameterization yields 62.4 kJ mol−1. Hence, when applying Eq. (17) to gas species with , considering additional information or constraints is recommended.
For our data set, the principal component analysis in Fig. S3 indicates no strong correlation between εr and . Figure 9 corroborates the negligible dependence of on εr. However, one would expect that greater μ, α, and εr result in larger due to enhanced molecular interactions. The derivation of our parameterization exploited the strong dependency of on α. We suggest that the underlying reason for this dependency is the competing effects of μ and α on as outlined below.
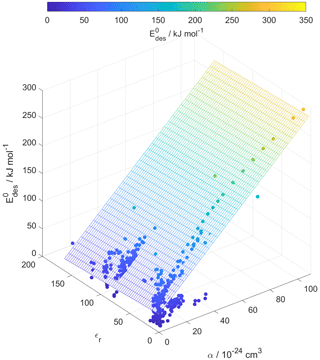
Figure 9Multilinear regression analysis of , substrate relative permittivity (εr), and gas species polarizability (α) using data from Tables A1–A15. Gridded surface shows regression model, and color shading indicates changes in .
Small molecules with polar groups can exert significant dipole moments, while the polarizability is still small. As depicted in Fig. S6, smaller molecules exert greater μ, while O : C values are high and α is low (see also Fig. 7). Note that alkanes and PAHs in the data set, following common convention, have zero dipole moments. Gas species with greater μ may interact more strongly with polarizable substrates expressed by εr, yielding larger . However, as the gas molecules become larger, their α increases, e.g., by the addition of methylene groups (Bosque and Sales, 2002), thereby dominating over the impact of μ on . Figure S6 supports this trend where molecules with largest α have low O : C and small μ. Hence, this data set yields a negative correlation between μ and α. As a consequence, for larger molecules the role of the molecule's μ interacting with the substrate becomes less important. Thus, in a way, the range of available desorption data could be responsible for the negligible correlation between and substrate εr (Fig. 9). In other words, polarizability α, which is strongest for molecules with small μ and low O : C, compensates and dominates the impact of the dipole moment on and, in turn, renders the substrate of less importance for parameterizing . This is also evident in Fig. 10, where the scatter of parameterization-derived values is largest for molecules with lower M and lower α. We can attribute the scatter in at lower M to the competing contributions of the gas species' μ, here accounted for by O : C, and α. These may be the reasons why can be reasonably parameterized from our data set without accounting for the substrate's εr and gas species' μ. Though, we would expect with more available data the role of gas species' μ and substrate's εr to likely be resolved in a parameterization.
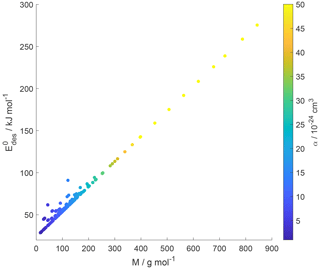
Figure 10Parameterized values as a function of gas species molar mass (M) and polarizability (α) given as a color bar following Eq. (17).
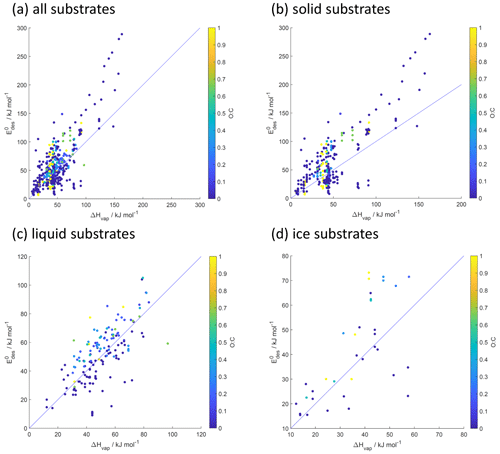
Figure 11Desorption energy () as a function of enthalpy of vaporization (ΔHvap) and its dependence on O : C for all (a), solid (b), liquid (c), and ice (d) substrates. Blue lines indicate 1:1 lines.
Considering the significant number of data and omission of substrate-specific properties in the parameterization, the scatter in is not very large. This suggests that this parameterization can serve as a reasonable first estimate of for a complex environmental substrate such as an aerosol particle. We would expect that, with an increasing number of desorption data that include larger molecules with larger O : C or μ and applied known standard states and absorbate models, the scatter in at lower molar masses can be resolved.
5.1 Relationship between desorption energy and enthalpy of vaporization
To examine the relationship between and ΔHvap, we have plotted the data given in supplemental tables (not the parameterized values) separated for the different substrate types in Fig. 11. Our data support a positive correlation between and ΔHvap, where for most instances is larger than ΔHvap. The role of O : C in the relationship between and ΔHvap is not clearly identifiable for the cases that include all, solid, and ice substrate data. However, for liquid substrates, the data suggest that, for given ΔHvap, larger O : C yields larger . Figure S7 provides a linear regression model for the case of liquid substrates. As shown above, larger O : C correlates with a larger μ, which may exert a greater impact on in the case of a liquid substrate. In fact, the interaction strength at the surface often exceeds the enthalpy of condensation between gas and its condensed liquid for the same species family, e.g., in the case of methyl-substituted benzenes (Raja et al., 2002; Bruant and Conklin, 2002), as well as for other species like alcohols, acids, amines, and ketones (Mmereki et al., 2000) and alkanes (Goss, 2009) and halogenated alkanes (Bruant and Conklin, 2001). This indicates that the aqueous solution–air interface allows for a two-dimensional environment in which the intermolecular interactions are as important as in the bulk condensed phase of the adsorbate alone (Valsaraj, 1988a, 2009).
5.2 Relationship between desorption energy and enthalpy of solvation for aqueous substrates
To examine the relationship between and ΔHsolv, we have plotted the data for liquid substrates, consisting mostly of water and few aqueous solutions (Tables A9 to A15) in Fig. 12. Despite the scatter in the data, a positive correlation between and ΔHsolv can be identified. The data fall symmetrically around the 1:1 line, indicating no strong bias. In the case of liquid substrates, the correlation between and ΔHsolv is comparable to that observed between and ΔHvap (Fig. 11c). Figure S8 provides a linear regression model for the data shown in Fig. 12.
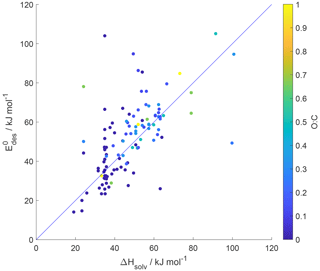
Figure 12Desorption energy () as a function of enthalpy of solvation (ΔHsolv) and its dependence on O : C for liquid substrates. Blue line indicates 1:1 line.
The relationship between and ΔHsolv shown in Fig. 12 can be understood in the following way. For large non-polar molecules, the free energy cost of entering the aqueous solution is mostly driven by enthalpic changes, because hydrogen bonds need to be disrupted to form a cavity around the molecule (Kronberg, 2016; Valsaraj, 1988a; Brini et al., 2017). The surface energy in that cavity is then driven by the surface energy of pure water and the hydrophobic interactions with the solute (Chandler, 2005). This is then somewhat similar to the situation when the same molecule is adsorbed at the aqueous solution–air interface. Thus, for the larger non-polar molecules, the contribution of the enthalpy of cavity formation can be identified as a dominating factor of the solvation process, which in turn depends on the intermolecular strength between adsorbing molecule and liquid. This, hence, can explain the correlation between and ΔHsolv for the case of the non-polar molecules.
For small non-polar molecules, the transfer to the aqueous phase is mostly entropy-driven, because the hydrogen bonds do not need to be disrupted but need to reorganize around the solute (Kronberg, 2016; Shinoda, 1992, 1977; Hvidt, 1983; Brini et al., 2017). Polar molecules would be comparable to ions, and in this case, the size and charge distribution determine the cost of solvation through the number and strength of hydrogen bonds to water, which lead to a correlation of ΔHsolv with the number of hydrophilic groups. The latter also determine (i.e., O : C correlates with μ). Among the small organic molecules contained in Fig. 12, with the increasing presence of hydrophilic functional groups, the larger O : C ratios lead to larger . For these reasons, the relationship between and ΔHsolv shown in Fig. 12 supports the specific and physical interaction model at the aqueous solution–air interface mentioned above: scales with the magnitude of hydrophobic interactions for non-polar molecules and with the presence of hydrophilic functional groups (i.e., O : C correlates with μ) for polar molecules, and thus the correlation with ΔHsolv is a logical consequence.
Note that since both and ΔHsolv are correlated and are mostly independent of temperature (Hildebrand and Scott, 1964) within the idealized concept presented here, the temperature dependence of τdes may apparently dominate the temperature dependence of solvation when . This idea of parallel behavior of desorption and solvation is also supported by a very recent experimental study that provides in situ measurements of the uptake of gas-phase water into ionic liquids at the gas–liquid interface using ambient pressure X-ray photoelectron spectroscopy (Broderick et al., 2019). These measurements indicate that, dependent on water mole fraction and temperature, solvation is governed by similar thermodynamics as relevant for crossing the gas–liquid interface during the mass-transfer process (Broderick et al., 2019). The positive correlation between the and ΔHsolv values displayed in Fig. 12 supports this notion, ascribing the molecular interactions controlling τdes and solvation an important role in the molecular understanding of gas–substrate interactions.
The discussion in the above sections demonstrated the importance of accurate knowledge of for the representation of multiphase chemical reactions across various environmental interfaces and phase states including aerosol particles. Analyses of experimentally conducted multiphase chemical kinetics studies as well modeling the detailed processes that lead to the physicochemical transformation of particles and define their atmospheric fate will greatly benefit from improved estimates of (Su et al., 2020; Zheng et al., 2020; Shiraiwa et al., 2017a, b; Shrivastava et al., 2017a, b; Li and Knopf, 2021; Kaiser et al., 2011; Springmann et al., 2009; Mu et al., 2018; Hems et al., 2021; Laskin et al., 2015). Below we discuss further relevant atmospheric chemistry processes that connect to and/or make use of , including gas–particle partitioning, secondary organic aerosol (SOA) formation, indoor air chemistry, and glass transition of OA particles.
6.1 Gas–particle partitioning of secondary organic aerosol
Organic aerosol is ubiquitous, consists of numerous chemical species, and represents a large mass fraction (20 %–90 %) of the total submicron particles in the troposphere (Nizkorodov et al., 2011; Jimenez et al., 2009; Hallquist et al., 2009; Kanakidou et al., 2005). The formation of SOA proceeds by complex pathways including reaction and mass transport in the gas and condensed phases. The equilibration timescale for gas–particle partitioning for SOA particles and particle–particle mixing of varying viscosity has been evaluated (Shiraiwa and Seinfeld, 2012; Berkemeier et al., 2020; Schervish and Shiraiwa, 2023; Li and Shiraiwa, 2019; Schervish et al., 2023). In some of those modeling studies a fixed s, which corresponds to about kJ mol−1 at 293 K, was applied. The simulation results shown in Fig. 5, however, demonstrated that we can expect significant changes in condensed phase equilibration times for gas–particle partitioning when and temperature change. Our tabulated data suggest that oxygenated VOCs will exert larger and, as such, longer τdes.
It has been shown that SOA oxidation products with a variety of functional groups fall into molecular corridors characterized by a tight inverse correlation between volatility (or saturation mass concentration, C0) and molar mass as depicted in Fig. 13 (Li et al., 2016; Shiraiwa et al., 2014). They are constrained by two boundary lines corresponding to the volatility of n-alkanes CnH2n+2 and sugar alcohols CnH2n+2On, which we now identify as “van der Waals” and “hydrogen-bonding”-dominated boundaries. This interpretation can be understood by the governing intermolecular forces. For example, using the EVAPORATION model (Compernolle et al., 2011), the vapor pressures for alkane, ketone, alcohol, and acid with a molecular weight of about 142 g mol−1 at 298 K yield the following: p0(C10H22) = 1.73 hPa, p0(H7C3C(O)C5H11) =0.084 hPa, p0(C9H19OH) = 0.023 hPa, and p0(C7H15COOH) = hPa, respectively. The decrease of about 3 orders of magnitude in the vapor pressure between the alkane and the carboxylic acid is mainly due to two carboxylic acid molecules forming hydrogen bonds, resulting in a dimer. A highly oxidized amide having ketone and alcohol groups such as N = CC(O)C(O)C(O)CO and M=149.146 g mol−1 has hPa. This is due to the fact that this molecule establishes not only the van der Waals forces such as London dispersion and Keesom forces but also hydrogen bonding with three hydrogen bond donors and multiple hydrogen bond acceptors. As can be seen in Fig. 13, the change in C0 derived from decane to C0 of the highly oxidized amide spans the identified molecular corridor around M=145 g mol−1, indicating that the van der Waals forces and the number of hydrogen bonds that can be established by a particular molecule may fundamentally describe the volatility range of the organic species.
Figure 13Molecular corridors of SOA formation showing saturation mass concentration (C0) as a function of molar mass (M). The small markers represent individual gas species color-coded by O : C ratio. Panel (a) displays data from Tables S1–S15. Panel (b) includes SOA precursor gases and oxidation products data discussed in Shiraiwa et al. (2014). The dotted lines represent linear alkanes CnH2n+2 (purple with ) and sugar alcohols CnH2n+2On (red with ). Inorganic species (diamonds) and organic species with similar molar mass but with different functional groups (circles) are plotted.
Keeping this approach in mind, we can ask the following: what are the extreme limits of the saturation mass concentration? The smallest organic molecule is methane, only prone to London dispersion forces. p0(CH4)=46 000 hPa with log 10(C0)=10.5, which corresponds to the upper bound of the molecular corridor. Ammonia (NH3) has a similar molar mass as CH4 but has lower vapor pressure, because NH3 can establish two hydrogen bonds. N2O5 does not form hydrogen bonds and is located above the alkane line. The lower bound of the molecular corridor is mainly defined by the molecule's permanent dipole moments and number of hydrogen bonds it can entertain. Clearly, these attributes are likely to be found in larger and highly oxidized compounds. Water constitutes a peculiarity when looking at its position in the C0–M framework depicted in Fig. 13. There is no other molecule with this small size that can form four hydrogen bonds. Sulfuric acid (H2SO4) can also form four hydrogen bonds and is located close to the lower bound of the molecular corridor. As molecules become larger, there are steric hindrances that likely inhibit stronger intermolecular bonding, whereas water with its small size is ideal. This reason may ultimately limit the lower bound of the molecular corridor and thus the lowest volatilities experienced by OA species.
As we have discussed above, and ΔHvap are positively correlated and in most cases is larger than ΔHvap (Fig. 11). Also, we found that gas species with higher O : C, and thus larger μ, exhibit larger values. This indicates that intermolecular interactions at the interface are as important as in the condensed phase of the adsorbate alone (Valsaraj, 2009, 1988a). We expect this also to hold for the case of SOA formation. It is generally observed that the composition of the organic matrix, barring any mass-transport limitations, has little influence on the gas–particle partitioning equilibrium (Donahue et al., 2011, 2012). Oxygenated VOCs have higher O : C and larger μ. Saturation vapor pressure or volatility provides guidance in this regard (Epstein et al., 2010). However, our study suggests that considering desorption, i.e., values, can impact equilibrium times of gas–particle partitioning as outlined in the gas uptake multilayer model simulations discussed in Sect. 4.
Figure 13a shows that the compiled data sets fall within the C0–M framework. In comparison, Fig. 13b shows the distribution of SOA oxidation products (916 different species) in the C0–M space evaluated previously by Shiraiwa et al. (2014). Since the gas species discussed in this work cover a similar C0 and M range as the SOA oxidation products, we can apply the parameterization of to provide estimates of for gas species typically involved in SOA gas–particle partitioning. This will allow a more detailed understanding and prediction of SOA formation, in particular for temperatures typically encountered in the troposphere during transport.
Figure 14Desorption energies () calculated for molecular corridor data of SOA precursor gases and oxidation products from Fig. 13. (Shiraiwa et al., 2014) as a function of molar mass and its dependence on O : C (a) and polarizability (b). This analysis applies the parameterizations given in Eqs. (15) and (18).
We derive of SOA oxidation products by application of Eq. (15). Since we know the molecular structure of the SOA oxidation products, we can calculate polarizability using the equation provided by Bosque and Sales (2002), instead of using Eq. (16):
where #C, #H, #O, #N, #S, #P, #F, #Cl, #Br, and #I represent the respective numbers of atoms in the molecule.
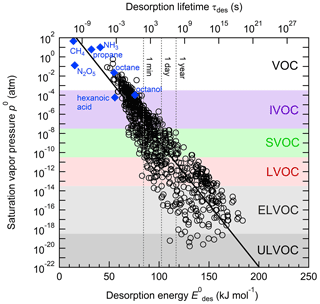
Figure 15Characteristic desorption energies (), desorption lifetimes (τdes), and saturation vapor pressures (p0) at 298 K for secondary organic aerosol (SOA) components and other selected compounds of atmospheric relevance. The blue markers show experimental literature data of and p0. The black markers correspond to the molecular corridor data of SOA formation displayed in Fig. 13 (Shiraiwa et al., 2014), for which p0 was estimated with the EVAPORATION model (Compernolle et al., 2011) and was estimated using Eq. (15). The solid black line represents an exponential fit to the SOA molecular corridor data. Blue markers show experimental data for selected other compounds of atmospheric relevance. Color shadings indicate widely used categories of SOA volatility basis set (VBS): volatile organic compounds (VOC), semi-volatile organic compounds (SVOC), low volatility organic compounds (LVOC), extremely low volatility organic compounds (ELVOC), and ultra-low volatility organic compounds (ULVOC) (Schervish and Donahue, 2020; Donahue et al., 2009).
Figure 14 displays values for the molecular corridor data of SOA precursors gases and oxidation products from Fig. 13 as a function of molar mass and its dependence on O : C and polarizability, following the molecular corridor approach using molar mass as the primary parameter characterizing the physicochemical properties of a molecule (Shiraiwa et al., 2014). Figure S9 provides the same analysis using parameterization as Eq. (17). For the majority of data points the predicted values are within ±10 % of the values shown in Fig. 14 and within the expected general uncertainty of as discussed above. For smallest molecules, Fig. 14a demonstrates the impact of O : C on , where alkanes, constituting the upper bound in the molecular corridor, have the lowest for a given molar mass. With increasing molecule O : C, increases as expected from our previous analyses and discussions. At larger molar masses the polarizability of the molecule dominates. Figure 14b further corroborates the strong correlation between molar mass and polarizability. Figure S9 depicts a tighter correlation of with molar mass and polarizability due to the linear representation of polarizability (Eq. 16). Furthermore, application of Eq. (16) yields alkanes having the lowest across the entire molar mass range (Fig. S9). Estimates of for these SOA oxidation products will allow refinement of gas–particle partitioning timescales, specifically when temperature changes are considered as outlined in our example shown in Fig. 5.
Figure 15 relates saturation vapor pressures (p0) at 298 K, estimated using the EVAPORATION model (Compernolle et al., 2011), to estimated , derived using Eq. (15), for selected compounds relevant for atmospheric chemistry and SOA molecular corridor data from Fig. 13 (Shiraiwa et al., 2014). The top axis of Fig. 15 shows the corresponding desorption lifetimes τdes at 298 K using the Frenkel equation (Eq. 1) with a pre-exponential factor Ades of 1013 s−1. The linear behavior in semi-logarithmic space (black solid line) reflects an exponential relation between p0 and and a linear relation between p0 and τdes. Similar relationships are known for p0 and ΔHvap (Epstein et al., 2010), which underscores the correlation of these two quantities as observed in Fig. 11. We find, however, a steeper slope of p0 with than previously found for p0 and ΔHvap, which suggests for large, oxygenated molecules with low vapor pressures. Note, however, that those gas species are lacking in our data sets. The relation of and ΔHvap and its consequences for gas–particle partitioning of SOA will be further investigated in follow-up studies.
Table 2 summarizes characteristic values of p0, , and τdes for the categories of a volatility basis set (VBS) widely used for the description of SOA: intermediate volatility organic compounds (IVOC), semi-volatile organic compounds (SVOC), low volatility compounds (LVOC), extremely low volatility compounds (ELVOC), and ultra-low volatility compounds (ULVOC) (Schervish and Donahue, 2020; Donahue et al., 2009). We obtain characteristic desorption lifetimes of nanoseconds to milliseconds for VOC, milliseconds to hours for IVOC, and seconds to months for SVOC, respectively. For LVOC, ELVOC, and ULVOC we obtain τdes values in the range of minutes to years and millennia. The latter, however, have to be considered as rough estimates, because the amounts of data available for parameterizing p0 and at low volatility are very sparse. Note that these VBS categories were originally defined in terms of saturation mass concentration C0. To express the categories in terms of p0, we applied a constant conversion factor of 10−10 atm m3 µg−1, i.e., assuming a molar mass of 244 g mol−1, for general orientation. For applications in which keeping the exact definition is required, a more nuanced conversion to vapor pressures could be achieved by parameterizing typical values of molar mass as a function of vapor pressure along the SOA molecular corridor. We provide an analogous figure displaying saturation mass concentrations in the Supplement (Fig. S10).
Table 2Characteristic estimates of desorption energies () and desorption lifetimes (τdes, at 298 K) for widely used categories of secondary organic aerosol volatility basis sets (SOA-VBS): volatile organic compounds (VOC), intermediate-volatile (IVOC), semi-volatile (SVOC), low-volatile (LVOC), and extremely/ultra-low volatile (ELVOC/ULVOC).

Gas–particle partitioning plays an important role in chemical transport models, which describe the long-distance transport and chemical degradation of atmospheric constituents. In these models, gas–particle partitioning is often treated with instantaneous-equilibration approaches. Desorption lifetimes crucially determine the position of partitioning steady states and thus affect chemical degradation rates. Moreover, they have a significant influence on the validity of the instantaneous-equilibration assumption (Wilson et al., 2021; Stolzenburg et al., 2018).
Adsorption and desorption processes of semi-volatile species are important in indoor environments, as large surface area-to-volume ratios indoors favor heterogeneous interactions. The deposition of semi-volatile organic compounds on impermeable indoor surfaces can lead to the formation of thin organic films (Weschler and Nazaroff, 2017). The desorption lifetime is a critical parameter for the initial film formation via multilayer adsorption and the subsequent film growth (Lakey et al., 2021). These surface films act as reservoirs of semivolatile compounds and also serve as reaction media, affecting indoor air composition (Wang et al., 2020; Lakey et al., 2023).
We have compiled computationally and experimentally derived desorption energy data to provide estimates of for a variety of gas species and solid, liquid, and ice substrates, thereby covering a range of relevant aerosol particle systems. The desorption energies have been placed in context with intermolecular forces. We were able to express as a function of molecular weight and O : C ratio only, facilitating the application of the proposed parameterization. The important roles of gas species' polarizability and dipole moment governing have been recognized. We demonstrated the importance of correct values for interpretation of multiphase chemical reactions and gas–particle partitioning, especially when extrapolating laboratory findings to atmospherically relevant temperature ranges. For example, assessment of chemical aging of aerosol particles during transport relies on values for various atmospheric oxidants.
The compiled literature data allowed us to correlate with the enthalpy of vaporization and solvation, thereby evaluating the role of desorption in these interfacial processes. We identified a positive correlation between and ΔHvap, where values are often larger than ΔHvap. For liquid substrates, we observe a correlation with molecule oxidation state as well, indicating the importance of intermolecular interactions when looking at interfacial processes.
A positive correlation has been observed between and ΔHsolv in liquid substrates. This trend could be related to the gas species' dipole moment and the interfacial interactions among the adsorbed gas species and molecules in the liquid phase.
We demonstrated the relevance of in gas–particle partitioning and its relationship to the concept of molecular corridors. values for many SOA components were derived allowing for in detail simulation of SOA formation and growth processes. Accurate representation of particle growth and SOA formation processes requires for typically oxygenated VOCs. The relevance of for application in indoor air chemistry has been highlighted. Furthermore, in the Appendix A1 we outline the correlation of glass transition points with , which adds another layer of complexity when modeling multiphase chemical reactions (through the potential of viscous phase states). Our findings identify the following areas of further research needs:
-
More adsorption and desorption data for environmentally relevant interfaces, including multicomponent aerosol particle surfaces, are needed. Experimental and computational approaches can yield necessary values.
-
Reporting and application of adsorption and/or desorption data should consider applied standard states and adsorption models to better constrain (Donaldson et al., 2012b; Savara, 2013; Campbell et al., 2016; Knopf and Ammann, 2021).
-
Desorption kinetic measurements involving liquids with high vapor pressure are needed. Furthermore, the role of solutes in aqueous solutions on the hydrogen bonding network and in turn on the desorption process is not well understood. For example, adsorbates with hydrophilic functional groups exert greater . Systematic examination of desorption kinetics as a function of varying solute concentration and gas species O : C and dipole moment are needed to improve our understanding of adsorption and desorption processes on liquid surfaces.
-
Experimental and theoretical multiphase chemical kinetics studies should aim to represent the typical atmospheric temperature range. This can add to further complications with regard to the underlying thermodynamics and kinetics in addition to possibly phase state changes of the substrate (Li and Knopf, 2021; Li et al., 2020; Slade et al., 2017; Knopf et al., 2005; Davies and Wilson, 2015; Chan et al., 2014; Hearn and Smith, 2007).
-
Advancing our understanding of the interfacial processes that govern mass accommodation, solvation, and vaporization is needed. Adsorption and desorption can play a role in these processes. However, the degree of how much impact has on gas species' solvation or vaporization depends on its relationship with ΔHvap and ΔHsolv. Considering that aerosol particles are chemically complex and exhibit multiple phases and phase states, these advances will improve representation of gas–particle partitioning.
This appendix provides a discussion of observed correlation between and Tg, nomenclature used in this study, and lists the applied data sets to develop the parameterization and to produce correlation plots. The parameters given in tables are also available electronically (Knopf et al., 2024).
A1 Glass transition
Molecular corridors yield also significant insight into particle phase state and viscosity. The glass transition temperature (Tg) characterizes the non-equilibrium phase change from a glassy solid state to a more pliable semi-solid state upon an increase of temperature or humidity (Koop et al., 2011). Tg depends primarily on the molar mass and secondarily on the O : C (Koop et al., 2011; Shiraiwa et al., 2017a). Organic compounds with greater molar mass and lower volatility have higher Tg, indicating that these compounds adopt an amorphous (semi-)solid phase with higher viscosity. For weakly functionalized compounds, viscosity and Tg are sensitive to addition of carboxylic acid (COOH) and hydroxyl (OH) groups compared to carbonyl (CO) and methylene (CH2) (Rothfuss and Petters, 2017; Galeazzo and Shiraiwa, 2022). It has been demonstrated that on average the addition of one OH group increases the viscosity by a factor of approximately 22 to 45 (Grayson et al., 2017). These studies imply that hydrogen bonding may play an important role in determining viscosity, which is consistent with its role in influencing glass transition temperatures (Nakanishi and Nozaki, 2011; van der Sman, 2013).
Recent studies have shown that a glassy surface can be much more dynamic with lower viscosity than anticipated based on Tg and bulk viscosity (Tian et al., 2022; Zhang and Fakhraai, 2017; Sikorski et al., 2010). The enhanced surface mobility, however, is mostly shown by two typical amorphous polymers of polystyrene and poly(methyl methacrylate) (Tian et al., 2022). Though it is likely that also enhanced mobility on the surface compared to the bulk is relevant for atmospheric organic matter, further studies are necessary to assess whether this is applicable to atmospheric glassy SOA particles, which are highly complex multicomponent mixtures that are very different from polymers.
Applying our parameterization of , we can now construct a relationship between and Tg of the SOA oxidation products shown in Fig. 13. Tg was derived applying the parameterization presented in Shiraiwa et al., (2017a) using molar mass and O : C as input variables. was derived applying Eqs. (15) and (18). Since both of our parameterizations of and Tg depend on molar mass and O : C ratio, it is reasonable to expect we can now construct a positive relationship between and Tg of the SOA oxidation products. Figure A1 shows that gas species with lower have lower Tg and vice versa. Figure A1a demonstrates that for gas species with same , an increase in O : C results in a significant increase of Tg, pointing to enhanced molecular interactions. Hence, alkanes represent species with lowest Tg at given . Figure A1b further corroborates this fact. Tg has a strong dependency on molar mass. However, for the same molar mass, Tg can vary by 100 K (which coincides with only small changes in ), which can now be attributed to the impact of O : C. In other words, increased molecular interactions can significantly increase Tg, when other parameters remain the same. Similar trends hold for , thereby allowing one to recognize that comparable molecular interactions control the properties of the amorphous phase state of a system and its . In absence of knowing the molecular structure, Fig. S11 provides the same analysis of the relationship between and Tg of the SOA oxidation products using parameterization Eq. (17) for comparison. We see that without knowing the molecular structure, a tighter correlation between and Tg is observed due to the linearization of the gas species' polarizability. Similarly to Figs. 14 and S6, the predicted values in Fig. S11 are within ±10 % of the values shown in Fig. A1 and within the expected general uncertainty of .
The correlation between and Tg serves as empirical and observational evidence. The theoretical and physical basis are yet to be established. It does not account for the potentially enhanced mobility on the surface of glassy matter (Tian et al., 2022; Zhang and Fakhraai, 2017; Sikorski et al., 2010). One would expect that surface mobility would similarly scale with the strength of intermolecular interactions. Molecules with high interact strongly with molecules of the same kind at the surface and in the bulk, and they are expected to also exhibit reduced dynamics in their own condensed phase (or in a mixture of similar molecules) and thus high viscosity. The presented correlation observed is meaningful for advancing our understanding of interfacial processes and supports further investigations.
A2 Nomenclature
| τdes | desorption lifetime |
| kdes | first-order desorption rate coefficient |
| Ades | pre-exponential factor |
| desorption energy with the energy reference of the gas molecule at rest at T=0 K | |
| γ | uptake coefficient |
| αs | surface accommodation coefficient |
| Γb | normalized loss rate in the bulk phase induced by solubility, diffusion and reaction |
| Γsb | normalized rate of surface to bulk transfer |
| Γs | normalized loss rate due to surface reaction |
| ks | first-order rate coefficient of chemical reaction at the surface |
| ksb | first-order rate coefficient for the transfer of molecules from the surface into the bulk (solvation) |
| kbs | first-order rate coefficient for the transfer of molecules from the bulk to the surface |
| αb | bulk accommodation coefficient |
| Gibbs free energy change of adsorption | |
| standard enthalpy change of adsorption | |
| standard entropy change of adsorption | |
| κ | transmission coefficient |
| standard concentration of molecules in the TS | |
| standard concentration of adsorbed molecules | |
| standard partition functions for the TS | |
| standard partition functions for the adsorbate | |
| partition functions for the TS | |
| qads | partition functions for the adsorbate |
| M | molar mass |
| ΔHvap | enthalpy of vaporization |
| α | polarizability |
| μ | dipole moment |
| O : C | oxygen-to-carbon ratio |
| ΔHsol | enthalpy of solvation |
| εr | relative permittivity of the substrate |
| TPD | temperature programmed desorption |
| TDS | thermal desorption spectroscopy |
| TG-DSC | thermal gravimetry with differential scanning calorimetry |
| KN | Knudsen cell |
| MB | molecular beam |
| GC | gas chromatography |
| IGC | inverse gas chromatography |
| VM | vacuum microbalance |
| DRIFT | diffuse reflectance infrared Fourier transform spectroscopy |
| FTIR | Fourier transform infrared spectroscopy |
| KU | kinetic uptake |
| VS | vibrational spectroscopy |
| ST | surface tension |
| MD | molecular dynamics |
| DFT | density functional theory |
| MC | Monte Carlo |
| GCMC | grand canonical Monte Carlo |
| CCSD(T) | coupled cluster singles and doubles theory, including perturbative triples |
| ECT | embedded cluster theory |
| DAM | dipped adcluster model |
Table A1Compiled absorbate–substrate data for water vapor and heavy water vapor adsorbed on various mineral and clay substrates, inorganics, organics, and carbonaceous substrates, including highly oriented pyrolytic graphite (HOPG) and self-assembled monolayers (SAM). Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.

* Applied the value for liquid phase of substrate species.
Table A2Compiled absorbate–substrate interaction energies for reactive gases on solid substrates. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
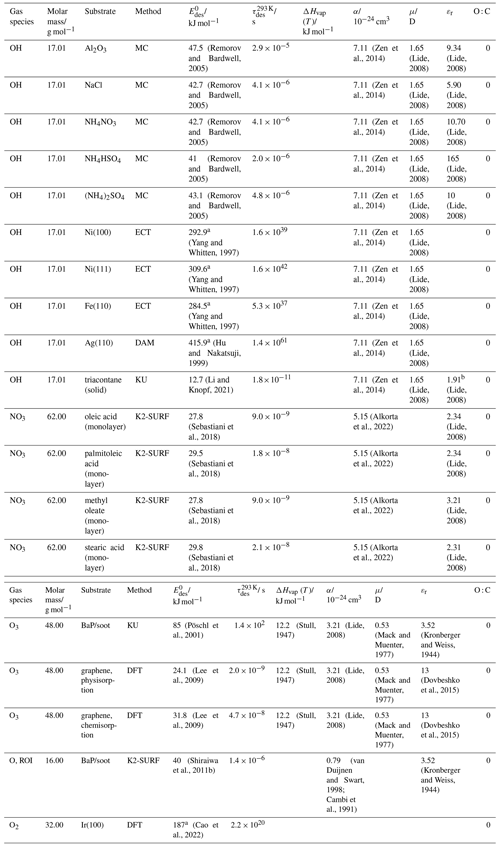
a Not applied in analysis. b Applied value for the liquid phase of substrate species.
Table A3Compiled absorbate–substrate interaction energies for reactive and non-reactive gases on soot of light-duty vehicle (LDV) and heavy-duty vehicle (HDV), Pyrex glass, steel, salt, mineral, clay, and highly oriented pyrolyzed graphite (HOPG). Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
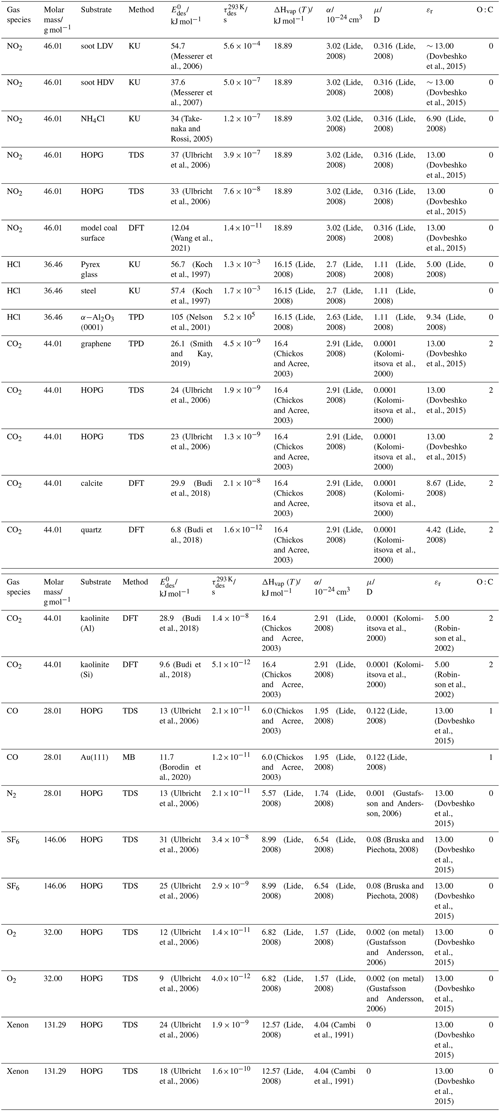
Table A4Compiled absorbate–substrate interaction energies for organic gases on self-assembled monolayers, salt, fly ash, and urban aerosol. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
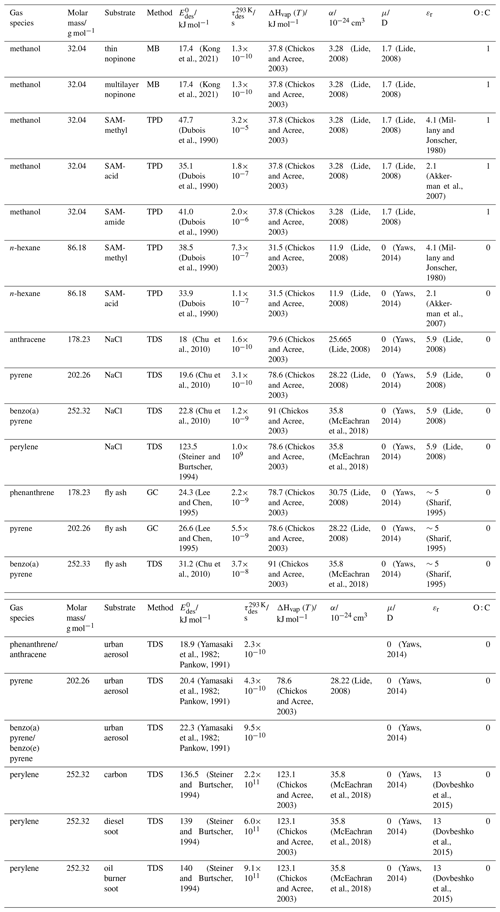
Table A5Compiled absorbate–substrate interaction energies of volatile organic compounds (VOCs) on graphite (C(0001)), highly oriented pyrolytic graphite (HOPG), granular activated carbon (GAC), and soot from combustion of kerosene. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.

Table A6Compiled absorbate–substrate interaction energies of volatile organic compounds (VOCs) on MgO(100), Pt(111), Ni(111), and Pd(111). Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
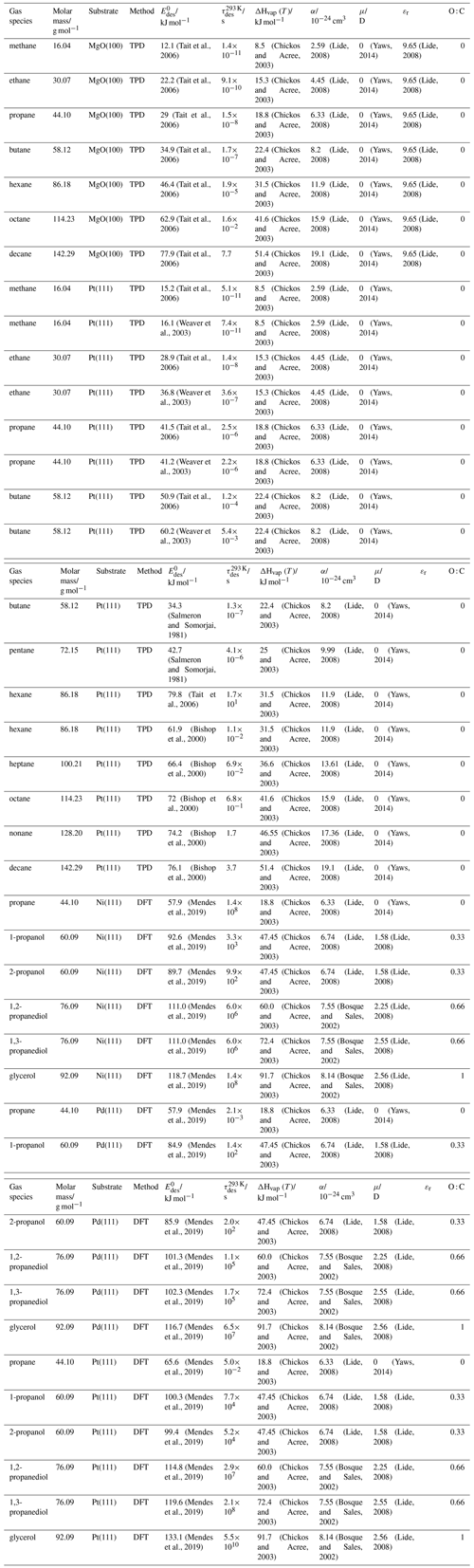
Table A7Compiled absorbate–substrate interaction energies of volatile organic compounds (VOCs) on mineral surrogates and minerals and clays. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.

Table A8Compiled absorbate–substrate interaction energies of inorganic and organic gas species on ice. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
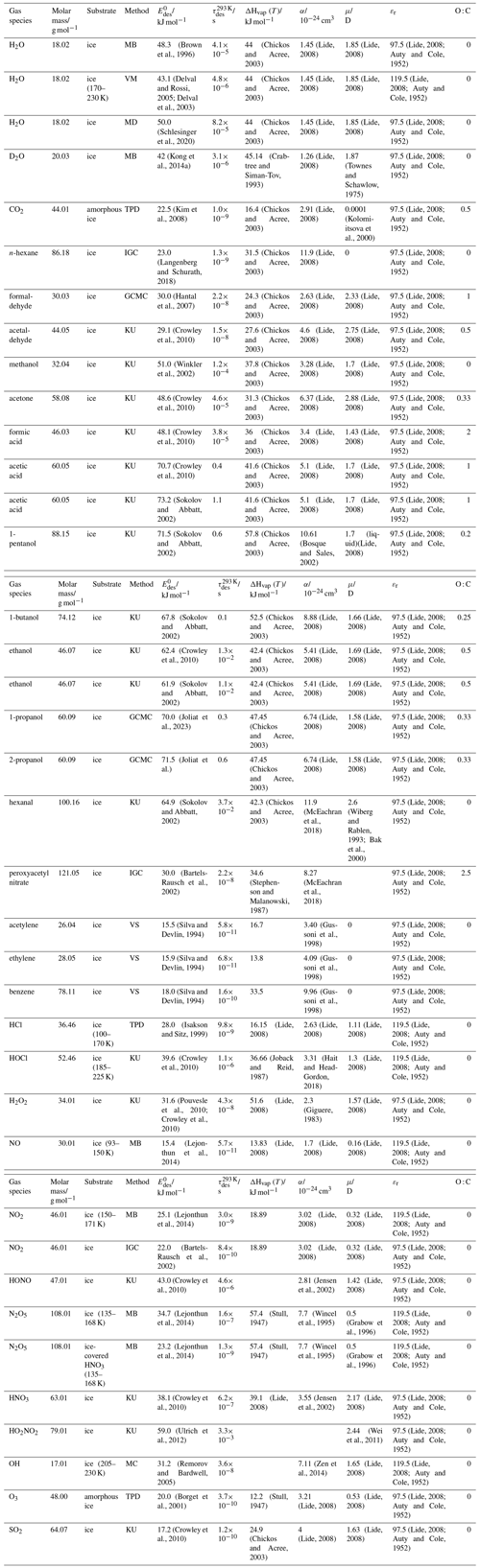
Table A9Compiled absorbate–substrate data for water vapor and inorganic gases adsorbed on water and aqueous substrates. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap) and solvation (ΔHsolv), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
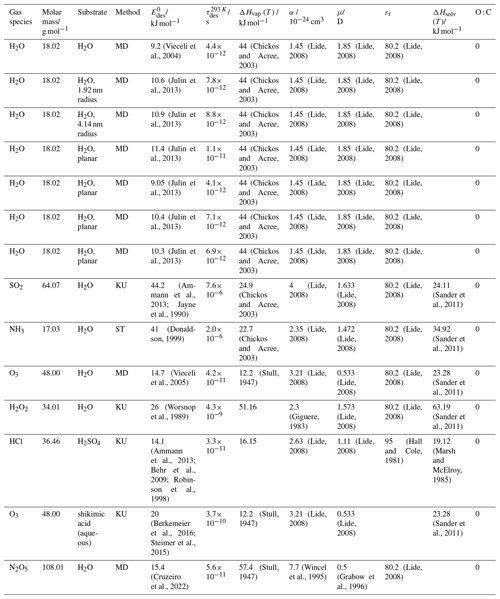
Table A10Compiled absorbate–substrate data for volatile aromatic gases adsorbed on water. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap) and solvation (ΔHsolv), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.

Table A11Compiled absorbate–substrate data for volatile amine and alcohol compounds adsorbed on water. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap) and solvation (ΔHsolv), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
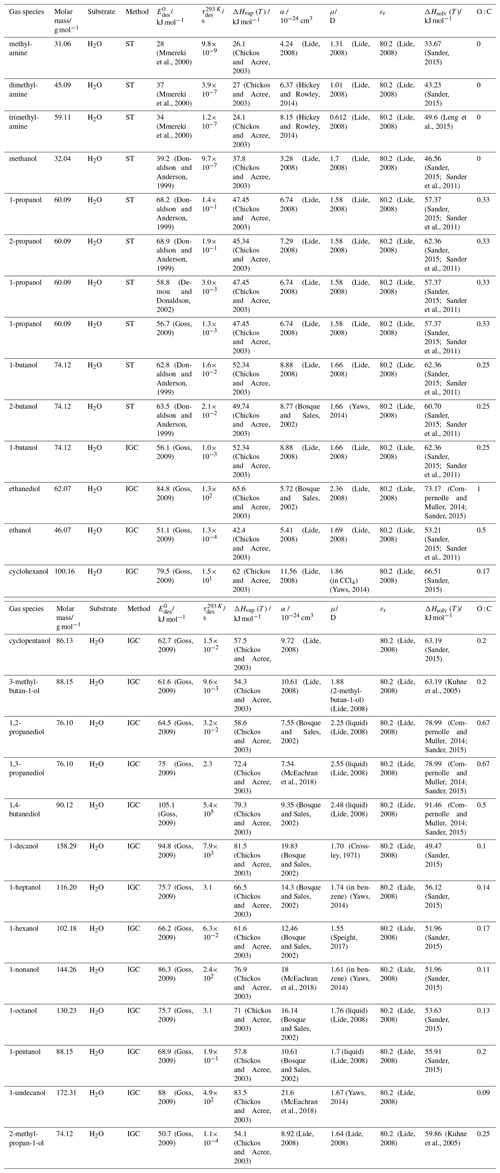
Table A12Compiled absorbate–substrate data for alkene and ketone compounds adsorbed on water. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap) and solvation (ΔHsolv), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
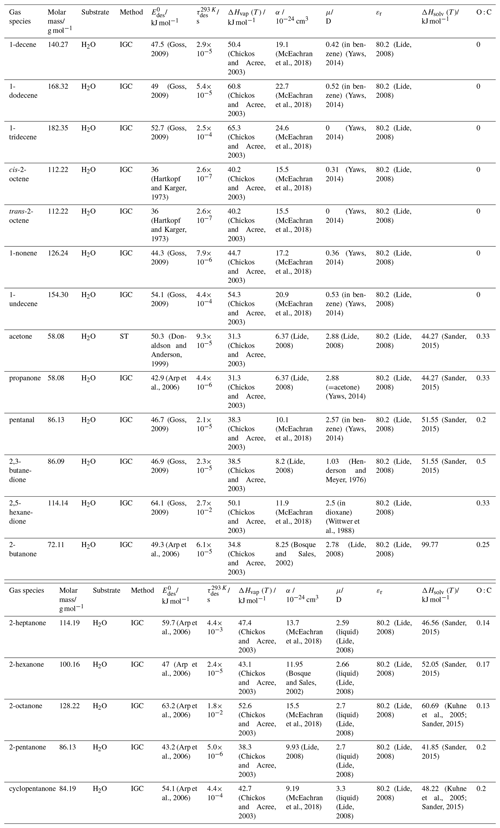
Table A13Compiled absorbate–substrate data for volatile acid and ether compounds adsorbed on water. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap) and solvation (ΔHsolv), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
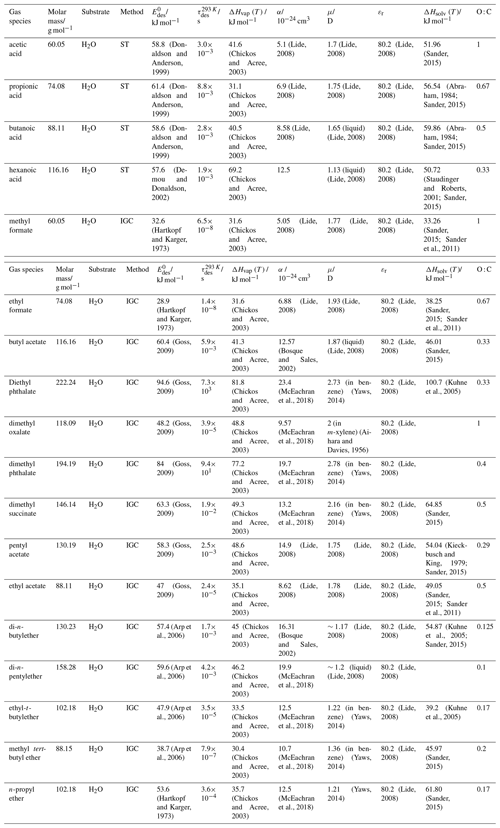
Table A14Compiled absorbate–substrate data for volatile alkane compounds adsorbed on water. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap) and solvation (ΔHsolv), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
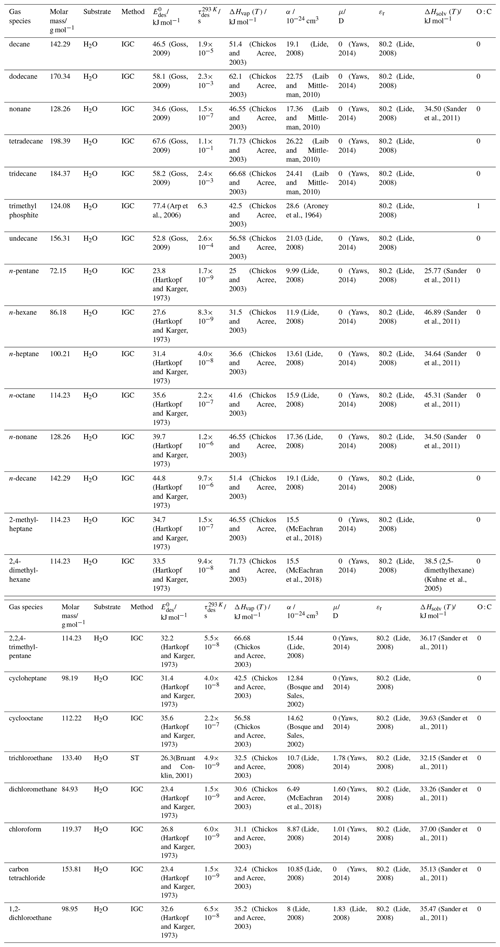
Table A15Compiled absorbate–substrate data for volatile acid and alcohol compounds adsorbed on aqueous solutions. Gas species, gas species' molar mass, substrate, experimental or theoretical method, desorption energy (), and desorption lifetimes (τdes) evaluated at 293 K using Ades=1013 s−1, enthalpy of vaporization (ΔHvap) and solvation (ΔHsolv), gas species' polarizability (α), gas species' dipole moment (μ), substrate's relative permittivity (εr), and gas species' oxygen-to-carbon ratios (O : C) are given.
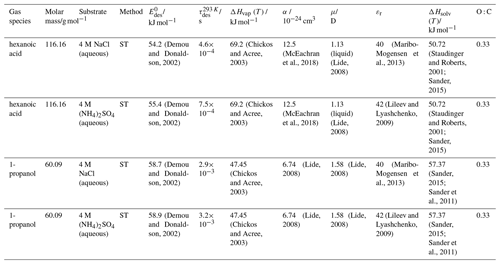
Data needed to draw the conclusions in the present study are given in the paper and in the Supplement. In addition, the data sets required to reproduce the results and corresponding figures are available on Zenodo (https://doi.org/10.5281/zenodo.8417534, Knopf et al., 2024).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-24-3445-2024-supplement.
DAK and MS envisioned the project. DAK supervised project, performed correlation analyses, and wrote the first draft of the manuscript. MS and TB performed kinetic flux modeling. MA, TB, and UP critically discussed analyses and results and were involved in representation of data. All authors discussed interpretation of the data and contributed to the writing of the paper.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Chemistry and Physics. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Daniel A. Knopf acknowledges support from the U.S. National Science Foundation (grant no. AGS-1446286) and the Max Planck Society for the sabbatical stay in 2014, which initiated this project. Manabu Shiraiwa acknowledges support from the U.S. National Science Foundation (grant nos. AGS-1654104, AGS-2246502) and the U.S. Department of Energy (grant no. DE-SC0022139). Markus Ammann acknowledges support from the Swiss National Science Foundation (grant no. 188662).
This research has been supported by the U.S. National Science Foundation (grant nos. AGS-1446286, AGS-2246502, and AGS-1654104), the U.S. Department of Energy (DE-SC0022139), and the Swiss National Science Foundation (grant no. 188662).
This paper was edited by Alexander Laskin and reviewed by two anonymous referees.
Abbatt, J. P. D. and Ravishankara, A. R.: Opinion: Atmospheric multiphase chemistry – past, present, and future, Atmos. Chem. Phys., 23, 9765–9785, https://doi.org/10.5194/acp-23-9765-2023, 2023.
Abbatt, J. P. D., Lee, A. K. Y., and Thornton, J. A.: Quantifying trace gas uptake to tropospheric aerosol: recent advances and remaining challenges, Chem. Soc. Rev., 41, 6555–6581, https://doi.org/10.1039/C2cs35052a, 2012.
Abraham, M. H.: Measurement of Enthalpies of Solution of Electrolytes, in: Thermochemistry and Its Applications to Chemical and Biochemical Systems. NATO ASI Series (Series C: Mathematical and Physical Sciences), edited by: Ribeiro da Silva, M. A. V., 119, Springer, Dordrecht, https://doi.org/10.1007/978-94-009-6312-2_20, 1984.
Ahmed, M., Blum, M., Crumlin, E. J., Geissler, P. L., Head-Gordon, T., Limmer, D. T., Mandadapu, K. K., Saykally, R. J., and Wilson, K. R.: Molecular Properties and Chemical Transformations Near Interfaces, J. Phys. Chem. B, 125, 9037–9051, https://doi.org/10.1021/acs.jpcb.1c03756, 2021.
Aihara, A. and Davies, M.: Dielectric relaxation times of some nonrigid polar molecules, J. Coll. Sci. Imp. U. Tok., 11, 671–687, https://doi.org/10.1016/0095-8522(56)90182-9, 1956.
Akkerman, H. B., Naber, R. C. G., Jongbloed, B., van Hal, P. A., Blom, P. W. M., de Leeuw, D. M., and de Boer, B.: Electron tunneling through alkanedithiol self-assembled monolayers in large-area molecular junctions, P. Natl. Acad. Sci. USA, 104, 11161–11166, https://doi.org/10.1073/pnas.0701472104, 2007.
Alcala-Jornod, C., van den Bergh, H., and Rossi, M. J.: Reactivity of NO2 and H2O on soot generated in the laboratory: a diffusion tube study at ambient temperature, Phys. Chem. Chem. Phys., 2, 5584–5593, 2000.
Alcala-Jornod, C., van den Bergh, H., and Rossi, M. J.: Can soot particles emitted by airplane exhaust contribute to the formation of aviation contrails and cirrus clouds?, Geophys. Res. Lett., 29, 4, https://doi.org/10.1029/2001gl014115, 2002.
Alkorta, I., Plane, J. M. C., Elguero, J., Davalos, J. Z., Acuna, A. U., and Saiz-Lopez, A.: Theoretical study of the NO3 radical reaction with CH2ClBr, CH2ICl, CH2BrI, CHCl2Br, and CHClBr2, Phys. Chem. Chem. Phys., 24, 14365–14374, https://doi.org/10.1039/d2cp00021k, 2022.
Allouche, A. and Bahr, S.: Acetic acid-water interaction in solid interfaces, J. Phys. Chem. B, 110, 8640–8648, https://doi.org/10.1021/jp0559736, 2006.
Ammann, M. and Pöschl, U.: Kinetic model framework for aerosol and cloud surface chemistry and gas-particle interactions – Part 2: Exemplary practical applications and numerical simulations, Atmos. Chem. Phys., 7, 6025–6045, https://doi.org/10.5194/acp-7-6025-2007, 2007.
Ammann, M., Pöschl, U., and Rudich, Y.: Effects of reversible adsorption and Langmuir-Hinshelwood surface reactions on gas uptake by atmospheric particles, Phys. Chem. Chem. Phys., 5, 351–356, 2003.
Ammann, M., Cox, R. A., Crowley, J. N., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume VI – heterogeneous reactions with liquid substrates, Atmos. Chem. Phys., 13, 8045–8228, https://doi.org/10.5194/acp-13-8045-2013, 2013.
Arangio, A. M., Slade, J. H., Berkemeier, T., Pöschl, U., Knopf, D. A., and Shiraiwa, M.: Multiphase Chemical Kinetics of OH Radical Uptake by Molecular Organic Markers of Biomass Burning Aerosols: Humidity and Temperature Dependence, Surface Reaction, and Bulk Diffusion, J. Phys. Chem. A, 119, 4533–4544, https://doi.org/10.1021/jp510489z, 2015.
Aroney, M. J., Saxby, J. D., Lefevre, R. J. W., and Chia, L. H. L.: Molecular polarisability. Dipole moments molar Kerr constants + conformations of 11 phosphate + phosphite triesters as solutes in benzene, J. Chem. Soc., 2948–2954, https://doi.org/10.1039/jr9640002948, 1964.
Arp, H. P. H., Goss, K. U., and Schwarzenbach, R. P.: Evaluation of a predictive model for air/surface adsorption equilibrium constants and enthalpies, Environ. Toxicol. Chem., 25, 45–51, https://doi.org/10.1897/05-291r.1, 2006.
Arrhenius, S. A.: Über die Dissociationswärme und den Einflusß der Temperatur auf den Dissociationsgrad der Elektrolyte, Z. Phys. Chem., 4, 96–116, 1889a.
Arrhenius, S. A.: Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren, Z. Phys. Chem., 4, 226–248, 1889b.
Artiglia, L., Edebeli, J., Orlando, F., Chen, S. Z., Lee, M. T., Arroyo, P. C., Gilgen, A., Bartels-Rausch, T., Kleibert, A., Vazdar, M., Carignano, M. A., Francisco, J. S., Shepson, P. B., Gladich, I., and Ammann, M.: A surface-stabilized ozonide triggers bromide oxidation at the aqueous solution-vapour interface, Nat. Commun., 8, 8, https://doi.org/10.1038/s41467-017-00823-x, 2017.
Asakawa, H., Sazaki, G., Nagashima, K., Nakatsubo, S., and Furukawa, Y.: Two types of quasi-liquid layers on ice crystals are formed kinetically, P. Natl. Acad. Sci. USA, 113, 1749–1753, https://doi.org/10.1073/pnas.1521607113, 2016.
Auty, R. P. and Cole, R. H.: Dielectric properties of ice and solid D2O, J. Chem. Phys., 20, 1309–1314, https://doi.org/10.1063/1.1700726, 1952.
Bak, K. L., Gauss, J., Helgaker, T., Jorgensen, P., and Olsen, J.: The accuracy of molecular dipole moments in standard electronic structure calculations, Chem. Phys. Lett., 319, 563–568, https://doi.org/10.1016/s0009-2614(00)00198-6, 2000.
Baron, M. and Arevalo, E. S.: Dipole-moment values from single-solution measurements, J. Chem. Educ., 65, 644–645, https://doi.org/10.1021/ed065p644, 1988.
Bartels-Rausch, T.: Ten things we need to know about ice and snow, Nature, 494, 27–29, https://doi.org/10.1038/494027a, 2013.
Bartels-Rausch, T., Huthwelker, T., Gaggeler, H. W., and Ammann, M.: Atmospheric pressure coated-wall flow-tube study of acetone adsorption on ice, J. Phys. Chem. A, 109, 4531–4539, https://doi.org/10.1021/jp045187l, 2005.
Bartels-Rausch, T., Jacobi, H.-W., Kahan, T. F., Thomas, J. L., Thomson, E. S., Abbatt, J. P. D., Ammann, M., Blackford, J. R., Bluhm, H., Boxe, C., Domine, F., Frey, M. M., Gladich, I., Guzmán, M. I., Heger, D., Huthwelker, Th., Klán, P., Kuhs, W. F., Kuo, M. H., Maus, S., Moussa, S. G., McNeill, V. F., Newberg, J. T., Pettersson, J. B. C., Roeselová, M., and Sodeau, J. R.: A review of air–ice chemical and physical interactions (AICI): liquids, quasi-liquids, and solids in snow, Atmos. Chem. Phys., 14, 1587–1633, https://doi.org/10.5194/acp-14-1587-2014, 2014.
Bartels-Rausch, T., Orlando, F., Kong, X. R., Artiglia, L., and Ammann, M.: Experimental Evidence for the Formation of Solvation Shells by Soluble Species at a Nonuniform Air-Ice Interface, ACS Earth Space Chem., 1, 572–579, https://doi.org/10.1021/acsearthspacechem.7b00077, 2017.
Bartels, T., Eichler, B., Zimmermann, P., Gäggeler, H. W., and Ammann, M.: The adsorption of nitrogen oxides on crystalline ice, Atmos. Chem. Phys., 2, 235–247, https://doi.org/10.5194/acp-2-235-2002, 2002.
Behr, P., Morris, J. R., Antman, M. D., Ringeisen, B. R., Splan, J. R., and Nathanson, G. M.: Reaction and desorption of HCl and HBr following collisions with supercooled sulfuric acid, Geophys. Res. Lett., 28, 1961–1964, https://doi.org/10.1029/2000gl012716, 2001.
Behr, P., Scharfenort, U., Ataya, K., and Zellner, R.: Dynamics and mass accommodation of HCl molecules on sulfuric acid-water surfaces, Phys. Chem. Chem. Phys., 11, 8048–8055, https://doi.org/10.1039/b904629a, 2009.
Beller, M., Renken, A., and van Santen, R. A.: Catalysis: From Principles to Applications, John Wiley & Sons, Inc., Hoboken, New Jersey, USA, ISBN 978-3-527-32349-4, 2012.
Berkemeier, T., Huisman, A. J., Ammann, M., Shiraiwa, M., Koop, T., and Pöschl, U.: Kinetic regimes and limiting cases of gas uptake and heterogeneous reactions in atmospheric aerosols and clouds: a general classification scheme, Atmos. Chem. Phys., 13, 6663–6686, https://doi.org/10.5194/acp-13-6663-2013, 2013.
Berkemeier, T., Steimer, S. S., Krieger, U. K., Peter, T., Pöschl, U., Ammann, M., and Shiraiwa, M.: Ozone uptake on glassy, semi-solid and liquid organic matter and the role of reactive oxygen intermediates in atmospheric aerosol chemistry, Phys. Chem. Chem. Phys., 18, 12662–12674, https://doi.org/10.1039/c6cp00634e, 2016.
Berkemeier, T., Takeuchi, M., Eris, G., and Ng, N. L.: Kinetic modeling of formation and evaporation of secondary organic aerosol from NO3 oxidation of pure and mixed monoterpenes, Atmos. Chem. Phys., 20, 15513–15535, https://doi.org/10.5194/acp-20-15513-2020, 2020.
Berkemeier, T., Mishra, A., Mattei, C., Huisman, A. J., Krieger, U. K., and Poschl, U.: Ozonolysis of Oleic Acid Aerosol Revisited: Multiphase Chemical Kinetics and Reaction Mechanisms, ACS Earth Space Chem., 5, 3313–3323, https://doi.org/10.1021/acsearthspacechem.1c00232, 2021.
Bertram, A. K., Martin, S. T., Hanna, S. J., Smith, M. L., Bodsworth, A., Chen, Q., Kuwata, M., Liu, A., You, Y., and Zorn, S. R.: Predicting the relative humidities of liquid-liquid phase separation, efflorescence, and deliquescence of mixed particles of ammonium sulfate, organic material, and water using the organic-to-sulfate mass ratio of the particle and the oxygen-to-carbon elemental ratio of the organic component, Atmos. Chem. Phys., 11, 10995–11006, https://doi.org/10.5194/acp-11-10995-2011, 2011.
Bishop, A. R., Girolami, G. S., and Nuzzo, R. G.: Structural models and thermal desorption energetics for multilayer assemblies of the n-alkanes on Pt(111), J. Phys. Chem. B, 104, 754–763, https://doi.org/10.1021/jp9926488, 2000.
Blank, M. and Ottewill, R. H.: Adsorption of aromatic vapors on water surfaces, J. Phys. Chem., 68, 2206–2211, https://doi.org/10.1021/j100790a030, 1964.
Bolis, V.: Fundamentals in Adsorption at the Solid-Gas Interface. Concepts and Thermodynamics, in: Calorimetry and Thermal Methods in Catalysis, edited by: Auroux, A., 154, Springer-Verlag Berlin Heidelberg, Berlin, 3–50, https://doi.org/10.1007/978-3-642-11954-5, 2013.
Bond, T. C., Doherty, S. J., Fahey, D. W., Forster, P. M., Berntsen, T., DeAngelo, B. J., Flanner, M. G., Ghan, S., Karcher, B., Koch, D., Kinne, S., Kondo, Y., Quinn, P. K., Sarofim, M. C., Schultz, M. G., Schulz, M., Venkataraman, C., Zhang, H., Zhang, S., Bellouin, N., Guttikunda, S. K., Hopke, P. K., Jacobson, M. Z., Kaiser, J. W., Klimont, Z., Lohmann, U., Schwarz, J. P., Shindell, D., Storelvmo, T., Warren, S. G., and Zender, C. S.: Bounding the role of black carbon in the climate system: A scientific assessment, J. Geophys. Res., 118, 5380–5552, https://doi.org/10.1002/jgrd.50171, 2013.
Borget, F., Chiavassa, T., Allouche, A., and Aycard, J. P.: Experimental and quantum study of adsorption of ozone (O3) on amorphous water ice film, J. Phys. Chem. B, 105, 449–454, https://doi.org/10.1021/jp001785y, 2001.
Borodin, D., Rahinov, I., Shirhatti, P. R., Huang, M., Kandratsenka, A., Auerbach, D. J., Zhong, T. L., Guo, H., Schwarzer, D., Kitsopoulos, T. N., and Wodtke, A. M.: Following the microscopic pathway to adsorption through chemisorption and physisorption wells, Science, 369, 1461–1465, https://doi.org/10.1126/science.abc9581, 2020.
Borrmann, S., Solomon, S., Dye, J. E., and Luo, B. P.: The potential of cirrus clouds for heterogeneous chlorine activation, Geophys. Res. Lett., 23, 2133–2136, 1996.
Bosque, R. and Sales, J.: Polarizabilities of solvents from the chemical composition, J. Chem. Inf. Comput. Sci., 42, 1154–1163, https://doi.org/10.1021/ci025528x, 2002.
Brastad, S. M., Albert, D. R., Huang, M. W., and Nathanson, G. M.: Collisions of DCl with a Solution Covered with Hydrophobic and Hydrophilic Ions: Tetrahexylammonium Bromide in Glycerol, J. Phys. Chem. A, 113, 7422–7430, https://doi.org/10.1021/jp900232v, 2009.
Brini, E., Fennell, C. J., Fernandez-Serra, M., Hribar-Lee, B., Luksic, M., and Dill, K. A.: How Water's Properties Are Encoded in Its Molecular Structure and Energies, Chem. Rev., 117, 12385–12414, https://doi.org/10.1021/acs.chemrev.7b00259, 2017.
Broderick, A., Rocha, M. A., Khalifa, Y., Shiflett, M. B., and Newberg, J. T.: Mass Transfer Thermodynamics through a Gas–Liquid Interface, J. Phys. Chem. B, 123, 2576–2584, https://doi.org/10.1021/acs.jpcb.9b00958, 2019.
Brown, D. E., George, S. M., Huang, C., Wong, E. K. L., Rider, K. B., Smith, R. S., and Kay, B. D.: H2O condensation coefficient and refractive index for vapor-deposited ice from molecular beam and optical interference measurements, J. Phys. Chem., 100, 4988–4995, https://doi.org/10.1021/jp952547j, 1996.
Bruant, R. G. and Conklin, M. H.: Adsorption of trichloroethene at the vapor/water interface, Environ. Sci. Technol., 35, 362–364, https://doi.org/10.1021/es000994t, 2001.
Bruant, R. G. and Conklin, M. H.: Adsorption of benzene and methyl-substituted benzenes at the vapor/water interface. 2. Single-component VHOC adsorption, J. Phys. Chem. B, 106, 2224–2231, https://doi.org/10.1021/jp0029156, 2002.
Bruska, M. K. and Piechota, J.: Density functional study of sulphur hexafluoride (SF6) and its hydrogen derivatives, Mol. Simul., 34, 1041–1050, https://doi.org/10.1080/08927020802258708, 2008.
Budi, A., Stipp, S. L. S., and Andersson, M. P.: Calculation of Entropy of Adsorption for Small Molecules on Mineral Surfaces, J. Phys. Chem. C, 122, 8236–8243, https://doi.org/10.1021/acs.jpcc.7b11860, 2018.
Caloz, F., Fenter, F. F., Tabor, K. D., and Rossi, M. J.: Paper I: Design and construction of a Knudsen-cell reactor for the study of heterogeneous reactions over the temperature range 130–750 K: Performances and limitations, Rev. Sci. Instrum., 68, 3172–3179, 1997.
Cambi, R., Cappelletti, D., Liuti, G., and Pirani, F.: Generalized correlations in terms of polarizability for vanderwaals interaction potential parameter calculations, J. Chem. Phys., 95, 1852–1861, https://doi.org/10.1063/1.461035, 1991.
Campbell, C. T., Sprowl, L. H., and Arnadottir, L.: Equilibrium Constants and Rate Constants for Adsorbates: Two-Dimensional (2D) Ideal Gas, 2D Ideal Lattice Gas, and Ideal Hindered Translator Models, J. Phys. Chem. C, 120, 10283–10297, https://doi.org/10.1021/acs.jpcc.6b00975, 2016.
Cao, X., Liu, C. L., Zhang, T. F., Xu, Q., Zhang, D. L., Liu, X. T., Jiao, H. J., Wen, X. D., Yang, Y., Li, Y. W., Niemantsverdriet, J. W., and Zhu, J. F.: Revisiting Oxygen Adsorption on Ir(100), J. Phys. Chem. C, 126, 10035–10044, https://doi.org/10.1021/acs.jpcc.2c01237, 2022.
Cappa, C. D., Onasch, T. B., Massoli, P., Worsnop, D. R., Bates, T. S., Cross, E. S., Davidovits, P., Hakala, J., Hayden, K. L., Jobson, B. T., Kolesar, K. R., Lack, D. A., Lerner, B. M., Li, S. M., Mellon, D., Nuaaman, I., Olfert, J. S., Petaja, T., Quinn, P. K., Song, C., Subramanian, R., Williams, E. J., and Zaveri, R. A.: Radiative Absorption Enhancements Due to the Mixing State of Atmospheric Black Carbon, Science, 337, 1078–1081, https://doi.org/10.1126/science.1223447, 2012.
Carslaw, K. S., Peter, T., and Muller, R.: Uncertainties in reactive uptake coefficients for solid stratospheric particles – 2. Effect on ozone depletion, Geophys. Res. Lett., 24, 1747–1750, https://doi.org/10.1029/97gl01684, 1997.
Chan, M. N., Zhang, H., Goldstein, A. H., and Wilson, K. R.: Role of Water and Phase in the Heterogeneous Oxidation of Solid and Aqueous Succinic Acid Aerosol by Hydroxyl Radicals, J. Phys. Chem. C, 118, 28978–28992, https://doi.org/10.1021/jp5012022, 2014.
Chandler, D.: Interfaces and the driving force of hydrophobic assembly, Nature, 437, 640–647, https://doi.org/10.1038/nature04162, 2005.
Charnawskas, J. C., Alpert, P. A., Lambe, A. T., Berkemeier, T., O'Brien, R. E., Massoli, P., Onasch, T. B., Shiraiwa, M., Moffet, R. C., Gilles, M. K., Davidovits, P., Worsnop, D. R., and Knopf, D. A.: Condensed-phase biogenic-anthropogenic interactions with implications for cold cloud formation, Faraday Discuss., 200, 164–195, https://doi.org/10.1039/C7FD00010C, 2017.
Chickos, J. S. and Acree, W. E.: Enthalpies of vaporization of organic and organometallic compounds, 1880–2002, J. Phys. Chem. Ref. Data, 32, 519–878, https://doi.org/10.1063/1.1529214, 2003.
China, S., Mazzoleni, C., Gorkowski, K., Aiken, A. C., and Dubey, M. K.: Morphology and mixing state of individual freshly emitted wildfire carbonaceous particles, Nat. Commun., 4, 2122, https://doi.org/10.1038/ncomms3122, 2013.
Cho, H., Shepson, P. B., Barrie, L. A., Cowin, J. P., and Zaveri, R.: NMR investigation of the quasi-brine layer in ice/brine mixtures, J. Phys. Chem. B, 106, 11226–11232, https://doi.org/10.1021/jp020449+, 2002.
Chorkendorff, I. and Niemantsverdriet, J. W.: Concepts of Modern Catalysis and Kinetics, 2nd, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 477 pp., ISBN 3527316728, 2007.
Chu, S. N., Sands, S., Tomasik, M. R., Lee, P. S., and McNeill, V. F.: Ozone Oxidation of Surface-Adsorbed Polycyclic Aromatic Hydrocarbons: Role of PAH-Surface Interaction, J. Am. Chem. Soc., 132, 15968–15975, https://doi.org/10.1021/ja1014772, 2010.
Collignon, B., Hoang, P. N. M., Picaud, S., and Rayez, J. C.: Ab initio study of the water adsorption on hydroxylated graphite surfaces, Chem. Phys. Lett., 406, 430–435, https://doi.org/10.1016/j.cplett.2005.03.026, 2005.
Compernolle, S. and Müller, J.-F.: Henry's law constants of polyols, Atmos. Chem. Phys., 14, 12815–12837, https://doi.org/10.5194/acp-14-12815-2014, 2014.
Compernolle, S., Ceulemans, K., and Müller, J.-F.: EVAPORATION: a new vapour pressure estimation methodfor organic molecules including non-additivity and intramolecular interactions, Atmos. Chem. Phys., 11, 9431–9450, https://doi.org/10.5194/acp-11-9431-2011, 2011.
Crabtree, A. and Siman-Tov, M.: Thermophysical properties of saturated light and heavy water for advanced neutron source applications, Oak Ridge National LaboratoryORNL/TM-12322, https://doi.org/10.2172/6306919, 1993.
Crossley, J.: Dielectric relaxation of 1-butanol and 1-decanol in several solvents, J. Phys. Chem., 75, 1790–1794, https://doi.org/10.1021/j100681a005, 1971.
Crossley, J.: Dielectric-relaxation of 1-alkenes, J. Chem. Phys., 58, 5315–5318, https://doi.org/10.1063/1.1679145, 1973.
Croteau, T., Bertram, A. K., and Patey, G. N.: Simulation of Water Adsorption on Kaolinite under Atmospheric Conditions, J. Phys. Chem. A, 113, 7826–7833, https://doi.org/10.1021/jp902453f, 2009.
Crowley, J. N., Ammann, M., Cox, R. A., Hynes, R. G., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume V – heterogeneous reactions on solid substrates, Atmos. Chem. Phys., 10, 9059–9223, https://doi.org/10.5194/acp-10-9059-2010, 2010.
Crowley, J. N., Ammann, M., Cox, R. A., Hynes, R. G., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Corrigendum to “Evaluated kinetic and photochemical data for atmospheric chemistry: Volume V – heterogeneous reactions on solid substrates” published in Atmos. Chem. Phys. 10, 9059–9223, 2010, Atmos. Chem. Phys., 13, 7359–7359, https://doi.org/10.5194/acp-13-7359-2013, 2013.
Cruzeiro, V. W. D., Galib, M., Limmer, D. T., and Gotz, A. W.: Uptake of N2O5 by aqueous aerosol unveiled using chemically accurate many-body potentials, Nat. Commun., 13, 7, https://doi.org/10.1038/s41467-022-28697-8, 2022.
Cussler, E. L.: Diffusion – Mass Transfer in Fluid Systems, ISBN 0521871212, 2009.
Cwiertny, D. M., Young, M. A., and Grassian, V. H.: Chemistry and photochemistry of mineral dust aerosol, Annu. Rev. Phys. Chem., 59, 27–51, https://doi.org/10.1146/annurev.physchem.59.032607.093630, 2008.
Daniels, D. J.: Ground Penetrating Radar, 2nd, The Institution of Engineering and Technology, London, United Kingdom, 726 pp., ISBN 978-0-86341-360-5, 2004.
Davidovits, P., Kolb, C. E., Williams, L. R., Jayne, J. T., and Worsnop, D. R.: Mass accommodation and chemical reactions at gas-liquid interfaces, Chem. Rev., 106, 1323–1354, https://doi.org/10.1021/cr040366k, 2006.
Davidovits, P., Kolb, C. E., Williams, L. R., Jayne, J. T., and Worsnop, D. R.: Update 1 of: Mass Accommodation and Chemical Reactions at Gas-Liquid Interfaces, Chem. Rev., 111, PR76-PR109, https://doi.org/10.1021/cr100360b, 2011.
Davies, J. F. and Wilson, K. R.: Nanoscale interfacial gradients formed by the reactive uptake of OH radicals onto viscous aerosol surfaces, Chem. Sci., 6, 7020–7027, https://doi.org/10.1039/c5sc02326b, 2015.
Delval, C. and Rossi, M. J.: Influence of monolayer amounts of HNO3 on the evaporation rate of H2O over ice in the range 179 to 208 K: A quartz crystal microbalance study, J. Phys. Chem. A, 109, 7151–7165, https://doi.org/10.1021/jp0505072, 2005.
Delval, C., Fluckiger, B., and Rossi, M. J.: The rate of water vapor evaporation from ice substrates in the presence of HCl and HBr: implications for the lifetime of atmospheric ice particles, Atmos. Chem. Phys., 3, 1131–1145, https://doi.org/10.5194/acp-3-1131-2003, 2003.
Demou, E. and Donaldson, D. J.: Adsorption of atmospheric gases at the air-water interface. 4: The influence of salts, J. Phys. Chem. A, 106, 982–987, https://doi.org/10.1021/jp0128628, 2002.
Desjonqueres, M.-C. and Spanjaard, D.: Concepts in Surface Physics, Springer-Verlag Berlin Heidelberg, https://doi.org/10.1007/978-3-642-61400-2, 1996.
Devlin, J. P., Joyce, C., and Buch, V.: Infrared spectra and structures of large water clusters, J. Phys. Chem. A, 104, 1974–1977, 2000.
Dickbreder, T., Lautner, D., Kohler, A., Klausfering, L., Bechstein, R., and Kuhnle, A.: How water desorbs from calcite, Phys. Chem. Chem. Phys., 25, 12694, https://doi.org/10.1039/d3cp01159c, 2023.
Donahue, N. M., Robinson, A. L., and Pandis, S. N.: Atmospheric organic particulate matter: From smoke to secondary organic aerosol, Atmos. Environ., 43, 94–106, https://doi.org/10.1016/j.atmosenv.2008.09.055, 2009.
Donahue, N. M., Epstein, S. A., Pandis, S. N., and Robinson, A. L.: A two-dimensional volatility basis set: 1. organic-aerosol mixing thermodynamics, Atmos. Chem. Phys., 11, 3303–3318, https://doi.org/10.5194/acp-11-3303-2011, 2011.
Donahue, N. M., Kroll, J. H., Pandis, S. N., and Robinson, A. L.: A two-dimensional volatility basis set – Part 2: Diagnostics of organic-aerosol evolution, Atmos. Chem. Phys., 12, 615–634, https://doi.org/10.5194/acp-12-615-2012, 2012.
Donaldson, D. J.: Adsorption of atmospheric gases at the air-water interface. I. NH3, J. Phys. Chem. A, 103, 62–70, 1999.
Donaldson, D. J. and Anderson, D.: Adsorption of atmospheric gases at the air-water interface. 2. C1–C4 alcohols, acids, and acetone, J. Phys. Chem. A, 103, 871–876, 1999.
Donaldson, D. J., Guest, J. A., and Goh, M. C.: Evidence For Adsorbed SO2 At the Aqueous Air Interface, J. Phys. Chem., 99, 9313–9315, 1995.
Donaldson, D. J., Ammann, M., Bartels-Rausch, T., and Pöschl, U.: Standard States and Thermochemical Kinetics in Heterogeneous Atmospheric Chemistry, J. Phys. Chem. A, 116, 6312–6316, https://doi.org/10.1021/jp212015g, 2012a.
Donaldson, D. J., Ammann, M., Bartels-Rausch, T., and Pöschl, U.: Standard States and Thermochemical Kinetics in Heterogeneous Atmospheric Chemistry, J. Phys. Chem. A, 116, 6312–6316, https://doi.org/10.1021/jp212015g, 2012b.
Dovbeshko, G. I., Romanyuk, V. R., Pidgirnyi, D. V., Cherepanov, V. V., Andreev, E. O., Levin, V. M., Kuzhir, P. P., Kaplas, T., and Svirko, Y. P.: Optical Properties of Pyrolytic Carbon Films Versus Graphite and Graphene, Nanoscale Res. Lett., 10, 234, https://doi.org/10.1186/s11671-015-0946-8, 2015.
Dubois, L. H., Zegarski, B. R., and Nuzzo, R. G.: Fundamental-studies of microscopic wetting on organic-surfaces. 2. interaction of secondary adsorbates with chemically textured organic monolayers, J. Am. Chem. Soc., 112, 570–579, https://doi.org/10.1021/ja00158a013, 1990.
Edebeli, J., Ammann, M., and Bartels-Rausch, T.: Microphysics of the aqueous bulk counters the water activity driven rate acceleration of bromide oxidation by ozone from 289–245 K, Environ. Sci.-Process Impacts, 21, 63–73, https://doi.org/10.1039/c8em00417j, 2019.
Edwards, K. C., Klodt, A. L., Galeazzo, T., Schervish, M., Wei, J. L., Fang, T., Donahue, N. M., Aumont, B., Nizkorodov, S. A., and Shiraiwa, M.: Effects of Nitrogen Oxides on the Production of Reactive Oxygen Species and Environmentally Persistent Free Radicals from alpha-Pinene and Naphthalene Secondary Organic Aerosols, J. Phys. Chem. A, 126, 7361–7372, https://doi.org/10.1021/acs.jpca.2c05532, 2022.
Ekholm, V., Caleman, C., Prytz, N. B., Walz, M. M., Werner, J., Ohrwall, G., Rubensson, J. E., and Bjorneholm, O.: Strong enrichment of atmospherically relevant organic ions at the aqueous interface: the role of ion pairing and cooperative effects, Phys. Chem. Chem. Phys., 20, 27185–27191, https://doi.org/10.1039/c8cp04525a, 2018.
Epstein, S. A., Riipinen, I., and Donahue, N. M.: A Semiempirical Correlation between Enthalpy of Vaporization and Saturation Concentration for Organic Aerosol, Environ. Sci. Technol., 44, 743–748, https://doi.org/10.1021/es902497z, 2010.
Fan, H. Y., Lakey, P. S. J., Frank, E. S., Tobias, D. J., Shiraiwa, M., and Grassian, V. H.: Comparison of the Adsorption-Desorption Kinetics of Limonene and Carvone on TiO2 and SiO2 Surfaces under Different Relative Humidity Conditions, J. Phys. Chem. C, 126, 21253–21262, https://doi.org/10.1021/acs.jpcc.2c06853, 2022.
Fang, Y., Riahi, S., McDonald, A. T., Shrestha, M., Tobias, D. J., and Grassian, V. H.: What Is the Driving Force behind the Adsorption of Hydrophobic Molecules on Hydrophilic Surfaces?, J. Phys. Chem. Lett., 10, 468–473, https://doi.org/10.1021/acs.jpclett.8b03484, 2019.
Faust, J. A. and Nathanson, G. M.: Microjets and coated wheels: versatile tools for exploring collisions and reactions at gas-liquid interfaces, Chem. Soc. Rev., 45, 3609–3620, https://doi.org/10.1039/c6cs00079g, 2016.
Faust, J. A., Dempsey, L. P., and Nathanson, G. M.: Surfactant-Promoted Reactions of Cl2 and Br2 with Br− in Glycerol, J. Phys. Chem. B, 117, 12602–12612, https://doi.org/10.1021/jp4079037, 2013.
Faust, J. A., Sobyra, T. B., and Nathanson, G. M.: Gas-Microjet Reactive Scattering: Collisions of HCl and DCl with Cool Salty Water, J. Phys. Chem. Lett., 7, 730–735, https://doi.org/10.1021/acs.jpclett.5b02848, 2016.
Fichthorn, K. A. and Miron, R. A.: Thermal desorption of large molecules from solid surfaces, Phys. Rev. Lett., 89, 4, https://doi.org/10.1103/PhysRevLett.89.196103, 2002.
Finlayson-Pitts, B. J. and Pitts, J. N.: Chemistry of the Upper and Lower Atmosphere: Theory, Experiments and Applications, Academic Press, San Diego, Calif., London, xxii, 969 pp., ISBN 012257060X, 2000.
Fogg, P. G. T. and Sangster, J. M.: Chemicals in the Atmosphere: Solubility, Sources and Reactivity, John Wiley & Sons Inc., Hoboken, New Jersey, ISBN 978-0-471-98651-5, 2003.
Foster, M. C. and Ewing, G. E.: Adsorption of water on the NaCl(001) surface. II. An infrared study at ambient temperatures, J. Chem. Phys., 112, 6817–6826, https://doi.org/10.1063/1.481256, 2000.
Frenkel, J.: Theory of the adsorption and related occurrences, Z. Phys., 26, 117–138, https://doi.org/10.1007/bf01327320, 1924.
Fuchs, N. A.: Mechanics of Aerosols, Pergamon, New York, https://doi.org/10.1002/qj.49709138822, 1964.
Fuchs, N. A. and Sutugin, A. G.: High-dispersed aerosols, in: Topics in current aerosol research, edited by: Hidy, G. M. and Brock, J. R., Pergamon, New York, https://doi.org/10.1016/B978-0-08-016674-2.50006-6, 1971.
Galeazzo, T. and Shiraiwa, M.: Predicting glass transition temperature and melting point of organic compounds via machine learning and molecular embeddings, Environ. Sci. – Atmospheres, 2, 362–374, https://doi.org/10.1039/d1ea00090j, 2022.
Galib, M. and Limmer, D. T.: Reactive uptake of N2O5 by atmospheric aerosol is dominated by interfacial processes, Science, 371, 921–925, https://doi.org/10.1126/science.abd7716, 2021.
Gao, X. F. and Nathanson, G. M.: Exploring Gas-Liquid Reactions with Microjets: Lessons We Are Learning, Accounts Chem. Res., 55, 3294–3302, https://doi.org/10.1021/acs.accounts.2c00602, 2022.
George, C., Ammann, M., D'Anna, B., Donaldson, D. J., and Nizkorodov, S. A.: Heterogeneous Photochemistry in the Atmosphere, Chem. Rev., 115, 4218–4258, https://doi.org/10.1021/cr500648z, 2015.
George, I. J. and Abbatt, J. P. D.: Heterogeneous oxidation of atmospheric aerosol particles by gas-phase radicals, Nat. Chem., 2, 713–722, https://doi.org/10.1038/Nchem.806, 2010.
Giguere, P. A.: Molecular association and structure of hydrogen-peroxide, J. Chem. Educ., 60, 399–401, https://doi.org/10.1021/ed060p399, 1983.
Giraudet, S., Pre, P., Tezel, H., and Le Cloirec, P.: Estimation of adsorption energies using physical characteristics of activated carbons and VOCs' molecular properties, Carbon, 44, 1873–1883, https://doi.org/10.1016/j.carbon.2006.02.018, 2006.
Goldstein, D. J.: Air and steam stripping of toxic pollutants, Appendix 3: Henry’s law constants, Tech. Rep. EPA-68-03-002, 114, Industrial Environmental Research Laboratory, Cincinnati, OH, USA, 1982.
Goodman, A. L., Bernard, E. T., and Grassian, V. H.: Spectroscopic study of nitric acid and water adsorption on oxide particles: Enhanced nitric acid uptake kinetics in the presence of adsorbed water, J. Phys. Chem. A, 105, 6443–6457, 2001.
Goss, K. U.: Adsorption of organic vapors on ice and quartz sand at temperatures below 0 °C, Environ. Sci. Technol., 27, 2826–2830, https://doi.org/10.1021/es00049a024, 1993.
Goss, K. U.: Adsorption of organic vapors on polar mineral surfaces and on a bulk water-surface – development of an empirical predictive model, Environ. Sci. Technol., 28, 640–645, https://doi.org/10.1021/es00053a017, 1994a.
Goss, K. U.: Predicting the enrichment of organic-compounds in fog caused by adsorption on the water-surface, Atmos. Environ., 28, 3513–3517, https://doi.org/10.1016/1352-2310(94)90008-6, 1994b.
Goss, K. U.: Predicting Adsorption of Organic Chemicals at the Air-Water Interface, J. Phys. Chem. A, 113, 12256–12259, https://doi.org/10.1021/jp907347p, 2009.
Goss, K. U. and Eisenreich, S. J.: Adsorption of VOCs from the gas phase to different minerals and a mineral mixture, Environ. Sci. Technol., 30, 2135–2142, https://doi.org/10.1021/es950508f, 1996.
Grabow, J. U., Andrews, A. M., Fraser, G. T., Irikura, K. K., Suenram, R. D., Lovas, F. J., Lafferty, W. J., and Domenech, J. L.: Microwave spectrum, large-amplitude motions, and ab initio calculations for N2O5, J. Chem. Phys., 105, 7249–7262, https://doi.org/10.1063/1.472586, 1996.
Grayson, J. W., Evoy, E., Song, M., Chu, Y., Maclean, A., Nguyen, A., Upshur, M. A., Ebrahimi, M., Chan, C. K., Geiger, F. M., Thomson, R. J., and Bertram, A. K.: The effect of hydroxyl functional groups and molar mass on the viscosity of non-crystalline organic and organic–water particles, Atmos. Chem. Phys., 17, 8509–8524, https://doi.org/10.5194/acp-17-8509-2017, 2017.
Grimm, R. L., Barrentine, N. M., Knox, C. J. H., and Hemminger, J. C.: D2O water interaction with mixed alkane thiol monolayers of tuned hydrophobic and hydrophilic character, J. Phys. Chem. C, 112, 890–894, https://doi.org/10.1021/jp710257q, 2008.
Groves, L. G. and Sudden, S.: The dipole moments of vapours – Part V Aromatic compounds, J. Chem. Soc., 1782–1784, https://doi.org/10.1039/jr9370001782, 1937.
Guilloteau, A., Bedjanian, Y., Nguyen, M. L., and Tomas, A.: Desorption of Polycyclic Aromatic Hydrocarbons from a Soot Surface: Three- to Five-Ring PAHs, J. Phys. Chem. A, 114, 942–948, https://doi.org/10.1021/jp908862c, 2010.
Guilloteau, A., Nguyen, M. L., Bedjanian, Y., and Le Bras, G.: Desorption of Polycyclic Aromatic Hydrocarbons from Soot Surface: Pyrene and Fluoranthene, J. Phys. Chem. A, 112, 10552–10559, https://doi.org/10.1021/jp803043s, 2008.
Gussoni, M., Rui, M., and Zerbi, G.: Electronic and relaxation contribution to linear molecular polarizability. An analysis of the experimental values, J. Mol. Struct., 447, 163–215, https://doi.org/10.1016/s0022-2860(97)00292-5, 1998.
Gustafsson, K. and Andersson, S.: Dipole active vibrations and dipole moments of N2 and O2 physisorbed on a metal surface, J. Chem. Phys., 125, 5, https://doi.org/10.1063/1.2218842, 2006.
Hai, P., Wu, C., Ding, X., and Li, Y.: Coverage-dependent adsorption and dissociation of H2O on Al surfaces, Phys. Chem. Chem. Phys., 25, 13041, https://doi.org/10.1039/d2cp04386f, 2023.
Hait, D. and Head-Gordon, M.: How accurate are static polarizability predictions from density functional theory? An assessment over 132 species at equilibrium geometry, Phys. Chem. Chem. Phys., 20, 19800–19810, https://doi.org/10.1039/c8cp03569e, 2018.
Hakem, I. F., Boussaid, A., Benchouk-Taleb, H., and Bockstaller, M. R.: Temperature, pressure, and isotope effects on the structure and properties of liquid water: A lattice approach, J. Chem. Phys., 127, 10, https://doi.org/10.1063/1.2804418, 2007.
Hall, D. G. and Cole, R. H.: Dielectric polarization of sulfuric-acid-solutions, J. Phys. Chem., 85, 1065–1069, https://doi.org/10.1021/j150608a029, 1981.
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009.
Hanefeld, U. and Lefferts, L.: Catalysis, John Wiley & Sons, Inc., Hoboken, New Jersey, USA, 384 pp., ISBN 978-3-527-81092-5, 2018.
Hanson, D. R.: Surface-specific reactions on liquids, J. Phys. Chem. B, 101, 4998–5001, 1997.
Hanson, D. R. and Lovejoy, E. R.: The Reaction of CIONO2 With Submicrometer Sulfuric-Acid Aerosol, Science, 267, 1326–1328, 1995.
Hanson, D. R. and Ravishankara, A. R.: The Loss of CF2O On Ice, Nat, and Sulfuric-Acid-Solutions, Geophys. Res. Lett., 18, 1699–1701, 1991.
Hanson, D. R., Ravishankara, A. R., and Solomon, S.: Heterogeneous Reactions in Sulfuric-Acid Aerosols – a Framework For Model-Calculations, J. Geophys. Res., 99, 3615–3629, 1994.
Hanson, D. R., Ravishankara, A. R., and Lovejoy, E. R.: Reaction of BrONO2 with H2O on submicron sulfuric acid aerosol and the implications for the lower stratosphere, J. Geophys. Res., 101, 9063–9069, 1996.
Hantal, G., Jedlovszky, P., Hoang, P. N. M., and Picaud, S.: Calculation of the adsorption isotherm of formaldehyde on ice by grand canonical Monte Carlo simulation, J. Phys. Chem. C, 111, 14170–14178, https://doi.org/10.1021/jp0742564, 2007.
Hao, H. X., Leven, I., and Head-Gordon, T.: Can electric fields drive chemistry for an aqueous microdroplet?, Nat. Commun., 13, 8, https://doi.org/10.1038/s41467-021-27941-x, 2022.
Hartkopf, A. and Karger, B. L.: Study of interfacial properties of water by gas-chromatography, Accounts Chem. Res., 6, 209–216, https://doi.org/10.1021/ar50066a006, 1973.
Hauxwell, F. and Ottewill, R. H.: Adsorption of toluene vapor on water surfaces, J. Colloid Interface Sci., 28, 514–521, https://doi.org/10.1016/0021-9797(68)90084-2, 1968.
Hearn, J. D. and Smith, G. A.: Ozonolysis of mixed oleic acid/n-docosane particles: The roles of phase, morphology, and metastable states, J. Phys. Chem. A, 111, 11059–11065, https://doi.org/10.1021/jp0755701, 2007.
Helburn, R., Albritton, J., Howe, G., Michael, L., and Franke, D.: Henry's law constants for fragrance and organic solvent compounds in aqueous industrial surfactants, J. Chem. Eng. Data, 53, 1071–1079, https://doi.org/10.1021/je700418a, 2008.
Hems, R. F., Schnitzler, E. G., Liu-Kang, C., Cappa, C. D., and Abbatt, J. P. D.: Aging of Atmospheric Brown Carbon Aerosol, ACS Earth Space Chem., 5, 722–748, https://doi.org/10.1021/acsearthspacechem.0c00346, 2021.
Henderson, G. L. and Meyer, G. H.: Intramolecular torsional potential and dielectric properties of 2,3-butanedione, J. Phys. Chem., 80, 2422–2425, https://doi.org/10.1021/j100562a020, 1976.
Hickey, A. L. and Rowley, C. N.: Benchmarking Quantum Chemical Methods for the Calculation of Molecular Dipole Moments and Polarizabilities, J. Phys. Chem. A, 118, 3678–3687, https://doi.org/10.1021/jp502475e, 2014.
Hildebrand, J. and Scott, R.: The solubility of nonelectrolytes, 3rd ed., Dover Publications, New York, 502 pp., ISBN 0486611256, 1964.
Hill, T. L.: An Introduction to Statistical Thermodynamics, Dover Publications, Inc., New York, 501 pp., ISBN 0486652424, 1986.
Hoffmann, M. R. and Edwards, J. O.: Kinetics of oxidation of sulfite by hydrogen-peroxide in acidic solution, J. Phys. Chem., 79, 2096–2098, https://doi.org/10.1021/j100587a005, 1975.
Hoffmann, M. R., Martin, S. T., Choi, W. Y., and Bahnemann, D. W.: Environmental Applications of Semiconductor Photocatalysis, Chem. Rev., 95, 69–96, https://doi.org/10.1021/cr00033a004, 1995.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
Hoskovec, M., Grygarova, D., Cvacka, J., Streinz, L., Zima, J., Verevkin, S. P., and Koutek, B.: Determining the vapour pressures of plant volatiles from gas chromatographic retention data, J. Chromatogr. A, 1083, 161–172, https://doi.org/10.1016/j.chroma.2005.06.006, 2005.
Houle, F. A., Wiegel, A. A., and Wilson, K. R.: Predicting Aerosol Reactivity Across Scales: from the Laboratory to the Atmosphere, Environ. Sci. Technol., 52, 13774–13781, https://doi.org/10.1021/acs.est.8b04688, 2018.
Hu, Z. M. and Nakatsuji, H.: Adsorption and disproportionation reaction of OH on Ag surfaces: dipped adcluster model study, Surf. Sci., 425, 296–312, https://doi.org/10.1016/s0039-6028(99)00215-0, 1999.
Huang, Y. Z., Mahrt, F., Xu, S., Shiraiwa, M., Zuend, A., and Bertram, A. K.: Coexistence of three liquid phases in individual atmospheric aerosol particles, P. Natl. Acad. Sci. USA, 118, 9, https://doi.org/10.1073/pnas.2102512118, 2021.
Huthwelker, T., Ammann, M., and Peter, T.: The uptake of acidic gases on ice, Chem. Rev., 106, 1375–1444, https://doi.org/10.1021/cr020506v, 2006.
Hvidt, A.: Interactions of water with non-polar solutes, Annu. Rev. Biophys. Bio., 12, 1–20, https://doi.org/10.1146/annurev.bb.12.060183.000245, 1983.
Ibrahim, S., Romanias, M. N., Alleman, L. Y., Zeineddine, M. N., Angeli, G. K., Trikalitis, P. N., and Thevenet, F.: Water Interaction with Mineral Dust Aerosol: Particle Size and Hygroscopic Properties of Dust, ACS Earth Space Chem., 2, 376–386, https://doi.org/10.1021/acsearthspacechem.7b00152, 2018.
Ingram, S., Rovelli, G., Song, Y. C., Topping, D., Dutcher, C. S., Liu, S. H., Nandy, L., Shiraiwa, M., and Reid, J. P.: Accurate Prediction of Organic Aerosol Evaporation Using Kinetic Multilayer Modeling and the Stokes-Einstein Equation, J. Phys. Chem. A, 125, 3444–3456, https://doi.org/10.1021/acs.jpca.1c00986, 2021.
Isaacman-VanWertz, G., Massoli, P., O'Brien, R., Lim, C., Franklin, J. P., Moss, J. A., Hunter, J. F., Nowak, J. B., Canagaratna, M. R., Misztal, P. K., Arata, C., Roscioli, J. R., Herndon, S. T., Onasch, T. B., Lambe, A. T., Jayne, J. T., Su, L., Knopf, D. A., Goldstein, A. H., Worsnop, D. R., and Kroll, J. H.: Chemical evolution of atmospheric organic carbon over multiple generations of oxidation, Nat. Chem., 10, 462–468, https://doi.org/10.1038/s41557-018-0002-2, 2018.
Isakson, M. J. and Sitz, G. O.: Adsorption and desorption of HCl on ice, J. Phys. Chem. A, 103, 2044–2049, https://doi.org/10.1021/jp984106g, 1999.
IUPAC, McNaught, A. D., and Wilkinson, A. (Eds.): Compendium of Chemical Terminology, (the “Gold Book”), 2nd, Blackwell Scientific Publications, Oxford, https://doi.org/10.1351/goldbook, 1997.
Jayne, J. T., Davidovits, P., Worsnop, D. R., Zahniser, M. S., and Kolb, C. E.: Uptake of SO2(g) By Aqueous Surfaces As a Function of Ph – the Effect of Chemical-Reaction At the Interface, J. Phys. Chem., 94, 6041–6048, 1990.
Jeffrey, G. A.: An Introduction to Hydrogen Bonding, Oxford University Press, Oxford, 303 pp., ISBN 0195095499, 1997.
Jeffrey, G. A. and Saenger, W.: Hydrogen Bonding in Biological Structures,, Springer-Verlag, Berlin, 569 pp., https://doi.org/10.1007/978-3-642-85135-3, 1991.
Jensen, L., Astrand, P. O., Osted, A., Kongsted, J., and Mikkelsen, K. V.: Polarizability of molecular clusters as calculated by a dipole interaction model, J. Chem. Phys., 116, 4001–4010, https://doi.org/10.1063/1.1433747, 2002.
Jeong, D., McNamara, S. M., Barget, A. J., Raso, A. R. W., Upchurch, L. M., Thanekar, S., Quinn, P. K., Simpson, W. R., Fuentes, J. D., Shepson, P. B., and Pratt, K. A.: Multiphase Reactive Bromine Chemistry during Late Spring in the Arctic: Measurements of Gases, Particles, and Snow, ACS Earth Space Chem., 6, 2877–2887, https://doi.org/10.1021/acsearthspacechem.2c00189, 2022.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, E. J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of Organic Aerosols in the Atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Joback, K. G. and Reid, R. C.: Estimation of pure-component properties from group-contributions, Chem. Eng. Commun., 57, 233–243, https://doi.org/10.1080/00986448708960487, 1987.
Johansson, S. M., Lovric, J., Kong, X. R., Thomson, E. S., Papagiannakopoulos, P., Briquez, S., Toubin, C., and Pettersson, J. B. C.: Understanding water interactions with organic surfaces: environmental molecular beam and molecular dynamics studies of the water-butanol system, Phys. Chem. Chem. Phys., 21, 1141–1151, https://doi.org/10.1039/c8cp04151b, 2019.
Johansson, S. M., Lovric, J., Kong, X. R., Thomson, E. S., Hallquist, M., and Pettersson, J. B. C.: Experimental and Computational Study of Molecular Water Interactions with Condensed Nopinone Surfaces Under Atmospherically Relevant Conditions, J. Phys. Chem. A, 124, 3652–3661, https://doi.org/10.1021/acs.jpca.9b10970, 2020.
Joliat, J., Lenoir, T., and Picaud, S.: Comparative Study of the Adsorption of 1-and 2-Propanol on Ice by Means of Grand Canonical Monte Carlo Simulations, ACS Earth Space Chem., 7, 850-−862, https://doi.org/10.1021/acsearthspacechem.2c00390, 2023.
Julin, J., Shiraiwa, M., Miles, R. E. H., Reid, J. P., Pöschl, U., and Riipinen, I.: Mass Accommodation of Water: Bridging the Gap Between Molecular Dynamics Simulations and Kinetic Condensation Models, J. Phys. Chem. A, 117, 410–420, https://doi.org/10.1021/jp310594e, 2013.
Jungwirth, P., Finlayson-Pitts, B. J., and Tobias, D. J.: Introduction: Structure and chemistry at aqueous interfaces, Chem. Rev., 106, 1137–1139, 2006.
Kahan, T. F., Kwamena, N. O. A., and Donaldson, D. J.: Heterogeneous ozonation kinetics of polycyclic aromatic hydrocarbons on organic films, Atmos. Environ., 40, 3448–3459, https://doi.org/10.1016/j.atmosenv.2006.02.004, 2006.
Kaiser, J. C., Riemer, N., and Knopf, D. A.: Detailed heterogeneous oxidation of soot surfaces in a particle-resolved aerosol model, Atmos. Chem. Phys., 11, 4505–4520, https://doi.org/10.5194/acp-11-4505-2011, 2011.
Kanakidou, M., Seinfeld, J. H., Pandis, S. N., Barnes, I., Dentener, F. J., Facchini, M. C., Van Dingenen, R., Ervens, B., Nenes, A., Nielsen, C. J., Swietlicki, E., Putaud, J. P., Balkanski, Y., Fuzzi, S., Horth, J., Moortgat, G. K., Winterhalter, R., Myhre, C. E. L., Tsigaridis, K., Vignati, E., Stephanou, E. G., and Wilson, J.: Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 5, 1053–1123, https://doi.org/10.5194/acp-5-1053-2005, 2005.
Kanji, Z. A., Ladino, L. A., Wex, H., Boose, Y., Burkert-Kohn, M., Cziczo, D. J., and Krämer, M.: Overview of Ice Nucleating Particles, in: Ice Formation and Evolution in Clouds and Precipitation: Measurement and Modeling Challenges, Meteorological Monographs, American Meteorological Society, 58, 1.1–1.33, https://doi.org/10.1175/AMSMONOGRAPHS-D-16-0006.1, 2017.
Kerbrat, M., Huthwelker, T., Gaggeler, H. W., and Ammann, M.: Interaction of Nitrous Acid with Polycrystalline Ice: Adsorption on the Surface and Diffusion into the Bulk, J. Phys. Chem. C, 114, 2208–2219, https://doi.org/10.1021/jp909535c, 2010.
Keyser, L. F., Moore, S. B., and Leu, M. T.: Surface-Reaction and Pore Diffusion in Flow-Tube Reactors, J. Phys. Chem., 95, 5496–5502, 1991.
Kieckbusch, T. G. and King, C. J.: Partition-coefficients for acetates in food systems, J. Agric. Food Chem., 27, 504–507, https://doi.org/10.1021/jf60223a033, 1979.
Kim, Y. K., Park, S. C., Kim, J. H., Lee, C. W., and Kang, H.: Interaction of Carbon Dioxide and Hydroxide Ion at the Surface of Ice Films, J. Phys. Chem. C, 112, 18104–18109, https://doi.org/10.1021/jp806643e, 2008.
Kisliuk, P.: The sticking probabilities of gases chemisorbed on the surfaces of solids, J. Phys. Chem. Solids, 3, 95–101, https://doi.org/10.1016/0022-3697(57)90054-9, 1957.
Kisliuk, P.: The sticking probabilities of gases chemisorbed on the surfaces of solids. 2, J. Phys. Chem. Solids, 5, 78–84, 1958.
Klassen, J. K., Fiehrer, K. M., and Nathanson, G. M.: Collisions of organic molecules with concentrated sulfuric acid: Scattering, trapping, and desorption, J. Phys. Chem. B, 101, 9098–9106, https://doi.org/10.1021/jp972329l, 1997.
Klassen, J. K., Hu, Z. J., and Williams, L. R.: Diffusion coefficients for HCl and HBr in 30 wt % to 72 wt % sulfuric acid at temperatures between 220 and 300 K, J. Geophys. Res.-Atmos., 103, 16197–16202, https://doi.org/10.1029/98jd01252, 1998.
Knopf, D. A. and Alpert, P. A.: Atmospheric ice nucleation, Nat. Rev. Phys., 5, 203–217, https://doi.org/10.1038/s42254-023-00570-7, 2023.
Knopf, D. A. and Ammann, M.: Technical note: Adsorption and desorption equilibria from statistical thermodynamics and rates from transition state theory, Atmos. Chem. Phys., 21, 15725–15753, https://doi.org/10.5194/acp-21-15725-2021, 2021.
Knopf, D. A. and Koop, T.: Heterogeneous nucleation of ice on surrogates of mineral dust, J. Geophys. Res., 111, D12201, https://doi.org/10.1029/2005jd006894, 2006.
Knopf, D. A., Anthony, L. M., and Bertram, A. K.: Reactive uptake of O3 by multicomponent and multiphase mixtures containing oleic acid, J. Phys. Chem. A, 109, 5579–5589, 2005.
Knopf, D. A., Forrester, S. M., and Slade, J. H.: Heterogeneous oxidation kinetics of organic biomass burning aerosol surrogates by O3, NO2, N2O5, and NO3, Phys. Chem. Chem. Phys., 13, 21050–21062, https://doi.org/10.1039/C1cp22478f, 2011.
Knopf, D. A., Pöschl, U., and Shiraiwa, M.: Radial Diffusion and Penetration of Gas Molecules and Aerosol Particles through Laminar Flow Reactors, Denuders, and Sampling Tubes, Anal. Chem., 87, 3746–3754, https://doi.org/10.1021/ac5042395, 2015.
Knopf, D. A., Alpert, P. A., and Wang, B.: The Role of Organic Aerosol in Atmospheric Ice Nucleation: A Review, ACS Earth Space Chem., 2, 168–202, https://doi.org/10.1021/acsearthspacechem.7b00120, 2018.
Knopf, D. A., Ammann, M., Berkemeier, T., Pöschl, U., and Shiraiwa, M.: Desorption Lifetimes and Activation Energies influencing Gas-Surface Interactions and Multiphase Chemical Kinetics, Zenodo [data set], https://doi.org/10.5281/zenodo.8417534, 2024.
Knox, C. J. H. and Phillips, L. F.: Capillary-wave model of gas-liquid exchange, J. Phys. Chem. B, 102, 8469–8472, https://doi.org/10.1021/jp973183t, 1998.
Koch, T. G. and Rossi, M. J.: Direct measurement of surface residence times: Nitryl chloride and chlorine nitrate on alkali halides at room temperature, J. Phys. Chem. A, 102, 9193–9201, https://doi.org/10.1021/jp982539d, 1998a.
Koch, T. G. and Rossi, M. J.: Direct measurement of surface residence times: Nitryl chloride and chlorine nitrate on alkali halides at room temperature, J. Phys. Chem. A, 102, 9193–9201, 1998b.
Koch, T. G., Fenter, F. F., and Rossi, M. J.: Real-time measurement of residence times of gas molecules on solid surfaces, Chem. Phys. Lett., 275, 253–260, 1997.
Kolasinski, K. W.: Surface Science: Foundations of Catalysis and Nanoscience, 3rd, John Wiley & Sons, Ltd., West Sussex, United Kingdom, 556 pp., https://doi.org/10.1002/9781119941798, 2012.
Kolb, C. E., Cox, R. A., Abbatt, J. P. D., Ammann, M., Davis, E. J., Donaldson, D. J., Garrett, B. C., George, C., Griffiths, P. T., Hanson, D. R., Kulmala, M., McFiggans, G., Pöschl, U., Riipinen, I., Rossi, M. J., Rudich, Y., Wagner, P. E., Winkler, P. M., Worsnop, D. R., and O' Dowd, C. D.: An overview of current issues in the uptake of atmospheric trace gases by aerosols and clouds, Atmos. Chem. Phys., 10, 10561–10605, https://doi.org/10.5194/acp-10-10561-2010, 2010.
Kolb, C. E., Worsnop, D. R., Zahniser, M. S., Davidovits, P., Keyser, L. F., Leu, M.-T., Molina, M. J., Hanson, D. R., Ravishankara, A. R., Williams, L. R., and Tolbert, M. A.: Laboratory Studies of Atmospheric Heterogeneous Chemistry, in: Progress and Problems in Atmospheric Chemistry, edited by: Barker, J. R., World Scientific, Singapore, 771–875, ISBN 978-981-02-1868-3, 1995.
Kolomiitsova, T. D., Lyaptsev, A. V., and Shchepkin, D. N.: Determination of parameters of the dipole moment of the CO2 molecule, Opt. Spectrosc., 88, 648–660, https://doi.org/10.1134/1.626856, 2000.
Kong, X. R., Thomson, E. S., Markovic, N., and Pettersson, J. B. C.: Dynamics and Kinetics of Methanol-Graphite Interactions at Low Surface Coverage, ChemPhysChem, 20, 2171–2178, https://doi.org/10.1002/cphc.201900457, 2019.
Kong, X. R., Lovri, J., Johansson, S. M., Prisle, N. L., and Pettersson, J. B. C.: Dynamics and Sorption Kinetics of Methanol Monomers and Clusters on Nopinone Surfaces, J. Phys. Chem. A, 125, 6263–6272, https://doi.org/10.1021/acs.jpca.1c02309, 2021.
Kong, X. R., Papagiannakopoulos, P., Thomson, E. S., Markovic, N., and Pettersson, J. B. C.: Water Accommodation and Desorption Kinetics on Ice, J. Phys. Chem. A, 118, 3973–3979, https://doi.org/10.1021/jp503504e, 2014a.
Kong, X. R., Thomson, E. S., Papagiannakopoulos, P., Johansson, S. M., and Pettersson, J. B. C.: Water Accommodation on Ice and Organic Surfaces: Insights from Environmental Molecular Beam Experiments, J. Phys. Chem. B, 118, 13378–13386, https://doi.org/10.1021/jp5044046, 2014b.
Kong, X. R., Waldner, A., Orlando, F., Artiglia, L., Huthwelker, T., Ammann, M., and Bartels-Rausch, T.: Coexistence of Physisorbed and Solvated HCI at Warm Ice Surfaces, J. Phys. Chem. Lett., 8, 4757–4762, https://doi.org/10.1021/acs.jpclett.7b01573, 2017.
Koop, T., Carslaw, K. S., and Peter, T.: Thermodynamic stability and phase transitions of PSC particles, Geophys. Res. Lett., 24, 2199–2202, 1997.
Koop, T., Bookhold, J., Shiraiwa, M., and Poeschl, U.: Glass transition and phase state of organic compounds: dependency on molecular properties and implications for secondary organic aerosols in the atmosphere, Phys. Chem. Chem. Phys., 13, 19238–19255, https://doi.org/10.1039/c1cp22617g, 2011.
Kroll, J. H., Donahue, N. M., Jimenez, J. L., Kessler, S. H., Canagaratna, M. R., Wilson, K. R., Altieri, K. E., Mazzoleni, L. R., Wozniak, A. S., Bluhm, H., Mysak, E. R., Smith, J. D., Kolb, C. E., and Worsnop, D. R.: Carbon oxidation state as a metric for describing the chemistry of atmospheric organic aerosol, Nat. Chem., 3, 133–139, https://doi.org/10.1038/nchem.948, 2011.
Kronberg, B.: The hydrophobic effect, Curr. Opin. Colloid Interface Sci., 22, 14–22, https://doi.org/10.1016/j.cocis.2016.02.001, 2016.
Kronberger, H. and Weiss, J.: Formation and structure of some organic molecular compounds. Part III. The dielectric polarisation of some solid crystalline molecular compounds, J. Chem. Soc., 464–469, https://doi.org/10.1039/jr9440000464, 1944.
Kuhne, R., Ebert, R. U., and Schuurmann, G.: Prediction of the temperature dependency of Henry's law constant from chemical structure, Environ. Sci. Technol., 39, 6705–6711, https://doi.org/10.1021/es050527h, 2005.
Kwamena, N. O. A., Thornton, J. A., and Abbatt, J. P. D.: Kinetics of surface-bound benzo a pyrene and ozone on solid organic and salt aerosols, J. Phys. Chem. A, 108, 11626–11634, https://doi.org/10.1021/jp046161x, 2004.
Laib, J. P. and Mittleman, D. M.: Temperature-Dependent Terahertz Spectroscopy of Liquid n-alkanes, J. Infrared Millim. Terahertz Waves, 31, 1015–1021, https://doi.org/10.1007/s10762-010-9678-0, 2010.
Laidler, K. J.: The mechanisms of some elementary surface reactions, J. Phys. Colloid Chem., 53, 712–732, https://doi.org/10.1021/j150470a010, 1949.
Laidler, K. J., Glasstone, S., and Eyring, H.: Application of the Theory of Absolute Reaction Rates to Heterogeneous Processes II. Chemical Reactions on Surfaces, J. Chem. Phys., 8, 667–676, https://doi.org/10.1063/1.1750737, 1940.
Lakey, P. S. J., Berkemeier, T., Krapf, M., Dommen, J., Steimer, S. S., Whalley, L. K., Ingham, T., Baeza-Romero, M. T., Pöschl, U., Shiraiwa, M., Ammann, M., and Heard, D. E.: The effect of viscosity and diffusion on the HO2 uptake by sucrose and secondary organic aerosol particles, Atmos. Chem. Phys., 16, 13035–13047, https://doi.org/10.5194/acp-16-13035-2016, 2016.
Lakey, P. S. J., Eichler, C. M. A., Wang, C. Y., Little, J. C., and Shiraiwa, M.: Kinetic multi-layer model of film formation, growth, and chemistry (KM-FILM): Boundary layer processes, multi-layer adsorption, bulk diffusion, and heterogeneous reactions, Indoor Air, 31, 2070–2083, https://doi.org/10.1111/ina.12854, 2021.
Lakey, P. S. J., Cummings, B. E., Waring, M. S., Morrison, G. C., and Shiraiwa, M.: Effective mass accommodation for partitioning of organic compounds into surface films with different viscosities, Environ. Sci.-Process Impacts, 25, 1464–1478, https://doi.org/10.1039/d3em00213f, 2023.
Langenberg, S. and Schurath, U.: Gas chromatography using ice-coated fused silica columns: study of adsorption of sulfur dioxide on water ice, Atmos. Chem. Phys., 18, 7527–7537, https://doi.org/10.5194/acp-18-7527-2018, 2018.
Langmuir, I.: A theory of adsorption, Phys. Rev., 6, 79–80, 1915.
Langmuir, I.: The evaporation, condensation and reflection of molecules and the mechanism of adsorption, Phys. Rev., 8, 149–176, https://doi.org/10.1103/PhysRev.8.149, 1916.
Langmuir, I.: The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 40, 1361–1403, https://doi.org/10.1021/ja02242a004, 1918.
Laskin, A., Laskin, J., and Nizkorodov, S. A.: Chemistry of Atmospheric Brown Carbon, Chem. Rev., 115, 4335–4382, https://doi.org/10.1021/cr5006167, 2015.
Lee, G., Lee, B., Kim, J., and Cho, K.: Ozone Adsorption on Graphene: Ab Initio Study and Experimental Validation, J. Phys. Chem. C, 113, 14225–14229, https://doi.org/10.1021/jp904321n, 2009.
Lee, M. T., Orlando, F., Artiglia, L., Chen, S. Z., and Ammann, M.: Chemical Composition and Properties of the Liquid-Vapor Interface of Aqueous C1 to C4 Monofunctional Acid and Alcohol Solutions, J. Phys. Chem. A, 120, 9749–9758, https://doi.org/10.1021/acs.jpca.6b09261, 2016.
Lee, M. T., Orlando, F., Khabiri, M., Roeselova, M., Brown, M. A., and Ammann, M.: The opposing effect of butanol and butyric acid on the abundance of bromide and iodide at the aqueous solution-air interface, Phys. Chem. Chem. Phys., 21, 8418–8427, https://doi.org/10.1039/c8cp07448h, 2019.
Lee, W. M. G. and Chen, J. C.: Partitioning coefficients of polycyclic aromatic-hydrocarbons in stack gas from a municipal incinerator, Environ. Int., 21, 827–831, https://doi.org/10.1016/0160-4120(95)00092-4, 1995.
Lejonthun, L., Andersson, P. U., Hallquist, M., Thomson, E. S., and Pettersson, J. B. C.: Interactions of N2O5 and Related Nitrogen Oxides with Ice Surfaces: Desorption Kinetics and Collision Dynamics, J. Phys. Chem. B, 118, 13427–13434, https://doi.org/10.1021/jp5053826, 2014.
Leluk, K., Orzechowski, K., Jerie, K., Baranowski, A., Slonka, T., and Glowinski, J.: Dielectric permittivity of kaolinite heated to high temperatures, J. Phys. Chem. Solids, 71, 827–831, https://doi.org/10.1016/j.jpcs.2010.02.008, 2010.
Leng, C. B., Kish, J. D., Roberts, J. E., Dwebi, I., Chon, N., and Liu, Y.: Temperature-Dependent Henry's Law Constants of Atmospheric Amines, J. Phys. Chem. A, 119, 8884–8891, https://doi.org/10.1021/acs.jpca.5b05174, 2015.
Li, G., Su, H., Kuhn, U., Meusel, H., Ammann, M., Shao, M., Pöschl, U., and Cheng, Y.: Technical note: Influence of surface roughness and local turbulence on coated-wall flow tube experiments for gas uptake and kinetic studies, Atmos. Chem. Phys., 18, 2669–2686, https://doi.org/10.5194/acp-18-2669-2018, 2018.
Li, J. and Knopf, D. A.: Representation of Multiphase OH Oxidation of Amorphous Organic Aerosol for Tropospheric Conditions, Environ. Sci. Technol., 55, 7266–7275, https://doi.org/10.1021/acs.est.0c07668, 2021.
Li, J., Forrester, S. M., and Knopf, D. A.: Heterogeneous oxidation of amorphous organic aerosol surrogates by O3, NO3, and OH at typical tropospheric temperatures, Atmos. Chem. Phys., 20, 6055–6080, https://doi.org/10.5194/acp-20-6055-2020, 2020.
Li, Y. and Shiraiwa, M.: Timescales of secondary organic aerosols to reach equilibrium at various temperatures and relative humidities, Atmos. Chem. Phys., 19, 5959-5971, https://doi.org/10.5194/acp-19-5959-2019, 2019.
Li, Y., Pöschl, U., and Shiraiwa, M.: Molecular corridors and parameterizations of volatility in the chemical evolution of organic aerosols, Atmos. Chem. Phys., 16, 3327–3344, https://doi.org/10.5194/acp-16-3327-2016, 2016.
Liang, Z., Li, K. J., Wang, Z. M., Bu, Y. S., and Zhang, J. L.: Adsorption and reaction mechanisms of single and double H2O molecules on graphene surfaces with defects: a density functional theory study, Phys. Chem. Chem. Phys., 23, 19071–19082, https://doi.org/10.1039/d1cp02595c, 2021.
Lide, D. R.: CRC Handbook of Chemistry and Physics, 82nd, CRC Press, Boca Raton, ISBN 0849304822, 2008.
Lileev, A. and Lyashchenko, A.: Dielectric properties of ammonium salt aqueous solutions, J. Mol. Liq., 150, 4–8, https://doi.org/10.1016/j.molliq.2009.08.008, 2009.
Longfellow, C. A., Imamura, T., Ravishankara, A. R., and Hanson, D. R.: HONO solubility and heterogeneous reactivity on sulfuric acid surfaces, J. Phys. Chem. A, 102, 3323–3332, 1998.
Mack, K. M. and Muenter, J. S.: Stark and Zeeman properties of ozone from molecular-beam spectroscopy, J. Chem. Phys., 66, 5278–5283, https://doi.org/10.1063/1.433909, 1977.
Mader, B. T., Goss, K. U., and Eisenreich, S. J.: Sorption of nonionic, hydrophobic organic chemicals to mineral surfaces, Environ. Sci. Technol., 31, 1079–1086, https://doi.org/10.1021/es960606g, 1997.
Maribo-Mogensen, B., Kontogeorgis, G. M., and Thomsen, K.: Modeling of Dielectric Properties of Aqueous Salt Solutions with an Equation of State, J. Phys. Chem. B, 117, 10523–10533, https://doi.org/10.1021/jp403375t, 2013.
Marsh, A. R. W. and McElroy, W. J.: The dissociation-constant and Henry law constant of HCl in aqueous-solution, Atmos. Environ., 19, 1075–1080, https://doi.org/10.1016/0004-6981(85)90192-1, 1985.
Marshall, F. H., Miles, R. E. H., Song, Y. C., Ohm, P. B., Power, R. M., Reid, J. P., and Dutcher, C. S.: Diffusion and reactivity in ultraviscous aerosol and the correlation with particle viscosity, Chem. Sci., 7, 1298–1308, https://doi.org/10.1039/c5sc03223g, 2016.
Marshall, F. H., Berkemeier, T., Shiraiwa, M., Nandy, L., Ohm, P. B., Dutcher, C. S., and Reid, J. P.: Influence of particle viscosity on mass transfer and heterogeneous ozonolysis kinetics in aqueous-sucrose-maleic acid aerosol, Phys. Chem. Chem. Phys., 20, 15560–15573, https://doi.org/10.1039/c8cp01666f, 2018.
Masel, R. I.: Principles of Adsorption and Reaction on Solid Surfaces, Wiley Series in Chemical Engineering, ISBN 978-0-471-30392-3, 1996.
McEachran, A. D., Mansouri, K., Grulke, C., Schymanski, E. L., Ruttkies, C., and Williams, A. J.: “MS-Ready” structures for non-targeted high-resolution mass spectrometry screening studies, J. Cheminformatics, 10, 16, https://doi.org/10.1186/s13321-018-0299-2, 2018.
McNamara, S. M., Chen, Q. J., Edebeli, J., Kulju, K. D., Mumpfield, J., Fuentes, J. D., Bertman, S. B., and Pratt, K. A.: Observation of N2O5 Deposition and CINO2 Production on the Saline Snowpack, ACS Earth Space Chem., 5, 1020–1031, https://doi.org/10.1021/acsearthspacechem.0c00317, 2021.
McNeill, V. F., Loerting, T., Geiger, F. M., Trout, B. L., and Molina, M. J.: Hydrogen chloride-induced surface disordering on ice, P. Natl. Acad. Sci. USA, 103, 9422–9427, https://doi.org/10.1073/pnas.0603494103, 2006.
McNeill, V. F., Geiger, F. M., Loerting, T., Trout, B. L., Molina, L. T., and Molina, M. J.: Interaction of hydrogen chloride with ice surfaces: The effects of grain size, surface roughness, and surface disorder, J. Phys. Chem. A, 111, 6274–6284, https://doi.org/10.1021/jp068914g, 2007.
McNeill, V. F., Grannas, A. M., Abbatt, J. P. D., Ammann, M., Ariya, P., Bartels-Rausch, T., Domine, F., Donaldson, D. J., Guzman, M. I., Heger, D., Kahan, T. F., Klán, P., Masclin, S., Toubin, C., and Voisin, D.: Organics in environmental ices: sources, chemistry, and impacts, Atmos. Chem. Phys., 12, 9653–9678, https://doi.org/10.5194/acp-12-9653-2012, 2012.
Mendes, P. C. D., Costa-Amaral, R., Gomes, J. F., and Da Silva, J. L. F.: The influence of hydroxy groups on the adsorption of three-carbon alcohols on Ni(111), Pd(111) and Pt(111) surfaces: a density functional theory study within the D3 dispersion correction, Phys. Chem. Chem. Phys., 21, 8434, https://doi.org/10.1039/c9cp00752k, 2019.
Meng, S., Wang, E. G., and Gao, S. W.: Water adsorption on metal surfaces: A general picture from density functional theory studies, Phys. Rev. B, 69, 13, https://doi.org/10.1103/PhysRevB.69.195404, 2004.
Merino, E. and Ribagorda, M.: Control over molecular motion using the cis-trans photoisomerization of the azo group, Beilstein J. Org. Chem., 8, 1071–1090, https://doi.org/10.3762/bjoc.8.119, 2012.
Messerer, A., Niessner, R., and Pöschl, U.: Comprehensive kinetic characterization of the oxidation and gasification of model and real diesel soot by nitrogen oxides and oxygen under engine exhaust conditions: Measurement, Langmuir-Hinshelwood, and Arrhenius parameters, Carbon, 44, 307–324, https://doi.org/10.1016/j.carbon.2005.07.017, 2006.
Messerer, A., Schmatloch, V., Pöschl, U., and Niessner, R.: Combined particle emission reduction and heat recovery from combustion exhaust – A novel approach for small wood-fired appliances, Biomass Bioenerg., 31, 512–521, https://doi.org/10.1016/j.biombioe.2007.01.022, 2007.
Meyer, H., Entel, P., and Hafner, J.: Physisorption of water on salt surfaces, Surf. Sci., 488, 177–192, https://doi.org/10.1016/s0039-6028(01)01136-0, 2001.
Mikhailov, E., Vlasenko, S., Martin, S. T., Koop, T., and Pöschl, U.: Amorphous and crystalline aerosol particles interacting with water vapor: conceptual framework and experimental evidence for restructuring, phase transitions and kinetic limitations, Atmos. Chem. Phys., 9, 9491–9522, https://doi.org/10.5194/acp-9-9491-2009, 2009.
Millany, H. M. and Jonscher, A. K.: Dielectric-properties of stearic-acid multilayers, Thin Solid Films, 68, 257–273, https://doi.org/10.1016/0040-6090(80)90151-0, 1980.
Mmereki, B. T., Hicks, J. M., and Donaldson, D. J.: Adsorption of atmospheric gases at the air-water interface. 3: Methylamines, J. Phys. Chem. A, 104, 10789–10793, https://doi.org/10.1021/jp0023258, 2000.
Moise, T., Flores, J. M., and Rudich, Y.: Optical properties of secondary organic aerosols and their changes by chemical processes, Chem. Rev., 115, 4400–4439, https://doi.org/10.1021/cr5005259, 2015.
Morris, J. R., Behr, P., Antman, M. D., Ringeisen, B. R., Splan, J., and Nathanson, G. M.: Molecular beam scattering from supercooled sulfuric acid: Collisions of HCl, HBr, and HNO3 with 70 wt % D2SO4, J. Phys. Chem. A, 104, 6738–6751, https://doi.org/10.1021/jp000105o, 2000.
Moussa, S. G., McIntire, T. M., Szori, M., Roeselova, M., Tobias, D. J., Grimm, R. L., Hemminger, J. C., and Finlayson-Pitts, B. J.: Experimental and Theoretical Characterization of Adsorbed Water on Self-Assembled Monolayers: Understanding the Interaction of Water with Atmospherically Relevant Surfaces, J. Phys. Chem. A, 113, 2060–2069, https://doi.org/10.1021/jp808710n, 2009.
Mu, Q., Shiraiwa, M., Octaviani, M., Ma, N., Ding, A. J., Su, H., Lammel, G., Poschl, U., and Cheng, Y. F.: Temperature effect on phase state and reactivity controls atmospheric multiphase chemistry and transport of PAHs, Sci. Adv., 4, 8, https://doi.org/10.1126/sciadv.aap7314, 2018.
Müller, R., Crutzen, P. J., Gross, J. U., Bruhl, C., Russell, J. M., Gernandt, H., McKenna, D. S., and Tuck, A. F.: Severe chemical ozone loss in the Arctic during the winter of 1995–96, Nature, 389, 709–712, 1997.
Nakanishi, M. and Nozaki, R.: Systematic study of the glass transition in polyhydric alcohols, Phys. Rev. E, 83, 5, https://doi.org/10.1103/PhysRevE.83.051503, 2011.
Nakatsuji, H.: Dipped adcluster model for chemisorptions and catalytic reactions on a metal-surface, J. Chem. Phys., 87, 4995–5001, https://doi.org/10.1063/1.452814, 1987.
Nathanson, G. M.: Molecular beam studies of gas-liquid interfaces, Annu. Rev. Phys. Chem., 55, 231–255, https://doi.org/10.1146/annurev.physchem.55.091602.094357, 2004.
Nathanson, G. M., Davidovits, P., Worsnop, D. R., and Kolb, C. E.: Dynamics and kinetics at the gas-liquid interface, J. Phys. Chem., 100, 13007–13020, 1996.
Nelson, C. E., Elam, J. W., Cameron, M. A., Tolbert, M. A., and George, S. M.: Desorption of H2O from a hydroxylated single-crystal alpha-Al2O3(0001) surface, Surf. Sci., 416, 341–353, https://doi.org/10.1016/s0039-6028(98)00439-7, 1998.
Nelson, C. E., Elam, J. W., Tolbert, M. A., and George, S. M.: H2O and HCl adsorption on single crystal alpha-Al2O3(0001) at stratospheric temperatures, Appl. Surf. Sci., 171, 21–33, 2001.
Nguyen, T. H., Goss, K.-U., and Ball, W. P.: Polyparameter Linear Free Energy Relationships for Estimating the Equilibrium Partition of Organic Compounds between Water and the Natural Organic Matter in Soils and Sediments, Environ. Sci. Technol., 39, 913–924, https://doi.org/10.1021/es048839s, 2005.
NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, Release 22, May 2022, Editor: Russell D. Johnson III, https://doi.org/10.18434/T47C7Z, 2022.
Nizkorodov, S. A., Laskin, J., and Laskin, A.: Molecular chemistry of organic aerosols through the application of high resolution mass spectrometry, Phys. Chem. Chem. Phys., 13, 3612–3629, https://doi.org/10.1039/c0cp02032j, 2011.
Ohrwall, G., Prisle, N. L., Ottosson, N., Werner, J., Ekholm, V., Walz, M. M., and Bjorneholm, O.: Acid-Base Speciation of Carboxylate Ions in the Surface Region of Aqueous Solutions in the Presence of Ammonium and Aminium Ions, J. Phys. Chem. B, 119, 4033–4040, https://doi.org/10.1021/jp509945g, 2015.
Oszust, J. and Ratajczak, H.: Dipole-moments and spectral features of some phenol-diethylamine complexes, J. Chem. Soc. Farad. T 1, 77, 1215–1221, https://doi.org/10.1039/f19817701215, 1981.
Pankow, J. F.: Common gamma-intercept and single compound regressions of gas particle partitioning data vs 1/t, Atmos. Environ. A-Gen., 25, 2229–2239, https://doi.org/10.1016/0960-1686(91)90098-r, 1991.
Paserba, K. R. and Gellman, A. J.: Effects of conformational isomerism on the desorption kinetics of n-alkanes from graphite, J. Chem. Phys., 115, 6737–6751, https://doi.org/10.1063/1.1398574, 2001.
Penkett, S. A., Jones, B. M. R., Brice, K. A., and Eggleton, A. E. J.: Importance of atmospheric ozone and hydrogen-peroxide in oxidizing sulfur-dioxide in cloud and rainwater, Atmos. Environ., 13, 123–137, https://doi.org/10.1016/0004-6981(79)90251-8, 1979.
Perraud, V., Bruns, E. A., Ezell, M. J., Johnson, S. N., Yu, Y., Alexander, M. L., Zelenyuk, A., Imre, D., Chang, W. L., Dabdub, D., Pankow, J. F., and Finlayson-Pitts, B. J.: Nonequilibrium atmospheric secondary organic aerosol formation and growth, P. Natl. Acad. Sci. USA, 109, 2836–2841, https://doi.org/10.1073/pnas.1119909109, 2012.
Peter, T.: Microphysics and heterogeneous chemistry of polar stratospheric clouds, Annu. Rev. Phys. Chem., 48, 785–822, 1997.
Petters, M. D., Prenni, A. J., Kreidenweis, S. M., DeMott, P. J., Matsunaga, A., Lim, Y. B., and Ziemann, P. J.: Chemical aging and the hydrophobic-to-hydrophilic conversion of carbonaceous aerosol, Geophys. Res. Lett., 33, L24806, https://doi.org/10.1029/2006gl027249, 2006.
Poe, S. H., Valsaraj, K. T., Thibodeaux, L. J., and Springer, C.: Equilibrium vapor-phase adsorption of volatile organic-chemicals on dry soils, J. Hazard. Mater., 19, 17–32, https://doi.org/10.1016/0304-3894(88)85071-4, 1988.
Pöschl, U. and Shiraiwa, M.: Multiphase Chemistry at the Atmosphere-Biosphere Interface Influencing Climate and Public Health in the Anthropocene, Chem. Rev., 115, 4440–4475, https://doi.org/10.1021/cr500487s, 2015.
Pöschl, U., Letzel, T., Schauer, C., and Niessner, R.: Interaction of ozone and water vapor with spark discharge soot aerosol particles coated with benzo a pyrene: O3 and H2O adsorption, benzo a pyrene degradation, and atmospheric implications, J. Phys. Chem. A, 105, 4029–4041, 2001.
Pöschl, U., Rudich, Y., and Ammann, M.: Kinetic model framework for aerosol and cloud surface chemistry and gas-particle interactions – Part 1: General equations, parameters, and terminology, Atmos. Chem. Phys., 7, 5989–6023, https://doi.org/10.5194/acp-7-5989-2007, 2007.
Pouvesle, N., Kippenberger, M., Schuster, G., and Crowley, J. N.: The interaction of H2O2 with ice surfaces between 203 and 233 K, Phys. Chem. Chem. Phys., 12, 15544–15550, https://doi.org/10.1039/c0cp01656j, 2010.
Raja, S., Yaccone, F. S., Ravikrishna, R., and Valsaraj, K. T.: Thermodynamic parameters for the adsorption of aromatic hydrocarbon vapors at the gas-water interface, J. Chem. Eng. Data, 47, 1213–1219, https://doi.org/10.1021/je025520j, 2002.
Rajyam, B. S. and Murty, C. R. K.: Dipole moments of some alkyl phenylacetates, Indian J. Pure Appl. Phys., 4, 327, 1966.
Rampi, M. A., Schueller, O. J. A., and Whitesides, G. M.: Alkanethiol self-assembled monolayers as the dielectric of capacitors with nanoscale thickness, Appl. Phys. Lett., 72, 1781–1783, https://doi.org/10.1063/1.121183, 1998.
Raso, A. R. W., Custard, K. D., May, N. W., Tanner, D., Newburn, M. K., Walker, L., Moore, R. J., Huey, L. G., Alexander, L., Shepson, P. B., and Pratt, K. A.: Active molecular iodine photochemistry in the Arctic, P. Natl. Acad. Sci. USA, 114, 10053–10058, https://doi.org/10.1073/pnas.1702803114, 2017.
Ravishankara, A. R.: Heterogeneous and multiphase chemistry in the troposphere, Science, 276, 1058–1065, 1997.
Redhead, P. A.: Thermal desorption of gases, Vacuum, 12, 203–211, https://doi.org/10.1016/0042-207X(62)90978-8, 1962.
Remorov, R. G. and Bardwell, M. W.: Model of uptake of OH radicals on nonreactive solids, J. Phys. Chem. B, 109, 20036–20043, 2005.
Rettner, C. T., Auerbach, D. J., Tully, J. C., and Kleyn, A. W.: Chemical dynamics at the gas-surface interface, J. Phys. Chem., 100, 13021–13033, https://doi.org/10.1021/jp9536007, 1996.
Ringeisen, B. R., Muenter, A. H., and Nathanson, G. M.: Collisions of DCl with liquid glycerol: Evidence for rapid, near-interfacial D → H exchange and desorption, J. Phys. Chem. B, 106, 4999–5010, https://doi.org/10.1021/jp013959x, 2002a.
Ringeisen, B. R., Muenter, A. H., and Nathanson, G. M.: Collisions of HCl, DCl, and HBr with liquid glycerol: Gas uptake, D → H exchange, and solution thermodynamics, J. Phys. Chem. B, 106, 4988–4998, https://doi.org/10.1021/jp013960w, 2002b.
Robinson, D. A., Cooper, J. D., and Gardner, C. M. K.: Modelling the relative permittivity of soils using soil hygroscopic water content, J. Hydrol., 255, 39–49, https://doi.org/10.1016/s0022-1694(01)00508-x, 2002.
Robinson, G. N., Worsnop, D. R., Jayne, J. T., Kolb, C. E., Swartz, E., and Davidovits, P.: Heterogeneous uptake of HCl by sulfuric acid solutions, J. Geophys. Res., 103, 25371–25381, 1998.
Romaner, L., Heimel, G., Ambrosch-Draxl, C., and Zojer, E.: The Dielectric Constant of Self-Assembled Monolayers, Adv. Funct. Mater., 18, 3999–4006, https://doi.org/10.1002/adfm.200800876, 2008.
Romanias, M. N., Ourrad, H., Thevenet, F., and Riffault, V.: Investigating the Heterogeneous Interaction of VOCs with Natural Atmospheric Particles: Adsorption of Limonene and Toluene on Saharan Mineral Dusts, J. Phys. Chem. A, 120, 1197–1212, https://doi.org/10.1021/acs.jpca.5b10323, 2016.
Rothfuss, N. E. and Petters, M. D.: Influence of Functional Groups on the Viscosity of Organic Aerosol, Environ. Sci. Technol., 51, 271–279, https://doi.org/10.1021/acs.est.6b04478, 2017.
Rouquerol, J. and Davy, L.: Automatic gravimetric apparatus for recording adsorption-isotherms of gases or vapors onto solids, Thermochim. Acta, 24, 391–397, https://doi.org/10.1016/0040-6031(78)80027-6, 1978.
Rowland, F. S.: Stratospheric ozone depletion, Annu. Rev. Phys. Chem., 42, 731–768, https://doi.org/10.1146/annurev.physchem.42.1.731, 1991.
Rudich, Y., Donahue, N. M., and Mentel, T. F.: Aging of organic aerosol: Bridging the gap between laboratory and field studies, Annu. Rev. Phys. Chem., 58, 321–352, https://doi.org/10.1146/annurev.physchem.58.032806.104432, 2007.
Salmeron, M. and Somorjai, G. A.: Adsorption and bonding of butane and pentane on the Pt(111) crystal-surfaces – effects of oxygen treatments and deuterium pre-adsorption, J. Phys. Chem., 85, 3835–3840, https://doi.org/10.1021/j150625a025, 1981.
Sander, R.: Compilation of Henry's law constants (version 4.0) for water as solvent, Atmos. Chem. Phys., 15, 4399–4981, https://doi.org/10.5194/acp-15-4399-2015, 2015.
Sander, R.: Compilation of Henry's law constants (version 5.0.0) for water as solvent, Atmos. Chem. Phys., 23, 10901–12440, https://doi.org/10.5194/acp-23-10901-2023, 2023.
Sander, S. P., Abbatt, J., Barker, J. R., Burkholder, J. B., Friedl, R. R., Golden, D. M., Huie, R. E., Kolb, C. E., Kurylo, M. J., Moortgat, G. K., Orkin, V. L., and Wine, P. H.: Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 17, JPL Publication 10-6, Jet Propulsion Laboratory, Pasadena, http://jpldataeval.jpl.nasa.gov (last access: 18 March 2024), 2011.
Savara, A.: Standard States for Adsorption on Solid Surfaces: 2D Gases, Surface Liquids, and Langmuir Adsorbates, J. Phys. Chem. C, 117, 15710–15715, https://doi.org/10.1021/jp404398z, 2013.
Savara, A., Schmidt, C. M., Geiger, F. M., and Weitz, E.: Adsorption Entropies and Enthalpies and Their Implications for Adsorbate Dynamics, J. Phys. Chem. C, 113, 2806–2815, https://doi.org/10.1021/jp806221j, 2009.
Schervish, M. and Donahue, N. M.: Peroxy radical chemistry and the volatility basis set, Atmos. Chem. Phys., 20, 1183–1199, https://doi.org/10.5194/acp-20-1183-2020, 2020.
Schervish, M. and Shiraiwa, M.: Impact of phase state and non-ideal mixing on equilibration timescales of secondary organic aerosol partitioning, Atmos. Chem. Phys., 23, 221–233, https://doi.org/10.5194/acp-23-221-2023, 2023.
Schervish, M., Donahue, N. M., and Shiraiwa, M.: Effects of volatility, viscosity, and non-ideality on particle-particle mixing timescales of secondary organic aerosols, Aerosol Sci. Technol., 1–16, https://doi.org/10.1080/02786826.2023.2256827, 2023.
Schlesinger, D., Lowe, S. J., Olenius, T., Kong, X. R., Pettersson, J. B. C., and Riipinen, I.: Molecular Perspective on Water Vapor Accommodation into Ice and Its Dependence on Temperature, J. Phys. Chem. A, 124, 10879–10889, https://doi.org/10.1021/acs.jpca.0c09357, 2020.
Schroder, E.: Methanol Adsorption on Graphene, J. Nanomater., 2013, 6, https://doi.org/10.1155/2013/871706, 2013.
Schwartz, S. E.: Mass-transport considerations pertinent to aqueous phase reactions of gases in liquid-water clouds, in: Chemistry of multiphase atmospheric systems, edited by: Jaeschke, W., NATO ASI Series, G6, Springer, Berlin, Heidelberg, 415–471, https://doi.org/10.1007/978-3-642-70627-1_16, 1986.
Sebastiani, F., Campbell, R. A., Rastogi, K., and Pfrang, C.: Nighttime oxidation of surfactants at the air–water interface: effects of chain length, head group and saturation, Atmos. Chem. Phys., 18, 3249–3268, https://doi.org/10.5194/acp-18-3249-2018, 2018.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Pysics. From Air Pollution to Climate Change, John Wiley, New York, 1326 pp., ISBN 0471178160, 1998.
Shaloski, M. A., Gord, J. R., Staudt, S., Quinn, S. L., Bertram, T. H., and Nathanson, G. M.: Reactions of N2O5 with Salty and Surfactant-Coated Glycerol: Interfacial Conversion of Br− to Br2 Mediated by Alkylammonium Cations, J. Phys. Chem. A, 121, 3708–3719, https://doi.org/10.1021/acs.jpca.7b02040, 2017.
Sharif, S.: Chemical and mineral-composition of dust and its effect on the dielectric-constant, IEEE T. Geosci. Remote, 33, 353–359, https://doi.org/10.1109/36.377935, 1995.
Shen, C. Y., Zhang, W., Choczynski, J., Davies, J. F., and Zhang, H. F.: Phase State and Relative Humidity Regulate the Heterogeneous Oxidation Kinetics and Pathways of Organic-Inorganic Mixed Aerosols, Environ. Sci. Technol., 56, 15398–15407, https://doi.org/10.1021/acs.est.2c04670, 2022.
Shi, Q., Jayne, J. T., Kolb, C. E., Worsnop, D. R., and Davidovits, P.: Kinetic model for reaction of ClONO2 with H2O and HCl and HOCl with HCl in sulfuric acid solutions, J. Geophys. Res., 106, 24259–24274, 2001.
Shinoda, K.: Iceberg formation and solubility, J. Phys. Chem., 81, 1300–1302, https://doi.org/10.1021/j100528a016, 1977.
Shinoda, K.: Characteristic property in aqueous-solutions – effect of iceberg formation of water surrounding solute on the solubility (or cmc) and its peculiar temperature-dependence, Adv. Colloid Interface Sci., 41, 81–100, https://doi.org/10.1016/0001-8686(92)80008-l, 1992.
Shiraiwa, M. and Pöschl, U.: Mass accommodation and gas–particle partitioning in secondary organic aerosols: dependence on diffusivity, volatility, particle-phase reactions, and penetration depth, Atmos. Chem. Phys., 21, 1565–1580, https://doi.org/10.5194/acp-21-1565-2021, 2021.
Shiraiwa, M. and Seinfeld, J. H.: Equilibration timescale of atmospheric secondary organic aerosol partitioning, Geophys. Res. Lett., 39, L24801, https://doi.org/10.1029/2012gl054008, 2012.
Shiraiwa, M., Garland, R. M., and Pöschl, U.: Kinetic double-layer model of aerosol surface chemistry and gas-particle interactions (K2-SURF): Degradation of polycyclic aromatic hydrocarbons exposed to O3, NO2, H2O, OH and NO3, Atmos. Chem. Phys., 9, 9571–9586, https://doi.org/10.5194/acp-9-9571-2009, 2009.
Shiraiwa, M., Pfrang, C., and Pöschl, U.: Kinetic multi-layer model of aerosol surface and bulk chemistry (KM-SUB): the influence of interfacial transport and bulk diffusion on the oxidation of oleic acid by ozone, Atmos. Chem. Phys., 10, 3673–3691, https://doi.org/10.5194/acp-10-3673-2010, 2010.
Shiraiwa, M., Ammann, M., Koop, T., and Pöschl, U.: Gas uptake and chemical aging of semisolid organic aerosol particles, P. Natl. Acad. Sci. USA, 108, 11003–11008, 2011a.
Shiraiwa, M., Sosedova, Y., Rouviere, A., Yang, H., Zhang, Y. Y., Abbatt, J. P. D., Ammann, M., and Pöschl, U.: The role of long-lived reactive oxygen intermediates in the reaction of ozone with aerosol particles, Nat. Chem., 3, 291–295, 2011b.
Shiraiwa, M., Pfrang, C., Koop, T., and Pöschl, U.: Kinetic multi-layer model of gas-particle interactions in aerosols and clouds (KM-GAP): linking condensation, evaporation and chemical reactions of organics, oxidants and water, Atmos. Chem. Phys., 12, 2777–2794, https://doi.org/10.5194/acp-12-2777-2012, 2012.
Shiraiwa, M., Zuend, A., Bertram, A. K., and Seinfeld, J. H.: Gas-particle partitioning of atmospheric aerosols: interplay of physical state, non-ideal mixing and morphology, Phys. Chem. Chem. Phys., 15, 11441–11453, https://doi.org/10.1039/c3cp51595h, 2013a.
Shiraiwa, M., Yee, L. D., Schilling, K. A., Loza, C. L., Craven, J. S., Zuend, A., Ziemann, P. J., and Seinfeld, J. H.: Size distribution dynamics reveal particle-phase chemistry in organic aerosol formation, P. Natl. Acad. Sci. USA, 110, 11746–11750, https://doi.org/10.1073/pnas.1307501110, 2013b.
Shiraiwa, M., Berkemeier, T., Schilling-Fahnestock, K. A., Seinfeld, J. H., and Pöschl, U.: Molecular corridors and kinetic regimes in the multiphase chemical evolution of secondary organic aerosol, Atmos. Chem. Phys., 14, 8323–8341, https://doi.org/10.5194/acp-14-8323-2014, 2014.
Shiraiwa, M., Li, Y., Tsimpidi, A. P., Karydis, V. A., Berkemeier, T., Pandis, S. N., Lelieveld, J., Koop, T., and Pöschl, U.: Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 8, 15002, https://doi.org/10.1038/ncomms15002, 2017a.
Shiraiwa, M., Ueda, K., Pozzer, A., Lammel, G., Kampf, C. J., Fushimi, A., Enami, S., Arangio, A. M., Frohlich-Nowoisky, J., Fujitani, Y., Furuyama, A., Lakey, P. S. J., Lelieveld, J., Lucas, K., Morino, Y., Poschl, U., Takaharna, S., Takami, A., Tong, H. J., Weber, B., Yoshino, A., and Sato, K.: Aerosol Health Effects from Molecular to Global Scales, Environ. Sci. Technol., 51, 13545–13567, https://doi.org/10.1021/acs.est.7b04417, 2017b.
Shklyarevskii, I. N. and Pakhomov, P. L.: Separation of contributions from free and coupled electrons into real and imaginary parts of a dielectric-constant of gold, Opt. Spektrosk., 34, 163–166, 1973.
Shrivastava, M., Lou, S. J., Zelenyuk, A., Easter, R. C., Corley, R. A., Thrall, B. D., Rasch, P. J., Fast, J. D., Simonich, S. L. M., Shen, H. Z., and Tao, S.: Global long-range transport and lung cancer risk from polycyclic aromatic hydrocarbons shielded by coatings of organic aerosol, P. Natl. Acad. Sci. USA, 114, E2263–E2263, https://doi.org/10.1073/pnas.1702221114, 2017a.
Shrivastava, M., Cappa, C. D., Fan, J. W., Goldstein, A. H., Guenther, A. B., Jimenez, J. L., Kuang, C., Laskin, A., Martin, S. T., Ng, N. L., Petaja, T., Pierce, J. R., Rasch, P. J., Roldin, P., Seinfeld, J. H., Shilling, J., Smith, J. N., Thornton, J. A., Volkamer, R., Wang, J., Worsnop, D. R., Zaveri, R. A., Zelenyuk, A., and Zhang, Q.: Recent advances in understanding secondary organic aerosol: Implications for global climate forcing, Rev. Geophys., 55, 509–559, https://doi.org/10.1002/2016rg000540, 2017b.
Sikorski, M., Gutt, C., Chushkin, Y., Lippmann, M., and Franz, H.: Dynamics at the Liquid-Vapor Interface of a Supercooled Organic Glass Former, Phys. Rev. Lett., 105, 4, https://doi.org/10.1103/PhysRevLett.105.215701, 2010.
Silva, S. C. and Devlin, J. P.: Interaction of acetylene, ethylene, and benzene with ice surfaces, J. Phys. Chem., 98, 10847–10852, https://doi.org/10.1021/j100093a027, 1994.
Slade, J. H. and Knopf, D. A.: Heterogeneous OH oxidation of biomass burning organic aerosol surrogate compounds: assessment of volatilisation products and the role of OH concentration on the reactive uptake kinetics, Phys. Chem. Chem. Phys., 15, 5898–5915, https://doi.org/10.1039/c3cp44695f, 2013.
Slade, J. H. and Knopf, D. A.: Multiphase OH oxidation kinetics of organic aerosol: The role of particle phase state and relative humidity, Geophys. Res. Lett., 41, 5297–5306, https://doi.org/10.1002/2014gl060582, 2014.
Slade, J. H., Thalman, R., Wang, J., and Knopf, D. A.: Chemical aging of single and multicomponent biomass burning aerosol surrogate particles by OH: implications for cloud condensation nucleus activity, Atmos. Chem. Phys., 15, 10183–10201, https://doi.org/10.5194/acp-15-10183-2015, 2015.
Slade, J. H., Shiraiwa, M., Arangio, A., Su, H., Pöschl, U., Wang, J., and Knopf, D. A.: Cloud droplet activation through oxidation of organic aerosol influenced by temperature and particle phase state, Geophys. Res. Lett., 44, 1583–1591, https://doi.org/10.1002/2016gl072424, 2017.
Slater, B. and Michaelides, A.: Surface premelting of water ice, Nat. Rev. Chem., 3, 172–188, https://doi.org/10.1038/s41570-019-0080-8, 2019.
Smith, R. S. and Kay, B. D.: Desorption Kinetics of Carbon Dioxide from a Graphene-Covered Pt(111) Surface, J. Phys. Chem. A, 123, 3248–3254 10.1021/acs.jpca.9b00674, 2019.
Sokolov, O. and Abbatt, J. P. D.: Adsorption to ice of n-alcohols (ethanol to 1-hexanol), acetic acid, and hexanal, J. Phys. Chem. A, 106, 775–782, 2002.
Sokolowska, Z., Jozefaciuk, G., Sokolowski, S., and Ourumovapesheva, A.: Adsorption of water-vapor by soils – investigations of the influence of organic-matter, iron, and aluminum on energetic heterogeneity of soil clays, Clay Clay Min., 41, 346–352, https://doi.org/10.1346/ccmn.1993.0410310, 1993.
Solomon, S.: Stratospheric ozone depletion: A review of concepts and history, Rev. Geophys., 37, 275–316, 1999.
Speight, J. G.: in: Lange's Handbook of Chemistry, 17th ed., McGraw-Hill Education, New York, ISBN 9781259586095, 2017.
Springmann, M., Knopf, D. A., and Riemer, N.: Detailed heterogeneous chemistry in an urban plume box model: reversible co-adsorption of O3, NO2, and H2O on soot coated with benzo[a]pyrene, Atmos. Chem. Phys., 9, 7461–7479, https://doi.org/10.5194/acp-9-7461-2009, 2009.
Sprowl, L. H., Campbell, C. T., and Arnadottir, L.: Hindered Translator and Hindered Rotor Models for Adsorbates: Partition Functions and Entropies, J. Phys. Chem. C, 120, 9719–9731, https://doi.org/10.1021/acs.jpcc.5b11616, 2016.
Staudinger, J. and Roberts, P. V.: A critical compilation of Henry's law constant temperature dependence relations for organic compounds in dilute aqueous solutions, Chemosphere, 44, 561–576, https://doi.org/10.1016/s0045-6535(00)00505-1, 2001.
Steimer, S. S., Berkemeier, T., Gilgen, A., Krieger, U. K., Peter, T., Shiraiwa, M., and Ammann, M.: Shikimic acid ozonolysis kinetics of the transition from liquid aqueous solution to highly viscous glass, Phys. Chem. Chem. Phys., 17, 31101–31109, https://doi.org/10.1039/c5cp04544d, 2015.
Steiner, D. and Burtscher, H. K.: Desorption of perylene from combustion, nacl, and carbon particles, Environ. Sci. Technol., 28, 1254–1259, https://doi.org/10.1021/es00056a012, 1994.
Steiner, T.: The hydrogen bond in the solid state, Angew. Chem.-Int. Edit., 41, 48–76, https://doi.org/10.1002/1521-3773(20020104)41:1<48::Aid-anie48>3.0.Co;2-u, 2002.
Stephenson, R. M. and Malanowski, S.: Handbook of the Thermodynamics of Organic Compounds, Elsevier Science Publishing Co., Inc., Dordrecht, https://doi.org/10.1007/978-94-009-3173-2, 1987.
Stolzenburg, D., Fischer, L., Vogel, A. L., Heinritzi, M., Schervish, M., Simon, M., Wagner, A. C., Dada, L., Ahonen, L. R., Amorim, A., Baccarini, A., Bauer, P. S., Baumgartner, B., Bergen, A., Bianchi, F., Breitenlechner, M., Brilke, S., Mazon, S. B., Chen, D. X., Dias, A., Draper, D. C., Duplissy, J., Haddad, I., Finkenzeller, H., Frege, C., Fuchs, C., Garmash, O., Gordon, H., He, X., Helm, J., Hofbauer, V., Hoyle, C. R., Kim, C., Kirkby, J., Kontkanen, J., Kuerten, A., Lampilahti, J., Lawler, M., Lehtipalo, K., Leiminger, M., Mai, H., Mathot, S., Mentler, B., Molteni, U., Nie, W., Nieminen, T., Nowak, J. B., Ojdanic, A., Onnela, A., Passananti, M., Petaja, T., Quelever, L. L. J., Rissanen, M. P., Sarnela, N., Schallhart, S., Tauber, C., Tome, A., Wagner, R., Wang, M., Weitz, L., Wimmer, D., Xiao, M., Yan, C., Ye, P., Zha, Q., Baltensperger, U., Curtius, J., Dommen, J., Flagan, R. C., Kulmala, M., Smith, J. N., Worsnop, D. R., Hansel, A., Donahue, N. M., and Winkler, P. M.: Rapid growth of organic aerosol nanoparticles over a wide tropospheric temperature range, P. Natl. Acad. Sci. USA, 115, 9122–9127, https://doi.org/10.1073/pnas.1807604115, 2018.
Stull, D. R.: Vapor pressure of pure substances – inorganic compounds, Ind. Eng. Chem., 4, 540-550, https://doi.org/10.1021/ie50448a023, 1947.
Su, H., Cheng, Y. F., and Poschl, U.: New Multiphase Chemical Processes Influencing Atmospheric Aerosols, Air Quality, and Climate in the Anthropocene, Accounts Chem. Res., 53, 2034–2043, https://doi.org/10.1021/acs.accounts.0c00246, 2020.
Svirbely, W. J., Ablard, J. E., and Warner, J. C.: Molar polarizations in extremely dilute solutions. The dipole moments of d-limonene, d-pinene, methyl benzoate and ethyl benzoate, J. Am. Chem. Soc., 57, 652–655, https://doi.org/10.1021/ja01307a015, 1935.
Tabai, S., Rogalski, M., Solimando, R., and Malanowski, S. K.: Activity coefficients of chlorophenols in water at infinite dilution, J. Chem. Eng. Data, 42, 1147–1150, https://doi.org/10.1021/je960336h, 1997.
Tabazadeh, A., Turco, R. P., and Jacobson, M. Z.: A Model for Studying the Composition and Chemical Effects of Stratospheric Aerosols, J. Geophys. Res., 99, 12897–12914, 1994.
Tait, S. L., Dohnalek, Z., Campbell, C. T., and Kay, B. D.: n-alkanes on Pt(111) and on C(0001)/Pt(111): Chain length dependence of kinetic desorption parameters, J. Chem. Phys., 125, 15, https://doi.org/10.1063/1.2400235, 2006.
Takenaka, N. and Rossi, M. J.: The heterogeneous reaction of NO2 with NH4Cl: A molecular diffusion tube study, J. Atmos. Chem., 50, 171–194, https://doi.org/10.1007/s10874-005-5898-4, 2005.
Tang, M. J., Cziczo, D. J., and Grassian, V. H.: Interactions of Water with Mineral Dust Aerosol: Water Adsorption, Hygroscopicity, Cloud Condensation, and Ice Nucleation, Chem. Rev., 116, 4205–4259, https://doi.org/10.1021/acs.chemrev.5b00529, 2016.
Tenhulscher, T. E. M., Vandervelde, L. E., and Bruggeman, W. A.: Temperature-dependence of henry law constants for selected chlorobenzenes, polychlorinated-biphenyls and polycyclic aromatic-hydrocarbons, Environ. Toxicol. Chem., 11, 1595–1603, https://doi.org/10.1897/1552-8618(1992)11[1595:Tdohlc]2.0.Co;2, 1992.
Thomas, J. M. and Williams, B. R.: Theory and applications of vacuum microbalance techniques, Q. Rev. Chem. Soc., 19, 251–253, https://doi.org/10.1039/qr9651900231, 1965.
Thomson, E. S., Kong, X. R., Andersson, P. U., Markovic, N., and Pettersson, J. B. C.: Collision Dynamics and Solvation of Water Molecules in a Liquid Methanol Film, J. Phys. Chem. Lett., 2, 2174–2178, https://doi.org/10.1021/jz200929y, 2011.
Thomson, E. S., Kong, X., Papagiannakopoulos, P., and Pettersson, J. B. C.: Deposition-mode ice nucleation reexamined at temperatures below 200 K, Atmos. Chem. Phys., 15, 1621–1632, https://doi.org/10.5194/acp-15-1621-2015, 2015.
Tian, H. K., Xu, Q. Y., Zhang, H. Y., Priestley, R. D., and Zuo, B.: Surface dynamics of glasses, Appl. Phys. Rev., 9, 25, https://doi.org/10.1063/5.0083726, 2022.
Tolbert, M. A., Rossi, M. J., Malhotra, R., and Golden, D. M.: Reaction of chlorine nitrate with hydrogen-chloride and water at antarctic stratospheric temperatures, Science, 238, 1258–1260, https://doi.org/10.1126/science.238.4831.1258, 1987.
Townes, C. H. and Schawlow, A. L.: Microwave Spectroscopy, Dover Publications, Inc., New York, 698 pp., ISBN 9780486617985, 1975.
Tully, J. C.: The dynamics of adsorption and desorption, Surf. Sci., 299, 667–677, https://doi.org/10.1016/0039-6028(94)90688-2, 1994.
Ulbricht, H., Zacharia, R., Cindir, N., and Hertel, T.: Thermal desorption of gases and solvents from graphite and carbon nanotube surfaces, Carbon, 44, 2931–2942, https://doi.org/10.1016/j.carbon.2006.05.040, 2006.
Ulrich, T., Ammann, M., Leutwyler, S., and Bartels-Rausch, T.: The adsorption of peroxynitric acid on ice between 230 K and 253 K, Atmos. Chem. Phys., 12, 1833–1845, https://doi.org/10.5194/acp-12-1833-2012, 2012.
Usher, C. R., Michel, A. E., and Grassian, V. H.: Reactions on mineral dust, Chem. Rev., 103, 4883–4939, 2003.
Valsaraj, K. T.: On the physicochemical aspects of partitioning of non-polar hydrophobic organics at the air-water-interface, Chemosphere, 17, 875–887, https://doi.org/10.1016/0045-6535(88)90060-4, 1988a.
Valsaraj, K. T.: Binding constants for non-polar hydrophobic organics at the air-water-interface – comparison of experimental and predicted values, Chemosphere, 17, 2049–2053, https://doi.org/10.1016/0045-6535(88)90015-x, 1988b.
Valsaraj, K. T.: Hydrophobic compounds in the environment – adsorption equilibrium at the air-water-interface, Water Res., 28, 819–830, https://doi.org/10.1016/0043-1354(94)90088-4, 1994.
Valsaraj, K. T.: Trace gas adsorption thermodynamics at the air-water interface: Implications in atmospheric chemistry, Pure Appl. Chem., 81, 1889–1901, https://doi.org/10.1351/pac-con-08-07-06, 2009.
Valsaraj, K. T. and Thibodeaux, L. J.: Equilibrium adsorption of chemical vapors on surface soils, landfills and landfarms – a review, J. Hazard. Mater., 19, 79–99, https://doi.org/10.1016/0304-3894(88)85075-1, 1988.
Valsaraj, K. T., Thoma, G. J., Reible, D. D., and Thibodeaux, L. J.: On the enrichment of hydrophobic organic-compounds in fog droplets, Atmos. Environ. A-Gen., 27, 203–210, https://doi.org/10.1016/0960-1686(93)90351-x, 1993.
van der Sman, R. G. M.: Predictions of Glass Transition Temperature for Hydrogen Bonding Biomaterials, J. Phys. Chem. B, 117, 16303–16313, https://doi.org/10.1021/jp408184u, 2013.
van Duijnen, P. T. and Swart, M.: Molecular and atomic polarizabilities: Thole's model revisited, J. Phys. Chem. A, 102, 2399–2407, https://doi.org/10.1021/jp980221f, 1998.
Vega, C. P., Pohjola, V. A., Samyn, D., Pettersson, R., Isaksson, E., Bjorkman, M. P., Martma, T., Marca, A., and Kaiser, J.: First ice core records of NO3- stable isotopes from Lomonosovfonna, Svalbard, J. Geophys. Res.-Atmos., 120, 313–330, https://doi.org/10.1002/2013jd020930, 2015.
Vieceli, J., Roeselova, M., and Tobias, D. J.: Accommodation coefficients for water vapor at the air/water interface, Chem. Phys. Lett., 393, 249–255, https://doi.org/10.1016/j.cplett.2004.06.038, 2004.
Vieceli, J., Roeselova, M., Potter, N., Dang, L. X., Garrett, B. C., and Tobias, D. J.: Molecular dynamics simulations of atmospheric oxidants at the air-water interface: Solvation and accommodation of OH and O3, J. Phys. Chem. B, 109, 15876–15892, https://doi.org/10.1021/jp051361, 2005.
Vinogradov, S. N. and Linnell, R. H.: Hydrogen Bonding, Van Nostrand Reinhold Company, London, 319 pp., ISBN 0442781857, 1971.
Virtanen, A., Joutsensaari, J., Koop, T., Kannosto, J., Yli-Pirila, P., Leskinen, J., Makela, J. M., Holopainen, J. K., Pöschl, U., Kulmala, M., Worsnop, D. R., and Laaksonen, A.: An amorphous solid state of biogenic secondary organic aerosol particles, Nature, 467, 824–827, https://doi.org/10.1038/nature09455, 2010.
Vlasenko, A., Huthwelker, T., Gaggeler, H. W., and Ammann, M.: Kinetics of the heterogeneous reaction of nitric acid with mineral dust particles: an aerosol flowtube study, Phys. Chem. Chem. Phys., 11, 7921–7930, https://doi.org/10.1039/b904290n, 2009.
Voigt, C., Schlager, H., Ziereis, H., Karcher, B., Luo, B. P., Schiller, C., Kramer, M., Popp, P. J., Irie, H., and Kondo, Y.: Nitric acid in cirrus clouds, Geophys. Res. Lett., 33, L05803, https://doi.org/10.1029/2005gl025159, 2006.
Voloshina, E., Usvyat, D., Schutz, M., Dedkov, Y., and Paulus, B.: On the physisorption of water on graphene: a CCSD(T) study, Phys. Chem. Chem. Phys., 13, 12041–12047, https://doi.org/10.1039/c1cp20609e, 2011.
von Domaros, M., Lakey, P. S. J., Shiraiwa, M., and Tobias, D. J.: Multiscale Modeling of Human Skin Oil-Induced Indoor Air Chemistry: Combining Kinetic Models and Molecular Dynamics, J. Phys. Chem. B, 124, 3836–3843, https://doi.org/10.1021/acs.jpcb.0c02818, 2020.
von Hessberg, P., Pouvesle, N., Winkler, A. K., Schuster, G., and Crowley, J. N.: Interaction of formic and acetic acid with ice surfaces between 187 and 227 K. Investigation of single species- and competitive adsorption, Phys. Chem. Chem. Phys., 10, 2345–2355, https://doi.org/10.1039/b800831k, 2008.
Wang, B. and Knopf, D. A.: Heterogeneous ice nucleation on particles composed of humic-like substances impacted by O3, J. Geophys. Res., 116, D03205, https://doi.org/10.1029/2010jd014964, 2011.
Wang, B., Lambe, A. T., Massoli, P., Onasch, T. B., Davidovits, P., Worsnop, D. R., and Knopf, D. A.: The deposition ice nucleation and immersion freezing potential of amorphous secondary organic aerosol: Pathways for ice and mixed-phase cloud formation, J. Geophys. Res., 117, D16209, https://doi.org/10.1029/2012jd018063, 2012.
Wang, C., Collins, D. B., Arata, C., Goldstein, A. H., Mattila, J. M., Farmer, D. K., Ampollini, L., DeCarlo, P. F., Novoselac, A., Vance, M. E., Nazaroff, W. W., and Abbatt, J. P. D.: Surface reservoirs dominate dynamic gas-surface partitioning of many indoor air constituents, Sci. Adv., 6, 11, https://doi.org/10.1126/sciadv.aay8973, 2020.
Wang, X., Qiao, L., Deng, C., et al.: Study on the characteristics of nitrogen dioxide adsorption and storage of coal residue in coal-fired power plants in goaf, Sci. Rep., 11, 8822, https://doi.org/10.1038/s41598-021-87855-y, 2021.
Weaver, J. F., Carlsson, A. F., and Madix, R. J.: The adsorption and reaction of low molecular weight alkanes on metallic single crystal surfaces, Surf. Sci. Rep., 50, 107–199, https://doi.org/10.1016/s0167-5729(03)00031-1, 2003.
Wei, W. M., Zheng, R. H., Jing, Y. Y., Liu, Y. T., Hu, J. C., Ye, Y., and Shi, Q.: Theoretical Study on Raman Spectra of Aqueous Peroxynitric Acid, Chin. J. Chem. Phys., 24, 625–630, https://doi.org/10.1088/1674-0068/24/05/625-630, 2011.
Weschler, C. J. and Nazaroff, W. W.: Growth of organic films on indoor surfaces, Indoor Air, 27, 1101–1112, https://doi.org/10.1111/ina.12396, 2017.
Whitten, J. L.: Theoretical-studies of surface-reactions – Embedded-cluster theory, Chem. Phys., 177, 387–397, https://doi.org/10.1016/0301-0104(93)80020-a, 1993.
Wiberg, K. B. and Rablen, P. R.: Comparison of atomic charges derived via different procedures, J. Comput. Chem., 14, 1504–1518, https://doi.org/10.1002/jcc.540141213, 1993.
Wiegel, A. A., Liu, M. J., Hinsberg, W. D., Wilson, K. R., and Houle, F. A.: Diffusive confinement of free radical intermediates in the OH radical oxidation of semisolid aerosols, Phys. Chem. Chem. Phys., 19, 6814–6830, https://doi.org/10.1039/c7cp00696a, 2017.
Willis, M. D. and Wilson, K. R.: Coupled Interfacial and Bulk Kinetics Govern the Timescales of Multiphase Ozonolysis Reactions, J. Phys. Chem. A, 126, 4991–5010, https://doi.org/10.1021/acs.jpca.2c03059, 2022.
Wilson, J., Pöschl, U., Shiraiwa, M., and Berkemeier, T.: Non-equilibrium interplay between gas–particle partitioning and multiphase chemical reactions of semi-volatile compounds: mechanistic insights and practical implications for atmospheric modeling of polycyclic aromatic hydrocarbons, Atmos. Chem. Phys., 21, 6175–6198, https://doi.org/10.5194/acp-21-6175-2021, 2021.
Wilson, K. R., Prophet, A. M., and Willis, M. D.: A Kinetic Model for Predicting Trace Gas Uptake and Reaction, J. Phys. Chem. A, 126, 7291–7308, https://doi.org/10.1021/acs.jpca.2c03559, 2022.
Wincel, H., Mereand, E., and Castleman, A. W.: Gas-Phase Reactions of N2O5 with NO(H2O), NO(H2O), and NOHNO2, J. Chem. Phys., 102, 9228–9234, https://doi.org/10.1063/1.468872, 1995.
Winkler, A. K., Holmes, N. S., and Crowley, J. N.: Interaction of methanol, acetone and formaldehyde with ice surfaces between 198 and 223 K, Phys. Chem. Chem. Phys., 4, 5270–5275, https://doi.org/10.1039/b206258e, 2002.
Wittwer, H., Pino, P., and Suter, U. W.: Dipole-moments and conformational-analysis of copolymers of ethylene and carbon-monoxide, Macromolecules, 21, 1262–1269, https://doi.org/10.1021/ma00183a015, 1988.
Woodill, L. A., O'Neill, E. M., and Hinrichs, R. Z.: Impacts of Surface Adsorbed Catechol on Tropospheric Aerosol Surrogates: Heterogeneous Ozonolysis and Its Effects on Water Uptake, J. Phys. Chem. A, 117, 5620–5631, https://doi.org/10.1021/jp400748r, 2013.
Worsnop, D. R., Zahniser, M. S., Kolb, C. E., Gardner, J. A., Watson, L. R., Vandoren, J. M., Jayne, J. T., and Davidovits, P.: Temperature-Dependence of Mass Accommodation of SO2 and H2O2 On Aqueous Surfaces, J. Phys. Chem., 93, 1159–1172, 1989.
Worsnop, D. R., Morris, J. W., Shi, Q., Davidovits, P., and Kolb, C. E.: A chemical kinetic model for reactive transformations of aerosol particles, Geophys. Res. Lett., 29, 57-1–57-4, https://doi.org/10.1029/2002GL015542, 2002.
Yamasaki, H., Kuwata, K., and Miyamoto, H.: Effects of ambient-temperature on aspects of airborne polycyclic aromatic-hydrocarbons, Environ. Sci. Technol., 16, 189–194, https://doi.org/10.1021/es00098a003, 1982.
Yang, H. and Whitten, J. L.: Energetics of hydroxyl and influence of coadsorbed oxygen on metal surfaces, J. Phys. Chem. B, 101, 4090–4096, https://doi.org/10.1021/jp9702311, 1997.
Yankova, R., Dimov, M., Dobreva, K., and Stoyanova, A.: Electronic structure, reactivity, and Hirshfeld surface analysis of carvone, J. Chem. Res, 43, 319–329, https://doi.org/10.1177/1747519819863957, 2019.
Yaws, C. L.: Thermophysical Properties of Chemicals and Hydrocarbons 2nd, Elsevier, Oxford, 1000 pp., ISBN 9780323286596, 2014.
You, Y. and Bertram, A. K.: Effects of molecular weight and temperature on liquid–liquid phase separation in particles containing organic species and inorganic salts, Atmos. Chem. Phys., 15, 1351–1365, https://doi.org/10.5194/acp-15-1351-2015, 2015.
You, Y., Renbaum-Wolff, L., Carreras-Sospedra, M., Hanna, S. J., Hiranuma, N., Kamal, S., Smith, M. L., Zhang, X. L., Weber, R. J., Shilling, J. E., Dabdub, D., Martin, S. T., and Bertram, A. K.: Images reveal that atmospheric particles can undergo liquid-liquid phase separations, P. Natl. Acad. Sci. USA, 109, 13188–13193, https://doi.org/10.1073/pnas.1206414109, 2012.
You, Y., Smith, M. L., Song, M. J., Martin, S. T., and Bertram, A. K.: Liquid-liquid phase separation in atmospherically relevant particles consisting of organic species and inorganic salts, Int. Rev. Phys. Chem., 33, 43–77, https://doi.org/10.1080/0144235x.2014.890786, 2014.
Zen, A., Trout, B. L., and Guidoni, L.: Properties of reactive oxygen species by quantum Monte Carlo, J. Chem. Phys., 141, 14, https://doi.org/10.1063/1.4885144, 2014.
Zhang, I. Y. and Grüneis, A.: Coupled Cluster Theory in Materials Science, Frontiers in Materials, 6, https://doi.org/10.3389/fmats.2019.00123, 2019.
Zhang, Y. and Fakhraai, Z.: Decoupling of surface diffusion and relaxation dynamics of molecular glasses, P. Natl. Acad. Sci. USA, 114, 4915–4919, https://doi.org/10.1073/pnas.1701400114, 2017.
Zhao, X. Y., Nathanson, G. M., and Andersson, G. G.: Experimental Depth Profiles of Surfactants, Ions, and Solvent at the Angstrom Scale: Studies of Cationic and Anionic Surfactants and Their Salting Out, J. Phys. Chem. B, 124, 2218–2229, https://doi.org/10.1021/acs.jpcb.9b11686, 2020.
Zheng, G. J., Su, H., Wang, S. W., Andreae, M. O., Poschl, U., and Cheng, Y. F.: Multiphase buffer theory explains contrasts in atmospheric aerosol acidity, Science, 369, 1374–1377, https://doi.org/10.1126/science.aba3719, 2020.
Zhou, S., Shiraiwa, M., McWhinney, R. D., Pöschl, U., and Abbatt, J. P. D.: Kinetic limitations in gas-particle reactions arising from slow diffusion in secondary organic aerosol, Faraday Discuss., 165, 391–406, https://doi.org/10.1039/c3fd00030c, 2013.
Zimmermann, S., Kippenberger, M., Schuster, G., and Crowley, J. N.: Adsorption isotherms for hydrogen chloride (HCl) on ice surfaces between 190 and 220 K, Phys. Chem. Chem. Phys., 18, 13799–13810, https://doi.org/10.1039/c6cp01962e, 2016.
Zobrist, B., Marcolli, C., Pedernera, D. A., and Koop, T.: Do atmospheric aerosols form glasses?, Atmos. Chem. Phys., 8, 5221–5244, https://doi.org/10.5194/acp-8-5221-2008, 2008.
Zobrist, B., Soonsin, V., Luo, B. P., Krieger, B. P., Marcolli, C., Peter, T., and Koop, T.: Ultra-slow water diffusion in aqueous sucrose glasses, Phys. Chem. Chem. Phys., 13, 3514–3526, 2011.
- Abstract
- Introduction
- Thermodynamic relations
- Compilation of desorption energies for solid and liquid substrates
- Impact of desorption lifetime on gas uptake
- Derivation of a parameterization of the desorption energy
- Atmospheric implications
- Summary and conclusions
- Appendix A
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Thermodynamic relations
- Compilation of desorption energies for solid and liquid substrates
- Impact of desorption lifetime on gas uptake
- Derivation of a parameterization of the desorption energy
- Atmospheric implications
- Summary and conclusions
- Appendix A
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement