The presence of clouds lowers climate sensitivity in the MPI-ESM1.2 climate model

Clouds affect the sensitivity of the climate system by changing their distribution, height, and optical properties under climate change. Although the precise magnitude remains uncertain, the direct cloud response to an external forcing is known to be destabilising. Additionally, clouds have a masking effect on CO₂ forcing and can influence other feedback mechanisms such as the surface albedo feedback. To understand the overall impact of clouds, we compute how much the equilibrium climate sensitivity (ECS) to a doubling of CO₂ changes when clouds are made transparent to radiation in an Earth system model (MPI-ESM1.2, the Max Planck Institute for Meteorology Earth System Model version 1.2). In practice, to stabilise the model climate at near-preindustrial temperatures, the solar constant was reduced by 8.8 %. Our experiments reveal that clouds exert a stabilising influence on the model, with a clear-sky ECS of 4.29 K, which is higher than the corresponding full-sky ECS of 2.84 K, contrasting with their direct destabilising effect. Detailed partial radiative perturbation diagnostics show that beyond directly amplifying warming by themselves, clouds also strengthen the negative lapse rate and positive water vapour feedbacks, while strongly damping the positive albedo feedback. These findings highlight the complex role of clouds in modulating climate sensitivity.

1 Introduction

The radiative balance at the top of the atmosphere (TOA) determines the state of the climate system. When the system is in equilibrium the mean imbalance is zero, but when the system is forced, a positive or negative imbalance can arise, resulting in warming or cooling of the system. The magnitude of climate change is usually quantified as the equilibrium climate sensitivity (ECS), which is defined as the long-term global mean temperature change when the system is forced by a doubling of the CO₂ concentration relative to preindustrial levels. The ECS assessed value by the IPCC AR6 (Intergovernmental Panel on Climate Change Sixth Assessment Report) is 3 K, with a likely range from 2.5 to 4 K (Forster et al., 2021). In recent years, after having been the main tool to assess the ECS for decades, climate model simulations have been largely shelved in favour of other lines of evidence that allowed the ECS uncertainty to be narrowed down by close to a factor of 2 (Sherwood et al., 2020; Forster et al., 2021). This seemed timely since the Coupled Model Intercomparison Project phase 6 (CMIP6) showed, across 27 global climate models (GCMs), a wider range of the ECS than in previous phases. The causes of this widening have been partly traced back to model representation of cloud processes, not all of which are completely understood (Zelinka et al., 2020; Flynn and Mauritsen, 2020).

Generally, ECS can be estimated elegantly in a linear framework (see Sect. 2.1) as the temperature change that would re-establish the radiation balance at the TOA, and it can be expressed as (minus) the ratio of a radiative forcing F to a linear response to temperature changes λ, the feedback parameter (Gregory et al., 2004). One approach, which generally goes by the name of process understanding, builds on this simple formula, separately estimating the forcing F and the feedback λ using different lines of evidence. Recent studies (Wilson and Gea-Banacloche, 2012; Jeevanjee et al., 2021; Stevens and Kluft, 2023) have shown how it is possible to derive analytical expressions for the feedback and the forcing in the spectral space by making only a few reasonable assumptions, mainly regarding the dependencies of relative humidity on temperature and on the spectral properties of water vapour and CO₂ absorption. For example, the works of Jeevanjee et al. (2021) and Stevens and Kluft (2023) have focused on the calculation of the clear-sky ECS by computing the effects of the atmospheric components on the feedback and the forcing. The effects of water vapour and CO₂ are computed one after the other; however, introducing the role of clouds into this analysis is intrinsically complicated due to the multitude of mechanisms associated with them. Therefore, Stevens and Kluft (2023) conclude that within their framework, it is not yet evident if clouds play more of a stabilising or a destabilising role, since cloud feedback and masking effects on both forcing and feedback push the ECS in different directions. As a consequence, the cloud effect on ECS can be seen as a correction to a clear-sky ECS, which itself depends mostly on physical mechanisms that are quantifiable with greater confidence than cloud-related processes.

Motivated by these ideas of estimating ECS without clouds influencing the result, we set out to test this idea in a global climate model. We achieved this by making clouds transparent to all radiation and compensating for the warming that results by adjusting the solar constant. Essentially, one can think of the present study as complementing the one-dimensional models proposed earlier, in that we additionally simulate the global circulation response to the presence (full-sky, FS) and absence of clouds (clear-sky, CS). We compare our findings with clear-sky diagnostics obtained within the full-sky simulations, which are indicative of the direct effect of clouds, without including the global circulation response (clear-sky from full-sky, CS_F), finding surprising agreement in the total feedback strength with our clear-sky experiment. We furthermore apply the partial radiative perturbation (PRP) technique to separate the feedbacks and forcing contributions, to elucidate which mechanisms differ between the two simulations.

We expect clouds to affect non-cloud feedback mechanisms in two ways: modifying the control climate state, e.g. the sea-ice extent, and affecting the general circulation response to increasing CO₂ concentration. Within our clear-sky framework, the two effects act simultaneously, while CS_F only diagnoses the effect of the cloud response to CO₂ concentration increases. Another method that has been extensively employed to address similar questions is cloud-locking (Mauritsen et al., 2013; Middlemas et al., 2020). Prescribing the cloud field from a control state under warming allows us to remove the role of cloud feedbacks without significantly altering the control state. However, this approach is less suitable for the assessment of the role of clouds as a whole, as fixing cloud radiative properties under warming does not ensure the removal of their masking effect on CO₂ forcing, water vapour, and albedo feedbacks (Kang et al., 2008), in contrast to our method. Our idea of removing the cloud radiative effect is not completely novel, and examples of a similar approach for the longwave component can be found in Slingo and Slingo (1988, 1991) and more recently in the COOKIE intercomparison experiment (Stevens et al., 2012), where fixed sea surface temperature (SST) simulations proved useful to study inter-model differences in precipitation climatology (Fläschner et al., 2018). In our setup, using coupled simulations without prescribing the SST patterns allows us to study how clouds affect climate sensitivity and the response to CO₂ in a more natural framework.

2 Methods

Our analysis was carried out by performing simulations with the Max Planck Institute for Meteorology Earth System Model version 1.2 (MPI-ESM1.2). The next sections describe the linear framework and the general procedure used for feedback and forcing estimations, the peculiarities of the model we used, the setup necessary for the clear-sky simulations, and the experiment design.

2.1 The linear framework and the regression method

To study the temperature response to a given forcing, a linear framework (Forster et al., 2021) is used, expressing the TOA imbalance N as the sum of an effective radiative forcing F (ERF in the following, Sherwood et al., 2015) and a contribution linearly proportional to the surface air temperature (SAT) change ΔT:

$$\begin{array}{}\text{(1)}& N=F+\mathit{\lambda }\mathrm{\Delta }T,\end{array}$$

where the strength of the effect that the temperature change feeds back to the TOA imbalance is given by the feedback parameter λ. Typically, if the applied forcing is small enough, it can be assumed that the feedback parameter is state and time-independent. This assumption, which is not always perfect (Ceppi and Gregory, 2019), is generally accepted when the magnitude of the forcing is small enough, as is the case with CO₂ concentration doubling.

In this framework it is often assumed that different feedback mechanisms act independently from each other, allowing for a separation of the total imbalance into as many terms as the number of mechanisms affecting it. Traditionally, the imbalance is separated into contributions from CO₂, temperature, water vapour, surface albedo, and clouds:

$$\begin{array}{}\text{(2)}& N=N_{{\mathrm{CO}}_{\mathrm{2}}}+N_{\mathrm{T}}+N_{\mathrm{WV}}+N_{\mathit{\alpha }}+N_{\mathrm{C}},\end{array}$$

where the temperature contribution is further divided into stratospheric (to separate effects of the well-known stratospheric cooling), Planck, and lapse rate tropospheric terms. In principle, additional feedback mechanisms may apply for forcings other than CO₂ concentration changes, which would result in corresponding contributions to the imbalance. Nevertheless, for our model configuration and CO₂ concentration changes, this separation adds up to the total imbalance. In accordance with this framework, the imbalance N is calculated at the TOA throughout the entirety of our analysis.

The established Gregory regression method (Gregory et al., 2004) is used to compute the ECS and the contributions to the total feedback from different mechanisms (see Sect. 2.5), whereby an ordinary least-squares linear regression is applied to the first 100 years of each simulation unless otherwise stated. Since the TOA imbalance goes to zero at the equilibrium, the ECS can be derived from Eq. (1) as

$$\begin{array}{}\text{(3)}& \mathrm{ECS}=-{\displaystyle \frac{F}{\mathit{\lambda }}}.\end{array}$$

Although great care was taken to stabilise the control simulations, these still had some drift. Therefore, yearly TOA imbalance and temperature differences are calculated with respect to contemporaneous 21-year running mean values from the control simulation (Caldwell et al., 2016; Zelinka et al., 2020), so that by TOA imbalance we actually mean the difference between the imbalances of the experiment and the control simulation $N=R_{\exp }-R_{\mathrm{ctrl}}$. Although after 100 years the climate system is still far from the equilibrium, and this might lead to an estimated ECS smaller than the true value, our model configuration is not particularly prone to show feedback time-dependency after 100 years (see Sect. 3). Therefore, for the scope of this paper we study feedback changes to 100-year regressions after CO₂ is doubled.

For the ERF contributions, we complement the Gregory-derived estimates with estimates based on the fixed-SST method (Hansen et al., 2005). In these experiments, the forcing is estimated from a fixed-SST simulation as

$$\begin{array}{}\text{(4)}& F_{\mathrm{S}}=N_{\mathrm{0}}-\mathit{\lambda }\mathit{\delta }{T}_{\mathrm{0}},\end{array}$$

with N₀ the average TOA imbalance over 30 simulation years, λ the feedback parameter from the regression method, and δT₀ the 30-year average global mean temperature change, which differs from zero since land temperatures are not fixed. The second term thus accounts for the small surface-temperature response to the forcing, although the λ from the coupled run may differ from the actual feedback parameter of the fixed-SST run due to a different warming pattern. Nevertheless, it still yields a good approximation of F_S since δT₀ is small and is likely to be more accurate than discarding the second term entirely, as noted by Hansen et al. (2005). Averaging over 30 years accounts for the internal variability in the climatology.

2.2 Model properties

MPI-ESM1.2, a coupled Earth system model, was used at its coarse resolution, i.e. CR (Mauritsen et al., 2019), to allow us to perform longer simulations and investigate the dependency of our results on slow adjustments and initial conditions. The atmosphere model uses T31 spectral truncation with a corresponding 96 × 48 atmospheric grid (about 3.75° × 3.75°) and 31 vertical levels, while the ocean component has a bipolar curvilinear grid with a nominal resolution of 3° × 1.8° and 40 vertical levels. MPI-ESM1.2-LR has an ECS of 2.77 K, and our computed value for MPI-ESM1.2-CR is 2.84 K, placing it near the 3 K best estimate by IPCC AR6 but in the lower half of the assessed likely range of 2.5–4.0 K (Forster et al., 2021).

Cloud mechanisms have been identified as one of the main sources of the ECS spread among different models (Bony et al., 2006, 2015; Zelinka et al., 2020; Flynn and Mauritsen, 2020), and for this reason, it is important to bear in mind how the model we use represents their behaviour under warming. MPI-ESM1.2 shows a positive cloud fast adjustment and an overall small but positive cloud feedback (Mauritsen et al., 2019), which is broadly in line with what other models do (Andrews and Forster, 2008; Zelinka and Hartmann, 2010; Kamae et al., 2015; Zelinka et al., 2020).

Given that both their feedback and forcing adjustment contributions are positive, clouds in MPI-ESM1.2-CR directly act to raise the model's ECS. We can quantify this effect by isolating the cloud contributions and computing the diagnostic clear-sky ECS that we would obtain if the effect of making the clouds transparent to radiation were only that of zeroing their feedback (λ_C) and fast-adjustment (f_C) contributions in the full-sky experiment:

$$\begin{array}{}\text{(5)}& {\mathrm{ECS}}_{\mathrm{CS}}^{⟂}={\mathrm{ECS}}_{\mathrm{FS}}\underset{{\mathit{\xi }}^{-\mathrm{1}}}{\underbrace{\left[{\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{FS}}}{{\mathit{\lambda }}_{\mathrm{FS}}-{\mathit{\lambda }}_{\mathrm{C}}}}\cdot {\displaystyle \frac{F_{\mathrm{FS}}-f_{\mathrm{C}}}{F_{\mathrm{FS}}}}\right]}}.\end{array}$$

The diagnostic estimate of the direct effect that clouds have on the ECS using PRP-derived λ_C and f_C (see Sect. 2.5) is $\mathit{\xi }=\mathrm{1.18}\pm \mathrm{0.04}$. As a value greater than 1, this indicates that the direct cloud effect is destabilising.

However, clouds not only play a direct role in the climate system through their radiative response to CO₂ increases and feedback to global warming but also can have a strong indirect effect in that they mask the response of non-cloud feedback mechanisms. The sum of these indirect and their direct effects on the climate system determines whether clouds ultimately stabilise or destabilise the climate. We calculate this total effect in two ways. The first one, which consists of looking at clear-sky fluxes from our full-sky simulation (CS_F), accounts for all of the clouds' effects except for their dynamical response to circulation changes. The second one, implying the calculation of the clear-sky ECS within our simulated transparent-cloud world, also accounts for their dynamical response to CO₂ increases and their alteration of the control climate. We introduced here ECS${}_{\mathrm{CS}}^{⟂}$ in the comparison with ECS_FS and ECS_CS to emphasise the difference between the effect on the ECS that clouds directly have through their feedbacks and the indirect effect that they produce affecting the other forcing and feedback mechanisms. In the majority of model intercomparison analyses, the focus is on the direct effect, although in our experiment the indirect cloud effect is of comparable magnitude.

2.3 Cloud transparency and solar constant adjustment

In the clear-sky simulations, the clouds are made transparent to radiation of every wavelength in order to remove the cloud radiative effect (CRE). This is achieved by setting the cloud water path equal to zero in the radiation calculations, such that the cloud optical depth is effectively zero. In the standard MPI-ESM1.2 control climate, the CRE calculated at the top of the atmosphere results in a strong cooling in the shortwave, as clouds reflect solar radiation, and warming to a lesser extent in the longwave, as is also the case in the real world (Boucher et al., 2013). The net global mean CRE being negative implies that removing clouds would lead to a much warmer climate, and our estimate from Gregory extrapolation is that it could stabilise at approximately 22 K warmer than the current climate. We thus deemed the results to be less relevant to the goals of the current study. For this reason, we chose to compensate for this warming, and we achieve this by reducing the solar constant.

The intensity of the reduction is first computed theoretically by matching the extrapolated ERF of the CRE removal with the reduction in the incoming shortwave radiation. Such simulations nevertheless resulted in a residual 4.7 W m⁻² imbalance that would lead to a prohibitive drift. Consequently, the solar constant was further reduced in an iterative tuning process aiming at getting as close as possible to initial zero imbalance. Our final value for the solar constant multiplication factor is 0.912, meaning a reduction by −8.8 % of its current magnitude. This value is then used for all the clear-sky simulations henceforth.

Given the strong differences in the spatial patterns of the two forcings we applied when compensating for the removal of cloud radiative effects by the reduced solar constant, we analyse how letting the system equilibrate on long timescales affects our findings. As shown in Sect. 3.1, waiting 800 years rather than 100 does not yield substantially different results and only marginally enhances differences that are already discernible after 100 years. In the following, clear-sky experiments spun-up after 800 years are considered.

2.4 Clear-sky simulation peculiarities

Whilst the ECS is a metric defined using global mean quantities, SAT patterns are known to affect climate feedbacks (Armour et al., 2013; Andrews et al., 2015; Ceppi and Gregory, 2017). Hence it is worth describing them in the clear-sky simulation. As the clear-sky system was tuned to aim at zero initial imbalance, we used surface air temperature time series of the clear-sky simulation to compare with the full-sky preindustrial control simulation. In the case of MPI-ESM1.2-CR, the full-sky preindustrial control simulation itself is the result of a spin-up from the ocean state of the previous model version and of fine tuning until quasi-stationarity is achieved (Mauritsen et al., 2019). From the same preindustrial control simulation, we started the clear-sky experiment by simultaneously applying the solar constant reduction and cloud transparency. In the clear-sky experiment, the sea surface and deep-ocean temperature responses to our perturbation are observed over decadal and centennial timescales, respectively, motivating the choice of performing CO₂ doubling experiments after either 100 or 800 years. However, the conclusions drawn from our results are independent of either of the choices.

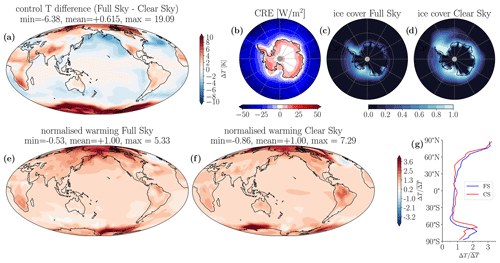
Figure 1 (a) SAT difference between the control simulations, 100-year average. Values for the clear-sky simulation are computed 800 years after its spin-up from the full-sky scenario. (b) Net cloud radiative effect in the full-sky experiment, showing positive values over Antarctica. (c, d) Yearly average Southern Ocean ice cover in the control simulation for the full-sky and clear-sky simulations. (e, f) SAT warming 100 years after the CO₂ concentration doubling, normalised to its global mean, for the full-sky and clear-sky simulations and (g) the latitudinal average.

Compensation for the CRE removal by the solar constant reduction ensured that the clear-sky simulation underwent only a slight cooling relative to the full-sky simulation, with a decrease in the global mean temperature by 0.61 K after 900–1000 years. The global pattern (Fig. 1) exhibits more-pronounced temperature differences over land (−2.08 K) and especially over dry regions, while midlatitude oceans are warmer (+0.59 K), particularly in correspondence with stratocumulus-covered regions such as the northeast Pacific. Clear-sky conditions also affect the sea-ice annual cycle, resulting in an increase in both its amplitude and annual mean in the Southern Hemisphere. Specifically, the Southern Ocean sea ice increases by almost 100 % in extent and more than 150 % in volume as a consequence of the removal of the cloud radiative effect, which is positive in the Antarctic region. As we shall see, this is a major cause of the albedo feedback increase and the Planck feedback intensification observed in the clear-sky experiments (see Sect. 3.1). The two effects partially compensate for each other, as the feedbacks have opposite signs. The clear-sky temperature pattern is a consequence of the different spatial pattern of the CRE removal and the compensating solar constant reduction. Despite these differences, the global pattern of warming shows good agreement between the two simulations, with the clear-sky simulation warming slightly more in the Southern Hemisphere.

2.5 Experiment design and feedback decomposition

Despite the ECS being defined as the temperature difference after CO₂ concentrations doubling, the standard experiment from CMIP5 and from CMIP6 onwards in the DECK (Diagnostic, Evaluation and Characterization of Klima) setup was the abrupt4xCO2 scenario (Eyring et al., 2016). This was chosen in order to obtain a higher signal-to-noise ratio in the Gregory plot, assuming the forcing from CO₂ doubling is half that of CO₂ quadrupling. Nevertheless, it has been shown that many models indicate a significant ECS increase with warming because of non-linearity that arises when the forcing of the system is not small enough (Jonko et al., 2013; Meraner et al., 2013). In our experiments, we want to disentangle the effect of cloud transparency on feedback mechanisms from the internal variability in the system. To overcome both problems, we account for the variability by performing an ensemble of 10 experiments (abrupt2xCO2) for each of the two configurations, with different initial conditions. This way, differences that stand out from the ensemble spread can be considered significant. The 10 ensemble members are simulations starting 20 years apart from each other, running for 100 years each. Initial conditions are taken after the system has equilibrated. For the clear-sky experiments, this is between 800 and 1000 years after spinning up from the full-sky state, which is quasi-stationary from the beginning (a detailed description is provided in Mauritsen et al., 2019, Sect. 8.1).

The feedback decomposition is achieved by making use of an online partial radiative perturbation technique (PRP; Wetherald and Manabe, 1988; Colman and McAvaney, 1997; Meraner et al., 2013). It is more computationally expensive than the radiative kernel method (Soden et al., 2008), but PRP is far more accurate and allows for direct computation of the feedback contribution from clouds, which in the standard kernel method is only computed as a residual (e.g. Soden et al., 2008). The application of the PRP technique with a time step for the PRP call in the radiation code of 10 h, resulting in a sampling of the diurnal cycle in 5 d, shows that the single-feedback contributions add up to the total feedback with just a 0.2 % error.

3 Results

By means of Gregory regression over the 10 ensemble members, we estimate the effective ECS of the full-sky and clear-sky experiments in two steps. First, we calculate feedback and forcing for each ensemble member, then, assuming the regressed feedbacks and forcings are taken from a Gaussian distribution whose standard deviation we estimate from the ensemble spread, we determine the ECS distributions. Our results (Fig. 2) show that the clear-sky ECS (4.29 K) is significantly higher than the full-sky ECS (2.84 K), with the clouds having an overall effect opposite in sign to that of just their direct feedback (diagnosed ECS^⟂ = 2.36 K). The picture is similar if, assuming that the clear-sky and the cloud-mediated TOA imbalances independently approach zero at the equilibrium, we calculate an ECS from the clear-sky fluxes within the full-sky simulation (4.80 K, a detailed description of this calculation is provided in Appendix A). The increase in the ECS is mainly caused by a significant reduction in the feedback strength without the clouds, a feature consistent between the values derived from the clear-sky experiment and the clear-sky fluxes within the full-sky simulation. We investigate the feedback changes in the next section before moving on to the forcing differences in Sect. 3.2.

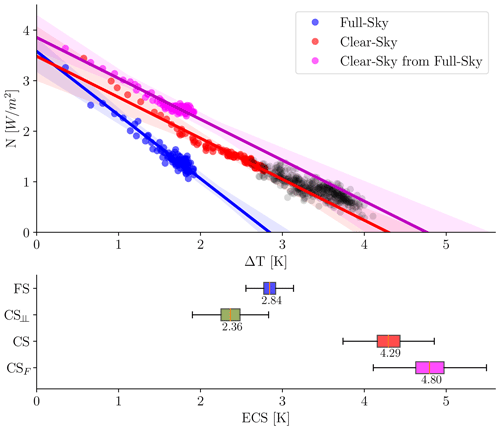
Figure 2 Gregory plot (yearly global mean TOA imbalance versus SAT change) for the full-sky (blue), clear-sky (red), and clear-sky fluxes from full-sky (purple) experiments. Regression lines are obtained from the ensemble average slope and intercept, with shaded areas covering their total spread. Using 500 simulation years (grey dots, single realisation) does not change the result substantially, albeit with a slight bending (ECS = 4.7 K). The bottom panel shows the computed ECS distributions. The green bar plot represents the diagnosed ECS${}_{\mathrm{CS}}^{⟂}$ of Eq. (5).

3.1 Feedbacks

In the clear-sky simulation, the total feedback parameter (${\mathit{\lambda }}_{\mathrm{CS}}=-\mathrm{0.81}\pm \mathrm{0.03}$ W m⁻² K⁻¹) is significantly weaker than in the full-sky simulation (${\mathit{\lambda }}_{\mathrm{FS}}=-\mathrm{1.30}\pm \mathrm{0.03}$ W m⁻² K⁻¹) and extremely close to the clear-sky fluxes from full-sky estimate (${\mathit{\lambda }}_{{\mathrm{CS}}_{\mathrm{F}}}=-\mathrm{0.80}\pm \mathrm{0.04}$ W m⁻² K⁻¹). In Fig. 3, the full-sky and clear-sky individual feedbacks are compared, together with the values obtained by regressing the clear-sky fluxes in the full-sky simulation (CS_F). We can consider the latter values as indicative of the immediate impact one would observe by swiftly removing the clouds without allowing the system to adjust to this change as in the clear-sky simulation (Appendix A). Differences between full-sky and CS_F values are representative of the masking effect of clouds, whereas clear-sky values account for both simple masking and the feedback mechanisms' alteration by the global circulation response to cloud transparency. The biggest differences between full-sky and clear-sky come from the positive variations in the surface albedo and lapse rate (LR) feedbacks, the latter being only partially compensated by the weakening of the water vapour (WV) feedback.

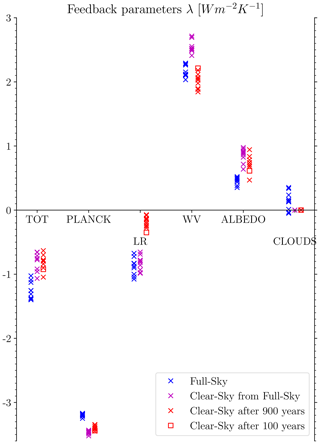
Figure 3 Feedback parameters across 10 ensemble members, diagnosed with the PRP technique for the full-sky (blue), clear-sky fluxes from full-sky (CS_F, purple), and clear-sky (red) experiments. The biggest differences between full-sky and clear-sky simulations are in the lapse rate and albedo feedbacks.

The weakening of the LR feedback is the most interesting result. It is mostly given by the weakening of the strongly negative LR feedback in the tropical region. The upper-tropospheric warming has already been found to be cloud-induced (Wetherald and Manabe, 1988; Langen et al., 2012), and Mauritsen et al. (2013) proposed that this could be due to a longwave flux convergence below the cloud tops, as warming the surface emits more radiation, while anvil clouds emit roughly the same (Hartmann and Larson, 2002), thus leading to flux convergence and heat accumulation aloft. If the flux convergence of heat, which is generated below the anvil tops but can propagate horizontally, disappears when clouds are made transparent, then there would be less heating aloft, ultimately leading to a weaker negative lapse rate feedback. This similarity in the lapse rate feedback strength between full-sky and CS_F in Fig. 3 is consistent with this hypothesis, as anvil clouds do not seem to significantly mask high-altitude tropical warming. A focus on the Indo-Pacific Warm Pool region (15° S–15° N, 110° E–160° W; e.g. in Jian et al., 2022), which is characterised by strong negative lapse rate feedback, shows the high-altitude warming, peaking between 300 and 200 hPa. The peak is located below the level of maximum cloudiness, where differences between clear-sky and full-sky cloudiness are the greatest (Fig. 4). This further suggests that high clouds play an important role in determining the strength of the lapse rate feedback.

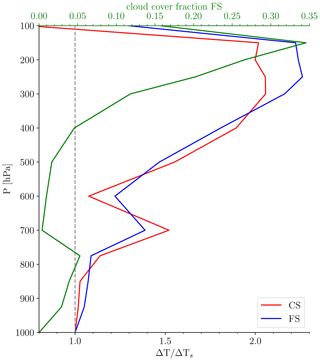
Figure 4 Warming 100 years after CO₂ concentration doubling, normalised to the surface values for the clear-sky and full-sky simulations in the Indo-Pacific Warm Pool, together with the average cloud cover fraction of the area in the full-sky simulation.

The WV feedback instead shows completely different behaviour. Because the water vapour is primarily located at lower altitudes and is thus masked by the clouds above it, the sudden removal of this masking, as for the CS_F value, results in a stronger WV feedback. Conversely, when the clouds are permanently made transparent to radiation (clear-sky), the weakening of the LR feedback also reduces the WV feedback originating from water vapour at higher altitudes; if there is less warming in the upper troposphere, where humidity can be considered temperature-constant, there would be less high-altitude water vapour increase with the same surface warming and hence a weaker WV feedback. This compensating effect, which is well-known in the literature (Colman and Soden, 2021), is better appreciated when comparing CS_F and clear-sky since in full-sky clouds mask the two feedbacks differently, and this is the main reason that the individual CS and CS_F feedbacks add up to nearly the same total feedback.

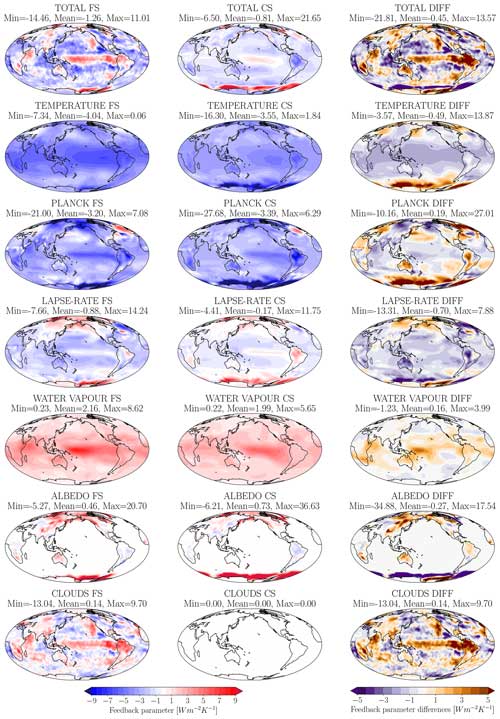
Figure 5 Local feedback parameters as averages over the 10 ensemble members and the differences between full-sky and clear-sky experiments. The total row is the sum of temperature, water vapour, and albedo and cloud feedbacks, while temperature is the sum of the Planck and lapse rate feedbacks and a negligible stratospheric component (not shown).

The albedo feedback is primarily caused by the snow and sea-ice melting in the polar regions. Those regions are generally cloudy, and hence removing cloud radiative effects allows more SW radiation to reach the surface, thus enhancing the surface albedo feedback with all other things being equal. The albedo feedback strength grows from 0.46 to 0.73 W m⁻² K⁻¹ from the full-sky to clear-sky experiments, which would become 0.80 W m⁻² K⁻¹ if normalised by the solar constant reduction in the latter experiment. The agreement between CS_F and clear-sky feedback strength might lead us to think that the effect of clouds is that of pure masking. However, this agreement is purely coincidental, as the increase in Antarctic sea ice in the clear-sky experiment is responsible for a widening of the area where a positive albedo feedback acts rather than an increase in feedback intensity in the same regions, as would be expected from masking (see Fig. 5 and the discussion in Sect. 3.3).

The Planck feedback shows minor differences, but it is slightly stronger under clear-sky conditions, possibly because the emission level is closer to the surface and thus warmer when clouds are transparent.

3.2 Effective radiative forcing

The differences in the ERF between full-sky and clear-sky simulations can be traced back to not only the direct CO₂ forcing but also stratospheric temperature and cloud adjustments that act to enhance the forcing. When separating the total imbalance into the single components, extra care should be taken in the interpretation of the fast adjustments. When analysing the single contributions using the Gregory method, deviations from linearity can lead to what we would think are fictitious adjustments because the regression method is extrapolating back to zero temperature change (the y-axis intercept). To take this into account, for our analysis we used three methods to assess the ERF. Here we highlight strengths and weaknesses of each of them.

1. Gregory regression across the entire 100 years of simulation (G100). As this is the same method as the one used to assess the feedback parameter, it allows us to explain the extent to which the contributions to the ERF in the full-sky and the clear-sky simulations lead to a different ECS. But because the regression is determined by interpolation of points that get denser further away from the y axis, the method leads to a low bias in the case of a gradually weakening time-dependent feedback.

2. Gregory regression for the first 20 years of the simulation, as in Block and Mauritsen (2013) (G20). Using points on a smaller temperature range closer to ΔT=0, where they are less affected by feedback time-dependency, is more representative of the initial forcing. However, it does not entirely explain ECS differences and is more susceptible to short-term variability, although the 10-ensemble method we use addresses the latter limitation.

3. Fixed-SST 30-year experiments, following the Hansen et al. (2005) method (H30). An advantage of this method is that a fixed SST results in most feedback mechanisms being effectively disabled. Nevertheless, land temperatures may change, and in particular, feedbacks occurring over land might be different in the full-sky and clear-sky simulations.

Consequently, when focusing on the impact on the ECS, G100 is preferable, while physical interpretation is more straightforward using G20 and H30.

Results for the total forcing with the three methods are presented in Fig. 6. What we would expect from the physically grounded argument of clouds masking the direct CO₂ forcing, is that their transparency should result in an increase in the total forcing. However, this forcing enhancement in the clear-sky simulation is only observed when using G20 and H30, although the differences are not statistically significant for any of the three methods. This is primarily attributable to the presence of a cloud adjustment that partially offsets the direct CO₂ forcing. The calculations also show notable agreement between the clear-sky experiment and the corresponding forcing estimated from the clear-sky fluxes in the full-sky simulation (CS_F) when using G20 and H30. Consistently with the physical interpretation that the difference between the two setups is solely attributable to the dynamical role of clouds, it appears reasonable to observe differences only in the feedback. Therefore, since there are other mechanisms that we expect to potentially be affected by the cloud transparency, we further analyse them by separating the total ERF in the direct CO₂ forcing and the fast adjustments using PRP, as shown in Fig. 7.

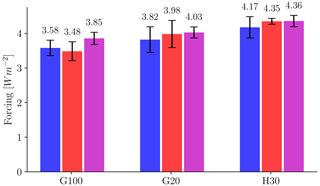
Figure 6 Total forcings from the full-sky experiment (blue), clear-sky experiment (red), and clear-sky fluxes from the full-sky experiment (purple) computed with three different methods. Error bars are plus and minus 1 standard deviation of the ensemble spread for G100 and G20 and 1 standard deviation of the yearly mean imbalances for H30.

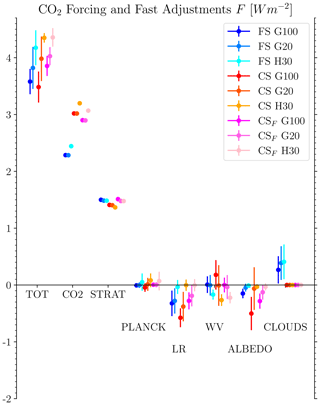
Figure 7 CO₂ direct forcing and fast adjustments assessed with the PRP technique for the full-sky experiment (shades of blue), clear-sky simulation (red to yellow), and clear-sky fluxes from the full-sky experiment (shades of pink) using the three methods described in Sect. 3.2. Error bars are 1σ of the ensemble spread for G100 and G20 and 1σ of the yearly mean imbalances for H30.

In the clear-sky simulation, the CO₂ direct forcing is enhanced with respect to the full-sky simulation. The three methods show good agreement, with clear-sky forcings always stronger than those of the full-sky simulation. The effect of clouds damping this forcing, which has long been known (e.g. Myhre et al., 1998), is explained well by Stevens and Kluft (2023): since the temperature of high clouds controls the emission of the CO₂ below them, they reduce the effects of changes in CO₂ concentration. Nevertheless, the presence of clouds also permits a cloud adjustment, that is, a change in cloudiness in direct response to the change in CO₂ concentration. In MPI-ESM1.2 there is a positive cloud fast adjustment (Fig. 7), primarily due to a reduction in the low-level stratiform clouds in the subtropics. Similar mechanisms have been found in other models (Andrews et al., 2012; Kamae et al., 2015). The removal of this cloud adjustment, however, only partially counterbalances the direct CO₂ forcing, such that other small changes to adjustments add up to the nearly identical ERF between the full-sky and clear-sky experiments (Fig. 6).

Differences in the diagnosed adjustments between the three different methods, (G100, G20, H30), can also be effects of the bending and feedback time-dependency in the Gregory diagram (Block and Mauritsen, 2013). Such behaviour is particularly evident for the lapse rate and water vapour feedbacks, which nearly cancel, as well as for the surface albedo feedback. These effects are larger in the clear-sky experiments. The G100 method is mostly affected by the bending, and in most cases the H30 method is least affected. As can be observed from Fig. 2, the feedback time dependency affects the CS experiment more than the FS, while being mainly limited to sub-centennial scales. Somewhat surprisingly, the water vapour adjustment computed with H30 is negative. This is due to the Hansen forcing definition, and we explain it in Sect. 3.3.

3.3 Spatial patterns of feedback and forcing

Following Hedemann et al. (2022) we used the global mean temperature definition of local feedback to represent the spatial differences between the full-sky and clear-sky simulations. In this way, local feedbacks are linearly additive and local differences can explain global feedback variations. Local feedback differences for each component are plotted in Fig. 5. Two details can be observed from the map of total feedback differences. First, the spatial pattern is strongly influenced by that of the cloud feedback, which is zero in the clear-sky scenario. Second, the strongest differences are in the Southern Ocean, where cloud transparency strongly enhances the albedo feedback as a consequence of the different ice distributions it induces in the control state (see panels (c) and (d) in Fig. 1). The different behaviour of Southern Ocean sea ice, which is subject to larger seasonal changes in the clear-sky experiment, also affects the temperature feedback. This feedback is generally stronger at high latitudes under clear-sky conditions. The removal of clouds also plays an important role in damping the positive water vapour feedback at low latitudes, reducing latitudinal variations.

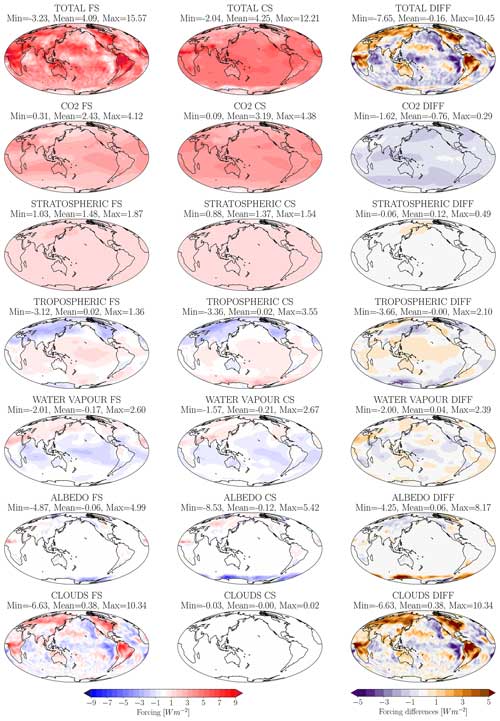
Figure 8 Local ERF contributions and the differences between the full-sky and clear-sky experiments, calculated using H30.

Spatial forcing contributions are shown in Fig. 8. As with the case of feedbacks, the rich spatial pattern observed in full-sky experiment is primarily attributed to the contribution of clouds, which is positive over land and predominantly negative over the oceans, especially in the eastern boundary regions and within the equatorial band. Contributions from other mechanisms exhibit greater spatial homogeneity. It is interesting to observe how the CO₂ forcing is influenced by high and thick clouds, with the forcing being more strongly damped in the regions of the Southern Ocean storm tracks and the Asian monsoon.

With respect to the water vapour feedback, it can be puzzling to see a negative global mean adjustment in the fixed-SST scenario. This is an artefact of the local application of Eq. (4). The term F₀ is positive over all land and nearly zero over the oceans (not shown), while the WV feedback is positive and stronger over the oceans (Fig. 5). This means that removing it from the oceans (where temperatures are held fixed and feedbacks are disabled) introduces a strong negative offset that adds to the less intense removal over lands, resulting in a negative F_S.

4 Conclusions

By comparing climate change simulations with abruptly doubled atmospheric CO₂ using the MPI-ESM1.2 global climate model in runs with and without cloud radiative effects, we have shown that clouds can exert a stabilising influence on the climate system. When clouds are made transparent to radiation in the model, the equilibrium climate sensitivity increases from 2.84 to 4.29 K. Whereas the effective radiative forcing is surprisingly close in magnitude, the total negative feedback is substantially weakened when clouds are made transparent.

At face value, this may seem surprising since the MPI-ESM1.2 model's diagnosed cloud feedback and the cloud adjustment to increasing CO₂ are both positive and so should act to enhance global warming. According to these diagnostics, the equilibrium climate sensitivity should have decreased to 2.36 K when clouds were made transparent. The reason is that clouds have more effects in the model. In addition to the positive cloud feedback and fast adjustment to CO₂, clouds also mask part of the direct CO₂ forcing, and they alter the strength of other feedback mechanisms, through either simple masking or altering the mechanism through changes in the control climate or the circulation.

When it comes to effective radiative forcing, the situation is fairly simple. The masking effect of clouds is to dampen the direct radiative forcing from a doubling of CO₂ by about 0.7 W m⁻². In simple terms, high clouds mask the CO₂ increase occurring below them. In MPI-ESM1.2 the clouds respond directly to a CO₂ increase with a decrease in cloudiness, thereby increasing the forcing by about 0.4 W m⁻². Together with a number of other small contributions, the net effect of clouds on the effective radiative forcing in this particular model is close to zero.

The situation is more complex when it comes to the effect of clouds on the total feedback. When including clouds, the total feedback is reduced by nearly −0.5 W m⁻² K⁻¹, despite the fact that the MPI-ESM1.2 model has a positive cloud feedback of about 0.1 W m⁻² K⁻¹.

A naive expectation might be that removing clouds should unmask a stronger surface albedo feedback. This simple idea is supported by the fact that the diagnosed clear-sky surface albedo feedback in the full-sky experiment is close in magnitude to that in the clear-sky experiment. However, upon closer inspection of the spatial distribution of the surface albedo feedback, this appears to be coincidental since there are substantial changes in the base climate with less snow and ice in the Northern Hemisphere and much more abundant sea ice in the Southern Ocean in the clear-sky experiment. The end result in both these cases is that the presence of clouds dampens the surface albedo feedback by about a factor of 2, or about −0.3 W m⁻² K⁻¹.

The largest single contribution to the change in the total feedback comes from the lapse rate feedback, about −0.7 W m⁻² K⁻¹. This is partially compensated for by shifts in the water vapour and Planck feedbacks, but if we add up all three feedbacks, the difference is still close to −0.3 W m⁻² K⁻¹. The much stronger lapse rate feedback is primarily associated with cloud-induced heating in the tropical upper troposphere and represents an effect that is not simply a cloud masking effect.

All in all, it should be remembered that the effect of clouds will be model dependent. But also, therefore, it is to be expected that inter-model differences for the models without cloud radiative effects will be smaller than inter-model differences for the models with them. In the present study, we propose a fairly simple protocol of reducing the solar constant to stabilise the climate near the preindustrial state, and so it could be easily replicated by other modelling groups.

Appendix A: Diagnosing clear-sky ECS from the full-sky simulation

What is the meaning of the clear-sky feedback and forcings that we obtain from the clear-sky fluxes in the full-sky simulation (CS_F)? The single calculation that the radiation code performs is exactly the same as the one performed in the clear-sky simulation, except for the fact that clear-sky values are not used to update physical quantities outside the radiation code in the full-sky simulation. This means that we can regard CS_F as an instantaneous “transient” value between the full-sky and the clear-sky simulation, which accounts only for the instantaneous cloud masking without the dynamical response to their radiative effect. In the clear-sky experiment instead, the system dynamically reacts to the absence of clouds. It is important to note that from the clear-sky fluxes within the full-sky simulation, inferring a clear-sky ECS is possible under one assumption. The Gregory regression method builds on the physical argument that the TOA imbalance goes to zero at the equilibrium, and in principle such an argument does not hold for the clear-sky fluxes since the clouds' contributions can be different at different states, and the two contributors to the equilibrium imbalance can change:

$$\begin{array}{}\text{(A1)}& \mathrm{\Delta }{N}_{\mathrm{eq}}=N_{{\mathrm{CS}}_{\mathrm{F}}}+N_{\mathrm{CL}}=\mathrm{0},\end{array}$$

namely $R_{{\mathrm{CS}}_{\mathrm{F}}}$ and R_CL being different for different equilibrium states (with higher CO₂ concentrations, the low clouds' radiative effect would be partly damped by the extra CO₂ above them), where $N=R-R_{\mathrm{0}}$ is the TOA imbalance and R₀ the TOA net flux of a reference equilibrium state. However, if the full-sky simulation were not to see N_CL, it would continue warming until $N_{{\mathrm{CS}}_{\mathrm{F}}}=\mathrm{0}$ alone, and consequently, the equilibrium temperature can be inferred with the same extrapolation method using $N_{{\mathrm{CS}}_{\mathrm{F}}}$ and temperature from the full-sky experiment. In other words, the decomposition of Eq. (A1) is an alternative to that of Eq. (2), with N_CL being the sum of the direct cloud contribution N_C and the masking effect on all other feedbacks.