the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A dynamic parameterization of sulfuric acid–dimethylamine nucleation and its application in three-dimensional modeling
Yuyang Li
Jiewen Shen
Runlong Cai
Shuxiao Wang
Manish Shrivastava
Da Gao
Jun Zheng
Markku Kulmala
Jingkun Jiang
Sulfuric acid (SA) is a governing gaseous precursor for atmospheric new particle formation (NPF), a major source of global ultrafine particles, in environments studied around the world. In polluted urban atmospheres with high condensation sinks (CSs), the formation of stable SA–amine clusters, such as SA–dimethylamine (DMA) clusters, usually initializes intense NPF events. Coagulation scavenging and cluster evaporation are dominant sink processes of SA–amine clusters in urban atmospheres, yet these loss processes are not quantitatively included in the present parameterizations of SA–amine nucleation. We herein report a parameterization of SA–DMA nucleation, based on cluster dynamic simulations and quantum chemistry calculations, with certain simplifications to greatly reduce the computational costs. Compared with previous SA–DMA nucleation parameterizations, this new parameterization was able to reproduce the dependences of particle formation rates on temperature and CSs. We then incorporated it in a three-dimensional (3-D) chemical transport model to simulate the evolution of the particle number size distributions. Simulation results showed good consistency with the observations in the occurrence of NPF events and particle number size distributions in wintertime Beijing and represented a significant improvement compared to that using a parameterization without coagulation scavenging. Quantitative analysis shows that SA–DMA nucleation contributes significantly to nucleation rates and aerosol population during the 3-D simulations in Beijing (>99 % and >60 %, respectively). These results broaden the understanding of NPF in urban atmospheres and stress the necessity of including the effects of coagulation scavenging and cluster stability in simulating SA–DMA nucleation in 3-D simulations. Representing these processes is thus likely to improve model performance in particle source apportionment and quantification of aerosol effects on air quality, human health, and climate.
- Article
(1948 KB) - Full-text XML
-
Supplement
(3778 KB) - BibTeX
- EndNote
New particle formation (NPF) is the major source of atmospheric particles in terms of their number concentration, which regulates the Earth's radiative balance and affects the climate (Kulmala et al., 2004; Gordon et al., 2017; Merikanto et al., 2009). The transformation from gaseous precursors to stable clusters and particles via nucleation is the initial step of NPF, and the new particle formation rate (J) is an essential parameter to characterize NPF intensity (Kulmala, 2003). Although nucleation processes would be suppressed by coagulation scavenging in urban atmospheres with high condensation sinks (CSs; Cai and Jiang, 2017; Cai et al., 2017b), intense NPF events have been frequently observed (Wu et al., 2007; Xiao et al., 2015; Deng et al., 2020). Recently, increasing evidence has been provided to show that those intense events are driven by the formation of stable sulfuric acid (SA)–amine clusters (Cai et al., 2022; Jen et al., 2014b; Yin et al., 2021), with a speed close to the collision limit for SA molecules, thus deriving high nucleation rates in urban atmospheres (Cai et al., 2021b; Yao et al., 2018; Chen et al., 2012). Furthermore, other molecules, such as HNO3 and NH3, could enhance the SA–dimethylamine (DMA) nucleation under certain conditions (Liu et al., 2021; Glasoe et al., 2015; Wang et al., 2021). Although a few previous three-dimensional (3-D) simulation studies have simulated NPF events in polluted urban atmospheres such as Beijing, they did not take the SA–amine nucleation into account (Chen et al., 2019; X. Chen et al., 2021). Thus, integrating SA–amine nucleation into 3-D models is essential for extending the understanding of NPF in polluted urban areas and quantifying its underlying impacts on the environment and climate. This requires a quantitative representation of particle formation rates through SA–amine nucleation for 3-D models.
Semi-empirical power law functions are widely used in SA-relevant nucleation rate studies to fit the experimental data, which has been shown to reproduce the measured J value in certain ambient observations or experimental conditions (Riccobono et al., 2014; Dunne et al., 2016; Bergman et al., 2015; Hanson et al., 2017; Semeniuk and Dastoor, 2018; Kürten et al., 2014, 2018). For SA–amine nucleation, Bergman et al. (2015) and Dunne et al. (2016) have presented semi-empirical parameterizations of good consistencies with chamber and flow-tube experimental results (Almeida et al., 2013; Jen et al., 2014b; Glasoe et al., 2015). In real urban atmospheres, recent advances have shown that coagulation scavenging would greatly suppress concentrations of molecular clusters and thus the nucleation rates (Cai and Jiang, 2017; Cai et al., 2021a, b; Marten et al., 2022). It has also been seen that the formation of the smallest SA–amine clusters, which is largely dependent on cluster stability, is the limiting step for SA–amine nucleation rates (Cai et al., 2022). However, the effects of coagulation scavenging and cluster stability vary with the environmental factors, e.g., CSs and temperature, while these effects have not been well represented in semi-empirical power law functions derived from certain experimental systems or ambient environments. Cluster kinetic simulations coupled with quantum chemistry calculations (Mcgrath et al., 2012), which take into account the effects of both coagulation scavenging and cluster stability, have been widely applied in zero-dimensional or one-dimensional simulations of SA–NH3 or SA–amine nucleation (Yang et al., 2021; Lu et al., 2020; Yao et al., 2018; Yu, 2006; Yu and Turco, 2001). Specifically, both cluster kinetic simulations and observations reveal that dimethylamine (DMA) is plausibly the most efficient for stabilizing SA clusters and is regarded as the key amine species that derives high particle formation rates in urban atmospheres (Jen et al., 2014b; Cai et al., 2022; Yao et al., 2018; Chen et al., 2012). However, no method with good representations of coagulation scavenging and cluster stabilities has been reported to explicitly simulate the SA–DMA nucleation rates in 3-D chemical transport models.
A challenge for setting up a parameterization based on cluster kinetic simulations for 3-D chemical transport models is to reduce the computational costs and yield explicit expressions. A plausible method to reduce the computational costs is to omit the unstable clusters with high evaporation rates from the nucleation pathway. Accordingly, different nucleation schemes were presented to represent the dominant source or sink processes of SA–DMA clusters in specific chamber experiments or ambient environments (Lu et al., 2020; Cai et al., 2021b). For polluted urban atmospheres, a kinetic model with a key pathway of particle formation in SA–DMA nucleation was constructed, yielding good predictions of measured SA cluster concentrations and 1.4 nm particle formation rates (J1.4) in urban Beijing (Cai et al., 2021b). Application of pseudo-steady-state assumptions is also an alternative method for reducing computational costs and yielding explicit expressions. The NPF occurrence indicator (I), based on the kinetic model with pseudo-steady-state assumptions, has shown good consistency with the qualitative estimations of NPF events in urban Beijing and Shanghai (Cai et al., 2021a). These results indicate the potential of deriving an explicit parameterization of particle formation rates by applying pseudo-steady-state assumptions to the kinetic model, although further quantitative analysis is still required to validate this parameterization.
In this study, we set up an SA–DMA nucleation parameterization, which is designed for application in 3-D chemical transport models. The parameterization is based on the pseudo-steady-state particle formation rate in the kinetic model, with a full representative of the effects of coagulation scavenging and cluster stability (Cai et al., 2021b). Generally, only four variables (temperature T, CS, gaseous DMA concentrations [B], and concentrations of SA molecules or clusters containing one SA molecule [SAtot]) are used in the parameterization, with the computational costs being greatly reduced. We then implement the parameterization in a 3-D chemical transport model and combine it with an integrated source–sink representation of DMA to simulate the evolution of the particle number size distributions (PNSDs) in wintertime Beijing. The precursor concentrations, PNSDs, NPF occurrence, and J1.4 values show relatively good consistencies between the simulations and observations. The simulations show that the SA–DMA nucleation contributes >99 % of the J1.4 value and >60 % of the total particle number concentration in wintertime Beijing, respectively. With this parameterization, 3-D chemical transport models could significantly improve the simulation of NPF, especially in urban environments, and thus the effects of NPF on particulate matter pollution or climate.
2.1 Derivation of parameterized formation rate in SA–DMA nucleation
Limited by computational quantum chemistry calculation results, SA–DMA nucleation is commonly simulated in the range of clusters containing not more than four SA or four DMA molecules (Olenius et al., 2013; Ortega et al., 2012). As unstable clusters would evaporate with higher rates, the formation of larger clusters potentially follows the pathways of the most stable clusters. In addition, as the SA–DMA clusters are increasingly stable along the main pathway of cluster formation, the clusters not smaller than A4B4 (hereafter AmBn refers to clusters containing m SA and n DMA molecules) are assumed to not evaporate back in these simulations. Although there are uncertainties in the pathways presented, based on different quantum chemistry methods, it is well accepted that the AmBm (m=1 to 4) and A2B1 clusters are relatively stable in the SA–DMA nucleation scheme (Olenius et al., 2013, 2017; Ortega et al., 2012; Myllys et al., 2019).
Based on previous studies under atmospheric conditions, the variations in the precursor concentrations, temperature, and CSs do not result in large deviations in the main pathway. Previous simulations under different [SA], [DMA], and temperature have shown that the main pathway was similar under the different conditions studied (Olenius et al., 2013). The effect of CS on the nucleation pathway is dependent on the relative relationship between the coagulation sink and the evaporation rate of a certain cluster. For most clusters out of the specified pathway, the evaporation rates are much higher than the typical CS range in urban atmospheres (Ortega et al., 2012); therefore, such clusters would not dominate the nucleation pathway no matter how low or high the CS is. Thus, in this study, the variation in the dominant pathway under different conditions was ignored.
Accordingly, the parameterization in this study is derived from the nucleation pathway, including A, B, and five other SA–DMA clusters (AmBm (m=1 to 4) and A2B1), consistent with a previous study (Cai et al., 2021b). The clusters, except for A4B4, are assumed to be in pseudo-steady states; i.e., the sink due to evaporation, coagulation scavenging, and cluster collision is equal to the source due to the collisions of molecules or smaller clusters. As the A4B4 clusters are estimated to be with an electrical mobility diameter of approximately 1.4 nm, the pseudo-steady-state formation rate of A4B4 was applied in the parameterization of the J1.4 value in this study. Although some studies have revealed that SA–DMA nucleation could also be enhanced by adding other molecules in certain conditions, a quantitative analysis of these effects in the relevant atmospheric conditions is still lacking; thus in this study, we set up this parameterization based only on the SA–DMA binary nucleation.
2.1.1 Derivation of collision coefficients, coagulation sink, and evaporation rates
In the nucleation pathway discussed above, A, B, and five SA–DMA clusters are included. The collision coefficients between them (βi,j) and the evaporation rate of A1B1 clusters (γ) vary with T during the simulation. The coagulation sinks (CoagSi) due to the coagulation scavenging of background aerosols are dependent on CSs. The work discussed in this section is focused on simplification of the derivation of these parameters to be updated in each simulation time interval to reduce the computational costs.
As the involved clusters and molecules are in the free molecular regime (Knudsen number >10), βi,j in SA–DMA nucleation processes can be calculated based on kinetic gas theory (Seinfeld and Pandis, 1998; Olenius et al., 2013; Ortega et al., 2012):
where m (kg) and V (m3) represent the molecular mass and molecular volume, respectively. The density of precursor molecules A and B was assumed to be 1830 and 680 kg m−3, respectively. T (K) represents the temperature. kb (J K−1) is the Boltzmann constant. Subscripts i and j refer to the index of the clusters or molecules (the numbers 1 to 7 refer to A, B, A1B1, A2B1, A2B2, A3B3, and A4B4, respectively, which are involved in the kinetic model). Ei,j is a dimensionless enhancement factor of the collision rates from Van de Waals forces between i and j. In this study, Ei,j is assumed to be 2.3 (Chan and Mozurkewich, 2001; Sceats, 1989), which is within the range of 2.3 to 2.7 predicted by the Brownian coagulation models and consistent with the value used in other cluster dynamics studies (Kürten et al., 2014; Lehtipalo et al., 2016; Stolzenburg et al., 2020).
Noting that mi and Vi are almost independent of the atmospheric conditions, and Ei,j is assumed to be constant, we can normalize different values of βi,j into β, and the normalizing factor is shown in a lookup table (Table S1 in the Supplement) as G(i,j).
where β represents the collision coefficients between two A1B1 clusters (β3,3) and could be calculated as follows:
where β0 is the value of β at the standard temperature T0=298.15 K, which is constant as m3 s−1.
Similarly, CoagSi could also be normalized to the CS using fixed ratios. The size-dependent coagulation sink (CoagS) is calculated with a power law exponent of −1.7, which is within the typical range of atmospheric aerosols (Lehtinen et al., 2007).
where the dimensionless factors H(i) are also recorded in Table S1 in the Supplement.
The evaporation rates of A1B1 could be derived based on the collision–evaporation equilibrium (Ortega et al., 2012), which is closely relevant to the free-energy barrier that forms A1B1 clusters (Olenius et al., 2013; Ortega et al., 2012).
where cref is the number concentrations under standard conditions (2.46×1025 m−3). ΔG is the formation of free energies of A1B1. Thus, if we take T0=298.15 as a reference, γ could also be calculated as follows:
where γ0′, with the value of 3.33 s−1, leads to the evaporation rates of A1B1 at T0, with kcal mol−1. ΔH is the formation enthalpy value of A1B1. In previous studies, several sets of ΔH and ΔG at specific temperatures were reported, based on different quantum chemistry models (Myllys et al., 2019; Ortega et al., 2012; Ge et al., 2020). Here we use kcal mol−1 and kcal mol−1, according to the results in Myllys et al. (2019). If the values of ΔG need to be updated in a future application of this parameterization, then the values of γ0 should be updated as well, based on Eq. (7). The sensitivity analysis of different values of ΔH and ΔG are discussed in Sect. 3.
Generally, with G(i,j) and H(i) being fixed into the parameterization formula, βi,j and CoagSi could be normalized to β and CS. Additionally, the values of γ and β could be updated in real time at any simulation time step, based on Eqs. (3) and (6).
2.1.2 Formula of the SA–DMA nucleation parameterization
Applying the pseudo-steady-state assumptions to the key pathway discussed above (Eqs. S1 to S9) and achieving real-time γ (s−1) and β (m3 s−1) values (Eqs. 3 and 6), we could derive an explicit formula of the parameterized value of J1.4 in this study (Eq. 8).
The above intermediate parameters are calculated as below:
In Eqs. (8) to (11), the four input variables which should be explicitly input to parameterize J1.4 are T (K), CS (s−1), [B] (m−3), and [SAtot] (m−3). Generally, only these four variable parameters are needed for the 3-D chemical transport models. Additionally, compared with directly coupling cluster dynamics simulations into 3-D chemical transport models, the parameterization of the pseudo-steady-state J1.4 value requires much less computational time.
2.2 Incorporating the parameterization into updated WRF-Chem/R2D-VBS model
The updated parameterization of SA–DMA nucleation was incorporated in the WRF-Chem (Weather Research and Forecasting model with Chemistry). Before adding the SA–DMA nucleation, we already incorporated seven other NPF mechanisms in the model (Zhao et al., 2020), including four inorganic pathways, with binary neutral/ion-induced SA–H2O nucleation and ternary neutral/ion-induced NH3–SA–H2O nucleation, and three organic pathways, including pure organic neutral/ion-induced organic nucleation and ternary nucleation involving organics and SA. The organic-containing nucleation pathways are driven by ultralow- and extremely low-volatility organic compounds (ULVOC and ELVOC), with O : C >0.4 being converted from monoterpene autoxidation. The chemical transformation and volatility distribution of monoterpene is represented in the model by R2D-VBS (radical two-dimensional volatility basis set framework) with constrained parameters against experiments. More details of the R2D-VBS model are given in our previous study (Zhao et al., 2020). The newly formed nanometer-sized particles and their initial size evolution are accounted for in the MOSAIC (MOdel for Simulating Aerosol Interactions and Chemistry) module by 20 size bins covering 1 nm to 10 µm. It is worth mentioning that the newly formed particles from SA–DMA nucleation are lumped into a lower-aerosol size bin in the model than that of other seven pathways. This should be attributed to the fact that our SA–DMA nucleation parameterization is formulated at a 1.4 nm sized particle formation rate, while the remaining ones are fitted based on measured particle formation rates from a cloud chamber at a mobility diameter of 1.7 nm. Given that condensation of gaseous SA and DMA on pre-existing aerosols and nucleation occurs simultaneously in the real atmosphere, we then use a time-integrated-average concentration of the precursors over each time step to drive SA–DMA nucleation in the model. The condensation sink for SA and DMA is calculated according to simulated real-time PNSDs. In addition, the consumption of both SA and DMA concentration during nucleation is also accounted in the model, in order to represent a comprehensive source–sink simulation scheme of two precursors in combination with other settings.
2.2.1 Sources and sinks of dimethylamine in the updated WRF-Chem/R2D-VBS model
A regional or global bottom-up emission inventory of DMA is currently lacking, mostly due to scarce direct measurements (Yang et al., 2022; Zhu et al., 2022). In previous 3-D model studies, amine NH3 emission ratios have often been used to estimate amine emissions due to the close correlation between NH3 and DMA emissions. However, a fixed amine NH3 ratio is likely to overestimate the concentrations of amines in rural areas, while underestimating those in urban areas, where high concentrations of amines have been reported (Yao et al., 2018; Bergman et al., 2015). Here, a set of source-dependent DMA NH3 emission ratios was used to develop the emission inventory of DMA, based on Mao et al. (2018). The ratios for different emission sectors were determined by a source apportionment analysis, based on a simultaneous observation of NH3, C1–C3 amines, NOx, and SO2 and also meteorological factors at a suburban site in Nanjing (Zheng et al., 2015a). We applied the source-dependent emission ratios (0.0070, 0.0018, 0.0015, 0.0100, and 0.0009 for chemical–industrial, other industrial, agricultural, residential, and transportation source types, respectively) to NH3 emissions in the ABaCAS-EI 2017 (emission inventory of the Air Benefit and Cost and Attainment Assessment System) for China mainland and the International Institute for Applied Systems Analysis (IIASA) 2015 emission inventory for other areas to build continental DMA emission inventory (Zheng et al., 2019; Li et al., 2017). In addition, the DMA emission for maritime area was developed by employing a DMA NH3 ratio derived from recent campaigns in offshore areas of China (see details in the Supplement; D. Chen et al., 2021).
DMA can be removed from the atmosphere through three main pathways, namely gas-phase chemical reaction, aerosol uptake, and wet deposition, which are all explicitly considered in our model. For the gas-phase chemical reactions, only the oxidation of DMA by •OH is included. Reactions with other oxidants (O3 and NO3) are much slower and therefore have negligible effects on DMA concentrations (Ge et al., 2011). The mechanism of DMA concentration depletion by aerosol uptake is still poorly understood, and the key parameter, the uptake coefficient γu, varies in a wide range, depending on many factors such as aerosol composition and relative humidity. In this study, we assumed γu = 0.001, which is approximately a median value among those reported by recent laboratory measurements (Qiu et al., 2011; Wang et al., 2010). Regarding DMA depletion by wet deposition, the treatment is similar to that of NH3, based on Henry's law. The key parameters for the above sink processes are summarized in Table S2 in the Supplement.
2.2.2 Configuration of the updated WRF-Chem/R2D-VBS model
The WRF-Chem model configured with the SA–DMA nucleation is applied to a domain covering eastern Asia with a horizontal resolution of 27 km, where Beijing is located close to the center. The simulations are performed for 2 winter months separately (December 2018 and January 2019), with a 5 d spin-up run for each month. The ABaCAS-EI 2017 and IIASA 2015 emission inventory were used for mainland China and other areas, respectively. The biogenic emission is calculated by the Model of Emissions of Gases and Aerosols from Nature (MEGAN) v2.04 (Guenther et al., 2006). Except for the monoterpene-related gas and aerosol chemistry that is traced by R2D-VBS, the remaining gas and aerosol chemical processes are simulated by the SAPRC-99 gas chemistry scheme coupled with the MOSAIC (MOdel for Simulating Aerosol Interaction and Chemistry) aerosol module and a one-dimensional VBS set for secondary organic aerosol (SOA) modeling (Zaveri et al., 2014; Shrivastava et al., 2011, 2019).
Four scenario simulations with different configurations of the NPF mechanisms were conducted in this study to examine how the SA–DMA nucleation affects the simulations of aerosol size distribution. These include the following: (1) eight NPF mechanisms with the SA–DMA nucleation rate at 1.4 nm (abbreviated as DMA1.4_Mech8); (2) eight NPF mechanisms with the SA–DMA nucleation rate at 1.7 nm converted using modified Kerminen–Kulmala equation (Lehtinen et al., 2007; DMA1.7_Mech8); (3) seven NPF mechanisms without the SA–DMA nucleation (NoDMA_Mech7); and (4) no NPF mechanism (NoDMA_Mech0). Among them, scenario 1 is our “best case”, with a full consideration of available nucleation mechanisms; scenario 2 is set to probe the feasibility to use modified Kerminen–Kulmala equation to simulate the initial particle growth; scenario 3 is the “base case” that represents the performance of the original model; and scenario 4 represents the evolution of the aerosol population only contributed by primary emissions. Scenarios 3 and 4 were set as controlling groups to assess the role of SA–DMA nucleation and other mechanisms.
2.3 Ambient measurements
Ambient observations were conducted at an urban site in Beijing from January to April 2018 and from October 2018 to March 2019. The site is located on the West Campus of the Beijing University of Chemical Technology. Details of the observation site can be found in previous studies (Liu et al., 2020; Deng et al., 2020). The concentrations of SA and involving clusters are measured using a chemical ionization high-resolution time-of-flight mass spectrometer (CI-HTOF-MS) and a chemical ionization time-of-flight mass spectrometer with a long mass analyzer (CI-LTOF-MS; Bertram et al., 2011; Jokinen et al., 2012). Other details in the sampling configurations have been reported in our previous study (Deng et al., 2020). Amine concentrations are measured using a modified time-of-flight mass spectrometer (TOF-MS; Zheng et al., 2015b; Cai et al., 2021b). A weather station was deployed to measure the meteorological data, including ambient temperature, relative humidity, and pressure. The PNSDs of particles from 1 nm to 10 µm were measured using a particle size distribution (PSD) and a diethyl glycol scanning mobility particle sizer (DEG-SMPS; Jiang et al., 2011; Liu et al., 2016; Cai et al., 2017a). CS is calculated from the measured PNSDs, and the J1.4 value is calculated using an improved aerosol population balance formula (Cai and Jiang, 2017). The details of instrument calibrations and data validations can be found in our previous study (Cai et al., 2021b).
3.1 Validation of parameterization
The reasonability of pseudo-steady-state assumptions in the SA–DMA nucleation pathway was tested through comparisons between the e-folding time of cluster dynamics (τ) in the kinetic simulation (see details in the Supplement) and the time interval of observational data (30 min in this study). The characteristic equilibrium time of involving clusters and simulated J1.4 values are shown in Fig. S1 in the Supplement. Generally, in either clean and cold circumstances or polluted and warm circumstances, the kinetically simulated J1.4 values could be well reproduced by parameterized pseudo-steady-state J1.4 values. Actually, τ values vary greatly with CoagS and γ and would be higher on cleaner and colder days, while even on extremely clean and cold days with CS =0.0001 s−1 and T=255 K, τ of A3B3 (longer than other clusters) is only ∼20 min, which is shorter than the data collection time interval of 30 min. Thus, for circumstances in which there are high atmospheric concentrations of DMA and SA, such as most typical polluted regions, we conclude that nucleation processes are rapid enough that kinetic J1.4 values can be represented by pseudo-steady-state J1.4 values.
Figure 1 presents the comparisons between parameterized J1.4 values in this study and those simulated in the kinetic models (hereafter referred to as KMs) presented by Cai et al. (2021b) and the cluster dynamic simulations containing all AmBn (m, n≤4) clusters (hereafter referred to as CDSs). Generally, there are good consistencies with the simulated J1.4 value between KMs and the parameterization with the correlation coefficient (R2) and normalized mean bias (NMB) of 0.9297 and 0.16, respectively. The simulated J1.4 value in the KMs can be reproduced by a parameterized J1.4 value within a ±50 % range for most of the cases in urban Beijing, with no systematic deviations found between them.
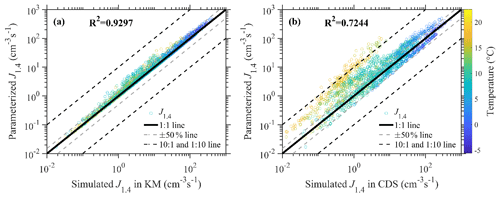
Figure 1A J1.4 value comparison of the simplified parameterization method with kinetic model (KM) results (a) and cluster dynamic simulation (CDS) results (b). The hollow red circles showed the simulation results according to atmospheric observation data. The straight gray line represents the 1:1 line, while the dashed gray line represents the ±50 % variation, and the dashed black lines represent 1:10 or 10:1 line. The circles are colored by the temperatures.
Figure 1b shows that, for most of the circumstances, deviations between the parameterized J1.4 value and the J1.4 value simulated in the CDS are within a range of 1 order of magnitude. The R2 and NMB of the simulated J1.4 value between this parameterization and the CDS are 0.7244 and 0.29, respectively. However, for circumstances with high temperatures, the parameterized J1.4 values were higher than those simulated in CDS, which might be due to the fact that the AkBk (k=2, 3, and 4) clusters are assumed to be non-evaporative in KMs while they would evaporate back in CDSs under high temperatures. The reasonability of the cluster stability assumptions under high temperatures relies mainly on the accuracy of quantum chemistry calculations, which require more experimental evidence and discussions. Additionally, due to the negative dependence of simulated J1.4 values on T, the simulated J1.4 values in this parameterization were mostly lower than 10 cm−3 s−1 under temperatures higher than 15 ∘C, which is lower than the median and mean value of particle formation rates measured during long-term observations in Beijing (Deng et al., 2021). Although they are relatively higher than those simulated in the CDS, the simulation results of the NPF occurrence did not show large deviations.
The computational costs of these three simulations have also been tested on the same personal computer with a MATLAB program. To achieve the steady-state J1.4 values in a specific atmospheric condition, the CDS and KM need ∼10 and ∼0.05 s CPU time, respectively, while the calculation of the parameterized pseudo-steady-state J1.4 value merely costs s CPU time. The CPU time was reduced by a factor of 5×107 and 4×104 when compared to CDS and KM, respectively. Thus, introducing this parameterization into 3-D chemical transport models could greatly reduce the computational costs.
3.2 The dependence of parameterized J1.4 values on input parameters
The correlation between parameterized SA–DMA nucleation J1.4 values and the input parameters is shown in Fig. 2. The parameters involved are T, CS, [DMA], and [SAtot]. The mean values of measured data during the observation period (281 K, 0.02 s−1, 3 ppt (parts per trillion), and 3.5×106 cm−3, respectively) are applied as typical conditions in the base case. Different from the semi-empirical power law functions only based on precursor concentrations presented by Dunne et al. (2016), the dependencies of particle formation rates on T and CS are represented in our parameterizations. With T increasing from −10 to 20 ∘C, γ would increase by ∼2 orders of magnitude, as shown in Fig. 2a, and thus the J1.4 value would decrease by over 2 orders of magnitude. This should be attributed to the positive dependence of evaporation rates of A1B1 clusters on the temperature. Under circumstances with high temperatures, the formation of A1B1 and the subsequent formation of larger clusters and 1.4 nm particles would be suppressed. The decreasing trend of the observed NPF rate (J1.5 value in this case) as a function of increasing T in urban Beijing has also been reported (Deng et al., 2020), which is consistent with our parameterizations.
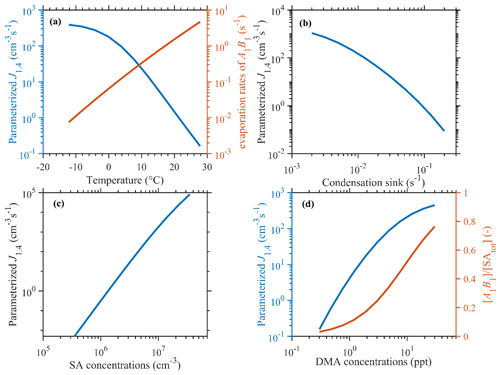
Figure 2Dependence of simulation results on varying T, CS, [DMA], and [SA] parameters. The values of fixed parameters are 281 K, 0.02 s−1, 3 ppt, and 3.5×106 cm−3, respectively, and are given as median values during NPF events in our simulation period.
Figure 2b shows that the J1.4 value would decrease by 2–4 orders of magnitude, with CS increasing by a factor of 10, and the logarithm dependence is higher in circumstances with higher CS, such as in urban Beijing, where CoagS dominates the sinks. This is consistent with the negative CS dependence of the measured particle formation rates and NPF occurrence demonstrated in previous observations in Beijing (Deng et al., 2021; Cai et al., 2021a, b). Note that the dependence of parameterized J1.4 values on CS is also sensitive to T due to the synergistic effect of evaporation and coagulation on the sink of A1B1 clusters, which are the key species in SA–DMA nucleation (Cai et al., 2022). If temperatures are higher, then evaporation would be the dominant sink of A1B1 clusters, while CS only suppresses the formation of larger clusters, whereas, under lower temperatures, such as in wintertime Beijing, CS would be the dominant sink of both A1B1 clusters and larger clusters.
The parameterized J1.4 value shows an increasing trend with increasing concentrations of SA and DMA. The parameterized J1.4 value is approximately proportional to [SA]4. This high dependence of the parameterized J1.4 value on [SA] could well reproduce the phenomenon that the rapid formation of new particles usually occurs at noon, which is when there is usually a strong formation of SA molecules in the atmosphere. The dependence of the J1.4 value on [DMA] is decreasing with increasing [DMA]. This is due to the near-saturation formation of A1B1 clusters, which is also found in kinetic model simulation results (Cai et al., 2021b). Generally, the parameterization could reproduce the fact that SA–DMA nucleation is driven by SA–DMA cluster formation, which is dominantly suppressed by cluster evaporation and coagulation sinks.
3.3 Comparison of 3-D model simulations with observations
As with [DMA], [SA] and CS are key input variables for the J1.4 value parameterization, so we first compare the simulated [DMA], [SA], and CS from the DMA1.4_Mech8 scenario with the observations (Fig. 3). Generally, there are good consistencies between both mean values and temporal variations, although there are still deviations at certain times. The mean simulated [DMA], [SA], and CS values are 1.9 ppt, 1.4×106 cm−3, and 0.040 s−1, respectively, which is close to the observed values of 2.0 ppt, 1.6×106 cm−3, and 0.043 s−1. In a quantitative view, the R2 values between the simulated and observed [DMA], [SA], and CS are 0.04, 0.37, and 0.40, respectively, while the coefficients during NPF periods increase to 0.12, 0.51, and 0.49. The normalized mean biases (NMBs) between the simulated and observed [DMA], [SA], and CS are , −0.22, and −0.36, respectively, while NMBs during NPF periods are −0.40, 0.01, and −0.66. Generally, the simulation of SA concentrations is good, especially during NPF periods with intense nucleation. We note that the correlation between simulated and observed DMA concentration is lower, which may be attributed to the large uncertainty in the diurnal variation in the amine emission. Nevertheless, during NPF periods, the differences between the observed DMA concentration (0.78±0.60 ppt) and our simulation (1.10±0.60 ppt) is relatively small. For [SA] and CS, to which J1.4 values are most sensitive, we compare the time series of simulated and observed [SA]4 CS2 (based on the approximate dependence of J1.4 values on [SA] and CS, as shown in Fig. 2) values during NPF periods to show the deviations of the combination of these two input parameters (Fig. S6). Generally, in most nucleation events, the simulated values would not deviate from the observed values by over an order of magnitude. This indicates the validity of the comprehensive representation of input parameters in the model.
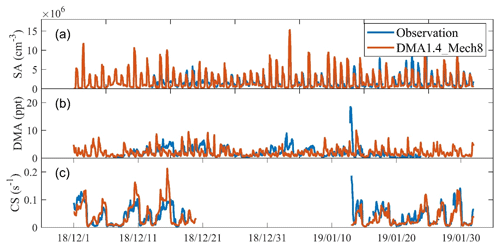
Figure 3Comparison of simulated concentrations of DMA (a), SA (b), and CS during periods with full PNSD observation (c) with field measurements for wintertime Beijing (December 2018 and January 2019).
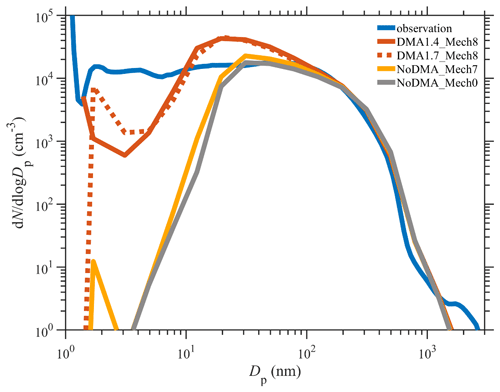
The time series of PNSDs for different simulation scenarios are presented in Fig. 4. When SA–DMA nucleation is considered, the typical PNSD shape on observed NPF days (7 December, 8 December, 9 December, 20 January, and 21 January), characterized as the burst of nanometer-sized particles and subsequent growth, is well captured by our best-case scenarios of DMA1.4_Mech8 and also DMA1.7_Mech8. In contrast, the scenarios without DMA-SA nucleation, NoDMA_Mech7 and NoDMA_Mech0, cannot reproduce the observed NPF events with a “vacancy band” for a 1–10 nm size range over the entire simulation period. Actually, although there are slightly higher sub-3 nm particle concentrations in NoDMA_Mech7 than in NoDMA_Mech0, which are generated from the seven nucleation pathways other than DMA–SA nucleation, the newly formed particle concentrations are too low to survive in the subsequent growth and be separated from background aerosols in the PNSDs. These results demonstrate that SA–DMA nucleation should be the dominant mechanism during NPF events in Beijing compared with other seven mechanisms.
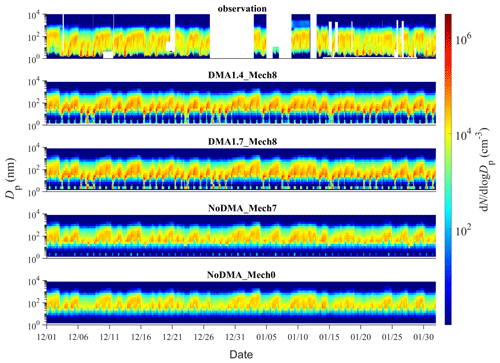
Figure 4Comparison of the time series of the particle number size distribution simulated by various scenarios with the observed one. A description of the four scenarios is detailed in Sect. 2.2.2.
Our results also reproduce the dependence of NPF occurrence on CS in Beijing. As shown in Fig. S2 in the Supplement, NPF generally occurs at low CS, while high CS results in nucleation rates that are too low to initiate NPF. The results were also validated through a comparison between the time series of the simulated and observed CS (Fig. 3c). Note that the simulated sub-3 nm particle concentrations also increase slightly on some non-NPF days in the DMA1.4_Mech8 and DMA1.7_Mech8 scenarios; however, the concentrations are ∼1 order of magnitude lower than those on NPF days, and the newly formed particles also fail to survive in the subsequent growth. The improvements of using the nucleation parameterization in this study is further stressed in the comparison between the DMA1.4_Mech8 scenario and the scenario (CLOUD), using the parameterization derived from the experimental data in CLOUD experiments from Dunne et al. (2016). Figure S3 shows that almost no rapid nucleation processes and NPF events are found in the simulation of CLOUD scenarios. In addition to the underestimation of nucleation rates, the simulated high nucleation rates usually occur on observed non-NPF days (Fig. S7), which should be attributed to the ignorance of CS dependence in the power law function parameterizations.
Figure 5 further compares the simulated and observed PNSDs averaged over the simulation period. The best-case scenario of DMA1.4_Mech8 brings the averaged PNSD in the 1–200 nm size range much closer to the observation than those of the base-case NoDMA_Mech7, and the latter only shows a minor change when compared to the scenario NoDMA_Mech0 without any nucleation. One may notice that the averaged PNSD in the 2–10 nm size range for the scenario DMA1.4_Mech8 is still lower than that of observation by ∼1 order of magnitude, despite the good agreement in the number concentrations of particles of ∼1.4 nm. This could be attributed to two possible reasons, namely that the model underestimates the actual nucleation rates or that newly formed particles of ∼1.4 nm grow too fast and reach larger size bins in the model (>10 nm). The first one can be excluded by a generally good agreement between the simulated nucleation rates and the ones derived from an observation, even with a slightly higher mean value for the former (shown in Sect. 3.4; Fig. 6). The observation–simulation comparison of averaged PNSDs is further conducted for individual NPF days. As shown in Fig. S8, the simulated PNSDs on all NPF days follow a similar pattern to the 2-month-averaged one in Fig. 6, indicating that the nucleation in each simulated NPF day is accompanied by subsequent rapid growth. The difference in the concentration of the 2–10 nm particles between observation and simulation is therefore a common feature on various days and is probably attributed to the simplified assumption in the particle growth simulation. Hence, the gap in the 2–10 nm size range might be attributed to the particle growth simulations in the model, which deserves further improvement. Moreover, in spite of a similar performance with respect to improving PNSD simulations compared to the best-case DMA1.4_Mech8, the scenario of DMA1.7_Mech8 presents a PNSD pattern that is shifted to larger size range. For these two scenarios including SA–DMA nucleation, scenario DMA1.4_Mech8 is more reasonable, since a systematic underestimation exists over the entire 1–10 nm range in scenario DMA1.7_Mech8. Still, the conversion from the 1.4 nm rate to those for larger particles through a modified Kerminen–Kulmala equation is an alternative way of depicting the SA–DMA nucleation for other models with different aerosol size settings. Overall, despite the aforementioned deficiencies, our updated WRF-Chem/R2D-VBS model configured with the SA–DMA nucleation parameterization shows substantial improvement in the representation of NPF events and the PNSDs.
3.4 Contribution from various pathways to nucleation rates and particle number concentrations
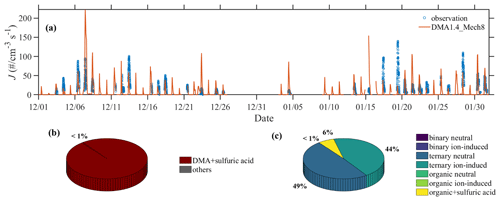
Quantitative analysis over various nucleation pathways is performed here to improve the understanding of NPF in Beijing. As presented in Fig. 6, the variation in the nucleation rates, which are derived from observed PNSD data, is well represented by the best-case scenario DMA1.4_Mech8. Compared to the majority contribution from SA–DMA nucleation, the nucleation rates from other nucleation mechanisms are lower by a factor of ∼100. In addition, SA–DMA nucleation contributes over 60 % to the aerosol population, reinforcing its dominant role in modulating the aerosol population in urban atmospheres.
3.5 Sensitivity analysis
Having shown the significant improvement of the model's performance in simulating the NPF by coupling the SA–DMA nucleation parameterization, we acknowledge that the simulation of the SA–DMA nucleation in 3-D model still has uncertainties in terms of both the source–sink representation of DMA and nucleation parameterization. Here, several key factors which may alter model performance were selected to perform sensitivity analysis.
First, the uncertainties brought by ΔG achieved from different quantum chemistry results are tested for both parameterized J1.4 values and the 3-D chemical transport model simulations. In previous studies, a number of ΔG values have been reported, namely −11.02 kcal mol−1 (Ge et al., 2020), −15.40 kcal mol−1 (Ortega et al., 2012), and −13.54 kcal mol−1 (Myllys et al., 2019). The ΔG of −14.00 kcal mol−1 that was applied in Cai et al. (2021b) to achieve good consistencies between simulated and measured J1.4 values is also applied in the sensitivity analysis. Figure S9 shows the variation in the parameterized J1.4 value by applying different ΔG values at 281 K, which is the median temperature of the observation period. For the DMA with median values of ∼3 ppt, different J1.4 values could vary by ∼5 orders of magnitude, with ΔG between −11.02 and −15.40 kcal mol−1, while J1.4 values with ΔG of −13.54 kcal mol−1 is also lower than that of −15.40 kcal mol−1 by a factor of ∼10. However, if the DMA concentrations are up to ∼30 ppt, then the differences in the J1.4 values, when ΔG varies between −13.54 and −15.40 kcal mol−1, would become much smaller, due to the saturated formation of A1B1 clusters. For the temperature of 298.15 K, the sensitivities of the parameterized J1.4 values are relatively larger because the formation of A1B1 clusters is far from saturation. Generally, the parameterized J1.4 value could be very sensitive to different ΔG values achieved from quantum chemistry results, due to the essential influence of cluster stabilities. As a result, using a lower ΔG value of −15.40 kcal mol−1 in the 3-D simulations with the DMA1.4_Mech8 scenario configuration could lead to much higher nucleation rates compared to the observation (Fig. S10). Thus, we call for a more systematic performance assessment of the quantum chemistry calculation methods to constrain the uncertainties in the cluster thermodynamic stabilities.
Moreover, for the DMA source, we conduct two sensitivity scenarios of doubling (DMA2) and halving (DMA0.5) the inputted DMA emission to test the influence of limited measurements on constraining the DMA NH3 emission ratio. As for the three sink processes, the parameters for the DMA-•OH reaction and wet deposition reported in the literature have relatively small differences, while the aerosol uptake coefficient of DMA covers a wide range that is over 2 orders of magnitude. We then conduct two sensitivity scenarios using the upper (; Upt4.4E-2) and lower (; Upt5.9E-4) limit of the aerosol uptake coefficient. All sensitivity scenarios are on the basis of the DMA1.4_Mech8 configuration. The influence of the scaled DMA emissions and varying uptake coefficients on the simulated DMA concentration, PNSDs, and nucleation rate is shown in Figs. S11–S21 in the Supplement. As expected, the DMA concentration, especially for the nighttime spikes, is sensitive to the emission change. In DMA0.5, the simulated J values are lower than those observed in almost all cases. In contrast, although the simulated J values in DMA2 are on average higher than the observations, they are comparable in some specific cases. Considering that during NPF cases, the observed [DMA] values are averagely 1.4 times higher than those simulated in DMA1.4_Mech8, we propose that the slight underestimation of DMA concentrations in this case might be the reason for the underestimation in J values in some cases. The sensitivity analysis for the uptake coefficient, however, shows different results. A higher uptake coefficient of leads to a much lower DMA concentration (10 % of the best case), while the DMA concentration only increases slightly when the lower limit of is used. Moreover, the changes in uptake coefficient show a limited effect on the PNSDs. The reason is that the DMA concentrations during NPF periods are much less affected by the changes in the uptake coefficient than those in non-NPF periods, since NPF usually occurs at low CS conditions when the uptake of DMA is weak.
The sensitivity analysis above shows that the parameters used in our simulation are reasonable, since perturbations within the ranges reported in the literature generally worsen the model performance. We also expect more field measurements of DMA emissions and its aerosol uptake to further constrain the key source–sink process parameters in the simulation of DMA, although some of them show a minor effect on the NPF and PNSD simulations.
This study presents a dynamically based SA–DMA nucleation parameterization for application in 3-D chemical transport models. Compared to the more widely used semi-empirical power law fitting parameterizations, this new parameterization is based on the key pathway of SA–DMA cluster formation and includes representations of the coagulation scavenging effect and cluster stability. Pseudo-steady-state assumptions were applied to reduce the computational time and were validated according to the short characteristic equilibrium time and through comparisons with the cluster dynamic simulations and the kinetic model. Relative to simulating the SA–DMA nucleation with cluster dynamic simulations or the kinetic model, the application of this new parameterization in 3-D chemical transport models greatly reduces the computational costs. We incorporated this new parameterization and the sources and sinks of DMA into the WRF-Chem/R2D-VBS model. Using the updated model, we simulated the DMA concentrations and PNSDs in Beijing during December 2018 and January 2019. Comparisons were made between 3-D model simulations and ambient measurements.
Good consistency was achieved when simulating the precursor concentrations, which validated the source–sink simulation of SA and DMA. Our quantitative analysis showed that compared to other nucleation mechanisms, SA–DMA nucleation contributed to >99 % of particle formation rates and >60 % of the particle number concentrations during the simulation period in urban Beijing. Although the uncertainties exist due to the excess rapid growth in the 3-D simulations, SA–DMA nucleation should be a dominant sources of aerosol populations due to the dominant contribution to new particle formation rates. Furthermore, the 3-D simulations with the new parameterization predicted the CS-dependent NPF occurrence in urban Beijing and quantitatively reproduced the particle size distributions. These results demonstrated that incorporating the SA–DMA nucleation parameterization, including the effect of coagulation scavenging and cluster stabilities, with 3-D chemical transport models can significantly improve the simulation of NPF and the particle size distributions.
Our results demonstrated that 3-D simulations with a new SA–DMA parameterization could reproduce the CS-dependent particle formation rates and NPF occurrence observed in Beijing. Given that CS varies widely between NPF days and non-NPF days in urban atmospheres (Xiao et al., 2015; Wu et al., 2007; Deng et al., 2021), compared to semi-empirical power law functions, this parameterization of the particle formation rates is likely more effective for predicting the NPF occurrence in urban atmospheres. Additionally, the particle formation rates from other nucleation mechanisms should also be suppressed by high CS, which needs further exploration and parameterizations. Our methodology of applying pseudo-steady-state assumptions to kinetic models could be important in reducing the computational costs of other SA–amine nucleation systems. For instance, quantum chemistry calculations indicate that other basic molecules like trimethylamine and diamines (Jen et al., 2014a, 2016) might also form relatively stable clusters with SA molecules; hence, the methodology of parameterizations in this study could be extended for them, or the basic molecules could also be treated as equivalent DMA concentrations. The improvements in the model simulations of particle size distributions are important for improving the simulations of cloud condensation nuclei and the climate effects of aerosols and NPF events. The improvements also provide more evidence for quantitatively evaluating the environmental and health effect of newly formed particles.
The simulation output data and codes needed for figure reproduction have been posted on Zenodo at https://doi.org/10.5281/zenodo.8194649 (Li et al., 2023).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-23-8789-2023-supplement.
YL, JS, BZ, and JJ designed the research. JZ, MK, and JJ collected the observational data. YL, RC, and JJ set up and tested the parameterization. JS, BZ, SW, and DG developed the 3-D model and performed the simulations. YL and JS analyzed the data, with the help of RC, BZ, and JJ. MS and YG presented important suggestions for the paper. YL, JS, BZ, and JJ wrote the paper, with input from all co-authors.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Chemistry and Physics. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Financial support from the National Natural Science Foundation of China (grant nos. 22188102 and 42275110), the Tencent Foundation through the XPLORER PRIZE, and Samsung PM2.5 SRP are acknowledged. Manish Shrivastava acknowledges the support from the U.S. Department of Energy (DOE), Office of Science, and Office of Biological and Environmental Research through the Early Career Research Program.
Financial support from the National Natural Science Foundation of China (grant nos. 22188102 and 42275110), the Tencent Foundation through the XPLORER PRIZE, and Samsung PM2.5 SRP are acknowledged.
This paper was edited by Kelley Barsanti and reviewed by two anonymous referees.
Almeida, J., Schobesberger, S., Kurten, A., Ortega, I. K., Kupiainen-Maatta, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurten, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppa, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petaja, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipila, M., Stozhkov, Y., Stratmann, F., Tome, A., Trostl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P. L., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamaki, H., and Kirkby, J.: Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 502, 359–363, 2013.
Bergman, T., Laaksonen, A., Korhonen, H., Malila, J., Dunne, E. M., Mielonen, T., Lehtinen, K. E. J., Kuhn, T., Arola, A., and Kokkola, H.: Geographical and diurnal features of amine-enhanced boundary layer nucleation, J. Geophys. Res.-Atmos., 120, 9606–9624, 2015.
Bertram, T. H., Kimmel, J. R., Crisp, T. A., Ryder, O. S., Yatavelli, R. L. N., Thornton, J. A., Cubison, M. J., Gonin, M., and Worsnop, D. R.: A field-deployable, chemical ionization time-of-flight mass spectrometer, Atmos. Meas. Tech., 4, 1471–1479, https://doi.org/10.5194/amt-4-1471-2011, 2011.
Cai, R. and Jiang, J.: A new balance formula to estimate new particle formation rate: reevaluating the effect of coagulation scavenging, Atmos. Chem. Phys., 17, 12659–12675, https://doi.org/10.5194/acp-17-12659-2017, 2017.
Cai, R., Chen, D.-R., Hao, J., and Jiang, J.: A miniature cylindrical differential mobility analyzer for sub-3 nm particle sizing, J. Aerosol Sci., 106, 111–119, https://doi.org/10.1016/j.jaerosci.2017.01.004, 2017a.
Cai, R., Yang, D., Fu, Y., Wang, X., Li, X., Ma, Y., Hao, J., Zheng, J., and Jiang, J.: Aerosol surface area concentration: a governing factor in new particle formation in Beijing, Atmos. Chem. Phys., 17, 12327–12340, https://doi.org/10.5194/acp-17-12327-2017, 2017b.
Cai, R., Yan, C., Worsnop, D. R., Bianchi, F., Kerminen, V.-M., Liu, Y., Wang, L., Zheng, J., Kulmala, M., and Jiang, J.: An indicator for sulfuric acid–amine nucleation in atmospheric environments, Aerosol Sci. Technol., 55, 1059–1069, https://doi.org/10.1080/02786826.2021.1922598, 2021a.
Cai, R., Yan, C., Yang, D., Yin, R., Lu, Y., Deng, C., Fu, Y., Ruan, J., Li, X., Kontkanen, J., Zhang, Q., Kangasluoma, J., Ma, Y., Hao, J., Worsnop, D. R., Bianchi, F., Paasonen, P., Kerminen, V.-M., Liu, Y., Wang, L., Zheng, J., Kulmala, M., and Jiang, J.: Sulfuric acid–amine nucleation in urban Beijing, Atmos. Chem. Phys., 21, 2457–2468, https://doi.org/10.5194/acp-21-2457-2021, 2021b.
Cai, R. L., Yin, R. J., Yan, C., Yang, D. S., Deng, C. J., Dada, L., Kangasluoma, J., Kontkanen, J., Halonen, R., Ma, Y., Zhang, X. H., Paasonen, P., Petaja, T., Kerminen, V. M., Liu, Y. C., Bianchi, F., Zheng, J., Wang, L., Hao, J. M., Smith, J. N., Donahue, N. M., Kulmala, M., Worsnop, D. R., and Jiang, J. K.: The missing base molecules in atmospheric acid-base nucleation, Natl. Sci. Rev., 9, 1–13, https://doi.org/10.1093/nsr/nwac137, 2022.
Chan, T. W. and Mozurkewich, M.: Measurement of the coagulation rate constant for sulfuric acid particles as a function of particle size using tandem differential mobility analysis, J. Aerosol. Sci., 32, 321–339, 2001.
Chen, D., Shen, Y., Wang, J., Gao, Y., Gao, H., and Yao, X.: Mapping gaseous dimethylamine, trimethylamine, ammonia, and their particulate counterparts in marine atmospheres of China's marginal seas – Part 1: Differentiating marine emission from continental transport, Atmos. Chem. Phys., 21, 16413–16425, https://doi.org/10.5194/acp-21-16413-2021, 2021.
Chen, M., Titcombe, M., Jiang, J., Jen, C., Kuang, C., Fischer, M. L., Eisele, F. L., Siepmann, J. I., Hanson, D. R., Zhao, J., and McMurry, P. H.: Acid-base chemical reaction model for nucleation rates in the polluted atmospheric boundary layer, P. Natl. Acad. Sci. USA, 109, 18713–18718, https://doi.org/10.1073/pnas.1210285109, 2012.
Chen, X., Yang, W., Wang, Z., Li, J., Hu, M., An, J., Wu, Q., Wang, Z., Chen, H., Wei, Y., Du, H., and Wang, D.: Improving new particle formation simulation by coupling a volatility-basis set (VBS) organic aerosol module in NAQPMS+APM, Atmos. Environ., 204, 1–11, https://doi.org/10.1016/j.atmosenv.2019.01.053, 2019.
Chen, X., Yu, F., Yang, W., Sun, Y., Chen, H., Du, W., Zhao, J., Wei, Y., Wei, L., Du, H., Wang, Z., Wu, Q., Li, J., An, J., and Wang, Z.: Global–regional nested simulation of particle number concentration by combing microphysical processes with an evolving organic aerosol module, Atmos. Chem. Phys., 21, 9343–9366, https://doi.org/10.5194/acp-21-9343-2021, 2021.
Deng, C., Cai, R., Yan, C., Zheng, J., and Jiang, J.: Formation and growth of sub-3 nm particles in megacities: impact of background aerosols, Faraday Discuss., 226, 348–363, https://doi.org/10.1039/d0fd00083c, 2021.
Deng, C. J., Fu, Y. Y., Dada, L., Yan, C., Cai, R. L., Yang, D. S., Zhou, Y., Yin, R. J., Lu, Y. Q., Li, X. X., Qiao, X. H., Fan, X. L., Nie, W., Kontkanen, J., Kangasluoma, J., Chu, B. W., Ding, A. J., Kerminen, V. M., Paasonen, P., Worsnop, D. R., Bianchi, F., Liu, Y. C., Zheng, J., Wang, L., Kulmala, M., and Jiang, J. K.: Seasonal Characteristics of New Particle Formation and Growth in Urban Beijing, Environ. Sci. Technol., 54, 8547–8557, 2020.
Dunne, E. M., Gordon, H., Kurten, A., Almeida, J., Duplissy, J., Williamson, C., Ortega, I. K., Pringle, K. J., Adamov, A., Baltensperger, U., Barmet, P., Benduhn, F., Bianchi, F., Breitenlechner, M., Clarke, A., Curtius, J., Dommen, J., Donahue, N. M., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Jokinen, T., Kangasluoma, J., Kirkby, J., Kulmala, M., Kupc, A., Lawler, M. J., Lehtipalo, K., Makhmutov, V., Mann, G., Mathot, S., Merikanto, J., Miettinen, P., Nenes, A., Onnela, A., Rap, A., Reddington, C. L. S., Riccobono, F., Richards, N. A. D., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Simon, M., Sipilaa, M., Smith, J. N., Stozkhov, Y., Tome, A., Trostl, J., Wagner, P. E., Wimmer, D., Winkler, P. M., Worsnop, D. R., and Carslaw, K. S.: Global atmospheric particle formation from CERN CLOUD measurements, Science, 354, 1119–1124, 2016.
Ge, P., Luo, G., Huang, W., Xie, H., Chen, J., and Luo, Y.: Theoretical study of the hydration effects on alkylamine and alkanolamine clusters and the atmospheric implication, Chemosphere, 243, 125323, https://doi.org/10.1016/j.chemosphere.2019.125323, 2020.
Ge, X., Wexler, A. S., and Clegg, S. L.: Atmospheric amines – Part I. A review, Atmos. Environ., 45, 524–546, https://doi.org/10.1016/j.atmosenv.2010.10.012, 2011.
Glasoe, W. A., Volz, K., Panta, B., Freshour, N., Bachman, R., Hanson, D. R., McMurry, P. H., and Jen, C.: Sulfuric acid nucleation: An experimental study of the effect of seven bases, J. Geophys. Res.-Atmos., 120, 1933–1950, 2015.
Gordon, H., Kirkby, J., Baltensperger, U., Bianchi, F., Breitenlechner, M., Curtius, J., Dias, A., Dommen, J., Donahue, N. M., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Frege, C., Fuchs, C., Hansel, A., Hoyle, C. R., Kulmala, M., Kurten, A., Lehtipalo, K., Makhmutov, V., Molteni, U., Rissanen, M. P., Stozkhov, Y., Trostl, J., Tsagkogeorgas, G., Wagner, R., Williamson, C., Wimmer, D., Winkler, P. M., Yan, C., and Carslaw, K. S.: Causes and importance of new particle formation in the present-day and preindustrial atmospheres, J. Geophys. Res.-Atmos., 122, 8739–8760, 2017.
Guenther, A., Karl, T., Harley, P., Wiedinmyer, C., Palmer, P. I., and Geron, C.: Estimates of global terrestrial isoprene emissions using MEGAN (Model of Emissions of Gases and Aerosols from Nature), Atmos. Chem. Phys., 6, 3181–3210, https://doi.org/10.5194/acp-6-3181-2006, 2006.
Hanson, D. R., Bier, I., Panta, B., Jen, C. N., and McMurry, P. H.: Computational Fluid Dynamics Studies of a Flow Reactor: Free Energies of Clusters of Sulfuric Acid with NH3 or Dimethyl Amine, J. Phys. Chem. A., 121, 3976–3990, 2017.
Jen, C. N., McMurry, P. H., and Hanson, D. R.: Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res.-Atmos., 119, 7502–7514, https://doi.org/10.1002/2014jd021592, 2014a.
Jen, C. N., McMurry, P. H., and Hanson, D. R.: Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res.-Atmos., 119, 7502–7514, 2014b.
Jen, C. N., Bachman, R., Zhao, J., McMurry, P. H., and Hanson, D. R.: Diamine-sulfuric acid reactions are a potent source of new particle formation, Geophys. Res. Lett., 43, 867–873, https://doi.org/10.1002/2015gl066958, 2016.
Jiang, J., Chen, M., Kuang, C., Attoui, M., and McMurry, P. H.: Electrical Mobility Spectrometer Using a Diethylene Glycol Condensation Particle Counter for Measurement of Aerosol Size Distributions Down to 1 nm, Aerosol Sci. Tech., 45, 510–521, https://doi.org/10.1080/02786826.2010.547538, 2011.
Jokinen, T., Sipilä, M., Junninen, H., Ehn, M., Lönn, G., Hakala, J., Petäjä, T., Mauldin III, R. L., Kulmala, M., and Worsnop, D. R.: Atmospheric sulphuric acid and neutral cluster measurements using CI-APi-TOF, Atmos. Chem. Phys., 12, 4117–4125, https://doi.org/10.5194/acp-12-4117-2012, 2012.
Kulmala, M.: How particles nucleate and grow, Science, 302, 1000–1001, 2003.
Kulmala, M., Vehkamaki, H., Petaja, T., Dal Maso, M., Lauri, A., Kerminen, V. M., Birmili, W., and McMurry, P. H.: Formation and growth rates of ultrafine atmospheric particles: a review of observations, J. Aerosol. Sci., 35, 143–176, 2004.
Kürten, A., Jokinen, T., Simon, M., Sipila, M., Sarnela, N., Junninen, H., Adamov, A., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Donahue, N. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hakala, J., Hansel, A., Heinritzi, M., Hutterli, M., Kangasluoma, J., Kirkby, J., Laaksonen, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Mathot, S., Onnela, A., Petaja, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schobesberger, S., Seinfeld, J. H., Steiner, G., Tome, A., Trostl, J., Winkler, P. M., Williamson, C., Wimmer, D., Ye, P. L., Baltensperger, U., Carslaw, K. S., Kulmala, M., Worsnop, D. R., and Curtius, J.: Neutral molecular cluster formation of sulfuric acid-dimethylamine observed in real time under atmospheric conditions, P. Natl. Acad. Sci. USA, 111, 15019–15024, 2014.
Kürten, A., Li, C., Bianchi, F., Curtius, J., Dias, A., Donahue, N. M., Duplissy, J., Flagan, R. C., Hakala, J., Jokinen, T., Kirkby, J., Kulmala, M., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Onnela, A., Rissanen, M. P., Simon, M., Sipilä, M., Stozhkov, Y., Tröstl, J., Ye, P., and McMurry, P. H.: New particle formation in the sulfuric acid–dimethylamine–water system: reevaluation of CLOUD chamber measurements and comparison to an aerosol nucleation and growth model, Atmos. Chem. Phys., 18, 845–863, https://doi.org/10.5194/acp-18-845-2018, 2018.
Lehtinen, K. E. J., Dal Maso, M., Kulmala, M., and Kerminen, V. M.: Estimating nucleation rates from apparent particle formation rates and vice versa: Revised formulation of the Kerminen-Kulmala equation, J. Aerosol. Sci., 38, 988–994, 2007.
Lehtipalo, K., Rondo, L., Kontkanen, J., Schobesberger, S., Jokinen, T., Sarnela, N., Kurten, A., Ehrhart, S., Franchin, A., Nieminen, T., Riccobono, F., Sipila, M., Yli-Juuti, T., Duplissy, J., Adamov, A., Ahlm, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Downard, A. J., Dunne, E. M., Flagan, R. C., Guida, R., Hakala, J., Hansel, A., Jud, W., Kangasluoma, J., Kerminen, V. M., Keskinen, H., Kim, J., Kirkby, J., Kupc, A., Kupiainen-Maatta, O., Laaksonen, A., Lawler, M. J., Leiminger, M., Mathot, S., Olenius, T., Ortega, I. K., Onnela, A., Petaja, T., Praplan, A., Rissanen, M. P., Ruuskanen, T., Santos, F. D., Schallhart, S., Schnitzhofer, R., Simon, M., Smith, J. N., Trostl, J., Tsagkogeorgas, G., Tome, A., Vaattovaara, P., Vehkamaki, H., Vrtala, A. E., Wagner, P. E., Williamson, C., Wimmer, D., Winkler, P. M., Virtanen, A., Donahue, N. M., Carslaw, K. S., Baltensperger, U., Riipinen, I., Curtius, J., Worsnop, D. R., and Kulmala, M.: The effect of acid-base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 7, 11594, https://doi.org/10.1038/ncomms11594, 2016.
Li, M., Zhang, Q., Kurokawa, J.-I., Woo, J.-H., He, K., Lu, Z., Ohara, T., Song, Y., Streets, D. G., Carmichael, G. R., Cheng, Y., Hong, C., Huo, H., Jiang, X., Kang, S., Liu, F., Su, H., and Zheng, B.: MIX: a mosaic Asian anthropogenic emission inventory under the international collaboration framework of the MICS-Asia and HTAP, Atmos. Chem. Phys., 17, 935–963, https://doi.org/10.5194/acp-17-935-2017, 2017.
Li, Y., Shen, J., Cai, R., Zhao, B., and Jiang, J.: Dataset for the new-SA-DMA-parameterization (Parameterization), Zenodo [data set], https://doi.org/10.5281/zenodo.8194649, 2023.
Liu, J., Jiang, J., Zhang, Q., Deng, J., and Hao, J.: A spectrometer for measuring particle size distributions in the range of 3 nm to 10 µm, Front. Env. Sci. Eng., 10, 63–72, https://doi.org/10.1007/s11783-014-0754-x, 2016.
Liu, L., Yu, F., Du, L., Yang, Z., Francisco, J. S., and Zhang, X.: Rapid sulfuric acid–dimethylamine nucleation enhanced by nitric acid in polluted regions, P. Natl. Acad. Sci. USA, 118, e2108384118, https://doi.org/10.1073/pnas.2108384118, 2021.
Liu, Y., Yan, C., Feng, Z., Zheng, F., Fan, X., Zhang, Y., Li, C., Zhou, Y., Lin, Z., Guo, Y., Zhang, Y., Ma, L., Zhou, W., Liu, Z., Dada, L., Dällenbach, K., Kontkanen, J., Cai, R., Chan, T., Chu, B., Du, W., Yao, L., Wang, Y., Cai, J., Kangasluoma, J., Kokkonen, T., Kujansuu, J., Rusanen, A., Deng, C., Fu, Y., Yin, R., Li, X., Lu, Y., Liu, Y., Lian, C., Yang, D., Wang, W., Ge, M., Wang, Y., Worsnop, D. R., Junninen, H., He, H., Kerminen, V.-M., Zheng, J., Wang, L., Jiang, J., Petäjä, T., Bianchi, F., and Kulmala, M.: Continuous and comprehensive atmospheric observations in Beijing: a station to understand the complex urban atmospheric environment, Big Earth Data, 4, 295–321, https://doi.org/10.1080/20964471.2020.1798707, 2020.
Lu, Y. Q., Liu, L., Ning, A., Yang, G., Liu, Y. L., Kurten, T., Vehkamaki, H., Zhang, X. H., and Wang, L.: Atmospheric Sulfuric Acid-Dimethylamine Nucleation Enhanced by Trifluoroacetic Acid, Geophys. Res. Lett., 47, https://doi.org/10.1029/2019GL085627, 2020.
Mao, J., Yu, F., Zhang, Y., An, J., Wang, L., Zheng, J., Yao, L., Luo, G., Ma, W., Yu, Q., Huang, C., Li, L., and Chen, L.: High-resolution modeling of gaseous methylamines over a polluted region in China: source-dependent emissions and implications of spatial variations, Atmos. Chem. Phys., 18, 7933–7950, https://doi.org/10.5194/acp-18-7933-2018, 2018.
Marten, R., Xiao, M., Rörup, B., Wang, M., Kong, W., He, X.-C., Stolzenburg, D., Pfeifer, J., Marie, G., Wang, D. S., Scholz, W., Baccarini, A., Lee, C. P., Amorim, A., Baalbaki, R., Bell, D. M., Bertozzi, B., Caudillo, L., Chu, B., Dada, L., Duplissy, J., Finkenzeller, H., Carracedo, L. G., Granzin, M., Hansel, A., Heinritzi, M., Hofbauer, V., Kemppainen, D., Kürten, A., Lampimäki, M., Lehtipalo, K., Makhmutov, V., Manninen, H. E., Mentler, B., Petäjä, T., Philippov, M., Shen, J., Simon, M., Stozhkov, Y., Tomé, A., Wagner, A. C., Wang, Y., Weber, S. K., Wu, Y., Zauner-Wieczorek, M., Curtius, J., Kulmala, M., Möhler, O., Volkamer, R., Winkler, P. M., Worsnop, D. R., Dommen, J., Flagan, R. C., Kirkby, J., Donahue, N. M., Lamkaddam, H., Baltensperger, U., and El Haddad, I.: Survival of newly formed particles in haze conditions, Environmental Science: Atmospheres, 2, 491–499, https://doi.org/10.1039/D2EA00007E, 2022.
McGrath, M. J., Olenius, T., Ortega, I. K., Loukonen, V., Paasonen, P., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 12, 2345–2355, https://doi.org/10.5194/acp-12-2345-2012, 2012.
Merikanto, J., Spracklen, D. V., Mann, G. W., Pickering, S. J., and Carslaw, K. S.: Impact of nucleation on global CCN, Atmos. Chem. Phys., 9, 8601–8616, https://doi.org/10.5194/acp-9-8601-2009, 2009.
Myllys, N., Kubečka, J., Besel, V., Alfaouri, D., Olenius, T., Smith, J. N., and Passananti, M.: Role of base strength, cluster structure and charge in sulfuric-acid-driven particle formation, Atmos. Chem. Phys., 19, 9753–9768, https://doi.org/10.5194/acp-19-9753-2019, 2019.
Olenius, T., Kupiainen-Maatta, O., Ortega, I. K., Kurten, T., and Vehkamaki, H.: Free energy barrier in the growth of sulfuric acid-ammonia and sulfuric acid-dimethylamine clusters, J. Chem. Phys., 139, 084312, https://doi.org/10.1063/1.4819024, 2013.
Olenius, T., Halonen, R., Kurten, T., Henschel, H., Kupiainen-Maata, O., Ortega, I. K., Jen, C. N., Vehkamaki, H., and Riipinen, I.: New particle formation from sulfuric acid and amines: Comparison of monomethylamine, dimethylamine, and trimethylamine, J. Geophys. Res.-Atmos., 122, 7103–7118, 2017.
Ortega, I. K., Kupiainen, O., Kurtén, T., Olenius, T., Wilkman, O., McGrath, M. J., Loukonen, V., and Vehkamäki, H.: From quantum chemical formation free energies to evaporation rates, Atmos. Chem. Phys., 12, 225–235, https://doi.org/10.5194/acp-12-225-2012, 2012.
Qiu, C., Wang, L., Lal, V., Khalizov, A. F., and Zhang, R.: Heterogeneous reactions of alkylamines with ammonium sulfate and ammonium bisulfate, Environ. Sci. Technol., 45, 4748–4755, https://doi.org/10.1021/es1043112, 2011.
Riccobono, F., Schobesberger, S., Scott, C. E., Dommen, J., Ortega, I. K., Rondo, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Downard, A., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hansel, A., Junninen, H., Kajos, M., Keskinen, H., Kupc, A., Kurten, A., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Petaja, T., Praplan, A. P., Santos, F. D., Schallhart, S., Seinfeld, J. H., Sipila, M., Spracklen, D. V., Stozhkov, Y., Stratmann, F., Tome, A., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Wimmer, D., Carslaw, K. S., Curtius, J., Donahue, N. M., Kirkby, J., Kulmala, M., Worsnop, D. R., and Baltensperger, U.: Oxidation Products of Biogenic Emissions Contribute to Nucleation of Atmospheric Particles, Science, 344, 717–721, 2014.
Sceats, M. G.: Brownian coagulation in aerosols – the role of long range forces, J. Colloid Interf. Sci., 129, 105–112, https://doi.org/10.1016/0021-9797(89)90419-0, 1989.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, ISBN 978-1-118-94740-1, 1998.
Semeniuk, K. and Dastoor, A.: Current state of aerosol nucleation parameterizations for air-quality and climate modeling, Atmos. Environ., 179, 77–106, 2018.
Shrivastava, M., Fast, J., Easter, R., Gustafson Jr., W. I., Zaveri, R. A., Jimenez, J. L., Saide, P., and Hodzic, A.: Modeling organic aerosols in a megacity: comparison of simple and complex representations of the volatility basis set approach, Atmos. Chem. Phys., 11, 6639–6662, https://doi.org/10.5194/acp-11-6639-2011, 2011.
Shrivastava, M., Andreae, M. O., Artaxo, P., Barbosa, H. M. J., Berg, L. K., Brito, J., Ching, J., Easter, R. C., Fan, J., Fast, J. D., Feng, Z., Fuentes, J. D., Glasius, M., Goldstein, A. H., Alves, E. G., Gomes, H., Gu, D., Guenther, A., Jathar, S. H., Kim, S., Liu, Y., Lou, S., Martin, S. T., McNeill, V. F., Medeiros, A., de Sá, S. S., Shilling, J. E., Springston, S. R., Souza, R. A. F., Thornton, J. A., Isaacman-VanWertz, G., Yee, L. D., Ynoue, R., Zaveri, R. A., Zelenyuk, A., and Zhao, C.: Urban pollution greatly enhances formation of natural aerosols over the Amazon rainforest, Nat. Commun., 10, 1046, https://doi.org/10.1038/s41467-019-08909-4, 2019.
Stolzenburg, D., Simon, M., Ranjithkumar, A., Kürten, A., Lehtipalo, K., Gordon, H., Ehrhart, S., Finkenzeller, H., Pichelstorfer, L., Nieminen, T., He, X.-C., Brilke, S., Xiao, M., Amorim, A., Baalbaki, R., Baccarini, A., Beck, L., Bräkling, S., Caudillo Murillo, L., Chen, D., Chu, B., Dada, L., Dias, A., Dommen, J., Duplissy, J., El Haddad, I., Fischer, L., Gonzalez Carracedo, L., Heinritzi, M., Kim, C., Koenig, T. K., Kong, W., Lamkaddam, H., Lee, C. P., Leiminger, M., Li, Z., Makhmutov, V., Manninen, H. E., Marie, G., Marten, R., Müller, T., Nie, W., Partoll, E., Petäjä, T., Pfeifer, J., Philippov, M., Rissanen, M. P., Rörup, B., Schobesberger, S., Schuchmann, S., Shen, J., Sipilä, M., Steiner, G., Stozhkov, Y., Tauber, C., Tham, Y. J., Tomé, A., Vazquez-Pufleau, M., Wagner, A. C., Wang, M., Wang, Y., Weber, S. K., Wimmer, D., Wlasits, P. J., Wu, Y., Ye, Q., Zauner-Wieczorek, M., Baltensperger, U., Carslaw, K. S., Curtius, J., Donahue, N. M., Flagan, R. C., Hansel, A., Kulmala, M., Lelieveld, J., Volkamer, R., Kirkby, J., and Winkler, P. M.: Enhanced growth rate of atmospheric particles from sulfuric acid, Atmos. Chem. Phys., 20, 7359–7372, https://doi.org/10.5194/acp-20-7359-2020, 2020.
Wang, L., Lal, V., Khalizov, A. F., and Zhang, R.: Heterogeneous Chemistry of Alkylamines with Sulfuric Acid: Implications for Atmospheric Formation of Alkylaminium Sulfates, Environ. Sci. Technol., 44, 2461–2465, https://doi.org/10.1021/es9036868, 2010.
Wang, Z.-Q., Liu, Y.-R., Wang, C.-Y., Jiang, S., Feng, Y.-J., Huang, T., and Huang, W.: Multicomponent nucleation of malonic acid involved in the sulfuric acid – dimethylamine system and its atmospheric implications, Atmos. Environ., 267, 118558, https://doi.org/10.1016/j.atmosenv.2021.118558, 2021.
Wu, Z. J., Hu, M., Liu, S., Wehner, B., Bauer, S., Ssling, A. M., Wiedensohler, A., Petaja, T., Dal Maso, M., and Kulmala, M.: New particle formation in Beijing, China: Statistical analysis of a 1-year data set, J. Geophys. Res.-Atmos., 112, D09209, https://doi.org/10.1029/2006JD007406, 2007.
Xiao, S., Wang, M. Y., Yao, L., Kulmala, M., Zhou, B., Yang, X., Chen, J. M., Wang, D. F., Fu, Q. Y., Worsnop, D. R., and Wang, L.: Strong atmospheric new particle formation in winter in urban Shanghai, China, Atmos. Chem. Phys., 15, 1769–1781, https://doi.org/10.5194/acp-15-1769-2015, 2015.
Yang, D., Zhu, S., Ma, Y., Zhou, L., Zheng, F., Wang, L., Jiang, J., and Zheng, J.: Emissions of Ammonia and Other Nitrogen-Containing Volatile Organic Compounds from Motor Vehicles under Low-Speed Driving Conditions, Environ. Sci. Technol., 56, 5440–5447, https://doi.org/10.1021/acs.est.2c00555, 2022.
Yang, S., Liu, Z., Clusius, P. S., Liu, Y., Zou, J., Yang, Y., Zhao, S., Zhang, G., Xu, Z., Ma, Z., Yang, Y., Sun, J., Pan, Y., Ji, D., Hu, B., Yan, C., Boy, M., Kulmala, M., and Wang, Y.: Chemistry of new particle formation and growth events during wintertime in suburban area of Beijing: Insights from highly polluted atmosphere, Atmos. Res., 255, 105553, https://doi.org/10.1016/j.atmosres.2021.105553, 2021.
Yao, L., Garmash, O., Bianchi, F., Zheng, J., Yan, C., Kontkanen, J., Junninen, H., Mazon, S. B., Ehn, M., Paasonen, P., Sipila, M., Wang, M. Y., Wang, X. K., Xiao, S., Chen, H. F., Lu, Y. Q., Zhang, B. W., Wang, D. F., Fu, Q. Y., Geng, F. H., Li, L., Wang, H. L., Qiao, L. P., Yang, X., Chen, J. M., Kerminen, V. M., Petaja, T., Worsnop, D. R., Kulmala, M., and Wang, L.: Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 361, 278–281, 2018.
Yin, R., Yan, C., Cai, R., Li, X., Shen, J., Lu, Y., Schobesberger, S., Fu, Y., Deng, C., Wang, L., Liu, Y., Zheng, J., Xie, H., Bianchi, F., Worsnop, D. R., Kulmala, M., and Jiang, J.: Acid–Base Clusters during Atmospheric New Particle Formation in Urban Beijing, Environ. Sci. Technol., 55, 10994–11005, https://doi.org/10.1021/acs.est.1c02701, 2021.
Yu, F.: From molecular clusters to nanoparticles: second-generation ion-mediated nucleation model, Atmos. Chem. Phys., 6, 5193–5211, https://doi.org/10.5194/acp-6-5193-2006, 2006.
Yu, F. Q. and Turco, R. P.: From molecular clusters to nanoparticles: Role of ambient ionization in tropospheric aerosol formation, J. Geophys. Res.-Atmos., 106, 4797–4814, 2001.
Zaveri, R. A., Easter, R. C., Shilling, J. E., and Seinfeld, J. H.: Modeling kinetic partitioning of secondary organic aerosol and size distribution dynamics: representing effects of volatility, phase state, and particle-phase reaction, Atmos. Chem. Phys., 14, 5153–5181, https://doi.org/10.5194/acp-14-5153-2014, 2014.
Zhao, B., Shrivastava, M., Donahue, N. M., Gordon, H., Schervish, M., Shilling, J. E., Zaveri, R. A., Wang, J., Andreae, M. O., Zhao, C., Gaudet, B., Liu, Y., Fan, J., and Fast, J. D.: High concentration of ultrafine particles in the Amazon free troposphere produced by organic new particle formation, P. Natl. Acad. Sci. USA, 117, 25344–25351, https://doi.org/10.1073/pnas.2006716117, 2020.
Zheng, H., Cai, S., Wang, S., Zhao, B., Chang, X., and Hao, J.: Development of a unit-based industrial emission inventory in the Beijing–Tianjin–Hebei region and resulting improvement in air quality modeling, Atmos. Chem. Phys., 19, 3447–3462, https://doi.org/10.5194/acp-19-3447-2019, 2019.
Zheng, J., Ma, Y., Chen, M., Zhang, Q., Wang, L., Khalizov, A. F., Yao, L., Wang, Z., Wang, X., and Chen, L.: Measurement of atmospheric amines and ammonia using the high resolution time-of-flight chemical ionization mass spectrometry, Atmos. Environ., 102, 249–259, https://doi.org/10.1016/j.atmosenv.2014.12.002, 2015a.
Zheng, J., Ma, Y., Chen, M. D., Zhang, Q., Wang, L., Khalizov, A. F., Yao, L., Wang, Z., Wang, X., and Chen, L. X.: Measurement of atmospheric amines and ammonia using the high resolution time-of-flight chemical ionization mass spectrometry, Atmos. Environ., 102, 249–259, 2015b.
Zhu, S., Yan, C., Zheng, J., Chen, C., Ning, H., Yang, D., Wang, M., Ma, Y., Zhan, J., Hua, C., Yin, R., Li, Y., Liu, Y., Jiang, J., Yao, L., Wang, L., Kulmala, M., and Worsnop, D. R.: Observation and Source Apportionment of Atmospheric Alkaline Gases in Urban Beijing, Environ. Sci. Technol., 56, 17545–17555, https://doi.org/10.1021/acs.est.2c03584, 2022.