Collision-sticking rates of acid–base clusters in the gas phase determined from atomistic simulation and a novel analytical interacting hard-sphere model

Kinetics of collision-sticking processes between vapor molecules and clusters of low-volatility compounds govern the initial steps of atmospheric new particle formation. Conventional non-interacting hard-sphere models underestimate the collision rate by neglecting long-range attractive forces, and the commonly adopted assumption that every collision leads to the formation of a stable cluster (unit mass accommodation coefficient) is questionable for small clusters, especially at elevated temperatures. Here, we present a generally applicable analytical interacting hard-sphere model for evaluating collision rates between molecules and clusters, accounting for long-range attractive forces. In the model, the collision cross section is calculated based on an effective molecule–cluster potential, derived using Hamaker's approach. Applied to collisions of sulfuric acid or dimethylamine with neutral bisulfate–dimethylammonium clusters composed of 1–32 dimers, our new model predicts collision rates 2–3 times higher than the non-interacting model for small clusters, while decaying asymptotically to the non-interacting limit as cluster size increases, in excellent agreement with a collision-rate-theory atomistic molecular dynamics simulation approach. Additionally, we calculated sticking rates and mass accommodation coefficients (MACs) using atomistic molecular dynamics collision simulations. For sulfuric acid, a MAC ≈1 is observed for collisions with all cluster sizes at temperatures between 200 and 400 K. For dimethylamine, we find that MACs decrease with increasing temperature and decreasing cluster size. At low temperatures, the MAC ≈1 assumption is generally valid, but at elevated temperatures MACs can drop below 0.2 for small clusters.

1 Introduction

In the first steps of atmospheric new particle formation (NPF), condensed-phase clusters (Vehkamäki and Riipinen, 2012) form from super-saturated vapors (Guo et al., 2014; Kirkby et al., 2011; Kulmala et al., 2000, 2013; Zhang et al., 2012). Precise quantification of the cluster formation rates is important to accurately assess global aerosol budgets and their impact on climate (Hallquist et al., 2009; Ramanathan et al., 2001; Seinfeld et al., 2016) and health (Pope and Dockery, 2006; Pöschl, 2005). Cluster formation is conventionally approximated as a microscopic kinetic process where the size evolution of the new-born clusters is driven by competing events of monomer acquisition and loss. This results in a set of pseudo-first-order kinetic equations (Schenter et al., 1999) (written here for a one-component system for simplicity):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{N}_i}{\mathrm{d}t}}& ={\mathit{\alpha }}_{i-\mathrm{1},\mathrm{1}}{k}_{i-\mathrm{1},\mathrm{1}}{N}_{i-\mathrm{1}}{N}_{\mathrm{1}}-{\mathit{\alpha }}_{i,\mathrm{1}}{k}_{i,\mathrm{1}}{N}_i{N}_{\mathrm{1}}\\ & -{\mathit{\gamma }}_i{N}_i+{\mathit{\gamma }}_{i+\mathrm{1}}{N}_{i+\mathrm{1}},i=\mathrm{1},\mathrm{2},\mathrm{\dots },\end{array}\end{array}$$

where N_i is the number concentration of clusters composed of i monomers (atoms or molecules), k_i,1 the monomer–cluster collision rate coefficient, γ_i the evaporation rate coefficient, and α_i,1 the mass accommodation coefficient which is a measure of the average probability for the monomer and cluster to “stick together” after a collision. The collision rate coefficient and mass accommodation coefficient can be combined into the sticking rate coefficient $s_{i,\mathrm{1}}={\mathit{\alpha }}_{i,\mathrm{1}}{k}_{i,\mathrm{1}}$. In principle, any cluster formation process can be accurately described by Eq. (1) and appropriate extensions (e.g., considering cluster dissociation or coagulation) if the associated rate coefficients are correctly determined. This work focuses particularly on the collision and sticking rate coefficients.

Precise determination of the collision and sticking rate coefficients is non-trivial, as they are sensitive to multiple variables including cluster size, structure, composition, system temperature, and vapor concentration. Conventional models, like the commonly used classical nucleation theory (CNT; Becker and Döring, 1935; Farkas, 1927), resort to crude assumptions to achieve generality. This inevitably sacrifices precision and leads to predictions agreeing with experiments only within a narrow range of saturation ratios and temperatures. In most conventional approaches, sticking rate coefficients are approximated by non-interacting hard-sphere collision rate coefficients derived from kinetic gas theory. By neglecting intermolecular interactions, kinetic gas theory may not predict accurate collision rate coefficients, as intermolecular long-range attractive forces can enhance collisions, especially for polar or polarizable molecules common in atmospheric aerosol formation. Moreover, using collision rate coefficients to approximate sticking rate coefficients may be questionable, especially for small clusters, as the formation of a stable product cluster after a collision may be unsuccessful in a significant number of events; i.e., the mass accommodation coefficient can be lower than unity. The non-interacting hard-sphere approximation thus potentially leads to significant errors in modeling the initial steps of cluster formation.

Molecular dynamics (MD) simulations allow us to study the time evolution of collision systems, where all intra- and intermolecular interactions are described through force fields. Recently, we have developed several atomistic molecular dynamics simulation frameworks (Yang et al., 2018; Halonen et al., 2019; Neefjes et al., 2022) to determine collision probabilities from sampling trajectories of atoms or molecules, which predict enhanced collision rate coefficients in good agreement with experiments (Lehtipalo et al., 2016; Stolzenburg et al., 2020). However, as the adequate sampling of collision probabilities requires simulating a large number of binary collisions, these approaches are computationally expensive. More efficient ways need to be proposed to systematically calculate rate coefficients, in particular for collisions involving molecules and clusters of different sizes.

Rate coefficients can also be obtained through analytical models that consider the interactions between the collision partners. These models usually require a fraction of the computational cost of MD simulations but generally still rely on significant approximations. In the central field approach, the collision partners are approximated by point particles interacting through an isotropic attractive potential. Along this line, Gioumousis and Stevenson (1958) developed a model to calculate the secondary ion–molecule reaction rates in mass spectrometers. Su and Bowers (1973) derived a theory to describe ion–permanent dipole interactions and combined it with the central field approach to model ion–polar molecule collisions. Several other authors (Moran and Hamill, 1963; Su et al., 1978; Clary, 1985) have also theoretically studied collision rate coefficients between ions and molecules by applying the central field approach.

We have previously shown that the central field approach yields very similar results to those from sampling collision trajectories using MD, provided that the attractive interaction used in the central field model is fitted to the tail of the potential of mean force (PMF) between the collision partners (Neefjes et al., 2022). The largest collision partners considered in that study were, however, dimers. For collisions involving larger clusters, it becomes increasingly difficult to obtain accurate PMFs. Additionally, in the central field model, a collision is only considered to have occurred when the center of mass distance between the collision partners is infinitesimal. Such a collision criterion may underestimate cluster formation rates, as in realistic systems, cluster formation can already occur at larger center-to-center distances, where the extended structures of the collision partner begin to overlap.

In this study, we present two extensions to the central field approach to efficiently predict collision rate coefficients between monomers and clusters of arbitrary sizes.

1. We consider an interacting hard-sphere model, in which the collision partners are still treated as point particles, interacting through an effective long-ranged isotropic attractive potential, but a collision is considered to have occurred if the center of mass distance between the collision partners is less than the sum of their hard-sphere radii to account for their extended structures.

2. We integrate the monomer–monomer attractive potential following the approach of Hamaker (Hamaker, 1937) to obtain an effective monomer–cluster attractive potential for which a well-defined collision cross section (CCS) can be determined and the monomer–cluster collision rate coefficients can be calculated. Parameters of the monomer–monomer attractive potential are taken from the PMF between the collision partners, calculated from well-tempered metadynamics simulations using atomistic force fields. To validate our analytical approach, we compared it to both atomistic MD collision simulations and MD simulations between two point particles interacting through the same effective potential.

Furthermore, we provide arguments from MD collision simulations for when a unit mass accommodation coefficient is valid and when this approximation fails. Sticking probabilities and sticking rate coefficients inferred from MD collision simulations can be used in Eq. (1) to model acid–base-induced atmospheric NPF and compare it to experimental results.

As test systems, we considered collisions between the monomers of sulfuric acid (H₂SO₄) and dimethylamine ((CH₃)₂NH) and clusters of dimethylammonium–bisulfate dimers ([${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n, $n=\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{8},\mathrm{16},\mathrm{32}$). Sulfuric acid is known to be a crucial component of continental NPF, while dimethylamine likely facilitates the formation of clusters through acid–base interactions (Kurtén et al., 2008; Sipilä et al., 2010). This paper is structured as follows: in Sect. 2.1, we present our analytical interacting hard-sphere collision rate model and show how the CCSs can be calculated for monomer–monomer and monomer–cluster collisions using a simple van der Waals potential and an effective potential derived from Hamaker's approach. In Sect. 2.2, we describe the well-tempered metadynamics calculations and the atomistic and point particle MD simulations. In Sect. 3, we validate the analytical model and present and discuss simulation results of the collision and sticking probabilities and rate coefficients for sulfuric acid–dimethylamine clusters. Section 4 summarizes and concludes the paper with an emphasis on its implications to atmospheric NPF modeling.

2 Theoretical and computational methods

2.1 Analytical methods

2.1.1 Central field approach

In the central field model, both collision partners are represented by point particles. We consider the initial condition where one particle remains at rest while the other particle approaches from infinitely far away with some initial relative velocity v₀. The perpendicular distance between the initial velocity of the moving particle and the center of the particle at rest defines the impact parameter b. The geometry of an example system is illustrated in Fig. 1. This typical two-dimensional two-body motion can be first reduced to a two-dimensional single-body orbital motion in a central field and then to a one-dimensional single-body motion along the particle center-to-center direction (Landau and Lifshitz, 1976), i.e.,

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}=U\left(r\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\mu }{v}^{\mathrm{2}}=U_{\mathrm{eff}}\left(r\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\mu }{v}_{\mathrm{r}}^{\mathrm{2}},\end{array}$$

where $U_{\mathrm{eff}}\left(r\right)=U\left(r\right)+\mathit{\mu }{v}_t^{\mathrm{2}}/\mathrm{2}=U\left(r\right)+\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}{b}^{\mathrm{2}}/\mathrm{2}{r}^{\mathrm{2}}$ is an effective potential resulting from reducing the two-dimensional orbital motion to the one-dimensional motion along the center-to-center direction, U(r) the attractive potential between the point particles, r the center-to-center distance, v the instantaneous relative velocity, v_r the component of the instantaneous relative velocity along the center-to-center direction, v_t the component of the instantaneous relative velocity perpendicular to the center-to-center direction, and μ the reduced mass.

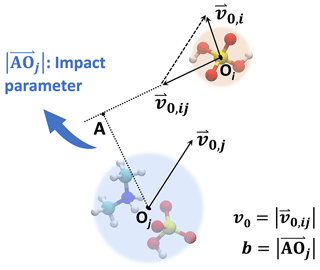
Figure 1 Central field model. The collision partners are described by point particles. In the frame of reference of the target particle, the collision geometry is fully described by the incoming particle's initial velocity v₀ and the impact parameter b.

Reducing the two-dimensional single-body orbital motion to a one-dimensional motion along the center-to-center direction introduces a centrifugal energy barrier (the repulsive part of the effective potential) between the point particles. In the central field model, a “collision” is defined by zero distance between the point particles. Crossing the centrifugal energy barrier in the center-to-center direction is, therefore, a necessary and sufficient condition for a collision. This condition is equivalent to the kinetic energy in the center-to-center direction $\mathrm{1}/\mathrm{2}\mathit{\mu }{v}_{\mathrm{r}}^{\mathrm{2}}$ being positive for all values of r>0; i.e., for a collision to happen, the following condition must hold for arbitrary r>0:

$$\begin{array}{}\text{(3)}& U_{\mathrm{eff}}\left(r\right)-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}\le \mathrm{0}.\end{array}$$

After substituting in the expression of the effective potential and rearranging the above equation, we obtain

$$\begin{array}{}\text{(4)}& b^{\mathrm{2}}\le r^{\mathrm{2}}\left[\mathrm{1}-{\displaystyle \frac{\mathrm{2}U\left(r\right)}{\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}}}\right]\equiv {\mathit{\omega }}_v\left(r\right),\end{array}$$

where the function ω_v(r) is defined for convenience. As Eq. (4) must hold for arbitrary r>0, it is apparent that the minimum value of function ω_v(r) in interval r>0 sets an upper boundary for the impact parameter b, below which a collision will happen and above which a collision is not possible. This upper boundary defines the critical impact parameter b_c,CF in the central field model:

$$\begin{array}{}\text{(5)}& b_{\mathrm{c},\mathrm{CF}}^{\mathrm{2}}={\mathit{\omega }}_v\left(R_{\mathrm{m}}\right),\end{array}$$

where ω_v(R_m) is the minimum of function ω_v(r) with R_m being the corresponding distance where the minimum is achieved. Physically, R_m is the closest distance that the collision partners can approach each other when the centrifugal barrier cannot be crossed.

Depending on the attractive potential U(r), Eq. (5) might, however, not provide a satisfactory definition for the critical impact parameter. Figure 2a shows the shape of ω_v(r) for general attractive potentials of the form $U\left(r\right)=-A(r/r_{\mathrm{0}}{)}^a$. For this general form, we can distinguish three cases.

• If $a<-\mathrm{2}$, ω_v(r) is a convex function exhibiting a single minimum at $r=R_{\mathrm{m}}=-r_{\mathrm{0}}\left[A\right(a+\mathrm{2})/\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}){]}^{-\mathrm{1}/a}>\mathrm{0}$ and ${\mathit{\omega }}_{v_{\mathrm{0}},a<-\mathrm{2}}\left(R_{\mathrm{m}}\right)=-a{r}_{\mathrm{0}}^{\mathrm{2}}\left[A\right(a+\mathrm{2})/\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}){]}^{-\mathrm{2}/a}/(a+\mathrm{2})$.

• If $a=-\mathrm{2}$, ω_v(r) monotonically increases with a minimum at $r=R_{\mathrm{m}}=\mathrm{0}$ and ${\mathit{\omega }}_{v,a=-\mathrm{2}}\left(R_{\mathrm{m}}\right)=\mathrm{2}A{r}_{\mathrm{0}}^{\mathrm{2}}/\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}$.

• If $-\mathrm{2}<a<\mathrm{0}$, ω_v(r) is a monotonically increasing function with a minimum at $r=R_{\mathrm{m}}=\mathrm{0}$ and ${\mathit{\omega }}_{v,-\mathrm{2}<a<\mathrm{0}}\left(R_{\mathrm{m}}\right)=\mathrm{0}$.

These cases indicate that (1) for $-\mathrm{2}<a<\mathrm{0}$, such as for the Coulombic potential, $b_{\mathrm{c},\mathrm{CF}}^{\mathrm{2}}={\mathit{\omega }}_{v,-\mathrm{2}<a<\mathrm{0}}\left(R_{\mathrm{m}}\right)=\mathrm{0}$ and the CCS is equally zero; the centrifugal barrier can never be crossed, and a collision is impossible regardless of the initial velocity and impact parameter. (2) For $a<-\mathrm{2}$ and large initial velocities v₀, $b_{\mathrm{c},\mathrm{CF}}^{\mathrm{2}}={\mathit{\omega }}_{v,a<-\mathrm{2}}\left(R_{\mathrm{m}}\right)=-a{r}_{\mathrm{0}}^{\mathrm{2}}\left[A\right(a+\mathrm{2})/\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}){]}^{-\mathrm{2}/a}/(a+\mathrm{2})$, and the CCS likewise becomes vanishingly small. These issues arise because the collision partners are approximated as point particles in the central field approach; a collision is only considered to have occurred when the distance between the particles is zero. In realistic systems, the collision partners have an extended structure. As a result, the point particle approximation is expected to give a lower collision rate than when the extent of the system is considered.

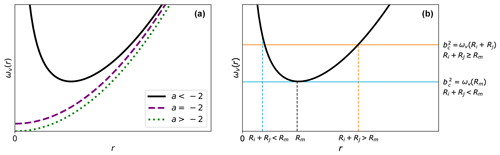
Figure 2 Shape of ω_v(r). (a) The general shape of the function ω_v(r) as a function of r≥0 depending on the interaction exponential a. (b) The general shape of ω_v(r) for $a<-\mathrm{2}$, together with two possible values for the critical impact parameter b_c. In the case $R_i+R_j<R_{\mathrm{m}}$, the critical impact parameter is determined solely by the interaction potential. However, if R_i+R_j≥R_m, the critical impact parameter is determined by the interaction potential and sum of the hard-sphere radii.

2.1.2 Interacting hard-sphere model

In the interacting hard-sphere model, the aforementioned situations are accounted for by using a revised collision criterion; i.e., if the distance between the collision partners is at any point smaller than the sum of their hard-sphere radii, R_i+R_j, a collision is considered to have occurred. It is apparent that when $R_i+R_j<R_{\mathrm{m}}$, this revised criterion will give an identical result as that in the central field model because in this case “reaching a distance smaller than R_i+R_j” is equivalent to “crossing the centrifugal barrier” for the point particles. The new criterion will make a difference only when R_i+R_j≥R_m, where even if the centrifugal barrier is not crossed, there is still a chance for the point particles to reach a distance smaller than R_i+R_j (see Fig. 2b). Using this revised criterion, we can define two cases for the critical impact parameter b_c:

$$\begin{array}{}\text{(6)}& b_{\mathrm{c}}^{\mathrm{2}}=\left\{\begin{array}{ll}{\mathit{\omega }}_v\left(R_{\mathrm{m}}\right),& \text{if}{R}_{\mathrm{m}}>R_i+R_j,\\ {\mathit{\omega }}_v(R_i+R_j),& \text{if}{R}_{\mathrm{m}}\le R_i+R_j.\end{array}\right.\end{array}$$

The concept of determining the critical impact parameter by examining the aforementioned two cases has been discussed by other authors (Ouyang et al., 2012; Fuchs and Sutugin, 1965), but explicit expressions using the hard-sphere radii, like Eq. (6), have not been presented in the existing literature to the best of our knowledge. Once the appropriate critical impact parameter is determined, the dynamical collision cross section (CCS) is given by the usual expression,

$$\begin{array}{}\text{(7)}& \mathrm{\Omega }\left(v_{\mathrm{0}}\right)=\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{b_{\mathrm{c}}\left(v_{\mathrm{0}}\right)}{\int }}b\mathrm{d}b=\mathit{\pi }{b}_{\mathrm{c}}^{\mathrm{2}}\left(v_{\mathrm{0}}\right),\end{array}$$

and the collision rate coefficient for interacting hard spheres is obtained as

$$\begin{array}{}\text{(8)}& k_{\mathrm{IHS}}=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathrm{\Omega }\left(v_{\mathrm{0}}\right)v_{\mathrm{0}}f\left(v_{\mathrm{0}}\right)\mathrm{d}{v}_{\mathrm{0}},\end{array}$$

where f(v₀) is the Maxwell–Boltzmann distribution. In the case of non-interacting hard spheres, the CCS is independent of the relative velocity, and the collision rate coefficient can be directly calculated by substituting $\mathrm{\Omega }\left(v\right)=\mathit{\pi }(R_i+R_j{)}^{\mathrm{2}}$ into the above equation:

$$\begin{array}{}\text{(9)}& k_{\mathrm{HS}}={\left({\displaystyle \frac{\mathrm{8}{k}_{\mathrm{B}}T}{\mathit{\pi }\mathit{\mu }}}\right)}^{\mathrm{1}/\mathrm{2}}\mathit{\pi }(R_i+R_j{)}^{\mathrm{2}},\end{array}$$

where k_B is the Boltzmann constant and T is the temperature.

To determine the critical impact parameter b_c in the interacting hard-sphere model, we first need to find the value of R_m for a given interaction potential U(r), which will be done in the following sections.

Solution for the monomer–monomer potential

Vapors relevant to atmospheric cluster formation are mostly composed of polar and polarizable molecules interacting through a van der Waals potential (Leite et al., 2012) which scales with the separation distance as

$$\begin{array}{}\text{(10)}& U_{\mathrm{mm}}\left(r\right)=-\mathrm{4}\mathit{ϵ}{\left({\displaystyle \frac{r}{\mathit{\sigma }}}\right)}^{-\mathrm{6}},\end{array}$$

where ϵ and σ are the characteristic energy and length of the attractive potential and the subscript “mm” denotes the monomer–monomer interaction. Substituting Eq. (10) into Eq. (4), the positive minimum of ω_v(r,U_mm) is found to be

$$\begin{array}{}\text{(11)}& {\mathit{\omega }}_v(R_{\mathrm{m}},U_{\mathrm{mm}})=\mathrm{3}{\mathit{\sigma }}^{\mathrm{2}}{\left({\displaystyle \frac{\mathrm{2}\mathit{ϵ}}{\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}}}\right)}^{\mathrm{1}/\mathrm{3}},\end{array}$$

located at

$$\begin{array}{}\text{(12)}& R_{\mathrm{m}}\left(U_{\mathrm{mm}}\right)=\mathit{\sigma }{\left({\displaystyle \frac{\mathrm{16}\mathit{ϵ}}{\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}}}\right)}^{\mathrm{1}/\mathrm{6}}.\end{array}$$

For a given pair of monomers, b_c can be readily evaluated from Eqs. (6) and (12) with respect to any given relative speed v₀. We obtained values for ϵ and σ from the potential of mean force (PMF) along the center of mass distance between the collision partners calculated from well-tempered metadynamics calculations using an empirical atomistic force field, presented in Sect. 2.2 (results are included in the Supplement).

Solution for the monomer–cluster potential

Following the approach of Hamaker (Hamaker, 1937), an effective monomer–cluster potential U_mc(r) can be obtained by integrating the monomer–monomer potential over the volume of a spherical cluster, in which uniform monomer number density is assumed:

$$\begin{array}{}\text{(13)}& \textcolor{red}{}\end{array}$$

where ρ_c is the monomer number density, R_c the radius of the cluster, dV=ρ²sin (ϕ)dθdϕdρ the volume element, V_c the total volume of the cluster, and n_c=ρ_cV_c the total number of monomers in the cluster. In Eq. (13), the effective monomer–cluster potential is essentially a sum over all individual contributions of the monomer–monomer potentials, which has two implications. First, the monomer–monomer potentials must be pairwise so that their individual contributions are additive. Hence, this approach is not suitable for non-pairwise interactions. Second, the approach can be conveniently extended to multi-component clusters containing several types of monomers. By using Eq. (13) in a similar manner, the corresponding multi-component monomer–cluster potential is $-\mathrm{4}{\sum }_i{n}_{\mathrm{c},i}{\mathit{ϵ}}_i{\mathit{\sigma }}_i^{\mathrm{6}}/{\left(r^{\mathrm{2}}-R_{\mathrm{c}}\right)}^{\mathrm{3}}$, where n_c,i is the number of monomers of type i in the cluster and ϵ_i and σ_i are the interaction parameters between a monomer of type i in the cluster and the free monomer colliding with the cluster. Note that further integrating U_mc(r) over the volume of another cluster recovers the well-known result of Hamaker for a van der Waals attractive potential between two spherical objects, which can be invoked to treat cluster–cluster collision rates. Integrated cluster–cluster potentials have previously been used to model collision rates, but the models usually resort to fitting against experimental data (Fuchs and Sutugin, 1965; Sceats, 1989). Replacing U(r) in Eq. (4) with U_mc(r), we find ω_v(r,U_mc) to be a convex function with a positive minimum (note that we require r>R_c). By taking the derivative of ω_v(r,U_mc) with respect to r, the minimum is found to be located at r=R_m(U_mc) and satisfies the following:

$$\begin{array}{}\text{(14)}& \sum _{i=\mathrm{0}}^{\mathrm{4}}{a}_i{R}_{\mathrm{m}}^{\mathrm{2}i}=\mathrm{0},\end{array}$$

with $a_{\mathrm{0}}=R_{\mathrm{c}}^{\mathrm{2}}(R_{\mathrm{c}}^{\mathrm{6}}-l_{\mathrm{c}}^{\mathrm{6}})$, $a_{\mathrm{1}}=-\mathrm{2}{l}_{\mathrm{c}}^{\mathrm{6}}-\mathrm{4}{R}_{\mathrm{c}}^{\mathrm{6}}$, $a_{\mathrm{2}}=\mathrm{6}{R}_{\mathrm{c}}^{\mathrm{4}}$, $a_{\mathrm{3}}=-\mathrm{4}{R}_{\mathrm{c}}^{\mathrm{2}}$, and a₄=1, where $l_{\mathrm{c}}\mathrm{\equiv }[\mathrm{8}{n}_{\mathrm{c}}\mathit{ϵ}{\mathit{\sigma }}^{\mathrm{6}}/(\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}){]}^{\mathrm{1}/\mathrm{6}}$ is a cluster size- and potential-dependent characteristic length. Equation (14) is a fourth-order (quartic) equation after writing it in terms of $R_{\mathrm{m}}^{\mathrm{2}}$, and it can be shown that only one real root exists for R_m>R_c (see Supplement). The solution is readily available:

$$\begin{array}{}\text{(15)}& R_{\mathrm{m}}^{\mathrm{2}}\left(U_{\mathrm{mc}}\right)=R_{\mathrm{c}}^{\mathrm{2}}+M+\sqrt{-M^{\mathrm{2}}-{\displaystyle \frac{q}{\mathrm{4}M}}},\end{array}$$

where $q=-\mathrm{2}{l}_{\mathrm{c}}^{\mathrm{6}}$, $M=\sqrt{(N+{\mathrm{\Delta }}_{\mathrm{0}}/N)/\mathrm{3}}/\mathrm{2}$, and $N=\sqrt[\mathrm{3}]{({\mathrm{\Delta }}_{\mathrm{1}}+\sqrt{{\mathrm{\Delta }}_{\mathrm{1}}^{\mathrm{2}}-\mathrm{4}{\mathrm{\Delta }}_{\mathrm{0}}^{\mathrm{3}}})/\mathrm{2}}$ with ${\mathrm{\Delta }}_{\mathrm{0}}=-\mathrm{36}{R}_{\mathrm{c}}^{\mathrm{2}}{l}_{\mathrm{c}}^{\mathrm{6}}$ and ${\mathrm{\Delta }}_{\mathrm{1}}=\mathrm{108}{l}_{\mathrm{c}}^{\mathrm{12}}$. With Eqs. (6) and (15), we can predict b_c for any monomer and cluster pair, as long as the monomer–monomer interaction parameters ϵ and σ are provided.

2.2 Computational methods

Computer simulations were used to

1. compute the PMF between monomer pairs to obtain the ϵ and σ parameter values required for the analytical collision rate coefficient model;

2. validate the analytical model by comparison with atomistic and point particle molecular dynamics (MD) collision simulations;

3. calculate predictions for the sticking probability, sticking rate coefficient, and mass accommodation coefficient by analyzing the atomistic MD collision simulations over a range of relative velocities and impact parameters.

2.2.1 Systems and force field

We considered the atmospherically relevant sulfuric acid (H₂SO₄) and dimethylamine ((CH₃)₂NH) molecules, as well as clusters consisting of 1, 2, 4, 8, 16, or 32 bisulfate–dimethylammonium dimers ([${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]). Clusters composed of n [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$] dimers were obtained by sintering and equilibrating two smaller clusters with $n/\mathrm{2}$ dimers.

In the PMF and atomistic MD simulations, these systems are described by a force field fitted according to the OPLS (optimized potentials for liquid simulations) all-atom procedure (Jorgensen et al., 1996). In the OPLS force field, the intramolecular interactions consist of harmonic bond potentials between covalently bonded atoms, harmonic angle potentials between atoms separated by two covalent bonds, and dihedral angle potentials between atoms separated by three covalent bonds,

$$\begin{array}{}\text{(16)}& \begin{array}{rl}{U}_{\mathrm{intra}}^{\mathrm{OPLS}}& =\sum _{i=\mathrm{1}}^{N_{\mathrm{bonds}}}{\displaystyle \frac{k_i^{\mathrm{b}}}{\mathrm{2}}}{\left(r_i-r_i^{\mathrm{0}}\right)}^{\mathrm{2}}+\sum _{j=\mathrm{1}}^{N_{\mathrm{angles}}}{\displaystyle \frac{k_j^{\mathit{\theta }}}{\mathrm{2}}}{\left({\mathit{\theta }}_j-{\mathit{\theta }}_j^{\mathrm{0}}\right)}^{\mathrm{2}}\\ & +\sum _{k=\mathrm{1}}^{N_{\mathrm{dihedrals}}}\sum _{n=\mathrm{1}}^{\mathrm{4}}{\displaystyle \frac{V_n}{\mathrm{2}}}\left[\mathrm{1}+\cos \left(n{\mathit{\varphi }}^k-{\mathit{\varphi }}_n^k\right)\right],\end{array}\end{array}$$

where $k_i^{\mathrm{b}}$, r_i, and $r_i^{\mathrm{0}}$ are the force constant, instantaneous, and equilibrium length of bond i; $k_j^{\mathit{\theta }}$, θ_j, and ${\mathit{\theta }}_j^{\mathrm{0}}$ are the force constant, instantaneous, and equilibrium value of angle j; and V_n, ${\mathit{\varphi }}_n^k$, and ϕ^k are the Fourier coefficients, phase angles, and instantaneous value of the dihedral angle k.

The intermolecular interactions, as well as intramolecular interactions between atoms separated by more than three covalent bonds, are described by Lennard-Jones potentials between atoms i and j separated by a distance r_ij, with distance and energy parameters σ_ij and ϵ_ij, as well as Coulomb interactions between the atoms' partial charges q_i and q_j:

$$\begin{array}{}\text{(17)}& \begin{array}{rl}{U}_{\mathrm{inter}}& =\sum _{i=\mathrm{1}}^{N_{\mathrm{1}}}\sum _{j=\mathrm{1}}^{N_{\mathrm{2}}}\mathrm{4}{\mathit{ϵ}}_{ij}\left[{\left({\displaystyle \frac{{\mathit{\sigma }}_{ij}}{r_{ij}}}\right)}^{\mathrm{12}}-{\left({\displaystyle \frac{{\mathit{\sigma }}_{ij}}{r_{ij}}}\right)}^{\mathrm{6}}\right]\\ & +\sum _{i=\mathrm{1}}^{N_{\mathrm{1}}}\sum _{j=\mathrm{1}}^{N_{\mathrm{2}}}{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }{\mathit{ϵ}}_{\mathrm{0}}}}{\displaystyle \frac{q_i{q}_j}{r_{ij}}},\end{array}\end{array}$$

where ϵ₀ is the vacuum permittivity.

The OPLS force field parameters used in this study were obtained from Loukonen et al. (2010). We note that in the original OPLS force field, Lennard-Jones and Coulomb interactions between atoms separated by three covalent bonds (“1–4 interactions”) are scaled by a factor 0.5. Loukonen et al. (2010) set this scaling factor to zero when fitting the force field parameters. For consistency, we have also set these interactions to zero in our simulations.

We have validated these force field parameters for MD collision simulations in our previous work (Halonen et al., 2019) by comparing predicted molecular structures, binding energies, and vibrational spectra of sulfuric acid molecules with ab initio results.

2.2.2 Potential of mean force calculations

To determine the thermally averaged interaction potential between the collision partners, we calculated the PMF as a function of their center of mass distance from well-tempered meta-dynamics simulations (Barducci et al., 2008), using the PLUMED plug-in (Tribello et al., 2014) for LAMMPS (Plimpton, 1995). Calculations were performed for five combinations of monomer pairs at 300 K: (CH₃)₂NH–(CH₃)₂NH, H₂SO₄–H₂SO₄, H₂SO₄–(CH₃)₂NH, H₂SO₄–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁, and (CH₃)₂NH–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁. We used the velocity Verlet integrator with a time step of 1 fs, where the Lennard-Jones interactions were cut off at 14 Å, while electrostatic interactions were evaluated with a cut-off at 40 Å. A total of 40 random walkers were employed to deposit Gaussians with a width of 0.1 Å and initial height of 2k_BT ($k_{\mathrm{B}}T/\mathrm{10}$ for the (CH₃)₂NH–(CH₃)₂NH system) every 500 time steps along the collective variable; a harmonic wall was used to restrict the collective variable to values below 35 Å. A bias factor of 20 (5 for the (CH₃)₂NH–(CH₃)₂NH system) was chosen, and a stochastic velocity rescaling thermostat with a time constant of 0.1 ps was used to maintain a constant temperature. Note that we used the PMF at 300 K to approximate cases at 200 and 400 K in deriving corresponding collision rate coefficients. Although there are slight differences in the PMFs at these temperatures, their influence on the analytical collision rate coefficients was found to be negligible. Results are summarized in Fig. S1 and Table S1 of the Supplement. The attractive interaction between (CH₃)₂NH and (CH₃)₂NH was too small to be distinguished from thermal noise in our calculations. It was therefore directly set to zero and is not shown in Fig. S1. The monomer–monomer interactions were assumed to take the form of a 12–6 Lennard-Jones potential. The depth of the potential well (or binding energy) ϵ was directly taken as the minimum energy of the PMF curve, and σ was determined from $\mathit{\sigma }=r_{\mathit{ϵ}}/\sqrt[\mathrm{6}]{\mathrm{2}}$, where r_ϵ is the corresponding distance for the minimum energy point on the PMF curve. The binding energy for the H₂SO₄–H₂SO₄ system was found to be −0.29 eV, which is in excellent agreement with previous ab initio results (Temelso et al., 2012) of −0.3 eV obtained from Boltzmann averaging over four energy minimum structure dimers at 298.15 K and is in good agreement with recent calculations (Elm et al., 2016; Myllys et al., 2017) of −0.23 and −0.26 eV at a higher level of theory. As the outcome of the collisions is already decided at a significant separation between the collision partners for the systems considered here, the role of proton transfer after a successful collision and other quantum effects can be ignored, and the classical force field approach is expected to capture the most important features of the collision.

We note that, though in the current paper the monomer–monomer interacting parameters were obtained from the PMF calculated by atomistic simulations, they could in principle be taken directly from literature values if available.

2.2.3 Atomistic molecular dynamics collision simulations

Atomistic simulations were performed with the LAMMPS code (Plimpton, 1995) for collisions of either H₂SO₄ or (CH₃)₂NH with [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n, where $n=\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{8},\mathrm{16}$, or 32 at temperatures of 200, 300, and 400 K. Equations of motion were integrated using a velocity Verlet algorithm with a time step of 1 fs, where Lennard-Jones and electrostatic interactions were evaluated with a cut-off at 280 Å. The collision partners are originally placed 550 Å apart along the x axis, well beyond the cut-off of the intermolecular potentials. At these positions, the collision partners were equilibrated for 50 ps using separate Langevin thermostats for each collision partner with a damping factor of 0.1 ps. The atomic velocities were drawn from the Maxwell–Boltzmann distribution at the target temperature with the center of mass motion of each collision partner and angular momentum of the combined system removed. After equilibration, the distance between the now orientationally randomized collision partners was decreased to 150 Å along the x axis, bringing them within range of the long-range intermolecular potentials. Both collision partners were then given a velocity along the x direction of $v_x=\pm v_{\mathrm{0}}/\mathrm{2}$ towards each other, where v₀ is the initial relative velocity. For each system, the range of relative velocities started at 50 m s⁻¹ and increased in steps of 50 m s⁻¹. The highest relative velocity was determined so that at least 99 % of the Maxwell–Boltzmann distribution was sampled. We sampled impact parameters starting from 0 up to 36 Å, in steps of 1 Å along the z axis. At initial relative velocities of 50 m s⁻¹, there is still some probability for a collision even beyond an impact parameter of 36 Å. These probabilities, however, do not contribute significantly to the collision rate coefficient.

For the collision systems with clusters containing 1, 2, 4, 8, 16, and 32 [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$] dimers, we performed N=1000, 1000, 800, 400, 200, and 100 independent trajectory simulations, respectively, for each combination of relative velocity and impact parameter. These result in statistically significant estimations of the collision probability. The resulting trajectories were analyzed to determine the collision probability: if the collision partners’ center of mass distance was smaller than R_i+R_j (determined once again from the mass and bulk density by assuming spherical shapes) in at least one time frame, then a collision event was identified. This definition is consistent with that in the analytical model, and it leads to the collision probability $P_{\mathrm{c}}(b,v_{\mathrm{0}})=N_{\mathrm{c}}/N$, where N_c is the numbers of identified collision events. The definition of the sticking probability is similar to that of the collision probability, i.e., $P_{\mathrm{s}}(b,v_{\mathrm{0}})=N_{\mathrm{s}}/N$, where the criterion for determining N_s is discussed in detail in Sect. 3.3.1.

2.2.4 Point particle molecular dynamics collision simulations

In the point particle molecular dynamics (PP MD) simulations, collision partners were treated as point masses interacting through effective pair potentials. The purpose of performing such simulations was to verify the critical impact parameters derived from the analytical interacting hard-sphere model. The collision simulation setup in this case is similar to that in the atomistic MD simulation. First, the point particles were placed 200 Å apart on the x axis, with a certain impact parameter along the y axis, and given an initial relative velocity along the x direction. Second, the equations of motion of the point particles were solved with the velocity Verlet algorithm. A dynamic time step interval was used to ensure that the displacement of the point particles at each time step cannot exceed 0.1 Å. A collision simulation was stopped when either of the following two situations happened: (1) the distance between the point particle pair is less that the sum of their hard-sphere radii (given in the analytical interacting hard-sphere model), or (2) the distance between the point particle pair is larger than the starting distance. Situation 1 corresponds to a collision event, while situation 2 indicates that a collision will not happen in that simulation. The critical impact parameter for a given initial relative speed was found by gradually increasing the impact parameter (starting from the summation of hard-sphere radii given in the interacting hard-sphere model) until the transition from situation 1 to situation 2 was observed. This procedure was used to simulate two example cases where point particle pairs interact through either a Coulomb or a Lennard-Jones potential. Simulated critical impact parameters as a function of initial relative speeds and their comparisons with those predicted from the analytical interacting hard-sphere model are discussed in Sect. 3.1.

2.2.5 Collision rate, sticking rate, and mass accommodation coefficients

The MD collision rate coefficient k_MD was calculated by numerically integrating the collision probability as a function of impact parameter and relative initial velocity obtained from the MD trajectory simulations over the impact parameter and relative speed distribution at the target temperature:

$$\begin{array}{}\text{(18)}& k_{\mathrm{MD}}=\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathrm{d}{v}_{\mathrm{0}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{v}_{\mathrm{0}}f\left(v_{\mathrm{0}}\right)b{P}_{\mathrm{c}}(b,v_{\mathrm{0}})\mathrm{d}b.\end{array}$$

Note that Eq. (18) reduces to Eq. (8) by letting $P_{\mathrm{c}}(b,v_{\mathrm{0}})=\mathrm{1}$ for b<b_c and $P_{\mathrm{c}}(b,v_{\mathrm{0}})=\mathrm{0}$ for b>b_c. Similarly, the sticking rate coefficient is calculated through

$$\begin{array}{}\text{(19)}& s_{\mathrm{MD}}=\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathrm{d}{v}_{\mathrm{0}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{v}_{\mathrm{0}}f\left(v_{\mathrm{0}}\right)b{P}_{\mathrm{s}}(b,v_{\mathrm{0}})\mathrm{d}b.\end{array}$$

The mass accommodation coefficient is defined as

$$\begin{array}{}\text{(20)}& {\mathit{\alpha }}_{\mathrm{MD}}={\displaystyle \frac{s_{\mathrm{MD}}}{k_{\mathrm{MD}}}},\end{array}$$

and it characterizes the average probability of sticking after collisions at the specified temperature.

3 Results and discussion

3.1 Validation of the analytical interacting hard-sphere model

To validate our analytical interacting hard-sphere model, we first compared the analytical critical impact parameter b_c predicted by Eq. (6) to molecular dynamics simulations of two point particles interacting through the same effective pair potential (i.e., PP MD). Two cases were considered: (1) collisions between the $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$ ion and ${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ion under the attractive Coulomb potential $U=-e^{\mathrm{2}}/\left(\mathrm{4}\mathit{\pi }{\mathit{ϵ}}_{\mathrm{0}}r\right)$, where e is the elementary charge and ϵ₀ the vacuum permittivity (Fig. 3a), and (2) collisions between the neutral sulfuric acid H₂SO₄ monomer and the neutral acid–base [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ dimer under the van der Waals potential $U=-\mathrm{4}\mathit{ϵ}(\mathit{\sigma }/r{)}^{\mathrm{6}}$, with parameters obtained from the potential of mean force (PMF) along the center of mass (COM) distance between the molecules (Fig. 3b). In the PP MD simulations, b_c was found for a specific relative speed by gradually increasing b until the distance r between the particles is never smaller than the sum of the hard-sphere radii. In the analytical model, R_m=0 for the attractive Coulomb potential and $R_{\mathrm{m}}=\mathit{\sigma }{\left[\mathrm{16}\mathit{ϵ}/\left(\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}\right)\right]}^{\mathrm{1}/\mathrm{6}}$ for the van der Waals potential.

Excellent agreement is observed in both cases (note that the dependent variable b_c is set as the x axis in Fig. 3). For the Coulomb potential, R_i+R_j is always larger than R_m, and $b_{\mathrm{c}}={\mathit{\omega }}_v(R_i+R_j{)}^{\mathrm{1}/\mathrm{2}}$ in the analytical model. The Coulomb potential case discussed here is only used to verify Eq. (6) but should not be implemented further in Eqs. (7) and (8) to calculate collision rate coefficients, as the Coulomb potential is non-negligible at distances comparable to the mean free path of the colliding ions at atmospheric pressures and hence violates the assumption of free molecular regime. For the van der Waals potential, $R_{\mathrm{m}}>R_i+R_j$ at low relative speeds, but at relative velocities over ∼ 800 m s⁻¹ the situation is reversed and $R_{\mathrm{m}}<R_i+R_j$. For velocities above ∼ 800 m s⁻¹, the analytical b_c transitions from ${\mathit{\omega }}_v(R_{\mathrm{m}}{)}^{\mathrm{1}/\mathrm{2}}$ to ${\mathit{\omega }}_v(R_i+R_j{)}^{\mathrm{1}/\mathrm{2}}$. It is important to note that for the H₂SO₄–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ system, relative speeds over ∼ 800 m s⁻¹ account for less than 1 % of the Boltzmann relative speed distribution. In this case, $b_{\mathrm{c}}={\mathit{\omega }}_v(R_{\mathrm{m}}{)}^{\mathrm{1}/\mathrm{2}}$ is a good approximation. However, as $R_{\mathrm{m}}\propto \mathit{\sigma }(\mathit{ϵ}/\mathit{\mu }{v}_{\mathrm{0}}^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{6}}$, smaller values of ϵ and σ or larger values of ω and v₀ can cause this transition to occur at lower relative speeds and increase the importance of the $b_{\mathrm{c}}={\mathit{\omega }}_v(R_i+R_j{)}^{\mathrm{1}/\mathrm{2}}$ case in the calculation of collision rate coefficients. In the Supplement, we show examples of collisions of carbon dioxide and water molecules, where considering ω_v(R_i+R_j) is important to obtain reasonable collision cross sections. These systems will be studied in further detail in a future publication.

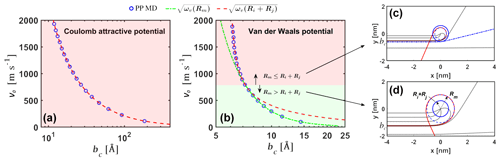
Figure 3 Critical impact parameter. Critical impact parameters b_c from the analytical model and from point particle molecular dynamics simulations (PP MD) for (a) Coulomb attractive potential for the $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$ and ${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ion pair and (b) van der Waals attractive potential for the H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ neutral pair. As the relative initial velocity v₀ increases, the system in panel (b) transitions from a regime where the critical impact parameter $b_{\mathrm{c}}=\sqrt{{\mathit{\omega }}_v\left(R_{\mathrm{m}}\right)}$ to $b_{\mathrm{c}}=\sqrt{{\mathit{\omega }}_v(R_i+R_j)}$. Example orbits for v₀=2000 m s⁻¹ and v₀=150 m s⁻¹ are shown in panels (c) and (d), respectively.

In Fig. 4, we compare the critical impact parameters obtained from the analytical model (Eq. 6) to the collision probability P_c(b,v₀) obtained from atomistic collision MD simulations, sampling the relevant range of impact parameters and relative velocities. We examine both “monomer–monomer” (H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁) and “monomer–cluster” (H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁₆) collisions. For the former, the effective interaction in the analytical model is obtained from the PMF as a function of the monomer–monomer COM distance (see Fig. S1 and Table S1 in the Supplement). For the latter, the effective interaction is obtained from Hamaker's approach (Eq. 13). Note that the atomistic force field describing the molecules and ions in the collision MD simulations is the same as in the PMF calculation, from which we derive the effective interaction parameters used to calculate the analytical critical impact parameters.

In general, P_c(b,v₀) exhibits a clear boundary between values of b and v₀ where collisions are highly probable (white region) and values where the probability is essentially 0 (black region). The location of this boundary depends on the intermolecular forces between the collision partners. An exception to this clear boundary can be seen at low relative speeds. Here, $P_{\mathrm{c}}(b,v_{\mathrm{0}})<\mathrm{1}$ even for small values of b, while at the same time, P_c(b,v₀) remains non-zero even for large values of b. This issue arises from the asymmetric structure of the molecules: due to the low relative speed, small but periodic repulsive interactions at certain collision angles can result in the molecules rebounding from each other before the orbit crosses the sum of the hard-sphere radii (Halonen et al., 2019). These low relative speeds, however, only account for a very small percentage of the Boltzmann speed distribution.

For both systems, the analytical b_c values obtained from ω_v(R_m) are in excellent agreement with the collision probabilities obtained from atomistic collision MD simulations over the relevant range of relative velocities at 300 K. The transition to $R_{\mathrm{m}}>R_i+R_j$ occurs for relative velocities around 800 ms⁻¹ for H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ and around 2300 m s⁻¹ for H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁₆. Once again, this indicates that the $b_{\mathrm{c}}={\mathit{\omega }}_v(R_i+R_j{)}^{\mathrm{1}/\mathrm{2}}$ case is not relevant for these systems at the studied temperature of 300 K. Most importantly, the excellent agreement between analytical b_c values and collision probabilities from atomistic collision MD simulations for the “monomer–cluster” collision demonstrates the validity of Hamaker's approach in modeling the effective monomer–cluster interactions of the studied systems.

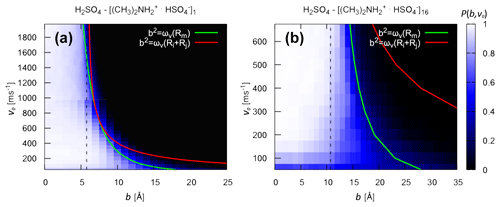
Figure 4 Collision probability and critical impact parameter. Collision probability P_c(b,v₀) from atomistic collision MD simulation and analytical critical impact parameters b_c (solid lines) for the collision of (a) H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ and (b) H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁₆ at 300 K. For the analytical monomer–cluster critical impact parameter in panel (b), the effective monomer–cluster interaction potential was obtained using Eq. (13). The dotted line represents the sum of the hard-sphere radii of the collision partners, obtained by assuming bulk density and spherical shape.

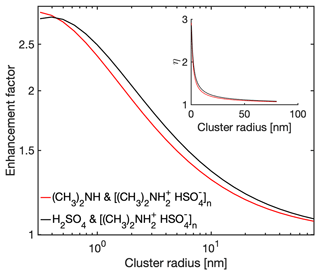
3.2 Collision rate enhancement factors predicted by the analytical interacting hard-sphere model

Having validated the analytical interacting hard-sphere model by comparison with MD simulations, we now use the model to predict enhancement factors η over the non-interacting hard-sphere model. We define $\mathit{\eta }=k_{\mathrm{IHS}}/k_{\mathrm{HS}}$ as the ratio between the collision rate coefficient obtained from the interacting and non-interacting hard-sphere model. Figure 5 shows η for H₂SO₄–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n collisions and (CH₃)₂NH–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n collisions at 300 K. Both monomer types have similar η: while the H₂SO₄ monomer has stronger intermolecular interactions, the (CH₃)₂NH monomer has larger thermal mean speeds. For both cases, the monomer–cluster collisions gradually approach non-interacting hard-sphere behavior as the size of the cluster increases, i.e., η→1 as n→∞. At smaller size ranges the non-interacting hard-sphere model can underestimate the collision rate coefficient by a factor of 2 to 3, potentially introducing non-negligible systematic errors in atmospheric NPF models. Hence, the correction due to long-range attractive forces may need to be included in NPF models.

Figure 5 Collision rate enhancement factor. Monomer–cluster collision rate enhancement factors gradually decay to 1 with increasing cluster radii, indicating a transition to hard-sphere-like behavior. The main plot shows the data with logarithmic radius axis and the inset with linear radius axis.

3.3 Analysis of molecular dynamics collision simulations

3.3.1 Timescale analysis and issues related to classical force field models

In this work, we use classical, atomistic molecular dynamics simulations to determine parameters used in the analytical model and to validate the analytical model by comparing them to collision MD simulations. It is therefore important to recall the limitations of classical force fields regarding the physico-chemical processes occurring in gas-phase collisions and the timescales on which these different processes occur.

Whether or not a collision will occur is typically determined at a relatively large intermolecular distance, where the collision partners can accurately be modeled using classical force field descriptions in a molecular dynamics simulation. Modeling the probability of the collision partners forming a stable product using MD simulations is, however, significantly more complex, as the “sticking” probabilities are influenced by the possibility of bond formation between the collision partners, which is not captured by non-reactive classical force fields. The acid–base clusters considered in this study can form hydrogen bonds upon collision, which is captured by the classical force field employed in the atomistic simulation; however, proton transfer between acids and bases cannot happen.

After a collision, the newly formed cluster will generally have some excess energy due to these bond formations. In the atmosphere, this energy will be removed from the cluster through collisions with surrounding gas molecules. In the collision MD simulations, however, no additional carrier gas is modeled. As such, the excess energy after a collision cannot be released.

Lastly, it is likely that the cluster dissociation process is unphysically enhanced due to the fact that in the classical atomistic model employed, each vibrational mode possesses $k_{\mathrm{B}}T/\mathrm{2}$ energy on average, while in a quantum-mechanical description of the same system, some high-frequency degrees of freedom would remain “frozen” at atmospherically relevant temperatures.

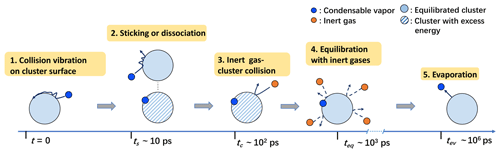
The mentioned limitations of MD simulations in modeling the sticking probability all enhance the dissociation of the formed cluster. As such, the sticking probability obtained from MD simulations can be seen as a limiting value. If the collision partners are able to stick together for a certain time after collision in the MD simulations, then it is likely that the same collision partners would be able to stick together for the same amount of time in the atmosphere. MD simulations are, however, limited in the timescale that they can model due to the computational cost. We, therefore, discuss some characteristic timescales in atmospheric cluster formation after collision.

We first differentiate the two types of monomer–cluster interactions influencing the cluster formation process: (1) the vibration and diffusion of a condensable vapor monomer on the cluster surface immediately after a collision, which, if successful, drives the cluster formation while storing excess energy due to bond formation (hydrogen bonds in this study), and (2) collisions between background carrier gas and the cluster, dissipating the excess energy and equilibrating/thermalizing the nascent cluster. We consider the following scenario: after a condensable vapor–cluster collision, the vapor monomer experiences a few rounds of unsteady vibrations on the cluster surface before forming stable hydrogen bonds (i.e., sticking) or rebounding from the cluster surface. In the former case, a stable cluster with excess thermal energy, distributed over its degrees of freedom, is produced. At this point, the captured monomer can only escape from the cluster through thermal fluctuation (i.e., evaporation), as the monomer has become thermally indistinguishable from other molecules in the cluster. At typical atmospheric conditions, the timescale t_s for the formation of stable bonds only requires a few vibrations of the impinging monomer on the cluster surface. Hence, t_s is commonly smaller than the mean free time t_c for the carrier gas–cluster collision and the time t_eq required to fully thermalize the cluster. Moreover, t_s, t_c, and t_eq can all be assumed to be orders of magnitude smaller than the time t_ev for a monomer to evaporate (see the schematic diagram in Fig. 6).

For example, for H₂SO₄–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$] and (CH₃)₂NH–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$] surrounded by air at standard atmospheric pressure and 300 K, $t_{\mathrm{s}}\sim \mathrm{2}{L}_{\mathrm{c}}/\overline{v}\sim \mathrm{10}$ ps, estimated based on its molecular neighbor separation distance L_c and the mean thermal speed $\overline{v}$. Based on the molecular collision frequency, t_c∼10² ps. As thermalization requires tens to hundreds of collisions (Yang et al., 2022), t_eq∼10³ ps. For these systems, by far the shortest evaporation timescale t_ev∼10⁶ ps is observed for the evaporation of a (CH₃)₂NH from the (CH₃)₂NH-[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$] cluster. The timescales of all other possible evaporation processes are significantly longer, $t_{\mathrm{ev}}\sim {\mathrm{10}}^{\mathrm{17}}-{\mathrm{10}}^{\mathrm{22}}$ ps (Ortega et al., 2012). Therefore, for the systems considered here, even the shortest t_ev is significantly larger than t_s, t_c, and t_eq.

The timescale analysis strongly indicates that a stable cluster is very likely to form if the impinging condensable vapor monomer can survive a very short window of unsteady vibration right after a collision.

Figure 6 Events of interest in atmospheric cluster growth. The schematic shows events of interest in the acid–base cluster growth process and the corresponding timescales at atmospherically relevant pressures and temperatures.

3.3.2 Collision and sticking criteria

To calculate collision and sticking probabilities in atomistic molecular dynamics simulations we need simple, but robust, criteria for when two collision partners have collided and when they are sticking together, as the large number of individual trajectories makes a manual inspection unfeasible. Collision and sticking criteria can be based on geometric and/or energetic properties of the system (Yang et al., 2018; Halonen et al., 2019; Neefjes et al., 2022). Here, we considered a criterion based on the center of mass distance between the collision partners, as this does not require knowledge of the detailed bonding between monomers and clusters of different sizes and can be directly related to the analytical interacting hard-sphere model.

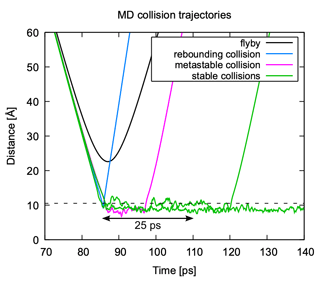
Figure 7 Classification of MD collision trajectories. Trajectories can be classified as “flyby” (no collision), “rebounding collision” (no formation of a metastable complex), collisions leading to the formation of a metastable complex that will re-dissociate on a timescale <25 ps, and “sticking collisions” leading to a cluster that remains stable for longer than 25 ps. The dashed black line indicates the sum of hard-sphere radii of the collision partners.

In analyzing the MD collision simulations, we broadly encounter four different kinds of trajectories: flyby, rebounding collision, collision with metastable product, and collision with stable product. An example of each of these types of trajectories is shown in Fig. 7. A flyby is characterized by a clearly parabolic curve when plotting the center of mass distance between the collision partners as a function of time. The curves of all collision trajectories show a bend towards a faster decrease in center of mass distance over time due to attractive interactions between the collision partners. In rebounding collisions, the trajectory sharply reverses direction after reaching its lowest intermolecular distance. In the two other collision types, a cluster is formed and the trajectory oscillates around some intermolecular distance. The collision partners can either dissociate after some time (metastable) or stay together longer than the assumed timescale for cluster equilibration (stable). As the impact parameter decreases, it becomes more difficult to distinguish between a flyby and a collision.

A distance criterion that is too strict runs the risk of miscounting collisions with relatively large center of mass distances arising from certain relative orientations as flybys. Conversely, a distance criterion that is too loose results in certain close flybys being counted as rebounding collisions. Generally, a good distance criterion would lie just above the largest amplitudes of the oscillating sticking trajectories in Fig. 7 and would need to be found for each combination of T, v₀, and b, which is not possible due to the large number of combinations that are analyzed. We found the sum of hard-sphere radii of the studied collision partners presented a surprisingly good distance criterion for the studied systems over a wide range of impact parameters and relative velocities. A comparison between the hard-sphere radii distance criterion and a manually optimized distance criterion yielded differences in collision probabilities of at most 1 %.

Based on our analyses, a collision is considered to have occurred if the center of mass distance between the collision partners is less than the sum of their hard-sphere radii in at least one time frame of the trajectory. Based on our timescale analyses in Sect. 3.3.1, a formed cluster is considered “sticking” if the center of mass distance between the collision partners is less than the sum of hard-sphere radii at any time between 25 ps after collision and the end of the simulation.

3.4 Collision and sticking rate coefficients from molecular dynamics simulations

Based on the above analysis, we monitored the center of mass distance between the impinging monomer and cluster during the atomistic MD simulations. Collision probabilities and sticking probabilities 25 ps or 50 ps after collision are shown in Fig. 8 for two different cases: (A) collisions between H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ and (B) collisions between (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁. The figure also shows the 1000 underlying trajectories at the relative velocity and impact parameter closest to the mode of the Maxwell–Boltzmann distribution and the sum of hard-sphere radii, respectively, for both systems. There are several implications of the results in Fig. 8. First, the collision and sticking probabilities are almost identical for the system of H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁, suggesting that most collisions lead to the formation of stable product clusters. For the system of (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁, the sticking probability is visibly lower than the collision probability, indicating that a significant portion of formed clusters dissociate in the first 25 ps after collision. This can largely be attributed to the fact that the hydrogen bond between the (CH₃)₂NH monomer and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n cluster is weaker than that between the H₂SO₄ monomer and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n cluster. Second, even though some dissociations can still be observed in the underlying trajectories of the system of (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ later than 25 ps after collision, the sticking probability at 25 ps is almost identical to that at 50 ps for both systems, indicating that increasing t_s beyond 25 ps has little effect on the sticking probability; 25 ps is sufficient for the formation of stable product clusters, which is consistent with our characteristic timescale analysis.

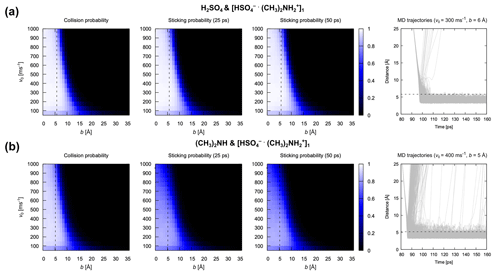
Figure 8 Collision and sticking probability. Collision probability P_c and sticking probabilities P_s after 25 and 50 ps for (a) the H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ pair and (b) the (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]₁ pair. The 1000 collision MD trajectories obtained for the most probable relative velocity and an impact parameter equal to the sum of hard-sphere radii are shown for both systems to illustrate the underlying dynamics of the collision. Dotted black lines represent the sum of collision pairs’ radii obtained by assuming the bulk density and spherical shape.

The sticking rate coefficients and rate enhancement factors for different clusters sizes and different temperatures are shown in Fig. 9a for H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n collisions and Fig. 9b for (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n collisions, where circles and squares correspond to results obtained at 25 and 50 ps, respectively. The sticking rate enhancement factor is an ad hoc quantity defined as the ratio between the sticking rate coefficient and the hard-sphere collision rate coefficient. For comparison, the collision rate coefficients from both the analytical model (solid line) and MD simulations (stars) are also shown in Fig. 9. For collisions between H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n (Fig. 9a), the collision rate coefficients and the sticking rate coefficients obtained at the two different times are all identical, as the hydrogen bonds are strong enough to “capture” all impinging monomers colliding with the cluster. For collisions between (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n (Fig. 9b), several interesting trends can be observed. At a low system temperature of 200 K, the collision rate coefficients are almost identical to the sticking rate coefficients except for a few data points at small cluster sizes. At this temperature, the binding energy of the hydrogen bond is large enough compared to the low kinetic energy of the impinging monomer to prevent rebounds. However, the deviation between the collision and sticking rate coefficients becomes visible with increasing system temperature, which leads to higher kinetic energies of the impinging monomer, resulting in more rebounding. At a system temperature of 300 K, this deviation is expected to be solely a consequence of the unsuccessful vibrational coupling events (i.e., rebounding), whereas at T=400 K, the characteristic evaporation time t_ev of the nascent product cluster has decreased to a value comparable to t_s. At 400 K, the deviation between collision and sticking rate coefficients is caused by the coupled effects of the unsuccessful vibrational coupling events and the evaporation of the nascent product cluster. Consequently, visible differences between sticking rate coefficients obtained at 25 and 50 ps appear at 400 K. Moreover, the deviation between sticking and collision rate coefficients decreases with increasing cluster size: larger sizes favor the formation of stable clusters. This is not surprising as larger clusters offer more potential sites for hydrogen bonds and more molecular neighbors to enhance mutual attractions. They also serve as more efficient sinks for dissipating the latent heat released during hydrogen bond formation upon collision (Yang et al., 2019, 2022).

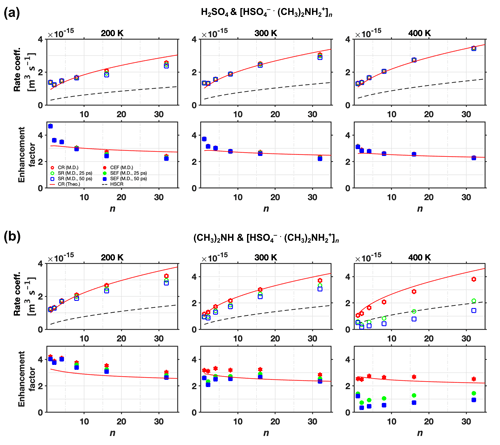
Figure 9 Rate coefficient and enhancement factor vs. cluster size (n) at various temperatures. Collision rate coefficient (CR), sticking rate coefficient (SR), hard-sphere collision rate coefficient (HSCR), collision rate enhancement factor (CEF = CR/HSCR), and sticking rate enhancement factor (SEF = SR/HSCR) for collisions of (a) H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n and (b) (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n at T=200, 300, and 400 K. The collision rate results are from both analytical predictions (Theo.) and molecular dynamics simulations (M.D.). The sticking rate results from molecular dynamics simulations were obtained with two different sticking timescale criteria, 25 and 50 ps.

It is important to remember the limitations of MD simulations using a classical force field description and the timescale analysis performed in Sect. 3.3.1 when predicting sticking rate coefficients. Overall, we expect our simulation approach to overestimate the probability of dissociation. Based on our simulations, it is therefore very likely that the H₂SO₄–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$] system indeed has a mass accommodation coefficient near unity. For the (CH₃)₂NH–[${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$] system, our simulations suggest a mass accommodation coefficient significantly less than unity at room temperature and above. Based on the weaker interactions between (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$] this is plausible, but the limitations of our simulation approach do not permit us to make a definitive statement. Ideally, collision would be studied using ab initio or at least reactive MD simulations in the presence of carrier gas, and for much longer timescales, to properly model all post-collision processes. Such calculations are, however, beyond the scope of current computational possibilities.

4 Conclusions

Precise rate coefficients are essential in modeling the gas-phase collisions which are the initial step in atmospheric new particle formation (NPF). The non-interacting hard-sphere model commonly adopted for neutral molecules and clusters may significantly underestimate collision rate coefficients due to neglecting long-range attractive forces. On the other hand, the assumption of a unit mass accommodation coefficient can overestimate the number of stable clusters formed, in particular for small clusters at elevated temperatures. It is important to note, however, that these two errors will not necessarily cancel each other out.

Simulation approaches based on atomistic modeling of the collision partners have recently been developed and shown to give reasonable estimates for collision rates and enhancement factors for collisions of individual molecules or ions. To systematically calculate rate coefficients for collisions between molecules and clusters of atmospherically relevant acid–base systems, we have developed a new analytical interacting hard-sphere model. The molecule–cluster interactions are obtained from Hamaker's approach by integrating monomer–monomer interactions over the volume of the cluster. Here, the underlying monomer–monomer interacting parameters were obtained from fitting Lennard-Jones potential to the monomer–monomer potential of mean force calculated from atomistic simulations, but we note that the monomer–monomer interacting parameters could also be obtained by other methods or taken directly from literature values if available. The critical impact parameter is determined using the sum of hard-sphere radii or the minimum distance between the point-like collision partners which cannot be crossed due to the centrifugal barrier in the central field model. The accuracy of the analytical model was validated against molecular dynamics collision simulations using the full atomistic model of the collision partners. The analytical model has an accuracy comparable to atomistic molecular dynamics simulations but can be applied efficiently for the systematic calculation of molecule–cluster collision rates required in atmospheric NPF models. The same approach can also be applied to calculate effective cluster–cluster interactions.

For collisions of sulfuric acid (H₂SO₄) or dimethylamine ((CH₃)₂NH) molecules with clusters consisting of 1-32 bisulfate–dimethylammonium ([${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]) dimers, we find that for cluster radii smaller than 2 nm, the non-interacting hard-sphere model underestimates the collision rate coefficient by a factor of 2 to 3 due to the neglect of the long-range attractive forces. The enhancement factor drops below 1.2 for cluster radii larger than 25 nm. This deviation from the non-interacting hard-sphere model can be large enough to introduce systematic errors in atmospheric NPF models. For all the systems considered in this study, the critical impact parameter was well described using the standard minimum distance criterion of the central field model.

The analytical interacting hard-sphere model cannot give the probability of sticking or rebounding after collisions. To assess the fraction of collisions leading to a stable product cluster, we analyzed the large data set of collisions obtained during the validation of the analytical interacting hard-sphere model, taking into account the limitations of the classical force fields employed, as well as the timescales of equilibration processes in the atmosphere, not simulated explicitly in the binary collision setup.

Our analysis shows that if a monomer can stay on the cluster surface for more than a characteristic time (typically tens of picoseconds) after a collision, then a stable product cluster is formed. With this criterion, the sticking probability, sticking rate coefficient, and mass accommodation coefficient can be calculated by analyzing a set of molecular dynamics collision trajectories where impact parameters and relative speeds are properly sampled.

The mass accommodation coefficient decreases with the increasing temperature and decreasing cluster size. For collisions between H₂SO₄ and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n, the unit mass accommodation coefficient assumption is generally valid in an atmospherically relevant temperature range of 200–400 K, regardless of the cluster size. However, the assumption may not hold if the temperature is further increased. For collisions between (CH₃)₂NH and [${\mathrm{HSO}}_{\mathrm{4}}^{-}$ ⋅ $({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}{\mathrm{NH}}_{\mathrm{2}}^{+}$]_n, the unit mass accommodation coefficient assumption is approximately valid at 200 K but becomes significantly worse at elevated temperatures; e.g., at 400 K it ranges from 0.1–0.6 for clusters with 1–32 monomers.

Future research directions include the investigation of systems where the transition between the two regimes defining the critical impact parameter occurs at lower and more relevant relative initial velocities, as well as the application of the analytical interacting hard-sphere model to cluster–cluster collisions. The model presented in this paper is expected to provide a useful tool for the atmospheric NPF community due to its relative simplicity, demonstrated good accuracy, and widespread applicability.