the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Very-long-period oscillations in the atmosphere (0–110 km) – Part 2: Latitude– longitude comparisons and trends
Dirk Offermann
Christoph Kalicinsky
Ralf Koppmann
Johannes Wintel
Measurements of atmospheric temperatures show a variety of long-term oscillations. These can be simulated by computer models and exhibit multi-annual, decadal, and even centennial periods. They extend from the ground up to the lower thermosphere. Recent analyses have shown that they exist in the models even if the model boundaries are kept constant with respect to influences of the sun, ocean, and greenhouse gases. Therefore, these parameters appear not to be responsible for the excitation of these oscillations, i.e. the oscillations might be rather self-excited. However, influences of land surface and vegetation changes had not been entirely excluded. This is studied in the present analysis. It turns out that such influences might be active in the lowermost atmospheric levels.
Long-term trends of atmospheric parameters such as the temperature are important for the understanding of the ongoing climate change. Their study is mostly based on data sets that are 1 to a few decades long. The trend values are generally small and so are the amplitudes of the long-period oscillations. It can therefore be difficult to disentangle these structures, especially if the interval of trend analysis is comparable to the period of the oscillations. If the oscillations are self-excited, there may be a non-anthropogenic contribution to the climate change which is difficult to determine. Long-term changes of the cold-point tropopause are analysed here as an example.
- Article
(2777 KB) - Full-text XML
- Companion paper
- BibTeX
- EndNote
Long-period temperature oscillations have been observed in atmospheric measurements and – surprisingly – in a very similar form in general circulation models (e.g. Meehl et al., 2013; Deser et al., 2014; Lu et al., 2014; Dai et al., 2015; Dijkstra et al., 2006; for further references, see Offermann et al., 2021). The latter authors have reported decadal to even centennial oscillation periods that not only existed at the surface but extended from the ground to the lower thermosphere. It was shown that they were not excited by the sun, the ocean, or greenhouse gases. The amplitudes of these oscillations are not large (i.e. fractions of 1 K). Nevertheless they may be important if long-term trends of temperature are analysed, as such trends are on this order of magnitude. Hence, these oscillations may be difficult to disentangle from the trends. This is especially important if the oscillations are part of the internal variability of the atmosphere. Internal and naturally forced variability – for instance, on decadal timescales – is discussed by Deser (2020) and in the IPCC Climate Change 2021 report (Eyring et al., 2021).
The analyses of Offermann et al. (2021) show very-long-period oscillations that appear to be of internal (self-excited) origin but whose detailed nature is as yet unknown. Therefore, that paper collected a number of characteristic structures which may help to clarify that question. This approach is further followed here by a comparative study of four locations in the Northern and Southern Hemispheres (at 50∘ N vs. 50∘ S, both at 7∘ E, and at 70 and 280∘ E, both at 75∘ N; coordinates are approximate).
The long-period oscillations of Offermann et al. (2021) were not excited by influences from the sun, ocean, and greenhouse gases. Therefore, self-excitation had been considered as a possibility. However, doubts remained as to a possible excitation by land surface–atmosphere interactions (see their Sect. 2.2). We therefore compare here locations and occasions with very different surface structures. The location 50∘ N is in middle of the European land mass. The location 50∘ S is about 15∘ S of the tip of South Africa in the Southern Ocean. The polar locations are in northernmost Canada and Siberia. Concerning land surface–atmosphere interaction, these locations should behave fairly differently. In a further comparison, two different seasons (summer and winter) at 50∘ N, 7∘ E are considered.
The results of Offermann et al. (2021) had been derived from several atmospheric computer models with special runs whose boundary conditions had been kept constant. In the present analysis, we again use two of these: HAMMONIA (38 123) and ECHAM6 (for details, see that paper). The models showed multi-annual, multi-decadal, and even centennial oscillation periods. These periods were found in a large altitude range, from the ground up to the lower thermosphere. The period values were about constant in this regime. The vertical profiles of oscillation amplitudes and phases, on the contrary, varied substantially. These variations were surprisingly similar for the different oscillation periods. An example of these vertical profiles is shown in Fig. 1. The amplitudes vary between maxima and minima. The phases show steps of about 180∘ which occur at the altitudes of the amplitude minima. For details, see Fig. 1 in Offermann et al. (2021). The pronounced vertical structures of the oscillations can possibly help us understand their nature proper.
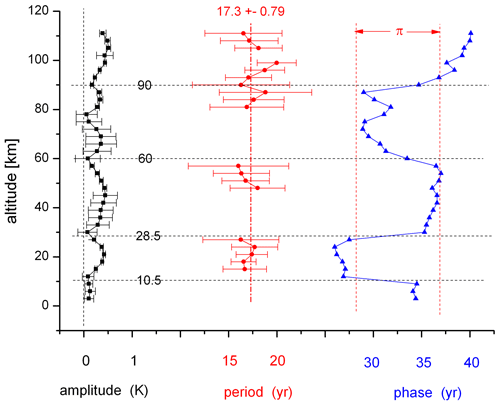
Figure 1Vertical structures of long-period oscillations near 17.3±0.8 yr from HAMMONIA temperatures.
Long-period oscillations may have important influences on the analysis of long-term trends, for instance of temperature. Such trends in the lower and middle atmosphere have been discussed frequently. They are positive or negative, depending on altitude. Recent analyses for the troposphere and stratosphere have been presented, for instance, by Steiner et al. (2020), based on numerous measured data. Such analyses generally cover only a few decades. Therefore, the changes are usually small and often comparable to the oscillation amplitudes mentioned. It can sometimes be difficult to analyse them.
Of special interest are temperature changes near the tropopause, as the tropopause is influenced by many parameters and is believed to show a robust “fingerprint” of climate change (Santer et al., 2004; Pisoft et al., 2021). Tropopause trend analyses have been presented several times (e.g. Zhou et al., 2001; Gettelman et al., 2009; Hu and Vallis, 2019). Long-term changes of tropopause and stratopause altitudes have been analysed by means of measured and modelled data by Pisoft et al. (2021). They find important changes, such as an increase in tropopause height and a contraction of the stratosphere, which they attribute mainly to long-term increases of greenhouse gases. The temperature at the tropopause is frequently studied as the “cold-point tropopause” (CPT), i.e. the lowest temperature between the troposphere and stratosphere. It is influenced by various atmospheric parameters and is therefore discussed as a climate indicator (Hu and Vallis, 2019; Gettelman et al., 2009).
Long-term changes of the CPT are of specific interest. They have been analysed in the tropics several times. Zhou et al. (2001) find a negative trend of K per decade in the time interval 1973–1998. RavindraBabu et al. (2020) find a trend of −1.09 K per decade in the time interval 2006–2018. Tegtmeier et al. (2020) report trends from −0.3 to −0.6 K per decade from reanalysis data in the time frame 1979–2005. However, positive trends of tropopause temperatures have also been discussed (Hu and Vallis, 2019). Positive and negative trends in the range −0.94 to +0.54 K per decade have been reported by Gettelman et al. (2009) in measured and model data. It is an open question as to what the reason for these differences and discrepancies in sign might be.
The present paper is organized as follows: Sect. 2 shows analyses from a HAMMONIA model run (Hamburg Model of the Neutral and Ionized Atmosphere; 34 years) with fixed boundaries for solar radiation, ocean, and greenhouse gases. Atmospheric oscillations at northern and southern locations are compared in terms of their periods and amplitudes. The periods are between 5 and 28 years. Section 3 shows corresponding results from a 400-year-long run of the ECHAM6 model (ECMWF Hamburg), also with fixed boundaries. Longer periods from 20 to 206 years are analysed here. Four locations at different latitudes and longitudes are compared. Section 4 discusses the results. A possible self-excitation of the atmospheric oscillations is considered again. Furthermore, the implications of the oscillations for the analysis of long-term trends are shown. As an example, the behaviour of the cold-point tropopause is discussed. Section 5 summarizes the results.
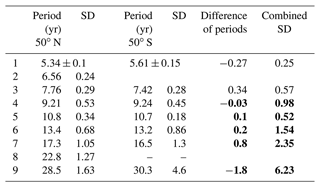
The HAMMONIA model (Schmidt et al., 2006) is based on the ECHAM5 general-circulation model (Roeckner et al., 2006) and extends vertically to 110 km. The simulation analysed here was run at a spectral resolution of T31 with 119 vertical layers. A 34-year run of the model (38 123) has been analysed here for long-period oscillations at Wuppertal (50∘ N, 7∘ E). Model details and harmonic-oscillation analysis have been described in Offermann et al. (2021). Model boundaries with respect to the sun, ocean, and greenhouse gases were held constant. Nine long-period oscillations with periods between 5 and 28 years have been detected (see Table 1). They were discussed in terms of self-excited (internal) atmospheric oscillations. Doubts concerning the self-excitation remained, however, because a possible land surface–atmosphere interaction could not be excluded. We therefore perform a corresponding analysis here for a conjugate geographic point at 50∘ S, 7∘ E. This location is about 15∘ S of the southernmost tip of South Africa in the middle of the ocean. Hence, the surface–atmosphere interaction should be quite different here from that in the middle of Europe. In case such an interaction plays a role, we hope to see this by comparing various atmospheric parameters. The analysis procedures in the north and the south are exactly the same.
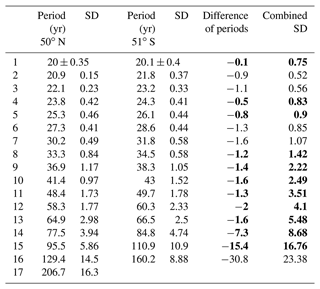
Table 1Oscillation periods and their standard deviations at 50∘ N, 7∘ E vs. 50∘ S, 7∘ E (HAMMONIA model). Bold font indicates agreement of periods within combined standard deviations.
Following Fig. 1, we study periods and amplitudes of the long-period oscillations. The figure shows that there are altitude ranges where a period could not be detected. This is attributed to the fact that the oscillation was not excited here or that it was too strongly damped to be detected (see Offermann et al., 2021). At these altitudes, the mean period value of the other altitudes is used as a proxy (dashed vertical red line, 17.3±0.79 yr in Fig. 1). The proxy is entered into the harmonic analysis and yields estimated values for amplitudes and phases of the oscillation at these altitudes. Details are given by Offermann et al. (2021). The statistical significance of the period values presented in this paper has been analysed in the preceding paper of Offermann et al. (2021, Sect. 3.2).
2.1 Periods
The above-mentioned nine periods found by Offermann et al. (2021) are repeated in Table 1 together with their standard deviations (SD). At 50∘ S, our analysis obtains seven oscillations that are also shown in Table 1. They all find a correspondence in the northern values. A close agreement is found that is well within the combined standard deviations in all but one case and is even within a single standard deviation in most cases. These cases are indicated in bold font in Table 1.
Table 1 holds a twofold surprise: first, it is interesting to see that long-period oscillations exist in the Southern Hemisphere and also in the Northern Hemisphere. Second, it is surprising that the values of the periods are so nearly the same. We would not expect this if the surface–atmosphere interaction did play a significant role. This is apparently not the case. Our data rather appear to hint at a global-oscillation mode that shows up in several periods.
2.2 Amplitudes
The vertical amplitude profile in Fig. 1 shows a pronounced structure. This offers a valuable tool for our north–south comparison. Offermann et al. (2021) showed that vertical amplitude profiles of the different oscillation periods were surprisingly similar at the northern location. Their maxima occurred at about the same altitudes and so did the minima. (See the accumulated amplitudes in Fig. 11 of that paper.) As a consequence, the temperature standard deviations can be used as proxies for the accumulated amplitudes. This is done for the location at 50∘ N, 7∘ E in Fig. 2 (black squares). For the southern location at 50∘ S, 7∘ E, we do the same for a comparison to the north (Fig. 2, red dots).
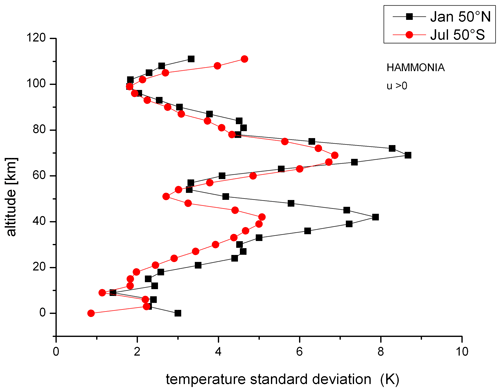
Figure 2Temperature standard deviations as proxies for oscillation amplitudes in winter. Data for January at 50∘ N (black squares) are compared to July at 50∘ S (red dots).
In the paper of Offermann et al. (2021), it was shown that the occurrence of the long-period oscillations was clearly dependent on the direction of the zonal wind: strong oscillation activity was not observed for easterly (westward) winds. In the middle atmosphere, the zonal wind during solstices is opposite in the Northern and the Southern Hemisphere. Hence, comparison of annual mean amplitudes at 50∘ N and 50∘ S could be misleading. Here, we therefore compare data of the same season: January at 50∘ N to July at 50∘ S (Fig. 2; zonal wind is eastward) and July at 50∘ N to January at 50∘ S (Fig. 3; zonal wind is westward).
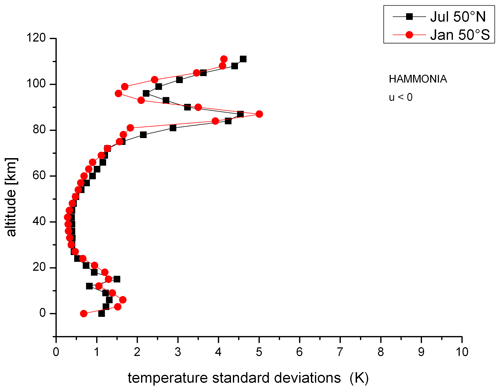
Figure 3Temperature standard deviations as proxies for oscillation amplitudes in summer. Data are for July at 50∘ N (black squares) and for January at 50∘ S (red dots).
As expected, a comparison of the two pictures shows a large difference in the profiles between summer and winter at a given latitude because of the opposite wind directions. The profiles in the same season, however, are surprisingly similar at 50∘ N and 50∘ S.
Taking together the results of periods and amplitudes, it appears that we see essentially the same atmospheric behaviour at 50∘ N and 50∘ S. We see no evidence of a possible interaction between the land surface and the atmosphere in the excitation of the oscillations, as the corresponding profiles are so similar. We therefore tend to believe that these oscillations are self-excited (internal). A deviation from this similarity occurs, however, at the lowest altitude in Figs. 2 and 3. This will be discussed in Sect. 4 below.
Much longer periods than those in HAMMONIA were found in the ECHAM6 model (Offermann et al., 2021). ECHAM6 is the successor of ECHAM5 (Stevens et al., 2013). As the atmospheric component of the Max Planck Institute Earth system model (MPI-ESM; Giorgetta et al., 2013), it has been used in a large number of model intercomparison studies related to the Coupled Model Intercomparison Project phase 5 (CMIP5). The ECHAM6 simulation analysed here was run at T63 spectral resolution with 47 vertical layers. For more details, see Offermann et al. (2021).
Our analyses were based on a 400-year run of the ECHAM6 model. In the long-period range, 17 oscillations were observed between 20 and 206 years (Table 2). They offer further north–south comparisons in the multi-decadal range and beyond.
Table 2Oscillation periods and their standard deviations at 50∘ N, 7∘ E vs. 50∘ S, 7∘ E (ECHAM6 model). Bold font indicates agreement of periods within combined standard deviations.
3.1 Periods
A harmonic analysis of the 400-year run at 50∘ S, 7∘ E is performed in the same way as described in Offermann et al. (2021) for the north. Sixteen periods can be identified here, with periods between 20 and 160 years. These are compared to the northern values in Table 2. (In some places of Tables 1–4, periods (counterparts) are missing. It is believed that, in these cases, the amplitudes were too small to be detected, as mentioned.)
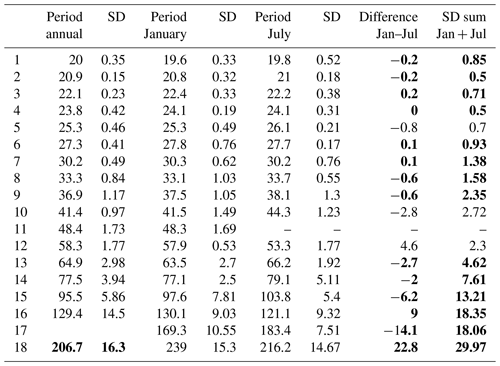
Table 3Temperature oscillation periods (year) at 50∘ N, 7∘ E; standard deviations (SD); and column differences. Bold font indicates agreement of periods within combined standard deviations.
We find corresponding oscillation values (“north–south pairs”) in all cases except one (206.7 year in the north). The second last column of Table 2 shows the pair differences, and the last column shows the combined standard deviations. An agreement of periods within the combined standard deviations is found in 11 cases (in bold font). In the remaining five cases, the periods agree within twice the standard deviations. This close agreement of the N–S pairs is similar to that given in Table 1. It is very remarkable that this close correspondence exists at these much longer periods, too. Together with the HAMMONIA results, this again suggests some kind of a three-dimensional global-oscillation mode.
The HAMMONIA data show substantial differences in terms of oscillation amplitudes between summer and winter. The oscillation periods of HAMMONIA and ECHAM6 in Tables 1 and 2, respectively, are annual values. As north and south are opposite in season, the good agreement of the corresponding period pairs suggests that seasonal differences of the periods should not be large. We verify this using the larger set of ECHAM6 data. We compare annual mean oscillation periods to January and July (mean) values, respectively (Table 3).
The comparison of the results at 50∘ N between annual periods and corresponding periods in the January data at 50∘ N yields 16 coincidences which agree within the combined standard deviations. The corresponding analysis of the annual 50∘ S data (Table 2) and the July data at 50∘ S gives 13 coincidences, 12 of which agreed within the combined standard deviations. (One agrees within the double standard deviations.) Hence, there is no essential difference between the annual and the summer and/or winter oscillation periods.
3.2 Amplitudes
Amplitudes of the long-period oscillations found in ECHAM6 are analysed in terms of temperature standard deviations, as has been done for the shorter periods of the HAMMONIA model. Also here, large seasonal differences are expected. Therefore, a north–south comparison is performed for corresponding seasons, i.e. January north is compared to July south as an example for winter. July north and January south are compared correspondingly for summer. This is shown in Figs. 4 and 5, respectively.
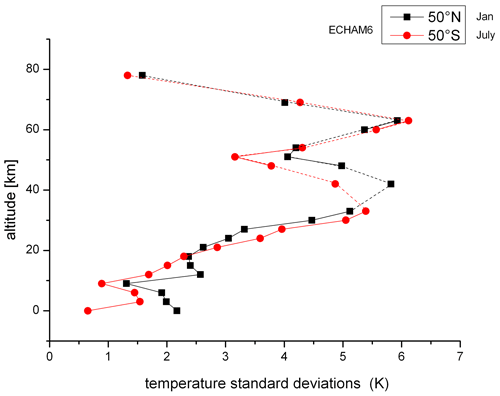
Figure 4Comparison of ECHAM6 temperature standard deviations in winter. January 50∘ N (black squares) and July 50∘ S (red dots) are given as examples.
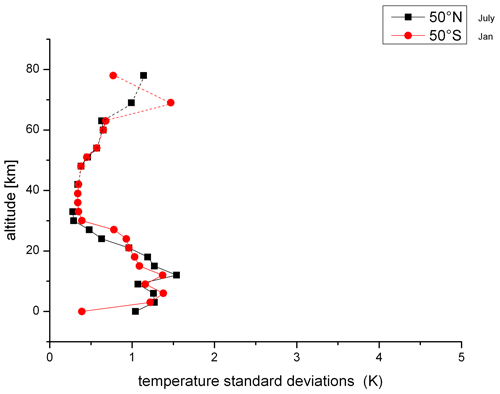
Figure 5Comparison of ECHAM6 temperature standard deviations in summer. July 50∘ N (black squares) and January 50∘ S (red circles) are given as examples.
Large seasonal differences are seen, indeed, and are similar to those in the shorter periods in Figs. 2 and 3. North and south profiles are, however, very similar if the same seasons are considered, as is observed for the shorter periods. Again, similarity is clearly lost at the lowest altitude.
It is also remarkable that the maxima near 40 and 70 km agree so well in Figs. 2 and 4.
3.3 Seasonal differences
If there were an appreciable influence of land surface and vegetation on the excitation of the long-period temperature oscillations in the atmosphere, one would expect a difference of the oscillations in relation to season at a given location. Such an analysis is in part implicitly contained in the north–south comparisons given above. We repeat it here in more detail. Oscillation periods in January (northern hemispheric winter) and July (northern hemispheric summer) are analysed in the ECHAM6 model at 50∘ N, 7∘ E. Seventeen pairs of oscillation periods can be identified at values similar to those of the annual analysis shown in the first column of Table 2. This is shown in Table 3. Standard deviations (SD) of the periods are also given. A period near 48 years could not be found in July. These results are compared to the annual values of Table 2. The second-to-last column in Table 3 shows the differences of the periods in January and July. The last column shows the sum of their standard deviations. A close agreement of the January and July periods is found: in 14 cases, the periods agree within the combined standard deviations, which is indicated by bold font in Table 3 (12 cases agree even within single standard deviations). In three cases, the periods agree within double standard deviations. The agreement of the monthly periods with the annual ones (first column in Table 3) is similarly close.
Given the close agreement of the monthly periods, it is interesting to compare their amplitudes.
These are shown in Fig. 6. Accumulated amplitudes are shown, i.e. the sum of all oscillation amplitudes obtained at a given altitude. The amplitudes could not be derived for each altitude. Hence, the curves shown in Fig. 6 are approximate. The two curves are quite different. The January curve has high values, is highly structured, and closely resembles in shape the winter temperature standard deviation profiles in Fig. 4. The values of the July curve are much smaller and resemble in shape the summer curves of the standard deviations given in Fig. 5. These agreements again justify the use of temperature standard deviations as proxies of the oscillation amplitudes.
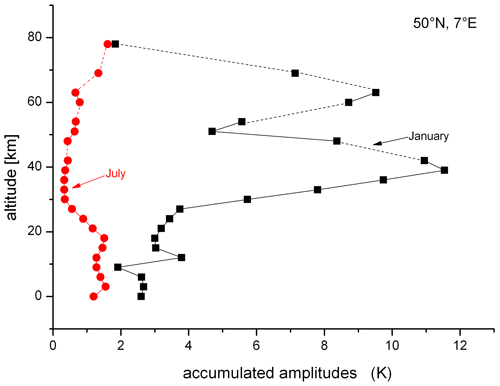
Figure 6Long-period temperature oscillations in the ECHAM6 model at 50∘ N, 7∘ E. Accumulated amplitudes are shown vs. altitude for the periods given in Table 3. Black squares are from monthly mean January data. Red bullets are from July.
The large difference in amplitudes in summer and winter in the stratosphere and mesosphere may be attributed to the opposite direction of zonal winds in the middle atmosphere in these seasons. It is surprising that, in spite of these large differences, the periods of the oscillations are so nearly the same. This demonstrates that the oscillation period is a robust parameter, as has been discussed by Offermann et al. (2021).
3.4 High latitudes
Considerable land surface and vegetation differences might also be expected at polar latitudes. We have therefore analysed ECHAM6 temperatures at 75∘ N, 70∘ E (northern Siberia) and 75∘ N, 280∘ E (northernmost Canada). Winter temperatures (January) have been searched for long-period oscillations in the same way as described above. The results are shown in Table 4. For comparison, January data at 50∘ N from Table 3 are also given.
Table 4Temperature oscillation periods (year) and their standard deviations (SD) at 50∘ N, 7∘ E; 75∘ N, 70∘ E; and 75∘ N, 280∘ E in January.
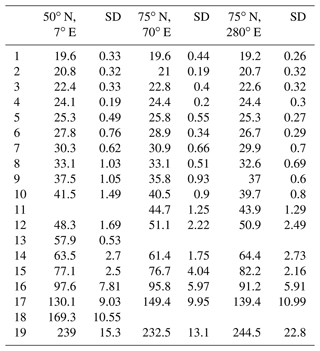
The results are quite interesting. The periods found at the two polar locations are very similar. Seventeen periods have been found at either station, and 16 of these agree within the combined standard deviations (12 agree even within single standard deviations). The periods at high latitudes are quite similar to those at middle latitudes (50∘ N, 7∘ E). The 18 periods seen at 50∘ N find 16 counterparts in either high-latitude station. Of these 15, 14 agree within the combined standard deviations for the 70∘ E (280∘ E) station. Eleven periods even agree within single standard deviations in either case. Hence, the comparison of middle to high latitudes does not show an influence on periods, either.
Deser et al. (2012) showed in their analysis that the variability of surface temperatures at high (northern) latitudes was considerably larger than that at middle and low latitudes. A similar result is obtained in the present data set for the upper atmosphere. We have calculated the temperature standard deviations at the two polar locations (75∘ N) and show them in Fig. 7. The results at the 70 and 280∘ E longitudes are fairly similar. However, as suspected, they are significantly larger than the mid-latitude values shown in Fig. 4.
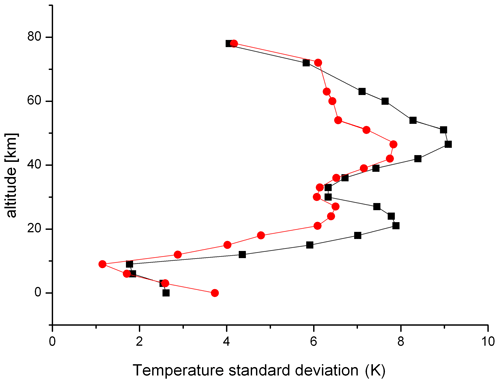
Figure 7Temperature standard deviations at polar latitudes – 75∘ N, 280∘ E (black squares) and 75∘ N, 70∘ E (red dots) – in January.
The profile forms shown in Fig. 7 are fairly different from those in Fig. 4. They are smeared, and the extrema occur at different altitudes. It appears that the profiles for different oscillation periods can be different for different latitudes, as well as for different longitudes. A detailed analysis is, however, beyond the scope of this paper.
4.1 Internal oscillations
The boundary conditions of the computer model runs used by Offermann et al. (2021) and in the present analysis were kept constant. This concerned solar irradiation, the ocean, and greenhouse gases. Nevertheless, the atmospheres in the models showed pronounced and consistent oscillations. It was therefore suggested that these oscillations were self-excited or internal in the atmosphere. Land surface and vegetation changes as external influences, however, were not completely excluded in the earlier paper. To check such possible influences, the models are analysed here at times and locations that have different land surface and vegetation conditions. These are, on the one hand, two corresponding locations in the Northern and Southern Hemispheres (50∘ N and S at 7∘ E). On the other, hand two different seasons are compared at the same location (50∘ N, 7∘ E). Finally, two polar locations (75∘ N at 70 and 280∘ E, respectively) are compared to the middle latitudes.
The results for all northern and southern locations and occasions are very similar as concerns the oscillation periods. Pairs of oscillations at two different locations are compared and show nearly the same values in many cases. Also, the amplitudes are found to be similar when comparing the corresponding seasons. However, amplitudes during different seasons (summer and winter) at the same location are quite different. Despite this discrepancy, their periods are very similar. We conclude from these various similarities that the long-period oscillation are not likely to originate from land surface and vegetation processes in most parts of our high vertical profiles. However, the similarity is lost at the lowest altitude, as mentioned above.
The large summer–winter difference in amplitudes (standard deviations) is shown here for one pair of north–south locations (50∘ N and S, 7∘ E) only. Deser et al. (2012) have shown global surface analyses which indicate, however, that this may be a global phenomenon (their Fig. 16). This is seen if their December–January data are compared to our January data: northern values are much larger than southern values. It thus appears that our north–south difference is part of an extended (global) structure.
However, there is a seeming disagreement between our data and those of Deser et al. (2012) in July: theses authors do not see much difference between 50∘ N and 50∘ S, whereas here in Figs. 2–5 the northern values are much smaller than those in the south if the entire profiles are considered.
The discrepancy disappears if only the lowest altitudes in our data are considered. Our north and south profiles are fairly similar at all altitudes, except in the case of the bottom values: at the lowest altitude, all of our southern amplitudes (given as standard deviations) are much smaller than their northern counterparts (Figs. 2–5). It needs to be emphasized that this difference is limited to the lowermost altitude and disappears at about the next higher level (3 km). This applies to the two different models HAMMONIA and ECHAM6. The difference of the two lowermost levels is surprising. It is, however, significant, as the statistical error of the standard deviations is 12 % for HAMMONIA and 3.5 % for ECHAM6. In numbers, Figs. 2–5 yield the following results. The January values are high in the north (2.2–3.0 K) and small in the south (0.39–0.68 K). Contrary to this, the July values are comparatively low in the north (1.04–1.12 K) and in the south (0.65–0.86 K). This is qualitatively similar to the results of Deser et al. (2012).
Desai et al. (2022) mention that land–atmosphere interactions should occur essentially in the lowest 1–2 km of the atmosphere (boundary layer). It thus appears interesting to interpret the large deviations from profile similarity at the lowermost levels of Figs. 2–5 as an indication of land–atmosphere interaction at these levels. The deviations are large and significant. They quickly disappear at the higher levels. This suggests that excitation of long-period oscillations by land surface–atmosphere interactions would be limited to the lowermost atmosphere.
Internal variability in the atmosphere has been discussed several times in the literature (see Deser, 2020, and references therein). This is thought to be caused by the chaotic dynamics of the atmosphere and oceans and to be generally unpredictable more than a few years ahead of time. It remains to be determined how this is related to our internal oscillations.
4.2 Implications of internal oscillations
4.2.1 Temperature trends
Long-term temperature changes are part of the ongoing climate change in the troposphere and in the upper atmosphere (Eyring et al., 2021). It is important to know whether there is a relationship between these trends and the internal (non-anthropogenic) atmospheric variability. We study this question by means of ECHAM6 data in the lower stratosphere, as the boundary values of the model runs were kept constant, and therefore the model variability is believed to be internal.
New long-term temperature trends in the troposphere and stratosphere have recently been presented by Steiner et al. (2020). Data cover about four decades (1980–2020). These authors find trends on the order of −0.2 K per decade in the lower stratosphere (near-global averages; their Fig. 8). For comparison, we show ECHAM6 data for 50∘ N, 7∘ E at 18 km altitude in our Fig. 8. These data are annual mean residues; i.e. the mean value has been subtracted from the annual data set. The series has been smoothed by a 16-point running mean. The figure shows trend-like increases or decreases of 0.2 K per decade or even steeper over 4-decade intervals. This is indicated by the slanted red lines that give an increase of 0.2 K per decade.
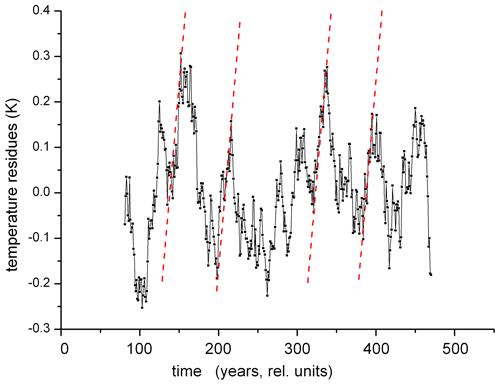
Figure 8ECHAM6 annual temperature residues at 50∘ N, 7∘ E and 18 km altitude. Data have been smoothed by a 16-point running mean. Time is in relative units. Inclined dashed (red) lines have a gradient of 0.2 K per decade.
The comparison with Steiner et al. (2020) is approximate because our data are local (50∘ N, 7∘ E), whereas Steiner et al. (2020) give global means. Such means tend to smooth all variability to some extent. Nevertheless, the results suggest that the long-term trends derived by Steiner et al. (2020) may contain some contribution of internal (i.e. non-anthropogenic) variability. This confirms a corresponding result of these authors saying that “… there may be a non-negligible internally generated component to the larger stratospheric trends …” (see their Sect. 5).
Care must therefore be taken if deriving climate trends from data sets of limited length (4 decades).
A similar caveat applies if internal oscillations with periods on this order are excited in the atmosphere.
4.2.2 Cold-point tropopause
The cold-point tropopause (CPT) is frequently discussed as a climate indicator (see e.g. Hu and Vallis, 2019; Gettelman et al., 2009; Han et al., 2017). A similar parameter is the lapse rate tropopause (LRT), which we do not discuss here, as it is generally close to and behaves similarly to the CPT (Pan et al., 2018; RavindraBabu et al., 2020).
We analyse long-term changes of the cold-point tropopause (CPT) in the ECHAM6 model with fixed boundaries at 50∘ N, 7∘ E and the corresponding Southern Hemisphere location (50∘ S, 7∘ E) as part of our north–south comparison. The lowest temperatures are found in this model at 11.5 km (208.67 hPa) and 12.4 km (181.16 hPa; this is the altitude resolution of the data). We have selected the lowest temperature at these two altitudes and thus formed a data set that approximates the cold-point tropopause, considering our limited altitude resolution.
The results are shown in Fig. 9. The figure compares our CPT data at the two locations. To study data that correspond, winter values are shown, i.e. January data in the Northern Hemisphere and July data in the Southern Hemisphere. The data have been smoothed by a 16-point running mean to suppress the short-term variability that is large (5 K peak to peak). The picture shows that the southern CPT are somewhat lower than the northern ones. Most interesting is the strong variability in either data set, including some apparent periodicity. The latter is indicated by the vertical dashed lines at 60-year intervals.
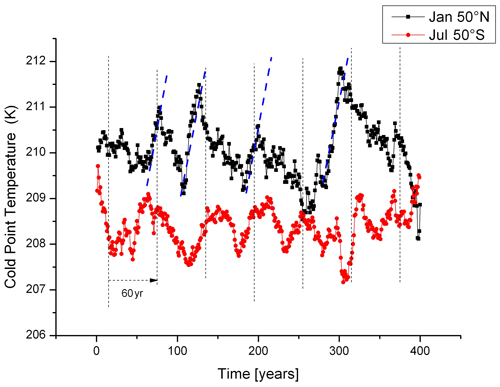
Figure 9Cold-point tropopause temperatures in ECHAM6. Winter data are shown for 50∘ N, January (black) and 50∘ S, July (red). Dotted vertical lines (black) indicate a 60-year periodicity. Inclined dashed lines (blue) show a trend of 1 K per decade. Time is in relative units.
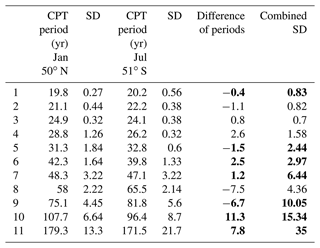
Table 5Cold-point tropopause oscillations in winter at 50∘ N and 51∘ S, standard deviations, and column differences. Bold font indicates agreement of periods within combined standard deviations.
On timescales of decades, positive and negative trends are seen. The positive trends are comparable to the dashed (blue) straight lines that have a gradient of 1 K per decade. The picture shows that such gradients or even steeper ones are not uncommon in the data. The decreasing branches show similar (negative) gradients.
Gradients on this order of magnitude are reported in the literature. Amazingly, both positive and negative values are found, as mentioned in Sect. 1. Recently, negative and positive trends in two subsequent 20-year time intervals (1980–2000; 2001–2020) have been discussed by Konopka et al. (2022). Figure 9 shows that this may not be surprising but may occur quite naturally depending on the time interval chosen for the trend determination. The quasi-periodic behaviour of the CPT plays a role here and suggests a possible connection to the internal oscillations of the atmosphere.
We therefore perform harmonic analyses of the CPT data similarly as those described above for annual temperatures in Table 2. The CPT data are monthly data of January and July, respectively. It was shown above that there is little difference between annual and monthly oscillation periods, and it was checked that this applies here, too.
Indeed, the harmonic analyses of the data yield a number of internal oscillation periods in the period range of Table 2. The results at the northern and southern locations are compared in Table 5. The table shows that the periods in the north and south form pairs similarly to those in Tables 1 and 2. A total of 11 coincidences are obtained. Seven of these agree within the combined standard deviations (bold font in the last two columns of Table 5). Four agree within the double standard deviations. All periods listed in Table 5 also find a counterpart in the corresponding (north or south) columns of Table 2. Also, these pairs agree within combined standard deviations (except one). It thus appears that the cold-point tropopause is at least partly controlled by the internal atmospheric oscillations. This applies to the north and also to the south; i.e. the north–south symmetry shown above is also found in this parameter.
The amplitudes of the CPT oscillations are found to be quite variable with the period (not shown here). The northern and the southern data both show strong amplitude peaks near 60 years. This fits with the data shown in Fig. 9.
Low-frequency oscillations (LFO) in the multi-decadal range (50–80 years) have frequently been discussed for surface temperatures. They have, for instance, been interpreted as internal Atlantic multidecadal variability or Pacific decadal oscillations and interdecadal Pacific oscillations (e.g. Meehl et al., 2013, 2016; Lu et al., 2014; Deser et al., 2014; Dai et al., 2015). It appears that internal oscillations also play a role here as contributors to the CPT variations in either hemisphere. Great caution is therefore advised when interpreting tropopause changes in the context of the anthropogenic long-term climate changes (e.g. Pisoft et al., 2021).
5.1 Self-excitation of oscillations
Present-day sophisticated atmospheric computer models exhibit long-period temperature oscillations in the multi-annual, decadal, and even centennial year range. Such oscillations may be found even if the model boundaries are kept constant concerning the influences of solar radiation, the ocean, and the variations of greenhouse gases (Offermann et al., 2021). A possible influence of land surface and vegetation changes, however, was yet undecided. Therefore, in the present analysis, oscillation periods are compared at locations and occasions with different land surface and vegetation behaviour with the hope of seeing possible differences in oscillation periods. Three cases are studied: first, a location in the Northern Hemisphere (50∘ N, 7∘ E) and its counterpart in the Southern Hemisphere (50∘ S, 7∘ E) are considered. The northern location is in the middle of Europe, whereas the southern location is 15∘ S of the tip of South Africa in the middle of the Southern Ocean. Second, two different seasons are compared in the northern location (January and July). Third, two polar latitude locations are studied at 75∘ N, 280∘ E and 75∘ N, 70∘ E. The land surface and vegetation conditions are quite different in all of these cases.
Two models are studied (HAMMONIA, ECHAM6) for medium and long oscillation periods (5 to beyond 200 years). The periods obtained for the contrasting cases are all found to be very similar.
The same holds for the vertical profiles (up to the mesopause) of the oscillation amplitudes at most altitudes. It is therefore concluded that the oscillations most likely are internally excited in the atmosphere.
There is, however, one exemption. Land–atmosphere interactions should mainly occur in the lowermost atmosphere (boundary layer). We therefore considered especially the lowest atmospheric levels. Here, indeed, the vertical amplitude profiles showed peculiar structures that we tentatively attribute to land–atmosphere interactions. The peculiarities quickly disappear at higher altitudes. Hence, we obtain the preliminary picture of self-excited oscillations in the upper atmosphere and possible land surface excitation at the lowest levels.
5.2 Trends and long periods
Long-term trends in atmospheric parameters are frequently analysed in the context of the ongoing climate change. Trend values are mostly small, and it is sometimes difficult to determine whether or to what extent they are anthropogenic in nature. In this context, internal oscillations can play a role, even if their amplitudes are small. If the oscillation period is on the order of the interval used for the trend analysis, it may become difficult to disentangle trend and oscillation. It is unimportant here whether the oscillations are self-excited or not.
As an example, the cold-point tropopause (CPT) in the 400-year run of the ECHAM6 model with fixed boundaries is analysed at two north–south locations. Strong trend-like increases or decreases of CPT values are seen on decadal timescales (order of 30 years). They are on the order of the trend values discussed in the literature. They are, however, not of anthropogenic origin, as is frequently assumed in the literature. Harmonic analysis of the CPT values yields oscillation periods that are very similar for the north and south locations and are similar to the values otherwise given in this analysis. Apparently, these internal oscillations are important contributors to the CPT variations observed.
The HAMMONIA and ECHAM6 data are available from Hauke Schmidt, MPI Meteorology, Hamburg.
DO performed the data analysis and prepared the paper with the help of all co-authors. JW managed the data collection and preparation. CK helped with the geographical analysis. RK provided interpretation and editing of the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Hauke Schmidt (MPI Meteorology, Hamburg, Germany) for the many helpful discussions. HAMMONIA and ECHAM6 simulations were performed at and supported by the German Climate Computing Centre (DKRZ), who are gratefully acknowledged.
This work was done within the CHIARA (CHaracterisation of the Internal vARiability of the Atmosphere) project as part of the ISOVIC (Impact of SOlar, Volcanic and Internal variability on Climate) project in the framework of the ROMIC II programme (Role of the Middle Atmosphere in Climate). The project was financially supported by the Federal Ministry for Education and Research within the ROMIC II programme under grant no. 01LG1909A and funded by the University of Wuppertal.
This open-access publication was funded by the University of Wuppertal.
This paper was edited by John Plane and reviewed by two anonymous referees.
Dai, A., Fyfe, J. C., Xie, S.-P., and Dai, X.: Decadal modulation of global surface temperature by internal climate variability, Nat. Clim. Change, 5, 555–559, 2015.
Desai, A. R., Paleri, S., Mineau, J., Kadum, H., Wanner, L., Mauder, M., Butterwoerth, B. J., Durden, D. J., and Metzger, S.: Scaling land-atmosphere interactions: Special or fundamental?, J. Geophys. Res.-Biogeo., 127, e2022JG007097, https://doi.org/10.1029/2022JG007097, 2022.
Deser, C.: Certain uncertainty: The role of internal climate variability in projections of regional climate change and risk management, Earth's Future, 8, e2020EF001854, https://doi.org/10.1007/s00382-010-0977-x, 2020.
Deser, C., Phillips, A., Bourdette, V., and Teng, H.: Uncertainty in climate change projections: the role of internal variability, Clim. Dynam., 38, 527–546, 2012.
Deser, C., Phillips, A. S., Alexander, M. A., and Smoliak, B. V.: Projecting North American climate over the next 50 years: Uncertainty due to internal variability, J. Climate, 27, 2271–2296, 2014.
Dijkstra, H. A., te Raa, L., Schmeits, M., and Gerrits, J.: On the physics of the Atlantic Multidecadal Oscillation, Ocean Dynam., 56, 36–50, https://doi.org/10.1007/s10236-005-0043-0, 2006.
Eyring, V., Gillett, N. P., Achuta Rao, K. M., Barimalala, R., Barreiro Parrillo, M., Bellouin, N., Cassou, C., Durack, P. J., Kosaka, Y., McGregor, S., Min, S., Morgenstern, O., and Sun, Y.: Human Influence on the Climate System, in: Climate Change 2021: The Physical Science Basis, Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S. L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M. I., Huang, M., Leitzell, K., Lonnoy, E., Matthews, J. B. R., Maycock, T. K., Waterfield, T., Yelekçi, O., Yu, R., and Zhou, B., Cambridge University Press, in press, August 2021.
Gettelman, A., Birner, T., Eyring, V., Akiyoshi, H., Bekki, S., Brühl, C., Dameris, M., Kinnison, D. E., Lefevre, F., Lott, F., Mancini, E., Pitari, G., Plummer, D. A., Rozanov, E., Shibata, K., Stenke, A., Struthers, H., and Tian, W.: The Tropical Tropopause Layer 1960–2100, Atmos. Chem. Phys., 9, 1621–1637, https://doi.org/10.5194/acp-9-1621-2009, 2009.
Giorgetta, M. A., Jungclaus, J., Reick, C. H., Legutke, S., Bader, J., Böttinger, M., Brovkin, V., Crueger, T., Esch, M., Fieg, K., Glushak, K., Gayler, V., Haak, H., Hollweg, H.-D., Ilyina, T., Kinne, S., Kornblueh, L., Matei, D., Mauritsen, T., Mikolajewicz, U., Mueller, W., Notz, D., Pithan, F., Raddatz, T., Rast, S., Redler, R., Roeckner, E., Schmidt, H., Schnur, R., Segschneider, J., Six, K. D., Stockhause, M., Timmreck, C., Wegner, J., Widmann, H., Wieners, K.-H., Claussen, M., Marotzke, J., and Stevens, B.: Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the coupled model intercomparison project phase 5, J. Adv. Model. Earth Syst., 5, 572–597, https://doi.org/10.1002/jame.20038, 2013.
Han, Y., Xie, F., Zhang, S., Zhang, R., Wang, F., and Zhang, J.: An analysis of tropical cold-point tropopause warming in 1999, Hindawi, Adv. Meteorol., 2017, 4572532, https://doi.org/10.1155/2017/4572532, 2017.
Hu, S. and Vallis, G. K.: Meridional structure and future changes of tropopause height and temperature, Q. J. Roy. Meteorol. Soc. 145, 2698–2717, 2019.
Konopka, P., Tao, M., Ploeger, F., Hurst, D. F., Santee, M. L., Wright, J. S., and Riese, M.: Stratospheric moistening after 2000, Geophys. Res. Lett., 49, e2022GL097609, https://doi.org/10.1029/2021GL097609, 2022.
Lu, J., Hu, A., and Zeng, Z.: On the possible interaction between internal climate variability and forced climate change, Geophys. Res. Lett., 41, 2962–2970, 2014.
Meehl, G. A., Hu, A., Arblaster, J., Fasullo, J., and Trenberth, K. E.: Externally forced and internally generated decadal climate variability associated with the Interdecadal Pacific Oscillation, J. Climate, 26, 7298–7310, 2013.
Meehl, G. A., Hu, A., Santer, B. D., and Xie, S.-P.: Contribution 35 of Interdecadal Pacific Oscillation to twentieth-century global surface temperature trends, Nat. Clim. Change, 6, 1005–1008, https://doi.org/10.1038/nclimate3107, 2016.
Offermann, D., Kalicinsky, C., Koppmann, R., and Wintel, J.: Very long-period oscillations in the atmosphere (0–110 km), Atmos. Chem. Phys., 21, 1593—1611, https://doi.org/10.5194/acp-21-1593-2021, 2021.
Pan, L. L., Honomichl, S. B., Bui, T. V., Thornberry, T., Rollins, A., Hintsa, E., and Jensen, E.: Lapse rate or cold point:The tropicaltropopause identified by in situ trace gas measurements, Geophys. Res. Lett., 45, 10756–10763, 2018.
Pisoft, P., Sacha, P., Polvani, L. M., Anel, J. A., de la Torre, L., Eichinger, R., Foelsche, U., Huszar, P., Jacobi, C., Karlicky, Kuchar, A., Miksovcky, J., Zak, M., and Rieder, H. E.: Stratospheric contraction caused by increasing greenhouse gases, Environ. Res. Lett., 16, 06438, https://doi.org/10.1088/1748-9326/abfe2b, 2021.
RavindraBabu, S., Akhil Raj, S. T., Basha, G., and Venkat Ratnam, M.: Recent trends in the UTLS temperature and tropical tropopause parameters over tropical South India region, J. Atmos. Sol.-Terr. Phy., 197, 105164, https://doi.org/10.1016/j.jastp.2019.105164, 2020.
Roeckner, E., Brokopf, R., Esch, M., Giorgetta, M., Hagemann, S., Kornblueh, L., Manzini, E., Schlese, U., and Schulzweida, U.: Sensitivity of simulated climate to horizontal and vertical resolution in the ECHAM5 atmosphere model, J. Climate, 19, 3771–3791, 2006.
Santer, B. D., Wigley, T. M. L., Simmons, A. J., Kallberg, P. W., Kelly, G. A., Uppala, S. M., Ammann, C., Boyle, J. S., Brüggemann, W., Doutriaux, C., Fiorino, M., Mears, C., Meehl, G. A., Sausen, R., Taylor, K. E., Washington, W. M., Wehner, M. F., and Wentz, F.: Identification of anthropogenic climate change using a second-generation reanalysis, J. Geophys. Res., 109, D21104, https://doi.org/10.1029/2004JD005075, 2004.
Schmidt, H., Brasseur, G. P., Charron, M., Manzini, E., Giorgetta, M. A., Diehl,T., Fomichev, V. I., Kinnison, D., Marsh, D., and Walters, S.: The HAMMONIA chemistry climate model: Sensitivity of the mesopause region to the 11-year solar cycle and CO2 doubling, J. Climate, 19, 3903–3931, https://doi.org/10.1175/JCLI3829.1, 2006.
Steiner, A. K., Ladstädter, F., Randel, W. J., Maycock, A. C., Fu, Q., Claud, C., Gleisner, H., Haimberger, L., Ho, S.-P., Keckhut, P., Leblanc, T., Mears, C., Polvani, M., Santer, B. D., Schmidt, T., Sofieva, V., Wing, R., and Zou, C.-Z.: Observed temperature changes in the troposphere and stratosphere from 1979 to 2018, J. Climate, 33, 8165–8194, 2020.
Stevens, B., Giorgetta, M., Esch, M., Mauritsen, T., Crueger, T., Rast, S., Salzmann, M., Schmidt, H., Bader, J., Block, K., Brokopf, R., Fast, I., Kinne, S., Kornblueh, L., Lohmann, U., Pincus, R., Reichler, T., and Roeckner, E.: The atmospheric component of the MPI-M earth system model: ECHAM6, J. Adv. Model. Earth Syst., 5, 1–27, 2013.
Tegtmeier, S., Anstey, J., Davis, S., Dragani, R., Harada, Y., Ivanciu, I., Pilch Kedzierski, R., Krüger, K., Legras, B., Long, C., Wang, J. S., Wargan, K., and Wright, J. S.: Temperature and tropopause characteristics from reanalyses data in the tropical tropopause layer, Atmos. Chem. Phys., 20, 753–770, https://doi.org/10.5194/acp-20-753-2020, 2020.
Zhou, X.-L., Geller, M. A., and Zhang, M.: Cooling trend of the tropical cold point tropopause temperatures and its implications, J. Geophys. Res., 106, 1511–1522, 2001.





