Comparison of six approaches to predicting droplet activation of surface active aerosol – Part 2: Strong surfactants

Surfactants have been a focus of investigation in atmospheric sciences for decades due to their ability to modify the water uptake and cloud formation potential of aerosols. Surfactants adsorb at the surface and can decrease the surface tension of aqueous solutions. In microscopic aqueous droplets with finite amounts of solute, surface adsorption may simultaneously deplete the droplet bulk of the surfactant. While this mechanism is now broadly accepted, the representation in atmospheric and cloud droplet models is still not well constrained. We compare the predictions of five bulk–surface partitioning models documented in the literature to represent aerosol surface activity in Köhler calculations of cloud droplet activation. The models are applied to common aerosol systems, consisting of strong atmospheric surfactants (sodium myristate or myristic acid) and sodium chloride in a wide range of relative mixing ratios. For the same particles, the partitioning models predict similar critical droplet properties at small surfactant mass fractions, but differences between the model predictions increase significantly with the surfactant mass fraction in the particles. Furthermore, significantly different surface tensions are predicted for growing droplets at given ambient conditions along the Köhler curves. The inter-model variation for these strong surfactant particles is different than previously observed for moderately surface active atmospheric aerosol components. Our results highlight the importance of establishing bulk–surface partitioning effects in Köhler calculations for a wide range of conditions and aerosol types relevant to the atmosphere. In particular, conclusions made for a single type of surface active aerosol and surface activity model may not be immediately generalized.

1 Introduction

The global climate is affected by atmospheric aerosols both directly through interaction with solar radiation and indirectly through their ability to serve as cloud condensation nuclei (CCN). The indirect effect from aerosol–cloud interactions still remains one of the largest sources of uncertainty in global radiative forcing estimates (IPCC, 2013, 2021). Surface active species (surfactants) are commonly found in atmospheric aerosols (e.g., Gérard et al., 2016; Petters and Petters, 2016; Nozière et al., 2017; Kroflič et al., 2018; Gérard et al., 2019). Aerosol surface activity has been shown to affect the critical point of cloud droplet activation, but a clear consensus has not yet been reached on the extent and specific mechanisms (e.g., Hänel, 1976; Shulman et al., 1996; Facchini et al., 1999, 2000; Li et al., 1998; Sorjamaa et al., 2004; Prisle et al., 2008, 2010, 2011; Topping, 2010; Raatikainen and Laaksonen, 2011; Ruehl and Wilson, 2014; Nozière et al., 2014; Ruehl et al., 2016; Petters and Petters, 2016; Ovadnevaite et al., 2017; Malila and Prisle, 2018; Lin et al., 2018; Prisle et al., 2019; Davies et al., 2019; Lowe et al., 2019; Lin et al., 2020; Bzdek et al., 2020; Prisle, 2021; Vepsäläinen et al., 2022).

Surfactants adsorb at the surface of a solution, resulting in enhanced surface concentrations compared to the interior (bulk) solution. The presence of surfactants in aqueous solutions can significantly reduce the surface tension, compared to pure water, which typically decreases with the concentration of surface active compounds (e.g., Wen et al., 2000; Hyvärinen et al., 2006; Vanhanen et al., 2008; Bzdek et al., 2020). The surface tension of a solution can be described in terms of either the surface or bulk composition, which are related via the bulk-to-surface concentration gradient for a given surface-active substance. The relation between surface tension and surface-specific composition is often unknown (Prisle et al., 2012b; Werner et al., 2014, 2018; Toribio et al., 2018), and experimentally based surface tension relations are therefore typically expressed in terms of the solution bulk composition. Measurements of surface tension are commonly performed for macroscopic solutions, where the bulk phase contains a sufficiently large amount of solute that the adsorption to the surface phase has negligible effect on the composition of the bulk. The surface tension of a macroscopic solution is therefore readily described in terms of the total solution composition.

In microscopic droplets, the surface adsorption of surfactants can significantly alter the bulk composition and therefore the composition-dependent droplet properties, due to the finite total amount of solute comprised in such small droplets (e.g., Prisle et al., 2010; Lin et al., 2018, 2020; Bzdek et al., 2020; Prisle, 2021). The distribution of surfactant mass between the surface and bulk phases is referred to as bulk–surface partitioning (Prisle et al., 2010; Vepsäläinen et al., 2022). Surface tension measurements for microscopic droplets (i.e., with diameters in the micrometer range or smaller) have only recently been achieved and for only a few droplet systems, including aqueous sodium chloride (NaCl), aqueous malonic or glutaric acid (Morris et al., 2015), aqueous NaCl or glutaric acid (Bzdek et al., 2016), and aqueous mixtures of strong surfactant Triton X-100 with glutaric acid or NaCl (Bzdek et al., 2020). Bzdek et al. (2020) showed that surface tension of aqueous Triton X-100 microscopic droplets (7–9 µm radius) suspended in air was significantly higher than for a macroscopic solution with identical composition. Their measurements provided the first direct experimental evidence of the influence of bulk-phase depletion due to bulk–surface partitioning in finite sized droplets.

Experimental data for composition-dependent properties of microscopic droplets are rare. Therefore, composition–property relations based on macroscopic data are used for estimating microscopic droplet properties, by accounting for the effect of bulk–surface partitioning on bulk composition with a partitioning model (e.g., Sorjamaa et al., 2004; Prisle et al., 2008, 2010; Malila and Prisle, 2018; Lin et al., 2018, 2020; Bzdek et al., 2020; Prisle, 2021). Several models have been developed to describe surfactant partitioning effects in aqueous droplets of atmospheric relevance. Most models either employ Gibbs surface thermodynamics, where the surface phase is approximated as a two-dimensional interface (e.g., Sorjamaa et al., 2004; Prisle et al., 2008, 2010; Topping, 2010; Raatikainen and Laaksonen, 2011; Petters and Petters, 2016; McGraw and Wang, 2021; Prisle, 2021), or assume a physical surface layer in the form of a molecular monolayer (e.g., Malila and Prisle, 2018), liquid–liquid phase separation (e.g., Ovadnevaite et al., 2017), a compressed film (e.g., Ruehl et al., 2016), or complete phase separation (e.g., Prisle et al., 2011; Ovadnevaite et al., 2017). Each surface partitioning model is based on specific assumptions and requirements for application. An overview of the most widely used partitioning models is given by Malila and Prisle (2018).

We have previously compared predictions with five bulk–surface partitioning models (Prisle et al., 2010, 2011; Ruehl et al., 2016; Ovadnevaite et al., 2017; Malila and Prisle, 2018) and a general bulk solution model (Prisle et al., 2010) for droplet activation of moderately surface active organic aerosol, comprised of malonic, succinic, or glutaric acid mixed with ammonium sulfate across a range of compositions (Vepsäläinen et al., 2022). Surfactant strength is here considered in terms of the ability to reduce the surface tension of aqueous solutions at a given concentration. We found that, for the same moderately surface active aerosol, the different models predict significantly different CCN activity, droplet surface tension, and degree of bulk–surface partitioning. However, these results cannot be immediately generalized to aerosols with significantly different surface activity. Here, we therefore compare predictions of cloud droplet activation with different surface activity models for strongly surface active aerosol in common conditions. Strong surfactants have different surface adsorption properties than moderately surface active compounds and a pronounced ability to reduce surface tension in macroscopic solutions (e.g., Campbell and Lakshminarayanan, 1965; Wen et al., 2000; Álvarez Silva et al., 2010; Petters and Petters, 2016). The mutual agreement between different surface activity models may therefore also be different than previously observed.

Strongly surface active aerosols are here represented by the atmospheric fatty acid myristic acid and its sodium salt (sodium myristate). Fatty acids have been found in atmospheric aerosol samples and are a major component of sea spray aerosol (SSA) (e.g., Mochida et al., 2002, 2007; Cheng et al., 2004; Wang et al., 2015; Cochran et al., 2016; Kirpes et al., 2019) and part of particle compositions associated with ice nucleation by SSA (e.g., DeMott et al., 2018; Perkins et al., 2020). Experiments by Wang et al. (2015) indicate that long-chain fatty acids are the dominant contributor to submicron organic SSA (aerodynamic diameter 0.56–1 µm). Cochran et al. (2016) tentatively identified over 280 organic compounds in nascent SSA, including saturated and unsaturated fatty acids and derivatives of fatty acids. Kirpes et al. (2019) observed thick organic coatings, consisting of marine saccharides, amino acids, fatty acids, and divalent cations, on Alaskan Arctic winter SSA, where 40 % of the particles containing surfactants matched only long-chain fatty acids, while the rest also contained short-chain fatty acids or saccharides. Fatty acid salts were the first atmospheric surfactants to be investigated in comprehensive experimental and partitioning modeling studies (Prisle et al., 2008, 2010, 2011) and have been subject of several subsequent similar studies (e.g., Nguyen et al., 2017; Forestieri et al., 2018).

2 Theory and modeling

We perform Köhler predictions of cloud droplet activation for surface active aerosol using six different models to describe possible surfactant effects during droplet growth, including five bulk–surface partitioning models and one bulk solution model. As a reference, we also include a classical Köhler model that does not consider any effects of surface activity. In addition, we estimate the relative change in cloud droplet number concentration from Köhler predictions with the surface activity models in comparison to the classical Köhler model.

Brief descriptions of the six surface activity models are given in the following sections. A conceptual figure of the models is shown in Fig. 1 of Vepsäläinen et al. (2022). For the most detailed documentation of each model, we refer the reader to the original publications.

2.1 Köhler theory

Cloud droplet activation is predicted with equilibrium Köhler theory (Köhler, 1936) in the form (Prisle et al., 2010)

$$\begin{array}{}\text{(1)}& S\equiv {\displaystyle \frac{p_{\mathrm{w}}}{p_{\mathrm{w}}^{\mathrm{0}}}}=a_{\mathrm{w}}\exp \left({\displaystyle \frac{\mathrm{4}{\stackrel{\mathrm{‾}}{v}}_{\mathrm{w}}\mathit{\sigma }}{RTd}}\right),\end{array}$$

where S is the equilibrium water vapor saturation ratio, p_w is the equilibrium partial pressure of water over the solution droplet, $p_{\mathrm{w}}^{\mathrm{0}}$ is the saturation vapor pressure over a flat surface of pure water, a_w is the droplet solution water activity, ${\stackrel{\mathrm{‾}}{v}}_{\mathrm{w}}=M_{\mathrm{w}}/{\mathit{\rho }}_{\mathrm{w}}$ is the molar volume of water, σ is the droplet surface tension, R is the universal gas constant, T is the temperature in Kelvin, and d is the spherical droplet diameter. Droplet activation is determined in terms of the critical saturation ratio (S_c) or the critical supersaturation (SS${}_{\mathrm{c}}=(S_{\mathrm{c}}-\mathrm{1})\cdot \mathrm{100}$ %), both corresponding to the maximum value of the Köhler curve described by Eq. (1).

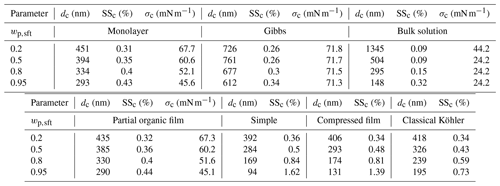
We calculate Köhler growth curves for particles comprising surfactants (abbreviated sft) sodium myristate (abbreviated NaC₁₄) or myristic acid mixed with NaCl in mass fractions of $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$–0.95 in dry particles with diameter D_p=50 nm. Compound properties used in the calculations are presented in Table 1 for water, NaC₁₄, myristic acid, and NaCl. The total amount of surfactant and NaCl in each particle is calculated from the respective solid-phase densities and relative mass fractions in the particle, which in turn determine the total amount of solute present in the growing aqueous droplet. All models assume spherical particles and droplets. Droplet solutions are described as ternary water–surfactant–inorganic salt mixtures, but the specific treatment of bulk–surface partitioning and the resulting droplet water activity and surface tension vary between the different models. Table 2 summarizes the surface tension and water activity calculation methods, as well as components considered in the droplet bulk and surface phases for the different models. For more details on the calculations, we refer the reader to Vepsäläinen et al. (2022).

2.2 Partitioning models

2.2.1 Gibbs adsorption model

In the Gibbs model of Prisle et al. (2010), the Gibbs adsorption equation,

$$\begin{array}{}\text{(2)}& \sum _j{n}_j^{\mathrm{T}}kT{\displaystyle \frac{\mathrm{d}\ln \left(a_j^{\mathrm{B}}\right)}{\mathrm{d}{n}_{\mathrm{sft}}^{\mathrm{B}}}}+A{\displaystyle \frac{\mathrm{d}\mathit{\sigma }}{\mathrm{d}{n}_{\mathrm{sft}}^{\mathrm{B}}}}=\mathrm{0},\end{array}$$

is solved iteratively for the bulk composition with the boundary condition that the molar ratio of water and NaCl is the same in both the bulk and surface phases. In Eq. (2), $n_j^{\mathrm{T}}$ is the total amount of species j in the droplet solution, k is the Boltzmann constant, $n_{\mathrm{sft}}^{\mathrm{B}}$ is the amount of surfactant in the droplet bulk, $a_j^{\mathrm{B}}$ is the activity of j in the droplet bulk solution, A is the spherical droplet surface area, and σ is the droplet surface tension, given as a function of bulk-phase composition. The position of the Gibbs diving surface is selected so that the droplet bulk-phase volume equals the total equimolar droplet volume and mass conservation ($n_j^{\mathrm{T}}=n_j^{\mathrm{S}}+n_j^{\mathrm{B}}$) is assumed for all components in the droplet (water, surfactant, NaCl).

Table 1 Molar mass (M), densities of the liquid (ρ_l) and solid (ρ_s) phases, and surface tension (σ) of the pure compounds.

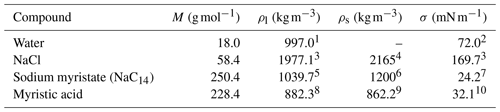
¹ Pátek et al. (2009). ² International Association for the Properties of Water and Steam (IAPWS) (2014). ³ Vanhanen et al. (2008) and Janz (1980). ⁴ Prisle et al. (2010). ⁵ Extended from binary aqueous density estimated via method of Calderón and Prisle (2021). ⁶ Estimate Prisle et al. (2011). ⁷ Value at CMC. ⁸ (Noureddini et al., 1992). ⁹ At 54 ^∘C (CRC Handbook, 2020). ¹⁰ The method of Zhang et al. (2018), using data from Di Nicola et al. (2016).

2.2.2 Simple complete partitioning model

The simple partitioning model of Prisle et al. (2011) assumes that all surfactants in the droplet are completely partitioned into an insoluble surface layer of pure surfactant and the remaining bulk phase is a binary mixture of water and NaCl. The surface tension of the droplet solution is assumed to be equal to that of pure water, representing that the surface coverage of the surfactant is insufficient to form a full monolayer.

2.2.3 Compressed film surface model

The compressed film model of Ruehl et al. (2016) divides the droplet into an organic surface and a ternary solution droplet bulk of water, surfactant, and NaCl. The surface tension is calculated as

$$\begin{array}{}\text{(3)}& \mathit{\sigma }=min\left({\mathit{\sigma }}_{\mathrm{w}},max\left({\mathit{\sigma }}_{\mathrm{w}}-(A_{\mathrm{0}}-A_{\mathrm{m}})m_{\mathit{\sigma }},{\mathit{\sigma }}_{\min }\right)\right),\end{array}$$

where σ_w is the surface tension of water, A₀ is the critical molecular area, A_m is the molecular area (Eq. 6), m_σ accounts for the interaction between surfactants at the interface, and σ_min is a lower limit imposed on the surface tension. The isotherm for the equation of state (EoS) of the compressed film is

$$\begin{array}{}\text{(4)}& \ln \left({\displaystyle \frac{C_{\mathrm{bulk}}}{C_{\mathrm{0}}}}\right)={\displaystyle \frac{(A_{\mathrm{0}}^{\mathrm{2}}-A_{\mathrm{m}}^{\mathrm{2}})m_{\mathit{\sigma }}{N}_{\mathrm{A}}}{\mathrm{2}RT}},\end{array}$$

where C₀ represents the surfactant bulk concentration at the phase transition, C_bulk represents the surfactant bulk concentration (Eq. 5), and N_A is Avogadro’s number, which is used to calculate the fraction of surfactant partitioned to the surface (f_surf). The parameters C_bulk and A_m can be expressed as functions of the NaCl seed (D_seed), dry particle (D_p) and droplet (d) diameters, and f_surf as

$$\begin{array}{}\text{(5)}& C_{\mathrm{bulk}}={\displaystyle \frac{(\mathrm{1}-f_{\mathrm{surf}})(D_{\mathrm{p}}^{\mathrm{3}}-D_{\mathrm{seed}}^{\mathrm{3}}){\stackrel{\mathrm{‾}}{v}}_{\mathrm{w}}}{d^{\mathrm{3}}{\stackrel{\mathrm{‾}}{v}}_{\mathrm{sft}}}}\end{array}$$

and

$$\begin{array}{}\text{(6)}& A_{\mathrm{m}}={\displaystyle \frac{\mathrm{6}{\stackrel{\mathrm{‾}}{v}}_{\mathrm{sft}}{d}^{\mathrm{2}}}{f_{\mathrm{surf}}(D_{\mathrm{p}}^{\mathrm{3}}-D_{\mathrm{seed}}^{\mathrm{3}})N_{\mathrm{A}}}}.\end{array}$$

The model-specific parameters A₀, C₀, m_σ, and σ_min are assumed to be compound-specific physical constants. The values used for parameters A₀=29.2 Ų, log ₁₀ $C_{\mathrm{0}}=-\mathrm{7.4}$, and m_σ=1.28 mJ m⁻² Å⁻² were obtained from Forestieri et al. (2018) for myristic acid. The minimum surface tension is assumed to be σ_min=0, as a conservative estimate, because it could not be determined experimentally (Forestieri et al., 2018). We use the same parameters for NaC₁₄ due to the lack of suitable data to fit parameters specifically for NaC₁₄.

2.2.4 Monolayer surface model

In the molecular monolayer model of Malila and Prisle (2018), the partitioning between the bulk and surface phases for each compound j is calculated iteratively from the semi-empirical relation

$$\begin{array}{}\text{(7)}& \mathit{\sigma }({\mathbf{x}}^{\mathrm{B}},T)={\displaystyle \frac{{\sum }_j{\mathit{\sigma }}_j{v}_j{x}_j^{\mathrm{S}}}{{\sum }_j{v}_j{x}_j^{\mathrm{S}}}},\end{array}$$

where v_j is the liquid-phase molecular volume, $x_j^{\mathrm{S}}$ is the droplet surface mole fraction of compound j, and σ_j is the surface tension of pure j. The vector x^B contains the bulk mole fractions $x_j^{\mathrm{B}}$ for water, surfactant, and NaCl. The thickness of the surface monolayer is calculated as

$$\begin{array}{}\text{(8)}& \mathit{\delta }={\left({\displaystyle \frac{\mathrm{6}}{\mathit{\pi }}}\sum _j{v}_j{x}_j^{\mathrm{S}}\right)}^{\mathrm{1}/\mathrm{3}}\end{array}$$

and the condition of mass conservation ($n_j^{\mathrm{T}}=n_j^{\mathrm{S}}+n_j^{\mathrm{B}}$) is imposed for each compound j.

2.2.5 Partial organic film model

In the partial organic film model of Ovadnevaite et al. (2017), all surfactants are assumed to reside in a NaCl- and water-free surface film, similar to the simple partitioning model of Prisle et al. (2011). The surface film is assumed to completely coat the droplet bulk until a minimum surface thickness is reached (δ_sft), where the surface film breaks, resulting in partial coverage of the droplet. The effective surface tension of the droplet is calculated as the surface-area-weighted mean of the surface tensions from the surface and bulk phases as

$$\begin{array}{}\text{(9)}& \mathit{\sigma }=(\mathrm{1}-c_{\mathrm{S}}){\mathit{\sigma }}^{\mathrm{B}}+c_{\mathrm{S}}{\mathit{\sigma }}^{\mathrm{S}},\end{array}$$

where

$$\begin{array}{}\text{(10)}& c_{\mathrm{S}}=min\left({\displaystyle \frac{V^{\mathrm{S}}}{V^{\mathit{\delta }}}},\mathrm{1}\right)\end{array}$$

is the surface coverage, V^S is the volume of the surface phase, and V^δ is the corresponding volume of a spherical shell of thickness δ_sft. Here, the surface thickness δ_sft is set equal to the corresponding values calculated with Eq. (8) of the monolayer model of Malila and Prisle (2018). A comparison between using a constant δ_sft vs. the values calculated with the monolayer model is presented in Sect. S1.3 in the Supplement. The surface tensions of individual liquid bulk (σ^B) and surface (σ^S) phases are calculated as volume fraction-weighted means of the pure-component surface tensions (Table 1).

2.3 Bulk surface activity model

In the bulk solution model (e.g., Prisle et al., 2010; Prisle, 2021), droplet properties are assumed to be equivalent to those for a macroscopic solution with the same total composition. The droplet bulk-phase composition is determined directly as the total composition of the droplet and the droplet surface tension is estimated from a macroscopic ternary solution surface tension parametrization (Sect. S2.2) using this composition.

2.4 Classical Köhler model

In the classical Köhler model (e.g., Prisle et al., 2010; Prisle, 2021), surface active aerosol components are treated as regular soluble solutes and specific effects of surface activity are not considered. The droplet surface tension is assumed to be constant and equal to that of pure water.

Table 2 Methods of calculating the droplet water activity (a_w) and surface tension (σ), and the composition of the droplet surface and bulk phases used with the different models. For more details on the calculations, we refer the reader to Vepsäläinen et al. (2022).

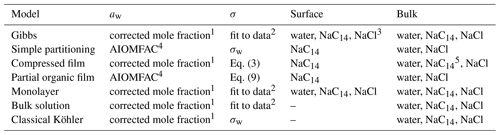
¹ Corresponding to the bulk-phase composition; see Sect. S2.1. For the bulk solution and classical Köhler models this calculated from the total composition of the droplet. ² Fit into the data of Wen et al. (2000) (Sect. S2.2 of the Supplement). ³ NaCl and water depletion from the surface balance the surfactant partitioning. ⁴ Fit into AIOMFAC-web (2023) calculations (Zuend et al., 2008, 2011); see Sect. S2.1. ⁵ Typically, all surfactants have partitioned to the surface at activation.

2.5 Critical micelle concentration

Above the so-called critical micelle concentration (CMC), some surfactants can self-aggregate to form structures here collectively referred to as micelles. The micellization process is highly dependent on the surfactant species (Langevin, 1992). In ternary water–surfactant–inorganic salt solutions, both the surfactant CMC and solution surface tension at the CMC can vary with inorganic salt concentration and may be further affected for ionic surfactants that share a common counterion with the inorganic salt. Accounting for these effects requires complex modeling (e.g., Kralchevsky et al., 1999; Calderón et al., 2020) with parameters obtained from experiments. The surfactant CMC often decreases with increasing inorganic salt concentration compared to a binary water–surfactant solution (Calderón and Prisle, 2021). However, for most ternary surfactant solutions, and in particular for atmospheric surfactants, the relevant interaction parameters are not known or readily accessible with existing experimental techniques.

In this work, the CMC of NaC₁₄ is estimated from binary water–NaC₁₄ surface tension data (Wen et al., 2000) and taken into account in the composition-dependent ternary surface tension function (Sect. S2.2) used for the Gibbs (Sect. 2.2.1), monolayer (Sect. 2.2.4), and bulk solution (Sect. 2.3) models. The surface tension at this concentration, σ_CMC=24.2 mN m⁻¹, is set as a lower limit for the droplet surface tension and assumed to be constant, such that NaCl has no effect on σ_CMC. For calculations with the Gibbs and monolayer models, the predicted droplet surface tension must be larger than σ_CMC for the Köhler curves to be calculated, because neither model explicitly treats micelle formation. With the bulk solution model, the CMC limits the maximum amount of surfactant dissolved in the bulk when the droplet surface tension is equal to σ_CMC. Any additional surfactant present in the droplets, as micelles or undissolved, is assumed to have negligible impact on the droplet volume and solution state. For the monolayer and partial organic film models, the surface tension of pure NaC₁₄ (in a hypothetical supercooled liquid state) is assumed to be equal to σ_CMC, due to lack of available data (Malila and Prisle, 2018). More information is given in Sect. S2.4.

2.6 Relative change in the cloud droplet number concentration

We estimate the relative change in cloud droplet number concentration caused by the differences in critical supersaturation (SS_c) predicted for the different partitioning models, as well as the bulk solution model, with respect to the classical Köhler model (SS${}_{\mathrm{c}}^{\mathrm{0}}$), using the method outlined by Bzdek et al. (2020). The cloud droplet number concentration N is assumed to depend on the supersaturation SS as N∝SS^k, where k≈0.5 (Facchini et al., 1999), and the relative change in cloud droplet number concentration is calculated as

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{\mathrm{\Delta }N}{N}}={\displaystyle \frac{({\mathrm{SS}}_{\mathrm{c}}^{\mathrm{0}}{)}^k-({\mathrm{SS}}_{\mathrm{c}}{)}^k}{({\mathrm{SS}}_{\mathrm{c}}{)}^k}}.\end{array}$$

3 Results and discussion

In the following sections, we present the results of Köhler calculations with the different models described above for common aerosol systems with dry diameters of D_p=50 nm and comprising NaC₁₄ and NaCl in various mixing ratios. Results for particles comprising myristic acid are presented in Sect. S1.1 in the Supplement. Furthermore, critical supersaturations and droplet diameters predicted for particles across the size range D_p=50–200 nm are presented in Sect. S1.4. With a given mass fraction of NaC₁₄, the inter-model variation between the different partitioning models is similar for particles of all sizes. The absolute differences in predicted SS_c between the models are larger for small particles, and therefore we here focus on the results for D_p=50 nm.

3.1 Köhler curves and droplet activation

Figure 1 shows the Köhler curves predicted with the different models in terms of supersaturation (SS) as a function of droplet size (d) for particles with initial dry diameter D_p=50 nm and NaC₁₄ mass fractions (w_p,sft) of 0.2, 0.5, 0.8, and 0.95 relative to NaCl. The critical points (d_c, SS_c) corresponding to the Köhler curves in Fig. 1 are given in Table 3. Figure 1 immediately highlights that the different models can predict significantly different Köhler growth curves and activation properties for the same dry particles. The differences in both SS_c and d_c predicted with the different bulk–surface partitioning models increase with w_p,sft. The simple partitioning and compressed film models consistently predict the highest SS_c and the smallest d_c for all w_p,sft. For the Gibbs model, predicted d_c are larger and SS_c are lower than for the other partitioning models. The monolayer and partial organic film models agree well and the predicted critical points are between the extremes for all models at each w_p,sft. There are generally large differences between the SS_c of the partitioning models and the bulk solution model, whereas the critical points of the classical Köhler model fall between the extremes of the different surface activity models.

3.1.1 Critical supersaturations

For particles with $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$ in Fig. 1a, the Köhler curves and SS_c values of the different models are comparable, except for the bulk solution model. The SS_c predicted with the monolayer and partial organic film models agree even as w_p,sft increases in Fig. 1b–d. We used the surface thickness predicted by the monolayer model (δ_ML) as input for the partial organic film model calculations, but this only slightly enhances the similarities of results from the two models. Using a constant surface thickness of 0.5 nm (δ_0.5) for the partial organic film model does not drastically change the SS_c. The largest differences were seen for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.5}$ and 0.8, where ${\mathrm{SS}}_{\mathrm{c}}^{{\mathit{\delta }}_{\mathrm{ML}}}/{\mathrm{SS}}_{\mathrm{c}}^{{\mathit{\delta }}_{\mathrm{0.5}}}=\mathrm{0.96}$. A detailed comparison is provided in Sect. S1.3.

The Gibbs model predicts lower SS_c than the monolayer and partial organic film models for all w_p,sft in Fig. 1. However, the critical points for the Gibbs model correspond to droplet sizes immediately after the droplet surface tension increases from the minimum value at the NaC₁₄ CMC (see Fig. 2), suggesting that predictions could be sensitive to the assumed value of the CMC. Experimentally determined CMC values can vary significantly for a given solution, depending on the measurement technique used (Álvarez Silva et al., 2010).

The SS_c of the simple partitioning and compressed film models increase more with w_p,sft than for the other models (Table 3). For particles with $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$–0.8 in Fig. 1a–c, the SS_c is only slightly higher for the simple partitioning model than for the compressed film model, but the difference between models increases for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.95}$ in Fig. 1d. Köhler calculations for myristic acid with the simple partitioning, compressed film, and partial film models (Sect. S1.1) predict higher SS_c and smaller d_c than for NaC₁₄, but the inter-model variation between the three models for myristic acid is similar to that for NaC₁₄ in Fig. 1. We assessed the sensitivity of the compressed film model predictions to the assumed molar volume of myristic acid, and found that the critical point is only significantly affected at $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.95}$ (Sect. S1.2).

In Fig. 1, the SS_c of the classical Köhler model is lower than for the simple and compressed film models but larger than for the monolayer, Gibbs, and partial film models. The bulk solution model predicts significantly lower SS_c than the partitioning models, analogously to several other results for strong surfactants (e.g., Sorjamaa et al., 2004; Prisle et al., 2008, 2010; Topping, 2010; Prisle et al., 2019; Prisle, 2021). For moderately surface active malonic, succinic, or glutaric acid and ammonium sulfate particles, we previously did not predict significantly lower SS_c with the bulk solution model than with the bulk–surface partitioning models (Vepsäläinen et al., 2022). Due to the moderate surface activity of these di- and polycarboxylic acids, the monolayer and Gibbs partitioning models predicted only a moderate extent of surface partitioning and consequently droplet bulk-phase compositions, surface tensions, and Köhler curves similar to the bulk solution model. The mutual agreement between the different models and in particular the significance of bulk–surface partitioning can therefore vary significantly with the surface active properties of the investigated aerosol.

For comparison, a critical supersaturation of SS${}_{\mathrm{c}}^{\exp }=\mathrm{0.965}$ % calculated from a fit to experimental SS_c data of Prisle et al. (2008) for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{1}$ and D_p=50 nm is included in Fig. 1d. The simple partitioning and compressed film models predict larger SS_c than this experimental value and the monolayer, Gibbs, partial organic film, bulk solution, and classical Köhler models predict smaller SS_c than this experimental value. For $w_{\mathrm{p},\mathrm{sft}}=\mathrm{1}$, the SS_c is higher than with $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.95}$, but the difference is minor compared to the difference between the SS_c for the monolayer, Gibbs, and partial organic film models and SS${}_{\mathrm{c}}^{\exp }$ in Fig. 1d. The simple model has previously been observed to overestimate SS_c at high w_p,sft and for less surface active aerosols (Prisle et al., 2011; Vepsäläinen et al., 2022).

Average supersaturations in low-level clouds range from 0.1 % to 0.4 % (e.g., Politovich and Cooper, 1988) but higher supersaturations of 0.7 % to 1.3 % can be reached during turbulent fluctuations in temperature and water vapor concentration (e.g., Siebert and Shaw, 2017). Only the simple partitioning, compressed film, and classical Köhler models predict SS_c above 0.7 % at high w_p,sft, while the other models predict considerably lower SS_c (Table 3). Therefore, the inter-model variation for the strongly surface active aerosol studied here is sufficiently pronounced to affect predictions of activation for the ambient conditions in low level clouds. The absolute differences between the highest and lowest SS_c in Fig. 1 are ΔSS_c=0.27 %, 0.41 %, 0.69 %, and 1.30 % for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$, 0.5, 0.8, and 0.95, respectively. However, excluding the bulk solution model, maximum differences in SS_c between the bulk–surface partitioning models are ΔSS_c=0.10 %, 0.24 %, 0.54 %, and 1.28 % for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$, 0.5, 0.8, and 0.95, respectively. This range of ΔSS_c for strongly surface active NaC₁₄ particles is similar to predictions for malonic acid by Vepsäläinen et al. (2022). The large differences between the SS_c of the different models for both strongly and moderately surface active aerosol means that representation of surface activity during Köhler calculations could cause significant changes in predictions of cloud droplet number concentrations (Fig. 4), with corresponding uncertainty in estimations of the cloud radiative effect.

3.1.2 Critical droplet diameters

In Fig. 1, the critical droplet diameters (d_c) predicted with the different models generally decrease as w_p,sft increases, except for the Gibbs model where d_c increases between $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$ and 0.5. The Gibbs model predicts the largest d_c of the bulk–surface partitioning models, and also larger d_c than for the bulk solution model, except for particles with $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$. However, as the critical point of cloud droplet activation predicted with the Gibbs model occurs close to the droplet size where the surface tension increases from the minimum value σ_CMC (Fig. 2), predictions may vary depending on the value used for the CMC of aqueous sodium myristate. For $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$ in Fig. 1a, the d_c values agree fairly well between the different bulk–surface partitioning models, except the Gibbs model. The monolayer and partial film models furthermore agree well for each w_p,sft value in Fig. 1 (see also Table 3). The simple partitioning and compressed film models predict similar d_c, only showing a significant difference for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.95}$ in Fig. 1d.

The Köhler curves predicted with the bulk solution model have a distinct shape with two local maxima, because the droplet surface tension is constant and equal to σ_CMC for the concentrated small droplet sizes before eventually increasing as the droplet grows and dilutes beyond the myristate CMC (Fig. 2). For $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$ in Fig. 1a, the critical point is reached at the maximum corresponding to the larger droplet size, where surface tension is higher than σ_CMC. For the classical Köhler model, predicted d_c are lower than for the monolayer and partial film models but higher than the simple and compressed film models.

The absolute differences between the largest and smallest d_c in Fig. 1 are $\mathrm{\Delta }{d}_{\mathrm{c}}=\mathrm{952},\mathrm{477},\mathrm{508}$, and 518 nm for particle compositions $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$, 0.5, 0.8, and 0.95, respectively. Differences between the bulk–surface partitioning models are however smaller, Δd_c=334 nm, for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$. The size of activating droplets will affect their liquid water content and in turn the optical properties of droplets and the cloud albedo (Twohy et al., 2013). Variations in d_c between the different models may therefore contribute to the uncertainty in estimations for radiative properties of clouds.

3.1.3 Inter-model variation

For particles containing strong surfactant NaC₁₄ with NaCl in Fig. 1, the simple partitioning and compressed film models predict the highest SS_c at high surfactant fractions w_p,sft. The monolayer and partial film models agree well for the entire range of particle compositions, while the Gibbs model predicts comparable SS_c. In previous Köhler calculations for particles containing moderately surface active malonic, succinic, or glutaric acid with ammonium sulfate (Vepsäläinen et al., 2022), the highest SS_c were predicted with the simple partitioning model, while the Gibbs, monolayer, and bulk solution models agreed well and predicted similar SS_c to the compressed film and partial film models for most w_p,sft. The inter-comparison of surface activity and partitioning models therefore shows several differences between strongly and moderately surface active aerosols. This suggests that effects of aerosol surface activity on cloud droplet formation captured by the different partitioning models cannot be robustly understood based on any single model or a few aerosol systems with similar surface activity. Therefore, assessments of bulk–surface partitioning effects in Köhler calculations should be based on predictions for a wide range of conditions and types of surface active aerosol relevant to the atmosphere.

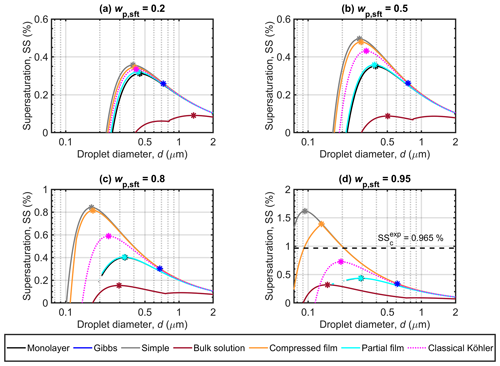
Figure 1 Köhler curves calculated with the different models for dry NaC₁₄–NaCl particles with D_p=50 nm. Each panel shows curves for droplets with different NaC₁₄ mass fractions (w_p,sft) in the particles. Critical points are also marked on each curve, and the experimental critical supersaturation reported by Prisle et al. (2008) corresponding to $w_{\mathrm{p},\mathrm{sft}}=\mathrm{1}$ is included in panel (d). Note that the vertical-axis scaling changes between the panels.

3.2 Droplet surface tension

Figure 2 shows the droplet surface tensions predicted along the corresponding Köhler curves in Fig. 1. The simple partitioning and classical Köhler models both assume a constant surface tension equal to that of pure water (σ_w). The surface tensions predicted during droplet growth vary significantly between the other models, but the surface tension curves for each model show similar characteristics between different w_p,sft.

Surface tensions at the critical point of cloud droplet activation (σ_c) predicted with the different models for each w_p,sft are given in Table 3. The σ_c differ significantly between the models and the differences increase with surfactant fraction w_p,sft in the particles. For $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.95}$ in Fig. 2d, σ_c spans the extremes from σ_CMC to σ_w between the different models. The monolayer and partial organic film models predict σ_c that significantly decreases with w_p,sft, while σ_c for the Gibbs model is close to σ_w. For the compressed film model, σ_c=σ_w for the investigated w_p,sft. The bulk solution model predicts σ_c=σ_CMC for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.5}$–0.95 and also the lowest σ_c among the models for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$.

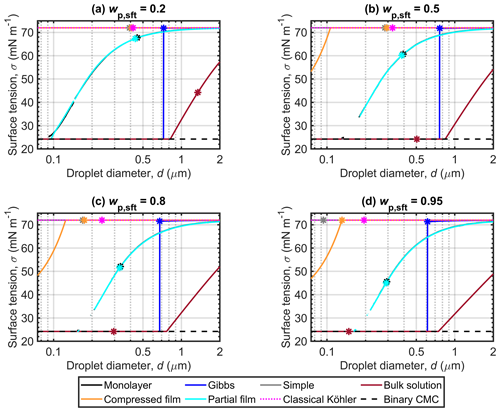
Figure 2 Droplet surface tensions along the Köhler curves, predicted with the different models for dry particles of D_p=50 nm with varying NaC₁₄ mass fractions (w_p,sft). The critical points evaluated for the Köhler curves in Fig. 1 are also marked. The surface tension at the CMC (σ_CMC) for NaC₁₄ in binary aqueous solution was estimated from the measurements of Wen et al. (2000) and is indicated as a lower limit for the droplet surface tension.

Droplet surface tensions predicted with the Gibbs model show a step increase from σ_CMC to values near σ_w for each w_p,sft in Fig. 2. The droplet diameter at (or immediately after) the step increase corresponds to the critical point, as discussed in connection with the Köhler curves. The surface tension curves of the monolayer and partial organic film models are similar for all w_p,sft in Fig. 2. The partial organic film model calculations were also performed with a constant surface thickness δ=0.5 nm, but changes to the results were minor (Sect. S1.3).

The droplet surface tension curves for the compressed film model behave differently for NaC₁₄ particles in Fig. 2 than for previous applications to other surface active aerosol systems (e.g., Ruehl et al., 2016; Forestieri et al., 2018; Vepsäläinen et al., 2022). Surface tension depression from σ_w before droplet activation is visible in Fig. 2b–d, but only for the highest NaC₁₄ fractions in Fig. 2d is d_c close to droplet size where the surface tension reaches σ_w, as was the typical observation of Ruehl et al. (2016) for dicarboxylic acids. Vepsäläinen et al. (2022) observed that the critical point and surface tension reaching σ_w occurred at different droplet sizes for particles with D_p=50 nm comprising moderately surface active di- and tricarboxylic acids and ammonium sulfate at $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$. Forestieri et al. (2018) made analogous observations as Vepsäläinen et al. (2022) for 80 nm NaCl particles coated with strongly surface active oleic acid at an organic volume fraction of 0.8. Predictions for myristic acid–NaCl particles (Sect. S1.1) show that the critical point and the surface tension reaching σ_w do not happen for similar droplet sizes at all w_p,sft values. Forestieri et al. (2018) used the same compressed film model parameters fitted for myristic acid as used here for both NaC₁₄ and myristic acid, at organic volume fractions of 0.40–0.98 for D_seed=180 and 200 nm and RH =99.83 %–99.93 %. The compressed film model parameters are fitted assuming pseudo-ideal droplet solutions, but aqueous fatty acids and their sodium salts can show significant deviations from an ideal solution (Michailoudi et al., 2020; Calderón et al., 2020). The present results suggest that the compressed film model is sensitive to the fitting conditions of the model parameters. The underlying assumption that the model parameters are compound-specific physical constants across varying surfactant mass fractions and dry particle sizes may not hold true for real droplet solutions.

The σ_c predicted for the monolayer, Gibbs, partial organic film, and bulk solution models in Fig. 2 decreases with increasing w_p,sft. For the monolayer, Gibbs, and partial organic film models, the mutual variations in σ_c are within 4.7, 11.8, 20.4, and 26.9 mN m⁻¹ of σ_w for particles with $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$, 0.5, 0.8, and 0.95, respectively (Table 3). For the monolayer and partial organic film models, σ_c shows large depressions from σ_w, in agreement with previous applications of the models (Ovadnevaite et al., 2017; Malila and Prisle, 2018; Lin et al., 2018, 2020; Vepsäläinen et al., 2022). For sodium myristate particles in Fig. 2, the Gibbs model predicts σ_c close to σ_w and σ_c=σ_w for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$–0.95 with the simple partitioning, compressed film, and classical Köhler models. The small or absent surface tension depression predicted with the Gibbs and compressed film models for NaC₁₄ is in agreement with other surface active aerosols (Prisle et al., 2008, 2010; Ruehl et al., 2016; Forestieri et al., 2018; Lin et al., 2018; Prisle, 2021; Vepsäläinen et al., 2022). The Gibbs model has been observed to predict significantly higher σ_c than the monolayer model for strongly surface active SDS–NaCl and moderately surface active ragweed pollenkitt–ammonium sulfate aerosol, as well as somewhat lower σ_c than the monolayer model for even more moderately surface active succinic acid–NaCl aerosol (Lin et al., 2018). The droplet σ_c for the bulk solution model shows a 27.8 mN m⁻¹ reduction from σ_w for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$ (Fig. 2a) and a 47.7 mN m⁻¹ reduction from σ_w for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.5}$–0.95 (Fig. 2b–d), where σ_c=σ_CMC.

Droplet surface tension impacts the conditions for growth and activation via the Kelvin term of the Köhler Eq. (1). The importance of surface tension in cloud droplet formation has been a topic of debate for decades (e.g., Li et al., 1998; Sorjamaa et al., 2004; Booth et al., 2009; Prisle et al., 2008, 2010; Nozière et al., 2014; Gérard et al., 2016; Ruehl et al., 2016; Ovadnevaite et al., 2017; Davies et al., 2019; Lowe et al., 2019; Bzdek et al., 2020). Here, we observe that different models predict diverging droplet surface tensions for strongly surface active aerosol, similarly to predictions for moderately surface active aerosol by Vepsäläinen et al. (2022). The σ_c of the monolayer and bulk solution models for strongly surface active aerosol is significantly lower than for moderately surface active aerosol, while the other partitioning models predict similar σ_c for both strongly and moderately surface active aerosol. The predicted droplet surface tensions reflect the underlying assumptions of the different models (Table 2), which do not account for all surfactant properties to the same degree. This suggests that varying conclusions about the importance of surface tension in cloud droplet activation could partly be due to differences between the various surface activity models applied. These model differences show that caution should be taken when interpreting the role of surface tension based on the predictions of any given model.

3.3 Bulk–surface partitioning of surfactant

Figure 3 shows the surface partitioning factors, in terms of the fraction of the total amount of NaC₁₄ that is partitioned to the surface ($n_{\mathrm{sft}}^{\mathrm{S}}/n_{\mathrm{sft}}^{\mathrm{T}}$), for growing droplets along the Köhler curves in Fig. 1. Both the simple partitioning and partial organic film models assume that all surfactant content is partitioned to the droplet surface throughout the droplet growth, such that $n_{\mathrm{sft}}^{\mathrm{S}}/n_{\mathrm{sft}}^{\mathrm{T}}=\mathrm{1}$. The bulk solution and classical Köhler models do not consider bulk–surface partitioning, and therefore $n_{\mathrm{sft}}^{\mathrm{S}}/n_{\mathrm{sft}}^{\mathrm{T}}=\mathrm{0}$. The constant partitioning factors for these models are not shown in Fig. 3.

Figure 3 shows that the compressed film model predicts the strongest bulk–surface partitioning of NaC₁₄ in growing droplets, followed by the Gibbs and monolayer models. For these models, the predicted partitioning factors are close, or equal, to unity throughout the respective Köhler curves, but the predicted droplet activation properties can vary significantly between the models (Table 3). For moderately surface active malonic, succinic, and glutaric acid particles, we previously found that the compressed film model predicted considerably larger partitioning factors than the monolayer and Gibbs models, whereas the different models could still predict similar droplet activation properties (Vepsäläinen et al., 2022). The strong partitioning predicted (or assumed) with the different partitioning models for NaC₁₄ means that inter-model differences in predicted droplet activation in Fig. 1 are mainly caused by differences in the droplet surface tension (Fig. 2). Surface activity could also have important implications for a variety of processes related to cloud microphysics, including aqueous droplet chemistry (Prisle, 2021). Chemical reactions in aqueous aerosols can be accelerated relative to macroscopic solutions (Marsh et al., 2019). Strong partitioning of surface-active species and the simultaneous depletion of the droplet bulk phase can affect the chemical environment in the droplet, in particular in the submicron range (Prisle et al., 2010), changing possible reaction pathways and rates in the surface (Prisle et al., 2012b; Öhrwall et al., 2015; Werner et al., 2018) and bulk (Prisle, 2021) phases of the droplet. Interfacial reactivity could be pronounced due to the large surface-area-to-volume ratios of finite volume droplets (Prisle et al., 2012b; Bzdek et al., 2020; Prisle, 2021).

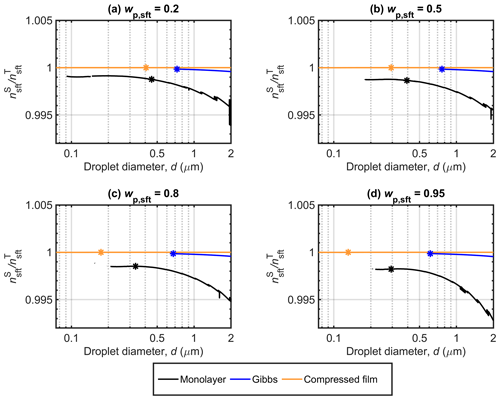
Figure 3 Surface partitioning factors ($n_{\mathrm{sft}}^{\mathrm{S}}/n_{\mathrm{sft}}^{\mathrm{T}}$) predicted with the monolayer, Gibbs, and compressed film bulk–surface partitioning models along the Köhler curves for NaC₁₄ particles with D_p=50 nm at different NaC₁₄ mass fractions (w_p,sft). The critical points of the corresponding Köhler curves in Fig. 1 are also marked.

Table 3 Critical droplet diameters (d_c), supersaturations (SS_c), and surface tensions (σ_c) predicted with the different models for NaC₁₄–NaCl particles with D_p=50 nm at 298.15 K. The simple partitioning, compressed film, and classical Köhler models all predict that σ_c = σ_w = 72.0 mN m⁻¹ for each w_p,sft, which is not shown in the table.

3.4 Relative change in the cloud droplet number concentration

Figure 4 shows the relative change in cloud droplet number concentration predicted with the different bulk–surface partitioning models and the bulk solution model to account for aerosol surface activity, with respect to predictions of the classical Köhler model (ΔNN⁻¹, Eq. 11), for NaC₁₄ particles in the size range D_p=50–200 nm. Implementations corresponding to the classical Köhler model are used in most larger-scale simulations, with a few exceptions (e.g., Prisle et al., 2012a; Lowe et al., 2019). The magnitude of ΔNN⁻¹ therefore highlights how variations in critical supersaturations predicted with the different surface activity models may translate into uncertainty in estimates of atmospheric cloud droplet number concentrations based on Köhler theory.

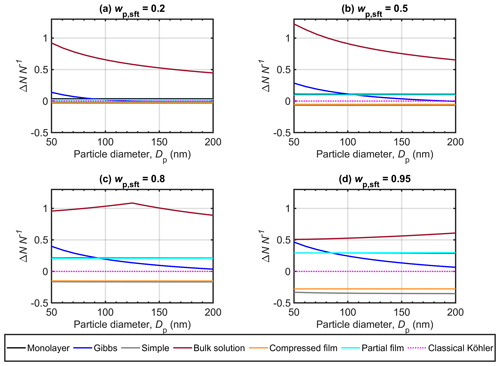
Figure 4 Relative change in cloud droplet number concentration (ΔNN⁻¹) predicted the different surface activity models, for D_p=50–200 nm at different NaC₁₄ mass fractions (w_p,sft) in the particles. The relative change is calculated with respect to predictions of the classical Köhler model.

In Fig. 4, the monolayer, simple partitioning, compressed film, and partial film models all show very little variation in ΔNN⁻¹ with particle size D_p for each w_p,sft. The differences in ΔNN⁻¹ between the surface activity model predictions increase with w_p,sft, as also seen with the SS_c in Fig. 1. For $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$, the monolayer, simple partitioning, compressed film, and partial film models each yield ΔNN⁻¹ within ±5 %. For $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.95}$, we predict 29 % more cloud droplets with the monolayer and partial film models than with the classical Köhler model, on average over the investigated particle size range. This is in reasonable agreement with results of Lowe et al. (2019), who used a partial film partitioning model combined with a cloud parcel model to predict an increase of 13 % in cloud droplet number concentrations for marine and an increase of 26 % for continental boreal aerosol populations compared to classical Köhler predictions. For $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.95}$, we however predict a 28 % decrease in cloud droplet number concentrations with the compressed film model and a decrease of 35 % with the simple model compared to the classical Köhler model. This shows that, for these strongly surface active particles, even the direction of the effects of surface activity as significant positive or negative ΔNN⁻¹ can vary with the choice of partitioning model.

With the Gibbs model, we here predict ΔNN⁻¹ of 2–21 % averaged over the particle size range for the surfactant fractions $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$–0.95. The bulk solution model predicts the lowest SS_c for the cases studied, resulting in the largest positive ΔNN⁻¹ of all the surface activity models. This is similar to the results of Prisle et al. (2012a), who implemented surfactant effects in the global circulation model (GCM) ECHAM5.5-HAM2. The bulk solution model here yields ΔNN⁻¹ which decreases (for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.2}$ and 0.5), increases (for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.95}$), or changes non-monotonically (for $w_{\mathrm{p},\mathrm{sft}}=\mathrm{0.8}$) with increasing D_p. This variation is due to the constraint on the droplet water activity imposed by the CMC, as well as the critical point of droplet activation moving between the two maxima of the Köhler curve, located at droplet sizes before and after the droplet surface tension increases from the minimum value σ_CMC (see Figs. 1 and 2). On overage over the investigated particle size range, the bulk solution model predicts ΔNN⁻¹ of 55 %–99 % for particles with different surfactant mass fractions. However, these very large ΔNN⁻¹ should be considered with some caution, as large relative changes in SS_c may conflict with the assumption of simple exponential dependence in Eq. (11). The bulk–surface partitioning models are considered to give more comprehensive and realistic representations of the droplet activation behavior, whereas the bulk solution model has been included in this comparison mainly for reference.

Results in Fig. 4 support previous estimates, showing that the surface activity of organic aerosol and its representation in calculations of cloud droplet activation have the potential to significantly influence global-scale predictions, at least for specific regions (Prisle et al., 2012a). Increased cloud droplet number concentrations would ultimately have a negative radiative effect and, therefore, a cooling effect on the climate. Decreased cloud droplet number concentrations would conversely lead to a warming effect. Facchini et al. (1999) estimated that a 20 % increase in the cloud droplet number concentration from consideration of aerosol surface activity would correspond to a change in cloud radiative forcing of −1 Wm⁻², in good agreement with the later full GCM predictions of Prisle et al. (2012a) for similar conditions. In the present work, the variation in ΔNN⁻¹ between the different model predictions for particles with high NaC₁₄ mass fractions suggests that the representation of surfactant effects could translate to significant uncertainty in larger-scale predictions of cloud radiative effects for regions where strongly surface active aerosol are prevalent. Consideration of surface activity could result in both significant warming or cooling effects, compared to the conventional predictions of a classical Köhler model, depending on the specific partitioning model used. Therefore, conclusions regarding bulk–surface partitioning effects on cloud droplet number concentrations and aerosol–cloud–climate effects based on any one model should be considered and extrapolated with caution.

4 Conclusions

We have applied five bulk–surface partitioning models (Prisle et al., 2010, 2011; Ruehl et al., 2016; Ovadnevaite et al., 2017; Malila and Prisle, 2018) currently in use in the atmospheric aerosol research community, together with a general bulk solution model and a classical Köhler model, in predictive Köhler modeling of droplet growth and activation for particles comprising strong surfactants sodium myristate or myristic acid mixed with NaCl across a range of particle compositions.

The different models can predict significantly different droplet activation properties (SS_c, d_c, and σ_c) for the same strongly surface active particles. Differences between the predictions of the bulk–surface partitioning models increase with the surfactant mass fraction in the particles. Each partitioning model predicts or assumes strong partitioning of surfactant to the droplet surface, leading to a small overall Raoult effect and small variations in the droplet bulk water activity between the different partitioning model predictions. Predicted differences in the critical droplet properties for the investigated strongly surface active aerosols mainly stem from the droplet surface tension and ensuing Kelvin effect. Our results further show that cloud droplet number concentrations predicted for strongly surface active aerosol can vary significantly between the different models. Relative changes in cloud droplet number concentrations with respect to a classical Köhler model range from −35 % to 29 % between the five partitioning models, corresponding to both considerable warming and cooling climate effects. These differences represent a significant uncertainty in estimating the cloud radiative effects for regions where strongly surface active aerosol are prevalent. Therefore, conclusions regarding aerosol–cloud–climate effects of aerosol surface activity and bulk–surface partitioning based on any one surface activity model should not be immediately generalized.

Comparison of inter-model variation for strongly and moderately (Vepsäläinen et al., 2022) surface active aerosol shows how the mutual agreement between the different surface activity and partitioning models varies with aerosol surface activity. Therefore, conclusions about the robustness of our understanding of the effects of aerosol surface activity, as captured by the inter-model variation, do not immediately translate between different surface active aerosol systems. This emphasizes the need to validate aerosol surface activity models for a range of surface active aerosol types and ambient conditions before establishing their broad applicability in atmospheric modeling. Generalization of Köhler predictions for only a few surface active aerosol systems and conditions could introduce significant bias in modeling larger-scale atmospheric processes.