the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantifying urban, industrial, and background changes in NO2 during the COVID-19 lockdown period based on TROPOMI satellite observations
Vitali Fioletov
Chris A. McLinden
Debora Griffin
Nickolay Krotkov
Henk Eskes
The COVID-19 lockdown had a large impact on anthropogenic emissions of air pollutants and particularly on nitrogen dioxide (NO2). While the overall NO2 decline over some large cities is well-established, understanding the details remains a challenge since multiple source categories contribute. In this study, a new method of isolation of three components (background NO2, NO2 from urban sources, and NO2 from industrial point sources) is applied to estimate the impact of the COVID-19 lockdown on each of them. The approach is based on fitting satellite data by a statistical model with empirical plume dispersion functions driven by a meteorological reanalysis. Population density and surface elevation data as well as coordinates of industrial sources were used in the analysis. The tropospheric NO2 vertical column density (VCD) values measured by the Tropospheric Monitoring Instrument (TROPOMI) on board the Sentinel-5 Precursor over 261 urban areas for the period from 16 March to 15 June 2020 were compared with the average VCD values for the same period in 2018 and 2019. While the background NO2 component remained almost unchanged, the urban NO2 component declined by −18 % to −28 % over most regions. India, South America, and a part of Europe (particularly, Italy, France, and Spain) demonstrated a −40 % to −50 % urban emission decline. In contrast, the decline over urban areas in China, where the lockdown was over during the analysed period, was, on average, only %. Emissions from large industrial sources in the analysed urban areas varied greatly from region to region from % for China to % for India. Estimated changes in urban emissions are correlated with changes in Google mobility data (the correlation coefficient is 0.62) confirming that changes in traffic were one of the key elements in the decline in urban NO2 emissions. No correlation was found between changes in background NO2 and Google mobility data. On the global scale, the background and urban components were remarkably stable in 2018, 2019, and 2021, with averages of all analysed areas all being within ±2.5 % and suggesting that there were no substantial drifts or shifts in TROPOMI data. The 2020 data are clearly an outlier: in 2020, the mean background component for all analysed areas (without China) was % and the mean urban component was % or 20σ below the baseline level from the other years.
- Article
(15433 KB) - Full-text XML
-
Supplement
(699 KB) - BibTeX
- EndNote
Nitrogen oxides are air pollutants that originate from various anthropogenic (fuel combustion) and natural (e.g. biomass burning, lightning) sources and whose emissions are regulated in many countries. Satellite measurements of one component of NOx, NO2, have a long history. In the stratosphere, the SAGE (Stratospheric Aerosol and Gas Experiment) instrument provided NO2 profile information through the stratosphere beginning in the mid-1980s (Cunnold et al., 1991). Satellite observations of tropospheric NO2 columns are more recent and began with the nadir-viewing GOME (Global Ozone Monitoring Experiment) in 1996 (Martin et al., 2002) with several successors, chief among these OMI (Ozone Monitoring Instrument) (Duncan et al., 2015; Krotkov et al., 2016; Lamsal et al., 2015, 2021; Levelt et al., 2018) and, most recently, TROPOMI (Tropospheric Monitoring Instrument) (van Geffen et al., 2020; Veefkind et al., 2012). Collectively these instruments have been used to better understand NO2 sources, sinks, distributions, and trends (Beirle et al., 2011, 2019; Liu et al., 2016; Lorente et al., 2019; Lu et al., 2015; Martin et al., 2002; McLinden et al., 2012; Stavrakou et al., 2020; Vîrghileanu et al., 2020) .
One primary NO2 characteristic provided by satellites is tropospheric vertical column density (VCD), a geophysical quantity representing the total number of molecules or total mass per unit of area in the troposphere. The main features of the tropospheric NO2 VCD distribution are well established. Due to its relatively short lifetime, a few hours within a plume during the day, NO2 is elevated near sources such as urban areas (Beirle et al., 2019; Lorente et al., 2019; Lu et al., 2015) and industrial locations such as power plants and oil refineries (Liu et al., 2016; McLinden et al., 2012). Over high mountains, NO2 VCDs are relatively small as the troposphere there is “thinner” with fewer emission sources. Ship tracks and major highways also create elevated NO2 values on satellite maps (Beirle et al., 2004; Georgoulias et al., 2020; Liu et al., 2020a; Richter et al., 2004).
The COVID-19 lockdown had an impact on tropospheric NO2 levels, first in China and then worldwide (Bao and Zhang, 2020; Bauwens et al., 2020; Ding et al., 2020; Gkatzelis et al., 2021; Kanniah et al., 2020; Keller et al., 2021; Koukouli et al., 2021; Liu et al., 2020a; Vadrevu et al., 2020; Vîrghileanu et al., 2020; Zhang et al., 2021). It was demonstrated that NO2 surface concentrations and VCDs significantly declined in the US and Canada after mid-March 2020 (Bauwens et al., 2020; Goldberg et al., 2020; Griffin et al., 2020). A decline of about −20 % to −25 % was observed in the US megacities as well as over some rural areas. A decline was also reported over Europe (e.g. Bar et al., 2021; Barré et al., 2021), India (Misra et al., 2021; Hassan et al., 2021), Pakistan (Ali et al., 2021; Mehmood et al., 2021), Brazil (Dantas et al., 2020; Siciliano et al., 2020), and other parts of the world (Ass et al., 2020; Aydın et al., 2020; Fu et al., 2020) as also discussed in overview papers (Gkatzelis et al., 2021; Levelt et al., 2021).
The impact of the lockdown on tropospheric NO2 VCD from satellite data was often estimated by comparing mean or median values over a certain area for the periods before and after the lockdown (e.g. Qu, et al., 2021; Barré et al., 2021; Mehmood et al., 2021; Hassan et al., 2021; see also online tool https://so2.gsfc.nasa.gov/no2/no2_index.html (last access: 18 December 2021) or as the values weighted according to the population density (Sannigrahi et al., 2021). This makes the results dependent on the area analysed and sensitive to the wind speed (Goldberg et al., 2020). There is also free-tropospheric NO2 that could mask the lockdown-related changes in anthropogenic emissions (Silvern et al., 2019). Moreover, meteorological variability was also a contributing factor to the differences (e.g. Barré et al., 2021; Griffin et al., 2020), although some studies found that its impact may not be very large (Bar et al., 2021).
An alternative approach is based on an estimation of NO2 emissions using satellite data and then comparing the emission estimates before and after the lockdown started (Lange et al., 2022). There are several methods to estimate the emissions (Streets et al., 2013). Methods such as inverse modelling (Konovalov et al., 2006; Mijling and van der A, 2012) and, more recently, flux divergence (Beirle et al., 2019, 2021) are used for such a purpose. One common technique is based on a rotation of satellite NO2 pixels around the source so the NO2 data would appear if the wind is from one common direction, allowing many overpasses to be combined. These rotated data are then integrated in the cross-wind direction, and then the results are fitted with an exponentially modified Gaussian (EMG) function (Lange et al., 2022; Pommier et al., 2013). The two unknown parameters, the emission strength and lifetime are estimated directly from the fit in one-dimensional space. The method works well for isolated stationary point sources and with steady winds (Beirle et al., 2021) but may not work in the areas where emissions from closely located multiple sources are mixed with urban emissions. Another approach employs a two-dimensional EMG plume function of the wind speed (Dammers et al., 2019; Fioletov et al., 2015; McLinden et al., 2020). The plume function depends on three parameters: the plume width, lifetime, and emission strengths. While all three parameters can be estimated from the fit, the algorithm works better if the plume width and lifetime are estimated in advance and then prescribed in the fit to estimate the emission strength. This algorithm was further improved to account for multiple sources or areas (Fioletov et al., 2017).
A different approach was used in this study. A statistical model was used to describe the TROPOMI NO2 data over areas (roughly, 330 km×330 km at 42∘ N) around major cities and isolate three components related to (1) plumes from urban sources, (2) plumes from industrial point sources, and (3) background NO2. The parameters of the statistical model link the satellite NO2 values to proxies related to elevation and population density as well as to locations of large industrial point sources. Then the three components in 2020 were compared to their values in 2018–2019 to study the COVID-19 lockdown impact. The parameters have simple physical interpretation such as point source or area emission rates and the background NO2 distribution. As the model only has a few parameters and their estimates are based on several hundreds of TROPOMI pixels in each area, statistical uncertainties of the parameter estimates are very small. The variability of urban, industrial, and background NO2 components due to meteorological or observational conditions was studied by comparing the estimates of the three components for 2018, 2019, and 2021 that were not affected by lockdowns.
This algorithm is based on a multi-source plume dispersion function fitting approach developed for sulfur dioxide (SO2) point and area sources (Fioletov et al., 2017; McLinden et al., 2020). It assumes that each source produces a plume that depends on unknown emission strength and these emission strengths are derived from the best fit to the satellite data. The algorithm was adapted for NO2 where emissions from urban areas, which tend to be dominated by residential and mobile emission sources, were often a major source sector. Since the approach is based on statistical methods it was necessary to have a sufficiently long data set to reduce the impact of natural factors such as meteorology that can cause NO2 VCD differences of ∼15 % over monthly timescales (Goldberg et al., 2020; Levelt et al., 2021). We use 3-month periods, with the averages for the period from 16 March to 15 June 2020, compared to those in 2018 and 2019 for the areas around 261 major cities worldwide. As the study is focused on relative NO2 changes due to the lockdown, possible systematic errors related to the TROPOMI retrievals (Verhoelst et al., 2021) and the algorithm fitting parameters (Fioletov et al., 2016) play a much smaller role than in the case of absolute emission estimates.
This paper is organized as follows: Sect. 2 describes various data sets used in the study; the analysis algorithm is discussed in Sect. 3. In Sect. 4, the COVID-19 lockdown impact is studied. The USA and Canada are analysed in detail to illustrate the method, then statistics for Europe are provided, and finally results for the entire world are presented. Discussion and conclusions are given in Sect. 5. The algorithm is described in Appendix A. Additional technical information and statistics are given in the Supplement.
2.1 TROPOMI NO2 VCD data
TROPOMI, onboard the European Space Agency (ESA) and EU Copernicus Sentinel-5 Precursor (S5p) satellite, was launched on 13 October 2017 (van Geffen et al., 2020; Veefkind et al., 2012). The satellite follows a Sun-synchronous, low-Earth (825 km) orbit with a daily Equator crossing time of approximately 13:30 local solar time (van Geffen et al., 2019). At nadir, TROPOMI pixel sizes were 3.5 km×7 km at the beginning of operation and were reduced to 3.5 km×5.6 km on 6 August 2019, and the swath width is 2600 km. TROPOMI NO2 VCD values represent the total number of molecules or total mass per unit area below the tropopause and are often given in molecules or moles (1 mole is equal to 6.022×1023 molecules) per square metre or centimetre as well as in Dobson units (DU, 1 DU molec. cm−2). In this study, level-2 TROPOMI data available from the Copernicus open-data access hub (https://s5phub.copernicus.eu, last access: 5 August 2021) were used. The reprocessed (RPRO) data version V1.2.2 was used for 2018, and offline-mode (OFFL) data of version V1.2.2 to version V1.3.2 were used for 2019–2020. The difference between these two versions is relatively minor, and therefore the combination is suitable to analyse NO2 changes during the period studied in this paper. The 2021 data (V1.4.0) were used only to estimate the interannual variability. The standard TROPOMI product, tropospheric vertical columns, based on air mass factors (AMFs) calculated using the vertical profile of NO2 from the TM5-MP model at resolution (Williams et al., 2017) was used. In the analysis, we use only data for which the quality assurance value is higher than 0.75 (van Geffen et al., 2018). Also, satellite pixels with snow on the ground, a solar zenith angle greater than 75∘ and with a cloud radiance fraction above 0.3 were excluded from the analysis.
The specified random uncertainty of a single TROPOMI tropospheric NO2 VCD measurement is 7×1014 molec. cm−2 (or 0.026 DU) (ESA EOP-GMQ, 2017). Tack et al. (2021) estimated this uncertainty and found it to be molec. cm−2. There is some evidence that TROPOMI NO2 is biased low by 14 %–40 % over polluted areas due to a limited spatial resolution of the model used to calculate the AMFs (Judd et al., 2020; Verhoelst et al., 2021; Zhao et al., 2020). This bias can be reduced by recalculation of AMFs with higher spatial resolution (Griffin et al., 2020; Ialongo et al., 2020; Zhao et al., 2020; Tack et al., 2021). In addition, the cloud pressures derived from the TROPOMI data have a positive bias in versions 1.2.x and 1.3.x, which has an impact on the NO2 tropospheric column retrieved (van Geffen et al., 2021). Both effects (biases) are expected to scale roughly linearly with the column amount (van Geffen et al., 2021), consistent with the validation results (Verhoelst et al., 2021). Therefore, the relative differences between 2018–2019 and 2020 data studied here should not be affected by these effects.
The TROPOMI NO2 distribution over the US and southern Canada is shown in Fig. 1. The data are stratified by the wind speed to highlight some of the features of the NO2 VCD distribution. NO2 values are elevated over highly populated areas, as is particularly evident from the maps for low wind speed where the NO2 remains close to the source before chemical or physical removal. Figure 1 also illustrates the fact that TROPOMI NO2 values over megacities are higher under calm winds and lower under high winds (e.g. Goldberg et al., 2020). Elevated NO2 values are also observed over power plants and mining operations (Goldberg et al., 2021). The NO2 VCD distribution also depends on local topography (Kim et al., 2021). For example, smaller values over elevated areas such as the Rocky Mountains and Appalachians and higher values over valleys such the California Central Valley are evident from the map. There is also some background NO2 that can be seen even over remote areas with no major anthropogenic sources: NO2 VCDs are not negligible (about 5×1014 cm−2) over vast remote areas such as national forests in Montana or Algonquin Provincial Park in Ontario as well as over the oceans.
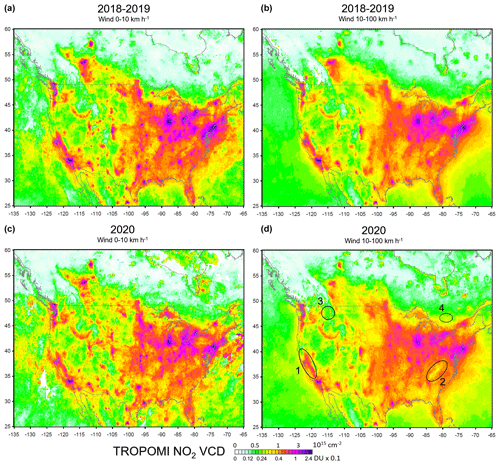
Figure 1Mean TROPOMI NO2 VCDs over the US and southern Canada for 16 March–15 June, in (a, b) 2018–2019 and (c, d) 2020. The main features of the NO2 distribution such as elevated NO2 values over large cities, industrial sources, and in the valleys such as the California Central Valley (1) and lower values over the mountains such as the Appalachians (2) are evident from the plot. Note that NO2 VCDs are not negligible (about 5×1014 cm−2) even over vast remote areas such as national forests in Montana (3) or Algonquin Provincial Park in Ontario (4) as well as the oceans. The maps are based on level-2 data gridded on a grid grouped by the wind speed: (a, c) less than 10 km h−1 and (b, d) more than 10 km h−1.
As TROPOMI has only one daily overpass at most locations, diurnal NO2 variations may affect emission estimates. Measurements from the ground demonstrate that, unlike surface concentrations, the diurnal variations in NO2 VCDs are relatively small, particularly in spring (Herman et al., 2009; Chong et al., 2018). However, since nighttime NO2 information is not available from satellite, we should say that all the results presented here are limited to daytime emissions only.
2.2 Wind data
As in several previous studies (Fioletov et al., 2015; McLinden et al., 2020; Zoogman et al., 2016) the plume dispersion function (discussed below in Sect. 3) is based on the wind speed and direction obtained from the meteorological reanalysis. For each satellite pixel, wind speed and direction were calculated based on European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 reanalysis data (C3S, 2017; Dee et al., 2011), which were merged with TROPOMI measurements. The wind profile data have 1 h temporal resolution and are available on a 0.25∘ horizontal grid. U and V (west–east and south–north respectively) wind-speed components were then linearly interpolated to the location of the centre of each TROPOMI pixel and to overpass time. The ERA5 wind components at 1000, 950, and 900 hPa were averaged to obtain the wind value used (that approximately corresponds to the mean winds between 0 and 1 km). This interval was comparable to the wind data used in other similar studies: Beirle et al. (2019) used data at 450 m, while Lange et al. (2022) used data from 100 m. The results are not very sensitive to the wind profile within this range as was previously investigated by Beirle et al. (2011) because the boundary layer wind is relatively constant, except close to the surface. Note that in ERA5 reanalysis in pressure coordinates, when the surface pressure is smaller than that at a given level (e.g. 1000 hPa), the values will simply duplicate the winds at the lowest pressure available.
2.3 Population density data
The Gridded Population of the World (GPW) data set (SEDAC, 2017) was used as a proxy for the urban component. GPW data are on a 0.042∘ (2.5 arcmin) grid and consist of estimates of human population density (number of persons per square kilometre) based on counts consistent with national censuses and population registers. When lower-resolution data were required, they were obtained by averaging the original data within the new grid cells. Information about large city location and population that was used to select cities for the analysis was obtained from the World Cities Database available from https://simplemaps.com/data/world-cities (last access: 10 May 2021).
2.4 Industrial point source locations
The algorithm of this study requires the coordinates of industrial point sources as an input. In addition, emission data from the US and Canada are used to verify the emissions estimated from TROPOMI data. For the US, 2018–2020 point source NOx emissions from the U.S. Environmental Protection Agency (EPA) National Emissions Inventory (NEI) (EPA, 2020) based on a continuous emission monitoring system (CEMS) are used. Note that the CEMS database is based on real emission measurements reported with 1 h resolution that were then averaged over the analysed period. This database includes most of the sources, including all large power plants. For sources that are not available from CEMS (e.g. oil refineries), emissions from the eGRID database (https://www.epa.gov/egrid/download-data, last access: 5 August 2021) for 2018 and 2019 were used. They are reported as annual emission estimates, and we assume that the emission rates are the same throughout the year. This database includes emissions from oil refineries and cement factories that are often not available from CEMS. Finally, US airport emissions are obtained from the 2017 NEI version released in January 2021 (https://www.epa.gov/air-emissions-inventories/2017-national-emissions-inventory-nei-data, last access: 5 August 2021). For Canada, annual emissions from the Canadian National Pollutant Release Inventory (NPRI, 2020) are used. Only Canadian and US sources with annual emissions greater than 0.5 kt yr−1 of NOx were selected and used in this study.
Coordinates of the European industrial point sources were obtained from the European Pollutant Release and Transfer Register (https://ec.europa.eu/environment/industry/stationary/eper/legislation.htm, last access: 5 August 2021) for 2007–2017 (last access: 2 March 2021), and those that emitted more than 0.5 kt yr−1 of NOx are included in the analysis. The world power plant database (https://globalenergymonitor.org/projects/global-coal-plant-tracker/, last access: 5 August 2021) was used to find locations of power plants for the global analysis. Missing sources were added based on the analysis of the NO2 residuals maps (see Sect. 3) and then confirmed using satellite imaginary as was previously done in other studies (e.g. McLinden et al., 2016; Fioletov et al., 2016; Dammers et al., 2019; Beirle et al., 2021). Satellite images from Google (https://www.google.com/maps, last access: 5 August 2021), Microsoft Bing (https://www.bing.com/maps, last access: 5 August 2021), and Sentinel 2 (https://apps.sentinel-hub.com/eo-browser/, last access: 5 August 2021) maps were used for this purpose. Multiple image sources were used since some of the images from Google maps are not always up to date and may not show recently built factories.
2.5 Elevation data
Elevation data were one of the proxies used in the statistical model. Elevation data used in this study are from the 2-Minute Gridded Global Relief Data (ETOPO2v2) database (NOAA, 2006). When lower-resolution data were required, they were obtained by averaging the original data within the new grid cells.
2.6 Google mobility data and analysed period
The lockdown periods due to the COVID restrictions varied from country to country, but in most countries, they started in the second half of March 2020. In the analysed Canadian cities, the lockdown started between 12 and 17 March. In the US, it started between 18–19 March (Atlanta, Los Angeles) and 2 April (Houston). In Europe, the lockdown started as early as on 8 March (Milan), but for most of the cities the lockdown was introduced after 14 March. The second half of March is also the time when the lockdown measures started in many other cities around the world including Auckland, Baghdad, Buenos Aires, Johannesburg, Lagos, Manila, New Delhi, Sydney, and many others (Levelt et al., 2021, their Appendix B).
It is more difficult to determine the time of return to normal activities because the restrictions were often lifted in phases. For example, in the US, a “stay at home” order was lifted between 30 April (Texas) and 11 June (New Hampshire). Moreover, there was no formal lockdown in some countries (Belarus, Japan, South Korea, Sweden, Taiwan), but a decline in public activities can be seen even in these countries as well. For example, there was an up to 40 % decline in road transport emissions in Sweden even in the absence of any formal lockdowns (Guevara et al., 2021). For this reason, we use mobility data as a proxy instead of the lockdown dates to select the analysed period.
The Google Community Mobility Report data (available from https://www.google.com/covid19/mobility/, last access: 1 March 2021) were used to determine a common time period for our analysis. These data represent the changes in the number of people at locations of various types compared to a baseline level. A baseline day represents a normal value for that day of the week. The baseline day is the median value from the 5-week period 3 January–6 February 2020. These mobility data can be used as a proxy for urban traffic (e.g. Guevara et al., 2021) and are known to be correlated with urban NOx emissions (Venter et al., 2020; Bar et al., 2021; Misra et al., 2021). In this study, they were compared to urban and background NO2 levels in different countries. The mobility data are available for several categories. Results for mobility for “retail and recreation” presented as this category demonstrated the highest correlation with estimated urban emissions. The retail and recreation category covers visits to restaurants, cafes, shopping centres, theme parks, museums, libraries, movie theatres, and similar locations. We will refer to this category as the “Google mobility data” for brevity.
Figure 2 shows changes in Google mobility data (available as deviations relative to the baseline period) for the regions analysed in this study (see Sect. 4). During the 3-month-long period from 16 March to 15 June 2020, the mobility data were below the baseline level in all analysed regions. Note that for China, Google mobility data are not available. In China, the lockdown occurred earlier (in February), except for Wuhan, where the lockdown was lifted only on 8 April. Note that there was no formal lockdown in the Japan, South Korea, and Taiwan region, although we still see some decline in mobility data there.
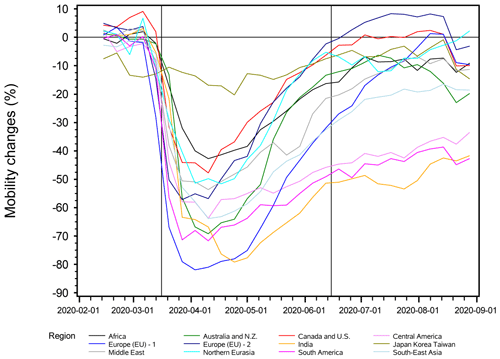
Figure 2Changes in weekly Google mobility data (for “retail and recreation” category) relative to the baseline period (3 January–6 February 2020) for 12 regions analysed in this study. The black vertical lines represent the beginning and the end of the period analysed in this study (16 March–15 June).
The technique used here is a further development of a point source emission estimation algorithm (Fioletov et al., 2015, 2016; McLinden et al., 2016; Dammers et al., 2019) that was later expanded to estimate multi-source and area-source emissions (Fioletov et al., 2017; McLinden et al., 2020). This section provides only a general description of the method. The calculation formulas are given in Appendix A. The approach used in this study is based on a linear regression model. All satellite measurements over a certain area during a certain period are linked to locations of industrial point sources as well as to population density and elevation-related proxies by a few parameters that characterize these links. Thus, information from thousands of satellite measurements is compressed into a handful of parameters and therefore their estimates can have very low statistical uncertainties. Then, satellite measurements can be reconstructed using the regression model, and the contribution of three terms of the model (industrial, urban, and background) can be studied. Such a model may not be very accurate in “predicting” values of individual satellite pixels, but we will show that it performs well when it is used to describe a 3-month mean NO2 VCD distribution over the analysed areas.
The method is adapted from the previously designed algorithm for multi-sources SO2 emission estimates (Fioletov et al., 2017) where the emissions are determined from the best fit of satellite observation by a set of plume functions (one per source) scaled by parameters of estimation representing the emission strength. Unlike SO2, where emissions are mostly generated by point sources, NO2 emissions also originate from area sources such as large cities. As shown in Fig. 1, landscape also has a major impact on the NO2 distribution. To accommodate these features, the statistical model was modified to
where α0, αp, αi, β0, β1, and β2 are the unknown regression parameters representing population-density-related proxies and emissions from individual point sources and a background with a contribution from the elevation; Ωp is the source plume function for the population-density-related distributed source (or area source); Ωi is the source plume functions for industrial point sources; H is the elevation above sea level, and the empirical scaling factor H0=1.0 km was introduced to make the exponential argument dimensionless and to account for altitudinal dependence better; and ε is the residual noise.
Equation (1) is a linear regression statistical model with unknown coefficient sets α and β. There are three main components in the model: the background term, , related to background and elevation (four fitted coefficients); the urban component term, αpΩp, related to the population density (one coefficient); and the industrial term, ΣαiΩi, which represents the contribution from industrial point sources (variable number of coefficients from zero to a few dozen). We will refer to them as background, urban, and industrial components.
The fitting was done for all satellite pixels centred within areas around large cities and collected during a 3-month period by minimization of the squares of the residuals (ε). The size of the area is based on the following considerations: the larger the area the less accurate assumptions about a linear gradient of background NO2 and constant emissions per capita are. The algorithm is based on fitting plumes. For typical plume characteristics (discussed below), the size of fitting area should be long, in the order of 100 km, to have enough data for the fit. Finally, the area should be large enough to avoid a correlation between the elevation and population density proxies.
As in Fioletov et al. (2017), the plume from an industrial point source i is described by a plume function where θ and φ are the satellite pixel coordinates; ω and s are the wind direction and speed for that pixel; and θi and φi are the source coordinates. An unknown parameter (αi) represents the total NO2 mass emitted from the source i. The emission rate for source i can be expressed as , where τ is a prescribed NO2 lifetime (or, more accurately, decay time, but we use the term “lifetime” because it is more common). Note that τ is different from the chemical lifetime (de Foy et al., 2015). Once the emission rate is established, it can be used to reconstruct how the distribution of NO2 emitted by that source would be seen by a satellite, i.e. to estimate the industrial component in satellite data. We expressed emission rates in kilotonnes per year in this study to make it easier to compare with the rates available from emission inventories. However, all emission calculations here are done for a 3-month period (from 16 March to 15 June).
The plume functions Ω are EMG functions that are commonly used to approximate plumes of VCDs of trace gases such as NO2, SO2, and ammonia (Beirle et al., 2011, 2014; Dammers et al., 2019; Fioletov et al., 2017, 2015; de Foy et al., 2015; Liu et al., 2016; McLinden et al., 2020). Similar in concept to a Gaussian plume function, they also take into account the finite physical size of the source and the spatial resolution of the satellite instrument being utilized. The lifetime τ reflects the rate at which NO2 is removed from the plume due to chemical conversion or physical removal such as deposition; it depends on several factors such as season and NO2 concentration. It is about 2–6 h in summer and longer in winter (de Foy et al., 2014; Liu et al., 2016). Moreover, for some sources, the lifetime may change over time (Laughner and Cohen, 2019) as NO2 concentration declines, although other studies suggest that such changes are minor (Stavrakou et al., 2020). Recent TROPOMI-based estimates show that a typical lifetime in urban areas is between 2 and 5 h in spring and autumn with shorter lifetimes at low latitudes (Lange et al., 2022). While the lifetime has a large impact on the emission estimates, relative changes are less sensitive to it. In addition to τ, the shape of the EMG function depends on the prescribed plume width (w), which depends on the size of the source and the size of satellite pixel. The value of w=8 km for plume width was used in this study for TROPOMI along with a constant value of τ=3.3 h. These values are based on a sensitivity study where TROPOMI data over Canada and the US were fitted by plume functions with various combinations of w and τ. The switch from 7 to 5.6 km along-track resolution in 2019 might have some impact on the optimal plume width, but the sensitivity analysis shows that small changes in w only have a minor impact on the results. We estimated that, for the urban component, on average, a 1 h deviation from the τ value used (3.33 h) or a 2 km variation in w changes the differences between 2020 and 2018–2019 values only by about 1 %.
Unlike many previous studies (Beirle et al., 2011; Fioletov et al., 2016; Lange et al., 2022) where the background offset was presumed to be constant and estimated from, for example, upwind NO2 data, we included a special term that is responsible for it. In Eq. (1), the term is assumed to be declining exponentially with elevation; i.e. within the analysed area, the higher the elevation is the lower the background tropospheric NO2 VCD is. It was also assumed that this contribution from elevation depends on geographical coordinates only and not on the winds. Even in the absence of any sources, there could be some gradient in tropospheric NO2 over the analysed area, as for example over some regions in northern Canada or along the east coast of the US (Fig. 1). To account for such gradients, the linear term , where θ0 and φ0 are the coordinates of the centre of the analysed area, was added. In other words, it was assumed that there is a linear gradient of background NO2 within the analysed area and NO2 VCD declines exponentially with height over elevated regions. Finally, α0 was added to the model to account for remaining free-tropospheric NO2 at high elevations where is very close to 0. Its presence gives a better agreement of the fitting results with the satellite data for areas with a high range of elevations. Since this term is part of the statistical model, all parameters α0, β0, β1, and β2 are estimated from the fitting. Once they are estimated, the term can be calculated for any place within the analysed area that gives a “background” value for that location that depends on the coordinates and elevation only. For simplicity, we will refer to the term discussed in this paragraph as the background component.
Finally, the apΩp term represents the emission contribution from factors related to urban activity. Such emissions can be estimated by establishing a regular grid and then estimating emissions for each grid point as was previously done for SO2 (Fioletov et al., 2017; McLinden et al., 2020). If, for example, we use a grid (i.e. 336 (16×21) grid cells) within the analysed area, this would mean that we need to add 336 unknown coefficients to Eq. (1). It would make the coefficient estimates less robust and prevent us from estimating emissions from individual industrial point sources because their plume functions would be highly correlated with the plume functions of the neighbouring grid cells. Instead, we assumed that emissions from each grid cell are proportional to the cell population and the coefficient of proportionality is the same for the entire analysed area. Thus, we just need to estimate one coefficient (αp), which is proportional annual emissions per capita. This makes the statistical uncertainty of such a coefficient very small. In fact, for most analysed areas, the uncertainty was at least 10 times less that the coefficient itself. The composite plume function Ωp is a sum of plume functions of all individual cell centres multiplied by the grid cell population. Thus, Ωp depends on geographical coordinates, population density, and local winds. The original population density data were converted to a grid by averaging population density data within each grid cell. Smaller grids such as were also considered, but it was found that the reduction of the grid size does not change the results, while it increases the computation time.
The downside of this approach is that the estimates would produce mean emissions per capita for a rather large area. This may not be very representative if there are cities with different economical conditions within the analysed area as, for example, at the border of North and South Korea. Such cases are easily identifiable from the maps of the fitting residuals: such cities would appear as areas of large positive and negative anomalies. We did find several such cases and manually adjusted the area to include only one highly populated area.
The proxy plume functions used in the model preferably should be uncorrelated because otherwise the coefficients have correlated errors making their interpretation difficult. For a typical urban area, the plume functions related to urban activity and to industrial sources are expected to be independent: high population density zones typically occupy a small part of the area and industrial sources are typically located away from such highly populated zones. Note that the NO2 lifetime is relatively short and the median wind speed in, for example, the eastern US is about 10 km h−1, so sources located 30–40 km apart typically have uncorrelated plume functions.
A high correlation between the population and landscape-related proxies is possible if a city is in a valley surrounded by mountains. The correlation could be reduced by increasing the size of the analysed area, but if the area is too large, the assumption that the background level has a linear gradient in the area may not be valid. Therefore, we limited the area to . The correlation coefficients between the site elevation and population density for areas are typically small. For example, in the US, correlations are positive over Florida (about 0.2), with the population density higher in the inland area, and negative in the Portland–Seattle–Vancouver area (about −0.35), where it is higher near the ocean and lower in the mountains. As the plume functions of individual industrial sources are very local (∼50 km footprint), they do not correlate with the elevation. With such low correlation coefficients, elevation does not affect estimates of other parameters of the regression model.
When industrial point sources are located in close proximity, their plume functions in the statistical model (Eq. 1) are highly correlated. In practice, it often appears if, for example, estimated emissions from one source are unrealistically high, while emissions from the other nearby source are low or even negative. In such cases, emissions from individual industrial sources often cannot be estimated. However, the sources can be grouped into independent clusters and total emissions from such clusters can be estimated. Such grouping could be done manually on a case-by-case basis, but it would be subjective and very time consuming. Instead, we applied an algorithm based on factor analysis. We would like to emphasize that the factor analysis, described in the next two paragraphs, was used to improve emission estimation for individual sources or clusters of sources. It is not required if only total emissions from all point sources in the area are estimated in order to separate them from urban emissions or if all industrial sources are isolated remote sources.
To group industrial sources into clusters, an orthogonalization process was applied to the plume functions of individual industrial sources. First, the correlation matrix for the plume functions of individual point sources (Ωi) was calculated and eigenvalues and eigenvectors (or “factors”) of the correlation matrix were determined. The correlation matrix was calculated just once using 16 March–15 June data from all 3 years. An isolated remote source would appear as an eigenvector with an eigenvalue of 1. Two (or more) sources that are closely located, but isolated from the other sources, have one corresponding eigenvector and an eigenvalue of 2 (or more). Eigenvalues lower than 1 mean that the corresponding sources are already partially included in other eigenvectors. To reduce the number of factors, only factors with eigenvalues >0.6 were kept.
The approach based on eigenvalues of the correlation matrix creates proxies that are not correlated and reduces the number of the fitting coefficients. While they correctly describe the total contribution of all industrial sources in the area in the total NO2 variability (or total emissions), individual eigenvectors, i.e. linear combinations of the original plume functions, may not have a clear interpretation. For example, they may include the original plume functions with negative coefficients. In order to avoid that and obtain proxies that have a meaningful interpretation, the eigenvectors were linearly transformed, so they became as close to the original plume functions as possible, while the correlation coefficients between them remained low. This was done using the varimax factor analysis method that is implemented in modern statistical software packages such as R and SAS (Belhekar, 2013). It orthogonally rotates the established factors to maximize the sum of squared correlations between the original variables and factors. Then, the algorithm uses a linear combination of the original variables that have the highest correlations with the rotated factors, i.e., the condition of orthogonality is removed in order to find the simplest linear combination of the original variables. In practice, the algorithm produces a set of “clusters”, i.e. linear combinations of the original plume functions that have low correlation coefficients (typically less than 0.2) between them, and each cluster has high correlation coefficient (typically more than 0.95) with one orthogonal factor. To simplify this further, if a linear combination has a weight for an original variable under 0.2, its weight was set to 0. As a result, all non-isolated point sources were grouped into small clusters, and emission estimates were done for such clusters instead of individual sources, while each isolated remote source forms a single-source cluster that corresponds to only that source. It is possible that a single source contributes to more than one cluster, which makes interpretation of emissions for such clusters more difficult, but such cases are rare.
As in any regression-analysis-based study, correlation between the proxies is one of the main obstacles in the result interpretation. The “orthogonalization” of plume functions from industrial sources greatly reduces cross-correlations between the proxies, but high correlations between industrial and population-density-related plume functions are still possible if industrial sources are located in highly populated areas. In such cases, it may be difficult to separate the industrial source signal from the contribution of the population-density-related proxy. For example, in one case (Edmonton, Canada) this correlation coefficient was as high as 0.94 and it was not possible to separate urban and industrial emissions. Without such separation, industrial emissions are counted as population-density-related, which makes Edmonton annual per capita emissions nearly twice as large as emissions for other cities. Note that for large cities and small industrial sources, high correlation means that the emissions from such industrial sources cannot be reliably estimated, although the impact on estimation of the population-density-related signal is small. For this reason, industrial point sources located in the cells where the population is greater than 600 000 people were excluded. This is an empirically estimated limit, and, in a few cases of very large cities (New York, Moscow), it was manually adjusted.
The fitting and parameter estimation was done using all individual TROPOMI level-2 pixels for the period from 16 March to 15 June four times: for 2018, 2019, 2020, and 2021. So, four sets of coefficients (one set per year) were obtained and then used to estimate the background levels and emissions. Then, the results for 2018 and 2019 were compared with these for 2020. We also performed the same analysis for 2021, but these results were only used to analyse interannual variability because COVID-19 lockdowns may still have some impact on NO2 in 2021.
As the regression model has three main terms (background, urban, and industrial), the NO2 VCD for each TROPOMI pixel is represented in Eq. (1) as a sum of three values (components) plus a residual error. Then the values of individual components and residuals can be analysed the same way as the original TROPOMI measurements; e.g. mean values over a certain period (in our case, 16 March–15 June) can be calculated as a function of latitude and longitude.
This is illustrated in Fig. 3, where individual terms of Eq. (1) are shown for an area centred on Montreal. The area includes two large cities, Montreal (4.2 million) and Ottawa (1.4 million, including the sister city of Gatineau). The terrain elevations in the analysed area are in the range from just a few metres above sea level along the Saint Lawrence River to more than 500 m at 100 km north of Montreal. For this plot (as well as for Fig. 1 and other figures), we used a non-linear scale that is more sensitive to small quantities in order to make small deviations more pronounced. Figure 3a–c shows the mean TROPOMI NO2 data (Fig. 3a), the fitting results (Fig. 3b), and the difference between them or the residuals (Fig. 3c). The background, urban, and industrial components are shown in Fig. 3d, e, and f respectively.
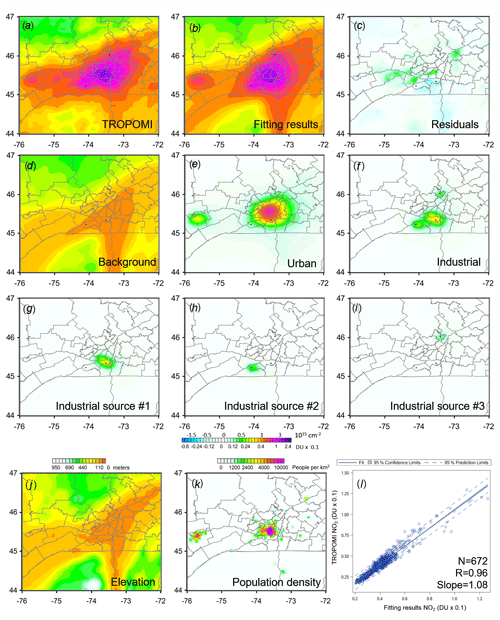
Figure 3(a) Mean TROPOMI NO2 for 16 March–15 June, 2018–2019, over the Montreal area, (b) the fitting results and (c) the residuals (i.e. the difference between a and b). Tropospheric NO2 VCDs have a large “background” level that is reflected by (d) the elevation-related component. (e) The population-density-related and (f) industrial-source-related components. Panel (b) is the sum of panels (d), (e), and (f). Emission point sources are shown by the black dots and the airport by the slightly larger grey dot. The industrial-source-related component is comprised of three clusters: one (g) with two sources and two (h, i) with one source each. The data are smoothed by the oversampling technique with the averaging radius R=10 km. Proxies used by the statistical model (Eq. 1): (j) elevation map on the colour scale that is similar to that for the elevation-related (background) component; (k) population density map. (l) Mean TROPOMI values (a) vs. the fitting results (b). Each dot represents the mean value for a cell on a 0.2×0.2 grid for 2018 or 2019. The number of data points (N), the correlation coefficient (R), and the slope are also shown.
The contribution of industrial point sources (ΣαiΩi) is illustrated by Fig. 3g–i. In the case of Montreal, total emissions from industrial sources are relatively small, less than 1.8 kt yr−1 from our estimates. Note that unlike the previous algorithm (Fioletov et al., 2017), where Ωi represented plume functions from individual sources, this new Ωi represents plume functions of clusters of closely located individual sources determined by factor analysis. The estimated parameter αi represents total NO2 mass of the entire cluster, while Ωi is a weighted sum of plume functions of individual sources in the cluster. The weighting coefficients are determined by the varimax technique, described above. In the case of Fig. 3, the first cluster is comprised of two sources and the second and third clusters are each just single point sources. The estimated parameter αi represents emissions from the entire cluster, required that αi≥0.
The background and urban component maps have a simple interpretation. Figure 3j and k show maps of the elevation and population density respectively. Not surprisingly, the background component, which is dominated by scaled elevation, looks similar to the elevation map itself. The urban component is the population density map convoluted with EMG functions, and therefore it looks like a smoothed population density map.
The suggested algorithm essentially finds the emission levels that give the best agreement with the TROPOMI data NO2 VCD and then uses these estimates to “reconstruct” the spatial NO2 distribution as well as the contribution from each source. As explained by Fioletov et al. (2017), the technique of satellite VCD reconstruction from fitted coefficients αi using Eq. (1) to isolate different components can be applied to the reported emissions Ei by using . This produces a map of VCD that would be seen by satellites if these reported emissions are the only sources of NO2. The same approach was employed here using US emission inventories. For such estimates, the ratio between NOx and NO2 is required. Beirle et al. (2021, their Fig. 2) have recently estimated the NOx-to-NO2 ratio for different parts of the world and found that the ratio is about 1.4 over the US and typically between 1.2 and 1.6. elsewhere. The value of 1.4 was used in this study.
The quality of a regression model (Eq. 1) can be described in terms of the correlation coefficient between the original and predicted values. In the case of Montreal, the correlation coefficient is about 0.55; i.e., a set of about half a million original TROPOMI observations over the area during a 3-month period can be described by just eight parameters (αp, α0, β0, β1, and β2 plus three coefficients αi for industrial sources) with that correlation coefficient. The model can be further improved by adding parameters responsible for workday–weekend differences, seasonal changes, and meteorological proxies (Goldberg et al., 2021; Kim et al., 2021). However, we focused on the mean NO2 changes over a 3-month period, and they can be successfully estimated without such additional parameters. Figure 3 shows that the fitting results are able to reproduce such mean data accurately: in the case of Montreal, the coefficient of determination (R2), i.e. the ratio of the variance of the residuals (Fig. 3c) to the variance of the averaged TROPOMI data (Fig. 3a), is between 0.9 (in 2019) to 0.93 (in 2020) meaning that fitting results “explain” from 90 % to 93 % of the observed variance. The Pearson correlation coefficient between the mean TROPOMI data and the fitting results is about 0.96 (Fig. 3l).
The necessity of both linear gradient- and elevation-related components in the background term in Eq. (1) is illustrated by Fig. 4. If the surface is nearly flat in the analysed area (as, for example, in the case of Minneapolis, Fig. 4g), the background component is dominated by the linear gradient. However, the elevation affects the NO2 distribution near mountain areas as, for example, in the case of Seattle, where mountains as high as 2000 m are located east of the city (Fig. 4i). It is interesting to note that the background components are practically identical for both periods, which gives a high confidence in the obtained results. The influence of the landscape on the NO2 distribution also explains why the distribution near Seattle does not look like a “hotspot” NO2 distribution near a typical large urban area. As Fig. 4 shows, the statistical model can successfully reproduce the NO2 VCD distribution in both areas. The Pearson correlation coefficient between the 3-month mean TROPOMI data and the fitting results for Minneapolis and Seattle are 0.96 and 0.94 respectively.
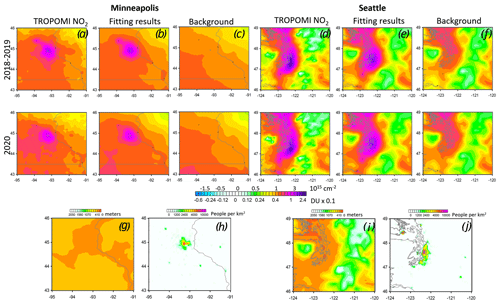
Figure 4Mean TROPOMI NO2 for 16 March–15 June over a flat area around Minneapolis and a mountain area around Seattle as indicated. The columns represent mean TROPOMI NO2 values (columns a, d), the fitting results (columns b, e), and the elevation-related background component (columns c, f). Elevation map on the colour scale that is similar to the background component (g, i) and the population density maps (h, j). The “hotspots” on the population density maps correspond to Minneapolis (h) and Seattle (j).
Since the fitting results are based on just a handful of parameters, the approach of this study is to investigate changes in these parameters or the three regression terms themselves between 2020 and 2018–2019.
To test the method, the described technique was applied to the 22 largest urban areas in the US and 5 in Canada (Fig. 5). Four examples with detailed analysis of the components of the NO2 distribution are discussed below with results shown in Fig. 6. Eight types of maps are shown. They include mean values for the analysed period for the actual TROPOMI data (column a), the fitting results (b), the residuals (c), i.e. (a) minus (b), and individual components of the fitting: the background (d) and urban (e) components and the industrial source clusters (f). Figure 6 is divided into four sections with the area name shown at the top of each cluster of plots.
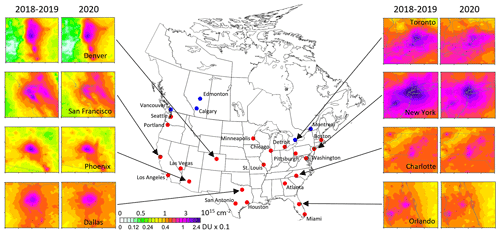
Figure 5The map of locations of the analysed 27 most populated urban cites in (red) the US and (blue) Canada (22 and 5 areas respectively). The analysis was done for 3∘ (latitude) by 4∘ (longitude) areas around the sites. The mean NO2 values for eight areas for the period from 16 March to 15 June in 2018–2019 and 2020 are also shown.
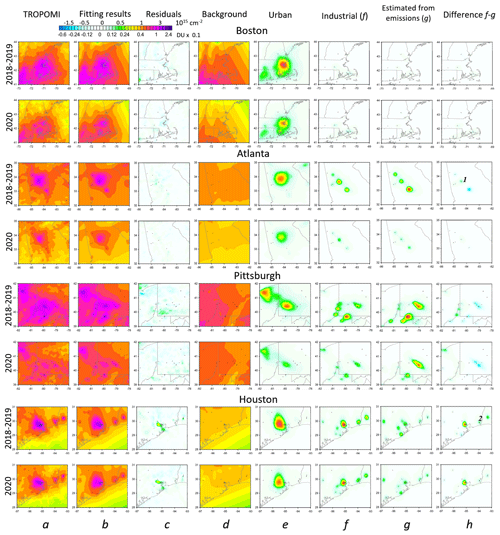
Figure 6Mean TROPOMI NO2 for 16 March–15 June over the four areas as indicated. For each area, the first row shows the 2018–2019 averages and the second row shown the 2020 averages. The columns represent mean TROPOMI NO2 VCD values (column a), the fitting results (column b), the residuals (column c) as well as individual components of the fitting: the background (elevation-related) (column d), the urban (population-density-related) (column e), and the industrial-source-related (column f) components. VCDs estimated from reported emissions are in column (g), and the difference between columns (f) and (g) is in column (h). 1 – Hartsfield–Jackson Atlanta International Airport; 2 – oil refineries near Houston.
As mentioned in Sect. 3, reported emissions can be used to reconstruct VCD distribution for NO2 emitted from these sources using Eq. (1). The maps of NO2 VCDs from the reported bottom–up emissions is shown in Fig. 6 (column g). We would like to emphasize that such a reconstruction is based on industrial emission data only, without any satellite NO2 observations (although τ and w in the plume functions were the same as in the satellite-based estimates). Finally, the maps of the difference between the TROPOMI industrial-source-related component (Fig. 6, column f) and NO2 VCD from the reported “bottom–up” emission-based reconstruction (Fig. 6, column g) is also shown in Fig. 6 (column h).
4.1 Case studies
Four examples that represent different cases of NO2 distributions around large urban areas are discussed below. In the case of Boston, there is a single urban source with no large industrial sources nearby and with relatively small impact from the terrain. The Atlanta area represents the case where the urban component is well-separated from industrial sources and the area also contains the world's largest airport. In the Pittsburgh area, industrial and urban sources have comparable contributions, and the TROPOMI-based industrial emission estimates can be validated by EPA NEI CEMS measured emissions. Multiple industrial sources in the Houston area are missing from the EPA NEI CEMS emission database used, and in this example emissions from the EPA eGRID database can be compared with TROPOMI-based estimates.
Boston is a major urban area with a population of more than 8 million (for the combined statistical area of Greater Boston). On the TROPOMI NO2 map (Fig. 6, column a), it appears as a large hotspot that can be successfully reproduced by the statistical model (Eq. 1) using the population density as a proxy. From our estimates, there is a % decline (the error bars correspond to 2σ for random uncertainty; see Sect. 4.3) in the urban emissions in 2020 compared to the 2018–2019 average. Our estimates of urban emission changes in 2020 are similar to the −22.8 % drop in TROPOMI NO2 values estimated by Goldberg et al. (2020) for the period from 15 March to 30 April and a −18.3 % drop estimated by Bar et al. (2021) for the period from 22 March to 30 May. Boston also shows one of the largest declines in the US in the background component (about 20±0.5 %). Although the background component is not linked to particular plumes, it is likely that very high emissions from the largest NO2 hotspot in the US over the New York–Philadelphia area contributed to the background NO2 over Boston, and a decline in emissions there caused changes in the background NO2 over Boston.
Our estimate of the urban emission decline for Atlanta is about %. This is higher than the −20 % decline estimated by Goldberg et al. (2020). However, changes in the background component were about %, while the background (Fig. 6, column d) component over Atlanta is comparable to the urban (Fig. 6, column e) component (both are about 0.04 DU), so the decline in the sum of the two components over Atlanta should be about −23 %. The urban component estimates are based on the fitting of the plume from the city itself where NO2 is dominated by on-road vehicle emissions. Kondragunta et al. (2021) estimated that the decline in on-road emissions is about −28 %, which is closer to our estimate. The Atlanta area also hosts the Hartsfield–Jackson Atlanta International Airport (labelled as “1” in Fig. 6, column h), the world's busiest airport with more than 100 million passengers per year in 2018–2019 (https://aci.aero/data-centre/annual-traffic-data/passengers/2017-passenger-summary-annual-traffic-data/, last access: 5 August 2021). The Atlanta airport NO2 signal can be easily isolated since the airport is located far away from industrial sources (the correlation coefficients between the plume functions are less than 0.2) and at a distance from Atlanta's most populated area (the correlation coefficient is 0.54). VCDs estimated for the industrial source clusters (column f in Fig. 6) are in line with those based on reported emissions (column g in Fig. 6). Our estimated annual emissions for the airport are 5.1±0.2, 6.4±0.2, and 2.9±0.2 kt yr−1 in 2018, 2019, and 2020 respectively, while the EPA emission inventory value is 3.7 kt yr−1 for 2017 (the last available year). Thus, our estimates show a 55 % decline in airport emissions between 2019 and 2020. The decline in aircraft operations for the analysed period was about 75 % for passenger flights and 25 % for cargo operations (according to the Department of Aviation, Hartsfield–Jackson Atlanta International Airport, https://www.atl.com/business-information/statistics/, last access: 15 November 2021). For illustration purposes only, for Hartsfield–Jackson Atlanta International Airport, the 2017 EPA emission inventory value was used to calculate NO2 VCD in column g of Fig. 6 for 2018 and 2019 and half that value for 2020.
The Pittsburgh area includes the cities Pittsburgh (population of ∼2.4 million) and Cleveland (∼3.6 million) and has one of the highest emissions from industrial sources among the analysed areas. Several coal-burning power plants are located east, west, and south of the city. Their emissions are comparable or even larger than from Pittsburgh itself. The NO2 distribution around major industrial sources reconstructed from the reported emissions (Fig. 6, column g) is similar to the NO2 distribution from industrial sources based on satellite estimates (Fig. 6, column f). The differences (column f minus column g) are small, although NO2 from the reported emissions is slightly larger for the cluster of power plans east of the city. The total reported emissions from all industrial sources in the Pittsburgh area are 43, 37, and 26 kt yr−1 for 2018, 2019, and 2020 respectively, while our estimates are 36, 34, and 24 kt yr−1 (with 2σ uncertainty of about 1.5 kt yr−1); i.e. the 2020 decline from our estimates is 35 %, while the decline in reported emissions is 31 %. The urban emissions declined from about 72±2.3 kt yr−1 in 2018 and 2019 to 36±1.2 kt yr−1 in 2020, i.e. by −50 %.
In the case of Houston, the EPA NEI CEMS emission inventory contains emissions from the power plants in the area but not from large oil refineries that are responsible for hotspots seen on the TROPOMI mean NO2 plot. Their coordinates and emission estimates were obtained from the eGRID inventory. The reported industrial emission values for the analysed Houston area in 2018–2019 are 17 kt yr−1, while our estimates are 36 and 31 kt yr−1 for 2018 and 2019 respectively, and the estimated value for 2020 is 33 kt yr−1. It appears that TROPOMI-based emission estimates agree with emissions from the power plants from CEMS but are noticeably larger that emissions from oil refineries available from the eGRID inventory (Fig. 6, column h). Our estimated changes in background and urban components for the Houston area are % and % respectively; i.e. we see a decline in the urban component and practically no changes in the two other components. Goldberg et al. (2020) estimated the decline over Houston as being −15.6 %, although the spread between the three methods of estimation used is large: from −26.3 % to −1.9 %. Note that the lockdown period in Houston was relatively short: from 2 April to 30 April.
4.2 Relative contribution of different components
NO2 VCD represents the total number of molecules and equivalently mass per area unit. When background, urban, and industrial components of the NO2 distribution are estimated as described in Sect. 3, it is possible to calculate the total NO2 mass of each of the components and estimate their relative contribution to the total NO2 mass. The diagram in Fig. 7 shows such a contribution of individual components for the Montreal area (Fig. 3d, e, f). Most NO2 mass is associated with the term related to the background component. For the Montreal area, the contribution of industrial sources is 4 times less than the contribution of the urban component, and these two components are responsible for less than one-quarter of the total NO2 mass in the area. The relative contribution of the three components in the other areas for the 2018–2019 period are shown in Fig. S1 in the Supplement. Most NO2 mass belongs to the background component that is not directly linked to plumes from urban and industrial sources. These plumes are responsible for about one-third of total satellite-estimated NO2 mass in New York and Los Angeles and far less in the other analysed urban areas in the US and Canada. This result depends on a particular size of the area, but the fraction of the background component is larger for larger areas as all major urban areas are already included in the analysis. Figure S1 also shows that NO2 mass emitted from cities is larger than emissions from the industrial sources for most of the analysed areas in the US and Canada. Note that characteristics such as the mean background value and annual emissions per capita are much less dependent on the area size, and the rest of the study is focused on them.
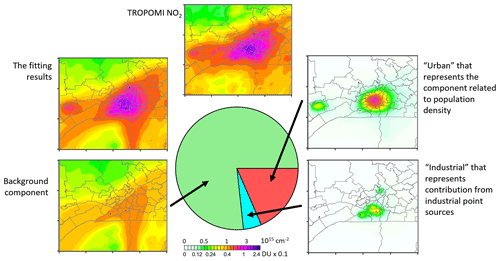
Figure 7The contribution of the three components to the total NO2 mass in the Montreal area for 16 March–15 June (average for 2018–2019). The total mass can be represented as a sum of three components shown in Fig. 2.
The mean NO2 distribution near major emission sources has sharp gradients that suggest that the NO2 lifetime is relatively short (on the order of a few hours), which is also confirmed by direct estimates (Beirle et al., 2011; de Foy et al., 2015). However, a large background component may suggest that the lifetime should be relatively long since NO2 distribution follows the terrain over large areas. This difference in the lifetime could be reconciled if we assume that a fraction of NO2 emitted from cities and industrial sources gets into the free troposphere and has a longer lifetime there than near the ground. Also, levels of the OH radical, the main chemical NOx sink, within a plume can be much larger than under “clean” conditions, and NO2 lifetime could be longer under such conditions than in the plume (Juncosa Calahorrano et al., 2021). Other sources, e.g. lightning or soil emissions, may contribute to background component NO2 directly. The background term can also include components of stratospheric NO2 that were imperfectly removed as part of the retrieval algorithm (von Geffen et al., 2020). Finally, estimates of NO2 lifetime from TROPOMI data (e.g. de Foy et al., 2015; Liu et al., 2016; Lange et al., 2022) are based on daytime observations only. However, the lifetime at night could be different (Kenagy et al., 2018), and nighttime emissions and NOx evolution during the nights are not reflected in our estimates.
4.3 Variability and uncertainty estimates
Two characteristics of uncertainties of the estimated NO2 components are calculated, and the results are presented in Table 1. Uncertainties related to the random measurement errors can be estimated assuming that the residuals ε in Eq. (1) are uncorrelated and have the same variance. Since the total number of satellite pixels in the statistical model is very large (several hundred thousand) and the number of parameters is small, such uncertainties are typically low. These uncertainties are calculated for the three components in each analysed year, and the average value for each area (in percent) is given in Table 1 as “random error”. On average, these random errors are about 0.25 %, 1 %, and 3 % for the baseline, urban, and industrial components respectively. The random uncertainty represents how precisely the component value is calculated and provides the lowest limit of the total uncertainty.
Table 1The standard deviations of the random errors and interannual variability for background, urban, and industrial components for the US and Canada in percent. The random errors are calculated as the averages of estimates for individual years. The interannual variability estimates are the standard deviations calculated from 3 years (2018, 2019, and 2021). Interannual variability of the industrial component is calculated for regions with estimated total emissions greater than 1 kt yr−1.
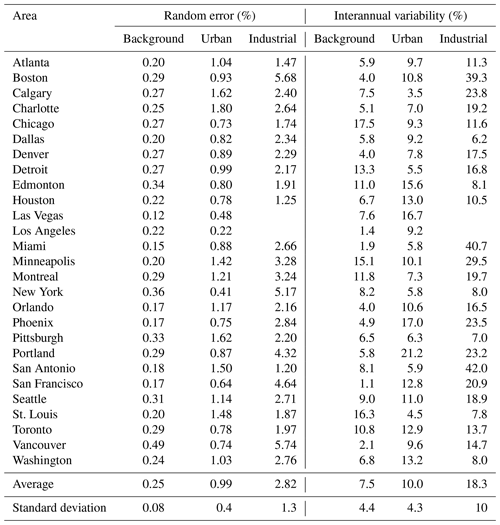
Interannual variability is another characteristic that reflects uncertainties related to the contributions from meteorology, possible instrument or algorithm-related issues, differences in sampling due to variations in cloud cover, and perhaps other factors. It is also affected by the changes in emissions themselves. Internal variability can be estimated by comparing the components, estimated for different years. The 2020 data are not used in this estimate since they were greatly affected by the lockdowns. Instead, we added estimates for 2021 and calculated the standard deviations from the three values (Table 1). Although estimates from just three data points are not very reliable, they show similar results for most of the analysed areas, and their average can be used as a characteristic of the interannual variability. The average standard deviation of the interannual variability for the background component is only 7.5 %. The interannual variabilities for the urban and industrial components are 10 % and 18 % respectively. The interannual variability represents the upper limit of the total uncertainty.
The uncertainty of the percentage change between 2018–2019 and 2020 values is a combination of the uncertainty of the baseline, estimated from just 2 years, and the uncertainty of the 2020 value. This gives the following values for 2-σ confidence limits for the percent changes: 18 %, 24 %, and 44 % for the baseline, urban, and industrial components respectively.
4.4 The COVID-19 lockdown impact: the US and Canada
The ability of the method to isolate individual components of the satellite-measured total NO2 mass makes it possible to estimate the impact of the COVID-19-related lockdown on these components separately. As mentioned, we compared the averages for the period from 16 March to 15 June in 2018 and 2019 to the same period averages for 2020.
To illustrate the changes in the background component, Fig. 8a–b show the mean VCD values of that component shown in Fig. 6, column d (or, in other words, the mean value of ) for the analysed areas for the two time intervals (a, c, e) as well as the percentage change in 2020 vs. 2018–2019 values (b, d, f). The mean value of decline for the background components among all urban areas is %. As mentioned, the largest decline in the background component was observed in Boston. The decline was also large (about −20 %) over two areas (Edmonton and Calgary) in the Canadian province of Alberta. It is unlikely that this decline is related to the lockdown; the restrictions in Alberta were not as tight as in many other areas: only some non-essential services were closed on 27 March and the restriction started to be eased in May (https://edmonton.citynews.ca/2020/12/24/2020-look-back-albertas-pandemic-response/, last access: 20 November 2021). In 2020, Alberta had a “historically low” level of forest fires: by June 2020, fires had burned just about 450 ha of forest, compared to, for example, 650 000 ha by June 2019 (https://globalnews.ca/news/7396849/alberta-2020-slow-wildfire-season/, last access: 10 November 2021), and therefore likely lower than normal natural NO2 emissions resulted in lower background levels.
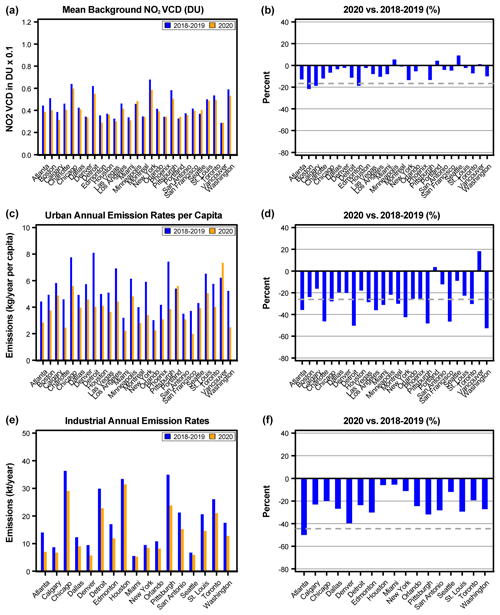
Figure 8(a, c, e) The background (a), urban (c), and industrial (e) components for all 27 analysed areas in the US and Canada in 2018–2019 (blue) and 2020 (orange). (b, d, f) The decline in 2020 values in percent from the 2018–2019 values for the same components. The background component is expressed as the mean value of that component for the analysed area. The urban component is expressed as annual emissions per capita, and the industrial component is expressed as total emissions from the point sources for the period from 16 March to 15 June. The grey dashed lines in (b), (d), and (f) indicate the 2σ level for the interannual variability.
The changes in the urban component are shown in Fig. 8c, d expressed as annual NO2 emissions per capita. Recall that emission rate is the mass divided by the constant lifetime; therefore, the percent changes in emissions per capita and the changes in total mass are identical. The relative changes for the urban component (Fig. 8d) are typically larger than those for the background component (Fig. 8b). The average total emissions per capita declined by −28 % in 2020 compared to the 2018–2019 average (from 5.6 to 4.2 kg yr−1). The median value of decline among all urban areas is −26 %, and the mean value of percentage decline is %. The changes in emissions per capita are rather uniform except in Vancouver, where 2020 emissions are 15 % larger than the average 2018–2019 emissions. This Vancouver anomaly is within the 2σ limits of natural variability as discussed in Sect. 4.3 (Table 1) and may be related to unusual meteorology and persistent cloud cover there in 2020. Edmonton is excluded from this panel because two industrial sources are located in the city itself, and, therefore, it is hard to separate their emissions from the urban emissions.
The number of large industrial sources and their emission strengths vary from area to area. Some areas, e.g. Las Vegas, do not have such emission sources at all. The total emissions from all large industrial emission sources and the percentage change in emissions are shown in Fig. 8e, f. The mean value of percentage decline in the areas with industrial sources is %. Unlike background and urban components, changes in emissions from industrial point sources demonstrate rather large scattering from one area to another. It is not a surprise since in addition to the difference in the strength and length of the lockdown between the areas, there is a difference in the lockdown impact on various industrial sectors.
Overall, the 2020 values for the baseline and industrial components at individual sites are within 2σ limits of the interannual variability (the grey dashed lines in Fig. 8b, d) with just a few exceptions, while 16 of 27 urban component values are outside these limits. As noted in Sect. 4.3, the interannual variability is rather large, and, therefore, the decline for individual areas is often not significant (Fig. 8f). For this reason, we analysed 27 individual areas covering a vast region with very different meteorological conditions, so the average of individual area estimates (i.e. the regional mean) can be calculated with high confidence. Indeed, the regionally mean values of the ratios of changes in 2020 urban and industrial components to the standard errors of these regional means are about 8.5 and 5.9 respectively (assuming that deviations for individual areas are not correlated), i.e. well outside the limits of interannual variability. The approach that is focused on regional statistics rather than on individual areas is used for all other regions in this study.
Since industrial point source emission estimates are obtained as part of our TROPOMI NO2 VCD data analysis, such estimated emissions can be compared to the reported ones. In general, there is an agreement between estimated and reported emissions, as was already demonstrated in Fig. 6a. The scatter plot of estimated vs. reported emissions in 2018–2019 is shown in Fig. 9 for the US urban areas. Each dot in the plot corresponds to industrial emissions from one area in either 2018 or 2019 with the total of 40 data points. The correlation coefficients between the two data sets from Fig. 9 is 0.84. The slope of the regression line is about 0.7 suggesting that, on average, our estimates are 30 % higher that reported emissions. The standard deviation of the residuals is about 5 kt yr−1. This value gives an approximate uncertainty for the point source of NO2 emission estimates for a 3-month period from TROPOMI data. As it is a direct comparison with the actual reported emissions, it includes all possible sources of errors. Then, the annual NO2 emissions are expected to be estimated with uncertainties of about 2.5 kt yr−1, which is twice less than about 5 kt yr−1 for SO2 emission uncertainties (Theys et al., 2021).
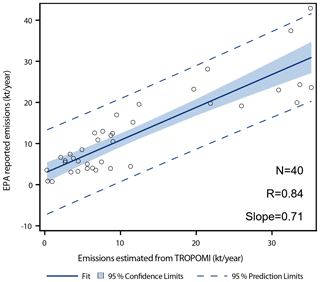
Figure 9Estimated and reported annual NO2 emission rates for US sources for 2018–2019. Each dot represents the sum of all emissions in one urban area in 2018 or 2019, and there are 40 dots in the plot. The emissions are expressed as annual rates. The correlation coefficient between the two data sets is 0.84, and the slope is 0.71±0.15. The standard deviation of the residuals is about 5 kt yr−1. The plot also shows the predicted regression line (blue), 95 % confidence intervals for the regression mean (the shaded area), and 95 % prediction intervals (dashed lines).
4.5 The COVID-19 lockdown impact: Europe
The described technique was applied to the European Union countries (plus non-members from former Yugoslavia) where detailed information about the industrial emission sources is available. The analysis was also done for areas around the 36 largest European cities with a population greater than 1 million plus some national capitals with a population of more than 500 000. Note that to avoid double-counting, if more than one city was located within an area, we used that area just once (e.g. Manchester and Birmingham are in one area).
The absolute and relative changes between 2018–2019 and 2020 for the three components are shown in Figs. 10 and 11. The NO2 decline in the urban component was particularly large (more than 50 %) for the countries in the most western part of the continent where the strictest lockdown measures were taken: France, Spain, and the UK (Fig. 10). In contrast, the decline in the German, Czech, and some other eastern European cities was only 20 %–25 % (Fig. 11). For this reason, two sub-regions were formed for the analysis: Europe-1 (Italy, France, Spain, Portugal, Belgium, Ireland, and the UK) and Europe-2 with all other countries. In general, the mean background values and estimated NO2 emission rates per capita in Europe are similar to those in the US and Canada. However, relative changes are somewhat different.
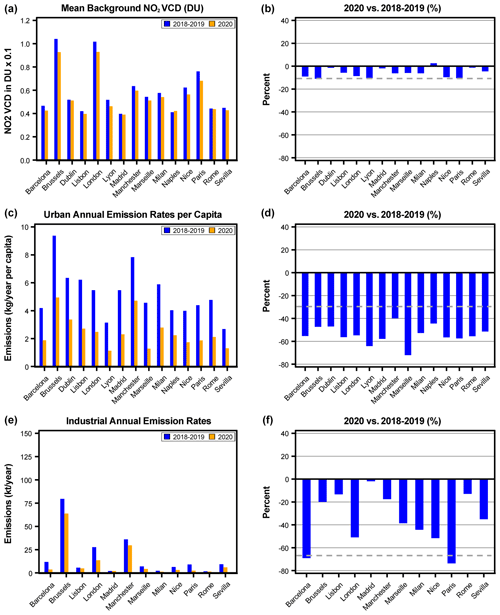
Figure 10The same as Fig. 8 but for the Europe-1 sub-region (Italy, France, Spain, Portugal, Belgium, Ireland, and the UK).
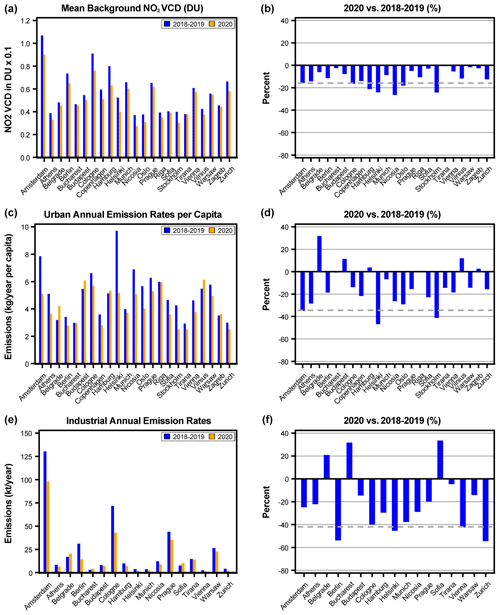
Figure 11The same as Fig. 8 but for the Europe-2 sub-region (other EU countries and non-members from former Yugoslavia).
In 2018–2019, the estimated annual emissions per capita for both European regions were very similar to those for the US and Canada. In 2020, the urban component declined in almost every analysed area. The average declines for the Europe-1 and Europe-2 regions were % and % respectively. This is in general agreement with total NOx emission reduction for these two European sub-regions: −50 % for Europe-1 countries (Italy, Spain, France) and −15 % to −25 % for Europe-2 countries (Germany, Sweden) with −85 % of the total reduction attributable to on-road transport (Guevara et al., 2021). The decline in Europe-1 was rather uniform with all but one area demonstrating a decline of more than −40 %. In contrast, only two areas demonstrated a −40 % decline in Europe-2, while most of the areas had a decline of under −20 %. Two areas in Europe-2 (Budapest and Belgrade) demonstrated an increase in NO2. They are located 320 km apart, and it is possible that relatively high NO2 values there were caused by some specific meteorological conditions in the spring of 2020: the NASA GEOS Composition Forecasting (GEOS-CF) simulations with constant anthropogenic emissions show a positive NO2 anomaly over Hungary in April–May 2020 (Liu et al., 2020b).
As in the case of the US and Canada, the mean background component in Europe shows a smaller decline than the urban component. On average, it was % and % lower in 2020 than in 2018–2019 for the Europe-1 and Europe-2 regions respectively, but it was pretty consistent as almost all individual areas demonstrated a decline. A large decline in population-related emissions and a relatively small decline in the background component for Europe-1 and the opposite for Europe-2 may create an impression that there is anticorrelation between the background level and population-related component, but this is not true. The large decline in average background for Europe-2 was caused by large negative background values for the Scandinavian countries in 2020, which also had large negative changes in the urban components. As discussed later in Sect. 4.6, there is no correlation between the changes in the background levels and the urban component.
The emissions from industrial sources also demonstrated a decline, although the scattering of the values is large as the changes varied from country to country and from sector to sector. Guevara et al. (2021) estimated that the emission decline in the energy industry was up to −30 % in Italy but under −5 % in Sweden. The emission decline from the manufacturing industry was smaller: from about −15 % in Italy, Spain, France, and the UK to −5 % in Germany and near zero in Sweden. Emissions from aviation were reduced by −90 % in all European countries (Guevara et al., 2021). We estimated changes in emissions only for industrial sources that are located in the analysed areas around major cities and therefore do not represent the entire industrial emissions, but our estimates also show a difference between the Europe-1 and Europe-2 regions: the average decline values are % and % respectively.
The uncertainty estimates are also in general similar to those for the US and Canada: the random uncertainty is about 0.25 % for the background component and 1 % for the urban component. The interannual variability estimates are also similar for the background component (5.6 %, 6.8 %, and 7.5 % for Europe-1, Europe-2, and Canada–US respectively). The interannual variability for the urban component for Europe-1 (12 %) is also the same as that for the Canada–US region but higher (15 %) for the Europe-2 region (Supplement, Tables S1 and S2). For Europe-1, the decline in the background component is within the 2σ level for all the areas and the decline in the urban component outside the 2σ level for all the areas. For Europe-2, however, the decline in the urban component is within the natural variability limits. For the industrial component, the variability is high and the 2020 decline is within the 2σ level for most of the areas.
For illustration purposes, four areas are examined in greater detail in Fig. 12. The Manchester map (Fig. 12 top row) illustrates a large area of high population density in central England with several power plants to the east. Recall that the urban component is essentially the population density convoluted with EMG functions, and the two large hotspots in the urban component corresponds to the Manchester and Liverpool area to the north and the Birmingham area at the south. Our TROPOMI data analysis shows a % decline in the urban component and about a % decline from total emissions from the power plants. These numbers are close to the decline in road traffic (−35 % and −50 % for April and May respectively) and industrial activity (−20 %) (Potts et al., 2021) reported by the UK Office of National Statistics. The estimated decline in the urban component is very close to the −42 % decline in the surface NO2 concentrations reported by Lee et al. (2020). In contrast, the background component shows almost no change in 2020 compared to 2018–2019. For this reason, the total decline in TROPOMI NO2 VCD over Manchester (−27 % according Barré et al., 2021, and −32 % according to Potts et al., 2021) is smaller than our estimates for the urban component alone.
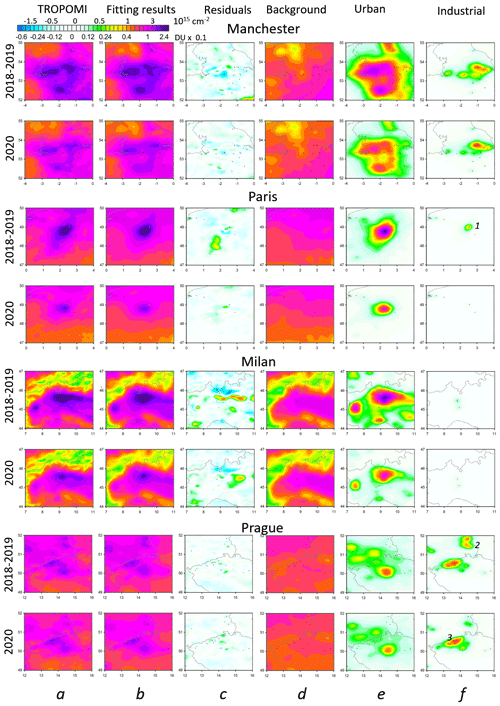
Figure 12Similar to Fig. 6 columns (a)–(f), for areas around four European cities: Manchester, Paris, Milan, and Prague. 1 – Charles de Gaulle Airport; 2 – power plants in Germany; 3 – power plants in the Czech Republic.
Paris is an example of a city that appears as a large, isolated urban source. The change between the two periods in the background component (Fig. 12, column d) is about %, while the decline in the urban component (Fig. 12, column e) is about %, as clearly seen in the plot. As in the other cases, this value of decline is larger than the decline from TROPOMI NO2 VCD data without separation of the two components and is closer to the changes in NO2 surface concentrations. The estimated decline in TROPOMI NO2 VCDs over Paris was about −30 % (Bauwens et al., 2020; Barré et al., 2021), while the estimated decline in NO2 concentrations was −40 % to 50 % (Keller et al., 2021; Barré et al., 2021). The terrain does not play a major role in the background component for the Paris area. There is a north–south gradient in the background component with higher values in the north-eastern corner of the area. The only relatively large industrial point source in the Paris area is Charles de Gaulle Airport which is evident on the 2018–2019 plot and practically disappears on the 2020 plot. Our estimates show an 90 % decline in NO2 emissions from 2018–2019 averages (from about 6.1±2.2 to 0.5±0.2 kt yr−1), which is in line with a more than −95 % decline in the passenger traffic of Charles de Gaulle Airport in April and May 2020 (https://www.parisaeroport.fr/en/group/finance/investor-relations/traffic, last access: 10 November 2021).
Milan was one of the first European cities where some lockdown measures were imposed in late February, and a −40 % to −60 % reduction in NO2 concentrations was reported (Collivignarelli et al., 2020). Complex terrain affects the NO2 distribution creating large differences between VCD values over the mountains and valleys and also makes it more difficult to fit the observations with the plume functions based on the assumption of straight-line plumes resulting in relatively high residuals. The background component shows practically no difference between the two periods. The contribution from industrial point sources for that area is small. The urban component demonstrates a % decline in 2020 that is similar to other TROPOMI-based estimates for Milan ( %, Bauwens et al., 2020; about −50 %, Barré et al., 2021), while the estimated decline in surface NO2 concentrations was only slightly larger at −41 % (Keller et al., 2021) and about −52 % (Barré et al., 2021). Such a small difference in decline between VCDs and surface concentrations may be due to a relatively small contribution of the background component to the total VCD: it is just about one-third of the urban component over Milan.
The maps for the Prague–Dresden area illustrate how changes in NO2 from industrial sources reflect differences in COVID-19 lockdown policies in Germany and the Czech Republic. The decline in the urban component was only about %. In addition to Prague that component also includes cities in east Germany (Dresden, Leipzig), but the changes over these cities and Prague are similar and close to −20 % (Barré et al., 2021). Otherwise, the difference would appear in the residuals (Fig. 12, column c). The main industrial sources in the Prague area are coal mines and coal-burning power plants in the Czech Republic west of Prague near the German border and in Germany north of Prague, near the Polish border. In the Czech Republic, the NO2 values of the industrial component remain unchanged, while the values over German industrial sources declined by a factor of 2. This is likely the result of different approaches to the coal power industry in the two countries. In the Czech case, power plants remained fully functioning and certain steps were taken to assure smooth operation and protect the workers: employees of power plants stayed on their job for longer periods, to avoid the risk of infection at home (EC, 2020). In Germany, the power generation from coal-burning plants was reduced by 60 % (from 13.4 TWh to 5.6 TWh per month) in April–May 2020 compared to 2019 (https://www.energy-charts.info/charts/energy/chart.htm?l=en&c=DE&year=2022, last access: 1 March 2021). As a result, we see a large difference in NO2 VCDs from the power plants in the two countries.
4.6 The global COVID-19 lockdown impact
To evaluate the COVID-19 lockdown impact worldwide, the analysis described earlier in Sect. 4 was performed for 261 urban areas around the world. All cities with a population greater than 1 million were considered. However, some of them, particularly in Africa, do not produce significant NO2 emissions that can be measured by TROPOMI over the 3-month period selected for this study. Another obstacle is in western Africa, where biomass burning made it difficult to estimate background levels as they were very different from year to year. Biomass burning areas appear as large anomalies on the maps of the residuals (such as shown in Fig. 3c) making the standard deviations of the residuals much higher than in the other African cities. For this reason, several areas with a population of over 1 million in western Africa were not included in the analysis. In the case of China, there are too many cities with a population of over 1 million. We raised the limit for China and considered only cities with a population greater than 6 million to keep the number of analysed areas similar to other regions.
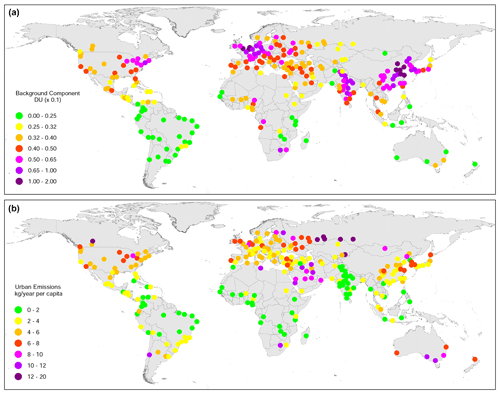
Figure 13(a) The map of the mean background component NO2 for all individual areas in 2018–2019 for the period 16 March–15 June estimated from TROPOMI. (b) The map of annual per capita urban NO2 emissions for the same period. The analysis was done using estimates for cities with a population greater than 6 million in China and 1 million for the rest of the world.
The analysis algorithm requires the coordinates of individual industrial sources in order to separate them from the urban component. The world power plant database (see Sect. 2.3) was used to locate most of the power plants. Other sources were identified from hotspots on the NO2 residual maps as typically corresponding to emission sources that are not included in the original fitting. Coordinates of such sources are determined from high-resolution satellite imagery and added to the point source list, and then the fitting process is repeated. A total of 357 such additional sources were identified. Most of them were cement and steel factories and oil refineries. In addition, the world's busiest airports were included as “industrial” emission sources. However, other sources, e.g. ship tracks or major highways, may still be missing, which may affect estimates for some areas. Some of these sources are identifiable in the residual maps and could be added to the statistical model in the future.
The map of the background and urban components for all 261 sites in 2018–2019 is shown in Fig. 13. The analysed period from mid-March to mid-June is close to spring in the Northern Hemisphere and autumn in the Southern Hemisphere, i.e. the seasons with very similar values of lifetime (Lange et al., 2022). Therefore, seasonal differences between the two hemispheres should be minimal, and maps of the main estimated components should represent their global distribution well. The highest background values are seen over east China and the northern part of central Europe, while the lowest are mostly over South America and East Africa.
The urban component demonstrates that the highest values are over the Siberian region of Russia. They are likely related to additional NOx emissions due to heating there since the climatological temperatures there are relatively low in March–April compared to other regions. Another hotspot is Edmonton, but as mentioned, its high value is due to poor separation of urban and industrial sources there. Annual emissions per capita are also high over the Middle East. However, in this region we found that the population density data in some areas including, for example, Riyadh may not be reliable and emissions per capita may be overestimated. The population density maps there do not match Google map satellite images and other proxies such as night light data. This requires further investigation.
As Fig. 13b shows, the lowest annual emissions per capita are in South America, Africa, and India (under 2 kg yr−1). Although emissions per capita were calculated for each area independently and the population and industrial sources vary greatly from area to area, the per capita values are uniform: for example, almost all areas in India are marked by green dots (0 to 2 kg yr−1), most European areas are orange (4 to 6 kg yr−1), etc. This gives further confidence in the obtained estimates. Figure 13 shows NO2 emissions based on the NO2 total mass estimates and a fixed lifetime. These could be further converted to the NOx emissions by applying a conversion factor that typically varies from 1.2 to 1.4 (Beirle et al., 2021).
Note that the urban NO2 “footprints” of cities with the same population vary greatly from region to region with the highest values in northern Eurasia and Australia and the smallest in Africa and India. To illustrate these large differences, Fig. S2 shows the examples of NO2 distribution near cities with a population of about 5–6 million with very large (Saint Petersburg, Russia) and very small (Dar es Salaam, Tanzania) per capita emissions. The total mass of NO2 per capita related to the urban component for Saint Petersburg was 40 times larger than for Dar es Salaam.
Figure 14 shows the maps of percent changes for individual areas for the background and urban components. Relative changes in the background component are typically within ±15 % and are much smaller than in the urban component. One of the regions with large negative changes in the background component is the Middle East. As mentioned, the population density data are not always accurate in that region and the background component may not be perfectly separated from the urban and industrial components. In contrast, the urban component demonstrates a much larger decline, particularly over Europe-1 and India. Note that the changes in the urban and background components are fairly independent: analysis of all 261 areas revealed that the correlation coefficient between them is −0.007.
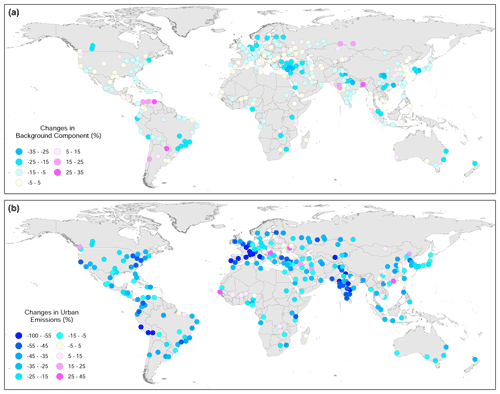
Figure 14The map of NO2 percent changes between 2018–2019 and 2020 for the period 16 March–15 June estimated from TROPOMI data for (a) the background component and (b) urban annual emissions per capita. The analysis was done using estimates for cities with a population greater than 6 million in China and greater than 1 million for the rest of the world.
The estimates for individual areas were then grouped into 13 large regions with 10–20 areas in each: the US and Canada, Europe-1 and Europe-2, China, India, South-East Asia (also includes Pakistan and Bangladesh), Japan with Taiwan and South Korea, northern Eurasia (former USSR countries and Mongolia), the Middle East, Africa, Australia and New Zealand, Central America, and South America. The regions are based on geographical location with similarities in economic development, and reactions to the COVID-19 pandemic were also considered. Then, the average characteristics of the background, urban, and industrial components were calculated for each region. Johannesburg (South Africa) and Pyongyang (North Korea) were not included in any particular region because their NO2 emissions were very different from those from neighbouring countries and therefore may bias regional statistics.
The summary results for the regions are shown in Fig. 15. The regions in Fig. 15 are sorted by relative decline in the urban component (from smallest to largest). The regional changes were calculated as the average of percent changes for individual areas for that region. The uncertainty values in Fig. 15 are based on variation in the values for individual areas within the region. The background component has the smallest variability among the three components, typically between 5 % and 9 %. The urban component variability is between 7 % and 17 %, and the decline observed in the urban component for South America, Europe-1, and India is outside the 3σ limits even for individual areas in these regions. The industrial component was added to separate emissions from large industrial sources in the urban areas from urban emissions themselves. Emissions from such industrial sources are typically similar to or smaller than urban emissions, and the variability of the industrial component (10 %–30 %) is similar to or larger than that for the urban component.
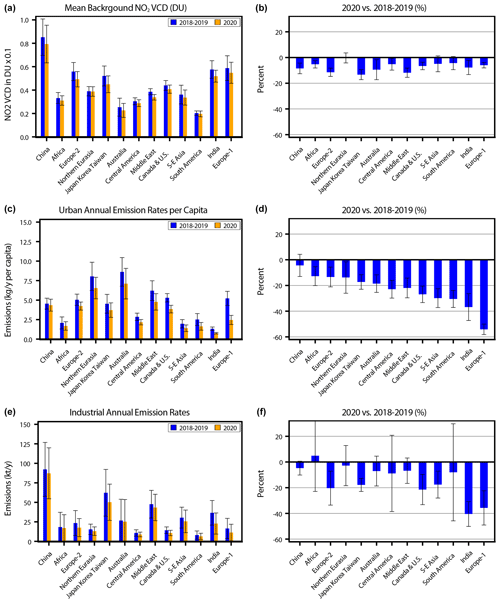
Figure 15(a, c, e) The mean values for 16 March–15 June in 2018–2019 (blue) and 2020 (orange) values for (a, b) the background, (c, d) urban, and (e, f) industrial components for the 13 regions. (b, d, f) The decline in 2020 mean values in percent from the mean 2018–2019 values. The data are sorted according to the changes between 2020 and 2018–2019 in the urban component (d). Mean values for each region were calculated as a mean of the values from all areas for that region. The uncertainty (σ) was calculated as a standard error of the mean. The error bars represent 2σ intervals.
China shows the smallest and non-significant decline in the urban component over the analysed period as the main COVID-19 lockdown in China occurred earlier (in February). Most of the regions demonstrated a statistically significant urban emission decline within the range of −18 % to −28 %. The decline was the largest (−36 % to −52 %) in three regions: Europe-1, South America, and India. The map of the urban emission changes (Fig. 14b) shows that the first two regions did indeed contain countries with a large decline in urban emissions. In the case of India, a similar decline can be seen in neighbouring Pakistan and Bangladesh. In Africa, a decline is seen in the south and the north of the continent, while countries in West Africa mostly show no decline and even some increase probably due to a contribution from forest fires.
As mentioned in Sect. 4.3, the industrial NO2 component varies from area to area and from one type of NO2 source to another, although there are some clear regional differences. Chinese cities demonstrated small changes in both urban and industrial components (−2.8 % and +5 % respectively) with one exception. Emissions from Wuhan, the city where the pandemic began, declined by more than −60 %. Industrial emissions there also declined but only by −30 %. The background component shows no change there. A very strict Wuhan lockdown ended on 8 April 2020, but during that lockdown, NO2 emissions in Wuhan declined by −82 % relative to the 2019 level (Ghahremanloo et al., 2021). That strict lockdown period lasted for less than one-third of the analysed period, but apparently it took some time for NO2 emissions to return to the pre-lockdown levels.
It is more difficult to interpret changes in industrial source emissions because they change over time for various reasons that may require an investigation on a case-by-case basis. For example, the large uncertainties in the industrial emission changes for Central America in Fig. 15 are caused by the doubling of emissions from power plants near Havana. This increase is likely caused by emissions from three power ships (power plants on ships) with a total capacity of 184 MW, which started their operation in Port de Mariel near Havana in the second half of 2019 (https://karpowership.com/en/project-cuba, last access: 4 November 2021). The largest regional industrial emission decline was observed over Europe-1 and India, i.e. where the largest urban emission decline was also observed. It is likely that the severe restrictions during the COVID-19 lockdown period there affected industrial activity. However, on a larger scale, this link is not that obvious. Although the lockdown had an impact on industrial sources, the correlation coefficient between changes in urban and industrial emissions among all analysed areas is −0.01.
As mentioned, statistical errors related to the fitting procedure are relatively small due to a very large number of satellite pixels used in the fit. For the urban component, they are between 1 % and 10 % for the cities analysed in this study. However, the year-to-year variability could be high. Table 2 summarizes the uncertainty for the 13 regions analysed in this study. It is similar to Table 1; however, individual rows contain the averages of uncertainty estimates for all individual areas in the region. The uncertainties for the background component are between 4.9 % and 9 %. The urban component demonstrates the interannual variability between 9 % and 22 % with the largest value over the Middle East, where, as mentioned, there could be a problem with the population density data quality. It is far more difficult to interpret the estimated interannual variability for the industrial sources because it depends on multiple factors from the meteorological conditions to the emission strength itself. The main conclusion here is that it is typically −10 % to −20 % for emissions from large (about 5 kt yr−1 or more) sources estimated based on 3 months of data.
Table 2The standard deviations of the random errors and interannual variability for background, urban, and industrial components for 13 regions in percent. The random errors and interannual variability are calculated from 3 years (2018, 2019, and 2021) for each area and then averaged for all areas in the region. Interannual variability of the industrial component is calculated for regions with estimated total emissions greater than 1 kt yr−1.
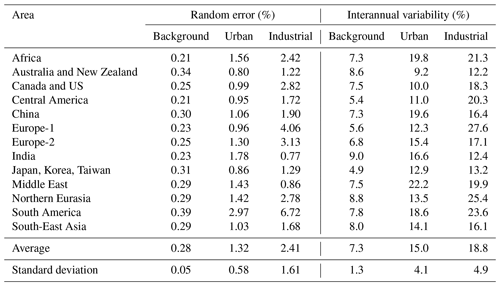
To demonstrate that the observed NO2 changes in urban emissions are indeed linked to the restricting measures taken by different countries, the estimated percent NO2 changes in annual emissions per capita were compared to the Google Earth Community Mobility Report data. The mobility data represent the changes in the number of people at locations of various type and can be used as a proxy for urban traffic. The changes in the background and urban components were calculated for every country and compared to changes in mobility data. Only countries with two or more cities were used in the comparison. Note that the mobility data were averages of all regions for the entire country, while the NO2 changes were estimated for areas around large cities only. Mobility data for China, North Korea, and some other countries were not available.
The scatter plot of the mobility and the NO2 VCD changes (Fig. 16) demonstrates a very different relationship between the urban and background components. Changes in mobility and urban components are correlated (Fig. 16a). As expected, the relative changes in the urban component are smaller than the mobility changes as the urban component includes more than just mobility-related traffic. The highest correlation is observed when changes in the NO2 urban component are compared with mobility for retail and recreation, covering visits to restaurants, cafes, shopping centres, theme parks, museums, libraries, movie theatres, and similar locations. The correlation coefficient between the percent changes in per capita emissions and retail and recreation mobility is 0.62 (the probability that there is no correlation is less than 0.0003). There is no statistically significant correlation (the correlation coefficient is −0.08) between the background NO2 and mobility data (Fig. 16b).
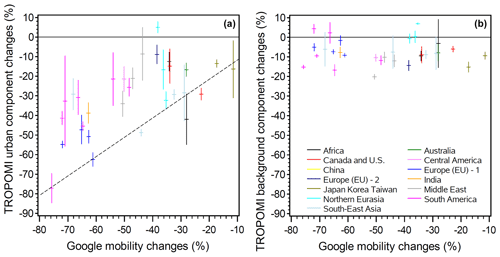
Figure 16A scatter plot of Google mobility statistic changes vs. TROPOMI NO2 VCD changes for (a) the urban and (b) background components during the period from 16 March to 15 June 2020 compared to the baseline period. The Google mobility statistic changes show the difference with the pre-lockdown period (3 January–6 February 2020) in percent. For TROPOMI, the difference is between the 2020 and the 2018–2019 average. Each symbol represents one country; the dot colour demonstrates the region as shown in the legend. Only countries with at least two cities used in this study are included in this plot. The correlation coefficient between the two data sets is 0.62. The dashed y=x line is shown for reference. The error bars represent the standard errors.
For individual areas, the uncertainties due to the interannual variability are rather large, so the observed 2020 decline in the urban component in many areas is within that uncertainty. Regional averages are more accurate and declines in urban emissions are statistically significant for all regions except China. Finally, mean 2020 declines in all areas (except China) are % and % for the background and urban components respectively, which corresponds to 10σ and 20σ levels (Supplement, Fig. S3). In 2018, 2019, and 2021, such global averages are remarkably stable, as all mean values are within ±2.5 % and are within ±5 % if the means are taken with the 2σ uncertainties. This suggests that there are no substantial drifts or shifts on the global scale in TROPOMI data, and the 2020 data are clearly an outlier.
Statistical regression analysis was used to separate the contribution from industrial sources, urban areas, and background levels to the satellite-observed tropospheric NO2 columns (VCDs) and to study the impact of the COVID-19 lockdown on each component separately. The analysis was done for 261 major urban areas around the world grouped into 13 large regions. The algorithm also estimates urban and industrial emissions assuming a constant NO2 lifetime (or, more accurately, decay time). A constant value of 3.3 h was used as the lifetime.
To verify the obtained emission estimates, we compared our result with the estimates from a similar study by Lange et al. (2022). In that study, TROPOMI NO2 data were used to estimate emissions from 45 sources worldwide, and then the results were compared with the available emission inventories and some other satellite-based emission estimates. There were 33 sources common to both works. In order to compare them we first calculated our total emissions, i.e. the sum of urban and industrial emissions, and then converted them to the same lifetimes as in Lange et al. (2022) and then multiplied them by 1.4 to calculate NOx emission. As expected, our emission estimates were higher than from Lange et al. (2022) because there is typically more than one emission source in the analysed areas of this study. Nevertheless, there is a 0.78 correlation coefficient between the two estimates.
Unlike other similar studies that simply removed the background offset (e.g. Beirle et al., 2011; Lange et al., 2022), this study included the background component as a function of the elevation in the analysis. On a scale of several hundred kilometres (as we analysed areas), most of the NO2 mass is typically related to the background component. Even in the areas such as New York City, the background component accounts for two-thirds of the total mass. This explains why the estimated impact of the COVID-19 lockdown in urban areas depends on the size of the analysed area: the larger the area the more background NO2 it includes and, therefore, the smaller the NO2 difference between the COVID-19 lockdown and reference periods.
In most of the analysed areas, changes in the background components between the COVID-19 lockdown period analysed here (from 16 March to 15 June 2020) were typically within 10 % from the 2018–2019 levels. In contrast, the urban component, based on population density, demonstrated a substantial and rather uniform decline of about −18 % to −28 % in most of the regions. Two regions (the most western part of Europe and India) demonstrated a larger decline: about −40 % to −50 %. China showed a much smaller decline ( %) because the lockdown there occurred prior to the analysed period. As for industrial point sources, emissions from them varied from region to region and from sector to sector. They demonstrate a decline of about −20 % or less except for the India and Europe-1 regions.
Abrupt changes in urban and industrial emissions due to the COVID-19 lockdown did not immediately result in a similar decline in the background component. This may explain why large changes in NO2 emissions in urban areas produced a relatively small, about 9 % decline in global NO2 (Bray et al., 2021). The importance of background NO2 VCD was previously noted by Qu et al. (2021) and Silvern et al. (2019) when they found that the observed satellite tropospheric NO2 VCD trends in remote areas do not match the expected changes. The origins of background NO2 are still largely related to urban and industrial sources as it is clearly higher in the Northern Hemisphere, particularly over China, central Europe, and the eastern US, than in the Southern Hemisphere and tropics. However, the analysed 3-month period may simply not be long enough for the lockdown to cause large changes in the background levels. There are also other NOx sources such as soil emissions (Hudman et al., 2012; Sha et al., 2021). They directly contribute to the background component as do sources aloft, such as lightning and to a lesser extent aircraft NOx. It is estimated that lightning is responsible for roughly 16 % of global production, and most of this NOx is found in the free troposphere (Bucsela et al., 2019). Furthermore, Zhang et al. (2012) estimated that sources such as lightning, soils, and wildfires account for about 20 % of emissions annually and up to 39 % in summer. Satellite measurements are also more sensitive to NO2 in the free troposphere than in the boundary layer and relatively small amounts of NO2 there produce a larger signal in satellite data. Another possible explanation is that low NO2 concentrations in the boundary layer and free troposphere may have longer lifetimes than in the plumes. The fact that NO2 fluctuations remain persistent over a longer time in clean conditions than over polluted areas (Vinnikov et al., 2017) indirectly confirms that.
Barré et al. (2021) noticed a different lockdown-related decline between NO2 VCDs and surface concentrations (−23 % and −43 % over Europe respectively). Moreover, Qu et al. (2021) reported that VCDs and surface concentrations had a similar decline between 2019 and 2020 at only 5 % of the most polluted sites. At the other sites, TROPOMI NO2 VCD data demonstrated, on average, a smaller decline than surface concentrations. Different changes in background and urban components in TROPOMI NO2 could explain this inconsistency between the surface and satellite VCD-based results. The urban component is directly linked to city plumes and therefore is a better proxy for surface concentrations in polluted areas, while the background component includes contributions from other sources that were not affected by the lockdown.
The urban and industrial components are based on plume dispersion functions that correspond to NO2 near the ground, almost always in the boundary layer. The urban component is based on the population density and the assumption that annual emissions per capita are uniform in the analysed area. There are very large differences, up to factor of 40, in estimated emissions per capita among the different areas. The estimates were done for 3-month periods. For such a short time interval, most of the cities with a population of more than 1 million produce a statistically significant signal that can be readily detected in TROPOMI NO2 data. As estimated emissions per capita are rather uniform, they can be used to account for the urban component outside large cities. Thus, it should be possible to estimate background, urban, and industrial components on the global scale and analyse the residuals in search of other factors contributing to the NO2 budget.
The approach described in this study can be used to estimate emissions from cities and industrial point sources. For the latter, only source coordinates are required. A comparison of reported and TROPOMI-derived NOx emissions for the US demonstrated a good correlation between them. As source coordinates can be also detected from satellite data alone (Beirle et al., 2019; Ding et al., 2020; McLinden et al., 2016), it may be possible to develop an independent “top–down” NOx emission inventory from satellite measurements to complement and improve available bottom–up inventories as was done for SO2 (Liu et al., 2018). This could be important for regions where no other emission information is available.
This appendix contains additional details of the fitting algorithm used that is largely based on the algorithm for multiple point source emission estimates (Fioletov et al., 2017). TROPOMI NO2 VCD can be expressed as a sum of contributions αi⋅Ωi from all individual industrial sources (i), a population-density-related term αpΩp, an elevation-related background, and noise (ε):
All Ω function are normalized (i.e. their total integral equals 1) plume functions: the value of that function for a particular pixel with latitude θ and longitude φ is proportional to the value of the plume parameterization from the source i located at the latitude θi and longitude (φi) (all in radians). The parameterization assumes that the plume is moving downwind along a straight line and has a Gaussian shape spread across that line. To describe the plume, we can rotate satellite pixels for a particular day around the source, so the plume would always be moving from north to south, apply the plume parameterization, and then rotate the pixels back. If (xi,yi) and are the pixel's Cartesian coordinates (km) in the system with the origin at the source i before and after the rotation respectively, then they can be calculated from the pixel and source latitudes and longitudes as
where (or for latitude and longitude in degrees); ω is the pixel wind direction (0 for north); and φi and θi are the source i longitude and latitude (all in radians). Note that there was a typo in this original formula for r in Fioletov et al. (2017).
Following Fioletov et al. (2017), the contribution from the source i can be expressed as , where
It is assumed that NO2 emitted from a point source declines exponentially (i.e. as exp(−λt)) with time (t) with a constant lifetime (or decay rate) . The second parameter is the plume width (σ).
Note that ; therefore the parameter αi represents the total observed number of NO2 molecules (or the NO2 mass) near the source i. If TROPOMI NO2 is in DU and σ is in kilometres, then a is in 2.69×1026 molecules or 0.021 T(NO2). Furthermore, the emission strength (E) can be calculated as assuming a simple mass balance.
As mentioned in Sect. 3, some of the sources used in the analysis are not point sources but clusters. In that case, , where Ωj is the plume function for source j and wj is the weighting coefficient established by the factor analysis.
Similarly, αpΩp represents the contribution from the population-density-related component, where Ωp is the plume function from an area-distributed source. Ωp is a weighted sum of plume functions from a grid with the weighting coefficients proportional to the population at the grid points , where θij and ϕij are the grid points coordinates and ρij is the population associated with that grid point. Thus, αp is the coefficient that represents the total NO2 mass which corresponds to one person. In our calculations we used a area with a grid with 336 (16×21) grid cells.
Finally, the elevation-related background term , where θ0 and φ0 are the coordinates of the centre of the analysed area and E is the elevation in kilometres and H0=1 km, is determined by three parameters.
Equation (A1) represents a linear regression model where the unknown parameters αp and αi can be estimated from the measured variable (TROPOMI NO2) at many pixels and known regressors. The fitting was done three times using all data for the analysed period (16 March–15 June) in 2018, 2019, and 2020.
The TROPOMI NO2 product is publicly available on the Copernicus Sentinel-5P data hub (https://s5phub.copernicus.eu, last access: 5 August 2021; S5P Data Hub, 2022). The reprocessed (RPRO) and offline mode (OFFL) data of version V1.2.2 to version V1.3.2 were used. The Gridded Population of the World (GPW) data set is available from the NASA Socioeconomic Data and Applications Center at https://sedac.ciesin.columbia.edu/data/collection/gpw-v4 (last access: 1 March 2021; SEDAC, 2017). The European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 reanalysis data are available from https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 (last access: 5 August 2021; C3S, 2017). Elevation data are from the gridded global relief ETOPO2v2 database (https://www.ngdc.noaa.gov/mgg/global/etopo2.html, last access: 1 March 2021; NOAA, 2006).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-22-4201-2022-supplement.
VF analysed the data and prepared the paper with input from CAM and critical feedback from all the co-authors. CAM and DG generated the TROPOMI data subsets for the analysis. NK and FL contributed to the interpretation of the results. HE provided the TROPOMI NO2 data product and related information. All authors read and agreed on the published version of the paper.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The Sentinel-5 Precursor TROPOMI level-2 product is developed with funding from the Netherlands Space Office (NSO) and processed with funding from the European Space Agency (ESA). We also thank two anonymous reviewers for their detailed comments that helped us to improve the paper.
This paper was edited by Tanja Schuck and reviewed by two anonymous referees.
Ali, G., Abbas, S., Qamer, F. M., Wong, M. S., Rasul, G., Irteza, S. M., and Shahzad, N.: Environmental impacts of shifts in energy, emissions, and urban heat island during the COVID-19 lockdown across Pakistan, J. Clean. Prod., 291, 125806, https://doi.org/10.1016/j.jclepro.2021.125806, 2021.
Ass, K. E., Eddaif, A., Radey, O., Aitzaouit, O., Yakoubi, M. E., and Chelhaoui, Y.: Effect of restricted emissions during Covid-19 lockdown on air quality in Rabat – Morocco, Global NEST Journal, 22, 348–353, https://doi.org/10.30955/gnj.003431, 2020.
Aydın, S., Nakiyingi, B. A., Esmen, C., Güneysu, S., and Ejjada, M.: Environmental impact of coronavirus (COVID-19) from Turkish perceptive, Environ. Dev. Sustain., 23, 7573–7580, https://doi.org/10.1007/s10668-020-00933-5, 2020.
Bao, R. and Zhang, A.: Does lockdown reduce air pollution? Evidence from 44 cities in northern China, Sci. Total Environ., 731, 139052, https://doi.org/10.1016/j.scitotenv.2020.139052, 2020.
Bar, S., Parida, B. R., Mandal, S. P., Pandey, A. C., Kumar, N., and Mishra, B.: Impacts of partial to complete COVID-19 lockdown on NO2 and PM2.5 levels in major urban cities of Europe and USA, Cities, 117, 103308, https://doi.org/10.1016/j.cities.2021.103308, 2021.
Barré, J., Petetin, H., Colette, A., Guevara, M., Peuch, V.-H., Rouil, L., Engelen, R., Inness, A., Flemming, J., Pérez García-Pando, C., Bowdalo, D., Meleux, F., Geels, C., Christensen, J. H., Gauss, M., Benedictow, A., Tsyro, S., Friese, E., Struzewska, J., Kaminski, J. W., Douros, J., Timmermans, R., Robertson, L., Adani, M., Jorba, O., Joly, M., and Kouznetsov, R.: Estimating lockdown-induced European NO2 changes using satellite and surface observations and air quality models, Atmos. Chem. Phys., 21, 7373–7394, https://doi.org/10.5194/acp-21-7373-2021, 2021.
Bauwens, M., Compernolle, S., Stavrakou, T., Müller, J.-F., van Gent, J., Eskes, H., Levelt, P. F., van der A, R., Veefkind, J. P., Vlietinck, J., Yu, H., and Zehner, C.: Impact of Coronavirus Outbreak on NO2 Pollution Assessed Using TROPOMI and OMI Observations, Geophys. Res. Lett., 47, e2020GL087978, https://doi.org/10.1029/2020GL087978, 2020.
Beirle, S., Platt, U., von Glasow, R., Wenig, M., and Wagner, T.: Estimate of nitrogen oxide emissions from shipping by satellite remote sensing, Geophys. Res. Lett., 31, L18102, https://doi.org/10.1029/2004GL020312, 2004.
Beirle, S., Boersma, K. F., Platt, U., Lawrence, M. G., and Wagner, T.: Megacity emissions and lifetimes of nitrogen oxides probed from space, Science, 333, 1737–1739, https://doi.org/10.1126/science.1207824, 2011.
Beirle, S., Hörmann, C., Penning de Vries, M., Dörner, S., Kern, C., and Wagner, T.: Estimating the volcanic emission rate and atmospheric lifetime of SO2 from space: a case study for Kīlauea volcano, Hawai`i, Atmos. Chem. Phys., 14, 8309–8322, https://doi.org/10.5194/acp-14-8309-2014, 2014.
Beirle, S., Borger, C., Dörner, S., Li, A., Hu, Z., Liu, F., Wang, Y., and Wagner, T.: Pinpointing nitrogen oxide emissions from space, Sci. Adv., 5, eaax9800, https://doi.org/10.1126/sciadv.aax9800, 2019.
Beirle, S., Borger, C., Dörner, S., Eskes, H., Kumar, V., de Laat, A., and Wagner, T.: Catalog of NOx emissions from point sources as derived from the divergence of the NO2 flux for TROPOMI, Earth Syst. Sci. Data, 13, 2995–3012, https://doi.org/10.5194/essd-13-2995-2021, 2021.
Belhekar, V. M.: Factor Analysis and Structural Equation Modeling, in: A Step-by-Step Approach to Using SAS® for Factor Analysis and Structural Equation Modeling, 2nd edn., edited by: O'Rourke, N. and Hatcher, L., SAS Institute, 314–361, IBSN 978-1599942308, 2013.
Bray, C. D., Nahas, A., Battye, W. H., and Aneja, V. P.: Impact of lockdown during the COVID-19 outbreak on multi-scale air quality, Atmos. Environ., 254, 118386, https://doi.org/10.1016/j.atmosenv.2021.118386, 2021.
Bucsela, E. J., Pickering, K. E., Allen, D. J., Holzworth, R. H., and Krotkov, N. A.: Midlatitude Lightning NOx Production Efficiency Inferred From OMI and WWLLN Data, J. Geophys. Res.-Atmos., 124, 13475–13497, https://doi.org/10.1029/2019JD030561, 2019.
C3S: Copernicus Climate Change Service (C3S): ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate, Copernicus Climate Change Service Climate Data Store (CDS) [data set], https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 (last access: 5 August 2021), 2017.
Chong, H., Lee, H., Koo, J. H., Kim, J., Jeong, U., Kim, W., Kim, S. W., Herman, J. R., Abuhassan, N. K., Ahn, J. Y., Park, J. H., Kim, S. K., Moon, K. J., Choi, W. J., and Park, S. S.: Regional Characteristics of NO2 Column Densities from Pandora Observations during the MAPS-Seoul Campaign, Aerosol Air Qual. Res., 18, 2207–2219, https://doi.org/10.4209/aaqr.2017.09.0341, 2018.
Collivignarelli, M. C., Abbà, A., Bertanza, G., Pedrazzani, R., Ricciardi, P., and Carnevale Miino, M.: Lockdown for CoViD-2019 in Milan: What are the effects on air quality?, Sci. Total Environ., 732, 139280–139280, https://doi.org/10.1016/j.scitotenv.2020.139280, 2020.
Cunnold, D. M., Zawodny, J. M., Chu, W. P., Pommereau, J. P., Goutail, F., Lenoble, J., McCormick, M. P., Veiga, R. E., Murcray, D., Iwagami, N., Shibasaki, K., Simon, P. C., and Peetermans, W.: Validation of SAGE II NO 2 measurements, J. Geophys. Res., 96, 12913–12925, https://doi.org/10.1029/91JD01344, 1991.
Dammers, E., McLinden, C. A., Griffin, D., Shephard, M. W., Van Der Graaf, S., Lutsch, E., Schaap, M., Gainairu-Matz, Y., Fioletov, V., Van Damme, M., Whitburn, S., Clarisse, L., Cady-Pereira, K., Clerbaux, C., Coheur, P. F., and Erisman, J. W.: NH3 emissions from large point sources derived from CrIS and IASI satellite observations, Atmos. Chem. Phys., 19, 12261–12293, https://doi.org/10.5194/acp-19-12261-2019, 2019.
Dantas, G., Siciliano, B., França, B. B., da Silva, C. M., and Arbilla, G.: The impact of COVID-19 partial lock- down on the air quality of the city of Rio de Janeiro, Brazil, Sci. Total Environ., 729, 139085, https://doi.org/10.1016/j.scitotenv.2020.139085, 2020.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
de Foy, B., Wilkins, J. L., Lu, Z., Streets, D. G., and Duncan, B. N.: Model evaluation of methods for estimating surface emissions and chemical lifetimes from satellite data, Atmos. Environ., 98, 66–77, https://doi.org/10.1016/j.atmosenv.2014.08.051, 2014.
de Foy, B., Lu, Z., Streets, D. G., Lamsal, L. N., and Duncan, B. N.: Estimates of power plant NOx emissions and lifetimes from OMI NO2 satellite retrievals, Atmos. Environ., 116, 1–11, https://doi.org/10.1016/j.atmosenv.2015.05.056, 2015.
Ding, J., van der A, R. J., Eskes, H. J., Mijling, B., Stavrakou, T., van Geffen, J. H. G. M., and Veefkind, J. P.: NOx Emissions Reduction and Rebound in China Due to the COVID-19 Crisis, Geophys. Res. Lett., 47, e2020GL089912, https://doi.org/10.1029/2020GL089912, 2020.
Duncan, B. N., Lamsal, L. N., Thompson, A. M., Yoshida, Y., Lu, Z., Streets, D. G., Hurwitz, M. M., and Pickering, K. E.: A space-based, high-resolution view of notable changes in urban NOx pollution around the world (2005–2014), J. Geophys. Res.-Atmos., 121, 976–996, https://doi.org/10.1002/2015JD024121, 2015.
EC (European Commission): COVID-19 in European coal regions, EC, https://ec.europa.eu/energy/sites/ener/files/documents/covid-19_in_european_coal_regions.pdf (last access: 1 March 2021), 2020.
EPA: U.S. Environmental Protection Agency (EPA) National Emissions Inventory, U.S. EPA, https://www.epa.gov/air-emissions-inventories, last access: 17 July 2020.
ESA EOP-GMQ: Sentinel-5 Precursor Calibration and Validation Plan for the Operational Phase, ESA, https://sentinel.esa.int/documents/247904/2474724/Sentinel-5P-Calibration-and-Validation-Plan.pdf (last access: 29 August 2021), 2017.
Fioletov, V., McLinden, C. A., Kharol, S. K., Krotkov, N. A., Li, C., Joiner, J., Moran, M. D., Vet, R., Visschedijk, A. J. H., and Denier van der Gon, H. A. C.: Multi-source SO2 emission retrievals and consistency of satellite and surface measurements with reported emissions, Atmos. Chem. Phys., 17, 12597–12616, https://doi.org/10.5194/acp-17-12597-2017, 2017.
Fioletov, V. E., McLinden, C. A., Krotkov, N., and Li, C.: Lifetimes and emissions of SO2 from point sources estimated from OMI, Geophys. Res. Lett., 42, 1969–1976, https://doi.org/10.1002/2015GL063148, 2015.
Fioletov, V. E., McLinden, C. A., Krotkov, N., Li, C., Joiner, J., Theys, N., Carn, S., and Moran, M. D.: A global catalogue of large SO2 sources and emissions derived from the Ozone Monitoring Instrument, Atmos. Chem. Phys., 16, 11497–11519, https://doi.org/10.5194/acp-16-11497-2016, 2016.
Fu, F., Purvis-Roberts, K. L., and Williams, B.: Impact of the COVID-19 pandemic lockdown on air pollution in 20 major cities around the world, Atmosphere, 11, 1189, https://doi.org/10.3390/atmos11111189, 2020.
Georgoulias, A. K., Boersma, K. F., Vliet, J. van, Zhang, X., van der A, R., Zanis, P., and de Laat, J.: Detection of NO2 pollution plumes from individual ships with the TROPOMI/S5P satellite sensor, Environ. Res. Lett., 15, 124037, https://doi.org/10.1088/1748-9326/abc445, 2020.
Ghahremanloo, M., Lops, Y., Choi, Y., and Mousavinezhad, S.: Impact of the COVID-19 outbreak on air pollution levels in East Asia, Sci. Total Environ., 754, 142226, https://doi.org/10.1016/j.scitotenv.2020.142226, 2021.
Gkatzelis, G. I., Gilman, J. B., Brown, S. S., Eskes, H., Gomes, A. R., Lange, A. C., McDonald, B. C., Peischl, J., Petzold, A., Thompson, C. R., and Kiendler-Scharr, A.: The Global Impacts of COVID-19 Lockdowns on Urban Air Quality: A Critical Review and Recommendations, Elementa: Science of the Anthropocene, 9, 00176, https://doi.org/10.1525/elementa.2021.00176, 2021.
Goldberg, D. L., Anenberg, S. C., Griffin, D., McLinden, C. A., Lu, Z., and Streets, D. G.: Disentangling the impact of the COVID-19 lockdowns on urban NO2 from natural variability, Geophys. Res. Lett., 47, e2020GL089269, https://doi.org/10.1029/2020GL089269, 2020.
Griffin, D., McLinden, C. A., Racine, J., Moran, M. D., Fioletov, V., Pavlovic, R., Mashayekhi, R., Zhao, X., and Eskes, H.: Assessing the impact of corona-virus-19 on nitrogen dioxide levels over southern Ontario, Canada, Remote Sens., 12, 4112, https://doi.org/10.3390/rs12244112, 2020.
Guevara, M., Jorba, O., Soret, A., Petetin, H., Bowdalo, D., Serradell, K., Tena, C., Denier van der Gon, H., Kuenen, J., Peuch, V.-H., and Pérez García-Pando, C.: Time-resolved emission reductions for atmospheric chemistry modelling in Europe during the COVID-19 lockdowns, Atmos. Chem. Phys., 21, 773–797, https://doi.org/10.5194/acp-21-773-2021, 2021.
Hassan, F., Chaudhry, M. U., Yasir, M., Asghar, M. N., and Sarkodie, S. A.: Monitoring the Impact of COVID-19 Lockdown on the Production of Nitrogen Dioxide (NO2) Pollutants Using Satellite Imagery: A Case Study of South Asia, Sustainability, 13, 7184, https://doi.org/10.3390/su13137184, 2021.
Herman, J., Cede, A., Spinei, E., Mount, G., Tzortziou, M., and Abuhassan, N.: NO2 column amounts from ground-based Pandora and MFDOAS spectrometers using the direct-sun DOAS technique: Intercomparisons and application to OMI validation, J. Geophys. Res., 114, D13307, https://doi.org/10.1029/2009JD011848, 2009.
Hudman, R. C., Moore, N. E., Mebust, A. K., Martin, R. V., Russell, A. R., Valin, L. C., and Cohen, R. C.: Steps towards a mechanistic model of global soil nitric oxide emissions: implementation and space based-constraints, Atmos. Chem. Phys., 12, 7779–7795, https://doi.org/10.5194/acp-12-7779-2012, 2012.
Ialongo, I., Virta, H., Eskes, H., Hovila, J., and Douros, J.: Comparison of TROPOMI/Sentinel-5 Precursor NO2 observations with ground-based measurements in Helsinki, Atmos. Meas. Tech., 13, 205–218, https://doi.org/10.5194/amt-13-205-2020, 2020.
Judd, L. M., Al-Saadi, J. A., Szykman, J. J., Valin, L. C., Janz, S. J., Kowalewski, M. G., Eskes, H. J., Veefkind, J. P., Cede, A., Mueller, M., Gebetsberger, M., Swap, R., Pierce, R. B., Nowlan, C. R., Abad, G. G., Nehrir, A., and Williams, D.: Evaluating Sentinel-5P TROPOMI tropospheric NO2 column densities with airborne and Pandora spectrometers near New York City and Long Island Sound, Atmos. Meas. Tech., 13, 6113–6140, https://doi.org/10.5194/amt-13-6113-2020, 2020.
Juncosa Calahorrano, J. F., Lindaas, J., O'Dell, K., Palm, B. B., Peng, Q., Flocke, F., Pollack, I. B., Garofalo, L. A., Farmer, D. K., Pierce, J. R., Collett, J. L., Weinheimer, A., Campos, T., Hornbrook, R. S., Hall, S. R., Ullmann, K., Pothier, M. A., Apel, E. C., Permar, W., Hu, L., Hills, A. J., Montzka, D., Tyndall, G., Thornton, J. A., and Fischer, E. V.: Daytime Oxidized Reactive Nitrogen Partitioning in Western U.S. Wildfire Smoke Plumes, J. Geophys. Res.-Atmos., 126, e2020JD033484, https://doi.org/10.1029/2020JD033484, 2021.
Kanniah, K. D., Kamarul Zaman, N. A. F., Kaskaoutis, D. G., and Latif, M. T.: COVID-19's impact on the atmospheric environment in the Southeast Asia region, Sci. Total Environ., 736, 139658, https://doi.org/10.1016/j.scitotenv.2020.139658, 2020.
Kenagy, H. S., Sparks, T. L., Ebben, C. J., Wooldrige, P. J., Lopez-Hilfiker, F. D., Lee, B. H., Thornton, J. A., McDuffie, E. E., Fibiger, D. L., Brown, S. S., Montzka, D. D., Weinheimer, A. J., Schroder, J. C., Campuzano-Jost, P., Day, D. A., Jimenez, J. L., Dibb, J. E., Campos, T., Shah, V., Jaeglé, L., and Cohen, R. C.: NOx lifetime and NOy partitioning during WINTER, J. Geophys. Res.-Atmos., 123, 9813–9827, https://doi.org/10.1029/2018JD028736, 2018.
Keller, C. A., Evans, M. J., Knowland, K. E., Hasenkopf, C. A., Modekurty, S., Lucchesi, R. A., Oda, T., Franca, B. B., Mandarino, F. C., Díaz Suárez, M. V., Ryan, R. G., Fakes, L. H., and Pawson, S.: Global impact of COVID-19 restrictions on the surface concentrations of nitrogen dioxide and ozone, Atmos. Chem. Phys., 21, 3555–3592, https://doi.org/10.5194/acp-21-3555-2021, 2021.
Kim, M., Kuhlmann, G., and Brunner, D.: Importance of satellite observations for high-resolution mapping of near-surface NO2 by machine learning, Remote Sens. Environ., 264, 112573, https://doi.org/10.1016/j.rse.2021.112573, 2021.
Kondragunta, S., Wei, Z., McDonald, B. C., Goldberg, D. L., and Tong, D. Q.: COVID-19 induced fingerprints of a new normal urban air quality in the United States, J. Geophys. Res.-Atmos., 126, e2021JD034797, https://doi.org/10.1029/2021JD034797, 2021.
Konovalov, I. B., Beekmann, M., Richter, A., and Burrows, J. P.: Inverse modelling of the spatial distribution of NOx emissions on a continental scale using satellite data, Atmos. Chem. Phys., 6, 1747–1770, https://doi.org/10.5194/acp-6-1747-2006, 2006.
Koukouli, M.-E., Skoulidou, I., Karavias, A., Parcharidis, I., Balis, D., Manders, A., Segers, A., Eskes, H., and van Geffen, J.: Sudden changes in nitrogen dioxide emissions over Greece due to lockdown after the outbreak of COVID-19, Atmos. Chem. Phys., 21, 1759–1774, https://doi.org/10.5194/acp-21-1759-2021, 2021.
Krotkov, N. A., McLinden, C. A., Li, C., Lamsal, L. N., Celarier, E. A., Marchenko, S. V., Swartz, W. H., Bucsela, E. J., Joiner, J., Duncan, B. N., Boersma, K. F., Veefkind, J. P., Levelt, P. F., Fioletov, V. E., Dickerson, R. R., He, H., Lu, Z., and Streets, D. G.: Aura OMI observations of regional SO2 and NO2 pollution changes from 2005 to 2015, Atmos. Chem. Phys., 16, 4605–4629, https://doi.org/10.5194/acp-16-4605-2016, 2016.
Lamsal, L. N., Duncan, B. N., Yoshida, Y., Krotkov, N. A., Pickering, K. E., Streets, D. G., and Lu, Z.: U.S. NO2 trends (2005–2013): EPA Air Quality System (AQS) data versus improved observations from the Ozone Monitoring Instrument (OMI), Atmos. Environ., 110, 130–143, https://doi.org/10.1016/j.atmosenv.2015.03.055, 2015.
Lamsal, L. N., Krotkov, N. A., Vasilkov, A., Marchenko, S., Qin, W., Yang, E.-S., Fasnacht, Z., Joiner, J., Choi, S., Haffner, D., Swartz, W. H., Fisher, B., and Bucsela, E.: Ozone Monitoring Instrument (OMI) Aura nitrogen dioxide standard product version 4.0 with improved surface and cloud treatments, Atmos. Meas. Tech., 14, 455–479, https://doi.org/10.5194/amt-14-455-2021, 2021.
Lange, K., Richter, A., and Burrows, J. P.: Variability of nitrogen oxide emission fluxes and lifetimes estimated from Sentinel-5P TROPOMI observations, Atmos. Chem. Phys., 22, 2745–2767, https://doi.org/10.5194/acp-22-2745-2022, 2022.
Laughner, J. and Cohen, R. C.: Direct observation of changing NOx lifetime in North American cities, Science, 366, 723–727, https://doi.org/10.1126/science.aax6832, 2019.
Lee, J. D., Drysdale, W. S., Finch, D. P., Wilde, S. E., and Palmer, P. I.: UK surface NO2 levels dropped by 42 % during the COVID-19 lockdown: impact on surface O3, Atmos. Chem. Phys., 20, 15743–15759, https://doi.org/10.5194/acp-20-15743-2020, 2020.
Levelt, P. F., Joiner, J., Tamminen, J., Veefkind, J. P., Bhartia, P. K., Stein Zweers, D. C., Duncan, B. N., Streets, D. G., Eskes, H., van der A, R., McLinden, C., Fioletov, V., Carn, S., de Laat, J., DeLand, M., Marchenko, S., McPeters, R., Ziemke, J., Fu, D., Liu, X., Pickering, K., Apituley, A., González Abad, G., Arola, A., Boersma, F., Chan Miller, C., Chance, K., de Graaf, M., Hakkarainen, J., Hassinen, S., Ialongo, I., Kleipool, Q., Krotkov, N., Li, C., Lamsal, L., Newman, P., Nowlan, C., Suleiman, R., Tilstra, L. G., Torres, O., Wang, H., and Wargan, K.: The Ozone Monitoring Instrument: overview of 14 years in space, Atmos. Chem. Phys., 18, 5699–5745, https://doi.org/10.5194/acp-18-5699-2018, 2018.
Levelt, P. F., Stein Zweers, D. C., Aben, I., Bauwens, M., Borsdorff, T., De Smedt, I., Eskes, H. J., Lerot, C., Loyola, D. G., Romahn, F., Stavrakou, T., Theys, N., Van Roozendael, M., Veefkind, J. P., and Verhoelst, T.: Air quality impacts of COVID-19 lockdown measures detected from space using high spatial resolution observations of multiple trace gases from Sentinel-5P/TROPOMI, Atmos. Chem. Phys. Discuss. [preprint], https://doi.org/10.5194/acp-2021-534, in review, 2021.
Liu, F., Beirle, S., Zhang, Q., Dörner, S., He, K., and Wagner, T.: NOx lifetimes and emissions of cities and power plants in polluted background estimated by satellite observations, Atmos. Chem. Phys., 16, 5283–5298, https://doi.org/10.5194/acp-16-5283-2016, 2016.
Liu, F., Choi, S., Li, C., Fioletov, V. E., McLinden, C. A., Joiner, J., Krotkov, N. A., Bian, H., Janssens-Maenhout, G., Darmenov, A. S., and da Silva, A. M.: A new global anthropogenic SO2 emission inventory for the last decade: a mosaic of satellite-derived and bottom-up emissions, Atmos. Chem. Phys., 18, 16571–16586, https://doi.org/10.5194/acp-18-16571-2018, 2018.
Liu, F., Page, A., Strode, S. A., Yoshida, Y., Choi, S., Zheng, B., Lamsal, L. N., Li, C., Krotkov, N. A., Eskes, H., Ronald Vander, A., Veefkind, P., Levelt, P., Joiner, J., and Hauser, O. P.: Abrupt declines in tropospheric nitrogen dioxide over China after the outbreak of COVID-19, Science Advances, 6, eabc2992, https://doi.org/10.1126/sciadv.abc2992, 2020a.
Liu, F., Page, A., Strode, S. A., Yoshida, Y., Choi, S., Smith, S., Knowland, K. E., Zheng, B., Lamsal, L. N., Li, C., and Krotkov, N. A.: Abrupt decline in tropospheric nitrogen dioxide after the outbreak of COVID-19, in: AGU Fall Meeting 2020, 1–17 December 2020, AGU, abstract A132-01, https://agu.confex.com/agu/fm20/meetingapp.cgi/Paper/664980 (last access: 1 March 2021), 2020b.
Lorente, A., Boersma, K. F., Eskes, H. J., Veefkind, J. P., van Geffen, J. H. G. M., de Zeeuw, M. B., Denier van der Gon, H. A. C., Beirle, S., and Krol, M. C.: Quantification of nitrogen oxides emissions from build-up of pollution over Paris with TROPOMI, Sci. Rep., 9, 20033, https://doi.org/10.1038/s41598-019-56428-5, 2019.
Lu, Z., Streets, D. G., de Foy, B., Lamsal, L. N., Duncan, B. N., and Xing, J.: Emissions of nitrogen oxides from US urban areas: estimation from Ozone Monitoring Instrument retrievals for 2005–2014, Atmos. Chem. Phys., 15, 10367–10383, https://doi.org/10.5194/acp-15-10367-2015, 2015.
Martin, R. V., Chance, K., Jacob, D. J., Kurosu, T. P., Spurr, R. J. D., Bucsela, E., Gleason, J. F., Palmer, P. I., Bey, I., Fiore, A. M., Li, Q., Yantosca, R. M., and Koelemeijer, R. B. A.: An improved retrieval of tropospheric nitrogen dioxide from GOME, J. Geophys. Res., 107, 4437, https://doi.org/10.1029/2001JD001027, 2002.
McLinden, C. A., Fioletov, V., Boersma, K. F., Krotkov, N., Sioris, C. E., Veefkind, J. P., and Yang, K.: Air quality over the Canadian oil sands: A first assessment using satellite observations, Geophys. Res. Lett., 39, L04804, https://doi.org/10.1029/2011GL050273, 2012.
McLinden, C. A., Fioletov, V., Shephard, M. W., Krotkov, N., Li, C., Martin, R. V., Moran, M. D., and Joiner, J.: Space-based detection of missing sulfur dioxide sources of global air pollution, Nat. Geosci., 9, 496–500, https://doi.org/10.1038/ngeo2724, 2016.
McLinden, C. A., Adams, C. L. F., Fioletov, V., Griffin, D., Makar, P. A., Zhao, X., Kovachik, A., Dickson, N. M., Brown, C., Krotkov, N., Li, C., Theys, N., Hedelt, P., and Loyola, D. G.: Inconsistencies in sulphur dioxide emissions from the Canadian oil sands and potential implications, Environ. Res. Lett., 16, 014012, https://doi.org/10.1088/1748-9326/abcbbb, 2020.
Mehmood, K., Bao, Y., Petropoulos, G. P., Abbas, R., Abrar, M. M., Saifullah, Mustafa, A., Soban, A., Saud, S., Ahmad, M., Hussain, I., and Fahad, S.: Investigating connections between COVID-19 pandemic, air pollution and community interventions for Pakistan employing geoinformation technologies, Chemosphere, 272, 129809, https://doi.org/10.1016/j.chemosphere.2021.129809, 2021
Mijling, B. and van der A, R. J.: Using daily satellite observations to estimate emissions of short-lived air pollutants on a mesoscopic scale, J. Geophys. Res., 117, 17302, https://doi.org/10.1029/2012JD017817, 2012.
Misra, P., Takigawa, M., Khatri, P., Dhaka, S. K., Dimri, A. P., Yamaji, K., Kajino, M., Takeuchi, W., Imasu, R., Nitta, K., Patra, P. K., and Hayashida, S.: Nitrogen oxides concentration and emission change detection during COVID-19 restrictions in North India, Scientific Reports, 11, 9800, https://doi.org/10.1038/s41598-021-87673-2, 2021.
NOAA: 2-Minute Gridded Global Relief Data (ETOPO2v2), World Data Service for Geophysics, Boulder [data set], https://www.ngdc.noaa.gov/mgg/global/etopo2.html (last access: 17 June 2020), 2006.
NPRI (National Pollutant Release Inventory): Sulfur oxide emissions for Canada, NPRI [data set], https://www.canada.ca/en/services/environment/pollution-waste-management/national-pollutant-release-inventory.html, last access: 17 July 2020.
Pommier, M., McLinden, C. A., and Deeter, M.: Relative changes in CO emissions over megacities based on observations from space, Geophys. Res. Lett., 40, 3766–3771, https://doi.org/10.1002/grl.50704, 2013.
Potts, D. A., Marais, E. A., Boesch, H., Pope, R. J., Lee, J., Drysdale, W., Chipperfield, M. P., Kerridge, B., Siddans, R., Moore, D. P., and Remedios, J.: Diagnosing air quality changes in the UK during the COVID-19 lockdown using TROPOMI and GEOS-Chem, Environ. Res. Lett., 16, 054031, https://doi.org/10.1088/1748-9326/abde5d, 2021.
Qu, Z., Jacob, D. J., Silvern, R. F., Shah, V., Campbell, P. C., Valin, L. C., and Murray, L. T.: US COVID-19 shutdown demonstrates importance of background NO2 in inferring NOx emissions from satellite NO2 observations, Geophys. Res. Lett., 48, e2021GL092783, https://doi.org/10.1029/2021GL092783, 2021.
Richter, A., Eyring, V., Burrows, J. P., Bovensmann, H., Lauer, A., Sierk, B., and Crutzen, P. J.: Satellite measurements of NO2 from international shipping emissions, Geophys. Res. Lett., 31, L23110, https://doi.org/10.1029/2004GL020822, 2004.
S5P Data Hub: Sentinel-5P Pre-Operations Data Hub, ESA, https://s5phub.copernicus.eu/ (last access: 5 August 2021), 2022.
Sannigrahi S., Kumar, P., Molter, A., Zhang, Q., Basu, B., Basu, A. S., and Pilla, F.: Examining the status of improved air quality in world cities due to COVID-19 led temporary reduction in anthropogenic emissions, Environ. Res., 196, 110927, https://doi.org/10.1016/j.envres.2021.110927, 2021
SEDAC: The Gridded Population of the World (GPW), NASA Socioeconomic Data and Applications Center (SEDAC) [data set], Palisades, NY, https://sedac.ciesin.columbia.edu/data/collection/gpw-v4 (last access: 10 May 2021), 2017.
Sha, T., Ma, X., Zhang, H., Janechek, N., Wang, Y., Wang, Y., Castro Garciá, L., Jenerette, G. D., and Wang, J.: Impacts of Soil NOx Emission on O3 Air Quality in Rural California, Environ. Sci. Technol., 55, 7113–7122, https://doi.org/10.1021/acs.est.0c06834, 2021.
Siciliano, B., Carvalho, G., Da Silva, C. M., and Arbilla, G.: The Impact of COVID-19 Partial Lockdown on Primary Pollutant Concentrations in the Atmosphere of Rio de Janeiro and São Paulo Megacities (Brazil), B. Environ. Contam. Tox., 105, 2–8, 2020.
Silvern, R. F., Jacob, D. J., Mickley, L. J., Sulprizio, M. P., Travis, K. R., Marais, E. A., Cohen, R. C., Laughner, J. L., Choi, S., Joiner, J., and Lamsal, L. N.: Using satellite observations of tropospheric NO2 columns to infer long-term trends in US NOx emissions: the importance of accounting for the free-tropospheric NO2 background, Atmos. Chem. Phys., 19, 8863–8878, https://doi.org/10.5194/acp-19-8863-2019, 2019.
Stavrakou, T., Müller, J. F., Bauwens, M., Boersma, K. F., and van Geffen, J.: Satellite evidence for changes in the NO2 weekly cycle over large cities, Sci. Rep., 10, 10066, https://doi.org/10.1038/s41598-020-66891-0, 2020.
Streets, D. G., Canty, T., Carmichael, G. R., De Foy, B., Dickerson, R. R., Duncan, B. N., Edwards, D. P., Haynes, J. A., Henze, D. K., Houyoux, M. R., Jacob, D. J., Krotkov, N. A., Lamsal, L. N., Liu, Y., Lu, Z., Martin, R. V., Pfister, G. G., Pinder, R. W., Salawitch, R. J., and Wecht, K. J.: Emissions estimation from satellite retrievals: A review of current capability, Atmos. Environ., 77, 1011–1042, https://doi.org/10.1016/j.atmosenv.2013.05.051, 2013.
Tack, F., Merlaud, A., Iordache, M.-D., Pinardi, G., Dimitropoulou, E., Eskes, H., Bomans, B., Veefkind, P., and Van Roozendael, M.: Assessment of the TROPOMI tropospheric NO2 product based on airborne APEX observations, Atmos. Meas. Tech., 14, 615–646, https://doi.org/10.5194/amt-14-615-2021, 2021.
Theys, N., Fioletov, V., Li, C., De Smedt, I., Lerot, C., McLinden, C., Krotkov, N., Griffin, D., Clarisse, L., Hedelt, P., Loyola, D., Wagner, T., Kumar, V., Innes, A., Ribas, R., Hendrick, F., Vlietinck, J., Brenot, H., and Van Roozendael, M.: A sulfur dioxide Covariance-Based Retrieval Algorithm (COBRA): application to TROPOMI reveals new emission sources, Atmos. Chem. Phys., 21, 16727–16744, https://doi.org/10.5194/acp-21-16727-2021, 2021.
Vadrevu, K. P., Eaturu, A., Biswas, S., Lasko, K., Sahu, S., Garg, J. K., and Justice, C.: Spatial and temporal variations of air pollution over 41 cities of India during the COVID-19 lockdown period, Sci. Rep., 10, 16574, https://doi.org/10.1038/s41598-020-72271-5, 2020.
van Geffen, J., Eskes, H., Boersma, K., Maasakkers, J., and Veefkind, J.: TROPOMI ATBD of the total and tropospheric NO2 data products (issue 1.2.0), De Bilt, the Netherlands, s5P-KNMI-L2-0005-RP, 2018.
van Geffen, J. H. G. M., Eskes, H. J., Boersma, K. F., Maasakkers, J. D., and Veefkind, J. P.: TROPOMI ATBD of the total and tropospheric NO2 data products, http://www.tropomi.eu/sites/default/files/files/publicS5P-KNMI-L2-0005-RP-ATBD_NO2_data_products-20190206_v140.pdf (last access: 17 June 2020), 2019.
van Geffen, J., Boersma, K. F., Eskes, H., Sneep, M., ter Linden, M., Zara, M., and Veefkind, J. P.: S5P TROPOMI NO2 slant column retrieval: method, stability, uncertainties and comparisons with OMI, Atmos. Meas. Tech., 13, 1315–1335, https://doi.org/10.5194/amt-13-1315-2020, 2020.
van Geffen, J., Eskes, H., Compernolle, S., Pinardi, G., Verhoelst, T., Lambert, J.-C., Sneep, M., ter Linden, M., Ludewig, A., Boersma, K. F., and Veefkind, J. P.: Sentinel-5P TROPOMI NO2 retrieval: impact of version v2.2 improvements and comparisons with OMI and ground-based data, Atmos. Meas. Tech. Discuss. [preprint], https://doi.org/10.5194/amt-2021-329, in review, 2021.
Veefkind, J. P. P., Aben, I., McMullan, K., Förster, H., de Vries, J., Otter, G., Claas, J., Eskes, H. J. J., de Haan, J. F. F., Kleipool, Q., van Weele, M., Hasekamp, O., Hoogeveen, R., Landgraf, J., Snel, R., Tol, P., Ingmann, P., Voors, R., Kruizinga, B., Vink, R., Visser, H., and Levelt, P. F. F.: TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications, Remote Sens. Environ., 120, 70–83, https://doi.org/10.1016/j.rse.2011.09.027, 2012.
Venter, Z. S., Aunan, K., Chowdhury, S., and Lelieveld, J.: COVID-19 lockdowns cause global air pollution declines, P. Natl. Acad. Sci. USA, 117, 18984–18990, https://doi.org/10.1073/pnas.2006853117, 2020.
Verhoelst, T., Compernolle, S., Pinardi, G., Lambert, J.-C., Eskes, H. J., Eichmann, K.-U., Fjæraa, A. M., Granville, J., Niemeijer, S., Cede, A., Tiefengraber, M., Hendrick, F., Pazmiño, A., Bais, A., Bazureau, A., Boersma, K. F., Bognar, K., Dehn, A., Donner, S., Elokhov, A., Gebetsberger, M., Goutail, F., Grutter de la Mora, M., Gruzdev, A., Gratsea, M., Hansen, G. H., Irie, H., Jepsen, N., Kanaya, Y., Karagkiozidis, D., Kivi, R., Kreher, K., Levelt, P. F., Liu, C., Müller, M., Navarro Comas, M., Piters, A. J. M., Pommereau, J.-P., Portafaix, T., Prados-Roman, C., Puentedura, O., Querel, R., Remmers, J., Richter, A., Rimmer, J., Rivera Cárdenas, C., Saavedra de Miguel, L., Sinyakov, V. P., Stremme, W., Strong, K., Van Roozendael, M., Veefkind, J. P., Wagner, T., Wittrock, F., Yela González, M., and Zehner, C.: Ground-based validation of the Copernicus Sentinel-5P TROPOMI NO2 measurements with the NDACC ZSL-DOAS, MAX-DOAS and Pandonia global networks, Atmos. Meas. Tech., 14, 481–510, https://doi.org/10.5194/amt-14-481-2021, 2021.
Vinnikov, K. Y., Dickerson, R. R., Krotkov, N. A., Edgerton, E. S., and Schwab, J. J.: The net decay time of anomalies in concentrations of atmospheric pollutants, Atmos. Environ., 160, 19–26, https://doi.org/10.1016/j.atmosenv.2017.04.006, 2017.
Vîrghileanu, M., Săvulescu, I., Mihai, B.-A., Nistor, C., and Dobre, R.: Nitrogen dioxide (NO2) pollution monitoring with sentinel-5p satellite imagery over europe during the coronavirus pandemic outbreak, Remote Sens., 12, 3575, https://doi.org/10.3390/rs12213575, 2020.
Williams, J. E., Boersma, K. F., Le Sager, P., and Verstraeten, W. W.: The high-resolution version of TM5-MP for optimized satellite retrievals: description and validation, Geosci. Model Dev., 10, 721–750, https://doi.org/10.5194/gmd-10-721-2017, 2017.
Zhao, X., Griffin, D., Fioletov, V., McLinden, C., Cede, A., Tiefengraber, M., Müller, M., Bognar, K., Strong, K., Boersma, F., Eskes, H., Davies, J., Ogyu, A., and Lee, S. C.: Assessment of the quality of TROPOMI high-spatial-resolution NO2 data products in the Greater Toronto Area, Atmos. Meas. Tech., 13, 2131–2159, https://doi.org/10.5194/amt-13-2131-2020, 2020.
Zhang, H., Lin, Y., Wei, S., Loo, B. P. Y., Lai, P. C., Lam, Y. F., Wan, L., and Li, Y.: Global association between satellite-derived nitrogen dioxide (NO2) and lockdown policies under the COVID-19 pandemic, Sci. Total Environ., 761, 144148, https://doi.org/10.1016/j.scitotenv.2020.144148, 2021.
Zhang, L., Jacob, D. J., Knipping, E. M., Kumar, N., Munger, J. W., Carouge, C. C., van Donkelaar, A., Wang, Y. X., and Chen, D.: Nitrogen deposition to the United States: distribution, sources, and processes, Atmos. Chem. Phys., 12, 4539–4554, https://doi.org/10.5194/acp-12-4539-2012, 2012.
Zoogman, P., Liu, X., Suleiman, R. M., Pennington, W. F., Flittner, D. E., Al-Saadi, J. A., Hilton, B. B., Nicks, D. K., Newchurch, M. J., Carr, J. L., Janz, S. J., Andraschko, M. R., Arola, A., Baker, B. D., Canova, B. P., Chan Miller, C., Cohen, R. C., Davis, J. E., Dussault, M. E., Edwards, D. P., Fishman, J., Ghulam, A., González Abad, G., Grutter, M., Herman, J. R., Houck, J., Jacob, D. J., Joiner, J., Kerridge, B. J., Kim, J., Krotkov, N. A., Lamsal, L., Li, C., Lindfors, A., Martin, R. V., McElroy, C. T., McLinden, C., Natraj, V., Neil, D. O., Nowlan, C. R., O'Sullivan, E. J., Palmer, P. I., Pierce, R. B., Pippin, M. R., Saiz-Lopez, A., Spurr, R. J. D., Szykman, J. J., Torres, O., Veefkind, J. P., Veihelmann, B., Wang, H., Wang, J., and Chance, K.: Tropospheric emissions: Monitoring of pollution (TEMPO), J. Quant. Spectrosc. Ra., 186, 17–39, https://doi.org/10.1016/j.jqsrt.2016.05.008, 2016.





