the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The role of organic acids in new particle formation from methanesulfonic acid and methylamine
Rongjie Zhang
Jiewen Shen
Hong-Bin Xie
Jingwen Chen
Jonas Elm
Atmospheric organic acids (OAs) are expected to enhance methanesulfonic acid (MSA)-driven new particle formation (NPF). However, the exact role of OAs in MSA-driven NPF remains unclear. Here, we employed a two-step strategy to probe the role of OAs in MSA–methylamine (MA) NPF. Initially, we evaluated the enhancing potential of 12 commonly detected OAs in ternary MA–MSA–OA cluster formation by considering the formation free energies of the (MSA)1(MA)1(OA)1 clusters and the atmospheric concentrations of the OAs. It was found that formic acid (ForA) has the highest potential to stabilize the MA–MSA clusters. The high enhancing potential of ForA results from its acidity, structural factors such as no intramolecular H bonds, and high atmospheric abundance. The second step is to extend the MSA–MA–ForA system to larger cluster sizes. The results indicate that ForA can indeed enhance MSA–MA NPF at atmospheric conditions (the upper limited temperature is 258.15 K), indicating that ForA might have an important role in MSA-driven NPF. The enhancing effect of ForA is mainly caused by an increased formation of the (MSA)2(MA)1 cluster, which is involved in the pathway of binary MSA–MA nucleation. Hence, our results indicate that OAs might be required to facilitate MSA-driven NPF in the atmosphere.
- Article
(1989 KB) - Full-text XML
-
Supplement
(1934 KB) - BibTeX
- EndNote
New particle formation (NPF) accounts for a substantial fraction of atmospheric aerosols (Elm et al., 2020; Zhang et al., 2012; Lee et al., 2019; Yin et al., 2021), which exert significant effects on air quality, human health, and the global climate (Ho et al., 2007; Heal et al., 2012; Zhang et al., 2015; An et al., 2016). Evidence from field observations, laboratory experiments, and simulations suggests that sulfuric acid (SA) is a key species in driving NPF over land (Lee et al., 2019; Elm et al., 2020; Yao et al., 2018; Sipila et al., 2010; Kirkby et al., 2011; Almeida et al., 2013; Nieminen et al., 2009). Recently, methanesulfonic acid (MSA)-driven NPF has received increasing attention with the implementation of stricter regulations on anthropogenic SO2 emissions globally (Dawson et al., 2012; Chen et al., 2015; Arquero et al., 2017a, b; Chen and Finlayson-Pitts, 2017; Xu et al., 2017; Wen et al., 2018; Chen et al., 2020b; Perraud et al., 2020a, b; Stahl et al., 2020), since MSA has a considerable contribution to NPF under the scenario that only natural sources of SO2 are kept (Perraud et al., 2015).
Atmospheric bases can enhance both SA-driven and MSA-driven NPF by stabilizing freshly formed molecular clusters via acid–base proton transfer reactions (Zhang et al., 2012; Almeida et al., 2013; Chen et al., 2020b; Perraud et al., 2020a, b; Kurten et al., 2008; Loukonen et al., 2010; Glasoe et al., 2015; Olenius et al., 2017; Ma et al., 2019b; Zuo et al., 2021; Shen et al., 2019, 2020; Chen et al., 2020a; Xu et al., 2020; Nishino et al., 2014). Amines have been shown to be much more efficient stabilizing species compared to ammonia for both SA–base and MSA–base cluster formation (Almeida et al., 2013; Kurten et al., 2008; Chen et al., 2020b; Perraud et al., 2020a; Shen et al., 2020; Chen et al., 2016). However, even considering the enhancing effect of bases, the SA-driven and MSA-driven nucleation mechanism still underestimates the nucleation rates compared to field observations (Zhang et al., 2012; Lee et al., 2019). This motivates the investigation of nucleation mechanisms involving other atmospheric relevant precursor vapors.
Atmospheric organic acids (OAs), originating from biogenic sources (vegetation) (Fehsenfeld et al., 1992; Chebbi and Carlier, 1996; Kavouras et al., 1998), anthropogenic sources (biomass burning and fossil fuel combustion) (Chebbi and Carlier, 1996; Chan et al., 2005; Falkovich et al., 2005; Cong et al., 2015; Friedman et al., 2017), and photochemical transformations from precursors, might be relevant for NPF (Zhang et al., 2004, 2012; Lee et al., 2019; Kavouras et al., 1998; Chebbi and Carlier, 1996; Paulot et al., 2009; Carlton et al., 2006). OAs cover a broad range of species in the atmosphere, with an estimated total atmospheric concentration above the parts per billion (ppb) level (Chebbi and Carlier, 1996; Veres et al., 2011). Although nucleation from OAs alone leads to a limited contribution to NPF (Zhang et al., 2012), previous studies have indicated that OAs might enhance SA-driven nucleation via hydrogen-bond (H-bond) interactions between OAs and SA (Zhang et al., 2004, 2012; Elm et al., 2020; Wang et al., 2019; Shi et al., 2019). Furthermore, OAs such as lactic, glyoxylic, glycolic, and malonic acid have been identified to enhance binary SA–base nucleation, especially at very low temperatures (218 K) (Zhang et al., 2017; Li et al., 2017; Liu et al., 2018; Zhang et al., 2018). Under certain conditions, the ternary SA–base–OA system might present higher nucleation rates compared to the binary systems of SA–base, SA–OA, and OA–base. In contrast to SA-driven NPF, MSA–base cluster formation is not very efficient on its own and thereby could be highly dependent on the enhancing effect of other contributing vapors (Dawson et al., 2012; Elm, 2021). While the SA-driven nucleation involving OAs has been extensively studied (Zhang et al., 2004; Elm et al., 2017; Li et al., 2017; Zhang et al., 2017, 2018; Liu et al., 2018; Wang et al., 2019; Shi et al., 2019), little is still known about the corresponding MSA-driven nucleation mechanism.
The potentially important role of OAs in MSA-driven nucleation has been pointed out by previous studies, which focused on the interaction between MSA and several OA monomers or role of oxalic acid in MSA–amine NPF (Zhao et al., 2017; Arquero et al., 2017a, b; Xu et al., 2017; Sheng et al., 2019). However, to date, the underlying enhancing effects from a broad range of OAs on MSA–amine nucleation have not been examined. Based on our recent work, the enhancing potential of other precursors on MSA-driven nucleation is quite sensitive to the specific molecular structure (Shen et al., 2020, 2019). In addition, there is a large difference in atmospheric abundance of various OAs, which also has an influence on the relative importance of different OAs in MSA–amine–OA cluster formation. Therefore, it is desirable to evaluate the role of OAs in MSA-driven NPF by considering the interaction of the different OAs with MSA–amine clusters and the atmospheric abundance of OAs.
Among the most commonly detected alkyl amines (methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA)), MA has been identified to be the strongest enhancing agent in MSA-driven NPF (Chen et al., 2016). Hence, in this study we will focus on the enhancing effect of OAs on binary MSA–MA nucleation. We initially evaluated the potential role of 12 commonly detected atmospheric OAs (formic (ForA), CH2O2; acetic (AceA), C2H4O2; glyoxylic (GlyA), C2H2O3; oxalic (OxaA), C2H2O4; pyruvic (PyrA), C3H4O3; malonic (MalA), C3H4O4; maleic (MaleA), C4H4O4; succinic (SucA), C4H6O4; glutaric (GluA), C5H8O4; adipic (AdiA), C6H10O4; benzoic (BenA), C7H6O2; and pinonic (PinA), C10H16O3 acids) in ternary MA–MSA–OA nucleation by examining the formation of the (MSA)1(MA)1(OA)1 clusters. Based on the calculated formation free energy (ΔG) of the (MSA)1(MA)1(OA)1 clusters and reported atmospheric concentrations of OAs, we rank the capability of different OAs to participate in ternary MSA–MA–OA nucleation. The OA with the highest capability was selected as a representative to further probe the enhancing potential of OAs on the MSA–MA NPF by considering the larger (MSA)x(MA)y(OA)z clusters.
2.1 Configurational sampling
A multi-step sampling scheme was used to search for the global minimum structures of the 12 (MA)1(MSA)1(OA)1 clusters, as well as the larger (MSA)x(MA)y(OA)z clusters. The binary MSA–MA cluster structures were taken from our previous work (Shen et al., 2020). Details of the scheme can be found in our previous studies addressing atmospheric cluster formation (Shen et al., 2019, 2020; Xie et al., 2017; Ma et al., 2019a). Briefly, around 1000–10 000 initial configurations for each cluster (fewer initial configurations for clusters with fewer molecules and more initial configurations for clusters with more molecules) were randomly generated and subsequently underwent a gradual screening process using various theoretical methods, to locate the clusters lowest in free energy. The employed theoretical methods for geometry optimization and single-point energy calculations include PM6, ωB97X-D/6-31, ωB97X-D/6-31, and DLPNO-CCSD(T)/aug-cc-pVTZ. The combination of ωB97X-D/6-31 and DLPNO-CCSD(T)/aug-cc-pVTZ has in several benchmarks shown good performance for studying the formation of atmospheric molecular clusters (Elm et al., 2013; Elm and Kristensen, 2017). All calculations employing semiempirical (PM6) and density functional theory (ωB97X-D functional) methods were performed in the GAUSSIAN 09 program package (Frisch et al., 2009), and DLPNO-CCSD(T)/aug-cc-pVTZ calculations were performed using the ORCA 4.0.0 program (Neese, 2012). The tight PNO and SCF convergence criteria were used in DLPNO-CCSD(T)/aug-cc-pVTZ calculations by employing keywords tightpno and tightscf. The binding free energy (ΔG) for each cluster was obtained by subtracting the Gibbs free energy of the constituent monomers (MA, MSA, and OA) from that of the cluster at 298.15 K. The ΔG values at other temperatures were also calculated under the assumption that the enthalpy and entropy change (ΔH and ΔS) are constant in the considered tropospheric temperature range (238.15–298.15 K).
2.2 Estimating the concentrations of the (MSA)1(MA)1(OA)1 clusters
The atmospheric relevance of the studied (MSA)1(MA)1(OA)1 clusters is not only determined by the thermodynamics of cluster formation, but also by the atmospheric abundance of the precursor molecules. The concentrations of the (MSA)1(MA)1(OA)1 clusters were estimated according to the law of mass balance by the following equation (Lin et al., 2019):
where [(MSA)1(MA)1(OA)1], [MSA], [MA] and [OA] are the atmospheric concentrations of the (MSA)1(MA)1(OA)1cluster, MSA, MA, and OA, respectively. ΔG is the calculated binding free energy, R is the molar gas constant, and T is the temperature (298.15 K).
The concentrations of precursors used in this study are based on reported values from field campaigns (see Table S1 in the Supplement). Notably, except for ForA and AceA, the concentrations of the OAs were estimated from those measured in the particle phase. Hence, the values in Table S1 may overestimate the gaseous concentrations of the remaining 10 OAs and should be considered as an upper limit. The concentration of the (MSA)2(MA)1 cluster was also calculated as a comparison. [MA] and [MSA] were set to be 2.5×108 (∼10 ppt) and 107 molecules cm−3 in the calculations, respectively. It should be noted that the choice of [MA] and [MSA] does not influence the calculated ranking of the OAs.
2.3 Atmospheric Cluster Dynamics Code (ACDC) simulations
ACDC was employed to study the time evolution of cluster formation rates, steady-state cluster concentrations, and growth pathways for the larger MSA–MA–OA cluster system (Mcgrath et al., 2012). We refer to our previous studies for further details of the theory behind ACDC (Shen et al., 2019, 2020). Briefly, the core of ACDC is to employ the birth–death equation (Eq. 2) to describe the time-dependent cluster distributions:
where subscripts ( and i+j) represent different clusters or monomers in the system, ci represents the number concentration of i, βi,j denotes the collision rate coefficient between i and j, and denotes the evaporation rate of a cluster i+j into smaller clusters (or monomer) i and j. Qi represents an additional outside source term of i, and Si represents other sink terms for i. The collision rate coefficients were calculated by hard-sphere kinetic gas theory as
where kb is the Boltzmann constant, T is the temperature, and mi and Vi are the mass and volume of i, respectively. The evaporation rates were calculated using detailed balance as
where ΔG is the formation free energy of the cluster, and cref is the reference monomer concentration at 1 atm, which is the pressure at which ΔG was calculated (Mcgrath et al., 2012). Here, the simulated system can be described as a “3×3 box” containing (MSA)x(MA)y(OA)z clusters, where 3 represents the maximal number of bases (MA) and acids (MSA and OA). We do not consider the MSA–MA–OA clusters that contain more bases than acids, as it has been shown that these usually have high evaporation rates and thereby are of little importance in NPF (Olenius et al., 2013). We used the calculated thermodynamic data of (MSA)x(MA)y(OA)z (0 3) clusters as input for ACDC simulations to obtain the cluster formation pathways and new particle formation rates. The selection of boundary clusters was based on the stability of clusters under the studied temperature (see details in the Supplement). As there have not been reported any coagulation coefficient of MSA from field campaigns, we set the coagulation sink to a constant value of s−1, corresponding to a typical value in polluted regions (Yao et al., 2018). In addition, the coagulation sink coefficients in the range from to s−1, covering possible values in clean and haze days, were selected to test the effect of coagulation sink coefficients on the main results. The temperature and concentrations of precursor gases (MSA, MA, and OA) were varied in the simulations to probe the effect of various atmospheric conditions. The simulations were performed at 238.15–298.15 K to investigate the effect of temperature. The test ranges for the OA precursor concentrations are 108–1012 cm−3. [MA] and [MSA] were set to be 1–100 ppt (–2.5×109cm−3) and 105–108 cm−3, respectively.
3.1 Analysis of the (MSA)1(MA)1(OA)1 clusters
The obtained global minima of 12 (MSA)1(MA)1(OA)1 clusters are presented in Fig. 1. For all (MSA)1(MA)1(OA)1 clusters, proton transfer from MSA to MA occurs, and the clusters are stabilized via both intermolecular H bonds and electrostatic interactions between positive and negative species. It should be noted that no proton transfer occurs from MSA to MA in the binary (MSA)1(MA)1 cluster (Shen et al., 2020). Thus, the addition of OAs to the (MSA)1(MA)1 cluster promotes the proton transfer. The formation of charged species could potentially enhance particle formation for ternary MSA–MA–OA nucleation compared to the binary MSA–MA system.
The clusters, all forming from monocarboxylic acid except PinA, present almost identical intermolecular interaction patterns. Four H bonds are formed in these clusters, and monomers are linked by two 10-membered rings and a six-membered ring. PinA differs from the other monocarboxylic acids as the additional carbonyl group (C=O) is involved in the H-bond formation in the (MSA)1(MA)1(PinA)1 cluster. For clusters forming from dicarboxylic acids, only MaleA and GluA can interact with the (MSA)1(MA)1 cluster via both −COOH groups in the (MA)1(MSA)1(OA)1 clusters. A previous study also found that dicarboxylic acids can interact with SA via both −COOH groups for SA–OA dimer clusters (Elm et al., 2017). However, other dicarboxylic acids follow a similar intermolecular interaction pattern as clusters containing monocarboxylic acids. For OxaA, the configuration involving the interaction of two −COOH groups with (MA)1(MSA)1 was not located. This results from the fact that the two −COOH groups in OxaA are directly linked, and thereby OxaA cannot adapt a conformation where both −COOH groups interact with other molecules in the clusters. For MalA, SucA, and AdiA, the binding free energies for the configuration with interactions of both −COOH groups with (MA)1(MSA)1 are higher than those for the configuration with the interaction of a single −COOH group with (MA)1(MSA)1. This could result from the high deformation energy penalty when these three OAs interact with (MA)1(MSA)1 via two −COOH groups. An interesting phenomenon was that MaleA and SucA have different interaction patterns although they have the same number of C atoms. Such a difference mainly results from the existence of a double-bond linker between the two −COOH groups of MaleA. The double-bond linker allows MaleA to interact with (MA)1(MSA)1 via two −COOH groups and slight deformation as shown in Fig. S1 in the Supplement.
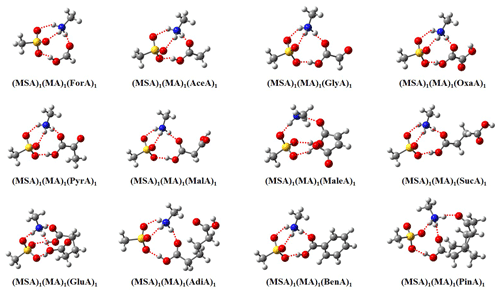
Figure 1Lowest Gibbs free energy conformations of 12 (MSA)1(MA)1(OA)1 clusters (OA is ForA, AceA, GlyA, OxaA, PyrA, MalA, MaleA, SucA, GluA, AdiA, BenA, and PinA) calculated at the ωB97X-D/6-31 level of theory, at 298.15 K and 1 atm. The red balls represent oxygen atoms, the blue balls represent nitrogen atoms, the gray balls represent carbon atoms, and the white balls represent hydrogen atoms. The dashed red lines indicate hydrogen bonds.
Figure 2a presents the ΔG values for 12 (MSA)1(MA)1(OA)1 clusters, along with the calculated value for the (MSA)2(MA)1 cluster as a comparison. Generally, the ΔG values of the (MSA)1(MA)1(OA)1 clusters vary from −12.69 to −17.87 kcal mol−1 and are 2.49–7.67 kcal mol−1 higher (i.e., less negative) than the ΔG value of the (MSA)2(MA)1 cluster. Based on previous studies, several factors such as the acidity and intramolecular H bond of OAs can affect their interaction energy with amine or SA (Elm et al., 2017). It should be noted that the structures of the simple monocarboxylic acids ForA, AceA, and BenA almost do not change during the interaction with the MSA–MA cluster, presenting the intrinsical interacting pattern of the −COOH group with the MSA–MA cluster. Therefore, the MSA–MA–OA systems with the simple monocarboxylic acids were initially selected to analyze which factors that affect the interaction between OAs and the MSA–MA cluster. As shown in Fig. 2b, the pKa of the OA presents a good linear relationship with the calculated ΔG values for the formation of the (MSA)1(MA)1(OA)1 clusters for the simple monocarboxylic acids, indicating the role of OA acidity in determining the ΔG value. This is the first time that such a linear relationship of pKa with ΔG for OAs with MSA(SA)–amine clusters is revealed. In the following part, the linear relationship of pKa with the ΔG value of the (MSA)1(MA)1(OA)1 was used as a baseline to discuss other factors that affect the ΔG values for the formation of the (MSA)1(MA)1(OA)1 clusters.
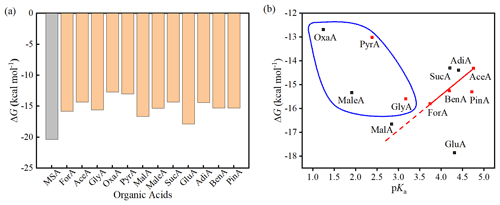
Figure 2Binding free energy (ΔG) (kcal mol−1) of the 12 (MSA)1(MA)1(OA)1 clusters and the (MSA)2(MA)1 cluster at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31 level of theory (the calculations are performed at 298.15 K and 1 atm) (a) and the relationship between the pKa of the organic acids with the binding free energy (ΔG) (kcal mol−1) of the 12 (MSA)1(MA)1(OA)1 clusters at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31 level of theory (the calculations are performed at 298.15 K and 1 atm) (b). The solid line in (b) is the fitted linear regression line of the ΔG on pKa value for the simplest monocarboxylic acids with r=0.996, and the dashed line is the extension of the solid line. The red squares represent monocarboxylic acids, the black squares represent dicarboxylic acids, and the circled species contain intramolecular H bonds.
As shown in Fig. 2b, the ΔG values of GluA and PinA lie under the baseline, indicating there are favorable structural factors besides acidity to enhance the interaction of these two OAs with the MSA–MA cluster. It was found that GluA and PinA form additional intermolecular H bonds with the MSA–MA cluster via additional −COOH and C=O, respectively. The formation of additional intermolecular H bonds explains why the ΔG values of GluA and PinA are lower than those predicted by their pKa (under the baseline).
The ΔG values of OxaA, PyrA, MaleA, GlyA, MalA, SucA, and AdiA lie above the baseline, indicating there are unfavorable structural factors to restrain the interaction of these seven OAs with the MSA–MA clusters. By comparing the structure of OAs in the (MSA)1(MA)1(OA)1 cluster and their corresponding isolated conformation (Fig. S2), it was found that the original intramolecular H bonds of GlyA, OxaA, MaleA and PyrA have been broken in the interaction with the MSA–MA cluster. Therefore, an energetic penalty should be paid for breaking the original intramolecular H bonds for these four acids, which should be the main reason that the ΔG values are higher than those evaluated by their pKa values (above the baseline). A similar phenomenon has previously been observed for α-keto carboxylic acids in SA–OA dimer clusters (Elm et al., 2017). The other three outliers (the dicarboxylic acids MalA, SucA and AdiA) interact with MSA–MA only via one −COOH group, behaving like a simple monocarboxylic acid. It was found that the structure of SucA and AdiA changes slightly during the interaction with the MSA–MA cluster compared to their corresponding isolated conformations. The calculated root-mean-square deviation (RMSD) of the OA structure in the MSA–MA–OA cluster relative to their corresponding isolated conformers is 0.046 and 0.353 Å for SucA and AdiA, respectively. Therefore, the structural change upon cluster formation cannot explain the outliers. The clustering ability of straight-chain dicarboxylic acids has been suggested to follow an alternating even/odd pattern by observing that the dimer formation for GluA (C5) is more efficient than SucA (C4) and AdiA (C6) (Elm et al., 2019). Therefore, it was speculated that the alternating even/odd pattern for the clustering ability of the dicarboxylic acids can explain SucA and AdiA as outliers. The structure of MalA changes significantly during the interaction with the MSA–MA cluster with a RMSD of 1.27 Å, which explains the reason for it behaving as an outlier. Overall, our results show that the acidity, hydrogen-bond-forming capacity, structural deformation energy of OA, and even/odd pattern if it is dicarboxylic acid are the main factors determining the formation free energy of the MSA–MA–OA cluster.
To evaluate the potential of the 12 OAs in ternary MA–MSA–OA nucleation, the atmospheric concentrations of (MSA)1(MA)1(OA)1 were calculated by Eq. (1). Figure 3 depicts the calculated [(MSA)1(MA)1(OA)1] along with [(MSA)2(MA)1]. As can be seen from Fig. 3, the [(MSA)1(MA)1(OA)1] spans many orders of magnitude (from to ∼1 molecules cm−3). Based on the mean values, [(MSA)1(MA)1(OA)1] decreases in the following order: ForA > AceA ≈ MSA > GluA > MalA > GlyA > BenA > PinA > SucA > MaleA > OxaA > AdiA > PyrA. Therefore, ForA should have the highest potential for participating in MSA–MA–OA cluster formation among the 12 considered OAs. More importantly, the calculated [(MSA)1(MA)1(ForA)1] is higher than [(MSA)2(MA)1], implying ForA could participate in MSA–MA nucleation by partly replacing MSA. In the following, larger MSA–MA–ForA clusters were investigated to further probe the possible enhancing potential of ForA on MSA–MA nucleation.
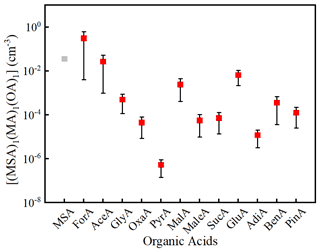
Figure 3The calculated [(MSA)1(MA)1(OA)1] and [(MSA)2(MA)1] (molecules cm−3) based on the mass balance equation and reported concentrations of precursors. The bars denote the minimum and the maximum of [(MSA)1(MA)1(OA)1], the red square denotes the mean values, and the gray square denotes [(MSA)2(MA)1].
3.2 Analysis of larger MSA–MA–ForA clusters
The pure (MSA)1−3 and binary (MSA)x(MA)y clusters have been discussed in our previous study (Shen et al., 2019, 2020). Here we mainly focus on the ForA-containing clusters. Figure S3 presents the obtained global minimum structures of the ForA-containing clusters. Similar to the pure (MSA)1−3 clusters, no proton transfer is observed in the pure acid clusters MSA-ForA and (ForA)1−3. For the binary MA-ForA clusters, proton transfer does not occur in the (MA)1(ForA)1−2 clusters, and a single MA is protonated in the (MA)1(ForA)3 and (MA)2(ForA)2 clusters. In the (MA)2(ForA)3 and (MA)3(ForA)3 clusters, we observe two and three proton transfers, respectively. For the ternary MSA–MA–ForA cluster systems, all MSA molecules have transferred a proton to MA, and ForA molecules have transferred a proton to the remaining MA when x≤y. When x>y only some of the MSA has transferred a proton to MA, and ForA is kept intact. Therefore, proton transfer from MSA to MA is more favorable than that from ForA to MA, which is in accordance with the lower acidity of ForA compared to MSA.
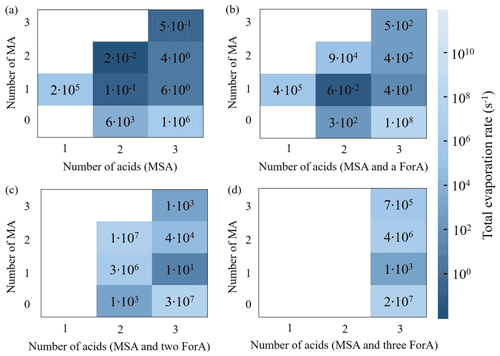
Figure S4 shows the calculated ΔG values of the (MSA)x(MA)y(ForA)z clusters. Generally, the more ForA monomers present in the cluster, the higher the ΔG value is when the number of total acids and ratio of acid to MA are equal. Based on calculated ΔG values of all considered clusters, the evaporation rates of the clusters were calculated. A previous study established that it is important to consider the concentration of precursor when evaluating the cluster stability (Xie et al., 2017). Generally, given higher concentration of precursors, the collision probability for a cluster is increased, and the balance between collision and evaporation is shifted forward, resulting in a higher cluster stability. Since the atmospheric concentration of ForA is much higher (about 103) than that of MA and MSA, an effective evaporation rate was used to evaluate cluster stability of ForA-containing clusters. The effective evaporation rates of the ForA-containing clusters were roughly obtained by scaling the original evaporation rate by 10−3, due to the concentration difference. The evaporation rates of binary MSA–MA clusters and effective ones of ForA-containing clusters are presented in Fig. 4. Among the ForA-containing clusters, only the evaporation rates of the (MSA)1(MA)1(ForA)1 and (MSA)1(ForA)1 clusters are lower than those of corresponding binary MSA–MA clusters with equal number of acids and bases. The evaporation rate of the (ForA)2 cluster is found to be comparable to that of (MSA)2. The remaining ForA-containing clusters have much higher evaporation rates compared to the corresponding binary MSA–MA clusters. Therefore, the (MSA)1(MA)1(ForA)1 and (MSA)1(ForA)1 clusters have the highest potential to participate in MSA–MA nucleation, followed by (ForA)2. It is worth mentioning that the evaporation rates of all ForA-containing clusters are higher than those of corresponding binary MSA–MA clusters if the concentration difference of precursors was not considered. Therefore, it is the high concentration of ForA that drives the stability of the clusters and not the intrinsic evaporation rate.
3.3 Enhancing effect of ForA
Here, we employed the enhancing coefficient R as the ratio of the cluster formation rate (J) for the ternary MSA–MA–ForA cluster system () relative to that of the binary MSA–MA cluster system (JMA−MSA) to present the enhancing effect of ForA. For R above 1, it can be inferred that ForA has an enhancing effect on the binary MSA–MA system. Previous studies have shown that the temperature and concentrations of precursors have a large influence on R of OAs for the ternary SA–base–OA systems (Elm et al., 2020; Zhang et al., 2017; Li et al., 2017; Liu et al., 2018; Zhang et al., 2018). Herein, the effects of temperature and precursor concentration on R were examined for the ternary MSA–MA–ForA cluster system. Two steps were employed to investigate the effects of temperature and precursor concentration on the R. The first step investigated the variation of R with [ForA] (108–1012 cm−3) at different temperature (238.15–298.15 K). The second step investigated the variation of R with [MA] (1–100 ppt) or [MSA] (105–108 cm−3) at fixed temperature and [ForA].
The variation of R with [ForA] at 238.15, 258.15, 278.15, and 298.15 K, [MA] = 10 ppt and [MSA] = 107 molecules cm−3 is presented in Fig. 5a. As seen from Fig. 5a, R almost remains as unity at all considered temperatures when [ForA] is less than 109 molecules cm−3. With increasing [ForA] when [ForA] is more than 109 molecules cm−3, R starts to obviously increase with [ForA] at low temperature (<258.15 K). However, the effect of [ForA] on R is much less pronounced when temperature is higher than 278.15 K, and the increase of R becomes nonnegligible only at 278.15 K and high [ForA] (>1011 cm−3). Therefore, both temperature and [ForA] can significantly affect R. Similar results were also reported in previous studies on the effect of OAs on SA–NH3 nucleation (Zhang et al., 2017, 2018; Liu et al., 2018). It is worth mentioning that the upper limited temperature at which ForA can effectively enhance MSA–MA NPF (258.15 K) is about 40 K higher than that of the previously studied OAs enhancing SA–NH3 NPF. In the following part, the condition with a reachable temperature (T=258.15 K) and [ForA] (1011 cm−3; ∼4 ppb) in the ambient atmosphere (Khwaja, 1995) was employed to investigate the effect of [MA] and [MSA] on R. It should be mentioned that these are not unrealistic conditions, for instance, at polluted sites in inland China.
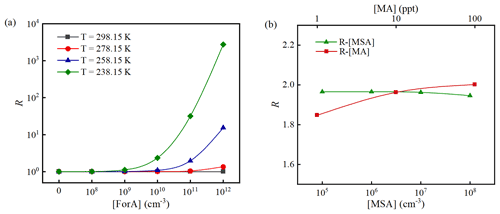
Figure 5The enhancing coefficient (R) as a function of [ForA] at [MA] = 10 ppt, [MSA] = 107 cm−3, and four temperatures (238.15, 258.15, 278.15, and 298.15 K) (a) and as a function of [MSA]/[MA] at [MA] = 10 ppt/[MSA] = 107 cm−3, [ForA] = 1011 cm−3, and T=258.15 K (b).
As can be seen in Fig. 5b, R shows a small but positive dependence on [MA]. However, R has little correlation with [MSA]. The difference between the relationships of R[MA] and R[MSA] can be explained by the difference in cluster stability and relative abundance of the precursors in the system. At [ForA] = 1011 molecules cm−3, the abundance of precursors in the system approximately decreases in the order ForA > MA > MSA. Due to the scarcity of MSA in the system, increased MA will prefer to participate in the formation of ForA-containing clusters. Therefore, increased [MA] has a small positive effect on R. Additionally, since the binding potential of MSA with the MA is much higher than that with MA-ForA clusters, the increased number of MSA molecules will primarily cluster with MA to form binary MSA–MA clusters, and consequently the influence on the ternary MSA–MA–ForA pathways is minor. As shown in Fig. S5, when coagulation sink coefficients change from to s−1, R almost remains constant, indicating the selection of coagulation sink coefficient has no significant effect on R. This is not surprising, as R represents the ratio of the new particle formation rates, and thereby the effect of the choice of coagulation sink largely cancels out.
3.4 Enhancement mechanism of ForA
The enhancement mechanism of ForA can be disclosed by a comparative analysis on the cluster growth pathway of ternary MSA–MA–ForA and binary MSA–MA cluster system. Figure 6a shows the main cluster growth pathways for the ternary MSA–MA–ForA cluster system at the conditions where ForA showed an enhancing effect (T=258.15 K, [MA] = 10 ppt, [MSA] = 107, and [ForA] = 1011 molecules cm−3). The cluster growth pathways for the binary MSA–MA system at the same condition (except for [ForA] =0 molecules cm−3) are shown in Fig. 6b.
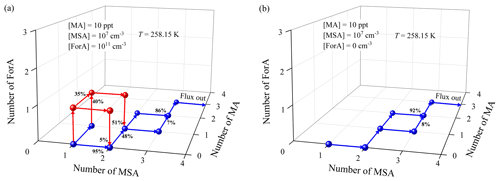
Figure 6Main cluster formation pathways for the ternary MSA–MA–ForA system (a) and the MSA–MA system (b) at T=258.15 K, [MA] = 10 ppt, [MSA] = 107, and [ForA] = 1011 molecules cm−3 (only for the ternary MSA–MA–ForA system).
For binary MSA–MA nucleation, the cluster growth mainly proceeds via the following route: MSA → (MSA)2 → (MSA)2(MA)1 → (MSA)2(MA)2 → (MSA)3(MA)2 → (MSA)3(MA)3, fluxing out of the system as the (MSA)4(MA)3 cluster, consistent with our previous findings (Shen et al., 2020). In addition, the (MSA)3(MA)1 cluster also has a nonnegligible contribution (8 %) to the formation of the (MSA)3(MA)2 cluster. As seen in Fig. 6a, when present at a concentration of 1011 molecules cm−3, ForA initially participates in the formation of smaller binary MSA–MA clusters and subsequently evaporates from them via three routes, i.e., MSA → (MSA)1(ForA)1 → (MSA)2(ForA)1 → (MSA)2; MSA → (MSA)1(ForA)1 → (MSA)1(ForA)1(MA)1 → (MSA)2(ForA)1(MA)1 → (MSA)2(MA)1; and MSA → (MSA)1(MA)1 → (MSA)1(ForA)1(MA)1 → (MSA)2(ForA)1(MA)1 → (MSA)2(MA)1. Therefore, ForA plays a catalytic role in the formation of the smaller binary MSA–MA clusters. In all ForA-containing clusters involved in the catalytic process, only (MSA)1(ForA)1 and (MSA)1(ForA)1(MA)1 can continue to grow, consistent with their stability. As the ForA-driven catalytic process is the only difference between formation pathway of the ternary MSA–MA–ForA and the binary MSA–MA cluster system, it should be the main reason that the presence of ForA can enhance the nucleation (R=1.96), compared to the case of the binary MSA–MA system. In addition, ForA mainly contributes to the formation of (MSA)2(MA)1 clusters (51 %) in the catalytic process. Therefore, ForA enhances the binary MSA–MA nucleation mainly via catalyzing the formation of the (MSA)2(MA)1 cluster. As can be seen from Fig. S6–S7, the catalyzed formation of the (MSA)2(MA)1 cluster is the main route for the ForA enhancing binary MSA–MA nucleation when [MA] and [MSA] change. In addition, as shown in Fig. S8, when coagulation sink coefficients and s−1 were employed, the formation pathway of the ternary MSA–MA–ForA clusters changes slightly compared to the case where a coagulation sink coefficient of s−1 was used. Therefore, the selection of coagulation sink coefficient has no effect on the predicted catalysis mechanism of ForA.
In this study, the potential of 12 commonly detected OAs in MSA–MA–OA nucleation has been systematically evaluated by examining the formation of the (MSA)1(MA)1(OA)1 clusters. It was found that ForA has the highest potential to participate in ternary MSA–MA–OA nucleation. This study also suggests that for a given OA to have highest potential in ternary MSA–MA–OA nucleation, the OA should have the following features: high atmospheric abundance, strong acidity, strong H-bond-forming capacity, weak or no intramolecular interaction in the monomer, and no/little structural deformation during clustering. It is noted that besides the simple OAs studied here, there are some complex organics with multi-functional groups including −COOH, e.g., highly oxygenated molecules (HOMs), in the atmosphere. These complex organics also might participate in the MSA–MA nucleation since they could interact with the MSA–MA cluster in a similar fashion as the simple OAs (H bonds and acid–base reaction). Therefore, studies on the role of the complex organics with multi-functional groups in MSA–MA NPF are warranted to further augment the current understanding of MSA-driven NPF.
This study for the first time reveals that ForA exerts a catalytic enhancing effect on binary MSA–MA nucleation by facilitating the formation of clusters in the initial stage of NPF. Based on reported energetic data of (SA)1(amine)1(OAs)1 (amine = MA and DMA, OAs = ForA, AceA, OxaA, PyrA, MalA, MaleA, SucA, GluA, AdiA, BenA, and PinA) and Eq. (1) (Li et al., 2020), (SA)1(amine)1(ForA)1 is calculated to have the (or second) highest concentration (see Table S3). Therefore, ForA could also have a high enhancing effect on SA-amine nucleation. A study on the enhancing effect of ForA on SA-driven NPF is warranted to further augment the current understanding of the contribution of OAs on NPF. The enhancing effect of ForA on binary MSA–MA nucleation is highly dependent on [ForA] and the temperature. At [ForA] = 1011 molecules cm−3 and 258.15 K, a reachable concentration and temperature in the ambient atmosphere, ForA can effectively enhance binary MSA–MA nucleation, clarifying its important role in MSA-driven NPF. In addition, the concentration of ForA could be even higher in regions with significant primary emission sources and/or intense chemical production (Franco et al., 2021). Therefore, as a ubiquitous organic acid in the atmosphere, the contribution of ForA to NPF involving MSA and amines deserves more attention in the future.
The data in this article are available from the corresponding author upon request (hbxie@dlut.edu.cn).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-22-2639-2022-supplement.
HBX designed the research; RZ, JS, and HBX performed research; RZ, JS, and HBX analyzed data; RZ, JS, HBX, JC, and JE wrote the paper; and HBX, JC, and JE reviewed and revised the paper.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The study was supported by the National Natural Science Foundation of China (21876024), the Major International (Regional) Joint Research Project (21661142001), and the Supercomputing Center of Dalian University of Technology. Jonas Elm thanks the Independent Research Fund Denmark (grant no. 9064-00001B).
This research has been supported by the National Natural Science Foundation of China (grant no. 21876024), the Major International (Regional) Joint Research Project (grant no. 21661142001), and the Independent Research Fund Denmark (grant no. 9064-00001B).
This paper was edited by Joachim Curtius and reviewed by two anonymous referees.
Almeida, J., Schobesberger, S., Kuerten, A., Ortega, I. K., Kupiainen-Maatta, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurten, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppa, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petaja, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipila, M., Stozhkov, Y., Stratmann, F., Tome, A., Troestl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamaki, H., and Kirkby, J.: Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 502, 359–363, https://doi.org/10.1038/nature12663, 2013.
An, P., Yuan, C.-Q., Liu, X.-H., Xiao, D.-B., and Luo, Z.-X.: Vibrational spectroscopic identification of isoprene, pinenes and their mixture, Chin. Chem. Lett., 27, 527–534, https://doi.org/10.1016/j.cclet.2016.01.036, 2016.
Arquero, K. D., Gerber, R. B., and Finlayson-Pitts, B. J.: The role of oxalic acid in new particle formation from methanesulfonic Acid, methylamine, and water, Environ. Sci. Technol., 51, 2124–2130, https://doi.org/10.1021/acs.est.6b05056, 2017a.
Arquero, K. D., Xu, J., Gerber, R. B., and Finlayson-Pitts, B. J.: Particle formation and growth from oxalic acid, methanesulfonic acid, trimethylamine and water: a combined experimental and theoretical study, Phys. Chem. Chem. Phys., 19, 28286–28301, https://doi.org/10.1039/c7cp04468b, 2017b.
Carlton, A. G., Turpin, B. J., Lim, H. J., Altieri, K. E., and Seitzinger, S.: Link between isoprene and secondary organic aerosol (SOA): Pyruvic acid oxidation yields low volatility organic acids in clouds, Geophys. Res. Lett., 33, 4, https://doi.org/10.1029/2005gl025374, 2006.
Chan, M. N., Choi, M. Y., Ng, N. L., and Chan, C. K.: Hygroscopicity of water-soluble organic compounds in atmospheric aerosols: Amino acids and biomass burning derived organic species, Environ. Sci. Technol., 39, 1555–1562, https://doi.org/10.1021/es049584l, 2005.
Chebbi, A. and Carlier, P.: Carboxylic acids in the troposphere, occurrence, sources, and sinks: A review, Atmos. Environ., 30, 4233–4249, https://doi.org/10.1016/1352-2310(96)00102-1, 1996.
Chen, D., Li, D., Wang, C., Liu, F., and Wang, W.: Formation mechanism of methanesulfonic acid and ammonia clusters: A kinetics simulation study, Atmos. Environ., 222, 117161, https://doi.org/10.1016/j.atmosenv.2019.117161, 2020a.
Chen, D., Li, D., Wang, C., Luo, Y., Liu, F., and Wang, W.: Atmospheric implications of hydration on the formation of methanesulfonic acid and methylamine clusters: A theoretical study, Chemosphere, 244, 125538, https://doi.org/10.1016/j.chemosphere.2019.125538, 2020b.
Chen, H. and Finlayson-Pitts, B. J.: New particle formation from methanesulfonic acid and amines/ammonia as a function of temperature, Environ. Sci. Technol., 51, 243–252, https://doi.org/10.1021/acs.est.6b04173, 2017.
Chen, H., Ezell, M. J., Arquero, K. D., Varner, M. E., Dawson, M. L., Gerber, R. B., and Finlayson-Pitts, B. J.: New particle formation and growth from methanesulfonic acid, trimethylamine and water, Phys. Chem. Chem. Phys., 17, 13699–13709, https://doi.org/10.1039/c5cp00838g, 2015.
Chen, H., Varner, M. E., Gerber, R. B., and Finlayson-Pitts, B. J.: Reactions of methanesulfonic acid with amines and ammonia as a source of new particles in air, J. Phys. Chem. B, 120, 1526–1536, https://doi.org/10.1021/acs.jpcb.5b07433, 2016.
Cong, Z., Kawamura, K., Kang, S., and Fu, P.: Penetration of biomass-burning emissions from South Asia through the Himalayas: new insights from atmospheric organic acids, Sci. Rep., 5, 9580, https://doi.org/10.1038/srep09580, 2015.
Dawson, M. L., Varner, M. E., Perraud, V., Ezell, M. J., Gerber, R. B., and Finlayson-Pitts, B. J.: Simplified mechanism for new particle formation from methanesulfonic acid, amines, and water via experiments and ab initio calculations, Proc. Natl. Acad. Sci. USA, 109, 18719–18724, https://doi.org/10.1073/pnas.1211878109, 2012.
Elm, J.: Clusteromics II: Methanesulfonic Acid–Base Cluster Formation, ACS Omega, 6, 17035–17044, https://doi.org/10.1021/acsomega.1c02115, 2021.
Elm, J. and Kristensen, K.: Basis set convergence of the binding energies of strongly hydrogen-bonded atmospheric clusters, Phys. Chem. Chem. Phys., 19, 1122–1133, https://doi.org/10.1039/c6cp06851k, 2017.
Elm, J., Bilde, M., and Mikkelsen, K. V.: Assessment of binding energies of atmospherically relevant clusters, Phys. Chem. Chem. Phys., 15, 16442–16445, https://doi.org/10.1039/c3cp52616j, 2013.
Elm, J., Myllys, N., and Kurten, T.: What is required for highly oxidized molecules to form clusters with sulfuric acid?, J. Phys. Chem. A, 121, 4578–4587, https://doi.org/10.1021/acs.jpca.7b03759, 2017.
Elm, J., Hyttinen, N., Lin, J. J., Kurten, T., and Prisle, N. L.: Strong Even/Odd Pattern in the Computed Gas-Phase Stability of Dicarboxylic Acid Dimers: Implications for Condensation Thermodynamics, J. Phys. Chem. A, 123, 9594–9599, https://doi.org/10.1021/acs.jpca.9b08020, 2019.
Elm, J., Kubecka, J., Besel, V., Jaaskelainen, M. J., Halonen, R., Kurten, T., and Vehkamaki, H.: Modeling the formation and growth of atmospheric molecular clusters: A review, J. Aerosol Sci., 149, 105621, https://doi.org/10.1016/j.jaerosci.2020.105621, 2020.
Falkovich, A. H., Graber, E. R., Schkolnik, G., Rudich, Y., Maenhaut, W., and Artaxo, P.: Low molecular weight organic acids in aerosol particles from Rondônia, Brazil, during the biomass-burning, transition and wet periods, Atmos. Chem. Phys., 5, 781–797, https://doi.org/10.5194/acp-5-781-2005, 2005.
Fehsenfeld, F., Calvert, J., Fall, R., Goldan, P., Guenther, A. B., Hewitt, C. N., Lamb, B., Liu, S., Trainer, M., Westberg, H., and Zimmerman, P.: Emissions of volatile organic compounds from vegetation and the implications for atmospheric chemistry, Glob. Biogeochem. Cycle, 6, 389–430, https://doi.org/10.1029/92gb02125, 1992.
Franco, B., Blumenstock, T., Cho, C., Clarisse, L., Clerbaux, C., Coheur, P. F., De Maziere, M., De Smedt, I., Dorn, H. P., Emmerichs, T., Fuchs, H., Gkatzelis, G., Griffith, D. W. T., Gromov, S., Hannigan, J. W., Hase, F., Hohaus, T., Jones, N., Kerkweg, A., Kiendler-Scharr, A., Lutsch, E., Mahieu, E., Novelli, A., Ortega, I., Paton-Walsh, C., Pommier, M., Pozzer, A., Reimer, D., Rosanka, S., Sander, R., Schneider, M., Strong, K., Tillmann, R., Van Roozendael, M., Vereecken, L., Vigouroux, C., Wahner, A., and Taraborrelli, D.: Ubiquitous atmospheric production of organic acids mediated by cloud droplets, Nature, 593, 233–237, https://doi.org/10.1038/s41586-021-03462-x, 2021.
Friedman, B., Link, M. F., Fulgham, S. R., Brophy, P., Galang, A., Brune, W. H., Jathar, S. H., and Farmer, D. K.: Primary and secondary sources of gas-phase organic acids from diesel exhaust, Environ. Sci. Technol., 51, 10872–10880, https://doi.org/10.1021/acs.est.7b01169, 2017.
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E.,Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Mennucci, B., Petersson, G. A., Nakatsuji, H., Caricato, M., Li, X.,Hratchian, H. P., Izmaylov, A. F., Bloino, J., Zheng, G., Sonnenberg, J. L., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J.,Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Montgomery, J. A. Jr., Peralta, J. E., Ogliaro, F., Bearpark, M.,Heyd, J. J., Brothers, E., Kudin, K. N., Staroverov, V. N., Kobayashi,R., Normand, J., Raghavachari, K., Rendell, A., Burant, J. C., Iyengar, S. S.,Tomasi, J., Cossi, M., Rega, N., Millam, J. M., Klene, M., Knox, J.E., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochterski, J. W., Martin, R. L., Morokuma, K., Zakrzewski, V. G., Voth, G. A., Salvador, P., Dannenberg, J. J., Dapprich, S., Daniels, A. D., Farkas, O., Foresman, J. B., Ortiz, J. V., Cioslowski, J., and Fox, D. J.: Gaussian 09, Gaussian Inc., Wallingford, CT, 2009.
Glasoe, W. A., Volz, K., Panta, B., Freshour, N., Bachman, R., Hanson, D. R., McMurry, P. H., and Jen, C.: Sulfuric acid nucleation: An experimental study of the effect of seven bases, J. Geophys. Res.-Atmos., 120, 1933–1950, https://doi.org/10.1002/2014jd022730, 2015.
Heal, M. R., Kumar, P., and Harrison, R. M.: Particles, air quality, policy and health, Chem. Soc. Rev., 41, 6606–6630, https://doi.org/10.1039/c2cs35076a, 2012.
Ho, K. F., Cao, J. J., Lee, S. C., Kawamura, K., Zhang, R. J., Chow, J. C., and Watson, J. G.: Dicarboxylic acids, ketocarboxylic acids, and dicarbonyls in the urban atmosphere of China, J. Geophys. Res.-Atmos., 112, D22S27, https://doi.org/10.1029/2006jd008011, 2007.
Kavouras, I. G., Mihalopoulos, N., and Stephanou, E. G.: Formation of atmospheric particles from organic acids produced by forests, Nature, 395, 683–686, https://doi.org/10.1038/27179, 1998.
Khwaja, H. A.: Atmospheric concentrations of carboxylic acids and related compounds at a semiurban site, Atmos. Environ., 29, 127–139, https://doi.org/10.1016/1352-2310(94)00211-3, 1995.
Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., Ehrhart, S., Franchin, A., Gagne, S., Ickes, L., Kuerten, A., Kupc, A., Metzger, A., Riccobono, F., Rondo, L., Schobesberger, S., Tsagkogeorgas, G., Wimmer, D., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Downard, A., Ehn, M., Flagan, R. C., Haider, S., Hansel, A., Hauser, D., Jud, W., Junninen, H., Kreissl, F., Kvashin, A., Laaksonen, A., Lehtipalo, K., Lima, J., Lovejoy, E. R., Makhmutov, V., Mathot, S., Mikkila, J., Minginette, P., Mogo, S., Nieminen, T., Onnela, A., Pereira, P., Petaja, T., Schnitzhofer, R., Seinfeld, J. H., Sipila, M., Stozhkov, Y., Stratmann, F., Tome, A., Vanhanen, J., Viisanen, Y., Vrtala, A., Wagner, P. E., Walther, H., Weingartner, E., Wex, H., Winkler, P. M., Carslaw, K. S., Worsnop, D. R., Baltensperger, U., and Kulmala, M.: Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 476, 429–433, https://doi.org/10.1038/nature10343, 2011.
Kurtén, T., Loukonen, V., Vehkamäki, H., and Kulmala, M.: Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia, Atmos. Chem. Phys., 8, 4095–4103, https://doi.org/10.5194/acp-8-4095-2008, 2008.
Lee, S.-H., Gordon, H., Yu, H., Lehtipalo, K., Haley, R., Li, Y., and Zhang, R.: New particle formation in the atmosphere: from molecular clusters to global climate, J. Geophys. Res.-Atmos., 124, 7098–7146, https://doi.org/10.1029/2018jd029356, 2019.
Li, H., Kupiainen-Maatta, O., Zhang, H., Zhang, X., and Ge, M.: A molecular-scale study on the role of lactic acid in new particle formation: Influence of relative humidity and temperature, Atmos. Environ., 166, 479–487, https://doi.org/10.1016/j.atmosenv.2017.07.039, 2017.
Li, Y., Zhang, H., Zhang, Q., Xu, Y., and Nadykto, A. B.: Interactions of sulfuric acid with common atmospheric bases and organic acids: Thermodynamics and implications to new particle formation, J. Environ. Sci., 95, 130–140, https://doi.org/10.1016/j.jes.2020.03.033, 2020.
Lin, Y., Ji, Y., Li, Y., Secrest, J., Xu, W., Xu, F., Wang, Y., An, T., and Zhang, R.: Interaction between succinic acid and sulfuric acid–base clusters, Atmos. Chem. Phys., 19, 8003–8019, https://doi.org/10.5194/acp-19-8003-2019, 2019.
Liu, L., Kupiainen-Maatta, O., Zhang, H., Li, H., Zhong, J., Kurten, T., Vehkamaki, H., Zhang, S., Zhang, Y., Ge, M., Zhang, X., and Li, Z.: Clustering mechanism of oxocarboxylic acids involving hydration reaction: Implications for the atmospheric models, J. Chem. Phys., 148, 214303, https://doi.org/10.1063/1.5030665, 2018.
Loukonen, V., Kurtén, T., Ortega, I. K., Vehkamäki, H., Pádua, A. A. H., Sellegri, K., and Kulmala, M.: Enhancing effect of dimethylamine in sulfuric acid nucleation in the presence of water – a computational study, Atmos. Chem. Phys., 10, 4961–4974, https://doi.org/10.5194/acp-10-4961-2010, 2010.
Ma, F., Xie, H.-B., Elm, J., Shen, J., Chen, J., and Vehkamaki, H.: Piperazine enhancing sulfuric acid-based new particle formation: implications for the atmospheric fate of piperazine, Environ. Sci. Technol., 53, 8785–8795, https://doi.org/10.1021/acs.est.9b02117, 2019a.
Ma, X., Sun, Y., Huang, Z., Zhang, Q., and Wang, W.: A density functional theory study of the molecular interactions between a series of amides and sulfuric acid, Chemosphere, 214, 781–790, https://doi.org/10.1016/j.chemosphere.2018.08.152, 2019b.
McGrath, M. J., Olenius, T., Ortega, I. K., Loukonen, V., Paasonen, P., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 12, 2345–2355, https://doi.org/10.5194/acp-12-2345-2012, 2012.
Neese, F.: The ORCA program system, Wiley Interdiscip. Rev.-Comput. Mol. Sci., 2, 73–78, https://doi.org/10.1002/wcms.81, 2012.
Nieminen, T., Manninen, H. E., Sihto, S. L., Yli-Juuti, T., Mauldin, I. R. L., Petäjä, T., Riipinen, I., Kerminen, V. M., and Kulmala, M.: Connection of Sulfuric Acid to Atmospheric Nucleation in Boreal Forest, Environ. Sci. Technol., 43, 4715–4721, https://doi.org/10.1021/es803152j, 2009.
Nishino, N., Arquero, K. D., Dawson, M. L., and Finlayson-Pitts, B. J.: Infrared studies of the reaction of methanesulfonic acid with trimethylamine on surfaces, Environ. Sci. Technol., 48, 323–330, https://doi.org/10.1021/es403845b, 2014.
Olenius, T., Kupiainen-Maatta, O., Ortega, I. K., Kurten, T., and Vehkamaki, H.: Free energy barrier in the growth of sulfuric acid-ammonia and sulfuric acid-dimethylamine clusters, J. Chem. Phys., 139, 084312, https://doi.org/10.1063/1.4819024, 2013.
Olenius, T., Halonen, R., Kurten, T., Henschel, H., Kupiainen-Maata, O., Ortega, I. K., Jen, C. N., Vehkamaki, H., and Riipinen, I.: New particle formation from sulfuric acid and amines: Comparison of monomethylamine, dimethylamine, and trimethylamine, J. Geophys. Res.-Atmos., 122, 7103–7118, https://doi.org/10.1002/2017jd026501, 2017.
Paulot, F., Crounse, J. D., Kjaergaard, H. G., Kroll, J. H., Seinfeld, J. H., and Wennberg, P. O.: Isoprene photooxidation: new insights into the production of acids and organic nitrates, Atmos. Chem. Phys., 9, 1479–1501, https://doi.org/10.5194/acp-9-1479-2009, 2009.
Perraud, V., Horne, J. R., Martinez, A. S., Kalinowski, J., Meinardi, S., Dawson, M. L., Wingen, L. M., Dabdub, D., Blake, D. R., Gerber, R. B., and Finlayson-Pitts, B. J.: The future of airborne sulfur-containing particles in the absence of fossil fuel sulfur dioxide emissions, Proc. Natl. Acad. Sci. USA, 112, 13514–13519, https://doi.org/10.1073/pnas.1510743112, 2015.
Perraud, V., Xu, J., Gerber, R. B., and Finlayson-Pitts, B. J.: Integrated experimental and theoretical approach to probe the synergistic effect of ammonia in methanesulfonic acid reactions with small alkylamines, Environ. Sci.-Processes Impacts, 22, 305–328, https://doi.org/10.1039/c9em00431a, 2020a.
Perraud, V., Li, X., Jiang, J., Finlayson-Pitts, B. J., and Smith, J. N.: Size-resolved chemical composition of sub-20 nm particles from methanesulfonic acid reactions with methylamine and ammonia, ACS Earth Space Chem., 4, 1182–1194, https://doi.org/10.1021/acsearthspacechem.0c00120, 2020b.
Shen, J., Xie, H.-B., Elm, J., Ma, F., Chen, J., and Vehkamaki, H.: Methanesulfonic Acid-driven New Particle Formation Enhanced by Monoethanolamine: A Computational Study, Environ. Sci. Technol., 53, 14387–14397, https://doi.org/10.1021/acs.est.9b05306, 2019.
Shen, J., Elm, J., Xie, H.-B., Chen, J., Niu, J., and Vehkamaki, H.: Structural effects of amines in enhancing methanesulfonic acid-driven new particle formation, Environ. Sci. Technol., 54, 13498–13508, https://doi.org/10.1021/acs.est.0c05358, 2020.
Sheng, X., Wang, B., Song, X., Ngwenya, C. A., Wang, Y., and Zhao, H.: Atmospheric Initial Nucleation Containing Carboxylic Acids, J. Phys. Chem. A, 123, 3876–3886, https://doi.org/10.1021/acs.jpca.9b01104, 2019.
Shi, X., Zhao, X., Zhang, R., Xu, F., Cheng, J., Zhang, Q., and Wang, W.: Theoretical study of the cis-pinonic acid and its atmospheric hydrolysate participation in the atmospheric nucleation, Sci. Total Environ., 674, 234–241, https://doi.org/10.1016/j.scitotenv.2019.03.479, 2019.
Sipila, M., Berndt, T., Petaja, T., Brus, D., Vanhanen, J., Stratmann, F., Patokoski, J., Mauldin, R. L. III., Hyvarinen, A.-P., Lihavainen, H., and Kulmala, M.: The role of sulfuric acid in atmospheric nucleation, Science, 327, 1243–1246, https://doi.org/10.1126/science.1180315, 2010.
Stahl, C., Cruz, M. T., Bañaga, P. A., Betito, G., Braun, R. A., Aghdam, M. A., Cambaliza, M. O., Lorenzo, G. R., MacDonald, A. B., Hilario, M. R. A., Pabroa, P. C., Yee, J. R., Simpas, J. B., and Sorooshian, A.: Sources and characteristics of size-resolved particulate organic acids and methanesulfonate in a coastal megacity: Manila, Philippines, Atmos. Chem. Phys., 20, 15907–15935, https://doi.org/10.5194/acp-20-15907-2020, 2020.
Veres, P. R., Roberts, J. M., Cochran, A. K., Gilman, J. B., Kuster, W. C., Holloway, J. S., Graus, M., Flynn, J., Lefer, B., Warneke, C., and de Gouw, J.: Evidence of rapid production of organic acids in an urban air mass, Geophys. Res. Lett., 38, 5, https://doi.org/10.1029/2011gl048420, 2011.
Wang, H., Zhao, X., Zuo, C., Ma, X., Xu, F., Sun, Y., and Zhang, Q.: A molecular understanding of the interaction of typical aromatic acids with common aerosol nucleation precursors and their atmospheric implications, RSC Adv., 9, 36171–36181, https://doi.org/10.1039/c9ra07398a, 2019.
Wen, H., Huang, T., Wang, C.-Y., Peng, X.-Q., Jiang, S., Liu, Y.-R., and Huang, W.: A study on the microscopic mechanism of methanesulfonic acid-promoted binary nucleation of sulfuric acid and water, Atmos. Environ., 191, 214–226, https://doi.org/10.1016/j.atmosenv.2018.07.050, 2018.
Xie, H.-B., Elm, J., Halonen, R., Myllys, N., Kurten, T., Kulmala, M., and Vehkamaki, H.: Atmospheric fate of monoethanolamine: enhancing new particle formation of sulfuric acid as an important removal process, Environ. Sci. Technol., 51, 8422–8431, https://doi.org/10.1021/acs.est.7b02294, 2017.
Xu, C. X., Jiang, S., Liu, Y. R., Feng, Y. J., Wang, Z. H., Huang, T., Zhao, Y., Li, J., and Huang, W.: Formation of atmospheric molecular clusters of methanesulfonic acid-diethylamine complex and its atmospheric significance, Atmos. Environ., 226, 9, https://doi.org/10.1016/j.atmosenv.2020.117404, 2020.
Xu, J., Finlayson-Pitts, B. J., and Gerber, R. B.: Proton transfer in mixed clusters of methanesulfonic acid, methylamine, and oxalic acid: implications for atmospheric particle formation, J. Phys. Chem. A, 121, 2377–2385, https://doi.org/10.1021/acs.jpca.7b01223, 2017.
Yao, L., Garmash, O., Bianchi, F., Zheng, J., Yan, C., Kontkanen, J., Junninen, H., Mazon, S. B., Ehn, M., Paasonen, P., Sipila, M., Wang, M., Wang, X., Xiao, S., Chen, H., Lu, Y., Zhang, B., Wang, D., Fu, Q., Geng, F., Li, L., Wang, H., Qiao, L., Yang, X., Chen, J., Kerminen, V.-M., Petaja, T., Worsnop, D. R., Kulmala, M., and Wang, L.: Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 361, 278–281, https://doi.org/10.1126/science.aao4839, 2018.
Yin, R., Yan, C., Cai, R., Li, X., Shen, J., Lu, Y., Schobesberger, S., Fu, Y., Deng, C., Wang, L., Liu, Y., Zheng, J., Xie, H., Bianchi, F., Worsnop, D. R., Kulmala, M., and Jiang, J.: Acid-Base Clusters during Atmospheric New Particle Formation in Urban Beijing, Environ. Sci. Technol., 55, 10994–11005, https://doi.org/10.1021/acs.est.1c02701, 2021.
Zhang, H., Kupiainen-Maatta, O., Zhang, X., Molinero, V., Zhang, Y., and Li, Z.: The enhancement mechanism of glycolic acid on the formation of atmospheric sulfuric acid-ammonia molecular clusters, J. Chem. Phys., 146, 184308, https://doi.org/10.1063/1.4982929, 2017.
Zhang, H., Li, H., Liu, L., Zhang, Y., Zhang, X., and Li, Z.: The potential role of malonic acid in the atmospheric sulfuric acid – Ammonia clusters formation, Chemosphere, 203, 26–33, https://doi.org/10.1016/j.chemosphere.2018.03.154, 2018.
Zhang, R., Suh, I., Zhao, J., Zhang, D., Fortner, E. C., Tie, X. X., Molina, L. T., and Molina, M. J.: Atmospheric new particle formation enhanced by organic acids, Science, 304, 1487–1490, https://doi.org/10.1126/science.1095139, 2004.
Zhang, R., Khalizov, A., Wang, L., Hu, M., and Xu, W.: Nucleation and growth of nanoparticles in the atmosphere, Chem. Rev., 112, 1957–2011, https://doi.org/10.1021/cr2001756, 2012.
Zhang, R., Wang, G., Guo, S., Zarnora, M. L., Ying, Q., Lin, Y., Wang, W., Hu, M., and Wang, Y.: Formation of Urban Fine Particulate Matter, Chem. Rev., 115, 3803–3855, https://doi.org/10.1021/acs.chemrev.5b00067, 2015.
Zhao, H., Jiang, X., and Du, L.: Contribution of methane sulfonic acid to new particle formation in the atmosphere, Chemosphere, 174, 689–699, https://doi.org/10.1016/j.chemosphere.2017.02.040, 2017.
Zuo, C., Zhao, X., Wang, H., Ma, X., Zheng, S., Xu, F., and Zhang, Q.: A theoretical study of hydrogen-bonded molecular clusters of sulfuric acid and organic acids with amides, J. Environ. Sci., 100, 328–339, https://doi.org/10.1016/j.jes.2020.07.022, 2021.