the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The number fraction of iron-containing particles affects OH, HO2 and H2O2 budgets in the atmospheric aqueous phase
Amina Khaled
Minghui Zhang
Reactive oxygen species (ROS), such as OH, HO2 and H2O2, affect the oxidation capacity of the atmosphere and cause adverse health effects of particulate matter. The role of transition metal ions (TMIs) in impacting the ROS concentrations and conversions in the atmospheric aqueous phase has been recognized for a long time. Model studies usually assume that the total TMI mass as measured in bulk aerosol or cloud water samples is distributed equally across all particles or droplets. This assumption is contrary to single-particle measurements that have shown that only a small number fraction of particles contain iron and other TMIs ( %), which implies that also not all cloud droplets contain TMIs. In the current study, we apply a box model with an explicit multiphase chemical mechanism to simulate ROS formation and cycling in aqueous aerosol particles and cloud droplets. Model simulations are performed for the range of 1 % ≤ FN,Fe ≤ 100 % for constant pH values of 3, 4.5 and 6 and constant total iron mass concentration (10 or 50 ng per cubic meter of air). Model results are compared for two sets of simulations with % (FeN<100) and 100 % (FeBulk). We find the largest differences between model results in OH and HO2 O concentrations at pH = 6. Under these conditions, HO2 is subsaturated in the aqueous phase because of its high effective Henry's law constant and the fast chemical loss reactions of the O radical anion. As the main reduction process of Fe(III) is its reaction with HO2 O, we show that the HO2 subsaturation leads to Fe(II) Fe(total) ratios for % that are lower by a factor of ≤ 2 as compared to bulk model approaches. This trend is largely independent of the total iron concentration, as both chemical source and sink rates of HO2 O scale with the iron concentration. We compare model-derived reactive uptake parameters γOH and for the full range of FN,Fe. While γOH is not affected by the iron distribution, the calculated values range from 0.0004 to 0.03 for FN,Fe = 1 % and 100 %, respectively. Implications of these findings are discussed for the application of lab-derived in models to present reactive HO2 uptake on aerosols. We conclude that the iron distribution (FN,Fe) should be taken into account to estimate the ROS concentrations and oxidation potential of particulate matter that might be overestimated by bulk sampling and model approaches. Our study suggests that the number concentration of iron-containing particles FN,Fe may be more important than the total iron mass concentration in determining ROS budgets and uptake rates in cloud and aerosol water.
- Article
(4487 KB) - Full-text XML
-
Supplement
(13028 KB) - BibTeX
- EndNote
The main oxidants in the atmospheric aqueous phases of cloud and aerosol particles include the hydroxyl radical (OH) and hydrogen peroxide (H2O2), whose concentration levels are closely linked to the hydroperoxy radical (HO2 O). The concentrations of these reactive oxygen species (ROS) are influenced by various redox reactions of transition metal ions (TMIs). Iron is the most abundant TMI in aerosol particles and cloud water. Its main sources include dust and coal combustion (Moffet et al., 2012) and biomass burning (Wang et al., 2015). Its concentration in cloud water ranges from nano- to micromolar levels (Cini et al., 2002; Deguillaume et al., 2005). Iron mass concentrations in aerosol samples reach from less than 1 ng m−3 to more than 100 ng m−3 (Schmücke, Germany) and sometimes up to several hundred nanograms per cubic meter (ng m−3) at other continental locations (Fomba et al., 2015, and references therein).
The role of transition metal ions in affecting the ROS concentration levels and redox reactions in clouds and particles has been explored in many model, lab and field studies, e.g., Deguillaume et al. (2004), Deguillaume et al. (2005) and Mao et al. (2013). Reactions of iron and other TMIs (e.g., copper) in the atmosphere have also been linked to the oxidative potential of particulate matter, causing oxidative stress in the respiratory tract and lungs (Saffari et al., 2014; Arangio et al., 2016; Tong et al., 2016; Molina et al., 2020; Wei et al., 2021). In particular, the oxidation of iron(II) by hydrogen peroxide (Fenton reaction) has been identified as one of the main chemical sources of the OH radical in cloud water (Ervens et al., 2003; Deguillaume et al., 2004; Tilgner et al., 2013), aqueous-phase aerosol particles (Al-Abadleh, 2015) and lung fluid (Charrier et al., 2015).
TMI concentrations in the cloud and aerosol phases are usually reported based on bulk measurements representing the total TMI mass per aqueous- or gas-phase volume. However, single-particle analyses have shown that iron is only present in a small number fraction of particles: Furutani et al. (2011) found that up to 15 % of particles in the diameter range between 0.5 and 1 µm contain iron. Similar number fractions (<1 %–15 %) were observed in Shanghai, where air masses were also affected by dust storms or biomass and coal burning (Zhang et al., 2014). A similar size range for iron-containing particles but smaller average number fraction (∼ 4 %) was found above the English Channel in air masses affected by steel works (Choël et al., 2007). As particles in this size range commonly act as cloud condensation nuclei (CCN), these analyses suggest that not all cloud droplets contain iron and that also the measured iron mass concentration in aerosol populations is not equally distributed among all particles. Drop-size-resolved cloud water measurements at a continental background site have shown that iron and copper are present in the same drop size range, whereas manganese is more abundant in larger droplets (Fomba et al., 2015). This may suggest that CCN were comprised of internal mixtures of iron and copper, whereas manganese-containing particles were externally mixed and of different hygroscopicity and/or different sizes.
The oxidation state of iron affects its solubility and thus its bioavailability and biogeochemical cycles in the atmosphere and oceans. Generally, ferrous salts are more soluble than ferric salts, with increasing solubility under acidic conditions, e.g., Ingall et al. (2018). Results from a global model study revealed large differences in predicted and observed iron solubility; observed Fe(II) Fe(total) ratios were on average between ∼ 1 % and ∼ 10 %, with larger variability in coarse than in fine particles (Luo et al., 2005). The Fe(II) fractions in particle samples above oceans have been shown to be above 30 %–75 % (Ingall et al., 2018). Measurement of the Fe(II) Fe(total) ratio on a single-particle basis revealed ratios of ≤ 20 % for particles from various sources (Takahama et al., 2008). In cloud water, Fe(II) often dominates the total iron concentration, in particular during daytime, when iron(III) hydroxy and organo complexes are reduced by photolysis processes (Deguillaume et al., 2005).
Multiphase chemistry models are usually initialized with bulk concentrations of iron to make predictions on the role of aqueous-phase chemistry in ROS levels (e.g., Ervens et al., 2003; Tilgner et al., 2013; Tong et al., 2017), sulfate formation (e.g., Alexander et al., 2009; Chang et al., 1987) or iron deposition (Myriokefalitakis et al., 2018). In a previous model study, we have demonstrated that such bulk approaches may not be appropriate for highly reactive compounds as redistribution and diffusion processes among droplets of chemical composition might lead to nonlinear effects impacting concentration levels (Khaled et al., 2021). While that study was focused on the biodegradation of organics by bacteria, which are only present in a small number fraction of cloud droplets, we apply the same idea in the present study to the ROS cycling, dependent on the number fraction of iron-containing particles.
We perform box model simulations with a detailed gas- and aqueous-phase chemical mechanism, in which a constant iron mass concentration mFe (nanograms per cubic meter of air) is distributed to a fraction of (i) cloud droplets or (ii) aqueous aerosol particles. We investigate the conditions in terms of pH, iron distribution and total iron mass, under which the number fraction of iron-containing particles significantly affects the concentration levels and phase transfer of OH, HO2 and H2O2 in the atmospheric multiphase system. We discuss the potential implications of these effects for the interpretation of measurements and model studies of the iron oxidation state, radical uptake rates onto aqueous aerosol particles and ROS budgets and oxidative potentials of aerosol and cloud water.
2.1 Model description
We use a box model with detailed gas- and aqueous-phase chemical mechanisms. The gas-phase chemical mechanism with 58 reactions is based on the NCAR Master Chemical Mechanism (Madronich and Calvert, 1989). The aqueous-phase chemical mechanism includes 43 reactions (Ervens et al., 2008; Tong et al., 2017) (Tables S1–S3 in the Supplement). Phase transfer processes for 14 species are described kinetically based on the resistance model (Schwartz, 1986; Nathanson et al., 1996) (Table S4). The model uses the standard equations for multiphase processes (Seinfeld and Pandis, 1998):
where both the gas-phase (Cg) and aqueous-phase (Caq) concentrations are expressed in units of moles per gram of air, LWC is the liquid water content (vol vol), KH(eff) is the (effective) Henry's law constant, and Saq, Sg and Laq, Lg are the chemical source and loss rates in the aqueous and gas phases (moles per gram of air per second). R and T are the constant for ideal gases (0.082058 L atm (K mol)−1) and absolute temperature (K). The mass transfer coefficient kmt (s−1) is defined as
where rd is the drop radius, Dg the gas-phase diffusion coefficient, α the mass accommodation coefficient, and Mg the molecular weight. The mass transfer coefficient kmt takes into account gas-phase diffusion and the mass accommodation, i.e., the probability that a molecule that hits the droplet (or particle) surface is taken up. It is the inverse of the characteristic time for these two resistances. Its full derivation can be found in the literature, e.g., by Nathanson et al. (1996), and is therefore not repeated here. In our model studies, it is assumed that all solutes are homogeneously mixed and no concentration gradients exist between the gas–aqueous interface and the bulk of the aqueous phase. This assumption is justified if chemical loss processes in the aqueous phase are comparatively slow, so that aqueous-phase diffusion can evenly distribute the species throughout the aqueous volume. The competition between aqueous-phase diffusion and chemical loss in the aqueous phase is commonly quantified by the dimensionless diffuso-reactive parameter q (Eq. S.1 in the Supplement, Seinfeld and Pandis, 1998). This parameter does not take into account chemical sources within the aqueous phase. As discussed in a previous study, the Fenton reaction can act as a such a source for the OH radical in aqueous solution (Ervens et al., 2014). A detailed comparison and discussion of the parameter q and the role of aqueous-phase diffusion can be found in the Supplement (Sect. S2).
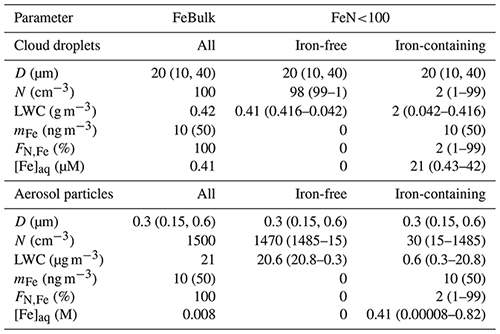
The box model considers monodisperse cloud droplet or wet aerosol particle populations with constant diameters (D) of 20 µm for cloud droplets and 300 nm for aqueous aerosol particles, respectively. The simulations are run at constant temperature (285.6 K), pressure (9.21 × 104 Pa) and air density (1.31 × 10−3 g cm−3).
2.2 Model simulations
The schematic of the model setup together with the main ROS formation and conversion processes are shown in Fig. 1. Results of two model approaches will be compared:
-
FeBulk. All droplets (particles) have the same chemical composition. The iron concentration is identical in all droplets (particles). The fraction of iron-containing droplets (particles) is FN,Fe = 100 %.
-
FeN<100. A subset of the number concentration (N) of droplets (or particles) is initialized with iron, whereas the remainder of the droplets (particles) is iron-free. In the base case simulations, we assume that the number fraction of iron-containing droplets (particles) is %; FN,Fe is varied from 1 %–99 % in sensitivity studies (Sect. 3.3).
We assume an iron mass concentration (mFe = 10 ng per cubic meter of air). (Some sensitivity studies for mFe = 50 ng per cubic meter of air are discussed.) Therefore, in the FeN<100 approach, the aqueous-phase iron concentration [M] is higher in the iron-containing droplets (particles) than in the FeBulk approach as the iron mass is distributed to fewer droplets (particles). Simulations are performed for constant values of pH = 3, 4.5 and 6. All model parameters are summarized in Table 1. Gas-phase species are initialized with the values in Table S5 and are not replenished throughout the simulations. Chemical and phase transfer rates are analyzed after a simulation time of 400 s. This timescale refers approximately to the lifetime of a single cloud droplet. It can be estimated based on updraft and downdraft velocities a cloud droplet experiences and on cloud thickness (e.g., average vertical velocity of 0.5 m s−1 throughout cloud that is 100 m thick, as typical values for shallow stratocumulus clouds). To demonstrate that our results and conclusions do not strongly depend on the choice of the timescale, we compare the main source and loss processes of the three species at t = 400 and t = 2000 s (Sect. 3.2). During even longer timescales, the concentrations may change in the box model; however, this may not be realistic since highly reactive gases are quickly depleted (e.g., SO2), whereas in the real atmosphere, emissions might replenish them.
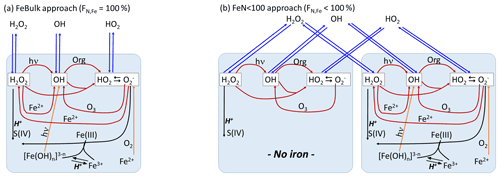
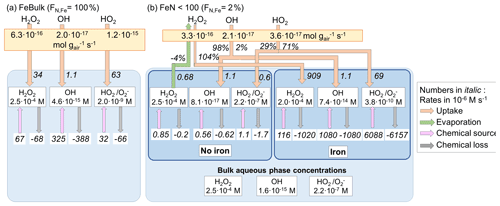
Figure 1Model schematic. (a) FeBulk: the total iron mass concentration (mFe = 10 ng m−3) is equally distributed among all droplets or particles (FN,Fe = 100 %). (b) FeN<100: the same iron mass concentration is distributed among a subset of droplets or particles (base case: FN,Fe = 2 %). Major ROS processes are phase transfer (blue), ROS net production (orange), ROS conversions (red) and ROS loss (black). Model parameters are summarized in Table 1.
Table 1Model parameters for multiphase simulations for cloud droplet and aerosol populations. D is the diameter, N the number concentration, LWC the liquid water content, mFe the total iron mass concentration, FN,Fe the number concentration of droplets or particles that contain iron and [Fe]aq the aqueous-phase concentration of iron. Numbers in parentheses denote values or parameter ranges of sensitivity studies.
3.1 Aqueous-phase concentrations and rates
3.1.1 Cloud droplets
Figure 2 summarizes the ROS concentrations and the chemical and phase transfer rates for the cloud case at pH = 4.5; the corresponding figures for simulations at pH = 3 and 6 are shown in Fig. S1 (Supplement). The net transfer rates (moles per gram of air per second) into the aqueous phase are shown in the yellow boxes. For FeN<100, the relative contributions (%) of this rate into the iron-free and iron-containing droplets are shown next to the arrows. The phase transfer rates are additionally shown in units of moles per liter per second (using the air density of 1.13 × 10−3 g cm−3 and LWCs in Table 1), together with the chemical source and loss rates in the aqueous phase (M s−1) and the corresponding aqueous-phase ROS concentrations (M) (white boxes). If the effect of iron is negligible on aqueous-phase concentrations and aqueous-phase rates, there should be no concentration difference between any droplets, neither between the results for FeBulk and FeN<100 nor between the iron-free and iron-containing droplets. In addition, the ratio of the phase transfer rates should also be equal to the ratio of the LWCs of the two drop classes (98 % : 2 %).
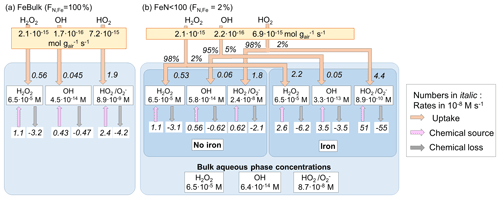
Figure 2Multiphase scheme for cloud water showing the phase transfer and chemical source and loss rates in the aqueous phase, mFe = 10 ng m−3, pH = 4.5. (a) FeBulk approach. (b) FeN<100 approach with a fraction of iron-containing droplets of FN,Fe = 2 %. Numbers below the species names are aqueous-phase concentrations (M), and chemical and phase transfer rates are shown in moles per liter per second. Net phase transfer rates near the top of the figure are expressed in gas-phase units (moles per gram of air per second); the relative contributions (%) into the iron-free and iron-containing droplets are shown next to the arrows. The bulk concentrations at the bottom of panel (b) represent the bulk concentrations weighted by the contributions of the two droplet classes to total LWC (98 % : 2 %).
All ROS are predicted to be taken up into cloud water, independently of the iron distribution at pH = 4.5 (Fig. 2), and also their ratio of the phase transfer rates nearly corresponds to the ratio of the LWCs of the two droplet classes (98 % : 2 %). Significant deviations from this theoretical value occur at pH = 3 for HO2 (Fig. S1b) and at pH = 6 for H2O2 that is predicted to evaporate from iron-free droplets (Fig. S1d).
The H2O2 concentrations in all droplets under all conditions and pH values (Fig. S1) correspond to the equilibrium concentrations according to Henry's law, in agreement with previous studies that have shown that H2O2 is at thermodynamic equilibrium in cloud water (Ervens, 2015). At pH = 3 and 4.5, the efficient H2O2 consumption is compensated by a relatively higher uptake rate, resulting in the efficient replenishment of H2O2 and equilibrium concentration. The uptake rates (in M s−1) between FeBulk and the iron-free droplets in the FeN<100 approach are similar (e.g., for H2O2 : 0.56 and 0.53 M s−1), whereas they are higher for uptake into the iron-containing droplets (2.2 M s−1). Since these droplets only comprise 2 % of the total LWC, this difference is not reflected in the net uptake rate. At pH = 6 (Fig. S1c and d), the majority of cloud droplets are predicted to be a source of H2O2; the only exception is the iron-containing droplets in the FeN<100 approach, from which H2O2 evaporates due to less efficient chemical H2O2 consumption in the aqueous phase.
The OH concentrations differ by nearly 1 order of magnitude between the iron-free and iron-containing cloud droplets (5.8 × 10−14 M vs. 3.3 × 10−13 M; Fig. 2b); the concentration in the FeBulk model is even slightly lower (4.5 × 10−14 M; Fig. 2a). The reasons for these differences are explored in Sect. 3.2, where the individual chemical processes affecting the concentrations are analyzed.
The bulk aqueous-phase OH concentration in the FeBulk approach is approximately 50 % higher (4.5 × 10−14 M) as compared to 6.4 × 10−14 M for FeN<100 (Fig. 2). A much greater discrepancy of nearly 1 order of magnitude between the two approaches is predicted at pH = 6, whereas the difference in the bulk concentrations at pH = 3 is smaller (Fig. S1). These concentrations corresponded to those in bulk cloud water samples from cloud droplet populations with FN,Fe = 2 %, provided that chemical processes in the sample upon sampling do not change the ROS levels (Sect. 3.3). For all cases, the chemical source and loss rates of the OH radical compensate for each other, leading to a relatively small uptake rate of the moderately soluble OH radical into the aqueous phase (∼ 10−16 mol g−1 s−1), which is not significantly affected by FN,Fe.
The concentration difference of HO2 O between iron-free and iron-containing droplets is nearly 2 orders of magnitude (2.4 × 10−8 M vs. 8.9 × 10−10 M), whereas the concentration for FeBulk is predicted to be between these two values (8.9 × 10−9 M) (Fig. 2). The difference in the concentrations is even greater (factor > 200) at pH = 6 (Fig. S1d), whereas it is less than a factor of 3 at pH = 3. These trends suggest that the concentrations are dependent on pH (Sect. 3.2). The comparison of the bulk aqueous-phase HO2 O concentrations resulting from the FeN<100 approach (bottom of Figs. 2b, S2b and d) to those in FeBulk shows that at pH = 4.5 and 6, the total HO2 O is underestimated by about 1 order of magnitude. At pH = 3, the chemical loss rate of HO2 O in iron-containing droplets is relatively larger than its chemical source rate (74 × 10−8 M s−1 vs. 66 × 10−8 M s−1; Fig. S1b). This imbalance in the chemical rates leads to a very efficient HO2 uptake into iron-containing droplets. Consequently, the phase transfer into these droplets comprises 13 % of the total uptake rate, whereas at higher pH values the contributions correspond to the ratio of LWCs between the two droplet classes (98 % : 2 %). The higher Henry's law constant of HO2 and rate constants of O reactions as compared to those of HO2 at higher pH lead to increasingly lower HO2 O concentrations with increasing pH.
3.1.2 Aqueous aerosol particles
Since the LWC of the aqueous aerosol particles is smaller by a factor of 2 × 105 than in clouds, the aqueous-phase iron concentration is accordingly higher, and so are all chemical rates of iron reactions. Similar to cloud water, the H2O2 concentration is neither significantly affected by the iron distribution nor by iron reactions; i.e., at a given pH value its aqueous-phase concentration is nearly the same in all particles. At pH = 4.5 and 6, evaporation of H2O2 is predicted for FeBulk and from the iron-free particles in FeN<100 (Figs. 3b and S2b and d). However, since the uptake rate of H2O2 into the iron-containing droplets is much higher, exceeding the evaporation rate by a factor of 25 (−4 % vs. 104 %, pH = 4.5) and ∼ 2 (−143 % vs. 243 % at pH = 6), aqueous particles represent a net sink of H2O2.
Similar to the cloud case, the OH concentrations in the aqueous phase of FeBulk are between those in the iron-free and iron-containing particles for FeN<100. The OH concentrations do not show a strong pH dependence, but their bulk values are about a factor of 3 lower for the FeN<100 approach (FN,Fe = 2 %) than for the FeBulk approach (1.6 × 10−15 M vs. ∼ 4.6 × 10−15 M). Even at the high iron concentrations as present in aerosol water (≤ 0.41 M), the chemical source and loss rates of OH nearly cancel out, leading to a relatively small uptake rate.
The HO2 O concentrations in the FeBulk approach are comparable to those as predicted for cloud water at the same pH value. However, the concentrations in the iron-free and iron-containing particles differ by 4 orders of magnitude at pH = 6 (1.5 × 10−6 and 1.3 × 10−10 M, Fig. S2d). The resulting bulk aqueous-phase concentrations are at least 1 order of magnitude underestimated by FeBulk (pH = 3); this difference is even a factor of 2000 at pH = 6 (Figs. 3d and S2d). While the chemical loss rate of HO2 O is nearly equal to or even larger than its source rate at pH = 4.5 and 6, at pH = 3 the source rate exceeds the loss rate resulting in evaporation of HO2 from the 2 % iron-containing particles (Fig. S2b). However, since the uptake rate into the iron-containing particles is larger than this evaporation rate, the net flux of HO2 is an uptake into the particle phase.
3.1.3 Gas-phase concentrations (OH, HO2) and mixing ratios (H2O2)
The gas-phase concentrations of OH and HO2 and mixing ratios of H2O2 are shown in Fig. S3 as a function of time (t≤7200 s) in the presence of cloud droplets and aerosol particles, respectively, at the three pH values considered here and for the two assumed iron distributions in the aqueous phase. The H2O2 mixing ratio in the presence of cloud water is very quickly reduced to about 50 % of its initial concentration (1 ppb) due to partitioning to the aqueous phase. Both the pH value and FN,Fe have a small effect on the H2O2 mixing ratio. The small increase of H2O2 over time is in agreement with findings in a recent multiphase box model intercomparison (Barth et al., 2021).
The OH concentrations are on the order of 106 cm−3, i.e., typical concentrations as found for continental daytime conditions. These concentrations build up within a few seconds and do not largely change over the time period considered here. The difference of up to a factor of 5 in the OH concentrations in the presence of cloud droplets with a pH value of 3 and 6, respectively, cannot be directly explained by any OH reactions in the aqueous phase but is rather a consequence of the OH–HO2 cycle in the multiphase system (Fig. 1). At pH = 6, the effective Henry's law constant for HO2 is highest, and therefore, most HO2 is partitioned to the aqueous phase, resulting in the lowest fractions of HO2 in the gas phase. The gas-phase HO2 concentrations are on the order of 108 cm−3, in agreement with predictions from other atmospheric multiphase chemistry models (e.g., Barth et al., 2021). Generally, the pH value and iron distributions cause smaller differences in the presence of aerosol particles as compared to the cloud case, since the liquid water content of particles is smaller by several orders of magnitude, and therefore a smaller fraction of the species is dissolved.
3.1.4 Partitioning coefficient ϵ
The partitioning coefficient ϵ is often used to describe the distribution of species between the aqueous and gas phases in the atmospheric multiphase system, e.g., Ervens (2015). It is defined as
with Caq and pg being the aqueous-phase concentration (M) and gas-phase partial pressure (atm) and KH(eff) the (effective) Henry's law constant (M atm−1). Accordingly, ϵ<1 indicates situations when the aqueous phase is subsaturated.
The ϵ values for the three ROS are summarized in Fig. 4 for the cloud and aerosol simulations at three pH values. The fact that is ∼ 1 shows that H2O2 is in thermodynamic equilibrium and explains why its concentrations do not differ among iron-containing and iron-free droplets (particles) (Figs. 2, 3 and S2).
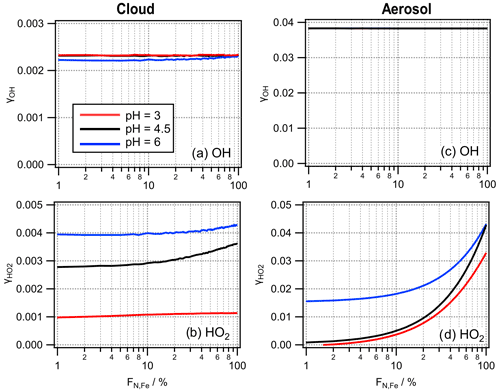
The ϵOH values in the presence of cloud droplets (red symbols, Fig. 4b) are on the order of ∼ 0.01–0.1. The values for iron-containing aerosol particles show a distinct trend with highest ϵOH values in iron-containing particles, whereas ϵOH in iron-free particles is lower by 2 and 3 orders of magnitude, respectively. The lack of a clear trend in ϵOH with pH suggests that the main formation and loss processes of OH are pH-independent. The differences in ϵOH scale with the OH concentrations in aerosol particles that differ by 3 orders of magnitude between iron-containing and iron-free particles in the FeN<100 approach and the concentration in the FeBulk case (Fig. 3). The ϵOH values in cloud water do not exhibit such strong differences, which is also reflected in the more similar concentrations in all droplets (Fig. 2).
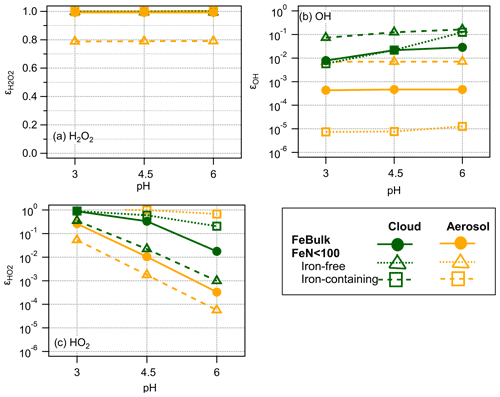
Figure 4Partitioning coefficients ϵ for (a) H2O2, (b) OH and (c) HO2 for pH = 3 , 4.5 and 6 for FeBulk (filled symbols) and FeN<100 in 98 % iron-free (squares) and 2 % iron-containing droplets (triangles). Results are shown for simulations of cloud droplets (green) and aerosol particles (orange) at three pH values (3, 4.5 and 6); lines are added to guide the eye.
The difference between the concentration in iron-free and iron-containing particles is up to 3 orders of magnitude (pH = 3, Fig. S2b), which is also reflected in the same difference in ϵ (Fig. 4b).
For the HO2 radical, iron reactions cause a significant deviation from thermodynamic equilibrium at high pH, resulting in decreasing with increasing pH. At high pH, HO2 is more efficiently consumed due to the higher rate constants of the O radical anion as compared to those with the undissociated HO2 radical. Unlike for OH, for which the smallest ϵ is seen in iron-free particles, the lowest is found for iron-containing particles – which shows that the concentration differences due to iron distribution for OH and HO2 have different reasons: whereas iron leads to efficient OH formation, it causes significant HO2 O loss.
3.2 Relative contributions of chemical reactions and phase transfer to ROS source and loss rates in the aqueous phase
To understand the trends in concentrations, reaction rates and partitioning coefficients with FN,Fe and pH as discussed in the previous section, Fig. 5 summarizes the main chemical pathways for the three ROS for the cloud and aerosol cases for the same conditions as in Figs. 2 and 3. The individual chemical source (S) and loss (L) processes are indicated between the figure panels for the cloud (top part of figure) and aerosol (bottom part) cases. Only chemical processes are listed that contribute to more than 1 % to the total rate in each simulation. As the phase transfer (PT) can be a source (i.e., uptake) or loss (i.e., evaporation) process for the aqueous-phase species, its contribution is placed between the chemical sources and losses. The total source and loss rates (mol g−1 s−1) are indicated in the boxes in the upper right of each panel.
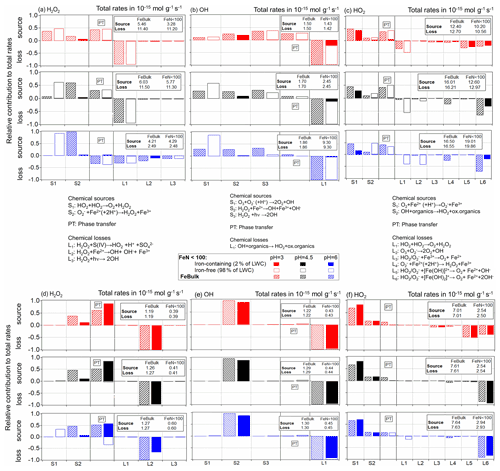
Figure 5Relative contributions of chemical and phase transfer rates to the total sources and losses of the three ROS. The total rates (moles per gram of air per second) are shown in boxes in the upper right of each panel. For the FeN<100 approach, the contributions in iron-free and iron-containing droplets (particles) are displayed as open and dashed bars and those for the FeBulk approach as solid filled bars. Simulations were performed at constant pH values of pH = 3 (red), 4.5 (black) and 6 (blue) for cloud conditions (a) H2O2, (b) OH and (c) HO2 and aerosol conditions (d) H2O2, (e) OH and (f) HO2. The chemical aqueous-phase source (S) and loss (L) reactions are listed between the panels.
Given its high Henry's law constant ( = 1.02 × 105 M atm−1), the H2O2 uptake contributes nearly 50 % to the total H2O2 source at pH ≤ 4.5 in cloud water (Fig. 5a) and even more in aerosol water (50 %–80 %) (Fig. 5d). However, the uptake occurs mostly (98 %) into iron-free cloud droplets, whereas in the aerosol case, most H2O2 is taken up by the iron-containing particles. This trend was already shown in the comparison of Figs. 2b and 3b. The main loss of H2O2 in cloud water is the pH-dependent reaction with sulfur(IV) (L1 in Fig. 5a), whose rate decreases with increasing pH (R4 in Table S1). Therefore, the chemical loss of H2O2 in cloud water is very inefficient at pH = 6 (2.4 × 10−15 mol g−1 s−1 at pH = 6 vs. ∼ 11 × 10−15 mol g−1 s−1 at pH ≤ 4.5; Fig. 5a). The rate of the recombination of H2O2 (S1 in Fig. 5a) increases with pH since the reaction of HO2 and O is much faster than with undissociated HO2 (100 × kR5 ∼ kR6; Table S1). Therefore, more H2O2 is formed at pH = 6 than at lower pH, leading to H2O2 evaporation from cloud droplets at pH = 6. Figure 5 represents a snapshot of the rates after a simulation time of 400 s. We have chosen this relatively short time, since gases are not replenished during the box model simulations as no emissions are considered. At longer timescales (after 2000 s), the conclusions would not be drastically different (Fig. S4); the only major difference is the loss of H2O2 by sulfur(IV) (L1 in Fig. S4a) as SO2 is consumed quickly within the first few minutes.
In aerosol water, the Fenton reaction (L2, Fig. 5a, d) is the main loss reaction of H2O2. The main H2O2 source process is the reaction of Fe2+ with O (S2), whose rate increases with increasing pH value. Since in iron-free particles, the chemical loss rate (L1) decreases with pH, but its source rate (S1) increases, H2O2 evaporates from iron-free particles. In iron-containing particles, both the main source and sink reactions are directly dependent on the Fe2+ concentration (S2, L2). As the iron concentration in the iron-containing particles is ∼ 50 times higher for FeN<100 than for FeBulk, it seems surprising at first that the chemical rates do not scale by this factor. Furthermore, the HO2 O concentration is much higher in iron-free than in iron-containing particles, in particular at pH = 6. Also this trend, thus, cannot explain the lower chemical H2O2 source rates of S2. Therefore, only a difference in the Fe2+ concentration can explain the differences in the chemical rates of the chemical H2O2 sources and sinks (Sect. 4.1).
Independently of the iron distribution, the relative importance of the uptake of the OH radical into aerosol particles' cloud water decreases with increasing pH, from ∼ 30 % at pH = 3 to <10 % at pH = 6 (Fig. 5b). As the rate of the O reaction with ozone (S1) increases with pH, the relative importance of this reaction increases with increasing pH value. The loss of OH in the aqueous phase is due to reactions with organic compounds; the rate of L1 in Fig. 5b and e represents the sum of all reaction rates of OH with organics in Table S1. As the rate constants of OH reactions with carboxylates are generally higher than those with their corresponding acids, the chemical loss rate in cloud water increases with pH. The most striking difference in the source and loss patterns of OH between cloud and aerosol water is the dominating role of the Fenton reaction (S2) as OH source in aerosol water. It contributes nearly 100 % of the sources at all pH values, making the OH uptake as a source negligible. Similar to the trends as described above for H2O2, the chemical rates of the Fenton reaction as OH source (S2) are much smaller in FeN<100 than for FeBulk, which can again be explained by the lower Fe(II) concentration at low FN,Fe. As the uptake rate of OH is fairly low as compared to its chemical rates due to its low Henry's law constant (KH,OH = 25 M atm−1; Table S4), the chemical source rate is nearly fully compensated for by the chemical loss rate that under all pH and LWC conditions results in (nearly) identical values.
The only major sources of HO2 O are the reactions of Fe2+ with molecular oxygen (S1) and the OH reactions with organics (S2) (Fig. 5c and f). The slight increase in the overall reaction rate of S2 with pH explains the highest chemical source rate in all droplets at the highest pH. Its main loss reactions are the reactions of Fe(III) (free Fe3+ and the hydroxy complexes [Fe(OH)n]3n−1 with n = 1, 2). The dominance of these processes for the loss of HO2 O leads to very efficient uptake into iron-containing droplets. The rate constants of these loss reactions with O are about 3 orders of magnitude higher than those with HO2 (R27, R28 and R35–R38 in Table S1). This results in the subsaturation of HO2 in the aqueous phase, i.e., decreasing with increasing pH (Fig. 4c). This effect is more pronounced in aerosol water than in cloud water because of the higher total Fe concentration in particles. The highly efficient loss of O at high pH results in the lowest HO2 O concentrations in the iron-containing droplets at pH = 6 (Fig. S2d). Since the reactions of Fe(III) with HO2 O are the main reduction processes of Fe(III), the lower HO2 O concentration leads to inefficient Fe(III) to Fe(II) conversion and relatively higher Fe(III) concentrations (Sect. 4.1).
3.3 Aqueous-phase concentrations as a function of FN,Fe
3.3.1 Comparison of bulk aqueous-phase concentrations
The values of FN,Fe = 2 % and 100 % likely represent extreme values for the iron distribution in cloud droplet or particle populations. Depending on abundance and proximity of iron emissions sources, fewer particles (and thus droplets) may also contain iron; this would translate into an even higher iron aqueous-phase concentration. Under such conditions, iron would not be completely dissolved and available for aqueous-phase reactions. Therefore, in the following, we limit our discussion to values of FN,Fe ≥ 1 %. In order to illustrate the total ROS budget in the aqueous phase, Fig. 6 shows the bulk aqueous-phase concentrations [ROS]aq,bulk (M) calculated based on the LWC-weighted average ROS concentration in the iron-containing and iron-free droplets or particles:
where [ROS]ironfree and [ROS]iron are the ROS concentrations in the iron-free and iron-containing droplets, respectively. (Note that the same calculation was performed for the bulk aqueous-phase concentrations in Figs. 2, 3, S1 and S2). Results are shown for the full range of 1 % ≤ FN,Fe ≤ 100 %.
The H2O2 concentrations do not show any dependence on the iron distribution FN,Fe (Fig. 6a and d). This trend can be explained because (i) in cloud water the main chemical source and loss processes are independent of iron, whereas (ii) in aerosol water, both the main chemical source and loss reactions are dependent on the Fe(II) concentration. The same set of processes can also explain why the resulting aqueous-phase H2O2 concentrations are independent of the total iron mass. In a sensitivity study, we increased mFe to 50 ng m−3, which results in very similar H2O2 concentrations (Fig. S5). Thus, a higher iron mass concentration increases both rates by the same factor, resulting in nearly equal H2O2 concentrations for both mFe.
The OH concentration in cloud water is underestimated by FeBulk by up to a factor of ∼ 5 (pH = 6, Fig. 6b). The large difference at the highest pH is the consequence of the more efficient OH formation at pH = 6 by the reaction of O with O3 (Sect. 3.2). Since in the FeN<100 approach the HO2 O concentration is about 1 order of magnitude higher at this pH value than for FeBulk, the OH concentration is generally underestimated by assuming FN,Fe = 100 %. It can be concluded that in clean conditions, i.e., when the pH value of cloud water is 5, even for relatively low iron mass concentrations, iron distribution should be taken into account to obtain the correct OH concentrations in cloud water. The deviations are only slightly higher for mFe = 50 ng m−3 than for 10 ng m−3 (Fig. S5). In aerosol water, the OH concentration is generally overestimated by FeBulk by factors of 2 and ∼ 5 for mFe = 10 and mFe = 50 ng m−3 (Figs. 6e and S5e), respectively. The lower OH concentration in the FeN<100 approach is a consequence of the lower Fe(II) concentration (Sect. 4.1), which leads to less OH formation by the Fenton reaction.
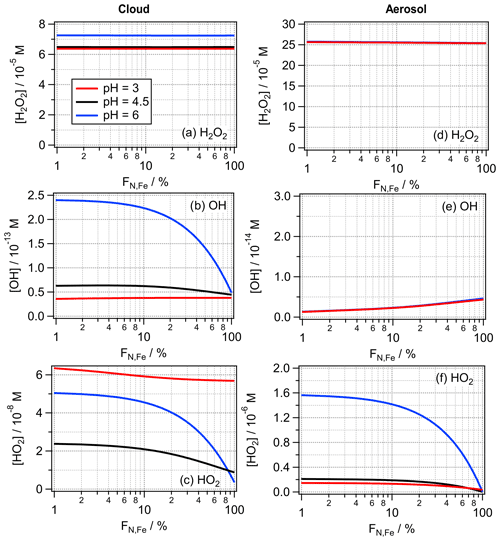
Figure 6Bulk aqueous-phase concentrations of H2O2, OH and HO2 for the cloud (a–c) and aerosol (d–f) cases as a function of FN,Fe using the model parameters listed in Table 1.
The HO2 O concentrations are underestimated in cloud water by the FeBulk approach, approximately by the same factors (∼ 2–5) as the OH radical, with the highest bias at pH = 6 (Fig. 6c). At pH = 3, the difference between the HO2 O concentrations for the two iron mass concentrations is much larger than for the other pH values. Unlike for the H2O2 and OH concentrations, that are very similar for both mFe, the HO2 O concentrations more clearly deviate for the two iron masses considered in Fig. S5. This can be explained by the less efficient Fe(III) reduction in the cloud droplets at mFe at all pH values (Sect. 4.1).
In aerosol water, the aqueous-phase HO2 O concentrations are nearly identical for wide ranges of FN,Fe at pH = 3 and 4.5, whereas the difference at FN,Fe = 1 % and 100 % is about 1 order of magnitude at pH = 6 (Fig. 6f). Thus, the aqueous-phase budget of HO2 O may be significantly underestimated – independently of mFe – with increasing pH if the iron distribution across the particle distribution is not properly accounted for.
3.3.2 Enhanced H2O2 partitioning into aerosol water: = 2.7 × 108 M atm−1
Strictly, Henry's law constants are not applicable to highly concentrated aqueous solutions such as aerosol water. Simultaneous measurements of particle-bound and gas-phase H2O2 concentrations suggest that it partitions much more efficiently to the particle phase than predicted based on its physical Henry's law constant ( = 1.02 × 105 M atm−1). Despite large uncertainties in such measurements and of related parameters such as the aerosol water content, various studies revealed that the partitioning of H2O2 between the gas and the aerosol aqueous phases may be more appropriately described with an effective Henry's law constant of ≤ 2.7 × 108 M atm−1 (Hasson and Paulson, 2003; Xuan et al., 2020). The observation by Hasson and Paulson (2003) of higher H2O2 concentrations in coarse-mode particles than in fine-mode particles might point to a size-dependent chemical particle composition with higher iron content in coarse particles that often contain dust.
To explore the effects of such enhanced partitioning, we performed a sensitivity study, using ≤ 2.7 × 108 M atm−1. In Fig. S6, the aqueous-phase concentrations and net phase transfer rates of the three ROS are compared to those using the physical Henry's law constant ( = 1.02 × 105 M atm−1). No other parameter was changed as to the best of our knowledge corresponding KH(eff) values for OH and/or HO2 are not available. We perform this comparison only for the aerosol case, as numerous measurements have shown that the partitioning of H2O2 into cloud water can be satisfactorily described by its KH (e.g., Ervens, 2015).
As expected, a higher results in higher H2O2 aqueous-phase concentrations by 3 orders of magnitude. Unlike for the low , the higher partitioning leads to smaller H2O2 concentrations for FeBulk than for FeN<100 by up to 1 order of magnitude and pH = 6. The OH concentration in the aqueous phase is predicted to decrease with increasing FN,Fe, unlike in the base case simulation where we showed the opposite trend (Fig. S6b). The higher H2O2 concentration generally increases the importance of the Fenton reaction and photolysis for OH production in the aqueous phase. While the HO2 O concentrations for the two values do not differ at low FN,Fe, they are significantly smaller by several orders of magnitude for the higher (Fig. S6c).
4.1 Oxidation state of iron: Fe(II) Fe(total)
The iron oxidation state determines its solubility and bioavailability since Fe(II) salts are usually more soluble than Fe(III) compounds. Fe(II) usually dominates during daytime because Fe(III) complexes are readily photolyzed (Deguillaume et al., 2005). Reported measurements are based on analyses that are performed on bulk samples, where redox reactions of iron can occur after collection and combination of all cloud droplets or aerosol particles, respectively. The trends and overall Fe(II) Fe(total) (or Fe(II) Fe(III)) ratios have been reproduced in several model studies that all assumed that iron is present in the complete aqueous phase (Ervens et al., 2003; Deguillaume et al., 2004; Luo et al., 2005; Tilgner et al., 2013; Ingall et al., 2018). Thus, the agreement between measured and predicted data is not surprising as both types of studies imply that the total soluble iron is evenly distributed throughout the total aqueous volume.
However, our study reveals that these Fe(II) Fe(total) ratios are not the true ratios present in the atmospheric aqueous phases if iron is only present in a small number fraction of particles or droplets. In cloud water, the soluble iron fraction (∼ Fe(II) Fe(total)) might be overestimated by up to factor of 2 (Fig. 7a), whereas this bias might be even higher in aerosol particles ( 2.5; Fig. 7b). The overview articles by Deguillaume et al. (2005) and Mao et al. (2017) show large ranges of the Fe(II) Fe(total) fraction (10 %–100 %). Interestingly the study by Takahama et al. (2008) that investigated single particles reports values at the lower end of this range (∼ 20 %). We cannot state with certainty that this finding is due to different aerosol composition or origin or indeed points to a more accurate representation of the Fe(II) Fe(total) ratio in individual particles rather than in bulk samples.
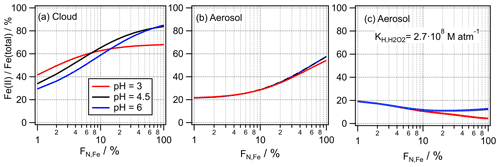
Figure 7Predicted Fe(II) Fe(total) ratios at pH = 3 , 4.5 and 6 and the conditions as given in Table 1. (a) Cloud, (b) aerosol and (c) aerosol with enhanced partitioning of H2O2 ( = 2.7×108 M atm−1; Sect. 3.3.2).
If the Fe(II) Fe(total) may be considered a measure of the bioavailability of iron, it might be actually lower than derived from ambient samples or model studies, if they apply a bulk approach. Our results suggest that parameterizations of the Fe(II) Fe(total) ratios, as, for example, suggested by Mao et al. (2017), might have to be further refined to account for the effects due to the iron distribution across particle populations. In aqueous media that consist of a bulk aqueous phase (e.g., oceans, lung fluid, to some extent also rainwater), the Fe(II) fraction will be appropriately represented by FN,Fe = 100 % (FeBulk). The timescales for the Fe(II) Fe(III) ratio to adjust from conditions of % to FN,Fe = 100 % will depend on the rates of iron redox processes and on the solubility and dissolution kinetics of ferrous and ferric salts, which, in turn, may be a function of other solutes and liquid water content. If H2O2 is more soluble in aerosol water than in cloud water ( = 2.7×108 M atm−1; Sect. 3.3.2), the Fe(II) Fe(total) ratio does not exceed ∼ 20 % for any FN,Fe (Fig. 7c). Thus, HO2 O is always efficiently consumed by Fe(III), even at the highest considered iron mass (50 ng m−3, Fig. S7c). This predicted independence of the Fe(II) Fe(total) ratio as a function of FN,Fe for the high in contrast to the predicted strong dependence using the physical may be used to guide future experiments to determine the “best” value of for aerosol water.
4.2 Reactive uptake parameters γ
4.2.1 Calculation of γOH and
The uptake of OH and HO2 into aerosol particles is often parameterized by the dimensionless reactive uptake coefficient γ that is derived as a function of the first-order radical loss (kloss) onto aerosol particles. For the derivation of γ based on lab studies, it is assumed that γ solely depends on the molecular speed and the droplet surface. However, it has been discussed that the reactive uptake coefficient in atmospheric applications should also include a term to account for gas-phase diffusion (Jacob, 2000):
with S being the total droplet surface area per air volume and ω the molecular speed,
where M is the molar mass (g mol−1), R is the gas constant and T is the absolute temperature (K) (e.g., Thornton and Abbatt, 2005; Pöschl et al., 2007). Accordingly, the phase transfer rate of radicals into the particle phase can be described as
and the reactive uptake coefficient γ can be derived as
The γ values for OH and HO2 as a function of FN,Fe are displayed in Fig. 8. If gas-phase diffusion is neglected in the derivation of γ, the last term in the denominator of Eq. (9) is set to zero (Eq. S.3). To demonstrate the impact of gas-phase diffusion on the reactive uptake parameter, we compare γ values calculated with Eq. (10) to values without consideration of gas-phase diffusion (Sect. S3 in the Supplement).
4.2.2 Reactive uptake coefficient of the hydroxy radical, γOH
The derived values for γOH over the full range of FN,Fe (∼ 2.2 × 10−3 ≤γOH(cloud) ≤ 6.4 × 10−3; γOH(aerosol) ∼ 3.8 × 10−2) are in good agreement with the average value suggested for pure water surfaces (γOH = 0.035) (Hanson et al., 1992). It should be noted that this latter experimental value was derived assuming a Henry's law constant of KH,OH ≥ 40 M atm−1 and [OH] ≥ 108 cm−3. If it were adjusted to atmospherically more relevant conditions ([OH] ∼ 106 cm−3) and KH,OH = 25 M atm−1 as used in our study (Table S4), the resulting γOH might be smaller by more than an order of magnitude than the reported one. Molecular dynamics simulations for the mass accommodation of OH on water surfaces showed αOH = 0.1, which can be considered the upper limit of reactive OH uptake onto water surfaces (Roeselová et al., 2003). The difference between such a value for pure water and the values from our model study demonstrates the high reactivity of the OH radical in the aqueous phase. As its solubility is limited, this high reactivity results in subsaturated conditions (ϵOH<1; Fig. 4b). The γOH values show little difference at different pH values and FN,Fe. Thus, the reactive uptake of OH into cloud droplets could be parameterized with a value of γOH∼ 2.3 × 10−3 for all conditions explored here. Similar to the findings for cloud water, the uptake of the OH radical could be parameterized by a single γ value for the conditions applied here (γOH∼ 0.0038). The comparison of the values in Fig. 8a and c to those in Fig. S8a and c reveals that the gas-phase diffusion leads to a significant decrease of γOH by a factor of ∼ 3 in clouds and ∼10 % in aerosol particles.
Several previous studies have determined γOH on surfaces other than pure water that are more comparable to atmospheric aerosol particles. Hanson et al. (1992) showed that γOH increases on acidic solutions from 0.07 (28 % H2SO4) to unity on 96 % H2SO4. On organic surfaces, γOH values are generally higher than on inorganic surfaces which demonstrates the high reactivity of OH with organics in the condensed phase and/or on organic surfaces. In several lab studies, squalane was used as a proxy for long-chain alkanes; the reactive uptake coefficients have been determined in a range of ∼ 0.2 (e.g., Che et al., 2009; Smith et al., 2009; Waring et al., 2011; Houle et al., 2015; Bianchini et al., 2018; Li and Knopf, 2021). A similar value range was also found for a wide variety of other organics (Bertram et al., 2001). In other experimental studies on organic particles, γOH>1 was found (γOH = 1.64 on wet succinic acid, Chan et al., 2014; 1.3 ± 0.4 on bis(2-ethylhexyl) sebacate, George et al., 2007). γOH on organic aerosols may decrease with increasing OH gas-phase concentration because the viscosity of the organic condensed phase prevents efficient uptake and diffusion of OH towards the particle center (Slade and Knopf, 2013; Arangio et al., 2015). Such effects were included in recently developed frameworks to parameterize γOH as a function of particle viscosity, size and gas-phase OH concentration (Renbaum and Smith, 2011; Houle et al., 2015).
We did not explore any of these parameters in detail in our current model study. However, the comparison of the tight range of our γOH values in Fig. 8, independently of FN,Fe and cloud or aerosol aqueous conditions, to the wide ranges of literature values leads us to the following conclusions: (i) the similarity of our γOH value based on an explicit chemical mechanism to that measured on pure water suggests that ∼ 10 ∼ 10−2 may be a good approximation under cloud conditions. (ii) The fact that we cannot reproduce the high γOH values as observed on organic aerosols suggests that organic reactions control the reactive uptake of OH, which are not included in our explicit chemistry scheme. (iii) Since organics are likely present in all aerosol particles, the effect of the iron distribution (FN,Fe) for γOH may be overestimated by our chemical mechanism on ambient aerosol particles.
4.2.3 Reactive uptake coefficient of the hydroxy peroxyl radical,
The values into cloud water are in the range of 0.001–0.004, with higher values at the highest pH (Fig. 8b). In aerosol water, shows a strong dependence on FN,Fe, leading to an overestimate of the reactive uptake by FeBulk by up to 2 orders of magnitude at pH = 3 (Fig. 8d). Note that at FN,Fe = 1 %. no value is shown as under such conditions, HO2 is predicted to evaporate. This evaporation is due to the inefficient chemical HO2 consumption in iron-free particles, whereas efficient uptake occurs into the iron-containing particles. This leads to a great imbalance of the phase transfer rates from and into the two droplet classes as shown in Fig. 2b. We use identical α values for droplet and aqueous particle surfaces. The mass accommodation coefficient α is the upper limit of the maximum value for the uptake coefficient γ. This limit can be seen in Fig. (8d), where approaches the value of = 0.05, i.e., the regime in which the uptake is fully controlled by the mass accommodation and not by the chemical loss in the aqueous phase. For the HO2 radical, gas-phase diffusion may decrease by a factor of ∼ 2 at pH = 6, whereas the two γ values are nearly identical at pH = 3 (Fig. S8b). In aerosol water, gas-phase diffusion has an insignificant impact on its reactive uptake coefficient onto aerosol water (Fig. S8d).
It has been shown in global model studies that the reactive loss of HO2 on aerosol surfaces can significantly impact the atmospheric oxidant budget (e.g., Haggerstone et al., 2005; Macintyre and Evans, 2011; Stadtler et al., 2018; Li et al., 2019). A value of = 0.2 based on the study by Jacob (2000) has been commonly used in global models, which has also been supported by molecular dynamics simulations (Morita et al., 2004). However, recent model studies suggest that this value may be an overestimate and that values on the order of = 0.05 or 0.08 may be more appropriate (Christian et al., 2017; Tan et al., 2020).
On dry aerosol surfaces, is usually low: for example, Bedjanian et al. (2005) measured = 0.075 ± 0.015 on dry soot surfaces, which is comparable to the value of ≤ 0.031 on dust (Matthews et al., 2014) and < 0.01 on dry NaCl (Remorov et al., 2002). increases by more than 1 order of magnitude when RH increases from ∼ 20 % to >90 % (Cooper and Abbatt, 1996; Taketani et al., 2008; Lakey et al., 2015, 2016; Moon et al., 2018). Lakey et al. (2015) showed much higher values on two humic acids ( and , respectively) than on pure long-chain carboxylic acids (). They ascribed the higher HO2 uptake to the small concentrations of copper and iron ions in the humic acids, in agreement with previous studies that showed the large impact of TMIs on HO2 reactive uptake (e.g., Mao et al., 2013, 2017). It was suggested by Lakey et al. (2015) that the HO2 uptake cannot be solely controlled by the TMI concentration as they did not see any correlation with . This lack of trend is similar to findings by Mozurkewich et al. (1987), who also did not find any clear relationship in on Cu-doped NH4HSO4 and LiNO3 particles with Cu concentration.
Based on our model results, the lack of such correlation can be qualitatively understood by simultaneous increase of the main chemical HO2 source and sink rates (Reactions S1 and L4–L6 in Fig. 5f). The absence of a dependence of HO2 uptake on wet particle diameter in the study by Mozurkewich et al. (1987) is also in agreement with our sensitivity studies in which we varied the particle diameter by a factor of ± 2 (Fig. S9). This implies that the interfacial mass transfer is not a limiting step in the HO2 uptake. The HO2 uptake on Cu-doped ammonium sulfate particles was observed to be higher under neutral ( = 0.2) as opposed to acidic conditions ( = 0.05) (Thornton and Abbatt, 2005). Similar results were observed by Mao et al. (2013) who generally found somewhat higher values than in our study () and highest values for the lowest ratios (i.e., highest iron concentration at a constant copper concentration) and highest pH. However, overall their differences in due to the ratio and/or pH are smaller than those that we predict for different FN,Fe (∼ 10−4 10−2, at pH = 3). This suggests that parameterizations that take into account the dependence on Cu concentration, total aerosol mass and particle size (e.g., Guo et al., 2019 and Song et al., 2020) should be further refined to also include the iron distribution.
We note that our results are not quantitatively comparable to those on Cu-doped particles, as our chemical scheme includes only reactions of iron as the only TMI. The corresponding reactions with generally have higher rate constants than those of iron reactions (Ervens et al., 2003; Deguillaume et al., 2004); however, as copper concentrations in ambient aerosols are usually lower than iron concentrations, the effect of both TMIs might be similar. We did not perform the equivalent simulations for copper in the present study as to our knowledge, there are no data available that give single-particle information on the distribution of iron and copper within droplet or particle populations. However, if iron and copper originated from different emission sources, the number concentration of TMI-containing particles might be relatively high. However, in such situations the synergistic effects of Fe and Cu affecting HOx cycling and uptake as suggested by Mao et al. (2013) might be reduced.
Measurements of on ambient aerosol populations showed ranges of 0.13 ≤ 0.34 (Mt. Tai) and 0.09 0.4 (Mt. Mang) (Taketani et al., 2012). No systematic trend with total iron concentration that exceeded 1 µg m−3 at Mt. Mang and 10 µg m−3 at Mt. Tai was observed. The acidity of the aerosols was not reported in that study; however, the derived values did not show any significant trend with the molar NH (SO NO) ratios that ranged from ∼ 1 to ∼ 2 and ∼ 2 to ∼ 3, pointing to moderately acidic to fully neutralized aerosol. The fact that the ambient data do not show any trend with acidity might either point to a high number fraction of TMI-containing particles and/or to a relatively high pH, i.e., to conditions under which our model results do not show a large effect of FN,Fe (Fig. 8d). Two studies of ambient aerosol at urban locations revealed similar average values as compared to the mountain sites, with = 0.23 ± 0.22 in Yokohama, Japan (Zhou et al., 2021), and 0.24 (0.08 ≤ 0.36) in Kyoto, Japan (Zhou et al., 2020). No significant trend in the γ values was observed as a function of aerosol or air mass characteristics (coastal or mainland).
Given the large ranges of values on lab-generated and ambient aerosol, it is difficult to reconcile differences between lab data and observations with our model results. However, our results might provide an explanation for the discrepancies of lab-derived or theoretical values in the range of 0.2–1 to those determined on ambient aerosol (<0.4). We cannot say for sure that these differences indeed stem from different assumptions of iron distribution or other factors affecting . However, our strong predicted decrease of values at low pH and FN,Fe suggests that applying lab-derived on aerosol particles with identical composition might lead to an overestimate of HO2 loss on atmospheric aerosol surfaces, even if all other aerosol properties (size, total iron mass, pH, etc.) are identical.
4.3 ROS budgets and oxidative potential (OP)
The formation and cycling of ROS in the aqueous phase are tightly linked to adverse health effects of particulate matter that are caused by oxidative stress in the respiratory tract and lungs (Stohs and Bagchi, 1995; Tong et al., 2017; Molina et al., 2020; Shahpoury et al., 2021). In addition, the oxidant content of ambient aerosol particles controls their aging timescales and interactions with the biosphere (Pöschl and Shiraiwa, 2015). Tong et al. (2020) found a positive trend of reactive species concentrations with total particle mass and increased OH concentrations as a function of transition metal content and the opposite trend for organic radicals at remote forest and polluted urban locations. Contrarily, Verma et al. (2012) did not find any correlation of the ROS formation potential with metal concentrations. Fang et al. (2016, 2017) suggested that sulfate may trigger metal solubility in highly acidic supermicron particles, which in turn leads to enhanced ROS formation. On a molar basis, quinones and TMIs may be equally efficient in producing ROS (Charrier and Anastasio, 2012; Lyu et al., 2018); however, as TMI concentrations are higher than those of quinones in aerosol water, TMIs are considered major drivers for ROS levels. In the overview study by Saffari et al. (2014) ROS activity was compared at different locations: at nearly all locations, the highest activity was observed in PM2.5 (as opposed to PM10) samples; this trend was explained with the higher fractions and solubilities of iron in particles of these sizes.
Based on such studies, the oxidative potential of atmospheric particulate matter has been related to the presence and number of TMIs in aerosol particles. Our model studies suggest that the total iron amount within an aerosol population may not be a sufficient parameter to constrain the oxidant concentrations within particulate matter in the atmosphere. However, the resulting health impacts of inhaled particles will likely not be largely affected by FN,Fe since upon inhalation, iron will likely dissolve in the lung fluid so that the particle-resolved effects of the iron distribution are diminished. While it may be possible that there are concentration gradients within the lung fluid due to dissolution and/or mixing kinetics, such effects cannot be quantified to date.
Generally all conclusions for oxidant budgets in aerosol water also apply to those in cloud water. However, the largest concentration differences for extreme values of FN,Fe are less than an order of magnitude (Sect. 3.1). Several model studies have explored the sources and production rates of OH in cloud water using chemical mechanisms of different complexities (e.g., Ervens et al., 2003; Deguillaume et al., 2004; Tilgner et al., 2013; Bianco et al., 2015). Our analysis shows that the chemical source and loss rates might be underestimated in bulk cloud water. While the overall oxidant content of the cloud water might not be significantly affected (“bulk aqueous-phase concentrations” in Figs. 2 and 6), the large differences of OH concentrations of about an order of magnitude in iron-containing and iron-free droplets may lead to very different oxidation rates of organics. Higher OH concentrations in the aqueous phase may also lead to more efficient formation of organics acids (aqSOA; Ervens et al., 2011, 2014). Generally, the highest OH concentrations in cloud water are predicted under clean (marine, remote) conditions (Herrmann et al., 2000; Tilgner et al., 2013). Our results suggest that the difference in OH concentrations might be even greater between low and high pH as we find the largest impact by FN,Fe for high pH. Even though in clean air masses, total iron concentrations might be lower, such trends might be robust as we do not find a strong dependence of the predicted OH concentrations on mFe. Given the close connections of OH and HO2 O, any conclusions for the OH concentrations in cloud water can be similarly drawn also for HO2 O. In contrast, the less reactive and more soluble H2O2 is not affected by the iron distribution.
The role of transition metal ion (TMI) reactions for impacting oxidant levels (OH, HO2, H2O2) in the atmospheric aqueous phase has been recognized for a long time. However, in atmospheric multiphase chemistry models, it usually assumed that all aerosol particles and droplets contain TMIs, and thus TMI-catalyzed reactions occur in all droplets. Single-particle analyses have shown that only a small number fraction of particles contain iron, which implies the same for cloud droplets that are formed on such particles.
Using a box model with a well-established chemical multiphase mechanism, we explored the importance of iron distribution across (i) aqueous aerosol particle or (ii) cloud droplet populations. We performed box model studies in which a constant iron concentration (10 ng m−3; in sensitivity studies also 50 ng m−3) is distributed to a number fraction FN,Fe of aerosol particles or droplets from 1 % to 100 % (“FeN<100” and “FeBulk” approaches, respectively).
We find that H2O2 concentrations in cloud water are not affected by FN,Fe. Its main source and loss processes include the recombination of HO2 and the reaction with S(IV), respectively. Since the loss process is slower than the uptake from the gas phase and the production in the aqueous phase, H2O2 is in thermodynamic equilibrium between the gas phase and all droplets. The same conclusions are drawn for H2O2 partitioning into aerosol water if the same Henry's law constant is applied ( = 1.02 × 105 M atm−1). However, since H2O2 has been found to partition more efficiently into aerosol water than into pure water, applying a higher effective Henry's law constant ( = 2.7 × 108 M atm−1) results in an overestimate of the H2O2 concentrations. These differences are largest at pH = 6, whereas the differences are negligible at pH = 3 or 4.5. The opposite trends are found for the OH radical, whose aqueous-phase concentration in cloud water might be overestimated by up to a factor of 5 using the FeBulk approach at pH = 6, whereas there might be an over- or underestimate by nearly an order of magnitude in aerosol water, depending on the choice of .
The concentrations of OH and HO2 radicals are closely linked. Generally we find that the HO2 O concentrations in the aqueous phase are underestimated by the FeBulk approach, again with the largest discrepancies at pH = 6 for FN,Fe = 1 % or 100 %. This trend can be explained by the increase of the effective Henry's law constant of HO2 at high pH ( = 1.5 × 105 M atm−1) and the higher rate constants of the O radical anion as compared to the corresponding reactions of the HO2 radical. The higher partitioning together with the quicker consumption of HO2 O at high pH leads to its subsaturation in the aqueous phase at high pH. This effect is strongest at low FN,Fe because the few iron-containing droplets (particles) are highly concentrated in iron. The reaction of Fe(III) ions or hydroxy complexes with HO2 O is the main sink of HO2 O in both the cloud and aerosol aqueous phases. At the same time it is also the main reduction pathway of Fe(III) to Fe(II). Since the HO2 O concentration in iron-containing droplets is up to 1 order of magnitude lower in the FeBulk approach, the Fe(III) reduction is less efficient. Our results are largely independent of the total iron mass concentration as both the chemical HO2 O sources and sinks are dependent on iron. Based on these results, we conclude that the Fe(II) Fe(total) ratio in cloud and aerosol water might be lower than implied by bulk samples. This finding has implications for the interpretation of modeled and measured Fe(II) Fe(total) (or Fe(II) Fe(III)) ratios that are often considered a measure of iron solubility and bioavailability. Our study demonstrates that multiphase chemistry models might not be able to properly predict OH and HO2 concentrations in the aqueous phase of cloud or aqueous particles, which might translate into biases in the predicted oxidation rates (e.g., aqSOA formation). While not explored in detail in the current study, further implications of iron distribution in cloud droplets might include differences in sulfate formation rates by metal-catalyzed processes.
The reactive uptake of OH and HO2 is often parameterized by γ. We derived γ values into cloud and aerosol water from our model studies. The values of γOH are not largely affected by the iron distribution and show values of γOH∼0.0023 for clouds and γOH∼ 0.038 for aerosol water. However, (aerosol) can be significantly reduced at low FN,Fe as compared to bulk samples, showing difference of up to 2 orders of magnitude at pH = 3 ( ∼ 0.03 for FN,Fe = 100 % and 0.0001 for FN,Fe = 2 %). This analysis demonstrates that γ values that are measured in lab studies using internally mixed aerosol particles might be too high as compared to those ambient aerosol populations. In addition to another factors that affect on various aerosol surfaces (chemical composition, particle size, water content, etc.), our results suggest that the iron distribution across particle populations can also add to the large variability of and to the mismatch of observed and modeled HO2 loss if lab-derived data are used. Similar considerations can also be applied to the interpretation of ROS formation and oxidative potential of aerosol particles. As ambient aerosol particles likely comprise external mixtures in terms of iron, neither results based on bulk sampling nor on modeling will correctly represent the oxidant budgets in ambient particulate matter.
Our study is to the best of our knowledge the first explicit chemical multiphase model study that systematically explores the role of iron distribution across individual aqueous aerosol particles or cloud droplets for the concentrations and uptake rates of reactive oxygen species. There are only few data available on the iron distribution in aerosol populations from single-particle analyses that may be used to constrain the number fraction of iron-containing particles and droplets. While we restricted our model studies to iron, similar conclusions may also be drawn for other transition metal ions, such as copper or manganese. We identified various potential implications of this parameter for, e.g., (i) oxidant budgets and particle mass formation (aqSOA, sulfate) in clouds and aerosols, (ii) reactive radical (OH, HO2) uptake onto aerosols, and (iii) oxidative potentials of aerosol particles, which should be further explored by experimental and model studies.
The model output is available at https://doi.org/10.5281/zenodo.5829360 (Ervens, 2022).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-22-1989-2022-supplement.
BE designed and led the study. AK performed the model studies. AK and BE wrote the manuscript. MZ contributed to the discussion of the results.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Chemistry and Physics. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Daniel Murphy (NOAA/ESRL) for useful discussions and for sharing data of single-particle measurements. We area also grateful to the two anonymous referees, whose comments have helped to improve the paper.
This research has been supported by the French National Research Agency (ANR) (grant no. ANR-17-MPGA-0013).
This paper was edited by John Liggio and reviewed by two anonymous referees.
Al-Abadleh, H. A.: Review of the bulk and surface chemistry of iron in atmospherically relevant systems containing humic-like substances, RSC Adv., 5, 45785–45811, https://doi.org/10.1039/C5RA03132J, 2015. a
Alexander, B., Park, R. J., Jacob, D. J., and Gong, S.: Transition metal-catalyzed oxidation of atmospheric sulfur: Global implications for the sulfur budget, J. Geophys. Res.-Atmos., 114, D02309, https://doi.org/10.1029/2008jd010486, 2009. a
Arangio, A. M., Slade, J. H., Berkemeier, T., Pöschl, U., Knopf, D. A., and Shiraiwa, M.: Multiphase Chemical Kinetics of OH Radical Uptake by Molecular Organic Markers of Biomass Burning Aerosols: Humidity and Temperature Dependence, Surface Reaction, and Bulk Diffusion, J. Phys. Chem. A, 119, 4533–4544, https://doi.org/10.1021/jp510489z, 2015. a
Arangio, A. M., Tong, H., Socorro, J., Pöschl, U., and Shiraiwa, M.: Quantification of environmentally persistent free radicals and reactive oxygen species in atmospheric aerosol particles, Atmos. Chem. Phys., 16, 13105–13119, https://doi.org/10.5194/acp-16-13105-2016, 2016. a
Barth, M. C., Ervens, B., Herrmann, H., Tilgner, A., McNeill, V. F., Tsui, W. G., Deguillaume, L., Chaumerliac, N., Carlton, A. G., and Lance, S.: Box Model Intercomparison of Cloud Chemistry, J. Geophys. Res.-Atmos., 126, e2021JD035486, https://doi.org/10.1029/2021JD035486, 2021. a, b
Bedjanian, Y., Lelièvre, S., and Le Bras, G.: Experimental study of the interaction of HO2 radicals with soot surface, Phys. Chem. Chem. Phys., 7, 334–341, https://doi.org/10.1039/B414217A, 2005. a
Bertram, A. K., Ivanov, A. V., Hunter, M., Molina, L. T., and Molina, M. J.: The reaction probability of OH on Organic Surfaces of Tropospheric Interest, J. Phys. Chem. A, 105, 9415–9421, https://doi.org/10.1021/jp0114034, 2001. a
Bianchini, R. H., Tesa-Serrate, M. A., Costen, M. L., and McKendrick, K. G.: Collision-Energy Dependence of the Uptake of Hydroxyl Radicals at Atmospherically Relevant Liquid Surfaces, J. Phys. Chem. C, 122, 6648–6660, https://doi.org/10.1021/acs.jpcc.7b12574, 2018. a
Bianco, A., Passananti, M., Perroux, H., Voyard, G., Mouchel-Vallon, C., Chaumerliac, N., Mailhot, G., Deguillaume, L., and Brigante, M.: A better understanding of hydroxyl radical photochemical sources in cloud waters collected at the puy de Dôme station – experimental versus modelled formation rates, Atmos. Chem. Phys., 15, 9191–9202, https://doi.org/10.5194/acp-15-9191-2015, 2015. a
Chan, M. N., Zhang, H., Goldstein, A. H., and Wilson, K. R.: Role of Water and Phase in the Heterogeneous Oxidation of Solid and Aqueous Succinic Acid Aerosol by Hydroxyl Radicals, J. Phys. Chem. C, 118, 28978–28992, https://doi.org/10.1021/jp5012022, 2014. a
Chang, J. S., Brost, R. A., Isaksen, I. S. A., Madronich, S., Middleton, P., Stockwell, W. R., and Walcek, C. J.: A three-dimensional Eulerian acid deposition model: Physical concepts and formulation, J. Geophys. Res.-Atmos., 92, 14681–14700, https://doi.org/10.1029/JD092iD12p14681, 1987. a
Charrier, J. G. and Anastasio, C.: On dithiothreitol (DTT) as a measure of oxidative potential for ambient particles: evidence for the importance of soluble transition metals, Atmos. Chem. Phys., 12, 9321–9333, https://doi.org/10.5194/acp-12-9321-2012, 2012. a
Charrier, J. G., Richards-Henderson, N. K., Bein, K. J., McFall, A. S., Wexler, A. S., and Anastasio, C.: Oxidant production from source-oriented particulate matter – Part 1: Oxidative potential using the dithiothreitol (DTT) assay, Atmos. Chem. Phys., 15, 2327–2340, https://doi.org/10.5194/acp-15-2327-2015, 2015. a
Che, D. L., Smith, J. D., Leone, S. R., Ahmed, M., and Wilson, K. R.: Quantifying the reactive uptake of OH by organic aerosols in a continuous flow stirred tank reactor, Phys. Chem. Chem. Phys., 11, 7885–7895, https://doi.org/10.1039/B904418C, 2009. a
Choël, M., Deboudt, K., Flament, P., Aimoz, L., and Mériaux, X.: Single-particle analysis of atmospheric aerosols at Cape Gris-Nez, English Channel: Influence of steel works on iron apportionment, Atmos. Environ., 41, 2820–2830, https://doi.org/10.1016/j.atmosenv.2006.11.038, 2007. a
Christian, K. E., Brune, W. H., and Mao, J.: Global sensitivity analysis of the GEOS-Chem chemical transport model: ozone and hydrogen oxides during ARCTAS (2008), Atmos. Chem. Phys., 17, 3769–3784, https://doi.org/10.5194/acp-17-3769-2017, 2017. a
Cini, R., Prodi, F., Santachiara, G., Porcu, F., Bellandi, S., Stortini, A., Oppo, C., Udisti, R., and Pantani, F.: Chemical characterization of cloud episodes at a ridge site in Tuscan Appennines, Italy, Atmos. Res., 61, 311–334, https://doi.org/10.1016/S0169-8095(01)00139-9, 2002. a
Cooper, P. L. and Abbatt, J. P. D.: Heterogeneous Interactions of OH and HO2 Radicals with Surfaces Characteristic of Atmospheric Particulate Matter, J. Phys. Chem., 100, 2249–2254, https://doi.org/10.1021/jp952142z, 1996. a
Deguillaume, L., Leriche, M., Monod, A., and Chaumerliac, N.: The role of transition metal ions on HOx radicals in clouds: a numerical evaluation of its impact on multiphase chemistry, Atmos. Chem. Phys., 4, 95–110, https://doi.org/10.5194/acp-4-95-2004, 2004. a, b, c, d, e
Deguillaume, L., Leriche, M., Desboeufs, K., Mailhot, G., George, C., and Chaumerliac, N.: Transition metals in atmospheric liquid particles: Sources, reactivity and sensitive parameters, Chem. Rev., 105, 3388–3431, https://doi.org/10.1021/cr040649c, 2005. a, b, c, d, e
Ervens, B.: Modeling the Processing of Aerosol and Trace Gases in Clouds and Fogs, Chem. Rev., 115, 4157–4198, https://doi.org/10.1021/cr5005887, 2015. a, b, c
Ervens, B.: Model output, Khaled et al., Iron distribution in the aqueous phase, Zenodo [data set], https://doi.org/10.5281/zenodo.5829360, 2022. a
Ervens, B., George, C., Williams, J. E., Buxton, G. V., Salmon, G. A., Bydder, M., Wilkinson, F., Dentener, F., Mirabel, P., Wolke, R., and Herrmann, H.: CAPRAM2.4 (MODAC mechanism): An extended and condensed tropospheric aqueous phase mechanism and its application, J. Geophys. Res., 108, 4426, https://doi.org/10.1029/2002JD002202, 2003. a, b, c, d, e
Ervens, B., Carlton, A. G., Turpin, B. J., Altieri, K. E., Kreidenweis, S. M., and Feingold, G.: Secondary organic aerosol yields from cloud-processing of isoprene oxidation products, Geophys. Res. Lett., 35, L02816, https://doi.org/10.1029/2007gl031828, 2008. a
Ervens, B., Turpin, B. J., and Weber, R. J.: Secondary organic aerosol formation in cloud droplets and aqueous particles (aqSOA): a review of laboratory, field and model studies, Atmos. Chem. Phys., 11, 11069–11102, https://doi.org/10.5194/acp-11-11069-2011, 2011. a
Ervens, B., Sorooshian, A., Lim, Y. B., and Turpin, B. J.: Key parameters controlling OH-initiated formation of secondary organic aerosol in the aqueous phase (aqSOA), J. Geophys. Res.-Atmos., 119, 3997–4016, https://doi.org/10.1002/2013JD021021, 2014. a, b
Fang, T., Verma, V., Bates, J. T., Abrams, J., Klein, M., Strickland, M. J., Sarnat, S. E., Chang, H. H., Mulholland, J. A., Tolbert, P. E., Russell, A. G., and Weber, R. J.: Oxidative potential of ambient water-soluble PM2.5 in the southeastern United States: contrasts in sources and health associations between ascorbic acid (AA) and dithiothreitol (DTT) assays, Atmos. Chem. Phys., 16, 3865–3879, https://doi.org/10.5194/acp-16-3865-2016, 2016. a
Fang, T., Guo, H., Zeng, L., Verma, V., Nenes, A., and Weber, R. J.: Highly Acidic Ambient Particles, Soluble Metals, and Oxidative Potential: A Link between Sulfate and Aerosol Toxicity, Environ. Sci. Technol., 51, 2611–2620, https://doi.org/10.1021/acs.est.6b06151, 2017. a
Fomba, K. W., van Pinxteren, D., Müller, K., Iinuma, Y., Lee, T., Collett Jr., J. L., and Herrmann, H.: Trace metal characterization of aerosol particles and cloud water during HCCT 2010, Atmos. Chem. Phys., 15, 8751–8765, https://doi.org/10.5194/acp-15-8751-2015, 2015. a, b
Furutani, H., Jung, J., Miura, K., Takami, A., Kato, S., Kajii, Y., and Uematsu, M.: Single-particle chemical characterization and source apportionment of iron-containing atmospheric aerosols in Asian outflow, J. Geophys. Res.-Atmos., 116, D18204, https://doi.org/10.1029/2011jd015867, 2011. a
George, I. J., Vlasenko, A., Slowik, J. G., Broekhuizen, K., and Abbatt, J. P. D.: Heterogeneous oxidation of saturated organic aerosols by hydroxyl radicals: uptake kinetics, condensed-phase products, and particle size change, Atmos. Chem. Phys., 7, 4187–4201, https://doi.org/10.5194/acp-7-4187-2007, 2007. a
Guo, J., Wang, Z., Wang, T., and Zhang, X.: Theoretical evaluation of different factors affecting the HO2 uptake coefficient driven by aqueous-phase first-order loss reaction, Sci. Total Environ., 683, 146–153, https://doi.org/10.1016/j.scitotenv.2019.05.237, 2019. a
Haggerstone, A.-L., Carpenter, L. J., N., C., and McFiggans, G.: Improved model predictions of HO2 with gas to particle mass transfer rates calculated using aerosol number size distributions, J. Geophys. Res., 110, , D04303, https://doi.org/10.1029/2004JD005282, 2005. a
Hanson, D. R., Burkholder, J. B., Howard, C. J., and Ravishankara, A. R.: Measurement of hydroxyl and hydroperoxy radical uptake coefficients on water and sulfuric acid surfaces, J. Phys. Chem., 96, 4979–4985, https://doi.org/10.1021/j100191a046, 1992. a, b
Hasson, A. S. and Paulson, S. E.: An investigation of the relationship between gas-phase and aerosol borne hydroperoxides in urban air, J. Aerosol Sci., 34, 459–468, https://doi.org/10.1016/S0021-8502(03)00002-8, 2003. a, b
Herrmann, H., Ervens, B., Jacobi, H.-W., Wolke, R., Nowacki, P., and Zellner, R.: CAPRAM2.3: A Chemical Aqueous Phase Radical Mechanism for Tropospheric Chemistry, J. Atmos. Chem., 36, 231–284, 2000. a
Houle, F. A., Hinsberg, W. D., and Wilson, K. R.: Oxidation of a model alkane aerosol by OH radical: the emergent nature of reactive uptake, Phys. Chem. Chem. Phys., 17, 4412–4423, https://doi.org/10.1039/C4CP05093B, 2015. a, b
Ingall, E. D., Feng, Y., Longo, A. F., Lai, B., Shelley, R. U., Landing, W. M., Morton, P. L., Nenes, A., Mihalopoulos, N., Violaki, K., Gao, Y., Sahai, S., and Castorina, E.: Enhanced Iron Solubility at Low pH in Global Aerosols, Atmosphere, 9, 201, https://doi.org/10.3390/atmos9050201, 2018. a, b, c
Jacob, D. J.: Heterogeneous chemistry and tropospheric ozone, Atmos. Environ., 34, 2131–2159, https://doi.org/10.1016/S1352-2310(99)00462-8, 2000. a, b
Khaled, A., Zhang, M., Amato, P., Delort, A.-M., and Ervens, B.: Biodegradation by bacteria in clouds: an underestimated sink for some organics in the atmospheric multiphase system, Atmos. Chem. Phys., 21, 3123–3141, https://doi.org/10.5194/acp-21-3123-2021, 2021. a
Lakey, P. S. J., George, I. J., Whalley, L. K., Baeza-Romero, M. T., and Heard, D. E.: Measurements of the HO2 Uptake Coefficients onto Single Component Organic Aerosols, Environ. Sci. Technol., 49, 4878–4885, https://doi.org/10.1021/acs.est.5b00948, 2015. a, b, c
Lakey, P. S. J., Berkemeier, T., Krapf, M., Dommen, J., Steimer, S. S., Whalley, L. K., Ingham, T., Baeza-Romero, M. T., Pöschl, U., Shiraiwa, M., Ammann, M., and Heard, D. E.: The effect of viscosity and diffusion on the HO2 uptake by sucrose and secondary organic aerosol particles, Atmos. Chem. Phys., 16, 13035–13047, https://doi.org/10.5194/acp-16-13035-2016, 2016. a
Li, J. and Knopf, D. A.: Representation of Multiphase OH Oxidation of Amorphous Organic Aerosol for Tropospheric Conditions, Environ. Sci. Technol., 55, 7266–7275, https://doi.org/10.1021/acs.est.0c07668, 2021. a
Li, K., Jacob, D. J., Liao, H., Shen, L., Zhang, Q., and Bates, K. H.: Anthropogenic drivers of 2013–2017 trends in summer surface ozone in China, P. Natl. Acad. Sci. USA, 116, 422–427, https://doi.org/10.1073/pnas.1812168116, 2019. a
Luo, C., Mahowald, N. M., Meskhidze, N., Chen, Y., Siefert, R. L., Baker, A. R., and Johansen, A. M.: Estimation of iron solubility from observations and a global aerosol model, J. Geophys. Res.-Atmos., 110, D23307, https://doi.org/10.1029/2005JD006059, 2005. a, b
Lyu, Y., Guo, H., Cheng, T., and Li, X.: Particle Size Distributions of Oxidative Potential of Lung-Deposited Particles: Assessing Contributions from Quinones and Water-Soluble Metals, Environ. Sci. Technol., 52, 6592–6600, https://doi.org/10.1021/acs.est.7b06686, 2018. a
Macintyre, H. L. and Evans, M. J.: Parameterisation and impact of aerosol uptake of HO2 on a global tropospheric model, Atmos. Chem. Phys., 11, 10965–10974, https://doi.org/10.5194/acp-11-10965-2011, 2011. a
Madronich, S. and Calvert, J. G.: The NCAR Master Mechanism of the Gas Phase Chemistry – Version 2.0, Tech. Rep., No. NCAR/TN-333+STR, University Corporation for Atmospheric Research, https://doi.org/10.5065/D6HD7SKH, 1989. a
Mao, J., Fan, S., Jacob, D. J., and Travis, K. R.: Radical loss in the atmosphere from Cu-Fe redox coupling in aerosols, Atmos. Chem. Phys., 13, 509–519, https://doi.org/10.5194/acp-13-509-2013, 2013. a, b, c, d
Mao, J., Fan, S., and Horowitz, L. W.: Soluble Fe in Aerosols Sustained by Gaseous HO2 Uptake, Environ. Sci. Technol. Lett., 4, 98–104, https://doi.org/10.1021/acs.estlett.7b00017, 2017. a, b, c
Matthews, P. S. J., Baeza-Romero, M. T., Whalley, L. K., and Heard, D. E.: Uptake of HO2 radicals onto Arizona test dust particles using an aerosol flow tube, Atmos. Chem. Phys., 14, 7397–7408, https://doi.org/10.5194/acp-14-7397-2014, 2014. a
Moffet, R. C., Furutani, H., Rödel, T. C., Henn, T. R., Sprau, P. O., Laskin, A., Uematsu, M., and Gilles, M. K.: Iron speciation and mixing in single aerosol particles from the Asian continental outflow, J. Geophys. Res.-Atmos., 117, D07204, https://doi.org/10.1029/2011JD016746, 2012. a
Molina, C., Toro A., R., Manzano, C. A., Canepari, S., Massimi, L., and Leiva-Guzmán, M. A.: Airborne Aerosols and Human Health: Leapfrogging from Mass Concentration to Oxidative Potential, Atmosphere, 11, 917, https://doi.org/10.3390/atmos11090917, 2020. a, b
Moon, D. R., Taverna, G. S., Anduix-Canto, C., Ingham, T., Chipperfield, M. P., Seakins, P. W., Baeza-Romero, M.-T., and Heard, D. E.: Heterogeneous reaction of HO2 with airborne TiO2 particles and its implication for climate change mitigation strategies, Atmos. Chem. Phys., 18, 327–338, https://doi.org/10.5194/acp-18-327-2018, 2018. a
Morita, A., Kanaya, Y., and Francisco, J. S.: Uptake of the HO2 radical by water: Molecular dynamics calculations and their implications for atmospheric modeling, J. Geophys. Res.-Atmos., 109, D09201, https://doi.org/10.1029/2003jd004240, 2004. a
Mozurkewich, M., H, M. P., Gupta, A., and Calvert, J. G.: Mass Accommodation Coefficient for HO2 Radicals on Aqueous Particles, J. Geophys. Res., 92, 4163–4170, 1987. a, b
Myriokefalitakis, S., Ito, A., Kanakidou, M., Nenes, A., Krol, M. C., Mahowald, N. M., Scanza, R. A., Hamilton, D. S., Johnson, M. S., Meskhidze, N., Kok, J. F., Guieu, C., Baker, A. R., Jickells, T. D., Sarin, M. M., Bikkina, S., Shelley, R., Bowie, A., Perron, M. M. G., and Duce, R. A.: Reviews and syntheses: the GESAMP atmospheric iron deposition model intercomparison study, Biogeosciences, 15, 6659–6684, https://doi.org/10.5194/bg-15-6659-2018, 2018. a
Nathanson, G. M., Davidovits, P., Worsnop, D. R., and Kolb, C. E.: Dynamics and Kinetics at the Gas-Liquid Interface, J. Phys. Chem., 100, 13007–13020, https://doi.org/10.1021/jp953548e, 1996. a, b
Pöschl, U. and Shiraiwa, M.: Multiphase Chemistry at the Atmosphere–Biosphere Interface Influencing Climate and Public Health in the Anthropocene, Chem. Rev., 115, 4440–4475, https://doi.org/10.1021/cr500487s, 2015. a
Pöschl, U., Rudich, Y., and Ammann, M.: Kinetic model framework for aerosol and cloud surface chemistry and gas-particle interactions – Part 1: General equations, parameters, and terminology, Atmos. Chem. Phys., 7, 5989–6023, https://doi.org/10.5194/acp-7-5989-2007, 2007. a
Remorov, R. G., Gershenzon, Y. M., Molina, L. T., and Molina, M. J.: Kinetics and Mechanism of HO2 Uptake on Solid NaCl, J. Phys. Chem. A, 106, 4558–4565, https://doi.org/10.1021/jp013179o, 2002. a
Renbaum, L. H. and Smith, G. D.: Artifacts in measuring aerosol uptake kinetics: the roles of time, concentration and adsorption, Atmos. Chem. Phys., 11, 6881–6893, https://doi.org/10.5194/acp-11-6881-2011, 2011. a
Roeselová, M., Jungwirth, P., Tobias, D. J., and Gerber, R. B.: Impact, Trapping, and Accommodation of Hydroxyl Radical and Ozone at Aqueous Salt Aerosol Surfaces, A Molecular Dynamics Study, J. Phys. Chem. B, 107, 12690–12699, https://doi.org/10.1021/jp030592i, 2003. a
Saffari, A., Daher, N., Shafer, M. M., Schauer, J. J., and Sioutas, C.: Global Perspective on the Oxidative Potential of Airborne Particulate Matter: A Synthesis of Research Findings, Environ. Sci. Technol., 48, 7576–7583, https://doi.org/10.1021/es500937x, 2014. a, b
Schwartz, S. E.: Mass-Transport Considerations Pertinent to Aqueous Phase Reactions of Gases in Liquid-Water Clouds, in: Chemistry of Multiphase Atmospheric Systems of Multiphase Atmospheric Systems, edited by: Jaeschke, W., NATO ASI Series, Series G: Ecological Sciences, Berlin, Heidelberg, Springer, 415–471, https://doi.org/10.1007/978-3-642-70627-1_16, 1986. a
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Physics, John Wiley & Sons, New York, ISBN 13 9780471178163, 1998. a, b
Shahpoury, P., Zhang, Z. W., Arangio, A., Celo, V., Dabek-Zlotorzynska, E., Harner, T., and Nenes, A.: The influence of chemical composition, aerosol acidity, and metal dissolution on the oxidative potential of fine particulate matter and redox potential of the lung lining fluid, Environ. Int., 148, 106343, https://doi.org/10.1016/j.envint.2020.106343, 2021. a
Slade, J. H. and Knopf, D. A.: Heterogeneous OH oxidation of biomass burning organic aerosol surrogate compounds: assessment of volatilisation products and the role of OH concentration on the reactive uptake kinetics, Phys. Chem. Chem. Phys., 15, 5898–5915, https://doi.org/10.1039/C3CP44695F, 2013. a
Smith, J. D., Kroll, J. H., Cappa, C. D., Che, D. L., Liu, C. L., Ahmed, M., Leone, S. R., Worsnop, D. R., and Wilson, K. R.: The heterogeneous reaction of hydroxyl radicals with sub-micron squalane particles: a model system for understanding the oxidative aging of ambient aerosols, Atmos. Chem. Phys., 9, 3209–3222, https://doi.org/10.5194/acp-9-3209-2009, 2009. a
Song, H., Chen, X., Lu, K., Zou, Q., Tan, Z., Fuchs, H., Wiedensohler, A., Moon, D. R., Heard, D. E., Baeza-Romero, M.-T., Zheng, M., Wahner, A., Kiendler-Scharr, A., and Zhang, Y.: Influence of aerosol copper on HO2 uptake: a novel parameterized equation, Atmos. Chem. Phys., 20, 15835–15850, https://doi.org/10.5194/acp-20-15835-2020, 2020. a
Stadtler, S., Simpson, D., Schröder, S., Taraborrelli, D., Bott, A., and Schultz, M.: Ozone impacts of gas–aerosol uptake in global chemistry transport models, Atmos. Chem. Phys., 18, 3147–3171, https://doi.org/10.5194/acp-18-3147-2018, 2018. a
Stohs, S. J. and Bagchi, D.: Oxidative mechanisms in the toxicity of metal ions, Free Radical Bio. Med., 18, 321–336, https://doi.org/10.1016/0891-5849(94)00159-h, 1995. a
Takahama, S., Gilardoni, S., and Russell, L. M.: Single-particle oxidation state and morphology of atmospheric iron aerosols, J. Geophys. Res.-Atmos., 113, D22202, https://doi.org/10.1029/2008JD009810, 2008. a, b
Taketani, F., Kanaya, Y., and Akimoto, H.: Kinetics of Heterogeneous Reactions of HO2 Radical at Ambient Concentration Levels with (NH4)2SO4 and NaCl Aerosol Particles, J. Phys. Chem. A, 112, 2370–2377, https://doi.org/10.1021/jp0769936, 2008. a
Taketani, F., Kanaya, Y., Pochanart, P., Liu, Y., Li, J., Okuzawa, K., Kawamura, K., Wang, Z., and Akimoto, H.: Measurement of overall uptake coefficients for HO2 radicals by aerosol particles sampled from ambient air at Mts. Tai and Mang (China), Atmos. Chem. Phys., 12, 11907–11916, https://doi.org/10.5194/acp-12-11907-2012, 2012. a
Tan, Z., Hofzumahaus, A., Lu, K., Brown, S. S., Holland, F., Huey, L. G., Kiendler-Scharr, A., Li, X., Liu, X., Ma, N., Min, K.-E., Rohrer, F., Shao, M., Wahner, A., Wang, Y., Wiedensohler, A., Wu, Y., Wu, Z., Zeng, L., Zhang, Y., and Fuchs, H.: No Evidence for a Significant Impact of Heterogeneous Chemistry on Radical Concentrations in the North China Plain in Summer 2014, Environ. Sci. Technol., 54, 5973–5979, https://doi.org/10.1021/acs.est.0c00525, 2020. a
Thornton, J. and Abbatt, J. P. D.: Measurements of HO2 uptake to aqueous aerosol: Mass accommodation coefficients and net reactive loss, J. Geophys. Res., 100, D08309, https://doi.org/10.1029/2004JD005402, 2005. a, b
Tilgner, A., Bräuer, P., Wolke, R., and Herrmann, H.: Modelling multiphase chemistry in deliquescent aerosols and clouds using CAPRAM3.0i, J. Atmos. Chem., 70, 221–256, https://doi.org/10.1007/s10874-013-9267-4, 2013. a, b, c, d, e
Tong, H., Arangio, A. M., Lakey, P. S. J., Berkemeier, T., Liu, F., Kampf, C. J., Brune, W. H., Pöschl, U., and Shiraiwa, M.: Hydroxyl radicals from secondary organic aerosol decomposition in water, Atmos. Chem. Phys., 16, 1761–1771, https://doi.org/10.5194/acp-16-1761-2016, 2016. a
Tong, H., Lakey, P. S. J., Arangio, A. M., Socorro, J., Kampf, C. J., Berkemeier, T., Brune, W. H., Pöschl, U., and Shiraiwa, M.: Reactive oxygen species formed in aqueous mixtures of secondary organic aerosols and mineral dust influencing cloud chemistry and public health in the Anthropocene, Faraday Discuss., 200, 251–270, https://doi.org/10.1039/C7FD00023E, 2017. a, b, c
Tong, H., Liu, F., Filippi, A., Wilson, J., Arangio, A. M., Zhang, Y., Yue, S., Lelieveld, S., Shen, F., Keskinen, H.-M. K., Li, J., Chen, H., Zhang, T., Hoffmann, T., Fu, P., Brune, W. H., Petäjä, T., Kulmala, M., Yao, M., Berkemeier, T., Shiraiwa, M., and Pöschl, U.: Aqueous-phase reactive species formed by fine particulate matter from remote forests and polluted urban air, Atmos. Chem. Phys., 21, 10439–10455, https://doi.org/10.5194/acp-21-10439-2021, 2021. a
Verma, V., Rico-Martinez, R., Kotra, N., King, L., Liu, J., Snell, T. W., and Weber, R. J.: Contribution of Water-Soluble and Insoluble Components and Their Hydrophobic/Hydrophilic Subfractions to the Reactive Oxygen Species-Generating Potential of Fine Ambient Aerosols, Environ. Sci. Technol., 46, 11384–11392, https://doi.org/10.1021/es302484r, 2012. a
Wang, R., Balkanski, Y., Boucher, O., Bopp, L., Chappell, A., Ciais, P., Hauglustaine, D., Peñuelas, J., and Tao, S.: Sources, transport and deposition of iron in the global atmosphere, Atmos. Chem. Phys., 15, 6247–6270, https://doi.org/10.5194/acp-15-6247-2015, 2015. a
Waring, C., King, K. L., Bagot, P. A. J., Costen, M. L., and McKendrick, K. G.: Collision dynamics and reactive uptake of OH radicals at liquid surfaces of atmospheric interest, Phys. Chem. Chem. Phys., 13, 8457–8469, https://doi.org/10.1039/C0CP02734K, 2011. a
Wei, J., Fang, T., Wong, C., Lakey, P. S. J., Nizkorodov, S. A., and Shiraiwa, M.: Superoxide Formation from Aqueous Reactions of Biogenic Secondary Organic Aerosols, Environ. Sci. Technol., 55, 260–270, https://doi.org/10.1021/acs.est.0c07789, 2021. a
Xuan, X., Chen, Z., Gong, Y., Shen, H., and Chen, S.: Partitioning of hydrogen peroxide in gas-liquid and gas-aerosol phases, Atmos. Chem. Phys., 20, 5513–5526, https://doi.org/10.5194/acp-20-5513-2020, 2020. a
Zhang, G., Bi, X., Lou, S., Li, L., Wang, H., Wang, X., Zhou, Z., Sheng, G., Fu, J., and Chen, C.: Source and mixing state of iron-containing particles in Shanghai by individual particle analysis, Chemosphere, 95, 9–16, https://doi.org/10.1016/j.chemosphere.2013.04.046, 2014. a
Zhou, J., Murano, K., Kohno, N., Sakamoto, Y., and Kajii, Y.: Real-time quantification of the total HO2 reactivity of ambient air and HO2 uptake kinetics onto ambient aerosols in Kyoto (Japan), Atmos. Environ., 223, 117189, https://doi.org/10.1016/j.atmosenv.2019.117189, 2020. a
Zhou, J., Sato, K., Bai, Y., Fukusaki, Y., Kousa, Y., Ramasamy, S., Takami, A., Yoshino, A., Nakayama, T., Sadanaga, Y., Nakashima, Y., Li, J., Murano, K., Kohno, N., Sakamoto, Y., and Kajii, Y.: Kinetics and impacting factors of HO2 uptake onto submicron atmospheric aerosols during the 2019 Air QUAlity Study (AQUAS) in Yokohama, Japan , Atmos. Chem. Phys., 21, 12243–12260, https://doi.org/10.5194/acp-21-12243-2021, 2021. a