The number fraction of iron-containing particles affects OH, HO₂ and H₂O₂ budgets in the atmospheric aqueous phase

Reactive oxygen species (ROS), such as OH, HO₂ and H₂O₂, affect the oxidation capacity of the atmosphere and cause adverse health effects of particulate matter. The role of transition metal ions (TMIs) in impacting the ROS concentrations and conversions in the atmospheric aqueous phase has been recognized for a long time. Model studies usually assume that the total TMI mass as measured in bulk aerosol or cloud water samples is distributed equally across all particles or droplets. This assumption is contrary to single-particle measurements that have shown that only a small number fraction of particles contain iron and other TMIs ($F_{\mathrm{N},\mathrm{Fe}}<\mathrm{100}$ %), which implies that also not all cloud droplets contain TMIs. In the current study, we apply a box model with an explicit multiphase chemical mechanism to simulate ROS formation and cycling in aqueous aerosol particles and cloud droplets. Model simulations are performed for the range of 1 % ≤ F_N,Fe ≤ 100 % for constant pH values of 3, 4.5 and 6 and constant total iron mass concentration (10 or 50 ng per cubic meter of air). Model results are compared for two sets of simulations with $F_{\mathrm{N},\mathrm{Fe}}<\mathrm{100}$ % (FeN<100) and 100 % (FeBulk). We find the largest differences between model results in OH and HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations at pH = 6. Under these conditions, HO₂ is subsaturated in the aqueous phase because of its high effective Henry's law constant and the fast chemical loss reactions of the O${}_{\mathrm{2}}^{-}$ radical anion. As the main reduction process of Fe(III) is its reaction with HO₂ $/$ O${}_{\mathrm{2}}^{-}$, we show that the HO₂ subsaturation leads to Fe(II) $/$ Fe(total) ratios for $F_{\mathrm{N},\mathrm{Fe}}<\mathrm{100}$ % that are lower by a factor of ≤ 2 as compared to bulk model approaches. This trend is largely independent of the total iron concentration, as both chemical source and sink rates of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ scale with the iron concentration. We compare model-derived reactive uptake parameters γ_OH and ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ for the full range of F_N,Fe. While γ_OH is not affected by the iron distribution, the calculated ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ values range from 0.0004 to 0.03 for F_N,Fe = 1 % and 100 %, respectively. Implications of these findings are discussed for the application of lab-derived ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ in models to present reactive HO₂ uptake on aerosols. We conclude that the iron distribution (F_N,Fe) should be taken into account to estimate the ROS concentrations and oxidation potential of particulate matter that might be overestimated by bulk sampling and model approaches. Our study suggests that the number concentration of iron-containing particles F_N,Fe may be more important than the total iron mass concentration in determining ROS budgets and uptake rates in cloud and aerosol water.

1 Introduction

The main oxidants in the atmospheric aqueous phases of cloud and aerosol particles include the hydroxyl radical (OH) and hydrogen peroxide (H₂O₂), whose concentration levels are closely linked to the hydroperoxy radical (HO₂ $/$ O${}_{\mathrm{2}}^{-}$). The concentrations of these reactive oxygen species (ROS) are influenced by various redox reactions of transition metal ions (TMIs). Iron is the most abundant TMI in aerosol particles and cloud water. Its main sources include dust and coal combustion (Moffet et al., 2012) and biomass burning (Wang et al., 2015). Its concentration in cloud water ranges from nano- to micromolar levels (Cini et al., 2002; Deguillaume et al., 2005). Iron mass concentrations in aerosol samples reach from less than 1 ng m⁻³ to more than 100 ng m⁻³ (Schmücke, Germany) and sometimes up to several hundred nanograms per cubic meter (ng m⁻³) at other continental locations (Fomba et al., 2015, and references therein).

The role of transition metal ions in affecting the ROS concentration levels and redox reactions in clouds and particles has been explored in many model, lab and field studies, e.g., Deguillaume et al. (2004), Deguillaume et al. (2005) and Mao et al. (2013). Reactions of iron and other TMIs (e.g., copper) in the atmosphere have also been linked to the oxidative potential of particulate matter, causing oxidative stress in the respiratory tract and lungs (Saffari et al., 2014; Arangio et al., 2016; Tong et al., 2016; Molina et al., 2020; Wei et al., 2021). In particular, the oxidation of iron(II) by hydrogen peroxide (Fenton reaction) has been identified as one of the main chemical sources of the OH radical in cloud water (Ervens et al., 2003; Deguillaume et al., 2004; Tilgner et al., 2013), aqueous-phase aerosol particles (Al-Abadleh, 2015) and lung fluid (Charrier et al., 2015).

TMI concentrations in the cloud and aerosol phases are usually reported based on bulk measurements representing the total TMI mass per aqueous- or gas-phase volume. However, single-particle analyses have shown that iron is only present in a small number fraction of particles: Furutani et al. (2011) found that up to 15 % of particles in the diameter range between 0.5 and 1 µm contain iron. Similar number fractions (<1 %–15 %) were observed in Shanghai, where air masses were also affected by dust storms or biomass and coal burning (Zhang et al., 2014). A similar size range for iron-containing particles but smaller average number fraction (∼ 4 %) was found above the English Channel in air masses affected by steel works (Choël et al., 2007). As particles in this size range commonly act as cloud condensation nuclei (CCN), these analyses suggest that not all cloud droplets contain iron and that also the measured iron mass concentration in aerosol populations is not equally distributed among all particles. Drop-size-resolved cloud water measurements at a continental background site have shown that iron and copper are present in the same drop size range, whereas manganese is more abundant in larger droplets (Fomba et al., 2015). This may suggest that CCN were comprised of internal mixtures of iron and copper, whereas manganese-containing particles were externally mixed and of different hygroscopicity and/or different sizes.

The oxidation state of iron affects its solubility and thus its bioavailability and biogeochemical cycles in the atmosphere and oceans. Generally, ferrous salts are more soluble than ferric salts, with increasing solubility under acidic conditions, e.g., Ingall et al. (2018). Results from a global model study revealed large differences in predicted and observed iron solubility; observed Fe(II) $/$ Fe(total) ratios were on average between ∼ 1 % and ∼ 10 %, with larger variability in coarse than in fine particles (Luo et al., 2005). The Fe(II) fractions in particle samples above oceans have been shown to be above 30 %–75 % (Ingall et al., 2018). Measurement of the Fe(II) $/$ Fe(total) ratio on a single-particle basis revealed ratios of ≤ 20 % for particles from various sources (Takahama et al., 2008). In cloud water, Fe(II) often dominates the total iron concentration, in particular during daytime, when iron(III) hydroxy and organo complexes are reduced by photolysis processes (Deguillaume et al., 2005).

Multiphase chemistry models are usually initialized with bulk concentrations of iron to make predictions on the role of aqueous-phase chemistry in ROS levels (e.g., Ervens et al., 2003; Tilgner et al., 2013; Tong et al., 2017), sulfate formation (e.g., Alexander et al., 2009; Chang et al., 1987) or iron deposition (Myriokefalitakis et al., 2018). In a previous model study, we have demonstrated that such bulk approaches may not be appropriate for highly reactive compounds as redistribution and diffusion processes among droplets of chemical composition might lead to nonlinear effects impacting concentration levels (Khaled et al., 2021). While that study was focused on the biodegradation of organics by bacteria, which are only present in a small number fraction of cloud droplets, we apply the same idea in the present study to the ROS cycling, dependent on the number fraction of iron-containing particles.

We perform box model simulations with a detailed gas- and aqueous-phase chemical mechanism, in which a constant iron mass concentration m_Fe (nanograms per cubic meter of air) is distributed to a fraction of (i) cloud droplets or (ii) aqueous aerosol particles. We investigate the conditions in terms of pH, iron distribution and total iron mass, under which the number fraction of iron-containing particles significantly affects the concentration levels and phase transfer of OH, HO₂ and H₂O₂ in the atmospheric multiphase system. We discuss the potential implications of these effects for the interpretation of measurements and model studies of the iron oxidation state, radical uptake rates onto aqueous aerosol particles and ROS budgets and oxidative potentials of aerosol and cloud water.

2 Multiphase box model

2.1 Model description

We use a box model with detailed gas- and aqueous-phase chemical mechanisms. The gas-phase chemical mechanism with 58 reactions is based on the NCAR Master Chemical Mechanism (Madronich and Calvert, 1989). The aqueous-phase chemical mechanism includes 43 reactions (Ervens et al., 2008; Tong et al., 2017) (Tables S1–S3 in the Supplement). Phase transfer processes for 14 species are described kinetically based on the resistance model (Schwartz, 1986; Nathanson et al., 1996) (Table S4). The model uses the standard equations for multiphase processes (Seinfeld and Pandis, 1998):

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}{C}_{\mathrm{aq}}}{\mathrm{d}t}}=\underset{\text{phase transfer rate}}{\underbrace{k_{\mathrm{mt}}\mathrm{LWC}\left(C_{\mathrm{g}}-{\displaystyle \frac{C_{\mathrm{aq}}}{\mathrm{LWC}{K}_{\mathrm{H}\left(\mathrm{eff}\right)}RT}}\right)}}+\underset{\text{chem rate}}{\underbrace{S_{\mathrm{aq}}-L_{\mathrm{aq}}}}\text{(2)}& {\displaystyle \frac{\mathrm{d}{C}_{\mathrm{g}}}{\mathrm{d}t}}=-\underset{\text{phase transfer rate}}{\underbrace{k_{\mathrm{mt}}\mathrm{LWC}\left(C_{\mathrm{g}}-{\displaystyle \frac{C_{\mathrm{aq}}}{\mathrm{LWC}{K}_{\mathrm{H}\left(\mathrm{eff}\right)}RT}}\right)}}+\underset{\text{chem rate}}{\underbrace{S_{\mathrm{g}}-L_{\mathrm{g}}}},\end{array}$$

where both the gas-phase (C_g) and aqueous-phase (C_aq) concentrations are expressed in units of moles per gram of air, LWC is the liquid water content (vol $/$ vol), K_H(eff) is the (effective) Henry's law constant, and S_aq, S_g and L_aq, L_g are the chemical source and loss rates in the aqueous and gas phases (moles per gram of air per second). R and T are the constant for ideal gases (0.082058 L atm (K mol)⁻¹) and absolute temperature (K). The mass transfer coefficient k_mt (s⁻¹) is defined as

$$\begin{array}{}\text{(3)}& k_{\mathrm{mt}}={\left({\displaystyle \frac{r_{\mathrm{d}}^{\mathrm{2}}}{\mathrm{3}{D}_{\mathrm{g}}}}+{\displaystyle \frac{r_{\mathrm{d}}}{\mathrm{3}\mathit{\alpha }}}\sqrt{{\displaystyle \frac{\mathrm{2}\mathit{\pi }{M}_{\mathrm{g}}}{RT}}}\right)}^{-\mathrm{1}},\end{array}$$

where r_d is the drop radius, D_g the gas-phase diffusion coefficient, α the mass accommodation coefficient, and M_g the molecular weight. The mass transfer coefficient k_mt takes into account gas-phase diffusion and the mass accommodation, i.e., the probability that a molecule that hits the droplet (or particle) surface is taken up. It is the inverse of the characteristic time for these two resistances. Its full derivation can be found in the literature, e.g., by Nathanson et al. (1996), and is therefore not repeated here. In our model studies, it is assumed that all solutes are homogeneously mixed and no concentration gradients exist between the gas–aqueous interface and the bulk of the aqueous phase. This assumption is justified if chemical loss processes in the aqueous phase are comparatively slow, so that aqueous-phase diffusion can evenly distribute the species throughout the aqueous volume. The competition between aqueous-phase diffusion and chemical loss in the aqueous phase is commonly quantified by the dimensionless diffuso-reactive parameter q (Eq. S.1 in the Supplement, Seinfeld and Pandis, 1998). This parameter does not take into account chemical sources within the aqueous phase. As discussed in a previous study, the Fenton reaction can act as a such a source for the OH radical in aqueous solution (Ervens et al., 2014). A detailed comparison and discussion of the parameter q and the role of aqueous-phase diffusion can be found in the Supplement (Sect. S2).

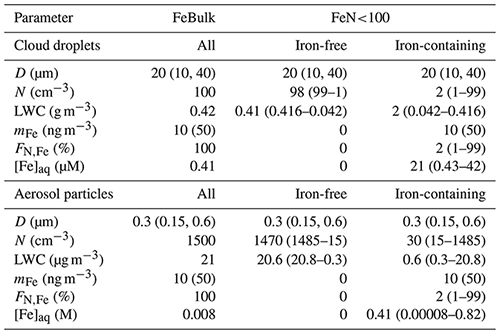
The box model considers monodisperse cloud droplet or wet aerosol particle populations with constant diameters (D) of 20 µm for cloud droplets and 300 nm for aqueous aerosol particles, respectively. The simulations are run at constant temperature (285.6 K), pressure (9.21 × 10⁴ Pa) and air density (1.31 × 10⁻³ g cm⁻³).

2.2 Model simulations

The schematic of the model setup together with the main ROS formation and conversion processes are shown in Fig. 1. Results of two model approaches will be compared:

• FeBulk. All droplets (particles) have the same chemical composition. The iron concentration is identical in all droplets (particles). The fraction of iron-containing droplets (particles) is F_N,Fe = 100 %.

• FeN<100. A subset of the number concentration (N) of droplets (or particles) is initialized with iron, whereas the remainder of the droplets (particles) is iron-free. In the base case simulations, we assume that the number fraction of iron-containing droplets (particles) is $F_{\mathrm{N},\mathrm{Fe}}=\mathrm{2}$ %; F_N,Fe is varied from 1 %–99 % in sensitivity studies (Sect. 3.3).

We assume an iron mass concentration (m_Fe = 10 ng per cubic meter of air). (Some sensitivity studies for m_Fe = 50 ng per cubic meter of air are discussed.) Therefore, in the FeN<100 approach, the aqueous-phase iron concentration [M] is higher in the iron-containing droplets (particles) than in the FeBulk approach as the iron mass is distributed to fewer droplets (particles). Simulations are performed for constant values of pH = 3, 4.5 and 6. All model parameters are summarized in Table 1. Gas-phase species are initialized with the values in Table S5 and are not replenished throughout the simulations. Chemical and phase transfer rates are analyzed after a simulation time of 400 s. This timescale refers approximately to the lifetime of a single cloud droplet. It can be estimated based on updraft and downdraft velocities a cloud droplet experiences and on cloud thickness (e.g., average vertical velocity of 0.5 m s⁻¹ throughout cloud that is 100 m thick, as typical values for shallow stratocumulus clouds). To demonstrate that our results and conclusions do not strongly depend on the choice of the timescale, we compare the main source and loss processes of the three species at t = 400 and t = 2000 s (Sect. 3.2). During even longer timescales, the concentrations may change in the box model; however, this may not be realistic since highly reactive gases are quickly depleted (e.g., SO₂), whereas in the real atmosphere, emissions might replenish them.

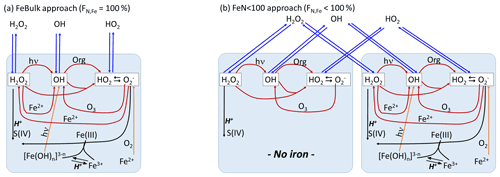
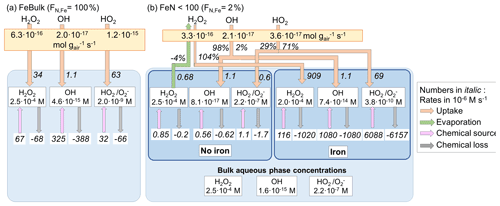
Figure 1 Model schematic. (a) FeBulk: the total iron mass concentration (m_Fe = 10 ng m⁻³) is equally distributed among all droplets or particles (F_N,Fe = 100 %). (b) FeN<100: the same iron mass concentration is distributed among a subset of droplets or particles (base case: F_N,Fe = 2 %). Major ROS processes are phase transfer (blue), ROS net production (orange), ROS conversions (red) and ROS loss (black). Model parameters are summarized in Table 1.

Table 1 Model parameters for multiphase simulations for cloud droplet and aerosol populations. D is the diameter, N the number concentration, LWC the liquid water content, m_Fe the total iron mass concentration, F_N,Fe the number concentration of droplets or particles that contain iron and [Fe]_aq the aqueous-phase concentration of iron. Numbers in parentheses denote values or parameter ranges of sensitivity studies.

3 Model results and discussion

3.1 Aqueous-phase concentrations and rates

3.1.1 Cloud droplets

Figure 2 summarizes the ROS concentrations and the chemical and phase transfer rates for the cloud case at pH = 4.5; the corresponding figures for simulations at pH = 3 and 6 are shown in Fig. S1 (Supplement). The net transfer rates (moles per gram of air per second) into the aqueous phase are shown in the yellow boxes. For FeN<100, the relative contributions (%) of this rate into the iron-free and iron-containing droplets are shown next to the arrows. The phase transfer rates are additionally shown in units of moles per liter per second (using the air density of 1.13 × 10⁻³ g cm⁻³ and LWCs in Table 1), together with the chemical source and loss rates in the aqueous phase (M s⁻¹) and the corresponding aqueous-phase ROS concentrations (M) (white boxes). If the effect of iron is negligible on aqueous-phase concentrations and aqueous-phase rates, there should be no concentration difference between any droplets, neither between the results for FeBulk and FeN<100 nor between the iron-free and iron-containing droplets. In addition, the ratio of the phase transfer rates should also be equal to the ratio of the LWCs of the two drop classes (98 % : 2 %).

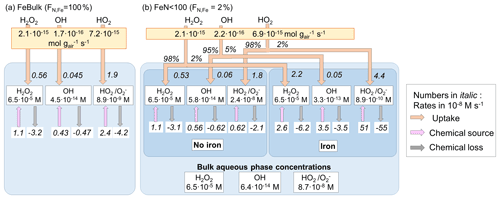
Figure 2 Multiphase scheme for cloud water showing the phase transfer and chemical source and loss rates in the aqueous phase, m_Fe = 10 ng m⁻³, pH = 4.5. (a) FeBulk approach. (b) FeN<100 approach with a fraction of iron-containing droplets of F_N,Fe = 2 %. Numbers below the species names are aqueous-phase concentrations (M), and chemical and phase transfer rates are shown in moles per liter per second. Net phase transfer rates near the top of the figure are expressed in gas-phase units (moles per gram of air per second); the relative contributions (%) into the iron-free and iron-containing droplets are shown next to the arrows. The bulk concentrations at the bottom of panel (b) represent the bulk concentrations weighted by the contributions of the two droplet classes to total LWC (98 % : 2 %).

All ROS are predicted to be taken up into cloud water, independently of the iron distribution at pH = 4.5 (Fig. 2), and also their ratio of the phase transfer rates nearly corresponds to the ratio of the LWCs of the two droplet classes (98 % : 2 %). Significant deviations from this theoretical value occur at pH = 3 for HO₂ (Fig. S1b) and at pH = 6 for H₂O₂ that is predicted to evaporate from iron-free droplets (Fig. S1d).

The H₂O₂ concentrations in all droplets under all conditions and pH values (Fig. S1) correspond to the equilibrium concentrations according to Henry's law, in agreement with previous studies that have shown that H₂O₂ is at thermodynamic equilibrium in cloud water (Ervens, 2015). At pH = 3 and 4.5, the efficient H₂O₂ consumption is compensated by a relatively higher uptake rate, resulting in the efficient replenishment of H₂O₂ and equilibrium concentration. The uptake rates (in M s⁻¹) between FeBulk and the iron-free droplets in the FeN<100 approach are similar (e.g., for H₂O₂ : 0.56 and 0.53 M s⁻¹), whereas they are higher for uptake into the iron-containing droplets (2.2 M s⁻¹). Since these droplets only comprise 2 % of the total LWC, this difference is not reflected in the net uptake rate. At pH = 6 (Fig. S1c and d), the majority of cloud droplets are predicted to be a source of H₂O₂; the only exception is the iron-containing droplets in the FeN<100 approach, from which H₂O₂ evaporates due to less efficient chemical H₂O₂ consumption in the aqueous phase.

The OH concentrations differ by nearly 1 order of magnitude between the iron-free and iron-containing cloud droplets (5.8 × 10⁻¹⁴ M vs. 3.3 × 10⁻¹³ M; Fig. 2b); the concentration in the FeBulk model is even slightly lower (4.5 × 10⁻¹⁴ M; Fig. 2a). The reasons for these differences are explored in Sect. 3.2, where the individual chemical processes affecting the concentrations are analyzed.

The bulk aqueous-phase OH concentration in the FeBulk approach is approximately 50 % higher (4.5 × 10⁻¹⁴ M) as compared to 6.4 × 10⁻¹⁴ M for FeN<100 (Fig. 2). A much greater discrepancy of nearly 1 order of magnitude between the two approaches is predicted at pH = 6, whereas the difference in the bulk concentrations at pH = 3 is smaller (Fig. S1). These concentrations corresponded to those in bulk cloud water samples from cloud droplet populations with F_N,Fe = 2 %, provided that chemical processes in the sample upon sampling do not change the ROS levels (Sect. 3.3). For all cases, the chemical source and loss rates of the OH radical compensate for each other, leading to a relatively small uptake rate of the moderately soluble OH radical into the aqueous phase (∼ 10⁻¹⁶ mol g⁻¹ s⁻¹), which is not significantly affected by F_N,Fe.

The concentration difference of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ between iron-free and iron-containing droplets is nearly 2 orders of magnitude (2.4 × 10⁻⁸ M vs. 8.9 × 10⁻¹⁰ M), whereas the concentration for FeBulk is predicted to be between these two values (8.9 × 10⁻⁹ M) (Fig. 2). The difference in the concentrations is even greater (factor > 200) at pH = 6 (Fig. S1d), whereas it is less than a factor of 3 at pH = 3. These trends suggest that the concentrations are dependent on pH (Sect. 3.2). The comparison of the bulk aqueous-phase HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations resulting from the FeN<100 approach (bottom of Figs. 2b, S2b and d) to those in FeBulk shows that at pH = 4.5 and 6, the total HO₂ $/$ O${}_{\mathrm{2}}^{-}$ is underestimated by about 1 order of magnitude. At pH = 3, the chemical loss rate of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ in iron-containing droplets is relatively larger than its chemical source rate (74 × 10⁻⁸ M s⁻¹ vs. 66 × 10⁻⁸ M s⁻¹; Fig. S1b). This imbalance in the chemical rates leads to a very efficient HO₂ uptake into iron-containing droplets. Consequently, the phase transfer into these droplets comprises 13 % of the total uptake rate, whereas at higher pH values the contributions correspond to the ratio of LWCs between the two droplet classes (98 % : 2 %). The higher Henry's law constant of HO₂ and rate constants of O${}_{\mathrm{2}}^{-}$ reactions as compared to those of HO₂ at higher pH lead to increasingly lower HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations with increasing pH.

3.1.2 Aqueous aerosol particles

Since the LWC of the aqueous aerosol particles is smaller by a factor of 2 × 10⁵ than in clouds, the aqueous-phase iron concentration is accordingly higher, and so are all chemical rates of iron reactions. Similar to cloud water, the H₂O₂ concentration is neither significantly affected by the iron distribution nor by iron reactions; i.e., at a given pH value its aqueous-phase concentration is nearly the same in all particles. At pH = 4.5 and 6, evaporation of H₂O₂ is predicted for FeBulk and from the iron-free particles in FeN<100 (Figs. 3b and S2b and d). However, since the uptake rate of H₂O₂ into the iron-containing droplets is much higher, exceeding the evaporation rate by a factor of 25 (−4 % vs. 104 %, pH = 4.5) and ∼ 2 (−143 % vs. 243 % at pH = 6), aqueous particles represent a net sink of H₂O₂.

Figure 3 Same as Fig. 2 but for the aerosol case (model parameters in Table 1).

Similar to the cloud case, the OH concentrations in the aqueous phase of FeBulk are between those in the iron-free and iron-containing particles for FeN<100. The OH concentrations do not show a strong pH dependence, but their bulk values are about a factor of 3 lower for the FeN<100 approach (F_N,Fe = 2 %) than for the FeBulk approach (1.6 × 10⁻¹⁵ M vs. ∼ 4.6 × 10⁻¹⁵ M). Even at the high iron concentrations as present in aerosol water (≤ 0.41 M), the chemical source and loss rates of OH nearly cancel out, leading to a relatively small uptake rate.

The HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations in the FeBulk approach are comparable to those as predicted for cloud water at the same pH value. However, the concentrations in the iron-free and iron-containing particles differ by 4 orders of magnitude at pH = 6 (1.5 × 10⁻⁶ and 1.3 × 10⁻¹⁰ M, Fig. S2d). The resulting bulk aqueous-phase concentrations are at least 1 order of magnitude underestimated by FeBulk (pH = 3); this difference is even a factor of 2000 at pH = 6 (Figs. 3d and S2d). While the chemical loss rate of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ is nearly equal to or even larger than its source rate at pH = 4.5 and 6, at pH = 3 the source rate exceeds the loss rate resulting in evaporation of HO₂ from the 2 % iron-containing particles (Fig. S2b). However, since the uptake rate into the iron-containing particles is larger than this evaporation rate, the net flux of HO₂ is an uptake into the particle phase.

3.1.3 Gas-phase concentrations (OH, HO₂) and mixing ratios (H₂O₂)

The gas-phase concentrations of OH and HO₂ and mixing ratios of H₂O₂ are shown in Fig. S3 as a function of time (t≤7200 s) in the presence of cloud droplets and aerosol particles, respectively, at the three pH values considered here and for the two assumed iron distributions in the aqueous phase. The H₂O₂ mixing ratio in the presence of cloud water is very quickly reduced to about 50 % of its initial concentration (1 ppb) due to partitioning to the aqueous phase. Both the pH value and F_N,Fe have a small effect on the H₂O₂ mixing ratio. The small increase of H₂O₂ over time is in agreement with findings in a recent multiphase box model intercomparison (Barth et al., 2021).

The OH concentrations are on the order of 10⁶ cm⁻³, i.e., typical concentrations as found for continental daytime conditions. These concentrations build up within a few seconds and do not largely change over the time period considered here. The difference of up to a factor of 5 in the OH concentrations in the presence of cloud droplets with a pH value of 3 and 6, respectively, cannot be directly explained by any OH reactions in the aqueous phase but is rather a consequence of the OH–HO₂ cycle in the multiphase system (Fig. 1). At pH = 6, the effective Henry's law constant for HO₂ is highest, and therefore, most HO₂ is partitioned to the aqueous phase, resulting in the lowest fractions of HO₂ in the gas phase. The gas-phase HO₂ concentrations are on the order of 10⁸ cm⁻³, in agreement with predictions from other atmospheric multiphase chemistry models (e.g., Barth et al., 2021). Generally, the pH value and iron distributions cause smaller differences in the presence of aerosol particles as compared to the cloud case, since the liquid water content of particles is smaller by several orders of magnitude, and therefore a smaller fraction of the species is dissolved.

3.1.4 Partitioning coefficient ϵ

The partitioning coefficient ϵ is often used to describe the distribution of species between the aqueous and gas phases in the atmospheric multiphase system, e.g., Ervens (2015). It is defined as

$$\begin{array}{}\text{(4)}& \mathit{ϵ}={\displaystyle \frac{C_{\mathrm{aq}}}{p_{\mathrm{g}}\cdot K_{\mathrm{H}\left(\mathrm{eff}\right)}}},\end{array}$$

with C_aq and p_g being the aqueous-phase concentration (M) and gas-phase partial pressure (atm) and K_H(eff) the (effective) Henry's law constant (M atm⁻¹). Accordingly, ϵ<1 indicates situations when the aqueous phase is subsaturated.

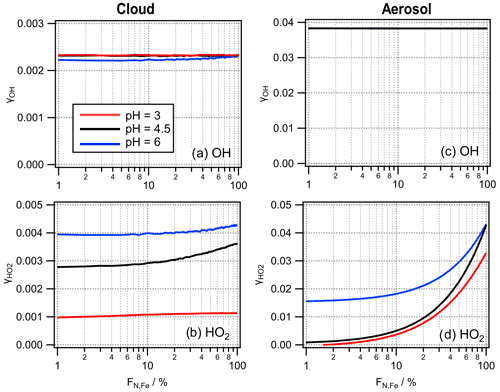
The ϵ values for the three ROS are summarized in Fig. 4 for the cloud and aerosol simulations at three pH values. The fact that ${\mathit{ϵ}}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ is ∼ 1 shows that H₂O₂ is in thermodynamic equilibrium and explains why its concentrations do not differ among iron-containing and iron-free droplets (particles) (Figs. 2, 3 and S2).

The ϵ_OH values in the presence of cloud droplets (red symbols, Fig. 4b) are on the order of ∼ 0.01–0.1. The values for iron-containing aerosol particles show a distinct trend with highest ϵ_OH values in iron-containing particles, whereas ϵ_OH in iron-free particles is lower by 2 and 3 orders of magnitude, respectively. The lack of a clear trend in ϵ_OH with pH suggests that the main formation and loss processes of OH are pH-independent. The differences in ϵ_OH scale with the OH concentrations in aerosol particles that differ by 3 orders of magnitude between iron-containing and iron-free particles in the FeN<100 approach and the concentration in the FeBulk case (Fig. 3). The ϵ_OH values in cloud water do not exhibit such strong differences, which is also reflected in the more similar concentrations in all droplets (Fig. 2).

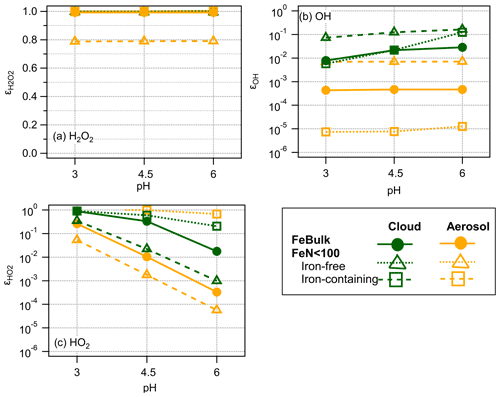
Figure 4 Partitioning coefficients ϵ for (a) H₂O₂, (b) OH and (c) HO₂ for pH = 3 , 4.5 and 6 for FeBulk (filled symbols) and FeN<100 in 98 % iron-free (squares) and 2 % iron-containing droplets (triangles). Results are shown for simulations of cloud droplets (green) and aerosol particles (orange) at three pH values (3, 4.5 and 6); lines are added to guide the eye.

The difference between the concentration in iron-free and iron-containing particles is up to 3 orders of magnitude (pH = 3, Fig. S2b), which is also reflected in the same difference in ϵ (Fig. 4b).

For the HO₂ radical, iron reactions cause a significant deviation from thermodynamic equilibrium at high pH, resulting in decreasing ${\mathit{ϵ}}_{{\mathrm{HO}}_{\mathrm{2}}}$ with increasing pH. At high pH, HO₂ is more efficiently consumed due to the higher rate constants of the O${}_{\mathrm{2}}^{-}$ radical anion as compared to those with the undissociated HO₂ radical. Unlike for OH, for which the smallest ϵ is seen in iron-free particles, the lowest ${\mathit{ϵ}}_{{\mathrm{HO}}_{\mathrm{2}}}$ is found for iron-containing particles – which shows that the concentration differences due to iron distribution for OH and HO₂ have different reasons: whereas iron leads to efficient OH formation, it causes significant HO₂ $/$ O${}_{\mathrm{2}}^{-}$ loss.

3.2 Relative contributions of chemical reactions and phase transfer to ROS source and loss rates in the aqueous phase

To understand the trends in concentrations, reaction rates and partitioning coefficients with F_N,Fe and pH as discussed in the previous section, Fig. 5 summarizes the main chemical pathways for the three ROS for the cloud and aerosol cases for the same conditions as in Figs. 2 and 3. The individual chemical source (S) and loss (L) processes are indicated between the figure panels for the cloud (top part of figure) and aerosol (bottom part) cases. Only chemical processes are listed that contribute to more than 1 % to the total rate in each simulation. As the phase transfer (PT) can be a source (i.e., uptake) or loss (i.e., evaporation) process for the aqueous-phase species, its contribution is placed between the chemical sources and losses. The total source and loss rates (mol g⁻¹ s⁻¹) are indicated in the boxes in the upper right of each panel.

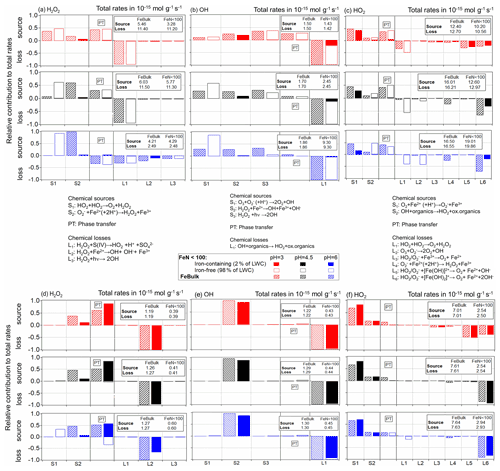
Figure 5 Relative contributions of chemical and phase transfer rates to the total sources and losses of the three ROS. The total rates (moles per gram of air per second) are shown in boxes in the upper right of each panel. For the FeN<100 approach, the contributions in iron-free and iron-containing droplets (particles) are displayed as open and dashed bars and those for the FeBulk approach as solid filled bars. Simulations were performed at constant pH values of pH = 3 (red), 4.5 (black) and 6 (blue) for cloud conditions (a) H₂O₂, (b) OH and (c) HO₂ and aerosol conditions (d) H₂O₂, (e) OH and (f) HO₂. The chemical aqueous-phase source (S) and loss (L) reactions are listed between the panels.

Given its high Henry's law constant ($K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ = 1.02 × 10⁵ M atm⁻¹), the H₂O₂ uptake contributes nearly 50 % to the total H₂O₂ source at pH ≤ 4.5 in cloud water (Fig. 5a) and even more in aerosol water (50 %–80 %) (Fig. 5d). However, the uptake occurs mostly (98 %) into iron-free cloud droplets, whereas in the aerosol case, most H₂O₂ is taken up by the iron-containing particles. This trend was already shown in the comparison of Figs. 2b and 3b. The main loss of H₂O₂ in cloud water is the pH-dependent reaction with sulfur(IV) (L1 in Fig. 5a), whose rate decreases with increasing pH (R4 in Table S1). Therefore, the chemical loss of H₂O₂ in cloud water is very inefficient at pH = 6 (2.4 × 10⁻¹⁵ mol g⁻¹ s⁻¹ at pH = 6 vs. ∼ 11 × 10⁻¹⁵ mol g⁻¹ s⁻¹ at pH ≤ 4.5; Fig. 5a). The rate of the recombination of H₂O₂ (S1 in Fig. 5a) increases with pH since the reaction of HO₂ and O${}_{\mathrm{2}}^{-}$ is much faster than with undissociated HO₂ (100 × k_R5 ∼ k_R6; Table S1). Therefore, more H₂O₂ is formed at pH = 6 than at lower pH, leading to H₂O₂ evaporation from cloud droplets at pH = 6. Figure 5 represents a snapshot of the rates after a simulation time of 400 s. We have chosen this relatively short time, since gases are not replenished during the box model simulations as no emissions are considered. At longer timescales (after 2000 s), the conclusions would not be drastically different (Fig. S4); the only major difference is the loss of H₂O₂ by sulfur(IV) (L1 in Fig. S4a) as SO₂ is consumed quickly within the first few minutes.

In aerosol water, the Fenton reaction (L2, Fig. 5a, d) is the main loss reaction of H₂O₂. The main H₂O₂ source process is the reaction of Fe²⁺ with O${}_{\mathrm{2}}^{-}$ (S2), whose rate increases with increasing pH value. Since in iron-free particles, the chemical loss rate (L1) decreases with pH, but its source rate (S1) increases, H₂O₂ evaporates from iron-free particles. In iron-containing particles, both the main source and sink reactions are directly dependent on the Fe²⁺ concentration (S2, L2). As the iron concentration in the iron-containing particles is ∼ 50 times higher for FeN<100 than for FeBulk, it seems surprising at first that the chemical rates do not scale by this factor. Furthermore, the HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentration is much higher in iron-free than in iron-containing particles, in particular at pH = 6. Also this trend, thus, cannot explain the lower chemical H₂O₂ source rates of S2. Therefore, only a difference in the Fe²⁺ concentration can explain the differences in the chemical rates of the chemical H₂O₂ sources and sinks (Sect. 4.1).

Independently of the iron distribution, the relative importance of the uptake of the OH radical into aerosol particles' cloud water decreases with increasing pH, from ∼ 30 % at pH = 3 to <10 % at pH = 6 (Fig. 5b). As the rate of the O${}_{\mathrm{2}}^{-}$ reaction with ozone (S1) increases with pH, the relative importance of this reaction increases with increasing pH value. The loss of OH in the aqueous phase is due to reactions with organic compounds; the rate of L1 in Fig. 5b and e represents the sum of all reaction rates of OH with organics in Table S1. As the rate constants of OH reactions with carboxylates are generally higher than those with their corresponding acids, the chemical loss rate in cloud water increases with pH. The most striking difference in the source and loss patterns of OH between cloud and aerosol water is the dominating role of the Fenton reaction (S2) as OH source in aerosol water. It contributes nearly 100 % of the sources at all pH values, making the OH uptake as a source negligible. Similar to the trends as described above for H₂O₂, the chemical rates of the Fenton reaction as OH source (S2) are much smaller in FeN<100 than for FeBulk, which can again be explained by the lower Fe(II) concentration at low F_N,Fe. As the uptake rate of OH is fairly low as compared to its chemical rates due to its low Henry's law constant (K_H,OH = 25 M atm⁻¹; Table S4), the chemical source rate is nearly fully compensated for by the chemical loss rate that under all pH and LWC conditions results in (nearly) identical values.

The only major sources of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ are the reactions of Fe²⁺ with molecular oxygen (S1) and the OH reactions with organics (S2) (Fig. 5c and f). The slight increase in the overall reaction rate of S2 with pH explains the highest chemical source rate in all droplets at the highest pH. Its main loss reactions are the reactions of Fe(III) (free Fe³⁺ and the hydroxy complexes [Fe(OH)_n]³ⁿ⁻¹ with n = 1, 2). The dominance of these processes for the loss of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ leads to very efficient uptake into iron-containing droplets. The rate constants of these loss reactions with O${}_{\mathrm{2}}^{-}$ are about 3 orders of magnitude higher than those with HO₂ (R27, R28 and R35–R38 in Table S1). This results in the subsaturation of HO₂ in the aqueous phase, i.e., decreasing ${\mathit{ϵ}}_{{\mathrm{HO}}_{\mathrm{2}}}$ with increasing pH (Fig. 4c). This effect is more pronounced in aerosol water than in cloud water because of the higher total Fe concentration in particles. The highly efficient loss of O${}_{\mathrm{2}}^{-}$ at high pH results in the lowest HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations in the iron-containing droplets at pH = 6 (Fig. S2d). Since the reactions of Fe(III) with HO₂ $/$ O${}_{\mathrm{2}}^{-}$ are the main reduction processes of Fe(III), the lower HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentration leads to inefficient Fe(III) to Fe(II) conversion and relatively higher Fe(III) concentrations (Sect. 4.1).

3.3 Aqueous-phase concentrations as a function of F_N,Fe

3.3.1 Comparison of bulk aqueous-phase concentrations

The values of F_N,Fe = 2 % and 100 % likely represent extreme values for the iron distribution in cloud droplet or particle populations. Depending on abundance and proximity of iron emissions sources, fewer particles (and thus droplets) may also contain iron; this would translate into an even higher iron aqueous-phase concentration. Under such conditions, iron would not be completely dissolved and available for aqueous-phase reactions. Therefore, in the following, we limit our discussion to values of F_N,Fe ≥ 1 %. In order to illustrate the total ROS budget in the aqueous phase, Fig. 6 shows the bulk aqueous-phase concentrations [ROS]_aq,bulk (M) calculated based on the LWC-weighted average ROS concentration in the iron-containing and iron-free droplets or particles:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\left[\mathrm{ROS}\right]}_{\mathrm{aq},\mathrm{bulk}}& =[\mathrm{ROS}{]}_{\mathrm{ironfree}}\cdot \left(\mathrm{1}-F_{\mathrm{N},\mathrm{Fe}}/\mathrm{100}\mathit{\%}\right)\\ & +[\mathrm{ROS}{]}_{\mathrm{iron}}\cdot F_{\mathrm{N},\mathrm{Fe}}/\mathrm{100}\mathit{\%},\end{array}\end{array}$$

where [ROS]_ironfree and [ROS]_iron are the ROS concentrations in the iron-free and iron-containing droplets, respectively. (Note that the same calculation was performed for the bulk aqueous-phase concentrations in Figs. 2, 3, S1 and S2). Results are shown for the full range of 1 % ≤ F_N,Fe ≤ 100 %.

The H₂O₂ concentrations do not show any dependence on the iron distribution F_N,Fe (Fig. 6a and d). This trend can be explained because (i) in cloud water the main chemical source and loss processes are independent of iron, whereas (ii) in aerosol water, both the main chemical source and loss reactions are dependent on the Fe(II) concentration. The same set of processes can also explain why the resulting aqueous-phase H₂O₂ concentrations are independent of the total iron mass. In a sensitivity study, we increased m_Fe to 50 ng m⁻³, which results in very similar H₂O₂ concentrations (Fig. S5). Thus, a higher iron mass concentration increases both rates by the same factor, resulting in nearly equal H₂O₂ concentrations for both m_Fe.

The OH concentration in cloud water is underestimated by FeBulk by up to a factor of ∼ 5 (pH = 6, Fig. 6b). The large difference at the highest pH is the consequence of the more efficient OH formation at pH = 6 by the reaction of O${}_{\mathrm{2}}^{-}$ with O₃ (Sect. 3.2). Since in the FeN<100 approach the HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentration is about 1 order of magnitude higher at this pH value than for FeBulk, the OH concentration is generally underestimated by assuming F_N,Fe = 100 %. It can be concluded that in clean conditions, i.e., when the pH value of cloud water is $\ge \sim$5, even for relatively low iron mass concentrations, iron distribution should be taken into account to obtain the correct OH concentrations in cloud water. The deviations are only slightly higher for m_Fe = 50 ng m⁻³ than for 10 ng m⁻³ (Fig. S5). In aerosol water, the OH concentration is generally overestimated by FeBulk by factors of $\le \sim$ 2 and ∼ 5 for m_Fe = 10 and m_Fe = 50 ng m⁻³ (Figs. 6e and S5e), respectively. The lower OH concentration in the FeN<100 approach is a consequence of the lower Fe(II) concentration (Sect. 4.1), which leads to less OH formation by the Fenton reaction.

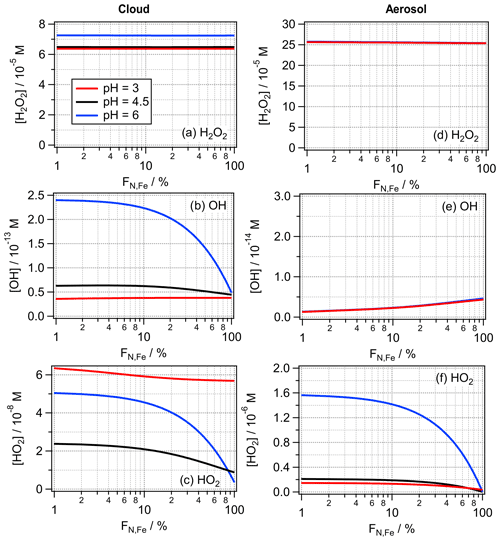
Figure 6 Bulk aqueous-phase concentrations of H₂O₂, OH and HO₂ for the cloud (a–c) and aerosol (d–f) cases as a function of F_N,Fe using the model parameters listed in Table 1.

The HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations are underestimated in cloud water by the FeBulk approach, approximately by the same factors (∼ 2–5) as the OH radical, with the highest bias at pH = 6 (Fig. 6c). At pH = 3, the difference between the HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations for the two iron mass concentrations is much larger than for the other pH values. Unlike for the H₂O₂ and OH concentrations, that are very similar for both m_Fe, the HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations more clearly deviate for the two iron masses considered in Fig. S5. This can be explained by the less efficient Fe(III) reduction in the cloud droplets at m_Fe at all pH values (Sect. 4.1).

In aerosol water, the aqueous-phase HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations are nearly identical for wide ranges of F_N,Fe at pH = 3 and 4.5, whereas the difference at F_N,Fe = 1 % and 100 % is about 1 order of magnitude at pH = 6 (Fig. 6f). Thus, the aqueous-phase budget of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ may be significantly underestimated – independently of m_Fe – with increasing pH if the iron distribution across the particle distribution is not properly accounted for.

3.3.2 Enhanced H₂O₂ partitioning into aerosol water: $K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ = 2.7 × 10⁸ M atm⁻¹

Strictly, Henry's law constants are not applicable to highly concentrated aqueous solutions such as aerosol water. Simultaneous measurements of particle-bound and gas-phase H₂O₂ concentrations suggest that it partitions much more efficiently to the particle phase than predicted based on its physical Henry's law constant ($K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ = 1.02 × 10⁵ M atm⁻¹). Despite large uncertainties in such measurements and of related parameters such as the aerosol water content, various studies revealed that the partitioning of H₂O₂ between the gas and the aerosol aqueous phases may be more appropriately described with an effective Henry's law constant of $K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ ≤ 2.7 × 10⁸ M atm⁻¹ (Hasson and Paulson, 2003; Xuan et al., 2020). The observation by Hasson and Paulson (2003) of higher H₂O₂ concentrations in coarse-mode particles than in fine-mode particles might point to a size-dependent chemical particle composition with higher iron content in coarse particles that often contain dust.

To explore the effects of such enhanced partitioning, we performed a sensitivity study, using $K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ ≤ 2.7 × 10⁸ M atm⁻¹. In Fig. S6, the aqueous-phase concentrations and net phase transfer rates of the three ROS are compared to those using the physical Henry's law constant ($K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ = 1.02 × 10⁵ M atm⁻¹). No other parameter was changed as to the best of our knowledge corresponding K_H(eff) values for OH and/or HO₂ are not available. We perform this comparison only for the aerosol case, as numerous measurements have shown that the partitioning of H₂O₂ into cloud water can be satisfactorily described by its K_H (e.g., Ervens, 2015).

As expected, a higher $K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ results in higher H₂O₂ aqueous-phase concentrations by 3 orders of magnitude. Unlike for the low $K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$, the higher partitioning leads to smaller H₂O₂ concentrations for FeBulk than for FeN<100 by up to 1 order of magnitude and pH = 6. The OH concentration in the aqueous phase is predicted to decrease with increasing F_N,Fe, unlike in the base case simulation where we showed the opposite trend (Fig. S6b). The higher H₂O₂ concentration generally increases the importance of the Fenton reaction and photolysis for OH production in the aqueous phase. While the HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations for the two $K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ values do not differ at low F_N,Fe, they are significantly smaller by several orders of magnitude for the higher $K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ (Fig. S6c).

4 Implications of $F_{\mathrm{N},\mathrm{Fe}}<\mathrm{100}$ % for model and field studies

4.1 Oxidation state of iron: Fe(II) $/$ Fe(total)

The iron oxidation state determines its solubility and bioavailability since Fe(II) salts are usually more soluble than Fe(III) compounds. Fe(II) usually dominates during daytime because Fe(III) complexes are readily photolyzed (Deguillaume et al., 2005). Reported measurements are based on analyses that are performed on bulk samples, where redox reactions of iron can occur after collection and combination of all cloud droplets or aerosol particles, respectively. The trends and overall Fe(II) $/$ Fe(total) (or Fe(II) $/$ Fe(III)) ratios have been reproduced in several model studies that all assumed that iron is present in the complete aqueous phase (Ervens et al., 2003; Deguillaume et al., 2004; Luo et al., 2005; Tilgner et al., 2013; Ingall et al., 2018). Thus, the agreement between measured and predicted data is not surprising as both types of studies imply that the total soluble iron is evenly distributed throughout the total aqueous volume.

However, our study reveals that these Fe(II) $/$ Fe(total) ratios are not the true ratios present in the atmospheric aqueous phases if iron is only present in a small number fraction of particles or droplets. In cloud water, the soluble iron fraction (∼ Fe(II) $/$ Fe(total)) might be overestimated by up to factor of 2 (Fig. 7a), whereas this bias might be even higher in aerosol particles ($\le \sim$ 2.5; Fig. 7b). The overview articles by Deguillaume et al. (2005) and Mao et al. (2017) show large ranges of the Fe(II) $/$ Fe(total) fraction (10 %–100 %). Interestingly the study by Takahama et al. (2008) that investigated single particles reports values at the lower end of this range (∼ 20 %). We cannot state with certainty that this finding is due to different aerosol composition or origin or indeed points to a more accurate representation of the Fe(II) $/$ Fe(total) ratio in individual particles rather than in bulk samples.

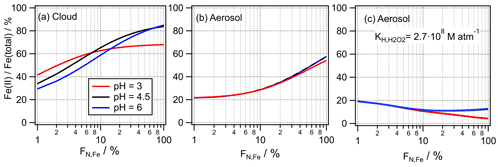
Figure 7 Predicted Fe(II) $/$ Fe(total) ratios at pH = 3 , 4.5 and 6 and the conditions as given in Table 1. (a) Cloud, (b) aerosol and (c) aerosol with enhanced partitioning of H₂O₂ ($K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ = 2.7×10⁸ M atm⁻¹; Sect. 3.3.2).

If the Fe(II) $/$ Fe(total) may be considered a measure of the bioavailability of iron, it might be actually lower than derived from ambient samples or model studies, if they apply a bulk approach. Our results suggest that parameterizations of the Fe(II) $/$ Fe(total) ratios, as, for example, suggested by Mao et al. (2017), might have to be further refined to account for the effects due to the iron distribution across particle populations. In aqueous media that consist of a bulk aqueous phase (e.g., oceans, lung fluid, to some extent also rainwater), the Fe(II) fraction will be appropriately represented by F_N,Fe = 100 % (FeBulk). The timescales for the Fe(II) $/$ Fe(III) ratio to adjust from conditions of $F_{\mathrm{N},\mathrm{Fe}}<\mathrm{100}$ % to F_N,Fe = 100 % will depend on the rates of iron redox processes and on the solubility and dissolution kinetics of ferrous and ferric salts, which, in turn, may be a function of other solutes and liquid water content. If H₂O₂ is more soluble in aerosol water than in cloud water ($K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ = 2.7×10⁸ M atm⁻¹; Sect. 3.3.2), the Fe(II) $/$ Fe(total) ratio does not exceed ∼ 20 % for any F_N,Fe (Fig. 7c). Thus, HO₂ $/$ O${}_{\mathrm{2}}^{-}$ is always efficiently consumed by Fe(III), even at the highest considered iron mass (50 ng m⁻³, Fig. S7c). This predicted independence of the Fe(II) $/$ Fe(total) ratio as a function of F_N,Fe for the high $K_{\mathrm{H},\mathrm{eff},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ in contrast to the predicted strong dependence using the physical $K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ may be used to guide future experiments to determine the “best” value of $K_{\mathrm{H},\mathrm{eff},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ for aerosol water.

4.2 Reactive uptake parameters γ

4.2.1 Calculation of γ_OH and ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$

The uptake of OH and HO₂ into aerosol particles is often parameterized by the dimensionless reactive uptake coefficient γ that is derived as a function of the first-order radical loss (k^loss) onto aerosol particles. For the derivation of γ based on lab studies, it is assumed that γ solely depends on the molecular speed and the droplet surface. However, it has been discussed that the reactive uptake coefficient in atmospheric applications should also include a term to account for gas-phase diffusion (Jacob, 2000):

$$\begin{array}{}\text{(6)}& k^{\mathrm{loss}}={\left({\displaystyle \frac{r_{\mathrm{d}}}{D_{\mathrm{g}}}}+{\displaystyle \frac{\mathrm{4}}{\mathit{\omega }\mathit{\gamma }}}\right)}^{-\mathrm{1}}S,\end{array}$$

with S being the total droplet surface area per air volume and ω the molecular speed,

$$\begin{array}{}\text{(7)}& \mathit{\omega }=\sqrt{{\displaystyle \frac{\mathrm{8}RT}{\mathit{\pi }M}}},\end{array}$$

where M is the molar mass (g mol⁻¹), R is the gas constant and T is the absolute temperature (K) (e.g., Thornton and Abbatt, 2005; Pöschl et al., 2007). Accordingly, the phase transfer rate of radicals into the particle phase can be described as

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\mathrm{d}[\mathrm{Radical}{]}_{\mathrm{g}}}{\mathrm{d}t}}=k^{\mathrm{loss}}[\mathrm{Radical}{]}_{\mathrm{g}},\end{array}$$

and the reactive uptake coefficient γ can be derived as

$$\begin{array}{}\text{(9)}& \mathit{\gamma }={\displaystyle \frac{\mathrm{4}}{\mathit{\omega }\left(\frac{S}{k^{\mathrm{loss}}}-\frac{r_{\mathrm{d}}}{D_{\mathrm{g}}}\right)}}.\end{array}$$

The γ values for OH and HO₂ as a function of F_N,Fe are displayed in Fig. 8. If gas-phase diffusion is neglected in the derivation of γ, the last term in the denominator of Eq. (9) is set to zero (Eq. S.3). To demonstrate the impact of gas-phase diffusion on the reactive uptake parameter, we compare γ values calculated with Eq. (10) to values without consideration of gas-phase diffusion (Sect. S3 in the Supplement).

Figure 8 Reactive uptake coefficients γ_OH and ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ derived from the multiphase model studies at three pH values for (a, b) cloud and (c, d) aerosol conditions.

4.2.2 Reactive uptake coefficient of the hydroxy radical, γ_OH

The derived values for γ_OH over the full range of F_N,Fe (∼ 2.2 × 10⁻³ ≤γ_OH(cloud) ≤ 6.4 × 10⁻³; γ_OH(aerosol) ∼ 3.8 × 10⁻²) are in good agreement with the average value suggested for pure water surfaces (γ_OH = 0.035) (Hanson et al., 1992). It should be noted that this latter experimental value was derived assuming a Henry's law constant of K_H,OH ≥ 40 M atm⁻¹ and [OH] ≥ 10⁸ cm⁻³. If it were adjusted to atmospherically more relevant conditions ([OH] ∼ 10⁶ cm⁻³) and K_H,OH = 25 M atm⁻¹ as used in our study (Table S4), the resulting γ_OH might be smaller by more than an order of magnitude than the reported one. Molecular dynamics simulations for the mass accommodation of OH on water surfaces showed α_OH = 0.1, which can be considered the upper limit of reactive OH uptake onto water surfaces (Roeselová et al., 2003). The difference between such a value for pure water and the values from our model study demonstrates the high reactivity of the OH radical in the aqueous phase. As its solubility is limited, this high reactivity results in subsaturated conditions (ϵ_OH<1; Fig. 4b). The γ_OH values show little difference at different pH values and F_N,Fe. Thus, the reactive uptake of OH into cloud droplets could be parameterized with a value of γ_OH∼ 2.3 × 10⁻³ for all conditions explored here. Similar to the findings for cloud water, the uptake of the OH radical could be parameterized by a single γ value for the conditions applied here (γ_OH∼ 0.0038). The comparison of the values in Fig. 8a and c to those in Fig. S8a and c reveals that the gas-phase diffusion leads to a significant decrease of γ_OH by a factor of ∼ 3 in clouds and ∼10 % in aerosol particles.

Several previous studies have determined γ_OH on surfaces other than pure water that are more comparable to atmospheric aerosol particles. Hanson et al. (1992) showed that γ_OH increases on acidic solutions from 0.07 (28 % H₂SO₄) to unity on 96 % H₂SO₄. On organic surfaces, γ_OH values are generally higher than on inorganic surfaces which demonstrates the high reactivity of OH with organics in the condensed phase and/or on organic surfaces. In several lab studies, squalane was used as a proxy for long-chain alkanes; the reactive uptake coefficients have been determined in a range of ∼ 0.2 $<{\mathit{\gamma }}_{\mathrm{OH}}<\mathrm{0.5}$ (e.g., Che et al., 2009; Smith et al., 2009; Waring et al., 2011; Houle et al., 2015; Bianchini et al., 2018; Li and Knopf, 2021). A similar value range was also found for a wide variety of other organics (Bertram et al., 2001). In other experimental studies on organic particles, γ_OH>1 was found (γ_OH = 1.64 on wet succinic acid, Chan et al., 2014; 1.3 ± 0.4 on bis(2-ethylhexyl) sebacate, George et al., 2007). γ_OH on organic aerosols may decrease with increasing OH gas-phase concentration because the viscosity of the organic condensed phase prevents efficient uptake and diffusion of OH towards the particle center (Slade and Knopf, 2013; Arangio et al., 2015). Such effects were included in recently developed frameworks to parameterize γ_OH as a function of particle viscosity, size and gas-phase OH concentration (Renbaum and Smith, 2011; Houle et al., 2015).

We did not explore any of these parameters in detail in our current model study. However, the comparison of the tight range of our γ_OH values in Fig. 8, independently of F_N,Fe and cloud or aerosol aqueous conditions, to the wide ranges of literature values leads us to the following conclusions: (i) the similarity of our γ_OH value based on an explicit chemical mechanism to that measured on pure water suggests that ∼ 10${}^{-\mathrm{3}}<{\mathit{\gamma }}_{\mathrm{OH}}$ ∼ 10⁻² may be a good approximation under cloud conditions. (ii) The fact that we cannot reproduce the high γ_OH values as observed on organic aerosols suggests that organic reactions control the reactive uptake of OH, which are not included in our explicit chemistry scheme. (iii) Since organics are likely present in all aerosol particles, the effect of the iron distribution (F_N,Fe) for γ_OH may be overestimated by our chemical mechanism on ambient aerosol particles.

4.2.3 Reactive uptake coefficient of the hydroxy peroxyl radical, ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$

The ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ values into cloud water are in the range of 0.001–0.004, with higher values at the highest pH (Fig. 8b). In aerosol water, ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ shows a strong dependence on F_N,Fe, leading to an overestimate of the reactive uptake by FeBulk by up to 2 orders of magnitude at pH = 3 (Fig. 8d). Note that at F_N,Fe = 1 %. no ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ value is shown as under such conditions, HO₂ is predicted to evaporate. This evaporation is due to the inefficient chemical HO₂ consumption in iron-free particles, whereas efficient uptake occurs into the iron-containing particles. This leads to a great imbalance of the phase transfer rates from and into the two droplet classes as shown in Fig. 2b. We use identical α values for droplet and aqueous particle surfaces. The mass accommodation coefficient α is the upper limit of the maximum value for the uptake coefficient γ. This limit can be seen in Fig. (8d), where ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ approaches the value of ${\mathit{\alpha }}_{{\mathrm{HO}}_{\mathrm{2}}}$ = 0.05, i.e., the regime in which the uptake is fully controlled by the mass accommodation and not by the chemical loss in the aqueous phase. For the HO₂ radical, gas-phase diffusion may decrease ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ by a factor of ∼ 2 at pH = 6, whereas the two γ values are nearly identical at pH = 3 (Fig. S8b). In aerosol water, gas-phase diffusion has an insignificant impact on its reactive uptake coefficient onto aerosol water (Fig. S8d).

It has been shown in global model studies that the reactive loss of HO₂ on aerosol surfaces can significantly impact the atmospheric oxidant budget (e.g., Haggerstone et al., 2005; Macintyre and Evans, 2011; Stadtler et al., 2018; Li et al., 2019). A value of ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ = 0.2 based on the study by Jacob (2000) has been commonly used in global models, which has also been supported by molecular dynamics simulations (Morita et al., 2004). However, recent model studies suggest that this value may be an overestimate and that values on the order of ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ = 0.05 or 0.08 may be more appropriate (Christian et al., 2017; Tan et al., 2020).

On dry aerosol surfaces, ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ is usually low: for example, Bedjanian et al. (2005) measured ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ = 0.075 ± 0.015 on dry soot surfaces, which is comparable to the value of ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ ≤ 0.031 on dust (Matthews et al., 2014) and ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ < 0.01 on dry NaCl (Remorov et al., 2002). ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ increases by more than 1 order of magnitude when RH increases from ∼ 20 % to >90 % (Cooper and Abbatt, 1996; Taketani et al., 2008; Lakey et al., 2015, 2016; Moon et al., 2018). Lakey et al. (2015) showed much higher ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ values on two humic acids ($\mathrm{0.0007}\le {\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}\le \mathrm{0.06}$ and $\mathrm{0.043}\le {\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}})\le \mathrm{0.09}$, respectively) than on pure long-chain carboxylic acids (${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}<\mathrm{0.004}$). They ascribed the higher HO₂ uptake to the small concentrations of copper and iron ions in the humic acids, in agreement with previous studies that showed the large impact of TMIs on HO₂ reactive uptake (e.g., Mao et al., 2013, 2017). It was suggested by Lakey et al. (2015) that the HO₂ uptake cannot be solely controlled by the TMI concentration as they did not see any correlation with ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$. This lack of trend is similar to findings by Mozurkewich et al. (1987), who also did not find any clear relationship in ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ on Cu-doped NH₄HSO₄ and LiNO₃ particles with Cu concentration.

Based on our model results, the lack of such correlation can be qualitatively understood by simultaneous increase of the main chemical HO₂ source and sink rates (Reactions S1 and L4–L6 in Fig. 5f). The absence of a dependence of HO₂ uptake on wet particle diameter in the study by Mozurkewich et al. (1987) is also in agreement with our sensitivity studies in which we varied the particle diameter by a factor of ± 2 (Fig. S9). This implies that the interfacial mass transfer is not a limiting step in the HO₂ uptake. The HO₂ uptake on Cu-doped ammonium sulfate particles was observed to be higher under neutral (${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ = 0.2) as opposed to acidic conditions (${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ = 0.05) (Thornton and Abbatt, 2005). Similar results were observed by Mao et al. (2013) who generally found somewhat higher values than in our study (${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}>\mathrm{0.4}$) and highest values for the lowest $\mathrm{Cu}/\mathrm{Fe}$ ratios (i.e., highest iron concentration at a constant copper concentration) and highest pH. However, overall their differences in ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ due to the $\mathrm{Fe}/\mathrm{Cu}$ ratio and/or pH are smaller than those that we predict for different F_N,Fe (∼ 10⁻⁴ $\le {\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ $\le \sim$ 10⁻², at pH = 3). This suggests that ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ parameterizations that take into account the dependence on Cu concentration, total aerosol mass and particle size (e.g., Guo et al., 2019 and Song et al., 2020) should be further refined to also include the iron distribution.

We note that our results are not quantitatively comparable to those on Cu-doped particles, as our chemical scheme includes only reactions of iron as the only TMI. The corresponding reactions with ${\mathrm{Cu}}^{+/\mathrm{2}+}$ generally have higher rate constants than those of iron reactions (Ervens et al., 2003; Deguillaume et al., 2004); however, as copper concentrations in ambient aerosols are usually lower than iron concentrations, the effect of both TMIs might be similar. We did not perform the equivalent simulations for copper in the present study as to our knowledge, there are no data available that give single-particle information on the distribution of iron and copper within droplet or particle populations. However, if iron and copper originated from different emission sources, the number concentration of TMI-containing particles might be relatively high. However, in such situations the synergistic effects of Fe and Cu affecting HO_x cycling and uptake as suggested by Mao et al. (2013) might be reduced.

Measurements of ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ on ambient aerosol populations showed ranges of 0.13 $\le {\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ ≤ 0.34 (Mt. Tai) and 0.09 $\le {\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}\le$ 0.4 (Mt. Mang) (Taketani et al., 2012). No systematic trend with total iron concentration that exceeded 1 µg m⁻³ at Mt. Mang and 10 µg m⁻³ at Mt. Tai was observed. The acidity of the aerosols was not reported in that study; however, the derived ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ values did not show any significant trend with the molar NH${}_{\mathrm{4}}^{+}$ $/$ (SO${}_{\mathrm{4}}^{\mathrm{2}-}+$ NO${}_{\mathrm{3}}^{-}$) ratios that ranged from ∼ 1 to ∼ 2 and ∼ 2 to ∼ 3, pointing to moderately acidic to fully neutralized aerosol. The fact that the ambient data do not show any trend with acidity might either point to a high number fraction of TMI-containing particles and/or to a relatively high pH, i.e., to conditions under which our model results do not show a large effect of F_N,Fe (Fig. 8d). Two studies of ambient aerosol at urban locations revealed similar average values as compared to the mountain sites, with ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ = 0.23 ± 0.22 in Yokohama, Japan (Zhou et al., 2021), and 0.24 (0.08 $\le {\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ ≤ 0.36) in Kyoto, Japan (Zhou et al., 2020). No significant trend in the γ values was observed as a function of aerosol or air mass characteristics (coastal or mainland).

Given the large ranges of ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ values on lab-generated and ambient aerosol, it is difficult to reconcile differences between lab data and observations with our model results. However, our results might provide an explanation for the discrepancies of lab-derived or theoretical ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ values in the range of 0.2–1 to those determined on ambient aerosol (<0.4). We cannot say for sure that these differences indeed stem from different assumptions of iron distribution or other factors affecting ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$. However, our strong predicted decrease of ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ values at low pH and F_N,Fe suggests that applying lab-derived ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ on aerosol particles with identical composition might lead to an overestimate of HO₂ loss on atmospheric aerosol surfaces, even if all other aerosol properties (size, total iron mass, pH, etc.) are identical.

4.3 ROS budgets and oxidative potential (OP)

The formation and cycling of ROS in the aqueous phase are tightly linked to adverse health effects of particulate matter that are caused by oxidative stress in the respiratory tract and lungs (Stohs and Bagchi, 1995; Tong et al., 2017; Molina et al., 2020; Shahpoury et al., 2021). In addition, the oxidant content of ambient aerosol particles controls their aging timescales and interactions with the biosphere (Pöschl and Shiraiwa, 2015). Tong et al. (2020) found a positive trend of reactive species concentrations with total particle mass and increased OH concentrations as a function of transition metal content and the opposite trend for organic radicals at remote forest and polluted urban locations. Contrarily, Verma et al. (2012) did not find any correlation of the ROS formation potential with metal concentrations. Fang et al. (2016, 2017) suggested that sulfate may trigger metal solubility in highly acidic supermicron particles, which in turn leads to enhanced ROS formation. On a molar basis, quinones and TMIs may be equally efficient in producing ROS (Charrier and Anastasio, 2012; Lyu et al., 2018); however, as TMI concentrations are higher than those of quinones in aerosol water, TMIs are considered major drivers for ROS levels. In the overview study by Saffari et al. (2014) ROS activity was compared at different locations: at nearly all locations, the highest activity was observed in PM_2.5 (as opposed to PM₁₀) samples; this trend was explained with the higher fractions and solubilities of iron in particles of these sizes.

Based on such studies, the oxidative potential of atmospheric particulate matter has been related to the presence and number of TMIs in aerosol particles. Our model studies suggest that the total iron amount within an aerosol population may not be a sufficient parameter to constrain the oxidant concentrations within particulate matter in the atmosphere. However, the resulting health impacts of inhaled particles will likely not be largely affected by F_N,Fe since upon inhalation, iron will likely dissolve in the lung fluid so that the particle-resolved effects of the iron distribution are diminished. While it may be possible that there are concentration gradients within the lung fluid due to dissolution and/or mixing kinetics, such effects cannot be quantified to date.

Generally all conclusions for oxidant budgets in aerosol water also apply to those in cloud water. However, the largest concentration differences for extreme values of F_N,Fe are less than an order of magnitude (Sect. 3.1). Several model studies have explored the sources and production rates of OH in cloud water using chemical mechanisms of different complexities (e.g., Ervens et al., 2003; Deguillaume et al., 2004; Tilgner et al., 2013; Bianco et al., 2015). Our analysis shows that the chemical source and loss rates might be underestimated in bulk cloud water. While the overall oxidant content of the cloud water might not be significantly affected (“bulk aqueous-phase concentrations” in Figs. 2 and 6), the large differences of OH concentrations of about an order of magnitude in iron-containing and iron-free droplets may lead to very different oxidation rates of organics. Higher OH concentrations in the aqueous phase may also lead to more efficient formation of organics acids (aqSOA; Ervens et al., 2011, 2014). Generally, the highest OH concentrations in cloud water are predicted under clean (marine, remote) conditions (Herrmann et al., 2000; Tilgner et al., 2013). Our results suggest that the difference in OH concentrations might be even greater between low and high pH as we find the largest impact by F_N,Fe for high pH. Even though in clean air masses, total iron concentrations might be lower, such trends might be robust as we do not find a strong dependence of the predicted OH concentrations on m_Fe. Given the close connections of OH and HO₂ $/$ O${}_{\mathrm{2}}^{-}$, any conclusions for the OH concentrations in cloud water can be similarly drawn also for HO₂ $/$ O${}_{\mathrm{2}}^{-}$. In contrast, the less reactive and more soluble H₂O₂ is not affected by the iron distribution.

5 Summary and conclusions

The role of transition metal ion (TMI) reactions for impacting oxidant levels (OH, HO₂, H₂O₂) in the atmospheric aqueous phase has been recognized for a long time. However, in atmospheric multiphase chemistry models, it usually assumed that all aerosol particles and droplets contain TMIs, and thus TMI-catalyzed reactions occur in all droplets. Single-particle analyses have shown that only a small number fraction of particles contain iron, which implies the same for cloud droplets that are formed on such particles.

Using a box model with a well-established chemical multiphase mechanism, we explored the importance of iron distribution across (i) aqueous aerosol particle or (ii) cloud droplet populations. We performed box model studies in which a constant iron concentration (10 ng m⁻³; in sensitivity studies also 50 ng m⁻³) is distributed to a number fraction F_N,Fe of aerosol particles or droplets from 1 % to 100 % (“FeN<100” and “FeBulk” approaches, respectively).

We find that H₂O₂ concentrations in cloud water are not affected by F_N,Fe. Its main source and loss processes include the recombination of HO₂ and the reaction with S(IV), respectively. Since the loss process is slower than the uptake from the gas phase and the production in the aqueous phase, H₂O₂ is in thermodynamic equilibrium between the gas phase and all droplets. The same conclusions are drawn for H₂O₂ partitioning into aerosol water if the same Henry's law constant is applied ($K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ = 1.02 × 10⁵ M atm⁻¹). However, since H₂O₂ has been found to partition more efficiently into aerosol water than into pure water, applying a higher effective Henry's law constant ($K_{\mathrm{H},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$ = 2.7 × 10⁸ M atm⁻¹) results in an overestimate of the H₂O₂ concentrations. These differences are largest at pH = 6, whereas the differences are negligible at pH = 3 or 4.5. The opposite trends are found for the OH radical, whose aqueous-phase concentration in cloud water might be overestimated by up to a factor of 5 using the FeBulk approach at pH = 6, whereas there might be an over- or underestimate by nearly an order of magnitude in aerosol water, depending on the choice of $K_{\mathrm{H},\mathrm{eff},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}}$.

The concentrations of OH and HO₂ radicals are closely linked. Generally we find that the HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentrations in the aqueous phase are underestimated by the FeBulk approach, again with the largest discrepancies at pH = 6 for F_N,Fe = 1 % or 100 %. This trend can be explained by the increase of the effective Henry's law constant of HO₂ at high pH ($K_{\mathrm{H},\mathrm{eff},{\mathrm{HO}}_{\mathrm{2}}}$ = 1.5 × 10⁵ M atm⁻¹) and the higher rate constants of the O${}_{\mathrm{2}}^{-}$ radical anion as compared to the corresponding reactions of the HO₂ radical. The higher partitioning together with the quicker consumption of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ at high pH leads to its subsaturation in the aqueous phase at high pH. This effect is strongest at low F_N,Fe because the few iron-containing droplets (particles) are highly concentrated in iron. The reaction of Fe(III) ions or hydroxy complexes with HO₂ $/$ O${}_{\mathrm{2}}^{-}$ is the main sink of HO₂ $/$ O${}_{\mathrm{2}}^{-}$ in both the cloud and aerosol aqueous phases. At the same time it is also the main reduction pathway of Fe(III) to Fe(II). Since the HO₂ $/$ O${}_{\mathrm{2}}^{-}$ concentration in iron-containing droplets is up to 1 order of magnitude lower in the FeBulk approach, the Fe(III) reduction is less efficient. Our results are largely independent of the total iron mass concentration as both the chemical HO₂ $/$ O${}_{\mathrm{2}}^{-}$ sources and sinks are dependent on iron. Based on these results, we conclude that the Fe(II) $/$ Fe(total) ratio in cloud and aerosol water might be lower than implied by bulk samples. This finding has implications for the interpretation of modeled and measured Fe(II) $/$ Fe(total) (or Fe(II) $/$ Fe(III)) ratios that are often considered a measure of iron solubility and bioavailability. Our study demonstrates that multiphase chemistry models might not be able to properly predict OH and HO₂ concentrations in the aqueous phase of cloud or aqueous particles, which might translate into biases in the predicted oxidation rates (e.g., aqSOA formation). While not explored in detail in the current study, further implications of iron distribution in cloud droplets might include differences in sulfate formation rates by metal-catalyzed processes.

The reactive uptake of OH and HO₂ is often parameterized by γ. We derived γ values into cloud and aerosol water from our model studies. The values of γ_OH are not largely affected by the iron distribution and show values of γ_OH∼0.0023 for clouds and γ_OH∼ 0.038 for aerosol water. However, ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$(aerosol) can be significantly reduced at low F_N,Fe as compared to bulk samples, showing difference of up to 2 orders of magnitude at pH = 3 (${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ ∼ 0.03 for F_N,Fe = 100 % and ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}\sim$ 0.0001 for F_N,Fe = 2 %). This analysis demonstrates that γ values that are measured in lab studies using internally mixed aerosol particles might be too high as compared to those ambient aerosol populations. In addition to another factors that affect ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ on various aerosol surfaces (chemical composition, particle size, water content, etc.), our results suggest that the iron distribution across particle populations can also add to the large variability of ${\mathit{\gamma }}_{{\mathrm{HO}}_{\mathrm{2}}}$ and to the mismatch of observed and modeled HO₂ loss if lab-derived data are used. Similar considerations can also be applied to the interpretation of ROS formation and oxidative potential of aerosol particles. As ambient aerosol particles likely comprise external mixtures in terms of iron, neither results based on bulk sampling nor on modeling will correctly represent the oxidant budgets in ambient particulate matter.

Our study is to the best of our knowledge the first explicit chemical multiphase model study that systematically explores the role of iron distribution across individual aqueous aerosol particles or cloud droplets for the concentrations and uptake rates of reactive oxygen species. There are only few data available on the iron distribution in aerosol populations from single-particle analyses that may be used to constrain the number fraction of iron-containing particles and droplets. While we restricted our model studies to iron, similar conclusions may also be drawn for other transition metal ions, such as copper or manganese. We identified various potential implications of this parameter for, e.g., (i) oxidant budgets and particle mass formation (aqSOA, sulfate) in clouds and aerosols, (ii) reactive radical (OH, HO₂) uptake onto aerosols, and (iii) oxidative potentials of aerosol particles, which should be further explored by experimental and model studies.