the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Constraining the particle-scale diversity of black carbon light absorption using a unified framework
Rajan K. Chakrabarty
Atmospheric black carbon (BC), the strongest absorber of visible solar radiation in the atmosphere, manifests across a wide spectrum of morphologies and compositional heterogeneity. Phenomenologically, the distribution of BC among diverse particles of varied composition gives rise to enhancement of its light absorption capabilities by over twofold in comparison to that of nascent or unmixed homogeneous BC. This situation has challenged the modeling community to consider the full complexity and diversity of BC on a per-particle basis for accurate estimation of its light absorption. The conventionally adopted core–shell approximation, although computationally inexpensive, is inadequate not only in estimating but also capturing absorption trends for ambient BC. Here we develop a unified framework that encompasses the complex diversity in BC morphology and composition using a single metric, the phase shift parameter (ρBC), which quantifies how much phase shift the incoming light waves encounter across a particle compared to that in its absence. We systematically investigate variations in ρBC across the multi-space distribution of BC morphology, mixing state, mass, and composition as reported by field and laboratory observations. We find that ρBC>1 leads to decreased absorption by BC, which explains the weaker absorption enhancements observed in certain regional BC compared to laboratory results of similar mixing state. We formulate universal scaling laws centered on ρBC and provide physics-based insights regarding core–shell approximation overestimating BC light absorption. We conclude by packaging our framework in an open-source Python application to facilitate community-level use in future BC-related research. The package has two main functionalities. The first functionality is for forward problems, wherein experimentally measured BC mixing state and assumed BC morphology are input, and the aerosol absorption properties are output. The second functionality is for inverse problems, wherein experimentally measured BC mixing state and absorption are input, and the morphology of BC is returned. Further, if absorption is measured at multiple wavelengths, the package facilitates the estimation of the imaginary refractive index of coating materials by combining the forward and inverse procedures. Our framework thus provides a computationally inexpensive source for calculation of absorption by BC and can be used to constrain light absorption throughout the atmospheric lifetime of BC.
- Article
(4227 KB) - Full-text XML
-
Supplement
(655 KB) - BibTeX
- EndNote
The contribution of aerosols to global radiative forcing remains one of the largest sources of uncertainty in current climate models (Reidmiller et al., 2018). Much of this uncertainty stems from disagreements between the predicted and observed radiative forcing by carbonaceous aerosols (Bond et al., 2013; Gustafsson and Ramanathan, 2016; Boucher et al., 2016). One of the most climatically relevant carbonaceous aerosols is black carbon (BC). Black carbon is widely considered to be a predominate light-absorbing atmospheric constituent (Bond et al., 2013; Bond and Bergstrom, 2006). Despite this, light absorption by BC is still significantly underestimated in current climate models, which stems from incorrect parameterization of BC optical properties (Bond et al., 2013; Gustafsson and Ramanathan, 2016; Boucher et al., 2016). Estimation of BC light absorption is particularly complicated, given that BC is often internally mixed with other species, which manifest as external coatings (China et al., 2013).
External coatings enhance light absorption by BC through a “lensing effect”, in which a portion of the incoming light is scattered by the coating into the BC core, where it is then absorbed (Chakrabarty and Heinson, 2018; Cappa et al., 2012; Peng et al., 2016; Saliba et al., 2016; Liu et al., 2017; Shiraiwa et al., 2010). However, previous studies on light absorption enhancement due to the lensing effect have had various results. Some studies find high absorption enhancement (up to a factor of 2.5), while others find little to no absorption enhancement with increasing coating amount (Cappa et al., 2012; Saliba et al., 2016; Shiraiwa et al., 2010; Liu et al., 2015; Cappa et al., 2019; Zhang et al., 2018; Denjean et al., 2020; Zanatta et al., 2018; Xie et al., 2019; Cui et al., 2016). The range of absorption enhancement from previous studies is evident in Fig. 1. Fierce et al. (2020) found that particle-to-particle heterogeneity reconciles a large portion of the observed discrepancies in light absorption enhancement (Fierce et al., 2020). However, even when particle-to-particle heterogeneity is considered, light absorption enhancement is still overestimated, and previous discrepancies cannot be fully resolved. Fierce et al. (2020) have also shown that representation of the complex morphology of BC further improves estimation of its optical properties, but systematic understanding of the effect of BC morphology on light absorption enhancement is understudied.
Here, we take a two-pronged approach to develop a simple yet rigorous unified framework for parameterizing the effects of particle size, morphology, and mixing state on BC light absorption. The first approach involves reducing the aforementioned multivariate space to a single parameter that captures causal relationships between BC's physiochemical properties and corresponding light absorption. Using this parameter, we next develop universal scaling laws for wavelength-dependent BC light absorption as a function of size, morphology, and mixing state. Previously, one would need to make assumptions regarding the morphology of BC, then select an appropriate model to calculate its light absorption properties. Our model is the first to allow for quick calculation of BC optical properties with any morphology. We validate these laws against observational datasets from 11 field campaigns which investigated global trends in BC absorption, as well as laboratory experiments that investigated light absorption enhancement. From the standpoint of practical applications of our framework, we package our scaling laws into open-source Python software which allows researchers to use our results to estimate absorption of BC aerosols based on their size, morphology, and mixing state, as well as to estimate the morphology of BC aerosols based on their size, absorption, and mixing state.
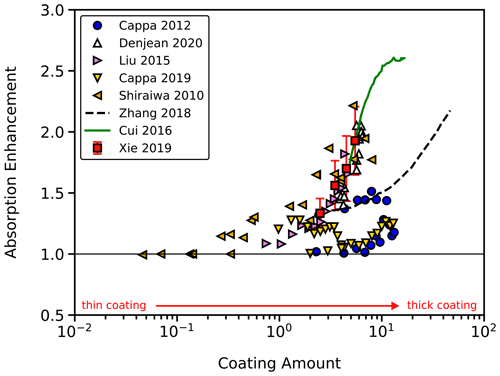
Figure 1Results from previous studies on light absorption enhancement. Some studies find high absorption enhancement, which have had large discrepancies. Some studies find that absorption is enhanced by over twofold, while other studies find little to no absorption enhancement with increased coating amount (Cappa et al., 2012; Denjean et al., 2020; Liu et al., 2015; Cappa et al., 2019; Shiraiwa et al., 2010; Zhang et al., 2018; Cui et al., 2016; Xie et al., 2019).
2.1 Representation of diverse black carbon morphologies
Black carbon is often modeled assuming a spherical core–shell configuration. However, soon after emission, BC aggregates have been found to have a lacy, fractal-like structure. Surface tension and capillary forces from the buildup of external coatings can cause BC aggregates to collapse and eventually take on a more spherical structure (China et al., 2013; Liu et al., 2017; Fierce et al., 2020; Wang et al., 2017). Recent studies have found that nonsphericity of BC-containing particles (partial encapsulation of BC) can decrease absorption enhancement (Hu et al., 2021, 2022). While these findings are notable, previous studies have not observed a prevalence of partially encapsulated BC, yet decreased light absorption enhancement is still observed (China et al., 2013; Fierce et al., 2020). Therefore, this study is focused on investigating the effects of core restructuring on light absorption enhancement, rather than the effects of partial BC encapsulation.
To model the evolution of BC morphology, we utilize three aggregation models which represent fresh, partially collapsed, and fully collapsed BC aggregates. Fresh BC aggregates were created using an off-lattice diffusion-limited cluster–cluster aggregation model, which has been shown to accurately represent BC aggregates produced by combustion systems, and have a fractal dimension (Df) of 1.83 ± 0.09 (Meakin, 1983, 1987). Partially and fully collapsed BC aggregates were respectively simulated with a percolation model and simple cubic lattice stacking and have Df of 2.11 ± 0.22 and 3.0. These particles resemble electron microscope images of moderately and heavily coated BC, respectively (Fierce et al., 2020). Each simulated BC particle is comprised of monomers with a radius equal to 20 nm (Bond et al., 2013). The amount of coating was quantified by the ratio of coating mass to BC mass (RBC). Under this definition, increased RBC represents increasing coating amount, and RBC=0 represents pure BC. The masses of the BC core and the coating material were determined per their volume and densities of 1.8 and 1.2 g cm−3, respectively (Bond and Bergstrom, 2006). This study utilized 345 aggregates, with BC masses between ∼ 1 and ∼ 70 fg, gyration radius between ∼ 50 and ∼ 300 nm, and RBC between 0 and 49. Figure 2 shows examples of simulated aggregates, which represent the range of observed BC morphology.
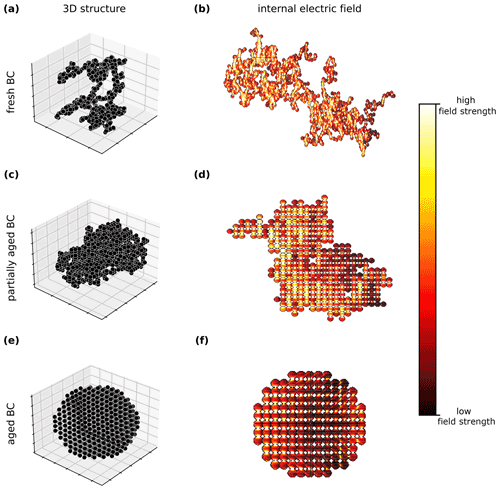
Figure 2The first column shows examples of the 3D structure of (a) freshly emitted, (c) partially aged, and (e) aged black carbon (BC) particles, which represent the range of BC morphology observed during atmospheric processing in field and laboratory studies. The second column shows internal light absorption distribution across these aggregates, with light incident from the left of the particle. As BC becomes more compact, areas of decreased light absorption begin to emerge in the interior of the aggregate, which in turn leads to decreased MACBC.
2.2 Calculation of optical properties
The optical properties of the generated aggregates were calculated using the Amsterdam Discrete Dipole Approximation (ADDA 1.3b4) algorithm (Yurkin and Hoekstra, 2011). The ADDA algorithm operates by breaking complex shapes into subvolumes small enough compared to the wavelength of light to be treated as point scatterers which interact with surrounding point scatterers. It is recommended that the wavelength of light be at least 10 times the size of individual subvolumes for accurate calculation of optical properties. For this study, the wavelength of light was approximately 100 times the size of individual subvolumes in order to reduce errors in calculation of optical properties. The ADDA algorithm calculated the absorption cross-section of each aggregate, which was then divided by the mass of the BC core to give the mass absorption cross-section (MACBC) of each aggregate. Much of the previous work which investigates light absorption by internally mixed BC measures absorption enhancement (Eabs). Absorption enhancement is commonly defined as absorption by internally mixed BC divided by absorption by pure BC (Fierce et al., 2020). There are three common methods for estimating light absorption by pure BC: direct measurement (using thermodenuders to remove coating material), extrapolation of best-fit lines of light absorption by internally mixed BC, and using literature values. All of these methods have challenges which can ultimately affect the reported value of Eabs. It has been found that thermodenuders may not remove low-volatility coating material, which leads to overestimation of light absorption by pure BC and underestimation of Eabs (Shetty et al., 2021). Extrapolation of absorption measurements by internally mixed BC either assumes that the morphology of BC does not affect light absorption or that the morphology of BC remains fixed as coating accumulates. Finally, use of literature values to approximate light absorption by pure BC assumes that light absorption by fractal aggregates is equivalent to literature values of absorption by bulk BC. The Rayleigh–Debye–Gans approximation of light absorption by fractal BC is significantly lower than commonly used literature values of absorption by pure BC (Bond and Bergstrom, 2006; Sorensen, 2001), indicating that use of literature values can also underestimate Eabs.
In order to avoid the errors associated with measurement of Eabs, we instead focus our efforts on quantification of MACBC. Absorption cross-section per BC mass is a common input of radiative transfer algorithms and is vital in converting BC mass concentration to absorption coefficient (Bond et al., 2013). Accurate scaling of MACBC as a function of aggregate size, morphology, and mixing state will allow for subsequent calculation of Eabs, which accounts for the evolution of BC morphology throughout its atmospheric lifetime.
2.3 Phase shift parameter is a unifying measure of size, morphology, and composition
Previous studies of Eabs have focused on the effects of a single dependent variable (absorption) as a function of a single independent variable (mixing state). However, detailed representation of the microphysical properties of BC leads to the introduction of several other measures which describe the size and morphology of BC, increasing the size of the variable set from two (absorption and mixing state) to four (size, morphology, absorption, and mixing state).
To reduce the size of the variable set, we utilize the phase shift parameter (ρ), which is a unifying measure of both aggregate size and morphology. Physically, ρ describes the amount of phase shift that light accumulates when passing through a particle (Heinson and Chakrabarty, 2016; Sorensen and Fischbach, 2000). When ρ is less than 1, there is not a significant amount of phase shift in the incident wave, and the particle–light interactions are well described by Rayleigh approximations. Conversely, when ρ is greater than 1, the particle–light interactions are well described by geometric optics (Sorensen and Fischbach, 2000). In this work, ρ is used to describe the size and morphology of the BC core, not the entire particle (BC core + coating). Therefore, in the remaining text we refer to the core phase shift parameter (ρBC) to distinguish from the phase shift parameter of the entire particle. The core phase shift parameter is given by (Debye, 1958)
where ρ is the wavelength of incident light, Rg is the particle radius of gyration (size metric), and meff is the effective complex index of refraction, which in turn is given by
Here, ϕ is the BC monomer packing fraction and m is the BC complex refractive index. The BC refractive index is fixed at 1.95 + 0.79i at all wavelengths (Bond and Bergstrom, 2006). The BC monomer packing fraction was calculated as the volume of BC which lies within a sphere of radius Rg (centered at the center of mass) divided by the volume of a sphere with radius Rg. It is important to note that all parameters used in Eqs. (1) and (2) describe the BC core, not the entire particle. It is also important to note that the dynamic compositional changes which a BC particle undergoes during atmospheric processing are captured by meff in Eq. (2) (Heinson et al., 2017). As coating accumulates on the surface of aggregates, the BC core will begin to collapse due to surface tension and capillary forces, and ρ will increase. This will affect meff and eventually ρBC. The aggregates in this study have ϕ between 0.029 and 0.52, representing the range observed in coated aggregates (Zangmeister et al., 2014; Chen et al., 2018). In general, for aggregates with an equal size parameter, higher ϕ leads to higher ρBC. A plot of ρBC normalized by size parameter can be found in Supplement Fig. S1.
The consequence of increased ρBC for light absorption can be seen in Fig. 2b, d, and f, which show internal fields of the BC aggregates shown in Fig. 1a, c, and e. For fresh aggregates (with ρBC≪1), light is able to fully illuminate the aggregate, and the entire volume contributes to light absorption. However, for fully collapsed aggregates (with ρBC>1), light is not able to illuminate the far interior of the particle, leading to areas of decreased light absorption. Therefore, if ρBC of a particle significantly increases, its light absorption properties will change significantly. It should be noted that since ρBC is a function of both the morphology and size of aggregates, full core collapse will not always lead to ρBC>1. Aggregates with a small number of monomers may never achieve ρBC>1, even when the monomer packing fraction reaches unity.
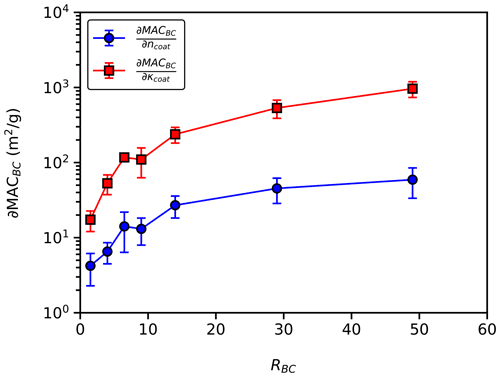
Figure 3Average change in MACBC per change in coating real refractive index (∂MAC) and average change in MACBC per change in coating imaginary refractive index (∂MAC) with constant ϕ. We find that ∂MAC is 4 to 16 times greater than ∂MAC, depending on RBC. These results imply that the choice of the coating imaginary refractive index is more important than the choice of the coating real refractive index when calculating MACBC. Error bars represent 1 standard deviation.
3.1 Sensitivity of MACBC to coating refractive index
To examine the effects of coating refractive index, we calculate MACBC of 30 randomly selected BC aggregates with a coating real refractive index (ncoat) of 1.45, 1.55, and 1.65 and a coating imaginary refractive index (κcoat) of 0.00, 0.05, and 0.1. Figure 3 shows the partial derivative of MACBC with respect to ncoat (∂MAC) and with respect to κcoat (∂MAC), with constant ϕ. We find that ∂MAC is always greater than ∂MAC and increases with increased RBC. These results show that the choice of κcoat is more important than the choice of ncoat when calculating MACBC. Given this, we further investigate scaling of MACBC with κcoat between 0.00 and 0.05, but ncoat remained fixed at 1.55 (Bond and Bergstrom, 2006). In the context of field and laboratory measurements, particles with κcoat=0.00 are representative of BC which is internally mixed with nonrefractory material, such as α-pinene secondary organic aerosol and sulfuric acid (Fierce et al., 2020). Particles with κcoat>0.00 are representative of BC which is internally mixed with absorbing material, such as brown carbon (Liu et al., 2015; Lu et al., 2015).
3.2 Phase shift parameter controls light absorption
Figure 4 shows MACBC as a function of ρBC and RBC for an incident wavelength (λ) of 532 nm. Figure 4b, d, and f show the clear emergence of two regimes separated by ρBC=1 (dashed line). For ρBC≤1, MACBC increases with increased RBC but is independent of ρBC. For ρBC>1, MACBC decreases with increased ρBC, and the rate of decrease is dependent on RBC. The finding of decreased light absorption for ρBC>1 is consistent with a recent study which also found decreased MACBC with increasing aggregate size (Romshoo et al., 2021). Best-fit lines for the scaling of MACBC as a function of RBC are shown as solid lines in Fig. 4 and are summarized by
where A, B, and C are constants, and κcoat is the imaginary part of the coating refractive index. The fitting parameters D and E are functions of RBC, given by
where X generically represents D or E, and denotes or .
The boundary condition for Eq. (3a) is that for RBC = 0, MACBC = MAC0()−AAE, where MAC0 is the average MACBC for uncoated aggregates with ρBC≤1 (6.8 m2 g−1), and AAE is the absorption Ångström exponent for pure BC (1.158). The boundary condition for Eq. (3b) is that at ρBC=1, MACBC must be equal to MACBC calculated using Eq. (3a).
The value of all constants used in Eqs. (3) and (4) can be found in Table 1. Details regarding the acquisition of AAE can be found in Supplement Fig. S2.
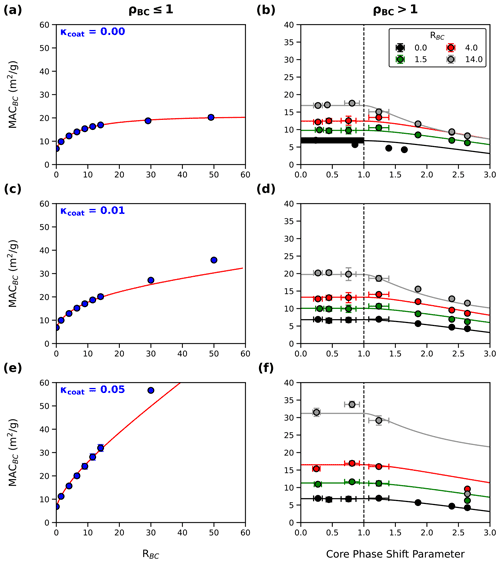
Figure 4Data and fitting of MACBC as a function of ρBC and RBC for BC internally mixed with a coating imaginary refractive index (κcoat) of 0.00 (a–b), 0.01 (c–d), and 0.05 (e–f). We find that for constant ρBC, MACBC increases with increasing RBC. Additionally, for constant RBC, MACBC decreases when ρBC surpasses unity. Solid lines show the scaling of MACBC given by Eq. (3).
We find AAE, which is consistent with previously reported values (Bond et al., 2013; Romshoo et al., 2021), and fitting parameter B, which is consistent with a previous numerical study of coated BC aggregates with ρBC≤1 (Chakrabarty and Heinson, 2018). The value of MAC0 is less than commonly used literature values of pure BC (7.75–8.0 m2 g−1) (Bond et al., 2013; Liu et al., 2020) but slightly greater than the Rayleigh–Debye–Gans approximation for MACBC, which accounts for the fractal morphology of BC (5.01 m2 g−1) (Sorensen, 2001). Figure 5a shows residual plots for the fitting of MACBC using Eq. (3). On average, Eq. (3) overestimates MACBC at λ = 532 nm by 0.47 %, with a standard deviation of 8.26 %. Generally, relative errors increase as RBC increases, as shown by Fig. 5b. It should also be noted that for thickly coated aggregates with κcoat>0.00, the scaling laws given in this work overestimate MACBC for aggregates with large ρBC and slightly underestimate MACBC for aggregates with ρBC<1. Underestimation of MACBC for large ρBC is likely due to accumulation of phase shift in the incident light as it passes through the coating material. This finding indicates that the scaling laws given by Eq. (3) are valid only when it can be assumed that the phase shift as light passes through coating materials is negligible.
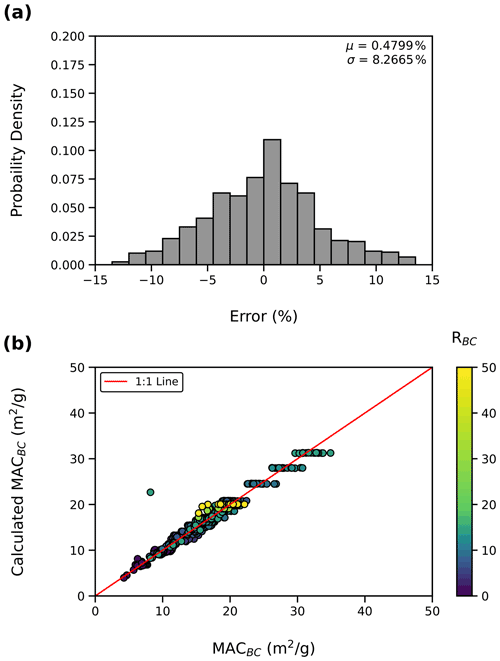
Figure 5(a) Residual plot of fitting of Eq. (3). On average, Eq. (3) overestimates MACBC by 0.47 %, with a standard deviation of 8.26 % (μ and σ, respectively). (b) MACBC calculated using Eq. (3) as a function of MACBC from ADDA. Equation (3) accurately predicts MACBC from the mixing state and morphology of the BC aggregates used to develop Eq. (3), but relative errors increase with increased RBC. It should be noted that the outlier point is a thickly coated aggregate with ρBC≫1 and κcoat>0.00, representing the limitations of the developed framework.
3.3 Wavelength dependency and limitations of core–shell Mie theory
Coated BC is conventionally modeled with a core–shell morphology using Mie theory to calculate its light absorption properties (Bond and Bergstrom, 2006). Our results indicate that misrepresentation of BC morphology will inevitably lead to errors in calculation of its light-absorbing properties. To highlight this point, Fig. 6 compares the accuracy of Eq. (3) in calculating MACBC of 15 randomly selected aggregates with λ = 405, 532, 880, and 1200 nm to Mie theory calculations for mass-equivalent spheres (with κcoat=0.00). Figure 6 shows that across wavelengths, Eq. (3) accurately calculates MACBC, with an average error of 9.08 ± 10.94 %. Figure 6 also shows that Mie theory is inconsistent in calculating MACBC for aggregates with fractal morphologies (Df≠3.0). Figure 6b shows that Mie theory overestimates MACBC at long wavelengths and underestimates MACBC at shorter wavelengths. These results are consistent with previous findings that Mie theory overestimates absorption by BC, given that BC absorption is commonly measured at longer wavelengths to avoid absorption by organic coatings (Cappa et al., 2019; Fierce et al., 2020). We also find that the accuracy of Mie theory improves significantly as Df approaches 3, which is analogous to the morphology of BC approaching that of a sphere. Conversely, Eq. (3) is more consistent in calculating MACBC with any morphology. It should be noted that the development of Eq. (3) involved only data points for λ = 532 nm. However, previous work has shown that enhancement of MACBC is independent of λ (Chakrabarty and Heinson, 2018), indicating that results obtained for λ = 532 nm are applicable to other wavelengths. Therefore, Fig. 6c–d also show the utility of Eq. (3) in calculating MACBC across wavelengths.
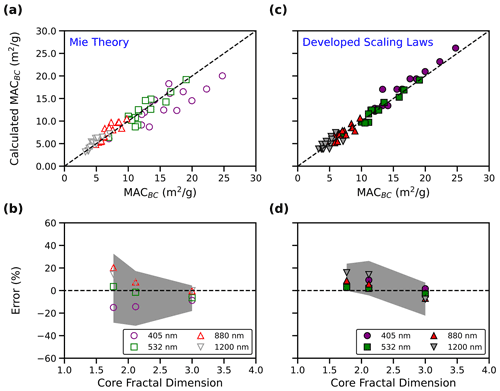
Figure 6(a–b) MACBC calculated using Mie theory (calculated MACBC) as a function of MACBC and error incurred by using Mie theory as a function of core fractal dimension (Df). (c–d) MACBC calculated using Eq. (3) (calculated MACBC) as a function of MACBC and error incurred by using Eq. (3) as a function of Df. In panels (b) and (d), the shaded region shows the range of errors (1 standard deviation). The scaling laws given in this work are more consistent than Mie theory in calculating MACBC for aggregates with arbitrary morphology.
3.4 Validation of scaling laws with field and laboratory observations
Figure 7 shows the scaling of MACBC with RBC for aggregates with ρBC≤1, along with data from studies which find significant increases in MACBC with increasing RBC (Yu et al., 2019; Saliba et al., 2016; Liu et al., 2015; Xie et al., 2019; Denjean et al., 2020; Zanatta et al., 2018). We find that MACBC from these studies closely matches the behavior of Eq. (3a), indicating that these studies were measuring light absorption properties of aggregates with ρBC≤1. It has been hypothesized that large values of MACBC in these studies could be the result of absorbing coatings. However, we find that the data from these studies closely match scaling of MACBC with κcoat fixed at 0.00. The assumption that κcoat=0.00 is bolstered by the fact that refractory organics absorb preferentially at ultraviolet wavelengths (Chakrabarty et al., 2010; Sumlin et al., 2018; Kirchstetter et al., 2004; Sengupta et al., 2018; Shamjad et al., 2018), and we have only included data from visible and near-infrared wavelengths.
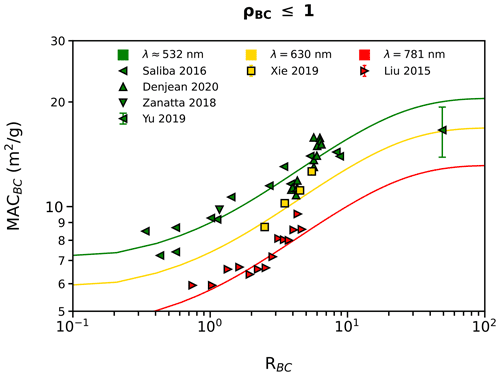
Figure 7Scaling of MACBC with RBC for aggregates with ρBC≤1 (Eq. 3a, solid lines) compared to the findings of several other studies which find significant MACBC (Yu et al., 2019; Saliba et al., 2016; Liu et al., 2015; Xie et al., 2019; Denjean et al., 2020; Zanatta et al., 2018). We find that measurements from these studies are well described by Eq. (3a), indicating that the aggregates measured in these studies had ρBC≤1.
Table 2Previous studies which find little to no increase in MACBC with increasing RBC and the corresponding average ρBC which replicates the measured MACBC. Using Eq. (3b), we are able to estimate ρBC of aggregates from studies which find values of MACBC that are significantly lower than that predicted by Eq. (3a) (Cappa et al., 2012; Shiraiwa et al., 2010; Cappa et al., 2019; Zhang et al., 2018; Cui et al., 2016). The error in ρBC is 1 standard deviation.
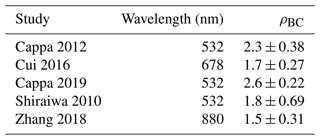
Table 2 shows previous studies which find little to no increase in MACBC with increasing RBC and the corresponding average ρBC which replicates the measured MACBC. The average ρBC was found by solving Eq. (3b), inserting each measured RBC and corresponding MACBC. The importance of ρBC in the estimation of MACBC is evident when comparing experimentally measured MACBC for the different studies shown in Table 2. For example, Cappa et al. (2019) sampled coated BC aggregates in Fontana and Fresno, California, and find little to no increase in MACBC, even with RBC>10 (Cappa et al., 2019). They postulate that the low value of MACBC is due to unequal distribution of coating material between BC particles. Separate studies have shown that uneven distribution of coating can cause decreased MACBC, but thorough consideration of heterogeneous coating amounts fails to fully explain low MACBC observed in the field (Fierce et al., 2020). Therefore, our results suggest that elevated ρBC due to core restructuring may be partially responsible for low MACBC observed by Cappa et al. (2019), further highlighting the importance of the diversity of BC morphology and mixing state in estimation of its light absorption properties.
3.5 Applications of the developed framework
The scaling laws given in this work allow experimentalists to carry out two procedures. The first is the forward procedure, wherein experimentally measured BC mass, mixing state, and coating refractive index are combined with assumed BC morphology and MACBC is calculated. The second is the inverse procedure, wherein experimentally measured BC mass, mixing state, and MACBC are inputs and BC morphology is output. Further, the inverse and forward procedures can be combined to estimate κcoat. We have developed an open-source Python package, called the “Python BC absorption package” (pyBCabs), which performs the forward and inverse functions. The following sections provide a brief overview of pyBCabs, as well as examples of inverse problems and estimation of κcoat. Further details regarding the functionality of the package, as well as more examples of forward and inverse problems for single BC particles and distributions of BC particles, can be found at https://pybcabs.readthedocs.io/en/latest/index.html, last access: 28 April 2022.
3.5.1 Forward procedure for light absorption properties
In the forward procedure, experimentally measured RBC and single-particle BC masses are first combined with the assumed morphology of BC and κcoat. Then, ρBC is calculated using Eqs. (1) and (2) based on the assumed morphology and BC mass. Finally, MACBC is calculated using Eqs. (3a) or (3b). A flowchart of the forward procedure is shown by the dashed lines in Fig. 8a. As an example, a fresh BC particle with mass-equivalent diameter of 300 nm and RBC=3.68 is input to the forward procedure along with the wavelength of interest (405 nm), and MACBC=16.703 m2 g−1 is output. A BC particle with the same characteristics of the previous example but with a fully collapsed BC core would have MACBC of 11.46 m2 g−1. This example demonstrates the utility of the developed framework in evaluating changes in MACBC as coating-induced restructuring occurs during atmospheric processing.
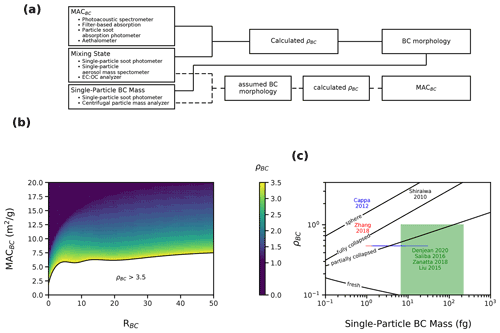
Figure 8(a) Flowchart for forward (dashed lines) and inverse (solid lines) procedures of the Python BC absorption module (pyBCabs), which uses three measured properties: mass absorption cross-section (MACBC), coating amount (RBC), and single-particle BC mass. In the forward procedure, the assumed BC morphology is combined with the single-particle BC mass to calculate MACBC (dashed lines). In the inverse procedure (solid lines), measurements of MACBC and RBC are first input to panel (b) in order to constrain the core phase shift parameter (ρBC). Then, ρBC and the single-particle BC mass are input to panel (c) to estimate the BC core structure. This procedure has been carried out for data from three studies, and we find that low MACBC from these studies can be explained by extensive compaction of the BC core (Cappa et al., 2012; Shiraiwa et al., 2010; Zhang et al., 2018). The procedure outlined in panel (a) has also been carried out for data from several studies, which found significant increases in MACBC with increasing RBC and that the core morphology lies between fresh and partially collapsed BC (Saliba et al., 2016; Liu et al., 2015; Denjean et al., 2020; Zanatta et al., 2018). The examples shown here are all calculated assuming κcoat=0.00.
3.5.2 Inverse procedure for morphology retrieval
In the inverse procedure, experimentally measured RBC and κcoat are first input to Eq. (3a), and MACBC is calculated. If the calculated MACBC replicates the measured MACBC, then it can be concluded that the measured BC has ρBC≤1, but the exact ρBC cannot be determined. If the measured MACBC is much less than that predicted by Eq. (3a), then Fig. 8b can be used to estimate ρBC. Alternatively, Eq. (3b) can be used to calculate ρBC directly. Finally, the single-particle BC mass and ρBC are combined with Fig. 8c to give insight into how much restructuring the BC core has undergone. A flowchart of the inverse procedure is shown by the solid lines in Fig. 8a. The inverse procedure has been carried out for seven previous studies (Cappa et al., 2012; Saliba et al., 2016; Shiraiwa et al., 2010; Liu et al., 2015; Zhang et al., 2018; Denjean et al., 2020; Zanatta et al., 2018), and the results are shown in Fig. 8c. Our results indicate that studies which find little to no increase in MACBC with increased RBC may be measuring BC aggregates which have undergone significant coating-induced restructuring, leading to ρBC>1, and may also be measuring particles which have significant heterogeneity in RBC. On the other hand, studies that find significant increases in MACBC may be measuring aggregates which have ρBC<1. This does not imply that these studies are measuring BC which has not been restructured, only that the product of the size parameter and core packing fraction of BC is not large enough such that ρBC>1.
3.5.3 Inverse procedure for coating refractive index retrieval
The inverse and forward procedures can be combined to estimate κcoat if MACBC is measured at multiple wavelengths. To accomplish this, ρBC is first found using the inverse procedure outlined above using MACBC measured at a near-infrared wavelength (where κcoat can be estimated as 0.00). Then, ρBC, RBC, and MACBC can be used to solve for κcoat at near-ultraviolet and visible wavelengths. This procedure is outlined in Fig. 9a and has been carried out for the Liu et al. (2015) study, which measured absorption enhancement for BC which was internally mixed with absorbing organics (Liu et al., 2015). We estimate that for this study, κcoat=0.056 at λ = 405 nm. Figure 9b shows data collected by Liu et al. (2015) at λ = 781 nm (red points) and λ = 405 nm (blue points). The solid lines show MACBC calculated using Eq. (3), inserting the appropriate λ and κcoat. Our estimation of κcoat is slightly greater than the reported κcoat in Liu et al. (2015). However, Liu et al. (2015) approximated κcoat using the Rayleigh–Debye–Gans approximations, not direct measurement (Liu et al., 2015). Additionally, our estimation of κcoat is consistent with previous studies of the refractive index of absorbing organics (Chakrabarty et al., 2010; Sumlin et al., 2018; Kirchstetter et al., 2004; Sengupta et al., 2018; Shamjad et al., 2018).
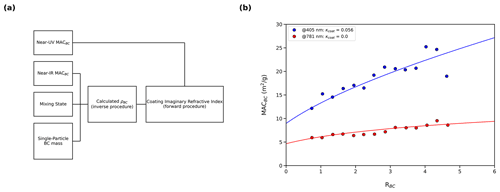
Figure 9(a) Flowchart for estimation of the coating refractive index. First, ρBC is determined using the inverse procedure with MACBC measured at the near-infrared (near-IR) wavelength, where the coating imaginary refractive index (κcoat) can be estimated as 0.00. Then, MACBC at the near-ultraviolet (near-UV) wavelength and calculated ρBC are input to Eq. (3) and κcoat is calculated using the forward procedure. (b) Example of coating imaginary refractive index retrieval for Liu et al. (2015) (Liu et al., 2015). First, measured MACBC at λ = 781 is used to retrieve BC morphology. We find that the BC in this study close matches the scaling of MACBC with ρBC≤1. Once ρBC is known, measured mixing state and MACBC at λ = 405 are input to Eq. (3a) and κcoat is solved for. We estimate that κcoat at λ = 405 is approximately 0.056. Data points show measurements made by Liu et al. (2015), and solid lines show the result of Eq. (3) with appropriate κcoat and λ.
This study comprehensively investigates the effect of BC morphology on light absorption, introduces ρBC as a central parameter in accurate estimation of MACBC, and develops improved scaling laws for MACBC. We find that for aggregates with ρBC≤1, MACBC increases with increasing RBC. For aggregates with ρBC>1, MACBC is a function of RBC and ρBC. Our work also shows that as ρBC increases past unity, MACBC decreases. We then provide a comparison of the scaling laws presented in this work with Mie theory calculations for mass-equivalent spheres. We find that Mie theory consistently overestimates MACBC of internally mixed BC with ρBC>1, which is consistent with previous studies which also find that Mie theory greatly overestimates absorption by BC (Cappa et al., 2012, 2019; Fierce et al., 2020). The scaling laws presented in this work account for the microphysical properties of BC and provide a new tool for estimating BC light absorption based on BC morphology.
Finally, we validate our findings with data from 11 previous studies which measure light absorption enhancement (Yu et al., 2019; Cappa et al., 2012; Saliba et al., 2016; Shiraiwa et al., 2010; Liu et al., 2015; Cappa et al., 2019; Zhang et al., 2018; Xie et al., 2019; Denjean et al., 2020; Zanatta et al., 2018; Cui et al., 2016). We find that studies which find significant absorption enhancement with increasing RBC agree well with our scaling laws for BC with ρBC≤1 (Saliba et al., 2016; Liu et al., 2015; Denjean et al., 2020; Zanatta et al., 2018; Xie et al., 2019; Yu et al., 2019). We also find that ρBC>1 is a possible explanation for studies which find little to no absorption enhancement (Cappa et al., 2012; Shiraiwa et al., 2010; Cappa et al., 2019; Zhang et al., 2018; Cui et al., 2016). These findings are significant because coating-induced restructuring of the BC core will lead to increases in the core packing fraction and consequent increases in ρBC. Our findings suggest that restructuring of the BC core and increased ρBC can lead to decreased absorption and may play a role in previous discrepancies in measured MACBC. Previous work has shown that heterogeneity in BC mixing state accounts for a large portion of the discrepancies in measured and modeled BC but does not fully reconcile previous discrepancies in BC absorption. Our study shows that particle-resolved mixing state and detailed representation of BC morphology are both necessary in order to fully parameterize absorption by internally mixed BC.
In order to make the results of this study readily available to experimentalists, we conclude by providing an open-source Python module, the “Python BC absorption package” (pyBCabs). This package has two functionalities. The first functionality is for forward problems, wherein BC mass and RBC of ambient and laboratory-generated BC are input, and MACBC is returned. The second functionality is for inverse problems, wherein BC mass, RBC, and MACBC of ambient and laboratory-generated BC are input, and the morphology of BC is returned. The forward and inverse functionalities can also be combined to estimate the imaginary part of the coating refractive index if MACBC is measured at multiple wavelengths.
The inverse functionality of this module allows for in situ inference of BC morphology, as opposed to ex situ methods of determining BC morphology, such as electron microscopy. Use of the inverse functionality of pyBCabs will allow for more detailed studies on the evolution of BC morphology during its atmospheric lifetime. Improved representation of BC morphology, as well as the improved scaling laws developed by this study, can then be incorporated into radiative transfer models and eventually aid in reducing the uncertainty of radiative forcing by carbonaceous aerosols.
All data from ADDA calculations are available for download at https://github.com/beelerpayton/ADDA_datasets (https://doi.org/10.5281/zenodo.7255194, Beeler and Chakrabarty, 2022a). Full details regarding the functionality of the developed Python package can be found at https://pybcabs.readthedocs.io/en/latest/index.html (last access: 26 October 2022, Beeler and Chakrabarty, 2022b).
The Supplement includes methods for converting absorption enhancement from previous field and laboratory studies to a mass absorption cross-section. It also includes two figures showing examples of a modeled partially collapsed BC particle (S1) and data used for calculation of the absorption Ångström exponent (S2). The supplement related to this article is available online at: https://doi.org/10.5194/acp-22-14825-2022-supplement.
RKC and PB conceived of the study and its design. RKC provided guidance and supervision for carrying out the research tasks and interpretation of results, as well as contributing to the preparation of the paper. PB performed the data analysis, developed the figures, and led the preparation of the paper. PB and RKC were involved in the editing and proofreading of the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the US National Science Foundation (AGS-1926817), the NASA ACCDAM program (NNH20ZDA001N), and the US Department of Energy (DE-SC0021011). Funding for collecting data during the 2010 CARES field campaign in California was provided by the Atmospheric Radiation Measurement (ARM) Program sponsored by the US Department of Energy (DOE), Office of Biological and Environmental Research (OBER). The authors thank William Heinson for insightful comments and assisting with getting this project off the ground.
This research has been supported by the US Department of Energy (grant no. DE-SC0021011) and the National Science Foundation (grant no. AGS-1926817).
This paper was edited by Dantong Liu and reviewed by three anonymous referees.
Beeler, P. and Chakrabarty, R. K.: ADDA_datasets (Version 1.0.0), Computer software, Zenodo [data set], https://doi.org/10.5281/zenodo.7255194, 2022a.
Beeler, P. and Chakrabarty, R. K.: Online user's guide for the Python Black Carbon Absorption package (pyBCabs), pyBCabsorption [code], https://pybcabs.readthedocs.io/en/latest/index.html, 2022b.
Bond, T. C. and Bergstrom, R. W.: Light Absorption by Carbonaceous Particles: An Investigative Review, Aerosol Sci. Tech., 40, 27–67, https://doi.org/10.1080/02786820500421521, 2006.
Bond, T. C., Doherty, S. J., Fahey, D. W., Forster, P. M., Berntsen, T., DeAngelo, B. J., Flanner, M. G., Ghan, S., Kärcher, B., Koch, D., Kinne, S., Kondo, Y., Quinn, P. K., Sarofim, M. C., Schultz, M. G., Schulz, M., Venkataraman, C., Zhang, H., Zhang, S., Bellouin, N., Guttikunda, S. K., Hopke, P. K., Jacobson, M. Z., Kaiser, J. W., Klimont, Z., Lohmann, U., Schwarz, J. P., Shindell, D., Storelvmo, T., Warren, S. G., and Zender, C. S.: Bounding the role of black carbon in the climate system: A scientific assessment: BLACK CARBON IN THE CLIMATE SYSTEM, J. Geophys. Res.-Atmos., 118, 5380–5552, https://doi.org/10.1002/jgrd.50171, 2013.
Boucher, O., Balkanski, Y., Hodnebrog, Ø., Myhre, C. L., Myhre, G., Quaas, J., Samset, B. H., Schutgens, N., Stier, P., and Wang, R.: Jury is still out on the radiative forcing by black carbon, P. Natl. Acad. Sci. USA, 113, E5092–E5093, https://doi.org/10.1073/pnas.1607005113, 2016.
Cappa, C. D., Onasch, T. B., Massoli, P., Worsnop, D. R., Bates, T. S., Cross, E. S., Davidovits, P., Hakala, J., Hayden, K. L., Jobson, B. T., Kolesar, K. R., Lack, D. A., Lerner, B. M., Li, S.-M., Mellon, D., Nuaaman, I., Olfert, J. S., Petaja, T., Quinn, P. K., Song, C., Subramanian, R., Williams, E. J., and Zaveri, R. A.: Radiative Absorption Enhancements Due to the Mixing State of Atmospheric Black Carbon, Science, 337, 1078–1081, https://doi.org/10.1126/science.1223447, 2012.
Cappa, C. D., Zhang, X., Russell, L. M., Collier, S., Lee, A. K. Y., Chen, C.-L., Betha, R., Chen, S., Liu, J., Price, D. J., Sanchez, K. J., McMeeking, G. R., Williams, L. R., Onasch, T. B., Worsnop, D. R., Abbatt, J., and Zhang, Q.: Light Absorption by Ambient Black and Brown Carbon and its Dependence on Black Carbon Coating State for Two California, USA, Cities in Winter and Summer, J. Geophys. Res.-Atmos., 124, 1550–1577, https://doi.org/10.1029/2018JD029501, 2019.
Chakrabarty, R. K. and Heinson, W. R.: Scaling Laws for Light Absorption Enhancement Due to Nonrefractory Coating of Atmospheric Black Carbon Aerosol, Phys. Rev. Lett., 121, 218701, https://doi.org/10.1103/PhysRevLett.121.218701, 2018.
Chakrabarty, R. K., Moosmüller, H., Chen, L.-W. A., Lewis, K., Arnott, W. P., Mazzoleni, C., Dubey, M. K., Wold, C. E., Hao, W. M., and Kreidenweis, S. M.: Brown carbon in tar balls from smoldering biomass combustion, Atmos. Chem. Phys., 10, 6363–6370, https://doi.org/10.5194/acp-10-6363-2010, 2010.
Chen, C., Enekwizu, O. Y., Fan, X., Dobrzanski, C. D., Ivanova, E. V., Ma, Y., Gor, G. Y., and Khalizov, A. F.: Single parameter for predicting the morphology of atmospheric black carbon, Environ. Sci. Technol., 52, 14169–14179, 2018.
China, S., Mazzoleni, C., Gorkowski, K., Aiken, A. C., and Dubey, M. K.: Morphology and mixing state of individual freshly emitted wildfire carbonaceous particles, Nat. Commun., 4, 2122, https://doi.org/10.1038/ncomms3122, 2013.
Cui, X., Wang, X., Yang, L., Chen, B., Chen, J., Andersson, A., and Gustafsson, Ö.: Radiative absorption enhancement from coatings on black carbon aerosols, Sci. Total Environ., 551/552, 51–56, https://doi.org/10.1016/j.scitotenv.2016.02.026, 2016.
Debye, P. P.: Light Scattering by Small Particles. HC Van de Hulst. Wiley, New York, Chapman and Hall, London, 1957, xiii+, 470 pp., Illus 12, Science, 127, 477–478, 1958.
Denjean, C., Brito, J., Libois, Q., Mallet, M., Bourrianne, T., Burnet, F., Dupuy, R., Flamant, C., and Knippertz, P.: Unexpected Biomass Burning Aerosol Absorption Enhancement Explained by Black Carbon Mixing State, Geophys. Res. Lett., 47, e2020GL089055, https://doi.org/10.1029/2020GL089055, 2020.
Fierce, L., Onasch, T. B., Cappa, C. D., Mazzoleni, C., China, S., Bhandari, J., Davidovits, P., Al Fischer, D., Helgestad, T., and Lambe, A. T.: Radiative absorption enhancements by black carbon controlled by particle-to-particle heterogeneity in composition, P. Natl. Acad. Sci. USA, 117, 5196–5203, 2020.
Gustafsson, Ö. and Ramanathan, V.: Convergence on climate warming by black carbon aerosols, P. Natl. Acad. Sci. USA, 113, 4243–4245, https://doi.org/10.1073/pnas.1603570113, 2016.
Heinson, W. R. and Chakrabarty, R. K.: Fractal morphology of black carbon aerosol enhances absorption in the thermal infrared wavelengths, Opt. Lett., 41, 808–811, https://doi.org/10.1364/OL.41.000808, 2016.
Heinson, W. R., Liu, P., and Chakrabarty, R. K.: Fractal scaling of coated soot aggregates, Aerosol Sci. Technol., 51, 12–19, 2017.
Hu, K., Liu, D., Tian, P., Wu, Y., Deng, Z., Wu, Y., Zhao, D., Li, R., Sheng, J., and Huang, M.: Measurements of the diversity of shape and mixing state for ambient black carbon particles, Geophys. Res. Lett., 48, e2021GL094522, https://doi.org/10.1029/2021GL094522, 2021.
Hu, K., Liu, D., Tian, P., Wu, Y., Li, S., Zhao, D., Li, R., Sheng, J., Huang, M., and Ding, D.: Identifying the Fraction of Core–Shell Black Carbon Particles in a Complex Mixture to Constrain the Absorption Enhancement by Coatings, Environ. Sci. Technol. Lett., 9, 272–279, https://doi.org/10.1021/acs.estlett.2c00060, 2022.
Kirchstetter, T. W., Novakov, T., and Hobbs, P. V.: Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon: SPECTRAL LIGHT ABSORPTION BY AEROSOLS, J. Geophys. Res., 109, D21208, https://doi.org/10.1029/2004JD004999, 2004.
Liu, D., Whitehead, J., Alfarra, M. R., Reyes-Villegas, E., Spracklen, D. V., Reddington, C. L., Kong, S., Williams, P. I., Ting, Y.-C., Haslett, S., Taylor, J. W., Flynn, M. J., Morgan, W. T., McFiggans, G., Coe, H., and Allan, J. D.: Black-carbon absorption enhancement in the atmosphere determined by particle mixing state, Nat. Geosci., 10, 184–188, https://doi.org/10.1038/ngeo2901, 2017.
Liu, F., Yon, J., Fuentes, A., Lobo, P., Smallwood, G. J., and Corbin, J. C.: Review of recent literature on the light absorption properties of black carbon: Refractive index, mass absorption cross section, and absorption function, Aerosol Sci. Technol., 54, 33–51, 2020.
Liu, S., Aiken, A. C., Gorkowski, K., Dubey, M. K., Cappa, C. D., Williams, L. R., Herndon, S. C., Massoli, P., Fortner, E. C., Chhabra, P. S., Brooks, W. A., Onasch, T. B., Jayne, J. T., Worsnop, D. R., China, S., Sharma, N., Mazzoleni, C., Xu, L., Ng, N. L., Liu, D., Allan, J. D., Lee, J. D., Fleming, Z. L., Mohr, C., Zotter, P., Szidat, S., and Prévôt, A. S. H.: Enhanced light absorption by mixed source black and brown carbon particles in UK winter, Nat. Commun., 6, 8435, https://doi.org/10.1038/ncomms9435, 2015.
Lu, Z., Streets, D. G., Winijkul, E., Yan, F., Chen, Y., Bond, T. C., Feng, Y., Dubey, M. K., Liu, S., and Pinto, J. P.: Light absorption properties and radiative effects of primary organic aerosol emissions, Environ. Sci. Technol., 49, 4868–4877, 2015.
Meakin, P.: Formation of Fractal Clusters and Networks by Irreversible Diffusion-Limited Aggregation, Phys. Rev. Lett., 51, 1119–1122, https://doi.org/10.1103/PhysRevLett.51.1119, 1983.
Meakin, P.: Fractal aggregates, Adv. Colloid Interfac., 28, 249–331, https://doi.org/10.1016/0001-8686(87)80016-7, 1987.
Peng, J., Hu, M., Guo, S., Du, Z., Zheng, J., Shang, D., Levy Zamora, M., Zeng, L., Shao, M., Wu, Y.-S., Zheng, J., Wang, Y., Glen, C. R., Collins, D. R., Molina, M. J., and Zhang, R.: Markedly enhanced absorption and direct radiative forcing of black carbon under polluted urban environments, P. Natl. Acad. Sci. USA, 113, 4266–4271, https://doi.org/10.1073/pnas.1602310113, 2016.
Reidmiller, D., Avery, C., Easterling, D., Kunkel, K., Lewis, K., Maycock, T., and Stewart, B.: Fourth national climate assessment, Vol. II, Impacts, risks, and adaptation in the United States, US Global Change Research Program, Washington, DC, USA, https://doi.org/10.7930/NCA4.2018, 2018.
Romshoo, B., Müller, T., Pfeifer, S., Saturno, J., Nowak, A., Ciupek, K., Quincey, P., and Wiedensohler, A.: Optical properties of coated black carbon aggregates: numerical simulations, radiative forcing estimates, and size-resolved parameterization scheme, Atmos. Chem. Phys., 21, 12989–13010, https://doi.org/10.5194/acp-21-12989-2021, 2021.
Saliba, G., Subramanian, R., Saleh, R., Ahern, A. T., Lipsky, E. M., Tasoglou, A., Sullivan, R. C., Bhandari, J., Mazzoleni, C., and Robinson, A. L.: Optical properties of black carbon in cookstove emissions coated with secondary organic aerosols: Measurements and modeling, Aerosol Sci. Technol., 50, 1264–1276, https://doi.org/10.1080/02786826.2016.1225947, 2016.
Sengupta, D., Samburova, V., Bhattarai, C., Kirillova, E., Mazzoleni, L., Iaukea-Lum, M., Watts, A., Moosmüller, H., and Khlystov, A.: Light absorption by polar and non-polar aerosol compounds from laboratory biomass combustion, Atmos. Chem. Phys., 18, 10849–10867, https://doi.org/10.5194/acp-18-10849-2018, 2018.
Shamjad, P., Satish, R., Thamban, N. M., Rastogi, N., and Tripathi, S.: Absorbing refractive index and direct radiative forcing of atmospheric brown carbon over Gangetic Plain, Acs Earth Space Chem., 2, 31–37, 2018.
Shetty, N., Beeler, P., Paik, T., Brechtel, F. J., and Chakrabarty, R. K.: Bias in quantification of light absorption enhancement of black carbon aerosol coated with low-volatility brown carbon, Aerosol Science and Technology, 55, 539–551, 2021.
Shiraiwa, M., Kondo, Y., Iwamoto, T., and Kita, K.: Amplification of Light Absorption of Black Carbon by Organic Coating, Aerosol Sci. Technol., 44, 46–54, https://doi.org/10.1080/02786820903357686, 2010.
Sorensen, C. and Fischbach, D.: Patterns in Mie scattering, Opt. Commun., 173, 145–153, 2000.
Sorensen, C. M.: Light Scattering by Fractal Aggregates: A Review, Aerosol Sci. Technol., 40, 648–687, 2001.
Sumlin, B. J., Heinson, Y. W., Shetty, N., Pandey, A., Pattison, R. S., Baker, S., Hao, W. M., and Chakrabarty, R. K.: UV–Vis–IR spectral complex refractive indices and optical properties of brown carbon aerosol from biomass burning, J. Quant. Spectrosc. Ra., 206, 392–398, https://doi.org/10.1016/j.jqsrt.2017.12.009, 2018.
Wang, Y., Liu, F., He, C., Bi, L., Cheng, T., Wang, Z., Zhang, H., Zhang, X., Shi, Z., and Li, W.: Fractal Dimensions and Mixing Structures of Soot Particles during Atmospheric Processing, Environ. Sci. Technol. Lett., 4, 487–493, https://doi.org/10.1021/acs.estlett.7b00418, 2017.
Xie, C., Xu, W., Wang, J., Liu, D., Ge, X., Zhang, Q., Wang, Q., Du, W., Zhao, J., Zhou, W., Li, J., Fu, P., Wang, Z., Worsnop, D., and Sun, Y.: Light absorption enhancement of black carbon in urban Beijing in summer, Atmospheric Environment, Atmos. Environ., 213, 499–504, https://doi.org/10.1016/j.atmosenv.2019.06.041., 2019.
Yu, P., Toon, O. B., Bardeen, C. G., Zhu, Y., Rosenlof, K. H., Portmann, R. W., Thornberry, T. D., Gao, R.-S., Davis, S. M., Wolf, E. T., de Gouw, J., Peterson, D. A., Fromm, M. D., and Robock, A.: Black carbon lofts wildfire smoke high into the stratosphere to form a persistent plume, Science, 365, 587–590, https://doi.org/10.1126/science.aax1748, 2019.
Yurkin, M. A. and Hoekstra, A. G.: The discrete-dipole-approximation code ADDA: Capabilities and known limitations, J. Quant. Spectrosc. Ra., 112, 2234–2247, https://doi.org/10.1016/j.jqsrt.2011.01.031, 2011.
Zanatta, M., Laj, P., Gysel, M., Baltensperger, U., Vratolis, S., Eleftheriadis, K., Kondo, Y., Dubuisson, P., Winiarek, V., Kazadzis, S., Tunved, P., and Jacobi, H.-W.: Effects of mixing state on optical and radiative properties of black carbon in the European Arctic, Atmos. Chem. Phys., 18, 14037–14057, https://doi.org/10.5194/acp-18-14037-2018, 2018.
Zangmeister, C. D., Radney, J. G., Dockery, L. T., Young, J. T., Ma, X., You, R., and Zachariah, M. R.: Packing density of rigid aggregates is independent of scale, P. Natl. Acad. Sci. USA, 111, 9037–9041, 2014.
Zhang, Y., Favez, O., Canonaco, F., Liu, D., Močnik, G., Amodeo, T., Sciare, J., Prévôt, A. S. H., Gros, V., and Albinet, A.: Evidence of major secondary organic aerosol contribution to lensing effect black carbon absorption enhancement, npj Clim. Atmos. Sci., 1, 47, https://doi.org/10.1038/s41612-018-0056-2, 2018.