Non-linear response of PM_2.5 to changes in NO_x and NH₃ emissions in the Po basin (Italy): consequences for air quality plans

Air pollution is one of the main causes of damages to human health in Europe, with an estimate of about 380 000 premature deaths per year in the EU28, as the result of exposure to fine particulate matter (PM_2.5) only. In this work, we focus on one specific region in Europe, the Po basin, a region where chemical regimes are the most complex, showing important non-linear processes, especially those related to interactions between NO_x and NH₃. We analyse the sensitivity of PM_2.5 concentration to NO_x and NH₃ emissions by means of a set of EMEP model simulations performed with different levels of emission reductions, from 25 % up to a total switch-off of those emissions. Both single and combined precursor reduction scenarios are applied to determine the most efficient emission reduction strategies and quantify the interactions between NO_x and NH₃ emission reductions. The results confirmed the peculiarity of secondary PM_2.5 formation in the Po basin, characterised by contrasting chemical regimes within distances of a few (hundred) kilometres, as well as non-linear responses to emission reductions during wintertime. One of the striking results is the slight increase in the PM_2.5 concentration levels when NO_x emission reductions are applied in NO_x-rich areas, such as the surroundings of Bergamo. The increased oxidative capacity of the atmosphere is the cause of the increase in PM_2.5 induced by a reduction in NO_x emission. This process could have contributed to the absence of a significant PM_2.5 concentration decrease during the COVID-19 lockdowns in many European cities. It is important to account for this process when designing air quality plans, since it could well lead to transitionary increases in PM_2.5 at some locations in winter as NO_x emission reduction measures are gradually implemented. While PM_2.5 chemical regimes, determined by the relative importance of the NO_x vs. NH₃ responses to emission reductions, show large variations seasonally and spatially, they are not very sensitive to moderate (up to 50 %–60 %) emission reductions. Beyond 25 % emission reduction strength, responses of PM2.5 concentrations to NO_x emission reductions become non-linear in certain areas of the Po basin mainly during wintertime.

1 Introduction

Air pollution is one of the main causes of damages to human health in Europe, with an estimate of about 380 000 premature deaths per year in the EU28, as the result of exposure to fine particulate matter (PM_2.5) only (EEA, 2020). Many of the exceedances to the EU limit values occur in urban areas where most of the population is exposed.

PM_2.5 is partly emitted directly (primary particles) and partly formed through photo-chemical reactions that involve gaseous precursors like SO_x, NO_x, NH₃ and non-methane volatile organic compounds (NMVOC) to form secondary inorganic and organic aerosol (SIA and SOA). The secondary fraction is often dominating the total concentration of particulate matter in urban areas as shown by e.g. Beekmann et al. (2015) for the Greater Paris region and by De Meij et al. (2006, 2009) or Larsen et al. (2012) in northern Italy, hence the importance of understanding the complex chemical processes that lead to its formation. In particular, it is key to identify the precursors involved in these reactions in order to target the right sectors of activity in air quality plans to effectively reduce pollution levels. According to the EDGAR estimates for 2015 for Italy, about 90 % of the NH₃ is directly emitted in the atmosphere by the agriculture sector, while SO_x precursors are predominantly released by the energy production and use (industrial) sectors (EDGAR, 2020). For NO_x, emissions are spread among various sectors, with transport (50 %), industry (40 %) and agriculture (4 %) being the main ones. The gaseous precursors of secondary organic aerosols (SOA) include a vast range of NMVOCs among which are biogenic terpenes and anthropogenic aromatics. The main sources of aromatics in Italy were in 2012 transport (58 %), use of fuels and solvents (32 %), and domestic heating (15 %) (EDGAR, 2020).

Regarding SIA, early works used box models with thermodynamic schemes to address the sensitivity of ammonium nitrate and sulfate concentrations to gaseous NH₃, NO_x and SO₂ emissions (Watson et al., 1994; Blanchard and Hidy, 2003; Pozzer et al., 2017; Guo et al., 2018; Nenes et al., 2020). These models were later on integrated into chemical transport models (CTMs), in particular to address the benefit of additional NH₃ emission reductions in addition to already ongoing SO₂ and NO_x emission reductions. For North America, Makar et al. (2009) simulated with a regional CTM that a 30 % reduction of ammonia emissions would lead to about 1 µg m⁻³ reduction in PM_2.5. For Europe, Bessagnet et al. (2014) simulated the effects of a 30 % NH₃ emission reduction in addition to those foreseen by the Gothenburg Protocol for 2030 and found that the G ratio defined as the ratio between free ammonia and total nitrate (Ansari and Pandis, 1998) was a good predictor for the efficiency of NH₃ reductions on SIA concentrations. These sensitivities to emission reductions are often governed by complex chemical mechanisms. A well-known phenomenon is the release of free ammonia as a result of decreased SO₂ emissions and sulfate formation, which allows for the formation of additional particulate nitrate, as described for example by Blanchard and Hidy (2003) and Shah et al. (2018) for wintertime PM_2.5 over the eastern United States. For eastern China, Fu et al. (2017) and Lachatre et al. (2019) showed both from modelling and satellite observations that such processes lead to strongly increased ammonia tropospheric columns. Finally, several works compared CTM simulations to specific observations. For instance, Pay et al. (2012) showed that the G ratio was generally underestimated over Europe, inducing that the Caliope model they used could probably overestimate the efficiency of NH₃ emission reductions. Petetin et al. (2016) came to a similar conclusion comparing CHIMERE CTM simulations to observations in the Paris region. They ascribed this underestimation to missing NH₃ emissions especially during warmer periods.

The formation of SOA results from even more complex reactions involving photo-chemical oxidation (as for SIA), nitration, fragmentation and oligomerisation of gaseous precursors or secondary products (Kroll and Seinfeld, 2008; Shrivastava et al., 2017). Models generally use simplified parameterisations to calculate the SOA formation yield from various classes of parent VOCs (Tsigaridis et al., 2014), and comparison with measurements often shows that SOA sources are still missing in models (Huang et al., 2020; Tsimpidi, 2016).

In this work, we focus on one specific region in Europe, the Po basin. In a companion paper (Clappier et al., 2021) that analyses PM secondary formation chemical regimes across Europe, the Po basin is clearly identified as a peculiar area where the chemical regime distributions are the most complex, showing non-linear processes (Thunis et al., 2013, 2015; Carnevale, 2020; Bessagnet, 2014), especially those related to interactions between NO_x and NH₃. The Po basin is also one of the pollution hot spots in Europe where the number of days above the limit values prescribed by the European Ambient Air Quality Directives (AAQD) for PM₁₀ is yet largely exceeded (EEA, 2020). This situation results from the high emission density in this region and also from the geographical setting of the area, in the border of the Alps and Apennines mountain ranges that lead to very weak winds in the area, favouring the accumulation of atmospheric pollutants.

We focus the present analysis on the NH₃–NO_x chemical processes and describe their spatial and seasonal variability, which could help to design more effective mitigation strategies. We start by describing the modelling set-up and detail the series of simulations required to perform our analysis. Section 3 provides a brief overview of the modelled base-case concentrations. In Sect. 4, we analyse the sensitivity of PM_2.5 concentrations to NH₃ and NO_x emissions. Section 5 provides an analysis of the non-linearity in PM_2.5 response to these emissions, while in Sect. 6 we discuss the implications of these results in terms of mitigation measures and design of air quality plans. Conclusions are finally proposed.

2 Methodology

2.1 Modelling set-up

The modelling study is performed with the EMEP air quality model, version rv4_17 (Simpson et al., 2012). The emission input consists of gridded annual national emissions (SO₂, NO, NO₂, NH₃, NMVOC, CO and primary PM_2.5) at 0.1×0.1^∘ resolution, based on data reported every year by parties to the Convention on Long-range Transboundary Air Pollution (CLRTAP). These emissions are provided for 10 anthropogenic source sectors classified by SNAP (Selected Nomenclature for Air Pollution) codes (EMEP, 2003). Meteorological input data are based on forecasts from the Integrated Forecasting System (IFS), a global operational forecasting model from the European Centre for Medium-Range Weather Forecasts (ECMWF). Meteorological fields are retrieved at a 0.1×0.1^∘ longitude–latitude resolution and are interpolated to the 50×50 km² polar stereographic grid projection (EMEP, 2011).

The gas-phase chemistry is based on the evolution of the so-called “EMEP scheme” as described in Simpson et al. (2012) and references therein. The chemical scheme couples the sulfur and nitrogen chemistry to the photochemistry using about 140 reactions between 70 species (Andersson-Sköld and Simpson, 1999; Simpson et al., 2012). In the EMEP Status Report 1/2004 (Fagerli et al., 2004) the reactions that cover acidification, eutrophication and ammonium chemistry are described. The aqueous-phase chemistry describes the formation of sulfate in clouds via SO₂ oxidation by ozone and H₂O₂ and catalysed by metal ions. An important pathway of particulate nitrate formation is through the hydrolysis of N₂O₅ on wet aerosol surfaces that converts NO_x into HNO₃. More information on the chemical equations is given in Simpson et al. (2012), Sect. 7.

The EMEP model has two size fractions for aerosols, fine aerosol (PM_2.5) and coarse aerosol (PM_10−2.5). The aerosol components presently accounted for are sulfate (SO${}_{\mathrm{4}}^{\mathrm{2}-}$), nitrate (NO${}_{\mathrm{3}}^{-}$), ammonium (NH${}_{\mathrm{4}}^{+}$), anthropogenic primary PM and sea salt.

For inorganic aerosols, EMEP uses the MARS equilibrium module to calculate the partitioning between gas and fine-mode aerosol phase in the system of SO${}_{\mathrm{4}}^{\mathrm{2}-}$, HNO₃, NO${}_{\mathrm{3}}^{-}$, NH₃ and NH${}_{\mathrm{4}}^{+}$ (Binkowski and Shankar, 1995). Aerosol water is calculated to account for particle water within the PM_2.5 mass, which depends on the mass of soluble PM fraction and on the type of salt mixture in particles. Sea salt (sodium chloride) and dust components are not accounted for by MARS, which might lead to PM underestimations close to coastal sites and where the dust contribution is important. More information on the gas and aerosol partitioning is given in Simpson et al. (2012), Sect. 7.6.

Regarding secondary organic aerosols (SOA), the EmChem09soa scheme is used, which is a simplified version of the so-called volatility basis set (VBS) approach (Robinson et al., 2007; Donahue et al., 2009). The VBS mechanism is discussed in detail in Bergström et al. (2012). The main difference between the VBS schemes and EmChem09soa is that all primary organic aerosol (POA) emissions are treated as non-volatile in EmChem09soa. This is done to keep the emission totals of both PM and VOC components the same as in the official emission inventories. The semi-volatile biogenic and anthropogenic SOA species are assumed to further oxidise (also known as ageing process) in the atmosphere by OH reactions. This will lead to a reduction in volatility for the SOA and thereby increased partitioning to the particle phase. More information on SOA is given in Simpson et al. (2012), Sect. 7.7.

The modelling domain covers the entire Po basin (Fig. 1) with a 0.1 by 0.1^∘ resolution (polar stereographic projection centred at 60^∘ N) and includes 20 vertical levels. The initial and background concentrations for ozone are based on Logan (1998) climatology, as described in Simpson et al. (2003). For the other species, background/initial conditions are set within the model using functions based on observations (Simpson et al., 2003; Fagerli et al., 2004). The simulations cover the entire meteorological year 2015. We will not discuss the validation of the base-case simulation, as this is available in other publications (e.g. Simpson et al., 2012) and regular status reports by EMEP (https://emep.int/mscw/mscw_publications.html, last access: 1 June 2021).

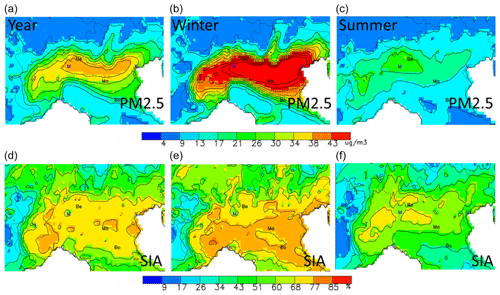
Figure 1 Seasonal variations of the base-case PM_2.5 (in µg m⁻³, a, b, c) and SIA (in percent of the PM_2.5 concentration, d, e, f). The abbreviations Be, Ma and Bo represent the locations selected for more detailed analysis: Bergamo (Be), Mantua (Ma) and Bologna (Bo). Other cities are indicated by their first letter for convenience: Venice, Milan, Turin and Genoa.

In this work, we simulated a series of 24 scenarios in which NO_x and NH₃ emissions were reduced independently or simultaneously by 25 %, 50 %, 75 % and 100 % from the base-case reference levels. Emission reductions were applied over the entire Po basin domain for a complete meteorological year (2015).

2.2 Spatial and temporal focus

Results are generally presented in terms of maps, but three locations within the domain were selected for a more detailed analysis. The locations are Bergamo (Be) in the northern part of the domain, Mantua (Ma; also known as Mantova) in the central eastern part of the Po basin and Bologna (Bo) in its southern part. As described in the following sections, we will see that these locations show very different behaviours in terms of response to emission changes.

We also aggregate results into two seasons: winter and summer, which cover the period from November to February and from April to September, respectively. These two seasons are characteristic of different chemical regimes as illustrated in the following sections. The process to define the temporal bounds of these two seasons is discussed in Appendix A. The two remaining months (March and October) represent transition periods and are not considered in our analysis.

As we only analyse processes involving inorganic gas-phase precursors, our focus is on secondary inorganic PM_2.5, although most of the results are expressed in terms of total PM_2.5 concentrations. The impact of NO_x emission reductions on SOA concentration is only briefly discussed in Sect. 5.

2.3 Indicators

To describe the interactions between NH₃ and NO_x emissions, we use the relationship proposed by Stein and Alpert (1993) and Thunis and Clappier (2014). This relation expresses the change in concentration resulting from a reduction of both precursors NO_x and NH₃ simultaneously, as the sum of two single concentration changes and an interaction term, as follows:

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }{C}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}=\mathrm{\Delta }{C}_{{\mathrm{NO}}_x}^{\mathit{\alpha }}+\mathrm{\Delta }{C}_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}+{\widehat{C}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }},\end{array}$$

where ΔC stands for the PM_2.5 concentration change (reference minus scenario) for a percentage α emission reduction (thus the term $\mathrm{\Delta }C/\mathit{\alpha }$ is defined as positive for a concentration reduction, consecutive to an emission reduction) and $\widehat{C}$ for the interaction term. We then scale each of these terms by the emission reduction (α) to generate potential impacts (P) (Thunis and Clappier, 2014).

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{\Delta }{C}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}}{\mathit{\alpha }}}& =P_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}=P_{{\mathrm{NO}}_x}^{\mathit{\alpha }}+P_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}+{\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}\\ & ={\displaystyle \frac{\mathrm{\Delta }{C}_{{\mathrm{NO}}_x}^{\mathit{\alpha }}}{\mathit{\alpha }}}+{\displaystyle \frac{\mathrm{\Delta }{C}_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}}{\mathit{\alpha }}}+{\displaystyle \frac{{\widehat{C}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}}{\mathit{\alpha }}}\end{array}\end{array}$$

This division by the factor α is a means to extrapolate virtually the impact resulting from any percentage emission reduction to 100 %. Potential impacts facilitate the comparison of concentration changes obtained for different emission reduction levels. Indeed, equal potential impacts imply a linear relationship between emission reductions and concentration changes. For example, $P^{\mathit{\alpha }}=P^{\mathit{\beta }}\Rightarrow \mathrm{\Delta }{C}^{\mathit{\alpha }}=\frac{\mathit{\alpha }}{\mathit{\beta }}\mathrm{\Delta }{C}^{\mathit{\beta }}$ for α and β, two emission reduction levels.

The overall potential impact is therefore the sum of two single potential impacts and one interaction term.

A relation between the potential impacts of combined emission reductions at two levels of intensity is obtained by writing Eq. (2) for two reduction levels α and β and subtracting the two equations. This leads to the following relation:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{P}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }}& =P_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}+\underset{{\widehat{P}}_{{\mathrm{NO}}_x}^{\mathit{\beta }-\mathit{\alpha }}}{\underbrace{P_{{\mathrm{NO}}_x}^{\mathit{\beta }}-P_{{\mathrm{NO}}_x}^{\mathit{\alpha }}}}+\underset{{\widehat{P}}_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }-\mathit{\alpha }}}{\underbrace{P_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }}-P_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}}}\\ & +\underset{{\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }-\mathit{\alpha }}}{\underbrace{{\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }}-{\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}}},\end{array}\end{array}$$

or equivalently via Eq. (2),

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{P}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }}& =P_{{\mathrm{NO}}_x}^{\mathit{\alpha }}+P_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}\\ & +\underset{\mathrm{non}-\mathrm{linear}\mathrm{terms}}{\underbrace{{\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}+{\widehat{P}}_{{\mathrm{NO}}_x}^{\mathit{\beta }-\mathit{\alpha }}+{\widehat{P}}_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }-\mathit{\alpha }}+{\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }-\mathit{\alpha }}}}.\end{array}\end{array}$$

While the two first terms on the right-hand side of Eq. (4) represent the single potential impacts, the remaining right-hand side terms quantify the magnitude of non-linearities. ${\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\alpha }}$ quantifies the NO_x–NH₃ interaction at level α; ${\widehat{P}}_{{\mathrm{NO}}_x}^{\mathit{\beta }-\mathit{\alpha }}$ and ${\widehat{P}}_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }-\mathit{\alpha }}$ are the single non-linearities associated with NO_x and NH₃ emissions, respectively, between levels α and β; and ${\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathit{\beta }-\mathit{\alpha }}$ represents the incremental change in the NO_x–NH₃ interaction between levels α and β.

Information about non-linearity is important to design air quality plans as it informs on the robustness of a given response, i.e. whether or not this response remains valid over a certain range and type of emission reductions. Because air quality models often provide responses for a limited set of scenarios that are then used as a basis to interpolate/extrapolate the responses to other emission reduction levels, robustness shall always be carefully assessed.

In the next section, we present the baseline results in terms of spatial and temporal variations.

3 Baseline concentrations of PM_2.5 and gaseous inorganic precursors

Before analysing the impact of emission changes on concentrations, it is worth having a look at the baseline concentration fields. In Fig. 1, the yearly averaged PM_2.5 concentration fields show a widespread pollution plume covering most of the area, with peak values extending in its central part. The maximum modelled yearly values reach 29 µgm⁻³, which represents an average between maximum winter values (maximum of 59 µgm⁻³) and minimum summer values (17 µgm⁻³).

The seasonal fields of PM_2.5 clearly show that high yearly average values mostly result from the winter season contributions when more stable atmospheric conditions lead to stagnant conditions, favouring the accumulation of particulate matter in the area (Pernigotti et al., 2014; Raffaelli et al., 2020). The increased emissions from the residential sector (heating, especially wood burning) foster this process (Ricciardelli et al., 2017; Hakimzadeh et al., 2020). Wintertime low temperatures also favour the partitioning of semi-volatile components (e.g. ammonium nitrate) towards the particulate phase. Overall, the relative contribution of secondary inorganic particles (SIA) ranges between 40 % and 50 %, regardless of the season, and is quite homogeneously distributed spatially over the entire area. Strategies targeting SIA have therefore the potential to abate about half of the total PM_2.5 concentration.

As mentioned earlier, the secondary inorganic fraction of PM_2.5 results from complex atmospheric processes that involve gaseous precursors (mainly SO₂, NO_x and NH₃), which can be summarised by the two following chemical pathways:

$$\begin{array}{}\text{(R1)}& {\displaystyle }\begin{array}{rl}& {\mathrm{NO}}_{\mathrm{2}}\left(\mathrm{g}\right)+\mathrm{OH}+\mathrm{M}\to {\mathrm{HNO}}_{\mathrm{3}}\left(\mathrm{g}\right)+\mathrm{M}\\ & {\mathrm{HNO}}_{\mathrm{3}}\left(\mathrm{g}\right)+{\mathrm{NH}}_{\mathrm{3}}\left(\mathrm{g}\right)\leftrightarrow {\mathrm{NH}}_{\mathrm{4}}^{+}\left(\mathrm{p}\right)+{\mathrm{NO}}_{\mathrm{3}}^{-}\left(\mathrm{p}\right),\end{array}\text{(R2)}& {\displaystyle }\begin{array}{rl}& {\mathrm{SO}}_{\mathrm{2}}\left(\mathrm{g}\right)+\mathrm{OH}\to \to {\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\left(\mathrm{g}\right)\\ & {\mathrm{SO}}_{\mathrm{2}}\left(\mathrm{aq}\right)+{\mathrm{O}}_{\mathrm{3}},{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\left(\mathrm{aq}\right)\to \to {\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\left(\mathrm{aq}\right)\\ & {\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\left(\mathrm{g}\right)\to {\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\left(\mathrm{p}\right)\to \to \mathrm{2}{\mathrm{H}}^{+}\left(\mathrm{p}\right)+{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\left(\mathrm{p}\right)\\ & {\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\left(\mathrm{p}\right)+\mathrm{2}{\mathrm{NH}}_{\mathrm{3}}\left(\mathrm{g}\right)\to \mathrm{2}{\mathrm{NH}}_{\mathrm{4}}^{+}\left(\mathrm{p}\right)+{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\left(\mathrm{p}\right)+{\mathrm{H}}_{\mathrm{2}}\mathrm{O},\end{array}\end{array}$$

where (g) means gas phase, (aq) means aqueous phase, and (p) means particulate matter, and the character $\to \to$ symbolises a chemical pathway that summarises a set of underlying reactions.

The second of these pathways (Reaction R2) is generally slower than the first one (Reaction R1), with the NO₂ oxidation specific time constant being typically some hours to a day and that of SO₂ being 1 to several days (Seinfeld and Pandis, 2006).

The spatial fields for the seasonal average concentrations of these precursors (Fig. 2) reflect their emission spatial patterns, resulting in a NO₂-rich area that comprises Milan plus its northern districts (and to a lesser extent, Turin), while NH₃ is more abundant in the central part of the Po basin, east of Milan, where intensive agriculture practices take place. Finally, high SO₂ concentrations are collocated with the NO₂-rich areas nearby Milan but with an additional zone around the harbour city of Genoa (also known as Genova; along the south coast), reflecting the more important SO₂ emissions from the shipping sector there. However, SO₂ concentrations are about 1 order of magnitude below those of NO₂. Seasonal variations are well marked for NO₂ and SO₂ concentrations – not so much in terms of minimum and maximum values but rather in terms of spread with an extended high-concentration zone during wintertime. In contrast, NH₃ concentrations remain very similar in summer and winter, both in terms of values and spatial distribution.

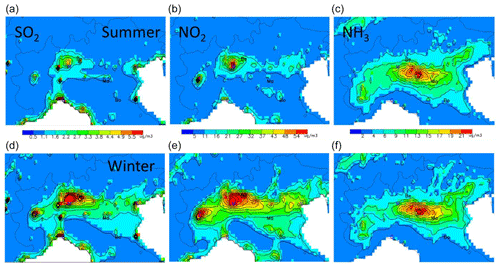
Figure 2 Summer (a, b, c) and winter (d, e, f) concentration base-case fields for SO₂ (a, d), NO₂ (b, e) and NH₃ (c, f) expressed in µg m⁻³. The abbreviations Be, Ma and Bo represent the locations selected for more detailed analysis: Bergamo (Be), Mantua (Ma) and Bologna (Bo). Other cities are indicated by their first letter for convenience: Venice, Milan, Turin and Genoa.

In next sections, we simulate a series of emission reduction scenarios to analyse the response of PM_2.5 concentration to single and combined reductions of NH₃ and NO_x.

4 Analysis of the SIA formation chemical regimes

4.1 Seasonal trends

From a strategic point of view, it is important to know whether NO_x (mostly emitted by the transport, industry and residential sectors) or NH₃ (mostly emitted by agriculture) needs to be reduced in priority in order to reach effective results on particulate pollution mitigation. In Clappier et al. (2021), we have observed a great heterogeneity in SIA formation chemical regimes across the Po basin, with different regimes being present in limited geographical areas. Here we intend to look at these regimes in more detail.

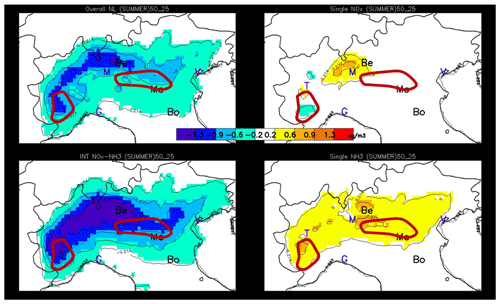
To analyse in detail the chemical regimes in the Po basin, we compare the two single potential impacts $P_{{\mathrm{NO}}_x}^{\mathrm{25}\mathit{\%}},P_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathrm{25}\mathit{\%}}$ obtained for moderate emission reductions of 25 %. Figure 3 provides a spatial overview of the difference between these two potential impacts ($P_{{\mathrm{NO}}_x}^{\mathrm{25}\mathit{\%}}-P_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathrm{25}\mathit{\%}}$). This indicator tells whether reductions of NO_x or NH₃ will lead to the greatest PM_2.5 concentration abatement, i.e. if the regime is rather NO_x- or NH₃-sensitive, with positive and negative values, respectively.

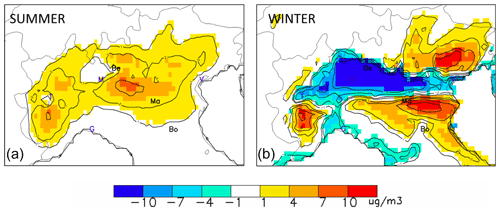
Figure 3 Winter (b) and summer (a) chemical regimes obtained from an emission reduction level of α=25 %. The maps represent the $P_{{\mathrm{NO}}_x}^{\mathrm{25}\mathit{\%}}-P_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathrm{25}\mathit{\%}}$ (unit: µg m⁻³) indicator that shows the NO_x- and NH₃-sensitive areas in yellow/red and blue, respectively. The abbreviations Be, Ma and Bo indicate the location of Bergamo, Mantua and Bologna, respectively. Other cities are indicated by their first letter for convenience: Venice, Milan, Turin and Genoa.

During summertime (Fig. 3 – left), the entire area is under weak NO_x-sensitive conditions with a maximum intensity in its central part, between Bergamo and Mantua.

During wintertime (Fig. 3 – right), the situation is contrasted with a wide and intense NH₃-sensitive area that appears around and south-eastwards of Bergamo. This area includes big cities like Milan. Other (not as marked) NH₃-sensitive regime zones appear near coastal areas. Most strongly NO_x-sensitive areas are located in the eastern parts of the domain, north of Bologna and Venice. NH₃-sensitive regimes are generally collocated with the NO₂- and SO₂-rich areas (Fig. 2), whereas NO_x-sensitive regimes coincide with NH₃-rich areas. The cases of the three selected cities (Bergamo, Mantua and Bologna) representative of the NH₃-sensitive, NO_x-sensitive and neutral regimes, respectively, are further analysed below.

The chemical regimes deducted from the results of emission reduction scenarios can be compared with the maps of the G ratio (Fig. 4), defined by Ansari and Pandis (1998) as the ratio between free ammonia (NH₃ and NH${}_{\mathrm{4}}^{+}$) and total nitrate (HNO₃+ NO${}_{\mathrm{3}}^{-}$) after neutralisation of H₂SO₄. Values of the G ratio below 1 indicate a NH₃-limited chemical regime, while values above 1 characterise a HNO₃-limited chemical regime.

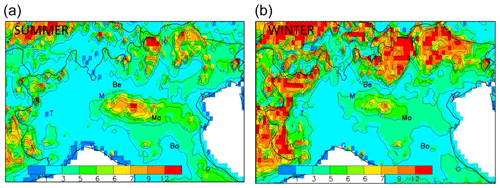
Figure 4 G ratio for winter (b) and summer (a) times. The abbreviations Be, Ma and Bo indicate the location of Bergamo, Mantua and Bologna, respectively. Other cities are indicated by their first letter for convenience: Venice, Milan, Turin and Genoa.

$$\begin{array}{}\text{(5)}& \mathrm{G}={\displaystyle \frac{{\mathrm{NH}}_{\mathrm{3}}\left(g\right)+{\mathrm{NH}}_{\mathrm{4}}^{+}\left(p\right)-\mathrm{2}{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\left(p\right)}{{\mathrm{HNO}}_{\mathrm{3}}\left(g\right)+{\mathrm{NO}}_{\mathrm{3}}^{-}\left(p\right)}}\end{array}$$

During summer, the G-ratio values well above unity indicate a HNO₃ limited chemical regime across the Po basin. This corresponds to a NO_x-sensitive chemical regime in this region (Fig. 3). Moreover, the location of the G-ratio maximum between Bergamo and Mantua spatially coincides with the most pronounced NO_x-sensitive regime and to a maximum of NH₃ concentrations of about 20 µg m⁻³ (Fig. 2). Indeed, NO_x emission reductions lead to HNO₃ concentration reductions, which is the limiting factor in NH₄NO₃ formation according to the G ratio. During winter, the G ratio still shows large values in the region south-east of Bergamo, but, contrary to summer, the chemical regime is clearly NH₃-sensitive (Fig. 3). More generally, G-ratio values remain above unity over the whole Po basin, while both NO_x- and NH₃-sensitive chemical regimes prevail in different areas. Therefore, the G ratio, related to the abundance of total free ammonia and total nitrate, provides information which differs from that obtained by determining the distribution of the NH₃- and NO_x-emission-sensitive chemical regimes. These differences illustrate the impossibility to directly use the G ratio for air quality management, an interesting result in itself. We will further discuss this interesting behaviour later when addressing non-linearity in Sect. 4.3.

4.2 Impact of the emission reduction strength

In this section, we repeat the analysis of Sect. 4.1 for yearly average concentrations but looking at the step changes of regimes as we progressively reduce emissions from the base-case situation. (Fig. 5). Chemical regimes are well in place for a 25 % level reduction (top left) and are only slightly perturbed from 25 % to 50 % with a reinforcement of the NO_x limited regime (top right). Despite this slight change in intensity, the regimes therefore keep the same spatial patterns. From 50 % onward, chemical regimes tend to attenuate and reverse themselves from 75 % to 100 % (bottom right).

In other words, locations that are NH₃-sensitive for the first steps emission reductions will become NO_x-sensitive for the last steps emission reductions, and vice versa.

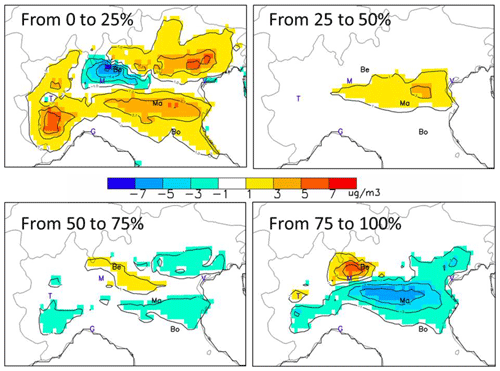
Figure 5 Yearly averaged chemical regimes obtained from a 25 % emission reduction starting at different levels of emissions corresponding to α=0, 25, 50 and 75. The maps represent the ($P_{{\mathrm{NO}}_x}-P_{{\mathrm{NH}}_{\mathrm{3}}}$) between the starting and ending levels (unit: µg m⁻³) showing the NO_x- and NH₃-sensitive areas in yellow/red and blue, respectively. The abbreviations Be, Ma and Bo indicate the location of Bergamo, Mantua and Bologna, respectively. Other cities are indicated by their first letter for convenience: Venice, Milan, Turin and Genoa.

4.3 A summarised overview: the PM_2.5 isopleths

Like isopleth plots that show the variations in the O₃ concentrations as a function of NO_x and VOC concentrations (Dodge, 1977), similar plots can be created for PM_2.5 concentrations as a function of NO_x and NH₃ emissions. Simulation results have indeed often been presented as 2D isopleths of PM_2.5 or nitrate as a function of precursor emissions, which allows showing in a comprehensive manner their sensitivity and also in a qualitative manner non-linear effects (for example Watson et al., 1994, over the USA; and Xing et al., 2018, over the Beijing–Tianjin–Hebei region in China). Figure 6 shows the PM_2.5 isopleths obtained through an interpolation among the 25 simulation concentration values (these 25 simulations correspond to the white square symbols in each isopleth diagram) at the three locations Be, Ma and Bo previously defined. The x and y axes represent the strengths of the NH₃ and NO_x emission sources, respectively. With this type of graphical representation, it is possible to visualise the response of PM_2.5 to a NO_x emission change by moving vertically, the reaction to a NH₃ emission change by moving horizontally or the reaction to a combined NO_x–NH₃ emission change by moving diagonally. The larger the number of isopleths we cross on the path (high gradient), the larger the expected impact from an emission reduction will be. A simple theoretical model to generate and interpret these isopleths is proposed in Appendix B.

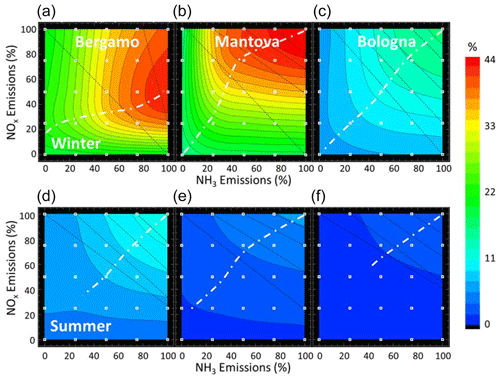
Figure 6 PM_2.5 isopleths during winter (a, b, c) and summer (d, e, f) at the three locations of interest (see maps). PM_2.5 concentrations are expressed in µg m⁻³ as a function of the intensity of the NO_x (y axis) and NH₃ (x axis) emissions, respectively. The overlaid dashed oblique lines on each diagram connect similar PM_2.5 concentration values for single NO_x and NH₃ reductions. The more vertical these lines are, the larger the NH₃ abatement impact compared to the NO_x abatement impact is; the more horizontal they are, the larger the NO_x abatement impact compared to the NH₃ abatement impact is. The dashed line delineates the ridge between the NH₃- and NO_x-sensitive areas.

From the analysis of the isopleths, we note the following points.

• In general, the isopleths show a regular pattern with a progressive decrease in PM_2.5 concentration when either the NO_x or NH₃ emissions are reduced, with the only exception being Bergamo during wintertime, where NO_x reductions up to 70 % lead to a small increase in PM_2.5 (Fig. 6 – top left), whatever the reduction in NH₃ emission is. We discuss this particular feature later in this section.

• The diagram areas can be divided into two zones separated by a ridge (dashed line in Fig. 6). Above the ridge line, PM_2.5 is more sensitive to NH₃, while below the ridge line, it is more sensitive to NO_x emission reductions. The orientation of the ridge (tending to vertical or horizontal) informs on the type of chemical regime (NO_x- or NH₃-sensitive, respectively).

• The efficiency of a NO_x vs. NH₃ emission reduction varies across locations. We can compare the efficiency of a given reduction by looking at the horizontal (for NO_x) and vertical (for NH₃) gradients. To support this comparison, we included in each diagram dashed oblique lines that connect similar PM_2.5 concentration values for single NO_x and NH₃ emission reductions. The more vertical these lines are, the larger the NH₃ abatement impact compared to the NO_x abatement impact is. Conversely, the more horizontal they are, the larger the NO_x abatement impact compared to the NH₃ abatement impact is. For moderate emission reductions (up to 50 %, top-right corner), different behaviours are observed: while in Bergamo PM_2.5 is more sensitive to NH₃ reductions, it is more sensitive to NO_x reductions in Mantua, and it is equally sensitive to both precursors in Bologna. This corresponds to the spatial patterns of NO_x- and NH₃-sensitive regimes depicted in Fig. 3.

• Winter- and summertime isopleths show completely different patterns in Bergamo, whereas at the two other locations, they remain similar.

• At Mantua where moderate NO_x reductions (e.g. 50 %) are the most efficient among the three sites, NH₃ emission reductions are more efficient than NO_x emission reductions for larger additional reductions (going for example from 75 % to 100 %). At Bergamo, NH₃ reductions are the most effective for moderate reductions, whereas NO_x reductions become more effective for larger reductions, as seen by the isopleths spacing. This confirms the finding of reversed chemical regimes for larger additional emission reductions detailed in the previous section and illustrated in Fig. 5.

The special pattern of Bergamo's PM_2.5 isopleths during wintertime needs some additional discussion. The increase in the inorganic fraction of PM_2.5 as a response to NO_x reductions during wintertime has already been noted by several authors (e.g. Le et al., 2020; Sheng et al., 2018). It has been related to an increase in the oxidising capacity of the atmosphere and in particular to increased ozone levels. This is due to the prevailing titration of O₃ by NO in wintertime high-NO_x conditions and in the absence of photochemical ozone production due to reduced solar radiation (Kleinman et al., 1991).

$$\begin{array}{}\text{(R3)}& \mathrm{NO}\left(\mathrm{g}\right)+{\mathrm{O}}_{\mathrm{3}}\left(\mathrm{g}\right)\to {\mathrm{NO}}_{\mathrm{2}}\left(\mathrm{g}\right)+{\mathrm{O}}_{\mathrm{2}}\left(\mathrm{g}\right)\end{array}$$

The impact of NO_x emission reductions on the concentration of various pollutants in Bergamo during wintertime is illustrated in Fig. 7. As expected, a 50 % reduction in NO_x emissions leads to a decrease in NO₂ concentration (from 47 to 28 µg m⁻³, i.e. a factor of 1.7). In contrast, O₃ concentration increases from 8 to 16 µg m⁻³, roughly a factor of 2. These compensating changes result in a small increase in NO₃ radical production (Reaction R4), which is the initial step of the major pathway of wintertime HNO₃ and particulate nitrate formation (Kenagy et al., 2018).

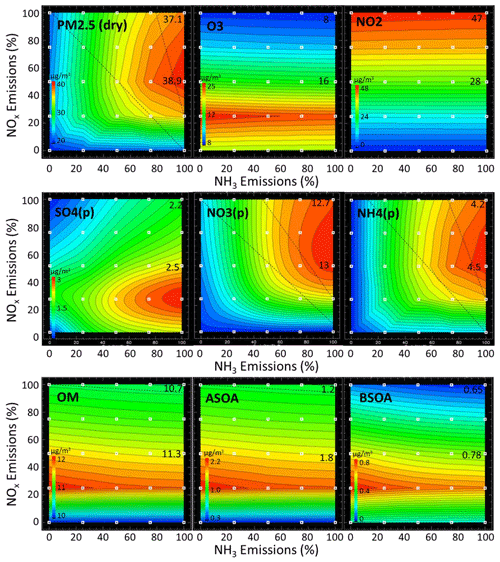
Figure 7 Wintertime isopleths in Bergamo for the species: dry PM_2.5, O₃, NO₂, sulfate (SO₄), nitrate (NO₃), ammonium (NH₄), organic matter (OM), and anthropogenic and biogenic secondary aerosols (ASOA and BSOA, respectively). The two numbers on the vertical axis indicate concentration values for the base case and at the 50 % NO_x emission level.

$$\begin{array}{}\text{(R4)}& {\mathrm{NO}}_{\mathrm{2}}\left(\mathrm{g}\right)+{\mathrm{O}}_{\mathrm{3}}\left(\mathrm{g}\right)\to {\mathrm{NO}}_{\mathrm{3}}\left(\mathrm{g}\right)+{\mathrm{O}}_{\mathrm{2}}\left(\mathrm{g}\right)\end{array}$$

In this pathway, the NO₃ radical formation is followed by combination with NO₂ to form N₂O₅, a reversible process, and heterogeneous HNO₃ formation on wet particle surfaces.

$$\begin{array}{}\text{(R5)}& {\displaystyle }{\mathrm{NO}}_{\mathrm{3}}\left(\mathrm{g}\right)+{\mathrm{NO}}_{\mathrm{2}}\left(\mathrm{g}\right)\leftrightarrow {\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}\left(\mathrm{g}\right)\text{(R6)}& {\displaystyle }{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}\left(\mathrm{g}\right)+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{aerosol}\mathrm{surface}\right)\to \mathrm{2}{\mathrm{HNO}}_{\mathrm{3}}\left(\mathrm{g}\right)\end{array}$$

The NO₃ radical has three major rapid sinks: reaction with NO, photolysis, and reaction with NMVOCs, especially terpenes.

$$\begin{array}{}\text{(R7)}& {\displaystyle }{\mathrm{NO}}_{\mathrm{3}}\left(\mathrm{g}\right)+\mathrm{NO}\left(\mathrm{g}\right)\to \mathrm{2}{\mathrm{NO}}_{\mathrm{2}}\left(\mathrm{g}\right)\text{(R8)}& {\displaystyle }{\mathrm{NO}}_{\mathrm{3}}\left(\mathrm{g}\right)+\mathrm{h}\mathit{\nu }\to {\mathrm{NO}}_{\mathrm{2}}\left(\mathrm{g}\right)+\mathrm{O}\left(\mathrm{g}\right)\text{(R9)}& {\displaystyle }{\mathrm{NO}}_{\mathrm{3}}\left(\mathrm{g}\right)+\mathrm{h}\mathit{\nu }\to {\mathrm{NO}}_{\mathrm{2}}\left(\mathrm{g}\right)+{\mathrm{O}}_{\mathrm{2}}\left(\mathrm{g}\right)\text{(R10)}& {\displaystyle }{\mathrm{NO}}_{\mathrm{3}}\left(\mathrm{g}\right)+\mathrm{NMVOC}\left(\mathrm{g}\right)\to \mathrm{products}\end{array}$$

Reactions (R3) to (R10) induce additional dependence of HNO₃ formation on NO_x species on top of Reaction (R1), but which partly cancel out, as they are both involved in formation and sink processes.

SOA is formed through a series of chemical reactions of gaseous precursors – mainly volatile, intermediate volatility or semi-volatile organic compounds (VOCs) with the oxidants O₃, OH and nitrate radical (NO₃) (Li et al., 2011).

$$\begin{array}{}\text{(R11)}& (\mathrm{S},\mathrm{I})\mathrm{VOC}\left(\mathrm{g}\right)+\mathrm{oxidants}\to (\mathrm{S},\mathrm{I})\mathrm{OVOC}\left(\mathrm{g}\right)\leftrightarrow \mathrm{SOA}\left(\mathrm{s}\right)\end{array}$$

Putting all the arguments together, it follows that wintertime ammonium nitrate formation over Bergamo is most probably controlled by NO₃ radical formation (Reaction R4). The fact that this behaviour is observed in Bergamo and not in Mantua or Bologna is due to the much larger NO₂ levels in the Bergamo–Milan area (above 50 µg m⁻³ during winter, Fig. 2). Such large NO₂ levels are also simulated locally over the Turin area and also lead to a slightly NH₃-sensitive regime there despite a G ratio well above unity. Beyond 50 % NO_x reduction, NH₄NO₃ formation decreases because NO₂ decreases more rapidly than ozone increases up to its maximum (at 75 % NO_x emission reduction; see Fig. 7).

The negative response of NH₄NO₃ to NO_x emission reductions in Be during wintertime explains the apparent discrepancies with the analysis of G ratio, which indicates that NH₄NO₃ is strongly HNO₃ limited. Simply, the HNO₃-limited chemical regime cannot be extrapolated to sensitivity to NO_x emissions in the case of the above shown negative response. Total nitrate is less abundant than free ammonia (defined as ${\mathrm{NH}}_{\mathrm{3}}\left(\mathrm{g}\right)+{\mathrm{NH}}_{\mathrm{4}}^{+}\left(\mathrm{p}\right)-\mathrm{2}{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\left(\mathrm{p}\right))$, but NO_x emission reductions up to about 50 % do not reduce its concentration, and NH₃ emission reductions are thus more efficient. In this respect, the G ratio cannot provide information about negative responses.

At Bergamo during winter, the increase in PM_2.5 (+1.8 µg m⁻³) arising from a 50 % reduction in NO_x emission also results from an increase in sulfate (+0.3 µg m⁻³) and in SOA (+0.6 µgm⁻³) concentrations. Both sulfate and SOA concentrations are closely related to O₃ concentrations (Fig. 7). The sulfate increase is comparable in magnitude to the nitrate increase, even if sulfate levels are much smaller than nitrate ones. Figure 7 actually shows a strikingly similar response of sulfate, SOA and ozone to NO_x emission reductions (given that SO₂ and NMVOC emissions are held constant). Indeed the prevailing wintertime aqueous production of H₂SO₄ requires oxidants and in particular ozone (Le et al., 2020; Sheng et al., 2018). In addition, the formation of SOA in both the gas and particulate phases also requires oxidants (Vahedpour et al., 2011; Huang et al., 2020; Feng et al., 2016, 2019; Li et al., 2011; Tsimpidi et al., 2010).

Pinder et al. (2008) also note an oxidant limitation for SIA formation over the eastern United states for the 2000 to 2020 period, but in their simulations, it mainly affects sulfate that increases as a result of NO_x emission reductions while nitrate decreases. This is due to a more important sulfate-to-nitrate ratio in the eastern United States than over the Po basin. Fu et al. (2020) derive from combined measurements and modelling that wintertime nitrate during haze events in the North China Plain (NCP) is nearly insensitive to 30 % NO_x emission reductions, because increased ozone levels increase the NO_x to HNO₃ conversion efficiency. Following these authors, this conversion also involves the homogeneous HNO₃ formation via the NO₂+OH. This reaction also could play a role in the Po basin, in addition to the heterogeneous pathway. Also Leung et al. (2020) simulate that wintertime nitrate abatement in the NCP is buffered with respect to emission reductions by increased oxidant build-up but also by sulfate to nitrate conversion by liberating free NH₃ through sulfate concentration reduction, which can then enhance nitrate formation. Womack et al. (2019) find an oxidant limitation of nitrate formation over wintertime Utah (USA) and show that nitrate concentration diminishes when reducing VOC emissions.

5 Analysis of non-linearities

Clappier et al. (2021) highlighted the specificities of the Po basin area within Europe. They showed that non-linearities are present in this region. One peculiarity of the Po basin is a marked difference between the chemical regimes encountered within a confined area, which have implications on the linearity of PM_2.5 responses to emission changes. In this section, we analyse in more details these non-linearities.

Information on the NO_x–NH₃ interaction term at the reduction level α=25 %, ${\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathrm{25}\mathit{\%}}[=P_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\mathrm{25}\mathit{\%}}-(P_{{\mathrm{NO}}_x}^{\mathrm{25}\mathit{\%}}+P_{{\mathrm{NH}}_{\mathrm{3}}}^{\mathrm{25}\mathit{\%}}\left)\right]$ (first non-linear term in Eq. 4), is provided in Fig. 8. At α= 25 %, the interaction term is negative (or null) across the entire modelling domain (most data points are below the 1:1 line) regardless of the chemical regimes and averages to approximately −10 %, as indicated by the linear fit slope (=0.9). In relative terms, this interaction term is also almost constant regardless of the season (not shown).

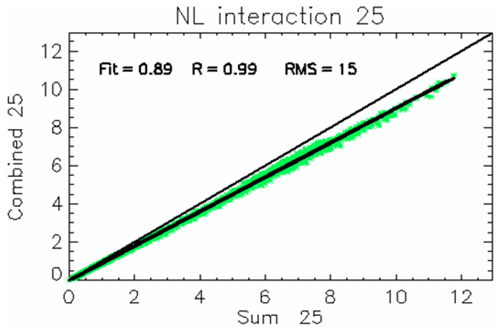
Figure 8 Yearly mean non-linear interaction term for a 25 % reduction in NO_x and NH₃. The scatter plot compares the sum of the potential impacts of the two single reductions (x axis) with the potential impact of the combined emission reduction (unit: µg m⁻³) (y axis). Departure from the 1:1 line quantifies the overall non-linearity. Each data point represents the yearly average values for a grid cell in the modelling domain.

This negativity can be explained by the fact that a reduction of only NO_x implies a reduction of both ${\mathrm{NO}}_{\mathrm{3}}^{-}$ and ${\mathrm{NH}}_{\mathrm{4}}^{+}$, and the same happens when reducing only NH₃; therefore a simultaneous reduction of both precursors is lower than the sum of the two. Single impacts would therefore lead to an overestimation (of about 10 %) in PM_2.5 reduction if added up to extrapolate linearly the impact of combined 25 % NO_x and NH₃ emission reductions on yearly averaged PM_2.5 concentrations. This result is expected for what concerns particulate NH₄NO₃, as a consequence of the gas–particle equilibrium described in Reaction (R1), although non-linear relationships between NO_x emissions and HNO₃ concentrations also play a role. Qualitatively, this negative interaction is also highlighted by the hyperbolic shapes of the PM_2.5 isopleths determined for three different sites of the domain (Fig. 6). As discussed in Appendix B, linearity would result in isopleths parallel to the descending diagonal lines.

When emission reductions increase from 25 % to 50 %, three additional non-linear terms are generated (three last terms in Eq. 4). Figures 9 and 10 provide an overview of these non-linear terms during wintertime and summertime, respectively. The top-left panel of each figure represents their sum, i.e. the total non-linearity generated between 25 % and 50 % emission reduction. The right column shows the non-linearities associated with NO_x and NH₃, while the bottom-left panel reports the non-linear interaction between the two precursors.

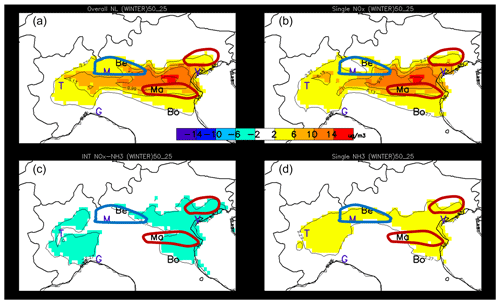
Figure 9 Wintertime maps of the overall non-linearity term (a) and of its components expressed as potential impacts between 25 % and 50 %: the single NO_x non-linearity term (a, b), the single NH₃ non-linearity term (d) and the NO_x–NH₃ interaction term (c). The three locations of interest, Bergamo, Mantua and Bologna, are indicated by their first two letters, while other cities are indicated with their first letter for convenience (Venice, Milan, Turin and Genoa). The hand-drawn contours roughly indicate the central position of the NH₃ (blue) and NO_x (red) sensitive regime areas (see Fig. 3 – right).

Figure 10 Same as Fig. 9 but for summertime.

Overall, non-linearities are more important during wintertime than during summertime. This is true both in absolute and relative (not shown) terms. Non-linearities tend to be the largest in between areas that are characterised by well-marked NH₃- or NO_x-sensitive regimes (indicated by the blue and red drawn contours). This can be explained by the fact that when one of the two components (NO_x or NH₃) is in large excess (compared to the other one), reductions of this compound have then generally only little impact, implying that both single and combined reductions only involve one compound and are therefore similar.

During wintertime, the overall non-linearity (Fig. 9 top left) is largely dominated by the single NO_x-related non-linearity (${\widehat{P}}_{{\mathrm{NO}}_x}^{\text{50\hspace{0.17em}\%–25\hspace{0.17em}\%}}$, Fig. 9 top right) – a singularity in Europe as the Po basin is the only area where this occurs to this extent (Clappier et al., 2021). In the region of Bergamo, the NO_x non-linearity remains weak despite the peculiar PM_2.5 responses to NO_x emission reductions (i.e. an increase in PM_2.5 concentrations for NO_x emission reduction up to 50 %, Fig. 7). In this NH₃-sensitive region, this behaviour can be explained by the strong oxidant limitation of HNO₃ formation outlined above (Fig. 7). It is worth mentioning that, although atypical, this behaviour is quasi-linear with PM_2.5 responses that remain proportional to the emission reduction strength (up to 50 %) but with a negative slope. Similarly to NO_x, NH₃ single non-linearities (Fig. 9, bottom right) are positive but weaker, indicating slightly larger potential impacts for emission reductions in the range 25 %–50 % than in the 0 %–25 % range. Finally, the NO_x–NH₃ non-linear interaction terms (Fig. 9, bottom left) are mostly negative, indicating that the interaction term for 50 % emission reductions is more negative than the corresponding term for 25 %, pointing out to a strengthening of the NO_x–NH₃ non-linearity when more intense emission reductions are considered.

In relative terms, the overall wintertime non-linearity terms increase by about 30 % when emission reductions increase from 25 % and 50 % (Fig. 11 top, blue points). Note that these non-linearity terms reach larger values in some places of the modelling domain as highlighted by the data point dispersion. In a previous work, Thunis et al. (2015) quantified the non-linearity of model responses to emission reductions in three areas in Europe, among which is the Po Basin. One of their conclusions was that non-linearities remain relatively low for yearly averaged responses. Although the results presented here show important non-linearities, these occur mainly during wintertime and are limited to specific areas. It is also worth noting that these non-linear responses (for moderate emission reductions up to 50 %) only occur in the Po Basin (Clappier et al., 2021).

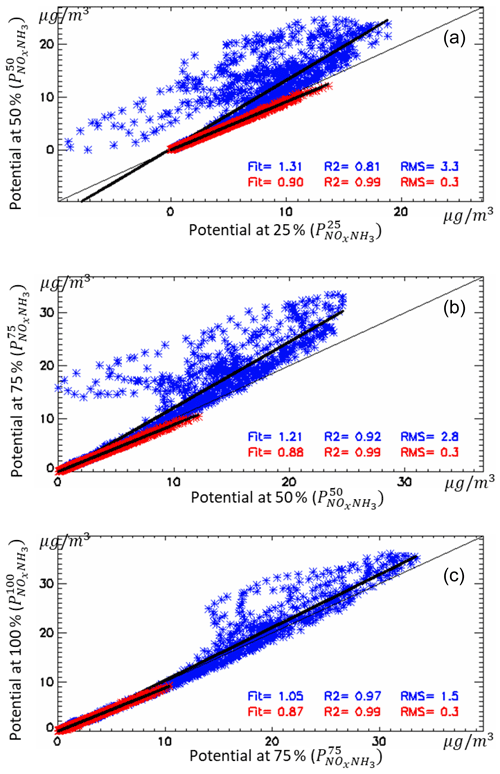
Figure 11 Changes in the overall non-linearity terms from 25 % to 50 % (a), from 50 % to 75 % (b) and from 75 % to 100 % (c) in NO_x and NH₃. The overall non-linearity is visualised as the distance from the 1:1 diagonal, i.e. the difference between the overall potential impact at two levels of emission reduction, x and y axis. Each point represents one land grid cell within the domain for wintertime (blue) and summertime (red). The “fit” parameter indicates the slope of the regression line, while R2 and RMS provide information on the coefficient of determination and the root mean square error, respectively.

During summertime, the magnitude of non-linear terms is smaller than during wintertime. The overall non-linearity term (top left) is dominated by the NH₃–NO_x non-linear interaction term (${\widehat{P}}_{{\mathrm{NO}}_x{\mathrm{NH}}_{\mathrm{3}}}^{\text{50\hspace{0.17em}\%–25\hspace{0.17em}\%}}$, Fig. 10, bottom left). In summer, the PM_2.5 concentration is NO_x-sensitive in almost all the domain (Fig. 3), and emission reductions do not lead to shifts in the chemical regimes. In this case, the interaction terms become more important. The non-linear interaction terms are negative everywhere in the Po basin, implying again that the interaction terms at 50 % are more negative than at 25 % emission reduction (reinforcement of the non-linearities when more intense emission reductions are considered). Most negative values appear in the western and northern part of domain.

Figure 11 shows the increase in the overall non-linear terms for emission reduction steps starting from different points, from 25 % to 50 %, from 50 % to 75 % and finally from 75 % to 100 %. Regardless of the emission reduction step, summertime non-linearities remain small all over the domain, with the regression slope close to 0.9 and very limited data point dispersions (i.e. low RMSE). Wintertime non-linearities further increase significantly from 50 % to 75 % reduction levels (regression fit parameter close to 1.21) but tend to stabilise between 75 % and 100 % reduction levels (regression fit parameter close to 1.05). It is interesting to note that potential impacts in winter increase for all segments (all winter points are above the 1:1 line), indicating that the same percentage reduction (25 %) gains progressively more impact when more intense reductions are considered.

6 Discussion

When designing air quality plans, it is important to identify the key precursors on which to act in priority to hit a specific air quality target but also to understand the consequences of these choices for various seasons (temporal variations), locations (spatial variability), emission reduction levels (strength) and strategies (combined or single emission reductions). As the information to make this decision is generally incomplete, assessing the robustness of the available model responses is essential. From the results presented here, a few key points appear.

The seasonal and spatial variabilities in the response of PM_2.5 to the reduction of NO_x and NH₃ emissions are extremely large, with different and sometimes opposite responses to emission changes. Yearly averages do not represent the appropriate time window to evaluate the impact of such emission reductions, and a focus on wintertime (November to February) seems to be the right option, especially because concentrations are larger during this period of the year.

The responses of PM_2.5 to emission reduction plans that cover the whole area (i.e. uniform emission reductions are applied everywhere in the domain) vary from location to location: opposite responses occur within a few hundred kilometres for some reduction levels. In the region of Bergamo, the PM_2.5 response to NO_x emission reductions can be negative, meaning an increase in PM_2.5 when reducing the NO_x emissions. It is important to combine NO_x and NH₃ emission reductions in winter or to go for stronger emission reductions to make sure these unwanted effects are limited.

Despite quite important non-linearities, PM_2.5 responses to emission reductions are not chaotic. Indeed, regardless of the emission reduction level, the non-linear terms related to NH₃ emission reduction and to NO_x–NH₃ interactions are quite uniform spatially. This is not the case of NO_x emission reduction, for which care must be taken to ensure that the detailed response of PM_2.5 is captured.

Although they are location specific, PM_2.5 isopleths represent an interesting tool to assess the impact of different NO_x and NH₃ emission reductions on PM_2.5 concentration. They indeed allow visualising in one single diagram the impact of any type of reductions on concentrations in a single grid cell (or set of grid cells). We must however remember that these isopleths derive from uniform emission reduction over the whole domain. Comparing sites where PM_2.5 responses to the same “domain-wide” policy are different, it appears challenging to define a single domain-wide policy efficiently reducing PM at all locations.

7 Conclusions

In this work, we analysed the sensitivity of PM_2.5 to NO_x and NH₃ emissions by means of a set of EMEP simulations performed with different levels of emission reductions, from 25 % up to a total switch-off of those emissions. Both single and combined precursor reduction scenarios were applied to determine the most efficient emission reduction strategies and quantify the interactions between NO_x and NH₃ emission reductions. Our results confirm the peculiarity of secondary inorganic PM_2.5 formation in the Po basin suggested by Clappier et al. (2021), characterised by contrasting chemical regimes within distances of a few (hundred) kilometres, as well as non-linear responses to emission reductions during wintertime. One of the striking results is the increase in the PM_2.5 concentration levels when NO_x emission reductions are applied in NO_x-rich areas, such as the surroundings of Bergamo. The isopleths in the graphs showing PM_2.5, nitrate, sulfate, SOA and O₃ concentrations as a function of NH₃ and NO_x emissions (Fig. 7) indicate that the increased oxidative capacity of the atmosphere is the cause of the increase in PM_2.5 induced by a reduction in NO_x emission of up to 50 %. This process can have contributed to the absence of significant PM_2.5 concentration decrease during the COVID-19 lockdowns in many European cities (EEA, 2020; Putaud et al., 2021). It is important to account for this process when designing air quality plans, since it could well lead to transitionary increases in PM_2.5 at some locations in winter as NO_x emission reduction measures are gradually implemented. At this type of location, mitigation measures that would be optimal in the long term might not be efficient in the short term.

Joint analyses of PM sensitivity to emissions and the G ratio can give a clue if a NH₃-sensitive chemical regime is due to either a lack of NH₃ or to a non-linear and negative response of HNO₃ concentration to NO_x emissions. In this latter case, the chemical regime is NH₃-sensitive in terms of NH₃ and NO_x emission reductions, but it can be HNO₃ limited in terms of the G ratio, as observed for the Bergamo–Milan region. Inversely, a G ratio greater than 1, indicating HNO₃ limitation to particulate nitrate formation, does not necessarily indicate a larger sensitivity to NO_x than to NH₃ emissions. Thus, our results show the impossibility to directly use the G ratio for air quality management, an interesting result in itself. While PM_2.5 chemical regimes (determined by the relative importance of the NO_x vs. NH₃ responses to emission reductions) show large variations seasonally and spatially, they are not very sensitive to moderate (up to 50 %) emission reductions. Beyond 25 % emission reduction strength, responses of PM_2.5 concentrations to NO_x emission reductions become non-linear in certain areas of the Po basin mainly during wintertime.

Since sulfate concentrations are low in the Po basin, the impact of SO₂ emission reductions was not evaluated here. However, the simulations performed in Clappier et al. (2021) indicate that air quality improvement plans addressing SO₂ emissions may still lead to additional PM_2.5 decreases. Further works should also test if NMVOC emission would further affect the concentration of oxidants and subsequently of nitrate (and sulfate) during winter. This depends on the fraction of ozone formed photochemically in the Po basin, compared to the one transported from outside by advection or entrainment.

Finally, it would be important to compare the results obtained in this work from the EMEPrv4_17 model with similar results obtained from other models. With its complex setting, the Po basin represents a good test case for such inter-comparisons.

Appendix A: Selection of seasons

Chemical regimes show a great variability with time. To select the extension of the seasons, we analyse the monthly behaviour of the NH₃ and NO_x responses as well as the interaction terms (Fig. A1). The analysis is performed for two locations: Bergamo, which lies in a NH₃-sensitive zone; and Mantua, which lies within a NO_x-sensitive zone. On these plots, we identify two major seasons with a consistent behaviour: winter from November to February and summer from April to September. These two seasons are similar at both locations. The two remaining months, March and October, are transition months and are not considered in the analysis. It is interesting to note that these two transition periods correspond more or less to the switching time between the NO_x and NH₃ concentration time profiles (Fig. 12 – right panel). On the latter figures, the SO₂ and NO₂ temporal evolutions are almost identical, in contrast to NH₃.

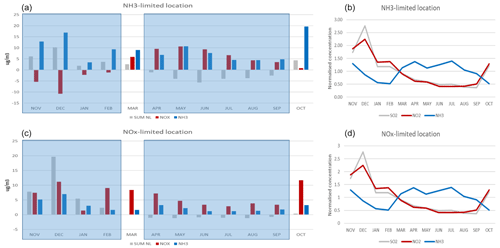
Figure A1 Monthly averaged responses to NH₃ (blue), NO_x (red) reductions (25 %) and interaction terms (grey) at two locations: Bergamo (a, b) and Mantua (c, d). Panels (b) and (d) shows the monthly evolution of the concentrations of NO₂, NH₃ and SO₂ at those two locations. Note that concentrations are normalised by their average values.

Appendix B: A theoretical example for the isopleths

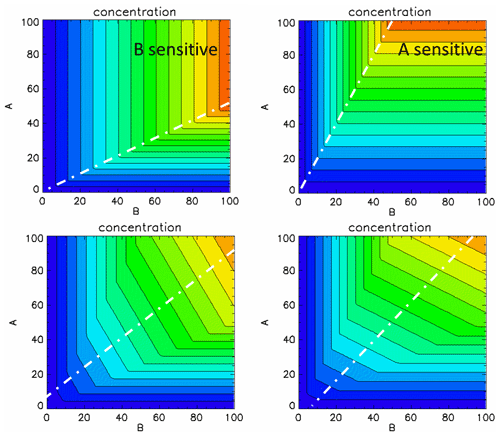
To facilitate the interpretation of the isopleths diagrams, we use a simple theoretical example that mimics the complex reactions process schematised by Reactions (R1) and (R2) above. Our simplified process is described by the following relation: $C_{\mathrm{c}}\left(x,y\right)=\min \left(E_{\mathrm{A}}\left[x\right],E_{\mathrm{B}}\left[y\right]\right)$, where C_c is the concentration of a compound “c” that is given by the minimum between two emitted species A and B. The concentration depends on the strengths of these emissions, specified by the parameters x and y. For each emission strength (x or y), the two emission species are proportional to their full-scale value (100 %): E_A(x)=xE_A[100] and E_B(y)=yE_B[100], respectively. If we choose E_A(100)≫E_B(100), we create a B-sensitive environment (Fig. B1 – left column) and inversely (Fig. 13 – right column). If we select mixed situations, representing for example an average of days, during which we alternate between A- and B-sensitive regimes, we obtain the two bottom isopleth diagrams that represent cases where a larger number of A-sensitive (right) or B-sensitive (left) events are recorded. Although extremely simple, these diagrams illustrate properties that are observed on the real test cases.

Let us take the example of an A-sensitive regime. Similar observations can be made in the case of a B-sensitive regime. We note the following points.

• The diagram area can roughly be divided into two zones separated by a ridge: a top-left triangle where the sensitivity to emission reductions of species “B” dominates and a bottom-right triangle where the sensitivity to A dominates. The slope of the ridge (larger or less than 1) informs on the type of regime.

• In the case of a single A-sensitive day (top right) with E_B(100)=2E_A(100), the concentration of compound “c” remains unchanged for emission reductions of B up to 50 %, while its concentration react in a linear way to emission changes in A from 0 % to 100 %. Between the base case and a reduction level of 50 %, the A gradient is therefore larger than the B gradient. This implies that the B gradient is larger than the A gradient between the 50 % and 100 % reduction levels because we know that for a 100 % reduction of A or B, the concentration must be zero. In our simple example, the gradient of B is zero from 0 % to 50 % but is twice as large as A between 50 % and 100 %.

• While the combination of several events (e.g. days) characterised by different regimes leads to smoother isopleths (bottom), the same characteristics can be noted. In particular, the inclination (tending to the horizontal or vertical) provides information on the type of chemical regime.

Figure B1 Isopleths for a simple theoretical system consisting of two emission precursors (A and B) competing through non-linear reactions to the concentration of a pollutant. See details in the text.