the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A predictive thermodynamic framework of cloud droplet activation for chemically unresolved aerosol mixtures, including surface tension, non-ideality, and bulk–surface partitioning
This work presents a thermodynamically consistent framework that enables self-contained, predictive Köhler calculations of droplet growth and activation with considerations of surface adsorption, surface tension reduction, and non-ideal water activity for chemically complex and unresolved surface-active aerosol mixtures. The common presence of surface-active species in atmospheric aerosols is now well-established. However, the impacts of different effects driven by surface activity, in particular bulk–surface partitioning and resulting bulk depletion and/or surface tension reduction, on aerosol hygroscopic growth and cloud droplet activation remain to be generally established. Because specific characterization of key properties, including water activity and surface tension, remains exceedingly challenging for finite-sized activating droplets, a self-contained and thermodynamically consistent model framework is needed to resolve the individual effects of surface activity during droplet growth and activation. Previous frameworks have achieved this for simple aerosol mixtures, comprising at most a few well-defined chemical species. However, atmospheric aerosol mixtures and more realistic laboratory systems are typically chemically more complex and not well-defined (unresolved). Therefore, frameworks which require specific knowledge of the concentrations of all chemical species in the mixture and their composition-dependent interactions cannot be applied. For mixtures which are unresolved or where specific interactions between components are unknown, analytical models based on retrofitting can be applied, or the mixture can be represented by a proxy compound or mixture with well-known properties. However, the surface activity effects evaluated by such models cannot be independently verified. The presented model couples Köhler theory with the Gibbs adsorption and Szyszkowski-type surface tension equations. Contrary to previous thermodynamic frameworks, it is formulated on a mass basis to obtain a quantitative description of composition-dependent properties for chemically unresolved mixtures. Application of the model is illustrated by calculating cloud condensation nuclei (CCN) activity of aerosol particles comprising Nordic aquatic fulvic acid (NAFA), a chemically unresolved and strongly surface-active model atmospheric humic-like substance (HULIS), and NaCl, with dry diameters of 30–230 nm and compositions spanning the full range of relative NAFA and NaCl mixing ratios. For comparison with the model presented, several other predictive Köhler frameworks, with simplified treatments of surface-active NAFA, are also applied. Effects of NAFA surface activity are gauged via a suite of properties evaluated for growing and activating droplets. The presented framework predicts a similar influence of surface activity of the chemically complex NAFA on CCN activation as was previously shown for single, strong surfactants. Comparison to experimental CCN data shows that NAFA bulk–surface partitioning is well-represented by Gibbs adsorption thermodynamics. Contrary to several recent studies, no evidence of significantly reduced droplet surface tension at the point of activation was found. Calculations with the presented thermodynamic model show that throughout droplet growth and activation, the finite amounts of NAFA in microscopic and submicron droplets are strongly depleted from the bulk, due to bulk–surface partitioning, because surface areas for a given bulk volume are very large. As a result, both the effective hygroscopicity and ability of NAFA to reduce droplet surface tension are significantly lower in finite-sized activating droplets than in macroscopic aqueous solutions of the same overall composition. The presented framework enables the influence of surface activity on CCN activation for other chemically complex and unresolved aerosol mixtures, including actual atmospheric samples, to be systematically explored. Thermodynamic input parameters can be independently constrained from measurements, instead of being either approximated by a proxy or determined by retrofitting, potentially confounding several mechanisms influenced by surface activity.
- Article
(2561 KB) - Full-text XML
-
Supplement
(2539 KB) - BibTeX
- EndNote
The surface activity of atmospheric aerosol components and its implications for cloud microphysics have been investigated for several decades. By definition, surface-active (surfactant) material adsorbs at the surface of a solution, leading to enhanced surface concentrations (activity), compared to the (interior) bulk, and a resulting radial concentration gradient between the surface and bulk phases. Due to this enhanced surface activity, surfactants can typically reduce surface tension of aqueous solutions more efficiently at a given concentration than homogeneously mixed solutes. Shulman et al. (1996) showed that reduced surface tension in aqueous droplets can alter the shape of their equilibrium growth curve as described by Köhler theory (Köhler, 1936) and thereby lower the critical supersaturation threshold for cloud droplet activation. Facchini et al. (1999, 2000) then demonstrated that surface-active material is indeed present in atmospheric cloud and fog samples, which can significantly reduce aqueous surface tension at concentrations comparable to those expected in activating droplets. Surface-active species have now been found in atmospheric aerosols from many different environments (e.g., Petters and Petters, 2016; Gérard et al., 2016; Kroflič et al., 2018).
To describe the evolving state of a growing droplet, calculations based on Köhler theory generally require knowledge of composition-dependent thermodynamic properties for the droplet in some form. The surface equation of state for a solution can be given in terms of either the surface or bulk composition, as these quantities are related via the equilibrium bulk-to-surface concentration gradient for a given surface-active substance. A number of techniques exist to experimentally determine the surface tension–composition relations for surfactant solutions, which almost exclusively require macroscopic (i.e., millimeter-scale or larger) sample sizes (Fainerman et al., 2002; Hyvärinen et al., 2006; Vanhanen et al., 2008; Alvarez et al., 2010; Kristensen et al., 2014; Bzdek et al., 2020). In these macroscopic solutions, the bulk phase can be considered an infinite reservoir, compared to the finite surface phase. Surface adsorption and enhanced surface activity therefore involve only a small fraction of the total amount of surface-active solute and have a negligible effect on the bulk composition. As a consequence, surface tension–composition relations reported in terms of total solute concentrations, which are readily constrained experimentally for macroscopic solutions, closely reflect the corresponding bulk composition. In microscopic and submicron activating cloud droplets, both surface and bulk phases are finite, and the surface area (A) to bulk volume (V) ratio may be orders of magnitude greater than for macroscopic solutions (Prisle et al., 2010; Lin et al., 2020). For example, a spherical droplet with diameter d=1 µm has m−1, whereas m−1 for a macroscopic droplet with d=1 mm. Because the finite-sized droplets comprise a finite total amount of surface-active solute, surface adsorption can therefore significantly deplete the droplet bulk phase. Furthermore, the highly sensitive variation of with the size of a finite solution introduces a size-dependent shift in both surface and bulk concentrations of a surface-active substance at the adsorption equilibrium.
The distribution of a surface-active substance between the distinct bulk and surface phases of a solution is referred to as its bulk–surface partitioning. Size-dependent partitioning has been predicted to in turn result in size-modulated composition-dependent properties for finite-sized solution droplets (Bianco and Marmur, 1992; Laaksonen, 1993; Sorjamaa et al., 2004; Prisle et al., 2010), including surface tension (a surface property) and water activity (a bulk property). These are key thermodynamic properties in Köhler theory determining aerosol water uptake, hygroscopic growth, and cloud droplet activation (e.g., Sorjamaa et al., 2004; Prisle et al., 2010). Until recently, experimental evidence for this effect in cloud microphysics has been indirect, from the reported inability of Köhler models directly using property–composition relations for macroscopic solutions to reproduce observed microscopic droplet activation. For example, a range of studies have consistently demonstrated that using surface tension and water activity relations based on total solution composition, without explicit consideration of the impact of bulk–surface partitioning on bulk composition, can lead to dramatic overestimations of cloud condensation nuclei (CCN) activity (Li et al., 1998; Sorjamaa et al., 2004; Prisle et al., 2008, 2010; Kristensen et al., 2014; Hansen et al., 2015; Petters and Petters, 2016; Lin et al., 2018; Forestieri et al., 2018; Prisle et al., 2019). Although previous work has measured the surface tension of micron-sized droplets or air bubbles suspended in a macroscopic surfactant solution medium (e.g., Jin et al., 2004; Alvarez et al., 2010), depletion of the bulk from surface adsorption is not significant in these conditions, as the bulk phase in such systems can be considered infinite, compared to the droplet or bubble surface. Bzdek et al. (2020) presented measurements of concentration-dependent surface tensions for finite-sized, surfactant-containing aqueous droplets suspended in air, which were significantly higher than those of macroscopic solutions with identical total compositions. These results provided the first direct experimental evidence for the influence of bulk-phase depletion from size-dependent bulk–surface partitioning on the air–solution surface tension of microscopic droplets.
Due to size-dependent effects of bulk–surface partitioning, in calculations of the cloud forming potential of surface-active aerosol using Köhler theory, macroscopic solution property–composition relations must be connected to those of growing microscopic droplets with changing via a partitioning model. An overview of the most widely used partitioning models in connection with Köhler theory is given by Malila and Prisle (2018). Thermodynamic partitioning models are typically based on a suitable adsorption isotherm and surface tension equation of state for the surface-active components. Furthermore, predictive models, such as those presented by Prisle et al. (2010), Topping (2010), Raatikainen and Laaksonen (2011), Petters and Kreidenweis (2013), and Ovadnevaite et al. (2017), generally require all droplet chemical components to be well-defined and input of compound-specific thermodynamic properties with well-characterized composition dependencies. Many process-level experimental and modeling studies of surface-active aerosols have therefore used sodium dodecyl sulfate (SDS) and similar industrial surfactants with relatively well-known properties as model compounds to represent the surface-active components of real atmospheric aerosols (e.g., Li et al., 1998; Sorjamaa et al., 2004; Harmon et al., 2010; Prisle et al., 2011; Raatikainen and Laaksonen, 2011; Petters and Kreidenweis, 2013). This has in part been due to the significant challenges involved in obtaining sufficient amounts of atmospheric samples and characterizing their composition and composition-dependent properties, including surface activity in aqueous solutions (e.g., Kroflič et al., 2018; Prisle et al., 2019). Furthermore, for the surface-active compounds which have so far been identified atmospheric samples, thermodynamic properties are typically not well-constrained, even in binary aqueous solutions or very simple mixtures (e.g., Prisle et al., 2008, 2010; Hansen et al., 2015).
The first atmospheric surfactants studied using predictive Köhler calculations together with a thermodynamic partitioning model were straight-chain fatty acid sodium salts (Prisle et al., 2008, 2010, 2011; Forestieri et al., 2018), which are widely identified in atmospheric aerosol samples (e.g., Yassaa et al., 2001; Mochida et al., 2002, 2003; Cheng et al., 2004). The predictive, thermodynamic Köhler models using detailed compound-specific solution properties have overall reproduced experimental observations of CCN activity well for the simple surface-active aerosols comprising a single or few well-defined compounds. Both SDS and the fatty acids and their salts are relatively strong surfactants; yet, contrary to expectations based on earlier studies (e.g., Shulman et al., 1996; Facchini et al., 1999), the modeled effect of surface tension on CCN activation was found to be very modest, due to strong depletion of the surfactant species from the bulk phase in activating droplets arising from surface partitioning. However, these results cannot immediately be generalized to describe the impact of surface activity for all aerosols in the atmosphere. First, the atmospherically relevant surfactants studied so far (see, e.g., overview by Petters and Petters, 2016) comprise only a narrow selection of often chemically simple, homologous molecules, which most likely do not represent the properties of all the different surface-active compounds present in the atmosphere. Second, atmospheric aerosol samples, as well as those generated in more elaborate laboratory experiments, often comprise chemically complex mixtures, which are either partially or entirely unresolved.
Several recent studies have presented results which are consistent with an enhancement of effective aerosol hygroscopic properties (i.e., derived based on observations of total water uptake) by surfactants, at least partly due to reduced surface tension, even when bulk–surface partitioning has been accounted for. George et al. (2009) found evidence for enhancement of CCN activity from reduced surface tension by surface-active oxidation products in complex aerosol mixtures formed by chemical aging of submicron bis-2-ethylhexyl sebacate (BES) and stearic acid particles in a reactor flow tube. By comparing measurements of CCN activity for surface-active limonene-derived organosulfate products (secondary organic aerosol (SOA) compounds) and water-soluble pollen extracts (primary organic aerosol (POA) compounds) in mixtures with ammonium sulfate to Köhler model predictions, Hansen et al. (2015) and Prisle et al. (2019) showed that experimentally determined droplet activation was consistent with the presence of both moderate bulk-phase depletion and reduced droplet surface tension. Ruehl et al. (2016) measured the sizes of activating droplets along the Köhler curves and at the point of CCN activation for ammonium sulfate particles coated by dicarboxylic acids or α-pinene ozonolysis SOA and found that the shape of the growth curves and the resulting critical droplet sizes were best described by accounting for both surface partitioning and reduced droplet surface tension. Ovadnevaite et al. (2017) used organic proxy mixtures, comprising well-known SOA components and dicarboxylic acids, to describe nascent ultrafine mode (NUM) particles measured in North Atlantic marine air masses at Mace Head, with diameters up to 50 nm and approximately equal amounts of organics and non-sea-salt sulfate. They showed that while surface tension and bulk depletion effects may cancel out for the larger particles, similarly to what was previously found for SDS and fatty acid salts (Prisle et al., 2008, 2010, 2011), surface tension lowering can for the NUM particles prevail over the reduction in the Raoult effect and lead to substantial increases in CCN activity. Similar mechanisms could also be present for the bacterial biopolymers investigated by Dawson et al. (2016) as a proxy for complex marine hydrogels. These substances produce significant surface tension reduction in macroscopic solutions (Lee et al., 2012), which is not reflected in experimental hygroscopic properties for aerosol mixtures with various salts. Dawson et al. (2016) suggested crosslinking between polymers and formation of insoluble complexes as a possible explanation. Another potential explanation could be bulk depletion from surface partitioning.
A major challenge in establishing general results for the role of surface-active aerosol in cloud microphysics relates to the composition-dependent thermodynamic description of chemically diverse and unresolved aerosol mixtures. Even in the hypothetical case where all aerosol components and their quantities would be known, it may not be realistic to obtain a well-constrained description of their interactions in all solution states corresponding to growing and activating droplets. Therefore, thermodynamic models based on explicit knowledge of chemical composition and composition-dependent properties for all species in the aerosol mixture cannot be directly applied. To enable predictive calculations for complex and unresolved aerosol mixtures, one approach has been to assume a well-known proxy compound or mixture to represent the properties of the complex system (e.g., Prisle et al., 2012a; Ovadnevaite et al., 2017; Lowe et al., 2019). A significant weakness of this approach is the uncertainty of how well the chosen proxy system represents the actual aerosol mixture. Simple binary and ternary aqueous droplet mixtures, such as those which have typically been the focus of thermodynamic process-level studies, may be too simplistic to capture the variation of surface activity and other properties displayed by chemically complex mixtures in response to changing ambient conditions. Alternatively, Prisle et al. (2011) proposed a very simple framework assuming that surface-active components are completely partitioned to the droplet surface with a resulting effective hygroscopicity parameter (Petters and Kreidenweis, 2007) of κ=0 and vanishing impact on droplets surface tension. This model is not thermodynamically consistent but can readily be applied to represent the overall effect of any surface-active aerosol, including chemically unresolved mixtures, on CCN activation. The simple representation was demonstrated to perform well for SDS and fatty acid salts with 8, 10, and 12 carbon atoms, but its general applicability to complex surface-active aerosol mixtures remains to be established. Instead of self-contained, independent predictions, thermodynamic modeling has also been achieved with analytical approaches (e.g., Ruehl et al., 2016; Forestieri et al., 2018), where model parameters are determined by first fitting the experimental data to be described. Here, the challenge is verifying that model parameters accurately describe the underlying thermodynamic properties of the system and in particular do not confound several interconnected effects of surface activity. The model may also not be applicable for systems and conditions other than the specific ones to which the model parameters were fitted.
This work presents a framework that enables predictive, thermodynamically consistent calculations of droplet growth and activation for chemically complex and unresolved surface-active aerosol mixtures. Analogous to the approach of Prisle et al. (2010) for simple, well-defined aerosol mixtures, Köhler theory is here coupled with a partitioning model based on the Gibbs adsorption and Szyszkowski-type surface tension equations. However, to obtain a quantitative description of chemically unresolved components in the droplets, the model is formulated on a mass basis. Continuous parametrizations of bulk water activity and surface tension in aqueous solutions, necessary for model input, are independently constructed from macroscopic measurements, where composition dependency is described in terms of mass concentrations without specific knowledge of the molecular identity of all solute species.
To illustrate its application, the presented mass-based model is used to evaluate a suite of properties, including critical supersaturation and droplet size, bulk-phase composition, water activity, surface tension, and the Kelvin effect, for growing and activating droplets formed from particles comprising Nordic aquatic fulvic acid (NAFA) mixed with sodium chloride (NaCl). NAFA is a complex mixture, which is not chemically well-defined. It is one of several commercial reference substances which has been used as models for atmospheric humic like substances (HULIS) (Kristensen et al., 2014). In addition to fatty acids, HULIS comprise another major group of atmospheric surface-active organics (e.g., Kiss et al., 2005; Dinar et al., 2006b; Graber and Rudich, 2006; Nguyen et al., 2014). A comprehensive data set, including measurements of surface tension and water activity for a large set of macroscopic aqueous NAFA–NaCl solutions with different concentrations and relative mixing ratios, to independently constrain necessary thermodynamic properties for the model calculations, as well as CCN activity for particles with a range of sizes comprising NAFA and NaCl in various mixing ratios, to validate the model predictions, has been reported (Kristensen et al., 2014; Lin et al., 2020). Similar to other model HULIS, NAFA significantly reduces surface tension in macroscopic aqueous solutions (e.g., Kiss et al., 2005; Aumann et al., 1967). However, Kristensen et al. (2014) found that CCN activity of both pure NAFA and mixed NAFA–NaCl particles was significantly overestimated by a Köhler model, where the impact of NAFA surface activity on droplet surface tension was assumed to be equivalent to that measured in the corresponding macroscopic solutions. This strongly suggests that size-dependent bulk–surface partitioning of NAFA in microscopic droplets also needs to be taken into account to fully explain the observed CCN activity, making it an interesting system for illustrating the application of the presented framework.
2.1 Köhler theory
Droplet hygroscopic growth and activation are calculated using a framework based on the Köhler equation in the form (Köhler, 1936; Prisle et al., 2010)
Equation (1) describes the equilibrium water vapor supersaturation (SS) over a spherical solution droplet as a function of its diameter (d), pw is the equilibrium partial pressure of water over the solution droplet, is the saturation vapor pressure over a planar surface of pure water, aw and σ are the water activity and surface tension of the droplet solution, νw is the partial molar volume of water in solution, approximated as the ratio of pure water molar mass and mass density , R is the universal gas constant, and T is the Kelvin temperature.
The solution droplet is formed as water condenses onto an initially dry particle. Only the dry particle itself, before any water uptake has occurred, is here referred to as a “particle”, and dry-particle diameters (as well as other properties) are designated by upper case symbols, as Dp. After water uptake, the wet aerosol particle is referred to as a (solution) droplet, and corresponding diameters (and other properties) are designated by lower case symbols, as d. For each dry-particle size and composition, the critical supersaturation (SSc) is evaluated as the maximum of the equilibrium droplet growth (Köhler) curve described by Eq. (1). The droplet size where SSc occurs is here referred to as the critical droplet diameter dc, or the point of activation. When droplets have grown past their respective critical point to sizes d>dc, they are described as activated cloud droplets. At earlier points d≤dc on the Köhler curves, droplets are considered to be in the process of activating.
The water activity (also called the Raoult term) describes the suppression of equilibrium water partial pressure over an aqueous solution by dissolved solutes, compared to the saturation vapor pressure of pure water, as
Here, xw is the water (mole or mass) fraction in solution, and γw is the corresponding (mole- or mass-fraction-based) activity coefficient of water. The exponential (or Kelvin) term describes the enhancement of vapor pressure over the convex side of a curved droplet surface, compared to a planar surface of the same liquid, and depends explicitly on the droplet surface tension. Both water activity and Kelvin term are functions of droplet composition, determining xw and thus γw=γw(xw) and aw=γwxw, as well as any concentration-dependent change in droplet solution surface tension from the pure water value, .
The total (T) amount of solute in the growing droplets remains constant and is determined from the dry-particle compositions in terms of relative mass fractions Wp,s of each solute component s, where . Assuming volume additivity in spherical particles, the total dry mass of each solute component is then given from their bulk mass densities ρs as
In calculations for NAFA–NaCl particles, values of ρNaCl=2.165 and were used. In the absence of an exact value, the NAFA density is assumed to be similar to that of Suwannee River fulvic acid, another common reference humic substance (Dinar et al., 2006a). The droplet temperature is assumed to be T=303 K, reflecting the range of effective temperatures from about 298–313 K in the CCN counter between measurements at different supersaturations (T. B. Kristensen, personal communication, 2012). The sensitivity of calculations to the assumed value of ρNAFA and variations in experimental droplet temperature is discussed in Sect. S6 of the Supplement.
At each droplet size, the total amount of water is calculated by assuming volume additivity also of water and dry-particle components within the droplet phase as
The total droplet composition is then given in terms of the mass fractions of each component as
2.2 Bulk–surface partitioning
When surface-active material adsorbs at the droplet surface, it leads to a partitioning of the total mass of surface-active solute between the surface (S) and bulk (B) phases of the solution droplet. This partitioning depletes the droplet bulk concentration, compared to the total concentration , and changes the overall bulk composition , compared to the total composition of the droplet xB≠xT. To calculate the resulting amount of solute in the droplet bulk (and surface), a partitioning model is used, based on the Gibbs adsorption equation (Gibbs et al., 1928) in the form
where A=πd2 is the droplet surface area, and Mi are the total and molar mass of each droplet component i, ai is the activity of each component in the droplet solution, and is the mass of surface-active (i.e., partitioning) species in the droplet bulk. For chemically well-defined components, here water and NaCl, Mi are well-known quantities. For NAFA, an average molar mass of g mol−1 is assumed, according to the experimentally based estimate of Mäkelä and Manninen (2008). This corresponds to an assumption of the average mass unit of surface-active solute partitioning between the bulk and surface of the solution. The sensitivity of calculations to variations in the assumed value of is discussed in Sect. S6 of the Supplement.
Non-ideal (ai≠xi, γi≠1) solution effects present in the droplets are taken into account via the composition-dependent droplet water activity aw, which also enters directly into Eq. (1), evaluated from an experimentally based parametrization as described in Sect. 2.3 below. Activities for non-volatile solutes are challenging to measure directly but can in binary solutions be inferred from measurements of the solvent activity via the Gibbs–Duhem equation. Since this is not possible for ternary and higher order mixtures, aNAFA and aNaCl are approximated as the corresponding mass fraction concentrations. Previous estimates for ternary surfactant–NaCl aqueous mixtures showed that this assumption had only minor effects in Köhler calculations (Prisle et al., 2010).
The bulk–surface partitioning equilibrium is solved iteratively from Eq. (6) at each point along the Köhler curve, corresponding to a given droplet size d and total composition xT. Constraints are applied in terms of mass conservation for all droplet components, , and by choosing the position of the Gibbs surface to yield the droplet bulk-phase volume equal to the total droplet volume (Prisle et al., 2010).
2.3 Ternary parametrizations
Evaluation of the Köhler curves from Eq. (1) in connection with a partitioning model requires fully continuous composition-dependent functions for surface tension and water activity of the growing droplets, with respect to independent variations in the amounts of each component in the droplets. By formulating both the Köhler (Sect. 2.1) and partitioning (Sect. 2.2) models on a mass basis, quantitative descriptions with respect to variations in the different solution components can be applied using mass-based concentrations, without specifically resolving the chemical species comprised within each component. This also enables continuous thermodynamic functions to be used for chemically unresolved fractions of the aerosol mixture, such as the NAFA component in the mixed NAFA–NaCl particles considered in this work. Mass-based concentrations of different aerosol fractions are often readily determined from experimental parameters related to aerosol characterization or sample preparation.
In the present implementation, both σ and aw are described as functions of the droplet bulk composition xB, which is the basis for using the Gibbs adsorption equation in the form given in Eq. (6). At equilibrium, the surface and bulk compositions of a given surface-active substance are related via the concentration gradient resulting from its surface activity and mass conservation within the solution, just as the respective activities of water and all other components are by definition the same in all phases of the solution. A major advantage of using bulk-composition-based relations for solution properties is that these can be obtained from conventional measurements for macroscopic solutions, where the bulk-phase composition is readily constrained in terms of the total dissolved mass. Although the surface tension of a solution may also be given in terms of the surface composition (e.g., Ruehl et al., 2016), the absolute surface composition is highly challenging to quantify by direct, independent measurements (e.g. Prisle et al., 2012b; Werner et al., 2014; Walz et al., 2016). Such a formulation is therefore less useful for self-contained, predictive modeling.
The partitioning model is the key to applying composition-dependent properties obtained for macroscopic systems to finite-sized droplets. The bulk (and surface) concentrations of surface-active droplet components change with droplet size along the Köhler growth curve in response to both dilution, as the droplet grows, and changing bulk–surface partitioning, for example expressed in terms of the surface partitioning factor , with changing ratio of the droplet surface area and bulk volume . When partitioning of surface-active components change, the relative mass fractions of each solute component s in the droplet bulk phase
where is the mass of solute in the droplet bulk and , therefore change in a continuous fashion from the corresponding dry-particle composition given by Wp,s. The effect of bulk–surface partitioning is to move the droplet bulk (and surface)-phase mixing state in the concentration domain, relative to the total mixing state of the droplet solution or to a macroscopic solution with the same composition. As a consequence, continuous parametrizations with respect to independent variations in all component concentrations are needed to evaluate droplet properties over the full range of mixing states realized during droplet growth and activation.
The Köhler and partitioning models are both fully predictive and can in principle be used with any functional form and number of fit parameters used to describe the mass-based composition variation of thermodynamic properties. For this work, parametrizations of both σ and aw were obtained here by fitting continuous functions of NAFA and NaCl aqueous concentrations to the experimental surface tensions and water activities reported by Kristensen et al. (2014) and Lin et al. (2020) for macroscopic solutions, using the least squares method.
2.3.1 Surface tension σ
NAFA–NaCl aqueous surface tensions (in mN m−1) were fitted with the Szyszkowski equation in the form (Meissner and Michaels, 1949)
where (Dillmann and Meier, 1991; Vanhanen et al., 2008) is the temperature-dependent surface tension of pure water (in mN m−1), and CNAFA is the mass concentration of NAFA (in g L−1). Dependency of σ on NaCl concentration enters through the fitting parameters qst1 (in mN m−1) and qst2 (in g L−1), which are both functions of the (dimensionless) mass fraction of NAFA solute relative to NaCl in the solution bulk phase (wNAFA, given in Eq. 7):
and
Fits were made with the constraints that qst1≥0 and qst2>0 for all . The overall goodness-of-fit to measured surface tensions is given by the sum of squares due to error, SSE = 78.54, R2=0.9357, and the root mean squared error, RMSE = 1.772.
To investigate the effect of the functional form of the parametrizations used, ternary fits were also made to the surface tension data using the Szyszkowski-type equation given by Prisle et al. (2010), which contains an additional term explicitly including the positive aqueous surface tension gradient with respect to NaCl concentration, as well as having both fitting parameters depend quadratically, instead of linearly, on wNAFA. Details are given in Sect. S6 of the Supplement. The more elaborate equations did not significantly improve the fit to macroscopic surface tension data, while introducing several additional fitting parameters to the calculations. The simpler Eq. (8) with implicit NaCl dependency and linear variation of the fit parameters with wNAFA was therefore used in the calculations for the present work.
2.3.2 Water activity aw
Osmolality-derived water activities were fitted as functions of NaCl and NAFA mass concentrations (CNaCl and CNAFA, both in g L−1) in the form
with fitting parameters L g−1 and L g−1. Goodness-of-fit is given by SSE = , R2=0.9963, and RMSE = . In addition to Eq. (11), fitting to several other, more complex functions were tested as well, but the simple linear relations gave the most reasonable fits to the data over the measured solution composition ranges. Water activities derived from osmometry in principle include all non-ideal solution effects, in particular concentration-dependent NAFA dissociation and effects of any non-ideal interactions among the resulting solute entities (e.g., Kiss and Hansson, 2004; Prisle, 2006). Still, the linear relationship on mass concentrations of solute with unknown molar content may not be thermodynamically consistent over the entire range of water–NAFA–NaCl mixing states. Indeed, for the limiting case of binary solutions, Eq. (11) does fail to comply with the Gibbs–Duhem relation in the limit of pure NAFA (). This state is, however, never realized in the calculations of this work, where droplet growth is initiated at a finite growth factor and tends toward infinite dilution. Zamora and Jacobson (2013) derived water activities from measured hygroscopic growth factors for NAFA–NaCl mixtures and also found near-linear relationships between water activity and total solute (molal) concentration.
2.4 Comparison to simplified predictive models
The framework presented in Sect. 2.1 and 2.2 enables predictive, thermodynamically consistent Köhler calculations of droplet growth and activation for chemically complex and unresolved surface-active aerosol mixtures. In this framework, droplet growth and activation is influenced by several simultaneous processes in the aqueous phase, including dilution, bulk–surface partitioning, reduced droplet surface tension, and non-ideal water activity. To highlight the interplay and relative roles of these different underlying mechanisms, Köhler calculations for NAFA–NaCl particles using the full mass-based partitioning model are compared to several simplified predictive approaches (outlined below and summarized in Table 1). Two frameworks are used, which consider bulk–surface partitioning in a simplified and not thermodynamically consistent way. Of these simplified partitioning frameworks, one (labeled I, as explained below) furthermore considers surface tension reduction in the droplet, however also in a not thermodynamically consistent way, whereas one (labeled S) does not consider reduced droplet surface tension. Additionally, two frameworks are used which do not consider bulk–surface partitioning in the droplets. These bulk solution models are thermodynamically consistent, but the application of thermodynamic relations derived from macroscopic measurements to describing microscopic droplets using these models is not. Of the two bulk models, one (labeled B) considers reduced droplet surface tension, and one (labeled K) does not.
The simplified predictive frameworks are implemented using the same mass-based Köhler model (Eq. 1) as the full partitioning model presented in this work (labeled P). For each NAFA–NaCl dry-particle composition and size, cloud droplet activation is therefore calculated from Eq. (1) according to five different representations:
- (P)
The full partitioning model. The thermodynamically consistent model presented in this work (Sects. 2.1, 2.2, and 2.3) considers both reduced droplet surface tension and non-ideal water activity. For each droplet size, the NAFA bulk–surface partitioning equilibrium is solved iteratively from Eq. (6) to determine the droplet bulk-phase composition , from which droplet surface tension, σ=σ(xB), and water activity, aw=aw(xB), are evaluated according to the concentration-dependent ternary parametrizations given in Eqs. (8) and (11), respectively. Calculations using this comprehensive thermodynamic model serve as a benchmark for evaluating the effects surface activity of chemically complex, unresolved NAFA in cloud droplet activation, as well as for the performance of the simplified representations.
- (S)
The simple partitioning model of Prisle et al. (2011). All surfactant solute is assumed to be completely partitioned to the droplet surface, such that for all droplet sizes and compositions, and the surface-active particle components do not affect either water activity or surface tension at the point of activation. This representation is an empirical model emulating the predictions of the thermodynamically consistent partitioning model of Prisle et al. (2010) for droplets comprising chemically simple and well-defined, strong surfactants (such as SDS) at the critical point of activation. However, because the surface-active components are assumed to not contribute to the composition-dependent droplet properties, and the partitioning equilibrium does not need iteration, this representation is computationally simple and immediately applicable to chemically complex, unresolved surface-active mixtures, such as NAFA. When all surfactant mass is depleted from the bulk, concentration-dependent droplet water activity is evaluated from a binary aqueous NaCl parametrization (Prisle, 2006) based on data from Low (1969):
Here, bNaCl is the molal concentration of NaCl, which is readily determined from the mass concentration via the well-known molar mass of NaCl. The droplet surface tension is constant, i.e., σ=σw.
- (I)
Insoluble surfactant model. Analogous to calculations with (S), all surfactant solute is assumed to be completely partitioned to the droplet surface (), but the surface tension is reduced by a constant amount throughout droplet growth, to either σ=0.95σw or 0.80σw. This corresponds to a simplified representation of an insoluble surfactant, where the surface-active component does not dissolve into the bulk solution but forms a phase-separated layer on the surface which reduces solution surface tension according to the surface coverage (Ruehl et al., 2016). Due to the lack of quantitative surface-composition-based surface tension relations for chemically unresolved NAFA, to enable predictive modeling, the surface tension reduction is represented here with a constant value, similar to the approach of Davies et al. (2019).
- (B)
Bulk solution model. The droplet is assumed to have the same properties as a macroscopic (bulk) solution of corresponding total composition, such that the droplet bulk-phase composition is determined directly from the total composition without iteration according to Eq. (6) (xB=xT). Similar approaches have been used in numerous previous works (e.g., Shulman et al., 1996; Facchini et al., 1999; Harmon et al., 2010; Kristensen et al., 2014) but have been demonstrated to lead to significant overestimations of CCN activity for simple particle mixtures comprising chemically well-defined, strong surfactants (Sorjamaa et al., 2004; Prisle et al., 2008, 2010). For the NAFA–NaCl particles, droplet surface tension and water activity are evaluated according to the same concentration-dependent mass-based ternary parametrizations (Eqs. 8 and 11) as for (P). However, the bulk compositions and consequently the evaluated surface tension and water activity values at each droplet size will generally differ between the two representations.
- (K)
Basic Köhler model. Effects of surface activity are disregarded altogether. As for (B), the droplet bulk-phase composition is equal to the total droplet composition, without correction for surface partitioning (xB=xT). The surface tension is assumed to be constant for all droplet sizes and compositions and equal to that of pure water (σ=σw). Similar approaches are commonly used in cloud microphysics when aerosol surface activity is unknown or considered to have a minor influence on CCN activity (see, e.g., Prisle et al., 2010, 2012a; Kristensen et al., 2014). In this work, water activity of droplets comprising NAFA and NaCl is, for consistency, still evaluated according to the concentration-dependent mass-based ternary parametrization in Eq. (11), using the total droplet composition aw=aw(xT).
In summary, the impact of bulk–surface partitioning of NAFA is considered in calculations with models (P), (S), and (I), whereas (B) and (K) are both bulk solution models. Droplet surface tension is reduced in models (P) and (B) according to Eqs. (8)–(10) and by a constant value in (I). The ternary water activity relation in Eq. (11) is used in models (P), (B), and (K), whereas a binary water activity relation for aqueous NaCl is used for models (S) and (I) because the surface-active component is assumed to be completely partitioned to the droplet surface.
Strictly, only the full partitioning model (P) requires the use of fully continuous ternary parametrizations developed for this work (Sect. 2.3), since only in these calculations does the relative NAFA–NaCl solute mixing ratio change from that of the dry particles () as the droplets grow. In models (S) and (I), the relative bulk-phase mixing state of NAFA and NaCl changes discontinuously at the onset of droplet growth, from the nominal dry-particle value to , when NAFA is completely partitioned to the surface. For calculations with the bulk models (B) and (K), the relative mixing ratio of NAFA and NaCl solutes remains equal to the nominal value of the dry particles and does not change with concentration of the growing droplets (). For consistency, the ternary parametrizations given in Eqs. (8) and (11) are used here in calculations with all models, at essentially no additional computational cost.
In the following, results are presented for modeled CCN activity and droplet properties during hygroscopic growth and at the critical point of activation for mixed NAFA–NaCl particles, using the mass-based full partitioning model presented in this work and the simplified models described in Sect. 2.4. By analyzing and comparing results of the full model presented with the simpler representations, the influence of various aspects of NAFA surface activity on predicted CCN activity is assessed. Sensitivity of predictions with the full partitioning model to selected input parameters, including assumed NAFA mass density and average molar mass, droplet temperature, choice of surface tension equation, and the effect of potential sample impurity in the droplet activation measurements of Kristensen et al. (2014), is discussed in Sect. S6 of the Supplement.
3.1 CCN activity
Modeled critical supersaturations (SSc) as functions of dry-particle diameter (Dp) are presented in Fig. 1 for particles with dry NAFA mass fractions (Wp,NAFA) of 0 % (blue), 20 %, (green), 50 % (red), 80 % (purple), and 100 % (black) relative to NaCl. Results of Köhler calculations with each of the four models (P), (S), (B), and (K) are shown in panels (a), (b), (c), and (d), respectively, together with the experimental values for particles with equivalent dry compositions reported by Kristensen et al. (2014). Error bars on the experimental data are estimated as ±1 standard deviations on measured SSc, as reported by Kristensen et al. (2014). Results for model (I) are shown in Sect. S1 of the Supplement.
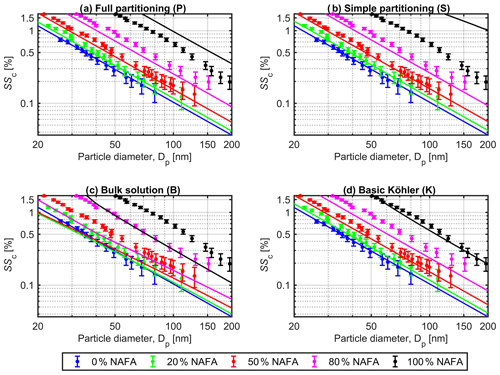
Figure 1Critical supersaturations (SSc) for mixed NAFA–NaCl particles, calculated (curves) using the different models described in Sect. 2.4: (a) full partitioning model (P), (b) simple partitioning model (S), (c) bulk solution model (B), and (d) basic Köhler model (K), in each case compared to experimental values (dots) measured by Kristensen et al. (2014). Colors indicate the original dry-particle fraction of NAFA (Wp,NAFA) relative to NaCl. Calculations are made using a NAFA mass density of ρNAFA=1.6 g cm−3. Error bars on experimental data represent ±1 standard deviations on SSc as reported by Kristensen et al. (2014).
All representations of NAFA surface activity give similar results in the limit of pure NaCl particles, as expected. For each model, the predicted CCN activity decreases (SSc increases) with increasing Wp,NAFA for a given particle size, in agreement with the experimental trend. This shows that upon varying the dry-particle composition from pure NaCl to pure NAFA, any effect of decreased droplet surface tension at the point of activation, from the presence of surface-active NAFA in the droplet phase, cannot overcome the simultaneous increase in water activity. The droplet water activity (Eq. 2) may increase from a potential combination of (i) increasing droplet non-ideality (specifically leading to increased γw>1), (ii) depletion of solute from the droplet bulk phase due to NAFA surface partitioning, and (iii) the much higher average molar mass of NAFA, compared to pure NaCl (both leading to increased ). Several studies have previously observed the same trend, experimentally or in model calculations, for aerosol systems comprising both simple strongly surface-active molecules, such as SDS and fatty acid sodium salts (Li et al., 1998; Sorjamaa et al., 2004; Prisle et al., 2008, 2010; Petters and Petters, 2016; Forestieri et al., 2018), as well as complex macromolecules and surface-active mixtures (Hansen et al., 2015; Dawson et al., 2016; Prisle et al., 2019), in various mixing ratios with inorganic salts.
The overall good performance of calculations using the mass-based full partitioning model (P) with respect to measured CCN activity is reassuring in terms of the ability to capture relevant properties of the activating droplets within the comprehensive thermodynamic description. Each of the models (P), (S), and (K) describe the experimental data fairly well, except in the case of pure NAFA particles, where the partitioning models (P) and (S) underestimate CCN activity well outside the reported experimental uncertainty. In the absence of hygroscopic NaCl, predictions with model (S) correspond to condensation of water into a pure aqueous droplet phase in the presence of insoluble material, which is adsorbed at the droplet surface without attaining full coverage. Calculations with the insoluble surfactant model (I), shown in Fig. S1 in the Supplement, rely on a similar assumption, but here the reduced surface tension brings predictions somewhat closer to experimental values for pure NAFA particles, compared to (S). To reconcile predictions of model (I) with measured SSc for pure NAFA particles would however require much stronger surface tension reductions than the 5 %–20 % included in the present calculations, at the expense of increasingly poor agreement with experimental values for all other particle compositions. In general, it is clear that model (I) does not represent experimental CCN data well across the full range of NAFA–NaCl particle sizes and compositions investigated. This suggests that discrepancies observed for the other partitioning models (P) and (S) for particles with the highest mass fractions of NAFA cannot be attributed to surface tension effects alone. It is possible that relatively small amounts of hygroscopic impurities could have been present in the experimental NAFA aerosol mixture and thus enhancing measured CCN activity, as first described by Bilde and Svenningsson (2004). The model sensitivity analysis presented in Sect. S6 of the Supplement shows that even 3 % by mass of impurities in the NAFA mixture with hygroscopic properties corresponding to those of NaCl would be sufficient to reconcile the calculations of model (P) with experimental data for pure NAFA particles. For the simple partitioning model (S), 5 % by mass of such impurities could similarly reproduce the measured CCN activity, whereas the agreement with experiments for both bulk solution models (K) and (B) decreases when assuming impurities in the NAFA mixture.
A prominent feature of Fig. 1 is how Köhler calculations using the bulk solution representation (B) with reduced droplet surface tension clearly and consistently underestimate experimental critical supersaturations for all particle sizes and compositions. Similar observations have been made in several previous studies at both sub- and supersaturated conditions, for particles comprising both chemically simple and complex surfactants and for both pure surfactant particles and in various mixtures with inorganic salts (Li et al., 1998; Rood and Williams, 2001; Sorjamaa et al., 2004; Prisle et al., 2008, 2010; Harmon et al., 2010; Ruehl et al., 2010; Zamora and Jacobson, 2013; Kristensen et al., 2014; Hansen et al., 2015; Petters and Petters, 2016; Forestieri et al., 2018; Prisle et al., 2019). The present results confirm that bulk–surface partitioning of strongly surface-active aerosol components must be taken duly into account if the impact on droplet surface tension is considered in predictions of CCN activity. The mass-based partitioning model (P) presented in this work enables thermodynamically consistent predictions with consideration of both bulk–surface partitioning and reduced droplet surface tension, also for chemically complex and unresolved surface-active aerosol components, in addition to the simple aerosol systems that have previously been described with such comprehensive approaches. Model (K) tends to overestimate mixed NAFA–NaCl experimental CCN activity slightly more than the partitioning models (P) and (S), further suggesting that NAFA bulk depletion from surface partitioning may indeed have a more significant impact on decreasing CCN activity than surface tension reduction has on increasing it.
Kristensen et al. (2014) originally compared their measured CCN activities to two simple bulk solution Köhler models based on similar assumptions as models (B) and (K) used here, with some differences in the actual model implementation. In the present work, calculations with models (B) and (K) are for consistency made with the continuous ternary surface tension and water activity parametrizations presented in Eqs. (8) and (11), even if these are not strictly needed in absence of bulk–surface partitioning calculations. Kristensen et al. (2014) used simpler parametrizations, with a 1-dimensional composition domain, which are not continuous with respect to variations in the relative NAFA–NaCl mass fractions in solution (wNAFA and wNaCl) and have slightly different functional forms than the parametrizations used here, even at the lines of intersection. Furthermore, the surface tension parametrizations used by Kristensen et al. (2014) are made for data points corresponding to measurement times t=0 s after the formation of the surface and therefore based on higher surface tension values for a given solution composition, compared to the data from measurement times t=600 s used in this work (see Sect. S5). As higher macroscopic surface tensions correspond to lower surface activity of NAFA, the predictions of SSc by Kristensen et al. (2014) are similarly biased higher, incidentally partially mimicking the elevated surface tension in droplets that would occur due to surface partitioning. However, as clearly seen from Fig. 7 of Kristensen et al. (2014), this effect still is not sufficient to bring the Köhler predictions even close to agreement with their measured CCN activities.
Similar to the model (K) used here, Kristensen et al. (2014) also find that a basic Köhler model, where effects of NAFA surface activity are completely ignored, gives good agreement with measured CCN activation for NAFA–NaCl particles with up to 50 % NAFA, as well as for pure NAFA but not for particle mixtures with 80 % NAFA. This seemingly counterintuitive result for particle mixtures comprising strongly surface-active material with significant ability to lower surface tension in macroscopic solutions has been observed also for simple, strong surfactants, such as SDS and C8–C12 fatty acid salts (Sorjamaa et al., 2004; Prisle et al., 2008, 2010, 2011). On the other hand, several recent studies have shown properties for both simple and complex aerosol mixtures, including secondary organic aerosol (George et al., 2009; Ruehl et al., 2016), limonene-derived organosulfate products (Hansen et al., 2015), marine primary organics (Ovadnevaite et al., 2017), and water-soluble pollen extracts (Prisle et al., 2019) which are consistent with an enhancement of aerosol water uptake by surfactants, at least partly due to reduced surface tension. This suggests that model (K) is too simple to fully capture CCN activity of different types of surface-active aerosol components and in all mixing states and that, generally, a full partitioning model is needed for robust predictions. In cases where the basic Köhler model (K) gives good agreement with experimental CCN activity for NAFA–NaCl particles, it also closely traces predictions with the mass-based full partitioning model (P).
3.2 Droplet properties at activation
Figure 2a presents critical supersaturations as a function of NAFA mass fraction Wp,NAFA in 50 nm dry particles, calculated with each model described in Sect. 2.4. Experimental values from Kristensen et al. (2014) for particles with similar dry sizes are shown for reference: immediate comparison is not always possible along the particle composition dimension because Kristensen et al. (2014) used an experimental setup that scanned a set of preselected supersaturations, rather than particle sizes and therefore did not measure the exact same particle sizes for each dry-particle composition. Corresponding to each value of SSc shown in panel (a), the other panels in Fig. 2 show, for the same 50 nm particles, also calculated at the critical point dc of the Köhler curve, (b) the individual Kelvin and Raoult terms, (c) the droplet diameter growth factor GF, and (d) the droplet surface tension σc. Qualitatively similar results were obtained for other dry-particle sizes (not shown). Differences between the models are more clearly seen for smaller particles, which generally activate for smaller critical sizes, corresponding to smaller critical growth factors, with more concentrated droplet compositions and larger surface area-to-bulk volume ratios, introducing more pronounced effects of surface partitioning for a given total composition.
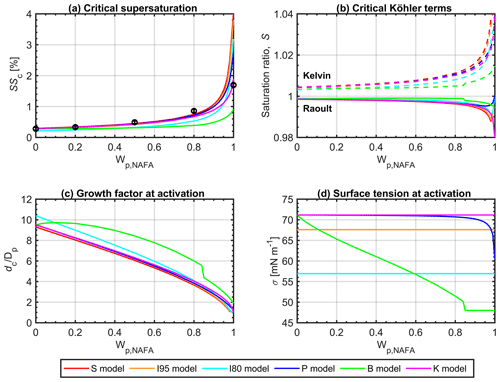
Figure 2Properties of activating droplets calculated with models (P), (S), (I), (B), and (K) at the critical point of droplet activation dc for 50 nm dry particles as functions of dry-particle NAFA mass fraction Wp,NAFA: (a) critical supersaturations SSc, (b) Kelvin and Raoult terms, (c) droplet diameter growth factor, and (d) droplet surface tension, all at the critical point of the Köhler curve corresponding to each SSc. In panel (a), experimental values from Kristensen et al. (2014) for particles with similar dry sizes are shown for reference.
Results in Fig. 2a illustrate how the full partitioning model (P) traces experimental CCN activity well, but they also highlight the strong sensitivity of model predictions to NAFA mass fraction for particles with the highest Wp,NAFA. As discussed in detail below, this sensitivity is due to predicted droplet states with highly depleted bulk phases, for which the partitioning of a single mass unit of surface-active solute leads to large changes in bulk (and surface) mass concentrations of the finite-sized droplets. A similar phenomenon was noted by Malila and Prisle (2018) and is further exaggerated for the present particle compositions due to the very large average molar mass of species comprised in the NAFA mixture (Mäkelä and Manninen, 2008).
Figure 2a shows that the simple partitioning models (S) and (I), as well as the basic Köhler bulk model (K), all predict very similar properties of activating droplets to those of the full partitioning model (P), for essentially the entire range of NAFA mass fractions in the particles. A similar close agreement between basic Köhler predictions and models that include comprehensive partitioning thermodynamics has also been observed in previous studies for particles comprising simple, well-defined, strong surfactant–salt mixtures (Prisle et al., 2010, 2011; Forestieri et al., 2018). For NAFA particles, the agreement between models here extends to even larger surfactant fractions (up to about 80 % by mass of NAFA) than seen in the earlier studies. Furthermore, not only critical supersaturations, but also the individual Kelvin and Raoult terms at the point of droplet activation in Fig. 2b and predicted droplet sizes at activation, as represented by the droplet growth factors in Fig. 2c, agree well between these models. This was not immediately expected, since model (S) was proposed to emulate specifically SSc, not necessarily other droplet properties at the critical point (Prisle et al., 2011), and since NAFA is seen from experimental data to give significant surface tension reductions in macroscopic solutions (Kristensen et al., 2014), contrary to the assumptions of both models (S) and (K). Figure 2d shows that the full partitioning model (P) predicts surface tensions of activating droplets, which are very close to that of pure water and within the range of constant values assumed in models (S), (I), and (K) for nearly the entire dry-particle composition range. The similarity between models of all activation parameters indicates that the underlying assumptions of both the simple partitioning representations and the basic Köhler model are reasonably representative of the critical droplet states for the NAFA particle systems in question, as predicted by the comprehensive model (P).
It is important to keep in mind that properties in Fig. 2 predicted for different Wp,NAFA correspond to critical droplets of different sizes dc. Variations of critical droplet properties with Wp,NAFA only represent states corresponding to the maxima of individual Köhler curves for each particle composition and therefore do not a priori reflect continuous variation in all underlying droplet properties. In addition to the overall variation in total solute composition given by Wp,NAFA, also the droplet dilution state, as seen by the varying activation growth factors GFc (panel c), and the ensuing size-dependent bulk–surface partitioning of NAFA, as predicted with model (P) according to the changing and dilution state, vary between the critical droplets. Total composition, dilution, and partitioning each affect the droplet bulk solution composition, from which the droplet surface tension (panel d) and Kelvin and Raoult terms (panel b) are evaluated.
3.2.1 Effects of surface activity on the Raoult term
The predicted Raoult terms shown in Fig. 2b vary for each model as functions of Wp,NAFA, when the mass of hygroscopic NaCl in the particles is gradually replaced with the significantly less hygroscopic component NAFA, and in response to the changing dilution state of the critical droplets. This influences both the overall amount of water and solute in the droplets at the respective dc and in the case of the models (P), (S), and (I) also the extent of bulk depletion from NAFA bulk–surface partitioning. Each of these mechanisms affects the composition of the droplet bulk phase, which governs aw according to Eq. (2) in general and Eqs. (11) or (12) for the present calculations in particular. The calculated critical Raoult terms are seen to be higher for the bulk solution model (B) than the other models, despite the partitioning models (P), (S), and (I) considering bulk depletion of NAFA, whereas the bulk model (B), like (K), does not. This is due to the significantly higher dilution factor of activating droplets predicted by (B), as is seen from GFc in Fig. 2c. For models (P), (S), and (I), both the predicted Raoult terms and growth factors of activating droplets are mutually very similar. For all models, the predicted reduction of water activity at droplet activation is modest across the full dry-particle composition range, reflecting the overall dilute critical droplet state and the modest impact of NAFA on predicted particle hygroscopicity.
For the partitioning models (P), (S), and (I), an inflection point is seen in the Raoult terms at very high Wp,NAFA, whereas for the bulk solution models (B) and (K), the Raoult terms decrease with increasing Wp,NAFA throughout the dry-particle composition range. In the absence of bulk–surface partitioning, predicted droplet concentrations continue to increase with decreasing dilution of the total solute mass, as seen from the growth factors GFc in Fig. 2c. When bulk–surface partitioning of NAFA is considered, the effect of decreasing dilution is first strong enough to overcome the decrease in the total amount of hygroscopic material, caused by increasing Wp,NAFA and the depletion of NAFA from the droplet bulk, due to surface partitioning, leading to decreasing Raoult terms. However, eventually the balance reverses, as the total amount of NaCl in the droplets becomes too small to compensate for the depletion of the surface-active component from the bulk. With the full partitioning model (P), the Raoult term for the critical droplets changes smoothly with Wp,NAFA, whereas sharp inflection points are seen for the simple partitioning models (S) and (I), where bulk–surface partitioning is described as a step function.
The predicted bulk compositions of activating droplets are presented in Fig. S2 and discussed in more detail in Sect. S2. The NAFA surface partitioning factor at droplet activation, in terms of the mass ratio of NAFA solute in the droplet surface and bulk, , calculated with the full partitioning model (P), is shown in Fig. S2c. In the models (S) and (I) with complete surface partitioning, this value is infinite at all droplet sizes, and in the bulk solution models (B) and (K), it is 0. Fig. S2d shows the resulting droplet bulk composition in terms of the mass fraction of solute comprised by NAFA, , at the point of droplet activation. For calculations with the bulk models (B) and (K), this ratio is identical to the dry-particle composition Wp,NAFA, as it should be in the absence of bulk depletion from surface partitioning of NAFA. With models (S) and (I), the predicted NAFA bulk solute fraction is vanishing, since CNAFA=0 g L−1. Model predictions show how bulk–surface partitioning of NAFA profoundly changes the droplet bulk-phase mixing state at the point of activation, compared to the relative NAFA–NaCl ratio in the original dry particles. For 50 nm particles, in activating droplets calculated with the comprehensive partitioning model (P) is larger than 500 for all particle compositions. For all dry-particle sizes and NAFA mass fractions investigated (Fig. 1), calculated with model (P) at the point of activation is greater than 2 orders of magnitude (not shown). As a result, except for the very largest dry-particle NAFA fractions, the concentration of NAFA (Fig. S2a) and the relative amount of droplet solute comprised by NAFA (Fig. S2d) in activating droplets are all but vanishing due to surface partitioning of NAFA. These calculations with the thermodynamically consistent framework (P) presented in this work support the extension of applications for the simple partitioning model (S), with the underlying assumptions that the surfactant bulk concentration at droplet activation is effectively 0 and the overall impact of NAFA on particle hygroscopicity is therefore vanishing, from the simple, strong surfactants previously investigated to strongly surface-active complex mixtures, such as NAFA.
For model (B), the predicted Raoult term of critical droplets has a step decrease with respect to the dry-particle composition at . The corresponding increasing concentrations of both NAFA and NaCl are clearly seen in Fig. S2a and b in the Supplement. This is caused by a predicted step decrease in the critical droplet growth factors GFc (Fig. 2c), leading to a simultaneous step increase in the Kelvin term (Fig. 2b). As seen in Fig. 2a, the opposing changes in the respective Kelvin and Raoult terms caused by decreasing dc cancel out, so that the resulting SSc values predicted with model (B) change smoothly with Wp,NAFA. At the same dry-particle composition, where the step change in GFc occurs, critical droplet surface tensions σc in Fig. 2d predicted with model (B) reach a constant minimum value. This corresponds to droplets reaching a critical-micelle-concentration-type transition for NAFA, which is estimated from the surface tension data of Kristensen et al. (2014) to occur for various NAFA–NaCl mixtures at approximately σ = 48 mN m−1. Figures 3 and 4 (discussed in more detail in Sect. 3.3 below) show how the critical point dc predicted with model (B) shifts between two local maxima on the Köhler curve, from the larger to the smaller droplet size, corresponding to droplets with surface tensions above, or at, the minimum value, respectively. This causes the discontinuous shift in predicted dc and other critical droplet properties seen for representation (B) in Figs. 2 and S2. A similar shift is not seen for calculations with the full partitioning model (P), which also considers reduced surface tension in the droplets because the surface tension never reaches the minimum value σ = 48 mN m−1 (Figs. 2d and 4) due to droplet bulk depletion.
3.2.2 Effects of surface activity on the Kelvin term
The Kelvin term predicted at droplet activation depends on the critical droplet size dc, determining the curvature effect, together with the droplet surface tension, according to Eq. (1). The critical Kelvin terms predicted with each model in Fig. 2b generally follow the corresponding trends in dc as given by GFc (Fig. 2c). Figure 2d shows how droplet surface tension at activation is reduced according to Eq. (8) in calculations with models (P) and (B) or fixed to constant values equal to σw for model (K) or mN m−1 and mN m−1 for model (I), in the following designated as (I95) and (I80), respectively. The composition-dependent droplet surface tension in models (P) and (B) is a function of the droplet bulk composition, which for each Wp,NAFA is governed by the droplet dilution state and for (P) also by size-dependent bulk–surface partitioning according to Eq. (6). When the critical surface tension is significantly reduced in calculations with (B) and (I80), the corresponding Kelvin terms are somewhat lower than for (P), (S), and (I95), where surface tension is only modestly reduced at activation or not at all.
Calculations with model (B) in Fig. 2d show how, despite higher predicted dilution states, NAFA can significantly reduce surface tension of activating droplets when they are considered similar to macroscopic solutions. However, in the comprehensive model (P), the predicted surface tensions of activating droplets are essentially the same as for pure water, when particles comprise less than 80 % by mass of NAFA. Only for the very highest mass fractions of NAFA () is the surface tension in model (P) reduced by more than 5 % from the pure water value. This is one of the fundamental assumptions underlying calculations with both models (S) and (K) – and the validity of this assumption, as predicted with comprehensive framework (P) for all but the largest dry-particle NAFA fractions, is one of the main drivers of the simultaneous close agreement between predictions with (S), (K), and (P). Furthermore, the effect of any modest surface tension reduction in model (P) at the point of droplet activation must be more than counterbalanced by bulk depletion due to NAFA surface partitioning, since the predicted SSc values are higher for (P) than for (K) but slightly higher in (S) than for (P), at the highest NAFA fractions. This is also reflected in the corresponding Raoult terms as discussed above.
3.3 Properties of growing droplets along Köhler curves
Figure 3 shows the Köhler curves for selected dry-particle compositions, Wp,NAFA, of (panel a) 0.20, (panel b) 0.50, (panel c) 0.80, and (panel d) 0.95, calculated with each model for the 50 nm particles described in Figs. 2 and S2. The droplet surface tensions evaluated along the Köhler curves are shown in Fig. 4, and the corresponding NAFA surface partitioning factors and water activities of the growing droplets are presented in Figs. S3 and S4 of the Supplement. All the predictive models used in this work produce meaningful Köhler curves and other solution properties for the growing droplets. For all curves representing calculated properties of the growing droplets, the respective critical points of droplet activation predicted with each model (corresponding to SSc presented in Figs. 1 and S1) are indicated with asterisks.
The close agreement between partitioning models (P), (S), and (I95) and the basic Köhler model (K) for calculated droplets properties at the point of activation dc (Fig. 2) is evident along the full Köhler curves in Fig. 3, except for particles with the highest NAFA fraction (panel d). Here, clear differences in the shapes of the calculated Köhler curves can be seen, when the representations of the surface-active NAFA component become more prominent relative to the still smaller amounts of hygroscopic NaCl in the droplets. For both models (B) and (I80), the predicted droplet surface tension in Fig. 4 is significantly reduced during droplet growth and well beyond the point of activation. At a given droplet size d, the equilibrium supersaturation SS is higher for representation (B) than for (I80), when the concentration-dependent droplet surface tension is higher in (B) than the fixed surface tension of σ=0.80σw in (I80), and vice versa. For models (P), (S), and (I95), the order of the Köhler curves, as well as the values of SSc at the critical points, do not simply follow the relative magnitudes of the droplet surface tensions at each d. In calculations with the full partitioning model (P), surface tension is reduced for the more concentrated droplets at the earlier stages of the Köhler growth curves, but only for the highest in Fig. 4d is the reduction maintained until the critical point. Even for droplets much smaller and more concentrated than at the point of activation (d<dc), surface tension is never reduced by more than about 10 % from the pure water value in the comprehensive model (P). This reflects the very small amounts of NAFA solute remaining in the finite-sized droplet bulk phase, when bulk–surface partitioning is taken into consideration.
The degree of NAFA partitioning to the surface is already significant at the much higher total droplet concentrations at the early stages of the Köhler curves, before activation takes place: the amount of NAFA in the droplet surface is generally 2–3 orders of magnitude higher than the amount left in the bulk (Fig. S4). Typically, is even higher for droplet sizes d<dc than at the critical point, reflecting that partitioning has an even greater effect on the droplet bulk concentration of NAFA than the lower degrees of dilution in the smaller droplets. As a consequence, even if NAFA is able to significantly reduce surface tension in macroscopic solutions, the same impact on surface tension is not seen in microscopic activating droplets, even at corresponding total droplet concentrations. The differences between surface tension variations predicted with Eq. (8) in macroscopic and microscopic droplet solutions due to changes in bulk composition from NAFA partitioning are further discussed in Sect. S4.
Figure S4 shows how the water activity increases as droplets grow and dilute along the Köhler curves. Predicted droplet aw only differs significantly between the different models when NAFA fractions in the dry particles are very large. The water activity is significantly reduced early in droplet growth but – except for the largest Wp,NAFA – is very close to 1 when droplets reach dc. As NAFA is much less hygroscopic than NaCl, and the resulting reduction of water activity is even smaller for submicron droplets due to strong bulk–surface partitioning, aw predicted with the comprehensive model (P) is governed by the hygroscopic salt, and variations along the Köhler curve mainly reflect the changing droplet dilution state.
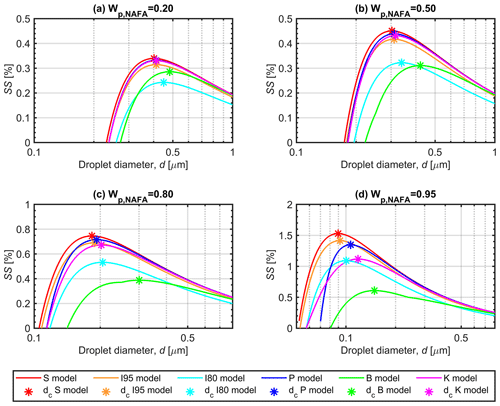
Figure 3Köhler curves for growing aqueous NAFA–NaCl droplets formed from 50 nm dry particles with NAFA mass fractions of (a) 0.20, (b) 0.50, (c) 0.80, and (d) 0.95, calculated with the different models described in Sect. 2.4. The critical points of droplet activation (SSc) presented in Figs. 1 and S1 are indicated with asterisks on each Köhler curve. Note that the supersaturation (SS) scale is different between the panels.
The comprehensive, mass-based framework introduced in this work enables self-contained, predictive, thermodynamically consistent evaluation of the different effects of surface activity for hygroscopic growth and cloud droplet activation of chemically complex, unresolved aerosol mixtures, analogously to what has previously been achieved only for a narrow range of chemically very simple and well-defined aerosol systems. The following section summarizes the main insights from predictions using the Köhler model presented with comprehensive considerations of bulk–surface partitioning, surface tension, and non-ideal water activity for chemically complex and unresolved, strongly surface-active NAFA mixtures, including the comparison to predictions with the simplified frameworks. Results of this work are contrasted with previous findings for the effects of surface activity on CCN activity of simple and complex aerosol mixtures. Furthermore, the predictive mass-based Gibbs adsorption model presented here is contrasted with other approaches recently used for evaluating detailed effects of bulk–surface partitioning and surface tension in cloud droplet activation. Finally, some of the potential implications of the present and previous results for understanding and modeling cloud microphysics of complex surface-active aerosol in the atmosphere and for the prospect to include effects of surface activity in large-scale atmospheric model applications are briefly discussed.
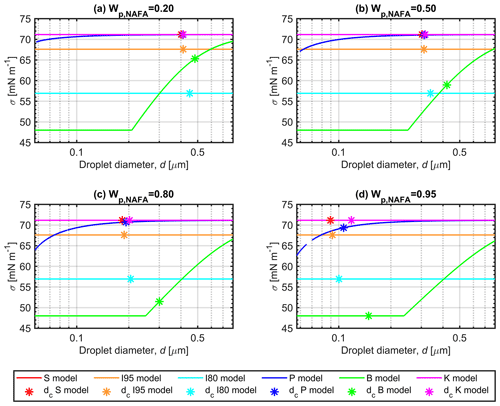
Figure 4Surface tension along Köhler curves for growing aqueous NAFA–NaCl droplets formed from 50 nm dry particles with NAFA mass fractions of (a) 0.20, (b) 0.50, (c) 0.80, and (d) 0.95, calculated with the different models described in Sect. 2.4. The critical points of droplet activation (corresponding to SSc presented in Figs. 1 and S1) are indicated with asterisks on each surface tension curve.
4.1 Effects of surface activity for the predicted CCN activity of NAFA
Results of the mass-based comprehensive model presented in this work show that the cloud droplet growth and activation behavior of chemically complex and unresolved NAFA mixtures is driven by very similar mechanisms as those found in earlier works for well-defined, strong surfactants in simple binary and ternary aqueous droplet mixtures: the comprehensive thermodynamic partitioning model (P) consistently during droplet growth and at the point of activation predicts the vast majority of NAFA in the droplet to be depleted from the bulk by partitioning to the surface. Except for particles with the very highest dry mass fractions, NAFA contributes next to none of the solute in the droplet bulk phase, which governs the equilibrium surface tension and water activity of the droplet. Therefore, even if NAFA effectively reduces surface tension in macroscopic solution, the droplet surface tension predicted at activation is barely reduced at all, for particles with less than 80 % NAFA. For even higher NAFA fractions, the maximum surface tension reduction only amounts to around 10 mN m−1 from the pure water value across the investigated dry-particle size range.
The basis for this seemingly counterintuitive droplet state is the comparatively very large surface areas (A) relative to the finite volume (V) of the bulk for microscopic activating cloud droplets, compared to a macroscopic solution. This has previously been demonstrated in predictive thermodynamic modeling (Prisle et al., 2008, 2010) and experiments (Bzdek et al., 2020) for chemically simple and well-defined strong surfactants. Even when essentially all the surface-active material is adsorbed at the droplet surface, the finite-sized solution droplets do not comprise enough surface-active solute altogether to generate sufficient surface (or bulk) concentrations to significantly reduce droplet surface tension. The equilibrium bulk-to-surface concentration gradient governing the adsorption of a surface-active substance is therefore established for a droplet solution state of dilute concentrations in both bulk and surface phases. The pronounced bulk-phase depletion further diminishes the low intrinsic hygroscopicity of the NAFA mixture, as seen in terms of impact on bulk water activity, to yield a nearly vanishing effective hygroscopicity in activating droplets. This leads to the strongly surface-active component effectively behaving in small droplets as an insoluble and only slightly or even non-surface-active substance.
4.1.1 Validity of assumptions in simplified predictive frameworks for NAFA
The detailed mechanisms of NAFA surface activity unraveled by the full partitioning model (P) explain the good performance of the simple partitioning model (S) with respect to both experimental data for NAFA particle mixtures and the comprehensive model: in model (S), contributions from NAFA to both water activity and surface tension reduction are effectively set to zero. Similar to previous results for the simple, strong surfactants SDS and fatty acid salts (Prisle et al., 2011), conditions predicted with the comprehensive thermodynamic model for a range of droplet sizes, including at the critical point of activation, are seen here to be closely represented by the simple partitioning model (S), also in the case of chemically complex, strongly surface-active NAFA. This establishes the simple partitioning model as a promising representation for other complex and unresolved surface-active aerosol mixtures relevant to the atmosphere.
In a macroscopic solution, a strong surfactant which is fully partitioned to the surface would be expected to significantly reduce solution surface tension, and the situation described by model (S) is of course quite unrealistic. However, the bulk solution model (B) is seen here to perform very poorly for NAFA–NaCl particles, compared to both reported CCN data (Kristensen et al., 2014) and predictions with the full partitioning model (P), in contrast to the good performance of the simple partitioning model (S). This shows that for the studied NAFA–NaCl mixtures, the most significant impact of surface activity on cloud droplet growth and activation is on bulk-phase depletion from surface partitioning and notably not on surface tension reduction in droplets. Calculations with model (P) use the same composition-dependent surface tension and water activity relations, independently constrained by measurements made for macroscopic solutions (Eqs. 8 and 11), as model (B). Several previous studies have concluded that application of macroscopic relations – without simultaneously correcting the droplet bulk composition for depletion of surface-active components due to bulk–surface partitioning onto the large droplet surfaces – fails to reproduce experimentally observed CCN activity for a variety of surface-active organic aerosol (e.g., Li et al., 1998; Prisle et al., 2008, 2010, 2011; Petters and Petters, 2016; Forestieri et al., 2018; Lin et al., 2018). The role of a partitioning model is to connect composition-dependent relations for surface tension, as well as other solution properties, derived for macroscopic systems to microscopic droplet states. Specifically, the effect of bulk–surface partitioning in droplets is to move the bulk-phase mixing state to a different point in the composition domain, compared to a macroscopic solution with the same total composition. This is illustrated in Figs. 2 and S2 for the present case of NAFA–NaCl droplet mixtures.
The model results presented here also show that including surface tension effects of NAFA without considering the altered bulk-phase composition from surface partitioning in droplets will lead to greater errors in estimating CCN activity than neglecting surface activity altogether. Similar conclusions have been made in several previous studies for simple particle mixtures comprising strong surfactants (SDS or fatty acid salts) with NaCl (Sorjamaa et al., 2004; Prisle et al., 2008, 2010; Forestieri et al., 2018). Detailed comparison to predictions with the comprehensive partitioning model (P) reveal that the good agreement of the basic Köhler model (K) with measured CCN activity is largely due to cancellation effects between the Kelvin and Raoult terms: by not accounting for the effects of NAFA surface activity, the basic Köhler model underestimates the surface tension depression and overestimates the water activity depression by NAFA in the droplets. This nearly full cancellation of the different effects of surface activity on Kelvin and Raoult terms may not be present in droplet activation for all types of surface-active aerosol components and mixtures but could rather prove to be a signature feature of CCN activity for relatively strong surfactants.
The presented mass-based comprehensive framework enables the detailed mechanisms of surface activity in hygroscopic growth and cloud droplet activation to be explored, in principle for any aerosol mixture. Resolving the different effects of surface activity using a thermodynamically consistent, predictive model avoids confounding multiple factors due to phenomenological resemblance of the simplified models to experimental observations.
4.1.2 Conditions favoring reduced droplet surface tension
Diverging observations have been made in different studies regarding the importance of surface tension for closure of CCN activity and number concentrations (e.g., Li et al., 1998; Sorjamaa et al., 2004; Wex et al., 2007; Varga et al., 2007; Prisle et al., 2008, 2010, 2019; Asa-Awuku et al., 2008; George et al., 2009; Booth et al., 2009; Poulain et al., 2010; Frosch et al., 2011; Noziere et al., 2014; Hansen et al., 2015; Ruehl et al., 2016; Ovadnevaite et al., 2017; Kroflič et al., 2018; Gérard et al., 2019, 2016; Frossard et al., 2019). This highlights that the role of surface activity in aerosol hygroscopic growth and cloud droplet activation is not yet fully constrained on a general level. The range of observations made for both complex aerosol mixtures and different simple, well-defined model compounds suggests that surface activity is likely to be manifested in a variety of ways for atmospheric aerosols and highly dependent on both ambient conditions and particle properties, including size and chemical mixing state, as well as surface activity and intrinsic hygroscopicity of the different components in the mixture. Results of the present work for strongly surface-active NAFA mixtures show that conditions favoring reduced surface tension, despite strong bulk depletion, are mainly present in the most concentrated droplets. Such highly concentrated droplet states are found for particles with the higher fractions of the surface-active NAFA component and at the earliest stages of droplet growth. For the smaller particles studied here, conditions favoring reduced droplet surface tension may extend to the point of activation. The influence of both surface partitioning and reduced surface tension on the shape of Köhler curves prior to the critical point of droplet activation has also been noted by Ruehl et al. (2016) and Davies et al. (2019).
Using a cloud parcel model, Lowe et al. (2019) similarly found that predictions of cloud microphysics and climate radiative forcing are sensitive to organic surface properties in pristine environments with ultrafine particle sources. The NUM particles observed by Ovadnevaite et al. (2017) were typically also significantly smaller than the NAFA–NaCl particles considered in this work. The strong bulk depletion of NAFA predicted with the full partitioning model in this work suggests that concentrations in the droplet bulk may actually be higher for more moderately strong surfactants, which are not fully depleted due to surface partitioning. For example, the previously studied dicarboxylic acids (Ruehl et al., 2016), organosulfates (Hansen et al., 2015), and α-pinene SOA (George et al., 2009; Ruehl et al., 2016), as well as the proxy mixture for NUM particles (Ovadnevaite et al., 2017) and pollen extracts (Prisle et al., 2019), are less surface-active and more intrinsically hygroscopic than NAFA. In these systems, the droplet state and CCN activation behavior may therefore be expected to be more sensitive to variations in the bulk–surface partitioning, as the droplet grows and changes, and in response to variations in organic–inorganic interactions with a changing mixing state.
4.2 Comparison to other bulk–surface partitioning models
Several bulk–surface partitioning models have been presented in recent years and deployed in connection with Köhler theory to evaluate CCN activity for various surface-active aerosol systems (see, e.g., Malila and Prisle, 2018). The models are each based on different assumptions and required forms of thermodynamic information. Therefore, a quantitative comparison of the performance of the different models for a common aerosol system under identical conditions is not straightforward. Vepsäläinen et al. (2021) recently made such a comparison of Köhler model predictions for particles comprising a set of well-known moderately surface-active dicarboxylic acids, using five different partitioning models. Common for the partitioning models is that bulk and surface phases of a growing solution droplet with changing are connected via a composition-dependent surface tension equation of state and an adsorption isotherm for the surface-active components. With specific choices of equations and input parameters, each model is tailored to capture certain properties of the surface-active aerosol components and has been successfully applied to describe cloud droplet activation of selected aerosol mixtures. However, altogether the different models have so far only been applied to a limited set of aerosol systems, and neither of the models fully captures all interactions of the surface-active solute across varying droplet states. Even if none of the models are currently broadly applicable to general aerosol mixtures, conditions, and modeling purposes, each provides valuable insight into the role of surface activity in growing and activating droplets.
Most of the frameworks described in the following have been presented in simplified versions, subject to various approximations. Curiously, several studies (Prisle et al., 2011; Ruehl et al., 2016; Ovadnevaite et al., 2017; Davies et al., 2019) note how the simplified version of a given model performs equally well against experimental data as the full model, as was also seen here for the simple model (S).
4.2.1 Compressed film model
Ruehl et al. (2016) used the “compressed film” model of Jura and Harkins (1946) to predict partitioning of surfactants into an organic surface layer. Using a surface-composition-based surface tension equation, they find quite a different surface tension variation with growing droplet size than seen using the Szyszkowski-type equation in this work. However, their study also involves particles comprising more moderately surface-active dicarboxylic acids and α-pinene SOA than the strongly surface-active NAFA mixtures. Furthermore, Ruehl et al. (2016) use a constant organic hygroscopicity parameter (Petters and Kreidenweis, 2007) and therefore do not include effects of concentration-dependent non-ideal water activity, which could also lead to differences, compared to the present work. In order to obtain the necessary surface tension and adsorption parameters, the model of Ruehl et al. (2016) must first be fitted to the experimental Köhler curves, in the form of measured droplet size–water saturation relations, being described. The model is therefore analytical, rather than predictive, and model parameters cannot immediately be applied to droplet systems and conditions which are different from those for which they have been obtained. For complex and unresolved aerosol mixtures, it may furthermore be challenging to independently verify that model parameters accurately describe the underlying thermodynamic properties and do not confound different effects of surface activity in the droplets.
Ruehl et al. (2016) found that droplet activation typically occurs after the droplet has reached a state where all surface-active solute is partitioned to the droplet surface, but the total amount is still less than what is necessary to reach the minimum surface concentration, expressed via the parameter δorg (interpreted as a minimum surface thickness), that enables full surface coverage and reduced surface tension. These observations are analogous to those of the present work for the comprehensive Gibbs adsorption (P) and simple (S) partitioning models. In the “gaseous film” region, the model of Ruehl et al. (2016) essentially describes the same conditions as the simple partitioning model (S) of Prisle et al. (2011).
4.2.2 Liquid–liquid phase separation model
The liquid–liquid phase separation (LLPS) model of Ovadnevaite et al. (2017) describes the partitioning equilibrium between separate aqueous and organic compartments representing the droplet bulk and surface, respectively. Partitioning is evaluated with considerations of composition-dependent solution non-ideality using the well-established AIOMFAC model. Where both the full and simple partitioning models of the present work and the model of Ruehl et al. (2016) in the compressed film region consider the surface to be comprised exclusively of the surface-active component, the LLPS model accounts for the presence of small amounts of organic material in the aqueous phase, as well as water and water-soluble components in the organic phase. Droplet surface tensions are evaluated from an empirical mixing rule, based on the volume-weighed composition of the organic (surface) phase. The LLPS model requires knowledge of the specific chemical identity, amount, and corresponding AIOMFAC parameters for all species in the droplet. Ovadnevaite et al. (2017) enabled predictive Köhler model calculations with the LLPS model for partially resolved aerosol mixtures by assuming simplified, well-defined proxy mixtures with well-known interaction parameters to represent the aerosol systems in question. This approach has inherent uncertainties related to the choice of proxy system and how well it represents the variation of all relevant solution interactions across the droplet states spanned during growth and activation. As discussed by Prisle et al. (2012a), if the proxy mixture is too simplistic, predicted properties may be more sensitive to variations in the droplet state, compared to the actual complex mixture.
Similar to the gaseous film model of Ruehl et al. (2016) and the simple partitioning model of Prisle et al. (2011), the simplified complete liquid–liquid phase separation (CLLPS) model (Ovadnevaite et al., 2017; Davies et al., 2019) also assumes that surface-active components are fully partitioned to the droplet surface. However, where the gaseous film and simple partitioning models assume droplet surface tension equal to that of pure water, the CLLPS model allows for composition-dependent reduced surface tension based on the fractional coverage of the droplet surface, using the volume-based mixing rule. Both the simple partitioning and CLLPS models also allow for representation of droplet solution non-ideality from solute species other than the surface-active components, with thermodynamic relations. The CLLPS model therefore captures properties of the droplets from both the simplified frameworks (S) and (B) used in this work.
4.2.3 Gibbs adsorption models
Partitioning models based on Gibbs adsorption with Szyszkowski-type surface tension equations have been the most widely used in predictive Köhler models (see, e.g., Malila and Prisle, 2018); however, the present framework is the first to implement this approach on a mass basis. This allows for thermodynamically consistent modeling of chemically complex and even unresolved mixtures, such as ambient aerosol particles, instead of a limited set of chemically simple systems, each comprising at most a few well-defined species. The present model is fully predictive and takes non-ideal interactions in droplets into account via continuous parametrizations, which are independently constrained by measurements. No additional parameters are introduced in the framework. A remaining disadvantage related to use of the model is that while water activity and surface tension can be accurately measured for complex and unresolved samples with standard instrumentation, these experiments require significant amounts of sample material to obtain a sufficient number of data points to construct robust continuous multi-dimensional parametrizations (e.g., Prisle et al., 2019; Lin et al., 2020). This may still pose a challenge related to ambient aerosol samples, especially for ultrafine particles sampled in pristine environments.
The simple partitioning model (Prisle et al., 2011) used in this work emulates the predictions of the full Gibbs-adsorption-based partitioning model for simple systems comprising well-known strong surfactants, with potential applications to complex, unresolved surface-active mixtures. Alternatively, Raatikainen and Laaksonen (2011) presented an analytical solution to the Gibbs adsorption model applicable to droplets comprising a single, chemically well-defined surface-active species and ignoring all droplet solution non-idealities. To model complex aerosol, it is therefore necessary to assume a suitable proxy compound.
4.2.4 Surface monolayer model
In the model of Malila and Prisle (2018), partitioning occurs between the droplet bulk and a surface monolayer with finite thickness. The partitioning equilibrium is evaluated according to an extension of the semi-empirical mixing rule of Laaksonen and Kulmala (1991), yielding a surface-composition-dependent surface tension, which is matched to that evaluated with a macroscopic relation for the corresponding droplet bulk-composition. Similar to the LLPS model, the monolayer model evaluates the partitioning of all droplet components between both bulk and surface phases. However, effects of non-ideality are accounted for by using composition-dependent thermodynamic functions independently constrained from experiments. The surface monolayer model is therefore predictive for the actual system to which it is applied, similar to the framework presented here. In the implementation presented by Malila and Prisle (2018), the monolayer model requires knowledge of specific chemical composition of the droplets. To enable predictive, thermodynamically consistent calculations also for chemically unresolved aerosol mixtures, the monolayer model could be formulated on a mass basis, using an approach analogous to this work.
The monolayer model has been found to predict lower droplet surface tensions than the Gibbs models, because the surface partitioning factor at a given droplet size is restricted to a finite value by the volume of the surface monolayer, leading to less strong depletion of the droplet bulk. This enhances the predicted potential impact of reduced surface tension, also at the point of droplet activation (Malila and Prisle, 2018; Lin et al., 2018, 2020; Bzdek et al., 2020).
4.3 Potential for large-scale applications
Thermodynamically consistent, comprehensive Köhler models including bulk–surface partitioning are generally not suitable or computationally feasible for applications to large-scale frameworks (Prisle et al., 2012a; Lowe et al., 2019). However, with simplified models, such as those described above, where the partitioning equilibrium does not require iteration for each droplet size, it is possible to explicitly consider effects of surface activity in large-scale simulations. So far, such studies have been sparse. The simple partitioning models of Raatikainen and Laaksonen (2011) and Prisle et al. (2011) have been successfully applied in a global climate model (Prisle et al., 2012a) and that of Ovadnevaite et al. (2017) in a cloud parcel model (Lowe et al., 2019).
Results of the present work show that both the simple partitioning representation (S) and the basic Köhler model (K) may represent CCN activity well for strongly surface-active mixtures with low intrinsic hygroscopicity, such as those with low solubility or high mean molar mass similar to NAFA, in alignment with the findings of Prisle et al. (2012a). Based on the good performance of model (S) with respect to both experimental CCN data and comprehensive calculations with the full Gibbs partitioning model for particles comprising the complex NAFA mixture, this model is a promising candidate to describe CCN potential of other strongly surface-active unresolved aerosol mixtures, including atmospheric aerosols. When reduced droplet surface tension prevails, the CLLPS will likely provide a better representation of the effects of aerosol surface activity, provided that a suitable proxy system can be identified to describe the aerosol mixture. To enable this, the applicability of various proxy mixtures across a range of atmospherically relevant aerosol compositions and ambient conditions must be carefully established. This could be achieved by comparing predictions with the CLLPS model for the chosen proxy system to self-contained, thermodynamically consistent modeling for the actual complex aerosol mixture, which is possible with the comprehensive mass-based framework presented here. For conditions where effects of intrinsic hygroscopicity and non-ideal solute interactions are more prominent than surface activity and reduced surface tension of an aerosol mixture, the basic Köhler model (K) with inclusion of a suitable thermodynamic representation of droplet non-ideality may still be preferable for large-scale applications, due to its ability to represent overall CCN activity and simplicity of implementation.
When the position of the partitioning equilibrium is highly sensitive to changes in conditions, due to moderate surface activity and non-ideal interactions in the aerosol mixtures, a comprehensive thermodynamic model is generally needed to fully capture variations in the droplet state with particle size and composition and in response to droplet growth and dilution. To explore and firmly establish which features are driving the impact of surface activity in cloud microphysics under various ambient conditions, thermodynamically consistent predictive modeling using independently derived mixture-specific model parameters will be needed for a wide range of atmospherically relevant aerosol systems. The presented mass-based framework allows this directly for chemically complex and unresolved mixtures, including actual atmospheric aerosol samples, without retrofitting of model parameters or assuming a proxy mixture to represent the actual system.
This work presents a thermodynamic framework for including bulk–surface partitioning of chemically unresolved surface-active aerosol components in predictive Köhler modeling of growing droplets, using mass-based Gibbs adsorption in combination with water activity and Szyszkowski surface tension equations. The role of aerosol surface activity in atmospheric cloud microphysics is still not generally established. Thermodynamically consistent, predictive modeling with independently constrained model parameters is necessary to resolve the different effects of surface activity occurring simultaneously during aerosol hygroscopic growth and cloud droplet activation and assess their relative impacts on CCN activity. Previous models have only achieved this for simple and chemically well-defined aerosol mixtures, which may not be broadly representative of atmospheric aerosol. The presented framework enables thermodynamically consistent, predictive Köhler modeling directly for chemically complex and unresolved surface-active aerosol mixtures, including actual atmospheric samples, without retrofitting model parameters or approximating thermodynamic properties with those of a proxy system. This will allow for a systematic exploration of the impact of surface activity in cloud microphysical processes for a broad range of atmospherically relevant complex aerosol systems and contribute to clarifying the conditions where cloud microphysics is governed by each of the effects of surface activity, as well as their most suitable representation in atmospheric modeling.
Application of the mass-based model presented was illustrated with predictive calculations of CCN activity for particles comprising chemically unresolved, surface-active NAFA mixtures, together with NaCl. As required input, fully continuous parametrizations of surface tension and water activity as functions of both NAFA and NaCl aqueous mass concentrations were constructed from independent measurements. Different conclusions have been reached in previous studies of the role of surface activity in hygroscopic growth and cloud droplet activation of atmospherically relevant surfactants and mixtures. With independently constrained thermodynamic functions for both water activity and aqueous NAFA surface activity, the thermodynamically consistent model presented predicts cloud microphysical properties for chemically complex, surface-active NAFA mixtures, which closely resembles those previously found for systems comprising simple, strong surfactants with well-defined molecular properties. NAFA has significant surfactant strength in macroscopic aqueous solutions, but predictions with the comprehensive framework show that, due to the very large surface-to-volume ratios of submicron activating droplets, the NAFA partitioning equilibrium is strongly shifted to the surface. Therefore, the same total compositions do not lead to similar reductions in droplet surface tension as in macroscopic solutions, if any at all. NAFA has a modest influence on water activity in both macroscopic aqueous solutions and activating droplets, at least in part due to its high average molar mass, compared to hygroscopic salts. Results of the presented model show that, in submicron droplets, the weak intrinsic impact on water activity is further reduced by surface partitioning of NAFA. Contrary to several recent works, results of the thermodynamically consistent mass-based model show that for the NAFA–NaCl mixtures, submicron droplet properties are governed by size-modulated influences of surface activity on both water activity and curvature terms of the Köhler curve. The “missing Raoult effect” from bulk-phase depletion due to surface adsorption overpowers any enhancement of droplet growth and activation from decreased surface tension.
The comprehensive, thermodynamically consistent predictions were used to benchmark four simplified models of the effect of NAFA surface activity in cloud droplet activation: (S) the simple partitioning representation proposed by Prisle et al. (2011), where NAFA is assumed to have zero intrinsic influence on both surface tension and water activity of droplets; (I) considering NAFA as a fully surface-partitioned, insoluble surfactant with fixed reduction of droplet surface tension; (B) assuming that droplets comprising NAFA and NaCl have identical properties to macroscopic bulk solutions of the same overall composition; and (K) treating NAFA and NaCl alike as regular soluble and homogeneously distributed (non-surface-active) solutes. Calculations with the presented comprehensive model for NAFA–NaCl particles confirm previous robust findings that assuming macroscopic solution properties for activating droplets in the micron and submicron size range without including effects of bulk–surface partitioning leads to gross overestimations of both thermodynamically consistent predictions and measurements of CCN activity. On the other hand, simplified frameworks assuming complete surface partitioning and/or omitting surface tension reduction each describe comprehensive model results and experimental CCN data for NAFA–NaCl particles well. Furthermore, these simple models also give similar results as the full partitioning framework for a number of other properties calculated for growing and activating droplets, when the conditions predicted with the full model are well-described by the underlying assumptions of the simplified frameworks.
Surface activity of aerosol components may also have important implications for other processes related to cloud microphysics, including aqueous chemistry taking place as droplets repeatedly shrink and grow during cloud processing in the atmosphere (Pruppacher and Jaenicke, 1995). For example, owing to the relatively large surface areas of submicron droplets, aqueous surface chemistry, such as the photosensitized limonene uptake by humic acid, another atmospheric model HULIS (Tsui and McNeill, 2018), may be significantly enhanced, compared to reactions in the bulk phase. Furthermore, extensive surface enrichment due to partitioning will change the chemical environment and possible chemical reaction pathways and rates of surface-active species in both the surface (Prisle et al., 2012b; Öhrwall et al., 2015; Werner et al., 2018) and for droplets in the submicron range (Prisle et al., 2010) also in the bulk phase. When depleted from the droplet bulk, surface-active compounds will not be as readily available for reactions with soluble species in the aqueous droplet phase, and the rate determining concentrations will be vastly different from a macroscopic solution with identical total composition. Finally, pressure-sensitive reactions in the droplet phase (Jenner, 1975) will be impacted by the elevated pressures inside microscopic systems from the finite curvature radii according to the Young–Laplace equation (Adamson and Gast, 1997). This pressure elevation, which is also the basis for the Kelvin effect in Eq. (1), depends directly on the droplet surface tension. The present work shows significant differences of up to roughly a factor of 2 between predicted surface tensions for submicron droplets and macroscopic solutions, translating to a factor of 4 difference in the curvature effect on changes in the chemical potential, which must be taken into account together with the explicit curvature variation in efforts to constrain such effects on yields and pathways of aerosol chemistry (e.g., Tu and Johnston, 2017; Winkler et al., 2012).
A comprehensive description of both droplet bulk and surface composition, by including size-dependent surface adsorption and its response to changing ambient humidity and droplet growth, may therefore be crucial for understanding the mechanisms and predicting the extent of chemical processes in microscopic atmospheric droplets.
Code and underlying research data are available upon request from the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-21-16387-2021-supplement.
The author declares that there is no conflict of interest.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author thanks Bjarke Mølgaard for his work on the surface tension and water activity parametrizations, Silvia Calderón, Jack J. Lin, Jussi Malila, Tomi Raatikainen, Sampo Vepsäläinen, and Taina Yli-Juuti for valuable discussions and technical support, and Thomas B. Kristensen and Merete Bilde for providing measurement data previously published by Kristensen et al. (2014) and Lin et al. (2020).
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation programme (project SURFACE, grant agreement no. 717022). Nønne L. Prisle also gratefully acknowledges funding from the Carlsberg Foundation (grant nos. 2009_01_0366 and 2010_01_0391) and Academy of Finland (grant nos. 257411, 308238, 314175, and 335649).
This paper was edited by Barbara Ervens and reviewed by three anonymous referees.
Adamson, A. and Gast, A.: Physical Chemistry of Surfaces, John Wiley & Sons, Inc., sixth edn., 808 pp., 1997. a
Alvarez, N. J., Walker, L. M., and Anna, S. L.: A Microtensiometer To Probe the Effect of Radius of Curvature on Surfactant Transport to a Spherical Interface, Langmuir, 26, 13310–13319, https://doi.org/10.1021/la101870m, 2010. a, b
Asa-Awuku, A., Sullivan, A. P., Hennigan, C. J., Weber, R. J., and Nenes, A.: Investigation of molar volume and surfactant characteristics of water-soluble organic compounds in biomass burning aerosol, Atmos. Chem. Phys., 8, 799–812, https://doi.org/10.5194/acp-8-799-2008, 2008. a
Aumann, E., Hildemann, L., and Tabazadeh, A.: Measuring and modeling the composition and temperature-dependence of surface tension for organic solutions, Atmos. Environ., 44, 329–337, 1967. a
Bianco, H. and Marmur, A.: The Dependence of the Surface Tension of Surfactant Solutions on Drop Size, Journal of Colloid and Interface Science, 151, 517–522, 1992. a
Bilde, M. and Svenningsson, B.: CCN Activation of Slightly Soluble Organics: The Importance of Small Amounts of Inorganic Salt and Particle Phase, Tellus B, 56, 128–134, 2004. a
Booth, A. M., Topping, D. O., McFiggans, G., and Percival, C. J.: Surface tension of mixed inorganic and dicarboxylic acid aqueous solutions at 298.15 K and their importance for cloud activation predictions, Phys. Chem. Chem. Phys., 11, 8021–8028, 2009. a
Bzdek, B. R., Reid, J. P., Malila, J., and Prisle, N. L.: The surface tension of surfactant-containing, finite volume droplets, P. Natl. Acad. Sci. USA, 117, 8335–8343, 2020. a, b, c, d
Cheng, Y., Li, S.-M., Leithead, A., Brickell, P. C., and Leaitch, W. R.: Characterizations of cis-pinonic acid and n-fatty acids on fine aerosols in the Lower Fraser Valley during Pacific 2001 Air Quality Study, Atmos. Environ., 38, 5789–5800, 2004. a
Davies, J. F., Zuend, A., and Wilson, K. R.: Technical note: The role of evolving surface tension in the formation of cloud droplets, Atmospheric Chemistry and Physics, 19, 2933–2946, 2019. a, b, c, d
Dawson, K. W., Petters, M. D., Meskhidze, N., Suda Petters, S., and Kreidenweis, S. M.: Hygroscopic growth and cloud droplet activation of xanthan gum as a proxy for marine hydrogels, J. Geophys. Res.-Atmos., 121, 11803–11818, 2016. a, b, c
Dillmann, A. and Meier, G. E. A.: A refined droplet approach to the problem of homogeneous nucleation from the vapor phase, The Journal of Chemical Physics, 94, 3872–3884, https://doi.org/10.1063/1.460663, 1991. a
Dinar, E., Mentel, T. F., and Rudich, Y.: The density of humic acids and humic like substances (HULIS) from fresh and aged wood burning and pollution aerosol particles, Atmos. Chem. Phys., 6, 5213–5224, https://doi.org/10.5194/acp-6-5213-2006, 2006a. a
Dinar, E., Taraniuk, I., Graber, E. R., Katsman, S., Moise, T., Anttila, T., Mentel, T. F., and Rudich, Y.: Cloud Condensation Nuclei properties of model and atmospheric HULIS, Atmos. Chem. Phys., 6, 2465–2482, https://doi.org/10.5194/acp-6-2465-2006, 2006b. a
Facchini, M., Mircea, M., Fuzzi, S., and Charlson, R.: Cloud Albedo Enhancement by Surface-Active Organic Solutes in Growing Droplets, Nature, 401, 257–259, https://doi.org/10.5194/acp-10-8219-2010, 1999. a, b, c
Facchini, M., Decesari, S., Mircea, M., Fuzzi, S., and Loglio, G.: Surface Tension of Atmospheric Wet Aerosol and Cloud/Fog Droplets in Relation to their Organic Carbon Content and Chemical Composition, Atmos. Environ., 34, 4853–4857, 2000. a
Fainerman, V. B., Miller, R., and Möhwald, H.: General Relationships of the Adsorption Behavior of Surfactants at the Water/Air Interface, J. Phys. Chem. B, 106, 809–819, 2002. a
Forestieri, S. D., Staudt, S. M., Kuborn, T. M., Faber, K., Ruehl, C. R., Bertram, T. H., and Cappa, C. D.: Establishing the impact of model surfactants on cloud condensation nuclei activity of sea spray aerosol mimics, Atmos. Chem. Phys., 18, 10985–11005, https://doi.org/10.5194/acp-18-10985-2018, 2018. a, b, c, d, e, f, g, h
Frosch, M., Prisle, N. L., Bilde, M., Varga, Z., and Kiss, G.: Joint effect of organic acids and inorganic salts on cloud droplet activation, Atmos. Chem. Phys., 11, 3895–3911, https://doi.org/10.5194/acp-11-3895-2011, 2011. a
Frossard, A. A., Gérard, V., Duplessis, P., Kinsey, J. D., Lu, X., Zhu, Y., Bisgrove, J., Maben, J. R., Long, M. S., Chang, R. Y. W., Beaupré, S. R., Kieber, D. J., Keene, W. C., Nozière, B., and Cohen, R. C.: Properties of Seawater Surfactants Associated with Primary Marine Aerosol Particles Produced by Bursting Bubbles at a Model Air-Sea Interface, Environ. Sci. Technol., 53, 9407–9417, https://doi.org/10.1021/acs.est.9b02637, 2019. a
George, I., Chang, R.-W., Danov, V., Vlasenko, A., and Abbatt, J.: Modification of cloud condensation nucleus activity of organic aerosols by hydroxyl radical heterogeneous oxidation, Atmos. Environ., 43, 5038–5045, https://doi.org/10.1016/j.atmosenv.2009.06.043, 2009. a, b, c, d
Gérard, V., Nozière, B., Baduel, C., Fine, L., Frossard, A. A., and Cohen, R. C.: Anionic, Cationic, and Nonionic Surfactants in Atmospheric Aerosols from the Baltic Coast at Askö, Sweden: Implications for Cloud Droplet Activation, Environ. Sci. Technol., 50, 2974–2982, https://doi.org/10.1021/acs.est.5b05809, 2016. a, b
Gérard, V., Nozière, B., Fine, L., Ferronato, C., Singh, D. K., Frossard, A. A., Cohen, R. C., Asmi, E., Lihavainen, H., Kivekäs, N., Aurela, M., Brus, D., Frka, S., and Cvitešić Kušan, A.: Concentrations and Adsorption Isotherms for Amphiphilic Surfactants in PM1 Aerosols from Different Regions of Europe., Environ. Sci. Technol., 53, 12379–12388, https://doi.org/10.1021/acs.est.9b03386, 2019. a
Gibbs, J., Bumstead, H., Longley, W., and Name, R. V.: The Collected Works of J. Willard Gibbs, Longmans, Green and Co., 434 pp., 1928. a
Graber, E. R. and Rudich, Y.: Atmospheric HULIS: How humic-like are they? A comprehensive and critical review, Atmos. Chem. Phys., 6, 729–753, https://doi.org/10.5194/acp-6-729-2006, 2006. a
Hansen, A. M. K., Hong, J., Raatikainen, T., Kristensen, K., Ylisirniö, A., Virtanen, A., Petäjä, T., Glasius, M., and Prisle, N. L.: Hygroscopic properties and cloud condensation nuclei activation of limonene-derived organosulfates and their mixtures with ammonium sulfate, Atmos. Chem. Phys., 15, 14071–14089, https://doi.org/10.5194/acp-15-14071-2015, 2015. a, b, c, d, e, f, g, h
Harmon, C., Grimm, R., McIntire, T., Peterson, M., Njegic, B., Angel, V., Alshawa, A., Underwood, J., Tobias, D., Gerber, R., Gordon, M., Hemminger, J., and Nizkorodov, S.: Hygroscopic growth and deliquescence of NaCl nanoparticles mixed with surfactant SDS, J. Phys. Chem. B, 114, 2435–2449, 2010. a, b, c
Hyvärinen, A.-P., Lihavainen, H., Gaman, A., Vairila, L., Ojala, H., Kulmala, M., and Viisanen, Y.: Surface Tensions and Densities of Oxalic, Malonic, Succinic, Maleic, Malic, and cis-Pinonic Acids, J. Chem. Eng., 51, 255–260, 2006. a
Jenner, G.: High Pressure Kinetic Investigations in Organic and Macromolecular Chemistry, Angewandte Chemie International Edition in English, 14, 137–143, https://doi.org/10.1002/anie.197501371, 1975. a
Jin, F., Balasubramaniam, R., and Stebe, K. J.: Surfactant adsorption to spherical particles: the intrinsic length scale governing the shift from diffusion to kinetic-controlled mass transfer, The Journal of Adhesion, 80, 773–796, https://doi.org/10.1080/00218460490480770, 2004. a
Jura, G. and Harkins, W. D.: Surfaces of Solids. XIV. A Unitary Thermodynamic Theory of the Adsorption of Vapors on Solids and of Insoluble Films on Liquid Subphases, Journal of the American Chemical Society, 68, 1941–1952, 1946. a
Kiss, G. and Hansson, H.-C.: Application of osmolality for the determination of water activity and the modelling of cloud formation, Atmos. Chem. Phys. Discuss., 4, 7667–7689, https://doi.org/10.5194/acpd-4-7667-2004, 2004. a
Kiss, G., Tombacz, E., and Hansson, H.-C.: Surface Tension Effects of Humic-Like Substances in the Aqueous Extract of Tropospheric Fine Aerosol, J. Atmos. Chem., 50, 279–294, 2005. a, b
Köhler, H.: The Nucleus in and the Growth of Hygroscopic Droplets, Transactions of the Faraday Society, 32, 1152–1161, 1936. a, b
Kristensen, T. B., Prisle, N. L., and Bilde, M.: Cloud droplet activation of mixed model HULIS and NaCl particles: Experimental results and κ-Köhler theory, Atmos. Res., 137, 167–175, 2014. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa
Kroflič, A., Frka, S., Simmel, M., Wex, H., and Grgić, I.: Size-resolved surface active substances of atmospheric aerosol: reconsideration of the impact on cloud droplet formation, Environ. Sci. Technol., 0, 30048123, https://doi.org/10.1021/acs.est.8b02381, 2018. a, b, c
Laaksonen, A.: The Composition Size Dependence of Aerosols Created by Dispersion of Surfactant Solutions, Journal of Colloid and Interface Science, 159, 517–519, 1993. a
Laaksonen, A. and Kulmala, M.: An explicit cluster model for binary nuclei in water-alcohol systems, The Journal of Chemical Physics, 95, 6745–6748, 1991. a
Lee, B.-B., Chan, E.-S., Ravindra, P., and Khan, T. A.: Surface tension of viscous biopolymer solutions measured using the du Nouy ring method and the drop weight methods, Polymer Bulletin, 69, 471–489, 2012. a
Li, Z., Williams, A., and Rood, M.: Influence of Soluble Surfactant Properties on the Activation of Aerosol Particles Containing Inorganic Solute, J. Atmos. Sci., 55, 1859–1866, 1998. a, b, c, d, e, f
Lin, J. J., Malila, J., and Prisle, N. L.: Cloud droplet activation of organic-salt mixtures predicted from two model treatments of the droplet surface, Environmental Science: Processes & Impacts, 20, 1611–1629, 2018. a, b, c
Lin, J. J., Kristensen, T. B., Calderón, S. M., Malila, J., and Prisle, N. L.: Effects of surface tension time-evolution for CCN activation of a complex organic surfactant, Environmental Science: Processes & Impacts, 22, 271–284, 2020. a, b, c, d, e, f
Low, R.: A Theoretical Study of Nineteen Condensation Nuclei, Journal de Recherches Atmospheriques, 65–78, 1969. a
Lowe, S. J., Partridge, D. G., Davies, J. F., Wilson, K. R., Topping, D., and Riipinen, I.: Key drivers of cloud response to surface-active organics, Nat. Commun., 10, 1–12, 2019. a, b, c, d
Mäkelä, J. and Manninen, P.: Molecular size distribution od structure investigations of humic substances in groundwater, working report 2008-36, Posiva Oy, Posiva Oy, Olkiluoto, FI-27160 Eurajoki, Finland, 2008. a, b
Malila, J. and Prisle, N. L.: A monolayer partitioning scheme for droplets of surfactant solutions, J. Adv. Model. Earth Sys., 10, 3233–3251, 2018. a, b, c, d, e, f, g
Meissner, H. P. and Michaels, A. S.: Surface Tensions of Pure Liquids and Liquid Mixtures, Industrial & Engineering Chemistry, 41, 2782–2787, https://doi.org/10.1021/ie50480a028, 1949. a
Mochida, M., Kitamori, Y., Kawamura, K., Nojiri, Y., and Suzuki, K.: Fatty acids in the marine atmosphere: Factors governing their concentrations and evaluation of organic films on sea-salt particles, J. Geophys. Res., 107, D17S4325, https://doi.org/10.1029/2001JD001278, 2002. a
Mochida, M., Kawamura, K., Umemoto, N., Kobayashi, M., Matsunaga, S., Lim, H.-J., Turpin, B., Bates, T., and Simoneit, B.: Spatial distributions of oxygenated organic compounds (dicarboxylic acids, fatty acids, and levoglucosan) in marine aerosols over the western Pacific and off the coast of East Asia: Continental outflow of organic aerosols during the ACE-Asia campaign, J. Geophys. Res., 108, D23S8638, https://doi.org/10.1029/2002JD003249, 2003. a
Nguyen, Q. T., Kristensen, T. B., Hansen, A. M. K., Skov, H., Bossi, R., Massling, A., Sørensen, L. L., Bilde, M., Glasius, M., and Nøjgaard, J. K.: Characterization of humic-like substances in Arctic aerosols, J. Geophys. Res.-Atmos,, 119, 5011–5027, https://doi.org/10.1002/2013JD020144, 2014. a
Noziere, B., Baduel, C., and Jaffrezo, J.-L.: The dynamic surface tension of atmospheric aerosol surfactants reveals new aspectsof cloud activation, Nat. Commun., 5, 1–7, 2014. a
Öhrwall, G., Prisle, N. L., Ottosson, N., Werner, J., Ekholm, V., Walz, M.-M., and Björneholm, O.: Acid-Base Speciation of Carboxylate Ions in the Surface Region of Aqueous Solutions in the Presence of Ammonium and Aminium Ions, The Journal of Physical Chemistry B, 119, 4033–4040, 2015. a
Ovadnevaite, J., Zuend, A., Laaksonen, A., Sanchez, K. J., Roberts, G., Ceburnis, D., Decesari, S., Rinaldi, M., Hodas, N., Facchini, M. C., Seinfeld, J. H., and O' Dowd, C.: Surface tension prevails over solute effect in organic-influenced cloud droplet activation, Nature, 546, 637–641, 2017. a, b, c, d, e, f, g, h, i, j, k, l
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity – Part 3: Including surfactant partitioning, Atmos. Chem. Phys., 13, 1081–1091, https://doi.org/10.5194/acp-13-1081-2013, 2013. a, b
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. a, b
Petters, S. S. and Petters, M. D.: Surfactant effect on cloud condensation nuclei for two-component internally mixed aerosols, J. Geophys. Res.-Atmos., 121, 1878–1895, 2016. a, b, c, d, e, f
Poulain, L., Wu, Z., Petters, M. D., Wex, H., Hallbauer, E., Wehner, B., Massling, A., Kreidenweis, S. M., and Stratmann, F.: Towards closing the gap between hygroscopic growth and CCN activation for secondary organic aerosols – Part 3: Influence of the chemical composition on the hygroscopic properties and volatile fractions of aerosols, Atmos. Chem. Phys., 10, 3775–3785, https://doi.org/10.5194/acp-10-3775-2010, 2010. a
Prisle, N.: Cloud Condensation Nuclei Properties of Organic Aerosol Particles: Effects of Acid Dissociation and Surfactant Partitioning, M.Sc. Thesis, Department of Chemistry, Faculty of Science, University of Copenhagen, 175 pp., 2006. a, b
Prisle, N. L., Raatikainen, T., Sorjamaa, R., Svenningsson, B., Laaksonen, A., and Bilde, M.: Surfactant partitioning in cloud droplet activation: a study of C8, C10, C12 and C14 normal fatty acid sodium salts, Tellus B, 60, 416–431, https://doi.org/10.1111/j.1600-0889.2008.00352.x, 2008. a, b, c, d, e, f, g, h, i, j, k, l
Prisle, N. L., Raatikainen, T., Laaksonen, A., and Bilde, M.: Surfactants in cloud droplet activation: mixed organic-inorganic particles, Atmos. Chem. Phys., 10, 5663–5683, https://doi.org/10.5194/acp-10-5663-2010, 2010. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y
Prisle, N. L., Dal Maso, M., and Kokkola, H.: A simple representation of surface active organic aerosol in cloud droplet formation, Atmos. Chem. Phys., 11, 4073–4083, https://doi.org/10.5194/acp-11-4073-2011, 2011. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Prisle, N. L., Asmi, A., Topping, D., Partanen, A.-I., Romakkaniemi, S., Dal Maso, M., Kulmala, M., Laaksonen, A., Lehtinen, K. E. J., McFiggans, G., and Kokkola, H.: Surfactant effects in global simulations of cloud droplet activation., Geophys. Res. Lett., 39, L05802, https://doi.org/10.1029/2011GL050467, 2012a. a, b, c, d, e, f
Prisle, N. L., Ottosson, N., Öhrwall, G., Söderström, J., Dal Maso, M., and Björneholm, O.: Surface/bulk partitioning and acid/base speciation of aqueous decanoate: direct observations and atmospheric implications, Atmos. Chem. Phys., 12, 12227–12242, https://doi.org/10.5194/acp-12-12227-2012, 2012b. a, b
Prisle, N. L., Lin, J. J., Purdue, S., Lin, H., Meredith, J. C., and Nenes, A.: Cloud condensation nuclei activity of six pollenkitts and the influence of their surface activity, Atmos. Chem. Phys., 19, 4741–4761, https://doi.org/10.5194/acp-19-4741-2019, 2019. a, b, c, d, e, f, g, h, i
Pruppacher, H. R. and Jaenicke, R.: The processing of water vapor and aerosols by atmospheric clouds, a global estimate, Atmos. Res., 38, 283–295, 1995. a
Raatikainen, T. and Laaksonen, A.: A simplified treatment of surfactant effects on cloud drop activation, Geosci. Model Dev., 4, 107–116, https://doi.org/10.5194/gmd-4-107-2011, 2011. a, b, c, d
Rood, M. J. and Williams, A. L.: Reply, J. Atmos. Sci., 58, 1468–1473, 2001. a
Ruehl, C. R., Chuang, P. Y., and Nenes, A.: Aerosol hygroscopicity at high (99 to 100 %) relative humidities, Atmos. Chem. Phys., 10, 1329–1344, https://doi.org/10.5194/acp-10-1329-2010, 2010. a
Ruehl, C. R., Davies, J. F., and Wilson, K. R.: An interfacial mechanism for cloud droplet formation on organic aerosols, Science, 351, 1447–1450, https://doi.org/10.1126/science.aad4889, 2016. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q
Shulman, M., Jacobson, M., Charlson, R., Synovec, R., and Young, T.: Dissolution Behavior and Surface Tension Effects of Organic Compounds in Nucleating Cloud Droplets, Geophys. Res. Lett., 23, 277–280, 1996. a, b, c
Sorjamaa, R., Svenningsson, B., Raatikainen, T., Henning, S., Bilde, M., and Laaksonen, A.: The role of surfactants in Köhler theory reconsidered, Atmos. Chem. Phys., 4, 2107–2117, https://doi.org/10.5194/acp-4-2107-2004, 2004. a, b, c, d, e, f, g, h, i, j
Topping, D.: An analytical solution to calculate bulk mole fractions for any number of components in aerosol droplets after considering partitioning to a surface layer, Geosci. Model Dev., 3, 635–642, https://doi.org/10.5194/gmd-3-635-2010, 2010. a
Tsui, W. G. and McNeill, V. F.: Modeling Secondary Organic Aerosol Production from Photosensitized Humic-like Substances (HULIS), Environ. Sci. Tech. Lett., 5, 255–259, https://doi.org/10.1021/acs.estlett.8b00101, 2018. a
Tu, P. and Johnston, M. V.: Particle size dependence of biogenic secondary organic aerosol molecular composition, Atmos. Chem. Phys., 17, 7593–7603, https://doi.org/10.5194/acp-17-7593-2017, 2017. a
Vanhanen, J., Hyvärinen, A.-P., Anttila, T., Raatikainen, T., Viisanen, Y., and Lihavainen, H.: Ternary solution of sodium chloride, succinic acid and water; surface tension and its influence on cloud droplet activation, Atmos. Chem. Phys., 8, 4595–4604, https://doi.org/10.5194/acp-8-4595-2008, 2008. a, b
Varga, Z., Kiss, G., and Hansson, H.-C.: Modelling the cloud condensation nucleus activity of organic acids on the basis of surface tension and osmolality measurements, Atmos. Chem. Phys., 7, 4601–4611, https://doi.org/10.5194/acp-7-4601-2007, 2007. a
Vepsäläinen, S., Calderón, S. M., Malila, J., and Prisle, N. L.: Droplet activation of moderately surface active organic aerosol predicted with six approaches to surface activity, Atmos. Chem. Phys. Discuss. [preprint], https://doi.org/10.5194/acp-2021-561, in review, 2021. a
Walz, M.-M., Werner, J., Ekholm, V., Prisle, N. L., Ohrwall, G., and Bjorneholm, O.: Alcohols at the aqueous surface: chain length and isomer effects, Phys. Chem. Chem. Phys., 18, 6648–6656, https://doi.org/10.1039/C5CP06463E, 2016. a
Werner, J., Julin, J., Dalirian, M., Prisle, N. L., Öhrwall, G., Persson, I., Björneholm, O., and Riipinen, I.: Succinic acid in aqueous solution: connecting microscopic surface composition and macroscopic surface tension, Phys. Chem. Chem. Phys., 16, 21486–21495, https://doi.org/10.1039/C4CP02776K, 2014. a
Werner, J., Persson, I., Björneholm, O., Kawecki, D., Saak, C.-M., Walz, M.-M., Ekholm, V., Unger, I., Valtl, C., Caleman, C., Öhrwall, G., and Prisle, N. L.: Shifted equilibria of organic acids and bases in the aqueous surface region, Phys. Chem. Chem. Phys., 20, 23281–23293, 2018. a
Wex, H., Hennig, T., Salma, I., Ocskay, R., Kiselev, A., Henning, S., Massling, A., Wiedensohler, A., and Stratmann, F.: Hygroscopic growth and measured and modeled critical supersaturations of an atmospheric HULIS sample, Geophys. Res. Lett., 34, L02818, https://doi.org/10.1029/2006GL028260, 2007. a
Winkler, P. M., Ortega, J., Karl, T., Cappellin, L., Friedli, H. R., Barsanti, K., McMurry, P. H., and Smith, J. N.: Identification of the biogenic compounds responsible for size-dependent nanoparticle growth, Geophys. Res. Lett., 39, https://doi.org/10.1029/2012GL053253, 2012. a
Yassaa, N., Meklati, B. Y., Cecinato, A., and Marino, F.: Particulate n-alkanes, n-alkanoic acids and polycyclic aromatic hydrocarbons in the atmosphere of Algiers City Area, Atmos. Environ., 35, 1843–1851, 2001. a
Zamora, I. R. and Jacobson, M. Z.: Measuring and modeling the hygroscopic growth of two humic substances in mixed aerosol particles of atmospheric relevance, Atmos. Chem. Phys., 13, 8973–8989, https://doi.org/10.5194/acp-13-8973-2013, 2013. a, b





