Mass accommodation and gas–particle partitioning in secondary organic aerosols: dependence on diffusivity, volatility, particle-phase reactions, and penetration depth

Mass accommodation is an essential process for gas–particle partitioning of organic compounds in secondary organic aerosols (SOA). The mass accommodation coefficient is commonly described as the probability of a gas molecule colliding with the surface to enter the particle phase. It is often applied, however, without specifying if and how deep a molecule has to penetrate beneath the surface to be regarded as being incorporated into the condensed phase (adsorption vs. absorption). While this aspect is usually not critical for liquid particles with rapid surface–bulk exchange, it can be important for viscous semi-solid or glassy solid particles to distinguish and resolve the kinetics of accommodation at the surface, transfer across the gas–particle interface, and further transport into the particle bulk.

For this purpose, we introduce a novel parameter: an effective mass accommodation coefficient α_eff that depends on penetration depth and is a function of surface accommodation coefficient, volatility, bulk diffusivity, and particle-phase reaction rate coefficient. Application of α_eff in the traditional Fuchs–Sutugin approximation of mass-transport kinetics at the gas–particle interface yields SOA partitioning results that are consistent with a detailed kinetic multilayer model (kinetic multilayer model of gas–particle interactions in aerosols and clouds, KM-GAP; Shiraiwa et al., 2012) and two-film model solutions (Model for Simulating Aerosol Interactions and Chemistry, MOSAIC; Zaveri et al., 2014) but deviate substantially from earlier modeling approaches not considering the influence of penetration depth and related parameters.

For highly viscous or semi-solid particles, we show that the effective mass accommodation coefficient remains similar to the surface accommodation coefficient in the case of low-volatility compounds, whereas it can decrease by several orders of magnitude in the case of semi-volatile compounds. Such effects can explain apparent inconsistencies between earlier studies deriving mass accommodation coefficients from experimental data or from molecular dynamics simulations.

Our findings challenge the approach of traditional SOA models using the Fuchs–Sutugin approximation of mass transfer kinetics with a fixed mass accommodation coefficient, regardless of particle phase state and penetration depth. The effective mass accommodation coefficient introduced in this study provides an efficient new way of accounting for the influence of volatility, diffusivity, and particle-phase reactions on SOA partitioning in process models as well as in regional and global air quality models. While kinetic limitations may not be critical for partitioning into liquid SOA particles in the planetary boundary layer (PBL), the effects are likely important for amorphous semi-solid or glassy SOA in the free and upper troposphere (FT–UT) as well as in the PBL at low relative humidity and low temperature.

1 Introduction

Secondary organic aerosols (SOA) are major constituents of atmospheric particulate matter, affecting air quality, climate, and public health (Jimenez et al., 2009; Kanakidou et al., 2005; Pöschl and Shiraiwa, 2015; Shrivastava et al., 2017a). Gas-phase reactions of volatile organic compounds (VOC) emitted from various anthropogenic and biogenic sources with oxidants such as ozone and OH radicals lead to the formation and growth of SOA (Kroll and Seinfeld, 2008). The oxidation of VOC forms a myriad of semi-volatile (SVOC) and low-volatility organic compounds (LVOC) that can condense on preexisting particles (Ziemann and Atkinson, 2012) or contribute to nucleation and new particle formation (Tröstl et al., 2016). The evolution of SOA is a complex multi-step process that involves chemical reactions and mass transport in the gas phase, at the particle surface and in the particle bulk, but the interplay of these processes and the rate-limiting steps in SOA formation have not yet been fully resolved or elucidated (Shiraiwa et al., 2014).

Traditionally, SOA particles were assumed to be homogeneous and well-mixed quasi-liquid droplets (Pankow, 1994). As demonstrated by recent atmospheric measurements and laboratory experiments, they can adopt glassy solid or amorphous semi-solid phase states, challenging the traditional views of SOA properties, interactions, and effects (Koop et al., 2011; Reid et al., 2018; Virtanen et al., 2010). Slow diffusion of water, oxidants, and organic molecules in viscous, semi-solid, or glassy particles may lead to kinetic limitations in heterogeneous and multiphase reactions (Alpert et al., 2019; Davies and Wilson, 2015; Kuwata and Martin, 2012; Shiraiwa et al., 2011; Zhang et al., 2018; Zhou et al., 2019). Global model calculations suggest that the phase state of atmospheric SOA may vary between liquid, semi-solid, and solid in the planetary boundary layer, while SOA should be mostly in a glassy state in the free troposphere (Shiraiwa et al., 2017). The occurrence of glassy SOA in the free troposphere may promote ice nucleation and cloud droplet activation (Knopf et al., 2018; Slade et al., 2017) and facilitate long-range transport of toxic organic compounds contained in SOA (Mu et al., 2018; Shrivastava et al., 2017b).

The formation and properties of SOA are large sources of uncertainty in the current understanding of global air quality, climate change, and public health. The development of SOA models is among the most challenging problems in atmospheric chemistry (Tsigaridis et al., 2014). In most current air quality, atmospheric chemistry, and climate models, the limiting step of SOA formation is assumed to be gas-phase oxidation of VOC to form semi-volatile and low-volatility products. Thus, gas-phase oxidation is described kinetically, while gas–particle partitioning is often approximated by quasi-instantaneous equilibrium partitioning of the oxidation products (Pankow, 1994; Shrivastava et al., 2017a; Tsigaridis et al., 2014). The assumption of quasi-instantaneous gas–particle equilibration, however, is in question if particles are highly viscous, semi-solid, or glassy – especially at low temperatures and low relative humidity (RH) (Li and Shiraiwa, 2019; Shiraiwa and Seinfeld, 2012). Experimental studies found kinetic limitations for gas uptake and particle evaporation at low RH (Liu et al., 2016; Perraud et al., 2012; Vaden et al., 2011; Yli-Juuti et al., 2017) but not for mixing in SOA at medium or high RH (Ye et al., 2016, 2018). An appropriate treatment of kinetic limitations depending on ambient conditions is critical for accurately reproducing particle size distribution dynamics in SOA growth (Shiraiwa et al., 2013a; Zaveri et al., 2018, 2020).

The dynamics of gas–particle partitioning have been considered in a wide range of atmospheric aerosol models, including aerosol dynamics models (Liu et al., 2019; McVay et al., 2014; Pandis et al., 1993; Riipinen et al., 2011; Zaveri et al., 2014), kinetic multilayer models (Berkemeier et al., 2016; Fowler et al., 2018; Roldin et al., 2014; Shiraiwa et al., 2012), GECKO-A (Aumont et al., 2005), the volatility basis set approach (Trump and Donahue, 2014; Trump et al., 2014), the statistical oxidation model (Cappa et al., 2016; Jathar et al., 2016), and particle evaporation models (Vaden et al., 2011; Yli-Juuti et al., 2017). Most model studies use the Fuchs–Sutugin approximation of mass-transport kinetics at the gas–particle interface with a fixed mass accommodation coefficient that does not vary with particle phase state nor with the volatility and diffusivity of the investigated organic compounds. Molecular dynamics simulations (Julin et al., 2014; Von Domaros et al., 2020) and a recent SOA chamber study (Liu et al., 2019) suggest that the mass accommodation coefficients for semi-volatile organic molecules on organic substrates are close to unity. Measurement-derived mass accommodation coefficients reported from thermodenuder investigations of SOA volatility distributions, however, were 1 to 3 orders of magnitude lower (Kostenidou et al., 2018; Lee et al., 2010; Saleh et al., 2011).

Overall, the relations between particle phase state, mass accommodation, and the growth and atmospheric evolution of SOA have not yet been resolved and continue to be a subject of scientific debate. In this study, we investigate the influence of volatility, diffusivity, and particle phase state on the mass accommodation and gas–particle partitioning of organic compounds in SOA by detailed and simplified kinetic modeling approaches, comparing the Fuchs–Sutugin approximation to a detailed kinetic multilayer model (kinetic multilayer model of gas–particle interactions in aerosols and clouds, KM-GAP; Shiraiwa et al., 2012) as well as approximate and transient two-film model solutions (Model for Simulating Aerosol Interactions and Chemistry, MOSAIC; Zaveri et al., 2014).

2 Theory and methods

Traditionally, dynamic models of aerosol chemistry and physics describe the rate of gas–particle partitioning by a first-order gas–particle mass transfer coefficient (k_gp in s⁻¹) based on the Fuchs–Sutugin approximation of gas diffusion in the transition regime (Seinfeld and Pandis, 2016):

$$\begin{array}{}\text{(1)}& {\displaystyle }{k}_{\mathrm{gp}}=\mathrm{4}\mathit{\pi }{D}_{\mathrm{g}}{r}_{\mathrm{p}}{N}_{\mathrm{p}}\mathit{\beta }\text{(2)}& {\displaystyle }\mathit{\beta }={\displaystyle \frac{\mathrm{0.75}\mathit{\alpha }(\mathrm{1}+Kn)}{K{n}^{\mathrm{2}}+Kn+\mathrm{0.283}Kn\mathit{\alpha }+\mathrm{0.75}\mathit{\alpha },}}\end{array}$$

where D_g (cm² s⁻¹) is the gas-phase diffusivity, r_p (cm) is the particle radius, N_p (cm⁻³) is the particle number concentration, Kn is the Knudsen number, and α is the mass accommodation coefficient which represents the probability for a gas molecule colliding with the surface of the particles to enter the condensed phase. k_gp is also often termed as condensation sink (CS). Kn is the ratio of the mean free path in the gas phase (λ), which can be calculated using the mean thermal velocity (ω), and the particle radius: Kn $=\mathit{\lambda }/r_{\mathrm{p}}=\mathrm{3}{D}_{\mathrm{g}}/\left(\mathit{\omega }{r}_{\mathrm{p}}\right)$ (Pöschl et al., 2007). The Fuchs–Sutugin correction is validated by experiments with ∼ 6 × 10⁻³ < Kn < 10 (Seinfeld and Pandis, 2016). With a typical mean free path of ∼ 100 nm for SOA compounds, this range corresponds to 10 nm < r_p < ∼ 17 µm, covering a typical size range of SOA particles observed in ambient atmosphere and laboratory experiments. β is the transition regime correction factor, which depends on Kn and α. This approach was demonstrated to work well for simulating the hygroscopic growth of sub-10 nm particles into few micron-size droplets, covering the kinetic and transition regimes (Winkler et al., 2006, 2004). Note that for larger particles with the limit of Kn → 0, β approaches 1, and the effect of mass accommodation coefficient becomes negligibly small in the continuum regime.

According to the absorptive partitioning theory under the assumption of ideal mixing (Pankow, 1994; Trump and Donahue, 2014), the rate of change of the gas- and particle-phase mass concentrations (C^g, C^p) of an organic compound in SOA partitioning can be expressed as

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{d}{C}^{\mathrm{g}}}{\mathrm{d}t}}=-k_{\mathrm{gp}}\left(C^{\mathrm{g}}-{\displaystyle \frac{C^{\mathrm{g}}}{C_{\mathrm{OA}}}}{C}^{\mathrm{0}}\right)\text{(4)}& {\displaystyle \frac{\mathrm{d}{C}^{\mathrm{p}}}{\mathrm{d}t}}=k_{\mathrm{gp}}\left(C^{\mathrm{g}}-{\displaystyle \frac{C^{\mathrm{p}}}{C_{\mathrm{OA}}}}{C}^{\mathrm{0}}\right)-k_{\mathrm{b}}{C}^{\mathrm{p}},\end{array}$$

where C_OA (µg m⁻³) is the organic aerosol particle mass concentration, C⁰ (µg m⁻³) is the gas-phase saturation mass concentration of the pure organic compound, and k_b (s⁻¹) is the first-order rate coefficient for its reaction in the particle bulk. The term $\frac{C^{\mathrm{p}}}{C_{\mathrm{OA}}}{C}^{\mathrm{0}}$ represents gas-phase concentration of Z right at the surface and condensation is driven by the gas-phase concentration gradient of Z between the gas and condensed phases.

While the term “mass accommodation coefficient” is widely used in atmospheric aerosol studies, its precise meaning is not always well defined. In particular, α is often applied without specifying if and how deep a molecule has to penetrate beneath the surface to have entered the condensed phase (adsorption vs. absorption). This aspect is usually not critical for liquid droplets with rapid surface–bulk exchange, fast bulk diffusion, and swift equilibration between the condensed phase and the surrounding gas phase. For viscous or solid particles, however, it can be essential to distinguish and resolve the kinetics of surface and bulk processes, including accommodation at the surface, transfer across the gas–particle interface, and further transport into the particle bulk (Kolb et al., 2010; Pöschl et al., 2007; Shiraiwa et al., 2012).

Building on the PRA (Pöschl–Rudich–Ammann) kinetic model framework (Pöschl et al., 2007) and the kinetic multilayer model of gas–particle interactions in aerosols and clouds (KM-GAP; Shiraiwa et al., 2012), we have derived an expression for the mass accommodation coefficient as a function of penetration depth into the particle bulk and related parameters (see step-by-step derivation in the Appendix):

$$\begin{array}{}\text{(5)}& \mathit{\alpha }\left(x\right)={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\frac{{\mathit{\alpha }}_{\mathrm{s}}\mathit{\omega }{C}^{\mathrm{0}}}{\mathrm{4}{D}_{\mathrm{b}}{\mathit{\rho }}_{\mathrm{p}}}x\times {\mathrm{10}}^{-\mathrm{12}}\frac{\mathrm{g}}{\mathrm{\mu }\mathrm{g}}\frac{{\mathrm{cm}}^{-\mathrm{3}}}{{\mathrm{m}}^{-\mathrm{3}}}}}.\end{array}$$

Here ω (cm s⁻¹) is the mean thermal velocity of the organic compound in the gas phase, D_b (cm² s⁻¹) is its diffusivity in the condensed phase, ρ_p (g cm⁻³) is the particle density, and x (cm) is the penetration depth. The scaling factor 10⁻¹² (g cm⁻³)∕(µg m⁻³) allows C⁰ to be inserted in the commonly used units of micrograms per cubic meter (µg m⁻³); it can be omitted when C⁰ is inserted in grams per cubic centimeter (g cm⁻³) or when all quantities are inserted with standard SI units (cgs or mks system of units).

The surface accommodation coefficient α_s, which corresponds to α(0) with the penetration depth of 0, is the probability for a gas molecule Z colliding with the surface not to be immediately scattered back to the gas phase but to be accommodated at the surface for period longer than the duration of an elastic scattering process (Pöschl et al., 2007). Various equivalent, similar, or closely related terms and parameters have been defined and used in the scientific literature, including (Kolb et al., 2010; Pöschl et al., 2007) the condensation coefficient (Pruppacher and Klett, 2012), the adsorption coefficient (Shi et al., 1999; Turco et al., 1989; Worsnop et al., 2002), the sticking coefficient (Hanson, 1997), the sticking probability (Clement et al., 1996; Garrett et al., 2006), trapping probability (Masel, 1996), the adsorptive mass accommodation coefficient (Elliott et al., 1991), and the thermal accommodation coefficient (Li et al., 2001; Worsnop et al., 2002).

When the penetration depth equals one or two molecular layers, i.e., once or twice the effective molecular length or diameter (δ), the corresponding penetration-depth-dependent mass accommodation coefficient is equivalent to the quasi-static surface accommodation coefficient (α_ss) or bulk accommodation coefficient (α_b), respectively, as defined in earlier kinetic multilayer model studies (Shiraiwa et al., 2012): α(δ)=α_ss and α(2δ)=α_b. A recent study has compared this kinetic multilayer (KM) modeling approach with molecular dynamics (MD) simulations to calculate mass accommodation coefficients for a variety of semi-volatile compounds with different volatilities in squalene (Von Domaros et al., 2020). The penetration depth was assumed to be equal to the sum of half of the molecule's own length and half of the length of a squalene molecule. For the evaluation of uncertainties and sensitivities, the penetration depth was also varied from the semi-volatile molecule's own length as a lower bound to the half-width of the nonuniform free energy region determined by the MD free energy profile as an upper bound. Within this range, the results of MD and KM simulations were in good agreement with each other, confirming the consistency and validity of the multilayer approach (Von Domaros et al., 2020).

Using the two-film theory of mass transfer between gas and particle phases, Zaveri et al. (2014) showed that the effects of a concentration gradient in the particle can be represented by a thin film adjacent to the surface with the following thickness or effective penetration depth for non-reactive partitioning and reactive uptake, respectively:

$$\begin{array}{}\text{(6)}& {\displaystyle }{x}_{\mathrm{eff}}=r_{\mathrm{p}}/\mathrm{5}\left(\text{non-reactive partitioning}\right)\text{(7)}& {\displaystyle }{x}_{\mathrm{eff}}=r_{\mathrm{p}}\left({\displaystyle \frac{\mathrm{1}-Q}{q\coth q-\mathrm{1}}}\right)\left(\text{reactive uptake}\right),\end{array}$$

where Q is the ratio of the average particle-phase concentration to the surface concentration at steady state, and q is a dimensionless diffusion–reaction parameter (Seinfeld and Pandis, 2016):

$$\begin{array}{}\text{(8)}& {\displaystyle }Q=\mathrm{3}\left({\displaystyle \frac{q\coth q-\mathrm{1}}{q^{\mathrm{2}}}}\right)\text{(9)}& {\displaystyle }q=r_{\mathrm{p}}\sqrt{{\displaystyle \frac{k_{\mathrm{b}}}{D_{\mathrm{b}}}}}.\end{array}$$

Note that q is the ratio of the particle radius to the so-called reacto-diffusive length, (D_b∕k_b)^0.5, representing the characteristic depth to which a species can penetrate while reacting in the particle bulk (Pöschl et al., 2007; Worsnop et al., 2002). The effective penetration depth represents the depth from the surface where concentration gradients are confined under a quasi-steady state (Zaveri et al., 2014). The timescale for molecules to travel the effective penetration depth (${\mathit{\tau }}_{x_{\mathrm{eff}}}$) can be estimated by Fick's law: ${\mathit{\tau }}_{x_{\mathrm{eff}}}=x_{\mathrm{eff}}^{\mathrm{2}}/D_{\mathrm{b}}$.

By inserting x_eff in Eq. (5), we obtain an effective mass accommodation coefficient that accounts for the influence of penetration depth and its dependence on the diffusivity and reactivity of the investigated chemical species in the particle:

$$\begin{array}{}\text{(10)}& {\mathit{\alpha }}_{\mathrm{eff}}=\mathit{\alpha }\left(x_{\mathrm{eff}}\right).\end{array}$$

α_eff can be combined into the transition regime correction factor (α=α_eff in Eq. 2) to account for the effective penetration depth in the Fuchs–Sutugin approach. This method should work after the effective penetration depth is established under quasi-steady-state conditions, while the method may underestimate condensation in transient conditions at shorter timescales as detailed below. Following up on the helpful comments of an anonymous reviewer (Anonymous Referee, 2020), we would like to clarify that we consider the surface accommodation coefficient to be a fundamental kinetic parameter as defined by the PRA framework (Pöschl et al., 2007) – regardless of the specific mass transfer regime – and not just as a parameter defined by Eq. (2). The effective accommodation coefficient, on the other hand, comprises both the fundamental quantity α_s and a flux correction depending on the effective penetration depth as defined by Eqs. (5)–(10).

3 Results and discussion

To investigate and demonstrate the relevance of the kinetics of mass accommodation and the applicability of α_eff, we simulate the temporal evolution of partitioning and equilibration of semi-volatile organic compounds (SVOC) with C⁰=100 µg m⁻³ and D_g=0.1 cm² s⁻¹ interacting with non-volatile seed particles, with a number concentration of 5000 cm⁻³, an initial diameter of 200 nm, and a surface accommodation coefficient ${\mathit{\alpha }}_{\mathrm{s}}=\mathit{\alpha }\left(\mathrm{0}\right)=\mathrm{1}$. For the SVOC, we assume initial gas- and particle-phase concentrations of 2 and 0 µg m⁻³, respectively. The particles are assumed to be either liquid with a bulk diffusion coefficient $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{7}}$ cm² s⁻¹ or semi-solid with $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{15}}$ cm² s⁻¹. These conditions were adopted from model simulations by Zaveri et al. (2014), representing typical conditions for SOA formation in laboratory experiments and ambient atmosphere.

Model calculations were performed with KM-GAP (Shiraiwa et al., 2012), with MOSAIC (Zaveri et al., 2014), and with an aerosol dynamic model using the simple Fuchs–Sutugin gas-phase diffusion model (F–S) with different values of α_m. Here, the KM-GAP results can be regarded as a benchmark because it explicitly resolves all relevant processes – including gas diffusion, reversible adsorption, surface–bulk exchange, bulk diffusion, and condensed-phase reactions – and has been successfully validated against experimental data of both non-reactive partitioning and reactive gas uptake in a wide range of aerosol and surrogate systems (Berkemeier et al., 2017; Shiraiwa et al., 2012). MOSAIC yields approximate and transient solutions, building on a less detailed representation of gas–particle interactions, which does not resolve reversible adsorption and surface–bulk exchange (Zaveri et al., 2014). In the F–S approximation, the kinetics of particle-phase mass transport are represented only by α_m as inserted into Eq. (2).

For liquid particles with fast surface–bulk exchange and bulk diffusion ($D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{7}}$ cm² s⁻¹), α(x) remains close to ${\mathit{\alpha }}_{\mathrm{s}}=\mathit{\alpha }\left(\mathrm{0}\right)=\mathrm{1}$, and all models yield the same result of fast mass transfer from the gas to particle phase and equilibration within 1 s (all model lines overlap with the dashed blue line (F–S, α=1) in Fig. 1a). For semi-solid particles with $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{15}}$ cm² s⁻¹, however, the temporal evolution of the SVOC gas-phase and particle-phase concentrations varies between different models and different values of α as shown in Fig. 1 on logarithmic scales.

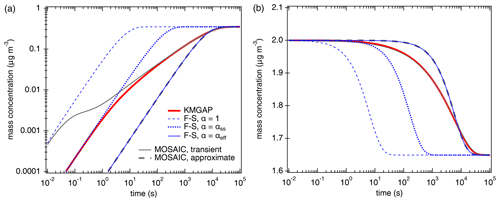
Figure 1 Temporal evolution of the particle-phase concentration (a) and the gas-phase concentration (b) of semi-volatile organic compounds (SVOC, C⁰= 100 µg m⁻³) interacting with semi-solid seed aerosol particles ($D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{15}}$ cm² s⁻¹, ω=2 × 10⁴ cm s⁻¹, ρ_p=1 g cm⁻³). The red lines are simulation results of KM-GAP, and the blue lines are the results of an aerosol dynamic model that employs the Fuchs–Sutugin approximation with $\mathit{\alpha }={\mathit{\alpha }}_{\mathrm{s}}=\mathrm{1}$ (dashed), $\mathit{\alpha }={\mathit{\alpha }}_{\mathrm{ss}}=\mathrm{3}$ × 10⁻² (dotted), and $\mathit{\alpha }={\mathit{\alpha }}_{\mathrm{eff}}=\mathrm{8}$ × 10⁻⁴ (solid). The gray lines represent the MOSAIC transient solution (solid) and approximate solution (dashed) (Zaveri et al., 2014).

According to KM-GAP (black line), the initial uptake of SVOC by the semi-solid particle phase is as fast as approximated by F–S, with α $={\mathit{\alpha }}_{\mathrm{ss}}=\mathit{\alpha }\left(\mathit{\delta }\right)=\mathrm{3}$ × 10⁻² corresponding to a penetration depth of only one molecular length (monolayer) below the particle surface. After 1 s, however, the uptake is limited by bulk diffusion and slows down substantially. After about 1 h corresponding to ${\mathit{\tau }}_{x_{\mathrm{eff}}}$ ($=\frac{x_{\mathrm{eff}}^{\mathrm{2}}}{D_{\mathrm{b}}}=\frac{(\mathrm{20}\mathrm{nm}{)}^{\mathrm{2}}}{{\mathrm{10}}^{-\mathrm{15}}{\mathrm{cm}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}}=\mathrm{4000}$ s), KM-GAP converges with the F–S approximation using $\mathit{\alpha }={\mathit{\alpha }}_{\mathrm{eff}}=\mathit{\alpha }(r_{\mathrm{p}}/\mathrm{5})=\mathrm{8}$ × 10⁻⁴. Notably, the F–S approximation with α_eff is identical to the MOSAIC approximation, although the latter is based on different rate equations using a unity mass accommodation coefficient like KM-GAP (α_s=1) and a two-film approach of bulk diffusion (Zaveri et al., 2014). The MOSAIC transient solution exhibits a very high and likely overestimated initial uptake corresponding to the F–S approximation with $\mathit{\alpha }={\mathit{\alpha }}_{\mathrm{s}}=\mathrm{1}$ because it does not resolve reversible adsorption and desorption at the surface (Shiraiwa et al., 2012). After ∼ 1 min, however, the MOSAIC transient solution converges with KM-GAP. Overall, Fig. 1 demonstrates that accurate modeling of SVOC partitioning and uptake into semi-solid particles requires an explicit treatment of reversible adsorption and desorption at short timescales (< 1 min) and an explicit treatment of bulk diffusion at intermediate timescales (∼ 1 min to ∼ 1 h) when bulk concentration gradients evolve within the effective penetration depth. At long timescales (> ${\mathit{\tau }}_{x_{\mathrm{eff}}}$ of 1 h), the partitioning is reasonably well captured by both the MOSAIC approximation using a two-film approach of bulk diffusion (Zaveri et al., 2014) and the simple F–S approximation, accounting for the influence of penetration depth with the effective mass accommodation coefficient, α_eff, newly introduced this study.

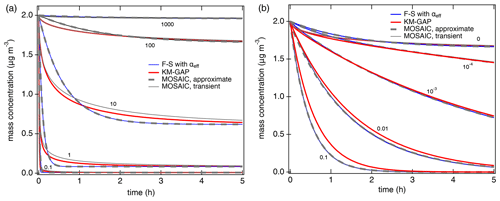
Figure 2 Temporal evolution of the gas-phase concentration of organic compounds interacting with semi-solid seed aerosol particles (α_s=1, ω=2 × 10⁴ cm s⁻¹, $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{15}}$ cm² s⁻¹, ρ_p=1 g cm⁻³). (a) Non-reactive partitioning of compounds with different volatilities (C⁰=0.1, 1, 10, 100, 1000 µg m⁻³). (b) Reactive uptake of semi-volatile compounds (C⁰=100 µg m⁻³) with different first-order bulk reaction rate coefficients (k_b=0, 10⁻⁴, 10⁻³, 0.01, 0.1 s⁻¹). The red lines are simulation results of KM-GAP, and the blue lines are the results of an aerosol dynamic model that employs the Fuchs–Sutugin approximation with ${\mathit{\alpha }}_{\mathrm{eff}}=\mathit{\alpha }(r_{\mathrm{p}}/\mathrm{5}$) for non-reactive partitioning (a) and with α_eff=α(x_eff) and x_eff from Eq. (5) for reactive uptake (b). The gray lines represent the MOSAIC transient solution (solid) and approximate solution (dashed) (Zaveri et al., 2014).

Figure 2a shows the temporal evolution of the gas-phase concentration of organic compounds with different volatilities (C⁰=0.1 to 1000 µg m⁻³) that undergo non-reactive partitioning into semi-solid seed aerosol particles ($D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{15}}$ cm² s⁻¹). At short timescales, substantial deviations can occur for semi-volatile compounds (C⁰=1 to 100 µg m⁻³), but at longer timescales KM-GAP and the F–S approximation with α_eff are in reasonably good agreement (relative deviations < 10 % after ∼ 1 h). For low-volatility compounds (C⁰ < 1 µg m⁻³), equilibration is achieved faster than for semi-volatile compounds because local thermodynamic equilibrium between the gas phase and the particle surface is quickly established by condensation without significant re-evaporation (Li and Shiraiwa, 2019; Zaveri et al., 2014). Semi-volatile compounds with reactive functional groups can undergo particle-phase reactions such as dimerization and oligomerization (Ziemann and Atkinson, 2012). Peroxide-containing highly oxidized molecules (HOM) are labile, with chemical half-lives shorter than 1 h (Krapf et al., 2016; Tong et al., 2019), corresponding to $k_{\mathrm{b}}>\sim$ 2 × 10⁻⁴ s⁻¹, and a recent study has shown that particle-phase reactions must be considered to describe HOM effects on particle growth (Pospisilova et al., 2020). First-order decomposition rate coefficients for organic hydroperoxides in SOA were reported in the range of 10⁻⁶–1.5 × 10⁻³ s⁻¹ (Tong et al., 2016, 2018; Wei et al., 2021) and can be enhanced by photolysis (Badali et al., 2015; Epstein et al., 2014) or Fenton-like reactions in the presence of transition metal ions (Goldstein and Meyerstein, 1999). Model results for SVOC partitioning plus reactive uptake with different rate coefficients in semi-solid aerosol particles are shown in Fig. 2b. The results of the Fuchs–Sutugin approximation with α_eff=α(x_eff) and x_eff from Eq. (7) are identical to the MOSAIC approximate and transient solutions. The uptake predicted by KM-GAP is similar but slightly slower in the case of high bulk reaction rate coefficients, which can be attributed to the influence of reversible adsorption and desorption at the surface. Additional simulations with α_s=0.1 confirm that the results of the Fuchs–Sutugin approximation with α_eff and the MOSAIC approximate solution are identical and that the results of KM-GAP and the MOSAIC transient solution are similar (Fig. S1 in the Supplement).

For a given surface accommodation coefficient of α_s=1, which is likely a good approximation for SVOC on organic surfaces (Julin et al., 2014; Von Domaros et al., 2020), Fig. 3a and b show how the effective mass accommodation coefficient α_eff depends on volatility and bulk diffusivity as related to particle phase state and viscosity according to the Stokes–Einstein relation (Shiraiwa et al., 2011). In the liquid phase with high bulk diffusivity ($D_{\mathrm{b}}>{\mathrm{10}}^{-\mathrm{10}}$ cm² s⁻¹), α_eff is essentially the same as α_s independent of volatility (${\mathit{\alpha }}_{\mathrm{eff}}\approx {\mathit{\alpha }}_{\mathrm{s}}\approx \mathrm{1}$). With a decrease of bulk diffusivity in viscous or semi-solid particles, α_eff decreases substantially for SVOC (0.3 < C⁰ < 300 µg m⁻³) and so-called intermediate-volatility organic compounds (IVOC; 300 < C⁰ < 3 × 10⁶ µg m⁻³) but not for LVOC (3 × 10⁻⁴ < C⁰ < 0.3 µg m⁻³) and so-called extremely low-volatility organic compounds (ELVOC; C⁰ < 3 × 10⁻⁴ µg m⁻³). The reason why compounds with higher volatility are more strongly affected by particle phase state and diffusivity is that they are more likely to desorb back to the gas phase when diffusion into the bulk is slow. Compounds with lower volatility exhibit much lower desorption rates and are less likely to re-evaporate, even if their diffusion into the bulk is slow. On the other hand, the influence of particle phase state and diffusivity increases with particle size because longer pathways of diffusion are required for effective accommodation, penetration, and absorption of gas molecules into larger particles, as illustrated in Fig. 3c and d.

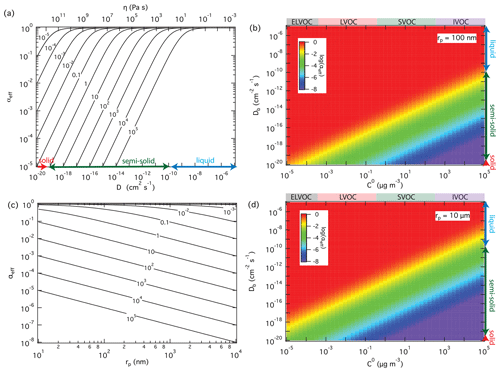
Figure 3 Effective mass accommodation coefficients, α_eff, for non-reactive partitioning of organic compounds Z (α_s=1, ω=2 × 10⁴ cm s⁻¹) with liquid, semi-solid, or solid aerosol particles (ρ_p=1 g cm⁻³) depending on pure compound volatility, C⁰, particle bulk diffusivity, D_b (corresponding to viscosity, η), and particle radius, r_p. α_eff calculated as a function of D_b for $C^{\mathrm{0}}={\mathrm{10}}^{-\mathrm{5}}$ to 10⁵ µg m⁻³ with r_p=100 nm (a); α_eff calculated as a function of C⁰ and D_b with r_p=100 nm (b) and 10 µm (d); α_eff calculated as a function of particle radius for $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{15}}$ cm² s⁻¹ and different levels of volatility ($C^{\mathrm{0}}={\mathrm{10}}^{-\mathrm{3}}$ to 10⁵ µg m⁻³) (c).

The theoretically predicted influence of volatility on effective mass accommodation is consistent with a recent experimental study of α-pinene SOA, reporting that the observed mass accommodation coefficients decreased from ∼ 1 for low-volatility compounds to ∼ 0.3 for semi-volatile compounds (Liu et al., 2019). Particle viscosity and bulk diffusivity were not reported for these experiments, but values around 10⁻¹³ to 10⁻¹⁴ cm² s⁻¹ had previously been estimated for the diffusion coefficient of organic compounds in α-pinene SOA under dry conditions (Zhou et al., 2013). As illustrated in Fig. 4a, theoretical predictions of α_eff using Eqs. (5) and (6) under the assumption of quasi-steady-state conditions with α_s=1 and $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{12}}$ to 10⁻¹⁴ cm² s⁻¹ can approximately capture the decrease and encompass the variability and uncertainty range of the experimentally derived mass accommodation coefficients reported by Liu et al. (2019). Indeed, the observational α values reported in Liu et al. (2019) and other experimental studies are usually obtained by fitting measurement data with the F–S approximation, and thus they should be directly compared to effective mass accommodation coefficient α_eff as derived by integration of the F–S approximation with detailed kinetic models of mass transport across the gas–particle interface. Figure 4b shows a wide range of other measurement-derived mass accommodation coefficients for various SOA and surrogate systems (data points/shaded areas) in comparison to generic values of α_eff (lines) calculated for characteristic experimental conditions (ω=2.0 × 10⁴ cm s⁻¹, ρ_p=1 g cm⁻³, and r_p=100 nm, and $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{19}}$ to 10⁻⁵ cm² s⁻¹). As indicated by molecular dynamics simulations and related studies, the surface accommodation coefficient (adsorption probability) for semi-volatile or low-volatility organic compounds on organic surfaces is likely close to unity, α_s=1 (Julin et al., 2014; Von Domaros et al., 2020). Accordingly, low observational values of α can be attributed to the penetration-depth dependence of mass accommodation and plausibly explained by different scenarios, combinations, or ratios of volatility and diffusivity, which can lead to a substantial decrease of α_eff relative to α_s in semi-solid particles. With regard to the dependence of α_eff on C⁰, mixing effects and non-ideality may lead to deviations between C⁰ and C^* (Zuend and Seinfeld, 2012), which should be taken into account in further investigations of mass accommodation and its influence on the formation and growth of SOA particles.

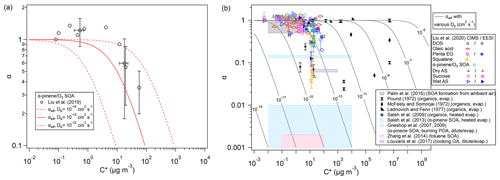
Figure 4 Effective mass accommodation coefficients, α_eff (lines, Eqs. 5–10) compared to measurement-derived mass accommodation coefficients, α (data points/shaded areas, Eqs. 1–2), plotted against effective saturation mass concentration, C^*, for various SOA and surrogate systems assuming α_s=1, ω=2 × 10⁴ cm s⁻¹, ρ_p=1 g cm⁻³, r_p=100 nm, and $C^{\mathrm{0}}=C^{*}$. (a) Observational results from laboratory experiments with semi-volatile components of SOA generated by ozonolysis of α-pinene (data points, Liu et al., 2019) compared to α_eff for $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{14}}$ to 10⁻¹² cm² s⁻¹ (lines). (b) Observational results from earlier experimental investigations of laboratory-generated and ambient samples (data points/shaded areas, compiled by Liu et al., 2019) compared to generic values of α_eff for $D_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{19}}$ to 10⁻⁵ cm² s⁻¹ (lines).

On the other hand, high reactivity can compensate for the influence of low diffusivity and mass-transport limitations in the particle phase, keeping α_eff close to α_s. In the case of non-reactive partitioning, the effective penetration depth used to calculate α_eff is one-fifth of the particle radius; i.e., $x_{\mathrm{eff}}/r_{\mathrm{p}}=\mathrm{0.2}$ (Eq. 6). In the case of reactive uptake, however, x_eff decreases with increasing reactivity and with decreasing diffusivity according to Eqs. (7) to (9). Figure 5a illustrates how the effective penetration depth normalized by the particle radius, x_eff∕r_p, decreases with increasing first-order bulk reaction rate coefficient, k_b, and with decreasing diffusion coefficient, D_b. The reduced effective penetration depths at high k_b and low D_b reflect that reactive uptake by semi-solid particles proceeds mainly through chemical reaction near the surface (Shiraiwa et al., 2013a). Figure 5b illustrates how α_eff depends on volatility and diffusivity for reactive uptake with α_s=1 and a first-order bulk reaction rate coefficient k_b=0.1 s⁻¹. In comparison to Fig. 3b for non-reactive partitioning, Fig. 5b shows that particle-phase reactivity leads to an extension of the volatility–diffusivity parameter space where α_eff≈α_s (red area): for semi-solid particles with low diffusivity, the parameter range of strong deviations between α_eff and α_s (yellow/green/blue area) is shifted towards higher volatility (lower right corner).

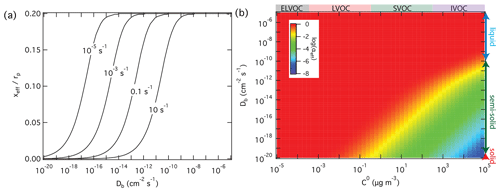
Figure 5 Effective penetration depths normalized by particle radius, x_eff, and mass accommodation coefficients, α_eff, for reactive uptake of organic compounds Z (α_s=1, ω=2 × 10⁴ cm s⁻¹) by liquid, semi-solid, or solid aerosol particles (r_p=100 nm, ρ_p=1 g cm⁻³) depending on pure compound volatility, C⁰, particle bulk diffusivity D_b, and first-order bulk reaction rate coefficient, k_b. (a) x_eff calculated as a function of D_b and $k_{\mathrm{b}}={\mathrm{10}}^{-\mathrm{5}}$ to 10 s⁻¹. (b) α_eff calculated as a function of C⁰ and D_b for k_b=0.1 s⁻¹.

4 Summary and conclusions

Traditional SOA modeling approaches often use the Fuchs–Sutugin approximation of mass-transport kinetics at the gas–particle interface in combination with mass accommodation coefficients that are not appropriately defined, leading to inconsistent results and conclusions. To overcome such deficiencies and difficulties, we have introduced an effective mass accommodation coefficient α_eff that depends on penetration depth and is a function of surface accommodation coefficient, volatility, bulk diffusivity, and particle-phase reaction rate coefficient. Application of α_eff in the traditional F–S approximation of SOA partitioning yields results that are consistent with detailed kinetic multilayer models (KM-GAP; Shiraiwa et al., 2012) and two-film models (MOSAIC; Zaveri et al., 2014).

We suggest that α_eff and its dependence on penetration depth and related parameters should be applied and considered when the F–S approximation is used to investigate and simulate gas–particle interactions in viscous or semi-solid organic aerosols. The simple parameterization can be incorporated into regional and global models for a more realistic representation of SOA processes in the atmosphere. While kinetic limitations of bulk diffusion may not be critical for partitioning into liquid particles in the planetary boundary layer (PBL) at high relative humidity and high temperature, their effects are important for amorphous semi-solid or glassy particles predicted for the free and upper troposphere (FT–UT) as well as for the PBL at low relative humidity and low temperature (Andreae et al., 2018; Maclean et al., 2017; Shiraiwa et al., 2017). Following up on the helpful comments of an anonymous reviewer (Anonymous Referee, 2020), we would like to emphasize that the effective mass accommodation coefficient offers a very efficient way of properly treating gas–particle partitioning in large-scale models because it is easily applicable for liquid, semi-solid, and solid particles as a function of standard physicochemical parameters.

In the analysis and interpretation of SOA chamber and laboratory experiments, α_eff provides a simply way of accounting for the potential impact of volatility, diffusivity, and particle phase state on the kinetics of gas–particle partitioning for analysis and interpretation of chamber experiments. In particular, it may help to address and resolve apparent inconsistencies between the definitions and parameter values of mass accommodation coefficients that are derived from experimental data and from molecular dynamics simulations.

At short timescales, before molecules diffuse to the effective penetration depth, however, α_eff is not sufficient to properly describe the kinetics of gas–particle interactions with the F–S approximation. The timescales to reach a quasi-steady state in the particle phase can be long (hours to days) for ultra-viscous and glassy phase states, low particle-phase reaction rate coefficients, and large particles (Shiraiwa et al., 2011; Zaveri et al., 2014). Such conditions require detailed kinetic model simulations with kinetic multilayer models or equivalent approaches explicitly resolving mass transport at the surface and in the bulk of the particle. The same applies for particles with layered structures such as surface crusts (solid/viscous surface layers) that may form upon chemical aging and can strongly impact the uptake of semi-volatile compounds and multiphase chemical processes in the particle phase (Pfrang et al., 2011; Vander Wall et al., 2018; Zhou et al., 2019). Moreover, mixed organic–inorganic particles often undergo liquid–liquid phase separation at moderate and high RH (Krieger et al., 2012; You et al., 2014; Zuend and Seinfeld, 2012), and liquid–liquid phase separation can also occur for purely organic particles (Song et al., 2017). For such particles with shell-core morphology, the effective penetration depth would be confined to particle shells, which could be smaller than the penetration depth estimated from the particle radius. The interplay of particle phase state and phase separation can further impact SOA partitioning (Shiraiwa et al., 2013b). In such complex particle morphologies with multiple phases, gradients and discontinuities of diffusivity may occur within the particle bulk and require more advanced modeling approaches of gas–particle interaction kinetics to be addressed in future studies.

Appendix A: Derivation of penetration-depth-dependent mass accommodation coefficient

Figure A1 illustrates the applied kinetic multilayer model framework, in which the structure and composition of a particle are described by a sorption layer (s), a quasi-static surface layer (ss), multiple bulk layers (b), and any volatile, semi-volatile, or low-volatility chemical species (Z) that can undergo gas–particle partitioning and transport between the different layers and chemical reactions with each other (Pöschl et al., 2007; Shiraiwa et al., 2012). At low gas-phase concentration levels or high surface–bulk exchange rates (e.g., for liquid particles under dilute atmospheric conditions), surface coverage and saturation effects can be neglected, and the surface accommodation coefficient (α_s) approaches the parameter value for an adsorbate-free surface (${\mathit{\alpha }}_{\mathrm{s}}\approx {\mathit{\alpha }}_{\mathrm{s},\mathrm{0}}$) (Pöschl et al., 2007; Shiraiwa et al., 2012). In the absence of condensed-phase reactions, a quasi-static surface accommodation coefficient (α_ss), i.e., the probability for a gas molecule colliding with the surface to enter the quasi-static surface layer, can be calculated as follows (Shiraiwa et al., 2012):

$$\begin{array}{}\text{(A1)}& {\mathit{\alpha }}_{\mathrm{ss}}={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{J_{\mathrm{s},\mathrm{ss}}}{J_{\mathrm{d}}+J_{\mathrm{s},\mathrm{ss}}}}={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{k_{\mathrm{s},\mathrm{ss}}}{k_{\mathrm{d}}+k_{\mathrm{s},\mathrm{ss}}}}.\end{array}$$

Here J_d is the desorption flux of Z, and k_d is the corresponding first-order rate coefficient; J_s,ss and k_s,ss represent the flux and first-order rate coefficient of transfer between the sorption layer and the quasi-static surface layer. The probability for an individual gas molecule colliding with the surface to enter the bulk with a penetration depth x can be described by a penetration-depth-dependent mass accommodation coefficient, α(x), defined as follows:

$$\begin{array}{}\text{(A2)}& \mathit{\alpha }\left(x\right)={\mathit{\alpha }}_{\mathrm{ss}}{\displaystyle \frac{{\mathrm{\Psi }}_{\mathrm{ss},\mathrm{b}x}}{\mathrm{1}-{\mathrm{\Psi }}_{\mathrm{ss},\mathrm{s}}{\mathrm{\Psi }}_{\mathrm{s},\mathrm{ss}}}}.\end{array}$$

Here Ψ_s,ss is the probability for Z in the sorption layer to enter the quasi-static surface layer, and Ψ_ss,bx and Ψ_ss,s are the probabilities for Z in the quasi-static surface layer to enter the bulk with the penetration depth of x or the sorption layer, respectively, which are determined by the corresponding fluxes and first-order rate coefficients of mass transport (Shiraiwa et al., 2012):

$$\begin{array}{}\text{(A3)}& {\displaystyle }{\mathrm{\Psi }}_{\mathrm{s},\mathrm{ss}}=J_{\mathrm{s},\mathrm{ss}}/(J_{\mathrm{s},\mathrm{ss}}+J_{\mathrm{des}})=k_{\mathrm{s},\mathrm{ss}}/(k_{\mathrm{s},\mathrm{ss}}+k_{\mathrm{d}})\text{(A4)}& {\displaystyle }{\mathrm{\Psi }}_{\mathrm{ss},\mathrm{s}}=J_{\mathrm{ss},\mathrm{s}}/(J_{\mathrm{ss},\mathrm{b}x}+J_{\mathrm{ss},\mathrm{s}})=k_{\mathrm{ss},\mathrm{s}}/(k_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{ss},\mathrm{s}})\text{(A5)}& {\displaystyle }{\mathrm{\Psi }}_{\mathrm{ss},\mathrm{b}x}=J_{\mathrm{ss},\mathrm{b}x}/(J_{\mathrm{ss},\mathrm{b}x}+J_{\mathrm{ss},\mathrm{s}})=k_{\mathrm{ss},\mathrm{b}x}/(k_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{ss},\mathrm{s}}).\end{array}$$

Inserting Eqs. (A3)–(A5) in Eq. (A2) leads to

$$\begin{array}{}\text{(A6)}& \begin{array}{rl}& \mathit{\alpha }\left(x\right)={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{k_{\mathrm{s},\mathrm{ss}}}{k_{\mathrm{d}}+k_{\mathrm{s},\mathrm{ss}}}}{\displaystyle \frac{\frac{k_{\mathrm{ss},\mathrm{b}x}}{k_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{ss},\mathrm{s}}}}{\mathrm{1}-\frac{k_{\mathrm{ss},\mathrm{s}}}{k_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{ss},\mathrm{s}}}\cdot \frac{k_{\mathrm{s},\mathrm{ss}}}{k_{\mathrm{s},\mathrm{ss}}+k_{\mathrm{d}}}}}\\ & ={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{k_{\mathrm{s},\mathrm{ss}}{k}_{\mathrm{ss},\mathrm{b}x}}{(k_{\mathrm{d}}+k_{\mathrm{s},\mathrm{ss}})(k_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{ss},\mathrm{s}})\left(\mathrm{1}-\frac{k_{\mathrm{ss},\mathrm{s}}}{k_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{ss},\mathrm{s}}}\cdot \frac{k_{\mathrm{s},\mathrm{ss}}}{k_{\mathrm{s},\mathrm{ss}}+k_{\mathrm{d}}}\right)}}\\ & ={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{k_{\mathrm{s},\mathrm{ss}}{k}_{\mathrm{ss},\mathrm{b}x}}{(k_{\mathrm{d}}+k_{\mathrm{s},\mathrm{ss}})\left(k_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{ss},\mathrm{s}}\right)-k_{\mathrm{ss},\mathrm{s}}{k}_{\mathrm{s},\mathrm{ss}}}}\\ & ={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{k_{\mathrm{s},\mathrm{ss}}{k}_{\mathrm{ss},\mathrm{b}x}}{k_{\mathrm{d}}{k}_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{s},\mathrm{ss}}{k}_{\mathrm{ss},\mathrm{b}x}+k_{\mathrm{d}}{k}_{\mathrm{ss},\mathrm{s}}}}={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\frac{k_{\mathrm{d}}{k}_{\mathrm{ss},\mathrm{s}}+k_{\mathrm{d}}{k}_{\mathrm{ss},\mathrm{b}x}}{k_{\mathrm{s},\mathrm{ss}}{k}_{\mathrm{ss},\mathrm{b}x}}}}\\ & ={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\frac{k_{\mathrm{d}}}{k_{\mathrm{s},\mathrm{ss}}}\frac{k_{\mathrm{ss},\mathrm{s}}+k_{\mathrm{ss},\mathrm{b}x}}{k_{\mathrm{ss},\mathrm{b}x}}}}={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\frac{k_{\mathrm{d}}}{k_{\mathrm{s},\mathrm{ss}}}\left(\mathrm{1}+\frac{k_{\mathrm{ss},\mathrm{s}}}{k_{\mathrm{ss},\mathrm{b}x}}\right)}}.\end{array}\end{array}$$

The first-order rate coefficients of adsorption and desorption are given by $k_{\mathrm{a}}={\mathit{\alpha }}_{\mathrm{s}}\mathit{\omega }/\mathrm{4}$ and $k_{\mathrm{d}}=\mathrm{1}/{\mathit{\tau }}_{\mathrm{d}}$, respectively, where ω (cm s⁻¹) is the mean thermal velocity of Z in the gas phase, and τ_d is the lifetime of desorption from the sorption layer (Pöschl et al., 2007; Shiraiwa et al., 2012). The rate coefficient of mass transfer between sorption layer and quasi-static surface layer can be estimated based on Fick's first law of diffusion considering that a molecule in the sorption layer needs to travel a distance of δ to move into the quasi-static surface layer: $k_{\mathrm{ss},\mathrm{s}}\approx D_{\mathrm{b}}/{\mathit{\delta }}^{\mathrm{2}}$ (Shiraiwa et al., 2012). An estimate for k_s,ss can be determined considering mass transport under equilibrium conditions, where mass balance implies $J_{\mathrm{s},\mathrm{ss}}=J_{\mathrm{ss},\mathrm{s}}$, i.e., $k_{\mathrm{s},\mathrm{ss}}[Z{]}_{\mathrm{s},\mathrm{eq}}=k_{\mathrm{ss},\mathrm{s}}[Z{]}_{\mathrm{ss},\mathrm{eq}}$, and J_des=J_ads, i.e., $k_{\mathrm{d}}[Z{]}_{\mathrm{s},\mathrm{eq}}=k_{\mathrm{a}}[Z{]}_{\mathrm{g},\mathrm{eq}}$ (Shiraiwa et al., 2012). Here [Z]_g,eq, [Z]_s,eq, and [Z]_ss,eq are the equilibrium or solubility saturation number concentrations of Z in the gas phase, on the sorption layer, and in the quasi-static surface layer, respectively:

$$\begin{array}{}\text{(A7)}& {\displaystyle }{k}_{\mathrm{s},\mathrm{ss}}=k_{\mathrm{ss},\mathrm{s}}{\displaystyle \frac{k_{\mathrm{d}}[Z{]}_{\mathrm{ss},\mathrm{eq}}}{k_{\mathrm{a}}[Z{]}_{\mathrm{g},\mathrm{eq}}}}\text{(A8)}& {\displaystyle \frac{k_{\mathrm{d}}}{k_{\mathrm{s},\mathrm{ss}}}}={\displaystyle \frac{k_{\mathrm{a}}}{k_{\mathrm{ss},\mathrm{s}}}}{\displaystyle \frac{[Z{]}_{\mathrm{g},\mathrm{eq}}}{[Z{]}_{\mathrm{ss},\mathrm{eq}}}}={\displaystyle \frac{k_{\mathrm{a}}}{k_{\mathrm{ss},\mathrm{s}}}}{\displaystyle \frac{[Z{]}_{\mathrm{g},\mathrm{eq}}}{[Z{]}_{\mathrm{b},\mathrm{eq}}\mathit{\delta }}}.\end{array}$$

In analogy, the first-order rate coefficient k_bx,ss can be estimated based on Fick's first law of diffusion, considering that a molecule Z at penetration depth x in the bulk needs to travel a distance of x−δ to move into the quasi-static surface layer (Fig. A1): $k_{\mathrm{b}x,\mathrm{ss}}\approx D_{\mathrm{b}}/(x-\mathit{\delta })$. Under equilibrium conditions, $J_{\mathrm{ss},\mathrm{b}x}=J_{\mathrm{b}x,\mathrm{ss}}$ and $k_{\mathrm{ss},\mathrm{b}x}[Z{]}_{\mathrm{ss},\mathrm{eq}}=k_{\mathrm{b}x,\mathrm{ss}}[Z{]}_{\mathrm{b},\mathrm{eq}}$ which leads to $k_{\mathrm{ss},\mathrm{b}x}=k_{\mathrm{b}x,\mathrm{ss}}/\mathit{\delta }=D_{\mathrm{b}}/\left(\mathit{\delta }\right(x-\mathit{\delta }\left)\right)$ assuming ideal mixing conditions and $[Z{]}_{\mathrm{b},\mathrm{eq}}=[Z{]}_{\mathrm{ss},\mathrm{eq}}/\mathit{\delta }$ (Shiraiwa et al., 2012). Thus, $k_{\mathrm{ss},\mathrm{s}}/k_{\mathrm{ss},\mathrm{b}x}=(D_{\mathrm{b}}/{\mathit{\delta }}^{\mathrm{2}})/(D_{\mathrm{b}}/(\mathit{\delta }(x-\mathit{\delta })\left)\right)=(x-\mathit{\delta })/\mathit{\delta }$.

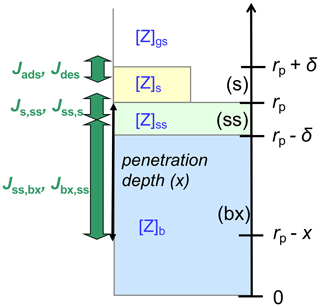
Figure A1 Schematic illustration of the kinetic multilayer modeling approach resolving mass-transport fluxes (J) between the near-surface gas phase (gs), the sorption layer (s), the quasi-static surface layer (ss), and the bulk layer at penetration depth x (bx) (Shiraiwa et al., 2012).

Based on the absorptive partitioning theory (Donahue et al., 2006; Pankow, 1994),

$$\begin{array}{}\text{(A9)}& C^{\mathrm{0}}={\displaystyle \frac{C^{\mathrm{g}}}{C^{\mathrm{p}}}}{C}_{\mathrm{OA}},\end{array}$$

where C⁰ (µg m⁻³) is the pure compound saturation mass concentration, C^g and C^p (µg m⁻³) are the gas-phase and particle-phase mass concentrations of the compound Z, respectively, and C_OA (µg m⁻³) is the total organic aerosol mass concentration. C^g and [Z]_g,eq are related through the following equation:

$$\begin{array}{}\text{(A10)}& C^{\mathrm{g}}={\displaystyle \frac{[Z{]}_{\mathrm{g},\mathrm{eq}}M}{N_{\mathrm{A}}}}\times {\mathrm{10}}^{\mathrm{12}}{\displaystyle \frac{\mathrm{\mu }\mathrm{g}}{\mathrm{g}}}{\displaystyle \frac{{\mathrm{m}}^{-\mathrm{3}}}{{\mathrm{cm}}^{-\mathrm{3}}}},\end{array}$$

where M is the molar mass of compound Z. [Z]_g,eq is the equilibrium (saturation) number concentration of Z in the gas phase. [Z]_g,eq can be calculated using the saturation vapor pressure p: $[Z{]}_{\mathrm{g},\mathrm{eq}}=p{N}_{\mathrm{A}}/(RT)$ where N_A is the Avogadro number, R is the gas constant, and T is the temperature. [Z]_b,eq corresponds to the ratio between the number concentration of Z in the particle phase (per cubic meter (m³) of air) to the particle volume concentration (m³ per m³ of air), which can be expressed using C^p and C_OA with the particle density ρ_p (g cm⁻³):

$$\begin{array}{}\text{(A11)}& [Z{]}_{\mathrm{b},\mathrm{eq}}={\displaystyle \frac{\frac{C^{\mathrm{p}}}{M}{N}_{\mathrm{A}}}{\frac{C_{\mathrm{OA}}}{{\mathit{\rho }}_{\mathrm{p}}}}}={\displaystyle \frac{C^{\mathrm{p}}{N}_{\mathrm{A}}{\mathit{\rho }}_{\mathrm{p}}}{C_{\mathrm{OA}}M}}.\end{array}$$

Combining Eqs. (A9)–(A11) would lead to

$$\begin{array}{}\text{(A12)}& \begin{array}{rl}& {\displaystyle \frac{[Z{]}_{\mathrm{g},\mathrm{eq}}}{[Z{]}_{\mathrm{b},\mathrm{eq}}}}={\displaystyle \frac{\frac{C^{\mathrm{g}}{N}_{\mathrm{A}}}{M}}{\frac{C^{\mathrm{p}}{N}_{\mathrm{A}}{\mathit{\rho }}_{\mathrm{p}}}{C_{\mathrm{OA}}M}}}\times {\mathrm{10}}^{-\mathrm{12}}={\displaystyle \frac{C^{\mathrm{g}}}{C^{\mathrm{p}}}}{C}_{\mathrm{OA}}{\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{p}}}}\times {\mathrm{10}}^{-\mathrm{12}}\\ & ={\displaystyle \frac{C^{\mathrm{0}}}{{\mathit{\rho }}_{\mathrm{p}}}}\times {\mathrm{10}}^{-\mathrm{12}}{\displaystyle \frac{\mathrm{g}}{\mathrm{\mu }\mathrm{g}}}{\displaystyle \frac{{\mathrm{cm}}^{-\mathrm{3}}}{{\mathrm{m}}^{-\mathrm{3}}}}.\end{array}\end{array}$$

Inserting Eq. (A8) into Eq. (A6) and combining this with Eq. (A12) leads to

$$\begin{array}{}\text{(A13)}& \begin{array}{rl}& \mathit{\alpha }\left(x\right)={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\frac{k_{\mathrm{a}}}{k_{\mathrm{ss},\mathrm{s}}}\frac{{\left[\mathrm{Z}\right]}_{\mathrm{g},\mathrm{eq}}}{{\left[Z\right]}_{\mathrm{b},\mathrm{eq}}\mathit{\delta }}\left(\mathrm{1}+\frac{x-\mathit{\delta }}{\mathit{\delta }}\right)}}\\ & ={\mathit{\alpha }}_{\mathrm{s}}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\frac{{\mathit{\alpha }}_{\mathrm{s}}\mathit{\omega }{C}^{\mathrm{0}}}{\mathrm{4}{D}_{\mathrm{b}}{\mathit{\rho }}_{\mathrm{p}}}x\times {\mathrm{10}}^{-\mathrm{12}}\frac{\mathrm{g}}{\mathrm{\mu }\mathrm{g}}\frac{{\mathrm{cm}}^{-\mathrm{3}}}{{\mathrm{m}}^{-\mathrm{3}}}}}.\end{array}\end{array}$$