Predictions of the glass transition temperature and viscosity of organic aerosols from volatility distributions

Volatility and viscosity are important properties of organic aerosols (OA), affecting aerosol processes such as formation, evolution, and partitioning of OA. Volatility distributions of ambient OA particles have often been measured, while viscosity measurements are scarce. We have previously developed a method to estimate the glass transition temperature (T_g) of an organic compound containing carbon, hydrogen, and oxygen. Based on analysis of over 2400 organic compounds including oxygenated organic compounds, as well as nitrogen- and sulfur-containing organic compounds, we extend this method to include nitrogen- and sulfur-containing compounds based on elemental composition. In addition, parameterizations are developed to predict T_g as a function of volatility and the atomic oxygen-to-carbon ratio based on a negative correlation between T_g and volatility. This prediction method of T_g is applied to ambient observations of volatility distributions at 11 field sites. The predicted T_g values of OA under dry conditions vary mainly from 290 to 339 K and the predicted viscosities are consistent with the results of ambient particle-phase-state measurements in the southeastern US and the Amazonian rain forest. Reducing the uncertainties in measured volatility distributions would improve predictions of viscosity, especially at low relative humidity. We also predict the T_g of OA components identified via positive matrix factorization of aerosol mass spectrometer (AMS) data. The predicted viscosity of oxidized OA is consistent with previously reported viscosity of secondary organic aerosols (SOA) derived from α-pinene, toluene, isoprene epoxydiol (IEPOX), and diesel fuel. Comparison of the predicted viscosity based on the observed volatility distributions with the viscosity simulated by a chemical transport model implies that missing low volatility compounds in a global model can lead to underestimation of OA viscosity at some sites. The relation between volatility and viscosity can be applied in the molecular corridor or volatility basis set approaches to improve OA simulations in chemical transport models by consideration of effects of particle viscosity in OA formation and evolution.

1 Introduction

Organic aerosols (OA) contribute substantially to the mass loadings of atmospheric fine particulate matter (Hallquist et al., 2009; Jimenez et al., 2009). OA formed from various anthropogenic or biogenic precursors have complex physicochemical properties (Goldstein and Galbally, 2007; Nizkorodov et al., 2011; Ditto et al., 2018), which makes predictions of their role in air quality, climate, and public health challenging (Kanakidou et al., 2005; Shrivastava et al., 2017). Volatility and viscosity are important properties of OA, both of which affect important aerosol processes such as gas–particle partitioning, new particle formation and evolution of size distribution, heterogeneous reactions, and cloud condensation and ice nucleation pathways of OA, as summarized in recent review articles (Krieger et al., 2012; Bilde et al., 2015; Pöschl and Shiraiwa, 2015; Knopf et al., 2018; Reid et al., 2018).

Recent measurements have shown that OA can exist in liquid (low dynamic viscosity η; η<10² Pa s), semisolid (10${}^{\mathrm{2}}\le \mathit{\eta }\le {\mathrm{10}}^{\mathrm{12}}$ Pa s), and amorphous solid (η>10¹² Pa s) states, depending on temperature (T), relative humidity (RH), and chemical composition (Reid et al., 2018). Even though there are several particle bounce measurements to infer ambient OA phase state, there are limited ambient measurements of particle phase state or viscosity (Virtanen et al., 2010; O'Brien et al., 2014; Bateman et al., 2016, 2017; Pajunoja et al., 2016; Liu et al., 2017; Ditto et al., 2019; Slade et al., 2019). Viscosity can be directly converted to bulk diffusivity of organic molecules using the Stokes–Einstein equation, which has been shown to work well for organic molecules diffusing through low-viscosity materials (Price et al., 2016; Chenyakin et al., 2017). This relation is inapplicable for predicting the bulk diffusivity of water and small molecules, and it may also underestimate the diffusivity of organic molecules in a highly viscous matrix, which can be corrected using a fractional Stokes–Einstein equation (Price et al., 2016; Evoy et al., 2019).

Viscosity can be related to the glass transition temperature (T_g), at which a phase transition between amorphous solid and semisolid states occurs (Koop et al., 2011). Ambient temperature varies through 100 K throughout the troposphere, greatly influencing the viscosity of the mixture. When the ambient temperature is below T_g, an amorphous particle behaves as a solid, while a particle would be semisolid or liquid when the ambient temperature is above T_g. OA particles contain a number of organic compounds and also a variable amount of liquid water depending on RH, which can act as a plasticizer to reduce T_g: these mixture effects can be estimated using the Gordon–Taylor relation (Mikhailov et al., 2009; Koop et al., 2011; Dette et al., 2014). In addition, ambient OA may often be internally mixed with inorganic species such as sulfate and nitrate, which would further lower T_g and viscosity if they were well mixed in one phase; when the phase separation occurs, the inorganic-rich and organic-rich phases may undergo glass transition at different temperatures (Dette and Koop, 2015).

For pure organic compounds with known molecular structure, viscosity can be predicted by group contribution approaches (Cao et al., 1993; Bosse, 2005; Y. C. Song et al., 2016; Rovelli et al., 2019; Gervasi et al., 2020); chemical composition of ambient OA is complex, and molecular specificity is often unavailable, which makes viscosity predictions of ambient OA challenging. We have recently developed a set of semiempirical parameterizations using molar mass (M) and atomic O:C ratio (Shiraiwa et al., 2017) or elemental composition (DeRieux et al., 2018) to predict T_g for compounds comprised of carbon, hydrogen, and oxygen (CHO compounds). These parameterizations have been applied to high-resolution mass spectrometry measurements to estimate viscosity of organic aerosols (DeRieux et al., 2018; Schum et al., 2018; Ditto et al., 2019; Song et al., 2019) and coupled into a thermodynamic model (Gervasi et al., 2020). Note that heteroatoms and the effects of molecular structure and functional groups on T_g are not considered in parameterizations of Shiraiwa et al. (2017) and DeRieux et al. (2018).

Viscosity of pure compounds has been found to be inversely correlated with vapor pressure (Thomas et al., 1979). The molecular-corridor-based analysis (Shiraiwa et al., 2014; Li et al., 2016) of hundreds of secondary organic aerosol (SOA) components has shown that compounds with lower pure-compound saturation mass concentration (C⁰) have higher T_g (Shiraiwa et al., 2017). Rothfuss and Petters (2017) found that there is a similar trend between the sensitivity of viscosity to functional group addition and the sensitivity of vapor pressure to functional group addition. Measurements of the evaporation kinetics of maleic acid showed that decreasing particle viscosity leads to a suppression in the effective vapor pressure of maleic acid (Marshall et al., 2018). Champion et al. (2019) found that SOA with higher condensed-phase fractions of extremely low volatility organic compounds (ELVOC) and low volatility organic compounds (LVOC) showed an increased viscosity. Zhang et al. (2019) measured T_g of isoprene SOA components including isoprene hydroxy hydroperoxide (ISOPOOH), isoprene-derived epoxydiol (IEPOX), 2-methyltetrols, and 2-methyltetrol sulfates (2-MT-OS), observing a tight correlation between T_g and vapor pressure.

Based on the above evidence showing a close relation between volatility and viscosity, in this study we develop the parameterizations predicting T_g as a function of C⁰ based on data from over 2000 compounds. Functional group contribution approaches are often used to predict C⁰ (Capouet and Müller, 2006; Pankow and Asher, 2008; Compernolle et al., 2011; O'Meara et al., 2014); thereby, using C⁰ to predict T_g would include the molecular structure effect indirectly. The developed parameterizations are applied to field observations of volatility distributions to predict viscosity of ambient OA.

2 Methods

2.1 Dataset of glass transition temperature

The training dataset used to develop the parameterizations of T_g include 2448 organic compounds classified into four classes (see the number of CH, CHO, CHON, and CHOS compounds in Table S1 in the Supplement). Measured T_g values are available for 42 CH compounds, 259 CHO compounds, 35 CHON compounds, and 1 CHOS compound (Koop et al., 2011; Rothfuss and Petters, 2017; Lessmeier et al., 2018; Zhang et al., 2019), among which there are 168 compounds with measured C⁰ available (Table S1). When T_g measurements are unavailable, T_g is estimated from the melting temperature (T_m) by applying the Boyer–Kauzmann rule of $T_{\mathrm{g}}=g\cdot T_{\mathrm{m}}$ (Kauzmann, 1948; Boyer, 1954) with g=0.70085 (±0.00375) (Koop et al., 2011), referred to as “estimated T_g” in this study (see good agreement of measured and estimated T_g in Fig. S1a in the Supplement). There are 1187 compounds (391 CH, 537 CHO, 241 CHON, and 18 CHOS compounds) with both measured T_m and C⁰ (Tables S1, S2) adopted from the MPBPWIN program test sets (http://esc.syrres.com/interkow/EpiSuiteData.htm, last access: 9 July 2020) included in the EPI Suite software version 4.1 (Estimation Programs Interface; US EPA, 2015). Measured T_g, T_m, or C⁰ for CHOS compounds is sparse and we adopt 850 CHOS compounds included in Li et al. (2016) with their T_m and C⁰ estimated by the EPI Suite software (Table S2). There are estimation limitations in the EPI Suite; for example, the disagreement between measured and estimated C⁰ is larger for compounds with $C^{\mathrm{0}}<\sim {\mathrm{10}}^{-\mathrm{2}}$ µg m⁻³ (Fig. S1b), which may affect the T_g predictions for compounds with low volatility. However, given the large number of data points with measured C⁰ included in the training dataset, the estimation bias introduced by the EPI Suite may not substantially impact the accuracy of the parameterization developed in this study.

The test dataset used to validate the performance of the parameterizations predicting T_g of SOA components includes 654 CHO compounds and 212 CHON compounds found in SOA oxidation products (Shiraiwa et al., 2014). The values of their C⁰ are estimated using the EVAPORATION model (Compernolle et al., 2011). Their T_m values are adopted from the EPI Suite. The T_g values predicted by our parameterizations are compared with the T_g estimated from the T_m by applying the Boyer–Kauzmann rule in the test dataset.

2.2 Parameterizations of T_g as a function of volatility

Figure 1a shows a dependence of T_g on C⁰ for 2448 organic compounds in the training dataset. The compounds with lower C⁰ have higher T_g, and the T_g appears to level off at around 420 K at $C^{\mathrm{0}}<\sim {\mathrm{10}}^{-\mathrm{10}}$ µg m⁻³. The dependence of T_g on the atomic O:C ratio is weaker (Figs. 1a and S2), in agreement with previous studies (Koop et al., 2011; Shiraiwa et al., 2017). Note that a tight correlation between T_g and the O:C ratio has been observed for oxidation products formed from specific precursors including α-pinene (Dette et al., 2014), n-heptadecane, and naphthalene (Saukko et al., 2012). Based on the trend shown in Fig. 1a, we develop a parameterization (Eq. 1) to predict T_g as a function of C⁰ and O:C, which are the parameters used in the two-dimensional volatility basis set (2D-VBS) framework (Donahue et al., 2011).

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{T}_{\mathrm{g}}=& \mathrm{289.10}-\mathrm{16.50}\times {\log }_{\mathrm{10}}\left(C^{\mathrm{0}}\right)-\mathrm{0.29}\times \left[{\log }_{\mathrm{10}}\right(C^{\mathrm{0}}){]}^{\mathrm{2}}\\ & +\mathrm{3.23}\times {\log }_{\mathrm{10}}\left(C^{\mathrm{0}}\right)\left(\mathrm{O}:\mathrm{C}\right)\end{array}\end{array}$$

The coefficients in Eq. (1) are obtained by fitting the T_g of 2448 compounds in Fig. 1a with multilinear least squares analysis with 68 % prediction and confidence intervals. The predicted T_g by Eq. (1) is plotted in Fig. 1a with the O:C ratios of 0, 0.5, and 1, showing that the predicted dependence of T_g on C⁰ follows the trend well in the training dataset. The O:C ratio mainly affects the predicted T_g of volatile compounds or extremely low volatility compounds. Figure 1b shows that the T_g values of those compounds are predicted well by Eq. (1) as indicated by a high correlation coefficient (R) of 0.92. The average absolute value of the relative error (AAVRE; Aiken et al., 2007) is 12 %.

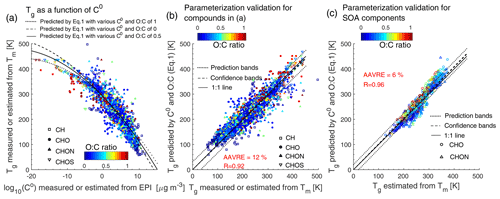
Figure 1 (a) T_g of organic compounds in the training dataset plotted against C⁰. The lines show the predictions of T_g (Eq. 1) by C⁰ and the O:C ratios of 0 (dashed), 0.5 (solid), and 1 (dotted). (b) Predicted T_g by C⁰ and the O:C ratio (Eq. 1) for compounds shown in (a) compared to measured or otherwise estimated T_g from T_m. (c) Predicted T_g for SOA components (Shiraiwa et al., 2014) using Eq. (1) plotted against estimated T_g from T_m with the Boyer–Kauzmann rule. The correlation coefficient (R) and the average absolute value of the relative error (AAVRE) are shown. In (b) and (c) the dashed and dotted lines show 68 % confidence and prediction bands, respectively.

Equation (1) is further evaluated using the test dataset for SOA components. Figure 1c compares T_g predicted by Eq. (1) with estimated T_g from T_m by applying the Boyer–Kauzmann rule, showing that Eq. (1) also presents a good performance for predicting T_g of these SOA components with R=0.96 and AAVRE =6 %. Note that C⁰ values of SOA components were estimated using the EVAPORATION model (Compernolle et al., 2011). The T_g values of individual SOA compounds can be predicted within ±20 K as indicated by the prediction band (dotted lines in Fig. 1c); however, this uncertainty may be much smaller for multicomponent SOA mixtures under ideal mixing conditions as indicated in the confidence band (dashed lines, almost overlapping with the 1:1 line) (Shiraiwa et al., 2017; DeRieux et al., 2018; Song et al., 2019).

We also develop a parameterization (Eq. 2) predicting T_g as a function of C⁰ solely, which can be applied to the information available with the one-dimensional VBS framework (1D-VBS; Donahue et al., 2006), and this can be used when the O:C ratio is not available in measurements.

$$\begin{array}{}\text{(2)}& T_{\mathrm{g}}=\mathrm{288.70}-\mathrm{15.33}\times {\log }_{\mathrm{10}}\left(C^{\mathrm{0}}\right)-\mathrm{0.33}\times \left[{\log }_{\mathrm{10}}\right(C^{\mathrm{0}}){]}^{\mathrm{2}}\end{array}$$

The coefficients in Eq. (2) are obtained following the procedures developing Eq. (1) and the same training dataset is used. Figures S3–S4 show that Eq. (2) gives very similar predictions as Eq. (1) particularly for the compounds with low O:C ratio. As Eqs. (1) and (2) are developed based on the compounds with their C⁰ higher than $\sim {\mathrm{10}}^{-\mathrm{20}}$ µg m⁻³, Eqs. (1) and (2) may not be applicable for compounds with $C^{\mathrm{0}}<\sim {\mathrm{10}}^{-\mathrm{20}}$ µg m⁻³ (Fig. 1a).

2.3 Predictions of T_g and viscosity of organic aerosols

For the application of T_g parameterizations in field observations of volatility distributions, T_g for each volatility bin (T_g,i) is calculated by Eq. (1). The term volatility refers to the effective saturation mass concentration (C^∗), and we assume ideal thermodynamic mixing in which case C^∗ is equal to C⁰ (Donahue et al., 2011). Note that there may be additional uncertainty in application of T_g parameterizations (which were developed based on pure compounds) to each volatility bin representing a surrogate of complex multicomponent mixtures. The isolines in Fig. 2 show the T_g,i predicted by Eq. (1) with the C^∗ and O:C defined in the 2D-VBS framework. T_g would be below ∼250 K for intermediate volatility organic compounds (IVOC; $\mathrm{300}<C^{\mathrm{0}}<\mathrm{3}\times {\mathrm{10}}^{\mathrm{6}}$ µg m⁻³), from ∼260 to 290 K for semivolatile organic compounds (SVOC; $\mathrm{0.3}<C^{\mathrm{0}}<\mathrm{300}$ µg m⁻³), and higher than 300 K for low-volatility organic compounds (LVOC; $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}<C^{\mathrm{0}}<\mathrm{0.3}$ µg m⁻³) and extremely low volatility organic compounds (ELVOC; $C^{\mathrm{0}}<\mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$ µg m⁻³). The T_g increases as the O:C ratio increases for SVOC and IVOC, which is consistent with previous studies (Koop et al., 2011; Saukko et al., 2012; Berkemeier et al., 2014). The T_g slightly decreases as the O:C ratio increases for LVOC and ELVOC compounds, which might be due to the uncertainties in Eq. (1) which is derived from a dataset containing fewer LVOC and ELVOC compounds as shown in Fig. 1a, which exhibits lower T_g with higher O:C.

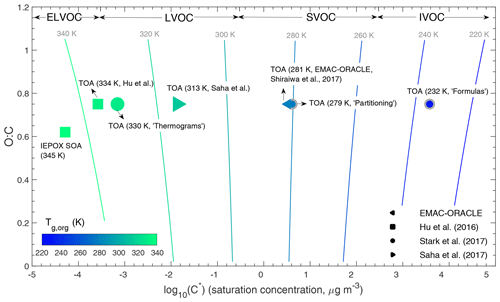
Figure 2 Predicted glass transition temperatures of organic aerosols under dry conditions (T_g,org) during the SOAS campaign placed into the 2-D VBS framework. The isopleths correspond to the T_g calculated using Eq. (1) with the effective saturation mass concentration (C^∗) and the O:C ratio defined in the 2D-VBS. The markers represent the T_g,org of total OA (TOA) and IEPOX SOA calculated from the volatility distributions simulated by a global chemical transport model (EMAC-ORACLE; Shiraiwa et al., 2017) or measured during the SOAS campaign (Hu et al., 2016; Saha et al., 2017; Stark et al., 2017). Three methods (Formulas, Partitioning, and Thermograms) are applied in Stark et al. (2017) to derive the C^∗ distributions, where the Thermograms method provides the most credible volatility distributions compared to Formulas and Partitioning (marker edge lines in gray).

The glass transition temperatures of organic aerosols under dry conditions (T_g,org) are calculated by the Gordon–Taylor equation (Gordon and Taylor, 1952) by assuming the Gordon–Taylor constant (k_GT) of 1 (Dette et al., 2014):

$$\begin{array}{}\text{(3)}& T_{\mathrm{g},\mathrm{org}}=\sum _i{w}_i{T}_{\mathrm{g},i},\end{array}$$

where w_i is the mass fraction in the particle phase for each volatility bin. The Gordon–Taylor approach has been validated for a wide range of mixtures including SOA compounds (Dette et al., 2014; Lessmeier et al., 2018). The Gordon–Taylor approach may fail in the case of adduct or complex formation (Koop et al., 2011), which is highly unlikely in multicomponent mixtures with myriads of SOA compounds with very small individual mole fractions and when particular interactions between individual compounds are more likely to average out (Shiraiwa et al., 2017); this aspect would need to be investigated in future studies.

The phase state of aerosol particles strongly depends on their water content (Mikhailov et al., 2009; Koop et al., 2011). Under humid conditions, the water content in OA can be estimated using the effective hygroscopicity parameter (κ) (Petters and Kreidenweis, 2007). The T_g of organic–water mixtures (T_g(w_org)) at given RH can be estimated using the Gordon–Taylor equation (Gordon and Taylor, 1952):

$$\begin{array}{}\text{(4)}& T_{\mathrm{g}}\left(w_{\mathrm{org}}\right)={\displaystyle \frac{(\mathrm{1}-w_{\mathrm{org}})T_{\mathrm{g},\mathrm{w}}+\frac{\mathrm{1}}{k_{\mathrm{GT}}}{w}_{\mathrm{org}}{T}_{\mathrm{g},\mathrm{org}}}{(\mathrm{1}-w_{\mathrm{org}})+\frac{\mathrm{1}}{k_{\mathrm{GT}}}{w}_{\mathrm{org}}}},\end{array}$$

where w_org is the mass fraction of organics in particles; T_g,w is the glass transition temperature of pure water (136 K; Kohl et al., 2005), and k_GT is the Gordon–Taylor constant for organic–water mixtures which is suggested to be 2.5 (Zobrist et al., 2008; Koop et al., 2011). Viscosity can then be calculated by applying the Vogel–Tammann–Fulcher (VTF) equation (Angell, 1991): $\mathit{\eta }={\mathit{\eta }}_{\mathrm{\infty }}{e}^{\frac{T_{\mathrm{0}}D}{T-T_{\mathrm{0}}}}$, where η_∞ is the viscosity at infinite temperature (10⁻⁵ Pa s; Angell, 1991), D is the fragility parameter which is assumed to be 10 (DeRieux et al., 2018), and T₀ is the Vogel temperature calculated as $T_{\mathrm{0}}=\frac{\mathrm{39.17}{T}_{\mathrm{g}}}{D+\mathrm{39.17}}$.

3 Application in field observations

3.1 Southern Oxidant and Aerosol Study (SOAS)

In this section we predict glass transition temperatures and phase state of ambient OA during the SOAS (Southern Oxidant and Aerosol Study) campaign, which took place in the southeastern United States (Centreville, Alabama) in summer 2013 (Carlton et al., 2018). The T_g of organic aerosols under dry conditions (T_g,org) is calculated using Eqs. (1) and (3) with measured volatility distributions. Figure 2 shows the calculated T_g,org placed in the 2D-VBS framework against the average log ₁₀(C^∗) calculated by $\sum _i{w}_i{\log }_{\mathrm{10}}(C_i^{\ast }$) (Kostenidou et al., 2018), and the measured O:C ratio is from Xu et al. (2015).

Figure 2 shows that T_g,org of total OA (TOA) range from 232 to 334 K, depending on volatility distributions measured by different methods, while the most credible predicted T_g,org values span in the range of 313–330 K. The reasons are stated below by comparing the different methods deriving the C^∗ distributions. Stark et al. (2017) used three methods (Thermograms, Partitioning, and Formulas) to derive volatility distributions by applying the measurements of organic acids (which were shown to account for about half of the total OA; Yatavelli et al., 2015) from a high-resolution chemical ionization time-of-flight mass spectrometer equipped with a filter inlet for gases and aerosols (Lopez-Hilfiker et al., 2014; Thompson et al., 2017). In the Thermograms method, C^∗ at 298 K is estimated from the desorption temperature after calibration with known species (Faulhaber et al., 2009). This method results in 93 % of OA mass distributed in the LVOC and ELVOC (Stark et al., 2017), and a high T_g,org of 330 K is predicted (Fig. 2). While this method may be influenced by thermal decomposition, the peak temperatures of decomposing species can be expected to relate closer to actual volatilities than any of the other two analysis methods (Stark et al., 2017). The result from the thermogram method is consistent with those measured by an aerosol mass spectrometer (AMS) with a thermodenuder, which also applied the thermogram method to estimate the C^∗ distributions (Hu et al., 2016). Saha et al. (2017) applied an evaporation kinetic model (Lee et al., 2011) based on the VBS approach to extract the C^∗ distributions, and the effects of enthalpy of vaporization and accommodation coefficient (α) are considered, resulting in the estimated T_g,org of 313 K. This study retrieved α of ∼0.5, which is consistent with recent experiments (Krechmer et al., 2017; Liu et al., 2019).

The lower T_g,org values (<280 K) calculated from the C^∗ distributions estimated from the Formulas and Partitioning methods (Stark et al., 2017) are less atmospherically relevant. The Formulas method used SIMPOL (simple group contribution method; Pankow and Asher, 2008) to calculate vapor pressures from the composition of the identified ions. While the specific functional group distributions needed for SIMPOL are unknown from mass spectrometer measurements, some assumptions can be made, leading to limits in the volatility distributions, all of which are showing the same behavior of high volatilities (Stark et al., 2017). This is because many of the detected species can be thermal decomposition products rather than actual SOA molecules (Stark et al., 2015, 2017), which can lead to overestimations of volatilities, resulting in the unlikely low T_g,org of 232 K. The Partitioning method used the measured particle-phase mass fractions of each species to estimate C^∗ based on the partitioning theory (Pankow, 1994). The estimated C^∗ is distributed mainly in the SVOC range (Stark et al., 2017), leading to a T_g,org of 279 K (Fig. 2). This value is very close to the T_g,org (281 K) simulated by a global chemical transport model, EMAC-ORACLE, in which a narrow distribution of C^∗ (1, 10, 10², and 10³ µg m⁻³) was applied (Shiraiwa et al., 2017). However, Stark et al. (2017) note that the partitioning-based volatility distribution is likely too high due to an artifact of signal-to-noise limitations, confining the C^∗ characterizable by the partitioning method to a relatively narrow range centered around the ambient OA concentration (by definition the semivolatile range). These analyses indicate that the volatility distributions derived from different methods, even when based on the same measurements, significantly affect the predicted T_g,org, and the most atmospherically relevant volatility distributions should be carefully chosen to reasonably predict the glass transition temperature of ambient OA. In summary, the T_g,org values during the SOAS campaign should be in the range of 313–330 K.

Figure 2 also includes T_g,org of isoprene-derived epoxydiol SOA (IEPOX-SOA) identified via positive matrix factorization (PMF) of AMS mass spectra (Lanz et al., 2007). IEPOX-SOA is predicted to have a T_g,org of 345 K with very low volatility with the average C^∗ lower than 10⁻⁴ µg m⁻³ (Hu et al., 2016; Lopez-Hilfiker et al., 2016; D'Ambro et al., 2019), which may be due to substantial formation of organosulfates and other oligomers (Lin et al., 2012; Hu et al., 2015; Riva et al., 2019). The predicted T_g,org of IEPOX-SOA is higher than previously reported T_g,org of 263–293 K for monoterpene-derived (α-pinene, 3-carene, myrcene, limonene, and ocimene) SOA (Petters et al., 2019).

We further calculate the viscosity of OA based on the T_g,org of TOA predicted above in order to compare with the ambient phase-state measurements during the SOAS campaign. Figure 3a shows the predicted viscosity of total OA at different RH; T is adopted as 298 K, the average value during the SOAS campaign (Hu et al., 2016). The effective hygroscopicity parameter (κ) is set to 0.14 for TOA based on measurements (Cerully et al., 2015). The characteristic timescale of mass transport and mixing by molecular diffusion (τ_mix) is also calculated: ${\mathit{\tau }}_{\mathrm{mix}}=d_{\mathrm{p}}^{\mathrm{2}}/\left(\mathrm{4}{\mathit{\pi }}^{\mathrm{2}}{D}_{\mathrm{b}}\right)$ (Seinfeld and Pandis, 2006), where d_p is the particle diameter, and the bulk diffusion coefficient D_b is calculated from the predicted viscosity by the fractional Stokes–Einstein relation (Evoy et al., 2019). We assume a radius of the diffusing molecule of 10⁻¹⁰ m and a particle diameter of 200 nm (Shiraiwa et al., 2011). Note that these estimated timescales represent rough estimations, as molecular interactions in complex mixtures are not considered.

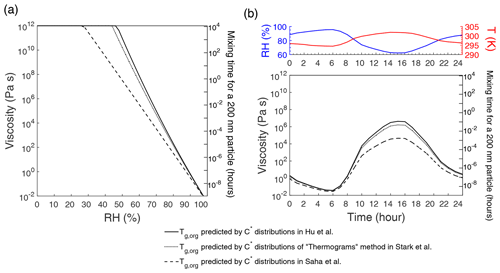
Figure 3 (a) Predicted viscosity of total OA measured during the SOAS campaign as a function of RH. (b) Diurnal variations of viscosity of total OA predicted employing the measured RH and T (Hu et al., 2016) during the SOAS campaign. T_g,org values are calculated using the volatility distributions measured in Hu et al. (2016), Saha et al. (2017), and the Thermograms method in Stark et al. (2017). Characteristic mixing timescales of organic molecules with a radius of 10⁻¹⁰ m within 200 nm particles are also shown on the right axis.

The viscosity of TOA at RH of 83 % (average RH during SOAS) is predicted to be less than 10² Pa s with τ_mix less than 1 s, which is consistent with the particle bounce measurements, suggesting that organic-dominated particles were mostly liquid during the SOAS campaign (Pajunoja et al., 2016). When RH was below ∼50 % in the sampling inlet, the particles were found to adopt a semisolid state (Pajunoja et al., 2016), which agrees with the predicted viscosity of 10⁷–10¹¹ Pa s, and τ_mix can be higher than 1 h at 50 % RH (Fig. 3a). The variations in T_g,org (313–330 K) due to the different measured C^∗ distributions (Fig. 2) have a more significant impact on the predicted viscosity at low and medium RH (Fig. 3a). When RH is higher than ∼70 %, the predicted viscosities calculated from different T_g,org values are very close; at high RH the condensed-phase water has a larger influence on the phase state than the volatility does, depending on the hygroscopicity of organic aerosols.

Figure 3b shows diurnal variations of predicted viscosity of total OA using measured T and RH during the SOAS campaign (Hu et al., 2016). During 10:00–20:00 LT (local time) when RH <70 % and T>298 K, three simulations using different T_g,org values predict that total OA occurs as semisolid with the predicted viscosity of 10²–10⁷ Pa s and the mixing times of less than 1 h. Particles are predicted to have a low viscosity of <1 Pa s, adopting a liquid phase during nighttime. The lowest viscosity occurs around 05:00–06:00 LT with RH >95 %. Here we did not consider the effects of the diurnal variations of volatility distributions, as they did not vary dramatically over the campaign period (Saha et al., 2017). Besides T and RH, diurnal variation of ambient aerosol phase state also depends on particle chemical composition and mixing states. Organic particles in the Amazon were found to be more viscous at night than the daytime due to the influence of biomass burning that may form nonliquid particles (Bateman et al., 2017). Particles in a mixed forest in northern Michigan, USA, were also found more viscous at night despite higher RH than the daytime, due to the formation of high molar mass organic compounds and smaller inorganic sulfate mass fractions (Slade et al., 2019). Phase-state measurements during daytime and nighttime at Atlanta, USA, suggested that the ambient particle phase state was influenced by OA composition, the presence of inorganic ions, aerosol liquid water, and particle mixing state (Ditto et al., 2019).

3.2 T_g,org at 11 global sites

Figure 4 summarizes T_g,org at 11 sites where the measured volatility distributions with volatility bins of four or more are available (Table S3). We did not include the data with narrower volatility ranges which may not correctly characterize the properties of ambient SOA (Bilde et al., 2015), and thus may not be appropriate for estimating volatility distributions or would result in unrealistically low T_g without considering realistically low C^∗ bins. Note that a narrow VBS may still be useful for efficiency in three-dimensional chemical transport models for SOA evaporation and condensation under a narrow range of ambient temperature variations (Kostenidou et al., 2018).

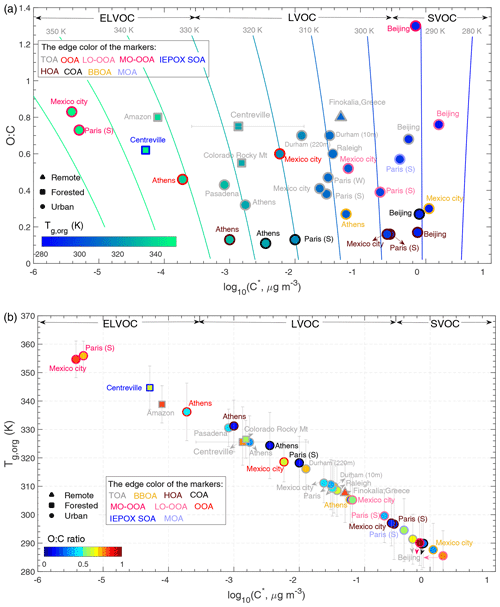
Figure 4 Predicted glass transition temperatures of organic aerosols under dry conditions (T_g,org) at 11 sites. The fill color of the markers represents T_g,org (a) or the O:C ratio (b). The marker edge color indicates the OA components identified via PMF of the AMS mass spectra. The isopleths in (a) correspond to T_g calculated using Eq. (1) with C^∗ and O:C defined in the 2D-VBS. The vertical error bars correspond to uncertainties in T_g,org considering parameterization uncertainties and error propagation. The horizontal error bars for the Centreville site correspond to the upper and lower limits of the average log₁₀(C^∗) calculated from different volatility distributions measured during the SOAS campaign (Hu et al., 2016; Saha et al., 2017; Stark et al., 2017).

Figure 4a shows the 2D-VBS framework of O:C vs. log₁₀C^∗ with the marker fill color representing T_g,org, whereas panel (b) shows T_g,org vs. log₁₀C^∗ with the marker fill color representing O:C. The marker edge color represents OA components identified via positive matrix factorization of AMS mass spectra (Lanz et al., 2007), including biomass-burning OA (BBOA), hydrocarbon-like OA (HOA), cooking OA (COA), and oxygenated OA (OOA), which is sometimes further separated into more oxygenated OA (MO-OOA) and less oxygenated OA (LO-OOA) factors. Note that these different OA factors may often be internally mixed in ambient atmosphere, and predicted T_g,org and particle viscosity would be irrelevant in such a case. Nevertheless, these predictions can be useful when particles are externally mixed or ambient OA are dominated by a certain OA factor.

T_g,org of total OA (TOA) varies from 290 to 339 K. The lower T_g,org occurs at Beijing, China, in June 2018 (Xu et al., 2019). OA in Beijing was found to be overall more volatile with the particle-phase semivolatile fraction of 63 %. This may be due to the higher total OA mass concentrations in Beijing (Xu et al., 2019), which facilitate greater partitioning of SVOC compounds into the particle phase, leading to a lower T_g,org. The predicted T_g,org of total OA at numerous other sites range between 300 and 320 K, including Paris (Paciga et al., 2016), Mexico City (Cappa and Jimenez, 2010), Centreville (Hu et al., 2016; Saha et al., 2017; Stark et al., 2017), Raleigh (Saha et al., 2017), and Durham (Saha et al., 2018) in southeastern US. The T_g,org value (316 K) at 220 m downwind from a highway in Durham is higher than the T_g,org (309 K) at 10 m downwind from a highway due to the dilution and mixing of traffic-sourced particles with background air and evaporation of semivolatile species during downwind transport (Saha et al., 2018). The T_g,org values are predicted to be high (>320 K) at the sites in Athens (Louvaris et al., 2017), Pasadena (Ortega et al., 2016), Colorado Rocky Mountain (Stark et al., 2017), and the Amazon (Hu et al., 2016). The T_g,org values for MO-OOA in Mexico City and Paris are predicted to be very high at ∼350 K, reflecting their very low volatility.

Figure 5 shows the OA viscosity variation of OA components against RH. The hygroscopic growth is considered based on hygroscopicity (κ), which is estimated as a function of the O:C ratio (Lambe et al., 2011) when κ was not measured (Table S3). The κ values of OA factors with low O:C ratio, i.e., HOA, COA, and BBOA, are estimated to be low (<0.08); they are predicted to undergo glass transition at RH between 25 % and 68 % and adopt a liquid phase only when RH is very high (∼80 %). The predicted behavior of BBOA is in line with bounce measurements observing that particles are semisolid in a biomass-burning plume (Bateman et al., 2017). OA factors with higher O:C ratios including LO-OOA, MO-OOA, and IEPOX SOA tend to become liquid (viscosity <10² Pa s) at intermediate RH (Fig. 5b).

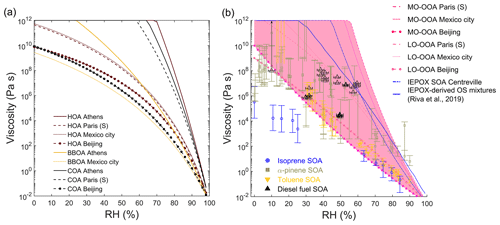
Figure 5 Predicted viscosity of (a) HOA, COA, and BBOA and (b) LO-OOA, MO-OOA, and IEPOX SOA in different locations at 298 K as a function of RH. Experimentally measured viscosity of laboratory-generated SOA formed from isoprene (Song et al., 2015), α-pinene (Abramson et al., 2013; Renbaum-Wolff et al., 2013; Kidd et al., 2014; Pajunoja et al., 2014; Bateman et al., 2015; Zhang et al., 2015; Grayson et al., 2016; Petters et al., 2019), toluene (M. Song et al., 2016), and diesel fuel (Song et al., 2019) are also shown. Predicted viscosity of IEPOX-derived OS mixtures (solid blue line) is from Riva et al. (2019). Note that in the case when these OA factors are internally mixed with other components, the predicted viscosity would not represent real ambient complex organic mixtures.

There have been growing measurements of RH-dependent viscosity of laboratory-generated SOA formed from different precursors, e.g., isoprene (Song et al., 2015), α-pinene (Abramson et al., 2013; Renbaum-Wolff et al., 2013; Kidd et al., 2014; Pajunoja et al., 2014; Bateman et al., 2015; Zhang et al., 2015; Grayson et al., 2016; Petters et al., 2019), toluene (M. Song et al., 2016), and diesel fuel (Song et al., 2019). As the OOA factors characterized from ambient AMS observations may represent ambient SOA (Jimenez et al., 2009), the predicted viscosities of OOA are compared with laboratory measurements of SOA viscosities in Fig. 5b. It shows that the majority of experimental values is well bounded by the predicted viscosities of OOA, represented by the pink shaded area. One exception is the measured viscosity of isoprene SOA is lower than the predicted viscosity of IEPOX SOA at low RH (<30 %). One possible reason is that the isoprene SOA in experiments was formed with high oxidant concentrations with a short reaction time in an oxidation flow reactor in the absence of inorganic seed particles (Song et al., 2015). In ambient environments heterogeneous reactions with acidic sulfate particles forming oligomers are suggested to be an important pathway (Surratt et al., 2010; Lin et al., 2013; Hu et al., 2015, 2016). These particle-phase organosulfates may contribute to a higher viscosity, as indicated by the predicted viscosity of IEPOX-derived organosulfate mixtures with their T_g,org estimated to be 313 K (Riva et al., 2019). Another reason could be the mass concentrations of isoprene SOA are much higher (100–1000 µg m⁻³; Song et al., 2015) compared to ambient OA concentrations (5 µg m⁻³ during SOAS; Stark et al., 2017). Higher mass concentrations can lead to lower viscosity, as more semivolatile compounds can partition into the particle phase (Grayson et al., 2016; Jain et al., 2018; Champion et al., 2019).

4 Comparison with global simulations

Shiraiwa et al. (2017) simulated the global distribution of annual averages of SOA phase state using the chemical transport model EMAC (Jöckel et al., 2006) coupled with the organic aerosol module ORACLE (Tsimpidi et al., 2014). ORACLE uses the 1D-VBS framework with four C^∗ bins (1, 10, 10², and 10³ µg m⁻³). To estimate T_g, the values of molar mass and O:C ratio were assigned for each volatility bin based on molecular corridors (Shiraiwa et al., 2014). Note that the molar mass assigned for the volatility bin of 1 µg m⁻³ was assumed to have relatively high molar mass to partially compensate for the fact that ORACLE does not consider lower volatility bins with higher molar mass. As shown in Fig. 6, global distributions of T_g∕T presented in Shiraiwa et al. (2017) are converted to viscosity using the VTF equation. Figure 6 also includes the viscosity of total OA at the 11 sites by applying measured volatility distributions and the global model-simulated 5-year-average T and RH with κ assumed to be 0.1 (Pringle et al., 2010). Figure 6b shows that the predicted viscosities at the 11 sites generally agree with the global simulations: the amorphous solid or semisolid phase occurs over relatively dry areas, including the sites in western US, Mexico City, Beijing, and coastal sites in Greece; the lower viscosity occurs in southeastern US and Paris.

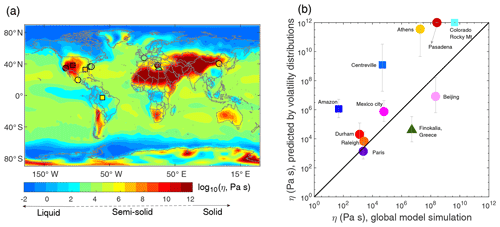
Figure 6 (a) Global distributions of SOA annually averaged viscosity at the surface simulated by a global chemical transport model (Shiraiwa et al., 2017) with the viscosity predicted by measured volatility distributions at 11 global sites (triangle, square, and circle represent remote, forested, and urban sites, respectively, Table S3). The color code indicates viscosity on a log scale. (b) Predicted viscosity based on measured volatility distributions compared against the viscosity in global simulations. The error bars correspond to uncertainties in viscosities calculated from uncertainties in predicted T_g,org shown in Fig. 4.

The global simulations show that the particles are liquid in the Amazon, while they occur as semisolid in our predictions based on measured volatility distributions (Fig. 6a). The reason for this disagreement may be mainly due to the substantial fraction of low volatility compounds observed in ambient measurements largely missing from global simulations. Hu et al. (2016) observed that 90 % of OA has volatilities lower than 1 µg m⁻³, which is the lowest C^∗ bin in the global simulations. The ambient phase-state measurements show that for background conditions of the Amazonian tropical forest particles are mostly liquid, while for the anthropogenic influence including both urban pollution and biomass burning they occur as semisolid or glassy (Bateman et al., 2016, 2017). The volatility distributions were measured in the dry season that is heavily influenced by biomass burning (Hu et al., 2016), which can lead to the higher predicted viscosity. Similar cases are observed in Athens and the two sites in the western US, that our predictions based on volatility distributions indicate the glassy phase state, while the global model predicts the occurrence of a semisolid phase.

5 Conclusions and implications

We have developed parameterizations to estimate the glass transition temperature of organic compounds using saturation mass concentration (C⁰) and atomic O:C ratio. They can be applied to ambient observations of volatility distributions to estimate viscosity of ambient organic aerosols. The T_g and viscosity prediction method can be applied in the volatility basis set or the molecular-corridor-based approach to improve OA simulations in chemical transport models by consideration of effects of particle viscosity on OA formation and evolution (Shiraiwa et al., 2017; Pye et al., 2017; Schmedding et al., 2019). Most of the current chemical transport models treat particles as a homogeneously well-mixed liquid without considering particle-phase diffusion limitations, which can lead to bias in simulations of SOA mass concentrations and evolution of size distributions (Shiraiwa and Seinfeld, 2012; Zaveri et al., 2018). The SOA simulations applying the VBS framework have not yet included the effects of viscosity on SOA formation and evolution. When the gas–particle partitioning is limited by bulk diffusion, kinetic treatments of SOA partitioning may need to be applied (Perraud et al., 2012; Liu et al., 2016; Yli-Juuti et al., 2017; Li and Shiraiwa, 2019). Some chamber experiments probing the mixing timescales of SOA particles formed from isoprene, α-pinene, and limonene did not observe significant kinetic limitations at moderate and high RH under room temperature conditions (Loza et al., 2013; Ye et al., 2016), while kinetic limitations of bulk diffusion of organic molecules in β-caryophyllene SOA have been observed at 75 % RH (Ye et al., 2018), warranting further investigations on the degree of kinetic limitations in ambient tropospheric conditions. In addition, the interplay of diffusion limitations and phase separation impacts heterogeneous and multiphase chemistry (Vander Wall et al., 2018; DeRieux et al., 2019; Zhou et al., 2019) and gas–particle partitioning (Zuend and Seinfeld, 2012; Shiraiwa et al., 2013; Freedman, 2017; Pye et al., 2017; Gorkowski et al., 2019a). The particle morphology and the degree of nonideal mixing and liquid–liquid phase separation can evolve upon atmospheric aging (Gorkowski et al., 2019b). These aspects may also need to be considered for better representation of organic aerosols in future studies.

Appendix A: Parameterizations of T_g based on elemental compositions

We recently developed a parameterization (Eq. A1) predicting T_g as a function of the number of carbon (n_C), hydrogen (n_H), and oxygen (n_O) atoms (DeRieux et al., 2018), similar to the formulation used to predict C⁰ (Donahue et al., 2011; Li et al., 2016):

$$\begin{array}{}\text{(A1)}& \begin{array}{rl}{T}_{\mathrm{g}}=& (n_{\mathrm{C}}^{\mathrm{0}}+\ln (n_{\mathrm{C}}\left)\right)b_{\mathrm{C}}+\ln \left(n_{\mathrm{H}}\right)b_{\mathrm{H}}+\ln \left(n_{\mathrm{C}}\right)\ln \left(n_{\mathrm{H}}\right)b_{\mathrm{CH}}\\ & +\ln \left(n_{\mathrm{O}}\right)b_{\mathrm{O}}+\ln \left(n_{\mathrm{C}}\right)\ln \left(n_{\mathrm{O}}\right)b_{\mathrm{CO}}.\end{array}\end{array}$$

Values of the coefficients $n_{\mathrm{C}}^{\mathrm{0}}$, b_C, b_H, b_CH, b_O, and b_CO are 1.96, 61.99, −113.33, 28.74, 0, and 0 for CH compounds and 12.13, 10.95, −41.82, 21.61, 118.96, and −24.38 for CHO compounds. We broaden the parameterizations for CH and CHO compounds (Eq. A1) to the following equations applicable to CHON (Eq. A2) and CHOS compounds (Eq. A3):

$$\begin{array}{}\text{(A2)}& {\displaystyle }\begin{array}{rl}{T}_{\mathrm{g}}=& (n_{\mathrm{C}}^{\mathrm{0}}+\ln (n_{\mathrm{C}}\left)\right)b_{\mathrm{C}}+\ln \left(n_{\mathrm{O}}\right)b_{\mathrm{O}}+\ln \left(n_{\mathrm{N}}\right)b_{\mathrm{N}}\\ & +\ln \left(n_{\mathrm{C}}\right)\ln \left(n_{\mathrm{O}}\right)b_{\mathrm{CO}}+\ln \left(n_{\mathrm{C}}\right)\ln \left(n_{\mathrm{N}}\right)b_{\mathrm{CN}}\\ & +\ln \left(n_{\mathrm{O}}\right)\ln \left(n_{\mathrm{N}}\right)b_{\mathrm{ON}},\end{array}\text{(A3)}& {\displaystyle }\begin{array}{rl}{T}_{\mathrm{g}}=& (n_{\mathrm{C}}^{\mathrm{0}}+\ln (n_{\mathrm{C}}\left)\right)b_{\mathrm{C}}+\ln \left(n_{\mathrm{O}}\right)b_{\mathrm{O}}+\ln \left(n_{\mathrm{S}}\right)b_{\mathrm{S}}\\ & +\ln \left(n_{\mathrm{C}}\right)\ln \left(n_{\mathrm{O}}\right)b_{\mathrm{CO}}+\ln \left(n_{\mathrm{C}}\right)\ln \left(n_{\mathrm{S}}\right)b_{\mathrm{CS}}\\ & +\ln \left(n_{\mathrm{O}}\right)\ln \left(n_{\mathrm{S}}\right)b_{\mathrm{OS}}.\end{array}\end{array}$$

Values of the coefficients $n_{\mathrm{C}}^{\mathrm{0}}$, b_C, b_O, b_N, b_CO, b_CN, and b_ON in Eq. (A2) are 5.34, 31.53, −7.06, 134.96, 6.54, −34.36, and −15.35, respectively. Values of the coefficients $n_{\mathrm{C}}^{\mathrm{0}}$, b_C, b_O, b_S, b_CO, b_CS, and b_OS in Eq. (A3) are 1.12, 68.41, 64.95, 35.77, −12.32, −9.85, and 13.80, respectively. These values are obtained by fitting the T_g of CHON and CHOS compounds included in the training dataset (Fig. 1a, Table S1) with multilinear least squares analysis. Figure A1a shows a fair agreement between the predicted T_g using Eq. (A2) and the measured or otherwise estimated T_g with R of 0.55 and relatively large AAVRE of 16 % for CHON compounds in the training dataset. Figure A1b shows a better prediction performance with R of 0.83 and AAVRE of 9 % for 212 CHON compounds included in the test dataset for SOA components with their T_g estimated by the Boyer–Kauzmann rule using the EPI-estimated T_m. Figure A1c shows that Eq. (A3) performs well for the CHOS compounds included in the training dataset with their T_g estimated by the Boyer–Kauzmann rule using the EPI-estimated T_m (R=0.87, AAVRE =8 %).

Figure S5 shows the comparison of T_g predicted by the elemental composition (Eqs. A1–A3) with the T_g predicted as a function of C⁰ and the O:C ratio (Eq. 1). The agreement between the two sets of parameterizations for nitrogen- and sulfur-containing compounds is not as good as that for CHO compounds, indicating that there are limitations of predicting T_g by the elemental composition for nitrogen- and sulfur-containing compounds with complex elemental compositions and molecular structures. As volatility depends significantly on functional groups contained in a molecule (Pankow and Asher, 2008; Compernolle et al., 2011), predicting T_g by volatility (Eq. 1) indirectly incorporates the molecular structure effects. As there are limited CHON and CHOS compounds with measured T_g available, future experiments measuring more T_g data for nitrogen- and sulfur-containing organics would help improve the T_g parameterizations by elemental composition.

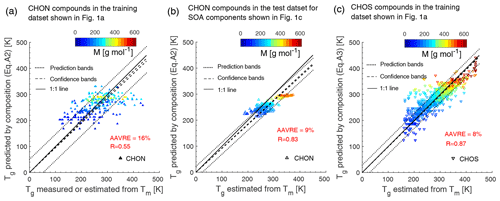
Figure A1 T_g predicted by elemental composition (Eq. A2) compared to (a) measured or otherwise estimated T_g by the Boyer–Kauzmann rule using measured T_m for CHON compounds in the training dataset and (b) estimated T_g by the Boyer–Kauzmann rule with T_m estimated by the EPI Suite for CHON compounds in the test dataset for SOA components. (c) T_g predicted by elemental composition (Eq. A3) compared to estimated T_g by the Boyer–Kauzmann rule with T_m estimated by the EPI Suite for CHOS compounds in the training dataset. The dashed and dotted lines show 68 % confidence and prediction bands, respectively. The correlation coefficient (R) and the average absolute value of the relative error (AAVRE) are included in each figure legend.

Appendix B: Comparison of T_g predictions with Zhang et al. (2019)

Recently Zhang et al. (2019) developed a semiempirical parameterization (Eq. B1) using vapor pressure (p₀ in atm) to predict T_g based on measured T_g of 11 SOA compounds:

$$\begin{array}{}\text{(B1)}& T_{\mathrm{g}}=\mathrm{480.1}-{\displaystyle \frac{\mathrm{54}\mathrm{395}}{({\log }_{\mathrm{10}}\left(p_{\mathrm{0}}\right)-\mathrm{1.7929}{)}^{\mathrm{2}}+\mathrm{116.49}}}.\end{array}$$

p₀ can be converted to C⁰ via $C^{\mathrm{0}}=\left({\mathrm{10}}^{\mathrm{6}}M{p}_{\mathrm{0}}\right)/\left(RT\right)$, where R is the ideal gas constant ($R=\mathrm{8.2}\times {\mathrm{10}}^{-\mathrm{5}}$ m³ atm mol⁻¹ K⁻¹), M is the molar mass (g mol⁻¹), and T is the temperature (K). Figure B1 compares the measured T_g included in the training dataset shown in Fig. 1a to T_g predicted by (a) C⁰ and the atomic O:C ratio (Eq. 1), (b) elemental composition (Eqs. A1–A3), and (c) Eq. (B1) by Zhang et al. (2019). While all three methods perform reasonably well, the predictions using elemental composition (Eqs. A1–A3) show better performance (Fig. B1b) with R of 0.93 and AAVRE of 11 %.

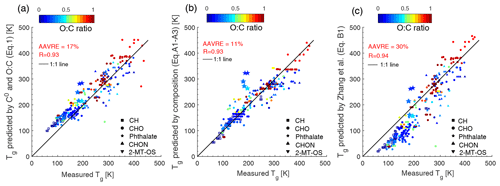
Figure B1 Comparison between measured T_g in the training dataset in Fig. 1a and T_g predicted by (a) C⁰ and O:C (Eq. 1), (b) elemental composition (Eqs. A1–A3), and (c) the parameterization (Eq. B1) in Zhang et al. (2019). The solid line shows the 1:1 line. The correlation coefficient (R) and the average absolute value of the relative error (AAVRE) are included in each figure legend.

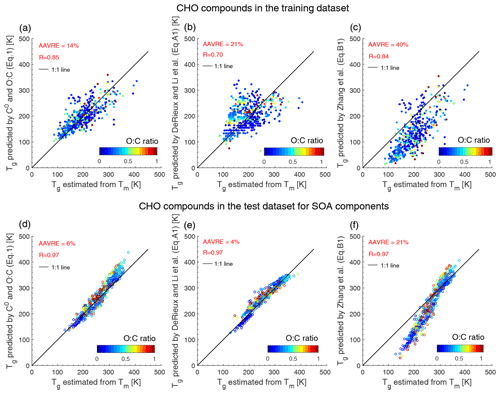
Figure B2 Predicted T_g by (a) C⁰ and O:C (Eq. 1), (b) elemental composition (Eq. A1), and (c) the parameterization (Eq. B1) in Zhang et al. (2019) plotted against estimated T_g from T_m applying the Boyer–Kauzmann rule. CHO compounds in (a)–(c) included in the training dataset shown in Fig. 1a are with measured T_m and C⁰ values; CHO compounds in (d)–(f) included in the test dataset for SOA components shown in Fig. 1c are with T_m and C⁰ values estimated by the EPI Suite and the EVAPORATION model, respectively. The correlation coefficient (R) and the average absolute value of the relative error (AAVRE) are shown.

The prediction performance is influenced by the training dataset used to develop parameterizations of T_g. The compounds shown in Fig. B1 contain mostly carboxylic acid and hydroxyl functional groups (Koop et al., 2011; Rothfuss and Petters, 2017) and are included in the training dataset used to develop Eqs. (1) and Eqs. (A1)–(A3). The training dataset used in Zhang et al. (2019) included 11 organic compounds, and their parameterization predicted T_g of isoprene SOA very well (Zhang et al., 2019), but underpredicted some low-T_g compounds (Fig. B1c). For compounds with their measured T_g higher than 200 K, predictions by Zhang et al. (2019) show good performance and are consistent with the predictions given by Eq. (1) as a function of C⁰ and the O:C ratio. Predicted T_g values of 2-MT-OS using the three methods are 297 K (Eq. 1, as a function of C⁰ and the O:C ratio), 275 K (Eq. A3, as a function of the elemental composition), and 280 K (Eq. B1, Zhang et al., 2019), comparable with the measured T_g of 276±15 K (Zhang et al., 2019).

Note that predictions using elemental composition (Eq. A1) overestimate the T_g of phthalate compounds (the star markers in Fig. B1). For instance, the observed T_g of dioctyl phthalate is 194 K (Zhang et al., 2018), while the prediction is higher than 300 K (Fig. B1b). The reason is that ester is not an effective functional group to increase viscosity compared to carboxylic acid and hydroxyl (Rothfuss and Petters, 2017). Parameterizations using volatility (Eqs. 1 and B1) improve the predicted T_g of phthalate compounds (Fig. B1a, c). Figure B2 shows, compared to the predictions using Eq. (B1) provided in Zhang et al. (2019), that predictions by C⁰ and the atomic O:C (Eq. 1) and elemental composition (Eq. A1) agree better with the T_g estimated from the Boyer–Kauzmann rule. Future experiments measuring more T_g data of SOA components would help verify the T_g predictions by different parameterizations.