the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
H migration in peroxy radicals under atmospheric conditions
Barbara Nozière
A large data set of rate coefficients for H migration in peroxy radicals is presented and supplemented with literature data to derive a structure–activity relationship (SAR) for the title reaction class. The SAR supports aliphatic RO2 radicals; unsaturated bonds and β-oxo substitutions both endocyclic and exocyclic to the transition state ring; and α-oxo (aldehyde), –OH, –OOH, and –ONO2 substitutions, including migration of O-based hydrogen atoms. Also discussed are –C(=O)OH and –OR substitutions. The SAR allows predictions of rate coefficients k(T) for a temperature range of 200 to 450 K, with migrations spans ranging from 1,4 to 1,9-H shifts depending on the functionalities. The performance of the SAR reflects the uncertainty of the underlying data, reproducing the scarce experimental data on average to a factor of 2 and the wide range of theoretical data to a factor of 10 to 100, depending also on the quality of the data. The SAR evaluation discusses the performance in multi-functionalized species. For aliphatic RO2, we also present some experimental product identification that validates the expected mechanisms. The proposed SAR is a valuable tool for mechanism development and experimental design and guides future theoretical work, which should allow for rapid improvements of the SAR in the future. Relative multi-conformer transition state theory (rel-MC-TST) kinetic theory is introduced as an aid for systematic kinetic studies.
- Article
(2058 KB) - Full-text XML
-
Supplement
(7570 KB) - BibTeX
- EndNote
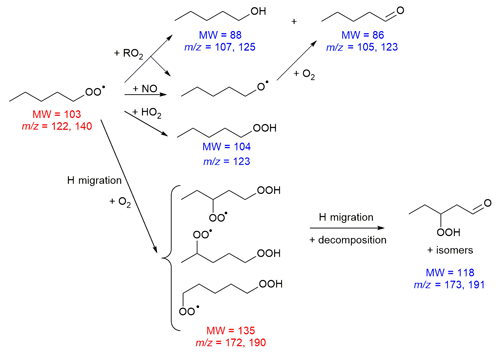
H migration in alkylperoxy radicals, RO2, is a well-known reaction in combustion processes, where it is a major path in OH radical generation in cool flames (Battin-Leclerc et al., 2011). Over the last few years, RO2 H migration has also been studied intensively at ambient temperatures, owing to its role in important atmospheric processes, such as the (re)generation of OH and HO2 radicals, and the formation of low-volatility oxygenated compounds and highly oxygenated molecules (HOMs) (Bianchi et al., 2019; Ehn et al., 2017; Hallquist et al., 2009; Jokinen et al., 2014; Vereecken et al., 2018). The wide range of implications of these reactions is due to the properties of the hydroperoxides formed in the H migration (Reaction R1).
Firstly, RO2 H migrations can be chained, having multiple H migration reactions that sequentially add O2 moieties to a molecule (Reactions R2 and R3). Secondly, via H bonding and inductive effects the –OOH group facilitates faster H migration reactions, enhancing the formation of highly oxidized molecules. The bond strength of the α-OOH hydrogen atoms is reduced, allowing for fast migration of these H atoms (Reaction R4); the resulting α-OOH alkyl radicals were shown to be theoretically unstable, decomposing spontaneously to a carbonyl compound with an OH radical co-product that acts as an important oxidant in the atmosphere (Vereecken et al., 2004) and is responsible for chain branching in low-temperature combustion (Battin-Leclerc et al., 2011). Finally, hydroperoxide-substituted RO2 radicals can rapidly scramble the peroxy H atoms (Reaction R5) (Jørgensen et al., 2016; Miyoshi, 2011; Nozière and Vereecken, 2019), allowing access to subsequent reactions and products that may not be accessible from the originally formed HOOQO2.
The RO2 H migration reactions have a comparatively high barrier and are often too slow to compete against the traditional atmospheric bimolecular reactions of peroxy at room temperature, i.e. their reaction with NO, HO2, and other RO2 radicals (Atkinson, 2007; Jenkin et al., 2019). These latter reactions have been studied extensively and are included in all chemical models, while their rate coefficients and products can be reasonably well predicted as a function of the RO2 molecular structure (Jenkin et al., 2019). The rate coefficient of the unimolecular reactions, however, depends strongly on the span of the H migration, the substitution pattern around the migrating H atom and peroxy radical moiety, and the nature of the substitution. In particular, unsaturated oxygenated RO2 radicals were found to have H migration reactions that are competitive in pristine environments. RO2 H migration reactions are typically not well represented in chemical atmospheric models, as they remain poorly characterized and no generally applicable quantitative structure–activity relationship (SAR) is available to aid in the construction of mechanisms (Vereecken et al., 2018).
Though high-quality theoretical work has been available for RO2 H migration for quite some time, as discussed below, direct experimental data on the rate coefficients remains limited. Recent work by Nozière and Vereecken (2019) studied H migration in aliphatic RO2, via combined experimental and theoretical methodologies, examining migration of primary, secondary, and tertiary H atoms over spans from 1,5-H to 1,8-H migrations. This experimental study of aliphatic RO2 H migration is currently the only available direct measurement of aliphatic RO2 H migration rate coefficients and thus represent important reference data in the development of SARs. H migration from aliphatic carbons is a critical step in the formation of highly oxygenated molecules where oxygen-to-carbon ratios (O:C) as high as 2 have been observed, implying that (nearly) all carbons have been oxygenated (Bianchi et al., 2019; Ehn et al., 2017). All other experimental studies we are aware of involve (unsaturated) oxygenated peroxy radicals, i.e. mostly RO2 radicals derived from isoprene and its oxidation products (Crounse et al., 2011, 2012, 2013; Jorand et al., 2003; Perrin et al., 1998; Praske et al., 2018, 2019; Xu et al., 2019). Modern explicit atmospheric models have extensive representations of this isoprene RO2 chemistry (Carter, 2010; Jenkin et al., 2015; Novelli et al., 2020; Wennberg et al., 2018), derived mostly from the Leuven Isoprene Mechanisms LIM0 and LIM1 (Peeters et al., 2009, 2014).
A recent review of RO2 chemistry by Jenkin et al. (2019), aimed at developing SARs for use in mechanism development, included a short list of recommendations for H migrations, but although the authors rely on theoretical data, they refrained from developing a generally applicable SAR based on the systematic theoretical studies available in the literature. More recently, Nozière and Vereecken (2019) proposed a simple SAR for aliphatic and OOH substituted RO2 radicals, combining their theoretical and experimental data with the systematic theoretical studies by Miyoshi (2011), Sharma et al. (2010), and Otkjær et al. (2018). Older work by Vereecken and Peeters (Vereecken, 2012; Vereecken and Peeters, 2010b) presented an extensive SAR, covering aliphatic, unsaturated, and oxygenated RO2, but these data were never formally published. Extensive theoretical data are also available on multi-functionalized RO2 radicals (e.g. Fuchs et al., 2018; Jørgensen et al., 2016; Møller et al., 2019; Novelli et al., 2020; Praske et al., 2018, 2019; da Silva, 2010a, b, 2011). Combined, this theory-based data set is sufficiently large to derive a first-order SAR covering many of the needs in atmospheric chemistry and serving as a basis for future improvements. If the rate coefficient predictions carry an uncertainty of an order of magnitude or less, many questions regarding the competitiveness of the RO2 H migration relative to other RO2 loss processes could be answered, and (semi-)quantitative models could be constructed.
In this work, we present an additional large theory-based data set, and derive a first-order SAR for RO2 H migration covering a wide range of chemical functionalities, with a reasonable level of reliability of ∼1 order of magnitude, depending on the molecular structure. We label this a first-order SAR, as we derive this SAR without rigorously incorporating all literature data available, by including lower-level theoretical predictions, and where needed build on reactivity trends of analogous classes without necessarily being able to validate the transferability of these trends. The current SAR is then a starting framework upon which to build a more complete and accurate SAR as more data becomes available, while retaining immediate usability within the expected accuracy. A full review of the RO2 literature is thus outside the scope of the current work, and only data used in deriving or validating our SAR are discussed. Work is ongoing to include more experimental data, to systematically re-evaluate the theoretical data at higher levels of theory, or to fill in missing data, and the current SAR helps to identify the most relevant reactions on which to dedicate limited computational and experimental resources. Where possible, experimental literature data will be used to validate and/or fine-tune the rate coefficient predictions. Unfortunately, not all experimental data are readily incorporated. For example, at high temperatures, the rate of reaction is determined strongly by the entropic changes from the reactant chain internal rotors to the cyclic transition states, while at lower temperatures the energy barrier height and tunnelling of the H atom are the most critical parameters. This transition leads to strongly non-linear Arrhenius behaviour, making extrapolation of the high-temperature data to ambient conditions more difficult. Similarly, the experimental data often provides bulk rate coefficients, convoluting multiple elementary reactions that may act on different timescales. One should bear in mind that the rate coefficient for H migration may not be sufficient to determine the impact of a reaction. Specifically, the reverse reaction must be slow enough to allow the (alkyl) reaction product to undergo a subsequent transition or chemical reaction rather than return to the parent RO2 radical. Examples of such subsequent capture reactions are O2 addition on the alkyl radical site (in the atmosphere, typically at a rate of s−1, Atkinson, 2007) or fast decomposition of the product. The reverse H migration is likewise slowed down by physicochemical effects such as allyl or vinoxy resonance stabilization of the radical electron or hydrogen bonding of the –OOH product moiety. Several authors have listed rate coefficients for reverse reactions (e.g. Jørgensen et al., 2016; Miyoshi, 2011; Otkjær et al., 2018); by and large, faster RO2 H migration reactions tend to have slower reverse reactions, such that in atmospheric conditions the reverse reactions are typically relevant only for those RO2 reactions already too slow to compete. The experimental data on RO2 H migration reactions are not only scarce, they are often also indirect and obtained for molecules with complex (oxygenated) substitution, with rate coefficients inferred from product observations without experimental confirmation that the assumed underlying mechanisms are correct and complete. A recent paper by Novelli et al. (2020), for example, briefly discusses how isoprene mechanisms have changed responding to new data. The recent experiments described in Nozière and Vereecken (2019) are the most direct measurements currently available of RO2 H migration reactions. In this work, we supplement these experiments with an analysis of the stable products, validating the expected reaction mechanisms.
2.1 Quantum chemical calculations
The Supplement lists a large data set for RO2 H migration reactions, as obtained over the last decade by our research group. Many levels of theory were employed for geometry optimization, ranging from older B3LYP/6-31G(d,p) to modern M06-2X-D3/aug-cc-pVTZ methodologies, and combined with single-point energy calculations ranging from the composite method CBS-QB3 to coupled cluster CCSD(T) calculations with extrapolations to the complete basis set limit. The Supplement lists the methodologies. Each methodology has its own advantages and drawbacks and unfortunately its own specific uncertainties and systematic bias. To reduce the method-induced scatter in the data set, we preferentially limit ourselves to data obtained at three levels of theory. The first is the CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ level of theory (wavenumber scaling factor of 0.971) (Bao et al., 2017; Dunning, 1989; Purvis and Bartlett, 1982; Zhao and Truhlar, 2008), a high-end methodology that has been used extensively by our group in recent publications (Fuchs et al., 2018; Novelli et al., 2020; Nozière and Vereecken, 2019) and was found by Nozière and Vereecken (2019) to reproduce the direct experimental data for RO2 H migration faithfully. A second set of calculations are based on CBS-QB3//B3LYP/6-31G(d,p) (5 d-orbitals, scaling factor of 0.977) (Bao et al., 2017; Becke, 1992; Lee et al., 1988; Montgomery et al., 2000). These calculations carry a somewhat larger error and scatter, but we find the obtained rate coefficients to mostly remain within a factor of 5 compared to more rigorous methodologies. A third set of data are based on CCSD(T)//M05-2X/6-311G(d,p) calculations (scaling factor of 0.964) (Bao et al., 2017; Purvis and Bartlett, 1982; Zhao et al., 2006) of a reliability that is an intermediate between the two earlier methods. Finally, relative rate estimates are based directly on B3LYP/6-31G(d,p) calculations; these relative rates estimates (see below) build solely on energy and entropic changes, not their absolute value, benefiting from cancellation of error.
The Supplement provides some more details on the calculation, including additional performance tests. It was found that CCSD(T) extrapolation to the complete basis set is not cost-effective at this time, considering the other contributions to the uncertainty of the SAR. IRCMax calculations show that the transition state (TS) geometries obtained using B3LYP are subject to larger additional errors, sometimes exceeding 1 kcal mol−1 on the absolute barrier height, compared to using more modern functionals such as M05-2X and M06-2X.
2.2 Absolute rate coefficient calculations
The rate coefficients of all reactions are calculated between 200 and 450 K using multi-conformer transition state theory (MC-TST) as described by Vereecken and Peeters (2003), and applied extensively and successfully in earlier work. The method is based on canonical transition state theory (CTST) calculations (Truhlar et al., 1996) in a rigid rotor harmonic oscillator approximation but explicitly includes all conformers of reactants and transition states to accommodate the effect of internal rotation and the differences in energy and entropy of each of the conformers. The calculations are performed at the high-pressure limit; earlier work has found that the rates of RO2 H migration are sufficiently slow to be negligibly affected by pressure fall-off at 1 atm (Miyoshi, 2012; Peeters et al., 2014; Xing et al., 2018; Zhang and Dibble, 2011). Tunnelling is incorporated using asymmetric Eckart tunnelling (Eckart, 1930; Johnston and Heicklen, 1962); for most H migrations, the reaction energy used in this tunnelling correction is estimated from an explicit product characterization (usually 1 conformer only). For the remaining reactions, the product energy is instead estimated based on the product energy of analogous reactions; as the relative energy of alkyl radicals is well understood, and as the tunnelling correction is not overly sensitive to this parameter, this reduced the computational effort without significantly influencing the rate predictions.
2.3 Relative rate coefficient calculations
Relative rate coefficient estimates were performed using the relative multi-conformer transition state theory (rel-MC-TST) described in the Supplement. Briefly, this method derives a rate coefficient from a full MC-TST prediction for a reference compound, and the change in rate induced by a modification of the molecular structure from the reference compound to the target compound, quantified by the characterization of a (small) subset of reactant and transition state conformers of the reference and target reaction. The method provides a cost-effective estimate of the rate coefficient, where the approximation becomes better as the molecular structure between reference and target reaction is more similar, and as more conformers are included in the relative rate change calculations. When including all conformers the method becomes the equivalent of a full MC-TST calculation. We have performed a set of calculations using heptane and octane as reference compounds, looking at the impact of methyl-, hydroxy-, and oxo-substitution and the impact of the double bond. This new methodology will be benchmarked in a separate paper.
2.4 Theoretical literature data
A few extensive theory-based data sets have been published over the last decade which, combined with the data set presented in this work and our earlier publications, form the basis of our current work. Several of these studies were aimed at combustion temperatures, and do not include data below 300 K. As a result, these rate equations are unlikely to properly describe the tunnelling-induced curvature in the Arrhenius plot below 300 K, possibly underestimating the rate coefficients at the lowest temperatures considered in this work (200 K). We briefly list some methodological aspects of a selection of papers.
Sharma et al. (2010) studied a systematic series of H migrations, using very high levels of methodology, explicitly accounting for quantum internal rotation but using less accurate Wigner tunnelling corrections, at temperatures ranging from 300 to 1500 K. This work contains aliphatic RO2 compounds, examining 1,3-H to 1,7-H shifts looking at abstraction of primary, secondary, and tertiary H atoms. A study by Miyoshi (2011) used similarly high levels of theory, with explicit consideration of internal rotation and applying more accurate Eckart tunnelling corrections, at temperatures 500–1250 K and pressures from 0.1 to 100 atm. This work examines aliphatic and hydroperoxy-substituted RO2, examining 1,4-H to 1,8-H migrations and categorizing the reactions based on substitution of the carbons bearing the –OO• radical and the migrating H atom; this categorization is adopted in the current work. The Sharma et al. (2010) and Miyoshi (2011) data sets form a large part of the current SAR and are considered to be generally reliable. Nozière and Vereecken (2019) recently derived a simple SAR based on these data sets, finding excellent agreement with experimental measurements. Data by Zang and Dibble (2011) cover a smaller set of migrations, mostly limited to 1,5-H migrations, but include a set of unsaturated hydrocarbons; the rate equations are derived for temperatures 300–2500 K. Otkjær et al. (2018) recently performed a systematic study of 1,4-H through 1,10-H migrations, examining a wide range of substitutions (alkyl, oxo, F atom, hydroxy, hydroperoxide, nitrate, methoxy, and unsaturated functionalities) at high levels of theory, with a MC-TST-based kinetic analysis. These authors examined the 290–320 K temperature range, but due to the chosen k(T) function, the temperature dependence can not be reliably extrapolated beyond this range. Mohamed et al. (2018a, b) performed a systematic study on hydroperoxide-substituted RO2 radicals in the temperature range 300–1500 K. The internal rotors are represented by a Pitzer and Gwinn approximation based on averaged barriers to rotation in the lowest-energy conformer, as obtained by explicit (partial) optimization of the rotational energy profile. At this time, we choose not to incorporate the results by Yao et al. (2017); their predictions for the 500–1200 K range are not compatible with the experimental data, overestimating the room temperature rate coefficients by several orders of magnitude.
In addition to these larger data sets, we include data from a number of other publications, which are cited in the relevant sections.
2.5 Theory-based rate coefficients
The theoretical predictions for ∼150 rate coefficient derived using MC-TST and rel-MC-TST rate theory are tabulated in the Sects. S2 and S3 in the Supplement. This data set collects rate coefficients obtained by our research group over the last decade, including some that have been presented before (Fuchs et al., 2018; Novelli et al., 2020; Vereecken, 2012; Vereecken and Peeters, 2010b). The rate coefficients published by other authors, representing a few hundred data points, are not replicated here but can be found in the respective publications.
2.6 Structure–activity relationship design
Merging the different data sets into a structure–activity relationship follows a set of steps for each rate coefficient in the data set. First, each reaction is categorized into one of the SAR classes based on the migration span and the substitution pattern around the migrating H atom and the –OO• moiety. Next, the rate coefficient is calculated across the temperature range 200–450 K or the temperature range where the kinetic expression is expected to be valid (e.g. 290–330 K for the data from Otkjær et al., 2018) to avoid introducing extrapolation errors. The k(298 K) target rate coefficient at 298 K is then obtained by geometrically averaging (equal weight) selected rate coefficients at that temperature. For three reactions, the experimental rate coefficients near 298 K were also included in the averaging, while for one reaction the target k(298 K) was set directly to the experimental value (see Table 9). Source rate coefficients are within a factor of 2 to 3 of the obtained k(298 K) average for aliphatic RO2, indicating good agreement of the data sets; for other functionalities there can be significantly more scatter. To determine the temperature profile of the SAR rate coefficient, the rate coefficients over the 200–450 K temperature range are geometrically averaged (equal weight). Any data that is deemed to be of insufficient quality is excluded in the previous steps; the selected data sets, however, contain little excluded data. The most common reason for rejection is suspicion of low-temperature rate under-prediction due to limitations in the tunnelling corrections and the extrapolation from higher temperatures. The subset of rate predictions in the k(T) profile prediction can be smaller than for determining k(298 K), as not all data sets are valid over the required temperature range or have limitations in their tunnelling corrections and extrapolation from higher temperatures. The obtained k(T) temperature-dependent profile is then shifted to match the target k(298 K) by altering the reaction barrier height, i.e. a correction term exp(Corr∕T) is factored into the k(T) profile. Finally, the shifted k(T) rate coefficients are then fitted to a modified Arrhenius expression (Kooij expression) K and listed in the SAR tables below. Figure 1 shows an example of this procedure, showing the original literature data, and the final k(T) SAR rate coefficient. Figure 2 shows an example of one of the SAR classes where many data points are available, showing the scatter on the literature data and the averaging effect of the SAR procedure. The Supplement contains a spreadsheet that has values and figures for all the underlying data and the derived SAR k(T).
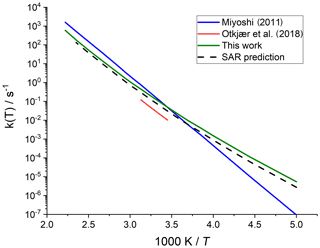
Figure 1Rate coefficient for 1,5-H migration in an aliphatic alkyl peroxy radical with a >CH(OO•) radical group and a tertiary (–CH<) migrating H atom. The SAR derivation matches a geometric average at 298 K and uses the most reliable temperature dependence, accounting for tunnelling at low temperatures.
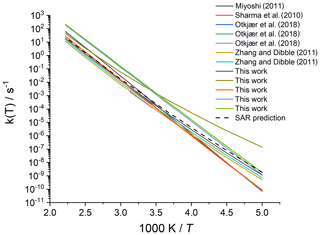
Figure 2Rate coefficient for 1,5-H migration in an aliphatic alkyl peroxy radical with a >CH(OO•) radical group and a secondary (–CH2–) migrating H atom. The literature data for the various reactions in this class are scattered over a factor of 22; the final SAR predictions are within a factor of 7 of all data at 298 K and incorporate the average temperature dependence of the five predictions that explicitly treat tunnelling corrections below 300 K.
The resulting k(T) expressions are expected to be less sensitive to the idiosyncrasies of the individual methodologies than using any specific theoretical method – at least where multiple data sets are available – and to provide a good prediction of the class-specific behaviour of RO2 H migration, especially when multiple molecules are included within the class, thus averaging out the molecular specifics. The use of geometric averaging and temperature-dependent correction factors reflects that the largest contributions to the uncertainty of theoretical predictions are due to uncertainties in the barrier height and tunnelling, both of which affect the rate coefficient non-linearly as a function of temperature. The transfer to the final SAR expression of temperature dependencies sourced from the most reliable k(T) predictions ensures the best possible temperature dependence, and avoids extrapolation problems from high-temperature data.
In some cases, there is insufficient data to derive a temperature dependence, even though room temperature data are available. In such cases, given that the temperature dependence is comparable in all RO2 H migration after correction by a shifting factor exp(Corr∕T), we resort to using the temperature dependence of a similar reaction, the average T dependence in the reaction class, or the average T dependence of a comparable reaction class to derive a rate expression. The applicability of using such a correction factor to transfer a T dependence between classes is illustrated in the Supplement. Finally, in cases where no data at room temperature are available for a SAR class with a particular substitution, we base a tentative rate expression on the rate difference at 298 K between the corresponding classes for aliphatic RO2. The uncertainty in these latter rate expressions is significantly larger than classes for which direct data are available and is likely no better than 2 orders of magnitude when factoring in the uncertainties on the underlying data and on transferability of kinetic properties. We provide such rate coefficients mostly in an attempt to provide a rough estimate, rather than providing no guidance at all. The different levels of approximations on the rate coefficient expressions are marked in the respective tables below.
The SAR parameters are presented as a set of lookup tables, showing both the k(298 K) value as the parameters for the modified Arrhenius rate expression K, combined with a few correction terms that only adjust the effective activation energy. The Supplement shows some examples of applying this SAR. An earlier H migration SAR for alkoxy radicals (Vereecken and Peeters, 2010a) presented the results as distinct contributing factors for ring strain, rigidity, conformers, tunnelling, etc. Other authors employed expressions factoring in a rate equation and a tunnelling correction (). These approaches are thought to be cumbersome in practice due to incompatibilities with existing tool chains, and we feel the current approach is significantly more accessible both for direct lookup by humans and for implementation in model generation software.
At this time, we choose not to focus the SAR on multi-functionalized compounds, i.e. we derive our SAR for aliphatic and mono-functionalized compounds, in as much as data are available for these. We also do not distinguish between stereo-isomers of chiral carbons (R/S-geometries) even though we find that the rate coefficients can differ by up to 2 orders of magnitude for complex, multi-functionalized species with multiple chiral carbons. As discussed below in more detail, we only include H migrations in cis- and gemini-substitutions in unsaturated species with a double bond; a more in-depth discussion is given below for other classes.
While not included in the derivation of the SAR, the data on multi-functionalized molecules is used to determine the performance of the SAR when extrapolated to more complex molecules. The scope of applicability for spectator functionalities, H migration affected by multiple functionalities, and cyclic compounds is examined in a later section.
2.7 Experimental methodology
For the experimental studies of the H migration reaction of aliphatic RO2, the methodology has been described in detail in earlier work (Nozière and Vereecken, 2019); we only provide a brief description here.
2.7.1 Radical generation
H migration reactions for a series of aliphatic RO2 (1-butylperoxy, 1-pentylperoxy, 1-hexylperoxy, ethyl-hexylperoxy and dimethyl-hexylperoxy) were studied experimentally at room temperature ( K) in a cylindrical flow reactor (Quartz, inner diameter 5 cm, length 120 cm). The RO2 was produced in a flow of synthetic air (3–4 sLm, standard temperature =273 K, and pressure =1 atm), to which an organic precursor 3×1015 to 5×1016 molecule cm−3 was added. For 1-butylperoxy, 1-pentylperoxy, 1-hexylperoxy, and ethyl-hexylperoxy, the precursor was the iodinated analogue: iodobutane, iodopentane, iodohexane, and 2-ethylhexyl iodide, respectively. For dimethyl-hexylperoxy it was 2,5-dimethylhexane. The radicals were produced by irradiating the flow mixture over 30–40 cm at middle of the reactor with four fluorescent lights (Philips TL12, 40 W, emitting over 280–400 nm). The iodinated precursors were photolysed directly, thus ensuring the formation of a single radical in each case. For instance, for 1-butylperoxy this was performed as follows:
For dimethyl-hexylperoxy, Cl2 (∼1015 molecule cm−3) was also added to the reactor and photolysed in the presence of dimethyl hexane:
2.7.2 Radical and stable product detection
A small fraction (50–100 sccm) of the reaction mixture was sampled through a sampling line at the output of the flow reactor and analysed with a quadrupole chemical ionization mass spectrometer (CIMS) using proton transfer at high pressure as ionizing technique (Hanson et al., 2004, 2003; Nozière and Hanson, 2017; Nozière and Vereecken, 2019). With this technique, the RO2 and their stable products were detected by reacting with proton–water clusters, H+(H2O)n with n=1 to 5, in the ionization region of the CIMS:
Thus, a compound of molecular weight M was typically detected at the ion masses M+1, M+19, M+37, and M+55. The typical resolution for the instrument was , and the detection limit was between 108 and 109 molecule cm−3. The radicals were unambiguously distinguished from potential stable isomers in the mass spectra by adding NO periodically in the reactor, resulting in their consumption. The periodic variation in other masses upon addition of NO also confirmed the identification of the stable compounds of the photochemical system, and allowed us to distinguish them from potential artefacts or pollution in the flow system.
3.1 Aliphatic RO2
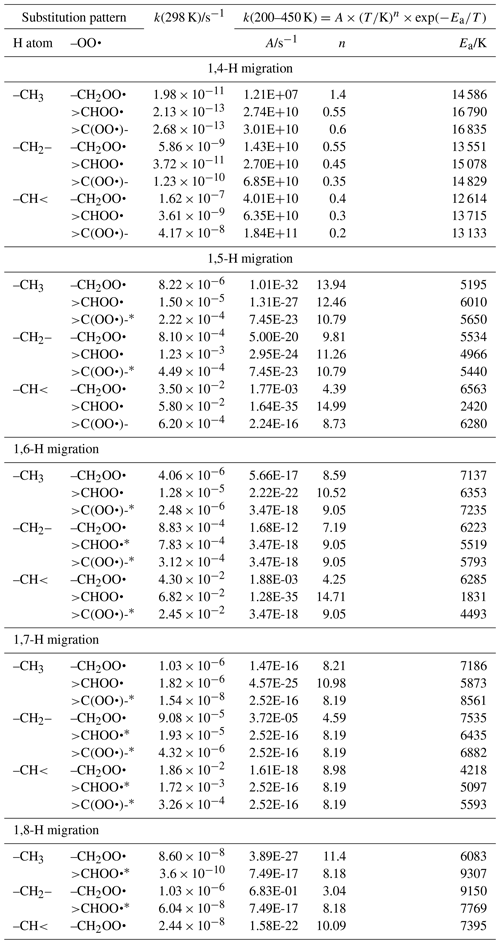
Linear and branched aliphatic peroxy radicals are described by the SAR rate coefficients in Table 1 and are derived based on our calculations (see Supplement) and selected literature data (Miyoshi, 2011; Otkjær et al., 2018; Praske et al., 2019; Sharma et al., 2010; Zhang and Dibble, 2011). No rate coefficients are included for 1,3-H migration, as these have been found to have high barriers and very low rate coefficients, k(298 K) s−1, making them irrelevant for atmospheric chemistry (Sharma et al., 2010). The 1,4-H migrations likewise have high barriers and low rate coefficients, k(298 K) s−1, for aliphatic compounds and are negligible in atmospheric conditions. Furthermore, the reaction barriers for 1,4-H migration tend to be higher than for the (also slow) HO2 elimination forming an alkene, making H migration a minor channel even if it is accessible. The 1,4-H migration is included here mostly to serve as a basis for substituted 1,4-H migration, such as aldehydic H migration where significantly lower barriers are found. Rate coefficients for 1,8-H migration are similarly low, k(298 K) s−1, due to the entropic disadvantage of losing a large number of internal rotors in the cyclic transition state; again, we include them here mostly for possible use as a reference rate coefficient. H migration at even larger spans, e.g. 1,9-H or 1,10-H shifts, have been studied by Otkjær et al. (2018), finding even lower rate coefficients and negligible contribution of these long-range migrations. Aliphatic RO2 H migration is then mostly governed by 1,5-H, 1,6-H, and 1,7-H migrations. The predicted rate coefficients in Table 1 show that substitution around the migrating H atom is of critical importance, with tertiary H atoms migrating several orders of magnitude faster than primary H atoms. Substitution around the –OO• moiety has less impact on the rate, and the impact varies with the substitution. We find no significant influence of the length of the spectator alkyl chain attached, in agreement with, e.g. Otkjaer et al. (2018).
3.2 Unsaturated RO2
To parameterize the impact of double bonds in the peroxy radicals, one should in principle account not only for the substitution around the peroxy and migrating H atom but also whether the double bond has zero, one, or both carbon atoms within the TS cycle and whether the product radical is stabilized by allyl resonance, and if so, what the substitution is on the second radical site and possibly on the centre carbon of the C•–C=C allylic group. Abstraction of vinyl H atoms, =CH–, is known to be negligibly slow at room temperature, of the order of k(298 K) s−1 (Zhang and Dibble, 2011), and is not considered in this work. There is little direct information on substitution on the central carbon of the allylic radical group, but the scarce data suggest the impact on k(298 K) to be of the order of a factor of ∼2 for H atom versus alkyl substitution. This comparatively small factor is not separable from the uncertainty in our data set, and our SAR reaction classes do not distinguish between these substitutions. Although it is technically feasible to migrate between trans-substituents, we find significant barriers for such processes even when forming allyl-stabilized alkyl radicals, e.g. 46 kcal mol−1 for 1,6-H migration in E-2-butene-1-peroxy radicals or 31 kcal mol−1 for 1,7-H migration in E-3-pentene-1-peroxy radicals. To reduce the strain in the transition states, very large migrations spans would then be required, leading again to low rate coefficients due to entropic disadvantage. Hence, in this work we focus only on substituents located on the same side of the double bond, i.e. gemini-substitution on the same carbon in the double bond or cis-substituents on the same side of the double-bond carbon atoms.
As already shown extensively, migration of an allylic H atom is found to be significantly faster than migration of an aliphatic carbon (Otkjær et al., 2018; Zhang and Dibble, 2011). The scatter between the available data sets is significantly larger than for aliphatic RO2, with differences of over an order of magnitude between methodologies and/or authors. The cases with the largest deviation from the average can often be traced to the absence of important (lower-energy) conformers in the multi-conformer analysis. In some compounds, we find large differences between the rate coefficients for endocyclic or exocyclic double bonds in the TS ring, up to 2 orders of magnitude on k(298 K), though for other H migrations the difference is negligible, making it hard to judge whether this is due to methodological scatter or due to the impact of ring strain and internal rotations on the entropy. At this time, we choose to distinguish between endocyclic and exocyclic double bonds until more data are available.
We only have a single data point, a 1,7-H migration in Z-2-heptene-1-peroxy, where a double bond is present in the TS ring but the migrating hydrogen is not an allylic H atom; the rate coefficient is indistinguishable from its aliphatic equivalent. As such, we only consider SAR classes for migration of allylic H atoms, until more information is available on the entropic effect of a non-allylic double bond in the TS ring.
3.2.1 Allylic H atom migration with a TS endocyclic double bond
The SAR expressions (see Table 2) for endocyclic double bonds in the TS ring are derived based on our calculations (see Supplement) and the data by Zhang and Dibble (2011).
Table 2Rate coefficients for allylic H migration in peroxy radicals with an endocyclic double bond within the TS ring, accounting for all abstractable H atoms in the group. These rates apply only to migration between cis- or gemini-substituents.
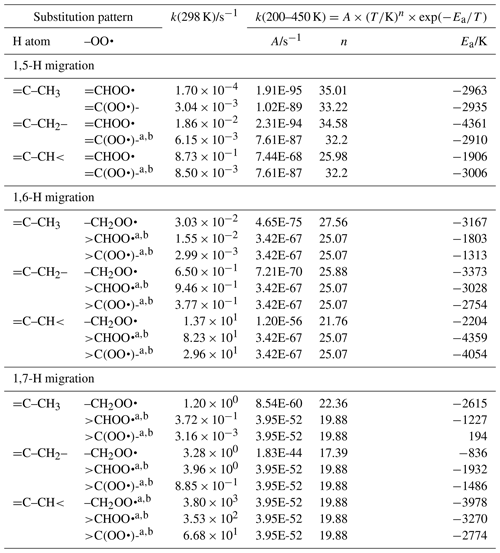
a Averaged temperature dependence from other reactions used. b k(298 K) anchor value derived from relative rates of aliphatic RO2, scaled to unsaturated RO2.
3.2.2 Allylic H atom migration with a TS exocyclic double bond
The SAR expressions (see Table 3) for exocyclic double bonds in the TS ring are derived based on our calculations (see Supplement) and selected literature data (Otkjær et al., 2018; Zhang and Dibble, 2011).
Table 3Rate coefficients for allylic H migration in peroxy radicals with a double bond outside the TS ring, accounting for all abstractable H atoms in the group.
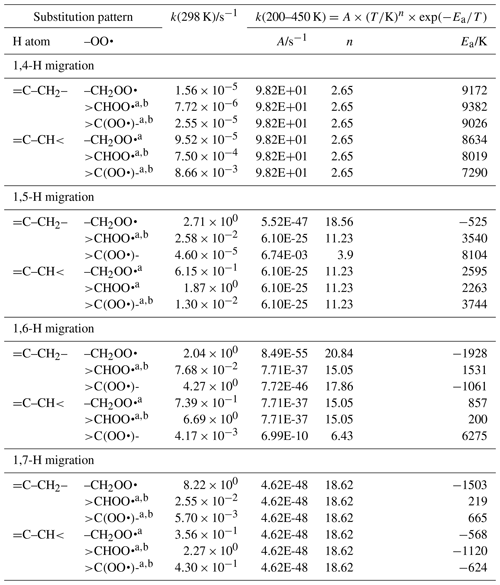
a Averaged temperature dependence from other reactions used. b k(298 K) anchor value derived from relative rates of aliphatic RO2, scaled to unsaturated RO2.
3.2.3 Allylic H migration with an endocyclic gemini-substituted double bond
The delocalizing double bond of the allylic H atom can have only a single carbon in the TS cycle, which occurs when the •OO-bearing and the migrating H-bearing substituent are in gemini-substitution (same carbon atom) of the double bond. This configuration is somewhat different to endocyclic double bonds with both carbons in the TS ring, due to differences in the number of internal rotors, rigidity, etc. A priori, one would expect these H migrations to be entropically disadvantaged compared to endocyclic double bonds, due to the loss of a higher number of internal rotors in the gemini-TS ring, and it is therefore slower than exocyclic double bonds. We have very few data points for such structures, mostly for methyl-H migrations in isoprene-derived peroxy radicals after reaction with OH or NO3, but the scarce data points do not indicate a significant difference between gemini-substituted and endocyclic double bonds, with rate coefficient differences of an order of magnitude at most. Until more systematic data are available, we recommend using the same rate coefficients for gemini-substitution as for endocyclic double bonds.
3.2.4 RO2 with conjugated double bonds
At this time, we have no systematic data available for RO2 with conjugated double bonds. Conjugated systems are virtually always more stable in their s-trans-conformer, with the orientation across the central single bond such that the double bonds are parallel (left-hand side of the diagram above). The H migration TS across such moieties, however, will force the central single bond to a less favourable s-cis- or s-gauche-orientation (central structure in the diagram above), incurring an increase in the barrier height and a decrease in the phenomenological rate coefficient. In the TS, the radical electron is involved in the H migration and is not yet free to be delocalized over the π system, and as such does not aid much in reducing the barrier height increase. However, the presence of the rigid double bonds reduces the number of degrees of freedom for internal rotation that are lost in the H shift TS, providing an entropic advantage compared to H migration in aliphatic RO2 radicals. It is unclear at this time whether this entropic advantage is able to overcome the energetic disadvantage for H migration across conjugated bonds, and we refrain from making recommendations for the rate coefficients until more data are available.
3.2.5 RO2 with trans-alkene, alkyne, allene, or cumulene, substitution
Allene, –C=C=C–, cumulene, –C=C=C=C–, or triple-bonded, –C≡C–, unsaturated groups are characterized by a rigid structure with at least three to four linearly aligned atoms. Similarly, trans-alkenes have four co-planar backbone atoms with diametrically positioned outer atoms. The smallest ring structures known with such unsaturated groups and still with a low enough ring strain to be isolable are trans-cyclooctane, cyclooctyne, 1,2-cyclooctadiene, and 1,2,3-cyclodecatriene, though smaller (hetero)rings are known (Barrows and Eberlein, 2005; Greenberg and Liebman, 1978; Johnson, 1989). H migrations across such subgroups, i.e. with the unsaturation within the TS cycle, are geometrically demanding, and only long-range migrations, i.e. 1,8-H migration or further, might be feasible. Indeed, with three co-planar carbons in the TS ring, at least two carbons are required to point the backbone back to the start without high ring strain (as in cyclohexane), followed by another two to three carbons reaching across the unsaturated moiety to potentially reach any H atoms on the other side. For trans-alkenes, eight-membered rings are not viable as an energetically accessible H migration TS due to the high ring strain, exceeding 10 kcal mol−1 over its cis-counterpart, and only at about 11 backbone atoms does the energy of a trans-cycloalkene become more favourable than its cis-cycloalkenes (Barrows and Eberlein, 2005). Similar energetic considerations pertain to the other unsaturated rings. In the H migration TS, the ring strain in the smaller rings will be further increased as the strained geometry requires that the O–H–C moiety must be strongly bent, whereas the energetically most favourable orientation is a (near-)linear O–H–C moiety. For all unsaturated moieties considered here, we thus estimate that at least 9 (but likely 10 or more) backbone atoms (including the peroxyl O atoms) are needed before the ring strain is reduced sufficiently for the TS to approach accessible energy barriers. Hence, only long-range migrations are accessible. Although the unsaturated bonds make these reactions entropically slightly more favourable, as one fewer degree of freedom for internal rotation is lost in the TS compared to aliphatic backbones, H migrations across these spans have typically low rate coefficients. We surmise that H migration reactions across these moieties are never competitive in atmospheric conditions, though validating calculations remain useful.
There is not enough information to reliably derive rate coefficients for these unsaturations when outside the TS cycle and leading to resonance-stabilized alkyl radicals; at this time, we propose applying the SAR for allylic H atom migration with exocyclic double bonds, though the uncertainty in the predicted rate coefficients is expected to be large.
3.3 Oxo-substituted RO2
3.3.1 Migration of aldehydic H atoms
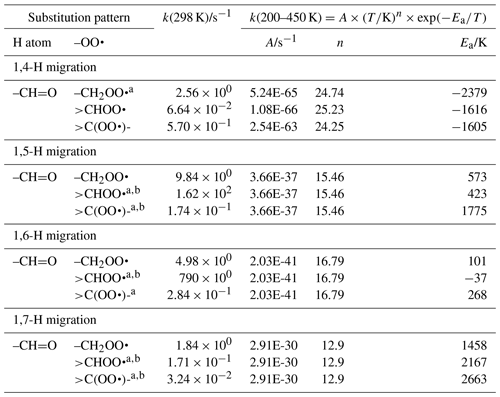
The abstraction of aldehydic H atoms is comparatively fast, k(298 K) ≥0.5 s−1, even for the short span of 1,4-H migrations. Our calculations are the only data points in our data sets for mono-substituted aldehydic RO2 radicals, and we resort to using information on hydroxy-substituted aldehydic RO2 for some of the aldehydic SAR classes. This includes acrolein and methacrolein, as found in our data set, the theoretical data by Møller et al. (2016) and da Silva (2011), and the methacrolein experimental rate determination by Crounse et al. (2012). As discussed in the section for OH-substituted RO2, the β-OH substitution of the peroxy radical moiety could affect the rate coefficient, and we should allow for an overestimation of a factor of 10 in our SAR predictions for 1,4-H migration. The OH substitution is likely also the cause for the low rate of 1,5-aldehyde H migration in 3-hydroxypropanal-3-peroxy described in Møller et al. (2016). Additional calculations on aldehydic compounds would be valuable. The SAR parameters are listed in Table 4.
3.3.2 Migration of β-oxo H atoms
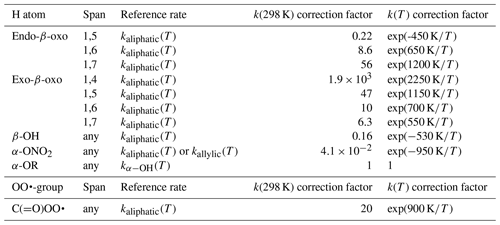
The data set of Otkjær et al. (2018) combined with our data set allows an approximate evaluation of the impact of β-oxo substitution of the migrating H atom, forming vinoxy-stabilized product radicals. The effect of this substitution has both an energetic component, due to the stabilization of the product radical, and an entropic component, where the carbonyl bond changes ring strain and rigidity. One should thus consider ring size and the endocyclic or exocyclic position of the > C=O moiety in the TS. Generally, we find that β-oxo substitution enhances the H migration rates compared to analogous aliphatic RO2. Exocyclic carbonyl bonds strongly enhance H migration rates with strained rings, have a more limited effect with rings with less strain and geometric constraints, and are expected to have no significant effect with very large rings. This is in agreement with, e.g. H abstraction rates from organic molecules by OH radicals, where a carbonyl group has little to no impact on the rate coefficient (e.g. ethane+OH versus acetone+OH). For endocyclic carbonyls, we find the opposite effect, where the presence of a rigid carbonyl group in an already strained ring decreases the rate coefficient but for large rings it has no strong effect. We summarized the scarce data as a set of correction factors (see Table 5) on the rate coefficient of the corresponding aliphatic RO2, as a function of the position of the carbonyl group and the migration span. We have no information available for 1,8-H migrations.
3.3.3 Migration in other oxo-substituted RO2 radicals
We have almost no data for peroxy radicals where the carbonyl is not in β position to the migrating H atom. For aliphatic H migration in acyl peroxy radicals, Møller et al. (2019) calculated rate coefficients in multi-substituted RO2, finding faster reactions compared to aliphatic peroxy radicals. We tentatively summarize the differences as a factor of exp(900 K∕T), as listed in Table 5. Knap and Jørgensen (2017) calculated an α-OOH 1,6-H migration in an acyl peroxy radical, finding a rate coefficient of 98 s−1, a factor 4×103 faster than the α-OOH 1,6-H migrations in aliphatic peroxy radicals; they also characterized aldehyde-H migrations by acyl peroxy radicals that are significantly faster than in regular RO2. Knap and Jørgensen (2017) also describe H scrambling in acyl peroxy radicals, finding rate coefficients ranging from 103 to 106 s−1 in agreement with or faster than the H-scrambling data described elsewhere in this work. At the same time, these authors find much slower reactions for the reverse H scrambling from peracid groups (–C(=O)OOH). The above data indicates strongly that acyl peroxy radicals are significantly more reactive towards H migration owing to the higher stability of the product peracid group, and should be investigated in more detail.
We have no systematic information for endocyclic oxo substituents that are in β position for the migrating H atom or the peroxy radical group. Our data set includes a single data point for an endo-β-oxo-substituted –OO• group; our relative MC-TST calculation on this latter 1,6-H migration indicates an impact of less than a factor of 5, but this value is not reliable enough to use as a basis for a SAR proposal. The study by da Silva (2010a) calculated a rate coefficient K∕T) s−1 for the 1,4-H shift in •OOC(=O)CH=O, i.e. k(298 K) =12 s−1, faster than the 1,4 aldehyde-H migration rate coefficients in the SAR. Due to the paucity of data, we currently make no recommendations for any of these types of RO2 H migrations with endocyclic oxo substitutions.
3.4 Hydroxy-substituted RO2
3.4.1 Migration of α-OH H atoms
α−OH substitution is known to reduce the C–H bond strength compared to an alkyl substitution, allowing for faster H abstraction (IUPAC Subcommittee on Atmospheric Chemical Kinetic Data Evaluation, 2017) or H migration (Vereecken and Peeters, 2010a). In RO2 radicals, we observe the same effect, with an increase in rate coefficient of about a factor of 10 at room temperature. The SAR predictions for migration of α-OH-H atoms are listed in Table 6, as derived from our calculations (see Supplement) and selected literature data (Jørgensen et al., 2016; Otkjær et al., 2018; Praske et al., 2018, 2019). There is direct experimental data available at higher temperatures, i.e. ∼450–525 K (Jorand et al., 2003; Perrin et al., 1998). Our theoretical calculations reproduce these experimental results well, within a factor of ∼5, and the SAR rate equations reproduce these values within a factor of 3.5, well within our SAR accuracy goal.
Table 6Rate coefficients for α-OH-substituted H migration in peroxy radicals, accounting for all abstractable H atoms in the group.
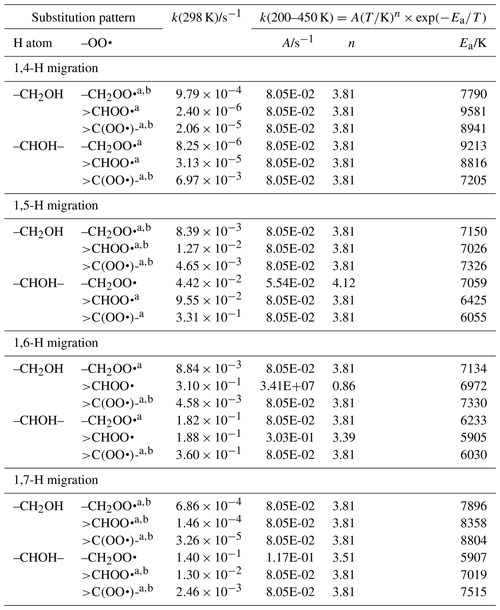
a Averaged temperature dependence from other reactions used. b k(298 K) anchor value derived from relative rates of aliphatic RO2, scaled to α-OH RO2.
There is very little information for gemini-di-hydroxy substitution; we are only aware of our own calculations on the 1,3-H and 1,4-H migration in hydroxy-methylperoxy versus dihydroxy-methylperoxy (see Supplement). These data do not provide a good reference for developing a generally applicable SAR correction, as the product radical decomposes, forming OH (1,3-H shift) or HO2 (1,4-H shift), respectively. The scarce data do suggest that adding a second –OH substitution increases the H migration rate significantly.
3.4.2 Migration of β-OH H atoms
The scarce data available on non-multi-functionalized RO2 with β-OH substitution next to the migrating H atom (this work, Praske et al., 2018, 2019; da Silva and Bozzelli, 2009) suggest that β-OH substitution next to the migrating H atom slows down H migration, on average by a factor of 0.17 at room temperature, both when the OH group is in endo- or exo-position on the TS ring. This corresponds to an increase in barrier height of about 1 kcal mol−1. The reason appears to be that the H bonding is absent or less favourable in the TS cycle due to geometric constraints, as opposed to the reactant where the peroxy radical group can interact freely with the –OH group. We propose that the rate coefficients for H migration of aliphatic H atoms with a β-OH substituent are corrected by a factor of exp (−528 K∕T) to account for this effect (see Table 5).
The information of β-OH substitution of the –OO• group is even more scarce (Jørgensen et al., 2016) and not entirely consistent across the reactions studied. Although the data suggests that the rate coefficient might increase by as much as a factor of 10, we do not propose a correction factor until more data become available.
3.4.3 Migration of hydroxyl-H atoms
H migration of a non-enolic hydroxy-H atom has been considered in many studies (e.g. this work, Asatryan et al., 2010; Fuchs et al., 2018; Jørgensen et al., 2016; Kuwata et al., 2007; Møller et al., 2019; Peeters et al., 2009; Piletic et al., 2019). The rate coefficients tend to be fairly low, k(298 K) s−1, and the reaction plays only a very small role in the atmosphere even in pristine conditions. Furthermore, the reverse reaction, i.e. the abstraction of a hydroperoxide OOH atom by an alkoxy radical, is rather fast, typically ≥1010 s−1, such that even if the reaction occurs, the regeneration of the original peroxy radical is often the main fate. Some exceptions to this reaction reversal have been reported though, such as the Waddington mechanism where the H shift is followed by fast decomposition of the resulting alkoxy radical (Lizardo-Huerta et al., 2016; Ray et al., 1973a, b). For example, Peeters et al. (2009) showed that 1,5-H migration in hydroxy-isoprene-peroxy radicals could not be reversed due to immediate dissociation of the β-unsaturated-β-OOH-alkoxy radical products. Given the generally low importance of hydroxy-H migrations, we do not derive a SAR for this reaction class at this time.
The abstraction of an enolic hydrogen atom, C=C–OH, forms a vinoxy-stabilized product radical, C•–C=O, which is more stable than the alkoxy products discussed above, thus preventing rapid reversal of the H migration. The rate coefficient is significantly faster than the reactions above, k(298 K) ≥104 s−1 for a 1,6-enol H migration (Peeters and Nguyen, 2012). A recent review by Jenkin et al. (2019) recommends K∕T).
Finally, we should note that α-OH peroxy radicals can undergo an HO2 elimination, forming a carbonyl compound with an HO2 co-product. Jenkin et al. (2019) tabulates these eliminations as a 1,4-H migration, but mechanistically these reactions occur by a concerted elimination characterized by a weakened, long C–OO bond in the transition state. These reactions have been studied in detail both theoretically and experimentally (Hermans et al., 2004, 2005a, b; Linguerri et al., 2017; Tomas et al., 2001; Veyret et al., 1989). The recent review by Jenkin et al. (2019) has recommendations for tertiary and quaternary carbons based on these studies; for secondary carbons, i.e. HO2 elimination from HOCH2OO•, we calculated a rate coefficient of 1.8×103 s−1, in agreement with these recommendations (see Supplement).
Table 7Rate coefficients for H migration of α-OOH H atoms in peroxy radicals, accounting for all abstractable H atoms in the group.
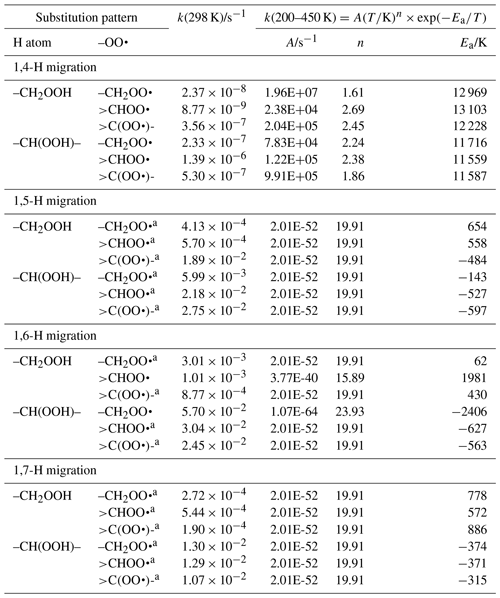
a Averaged temperature dependence from other reactions used. b k(298 K) anchor value derived from relative rates of aliphatic RO2, scaled to α-OOH RO2.
3.5 Hydroperoxide-substituted RO2
3.5.1 Migration of α-OOH H atoms
For many of the α-OOH H migrations, there are significant differences between the different literature sources (this work; Miyoshi, 2011; Mohamed et al., 2018a, b; Otkjær et al., 2018; Praske et al., 2019; Sharma et al., 2010) of up to several orders of magnitude for some of the reactions considered, though for some of the reactions near-identical values are found by all authors. This scatter reduces the reliability of the SAR predictions significantly, and in many cases the k(298 K) geometric average of the literature rate coefficients will have an uncertainty exceeding an order of magnitude. Furthermore, most of the data sets are derived at high temperatures, ≥300 K, and do not reproduce the curvature in the Arrhenius plot that is evident in our predictions down to 200 K. To improve the prediction of the rate coefficients below room temperature, we apply the temperature dependence of our work (α-OOH 1,6-H migrations) to all 1,5-H through 1,7-H migrations. This does not affect the SAR rate coefficient above 300 K appreciably and thus remains in agreement with the literature values at higher temperatures. The 1,4-H migrations have high barriers and their Arrhenius plots are more linear due to different tunnelling properties; we do not apply the k(T) curvature as above but instead solely rely on the geometric average of the reported k(T) values.
The product α-OOH alkyl radical formed after migration of the α-OOH hydrogen atom is unstable and falls apart spontaneously to a carbonyl compound with an OH radical co-product; the addition of O2 on this radical is not competitive (Vereecken et al., 2004).
3.5.2 Migration of hydroperoxide H atoms (scrambling)
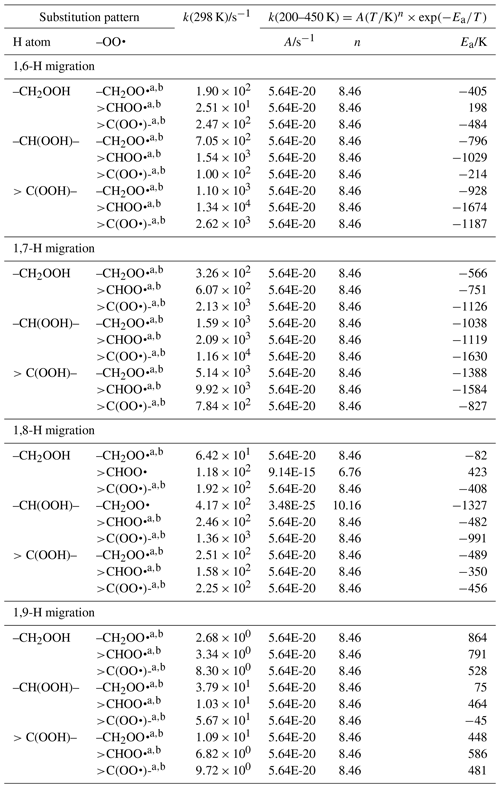
The available theoretical data on migration of hydroperoxide-H atoms can be divided into two groups. On one hand are the studies by Miyoshi (2011) and Mohamed et al. (2018b), who find comparatively slow H atom exchange between hydroperoxide group and the –OO• radical, with rate coefficients of the order of 1 to 10−5 s−1, depending on the migration span (1,6-H to 1,8-H migration) and substitution around the oxygenated moieties. These calculations are based on single-conformer CBS-QB3 calculations with explicit treatment of internal rotation. Our own calculations (Novelli et al., 2020; Nozière and Vereecken, 2019), however, find rate coefficients ≥102 s−1, as do theoretical calculations by Jørgensen et al. (2016), Møller et al. (2019), and Praske et al. (2019), who find k(298 K) of 102 to 106 s−1, for a large set of H exchange reactions. These latter group of calculations are all based on multi-conformer TST calculations based on higher-level CCSD(T)//M06-2X or CCSD(T)-F12//ωB97X-D calculations. Experimental data by Praske et al. (2019), constrained by observed products as a function of the competing reaction with NO, finds rate coefficients k(296 K) ∼102 s−1 for a 1,6-H migration and even k(296 K) >104 s−1 for a 1,7-H migration, corroborating the higher values in the second group of theoretical data. The reason for this dichotomy in theoretical data is apparently due to the use of B3LYP geometries in the Miyoshi (2011) and Mohamed et al. (2018b) studies: this methodology is known to underestimate H migration energy barriers, typically by a few kcal mol−1, which can mostly be rectified by the subsequent CBS-QB3 energy calculations. For scrambling reaction specifically, however, our test calculations show that B3LYP underestimates the barrier height by as much as 5 kcal mol−1, a very large error that probably leads to incorrectly optimized geometries affecting subsequent single-point energy calculations. This, and the fact that these studies do not explicitly consider all conformers, suggests that their low rate coefficients are the result of not using the lowest-energy geometries for the transition states.
Unfortunately, the study by Miyoshi (2011) is the only extensive systematic study of the scrambling reactions available (1,6-H through 1,9-H migration, for all nine substitution patterns around the active sites). Nozière and Vereecken (2019) pragmatically scaled up the rate coefficients of Miyoshi by a factor of 104, the average difference between the Miyoshi predictions and the observations of Praske et al. (2019). In this work, we apply a similar procedure, where we use the systematic study of Miyoshi (2011) as a basis but scale the rate coefficients at 298 K for 1,6-H migration upwards by a factor of 4.8×102, as obtained by taking the ratio of the experimental value of Praske et al. (2019) of 102 s−1 and the theoretical s−1 (under)estimate by Miyoshi. Likewise, 1,7-H migrations k(298 K) are scaled up by a factor of 5.6×103, based on the experimental lower limit of 104 s−1 of Praske et al. (2009) and the corresponding value of Miyoshi. Theoretically predicted rate coefficients are typically another factor of ∼102 higher, suggesting that we will underestimate H scrambling rates. Finally, 1,8-H and 1,9-H migrations are scaled up by a factor of 1.6×105, by comparing the predictions from Miyoshi against the Nozière and Vereecken (2019) predictions for 1,8-H migrations. Additionally, we apply the temperature dependence derived from these latter calculations to incorporate the impact of entropy and tunnelling on the rate coefficient curvature in the low-temperature range. Where available, data by Mohamed et al. (2018b), Praske et al. (2019), and Nozière and Vereecken (2019) are included when calculating the rate coefficient.
For 1,5-H migration no data are available; this reaction class implies gemini-OOH/OO• groups for which there is no obvious atmospheric formation pathway, so we ignore these reactions at this time.
The above scaling procedure is, overall, rather unsatisfactory, and it is clear that more theoretical and experimental data are needed to reduce the uncertainties and avoid the poorly founded corrections. One redeeming factor, however, is that the experimental data and much of the theoretical calculations suggest that H scrambling reactions across –OOH and –OO• groups are significantly faster than most, if not all, other RO2 H migration reactions. Hence, for many practical purposes, the hydroperoxide hydrogens can be considered mobile at the timescale of other product-forming H migration reactions, and the reactants can be merged into a single reactant pool reacting at bulk reaction rates. This is discussed in more detail in Sect. 5.
3.6 Carboxylic acid-substituted RO2
The migration of acidic H atoms was shown by da Silva (2010b) to be a potential route to OH regeneration in the atmosphere. The migration of the acid H atom is aided by the formation of a resonance-stabilized acyloxy radical, –C(=O)O•, which readily eliminates CO2, thus preventing reversal of the H migration. In the case of a β-peroxy radical, e.g. •OOCH2C(=O)OH, the resulting α-OOH alkyl radical product is even intrinsically unstable, spontaneously falling apart to CO2, an OH radical, and a carbonyl compound (da Silva, 2010b; Vereecken et al., 2004). Our own calculations on ethanoic acid-2-peroxy and 3-hydroxy-2-methyl-propanoic acid-2-peroxy radicals (derived from methacrylic acid by addition of OH and O2) are in good agreement with the data by da Silva (2010b) on ethanoic-acid-2-peroxy, propanoic-acid-2-peroxy, and 3-hydroxy-propanoic-acid-2-peroxy radicals (derived from acrylic acid by addition of OH and O2), with rate coefficients ranging from to 6 s−1. As information is only available on β-carboxylperoxy radicals, we can not derive generally applicable SAR expressions at this time; studies on the atmospheric oxidation of (unsaturated) carboxylic acids could benefit from more information on this pathway.
3.7 α-nitrate-substituted RO2
The data set of Otkjær et al. (2018) contains a number of α-ONO2-substituted H migrations, while our data set (see Supplement) has some information for unsaturated nitrated RO2 derived from isoprene + NO3 + O2 reactions. Compared to an alkyl group, a nitrate group reduces the rate coefficient somewhat, in agreement with, e.g. the known inhibiting effect for H abstraction by OH radicals from nitrate-substituted compounds. The inhibition is similar for H migrations across all spans in both aliphatic and unsaturated RO2, ranging from 0.001 to 0.9 at room temperature, with an average across the data sets of a factor of ∼0.04. We include this effect in the SAR by a temperature-dependent correction factor K∕T) (see Table 5).
The product α-ONO2 alkyl radical formed after migration of the α-nitrate hydrogen atom is unstable and falls apart spontaneously to a carbonyl compound with an NO2 radical co-product; the addition of O2 on this radical is not competitive (Vereecken, 2008).
3.8 Other substitutions
Otkjær et al. (2018) has some information on F atom substitution for a range of H migrations; at this time we do not include halogen atom substitution in our SAR. We have not found systematic data on other relevant substitutions, such as the nitrogen oxides –NO, –NO2, –ONO, –OONO, and –OONO2, or for peroxides, such as –OOR. Otkjær et al. (2018) lists a set of rate coefficients for ether substitution on the migrating H atom, α-OR, finding rate coefficients within a factor of 3 up or down from the corresponding α-OH-substituted H migration. At this time, we recommend using the kαOH(T) values for these α-OR-substituted H atoms (see Table 5).
Aside from a comparison against the scarce experimental data, it is not overly useful to examine the agreement between the SAR predictions and the data used to derive the SAR, as the SAR parameters are typically derived using only a few data points, ensuring good apparent agreement between SAR and training data. Occasionally, the underlying data have been intentionally strongly corrected (e.g. H scrambling), such that the predictions will not match the data. Hence, the SAR parameters are subject more to the (sometimes large) uncertainties on the training set data points than the fitting procedure, making a visual comparison or statistical goodness-of-fit analysis unrewarding. It is more useful to validate the SAR to its robustness, examining the reproduction of data points that were not part of the training data; we refer to Vereecken et al. (2018) for a more in-depth discussion of SAR validation needs in atmospheric chemistry. In this work, we specifically aim to test the scope of applicability of the SAR, applying it to a test set of over 100 data points that were not in the training set and that are furthermore multi-functionalized and thus represent data points that are outside the coverage of the training set. We distinguish between three groups of data. The first are rate coefficients for reactions that formally work on multi-functionalized RO2, but where only one functionality is expected to influence the reactivity strongly, the impact of all other functionalities, or of substituents that are not included in the SAR, are neglected (“spectator” groups). A second group of data are those where multiple functionalities affect the reaction rate, e.g. two substituents located in the α and β positions of the migrating H atom. Thirdly, we visualize the results for cyclic species, where the H migration involves a peroxy radical or migrating H atom on the parent molecule cycle or where the migration spans carbons part of the (mono- or multi-cyclic) ring structure. The resulting changes in ring strain or geometric constraints are not accounted for in the SAR, and we explicitly expect the SAR to perform poorly for such compounds.
4.1 Comparison against experimental data
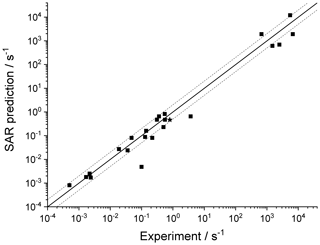
Table 9 lists the available literature experimental rate coefficients, and compares them to the SAR predictions at the appropriate temperature, accounting for multiple channels where necessary. A later section provides additional experimental validation for RO2 H migrations. For nearly all available values, the performance is excellent, reproducing the values on average by a factor of 2 (see Fig. 3). Only a single, multi-functionalized molecule, •OO-CH(CH3)-C(=O)-CH(OOH)-CH3, does not match the predictions by a large factor of ∼102. The direct theoretical calculations of 0.25 and 0.54 s−1 by Møller et al. (2019) conform to the lower limit found by Crounse et al. (2013), ≥0.1 s−1, so clearly the SAR does not behave as desired for this compound. As our SAR matches the theoretical predictions for α-OOH-substituted RO2 well, the likely culprit for the failure is the SAR correction for endo-β-oxo 1,5-H migrations (see Table 5). It is the only β-oxo correction to slow down the reaction and was derived from a single data point and obtained by a rel-MC-TST calculations using only three conformers, making it one of the least reliable values used for the SAR. An alternative source of error could be that the SAR should account for interactions between β-oxo and α-OOH substitutions. Additional training data are needed to resolve this issue.
Table 9Comparison of the SAR predictions, kSAR(T), against the experimental values, kexp(T). Values marked with an asterisk are used in the derivation of the SAR, usually by geometric averaging with theoretical data.
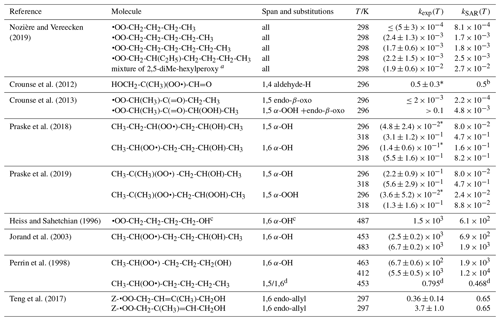
a SAR prediction for a mixture of of 2,5-dimethylhexyl-1-, 2-,
and 3-peroxy, respectively, following the procedure in Nozière and
Vereecken (2019) for a reaction time
of 1 min.
b SAR matches experimental value by design. Excluding experimental
value from the SAR derivation yields 0.23 s−1, showing good agreement
between theoretical
and experimental data.
c The observed reaction is identified based on the product study by
Jorand et al. (1996).
d Ratio of the 1,5-H over 1,6-H migration rate.
4.2 Performance with spectator substitution
To keep the number of SAR parameters manageable and make the SAR easily applicable, one hopes that each SAR class is applicable to a wide range of compounds, without having to resort to explicitly examining all possible permutations of functionalities on the reactant. Due to the nature of the title reaction, a fairly large number of SAR classes is unavoidable, as the reaction acts from short to long ranges and is dependent on two reactive sites (–OO• moiety and migrating H atom) that can be influenced by their neighbours (even long-range neighbours in case of delocalization). In this test set, we include those compounds that have non-aliphatic “spectator” substituents located such that they are not expected to have an overly large effect on the H migration reaction. Examples include substituents outside the TS cycle or located sufficiently far from both reaction sites.
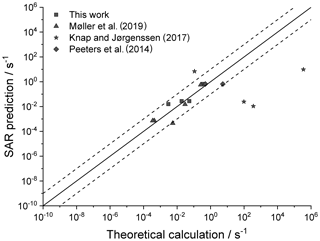
Figure 4 shows the agreement between the SAR predictions and our theory-based data set (see Supplement) for those reactions of non-cyclic RO2 not included in the training set. The performance is comparatively good, with most predictions within an order of magnitude. Given that this set includes stereo-isomers where direct calculations show rate coefficient differences of almost 2 orders of magnitude, this indicates that the SAR performs well and that spectator functionalities can be well approximated by aliphatic substituents. The largest scatter is found for a very slow H migration, ktheory (298 K) s−1, which is not relevant in the atmosphere, and for H-scrambling reactions, which have been discussed earlier as suffering from large discrepancies between the predictions in the various literature sources. As expected (see above), we typically under-predict H-scrambling rates; despite this we still find that the scrambling reactions are several orders of magnitude faster than other H migrations, supporting pooling hydroperoxide-substituted RO2 radicals, as discussed in Sect. 5. A similar analysis of selected literature data is shown in Fig. 5 (D'Ambro et al., 2017; Jørgensen et al., 2016; Knap et al., 2015, 2016; Knap and Jørgensen, 2017; Kurtén et al., 2015; Møller et al., 2016, 2019; Piletic et al., 2019; Praske et al., 2018, 2019; Wang et al., 2018; Xing et al., 2018). The SAR predictions show a significantly wider scatter than for the previous test set. However, one should take into account that these data are based on a wider range of theoretical methodologies, and the wider scatter is at least partly caused by the use of MC-TST calculations based on a limited number of conformers, or from the use of density-functional theory-based energies that carry a larger uncertainty. At this point, we anticipate that the scatter relative to the SAR prediction will decrease strongly when applying better quantum chemical methodologies and by incorporating more conformers in the kinetic analysis, either by full MC-TST or rel-MC-TST.
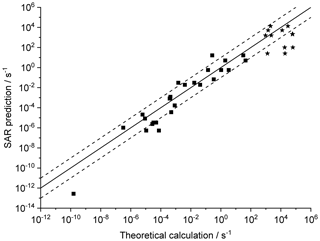
Figure 4k(298 K) H migration in multi-functionalized species with spectator substituents. The data shown are derived in this work or our earlier publications, using MC-TST incorporating all conformers compared against the SAR prediction. The stars indicate OOH/ OO• H-scrambling reactions. The solid line shows 1:1 correspondence, with the dotted lines delineating an order of magnitude of uncertainty.
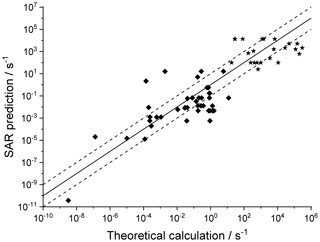
Figure 5Literature theory-based k(298 K) rate coefficients compared against the SAR predictions (see text for references) in multi-functionalized species with spectator substituents. The stars are OOH∕OO• H-scrambling reactions. The solid line shows 1:1 correspondence, with the dotted lines delineating an order of magnitude of uncertainty
4.3 Multi-functionalized compounds
Our SAR currently does not directly support the prediction of rate coefficients for RO2 radicals when the H migration is affected by more than one functionality, due to the lack of data to derive reliable cross-terms accommodating two or more simultaneous functionalities. As a test case, however, here we examine the 1,6-H migration in methyl-4-hydroxy-2-butene-1-peroxy, i.e. the Z-δ-1-OH-isoprene-4-peroxy (Z-HO-CH2-C(CH3)=CH-CH2OO•, Z-δ-RO2-1) and Z-δ-4-OH-isoprene-1-peroxy (Z-•OO-CH2-C(CH3)=CH-CH2OH, Z-δ-RO2-4) radicals of critical importance in the isoprene oxidation (Bianchi et al., 2019; Nguyen et al., 2010; Novelli et al., 2020; Peeters et al., 2009, 2014; Wennberg et al., 2018). Teng et al. (2017) derived rate coefficients for these unimolecular reactions from experiments, finding rates of 0.36±0.14 s−1 (Z-δ-RO2-1) and 3.7±1.0 s−1 (Z-δ-RO2-4), in good agreement with the theoretical data, e.g. 0.49 and 5.4 s−1, as derived by Peeters et al. (2014) for the LIM1 mechanism. These values have been incorporated in atmospheric models (e.g. Wennberg et al., 2018), though some models use lower rate coefficients; the MCM v3.3.1 (Jenkin et al., 2015), for example, uses 0.11 and 1.2 s−1. The overall kinetics is mostly sensitive (Novelli et al., 2020) to the ratio of the H migration rate over O2 elimination and other reactions, whose rate coefficients are also different in these models. The rate coefficient for 1,6-H migration is significantly faster than in the corresponding aliphatic compounds and is accelerated by the formation of a stable α-OH allyl radical. The main impact is due to the allylic resonance, which enhances the rate by over a factor of 700 (see Table 2); the α-OH substitution has an impact of a factor of ∼10 in our SAR (see Table 6). A SAR prediction including only the TS endocyclic double bond, 0.65 s−1, reproduces the experimental and direct theoretical results within a factor of 6 to 8; bearing in mind that our SAR does not distinguish between substitutions on the second allylic radical site, which in this case has an impact of a factor of 10, which is remarkably good. Applying corrections for both the allylic and α-OH functionalities, yielding 6.5 s−1, apparently overestimates the rate coefficients by up to a factor of 20. This test suggests that there is mutual influence between multiple functionalities beyond a purely additive or multiplicative combination. However, within the uncertainties of our SAR, i.e. allowing for the scatter on the underlying data and the simplifications in the SAR such as ignoring stereochemistry and secondary allylic sites, we would be hard-pressed to make a case for including a second-order bi-functional correction on the basic SAR at this time.
Figure 6 shows an analysis of available rate coefficients on multi-functionalized species (this work; Knap and Jørgensen, 2017; Møller et al., 2019; Peeters et al., 2009), approximating the rate coefficient using only the existing SAR parameters for mono-functional RO2 radicals. We find that the agreement is generally good; the large scatter on the Knap and Jørgensen (2017) data appears to be due to the use of lower-level, density-functional theory-based reaction energies.
4.4 Cyclic structures
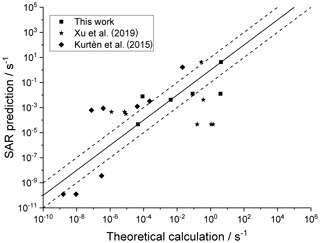
For completeness, Fig. 7 depicts the SAR performance for a set of H migrations in cyclic species, such as substituted menthenyl-peroxy radicals, pinonaldehyde-peroxy radicals, and bicyclic peroxide-peroxy radicals (this work; Kurtén et al., 2015; Xu et al., 2019). As the SAR has no provisions for strained bicyclic structures, these predictions are not expected to be particularly good.
4.5 Untestable SAR parameters
Much of the uncertainty in the SAR predictions is not shown in the above tests. In particular, the values in the SAR that are inferred only by relative rate considerations – either the temperature dependence k(T) and/or absolute value at 298 K – can not be tested due to lack of data for comparison. While the other SAR predictions are seen above to be somehow “average” in comparison to the available data, albeit possibly with a large uncertainty, a critical difference with the estimated values is that these could have a (large) systematic bias that influences how we perceive the importance of these reactions. In this respect, it is important that further systematic studies are performed to provide a reference value in each of the SAR categories. Until then, we rely solely on the assumption that the reactivity trends are applicable across SAR classes.
The rapid migration of hydroperoxide-H atoms in HOO-substituted peroxy radicals has some interesting ramifications for the chemistry and kinetics of these radicals. As already mentioned earlier, the scrambling reactions are typically several orders of magnitude faster than other RO2 H migration reactions. As a result, the HOO-RO2 isomeric population will readily equilibrate and re-equilibrate to compensate for loss (or gain) of specific isomers; for the reaction rates at play, this typically means that the isomers are present in their Boltzmann equilibrium relative concentrations. It then becomes convenient to describe the isomers as a single equilibrated pool of HOO-RO2 molecules (see Fig. 8). As the effective contribution of an isomer is then no longer equal to the total concentration (or its original concentration implied by any formation processes), the elementary rate coefficient is not a good measure of the rate of product formation unless the isomer-specific contribution is explicitly accounted for. This is done by “bulk” rate coefficients, operating on the pool of HOO-RO2 molecules.
Figure 8Illustration of fast scrambling and the use of bulk rate coefficients to reduce the complexity of the kinetic model, with (a) the explicit model and (b) the model using a single lumped pool (in square brackets). In the example above, k2(bulk) is the sum of the bulk rate coefficients for each of the two channels. The scheme is trivially extended to more isomers and reaction channels.
For a specific elementary reaction, one then finds a bulk rate coefficient as follows:
which can be used to convert elementary rate coefficients to population-weighted rate coefficients (Vereecken et al., 2017), with Qi(T) the partition functions of each of the isomers, Ei their relative energy, and k1 the elementary rate coefficient for a reaction starting from isomer 1. If a product is formed in more than one channel, the bulk rate coefficients are summed. Using the equilibrium constant expressed as a ratio of partition functions and relative energies and using the resulting contributing fractions of each isomer in the total concentration, we can rewrite this equation as follows:
where fi(T) is the temperature-dependent fraction of reactant i in the isomer pool and performing reaction 1 with the elementary rate coefficient k1(T).
These formulae imply that the effective bulk rate coefficient is less than the elementary rate coefficients obtained by the theoretical rate calculations and SAR predictions for a single isomer. Bulk rate coefficients have been described and applied earlier, both based on HOO-RO2 scrambling and other RO2-equilibrating mechanisms (Novelli et al., 2020; Nozière and Vereecken, 2019; Peeters et al., 2009, 2014), and they have proven necessary to connect the elementary reaction kinetics to the phenomenological observations.
The ability to describe the pool of HOO-RO2 as a single species in a kinetic model could lead to significant simplification and a more natural implementation for comparison against experiment. For studying the formation of highly oxidized molecules (HOM), multi-OOH-substituted molecules typically formed through multiple RO2-H migrations + O2 addition sequences, and the pooling could provide a more direct link to aerosol models, which often lump species in similarity classes. Unfortunately, there is no simple method to predict the relative contributions of the HOO-RO2 in a pool and thus obtain kpool(T). A pragmatic solution proposed by Nozière and Vereecken (2019) involves simply counting the number of isomers n contributing to the pool, assigning an equal population fraction to each, and using this as a measure for the bulk rate coefficient ratio relative to the elementary rate coefficient kj(T) :
This solution is readily implemented both manually and in automated mechanisms, but it implies that the isomers should be present in roughly equal concentrations. In some cases, one or some of the isomers could be dominant or negligible, e.g. due to stabilization by H bonding, or by formation of more stable hydroperoxides (e.g. peracids). The simplified approach above thus carries a larger uncertainty if the isomers are not sufficiently “similar”.
A corollary of the fast re-equilibration is that the HOO-RO2 molecules have access to all exit channels in the pool, irrespective of the isomer that was originally formed. An example of such a system has been recently described by Novelli et al. (2020), where di-HPCARP-RO2, a dihydroperoxy-aldehyde-peroxy radical formed from isoprene (three isomers per pool), initially does not have access to a fast aldehyde-H migration pathway (only a slow 1,4-H shift), but fast scrambling allowed access to much faster 1,5-aldehyde-H and 1,6-aldehyde-H migration channels, leading to acyl radical formation as the dominant channel. Again, this could allow reductions in mechanism complexity, as less favourable exit channels for some of the isomers can be omitted in favour of dominant exit channels through other isomers in the HOO-RO2 pool. Such mechanism reductions are readily implemented.
Unfortunately, there are conditions where the reduction of the mechanism by pooling isomers is unlikely to work. An example is a mechanism that should be applicable across a large range of RO2 co-reactant (e.g. NO) concentrations. At low concentrations where the bimolecular reaction is slower than the H atom scrambling, use of an HOO-RO2 pool will be appropriate, but for increasingly high concentrations the bimolecular reaction will compete with and eventually overwhelm the equilibration by H scrambling, leading to product yields that are determined by the nascent isomeric contributions rather than the equilibrium contributions. For such broadly applicable models, an explicit multi-conformer mechanism must be constructed (as in Fig. 8a), though some model reduction may still be possible by omission of some of the slower H migration channels.
In atmospheric chemistry, the unimolecular reactions of the alkyl radical products are typically not considered explicitly, and mechanisms such as the Master Chemical Mechanism assume, by default, O2 addition for all alkyl radicals unless a special reaction is known to occur (Saunders et al., 2003). Examples of the latter includes > C•(OH) + O2, epoxide formation in C•-COOH, or OH elimination in C•OOH. For aliphatic alkyl radicals, the rate of H migration or elimination reactions rarely reaches 104 s−1 at room temperature, such that O2 addition is dominant (Miyoshi, 2011; Villano et al., 2011; Wang et al., 2015). The weaker OO–H bond in hydroperoxides as formed in the currently considered reactions, however, facilitates H migration in •QOOH radicals, possibly allowing reversal of the RO2 H migration. If we assume that only the reverse •QOOH to RO2 reaction can occur in competition with O2 addition, the effective rate of HOOQO2 formation will be dependent on the rate of •QOOH formation, k1 and the reverse reaction k−1 competing against the O2 addition, [O2]:
i.e. the faster the reverse reaction, the slower effective product formation keff will be for a given [O2] value. A structure–activity relationship for RO2 H migration can not account for the effect of the reverse H migration reaction, as other reaction paths may be accessible, such as alkyl ring closure reactions, epoxidation, HO2 elimination forming alkenes, and other rearrangements that have been amply studied at the higher temperatures found in combustion systems (see, e.g. Miyoshi, 2011). A full analysis of the fate of the •QOOH intermediates is outside the scope of the present paper, and we refer the reader to the cited papers for reaction rate rules.
The experimental studies by Nozière and Vereecken (2019) examined migration of aliphatic H atoms, which are comparatively slow, have a high forward barrier, and are endoergic by ∼15 kcal mol−1, leading to reverse barriers of 10 kcal mol−1 or less. They concomitantly have a rather high reverse rate coefficient k−1 and are thus potentially affected by •QOOH H migration. A theory-based comparison by Miyoshi (2011) found that for 1,7-H shift spans or larger, the entropic disadvantage of the cyclic H migration TS against the more facile O2 addition (0.2 atm O2) allows the latter to dominate at room temperature by a factor of ∼103 or higher. For 1,5 to 1,6-H migrations, however, the ratio k−1(298 K)(298 K)[O2] is closer to 10, indicating that the effective rate of product formation keff(298 K) could be reduced by ∼10 % compared to the elementary reaction rate for RO2 H migration. Since 1,5-H and 1,6-H migrations are typically the most favourable H migration spans, this reverse reaction may need to be taken into account for highly accurate analyses. Future work could examine this aspect in more detail; at present, the estimated impact is smaller than the total uncertainties on the measurements (Nozière and Vereecken, 2019) Experiments at varying elevated O2 concentrations could directly probe the impact of the competition between k−1 and on the phenomenological rate coefficient.
The RO2 H migration reaction rates are subject to Bell–Evans–Polanyi relationships, where more exothermic reactions have lower forward energy barriers and higher reverse barriers. A good correlation is only found within a single substituent group as, for example, allyl resonance stabilization and other effects can affect the post-TS stabilization of the product energy by a larger amount than in the transition state. Faster H migration reactions then tend to have slower reverse reactions, and RO2 reactions fast enough to be important in atmospheric conditions are likely to have slow enough reverse reactions to safely assume that O2 addition in the product alkyl radical is dominant. The experiments by Nozière and Vereecken (2019) then appear to be a worst case scenario regarding the difference between elementary and phenomenological rates, and we propose that reverse H migration generally has a very limited impact under atmospheric conditions. For some radicals, such as allyl-stabilized or aromatic radicals, effective O2 addition is significantly slower than for aliphatic alkyl radicals (Peeters et al., 2009; Vereecken, 2019). Furthermore, such stabilized radicals are readily formed, with the SAR described in this paper showing that unsaturated functionalities generally lead to fast RO2 migration of the β-H atoms. The same electronic stabilization that hampers O2 addition, however, also reduces the rate of the reverse alkyl radical H migration, mitigating the slower HOOQOO• formation.
Many of the organic compounds emitted to the atmosphere are (multi-)unsaturated, allowing for the possibility of alkyl cycloaddition reactions. The predicted rate coefficients near room temperature are of the order of 106 s−1 or less and are not effectively competing against O2 addition (Wang et al., 2015).
In addition to RO2 and HOOQO2, a number of stable products were detected in the experiments described earlier by Nozière and Vereecken (2019). For all the RO2 studied, the carbonyl compound corresponding to initially formed RO2 was observed and represented by far the main reaction product, evidencing the importance of the keto-hydroxy channel in the self-reaction of RO2 in all cases. These products were mostly observed at mass M+19 and at lower intensities at M+37 and sometimes even M+55. Thus, in the 1-butylperoxy system, butanal (MW =72 g mol−1) was mostly observed at and 109; in the 1-pentylperoxy system, pentanal (MW =86 g mol−1) was observed at and 123; in the 1-hexylperoxy system, hexanal (MW =100 g mol−1) was observed at and 137; and in the ethylhexylperoxy system, ethylhexanal (MW =128 g mol−1) was observed at . For dimethylhexylperoxy, 2,5-dimethyl-hexanal and isomers (MW =128 g mol−1) were mostly observed at M+1 () and M+19 (). Note, however, that the technique does not distinguish between isomers; therefore, the position of the carbonyl groups in these compounds (and of the other substituents in the other types of products discussed below) could not be confirmed. The ROOH hydroperoxides produced by the RO2 + HO2 reactions were also observed in most systems, but their main peak at M+19 (Nozière and Hanson, 2017) overlapped with the M+37 peaks for the main carbonyl products: butylhydroperoxide, MW =90 g mol−1 and M+19 was ; pentylhydroperoxide, MW =104 g mol−1 and M+19 was ; hexylhydroperoxide, MW =118 g mol−1 and M+19 was ; 2,5-dimethyl-hexylhydroperoxide, MW =146 g mol−1 and M+19 was . The contribution of the hydroperoxides to these signals was thus determined by adding NO periodically in the reactor. The systematic decrease in these signals in the presence of NO confirmed the significant contribution of hydroperoxides, as these compounds are formed only in the absence of NO. In the 1-butylperoxy, 1-pentylperoxy, and 1-hexylperoxy systems, peaks corresponding the alcohols produced by the self-reaction of RO2 were also observed at their M+19 and M+37 peaks: in the 1-butylperoxy system butanol (MW =74 g mol−1) was thus observed at and 111; in the 1-pentylperoxy system, pentanol (MW =88 g mol−1) was observed at and 125; and in the 1-hexylperoxy system, hexanol (MW =102 g mol−1) was observed at and 139. These peaks were found to disappear systematically when NO was added to the reactor, confirming that they were produced by the reaction of the RO2 radicals in the absence of NO, in agreement to known RO2 + RO2 chemistry. Finally, in the 1-pentylperoxy, 1-hexylperoxy, and dimethylhexylperoxy systems, peaks corresponding to the carbonyl analogues of HOOQO2 were observed. Interestingly, where the HOOQO2 radicals were exclusively observed at their M+55 peaks due to water clustering (Nozière and Vereecken, 2019), these carbonyls were also observed at their M+55 and even M+73 peaks. In the 1-pentylperoxy system, pentanonylhydroperoxide (MW =118 g mol−1) was thus observed at and 191; in the 1-hexylperoxy system, hexanonylhydroperoxide (MW =132 g mol−1) was observed at and 205; and in the dimethylhexylperoxy system dimethylhexanonylhydroperoxide (MW =146 g mol−1) was observed at and 219. The formation of these carbonyl compounds was consistent with the fast decomposition of the α-OOH alkyl radicals produced by the fast H migration from the HOOQO2 (pathway R4 shown in the Introduction). The observation of all of these products is illustrated for the case of the 1-pentylperoxy system in Figs. 9 and 10. These products thus confirmed the main expected reaction pathways for RO2 and HOOQO2.
Figure 9Main product peaks in the 1-pentylperoxy system (experiments from 8 November 2018). See Fig. 10 for Lewis structures of the molecules (without complexed H2O): is C5H10=O; is C5H11OH; is mostly C5H11OH with some contribution of C5H10=O; is C5H11OH; and are HOOC5H9=O.
In this work, an extensive SAR is presented for predicting the temperature-dependent rate coefficient for H migration in substituted alkylperoxy radicals. The SAR is mostly based on theoretical data at various levels of theory, using both newly presented and literature data. The theoretical methodology used to predict the rate coefficient is evaluated, taking the best available data into account when deriving the absolute rate coefficient and its temperature dependence, thus leading to the best available estimates. Modified Arrhenius parameters are presented for the temperature range 200–450 K, sufficient to cover all relevant atmospheric conditions. Experimental data are scarce but is used when available. The SAR generalized earlier work on RO2 H migration, and can provide valuable guidance for mechanism development in atmospheric conditions. The reliability of the SAR depends strongly on the SAR reaction class. For aliphatic RO2, there is ample theoretical data, which tends to agree well, allowing for robust predictions across the entire temperature range. The experimental data by Nozière and Vereecken on aliphatic RO2 H migration were not used in the derivation but provide very valuable verification of the a priori predictions, as aliphatic RO2 serves as the core of the SAR, representing the main features of the carbon backbone of the molecules. Migration spans from 1,4 to 1,8 are considered.
For unsaturated RO2, we have generated a large number of characterizations and find that allylic stabilization of the alkyl radical greatly enhanced the H migration rate. The SAR distinguishes between endocyclic and exocyclic double bonds in the cyclic transition state. Likewise, β-oxo substitution on the migrating H atom, either endocyclic or exocyclic in the TS, can enhance the rate of migration. Hydroxy and hydroperoxide-substituted RO2 radicals show enhanced abstraction rates for the α-H atoms. Migration of aldehydic and acidic H atoms are likewise fast, whereas nitrate substitution slows down migration of the α-H atoms. For none of the latter SAR classes is full coverage available, with several reaction types that have no (reliable) rate predictions available in the literature. The current SAR derivation thus also serves as a good guide for future studies, indicating where efforts are best applied. A case in point would be the H atom scrambling in hydroperoxide-substituted RO2 radicals, for which the available data splits into two groups, predicting rate coefficients separated by 4 orders of magnitude or more. Targeted calculations could prove very valuable to resolve this issue. Other important reactions that could benefit specifically from additional data are the migration of aldehydic H atoms, and the migration of β-oxo H atoms, for which very few data are available for some of the migration spans that have fast reaction rates that could be of importance in the atmosphere. In this work we introduce relative multi-conformers transition state theory, rel-MC-TST, a technique for reducing the computational cost of systematic rate studies that appears well suited to aid in the characterizing the many reaction rates needed to enhance the current SAR.
Compared to the scarce available experimental data, the SAR performs very well, reproducing the data within a factor of 2 on average, which is comparable to the experimental uncertainty. While in some cases the experimental data were used in the SAR training data, most of the predictions are based primarily on theoretical data, suggesting that the theoretical data provides a good basis for the SAR. A further analysis of the performance of the SAR focused on its application to multi-functionalized RO2 radicals, probing the scope of applicability beyond the mono-functionalized training set. By and large, the SAR performs well, showing a scatter relative to the available theoretical data of about an order of magnitude; it should be noted here that the underlying data are expected to show scatter of this magnitude, and the SAR can thus not be tested beyond this accuracy. The SAR also suffers somewhat from pragmatic simplifications, such as the lumping of stereo-isomers that can show rate coefficients differing by up to 2 orders of magnitude.
In this work, we also report experimental verification of the reaction mechanisms by direct measurements of the products as a function of the reaction conditions; earlier experimental work is often indirect, relying to some extent on mechanistic assumptions to derive the rate coefficients of the elementary or bulk rate coefficients. We discuss the impact of fast isomerization reactions by H scrambling in hydroperoxide-RO2 in some detail, which affects the apparent rate coefficient and product distribution. Under conditions with sufficiently slow competing bimolecular reactions such as with NO, HO2, and RO2, the unimolecular decay of such HOO-RO2 is better described using bulk rate coefficients acting on an equilibrated pool of peroxy radicals.
Though we anticipate that the SAR parameters will be improved rapidly over the next few years, the current SAR can already provide guidance in the generation of kinetic models, experimental design, and theoretical studies. Further literature review can also provide additional points of reference, though the status appears that the published data have quite a lot of scatter for rather similar reactions, and adding more sources may thus not necessarily increase the reliability. Extension and refinement of the SAR should thus be based on combined literature data, new theoretical calculations at high levels of theory, and especially experimental work. We feel improvement for aldehydic H migration and unsaturated compounds are most needed, as these reactions have the highest rate coefficients and the functionalities are the most common, affecting atmospheric chemistry most.
All data is available in the supporting information or in the cited literature.
The supplement related to this article is available online and contains examples of the SAR application, additional information on methodologies, the theoretically derived rate coefficients for ∼150 compounds, the description of the rel-MC-TST methodology, a documented spreadsheet implementing the SAR derivation, and the raw quantum chemical data. The supplement related to this article is available online at: https://doi.org/10.5194/acp-20-7429-2020-supplement.
The quantum chemical calculations, theoretical kinetic calculations, literature study, and SAR analysis were performed by LV. The experiments and their analysis were done by BN. Both authors contributed to the discussion and writing of the manuscript.
The authors declare that they have no conflict of interest.
Luc Vereecken gratefully acknowledges the Max Planck Graduate Center–Johannes Gutenberg University Mainz (MPGC). He also thanks Astrid Kiendler-Scharr and Andreas Wahner (Forschungszentrum Jülich) for supporting this project.
The article processing charges for this open-access publication were covered by a Research Centre of the Helmholtz Association.
This paper was edited by James B. Burkholder and reviewed by three anonymous referees.
Asatryan, R., da Silva, G., and Bozzelli, J. W.: Quantum Chemical Study of the Acrolein (CH2CHCHO) + OH + O2 Reactions, J. Phys. Chem. A, 114, 8302–8311, https://doi.org/10.1021/jp104828a, 2010.
Atkinson, R.: Gas-phase tropospheric chemistry of organic compounds: a review, Atmos. Environ., 41, Supplement, 200–240, https://doi.org/10.1016/j.atmosenv.2007.10.068, 2007.
Bao, J. L., Zheng, J., Alecu, I. M., Lynch, B. J., Zhao, Y., and Truhlar, D. G.: Database of Frequency Scale Factors for Electronic Model Chemistries (Version 3 Beta 2), available at: http://comp.chem.umn.edu/freqscale/index.html (last access: 18 June 2020), 2017.
Barrows, S. E. and Eberlein, T. H.: Cis and trans isomers of cycloalkenes, J. Chem. Educ., 82, 1334–1339, https://doi.org/10.1021/ed082p1334, 2005.
Battin-Leclerc, F., Blurock, E., Bounaceur, R., Fournet, R., Glaude, P.-A., Herbinet, O., Sirjean, B., and Warth, V.: Towards cleaner combustion engines through groundbreaking detailed chemical kinetic models, Chem. Soc. Rev., 40, 4762–4782, https://doi.org/10.1039/c0cs00207k, 2011.
Becke, A. D.: Density-functional thermochemistry. II. The effect of the Perdew–Wang generalized-gradient correlation correction, J. Chem. Phys., 97, 9173–9177, https://doi.org/10.1063/1.463343, 1992.
Bianchi, F., Kurtén, T., Riva, M., Mohr, C., Rissanen, M. P., Roldin, P., Berndt, T., Crounse, J. D., Wennberg, P. O., Mentel, T. F., Wildt, J., Junninen, H., Jokinen, T., Kulmala, M., Worsnop, D. R., Thornton, J. A., Donahue, N., Kjaergaard, H. G., and Ehn, M.: Highly Oxygenated Organic Molecules (HOM) from Gas-Phase Autoxidation Involving Peroxy Radicals: A Key Contributor to Atmospheric Aerosol, Chem. Rev., 119, 3472–3509, https://doi.org/10.1021/acs.chemrev.8b00395, 2019.
Carter, W. P. L.: Development of the SAPRC-07 chemical mechanism, Atmos. Environ., 44, 5324–5335, https://doi.org/10.1016/j.atmosenv.2010.01.026, 2010.
Crounse, J. D., Paulot, F., Kjaergaard, H. G., and Wennberg, P. O.: Peroxy radical isomerization in the oxidation of isoprene, Phys. Chem. Chem. Phys., 13, 13607–13613, https://doi.org/10.1039/c1cp21330j, 2011.
Crounse, J. D., Knap, H. C., Ørnsø, K. B., Jørgensen, S., Paulot, F., Kjaergaard, H. G., and Wennberg, P. O.: Atmospheric Fate of Methacrolein. 1. Peroxy Radical Isomerization Following Addition of OH and O2, J. Phys. Chem. A, 116, 5756–5762, https://doi.org/10.1021/jp211560u, 2012.
Crounse, J. D., Nielsen, L. B., Jørgensen, S., Kjaergaard, H. G., and Wennberg, P. O.: Autoxidation of Organic Compounds in the Atmosphere, J. Phys. Chem. Lett., 4, 3513–3520, https://doi.org/10.1021/jz4019207, 2013.
D'Ambro, E. L., Møller, K. H., Lopez-Hilfiker, F. D., Schobesberger, S., Liu, J., Shilling, J. E., Lee, B. H., Kjaergaard, H. G. and Thornton, J. A.: Isomerization of Second-Generation Isoprene Peroxy Radicals: Epoxide Formation and Implications for Secondary Organic Aerosol Yields, Environ. Sci. Technol., 51, 4978–4987, https://doi.org/10.1021/acs.est.7b00460, 2017.
da Silva, G.: Hydroxyl radical regeneration in the photochemical oxidation of glyoxal: kinetics and mechanism of the HC(O)CO + O2 reaction, Phys. Chem. Chem. Phys., 12, 6698, https://doi.org/10.1039/b927176g, 2010a.
da Silva, G.: Oxidation of Carboxylic Acids Regenerates Hydroxyl Radicals in the Unpolluted and Nighttime Troposphere, J. Phys. Chem. A, 114, 6861–6869, https://doi.org/10.1021/jp101279p, 2010b.
da Silva, G.: Kinetics and Mechanism of the Glyoxal + HO2 Reaction: Conversion of HO2 to OH by Carbonyls, J. Phys. Chem. A, 115, 291–297, https://doi.org/10.1021/jp108358y, 2011.
da Silva, G. and Bozzelli, J. W.: Role of the α-hydroxyethylperoxy radical in the reactions of acetaldehyde and vinyl alcohol with HO2, Chem. Phys. Lett., 483, 25–29, https://doi.org/10.1016/j.cplett.2009.10.045, 2009.
Dunning, T. H.: Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 90, 1007–1023, https://doi.org/10.1063/1.456153, 1989.
Eckart, C.: The penetration of a potential barrier by electrons, Phys. Rev., 35, 1303–1309, https://doi.org/10.1103/PhysRev.35.1303, 1930.
Ehn, M., Berndt, T., Wildt, J., and Mentel, T.: Highly Oxygenated Molecules from Atmospheric Autoxidation of Hydrocarbons: A Prominent Challenge for Chemical Kinetics Studies, Int. J. Chem. Kinet., 49, 821–831, https://doi.org/10.1002/kin.21130, 2017.
Fuchs, H., Albrecht, S., Acir, I., Bohn, B., Breitenlechner, M., Dorn, H.-P., Gkatzelis, G. I., Hofzumahaus, A., Holland, F., Kaminski, M., Keutsch, F. N., Novelli, A., Reimer, D., Rohrer, F., Tillmann, R., Vereecken, L., Wegener, R., Zaytsev, A., Kiendler-Scharr, A., and Wahner, A.: Investigation of the oxidation of methyl vinyl ketone (MVK) by OH radicals in the atmospheric simulation chamber SAPHIR, Atmos. Chem. Phys., 18, 8001–8016, https://doi.org/10.5194/acp-18-8001-2018, 2018.
Greenberg, A. and Liebman, J. F.: Strained organic molecules, Academic Press, San Diego, available at: https://public.ebookcentral.proquest.com/choice/publicfullrecord.aspx?p=1822362 (last access: 26 April 2020), 1978.
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009.
Hanson, D., Orlando, J., Noziere, B., and Kosciuch, E.: Proton transfer mass spectrometry studies of peroxy radicals, Int. J. Mass Spectrom., 239, 147–159, https://doi.org/10.1016/j.ijms.2004.07.021, 2004.
Hanson, D. R., Greenberg, J., Henry, B. E., and Kosciuch, E.: Proton transfer reaction mass spectrometry at high drift tube pressure, Int. J. Mass Spectrom., 223–224, 507–518, https://doi.org/10.1016/S1387-3806(02)00924-7, 2003.
Heiss, A. and Sahetchian, ,K.: Isomerization reactions of the n-C4H9O and n-OOC4H8OH radicals in oxygen, Int. J. Chem. Kinet., 28, 531–544, https://doi.org/10.1002/(SICI)1097-4601(1996)28:7<531::AID-KIN5>3.0.CO;2-W, 1996.
Hermans, I., Nguyen, T. L., Jacobs, P. A., and Peeters, J.: Tropopause Chemistry Revisited: HO2•-Initiated Oxidation as an Efficient Acetone Sink, J. Am. Chem. Soc., 126, 9908–9909, https://doi.org/10.1021/ja0467317, 2004.
Hermans, I., Nguyen, T. L., Jacobs, P. A., and Peeters, J.: Autoxidation of Cyclohexane: Conventional Views Challenged by Theory and Experiment, ChemPhysChem, 6, 637–645, https://doi.org/10.1002/cphc.200400211, 2005a.
Hermans, I., Müller, J.-F., Nguyen, T. L., Jacobs, P. A., and Peeters, J.: Kinetics of α-Hydroxy-alkylperoxyl Radicals in Oxidation Processes, HO2•-Initiated Oxidation of Ketones/Aldehydes near the Tropopause, J. Phys. Chem. A, 109, 4303–4311, https://doi.org/10.1021/jp044080v, 2005b.
IUPAC Subcommittee on Atmospheric Chemical Kinetic Data Evaluation: Evaluated Kinetic Data, available at: http://iupac.pole-ether.fr/index.html (last access: 18 June 2020), 2017.
Jenkin, M. E., Young, J. C., and Rickard, A. R.: The MCM v3.3.1 degradation scheme for isoprene, Atmos. Chem. Phys., 15, 11433–11459, https://doi.org/10.5194/acp-15-11433-2015, 2015.
Jenkin, M. E., Valorso, R., Aumont, B., and Rickard, A. R.: Estimation of rate coefficients and branching ratios for reactions of organic peroxy radicals for use in automated mechanism construction, Atmos. Chem. Phys., 19, 7691–7717, https://doi.org/10.5194/acp-19-7691-2019, 2019.
Johnson, R. P.: Strained Cyclic Cumulenes, Chem. Rev., 89, 1111–1124, https://doi.org/10.1021/cr00095a009, 1989.
Johnston, H. S. and Heicklen, J.: Tunneling corrections for unsymmetrical Eckart potential energy barriers, J. Phys. Chem., 66, 532–533, https://doi.org/10.1021/j100809a040, 1962.
Jokinen, T., Sipila, M., Richters, S., Kerminen, V.-M., Paasonen, P., Stratmann, F., Worsnop, D., Kulmala, M., Ehn, M., Herrmann, H., and Berndt, T.: Rapid Autoxidation Forms Highly Oxidized RO2 Radicals in the Atmosphere, Angew. Chem.-Int. Ed., 53, 14596–14600, https://doi.org/10.1002/anie.201408566, 2014.
Jorand, F., Heiss, A., Sahetchian, K., Kerhoas, L. and Einhorn, J.: Identification of an unexpected peroxide formed by successive isomerization reactions of the n-butoxy radical in oxygen, J. Chem. Soc. Faraday T., 92, 4167–4171, https://doi.org/10.1039/ft9969204167, 1996.
Jorand, F., Heiss, A., Perrin, O., Sahetchian, K., Kerhoas, L., and Einhorn, J.: Isomeric hexyl-ketohydroperoxides formed by reactions of hexoxy and hexylperoxy radicals in oxygen, Int. J. Chem. Kinet., 35, 354–366, https://doi.org/10.1002/kin.10136, 2003.
Jørgensen, S., Knap, H. C., Otkjær, R. V., Jensen, A. M., Kjeldsen, M. L. H., Wennberg, P. O., and Kjaergaard, H. G.: Rapid Hydrogen Shift Scrambling in Hydroperoxy-Substituted Organic Peroxy Radicals, J. Phys. Chem. A, 120, 266–275, https://doi.org/10.1021/acs.jpca.5b06768, 2016.
Knap, H. C. and Jørgensen, S.: Rapid Hydrogen Shift Reactions in Acyl Peroxy Radicals, J. Phys. Chem. A, 121, 1470–1479, https://doi.org/10.1021/acs.jpca.6b12787, 2017.
Knap, H. C., Jørgensen, S., and Kjaergaard, H. G.: Theoretical investigation of the hydrogen shift reactions in peroxy radicals derived from the atmospheric decomposition of 3-methyl-3-buten-1-ol (MBO331), Chem. Phys. Lett., 619, 236–240, https://doi.org/10.1016/j.cplett.2014.11.056, 2015.
Knap, H. C., Schmidt, J. A., and Jorgensen, S.: Hydrogen shift reactions in four methyl-buten-ol (MBO) peroxy radicals and their impact on the atmosphere, Atmos. Environ., 147, 79–87, https://doi.org/10.1016/j.atmosenv.2016.09.064, 2016.
Kurtén, T., Rissanen, M. P., Mackeprang, K., Thornton, J. A., Hyttinen, N., Jorgensen, S., Ehn, M., and Kjaergaard, H. G.: Computational Study of Hydrogen Shifts and Ring-Opening Mechanisms in α-Pinene Ozonolysis Products, J. Phys. Chem. A, 119, 11366–11375, https://doi.org/10.1021/acs.jpca.5b08948, 2015.
Kuwata, K. T., Dibble, T. S., Sliz, E., and Petersen, E. B.: Computational Studies of Intramolecular Hydrogen Atom Transfers in the β-Hydroxyethylperoxy and β-Hydroxyethoxy Radicals, J. Phys. Chem. A, 111, 5032–5042, https://doi.org/10.1021/jp0704113, 2007.
Lee, C., Yang, W., and Parr, R. G.: Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 37, 785–789, https://doi.org/10.1103/PhysRevB.37.785, 1988.
Linguerri, R., Puzzarini, C., Al Mogren, M. M., Francisco, J. S., and Hochlaf, M.: Benchmark study of the structural and spectroscopic parameters of the hydroxymethyl peroxy (HOCH2OO) radical and its decomposition reaction to HO2 and H2CO, J. Chem. Phys., 146, 144303, https://doi.org/10.1063/1.4979573, 2017.
Lizardo-Huerta, J. C., Sirjean, B., Bounaceur, R., and Fournet, R.: Intramolecular effects on the kinetics of unimolecular reactions of β-HOROO• and HOQ•OOH radicals, Phys. Chem. Chem. Phys., 18, 12231–12251, https://doi.org/10.1039/c6cp00111d, 2016.
Miyoshi, A.: Systematic Computational Study on the Unimolecular Reactions of Alkylperoxy (RO2), Hydroperoxyalkyl (QOOH), and Hydroperoxyalkylperoxy (O2QOOH) Radicals, J. Phys. Chem. A, 115, 3301–3325, https://doi.org/10.1021/jp112152n, 2011.
Miyoshi, A.: Molecular size dependent falloff rate constants for the recombination reactions of alkyl radicals with O2 and implications for simplified kinetics of alkylperoxy radicals, Int. J. Chem. Kinet., 44, 59–74, https://doi.org/10.1002/kin.20623, 2012.
Mohamed, S. Y., Davis, A. C., Al Rashidi, M. J., and Sarathy, S. M.: Computational Kinetics of Hydroperoxybutylperoxy Isomerizations and Decompositions: A Study of the Effect of Hydrogen Bonding, J. Phys. Chem. A, 122, 6277–6291, https://doi.org/10.1021/acs.jpca.8b04415, 2018a.
Mohamed, S. Y., Davis, A. C., Al Rashidi, M. J., and Sarathy, S. M.: High-Pressure Limit Rate Rules for α-H Isomerization of Hydroperoxyalkylperoxy Radicals, J. Phys. Chem. A, 122, 3626–3639, https://doi.org/10.1021/acs.jpca.7b11955, 2018b.
Møller, K. H., Otkjær, R. V., Hyttinen, N., Kurtén, T., and Kjaergaard, H. G.: Cost-Effective Implementation of Multiconformer Transition State Theory for Peroxy Radical Hydrogen Shift Reactions, J. Phys. Chem. A, 120, 10072–10087, https://doi.org/10.1021/acs.jpca.6b09370, 2016.
Møller, K. H., Bates, K. H., and Kjaergaard, H. G.: The Importance of Peroxy Radical Hydrogen-Shift Reactions in Atmospheric Isoprene Oxidation, J. Phys. Chem. A, 123, 920–932, https://doi.org/10.1021/acs.jpca.8b10432, 2019.
Montgomery, J. A., Frisch, M. J., Ochterski, J. W., and Petersson, G. A.: A complete basis set model chemistry. VII. Use of the minimum population localization method, J. Chem. Phys., 112, 6532–6542, https://doi.org/10.1063/1.481224, 2000.
Nguyen, T. L., Vereecken, L. and Peeters, J.: HOx Regeneration in the Oxidation of Isoprene III: Theoretical Study of the key Isomerisation of the Z-δ-hydroxy-peroxy Isoprene Radicals, ChemPhysChem, 11, 3996–4001, https://doi.org/10.1002/cphc.201000480, 2010.
Novelli, A., Vereecken, L., Bohn, B., Dorn, H.-P., Gkatzelis, G. I., Hofzumahaus, A., Holland, F., Reimer, D., Rohrer, F., Rosanka, S., Taraborrelli, D., Tillmann, R., Wegener, R., Yu, Z., Kiendler-Scharr, A., Wahner, A., and Fuchs, H.: Importance of isomerization reactions for OH radical regeneration from the photo-oxidation of isoprene investigated in the atmospheric simulation chamber SAPHIR, Atmos. Chem. Phys., 20, 3333–3355, https://doi.org/10.5194/acp-20-3333-2020, 2020.
Nozière, B. and Hanson, D. R.: Speciated Monitoring of Gas-Phase Organic Peroxy Radicals by Chemical Ionization Mass Spectrometry: Cross-Reactions between CO2, and c-C6H11O, J. Phys. Chem. A, 121, 8453–8464, https://doi.org/10.1021/acs.jpca.7b06456, 2017.
Nozière, B. and Vereecken, L.: Direct Observation of Aliphatic Peroxy Radical Autoxidation and Water Effects: an Experimental and Theoretical Study, Angew. Chem. Int. Edit., 58, 13976–13982, https://doi.org/10.1002/anie.201907981, 2019.
Otkjær, R. V., Jakobsen, H. H., Tram, C. M., and Kjaergaard, H. G.: Calculated Hydrogen Shift Rate Constants in Substituted Alkyl Peroxy Radicals, J. Phys. Chem. A, 112, 8665–8673, https://doi.org/10.1021/acs.jpca.8b06223, 2018.
Peeters, J. and Nguyen, T. L.: Unusually Fast 1,6-H Shifts of Enolic Hydrogens in Peroxy Radicals: Formation of the First-Generation C2 and C3 Carbonyls in the Oxidation of Isoprene, J. Phys. Chem. A, 116, 6134–6141, https://doi.org/10.1021/jp211447q, 2012.
Peeters, J., Nguyen, T. L., and Vereecken, L.: HOx radical regeneration in the oxidation of isoprene, Phys. Chem. Chem. Phys., 11, 5935–5939, https://doi.org/10.1039/b908511d, 2009.
Peeters, J., Müller, J.-F. J., Stavrakou, T., and Nguyen, V. S.: Hydroxyl Radical Recycling in Isoprene Oxidation Driven by Hydrogen Bonding and Hydrogen Tunneling: the Upgraded LIM1 Mechanism, J. Phys. Chem. A, 118, 8625–8643, https://doi.org/10.1021/jp5033146, 2014.
Perrin, O., Heiss, A., Sahetchian, K., Kerhoas, L., and Einhorn, J.: Determination of the isomerization rate constant HOCH2CH2CH2CH(OO.)CH3 → HOC.HCH2CH2CH(OOH)CH3, Importance of intramolecular hydroperoxy isomerization in tropospheric chemistry, Int. J. Chem. Kinet., 30, 875–887, https://doi.org/10.1002/(SICI)1097-4601(1998)30:12<875::AID-KIN2>3.0.CO;2-8, 1998.
Piletic, I. R., Howell, R., Bartolotti, L. J., Kleindienst, T. E., Kaushik, S. M., and Edney, E. O.: Multigenerational Theoretical Study of Isoprene Peroxy Radical 1-5-Hydrogen Shift Reactions that Regenerate HOx Radicals and Produce Highly Oxidized Molecules, J. Phys. Chem. A, 123, 906–919, https://doi.org/10.1021/acs.jpca.8b09738, 2019.
Praske, E., Otkjær, R. V., Crounse, J. D., Hethcox, J. C., Stoltz, B. M., Kjaergaard, H. G., and Wennberg, P. O.: Atmospheric autoxidation is increasingly important in urban and suburban North America, P. Natl. Acad. Sci. USA, 115, 64–69, https://doi.org/10.1073/pnas.1715540115, 2018.
Praske, E., Otkjær, R. V., Crounse, J. D., Hethcox, J. C., Stoltz, B. M., Kjaergaard, H. G., and Wennberg, P. O.: Intramolecular Hydrogen Shift Chemistry of Hydroperoxy-Substituted Peroxy Radicals, J. Phys. Chem. A, 123, 590–600, https://doi.org/10.1021/acs.jpca.8b09745, 2019.
Purvis, G. D. and Bartlett, R. J.: A full coupled-cluster singles and doubles model: The inclusion of disconnected triples, J. Chem. Phys., 76, 1910, https://doi.org/10.1063/1.443164, 1982.
Ray, D., Redfearn, A., and Waddington, D. J.: Gas-Phase Oxidation of Alkenes- Decomposition of Hydroxy-Substituted Peroxyl Radicals, J. Chem. Soc. Perkin T., 2, 540–543, https://doi.org/10.1039/p29730000540, 1973a.
Ray, D. J. M., Ruiz Diaz, R., and Waddington, D. J.: Gas-phase oxidation of butene-2: The role of acetaldehyde in the reaction, Symp. Int. Combust., 14, 259–266, https://doi.org/10.1016/S0082-0784(73)80026-8, 1973b.
Saunders, S. M., Jenkin, M. E., Derwent, R. G., and Pilling, M. J.: Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part A): tropospheric degradation of non-aromatic volatile organic compounds, Atmos. Chem. Phys., 3, 161–180, https://doi.org/10.5194/acp-3-161-2003, 2003.
Sharma, S., Raman, S., and Green, W. H.: Intramolecular Hydrogen Migration in Alkylperoxy and Hydroperoxyalkylperoxy Radicals: Accurate Treatment of Hindered Rotors, J. Phys. Chem. A, 114, 5689–5701, https://doi.org/10.1021/jp9098792, 2010.
Teng, A. P., Crounse, J. D., and Wennberg, P. O.: Isoprene Peroxy Radical Dynamics, J. Am. Chem. Soc., 139, 5367–5377, https://doi.org/10.1021/jacs.6b12838, 2017.
Tomas, A., Villenave, E., and Lesclaux, R.: Reactions of the HO2 radical with CH3CHO and CH3C(O)O2 in the gas phase, J. Phys. Chem. A, 105, 3505–3514, https://doi.org/10.1021/jp003762p, 2001.
Truhlar, D. G., Garrett, B. C., and Klippenstein, S. J.: Current Status of Transition-State Theory, J. Phys. Chem., 100, 12771–12800, https://doi.org/10.1021/jp953748q, 1996.
Vereecken, L.: Computational study of the stability of α-nitroxy-substituted alkyl radicals, Chem. Phys. Lett., 466, 127–130, https://doi.org/10.1016/j.cplett.2008.10.042, 2008.
Vereecken, L.: H-migration in Alkylperoxy Radicals in the Atmosphere: Theory-based SAR Development, in: 22nd International Symposium on Gas Kinetics, Boulder, CO, US, 2012.
Vereecken, L.: Reaction mechanisms for the atmospheric oxidation of monocyclic aromatic compounds, in: Advances in Atmospheric Chemistry: Volume 2: Organic Oxidation and Multiphase Chemistry, vol. 1, edited by: Barker, J. R., Steiner, A. L., and Wallington, T. J., World Scientific Publishing Co. Pte. Ltd., Singapore, 377–527, 2019.
Vereecken, L. and Peeters, J.: The 1,5-H-shift in 1-butoxy: A case study in the rigorous implementation of transition state theory for a multirotamer system, J. Chem. Phys., 119, 5159–5170, https://doi.org/10.1063/1.1597479, 2003.
Vereecken, L. and Peeters, J.: A structure–activity relationship for the rate coefficient of H-migration in substituted alkoxy radicals, Phys. Chem. Chem. Phys., 12, 12608–12620, https://doi.org/10.1039/c0cp00387e, 2010a.
Vereecken, L. and Peeters, J.: Hydrogen migration in alkoxy and alkylperoxy radicals, in: 21th International Symposium on Gas Kinetics, Leuven, Belgium, 2010b.
Vereecken, L., Nguyen, T. L., Hermans, I., and Peeters, J.: Computational study of the stability of alpha-hydroperoxyl- or alpha-alkylperoxyl substituted alkyl radicals, Chem. Phys. Lett., 393, 432–436, https://doi.org/10.1016/j.cplett.2004.06.076, 2004.
Vereecken, L., Novelli, A., and Taraborrelli, D.: Unimolecular decay strongly limits concentration of Criegee intermediates in the atmosphere, Phys. Chem. Chem. Phys., 19, 31599–31612, https://doi.org/10.1039/C7CP05541B, 2017.
Vereecken, L., Aumont, B., Barnes, I., Bozzelli, J. W., Goldman, M. J., Green, W. H., Madronich, S., Mcgillen, M. R., Mellouki, A., Orlando, J. J., Picquet-Varrault, B., Rickard, A. R., Stockwell, W. R., Wallington, T. J., and Carter, W. P. L.: Perspective on Mechanism Development and Structure-Activity Relationships for Gas-Phase Atmospheric Chemistry, Int. J. Chem. Kinet., 50, 435–469, https://doi.org/10.1002/kin.21172, 2018.
Veyret, B., Lesclaux, R., Rayez, M.-T., Rayez, J.-C., Cox, R. A., and Moortgat, G. K.: Kinetics and Mechanism of the Photooxidation of Formaldehyde .1. Flash-Photolysis Study, J. Phys. Chem., 93, 2368–2374, https://doi.org/10.1021/j100343a033, 1989.
Villano, S. M., Huynh, L. K., Carstensen, H.-H., and Dean, A. M.: High-Pressure Rate Rules for Alkyl + O-2 Reactions. 1. The Dissociation, Concerted Elimination, and Isomerization Channels of the Alkyl Peroxy Radical, J. Phys. Chem. A, 115, 13425–13442, https://doi.org/10.1021/jp2079204, 2011.
Wang, K., Villano, S. M., and Dean, A. M.: Reactivity–Structure-Based Rate Estimation Rules for Alkyl Radical H Atom Shift and Alkenyl Radical Cycloaddition Reactions, J. Phys. Chem. A, 119, 7205–7221, https://doi.org/10.1021/jp511017z, 2015.
Wang, S., Riva, M., Yan, C., Ehn, M., and Wang, L.: Primary Formation of Highly Oxidized Multifunctional Products in the OH-Initiated Oxidation of Isoprene: A Combined Theoretical and Experimental Study, Environ. Sci. Technol., 52, 12255–12264, https://doi.org/10.1021/acs.est.8b02783, 2018.
Wennberg, P. O., Bates, K. H., Crounse, J. D., Dodson, L. G., McVay, R. C., Mertens, L. A., Nguyen, T. B., Praske, E., Schwantes, R. H., Smarte, M. D., St Clair, J. M., Teng, A. P., Zhang, X. and Seinfeld, J. H.: Gas-Phase Reactions of Isoprene and Its Major Oxidation Products, Chem. Rev., 118, 3337–3390, https://doi.org/10.1021/acs.chemrev.7b00439, 2018.
Xing, L., Lucas, J., Wang, Z., Wang, X., and Truhlar, D. G.: Hydrogen shift isomerizations in the kinetics of the second oxidation mechanism of alkane combustion. Reactions of the hydroperoxypentylperoxy OOQOOH radical, Combust. Flame, 197, 88–101, https://doi.org/10.1016/j.combustflame.2018.07.013, 2018.
Xu, L., Moller, K. H., Crounse, J. D., Otkjwr, R., Kjaergaard, H. G., and Wennberg, P. O.: Unimolecular Reactions of Peroxy Radicals Formed in the Oxidation of α-Pinene and β-Pinene by Hydroxyl Radicals, J. Phys. Chem. A, 123, 1661–1674, https://doi.org/10.1021/acs.jpca.8b11726, 2019.
Yao, Q., Sun, X.-H., Li, Z.-R., Chen, F.-F., and Li, X.-Y.: Pressure-Dependent Rate Rules for Intramolecular H-Migration Reactions of Hydroperoxyalkylperoxy Radicals in Low Temperature, J. Phys. Chem. A, 121, 3001–3018, https://doi.org/10.1021/acs.jpca.6b10818, 2017.
Zhang, F. and Dibble, T. S.: Effects of Olefin Group and Its Position on the Kinetics for Intramolecular H-Shift and HO2 Elimination of Alkenyl Peroxy Radicals, J. Phys. Chem. A, 115, 655–663, https://doi.org/10.1021/jp1111839, 2011.
Zhao, Y. and Truhlar, D. G.: The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 120, 215–241, https://doi.org/10.1007/s00214-007-0310-x, 2008.
Zhao, Y., Schultz, N. E., and Truhlar, D. G.: Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions, J. Chem. Theory Comput., 2, 364–382, https://doi.org/10.1021/ct0502763, 2006.
- Abstract
- Introduction
- Methodology
- Structure–activity relationship
- SAR validation and scope of applicability
- Implications of rapid H atom scrambling in HOO-RO2
- The post-H-migration reaction dynamics
- Further experimental verification of peroxy radical reaction mechanisms
- Discussion and conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Methodology
- Structure–activity relationship
- SAR validation and scope of applicability
- Implications of rapid H atom scrambling in HOO-RO2
- The post-H-migration reaction dynamics
- Further experimental verification of peroxy radical reaction mechanisms
- Discussion and conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement