Thermodynamic properties of isoprene- and monoterpene-derived organosulfates estimated with COSMOtherm

Organosulfates make significant contributions to atmospheric secondary organic aerosol (SOA), but little is known about the thermodynamic properties of atmospherically relevant organosulfates. We have used the COSMOtherm program to calculate both the gas- and condensed-phase properties of previously identified atmospherically relevant monoterpene- and isoprene-derived organosulfates. Properties include solubilities, activities and saturation vapor pressures, which are critical to the aerosol-phase stability and atmospheric impact of organosulfate SOA. Based on the estimated saturation vapor pressures, the organosulfates of this study can all be categorized as semi-volatile or low-volatile, with saturation vapor pressures 4 to 8 orders of magnitude lower than that of sulfuric acid. The estimated pK_a values of all the organosulfates indicate a high degree of dissociation in water, leading in turn to high dissociation-corrected solubilities. In aqueous mixtures with inorganic sulfate, COSMOtherm predicts a salting-out of both the organosulfates and their sodium salts from inorganic co-solutes. The salting-out effect of ammonium sulfate (less acidic) is stronger than of ammonium bisulfate (more acidic). Finally, COSMOtherm predicts liquid–liquid-phase separation in systems containing water and monoterpene-derived organosulfates. The COSMOtherm-estimated properties support the observed stability of organosulfates as SOA constituents and their long-range transport in the atmosphere but also show significant variation between specific compounds and ambient conditions.

1 Introduction

Organosulfates (R−OSO₃H, OS) have been identified as components of atmospheric secondary organic aerosol (SOA) from a variety of environments (Surratt et al., 2007; Glasius et al., 2018a, b). In the Amazon, the contribution of organic sulfate was found to be 3 %–42 % of the total aerosol sulfate for the compounds measured using aerosol mass spectrometry (Glasius et al., 2018a). In Atlanta, Georgia, organosulfates accounted for 16.5 % of the total organic carbon of fine particulate matter (PM_2.5) (Hettiyadura et al., 2019).

Multiple laboratory studies have shown that organosulfates are formed in the condensed phase from reactions between organic molecules and either a sulfate ion (${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$) (Iinuma et al., 2009; Minerath and Elrod, 2009) or a sulfate radical (${\mathrm{SO}}_{\mathrm{4}}^{\cdot -}$) (Schindelka et al., 2013; Wach et al., 2019). Organosulfates have been seen to form, for instance, from oxidation products of monoterpenes (Surratt et al., 2008) and pinonaldehyde (Liggio and Li, 2006) in the presence of acidified sulfate seed and from isoprene-derived organosulfates in the presence of sulfate (Darer et al., 2011). Some studies have suggested that the formation of organosulfate correlates with the acidity of the aerosol particles (Chan et al., 2011) such that more dilute acidic sulfate aerosol leads to a lower reactive uptake of isoprene epoxydiol (C₅H₁₀O₃, IEPOX) (Zhang et al., 2018), while other studies suggest that the abundance of the formed organosulfates correlates only with the sulfate content in the aerosol (Xu et al., 2015; Budisulistiorini et al., 2015).

Recent measurements close to Beijing using a Filter Inlet for Gas and Aerosol (FIGAERO) chemical ionization mass spectrometer (CIMS) have shown that sulfur-containing organic compounds, such as organosulfates, organosulfonates and nitrooxy organosulfates, can also be present in the gas phase (Le Breton et al., 2018). Higher temperatures promote the presence of sulfur compounds in the gas phase, and furthermore the partitioning to the particle phase was found to be dependent on ambient relative humidity. In urban areas, such as Xi'an in northwestern China, organosulfates are primarily of anthropogenic origin (Huang et al., 2018), but in semirural locations 40 km northwest of Beijing, up to 19 % of the sulfur-containing organics have been identified to be of biogenic origin (Le Breton et al., 2018).

Very little is known of the physicochemical properties of specific atmospherically relevant organosulfates and how they affect the properties of SOA. This is in part due to challenges related to sampling and isolating sufficient amounts of organosulfate material from atmospheric organic aerosol for the subsequent analysis of single component properties, as well as synthesizing adequate amounts of known organosulfate reference compounds. The hygroscopic properties of organosulfate-containing aerosol have been measured using sodium salts of alkane sulfates (Woods III et al., 2007; Estillore et al., 2016) and limonene-derived organosulfates (Hansen et al., 2015). Limonene-derived organosulfate was demonstrated to lower the surface tension of aqueous solutions even more effectively than atmospherically relevant strong organic acids (Hansen et al., 2015). The effect of surface activity was evident in both subsaturated hygroscopic growth and measured cloud condensation nuclei (CCN) properties of limonene-derived organosulfate and its mixtures with ammonium sulfate (Hansen et al., 2015). The addition of organosulfates lowers the relative humidity of deliquescence and efflorescence transitions of sodium chloride aerosol (Estillore et al., 2016). In addition, Nguyen et al. (2014a, b) have seen indications of the long-range transport of organosulfates, suggesting that organosulfates must have sufficiently low volatilities to remain in the aerosol phase over a wide range of atmospheric conditions.

In this study, we use the COSMOtherm program to estimate different thermodynamic properties related to the gas- and condensed-phase equilibrium of organosulfates and IEPOX in both pure water and aqueous mixtures with ammonium sulfate ((NH₄)₂SO₄, AS) and bisulfate (NH₄HSO₄, ABS). The accuracy of COSMOtherm pK_a calculations (parameterization BP_TZVPD_FINE_C30_1601) is 0.65 log units (root mean square deviation – RMSD) (Klamt et al., 2016), and experimental saturation vapor pressures can be predicted within a factor of 2 with a tendency to overpredict experimental values of carboxylic acids (Schröder et al., 2016).

Figures 1 and 2 show the monoterpene- and isoprene-derived organosulfates, respectively, studied here. These compounds have previously been identified as components of atmospheric aerosol (Surratt et al., 2007, 2008, 2010; Iinuma et al., 2009; Hansen et al., 2015). α-Pinene-OS-1 and α-pinene-OS-2, and all of the β-pinene- and limonene-derived organosulfates are products of the monoterpene + OH reaction. α-Pinene-OS-3 is formed from pinonaldehyde, α-pinene-OS-4 from an oxidation product of α-pinene + OH, and α-pinene-OS-5 and α-pinene-OS-6 are derived from pinonic acid. Isoprene-OS-1 and isoprene-OS-2 are proposed to be formed from the aldehyde–keto form of an isoprene OH oxidation product in low-NO_x conditions. Isoprene-OS-3 and isoprene-OS-4 are likely formed from a nucleophilic attack by sulfate on the epoxy group of IEPOX (Darer et al., 2011). In field measurements in the US (Hettiyadura et al., 2017, 2019), an organosulfate corresponding to the chemical formula of isoprene-OS-3 and isoprene-OS-4 dominated the bisulfate mass of PM_2.5. Since primary organosulfates are more stable against hydrolysis than tertiary organosulfates (Darer et al., 2011), isoprene-OS-3 is likely the more abundant isomer, compared to isoprene-OS-4, in acidic aerosol.

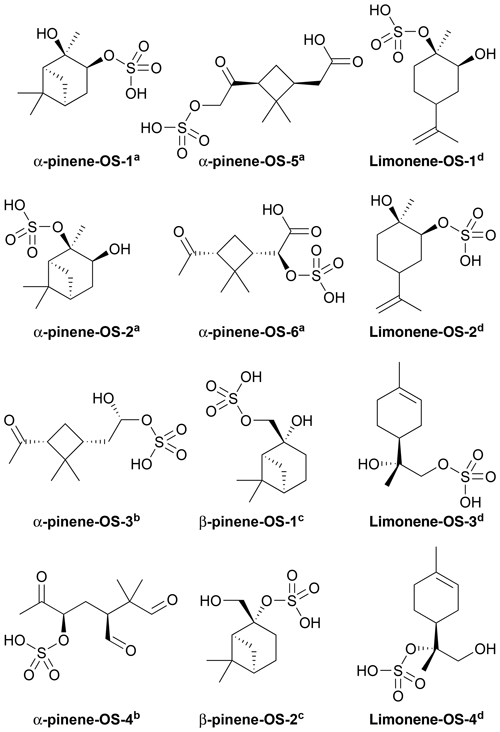
Figure 1 Structures of the studied monoterpene-derived organosulfates, provided by ^aSurratt et al. (2008), ^bSurratt et al. (2007), ^cIinuma et al. (2009) and ^dHansen et al. (2015).

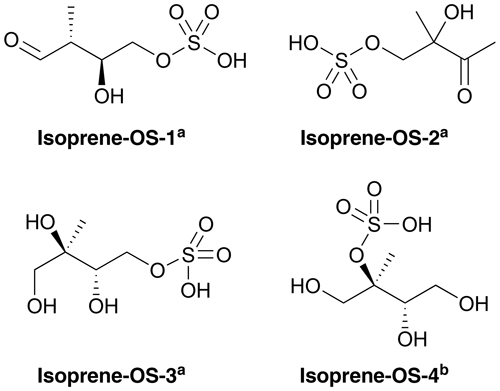
Figure 2 Structures of the studied isoprene-derived organosulfates, provided by ^aSurratt et al. (2007) and ^bSurratt et al. (2010). Isoprene-OS-3 and isoprene-OS-4 are IEPOX-derived organosulfates.

For comparison to monoterpene- and isoprene-derived organosulfate, we also studied the atmospherically abundant IEPOX (C₅H₁₀O₃; see the different isomers in Fig. S1 of the Supplement) and the smallest organosulfate, methyl bisulfate (CH₃OSO₃H).

2 Computational methods

We used COSMOtherm release 19 (COSMOtherm, 2019) to estimate several thermodynamic properties, such as acidity (pK_a), Henry's law solubility, activity and vapor pressure. The COSMOtherm program is based on the conductor-like screening model for real solvents (COSMO-RS; Klamt, 1995; Klamt et al., 1998; Eckert and Klamt, 2002). COSMOtherm combines quantum chemistry and statistical thermodynamics to predict the condensed-phase properties of liquids as well as partitioning between condensed and gas phases. Quantum chemical calculations provide input files (cosmo-files) for COSMOtherm, and the same files can be used to estimate properties in various solutions. In addition, multiple conformers can be included in COSMOtherm calculations to improve the description of conformer distributions in different solutions. Below we explain in detail how the input files for the COSMOtherm calculations were computed and give definitions used by COSMOtherm to estimate each of the properties. More detailed explanations for all of the methods can be found in the COSMOtherm reference manual (Eckert and Klamt, 2019). Without experimental reference data, we are not able to estimate the error for individual compounds. The error estimates are the same for all studied compounds, and we therefore do not show error bars in the figures.

2.1 COSMO input file generation

To generate the input files for the COSMOtherm calculations, we used the COSMOconf program version 4.3 (COSMOconf, 2013). COSMOconf contains conformer generation algorithms, different levels of theory of quantum chemical calculations for both the condensed and the gas phase, and various methods for reducing the number of conformers in a way that does not compromise the accuracy of the COSMOtherm calculations.

Including multiple conformers in the COSMOtherm calculations is important when the conformers have different polarities, as is the case for molecules that are able to form intramolecular hydrogen bonds (Eckert and Klamt, 2019). For finding an initial set of conformers, COSMOconf uses various conformer-generating algorithms. However, none of these methods allow for the systematic conformer sampling of the molecules. The nonsystematic conformer generation in COSMOconf has been shown to lead to significantly different results in COSMOtherm depending on the initial geometry with molecules containing hydroxy and hydroperoxy functional groups (Kurtén et al., 2018). Based on the recommendation by Kurtén et al. (2018), we therefore used the systematic conformer sampling with the Merck molecular force field (MMFF94) in the Spartan '14 program (Wavefunction Inc., 2014). In addition to the most common carbon and oxygen atom types, the MMFF94 is parameterized for the atom types of a sulfate group sulfur and oxygens (Halgren, 1996). This ensures that all unique conformers are found using the systematic sampling.

The conformers from Spartan '14 were used as input to COSMOconf, and the TURBOMOLE program package version 7.11 (TURBOMOLE, 2010) was used for the quantum chemical calculations. Our calculation template in COSMOconf follows the BP-TZVPD-FINE-COSMO.xml template found in the program, omitting the conformational sampling step at the beginning and setting the cutoffs (based on energy and the number of conformers) of conformers high enough that no conformers were discarded. The gas-phase conformers were obtained by BP/def-TZVP gas-phase geometry optimizations and BP/def2-TZVPD single-point energy calculations of the condensed-phase geometries from COSMOconf using the calculate function in TURBOMOLE. The BP/def2-TZVPD-FINE//BP/def-TZVP level .cosmo and .energy files from COSMOconf and TURBOMOLE were used in COSMOtherm calculations. In addition, .cosmo, .energy and .vap files for H₂O and the inorganic ions were taken from the COSMObase17 database (COSMObase, 2011).

2.2 COSMOtherm calculations

In our COSMOtherm calculations, we have used the most recent BP_TZVPD_FINE_19 parameterization. All calculations were done at 298.15 K. To the best of our knowledge, experimental information on the pure component phase state of most atmospherically relevant organics is not available. We therefore assume that all of the organosulfates (OS) and the isoprene epoxydiols (IEPOX) are liquid at 298.15 K. Without melting point and heat of fusion data, we are not able to accurately estimate the solubilities of solid-phase organosulfates. If the OS and IEPOX are solid at 298.15 K, the solubility results shown here are the mole fractions of the virtual liquid of the solute in the two liquid phases of a solid–liquid–liquid equilibrium. Sodium salts of the organosulfates (R−OSO₃Na, NaOS) are similar to sodium dodecyl sulfate (SDS) with regard to molar mass and functionality. SDS is solid at 298.15 K, and we therefore assume that NaOS is solid at this temperature. The organic compounds are treated as solutes and the aqueous solutions (pure water or binary aqueous ammonium salt mixtures) as the solvent.

To select the maximum number of conformers needed for COSMOtherm calculations, convergence on the number of conformers was tested by calculating the activities of isoprene-OS-1. In these test calculations, the change in activity of isoprene-OS-1 and H₂O (in different mole fractions of isoprene-OS-1 in water) was at most 0.005 between 40 and 45 conformers of isoprene-OS-1. Based on this, the maximum number of conformers was set to 40 for larger monoterpene-derived organosulfates and 50 for the smaller isoprene-derived molecules.

In COSMOtherm calculations, conformers are weighted according to the Boltzmann distribution based on the sum of their solvated energy and chemical potential in the solution. However, normally only conformers with the lowest solvated energies are selected for COSMOtherm calculations. If the total number of unique conformers is high, not all conformers can be included in the COSMOtherm calculation. When only a fraction of all conformers is used in a COSMOtherm calculation, only those containing intramolecular hydrogen bonds are used, as they have the lowest solvated energies. However, the interaction between a compound and water is more favorable for conformers containing no intramolecular hydrogen bonds. Therefore, in aqueous solutions, the chemical potential of conformers containing no intramolecular hydrogen bonds is much lower than that of conformers that contain multiple hydrogen bonds. If a compound contains more unique conformers than can be included in COSMOtherm calculations, more attention should be paid to selecting the conformers to represent the conformer distribution in the studied solutions.

Kurtén et al. (2018) found that COSMOtherm (release 18; COSMOtherm, 2018) overestimates the effect of intramolecular hydrogen bonds and recommended that only conformers containing no intramolecular hydrogen bonds should be used in saturation vapor pressure calculations. We tested the difference in saturation vapor pressures calculated using releases 18 and 19 (parameterizations BP_TZVPD_FINE_18 and BP_TZVPD_FINE_19, respectively) and found that differences between the two parameterizations are larger using all conformers than when only conformers containing no intramolecular hydrogen bonds are used. Variation between estimates using different conformer sets is also smaller in release 19 than in release 18. We therefore omitted all conformers containing intramolecular hydrogen bonds from the calculations of OS and IEPOX. Generally, the omission of conformers containing intramolecular hydrogen bonds leads to lower saturation vapor pressures (Kurtén et al., 2018).

The number of intramolecular hydrogen bonds in the condensed phase was determined using release 18 of COSMOtherm. For isoprene-OS-3 and isoprene-OS-4, we only found two and zero conformers containing no hydrogen bonds, respectively. For these two species, we used all conformers containing no full and any number of partial intramolecular hydrogen bonds or one full and no partial intramolecular hydrogen bonds. Many of the deprotonated organosulfates (sodium salt anions) have only conformers that contain intramolecular hydrogen bonds. For this reason, we chose to use all of their lowest-energy conformers in the COSMOtherm calculations involving the NaOS. In the calculation of pK_a we used all conformers, since the calculation uses both the neutral and the ionic species.

2.2.1 Chemical potential

The chemical potential (μ) of a component i in a mixture is defined with respect to the chemical potential in a given reference state μ_i^∘ with constant temperature T and pressure P as

$$\begin{array}{}\text{(1)}& {\mathit{\mu }}_i\left(x_i\right)={\mathit{\mu }}_i{}^{\circ }(T,P)+RT\ln a_i,\end{array}$$

where R is the gas constant, and a_i=a_i(x_i) is the activity of component i at a given actual mole fraction x_i with respect to the chosen reference state. COSMOtherm uses the pseudo-chemical potential (Ben-Naim, 1987) ${\mathit{\mu }}_i^{*}$, which is defined as

$$\begin{array}{}\text{(2)}& {\mathit{\mu }}_i^{*}\left(x_i\right)={\mathit{\mu }}_i{}^{\circ }(T,P)+RT\ln {\mathit{\gamma }}_i,\end{array}$$

where γ_i ($=a_i/x_i$) is the activity coefficient of component i at mole fraction x_i. By definition, the activity coefficient is 1 when component i is in the reference state (${\mathit{\gamma }}_i\left(x_i{}^{\circ }\right)=\mathrm{1}$). This means that in the reference state, chemical potential and pseudo-chemical potential are equal:

$$\begin{array}{}\text{(3)}& {\mathit{\mu }}_i^{*}{}^{\circ }(T,P)={\mathit{\mu }}_i{}^{\circ }(T,P).\end{array}$$

In COSMOtherm, the pseudo-chemical potential of component i in system S is calculated using the σ potential:

$$\begin{array}{}\text{(4)}& {\mathit{\mu }}_i^{*}={\mathit{\mu }}_i^{C,S}+\int p_i\left(\mathit{\sigma }\right){\mathit{\mu }}_{\mathrm{S}}\left(\mathit{\sigma }\right)d\mathit{\sigma },\end{array}$$

where p_i(σ) is the un-normalized σ profile, and μ_S(σ) is the chemical potential of a surface segment with the screening charge density σ (the σ potential), which describes the affinity of the system S to a surface of screening charge density σ. The combinatorial contribution to the chemical potential (${\mathit{\mu }}_i^{C,S}$),

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\mathit{\mu }}_i^{C,S}& =RT\left[\right({\widehat{\mathit{\lambda }}}_{\mathrm{0}}-{\widehat{\mathit{\lambda }}}_{\mathrm{1}}\left)\ln \right(r_i)+{\widehat{\mathit{\lambda }}}_{\mathrm{1}}(\mathrm{1}-{\displaystyle \frac{r_i}{\stackrel{\mathrm{‾}}{r}}}+\ln {\displaystyle \frac{r_i}{\stackrel{\mathrm{‾}}{r}}})\\ & +{\widehat{\mathit{\lambda }}}_{\mathrm{2}}(\mathrm{1}-{\displaystyle \frac{q_i}{\stackrel{\mathrm{‾}}{q}}}+\ln {\displaystyle \frac{q_i}{\stackrel{\mathrm{‾}}{q}}})-{\widehat{\mathit{\lambda }}}_{\mathrm{3}}\ln \left(r_i\right)],\end{array}\end{array}$$

is derived from the similar combinatorial free energy expression. The prefactors ${\widehat{\mathit{\lambda }}}_{\mathrm{0}}$, ${\widehat{\mathit{\lambda }}}_{\mathrm{1}}$ and ${\widehat{\mathit{\lambda }}}_{\mathrm{2}}$ have fixed values, while ${\widehat{\mathit{\lambda }}}_{\mathrm{3}}$ is adjustable. The total volume ($\stackrel{\mathrm{‾}}{r}$) and area ($\stackrel{\mathrm{‾}}{q}$) of all components i are calculated as the mole-fraction-weighted sums of the dimensionless molecular volume (r_i) and area (q_i) of component i, respectively.

2.2.2 Activity coefficient

The activity coefficient of component i at mole fraction x_i in a mixture can be calculated using Eq. (2) as

$$\begin{array}{}\text{(6)}& \ln \left({\mathit{\gamma }}_i\right(x_i\left)\right)={\displaystyle \frac{{\mathit{\mu }}_i^{*}\left(x_i\right)-{\mathit{\mu }}_i{}^{\circ }(T,P)}{RT}}.\end{array}$$

The value of the activity coefficient in a given solution state {x_i} depends on the choice of reference state. As the default reference state, COSMOtherm uses the pure compound ($x_i{}^{\circ }=\mathrm{1}$, labeled as convention I in the following; Levine, 2009) at 10⁵ Pa pressure and 298.15 K temperature. According to Eq. (3), with respect to this reference state, the pseudo-chemical potential is equal to the chemical potential when the system is in the reference state, ${\mathit{\mu }}_i^{*,\mathrm{I}}{}^{\circ }(x_i=\mathrm{1})={\mathit{\mu }}_i^{\mathrm{I}}{}^{\circ }(x_i=\mathrm{1})$, giving

$$\begin{array}{}\text{(7)}& \ln \left({\mathit{\gamma }}_i^{\mathrm{I}}\right(x_i\left)\right)={\displaystyle \frac{{\mathit{\mu }}_i^{*}\left(x_i\right)-{\mathit{\mu }}_i^{*,\mathrm{I}}{}^{\circ }(T,P)}{RT}}.\end{array}$$

Activity coefficient values derived from experiments are often determined with respect to an ideal infinite dilution reference state ($x_i{}^{\circ }\to \mathrm{0}$, labeled as convention II; Levine, 2009). For comparison with such experimentally derived values, activity coefficients for a given actual state {x_i} determined with respect to the pure component reference state (γ^I) can be converted to the infinite dilution reference state (γ^II) as

$$\ln {\displaystyle \frac{{\mathit{\gamma }}_i^{\mathrm{I}}\left(x_i\right)}{{\mathit{\gamma }}_i^{\mathrm{I}}(x_i\to \mathrm{0})}}=\ln {\mathit{\gamma }}_i^{\mathrm{I}}\left(x_i\right)-\ln {\mathit{\gamma }}_i^{\mathrm{I}}(x_i\to \mathrm{0})$$

$$={\displaystyle \frac{{\mathit{\mu }}_i^{*}\left(x_i\right)-{\mathit{\mu }}_i^{*,\mathrm{I}}{}^{\circ }(T,P)}{RT}}-{\displaystyle \frac{{\mathit{\mu }}_i^{*}(x_i=\mathrm{0})-{\mathit{\mu }}_i^{*,\mathrm{I}}{}^{\circ }(T,P)}{RT}}$$

$$={\displaystyle \frac{{\mathit{\mu }}_i^{*}\left(x_i\right)-{\mathit{\mu }}_i^{*}(x_i=\mathrm{0})}{RT}}$$

$$={\displaystyle \frac{{\mathit{\mu }}_i^{*}\left(x_i\right)-{\mathit{\mu }}_i^{*,\mathrm{II}}{}^{\circ }(T,P)}{RT}}$$

$$\begin{array}{}\text{(8)}& =\ln {\mathit{\gamma }}_i^{\mathrm{II}}\left(x_i\right),\end{array}$$

where ${\mathit{\mu }}_i^{*}(x_i=\mathrm{0})={\mathit{\mu }}_i^{*,\mathrm{II}}{}^{\circ }(T,P)$ follows from Eq. (2), since γ^II=1 at the reference state ($x_i{}^{\circ }\to \mathrm{0}$).

To the best of our knowledge, no experimental data on the isoprene- and monoterpene-derived organosulfates are currently available. Here, we therefore do not show activity coefficients for these compounds with respect to the infinite dilution reference state, but they can be calculated from our data using Eq. (8).

2.2.3 Solubility

We calculate both the absolute and relative solubilities of organosulfate solutes. The absolute solubilities are estimated by finding the liquid–liquid equilibrium (LLE; for liquid solutes) or the solid–liquid equilibrium (SLE; for solid solutes) using the solid–liquid equilibrium solver (SLESOL) in COSMOtherm. For liquid solutes, the SLESOL finds the LLE between two phases (α and β) using the liquid-phase equilibrium condition4:

$$\begin{array}{}\text{(9)}& a_i^{\mathrm{I},\mathit{\alpha }}=a_i^{\mathrm{I},\mathit{\beta }}.\end{array}$$

In the LLE, Eq. (9) is true for both the solute and the solvent. Equation (9) is equivalent to the chemical potential of the solute being equal at the solubility limit in both phases, as opposed to the definition of the solubility of a solid solute in which the chemical potential of the solute at the solubility limit is equal to its chemical potential in the pure solute.

Based on their molecular structures, we expect organosulfates to have Brønsted acid properties. The acidity, in terms of the acid constant pK_a (−log ₁₀K_a for the equilibrium constant K_a corresponding to the equilibrium $\mathrm{R}-{\mathrm{OSO}}_{\mathrm{3}}\mathrm{H}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ ⇌ $\mathrm{R}-{\mathrm{OSO}}_{\mathrm{3}}^{-}+{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$), is estimated using the deprotonated organosulfate species. COSMOtherm estimates the pK_a of compound i from the molar free energy (G; kJ mol⁻¹) of the neutral and ionic species at infinite dilution using the linear free energy relationship (LFER):

$$\begin{array}{}\text{(10)}& \mathrm{p}{K}_{\mathrm{a}}^i=c+d(G_i^{\mathrm{anion}}-G_i^{\mathrm{neutral}}).\end{array}$$

The LFER parameters for solvent water ($c=-\mathrm{130.152}$ and d=0.116 mol kJ⁻¹) are taken from COSMOtherm's parameter file. The energy difference ($G_i^{\mathrm{anion}}-G_i^{\mathrm{neutral}}$) is always positive because in a neutral solvent, a neutral compound is more favorable than a charged compound. Relatively lower anion energy (more favorable deprotonation) leads to a smaller energy difference, leading to lower pK_a. The parameterization in COSMOtherm currently enables the calculation of pK_a only in water, dimethylsulfoxide, acetonitrile or heptane. We are therefore not able to estimate pK_a values of the organosulfates in other solvents relevant to this work, specifically aqueous ammonium sulfate and bisulfate solutions.

Dissociation in aqueous solution is expected to enhance solubility compared to the undissociated species. We use pK_a values to calculate a dissociation correction to solubilities. The molar concentration of acid anion (A⁻) after dissociation is calculated using the pH of the solvent (pH=7.0 for water) and pK_a for the solute:

$$\begin{array}{}\text{(11)}& c_i^{A^{-}}=-\mathrm{0.5}\times {\mathrm{10}}^{-\mathrm{pH}}+\sqrt{\mathrm{0.25}\times {\mathrm{10}}^{-\mathrm{2}\mathrm{pH}}+c_i^{\mathrm{HA}}{\mathrm{10}}^{-\mathrm{p}{K}_{\mathrm{a}}}}.\end{array}$$

Here, the molar concentration of dissolved undissociated molecular organosulfate (HA) is calculated from the solubility mole fraction estimated using the SLESOL method, the mole-fraction-weighted density (ρ) of the system and the average molar mass of the solution ($M_{\mathrm{solution}}={\sum }_i{x}_i{M}_i$, where M_i is the molar mass of component i):

$$\begin{array}{}\text{(12)}& c_i^{\mathrm{HA}}=x_i{\displaystyle \frac{\mathit{\rho }}{M_{\mathrm{solution}}}}.\end{array}$$

The calculation of composition-dependent solution densities is explained in Sect. S1 of the Supplement. The dissociation-corrected mole fraction solubility (x^DC) is then calculated from the sum of the anionic and molecular molar concentrations using Eq. (12):

$$\begin{array}{}\text{(13)}& x_i^{\mathrm{DC}}=(c_i^{\mathrm{HA}}+c_i^{{\mathrm{A}}^{-}}){\displaystyle \frac{M_{\mathrm{solution}}}{\mathit{\rho }}}.\end{array}$$

The average molar mass and composition-weighted density of the solution can be expressed using the mole fraction of the organic compound (see Sect. S1 for the equations), which is calculated iteratively from the dissociation-corrected molar concentration $c_i^{\mathrm{HA}}+c_i^{{\mathrm{A}}^{-}}$.

For solid solutes, here the organosulfate sodium salts, the SLESOL finds the solid–liquid equilibrium (SLE) using the solid–liquid-phase equilibrium condition:

$$\begin{array}{}\text{(14)}& {\log }_{\mathrm{10}}\left(x_{\mathrm{SOL},i}\right)={\displaystyle \frac{{\mathit{\mu }}_i^{*,\mathrm{I}}{}^{\circ }-{\mathit{\mu }}_i^{*}\left(x_i\right)-\mathrm{\Delta }{G}_{\mathrm{fus}}\left(T\right)}{RT\ln \left(\mathrm{10}\right)}}.\end{array}$$

The temperature-dependent molar free energy of fusion (ΔG_fus>0 kJ mol⁻¹ for solid solutes) is an experimentally determined parameter, which can also be calculated from the experimental molar heat of fusion (ΔH_fus) and melting temperature (T_melt) using the Schröder–van Laar equation (Prigogine and Defay, 1954):

$$\begin{array}{}\text{(15)}& \begin{array}{rl}\mathrm{\Delta }{G}_{\mathrm{fus}}\left(T\right)& =\mathrm{\Delta }{H}_{\mathrm{fus}}(\mathrm{1}-{\displaystyle \frac{T}{T_{\mathrm{melt}}}})-\mathrm{\Delta }{C}_{p,\mathrm{fus}}(T_{\mathrm{melt}}-T)\\ & +\mathrm{\Delta }{C}_{p,\mathrm{fus}}T\ln {\displaystyle \frac{T_{\mathrm{melt}}}{T}}.\end{array}\end{array}$$

The heat capacity of fusion (ΔC_p,fus) can be obtained from experiments, estimated as

$$\begin{array}{}\text{(16)}& \mathrm{\Delta }{C}_{p,\mathrm{fus}}={\displaystyle \frac{\mathrm{\Delta }{H}_{\mathrm{fus}}}{T_{\mathrm{melt}}}},\end{array}$$

or assumed to be zero. Equation (16) is physically a better estimate than $\mathrm{\Delta }{C}_{p,\mathrm{fus}}=\mathrm{0}$ $\mathrm{kJ}{\mathrm{mol}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$ for nonspherical and neutral compounds at temperatures above 150 K and within 200 K of the melting point (Eckert and Klamt, 2019). Since experimental data are not available for the organosulfate sodium salts, we use the COSMOtherm estimate of ΔC_p,fus in solubility calculations for solid solutes. As the melting point and heat of fusion, we use the experimental values of a related organosulfate compound, SDS, T_melt=478.15 K (Rumble, 2018) and ΔH_fus=50 kJ mol⁻¹ (the heat of fusion of hydrated solid surfactant to micellar state; Shinoda et al., 1966).

In COSMOtherm, small atomic metal ions have extreme screening charge densities ($\mathit{\sigma }<-\mathrm{0.025}$ e Å⁻² or σ>0.025 e Å⁻²). In reality, extreme screening charge densities of ions would lead to the formation of a solvation shell, whereby polar solvent molecules form strong hydrogen bonds with the ion. This is not accounted for in COSMOtherm, which leads to unrealistic behavior of the sodium ion in water. To improve the description of sodium cation solvation in the case of the organosulfate sodium salts, we use a hydrated sodium cation instead of the dry sodium cation. Hydration of ions has previously been used in a model combining COSMOtherm to describe the short-range ion–molecule and molecule–molecule interactions in combination with the Pitzer–Debye–Hückel solvation model (PDHS) to describe long-range ion–ion interactions (Toure et al., 2014). The choice of hydration number for sodium is explained in more detail in Sect. S2 and Fig. S2. The screening charge densities of larger ions, such as ammonium, sulfate and bisulfate, are less extreme (−0.025 e Å${}^{-\mathrm{2}}<\mathit{\sigma }<\mathrm{0.025}$ e Å⁻²; see Fig. S4), and the non-hydrated ions can be used in COSMOtherm calculations.

We also calculate solubilities in ternary systems containing water, organosulfate (OS or NaOS) and inorganic salt ((NH₄)₂SO₄ or NH₄HSO₄). In these cases, the inorganic salt is considered part of the solvent and treated here in the form of its individual dissociated ions, leading to differently scaled mole fractions. The conversion of results from COSMOtherm's framework to the ternary system framework is explained in Sect. S2 and Fig. S3.

Relative organic solubilities with respect to either the binary water–organic system or the ternary water–organic–inorganic salt system are calculated using the relative screening option in COSMOtherm. The relative solubilities are estimated using a zeroth-order approximation of the solubility ($x_{\mathrm{SOL},i}^{\left(\mathrm{0}\right)}$):

$$\begin{array}{}\text{(17)}& {\log }_{\mathrm{10}}\left(x_{\mathrm{SOL},i}^{\left(\mathrm{0}\right)}\right)={\displaystyle \frac{{\mathit{\mu }}_i^{*,\mathrm{I}}{}^{\circ }-{\mathit{\mu }}_i^{*}(x_i=\mathrm{0})-max(\mathrm{0},\mathrm{\Delta }{G}_{\mathrm{fus}}(T\left)\right)}{RT\ln \left(\mathrm{10}\right)}},\end{array}$$

where the solubility of component i (in our case OS or NaOS) is assumed to be small enough to consider the component in a state of infinite dilution (x_i=0) instead of the actual composition at the solubility limit (x_i=x_SOL). In this approximation, the concentration of solute in the solvent is therefore assumed to be very small. The advantage of this zeroth-order approximation in the solubility calculation of solid solutes is that the solubility is calculated using only the chemical potential of the solute in the infinite dilution of the solvent, while the reference-state (pure solute) chemical potential and the free energy of fusion cancel out. For a solute i in two different systems with solvents S1 and S2,

$$\begin{array}{}\text{(18)}& \begin{array}{rl}{\log }_{\mathrm{10}}\left(x_{\mathrm{SOL},i}^{S\mathrm{1},\left(\mathrm{0}\right)}\right)& -{\log }_{\mathrm{10}}\left(x_{\mathrm{SOL},i}^{S\mathrm{2},\left(\mathrm{0}\right)}\right)\\ & ={\displaystyle \frac{{\mathit{\mu }}_i^{*,\mathrm{I}}{}^{\circ }-{\mathit{\mu }}_i^{*,S\mathrm{1}}(x_i=\mathrm{0})-\mathrm{\Delta }{G}_{\mathrm{fus}}\left(T\right)}{RT\ln \left(\mathrm{10}\right)}}\\ & -{\displaystyle \frac{{\mathit{\mu }}_i^{*,\mathrm{I}}{}^{\circ }-{\mathit{\mu }}_i^{*,S\mathrm{2}}(x_i=\mathrm{0})-\mathrm{\Delta }{G}_{\mathrm{fus}}\left(T\right)}{RT\ln \left(\mathrm{10}\right)}}\\ & ={\displaystyle \frac{-{\mathit{\mu }}_i^{*,S\mathrm{1}}(x_i=\mathrm{0})+{\mathit{\mu }}_i^{*,S\mathrm{2}}(x_i=\mathrm{0})}{RT\ln \left(\mathrm{10}\right)}}.\end{array}\end{array}$$

The relative screening is especially useful in cases in which the solute is solid and the experimental free energy of fusion is unknown.

2.2.4 Vapor pressure and Henry's law

The saturation vapor pressure (P_sat) of a pure compound (i) is estimated from the molar free energy of the compound in the liquid phase ($G_i^{\left(l\right)}$) and the gas phase ($G_i^{\left(g\right)}$):

$$\begin{array}{}\text{(19)}& P_{\mathrm{sat},i}=e^{-\frac{G_i^{\left(l\right)}-G_i^{\left(g\right)}}{RT}}\times {\mathrm{10}}^{\mathrm{5}}\mathrm{Pa}.\end{array}$$

COSMOtherm calculates the infinite dilution Henry's law volatility ($H_{\mathrm{vol}}^{\mathrm{\infty }}$, in pressure units) as a product of the pure solute saturation vapor pressure and the activity coefficient of the solute in the infinite dilution state (${\mathit{\gamma }}_i^{\mathrm{I}}(x_i\to \mathrm{0})$):

$$\begin{array}{}\text{(20)}& H_{\mathrm{vol},i}^{\mathrm{\infty }}=P_{\mathrm{sat},i}\cdot {\mathit{\gamma }}_i^{\mathrm{I}}(x_i\to \mathrm{0}).\end{array}$$

This formula is based on the assumption that the solubility of compound i in the solvent is small, allowing for the use of the zeroth-order solubility approximation ($x_{\mathrm{SOL},i}^{\left(\mathrm{0}\right)}\cong \mathrm{1}/{\mathit{\gamma }}_i^{\mathrm{I}}(x_i\to \mathrm{0})$). Note that ${\mathit{\gamma }}_i^{\mathrm{I}}(x_i\to \mathrm{0})$ is evaluated at infinite dilution but with respect to the pure component reference state.

Using the density and molar mass of the pure solvent, Henry's law volatilities in units of pressure can be converted to Henry's law solubilities ($H_{\mathrm{sol}}^{\mathrm{\infty }}$; $\mathrm{mol}{\mathrm{m}}^{-\mathrm{3}}{\mathrm{Pa}}^{-\mathrm{1}}$):

$$\begin{array}{}\text{(21)}& H_{\mathrm{sol},i}^{\mathrm{\infty }}={\displaystyle \frac{\mathit{\rho }}{M_{\mathrm{solvent}}\cdot H_{\mathrm{vol},i}^{\mathrm{\infty }}}}.\end{array}$$

The solvent density and molar mass are equal to the corresponding values for the solution under the assumption of infinite dilution. Densities (g cm⁻³) of aqueous (NH₄)₂SO₄ and NH₄HSO₄ solvents in the conversion of Henry's law volatility into Henry's law solubility are calculated using the experimental polynomial fit by Tang and Munkelwitz (1994):

$$\begin{array}{}\text{(22)}& \mathit{\rho }=\mathrm{0.9971}+\sum _{i=\mathrm{1}}^{\mathrm{3}}{A}_i(wt\mathit{\%}{)}^i.\end{array}$$

For ammonium sulfate, $A_{\mathrm{1}}=\mathrm{5.92}\times {\mathrm{10}}^{-\mathrm{3}}$, $A_{\mathrm{2}}=-\mathrm{5.036}\times {\mathrm{10}}^{-\mathrm{6}}$ and $A_{\mathrm{3}}=\mathrm{1.024}\times {\mathrm{10}}^{-\mathrm{8}}$, and for ammonium bisulfate, $A_{\mathrm{1}}=\mathrm{5.87}\times {\mathrm{10}}^{-\mathrm{3}}$, $A_{\mathrm{2}}=-\mathrm{1.89}\times {\mathrm{10}}^{-\mathrm{6}}$ and $A_{\mathrm{3}}=\mathrm{1.763}\times {\mathrm{10}}^{-\mathrm{7}}$.

In addition, we calculate an alternative LLE-based Henry's law solubility using the molar concentration of the solute ($c_i^{\mathrm{HA}}$) obtained from the LLE solubility calculation. This gives an estimate of the Henry's law solubility in a non-dilute solution:

$$\begin{array}{}\text{(23)}& H_{\mathrm{sol},i}^{\mathrm{LLE}}={\displaystyle \frac{c_i^{\mathrm{HA}}}{P_{\mathrm{sat},i}}}.\end{array}$$

This definition also allows for the calculation of the effective Henry's law solubility, whereby the dissociation of the solute is included in the total molar concentration:

$$\begin{array}{}\text{(24)}& H_{\mathrm{sol},i}^{\mathrm{eff}}={\displaystyle \frac{c_i^{\mathrm{HA}}+c_i^{{\mathrm{A}}^{-}}}{P_{\mathrm{sat},i}}}.\end{array}$$

3 Results and discussion

3.1 Solubility in pure water

Solubilities of organics in pure water and of water in the organic-rich phase were calculated using COSMOtherm as the respective mole fractions at the liquid–liquid equilibrium of OS–water mixtures. Results are shown in Fig. 3.

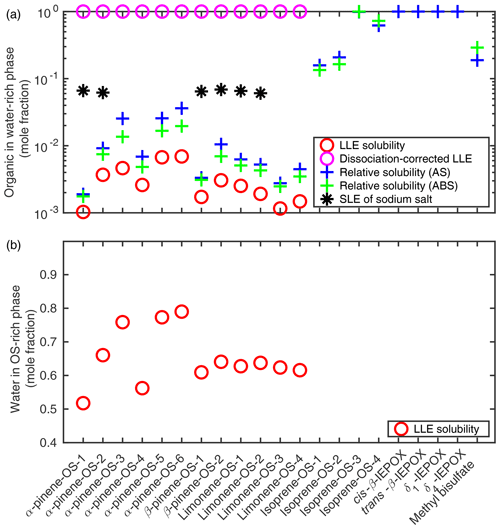
Figure 3 (a) The solubility of organosulfates and their sodium salts in pure water; (b) the solubility of water in the organosulfate phase (T=298.15 K). Solubilities were estimated using the SLESOL method to solve the liquid–liquid (LLE) or solid–liquid (SLE) equilibrium in COSMOtherm. LLE∕SLE was not found for the systems with missing points, indicating that the solute is fully miscible with the solvent. Relative solubilities of organosulfates and IEPOX were calculated using the LLE solubility of each compound in 0.09 mole fraction of the inorganic salt (AS or ABS) as a reference for the pure water solubility.

The LLE was not found for isoprene-derived organosulfates, IEPOX isomers or methyl bisulfate, indicating that these compounds are fully miscible with pure water at 298.15 K. We therefore also calculated the pure water solubilities relative to the organosulfate solubility in a 0.09 mole fraction salt solution by solving the LLE of ternary systems in which the solvent contains 0.09 mole fraction of either ammonium sulfate (AS, (NH₄)₂SO₄) or ammonium bisulfate (ABS, NH₄HSO₄). Solubility calculations for ternary systems are described in more detail in Sect. 3.2. This is done to get a quantitative estimate of the relative solubilities of the compounds that are fully soluble in pure water. The 0.09 mole fraction is below the solubility limit of both (NH₄)₂SO₄ ($x_{\mathrm{SOL},\mathrm{AS}}=\mathrm{0.094}$) and NH₄HSO₄ ($x_{\mathrm{SOL},\mathrm{ABS}}=\mathrm{0.33}$) in water at 298.15 K (Tang and Munkelwitz, 1994). The specific inorganic salt mole fraction was chosen to be as high as possible while within the aqueous solubility limit of the salt to ensure that the organic compounds are typically not fully miscible with the salt solution. Results are shown in Fig. 3 together with corresponding binary organic solubilities. Compared to the binary LLE solubility, the aqueous solubility calculated as a relative solubility for monoterpene-derived organosulfates is on average 3.1 times higher (1.8–5.5) using (NH₄)₂SO₄ solutions as a reference and 2.2 times higher (1.7–2.9) using NH₄HSO₄ solutions. The LLE was not found in the ternary systems containing IEPOX and 0.09 mole fraction of NH₄HSO₄.

Based on LLE calculations, the monoterpene-derived organosulfates are less soluble in the ammonium sulfate and bisulfate solutions than in pure water, which means that the ammonium salts have a salting-out effect on the OS. From the solubilities calculated as relative solubility compared to (NH₄)₂SO₄ and NH₄HSO₄ solutions, we can see that the relative solubility calculation in COSMOtherm overestimates the salting-out effect of both ammonium salts compared to the more accurate LLE calculation. In addition, the salting-out effect of (NH₄)₂SO₄ is overestimated more than that of NH₄HSO₄. The relative solubility calculation uses the zeroth-order solubility approximation, which means that the estimate is less accurate when the absolute solubility of the solute is high. The largest difference between the aqueous LLE and the solubility calculated relative to the ternary LLE is seen for the OS with the higher absolute solubilities.

We see in Fig. 3 that α-pinene-OS-1 has the lowest solubility of all the organosulfates. There are only minor structural differences between α-pinene-OS-1 and α-pinene-OS-2, but this still leads to a factor of 3.6 difference in the calculated solubility. All the β-pinene and limonene organosulfates, with the same functional groups as α-pinene-OS-1 and α-pinene-OS-2, have solubilities between those of α-pinene-OS-1 and α-pinene-OS-2. These results show that even minor differences in the molecular structure, such as the placement of functional groups, can have a large impact on the solubility of organosulfates.

The most soluble monoterpene-derived organosulfates are α-pinene-OS-5 and α-pinene-OS-6, which each have both a carboxylic acid group and a carbonyl group. α-Pinene-OS-4 has a flexible carbon backbone and three carbonyl functionalities; however, it still has a relatively low solubility compared to the other α-pinene-OS. The effect of the different types of oxygen-containing functional groups on the solubilities is caused by their ability to form intermolecular hydrogen bonds with the solvent water. This explains the lower solubility of α-pinene-OS-4, which has mainly hydrogen-bond-accepting carbonyl groups, compared to α-pinene-OS-3, α-pinene-OS-5 and α-pinene-OS-6, which contain hydroxy groups that can act as both H-bond acceptors and donors.

We calculated acid constants (pK_a) for all organosulfates to capture the effect of the dissociation of the neutral molecules in water. Estimated pK_a values of the organosulfates are between −4.57 and −2.37, indicating that all of the organosulfates are strong acids that will likely be strongly dissociated in water. For comparison, we estimated the first pK_a of sulfuric acid with COSMOtherm to be −3.51. The organosulfates are therefore estimated to be of equivalent strength or even stronger acids than H₂SO₄, and thus for all practical purposes they fully dissociate in near-neutral solutions and even solutions at the most atmospherically relevant pH. The pK_a values for all organosulfates and sulfuric acid are shown in Table S1 of the Supplement.

Dissociation-corrected solubilities were calculated from Eq. (11) using the LLE solubilities in pure water and pK_a estimated with COSMOtherm. Molar liquid volumes of the pure organic compounds used to calculate the densities of organic-water solutions for Eq. (12) are shown in Table S7. For all organic compounds, dissociation-corrected solubilities correspond to mole fractions higher than 1. This unphysical result is likely caused by the inability of Eq. (11) to accurately capture the solution behavior of very strongly acidic compounds. This equation is only used to calculate dissociation-corrected solubilities and has no effect on other property calculations. The dissociation of strong acids is expected to be high in solutions with higher pH than the pK_a of the solute (Clayden et al., 2001), as is the case here.

Since the organosulfates strongly dissociate in water, we also calculated the aqueous solubilities of their sodium salts (NaOS). For these sodium organosulfate salts, we used the heat capacity of fusion estimate ($\mathrm{\Delta }{C}_{p,\mathrm{fus}}=\mathrm{\Delta }{H}_{\mathrm{fus}}/T_{\mathrm{melt}}$) with a melting point of 478.15 K (Rumble, 2018) and a heat of fusion of 50 kJ mol⁻¹ (Shinoda et al., 1966). Calculated solubilities of the NaOS salts are shown in Fig. 3 and Table S1. For systems in which a solid–liquid equilibrium was found, the solubility of the organosulfate sodium salt is around 0.065 mole fraction.

3.2 Solubility in aqueous ammonium sulfate and bisulfate solutions

Solubilities of both OS and NaOS were calculated by solving the LLE or the SLE, respectively, in aqueous solvents containing 0.09 mole fraction of either ammonium sulfate or ammonium bisulfate. Solubility values for the OS and NaOS in these solvents, and the aqueous ammonium sulfate and bisulfate salt solutions in the OS phase, are given in Table S2.

Organic solubilities in aqueous inorganic solutions ranging from pure water to 0.09 mole fraction of inorganic salt were calculated using relative screening. These relative solubilities were then scaled using the absolute solubility values of the 0.09 mole fraction binary solvents to obtain the final relative solubilities of the OS and NaOS with respect to each binary system at the different inorganic salt mole fractions. The procedure is described in detail in Sect. S2. Relative solubilities are shown in Fig. 4 (OS in (NH₄)₂SO₄), Fig. 5 (NaOS in (NH₄)₂SO₄), Fig. S7 (OS in NH₄HSO₄) and Fig. S8 (NaOS in NH₄HSO₄).

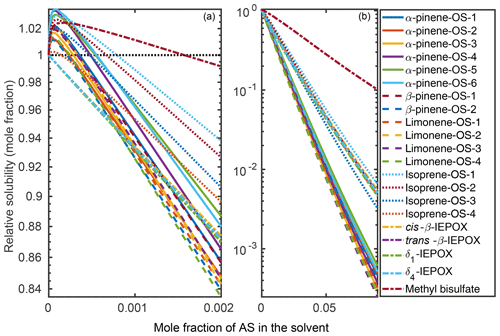
Figure 4 Relative solubilities of OS in (NH₄)₂SO₄ (aq) solutions (T=298.15 K relative to pure water) estimated in COSMOtherm using relative screening. (a) Results for the lower binary salt mole fraction range from 0 to $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$ and (b) the whole range between 0 and 0.09 mole fraction of the salt. The black dotted line in (a) shows the relative solubility of 1, equivalent to the solubility of the OS in pure water.

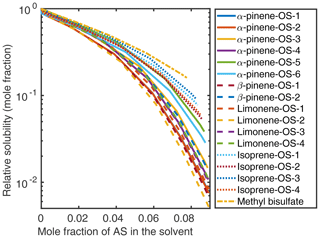
Figure 5 Relative solubilities of NaOS salts in (NH₄)₂SO₄ (aq) solutions (T=298.15 K relative to pure water) estimated using relative screening in COSMOtherm.

At low ($<{\mathrm{10}}^{-\mathrm{3}}$) (NH₄)₂SO₄ mole fractions, the molecular organosulfates salt in, meaning that the presence of the inorganic salt enhances the total amount of the organosulfate soluble in the aqueous phase. At higher inorganic salt mole fractions the organosulfates salt out. All IEPOX isomers and NaOS salts salt out in the presence of co-solvated (NH₄)₂SO₄ across the whole concentration range. At 0.09 mole fraction of (NH₄)₂SO₄, the organic compounds can be grouped into three categories based on their relative solubilities: methyl bisulfate with the highest relative solubility, isoprene-derived organosulfates and IEPOX in the middle, and all monoterpene-derived organosulfates with the lowest relative solubilities with respect to the pure aqueous solubility.

All of the organic compounds salt out in ternary aqueous solutions with NH₄HSO₄ (see Figs. S7 and S8), but the salting-out effect of NH₄HSO₄ on the organic compounds is weaker than that of (NH₄)₂SO₄. This is due to the stronger salting interactions of the doubly charged sulfate ion compared to the singly charged bisulfate ion.

As was mentioned above, the salting-out of organosulfates from 0.09 mole fraction (NH₄)₂SO₄ solution is overestimated by a factor of 3.1 using the relative solubility calculation compared to the LLE calculation. Wang et al. (2014) found that COSMOtherm overestimates the salting-out effect of (NH₄)₂SO₄ on average by a factor of 3 compared to experiments. They described the salting behavior using Setschenow constants calculated from COSMOtherm-estimated (release 14) partition coefficients, which are comparable to relative solubilities. We used COSMOtherm19-estimated relative solubilities to calculate corresponding Setschenow constants for the compounds used by Wang et al. (2014) that are in COSMObase17 and the same 5 % (NH₄)₂SO₄ solution (w∕v, corresponding to x_AS=0.007) with solvent densities by Tang and Munkelwitz (1994). We found that COSMOtherm19 overestimates the experimental Setschenow constant of these compounds in 5 % (NH₄)₂SO₄ solution on average by a factor of 1.5 (see Fig. S11), which is an improvement to the factor of 3 of COSMOtherm14. The overestimation might be decreased by calculating LLE solubilities as opposed to relative solubilities that use the zeroth-order solubility approximation. However, finding the LLE of multiple systems is computationally infeasible and not certain to improve the results.

Liquid–liquid-phase separation (LLPS) has been detected in several aerosol experiments (Song et al., 2012, 2018; Rastak et al., 2017; Ham et al., 2019). For example, Song et al. (2012) observed LLPS for ammonium sulfate aerosol that contained organic compounds with O:C below 0.8, whereas no LLPS was seen with O:C above 0.8, depending on the functional groups. In these experiments, organic compounds contained hydroxy, carbonyl and carboxylic acid groups (Song et al., 2012). In binary aerosol systems containing water and organic compounds (without inorganic salt), Song et al. (2018) observed LLPS for O:C below 0.44 or 0.58 in systems with one or two different organic compounds, respectively. The compounds in this study contain ester, ether and hydroxy functional groups (Song et al., 2018). With O:C ratios of the monoterpene- and isoprene-derived organosulfates in the ranges 0.5–0.7 and 1.2–1.4, respectively, these results are consistent with the present work. On the other hand, in experiments with an OH-oxidized α-pinene and water system (Ham et al., 2019) only a single organic-rich phase was observed, whereas LLPS was seen between water and ozone-oxidized α-pinene products (Ham et al., 2019) or OH-oxidized isoprene products (Rastak et al., 2017). There are small differences in the partial charges of the oxygen atoms associated with a sulfate group compared to a carboxylic acid group (see Sect. S3 for a comparison of the σ potentials) that may influence the O:C ratio of organosulfates required for LLPS. From our results we can also see that other structural factors further affect the thermodynamic properties, in addition to the O:C ratio or the types of functional groups.

3.3 Activity

Activities were calculated for organosulfates, IEPOX isomers and water in binary aqueous mixtures with different organic-to-water molar ratios (see Table S3). Figure 6 shows, as examples, binary mixing diagrams similar to that presented by Prisle et al. (2010) for water and (a) α-pinene-OS-5, (b) β-pinene-OS-1, (c) limonene-OS-1, (d) isoprene-OS-2, and (e) δ₁-IEPOX. Diagonal dashed lines illustrate the ideal mole-fraction-based activities (a_i=x_i) with respect to a pure compound (i=OS, water) reference state. Since the solubility of the organics in water is much smaller than the solubility of water in the organics, the mixing diagrams for monoterpene-derived organosulfates (Fig. 6a–c) are divided into two sections (note the different scales of the two phase regions): the aqueous phase (left sides) and the organic phase (right sides). In between is a composition range corresponding to the miscibility gap. From Fig. 6a–c we see how the calculated water and organosulfate activities fulfill the liquid-phase equilibrium condition of Eq. (9) at the solubility limit.

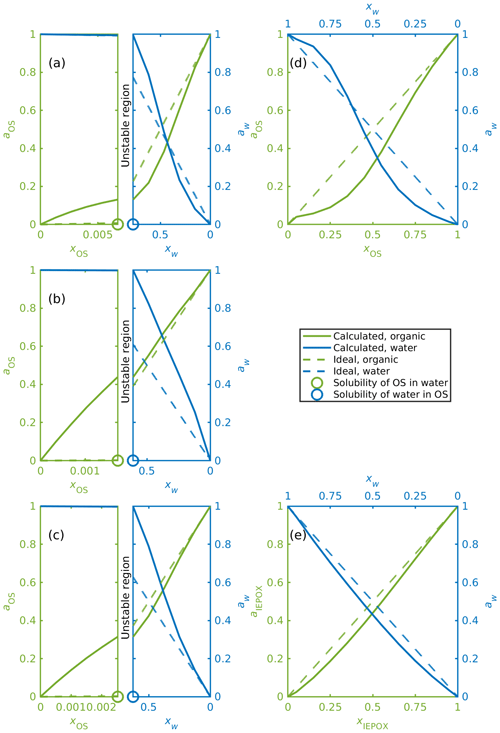
Figure 6 Activities of OS, IEPOX and water in binary mixtures; (a) α-pinene-OS-5, (b) β-pinene-OS-1, (c) limonene-OS-1, (d) isoprene-OS-2, (e) δ₁-IEPOX. The left-hand sides of panels (a–c) show the water-rich phase, and the right-hand sides show the corresponding organic-rich phase.

Activities for the monoterpene-derived organosulfates display three different types of behavior. The most common is exemplified in Fig. 6a, where in the organic-rich phase, the organosulfate activity is lower than the mole fraction of the organics (a_OS≤x_OS). A low activity indicates that the organosulfate is more stable in the organic-rich phase than in the ideal pure organosulfate. The water activity is below the ideal activity (a_w<x_w) at low mole fractions of water and above the ideal activity (a_w>x_w) at higher water mole fractions in the organic-rich phase. The organic activity at the solubility limit is low (a_OS<0.28 when x_OS=x_SOL) compared to the other monoterpene-derived organosulfates. Similar behavior is seen in α-pinene-OS-3, α-pinene-OS-4, α-pinene-OS-6, β-pinene-2 and limonene-OS-4. A comparison between the activities of α-pinene-OS-5 and H₂SO₄ calculated using COSMOtherm and literature values of H₂SO₄ activities are shown in Fig. S9.

The opposite is seen in α-pinene-OS-1, β-pinene-OS-1 (Fig. 6b) and limonene-OS-3, for which the activity of the organosulfate in the organic-rich phase is very close to or above the ideal activity. In addition, the activity at the solubility limit (both the solubility of the water and the organic) for these compounds is above 0.36. The third behavior type seen in Fig. 6c is between the first two cases, in which the water activity follows the ideal activity in small mole fractions of water. Here the organic activity at the solubility limit is around 0.3. The other compounds in this group are α-pinene-OS-2 and limonene-OS-2.

Since the isoprene-derived organosulfates, IEPOX isomers and methyl bisulfate are fully miscible with pure water, liquid–liquid-phase separation was not observed for these systems. The mixing diagrams for all isoprene-derived organosulfates and methyl bisulfate are similar to the one shown in Fig. 6d. Calculated activities for all IEPOX isomers are close to the ideal activities at all mixing states (Fig. 6e).

Figure 7a–e show mixing diagrams for the same organic compounds as Fig. 6a–e but now with a solvent that is a 0.09 mole fraction binary aqueous solution of NH₄HSO₄ instead of pure water. Here, COSMOtherm also predicts LLPS for systems containing the isoprene-derived organosulfates (Fig. 7d). Again, activities for the organosulfates are higher than their mole fractions in the water-rich phase. Here we can also see that the predicted activity of water in the binary solvent is 0.78. The corresponding activity coefficients ${\mathit{\gamma }}_i=a_i/x_i$ for the organic compounds and water in each system in Fig. 7 are tabulated in Table S4.

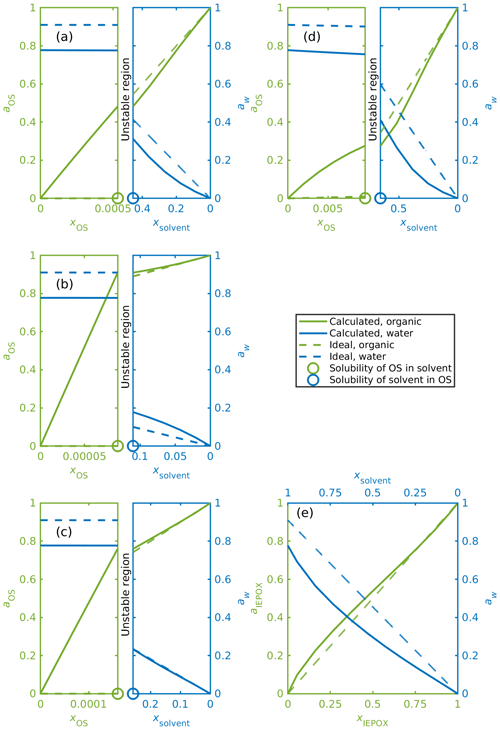
Figure 7 Activities for OS, IEPOX and water in ternary aqueous mixtures. The solvent is a 0.09 mole fraction ammonium bisulfate solution, and the ideal water activity is equal to the mole fraction of water; (a) α-pinene-OS-5, (b) β-pinene-OS-1, (c) limonene-OS-1, (d) isoprene-OS-2, (e) δ₁-IEPOX. The left-hand sides of panels (a–d) show the solvent-rich phase, and the right-hand sides show the organic-rich phase. The ABS-to-water ratio is kept constant in all calculated mixing states, which means that ammonium bisulfate and water are not individually at equilibrium at the solubility limits.

The calculated activity of each organic compound in the aqueous phase is higher in the ternary OS+aqueous ammonium bisulfate systems compared to the binary OS+water systems. This means that the inorganic salt decreases the stability of the organosulfate in the aqueous phase. At the same time, the stability of the organosulfate in the organic-rich phase also decreases in the presence of the inorganic salt.

Similar mixing diagrams for 0.09 mole fraction aqueous ammonium sulfate solvent are shown in Fig. S10 and tabulated values in Table S5. In ammonium sulfate solutions, COSMOtherm predicts a water activity of 1.14 in the aqueous solvent-rich phase, indicating that according to COSMOtherm, the 0.09 mole fraction aqueous solution of ammonium sulfate is unstable. This discrepancy with the experimental solubility of $x_{\mathrm{SOL},\mathrm{AS}}=\mathrm{0.094}$ (Tang and Munkelwitz, 1994) is possibly caused by an inadequate representation of the solvation of ionic liquids in COSMO-RS theory (Toure et al., 2014).

3.4 Saturation vapor pressure

We calculated saturation vapor pressures for the neutral organic compounds at 298.15 K (Table 1). Comparing the studied organosulfate compounds based on their functional groups, those containing carboxylic acid groups, i.e., α-pinene-OS-5 and α-pinene-OS-6, have the lowest saturation vapor pressures. α-Pinene-OS-4, also having an O:C ratio of 0.7, has an order of magnitude higher saturation vapor pressure, indicating that two carbonyl groups are less effective at lowering the vapor pressure than a single carboxylic acid group. In addition, α-pinene-OS-3 (one carbonyl and one hydroxy group) has a lower saturation vapor pressure than α-pinene-OS-4 with one more oxygen atom.

Table 1 Estimated saturation vapor pressures of the pure compounds and the ratio between the saturation vapor pressures of the organic compound and sulfuric acid.

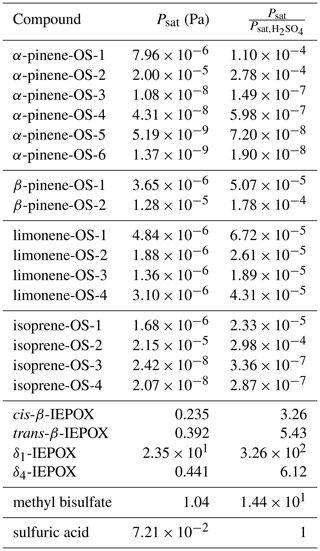
The saturation vapor pressure of sulfuric acid (extrapolated from experimental data using ab initio data) is $\mathrm{2.10}\times {\mathrm{10}}^{-\mathrm{3}}$ Pa at 298.15 K (Ayers et al., 1980; Kulmala and Laaksonen, 1990; Noppel et al., 2002), while COSMOtherm estimates the vapor pressure of the pure sulfuric acid to be $\mathrm{7.21}\times {\mathrm{10}}^{-\mathrm{2}}$ Pa (about 34 times higher). Due to the previously demonstrated systematic overestimation of absolute saturation vapor pressures by COSMOtherm (Kurtén et al., 2016), we show both absolute vapor pressures and the vapor pressures relative to the estimated sulfuric acid saturation vapor pressure in Table 1. The saturation vapor pressures of monoterpene- and isoprene-derived organosulfates are all 4 to 8 orders of magnitude lower than that of sulfuric acid. On the other hand, the saturation vapor pressures of IEPOX isomers and methyl bisulfate are higher than for sulfuric acid.

Compared to previously calculated saturation vapor pressures for α-pinene autoxidation products using COSMOtherm, the organosulfates studied here are significantly less volatile (Kurtén et al., 2016). It should be noted, however, that in the study of Kurtén et al. (2016), the number of intramolecular hydrogen bonds was not limited in the COSMOtherm calculations, which likely led to higher saturation vapor pressure estimates (Kurtén et al., 2018). Furthermore, as we have seen here, the acidic organosulfates readily dissociate in the particle phase, forming ionic species, which will effectively suppress their partitioning to the gas phase.

δ₁-IEPOX has a higher saturation vapor pressure than the other IEPOX isomers. This can be understood from a structural point of view, as the lowest-energy conformer (highest weight in the COSMOtherm calculations) of δ₁-IEPOX seems to have two intramolecular hydrogen bonds. COSMOtherm does not count either of these as full or partial intramolecular hydrogen bonds in the condensed phase. However, the gas-phase free energy (G^(g)) of the conformer is lower than for the other IEPOX conformers, leading to about 5 kJ mol⁻¹ of difference in the energy between the condensed and gas phase of δ₁-IEPOX and δ₄-IEPOX. This in turn leads to a relatively higher saturation vapor pressure (Eq. 19) compared to the other IEPOX isomers.

3.5 Henry's law solubility

The activity coefficients at infinite dilution in water, the free energies of solvation and Henry's law solubilities in pure water calculated using the different methods (explained in Sect. 2.2.4) at 298.15 K are given in Table S6. Among the studied organics, Henry's law solubility is the highest for monoterpene- and isoprene-derived organosulfates containing the highest number of oxygen atoms and the lowest for methyl bisulfate and the IEPOX isomers. The infinite dilution Henry's law solubilities ($H_{\mathrm{sol}}^{\mathrm{\infty }}$) were calculated by COSMOtherm using Eq. (21). We also calculated LLE-based Henry's law solubilities ($H_{\mathrm{sol}}^{\mathrm{LLE}}$) using Eq. (23) with the pure water solubilities of the organic compounds. A comparison between the infinite dilution and the LLE-based Henry solubilities is shown in Fig. 8. The LLE-based Henry's law solubility for monoterpene-derived OS+water is on average 4.4 times lower than the corresponding infinite dilution Henry's law solubility. Henry's law solubility is the equilibrium ratio between the abundance in the gas phase and in the aqueous phase for a dilute solution. For the fully miscible compounds, including the dissociation correction, the solution is no longer dilute. We therefore did not calculate the LLE-based Henry's law solubility of the isoprene-derived compounds and methyl bisulfate, which are fully miscible with pure water at 298.15 K.

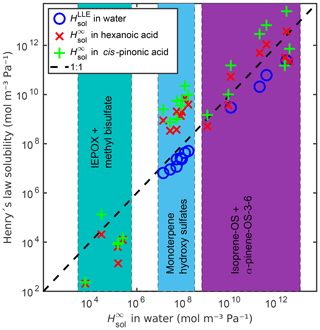
Figure 8 Comparison between infinite dilution Henry's law solubility ($H_{\mathrm{sol}}^{\mathrm{\infty }}$) in water, hexanoic acid and cis-pinonic acid, and LLE based Henry's law solubility ($H_{\mathrm{sol}}^{\mathrm{LLE}}$) in water. The dashed line shows the 1:1 ratio between $H_{\mathrm{sol}}^{\mathrm{\infty }}$ in water and the other Henry's law solubilities.

Additionally, we calculated the infinite dilution Henry's law solubilities of all compounds in two organic solvents, hexanoic and cis-pinonic acids (see Fig. 8 and Table S6). The densities of these organic acids (ρ_hexanoic=0.9400 g cm⁻³ and ${\mathit{\rho }}_{\mathrm{cis}-\mathrm{pinonic}}=\mathrm{1.0739}$ g cm⁻³) were estimated using COSMOtherm. The Henry's law solubilities of the monoterpene-derived organosulfates are the lowest in water and the highest in cis-pinonic acid. The isoprene-derived compounds (OS and IEPOX) are all less soluble in hexanoic acid than in water. The more oxygenated isoprene-OS-3 and isoprene-OS-4 are also less soluble in cis-pinonic acid than in water, opposite to the less oxygenated isoprene-OS-1 and isoprene-OS-2, which are the most soluble in cis-pinonic acid. The epoxydiols are least soluble in hexanoic acid and the most soluble in water. This means that the phase separation behavior of OS from different precursors will be different in multiphase atmospheric aerosol, leading to different OS aerosol-phase states depending on the predominant precursor.

Figure 9 shows the infinite dilution Henry's law solubilities for the organic compounds in the aqueous mixtures with different mole fractions of ammonium sulfate (panel a) and ammonium bisulfate (panel b). The decrease in Henry's law solubility is steeper with the increase in ammonium sulfate than in ammonium bisulfate. This is due to the stronger salting-out effect on the organics of ammonium sulfate than of ammonium bisulfate, also seen in the relative solubility calculations. In the case of both inorganic salts, all of the hydroxy sulfates, i.e., α-pinene-OS-1 and α-pinene-OS-2, and all β-pinene and limonene isomers have similar Henry's law solubilities and trends as a function of salt mole fractions. In ammonium sulfate solutions, the Henry's law solubility of isoprene-derived organosulfates decreases more slowly with the increase in ammonium salt concentration than the solubility of monoterpene-derived organosulfates.

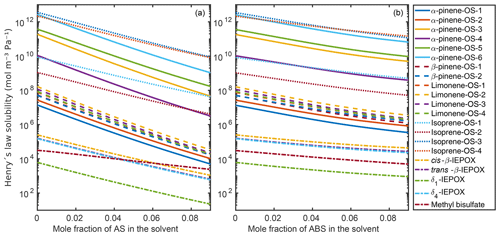
Figure 9 Infinite dilution Henry's law solubilities in aqueous solutions of (a) (NH₄)₂SO₄ and (b) NH₄HSO₄ at 298.15 K.

COSMOtherm-estimated Henry's law solubility has previously been reported for isoprene-derived 2-methyltetrol (D'Ambro et al., 2019), which is similar to isoprene-OS-3 and isoprene-OS-4 with the difference that the sulfate group is replaced by a hydroxy group. We calculated the Henry’s law solubility of 2-methyltetrol in water using COSMOtherm19 and found that the compounds containing a sulfate group (isoprene-OS-3 and isoprene-OS-4) have Henry's law solubilities that are 4 orders of magnitude higher than the compound containing only hydroxy groups (2-methyltetrol). The higher Henry's law solubility of the organosulfate compared to 2-methyltetrol is caused by 5 orders of magnitude lower saturation vapor pressure and an order of magnitude higher activity coefficient at the infinite dilution of the solute. Similar differences are seen between the IEPOX isomers, isoprene-OS-1 and isoprene-OS-2, although the functional groups in isoprene-OS-1 and isoprene-OS-2 (hydroxy and carbonyl) are different than those in IEPOX (hydroxy and epoxy). This means that the presence of sulfate in SOA and the formation of organosulfate compounds enhance SOA formation, since organosulfates are less likely to evaporate than non-sulfate organics.

4 Conclusions

We have used COSMOtherm to evaluate the thermochemical properties (pK_a, solubility, activity, Henry's law solubility and saturation vapor pressure) of organosulfates derived from isoprene, α-pinene, β-pinene and limonene. These properties are key to governing the phase state behavior and stability of organosulfates as components of atmospheric SOA.

Interactions with atmospheric water are critical processes determining the growth of SOA and in turn any size-dependent effects, such as heterogeneous chemistry mediated by available surface area and both the direct and indirect climate effects of aerosols. The studied organosulfates have several polar functional groups and in many cases amphiphilic structures. Overall, the organosulfates display both favorable (a_OS<x_OS) and unfavorable (a_OS>x_OS) interactions with water in the condensed phase. Both behaviors are seen for the same compound in different regions of the mixing diagram. In water+monoterpene-derived organosulfate mixtures, COSMOtherm predicts phase separation into organic-rich and water-rich phases. Particles with LLPS have already been detected in field samples and generated in numerous laboratory experiments when mixing inorganic sulfate salts and organic compounds (e.g., carboxylic acids and electrolytes, organosulfates from the oxidation of volatile organic compounds – VOCs) (Wu et al., 2018; Bondy et al., 2018). When a miscibility gap exists, water uptake to the organic-rich aerosol phase, as well as organosulfate formation in the aqueous aerosol, is not a continuous function of relative humidity or organosulfate precursor availability.

In the particular case of cloud condensation nuclei (CCN) activation, elevated water activities in a water-rich phase due to the presence of organosulfate solute will suppress water uptake from a decreased Raoult effect (a_w>x_w) and decrease SOA CCN activity. However, interactions may not be constant across the phase diagram. Variations between organic-rich and water-rich phases, as well as between the organosulfates, can contribute to explaining the variation in the limonene-derived OS hygroscopicity parameter between subsaturated and supersaturated conditions observed by Hansen et al. (2015). They also found a nonlinear composition dependence of the CCN activity of mixed OS–AS aerosols and connected the inability of their Köhler model to capture this trend with the nonideal behavior of the droplet solutions (Hansen et al., 2015). The COSMOtherm-estimated activities can be used in Köhler calculations to model the nonideality of aqueous droplet solutions. For instance, the hygroscopic growth factor (calculated as a ratio between wet and dry particle diameter) is higher for particles with lower water activity than for particles with higher water activity. From our calculation we can see that for some of the organosulfates, water activity in the organic phase is above ideality (a_w>x_w), meaning a lower water uptake compared to the organosulfates with water activities below ideality (a_w<x_w). Additionally, a miscibility gap means that the aerosol system has inaccessible mixing states. Therefore, not all conditions, including the CCN activation threshold, may be reached in a continuous fashion during cloud processing but could instead be short-circuited by aerosol LLPS.

Our calculations predict limited organosulfate solubility in pure water and even lower solubility in the aqueous solutions of ammonium sulfate and ammonium bisulfate. Solubility, however, is strongly enhanced by the formation of the corresponding organosulfate anionic species in aqueous environments that are not very strongly acidic. Previous experimental, modeling and computational studies (Wang et al., 2014, 2016) have shown that ammonium sulfate has a salting-out effect on organic compounds. This is seen in our calculations for the IEPOX isomers, whereas a weak (at most 3.5 %) salting-in effect on the organosulfates is predicted at low concentrations of ammonium sulfate. COSMOtherm has previously been shown to overestimate the salting-out effect of ammonium sulfate on diverse organic compounds (Wang et al., 2014; Toivola et al., 2017). Based on this, it is possible that the salting-in of organosulfates may be underestimated in our present calculations. The presence of additional inorganic salt in the aerosol where organosulfate is formed may therefore enhance or decrease the SOA phase stability of the organosulfate, depending on the organic:inorganic sulfate mixing ratio and relative humidity.

Calculated saturation vapor pressures are lower for organosulfates than isoprene-derived dihydroxy dihydroperoxides, dihydroperoxy hydroxy aldehydes (Kurtén et al., 2018) and α-pinene-derived oxidized compounds (Kurtén et al., 2016). Based on this, organosulfates are more stable in the condensed phase than non-sulfate organic compounds. In addition, the saturation vapor pressure of H₂SO₄ is higher than all of the organosulfates. Due to the low pK_a of all organosulfates (and H₂SO₄), if the aerosol contains molecules or ions capable of acting as bases, the effective vapor pressure (equilibrium vapor pressure) of OS SOA will be many orders of magnitude lower than the saturation vapor pressures. Overall, organosulfates are thus unlikely to evaporate from an aerosol in which they are formed. This means that the formation of organosulfates, in particular the formation of their salts, can significantly contribute to increasing the SOA mass in regions with high sulfate aerosol content. Not only will OS add to SOA, but this SOA will also be stable over a wide range of conditions, including salinity and acidity.

The results of this work show that COSMOtherm is a viable path to obtaining compound-specific thermochemical properties of atmospheric organic aerosol, which may not be available through experimental methods anytime soon. We have calculated values for selected properties that are overall consistent with observations from a variety of aerosol measurements from both fieldwork and laboratory work. However, we also see that oxidized atmospheric organics from similar precursors and with similar chemical functionalities may exhibit surprisingly different compound-specific phase state properties. In combination with the variation of these properties across a range of conditions, this thermochemical heterogeneity of atmospheric organosulfates – and of other compound classes that may display similar variation – poses a real challenge for large-scale atmospheric simulations. In particular, we note that great caution must be taken when using single compounds to represent the properties of an entire group.