the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A model-based analysis of foliar NOx deposition
Erin R. Delaria
Foliar deposition of NO2 removes a large fraction of the global soil-emitted NOx. Understanding the mechanisms of NOx foliar loss is important for constraining surface ozone, constraining NOx mixing ratios, and assessing the impacts of nitrogen inputs to ecosystems. We have constructed a 1-D multibox model with representations of chemistry and vertical transport to evaluate the impact of leaf-level processes on canopy-scale concentrations, lifetimes, and canopy fluxes of NOx. Our model is able to closely replicate canopy fluxes and above-canopy NOx daytime mixing ratios observed during two field campaigns, one in a western Sierra Nevada pine forest (BEARPEX-2009) and the other in a northern Michigan mixed hardwood forest (UMBS-2012). We present a conceptual argument for the importance of NO2 dry deposition and demonstrate that NO2 deposition can provide a mechanistic explanation for the canopy reduction of NOx. We show that foliar deposition can explain observations suggesting as much as ∼60 % of soil-emitted NOx is removed within forest canopies. Stomatal conductances greater than 0.1 cm s−1 result in modeled canopy reduction factors in the range of those used in global models, reconciling inferences of canopy NOx reduction with leaf-level deposition processes. We show that incorporating parameterizations for vapor pressure deficit and soil water potential has a substantial impact on predicted NO2 deposition in our model, with the percent of soil NOx removed within one canopy increasing by ∼15 % in wet conditions compared to dry conditions. NO2 foliar deposition was also found to have a significant impact on ozone and nitrogen budgets under both high- and low-NOx conditions.
- Article
(6296 KB) - Full-text XML
-
Supplement
(1093 KB) - BibTeX
- EndNote
The chemistry of nitrogen oxides () has a large impact on the oxidative capacity of the atmosphere and the budget of global surface ozone (Crutzen, 1979). NOx is primarily removed from the atmosphere by chemical reactions to form nitric acid, alkyl nitrates, and peroxynitrates, as well as by dry deposition of NO2 (Crutzen, 1979; Jacob and Wofsy, 1990; Romer et al., 2016). The chemical loss pathways of NOx have been extensively studied, but the physical loss of NO2 to dry deposition remains much more uncertain. Globally, foliar deposition of NO2 removes 20 %–50 % of soil-emitted NO (Jacob and Wofsy, 1990; Yienger and Levy, 1995) and constrains near-surface NOx concentrations and input to ecosystems (Hardacre et al., 2015). Understanding the processes that control this removal of NOx by the biosphere is important for predicting anthropogenic surface ozone and understanding flows in the nitrogen cycle.
Reactive nitrogen oxides also serve as an important nutrient in ecosystems. Exchange processes cycle nitrogen between the biosphere and atmosphere, influencing the availability of nitrogen to ecosystems (Townsend et al., 1996; Holland et al., 1997, 2005; Galloway et al., 2004). Deposition of atmospheric reactive nitrogen species can fertilize ecosystems with limited nitrogen availability (Ammann et al., 1995; Townsend et al., 1996; Williams et al., 1996; Holland et al., 1997; Galloway et al., 2004; Teklemariam and Sparks, 2006). Although nitrogen is often the limiting nutrient for plant growth (Oren et al., 2001; Galloway et al., 2004), anthropogenic activities have in some cases caused an excess loading of nitrogen to ecosystems, leading to dehydration, chlorosis, soil acidification, and a decline in productivity (Vitousek et al., 1997; Fenn et al., 1998; Galloway et al., 2004).
The current understanding of the exchange of nitrogen oxides between the atmosphere and biosphere remains incomplete. Despite the importance of dry-deposition processes, they are among the most uncertain and poorly constrained aspects of atmosphere–biosphere nitrogen exchange and the tropospheric budgets of O3 and NOx (Wild, 2007; Min et al., 2014; Hardacre et al., 2015). This uncertainty arises from the complex dependence of dry-deposition processes on surface cover, meteorology, seasonal changes in leaf area index (LAI), species of vegetation, and the chemical species carrying odd N. Developing a mechanistic understanding of dry deposition of NO2 has largely depended on inferences from scarce long-term field observation data and a limited number of laboratory studies on the effects of environmental factors on deposition at the leaf level. This understanding is represented by a deposition velocity, Vd. Many global-scale chemical transport models (Wesely, 1989; Jacob and Wofsy, 1990; Ganzeveld and Lelieveld, 1995; Wang and Leuning, 1998; Ganzeveld et al., 2002a) parameterize Vd using the resistance-in-series approach similar to that developed by Baldocchi et al. (1987). These treatments are heavily parameterized, leading to a large degree of uncertainty, and many (Jacob and Wofsy, 1990; Wesely, 1989) do not account for the effects of vapor pressure deficit (VPD), soil water potential (SWP), CO2 mixing ratio, or other factors known to influence stomatal conductance (Hardacre et al., 2015). A common approach for modeling canopy uptake of trace gases is with a one- or two-layer big-leaf dry-deposition model, in which the forest is treated as having a characteristic average deposition velocity (Hicks et al., 1987; Wesely, 1989; Ganzeveld and Lelieveld 1995; Wang and Leuning, 1998; Zhang et al., 2002). However, Ganzeveld et al. (2002b) implemented a multilayer column model in a global chemistry and general circulation model GCM-ECHAM (European Centre Hamburg Model) to study the role of canopy interactions in global atmosphere–biosphere NOx exchange and demonstrated the importance of considering interactions within the canopy, particularly in pristine forest sites. More comprehensive treatments of atmosphere–biosphere exchange are thus needed in global models.
The deposition velocity of NO2 to vegetation is largely regulated by stomatal conductance (Johansson, 1987; Thoene et al., 1991; Rondon and Granat, 1994; Teklemariam and Sparks, 2006; Chaparro-Suarez et al., 2011; Breuninger et al., 2012; Delaria et al., 2018), which varies with tree species, photosynthetically active radiation (PAR), VPD, temperature (T), SWP and seasonality of leaf phenology (Emberson et al., 2000; Zhang et al., 2003; Altimir et al., 2004; Hardacre et al., 2015; Kavassalis and Murphy, 2017). NO2 deposition remains even more uncertain than deposition of O3, where stomatal response has been shown to be the primary regulator of foliar deposition, and mesophyllic resistance to deposition is negligible. Observations from leaf-level laboratory studies suggest the deposition of NO2 is also controlled by stomatal aperture (Hanson and Lindberg, 1991; Rondon and Granat, 1994; Hereid and Monson, 2001; Teklemariam and Sparks, 2006; Pape et al., 2009; Chaparro-Suarez et al., 2011; Breuninger et al., 2012; Delaria et al., 2018); however, reactions in the mesophyll may also be important for controlling the deposition velocity of NO2 (Teklemariam and Sparks, 2006; Breuninger et al., 2012). A failure to consider the effects of relevant meteorology on stomatal conductance, as well as our deficient understanding of mesophyllic resistances and the diversity of ecosystem responses, severely limits our ability to understand dry-deposition processes and how they will be affected by feedbacks from changes in climate, land use, and air pollution.
The importance of these considerations has recently been illustrated by Kavassalis and Murphy (2017), who found a significant correlation between VPD and ozone loss and demonstrated that modeling using VPD-dependent parameterizations of deposition better predicted the correlation they observed. Previous work by Altimir et al. (2004) and Gunderson et al. (2002) have described the effects of VPD and other environmental parameters on the stomatal conductance to O3 of Pinus sylvestris and Liquidambar styraciflua, respectively. More recent models, like the DO3SE (Deposition of Ozone for Stomatal Exchange) model for estimating stomatal conductance to predict ozone deposition velocities, fluxes, and damage to plants, incorporate the effects of VPD and SWP on stomatal conductance. No similar model exists for assessing these effects on NOx deposition, although Ganzeveld et al. (2002b) included the effect of soil moisture availability for evaluating the role of canopy NOx uptake on canopy NOx fluxes. The DO3SE has successfully been implemented in the European Monitoring and Evaluation Programme (EMEP) regional model (Simpson et al., 2012). Modeling studies by Buker et al. (2007) and Emberson et al. (2000) have also demonstrated the success of regional-scale parameterizations using observed relationships between meteorology and stomatal conductance for application to O3. Such treatments of VPD and SWP were incorporated into a regional air quality model by Zhang et al. (2002, 2003).
In this study we present a simplified multilayer atmosphere–biosphere exchange model and investigate the sensitivity of NOx canopy fluxes, ozone production, NOx vertical profiles, and NOx lifetimes to different parameterizations of stomatal conductance and deposition velocity. We consider here both the Wesely model and the similarly simplistic approach of Emberson et al. (2000) that incorporates effects of VPD and SWP. We restrict our considerations to the effects of different stomatal resistance parameterizations on predicted deposition velocities, as the magnitude of the mesophyllic resistance remains uncertain and is assumed to be comparatively small in atmospheric models (Zhang et al., 2002). We also restrict our considerations to NO2 deposition, as NO deposition has been shown to be negligible in comparison (Delaria et al., 2018). There have been many studies investigating the effects of dry-deposition parameterizations on deposition velocities – particularly of ozone – and the abilities of different modeling schemes to reproduce observational data for other molecules such as NO2, NO, H2O2, HNO3, hydroxy nitrates, alkyl nitrates, and peroxyacyl nitrates (Zhang et al., 1996; Wang et al., 1998b; Emberson et al., 2000; Ganzeveld 2002a; Buker et al., 2007; Wolfe et al., 2011; Hardacre et al., 2015; Nguyen et al., 2015). However, there has been little evaluation of how changes in dry deposition of NO2 may affect the surface mixing ratios and chemistry of important atmospheric species. Assessing the sensitivity to NO2 deposition is crucial not only for evaluating the potential impact of uncertainties in dry-deposition parameterizations for global and regional models, but also for understanding how a changing climate may influence NOx, surface ozone, and the nitrogen cycle.
We have constructed a simple atmospheric model for investigating the influence of leaf-level NO2 foliar deposition on canopy-scale NOx lifetimes and concentrations. The model consists of three canopy layers and a total of eight vertical boxes within the planetary boundary layer (PBL), taken to be 1000 m during the day and 60 m at night (Wolfe and Thornton, 2011; Wolfe et al., 2011). The increase in PBL height during the day is treated as a Gaussian function of time with 98 % of the integrated area contained between sunrise and sunset, with the maximum height reached at the time of maximum daily temperature (Fig. 1). The first two boxes above the canopy were kept at a constant altitude, as the evolution of these layers was found to have a minimal effect on the model results discussed. The model was designed to be representative of a homogenous forest environment with the aim of simulating observations at forest tower sites.
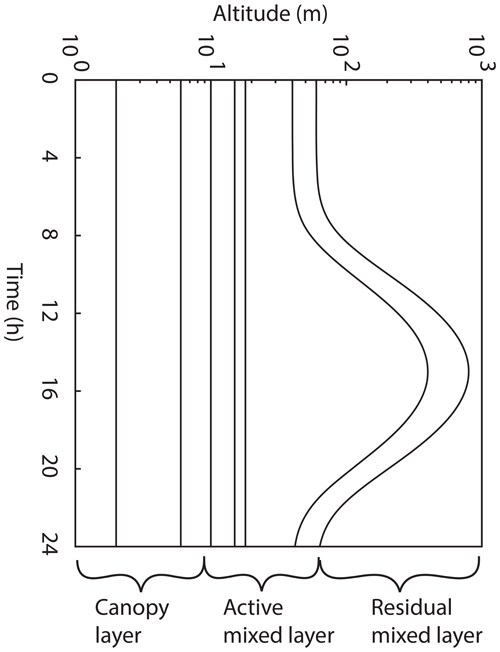
Figure 1Planetary boundary dynamics in the 1-D multibox model. The model domain consists of three boxes in the canopy layer, four in the active mixed layer, and one in the residual mixed layer. The lower five boxes have fixed heights, while the sixth and seventh boxes evolve throughout the day, in the form of a Gaussian function.
In each box, the change in concentration (C) of species i is calculated using the time-dependent continuity equation:
where the terms on the right are the chemical production, chemical loss, emission, deposition, advection, and turbulent flux, respectively. In each box (k=1–8) the altitude (z) is considered to be the average of the altitudes at the upper boundaries of boxes k and k−1 (i.e., the midpoint of box k). The change in concentration for species i is calculated for each time step Δt=2 s (Table 1).
where Δhk is the width of box k. The only species not treated in this manner is the hydroxyl radical (OH), which is calculated using a steady-state approximation.
Table 1Parameters used in the model for comparison to observations from UMBS and BEARPEX-2009.
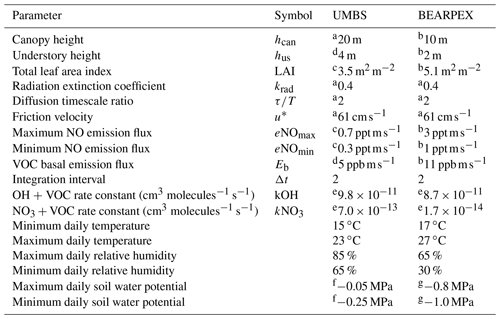
a Geddes and Murphy (2014). b Wolfe and Thornton (2011). c Seok et al. (2013). d Estimated from Bryan et al. (2015). e See text; calculated assuming the dominant volatile organic compound (VOC) is 2-methyl-3-buten-2-ol (MBO) for Blodgett Forest and isoprene for UMBS. f Estimated from Matheny et al. (2015). g Estimated from Ishikawa and Bledsoe (2000) and Stern et al. (2018).
2.1 Deposition
The deposition flux (Fdep) of each depositing species i in the canopy is calculated according to
where LAI is the leaf area index, and Vd is the deposition velocity. The deposition velocities are calculated according to
where R is the total resistance to deposition.
where Ra, Rb, Rcut, Rst, and Rm are the aerodynamic, boundary layer, cuticular, stomatal, and mesophilic resistances, respectively. These resistances describe the turbulent transport of a gas to the surface (Ra), molecular transport through a thin layer of air above the leaf surface (Rb), and deposition to the leaf surface (Rleaf) (Baldocchi et al., 1987). Rleaf is dependent upon plant physiology and the chemical and physical properties of the depositing compounds. Rleaf is determined by deposition to the leaf cuticles (Rcut), diffusion through the stomata (Rst), and chemical processing within the mesophyll (Rm). We do not allow for emission of NO or NO2 from leaves, consistent with recent laboratory observations that have observed negligible compensation points for these molecules (Chaparro-Suarez et al., 2011; Breuninger et al., 2013; Delaria et al., 2018).
All boundary, aerodynamic, cuticular, and soil resistances of O3, HNO3, CH2O, alkyl nitrates (ANs), acyl peroxy nitrates (APNs), HC(O)OH, ROOH, and H2O2 are calculated according to Wolfe et al. (2011). The cuticular and mesophyllic resistances for NO2 and NO are adjustable input parameters. Stomatal resistances are determined from the stomatal conductance to water vapor (gs) calculated using either Eq. (7) (Wesely, 1989) or Eq. (8) (Jarvis et al., 1976; Emberson et al., 2000), hereafter referred to as the Wesely and Emberson schemes, respectively:
where gmax is the species-specific maximum stomatal conductance; fmin is a species-specific scaling factor to the minimum stomatal conductance; SR is the solar radiation in watts per square meter (W m−2); and fphen, fSWP, flight, ftemp, and fVPD are functions representing modifications to the stomatal conductance due to leaf phenology, soil water content, irradiance, temperature, and vapor pressure deficit, respectively (Eqs. 9–12).
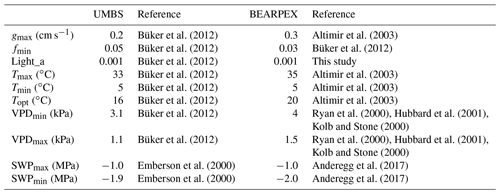
Topt and Tmin are the optimal and minimum temperature required for stomatal opening. PPFD is the photosynthetic photon flux density, and Lighta is a species-specific light response parameter. VPDmin and VPDmax are the vapor pressure deficit at which stomatal opening reaches a minimum and maximum, respectively. SWPmin and SWPmax are the soil water potentials at which stomatal opening reaches a minimum and maximum, respectively. All model calculations represented the peak growing season when fphen=1. ftemp, fVPD, and flight were calculated according to Emberson et al. (2000) using parameters found in Table 2.
2.2 Site description
The model was evaluated with comparison to observations from the Biosphere Effects on Aerosols and Photochemistry 2009 (BEARPEX-2009) field campaign from 15 June to 31 July 2009 at Blodgett Forest (Min et al., 2014) and the University of Michigan Biological Station (UMBS) during 5–10 August 2012 (Geddes and Murphy, 2014). For the BEARPEX-2009 calculations, the modeled canopy included an overstory height of 10 m with a one-sided leaf area index of 3.2 m2 m−2 (LAIos) and an understory height of 2 m with a LAI of 1.9 m2 m−2 (LAIus). Model simulations were run for 30 June 2009 using conditions from the BEARPEX-2009 ponderosa pine forest site located in the western foothills of the Sierra Nevada Mountains, CA (38∘58′42.9′′ N, 120∘57′57.9′′ W; elevation 1315 m) (Table 1) (Fig. 2a). Meteorological conditions and soil NO emissions used in the model simulation were those reported by Min et al. (2014). Diurnal soil water potentials (SWPs) were values reported in a geological survey of nearby Sierra sites in a comparatively wet year (Ishikawa and Bledsoe, 2000; Stern et al., 2018).
Figure 2Satellite images showing the locations of (a) the BEARPEX-2009 campaign and (b) the University of Michigan Biological Station (UMBS). Red triangles show the specific site locations. Measurements of chemical species and local meteorological variables from the two campaigns were used to validate our 1-D canopy multibox model.
For UMBS-2012 calculations, the modeled canopy included an overstory height of 20 m with a one-sided LAI of 2.5 m2 m−2 and an understory height of 4 m with a LAI of 1 m2 m−2 (Bryan et al. 2015). Model simulations were run for 8 August 2012 using conditions from the UMBS mixed hardwood forest located in northern Michigan (45∘33′32′′ N, 84∘42′52′′ W) (Table 1) (Fig. 2b). Daily temperatures, VPDs, soil NO emissions, and site-specific parameters used in the model simulations were those reported in Geddes and Murphy (2014) and Seok et al. (2013).
Temperature and relative humidity used in the model were sinusoidal fits to observations of minimum and maximum daily temperature and relative humidity from the corresponding field measurement site. The relative temperature decrease as a function of altitude was calculated using a fit to observations during BEARPEX-2007, as presented by Wolfe and Thornton (2011). Solar zenith angles (SZAs) and photosynthetically active radiation (PAR) were calculated every 0.5 h for each location and time period using the National Center for Atmospheric Research TUV calculator (Madronich and Flocke, 1999) and fit using a smoothed spline interpolation. Within the canopy, extinction of radiation (ER) was calculated following Beer's law:
where krad is the radiation extinction coefficient, SZA is the solar zenith angle, and LAIcum is the cumulative LAI calculated as the sum of one-half the LAI in box k and the total LAI in the boxes above box k.
2.3 Vertical transport and advection
The turbulent diffusion flux (F(z)) is represented in the model using K-theory, according to the Chemistry of Atmosphere-Forest Exchange (CAFE) Model (Wolfe and Thornton, 2011).
where ΔCi,k is the change in concentration in species i in box k during each time step, and Δz is the difference between the midpoints of boxes k and k+1. K(z) above the canopy is based on the values from Gao et al. (1993), and below the canopy it is a function of friction velocity calculated according to Wolfe et al. (2011) and is a function of the diffusion timescale ratio (τ∕TL) – defined as the ratio of the time since emission of a theoretical diffusing plume (τ) and the Lagrangian timescale (TL) – and the friction velocity (u∗) (Wolfe and Thornton, 2011). The details of the parameterization of turbulent diffusion fluxes are documented elsewhere (Wolfe and Thornton, 2011) and based on the works of Raupach (1989) and Makar et al. (1999). The height-dependent friction velocity (u(z)∗) is attenuated from the above-canopy u∗ according to Yi et al. (2008). Although Finnigan et al. (2015) identified flaws in this treatment, we believe it is sufficient for our focus on illustrating generalizable qualitative trends.
The resulting residence time in the canopy is approximately 2–3 min for model conditions during the day. Our model is a simple parameterization of turbulent processes and as such will only capture mean vertical diffusion. Other works (Collineau and Brunet, 1993a; Raupach et al., 1996; Brunet and Irvine, 2000; Thomas and Foken, 2007; Sörgel et al., 2011; Steiner et al., 2011) have shown that near-field effects of individual canopy elements and coherent turbulent structures can play an important role in canopy exchange. These more intricate processes are not captured explicitly by our simple model. Previous works (Gao et al., 1993; Makar et al., 1999; Stroud et al., 2005; Wolfe et al., 2011) have also utilized fairly simple representations of canopy exchange in local and regional models, and as such K-theory is likely sufficient to represent average vertical diffusion for the purposes of our study.
Advection in the model is treated as a simple mixing process in each model layer.
where kmix=0.3 h−1 (Wolfe and Thornton, 2011), and Ci(adv) is the advection concentration of species i. Advection concentrations are set to fit with the observations during BEARPEX-2009 (Min et al., 2014) or UMBS-2012 (Geddes and Murphy, 2014; Seok et al., 2013) and are used to maintain reasonable background concentrations (Table S1 in the Supplement). Concentrations of NOx, O3, and some volatile organic compounds (VOCs) at both sites were influenced by emissions from nearby cities and consequently had sources outside the canopy. For the BEARPEX-2009 model runs, the maximum daily advection concentration was reached at around 17 h, based on field observations of higher NOx plumes from nearby Sacramento in the afternoon (Wolfe et al., 2011; Min et al., 2014). The diurnal advection concentrations of NOx were modeled with a sinusoidal function in the range 0.1–0.35 ppb (Table S1). For UMBS all advection concentrations were constant.
2.4 Chemistry
Chemistry in the model is based on reaction rate constants from the JPL Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies evaluation no. 18 (Burkholder et al., 2015). Photolysis rates are calculated as a function of solar zenith angle (SZA), which was constructed using a smoothed spline interpolation fit of photolysis rates calculated with the TUV calculator (Madronich and Flocke, 1999) at every 10∘ interval of the zenith angle. The simplified reaction scheme included in the model is based on the model presented in Browne and Cohen (2012). The model includes both daytime and nighttime NOx chemistry and a simplified oxidation scheme. In this simplified case, oxidation of VOCs during the daytime results in the production of peroxy radicals (RO2), treated as a uniform chemical family. To be applicable to a range of forest types, we also include adjustable parameters, kOH and kNO3 for the average rate constant for reaction of VOCs with OH and NO3, respectively. kOH and kNO3 are effective values adjusted in the model based on site-specific VOC composition and observations of OH reactivity. A complete list of reactions and rate constants included in the model is shown in Table S2.
2.5 BVOC emissions
Emissions rates (molecules ) of biogenic volatile organic compounds (BVOCs) in the canopy are calculated via
where Eb (molecules cm(leaf)−2 s−1) is the basal emission rate of VOC, Δh is the total height of the box, and CL and CT are corrections for light and temperature (Guenther et al., 1995).
2.6 Evaluation of NOx fluxes and lifetimes
The model was used to assess the impact of NO2 deposition parameters on the NOx budget, lifetime, loss, and vertical profile within a forested environment. In each box, the rates of NOx loss with respect to nitric acid formation, alkyl nitrate formation, and deposition were calculated from Eqs. (17)–(19).
α is the fraction of the NO+RO2 reaction that forms alkyl nitrates, and β is the fraction of the NO3+BVOC reaction that forms alkyl nitrates. The NOx lifetime was then scaled to the entire boundary layer by summing over the products of the lifetime and boundary layer fraction (Δhk∕PBL) in each box.
NOx was treated as the sum of NO, NO2, and all short-lived products, including NO3, 2N2O5, and peroxyacetyl nitrate (PAN) (Romer et al., 2016). Deposition of PAN was not considered.
We also calculated the 24 h average vertical fluxes (Eq. 14) of NOx and used the flux through the canopy to estimate the fraction of soil-emitted NOx ventilated to the troposphere above. Because PAN formed during the nighttime is expected to rerelease NOx to the atmosphere during the day, in this calculation, PAN was included as part of the NOx budget.
We assessed the sensitivity of the model to τ∕TL, the radiation extinction coefficient (krad), the aerodynamic leaf width (lw), LAI, soil NO emission (eNO), and α. These parameters are simplifications of complex physical processes and not always easily constrained by observations. The total deposition velocity of NO2 chosen for these assessments was 0.2 cm s−1 during the daytime and 0.02 cm s−1 during the nighttime, based on values of gmax and gmin chosen for Blodgett Forest (discussed above) and typical values for deposition velocity observed for a variety of species in the laboratory (Teklemariam and Sparks, 2006; Chaparro Suarez et al., 2011; Breuninger et al., 2013; Delaria et al., 2018).
The largest effects were observed for changes in α, LAI, and soil NO emission. LAIos and LAIus were scaled from their values of 1.9 and 3.2 m2 m−2, respectively, by a factor of 0.25 and 1.5. Increasing the scaling factor from 0.25 to 1.5 resulted in a decrease in NOx lifetimes, above-canopy concentration, and average canopy flux of 24 %, 27 %, and 36 %, respectively (Fig. S1 in the Supplement). Increasing α from 0.01 to 0.1 resulted in a decrease in NOx lifetimes, above-canopy concentrations, and average canopy fluxes of 75 %, 38 %, and 39 %, respectively (Fig. S2). For all other model runs an α of 0.075 was chosen, in accordance with observations from regions primarily influenced by BVOCs (e.g., monoterpenes, isoprene, 2-methyl-3-buten-2-ol). Increasing the maximum soil NO emission from 1 to 10 ppt m s−1 increased the in-canopy enhancement from 28 % to 140 % relative to above-canopy NOx concentrations (Fig. S3b). The fraction of soil-emitted NOx ventilated through the canopy also increased from 45 % to 64 % (Fig. S3a). The large effect of soil NO emission on NOx fluxes implies that this highly variable parameter (Vinken et al., 2014) is also important to constrain in chemical transport models. Further discussion of soil NO emission is, however, beyond the scope of this study.
Very small effects on NOx were observed for changes in the parameters τ∕TL, krad, or lw. The minor changes caused by variations in these parameters are listed below for completeness.
τ∕TL represents the diffusion timescale ratio, a full description of which can be found in Wolfe and Thornton (2011). A larger τ∕TL represents faster diffusion and vertical transport within the canopy layer, as well as shorter residence times in the canopy. We find that altering this parameter from 1.2 to 8 (representing a change in residence time from 650 to 62 s) caused a 9.9 %, 4.4 %, and 8.7 % increase in average canopy fluxes, NOx lifetimes, and above-canopy concentration, respectively (Fig. S4). For all subsequent model runs, a value of 2 for τ∕TL was chosen, resulting in a canopy residence time during the day of 152 and 194 s for Blodgett Forest and UMBS, respectively, calculated using Eq. (21).
The boundary layer resistance, or laminar sublayer resistance, Rb, is dependent upon the aerodynamic leaf width, lw (Eq. 22):
where ν=0.146 cm2 s−1 is the kinematic viscosity of air, D is the species-dependent molecular diffusion coefficient, c is a tunable constant set to 1 for this study, and u∗(z) is the height-dependent friction velocity that is a function of u∗ and LAIcum (Wolfe and Thornton, 2011). lw depends upon the vegetation species. A value of 1 cm was chosen for the overstory and 2 cm for the understory, as these widths are characteristic of pine trees and understory shrubs in a ponderosa pine forest (Wolfe and Thornton, 2011). Species with rapid deposition to the cuticles or the stomata are expected to be more sensitive to errors in lw, such as HNO3 or H2O2. An increase in NOx lifetime, average canopy flux, and above-canopy concentration of 1.4 %, 2.4 %, and 2.8 %, respectively, was predicted for a change in lw scaling factor from 0.1 to 2 (Fig. S5). These changes are expected to be greater in forests with a larger average deposition velocity, where Rb makes a greater contribution to the total resistance.
The rates of stomatal gas exchange and photolysis are regulated by the intensity of light that penetrates the canopy. The extinction of radiation by the canopy, treated as a Beer law parameterization (Eq. 13), is exponentially proportional to the radiation extinction coefficient, krad. krad ranging from 0.4–0.65 has been measured for coniferous forests and understory shrubs (Wolfe and Thornton, 2011). The NOx lifetime increased by 2.7 %, and the canopy fluxes and above-canopy concentrations decreased by 0.7 % and 0.6 %, respectively, for a change in krad from 0 to 0.6 (Fig. S6). This effect is expected to be greater for forests with a larger LAI. The minimal effect of krad on model results was also observed for multiple canopy profile shapes of equivalent LAI.
4.1 Model validation: comparison to field observations
To evaluate the applicability of our 1-D multilayer canopy model for predicting NOx concentrations and vertical fluxes in a variety of forest environments, we compared the model to observations from BEARPEX-2009 and UMBS-2012. Parameters used in each calculation are shown in Table 1. The model was run using both the Emberson and Wesely stomatal conductance models. Parameters for temperature, drought stress, and maximum and minimum stomatal conductances used in the Emberson model were input for the dominant tree species in the region (Table 2). At the BEARPEX-2009 site, the dominant tree species was ponderosa pine. For this site, gmax and parameters for fSWP and fVPD were inferred from ponderosa pine stomatal conductance data (Kelliher et al., 1995; Ryan et al., 2000; Hubbard et al., 2001; Johnson et al., 2009; Anderegg et al., 2017), and flight was inferred from measurements of the canopy conductance during BEARPEX-2009 (Fig. 3a). ftemp was represented by observations for Scots pine (Altimir et al., 2004; Emberson et al., 1997; Buker et al., 2012) and validated with comparison to stomatal conductance measured via sap flow during BEARPEX-2009 (Fig. 3a). At UMBS the dominant species are quaking aspen and bigtooth aspen, with many birch, beech, and maple species also present (Seok et al., 2013). Data for a European beech tree species were used to represent stomatal conductance parameters (Buker et al., 2007; Buker et al., 2012) and SWP stress (Emberson et al., 2000). These parameters were validated with comparison to stomatal conductance calculated from water vapor and latent heat flux measurements during UMBS-2012 using an energy-balance method according to Mallick et al. (2013) (Fig. 4a).
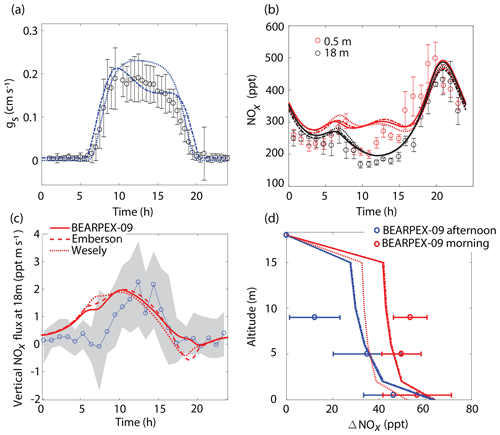
Figure 3Comparison of model results to BEARPEX-2009 hourly averaged observations of (a) stomatal conductances, (b) NOx mixing ratios at 18 m (black) and 0.5 m (red), and (c) vertical fluxes at 18 m. (d) Averaged observations of in-canopy NOx enhancements from 09:00 to 12:00 (blue) and from 13:00 to 16:00 (red) compared with modeled NOx enhancements, defined as the difference between NOx below the canopy and NOx measured at 18 m. Observations from BEARPEX-2009 are from Min et al. (2014). In all panels solid lines, dotted lines, and dashed lines represent results from our model with stomatal conductances parameterized using observed conductances, the Wesely model, and the Emberson model, respectively. Circles, error bars, and grey shaded regions represent observations, standard errors of the mean, and the interquartile range of data, respectively.
The model replicates key features of the canopy fluxes and above-canopy NOx daytime mixing ratios from the 2009 BEARPEX campaign (Fig. 3). The average daytime above-canopy NOx mixing ratios during the duration of BEARPEX-2009 was 253 ppt, with observations ranging from 80 to 550 ppt of NO2 and from 10 to 100 ppt of NO (Min et al., 2014). The general daily trends in observations of NOx mixing ratios are captured by both the Wesely and Emberson cases – with minimum NOx mixing ratios occurring in the late morning, an increase in NOx in the afternoon, and maximum NOx concentrations of 450–500 ppt reached in the evenings, primarily as a result of high-NOx plumes from nearby Sacramento in the afternoon (Wolfe et al., 2011; Min et al., 2014) (Fig. 3b). However, both model scenarios predict a slower-than-observed decrease in NOx mixing ratios from the evening to the early morning, predict larger midmorning fluxes than observed (by ∼0.5–1.5 ppt m s−1), and fail to represent the in-canopy enhancement of NOx (∼50 ppt), relative to above-canopy mixing ratios, observed in the evening (Fig. 3). The above-canopy vertical NOx flux predicted in both model cases also agrees reasonably well with observations, with the Emberson case representing morning and midday NOx fluxes slightly better than the Wesely case. This relatively good agreement between the Emberson case and observed fluxes is also demonstrated in Fig. 3d by the agreement between modeled and observed canopy NOx enhancements. There is, however, generally little difference between Emberson and Wesely model cases for this site during the period considered (Fig. 3). This is likely due to the good agreement in both the Emberson and Wesely cases with observations of stomatal conductance (Fig. 3a).
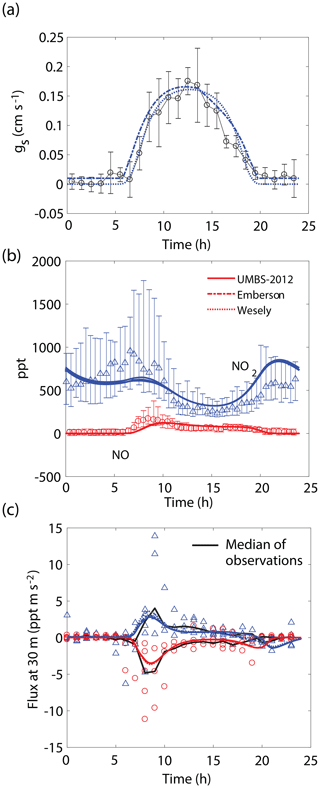
Figure 4Comparison of model results to (a) hourly averaged observed stomatal conductances, (b) NO and NO2 mixing ratios at 30 m, and (c) median (black lines) and hourly averaged NO and NO2 vertical fluxes at 30 m observed during UMBS-2012 for 8 August 2012. In all panels solid lines, dotted lines, and dashed lines represent results from our model with stomatal conductances parameterized using observed conductances, the Wesely model, and the Emberson model, respectively. Blue triangles and red circles represent NO2 and NO observations, respectively. Error bars represent the interquartile range of data.
We also observe similar correspondence between the model and key features of the UMBS-2012 observations (Fig. 4). NO and NO2 mixing ratios and canopy fluxes are both within the range of observations. The model predicts a maximum of ∼40 % lower NO2 in the morning and ∼30 % higher NO2 at night than what was observed (Fig. 4b). It should also be noted that this agreement was achieved without inclusion of an NO2 compensation point, whereas Seok et al. (2013) had proposed the importance of considering foliar NO2 emission at this location. Differences between the Wesely model and Emberson model were negligible for this site. This is likely due to a higher humidity in the summer in this region and larger soil moisture, reducing the prediction for midday and late afternoon VPD stress by the Emberson model, as can be seen by the similarity in the predicted gs by the Emberson and Wesely models (Fig. 4a).
4.2 Effects of maximum stomatal conductance
The BEARPEX-2009 case was simulated using the Wesely model for different values of the maximum stomatal conductance (gmax) (Fig. 5), with advection concentrations of NOx set to zero. The range of gmax currently represented in the literature during the peak growing season for forested regions ranges from 0.2 to 0.8 cm s−1 (Kelliher et al., 1995; Emberson et al., 1997; Emberson et al., 2000; Ryan et al., 2000; Hubbard et al., 2001; Altimir et al., 2003; Fares et al., 2013). This range reflects differences in forest types and a wide variety of tree species. Global chemical transport models (CTMs) using the Wesely parameterization currently include gmax of 1.4, 0.77, and 1 cm s−1 for deciduous, coniferous, and mixed forests, respectively (Wesely, 1989; Wang et al., 1998a). Figure 5b demonstrates the impact of gmax on the average daily vertical flux of NOx through the canopy. A total of 96 % of soil-emitted NOx is ventilated through the canopy with no foliar deposition (gmax=0 cm s−1). In contrast, 44 % of soil-emitted NOx is taken up by the forest and 56 % is ventilated through the canopy when the maximum stomatal conductance is 1.4 cm s−1. Figure 5c and d show the effects of gmax on the diurnal flux through the canopy and the diurnal above-canopy NOx mixing ratio, respectively. Compared with no foliar deposition, a gmax of 1.4 cm s−1 results in ∼60 % reduction in the canopy flux and ∼50 % reduction in the above-canopy NOx mixing ratio at noon. (Fig. 5c and d). In Fig. 6a we show the fraction of soil-emitted NOx ventilated through the canopy as a function of gmax. The model suggests a maximum foliar reduction of NOx of ∼60 % for a canopy of 10 m and total LAI of 5.1 m2 m−2. Our model also predicts that changes in gmax have a greater overall impact on canopy NOx fluxes at larger leaf resistances and slower foliar uptake. In the range for gmax of ∼0–0.5 cm s−1, variation in gmax can have a large impact on the predicted canopy fluxes of NOx, which would in turn have a large impact on concentrations and fluxes of O3. These values of gmax result in deposition velocities in the range expected for most forests, based on laboratory measurements of leaf-level deposition (Hanson and Lindberg, 1991; Rondon and Granat, 1994; Hereid and Monson, 2001; Teklemariam and Sparks, 2006; Pape et al., 2009; Chaparro-Suarez et al., 2011; Breuninger et al., 2013; Delaria et al., 2018) and global analysis suggesting 20–50 % reductions in soil-emitted NOx by vegetation (Jacob and Wofsy, 1990; Yienger and Levy, 1995; Ganzeveld et al., 2002a, b). Model calculations also predict a strong effect on the lifetimes of NOx, as shown in Fig. 6b, with maximum stomatal conductances of 0.1, 0.3, and 1.4 cm s−1 reducing the NOx lifetime by ∼0.7 h (∼7 %), ∼1.8 h (∼18 %), and ∼3.6 h (∼36 %), respectively, compared with no deposition. Similar trends (not shown) were also observed using parameters for UMBS.
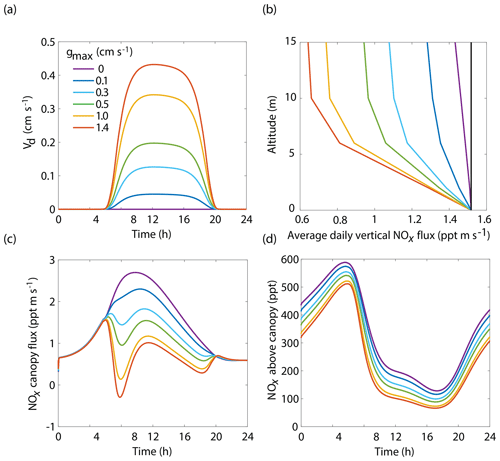
Figure 5Model results of (a) diurnal NO2 deposition velocities, (b) average daily vertical fluxes of NOx and a conserved tracer (black line), (c) diurnal canopy fluxes at 10 m, and (d) diurnal above-canopy NOx mixing ratios at 15 m for different values of maximum stomatal conductance (gmax) using the Wesely scheme to calculate stomatal conductance.
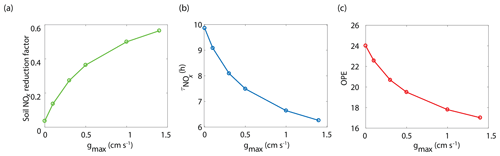
Figure 6Model-predicted dependence of (a) the fraction of soil-emitted NOx removed in the canopy, (b) the average daily NOx lifetime () in the planetary boundary layer, and (c) ozone production efficiency (OPE) on maximum stomatal conductance (gmax) using the Wesely scheme to calculate stomatal conductance.
4.3 Emberson model vs. Wesely model comparison
The relative importance of including parameterizations of VPD and SWP in the calculation of stomatal conductance and overall deposition velocity is expected to be regionally variable, along with regional variations in dominant tree species, soil types, and meteorology. We ran the model using BEARPEX-2009 conditions using both the Wesely and Emberson stomatal conductance models under “dry” and “wet” conditions. Here we use “dry” to refer to conditions of low humidity and low soil moisture and “wet” to refer to conditions with high humidity and high soil moisture. Under the dry scenario the SWP daily minimum and maximum were −2.0 and −1.7 MPa, respectively, with the daily minimum reached at sunset. A minimum daily RH of 40 % occurred at noon, with a maximum at midnight of 65 %. Summertime is often even drier in regions of the western United States, so these dry parameters are conservative estimates for many forests. Under the wet scenario the SWP daily minimum and maximum were −0.5 and −0.1 MPa, respectively. The maximum and minimum RH were 90 % and 80 %, respectively. The values for soil moisture and relative humidity chosen were based on observations of SWP by Ishikawa and Bledsoe (2000) and the long-term climate data record at Auburn Municipal Airport (38.9547∘ N, −121.0819∘ W) from the NOAA National Centers for Environmental Information.
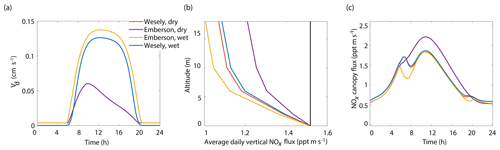
Figure 7Modeled results of (a) diurnal NO2 deposition velocities, (b) average daily vertical fluxes compared to a conserved tracer (black line), and (c) diurnal canopy fluxes at 10 m for wet and dry scenarios using either the Wesely or Emberson models to calculate stomatal conductance.
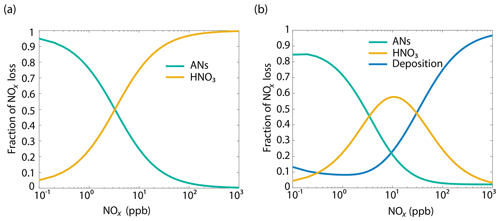
The results of the Wesely and Emberson wet and dry model runs are shown in Fig. 8. There was only a slight decrease in the in-canopy NOx enhancement and the canopy flux in the Wesely wet case, presumably due to a slight increase in OH radicals at higher RH. Predictably, the difference in the modeled deposition velocities was quite dramatic between the Emberson wet and dry cases. In the dry scenario, the deposition velocity reached a maximum in the late morning but rapidly declined after noon. The maximum deposition velocity reached was also substantially reduced (Fig. 7a). Using the wet Emberson stomatal conductance model, the NOx flux out of the forest was reduced by 16 % midday compared to the dry case, and the percent of soil NOx removed within the canopy was increased from 18 % to 30 % (Fig. 7). The model calculates a substantial impact on above-canopy NOx mixing ratios (Fig. 8), with a maximum of ∼30 % difference in NOx in the afternoon between wet and dry days using the Emberson parameterization, compared with ∼10 % difference using the Wesely model. Using the Emberson parameterization of stomatal conductance, deposition during wet days is predicted to contribute substantially more to the total NOx loss (∼40 %), with only ∼15 % contribution predicted for dry days (Fig. 9).
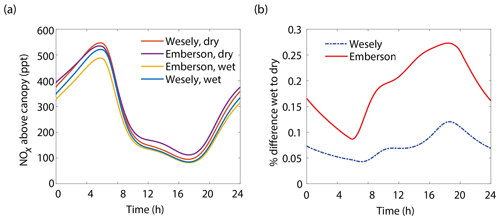
Figure 8(a) Modeled NOx mixing ratios above the canopy at 18 m for wet and dry scenarios using either the Wesely or Emberson models to calculate stomatal conductance. (b) Percent difference between NOx mixing ratios on wet and dry days using either the Wesely (dashed blue line) or Emberson (solid red line) parameterization of stomatal conductance.
Under the Wesely model, where stomatal conductance is parameterized only with temperature and solar radiation, the predicted deposition velocity would be nearly identical between the spring and fall in the western United States and similar semiarid regions (with comparatively minor temperature effects). While the Emberson model predicts large seasonal differences, the Wesely model fails to account for the dramatic decrease in stomatal conductance seen in the dry seasons in such regions caused by significant reductions in relative humidity and soil water potential (Prior et al., 1997; Panek and Goldstein, 2001; Chaves, 2002; Beedlow et al., 2013). We recognize that the multibox model presented in this work is a simplified representation of physical processes and as such is not likely to (and is not intended to) provide quantitative exactitude for the trends described above. However, we argue for the necessity of incorporating these conceptual advances for accurately representing canopy processes and predicting their effect on the NOx cycle.
5.1 Implications for modeling NO2 dry deposition
As in our multilayer canopy model, the most common current method of parameterizing stomatal and cuticular deposition in large-scale chemical transport models (CTMs) is through the resistance model framework of Baldocchi et al. (1987). Many global (e.g., WRF-Chem and GEOS-Chem) and regional (e.g., MOZART and CAMx) CTMs calculate the stomatal component of the total deposition resistance using the representation of Wesely (1989), where stomatal conductance is dependent only on the type of vegetation, temperature, and solar radiation. The limitations of this parameterization have been highlighted by observations of a strong dependence of foliar deposition on soil moisture and vapor pressure deficit (VPD) (Kavassalis and Murphy, 2017; Rydsaa et al., 2016). Inadequate descriptions of vegetative species, soil moisture, drought stress, etc., can have a dramatic impact on model results and can result in significant discrepancies between models and observations (Wesely and Hicks, 2000). Failure to account for effects of plant physiology on deposition may result in misrepresentation of deposition velocities, which, as we demonstrate, can have a substantial impact on NOx lifetimes and mixing ratios above and within a forest canopy. This effect will be especially pronounced in areas such as much of the western United States, where there are frequent periods of prolonged drought. Parameterizations of stomatal conductance, such as those presented in Emberson et al. (2000) and incorporated into some regional-scale CTMs (e.g., EMEP, MSC-W, and CHIMERE), if incorporated into global atmospheric models, could more accurately reflect the dependence of foliar deposition on meteorology and soil conditions. However, additional laboratory and field measurements on diverse plant species are also needed to determine appropriate, ecosystem-specific inputs to these parameterizations.
It should be noted that there have been significant recent advances in optimization approaches of stomatal modeling based on the theory that stomata maximize CO2 assimilation per molecule of water vapor lost via transpiration (Medlyn et al., 2011; Bonan et al., 2014; Franks et al., 2017; Miner et al., 2017; Franks et al., 2018). Medlyn et al. (2011) reconciled the empirical widely utilized Ball–Berry model with a theoretical framework optimizing ribulose-1,5-bisphosphate (RuBP) regeneration-limited photosynthesis. However, such methods of water use efficiency optimization do not account for stomatal closure as a result of soil moisture stress. Bonan et al. (2014) further developed a model considering water use efficiency optimization and water transport between the soil, plant, and atmosphere. Such parameterizations are utilized in the Community Land Model (CLM) – a land surface model often incorporated into regional and global climate–chemistry models (Lombardozzi et al., 2015; Kennedy et al., 2019). Although this model provides a physiological and mechanistic basis for stomatal behavior, it is heavily parameterized, relying on inputs of plant and soil parameters that could be expected to vary significantly across ecosystem types. For this reason, we view these methods as aspirational for incorporation into atmospheric global CTMs. We find the relative simplicity of the Emberson approach more useful for the purpose and scope of parameters for large-scale atmospheric models.
5.2 Implications for modeling ozone
NO2, as well as O3, deposition budgets are frequently calculated through inferential methods whereby the deposition velocity is constrained with ambient observations (Holland et al., 2005; Geddes and Murphy, 2014). These inferential models are often complicated by the fast reaction of the NO2–NO–O3 triad, making it difficult to separate chemical and physical processes. Further, these inferential models for determining dry deposition constrained with observations of chemical concentrations and eddy-covariance measurements of fluxes are difficult to interpret because of similar chemical and turbulent timescales (Min et al., 2014; Geddes and Murphy, 2014). Emission of NO from soils, rapid chemical conversion to NO2, and subsequent in-air reactions of NOx must be evaluated accurately in order to correctly infer NOx and O3 atmosphere–biosphere exchange from observations. Our multilayer canopy model applies a simple method of representing these processes and evaluating the separate effects of chemistry and dry deposition on the NOx budget in forests.
Since the foliar deposition of NO2 reduces the NOx lifetime and NOx that is transported out of the canopy, it will also reduce the amount of ozone that is produced both within and above the canopy. Ozone production efficiency (OPE) in the canopy is calculated using Eqs. (23)–(25):
where P(O3) is the ozone production rate and L(NOx) is the NOx loss rate. The effect of stomatal conductance to NO2 on OPE is shown in Fig. 6c. An increase in gmax from 0 to 0.3 cm s−1 results in a decrease in OPE for the PBL from 24.0 to 20.7 (∼14 %) and a decrease to 17.0 (∼30 %) if gmax is 1.4 cm s−1. This is similar to OPE calculations that have been reported for forests and environments with NOx mixing ratios less than 1 ppb and heavily influenced by BVOC emissions (Marion et al., 2001; Browne and Cohen, 2012; Ninneman et al., 2017).
NO2 deposition and the in-canopy chemistry of NO2–NO–O3 also impact O3 production and removal. O3 deposition is frequently inferred from measurements of O3 concentrations or eddy-covariance measurements (Wesely and Hicks, 2000; Kavassalis and Murphy, 2017). However, because NO2 has a direct impact on ozone production, deposition of NO2 can affect inferences of O3 deposition from observations. The 14 % reduction of OPE and the more-than-20 % reduction in daytime NOx resulting from an increase in gmax from 0 to 0.3 cm s−1 can cause a parallel decrease in O3 concentrations and fluxes independent of O3 chemical loss or deposition. Thus, deposition of NO2 must be taken into account when evaluating O3 deposition losses from observed canopy fluxes.
5.3 Implications for near-urban forests
The analysis above suggests that the relative importance of chemical sinks and deposition will vary with NOx concentration. To evaluate the relative importance of NO2 foliar deposition and chemistry as a function of NOx mixing ratio, a simplified single-box model was also constructed with a simplified reaction scheme (Table S3), VOC reactivity of 8 s−1, α of 0.075, and a HOx () production rate ( of 2×106 molecules (similar to conditions observed during BEARPEX-09). RO2, OH, and HO2 were solved for steady-state concentrations, and NOx loss pathways were calculated via Eqs. (26)–(29).
where hcan is the canopy height (15 m), hPBL is the planetary boundary layer height (1000 m), and LAI is 5 m2 m−2.
where
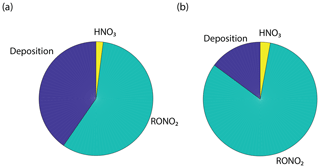
The results from this simplified box model are shown in Fig. 9 and agree well with our 1-D multibox model near 10 ppb NOx (Fig. S7). With deposition set to zero, nitric acid formation becomes a more significant sink of NOx than alkyl nitrate formation at around 1 ppb, and nitric acid formation accounts for more than 70 % of the total loss at 100 ppb. With a deposition pathway included, deposition acts as the dominant NOx sink above 30 ppb and at 10 ppb deposition, and AN formations are each 20 % of the NOx sink. Deposition is approximately 10 % of the sink over a wide range of concentrations. Forests in close proximity to urban centers (Fig. S9) may result in a substantial local decrease in NOx (Fig. S8, Fig. 10). Although the influence of urban or near-urban trees on NOx concentrations would be heavily dependent on meteorological factors (i.e., wind speed and direction), proximity to emission sources, and LAI, it may have some importance on a local or neighborhood scale. This effect may be relevant for understanding and predicting the effects of NOx reduction policies within and near cities. It may also be useful in considering NO2 deposition as a direct nitrogen input to the biosphere not mediated by soil processes.
We have constructed a 1-D multibox model with representations of chemistry and vertical transport to evaluate the impact of leaf-level processes on canopy-scale concentrations, lifetimes, and canopy fluxes of NOx. Our model is able to closely replicate canopy fluxes and above-canopy NOx daytime mixing ratios during two field campaigns that took place in a Sierra Nevada pine forest (BEARPEX-2009) and a northern Michigan mixed hardwood forest (UMBS-2012). We conclude that the widely used canopy reduction factor approach to describing soil NOx removal from the atmosphere within plant canopies is consistent with a process-based model that utilizes stomatal uptake, and we recommend that the canopy reduction factor (CRF) parameter be replaced with stomatal models for NO2 uptake.
We demonstrate with our 1-D multibox model that NO2 deposition provides a mechanistic explanation behind CRFs that are widely used in CTMs. We predict a maximum of ∼60 % reduction in the fraction of soil-emitted NOx ventilated through the canopy when stomatal conductances are greater than 0.075 cm s−1, consistent with the range of global CRFs used in current CTMs (Jacob and Wofsy, 1990; Yienger and Levy, 1995). Our model also predicts that changes in gmax have a greater overall impact on canopy NOx fluxes at larger leaf resistances to uptake (slower foliar uptake). In the range for gmax of ∼0–0.5 cm s−1, errors or variability in stomatal conductance can have a large impact on the predicted canopy concentrations and fluxes of NOx, which would in turn have a large impact on concentrations and fluxes of O3. This range of deposition velocities describes the range of uptake rates measured for many tree species and forest ecosystems (Hanson and Lindberg, 1991; Rondon and Granat, 1994; Hereid and Monson, 2001; Teklemariam and Sparks, 2006; Pape et al., 2008; Chaparro-Suarez et al., 2011; Delaria et al., 2018). Model calculations also predict a similar trend on the lifetimes of NOx, with a maximum reduction in the NOx lifetime by ∼4 h (>40 %) compared with no deposition.
The large effect that small changes in stomatal conductance can have on NOx lifetimes, concentrations, budget, and O3 production makes it very important to accurately parameterize in atmospheric models. Most global-scale chemical transport models parameterize stomatal conductance using the representation developed by Wesely (1989) (Jacob and Wofsy, 1990; Verbeke et al., 2015). These do no account for the effects of VPD, SWP, CO2 mixing ratio, or other factors known to influence stomatal conductance (Hardacre et al., 2015). We show that incorporating vapor pressure deficit and soil water potential – using the parameterization of Emberson et al. (2000) – has a substantial impact on predicted NO2 deposition, with the percent of soil NOx removed within the canopy increasing from 18 % to 30 % in wet (low VPD and high SWP) conditions compared to dry conditions in the location of BEARPEX-2009. Under the Wesely model, where stomatal conductance is parameterized only with temperature and solar radiation, the predicted deposition velocity would be nearly identical between wet and dry days and between the spring and fall in semiarid regions (e.g., much of the western United States, the Mediterranean Basin, the west coast of South America, parts of northwest Africa, parts of western and southern Australia, and parts of South Africa). The dominant effect of stomatal opening on NO2 deposition causes an important time of day and seasonal behavior that should be extensively explored with observations of NOx fluxes and concurrent models to confirm the role of deposition in a wider range of environments and more thoroughly vet the conceptual model proposed here.
The model reported in this paper has been deposited in GitHub (https://github.com/erd02011/NOxmodel_ACP2019) and Zenodo (https://doi.org/10.5281/zenodo.3666813; Delaria et al., 2019, 2020).
The data presented in this study from Blodgett Forest and the University of Michigan Biological Station were published in earlier works by Min et al. (2014; https://doi.org/10.5194/acp-14-5495-2014) and Geddes and Murphy (2014; https://doi.org/10.5194/acp-14-2939-2014), respectively.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-20-2123-2020-supplement.
ERD built the model, preformed data analysis, and prepared all figures. ERD wrote the paper in consultation with RCC. RCC supervised the project.
The authors declare that they have no conflict of interest.
We would like to thank the three reviewers for their constructive comments. We would also like to give a special thanks to Jennifer G. Murphy, University of Toronto, and Jeffrey Geddes, Boston University, for providing data from the UMBS field site and for constructive comments that improved the paper. We appreciate use of local climatological data (Auburn Municipal Airport, CA, USA) provided by the National Centers for Environmental Information (NCEI) of the National Oceanic and Atmospheric Administration (NOAA), available at: https://www.ncdc.noaa.gov/cdo-web/datasets/LCD/stations/WBAN:23224/detail (last access: 28 October 2019).
This research has been supported by the National Science Foundation (grant no. AGS-1352972) and the NOAA Climate Program Office's Atmospheric Chemistry, Carbon Cycle, and Climate program (grant no. NA18OAR4310117). Additional support was provided by an NSF Graduate Research Fellowship to Erin R. Delaria (grant no. DGE 1752814).
This paper was edited by Laurens Ganzeveld and reviewed by Kirsti Ashworth and two anonymous referees.
Altimir, N., Tuovinen, J.-P., Vesala, T., Kulmala, M., and Hari, P.: Measurements of ozone removal by Scots pine shoots: calibration of a stomatal uptake model including the non-stomatal component, Atmos. Environ., 38, 2387–2398, https://doi.org/10.1016/j.atmosenv.2003.09.077, 2004.
Ammann, M., Ballmoos, P. V., Stalder, M., Suter, M., and Brunold, C.: Uptake and assimilation of atmospheric NO2–N by spruce needles (Picea abies): A field study, Water Air Soil Pollut., 85, 1497–1502, https://doi.org/10.1007/BF00477193, 1995.
Anderegg, W. R., Wolf, A., Arango-Velez, A., Choat, B., Chmura, D. J., Jansen, S., Kolb, T., Li, S., Meinzer, F., Pita, P., Resco de Dios, V., Sperry, J. S., Wolfe, B. T., and Pacala, S.: Plant water potential improves prediction of empirical stomatal models, PLoS ONE, 12, e0185481f, https://doi.org/10.1371/journal.pone.0185481, 2017.
Baldocchi, D. D., Hicks, B. B., and Camara, P.: A Canopy Stomatal-Resistance Model for Gaseous Deposition to Vegetated Surfaces, Atmos. Environ., 21, 91–101, https://doi.org/10.1016/0004-6981(87)90274-5, 1987.
Beedlow, P. A., Lee, E. H., Tingey, D. T., Waschmann, R. S., and Burdick, C. A.: The importance of seasonal temperature and moisture patterns on growth of Douglas-fir in western Oregon, USA, Agr. Forest Meteorol., 169, 174–185, https://doi.org/10.1016/j.agrformet.2012.10.010, 2013.
Bonan, G. B., Williams, M., Fisher, R. A., and Oleson, K. W.: Modeling stomatal conductance in the earth system: linking leaf water-use efficiency and water transport along the soil–plant–atmosphere continuum, Geosci. Model Dev., 7, 2193–2222, https://doi.org/10.5194/gmd-7-2193-2014, 2014.
Breuninger, C., Oswald, R., Kesselmeier, J., and Meixner, F. X.: The dynamic chamber method: trace gas exchange fluxes (NO, NO2, O3) between plants and the atmosphere in the laboratory and in the field, Atmos. Meas. Tech., 5, 955–989, https://doi.org/10.5194/amt-5-955-2012, 2012.
Breuninger, C., Meixner, F. X., and Kesselmeier, J.: Field investigations of nitrogen dioxide (NO2) exchange between plants and the atmosphere, Atmos. Chem. Phys., 13, 773–790, https://doi.org/10.5194/acp-13-773-2013, 2013.
Browne, E. C. and Cohen, R. C.: Effects of biogenic nitrate chemistry on the NOx lifetime in remote continental regions, Atmos. Chem. Phys., 12, 11917–11932, https://doi.org/10.5194/acp-12-11917-2012, 2012.
Brunet, Y. and Irvine, M. R.: The control of coherent eddies in vegetation canopies: Streamwise structure spacing, canopy shear scale and atmospheric stability, Bound.-Lay. Meteorol., 94, 139–163, 2000.
Bryan, A. M., Cheng, S. J., Ashworth, K., Guenther, A. B.,Hardiman, B. S., Bohrer, G., and Steiner, A. L.: Forest-atmosphere BVOC exchange in diverse and structurally complex canopies: 1-D modeling of a mid-successional forest in northern Michigan, Atmos. Environ., 120, 217–226, https://doi.org/10.1016/j.atmosenv.2015.08.094, 2015.
Büker, P., Emberson, L. D., Ashmore, M. R., Cambridge, H. M., Jacobs, C. M. J., Massman, W. J., Muller, J., Nikolov, N., Novak, K., Oksanen, E., Schaub, M., and de la Torre, D.: Comparison of different stomatal conductance algorithms for ozone flux modelling, Environ. Pollut., 146, 726–735, https://doi.org/10.1016/j.envpol.2006.04.007, 2007.
Büker, P., Morrissey, T., Briolat, A., Falk, R., Simpson, D., Tuovinen, J.-P., Alonso, R., Barth, S., Baumgarten, M., Grulke, N., Karlsson, P. E., King, J., Lagergren, F., Matyssek, R., Nunn, A., Ogaya, R., Peñuelas, J., Rhea, L., Schaub, M., Uddling, J., Werner, W., and Emberson, L. D.: DO3SE modelling of soil moisture to determine ozone flux to forest trees, Atmos. Chem. Phys., 12, 5537–5562, https://doi.org/10.5194/acp-12-5537-2012, 2012.
Burkholder, J. B., Sander, S. P., Abbatt, J., Barker, J. R., Huie, R. E., Kolb, C. E., Kurylo, M. J., Orkin, V. L., Wilmouth, D. M., and, Wine, P. H.: Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 18, JPL Publication 15-10, Jet Propulsion Laboratory, Pasadena, available at: http://jpldataeval.jpl.nasa.gov (last access: 28 September 2018), 2015.
Chaparro-Suarez, I. G., Meixner, F. X., and Kesselmeier, J.: Nitrogen dioxide (NO2) uptake by vegetation controlled by atmospheric concentrations and plant stomatal aperture, Atmos. Environ., 45, 5742–5750, https://doi.org/10.1016/j.atmosenv.2011.07.021, 2011.
Chaves, M. M.: How Plants Cope with Water Stress in the Field? Photosynthesis and Growth, Ann. Bot.-London, 89, 907–916, https://doi.org/10.1093/aob/mcf105, 2002.
Collineau, S. and Brunet, Y.: Detection of turbulent coherent motions in a forest canopy, 1. Wavelet analysis, Bound.-Lay. Meteorol., 65, 357–379, 1993.
Crutzen, P. J.: The Role of NO and NO2 in the Chemistry of the Troposphere and Stratosphere, Annu. Rev. Earth Pl. Sc., 7, 443–472, https://doi.org/10.1146/annurev.ea.07.050179.002303, 1979.
Delaria, E. R., Vieira, M., Cremieux, J., and Cohen, R. C.: Measurements of NO and NO2 exchange between the atmosphere and Quercus agrifolia, Atmos. Chem. Phys., 18, 14161–14173, https://doi.org/10.5194/acp-18-14161-2018, 2018.
Delaria, E. R.: Multibox forest model for assessing impacts of NO2 stomatal deposition on NOx above a canopy, https://github.com/erd02011/NOxmodel_ACP2019 (last access: 20 February 2020), 2019.
Delaria, E. R.: Multibox forest model for assessing impacts of NO2 stomatal deposition on NOx above a canopy, https://doi.org/10.5281/zenodo.3666813, 2020.
Emberson, L., Ashmore, M., Cambridge, H., Simpson, D., and Tuovinen, J.-P.: Modelling stomatal ozone flux across Europe, Environ. Pollut., 109, 403–413, https://doi.org/10.1016/S0269-7491(00)00043-9, 2000.
Emberson, L. D.: Defining and mapping relative potential sensitivity of European vegetation to ozone, PhD Thesis, Imperial College, University of London, UK, 1997.
Fares, S., Matteucci, G., Mugnozza, G. S., Morani, A., Calfapietra, C., Salvatori, E., Fursao, L., Manes, F., and Loreto, F.: Testing of models of stomatal ozone fluxes with field measurements in a mixed Mediterranean forest, Atmos. Environ., 67, 242–251, https://doi.org/10.1016/j.atmosenv.2012.11.007, 2013.
Fenn, M. E., Poth, M. A., Aber, J. D., Baron, J. S., Bormann, B. T., Johnson, D. W., Lemly, D. A., McNulty, S. G., Ryan, D. F., and Stottlemyer, R.: Nitrogen Excess in North American Ecosystems: Predisposing Factors, Ecosystem Responses, and Management Strategies, Ecol. Appl., 8, 706–733, https://doi.org/10.1890/1051-0761(1998)008[0706:NEINAE]2.0.CO;2, 1998.
Finnigan, J., Harman, I., Ross, A., and Belcher, S.: First-order turbulence closure for modelling complex canopy flows, Q. J. R. Meteorol. Soc., 141, 2907–2916, https://doi.org/10.1002/qj.2577, 2015.
Franks, P. J., Berry, J. A., Lombardozzi, D. L., and Bonan, G. B.: Stomatal Function across Temporal and Spatial Scales: Deep-Time Trends, Land-Atmosphere Coupling and Global Models, Plant Physiol., 174, 583–602, https://doi.org/10.1104/pp.17.00287, 2017
Franks, P., Bonan, G., Berry, J., Lombardozzi, D., Holbrook, N., Herold, N., and Oleson, K.: Comparing optimal and empirical stomatal conductance models for application in Earth system models, Glob. Change Biol., 24, 5708–5723, https://doi.org/10.1111/gcb.14445, 2018.
Galloway, J. N., Dentener, F. J., Capone, D. G., Boyer, E. W., Howarth, R. W., Seitzinger, S. P., Asner, G. P., Cleveland, C. C., Green, P. A., Holland, E. A., Karl, D. M., Michaels, A. F., Porter, J. H., Townsend, A. R., and Vörösmarty, C. J.: Nitrogen cycles: Past, present, and future, Biogeochemistry, 70, 153–226, https://doi.org/10.1007/s10533-004-0370-0, 2004.
Ganzeveld, L. and Lelieveld, J.: Dry Deposition Parameterization In A Chemistry General-circulation Model and Its Influence On the Distribution of Reactive Trace Gases, J. Geophys. Res.-Atmos., 100, 20999–21012, https://doi.org/10.1029/95JD02266, 1995.
Ganzeveld, L. N., Lelieveld, J., Dentener, F. J., Krol, M. C., and Roelofs, G. J.: Atmosphere-biosphere trace gas exchanges simulated with a single-column model, J. Geophys. Res.-Atmos., 107, 4297, https://doi.org/10.1029/2001jd000684, 2002a.
Ganzeveld, L. N., Lelieveld, J., Dentener, F. J., Krol, M. C., Bouwman, A. J., and Roelofs, G. J.: Global soil-biogenic NOx emissions and the role of canopy processes, J. Geophys. Res.-Atmos., 107, 4298, https://doi.org/10.1029/2001jd001289, 2002b.
Gao, W., Wesely, M. L., and Doskey, P. V.: Numerical modelling of the turbulent diffusion and chemistry of NOx, O3, isoprene, and other reactive trace gases in and above a forest canopy, J. Geophys. Res.-Atmos., 98, 18339–18353, 1993.
Geddes, J. A. and Murphy, J. G.: Observations of reactive nitrogen oxide fluxes by eddy covariance above two midlatitude North American mixed hardwood forests, Atmos. Chem. Phys., 14, 2939–2957, https://doi.org/10.5194/acp-14-2939-2014, 2014.
Guenther, A., Hewitt, C. N., Erickson, D., Fall, R., Geron, C., Graedel, T., Harley, P., Klinger, L., Lerdau, M. T., McKay, W. A., Pierce, T., Scholes, B., Steinbrecher, R., Tallamraju, R., Taylor, J., and Zimmerman, P.: A global model of natural volatile organic compound emissions, J. Geophys. Res., 100, 8873–8892, https://doi.org/10.1029/94JD02950, 1995.
Gunderson, C. A., Sholtis, J. D., Wullschleger, S. D., Tissue, D. T., Hanson, P. J., and Norby, R. J.: Environmental and stomatal control of photosynthetic enhancement in the canopy of a sweetgum (Liquidambar styraciflua L.) plantation during 3 years of CO2 enrichment, Plant Cell Environ., 25, 379–393, https://doi.org/10.1046/j.0016-8025.2001.00816.x, 2002.
Hanson, P. J. and Lindberg, S. E.: Dry Deposition of Reactive Nitrogen-Compounds – a Review of Leaf, Canopy and Non-Foliar Measurements, Atmos. Environ. A-Gen., 25, 1615–1634, https://doi.org/10.1016/0960-1686(91)90020-8, 1991.
Hardacre, C., Wild, O., and Emberson, L.: An evaluation of ozone dry deposition in global scale chemistry climate models, Atmos. Chem. Phys., 15, 6419–6436, https://doi.org/10.5194/acp-15-6419-2015, 2015.
Hereid, D. P. and Monson, R. K.: Nitrogen oxide fluxes between corn (Zea mays L.) leaves and the atmosphere, Atmos. Environ., 35, 975–983, https://doi.org/10.1016/S1352-2310(00)00342-3, 2001.
Hicks, B., Baldocchi, D., Meyers, T., Hosker, R., and Matt, D.: A Preliminary multiple resistance routine for deriving dry deposition velocitiesfrom measured quantities, Water Air Soil Pollut., 36, 311–330, https://doi.org/10.1007/BF00229675, 1987.
Holland, E. A., Braswell, B. H., Lamarque, J.-F., Townsend, A., Sulzman, J., Müller, J.-F., Dentener, F., Brasseur, G., Levy II, H., Penner, J. E., and Roelofs, G.-J.: Variations in the predicted spatial distribution of atmospheric nitrogen deposition and their impact on carbon uptake by terrestrial ecosystems, J. Geophys. Res.-Atmos., 102, 15849–15866, https://doi.org/10.1029/96JD03164, 1997.
Holland, E. A., Braswell, B. H., Sulzman, J., and Lamarque, F.: Nitrogen deposition onto the United States and western Europe: Synthesis of observations and models, Ecol. Appl., 15, 38–57, https://doi.org/10.1890/03-5162, 2005.
Hubbard, R. M., Ryan, M. G., Stiller, V., and Sperry, J. S.: Stomatal conductance and photosynthesis vary linearly with plant hydraulic conductance in ponderosa pine, Plant Cell Environ., 24, 113–121, https://doi.org/10.1046/j.1365-3040.2001.00660.x, 2001.
Ishikawa, C. M. and Bledsoe, C.: Seasonal and diurnal patterns of soil water potential in the rhizosphere of blue oaks: evidence for hydraulic lift, Oecologia, 125, 459–465, https://doi.org/10.1007/s004420000470, 2000.
Jacob, D. J. and Wofsy, S. C.: Budgets of reactive nitrogen, hydrocarbons, and ozone over the Amazon forest during the wet season, J. Geophys. Res., 95, 16737, https://doi.org/10.1029/JD095iD10p16737, 1990.
Jarvis, P. G., Monteith, J. L., and Weatherley, P. E.: The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field, Philos. T. R. Soc. B, 273, 593–610, https://doi.org/10.1098/rstb.1976.0035, 1976.
Johansson, C.: Pine forest: a negligible sink for atmospheric NOx in rural Sweden, Tellus B, 39, 426–438, 1987.
Johnson, D., Woodruff, D., Mcculloh, K., and Meinzer, F.: Leaf hydraulic conductance, measured in situ, declines and recovers daily: leaf hydraulics, water potential and stomatal conductance in four temperate and three tropical tree species, Tree Physiol., 29, 879–887, https://doi.org/10.1093/treephys/tpp031, 2009.
Kavassalis, S. C. and Murphy, J. G.: Understanding ozone-meteorology correlations: A role for dry deposition, Geophys. Res. Lett., 44, 2922–2931, https://doi.org/10.1002/2016GL071791, 2017.
Keilliher, F. F., Leuning, R., Raupach, M. R., and Schulze, E.-D.: Maximum conductances for evaporation from global vegetation types, Agr. Forest Meteorol., 73, 1–16, https://doi.org/10.1016/0168-1923(94)02178-M, 1995.
Kennedy, D., Swenson, S., Oleson, K. W., Lawrence, D. M., Fisher, R., Lola da Costa, A. C., and Gentine, P.: Implementing plant hydraulics in the Community Land Model, version 5, J. Adv. Model. Earth Sy., 11, 485–513, https://doi.org/10.1029/2018MS001500, 2019.
Kolb, T. and Stone, J.: Differences in leaf gas exchange and water relations among species and tree sizes in an Arizona pine-oak forest, Tree Physiol., 20, 1–12, https://doi.org/10.1093/treephys/20.1.1, 2000.
Lombardozzi, D. L., Bonan, G. B., Smith, N. G., Dukes, J. S., and Fisher, R. A.: Temperature acclimation of photosynthesis and respiration: A key uncertainty in the carbon cycle-climate feedback, Geophys. Res. Lett., 42, 8624–8631, https://doi.org/10.1002/2015GL065934, 2015.
Madronich, S. and Flocke, S.: The Role of Solar Radiation in Atmospheric Chemistry, in: Environmental Photochemistry, The Handbook of Environmental Chemistry (Reactions and Processes), edited by: Boule, P., vol. 2/2L. Springer, Berlin, Heidelberg, https://doi.org/10.1007/978-3-540-69044-3_1 1999.
Makar, P. A., Fuentes, J. D., Wang, D., Staebler, R. M., and Wiebe, H. A.: Chemical processing of biogenic hydrocarbons within and above a temperate deciduous forest, J. Geophys. Res., 104, 3581–3603, 1999.
Mallick, K., Jarvis, A., Fisher, J. B., Tu, K. P., Boegh, E., and Niyogi, D.: Latent Heat Flux and Canopy Conductance Based on Penman–Monteith, Priestley–Taylor Equation, and Bouchet's Complementary Hypothesis, J. Hydrometeorol., 14, 419–442, https://doi.org/10.1175/JHM-D-12-0117.1, 2013.
Marion, T., Perros, P., Losno, R., and Steiner, E.: Ozone Production Efficiency in Savanna and Forested Areas during the EXPRESSO Experiment, J. Atmos. Chem., 38, 3–30, https://doi.org/10.1023/A:1026585603100, 2001.
Matheny, A. M., Bohrer, G., Garrity, S. R., Howard, C. J., and Vogel, C. S.: Observations of stem water storage in trees of opposing hydraulicstrategies, Ecosphere, 6, 1–13, https://doi.org/10.1890/ES15-00170.1, 2015.
Medlyn, B. E., Duursma, R. A., Eamus, D., Ellsworth, D. S., Prentice, I. C., Barton, C. V., Crous, K. Y., De Angelis, P., Freeman, M., and Wingate, L.: Reconciling the optimal and empirical approaches to modelling stomatal conductance, Glob. Change Biol., 17, 2134–2144, https://doi.org/10.1111/j.1365-2486.2010.02375.x, 2011.
Min, K.-E., Pusede, S. E., Browne, E. C., LaFranchi, B. W., and Cohen, R. C.: Eddy covariance fluxes and vertical concentration gradient measurements of NO and NO2 over a ponderosa pine ecosystem: observational evidence for within-canopy chemical removal of NOx, Atmos. Chem. Phys., 14, 5495–5512, https://doi.org/10.5194/acp-14-5495-2014, 2014.
Miner, G. L., Bauerle, W. L., and Baldocchi, D. D.: Estimating the sensitivity of stomatal conductance to photosynthesis: a review, Plant Cell Environ., 40, 1214–1238, https://doi.org/10.1111/pce.12871, 2017.
Nguyen, T. B., Crounse, J. D., Teng, A. P., St. Clair, J. M., Paulot, F., Wolfe, G. M., and Wennberg, P. O.: Rapid deposition of oxidized biogenic compounds to a temperate forest, P. Natl. Acad. Sci. USA, 112, E392–E401, https://doi.org/10.1073/pnas.1418702112, 2015.
Ninneman, M., Lu, S., Lee, P., McQueen, J., Huang, J., Demerjian, K., and Schwab, J.: Observed and Model-Derived Ozone Production Efficiency over Urban and Rural New York State, Atmosphere, 8, 126, https://doi.org/10.3390/atmos8070126, 2017.
Oren, R., Ellsworth, D. S., Johnsen, K. H., Phillips, N., Ewers, B. E., Maier, C., Schafer, K. V. R., McCarthy, H. Hendrey, G. McNulty, S. G., and Katul, G. G.: Soil fertility limits carbon sequestration by forest ecosystems in a CO2-enriched atmosphere, Nature, 411, 469–472, https://doi.org/10.1038/35078064, 2001.
Panek, J. A. and Goldstein, A. H.: Response of stomatal conductance to drought in ponderosa pine: implications for carbon and ozone uptake, Tree Physiol., 21, 337–344, https://doi.org/10.1093/treephys/21.5.337, 2001.
Pape, L., Ammann, C., Nyfeler-Brunner, A., Spirig, C., Hens, K., and Meixner, F. X.: An automated dynamic chamber system for surface exchange measurement of non-reactive and reactive trace gases of grassland ecosystems, Biogeosciences, 6, 405–429, https://doi.org/10.5194/bg-6-405-2009, 2009.
Prior, L. D., Eamus, D., and Duff, G. A.: Seasonal and Diurnal Patterns of Carbon Assimilation, Stomatal Conductance and Leaf Water Potential in Eucalyptus tetrodonta Saplings in a Wet-Dry Savanna in Northern Australia, Austral. J. Bot., 45, 241, https://doi.org/10.1071/BT96017, 1997.
Raupach, M. R.: A practical Lagrangian method for relating scalar concentrations to source distributions in vegetation canopies, Q. J. Roy. Meteor. Soc., 115, 609–632, 1989.
Raupach, M. R., Finnigan, J. J., and Brunet, Y.: Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy, Bound.-Lay. Meteorol., 78, 351–382, 1996.
Romer, P. S., Duffey, K. C., Wooldridge, P. J., Allen, H. M., Ayres, B. R., Brown, S. S., Brune, W. H., Crounse, J. D., de Gouw, J., Draper, D. C., Feiner, P. A., Fry, J. L., Goldstein, A. H., Koss, A., Misztal, P. K., Nguyen, T. B., Olson, K., Teng, A. P., Wennberg, P. O., Wild, R. J., Zhang, L., and Cohen, R. C.: The lifetime of nitrogen oxides in an isoprene-dominated forest, Atmos. Chem. Phys., 16, 7623–7637, https://doi.org/10.5194/acp-16-7623-2016, 2016.
Rondon, A. and Granat, L.: Studies on the Dry Deposition of NO2 to Coniferous Species at Low NO2 Concentrations, Tellus B, 46, 339–352, https://doi.org/10.1034/j.1600-0889.1994.t01-4-00001.x, 1994.
Ryan, M., Bond, B., Law, B., Hubbard, R., Woodruff, D., Cienciala, E., and Kucera, J.: Transpiration and whole-tree conductance in ponderosa pine trees of different heights, Oecologia, 124, 553–560, https://doi.org/10.1007/s004420000403, 2000.
Rydsaa, J., Stordal, F., Gerosa, G., Finco, A., and Hodnebrog, Ø.: Evaluating stomatal ozone fluxes in WRF-Chem: Comparing ozone uptake in Mediterranean ecosystems, Atmos. Environ., 143, 237–248, https://doi.org/10.1016/j.atmosenv.2016.08.057, 2016.
Seok, B., Helmig, D., Ganzeveld, L., Williams, M. W., and Vogel, C. S.: Dynamics of nitrogen oxides and ozone above and within a mixed hardwood forest in northern Michigan, Atmos. Chem. Phys., 13, 7301–7320, https://doi.org/10.5194/acp-13-7301-2013, 2013.
Simpson, D., Benedictow, A., Berge, H., Bergström, R., Emberson, L. D., Fagerli, H., Flechard, C. R., Hayman, G. D., Gauss, M., Jonson, J. E., Jenkin, M. E., Nyíri, A., Richter, C., Semeena, V. S., Tsyro, S., Tuovinen, J.-P., Valdebenito, Á., and Wind, P.: The EMEP MSC-W chemical transport model – technical description, Atmos. Chem. Phys., 12, 7825–7865, https://doi.org/10.5194/acp-12-7825-2012, 2012.
Sörgel, M., Trebs, I., Serafimovich, A., Moravek, A., Held, A., and Zetzsch, C.: Simultaneous HONO measurements in and above a forest canopy: influence of turbulent exchange on mixing ratio differences, Atmos. Chem. Phys., 11, 841–855, https://doi.org/10.5194/acp-11-841-2011, 2011.
Steiner, A. L., Pressley, S. N., Botros, A., Jones, E., Chung, S. H., and Edburg, S. L.: Analysis of coherent structures and atmosphere-canopy coupling strength during the CABINEX field campaign, Atmos. Chem. Phys., 11, 11921–11936, https://doi.org/10.5194/acp-11-11921-2011, 2011.
Stern, M. A., Anderson, F. A., Flint, L. E., and Flint, A. L.: Soil moisture datasets at five sites in the central Sierra Nevada and northern Coast Ranges, California, Data Series, U.S. Geological Survey, Reston, Virginia, https://doi.org/10.3133/ds1083, 2018.
Stroud, C., Makar, P., Karl, T., Guenther, A., Geron, C., Turnipseed, A. A., Nemitz, E., Baker, B., Potosnak, M., and Fuentes, J. D.: Role of canopy-scale photochemistry in modifying biogenicatmosphere exchange of reactive terpenoid species: Results from the CELTIC field study, J. Geophys. Res., 110, D17303, https://doi.org/10.1029/2005JD005775, 2005.
Teklemariam, T. A. and Sparks, J. P.: Leaf fluxes of NO and NO2 in four herbaceous plant species: The role of ascorbic acid, Atmos. Environ., 40, 2235–2244, https://doi.org/10.1016/j.atmosenv.2005.12.010, 2006.
Thoene, B., Schroder, P., Papen, H., Egger, A., and Rennenberg, H.: Absorption of Atmospheric No2 by Spruce (Picea-Abies L Karst) Trees 1, NO2 Influx and Its Correlation with Nitrate Reduction, New Phytol., 117, 575–585, https://doi.org/10.1111/j.1469-8137.1991.tb00962.x, 1991.
Thomas, C. and Foken, T.: Flux contribution of coherent structures and its implications for the exchange of energy and matter in a tall spruce canopy, Bound.-Lay. Meteorol., 123, 317–337, 2007.
Townsend, A. R., Braswell, B. H., Holland, E. A., and Penner, J. E.: Spatial and Temporal Patterns in Terrestrial Carbon Storage Due to Deposition of Fossil Fuel Nitrogen, Ecol. Appl., 6, 806–814, https://doi.org/10.2307/2269486, 1996.
Verbeke, T., Lathière, J., Szopa, S., and de Noblet-Ducoudré, N.: Impact of future land-cover changes on HNO3 and O3 surface dry deposition, Atmos. Chem. Phys., 15, 13555–13568, https://doi.org/10.5194/acp-15-13555-2015, 2015.
Vinken, G. C. M., Boersma, K. F., Maasakkers, J. D., Adon, M., and Martin, R. V.: Worldwide biogenic soil NOx emissions inferred from OMI NO2 observations, Atmos. Chem. Phys., 14, 10363–10381, https://doi.org/10.5194/acp-14-10363-2014, 2014.
Vitousek, P. M., Aber, J. D., Howarth, R. W., Likens, G. E., Matson, P. A., Schindler, D. W., Schlesinger, W. H. and Tilman, D. G.: Human Alteration of the Global Nitrogen Cycle: Sources and Consequences, Ecol. Appl., 7, 737–750, https://doi.org/10.1890/1051-0761(1997)007[0737:HAOTGN]2.0.CO;2, 1997.
Wang, Y., Jacob, D. J., and Logan, J. A.: Global simulation of tropospheric O3-NOx-hydrocarbon chemistry: 1. Model formulation, J. Geophys. Res.-Atmos., 103, 10713–10725, https://doi.org/10.1029/98JD00158, 1998a.
Wang, Y., Logan, J. A., and Jacob, D. J.: Global simulation of tropospheric O3-NOx-hydrocarbon chemistry: 2. Model evaluation and global ozone budget, J. Geophys. Res.-Atmos., 103, 10727–10755, https://doi.org/10.1029/98JD00157, 1998b.
Wang, Y.-P. and Leuning, R.: A two-leaf model for canopy conductance, photosynthesis and partitioning of available energy I, Agr. Forest Meteorol., 91, 89–111, https://doi.org/10.1016/S0168-1923(98)00061-6, 1998.
Wesely, M.: Parameterization of surface resistances to gaseous dry deposition in regional-scale numerical models, Atmos. Environ., 23, 1293–1304, https://doi.org/10.1016/0004-6981(89)90153-4, 1989.
Wesely, M. L. and Hicks, B. B.: A review of the current status of knowledge on dry deposition, Atmos. Environ., 34, 2261–2282, 2000.
Wild, O.: Modelling the global tropospheric ozone budget: exploring the variability in current models, Atmos. Chem. Phys., 7, 2643–2660, https://doi.org/10.5194/acp-7-2643-2007, 2007.
Williams, M., Rastetter, E. B., Fernandes, D. N., Goulden, M. L., Wofsy, S. C., Shaver, G. R., Melillo, J. M., Munger, J. W., Fan, S., and Nadelhoffer, K. J.: Modelling the soil-plant-atmosphere continuum in a Quercus-Acer stand at Harvard Forest: the regulation of stomatal conductance by light, nitrogen and soil/plant hydraulic properties, Plant Cell Environ., 19, 911–927, https://doi.org/10.1111/j.1365-3040.1996.tb00456.x, 1996.
Wolfe, G. M. and Thornton, J. A.: The Chemistry of Atmosphere-Forest Exchange (CAFE) Model – Part 1: Model description and characterization, Atmos. Chem. Phys., 11, 77–101, https://doi.org/10.5194/acp-11-77-2011, 2011.
Wolfe, G. M., Thornton, J. A., Bouvier-Brown, N. C., Goldstein, A. H., Park, J.-H., McKay, M., Matross, D. M., Mao, J., Brune, W. H., LaFranchi, B. W., Browne, E. C., Min, K.-E., Wooldridge, P. J., Cohen, R. C., Crounse, J. D., Faloona, I. C., Gilman, J. B., Kuster, W. C., de Gouw, J. A., Huisman, A., and Keutsch, F. N.: The Chemistry of Atmosphere-Forest Exchange (CAFE) Model – Part 2: Application to BEARPEX-2007 observations, Atmos. Chem. Phys., 11, 1269–1294, https://doi.org/10.5194/acp-11-1269-2011, 2011.
Yi, C.: Momentum Transfer within Canopies, J. Appl. Meteorol. Clim., 47, 262–275, https://doi.org/10.1175/2007JAMC1667.1, 2008.
Yienger, J. J. and Levy, H.: Empirical model of global soil-biogenic NOx emissions, J. Geophys. Res., 100, 11447–11464, https://doi.org/10.1029/95JD00370, 1995.
Zhang, L., Padro, J., and Walmsley, J.: A multi-layer model vs single-layer models and observed O3 dry deposition velocities, Atmos. Environ., 30, 339–345, https://doi.org/10.1016/1352-2310(95)00286-8, 1996.
Zhang, L., Moran, M., Makar, P., Brook, J., and Gong, S.: Modelling Gaseous Dry Deposition in AURAMS A Unified Regional Air-quality Modelling System, Atmos. Environ., 36, 537–560, 2002.
Zhang, L., Brook, J. R., and Vet, R.: A revised parameterization for gaseous dry deposition in air-quality models, Atmos. Chem. Phys., 3, 2067–2082, https://doi.org/10.5194/acp-3-2067-2003, 2003.