the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Gravitational separation of Ar∕N2 and age of air in the lowermost stratosphere in airborne observations and a chemical transport model
Martyn P. Chipperfield
Eric J. Morgan
Britton B. Stephens
Marianna Linz
Wuhu Feng
Chris Wilson
Jonathan D. Bent
Steven C. Wofsy
Jeffrey Severinghaus
Ralph F. Keeling
Accurate simulation of atmospheric circulation, particularly in the lower stratosphere, is challenging due to unresolved wave–mean flow interactions and limited high-resolution observations for validation. Gravity-induced pressure gradients lead to a small but measurable separation of heavy and light gases by molecular diffusion in the stratosphere. Because the relative abundance of Ar to N2 is exclusively controlled by physical transport, the argon-to-nitrogen ratio (Ar∕N2) provides an additional constraint on circulation and the age of air (AoA), i.e., the time elapsed since entry of an air parcel into the stratosphere. Here we use airborne measurements of N2O and Ar∕N2 from nine campaigns with global coverage spanning 2008–2018 to calculate AoA and to quantify gravitational separation in the lowermost stratosphere. To this end, we develop a new N2O–AoA relationship using a Markov chain Monte Carlo algorithm. We observe that gravitational separation increases systematically with increasing AoA for samples with AoA between 0 and 3 years. These observations are compared to a simulation of the TOMCAT/SLIMCAT 3-D chemical transport model, which has been updated to include gravitational fractionation of gases. We demonstrate that although AoA at old ages is slightly underestimated in the model, the relationship between Ar∕N2 and AoA is robust and agrees with the observations. This highlights the potential of Ar∕N2 to become a new AoA tracer that is subject only to physical transport phenomena and can supplement the suite of available AoA indicators.
- Article
(4102 KB) - Full-text XML
-
Supplement
(8996 KB) - BibTeX
- EndNote
Transport in the middle atmosphere is driven by a combination of advection by the Brewer–Dobson circulation (BDC) (Brewer, 1949; Dobson, 1956) and quasi-horizontal, two-way mixing by breaking waves (Holton et al., 1995). Models consistently predict an acceleration of the BDC due to climate change (Butchart, 2014), but subgrid-scale mixing processes and momentum transfer by unresolved buoyancy waves limit our ability to accurately simulate circulation in the stratosphere (Haynes, 2005; Plumb, 2007). An acceleration of the BDC has important repercussions for stratosphere–troposphere exchange (STE) and thus recovery of the ozone layer and the greenhouse effect of stratospheric water vapor; however, observational evidence of an acceleration of the BDC is weak (Engel et al., 2009, 2017; Waugh, 2009; Ray et al., 2010, 2014).
The mean age of air (AoA) is a widely used indicator of stratospheric circulation (Hall and Plumb, 1994; Waugh and Hall, 2002; Linz et al., 2016). Air can be transported to any location r in the stratosphere via a myriad of different paths, and each path will have an associated transit time. The probability density function that describes the likelihood of air reaching location r with a specific transit time is called the age spectrum. Although the age spectrum is not directly observable, some aspects of its shape can be inferred from observations of short- and long-lived tracers (Andrews et al., 1999, 2001; Schoeberl et al., 2005; Hauck et al., 2019, 2020; Podglajen and Ploeger, 2019). For tracers that are conserved in the stratosphere and whose concentrations increase approximately linearly with time in the troposphere, such as SF6 and CO2, the mean AoA, i.e., the first moment of the distribution, can simply be calculated as the time difference, or “lag time”, to when tracer concentrations in the upper troposphere last had comparable values as measured in a stratospheric sample (Hall and Plumb, 1994; Boering et al., 1996; Waugh and Hall, 2002). The stratospheric concentration of N2O has also been calibrated as an independent AoA tracer by relating the gradual photolytic loss of N2O in the stratosphere to AoA as determined from CO2 (Boering et al., 1996; Andrews et al., 2001; Linz et al., 2017).
In contrast to early measurements made on rocket samples (Bieri and Koide, 1970), Ishidoya et al. (2008, 2013) have shown using a balloon-borne sampling system that stratospheric air is detectably fractionated by gravitational settling (GS), with the degree of fractionation strongly correlated to AoA (Ishidoya et al., 2008, 2013, 2018; Sugawara et al., 2018; Belikov et al., 2019). GS leads to depletion of heavier gases in the stratosphere yielding lower ratios of heavy to light gases, e.g., Ar∕N2, 18O∕16O of O2 and 15N∕14N of N2, with increasing elevation. The vertical gradients induced by gravimetric separation are steeper at higher latitudes (Ishidoya et al., 2008, 2013, 2018; Sugawara et al., 2018), and consistent with patterns observed in stratospheric AoA (Sugawara et al., 2018; Belikov et al., 2019). Gravimetric settling in the stratosphere has also been simulated in 1-D (Keeling, 1988; Ishidoya et al., 2008), 2-D (Ishidoya et al., 2013, 2018; Sugawara et al., 2018), and 3-D stratospheric models (Belikov et al., 2019); 2-D and 3-D models both show a pattern of GS which increases with altitude and latitude, similar to the patterns observed in tracers with a significant stratospheric sink such as N2O, and consistent with a positive correlation with AoA (Ishidoya et al., 2013; Sugawara et al., 2018; Belikov et al., 2019). Here we attempt to calibrate GS of Ar∕N2 as an AoA tracer similar to previous work on the N2O–AoA relationship.
Observing GS in the stratosphere is challenging, however, as the signals are small and because of the need to avoid artifacts caused by temperature- and pressure-induced fractionation near the sampling inlet (Blaine et al., 2006; Ishidoya et al., 2008, 2013). The resulting scatter in existing balloon-based measurements precludes a clear evaluation of the relationship between GS and AoA (Belikov et al., 2019).
Here we present a dataset of gravitational fractionation of Ar∕N2 and AoA observations made on flask samples from three airborne research projects, totaling nine campaigns in the lowermost stratosphere with mean AoA <3 years (Wofsy et al., 2017, 2018; Stephens, 2017). The HIAPER Pole-to-Pole Observations (HIPPO) project was a global survey of the Pacific troposphere to lower stratosphere on the NSF/NCAR Gulfstream-V aircraft (Wofsy et al., 2011), composed of five individual campaigns from 2008 to 2011. The O2∕N2 Ratio and CO2 Airborne Southern Ocean (ORCAS) study was conducted using the same aircraft but focused on the Drake Passage and Antarctic Peninsula during January–February 2016 (Stephens et al., 2018). The Atmospheric Tomography (ATom) project was a survey of the troposphere and lower stratosphere of the Pacific and Atlantic Ocean basins on the NASA DC-8 aircraft, composed of four individual campaigns from 2016 to 2018 (Prather et al., 2017). The observations are compared to new simulations of GS with the TOMCAT/SLIMCAT (Chipperfield, 2006) tracer transport model. Our goals are to demonstrate the consistency of our data with gravitational fractionation, to evaluate model performance, and to highlight the potential of Ar∕N2 as a new age tracer.
2.1 Measurements
Discrete 1.5 L flask samples were taken with the NCAR/Scripps Medusa Whole Air Sampler (Bent, 2014; Stephens et al., 2020) (https://www.eol.ucar.edu/instruments/ncar-scripps-airborne-flask-sampler, last access: 7 June 2020). Medusa holds 32 borosilicate glass flasks sealed with Viton o-rings and uses active pressure control to fill the flasks with cryogenically dried air to ∼760 torr. Flasks are shipped to the Scripps Institution of Oceanography (SIO) for analysis of Ar∕N2 ratios on an IsoPrime Mass Spectrometer. We report changes in Ar∕N2 ratios in delta notation:
where RSA is the mixing or isotope ratio in the sample and RREF the ratio in a reference mixture. Measurements are made on the Scripps O2 Program Argon Scale, as defined on 21 January 2020. δ(Ar∕N2) values are reported after applying an offset to the data to yield a mean of zero in the tropical airborne observations of the free troposphere between 3 and 8 km.
Uncertainty in δ(Ar∕N2) observations arises from a combination of analytical limitations and artifactual fractionation during sampling. Replicate agreement of surface flasks shows a 1σ repeatability of ±6.1 per meg for δ(Ar∕N2), but additional scatter in the data may be introduced by small leaks in the Medusa system and thermal or pressure gradient fractionation at the sample intake (Morgan et al., 2020; Stephens et al., 2020). For further details, see Bent (2014). These effects are challenging to separate from true atmospheric variability and differ between campaigns because sampling strategies have generally improved over time. To constrain uncertainty due to aircraft sampling, we quantify total variability in observations from the presumably fairly homogeneous tropical troposphere between 3 and 8 km (Fig. S1 in the Supplement). Data from the earlier campaigns HIPPO 1–5 show a pooled standard deviation of 24 per meg, whereas data from ATom 2–4 yield a pooled standard deviation of 9 per meg, illustrating advances in sampling and sample handling. While no ORCAS samples are available in the tropical troposphere, ORCAS data show similar scatter to ATom 2–4 data between 20 and 50∘ S. For all campaigns, the uncertainty is small compared to the stratospheric signal of tens to hundreds per meg shown below. We also show that the stratospheric signal in δ(Ar∕N2) is not due to pressure-dependent inlet fractionation by evaluating the residual δ(Ar∕N2), which has been corrected for the natural gravitational signal (Fig. S2).
We have compiled available simultaneous, high-frequency measurements of a range of other trace gases, including N2O, CO2, O3, CH4, and CO, to identify Medusa samples with stratospheric influence and calculate mean AoA. N2O was measured continuously with a precision of 0.09 ppb at 1 Hz frequency using the Harvard Quantum Cascade Laser Spectrometer (QCLS) (Santoni et al., 2014) during HIPPO and ORCAS and measured every 1–3 min using the NOAA gas chromatograph PAN and Trace Hydrohalocarbon ExpeRiment (PANTHER) during ATom. The Unmanned Aircraft Systems Chromatograph for Atmospheric Trace Species (UCATS) was used to measure O3 during HIPPO and ATom. O3 was not measured on ORCAS. We use continuous H2O data from the NCAR open-path near-infrared multi-pass spectrometer Vertical Cavity Surface Emitting Laser (VCSEL) (Zondlo et al., 2010) for HIPPO and ORCAS, whereas H2O was measured using the NASA Diode Laser Hygrometer (DLH) (Diskin et al., 2002) during ATom flights. CH4, CO2, and CO were measured by QCLS during HIPPO and ORCAS and by the NOAA Picarro (Karion et al., 2013) during ATom. An averaging kernel is applied to the continuous and semi-continuous aircraft data, such as N2O, O3, and H2O, to match it to Medusa samples. The kernel multiplies a weighting function wi(t) by all continuous data before time ts, when Medusa switched from sample flask i to sample flask i+1. wi(t) for each sample i is given by
where t is each 1 s increment of the continuous data and is the flushing time of air in a Medusa flask determined by the flask volume V and airflow Q.
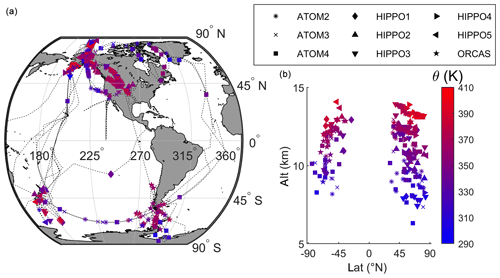
Figure 1Horizontal (a) and vertical (b) distributions of airborne flask sample locations identified as being of stratospheric origin (see text). Thin dashed black lines on the map illustrate the flight tracks of all nine campaigns. Symbols indicate the campaigns during which the stratospheric samples were collected, and colors show the potential temperature at which the sample was taken.
Stratospheric samples are identified based on their N2O, O3, and water vapor levels. Classification based on chemical composition rather than potential temperature or altitude effectively selects samples with a clear stratospheric signature in the lowermost stratosphere and excludes air which has experienced substantial mixing with tropospheric air masses. We label samples as “stratospheric” if (i) water vapor levels are below 15 ppm and either (ii.a) O3 values exceed 140 ppb or (ii.b) N2O (detrended to a reference year of 2009) is below 315 ppb. These criteria yield 234 lower stratospheric samples with high-quality N2O and δ(Ar∕N2) data, spanning a wide range of latitudes poleward of 40∘ in both the Northern Hemisphere and Southern Hemisphere (Fig. 1). We use Medusa samples from all five HIPPO campaigns, ORCAS, and ATom 2–4. We do not use samples from ATom 1 because inlet fractionation due to the unique inlet design and location on the DC-8 on this campaign introduced apparent biases on the order of 30 per meg. An additional 25 stratospheric samples are available from the START-08 campaign on the NSF/NCAR GV, but we have not used these here because of the limited number of flasks collected and greater scatter in the data.
2.2 AoA calculation
Stratospheric (mean) AoA for Medusa samples is calculated from N2O using an updated hemisphere-specific N2O–AoA relationship. Our method broadly follows Andrews et al. (2001), who assumed a bimodal age spectrum and used multiple observations of CO2 binned by N2O values to resolve the seasonal cycle of CO2 in each bin. Properties of the age spectrum for each N2O bin, including mean AoA, were constrained by optimizing the agreement between observed CO2 concentrations and concentrations implied by randomly generated age spectra in each N2O bin. Andrews et al. (2001) used a highly efficient “genetic algorithm” to yield the most likely relationship between mean AoA and N2O in each bin. In contrast, we use a more computationally costly Markov chain Monte Carlo (MCMC) method that allows us to obtain more robust uncertainties for all estimated parameters of the age spectrum. Following Malinverno (2002) and Green (1995), our algorithm builds on a Metropolis–Hastings sampler (Metropolis et al., 1953; Hastings, 1970) to evaluate probability distributions for each age spectrum parameter and automatically chooses whether a unimodal or bimodal representation of the age spectrum is more appropriate in each N2O bin. Finally, we constructed a new tropical upper troposphere reference time series for CO2 in this study to ensure maximum consistency between all observations used. Analytical and methodological uncertainties are propagated thoroughly and reported as the 95 % confidence interval around a mean.
We consider the tropical upper troposphere to be the single entry point of air into the stratosphere for our AoA calculation. Mixing between tropospheric and lower stratospheric air can occur outside the tropics, leading to air masses that are transitional between stratospheric and tropospheric in the lowermost extratropical stratosphere (e.g., Škerlak et al., 2014). This additional pathway for tropospheric entry has been accounted for in previous studies via additional model information and/or multiple tracers (Ray et al., 1999; Hoor et al., 2004; Bönisch et al., 2009; Hauck et al., 2020). However, we are limited by the number of tracers available to us and therefore instead aim to largely exclude samples influenced through this additional pathway by using thresholds in N2O, O3, and H2O when identifying stratospheric samples. Because of this sample selection strategy, we note that the ages calculated here should not be considered representative of the region that air was sampled in.
Our upper troposphere reference time series (TRTS) consists of a long-term trend and a representation of the mean seasonal cycle. Because direct CO2 observations in the region are limited, the long-term trend and a first guess of the mean seasonal cycle are estimated from monthly mean surface observations at the Mauna Loa station in Hawaii (MLO, 19∘ N, 155∘ W; Fig. 2a) (Keeling et al., 2001) which are later adjusted to match airborne observations in the tropics (20∘ S–20∘ N) above 8 km (Fig. 2c). The adjustment includes (i) a constant offset, (ii) a reduced amplitude of the seasonal cycle, and (iii) a phase lag of 1 month. As shown in Fig. 2, after these adjustments the TRTS matches the mean seasonal cycle and absolute value of the airborne data, thus accounting for known vertical gradients of CO2 and reduced seasonality in the upper troposphere (Fig. 2d). The amplitude of the seasonal cycle in our time series is also in good agreement with the boundary condition used by Andrews et al. (1999, 2001).
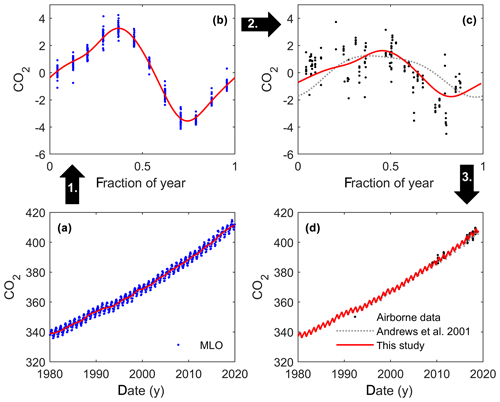
Figure 2Illustration of the major steps in deriving a tropical upper tropospheric reference time series. Panel (a) shows the monthly mean surface CO2 concentrations at Mauna Loa (MLO) (Keeling et al., 2001) with a stiff spline trend shown in red. Panel (b) shows a fit of the mean seasonal cycle at MLO compared to detrended observations from 1980 to 2019. Panel (c) shows the 1-month lagged seasonal cycle (red line) rescaled in amplitude to match detrended airborne observations in the equatorial upper troposphere (20∘ S < lat < 20∘ N, alt >8 km, black). The seasonal cycle derived by Andrews et al. (2001) is presented as a dotted grey line for reference. Panel (d) shows the resulting upper tropospheric mean reference time series (TRTS, red) used for CO2 in the age-of-air algorithm with the airborne observations from the tropical upper troposphere (black dots) and the time series (grey dotted line) of Andrews et al. (2001).
The new TRTS is used to estimate the age spectrum in 13 N2O bins of 5 or 10 ppb width (320–325, ..., 290–295, 280–290, ..., 230–240 ppb) using a Markov chain Monte Carlo (MCMC) algorithm which compares observed CO2 concentrations in the bin to concentration expected from the TRTS. To maximize data availability, we use high-frequency data (see Sect. 2.1) identified as stratospheric according to the criteria above from the 10 s merged products available for HIPPO, ORCAS, and ATom rather than data averaged to the lower Medusa sampling interval for this calibration exercise. Small corrections are applied to the observed CO2 concentrations (<0.2 ppm) to account for oxidation of CH4 and CO in the stratosphere.
The MCMC algorithm considers random noise in the TRTS and uses a unimodal or bimodal inverse Gaussian shape of the age spectrum characterized by mean ages Γ1 and Γ2 and shape parameters λ1 and λ2:
where factor A determines the relative weight of each peak and a value of A=1 yields a unimodal spectrum (Hall and Plumb, 1994; Andrews et al., 2001; Bönisch et al., 2009). Though more complex representations of the age spectrum have recently been proposed, accounting for multiple modes and seasonal variations (e.g., Bönisch et al., 2009; Li et al., 2012; Hauck et al., 2019, 2020; Podglajen and Ploeger, 2019), these require additional information from multiple tracers or models and good seasonal data coverage that is not available here. In any case, we only rely on the first moment of the age distribution (i.e., the mean age) for calibrating the N2O–AoA relationship, and the mean age is not particularly sensitive to the assumed shape of the age spectrum (Andrews et al., 2001). By setting A=1 for 50 % of all tested age spectra, the MCMC algorithm automatically selects whether a unimodal or bimodal representation of the age spectrum is optimal for matching observations. Although bimodal solutions with five instead of two free parameters will always be able to fit the data better, a larger number of parameters also decreases the likelihood of randomly selecting a combination of parameters that match the observations well because the fraction of the total parameter space region which yields good agreement with the observation decreases as more parameters are added (Malinverno, 2002). The algorithm is thus able to make an appropriate choice between unimodal and bimodal distributions from the data themselves, without any further a priori assumptions. The MCMC algorithm is set up separately with 2000 independent chains for each N2O bin to account for uncertainty in the TRTS and obtain best estimates of the mean AoA, i.e., the first moment of Eq. (3). To simplify the algorithm, possible values of , and λ2 are repeatedly sampled from the same N2O bin-specific prior distributions. Details of the algorithm are presented in Appendix A.
Finally, the resulting relationship between mean AoA and the N2O concentration of each bin is fit separately for each hemisphere by a quadratic polynomial, and the polynomial is evaluated at the N2O value of each Medusa sample to pair every observation of δ(Ar∕N2) with an AoA. Uncertainty in N2O and the polynomial fits are propagated by a Monte Carlo scheme. Overall, our method estimates the most likely mean AoA for each Medusa sample and improves upon previous methods by providing a framework for the treatment of uncertainty resulting from (i) analytical error, (ii) uncertainty in the shape of the age spectrum, and (iii) uncertainty in the composition of source gas introduced into the stratosphere.
2.3 TOMCAT/SLIMCAT model
TOMCAT/SLIMCAT (hereafter TOMCAT) is an offline 3-D chemical tracer transport model that has been used extensively for studies of stratospheric ozone depletion and circulation (e.g., Chipperfield, 2006; Chipperfield et al., 2017; Krol et al., 2018). For this study, TOMCAT was run over 31 years, from 1988 to 2018, with a timestep of 30 min at horizontal resolution forced by the ERA-Interim reanalysis (Dee et al., 2011) at 60 vertical hybrid sigma-pressure (σ–p) levels up to ∼60–65 km. The first 20 years (i.e., before the first flask observation) were treated as spin-up. The TOMCAT AoA tracer is initialized at the surface and corrected to a value of AoA =0 just below the tropical tropopause. Vertical motion was calculated from the divergence of the horizontal mass fluxes. Although this approach gives slightly younger stratospheric AoA than using isentropic levels and radiative heating rates, it allows a more detailed treatment of tropospheric transport (Chipperfield, 2006; Monge-Sanz et al., 2007). The model simulation was sampled at the times and locations of the Medusa flask observations to provide a direct comparison between the measurements and model.
Following the methodology of Belikov et al. (2019), we include an additional vertical flux term in the model representing the GS of gases in the atmosphere. The vertical flux fi (mol m−2 s−1) of tracer i due to molecular diffusion in Earth's gravitational field is given as (Banks and Kockarts, 1973; Belikov et al., 2019)
where Di is the tracer-specific binary molecular diffusivity in air (m2 s−1), N is the number density of air (mol m−3), Ci is the mixing ratio, is the tracer-specific atmospheric equilibrium scale height (m), R is the fundamental gas constant (J K−1 mol−1), g is the gravitational constant (m s−2), Mi is the tracer-specific atomic or molecular mass (kg mol−1), αi is the tracer-specific thermal diffusivity (m2 s−1), and T is temperature (K). The three terms in Eq. (4) represent molecular diffusion driven by (i) vertical gradients in the mole fraction of i, (ii) pressure gradients caused by gravity and described by the barometric law, and (iii) temperature gradients (left to right). We neglect the first and third terms in the brackets in Eq. (4), leaving only the gravitational settling term on the basis that both terms are orders of magnitude less important than the gravitational separation term under stratospheric conditions (see Appendix B) (Ishidoya et al., 2013; Belikov et al., 2019). No fluxes are allowed through the top boundary, and Ci is held constant at the Earth's surface.
To simplify the numerical treatment, we simulate an idealized reference tracer of gravitational fractionation δGST, which has a molecular mass 1 amu greater than air and diffusivity equal to that of Ar (see Appendices B and C). This tracer can be scaled offline to obtain the gravitational separation signal in any other species, including δ(Ar∕N2), e.g.,
The appropriate diffusivity values DAr and for Ar and N2 in air are derived in Appendix B for a ternary mixture of Ar, O2, and N2, extending previous work (Ishidoya et al., 2013; Belikov et al., 2019). δGST is divided by DGST in Eq. (5) and therefore does not depend on the exact value chosen for DGST.
2.4 NIES TM model
We compare our results to previous simulations of GS using the National Institute for Environmental Studies chemical transport model (NIES TM) published recently by Belikov et al. (2019). The NIES TM is a 3-D transport model of similar complexity to TOMCAT driven by the Japanese 25-year Reanalysis (JRA-25) with a hybrid sigma–isentropic (σ–θ) vertical coordinate up to 5 hPa or ∼35 km. The model and GS results are described in detail in Belikov et al. (2013, 2019), respectively.
3.1 N2O–AoA calibration
Our new relationships between N2O and mean AoA for the Northern Hemisphere and Southern Hemisphere (NH and SH) are well constrained by the observations and generally follow the mid-latitude NH calibration curve of Andrews et al. (2001) (Fig. 3d). At mean AoA >2.5, the N2O–AoA relationship yields slightly younger ages in the NH than in the SH and compared to the previously published curve, suggesting there might be a latitudinal dependence of the relationship. Such a latitude dependence is, in fact, expected based on theory (Plumb, 2007). We expect curvature and a latitudinal difference in the N2O–AoA relationship because photolysis of N2O depends on latitude and altitude due to local sunlight availability. Furthermore, mixing of young and old air results in a mixture with an anomalously low N2O concentration for a given age. Since the SH, NH, and tropics feature different photolysis rates and show different degrees of mixing/isolation, different N2O–AoA relationships are expected.
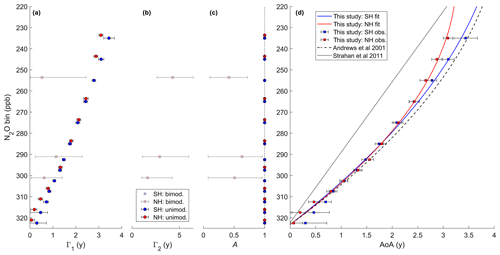
Figure 3Hemisphere-specific properties of the age spectra in different N2O bins from the 10 s averaged airborne observations estimated by Markov chain Monte Carlo. Panels (a)–(c) show the value and 95 % confidence interval of Γ1 Γ2 and A in each bin for either a unimodal (blue and red circles) or bimodal (faint blue and faint red stars) age spectrum depending on which type was preferentially selected by the algorithm. N2O values are offset by 1.4 ppb for all Northern Hemisphere estimates (NH, red) for visual clarity in panels (a)–(c). Panel (d) shows the mean AoA and confidence interval of the age spectra ensemble in each bin (i.e., unimodal and bimodal together). These data are fit by a quadratic polynomial for each hemisphere with a fixed y intercept (NH AoA ; SH AoA ). Previous relationships published by Andrews et al. (2001) and Strahan et al. (2011) are given as a dashed and dotted line for reference. y-intercept values of the previously published N2O–AoA calibrations have been updated to reflect the gradual increase in tropospheric N2O between 1997 and the new reference year 2009.
Unimodal age spectra are generally preferentially selected by the algorithm, in particular for the SH (Fig. 3a–c), but unimodal age spectra dominate the solution ensemble by a small margin except for AoA <0.5 years (Fig. S3). Confidence intervals on age spectra parameters from bimodal spectra are considerably wider than for unimodal spectra. This implies that the parameters in a bimodal distribution are redundant and the shape of the age spectrum is not sufficiently constrained by the observations used. The width of the spectrum in each N2O bin varies widely within the prescribed bounds for most unimodal and bimodal age spectra (Fig. S3). It appears that not enough data are available from the airborne campaigns to determine the amplitude of the seasonal cycle with enough confidence to constrain the width of the age spectrum and distinguish the relative contribution of the old peak (influencing primarily the mean concentration difference to the troposphere) and the young peak (controlling the amplitude of seasonality) in bimodal age spectra. Additional observations with less scatter or information from different age tracers are needed to properly resolve the shape of the age spectra. Despite the limited resolution of the seasonal cycle, the observations are sufficient to place tight limits on the mean AoA in each N2O bin and yield a well-characterized relationship between N2O and mean AoA for each hemisphere.
3.2 The relationship between mean AoA and GS in models and observations
A comparison of the AoA–GS relationship with observations yields good agreement for the TOMCAT model results within the observational uncertainties (Fig. 4a), but the observations fall outside the range of GS predicted by the NIES TM (Belikov et al., 2019) for mean AoA >1 year (Fig. 4b). For young samples with mean AoA <3 years, GS of δ(Ar∕N2) increases by roughly 35–45 per meg per year of AoA in both TOMCAT and observations and converges to zero for the youngest samples. In the upper stratosphere, TOMCAT does not obtain any ages as old as observed by Ishidoya et al. (2008, 2013, 2018) and therefore cannot reproduce these observations directly. Changing the vertical coordinate system of TOMCAT or forcing the model with a different reanalysis product could improve agreement with the observations for old ages because TOMCAT in the configuration used here is known to slightly underestimate AoA in the upper stratosphere (Monge-Sanz et al., 2007; Chabrillat et al., 2018). The very steep AoA–GS relationship for the oldest simulated air is however seen in TOMCAT and the balloon observations.
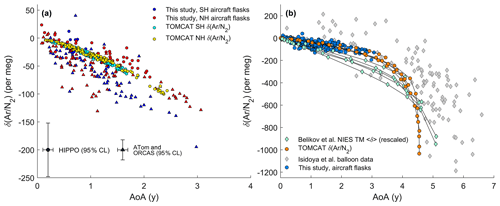
Figure 4Comparison of age of air (AoA) and gravitational settling (GS) of δ(Ar∕N2) in models and observations. Panel (a) shows observations from the Northern Hemisphere (red) and Southern Hemisphere (blue) together with TOMCAT model output (SH: cyan; NH: yellow) selected from the closest model grid box in time and space. Because uncertainty for AoA is similar for all stratospheric samples but δ(Ar∕N2) uncertainty differs between campaigns, representative error bars (95 % confidence interval) are shown for HIPPO (triangles) and ATom/ORCAS (circles) at an arbitrary AoA. δ(Ar∕N2) is normalized to yield a delta value of zero in the equatorial free troposphere. In panel (b), observations from airborne campaigns (this study) and the balloon sampling system (Ishidoya et al., 2008, 2013, 2018; Sugawara et al., 2018) are plotted with the AoA–GS relationship observed in TOMCAT and the NIES TM (Belikov et al., 2019) as lines for each of the latitude bands shown in Fig. 5 and points for different altitude bins between 10 and 35 km. To yield an equivalent estimate of δ(Ar∕N2), δ(13CO2∕12CO2) results from the NIES TM (Belikov et al., 2019) have been rescaled according to Eq. (5) and offset by ∼10 per meg to account for the different tropospheric reference region in the definition of δ.
A comparison of δ(Ar∕N2) and AoA between flask samples and TOMCAT is shown in Fig. S4. However, the direct comparison should not be considered a good test of model performance because our stratospheric composition criteria intentionally target unusually old air in the lowermost stratosphere. For the same reason, profiles of δ(Ar∕N2) and AoA are not evaluated here. Instead, we suggest the AoA–GS relationship provides a more robust metric for comparison. Overall, our observations validate the implementation of GS for young (<3 years) ages in TOMCAT.
The relationship between mean AoA and GS differs between TOMCAT and the NIES TM (Fig. 5). The NIES TM shows weaker curvature in the relationship overall and produces larger declines in Ar∕N2 at ages less than 4.5 years compared to TOMCAT. In TOMCAT's mesosphere (which is at the limit of the domain covered by the ERA-Interim reanalyses forcing the model), AoA is near uniform, but GS continues to increase with increasing altitude, changing the relationship between mean AoA and GS in this region. The AoA–GS relationship in TOMCAT is very similar in all non-tropical regions (outside 15∘ > lat ∘), whereas the curvature of the relationship is slightly stronger in the tropics. In contrast, the NIES TM has a clear dependence of the AoA–GS relationship on latitude. There is also some evidence in the observations of a dependence of the AoA–GS relationship on hemisphere. In the observations, δ(Ar∕N2) values appear to be slightly more negative in the SH than in the NH for the same age, particularly for AoA >1.5 years. However, almost all SH samples with mean AoA older than 1.5 years come only from the ORCAS campaign. This campaign used a different inlet design than HIPPO and ATom, which could cause a small artifactual offset, but the scatter in our observations generally makes it difficult to separate signal from noise for small interhemispheric differences.
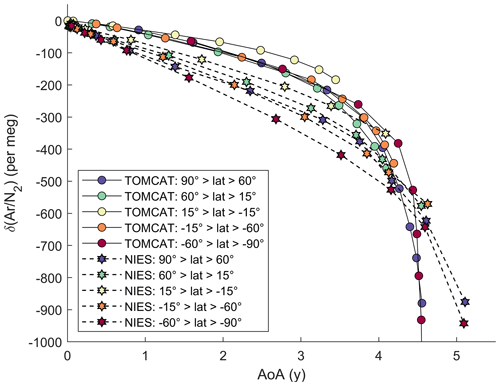
Figure 5Comparison of the annual and zonal mean age of air (AoA) relationship with gravitational settling simulated in TOMCAT and the NIES TM. The relationship is plotted as lines for the latitude bands indicated by marker color. For the NIES TM, markers show the vertical profile using all grid boxes available between ∼10 and 35 km. For TOMCAT, markers instead correspond to binned altitude bands between 10 and 35 km with a spacing of 2.5 km because of the finer vertical resolution of the model. To yield an equivalent estimate of δ(Ar∕N2), δ(13CO2∕12CO2) results from the NIES TM (Belikov et al., 2019) have been rescaled according to Eq. (5) and offset by ∼10 per meg to account for the different tropospheric reference region in the definition of δ.
3.3 GS and AoA in TOMCAT
Annual mean δ(Ar∕N2) in TOMCAT follows the typical pattern of a tracer with a stratospheric sink (Chipperfield, 2006), as previously found in simulations using the NIES TM (Belikov et al., 2019) and the SOCRATES model (Ishidoya et al., 2013; Sugawara et al., 2018) (Fig. 6). δ(Ar∕N2) is zero in the troposphere and decreases with elevation. The most depleted δ(Ar∕N2) is observed at high latitudes where sinking air of the Brewer–Dobson circulation advects strongly fractionated air downward. In the tropics, δ(Ar∕N2) values are considerably less fractionated at the same altitude due to upwelling of unfractionated tropospheric air. Vertical gradients in δ(Ar∕N2) generally increase with altitude and are largest in the mesosphere (>50 km) because molecular diffusion increases with decreasing pressure and eventually dominates above the turbopause (not shown). There are strong seasonal changes in δ(Ar∕N2) depletion on the order of several thousand per meg, in particular in the high-latitude mesosphere, with the strongest fractionation occurring during the winter season (see movie available with online version of the paper).
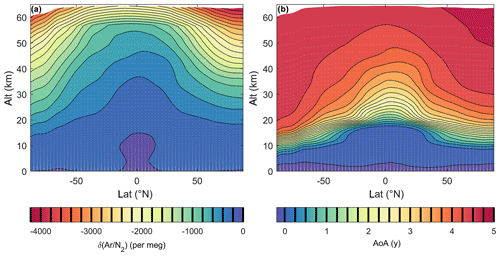
Figure 6Annual and zonal means of δ(Ar∕N2) (a) and age of air (AoA) (b) simulated by TOMCAT. Values of the contour lines are shown as black vertical lines on the color bar. Grey dots indicate the center of a grid box in TOMCAT. A video of this figure highlighting the natural variability in monthly-mean values is available in the Supplement.
The AoA tracer in TOMCAT shows a similar pattern to δ(Ar∕N2), with younger ages at low altitude and in the tropics and the oldest ages in the mesosphere. Vertical gradients in mean AoA are largest at high latitudes close to the tropopause. At high latitudes above 20 km and at low latitudes above 50 km, vertical gradients of AoA mostly disappear and AoA becomes nearly uniform.
4.1 Difference between TOMCAT and the NIES TM
We hypothesize that an adequate representation of the mesosphere in models is critical in determining the curvature of the AoA–GS relationship. The residence time of air above ∼40 km is rather short in TOMCAT, and AoA is nearly constant with altitude in this region. GS in contrast continues to increase with altitude because of the diffusivity dependence on pressure allowing gases to separate more effectively. The much lower top of the NIES TM (∼35 km vs. 60–65 km) reduces its ability to capture this effect, which impacts the AoA–GS relationship because the mesospheric signal is exported into the stratosphere, in particular in polar regions where mesospheric air descends. TOMCAT furthermore produces a less negative slope of the AoA–GS relationship for young air (mean AoA <3 years) and greater similarity in the AoA–GS relationship between latitude bands than the NIES TM as shown in Fig. 5. This could in part be a consequence of using a different meteorological reanalysis product for forcing the two models (Chabrillat et al., 2018) or could indicate differences between the models in vertical and horizontal mixing intensity.
4.2 Estimating mean AoA from observed δ(Ar∕N2)
Different tracers of AoA all have unique strengths and weaknesses. Estimating AoA in the lowermost stratosphere from CO2 for example is limited by complexities involving seasonality and the possibility of multiple entry points of air into the stratosphere due to isentropic mixing with the midlatitude troposphere (Hall and Plumb, 1994; Andrews et al., 2001; Waugh and Hall, 2002). SF6-derived AoA in contrast is biased high at mid and high latitudes due to the influence of mesospheric air which has been photochemically depleted in SF6 (Kovács et al., 2017; Linz et al., 2017). N2O as an AoA tracer relies on the photolytic destruction of N2O in the stratosphere, which may depend strongly on location and had only been empirically calibrated for young ages at mid latitudes so far (Andrews et al., 2001; Linz et al., 2017).
Thanks to the robust relationship between mean AoA and δ(Ar∕N2) and the small seasonal cycle amplitude of per meg in the upper troposphere (Fig. S1), mean AoA could also be estimated from δ(Ar∕N2). Using the current analytical δ(Ar∕N2) uncertainty of 12.2 per meg (2σ) and the AoA–δ(Ar∕N2) relationship seen in TOMCAT (including variability from seasonal and latitudinal differences), we estimate that mean AoA could be calculated to within about ±0.4 years (2σ, Fig. S5). This is still considerably worse than the ±0.1-year confidence interval in mean AoA estimated from N2O. However, the uncertainty can be improved with future improvements in sampling, and the accuracy and precision of the measurements.
The heavy noble gases krypton and xenon will be roughly 3.6× and 5.8× more strongly fractionated in the stratosphere than Ar but are also more challenging to measure due to their ∼ 8000× and 100 000× lower abundance in the atmosphere. Nevertheless, future analysis of these gases in stratospheric air samples might further improve our ability to estimate AoA from the gravitational fractionation of gases and help diagnose artifactual fractionation, because heavier noble gases are more strongly fractionated under the influence of gravity and less sensitive to thermal fractionation (Seltzer et al., 2019).
4.3 Future directions
An open question in climate applications of noble gases is whether there could be a stratospheric influence on tropospheric δ(Ar∕N2). Tropospheric observations of δ(Ar∕N2) and other noble gas-elemental ratios have been used to infer ocean heat content changes by capitalizing on the temperature dependency of gas solubility in the oceans (Keeling et al., 2004; Headly and Severinghaus, 2007; Ritz et al., 2011; Bereiter et al., 2018). However, long-term trends (Butchart, 2014) and natural variability in stratospheric circulation and stratosphere–troposphere exchange (STE) such as the Quasi-Biennial Oscillation (QBO) (Baldwin et al., 2001) could advect a stratospheric GS signal into the troposphere and alias onto surface observations of these gases. To this end, we calculate the volumetric Ar deficit in the atmosphere in moles using TOMCAT (Fig. 7) relative to a hypothetical, unfractionated atmosphere with a homogenous mixing ratio () at all elevations. Ar deficit is
where CAr is the simulated Ar mixing ratio and Nair is the number density of air.
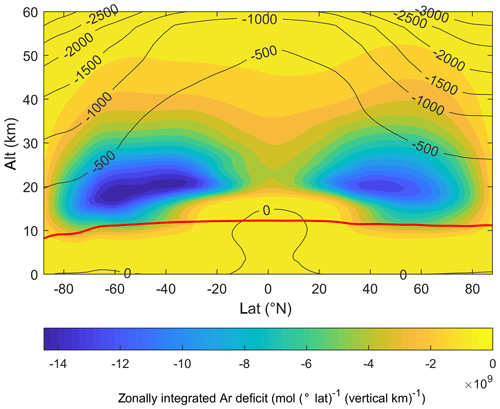
Figure 7Color map of annual mean and zonally integrated Ar deficit in TOMCAT. Overlain black contour lines show δ(Ar∕N2) (per meg). The red solid line highlights the mean position of the 200 hPa isobar.
The Ar deficit is concentrated in the lower stratosphere at around 20 km and at mid to high latitudes. Although the GS signal is considerably stronger in the mesosphere, the potential for perturbing the troposphere is low given the low molar density of air in the mesosphere. The region with the greatest potential to influence the troposphere therefore lies in the lower stratosphere. The total Ar deficit of the atmosphere above 200 hPa is approximately mol and the atmosphere below 200 hPa contains roughly 1.3×1018 mol of Ar. Perturbing STE and/or the stratospheric circulation by 10 %, consistent with interannual to decadal variability of STE in models (Salby and Callaghan, 2006; Flury et al., 2013; Ray et al., 2014; Montzka et al., 2018), thus should lead to a detectable signal of roughly 2.2 per meg () in tropospheric δ(Ar∕N2). Corresponding advection of stratospheric GS signals in N2 amplifies the pure Ar signal by roughly 10 %. A careful investigation of such a signal in the δ(Ar∕N2) surface network data (Keeling et al., 2004) is needed because secular trends of δ(Ar∕N2) caused by degassing of Ar and N2 from a warming ocean are also expected to be on the order of 2–3 per meg per decade. Previous studies have also used ratios involving heavier noble gases (Xe∕N2, Kr∕N2) to reconstruct mean ocean temperature changes over glacial–interglacial timescales (Headly and Severinghaus, 2007; Bereiter et al., 2018; Baggenstos et al., 2019). Simultaneous changes in stratospheric circulation and STE affect heavier noble gases more strongly than Ar∕N2 and will need to be accounted for in such applications of noble gas thermometry.
With improvements in data treatment, measurement quality, and modeling constraints, we have shown that gravitational fractionation of Ar relative to N2 in the stratosphere and mesosphere is a potentially powerful constraint on circulation. High-precision observations of δ(Ar∕N2) in air samples of the lowermost stratosphere from nine airborne campaigns are well captured by the TOMCAT/SLIMCAT 3-D chemical transport model, which has been updated to account for the influence of gravity on air composition through molecular diffusion. In the observations and the model, δ(Ar∕N2) is directly related to stratospheric mean age of air (AoA) derived here using a new calibration of N2O. Our observations for mean AoA <3 years produce a slope of roughly 35–45 per meg of δ(Ar∕N2) per year of AoA. TOMCAT/SLIMCAT shows better agreement with the new observations than the NIES transport model (Belikov et al., 2019), and we speculate that the model disagreement could be explained by (i) the factor of 2 lower top of the NIES transport model, (ii) the use of different reanalysis products, and/or (iii) differences in vertical and horizontal mixing. In this context, further work is also needed to study the influence of unresolved turbulence on AoA and δ(Ar∕N2) in chemical transport models.
As the importance of stratospheric circulation for ozone recovery, climate projections, and evaluation of tropospheric trends in halocarbons is increasingly recognized, a need for new observations from the still undersampled stratosphere is becoming evident. Combining δ(Ar∕N2) with other tracers of circulation could lead to new insights into atmospheric mixing and transport. δ(Ar∕N2) has potential advantages over existing approaches based on transient tracers such as CO2 or N2O since δ(Ar∕N2) is only influenced by the physics of transport and mostly unaffected by seasonality in the tropical upper troposphere. Furthermore, because of its large gradients at high altitudes, δ(Ar∕N2) observations from the upper stratosphere and mesosphere could improve our understanding of circulation on seasonal and interannual timescales in a region where AoA becomes near uniform, and some photochemical age tracers such as N2O are almost fully depleted and thus lose sensitivity to circulation changes.
The following list outlines key steps in our MCMC algorithm to calculate AoA from CO2 for each N2O bin.
-
Start a new Markov chain and allow for uncertainty in TRTS by adding white noise with an amplitude given by the scatter of upper tropospheric observations around the mean TRTS in Fig. 2.
-
With a 50 % chance, peak weighting factor A is set to zero and a unimodal spectrum is tested (k=1). Alternatively, A is allowed to vary between 0 and 1 for a bimodal distribution (k=2).
-
The other age spectrum parameters are selected from N2O bin-dependent prior distributions: Γ1 is sampled from a uniform prior distribution with a mean AoA predicted by the N2O–AoA relationship of Andrews et al. (2001) and with generous width (>1.5 years). Γ2 is sampled from a uniform prior distribution with values between 1 and 6 years representing older stratospheric air. The shape parameters are defined as , and γi is chosen randomly for each peak with values between 0.1 and 1, as observed in previous studies (Hall and Plumb, 1994; Andrews et al., 2001; Waugh and Hall, 2002).
-
Convolve the age spectrum calculated from the parameters ( with the perturbed TRTS to obtain a possible time series of CO2 in the N2O bin and calculate the misfit (e) between the CO2 time series and observations.
-
Calculate the likelihood function P(d|k,m) for the set of parameters m and k, given a total of n observations (d):
where is the covariance matrix. We assume that all n observations are independent. Thus, has only diagonal entries of and simplifies to . The value of is different for each bin and determined iteratively as the approximate root mean square error of the observations around the final time series for each bin obtained at the end of the MCMC algorithm. Typical values of are between 0.18 and 1.28 ppm and generally decrease with increasing AoA of a N2O bin.
-
If this is the first pass of the chain, define ksaved and msaved to equal k and m. Otherwise, calculate the selection criterion and accept k and m as new saved values (ksavedmsaved) with probability α. Sampling from the same prior distributions on each pass of the chain simplifies our expression of α compared to that presented by Malinverno (2002), making it only dependent on the likelihood ratio.
-
Repeat steps 2–6 1000 times, sampling parameter values from the same prior distributions, and store the final values of ksaved and msaved obtained after the 1000th iteration (i.e., a plausible solution produced past the burn-in period) for later use.
-
To sample the full posterior pdf (i.e., the full uncertainty about the age spectrum parameters), initialize 2000 different Markov chains by repeating steps 1–7. Each stored value of m characterizes one age spectrum that is likely not far from the best solution, given the data d, yielding an ensemble of 2000 age spectra from which statistics can be computed. Note that each Markov chain is fully independent, so the algorithm can be easily parallelized to minimize computational costs.
We start by approximating air as a ternary mixture of N2, O2, and Ar and later generalize to consider additional trace species. According to the Maxwell–Stefan equations (Taylor and Krishna, 1993), diffusion in this ternary mixture is governed by
where is the mole fraction, ni is molar or number density (mol m−3), N is the total number density (mol m−3), fi is the molecular diffusion flux (mol m2 s−1) relative to the molar average velocity of the mixture, di is the thermodynamic driving force for molecular diffusion (m−1), and Di:j is the binary diffusion coefficient of the (i:j) pair. An equation for O2 that is analogous to Eq. (B1) is not needed because changes in O2 are governed by the conservation Eqs. (B3) and (B4). Binary diffusivity coefficients (cm2 s−1) can be calculated using the method of Fuller et al. as reported in Reid et al. (1987):
where P is pressure (atm), νi is the molecular diffusion volume of a trace gas or air (Table B1), and Mi is the molecular mass (g mol−1) of a gas.
For an ideal gas, di is given by
where is the mass fraction of gas i, ρi is density of i (kg m−3), P is pressure (Pa), T is temperature (K), is the thermal-diffusion ratio of i, Mi is the molecular mass of i (kg mol−1), and Fi the external body force per mole (N mol−1) for i (Chapman et al., 1990; Taylor and Krishna, 1993).
In the atmosphere, (vertical) pressure gradients are caused by gravity and well approximated by hydrostatic balance
The gravitational force per mole Fi is
Substituting Eqs. (B7) and (B8) into Eq. (B6) yields
where we use the definition of the scale height . The two terms involving the body force cancel because all species experience the same gravitational force per unit mass. The tendency for gravimetric separation instead arises from the pressure gradient term proportional to .
Equations (B1) and (B2) can be inverted to solve for and fAr (Taylor and Krishna, 1993):
where
Here and are the effective diffusivities of N2 and Ar in air, while and reflect ternary cross-interactions, such as the tendency of N2 to be impacted by any process that drives a diffusive flux of Ar.
Table B2Characteristic values of variables in Eqs. (B19) and (B20).
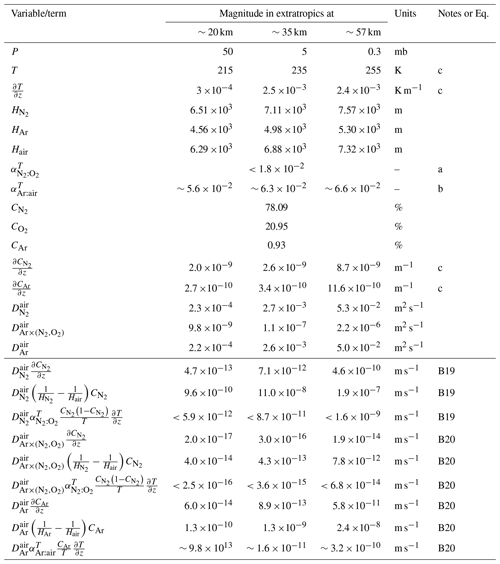
a observed at 293 K (Waldmann, 1947). b Assuming . c Estimated from TOMCAT results.
In air, Ar is a minor gas (), and therefore interactions of N2 with Ar can be neglected in the N2 flux and the diffusive fluxes of N2 and O2 must balance approximately, as in the case of a binary mixture of the two gases:
Combining Eqs. (B10) and (B17) with Eq. (B9) yields
where we have replaced the thermal diffusion ratio with the better empirically constrained thermal diffusion factor defined as such only in binary mixtures. Therefore, and . Table B2 presents rough estimates of the magnitudes of the terms in Eqs. (B19) and (B20) in the stratosphere, showing that the thermal diffusion and cross-diffusion terms involving are at least 2 orders of magnitude smaller than the remaining terms. Neglecting these smaller terms yields the governing Eq. (4) used in our model simulation:
where we introduced , the molecular mass difference to air (kg mol−1), as a shorthand. Equation (B21) is equally valid for trace gases such as Ar and major gases N2 and O2 when the appropriate diffusivities given by Eqs. (B12) and (B14) are used. In our case for N2 and for Ar.
The conservation equation of gas i with mixing ratio Ci accounting for advection (first term RHS), eddy mixing (second term RHS), and molecular diffusion (third term RHS, using the simplified Eq. B21) is given by
where u is the velocity vector (m s−1), De is the eddy diffusivity tensor (m2 s−1), Di is the molecular diffusivity of species i in air (i.e., m2 s−1), g is the gravitational acceleration, R is the fundamental gas constant (J K−1 mol−1), and T is temperature (K). “∇⋅” represents the divergence operator. u, De, Di, N, and T depend on x, y, z, and t and the largest gradients for these variables generally occur in the vertical direction.
Dividing Eq. (C1) by a reference value Ci,0, separating Ci into a constant and a perturbation component (i.e., ), and using the chain rule yields
To simplify Eq. (C2), we assume that the perturbations in the mixing ratio are small (i.e., δi≪1), which is true at the 1 % level for δ(Ar∕N2) even in the mesosphere. Furthermore, we assume that (U is a characteristic velocity scale, De is a characteristic eddy diffusivity, and L is a characteristic length scale; ) or, equivalently stated in terms of the Peclet number, . We estimate typical values of the vertical Peclet number in the stratosphere to be between 1000 and 10 000 based on the height (∼20 km) and turnover time (∼5 years) of the stratosphere and the range of molecular diffusivities given in Table B1. In the mesosphere, AoA is near uniform, and we conservatively assume a turnover time of 0.5 years and a height of 20 km. This implies a Peclet number of ∼500 for the mesosphere. Under these conditions, the third term on the RHS can be eliminated because it is O(Pe) smaller than the first and second terms and because it is O(δi) smaller than the fourth term. Thus, we obtain
where the last term approximates the vertical divergence of the gravitational flux. At the top of the atmosphere and Earth's surface, the gravitational flux abruptly vanishes, and its divergence becomes large. If its divergence is small in the interior, Eq. (C3) can be conceptually interpreted as an advection–diffusion problem with large apparent sources or sinks at the bottom and top boundaries due to diffusive flux divergence. The steady-state solution to Eq. (C3) for a tracer δi with no additional sources and sinks (other than the apparent sources from diffusive flux divergence) yields the steady-state profile for species i. This solution can be scaled to yield the steady-state solution for any other tracer δj as
as can easily be validated by solving Eq. (C4) for δi and substitution into Eq. (C3). Note that does not depend on x, y, and z.
Furthermore, ratios of passive tracers k and l can be calculated directly from δi by recognizing that for . Hence, we obtain the general version of Eq. (5) in the main text:
All data from the ORCAS, HIPPO, and ATom airborne campaigns are freely available at https://doi.org/10.5065/D6SB445X (Stephens, 2017), https://doi.org/10.3334/CDIAC/HIPPO_014 (Wofsy et al., 2017), and https://doi.org/10.3334/ornldaac/1581 (Wofsy et al., 2018). All of the primary data used here are consistent with the associated merged data products in Wofsy et al. (2017, 2018) and Stephens (2017). For Medusa samples identified as stratospheric, CO2, δ(Ar∕N2), AoA, and kernel-averaged N2O, O3, H2O, CO, CH4, as well as additional metadata are available at https://doi.org/10.3334/ORNLDAAC/1788 (Birner et al., 2020). A movie highlighting the variability of monthly and zonal means of (a) δ(Ar∕N2) and (b) age of air (AoA) in TOMCAT is available in the Supplement. The video corresponds to Fig. 6 in the paper.
NIES TM modeling results (Belikov et al., 2019) and stratospheric observations of GS from the cryogenic balloon sampling system (Ishidoya et al., 2008, 2013, 2018; Sugawara et al., 2018) were provided directly by the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-20-12391-2020-supplement.
MPC, WF, and CW set up and ran the TOMCAT model simulations. EJM, JDB, BBS, and SCW collected samples and curated data. BB carried out the data analysis with important input from MPC, JS, RFK, SCW, ML, and EJM. BB prepared the manuscript with contributions from all the co-authors.
The authors declare that they have no conflict of interest.
We would like to thank the pilots and crew of the GV and DC-8 research aircraft as well as NCAR and NASA project managers, field support staff, and logistics experts that were integral to the success of the ORCAS, HIPPO, and ATom campaigns. We are grateful to Andy Watt at NCAR, who helped prepare the Medusa sampler for the field and assisted with its operation. Bill Paplawsky, Sara Afshar, Shane Clark, Stephen Walker, and Adam Cox facilitated sample analysis, gas cylinder preparation, and data management and performed instrument maintenance at the Scripps Institution of Oceanography (SIO). Special thanks go to Eric Hintsa, Fred Moore, Jim Elkins, Mark Zondlo, Stuart Beaton, Minghui Diao, Glenn Diskin, Glen Sachse, Joshua DiGangi, John Nowak, James Flynn, Sergio Alvarez, Kathryn McKain, and Colm Sweeney for sharing O3, N2O, H2O, CO, and CH4 data used in this paper.
For the VCSEL hygrometer, field support, laboratory calibrations, and QA/QC were provided by Minghui Diao, Josh DiGangi, Mark Zondlo, and Stuart Beaton in HIPPO; Stuart Beaton provided field support and Minghui Diao provided laboratory calibrations and QA/QC in ORCAS.
This material is based upon work supported by the National Center for Atmospheric Research (NCAR), which is a major facility sponsored by the National Science Foundation (NSF) under cooperative agreement no. 1852977. The TOMCAT simulations were performed on the UK Archer and University of Leeds ARC HPC facilities. The modeling work in Leeds was supported by a NERC SISLAC. Martyn P. Chipperfield was also supported by a Royal Society Wolfson Merit award.
We thank Dimitry Belikov, Satoshi Sugawara, Shigeyuki Ishidoya, and colleagues for sharing the NIES TM modeling results and stratospheric observations from the balloon sampling system with us.
This research has been supported by NASA (grant nos. NNX17AE74G and NNX15AJ23G), the National Science Foundation (grant nos. ATM-0628575, ATM-0628519, ATM-0628388, AGS-1547797, AGS-1623748, 1501993, 1501997, 1501292, 1502301, and 1543457), and the Natural Environment Research Council (grant no. NE/R001782/1).
This paper was edited by Andreas Engel and reviewed by two anonymous referees.
Andrews, A. E., Boering, K. A., Daube, B. C., Wofsy, S. C., Hintsa, E. J., Weinstock, E. M., and Bui, T. P.: Empirical age spectra for the lower tropical stratosphere from in situ observations of CO2: Implications for stratospheric transport, J. Geophys. Res., 104, 26581–26595, https://doi.org/10.1029/1999JD900150, 1999.
Andrews, A. E., Boering, K. A., Wofsy, S. C., Daube, B. C., Jones, D. B., Alex, S., Loewenstein, M., Podolske, J. R., and Strahan, S. E.: Empirical age spectra for the midlatitude lower stratosphere from in situ observations of CO2: Quantitative evidence for a subtropical “barrier” to horizontal transport, J. Geophys. Res., 106, 10257–10274, https://doi.org/10.1029/2000JD900703, 2001.
Baggenstos, D., Häberli, M., Schmitt, J., Shackleton, S. A., Birner, B., Severinghaus, J. P., Kellerhals, T., and Fischer, H.: Earth's radiative imbalance from the Last Glacial Maximum to the present, P. Natl. Acad. Sci. USA, 116, 14881–14886, https://doi.org/10.1073/pnas.1905447116, 2019.
Baldwin, M. P., Gray, L. J., Dunkerton, T. J., Hamilton, K., Haynes, P. H., Randel, W. J., Holton, J. R., Alexander, M. J., Hirota, I., Horinouchi, T., Jones, D. B. A., Kinnersley, J. S., Marquardt, C., Sato, K., and Takahashi, M.: The quasi-biennial oscillation, Rev. Geophys., 39, 179–229, 2001.
Banks, P. M. and Kockarts, G.: Aeronomy, Part B, 1st edn., Academic Press, New York, USA and London, UK, 1973.
Belikov, D. A., Maksyutov, S., Sherlock, V., Aoki, S., Deutscher, N. M., Dohe, S., Griffith, D., Kyro, E., Morino, I., Nakazawa, T., Notholt, J., Rettinger, M., Schneider, M., Sussmann, R., Toon, G. C., Wennberg, P. O., and Wunch, D.: Simulations of column-averaged CO2 and CH4 using the NIES TM with a hybrid sigma-isentropic (σ−θ) vertical coordinate, Atmos. Chem. Phys., 13, 1713–1732, https://doi.org/10.5194/acp-13-1713-2013, 2013.
Belikov, D., Sugawara, S., Ishidoya, S., Hasebe, F., Maksyutov, S., Aoki, S., Morimoto, S., and Nakazawa, T.: Three-dimensional simulation of stratospheric gravitational separation using the NIES global atmospheric tracer transport model, Atmos. Chem. Phys., 19, 5349-5361, https://doi.org/10.5194/acp-19-5349-2019, 2019.
Bent, J. D.: Airborne Oxygen Measurements over the Southern Ocean as an Integrated Constraint of Seasonal Biogeochemical Processes, University of California, San Diego, USA, 2014.
Bereiter, B., Shackleton, S., Baggenstos, D., Kawamura, K., and Severinghaus, J.: Mean global ocean temperatures during the last glacial transition, Nature, 553, 39–44, https://doi.org/10.1038/nature25152, 2018.
Bieri, R. H. and Koide, M.: Noble gases in the atmosphere between 43 and 63 kilometers, J. Geophys. Res., 75, 6731–6735, https://doi.org/10.1029/jc075i033p06731, 1970.
Birner, B., Chipperfield, M., Morgan, E. J., and Keeling, R. F.: ATom: Age of Air, Ar∕N2 Ratio, and Trace Gases in Stratospheric Samples, 2009–2018, ORNL DAAC, Oak Ridge, Tennessee, USA, https://doi.org/10.3334/ORNLDAAC/1788, 2020.
Blaine, T. W., Keeling, R. F., and Paplawsky, W. J.: An improved inlet for precisely measuring the atmospheric Ar∕N2 ratio, Atmos. Chem. Phys., 6, 1181–1184, https://doi.org/10.5194/acp-6-1181-2006, 2006.
Boering, K. A., Wofsy, S. C., Daube, B. C., Schneider, H. R., Loewenstein, M., Podolske, J. R., and Conway, T. J.: Stratospheric mean ages and transport rates from observations of carbon dioxide and nitrous oxide, Science, 274, 1340–1343, https://doi.org/10.1126/science.274.5291.1340, 1996.
Bönisch, H., Engel, A., Curtius, J., Birner, Th., and Hoor, P.: Quantifying transport into the lowermost stratosphere using simultaneous in-situ measurements of SF6 and CO2, Atmos. Chem. Phys., 9, 5905–5919, https://doi.org/10.5194/acp-9-5905-2009, 2009.
Brewer, A. W.: Evidence for a world circulation provided by the measurements of helium and water vapour distribution in the stratosphere, Q. J. Roy. Meteor. Soc., 75, 351–363, 1949.
Butchart, N.: The Brewer-Dobson circulation, Rev. Geophys., 52, 157–184, https://doi.org/10.1002/2013RG000448, 2014.
Chabrillat, S., Vigouroux, C., Christophe, Y., Engel, A., Errera, Q., Minganti, D., Monge-Sanz, B. M., Segers, A., and Mahieu, E.: Comparison of mean age of air in five reanalyses using the BASCOE transport model, Atmos. Chem. Phys., 18, 14715–14735, https://doi.org/10.5194/acp-18-14715-2018, 2018.
Chapman, S., Cowling, T. G., and Burnett, D.: The mathematical theory of non-uniform gases: an account of the kinetic theory of viscosity, thermal conduction and diffusion in gases, 3rd edn., Cambridge University Press, New York, USA, 1990.
Chipperfield, M. P.: New version of the TOMCAT/SLIMCAT off-line chemical transport model: Intercomparison of stratospheric tracer experiments, Q. J. Roy. Meteor. Soc., 132, 1179–1203, https://doi.org/10.1256/qj.05.51, 2006.
Chipperfield, M. P., Bekki, S., Dhomse, S., Harris, N. R. P., Hassler, B., Hossaini, R., Steinbrecht, W., Thiéblemont, R., and Weber, M.: Detecting recovery of the stratospheric ozone layer, Nature, 549, 211–218, https://doi.org/10.1038/nature23681, 2017.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., Mcnally, A. P., Monge-Sanz, B. M., Morcrette, J. J., Park, B. K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Diskin, G. S., Podolske, J. R., Sachse, G. W., and Slate, T. A.: Open-path airborne tunable diode laser hygrometer, in Diode Lasers and Applications in Atmospheric Sensing, edited by: Fried, A., Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE), 4817, 196–204, https://doi.org/10.1117/12.453736, 2002.
Dobson, G. M. B.: Origin and distribution of the polyatomic molecules in the atmosphere, P. Roy. Soc. Lond. A Mat., 236, 187–193, https://doi.org/10.1098/rspa.1956.0127, 1956.
Engel, A., Möbius, T., Bönisch, H., Schmidt, U., Heinz, R., Levin, I., Atlas, E., Aoki, S., Nakazawa, T., Sugawara, S., Moore, F., Hurst, D., Elkins, J., Schauffler, S., Andrews, A., and Boering, K.: Age of stratospheric air unchanged within uncertainties over the past 30 years, Nat. Geosci., 2, 28–31, https://doi.org/10.1038/ngeo388, 2009.
Engel, A., Bönisch, H., Ullrich, M., Sitals, R., Membrive, O., Danis, F., and Crevoisier, C.: Mean age of stratospheric air derived from AirCore observations, Atmos. Chem. Phys., 17, 6825–6838, https://doi.org/10.5194/acp-17-6825-2017, 2017.
Flury, T., Wu, D. L., and Read, W. G.: Variability in the speed of the Brewer–Dobson circulation as observed by Aura/MLS, Atmos. Chem. Phys., 13, 4563–4575, https://doi.org/10.5194/acp-13-4563-2013, 2013.
Green, P. J.: Reversible jump Markov chain monte carlo computation and Bayesian model determination, Biometrika, 82, 711–732, https://doi.org/10.1093/biomet/82.4.711, 1995.
Hall, T. M. and Plumb, R. A.: Age as a diagnostic of stratospheric transport, J. Geophys. Res., 99, 1059–1070, https://doi.org/10.1029/93JD03192, 1994.
Hastings, W. K.: Monte carlo sampling methods using Markov chains and their applications, Biometrika, 57, 97–109, 1970.
Hauck, M., Fritsch, F., Garny, H., and Engel, A.: Deriving stratospheric age of air spectra using an idealized set of chemically active trace gases, Atmos. Chem. Phys., 19, 5269–5291, https://doi.org/10.5194/acp-19-5269-2019, 2019.
Hauck, M., Bönisch, H., Hoor, P., Keber, T., Ploeger, F., Schuck, T. J., and Engel, A.: A convolution of observational and model data to estimate age of air spectra in the northern hemispheric lower stratosphere, Atmos. Chem. Phys., 20, 8763–8785, https://doi.org/10.5194/acp-20-8763-2020, 2020.
Haynes, P.: Stratospheric Dynamics, Annu. Rev. Fluid Mech., 37, 263–293, 2005.
Headly, M. A. and Severinghaus, J. P.: A method to measure Kr∕N2 ratios in air bubbles trapped in ice cores and its application in reconstructing past mean ocean temperature, J. Geophys. Res., 112, D19105, https://doi.org/10.1029/2006JD008317, 2007.
Holton, J. R., Haynes, P. H., Mcintyre, M. E., Douglass, A. R., and Rood, B.: Stratosphere-Troposphere, Rev. Geophys., 95, 403–439, 1995.
Hoor, P., Gurk, C., Brunner, D., Hegglin, M. I., Wernli, H., and Fischer, H.: Seasonality and extent of extratropical TST derived from in-situ CO measurements during SPURT, Atmos. Chem. Phys., 4, 1427–1442, https://doi.org/10.5194/acp-4-1427-2004, 2004.
Ishidoya, S., Sugawara, S., Morimoto, S., Aoki, S., and Nakazawa, T.: Gravitational separation of major atmospheric components of nitrogen and oxygen in the stratosphere, Geophys. Res. Lett., 35, L03811, https://doi.org/10.1029/2007GL030456, 2008.
Ishidoya, S., Sugawara, S., Morimoto, S., Aoki, S., Nakazawa, T., Honda, H., and Murayama, S.: Gravitational separation in the stratosphere – a new indicator of atmospheric circulation, Atmos. Chem. Phys., 13, 8787–8796, https://doi.org/10.5194/acp-13-8787-2013, 2013.
Ishidoya, S., Sugawara, S., Inai, Y., Morimoto, S., Honda, H., Ikeda, C., Hashida, G., Machida, T., Tomikawa, Y., Toyoda, S., Goto, D., Aoki, S., and Nakazawa, T.: Gravitational separation of the stratospheric air over Syowa, Antarctica and its connection with meteorological fields, Atmos. Sci. Lett., 19, 1–7, https://doi.org/10.1002/asl.857, 2018.
Karion, A., Sweeney, C., Wolter, S., Newberger, T., Chen, H., Andrews, A., Kofler, J., Neff, D., and Tans, P.: Long-term greenhouse gas measurements from aircraft, Atmos. Meas. Tech., 6, 511–526, https://doi.org/10.5194/amt-6-511-2013, 2013.
Keeling, C. D., Stephen, C., Piper, S. C., Bacastow, R. B., Wahlen, M., Whorf, T. P., Heimann, M., and Meijer, H. A.: Exchanges of atmospheric CO2 and 13CO2 with the terrestrial biosphere and oceans from 1978 to 2000, Global Aspects, SIO Reference Series, 01–06, 83–113, 2001.
Keeling, R. F.: Development of an interferometric oxygen analyzer for precise measurement of the atmospheric O2 mole fraction, Harvard University, Cambridge, USA, 1988.
Keeling, R. F., Blaine, T., Paplawsky, B., Katz, L., Atwood, C., and Brockwell, T.: Measurement of changes in atmospheric Ar∕N2 ratio using a rapid-switching, single-capillary mass spectrometer system, Tellus B, 56, 322–338, 2004.
Kovács, T., Feng, W., Totterdill, A., Plane, J. M. C., Dhomse, S., Gómez-Martín, J. C., Stiller, G. P., Haenel, F. J., Smith, C., Forster, P. M., García, R. R., Marsh, D. R., and Chipperfield, M. P.: Determination of the atmospheric lifetime and global warming potential of sulfur hexafluoride using a three-dimensional model, Atmos. Chem. Phys., 17, 883–898, https://doi.org/10.5194/acp-17-883-2017, 2017.
Krol, M., de Bruine, M., Killaars, L., Ouwersloot, H., Pozzer, A., Yin, Y., Chevallier, F., Bousquet, P., Patra, P., Belikov, D., Maksyutov, S., Dhomse, S., Feng, W., and Chipperfield, M. P.: Age of air as a diagnostic for transport timescales in global models, Geosci. Model Dev., 11, 3109–3130, https://doi.org/10.5194/gmd-11-3109-2018, 2018.
Li, F., Waugh, D. W., Douglass, A. R., Newman, P. A., Pawson, S., Stolarski, R. S., Strahan, S. E., and Nielsen, J. E.: Seasonal variations of stratospheric age spectra in the Goddard Earth Observing System Chemistry Climate Model (GEOSCCM), J. Geophys. Res.-Atmos., 117, D05134, https://doi.org/10.1029/2011JD016877, 2012.
Linz, M., Plumb, R. A., Gerber, E. P., and Sheshadri, A.: The relationship between age of air and the diabatic circulation of the stratosphere, J. Atmos. Sci., 73, 4507–4518, https://doi.org/10.1175/JAS-D-16-0125.1, 2016.
Linz, M., Plumb, R. A., Gerber, E. P., Haenel, F. J., Stiller, G., Kinnison, D. E., Ming, A., and Neu, J. L.: The strength of the meridional overturning circulation of the stratosphere, Nat. Geosci., 10, 663–667, https://doi.org/10.1038/ngeo3013, 2017.
Malinverno, A.: Parsimonious Bayesian Markov chain Monte Carlo inversion in a nonlinear geophysical problem, Geophys. J. Int., 151, 675–688, 2002.
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E.: Equation of state calculations by fast computing machines, J. Chem. Phys., 21, 1087–1092, 1953.
Monge-Sanz, B. M., Chipperfield, M. P., Simmons, A. J., and Uppala, S. M.: Mean age of air and transport in a CTM: Comparison of different ECMWF analyses, Geophys. Res. Lett., 34, L04801, https://doi.org/10.1029/2006GL028515, 2007.
Montzka, S. A., Dutton, G. S., Yu, P., Ray, E., Portmann, R. W., Daniel, J. S., Kuijpers, L., Hall, B. D., Mondeel, D., Siso, C., Nance, J. D., Rigby, M., Manning, A. J., Hu, L., Moore, F., Miller, B. R., and Elkins, J. W.: An unexpected and persistent increase in global emissions of ozone-depleting CFC-11, Nature, 557, 413–417, 2018.
Morgan, E. J., Stephens, B. B., Birner, B., and Keeling, R. F.: Observational Constraints on the Vertical and Interhemispheric Gradient of the Ar∕N2 Ratio in the Troposphere, Abstract CT14A-0845, presented at: Ocean Sciences Meeting 2020, 16–21 February 2020, San Diego, USA, AGU, 2020.
Plumb, R. A.: Tracer interrelationships in the stratosphere, Rev. Geophys., 45, RG4005, https://doi.org/10.1029/2005RG000179, 2007.
Podglajen, A. and Ploeger, F.: Retrieving the age of air spectrum from tracers: principle and method, Atmos. Chem. Phys., 19, 1767–1783, https://doi.org/10.5194/acp-19-1767-2019, 2019.
Prather, M. J., Zhu, X., Flynn, C. M., Strode, S. A., Rodriguez, J. M., Steenrod, S. D., Liu, J., Lamarque, J.-F., Fiore, A. M., Horowitz, L. W., Mao, J., Murray, L. T., Shindell, D. T., and Wofsy, S. C.: Global atmospheric chemistry – which air matters, Atmos. Chem. Phys., 17, 9081–9102, https://doi.org/10.5194/acp-17-9081-2017, 2017.
Ray, E. A., Moore, F. L., Elkins, J. W., Dutton, G. S., Fahey, D. W., Vömel, H., Oltmans, S. J., and Rosenlof, K. H.: Transport into the Northern Hemisphere lowermost stratosphere revealed by in situ tracer measurements, J. Geophys. Res.-Atmos., 104, 26565–26580, https://doi.org/10.1029/1999JD900323, 1999.
Ray, E. A., Moore, F. L., Rosenlof, K. H., Davis, S. M., Boenisch, H., Morgenstern, O., Smale, D., Rozanov, E., Hegglin, M., Pitari, G., Mancini, E., Braesicke, P., Butchart, N., Hardiman, S., Li, F., Shibata, K., and Plummer, D. A.: Evidence for changes in stratospheric transport and mixing over the past three decades based on multiple data sets and tropical leaky pipe analysis, J. Geophys. Res.-Atmos., 115, D21304, https://doi.org/10.1029/2010JD014206, 2010.
Ray, E. A., Moore, F. L., Rosenlof, K. H., Davis, S. M., Sweeney, C., Tans, P., Wang, T., Elkins, J. W., Bönisch, H., Engel, A., Sugawara, S., Nakazawa, T., and Aoki, S.: Improving stratospheric transport trend analysis based on SF6 and CO2 measurements, J. Geophys. Res.-Atmos., 119, 14110–14128, https://doi.org/10.1002/2014JD021802, 2014.
Reid, R. C., Prausnitz, J. M., and Poling, B. E.: The properties of gases and liquids, 4th edn., edited by: Sun, B. and Fleck, G. H., McGraw-Hill, New York, USA, 1987.
Ritz, S. P., Stocker, T. F., and Severinghaus, J. P.: Noble gases as proxies of mean ocean temperature: Sensitivity studies using a climate model of reduced complexity, Quaternary Sci. Rev., 30, 3728–3741, 2011.
Salby, M. L. and Callaghan, P. F.: Influence of the Brewer-Dobson circulation on stratosphere-troposphere exchange, J. Geophys. Res.-Atmos., 111, 1–9, 2006.
Santoni, G. W., Daube, B. C., Kort, E. A., Jiménez, R., Park, S., Pittman, J. V., Gottlieb, E., Xiang, B., Zahniser, M. S., Nelson, D. D., McManus, J. B., Peischl, J., Ryerson, T. B., Holloway, J. S., Andrews, A. E., Sweeney, C., Hall, B., Hintsa, E. J., Moore, F. L., Elkins, J. W., Hurst, D. F., Stephens, B. B., Bent, J., and Wofsy, S. C.: Evaluation of the airborne quantum cascade laser spectrometer (QCLS) measurements of the carbon and greenhouse gas suite – CO2, CH4, N2O, and CO – during the CalNex and HIPPO campaigns, Atmos. Meas. Tech., 7, 1509–1526, https://doi.org/10.5194/amt-7-1509-2014, 2014.
Schoeberl, M. R., Douglass, A. R., Polansky, B., Bonne, C., Walker, K. A., and Bernath, P.: Estimation of stratospheric age spectrum from chemical tracers, J. Geophys. Res.-Atmos., 110, D21303, https://doi.org/10.1029/2005JD006125, 2005.
Seltzer, A. M., Ng, J., Danskin, W. R., Kulongoski, J. T., Gannon, R. S., Stute, M., and Severinghaus, J. P.: Deglacial water-table decline in Southern California recorded by noble gas isotopes, Nat. Commun., 10, 1–6, 2019.
Škerlak, B., Sprenger, M., and Wernli, H.: A global climatology of stratosphere–troposphere exchange using the ERA-Interim data set from 1979 to 2011, Atmos. Chem. Phys., 14, 913–937, https://doi.org/10.5194/acp-14-913-2014, 2014.
Stephens, B.: ORCAS Merge Products. Version 1.0, UCAR/NCAR – Earth Observing Laboratory, https://doi.org/10.5065/D6SB445X, 2017.
Stephens, B. B., Long, M. C., Keeling, R. F., Kort, E. A., Sweeney, C., Apel, E. C., Atlas, E. L., Beaton, S., Bent, J. D., Blake, N. J., Bresch, J. F., Casey, J., Daube, B. C., Diao, M., Diaz, E., Dierssen, H., Donets, V., Gao, B. C., Gierach, M., Green, R., Haag, J., Hayman, M., Hills, A. J., Hoecker-Martínez, M. S., Honomichl, S. B., Hornbrook, R. S., Jensen, J. B., Li, R. R., McCubbin, I., McKain, K., Morgan, E. J., Nolte, S., Powers, J. G., Rainwater, B., Randolph, K., Reeves, M., Schauffler, S. M., Smith, K., Smith, M., Stith, J., Stossmeister, G., Toohey, D. W., and Watt, A. S.: The O2∕N2 ratio and CO2 airborne Southern Ocean study, B. Am. Meteorol. Soc., 99, 381–402, https://doi.org/10.1175/BAMS-D-16-0206.1, 2018.
Stephens, B. B., Morgan, E. J., Bent, J. D., Keeling, R. F., Watt, A. S., Shertz, S. R., and Daube, B. C.: Airborne measurements of oxygen concentration from the surface to the lower stratosphere and pole to pole, Atmos. Meas. Tech. Discuss., https://doi.org/10.5194/amt-2020-294, in review, 2020.
Strahan, S. E., Douglass, A. R., Stolarski, R. S., Akiyoshi, H., Bekki, S., Braesicke, P., Butchart, N., Chipperfield, M. P., Cugnet, D., Dhomse, S., Frith, S. M., Gettelman, A., Hardiman, S. C., Kinnison, D. E., Lamarque, J. F., Mancini, E., Marchand, M., Michou, M., Morgenstern, O., Nakamura, T., Olivié, D., Pawson, S., Pitari, G., Plummer, D. A., Pyle, J. A., Scinocca, J. F., Shepherd, T. G., Shibata, K., Smale, D., Teyssèdre, H., Tian, W., and Yamashita, Y.: Using transport diagnostics to understand chemistry climate model ozone simulations, J. Geophys. Res.-Atmos., 116, 1–18, 2011.
Sugawara, S., Ishidoya, S., Aoki, S., Morimoto, S., Nakazawa, T., Toyoda, S., Inai, Y., Hasebe, F., Ikeda, C., Honda, H., Goto, D., and Putri, F. A.: Age and gravitational separation of the stratospheric air over Indonesia, Atmos. Chem. Phys., 18, 1819–1833, https://doi.org/10.5194/acp-18-1819-2018, 2018.
Taylor, R. and Krishna, R.: Multicomponent mass transfer, 2nd edn., John Wiley & Sons, New York, USA, 1993.
Waldmann, L.: Die Temperaturerscheinungen bei der Diffusion in ruhenden Gasen und ihre meßtechnische Anwendung, Z. Phys., 124, 2–29, https://doi.org/10.1007/BF01374919, 1947.
Waugh, D.: Atmospheric dynamics: The age of stratospheric air, Nat. Geosci., 2, 14–16, https://doi.org/10.1038/ngeo397, 2009.
Waugh, D. W. and Hall, T. M.: Age of stratospheric air: Theory, observations, and models, Rev. Geophys., 40, 1-1–1-26 https://doi.org/10.1029/2000RG000101, 2002.
Wofsy, S. C., the HIPPO science team, cooporating modelers and satellite teams: HIAPER Pole-to-Pole Observations (HIPPO): Fine-grained, global-scale measurements of climatically important atmospheric gases and aerosols, Philos. T. Roy. Soc. A Mat., 369, 2073–2086, https://doi.org/10.1098/rsta.2010.0313, 2011.
Wofsy, S., Daube, B., Jimenez, R., Kort, E., Pittman, J., Park, S., Commane, R., Xiang, B., Santoni, G., Jacob, D., Fisher, J., Pickett-Heaps, C., Wang, H., Wecht, K., Wang, Q., Stephens, B., Shertz, S., Watt, A., Romashkin, P., Campos, T., Haggerty, J., Cooper, W., Rogers, D., Beaton, S., Hendershot, R., Elkins, J., Fahey, D., Gao, R., Moore, F., Montzka, S., Schwarz, J., Perring, A., Hurst, D., Miller, B., Sweeney, C., Oltmans, S., Nance, D., Hintsa, E., Dutton, G., Watts, L., Spackman, J., Rosenlof, K., Ray, E., Hall, B., Zondlo, M., Diao, M., Keeling, R., Bent, J., Atlas, E., Lueb, R. and Mahoney, M. J. (Deceased): HIPPO MEDUSA Flask Sample Trace Gas And Isotope Data, Version 1.0, https://doi.org/10.3334/CDIAC/HIPPO_014, 2017.
Wofsy, S. C., Afshar, S., Allen, H. M., Apel, E., Asher, E. C., Barletta, B., Bent, J., Bian, H., Biggs, B. C., Blake, D. R., Blake, N., Bourgeois, I., Brock, C. A., Brune, W. H., Budney, J. W., Bui, T. P., Butler, A., Campuzano-Jost, P., Chang, C. S., Chin, M., Commane, R., Correa, G., Crounse, J. D., Cullis, P. D., Daube, B. C., Day, D. A., Dean-Day, J. M., Dibb, J. E., Digangi, J. P., Diskin, G. S., Dollner, M., Elkins, J. W., Erdesz, F., Fiore, A. M., Flynn, C. M., Froyd, K., Gesler, D. W., Hall, S. R., Hanisco, T. F., Hannun, R. A., Hills, A. J., Hintsa, E. J., Hoffman, A., Hornbrook, R. S., Huey, L. G., Hughes, S., Jimenez, J. L., Johnson, B. J., Katich, J. M., Keeling, R., Kim, M. J., Kupc, A., Lait, L. R., Lamarque, J. F., Liu, J., McKain, K., McLaughlin, R. J., Meinardi, S., Miller, D. O., Montzka, S. A., Moore, F. L., Morgan, E. J., Murphy, D. M., Murray, L. T., Nault, B. A., Neuman, J. A., Newman, P. A., Nicely, J. M., Pan, X., Paplawsky, W., Peischl, J., Prather, M. J., Price, D. J., Ray, E., Reeves, J. M., Richardson, M., Rollins, A. W., Rosenlof, K. H., Ryerson, T. B., Scheuer, E., Schill, G. P., Schroder, J. C., Schwarz, J. P., St.Clair, J. M., Steenrod, S. D., Stephens, B. B., Strode, S. A., Sweeney, C., Tanner, D., Teng, A. P., Thames, A. B., Thompson, C. R., Ullmann, K., Veres, P. R., Vizenor, N., Wagner, N. L., Watt, A., Weber, R., Weinzierl, B., Wennberg, P. O., Williamson, C. J., Wilson, J. C., Wolfe, G. M., Woods, C. T., and Zeng, L. H.: ATom: Merged Atmospheric Chemistry, Trace Gases, and Aerosols, ORNL DAAC, Oak Ridge, Tennessee, USA, https://doi.org/10.3334/ORNLDAAC/1581, 2018.
Zondlo, M. A., Paige, M. E., Massick, S. M., and Silver, J. A.: Vertical cavity laser hygrometer for the National Science Foundation Gulfstream-V aircraft, J. Geophys. Res.-Atmos., 115, D20309, https://doi.org/10.1029/2010JD014445, 2010.
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Conclusions
- Appendix A: Description of the Markov chain Monte Carlo algorithm
- Appendix B: Derivation of Eq. (4) from the Maxwell–Stefan equations
- Appendix C: Calculating δ(Ar∕N2) from δ(GST)
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Conclusions
- Appendix A: Description of the Markov chain Monte Carlo algorithm
- Appendix B: Derivation of Eq. (4) from the Maxwell–Stefan equations
- Appendix C: Calculating δ(Ar∕N2) from δ(GST)
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement