Peroxy radical chemistry and the volatility basis set

Gas-phase autoxidation of organics can generate highly oxygenated organic molecules (HOMs) and thus increase secondary organic aerosol production and enable new-particle formation. Here we present a new implementation of the volatility basis set (VBS) that explicitly resolves peroxy radical (RO₂) products formed via autoxidation. The model includes a strong temperature dependence for autoxidation as well as explicit termination of RO₂, including reactions with NO, HO₂, and other RO₂. The RO₂ cross-reactions can produce dimers (ROOR). We explore the temperature and NO_x dependence of this chemistry, showing that temperature strongly influences the intrinsic volatility distribution and that NO can suppress autoxidation under conditions typically found in the atmosphere.

1 Introduction

Atmospheric particles have dangerous health effects and influence the environment both through their direct scattering of incoming radiation and their indirect effect on clouds as cloud condensation nuclei. New-particle formation (secondary particle production) constitutes the largest source of particles in the atmosphere; furthermore many if not most particles with significant health or climate effects consist largely of secondary material, having grown via condensation from a much smaller initial size. Organic vapors contribute to both nucleation and growth of new particles as well as growth of primary nanoparticles, all of which constitute secondary organic aerosol (SOA). Especially for condensation to the smallest particles, the volatility of those condensible organics is important. Therefore it is of interest to investigate and model how volatile precursors oxidize in the atmosphere to low-volatility or extremely low volatility products (LVOCs and ELVOCs) that will contribute to SOA. Furthermore, organic oxidation products alone can drive pure biogenic nucleation (Kirkby et al., 2016), and so the formation mechanisms and nucleation rates of a new class of ultra-low-volatility products (ULVOCs) that can drive nucleation are also of interest.

One important class of condensible organics is the group known as highly oxygenated organic molecules (HOMs). HOMs are organic compounds containing at least six oxygen atoms formed through peroxy radical (RO₂) isomerization and subsequent addition of molecular oxygen, which preserves RO₂ functionality in a recursive process known as autoxidation, followed by RO₂ termination to molecular products (Crounse et al., 2013; Ehn et al., 2014; Bianchi et al., 2019). HOMs open up a rich space for gas-phase organic oxidation chemistry to strongly influence new-particle formation involving condensible organic products. Because the chemistry involves competition between internal isomerization (which typically will have a relatively high energy barrier and thus a strong temperature dependence) and radical-radical termination reactions (which typically have low barriers and thus only a modest temperature dependence), we expect a strong temperature dependence to HOM formation. Furthermore, because NO_x (especially NO) can greatly shorten RO₂ lifetimes, we also expect a strong NO_x dependence to HOM formation. Finally, to the extent that RO₂-RO₂ cross-reactions between radicals from different organic precursors can be important, there may be a rich interplay among the oxidation mechanisms for a host of different organic compounds.

The volatility basis set (VBS) has been developed and used widely as a framework to represent, track, and model the oxidation of volatile organic precursors, the subsequent production of condensible products, and their evolution through multiple generations of oxidation chemistry and fragmentation (Donahue et al., 2005, 2006, 2011, 2012b, 2013; Chuang and Donahue, 2016). For numerical calculations, the 2D-VBS space is discretized into bins, with each C^∗ (300 K) bin typically separated by 1 order of magnitude and each O : C bin separated by 0.1. It is not necessary to know the identity of molecules in these bins, but this can be inferred by application of composition activity relations such as SIMPOL (Pankow and Asher, 2007). In general, the perspective of the VBS has been to explicitly track the most important observable properties of organics with respect to organic aerosol formation – volatility (C^∘ (T)) and the degree of oxidation (O : C) – forming the so-called two-dimensional volatility basis set (2D-VBS). Where specific products have known properties, those molecules can be located individually in the 2D-VBS. Where specific products are not known, the 2D-VBS can still track the overall carbon in a reactive system, with properties (C^∘ and O : C) evolving following known chemistry during photochemical aging. In this work, we plot everything using a C^∗ (300 K) x axis so as to visualize how the products of the chemistry are changing rather and inferring how this would affect condensation.

The importance of RO₂ branching chemistry has so far been recognized implicitly in VBS formulations (Presto and Donahue, 2006; Henry and Donahue, 2011) but not explicitly. Instead, the product (volatility) distribution in the VBS has been based on some measure of the RO₂ branching (i.e., VOC : NO_x or RO₂ branching in an explicit mechanism). Consequently, there have been high-NO_x products and low-NO_x products (volatility distributions) (Presto and Donahue, 2006), or even high-HO₂ and high-RO₂ products (Henry and Donahue, 2011), that can be mixed to form products at intermediate NO_x (or HO_x:RO_x) based on this indirect measure of RO₂ branching. Further, relatively little has been done to represent any temperature dependence of VOC oxidation in VBS implementations.

The purpose of this paper is to extend the 2D-VBS to explicitly represent RO₂ chemistry, including RO₂ oxidation and HOM formation as well as all forms of RO₂ termination, and only distribute products into volatility bins after RO₂ termination in an explicit gas-phase chemical mechanism. In this way we can represent the gas-phase HOM formation mechanism, its temperature dependence, and the rich array of competing RO₂ termination processes in a scheme that can merge seamlessly with any gas-phase chemical mechanism (MCM, etc.) while maintaining the generality of the VBS and its ability to represent the ongoing chemistry of organic species associated with organic aerosol formation and particle growth.

2 Background

HOMs and their properties have been measured in multiple laboratory and field studies. HOMs can drive pure biogenic nucleation indicating that, in the VBS context, at least some of them must be ELVOCs/ULVOCs. Stolzenburg et al. (2018) and Tröstl et al. (2016) report measurements of HOMs in the LVOC and SVOC range during experiments in the CLOUD chamber at CERN, showing that these HOMs (especially LVOCs) drive growth during new-particle formation, providing a significant reservoir of condensible species to stabilize particles after initial clustering (Stolzenburg et al., 2018; Tröstl et al., 2016). From these data, both collected under NO_x-free conditions, HOM products are expected to be distributed in the SVOC, LVOC, and ELVOC range, with the largest concentration as LVOCs.

The composition and properties of HOMs produced during oxidation of a precursor such as α-pinene (as well as their quantitative yields) depend on the conditions under which they are formed. Frege et al. (2018), again at CLOUD, found that at lower temperatures fewer total HOMs are formed, with dimers seeing the sharpest falloff (Frege et al., 2018). Lehtipalo et al. (2018) showed that increasing NO_x concentrations suppress the ELVOC HOMs but have less of an effect on the LVOC and SVOC HOMs (Lehtipalo et al., 2018).

There are two important elements to HOM formation and its volatility distribution. The first is autoxidation itself, which produces progressively more oxidized peroxy radicals via H-atom transfer and thus –OOH functionalization before the radicals ultimately terminate to form stable products. The second is dimerization, which is one of the termination processes, where these functionalized RO₂ associate to form a covalently bonded dimer (presumably a peroxide, ROOR). The first process plays a key role in particle growth and the temperature dependence of condensible vapor yields. The second process may be rate limiting for pure biogenic nucleation.

Autoxidation involves an internal H-atom transfer, which almost certainly has a significant activation energy. Further, the process is observed to be competitive with bimolecular reactions on a timescale of 1 s or longer (Ehn et al., 2014). Unimolecular reactions have an intrinsic rate constant (A factor) given by molecular vibrational frequencies, and even loose bending modes in molecules have frequencies of THz. To slow down unimolecular reactions to 1 s⁻¹ or so, a high activation energy is thus almost essential. Rate coefficients for competitive reactions suggest an autoxidation energy barrier in the range of 15–18 kcal mol⁻¹ (7500–9000 K). This is also consistent with quantum chemical calculations as well as experimental data fitted to an extended MCM model (Rissanen et al., 2014; Molteni et al., 2019). This high activation energy also means that the RO₂ isomerization reactions will have a strong temperature dependence, becoming very slow at low temperature.

In contrast to the strong temperature dependence of autoxidation, the two canonical RO₂ loss reactions, with HO₂ and NO, both have only a weak temperature dependence with similar rate coefficients near 10⁻¹¹ cm³ molecules⁻¹ s⁻¹ largely independent of RO₂ structure (Atkinson et al., 2008). HO₂ levels typical in the lower atmosphere are roughly 3 pptv, or 10⁸ molecules cm⁻³, giving a first-order low-NO_x loss frequency of 10⁻³ s⁻¹. NO in polluted areas can go much higher, increasing the high-NO_x loss to 0.1 s⁻¹ or even higher. This establishes the competitive range for RO₂ first-order loss in the 0.001–1 s⁻¹ range in the atmosphere. Because these rate coefficients are only weakly sensitive to temperature, the high activation energy for the H-atom transfer in autoxidation means we expect the reactions with HO₂ and NO to be more competitive at low temperature.

Another RO₂ loss is to react with other RO₂. Unlike their reactions with HO₂ and NO, in which the rate coefficients depend only weakly on the nature of the R group, the rate coefficients for RO₂–RO₂ self- and cross-reactions are extremely sensitive to the nature of the R group. This has been well established for decades for the self-reactions of different small RO₂ (Madronich and Calvert, 1990; Donahue and Prinn, 1990; Wallington et al., 1992; Tyndall et al., 2001). However, because ambient RO₂ concentrations rarely exceed ambient HO₂ (Mihelcic et al., 2003; Tan et al., 2018), reactions with other RO₂ will only be a major RO₂ loss pathway in the atmosphere when the rate coefficient equals or exceeds 10⁻¹¹ cm³ molecules⁻¹ s⁻¹. This is in contrast to low-NO_x chamber experiments, where RO₂ concentrations can greatly exceed HO₂ concentrations, potentially biasing the chambers away from reactions important in the atmosphere.

At least for highly oxygenated peroxy radicals, association to form dimers has been found in some experimental studies to proceed with a rate coefficient near the collisional limit ($k>{\mathrm{10}}^{-\mathrm{10}}$ cm³ molecules⁻¹ s⁻¹) (Berndt et al., 2018; Molteni et al., 2019). However, Zhao et al. (2017) find that the typical rate coefficient for presumably similar RO₂+RO₂ association reactions is at least an order of magnitude slower (Zhao et al., 2017). These findings may or may not be directly in conflict given the wide range of peroxy radical rate coefficients. The general tendency is that electron-withdrawing groups (i.e., acyl groups in peroxy acyl radicals) increase the RO₂ self-reaction rate coefficients while electron-donating groups (i.e., tert-butyl in tert-butyl peroxy radicals) lower the rate coefficients. Thus, very fast cross-reaction rate coefficients for highly oxygenated RO₂ radicals are consistent with the general trend.

Autoxidation includes a unimolecular hydrogen shift reaction in which a peroxy moiety abstracts a hydrogen elsewhere on the molecule, generating an alkyl radical, which molecular oxygen will add to in turn, regenerating a peroxy radical functionality on a now-more-oxidized carbon backbone. This process is significant in its ability to rapidly generate multifunctional oxygenation products in only a single generation of chemistry (stable molecule to stable molecule). However, experimental and theoretical evidence suggests that not every peroxy radical is readily capable of undergoing autoxidation. The fraction of peroxy radicals that will autoxidize will be different depending on the precursor of interest; for α-pinene three of the four peroxy radicals from ozonolysis can autoxidize. Ehn et al. (2014) found that the yield of highly oxidized peroxy radicals from OH oxidation of α-pinene was lower than from ozonolysis, indicating that while OH-radical-derived peroxy radicals can autoxidize, the process is either slower or there are fewer that autoxidize readily (Ehn et al., 2014).

To summarize, three important characteristics of a strongly autoxidizing system such as O₃+α-pinene are emerging. First, most of the products under atmospheric conditions are likely to be traditional oxidation products formed without an autoxidation step. Second, the amount of autoxidation is likely to be strongly temperature dependent, with more at higher temperature. Third, some termination of at least the highly oxygenated RO₂ results in covalently bound (and highly oxygenated) dimers, which will have extraordinarily low vapor pressures.

Each consequence has an important implication, which we give in reverse order. First, the dimerization may be the rate-limiting step for pure organic nucleation; because it involves a cross-reaction, this means that organic nucleation may also be highly sensitive to interactions between different hydrocarbon oxidation sequences, especially at low NO_x. It remains somewhat unclear how important this termination is in the real atmosphere vs. chambers, given the high RO₂:HO₂ in chambers; however, the characteristic dimer products are observed in the atmosphere. This strongly suggests that these association reactions are important in the atmosphere.

Second, the temperature dependence of the monomer autoxidation products may well be counterbalanced by the simple temperature dependence of vapor pressures. Both of these govern organic condensation, especially to very small particles. Consequently, particle growth rates from organic oxidation (as well as secondary organic aerosol mass yields) are likely to be less sensitive to temperature than one would otherwise expect. They are also likely to be less sensitive to interactions between different hydrocarbon oxidation sequences. Particle nucleation and growth may thus be partially decoupled, making the treatment of each separately important, especially in the “valley of death” region below 3–5 nm where highly diffusive particles are most vulnerable to coagulation loss.

Third, the large majority of organic oxidation products are likely to be oxygenated species with lower vapor pressure than the precursors that remain in the gas phase (traditional SVOCs). Later-generation chemistry of these products remains an important topic that cannot be forgotten (Donahue et al., 2005, 2012a); these subsequent steps have already been shown to be efficient sources of HOMs (Schobesberger et al., 2013; Ye et al., 2018).

3 The model

For this work we will model an idealized batch reactor with oxidation of α-pinene leading to HOM products. The model is split into two pieces: a general chemical mechanism and a specific implementation for the batch reactor. Here we only simulate the gas-phase chemistry, culminating in formation (and loss) of RO₂ species, with RO₂ termination mapping into the 2D-VBS via a succession of kernels specific to each termination step.

3.1 Chemical mechanism

The model we use here is an explicit gas-phase photochemical box model using a custom-written Perl mechanism parser that produces Matlab code for the coupled differential equations describing an arbitrary set of input reactions. The reaction set here is relatively standard small-molecule HO_x chemistry with added α-pinene. We list the full set of reactions and rate coefficients in the Supplement.

The reactions begin with oxidation of a precursor, in this case α-pinene via ozonolysis, OH, and the nitrate radical (when NO_x is present). Most of the products of these oxidation reactions will be peroxy radicals, with 10 carbons each, which will undergo two types of reactions: autoxidation or radical termination. Autoxidation, as described previously, is a unimolecular reaction followed by O₂ addition that generates a more oxidized peroxy radical that will have the same reaction pathways available to it again as the parent RO₂. It is thus effectively recursive. The radical termination reactions available to a peroxy radical are reaction with HO₂, NO, or another peroxy radical.

It is likely that peroxy radicals have a diversity of H-transfer activation energies (and A factors) and that this diversity is important to the overall system behavior. We currently lack sufficient kinetic information to constrain this, and so we adopt a simple approach. For the initial RO₂ (without additional –OOH functionality), we assume that some fraction can undergo autoxidation and the remainder cannot (it is a binary choice). All of the RO₂ that can autoxidize does so with a single barrier height and A factor, and this is common to all of the subsequent oxidized RO₂.

A second complication is the role of alkoxy radicals (RO), which can be chain propagating (including a much more widely recognized 1–4 H shift that is broadly similar to the H shift in autoxidation) (Atkinson, 1997; Lim and Ziemann, 2009) However, for this set of simulations only we shall assume that RO radicals effectively terminate to molecular products; that is consistent with our broad objective to upgrade the 2D-VBS from simply generating (NO_x-dependent) products from a precursor (i.e., α-pinene) to allow the products to be controlled by peroxy radicals. In the future we shall relax this assumption and permit regeneration of RO₂ from RO.

3.1.1 α-pinene reactions

We are simulating α-pinene ozonolysis, but this chemistry will produce OH radicals and, with added NO_x, NO₃ as well. Consequently, we have three oxidants to consider. It has been found that OH oxidation of α-pinene produces far fewer HOMs than O₃ (Kirkby et al., 2016), presumably because the OH addition does not immediately cleave the six-member ring in α-pinene. Further, oxidation of α-pinene by NO₃ has been shown to produce very little first-generation SOA (Fry et al., 2014; Ng et al., 2017). However, almost all primary oxidation results in peroxy radicals (with the exception of some small fraction of stabilized Criegee intermediates), though only some of those may have rapid autoxidation pathways. To address this, we assign two first-generation RO₂ radicals to each oxidation pathway; one, Ox₀RO₂, has the potential for autoxidation, while the second, RO₂, does not.

$$\mathit{\alpha }\text{-pinene}+\mathrm{Ox}\to {\mathit{\alpha }}_{\mathrm{ox}}{\mathrm{Ox}}_{\mathrm{0}}{\mathrm{RO}}_{\mathrm{2}}+(\mathrm{1}-{\mathit{\alpha }}_{\mathrm{ox}}){\mathrm{RO}}_{\mathrm{2}}+y_{\mathrm{ox}}\mathrm{OH}$$

Here we assume that ${\mathit{\alpha }}_{{\mathrm{O}}_{\mathrm{3}}}=\mathrm{0.25}$, α_OH=0.1, and ${\mathit{\alpha }}_{{\mathrm{NO}}_{\mathrm{3}}}=\mathrm{0}$. Further, $y_{{\mathrm{O}}_{\mathrm{3}}}=\mathrm{0.8}$ (Presto and Donahue, 2004), y_OH=0, and $y_{{\mathrm{NO}}_{\mathrm{3}}}=\mathrm{0}$.

3.1.2 Autoxidation

The autoxidation process involves an internal H-atom transfer in an RO₂ radical, immediately followed by O₂ addition to reform a new RO₂ radical with an added –OOH group. Broadly, we label these reactions

$${\mathrm{Ox}}_n{\mathrm{RO}}_{\mathrm{2}}\to {\mathrm{Ox}}_{n+\mathrm{1}}{\mathrm{RO}}_{\mathrm{2}}k=A\exp (-{\mathit{\theta }}_{\mathrm{a}}/T),$$

where n is the number of –OOH groups (the number of generations of autoxidation). The rate-limiting kinetic parameter is the unimolecular rate constant for H-atom transfer, which we express as an Arrhenius rate coefficient with a pre-exponential A=10⁸ s⁻¹ for the Ox₀RO₂, which decreases to $A=\mathrm{7}\times {\mathrm{10}}^{\mathrm{7}}$ and $A=\mathrm{6}\times {\mathrm{10}}^{\mathrm{7}}$ for the Ox₁RO₂ and the Ox₂RO₂, respectively, and an activation energy θ_a=7500 K that is consistent for all autoxidation steps in our base-case simulation. This gives an H-atom transfer rate coefficient for Ox₀RO₂ of 0.01 s⁻¹ at 298 K and 10⁻⁷ s⁻¹ at 248 K for the Ox₀RO₂. Raising the activation energy to ${\mathit{\theta }}_{\mathrm{a}}=E_{\mathrm{a}}/R=\mathrm{8000}$ K gives an H-atom transfer rate coefficient of $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹ at 298 K and $\mathrm{7}\times {\mathrm{10}}^{-\mathrm{7}}$ s⁻¹ at 248 K. Even though each H-atom transfer step proceeds with different rate coefficients, we are still likely missing a large amount of the diversity of barriers and rate constants. In addition it is plausible that the barriers drop with increasing extent of autoxidation.

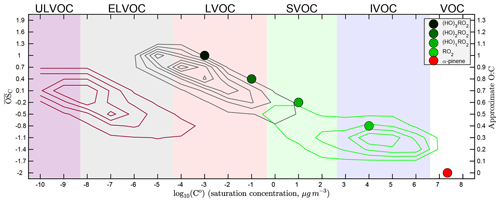
Figure 1 Basic α-pinene oxidation and the two-dimensional volatility basis set (2D-VBS), including explicitly treated peroxy radicals (RO₂). Axes are volatility log ₁₀C^∘(300 K) and O : C. Broad colored bands are volatility classes, indicated along the top: ULVOCs are efficient nucleators. α-Pinene (red, lower right) oxidizes to produce a succession of peroxy radicals – first a traditional radical (RO₂, in light green) and then a succession of oxidized RO₂ via autoxidation (Ox_nRO₂, darker shades of green). RO₂ radicals ultimately terminate into molecular products, represented here by contours depending on whether they derive from the traditional RO₂ (green contours), autoxidation (C₁₀ monomers, gray contours), or Ox_nRO₂ dimerization (C₂₀ ROOR, maroon contours).

There are multiple peroxy radical structures formed both initially and via every autoxidation reaction. Furthermore, HOM RO₂ radicals with multiple –OOH groups can rapidly interconvert, and even the exact same peroxy radical can react with other radicals to produce different product structures. This leads to a large and complex distribution of final product structures. In order to reduce this complexity, we represent the peroxy radicals as individual surrogate molecules – points in the 2D-VBS space – with autoxidation moving the surrogate to lower volatility and higher O : C. We thus explicitly represent the volatility of the RO₂ radicals, which we show in Fig. 1 as a sequence of four colored circles (along with α-pinene itself as a red circle), ranging from light green for all traditional RO₂ that have not undergone autoxidation through a succession of deeper green colors for Ox_nRO₂ that have undergone n=1–3 generations of autoxidation.

3.1.3 Unimolecular RO₂ termination

Peroxy radicals may undergo unimolecular termination at any point in the autoxidation chain, but exact barrier height and prefactors for these reactions remain unknown. For example, radical termination may occur via OH loss following a H abstraction from a carbon with an –OOH group attached. Assuming that the termination involves a bond scission and potentially an H-atom transfer between neighboring groups, this termination is likely to have a higher A factor but a higher activation energy than the internal isomerization (which has a long cyclic transition state and thus a relatively low A factor). Here we represent this process with a prefactor of 10¹⁵ s⁻¹ and a barrier of 13 000 K. This gives a termination rate coefficient of 10⁻⁴ s⁻¹ at 298 K and $\mathrm{1.7}\times {\mathrm{10}}^{-\mathrm{8}}$ s⁻¹ at 248 K. As with autoxidation, there is every reason to believe that different functional groups on the peroxy radical would hinder or enhance the unimolecular termination pathway, but we use a consistent prefactor and barrier for every peroxy radical to represent a complicated reaction pathway more simply.

In our framework, unimolecular termination products are treated as monomer products previously discussed. They may or may not be HOMs depending on whether the peroxy radical that produced them underwent autoxidation to any extent.

3.1.4 RO₂ cross-reaction kinetics

Based on the available evidence that RO₂ self-reaction rate constants accelerate with the presence of electron-withdrawing functional groups near the –OO moiety, we assume that the self-reaction rate constants for the Ox_nRO₂ are given as shown in Table 1.

Table 1 Self-reaction rate constants for RO₂ and Ox_nRO₂ are shown. As peroxy radicals become more oxidized, the assumption is that their association rate constants increases.

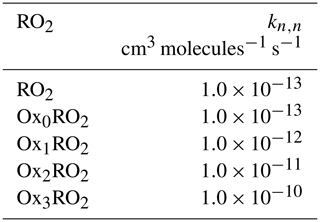
Given the enormous number of possible cross-reactions (and paucity of kinetic data), Madronich (Madronich and Calvert, 1990) proposed a simple parameterization to estimate the cross-reaction rate coefficient for two dissimilar RO₂ radicals as the geometric mean of their self-reaction rate constants, $k_{n,m}=\mathrm{2}\sqrt{k_{n,n}{k}_{m,m}}$. The factor of 2 is due to the different symmetry of the self- and cross-reactions.

3.1.5 RO₂ dimerization

The mechanism for RO₂ dimerization is unknown. It is a theoretical puzzle because RO₂ reactions are thought to proceed through a weakly bound tetroxide intermediate, ROO–OOR, which is a singlet closed-shell species (Lee et al., 2016). If by whatever (presumably multiple step) process this singlet species eliminates molecular oxygen, O₂(³Σ), the singlet peroxide ROOR is spin forbidden. In the more common radical pathway, which produces $\mathrm{RO}+\mathrm{RO}+{\mathrm{O}}_{\mathrm{2}}$, the two RO radicals are spin entangled in a triplet state. They cannot re-combine into a peroxide (ROOR) without first crossing to the singlet state.

Here we model the RO₂ cross-reactions as

$${\mathrm{RO}}_{\mathrm{2}}+{\mathrm{R}}^{\prime }{\mathrm{O}}_{\mathrm{2}}\to \mathit{\gamma }{\mathrm{ROOR}}^{\prime }+(\mathrm{1}-\mathit{\gamma })(\mathrm{RO}+{\mathrm{R}}^{\prime }\mathrm{O})+{\mathrm{O}}_{\mathrm{2}},$$

with products being treated as stable molecules within the volatility basis set. A more general treatment would also include both the radical (RO) and molecular (alcohol + carbonyl) pathways, which are treated with a branching ratio β (Tyndall et al., 2001); here we assume that β=1 for all of these peroxy radicals, consistent with findings that the radical pathway is favored for peroxy radicals with electron-withdrawing functional groups near the –OO moiety.

It may be that the ability to form dimers is directly dependent on additional functional groups in the RO₂ molecules or it may be an indirect consequence, for example related to volatility and possibly cluster lifetime when two RO₂ radicals interact. Because we are explicitly tracking the volatility of the RO₂ radicals produced via autoxidation (and because some have very low volatility), here we shall explore the possibility that dimerization is somehow tied to the volatility of the reacting RO₂ radicals. Specifically, we hypothesize that when low-volatility RO₂ species collide they will form a short-lived (radical) cluster, both before and after reacting. We further assume that ROOR dimer formation in this cluster follows the more traditional radical (RO) step and that the product cluster must be long enough lived for collisions with air molecules to induce a spin flip in the initially triplet entangled system. As a rough measure of cluster lifetime we will use the geometric mean volatility of two interacting RO₂ species (i.e., the average of the log C^∘ values).

If dimerization is volatility dependent, the probability of dimerization occurring when two peroxy radicals interact may be approximated by

$$\begin{array}{}\text{(1)}& \mathit{\gamma }={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+C_{\mathrm{GM}}^{\circ }/C_{\mathrm{ref}}^{\circ }}},\end{array}$$

where $C_{\mathrm{GM}}^{\circ }$ is the geometric mean of the effective saturation concentrations of the two reacting peroxy radicals and $C_{\mathrm{ref}}^{\circ }$ is a temperature-dependent reference saturation concentration representing where we expect half of the reacting peroxy radicals to dimerize. The value of $C_{\mathrm{ref}}^{\circ }$ used in this work is 10⁻² at 298 K and moves 1 order of magnitude lower in volatility per 10 K reduction in temperature. In our base case we assume a rate coefficient for highly oxidized α-pinene peroxy radical reactions near the collisional limit, but given the branching ratio in Eq. (1) the dimerization product yield can be much lower (depending on RO₂ volatility).

3.2 RO₂ termination kernels and the VBS

Following α-pinene oxidation, the initial, traditional RO₂ is a dicarbonyl peroxy radical (C₁₀H₁₅O₄). Each carbonyl functional group reduces the volatility by about 1 order of magnitude (Pankow and Asher, 2007), and we assume that the –OO moiety decreases the volatility by roughly another 1.5 orders of magnitude; consequently, this RO₂ has a $C^{\circ }\left(\mathrm{300}\mathrm{K}\right)\simeq {\mathrm{10}}^{\mathrm{4}}$ µg m⁻³. Each successive Ox_nRO₂ differs from its predecessor by having an additional –OOH functional group. These nominally decrease volatility by 2.5 orders of magnitude (Pankow and Asher, 2007); however, there is evidence that multifunctional molecules with opportunities for internal hydrogen bonding have higher volatilities than simple composition activity relations suggest (Kurtén et al., 2016). To crudely represent this we assign $C^{\circ }\left(\mathrm{300}\mathrm{K}\right)\simeq \mathrm{10}$ µg m⁻³ for Ox₁RO₂ but assume that each successive generation of autoxidation decreases volatility by only 2 orders of magnitude, as shown in Fig. 1. It is interesting to note that Ox₂RO₂ reactions up on the autoxidation sequence have a low enough volatility that they are likely to remain in particles if they collide with them.

Figure 1 also shows the broad XVOC ranges as colored bands. This includes the new ULVOCs in purple, which have a sufficiently low volatility ($C^{\circ }\left(T\right)\le \mathrm{3}\times {\mathrm{10}}^{-\mathrm{9}}$ µg m⁻³) to nucleate efficiently under typical conditions (it is supersaturation that ultimately drives this). The ELVOCs, in contrast, will stick to any particle of any size they hit but may not contribute significantly to nucleation itself (in practice it may be the geometric mean of C^∘(T) for two colliding vapors that govern nucleation, just as we hypothesize for ROOR formation).

We represent RO₂ termination reactions to products as kernels anchored to the peroxy radical point that produced them. These kernels allow us to represent a wide variety of stabilization pathways producing a wide variety of different products through one surrogate species; the variety of species that the surrogate represents are instead mapped to a distribution of products within the 2D-VBS defined by a transformation relative to the surrogate RO₂ volatility and O : C. In Fig. 1 we show the sum of these kernels (weighted by branching) for the three broad classes of products defined earlier: traditional oxidation products, monomers involving at least one generation of autoxidation, and ROOR dimers. We provide the individual kernels (relative to the C^∘ and O : C values for each RO₂) in the Supplement. The net effect is a concentration of traditional products with O : C modes in the SVOC and IVOC range, which in earlier VBS parameterizations of α-pinene SOA have constituted all of the products (Presto and Donahue, 2006; Jimenez et al., 2009; Donahue et al., 2012b), augmented by a tongue of HOM monomer products extending through the LVOC range and up to O : C >1, and finally with a parallel shoal of HOM dimer products spanning the ELVOC range and extending into the ULVOC range (causing pure biogenic nucleation; Kirkby et al., 2016).

We fully resolve the reaction products and then take the final concentration of every surrogate species (for example “Ox₂RONO₂” represents all organonitrates derived from second-generation autoxidized peroxy radicals) and map those to a distribution of products in the 2D-VBS using the appropriate kernel. This can readily be adapted to form a module (operator) within a larger framework representing particle microphysics, transport, wall loss, etc.

3.3 Ideal reactor

Here we model an ideal batch reactor with an initial input of precursor α-pinene that is oxidized over time, leaving only stable oxidation products, with essentially no precursor remaining at the end of the simulation. There is no wall loss, ventilation, additional vapors added after the initialization, or particle condensation or nucleation; our goal here is to just probe the chemistry of interest without interference of the physics of typical chamber experiments. We present results varying the temperature, NO_x, and barrier height dependence of the yields of α-pinene ozonolysis. We simulate 600 ppt of α-pinene (1.5×10¹⁰ molecules cm⁻³) reacting with 40 ppb of ozone, which corresponds to a lifetime of approximately 4 h (1.4×10⁴ s) at 298 K. When we simulate NO_x chemistry we add the NO_x to the system as NO, after which it undergoes reaction to NO₂ and reaches an equilibrium ratio of $\mathrm{NO}:{\mathrm{NO}}_{\mathrm{2}}\simeq \mathrm{1}:\mathrm{10}$. The value we report as the concentration of NO_x is the amount of NO initially added into the system. All the simulations here are run in light so that photochemistry is able to occur.

4 Results

We present results showing the final products of the chemistry described above and how they resolve within the 2D-VBS. We make qualitative comparisons with previous experimental results to show the validity of our approaches.

4.1 Base-case run

We will start with a base-case run at 298 K without NO_x to demonstrate the model and its output. As the α-pinene reacts, the peroxy radicals quickly build up to a steady state and then decay in consort with the α-pinene as they autoxidize and form stable products. As Fig. 2 shows, each of the successively more oxidized peroxy radicals reaches a maximum concentration at a similar time but to progressively lower maximum values. The stable products are formed via the various peroxy radical termination processes, and in this simulation they have no sinks and so simply accumulate. Their yields are thus simply their final concentrations divided by the initial α-pinene concentration.

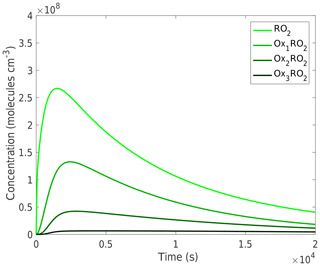
Figure 2 Concentration time series of peroxy radicals (RO₂). The peroxy radical concentrations over the course of a simulation peak early as they are produced via α-pinene oxidation and decrease as α-pinene decays and the RO₂ react away. This simulation is run at 298 K and with no NO_x, although the trends are similar across the temperatures and NO_x concentrations investigated here, with the difference being in the absolute concentrations, especially those of the more oxidized peroxy radicals.

In Fig. 3a we show one such set of terminal products, labeled Ox_n, to indicate the number of autoxidation steps. These products form from both RO₂+NO and RO₂+RO₂ reactions and so scale with the RO₂ radicals themselves, but because they are not lost in the batch reaction (here we do not simulate aging with the 2D-VBS) their concentrations accumulate over time.

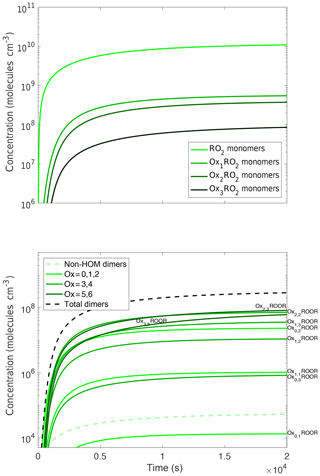
Figure 3 Concentration time series of monomer and dimer products. Ox_n indicates the number of autoxidation steps. All of these products are formed via peroxy radical chemistry, but the products are still predominantly non-HOM. This trend persists for hydroperoxides and organonitrates when NO_x is present. The dimers do not follow the same trend of forming more from the less oxidized peroxy radical as the other species do. The dimer plot is colored by the sum of how oxidized the two peroxy radicals that reacted to form the dimer are (i.e., the dimerization of an Ox₁RO₂ and an Ox₂RO₂ would be considered the sum of Ox = 3). However, they also do not follow the exact opposite trend. This is due to the branching ratio to dimers being larger for low-volatility peroxy radicals but those peroxy radicals being less common, leading to midrange oxidized peroxy radicals forming the most dimers.

In Fig. 3b we show the corresponding dimer (ROOR) concentrations. We identify the dimers by a number pair (n,m) indicating the autoxidation extent of the associated Ox_nRO₂. Here the situation is more nuanced because the dimers are formed exclusively through cross-reactions, and we assume (Eq. 1) that the dimer yields depend on the RO₂ volatility. Consequently, even though the most oxidized RO₂ have lower concentrations, they produce dimers with higher yields. The 2–2 and 3–3 symmetric dimers, along with the 2–3 cross dimer, are the most abundant.

The ultimate product distribution is dependent on the competition between autoxidation and termination via other radical species. Thus it is important to fully implement HO_x and NO_x chemistry, and it is informative to see how the concentrations of these radicals vary throughout the simulation. We show HO₂ and NO for various levels of added NO_x in Fig. 4, along with the sum of oxidized RO₂ (∑Ox_nRO₂). Characteristically for chamber experiments, HO₂ remains at a low level (≲10⁷ molecules cm⁻³) compared to the atmosphere due to the relative scarcity of species such as CO and CH₂O that directly convert OH into HO₂ and also photolyze to produce HO₂. Thus HO₂ remains far rarer than even the OxRO₂ while most α-pinene is oxidized, with ${\mathrm{OxRO}}_{\mathrm{2}}:{\mathrm{HO}}_{\mathrm{2}}\simeq \mathrm{40}$ as shown in Fig. 4. Including the RO₂ that was not oxidized, shown in Fig. 2, then we increase that ratio, all ${\mathrm{RO}}_{\mathrm{2}}:{\mathrm{HO}}_{\mathrm{2}}\simeq \mathrm{80}$. Because in our simulation we add NO_x as NO, at first the NO levels drop rapidly via reaction with HO₂ and RO₂ but then reach a steady state as NO₂ photolysis replenishes NO. In general for batch chamber experiments, NO_x is not added at the steady-state NO:NO₂, and it is common to add NO as we simulate here; the rapidly evolving NO concentrations complicate interpretation of the results as the conditions can move from high NO early in the experiment to low NO later on. However, in this simulation, for 100 pptv of added NO_x the NO stabilizes near 3 pptv. This is sufficient to slightly suppress the HO₂, to more significantly reduce the oxidized RO₂, and to dominate RO₂ termination.

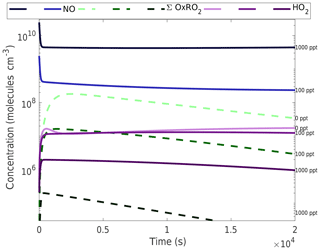
Figure 4 Concentration time series of HO₂, NO, and oxidized RO₂ at various NO_x levels. The numbers along the right-hand y axis refer to the NO_x concentration for each simulation, which is also indicated by the shading of each curve, going from light at low NO_x to dark at high NO_x. HO₂ remains reasonably stable near 10⁷ molecules cm⁻³ (0.3 pptv). NO_x is introduced as NO and drops to a steady state as it reacts with HO₂ and RO₂ to form NO₂, which in turn photolyzes. By 1000 pptv of added NO_x the NO greatly exceeds the HO₂ and somewhat suppresses HO₂ concentrations. The oxidized RO₂ (∑Ox_nRO₂) reaches a peak just over 10⁸ molecules cm⁻³ at zero NO_x before gradually decaying as a function of time.

The OxRO₂ curves in Fig. 4 allow one to assess RO₂ termination in general, remembering that the rate coefficients for HO₂ and NO termination are similar and (in our model) the OxRO₂ self-reaction rate coefficients are up to 10 times faster. This means that HO₂ is never an important RO₂ sink under these conditions, while NO becomes competitive between 50 and 100 ppt added NO_x (the NO concentration must be 10 times higher than the OxRO₂ to compete). Increasing NO significantly suppresses OxRO₂, and so by 1000 ppt of NO_x the NO pathway is dominant at all times.

4.2 Temperature dependence

The temperature dependence of the HOM formation chemistry is a key diagnostic with great atmospheric significance. Experimental data indicate that HOM yields decrease with decreasing temperature and that HOM dimers especially follow this trend. This does not mean that condensible LVOC products necessarily decrease as products with a higher C^∘(300 K) will condense when it is cold; the XVOC color patches in the 2D-VBS figures show this volatility temperature dependence. Each XVOC region shifts to higher C^∘(300 K) at lower temperatures, meaning that a compound with a $\log \left(C^{\circ }\right(\mathrm{300}\mathrm{K}\left)\right)=-\mathrm{4}$ would be in the LVOC range at 298 K, the ELVOC range at 278 K, and the ULVOC range at 248 K. However, since essentially all of the (room temperature) ULVOCs and ELVOCs are dimers, their yields will follow the dimer trends.

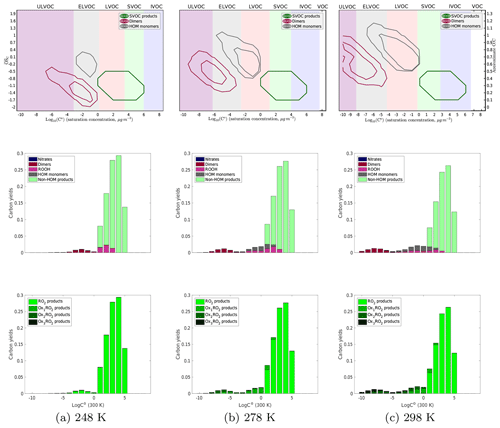
Figure 5 Yields of α-pinene oxidation products without any NO_x present at 248, 278, and 298 K. As temperature decreases, in the top, contour plots the dimer products shift to higher volatilities and lower O : C, even to the point where the dimers have approximately the same C^∗ (300 K) as the monomer products, which is supported by experimental data. In addition, the diversity of both monomer and dimer products decreases with decreasing temperature. In the middle row of plots, where we color the yields by what type of product they are, we again see that shift of the products to higher volatilities. In addition, we see fewer dimers formed at lower temperatures. It is also of note that the formation of hydroperoxides is not a significant fraction of the yield at any temperature due to the low concentration of HO₂. The bottom plots, colored by the extent of autoxidation the products underwent before terminating, show that as we decrease temperature, the extent of autoxidation that the peroxy radicals undergo decreases. At 248 K, we see almost no products that have undergone any autoxidation.

In Fig. 5 we show the temperature-dependent results for our base-case NO_x-free simulation. Each column is a different temperature (248, 278, and 298 K). The top row is a 2D-VBS contour plot of the products, recapitulating Fig. 1 with the volatility classes (defined by C^∘(T)) shifting with temperature following Stolzenburg (Stolzenburg et al., 2018). The middle row is a 1D-VBS plot (summing the top plots over O : C) with histograms of carbon yields in each volatility bin, colored by the RO₂ termination process (NO, dimerization, HO₂, etc.). The bottom row is color coded by the generation of autoxidation, with darker colors corresponding to products of RO₂ that have undergone more autoxidation steps.

In the bottom row of Fig. 5 we can clearly see that the amount of products formed from autoxidized peroxy radicals decreases with decreasing temperature to the point where at 248 K there is no significant contribution of autoxidation to the yields at all. This is expected from the temperature dependence of the autoxidation rate coefficient, and the trend is supported with experimental data. In the middle plots, we see a reduction in HOM monomers at lower temperatures, but because the volatility classes shift toward higher C^∘(300 K) at lower temperature, there are still relatively high LVOC yields, which is consistent with previous growth rate measurements indicating large contributions from LVOCs to growth even at low temperature. We also see that at lower temperatures dimer yields are greatly reduced. This makes sense based on the hypothesis that when two peroxy radicals react the probability that they formed a dimer is dependent on their volatility and thus dependent on the extent of autoxidation. However, at 248 K, we see an emergence of non-HOM dimers, dimers formed via reaction between two non-autoxidized peroxy radicals. These are non-HOM dimers as the definition of “HOMs” requires there to be an autoxidation step in the formation process. They are a consequence of our hypothesis that dimer formation is related to RO₂ complex lifetime, as expressed in Eq. (1); any temperature dependence of dimer yields (and their O : C) is thus a test of this hypothesis.

In addition, we see almost no formation of products from an RO₂+HO₂ pathway. This is not a major pathway for peroxy radical termination at any temperature, given our base-case assumption of a fast RO₂+RO₂ reaction and the high RO₂:HO₂ in low-NO_x chamber conditions. There is, however, a slight temperature dependence of hydroperoxide formation as at low temperatures (with no NO_x) there is a larger buildup of the Ox₀RO₂, which have a relatively slow self-reaction rate constant and thus do terminate with HO₂.

4.3 NO_x dependence

Experimental data indicate that ULVOC/ELVOC yields are strongly reduced with increasing NO_x while LVOC and SVOC yields are less affected. In addition, at intermediate NO_x concentrations, HOM organonitrates will be formed, contributing HOMs in the SVOC to LVOC range not found under low-NO_x conditions.

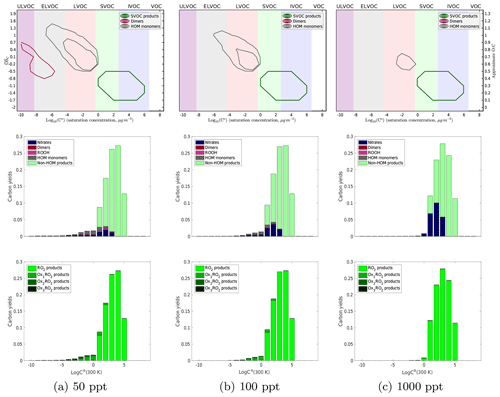
Figure 6 Yields of α-pinene oxidation products at 298 K with 50, 100, and 1000 ppt of NO introduced into the system. There are similar trends seen in the contour plot with an increase in the volatility of both HOM monomer and dimer products as well as a decrease in the diversity of both with increasing NO_x. In the second row of plots, we see an increase in the amount of nitrates formed and the depletion of dimers formed with increasing NO_x. Similarly to the temperature trend, as we increase NO_x the products shift to higher volatilities. However, once we reach a high enough NO_x concentration to produce essentially no dimers, we still see some LVOC products that include nitrates. This is consistent with experimental evidence that NO_x suppresses nucleation but not necessarily growth. From the last plots, we can clearly see fewer autoxidation products at higher NO_x concentrations with a nearly complete suppression of autoxidation between 500 and 1000 ppt of NO_x.

We show the NO_x-dependent results for our 298 K simulation in Fig. 6, which follows the temperature-dependent results in Fig. 5 in form. Each column is a different NO_x concentration (50, 100, and 1000 ppt), but the results show the same qualitative pattern as those in Fig. 5, with high NO_x taking the place of low temperature. NO suppresses autoxidation and HOM formation just as low temperature does, but normal hydroperoxides (formed via HO₂ termination) are replaced by organonitrates. Further, because the temperature is not reduced, the high-NO_x products remain largely in the SVOC class, so high NO_x will suppress nucleation.

At very low NO_x (<20 ppt), we see relatively little effect on yields, either type or autoxidation, compared to the zero-NO_x 298 K results in Fig. 5. There is, however, some suppression of dimers. In our simulation, NO_x becomes competitive with autoxidation around 500 ppt and completely overpowers autoxidation around 1000 ppt. This is based on an RO₂+NO rate coefficient of 10⁻¹¹ cm³ molecules⁻¹ s⁻¹ and an activation barrier to autoxidation producing a rate coefficient of about 10⁻³ s⁻¹ at 298 K. In this simulation we do not incorporate any variation in kinetics with the RO₂ classes (e.g., the isomerization activation energy) other than the dependence of dimerization on the geometric mean of RO₂ volatility expressed in Eq. (1) and the small change in the prefactor for autoxidation discussed in Sect. 3.1.2. Therefore, we caution against making quantitative comparisons to experimental results such as Zhao et al., who found that competition between autoxidation and NO_x termination begins to favor the NO_x pathway at about 20 ppbv of NO_x. It is highly likely that the RO₂ kinetics vary considerably depending on the exact RO₂ structure, and it is very possible that more of this will need to be represented to obtain quantitative agreement with experimental observations.

In Fig. 7 we show the NO_x effects on HOM monomers and dimers at different temperatures. For the NO_x range we simulate here, the major effect of NO is to suppress the total HOMs uniformly by roughly a factor of 10. In this plot we see that while temperature has a relatively uniform effect of suppressing HOM monomers and dimers, NO_x suppresses dimer yields more aggressively than it does HOM monomer yields. This can be explained due to the emergence of HOM nitrates, which are included in the monomer yields, as well as the consequence of NO reducing total OxRO₂ and thus the rate of peroxy radical association reactions.

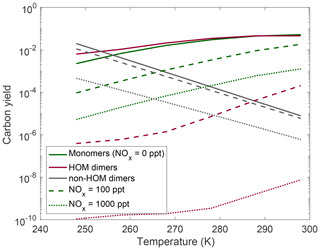
Figure 7 Yields at different temperatures and various NO_x levels: no NO_x present (solid curves), 100 ppt of NO_x present (dashed curves), and 1000 ppt of NO_x present (dotted curves). Very low NO_x concentrations have little effect on HOM yields; however, NO_x eventually becomes competitive with HOM-producing pathways, and there is a significant reduction in both dimer and HOM monomer yields accompanied by an increase in non-HOM dimers. HOM dimers are more strongly affected by suppression of autoxidation than HOM monomers.

It is important to note that the relatively low HO₂ concentrations in these runs may be enhancing the importance of NO_x chemistry here. With higher HO₂ concentrations, the RO₂+HO₂ reaction will compete with the RO₂+NO and reduce the nitrate yields. However, the HO₂ concentrations simulated here line up with what is often seen in very clean chamber experiments, and thus our NO_x conclusions hold for those cases.

4.4 Sensitivity studies

As stated, the energy barrier to autoxidation is an important unknown in this model. It is constrained experimentally by the competition with the RO₂+NO reaction, but the coefficient associated with autoxidation could span orders of magnitude for different peroxy radicals. In all the simulations described so far, we used a single barrier for autoxidation for every peroxy radical and reduced the prefactor as n, the extent of autoxidation, increased.

We employ two methods to investigate the barrier height dependence of the yields: fixing the rate coefficient at 298 K and varying its activation energy (in a Clausius–Clapeyron-like expression) and allowing the rate coefficient to vary within an order of magnitude of what was used in the base-case scenario over the whole temperature range. This is to see the effect of the autoxidation barrier height on the HOM and dimer yields as well as to provide a context for the error associated with our assumption regarding the barrier height. The effect of these methods on the autoxidation rate constant is shown in the Supplement.

As shown in Fig. 8, changing the barrier height strongly affects the calculated amount of autoxidation, especially at low temperatures. There is little effect near 298 K because that is where we prescribe the rate coefficient. In Fig. 9, we show results from allowing the rate coefficient to vary an order of magnitude over the entire temperature range, producing dimer and monomer yields that span orders of magnitude. The solid curves indicate the base-case scenario described above. This allows us to put some bounds on the rate coefficient of autoxidation as experimentally dimer and monomer yields fall well within the shaded region of the plot.

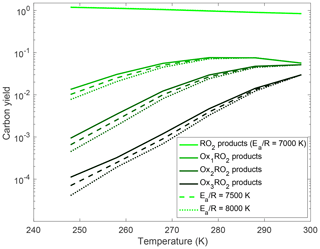
Figure 8 Variation in carbon yields of the OxRO₂s with temperature for different autoxidation barrier heights. Here the autoxidation rate coefficient at 298 K is fixed at 0.01 s⁻¹, and we vary the activation energy. The dashed curve shows the results for the rate coefficient in our base-case simulation. The solid curve has a lower activation energy and thus a weaker temperature dependence, while the dotted curve has a higher activation anergy and thus a stronger temperature dependence. As expected autoxidation is suppressed more quickly as temperature drops when the activation energy is higher; this translates to lower HOM yields.

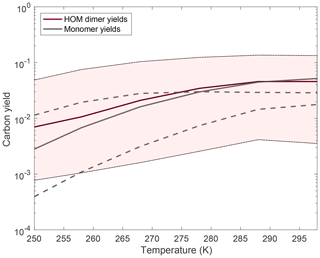
Figure 9 Changes to HOM monomer and dimer yields with an order of magnitude variation in the rate coefficient at 298 K by changing the autoxidation A factor. The rate coefficient at temperatures other than 298 K is calculated in the same manner as described above. Almost all of the yields at a particular temperature are increased relative to the traditional case when we assume the rate coefficient at 298 K is higher than the traditional case, and the yields decrease at a particular temperature when we assume the rate coefficient is lower than the traditional case. The monomer yields decrease with a faster autoxidation rate constant at high temperatures because with more autoxidation more association reactions successfully form dimers, thus reducing the monomer yields. Quantitatively, as we vary the rate coefficient of autoxidation by an order of magnitude, we are seeing a corresponding increase or decrease in the HOM product also by about an order of magnitude. The monomer yields are shown in dashed lines and show a more complicated trend, with the low barrier monomer yields being higher than the base-case yields at lower temperatures but lower at high temperatures.

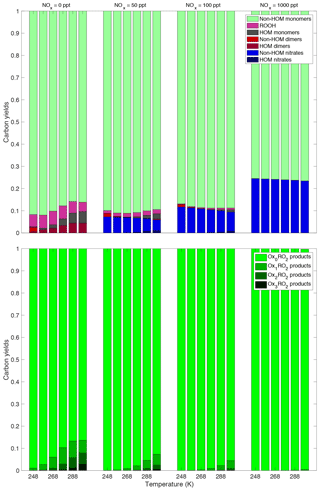
Figure 10 This plot shows the synergistic effect of the NO_x and temperature on the product yields. The same trend persists at every NO_x concentration, specifically the decrease in the amount of HOMs – both monomers and dimers with decreasing temperature. Of note is that at the highest NO_x concentration shown here (1000 ppt NO added), the HOM production is close to 0 at every temperature. Thus complete suppression of HOMs occurs around this NO_x concentration. This plot shows both the temperature dependence and the NO_x dependence again, but colors are based on how oxidized the peroxy radical that produced the products was. The products represented by the darker colors underwent more autoxidation before terminating than those represented by the lighter colors. We can see that autoxidation is suppressed both by temperature and by NO_x. Once again, we see that at a high enough NO_x concentration autoxidation is effectively suppressed at all the temperatures investigated here.

There is ample evidence in the kinetic literature for a high degree of variability in the autoxidation rate. Therefore, it is possible that to adequately describe autoxidation; its effects on new-particle formation as well as SOA formation; and the sensitivity of both to NO, T, HO₂, etc., we will need to treat fast- and slow-reacting RO₂. While it is possible for us to put bounds on autoxidation with the assumptions made here, it is very likely that the autoxidation of specific peroxy radicals lies outside these bounds. For example, the low barrier shown in Fig. 9 is likely outside these bounds as at the highest temperatures the monomer yields are lower than the dimer yields, which contradicts experimental evidence. However, with relatively minor changes to other parameters (e.g., the dimerization rate coefficient, the branching ratio to dimers γ, the unimolecular termination rate coefficient), this barrier height would be completely reasonable and therefore still represents a good lower bound for the autoxidation barrier height. The Ox_nRO₂ represents a variety of peroxy radicals, and therefore these bounds are representative of the general behavior of these peroxy radicals rather than being bounds for any specific peroxy radical species.

4.4.1 NO_x dependence of temperature dependence

We also want to investigate how the similar trends of decreasing temperature and increasing NO_x work together. The bottom plot of Fig. 10 clearly shows this synergistic effect on autoxidation, as products that have undergone any autoxidation are almost completely suppressed at the highest NO_x concentration and the lowest temperature investigated here. The top plot of Fig. 10 shows once again that decreasing temperature and increasing NO_x work together to suppress both HOM monomers and HOM dimers as well as a few other trends. As NO_x is increased, the yield of nitrates increases, but at any specific NO_x concentration the amount of nitrate formed is effectively temperature independent. However, HOM nitrates are only formed at the highest temperature and at lower NO_x concentrations; obviously, to form nitrates some NO_x needs to be present, but if too much is present, the peroxy radicals will terminate before they can autoxidize to form HOM nitrates. At low NO_x concentrations the HOM formation is dependent on temperature as discussed previously, but at high NO_x concentrations the yields are completely dominated by termination with NO. We can also see at low NO_x and low temperatures the appearance of non-HOM dimers; formation of these less oxidized peroxides is a consequence of our assumption that a long-lived RO₂ molecular cluster is required to allow the products to cross to the singlet spin surface. This plot also shows the temperature and NO_x dependence of yields from the RO₂+HO₂ reaction. While never a large portion of the total yield, products of this reaction increase under low-temperature and low-NO_x conditions. When the temperature is low, most of the peroxy radicals present are Ox₀RO₂, which, based on our association rate constants, will react the slowest with each other. This allows for more of the peroxy radicals to react with HO₂, even at the relatively low HO₂ concentrations present. At high NO_x, the RO₂+NO reactions dominate everything including the RO₂+HO₂ reaction and very few to no ROOH products are formed.

5 Conclusions

Here we present a model that represents peroxy radical chemistry semiexplicitly and maps the products of that chemistry onto the 2D-VBS. We investigate the dependence of the product yields on temperature, NO_x, and the energy barrier to autoxidation. Ultimately both HOM and dimers are suppressed under conditions when autoxidation is suppressed via the competition with radical termination processes. Competition with bimolecular termination processes is enhanced when the RO₂ lifetime with respect to bimolecular radical termination is shortened (higher radical concentrations) or when autoxidation is slower (higher energy barrier). Therefore, HOM and dimer production is highest under high-temperature, low-NO_x conditions and if we assume a lower energy barrier to autoxidation. These simulations were conducted assuming relatively fast dimerization rate constants. Therefore should some or all peroxy radicals dimerize slower, another important competition, which is not discussed at length here due to its relatively low impact, the RO₂+HO₂ reaction, could be much more important.

Overall, our simulation results are consistent with emerging experimental observations and strongly suggest that HOM formation will be strongly temperature dependent under atmospheric conditions, as well as highly sensitive to NO. The new radical VBS allows us to explicitly simulate the RO₂ termination without making ad hoc assumptions about high- or low-NO conditions and also enables general consideration of RO₂ termination chemistry, including cross-reactions among RO₂ derived from many hydrocarbon precursors. It is thus well suited to describe these rich chemical systems.