the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
New particle formation from sulfuric acid and ammonia: nucleation and growth model based on thermodynamics derived from CLOUD measurements for a wide range of conditions
Andreas Kürten
Understanding new particle formation and growth is important because of the strong impact of these processes on climate and air quality. Measurements to elucidate the main new particle formation mechanisms are essential; however, these mechanisms have to be implemented in models to estimate their impact on the regional and global scale. Parameterizations are computationally cheap ways of implementing nucleation schemes in models, but they have their limitations, as they do not necessarily include all relevant parameters. Process models using sophisticated nucleation schemes can be useful for the generation of look-up tables in large-scale models or for the analysis of individual new particle formation events. In addition, some other important properties can be derived from a process model that implicitly calculates the evolution of the full aerosol size distribution, e.g., the particle growth rates. Within this study, a model (SANTIAGO – Sulfuric acid Ammonia NucleaTIon And GrOwth model) is constructed that simulates new particle formation starting from the monomer of sulfuric acid up to a particle size of several hundred nanometers. The smallest sulfuric acid clusters containing one to four acid molecules and a varying amount of base (ammonia) are allowed to evaporate in the model, whereas growth beyond the pentamer (five sulfuric acid molecules) is assumed to be entirely collision-controlled. The main goal of the present study is to derive appropriate thermodynamic data needed to calculate the cluster evaporation rates as a function of temperature. These data are derived numerically from CLOUD (Cosmics Leaving OUtdoor Droplets) chamber new particle formation rates for neutral sulfuric acid–water–ammonia nucleation at temperatures between 208 and 292 K. The numeric methods include an optimization scheme to derive the best estimates for the thermodynamic data (dH and dS) and a Monte Carlo method to derive their probability density functions. The derived data are compared to literature values. Using different data sets for dH and dS in SANTIAGO detailed comparison between model results and measured CLOUD new particle formation rates is discussed.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(1859 KB)
- Corrigendum
-
Supplement
(442 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(1859 KB) - Full-text XML
- Corrigendum
-
Supplement
(442 KB) - BibTeX
- EndNote
The formation of new aerosol particles from the gas phase (nucleation) is the most important source of cloud condensation nuclei (CCN) in the free and upper troposphere (Dunne et al., 2016; Gordon et al., 2017). Binary new particle formation (NPF) from sulfuric acid and water is thought to be an important mechanism at cold conditions that can be enhanced by ions (Lee et al., 2003; Kirkby et al., 2011; Duplissy et al., 2016). The ternary system involving ammonia besides sulfuric acid and water can yield significantly enhanced NPF rates (Ball et al., 1999; Benson et al., 2009; Glasoe et al., 2015; Kirkby et al., 2011; Kürten et al., 2016). The addition of only a few parts per trillion by volume of ammonia can increase NPF rates by several orders of magnitude compared with the pure binary system (Kürten et al., 2016). The importance of ammonia in terms of NPF is highlighted by recent modeling studies, where a large fraction of CCN originates from ternary H2SO4-H2O-NH3 nucleation (Dunne et al., 2016; Gordon et al., 2017). The detection of ammonia above several parts per trillion by volume in the upper troposphere by recent satellite measurements supports these findings (Höpfner et al., 2016). Furthermore, an aircraft campaign up to ∼5 km altitude measured elevated NH3 concentrations over Texas (Nowak et al., 2010). Therefore, it is likely that ammonia plays an important role in new particle formation in the free troposphere. An expected future increase in the anthropogenic ammonia emissions could even increase the significance of ammonia in terms of NPF (Clarisse et al., 2009).
At cold conditions, NPF from H2SO4-H2O-NH3 is efficient enough to explain NPF at atmospherically relevant concentrations of sulfuric acid and ammonia (Kirkby et al., 2011; Dunne et al., 2016; Kürten et al., 2016). However, the involvement of ammonia in the formation of new particles at the relatively warm conditions close to the surface is not clear yet. A recent study indicates that ion-induced ternary nucleation can explain some new particle formation events in the boreal forest in Finland (Yan et al., 2018); evidence that NH3 is important in polluted boundary layer environments has been presented earlier (Chen et al., 2012). Most recently, Jokinen et al. (2018) showed that ion-induced ternary nucleation is important in coastal Antarctica. The importance of ammonia in enhancing boundary layer nucleation in the presence of highly oxygenated molecules (HOMs) from monoterpenes and sulfuric acid has recently been described (Lehtipalo et al., 2018).
In order to model nucleation, knowledge about cluster evaporation rates is required. This can either be gained by measurements in a flow tube (Hanson and Eisele, 2002; Jen et al., 2014, 2016; Hanson et al., 2017) or in a chamber such as CLOUD (Cosmics Leaving OUtdoor Droplets; Kürten et al., 2015a). Another possibility is to apply quantum chemical (QC) calculations (Kurtén et al., 2007; Nadykto and Yu, 2007; Ortega et al., 2012; Elm et al., 2013; Elm and Kristensen, 2017; Yu et al., 2018). Comparison between experimental data measured at the CLOUD chamber and modeled formation rates using the ACDC (Atmospheric Cluster Dynamics Code) model (McGrath et al., 2012) with evaporation rates from quantum chemistry (Ortega et al., 2012) yielded good agreement for some conditions (208 and 223 K). For higher temperatures (≥248 K), the model generally overestimated the formation rates up to several orders of magnitude. A more recently developed nucleation model, also relying on evaporation rates from QC calculations, yields good agreement with the CLOUD data for some conditions (Yu et al., 2018).
For the global modeling studies by Dunne et al. (2016) and Gordon et al. (2017), CLOUD data have been parameterized to yield nucleation rates for four different channels (binary neutral and ion-induced and ternary neutral and ion-induced). The parameterization works well and describes the nucleation rates over a wide range of conditions (Dunne et al., 2016), but it also has its limitations. First, it does not give any insight into the stability of individual sulfuric acid–ammonia clusters. Second, the influence of other parameters on nucleation (e.g., the condensation sink) cannot be tested, while the model by Yu et al. (2018) considers the effect of the condensation sink on the nucleation rate. Third, the parameterization provides only the nucleation rate, while a full nucleation model utilizing size bins over a wide diameter range can also yield the particle growth rates (Li and McMurry, 2018).
In the present study a model covering the aerosol size distribution over a wide size range, i.e., from the monomer of sulfuric acid up to several hundred nanometers, is constructed. The model simulates acid–base nucleation and considers evaporation rates for the clusters containing one to four sulfuric acid molecules and variable number of base molecules. The model allows for calculating new particle formation and growth rates at different sizes and considers sinks like wall loss, dilution and coagulation. SANTIAGO (Sulfuric acid Ammonia NucleaTIon And GrOwth model) is an extension of a previous simpler model version used to simulate acid–base nucleation involving dimethylamine (Kürten et al., 2014, 2018). The model extension in the present study is a prerequisite for the main goal of deriving the thermochemical parameters (dH and dS) for the sulfuric acid–ammonia system from CLOUD chamber data (Dunne et al., 2016; Kürten et al., 2016). The data cover electrically neutral conditions for the clusters up to the tetramer (containing four sulfuric acid molecules and up to four ammonia molecules). First, a model has been developed that uses molecular and geometric size bins to cover a wide particle size range (starting with the monomer of sulfuric acid). Second, two numeric algorithms yield a best fit for the dH and dS values and their probability density functions (pdf's). The pdf's are obtained by using a Monte Carlo method introduced by Kupiainen-Määttä (2016). In total, CLOUD data from 125 experiments are considered; these cover the range from 208 to 292 K and a wide range of atmospherically relevant sulfuric acid and ammonia concentrations. The results of the model are compared to the measured CLOUD data, and further comparison regarding the thermochemical data from literature (Ortega et al., 2012; Hanson et al., 2017; Yu et al., 2018) is presented.
The aim of the present study is to find values for dH and dS of selected clusters (11 different clusters) such that modeled new particle formation (NPF) rates represent measured NPF rates from the CLOUD experiment with a small error. In order to perform this task, a model has been developed that calculates the NPF rates based on given concentrations of sulfuric acid and ammonia, relative humidity (RH), and temperature (T; Sect. 2.2). The data set from Kürten et al. (2016) for 125 neutral NPF rates is used to derive dH and dS. A best-fit thermodynamic data set is obtained by using an optimization method (Sect. 2.4). Moreover, the distributions of the probability density functions for each cluster are explored with a Monte Carlo method (Kupiainen-Määttä, 2016, and Sect. 2.5). The thermodynamic parameters (enthalpy change dH and entropy change dS due to the addition or removal of a molecule) are required in order to obtain the evaporation rate of a cluster. The mathematical relationship between dH, dS, and the evaporation rate are provided in the supplementary information (Supplement Sect. S2).
2.1 Experimental data from the CLOUD experiment
The experimental data used to develop the model were taken at the CLOUD chamber at CERN (European Organization for Nuclear Research). The 26.1 m3 stainless steel chamber allows for conducting nucleation and growth experiments under atmospherically relevant conditions regarding the trace gas concentrations, temperature, relative humidity, and ion concentrations (Kirkby et al., 2011). The chamber and the results for different chemical systems have been described elsewhere in the literature (e.g., Kirkby et al. 2011; Almeida et al., 2013; Duplissy et al., 2016). In the present study no new data are presented from CLOUD; instead the data from the Dunne et al. (2016) and Kürten et al. (2016) studies are used. Whereas in the previous publications the influence of the ion concentration on nucleation was also discussed, this study focuses on neutral nucleation only. The parameter space covers temperatures between 208 and 292 K (five different temperatures) and a wide range of atmospherically relevant sulfuric acid and ammonia concentrations. No systematic investigation of the relative humidity was carried out; for most experiments, the relative humidity was at 38 %. The new particle formation rates are reported for a mobility diameter of 1.7 nm (1.4 nm geometric diameter; see Ku and Fernandez de la Mora, 2009). All data shown in the figures of the present study are available for download (see Kürten, 2019).
2.2 Acid–base model
The model used in the present study solves a set of differential equations describing the concentrations of clusters and particles (McMurry, 1980; Kürten et al., 2014, 2015a, 2018; McMurry and Li, 2017). The model from Kürten et al. (2018) describes nucleation for the system of sulfuric acid and dimethylamine, where the formed clusters are stable against evaporation at a temperature of 278 K. For this reason, the sulfuric acid–dimethylamine system can be treated as quasi-unary, and the kinetic approach (all cluster evaporation rates equal zero) yields very good agreement between modeled and measured particle concentrations and formation rates over a wide range of particle diameters. The model treats the smallest clusters in molecular size bins, based on the number of sulfuric acid molecules in a cluster, while geometric size bins are used for the larger particles (Kürten et al., 2018). In the present study 12 molecular bins and 25 geometric bins with a geometric growth factor of 1.25 result in a maximum particle diameter of 295 nm. Choosing a larger number of bins and/or geometric factor would result in a larger upper size limit, which was, however, not necessary in the present study. Compared with the earlier study by Kürten et al. (2018) the number of bins is reduced in order to reduce computation time; the simulation of one new particle formation event (several hours of nucleation) takes ∼0.1 s on a personal computer with a 3.4 GHz processor.
While the approach of using a quasi-unary system with zero evaporation works well for sulfuric acid–dimethylamine, this assumption cannot be used for sulfuric acid and ammonia because some small clusters evaporate rapidly (Nadykto and Yu, 2007; Ortega et al., 2012; Jen et al., 2014). In the following, the number of sulfuric acid molecules denotes the clusters as monomers (one sulfuric acid), dimers (two sulfuric acids), trimers (three sulfuric acids), etc. The clusters from the monomer to the tetramer can contain different numbers of ammonia molecules, where the maximum number of ammonia molecules is not allowed to exceed the number of acid molecules. The assumption that no clusters are allowed that contain more base than acid is based on fast evaporation rates that have been found for such clusters from quantum chemical calculations (Schobesberger et al., 2015; Elm et al., 2017; Yu et al., 2018); the assumption is further supported by mass spectrometric measurements that could not identify such clusters (Kirkby et al., 2011; Schobesberger et al., 2015). This results in the acid–base reaction scheme shown in Fig. 1, where A1 denotes the sulfuric acid monomer concentration and B1 the ammonia concentration. For the larger clusters and particles (starting with the pentamer), no differentiation regarding the base content is applied. The full set of differential equations used in SANTIAGO is listed in Sect. S1. Compared with its previous version SANTIAGO can more accurately describe nucleation from sulfuric acid and ammonia because of the consideration of clusters with different amounts of acid and base that are allowed to evaporate.
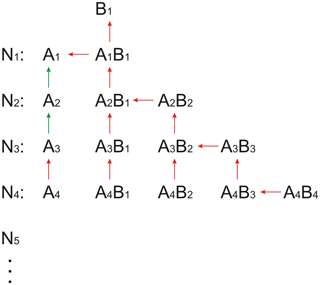
Figure 1Acid–base scheme implemented in SANTIAGO (Sulfuric acid Ammonia NucleaTIon And GrOwth model). AxBy denotes a cluster of sulfuric acid and ammonia with x sulfuric acid molecules and y ammonia molecules. The arrows indicate the considered evaporation rates. Red colors mark the evaporation channels optimized with numeric methods in the present study. Evaporation rates for the channels marked with green arrows were taken from Hanson and Lovejoy (2006). Forward reactions are not shown, but the model considers all possible collisions, i.e., cluster–cluster collisions and not just the additions of monomers. Clusters and/or particles beyond the pentamer (with concentration N5) are not allowed to evaporate; for these larger clusters, the base content is not considered.
While a mixed acid–base cluster can in principle lose either acid or base, the following rule was implemented in the model: clusters containing more acid than base can only evaporate an acid molecule, while clusters containing equal numbers of acid and base can lose a base molecule only. While this is a simplification of the reality, quantum chemical calculations support that this assumption generally considers the dominant evaporation processes (Yu et al., 2018). In principle, acid and base evaporation could be implemented for each cluster in the model, but this would increase the number of free parameters from 22 (with the simplification) to 40 (with all possible evaporations), which would probably not lead to better results but would increase the computation time significantly. The existence of clusters containing more base than acid is excluded in SANTIAGO, which is also supported by quantum chemical calculations (Ortega et al., 2012; Yu et al., 2018).
The thermodynamic parameters for the two smallest pure acid clusters (A2 and A3) are taken from a study where the parameters were derived from flow tube measurements (Hanson and Lovejoy, 2006). Ehrhart et al. (2016) showed that a numeric model for sulfuric acid–water binary nucleation using those data can replicate new particle formation rates measured at CLOUD well. In their study, Hanson and Lovejoy report dependencies of the dimer and trimer evaporation rates regarding the relative humidity, which are also adopted in the present study (evaporation rate proportional to (20 %/RH)0.5 for the dimer and (20 %/RH)1.5 for the trimer). The same dependency was used here, and the evaporation rate for the pure tetramer (A4) was scaled by the same RH-dependent factor as for the pure acid trimer. Further humidity effects are not applied; therefore, the results for the thermodynamic data can be interpreted as a weighted average over the range of the different water contents for each cluster. The equations for calculating an evaporation rate from dH and dS are given in Sect. S2 (see also Ortega et al., 2012). In general, slower evaporation rates result from more negative values of dH and from less negative values of dS; the evaporation rate varies exponentially with dH and dS. How strong the evaporation rate varies with temperature is determined by the value of dH.
Forward reaction rates are calculated based on the equations for the collision frequency function by Chan and Mozurkewich (2001), with a value of for the Hamaker constant (Hamaker, 1937). An enhanced collision-rate between small clusters and particles due to van der Waals forces was reported in recent CLOUD publications (Kürten et al., 2014, 2018; Lehtipalo et al., 2016). SANTIAGO takes dilution and wall loss into account, which are relevant loss processes in the CLOUD chamber (Kirkby et al., 2011; Kürten et al., 2015a; Sect. S1). The value of the modeled new particle formation rate, Jmodel, is taken for the nonamer (Kürten et al., 2015b):
The nonamer (m=9) has approximately a mobility diameter of 1.7 nm for which CLOUD new particle formation rates are derived (Kirkby et al., 2011; Dunne et al., 2016). The formation rate calculation takes into account that the collision of two smaller clusters with concentrations Ni and Nj yield a particle equal or larger than the nonamer. The differential equations are integrated over the same time that each of the 125 individual CLOUD runs lasted; this time varied between roughly half an hour and several hours, depending on the gas concentrations. The latest value of the calculated nucleation rate defines the modeled NPF rate. Further details regarding the model can be found in Kürten et al. (2015b, 2018) and in Sect. S1.
The particle growth rate (GR) can be calculated using the monomer and cluster concentrations in SANTIAGO:
The increase in diameter depends on the particle diameter for which the growth rate is determined, dp,m, and the colliding cluster and/or particle diameter, dp,i (Nieminen et al., 2010). Note that Eq. (2) does not only consider the growth due to monomer additions (i=1) but also the gain due to collisions with all clusters and/or particles smaller than the considered diameter. Lehtipalo et al. (2016) highlighted the importance of such cluster–cluster or cluster–particle collisions, especially for systems containing high cluster concentrations like the sulfuric acid–dimethylamine system. In the present study the GR is calculated for a mobility diameter of 2.4 nm.
2.3 Metric for average error of the model
In order to optimize the thermodynamic parameters, it is necessary to define a criterion that describes the overall deviation between the 125 measured and modeled new particle formation rates. Since the NPF rates span a large range (from roughly 10−3 to 102 cm−3 s−1), it is reasonable to compare the ratios between modeled and measured rates rather than the absolute differences. This way, mainly the high values of the NPF rates being brought into agreement is avoided. In addition, it is taken into account that the data cover five different temperatures (208, 223, 248, 278, and 292 K) with different numbers of experiments conducted at each of the temperatures. In order to weigh each of the temperatures equally and not to bias the error calculation towards the temperature at which most of the experiments were conducted, the following error function, f, is defined:
In this equation the values n1 to n5 indicate the number of experiments at each temperature.
2.4 Optimization method
The optimization method used was introduced by Steihaug (1983) and uses an approximation for the function, f, that should be minimized. A quadratic model (second-order Taylor expansion) approximates the function
In this study, the point xk is the current set of thermodynamic parameters (11 dH and 11 dS values, i.e., 22 parameters in total), and sk is the vector that moves the point to a new position that ideally yields a smaller error (i.e., a smaller value for f). The gradient vector is denoted by gk and the Hessian matrix by Hk. Steihaug's conjugated gradient method finds the sk that minimizes M (Steihaug, 1983; Nocedal and Wright, 2006). The algorithm takes into account that the length of the vector sk stays within a certain trust region, Δk (i.e., ). The following value is used to decide whether Δk can be increased, stays unchanged, or should be reduced after each iteration, k:
The empirical factor η1 is used to determine, after each iteration, whether a step should be taken or not:
The trust region radius is updated by using the following rules:
where the empirical parameters η2, η3, t1, and t2 are used. The algorithm in this study was run with parameters Δ0=0.5, Δmax=2, t1=0.25, t2=2.0, η1=0.20, η2=0.25, and η3=0.75 and converged approximately after 20 steps. The values for x0 (initialization) are the dH and dS values from Ortega et al. (2012).
2.5 Monte Carlo method
With the Monte Carlo method (Differential Evolution–Markov Chain algorithm – DE–MC; see Ter Braak, 2006; Ter Braak and Vrugt, 2008; Kupiainen-Määttä, 2016) the pdf's of the thermodynamic parameters are explored. The pdf's give information on the uncertainties of the parameters found by the optimization algorithm, as it is very likely that the optimized values represent a local minimum in the parameter space that is just one possible solution out of many others. The DE–MC algorithm aims at finding the most probable values for the parameters instead of finding the optimal values (Kupiainen-Määttä, 2016). Therefore, the Monte Carlo solutions can be used to evaluate if the optimized values are within the range of the most probable solutions.
2.5.1 Initialization for generating the prior distributions
At the start of the Monte Carlo simulation, the parameters dH and dS are initialized, where each value is randomly selected from a range of possible values. In this study, this range was defined by the values from Ortega et al. (2012), ±10 kcal mol−1 for dH and ±10 cal mol−1 K−1 for dS. For these randomly selected thermodynamic parameters, the initial error (Eq. 3) is calculated.
2.5.2 Main loop
Within the main loop (iterated 5000 times), the first step involves the random variation of the parameters. The value for each dH and dS is updated with a probability of 0.2. Given that 22 parameters are used, this means that on average, 4.4 parameters changed during each iteration. If, however, the situation occurs that no update for any of the parameters is requested, the selection process is repeated until at least one thermodynamic parameter is updated (Kupiainen-Määttä, 2016). If a value should be updated, its step width is chosen from a normal distribution with a standard deviation of 0.05 times the width of the allowed range (i.e., 20 kcal mol−1 for dH and 20 cal mol−1 K−1 for dS). If a step would lead to the crossing of the upper or lower bound for any of the parameters, a new random value is chosen until the updated value stays within its allowed range. With the new set of parameters, the new error, f(xk+sk), is calculated. If f(xk+sk) < f(xk), then the new set of parameters is accepted. However, even if f(xk+sk) is larger than f(xk), the step might still be accepted with the probability
where a σ of 0.2 has been chosen (same as by Kupiainen-Määttä, 2016). This means that even steps in the “wrong” direction (making the error larger) have a chance of being taken. This can avoid the parameters becoming trapped in a local minimum, which can, for example, be the case with minimization methods. In any case, xk+1 is set to xk+sk if a step is taken before a new iteration starts. The error and the full set of parameters are recorded after each iteration.
2.5.3 Generation of the prior distribution
In total 20 data sets (each containing 5000 steps) are generated with the methods described in Sect. 2.5.1 and 2.5.2. From each of the 20 data sets the average error was determined from the last 2500 points. Whenever the error for one data set is smaller than the geometric mean from all 20 errors, the data set was selected (Kupiainen-Määttä, 2016). All selected data sets combined and thinned to 5000 data points represent the prior distribution, Z0. For each parameter, the standard deviation σini is determined.
2.5.4 DE–MC algorithm
In the DE–MC algorithm, five Markov chains are run in parallel, where each of the chains starts from a random point of the joint history, Z0 (Ter Braak, 2006; Ter Braak and Vrugt, 2008; Kupiainen-Määttä, 2016). In the algorithm, the probability to jump from an old point, xold, to a new point, xnew, should be the same as moving from xnew to xold. This is achieved by calculating the new position vector according to
where x1 and x2 are randomly selected points from the joint history, Z0. The factor γ is taken as (Ter Braak, 2006)
or 0.98 (at every fifth step). Each individual dH and dS value for the new point is updated with a probability of 0.2 (see Sect. 2.3.2). δ is drawn from a normal distribution with (calculated from the prior distribution; see above). The decision process of whether a step should be accepted or not is the same as in Sect. 2.5.2 (Eq. 8).
The points from the five chains are appended to the joint history, Z0, and the new points in the following iterations are drawn from the updated history. This way, eventually convergence should be reached after many iterations, resulting in the posterior distributions (probability density functions) for all parameters. The metric indicating convergence is given by the following (Kupiainen-Määttä, 2016):
with the parameter k indicating the step index; the number of chains is c=5. The variance of the means for each parameter, b, is calculated from
where is the average of a parameter over all chains and μl is the average for each of the chains, l. The mean of the variances, W, is calculated from
where Varl is the variance for each parameter in one of the chains. Convergence is assumed when (for each of the 22 parameters) reaches a value of < 1.1. In the present study, this was the case after more than 105 iterations.
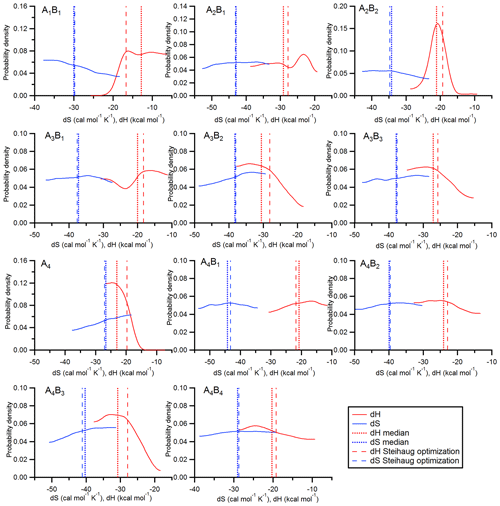
Figure 2Probability density functions of dH and dS values for 11 clusters in the acid–base system (AxBy is cluster of sulfuric acid and ammonia with x sulfuric acid molecules and y ammonia molecules). The vertical lines indicate the values from the optimization method (dashed lines) and the medians of the probability density functions (dotted lines).
3.1 Thermodynamic data
The results for the thermodynamic parameters are shown in Fig. 2. This figure indicates the results from the optimization method (dashed lines) and the pdf's (solid lines) along with their medians (dotted lines) for the 11 different clusters. A comparison between the pdf's and the values from Ortega et al. (2012) and Hanson et al. (2017) is shown in Supplement Fig. S1. The pdf's result from generating histograms of the values from Z0, where the first 5000 points are neglected (see Sect. 2.5.4). Discussion on the thermodynamic data follows in Sect. 4.
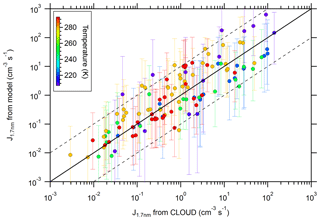
Figure 3Calculated new particle formation (NPF) rates vs. measured NPF rates (from Kürten et al., 2016). The color code indicates the temperature (between 208 and 292 K). The calculated values are from the model using the thermodynamic data from Steihaug's optimization method. The solid line indicates the one-to-one correspondence, while the dashed lines indicate a deviation by a factor of 10 from the one-to-one line. The error bars include the uncertainty of the [H2SO4] (factor of 2) and the [NH3] (see Kürten et al., 2016).
An overall comparison between modeled and measured NPF rates is shown in Fig. 3. SANTIAGO uses the thermodynamic data from Steihaug's optimization method. The maximum ratio for the deviation between the modeled and measured nucleation rates is below a factor of 10, with only a few exceptions. The average deviation is a factor of ∼4. Some of the cases where the ratio deviates by more than a factor of 10 correspond to the lowest temperature (208 K) binary experiments where the model overestimates the measured NPF rates (Sect. 3.2). As intended (Sect. 2.3), the data in Fig. 3 do not indicate an apparent bias.
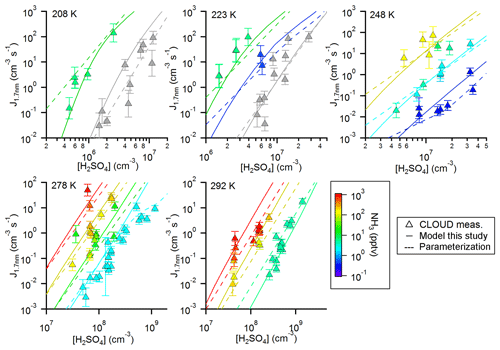
Figure 4Comparison between simulated and measured new particle formation rates for five different temperatures. The color code indicates the ammonia mixing ratio (for the respective temperatures indicated in the figure panels and a pressure of 1 bar); the grey symbols indicate pure binary conditions. The model (solid lines) uses thermodynamic data from the optimization scheme according to Steihaug (1983, Sect. 2.4). The average ratio for the deviation is ∼4. In comparison, the results from the parameterization are also shown (dashed lines; Gordon et al., 2017).
3.2 Comparison between modeled and experimental data: J1.7 nm vs. [H2SO4]
To further evaluate the performance of SANTIAGO the calculated NPF rates are shown together with the measured rates as a function of the sulfuric acid concentration for the five different temperatures (Fig. 4). The color code represents the ammonia mixing ratio, while grey symbols indicate pure binary nucleation (see Kürten et al., 2016; Duplissy et al., 2016). Again, as in Fig. 3, the agreement between modeled and measured data is good. The same applies to the parameterization; in some cases, the parameterization yields even better agreement compared with the model. This is the case, for example, for the binary nucleation at 208 K and the data at 278 and 292 K for the lowest ammonia mixing ratios. However, one clear advantage of SANTIAGO is that it describes the functional behavior of the system more accurately. At a temperature of 208 K for the high ammonia mixing ratio, the model line shows a pronounced curvature, whereas the parameterization yields a straight line on the log–log plot. The curvature is due to the fact that the survival probability of subcritical clusters (i.e., clusters below the nonamer) can be strongly affected by losses to walls or pre-existing particles (Ehrhart and Curtius, 2013). This effect is most strongly pronounced when the concentration of the nucleating vapor is relatively low, which results in slow cluster and/or particle growth rates. Other thermodynamic data sets can be used to generate model curves similar to the ones in Fig. 4. Using the data from Ortega et al. (2012) and Hanson et al. (2017) generates Figs. S3 and S4. Figure S2 shows the model curves using dH and dS from the medians of the Monte Carlo simulation. The medians also give good results, except for an overestimation at 248 and 278 K at the lowest NH3 concentration. This is probably due to comparatively low dG values for the sulfuric acid tetramer (Table 1). Unfortunately, Yu et al. (2018) did not provide dH and dS values but only dG values at 298 K; therefore, their data set could not be tested.
Table 1dH and dS values from this study and from the literature. a Optimization method. b Medians from Monte Carlo simulation. dG values at 298 K. c Data from Ortega et al. (2012). d Data from Hanson et al. (2017). e Data from Yu et al. (2018). f Value applies for cluster without involvement of water; with different amounts of water molecules, this value varies between 11.52 and 12.59 kcal mol−1. g Value applies for cluster without involvement of water; with different amounts of water molecules, this value varies between 5.71 and 8.37 kcal mol−1. NA stands for not available.

3.3 Comparison between modeled and experimental data: J1.7 nm vs. [NH3]
SANTIAGO can yield the dependency of the NPF rates for varying ammonia concentrations at fixed sulfuric acid concentration. Figure 5 shows these data for five different temperatures over a wide range of NH3 concentrations. The modeled data agree overall very well with the experimental CLOUD data. The data points indicated in Fig. 5 are obtained by normalizing the CLOUD data to one sulfuric acid concentration for each of the temperatures (see Kürten et al., 2016); the sulfuric acid concentrations for the normalization are indicated in the figure annotation.
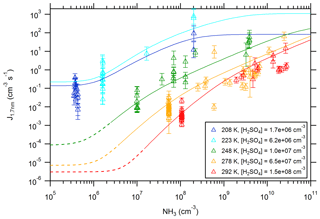
Figure 5New particle formation rates as a function of the ammonia concentration. The triangles show the neutral formation rates from the CLOUD experiment normalized to the indicated sulfuric acid concentration for five different temperatures (Kürten et al., 2016). The lines show calculated NPF rates from the model using the thermodynamic data from the optimization method (Table 1). The dashed sections (for 248, 278, and 292 K) indicate regions of the parameter space where the model does not give accurate results, as the true binary rates are expected to be lower (Ehrhart et al., 2016).
For the lowest temperature (208 K) the new particle formation rates show almost no increase with [NH3] when ammonia is present at low concentrations (≤106 cm−3); this indicates that NPF is dominated by the pure binary channel. The data points for pure binary conditions are placed at the estimated NH3 background concentrations for 208 and 223 K in Fig. 5 (Kürten et al., 2016). However, in the model for generating the lines at pure binary conditions (Fig. 4), zero NH3 is assumed. For larger [NH3] the NPF rates increase until they reach a plateau at ≥109 cm−3. In this case new particle formation is only limited by the availability of sulfuric acid; evaporating ammonia molecules from clusters are, however, rapidly replaced because the arrival rate of ammonia is similar or faster than the ammonia evaporation rate. For the data at 223 K the situation is very similar. The plateau values agree very well with the calculated values for collision-controlled new particle formation (Kürten et al., 2018), which can be seen as a validation of SANTIAGO.
For both temperatures (208 and 223 K) the experimental pure binary new particle formation rates are represented well by the model. At 248 K and above, the modeled rates at low [NH3] very likely overestimate the NPF rates (dashed sections of the curves; see discussion in Sect. 4) because the model considers only evaporation up to the sulfuric acid tetramer, which is not sufficient to accurately model binary nucleation at these conditions. However, the slow rates of or s−1 are not atmospherically relevant near the ground in most cases. Beyond the regions where binary nucleation dominates, the rates increase steeply with [NH3]. Although the slopes of the curves flatten somewhat towards high ammonia concentrations, no plateau is reached, even at concentrations of 1011 cm−3 (approximately 4 ppbv).
3.4 Particle growth rates
Figure 6 shows calculated growth rates as a function of the sulfuric acid concentration according to Eq. (2). Additionally, a curve from the equations given by Nieminen et al. (2010) is included. The model results from the present study show a linear increase in the GR as a function of the sulfuric acid monomer concentration as expected (Nieminen et al., 2010). The higher values from SANTIAGO can be explained by the different methods for calculating the collision rate constant that include the van der Waals enhancement for the model of the present study (see Kürten et al., 2018). The increase in GR at a low temperature (208 K) is not intuitive, as the collision rates decrease somewhat with temperature, which should lead to slower GR. However, the clusters are more stable at low temperature and their elevated concentrations can contribute to particle growth (Lehtipalo et al., 2016). This effect is pronounced at 208 K with some ammonia, which indicates that considering only the condensation of monomers is not sufficient for some conditions. Not only can growth be effected by coagulation but also new particle formation rates; therefore, the implementation of a full coagulation scheme (Sect. S1) is important for the present study. The possibility of deriving growth rates with the model is an important feature that is not included in the parameterization for the CLOUD new particle formation rates by Dunne et al. (2016). The modeled growth rates enable further comparison to experimental data and the future study of particle growth to climatically relevant diameters.
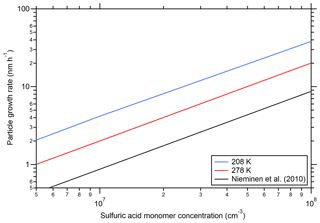
Figure 6Particle growth rates as a function of the sulfuric acid monomer concentration. The black line indicates the theoretical curve from Nieminen et al. (2010) for a temperature of 278 K and for sulfuric acid vapor. The other lines show the calculated particle growth rates at two different temperatures (indicated in the figure legend). The NH3 concentration was set to 1×108 cm−3 (blue and red curve); for all calculations a density of 1615 kg m−3 and a particle mobility diameter of 2.4 nm was used, and the diameter of the particles was calculated assuming a molecular mass of 151 amu (two water molecules and one ammonia molecule per sulfuric acid molecule).
4.1 General discussion on the thermodynamic values
4.1.1 Results from the optimization and Monte Carlo method
The posterior distributions with the median values for dH and dS for all clusters are shown in Fig. 2. For comparison, the values from Steihaug's optimization method are also shown. For the dS values, the medians and the optimized values agree very well. However, the distributions are rather flat, indicating that there is a wide possible range of entropies that lead to reasonable agreement between modeled and measured NPF rates. This is also reflected in Table 1 when comparing the dS to the Ortega et al. (2012) data. These were used to initialize the optimization method. However, no large differences can be found between the initialized and optimized values, which can be interpreted such that the quantum chemical calculations yield accurate results for dS.
The distributions for the dH values show more structure. However, the only cluster where a clear peak can be found is the A2B2 cluster (for the B evaporation). The median value of the distribution is somewhat lower (by ∼2 kcal mol−1) compared with the optimized value, but it is well within the half-width of the distribution. For most dH values flat regions of the probability density function exist, for example, for the A2B1 cluster (A evaporation) between −28 and −39 kcal mol−1. In this range the evaporation rate varies between and s−1 (at 278 K and d cal mol−1 K−1; Sect. S2). In practice, it does not matter which one of these evaporation rates is used; the magnitude of the evaporation rate in this range has essentially no effect on the outcome because the cluster is stable on the considered timescale (Kupiainen-Määttä, 2016).
For some clusters, limits seem to exist for dH. For example, the dH value for the A4 is below −15 kcal mol−1, and for the A4B3 clusters (A evaporation), the upper limit is approximately −19 kcal mol−1. The pdf's for the A1B1 and the A2B1 clusters show local maxima, which indicate elevated probability densities around −16.5 and −23 kcal mol−1.
4.1.2 Comparison of dH and dS to literature data
For most of the clusters, the agreement between the Ortega et al. (2012) data and the data from the present study is quite good. One exception is the A4 cluster, where the pdf indicates a median value of −23.1 kcal mol−1 for dH (−19.7 kcal mol−1 from the optimization method) in contrast to −16.78 kcal mol−1 by the Ortega et al. (2012) study. The much lower value found in the present study is reasonable, since Ortega et al. (2012) did not include water vapor in their calculations. The available water in the CLOUD experiment can lead to significantly slower evaporation rates indicated by the lower dH value. The difference from the Hanson et al. (2017) data is generally much larger. Especially, the trimer and tetramer with one ammonia (A3B1 and A4B1) evaporate significantly slower for the Hanson et al. (2017) data. This might explain the much higher NPF rates observed at the warm temperatures for the Hanson et al. (2017) predictions compared with the CLOUD data (Fig. S4). Yu et al. (2018) report dG values (Table 1) in their study. While the agreement between their model and CLOUD data is generally good for ion-induced conditions, the agreement for neutral conditions is only good for low temperature conditions. At temperatures ≥248 K the Yu et al. (2018) model underestimates the measurements by up to many orders of magnitude. This can at least partly be explained by the significantly higher dG values for some clusters (e.g., A2B1 and A4B1) in comparison to the other literature data and the values from the present study.
4.2 Uncertainties and limitations of SANTIAGO
One limitation of the model from the present study is that the effect of water vapor is not taken into account explicitly, i.e., no clusters containing different amounts of water molecules are considered. However, for the clusters containing no ammonia, to some extent humidity effects are included. This is achieved by scaling the evaporation rates of the sulfuric acid dimer, trimer and tetramer by a factor (20 %/RH)p with p=0.5 for the dimer and 1.5 for the trimer and tetramer. The first two values for the parameter p are from Hanson and Lovejoy (2006). For the tetramer the same dependency as for the trimer is assumed, which introduces uncertainty. The reported dH and dS values for the sulfuric acid tetramer are therefore derived for a relative humidity of 20 % in order to be consistent with the Hanson and Lovejoy (2006) data. In Fig. 4 the agreement between the modeled and measured pure binary data (at 208 and 223 K) is relatively good, especially for the 223 K data. For the 208 K data SANTIAGO overestimates the measured data. It has to be noted that the model calculations assume an average RH (33 % at 208 K and 28 % at 223 K), whereas the measurement conditions cover varying relative humidities (12 % to 57 % at 208 K and 11 % to 52 % at 223 K). This can explain some of the scatter in the measured data but not the systematic overestimation for the 208 K data by the model. However, the general agreement between model and measurement at ≤223 K is considered good for both ternary and binary conditions. For the warmer temperatures (≥248 K) the pure binary conditions can currently not be accurately represented by the model. This can be seen in Fig. 5 for the dashed sections of the curves, which approximately mark the limit of the parameter space regarding the allowed NH3 concentrations. For the very low NH3 concentrations, the modeled NPF rates approach the “pure” binary conditions. However, comparison with the data by Ehrhart et al. (2016) who simulated pure binary nucleation for the CLOUD chamber with the SAWNUC (Sulfuric Acid Water NUCleation) model indicates that the apparent binary data in Fig. 5 are significantly overestimating the true binary NPF rates. For 248 K the overestimation seems to be within a factor of 10, but for 278 and 292 K, the overestimation amounts to many orders of magnitude (Ehrhart et al., 2016). For this reason, the solid line sections for 248 K and warmer have been defined such that the contribution from the overestimated binary conditions is in any case less than 10 %. This means that SANTIAGO can be applied, e.g., at 292 K for NH3 concentrations above ca. 1×107 cm−3 (≈0.4 pptv at 292 K and 1 bar). It can be seen that NH3 has a large effect even at these tiny concentrations, which are below the measurable range of ammonia in the atmosphere.
The effect of water vapor on particle growth rates needs to be studied in the future. Comparison between measured and modeled growth rates at small diameters (2 nm) in the acid–base system (sulfuric acid–dimethylamine and sulfuric acid–ammonia) indicates that water has no significant effect on particle growth (Lehtipalo et al., 2016). The same can be concluded for the sulfuric acid–ammonia system at larger diameters (∼10 nm; see Chen et al., 2018).
The fact that no larger clusters than the tetramers can evaporate in SANTIAGO apparently leads to truncation errors as discussed before for the binary conditions. This truncation leads to the overestimation of new particle formation rates for the pure binary conditions at the warm temperatures. The extent to which truncation affects the ternary new particle formation can be discussed based on the cluster evaporation rates for the tetramers at the warmest temperature (292 K). The evaporation rates are ∼3000 s−1 (A4B1), ∼75 s−1 (A4B2), and ∼0.02 s−1 (A4B3) when using the thermodynamic parameters from Table 1 (first columns) and the equations to convert dH and dS to an evaporation rate (see Sect. S2). This indicates that new particle formation proceeds most efficiently via the clusters containing at least three base molecules. For this cluster the forward reaction rate is larger than the evaporation rate when the total sulfuric acid concentration is larger than cm−3. If the A4B3 and A4B4 clusters are the dominant ones, this indicates that even if a pentamer with a small number of base molecules evaporates rapidly, it is probably not very important in terms of contributing to the new particle formation rates, as the main nucleation pathway will follow the clusters with high ammonia content. If truncation nevertheless plays a role, it can lead to an overestimation of evaporation for a smaller cluster, thereby compensating for the missing evaporation of the larger clusters. Therefore, it is possible that some evaporation rates in the present study could be overestimated. However, the data that are shown in Table 1 for a comparison have been derived from similar methods, where the effect of evaporation is also considered only up to a certain cluster size limit. Truncation effects are discussed in detail by Hanson et al. (2017).
Similarly, to truncation the negligence of evaporation of either acid or base for all considered clusters can potentially lead to errors (see Sect. 2.2). The model includes only the cluster evaporation rates, which seem to be most relevant (see Fig. 1; Ortega et al., 2012; Yu et al., 2018). For each cluster, one evaporation rate is included (either acid or base). This means that the negligence of the second evaporation channel can lead to an overestimation of the cluster concentration. However, in case the omitted evaporation rate is smaller than the considered one, this effect is very likely small. The selection of the considered evaporation rates are guided by the literature data on QC calculations (Ortega et al., 2012; Yu et al., 2018). This does, however, not rule out that important evaporation channels could be neglected. On the other hand, increasing the number of free parameters does not necessarily improve the accuracy of the model but only its complexity and the computational demands for the optimization and Monte Carlo calculations.
4.3 Implementation of literature data in SANTIAGO
The previous study by Kürten et al. (2016) compares the CLOUD data with ACDC (McGrath et al., 2012) model calculations using the thermodynamic data from Ortega et al. (2012). Using the same data, Fig. S3 shows this comparison using the model from the present study. Surprisingly the agreement between the model and measurement is better than in the study by Kürten et al. (2016). One difference between the two studies is that the ACDC model used the formation rate for neutral clusters containing six sulfuric acid molecules instead of nine in the present study. This difference was tested with the present model, but it only leads to a very small change in the simulated formation rates. An effect that can, however, explain the discrepancy is that the ACDC model calculations did not consider a wide range of particle sizes. This could lead to inaccuracies regarding the coagulation sink for the formed clusters. Especially at high acid concentrations when growth and nucleation rates are large, the particles can create a significant sink that can reach a similar magnitude to the wall loss rate in the CLOUD chamber (Kürten et al., 2015b). Neglecting the full size distribution can lead to an overestimation of cluster concentrations and formation rates (Sect. S1). This effect needs to be studied in more detail in the future. In any case, taking into account particles over a wide size range should improve the accuracy of a model due to the described effect.
The comparison between the CLOUD data and SANTIAGO using the Hanson et al. (2017) data is shown in Fig. S4. Hanson et al. (2017) base their data on flow tube measurements performed at rather warm temperatures (∼295 K). The agreement between the modeled and measured data is good, however, mostly at the low temperatures (208 and 223 K); for the warmer temperatures, the model using the literature data significantly overestimates the NPF rates. This can partly be due to the fact that the model does not include all possible evaporation effects (acid and base for each cluster). Hanson et al. (2017) derived their data, however, by including many more possible evaporation channels. Their negligence shifts the new particle formation rates to higher values. It is likely that this effect is stronger at warm temperatures because at very cold conditions the evaporation rates for the clusters are generally very low except for the A1B1 cluster. For this cluster only one possible evaporation channel exists that is included in the model. By including the new particle formation rates reported by Hanson et al. (2017) for 278 K at CLOUD chamber conditions (additional symbols in Fig. S4 at 278 K), the agreement is somewhat better but still significantly higher than the CLOUD data. Therefore, the missing evaporation channels in this study cannot explain the full extent of the discrepancy.
The model SANTIAGO (Sulfuric acid Ammonia NucleaTIon And GrOwth model) describes new particle formation and growth from the reactions between sulfuric acid and ammonia. The effect of water vapor is taken into account, but the capability of simulating binary nucleation is limited to low temperatures (≤223 K) because cluster evaporation rates are only considered up to the tetramer; at warmer temperatures evaporation of larger pure acid clusters becomes important.
SANTIAGO implements evaporation of the smallest clusters, containing one to four sulfuric acid molecules and a variable number of ammonia molecules. The thermodynamic data (dH and dS) for 11 different channels are used to calculate evaporation rates as a function of temperature. Two numeric methods have been applied to find the best set of parameters (Steihaug algorithm) and their probability density functions (Differential Evolution–Markov Chain algorithm – DE–MC). This is achieved by comparing the model output to the CLOUD data set for neutral nucleation in the ternary system of sulfuric acid–water–ammonia (Dunne et al., 2016; Kürten et al., 2016). The average ratio between modeled and measured data is found to be as small as a factor of ∼4 (mean error) for a wide range of conditions (208 to 292 K, sulfuric acid at atmospherically relevant concentrations, e.g., cm−3 at 208 K and at 292 K) when using the best-fit parameters. SANTIAGO can represent the neutral measured CLOUD data very well for all tested conditions. This means that even binary neutral nucleation at the lowest temperatures (208 and 223 K) can be described well.
The optimization and the Monte Carlo method were successfully applied to explore the landscape of the cluster thermodynamics for the nucleating system of sulfuric acid and ammonia. However, the probability density functions from the DE–MC algorithm do not yield a very clear picture of the most likely values for dH and dS, as the derived probability density functions are rather flat and indicate a wide range of probable values. Therefore, the parameters reported in the present study have a rather high uncertainty. Future experiments and quantum chemical calculations are necessary to narrow down these uncertainties.
Implementation of the literature data in the model indicates that the Ortega et al. (2012) thermodynamic data describes the CLOUD data better than previously thought (Kürten et al., 2016). This could be because of the negligence of large particles in the previous study. It seems essential to include the larger nucleated particles in the model, as these contribute to the sink for the small nucleating clusters and particles. The Hanson et al. (2017) data overestimate the new particle formation rates for the warm temperatures (278 and 292 K). No direct comparison to the Yu et al. (2018) is possible, as no temperature-dependent evaporation rates can be calculated from their reported dG values at 298 K.
SANTIAGO allows for calculating new particle formation rates for a wide range of experimental conditions (T, RH, sulfuric acid, and ammonia concentration). In contrast to the parameterization from Dunne et al. (2016) for the CLOUD data, it is also capable of considering different external sinks (e.g., due to chamber and/or flow tube walls in laboratory experiments or the presence of pre-existing particles in the atmosphere) that can affect nucleation and particle growth (Kerminen and Kulmala, 2002; Ehrhart and Curtius, 2013). With the model, growth rates can also be determined.
Finally, the strong dependence on [NH3] regarding NPF even at levels below 1 pptv highlights the need for improved instrumentation when one wants to understand the impact of ammonia on nucleation, as no available technique can measure such low atmospheric ammonia concentrations in real time.
Data can be downloaded from https://doi.org/10.5281/zenodo.2634985 (Kürten, 2019) and are also available upon request by sending an email to the corresponding author.
| b | Variance of the means for each parameter (dH or dS) |
| B | Hessian matrix of f regarding all dH and dS values |
| c | Number of chains |
| dp | Particle diameter |
| dH | Enthalpy for one of the reactions (see Table 1) |
| dS | Entropy for one of the reactions (see Table 1) |
| f | Average error for all modeled and measured particle formation rates |
| g | Gradient vector of f regarding all dH and dS values |
| GR | Particle growth rate |
| i | Index |
| j | Index |
| Jexp | Experimental formation rate (from CLOUD experiment) |
| Jmodel | Modeled formation rate |
| k | Iteration index in numeric algorithms |
| K | Collision rate constant for clusters and/or particles |
| l | Index |
| m | Index for critical cluster size (m=9) |
| M | Approximated function value in Steihaug's method |
| n | Number of experiments (n1 for 208 K, n2 for 223 K, n3 for 248 K, n4 for 278 K, and n5 for 298 K) |
| ncoefs | Total number of coefficients, i.e., all dH and dS values (ncoefs=22) |
| N | Cluster and/or particle number density |
| p | Power dependency of an evaporation rate regarding the relative humidity |
| P | Acceptance probability in Monte Carlo algorithm |
| Statistical metric to indicate convergence for the Monte Carlo simulation | |
| RH | Relative humidity |
| s | Vector of step changes (all dH and dS values) in one iteration |
| t | Empirical parameter needed in Steihaug's optimization algorithm (t1, t2) |
| T | Temperature |
| Var | Variance for a parameter in one of the chains |
| W | Mean of the variances over all chains for one parameter |
| x | Current vector of all dH and dS values (Monte Carlo simulation) |
| x1, x2 | Drawn vectors of all dH and dS values from history (Monte Carlo simulation) |
| xnew | New vector of all dH and dS values (Monte Carlo simulation) |
| xold | Old vector of all dH and dS values (Monte Carlo simulation) |
| Z0 | Joint history for all chains in the Monte Carlo simulation |
| δ | Term in the calculation of the new vector in the Monte Carlo algorithm |
| Δ | Radius of trust region in Steihaug's method |
| Δmax | Maximum allowed radius of trust region in Steihaug's method |
| γ | Scaling factor in the calculation of the new vector in the Monte Carlo algorithm |
| η | Empirical parameter needed in Steihaug's optimization algorithm (η1, η2, η3) |
| μ | Mean value for one parameter |
| Mean value over all chains for one parameter | |
| ρ | Ratio between actual and predicted function reduction in Steihaug's method |
| σ | Standard deviation |
| σini | Standard deviation of the parameters from the prior distribution |
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-5033-2019-supplement.
The author declares that there is no conflict of interest.
This article is part of the special issue “The CERN CLOUD experiment (ACP/AMT inter-journal SI)”. It is not associated with a conference.
Funding from the German Federal Ministry of Education and Research (project “CLOUD-16” 01LK1601A) is gratefully acknowledged.
This paper was edited by Jonathan Abbatt and reviewed by two anonymous referees.
Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurtén, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppä, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petäjä, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamäki, H., and Kirkby, J.: Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 502, 359–363, https://doi.org/10.1038/nature12663, 2013.
Ball, S. M., Hanson, D. R., Eisele, F. L., and McMurry, P. H.: Laboratory studies of particle nucleation: Initial results for H2SO4, H2O, and NH3 vapors, J. Geophys. Res.-Atmos., 104, 23709–23718, https://doi.org/10.1029/1999JD900411, 1999.
Benson, D. R., Erupe, M. E., and Lee, S.-H.: Laboratory-measured H2SO4-H2O-NH3 ternary homogeneous nucleation rates: Initial observations, Geophys. Res. Lett., 36, L15818, https://doi.org/10.1029/2009GL038728, 2009.
Chan, T. W. and Mozurkewich, M.: Measurement of the coagulation rate constant for sulfuric acid particles as a function of particle size using tandem differential mobility analysis, J. Aerosol Sci., 32, 321–339, https://doi.org/10.1016/S0021-8502(00)00081-1, 2001.
Chen, H., Chee, S., Lawler, M. J., Barsanti, K. C., Wong, B. M., and Smith, J. N.: Size resolved chemical composition of nanoparticles from reactions of sulfuric acid with ammonia and dimethylamine, Aerosol Sci. Tech., 52, 1120–1133, https://doi.org/10.1080/02786826.2018.1490005, 2018.
Chen, M., Titcombe, M., Jiang, J., Jen, C., Kuang, C., Fischer, M. L., Eisele, F. L., Siepmann, J. I., Hanson, D. R., Zhao, J., and McMurry, P. H.: Acid–base chemical reaction model for nucleation rates in the polluted atmospheric boundary layer, P. Natl. Acad. Sci. USA, 109, 18713–18718, https://doi.org/10.1073/pnas.1210285109, 2012.
Clarisse, L., Clerbaux, C., Dentener, F., Hurtmans, D., and Coheur, P.-F.: Global ammonia distribution derived from infrared satellite observations, Nat. Geosci., 2, 479–483, https://doi.org/10.1038/NGEO551, 2009.
Dunne, E. M., Gordon, H., Kürten, A., Almeida, J., Duplissy, J., Williamson, C., Ortega, I. K., Pringle, K. J., Adamov, A., Baltensperger, U., Barmet, P., Benduhn, F., Bianchi, F., Breitenlechner, M., Clarke, A., Curtius, J., Dommen, J., Donahue, N. M., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Jokinen, T., Kangasluoma, J., Kirkby, J., Kulmala, M., Kupc, A., Lawler, M. J., Lehtipalo, K., Makhmutov, V., Mann, G., Mathot, S., Merikanto, J., Miettinen, P., Nenes, A., Onnela, A., Rap, A., Reddington, C. L. S., Riccobono, F., Richards, N. A. D., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Simon, M., Sipilä, M., Smith, J. N., Stozkhov, Y., Tomé, A., Tröstl, J., Wagner, P. E., Wimmer, D., Winkler, P. M., Worsnop, D. R., and Carslaw, K. S.: Global atmospheric particle formation from CERN CLOUD measurements, Science, 354, 1119–1124, https://doi.org/10.1126/science.aaf2649, 2016.
Duplissy, J., Merikanto, J., Franchin, A., Tsagkogeorgas, G., Kangasluoma, J., Wimmer, D., Vuollekoski, H., Schobesberger, S., Lehtipalo, K., Flagan, R. C., Brus, D., Donahue, N. M., Vehkämäki, H., Almeida, J., Amorim, A., Barmet, P., Bianchi, F., Breitenlechner, M., Dunne, E. M., Guida, R., Henschel, H., Junninen, H., Kirkby, J., Kürten, A., Kupc, A., Määttänen, A., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Praplan, A. P., Riccobono, F., Rondo, L., Steiner, G., Tome, A., Walther, H., Baltensperger, U., Carslaw, K. S., Dommen, J., Hansel, A., Petäjä, T., Sipilä, M., Stratmann, F., Vrtala, A., Wagner, P. E., Worsnop, D. R., Curtius, J., and Kulmala, M.: Effect of ions on sulfuric acid-water binary particle formation II: Experimental data and comparison with QC-normalized classical nucleation theory, J. Geophys. Res.-Atmos., 121, 1752–1775, https://doi.org/10.1002/2015JD023539, 2016.
Ehrhart, S. and Curtius, J.: Influence of aerosol lifetime on the interpretation of nucleation experiments with respect to the first nucleation theorem, Atmos. Chem. Phys., 13, 11465–11471, https://doi.org/10.5194/acp-13-11465-2013, 2013.
Ehrhart, S., Ickes, L., Almeida, J., Amorim, A., Barmet, P., Bianchi, F., Dommen, J., Dunne, E. M., Duplissy, J., Franchin, A., Kangasluoma, J., Kirkby, J., Kürten, A., Kupc, A., Lehtipalo, K., Nieminen, T., Riccobono, F., Rondo, L., Schobesberger, S., Steiner, G., Tomé, A., Wimmer, D., Baltensperger, U., Wagner, P. E., and Curtius, J.: Comparison of the SAWNUC model with CLOUD measurements of sulphuric acid-water nucleation, J. Geophys. Res.-Atmos., 121, 12401–12414, https://doi.org/10.1002/2015JD023723, 2016.
Elm, J. and Kristensen, K.: Basis set convergence of the binding energies of strongly hydrogen-bonded atmospheric clusters, Phys. Chem. Chem. Phys., 19, 1122, https://doi.org/10.1039/c6cp06851k, 2017.
Elm, J., Bilde, M., and Mikkelsen, K. V.: Assessment of binding energies of atmospherically relevant clusters, Phys. Chem. Chem. Phys., 15, 16442, https://doi.org/10.1039/c3cp52616j, 2013.
Glasoe, W. A., Volz, K., Panta, B., Freshour, N., Bachman, R., Hanson, D. R., McMurry, P. H., and Jen, C.: Sulfuric acid nucleation: An experimental study of the effect of seven bases, J. Geophys. Res.-Atmos., 120, 1933–1950, https://doi.org/10.1002/2014JD022730, 2015.
Gordon, H., Kirkby, J., Baltensperger, U., Bianchi, F., Breitenlechner, M., Curtius, J., Dias, A., Dommen, J., Donahue, N. M., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Frege, C., Fuchs, C., Hansel, A., Hoyle, C. R., Kulmala, M., Kürten, A., Lehtipalo, K., Makhmutov, V., Molteni, U., Rissanen, M. P., Stozkhov, Y., Tröstl, J., Tsagkogeorgas, G., Wagner, R., Williamson, C., Wimmer, D., Winkler, P. M., Yan, C., and Carslaw, K. S.: Causes and importance of new particle formation in the present-day and preindustrial atmospheres, J. Geophys. Res.-Atmos., 122, 8739–8760, https://doi.org/10.1002/2017JD026844, 2017.
Hamaker, H. C.: The London?van der Waals attraction between spherical particles, Physica, 4, 1058–1072, https://doi.org/10.1016/S0031-8914(37)80203-7, 1937.
Hanson, D. R., and Eisele, F. L.: Measurement of prenucleation molecular clusters in the NH3, H2SO4, H2O system, J. Geophys. Res.-Atmos., 107, 4158, https://doi.org/10.1029/2001JD001100, 2002.
Hanson, D. R. and Lovejoy, E. R.: Measurement of the thermodynamics of the hydrated dimer and trimer of sulfuric acid, J. Phys. Chem. A, 110, 9525–9528, https://doi.org/10.1021/jp062844w, 2006.
Hanson, D. R., Bier, I., Panta, B., Jen, C. N., and McMurry, P. H.: Computational Fluid Dynamics Studies of a Flow Reactor: Free Energies of Clusters of Sulfuric Acid with NH3 or Dimethyl Amine, J. Phys. Chem. A, 121, 3976–3990, https://doi.org/10.1021/acs.jpca.7b00252, 2017.
Höpfner, M., Volkamer, R., Grabowski, U., Grutter, M., Orphal, J., Stiller, G., von Clarmann, T., and Wetzel, G.: First detection of ammonia (NH3) in the Asian summer monsoon upper troposphere, Atmos. Chem. Phys., 16, 14357–14369, https://doi.org/10.5194/acp-16-14357-2016, 2016.
Jen, C., McMurry, P. H., and Hanson, D. R.: Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res.-Atmos., 119, 7502–7514, https://doi.org/10.1002/2014JD021592, 2014.
Jen, C. N., Zhao, J., McMurry, P. H., and Hanson, D. R.: Chemical ionization of clusters formed from sulfuric acid and dimethylamine or diamines, Atmos. Chem. Phys., 16, 12513–12529, https://doi.org/10.5194/acp-16-12513-2016, 2016.
Jokinen, T., Sipilä, M., Kontkanen, J., Vakkari, V., Tisler, P., Duplissy, E.-M., Junninen, H., Kangasluoma, J., Manninen, H. E., Petäjä, T., Kulmala, M., Worsnop, D. R., Kirkby, J., Virkkula, A., and Kerminen, V.-M.: Ion-induced sulfuric acid–ammonia nucleation drives particle formation in coastal Antarctica, Sci. Adv., 4, eaat9744, https://doi.org/10.1126/sciadv.aat9744, 2018.
Kerminen, V.-M., and Kulmala, M.: Analytical formulae connecting the “real” and the “apparent” nucleation rate and the nuclei number concentration for atmospheric nucleation events, J. Aerosol Sci., 33, 609–622, https://doi.org/10.1016/S0021-8502(01)00194-X, 2002.
Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., Ehrhart, S., Franchin, A., Gagné, S., Ickes, L., Kürten, A., Kupc, A., Metzger, A., Riccobono, F., Rondo, L., Schobesberger, S., Tsagkogeorgas, G., Wimmer, D., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Downard, A., Ehn, M., Flagan, R.C., Haider, S., Hansel, A., Hauser, D., Jud, W., Junninen, H., Kreissl, F., Kvashin, A., Laaksonen, A., Lehtipalo, K., Lima, J., Lovejoy, E. R., Makhmutov, V., Mathot, S., Mikkilä, J., Minginette, P., Mogo, S., Nieminen, T., Onnela, A., Pereira, P., Petäjä, T., Schnitzhofer, R., Seinfeld, J. H., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Vanhanen, J., Viisanen, Y., Vrtala, A., Wagner, P. E., Walther, H., Weingartner, E., Wex, H., Winkler, P. M., Carslaw, K. S., Worsnop, D. R., Baltensperger, U., and Kulmala, M.: Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 476, 429–435, https://doi.org/10.1038/nature10343, 2011.
Ku, B. K. and Fernandez de la Mora, J.: Relation between electrical mobility, mass, and size for nanodrops 1–6.5 nm in diameter in air, Aerosol Sci. Tech., 43, 241–249, https://doi.org/10.1080/02786820802590510, 2009.
Kupiainen-Määttä, O.: A Monte Carlo approach for determining cluster evaporation rates from concentration measurements, Atmos. Chem. Phys., 16, 14585–14598, https://doi.org/10.5194/acp-16-14585-2016, 2016.
Kürten, A.: Data set for “New particle formation from sulfuric acid and ammonia: nucleation and growth model based on thermodynamics derived from CLOUD measurements for a wide range of conditions”, https://doi.org/10.5281/zenodo.2634985, 2019.
Kürten, A., Jokinen, T., Simon, M., Sipilä, M., Sarnela, N., Junninen, H., Adamov, A., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Donahue, N. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hakala, J., Hansel, A., Heinritzi, M., Hutterli, M., Kangasluoma, J., Kirkby, J., Laaksonen, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Mathot, S., Onnela, A., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schobesberger, S., Seinfeld, J. H., Steiner, G., Tomé, A., Tröstl, J., Winkler, P. M., Williamson, C., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K. S., Kulmala, M., Worsnop, D. R., and Curtius, J.: Neutral molecular cluster formation of sulfuric acid-dimethylamine observed in real-time under atmospheric conditions, P. Natl. Acad. Sci. USA, 111, 15019–15024, https://doi.org/10.1073/pnas.1404853111, 2014.
Kürten, A., Münch, S., Rondo, L., Bianchi, F., Duplissy, J., Jokinen, T., Junninen, H., Sarnela, N., Schobesberger, S., Simon, M., Sipilä, M., Almeida, J., Amorim, A., Dommen, J., Donahue, N. M., Dunne, E. M., Flagan, R. C., Franchin, A., Kirkby, J., Kupc, A., Makhmutov, V., Petäjä, T., Praplan, A. P., Riccobono, F., Steiner, G., Tomé, A., Tsagkogeorgas, G., Wagner, P. E., Wimmer, D., Baltensperger, U., Kulmala, M., Worsnop, D. R., and Curtius, J.: Thermodynamics of the formation of sulfuric acid dimers in the binary (H2SO4-H2O) and ternary (H2SO4-H2O-NH3) system, Atmos. Chem. Phys., 15, 10701–10721, https://doi.org/10.5194/acp-15-10701-2015, 2015a.
Kürten, A., Williamson, C., Almeida, J., Kirkby, J., and Curtius, J.: On the derivation of particle nucleation rates from experimental formation rates, Atmos. Chem. Phys., 15, 4063–4075, https://doi.org/10.5194/acp-15-4063-2015, 2015b.
Kürten, A., Bianchi, F., Almeida, J., Kupiainen-Määttä, O., Dunne, E. M., Duplissy, J., Williamson, C., Barmet, P., Breitenlechner, M., Dommen, J., Donahue, N. M., Flagan, R. C., Franchin, A., Gordon, H., Hakala, J., Hansel, A., Heinritzi, M., Ickes, L., Jokinen, T., Kangasluoma, J., Kim, J., Kirkby, J., Kupc, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Onnela, A., Ortega, I. K., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schnitzhofer, R., Schobesberger, S., Smith, J. N., Steiner, G., Stozhkov, Y., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Wagner, P. E., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K., Kulmala, M., and Curtius, J.: Experimental particle formation rates spanning tropospheric sulfuric acid and ammonia abundances, ion production rates and temperatures, J. Geophys. Res.-Atmos., 121, 12377–12400, https://doi.org/10.1002/2015JD023908, 2016.
Kürten, A., Li, C., Bianchi, F., Curtius, J., Dias, A., Donahue, N. M., Duplissy, J., Flagan, R. C., Hakala, J., Jokinen, T., Kirkby, J., Kulmala, M., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Onnela, A., Rissanen, M. P., Simon, M., Sipilä, M., Stozhkov, Y., Tröstl, J., Ye, P., and McMurry, P. H.: New particle formation in the sulfuric acid-dimethylamine-water system: reevaluation of CLOUD chamber measurements and comparison to an aerosol nucleation and growth model, Atmos. Chem. Phys., 18, 845–863, https://doi.org/10.5194/acp-18-845-2018, 2018.
Kurtén, T., Torpo, L., Ding, C.-G., Vehkamäki, H., Sundberg, M. R., Laasonen, K., and Kulmala, M.: A density functional study on water-sulfuric acid-ammonia clusters and implications for atmospheric cluster formation, J. Geophys. Res-Atmos., 112, D04210, https://doi.org/10.1029/2006JD007391, 2007.
Lee, S.-H., Reeves, J. M., Wilson, J. C., Hunton, D. E., Viggiano, A. A., Miller, T. M., Ballenthin, J. O., and Lait, L. R.: Particle formation by ion nucleation in the upper troposphere and lower stratosphere, Science, 301, 1886–1889, https://doi.org/10.1126/science.1087236, 2003.
Lehtipalo, K., Rondo, L., Kontkanen, J., Schobesberger, S., Jokinen, T., Sarnela, N., Kürten, A., Ehrhart, S., Franchin, A., Nieminen, T., Riccobono, F., Sipilä, M., Yli-Juuti, T., Duplissy, J., Adamov, A., Ahlm, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Downard, A. J., Dunne, E. M., Flagan, R. C., Guida, R., Hakala, J., Hansel, A., Jud, W., Kangasluoma, J., Kerminen, V.-M., Keskinen, H., Kim, J., Kirkby, J., Kupc, A., Kupiainen-Määttä, O., Laaksonen, A., Lawler, M. J., Leiminger, M., Mathot, S., Olenius, T., Ortega, I. K., Onnela, A., Petäjä, T., Praplan, A., Rissanen, M. P., Ruuskanen, T., Santos, F. D., Schallhart, S., Schnitzhofer, R., Simon, M., Smith, J. N., Tröstl, J., Tsagkogeorgas, G., Tomé, A., Vaattovaara, P., Vehkamäki, H., Vrtala, A. E., Wagner, P. E., Williamson, C., Wimmer, D., Winkler, P. M., Virtanen, A., Donahue, N. M., Carslaw, K. S., Baltensperger, U., Riipinen, I., Curtius, J., Worsnop, D. R., and Kulmala, M.: The effect of acid–base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 7, 11594, https://doi.org/10.1038/ncomms11594, 2016.
Lehtipalo, K., Yan, C., Dada, L., Bianchi, F., Xiao, M., Wagner, R., Stolzenburg, D., Ahonen, L. R., Amorim, A., Baccarini, A., Bauer, P. S., Baumgartner, B., Bergen, A., Bernhammer, A.-K., Breitenlechner, M., Brilke, S., Buchholz, A., Mazon, S. B., Chen, D., Chen, X., Dias, A., Dommen, J., Draper, D. C., Duplissy, J., Ehn, M., Finkenzeller, H., Fischer, L., Frege, C., Fuchs, C., Garmash, O., Gordon, H., Hakala, J., He, X., Heikkinen, L., Heinritzi, M., Helm, J. C., Hofbauer, V., Hoyle, C. R., Jokinen, T., Kangasluoma, J., Kerminen, V.-M., Kim, C., Kirkby, J., Kontkanen, J., Kürten, A., Lawler, M. J., Mai, H., Mathot, S., Mauldin III, R. L., Molteni, U., Nichman, L., Nie, W., Nieminen, T., Ojdanic, A., Onnela, A., Passananti, M., Petäjä, T., Piel, F., Pospisilova, V., Quéléver, L. L. J., Rissanen, M. P., Rose, C., Sarnela, N., Schallhart, S., Schuchmann, S., Sengupta, K., Simon, M., Sipilä, M., Tauber, C., Tomé, A., Tröstl, J., Väisänen, O., Vogel, A. L., Volkamer, R., Wagner, A. C., Wang, M., Weitz, L., Wimmer, D., Ye, P., Ylisirniö, A., Zha, Q., Carslaw, K. S., Curtius, J., Donahue, N. M., Flagan, R. C., Hansel, A., Riipinen, I., Virtanen, A., Winkler, P. M., Baltensperger, U., Kulmala, M., and Worsnop, D. R.: Multicomponent new particle formation from sulfuric acid, ammonia, and biogenic vapors, Sci. Adv., 12, eaau5363, https://doi.org/10.1126/sciadv.aau5363, 2018.
Li, C. and McMurry, P. H.: Errors in nanoparticle growth rates inferred from measurements in chemically reacting aerosol systems, Atmos. Chem. Phys., 18, 8979–8993, https://doi.org/10.5194/acp-18-8979-2018, 2018.
McGrath, M. J., Olenius, T., Ortega, I. K., Loukonen, V., Paasonen, P., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 12, 2345–2355, https://doi.org/10.5194/acp-12-2345-2012, 2012.
McMurry, P. H.: Photochemical Aerosol Formation from SO2: A theoretical analysis of smog chamber data, J. Colloid Interf. Sci., 78, 513–527, https://doi.org/10.1016/0021-9797(80)90589-5, 1980.
McMurry, P. H. and Li, C.: The dynamic behavior of nucleating aerosols in constant reaction rate systems: Dimensional analysis and generic numerical solutions, Aerosol Sci. Tech., 51, 1057–1070, https://doi.org/10.1080/02786826.2017.1331292, 2017.
Nadykto, A. B. and Yu, F.: Strong hydrogen bonding between atmospheric nucleation precursors and common organics, Chem. Phys. Lett., 435, 14–18, https://doi.org/10.1016/j.cplett.2006.12.050, 2007.
Nieminen, T., Lehtinen, K. E. J., and Kulmala, M.: Sub-10 nm particle growth by vapor condensation – effects of vapor molecule size and particle thermal speed, Atmos. Chem. Phys., 10, 9773–9779, https://doi.org/10.5194/acp-10-9773-2010, 2010.
Nocedal, J. and Wright, S. J.: Numerical Optimization, Second edition, Algorithm 7.2, Springer, 2006.
Nowak, J. B., Neuman, J. A., Bahreini, R., Brock, C. A., Middlebrook, A. M., Wollny, A. G., Holloway, J. S., Peischl, J., Ryerson, T. B., and Fehsenfeld, F. C.: Airborne observations of ammonia and ammonium nitrate formation over Houston, Texas, J. Geophys. Res.-Atmos., 115, D22304, https://doi.org/10.1029/2010JD014195, 2010.
Ortega, I. K., Kupiainen, O., Kurtén, T., Olenius, T., Wilkman, O., McGrath, M. J., Loukonen, V., and Vehkamäki, H.: From quantum chemical formation free energies to evaporation rates, Atmos. Chem. Phys., 12, 225–235, https://doi.org/10.5194/acp-12-225-2012, 2012.
Schobesberger, S., Franchin, A., Bianchi, F., Rondo, L., Duplissy, J., Kürten, A., Ortega, I. K., Metzger, A., Schnitzhofer, R., Almeida, J., Amorim, A., Dommen, J., Dunne, E. M., Ehn, M., Gagné, S., Ickes, L., Junninen, H., Hansel, A., Kerminen, V.-M., Kirkby, J., Kupc, A., Laaksonen, A., Lehtipalo, K., Mathot, S., Onnela, A., Petäjä, T., Riccobono, F., Santos, F. D., Sipilä, M., Tomé, A., Tsagkogeorgas, G., Viisanen, Y., Wagner, P. E., Wimmer, D., Curtius, J., Donahue, N. M., Baltensperger, U., Kulmala, M., and Worsnop, D. R.: On the composition of ammonia-sulfuric-acid ion clusters during aerosol particle formation, Atmos. Chem. Phys., 15, 55–78, https://doi.org/10.5194/acp-15-55-2015, 2015.
Steihaug, T.: The Conjugate Gradient Method and Trust Regions in Large Scale Optimization, Society for Industrial and Applied Mathematics, 20, 626–637, 1983.
Ter Braak, C. J. F.: A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: easy Bayesian computing for real parameter spaces, Stat. Comput., 16, 239–249, https://doi.org/10.1007/s11222-006-8769-1, 2006.
Ter Braak, C. J. F. and Vrugt, J. A.: Differential Evolution Markov Chain with snooker updater and fewer chains, Stat. Comput., 18, 435–446, https://doi.org/10.1007/s11222-008-9104-9, 2008.
Yan, C., Dada, L., Rose, C., Jokinen, T., Nie, W., Schobesberger, S., Junninen, H., Lehtipalo, K., Sarnela, N., Makkonen, U., Garmash, O., Wang, Y., Zha, Q., Paasonen, P., Bianchi, F., Sipilä, M., Ehn, M., Petäjä, T., Kerminen, V.-M., Worsnop, D. R., and Kulmala, M.: The role of H2SO4-NH3 anion clusters in ion-induced aerosol nucleation mechanisms in the boreal forest, Atmos. Chem. Phys., 18, 13231–13243, https://doi.org/10.5194/acp-18-13231-2018, 2018.
Yu, F., Nadykto, A. B., Herb, J., Luo, G., Nazarenko, K. M., and Uvarova, L. A.: H2SO4-H2O-NH3 ternary ion-mediated nucleation (TIMN): kinetic-based model and comparison with CLOUD measurements, Atmos. Chem. Phys., 18, 17451–17474, https://doi.org/10.5194/acp-18-17451-2018, 2018.
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(1859 KB) - Full-text XML
- Corrigendum
-
Supplement
(442 KB) - BibTeX
- EndNote





