The global climatology of the intensity of the ionospheric sporadic E layer

On the basis of S4max data retrieved from COSMIC GPS radio occultation measurements, the long-term climatology of the intensity of E_s layers is investigated for the period from December 2006 to January 2014. Global maps of E_s intensity show the high-spatial-resolution geographical distribution and strong seasonal dependence of E_s layers. The maximum intensity of E_s occurs over the mid-latitudes, and its value in summer is 2–3 times larger than that in winter. A relatively strong E_s layer is observed at the North Pole and South Pole, with a distinct boundary dividing the mid-latitudes and high latitudes along the 60–80^∘ geomagnetic latitude band. The simulation results show that the convergence of vertical ion velocity could partially explain the seasonal dependence of E_s intensity. Furthermore, some disagreements between the distributions of the calculated divergence of vertical ion velocity and the observed E_s intensity indicate that other processes, such as the vertical motions of gravity waves, magnetic-field effects, meteoric mass influx into Earth's atmosphere, and the chemical processes of metallic ions, should also be considered as they may also play an important role in the spatial and seasonal variations in E_s layers.

1 Introduction

Ionospheric sporadic E (E_s) layers are thin-layered structures with intense, high electron densities at 90–130 km altitudes. Rocket-borne mass-spectrometric measurements have shown that the E_s layer mostly result from the ionisation of metal atoms, such as Fe⁺, Mg⁺, and Na⁺ (Kopp, 1997; Grebowsky and Aikin, 2002). The E_s layer mainly resides over mid-latitudes and is relatively absent at the geomagnetic equator and high latitudes (Whitehead, 1989). It is widely accepted that the mechanism responsible for E_s layer formation at mid-latitudes is wind shear, in which the zonal and meridional winds provide vertical wind shear convergence nodes. As a result, long-lived metallic ions are forced to converge towards the wind shear null to form a thin layer of intense metallic ionisation (Whitehead, 1961, 1970, 1989; Macleod, 1966; Nygren et al., 1984; Haldoupis, 2012). In the equatorial region, the physical process of E_s irregularities is attributed to the gradient-drift instabilities associated with the equatorial electrojet (Tsunoda, 2008). At high magnetic latitudes, the vertical motion of gravity waves is very efficient in concentrating the ionisation of E_s because the magnetic-field lines are nearly vertical in the polar gap (Bautista et al., 1998; MacDougall et al., 2000a, b; MacDougall and Jayachandran, 2005). The E_s layer generally has a vertical scale of 1 km or less, but its horizontal scale can extend up to several hundreds of kilometres. Consequently, intense E_s plasma irregularities and their sharp vertical electron density gradients seriously affect radio communications and navigation systems (Pavelyev et al., 2007). Furthermore, these effects on global positioning system (GPS) radio occultation (RO) signals detected by low-Earth-orbit (LEO) satellites can be exploited for lower-level atmospheric and ionospheric global investigations (Rocken et al., 2000; Hocke and Tsuda, 2001; Schreiner et al., 2007; Yue et al., 2010, 2011).

Observations of E_s layers have been widely investigated from ground-based radars (e.g. Farley, 1985; Whitehead, 1989; Kelly, 1989; Chu and Wang, 1997; Mathews, 1998). In addition to ground-based radars, the scintillations of GPS-RO were employed to extensively investigate E_s layers over the past few decades (Wu et al., 2005; Arras et al., 2008; Zeng and Sokolovskiy, 2010; Chu et al., 2011). A global map of E_s layers was first presented based on a meridional chain of ionosonde stations (Leighton et al., 1962). In recent years, based on GPS-RO measurements, knowledge of the global E_s layer occurrence rate (hereafter called E_sOR) has been advanced remarkably. Wu et al. (2005) used phase and signal-to-noise ratio (SNR) variations from ∼6000 GPS–Challenging Minisatellite Payload (CHAMP) occultations to study the global climatology of E_sOR. Arras et al. (2008) investigated the global E_sOR distribution, with a resolution of $\mathrm{5}{}^{\circ }\times \mathrm{5}{}^{\circ }$, based on CHAMP, GRACE (Gravity Recovery and Climate Experiment), and COSMIC (Constellation Observing System for Meteorology, Ionosphere, and Climate) occultation data. These previous studies of global E_sOR maps show a strong seasonal variation, with a summer maximum in the mid-latitudes. Chu et al. (2014) employed COSMIC measurements to study the global morphology of E_sOR and the results of the theoretical simulations suggested that the E_sOR seasonal variation is likely attributed to the convergence of the metallic ion flux caused by vertical wind shear. Shinagawa et al. (2017) calculated the global distribution of the vertical ion convergence and showed that local and seasonal variations in wind shear distribution could partially account for the geographical and seasonal variation in E_sOR.

Many papers have reported the geographical distribution and seasonal variation in global E_s layers retrieved from GPS-RO signals, and nearly all of these works focused on the E_sOR. The global climatology of the intensity of E_s layers has not been fully studied. The purpose of this paper is to study the global intensity of E_s layers and compare the results of E_s intensity with previous studies on the E_sOR. The occurrence of E_s layers can cause both SNR fluctuations and relative slant total electron content (TEC) peaks (Yue et al., 2015). Sometimes, the SNR has specific U-shaped structures in the amplitude of GPS-RO signals, as reported by Zeng and Sokolovskiy (2010) and Yue et al. (2015). The obvious increase in slant TEC occurring at approximately 92 km implies ionisation enhancement in E_s. In this study, the scintillation index (S4 index) data, measured from SNR fluctuations in the L1 channel of the COSMIC GPS-RO profiles at altitudes between 90 and 130 km for the period from December 2006 to January 2014, are employed to study the global climatology of the ionisation of E_s layers. Section 2 describes the used data sets and procedures adopted to derive the S4 index. In Sect. 3, the global long-term behaviours of E_s layers with a high spatial resolution are presented and compared with the previous E_sOR results, including the latitude–day, latitude–longitude, and altitude–latitude distributions; seasonal variations; and geomagnetic dependence of E_s layers. In Sect. 4, on the basis of the wind shear combined with several global-scale models, namely the Whole Atmosphere Community Climate Model (WACCM) (Marsh et al., 2013), the Naval Research Laboratory (NRL) Mass Spectrometer and Incoherent Scatter (MSIS)-00 atmospheric model (Picone et al., 2002), and the International Geomagnetic Reference Field (IGRF)-12 geomagnetic-field model (Thébault et al., 2015), we calculate the global distribution of the divergence of metallic ion velocity for comparison with the observations of E_s layers from COSMIC satellites. The effect of the magnetic declination angle on the divergence of the metallic ion velocity in the simulation of E_s is investigated for the first time. Section 5 presents the discussion and conclusions of this paper.

2 Data and procedure of deriving the S4 index

The COSMIC global data sets used in this study are the COSMIC-GPS amplitude S4 indices. The GPS radio signals are received by the precise orbit determination antennas of COSMIC for each GPS-RO when a GPS sets or rises behind Earth's atmosphere, as seen by the LEO satellite. Once the GPS signal is received at the LEO satellite, the onboard algorithm of the GPS receiver measures SNR intensity fluctuations from the raw 50 Hz L1 amplitude measurements, which are then recorded in the data stream at a 1 Hz rate at the ground receiver to minimise the data record size (Syndergaard et al., 2006). The raw scintillation measurements from the receiver are therefore the root mean square (rms) of the SNR intensity fluctuation in 1 s (i.e. σ_I), which can be expressed as ${\mathit{\sigma }}_I=\sqrt{〈(I-〈I〉{)}^{\mathrm{2}}〉}$. I represents the square of the L1 SNR, and the bracket 〈〉 denotes the 1 s averaged value. The S4 indices are reconstructed by the COSMIC Data Analysis and Archive Center (CDAAC) ground processing after these σ_I data are downloaded (Rocken et al., 2000). During the procedure of deriving the S4 indices, two additional steps are included in the ground processing. The first step is to assume that the SNR intensity fluctuations have Gaussian distributions to calculate an approximate value of 〈I〉 from σ_I and 〈SNR〉. The second is to apply a low-pass filter to the time series of 〈I〉 to obtain a new average of the intensity 〈I〉_new at each second to replace the 〈I〉 in the calculation of the S4 indices. After these steps, a long-term detrended S4 index can be reconstructed by CDAAC ground processing. Further details on the procedure of deriving the S4 index, along with some individual example figures, can be found in the report of Ko and Yeh (2010).

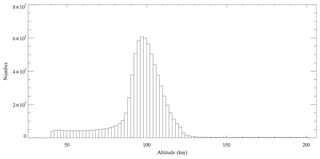
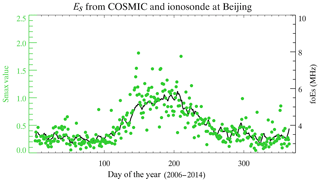
In the present study, the COSMIC global data sets specifically denote the maximum value of S4 (S4max). The COSMIC global S4max data include the S4max value and geographic latitude, longitude, altitude and local time at which S4max was detected. The computed detrended S4max index is available from 28 December 2006 onwards on the CDAAC website (http://cdaac-www.cosmic.ucar.edu/cdaac, last access: 30 December 2017). The long-term global climatology of the E_s intensity is investigated based on the global S4max data from December 2006 to January 2014. Figure 1 shows the altitude distribution of the COSMIC S4max profiles. A considerable number of profiles are distributed at altitudes between 40 and 130 km, with a peak number at approximately 100 km. Information on E_s layers can be extracted from amplitude fluctuations in the SNR profiles (Wu et al., 2005). Please note that as a result of the integrated influence either in the SNR or the slant TEC along the LEO-GPS ray, the effect of E_s layers at high altitudes could map down to the lower tangent point altitudes, which may virtually induce multiple peaks in one RO event (Zeng and Sokolovskiy, 2010; Yue et al., 2015). In Fig. 1, the occurrence of sporadic E can be seen down to 40 km as a result of an integral problem with using RO measurements. In fact, E_s layers could not be formed by the wind shear below 90 km because of the high ion-neutral collision frequencies. The E_s layer over lower altitudes (between 40 and 90 km) should be some artefact resulting from the mapping effect integrated along the LEO-GPS ray. Therefore, the S4max values that appear in altitudes ranging between 90 and 130 km are used to study the E_s layers in the lower ionosphere region. Figure 2 shows the entire distribution of the daily average E_s intensity from 2006 to 2014 retrieved from COSMIC within $\pm \mathrm{2.5}{}^{\circ }$ latitude and longitude of one ionosonde station in Beijing (40.3^∘ N, 116.2^∘ E), which agrees with the ionosonde measurements (f_oE_s). The global morphology of the E_s intensity is presented, and its altitude and seasonal dependences are given at a high spatial resolution because of the large COSMIC RO data sets that have high vertical resolutions.

Figure 1 The altitude distribution of COSMIC S4max profiles from December 2006 to January 2014.

Figure 2 The entire distribution of the daily average E_s intensity retrieved from COSMIC within ±2.5^∘ latitude and longitude of one ionosonde station and ionosonde data (f_oE_s) in Beijing from 2006 to 2014.

3 Observations

Figure 3 shows the long-term time series of the E_s values, with a resolution of 5^∘ latitude × 5 days. As shown, the E_s layer is mainly a sporadic-layered phenomenon in the summer hemisphere, as is known from former E_sOR studies (Leighton et al., 1962; Wu, 2006; Arras et al., 2008; Chu et al., 2014). In Fig. 3, it is clear that the intensity of E_s is enhanced in the northern (southern) summer hemisphere from May to September (from November to March), with a maximum in June (December) (i.e. 1 month ahead of the E_sOR maximum, Chu et al., 2014). In addition, the seasonal E_s layer also has inter-annual variability. Compared with the intense E_s activity in the summers of 2010 and 2011, the intensity of E_s is lower in the northern summers of 2012 and 2013, respectively. This result may be caused by anomalies in the wind field in the upper atmosphere and a corresponding reduction in the vertical wind shear associated with E_s formation.

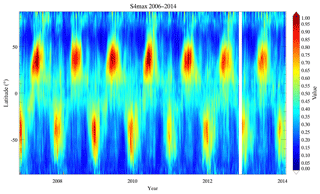
Figure 3 Time series of E_s intensity with a resolution of 5^∘ latitude × 5 days for the period from December 2006 to January 2014.

The map in Fig. 4 shows the global geographical distributions of the E_s average intensity, using a significantly improved spatial resolution of $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$. The red and green solid curves represent the northern and southern geomagnetic latitude contours of 60, 70, and 80^∘, respectively. The geomagnetic equator is also plotted with a yellow curve. The E_s layers are predominantly distributed with S4max values exceeding 0.7 at mid-latitudes. Because of the increased spatial resolution, the regional features and longitudinal variations become visible. The intensity of E_s is much weaker at the lower latitudes in both hemispheres, especially in the noticeable gap near the magnetic equator. When the magnetic field is horizontal at the geomagnetic equator, below the zonal wind shear action, ions move vertically due to the Lorentz force. However, they fail to converge into a layer because they are withheld by magnetised electrons. The plasma remains locally neutral. For a meridional wind shear process, ions move along the magnetic-field lines without being acted upon by Lorentz forces (Haldoupis, 2012). Therefore, a noticeable gap near the magnetic equator could be expected, which is explained by the vanishing vertical component of the geomagnetic-field lines, keeping the ionised particles from effectively vertically converging. This gap could also be found in the distribution of E_sOR, although it is not as evident in Arras et al. (2008).

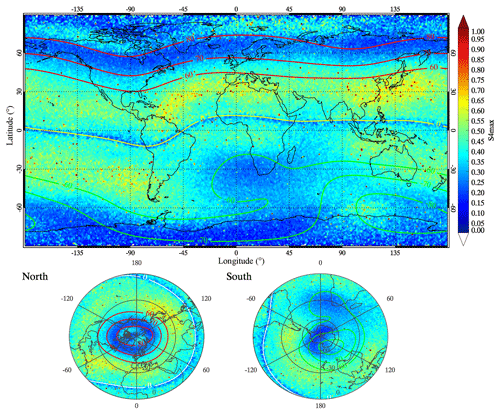
Figure 4 Global geographical distributions of the E_s average intensity from 2006 to 2014, with the spatial resolution of a $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid. The red and green curves signify the geomagnetic latitude contours of 60, 70, and 80^∘, and the yellow curve represents the geomagnetic equator.

Furthermore, the E_s longitudinal variations in the geomagnetic field are also clearly shown. The decrease in E_s intensity can be seen clearly in the South Atlantic Anomaly (SAA) zone and the North American region with geomagnetic latitude. The region of large E_s intensity exists in the North African and North Atlantic regions, Southeast Asian region, southern African and South Pacific regions. There is a difference between the E_s intensity and E_sOR distributions at high latitudes: that is, the occurrence rates of E_s are generally low (Arras et al., 2008), but the intensity of E_s is relatively high. This pattern is more evident over the magnetic poles, which is likely the result of vertical motions of gravity waves in concentrating the ionisation of E_s layers (MacDougall et al., 2000a, b). The lower panels depict the northern and southern polar views of the distributions of E_s intensity, and these views make the features clearer.

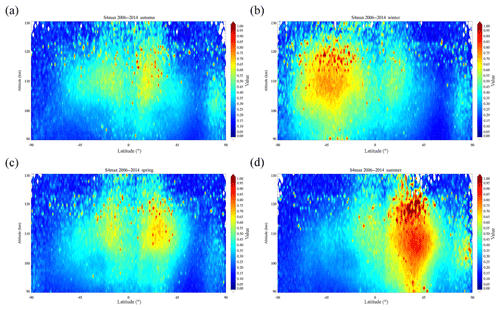
The maps in Fig. 5 show the geographical distribution of E_s intensity for four different seasons in a $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid. The distribution of E_s layers shows a significant seasonal dependence. The intensity of the E_s layers in the mid-latitudes of the summer hemisphere is 2–3 times larger than that in the winter hemisphere. During spring and autumn, the intensity of the E_s layers is moderate, covering the entire globe, and a distinct boundary dividing the mid-latitudes and high latitudes is visible along the 60–80^∘ geomagnetic latitude band. From the polar views during each season, it can be seen that the E_s layers remain at a relatively high level at the North Pole and South Pole. This characteristic could be attributed to high energy radiation, particle precipitation, and polar gap gravity waves.

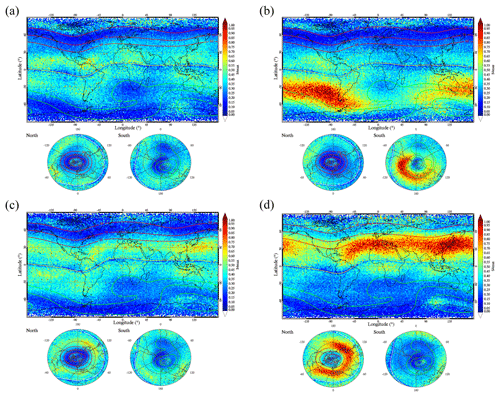
Figure 5 Seasonal variations in E_s intensity from 2006 to 2014, with the spatial resolution of a $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid. Plots for (a) autumn (September, October, November), (b) winter (December, January, February), (c) spring (March, April, May), and (d) summer (June, July, August).

Figure 6 shows the altitude–latitude distribution of the E_s intensity with a resolution of 1 km altitude $\times \mathrm{1}{}^{\circ }$ latitude. The intensity of E_s is distributed at altitudes between 95 and 125 km. The densest patches of E_s exist at altitudes exceeding 110 km, which is different from the E_sOR altitude–latitude distribution that dominates at 95–110 km, with a peak at approximately 105 km in the mid-latitudes of 25–45^∘ (Arras et al., 2008). The E_s intensity has a broader latitudinal extent of 10–75^∘ S in the Southern Hemisphere, compared with 10–60^∘ N in the Northern Hemisphere.

Figure 7 presents the seasonal variation in the altitude–latitude distributions of the E_s intensity for the same temporal period and spatial resolution as those in Fig. 6. The E_s intensity for the summer and winter solstices clearly has a significantly broader latitudinal extent towards the high-latitude region. In addition, the overall intensities of the E_s layers increase, spanning a larger vertical extent during the solstices. In general, the E_s intensity exceeding 0.65 values is distributed at altitudes of 100–125 km in the southern summer and at altitudes of 90–130 km in the northern summer. During equinox seasons, the E_s intensity is moderate and its altitude–latitude distribution is relatively symmetrical.

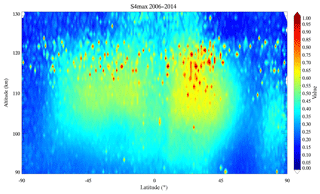
Figure 6 Altitude–latitude distribution of the E_s intensity from 2006 to 2014, with a resolution of 1 km altitude $\times \mathrm{1}{}^{\circ }$ latitude.

Figure 7 Seasonal variations in altitude–latitude distributions of E_s intensity from 2006 to 2014 for four different seasons: (a) autumn, (b) winter, (c) spring, and (d) summer.

4 Wind shear explanation for E_s seasonal variation

The global climatology of the intensity of E_s layers is investigated from the COSMIC occultation data, employing the GPS-RO technique. One of the pronounced variabilities in E_s layers is the seasonal variation, with a maximum appearance in the summer hemisphere. Although the mechanism for E_s layer formation is widely accepted, these dense and thin layers of metallic ion plasma are formed by the vertical ion convergence of neutral wind shear. The overall morphology of E_s layers cannot be explained by the wind shear. One of the unsolved issues in the ionosphere is that the overall morphology, including the seasonal dependence of E_s layers, does not have a comprehensive explanation (Whitehead, 1989; Haldoupis et al., 2007).

Seasonal dependence is found not only in the E_s intensity but also in previous studies of E_sOR variations (Wu et al., 2005; Arras et al., 2008; Chu et al., 2014). Chu et al. (2014) simulated the global distribution of the convergence of metallic ion flux caused by vertical wind shear, suggesting that the maximum E_s in summer and minimum of E_s in winter are likely caused by the vertical wind shear effect.

From the wind shear (e.g. Nygren et al., 1984; Mathews, 1998; Kirkwood and Nilsson, 2000), the vertical ion velocity w_i induced by the neutral wind is described by Eq. (1):

$$\begin{array}{}\text{(1)}& {\displaystyle }{w}_{\mathrm{i}}={\displaystyle \frac{r_{\mathrm{i}}\cos I}{\mathrm{1}+r_{\mathrm{i}}^{\mathrm{2}}}}\times U-{\displaystyle \frac{\sin I\cos I}{\mathrm{1}+r_{\mathrm{i}}^{\mathrm{2}}}}\times V+{\displaystyle \frac{r_{\mathrm{i}}^{\mathrm{2}}+{\sin }^{\mathrm{2}}I}{\mathrm{1}+r_{\mathrm{i}}^{\mathrm{2}}}}\times W,\end{array}$$

where I represents the magnetic inclination angle that is defined as positive (i.e. downward direction) in the Northern Hemisphere; r_i represents the ratio of the ion-neutral collision frequency (ν_i) to the ion gyrofrequency (ω_i); and the neutral wind velocity $V_{\mathrm{n}}=(U,V,W)$ components are in the zonal (positive for eastward), meridional (positive for northward), and vertical (positive for upward) directions. Therefore, the favourable wind field for E_s layer formation is where there is a negative $\frac{\mathrm{d}{w}_{\mathrm{i}}}{\mathrm{d}z}$ relationship, indicating an ion-convergence region.

Version 4 of the WACCM (WACCM4) is a global climate model with interactive chemistry, developed at the National Center for Atmospheric Research (NCAR) (Marsh et al., 2013). A specified dynamics run of WACCM4 (SD-WACCM4) was constrained by the Modern-Era Retrospective Analysis for Research and Applications (MERRA). SD-WACCM4 is used to simulate the global distribution of the divergence of ion velocity from the period of 2006 to 2014, which is consistent with the period of E_s observations from the COSMIC occultation data. To compare with previous studies, the neutral wind is provided by the output from WACCM, and the ion-neutral frequency is calculated by the atmospheric composition from the MSIS-00 atmospheric model in accordance with Chu et al. (2014). The global distributions of the geomagnetic field and magnetic inclination angle at 100 km are estimated from the IGRF-12 model. The calculation of ion velocity is binned and averaged in a 1^∘ latitude $\times \mathrm{1}{}^{\circ }$ longitude grid at WACCM altitude levels from 0 to 130 km.

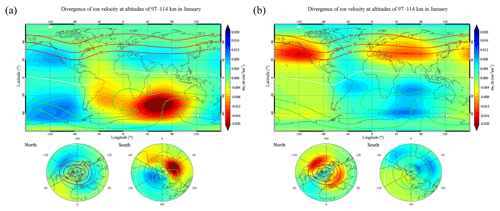
Figure 8 presents simulation results of the global distributions of the monthly mean divergence in vertical ion velocity in the altitude range between 97 and 114 km in January and July. The negative (positive) $\frac{\mathrm{d}{w}_{\mathrm{i}}}{\mathrm{d}z}$ ratio represents the convergence (divergence) of ions in units of m s⁻¹ km⁻¹. The results show a good correlation between the simulated distributions of the monthly mean divergence of vertical ion velocity in Fig. 8 and the geographical distribution of E_s intensity measured from the COSMIC GPS-RO profiles in Fig. 5. Chu et al. (2014) simulated the global distributions of the mean divergence of the Fe⁺ concentration flux at altitudes of 94–115 km in all four seasons. The study also showed a similar simulation result for the distributions of divergence in the Fe⁺ concentration flux, which is well correlated with the COSMIC-measured E_sOR distribution. The simulation of the divergence of vertical ion velocity supports the wind shear of E_s formation and indicates that the seasonal dependence of E_s layers is likely attributed to the convergence of vertical ion velocity driven by neutral wind.

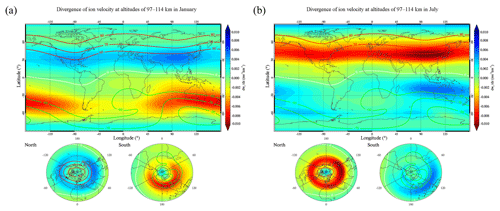
Figure 8 Simulation results of the global distributions of the monthly mean divergence of vertical ion velocity from 2006 to 2014 (units of m s⁻¹ km⁻¹) at altitudes ranging between 97 and 114 km in January (a) and July (b). The red and green curves signify 60, 70, and 80^∘ geomagnetic latitude contours, and the yellow curve represents the geomagnetic equator.

Furthermore, we also notice that the E_s intensity is distributed at relatively high altitudes of 95–125 km compared with the E_sOR at 90–120 km. The densest patches of E_s exist above 115 km, and the E_s layer has a broader vertical extent in summer, as shown in Fig. 7. In the simulation, the distributions of the monthly mean divergence of the vertical ion velocity at an altitude range of 114–128 km in January and July are shown in Fig. 9. In contrast with the distributions of the divergence of vertical ion velocity between 97 and 114 km in Fig. 8, Fig. 9 shows an ion-divergence region at altitudes of 114–128 km in summer over mid-latitudes as a result of different zonal and meridional winds. These results suggest that the wind shear alone has difficulty explaining the E_s seasonal dependence at higher altitudes (114–128 km), although the wind shear is considered the primary theory for explaining the physical production of E_s layers (Whitehead, 1989; Haldoupis et al., 2007).

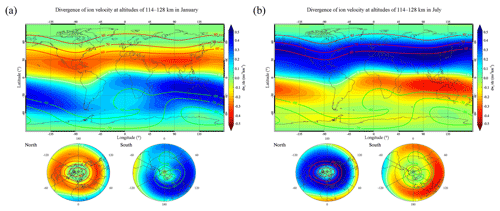
Figure 9 Same as Fig. 8 but for the altitude range between 114 and 128 km in January (a) and July (b).

In previous studies on the wind shear of E_s layer formation, the magnetic declination angle effect is neglected in the calculation of the vertical ion velocity w_i induced by the neutral wind. The steady-state ion momentum equation is as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }{m}_{\mathrm{i}}{\displaystyle \frac{\mathrm{d}{\mathit{v}}_{\mathrm{i}}}{\mathrm{d}t}}=\mathrm{0}=e(\mathit{E}+{\mathit{v}}_{\mathrm{i}}\times \mathit{B})-m_{\mathrm{i}}{\mathit{\nu }}_{\mathrm{in}}({\mathit{v}}_{\mathrm{i}}-{\mathit{V}}_{\mathrm{n}}).\end{array}$$

On the basis of the steady-state ion momentum equation, the Eq. (1) for the vertical ion velocity w_i is extended to take the magnetic declination angle D into consideration as follows:

$$\begin{array}{ll}{\displaystyle }{w}_{\mathrm{i}}& {\displaystyle }={\displaystyle \frac{r_{\mathrm{i}}\cos D\cos I-\sin D\sin I\cos I}{\mathrm{1}+r_{\mathrm{i}}^{\mathrm{2}}}}\times U\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{r_{\mathrm{i}}\sin D\cos I+\cos D\sin I\cos I}{\mathrm{1}+r_{\mathrm{i}}^{\mathrm{2}}}}\times V\\ \text{(3)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{r_{\mathrm{i}}^{\mathrm{2}}+{\sin }^{\mathrm{2}}I}{\mathrm{1}+r_{\mathrm{i}}^{\mathrm{2}}}}\times W.\end{array}$$

The magnetic declination angle currently ranges from $-\mathrm{30}{}^{\circ }$ W to 26^∘ E; therefore, it is expected to have an influence on the vertical ion velocity w_i. The effect of the magnetic declination angle on the divergence in ion velocity in the simulation of E_s is investigated. Figure 10 presents the global distributions of the monthly mean divergence in vertical ion velocity at altitudes ranging from 97 to 114 km with the consideration of the magnetic declination angle. The figure shows a seasonal dependence, with ion-convergence regions in summer and ion-divergence regions in winter. However, the morphology of the divergence of the vertical ion velocity is different from that without the magnetic declination angle considered in Fig. 8. In January, strong ion convergence appears in the SAA region. In July, Asia, Europe, and the North Pacific tend to be regions of ion convergence. The agreement with the observations becomes worse, which could imply that the cause of global E_s layers remains a mystery because it cannot be fully accounted for by the wind shear effect (Whitehead, 1989; Haldoupis et al., 2007). The formation of mid-latitude E_s layers could be partially explained by the wind shear. The investigation of the causes of seasonal variability in E_s should lead to more detailed studies so that we can fully understand and properly quantify the properties of E_s layers.

Figure 10 Same as Fig. 8 but with the consideration of the effect of the magnetic declination angle on the vertical ion velocity in January (a) and July (b).

5 Discussion

The seasonal and geographical dependences of E_sOR have been widely studied by ionospheric observations since the 1960s (Leighton et al., 1962; Smith, 1978; Wu et al., 2005; Arras et al., 2008; Zeng and Sokolovskiy, 2010), but, thus far, the overall morphology of E_s is still not well explained. The seasonal dependence of E_s layers remains an ongoing mystery, as it is unexpected in the classical wind shear reported in the review article of Whitehead (1989). Recently, Chu et al. (2014) simulated the distribution of the convergence of the Fe⁺ concentration flux and indicated that the vertical ion convergence caused by neutral wind could be responsible for the seasonal dependence of E_s.

In our investigations, the global climatology of the intensity of E_s layers is found to also have a seasonal dependence, with a pronounced maximum over mid-latitudes in the summer hemisphere, as shown in Fig. 5. The E_s intensity has similar seasonal and spatial distributions to the E_sOR, but the E_s layer has a relatively large intensity and a small E_sOR value at the North Pole and South Pole. The wind shear mechanism does not work efficiently at either auroral zones or the magnetic equator (Haldoupis, 2012); therefore, the strong E_s layers in the Earth's polar regions could be initially caused by gravity waves (Bautista et al., 1998; MacDougall et al., 2000a, b). In the simulations, the gravity waves with horizontal wavelengths smaller than ∼200 km are not explicitly resolved in WACCM (Liu et al., 2014). In particular, the vertical motion of gravity waves dominates the formation of the E_s layer on the polar cap, where the near-vertical magnetic field significantly reduces the effectiveness of wind-shear in converging ions into layers. Polar-cap gravity waves have been studied by Johnson et al. (1995) and MacDougall et al. (1997). These layers are maintained in an ionised state through charge exchange of neutral metal atoms with NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ ions by photoionisation. These studies found that the vertical motion of gravity waves is very efficient in concentrating polar-cap E_s layers. The short-lived polar-cap E_s layers in winter appear to be associated with gravity waves. In summer the polar-cap E_s layers are long-lasting and thin. These initial concentrations of metallic ions persist and change into long-lived E_s because of ambient metallic ions produced by photoionisation in the sunlit E region (MacDougall et al., 2000a). The E_s layers at the cusp latitude are relatively different from those at the polar cap. The cusp E_s could be associated with the convergence of ionisation by the electric fields (MacDougall and Jayachandran, 2005).

On the other hand, simulating the global distributions of the monthly mean divergence of vertical ion velocity in an altitude range between 97 and 114 km shows an ion-convergence region in the summer mid-latitudes, which is similar to the simulation results of Chu et al. (2014). This result suggests that the seasonal dependence of E_s is likely attributed to the vertical convergence of ions driven by neutral wind. However, some disagreements between the distributions of the calculated divergence of vertical ion velocity and observed E_s intensity are found. For example, there are ion-divergence regions in the mid-latitudes in winter in Fig. 8, but the dissipation of E_s is observed in the 60–80^∘ geomagnetic latitude band. The densest E_s layer appears above 115 km, which is higher than the E_sOR. Another discrepancy is that the simulated divergence of vertical ion velocity in an altitude range between 114 and 128 km has a positive $\frac{\mathrm{d}{w}_{\mathrm{i}}}{\mathrm{d}z}$ ratio in the summer hemisphere, which indicates an ion-divergence region of ions in contrast with the observed summer maximum of E_s intensity in the summer mid-latitudes.

The effect of the magnetic declination angle on the divergence of metallic ion velocity is investigated in the simulation of E_s for the first time in Fig. 10. Though the figure shows marked seasonal dependence, with a strong summer ion-convergence region, the morphology of the divergence of vertical ion velocity is different from the distribution of the observed E_s intensity in Fig. 5. Thus, the vertical ion convergence by itself is far from sufficient for explaining the strong E_s summer maximum. Other physical processes should also be considered in the geographical distribution and spatial variations in E_s layers, as they play important roles in determining the global morphology of E_s, such as the magnetic field, ionospheric electric field, the chemical processes of metallic ions, large geomagnetic storms, and meteorological processes in the lower atmosphere (e.g. Bautista et al., 1998; Mathews, 1998; Carter and Forbes, 1999; MacDougall et al., 2000a, b; Davis and Johnson, 2005; MacDougall and Jayachandran, 2005; Johnson and Davis, 2006; Haldoupis, 2012; Yue et al., 2012; Feng et al., 2013; Yu et al., 2015).

Haldoupis et al. (2007) proposed that the seasonal dependence of E_s could be explained by the seasonal variation in the meteor influx into the upper atmosphere. However, it has been largely accepted that sporadic meteoroids provide a much greater meteor mass on average than meteor showers (Ceplecha et al., 1998; Baggaley, 2002; Janches et al., 2002; Williams and Murad, 2002). The meteoric mass influx caused by sporadic meteoroids reaches a maximum in autumn rather than summer (Janches et al., 2006). The global input of meteoric material is well established to enhance the mesospheric metal layers and E_s layers (Plane, 2004; Plane et al., 2015). Carrillo-Sánchez et al. (2016) estimated the global interplanetary dust particles (IDPs) to be 43±14 t d−1; this was taken from three different observations in order to constrain the relative contributions of each dust source to lidar observations of the vertical Na and Fe fluxes. However, the daily amount is still not well defined. Estimates of the IDP range from 5 to 270 t d−1, depending on the different methods used to make the estimate (Plane, 2012). These effects of meteoric ablation are significantly influenced by the magnitude of the IDP input with 2 orders of magnitude uncertainty. On the other hand, this fact also highlights the importance of a fundamental understanding of the global climatology of E_s layers.

6 Conclusions

In this study, we investigate the long-term climatology of the intensity of E_s layers on the basis of S4max data retrieved from COSMIC GPS-RO measurements. The resulting global E_s maps with a high spatial resolution present the geographical distributions and strong seasonal dependence of E_s intensity, which agrees with former studies of global E_sOR maps (Wu, 2006; Arras et al., 2008; Chu et al., 2014). The high E_s intensity in summer exists at altitudes of 115–125 km at 10–60^∘ latitude in the Northern Hemisphere and at altitudes of 115–120 km at 10–75^∘ latitudes in the Southern Hemisphere.

Furthermore, the simulation results of the global distributions of the monthly mean divergence of vertical ion velocity could partially explain the seasonal dependence of E_s intensity. We show that the elemental mechanism responsible for E_s layers based on wind shear could explain the seasonal dependence of E_s intensity (97–114 km), but it is hard to explain the E_s seasonal dependence at higher altitudes (114–128 km). To further investigate the magnetic-field effects on the wind shear processes of E_s formation, the effect of the magnetic declination angle on the divergence of metallic ion velocity in the simulation of E_s is investigated, and we discuss some disagreements between the distributions of the calculated divergence of vertical ion velocity and the observed E_s intensity. Although the wind shear of E_s formation was conceived and formulated in the 1960s (Whitehead, 1961), its importance for understanding the formation of E_s must have escaped attention. This study implies that, in addition to the vertical wind shear effects, other processes, such as the vertical motion of gravity waves, magnetic-field effects, meteoric mass influx into Earth's atmosphere, and the chemical processes of metallic ions, should also be considered, which could play a dominant role in the geographical and seasonal variations in E_s layers. To accurately understand and properly quantify the properties of E_s layers on a global scale that are also associated with the distribution of global metallic ions, we need to combine more ground-based ionosonde data with satellite observations and extensively study the geographical and seasonal variations in E_s layers.