the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel approach for characterizing the variability in mass–dimension relationships: results from MC3E
Joseph A. Finlon
Stephen W. Nesbitt
Robert M. Rauber
Hugh Morrison
Pengfei Zhang
Mass–dimension (m–D) relationships determining bulk microphysical properties such as total water content (TWC) and radar reflectivity factor (Z) from particle size distributions are used in both numerical models and remote sensing retrievals. The a and b coefficients representing m=aDb relationships, however, can vary significantly depending on meteorological conditions, particle habits, the definition of particle maximum dimension, the probes used to obtain the data, techniques used to process the cloud probe data, and other unknown reasons. Thus, considering a range of a,b coefficients may be more applicable for use in numerical models and remote sensing retrievals. Microphysical data collected by two-dimensional optical array probes (OAPs) installed on the University of North Dakota (UND) Citation aircraft during the Mid-latitude Continental Convective Clouds Experiment (MC3E) were used in conjunction with TWC data from a Nevzorov probe and ground-based S-band radar data to determine a and b using a technique that minimizes the chi-square difference between the TWC and Z derived from the OAPs and those directly measured by a TWC probe and radar. All a and b values within a specified tolerance were regarded as equally plausible solutions. Of the 16 near-constant-temperature flight legs analyzed during the 25 April, 20 May, and 23 May 2011 events, the derived surfaces of solutions on the first 2 days where the aircraft-sampled stratiform cloud had a larger range in a and b for lower temperature environments that correspond to less variability in N(D), TWC, and Z for a flight leg. Because different regions of the storm were sampled on 23 May, differences in the variability in N(D), TWC, and Z influenced the distribution of chi-square values in the (a,b) phase space and the specified tolerance in a way that yielded 2.8 times fewer plausible solutions compared to the flight legs on the other dates. These findings show the importance of representing the variability in a,b coefficients for numerical modeling and remote sensing studies, rather than assuming fixed values, as well as the need to further explore how these surfaces depend on environmental conditions in clouds containing ice hydrometeors.
- Article
(6377 KB) - Full-text XML
-
Supplement
(114 KB) - BibTeX
- EndNote
Mass–dimension (m–D) relations are required to link bulk microphysical properties, such as total water content (TWC) and the forward model radar reflectivity factor (Z), to ice crystal particle size distributions (PSDs). These relations are extensively assumed in both numerical models and remote sensing retrievals and relate a particle's mass (m) to its size, typically defined by its maximum dimension projected onto a 2-D plane (D), by means of a power law in the form m=aDb. Past studies have suggested that the exponent b is related to the exponent in surface area–dimension relationships (Fontaine et al., 2014) or to a particle's fractal dimension (Schmitt and Heymsfield, 2010). The prefactor a has some dependence on b and on the particle density.
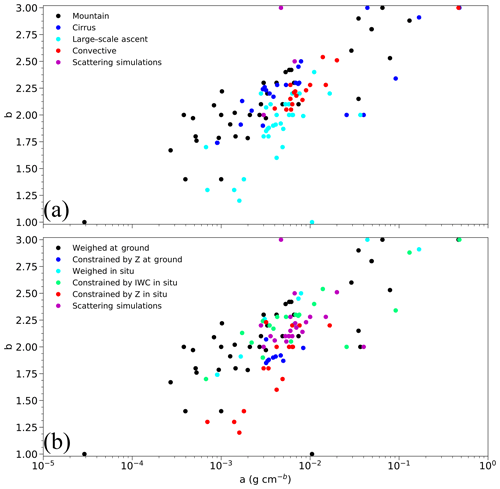
Figure 1Distribution of a and b coefficients used for characterizing m=aDb relationship from past studies. Points colored by the (a) environment in which measurements were taken and (b) technique used to derive the relations.
Prior m–D relationships have been determined using cloud probe data obtained in a variety of environmental conditions. Figure 1a shows how m–D coefficients derived from previous studies vary depending on the types of clouds sampled. A full list of these m–D coefficients and their corresponding references is available as a supplement. Coefficients derived using data over mountainous terrain (e.g., Nakaya and Terada, 1935; Locatelli and Hobbs, 1974), cirrus clouds (e.g., Heymsfield, 1972; Hogan et al., 2000), convective clouds (e.g., Liu and Curry, 2000; Cazenave et al., 2016; Leroy et al., 2016), regions of large-scale ascent (e.g., Szyrmer and Zawadzki, 2010), and computer-generated shapes (e.g., Matrosov, 2007; Olson et al., 2016) are shown. A total of 119 relations are shown in Fig. 1. The range of a in Fig. 1a spans 5 orders of magnitude, with variations in a spanning 3 orders of magnitude or more, even for measurements obtained in the same cloud type. The exponent b ranges between 1 and 3 within the same environments. The relations in Fig. 1 were derived using data collected by different types and versions of cloud probes, using different algorithms to process the data. McFarquhar et al. (2017) showed that it can be difficult to disentangle the dependence of derived microphysical parameters on environmental conditions from the dependence on the probes used to collect and the methods to process the data.
Figure 1b shows that m–D coefficients also vary depending on the technique used to derive the m–D relations. In some studies the maximum dimension of frozen hydrometeors was recorded before the crystal was melted and the single particle mass was subsequently measured (Magono and Nakamura, 1965; Zikmunda and Vali, 1972; Mitchell et al., 1990), whereas other studies used measurements of either bulk mass measured by an evaporation probe (Heymsfield et al., 2002; Cotton et al., 2013; Xu and Mace, 2017) or bulk Z values observed by a collocated radar measurement (McFarquhar et al., 2007a; Maahn et al., 2015) in combination with in situ measured PSDs. Furthermore, Wu and McFarquhar (2016) showed that inconsistencies in how D is defined (Mitchell and Arnott, 1994; Brown and Francis, 1995; McFarquhar and Heymsfield, 1996; Heymsfield et al., 2013; Lawson et al., 2015; Korolev and Field, 2015) can also impact m–D relations. For example, they noted that ice water content (IWC) values derived using various definitions of D ranged between 60 % and 160 % of the IWC derived using a smallest enclosing circle to define D.
Remote sensing retrieval schemes and model microphysical parameterization schemes are sensitive to the choice of m–D relationship. For example, Delanoë and Hogan (2010) showed that differences in the mean extinction, IWC, and effective radius retrieved from spaceborne remote sensors were 28 %, 9 %, and 30 %, respectively, depending on whether m–D relations of spherical aggregates (Brown and Francis, 1995, hereafter BF95) or bullet rosettes (Mitchell, 1996) were used. McCumber et al. (1991) showed time series of modeled precipitation rate with differences of 20 % to 50 % depending on assumptions about particle density, which are affected by the m–D relation. Later studies (e.g., Mitchell, 1996; Erfani and Mitchell, 2016) attributed differences in model output to the influence of particle mass on terminal fall velocities.
Although many studies have established m–D relations for specific cases, a universal m–D relationship has not been found, and a single relation cannot be expected to represent the wide range of crystal habits and sizes within clouds occurring at different temperatures and locations or those formed by different mechanisms. Moreover, a single relationship cannot account for the natural variability in cloud properties such as particle size, shape, and density that occurs even in similar environmental conditions. Thus, an alternate approach is more appropriate for modeling and remote sensing studies that considers multiple m–D relations over many retrievals or model simulations to evaluate the variability in the ensemble results.
While previous studies (e.g., McFarquhar et al., 2007b; Heymsfield et al., 2010; Mascio et al., 2017) have considered how m–D relations vary with environmental conditions, such as temperature, the derived relations were fixed regardless of potential fluctuations for that environment. Further uncertainties were associated with measurement errors induced by shattering of large ice crystals on probe tips and subsequent detection within the probe's sample volume (Field et al., 2003), from the processing techniques used (McFarquhar et al., 2017), and from the statistical counting of particles (e.g., Hallett, 2003; McFarquhar et al., 2007a). The approach by Fontaine et al. (2014) evaluated the variability in the prefactor a for an assumed exponent b for two field projects but ultimately still derived a single m–D relationship for each dataset based on the mean conditions.
Extending the approach of McFarquhar et al. (2015), which derived a volume of equally realizable solutions within the phase space of the three gamma fit parameters (concentration N0, shape μ, and slope λ) characterizing PSDs, a novel approach is used here to determine equally valid m–D relations for a given environment. Data from a variety of environments sampled during the Mid-latitude Continental Convective Clouds Experiment (MC3E) are used to establish a surface of equally plausible a and b coefficients in the (a,b) phase space using a technique that minimizes the chi-square difference between the TWC and Z derived from the PSDs measured by optical array probes (OAPs) and those directly measured by a TWC probe and radar.
The remainder of this paper is organized as follows. Section 2 outlines the datasets used and the methodology to process the radar and microphysics data, while Sect. 3 describes the technique employed to determine the surfaces of m–D coefficients. A brief description of the MC3E cases used in this study is provided in Sect. 4, and the surfaces of coefficients are derived and discussed in Sect. 5. A summary of the technique and its implications for numerical modeling and remote sensing retrieval schemes are given in Sect. 6.
The data in this study were collected within mesoscale convective systems (MCSs) during the 2011 MC3E (Jensen et al., 2016). The study presented here uses data from cloud microphysical instruments aboard the University of North Dakota (UND) Cessna Citation II aircraft and from the Vance Air Force Base, OK (KVNX), Weather Surveillance Radar 1988 Doppler (WSR-88D) radar.
2.1 Identification of coincident aircraft and radar data
The use of airborne microphysical measurements and radar data collected from the ground allowed sampling of the same region of the cloud from microphysical and remote sensing perspectives. Use of the Airborne Weather Observation Toolkit (Nesbitt et al., 2019) radar matching algorithm and the Python ARM Radar Toolkit (Py-ART; Helmus and Collis, 2016) permitted calculation of radar Z in the vicinity of the aircraft for each second of in situ cloud distributions measured during flight. The algorithm organizes all radar gates in a 3-D space (Maneewongvatana and Mount, 1999) for efficient acquisition of radar parameters at nearby radar range gates. The Barnes (1964) interpolation technique is then applied to data at the eight nearest gates within 500 m of the aircraft's location, ignoring vertically adjacent gates beyond a range of 65 km as the beamwidth exceeds the 500 m threshold to obtain an averaged Z at the aircraft location.
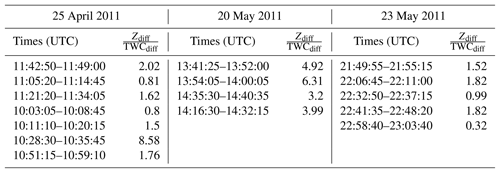
Table 1List of constant-temperature flight legs used in the analysis for which coincident data between the ground-based radar and UND Citation exist. Start and end times, mean altitude, and temperature are displayed.
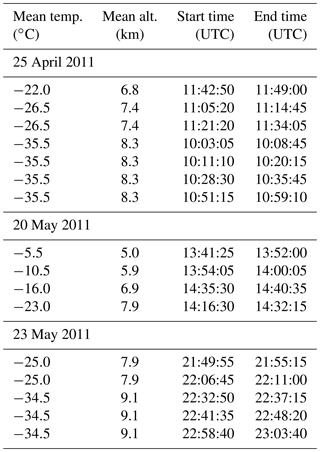
To compare microphysical properties with radar-measured Z for constant altitude flight legs at a similar environmental temperature, only those times when the radar and microphysical datasets are coincident and the temperature varies by less than 1 ∘C were considered. To reduce uncertainty due to counting statistics in the measured PSDs, microphysical data were averaged over a 10 s period. Each 10 s period determined required radar echo and microphysical data for all 1 s samples to ensure that the aircraft and matched radar Z were completely in cloud during the 10 s period. The TWC measurements and matched radar Z were then averaged over the same 10 s period, with each 10 s interval assigned as a coincident point. Table 1 lists the start and end times, mean altitude, and temperature for each of the 16 constant-temperature flight legs flown when the UND Citation was in cloud. Observations where the mean TWC for a 10 s interval <0.05 g m−3 were ignored as the values were considered either below the noise threshold of the Nevzorov probe or optically thin cloud. To further constrain the study to periods when clouds were dominated by ice-phase hydrometeors such that TWC ≈ IWC and to reduce the impact of liquid-phase hydrometeors on the derived TWC and Z, observations were excluded from the analysis if the concentration from the cloud droplet probe exceeded 10 cm−3 at any point during the 10 s interval, which usually corresponds to the presence of water (Heymsfield et al., 2011). Of the coincident observations considered, 13 % were excluded from the analysis based on these criteria. A total of 489 coincident observations were retained for this analysis.
2.2 Radar measurements
Data from the KVNX S-band (10 cm wavelength) radar were used in this study. Although the NASA dual-polarization (N-Pol) S-band Doppler radar was deployed during MC3E, mechanical issues prevented reliable collection of data for two of the three events examined here. Radars at other wavelengths collected data during MC3E. However, attenuation through liquid portions of the cloud (e.g., Bringi et al., 1990; Park et al., 2005; Matrosov, 2008) and non-Rayleigh scattering by larger particles (e.g., Lemke and Quante, 1999; Matrosov, 2007) could not be accounted for and prompted exclusive use of the S-band radar.
Radar reflectivity factor values for gates near the UND Citation (Sect. 2.1) were used to obtain the average value of Z, using the radar matching algorithm only if the following criteria were met: the correlation coefficient ρHV≥0.75, sigma differential phase SDP ≤12 deg2 km−2, differential reflectivity is represented by dB, and reflectivity texture (defined as the standard deviation in Z of the nearest five gates) <7 dBZ. These ranges represent acceptable values for echoes based on previous studies (Bringi and Chandrasekar, 2001). Radar gates not meeting these criteria were masked, reducing the likelihood of including gates with excessive signal noise due to clutter or a weak signal, contamination by the aircraft, or other factors. For instances where the matched Z changed by more than 2 dBZ for subsequent 1 s points (fewer than 1 % of the observations), all radar gates factored into the radar matching algorithm were inspected by eye to ensure that no outlier values were responsible for the jump in the matched Z. Of the observations that were manually inspected, all appeared spatially consistent with no outliers present and as such remained in the averaging routine of the matching algorithm discussed in Sect. 2.1.
2.3 Microphysical measurements
During MC3E the Citation aircraft sampled clouds in situ, with most data collected in ice-phase clouds between the melting layer and cloud top (Jensen et al., 2016). A suite of microphysical instruments was installed on the aircraft, including OAPs, which were used to image particles and derive PSDs, and a TWC probe. Specifics on the instrumentation and steps used to process the data are described below.
2.3.1 OAP data
A cloud imaging probe (CIP), a 2D cloud (2D-C) probe, and a High Volume Precipitation Spectrometer (HVPS), version 3 (HVPS-3), sized particles by shadowing photodiode arrays attached to fast response electronics. Data from the 2D-C and HVPS-3 were combined to create a composite PSD, permitting particles between 150 µm and 19.2 mm to be considered in the analysis. The 2D-C was used instead of the CIP in the analysis, even though the CIP has a larger sample volume, because the inclusion of anti-shattering tips on the 2D-C reduced the impact of shattered artifacts (e.g., Korolev et al., 2011). Previous studies (Korolev et al., 2011, 2013a; Jackson et al., 2014) showed that use of algorithms to identify shattered artifacts is sometimes needed even when the OAP is equipped with anti-shattering tips. Artifacts are identified by examining the frequency distribution of the times between which particles enter the sample volume (inter-arrival time; Field et al., 2006). When artifacts are present, this distribution follows a bimodal distribution, with naturally occurring particles having a mode with longer inter-arrival times and shattered artifacts having a mode with shorter inter-arrival times (e.g., Field et al., 2003). During MC3E there was only one mode in the inter-arrival time distribution corresponding to the naturally occurring particles (Wu and McFarquhar, 2016) at all times, suggesting that there were few shattered artifacts. Therefore, no shattering removal algorithm was used for the 2D-C and HVPS. Following Wu and McFarquhar (2016), the number distribution function N(D) was determined using the 2D-C for particles with D<1 mm and the HVPS-3 for D>1 mm. The 1 mm cutoff was chosen since N(D) for the two OAPs agreed within 5 % on average for mm and was used for all PSDs irrespective of periods when the difference between N(D) for the OAPs exceeded 5 % in the overlap region. Given uncertainties in the probe's sample area and limitations of its depth of field for smaller particle sizes (Baumgardner and Korolev, 1997), particles with D<150 µm were not included in the analysis.
The OAP data were processed using the University of Illinois/Oklahoma OAP Processing Software (UIOOPS; McFarquhar et al., 2018). Numerous morphological properties were calculated (e.g., particle maximum dimension, projected area, perimeter, area ratio, and habit) for individual particles, and PSDs were determined for each second of flight. Following Heymsfield and Baumgardner (1985) and Field (1999), only particles imaged with their center within the OAP's field of view were considered, as otherwise there is too much uncertainty in particle size. Particles were identified as having their center within the field of view if their maximum dimension along the time direction exceeded the largest length where the particle potentially touched the edge of the photodiode array.
2.3.2 TWC data
The TWC was determined from the Nevzorov probe using the power required to melt or evaporate ice particles impinging on the inside of a cone (e.g., Nevzorov, 1980; Korolev et al., 1998). The probe used had a deeper cone than previous designs, with a 60∘ vertex angle (as opposed to a 120∘ angle) that prevented many particles from bouncing out of the cone. Because previous studies suggested that particles with D>4 mm can bounce out of even the deeper cone (Wang et al., 2015), TWC may be underestimated when such particles are present. However, Korolev et al. (2013b) showed that the ratio of the Nevzorov IWC to that derived from the measured PSDs using the BF95 relation did not significantly vary with particle maximum dimension. Of the coincident points belonging to constant altitude flight legs in this study, 79.2 % of the observations had cumulative mass estimates using the BF95 relation from particles with D≤4 mm contributing at least 80 % to the total mass. Therefore, measurements of TWC were included irrespective of whether Dmax>4 mm.
In this section, a method for determining a surface of equally realizable solutions for m–D coefficients in the phase space of (a,b) coefficients is described. The surface of these coefficients is determined through a procedure that minimizes the χ2 differences between the TWC and Z derived from N(D) and those directly measured by the Nevzorov and ground-based radar, respectively. The minimization procedure is carried out for each constant-temperature flight leg (defined by temperature varying by less than 1 ∘C) for the MC3E cases studied. This approach follows that of McFarquhar et al. (2015), who developed volumes of equally realizable N0, μ, and λ characterizing the observed N(D) as gamma distributions for observations obtained during the Indirect and Semi-Direct Aerosol Campaign (ISDAC) and the NASA African Monsoon Multidisciplinary Analyses project (NAMMA).
Table 2List of constant-temperature flight legs and the ratio between Zdiff and TWCdiff valid at the (a,b) values that minimize χ2.
For an individual 10 s sample, the TWC and Z derived from the PSD for a specific a and b are given by TWCSD and ZSD, respectively, as
and
following the method of Hogan et al. (2006) and accounting for the different dielectric constants for water () and ice (). Uncertainties in TWCSD and ZSD are discussed later in this section. The metric defining the difference between the TWC and Z derived from N(D) for a specific a and b and those directly measured by the Nevzorov and ground-based radar, respectively, is given by TWCdiff and Zdiff as follows:
and
In this study, TWCdiff and Zdiff are computed for all points in the domain of values encompassing g cm−b and at increments of g cm−b and 0.01, respectively.
Given a priori assumptions of Z being proportional to the square of a particle's mass, the square root of reflectivity was used in Eq. (4) so that TWCdiff would be similar to Zdiff on average and so that each would have approximately equal weight in determining a and b. Although radar Z measurements involve a significantly greater sample volume than that of OAPs and a bulk content probe, TWCdiff and Zdiff were not weighted proportionally to the sample volume in order to ensure that both bulk moments had some impact on the derived a and b. Given that larger ice crystals are fractionally more important than small crystals in determining ZSD compared to TWCSD and given varying contributions of larger crystals to ZSD and TWCSD, TWCdiff has a greater impact on the χ2 minimization procedure some of the time, while Zdiff has a greater impact at other times. The ratios between Zdiff and TWCdiff for each flight leg are given in Table 2 and range between 0.32 and 8.58, with a mean of 2.62 for the 16 flight legs. No attempt is made to force equal weight for Zdiff and TWCdiff for each coincident point because there are periods when cloud properties influence TWC differently than Z.
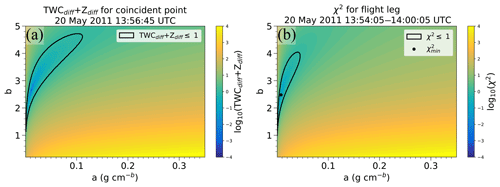
Figure 2TWCdiff+Zdiff in (a,b) phase space for (a) a 10 s coincident point beginning at 13:56:15 UTC on 20 May 2011, (b) integrated over the encompassing flight leg between 13:54:14 and 13:59:35 UTC, and normalized by the number of observations N. The black dot in (b) denotes the a and b minimizing χ2.
At first, the sum of TWCdiff+Zdiff is used to identify (a,b) values that characterize an individual 10 s data point. An example of TWCdiff+Zdiff computed in the (a,b) phase space for a 10 s averaged PSD measured beginning at 13:56:45 UTC on 20 May 2011 is shown in Fig. 2a. The color representing TWCdiff+Zdiff is shaded on a logarithmic scale to more easily show the range of values. The smallest swath of values, arbitrarily chosen as being TWC within the region outlined in black, spans b values from 1.13 to 4.72. The curvature in the outlined region highlights the correlation of a and b, showing that a similar m can be obtained using very different b values by adjusting a accordingly. Considering both TWCdiff and Zdiff allows the shape and placement of the smallest swath of values to be adjusted according to two different moments of the PSD, since conditions impact TWC differently than Z. Using two constraints on the χ2 minimization technique therefore provides additional insight into the microphysical properties as discussed in Sect. 5.
The chi-square statistic for a flight leg, defined as
involves a summation over all N 10 s coincident observations represented by the index i and normalized by N. When χ2 is computed by summing over all N points in the flight leg, the region with the smallest χ2 (χ2≤1; outlined region in Fig. 2b) is smaller than the region in Fig. 2a, which shows χ2 for a single point, because different (a,b) values minimize χ2 for each of the individual PSDs in the 5 min period depicted. Therefore, overall the χ2 values are higher than the TWCdiff+Zdiff computed for each (a,b). The point in Fig. 2b corresponds to the a and b point that minimizes χ2, represented hereafter as , which represents the most likely a and b value.
To represent the uncertainty in the derived coefficients for each flight leg, all a and b values fulfilling are assumed to be equally plausible solutions. Analogous to McFarquhar et al. (2015), the confidence region is defined as . The characterizes the robustness of the minimization procedure affected by the natural parameter variability over a flight leg, represents uncertainties in the PSD due to statistical sampling uncertainties, and represents measurement uncertainties. Similar to their study, is determined here as
The different terms in Eq. (6) represent the difference in the minimum and maximum TWC or Z derived from the minimum and maximum N(D) using the most likely (a,b) values minimizing χ2 (TWCSD,min and TWCSD,max or ZSD,min and ZSD,max) and those derived from the measured N(D) (TWCSD or ZSD). Following McFarquhar et al. (2015), the minimum and maximum N(D) values are determined by subtracting or adding the square root of the number of particles counted in each size bin to the number of particles counted in the bin when computing N(D). This technique represents uncertainty in the actual particle counts for each size bin as given by Poisson statistics (Hallett, 2003; McFarquhar et al., 2007a).
Estimates of the measurement uncertainty from the OAPs, Nevzorov probe, and ground-based radar also influence the uncertainty in the derived coefficients. The uncertainty due to measurement error is defined as
The terms TWC, TWC, , and represent the minimum and maximum TWC or Z derived using a 50 % uncertainty in the measured N(D). This uncertainty follows Heymsfield et al. (2013), where up to a 50 % difference in the number concentration for particles with D>0.1 mm was determined. Uncertainties in the bulk measurements of TWC and Z must also be considered in the generation of the uncertainty surfaces, with the minimum and maximum possible bulk values represented as TWC, TWC, , and . Following Korolev et al. (2013b), it was assumed that there was a 2 % uncertainty when Dmax≤4 mm and an 8 % uncertainty for other periods to address the possibility of particles bouncing out of the cone of the Nevzorov probe. A radar reflectivity uncertainty of 1 dB (Krajewski and Ciach, 2003) is subtracted from or added to the measured Z to determine and .
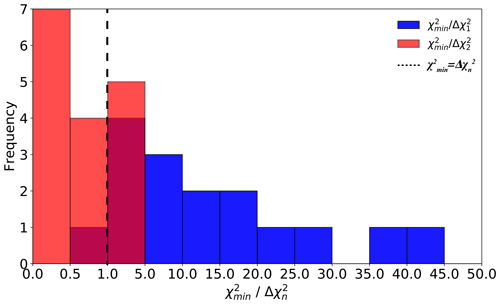
Figure 3Frequency of (blue shading) and (red shading), where , , and are derived for each flight leg used in analysis.
Figure 3 illustrates the frequency distribution of the ratio between and (blue shading) and between and (red shading) for all 16 flight legs. Of all 16 legs considered, 15 have a ratio between and greater than 1, meaning that , and 50 % of the observations have ratios greater than 10. For 5 of the 16 legs, the ratio between and is greater than 1, indicating that the χ2 obtained from the (a,b) minimization procedure is greater than the difference between moments derived from the minimum and maximum N(D) and from the minimum and maximum TWC and Z due to measurement errors for nearly one-third of the periods in this study. This means that the natural parameter variability over a flight leg is sometimes more important for the derived uncertainty of m–D coefficients, whereas at other times measurement errors are more important. This is further discussed in Sect. 5.
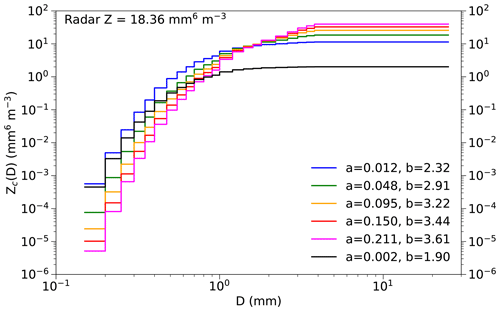
Figure 4Zc(D) as a function of D derived using modified m–D coefficients from BF95 (black) and from the 5th (blue), 25th (green), 50th (orange), 75th (red), and 95th (magenta) percentiles from the set of equally plausible m–D coefficients in the order of increasing b and a values for the 14:16:30–14:32:15 UTC flight leg on 20 May 2011. Mean radar reflectivity matched at the aircraft's position for the same period is listed in top left.
At first, the b coefficients greater than 3 shown in Fig. 2 may seem counterintuitive as the mass of a particle cannot be greater than that of an ice sphere. Furthermore, a particle's density would increase with increasing D for b>3. But, due to the covariability in a and b, b>3 does not necessarily imply that the particle has a mass greater than a sphere. Nevertheless, equally plausible b values greater than 3 were closely inspected, as past studies (e.g., Fontaine et al., 2014) have disregarded b>3 as a possible exponent in an m–D relation. To investigate the impact of b>3, a linear sequence of b values in the plausible surface was generated for each flight leg, and the 5th, 25th, 50th, 75th, and 95th percentiles of b were determined. The corresponding a from each of these b values was identified, and the cumulative reflectivity distribution functions, defined as
were computed using the mean N(D) for the period and the particle mass derived with these a and b values. Figure 4 shows an example of the Zc(D) over the range of particle sizes observed from the −23 ∘C flight leg on 20 May 2011 using these a and b coefficients. The Zc(D) derived using BF95 coefficients, with the prefactor a (=0.002 g cm−1.9) modified following the correction factor of Hogan et al. (2012) applicable for the definition of D used here, is also shown for reference. It is worth noting that the modified BF95 coefficients may reasonably resolve the particle mass for some particle sizes for the PSD depicted in Fig. 4. While the lower values of a and b yield larger Zc(D) for smaller D than the larger values of a and b, the derived total reflectivity for the 5th and 95th percentiles of b are within 11.38 mm6 m−3 of the mean matched radar Z of 18.36 mm6 m−3 (12.64 dBZ), a difference of 62 % in the mean. In contrast, the difference in the mean from the Zt computed with modified BF95 coefficients is much higher, 88.6 %, suggesting values of b>3 are indeed giving plausible results for the range of particle sizes observed.
When the seven flight legs that have some values of b>3 in the surface of equally plausible solutions are considered, Z values for the 5th and 95th percentiles of b are within 82.4 % of the mean matched radar Z. While this value is greater than the 50.5 % difference for the other flight legs and for the period illustrated in Fig. 4, Z values for the 5th and 95th percentiles are more consistent with the mean matched radar Z compared to that computed with the modified BF95 relationship.
Thus, the bulk variables such as Z derived using b>3 are physically plausible for the distributions examined here, given the covariability in a and b. However, this conclusion may only apply when the coefficients are applied over the range of particle sizes observed during MC3E and assuming PSDs with similar shapes. For example, for the 95th percentile of b (b=3.61) and the corresponding value of a used to construct Fig. 4, ice particles with D<3.83 cm have particle masses less than those of spherical particles with a density of solid ice for the same maximum dimension. In contrast, if the covariability in a and b was not taken into account when choosing the corresponding a value, then a particle could have a mass greater than that of a spherical particle for a much smaller D. While the technique highlights the possibility of a wide range of m–D coefficients for a given environment, equally plausible solutions containing b>3 are still not considered in the remainder of this study to remain consistent with previous studies and to avoid any chance of unphysical behavior should the equally plausible coefficients be extrapolated to PSDs from remote sensing retrievals or microphysics parameterization schemes that extend to particle sizes larger than in the original dataset.
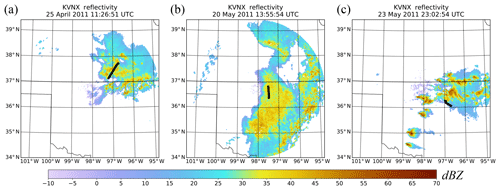
Figure 50.5∘ PPI scan of corrected radar reflectivity from the KVNX radar for (a) 11:26:51 UTC on 25 April 2011, (b) 14:04:34 UTC on 20 May 2011, and (c) 23:02:54 UTC on 23 May 2011. Black lines denote the Citation flight track for the constant-temperature leg corresponding to the radar image shown.
The Citation aircraft sampled different ice-phase environments during the 25 April, 20 May, and 23 May 2011 flights. Jensen et al. (2016) provide an overview of all MC3E cases, while Jensen et al. (2014) give a synoptic scale overview of the MCSs examined in this study. These particular events were chosen because of variations in how the storms evolved and the location of in situ measurements relative to the convective system. Figure 5 shows a 0.5∘ plan-position indicator (PPI) scan of corrected radar reflectivity from the KVNX radar for each event. The PPI was obtained during the middle of the UND Citation flight leg, depicted by the black line in Fig. 5.
The first event involved an upper-level trough that produced ascent aloft and generated thunderstorms across northern Oklahoma around 06:00 UTC on 25 April 2011. As these storms traversed northward along an elevated frontal boundary overnight, their bases decoupled from the boundary layer as daytime solar radiation ceased. The discrete cells evolved into an MCS and moved into southern Kansas by 11:00 UTC (Fig. 5a), when the Citation sampled weaker embedded convection and broader stratiform precipitation. The second MCS, with a north-to-south-oriented squall line which was part of a larger system, developed from a line of convective cells originating in western Texas along a dry line around 10:00 UTC on 20 May 2011 and propagated into the deployment region in northern central Oklahoma. The Citation aircraft primarily flew within the trailing stratiform region of the MCS (Fig. 5b). The third MCS originated as a series of discrete supercell thunderstorms along a surface dry line in western Oklahoma and moved eastward into the MC3E domain by 21:00 UTC on 23 May 2011 before transitioning to a more linear MCS feature. Microphysical measurements were made in the anvil region of these strong thunderstorms (Fig. 5c).
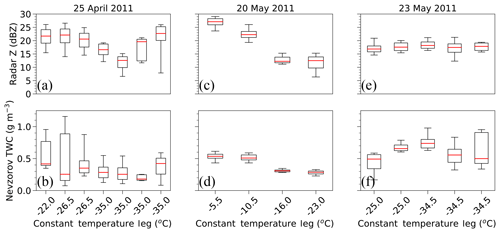
Figure 6Distribution of matched Z (a, c, e) and TWC from the Nevzorov probe (b, d, f) for each constant-temperature leg on 25 April (a, b), 20 May (c, d), and 23 May 2011 (e, f). Whiskers represent the 5th and 95th percentiles, box edges are the 25th and 75th percentiles, and the line in the middle is the median. Cases where multiple legs of the same temperature exist are shown in chronological order.
To provide context for the bulk characteristics sampled during each event, box plots of Z matched at the aircraft's location, and TWC values from the Nevzorov probe for each constant-temperature flight leg are given in Fig. 6. The whiskers represent the 5th and 95th percentiles from coincident observations, the box edges denote the 25th and 75th percentiles, and the red line in the middle is the median. Distributions are listed in the order of decreasing temperature, with instances of multiple legs having the same average temperature shown in chronological order. While the bulk TWC and Z may differ for flight legs of similar average temperature on a given day, as in the −26.5 and −35 ∘C environments on 25 April (Fig. 6a–b), a greater or smaller TWC correlates with a greater or smaller Z for most cases. The variability in the TWC and Z as it relates to the construction of surfaces of equally plausible m–D coefficients is discussed in the next section.
This section discusses how the (a,b) surfaces vary between different cases, as a function of temperature, depending on the determination of radar reflectivity and depending on whether PSDs had large mass contributions from particles with D>4 mm.
5.1 Radar absolute Z calibration
While S-band radars within the Next Generation Weather Radar (NEXRAD) WSR-88D network are calibrated individually and among one another upon initial installation, biases in Z can develop over time (Ice et al., 2017). Zhang et al. (2013) described a technique that uses self-similarity in the Z, ZDR, and specific differential phase (KDP) fields to estimate the absolute Z bias for events in rain. This method was employed for the cases in this study, and biases in Z of −1.08 (25 April), −0.65 (20 May), and 1.43 dBZ (23 May 2011) were found. These corrections were applied to the value of Z calculated as explained in Sect. 3. The surfaces of m–D coefficients derived using the matched radar Z and those with the bias corrections applied were similar, with the range of equally plausible b values differing, on average, by 6.4 % after the corrections were made.
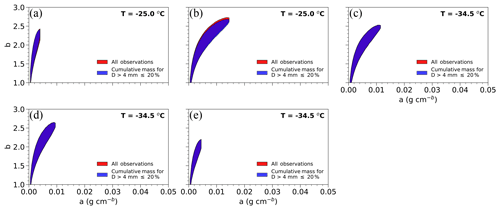
Figure 7Surfaces of equally plausible a and b values from the m=aDb relation from each near-constant-temperature leg on 23 May 2011 for all coincident observations (red) and only those where cumulative mass for D>4 mm is ≤20 % (blue). Flight legs of the same temperature are shown in chronological order.
5.2 Accounting for mass contributions from larger particles
As discussed in Sect. 2.3.2, the Nevzorov probe is prone to larger particles (D>4 mm) bouncing out of the collection cone, resulting in potential TWC underestimations. Mass contents were derived from the PSDs using the modified BF95 coefficients to identify time periods in which the contribution of mass from particles with D>4 mm was likely greater than 20 %. Of all 10 s PSDs used in this study, 20.9 % had mass contributions from the larger particles exceeding 20 % of the total mass. Figure 7 illustrates the similarity in the (a,b) surfaces generated using all coincident observations (red shading) and only those using observations with mass from larger particles contributing ≤20 % of the total mass (blue shading) for the 23 May 2011 event. Regions of overlap between the two approaches only appear as purple shading. The sensitivity test shows that omitting observations where larger particles contribute fractionally more to the total mass yields an area of equally plausible (a,b) surfaces for the 23 May event, differing, on average, by 1.4 %. As such, all coincident observations are used for this study irrespective of the fractional contributions of particles with D>4 mm to the mass.
5.3 Environmental impact on m–D coefficients
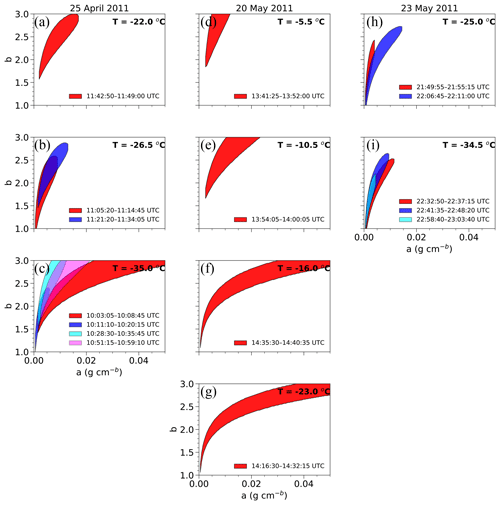
Surfaces of equally plausible m–D coefficients in the (a,b) phase space from all flight legs outlined in Table 1 are shown in Fig. 8. For each event, flight legs are grouped by the same environmental temperature, with the different colors corresponding to the time periods given in each panel. These surfaces are influenced by how TWC and Z derived from the PSDs relate to observed TWC and Z and by the variability in each within a flight leg. The observed trends in the (a,b) surfaces and how they are affected by N(D), TWC, and Z are discussed further below.
To compare surfaces of equally plausible solutions between different environments and also between periods with the same temperature, the percentage of overlap between any two flight legs is computed and shown as a matrix in Fig. 9. The percentage of overlap is determined by counting the number of (a,b) pairs contained in both equally plausible surfaces for the conditions listed in the row and column in the matrix and dividing by the number of (a,b) pairs in the surface for the condition listed in the row multiplied by 100 %. There are two values in the matrix corresponding to each comparison between two flight legs, with differences between the two values resulting from dividing the area of the equally plausible surface from the corresponding column by that in the corresponding row in the matrix. Thus, it is possible for the percentage of overlap between two flight legs to be greater when normalized by an equally plausible surface that is smaller in area and to be smaller when normalized by a larger equally plausible surface. It is worth noting that the percentage of overlap does not always follow an organized trend with respect to moving away from the gray diagonal line in the matrix, as depicted in the top right corner of Fig. 9a. The lack of organized overlap values in some regions of the matrix could be influenced by the sensitivity in computing the overlap region over a fine resolution of (a,b) values within the domain described in Sect. 3 or perhaps could change in a more organized manner if there were a more statistically representative sample for these calculations to be made. Using the (a,b) surfaces from the −26.5 ∘C flight legs on 25 April (Fig. 8b) as an example, 62 % of the (a,b) surface for the 11:05:20–11:14:45 UTC period (labeled −26.5 ∘C, I; Fig. 9a) overlaps with the later −26.5 ∘C flight leg, while 65 % of the (a,b) surface for the 11:21:20–11:34:05 UTC period (labeled −26.5 ∘C, II) overlaps with the earlier −26.5 ∘C flight leg. The difference occurs because there are 1132 (a,b) pairs in the surface for the 11:05:20–11:14:45 UTC period and 1077 (a,b) pairs in the surface for the 11:21:20–11:34:05 UTC period. Flight legs having the same temperature are ordered chronologically as in Fig. 8 and are differentiated with a Roman numeral. Differences of the (a,b) surfaces between flight legs are further discussed below.
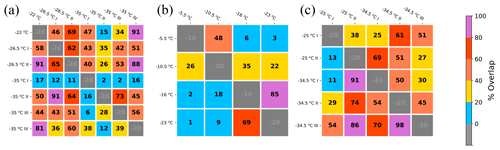
Figure 9Matrix of overlap area between the equally plausible (a,b) surfaces corresponding to each row and column for (a) 25 April, (b) 20 May, and (c) 23 May 2011. The overlap area for each square is normalized by the area of the (a,b) surface corresponding to the flight leg listed in each row.
5.3.1 25 April case
While differences exist between the (a,b) surfaces for the near-constant-temperature legs on 25 April (Fig. 9a), these surfaces have considerable overlap with each other for a<0.01 g cm−b and b<2.5 (Fig. 8a–c). The −22 and −26.5 ∘C legs have similar sets of equally plausible solutions, with (a,b) surfaces overlapping between 46 % and 91 % (Fig. 9a). Less agreement in the (a,b) surfaces is observed among the −35 ∘C flight legs, with the surfaces overlapping by an average of 27.8 % among the different combinations. The differences in the size of the surfaces is primarily influenced by the natural variability within cloud () for five of the seven legs and by the uncertainty due to measurement errors () for the remaining legs. The areas of the (a,b) surfaces for the −22 and −26.5 ∘C legs were, on average, 31.2 % smaller than the surfaces associated with the −35 ∘C environment (Fig. 8a–c). Three of the four −35 ∘C legs have surfaces larger than the −22 and −26.5 ∘C environments, as the surface of equally plausible m–D coefficients extends beyond the maximum value a of 0.017 g cm−b and b of 3.00 found for the −22 and −26.5 ∘C legs. To explain the variation in these (a,b) surfaces for the different temperatures, the distributions of microphysical quantities for the times corresponding to these surfaces were examined.
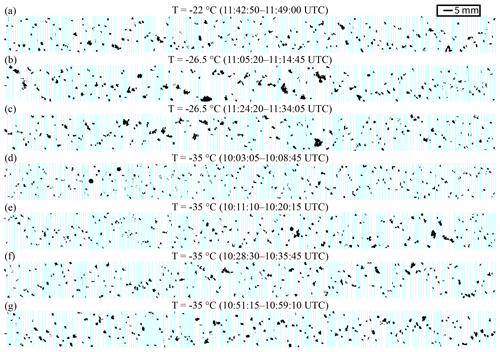
Figure 10Representative particle images from the HVPS-3 for each near-constant-temperature flight leg on 25 April 2011.
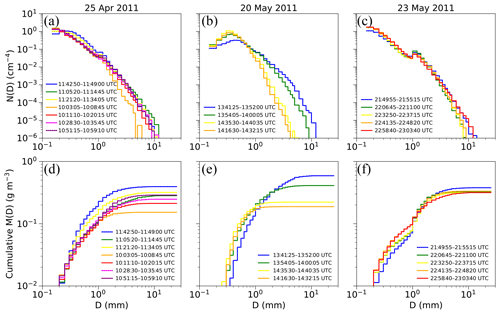
Figure 11Mean N(D) (a, b, c) and cumulative M(D) (d, e, f) for each constant-temperature leg on 25 April (a, d), 20 May (b, e), and 23 May 2011 (c, f). Cases where multiple legs of the same temperature exist are shown in chronological order.
To examine the variability in hydrometeors, particle images and distributions of bulk microphysical properties were analyzed for each flight leg. Example particle images from the HVPS-3, which provide information on the size and habit of ice-phase particles with D>1 mm, are plotted in Fig. 10. The pictured particles represent a subset of those imaged for the time period given and were chosen at random in an attempt to obtain a representative sample of hydrometeors. Figure 11 shows the mean N(D) and cumulative mass distribution function M(D) using the modified BF95 relationship for each flight leg analyzed in this study. Figure 12 details the distribution of number concentration Nt, median mass diameter Dmm, and a metric for particle sphericity obtained from the PSDs derived from the 2D-C and HVPS-3 data at each 10 s coincident observation. The Dmm is derived using the modified BF95 coefficients for comparison among the different flight legs. The whisker and box edges are the same as in Fig. 6. Particle sphericity ζ (McFarquhar et al., 2005; Finlon et al., 2016) is defined by
where a is the cross-sectional area directly measured by the probe and P is the perimeter determined from the sum of all pixels within a width of one diode of the edge of the particle and the diode resolution. Finlon et al. (2016) described how a higher ζ denotes more-circular particles. Sphericity values shown in Fig. 12 represent a mass-weighted mean of ζ for all particles using mass estimated from the modified BF95 relation within each 10 s observation. Figures 10, 11, and 12 are ordered in the same manner as in Fig. 6, with instances of multiple legs having the same average temperature shown in chronological order.
As evidenced by the particle images and mean N(D) at and −26.5 ∘C (Figs. 10a–c, 11a), the presence of aggregates exceeding 5 mm is more common compared to lower temperatures (Fig. 10d–g), where the ice crystals and aggregates appear to be skewed towards smaller sizes. Distributions of Dmm (Fig. 12b) and TWC (Fig. 6b) also indicate this trend, with a median Dmm for the 11:05:20–11:14:45 UTC ( ∘C) flight leg of 2.2 mm, while the −35 ∘C periods have a median Dmm ranging between 1.1 and 1.7 mm.
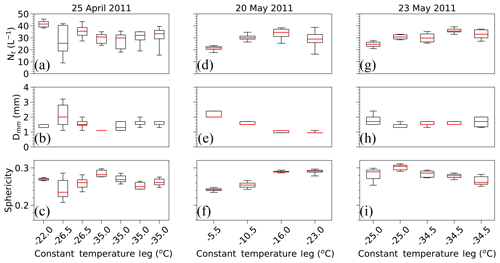
Figure 12As in Fig. 6, but for number concentration Nt, median mass diameter Dmm, and mass-weighted mean sphericity.
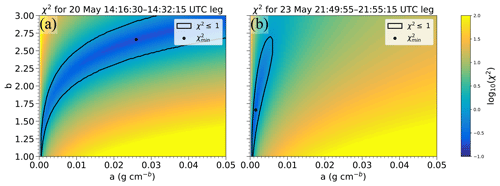
To illustrate that the range of equally plausible (a,b) coefficients is sometimes explained more by the variability in cloud parameters than the uncertainty in measurement errors, the distributions of bulk microphysical variables, TWC, and Z are compared between the 11:05:20–11:14:45 UTC ( ∘C) and 10:03:05–10:08:45 UTC ( ∘C) periods. The −26.5 ∘C flight leg had ranges in Nt, Dmm, sphericity, Z, and TWC between the 25th and 75th percentiles (interquartile range hereafter) of 21.5 L−1, 1.3 mm, 0.04, 5.2 dBZ, and 0.73 g m−3, respectively, while the same variables for the −35 ∘C period had smaller interquartile ranges of 7.4 L−1, 0.1 mm, 0.02, 4.0 dBZ, and 0.17 g m−3 (Figs. 6a, b; 12a–c). The distribution of χ2 in the (a,b) phase space is expected to differ when the variability in N(D) throughout a flight leg is different between two periods since different a and b values are likely to yield TWCSD and ZSD similar to the observed TWC and Z. Figure 13 illustrates the distribution of χ2 for the two periods, with the outlined region representing χ2 values that are ≤2 for comparison. The region containing χ2≤2 is 90.8 % smaller for the −26.5 ∘C flight leg compared to the −35 ∘C period and indicates that the TWCSD and ZSD derived from all possible a and b values remain fairly consistent over the course of the −26.5 ∘C flight leg due to the smaller interquartile ranges in the TWC, Z, and bulk microphysical properties. As such, low χ2 values are present over a larger range of m–D coefficients for the −35 ∘C leg.
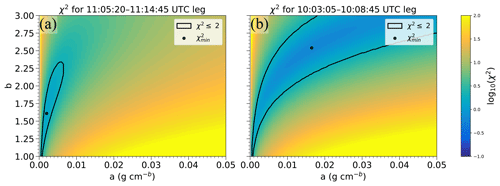
Figure 13χ2 statistic in (a,b) phase space for the (a) 11:05:20–11:14:45 UTC and (b) 10:03:05–10:08:45 UTC flight legs on 25 April 2011. Outlined regions represent χ2≤2, and the dots represent .
Although the distribution of χ2 is an important factor in determining the area of an equally plausible surface, the Δχ2 confidence region, which is equal to for four of the flight legs on this day and equal to for three of the flight legs on this day, can also influence the area of (a,b) surfaces. While the allowable tolerance is greater by factor of 2 for the −26.5 ∘C leg, the equally plausible (a,b) surface is 3.4 times smaller compared to the −35 ∘C flight leg (Fig. 8b, c) because of the magnitude and distribution of χ2 values in the (a,b) phase space. Put another way, more χ2 values considered within the (a,b) phase space are greater than the criteria to be considered equally plausible solutions compared to the −35 ∘C leg.
5.3.2 20 May case
The wide range of temperatures sampled during the 20 May event was associated with a large variation in Z (Fig. 6c), with median values ranging between 12.5 dBZ ( ∘C) and 27.1 dBZ ( ∘C). Representative particle images (Fig. 14) highlight differences in particle size and habit between the higher temperature flight legs ( and −10.5 ∘C) and the lower temperature periods ( and −23 ∘C), with images and mean N(D) (Fig. 11b) from the −5.5 and −10.5 ∘C legs indicating a greater frequency of larger ice crystals and aggregates with D≥2 mm. A Mann–Whitney U test confirms that Dmm (Fig. 12e) and sphericity (Fig. 12f) between the higher and lower temperature environments are statistically different at the 99 % confidence level, with notably larger and fewer spherical particles observed during the −5.5 and −10.5 ∘C flight legs. Furthermore, median Z values for the −5.5 and −10.5 ∘C periods (22.3–27.1 dBZ) are up to 30.7 times greater than for the −16 and −23 ∘C legs (12.2–12.5 dBZ), while the median TWC is up to 1.9 times (0.3 g m−3) greater for the −5.5 and −10.5 ∘C legs. Thus, the difference in particle properties and bulk properties TWC and Z can be used to explain differences in (a,b) coefficients observed between the legs on this day.
Microphysical properties such as the effective density ρe of ice hydrometeors can impact TWC differently than they do Z. The ρe, defined here as the ratio of TWC derived assuming the modified BF95 relationship to the integrated volume of particles enclosed by an oblate spheroid with an aspect ratio of 0.6 (e.g., Hogan et al., 2012), is estimated to evaluate its influence on TWC and Z. Median ρe ranges between 0.05 and 0.08 g cm−3 for the −5.5 and −10.5 ∘C periods and between 0.18 and 0.21 g cm−3 for the −16 and −23 ∘C flight legs. These trends along with minimal riming evident from the 2D-C particle images suggest that particles are on average less compact for the higher temperature legs. Furthermore, the presence of larger aggregates as suggested by greater values of Dmm (Fig. 12e), lower sphericity (Fig. 12f) and ρe, and the representative particle images from the HVPS-3 (Fig. 14a, b) are consistent with an increasing Z when observed by longer wavelength radars (e.g., Giangrande et al., 2016).
Since differences in ρe appear to affect the TWC and Z on 20 May, the variability in N(D) is not the only factor influencing the equally plausible (a,b) surfaces depicted in Fig. 8d–g. Figure 9b illustrates that only the −16 and −23 ∘C legs have similar (a,b) surfaces, with 85 % of the (a,b) coefficients from the −16 ∘C leg overlapping with the −23 ∘C flight leg. Minimum values of b for the −5.5 and −10.5 ∘C flight legs, where less compact particles were observed, were 1.84 and 1.66, respectively, while minimum b values for the −16 and −23 ∘C legs were 1.09 and 1.06 for similar a values (Fig. 8d–g). Looking at the (a,b) surfaces another way, values of a for the −5.5 and −10.5 ∘C legs were as large as 0.031 g cm−b, while a exceeds 0.05 g cm−b for b=3 during the −16 and −23 ∘C flight legs. Although the Δχ2 confidence region is equal to for the four flight legs on this day and has Δχ2 values that are within 1 % of each other, the distribution of χ2 greatly influences the extent of these surfaces in the (a,b) phase space, with an area for the −5.5 and −10.5 ∘C flight legs that is on average 2.9 times smaller than the −16 and −23 ∘C periods. When considering the m=aDb relation whose size D and exponent b are held fixed, lower values of a as observed during the −5.5 and −10.5 ∘C legs suggest that particles on average have smaller m compared to the −16 and −23 ∘C legs and are consistent with smaller ρe observed for the −5.5 and −10.5 ∘C periods.
5.3.3 23 May case
The 23 May case was unique from the other two cases in that the bulk Z varied less between the different temperature environments (Fig. 6e), with median Z ranging only between 16.9 and 18.2 dBZ. Representative particle images (Fig. 15) in addition to the mean N(D) (Fig. 11c) and the cumulative M(D) (Fig. 11f) indicate that the sizes and shapes of ice hydrometeors are similar for all five flight legs. Additionally, distributions of Dmm (Fig. 12h) and sphericity (Fig. 12i), with median values of each varying by 0.4 mm and 0.04, respectively, further support this similarity in cloud properties between the different environments. Equally plausible (a,b) surfaces were also similar irrespective of temperature (Fig. 8h, i), with the four flight legs after the 21:49:55–21:55:15 UTC period having surfaces that overlap on average 62.1 % among the different combinations (Fig. 9c). The 21:49:55–21:55:15 UTC leg is the only period on this day where the Δχ2 confidence region is determined by the natural variability in the cloud () rather than the uncertainty due to measurement errors (). As such, the (a,b) surface for this period has minimal overlap with the other equally plausible surfaces. Closer examination of the bulk TWC (Fig. 6f) indicates that values at the fifth percentile for the 21:49:55–21:55:15 UTC period are 65.2 % less than the remaining flight legs, which impacts the distribution of χ2 values and the (a,b) values that are within the threshold.
Although surfaces of equally plausible solutions trend larger in area for lower temperature environments on 25 April and 20 May, the area of (a,b) surfaces among the five flight legs on 23 May are on average 2.2 (3.8) times smaller compared to the 25 April (20 May) event. To examine how the distribution of χ2 in the (a,b) phase space is affected by differences in the variability in TWC and Z throughout a flight leg, the 14:16:30–14:32:15 UTC period on 20 May and the 21:49:55–21:55:15 UTC period on 23 May are compared because of their similar temperature and the threshold used to determine the (a,b) surfaces. Figure 16 illustrates the distribution of χ2 for the two periods, with the outlined region representing χ2 values that are ≤1 for the purpose of comparison. The region containing χ2 ≤1 is 88.2 % smaller for the 23 May flight leg compared to the 20 May period and highlights how different a and b values can yield a χ2 value that is within the given tolerance based on differences in the observed TWC and Z distributions. When bulk TWC and Z values are compared against the 25 April (20 May) events, the median Z from flight legs on 23 May is on average 34.4 % (25.9 %) lower, while the median TWC is 90.3 % (43.9 %) greater. As mentioned in Sect. 4, the sampling strategy on 23 May was different from the stratiform clouds observed with the previous two events in that measurements were primarily made in the anvil region of supercell thunderstorms. Previous studies (e.g., Heymsfield et al., 2007) noted that the prefactor a had less of a temperature dependence within anvil cirrus clouds, consistent with trends in a for the 23 May flight legs.
This paper presented a novel approach for characterizing the variability in mass–dimension (m–D) coefficients characterizing particle size distributions (PSDs) during the Mid-latitude Continental Convective Clouds Experiment (MC3E). The technique outlined here extends the approach of McFarquhar et al. (2015), who derived a volume of equally realizable solutions in the phase space of gamma fit parameter coefficients for characterizing PSDs. Ground-based radar measurements of reflectivity Z from the Vance Air Force Base, OK, radar were matched to the location of the Cessna Citation II aircraft, where total water content (TWC) measurements from the Nevzorov probe were made and PSDs were derived from optical array probe data. These collocated datasets permitted use of a χ2 minimization technique where all χ2 values within a tolerance Δχ2 of the minimum χ2 were considered equally plausible solutions to the m=aDb relationship for a flight leg of similar temperature. The tolerance was determined by considering uncertainties due to natural variability in cloud conditions for a particular environment, the statistical sampling of particles from the PSDs, and uncertainties in the measurements themselves.
The key findings of the paper are as follows:
-
The distribution of χ2 values in the (a,b) phase space shows that the a and b parameters are highly correlated, as expected. The degree to which these χ2 values vary throughout a flight leg is influenced by how the PSDs, TWC from the Nevzorov probe, and Z from radar vary within a flight leg of similar temperature. Flight legs that have little variability in the microphysical properties and an allowable tolerance equal to the minimum χ2 in the (a,b) phase space, such as the 10:03:05–10:08:45 UTC period on 25 April, occupy a surface area in the (a,b) phase space that is up to 8.7 times larger than flight legs where microphysical properties vary more, such as the 11:05:20–11:14:45 UTC leg on the same day.
-
Surfaces of equally plausible solutions appear dependent on temperature for the 25 April and 20 May events. The range of plausible a and b coefficients is larger for flight legs of lower temperature, and 80 % of the surfaces compared between the lowest and highest temperature for each day overlap by less than 50 %.
-
Cases with little dependence of the surfaces of equally plausible solutions on temperature, like the flight legs analyzed on 23 May, can be explained in terms of the regions of cloud sampled and the types of ice hydrometeors observed. A mean overlap of 62.1 % between four of the five (a,b) surfaces on that day is consistent with previous studies (e.g., Heymsfield et al., 2007) that note little dependence in the a coefficient on temperature in anvil cirrus clouds.
-
The minimum χ2 in the (a,b) phase space determines the allowable tolerance Δχ2 for 5 of the 16 flight legs when determining the set of equally plausible a and b coefficients, whereas the combined uncertainty due to measurement error from the OAPs, Nevzorov TWC probe, and radar determines the Δχ2 for the remaining 11 flight legs. This means that the uncertainty in the m–D coefficients is driven by uncertainties in the measurements the majority of the time, with the natural parameter variability over a flight leg being a driving factor for 31 % of the flight legs observed. Thus, efforts to reduce measurement errors could reduce the uncertainty in derived (a,b) coefficients.
-
The covariability in a and b permits possible solutions of b>3 for the ranges of particle sizes observed in 7 of the 16 flight legs analyzed. For these flight legs this covariability means that the Z derived from a and b and the PSDs is still within 82.4 % of the mean matched radar Z, which is marginally greater than the 50.5 % difference when b is not greater than 3.
-
Flight legs where the cloud particles have lower effective density ρe, such as the −5.5 and −10.5 ∘C flight legs on 20 May, yield minimum b values in the (a,b) phase space as much as 0.78 larger than clouds with a higher ρe like the −16 and −23 ∘C legs on the same day. These differences can be explained by the different impacts of ρe on TWC compared to Z.
A key finding of this study is that a range of a and b coefficients should be considered equally plausible for a given environment due to the natural variability in cloud conditions and measurement uncertainties, even within a similar temperature range. This variability results in a large range of a and b as equally plausible solutions (as indicated in this study) and could explain the range in m–D coefficients determined in past studies (Fig. 1), where a coefficients can vary by 3 orders of magnitude and b coefficients can vary in value between 1 and 3 for measurements taken in similar environmental conditions. The technique used in this study provides insight into how equally plausible m–D coefficients can arise because the dependence of derived microphysical parameters on environmental conditions is sometimes more important than measurement uncertainties based on the instruments used to collect the data, but this is not always the case. Furthermore, it is shown that the dependence of the (a,b) coefficients on temperature is still notable even when considering the ranges of equally plausible solutions. Future studies should further ascertain the extent to which the dependence of (a,b) on other environmental parameters is robust enough to be distinguished from the natural variability in the surface or its variability due to measurement errors.
While representing m–D coefficients as a range of equally plausible solutions may address shortcomings of microphysical parameterization schemes and remote sensing retrievals that employ a single m–D relationship for a given ice species or environment, caution should be taken if the results presented here are applied to ranges of particle size or environments outside of those sampled (e.g., ones with different observed habits or various degrees of riming). The results presented here illustrate that a similar TWC and Z can be obtained regardless of the a and b values chosen, with coefficients randomly selected from a surface of solutions allowing one to represent how the uncertainty in (a,b) impacts any derived quantity. Thus, the large variability in the derived (a,b) for an equally plausible surface does not necessarily indicate that there is a large uncertainty in quantities derived using the a and b coefficients. Future work should assess how the representation of modeled processes and retrieved quantities are influenced by the variability in a and b coefficients as well as which environmental drivers and cloud microphysical properties influence the size of derived surfaces of equally plausible solutions and the extent to which measurement errors need to be reduced to better refine these surfaces. The approach presented in this study can be applied to additional studies that make use of collocated radar and microphysical measurements in other cloud and meteorological environments and improve the statistical robustness of plausible m–D parameters for given environmental conditions. Such studies may help us to further understand how surfaces of equally plausible (a,b) solutions are affected by different environments and the variability in cloud conditions therein, as well as the dependence of these solutions as a function of other cloud or environmental properties.
The radar (National Weather Service, 2014) and OAP (Delene and Poellot, 2012) data used in this study are found on the NASA GHRC MC3E data archive. The software packages used to match the radar data to the aircraft's location (Nesbitt et al., 2019) and to process the OAP data (McFarquhar et al., 2018) are openly available as GitHub repositories. The data containing the matched radar and microphysical properties (Finlon, 2018) used in this study are archived and available online.
| a | Prefactor component in mass–dimension relationship |
| a | Particle cross-sectional area |
| b | Exponent component in mass–dimension relationship |
| χ2 | Chi-square statistic for each (a,b) over a flight leg |
| Lowest χ2 value in the (a,b) phase space for a flight leg | |
| Threshold determined from uncertainty in the particle size distribution due to sampling statistics | |
| Threshold determined from combined uncertainty due to measurement errors | |
| Δχ2 | Maximum value of , , or |
| D | Particle maximum dimension |
| Dmm | Median mass diameter |
| IWC | Ice water content |
| KDP | Specific differential phase |
| Dielectric constant for ice | |
| Dielectric constant for water | |
| M(D) | Mass distribution function |
| N(D) | Number distribution function |
| Nt | Total number concentration |
| P | Particle perimeter |
| ρe | Effective density |
| SDP | Sigma differential phase |
| T | Environmental temperature |
| TWC | Total water content measurement |
| TWCdiff | Measure of normalized difference between the Nevzorov TWC and that derived from the N(D) for a given (a,b) defined by Eq. (3) |
| TWCSD | TWC derived from the N(D) for a given (a,b) |
| ζ | Particle sphericity |
| Z | Radar reflectivity factor |
| Zc(D) | Cumulative reflectivity distribution function up to size D′ |
| Z(D) | Reflectivity distribution function |
| Zdiff | Measure of normalized difference between the radar Z and that derived from the N(D) for a given (a,b) defined by Eq. (4) |
| ZDR | Differential reflectivity |
| ZSD | Z derived from the N(D) for a given (a,b) |
| Zt | Derived total reflectivity from the mean N(D) for a given (a,b) |
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-3621-2019-supplement.
JF prepared the paper and performed all the calculations, with contributions from all co-authors. GM provided the idea and formulated the framework for the study, SN provided the framework for matching radar gates to an aircraft's position, WW processed particle data from the optical array probes, PZ conducted the radar bias calculations used in this study, and RR and HM provided feedback on the ideas and calculations presented.
The authors declare that they have no conflict of interest.
This research was supported by the US Department of Energy grants
DE-SC0014065 and DE-SC0016476 (through UCAR subcontract SUBAWD000397), by the
NASA Precipitation Measurement Missions grant NNX16AD80G, and by the National
Science Foundation grant AGS-1247404. We thank all participants of MC3E for
collecting the data used in this study.
Edited by: Martina Krämer
Reviewed by: Darrel Baumgardner and one anonymous referee
Barnes, S. L.: A Technique for Maximizing Details in Numerical Weather Map Analysis, J. Appl. Meteorol., 3, 396–409, https://doi.org/10.1175/1520-0450(1964)003<0396:ATFMDI>2.0.CO;2, 1964. a
Baumgardner, D. and Korolev, A.: Airspeed Corrections for Optical Array Probe Sample Volumes, J. Atmos. Ocean. Tech., 14, 1224–1229, https://doi.org/10.1175/1520-0426(1997)014<1224:ACFOAP>2.0.CO;2, 1997. a
Bringi, V. N. and Chandrasekar, V.: Polarimetric Doppler Weather Radar: Principles and Applications, Cambridge University Press, 2001. a
Bringi, V. N., Chandrasekar, V., Balakrishnan, N., and Zrnic, D. S.: An Examination of Propagation Effects in Rainfall on Radar Measurements at Microwave Frequencies, J. Atmos. Ocean. Tech., 7, 829–840, https://doi.org/10.1175/1520-0426(1990)007<0829:AEOPEI>2.0.CO;2, 1990. a
Brown, P. R. A. and Francis, P. N.: Improved Measurements of the Ice Water Content in Cirrus Using a Total-Water Probe, J. Atmos. Ocean. Tech., 12, 410–414, https://doi.org/10.1175/1520-0426(1995)012<0410:IMOTIW>2.0.CO;2,1995. a, b
Cazenave, F., Gosset, M., Kacou, M., Alcoba, M., Fontaine, E., Duroure, C., and Dolan, B.: Characterization of Hydrometeors in Sahelian Convective Systems with an X-Band Radar and Comparison with In Situ Measurements. Part I: Sensitivity of Polarimetric Radar Particle Identification Retrieval and Case Study Evaluation, J. Appl. Meteorol. Clim., 55, 231–249, https://doi.org/10.1175/JAMC-D-15-0013.1, 2016. a
Cotton, R. J., Field, P. R., Ulanowski, Z., Kaye, P. H., Hirst, E., Greenaway, R. S., Crawford, I., Crosier, J., and Dorsey, J.: The effective density of small ice particles obtained from in situ aircraft observations of mid-latitude cirrus, Q. J. Roy. Meteor. Soc., 139, 1923–1934, https://doi.org/10.1002/qj.2058, 2013. a
Delanoë, J. and Hogan, R. J.: Combined CloudSat-CALIPSO-MODIS retrievals of the properties of ice clouds, J. Geophys. Res., 115, D00H29, https://doi.org/10.1029/2009JD012346, 2010. a
Delene, D. and Poellot, M. R.: GPM Ground Validation UND Citation Cloud Microphysics MC3E, NASA Glob. Hydrol. Resour. Cent. DAAC, https://doi.org/10.5067/GPMGV/MC3E/MULTIPLE/DATA201, 2012. a
Erfani, E. and Mitchell, D. L.: Developing and bounding ice particle mass- and area-dimension expressions for use in atmospheric models and remote sensing, Atmos. Chem. Phys., 16, 4379–4400, https://doi.org/10.5194/acp-16-4379-2016, 2016. a
Field, P. R.: Aircraft Observations of Ice Crystal Evolution in an Altostratus Cloud, J. Atmos. Sci., 56, 1925–1941, https://doi.org/10.1175/1520-0469(1999)056<1925:AOOICE>2.0.CO;2, 1999. a
Field, P. R., Wood, R., Brown, P. R. A., Kaye, P. H., Hirst, E., Greenaway, R., and Smith, J. A.: Ice Particle Interarrival Times Measured with a Fast FSSP, J. Atmos. Ocean. Tech., 20, 249–261, https://doi.org/10.1175/1520-0426(2003)020<0249:IPITMW>2.0.CO;2, 2003. a, b
Field, P. R., Heymsfield, A. J., and Bansemer, A.: Shattering and Particle Interarrival Times Measured by Optical Array Probes in Ice Clouds, J. Atmos. Ocean. Tech., 23, 1357–1371, https://doi.org/10.1175/JTECH1922.1, 2006. a
Finlon, J. A.: Matched Radar and Microphysical Properties During MC3E, https://doi.org/10.13012/B2IDB-6396968_V1, 2018. a
Finlon, J. A., McFarquhar, G. M., Rauber, R. M., Plummer, D. M., Jewett, B. F., Leon, D., and Knupp, K. R.: A Comparison of X-Band Polarization Parameters with In Situ Microphysical Measurements in the Comma Head of Two Winter Cyclones, J. Appl. Meteorol. Clim., 55, 2549–2574, https://doi.org/10.1175/JAMC-D-16-0059.1, 2016. a, b
Fontaine, E., Schwarzenboeck, A., Delanoë, J., Wobrock, W., Leroy, D., Dupuy, R., Gourbeyre, C., and Protat, A.: Constraining mass-diameter relations from hydrometeor images and cloud radar reflectivities in tropical continental and oceanic convective anvils, Atmos. Chem. Phys., 14, 11367–11392, https://doi.org/10.5194/acp-14-11367-2014, 2014. a, b, c
Giangrande, S. E., Toto, T., Bansemer, A., Kumjian, M. R., Mishra, S., and Ryzhkov, A. V.: Insights into riming and aggregation processes as revealed by aircraft, radar, and disdrometer observations for a 27 April 2011 widespread precipitation event, J. Geophys. Res.-Atmos., 121, 5846–5863, https://doi.org/10.1002/2015JD024537, 2016. a
Hallett, J.: Handbook of Weather, Climate, and Water, John Wiley & Sons, Inc., Hoboken, NJ, USA, https://doi.org/10.1002/0471721603, 2003. a, b
Helmus, J. and Collis, S.: The Python ARM Radar Toolkit (Py-ART), a Library for Working with Weather Radar Data in the Python Programming Language, J. Open Res. Softw., 4, e25, doi:10.5334/jors.119, 2016. a
Heymsfield, A.: Ice Crystal Terminal Velocities, J. Atmos. Sci., 29, 1348–1357, https://doi.org/10.1175/1520-0469(1972)029<1348:ICTV>2.0.CO;2, 1972. a
Heymsfield, A. J. and Baumgardner, D.: Summary of a workshop on processing 2-D probe data, B. Am. Meteorol. Soc., 66, 437–440, 1985. a
Heymsfield, A. J., Lewis, S., Bansemer, A., Iaquinta, J., Miloshevich, L. M., Kajikawa, M., Twohy, C., and Poellot, M. R.: A General Approach for Deriving the Properties of Cirrus and Stratiform Ice Cloud Particles, J. Atmos. Sci., 59, 3–29, https://doi.org/10.1175/1520-0469(2002)059<0003:AGAFDT>2.0.CO;2, 2002. a
Heymsfield, A. J., Bansemer, A., and Twohy, C. H.: Refinements to Ice Particle Mass Dimensional and Terminal Velocity Relationships for Ice Clouds, Part I: Temperature Dependence, J. Atmos. Sci., 64, 1047–1067, https://doi.org/10.1175/JAS3890.1, 2007. a, b
Heymsfield, A. J., Schmitt, C., Bansemer, A., and Twohy, C. H.: Improved Representation of Ice Particle Masses Based on Observations in Natural Clouds, J. Atmos. Sci., 67, 3303–3318, https://doi.org/10.1175/2010JAS3507.1, 2010. a
Heymsfield, A. J., Field, P. R., Bailey, M., Rogers, D., Stith, J., Twohy, C., Wang, Z., and Haimov, S.: Ice in Clouds Experiment-Layer Clouds, Part I: Ice Growth Rates Derived from Lenticular Wave Cloud Penetrations, J. Atmos. Sci., 68, 2628–2654, https://doi.org/10.1175/JAS-D-11-025.1, 2011. a
Heymsfield, A. J., Schmitt, C., and Bansemer, A.: Ice Cloud Particle Size Distributions and Pressure-Dependent Terminal Velocities from In Situ Observations at Temperatures from 0∘ to −86 ∘C, J. Atmos. Sci., 70, 4123–4154, https://doi.org/10.1175/JAS-D-12-0124.1, 2013. a, b
Hogan, R. J., Illingworth, A. J., and Sauvageot, H.: Measuring crystal size in cirrus using 35- and 94-GHz radars, J. Atmos. Ocean. Tech., 17, 27–37, https://doi.org/10.1175/1520-0426(2000)017<0027:MCSICU>2.0.CO;2, 2000. a
Hogan, R. J., Mittermaier, M. P., and Illingworth, A. J.: The Retrieval of Ice Water Content from Radar Reflectivity Factor and Temperature and Its Use in Evaluating a Mesoscale Model, J. Appl. Meteorol. Clim., 45, 301–317, https://doi.org/10.1175/JAM2340.1, 2006. a
Hogan, R. J., Tian, L., Brown, P. R. A., Westbrook, C. D., Heymsfield, A. J., and Eastment, J. D.: Radar Scattering from Ice Aggregates Using the Horizontally Aligned Oblate Spheroid Approximation, J. Appl. Meteorol. Clim., 51, 655–671, https://doi.org/10.1175/JAMC-D-11-074.1, 2012. a, b
Ice, R. L., Richardson, L. M., Daniel, A. E., Free, A. D., Macemon, R. W., Krause, J. C., Secrest, G., Lee, R. R., Melnikov, V. M., and Hubbert, J. C.: Monitoring the Performance of the Polarimetric WSR-88D-Calibration and Sensitivity, in: 33rd Conference on Environmental Information Processing Technologies, American Meteorological Society, 2017. a
Jackson, R. C., McFarquhar, G. M., Stith, J., Beals, M., Shaw, R. A., Jensen, J., Fugal, J., and Korolev, A.: An Assessment of the Impact of Antishattering Tips and Artifact Removal Techniques on Cloud Ice Size Distributions Measured by the 2D Cloud Probe, J. Atmos. Ocean. Tech., 31, 2567–2590, https://doi.org/10.1175/JTECH-D-13-00239.1, 2014. a
Jensen, M. P., Giangrande, S. E., and Kollias, P.: The Mid-latitude Continental Convective Clouds Experiment (MC3E) Final Campaign Report, 1–13, 2014. a
Jensen, M. P., Petersen, W. A., Bansemer, A., Bharadwaj, N., Carey, L. D., Cecil, D. J., Collis, S. M., Del Genio, A. D., Dolan, B., Gerlach, J., Giangrande, S. E., Heymsfield, A., Heymsfield, G., Kollias, P., Lang, T. J., Nesbitt, S. W., Neumann, A., Poellot, M., Rutledge, S. A., Schwaller, M., Tokay, A., Williams, C. R., Wolff, D. B., Xie, S., Zipser, E. J., Jensen, M. P., Petersen, W. A., Bansemer, A., Bharadwaj, N., Carey, L. D., Cecil, D. J., Collis, S. M., Genio, A. D. D., Dolan, B., Gerlach, J., Giangrande, S. E., Heymsfield, A., Heymsfield, G., Kollias, P., Lang, T. J., Nesbitt, S. W., Neumann, A., Poellot, M., Rutledge, S. A., Schwaller, M., Tokay, A., Williams, C. R., Wolff, D. B., Xie, S., and Zipser, E. J.: The Midlatitude Continental Convective Clouds Experiment (MC3E), B. Am. Meteorol. Soc., 97, 1667–1686, https://doi.org/10.1175/BAMS-D-14-00228.1, 2016. a, b, c
Korolev, A. and Field, P. R.: Assessment of the performance of the inter-arrival time algorithm to identify ice shattering artifacts in cloud particle probe measurements, Atmos. Meas. Tech., 8, 761–777, https://doi.org/10.5194/amt-8-761-2015, 2015. a
Korolev, A., Emery, E., and Creelman, K.: Modification and Tests of Particle Probe Tips to Mitigate Effects of Ice Shattering, J. Atmos. Ocean. Tech., 30, 690–708, https://doi.org/10.1175/JTECH-D-12-00142.1, 2013a. a
Korolev, A., Strapp, J. W., Isaac, G. A., and Emery, E.: Improved Airborne Hot-Wire Measurements of Ice Water Content in Clouds, J. Atmos. Ocean. Tech., 30, 2121–2131, https://doi.org/10.1175/JTECH-D-13-00007.1, 2013b. a, b
Korolev, A. V., Strapp, J. W., Isaac, G. A., and Nevzorov, A. N.: The Nevzorov Airborne Hot-Wire LWC-TWC Probe: Principle of Operation and Performance Characteristics, J. Atmos. Ocean. Tech., 15, 1495–1510, https://doi.org/10.1175/1520-0426(1998)015<1495:TNAHWL>2.0.CO;2, 1998. a
Korolev, A. V., Emery, E. F., Strapp, J. W., Cober, S. G., Isaac, G. A., Wasey, M., and Marcotte, D.: Small Ice Particles in Tropospheric Clouds: Fact or Artifact? Airborne Icing Instrumentation Evaluation Experiment, B. Am. Meteorol. Soc., 92, 967–973, https://doi.org/10.1175/2010BAMS3141.1, 2011. a, b
Krajewski, W. F. and Ciach, G. J.: Towards Probabilistic Quantitative Precipitation WSR88D Algorithms: Preliminary Studies and Problem Formulation, Tech. Rep., DG133W-02-CN-0089, NOAA/NWS, 2003. a
Lawson, R. P., Woods, S., and Morrison, H.: The Microphysics of Ice and Precipitation Development in Tropical Cumulus Clouds, J. Atmos. Sci., 72, 2429–2445, https://doi.org/10.1175/JAS-D-14-0274.1, 2015. a
Lemke, H. M. and Quante, M.: Backscatter characteristics of nonspherical ice crystals: Assessing the potential of polarimetric radar measurements, J. Geophys. Res.-Atmos., 104, 31739–31751, https://doi.org/10.1029/1999JD900490, 1999. a
Leroy, D., Fontaine, E., Schwarzenboeck, A., and Strapp, J. W.: Ice Crystal Sizes in High Ice Water Content Clouds. Part I: On the Computation of Median Mass Diameter from In Situ Measurements, J. Atmos. Ocean. Tech., 33, 2461–2476, https://doi.org/10.1175/JTECH-D-15-0151.1, 2016. a
Liu, G. and Curry, J. A.: Determination of Ice Water Path and Mass Median Particle Size Using Multichannel Microwave Measurements, J. Appl. Meteorol., 39, 1318–1329, https://doi.org/10.1175/1520-0450(2000)039<1318:DOIWPA>2.0.CO;2, 2000. a
Locatelli, J. D. and Hobbs, P. V.: Fall speeds and masses of solid precipitation particles, J. Geophys. Res., 79, 2185–2197, https://doi.org/10.1029/JC079i015p02185, 1974. a
Maahn, M., Löhnert, U., Kollias, P., Jackson, R. C., and McFarquhar, G. M.: Developing and Evaluating Ice Cloud Parameterizations for Forward Modeling of Radar Moments Using in situ Aircraft Observations, J. Atmos. Ocean. Tech., 32, 880–903, https://doi.org/10.1175/JTECH-D-14-00112.1, 2015. a
Magono, C. and Nakamura, T.: Aerodynamic Studies of Falling Snowflakes, J. Meteorol. Soc. Jpn., 43, 139–147, 1965. a
Maneewongvatana, S. and Mount, D. M.: It's okay to be skinny, if your friends are fat, in: 4th Annual CGC Workshop on Computational Geometry, 1999. a
Mascio, J., Xu, Z., and Mace, G. G.: The Mass-Dimensional Properties of Cirrus Clouds During TC4, J. Geophys. Res.-Atmos., 122, 10402–10417, https://doi.org/10.1002/2017JD026787, 2017. a
Matrosov, S. Y.: Modeling Backscatter Properties of Snowfall at Millimeter Wavelengths, J. Atmos. Sci., 64, 1727–1736, https://doi.org/10.1175/JAS3904.1, 2007. a, b
Matrosov, S. Y.: Assessment of Radar Signal Attenuation Caused by the Melting Hydrometeor Layer, IEEE T. Geosci. Remote, 46, 1039–1047, https://doi.org/10.1109/TGRS.2008.915757, 2008. a
McCumber, M., Tao, W.-K., Simpson, J., Penc, R., Soong, S.-T., McCumber, M., Tao, W.-K., Simpson, J., Penc, R., and Soong, S.-T.: Comparison of Ice-Phase Microphysical Parameterization Schemes Using Numerical Simulations of Tropical Convection, J. Appl. Meteorol., 30, 985–1004, https://doi.org/10.1175/1520-0450-30.7.985, 1991. a
McFarquhar, G. M. and Heymsfield, A. J.: Microphysical Characteristics of Three Anvils Sampled during the Central Equatorial Pacific Experiment, J. Atmos. Sci., 53, 2401–2423, https://doi.org/10.1175/1520-0469(1996)053<2401:MCOTAS>2.0.CO;2, 1996. a
McFarquhar, G. M., Timlin, M. S., Nousiainen, T., and Yang, P.: A New Representation of the Single-Scattering Properties for Mid-latitude Clouds and its Impacts, in: Fifteenth ARM Science Team Meeting Proceedings, 2005. a
McFarquhar, G. M., Timlin, M. S., Rauber, R. M., Jewett, B. F., Grim, J. A., and Jorgensen, D. P.: Vertical Variability of Cloud Hydrometeors in the Stratiform Region of Mesoscale Convective Systems and Bow Echoes, Mon. Weather Rev., 135, 3405–3428, https://doi.org/10.1175/MWR3444.1, 2007a. a, b, c
McFarquhar, G. M., Zhang, G., Poellot, M. R., Kok, G. L., McCoy, R., Tooman, T., Fridlind, A., and Heymsfield, A. J.: Ice properties of single-layer stratocumulus during the Mixed-Phase Arctic Cloud Experiment: 1. Observations, J. Geophys. Res.-Atmos., 112, 1–19, https://doi.org/10.1029/2007JD008633, 2007b. a
McFarquhar, G. M., Hsieh, T.-L., Freer, M., Mascio, J., and Jewett, B. F.: The Characterization of Ice Hydrometeor Gamma Size Distributions as Volumes in N0-μ-λ Phase Space: Implications for Microphysical Process Modeling, J. Atmos. Sci., 72, 892–909, https://doi.org/10.1175/JAS-D-14-0011.1, 2015. a, b, c, d, e
McFarquhar, G. M., Baumgardner, D., Bansemer, A., Abel, S. J., Crosier, J., French, J., Rosenberg, P., Korolev, A., Schwarzoenboeck, A., Leroy, D., Um, J., Wu, W., Heymsfield, A. J., Twohy, C., Detwiler, A., Field, P., Neumann, A., Cotton, R., Axisa, D., Dong, J., McFarquhar, G. M., Baumgardner, D., Bansemer, A., Abel, S. J., Crosier, J., French, J., Rosenberg, P., Korolev, A., Schwarzoenboeck, A., Leroy, D., Um, J., Wu, W., Heymsfield, A. J., Twohy, C., Detwiler, A., Field, P., Neumann, A., Cotton, R., Axisa, D., and Dong, J.: Processing of Ice Cloud In Situ Data Collected by Bulk Water, Scattering, and Imaging Probes: Fundamentals, Uncertainties, and Efforts toward Consistency, Meteorol. Monogr., 58, 11.1–11.33, https://doi.org/10.1175/AMSMONOGRAPHS-D-16-0007.1, 2017. a, b
McFarquhar, G. M., Finlon, J. A., Stechman, D. M., Wu, W., Jackson, R. C., and Freer, M.: University of Illinois/Oklahoma Optical Array Probe (OAP) Processing Software, https://doi.org/10.5281/zenodo.1285969, 2018. a, b
Mitchell, D. L.: Use of Mass- and Area-Dimensional Power Laws for Determining Precipitation Particle Terminal Velocities, J. Atmos. Sci., 53, 1710–1723, https://doi.org/10.1175/1520-0469(1996)053<1710:UOMAAD>2.0.CO;2, 1996. a, b
Mitchell, D. L. and Arnott, W. P.: A Model Predicting the Evolution of Ice Particle Size Spectra and Radiative Properties of Cirrus Clouds, Part II: Dependence of Absorption and Extinction on Ice Crystal Morphology, J. Atmos. Sci., 51, 817–832, https://doi.org/10.1175/1520-0469(1994)051<0817:AMPTEO>2.0.CO;2, 1994. a
Mitchell, D. L., Zhang, R., and Pitter, R. L.: Mass-Dimensional Relationships for Ice Particles and the Influence of Riming on Snowfall Rates, J. Appl. Meteorol., 29, 153–163, https://doi.org/10.1175/1520-0450(1990)029<0153:MDRFIP>2.0.CO;2, 1990. a
Nakaya, U. and Terada, T. J.: Simultaneous Observations of the Mass, Falling Velocity and Form of Individual Snow Crystals, Journal of the Faculty of Science, Hokkaido Imperial University, 1, 191–200, 1935. a
National Weather Service: GPM Ground Validation KVNX NEXRAD MC3E, NASA Glob. Hydrol. Resour. Cent. DAAC, https://doi.org/10.5067/MC3E/NEXRAD/DATA202, 2014. a
Nesbitt, S., Guy, N., Lang, T., Lyons, A. and Finlon, J.: Airborne Weather Observation Toolkit (AWOT), https://doi.org/10.5281/ZENODO.2587168, 2019. a, b
Nevzorov, A. N.: Aircraft cloud water content meter, in: Communications a la VIIIeme Conference Internationale sur la Physique des Nuages, AIMPA, 701–703, 1980. a
Olson, W. S., Tian, L., Grecu, M., Kuo, K.-S., Johnson, B. T., Heymsfield, A. J., Bansemer, A., Heymsfield, G. M., Wang, J. R., and Meneghini, R.: The Microwave Radiative Properties of Falling Snow Derived from Nonspherical Ice Particle Models, Part II: Initial Testing Using Radar, Radiometer and In Situ Observations, J. Appl. Meteorol. Clim., 55, 709–722, https://doi.org/10.1175/JAMC-D-15-0131.1, 2016. a
Park, S.-G., Bringi, V. N., Chandrasekar, V., Maki, M., and Iwanami, K.: Correction of Radar Reflectivity and Differential Reflectivity for Rain Attenuation at X Band, Part I: Theoretical and Empirical Basis, J. Atmos. Ocean. Tech., 22, 1621–1632, https://doi.org/10.1175/JTECH1803.1, 2005. a
Schmitt, C. G. and Heymsfield, A. J.: The Dimensional Characteristics of Ice Crystal Aggregates from Fractal Geometry, J. Atmos. Sci., 67, 1605–1616, https://doi.org/10.1175/2009JAS3187.1, 2010. a
Szyrmer, W. and Zawadzki, I.: Snow Studies, Part II: Average Relationship between Mass of Snowflakes and Their Terminal Fall Velocity, J. Atmos. Sci., 67, 3319–3335, https://doi.org/10.1175/2010JAS3390.1, 2010. a
Wang, J., Dong, X., and Xi, B.: Investigation of ice cloud microphysical properties of DCSs using aircraft in situ measurements during MC3E over the ARM SGP site, J. Geophys. Res.-Atmos., 120, 3533–3552, https://doi.org/10.1002/2014JD022795, 2015. a
Wu, W. and McFarquhar, G. M.: On the Impacts of Different Definitions of Maximum Dimension for Nonspherical Particles Recorded by 2D Imaging Probes, J. Atmos. Ocean. Tech., 33, 1057–1072, https://doi.org/10.1175/JTECH-D-15-0177.1, 2016. a, b, c
Xu, Z. and Mace, G. G.: Ice Particle Mass-Dimensional Relationship Retrieval and Uncertainty Evaluation Using the Optimal Estimation Methodology Applied to the MACPEX Data, J. Appl. Meteorol. Clim., 56, 767–788, https://doi.org/10.1175/JAMC-D-16-0222.1, 2017. a
Zhang, P., Zrnic, D., and Ryzhkov, A.: Partial Beam Blockage Correction Using Polarimetric Radar Measurements, J. Atmos. Ocean. Tech., 30, 861–872, https://doi.org/10.1175/JTECH-D-12-00075.1, 2013. a
Zikmunda, J. and Vali, G.: Fall Patterns and Fall Velocities of Rimed Ice Crystals, J. Atmos. Sci., 29, 1334–1347, https://doi.org/10.1175/1520-0469(1972)029<1334:FPAFVO>2.0.CO;2, 1972. a
equally realizableparameters based on the natural variability in cloud conditions observed by aircraft over the Great Plains. Results from this approach address shortcomings of microphysical parameterization schemes and remote sensing retrievals that employ a single m–D relation for a given ice species or environment.