Accounting for the effects of nonideal minor structures on the optical properties of black carbon aerosols

Black carbon (BC) aerosol is the strongest sunlight-absorbing aerosol, and its optical properties are fundamental to radiative forcing estimations and retrievals of its size and concentration. BC particles exist as aggregate structures with small monomers and are widely represented by the idealized fractal aggregate model. In reality, BC particles possess complex and nonideal minor structures besides the overall aggregate structure, altering their optical properties in unforeseen ways. This study introduces the parameter “volume variation” to quantify and unify different minor structures and develops an empirical relationship to account for their effects on BC optical properties from those of ideal aggregates. Minor structures considered are as follows: the polydispersity of monomer size, the irregularity and coating of the individual monomer, and necking and overlapping among monomers. The discrete dipole approximation is used to calculate the optical properties of aggregates with these minor structures. Minor structures result in scattering cross-section enhancement slightly more than that of absorption cross section, and their effects on the angle-dependent phase matrix as well as asymmetry factor are negligible. As expected, the effects become weaker with the increase in wavelength. Our results suggest that a correction ratio of 1.05 is necessary to account for the mass or volume normalized absorption and scattering of nonideal aggregates in comparison to ideal ones, which also applies to aggregates with multiple minor structures. In other words, the effects of minor structures are mainly contributed by their influence on particle volume/mass that cannot be ignored, and a relative difference of approximately 5 % is noticed after removing the volume effects. Thus, accurate knowledge and evaluation of BC volume/mass are more important than those of the minor structures themselves. Most importantly, the simulations of optical properties of nonideal aggregates are greatly simplified by applying the empirical relationship because they can be directly obtained from those of the corresponding ideal aggregates, a volume/mass difference parameter, and the correction factor, i.e., 1.05, not the detailed minor structure information. We expect this convenient treatment to find wide applications for the accounting for the effects of nonideal minor structures on BC optical properties.

1 Introduction

Black carbon (BC), produced by incomplete combustion of fossil fuels, biofuels, and biomass, is one of the strongest sunlight-absorbing atmospheric constituents (Jacobson, 2001; Andreae and Gelencsér, 2006). BC particles affect the radiative balance at global and regional scales by absorbing solar radiation and reducing the radiation reaching the surface (Crutzen and Andreae, 1990; Menon et al., 2002; Kahnert and Devasthale, 2011). Thus, the optical properties of BC particles are fundamental not only to radiative forcing estimations but also to retrievals of their size and concentration, whereas they are, in turn, highly dependent on the complex and heterogeneous morphology of BC particles.

Fractal aggregates have been widely used to represent BC geometries and to obtain their optical properties (Farias et al., 1996; Liu et al., 2012; Bescond et al., 2013). In the fractal aggregate model, aggregates are formed by numerous perfect same-sized spheres, also called monomers, that are in point contact. Mathematically, fractal aggregates are described by the following statistic scaling rule (Sorensen, 2001):

$$\begin{array}{}\text{(1)}& N=k_{\mathrm{f}}{\left({\displaystyle \frac{R_{\mathrm{g}}}{a_o}}\right)}^{D_{\mathrm{f}}},\end{array}$$

where N is the number of monomers in an aggregate, a_o is the radius of primary monomers, and R_g is the gyration radius. k_f (fractal prefactor) and D_f (fractal dimension) are parameters describing the aggregate overall structure, i.e., lacy or compact. A large amount of experimental evidence confirms that freshly emitted BC particles are normally chain-like, lacy aggregates with D_f less than 2, whereas aged BC aggregates tend to be more compact, with D_f values even close to 3 (Sorensen, 2001; Chakrabarty et al., 2009; Wang et al., 2017).

Figure 1 Examples of TEM/SEM images of BC particles from different in situ or laboratory observations (Gwaze et al., 2006; Kamimoto et al., 2007; Chakrabarty et al., 2009; Yon et al., 2015; Wang et al., 2017).

BC particles in the ambient atmosphere show significant diversities in their morphologies and are much more complex than the idealized fractal-like aggregates specified by Eq. (1), which only describe their general morphology (Wu et al., 2015a; Pirjola et al., 2017). Figure 1 shows some examples of transmission electron microscope and scanning electron microscope (TEM/SEM) images of BC particles sampled under different real-world scenarios (Gwaze et al., 2006; Kamimoto et al., 2007; Chakrabarty et al., 2009; Yon et al., 2015; Wang et al., 2017). The particles are obviously highly complex, not only in their overall morphology but also concerning their detailed structures. As is apparent, actual BC particles display features that are quite different from the assumptions used for fractal aggregates (e.g., same-sized, perfectly spherical, and point contacting), such as polydispersity of monomer size and necking and overlapping among monomers. Furthermore, BC aggregates also get mixed with organic or inorganic aerosols in varying proportions during transport and aging (e.g., the left column of Fig. 1), and the mixing can alter their morphology as well. Several studies have been carried out to quantify these detailed structures to better represent them in numerical models (Cheng et al., 2014; Moteki, 2016). Among them, the polydispersity of monomer size is the most well studied (Chakrabarty et al., 2006, 2007; Bescond et al., 2014; Wu et al., 2015b), and a complete set of methods have been established to characterize monomer size distribution. Bourrous et al. (2018) developed a semiautomatic analysis to obtain the overlap coefficient and specific surface areas of aggregates. All these studies show clearly and quantitatively the existence of detailed minor structures of actual BC aggregates.

The overall fractal aggregate morphologies and their influences on the optical properties of BC particles have been well studied (Sorensen, 2001; Liu and Mishchenko, 2005; Kahnert and Devasthale, 2011). The minor structures mentioned above, which have even smaller length scales than the aggregate overall size, also gain significant attention for their influence on aggregate optical properties (Farias et al., 1996; Bond et al., 2006; Scarnato et al., 2013). As a consequence, more realistic and detailed models have been developed to improve our knowledge of the optical properties of BC aggregates. Farias et al. (1996) confirmed the effects of particle polydispersity on mean optical cross sections, with an amplification ratio of 1.2 and 1.8 for absorption and scattering, respectively; however, a recent study by Liu et al. (2015) found the ratios to be 1 and 2.5, respectively. The significant differences of the amplification ratios are mainly caused by different monomer size distributions as well as aggregate parameters considered in the studies. Bescond et al. (2013) evaluated the impact of overlapping and necking on the radiative properties of soot aggregates, with the main focus of their effects being on depolarization. Skorupski and Mroczka (2014) extended the investigation to the effects of overlapping and necking on the absorption and scattering properties and found that the effects of “small” necking can be ignored, but when overlap occurs the effects are pronounced. However, Yon et al. (2015) showed that overlapping and necking may significantly affect the absorption and scattering properties with the amplification factor being up to 2 at a wavelength of 266 nm. Meanwhile, small- to moderate-scale coating in different forms have been considered in numerical models to study their effects on the optical properties, and the impact of coating on absorption was found to be, on average, 1.1 in the visible spectral range (Scarnato et al., 2013; Dong et al., 2015; Doner et al., 2017). For a relatively small amount of coating, the extinction and absorption cross sections are approximately enhanced, respectively, by 5 % and 3 % as the volume fraction of coating increases from 0.01 to 0.2, as shown by Liu et al. (2012). However, Dong et al. (2015) indicated that the amplification factors of absorption and scattering increase to 1.15 and 2 for a partial coating with a volume fraction of 0.5.

Table 1 Comparison of the previous studies on effects of minor structures on optical properties of fractal aggregates.

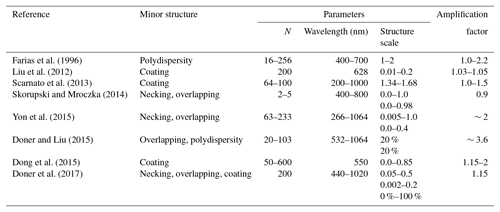
Table 1 summarizes some of the previous studies investigating the effects of nonideal minor structures on BC optical properties (Farias et al., 1996; Liu et al., 2012; Scarnato et al., 2013; Skorupski and Mrocz, 2014; Yon et al., 2015; Dong et al., 2015; Doner and Liu, 2017; Doner et al., 2017). Key parameters for simulations, including the monomer number, wavelength, structure scale, and the key conclusions are given in the table. The average amplification factor of optical properties caused by these minor structures is used to specify these effects. Obviously, quite different conclusions are found, and this can be attributed to the different assumptions and parameters used in the numerical models. Because of the lack of a unified approach and criterion to quantify the effects of various minor structures, it is difficult to gain an overall quantitative understanding of such effects and to incorporate these effects in numerical models for climate modeling and the retrieval of BC concentrations in optical diagnostics. The relevant investigations will also likely continue to focus on the effects of certain specific structures. Furthermore, with a clear knowledge that the minor structures of aggregates do influence their optical properties, the numerical simulations and applications for radiative properties of BC particles become more difficult because more sophisticated and less computationally efficient numerical models are required to accurately capture the effects of such nonideal structures. Thus, it becomes an open question as to how we should deal with these different structures and apply them to practical applications in the future.

This study systematically investigates the effects of several minor structures on the optical properties of BC aggregates, including the polydispersity of monomer size, monomer surface irregularity, coating, necking, and overlapping and develops a simple method to account for their effects from the optical properties of the corresponding idealized fractal aggregates. This paper is organized as follows. Section 2 introduces the numerical models of BC aggregates with different minor structures and unifies them by introducing a parameter of “volume variation”. The effects of the minor structures and the empirical relationship to consider them in practical applications are discussed in Sect. 3. Section 4 concludes this study.

2 Minor structures

Actual BC aggregates always possess imperfectly detailed structures, and, to account for their effects on the optical properties of BC aggregates in numerical simulations, accurate numerical models to adequately represent such structures are needed. We define the imperfect geometries, such as monomer size polydispersity, monomer nonsphericity (or irregular monomer surface), thin coating, necking, and overlapping, as “minor structures” in this paper. First, the “minor” indicates that the structures are relevant at the monomer scale and do not strongly alter the overall fractal aggregate structure. Secondly, the structures are assumed to change the aggregate total volume/mass slightly, e.g., a difference less than 20 % from the idealized aggregate. The following introduces the five minor structures that will be considered in this study.

The monomers are often assumed to be same-sized spheres for simplification in numerical studies on BC optical properties. However, measurements of sampled BC particles reveal that BC monomers have clear variations in their sizes, ranging from approximately 10 nm up to even 100 nm (Dankers and Leipertz, 2004; Chakrabarty et al., 2006; Bescond et al., 2014). Thus, the polydispersity of monomer size is defined as the first minor structure, i.e., M₁. Based on various observations (Köylü and Faeth, 1994; Lehre et al., 2003), a lognormal size distribution provides a close representation of realistic monomer size distribution:

$$\begin{array}{}\text{(2)}& P\left(a_{\mathrm{1}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{a}_{\mathrm{1}}\sqrt{\mathrm{2}\mathit{\pi }}\ln c_{\mathrm{1}}}}\exp \left[-{\left({\displaystyle \frac{\ln \left(a_{\mathrm{1}}/a_o\right)}{\sqrt{\mathrm{2}}\ln c_{\mathrm{1}}}}\right)}^{\mathrm{2}}\right],\end{array}$$

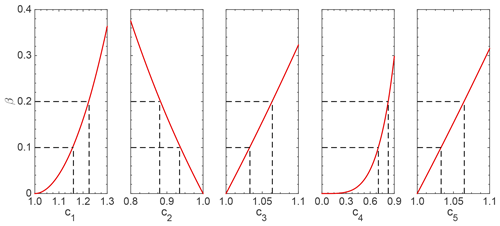
where a_o and c₁ are the geometric mean radius and geometric standard deviation, respectively, and a₁ indicates the radii defined for M₁. The M₁ shown in Fig. 2 schematically gives the two-dimensional illustration of aggregates with polydisperse monomers. As aggregate size N becomes larger, the monomer sizes should follow the aforementioned size distribution. We fix a_o to be the same as that of the same-sized monomers, and the geometric standard deviation c₁ is the only variable to specify the polydispersity. For c₁ larger than 1, the monomer radii distribute over a wider range. More details of the definition of the monomer size distribution can be found in Liu et al. (2015).

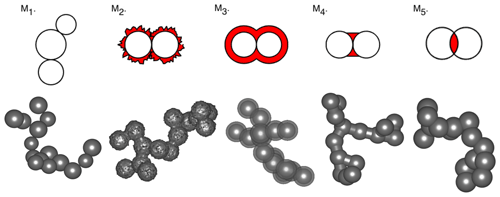
Figure 2 Two- and three-dimensional models of five minor structures. Aggregates with 15 monomers and a fractal dimension of 1.8 are considered for an example.

Secondly, the actual BC monomers in the atmosphere will never be perfectly spherical, and there must be irregularity or surface roughness to some degree for BC monomers. Therefore, we consider the irregularity of BC  monomers as the second structure feature M₂ in this study. Various numerical models, either stochastic or regular, have been developed to represent the rough surface of aerosols or ice crystals (Li et al., 2004; Kahnert et al., 2012a), and some of them can also be adopted for BC monomers. The surface roughness is a morphological feature with a random nature, and the model introduced by Muinonen et al. (1996) is used for each BC monomer. The model uses multivariate lognormal statistics (Gaussian random shape), and the monomer surface can be expressed by

$$\begin{array}{}\text{(3)}& a_{\mathrm{2}}\left(\mathit{\vartheta },\mathit{\phi }\right)={\displaystyle \frac{a_o}{\sqrt{c_{\mathrm{2}}}}}\exp \left(s\left(\mathit{\vartheta },\mathit{\phi }\right)\right).\end{array}$$

Similarly, a₂(ϑ,φ) is the function for defining monomer surface in the model M₂. ϑ and φ are the azimuth and elevation angles for given spherical coordinates. s(ϑ,φ) is the random variable obeying the Gaussian distribution with the mean value of 0 and a fixed variance of 0.05, and the same definitions are given in Muinonen et al. (1996). The degree of roughness or irregularity of each monomer is directly controlled by the standard variance of Gaussian distribution, i.e., parameter c₂. With the decrease of c₂, the surface of the monomer becomes more rough, and spikes on the surface become sharper. Following Eq. (3), an example of M₂ for two monomers is illustrated in Fig. 2, and the spikes on monomer spheres can be either outward or inward due to its randomness. The changes from that of the perfect aggregate in the aggregate volume due to irregularity are clearly represented by the red region of M₂ in Fig. 2.

Once emitted into the atmosphere, BC particles are unavoidably mixed with non-absorbing or weakly absorbing aerosols, such as sulfates, nitrates, and organic carbon, which significantly affects the absorption and scattering properties of BC particles (Jacobson, 2000; Schwarz et al., 2008; Liu et al., 2013). The third minor structure (M₃) considered is coating. The mixing states are diverse under different situations, so various complex coating models have been developed (Scarnato et al., 2013; Dong et al., 2015). Since this study focuses on monomer minor structures, a thin coating model, i.e., M₃ shown in Fig. 2, is considered by wrapping each monomer with a spherical coating shell. Thus, the radius of the coated sphere can be described by a coating parameter c₃:

$$\begin{array}{}\text{(4)}& a_{\mathrm{3}}=c_{\mathrm{3}}\cdot a_o,\end{array}$$

where c₃ is a dimensionless parameter greater than 1. The red region of M₃ in Fig. 2 indicates the coating material. As c₃ increases, the coating becomes thicker and its fraction also increases. Note that we consider only non-absorbing materials as coating in this study because absorbing aerosols will introduce additional complications.

Besides the minor structures for individual monomer discussed above, structures between neighboring monomers also exist and affect the radiative properties of BC aggregates. The fourth minor structure (M₄) is defined as “necking” between neighboring monomers, which is a result of sintering processes or surface growth around the contact point (Zaitone et al., 2009; Bescond et al., 2013). We introduce one of the simplest necking forms, i.e., a cylindrical connector, and, in other words, cylinders are added around the contact point of two neighboring monomers along their centers. A dimensionless parameter c₄ is used to quantify the radius of the circular cylinders a₄:

$$\begin{array}{}\text{(5)}& a_{\mathrm{4}}=c_{\mathrm{4}}\cdot a_o.\end{array}$$

The red region of M₄ in Fig. 2 shows the necking between two neighboring monomers. When c₄=0, the connection does not exist, and, for c₄=1, the radius of the cylinder is equal to the monomer radius.

The last minor structure (M₅) considered is overlapping between two connected monomers. Two general ways are used to generate overlapping: one is to reduce the distance between the centers of two connected monomers (Brasil et al., 1999; Yon et al., 2015), which will influence the aggregate overall compactness significantly; another is to enlarge the radius of primary monomers but keep their centers unchanged (Doner and Liu, 2017), and the aggregate overall compactness is less influenced. To keep the morphology of aggregates unchanged and consistent with that of other minor structures mentioned above, we generate the overlapping using the latter way in this paper. The enlarged monomer radius is expressed as follows:

$$\begin{array}{}\text{(6)}& a_{\mathrm{5}}=c_{\mathrm{5}}\cdot a_o.\end{array}$$

When c₅=1, the monomers are in point contact, as in the ideal fractal aggregates. With the increase of c₅, the monomers become larger and there is overlapping between connected monomers. Although overlapping leads to a decrease in the aggregate volume, as shown in the red region of M₅ in Fig. 2, the total volume still increases as the volume of each monomer is larger.

To summarize, the top row of Fig. 2 schematically illustrates the definitions of the five numerical models in two dimensions. With these basic minor structures defined quantitatively, it is straightforward to build fractal aggregates with these structures. First, idealized fractal aggregates with same-sized spheres in point contact are generated using a tunable cluster–cluster aggregation algorithm (Filippov et al., 2000). From the generated ideal aggregate, we modify each monomer with different minor structures as discussed above to develop the nonideal aggregates. The bottom row of Fig. 2 shows some examples of aggregates with minor structures, which are modified from ideal aggregates generated using fractal dimension and fractal prefactor of 1.8 and 1.2, respectively (Sorensen and Roberts, 1997; Sorensen, 2001; Kahnert and Devasthale, 2011). The aggregates with only 15 monomers are displayed to better highlight the details of minor structures in each case.

Geometrically, different numerical models have to be developed for different minor structures, which make direct comparisons between these different minor structures challenging since these structures can lead to different effects on the optical properties and their effects are seemingly not directly comparable. Only when these minor structures are defined in a unified manner can their influences on the BC optical properties be quantitatively compared and the nature of their effects be better understood. For the five minor structures considered, five different dimensionless parameters are used to quantify them independently. To this end, we have to find a unified parameter that can be connected to the effects of all the five structures in order to quantify them. Considering that all minor structures influence not only the geometry but also overall particle volume/mass, we convert geometrical differences into volume/mass differences in this study. Thus, a unified parameter β, called the volume variation, is defined, and it simply represents the relative volume difference between an aggregate with minor structures and the corresponding perfect one:

$$\begin{array}{}\text{(7)}& \mathit{\beta }={\displaystyle \frac{V_{\mathit{\beta }}-V_o}{V_o}},\end{array}$$

where V_o is the volume of idealized fractal aggregates, and V_β is the volume of aggregates with minor structures. Because the particle volume is one of the most prominent factors affecting particle optical properties, especially for particles much smaller than the incident wavelength (e.g., single monomer), the parameter of volume variation will not only unify the definition of the minor structures for comparison but also provide a simple quantitative method to account for their effects on BC optical properties.

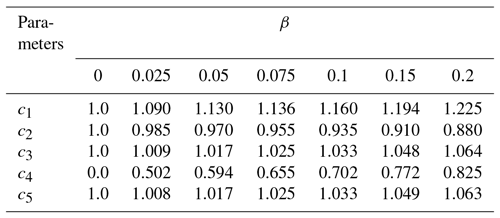
Figure 3 illustrates the relationships between the volume variation β and different structure parameters. The volume of aggregates with minor structures can be calculated numerically in a discretized space domain with a sufficiently high spatial resolution, which will also be used for optical property simulations in the following section. Obviously, the total volume variation β varies rapidly with the change of structure parameters, and these structure parameters under different volume variations can be uniquely identified by their clear relationships. When β is 0, the BC aggregates are the original ideal ones. The volume variation range from 0 to 0.2 is considered in this paper. The relationship between the volume variation and the parameters at a given level of volume variation is also illustrated in Table 2, in which the five dimensionless parameters leading to the given β values are listed. Here it is seen that these values correspond to conditions wherein only one minor structure is allowed in each case. Meanwhile, the relationship may vary slightly for different aggregates due to their irregular natures, so the β value of each aggregate will be calculated in the following section.

Figure 3 Relationships between geometry parameters and volume variations.

Table 2 Relationship between different minor structure parameters (c_i with i from 1 to 5) and unified parameter volume variation β.

3 Effects of minor structures

We use the discrete dipole approximation (DDA) method to simulate the optical properties of BC aggregates with those minor structures, because it is highly flexible in term of defining particle shape and composition (Yurkin and Hoekstra, 2007; Kahnert et al., 2012b). The Amsterdam DDA (ADDA) code developed by Yurkin and Hoekstra (2007, 2011) is used. In the DDA simulations, the scatterers are discretized into numerous small sub-volumes, namely dipoles, and particles with complex shapes can be accurately described via such dipoles as long as the dipoles are sufficiently small in comparison to the particle size. Note that the surface granularity inherent to the DDA model may limit the accuracy of the resulting optical properties, due to the small-sized scale of monomers and the minor structures (Draine, 1988; Moteki, 2016). To ensure that the detailed monomer structures are adequately represented in the DDA simulations, we discretize the particles using 200 dipoles per wavelength (dpl), and this leads to over 900 dipoles per monomer. Liu et al. (2018b) developed a systematic and comprehensive study to evaluate the performance of the DDA for simulating the optical properties of BC aggregates by comparing with the multiple-sphere T matrix (MSTM) results. Their results indicate that a systematic relative error (∼3 % with a dpl of 200) does exist between the DDA and MSTM, whereas such a systematic and small error will not influence our discussions that mainly focus on the relative values. This paper mainly discusses the optical properties at an incident wavelength of 500 nm, and the BC refractive index is assumed to be 1.8+0.6i; we will also briefly discuss the effects of refractive index on our results. The original monomer radius for the ideal aggregate is assumed to be a_o=15 nm. For the overall geometry, we consider the fractal dimension values obtained from Wang et al. (2017) and build both lacy aggregates (D_f=1.8) and aged ones with compact structures (D_f=2.3) for optical studies. For practical applications, aerosols are normally considered to be randomly oriented in the ambient atmosphere, and all the optical properties discussed will be those averaged over a sufficiently large number of orientations.

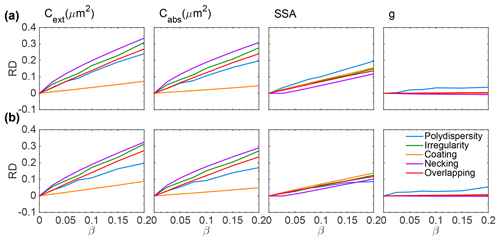
Figure 4 Relative differences of optical properties for aggregates with minor structures compared to those with perfect fractal aggregate structures at a wavelength of 500 nm. Aggregates with 200 monomers and a fractal dimension of 1.8 (a) and 2.3 (b) are considered.

Figure 4 compares the relative differences (RDs) between optical properties of the idealized aggregates and those with different minor structures as a function of volume variation β. Here, aggregates with 200 monomers are considered, and Fig. 4a and b show results of aggregates with D_f=1.8 and D_f=2.3, respectively. Positive RDs mean that the minor structures enhance the corresponding optical properties. With the increase of volume variation, the RDs in the extinction and absorption cross sections increase almost linearly, and different minor structures tend to have obvious enhancement in extinction and absorption cross sections to varying degrees. The effects of necking are largest with ∼35 % RDs as β increases to 0.2, while the effects of coating are smallest with RDs less than 10 %. The RDs of single scattering albedo (SSA) also become larger with the increase of β (up to ∼15 % at β=0.2), whereas these differences for different minor structures are less significant than those in extinction and absorption cross sections. The results of asymmetry factors for different minor structures display very small differences, and the RDs, less than 3 % even for the largest β value considered, are close to zero over the entire range of β considered, suggesting that it is nearly unaffected by the type and magnitude of minor structures. Furthermore, results for lacy and compact aggregates are similar, and only the polydispersity of monomer size shows a relatively lower impact on the SSA.

With almost no influence on the asymmetry factors, the effects of these minor structures on the angle-dependent scattering matrix elements are also expected to be minor. Figure 5 shows the normalized phase function and two nonzero scattering matrix elements (P₂₂ and P₃₄) for aggregates with minor structures at a volume variation of β=0.1, and those of perfect aggregates are given as a direct comparison. Because minor structures show even lower impacts on other nonzero scattering matrix elements (P₁₂, P₃₃, and P₄₄), they will not be shown here. The normalized phase functions and P₃₄ of aggregates with different minor structures agree closely with those of idealized aggregates. The polydispersity (the blue lines) has essentially no influence on P₁₁ but shows impacts on backward scattering with scattering angles larger than 90^∘, and the effects are slightly larger for compact aggregates. For P₂₂, the necking causes the largest decreases among the five structures, whereas the overall differences remain small (note that the range of P₂₂ values plotted are between 0.96 and 1). To summarize, minor structures have negligible effects on the angle-dependent scattering, even at a volume variation of 0.1. Thus, the scattering matrix elements of aggregates will not be further considered and the following discussion will focus only on the integral scattering properties (i.e., those shown in Fig. 4).

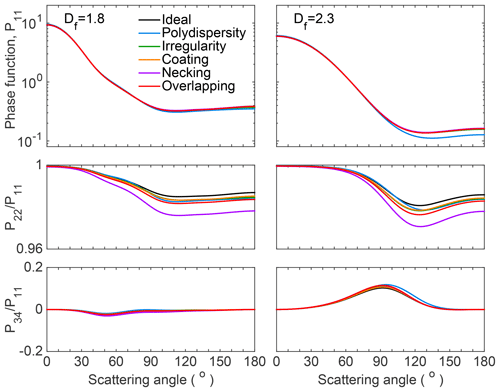
Figure 5 Three normalized scattering matrix elements (P₁₁, P₁₂, and P₃₄) of fractal aggregates with minor structures.

Different from perfect aggregates, whose optical properties can be calculated conveniently by accurate models such as the MSTM method (Mackowski, 2014) and the generalized multiparticle Mie-solution (GMM) method (Xu, 1995), modeling the optical properties of aggregates with minor structures is much more tedious. This also makes its applications challenging due to the time-consuming simulations and uncertainties in the definition of minor structure parameters. Thus, it is important and necessary to find an empirical relationship between optical properties of aggregates with and without minor structures. The relationship, which can estimate the optical properties of aggregates with minor structures from those of idealized ones, should be general and simple for the purpose of practical application. Fortunately, Figs. 4 and 5 indicate that although the minor structures have different influences on aggregate optical properties, they do have some similar features. For example, their effects on the extinction and absorption cross sections are almost proportional to the volume variation, and the effects on the scattering matrix are ignorable. Those features can be applied for the empirical relationship.

To develop the empirical relationship based on the current DDA results, the significant influence of the volume variation on the cross sections should be considered first. This is reasonable because minor structures only change monomer shapes. In the visible and shortwave infrared spectra ranges, BC monomers are normally in the Rayleigh regime, and the corresponding absorption and scattering cross sections are proportional to the volume and volume square, respectively. Considering the linear relationship shown in the absorption cross section in Fig. 4, it is reasonable to approximate the absorption cross section of aggregates with minor structures as follows:

$$\begin{array}{}\text{(8)}& {\mathrm{ABS}}_{\mathit{\beta }}=B_{\mathrm{ABS}}\cdot {\displaystyle \frac{V_{\mathit{\beta }}}{V_o}}\cdot {\mathrm{ABS}}_o=B_{\mathrm{ABS}}\cdot (\mathrm{1}+\mathit{\beta })\cdot {\mathrm{ABS}}_o,\end{array}$$

where ABS_β is the absorption cross section of the imperfect aggregate with a volume of V_β and volume variation of β, and ABS_o and V_o are the values of the corresponding perfect aggregate. The 1+β term indicates the change in overall volume due to minor structures, and the parameter B_ABS can be understood as a “correction ratio” indicating the direct effects of minor structures on the absorption cross section. Similarly, the relationship for the scattering cross section can be given as follows:

$$\begin{array}{}\text{(9)}& {\mathrm{SCA}}_{\mathit{\beta }}=B_{\mathrm{SCA}}\cdot {\left({\displaystyle \frac{V_{\mathit{\beta }}}{V_o}}\right)}^{\mathrm{2}}\cdot {\mathrm{SCA}}_o=B_{\mathrm{SCA}}\cdot (\mathrm{1}+\mathit{\beta }{)}^{\mathrm{2}}\cdot {\mathrm{SCA}}_o.\end{array}$$

Meanwhile, the extinction cross section can be obtained by the sum of the scattering and absorption cross section. Note that similar relationships to Eqs. (8) and (9) have been proposed by Farias et al. (1996) to account for the effect of monomer polydispersity but without the terms B_ABS and B_SCA. Based on the results shown in Figs. 4 and 5, the scattering matrix and asymmetry factor are unchanged. Because the volume of BC, absorbing material, is not changed in the coating case, the volume variation term (1+β) in Eq. (8) is removed in the empirical approximation.

The next step is to determine the values of B_ABS and B_SCA for different minor structures. We approximate the two correction ratios based on the results shown in Fig. 4, and the results are listed in Table 3. All values in the table are larger than 1, meaning that the minor structures also enhance the equivalent mass absorption and scattering of aggregates. Larger values of B_ABS or B_SCA mean that the minor structure has a stronger influence. The B_ABS of necking is the largest with a value up to 1.08, and the  B_ABS of polydispersity is the smallest (1.02). The correction ratios are all in the range between 1.01 and 1.08 for absorption and scattering, so the empirical relationships in Eqs. (8) and (9) can be further simplified by assigning a constant correction ratio of $B_{\mathrm{ABS}}=B_{\mathrm{SCA}}=\mathrm{1.05}$ for all cases. In other words, we specify an average enhancement rate in the scattering and absorption of aggregates with minor structures after considering volume variation. The resulting cross sections can be used to obtain the new single-scattering albedo of aggregates with minor structures as well. Another advantage of the proposed relationships is that only a volume or mass variation is needed for the approximation, whereas evaluation of the geometric parameters of the minor structure is much more challenging.

Table 3 Correction ratio obtained from results in Fig. 4 to give the absorption and scattering cross sections of aggregates with different minor structures.

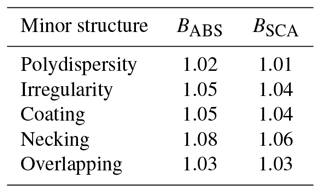
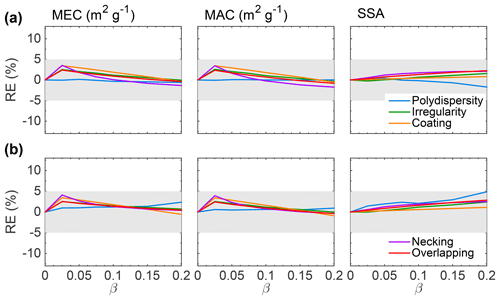
Figure 6 Relative error of optical properties for aggregates with minor structures between direct DDA simulations and those modified from ideal fractal aggregates using the empirical correction factors and volume/mass variation.

To evaluate the performance of the empirical relationship, Fig. 6 replots the results of Fig. 4 and directly compares the results using the aforementioned correction relationships (with the help of those of perfect aggregates) and those of the rigorous DDA simulations for nonideal aggregates. To remove the effects of differences in volume in the following evaluations, mass extinction and absorption cross sections (MEC and MAC), i.e., values per unit BC mass, are considered instead of absolute cross sections, and we use a BC density of 1.8 g cm⁻³ (Bond and Bergstrom, 2006). Thus, the relative errors (REs) in Fig. 6 show the relative errors of empirical relationships for approximating the optical properties of BC aggregates with minor structures. The gray shaded regions indicate REs of between ±5 %. Again, Fig. 6a shows lacy aggregates, and Fig. 6b shows compact aggregates. Obviously, the relative errors between direct DDA simulations of imperfect aggregates and results from empirical relationships are well under the ±5 %. This indicates that the empirical relationships can provide a good approximation of the optical properties of BC aggregates with minor structures, at least for cases considered in this study.

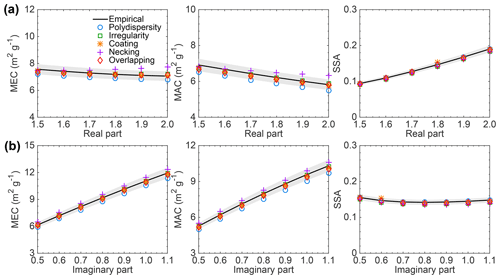
Figure 7 Comparison of the optical properties of aggregates with minor structures from direct simulations (markers) and those corrected from empirical relationships (black lines) as functions of refractive indices.

All the studies above are based on an assumed refractive index of 1.8+0.6i (but close to the real one), whereas the refractive index is not only one of the most important parameters for determining BC optical properties but also one of the most uncertain physical properties (Bond and Bergstrom, 2006; Liu et al., 2018a). To investigate the influence of BC refractive index on the minor structure effects, Fig. 7 compares the optical properties of BC aggregates with minor structures with those from empirical relationships as functions of the real part (Fig. 7a) and the imaginary part (Fig. 7b) of refractive index. Aggregates with 200 monomers and a fractal dimension of 1.8 are considered, and the volume variation due to minor structures is set to 0.1. Figure 7 indicates that the refractive indices do affect optical properties significantly, whereas the relative differences caused by the minor structures do not change too much. Only the necking causes optical properties slightly out the ranges given by the empirical results (shadow regions) due to change of the real part of refractive index. In other words, the minor structures show similar effects on BC optical properties at different refractive indices, and our empirical method can be extended to a wider range of BC refractive indices.

The performance of this simple approximation utilizing the optical properties of perfect aggregates is further evaluated for differently sized aggregates at different wavelengths. Figure 8 compares the optical properties from direct simulations of aggregates with minor structures (markers) and empirical approximations based on properties of perfect aggregates (solid black lines). Here, we consider only lacy aggregates with a fractal dimension of 1.8 and aggregates containing 50 to 1500 monomers are considered. Again, the volume variation is 0.1. Thus, the volume equivalent diameter up to ∼350 nm is included to cover a wide range of BC size distribution (Schnaiter et al., 2005; Reddington et al., 2013). The gray shaded regions indicate ±5 % relative errors within the results from the empirical relationships. As expected, the effects of minor structures are less sensitive to particle size. The MEC and MAC for aggregates with monomer polydispersity and necking are slightly smaller and larger than the empirical results, respectively. Nevertheless, all of the markers, i.e., results from direct simulations of aggregates with minor structures, lie within the ±5 % gray shaded areas. The empirical results of SSA agree more closely with direct simulation results. As expected, the asymmetry factor is least affected by minor structures with average REs of less than 2 %. The monomer polydispersity shows some effects on the asymmetry factor, with REs reaching almost 6.5 % for relatively small aggregates containing 100 monomers or less. Considering the significant uncertainties of BC parameters, a relative error of 5 % is acceptable for most applications; furthermore, Fig. 8 validates that the average volume correction ratio and empirical relationships can be applied confidently to account for the effects of minor structures on the optical properties of BC aggregates. Results for compact aggregates are similar and will not be shown here.

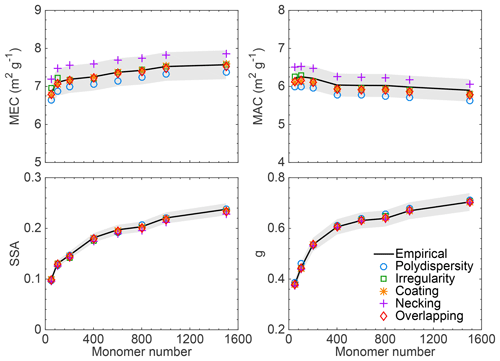
Figure 8 Comparison of the optical properties of aggregates with minor structures from direct simulations (markers) and those from ideal aggregates but with corrections accounting for the minor structures (black lines).

Table 4 Bulk scattering properties for lacy aggregates with minor structures (β=0.1) of direct simulations and those from perfect aggregate structures but with corrections. The values in parentheses represent the relative error (%) from the empirical results.

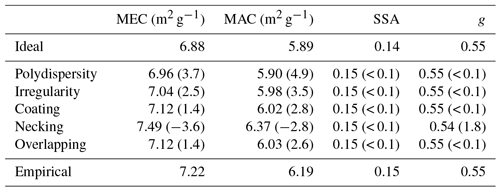
Table 4 shows the bulk optical properties of BC aggregates with minor structures from direct DDA simulations and those from the empirical approximations, and the optical properties of ideal fractal aggregates are also given as a reference. A lognormal size distribution with a geometric mean diameter and a standard deviation of 120 nm and 1.5, respectively, are used for aggregate sizes (Alexander et al., 2008; Chung et al., 2012). It is clear from Table 4 that the bulk optical properties of ideal aggregates are significantly lower than those of aggregates with minor structures, especially for MEC and MAC. With an average over the aggregate size, the empirical approximation should give even better approximations. The bulk MEC and MAC are approximately 7 and 6 m² g⁻¹, respectively, at 500 nm, which is in reasonable agreement with observations (Bond and Bergstrom, 2006; Kahnert et al., 2010; Liu et al., 2010; Xu et al., 2017). The empirical results overestimate MEC and MAC of polydispersity by 3.7 % and 4.9 %, respectively, and underestimate those of necking by 3.6 % and 2.8 %. Again, minor structures show less impact on the bulk asymmetry factor and SSA, and the relative errors from those of idealized aggregates are always less than 2 %. Clearly, after scaling with the empirical relationship, results from the perfect aggregates can be readily used to represent the bulk optical properties of aggregates with minor structures.

The results discussed above are at a wavelength of 500 nm and results at different incident wavelengths between 300 and 700 nm are illustrated in Fig. 9. Aggregates with 200 monomers and the fractal dimension of 1.8 are considered for these simulations at a volume variation of 0.1. Obviously, all the optical properties decrease with the increase of wavelength because the particles become relatively small compared to the longer wavelength. The empirical relationship with the same correction ratio 1.05 is applicable for different wavelengths. Again, all the optical properties of BC aggregates with different minor structures (markers) are within the range of ±5 % from the results of empirical approximations (the solid black lines).

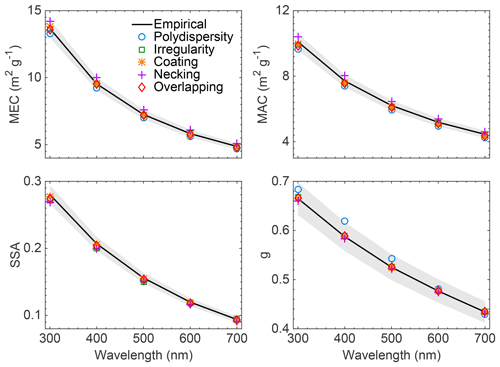
Figure 9 Same as Fig. 8 but for optical properties of aggregates with 200 monomers at different wavelengths.

Most previous studies, as well as the aforementioned results, consider minor structures individually; i.e., the BC aggregates deviate from the ideal ones through only one of the five structures, whereas atmospheric BC aggregates in general contain more than one structure simultaneously. To develop more realistic models to represent actual BC particles, we further investigate whether the effects of a combination of different minor structures can still be accounted for by simple empirical relationships. To this end, we include multiple minor structures in a single aggregate and use the volume variation to constrain the combination. For a given total volume variation, the contribution of each minor structure can be randomly generated. Figure 10 shows 10 examples of aggregates containing 15 monomers with random combinations of minor structures to represent their detail morphologies, and 5 examples of aggregates containing 100 monomers, which are more close to actual BC aggregates, are given in the bottom row. Different combinations show clearly different geometries, though they all have the same total volume variation of 0.1 from the corresponding perfect aggregate.

Figure 10 Examples of aggregates with random combinations of minor structures. The aggregates are generated to have the same volume variation of 0.1 compared to their perfect counterparts.

Figure 11 compares the optical properties of aggregates with multiple minor structures calculated by the DDA (blue bars) and those from empirical approximations (yellow bars). For each case, 20 random aggregates are built and calculated, and the same volume variation of 0.1 is imposed for imperfect aggregates. The averaged optical properties as well as their variances (vertical red error bars) are shown in the figure. Surprisingly, even with different combinations of minor structures, the variances are quite small, indicating that the differences between the 20 random cases are minor. The asymmetry factor shows the largest variance, which agrees with the results of ideal aggregates (Liu et al., 2015). Comparing the blue and yellow bars, we can find that the empirical results agree closely with the accurate calculations as all of the relative errors are less than 3 %. Therefore, even for BC aggregates with multiple minor structures, their combined effects can still be accurately accounted for by the empirical relationships proposed in this study due to the consistent volume variation.

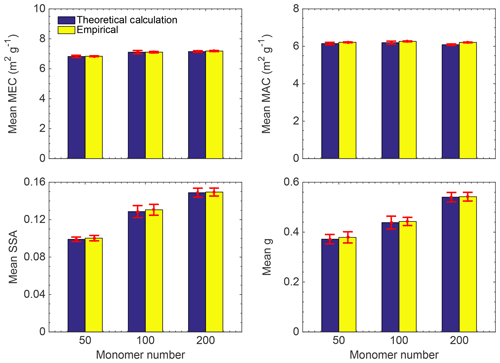
Figure 11 Comparison of the optical properties from direct simulations of aggregates with combined multiple minor structures (blue) and those from perfect aggregate structures but with corrections to account for the minor structures (yellow).

Table 5 BC radiative forcings calculated based on different assumptions of BC optical properties or column amounts.

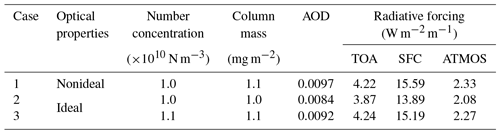
To understand the impact of aggregate minor structures on BC radiative forcing estimations, we compare the direct radiative forcing of BC aerosols with and without considering minor structures. We perform a simple radiative transfer simulation for a semiquantitative discussion, and the Santa Barbara DISORT Atmospheric Radiative Transfer Model is used to calculate BC forcing at a visible wavelength (Ricchiazzi et al., 1998; Zeng et al., 2019). Similar to the settings used by Zeng et al. (2019), the midlatitude summer atmosphere profile is considered, and the surface albedo is set to 0.15. The solar zenith angle is 60^∘. We assume BC particles to be located uniformly at the bottom layer of the atmosphere with a height between 0 and 1 km and a BC number concentration of 10¹⁰ particles m⁻³ following Reche et al. (2011). Table 5 compares the input BC properties (optical properties and aerosol loading) and the corresponding radiative forcings, including those at the top of the atmosphere (TOA) and the surface (SFC) and in the atmosphere (ATMOS). The same BC size distribution as well as the corresponding bulk optical properties given in Table 4 is used. We consider aggregates with the minor structures that lead to a 10 % difference in the volume. For the ideal aggregates, we consider two BC number concentrations: (1) the same as that for BC with minor structures, and (2) 10 % larger to account for the volume increase due to minor structures, whereas both cases used the optical properties of ideal aggregates. Here, the optical properties of aggregates with minor structures are directly transformed from those of the ideal ones through the empirical relationship because those from accurate simulations show relative differences of less than 5 % (see Table 4) and will not change the forcing values significantly. The table indicates that the effects of aggregate minor structures on BC radiative forcing are in similar orders to the effects on the optical properties, i.e., relative differences approximately ∼12 % between the results of Cases 1 and 2. Again, the differences are mainly contributed by the differences of BC amount/volume because, after assuming the same BC mass between Cases 1 and 3, the forcings become close to each other. However the effects are interpreted, the effects of minor structures can be easily accounted for without the tedious simulations of the optical properties for particles with minor structures or without even knowing their details.

4 Conclusion

This study investigates the effects of different minor structures on the optical properties of BC aggregates and develops a simple empirical treatment to account for their effects from the optical properties of the corresponding ideal fractal aggregates. The structures considered in this study include polydispersity, irregularity, coating, necking, and overlapping, all of which are for monomers and not the aggregate overall structure. The volume variation can be used to unify the effects of different minor structures. Minor structures significantly affect the optical properties of BC aggregates with different fractal dimensions and aggregate sizes, and with the increase of wavelength, these effects become slightly weaker. Among the five minor structures, necking shows the strongest effect. The asymmetry factor and the scattering matrix are almost unaffected by these minor structures. For easy and accurate estimation of BC aggregates involving these minor structures, a simple empirical relationship is developed to account for their effects on the optical properties based on a constant correction ratio of 1.05 and volume variation from that of the corresponding ideal aggregate. Results show that the empirical relationships can accurately represent the optical properties of BC aggregates with minor structures. Additionally, the effects of multiple minor structures are found to be similar to those of a single structure with the same volume variation and the empirical relation is also applicable. Overall, the effects of minor structures on BC aggregate optical properties are mainly caused by their influences on the total overall volume/mass, and the minor structure effects merely result in ∼5 % differences in the mass optical properties. Thus, future studies should pay more attention to BC total volume/mass, and the details of the minor structures may not need to be considered with the empirical relationship developed by this study.

For practical applications, the detailed parameters of fractal aggregates as well as the minor structures should be known, and such knowledge can be obtained via the analysis of aggregate images (Brasil et al., 2000; Chakrabarty et al., 2006). Among the minor structures, the monomer size polydispersity and overlapping have been most widely considered (Bescond et al., 2014; De Temmerman et al., 2014; Bourrous et al., 2018). However, with the proposed empirical relationship, only simple estimations of the volume or mass variation are sufficient to account for the change in optical properties. The methodology proposed in this study enables efficient and accurate prediction of the optical properties of BC aggregates with minor structures based on those of the corresponding ideal aggregates that can be calculated using the MSTM and GMM methods with much less computational effort than the DDA, and the optical properties of those ideal aggregates have been taken from a comprehensive database (Liu et al., 2019). This will make the applications more practical and instructive for experimental analysis.