Complex refractive indices and single-scattering albedo of global dust aerosols in the shortwave spectrum and relationship to size and iron content

The optical properties of airborne mineral dust depend on its mineralogy, size distribution, and shape, and they might vary between different source regions. To date, large differences in refractive index values found in the literature have not been fully explained. In this paper we present a new dataset of complex refractive indices ($m=n-ik$) and single-scattering albedos (SSAs) for 19 mineral dust aerosols over the 370–950 nm range in dry conditions. Dust aerosols were generated from natural parent soils from eight source regions (northern Africa, Sahel, Middle East, eastern Asia, North and South America, southern Africa, and Australia). They were selected to represent the global-scale variability of the dust mineralogy. Dust was resuspended into a 4.2 m³ smog chamber where its spectral shortwave scattering (β_sca) and absorption (β_abs) coefficients, number size distribution, and bulk composition were measured. The complex refractive index was estimated by Mie calculations combining optical and size data, while the spectral SSA was directly retrieved from β_sca and β_abs measurements. Dust is assumed to be spherical in the whole data treatment, which introduces a potential source of uncertainty. Our results show that the imaginary part of the refractive index (k) and the SSA vary widely from sample to sample, with values for k in the range 0.0011 to 0.0088 at 370 nm, 0.0006 to 0.0048 at 520 nm, and 0.0003 to 0.0021 at 950 nm, as well as values for SSA in the range 0.70 to 0.96 at 370 nm, 0.85 to 0.98 at 520 nm, and 0.95 to 0.99 at 950 nm. In contrast, the real part of the refractive index (n) is mostly source (and wavelength) independent, with an average value between 1.48 and 1.55. The sample-to-sample variability in our dataset of k and SSA is mostly related to differences in the dust iron content. In particular, a wavelength-dependent linear relationship is found between the magnitude of k and SSA and the mass concentrations of both iron oxide and total elemental iron, with iron oxide better correlated than total elemental iron with both k and SSA. The value of k was found to be independent of size. When the iron oxide content exceeds 3 %, the SSA linearly decreases with an increasing fraction of coarse particles at short wavelengths (< 600 nm).

Compared to the literature, our values for the real part of the refractive index and SSA are in line with past results, while we found lower values of k compared to most of the literature values currently used in climate models.

We recommend that source-dependent values of the SW spectral refractive index and SSA be used in models and remote sensing retrievals instead of generic values. In particular, the close relationships found between k or SSA and the iron content in dust enable the establishment of predictive rules for spectrally resolved SW absorption based on particle composition.

1 Introduction

With teragram amounts of annual emissions, a residence time of about 1–2 weeks in the atmosphere, and a planetary-scale transport, mineral dust aerosols are a global phenomenon (Uno et al., 2009; Ginoux et al., 2012) and contribute significantly to the global and regional aerosol loading (Ridley et al., 2016) and direct radiative effect (Miller et al., 2014).

However, large uncertainties still persist on the magnitude and overall sign of the dust direct radiative effect (Boucher et al., 2013; Highwood and Ryder, 2014; Kok et al., 2017). One of the major sources of this uncertainty is our insufficient knowledge of dust absorption properties in the shortwave (SW) and longwave (LW) spectral ranges (e.g., Balkanski et al., 2007; Samset et al., 2018), given that mineral dust contains large particles and a variety of minerals absorbing over both spectral regions (e.g., iron oxides, clays, quartz, and calcium-rich species; Sokolik and Toon, 1999; Lafon et al., 2006; Di Biagio et al., 2014a, b). Global- and regional-scale mapping of dust absorption remains limited and more information is required (Samset et al., 2018).

Aerosol absorption is represented by both the imaginary part (k) of the complex refractive index ($m=n-ik$) of its constituent material and by the single-scattering albedo (SSA; i.e., the ratio of the scattering to extinction coefficient) of the particle population, as well as by the mass absorption efficiency (MAE; m² g⁻¹), i.e., the aerosol absorption coefficient per unit mass concentration.

In the shortwave spectral range, absorption by dust accounts for up to ∼10 %–20 % of its total extinction. Dust absorption is highest in the ultraviolet–visible (UV–Vis) and almost nil towards the near infrared (IR) (Cattrall et al., 2003; Redmond et al., 2010) due to the combined contribution of large particles in the size distribution and the dust mineralogy, notably the presence of iron oxides (Karickhoff and Bailey, 1973; Lafon et al., 2006; Derimian et al., 2008; Moosmüller et al., 2012; Formenti et al., 2014a, b; Engelbrecht et al., 2016; Caponi et al., 2017). The mineralogy of airborne mineral dust varies according to that of the parent soils (Nickovic et al., 2012; Journet et al., 2014). Consequently, dust aerosols of different origins should be more or less absorbing in the SW and have a different imaginary spectral refractive index and SSA. Field and laboratory measurements, including ground-based and spaceborne remote sensing, show that k varies at a regional scale by almost 2 orders of magnitude (0.0001–0.008 at 550 nm) with corresponding SSAs between 0.80 and 0.99 at 550 nm (Volz, 1972; Patterson et al., 1977; Shettle and Fenn, 1979; Dubovik et al., 2002; Haywood et al., 2003; Sinyuk et al., 2003; Linke et al., 2006; Osborne et al., 2008; Müller et al., 2009; Otto et al., 2009; Petzold et al., 2009; Schladitz et al., 2009; McConnell et al., 2010; Formenti et al., 2011; Wagner et al., 2012; Ryder et al., 2013a; Engelbrecht et al., 2016; Rocha-Lima et al., 2018). Despite some variability being instrumental or analytical (differences in the sampled size fraction or in the method used to retrieve optical parameters), geographic differences persist when the same measurement approach and retrieval method are applied, e.g., in AERONET inversions, supporting the dependence of dust k and SSA on its origin (Dubovik et al., 2002; Koven and Fung, 2006; Su and Toon, 2011). In contrast, the real part (n) of the dust refractive index, mostly related to particle scattering, is less variable, with values between 1.47 and 1.56 at 550 nm (e.g., Volz, 1972; Patterson et al., 1977; Balkanski et al., 2007; Petzold et al., 2009).

Differences in k or SSA caused by the spatial variability of the iron content may affect the sign of the dust radiative effect (heating vs. cooling) (Liao and Seinfeld, 1998; Claquin et al., 1999; Miller et al., 2014) and its global and regional implications (Myhre and Stordal, 2001; Colarco et al., 2014; Das et al., 2015; Jin et al., 2016; Bangalath and Stenchikov, 2016; Strong et al., 2018). The direct radiative effect of dust has a strong impact on the western African monsoon (Yoshioka et al., 2007; Konaré et al., 2008) and the Indian summer monsoon (Vinoj et al., 2014; Das et al., 2015; Jin et al., 2016). However, there is no consensus on whether dust increases or decreases precipitation over these regions (Solmon et al., 2008; Jin et al., 2016; Strong et al., 2018). As an example, Solmon et al. (2008) indicate that dust reduces precipitation over most of the Sahelian region but increases it over the northern Sahel–southern Sahara. This pattern is, however, very sensitive to the dust absorbing properties, and a decrease of a few percent in dust absorption may even cancel out the increase in precipitation over the Sahel. Similarly, Jin et al. (2016) show that by varying k from zero to 0.008 at 600 nm (i.e., the highest value currently used in models) the dust effect on the Indian summer monsoon may shift from negative (reduction of precipitation) to positive (increase in precipitation) values.

In spite of this sensitivity, present climate models adopt a globally constant spectral complex refractive index (and SSA) for dust and hence still implicitly assume the same dust mineralogical composition at the global scale. This is mainly due to the lack of a globally consistent dataset providing information on the geographical variability of the dust scattering and absorption properties (e.g., Samset et al., 2018). Reference values for the refractive index are usually taken from Volz (1972), Patterson et al. (1977), D'Almeida et al. (1991), Shettle and Fenn (1979), Sokolik et al. (1993), Sinyuk et al. (2003), or OPAC (Optical Properties of Aerosols and Clouds; Hess et al., 1998; Koepke et al., 2015). A parameterization of the spectrally resolved dust refractive index as a function of the mineralogical composition of the particles is desirable to replace the globally constant values in current climate models, in particular for those models that started to incorporate the representation of dust mineralogy into their schemes (Scanza et al., 2015; Perlwitz et al., 2015a, b).

Improving our knowledge of the spectral SW refractive index of mineral dust and its relation to particle composition (henceforth origin) is also key for the detection of dust aerosols in the atmosphere and the quantification of its mass loading, as well as total or absorption spectral optical depth from active and passive remote sensing (e.g., Ridley et al., 2016). As an example, the retrieval of the dust SSA and optical depth over bright desert surfaces with the MODIS (Moderate Imaging Resolution Spectroradiometer) Deep Blue algorithm (Hsu et al., 2004) applies the critical surface reflectance method (Kaufman, 1987) to retrieve dust properties from measured top-of-atmosphere (TOA) spectral reflectance. This algorithm depends critically on a priori information on the spectral refractive index (Kaufman et al., 2001; Yoshida et al., 2013). Similarly, active remote sensing techniques (lidar, light detection and ranging) require knowledge of the extinction-to-backscatter ratio (the lidar ratio), which is also a strong function of the complex index of the refraction or SSA of the aerosol particles (e.g., Gasteiger et al., 2011; Shin et al., 2018). Gasteiger et al. (2011) have shown that a 5 % change in the SSA at 532 nm can modify by up to 20 % the lidar ratio of dust, which means a 20 % change in the estimated profile of the dust extinction coefficient and retrieved optical depth from lidar measurements.

In this paper we address these issues by reporting a new laboratory investigation of the shortwave refractive index and SSA of dust from various source regions worldwide in the framework of the RED-DUST project (Di Biagio et al., 2017a; hereafter DB17; Caponi et al., 2017; hereafter C17). Dust optical properties at discrete wavelengths between 370 and 950 nm are derived in conjunction with the particle elemental and mineralogical composition, including total elemental iron and iron oxides. We investigate the relationship of k and SSA to the iron content to provide a parameterization of the dust absorption as a function of its mineralogy, which can be applied to climate models. The dependence of dust absorption on the particle coarse size fraction is also investigated to evaluate the change in dust absorption with atmospheric transport time.

2 Experimental setup and instrumentation

As previously described in DB17 and C17, all experiments discussed here were conducted in the 4.2 m³ stainless-steel CESAM chamber (French acronym for Experimental Multiphasic Atmospheric Simulation Chamber) (Wang et al., 2011). Mineral dust aerosols were generated through the mechanical shaking of parent soils using about 15 g of soil sample (first sieved to < 1000 µm and then dried at 100 ^∘C) placed in a 1 L Büchner flask and shaken for about 30 min at 100 Hz by means of a sieve shaker (Retsch AS200). The dust suspension in the flask was injected into the chamber by flushing with N₂ at 10 L min⁻¹ for about 10–15 min. After injection in the chamber, the largest fraction of the dust aerosol (> 1.5 µm diameter) remained in suspension for approximately 60 to 120 min thanks to a four-blade stainless-steel fan located at the bottom of the chamber, which also ensured homogeneous conditions within the chamber volume. The submicron dust fraction instead remained constant with time during the experiments (see Sect. 4.1.1). The evolution of the physicochemical and optical properties of the suspended dust was measured by different instruments connected to the chamber. The spectral particle volume dry scattering (β_sca) and absorption (β_abs) coefficients were respectively measured by a three-wavelength nephelometer (TSI Inc. model 3563, operating at 450, 550, and 700 nm; 2 L min⁻¹ flow rate, 2 s time resolution) and a seven-wavelength aethalometer (Magee Sci. model AE31, operating at 370, 470, 520, 590, 660, 880, and 950 nm; 2 L min⁻¹ flow rate, 2 min time resolution). The size distribution of aerosols was measured by means of a scanning mobility particle sizer (SMPS, TSI, DMA model 3080, CPC model 3772; mobility diameter range 0.019–0.882 µm; 2.0 and 0.2 L min⁻¹ sheath–aerosol flow rates, 135 s time resolution), a WELAS optical particle counter (OPC) (PALAS, model 2000, white light source between 0.35 and 0.70 µm; optical-equivalent diameter range 0.58–40.7 µm; 2 L min⁻¹ flow rate, 1 min time resolution), and a SkyGrimm OPC (Grimm Inc., model 1.129, 0.655 µm operating wavelength; optical-equivalent diameter range 0.25–32 µm; 1.2 L min⁻¹ flow rate, 6 s time resolution). Aerosol elemental and mineralogical composition, including iron oxides, was derived from the analysis of dust samples collected on polycarbonate filters (47 mm diameter Nuclepore, Whatman, nominal pore size 0.4 µm) mounted in a custom-made stainless-steel sample holder (operated at 6 L min⁻¹) for most of the duration of each experiment.

All instruments (size, SW optics, filters) sampled air from the chamber. To equalize the airflow extracted by the different instruments, a particle-free N₂∕O₂ mixture airflow was continuously injected into the chamber. Inlets for all extractive measurements consisted of a stainless-steel tube located inside the CESAM chamber and an external connection of silicone tubing (TSI Inc.) from the chamber to the instruments for a total length varying between 0.4 and 1.2 m. As detailed in DB17 and shown in Fig. S1 in the Supplement, the transmission efficiency due to aspiration and transmission in the sampling lines as a function of particle diameter was estimated to calculate the effective dust fraction sensed by each instrument, taking into account the sampling flow rate, tubing diameter, tubing geometry, and particle shape and density. For the nephelometer and the aethalometer, the length of the sampling line from the intake point in the chamber to the instrument entrance was about 1.2 m, which resulted in a 50 % cutoff of the transmission efficiency at 3.9 µm particle geometric diameter and 100 % cutoff at 10 µm. For the filter sampling system, the length of the sampling line of about 0.5 m resulted in a 50 % (100 %) cutoff at 6.5 µm (15 µm) particle geometric diameter (or 50 % cutoff at 10.6 µm aerodynamic diameter as indicated in C17; therefore, compositional analyses refer to the PM_10.6 size fraction). For the WELAS, the only OPC considered for size distribution in the coarse fraction (see Sect. 2.2), the 50 % (100 %) cutoff was reached for particles of 5 µm (8 µm) diameter.

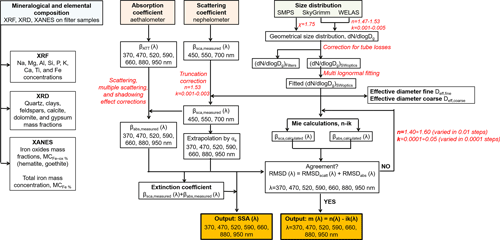
Figure 1 Flowchart illustrating the procedure for data treatment and retrieval of the physical and chemical (size, composition) as well as spectral optical properties (single-scattering albedo (SSA) and complex refractive index) of mineral dust aerosols. In red we mention the different corrections performed and the values adopted in the calculations. The α_s symbol in the scheme indicates the SAE_450–550 and the SAE_550–700 Ångström exponents used to extrapolate the nephelometer data at the aethalometer wavelengths.

All experiments were conducted at ambient temperature and relative humidity < 2 %. In addition to overnight evacuation, the chamber was manually cleaned between experiments to avoid contamination from remaining dust. Background concentrations of aerosols in the chamber were less than 2.0 µg m⁻³ (that is, 10² to 10⁵ times smaller than the concentration of dust aerosols in suspension in the chamber during experiments)

A flowchart of the procedure used to treat and combine optical, size, and compositional data, as well as the algorithm for SSA and complex refractive index retrieval, is shown in Fig. 1. Full details on the data treatment for size distribution measurements and filter compositional data are provided in DB17 and C17, and in the following we only mention the main points of interest for the present paper. Full details on the data treatment of the SW optical data are provided in Sects. 2.1 and 3.

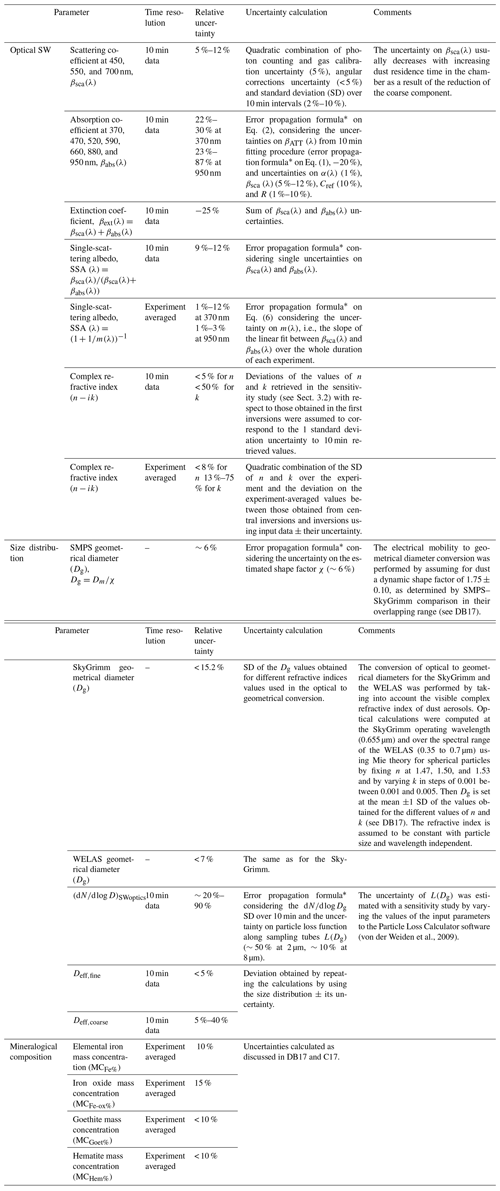
Table 1 Measured and retrieved quantities and their estimated relative uncertainties. For further details, refer to Sect. 2, as well DB17 and C17.

^* ${\mathit{\sigma }}_f=\sqrt{\sum _{i=\mathrm{1}}^n{\left(\frac{\partial f}{\partial x_i}{\mathit{\sigma }}_{x_i}\right)}^{\mathrm{2}}}$.

The optical and size datasets were acquired at different temporal resolutions and then averaged over compatible 10 min intervals, whereas the compositional data represent the experiment integral. The SSA and complex refractive index data were retrieved both at 10 min resolution and as experiment averages to relate them to both size and compositional data. Table 1 summarizes the uncertainties on the measured and derived parameters described in the following.

2.1 SW optical measurements

2.1.1 Aerosol scattering coefficient

The aerosol scattering coefficients (β_sca) at 450, 550, and 700 nm were measured by the nephelometer at angles between 7 and 170^∘ and needed to be corrected for the restricted field of view of the instrument (truncation correction) to retrieve β_sca at 0–180^∘. The truncation correction factor (C_trunc), i.e., the ratio of the β_sca at 0–180 and 7–170^∘, was estimated by Mie calculations for homogeneous spherical particles using the size distribution measured simultaneously behind SW inlets (see Sect. 2.2). In the calculations, the real part of the complex refractive index of dust was assumed to be wavelength independent and fixed at a value of 1.53, while the imaginary part was set to 0.003 at 450 and 550 nm and to 0.001 at 700 nm, according to preexisting information (Sinyuk et al., 2003; Schladitz et al., 2009; Formenti et al., 2011; Rocha-Lima et al., 2018). For the different dust samples, C_trunc ranged between 1.2 and 1.7 and decreased with wavelength and the dust residence time in the chamber, following the relative importance of the coarse component in the dust population. The uncertainty on C_trunc, calculated by repeating the optical calculations by using the size distribution of dust within its error bars as input to the optical code, is less than ±5 % at all wavelengths. In order to assess the consistency of the derived truncation correction, we made a sensitivity study in which we recalculated C_trunc by varying the refractive index used as input to the Mie calculations in the range of n and k values obtained in this study (i.e., values at 10 % and 90 % as reported in Table 5 for the whole dataset; that is, n between 1.49 and 1.54 and k between 0.001 and 0.006 at 450, 550, and 700 nm). The results of this sensitivity study indicate that, for a fixed dust size distribution, the truncation correction C_trunc varies less than 1 % for n between 1.49 and 1.54 and < 5 % for k between 0.001 and 0.006, so it is quite insensitive to the exact assumed n and k values.

Once corrected for truncation, the spectral β_sca was extrapolated at the aethalometer wavelengths. With this aim, the scattering Ångström exponents, SAE_450–550 and SAE_550–700, were calculated as the linear fit of β_sca vs. λ at 450–550 nm and 550–700 nm, respectively. The SAE_450–550 and SAE_550–700 coefficients were used to extrapolate β_sca at wavelengths respectively lower and higher than 550 nm. Extrapolated β_sca values were used to derive an average SAE of dust for the entire investigated spectral range.

2.1.2 Aerosol absorption coefficient

The aerosol absorption coefficient (β_abs) at 370, 470, 520, 590, 660, 880, and 950 nm was retrieved from aethalometer measurements. The aethalometer measures the attenuation (ATT) through an aerosol-laden quartz filter, related to the spectral attenuation coefficient (β_ATT) as

$$\begin{array}{}\text{(1)}& {\mathit{\beta }}_{\mathrm{ATT}}\left(\mathit{\lambda }\right)={\displaystyle \frac{\mathrm{\Delta }\mathrm{ATT}\left(\mathit{\lambda }\right)}{\mathrm{\Delta }t}}{\displaystyle \frac{A}{V}},\end{array}$$

where A is the area of the aerosol collection spot (0.5±0.1) cm² and V the air sample flow rate (0.002 m³ min⁻¹). The slope $\frac{\mathrm{\Delta }\mathrm{ATT}\left(\mathit{\lambda }\right)}{\mathrm{\Delta }t}$ is the linear fit of the measured attenuation as a function of time calculated over 10 min intervals. The spectral attenuation coefficient was converted into an absorption coefficient β_abs following the formula by Collaud Coen et al. (2010):

$$\begin{array}{}\text{(2)}& {\mathit{\beta }}_{\mathrm{abs}}\left(\mathit{\lambda }\right)={\displaystyle \frac{{\mathit{\beta }}_{\mathrm{ATT}}\left(\mathit{\lambda }\right)-\mathit{\alpha }\left(\mathit{\lambda }\right){\mathit{\beta }}_{\mathrm{sca}}\left(\mathit{\lambda }\right)}{C_{\mathrm{ref}}R\left(\mathit{\lambda }\right)}}.\end{array}$$

The α(λ)β_sca(λ) term accounts for the fraction of the measured attenuation due to side and backward scattering and not to light absorption. The Collaud Coen correction scheme has been recently shown to yield quite accurate values of the absorption coefficients and absorption Ångström exponents from aethalometer data (Saturno et al., 2017). The value of α(λ) was calculated with the formula by Arnott et al. (2005) and varied between 0.002 and 0.02 (< ±1 % from formal error propagation on the Arnott formula), while β_sca(λ) is the scattering coefficient from the nephelometer extrapolated to the aethalometer wavelengths. The C_ref term accounts for multiple scattering by the filter fibers, aerosol laden or not. Its spectral value, obtained by the linear extrapolation of C_ref at 450 and 660 nm estimated for mineral dust by Di Biagio et al. (2017b), varied between 4.30 at 370 nm and 3.32 at 950 nm. We assume for the extrapolated C_ref an uncertainty of ±10 % as estimated in Di Biagio et al. (2017b). The correction factor, R, accounts for the decrease in the aethalometer sensitivity with the increase in the aerosol filter loading. The value of R depends on the absorptivity properties of the sampled aerosol and can be calculated as a function of the particle SSA. In this study, we calculated R by estimating a first-guess SSA^∗ as the ratio of the nephelometer-corrected β_sca and β_ext obtained as the sum of β_sca and the β_abs non-corrected for filter loading effect. The R was estimated by using the Collaud Coen et al. (2010) formulation. For the range of estimated SSA^∗ (about 0.60 to 0.99), R varied between 0.5 and 1.0 (±1 %–10 %).

The absorption Ångström exponent (AAE) was calculated as the power-law fit of β_abs versus λ.

Due to an instrumental problem, aethalometer data were not always available, with a typical 30 min interruption usually 10 to 30 min after the beginning of experiments.

2.2 Size distribution

The aerosol number size distribution was obtained from SMPS, WELAS, and SkyGrimm measurements over different diameter ranges. The measured electrical mobility and optical equivalent diameters from the SMPS and the OPCs were first converted into geometrical diameters (D_g) as described in DB17 and summarized in Table 1. The OPC conversion assumes a dust complex refractive index that in our study was set in the range 1.47–1.53 for n and 0.001–0.005 for k for both the SkyGrimm and the WELAS (following DB17; for more details see Table 1). After conversion, the estimated D_g range was 0.01–0.50 µm for the SMPS, 0.65–73.0 µm for the WELAS, and 0.29–68.2 µm for the SkyGrimm. Due to a calibration issue, data for the SkyGrimm in the range D_g > 1 µm were discarded so that the WELAS is the only instrument considered in the super-micron range. A very low counting efficiency was observed for the WELAS below 1 µm, and data in this size range were also discarded.

The SMPS, WELAS, and SkyGrimm data were combined, as detailed in DB17, to obtain the full size distribution of the dust aerosols suspended in the CESAM chamber, (dN∕dlog D_g)_CESAM, and the size distribution behind SW optical instruments inlets, (dN∕dlog D_g)_SWoptics, after taking into account particle losses along sampling lines (see Fig. S1). As previously discussed, due to the particle losses in the sampling line from the chamber to the nephelometer and the aethalometer, the (dN∕dlog D_g)_SWoptics size distribution is cut at 10 µm, so no particles above this diameter reach the SW instruments.

The measured size distributions, (dN∕dlog D_g)_CESAM and (dN∕dlog D_g)_SWoptics, were used to estimate the mass concentration of aerosols and their effective diameter (D_eff) in the CESAM chamber and behind the SW instrument inlets as

$$\begin{array}{}\text{(3)}& {\displaystyle }\text{mass\hspace{0.17em}concentration}=\int {\displaystyle \frac{\mathit{\pi }}{\mathrm{6}}}{D}_{\mathrm{g}}^{\mathrm{3}}{\displaystyle \frac{\mathrm{d}N}{\mathrm{d}\log D_{\mathrm{g}}}}\mathit{\rho }\cdot \mathrm{d}\log D_{\mathrm{g}},\text{(4)}& {\displaystyle }{D}_{\mathrm{eff}}={\displaystyle \frac{\int D_{\mathrm{g}}^{\mathrm{3}}\frac{\mathrm{d}N}{\mathrm{d}\log D_{\mathrm{g}}}\mathrm{d}\log D_{\mathrm{g}}}{\int D_{\mathrm{g}}^{\mathrm{2}}\frac{\mathrm{d}N}{\mathrm{d}\log D_{\mathrm{g}}}\mathrm{d}\log D_{\mathrm{g}}}}.\end{array}$$

The effective dust density ρ in Eq. (3) was set at 2.5 g cm⁻³, a value that is approximately in the middle of the range of desert dust densities reported in the literature, i.e., 2.1–2.75 g cm⁻³ (Maring et al., 2000; Iwasaka et al., 2003; Reid et al., 2003). The effective diameter was evaluated separately for the fine and coarse fractions of dust by integrating Eq. (4) for diameters ≤1 µm (D_eff,fine) and > 1 µm (D_eff,coarse), respectively. For D_eff,coarse the upper limit of the calculation is 10 µm when calculated from (dN∕dlog D_g)_SWoptics, i.e., measured behind the SW inlets.

The dust size distribution, (dN∕dlog D)_SWoptics, measured at each 10 min time step for each sample was fitted with a sum of five lognormal functions to smooth data inhomogeneities linked to the different instrument operating principles and artifacts. Fitting was performed using the Levenberg–Marquardt algorithm. For each mode, the parameters of the lognormal functions, i.e., the total number concentration (N_i), the geometric median diameter (D_g,i), and the geometric standard deviation of the distribution (σ_i), were retrieved. The uncertainties in the retrieved parameters were estimated by repeating the fit using size data within their uncertainties. The resulting parameters of the fits at the peak of the injection in the chamber are reported in Table S1, and an example of size fitting is shown in Fig. S2.

The procedure described here to estimate (dN∕dlog D_g)_CESAM and (dN∕dlog D_g)_SWoptics implies that assumptions are made on the values of n and k to correct OPC data, and this may introduce a circularity in the estimates of the refractive index of dust that use (dN∕dlog D_g)_SWoptics as input in optical calculations (see Sect. 3.2). In order to analyze the dependence of the results on this assumption, we made a sensitivity calculation by varying the values of n and k used for OPC corrections within the range of values retrieved in this study (10 % and 90 % in Table 4, i.e., 1.49–1.54 for n and 0.001–0.006 for k). We concluded that changing n and k in this range has a very low impact on the retrieved number size distribution behind the SW inlets (dN∕dlog D_g)_SWoptics compared to the original assumptions made in our calculations (< 5 % changes in the retrieved size number distribution at the different diameters between the original correction and the correction by varying n and k). This is due to the fact that when changing D_g due to changes in the n and k in the OPC correction, the loss function also modifies to values corresponding to the new D_g. Given that the loss function increases–decreases for increasing–decreasing D_g, the combined changes in D_g and the loss function compensate so that the net number concentration behind the SW inlets varies less than a few percent. These results therefore suggest that the procedure to estimate the complex refractive index of dust is nearly independent of the assumed OPC correction.

Other sources of uncertainties are linked to the spherical assumption to perform the optical to geometrical diameter conversion (discussed in Sect. 3.3) as well as those due to Mie resonance oscillations of the calculated scattering intensities. Concerning Mie resonances, a sensitivity study was performed varying the size resolution of our calculations (high–low diameter resolution in the calculations to have a better–worse reproduction of Mie resonance oscillations) and show that Mie resonances impact the optical to geometrical diameter correction by less than 1 %.

Dust elemental and mineralogical composition and iron content

The elemental and mineralogical composition of the dust aerosols in the PM_10.6 size fraction was estimated by combining different techniques: X-ray diffraction (XRD; Panalytical model Empyrean diffractometer) to estimate the particle mineralogical composition in terms of clays, quartz, calcite, dolomite, gypsum, and feldspars; wavelength dispersive X-ray fluorescence (WD-XRF; Panalytical PW-2404 spectrometer) to determine the dust elemental composition (Na, Mg, Al, Si, P, K, Ca, Ti, Fe); and X-ray absorption near-edge structure (XANES) to retrieve the content of iron oxides and their speciation between hematite and goethite. The dust mass collected on Nuclepore filters during the experiments varied between 0.3 and 6 mg m⁻³ as calculated from elemental concentrations according to Lide (1992).

Full details on the XRD, WD-XRF, and XANES measurements and data analysis are provided in DB17 and C17. In this study, we discuss the dust elemental iron mass concentration, MC_Fe%, i.e., the percent mass of elemental iron with respect to the total dust mass concentration, and the iron oxides mass concentration, MC_Fe-ox%, i.e., the percent mass fraction of iron oxides with respect to the total dust mass concentration, estimated as the sum of goethite (MC_Goet%) and hematite (MC_Hem%) species.

3 Strategy for data analysis

3.1 Calculation of the spectral extinction coefficient and SSA from scattering and absorption coefficients

The spectral scattering and absorption coefficients, β_sca(λ) and β_abs(λ), measured by the nephelometer and the aethalometer were used to estimate 10 min averages of the spectral extinction coefficient, β_ext(λ), at the 7λ of the aethalometer between 370 and 950 nm as

$$\begin{array}{}\text{(5)}& {\mathit{\beta }}_{\mathrm{ext}}\left(\mathit{\lambda }\right)={\mathit{\beta }}_{\mathrm{abs}}\left(\mathit{\lambda }\right)+{\mathit{\beta }}_{\mathrm{sca}}\left(\mathit{\lambda }\right).\end{array}$$

The extinction Ångström exponent (EAE) was calculated as the power-law fit of β_ext versus λ.

The spectral single-scattering albedo of dust at 10 min resolution (SSA_10 min) was retrieved as

$$\begin{array}{}\text{(6)}& {\mathrm{SSA}}_{\mathrm{10}\min }\left(\mathit{\lambda }\right)={\displaystyle \frac{{\mathit{\beta }}_{\mathrm{sca}}\left(\mathit{\lambda }\right)}{{\mathit{\beta }}_{\mathrm{ext}}\left(\mathit{\lambda }\right)}}.\end{array}$$

The experiment-averaged SSA (λ) was calculated for each soil type based on the following formula (Moosmüller et al., 2012):

$$\begin{array}{}\text{(7)}& \mathrm{SSA}\left(\mathit{\lambda }\right)={\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{m\left(\mathit{\lambda }\right)}}\right)}^{-\mathrm{1}},\end{array}$$

where m(λ) represents the slope of the linear fit between the 10 min averages of β_sca(λ) and β_abs(λ) measured along the whole duration of each experiment. An example of β_sca(λ) versus β_abs(λ) fitting to retrieve the spectral SSA is shown in Fig. S3. The correlation coefficient R² of the β_sca(λ) versus β_abs(λ) fit usually ranges between 0.97 and 1 at all wavelengths. As will be discussed later in the paper, the single-scattering albedo of dust depends on the particle coarse size fraction, and during our experiments SSA_10 min was not derived continuously for the different samples due to the aethalometer measurement interruptions. The application of Eq. (7) avoids any bias in the calculated averaged SSA for different soils due to size effects. For two of the analyzed samples (Tunisia and Namib-2), however, the linear fitting procedure was not applicable due to the fact that only two absorption measurements and one absorption measurement, respectively, from the aethalometer were available just after the peak of the injection, with no data afterwards. Average SSA data for Tunisia were thus estimated as the mean of the two available SSA_10 min data points, while the single SSA_10 min measurement at the peak of the injection was reported for Namib-2. This difference in time sampling should be kept in mind when comparing data for these two samples to the rest of the dataset.

3.2 Retrieval of the spectral complex refractive index

An optical calculation was performed to estimate the complex refractive index ($m=n-ik$) of dust aerosols based on optical and size data. The retrieval algorithm consisted of recalculating the spectral scattering β_sca(λ) and absorption β_abs(λ) coefficients measured at each 10 min interval by using the fitted (dN∕dlog D)_SWoptics size distribution as input and by varying the real and imaginary parts of the complex refractive index in the calculations until the best agreement between measurements and calculations was found. At each wavelength the root mean square deviation (RMSD) was calculated as

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathrm{RMSD}\left(\mathit{\lambda }\right)& =\sqrt{{\left[{\displaystyle \frac{{\mathit{\beta }}_{\mathrm{sca},\mathrm{measured}}\left(\mathit{\lambda }\right)-{\mathit{\beta }}_{\mathrm{sca},\mathrm{calculated}}\left(\mathit{\lambda }\right)(n,k)}{{\mathit{\beta }}_{\mathrm{sca},\mathrm{calculated}}\left(\mathit{\lambda }\right)(n,k)}}\right]}^{\mathrm{2}}}\\ & \stackrel{\mathrm{‾}}{+{\left[{\displaystyle \frac{{\mathit{\beta }}_{\mathrm{abs},\mathrm{measured}}\left(\mathit{\lambda }\right)-{\mathit{\beta }}_{\mathrm{abs},\mathrm{calculated}}\left(\mathit{\lambda }\right)(n,k)}{{\mathit{\beta }}_{\mathrm{abs},\mathrm{calculated}}\left(\mathit{\lambda }\right)(n,k)}}\right]}^{\mathrm{2}}}.\end{array}\end{array}$$

The RMSD was minimized at each wavelength to obtain n–k pairs that most closely reproduce the measured scattering and absorption coefficients. Optical calculations were performed at the seven wavelengths of the aethalometer between 370 and 950 nm using Mie theory. In the calculations, the real part of the refractive index was varied in the range 1.40–1.60 at steps of 0.01, while the imaginary part was varied in the range 0.0001–0.050 at steps of 0.0001. For each sample, this resulted in 10 500 computations per wavelength and per 10 min time step. The uncertainty on the real and imaginary parts of the refractive index was estimated with a sensitivity study. For this purpose, the values of n and k were also obtained by using as input the observed β_sca(λ), β_abs(λ), and (dN∕dlog D)_SWoptics, plus or minus 1 SD on their measurement. The deviations of the values of n and k retrieved in the sensitivity study with respect to those obtained in the first inversions were assumed to correspond to the 1 SD uncertainty of 10 min retrieved values.

Experiment-averaged values of the spectral n and k were estimated as the average of single n and k values retrieved at 10 min steps (indicated as n_10 min and k_10 min). In fact, differently from the SSA, the refractive index did not seem to depend on the particle coarse size fraction (Sect. 4.5).

A control experiment was performed with submicron ammonium sulfate aerosols (see DB17 and Fig. S4) with the aim of validating the proposed methodology to estimate the aerosol complex refractive index for a nonabsorbing aerosol type. For ammonium sulfate particles with a mono-modal size distribution centered at 0.06 µm, as measured with the SMPS, the retrieved real part of the refractive index was 1.56 (±0.01) in the 450–700 nm wavelength range, as expected from the literature (Toon et al., 1976; Flores et al., 2009; Denjean et al., 2014).

3.3 Assumptions on the retrieval of SSA and complex refractive index

The approach used to retrieve the SSA and the complex refractive index of dust and the accuracy of the results depend on the accuracy of the input data and the assumptions in the optical calculations. We discuss here two points of the applied procedure, in part already mentioned in the previous paragraphs.

1. The size distribution from OPCs and also the scattering coefficient from the nephelometer used as input to the n and k retrieval procedure and SSA calculation depend more or less directly on the dust refractive index. These instruments, in fact, need to be corrected for instrumental artifacts, and these corrections require a priori knowledge of the n and k, which in our approach were set to fixed values (1.47–1.53 for n and 0.001–0.005 for k for OPC optical to geometrical diameter conversion; 1.53 for n and 0.001–0.003 for k for nephelometer truncation correction). This choice may in principle introduce a certain degree of uncertainty and circularity into the derived n, k, and SSA for dust. Nonetheless, we note that the range of refractive index values used to correct OPCs and nephelometer data falls in the range of variability of the refractive index values obtained in this study (see Sect. 4.3), which suggests that the values used for the corrections are appropriate. Additionally, as previously discussed, both the size distribution (dN∕dlog D_g)_SWoptics and the scattering coefficient are not very sensitive to the assumptions about n and k used for the calculations (less than 5 % changes in both the number size distribution behind SW inlets and the scattering coefficient from changing n and k within the range of estimated values in this study) which further demonstrates the robustness of the proposed approach.

2. The retrieval procedure for n and k, as well as the calculations for OPC optical-to-geometrical diameter and the nephelometer truncation correction, simplifies the nonspherical heterogeneous dust aerosols (e.g., Chou et al., 2008; Okada et al., 2001; Nousiainen and Kandler, 2015) into homogeneous spherical particles that can be represented by Mie theory. In the present study, we decided not to use a more advanced shape-representing theory for three main reasons. First, the spherical model has been shown to produce only moderate errors when computing angular-integrated quantities (Mishchenko et al., 1995; Otto et al., 2009; Sorribas et al., 2015) such as those we calculate in this study to retrieve the OPC and truncation corrections and for n and k retrieval. For instance, Sorribas et al. (2015) showed that using a spheroidal model has a limited effect on the truncation correction. These authors estimated that using a spheroidal model permits a 4 % to 13 % improvement in the agreement between the modeled and measured spectral scattering coefficient at 450–700 nm but only for super-micron particles. Conversely, for submicron dust the spherical approximation is better suited than the spheroidal model to reproduce the scattering coefficients by the nephelometer. The study by Mogili et al. (2007) also found an excellent agreement between measured shortwave extinction spectra and those calculated from Mie theory simulations for dust minerals, supporting the use of Mie theory for dust optical modeling. On the other side, other studies point to the need for a nonspherical assumption to improve the modeling of dust optical properties (e.g., Otto et al., 2009). Second, we used Mie theory for the sake of comparison with the large majority of previous field and laboratory data published so far, which have used calculations with the spherical approximation. Third, the shape distribution and morphology of the dust samples were not measured during experiments. Improper assumptions on the particle shape and morphology may induce even larger errors than using Mie theory, in particular for super-micron aerosols (Kalashnikova and Sokolik, 2004; Nousiainen and Kandler, 2015). It should be pointed out, however, that dust is usually assumed to be spherical in global climate models (e.g., Myhre and Stordal, 2001; Balkanski et al., 2007; Jin et al., 2016), and different studies still show contradictory results on the true impact of dust nonsphericity on radiative fluxes and heating rates from global model simulations (Mishchenko et al., 1995; Yi et al., 2011; Räisänen et al., 2012; Colarco et al., 2014). On the other hand, shape effects can be important for the retrieval of aerosol properties from remote sensing techniques using spectral, angular, and polarized reflectance measurements (e.g., Feng et al., 2009). In synthesis, accounting for shape effects is still controversial for dust modeling and also a complex issue beyond the scope of this paper. Thus, while we acknowledge the potential uncertainties induced by spherical assumptions in our study, we do not quantify the overall impact of this assumption on our results here.

Table 2 Summary of information on the soil samples and sediments used in this study.

4 Results

A total of 19 soil samples from different desert areas in northern Africa, Sahel, eastern Africa and the Middle East, eastern Asia, North America, South America, southern Africa, and Australia were selected for experiments from a collection of 137 soil samples from source areas worldwide. The main information on the provenance of these soils is provided in Table 2. The 19 selected soils, the same as analyzed in DB17, represent the major dust source regions depicted in Ginoux et al. (2012). Amongst the database of 137 samples from all the world regions that constitute significant dust emitters, the range in mineralogical composition obtained for the chosen samples represents the largest variability in iron oxide contents that can be found worldwide. This is illustrated in Fig. 2 where we represent the variability of hematite and goethite content in the 19 selected soils and compare it with the range of variability of the global desert soils from the database of Journet et al. (2014).

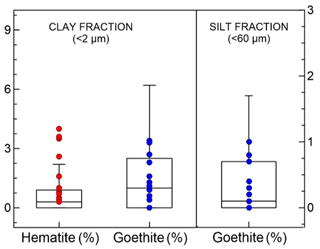
Figure 2 Box-and-whisker plot showing the full variability of hematite and goethite mass fractions in the soils for the clay-sized (< 2 µm diameter) and silt-sized (< 60 µm diameter) fractions as retrieved from the global soil mineralogical database by Journet et al. (2014). The box-and-whisker plot includes data for the nine desert source areas depicted in Ginoux et al. (2012) and DB17 (northern Africa, Sahel, eastern Africa and the Middle East, central Asia, eastern Asia, North America, South America, southern Africa, and Australia). Dots indicate hematite and goethite content in clay-sized and silt-sized soils (always from Journet et al.) extracted in correspondence to the geographical coordinates at which the 19 soils used in the CESAM experiments were collected. The Journet et al. database assumes that the iron oxides in the silt fraction consist only of goethite.

4.1 Physical and chemical properties of analyzed dust samples

4.1.1 Dust mass concentration and size distribution

Figure 3 shows a typical example of a time series of aerosol mass concentration and effective fine and coarse diameters measured inside the CESAM chamber and behind the SW instruments inlets during the experiments, as well as the corresponding β_sca and β_abs at 370 nm. The figure shows the rapid increase in the mass concentration within CESAM during dust injection in the chamber and its subsequent decrease during the experiments due to both size-selective gravitational settling, occurring mostly within the first 30 min of the experiments, and dilution by sampling. The scattering and absorption coefficients of dust decrease with time after injection in tandem with the decrease in the mass concentration and the size-dependent depletion in the chamber. The dust mass concentration inside CESAM at the peak of the injection is between 2 (Mali) and 310 mg m⁻³ (Bodélé) and falls to values between 0.9 (Mali) and 20 mg m⁻³ (Bodélé) behind the SW instruments inlets. These values are comparable to those measured close to sources during dust storms (Rajot et al., 2008; Kander et al., 2009). After 2 h, the dust mass concentration has decreased to values of 0.2 to 2.5 mg m⁻³ (inside CESAM) and 0.1 to 1.9 mg m⁻³ (behind the SW inlets), as after medium- to long-range dust transport in the real atmosphere (Weinzierl et al., 2011; Denjean et al., 2016b). This indicates that in a 2 h experiment in CESAM it is possible to reproduce the temporal changes in the dust mass load observed in the real atmosphere from emission to medium- to long-range transport.

As the mass concentration, the effective diameter of the coarse fraction, D_eff,coarse, also rapidly decreases with time due the progressive deposition of the coarsest particles in the chamber. For the various soils, D_eff,coarse varies in the range of 4–8 µm (peak of injection) to 3–4 µm (after 2 h) inside the CESAM chamber and in the range of 3–4 µm (peak of injection) to 2–3 µm (after 2 h) behind the SW inlets. In contrast, D_eff,fine remains quite constant during the experiments, with a value between 0.6 and 0.7 µm for all soils. The values of D_eff,coarse obtained in this study inside the CESAM chamber are in line with those measured close to African sources (4–12 µm; Rajot et al., 2008; Weinzierl et al., 2009; Ryder et al., 2013a) and for dust transported across the Mediterranean (5–8 µm; Denjean et al., 2016a). Conversely, the values of D_eff,coarse behind the SW instrument inlets are mostly in agreement with those reported for dust transported at Cape Verde and across the Atlantic Ocean (∼3 µm; Maring et al., 2003; Müller et al., 2011; Denjean et al., 2016b). Our values of D_eff,fine are higher compared to values reported by Denjean et al. (2016a) for dust aerosols transported over the Mediterranean (0.2 to 0.5 µm), reflecting the fact that we analyze pure dust, whereas these authors often encountered dust externally mixed with pollution particles.

The comparison of D_eff,coarse values suggests that while the size distribution in CESAM is mostly representative of dust close to sources (see DB17), the size measured behind the SW instrument inlets is mostly representative of transport conditions. Figure 4 illustrates this point by showing the volume size distributions of the generated dust aerosols at the peak of injection seen by the SW optical instruments compared to the average size of dust measured in CESAM (DB17) and field observations close to sources (e.g., Niger) and after long-range transport (Cape Verde, Suriname, Puerto Rico, and Barbados). The size distribution of dust inside CESAM includes a coarse mode up to 50 µm and reproduces field observations close to sources well, as shown in comparison to the Niger case. Due to particle losses along tubes, particles above 10 µm diameter are not seen by the SW instruments. The overall shape of the dust size distribution sensed by the SW instruments is comparable to that measured after atmospheric long-range transport, even if the fraction of particles above 3.9 µm diameter, which is at the 50 % cutoff of the transmission efficiency for the SW optical instruments, is significantly underrepresented compared to observations (i.e., Betzer et al., 1988; Formenti et al., 2001; Maring et al., 2003; Ryder et al., 2013b, 2018; Jeong et al., 2014; Denjean et al., 2016b). It should be keep in mind that field data are also often affected by inlet restrictions so that they cannot measure the whole coarse dust fraction (see Table 1 in Ryder et al., 2018). The lowest cutoffs for field data shown in Fig. 4 are for the NAMMA and PRIDE datasets and correspond to upper size limits at 5 and 10 µm in diameter, respectively. These values being above our cutoff of 3.9 µm means that the comparison with our size dataset is meaningful within the range of our measurements. Only the data from AER-D did not suffer from significant inlet restrictions, thus leading to the observation of giant dust particles up to tens of microns in the Saharan Air Layer off the coasts of western Africa.

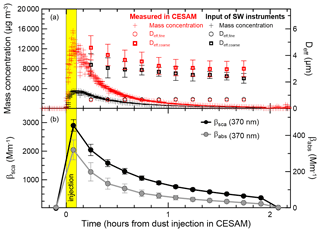
Figure 3 (a) Time series of the aerosol mass concentration (cross symbols) and effective fine (D_eff,fine, open dots) and coarse diameter (D_eff,coarse, open squares) measured inside the CESAM chamber (red symbols) and at the input of the SW instruments (black symbols) for one experiment (Morocco dust). (b) Time series of the scattering β_sca and absorption β_abs coefficients at 370 nm for the same experiment. Mass concentrations are reported as 6 s data, while all other quantities are 10 min averages.

Table 3 Chemical characterization of the dust aerosols in the PM_10.6 size fraction. Column 3 shows MC_Fe%, the fractional mass of elemental iron with respect to the total dust mass concentration (±10 % relative uncertainty), and column 4 reports MC_Fe-ox%, the mass fraction of iron oxides with respect to the total dust mass concentration (±15 % relative uncertainty) and its speciation in hematite MC_Hem% and goethite MC_Goeth% (< ±10 % relative uncertainty). The iron oxide measurements were not made on the Taklimakan sample. Mean values and standard deviations (SDs) based on single-sample data are reported for the full dataset.

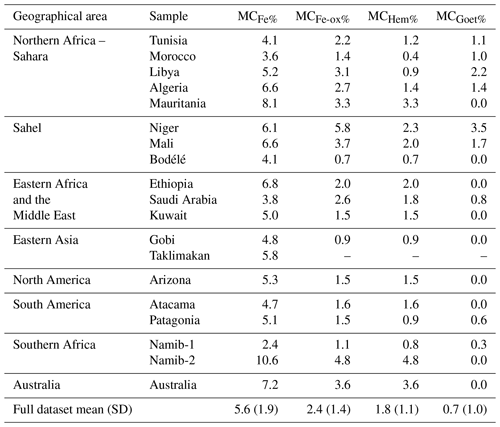
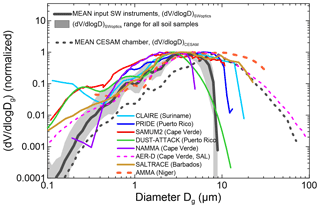
Figure 4 Comparison of dust size distributions sensed by the SW optical instruments (i.e., behind the SW instrument inlet (dV∕dlog D_g)_SWoptics), with field data for long-range-transported dust. The thick black line represents the mean value of (dV∕dlog D_g)_SWoptics at the peak of the dust injection in CESAM for experiments with the different samples. The grey shaded area indicates the range of (dV∕dlog D_g)_SWoptics for all samples. The dotted black line shows the average of the dust size distribution at the peak of the injection inside the CESAM chamber from DB17. Field data are from the following: Formenti et al. (2001) (CLAIRE campaign in Suriname, South America), Maring et al. (2003), and Denjean et al. (2016b) (PRIDE and DUST-ATTACK campaigns in Puerto Rico, Caraibes); Müller et al. (2011), Chen et al. (2011), and Ryder et al. (2018) (SAMUM2, NAMMA, and AER-D campaigns in Cape Verde, eastern Atlantic); and Weinzierl et al. (2017) (SALTRACE campaign, data from Barbados). For comparison, data taken close to the source in Niger from Formenti et al. (2011) during the AMMA campaign are also shown. SAL stands for Saharan Air Layer. All data are reported as volume size distributions normalized at the maximum. The different acronyms are spelled out as follows. AER-D: AERosol Properties – Dust; AMMA: African Monsoon Multidisciplinary Analysis; CLARE: Cooperative LBA Airborne Regional Experiment; DUST-ATTACK: Dust Aging and TransporT from Africa to the Caribbean; NAMMA: NASA African Monsoon Multidisciplinary Analysis; PRIDE: Puerto Rico Dust Experiment; SALTRACE: Saharan Aerosol Long–range Transport and Aerosol–Cloud–Interaction Experiment; SAMUM: Saharan Mineral Dust Experiment.

4.1.2 Iron and iron oxide dust content

Elemental iron includes iron in the form of iron oxides and hydroxides, i.e., hematite and goethite (the so-called free iron, mostly controlling SW absorption), as well as the iron incorporated in the crystal structure of silicates and aluminosilicates (illite, smectite), which does not substantially contribute to SW absorption (Karickhoff and Bailey, 1973; Lafon et al., 2004). The mass concentrations of these components (total iron oxides, hematite, goethite, and total elemental iron) for the different analyzed samples are reported in Table 3. There is a considerable variability in the iron and iron oxide content for our samples. Total iron in the dust samples is in the range from 2.4 % (Namib-1) to 10.6 % (Namib-2). Iron oxides account for 11 % to 62 % of the iron mass (calculated following C17, not reported in Table 3), whereas the percent of iron oxides to the total dust mass varies between 0.7 % (Bodélé Depression) and 5.8 % (Niger). These data are in the range of values reported in the literature (Reid et al., 2003; Scheuvens et al., 2013; Formenti et al., 2011, 2014a). For the samples from the Sahara and the Sahel, goethite is the dominant iron oxide species, in agreement with Lafon et al. (2006) and Formenti et al. (2014a, b). Elsewhere, hematite dominates over goethite, as reported by some studies (Arimoto et al., 2002; Shen et al., 2006; Lu et al., 2011).

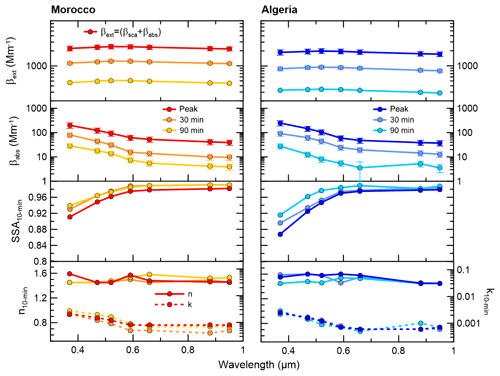
Figure 5 Spectral extinction coefficient, absorption coefficient, SSA, and real (n) and imaginary (k) parts of the refractive index at the peak of the dust injection in the chamber and after 30 and 90 min for Morocco and Algeria dust samples. Data are reported at the seven aethalometer wavelengths (370, 470, 520, 590, 660, 880, and 950 nm) as 10 min averages. In the top panels we report the extinction calculated as the sum of scattering and absorption coefficients. For the sake of clarity error bars are not shown for SSA, n, and k data.

4.2 Spectral- and time-dependent dust extinction and absorption coefficients, complex refractive index, and SSA

Figure 5 illustrates a typical spectral- and time-dependent set of measured optical properties. The spectral extinction coefficient, absorption coefficient, SSA, and real and imaginary parts of the complex refractive index obtained at 10 min resolution for the Morocco and Algeria samples are shown at the peak of the dust injection in CESAM and 30 and 90 min after the peak. Figure 5 shows that absorption decreases with wavelength but not extinction. The SSA increases from 370 to 590 nm, while it is almost constant between 590 and 950 nm. The imaginary part of the refractive index decreases with λ following the decrease in β_abs. The real part of the refractive index does not depend on wavelength.

The extinction and absorption coefficients decrease in absolute value with time, as already shown in Fig. 3. Their spectral dependence remains quite constant with time but varies from soil to soil. The experiment-averaged absorption, scattering, and extinction Ångström exponents in the 370–950 nm spectral range, representing the spectral variation of the absorption, scattering, and extinction coefficients, vary between values of 1.5 and 2.4 (AAE), −0.4 and 0.4 (SAE), and −0.2 and +0.5 (EAE) for the different samples. These values are in line with those previously reported by Moosmüller et al. (2012) and C17 for dust from various locations. The retrieved n and k also show negligible changes in their spectral shape with time, and their magnitude remains approximately constant. In contrast, the SSA increases with time, in particular below the 600 nm wavelength, and its spectral shape changes. This is mostly due to the decrease in the coarse size fraction with residence time in the chamber, as will be analyzed in Sect. 4.5. Similarly to the absorption, scattering, and extinction coefficients, the spectral shape of k and SSA is somewhat different between the various samples, with the sharpest spectral variations observed for the most absorbing samples and a less pronounced spectral variation for the less absorbing ones, as is evident, for example, by comparing the SSA data for Morocco and Algeria in Fig. 5.

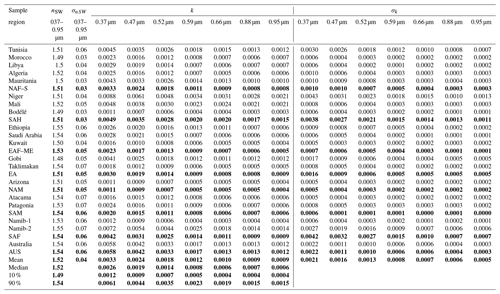
Table 4 Real (n) and imaginary (k) parts of the refractive index estimated for the 19 analyzed dust samples and mean values calculated for the eight regions and for the full dataset. Data for single soils are reported as experiment-averaged values, and their uncertainty is calculated as indicated in Table 1. Mean values and standard deviations (SDs) at each wavelength based on single-sample data are reported for the eight regions and the full dataset. The median and 10 % and 90 % percentile are also reported for the full dataset. For North America and Australia, for which only one dust sample was analyzed, the reported data correspond to the single sample available from these regions. For the real part, the average over the whole shortwave range (n_SW) is indicated. Mean (± SD), median, and 10 % and 90 % values are indicated in bold font. The region acronyms are as follows. NAF–S: northern Africa–Sahara, SAH: Sahel, EAF–ME: eastern Africa and the Middle East, EA: eastern Asia, NAM: North America, SAM: South America, SAF: southern Africa, AUS: Australia.

4.3 Spectral complex refractive index and SSA for the different source regions and comparison to literature data

Figures 6 and 7 show the experiment-averaged n, k, and SSA between 370 and 950 nm for the 19 aerosol samples analyzed in this study. Data for n, k, and SSA and their uncertainties are reported in Tables 4 and 5 for each sample together with the average values for each of the eight different source regions and for the full dataset. Figures 6 and 7 show that there are significant differences, both in magnitude and spectral shape, between the imaginary refractive index and SSA for the different samples. The highest values of k (0.0048–0.0088 at 370 nm and 0.0012–0.0021 at 950 nm) and lowest values of SSA (0.70–0.75 at 370 nm and 0.95–0.97 at 950 nm) are obtained for the Niger, Mali, Namib-2, and Australia samples, which also show the highest values of both the iron oxide content between 3.6 % and 5.8 % and hematite content between 2.0 % and 4.8 %. The lowest values (k is 0.0011–0.0012 at 370 and 0.0003–0.0004 at 950 nm, and SSA is in the range 0.91–0.96 at 370 nm and 0.97–0.99 at 950 nm) are obtained for the Bodélé, Namib-1, and Arizona samples, which have iron oxide contents between 0.7 % and 1.5 %. Both k and SSA vary from region to region, with the largest absorptions (highest k, lowest SSA) for the Sahel and Australia and the lowest absorption (lowest k, highest SSA) in North and South America and the Middle East; k and SSA values also vary within the same region, as illustrated for the Sahelian and southern African samples. The real part of the refractive index, on the other hand, is not only almost wavelength independent, as anticipated, but also relatively invariant from sample to sample. Its average over the 370–950 nm spectral range is between 1.48 (Gobi) and 1.55 (Ethiopia and Namib-2).

Table 5 As in Table 4 for the single-scattering albedo (SSA) data. Mean, median, and 10 % and 90 % values are indicated in bold font.

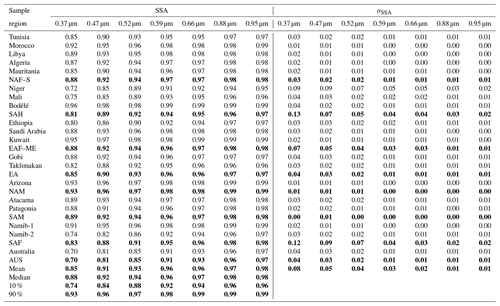
The full envelope of n, k, and SSA obtained for the entire set of analyzed samples is shown in Fig. 8. The real refractive index is relatively invariant, while the spectral k varies by up to an order of magnitude (0.001–0.009 at 370 nm and 0.0003–0.002 at 950 nm). The SSA changes accordingly for the different dust samples at the different wavelengths (30 % change at 370 nm corresponding to values between 0.70 and 0.96 and a 4 % change at 950 nm for values within 0.95–0.99). The population mean is 1.52 for n (as spectral average) and varies in the range 0.0033–0.0009 for k and 0.85–0.98 for the SSA between 370 and 950 nm (0.0016 and 0.94 as spectral averages for k and SSA) (Fig. 8 and Tables 4 and 5).

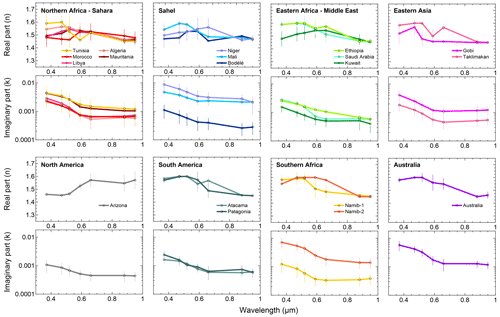
Figure 6 Real (n) and imaginary (k) parts of the dust complex refractive index at seven wavelengths between 370 and 950 nm obtained for the 19 aerosol samples analyzed in this study. Data correspond to the time average of the 10 min values obtained between the peak of the injection and 120 min later. The error bar corresponds to the absolute uncertainty in n and k, estimated to be < 8 % for n and between 13 and 75  % for k.

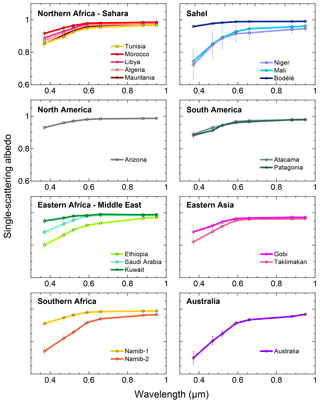
Figure 7 Single-scattering albedo (SSA) at seven wavelengths between 370 and 950 nm obtained for the 19 aerosol samples analyzed in this study. Data correspond for each sample (with the exception of Tunisia and Namib-2; see Sect. 3.1) to the fit of the 10 min values of β_sca versus β_abs, and the uncertainty is between 1 % and 12 % at 370 nm and between 1 % and 3 % at 950 nm.

The comparison between the full envelope of n, k, and SSA in this study with literature data is also shown in Fig. 8. Literature values considered for comparison include estimates from ground-based, aircraft, and satellite observations, laboratory studies, AERONET inversions, and estimates from mixing rules based on the dust mineralogical composition. Given that the sample selection in our experiments fully envelopes the global variability of the mineralogy of natural dust, we could expect that our dataset would also fully envelope the global-scale variability of the dust absorption and scattering properties in the SW. When comparing with available literature data we found that our n and SSA datasets encompass the range of values indicated in the literature very well, with only a few outlier points. In contrast, for the imaginary refractive index the reported range of variability from the literature is significantly larger than that found in our study, with our range of k being mostly at the lower bound of previous results. Nonetheless, our range of k values fully envelopes the ensemble of remote sensing and field campaign data on airborne dust from the previous literature reported in Fig. 8a. The global average spectral values for k in our study (thick black line) perfectly match the Dubovik et al. (2002) dataset from a synthesis of AERONET observations from various locations worldwide. Likewise, our k average is also very close to the dataset by Balkanski et al. (2007) estimated from mineralogical composition assuming 1.5 % (by volume) hematite in dust, a value shown to allow for a reconciliation of climate modeling and satellite observations of the dust direct SW radiative effect. By comparison, the average dust hematite content for the ensemble of our analyzed samples is 1.8 % (in mass), close to the 1.5 % value proposed by Balkanski et al. (2007).

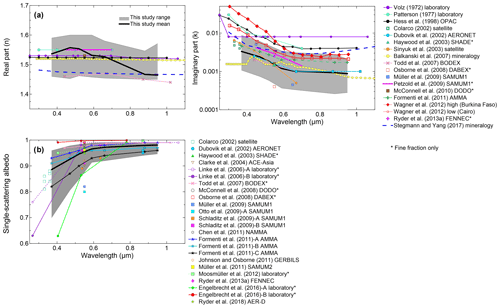
Figure 8 Comparison of the results obtained in this study with literature-compiled values of the (a) dust real and imaginary parts of the refractive index (n, k) and (b) single-scattering albedo (SSA) in the SW spectral range. The regions in grey indicate the full range of variability obtained in this study, and the thick black lines are the means of n, k, and SSA obtained for the different aerosol samples. Literature values include estimates from ground-based and aircraft observations during field campaigns, laboratory studies, AERONET inversions, and estimates from dust mineralogical composition. Data are in some cases for the full dust size distribution, while in others only the fine fraction below about 2 µm is represented (identified with *). The main provenance of the dust and datasets from the literature is provided in the following: Volz et al. (1972) data are for rainout dust collected in Germany; Patterson et al. (1977) data are for Saharan dust; Hess et al. (1998) data are from the OPAC database; Colarco et al. (2002) data are for dust from Dakar, SAL, and Tenerife; Dubovik et al. (2002) include data from the Bahrain–Persian Gulf and Solar Village–Saudi Arabia AERONET stations; Haywood et al. (2003) include dust from Mauritania; Sinyuk et al. (2003) data are from Cape Verde, Dakar, and Burkina Faso; Clarke et al. (2004) include Asian dust offshore of China, Japan, and Korea; Linke et al. (2006)-A includes dust from Cairo; Linke et al. (2006)-B includes dust from Morocco; Balkanski et al. (2007) calculated data from the mineralogical composition assuming a 1.5 % hematite mass fraction in dust; Todd et al. (2007) data are from Bodélé; Osborne et al. (2008) data are from Niger; Otto et al. (2009), Petzold et al. (2009), Schladitz et al. (2009), and Müller et al. (2009, 2011) include dust originated mostly in Morocco; McConnell et al. (2008, 2010) include dust from Niger–Senegal; Chen et al. (2011) include dust from the western Sahara; Formenti et al. (2011) in the k plot represents an average of airborne observations for the AMMA campaign in Niger, while for the SSA plot, Formenti et al. (2011)-A represents observations in the Saharan Air Layer, Formenti et al. (2011)-B data are from Bodélé–Sudan, and Formenti et al. (2011)-C represents a Sahelian uplift episode; Johnson and Osborne (2011) include dust from the western Sahara; Moosmüller et al. (2012) analyzed samples from the Middle East, Mali, and Spain, and here we report the average of their obtained values; Wagner et al. (2012) obtained k values for several samples from Burkina Faso, Cairo, and the SAMUM campaign, and here we report the values for the maximum of their spectral k (Burkina Faso) and the minimum (Cairo); Ryder et al. (2013a) include dust from the western Sahara and Mauritania, and we report in both the k and SSA plots the average of their observations; Engelbrecht et al. (2016) analyzed many dust samples from all over the world, and here we report their estimated minimum and maximum of the dust SSA (A) from California and (B) from the Etosha Pan in Namibia; Stegmann and Yang (2017) modeled the refractive index of dust based on assumed mineralogical compositions typical for the northern and southern Sahara and western and eastern Asia dust, and here we report the average of their results for both n and k. Uncertainties in the field observations have been omitted for the sake of clarity. The legend identifies the line styles used in the plots. The different acronyms are spelled out as follows (see also the caption of Fig. 4). AERONET: Aerosol Robotic Network; OPAC: Optical Properties of Aerosols and Clouds; SHADE: Saharan Dust Experiment; BODEX: the Bodélé Dust Experiment; DABEX: Dust and Biomass Experiment; SAMUM1 and SAMUM2 refer to the two SAMUM campaigns in Morocco and Cape Verde, respectively, SAMUM: Saharan Mineral Dust Experiment; DODO: Dust Outflow and Deposition to the Ocean; ACE-Asia: Asian Pacific Regional Aerosol Characterization Experiment; GERBILS: Geostationary Earth Radiation Budget Intercomparison of Longwave and Shortwave radiation.

Looking at Fig. 8, the datasets that show the largest values, which also fall outside our estimated range of k over the entire considered wavelength range, are the ones by Wagner et al. (2012) obtained from laboratory chamber experiments, especially deviating below the 600 nm wavelength from our range of k, and the ones by Volz (1972), Patterson et al. (1977), and Hess et al. (1998; i.e., the OPAC 3.1 version database, which is the same k dataset used in the new OPAC 4.0 version; Koepke et al., 2015). The Volz (1972), Patterson et al. (1977), and OPAC datasets are amongst the most commonly used references for the dust imaginary refractive index in many climate models. The reasons for these discrepancies in the k values are difficult to assess, since they could be related to both instrumental and analytical aspects. In the studies by Volz (1972) and Patterson et al. (1977), for instance, the complex refractive index was obtained by transmittance and diffuse reflectance on pellet samples, a technique that requires the dust to be pressed in a matrix of nonabsorbing material. In this case a discrepancy arises from the different optical behavior between dust compressed in a pellet and the airborne particles. Moreover, Volz (1972) and Patterson et al. (1977) analyze dust aerosols collected after mid- to long-range transport, thus after the dust has possibly been mixed with absorbing species.

For the case of Wagner et al. (2012) the imaginary refractive index was retrieved from laboratory chamber experiments on suspended dust, as in our study. Nonetheless, their approach differs in various aspects from the one applied here and this can lead to the observed differences in the retrieved k. First, the aerosol generation technique is different between the two works, and this possibly leads to particles with different physicochemical features compared to our study. In Wagner et al. (2012) the dust aerosol was generated by a rotating brush disperser using only the 20–75 µm sieved fraction of the soils. This system acts to disaggregate the finest particles of the soil by passing it through a nozzle. Then the largest aerosol grains were removed by a cyclone system (50 % cutoff at 1.2 µm aerodynamic diameter) so that only the submicron size fraction was measured. We show in Sect. 4.5 that k is independent of size for the range of investigated effective coarse diameters between 2 and 4 µm, but the range of sizes analyzed in Wagner et al. (2012) is significantly lower than in our study and a size effect cannot be excluded. In fact, the relationship between dust absorption and iron content may vary depending on the considered size fraction (see C17) due to the fact that iron-bearing minerals are more concentrated in the clay fraction (< 2.0 µm) of the dust (Kandler et al., 2009). Moreover, generating dust in a different way may lead to differences in the chemical and mineralogical size-dependent composition of the sample, therefore contributing to the observed differences. The impact of this, however, is difficult to evaluate. Another difference concerns the choice of the optical theory to retrieve k (T matrix in Wagner et al. instead of Mie theory as used in our work). This can contribute to the observed differences, even if in a limited way (Mogili et al., 2007; Sorribas et al., 2015). Third, in their retrieval Wagner et al. fixed the real refractive index to a wavelength-independent value of 1.53 (as done in several other field and laboratory studies in Fig. 8), and this assumption can bias high–low the retrieved k if the actual n is higher–lower than the assumed 1.53 value. So, in summary, while multiple factors could contribute to the discrepancy, it remains difficult to assess which source of discrepancy is dominant.

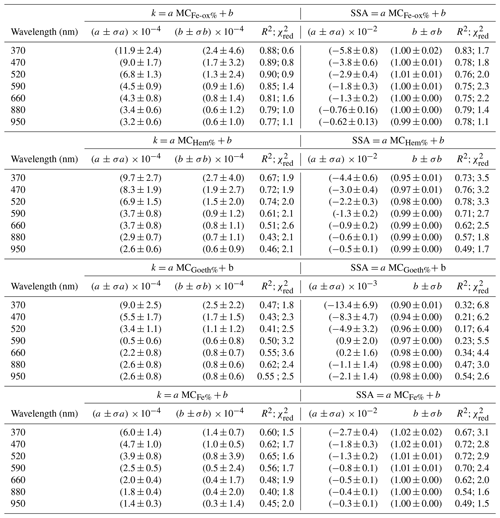
Table 6 Results of the linear fit between k, SSA, and the mass concentration of iron oxides (MC_Fe-ox%), hematite (MC_Hem%), goethite (MC_Goeth%), and elemental iron (MC_Fe%) in dust. Column 1 indicates the wavelength; (a±σa) indicates the retrieved slope and its estimated uncertainty; (b±σb) indicates the retrieved intercept and its estimated uncertainty; R² denotes the correlation coefficient; and ${\mathit{\chi }}_{\mathrm{red}}^{\mathrm{2}}$ is the reduced chi square of the fit.

4.4 Imaginary refractive index and SSA versus iron and iron oxide content

The sample-to-sample variability of the imaginary part of the refractive index k and the SSA observed in Figs. 6 and 7 is related to the dust composition by investigating the dependence on the particle iron content. In Fig. 9 we show the experiment-averaged k and SSA at 370, 520, and 950 nm versus the mass concentration of iron oxides (hematite+goethite, MC_Fe-ox%), hematite (MC_Hem%), goethite (MC_Goeth%), and total elemental iron (MC_Fe%) measured for the different dust samples in this study. The data are linearly fitted to relate k and SSA to MC_Fe-ox%, MC_Hem%, MC_Goeth%, and MC_Fe%. The results of the fits at all wavelengths between 370 and 950 nm are reported in Table 6, together with statistical indicators of the goodness of fit (correlation coefficient, R², and reduced chi square, ${\mathit{\chi }}_{\mathrm{red}}^{\mathrm{2}}$, i.e., the obtained chi square divided by the number of degrees of freedom). There is an excellent correlation between MC_Fe-ox% and both k and SSA at the different wavelengths (R²> 0.75). A weaker correlation is found when relating k and SSA to MC_Hem% and MC_Fe% (R² between 0.40 and 0.74 for k and between 0.49 and 0.78 for SSA), as well as MC_Goeth% (R² between 0.17 and 0.62). The better correlation of k and SSA with MC_Fe-ox% compared to MC_Fe% is expected since dust optical properties in the visible wavelengths are mostly sensitive to the fraction of iron oxides, rather than to iron incorporated into the crystal structure of silicates (Karickhoff and Bailey, 1973; Lafon et al., 2006; Moosmüller et al., 2012; Klaver et al., 2011; Engelbrecht et al., 2016; C17). The quantities that most robustly satisfy a linear relationship are k and MC_Fe-ox%, as indicated by the reduced chi square ${\mathit{\chi }}_{\mathrm{red}}^{\mathrm{2}}$ that is around 1 at all different wavelengths. The ${\mathit{\chi }}_{\mathrm{red}}^{\mathrm{2}}$ increases to values also larger than 2 in the other cases, indicating the poorer robustness of the fit in these cases.

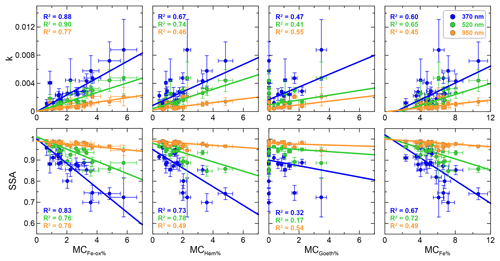
Figure 9 Experiment-averaged imaginary part of the refractive index (k, top panels) and single-scattering albedo (SSA, bottom panels) at 370, 520, and 950 nm versus the mass concentration of iron oxides (MC_Fe-ox%), hematite (MC_Hem%), goethite (MC_Goeth%), and elemental iron (MC_Fe%) measured for the different dust samples analyzed in this study. The calculated linear fit regression lines are shown, together with the correlation coefficients of the fits (R²). The legend indicates the line styles used in the plots. Data for the Taklimakan sample were excluded from the k and SSA plots versus MC_Fe-ox%, MC_Hem%, and MC_Goeth% due to the absence of iron oxide data for this sample.

We also investigated the dependence of the spectral k and SSA on the mass concentration of other minerals, such as clays, calcite, quartz, and feldspars, as well as on the mass concentration of different elements. We found that there is no statistically significant correlation between k or SSA and the mass concentration of any of these compounds (not shown), with R² values between 0.002 and 0.46 at the different wavelengths for all cases.

These results therefore clearly show that iron, particularly in the form of iron oxides (hematite+goethite), is the main driver of dust shortwave absorption. Measuring only the hematite mass fraction to estimate the dust absorption, as is sometimes done, is therefore not sufficient.

4.5 Imaginary refractive index and SSA versus dust coarse size fraction

The dependence of the spectral k and SSA on the dust coarse fraction is investigated by relating it to the D_eff,coarse calculated from the size distribution data behind the SW instruments inlets. The k_10 min and SSA_10 min at 370, 520, and 950 nm versus D_eff,coarse are shown in Fig. 10 for all experimental data, which we separated into three classes based on their iron oxide content (MC_Fe-ox%≤1.5 %, 1.5 % < MC_Fe-ox% < 3 %, MC_Fe-ox%≥3 %). Figure 10 shows that even if the correlation is not very strong (R² < 0.54), there is a clearly decreasing tendency for the SSA_10 min with increasing D_eff,coarse, particularly at 370 and 520 nm for strongly absorbing samples with iron oxide content larger than 3 %. The SSA_10 min is mostly independent of changes in D_eff,coarse at 950 nm. Conversely, k_10 min has a very poor correlation with D_eff,coarse (R² < 0.35) and thus does not depend on size. Similar results were also obtained for the real part (not shown).

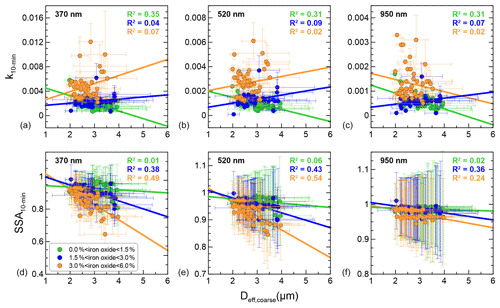
Figure 10 The 10 min averaged imaginary refractive index (k_10 min, a, b, c) and single-scattering albedo (SSA_10 min, d, e, f) at 370, 520, and 950 nm versus effective coarse diameter (D_eff,coarse) estimated at the input of the SW instruments. Data were classified into three classes based on the iron oxide content of the dust samples. The linear fit curves and the correlation coefficients for the linear regression fits for each dataset are also reported. The legend identifies the line styles used in the plots.

These results confirm previous observations (Sokolik and Toon, 1999; McConnell et al., 2008, 2010; Ryder et al., 2013a, b) that the refractive index is independent of size. This suggests that size-dependent mineralogical composition is not sufficient to affect k (in the limit of our measurement and retrieval procedure precision). It is worth mentioning that only a few past studies evidenced a dependence of k on the size distribution of dust aerosols (i.e., Kandler et al., 2009, 2011  Otto et al., 2009); this may be because the refractive index was retrieved in these studies from mixing rules based on the estimated size-dependent mineralogical composition.

Differently from k, the SSA increases as the coarse dust size fraction decreases. This is due to the fact that absorption efficiency for a single particle (Q_abs) increases with particle diameter, while the scattering efficiency (Q_sca) decreases. Ryder et al. (2013a) also showed that the dependence of SSA on size is linear but important only when the coarse fraction is high (if particles larger than about 3 µm in diameter are present); otherwise, the SSA depends mainly on composition, also in agreement with more recent field observations by Ryder et al. (2018).

5 Summary

In this paper we presented new measurements of the spectral SW complex refractive index ($m=n-ik$) and single-scattering albedo (SSA) for 19 mineral dust aerosols generated in the laboratory from natural soil samples from major desert dust source areas in northern Africa, the Sahel, Middle East, eastern Asia, North and South America, southern Africa, and Australia. These were selected to represent the heterogeneity of dust composition at the global scale, in particular the range of iron oxide concentrations. The envelope of refractive indices and SSA data obtained in this study can thus be taken as representative of the variability of global dust aerosols.

The experiments described here were conducted in the 4.2 m³ CESAM chamber, a dynamic environment in which dust aerosols are generated and maintained in suspension for several hours while monitoring the evolution of their physical, chemical, and optical properties. The generated dust aerosols are characterized by a realistic size distribution, including both the submicron and the super-micron fraction, and they have an atmospherically representative mass concentration and composition, including iron oxides and elemental iron content.

Some other laboratory studies have been performed in the past to investigate the shortwave SSA of dust from different sources worldwide and its dependence on composition (Linke et al., 2006; Moosmüller et al., 2012; Engelbrecht et al., 2016). Conversely, for the refractive index there is to our knowledge only one other chamber study (Wagner et al., 2012) that retrieved the imaginary part k between 305 and 955 nm for dust aerosols from a limited number of source areas in Africa (Burkina Faso, Egypt, and Morocco). As a matter of fact, our work provides the first consistent simulation chamber study of the complex refractive index of global dust.

The results of the present study can be summarized as follows.

1. The spectral k and SSA retrieved in this study vary from sample to sample within the same region but also from one region to another. For k, values vary from 0.0011 to 0.0088 at 370 nm, 0.0006 to 0.0048 at 520 nm, and 0.0003 to 0.002 at 950 nm. For SSA, values vary from 0.70 to 0.96 at 370 nm, 0.85 to 0.98 at 520 nm, and from 0.95 to 0.99 at 950 nm. In contrast, n is wavelength independent and almost uniform for the different sources, with values between 1.48 and 1.55. Values for n and SSA fall within the range of published literature estimates, while for k we obtain a much narrower range of variability than the ensemble of literature results, as illustrated in Fig. 8. In particular, we found lower values of k compared to most of the literature values currently used in climate models, such as Volz et al. (1972), Patterson et al. (1977), and the OPAC database (Hess et al., 1998; Koepke et al., 2015). In their study, Miller et al. (2014) state that the values of Dubovik et al. (2002) from AERONET, Patterson et al. (1977) for far-traveled dust, and OPAC probably encompass global solar absorption by dust. In contrast, our results indicate that dust absorption is lower than previously thought, and its average is close to the values reported by Dubovik et al. (2002) from AERONET observations and Balkanski et al. (2007) for dust with a 1.5 % volume fraction of hematite. Our range of variability of an order of magnitude for k and between 4 % and 30 % for the spectral SSA is actually large enough to change the sign of the global dust direct effect at the TOA (Miller et al., 2004), as well as its regional implications (e.g., Solmon et al., 2008; Jin et al., 2016), and has to be taken into account in climate modeling.

2. The documented changes in k and SSA also impact remote sensing retrievals. To give an example, following Gasteiger et al. (2011), our observed variability of about 10 % for the SSA at 532 nm would translate to about 40 % variability in the retrieved extinction profiles and optical depths from lidar observations for dust from varying sources.

3. The sample-to-sample variability observed in this study is mostly related to the iron oxide and elemental iron content in dust. At each investigated wavelength the magnitude of k and SSA is linearly correlated with the mass concentration of total iron oxides, hematite, goethite, and total elemental iron. Small variations of these compounds translate into large variations of k and SSA.

4. We also investigated the dependence of k and SSA on the size distribution of dust. While k is independent of size (suggesting that a constant value can be used along transport), below 600 nm the SSA linearly decreases for increasing D_eff,coarse for strongly absorbing samples with more than 3 % iron oxide content. The investigated range of D_eff,coarse is within about 2 and 4 µm and thus comparable to values obtained along a transport path over the Atlantic Ocean for dust during about 2 to 6 d following emission (Denjean et al., 2016a).

5. The observations of points (3) and (4) suggest that while it is sufficient to know the content of iron oxide (or elemental iron) in dust to predict its spectral k, which means that only one tracer is needed in models to parameterize its regional and global variability, for the spectral SSA both composition and size distribution are required.

6 Concluding remarks

Based on our results, we recommend that dust simulations, as well as remote sensing retrievals, use source-dependent values of the spectral SW refractive index and SSA instead of generic values. We propose, as a first step, a set of regionally averaged n, k, and SSA values to represent dust from each of the eight regions analyzed here as well as a global average value from the ensemble of our data (Tables 4 and 5). Furthermore, the relationships found between k, SSA, and the iron oxides or elemental iron content in dust create an opportunity to establish predictive rules to estimate the spectrally resolved SW absorption of dust based on composition. We recommend the use of iron oxide content rather than iron content as it is better correlated with k and SSA. The relationship found in this study nonetheless refers to the bulk composition of the dust aerosols and to a size range typical of 2 to 6 d of transport in the atmosphere. As demonstrated in C17 for the mass extinction efficiency, the relationships linking dust absorption to iron content vary as a function of the analyzed size fraction due to the fact that iron-bearing minerals are more concentrated in the clay fraction (< 2.0 µm) than in the coarsest fraction of the dust (Kandler et al., 2009; C17). Further investigation should therefore evaluate the dependence of the spectral k and SSA versus iron content as a function of the size distribution of the particles, in particular extending to a wider range of D_eff,coarse compared to the one investigated in the present study. This will allow for the determination of whether the k and SSA versus iron relationship changes or not in different phases of the aerosol lifetime and therefore whether it is valid close to source areas (when the coarsest fraction is dominant, i.e., D_eff,coarse up to 15 µm; Ryder et al., 2013b) and in long-range transport conditions (when most of the coarse particle fraction above a few micrometers has settled out, i.e., D_eff,coarse of 2–3 µm or lower; Denjean et al., 2016b).

We point out, however, that the use of mineralogy to estimate k and SSA based on linear relationships, as obtained in our study, requires the model-predicted dust composition to accurately reflect that of natural atmospheric aerosols. For this aim, realistic soil mineralogy databases and accurate modeling of the soil to aerosol size fractionation need to be developed in model schemes. In this sense we mention the EMIT project (Earth Surface Mineral Dust Source Investigation) as a potential near-future source of high-resolution surface mineralogy data for arid and semiarid regions based on imaging spectroscopy satellite data (Green et al., 2018). Also, a realistic representation of the size distribution, in particular the coarse mode fraction of dust and its retention during atmospheric transport, should be provided in models given its importance in affecting the SSA, as shown in this study and previously reported in other papers (Ryder et al., 2013a, b, 2018).

Our study focuses on the dust spectral optical properties between 370 and 950 nm. Further work is required to extend the range of spectral refractive index and SSA data to wavelengths lower than 370 nm or higher than 950 nm given that these data are often required in global circulation models and numerical weather prediction models.

We do not provide any quantification of the uncertainty associated with the assumption of spherical particles in our study, even if we acknowledge the potential role of nonsphericity in affecting our data treatment and results. Additional work is foreseen to better investigate the shape of our generated dust and the impact of nonsphericity on retrieved spectral refractive indices and SSA.

Finally, this study had the objective to investigate the variability of dust SW optical properties at the global scale linked to the global variability of dust composition. It is noteworthy that observations over southern Africa and the Sahel from the present study indicate that the k and SSA variability over these regions is comparable to the one obtained for the global scale. For other regions, such as North America and Australia, only one sample was analyzed, with no information on the regional-scale variability of k and SSA. Additionally, for some of the analyzed areas, such as the Bodélé depression, even local-scale variability (on the order of a few kilometers) may be of relevance given the documented local-scale changes in the particle mineralogy and iron content (Bristow et al., 2010). More efforts should therefore be devoted to better characterizing the variability of dust spectral optical properties at the regional and subregional scale with the aim of better assessing the dust impact on the climate of different areas of the world.