the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Fundamentals of data assimilation applied to biogeochemistry
Anna M. Michalak
Frédéric Chevallier
This article lays out the fundamentals of data assimilation as used in biogeochemistry. It demonstrates that all of the methods in widespread use within the field are special cases of the underlying Bayesian formalism. Methods differ in the assumptions they make and information they provide on the probability distributions used in Bayesian calculations. It thus provides a basis for comparison and choice among these methods. It also provides a standardised notation for the various quantities used in the field.
The task of improving current knowledge by considering observed phenomena is a fundamental part of the scientific process. The mechanics of the process are a matter for historians of science and a matter of fierce debate, while its fundamental reliability is a matter for philosophers, literally a metaphysical question. Here we are concerned with building and using algorithms for the process. The step by step construction of such algorithms from agreed upon logical premises is beyond our scope here but is masterfully presented by Jaynes and Bretthorst (2003).
It is important to note at the outset the generality of the machinery we will present, especially because many of the common objections to the methods spring from misunderstandings of this generality. For example, it is a common complaint that data assimilation can improve a model but cannot test it. The methods are, however, capable of considering multiple models and assigning probabilities to them; a test of their relative performance.
At the outset we should settle some questions of terminology. The phrases “data assimilation”, “parameter estimation”, “inverse modelling” and “model–data fusion” are used with overlapping meanings in the literature. “Inversion” is most commonly used to describe improving knowledge of the inputs of a model given observations of its output. The term arises since the technique reverses the normal direction of causality (Enting, 2002, p. 10). Data assimilation most commonly refers to the correction of the trajectory of a running model given observations. There are many exceptions to this categorisation and other distinctions could be made. We will use the term data assimilation throughout but readers should interpret the name broadly.
We are concerned with algorithms to improve the performance of models through the use of data. The improvement will come via knowledge of the state (quantities the model calculates), boundary conditions (quantities we insert into the model) or structure of the model. Performance will be assessed by the model's ability to reproduce observations, especially those not included in the data assimilation algorithm.
The application of data assimilation to biogeochemistry has proceeded from informality to formal methods and from small to larger problems. One can see the study of Fung et al. (1987) as a data assimilation experiment. These authors adjusted respiration parameters in a simple biosphere model so that the seasonal cycle of atmospheric CO2 concentration better matched the observed seasonal cycle at some stations. About 15 years later, Kaminski et al. (2002) performed a similar study on a similar model with more stations and a formal algorithm. We see similar developments in the estimation of CO2 fluxes (e.g. Tans et al., 1990 vs Chevallier et al., 2010) and ocean productivity (Balkanski et al., 1999 cf. Brasseur et al., 2009).
The flourishing of the general approach has also led to a great diversification of methods, reflecting repeated borrowings from other fields. This has been extremely fruitful, but can be confusing for a novice. Our aim in this paper is to reintroduce the fundamental theory and demonstrate how these methods are implementations of that theory. We will aim to tread a careful path between generality and simplicity. If we succeed, a reader should be well-placed to understand the relationships among the methods and applications presented later. We will also introduce a consistent notation that is sufficiently general as to capture the range of possible applications.
The structure of the paper is as follows. In Sect. 2 we introduce the general theory. There is no new material here, but we need a basis for the subsequent discussion. Section 3 introduces a consistent notation. Section 4 presents an overall approach to the solution to the data assimilation problem through the use of a simple example. Section 5 describes the construction of inputs to the problem. Section 6 describes solution methods and how they are special cases of the general theory but take advantage of the circumstances of a particular problem. Section 7 describes some computational aspects related to the solution of data assimilation problems. Finally, Sect. 8 introduces a range of example applications which illustrate the historical development of the field.
In what follows we will not be using mathematically precise language. We think the trade-off of ambiguity for simplicity suits our introductory task. Some of the key concepts are introduced in Tarantola and Valette (1982) and elaborated further in Tarantola (1987). In addition, Evans and Stark (2002) sought to unify the languages of applied mathematics and statistics used to describe the methods. Jaynes and Bretthorst (2003) gave a thorough exposition on the underlying ideas while Tarantola (2005) provided a comprehensive treatment of both motivations and methods. Other presentations that focus on particular applications include Kalnay (2003) for numerical weather prediction, Rodgers (2000) for atmospheric remote sensing, Enting (2002) and Bocquet et al. (2015) for atmospheric composition, and Carrassi et al. (2018) for the geosciences more generally.
2.1 Events and probability
For our purposes, we define an event as a statement about the condition of a system. This is deliberately general; such statements can take many forms. Examples include categorical or discrete statements (e.g. “including isopycnal mixing improves ocean circulation models”), logical propositions (e.g. “increasing soil temperatures lead to increased soil respiration”) or quantitative statements like “the Amazon forest is a sink of between 1 and 2 Pg C yr−1”. The choice of the set of events we consider is the first one we make in setting up any data assimilation problem. We require that any events that are logically incompatible be disjoint (mutually exclusive) and that the set of events be complete.1
The concept of probability is so simple and universal that it is hard to find a definition that is more than a tautology. It is a function mapping the set of events onto the interval [0,1]. Its simplest properties, often called the Kolmogorov axioms (Jaynes and Bretthorst, 2003, Appendix A) reflect the definition of events, i.e that the probability of the whole domain is 1, and that the probability of the union of two disjoint events is the sum of their individual probabilities. The most common case in natural science is learning about some numerical quantity like a rate constant or a flux. We term the set of these quantities the “target variables” of the problem. They are also called unknowns, parameters or control variables. In this continuous case, events are usually membership of some set (e.g. ). If our target variables are continuous, we can define a probability density function p (usually abbreviated PDF) such that the probability P that a target variable x is in some region R is the integral of p over R. In one dimension this simplifies to
2.2 Bayesian and non-Bayesian inference
At this point, any discussion of statistics bifurcates into two apparently incompatible methodologies, roughly termed frequentist and Bayesian. Debate between the two schools has been carried on with surprising vigour. See Salsburg (2001) for a general history and Jaynes and Bretthorst (2003) for a partisan view. Characterising the two schools is far beyond our scope here, especially as we will follow only one of them in much detail, but since even the language of the methods is almost disjoint it is worth introducing the new reader to the major concepts.
Frequentists generally pose problems as the quest for some property of a population. The property must be estimated from a sample of the population. Estimators are functions that compute these estimates from the sample. The design of estimators with desirable properties (no bias, minimum uncertainty, etc.) is a significant part of the technical apparatus of frequentist inference. Often we seek a physical parameter. This is not a bulk property but a single value that must be deduced from imperfect data. Here we treat each experiment as observing a member of a population so that we can use the same apparatus.
Bayesian statisticians concern themselves with the state of knowledge of a system. They regard the task of inference as improving this state of knowledge. We generate knowledge of some property of the system by applying some mathematical operation to the state of knowledge of the underlying system. Although we may call this estimating some property of the system, the calculations involved are quite different from the estimators of frequentist statistics. As a practical example a frequentist may estimate a mean by averaging their sample while a Bayesian may calculate an integral over their probability density. It is also important to note that for a Bayesian the state of knowledge does not necessarily come only from the sample itself. This use of information external or prior to the data is the most important practical difference between the two methods. Throughout this paper we will generally follow a Bayesian rather than frequentist approach. This represents the balance of activity in the field but is not a judgement on their relative merits.
The notation in use in this field is as varied as the nomenclature. This is unavoidable where similar techniques have been developed independently to answer the needs of many different fields. This diversity complicates the task for novices and experts alike as they compare literature from different fields. Producing a notation at once compact enough to be usable and general enough to cover all cases is a difficult task. Ide et al. (1997) made an attempt focused on numerical weather and ocean prediction. Experience has shown their notation to be sufficient for most practical cases and we have followed it here as closely as possible. The notation does have an explicitly Bayesian flavour. For example we eschew the use of hats to describe estimates because we regard estimation as an operation on a probability density. The notation used in this paper and the rest of the issue derives from Table 1 and readers should refer to this table for definitions of symbols.
Table 1Table of notation used throughout the issue. Borrows heavily from Ide et al. (1997) Appendix 1.
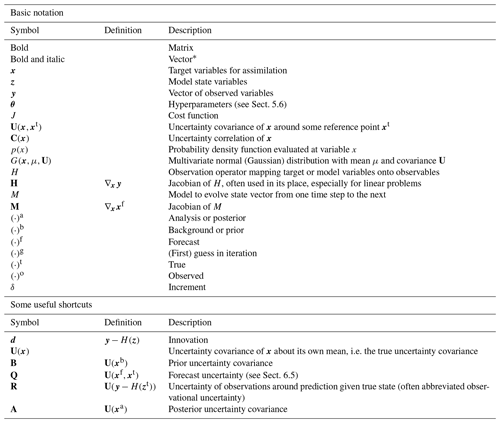
* We diverge here from Ide et al. (1997) for consistency with the Copernicus convention for mathematical notation.
In this section we will sketch the fundamental solution of the inverse problem. This will motivate a more detailed description of the various inputs in the following section.
Tarantola (2005) states at the outset of his book that the state of knowledge of a system can be described by a probability distribution or corresponding probability density. Our task is to combine knowledge from measurements with pre-existing knowledge on the system's state to improve knowledge of the system.2
The recipe for combining these two sources of knowledge is traditionally introduced via conditional probabilities and expressed as Bayes' theorem (Laplace, 1774). Here we follow Tarantola (2005) and Jaynes and Bretthorst (2003), who derive the machinery directly from the axioms of probability.
We postulate that the true state of the system is consistent with our prior knowledge of it and the measurements we take. The link between the system's state and the observations is created by an observation operator (often called a forward operator).3 Both observations and observation operators are imperfect and we describe the state of knowledge of them both with probability densities.
The case for one target variable and one observation is described in Fig. 1, slightly adapted from Rayner (2010). Figure 1a shows the joint probability distribution for the target variable (blue rectangle) and the measured quantity (red rectangle). Our imperfect knowledge of the mapping between them is shown by the green rectangle. In this simple case the three PDFs are uniform, meaning all values within the interval are equally likely.
The solution of the problem is the intersection or multiplication of the three PDFs. Adding the requirement that the system state must take a value, we obtain the solution (panel b) by projecting the joint PDF onto the x axis and normalising it. We write the multiplication as
where we have extended the case with one variable and one observation to the usual case where both are vectors. We generate the posterior distribution for x by integrating over possible values of the observed quantity
The constant of proportionality follows from normalisation . The last term in Eq. (2) is the probability of a value y given a value of the target variable x and is often termed the likelihood. We stress that the generated PDFs are the most complete description of the solution. What we usually think of as the estimated target variable xa is some derived property of p(x), e.g. its mode or mean. Note that if any PDF is mischaracterised, xa can correspond to a very small probability, possibly even smaller than for xb. Such a situation may remain unnoticed in the absence of independent direct validation data for xa, as is currently the case for global atmospheric inversions. This issue underlines the necessity to keep a clear link with the statistical framework, despite the possible technical complexity of data assimilation systems.
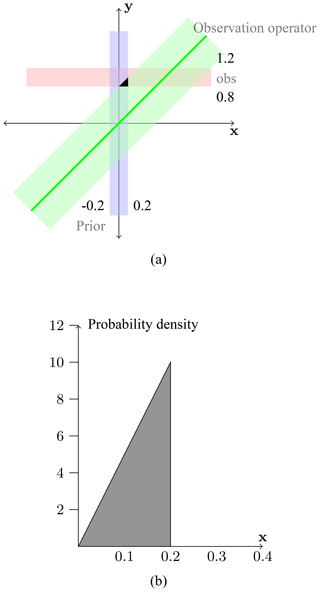
Figure 1Illustration of Bayesian inference for a system with one target variable and one observation. Panel (a) shows the joint probability distribution for target variable (x axis) and measurement (y axis). The light-blue rectangle (which extends to infinity in the y direction) represents the prior knowledge of the target variable (uniformly distributed between −0.2 and 0.2). The light-red rectangle (which extends to infinity in the x direction) represents the knowledge of the true value of the measurement (uniformly distributed between 0.8 and 1.2). The green rectangle (extending to infinity along the one-to-one line) represents the state of knowledge of the observation operator. The observation operator is a simple one-to-one mapping represented by the heavy green line. The black triangle (the intersection of the three PDFs) represents the solution as the joint PDF. Panel (b) shows the PDF for target variables obtained by projecting the black triangle from (a) onto the x axis (i.e. integrating over all values of the observation). Figure modified from Rayner (2010).
In this section we describe the various inputs to Eq. (2) along with some closely related quantities.
5.1 Deciding on target variables
It is important at the outset to distinguish between target variables x and state variables z. Target variables are the set of quantities we wish to learn more about in the assimilation. State variables are the set of quantities calculated by a model. As an example, a chemical transport model may have specified inputs of various tracers and will calculate the evolution of those (and other) tracers subject to atmospheric transport and chemical transformation. We will frequently wish to learn about the inputs but not about the concentrations. In that case the inputs are target variables while the concentrations are state variables. We might also choose to learn about the concentrations in the assimilation, in which case they become both state and target variables. Although not usually considered part of the problem, the decision on target variables preconditions much of what follows. In general the target variables should include anything which is important to the behaviour of the system and is not perfectly known. A common misunderstanding is to limit the target variables to the smallest possible set. This is risky for three reasons.
-
We often wish to calculate the uncertainty in some predicted quantity. We may inadvertently eliminate a target variable whose uncertainty contributes to that of our quantity of interest.
-
We are not always capable of guessing in advance which target variables will be well-constrained by the assimilation. We should let the observations determine which variables can be constrained rather than guessing in advance (Wunsch and Minster, 1982).
-
If a target variable that should be important for explaining an observation is removed, the information from that observation may contaminate other target variables (Trampert and Snieder, 1996; Kaminski et al., 2001). This usually happens when we limit the detail or resolution in our target variables.
These considerations push us towards complex rather than simple models. A common critique is that we will overfit the data. This can certainly happen but will be revealed by proper consideration of the posterior uncertainty. We can always post-treat the target variables to seek combinations with lower uncertainty (Wunsch and Minster, 1982). An example is aggregating a gridded field to lower resolution, which is often better constrained by the observations. It is possible, especially for approximate methods and nonlinear models, that overfitting may not be reflected in higher uncertainty.
Point three above has been the subject of much work in the flux inversion community in which our target variables are gridded surface fluxes of some atmospheric tracer. Often we group or aggregate grid cells into regions and assume the flux pattern inside these regions is perfectly known. Our target variables comprise multiples or scaling factors for these patterns. Kaminski et al. (2001) showed that incorrect specification of these patterns led to errors in the retrieved multipliers. Following Trampert and Snieder (1996) such errors are known as aggregation errors. Kaminski et al. (2001) proposed an algorithm for deweighting observations most strongly contaminated by aggregation errors. The more common solution is to solve at higher resolution (see Sect. 7.1). Bocquet (2005) pointed out some limitations of this approach with the information from observations being focused more tightly around observing sites as resolution increased. (Rodgers, 2000, Sect. 3.2.1) also noted an increased impact of the prior as more detail in the target variables meant that more remained unobserved. This has led to various approaches to designing structures for the target variables consistent with the capabilities of the observing system. Wu et al. (2011), Turner and Jacob (2015), and Lunt et al. (2016) chose different methods for doing this with Lunt et al. (2016) showing how to include the uncertainty in the choice of target variables in their assimilation.
We use an example to illustrate the process. Bodman et al. (2013) used the simple carbon cycle–climate model MAGICC (Meinshausen et al., 2008) and historical observations of temperature and CO2 concentration to estimate the global mean temperature and integrated carbon uptake for 2100. The steps involved in choosing which parameters of MAGICC to use as target variables were as follows.
-
Decide on a quantity of interest. This will be driven by the science question we are addressing, e.g. the global mean temperature in 2100 or the biospheric carbon uptake of North America. Often it will not be a target variable but the result of a forecast or diagnostic calculation.
-
Use sensitivity analysis to find variables to which the quantity of interest is sensitive (e.g. Moore et al., 2012). This may often include forcings that are usually neglected. It is often a brute force calculation performed by changing the variable a small amount, though the adjoint analysis discussed in Sect. 7.1 can also be used.
-
Generate prior PDFs for the most sensitive variables and, with these, calculate the prior PDF in the quantity of interest generated by each potential target variable. This and the previous steps should never be separated; the sensitivity to a given target variable is best expressed in uncertainty units for that variable. This provides a common basis for comparing sensitivities of different variables in different units. For example, Bodman et al. (2013) used realisations of the simple climate model MAGICC to calculate the contribution of uncertainties in model parameters (such as climate sensitivity or carbon cycle feedback parameters) to uncertainty in temperature in 2100.
-
Target the most important variables for our quantity of interest with the cut-off being computationally driven. This led Bodman et al. (2013) to choose a set of 11 target variables.
It is noteworthy how much calculation may be required before we start an assimilation.
5.2 Possible prior information
The PDF for the prior p(x|xb) should reflect whatever information we have about the quantity before a measurement is made. This is not always easy given that science is in continual dialogue between existing knowledge and new measurements and it is likely that measurements quite similar to the ones we are about to use have already informed the prior. We should also use any information we have, even if this is only obvious constraints such as positivity. Some of the reluctance to use Bayesian methods comes from the possible impact of the prior PDF on the posterior. This influence can be subtle. For example, if we wish to constrain some physical value K and we approach this by solving for a scaling factor s so that sK appears in our physical problem. We can reasonably expect that s is positive. Choosing a uniformly distributed random positive s is far more likely to increase rather than decrease the magnitude of sK compared to K. Solving for log (s) as a target variable means we can make increase or decrease equally likely. This was first noted by Jeffreys (1939) and is explained in more detail in Jaynes and Bretthorst (2003) Sect. 6.15.
In practice, prior information is most often taken from a model providing a mechanistic or process-based representation of the system (e.g. Gurney et al., 2002). The advantage of this approach is that it explicitly incorporates scientific understanding of the functioning of the system into the data assimilation process. Further, model outputs can easily be tailored to the data assimilation we are performing, e.g. prior information can be provided at whatever time and space resolution we need. The disadvantage is that many alternate representations often exist, and that the choice among them can have a major and scale-dependent influence on the final PDFs (e.g. Lauvaux et al., 2012; Carouge et al., 2010a), while the relative merits of such alternate priors is difficult to objectively and quantitatively determine when no ground truth is available. The availability of ground truth allows one to draw the statistics of model performance, but not necessarily directly at the spatial and temporal scales of the prior information. In this case, one needs to study how the uncertainties of the target variables change as they are aggregated or disaggregated. These scaling properties are controlled by uncertainty correlations (e.g. Chevallier et al., 2012). The parameters that encapsulate this prior information (such as uncertainty magnitudes or correlation lengths) are also imperfectly known and Sect. 5.6 describes how they can be incorporated into the formalism. Michalak et al. (2017) describes how they may be diagnosed from the assimilation system.
Alternatives that reduce the reliance on potentially subjective prior information do exist, where less restrictive prior assumptions are made. The case of uniform priors described above is one such example. One practical example in biogeochemical data assimilation is the “geostatistical” approach (e.g. Michalak et al., 2004), where the prior is described as a function of unknown hyperparameters that link ancillary data sets to the state, and where the prior uncertainty covariance is formally described through spatial and temporal correlation analysis that is based as strongly as possible on available observations. The advantage here is the replacement of possibly subjective prior with empirical information (e.g. Gourdji et al., 2012; Miller et al., 2013), while the disadvantage is a more limited formal link to scientific process-based prior understanding of the system.
It is important to note that the various approaches used to construct the prior in data assimilation problems are not disjoint options, but rather can be thought of as points along a continuum of options that reflect different choices about the assumptions that a researcher is willing to make about the system (e.g. Fang et al., 2014; Fang and Michalak, 2015). The choice of prior is an expression of a choice of assumptions. With a careful framing of the specific question to be addressed, and with an explicit examination of the assumptions inherent to different possible approaches, one can design a set of priors that optimally blends existing approaches for a given application.
We also note that often much more attention is paid to the parameters that define the location of the prior PDF (such as the mode) while less attention is paid to its spread (e.g. the variance in the case of Gaussian distributions). The two are equally important as they both control the intersection of PDFs in Fig. 1.
5.3 Observations
The PDF for the observation p(y|yo) represents our knowledge of the true value of the measured quantity given the measurement. The characterisation of this PDF is the task of metrology discussed by Scholze et al. (2017). An important point to make at this stage is that verification of a measurement means, for our purposes, verification of the PDF (including its mean, i.e. studying possible systematic errors in measurements). That is, it is more important that the PDF we use properly represents the state of knowledge of the true value than that the value is as precise as possible.
5.4 Observation operators
The PDF for the observation operator p(y|H(x)) represents our state of knowledge of the true value of a modelled quantity that arises from a given state of the system. It includes any artefact caused by the resolution of the target variables (Kaminski et al., 2001; Bocquet, 2005). It also includes uncertain choices about model structure and numerical implementation as well as model parameters that are not included among the target variables. The PDF for the observation operator is often hard to verify because there are few cases where we know precisely the relevant values of the system state. Without this knowledge it is hard to ascribe a difference between the simulated and true value to an error in the observation operator or an error in the prior. Frequently we must abstract the observation operator and run it under controlled conditions. An example is deliberate tracer release experiments (e.g. van Dop et al., 1998). Absent such direct verification, calculations like sensitivity analyses or ensemble experiments (e.g. Law et al., 1996) give incomplete guidance. It is important to note that if the PDFs are Gaussian then the errors due to observations and observation operators may be added by adding their covariances (Tarantola, 2005, Eq. 1.101). We frequently shorthand this as the data uncertainty (or worse data error) when it is usually dominated by the observation operator. The resulting PDF describes the difference we might expect between the simulated result of the observation operator and the measured value. Thus analysis of the residuals (observation − simulated quantity) can help test the assumed errors (e.g. Desroziers et al., 2005; Kuppel et al., 2013). This forms part of the diagnostics of data assimilation treated in Michalak et al. (2017) and touched on in Sect. 5.6.
In some cases it may be possible to calculate uncertainty in the observation operator in advance rather than diagnosing it from the assimilation. If there is an ensemble of observation operators available (e.g. Gurney et al., 2002) we can use the spread among their outputs as a measure of spread, including likely consistent or systematic errors arising from shared history and components (Bishop and Abramowitz, 2013). We may also perturb parameters in the observation operator to calculate their contribution to uncertainty.
5.5 Dynamical models
Although they are not one of the ingredients in Fig. 1, dynamical models are so common in this field that we include them here. Many of the systems studied are dynamical in that they involve the evolution of the system state through time. We reserve the term dynamical model (often shorthanded to model) for the mathematical function or computer system that performs this evolution. We frequently consider the dynamical model to be deterministic, in which case the set of system states as a function of time is a unique function of the boundary and initial conditions. Some formulations relax this condition, in which case we need a PDF for the model. In the most common case of a first-order model, the PDF represents our state of knowledge of the true state of the system at time step i+1 given its state at time step i and perfect knowledge of all relevant boundary conditions. As with observation operators this is hard to generate in practice since we rarely know the preexisting state or boundary conditions perfectly. In repeated assimilation cases like numerical weather prediction the statistics of many cases can give guidance. The PDF can also be deduced from the analysis of the model–data misfits when the statistics of the uncertainty of the model inputs and of the measurement errors are known (Kuppel et al., 2013).
The boundary between the observation operator and the dynamical model depends on our choice of target variables. If we consider only the initial state and assimilate observations over a time window (the classic case of four-dimensional variational data assimilation, 4D-Var) then the dynamical model forms part of the mapping between the unknowns and the observations so is properly considered part of the observation operator. If we include the system state from the assimilation window (weak-constraint 4D-Var) then the dynamical model enters as a separate object with its own PDF. We will see shortly how this can be incorporated explicitly into the statistical framework. One confusing outcome of this distinction is that the same model could play the role of an observation operator or a dynamical model depending on how it is used.
5.6 Hierarchical methods and hyperparameters
The solution to the data assimilation problem depends on many inputs that are themselves uncertain. These include parameters of the input PDFs such as variances or choices of observation operators. Frequently we regard these as fixed, which is likely to underestimate the uncertainty of the estimates. One solution is to incorporate these extra variables into the data assimilation process. The problem is to deal with the complex relationships such as the dependence of the likelihood p(y|H(x)) on H as well as x. An explanation and evaluation of methods for such problems is given by Cressie et al. (2009); here we sketch the problem and note some applications in the field.
The chain rule of probabilities (Jaynes and Bretthorst, 2003, Eq. 14.5) can be stated as follows. For two events A and B
If the events are regions in parameter space we can develop similar relations with PDFs. We can go further if there are more than two parameters involved, building a hierarchy in which we construct the joint PDF from a base probability and a cascading set of conditional probabilities. For this reason the approach is described as hierarchical.
In our case we extend our target variables x by a new set of unknowns θ. θ contains quantities that may affect our data assimilation problem but are not themselves target variables. Examples include parameters describing PDFs (variances, correlation lengths, etc.), choices of dynamical models, or observation operators or even the complexity of the target variables themselves. Some elements in θ may not even concern x such as the observational uncertainties treated in Michalak et al. (2005).
For our case Eq. (4) becomes
We can then solve Eq. (2) for the extended set of target variables x,θ to obtain P(x,θ) and then if we are not interested in θ may integrate Eq. (5) to remove it. θ may appear in several places with Eq. (2). For example if we are unsure of the uncertainty we should attach to the prior, we may include parameters describing the uncertainty in the first term on the right of Eq. (2). The same holds for the measurement process and the second term on the right. Finally if we have more than one potential observation operator we can include a collection of these in the third term on the right.
A prototype of this approach was given by Michalak et al. (2005). They included parameters describing R (often called hyperparameters) in an atmospheric flux assimilation. While they did not solve for the PDF of these hyperparameters, they did calculate the mode of their distribution and recalculated the distributions of fluxes accordingly. This calculation did not include the impact of uncertainties in the hyperparameters on uncertainties in the fluxes. Michalak et al. (2005) and Wu et al. (2013) used the same approach to solve for correlation length scales among flux errors in their assimilation. Ganesan et al. (2014) took account of uncertainties in diagonal elements of B and R and temporal autocorrelations in R. Ganesan et al. (2014) did consider the impact of uncertainties in θ on estimated fluxes but at considerable computational cost. Finally Rayner (2017) considered the uncertainty introduced by an ensemble of observation operators in the Transport Model Comparison (TransCom) described in Gurney et al. (2002).
Finally we should note that the hierarchical approach outlined here subsumes the description in Sect. 4. For this reason, and as a continual reminder of the assumptions implicit in selecting models and other inputs, Wikle and Berliner (2007) write the whole methodology in hierarchical form.
6.1 General principles
We saw in Sect. 4 that the solution of the assimilation problem consisted of the multiplication of three PDFs to generate the posterior PDF. Before describing solution methods applicable in various circumstances, we point out some general consequences of Eq. (2). We begin by stressing that the posterior PDF generated in Eq. (2) is the most general form of the solution. Derived quantities are generated by operations on this PDF.
Second, we see that the only physical model involved is the observation operator. All the sophisticated machinery of assimilation is not fundamental to the problem, although we need it to derive most of the summary statistics.
Third there is no requirement that a solution exists or, if it does, it can have vanishingly low probability. In Fig. 1 this would occur if the PDFs were made tighter (smaller rectangles for example) so that they did not overlap. This is a critical scientific discovery because it tells us our understanding of the problem is not consistent with the data, notwithstanding all the uncertainties of the inputs. It points out a boundary of “normal science” as defined by Kuhn (1962).4 Michalak et al. (2017) focus on diagnosing such inconsistencies.
6.2 Sampling methods
A general approach for characterising the posterior probability distribution of the target variables is to devise an approach for generating a large number of samples, or realisations, from this multivariate posterior distribution. We briefly describe a few example approaches that fall under this umbrella.
One approach to solving Eq. (2) is direct calculation of the product for a large number of realisations drawn from the constituent PDFs. Most simply, one can treat the PDF like any other scalar function and map it. This is often achieved by graphs or contour plots of a transformation of the PDF such as the least-squares cost function (e.g. Kaminski et al., 2002, Fig. 12). This mapping approach requires one computation of the forward model for each parameter set, so is infeasible for even moderately dimensioned problems. In addition, most of these parameter sets will lie in very low-probability regions.
A range of more sophisticated Monte Carlo sampling approaches exist for multidimensional problems. The most straightforward of these is direct sampling of the posterior PDF, feasible for the case where this posterior PDF is sufficiently simple to allow sampling from the distribution. This would be the case, for example, for multivariate Gaussian or lognormal distributions.
In cases where direct sampling is not feasible, the strategy often becomes one of sequentially sampling from a surrogate distribution (often termed the proposal distribution) in such a way that the ensemble of samples ultimately represents a sample from the more complex target distribution. Arguably, the simplest of the approaches falling under this umbrella is rejection sampling. In this approach, a sample is generated from a proposal distribution that is simple enough to be sampled directly, and that sample is accepted or rejected with a probability equal to the ratio between the likelihood of the sampled value based on the target versus the proposal distribution, normalised by a constant (e.g. Robert and Casella, 2004).
A particularly useful class of Monte Carlo sampling strategies are Markov chain Monte Carlo (MCMC) approaches. In these approaches, the samples form a Markov chain, such that each sample is not obtained independently, but rather as a perturbation of the last previously accepted sample. Rather than sampling the posterior PDF directly, one can also sample each of three PDFs sequentially (Fig. 1), e.g. with the cascaded Metropolis algorithm (see Tarantola, 2005, Sect. 6.11).
Another commonly used MCMC algorithm, the Gibbs sampler, can be seen as a special case of the Metropolis–Hastings algorithm where the target variables are sampled individually and sequentially, rather than sampling the full multivariate PDF of target variables as a single step (e.g. Casella and George, 1992). An advantage of the Gibbs sampler is that it can lead to higher rates of acceptance because defining strategic approaches for generating perturbations is more straightforward for univariate distributions. A disadvantage is that the overall computational cost can still be higher due to the need to perform sampling multiple times for each overall realisation.
The most important implementation detail for applying MCMC approaches is the choice of the perturbation. Good strategies are adaptive, lengthening the step size to escape from improbable regions of the parameter space and shortening it to sample probable parts (noting the comments on independence above).
Note that it takes at least one forward run for every accepted point, meaning only inexpensive observation operators can be treated this way. Furthermore the original algorithm cannot be parallelised because each calculation requires the previous one. Some related techniques are amenable to parallel computation (e.g. Jacob et al., 2011). On the other hand MCMC makes few assumptions about the posterior PDF, can handle a wide variety of input PDFs and requires no modification to the forward model.
6.3 Summary statistics
We often describe the solution of the assimilation problem using summary statistics of the posterior PDF. This can be because we assume that the posterior PDF has an analytic form with a few parameters that can describe it (e.g. the mean and standard deviation of the Gaussian) or because we need a numerical representation for later processing or comparison. This nearly universal practice is valuable but requires care. For example, consider a target variable in the form of a time series. We can represent the mode of the posterior PDF as a line graph and the posterior uncertainty as a band around this line. The true time series is a realisation drawn from within this band. Any statements about the temporal standard deviation of the true time series must be based on PDFs generated from these realisations. These estimates will generally yield larger variability than that from our most likely realisation.
The linear Gaussian case is so common that it deserves explicit treatment, however, provided the caveat above is borne in mind.
6.4 The linear Gaussian case
If H is linear and the PDFs of the prior, data and model are Gaussian then the posterior PDF consists of the multiplication of three Gaussians. We multiply exponentials by adding their exponents so it follows that the exponent of the posterior has a quadratic form and hence the posterior is Gaussian.
The Gaussian form for the inputs allows one important simplification without approximation. We noted in Sect. 4 that the solution to the assimilation problem consists of finding the joint posterior PDF for unknowns and observed quantities and then projecting this into the subspace of the unknowns. As we saw in Sect. 4 we also calculate the posterior PDF for y the observed quantity. If there are very large numbers of observations this is computationally prohibitive and usually uninteresting. If the PDFs are Gaussian, Tarantola (2005, Sect. 6.21) showed that the last two terms of Eq. (2) can be combined into a single PDF , where , i.e. by adding the two variances. The PDF now includes only the unknowns x and the posterior PDF can be written
This generates a Gaussian for x whose mean and variance can be calculated by a range of methods (Rodgers, 2000, chap. 1). The posterior covariance A does not depend on xb or yo so that one can calculate posterior uncertainties before measurements are taken (Hardt and Scherbaum, 1994). This is the basis of the quantitative network design approaches described in Krause et al. (2008) and Kaminski and Rayner (2017).
The largest computation in this method is usually the calculation of H, which includes the response of every observation to every unknown. This may involve many runs of the forward model. Once completed, H is the Green's function for the problem and instantiates the complete knowledge of the resolved dynamics. It enables a range of other statistical apparatuses, e.g. Michalak et al. (2005) or Rayner (2017).
Following the introduction of formal Bayesian methods to atmospheric assimilations by Enting et al. (1993, 1995), these analytical methods became the most common method for this field. Rayner et al. (1999), Bousquet et al. (2000), Roy et al. (2003) and Patra et al. (2005, 2006) used repeated forward runs of a single transport model while the series of papers from TransCom (Gurney et al., 2002, 2003; Law et al., 2003; Gurney et al., 2004; Baker et al., 2006) used repeated runs of an ensemble of models. Meanwhile Kaminski et al. (1999a, b), Rödenbeck et al. (2003), Peylin et al. (2005), Gerbig et al. (2009), Lauvaux et al. (2009), Turnbull et al. (2011), Gourdji et al. (2012), Fang et al. (2014), Fang and Michalak (2015), Lauvaux et al. (2012) and Schuh et al. (2013) (among many others) used various forms of a transport model in reverse mode. These calculate the same Jacobian but require one run per observation rather than per unknown. The advent of more atmospheric data (especially satellite measurements of concentration) and the need for a higher resolution of unknowns have seen these methods largely replaced by the matrix-light methods described in Sect. 7.1.
6.5 Dynamically informed priors: the Kalman filter
A common case in physical systems has the state of the system evolving according to some dynamical model M. This is usually (though not necessarily) some form of first-order differential equation. In such a case a natural algorithm for constraining the evolution of the system with data is as follows.
-
At any time step n our knowledge of the system is contained in the probability distribution p(xn).
-
Calculate a probability distribution for the new state of the system using the dynamical model M where the superscript f (forecast) indicates the application of the dynamical model.
-
Use as the prior PDF for the assimilation step described in Sect. 4.
-
This yields a posterior PDF p(xn+1) which we use as the input for the next iteration of step 1.
For the simplest case of linear M and H with Gaussian PDFs the algorithm was derived by Kalman (1960). The most difficult step is the generation of p(xf,n). For the original Gaussian case where this is given by
where Q, the forecast error covariance, represents the uncertainty added to the state of the system by the model itself, i.e. not including uncertainties in the state. The matrix product in Eq. (7) makes this approach computationally intractable for large numbers of unknowns and various approaches have been tried using a well-chosen subspace. The ensemble methods discussed in Sect. 7.3 have generally supplanted these. This also holds for nonlinear variants of the system.
The original conception of the Kalman filter was for dynamical control in which the state of the system is continually adjusted in accordance with arriving observations. For data assimilation applied to biogeochemistry our motivation is to hindcast the state of the system and, optionally, infer some underlying constants (e.g. Trudinger et al., 2007, 2008). A consequence of making inferences at each time separately is that the system may be forced to follow an erroneous observation. For a hindcast we can counter this by expanding our set of unknowns to include not only the current state but also the state for several time steps into the past, and therefore to smooth their previous analyses. This technique is known as the Kalman smoother (Jazwinski, 1970) and also exists in ensemble variants (Evensen, 2009) and in variational ones (see Sect. 7.1). Evensen (2009) also showed that the Kalman filter described above is a special case of the Kalman smoother with only one time level considered.
Note that by default, the time series of the maximum a posteriori estimates is not physically consistent; e.g. it does not conserve tracer mass from one assimilation step to another. However, the time series of the full PDFs includes trajectories that are physically consistent.
Much of the computational machinery of data assimilation aims to calculate various summary statistics of the posterior PDF. The utility of this approach depends on whether these parameters accurately summarise the posterior PDF. It is best to choose the target summary statistic based on knowledge of the posterior PDF; there is no point estimating two parameters if the posterior distribution is described by only one (e.g. the Poisson distribution). Here we limit ourselves to discussions of the two most common parameters: the maximum a posteriori estimate and the posterior covariance. Solving for these parameters does not itself assume a Gaussian posterior but we often do assume such normality.
7.1 Iterative solution for the mode: variational methods
The mode of the posterior PDF is the value of the unknowns that maximises the posterior probability. It is often summarised as the maximum a posteriori or MAP estimate. If p is a product of exponentials then we can write
Then maximising p is equivalent to minimising J.5 In the linear Gaussian case J is quadratic so minimising it is termed a least-squares solution. It is perhaps unfortunate that many treatments of data assimilation start from the discussion of a least-squares problem and thus hide many of the assumptions needed to get there.
The minimisation of J takes us into the realm of numerical methods, beyond our scope. From the numerical viewpoint J is a scalar function of the unknowns x. Minimising J is a problem in the calculus of variations and so the methods are commonly termed variational.
The quadratic form is sufficiently common to warrant more development. From Eq. (6), J takes the form
Most efficient minimisation algorithms require the gradient of J(x) (∇xJ). In general these gradients are precisely calculated by the use of adjoint methods (Griewank, 2000), but they involve the analytical derivation of each line of code of H beforehand. The only matrices left that are potentially large in this approach are B and R.
7.2 Calculation of posterior uncertainty
Any reasonable summary of a posterior PDF will involve a parameter describing its spread as well as location. This spread almost always has a higher dimension than the mode because it must describe the joint probabilities of parameters. This immediately raises a problem of storage and computation because even moderate assimilation problems may include 100 000 unknowns for which representation of the joint PDF is intractable. In purely Gaussian problems it can be shown that the Hessian or second derivative evaluated at the minimum is the inverse covariance of the posterior PDF. This is promising given that many gradient-based algorithms for minimisation calculate low-rank approximations of the Hessian (Meirink et al., 2008; Bousserez et al., 2015). Unfortunately they usually commence with the largest eigenvalues of the Hessian corresponding to the lowest eigenvalues (best-constrained parts) of the covariance. When convergence is achieved we are left with a subspace of the unknowns for which we can comment on the posterior uncertainty and ignorance beyond this. Properly we should restrict analysis of the results to this limited subspace but it usually does not map conveniently onto the physical problem we are studying (Chevallier et al., 2005).
An alternative approach is to generate an ensemble of modes using realisations of the prior and data PDFs (Fisher, 2003; Chevallier et al., 2007). The resulting realisations of the posterior PDF can be used as a sample for estimating population statistics. For Gaussian problems it can be shown that the sample covariance so generated is an unbiased estimator of the posterior covariance. For non-Gaussian problems we can use the ensemble of realisations to estimate a parameter representing the spread of the distribution or calculate an empirical measure (commonly the ensemble standard deviation).
7.3 The ensemble Kalman filter
The main limitations of the traditional Kalman filter for data assimilation are its assumption of Gaussian PDFs, the requirement for linear M and H, and the difficulty of projecting the state covariance matrix forward in time. The ensemble approach described in Sect. 7.2 can also be used to circumvent these problems. The hierarchy of approaches is reviewed in Chen (2003). The most prominent (and most closely related to the original) is the ensemble Kalman filter (EnKF) (Evensen, 2003, 2009). Instead of exactly representing the PDF by its mean and covariance we generate an ensemble of realisations. We replace Eq. (7) by advancing each realisation with the dynamical model then perturbing the result with noise generated from Q. We then update each ensemble member using the Gaussian theory described in Sect. 6.4. Equation (6) shows that, as well as a prior estimate (for which we use the ensemble member), we need observations, an observational covariance and a prior covariance. The prior covariance we calculate from the ensemble itself. The observational covariance we assume. In the simplest version of the EnKF we do not use the observations directly but rather perturb these with the observational noise. More recent versions (e.g. Tippett et al., 2003) avoid perturbing the observations but produce the same posterior uncertainty.
Computationally we need to run a dynamical model for each realisation of the ensemble. This differs from Eq. (7) for which we need a run of the dynamical model for every unknown. Another advantage is that, while Eq. (7) is exact only for linear models, the ensemble method may capture nonlinear impacts on the state covariance. The biggest disadvantage is the sampling problem for the posterior PDF. The limited ensemble size introduces errors in the magnitudes of the variances and spurious correlations among state variables. Often the covariance must be inflated ad hoc to prevent the ensemble from collapsing to an artificially small variance. Similarly the spurious correlations between, for example, spatially separated points mean that observations can artificially influence target variables at long distances. This is handled by limiting the range of influence of observations (see Houtekamer and Zhang, 2016, for a review of these techniques for numerical weather prediction), but this fix has also unwanted effects at short distances and is questionable for long-lived tracers (e.g. Miyazaki et al., 2011).
7.4 Combining filtering and sampling: the particle filter
Particle filters or sequential Monte Carlo methods relax the assumptions inherent in the EnKF. Like the EnKF, the particle filter samples the underlying PDFs with a series of realisations rather than propagating the mean and variance of the PDF. There are steps in the EnKF that assume Gaussian probability distributions and the particle filter avoids these, seeking to fit the true underlying PDF. We parallel the description of the Kalman filter algorithm (Sect. 6.5) to highlight the differences.
-
At any time step n our knowledge of the system is contained in the probability distribution p(xn). Generate a set of realisations (usually called particles) drawn from p(xn).
-
Propagate each realisation forward in time using the dynamical model M to generate realisations of the forecast state .
-
Account for the uncertainty in the dynamical model by perturbing according to the model PDF to generate realisations consistent with the dynamical model and its uncertainty.
-
For each , generate the simulated observations yi using the observation operator H then evaluate the PDF for the observations p(y) at the point yi; these probabilities act as weights for .
-
Using some numerical procedure with inputs of and p(yi) generate a posterior PDF p(xn+1), which we use as the prior PDF for the next iteration.
We see that the last three steps mirror the multiplication of PDFs described in Eq. (2). Also, the difference between the EnKF and particle filter lies chiefly in how we generate the posterior PDF from the ensemble of forecast states; the EnKF uses the linear Gaussian approximation while the particle filter uses some kind of sampling. Thus the particle filter is a hybrid of the Kalman filter and sampling approaches.
The relaxation of the Gaussian assumption is at once a strength and weakness of the particle filter. It can handle more complex PDFs than the EnKF but it also requires many more samples because it samples the posterior PDF rather blindly while the EnKF is guided by the Kalman update step into regions of high probability. This difference has meant that, while the EnKF has been used successfully on some very large problems (such as numerical weather prediction) the particle filter has been limited to the same problem sizes as the approaches described in Sect. 6.2. More recent developments such as the marginal particle filter (Klaas et al., 2005) or the equivalent-weights particle filter (Ades and van Leeuwen, 2015) try to overcome the sampling problem by introducing additional steps for the resampling of the particles.
An overview of the principal ideas of particle filtering and improvements upon the basic filter is given by Doucet et al. (2001) while van Leeuwen (2009) reviews its application in geophysical systems. Stordal et al. (2011) point to some further generalisations which may combine advantages of the EnKF and particle filter.
7.5 Time window
A common feature of biogeochemical systems is a large range of timescales. For example, terrestrial models may include both photosynthesis (sub-seconds) to forest succession (centuries). Slow processes often couple weakly to instantaneous observations so they must be constrained by long observational series. This can make the problem computationally intractable. A common solution is to break the problem into shorter assimilation windows. This is different from the case of numerical weather prediction where the main consideration is the need for a new forecast every few hours and the advantage that the dynamical model can be considered perfect for short enough times.
The choice of assimilation window for biogeochemical applications is guided by several factors.
-
Computational cost. If our target variables change with time, then longer assimilation windows imply higher dimensions for x with corresponding space requirements. Any scheme that requires multiple runs over the assimilation window (such as the EnKF or iterative methods) will also take longer.
-
Sensitivity of observations to target variables. These often decrease with time, especially for initial conditions. Once they become either too small or too unreliable (because of accumulating model error), there is little added value in assimilating observations further into the future. We may thus break the problem into several parallel assimilations.
The first point above means the assimilation window must also consider the time resolution for which we wish to solve. If we believe the value of some physical parameter only holds for a finite time (e.g. a month) there is little point exposing it to observations several years later. In practice the assimilation window is usually set by a trade-off between computational constraints and the timescale of the slowest processes studied.
Throughout this paper we have adopted a thematic structure. Here we switch views to a narrative description. This is partly to situate the various methods we have described but also to give some signposts for the future. We cannot hope to be exhaustive, nor to trace the rise and fall of each method. Rather, we will identify drivers for these developments and show examples of how they have guided the field. Our intention is to support the rest of the paper rather than provide a comprehensive review.
We can identify four major drivers for the development of biogeochemical data assimilation:
-
development of the underlying methods and their percolation into the field,
-
rise in the scale and complexity of models and data sets,
-
rise in computational power,
-
diversifying needs within and beyond science.
These drivers do not always pull in the same direction, e.g. increases in scale may require simplification of techniques while computational power may allow more sophistication. Different practitioners will also make different choices faced with the same trade-offs so our narrative is not a single thread but some large-scale patterns are evident.
One of the first clearly recognisable applications of data assimilation to biogeochemistry (Bolin and Keeling, 1963) used a set of measurements of CO2 concentrations to estimate the meridional diffusion of this gas and the distribution of its sources. It is now clear that the assumptions of Bolin and Keeling (1963) were wrong but, to quote Keeling (1998), “our results could not be seriously challenged, however, until digital computers, atmospheric circulation models, and considerably more CO2 data all became available two decades later”.
Bolin and Keeling (1963) confronted the problem that information is generally lost in the transformation of the inputs we seek to the outputs we observe. Approaches to this problem have guided the field since. Other fields face the same problem. Atmospheric remote sensing (Rodgers and Walshaw, 1966) and seismic studies (Backus and Gilbert, 1968) addressed it in related fields and their approaches, refracted through later developments, would eventually enter biogeochemistry. Approaches can be roughly divided into two classes: identifying and limiting the solution to those parts constrained by the data or the addition of ancillary information. The former approach is exemplified by the studies of Brown (1993, 1995), who used the singular value decomposition to establish flux patterns most strongly projected onto the data and limited her analysis to those components. Later studies which intentionally limited the number of unknowns (e.g. Fan et al., 1998; Gloor et al., 2000) can be regarded as less formal examples of this approach while bearing in mind the caution of Wunsch and Minster (1982) about allowing the data to choose the subspace of unknowns we constrain. Other approaches considered the observability of target variables by the available data. Target variables could be aggregated where they were not individually constrained sufficiently. Manning et al. (2011) aggregated pixels in their flux assimilation until they reached some threshold of observability while Wu et al. (2011) included observability as a design criterion for their choice of target variables.
The addition of ancillary information is frequently termed regularisation since its practical purpose is to limit implausible solutions in poorly constrained parts of parameter space. For most problems, solving inverse problems meant solving a version of Eq. (9) which ignored the first term on the right-hand side. Regularisation consisted of adding some other term, which penalised undesirable solutions. Possibilities included “shrinkage estimators” which penalised the overall size of the solution (Shaby and Field, 2006), or smoothing operators, which penalised rapid variations in the solution (e.g. Enting, 1987; McIntosh and Veronis, 1993).
The importation of the explicit Bayesian methods which we have reviewed here largely supplanted the alternative regularisation methods, though some studies (e.g. Krakauer et al., 2004; Issartel, 2005; Manning et al., 2011; Vanoye and Mendoza, 2014) followed other approaches. Also, the geostatistical methods introduced into the field by Michalak et al. (2004) remain in use (e.g. Gourdji et al., 2008; Miller et al., 2013). Bayesian methods entered biogeochemistry through atmospheric inverse studies (Enting et al., 1993, 1995). Most work since has elaborated different methods of solution or forms of prior knowledge. Almost all methods described in Sect. 6 have found some application. Often a method will be tried and left until an algorithmic advance or computational improvement makes it feasible.
Classical analytical methods (Sect. 6.4) were the first workhorse for flux assimilations of inert tracers like CO2 where the problem is linear. They are still widely used (e.g. Fang et al., 2014; Fang and Michalak, 2015; Henne et al., 2016; Saeki and Patra, 2017; Chen et al., 2017; Shiga et al., 2018; Wang et al., 2018). Originally Jacobians were generated with multiple forward runs, each run corresponding to a desired source component. The development of adjoint transport models allowed one run per observation (e.g. Kaminski et al., 1999a, b; Rödenbeck et al., 2003; Carouge et al., 2010a, b; Thompson et al., 2011; Gourdji et al., 2012; Fang et al., 2014; Fang and Michalak, 2015). This is more efficient in the usual case of more unknowns than observations. The task of generating Jacobians is inherently parallel so the ultimate limitation on these methods is the storage and manipulation of large matrices. These limitations recede with increasing computational power, and recent algorithmic advances (e.g. Yadav and Michalak, 2013) have also expanded their domain. Analytical methods are prized for exact calculation of posterior covariance and so are widely used in network design (e.g. Gloor et al., 2000; Patra et al., 2003; Hungershoefer et al., 2010; Kaminski and Rayner, 2017). Matrix methods are also often used where more sophisticated statistics require more complex calculations such as the hierarchical calculations of Michalak et al. (2004), Ganesan et al. (2014) and Rayner (2017). They may also be used in weakly nonlinear forms where dimensionality is low enough to permit finite difference sensitivity calculations for each unknown (e.g. Kuppel et al., 2012; Bacour et al., 2015; MacBean et al., 2018; Norton et al., 2018).
Once the number of both observations and target variables renders computation of Jacobians unfeasible, variational methods (Sect. 7.1) are a natural extension of the matrix methods. This evolution is particularly evident in atmospheric problems, driven by increases in satellite data and a drive for higher resolution. Several groups have developed similar systems around adjoints of atmospheric transport models for global models (e.g. Rödenbeck, 2005; Chevallier et al., 2005; Henze et al., 2007; Bergamaschi et al., 2007; Liu et al., 2014; Wilson et al., 2014) and for regional models (e.g. Brioude et al., 2011; Broquet et al., 2011; Guerrette and Henze, 2015; T. Zheng et al., 2018). Most of the effort has centred on improving knowledge of sources and sinks (e.g. Basu et al., 2013; Escribano et al., 2016; Lu et al., 2016; B. Zheng et al., 2018) but some has focused on improving state estimation for forecasting (e.g. Elbern and Schmidt, 2001; Wang et al., 2011; Park et al., 2016). To achieve high resolution while maintaining global consistency, some authors also combine methods, using one for the large-scale domain and, potentially, a different method for a nested domain. This approach was introduced by Rödenbeck et al. (2009) and has been recently used by Kountouris et al. (2018).
Versions of the Kalman filter are some of the natural choices whenever the dynamical evolution of the model state is explicitly included. Few atmospheric studies have exploited this capability, though Miyazaki et al. (2011) solved for both fluxes and concentrations. More common is a random walk or persistence model in which state variables evolve without dynamical guidance. This was implemented for atmospheric flux assimilation by Mulquiney et al. (1995, 1998) and Mulquiney and Norton (1998). Trudinger et al. (2002a, b) later used the Kalman smoother to estimate global fluxes from ice core concentration and isotopic measurements. Peters et al. (2005) introduced the CarbonTracker system using a simplified version of the EnKF and the global atmospheric model TM5 (Krol et al., 2005). TM5's global nested capability has allowed a large suite of global and regional applications for CarbonTracker (e.g. Peters et al., 2010) for Europe or Kim et al. (2014) for Asia. Other applications of the EnKF to the estimation of surface sources include Zupanski et al. (2007) and Feng et al. (2009). One problem common to all these models was a potential time delay between target variables and observations. This does not fit immediately into the original formalism of Kalman (1960). A solution was to keep several time steps in a moving assimilation window but one may need many steps if the time delay is long. This can vitiate some of the computational advantages of the EnKF.
Kalman filters were frequently limited by the need to calculate Jacobians for each target variable. This was circumvented by the introduction of the EnKF. Provided one accounts for the problems of ensemble size, the EnKF's combination of efficiency and simplicity has led it to supplant other KF approaches.
The movement towards inclusion of explicit dynamics in biogeochemical inverse problems has increased the use of EnKF and variational methods since both handle the nonlinear formulations common in biogeochemical models. In terrestrial models, Williams et al. (2005) and Quaife et al. (2008) included state variables of a simple terrestrial model in an ensemble system while Dutta et al. (20198) solved for parameters. Trudinger et al. (2008) considered the joint estimation of parameters and state variables using an EnKF and pseudo-observations at a site. Barrett (2002) and Braswell et al. (2005) used variational approaches to optimise parameters of simple biosphere models against various site data. Rayner et al. (2005) and the papers that followed it (e.g. Scholze et al., 2007; Knorr et al., 2010; Kaminski et al., 2012; Scholze et al., 2016) used an adjoint of a more comprehensive (though incomplete) biosphere model coupled to various observation operators in their variational approach.
There have been some attempts to compare the strengths and weaknesses of the various approaches above. Meirink et al. (2008) or Kopacz et al. (2009) illustrated the equivalence of the variational and the analytical approaches for a given definition of x, while Liu et al. (2016) showed some convergence of the variational approach and of the ensemble Kalman filter for increasing observation coverage. Trudinger et al. (2007) used a simplified terrestrial model and a fairly rigorous protocol to test the efficiency and robustness of several estimation methods. They found no clear differences among methods but did note the importance of careful analysis of assimilation performance (e.g. do the differences between posterior simulation and data agree with the assumed PDF?). Chatterjee and Michalak (2013) compared the variational and EnKF approaches to estimating surface fluxes and also noticed that each had comparative strengths and weaknesses. Trudinger et al. (2007) suggest that any of these algorithms are capable of performing well if well handled and analysed.
In previous sections, we have described how many assimilation methods are alternative algorithms for the same underlying problem. Different methods have risen to prominence in response to combinations of the four drivers mentioned above. Discussion of future directions is necessarily speculative but we can suggest how some of the drivers will evolve and their corresponding influence.
Computational constraints are less active now and likely to remain so. This is true even when we consider the increases in data size and complexity. The increased availability of large numbers of processors rather than their individual speed will likely privilege naturally parallel algorithms such as ensemble methods.
The rising complexity and diversity of models will also promote ensemble approaches. The strongest analogy is with climate prediction and seasonal forecasting where ensembles frequently include different dynamical formulations as well as different parameter settings. As of yet there have been few attempts at multi-model ensemble data assimilation in biogeochemistry with the TransCom project being the highest profile example. One reason for this is the scarcity of biogeochemical models with data assimilation capability. Another advantage of ensemble methods is a reduced entry barrier.
A more likely brake on the evolution of data assimilation in biogeochemistry is the quality of the models themselves. A precondition for the utility of data assimilation is that information learned in one environment or regime is applicable elsewhere, or that a model can make coherent inferences from different observations of the same system. As examples, Medvigy et al. (2009) found it difficult to transfer inferences made at one ecosystem site to another while Bacour et al. (2015) found it difficult to fit multiple streams of data with a single set of parameters. We would recommend tighter integration of data assimilation with model development so that components can be tested as they are developed.
Finally, the distinctions we have drawn between methods here represent a snapshot in time. Methods are likely to be matched and combined differently in future. At the moment most assimilation studies choose either external inputs (boundary conditions or parameters) or model state as target variables (Sect. 5.1). This distinction is convenient but artificial since both are usually uncertain. Both weak-constraint variational methods and dual-state Kalman filters can handle both types of target variables and we may expect to see them used increasingly. Other merged approaches, for instance by constructing optimal low-rank solutions even for highly dimensional problems in new systems, also seems a promising way forward (Bousserez and Henze, 2018).
There is a wide range of techniques available for assimilating data into models such as those used in biogeochemistry. Most of these, however, inherit the basic formalism of Bayesian inference in which posterior probabilities are constructed as conjunctions or multiplications of probability distributions describing prior knowledge, measured quantities and models relating the two. The methods differ in the information they assume or adopt on the various components. In general the more restrictive the assumptions the more powerful the statistical apparatus available to analyse the system.
This paper contains some sketches of mathematical development but does not rely on any particular piece of code or data set.
PJR led the writing of the paper, AMM wrote several sections and redacted the whole paper. FC wrote several sections, redacted the whole paper and was primarily responsible for regularising the notation.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Data assimilation in carbon/biogeochemical cycles: consistent assimilation of multiple data streams (BG/ACP/GMD inter-journal SI)”. It is not associated with a conference.
We acknowledge the support from the International Space Science Institute (ISSI). This publication is an outcome of the ISSI's Working Group on “Carbon Cycle Data Assimilation: How to consistently assimilate multiple data streams”.
This research was supported by the Australian Research Council (grant no. DP1096309).
This paper was edited by Marko Scholze and reviewed by three anonymous referees.
Ades, M. and van Leeuwen, P. J.: The equivalent-weights particle filter in a high-dimensional system, Q. J. Roy. Meteor. Soc., 141, 484–503, https://doi.org/10.1002/qj.2370, 2015. a
Backus, G. and Gilbert, F.: The resolving power of gross earth data, Geophys. J. Roy. Astr. S., 13, 247–276, 1968. a
Bacour, C., Peylin, P., MacBean, N., Rayner, P. J., Delage, F., Chevallier, F., Weiss, M., Demarty, J., Santaren, D., Baret, F., and Prunet, P.: Joint assimilation of eddy-covariance flux measurements and FAPAR products over temperate forests within a process-oriented biosphere model, J. Geophys. Res., 120, 1839–1857, https://doi.org/10.1002/2015JG002966, 2015. a, b
Baker, D. F., Law, R. M., Gurney, K. R., Rayner, P., Peylin, P., Denning, A. S., Bousquet, P., Bruhwiler, L., Chen, Y.-H., Ciais, P., Fung, I. Y., Heimann, M., John, J., Maki, T., Maksyutov, S., Masarie, K., Prather, M., Pak, B., Taguchi, S., and Zhu, Z.: TransCom 3 inversion intercomparison: Impact of transport model errors on the interannual variability of regional CO2 fluxes, 1988–2003, Global Biogeochem. Cy., 20, GB1002, https://doi.org/10.1029/2004GB002439, 2006. a
Balkanski, Y., Monfray, P., Battle, M., and Heimann, M.: Ocean primary production derived from satellite data: An evaluation with atmospheric oxygen measurements, Global Biogeochem. Cy., 13, 257–271, 1999. a
Barrett, D. J.: Steady state turnover time of carbon in the Australian terrestrial biosphere, Global Biogeochem. Cy., 16, 1108, https://doi.org/10.1029/2002GB001860, 2002. a
Basu, S., Guerlet, S., Butz, A., Houweling, S., Hasekamp, O., Aben, I., Krummel, P., Steele, P., Langenfelds, R., Torn, M., Biraud, S., Stephens, B., Andrews, A., and Worthy, D.: Global CO2 fluxes estimated from GOSAT retrievals of total column CO2, Atmos. Chem. Phys., 13, 8695–8717, https://doi.org/10.5194/acp-13-8695-2013, 2013. a
Bergamaschi, P., Frankenberg, C., Meirink, J. F., Krol, M., Dentener, F., Wagner, T., Platt, U., Kaplan, J. O., Körner, S., Heimann, M., Dlugokencky, E. J., and Goede, A.: Satellite chartography of atmospheric methane from SCIAMACHY on board ENVISAT: 2. Evaluation based on inverse model simulations, J. Geophys. Res., 112, D02304, https://doi.org/10.1029/2006JD007268, 2007. a
Bishop, C. H. and Abramowitz, G.: Climate model dependence and the replicate Earth paradigm, Clim. Dynam., 41, 885–900, 2013. a
Bocquet, M.: Grid resolution dependence in the reconstruction of an atmospheric tracer source, Nonlin. Processes Geophys., 12, 219–233, https://doi.org/10.5194/npg-12-219-2005, 2005. a, b
Bocquet, M., Elbern, H., Eskes, H., Hirtl, M., Žabkar, R., Carmichael, G. R., Flemming, J., Inness, A., Pagowski, M., Pérez Camaño, J. L., Saide, P. E., San Jose, R., Sofiev, M., Vira, J., Baklanov, A., Carnevale, C., Grell, G., and Seigneur, C.: Data assimilation in atmospheric chemistry models: current status and future prospects for coupled chemistry meteorology models, Atmos. Chem. Phys., 15, 5325–5358, https://doi.org/10.5194/acp-15-5325-2015, 2015. a
Bodman, R. W., Rayner, P. J., and Karoly, D. J.: Uncertainty in temperature projections reduced using carbon cycle and climate observations, Nat. Clim. Change, 3, p. 725, https://doi.org/10.1038/NCLIMATE1903, 2013. a, b, c
Bolin, B. and Keeling, C. D.: Large-scale atmospheric mixing as deduced from the seasonal and meridional variations of carbon dioxide, J. Geophys. Res., 68, 3899–3920, 1963. a, b, c
Bousquet, P., Peylin, P., Ciais, P., Le Quéré, C., Friedlingstein, P., and Tans, P. P.: Regional changes in carbon dioxide fluxes of land and oceans since 1980, Science, 290, 1342–1346, 2000. a
Bousserez, N. and Henze, D. K.: Optimal and scalable methods to approximate the solutions of large-scale Bayesian problems: theory and application to atmospheric inversion and data assimilation, Q. J. Roy. Meteor. Soc., 144, 365–390, 2018. a
Bousserez, N., Henze, D., Perkins, A., Bowman, K., Lee, M., Liu, J., Deng, F., and Jones, D.: Improved analysis-error covariance matrix for high-dimensional variational inversions: application to source estimation using a 3D atmospheric transport model, Q. J. Roy. Meteor. Soc., 141, 1906–1921, 2015. a
Brasseur, P., Gruber, N., Barciela, R., Brander, K., Doron, M., El Moussaoui, A., Hobday, A. J., Huret, M., Kremeur, A.-S., Lehodey, P., Matear, R., Moulin, C., Murtugudde, R., Senina, I., and Svendsen, E.: Integrating biogeochemistry and ecology into ocean data assimilation systems, Oceanography, 22, 206–215, 2009. a
Braswell, B. H., Sacks, W. J., Linder, E., and Schimel, D. S.: Estimating diurnal to annual ecosystem parameters by synthesis of a carbon flux model with eddy covariance net ecosystem exchange observations, Glob. Change Biol., 11, 335–355, 2005. a
Brioude, J., Kim, S.-W., Angevine, W. M., Frost, G., Lee, S.-H., McKeen, S., Trainer, M., Fehsenfeld, F. C., Holloway, J., Ryerson, T., Williams, E. J., Petron, G., and Fast, J. D.: Top-down estimate of anthropogenic emission inventories and their interannual variability in Houston using a mesoscale inverse modeling technique, J. Geophys. Res.-Atmos., 116, 20305, https://doi.org/10.1029/2011JD016215, 2011. a
Broquet, G., Chevallier, F., Rayner, P., Aulagnier, C., Pison, I., Ramonet, M., Schmidt, M., Vermeulen, A. T., and Ciais, P.: A European summertime CO2 biogenic flux inversion at mesoscale from continuous in situ mixing ratio measurements, J. Geophys. Res., 116, D23303, https://doi.org/10.1029/2011JD016202, 2011. a
Brown, M.: Deduction of Emissions of Source Gases Using an Objective Inversion Algorithm and a Chemical Transport Model, J. Geophys. Res., 98, 12639–12660, 1993. a
Brown, M.: The singular value decomposition method applied to the deduction of the emissions and the isotopic composition of atmospheric methane, J. Geophys. Res., 100, 11425–11446, 1995. a
Carouge, C., Bousquet, P., Peylin, P., Rayner, P. J., and Ciais, P.: What can we learn from European continuous atmospheric CO2 measurements to quantify regional fluxes – Part 1: Potential of the 2001 network, Atmos. Chem. Phys., 10, 3107–3117, https://doi.org/10.5194/acp-10-3107-2010, 2010a. a, b
Carouge, C., Rayner, P. J., Peylin, P., Bousquet, P., Chevallier, F., and Ciais, P.: What can we learn from European continuous atmospheric CO2 measurements to quantify regional fluxes – Part 2: Sensitivity of flux accuracy to inverse setup, Atmos. Chem. Phys., 10, 3119–3129, https://doi.org/10.5194/acp-10-3119-2010, 2010b. a
Carrassi, A., Bocquet, M., Bertino, L., and Evensen, G.: Data assimilation in the geosciences: An overview of methods, issues, and perspectives, Wires Clim. Change, 9, e535, https://doi.org/10.1002/wcc.535, 2018. a
Casella, G. and George, E. I.: Explaining the gibbs sampler, Am. Stat., 46, 167–174, https://doi.org/10.2307/2685208, 1992. a
Chatterjee, A. and Michalak, A. M.: Technical Note: Comparison of ensemble Kalman filter and variational approaches for CO2 data assimilation, Atmos. Chem. Phys., 13, 11643–11660, https://doi.org/10.5194/acp-13-11643-2013, 2013. a
Chen, J. M., Mo, G., and Deng, F.: A joint global carbon inversion system using both CO2 and 13CO2 atmospheric concentration data, Geosci. Model Dev., 10, 1131–1156, https://doi.org/10.5194/gmd-10-1131-2017, 2017. a
Chen, Z.: Bayesian filtering: From Kalman filters to particle filters, and beyond, Statistics, 182, 1–69, 2003. a
Chevallier, F., Fisher, M., Peylin, P., Serrar, S., Bousquet, P., Breon, F.-M., Chedin, A., and Ciais, P.: Inferring CO2 sources and sinks from satellite observations: method and application to TOVS data, J. Geophys. Res., 110, D24309, https://doi.org/10.1029/2005JD006390, 2005. a, b
Chevallier, F., Bréon, F.-M., and Rayner, P. J.: The Contribution of the Orbiting Carbon Observatory to the Estimation of CO2 Sources and Sinks: Theoretical Study in a Variational Data Assimilation Framework, J. Geophys. Res., 112, D09307, https://doi.org/10.1029/2006JD007375, 2007. a
Chevallier, F., Ciais, P., Conway, T. J., Aalto, T., Anderson, B. E., Bousquet, P., Brunke, E. G., Ciattaglia, L., Esaki, Y., Frohlich, M., Gomez, A., Gomez-Pelaez, A. J., Haszpra, L., Krummel, P. B., Langenfelds, R. L., Leuenberger, M., Machida, T., Maignan, F., Matsueda, H., Morgu, J. A., Mukai, H., Nakazawa, T., Peylin, P., Ramonet, M., Rivier, L., Sawa, Y., Schmidt, M., Steele, L. P., Vay, S. A., Vermeulen, A. T., Wofsy, S., and Worthy, D.: CO2 surface fluxes at grid point scale estimated from a global 21 year reanalysis of atmospheric measurements, J. Geophys. Res.-Atmos., 115, D21307, https://doi.org/10.1029/2010JD013887, 2010. a
Chevallier, F., Wang, T., Ciais, P., Maignan, F., Bocquet, M., Altaf Arain, M., Cescatti, A., Chen, J., Dolman, A. J., Law, B. E., Margolis, H. A., Montagnani, L., and Moors, E. J.: What eddy-covariance measurements tell us about prior land flux errors in CO2-flux inversion schemes, Global Biogeochem. Cy., 26, GB1021, https://doi.org/10.1029/2010GB003974, 2012. a
Cressie, N., Calder, C. A., Clark, J. S., Hoef, J. M. V., and Wikle, C. K.: Accounting for uncertainty in ecological analysis: the strengths and limitations of hierarchical statistical modeling, Ecol. Appl., 19, 553–570, https://doi.org/10.1890/07-0744.1, 2009. a
Desroziers, G., Berre, L., Chapnik, B., and Poli, P.: Diagnosis of observation, background and analysis-error statistics in observation space, Q. J. Roy. Meteor. Soc., 131, 3385–3396, https://doi.org/10.1256/qj.05.108, 2005. a
Doucet, A., de Freitas, N., and Gordon, N. (Eds.): Sequential Monte Carlo Methods in Practice, Springer New York, https://doi.org/10.1007/978-1-4757-3437-9, 2001. a
Dutta, D., Schimel, D. S., Sun, Y., van der Tol, C., and Frankenberg, C.: Optimal inverse estimation of ecosystem parameters from observations of carbon and energy fluxes, Biogeosciences, 16, 77–103, https://doi.org/10.5194/bg-16-77-2019, 2019. a
Elbern, H. and Schmidt, H.: Ozone episode analysis by four-dimensional variational chemistry data assimilation, J. Geophys. Res.-Atmos., 106, 3569–3590, 2001. a
Enting, I. G.: On the use of smoothing splines to filter CO2 data, J. Geophys. Res., 92D, 10977–10984, 1987. a
Enting, I. G.: Inverse Problems in Atmospheric Constituent Transport, Cambridge University Press, 2002. a, b
Enting, I. G., Trudinger, C. M., Francey, R. J., and Granek, H.: Synthesis Inversion of Atmospheric CO2 Using the GISS Tracer Transport Model, Tech. Paper No. 29, CSIRO Div. Atmos. Res., 1993. a, b
Enting, I. G., Trudinger, C. M., and Francey, R. J.: A synthesis inversion of the concentration and δ13C of atmospheric CO2, Tellus, 47B, 35–52, 1995. a, b
Escribano, J., Boucher, O., Chevallier, F., and Huneeus, N.: Subregional inversion of North African dust sources, J. Geophys. Res.-Atmos., 121, 8549–8566, 2016. a
Evans, S. N. and Stark, P.: Inverse Problems as Statistics, Inverse Probl., 18, R55–R97, 2002. a
Evensen, G.: The ensemble Kalman filter: Theoretical formulation and practical implementation, Ocean Dynam., 53, 343–367, 2003. a
Evensen, G.: The ensemble Kalman filter for combined state and parameter estimation, IEEE Contr. Syst. Mag., 29, 83–104, https://doi.org/10.1109/MCS.2009.932223, 2009. a, b, c
Fan, S., Gloor, M., Mahlman, J., Pacala, S., Sarmiento, J., Takahashi, T., and Tans, P.: A Large Terrestrial Carbon Sink in North America Implied by Atmospheric and Oceanic CO2 Data and Models, Science, 282, 442–446, 1998. a
Fang, Y. and Michalak, A. M.: Atmospheric observations inform CO2 flux responses to enviroclimatic drivers, Global Biogeochem. Cy., 29, 555–566, 2015. a, b, c, d
Fang, Y., Michalak, A. M., Shiga, Y. P., and Yadav, V.: Using atmospheric observations to evaluate the spatiotemporal variability of CO2 fluxes simulated by terrestrial biospheric models, Biogeosciences, 11, 6985–6997, https://doi.org/10.5194/bg-11-6985-2014, 2014. a, b, c, d
Feng, L., Palmer, P. I., Bösch, H., and Dance, S.: Estimating surface CO2 fluxes from space-borne CO2 dry air mole fraction observations using an ensemble Kalman Filter, Atmos. Chem. Phys., 9, 2619–2633, https://doi.org/10.5194/acp-9-2619-2009, 2009. a
Fisher, M.: Estimation of Entropy Reduction and Degrees of Freedom for Signal for Large Variational Analysis Systems, ECMWF technical memorandum, European Centre for Medium-Range Weather Forecasts, available at: http://books.google.com.au/books?id=anikQwAACAAJ (last access: 10 September 2019), 2003. a
Fung, I. Y., Tucker, C. J., and Prentice, K. C.: Application of Advanced Very High Resolution Radiometer Vegetation Index to Study Atmosphere-Biosphere Exchange of CO2, J. Geophys. Res., 92, 2999–3015, 1987. a
Ganesan, A. L., Rigby, M., Zammit-Mangion, A., Manning, A. J., Prinn, R. G., Fraser, P. J., Harth, C. M., Kim, K.-R., Krummel, P. B., Li, S., Mühle, J., O'Doherty, S. J., Park, S., Salameh, P. K., Steele, L. P., and Weiss, R. F.: Characterization of uncertainties in atmospheric trace gas inversions using hierarchical Bayesian methods, Atmos. Chem. Phys., 14, 3855–3864, https://doi.org/10.5194/acp-14-3855-2014, 2014. a, b, c
Gerbig, C., Dolman, A. J., and Heimann, M.: On observational and modelling strategies targeted at regional carbon exchange over continents, Biogeosciences, 6, 1949–1959, https://doi.org/10.5194/bg-6-1949-2009, 2009. a
Gloor, M., Fan, S. M., Pacala, S., and Sarmiento, J.: Optimal sampling of the atmosphere for purpose of inverse modeling: A model study, Global Biogeochem. Cy., 14, 407–428, 2000. a, b
Gourdji, S. M., Mueller, K. L., Schaefer, K., and Michalak, A. M.: Global Monthly-Averaged CO2 Fluxes Recovered Using a Geostatistical Inverse Modeling Approach: 2. Results Including Auxiliary Environmental Data, J. Geophys. Res., 113, D21114, https://doi.org/10.1029/2007JD009734, 2008. a
Gourdji, S. M., Mueller, K. L., Yadav, V., Huntzinger, D. N., Andrews, A. E., Trudeau, M., Petron, G., Nehrkorn, T., Eluszkiewicz, J., Henderson, J., Wen, D., Lin, J., Fischer, M., Sweeney, C., and Michalak, A. M.: North American CO2 exchange: inter-comparison of modeled estimates with results from a fine-scale atmospheric inversion, Biogeosciences, 9, 457–475, https://doi.org/10.5194/bg-9-457-2012, 2012. a, b, c
Griewank, A.: Evaluating Derivatives: Principles and Techniques of Automatic Differentiation, SIAM, Philadelphia, Pa., 2000. a
Guerrette, J. J. and Henze, D. K.: Development and application of the WRFPLUS-Chem online chemistry adjoint and WRFDA-Chem assimilation system, Geosci. Model Dev., 8, 1857–1876, https://doi.org/10.5194/gmd-8-1857-2015, 2015. a
Gurney, K. R., Law, R. M., Denning, A. S., Rayner, P. J., Baker, D., Bousquet, P., Bruhwiler, L., Chen, Y.-H., Ciais, P., Fan, S., Fung, I. Y., Gloor, M., Heimann, M., Higuchi, K., John, J., Maki, T., Maksyutov, S., Masarie, K., Peylin, P., Prather, M., Pak, B. C., Randerson, J., Sarmiento, J., Taguchi, S., Takahashi, T., and Yuen, C.-W.: Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models, Nature, 415, 626–630, 2002. a, b, c, d
Gurney, K. R., Law, R. M., Denning, A. S., Rayner, P. J., Baker, D., Bousquet, P., Bruhwiler, L., Chen, Y.-H., Ciais, P., Fan, S., Fung, I. Y., Gloor, M., Heimann, M., Higuchi, K., John, J., Kowalczyk, E., Maki, T., Maksyutov, S., Peylin, P., Prather, M., Pak, B. C., Sarmiento, J., Taguchi, S., Takahashi, T., and Yuen, C.-W.: TransCom 3 CO2 inversion intercomparison: 1. Annual mean control results and sensitivity to transport and prior flux information, Tellus, 55B, 555–579, https://doi.org/10.1034/j.1600-0560.2003.00049.x, 2003. a
Gurney, K. R., Law, R. M., Denning, A. S., Rayner, P. J., Pak, B. C., Baker, D., Bousquet, P., Bruhwiler, L., Chen, Y.-H., Ciais, P., Fung, I. Y., Heimann, M., John, J., Maki, T., Maksyutov, S., Peylin, P., Prather, M., and Taguchi, S.: Transcom 3 inversion intercomparison: Model mean results for the estimation of seasonal carbon sources and sinks, Global Biogeochem. Cy., 18, GB1010, https://doi.org/10.1029/2003GB002111, 2004. a
Hardt, M. and Scherbaum, F.: The Design of Optimum Networks for Aftershock Recordings, Geophys. J. Int., 117, 716–726, 1994. a
Henne, S., Brunner, D., Oney, B., Leuenberger, M., Eugster, W., Bamberger, I., Meinhardt, F., Steinbacher, M., and Emmenegger, L.: Validation of the Swiss methane emission inventory by atmospheric observations and inverse modelling, Atmos. Chem. Phys., 16, 3683–3710, https://doi.org/10.5194/acp-16-3683-2016, 2016. a
Henze, D. K., Hakami, A., and Seinfeld, J. H.: Development of the adjoint of GEOS-Chem, Atmos. Chem. Phys., 7, 2413–2433, https://doi.org/10.5194/acp-7-2413-2007, 2007. a
Houtekamer, P. and Zhang, F.: Review of the ensemble Kalman filter for atmospheric data assimilation, Mon. Weather Rev., 144, 4489–4532, 2016. a
Hungershoefer, K., Breon, F.-M., Peylin, P., Chevallier, F., Rayner, P., Klonecki, A., Houweling, S., and Marshall, J.: Evaluation of various observing systems for the global monitoring of CO2 surface fluxes, Atmos. Chem. Phys., 10, 10503–10520, https://doi.org/10.5194/acp-10-10503-2010, 2010. a
Ide, K., Courtier, P., Ghil, M., and Lorenc, A. C.: Unified Notation for Data Assimilation: Operational, Sequential and Variational, J. Meteorol. Soc. Jpn. Ser. II, 75, 181–189, 1997. a, b, c
Issartel, J.-P.: Emergence of a tracer source from air concentration measurements, a new strategy for linear assimilation, Atmos. Chem. Phys., 5, 249–273, https://doi.org/10.5194/acp-5-249-2005, 2005. a
Jacob, P., Robert, C. P., and Smith, M. H.: Using parallel computation to improve independent Metropolis–Hastings based estimation, J. Comput. Graph. Stat., 20, 616–635, 2011. a
Jaynes, E. and Bretthorst, G.: Probability Theory: The Logic of Science, Cambridge University Press, available at: http://books.google.com.au/books?id=tTN4HuUNXjgC (last access: 18 September 2018), 2003. a, b, c, d, e, f, g
Jazwinski, A. H.: Stochastic processes and filtering theory, Academic Press, New York, 1970. a
Jeffreys, H.: Theory of Probability, The International series of monographs on physics, 380 pp., Oxford, UK, 1939. a
Kalman, R. E.: A new approach to linear filtering and prediction problems, J. Basic Eng.-T.-ASME, 82D, 35–45, 1960. a, b
Kalnay, E.: Atmospheric modelling, data assimilation and predictability, Cambridge University Press, 2003. a
Kaminski, T. and Rayner, P. J.: Reviews and syntheses: guiding the evolution of the observing system for the carbon cycle through quantitative network design, Biogeosciences, 14, 4755–4766, https://doi.org/10.5194/bg-14-4755-2017, 2017. a, b
Kaminski, T., Heimann, M., and Giering, R.: A coarse grid three-dimensional global inverse model of the atmospheric transport, 1, Adjoint Model and Jacobian Matrix, J. Geophys. Res., 104, 18535–18553, 1999a. a, b
Kaminski, T., Heimann, M., and Giering, R.: A coarse grid three-dimensional global inverse model of the atmospheric transport, 2, Inversion of the transport of CO2 in the 1980s, J. Geophys. Res., 104, 18555–18582, 1999b. a, b
Kaminski, T., Rayner, P. J., Heimann, M., and Enting, I. G.: On Aggregation Errors in Atmospheric Transport Inversions, J. Geophys. Res., 106, 4703–4715, 2001. a, b, c, d
Kaminski, T., Knorr, W., Rayner, P., and Heimann, M.: Assimilating Atmospheric data into a Terrestrial Biosphere Model: A case study of the seasonal cycle, Global Biogeochem. Cy., 16, 1066, https://doi.org/10.1029/2001GB001463, 2002. a, b
Kaminski, T., Rayner, P. J., Voßbeck, M., Scholze, M., and Koffi, E.: Observing the continental-scale carbon balance: assessment of sampling complementarity and redundancy in a terrestrial assimilation system by means of quantitative network design, Atmos. Chem. Phys., 12, 7867–7879, https://doi.org/10.5194/acp-12-7867-2012, 2012. a
Keeling, C. D.: Rewards and Penalties of Monitoring the Earth, Annu. Rev. Energ. Env., 23, 25–82, 1998. a
Kim, J., Kim, H. M., and Cho, C.-H.: The effect of optimization and the nesting domain on carbon flux analyses in Asia using a carbon tracking system based on the ensemble Kalman filter, Asia-Pac. J. Atmos. Sci., 50, 327–344, 2014. a
Klaas, M., de Freitas, N., and Doucet, A.: Toward Practical N2 Monte Carlo: the Marginal Particle Filter, in: Proceedings of the Twenty-First Conference Annual Conference on Uncertainty in Artificial Intelligence (UAI-05), AUAI Press, Arlington, Virginia, 308–315, 2005. a
Knorr, W., Kaminski, T., Scholze, M., Gobron, N., Pinty, B., Giering, R., and Mathieu, P.-P.: Carbon cycle data assimilation with a generic phenology model, J. Geophys. Res.-Biogeo., 115, G04017, https://doi.org/10.1029/2009JG001119, 2010. a
Kopacz, M., Jacob, D. J., Henze, D. K., Heald, C. L., Streets, D. G., and Zhang, Q.: Comparison of adjoint and analytical Bayesian inversion methods for constraining Asian sources of carbon monoxide using satellite (MOPITT) measurements of CO columns, J. Geophys. Res.-Atmos., 114, D04305, https://doi.org/10.1029/2007JD009264, 2009. a
Kountouris, P., Gerbig, C., Rödenbeck, C., Karstens, U., Koch, T. F., and Heimann, M.: Technical Note: Atmospheric CO2 inversions on the mesoscale using data-driven prior uncertainties: methodology and system evaluation, Atmos. Chem. Phys., 18, 3027–3045, https://doi.org/10.5194/acp-18-3027-2018, 2018. a
Krakauer, N. Y., Schneider, T., Randerson, J. T., and Olsen, S. C.: Using generalized cross-validation to select parameters in inversions for regional carbon fluxes, Geophys. Res. Lett., 31, 19108, https://doi.org/10.1029/2004GL020323, 2004. a
Krause, A., Singh, A., and Guestrin, C.: Near-optimal sensor placements in Gaussian processes: Theory, efficient algorithms and empirical studies, J. Mach. Learn. Res., 9, 235–284, 2008. a
Krol, M., Houweling, S., Bregman, B., van den Broek, M., Segers, A., van Velthoven, P., Peters, W., Dentener, F., and Bergamaschi, P.: The two-way nested global chemistry-transport zoom model TM5: algorithm and applications, Atmos. Chem. Phys., 5, 417–432, https://doi.org/10.5194/acp-5-417-2005, 2005. a
Kuhn, T. S.: The structure of scientific revolutions, University of Chicago, 172 pp., 1962. a
Kuppel, S., Peylin, P., Chevallier, F., Bacour, C., Maignan, F., and Richardson, A. D.: Constraining a global ecosystem model with multi-site eddy-covariance data, Biogeosciences, 9, 3757–3776, https://doi.org/10.5194/bg-9-3757-2012, 2012. a
Kuppel, S., Chevallier, F., and Peylin, P.: Quantifying the model structural error in carbon cycle data assimilation systems, Geosci. Model Dev., 6, 45–55, https://doi.org/10.5194/gmd-6-45-2013, 2013. a, b
Laplace, P. S.: Mémoire sur la probabilité des causes par les événements, Mem. Acad. Roy. Sci., 6, 621–656, 1774. a
Lauvaux, T., Pannekoucke, O., Sarrat, C., Chevallier, F., Ciais, P., Noilhan, J., and Rayner, P. J.: Structure of the transport uncertainty in mesoscale inversions of CO2 sources and sinks using ensemble model simulations, Biogeosciences, 6, 1089–1102, https://doi.org/10.5194/bg-6-1089-2009, 2009. a
Lauvaux, T., Schuh, A. E., Uliasz, M., Richardson, S., Miles, N., Andrews, A. E., Sweeney, C., Diaz, L. I., Martins, D., Shepson, P. B., and Davis, K. J.: Constraining the CO2 budget of the corn belt: exploring uncertainties from the assumptions in a mesoscale inverse system, Atmos. Chem. Phys., 12, 337–354, https://doi.org/10.5194/acp-12-337-2012, 2012. a, b
Law, R. M., Rayner, P. J., Denning, A. S., Erickson, D., Fung, I. Y., Heimann, M., Piper, S. C., Ramonet, M., Taguchi, S., Taylor, J. A., Trudinger, C. M., and Watterson, I. G.: Variations in modelled atmospheric transport of carbon dioxide and the consequences for CO2 inversions, Global Biogeochem. Cy., 10, 783–796, 1996. a
Law, R. M., Chen, Y.-H., Gurney, K. R., and TransCom 3 modellers: TransCom 3 CO2 inversion intercomparison: 2. Sensitivity of annual mean results to data choices, Tellus, 55B, 580–595, https://doi.org/10.1034/j.1600-0560.2003.00053.x, 2003. a
Liu, J., Bowman, K. W., Lee, M., Henze, D. K., Bousserez, N., Brix, H., James Collatz, G., Menemenlis, D., Ott, L., Pawson, S., Jones, D., and Nassar, R.: Carbon monitoring system flux estimation and attribution: impact of ACOS-GOSAT XCO2 sampling on the inference of terrestrial biospheric sources and sinks, Tellus B, 66, 22486, https://doi.org/10.3402/tellusb.v66.22486, 2014. a
Liu, J., Bowman, K. W., and Lee, M.: Comparison between the Local Ensemble Transform Kalman Filter (LETKF) and 4D-Var in atmospheric CO2 flux inversion with the Goddard Earth Observing System-Chem model and the observation impact diagnostics from the LETKF, J. Geophys. Res.-Atmos., 121, 13066–13087, https://doi.org/10.1002/2016JD025100, 2016. a
Lu, S., Lin, H., Heemink, A., Fu, G., and Segers, A.: Estimation of volcanic ash emissions using trajectory-based 4D-Var data assimilation, Mon. Weather Rev., 144, 575–589, 2016. a
Lunt, M. F., Rigby, M., Ganesan, A. L., and Manning, A. J.: Estimation of trace gas fluxes with objectively determined basis functions using reversible-jump Markov chain Monte Carlo, Geosci. Model Dev., 9, 3213–3229, https://doi.org/10.5194/gmd-9-3213-2016, 2016. a, b
MacBean, N., Maignan, F., Bacour, C., Lewis, P., Peylin, P., Guanter, L., Köhler, P., Gómez-Dans, J., and Disney, M.: Strong constraint on modelled global carbon uptake using solar-induced chlorophyll fluorescence data, Sci. Rep., 8, 1973, https://doi.org/10.1038/s41598-018-20024-w, 2018. a
Manning, A., O'Doherty, S., Jones, A., Simmonds, P., and Derwent, R.: Estimating UK methane and nitrous oxide emissions from 1990 to 2007 using an inversion modeling approach, J. Geophys. Res.-Atmos., 116, D02305, https://doi.org/10.1029/2010JD014763, 2011. a, b
McIntosh, P. C. and Veronis, G.: Solving Underdetermined Tracer Inverse Problems by Spatial Smoothing and Cross Validation, J. Phys. Oceanogr., 23, 716–730, 1993. a
Medvigy, D., Wofsy, S. C., Munger, J. W., Hollinger, D. Y., and Moorcroft, P. R.: Mechanistic scaling of ecosystem function and dynamics in space and time: Ecosystem Demography model version 2, J. Geophys. Res., 114, G01002, https://doi.org/10.1029/2008JG000812, 2009. a
Meinshausen, M., Raper, S. C. B., and Wigley, T. M. L.: Emulating coupled atmosphere-ocean and carbon cycle models with a simpler model, MAGICC6 – Part 1: Model description and calibration, Atmos. Chem. Phys., 11, 1417–1456, https://doi.org/10.5194/acp-11-1417-2011, 2011. a
Meirink, J. F., Bergamaschi, P., and Krol, M. C.: Four-dimensional variational data assimilation for inverse modelling of atmospheric methane emissions: method and comparison with synthesis inversion, Atmos. Chem. Phys., 8, 6341–6353, https://doi.org/10.5194/acp-8-6341-2008, 2008. a, b
Michalak, A. M., Bruhwiler, L., and Tans, P. P.: A geostatistical approach to surface flux estimation of atmospheric trace gases, J. Geophys. Res., 109, D14109, https://doi.org/10.1029/2003JD004422, 2004. a, b, c
Michalak, A. M., Hirsch, A., Bruhwiler, L., Gurney, K. R., Peters, W., and Tans, P. P.: Maximum likelihood estimation of covariance parameters for Bayesian atmospheric trace gas surface flux inversions, J. Geophys. Res., 110, D24107, https://doi.org/10.1029/2005JD005970, 2005. a, b, c, d
Michalak, A. M., Randazzo, N. A., and Chevallier, F.: Diagnostic methods for atmospheric inversions of long-lived greenhouse gases, Atmos. Chem. Phys., 17, 7405–7421, https://doi.org/10.5194/acp-17-7405-2017, 2017. a, b, c
Miller, S. M., Wofsy, S. C., Michalak, A. M., Kort, E. A., Andrews, A. E., Biraud, S. C., Dlugokencky, E. J., Eluszkiewicz, J., Fischer, M. L., Janssens-Maenhout, G., Miller, B. R., Miller, J. B., Montzka, S. A., Nehrkorn, T., and Sweeney, C.: Anthropogenic emissions of methane in the United States, P. Natl. Acad. Sci. USA, 110, 20018–20022, https://doi.org/10.1073/pnas.1314392110, 2013. a, b
Miyazaki, K., Maki, T., Patra, P., and Nakazawa, T.: Assessing the impact of satellite, aircraft, and surface observations on CO2 flux estimation using an ensemble-based 4-D data assimilation system, J. Geophys. Res.-Atmos., 116, D16306, https://doi.org/10.1029/2010JD015366, 2011. a, b
Moore, A. M., Arango, H. G., and Broquet, G.: Estimates of analysis and forecast error variances derived from the adjoint of 4D-Var, Mon. Weather Rev., 140, 3183–3203, 2012. a
Mulquiney, J. E. and Norton, J. P.: A new inverse method for trace gas flux estimation 1. State-space model identification and constraints, J. Geophys. Res., 103D, 1417–1427, 1998. a
Mulquiney, J. E., Norton, J. P., Jakeman, A. J., and Taylor, J. A.: Random walks in the Kalman filter: Implications for greenhouse gas flux deductions, Environmetrics, 6, 473–478, 1995. a
Mulquiney, J. E., Taylor, J. A., Jakeman, A. J., Norton, J. P., and Prinn, R. G.: A new inverse method for trace gas flux estimation 2. Application to tropospheric CFCl3 fluxes, J. Geophys. Res., 103D, 1429–1442, 1998. a
Norton, A. J., Rayner, P. J., Koffi, E. N., and Scholze, M.: Assimilating solar-induced chlorophyll fluorescence into the terrestrial biosphere model BETHY-SCOPE v1.0: model description and information content, Geosci. Model Dev., 11, 1517–1536, https://doi.org/10.5194/gmd-11-1517-2018, 2018. a
Park, S.-Y., Kim, D.-H., Lee, S.-H., and Lee, H. W.: Variational data assimilation for the optimized ozone initial state and the short-time forecasting, Atmos. Chem. Phys., 16, 3631–3649, https://doi.org/10.5194/acp-16-3631-2016, 2016. a
Patra, P. K., Maksyutov, S., Baker, D., Bousquet, P., Bruhwiler, L., Chen, Y.-H., Ciais, P., Denning, A. S., Fan, S., Fung, I. Y., Gloor, M., Gurney, K. R., Heimann, M., Higuchi, K., John, J., Law, R. M., Maki, T., Peylin, P., Prather, M., Pak, B., Rayner, P. J., Sarmiento, J. L., Taguchi, S., Takahashi, T., and Yuen, C.-W.: Sensitivity of optimal extension of CO2 observation networks to model transport, Tellus B, 55, 498–511, 2003. a
Patra, P. K., Maksyutov, S., Ishizawa, M., Nakazawa, T., Takahashi, T., and Ukita, J.: Interannual and decadal changes in the sea-air CO2 flux from atmospheric CO2 inverse modeling, Global Biogeochem. Cy., 19, GB4013, https://doi.org/10.1029/2004GB002257, 2005. a
Patra, P. K., Gurney, K. R., Denning, A. S., Maksyutov, S., Nakazawa, T., Baker, D., Bousquet, P., Bruhwiler, L., Chen, Y.-H., Ciais, P., Fan, S., Fung, I., Gloor, M., Heimann, M., Higuchi, K., John, J., Law, R. M., Maki, T., Pak, B. C., Peylin, P., Prather, M., Rayner, P. J., Sarmiento, J., Taguchi, S., Takahashi, T., and Yuen, C.-W.: Sensitivity of inverse estimation of annual mean CO2 sources and sinks to ocean-only sites versus all-sites observational networks, Geophys. Res. Lett., 33, 05814, https://doi.org/10.1029/2005GL025403, 2006. a
Peters, W., Miller, J. B., Whitaker, J., Denning, A. S., Hirsch, A., Krol, M. C., Zupanski, D., Bruhwiler, L., and Tans, P. P.: An ensemble data assimilation system to estimate CO2 surface fluxes from atmospheric trace gas observations, J. Geophys. Res., 110, 24304, https://doi.org/10.1029/2005JD006157, 2005. a
Peters, W., Krol, M., Van Der Werf, G., Houweling, S., Jones, C., Hughes, J., Schaefer, K., Masarie, K., Jacobson, A., Miller, J., Cho, C. H., Ramonet, M., Schmidt, M., Ciattaglia, L., Apadula, F., Heltai, D., Meinhardt, F., Di Sarra, A. G., Piacentino, S., Sferlazzo, D., Aalto, T., Hatakka, J., Ström, J., Haszpra, L., Meijer, H. A. J., van der Laan, S., Neubert, R. E. M., Jordan, A., Rodó, X., Morguí, J. A., Vermeulen, A. T., Popa, E., Rozanski, K., Zimnoch, M., Manning, A. C., Leuenberger, M., Uglietti, C., Dolman, A. J., Ciais, P., Heimann, M., and Tans, P. P.: Seven years of recent European net terrestrial carbon dioxide exchange constrained by atmospheric observations, Glob. Change Biol., 16, 1317–1337, 2010. a
Peylin, P., Rayner, P. J., Bousquet, P., Carouge, C., Hourdin, F., Heinrich, P., Ciais, P., and AEROCARB contributors: Daily CO2 flux estimates over Europe from continuous atmospheric measurements: 1, inverse methodology, Atmos. Chem. Phys., 5, 3173–3186, https://doi.org/10.5194/acp-5-3173-2005, 2005. a
Quaife, T., Lewis, P., De Kauwe, M., Williams, M., Law, B. E., Disney, M., and Bowyer, P.: Assimilating canopy reflectance data into an ecosystem model with an Ensemble Kalman Filter, Remote Sens. Environ., 112, 1347–1364, 2008. a
Rayner, P.: Data Assimilation using an Ensemble of Models: A hierarchical approach, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2017-10, in review, 2017. a, b, c
Rayner, P. J.: The Current State of Carbon Cycle Data Assimilation, Curr. Opin. Env. Sust., 2, 289–296, https://doi.org/10.1016/j.cosust.2010.05.005, 2010. a, b
Rayner, P. J., Enting, I. G., Francey, R. J., and Langenfelds, R. L.: Reconstructing the recent carbon cycle from atmospheric CO2, δ13C and O2∕N2 observations, Tellus, 51B, 213–232, 1999. a
Rayner, P. J., Scholze, M., Knorr, W., Kaminski, T., Giering, R., and Widmann, H.: Two decades of terrestrial Carbon fluxes from a Carbon Cycle Data Assimilation System (CCDAS), Global Biogeochem. Cy., 19, 2026, https://doi.org/10.1029/2004GB002254, 2005. a
Rayner, P. J., Raupach, M. R., Paget, M., Peylin, P., and Koffi, E.: A new global gridded dataset of CO2 emissions from fossil fuel combustion: 1: Methodology and evaluation, J. Geophys. Res., 115, D19306, https://doi.org/10.1029/2009JD013439, 2010. a
Robert, C. P. and Casella, G.: Monte Carlo Statistical Methods, chap. 2.3.2, Springer, 2nd Edn., 51–53,2004. a
Rödenbeck, C.: Estimating CO2 sources and sinks from atmospheric mixing ratio measurements using a global inversion of atmospheric transport, no. 06, Max Planck Institute for biogeochemistry Technical Reports, Max Planck Society, 2005. a
Rödenbeck, C., Houweling, S., Gloor, M., and Heimann, M.: Time-dependent atmospheric CO2 inversions based on interannually varying tracer transport, Tellus, 55B, 488–497, 2003. a, b
Rödenbeck, C., Gerbig, C., Trusilova, K., and Heimann, M.: A two-step scheme for high-resolution regional atmospheric trace gas inversions based on independent models, Atmos. Chem. Phys., 9, 5331–5342, https://doi.org/10.5194/acp-9-5331-2009, 2009. a
Rodgers, C. D.: Inverse methods for atmospheric sounding: Theory and practice, World Scientific Publishing Co. Pte. Ltd. 2000. a, b, c
Rodgers, C. D. and Walshaw, C. D.: The computation of infra-red cooling rate in planetary atmosphere, Q. J. Roy. Meteor. Soc., 92, 67–92, 1966. a
Roy, T., Rayner, P., Matear, R., and Francey, R.: Southern hemisphere ocean CO2 uptake: reconciling atmospheric and oceanic estimates, Tellus, 55B, 701–710, https://doi.org/10.1034/j.1600-0560.2003.00058.x, 2003. a
Saeki, T. and Patra, P. K.: Implications of overestimated anthropogenic CO2 emissions on East Asian and global land CO2 flux inversion, Geoscience Letters, 4, 9, https://doi.org/10.1186/s40562-017-0074-7, 2017. a
Salsburg, D.: The lady tasting tea: How statistics revolutionized science in the twentieth century, Macmillan, 2001. a
Scholze, M., Kaminski, T., Rayner, P., Knorr, W., and Geiring, R.: Propagating uncertainty through prognostic CCDAS simulations, J. Geophys. Res., 112, d17305, https://doi.org/10.1029/2007JD008642, 2007. a
Scholze, M., Kaminski, T., Knorr, W., Blessing, S., Vossbeck, M., Grant, J., and Scipal, K.: Simultaneous assimilation of SMOS soil moisture and atmospheric CO2 in-situ observations to constrain the global terrestrial carbon cycle, Remote Sens. Environ., 180, 334–345, 2016. a
Scholze, M., Buchwitz, M., Dorigo, W., Guanter, L., and Quegan, S.: Reviews and syntheses: Systematic Earth observations for use in terrestrial carbon cycle data assimilation systems, Biogeosciences, 14, 3401–3429, https://doi.org/10.5194/bg-14-3401-2017, 2017. a
Schuh, A. E., Lauvaux, T., West, T. O., Denning, A. S., Davis, K. J., Miles, N., Richardson, S., Uliasz, M., Lokupitiya, E., Cooley, D., Andrews, A., and Ogle, S.: Evaluating atmospheric CO2 inversions at multiple scales over a highly inventoried agricultural landscape, Glob. Change Biol., 19, 1424–1439, https://doi.org/10.1111/gcb.12141, 2013. a
Shaby, B. A. and Field, C. B.: Regression tools for CO2 inversions: application of a shrinkage estimator to process attribution, Tellus B, 58, 279–292, 2006. a
Shiga, Y. P., Tadić, J. M., Qiu, X., Yadav, V., Andrews, A. E., Berry, J. A., and Michalak, A. M.: Atmospheric CO2 Observations Reveal Strong Correlation Between Regional Net Biospheric Carbon Uptake and Solar-Induced Chlorophyll Fluorescence, Geophys. Res. Lett., 45, 1122–1132, https://doi.org/10.1002/2017GL076630, 2018. a
Stordal, A. S., Karlsen, H. A., Nævdal, G., Skaug, H. J., and Vallès, B.: Bridging the ensemble Kalman filter and particle filters: the adaptive Gaussian mixture filter, Comput. Geosci., 15, 293–305, 2011. a
Tans, P. P., Fung, I. Y., and Takahashi, T.: Observational constraints on the global atmospheric CO2 budget, Science, 247, 1431–1438, 1990. a
Tarantola, A.: Inverse Problem Theory: Methods for Data Fitting and Parameter Estimation, Elsevier, Amsterdam, 1987. a
Tarantola, A.: Inverse problem theory and methods for model parameter estimation, Society for Industrial and Applied Mathematics, 89, 339 pp., 2005. a, b, c, d, e, f, g
Tarantola, A. and Valette, B.: Generalized nonlinear inverse problem solved using the least squares criterion, Rev. Geophys., 20, 219–232, 1982. a
Thompson, R. L., Gerbig, C., and Rödenbeck, C.: A Bayesian inversion estimate of N2O emissions for western and central Europe and the assessment of aggregation errors, Atmos. Chem. Phys., 11, 3443–3458, https://doi.org/10.5194/acp-11-3443-2011, 2011. a
Tippett, M. K., Anderson, J. L., Bishop, C. H., Hamill, T. M., and Whitaker, J. S.: Ensemble square root filters, Mon. Weather Rev., 131, 1485–1490, 2003. a
Trampert, J. and Snieder, R.: Model Estimations Biased by Truncated Expansions: Possible Artifacts in Seismic Tomography, Science, 271, 1257–1260, 1996. a, b
Trudinger, C., Raupach, M., Rayner, P., Kattge, J., Liu, Q., Pak, B., Reichstein, M., Renzullo, L., Richardson, A. D., Roxburgh, S., Styles, J., Wang, Y. P., Briggs, P., Barrett, D., and Nikolova, S.: The OptIC project: An intercomparison of optimisation techniques for parameter estimation in terrestrial biogeochemical models, J. Geophys. Res., 112, 2027, https://doi.org/10.1029/2006JG000367, 2007. a, b, c
Trudinger, C. M., Enting, I. G., and Rayner, P. J.: Kalman filter analysis of ice core data: 1. Method development and testing the statistics, J. Geophys. Res., 107(D20), https://doi.org/10.1029/2001JD001111, 2002a. a
Trudinger, C. M., Enting, I. G., Rayner, P. J., and Francey, R. J.: Kalman filter analysis of ice core data: 2. Double deconvolution of CO2 and δ13C measurements, J. Geophys. Res., 107, ACH 5-1–ACH 5-24, https://doi.org/10.1029/2001JD001112, 2002b. a
Trudinger, C. M., Raupach, M. R., Rayner, P. J., and Enting, I. G.: Using the Kalman filter for parameter estimation in biogeochemical models, Environmetrics, 19, 849–870, https://doi.org/10.1002/env.910, 2008. a, b
Turnbull, J. C., Karion, A., Fischer, M. L., Faloona, I., Guilderson, T., Lehman, S. J., Miller, B. R., Miller, J. B., Montzka, S., Sherwood, T., Saripalli, S., Sweeney, C., and Tans, P. P.: Assessment of fossil fuel carbon dioxide and other anthropogenic trace gas emissions from airborne measurements over Sacramento, California in spring 2009, Atmos. Chem. Phys., 11, 705–721, https://doi.org/10.5194/acp-11-705-2011, 2011. a
Turner, A. J. and Jacob, D. J.: Balancing aggregation and smoothing errors in inverse models, Atmos. Chem. Phys., 15, 7039–7048, https://doi.org/10.5194/acp-15-7039-2015, 2015. a
van Dop, H., Addis, R., Fraser, G., Girardi, F., Graziani, G., Inoue, Y., Kelly, N., Klug, W., Kulmala, A., Nodop, K., and Pretel, J.: ETEX A European tracer experiment observations, dispersion modelling and emergency response, Atmos. Environ., 32, 4089–4094, 1998. a
van Leeuwen, P. J.: Particle Filtering in Geophysical Systems, Mon. Weather Rev., 137, 4089–4114, https://doi.org/10.1175/2009MWR2835.1, 2009. a
Vanoye, A. Y. and Mendoza, A.: Application of direct regularization techniques and bounded–variable least squares for inverse modeling of an urban emissions inventory, Atmos. Pollut. Res., 5, 219–225, 2014. a
Wang, J. S., Kawa, S. R., Collatz, G. J., Sasakawa, M., Gatti, L. V., Machida, T., Liu, Y., and Manyin, M. E.: A global synthesis inversion analysis of recent variability in CO2 fluxes using GOSAT and in situ observations, Atmos. Chem. Phys., 18, 11097–11124, https://doi.org/10.5194/acp-18-11097-2018, 2018. a
Wang, X., Mallet, V., Berroir, J.-P., and Herlin, I.: Assimilation of OMI NO2 retrievals into a regional chemistry-transport model for improving air quality forecasts over Europe, Atmos. Environ., 45, 485–492, 2011. a
Wikle, C. K. and Berliner, L. M.: A Bayesian tutorial for data assimilation, Physica D, 230, 1–16, 2007. a
Williams, M., Schwarz, P. A., Law, B. E., Irvine, J., and Kurpius, M. R.: An improved analysis of forest carbon dynamics using data assimilation, Glob. Change Biol., 11, 89–105, 2005. a
Wilson, C., Chipperfield, M. P., Gloor, M., and Chevallier, F.: Development of a variational flux inversion system (INVICAT v1.0) using the TOMCAT chemical transport model, Geosci. Model Dev., 7, 2485–2500, https://doi.org/10.5194/gmd-7-2485-2014, 2014. a
Wu, L., Bocquet, M., Lauvaux, T., Chevallier, F., Rayner, P., and Davis, K.: Optimal Representation of Source-Sink Fluxes for Mesoscale Carbon Dioxide Inversion with Synthetic Data, J. Geophys. Res., 116, D21304, https://doi.org/10.1029/2011JD016198, 2011. a, b
Wu, L., Bocquet, M., Chevallier, F., Lauvaux, T., and Davis, K.: Hyperparameter Estimation for Uncertainty Quantification in Mesoscale Carbon Dioxide Inversions, Tellus, 65b, 20894, https://doi.org/10.3402/tellusb.v65i0.20894, 2013. a
Wunsch, C. and Minster, J.-F.: Methods for box models and ocean circulation tracers: Mathematical programming and non-linear inverse theory, J. Geophys. Res., 87, 5647–5662, 1982. a, b, c
Yadav, V. and Michalak, A. M.: Improving computational efficiency in large linear inverse problems: an example from carbon dioxide flux estimation, Geosci. Model Dev., 6, 583–590, https://doi.org/10.5194/gmd-6-583-2013, 2013. a
Zheng, B., Chevallier, F., Ciais, P., Yin, Y., Deeter, M. N., Worden, H. M., Wang, Y., Zhang, Q., and He, K.: Rapid decline in carbon monoxide emissions and export from East Asia between years 2005 and 2016, Environ. Res. Lett., 13, 4, https://doi.org/10.1088/1748-9326/aab2b3, 2018. a
Zheng, T., French, N. H. F., and Baxter, M.: Development of the WRF-CO2 4D-Var assimilation system v1.0, Geosci. Model Dev., 11, 1725–1752, https://doi.org/10.5194/gmd-11-1725-2018, 2018. a
Zupanski, D., Denning, A. S., Uliasz, M., Zupanski, M., Schuh, A. E., Rayner, P. J., Peters, W., and Corbin, K.: Carbon flux bias estimation employing Maximum Likelihood Ensemble Filter (MLEF), J. Geophys. Res., 112, d17107, https://doi.org/10.1029/2006JD008371., 2007. a
This definition of event already takes us down one fork of the major distinction in statistics roughly described as Bayesians vs. frequentists. This is a Bayesian definition; a frequentist will usually refer to an event as the outcome of an experiment.
Tarantola (2005) uses the term information instead of knowledge. We avoid it here because it has a technical meaning.
Rayner et al. (2010) refer to this as a model but here we reserve that term for the dynamical evolution of the system.
We thank Ian Enting for pointing this out.
- Abstract
- Introduction
- Data assimilation as statistical inference
- Towards a consistent notation
- Fundamental Bayesian theory
- The ingredients
- Solving the assimilation problem
- Computational aspects
- Historical overview
- Future developments
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Data assimilation as statistical inference
- Towards a consistent notation
- Fundamental Bayesian theory
- The ingredients
- Solving the assimilation problem
- Computational aspects
- Historical overview
- Future developments
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References





