the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical note: Effects of uncertainties and number of data points on line fitting – a case study on new particle formation
Mikko R. A. Pitkänen
Tuomo Nieminen
Antti Lipponen
Sini Isokääntä
Antti Arola
Kari E. J. Lehtinen
Fitting a line to two measured variables is considered one of the simplest statistical procedures researchers can carry out. However, this simplicity is deceptive as the line-fitting procedure is actually quite a complex problem. Atmospheric measurement data never come without some measurement error. Too often, these errors are neglected when researchers make inferences from their data.
To demonstrate the problem, we simulated datasets with different numbers of data points and different amounts of error, mimicking the dependence of the atmospheric new particle formation rate (J1.7) on the sulfuric acid concentration (H2SO4). Both variables have substantial measurement error and, thus, are good test variables for our study. We show that ordinary least squares (OLS) regression results in strongly biased slope values compared with six error-in-variables (EIV) regression methods (Deming regression, principal component analysis, orthogonal regression, Bayesian EIV and two different bivariate regression methods) that are known to take errors in the variables into account.
- Article
(1438 KB) - Full-text XML
-
Supplement
(413 KB) - BibTeX
- EndNote
Atmospheric measurements always come with some measurement error. Too often, these errors are neglected when researchers make inferences based on their data. Describing the relationship between two variables typically involves making deductions in a more general context than that in which the variables were directly studied. If the relationship is not defined correctly, the inference is also not valid. In some cases, the bias in the analytical method is even given a physical meaning.
When analysing the dependencies of two or more measured variables, regression models are usually applied. Regression models can be linear or non-linear, depending on the relationship between the datasets that are analysed. Standard regression models assume that the independent variables of the model have been measured without error and that the model only accounts for errors in the dependent variables or responses. In cases where the measurements of the predictors contain error, estimating using standard methods (usually ordinary least squares, OLS) does not tend to provide the true parameter values, even when a very high number of data points is used. In linear models, the coefficients are underestimated (e.g. Carroll et al., 2006); however, in non-linear models, the bias is likely to be more complicated (e.g. Schennach, 2004). If predictor variables in regression analyses contain any measurement error, methods that account for errors should be applied – particularly when errors are large. Thus, test variables in this study were chosen such that they included significant uncertainties in both the independent and dependent variables.
The sulfuric acid concentration (H2SO4) is known to strongly affect the formation rates (J) of aerosol particles (Kirkby et al., 2016; Kuang et al., 2008; Kulmala et al., 2006; Kürten et al., 2016; Metzger et al., 2010; Riccobono et al., 2014; Riipinen et al., 2007; Sihto et al., 2006; Spracklen et al., 2006). The relationship between J (cm−3 s−1) and H2SO4 (molec cm−3) is typically assumed to be in the following form: log(H2SO4)+α (Seinfeld and Pandis, 2016). In addition, parameterisations based on the results from these fits have been implemented in global models (e.g. in Dunne et al., 2016, Metzger et al., 2010 and Spracklen et al., 2006) to estimate the effects of new particle formation on global aerosol amounts and characteristics. Theoretically, in homogeneous nucleation, the slope of this relationship is related to the number of sulfuric acid molecules in the nucleating critical cluster, based on the first nucleation theorem (Vehkamäki, 2006).
Some published results have shown discrepancies in the expected J vs. H2SO4 dependence. Analysing data from Hyytiälä in 2003, Kuang et al. (2008) used an unconstrained least squares method, which was not specified in the paper, and obtained a β value of 1.99 for the slope, whereas Sihto et al. (2006) reported a β value of 1.16 using OLS from the same field campaign. The studies had some differences in pre-treatment of the data and used different time windows, but a significant proportion of this inconsistency is very likely due to the use of different fitting methods. The problem regarding the relationship of H2SO4 and J was previously acknowledged in Paasonen et al. (2010), who noted that the bivariate fitting method, as presented in York et al. (2004), should be applied; however, this method could not be used due to the lack of proper error estimates for each quantity. They were not aware of methods that did not require knowledge of the errors in advance, and instead made use of estimated variances. Here, we present the appropriate tools required for the above-mentioned approach.
Multiple attempts have been made to present methods that account for errors in the predictor variables for regression-type analyses, going back to Deming (1943). However, the traditional least squares fitting method is still the de facto line-fitting method due to its simplicity and common availability in frequently used software. In atmospheric sciences, Cantrell (2008) drew attention to the method introduced by York (1966) and York et al. (2004) and listed multiple other methodological papers utilising similar methodology. Pitkänen et al. (2016) raised awareness of the fact that errors are not accounted for in the predictor variables in the remote-sensing community, and this study partly follows their approach and introduces multiple methods to account for the errors in predictors. Cheng and Riu (2006) studied methods involving heteroscedastic errors, whereas Wu and Yu (2018) approached the problem with measurement errors via weighted regression and applied some techniques that are also used in our study.
Measurement errors in each variable must be taken into account using approaches known as errors-in-variables (EIV) regression. EIV methods simply mean that errors in both variables are accounted for. In this study, we compared OLS regression results to six different regression methods (Deming regression, principal component analysis regression, orthogonal regression, Bayesian EIV regression and two different bivariate regression methods) that are known to be able to take errors in variables into account and provide (at least asymptotically) unbiased estimates. In this study, we focus exclusively on linear EIV methods, but it is important to acknowledge that non-linear methods also exist, e.g. ORDPACK introduced in Boggs et al. (1987) and implemented in Python SciPy and R (Boggs et al., 1989; Spiess, 2015). ORDPACK is a somewhat improved version of classical orthogonal regression, in that arbitrary covariance structures are acceptable, and it is specifically set up so that a user can specify measurement error variance and covariance point by point; some of the methods in this study carry out the same process in linear analysis.
2.1 Data illustrating the phenomenon
Measurement data contain different types of errors. Usually, the errors are divided to two main class: systematic error and random error.
Systematic errors, commonly referred as bias, in experimental observations usually come from the measurement instruments. They may occur because something is wrong with the instrument or its data handling system, or due to operator error. In line fitting, bias cannot be taken into account and needs to be minimised by way of careful and regular instrument calibrations and zeros or data preprocessing. The random error, in comparison, may have different components; the two components discussed here are the natural error and the measurement error. In addition, one should note the existence of equation error (discussed in Carroll and Ruppert, 1996), which refers to using an inappropriate form of a fitting equation. Measurement error is more generally understood; it is where measured values do not fully represent the true values of the variable being measured. This also contains sampling error (e.g. in the case of H2SO4 measurement, the sampled air in the measurement instrument is not a representative sample of the outside air due to losses of H2SO4 occurring in the sampling lines, among other factors). Natural error is the variability caused by natural or physical phenomenon (e.g. a specific amount of H2SO4 does not always cause the same number of new particles to be formed).
In the analysis of the measurement data, some amount of these errors are known or can be estimated, but some of the error will usually remain unknown; this should be kept in mind when interpreting fits. Even though the measurement error is taken into account, the regression fit may be biased due to unknown natural error. In this study, we assume that the errors of the different variables are uncorrelated, but in some cases this has to be accounted for, as noted, for example, in Trefall and Nordö (1959) and Mandel (1984). The correlation between the errors of two variables, measured with separate instruments, independent of each other, such as formation rate and H2SO4, may come from factors such as environmental variables that affect both of the variables at the same time. Factors affecting the formation of sulfuric acid have been studied in various papers, e.g. in Weber et al. (1997) and Mikkonen et al. (2011). New particle formation rates, in turn, have been studied in works such as Boy et al. (2008) and Hamed et al. (2011) and similarities between the affecting factors can be seen. In addition, factors like room temperature in the measurement space and atmospheric pressure may affect the performance of instrumentation, thereby causing additional error.
The data used in this study consist of simulated new particle formation rates at 1.7 nm (J1.7) and sulfuric acid (H2SO4) concentrations mimicking observations of pure sulfuric acid in nucleation experiments from the CLOUD chamber at CERN (Kürten et al. 2016; https://home.cern/about/experiments/cloud, last access: 16 August 2019), including the corresponding expected values, their variances and covariance structures. The Proton Synchrotron at CERN provides an artificial source of “cosmic rays” that simulates the natural ionisation conditions between the ground level and the stratosphere. The core is a large (volume 26 m3) electro-polished stainless-steel chamber with temperature control (temperature stability better than 0.1 K) at any tropospheric temperature, precise delivery of selected gases (SO2, O3, NH3 and various organic compounds) and ultra-pure humidified synthetic air, as well as very low gas-phase contaminant levels. The existing data on new particle formation include what are believed to be the most important formation routes that involve sulfuric acid, ammonia and water vapour (Kirkby et al., 2011); sulfuric acid and amine (Almeida et al., 2013); and ion-induced organic nucleation (Kirkby et al., 2016). The actual nucleation of new particles occurs at a slightly smaller size. After formation, particles grow by condensation to reach the detection limit (1.7 nm) of the instrument; thus, J1.7 refers to the formation rate of particles as the instrument detects them, accounting for the known particle losses due to coagulation and deposition on the chamber walls. The relationships between precursor gas-phase concentrations and particle formation rates were chosen because they are both known to have considerable measurement errors and their relationship has been well-studied using regression-based analyses (Kirkby et al., 2016; Kürten et al., 2016; Riccobono et al., 2014; Tröstl et al., 2016). Additionally, many of the published papers on this topic do not describe how they accounted for the uncertainties in the analysis, which casts doubt on the fact that errors were treated properly. However, it should be kept in mind that the data could be any set of numbers assumed to have a linear relationship, but, in order to raise awareness in the aerosol research community, in this study we relate our analysis to the important problem of understanding new particle formation.
2.2 Regression methods
We carried out fits for the linear dependency of the logarithms of the two study variables, such that the equation for the fit was given by
where y represents log10(J1.7), x is log10(H2SO4), β values are the coefficients estimated from the data and ε is the error term. In order to demonstrate the importance of taking the measurement errors into account in the regression analysis, we tested seven different line-fitting methods: ordinary least squares (OLS), not taking the uncertainty in x variable into account; orthogonal regression (ODR; Boggs et al., 1987); Deming regression (DR; Deming, 1943); principal component analysis (PCA; Hotelling, 1957) regression; Bayesian EIV regression (Kaipio and Somersalo, 2005); and two different bivariate least squares methods by York et al. (2004) and Francq and Govaerts (2014, BLS), respectively, which are known to be able to account for errors in variables and provide (at least asymptotically) unbiased estimates. The differences between the methods stem from the criterion they minimise when calculating the coefficients and how they account for measurement errors. The minimising criteria for all methods are given in Appendix A1, but in the following we give the principles of the methods.
OLS minimises the squared distance of the observation and the fit line either in the x or y direction, but not both at the same time, whereas ODR minimises the sum of the squared weighted orthogonal distances between each point and the line. DR was originally an improved version of orthogonal regression, accounting for the ratio of the error variances, λxy, of the variables, (in classical non-weighted ODR λxy=1), and it is the maximum likelihood estimate (MLE) for the model (given in Eq. 1) when λxy is known. The PCA approach is the same as in ODR, but the estimation procedure is somewhat different as can be seen in Table S1 in the Supplement. The bivariate algorithm by York et al. (2004) provides a simple set of equations for iterating the MLE of the slope and intercept with weighted variables, which makes it similar to ODR in this case. However, using ODR allows for a regression to be performed on a user-defined model, whereas the York (2004) solution only works on linear models. This, for instance, enables the use of linear-scale uncertainties in ODR in this study, whereas the York (2004) approach could only use log-scale uncertainties. In Bayes EIV, statistical models for the uncertainties in the observed quantities are used and probability distributions for the line slope and intercept are computed according to Bayes' theorem. In this study, we computed the Bayesian maximum a posteriori (MAP) estimates for the slope and intercept that are the most probable values given the likelihood and prior models (see Appendix A1 for more details on models used in Bayes EIV). BLS takes errors and heteroscedasticity into account, i.e. unequal variances, in both variables; thus, it is a more advanced method than DR (under normality and equal variances, BLS is exactly equivalent to DR). PCA only accounts for the observed variance in data, whereas ODR, Bayes EIV and York bivariate regression require known estimates for measurement errors, although for Bayes EIV the error can be approximated with a distribution. DR and BLS can be applied with both errors given by the user and measurement variance-based errors. In this study, we applied measurement variance-based errors for these methods. The analyses for OLS and PCA were calculated with the “lm” and “prcomp” R functions (R Core Team, 2018), respectively, DR was calculated with the “deming” package (Therneau, 2018) and BLS was calculated with the “BivRegBLS” package (Francq and Berger, 2017) in R. The ODR-based estimates were obtained using the “scipy.odr” Python package (Jones et al., 2001), while the “PyStan” Python package (Stan Development Team, 2018) was used for calculating the Bayesian regression estimates. Finally, the York bivariate estimates were produced with a custom Python implementation of the algorithm presented by York et al. (2004).
3.1 Simulated data
In measured data, the variables that are observed are not x and y, but (x+ex) and (y+ey), where ex and ey are the uncertainty in the measurements, and the true x and y cannot be exactly known. Thus, we used simulated data, where the true, i.e. noise-free, x and y were known to illustrate how the different line-fitting methods perform in different situations.
We simulated a dataset mimicking the new particle formation rates (J1.7) and sulfuric acid concentrations (H2SO4) reported from CLOUD-chamber measurements at CERN. Both variables are known to have substantial measurement error and, thus, they are good test variables for our study. Additionally, the relationship of the logarithms of these variables is quite often described with linear OLS regression and, thus, the inference may be flawed.
We generated 1000 random noise-free H2SO4 concentration values assuming a log-normal distribution with a median of 2.0×106 (molec cm−3) and a standard deviation of 2.4×106 (molec cm−3). The corresponding noise-free J1.7 was calculated using model log10((H2SO4)+α with the noise-free slope β=3.3 and , which are both realistic values presented by Kürten et al. (2016, Table 2 in their paper, for the no added ammonia cases).
Simulated observations of the noise-free H2SO4 concentrations were obtained by adding random errors that have a random absolute component normal() and a random component relative to the observation x itself erel,xx, where normal(). Similar definitions apply for the noise-free J1.7, ey, σabs,y and σrel,y. The standard deviations of the measurement error components were chosen as , , σabs,y = and , which are subjective estimates based on measurement data. The resulting total errors were occasionally about as large as the data values themselves; however, they are not unusually large error values with respect to corresponding real datasets, where overall uncertainties may reach 150 % for H2SO4 concentrations and 250 % for nucleation rates (e.g. Dunne et al., 2016).
These choices regarding generating simulated data reflect what real dataset can often be like: the bulk of the data approximates a log-normal distribution with one of the tails possibly being thinned or cut close to a limit of detection of an instrument or close to a limit of the data filtering criterion. In our simulated data, each negative observation and each negative noise-free value was replaced with a new random simulated value, which only slightly offsets the final distribution from a perfectly symmetric log-normal shape.
Simulating the observations tends to generate infrequent extreme outlier observations from the infinite tails of the normal distribution. We discarded outliers with an absolute error larger than 3 times the combined standard uncertainty of the observation in order to remove the effect of outliers from the regression analysis. This represents the quality control procedure in data analysis and also improves the stability of our results between different simulations.
3.2 Case study on measured data
In order to show that the results gained with simulated data are also applicable in real measurement data, we applied our methods to data measured in the CLOUD chamber and published by Dunne et al. (2016). Fig. 1 in Dunne et al. (2016) shows nucleation rates (J) at a 1.7 nm mobility diameter as a function of the sulfuric acid concentration. We used their measurements with no added ammonia at two different temperatures, 278 and 292 K, as shown in their Fig. 1D and E and given in their Supplementary material.
4.1 Fits for simulated data
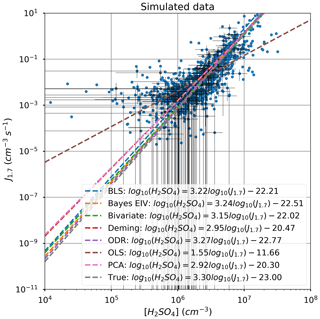
Differences between the regression methods are illustrated in four different ways: firstly, by showing line fits on a scatterplot of simulated data; secondly, by illustrating how the slopes change when the uncertainty in the measured variables increase; thirdly, by showing the sensitivity of the fits on number of observations; and finally, by showing how the fits are affected by adding outliers in the data. Regression fits using each of the respective methods are shown in Fig. 1.
As we know that the noise-free slope βtrue is 3.30, we can easily see how the methods perform. The worst performing method was OLS, with a βols value of 1.55, which is roughly half of the βtrue. The best performing methods that displayed equal accuracy, i.e. within 2 % range, were ODR (βODR=3.27), Bayes EIV (βBEIV=3.24) and BLS (βBLS=3.22), whereas York (βYork=3.15) was within a range of 5 %; Deming (βDR=2.95) and PCA (βPCA=2.92), in comparison, slightly underestimated the slope.
The sensitivity of the methods was first tested by varying the uncertainty in the H2SO4 observations. We simulated six datasets with 1000 observations and with varying absolute and relative uncertainties (as listed in Table 1), and then performed fits with each method on all of these datasets. The performance of the methods is shown in Fig. 2, with the results corresponding to Fig. 1 marked in black. The results show that when the uncertainty is small, the bias in the OLS fit is smaller, but when more uncertainty is added to data, the bias increases significantly. A decrease in performance can also be seen with ODR, which overestimates the slope, and PCA, DR and Bayes EIV, which all underestimate the slope. The bivariate methods, BLS and York, seem to be quite robust with increasing uncertainty, as the slopes do not change significantly.
Table 1The uncertainties used in the simulation for the sensitivity test for increasing uncertainty.
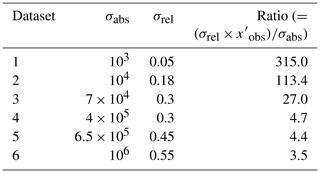
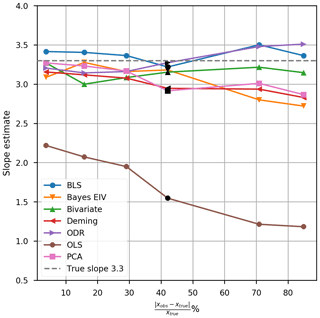
Figure 2Sensitivity test for increasing uncertainty in simulated data. Black markers show the initial dataset described in Sect. 3. The dashed line indicates the noise-free slope.
The sensitivity of the methods to the decreasing n (number of observations) was tested by picking 100 random samples from the 1000-sample simulation dataset with n of 3, 5, 10, 20, 30, 50, 70, 100, 300 and 500 and carrying out fits for all samples using all methods. The average slopes and their standard errors are shown in Fig. 3. It is clear that when the n≤10, the variation in the estimated slopes can be considerably high. When n≥30 the average slopes stabilised close to their characteristic levels (within 5 %), except for Bayes EIV and York bivariate, which needed more than 100 observations. The most sensitive methods for a small n were Bayes EIV, ODR and PCA; thus, these methods should not be applied for data with a small n and a similar type of uncertainty to that presented here. However, the reader is reminded that number of points needed for a good fit depends on the uncertainties in the data.
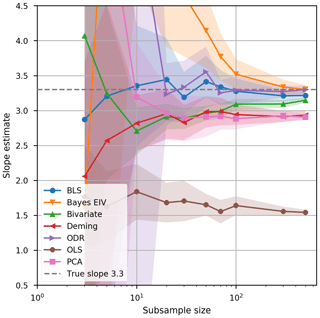
Figure 3Effect of sample size on the uncertainty of different fits. Lines show the median and shading illustrates the 1 standard deviation range of slope estimates for 40 repeated random samples. The dashed line indicates the noise-free slope.
The sensitivity of the predictor variable H2SO4 to outliers was tested using two different scenarios. In the first scenario, outliers were randomly allowed to be at either the high or low end of the distribution. In the second scenario, outliers were only allowed to be large numbers, which is often the case in H2SO4 and aerosol concentration measurements as numbers are removed from the data when they are smaller than the detection limit of the measurement instrument. Five cases with an n of 1000 were simulated with an increasing number of outliers (0, 5, 10, 20 and 100) and 10 repetitions of H2SO4 values with a different set of outliers. Outliers were defined such that the combined standard uncertainty. The methods most sensitive to outliers in both scenarios were OLS and Bayes EIV. A high number of outliers caused underestimations in PCA and DR, especially when using the outliers with high values (second scenario mentioned above), and a slight overestimation in BLS in the random outlier case (first scenario mentioned above). York bivariate and ODR were not affected in either case, and BLS only showed small variation between the 10 replicates in the estimated slope. We did not explore how large a number of outliers would needed to be to seriously disrupt the fits for the various methods. We felt that it is likely not realistic to have situations that have more than 10 % outliers.
We also applied an alternative method for simulating the data to different testing methods. The main difference compared with our method was that the distribution of noise-free H2SO4 followed a uniform distribution in log-space. With this assumption, it could be seen that OLS works almost as well as the EIV methods introduced here if the range of the data is wide (H2SO4 concentration in the range of 106–109). However, when scaled to concentrations usually measured in the atmosphere (104–107), the high uncertainties caused similar behaviour to the data seen in our previous simulations. Details of these results can be seen in Supplement S1.
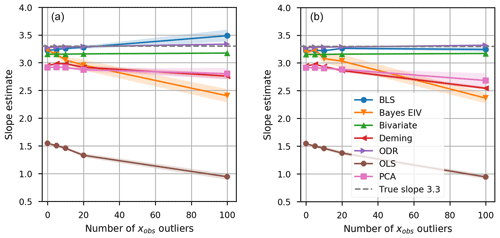
Figure 4Effect of outliers in the data. (a) The random outliers case and (b) the only high positive values case. Lines show the median and the shading shows ±1 standard deviation of the slope estimates in the 10 repeated studies. The dashed line indicates the noise-free slope.
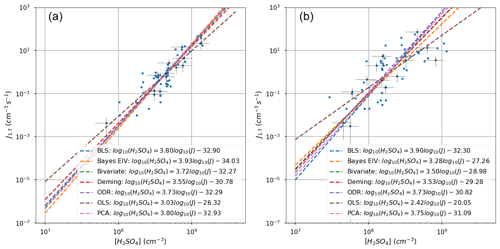
4.2 Results of the case study
Figure 5 shows the fits of the data from Dunne et al. (2016). As expected, the fit using OLS is underestimated at both temperatures: βols(278 K) was 2.4 and βols(292 K) was 3.0. The regression equations for all methods are shown in Fig. 5. Dunne et al. (2016) did not use a linear fit in their study and instead applied a non-linear Levenberg–Marquardt algorithm (Moré, 1978) on function where k is a temperature-dependent rate coefficient with a non-linear function including three estimable parameters (see Sect. 8 of their Supplement for details). Thus, the results are not directly comparable as, for simplicity, we fit the data measured at different temperatures separately. However, their β value for the fit (β=3.95) is quite close to our results using EIV methods, especially as slopes from Bayes EIV at 292 K and BLS and PCA at both temperatures were within a range of 5 %. We also carried out some tests on data measured at lower temperatures (results not shown here). However, the slopes did not vary drastically from those at βols(278 K) and βols(292 K) when the other conditions were similar, even though the lower number of observations at lower temperatures increased uncertainty in the data. Nevertheless, the intercepts β0(T) varied between temperatures.
Ordinary least squares regression can be used to answer some simple questions regarding data, such as “How is y related to x?”. However, if we are interested in the strength of the relationship and the predictor variable X contains some error, then error-in-variables methods should be applied. There is no single correct method to make the fit, as the methods behave slightly differently with different types of error. The choice of method should be based on the properties of data and the specific research question. There are usually two types of error in the data: natural and measurement error, where natural error refers to stochastic variation in the environment. Even if the natural error in the data is not known, taking the measurement error into account improves the fit significantly. Weighting the data based on some factor, typically the inverse of the uncertainty, reduces the effect of outliers and makes the regression more depend on the data that are more certain (see e.g. Wu and Yu, 2018), but it does not solve the problem completely.
As a test study, we simulated a dataset mimicking the dependence of the atmospheric new particle formation rate on the sulfuric acid concentration. We introduced three major sources of uncertainty when establishing inference from scatterplot data: the increasing measurement error, the number of data points and the number of outliers. In Fig. 1, we showed that for simulations where errors are taken from real measurements of J1.7 and H2SO4 four of the methods gave slopes within 5 % of the known noise-free value: BLS, York bivariate, Bayes EIV and ODR. Estimates from BLS and York bivariate even remained stable when the uncertainty in the simulated H2SO4 concentration was increased drastically, as seen in Fig. 2. The main message to take away from Fig. 3, in comparison, is that if the data contain some error, all fit methods are highly uncertain when small numbers of observations are used. BLS was the most accurate with the smallest sample sizes (10 or less), ODR stabilised with 20 observations, and York bivariate and Bayes EIV needed 100 or more data points to become accurate. After that, these methods approached the noise-free value asymptotically, whereas the OLS slope converged towards an incorrect value. With an increasing number of outliers (Fig. 4), ODR and York bivariate were the most stable methods, even when 10 % of observations were classified as outliers in both test cases. BLS remained stable in the scenario with only high outlier values. Bayes EIV was the most sensitive to outliers after OLS.
From this, we can recommend that if the uncertainty in the predictor variable is known, York bivariate, or another method able to use known variances, should be applied. If the errors are not known, and they are estimated from data, BLS and ODR were found to be the most robust in cases with increasing uncertainty (relative error, rE > 30 % in Fig. 2) and with a high number of outliers. In our test data, BLS and ODR remained stable up to rE > 80 % (Fig. 2), whereas DR and PCA began to become more uncertain when rE > 30 % and Bayes EIV when rE > 50 %. If the number of observations is less than 10 and the uncertainties are high, we would recommend considering if a regression fit is appropriate at all. However, with the chosen uncertainties in our simulation tests, BLS was found to be the most robust with small numbers of data points. Bayes EIV displayed significant advantages if the number of observations was high enough and there were not too many outliers, as it did not require an explicit definition of the errors and could treat them as unknown parameters given their probability distributions.
We also carried out a case study on data measured in the CLOUD chamber and published by Dunne et al. (2016). In these analyses, we saw that our above-mentioned recommended methods also performed best for these data. Our tests indicated that the slope β1 for the fit is not highly sensitive to changes in temperature in the chamber but the intercept β0 in linear fit is. This dependency was also seen, and taken into account, in Dunne et al. (2016).
Python code for running the methods can be found on GitHub: https://gist.github.com/mikkopitkanen/da8c949571225e9c7093665c9803726e (Pitkänen, 2019).
Simulated datasets used in the example analysis are given in the Supplement.
In this appendix, we introduce the minimising criteria (Cmethod) for all methods applied in the main text. We also give the equations for the regression coefficients ( and ) for the methods.
A1 Ordinary least squares (OLS)
OLS minimises the sum of squares vertical distances (residuals) between each point and the fitted line. OLS regression minimises the following criterion:
where and refer to estimators calculated from the data. These estimations are given by
where observed variances for and for , and observed covariance for x and y .
A2 Orthogonal regression (ODR)
ODR (https://docs.scipy.org/doc/external/odrpack_guide.pdf, last access: 16 August 2019, https://docs.scipy.org/doc/scipy/reference/odr.html, last access: 27 July 2018) minimises the sum of the square of the orthogonal distances between each point and the line. The criteria is given by
where
and
ODR accounts for the fact that errors exist in both axes but does not account for the exact values of the variances of variables. Thus, only the ratio between the two error variances (λxy) is needed to improve the methodology. With notation of Francq and Govaerts (2014), this ratio is given by the following:
where the numerator of the ratio is the error variance in the data in the y axis and the denominator is the error variance in the data in the x axis.
A3 Deming regression (DR)
DR is the ML (maximum likelihood) solution of Eq. 1 when λxy is known. In practice, λxy is unknown and it is estimated from the variances of x and y calculated from the data.
The DR minimises the criterion CDR, which is the sum of the square of (weighted) oblique distances between each point to the line:
where
and
A4 Bivariate least squares regression (BLS)
BLS is a generic name but here we refer to the formulation described in Francq and Govaerts (2014) and references therein. BLS takes errors and heteroscedasticity in both axes into account and is usually written in matrix notation. BLS minimises the criterion CBLS, which is the sum of weighted residuals WBLS given by the following:
with
Estimators for the parameters are computed by iterations using the following formulas:
where known uncertainties and are replaced with estimated variances Sx and Sy in this study.
A second bivariate regression method that was used in this study is an implementation of the regression method described by York et al. (2004, Section III). The minimisation criterion is described in York (1968):
where and are the weight coefficients for x and y, respectively, and r is the correlation coefficient between x and y. xi,adj and yi,adj are adjusted values of xi, yi, which fulfil the requirement
The solution for and is found iteratively following the 10-step algorithm presented in York et al. (2004, Section III).
A5 The principal component analysis-based regression (PCA)
PCA can be applied for bivariate and multivariate cases.
For one independent and one dependent variable, the regression line is
where the error between the observed value yi and the estimated value a+bxi is minimum. For n data points, we compute a and b using the method of least squares that minimises
This is a standard technique that gives the regression coefficients α and β.
A6 Bayesian error-in-variables regression (Bayes EIV)
Bayes EIV regression estimate applies Bayesian inference using the popular Stan software tool (http://mc-stan.org/users/documentation/, last access: 27 July 2018), which allows the use of prior information of the model parameters. We assumed
where μ and σ are the respective mean and standard deviation of xtrue and ytrue and are treated as unknowns. The observations xobs and yobs of xtrue and ytrue, respectively, were defined as follows:
where σrel and σabs are the relative and absolute components of standard uncertainties, respectively.
The Stan tool solved regression problems using 1000 iterations, and it provided a posteriori distributions for the model parameters βBEIV and αBEIV. For the definitions of given Student t, log-normal and normal probability distributions, see Stan documentation. In our regression analysis, we used the maximum a posteriori estimates for βBEIV and αBEIV provided by the software tool.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-12531-2019-supplement.
SM prepared the paper with contributions from all co-authors. SM, MRAP and SI performed the formal analysis. MRAP simulated the data. SM, AA and KEJL formulated the original idea. SM, MRAP and AL developed and implemented the methodology. SM, MRAP, TN and AL were responsible for the investigation and validation of the data and methods.
The authors declare that they have no conflict of interest.
This research has been supported by the Nessling Foundation and the Academy of Finland (grant no. 307331).
This paper was edited by Fangqun Yu and reviewed by three anonymous referees.
Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurtén, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppä, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petäjä, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamäki, H., and Kirkby, J.: Molecular understanding of sulphuric acid–amine particle nucleation in the atmosphere, Nature, 502, 359–363, https://doi.org/10.1038/nature12663, 2013.
Boggs, P. T., Byrd, R. H., and Schnabel, R. B.: A Stable and Efficient Algorithm for Nonlinear Orthogonal Distance Regression, SIAM J. Sci. Stat. Comput., 8, 1052–1078, https://doi.org/10.1137/0908085, 1987.
Boggs, P. T., Donaldson, J. R., Byrd, R. H., and Schnabel, R. B.: Algorithm 676 ODRPACK: software for weighted orthogonal distance regression, ACM Trans. Math. Softw., 15, 348–364, https://doi.org/10.1145/76909.76913, 1989.
Boy, M., Karl, T., Turnipseed, A., Mauldin, R. L., Kosciuch, E., Greenberg, J., Rathbone, J., Smith, J., Held, A., Barsanti, K., Wehner, B., Bauer, S., Wiedensohler, A., Bonn, B., Kulmala, M., and Guenther, A.: New particle formation in the Front Range of the Colorado Rocky Mountains, Atmos. Chem. Phys., 8, 1577–1590, https://doi.org/10.5194/acp-8-1577-2008, 2008.
Cantrell, C. A.: Technical Note: Review of methods for linear least-squares fitting of data and application to atmospheric chemistry problems, Atmos. Chem. Phys., 8, 5477–5487, https://doi.org/10.5194/acp-8-5477-2008, 2008.
Carroll, R. J. and Ruppert, D.: The Use and Misuse of Orthogonal Regression in Linear Errors-in-Variables Models, Am. Stat., 50, 1–6, https://doi.org/10.1080/00031305.1996.10473533, 1996.
Carroll, R. J., Ruppert, D., Stefanski, L. A., and Crainiceanu, C. M.: Measurement error in nonlinear models?: a modern perspective, 2nd Edn., Chapman & Hall/CRC, 41–64, 2006.
Cheng, C.-L. and Riu, J.: On Estimating Linear Relationships When Both Variables Are Subject to Heteroscedastic Measurement Errors, Technometrics, 48, 511–519, https://doi.org/10.1198/004017006000000237, 2006.
Deming, W. E.: Statistical adjustment of data, Wiley, New York, 128–212, 1943.
Dunne, E. M., Gordon, H., Kürten, A., Almeida, J., Duplissy, J., Williamson, C., Ortega, I. K., Pringle, K. J., Adamov, A., Baltensperger, U., Barmet, P., Benduhn, F., Bianchi, F., Breitenlechner, M., Clarke, A., Curtius, J., Dommen, J., Donahue, N. M., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Jokinen, T., Kangasluoma, J., Kirkby, J., Kulmala, M., Kupc, A., Lawler, M. J., Lehtipalo, K., Makhmutov, V., Mann, G., Mathot, S., Merikanto, J., Miettinen, P., Nenes, A., Onnela, A., Rap, A., Reddington, C. L. S., Riccobono, F., Richards, N. A. D., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Simon, M., Sipilä, M., Smith, J. N., Stozkhov, Y., Tomé, A., Tröstl, J., Wagner, P. E., Wimmer, D., Winkler, P. M., Worsnop, D. R., and Carslaw, K. S.: Global atmospheric particle formation from CERN CLOUD measurements, Science, 354, 1119–1124, https://doi.org/10.1126/science.aaf2649, 2016.
Francq, B. G. and Berger, M.: BivRegBLS: Tolerance Intervals and Errors-in-Variables Regressions in Method Comparison Studies, R package version 1.0.0, available at: https://rdrr.io/cran/BivRegBLS/ (last access: 2 October 2019), 2017.
Francq, B. G. and Govaerts, B. B.: Measurement methods comparison with errors-in-variables regressions, From horizontal to vertical OLS regression, review and new perspectives, Chemom. Intell. Lab. Syst., 134, 123–139, https://doi.org/10.1016/j.chemolab.2014.03.006, 2014.
Hamed, A., Korhonen, H., Sihto, S.-L., Joutsensaari, J., Järvinen, H., Petäjä, T., Arnold, F., Nieminen, T., Kulmala, M., Smith, J. N., Lehtinen, K. E. J., and Laaksonen, A.: The role of relative humidity in continental new particle formation, J. Geophys. Res., 116, D03202, https://doi.org/10.1029/2010JD014186, 2011.
Hotelling, H.: The Relations of the Newer Multivariate Statistical Methods to Factor Analysis, Br. J. Stat. Psychol., 10, 69–79, https://doi.org/10.1111/j.2044-8317.1957.tb00179.x, 1957.
Jones, E., Oliphant, T., and Peterson, P.: SciPy: Open Source Scientific Tools for Python, available at: http://www.scipy.org/ (last access: 16 August 2019), 2001.
Kaipio, J. and Somersalo, E.: Statistical and Computational Inverse Problems, Springer-Verlag, New York, 145–188, 2005.
Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., Ehrhart, S., Franchin, A., Gagné, S., Ickes, L., Kürten, A., Kupc, A., Metzger, A., Riccobono, F., Rondo, L., Schobesberger, S., Tsagkogeorgas, G., Wimmer, D., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Downard, A., Ehn, M., Flagan, R. C., Haider, S., Hansel, A., Hauser, D., Jud, W., Junninen, H., Kreissl, F., Kvashin, A., Laaksonen, A., Lehtipalo, K., Lima, J., Lovejoy, E. R., Makhmutov, V., Mathot, S., Mikkilä, J., Minginette, P., Mogo, S., Nieminen, T., Onnela, A., Pereira, P., Petäjä, T., Schnitzhofer, R., Seinfeld, J. H., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Vanhanen, J., Viisanen, Y., Vrtala, A., Wagner, P. E., Walther, H., Weingartner, E., Wex, H., Winkler, P. M., Carslaw, K. S., Worsnop, D. R., Baltensperger, U., and Kulmala, M.: Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 476, 429–433, https://doi.org/10.1038/nature10343, 2011.
Kirkby, J., Duplissy, J., Sengupta, K., Frege, C., Gordon, H., Williamson, C., Heinritzi, M., Simon, M., Yan, C., Almeida, J., Tröstl, J., Nieminen, T., Ortega, I. K., Wagner, R., Adamov, A., Amorim, A., Bernhammer, A.-K., Bianchi, F., Breitenlechner, M., Brilke, S., Chen, X., Craven, J., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Hakala, J., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Kim, J., Krapf, M., Kürten, A., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Molteni, U., Onnela, A., Peräkylä, O., Piel, F., Petäjä, T., Praplan, A. P., Pringle, K., Rap, A., Richards, N. A. D., Riipinen, I., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Scott, C. E., Seinfeld, J. H., Sipilä, M., Steiner, G., Stozhkov, Y., Stratmann, F., Tomé, A., Virtanen, A., Vogel, A. L., Wagner, A. C., Wagner, P. E., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Zhang, X., Hansel, A., Dommen, J., Donahue, N. M., Worsnop, D. R., Baltensperger, U., Kulmala, M., Carslaw, K. S., and Curtius, J.: Ion-induced nucleation of pure biogenic particles, Nature, 533, 521–526, https://doi.org/10.1038/nature17953, 2016.
Kuang, C., McMurry, P. H., McCormick, A. V., and Eisele, F. L.: Dependence of nucleation rates on sulfuric acid vapor concentration in diverse atmospheric locations, J. Geophys. Res., 113, D10209, https://doi.org/10.1029/2007JD009253, 2008.
Kulmala, M., Lehtinen, K. E. J., and Laaksonen, A.: Cluster activation theory as an explanation of the linear dependence between formation rate of 3 nm particles and sulphuric acid concentration, Atmos. Chem. Phys., 6, 787–793, https://doi.org/10.5194/acp-6-787-2006, 2006.
Kürten, A., Bianchi, F., Almeida, J., Kupiainen-Määttä, O., Dunne, E. M., Duplissy, J., Williamson, C., Barmet, P., Breitenlechner, M., Dommen, J., Donahue, N. M., Flagan, R. C., Franchin, A., Gordon, H., Hakala, J., Hansel, A., Heinritzi, M., Ickes, L., Jokinen, T., Kangasluoma, J., Kim, J., Kirkby, J., Kupc, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Onnela, A., Ortega, I. K., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schnitzhofer, R., Schobesberger, S., Smith, J. N., Steiner, G., Stozhkov, Y., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Wagner, P. E., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K., Kulmala, M., and Curtius, J.: Experimental particle formation rates spanning tropospheric sulfuric acid and ammonia abundances, ion production rates, and temperatures, J. Geophys. Res., 121, 12377–12400, https://doi.org/10.1002/2015JD023908, 2016.
Mandel, J.: Fitting Straight Lines When Both Variables are Subject to Error, J. Qual. Technol., 16, 1–14, https://doi.org/10.1080/00224065.1984.11978881, 1984.
Metzger, A., Verheggen, B., Dommen, J., Duplissy, J., Prevot, A. S. H., Weingartner, E., Riipinen, I., Kulmala, M., Spracklen, D. V, Carslaw, K. S., and Baltensperger, U.: Evidence for the role of organics in aerosol particle formation under atmospheric conditions., P. Natl. Acad. Sci. USA, 107, 6646–51, https://doi.org/10.1073/pnas.0911330107, 2010.
Mikkonen, S., Romakkaniemi, S., Smith, J. N., Korhonen, H., Petäjä, T., Plass-Duelmer, C., Boy, M., McMurry, P. H., Lehtinen, K. E. J., Joutsensaari, J., Hamed, A., Mauldin III, R. L., Birmili, W., Spindler, G., Arnold, F., Kulmala, M., and Laaksonen, A.: A statistical proxy for sulphuric acid concentration, Atmos. Chem. Phys., 11, 11319–11334, https://doi.org/10.5194/acp-11-11319-2011, 2011.
Moré, J. J.: The Levenberg-Marquardt algorithm: Implementation and theory, Springer, Berlin, Heidelberg, 105–116, 1978.
Paasonen, P., Nieminen, T., Asmi, E., Manninen, H. E., Petäjä, T., Plass-Dülmer, C., Flentje, H., Birmili, W., Wiedensohler, A., Hõrrak, U., Metzger, A., Hamed, A., Laaksonen, A., Facchini, M. C., Kerminen, V. M., and Kulmala, M.: On the roles of sulphuric acid and low-volatility organic vapours in the initial steps of atmospheric new particle formation, Atmos. Chem. Phys., 10, 11223–11242, https://doi.org/10.5194/acp-10-11223-2010, 2010.
Pitkänen, M. R. A., Mikkonen, S., Lehtinen, K. E. J., Lipponen, A., and Arola, A.: Artificial bias typically neglected in comparisons of uncertain atmospheric data, Geophys. Res. Lett., 43, 10003–10011, https://doi.org/10.1002/2016GL070852, 2016.
Pitkänen, M.: Regression estimator calculator, GitHub repository, https://gist.github.com/mikkopitkanen/da8c949571225e9c7093665c9803726e, last access: 3 October 2019.
R Core Team: R: A language and environment for statistical computing, available at: http://www.r-project.org (16 August 2019), 2018.
Riccobono, F., Schobesberger, S., Scott, C. E., Dommen, J., Ortega, I. K., Rondo, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Downard, A., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hansel, A., Junninen, H., Kajos, M., Keskinen, H., Kupc, A., Kürten, A., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Petäjä, T., Praplan, A. P., Santos, F. D., Schallhart, S., Seinfeld, J. H., Sipilä, M., Spracklen, D. V, Stozhkov, Y., Stratmann, F., Tomé, A., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Wimmer, D., Carslaw, K. S., Curtius, J., Donahue, N. M., Kirkby, J., Kulmala, M., Worsnop, D. R., and Baltensperger, U.: Oxidation products of biogenic emissions contribute to nucleation of atmospheric particles, Science, 344, 717–721, https://doi.org/10.1126/science.1243527, 2014.
Riipinen, I., Sihto, S.-L., Kulmala, M., Arnold, F., Dal Maso, M., Birmili, W., Saarnio, K., Teinilä, K., Kerminen, V.-M., Laaksonen, A., and Lehtinen, K. E. J.: Connections between atmospheric sulphuric acid and new particle formation during QUEST III–IV campaigns in Heidelberg and Hyytiälä, Atmos. Chem. Phys., 7, 1899–1914, https://doi.org/10.5194/acp-7-1899-2007, 2007.
Schennach, S. M.: Estimation of Nonlinear Models with Measurement Error, Econometrica, 72, 33–75, https://doi.org/10.1111/j.1468-0262.2004.00477.x, 2004.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric chemistry and physics: From air pollution to climate change, available at: https://www.wiley.com/en-fi/Atmospheric+Chemistry+and+Physics:+From+Air+Pollution+to+Climate+Change,+3rd+Edition-p-9781118947401 (last access: 26 September 2018), 2016.
Sihto, S.-L., Kulmala, M., Kerminen, V.-M., Dal Maso, M., Petäjä, T., Riipinen, I., Korhonen, H., Arnold, F., Janson, R., Boy, M., Laaksonen, A., and Lehtinen, K. E. J.: Atmospheric sulphuric acid and aerosol formation: implications from atmospheric measurements for nucleation and early growth mechanisms, Atmos. Chem. Phys., 6, 4079–4091, https://doi.org/10.5194/acp-6-4079-2006, 2006.
Spiess, A.: Orthogonal Nonlinear Least-Squares Regression in R, available at: https://cran.hafro.is/web/packages/onls/vignettes/onls.pdf (last access: 17 July 2018), 2015.
Spracklen, D. V., Carslaw, K. S., Kulmala, M., Kerminen, V.-M., Mann, G. W., and Sihto, S.-L.: The contribution of boundary layer nucleation events to total particle concentrations on regional and global scales, Atmos. Chem. Phys., 6, 5631–5648, https://doi.org/10.5194/acp-6-5631-2006, 2006.
Stan Development Team: PyStan: the Python interface to Stan, Version 2.17.1.0., available at: http://mc-stan.org, last access: 27 July 2018.
Therneau, T.: deming: Deming, Theil-Sen, Passing-Bablock and Total Least Squares Regression, R package version 1.4., available at: https://cran.r-project.org/package=deming (last access: 16 August 2019), 2018.
Trefall, H. and Nordö, J.: On Systematic Errors in the Least Squares Regression Analysis, with Application to the Atmospheric Effects on the Cosmic Radiation, Tellus, 11, 467–477, https://doi.org/10.3402/tellusa.v11i4.9324, 1959.
Tröstl, J., Chuang, W. K., Gordon, H., Heinritzi, M., Yan, C., Molteni, U., Ahlm, L., Frege, C., Bianchi, F., Wagner, R., Simon, M., Lehtipalo, K., Williamson, C., Craven, J. S., Duplissy, J., Adamov, A., Almeida, J., Bernhammer, A.-K., Breitenlechner, M., Brilke, S., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Gysel, M., Hansel, A., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Keskinen, H., Kim, J., Krapf, M., Kürten, A., Laaksonen, A., Lawler, M., Leiminger, M., Mathot, S., Möhler, O., Nieminen, T., Onnela, A., Petäjä, T., Piel, F. M., Miettinen, P., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Sipilä, M., Smith, J. N., Steiner, G., Tomè, A., Virtanen, A., Wagner, A. C., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Carslaw, K. S., Curtius, J., Dommen, J., Kirkby, J., Kulmala, M., Riipinen, I., Worsnop, D. R., Donahue, N. M., and Baltensperger, U.: The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 533, 527–531, https://doi.org/10.1038/nature18271, 2016.
Vehkamäki, H.: Classical nucleation theory in multicomponent systems, Springer-Verlag, Berlin/Heidelberg, 119–159, 2006.
Weber, R. J., Marti, J. J., McMurry, P. H., Eisele, F. L., Tanner, D. J., and Jefferson, A.: Measurements of new particle formation and ultrafine particle growth rates at a clean continental site, J. Geophys. Res.-Atmos., 102, 4375–4385, https://doi.org/10.1029/96JD03656, 1997.
Wu, C. and Yu, J. Z.: Evaluation of linear regression techniques for atmospheric applications: the importance of appropriate weighting, Atmos. Meas. Tech., 11, 1233–1250, https://doi.org/10.5194/amt-11-1233-2018, 2018.
York, D.: Least-sqares fitting of a straight line, Can. J. Phys., 44, 1079–1086, https://doi.org/10.1139/p66-090, 1966.
York, D., Evensen, N. M., Martínez, M. L., and De Basabe Delgado, J.: Unified equations for the slope, intercept, and standard errors of the best straight line, Am. J. Phys., 72, 367–375, https://doi.org/10.1119/1.1632486, 2004.