Cloud feedbacks in extratropical cyclones: insight from long-term satellite data and high-resolution global simulations

A negative extratropical shortwave cloud feedback driven by changes in cloud optical depth is a feature of global climate models (GCMs). A robust positive trend in observed liquid water path (LWP) over the last two decades across the warming Southern Ocean supports the negative shortwave cloud feedback predicted by GCMs. This feature has been proposed to be due to transitions from ice to liquid with warming. To gain insight into the shortwave cloud feedback we examine extratropical cyclone variability and the response of extratropical cyclones to transient warming in GCM simulations. Multi-Sensor Advanced Climatology Liquid Water Path (MAC-LWP) microwave observations of cyclone properties from the period 1992–2015 are contrasted with GCM simulations, with horizontal resolutions ranging from 7 km to hundreds of kilometers. We find that inter-cyclone variability in LWP in both observations and models is strongly driven by the moisture flux along the cyclone's warm conveyor belt (WCB). Stronger WCB moisture flux enhances the LWP within cyclones. This relationship is replicated in GCMs, although its strength varies substantially across models. It is found that more than 80 % of the enhancement in Southern Hemisphere (SH) extratropical cyclone LWP in GCMs in response to a transient 4 K warming can be predicted based on the relationship between the WCB moisture flux and cyclone LWP in the historical climate and their change in moisture flux between the historical and warmed climates. Further, it is found that that the robust trend in cyclone LWP over the Southern Ocean in observations and GCMs is consistent with changes in the moisture flux. We propose two cloud feedbacks acting within extratropical cyclones: a negative feedback driven by Clausius–Clapeyron increasing water vapor path (WVP), which enhances the amount of water vapor available to be fluxed into the cyclone, and a feedback moderated by changes in the life cycle and vorticity of cyclones under warming, which changes the rate at which existing moisture is imported into the cyclone. Both terms contribute to increasing LWP within the cyclone. While changes in moisture flux predict cyclone LWP trends in the current climate and the majority of changes in LWP in transient warming simulations, a portion of the LWP increase in response to climate change that is unexplained by increasing moisture fluxes may be due to phase transitions. The variability in LWP within cyclone composites is examined to understand what cyclonic regimes the mixed-phase cloud feedback is relevant to. At a fixed WCB moisture flux cyclone LWP increases with increasing sea surface temperature (SST) in the half of the composite poleward of the low and decreases in the half equatorward of the low in both GCMs and observations. Cloud-top phase partitioning observed by the Atmospheric Infrared Sounder (AIRS) indicates that phase transitions may be driving increases in LWP in the poleward half of cyclones.

1 Introduction

Constraining the change in cloud reflectivity in response to warming is key to offering a more accurate prediction of 21st century climate change. Caldwell et al. (2016) showed that uncertainty in shortwave cloud feedback represented the largest contribution to uncertainty in climate sensitivity in the Coupled Model Intercomparison Project Phase 5 (CMIP5) generation of models. Model uncertainty in the shortwave cloud feedback is driven by differences in the representation of clouds in the planetary boundary layer, which contribute strongly to albedo, but not to outgoing longwave radiation (Hartmann and Short, 1980). These clouds exist at a timescale and length scale that is much finer than even the highest-resolution simulation and are thus parameterized, leading to substantial disagreement in feedback from one model to another.

The shortwave cloud feedback, while highly variable across models, does have some qualitatively similar features that appear in many CMIP-class global climate models (GCMs). The most salient of these is the dipole pattern in the shortwave cloud feedback (Zelinka et al., 2012a, b, 2013, 2016). The shortwave cloud feedback dipole is characterized by decreasing cloud coverage in the subtropics (a positive feedback) and increasing cloud optical depth in the extratropics (a negative feedback) in response to warming. There is a growing consensus that the positive lobe of the dipole, where subtropical cloud fraction decreases, is a robust feature of the climate system. Both empirical analysis of observations (McCoy et al., 2017a; Clement et al., 2009; Klein et al., 1995; Myers and Norris, 2015, 2016; Norris et al., 2016) and very high-resolution simulations (Blossey et al., 2013; Bretherton, 2015; Bretherton and Blossey, 2014; Bretherton et al., 2013; Rieck et al., 2012) have substantiated the subtropical positive feedback predicted by GCMs, although it appears that traditional GCMs somewhat underpredict the decrease in subtropical cloud cover in response to warming and thus underestimate the positive feedback (Klein et al., 2017).

With the growing consensus surrounding the positive lobe of the dipole, a constraint on the negative lobe, where extratropical cloud optical depth increases with warming, has increased in importance as a significant source of uncertainty in the global-mean shortwave cloud feedback. Evaluation of model behavior and some observations indicate that the negative lobe is related to a transition from a more ice-dominated to a more liquid-dominated state – the so-called mixed-phase cloud feedback (McCoy et al., 2017b; Ceppi et al., 2016a; Tsushima et al., 2006; Cheng et al., 2012; Naud et al., 2006; Choi et al., 2014). This transition results in an increase in small, bright liquid droplets at the expense of ice crystals and thus an increase in albedo (Zelinka et al., 2012a; McCoy et al., 2014). It is possible that this transition also decreases precipitation efficiency by decreasing the number of frozen hydrometeors (Field and Heymsfield, 2015; Morrison et al., 2011; Heymsfield et al., 2009) and enhancing the total condensate.

GCMs struggle to realistically simulate mixed-phase clouds. Evaluation of ice–liquid partitioning in GCMs participating in CMIP5 showed that there was a 30 K temperature range in which different models predicted an equal mixture of ice and liquid within clouds (McCoy et al., 2016). This model diversity in partitioning leads to a diversity in liquid water path (LWP) response to warming and ultimately shortwave cloud feedback in the extratropics (Tan et al., 2016). Models that glaciate at a warmer temperature transition more ice to liquid with warming, simply because they have a large reservoir of susceptible cloud ice in the climate mean state (McCoy et al., 2015b).

The mixed-phase cloud transition mechanism is partially supported by the observationally inferred response of extratropical clouds to warming. Several studies have substantiated that cloud optical depth responds to atmospheric and surface temperature in the midlatitudes, particularly the Southern Ocean (SO) (Ceppi et al., 2016b; Terai et al., 2016; Gordon and Klein, 2014). Multiple linear regression of cloud optical depth on atmospheric stability and temperature shows that increasing surface temperature tends to decrease cloud optical depth (Terai et al., 2016). These investigations examined the variability across the midlatitudes in a non-phenomenological sense, making it difficult to assign a mechanism to their diagnosed covariability between optical depth, LWP, and temperature. Overall, it remains unclear if this optical depth change is directly related to shifts in cloud phase because it is difficult to accurately measure the phase of water in clouds and the total amount of frozen water (Jiang et al., 2012). In addition to the difficulties in measuring ice-phase cloud properties, the diversity in synoptic states in the midlatitudes further complicates this analysis. Bodas-Salcedo (2018) demonstrated that the radiative signal from increased LWP associated with phase transitions is masked by ice cloud within low-pressure systems. This shows that extratropical variability in LWP needs to be considered in the context of the regime it is occurring in. This is supported by earlier studies that demonstrated that there was strong regime dependence in the bias in reflected shortwave radiation across Southern Hemisphere (SH) extratropical cyclones (Bodas-Salcedo et al., 2014). Shifts in cyclonic regimes have been suggested as a possible explanation for negative midlatitude shortwave cloud feedback. Tselioudis and Rossow (2006) proposed that changes in cyclone frequency and surface pressure in response to a doubling in CO₂ could increase reflected shortwave radiation over the midlatitudes by 1.9 to 4.9 W m⁻². Despite the complexity of midlatitude feedback processes, robust increases in extratropical cloud cover (Norris et al., 2016) and liquid water path (Manaster et al., 2017) have been observed over the 25 years covered by satellite observations. It is reasonable to hypothesize that warming in the extratropics might be driving these trends partly via changes in cloud phase from ice to liquid. Can our understanding of the large synoptic systems that dominate the extratropics assist us in interpreting the long-term cloud property trends observed across these regions?

In this study we follow a similar technique to Tselioudis and Rossow (2006) and examine observations of midlatitude cyclones to infer a feedback. However, this is difficult to interpret in a causal sense. GCMs are used to support inferences made by examining observed covariability in the current climate. The cloud organization within midlatitude cyclone systems exists on a variety of length scales from synoptic (thousands of kilometers) to mesoscale cellular convection (kilometers). Traditional GCMs are able to capture the overall synoptic length scale, but are typically too coarse to capture the finer structures. Here, we utilize a diverse selection of GCMs with resolutions as fine as 7 km to examine the impact of resolving these features. From these simulations we hope to offer guidance as to what aspects of models are important to capturing midlatitude variability and cloud feedback.

We will show that the mixed-phase cloud feedback does not explain all of the observed variability or trends in extratropical LWP within cyclones in both observations and GCMs by showing that changes in moisture flux into the cyclones predict the majority of the change in LWP in response to warming. This is done by sorting our observations and simulations into cyclonic regimes across the extratropics. We show how clouds in cyclones have their LWP variability explained by meteorological variability and that trends in meteorological variability predict the majority of decadal trends in cyclone LWP. Similarly, changes in cyclone LWP between simulations forced with observed sea surface temperature (SST) and simulations with enhanced SST can be explained by changes in moisture flux into cyclones. This work builds on earlier insight by Kodama et al. (2014) who utilized aquaplanet simulations to posit that a relationship between SST and water vapor path (WVP) modulated by Clausius–Clapeyron within extratropical cyclones should lead to a negative cloud feedback, in keeping with Betts and Harshvardhan (1987). We hope that the relationships between synoptic state and cyclone cloud LWP in this work provide a clear benchmark that models may be evaluated against and will reduce uncertainty related to the extratropical shortwave cloud feedback in models.

2 Methods

In this section we discuss the methodology used to identify the low-pressure centers of midlatitude cyclones. We compare microwave observations of cyclone properties to global model simulations ranging from CMIP5 GCMs with horizontal resolution in excess of 100 km to convection-permitting GCMs with a resolution of approximately 7 km. The methodology used to create the unified microwave observations and cloud-top phase and the model setup for the global simulations are described in this section as well.

2.1 Data analysis

2.1.1 Cyclone compositing

Numerous studies have examined midlatitude variability by compositing around cyclone centers (Field et al., 2011; Field and Wood, 2007; Naud et al., 2016; Catto, 2016; Naud et al., 2017; Grandey et al., 2013). Identification of cyclone centers may be achieved by using pressure (Jung et al., 2006; Löptien et al., 2008; Hoskins and Hodges, 2002; Field et al., 2008); geopotential height (Blender and Schubert, 2000); or vorticity (Sinclair, 1994; Hoskins and Hodges, 2002; Catto et al., 2010). Here we follow the methodology described in Field and Wood (2007). As in Field and Wood (2007) sea-level pressure (SLP) is averaged to 2.5^∘ resolution. Daily-mean anomalies in SLP ($p_{\mathrm{0}}^{\prime }$) are calculated by subtracting the average of SLP starting from 15 days before to 15 days after from each day for each 2.5^∘ × 2.5^∘ region. Candidate 2.5^∘ × 2.5^∘ grid points were found using the following criterion:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}{p}_{\mathrm{0}}^{\prime }}{\mathrm{d}x}}{\displaystyle \frac{\mathrm{d}{p}_{\mathrm{0}}^{\prime }}{\mathrm{d}y}}<\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}\mathrm{hPa}{\mathrm{km}}^{-\mathrm{2}}\end{array}$$

and

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}{p}_{\mathrm{0}}^{\prime }}{\mathrm{d}{x}^{\mathrm{2}}}}+{\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}{p}_{\mathrm{0}}^{\prime }}{\mathrm{d}{y}^{\mathrm{2}}}}>\mathrm{6}\times {\mathrm{10}}^{-\mathrm{5}}\mathrm{hPa}{\mathrm{km}}^{-\mathrm{2}},\end{array}$$

where SLP <1015 hPa. These candidate 2.5^∘ × 2.5^∘ grid points are filtered to find the maximum negative anomaly within a 2000 km radius of each grid point. Each composite is 4000 km across. Composited data are averaged onto an equal-area grid centered around the maximum negative anomaly. The averaging grid was 18 zonal bins by 19 meridional bins. In this study we examine Northern Hemisphere (NH) and SH cyclones. For consistency with previous studies utilizing the Field and Wood (2007) cyclone compositing algorithm, cyclone centers must have their center between 30 and 80^∘ latitude. SH cyclones are flipped in the north–south direction so that all cyclones are oriented with the pole to the top of the figure. This is done to allow easy comparison of cyclone composites in the NH and SH. All cyclone means are the average of all data within 2000 km of the cyclone center. More complex analysis techniques exist that allow the definition of the edge of a cyclonic system (Pfahl and Sprenger, 2016). We have chosen to take averages around low-pressure centers with a set radius.

Some microwave radiometer products are unavailable over land or ice (e.g., surface wind), while others have larger uncertainty resulting from atmospheric emission signals being occasionally overwhelmed by land or ice emission (e.g., cloud liquid water). Therefore, only cyclone centers with 50 % or more of the composite area located over ice-free ocean are considered valid in cyclone composites from observations or models. Model data over sea ice or land are removed from the composite to ensure parity with the observations.

2.1.2 Regression analysis

In this work we examine observed and simulated extratropical variability in the current climate in the context of linear regressions. This framework is used to infer a climate feedback from changes in cyclone properties, and these inferred feedbacks are tested in a set of simulations of transient warming following Qu et al. (2015).

In the cyclone compositing framework that this paper is built on we examine (i) the variability of different variables between cyclones within the coordinate system of the cyclone composite (e.g., the inter-cyclone variability in some region of the composite); (ii) the variability in mean cyclone properties across many cyclones; and (iii) the seasonal and regional mean variability in cyclone means (e.g., the average cyclone LWP for all cyclones in a given region). To add clarity to our analysis we will refer to a given cyclone property X as X_CM when a cyclone-wide mean is taken (where the mean of all data is within a 2000 km radius of the low-pressure center) and X_RM when we are examining the regional mean of many different cyclones. In the case in which we will investigate the spatial variability around the low-pressure center, we will write X_ij to signify the different averaging regions within the composite. In the case of some variables, only cyclone means are defined (e.g., WCB moisture flux into the cyclone) and the “CM” subscript is not written. A list of acronyms and subscripts is given in Table 1.

Table 1 Acronyms and subscripts used in this work.

2.2 Observations and reanalysis

2.2.1 MAC-LWP

The Multi-Sensor Advanced Climatology (MAC) framework used for developing monthly cloud water products (Elsaesser et al., 2017) is adapted for use here to create diurnal-cycle-corrected and bias-corrected daily data sets for liquid water path (LWP, where path is the mass in an atmospheric column), 10 m wind speed, and water vapor path (WVP). Bias correction was performed using observations from Aqua MODIS. As a function of WVP and 10 m surface wind, Aqua MODIS was used to determine clear-sky (here, by definition, LWP =0) scenes, and these scenes were compared to AMSR-E LWP. If a nonzero difference was computed between AMSR-E and MODIS LWP, this difference was removed from all individual input LWP records (as a function of WVP and wind) prior to processing in the MAC algorithm. This LWP bias correction is discussed in more detail in Elsaesser et al. (2017).

Because passive microwave cloud liquid water retrievals must make assumptions regarding the partitioning of precipitating and nonprecipitating liquid, there is a systematic uncertainty in the microwave LWP data set. The cyclone LWP observations from this data set that are used in this study are the estimated nonprecipitating liquid water averaged over both cloudy and clear sky, with the bias (largely due to the aforementioned precipitation partitioning errors) estimated to be ∼0.01–0.02 kg m⁻² for the midlatitude regions analyzed here (Greenwald et al., 2018).

MAC-LWP uses data from multiple microwave radiometers to create a data set spanning 1988–2016. However, up until 1991 the only data source was F08 SSM/I, which therefore implies greater uncertainty in daily averages prior to 1992 (since only two satellite overpasses per day would go into such estimates). Thus, we consider this period less reliable and only observations from 1992 onwards are considered in this study. Because sea surface temperature and sea ice coverage are only available through 2015 we do not examine extratropical cyclones after this period.

One possible caveat in our analysis is that the radiative signal used to retrieve LWP may partly arise from upwelling radiation due to wind roughening of the ocean surface or emission from WVP. In such cases, LWP is biased in one direction, while wind and/or WVP may be biased in an opposite direction (Elsaesser et al., 2017). However, retrievals of WVP and wind speed have been shown to be unbiased relative to in situ observations, and thus such issues are likely minimal (Mears et al., 2001; Wentz, 2015; Trenberth et al., 2005; Meissner et al., 2001; Elsaesser et al., 2017).

2.2.2 MERRA-2

The Modern-Era Retrospective Analysis for Research and Applications Version 2 (Bosilovich et al., 2015) (MERRA-2) daily-mean sea-level pressure (SLP) was used to locate cyclone centers in the observational record from 1992 to 2015 using the algorithm described above.

2.2.3 AIRS cloud-top phase partitioning

The Atmospheric Infrared Sounder (AIRS) instrument on NASA's EOS Aqua satellite provides estimates of cloud thermodynamic phase (liquid, ice, and unknown categories) (Kahn et al., 2014). The cloud-phase algorithm is based on a channel selection that exploits differences in the index of refraction for liquid and ice (Nasiri and Kahn, 2008), while more ambiguous spectral signatures are classified as unknown phase. Jin and Nasiri (2014) showed that ice cloud within the AIRS field of view is correctly identified in excess of 90 % of the time when compared to estimates of thermodynamic phase from Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO; Hu et al., 2010). Liquid-phase clouds dominate subtropical stratocumulus regimes (Kahn et al., 2017), while unknown-phase clouds are found most frequently in trade cumulus regimes and the cold sector of extratropical cyclones (Naud and Kahn, 2015). Observations from the ascending and descending orbits of AIRS were averaged together to approximate a daily mean.

2.2.4 SST and sea ice

The Met Office Hadley Centre sea ice and sea surface temperature data set (HadISST.2.1.0.0, Titchner and Rayner, 2014) was used to provide sea ice coverage and sea surface temperature (SST) within the cyclone composite for both models and observations up until 2015. HadISST.2.1.0.0 SST and sea ice cover was also used to provide boundary conditions for the atmosphere-only PRIMAVERA simulations described below.

Table 2 Brief descriptions of the models used in this study. The label in the left column is used in some figures for brevity in labeling. The observations used in this study are discussed more completely in the Methods section.

¹ CFMIP2, ² PRIMAVERA.

2.3 Simulations

In this study we have assembled a broad array of GCMs to examine their midlatitude variability. Model resolutions range from quite coarse, consistent with long integrations performed as part of CMIP5, to high-resolution simulations performed under the auspices of PRIMAVERA for CMIP6, UM-CASIM, ICON, and NICAM. These simulations have long integration records and their trends may be compared to observations. Two very high-resolution simulations (nearer to 7 km horizontal resolution) are also considered. Because of their demand on computational resources only short integrations are available, but they allow insight into the representation of midlatitude processes in the convective grey zone (Field et al., 2017). Simulations are described in detail in the Supplement and are listed in Table 2. Short descriptions of the CFMIP2 and PRIMAVERA model intercomparisons are provided below.

2.3.1 CFMIP2

We consider several models from the CMIP5 models participating in CFMIP2. These models are listed in Table 2. Atmosphere-only (AMIP) simulations using observed SST as a boundary condition are available for the period 1979–2008. In addition, simulations were performed with SST uniformly increased by 4 K (AMIP +4 K). The contrast between these sets of simulations will be used to investigate warming-induced changes in extratropical cyclones.

2.3.2 PRIMAVERA

The PRocess-based climate sIMulation: AdVances in high-resolution modeling and European climate Risk Assessment (PRIMAVERA) project is intended to develop high-resolution GCMs. Several European modeling centers have coordinated with each other to run instances of their CMIP6 models at increased horizontal resolution. These simulations use Easy Aerosol (Voigt et al., 2014) to unify aerosol perturbations across the models. At the time of writing, historical simulations with prescribed SST and sea ice have been completed for the models analyzed here. These simulations allow insight into whether increasing horizontal resolution impacts the ability of models to realistically represent midlatitude variability. High-resolution models are labeled HR, and low resolution is labeled LR, with the exception of HadGEM3, which has three resolutions (low resolution is labeled LM, middle resolution is labeled MM, and high resolution is labeled HM). PRIMAVERA simulations are performed under the HighResMIP protocols outlined by the Coupled Model Intercomparison Project panel.

3 Results

3.1 Precipitation and WCB moisture flux

The majority of moisture ingested into extratropical cyclones is imported along the warm conveyor belt (WCB) (Eckhardt et al., 2004; Field and Wood, 2007). The WCB moisture flux is defined as

$$\begin{array}{}\text{(3)}& \mathrm{WCB}=k\cdot {\mathrm{WVP}}_{\mathrm{CM}}\cdot {\mathrm{WS}}_{\mathrm{10}\mathrm{m}\mathrm{CM}},\end{array}$$

where WVP_CM is the cyclone-mean water vapor path in kg m⁻², WS_10 m CM is the cyclone-mean wind speed at 10 m in m s⁻¹, and k is a constant parameterizing the width of the WCB as defined in Field and Wood (2007) and is calculated by linear regression of the precipitation rate on WVP_CM⋅WS_10 m CM. Cyclone means are the average of all data within a 2000 km radius of the cyclone center. We note that the k in Field and Wood (2007) was based on AMSR-E data. AMSR-E observes half the precipitation rate in cyclones that CloudSat does (Naud et al., 2018; Field et al., 2011). For consistency with previous literature we have chosen to use the k based on AMSR-E observations ($k=\mathrm{2.66}\times {\mathrm{10}}^{-\mathrm{7}}$ m⁻¹) as calculated by Field and Wood (2007). Our results might change slightly in a quantitative sense if another k is used, but will remain qualitatively the same.

Although the moisture imported along the WCB may condense and form clouds within the cyclone, in order to maintain water mass balance in extratropical cyclones, the moisture flux into a cyclone must match the precipitation out of the cyclone over a 2000 km radius. We find that the product of WVP and wind speed within cyclones is a good predictor of precipitation rate in the GCMs considered in this study (Table 2, Fig. S1 in the Supplement), in agreement with what has been found for observations (Field and Wood, 2007). Thus the WCB flux is a proxy for the moisture flux into a midlatitude cyclone that is balanced by the precipitation for a quasi-steady state. Model values of the WCB width parameter (k) (Eq. 3) range from 2.41 to $\mathrm{4.11}\times {\mathrm{10}}^{-\mathrm{7}}$ m⁻¹ and are near to the k trained on AMSR-E data (Field and Wood, 2007). It is interesting to note that the k value does not appear to depend on model resolution and the lowest and highest ks come from the high-resolution simulations in ICON and UM-CASIM, respectively. However, this range in k is within the observational uncertainty in precipitation rate (Field et al., 2011). Naud et al. (2018) examined the observed precipitation rate in extratropical cyclones and found that the mean extratropical cyclone precipitation rate differed substantially depending on whether a microwave radiometer (0.08 mm hr⁻¹; AMSR-E) or radar (0.17 mm hr⁻¹; CloudSat) was used to measure precipitation rate. If we rescale the AMSR-E precipitation rates so that the cyclone-mean precipitation rate is consistent with radar measurements, k should be $\mathrm{5.67}\times {\mathrm{10}}^{-\mathrm{7}}$ m⁻¹. Overall, the GCM cyclone precipitation flux that is predicted by the simple model of WCB moisture flux and the k inferred from the GCMs are well within the observational uncertainty.

The WCB moisture flux provides a useful predictor of precipitation – both in the climate mean state and in projected changes in rain rate via dynamical alterations (in wind speed) and Clausius–Clapeyron-driven changes (in WVP). We compare the distributions of WCB moisture flux, WS_10 m CM, and WVP_CM in models and observations. The mean WCB moisture flux in the GCMs considered in this study is generally lower than the observations (Fig. S2a, b), with model biases ranging from −1.16 to −0.31 mm day⁻¹ in the SH and from −0.79 to +0.24 mm day⁻¹ in the NH. This bias appears to be linked to low 10 m wind speed in cyclones in models (Fig. S2c, d) as GCM WVP_CM is near to the observed distribution (Fig. S2e, f). One possibility is that this issue is related to excessive surface drag over oceans, which is a known issue in modeling tropical cyclones (Donelan et al., 2004; Soloviev et al., 2014). Anecdotally, the CNRM-CM6 LR and HR GCMs cap surface drag and are the only two GCMs whose mean wind speed is greater than or equal to the observed wind speed. Based on this we suggested sensitivity tests in GCMs to the capping of surface drag as a step toward a realistic representation of midlatitude precipitation rates. If this is the cause of lower surface wind speed in cyclones, then it means that modeled midlatitude cyclones have been systematically underestimating precipitation through decreased flux of moisture into the cyclone. It is also possible that the low WS_10 m CM in some of the GCMs reflects deficient horizontal resolution (Strachan et al., 2013). The most biased cyclone-mean WS_10 m speeds are the IPSL-CM5 and CNRM-CM5 models, which have relatively low horizontal resolutions. This may be coincidental as there does not appear to be a systematic trend in different resolution instances of the same model within the PRIMAVERA GCMs.

3.2 LWP and WCB moisture flux

As shown in Sect. 3.1, precipitation within midlatitude cyclones is predicted by the WCB moisture flux. This provides a useful way to understand changes in cyclone properties as it gives a predictor of precipitation rate that can be decomposed into a contribution from dynamics (the wind speed) and thermodynamics (the WVP).

In McCoy et al. (2018b) it was proposed that when averaged over a sufficiently long period of time, cyclones were in a steady state in which the environment – in particular the moisture flux – dictated the precipitation rate out of the cyclone. If extratropical cyclones are in a steady state, then we expect that an increased moisture flux should enhance cyclone LWP, providing that precipitation processes are dominated by the warm rain process. This is because a higher in-cloud LWP is needed to generate a higher rain rate below cloud (Wood et al., 2009; Hill et al., 2015). Thus, an areally averaged rain rate should increase as LWP increases, either by increasing coverage of cloud or by increasing in-cloud LWP. Both effects should translate to an enhancement in cyclone albedo (at a fixed solar zenith angle; see the discussion in McCoy et al., 2018b). This makes understanding the efficiency with which extratropical cyclones can convert moisture flux to precipitation via cloud water key in understanding variability in extratropical albedo. We note that in this study we utilize microwave observations of LWP, which are the average of cloudy and clear regions, so increases in either in-cloud LWP or cloud coverage should translate to an increase in microwave-observed LWP. Similarly, the GCM LWP is the average of clear and cloudy regions.

Extratropical cyclone LWP represents a key variable in determining extratropical albedo, but does it scale with the WCB moisture flux? A linkage between the moisture flux into an extratropical cyclone and the total column liquid in the cyclone has been demonstrated previously in McCoy et al. (2018b). A caveat to this is that in McCoy et al. (2018b) total liquid water path (TLWP, precipitating and nonprecipitating liquid) was examined. Here, we examine the fraction of the TLWP which is suspended in clouds (referred to as LWP here).

Does LWP_CM increase with the WCB moisture flux in the same way that TLWP_CM does? The efficiency with which extratropical cyclones can shift vapor to rain determines the relation between WCB moisture flux and LWP_CM. In the limiting case this efficiency might increase sufficiently rapidly with the moisture flux that LWP_CM would not increase in step with the WCB moisture flux (all additional liquid becomes rain). Because we cannot directly observe how extratropical cyclones partition precipitating and nonprecipitating liquid (see Methods section), we cannot directly evaluate how precipitation efficiency scales with the WCB moisture flux. This represents an uncertainty in our analysis. However, we can evaluate extratropical cyclone rain and cloud partitioning in high-resolution simulations as a check on the calculations used in the MAC-LWP data set. LWP_CM, TLWP_CM (rain + cloud liquid), and the WCB moisture flux are calculated for extratropical cyclones observed using MAC-LWP and as simulated by UM-CASIM (see Table 2). The parameterization that partitions cloud and rain water paths in the MAC-LWP observations results in a decrease in the fraction of liquid water path that is in clouds (LWP_CM∕TLWP_CM) as the WCB moisture flux decreases by −0.075 day mm⁻¹ (see the slope of the line in Fig. S3). Comparison to UM-CASIM simulations shows a similar decrease in the fraction of liquid water that is suspended in clouds (−0.087 day mm⁻¹, Fig. S3). Ultimately, the partitioning of rain and cloud water in MAC-LWP and the microphysics scheme in UM-CASIM both lead to an increase in LWP with the increasing WCB moisture flux. This is likely due to autoconversion becoming more efficient at higher LWP, leading to a more pronounced flattening of the curve at higher LWP. It was shown in McCoy et al. (2018b) that this behavior could be fit as LWP∝WCB^p or LWP∝RR^p, where RR is the rain rate, since the WCB moisture flux and rain rate are linearly related.

We have examined how the WCB moisture flux predicts precipitation. We have also examined how the partitioning between rain and cloud changes as a function of the WCB moisture flux. Now we will embark on an examination of the relationship between the WCB moisture flux and LWP. We will focus on the behavior of cyclones within the SH. This is done for the following reasons: (1) the SH has a large, unbroken expanse of midlatitude ocean to investigate; (2) GCMs have well-documented and ongoing issues in accurately representing cloudiness in these regions (Trenberth and Fasullo, 2010; McCoy et al., 2016; Grise et al., 2015); (3) the GCM-predicted negative cloud optical depth feedback that is the primary subject of this paper is most pronounced in the SH (Zelinka et al., 2012a, 2016); and (4) observations and GCMs show a robust trend in LWP in this region that is likely driven by warming (Manaster et al., 2017; Norris et al., 2016). Ultimately, we focus on the SH for the sake of brevity. We find extremely similar behavior in the NH and the plots in the paper are reproduced in the Supplement for the NH.

With the caveat in mind that we must infer the partitioning of liquid between rain and cloud in the observations, we evaluate the ability of a wide array of GCMs to simulate the response of cyclone-mean LWP (LWP_CM) to the WCB moisture flux in the Southern Ocean (30–80^∘ S). We compare the WCB moisture flux dependence of LWP_CM in the models listed in Table 2 and observations from MAC-LWP (Fig. 1). Increasing the WCB moisture flux increases LWP_CM in both observations and models. As noted above, we should expect this based on the warm rain process. A greater LWP is required to yield a larger precipitation rate (Wood et al., 2009; Hill et al., 2015). As shown in Sect. 3.1 the precipitation rate is well predicted by the WCB moisture flux. While the high-resolution models (<100 km horizontal resolution) have a slope of the WCB–LWP_CM relationship that is in keeping with the observed slope, they tend to have too low a LWP_CM for a given WCB moisture flux. However, if the maximum bias in observed LWP_CM of 0.03 kg m⁻² is assumed based on an estimated range 0.01–0.02 kg m⁻² (Greenwald et al., 2018), then many of these models are in the possible observational range. It is also reasonable to suspect that models that only generate clouds when the entire grid box is saturated (e.g., there is no convection parameterization or cloud scheme) will underestimate cloudiness.

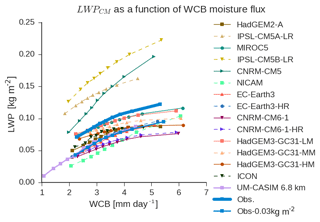
Figure 1 Cyclone-mean LWP (LWP_CM) as a function of the WCB moisture flux in models and observations. LWP_CM is shown averaged into nine equal quantiles for the observations and each GCM. The maximum bias in the observations (∼0.03 kg m⁻²) is shown by a lighter blue line.

It is suggested that the lower-resolution CFMIP2 models tend to have a much wider diversity in slopes than the higher-resolution PRIMAVERA models, UM-CASIM, NICAM, and ICON. This may reflect parametric uncertainty in the representation of convection. UM-CASIM, NICAM, and ICON do not parameterize convection and have extremely similar relationships between the WCB moisture flux and LWP. Based on this we suggest that the relationship between the moisture flux and LWP may offer a possible evaluation tool for the realism of convection within GCMs. However, this may also just by chance be related to the selection of models presented here as the low-resolution HadGEM3-GC31-LM has a reasonably close behavior to the higher-resolution instances of that model (HadGEM3-GC31-MM, and HadGEM3-GC31-HM). Overall, the constraint provided by the WCB–LWP_CM relationship shown here provides a useful tool for GCMs to evaluate their climate mean-state behavior in the extratropics.

As discussed in the paragraph above, the partitioning between rain and cloud shifts toward rain at higher moisture fluxes (Fig. S3). This leads to the asymptotic nature of the curves shown in Fig. 1. Presumably differences in the degree to which the curve flattens at higher LWP as precipitation becomes more efficient in some models reflect differences in the way that precipitation is treated in the different GCMs, with (for example) autoconversion being stronger in some models, leading to a more pronounced flattening of the LWP–WCB curve (and vice versa). The asymptotic behavior of the WCB–LWP_CM curve is a second-order effect in our analysis (we will return to this discussion in Sect. 3.3.3).

3.3 Long-term variability in observed cloud properties

3.3.1 Monthly-mean regional variability in extratropical cyclone properties

The moisture flux into extratropical cyclones plays a dominant role in determining their LWP and, ultimately, precipitation rate. How does this mechanism influence the cloud feedback in the midlatitudes? In keeping with earlier studies (Myers and Norris, 2016; Qu et al., 2015) we examine observed anomalous variability from 1992 to 2015 to infer the cloud feedback in these regions within cyclones. We will then utilize transient warming simulations in which SSTs have been increased by 4 K to see if variability within the current climate has the capability to predict the change in cyclone properties in a warmed climate. This technique follows the analysis of stratocumulus clouds in Qu et al. (2015). The Indian, Pacific, and Atlantic oceans between 30 and 80^∘ S are each examined individually (precise regions are shown in Fig. S4). In this section we discuss cyclone means in the context of the monthly means across all the cyclones in each region. For each region the monthly-mean anomaly relative to the monthly-mean climatology is calculated. Variables averaged to regional means are denoted RM (see Table 1 for a list of acronyms and subscripts).

Figure 2 shows the relation between the regional and monthly mean of various cyclone properties. For each ocean basin the average of the LWP_CM for all cyclones for each month is taken (LWP_RM). The climatological LWP_RM is subtracted for each month to yield anomalies. The same procedure is repeated for the WCB moisture flux. The relation between anomalies in LWP_RM and WCB moisture flux anomalies is shown in Fig. 2a. This allows us to examine the relation of various predictors across the population of cyclones within a given basin in the Southern Ocean.

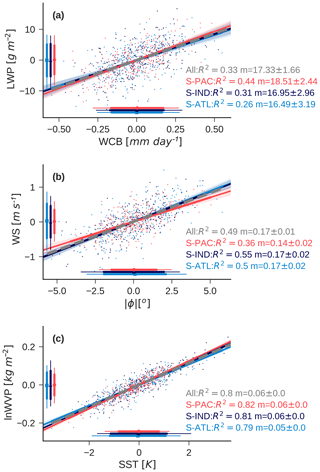
Figure 2 Observed monthly- and regional-mean anomalies in extratropical cyclone properties in the SH oceans (NH oceans are shown in Fig. S5). (a) Cyclone monthly-mean LWP_RM as a function of WCB_RM; (b) regional- and monthly-mean wind speed as a function of regional- and monthly-mean cyclone absolute (poleward) latitude; (c) monthly-mean ln(WVP)_RM as a function of SST_RM. Each data point in the plot represents the monthly- and regional-mean anomaly in a given variable within extratropical cyclones relative to the monthly-mean climatology. The shaded area corresponds to the 95 % confidence interval on the fit. The R² and best fit line are listed for each subplot and for each ocean region. The R² of all monthly- and regional-mean anomalies is also noted (the variability in regional- and monthly-mean anomalies is weighted equally between regions to calculate the overall R²). Bars on the sides of the plot show the mean (marker), standard deviation (thick lines), and 90th percentile range (thin lines) of monthly- and regional-mean anomalies for each region.

Anomalous variability in LWP_RM in the SH extratropical oceans correlates with variability in the WCB moisture flux (Fig. 2a). The South Pacific region has 42 % of monthly-mean LWP_RM anomalies explained by moisture flux anomalies, the South Atlantic and Indian oceans have approximately 30 % of their monthly anomalies in LWP_RM explained by the moisture flux. Overall, the slope of the relation between anomalies in monthly-mean extratropical cyclone LWP_RM and WCB moisture flux monthly means is quite similar across these regions and the slope has very little uncertainty.

Why do the different ocean basins have such different explained variances (R²s) in the relationship ${\mathrm{LWP}}_{\mathrm{RM}}=a\cdot {\mathrm{WCB}}_{\mathrm{RM}}+c+\mathrm{residual}$? Presumably this relates to some unconsidered predictor in our analysis expressed through the residual term. For example, cloud droplet number concentration (CDNC) variability in cyclones substantially affects LWP (McCoy et al., 2018b). The explained variances in the different ocean basins are consistent with this. The explained variance by the WCB moisture flux is higher in the South Pacific compared to the rest of the Southern Ocean where intermittent phytoplankton blooms dramatically vary CDNC (McCoy et al., 2015a; Meskhidze and Nenes, 2006; Charlson et al., 1987) and the NH where anthropogenic emissions vary from year to year (McCoy et al., 2018a; Bennartz et al., 2011). The global climate models that we focus on in this study to do not provide CDNC as an output and we will reserve partitioning interannual variability in cyclone behavior into contributions from meteorology and microphysics for future study.

A large fraction ($\sim \mathrm{1}/\mathrm{3}$) of SH ocean anomalies in monthly- and regional-mean LWP_RM may be explained by WCB moisture flux anomalies alone and the sensitivity of LWP to WCB moisture flux is robust and differs very little from basin to basin. What in turn explains moisture flux variability? As shown in Eq. (3), the WCB moisture flux is the product of WVP and wind speed. We will discuss the contributions of each of these terms below.

Monthly-mean cyclone WS_10 m RM, which is a proxy for the input rate of moisture into the cyclone, enhances as cyclones move poleward (Figs. 2b and S6). In the Southern Ocean 36 %–55 % of anomalous monthly variability in wind speed is linearly related to cyclone latitude. Examination of cyclone-mean wind speed as a function of latitude shows agreement in models and observations. In models and observations cyclone-mean wind speed increases toward 60^∘, and then decreases poleward of 60^∘ in both hemispheres (Fig. S6). Overall, the explained variance in anomalous monthly- and regional-mean wind speed is 49 % across all SH ocean basins (weighting all ocean basins equally). This reflects the genesis and development of an extratropical cyclone. The genesis of extratropical cyclones occurs toward the tropics and then over their life cycle cyclones move toward the pole. During this life cycle they intensify, leading to enhancement in near-surface wind speed (Tamarin and Kaspi, 2017; Beare, 2007; Bengtsson et al., 2009). Two important questions stand out in regards to our analysis: will the genesis region of extratropical cyclones shift in a warmed climate? Will extratropical cyclones develop differently in a warmed climate?

The complexity of changes in the life cycle, frequency, and intensity of extratropical cyclones under warming makes it difficult to say confidently how their vorticity and surface wind speed will change. There is a general consensus that storm tracks will shift toward the poles as the climate warms (Barnes and Polvani, 2013; Yin, 2005; Lorenz and DeWeaver, 2007; Bender et al., 2011b), but the mechanism that prompts this poleward movement remains unclear (Shaw et al., 2016). As they shift poleward storm tracks intensify (Lorenz and DeWeaver, 2007; Yin, 2005; Ulbrich et al., 2009). Simulations with greenhouse gas warming generally show decreased frequency of midlatitude cyclones, but increases in cyclone intensity (Lambert and Fyfe, 2006; Bengtsson et al., 2006; Geng and Sugi, 2003). This may be related to changes in cyclone life cycle, with cyclones taking longer to reach peak intensity over a longer propagation in a warming world (Tamarin and Kaspi, 2017; Tamarin-Brodsky and Kaspi, 2017). We will discuss the response to a transient warming within CFMIP2 GCMs, for which the prescribed SST is enhanced by 4 K in the following section.

Monthly-mean variability in extratropical cyclones ln(WVP)_RM is explained by SST_RM, with 80 % of anomalous monthly mean variability in ln(WVP)_RM predicted by SST_RM (Fig. 2c). This linkage between anomalies in cyclone-mean SST and anomalies in ln(WVP) via Clausius–Clapeyron has been shown previously in Field et al. (2008).

In summary, we propose that Southern Ocean cloud feedbacks in cyclonic systems are not only related to the so-called mixed-phase cloud feedback, but are contributed to by changes in WVP and wind speed. Because increasing SST increases WVP via Clausius–Clapeyron, which in turn increases condensed water, this response to increasing SST is easy to conflate with ice to liquid transitions. However, SST alone is a poor predictor of LWP_RM (Fig. S7). The variance in LWP_RM explained by SST alone is less than 10 % in any basin and the fits in the different basins are different at 95 % confidence. This is consistent with the weak negative dependence of cloud optical depth on SST shown by Terai et al. (2016). In the following sections we will continue to investigate the dependence of cyclone LWP on the WCB moisture flux in the current climate and investigate how this mechanism might affect the extratropical cloud feedback.

3.3.2 Model–observation comparisons of extratropical cyclone behavior

As shown above, observed extratropical cyclone LWP_CM depends on the WCB moisture flux. This translates to anomalous regional- and monthly-mean variability in the WCB moisture flux covarying with regional- and monthly-mean anomalous variability in extratropical cyclone LWP_RM. As we saw in Fig. 1, climate model extratropical cyclone LWP also depends on the WCB moisture flux, but models do not agree on how sensitive cyclone LWP_CM is to moisture flux. In this section we examine how GCM regional- and monthly-mean anomalous variability in extratropical cyclone properties compares to observations within the current climate.

First, we examine the ability of models to reproduce the WCB moisture flux–LWP_RM relation observed in the SH. As in Fig. 2a, the slope of the best fit linear line between monthly-mean anomalies in cyclone LWP_RM and the WCB moisture flux is computed in each SH ocean basin, and is summarized in Fig. 3a. The 95 % confidence on the best fit line is also shown. All the models and the observations have a nonzero slope at 95 % confidence. The slope of the WCB moisture flux–LWP relationship in IPSL-CM5B-LR and CNRM-CM5 models is more than twice the slope inferred from observations, while the CNRM-CM6 and HadGEM3 models have around half the observed slope. NICAM, HadGEM2, IPSL-CM5A-LR, and the EC-Earth models compare favorably to the observations. Evaluation of model variability shows that all models have over 20 % of their LWP_RM variability explained by WCB in the SH, with some models able to explain up to 70 % of their anomalous monthly- and regional-mean variability using the WCB moisture flux (Fig. S8). Despite low explained variance in some models, the relationship between the WCB moisture flux and LWP is significant at 95 % confidence in all of the models. As discussed in the previous section, variability in warm cloud microphysics (e.g., CDNC) has been shown to substantially affect cyclone LWP (McCoy et al., 2018b). The inclusion of these or other processes as predictors should increase explained variance by the regression model. For example, NICAM, which has no aerosol–cloud adjustments, has the highest variance explained by the WCB moisture flux alone (50 %–75 %, depending on the basin; Fig. S8). Overall, the variance explained in the current climate is of secondary interest to the confidence in the slope of the relationship.

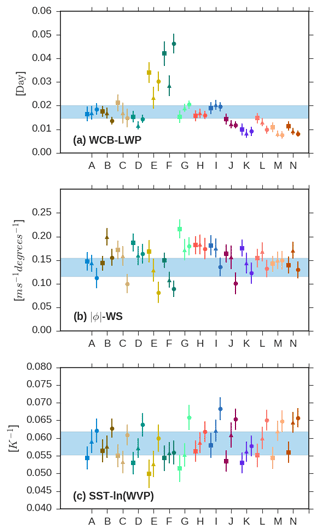
Figure 3 The slope of the best fit line between monthly- and regional-mean anomalies of different cyclone-mean properties. Symbols denote different SH ocean basins (South Atlantic: squares, South Indian: triangles, and South Pacific: circles). Model colors are as in Fig. 1. Each model is labeled with a letter on the ordinate (see Table 2). The observations are shown as “A”. The 95 % confidence on the slope is noted for each basin. The shaded area shows the 95 % confidence on the mean of the observed slope based on the SH ocean basins. Panel (a) shows the slope of the regression of cyclone LWP_RM on WCB moisture flux, panel (b) shows the regression slope of the mean wind speed in cyclones on mean poleward latitude, and panel (c) shows the regression slope of ln(WVP)_RM on SST_RM.

Next, we investigate the relation between mean absolute (poleward) cyclone latitude and WS_10 m in cyclones. All models have a correlation between anomalous monthly-mean poleward latitude and WS_10 m RM at 95 % confidence (Fig. 3b), in keeping with the agreement in the latitudinal dependence of WS_10 m CM shown in Fig. S6. The agreement between the observed and modeled sensitivities is good and most models overlap with the 95 % confidence on the observational sensitivity. This supports the idea that the models presented here have a fairly consistent representation of the cyclone life cycle in the current climate.

Finally, we examine the relation between ln(WVP)_RM and SST_RM in the GCMs as in Field et al. (2008). The relation between SST and column water vapor in the models and in the observations is quite similar (Fig. 3c), indicating that all the models are able to somewhat accurately reproduce the response in WVP associated with Clausius–Clapeyron and warming.

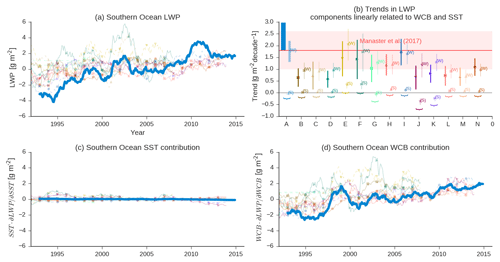
Figure 4 (a) SH cyclone LWP_RM in observations (thick blue line) and models (colors as in Fig. 1) for which cyclones are centered between 44.5 and 59.5^∘ S. A 2-year running mean has been applied to simplify the plot. (b) The red shaded area shows the zonal-mean Southern Ocean LWP trend calculated in Manaster et al. (2017) (Southern Ocean defined as 44.5–59.5^∘ S therein). Trends in cyclone LWP_RM from observations and models are shown in dark colors (where LWP_RM is calculated using cyclones centered in the same region as Manaster et al., 2017). Models and observations are labeled by a letter on the ordinate (see Table 2). Observations are labeled as “A”. The 95 % confidence in each trend is shown using error bars. A multiple linear regression of LWP_CM on SST_CM and WCB moisture flux is used to partition the trend into contributions from WCB and SST changes. The trend in LWP_RM predicted by the regression model (Eq. 4) and changes in SST_RM are shown in (c), and the trend in LWP_RM associated with WCB is shown in (d). The trend from models and observations consistent with their multiple linear regression models and changes in SST_RM and WCB are shown in (b) using lighter colors and labeled as (S) for SST and (W) for WCB.

3.3.3 Decadal trends in extratropical cyclone properties

In Sect. 3.3.1 and 3.3.2 we discussed how monthly variability in LWP_RM may be predicted by moisture flux. This examination of the variability within the system suggests that warming will lead to enhanced LWP across the midlatitude ocean via enhanced WVP that may be fluxed into cyclones. This means that the shortwave cloud feedback in the Southern Ocean (SO) may be partially driven by changes in WCB moisture flux and not only by ice to liquid transitions. To support this argument we examine whether warming on a decadal scale across the midlatitudes is accompanied by an increase in WCB moisture flux and cyclone LWP. This LWP behavior has already been shown within the data record. Examination of zonal-mean LWP anomalies in the MAC-LWP data record and in GCMs by Manaster et al. (2017) showed a robust positive trend in LWP. In this section we will examine the trend in cyclone LWP during the period 1992–2015 in the context of trends in moisture flux. This will be contrasted with the zonal-mean trend diagnosed by Manaster et al. (2017).

In this study we are pursuing a regime-oriented approach to understanding extratropical variability. Do the zonal-mean trends in Manaster et al. (2017) agree with the trends in extratropical cyclone behavior? Because Manaster et al. (2017) investigated trends in the latitude band 44.5–59.5^∘ S we subset our data record to only consider cyclones centered in this latitude band so that a more direct comparison can be made. Trends in Southern Ocean regional-mean cyclone LWP_RM and zonal-mean LWP as calculated by Manaster et al. (2017) over the last two decades are similar (Fig. 4a, b; 2.40±0.58 g m⁻² decade⁻¹ within extratropical cyclones versus 1.8±0.8 g m⁻² decade⁻¹ in the zonal-mean (Manaster et al., 2017), where uncertainty is the 95 % confidence interval). Given that cyclones cover approximately half the Southern Ocean (Bodas-Salcedo et al., 2014), this in-cyclone trend can account for a good portion of the overall zonal-mean signal.

We have shown in the previous section that around a third of the monthly- and regional-mean variability in cyclone LWP_CM is related to variability in the WCB moisture flux (Fig. 2a). A regression on SST alone explains less than a tenth of the variance (Fig. S7). Consistent with this, we could use the simple regression model ${\mathrm{LWP}}_{\mathrm{CM}}=a\cdot \mathrm{WCB}+c+\mathrm{residual}$ trained on the observational record to see if the LWP trend in the Southern Ocean is consistent with the trend in the WCB moisture flux. It is possible that some of this trend that is related to changes from ice to liquid phase that is being obscured by WCB moisture flux variability. Both changes from ice to liquid and the WCB moisture flux (via WVP and Clausius–Clapeyron) will be associated with variability in atmospheric temperature. To examine this we need to disentangle changes related to the synoptic state and changes in SST in the observational record. We attempt this utilizing a simple regression model fitting to a two-dimensional plane in WCB moisture flux and SST space. This fit splits the variability into a WCB moisture flux term and a term associated with SST variations around a given WCB moisture flux (Fig. 5). If changes from ice to liquid water are an important factor in the cloud feedback in this region, then increasing SST at a fixed WCB moisture flux should correspond to an increase in LWP.

Regressing on WCB moisture flux and SST simultaneously is problematic as SST changes ultimately drive a significant fraction of WCB moisture flux changes via Clausius–Clapeyron. Analogously, SST and atmospheric stability covary, but have differing effects on cloud cover, and similar linear regression analysis has been undertaken to disentangle their contributions and infer the shortwave cloud feedback (Qu et al., 2015; Klein et al., 2017; Terai et al., 2016).

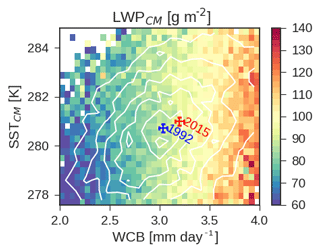
Figure 5 Average Southern Ocean cyclone LWP_CM binned as a function of SST_CM and WCB moisture flux for the latitude band 44.5 to 59.5^∘ S, following Manaster et al. (2017). Contours of cyclone distribution are shown in white. The mean cyclone WCB moisture flux and SST_CM for 1992 and 2015 are shown as blue and red points, respectively. Error bars show the 95 % confidence on the mean.

To try and partition variance in the Southern Ocean into components related to synoptic variability and a component related to the variance in SST around the synoptic state, we train the regression model

$$\begin{array}{}\text{(4)}& {\mathrm{LWP}}_{\mathrm{CM}}=a\cdot \mathrm{WCB}+b\cdot {\mathrm{SST}}_{\mathrm{CM}}+c+\mathrm{residual}.\end{array}$$

This regression model is trained on the population of SH cyclone means from 1992 to 2015 and centered in the latitude band considered in Manaster et al. (2017). In this analysis we ignore the power law dependence of LWP on the WCB moisture flux (Fig. 1). In the following section we show that this assumption does not substantially affect the predictability of the change in cyclone LWP in response to warming. The regression model trained on the observational record has coefficients

$$\begin{array}{ll}{\displaystyle }{\mathrm{LWP}}_{\mathrm{CM}}& {\displaystyle }=(\mathrm{28.71}\pm \mathrm{0.42})\cdot \mathrm{WCB}-(\mathrm{0.29}\pm \mathrm{0.1})\cdot {\mathrm{SST}}_{\mathrm{CM}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }+\mathrm{3.70}\pm \mathrm{1.21},n=\mathrm{18842},R^{\mathrm{2}}=\mathrm{0.53}.\end{array}$$

As can be seen in Fig. 5 LWP_CM primarily depends on the WCB moisture flux. At a fixed WCB moisture flux, changes of ±5 K in the SST do not correspond to significant changes in LWP. Because of this most of the long-term trend in LWP_CM averaged across the Southern Ocean can be explained by changes in the WCB moisture flux alone (Fig. 4b, d). This is not to say that changes in SST do not have any effect – clearly they do via the WVP term in the WCB moisture flux. Most of the increase in the WCB moisture flux may be explained by steadily increasing cyclone WVP, driven by enhanced SST (Fig. S9). However, changes in SST independent of WCB do not predict the trend in LWP. This is also shown in schematic form in Fig. 5: between 1992 and 2015 SST increases and the WCB moisture flux increases, driven by Clausius–Clapeyron, but the shift in SST has relatively little effect independent of the shift to a higher WCB moisture flux.

The regression model in Eq. (5) uses variability in the WCB moisture flux and SST to predict variability in cyclone LWP. As discussed above, SST variability drives changes in WVP via Clausius–Clapeyron, leading to covariability between the WCB moisture flux and SST_CM (r=0.84 over the 1992–2015 period in both hemispheres; see also the contours of cyclone population in Fig. 5). While the WCB moisture flux and SST_CM are fairly colinear, SST_CM is only poorly correlated with LWP_CM (r=0.25). The correlation between LWP_CM and WCB moisture flux is much stronger (r=0.63). As discussed in Sect. 3.3.1, the correlation between monthly- and regional-mean anomalies in SST and LWP are also weak and are inconsistent between basins. Thus, despite being a good predictor of the WVP component of WCB moisture flux, SST_CM, it is a poor predictor of cyclone LWP_CM, which is consistent with the lack of a trend associated with SST variability independent of WCB moisture flux variability in Fig. 4.

The coefficient relating the WCB moisture flux and LWP in Eq. (5) is relatively insensitive to whether or not SST is included as a predictor. If WCB moisture flux is used as the only predictor, then the coefficient relating WCB moisture flux to LWP changes to 28.13±0.40 g m⁻² day mm⁻¹. If only SST is used as predictor, then the coefficient relating SST and LWP changes sign ($+\mathrm{2.90}\pm \mathrm{0.12}$ g m⁻² K⁻¹). This is because SST is a good predictor of the WCB moisture flux so if the WCB moisture flux is not held constant in the regression, the coefficient relating SST to LWP absorbs variability related to the WCB moisture flux. This also shows that studies using SST alone to infer the climate feedback in this region will lead to non-robust predictions of the change in LWP because SST will covary with the WCB moisture flux in the mean climate, but the change in SST in response to greenhouse-gas-driven warming will not be the same as the change in the WCB moisture flux. This argument infers the change in LWP from current variability – to further support this analysis we will turn to transient warming simulations in Sect. 3.3.4.

Once the trend in the WCB moisture flux is accounted for, relatively little room is left for an effect related to phase changes (Fig. 4b). SST was included as a predictor in Eq. (4) to see if variations in SST at a constant WCB moisture flux led to an increase in LWP consistent with a transition from ice to liquid. It was found that SST increases corresponded to a slight decrease in LWP at a given WCB moisture flux. This is consistent with SST acting as a proxy for several other boundary-layer processes such as weakening the inversion strength and the buoyancy-driven reductions in cloud cover (Bretherton and Blossey, 2014). Overall, we cannot take the trends in the observational record of cyclone LWP as a sign of a strong mixed-phase cloud feedback because most of the trend is predicted by changes in synoptic state.

Comparison of the trend in Southern Ocean LWP_RM for the models listed in Table 2 is shown in Fig. 4b. Despite the models being run in AMIP mode with prescribed SSTs, there is significant variability in the trend in LWP_RM in the period 1992–2015 (note that CFMIP2 models simulated 1979–2008). The GCMs all show a positive trend that is significant at 95 % confidence, but generally underpredict the strength of the trend. It is also interesting to note that the trend in LWP_RM across the Southern Ocean is almost completely explained by WCB moisture flux variability in all the GCMs. In the following section we will revisit this puzzle and use spatial variability within cyclone composites and cloud-top phase to attempt to disentangle the contributions of ice-to-liquid transitions and WCB moisture flux.

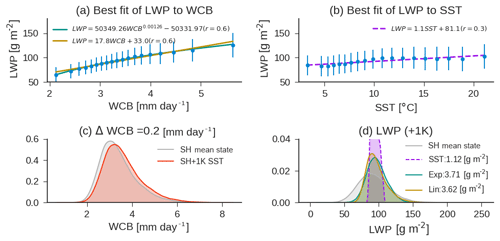
Figure 6 (a) The LWP_CM observed in SH as a function of the WCB moisture flux; the best fit line to the observations using the form ${\mathrm{LWP}}_{\mathrm{CM}}=a\cdot {\mathrm{WCB}}^b+c$ is shown using a green line. A simple linear fit is shown in yellow. The observations are binned into equal quantiles for visual clarity. Error bars show a standard deviation within each bin. (b) The fit of cyclone LWP_CM to SST_CM. (c) The distribution of SH WCB moisture flux in the current climate, and when the WVP moisture flux is scaled by 1.06 consistent with a uniform 1 K increase in SST. The difference in the WCB moisture flux is noted in the title. (c) The distribution of LWP_CM in the current climate and as predicted by the fits shown in (a) and (b). The LWP_CM when SST is increased by 1 K as predicted by the fits in (a) is based on scaling WVP by 1.06. The LWP_CM predicted by the fit shown in (b) is based on SST increasing uniformly by 1 K. The mean difference of LWP_CM between the prediction and the climate mean state is noted in the legend.

Of course this only examines variability within extratropical cyclones. One possibility is that in anticyclones all long-term trends relate to phase transitions consistent with the mixed-phase cloud feedback. However, this seems unlikely given the extensive analysis performed by Terai et al. (2016) demonstrating a substantial contribution to cloud optical depth variability in the Southern Ocean from variability in estimated inversion strength (Wood and Bretherton, 2006), and a lesser contribution linearly related to SST. It is also worth noting that increased SST predicted decreased cloud optical depth (Terai et al., 2016). Thus, it is unlikely that all the change in cloud properties in anti-cyclonic regions is related to phase transitions and it is more likely that the change in cloud properties in these regions is dominated by changes in boundary-layer cloudiness, consistent with enhancing inversion strength (Terai et al., 2016), which is a well-quantified feature of boundary-layer cloud cover (Wood and Bretherton, 2006; Klein and Hartmann, 1993). We reserve a more complete examination of cloud variability composited around both high- and low-pressure centers for a future paper and will focus on examining low-pressure centers in the present work.

The WCB moisture flux and cyclone LWP are covariable (Fig. 2a). This infers that warming over the midlatitudes should result in an increase in LWP as the WCB moisture flux increases following Clausius–Clapeyron. The trend in cyclone LWP over the Southern Ocean in response to warming agrees with this inference made from internal variability (Fig. 4a). We will now examine a simplified prediction of what the change in cyclone LWP might look like in response to a uniform warming. If we assume that the distribution of wind speed remains unchanged, that frequency of occurrence of cyclones remains unchanged, and that WVP increases by 6 % K⁻¹ due to increasing SST (Fig. 3c), we can estimate the change in the WCB moisture flux consistent with a uniform 1 K warming (Fig. 6). In this paper we have been utilizing a linear fit between the WCB moisture flux and cyclone LWP. As can be seen in Fig. 6a the shape of the relationship between WCB moisture flux and cyclone LWP is better represented by an exponential fit (as in McCoy et al., 2018b). However, the variance in LWP explained by either function is nearly identical. The linear relationship between the WCB moisture flux and LWP_CM predicts an increase of 3.62 g m⁻² in the SH (Fig. 6d) in response to the change in WCB moisture flux shown in Fig. 6c. If the exponential fit is used the change in cyclone LWP is 3.71 g m⁻². Thus, use of a linear relationship between the WCB moisture flux and LWP may slightly underestimate the change in cyclone LWP to warming.

Does this prediction offer any more information than an analysis using SST alone? The dependence of LWP_CM on SST_CM in the SH is shown in Fig. 6b. The relationship appears to be somewhat non-monotonic (LWP increases with SST until 10 ^∘C and then decreases) and the correlation is substantially weaker than between the WCB moisture flux and LWP_CM. Linear regression of LWP_CM on SST_CM and a 1 K increase in SST_CM predict a 1.12 g m⁻² increase in LWP_CM, nearly a third of the prediction based on changes in the WCB moisture flux. We offer this quick estimate in order to provide an approximate scale to the potential of the WVP-mediated changes in extratropical cyclone LWP in a warming climate. An estimate of the change in reflectivity consistent with this change in cyclone LWP will be offered in Sect. 3.4, when we examine the change in cyclone structure in response to change in the WCB moisture flux. In the following section we will investigate whether WCB-moisture-flux-driven increases in LWP can explain the warming response in GCMs.

3.3.4 Predicting the cyclone LWP response in transient warming simulations

In Sect. 3.3.1 and 3.3.2 we examined month-to-month regional variability. In Sect. 3.3.3 we examined whether trends in SST, WCB moisture flux, and cyclone LWP from 1992 to 2015 were consistent with the predictions based on month-to-month variability. The analysis in these sections inferred that the increasing WCB moisture flux should increase cyclone LWP in a warming world. In this section we will test the assumption that the relationship between the WCB moisture flux and LWP can predict the warming response of a model. At the time of writing the only GCMs considered in this study that have simulated a global increase in temperature (outside of the observational record) are the GCMs participating in CFMIP2 (see Table 2). The CFMIP2 GCMs performed a set of simulations in which the specified SST in the atmosphere-only (AMIP) runs was increased by 4 K (AMIP + 4 K). The CFMIP2 GCMs represent a wide array of different relationships between the WCB moisture flux and cyclone LWP and it is hoped that even though we have limited our analysis of cyclone behavior in a warmed climate to these models, it still provides insight into the broader collection of models examined in the rest of this study.

Comparison of the WCB moisture flux–LWP relationship (see Fig. 1) between the AMIP and AMIP + 4 K CFMIP2 simulations shows that they are fairly similar in the SH (Fig. 7). Only IPSL-CM5A-LR has a substantially different relationship between LWP_CM and the WCB moisture flux in the AMIP and AMIP + 4 K simulations. Examination of the NH shows that all the models display a downward shift in the WCB moisture flux–LWP relationship in the warmed simulations (Fig. S10). It is unclear why the WCB moisture flux–LWP relationship in the NH shifts downward, while it shifts upward in the SH in only one of the GCMs. At least in the SH this upward shift is conceptually consistent with a decrease in precipitation efficiency due to decreased ice-phase precipitation. In this case an increase in cyclone LWP would be in line with the necessity of balancing precipitation out of the cyclone and moisture flux into the cyclone (McCoy et al., 2018b).

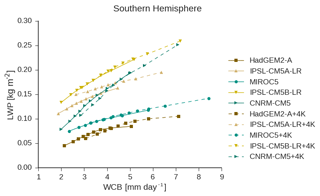
Figure 7 As in Fig. 1, but contrasting the AMIP and AMIP + 4 K simulations in the CFMIP2 simulations.

To test whether the current climate's variability can be used to predict the future (as in Qu et al., 2015) we train a linear regression model of the form ${\mathrm{LWP}}_{\mathrm{CM}}=a\cdot \mathrm{WCB}+c+\mathrm{residual}$ for each GCM. The regression model is fit using the variability in the present-day AMIP simulations. Cyclone LWP in the AMIP + 4 K simulations is predicted based on the regression model and the WCB moisture flux in the AMIP + 4 K simulations. To reiterate, if we know the relationship between the moisture flux and cyclone LWP in the current climate, and we know how moisture flux changes, then can we predict the change in cyclone LWP?

Changes in the WCB moisture flux explain the majority of cyclone LWP difference between the AMIP + 4 K and AMIP simulations (Fig. 8). Over 80 % of the difference in Southern Hemisphere cyclone LWP between AMIP and AMIP + 4 K is explained by differences in the WCB moisture flux in four out of five of the models. The change in cyclone LWP in IPSL-CM5A-LR is 30 % greater than the change predicted by the WCB moisture flux alone, consistent with a potential phase-transition-driven increase in LWP. For completeness the same calculation was carried out in the NH. Differences in Northern Hemisphere cyclone LWP between AMIP and AMIP + 4 K are within 25 % of the prediction based on the AMIP WCB moisture flux–LWP relationship and the difference in the WCB moisture flux (Fig. S11).

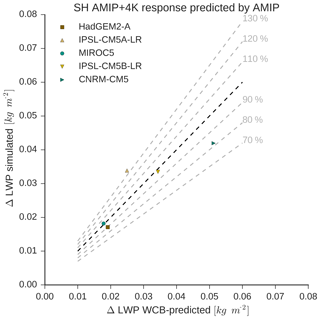
Figure 8 The difference in cyclone LWP in the SH between AMIP and AMIP + 4 K simulations versus the difference in SH cyclone LWP inferred from changes in the WCB moisture flux and the relationship between the WCB moisture flux and LWP_CM in the current climate. The 1-to-1 line is shown as a dark dashed line.

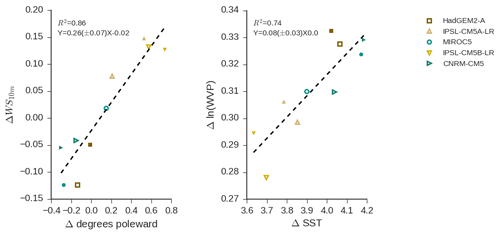
Figure 9 Changes in cyclone-mean wind speed at 10 m (WS_10 m) and the natural log of WVP between AMIP and AMIP + 4 K simulations plotted against changes in mean poleward cyclone latitude and SST, respectively. Open symbols show the change over the NH and closed symbols show the change over the SH. The best fit line to the NH and SH is noted in each plot along with 95 % confidence in the slope.

The ability of the regression model to explain changes in LWP is quite high, although its ability to explain monthly- and regional-mean variability is not exceptionally high in some of the GCMs (Fig. S8). As discussed in Sect. 3.3.1, the residual term in Eq. (4) is generated by predictors not considered in our analysis, for example, cloud droplet number concentration (CDNC), which has been shown to have substantial predictive ability (McCoy et al., 2018b). These unconsidered predictors might contribute to the variance in the current climate, leading to a lower explained variance by the regression model, but if these other predictors do not change between the AMIP and AMIP + 4 K simulations then the regression model will be able to accurately predict the change in LWP between these simulations. For example, aerosol emissions do not change between AMIP and AMIP + 4 K. By extension CDNC is unlikely to change so variance unexplained by this factor in the historical climate is unimportant for explaining the change in LWP between AMIP and AMIP + 4 K.

It appears that the relationships between extratropical cyclone latitude and wind speed and between SST and cyclone WVP from the current climate hold in a warmed climate. As cyclones shift poleward in response to warming, their mean wind speed increases (Fig. 9). Similarly, as SSTs rise, WVP increases. As prescribed by the AMIP + 4 K simulations, the SST rises in both hemispheres, leading to increasing WVP. The response in mean cyclone position is varied and difficult to interpret in the context of a greenhouse-gas-induced warming due to the fixed SST imposed in these simulations. The mechanism that links the mean cyclone latitude and cyclone wind speed is not clear, but one possibility is that cyclone life cycle changes in response to warming, leading to changes in the average wind speed within a cyclone as the average latitude range in which cyclones exist changes. We reserve understanding why mean cyclone location and wind speed change in this way for a future paper using both uniform increases in SST and a more realistic warming pattern.

In summary, we find that most of the cyclone LWP trend in the SH observational record can be explained by a steady increase in the WCB moisture flux, as opposed to a transition to less-glaciated clouds. We support this result by contrasting CFMIP2 AMIP and AMIP + 4 K simulations. More than 80 % of the difference in SH cyclone LWP between these simulations can be explained by changes in the WCB moisture flux. In the next section we will utilize observations of cloud-top phase to further examine how cloud glaciation might affect cyclone LWP.

3.4 The spatial distribution of LWP within cyclones

3.4.1 Sensitivity to the WCB moisture flux and SST

In Sect. 3.3 we have investigated the link between large-scale meteorology, as characterized by the WCB moisture flux, and extratropical cyclone LWP averaged to a cyclone mean, or the regional scale. The moisture flux along the WCB explains a great deal of the variability in cyclone LWP in models and observations. Increases in the WCB moisture flux also predict the decadal trend in SH LWP_RM. Over 80 % of the cyclone LWP response in the SH can be explained using the GCM's current variability and the predicted change in the WCB moisture flux. All of these lines of evidence show that mixed-phase transitions do not account for the majority of the increase in LWP in response to warming, and ultimately the negative feedback in extratropical cyclones. In this section we will use observations of cloud-top phase to examine whether any variability in extratropical cyclone LWP can be linked to a transition from ice to liquid consistent with a warming signal (that is to say, phase transitions consistent with the mixed-phase cloud feedback).

We will examine the response of LWP within the cyclone composite (LWP_ij) based on multiple linear regression on the WCB moisture flux into the cyclone and SST_ij. Similarly to Eq. (4), the regression model considered here is

$$\begin{array}{}\text{(6)}& {\mathrm{LWP}}_{ij}=a_{ij}\cdot \mathrm{WCB}+b_{ij}\cdot {\mathrm{SST}}_{ij}+c_{ij}+{\mathrm{residual}}_{ij},\end{array}$$

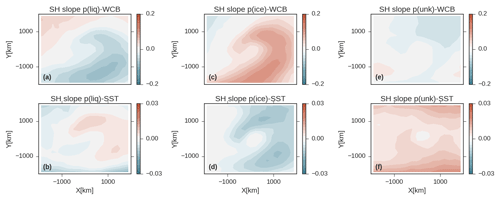
where the subscripts i and j refer to areal averages within the composites in the longitudinal and poleward directions (see Table 1). Each averaging region is approximately 200 km × 200 km. Values for the coefficients are calculated by fitting the regression model across cyclones in each averaging region ij. To simplify our presentation and compare across GCMs and observations, we show the regression coefficients for the GCMs in Table 2 and the observations averaged in the longitudinal direction. The zonal means of coefficient values of a_ij and b_ij are shown in Fig. 10 (full composite maps of a_ij and b_ij are shown in Fig. S12, but show little additional structure in the longitudinal direction). Unsurprisingly, there is a strong positive relationship between the WCB moisture flux and LWP_ij throughout the cyclone (e.g., the coefficient a_ij in Eq. 6). Increasing SST_ij tends to covary with increased LWP_ij in the part of the composite poleward of the low and with decreased LWP_ij in the portion of the composite equatorward of the low (e.g., b_ij).

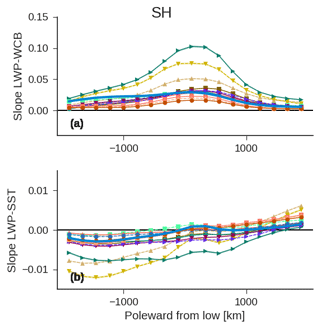
Figure 10 The multiple linear regression slopes from Eq. (6) averaged zonally across the composite. The x axis shows distance from the low-pressure center oriented toward the pole. Regression slopes from the NH are shown in (Fig. S13). Panel (a) shows the slope relating the WCB moisture flux into the cyclone and LWP_ij (units are kg mm day⁻¹ m⁻²). Panel (b) shows the slope of the regression relating SST_ij and LWP_ij (kg m⁻² K⁻¹). The 95 % confidence intervals in the zonal-mean regression slope are shown as shading.

Comparison between models and observations shows that there is variability between models and observations regarding the sensitivity of LWP_ij to the WCB moisture flux into the cyclone (Fig. 10a), which is consistent with the range of slopes shown in Fig. 1. However, the relation between LWP_ij and SST_ij within the composite is fairly similar across models (Fig. 10b). Increasing SST in the equatorward part of the composite tends to covary with decreasing LWP_ij and increasing SST_ij in the poleward part of the composite covaries with increases in LWP_ij.

This negative relationship between local changes in SST_ij and LWP_ij within the part of the composite that is equatorward of the low agrees with previous studies showing breakup in midlatitude stratocumulus with advection over warmer SSTs due to decoupling of the subcloud layer (Norris and Iacobellis, 2005), and is consistent with the prevailing hypothesis regarding warm clouds in the subtropical trade cumulus and stratocumulus regions (Klein et al., 2017). It is possible that the poleward enhancement in LWP_ij in response to enhancement in SST_ij may relate to shifts from ice to liquid cloud, but it might also relate to other meteorological controls on cloud cover and thickness (Grise and Medeiros, 2016).

Do the changes in LWP inferred from Eq. (6) translate into a meaningful change in reflected shortwave radiation? As shown in Bodas-Salcedo (2018) and Bodas-Salcedo et al. (2016), the effect of changes in LWP is highly dependent on the cloud regime that they are occurring in. In particular, overlying cloud can act to blunt the effect of changes in LWP on top-of-the-atmosphere reflected shortwave radiation. For example, an optically thick layer of ice cloud over the liquid in the cyclone would result in very little impact from LWP variability. We offer an approximate calculation of the change in reflected shortwave radiation consistent with the coefficients calculated in Eq. (6) using observations from CERES. The idea underlying this calculation is that the CERES top-of-the-atmosphere reflected shortwave radiation will include the effects of overlying ice cloud. The sensitivity in reflected shortwave radiation to LWP will be lowered by the effects of ice cloud. Daily-mean all-sky albedo from CERES SYN1DEG (Doelling et al., 2016; Wielicki et al., 1996) was calculated from 3-hourly data from 2003 to 2015, for which the solar zenith angle does not exceed 45^∘ (see McCoy et al., 2018b for a full discussion of these data). Regression of albedo on LWP variability gives an empirical relationship between LWP and albedo (Fig. S14). Radiative fluxes are more readily comparable to previous studies of cloud feedbacks. Thus, the change in albedo is scaled by the annual mean insolation taken from the CERES EBAF-TOA edition 4 data set (Loeb et al., 2009) averaged over 30–80^∘ to give the change in W m⁻² per change in LWP. While empirical, this is a relatively simple way to examine the effects of overlying ice cloud blunting the effects of underlying liquid variability on top-of-the-atmosphere albedo.

We find that LWP is always positively correlated with albedo (Fig. S14). At zeroth order we expect this based on the robust positive relationship between cloud fraction and all-sky albedo (Bender et al., 2011a, 2017), and remembering that microwave LWP is the average of in-cloud liquid and clear sky. If we multiply the relationships for the SH from the regression model (Eq. 6, Fig. S12a, b) by the slope of the regression between LWP and albedo, then this gives the change in albedo across the cyclone composite consistent with a unit increase in the WCB moisture flux or SST. The WCB moisture flux increases by approximately 0.2 mm day⁻¹ for a 1 K increase in SST in the SH if wind speed is held constant and WVP increases following Clausius–Clapeyron (Fig. 6c). Thus, we scale the change in albedo per unit change in the WCB moisture flux by 0.2 mm day⁻¹ to give a change in albedo related to changes in the WCB moisture flux consistent with a 1 K SST increase (assuming no change in wind speed). In the context of Eq. (6) the net change in reflected shortwave radiation that is implied by a 0.2 mm day⁻¹ increase in the WCB moisture flux is 0.87 W m⁻² and reflected shortwave radiation decreases by 0.23 W m⁻² for a 1 K SST increase. Again, these empirical calculations are simplistic and are only intended to approximate the effect of the blunting of the efficacy of liquid on driving changes in top-of-the-atmosphere albedo. Overall, we find that the changes in LWP that are empirically linked to changes in the WCB moisture flux and SST in the multiple regression shown in Eq. (6) translate to reasonably large negative and positive feedbacks, respectively. These implied feedbacks may be contrasted with the zonal-mean cloud feedbacks from the CFMIP2 and CFMIP1 models, with a strongest value for the negative lobe of the shortwave cloud feedback dipole of −2 W m⁻² in some GCMs (Zelinka et al., 2013, 2016).

3.4.2 Insight from cloud phase observed by AIRS

We have shown that LWP covaries with the WCB moisture flux at a fixed SST and how SST and LWP covary at a fixed WCB moisture flux within cyclones. It is also shown that the LWP changes associated with changes in SST, and the moisture flux could have the capability to appreciably change the reflected shortwave flux in extratropical cyclones. Is this increase in LWP_ij with increasing SST_ij at a fixed WCB moisture flux in the poleward half of the composite from phase transitions? We examine the sensitivity of cloud top phase to SST_ij and WCB to see if there is any consistency in regions where clouds become more liquid dominated and regions where the LWP_ij sensitivity to SST_ij suggests a phase transition. Cloud-top phase was measured by the AIRS instrument during the period 2003–2015. It is important to caveat the following analysis by noting that, unlike the other observational data sets used in this paper (MAC-LWP and CERES), data from AIRS are not diurnally averaged. Data are only available for the Aqua satellite's overpass times. The effects of this temporal subsetting of the data are not clear. However, the goal of the analysis we are pursuing is qualitative. Our intention is to see if liquid cloud phase increases at the expense of ice phase with increasing SST in the same regions that LWP increases with increasing SST. Figure S15 shows cyclone-composited AIRS observations. The structure of the ice and liquid phase exhibits a reasonable ice cloud shield and liquid warm sector – indicating that it may shed at least some light on variability in cloud-top phase within cyclones.

As discussed in the Methods section, when the cloud is broken, mixed-phased, or possibly supercooled liquid, the infrared signature becomes weak and the cloud top is flagged as unknown by AIRS. Here, we examine the probability that a given cloud-top phase (liquid, ice, or unknown) was detected by AIRS given that any phase detection was made in a cyclone composite framework. We examine how phase depends on the WCB moisture flux and how it depends on SST_ij. This is done analogously to the analysis performed in Sect. 3.4.1 in the context of multiple linear regression.

$$\begin{array}{}\text{(7)}& p{\left(x\right)}_{ij}=a_{ij}\cdot \mathrm{WCB}+b_{ij}\cdot {\mathrm{SST}}_{ij}+c_{ij}+{\mathrm{residual}}_{ij},\end{array}$$

where p(x)_ij is the probability of a cloud-top phase being an arbitrary phase x (ice, liquid, or unknown) given that a phase detection was made.

In this work we have focused on the SH for brevity because it is interesting from a modeling perspective and because the behavior of cyclone LWP as a function of the WCB moisture flux in the NH is approximately the same, giving little additional explanatory value to including it. However, the preponderance of unknown-topped cloud observed by AIRS in the SH necessitates contrasting NH and SH midlatitude oceans to offer insight into whether cloud-top phase changes might explain some of the response of LWP to SST within cyclones.

Figure 11 The coefficients in the multiple linear regression relating the probability of liquid, ice, and unknown cloud-top phase to the WCB moisture flux (units are day mm⁻¹) into the cyclone and SST_ij within the cyclone (units are K⁻¹, Eq. 6). All data are from the NH. Panels (a, b) relate to the probability of liquid topped clouds, panels (c, d) to ice-topped clouds, and panels (e, f) to unknown phase. Note that all probabilities are the probability of detecting a specific phase, given that a phase detection has been made. The first row shows the coefficient relating the WCB moisture flux into the cyclone to cloud-top phase probability. The second row shows the coefficient between SST_ij and cloud-top phase.

Figure 12 As in Fig. 11, but for the SH.

The coefficients from training Eq. (6) across cyclones in the SH are shown in Fig. 12. Overall, the effect of increasing moisture flux into the cyclone is to increase the frontal cloud which is ice-topped (Fig. 12c). The ice cloud is anti-correlated with SST – as one would intuitively expect (Figs. 11d and 12d). However, most of this is along the comma-shaped frontal region, consistent with Bodas-Salcedo (2018). In the SH increasing SSTs covary with enhancement in the prevalence of unknown cloud tops at the expense of the liquid and ice fraction across the entire cyclone composite (Fig. 12b, d, f).

While the SST dependence of LWP_ij is quite similar across models and observations in both hemispheres (Figs. 10b, S14), the dependence of observed cloud-top phase on SST_ij is different in the NH and SH. This because AIRS identifies a very large fraction of the SH clouds as unknown phase.

In the NH, the probability of liquid-topped clouds increases with increasing SST in the poleward part of the composite (Fig. 11b). Toward the Equator, increasing SST increases the fraction of unknown cloud tops (Fig. 11f). Increasing liquid fraction in the poleward half of NH cyclones over warmer SSTs (Fig. 11b) is consistent with transitions from a more ice-dominated to a more liquid-dominated state. The covariance of LWP_ij and SST_ij in these regions (Figs. 10b, S12b, d, S13b) appears to bear out this explanation. This may simply reflect an increase in liquid at the expense of ice, or it may reflect an increase in overall condensate via suppression of the efficient depletion of cloud condensate via ice-phase precipitation (Field and Heymsfield, 2015).

The decrease in both liquid and ice fraction and the increase in unknown cloud tops over warmer SSTs in the equatorward portion of NH cyclones and in the entirety of SH cyclone composites is perplexing. One possibility is that it may be linked to transitions from closed to open mesoscale cellular convection (McCoy et al., 2017c; Norris and Iacobellis, 2005), leading to weaker infrared signals and thus unknown cloud-top phase classification from AIRS (Nasiri and Kahn, 2008; Kahn et al., 2011). This may point toward the pathway of higher SST, more cumuliform cloud, and more broken cloud (Norris and Iacobellis, 2005), which is also consistent with other empirical studies of low cloud cover in the subtropics (Klein et al., 2017). Another possibility is that the Southern Ocean is much more dominated by supercooled liquid cloud (Chubb et al., 2013; Kanitz et al., 2011; Hu et al., 2010; Tan et al., 2014) and it does not have the same phase transition sensitivity as the NH oceans.

4 Conclusions

We have examined the behavior of extratropical cyclones (centered 30–80^∘) in models and long-term microwave observations for the period 1992–2015. We use the warm conveyor belt (WCB) moisture flux to characterize the synoptic state of these cyclones. The WCB moisture flux is the product of water vapor path (WVP) and wind speed at 10 m (WS_10 m) averaged within 2000 km of the cyclone center. As the moisture flux along the WCB increases, the liquid water path (LWP) within the cyclone increases (Figs. 1, 2a). The ability of GCMs to reproduce this relationship is examined using an array of models from high-resolution simulations within the convective grey zone to coarse resolutions typical of fully coupled GCMs performing climate integration. It is found that the sensitivity of cyclone LWP to the WCB moisture flux in these GCMs varies by a factor of 2 around the observed sensitivity. There was not a systematic dependence of this relationship on resolution (Fig. 1). However, convection-permitting models agreed well with each other and the observations – indicating that parametric uncertainty within convective parameterizations may contribute to uncertainty in the relationship between the WCB moisture flux and cyclone LWP in GCMs.

The WCB moisture flux into cyclones will increase as the planet warms because WVP scales with temperature following Clausius–Clapeyron. Because cyclone LWP increases with the WCB moisture flux, this is projected to lead to a negative shortwave cloud feedback. A simple calculation holding wind speed and cyclone frequency of occurrence fixed and assuming that WVP changes by 6 % estimates an increase in cyclone LWP of 3.62 g m⁻² in the SH (Fig. 6). An empirical calculation of brightening estimates that changes in cyclone LWP due to the enhanced WCB moisture flux would equate to a brightening of 0.87 W m⁻² within Southern Ocean cyclones, which is an appreciable fraction of the multimodel mean shortwave cloud feedback (McCoy et al., 2016; Zelinka et al., 2013).

Within the observational record we can only infer feedbacks from covariability, but by using model simulations of transient warming we can see if these inferences have predictive ability. Analysis of simulations performed with observed SSTs and SST enhanced by 4 K shows that differences in the WCB moisture flux can explain the majority of the change in simulated cyclone LWP between the current climate and the warmed climate (Fig. 8). Thus, the relationship between the WCB moisture flux and cyclone LWP in the current climate may be used to understand cloud feedbacks. Based on this, we propose two extratropical cloud feedbacks within cyclone systems:

1. The first is a Clausius–Clapeyron-mediated local feedback whereby increasing atmospheric temperature enhances the available moisture to be fluxed into the cyclone. This feedback is in line with the feedback proposed in Betts and Harshvardhan (1987), but is expressed in the framework of a midlatitude cyclone, which imposes a structure on the derivative of the moist adiabat with respect to temperature.

2. The second is a dynamical feedback related to changes in the genesis and development of cyclones in response to warming, which in turn affects the wind speed and thus the flux of moisture into the cyclone. The sign of the wind-speed-driven feedback appears to be uncertain in a warming climate, but this relationship creates a pathway between synoptic-scale dynamics and the cloud feedback.

Cloud-top phase observed by AIRS was used to investigate whether changes in LWP within cyclones unexplained by the WCB moisture flux were consistent with a transition from ice to liquid phase. In the equatorward half of cyclones LWP decreases with increasing SST, and in the poleward half of cyclones LWP increases with increasing SST. Utilizing cloud-top phase data from AIRS, we show that changes from ice to liquid cloud could contribute to increasing LWP with increasing SST in the poleward half of cyclone composites (Figs. 11b and 12b). In the equatorward half of NH cyclone composites and across all of SH cyclones, unknown phase (broken or mixed-phase) cloud tops become more frequent as SST increases (Fig. 11f). This may be consistent with the breakup of stratocumulus over warmer SSTs (Norris and Iacobellis, 2005).

In summary, we find a robust relationship between the moisture flux into extratropical cyclones and their LWP in observations and GCMs (Fig. 3a). This relationship has the ability to explain cyclone-to-cyclone variability, regional- and monthly-mean variability across ocean basins (Fig. 2a), and the observed trend in Southern Ocean LWP from 1992 to 2015 (Fig. 4). While we can only examine covariability within the observational record, we can examine the transient climate response within GCMs to see if this relationship has utility in predicting the response of extratropical cyclone LWP to climate change. It is found that over 80 % of the LWP change in extratropical cyclones can be explained using their change in the WCB moisture flux and the relationship between the WCB moisture flux and cyclone LWP in their simulations of the present climate. We propose that the relationship between the WCB moisture flux and liquid water path in midlatitude cyclones is a key aspect of whether a GCM will have a strongly or weakly negative shortwave cloud feedback in the extratropics and thus acts as a useful constraint on climate sensitivity (Caldwell et al., 2016).