Predictions of diffusion rates of large organic molecules in secondary organic aerosols using the Stokes–Einstein and fractional Stokes–Einstein relations

Information on the rate of diffusion of organic molecules within secondary organic aerosol (SOA) is needed to accurately predict the effects of SOA on climate and air quality. Diffusion can be important for predicting the growth, evaporation, and reaction rates of SOA under certain atmospheric conditions. Often, researchers have predicted diffusion rates of organic molecules within SOA using measurements of viscosity and the Stokes–Einstein relation ($D\propto \mathrm{1}/\mathit{\eta }$, where D is the diffusion coefficient and η is viscosity). However, the accuracy of this relation for predicting diffusion in SOA remains uncertain. Using rectangular area fluorescence recovery after photobleaching (rFRAP), we determined diffusion coefficients of fluorescent organic molecules over 8 orders in magnitude in proxies of SOA including citric acid, sorbitol, and a sucrose–citric acid mixture. These results were combined with literature data to evaluate the Stokes–Einstein relation for predicting the diffusion of organic molecules in SOA. Although almost all the data agree with the Stokes–Einstein relation within a factor of 10, a fractional Stokes–Einstein relation ($D\propto \mathrm{1}/{\mathit{\eta }}^{\mathit{\xi }}$) with ξ=0.93 is a better model for predicting the diffusion of organic molecules in the SOA proxies studied. In addition, based on the output from a chemical transport model, the Stokes–Einstein relation can overpredict mixing times of organic molecules within SOA by as much as 1 order of magnitude at an altitude of ∼3 km compared to the fractional Stokes–Einstein relation with ξ=0.93. These results also have implications for other areas such as in food sciences and the preservation of biomolecules.

1 Introduction

Atmospheric aerosols, suspensions of micrometer and sub-micrometer particles in the Earth's atmosphere, modify climate by interacting with incoming solar radiation and by altering cloud formation and cloud properties (Stocker et al., 2013). These aerosols also negatively impact air quality and may facilitate the long-range transport of pollutants (Friedman et al., 2014; Mu et al., 2018; Shrivastava et al., 2017a; Vaden et al., 2011; Zelenyuk et al., 2012).

A large fraction of atmospheric aerosols are classified as secondary organic aerosol (SOA). SOA is formed in the atmosphere when volatile organic molecules, emitted from both anthropogenic and natural sources, are oxidized and partition to the particle phase (Ervens et al., 2011; Hallquist et al., 2009). The exact chemical composition of SOA remains uncertain; however, measurements have shown that SOA contains thousands of different organic molecules, and the average oxygen-to-carbon (O:C) ratio of organic molecules in SOA ranges from 0.3 to 1.0 or even higher (Aiken et al., 2008; Cappa and Wilson, 2012; Chen et al., 2009; DeCarlo et al., 2008; Ditto et al., 2018; Hawkins et al., 2010; Heald et al., 2010; Jimenez et al., 2009; Laskin et al., 2018; Ng et al., 2010; Nozière et al., 2015; Takahama et al., 2011; Tsimpidi et al., 2018). SOA also contains a range of organic functional groups including alcohols and carboxylic acids (Claeys et al., 2004, 2007; Edney et al., 2005; Fisseha et al., 2004; Glasius et al., 2000; Liu et al., 2011; Surratt et al., 2006, 2010).

In order to accurately predict the impacts of SOA on climate, air quality, and the long-range transport of pollutants, information on the rate of diffusion of organic molecules within SOA is needed. For example, predictions of SOA particle size, which has implications for climate and visibility, vary significantly in simulations as the diffusion rate of organic molecules is varied from 10⁻¹⁷ to 10⁻¹⁹ m² s⁻¹ (Zaveri et al., 2014). Lifetimes of polycyclic aromatic hydrocarbons (PAHs) in an SOA particle increase as the bulk diffusion coefficient of PAHs decreases from 10⁻¹⁶ m² s⁻¹ at a relative humidity of 50 % to 10⁻¹⁸ m² s⁻¹ under dry conditions (Zhou et al., 2019). Shrivastava et al. (2017a) have shown that including shielding by a viscous organic aerosol coating (equivalent to a bulk diffusion limitation) results in better model predictions of observed concentrations of PAHs. Reactivity in SOA can also depend on the diffusion rates of organic molecules (Davies and Wilson, 2015; Lakey et al., 2016; Li et al., 2015; Liu et al., 2018; Shiraiwa et al., 2011; Zhang et al., 2018; Zhou et al., 2013). For the cases discussed above, the diffusion of organic molecules within SOA becomes a rate-limiting step only when diffusion rates are small.

In some cases, the diffusion rates of organic molecules in SOA have been measured or inferred from experiments (Abramson et al., 2013; Liu et al., 2016; Perraud et al., 2012; Ullmann et al., 2019; Ye et al., 2016). However, in most cases researchers have predicted diffusion rates of organic molecules within SOA using measurements of viscosities and the Stokes–Einstein relation (Booth et al., 2014; Hosny et al., 2013; Koop et al., 2011; Maclean et al., 2017; Power et al., 2013; Renbaum-Wolff et al., 2013; Shiraiwa et al., 2011; Song et al., 2015, 2016a). This is due to the development and application of several techniques that can measure the viscosity of ambient aerosol or small volumes in the laboratory (Grayson et al., 2015; Pajunoja et al., 2014; Renbaum-Wolff et al., 2013; Song et al., 2016b; Virtanen et al., 2010). The Stokes–Einstein relation (Eq. 1) states that diffusion is inversely related to viscosity:

$$\begin{array}{}\text{(1)}& D={\displaystyle \frac{kT}{\mathrm{6}\mathit{\pi }\mathit{\eta }{R}_{\mathrm{H}}}},\end{array}$$

where D is the diffusion coefficient, k is the Boltzmann constant, T is the temperature in Kelvin, R_H is the hydrodynamic radius of the diffusing species, and η is the viscosity of the matrix. Until now, only a few studies have investigated the accuracy of the Stokes–Einstein relation for predicting the diffusion coefficients of organic molecules in SOA, and almost all of these studies relied on sucrose as a proxy for SOA particles (Bastelberger et al., 2017; Chenyakin et al., 2017; Price et al., 2016). Sucrose was used as a proxy for SOA in these studies because (1) sucrose has an O:C ratio similar to that of highly oxidized components of SOA, and (2) viscosity and diffusion data for sucrose exist in the literature (mainly from the food science literature, as well as from Power et al., 2013, who reported viscosities far outside the range of what had previously been reported). However, studies with other proxies of SOA are required to determine if the Stokes–Einstein relation can accurately represent the diffusion of organic molecules in SOA and to more accurately predict the role of SOA in climate, air quality, and the transport of pollutants (Reid et al., 2018; Shrivastava et al., 2017b).

In the following, we expand on previous studies with sucrose matrices by testing the Stokes–Einstein relation in the following proxies for SOA: 2-hydroxypropane-1,2,3-tricarboxylic acid (i.e., citric acid), 1,2,3,4,5,6-hexanol (i.e., sorbitol), and a mixture of citric acid and sucrose. These proxies have functional groups that have been identified in SOA and O:C ratios similar to those ratios found in the most highly oxidized components of SOA in the atmosphere (1.16, 1.0, and 0.92 for citric acid, sorbitol, and sucrose, respectively). To test the Stokes–Einstein relation, we first determined the diffusion coefficients of fluorescent organic molecules as a function of water activity (a_w) in these SOA proxies using rectangular area fluorescence recovery after photobleaching (rFRAP; Deschout et al., 2010). Studies as a function of a_w are critical because as the relative humidity (RH) changes in the atmosphere, a_w (and hence water content) in SOA will change to maintain equilibrium with the gas phase. The diffusing organic molecules studied in this work were the fluorescent organic molecules rhodamine 6G and cresyl violet (Fig. S1 in the Supplement). Details of the experiments are given in the Methods section. The experimental diffusion coefficients are compared with predictions using literature viscosities (Rovelli et al., 2019; Song et al., 2016b) and the Stokes–Einstein relation. The results from the current study are then combined with literature diffusion (Champion et al., 1997; Chenyakin et al., 2017; Price et al., 2016; Rampp et al., 2000; Ullmann et al., 2019) and viscosity (Först et al., 2002; Grayson et al., 2017; Green and Perry, 2007; Haynes, 2015; Lide, 2001; Migliori et al., 2007; Power et al., 2013; Quintas et al., 2006; Rovelli et al., 2019; Swindells et al., 1958; Telis et al., 2007; Ullmann et al., 2019) data to assess the ability of the Stokes–Einstein relation to predict the diffusion of organic molecules in atmospheric SOA. The ability of the fractional Stokes–Einstein relation (see below) to predict diffusion is also tested.

In addition to atmospheric applications, the results from this study have implications for other areas in which the diffusion of organic molecules within organic–water matrices is important, such as the cryopreservation of proteins (Cicerone and Douglas, 2012; Fox, 1995; Miller et al., 1998), the storage of food products (Champion et al., 1997; van der Sman and Meinders, 2013), and the viability of pharmaceutical formulations (Shamblin et al., 1999). The results also have implications for our understanding of the properties of deeply supercooled and supersaturated glass-forming solutions, which are important for a wide range of applications and technologies (Angell, 1995; Debenedetti and Stillinger, 2001; Ediger, 2000).

2 Methods

2.1 Preparation of fluorescent organic–water films

The technique used here to determine diffusion coefficients required thin films containing the organic matrix (i.e., citric acid or sorbitol or a mixture of citric acid and sucrose), water, and trace amounts of the diffusing organic molecules (i.e., fluorescent organic molecules). Citric acid (≥99 % purity) and sorbitol (≥98 % purity) were purchased from Sigma-Aldrich and used as received. Rhodamine 6G chloride (≥99 % purity) and cresyl violet acetate (≥75 % purity) were purchased from Acros Organics and Santa Cruz Biotechnology, respectively, and used as received. Solutions containing the organic matrix, water, and the diffusing molecules were prepared gravimetrically; 55 wt % citric acid solutions and 30 wt % sorbitol and sucrose–citric acid solutions were used to prepare the citric acid, sorbitol, and sucrose–citric acid thin films, respectively. A mass ratio of 60:40 sucrose to citric acid was used for the sucrose–citric acid matrix. The concentrations of rhodamine 6G and cresyl violet in the solutions were 0.06 and 0.08 mM, respectively. After the solutions were prepared gravimetrically, the solutions were passed through a 0.02 µm filter (Whatman^™) to eliminate impurities. Droplets of the solution were placed on cleaned siliconized hydrophobic slides (Hampton Research), by either nebulizing the bulk solution or using the tip of a sterilized needle (BD PrecisionGlide Needle, Franklin Lakes, NJ, USA). The generated droplets ranged in diameter from ∼100 to ∼1300 µm. After the droplets were located on the hydrophobic slides, the hydrophobic slides were placed inside sealed glass containers with a controlled water activity (a_w). The a_w was set by placing saturated inorganic salt solutions with known a_w values within the sealed glass containers. The a_w values used ranged from 0.14 to 0.86. When the a_w values were higher than 0.86, recovery times were too fast to measure with the rFRAP setup. When the a_w values were lower than 0.14 or 0.23, depending on the organic solute, solution droplets often crystallized. The slides holding the droplets were left inside the sealed glass containers for an extended period of time to allow the droplets to equilibrate with the surrounding a_w. The method used to calculate equilibration times is explained in Sect. S1 in the Supplement, and conditioning times for all samples are given in Tables S2–S5 in the Supplement. Experimental times for conditioning were a minimum of 3 times longer than the calculated equilibration times.

After the droplets on the slides reached equilibrium with the a_w of the airspace over the salt solution, the sealed glass containers holding the slides and conditioned droplets were brought into a Glove Bag^™ (Glas-Col). The a_w within the Glove Bag was controlled using a humidified flow of N₂ gas and monitored using a handheld hygrometer. The a_w within the Glove Bag^™ was set to the same a_w as used to condition the droplets to prevent the droplets from being exposed to an unknown and uncontrolled a_w. To form a thin film, aluminum spacers were placed on the siliconized glass slide holding the droplets, followed by another siliconized glass slide, which sandwiched the droplets and the aluminum spacers. The thickness of the aluminum spacers (30–50 µm) determined the thickness of the thin film. The two slides were sealed together by vacuum grease spread around the perimeter of one slide before sandwiching (see Fig. S2 for details).

The organic matrices were often supersaturated with respect to crystalline citric acid or sorbitol. Nevertheless, crystallization was not observed in most cases until a_w values 0.14–0.23, depending on the organic matrix, because the solutions were passed through a 0.02 µm filter and the glass slides used to make the thin films were covered with a hydrophobic coating. Filtration likely removed heterogeneous nuclei that could initiate crystallization, and the hydrophobic coating reduced the ability of these surfaces to promote heterogeneous nucleation (Bodsworth et al., 2010; Pant et al., 2006; Price et al., 2014; Wheeler and Bertram, 2012). In the cases in which crystallization was observed, determined using optical microscopy, the films were not used in rFRAP experiments. An image demonstrating the difference in appearance between crystallized and noncrystallized droplets is given in Fig. S3. We did not condition droplets without fluorescent organic molecules to determine the effect of the tracer molecules on crystallization. However, previous studies have shown that droplets with the compositions and range of a_w values studied here can exist in the metastable liquid state if heterogeneous nucleation by surfaces is reduced. Furthermore, since the concentration of the tracers in the droplets were so low, the tracers are not expected to change the driving force for crystallization in the droplets.

2.2 Rectangular area fluorescence recovery after photobleaching (rFRAP) technique and extraction of diffusion coefficients

Diffusion coefficients were determined using the rFRAP technique reported by Deschout et al. (2010). The technique uses a confocal laser scanning microscope to photobleach fluorescent molecules in a specified volume of an organic thin film containing fluorescent molecules. The photobleaching event initially reduces the fluorescence intensity within the bleached volume. Afterward, the fluorescence intensity within the photobleached volume recovers due to the diffusion of fluorescent molecules from outside the bleached region. From the time-dependent recovery of the fluorescence intensity, diffusion coefficients are determined. All diffusion experiments here were performed at 295±1 K.

The rFRAP experiments were performed on a Zeiss Axio Observer LSM 510MP laser scanning microscope with a 10X, 0.3 NA objective, and a pinhole setting between 80 and 120 µm. Photobleaching and the subsequent acquisition of recovery images were done using a 543 nm helium–neon (HeNe) laser. The bleach parameters (e.g., laser intensity, iterations, laser speed) were varied for each experiment so that the fraction of fluorescent molecules being photobleached in the bleach region was about 30 %. A photobleaching of about 30 % was suggested by Deschout et al. (2010), who report that diffusion coefficients determined using the rFRAP technique are independent of the extent of photobleaching up to a bleach depth of 50 %. The energy absorbed by the thin film during photobleaching is not expected to affect experimental diffusion coefficients. Although local heating may occur during photobleaching, the thermal diffusivity in the samples is orders of magnitude greater than the molecular diffusivity, and the heat resulting from photobleaching will dissipate to the surroundings on a timescale much faster than the diffusion of molecules will occur (Chenyakin et al., 2017). Measurements as a function of photobleaching size and power are consistent with this expectation (Chenyakin et al., 2017; Ullmann et al., 2019).

Bleached areas ranged from 20 to 400 µm². The geometry of the photobleached region was a square with sides of length l_x and l_y ranging from 4.5 to 20 µm. Smaller bleach areas were used in experiments in which diffusion was slower in order to shorten recovery times. Chenyakin et al. (2017) showed that experimental diffusion coefficients varied by less than the experimental uncertainty when the bleach area was varied from 1 to 2500 µm² in sucrose–water films. Similarly, Deschout et al. (2010) demonstrated that diffusion coefficients varied by less than the experimental uncertainty when the bleach area was varied from approximately 4 to 144 µm² in sucrose–water films. The images collected during an rFRAP experiment represent fluorescence intensities as a function of x and y coordinates and are taken at regular time intervals after photobleaching. An example of images recorded during an rFRAP experiment is shown in Fig. S4. Every image taken following the photobleaching event is normalized relative to an image taken before photobleaching. To reduce noise, all images are downsized by averaging from a resolution of 512×512 to 128×128 pixels.

The mathematical description of the fluorescence intensity as a function of position (x and y) and time (t) after photobleaching a rectangular area in a thin film was given by Deschout et al. (2010):

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\displaystyle \frac{F(x,y,t)}{F_{\mathrm{0}}(x,y)}}& =\left[\mathrm{1}-{\displaystyle \frac{K_{\mathrm{0}}}{\mathrm{4}}}\cdot \left(\mathrm{erf}\left({\displaystyle \frac{x+\frac{l_x}{\mathrm{2}}}{\sqrt{r^{\mathrm{2}}+\mathrm{4}Dt}}}\right)\right.\right.\\ & \left.-\mathrm{erf}\left({\displaystyle \frac{x-\frac{l_x}{\mathrm{2}}}{\sqrt{r^{\mathrm{2}}+\mathrm{4}Dt}}}\right)\right)\cdot \left(\mathrm{erf}\left({\displaystyle \frac{y+\frac{l_y}{\mathrm{2}}}{\sqrt{r^{\mathrm{2}}+\mathrm{4}Dt}}}\right)\right.\\ & \left.\left.-\mathrm{erf}\left({\displaystyle \frac{y-\frac{l_y}{\mathrm{2}}}{\sqrt{r^{\mathrm{2}}+\mathrm{4}Dt}}}\right)\right)\right],\end{array}\end{array}$$

where $F(x,y,t)$ is the fluorescence intensity at position x and y after a time t, F₀(x,y) corresponds to the initial intensity at position x and y before photobleaching, K₀ is related to the initial fraction of photobleached molecules in the bleach region, and l_x and l_y correspond to the size (length) of the bleach region in the x and y directions. The parameter r represents the resolution of the microscope, t is the time after photobleaching, and D is the diffusion coefficient.

The entire images (128×128 pixels following downsizing) collected during an rFRAP experiment were fit to Eq. (2) using a MATLAB script (The Mathworks, Natick, MA, USA), with the terms K₀ and r²+4Dt left as free parameters. An additional normalization factor was also left as a free parameter and returned a value close to 1, since images recorded after photobleaching were normalized to the pre-bleach image before fitting. To determine the bleach width (l_x, l_y), Eq. (2) was fit to the first five images recorded after photobleaching a film with the bleach width (l_x,l_y) left as a free parameter. The bleach width returned by the fit to the first five frames was then used as input in Eq. (2) to analyze the full set of images.

From the fitting procedure, a value for r²+4Dt was determined for each image and plotted as a function of time after photobleaching. A straight line was then fit to the r²+4Dt vs. t plot, and from the slope of the line D was calculated. An example is shown in Fig. S5. As the intensity of the fluorescence in the bleached region recovers, the noise in the data becomes large relative to the difference in fluorescence intensity between the bleached and non-bleached regions (i.e., signal). To ensure that we only use data with a reasonable signal-to-noise ratio, images were not used if this signal was less than 3 times the standard deviation of the noise.

Figure S6 shows a cross section of the fluorescence intensity along the x direction from the data in Fig. S4. Figure S6 is given only to visualize the fit of the equation to the data, and the cross-sectional fit was not used to determine diffusion coefficients. As mentioned above, the entire images (128×128 pixels following downsizing) were used to determine diffusion coefficients. To generate the cross-sectional view, at each position x, the measured fluorescence intensity is averaged over the width of the photobleached region in the y direction (black squares). Also included in Fig. S6 are cross-sectional views of the calculated fluorescence intensity along the x direction generated from the fitting procedure (solid red lines). To generate the line, Eq. (2) was first fit to the images. The resulting fit was then averaged over the width of the photobleached region in the y direction. The good agreement between the measured cross section and the predicted cross section illustrates that Eq. (2) describes the rFRAP data well.

Equation (2) assumes that there is no net diffusion in the axial direction (i.e., z direction). Deschout et al. (2010) have shown that Eq. (2) gives accurate diffusion coefficients when the numerical aperture of the microscope is low (≤0.45) and the thickness of the fluorescent films is small (≤120 µm), which is consistent with the numerical aperture of 0.30 and film thickness of 30–50 µm used here.

3 Results and discussion

3.1 Diffusion coefficients of organic molecules in citric acid, sorbitol, and sucrose–citric acid matrices

The experimental diffusion coefficients of organic molecules in matrices of citric acid, sorbitol, and sucrose–citric acid as a function of water activity (a_w) are shown in Fig. 1 (and listed in Tables S2–S5). The experimental diffusion coefficients depend strongly on a_w for all three proxies of SOA. As a_w increases from 0.23 (0.14 in one case) to 0.86, diffusion coefficients increase by between 5 and 8 orders of magnitude. This dependence on a_w arises from the plasticizing influence of water on these matrices; as a_w increases (and hence the water content increases) the viscosity decreases (Koop et al., 2011). In addition, the experimental diffusion coefficients varied significantly from matrix to matrix at the same a_w (Fig. 1). As an example, at a_w=0.23 the diffusion coefficient of rhodamine 6G is about 4 orders of magnitude larger in citric acid compared to the sucrose–citric acid mixture.

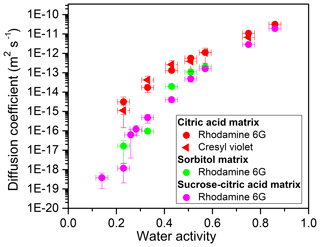
Figure 1 Experimental diffusion coefficients of fluorescent organic molecules in various organic matrices as a function of water activity (a_w). The x error bars represent the uncertainty in the measured a_w (±0.025) and y error bars correspond to 2 times the standard deviation in the diffusion measurements. Each data point is the average of a minimum of four measurements. Indicated in the legend are the fluorescent organic molecules studied and the corresponding matrices.

We also considered the relationship between $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}}$) and log (η), a comparison that allows for the identification of deviations from the Stokes–Einstein relation (Fig. 2). By plotting $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}})$, we account for differences in the hydrodynamic radii of diffusing species and small differences in temperature (within a range of 6 K). The viscosity corresponding to each diffusion coefficient was determined from relationships between a_w and viscosity developed from literature data (Figs. S7–S9). The solid line in Fig. 2 corresponds to the relationship between $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}})$ and log (η) if the Stokes–Einstein relation (Eq. 1) is obeyed. Figure 2 shows that the diffusion coefficients of the fluorescent organic molecules depend strongly on viscosity, with the diffusion coefficients varying by approximately 8 orders of magnitude as viscosity varied by 8 orders of magnitude. If the uncertainties of the measurements are considered, all the data points except three (89 % of the data) are consistent with predictions from the Stokes–Einstein relation (meaning that the error bars on the measurements overlap the solid line in Fig. 2) over 8 orders of magnitude of change in diffusion coefficients. This finding is remarkable considering the assumptions inherent in the Stokes–Einstein relation (e.g., the diffusing species is a hard sphere that experiences the fluid as a homogeneous continuum and no slip at the boundary of the diffusing species).

3.2 Comparison with relevant literature data

Previous studies have used sucrose to evaluate the ability of the Stokes–Einstein relation to predict the diffusion coefficients of organic molecules in SOA (Bastelberger et al., 2017; Chenyakin et al., 2017; Price et al., 2016). In addition, a recent study (Ullmann et al., 2019) used SOA generated in the laboratory from the oxidation of limonene, subsequently exposed to NH_3(g) (i.e., brown limonene SOA), to evaluate the Stokes–Einstein relation. Although studies with SOA generated in the laboratory are especially interesting, that previous study was limited to relatively low viscosities (≤10² Pa s), whereby a breakdown of the Stokes–Einstein relation is less expected. In Fig. 3a, we have combined the results from the current study (i.e., the results from Fig. 2) with previous studies of diffusion and viscosity in sucrose and brown limonene SOA (Champion et al., 1997; Chenyakin et al., 2017; Price et al., 2016; Rampp et al., 2000; Ullmann et al., 2019). To be consistent with the current study, we have not included data in Fig. 3a if the diffusion coefficients and viscosities were measured at, or calculated using, temperatures outside the range of 292–298 K and if the radius of the diffusing molecule was smaller than the radius of the organic molecules in the fluid matrix. Previous work has shown that the Stokes–Einstein relation is not applicable when the radius of the diffusing molecule is less than the radius of the matrix molecules, and those cases are beyond the scope of this work (Bastelberger et al., 2017; Davies and Wilson, 2016; Marshall et al., 2016; Power et al., 2013; Price et al., 2016; Shiraiwa et al., 2011). Additional details for the data shown in Fig. 3a are included in Sect. S2 and Table S6.

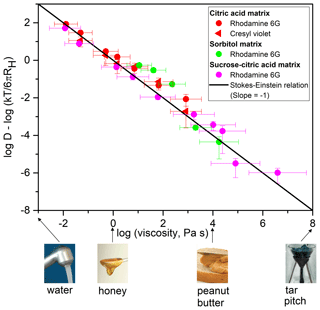
Figure 2 Plot of $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}})$ as a function of log (η) for the diffusion coefficients shown in Fig. 1. Viscosities (η) were determined from relationships between viscosity and a_w (Figs. S7–S9). T corresponds to the experimental temperature and R_H corresponds to the radius of each diffusing species (see Table S6). The x error bars were calculated using the uncertainty in a_w at which the samples were conditioned (±0.025) and uncertainties in the viscosity–a_w parameterizations. The y error bars represent 2 times the standard deviation of the experimental diffusion coefficients. The black line represents the relationship between $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}})$ and log (η) predicted by the Stokes–Einstein relation (slope $=-\mathrm{1}$). Shown at the bottom of the figure are various substances and their approximate room temperature viscosities to provide context, as in Koop et al. (2011). The image of tar pitch is part of an image from the pitch drop experiment (image courtesy of Wikimedia Commons, GNU Free Documentation License, University of Queensland, John Mainstone).

Based on Fig. 3a the diffusion coefficients of the organic molecules in sucrose matrices and matrices consisting of SOA generated in the laboratory depend strongly on viscosity, similar to the results shown in Fig. 2. In addition, almost all the data agree with the Stokes–Einstein relation (solid line in Fig. 3a) within a factor of 10. This finding is in stark contrast to the diffusion of water in organic–water mixtures, wherein much larger deviations between experimental and predicted diffusion coefficients were observed over the same viscosity range (Davies and Wilson, 2016; Marshall et al., 2016; Price et al., 2016).

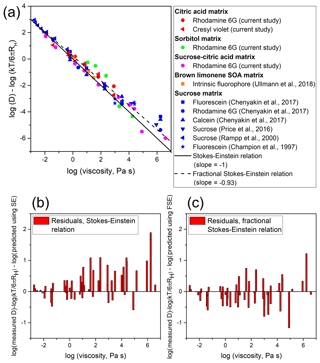
Figure 3 (a) Plot of $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}})$ as a function of log (η) for experimental diffusion coefficients reported in this work and literature data. Indicated in the legend are the diffusing organic molecules studied and the corresponding matrices. T corresponds to the experimental temperature of each diffusion coefficient and R_H corresponds to the radius of each diffusing species (Sect. S2 and Table S6). The symbols represent experimental data points. The solid line represents the relationship between $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}})$ and log (η) predicted by the Stokes–Einstein relation, while the dashed line represents the relationship between $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}})$ and log (η) predicted by a fractional Stokes–Einstein relation with a slope of −0.93 and crossover viscosity of 10⁻³ Pa s. Panels (b) and (c) are plots of the differences (i.e., residuals) between experimental and predicted values of $\log \left(D\right)-\log (kT/\mathrm{6}\mathit{\pi }{R}_{\mathrm{H}})$ using the Stokes–Einstein relation and the fractional Stokes–Einstein relation, respectively. The sum of squared residuals for the Stokes–Einstein relation is 19.7 and the sum of squared residuals for the fractional Stokes–Einstein relation is 10.8.

In Fig. 3b, we show the differences between the experimental values and the solid line in Fig. 3a as a function of viscosity. If the Stokes–Einstein relation describes the data well, these differences (i.e., residuals) should be scattered symmetrically about zero, while the magnitude of the residuals should be less than or equal to the uncertainty in the measurements. However, the residuals are skewed to be positive, especially as viscosity increases, with experimental diffusion faster than expected based on the Stokes–Einstein relation. Figure 3b suggests that the Stokes–Einstein relation may not be the optimal model for predicting diffusion coefficients in SOA, particularly at high viscosities.

3.3 Fractional Stokes–Einstein relation

When deviation from the Stokes–Einstein relation has been observed in the past, a fractional Stokes–Einstein relation ($D\propto \mathrm{1}/{\mathit{\eta }}^{\mathit{\xi }}$, where ξ is an empirical fit parameter) has often been used to quantify the relationship between diffusion and viscosity. For example, Price et al. (2016) showed that a fractional Stokes–Einstein relation can accurately represent the diffusion of sucrose in a sucrose matrix over a wide range of viscosities (from roughly 10⁰–10⁶ Pa s) with ξ=0.90. Building on that work, the data in Fig. 3a were fit to the following fractional Stokes–Einstein relation:

$$\begin{array}{}\text{(3)}& D=D_{\mathrm{c}}{\left({\displaystyle \frac{{\mathit{\eta }}_{\mathrm{c}}}{\mathit{\eta }}}\right)}^{\mathit{\xi }},\end{array}$$

where ξ is an empirical fit parameter, η_c is the crossover viscosity, and D_c is the crossover diffusion coefficient. The crossover viscosity is the viscosity at which the Stokes–Einstein relation and the fractional Stokes–Einstein relation predict the same diffusion coefficient. Based on the data in Fig. 3 we have chosen ${\mathit{\eta }}_{\mathrm{c}}={\mathrm{10}}^{-\mathrm{3}}$ Pa s. The crossover diffusion coefficient corresponds to the diffusion coefficient at η_c (which can be calculated with the Stokes–Einstein relation). The value of ξ is determined as the slope of the dashed line in Fig. 3a. The best fit to the data (represented by the dashed line in Fig. 3a) resulted in a ξ value of 0.93. Each data point was weighted equally when performing the fitting.

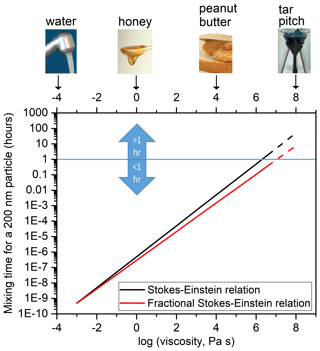
Figure 4 Mixing times of organic molecules within a 200 nm particle as a function of viscosity using the Stokes–Einstein relation (black line) and a fractional Stokes–Einstein relation (red line). The dashed lines indicate that the relations were extrapolated to viscosities beyond the tested range of viscosities ($\ge \mathrm{4}\times {\mathrm{10}}^{\mathrm{6}}$ Pa s).

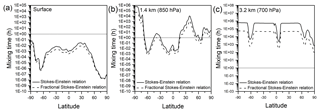
Figure 5 Mixing times (in hours) of organic molecules in 200 nm SOA particles at (a) the surface, (b) 850 hPa or ∼1.4 km of altitude, and (c) 700 hPa or ∼3.2 km of altitude using diffusion coefficients calculated with the Stokes–Einstein relation (solid black lines) and the fractional Stokes–Einstein relation (dashed black lines). A 1 h mixing time, which is often assumed in chemical transport models, is also indicated in each figure with a horizontal dotted line.

In Fig. 3c, we plotted the difference between the experimental values shown in Fig. 3a and the predicted values using the fractional Stokes–Einstein relation (dashed line in Fig. 3a). These residuals are more symmetrically scattered about zero compared to the residuals plotted in Fig. 3b. In addition, the sum of squared residuals (r²) in Fig. 3c was less than the sum of squared residuals in Fig. 3b (r²=10.8 compared to 19.7). Beyond the sum of squared residuals test we have performed a reduced chi-squared (χ²) test, which takes into account the extra fitting variable present in the fractional Stokes–Einstein relation. Assuming a variance of 0.25, the reduced χ² value is 1.24 for the Stokes–Einstein relation and 0.67 for the fractional Stokes–Einstein relation. This information suggests that the fractional Stokes–Einstein relation with an exponent value of ξ=0.93 may be the better model for predicting the diffusion coefficients of organic molecules in SOA compared to the traditional Stokes–Einstein relation. This is in close agreement with the findings of Price et al. (2016), who showed that the diffusion of sucrose in a sucrose–water matrix could be modeled using a fractional Stokes–Einstein relation with ξ=0.90 over a large range in viscosity. The new fractional Stokes–Einstein relation, which builds on the work of Price et al. (2016), was derived using diffusion data of several large organic molecules in several types of organic–water matrices and thus demonstrates a broader utility of the fractional Stokes–Einstein relation.

For the case of large diffusing molecules such as those included in this work (i.e., the radius of the diffusing molecule is equal to or larger than the radius of the organic molecules in the matrix), we do not observe a strong dependence of ξ on the size or nature of the diffusing molecule. For smaller molecules, ξ is expected to change significantly. For example, Price et al. (2016) showed that ξ=0.57 for the diffusion of water in a sucrose–water matrix, and Pollack (1981) showed that ξ=0.63 for the diffusion of xenon in a sucrose–water matrix. The development of a relationship between ξ and the size of small diffusing molecules is beyond the scope of this work.

3.4 Implications for atmospheric mixing times

To investigate the atmospheric implications of these results, we considered the mixing times of organic molecules within SOA in the atmosphere as a function of viscosity using both the Stokes–Einstein relation (Eq. 1) and the fractional Stokes–Einstein relation (Eq. 3) with ξ=0.93. Mixing times were calculated with the following equation (Seinfeld and Pandis, 2006; Shiraiwa et al., 2011):

$$\begin{array}{}\text{(4)}& {\mathit{\tau }}_{\mathrm{mix}}={\displaystyle \frac{d_{\mathrm{p}}^{\mathrm{2}}}{\mathrm{4}{\mathit{\pi }}^{\mathrm{2}}D}},\end{array}$$

where τ_mix is the characteristic mixing time, d_p is the SOA particle diameter, and D is the diffusion coefficient. τ_mix corresponds to the time at which the concentration of the diffusing molecules at the center of the particle deviates by less than a factor of 1∕e from the equilibrium concentration. We assumed a d_p of 200 nm, which is roughly the median diameter in the volume distribution of ambient SOA (Martin et al., 2010; Pöschl et al., 2010; Riipinen et al., 2011). We assumed a value of 0.38 nm for R_H based on literature values for molecular weight (175 g mol⁻¹; Huff Hartz et al., 2005) and the density (1.3 g cm⁻³; Chen and Hopke, 2009; Saathoff et al., 2009) of SOA molecules and assuming a spherical symmetry of the diffusing species.

Figure 4 shows the calculated mixing times of 200 nm particles as a function of the viscosity of the matrix. The mixing time of 1 h is highlighted, since when calculating the growth and evaporation of SOA and the long-range transport of pollutants using chemical transport models, a mixing time of < 1 h for organic molecules within SOA is often assumed (Hallquist et al., 2009). At a viscosity of 5×10⁶ Pa s, the mixing time is > 1 h based on the Stokes–Einstein relation but remains < 1 h based on the fractional Stokes–Einstein relation. Furthermore, at high viscosities > 5×10⁶ Pa s, the mixing times predicted with the traditional Stokes–Einstein relation are at least a factor of 5 greater than those predicted with the fractional Stokes–Einstein relation.

Recently, Shiraiwa et al. (2017) estimated mixing times of organic molecules in SOA particles in the global atmosphere using the global chemistry climate model EMAC (Jöckel et al., 2006) and the organic module ORACLE (Tsimpidi et al., 2014). Glass transition temperatures of SOA compounds were predicted based on molar mass and the O:C ratio of SOA components, followed by predictions of viscosity. Diffusion coefficients and mixing times were predicted using the Stokes–Einstein relation. To further explore the implications of our results, we calculated mixing times of organic molecules in SOA globally using the same approach as Shiraiwa et al. (2017) and compared predictions using the Stokes–Einstein relation and predictions using the fractional Stokes–Einstein relation with ξ=0.93. Shown in Fig. 5 are the results from these calculations. At all latitudes at the surface, the mixing times are well below the 1 h often assumed in chemical transport models regardless of whether the Stokes–Einstein relation or the fractional Stokes–Einstein relation is used (Fig. 5a). On the other hand, at an altitude of approximately 1.4 km, the latitudes at which the mixing times exceed 1 h will depend on whether the Stokes–Einstein relation or fractional Stokes–Einstein relation is used (Fig. 5b). At an altitude of 3.2 km the mixing times are well above the 1 h cutoff regardless of what relation is used, and the Stokes–Einstein relation can overpredict mixing times of SOA particles by as much as 1 order of magnitude compared to the fractional Stokes–Einstein relation (Fig. 5c). A caveat is that the predictions at 3.2 km are based on viscosities higher than the viscosities studied in the current work. Hence, at 3.2 km the Stokes–Einstein and fractional Stokes–Einstein relations are being used outside the viscosity range tested here. Although experimentally challenging, additional studies are recommended to determine if the fractional Stokes–Einstein relation with ξ=0.93 is able to accurately predict the diffusion coefficients of organic molecules in proxies of SOA at viscosities higher than investigated in the current study.

4 Summary and conclusions

We report experimental diffusion coefficients of fluorescent organic molecules in a variety of SOA proxies. The reported diffusion coefficients varied by about 8 orders of magnitude as the water activity in the SOA proxies varied from 0.23 (0.14 in one case) to 0.86. By combining the new diffusion coefficients with literature data, we have shown that, in almost all cases, the Stokes–Einstein relation correctly predicts the diffusion coefficients of organic molecules in SOA proxies within a factor of 10. This finding is in stark contrast to the diffusion of water in SOA proxies, whereby much larger deviations between experimental and predicted diffusion coefficients have been observed over the same viscosity range. Even though the Stokes–Einstein relation correctly predicts the diffusion of organic molecules in the majority of cases within a factor of 10, both a sum of squared residuals analysis and a reduced chi-squared test show that a fractional Stokes–Einstein relation with an exponent of ξ=0.93 is a better model for predicting diffusion coefficients in SOA proxies for the range of viscosities included in this study. This is consistent with earlier work that showed the fractional Stokes–Einstein relation is able to reproduce experimental diffusion coefficients of sucrose in sucrose–water matrices. The fractional Stokes–Einstein relation predicts faster diffusion coefficients and therefore shorter mixing times of SOA particles in the atmosphere. At an altitude of ∼3.2 km, the difference in mixing times predicted by the two relations is as much as 1 order of magnitude.